1996年全国Ⅱ高考数学试题(文)

合集下载

1996年全国Ⅱ高考数学试题(理)

1996年普通高等数学招生全国统一考试（全国Ⅱ）理科数学参考公式：三角函数的积化和差公式：[]1sin cos sin()sin()2αβαβαβ=++- []1cos sin sin()sin()2αβαβαβ=+--[]1cos cos cos()cos()2αβαβαβ=++-[]1sin sin cos()cos()2αβαβαβ=-+--正棱台、圆台的侧面积公式1()2S c c l ='+台侧其中c '、c 分别表示上、下底面周长，l 表示斜高或母线长．球的体积公式：343V r π=球，其中R 表示球的半径．第Ⅰ卷（选择题共65分）一、选择题：本大题共15小题，第1－10题第小题4分，第11－15题每小题5分，共65分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集I N =，集合{}|2,A x x n n N ==∈，{}|4,B x x n n N ==∈，则A ．I AB =B ．I A B =C ．I A B =D ．I A B =2．当1a >时，在同一坐标系中，函数x y a -=与logy x =的图像是3．若22sin cos x x >，则x 的取值范围是A ．322,44x k x k k Z ππππ⎧⎫-<<+∈⎨⎬⎩⎭B ．522,44x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭C ．22,44x k x k k Z ππππ⎧⎫-<<+∈⎨⎬⎩⎭D ．322,44x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭4．复数4A．1+ B．1-+ C．1- D．1--5．如果直线,l m 与平面,,αβγ满足：l βγ= ，l ∥α，m α⊂和m γ⊥，那么必有A ．a γ⊥且l m ⊥B ．αγ⊥且m ∥βC ．m ∥β且l m ⊥D ．α∥β且αγ⊥ 6．当22x ππ-≤≤时，函数()sin f x x x =+的A ．最大值是1，最小值是－1B ．最大值是1，最小值是12-C ．最大值是2，最小值是－2D ．最大值是2，最小值是－17．椭圆33cos ,15sin ,x y ϕϕ=+⎧⎨=-+⎩的两个焦点的坐标是A ．(3,5)-，(3,3)--B ．(3,3)，(3,5)-C ．(1,1)，(7,1)-D ．(7,1)-，(1,1)--8．若02πα<<，则arcsin[cos()]arccos[sin()]2παπα+++等于A ．2πB ．2π-C ．22πα- D ．22πα--9．将边长为a 的正方形A B C D 沿对角线A C 折起，使得B D a =，则三棱锥D A B C -的体积为A ．36aB ．312aC12D．31210．等比数列{}n a 的首项11a =-，前n 项和为n S ，若1053132S S =，则lim n n S →∞等于A ．23B ．23-C ．2D ．2-11．椭圆的极坐标方程为32cos ρθ=-，则它的短轴上的两个顶点的极坐标是A ．(3,0)，(1,)πB．)2π，3)2πC ．(2,)3π，5(2,)3π D．arctan2，2arctan2π-12．等差数列{}n a 的前m 项和为30，前2m 项和为100，则它的前3m 项和为A ．130B ．170C ．210D ．26013．设双曲线22221(0)x y a b ab-=<<的半焦距为c ，直线l 过(,0)a ，(0,)b 两点，已知原点到直线l4，则双曲线的离心率为A ．2 B． CD．314．母线长为1，的圆锥体积最大时，其侧面展开图圆心角ϕ等于A．3B．3C． D315．设()f x 是(,)-∞+∞上的奇函数，(2)()f x f x +=-，当01x ≤≤时，()f x x =，则(7.5)f 等于A ．0.5B ．0.5-C ．1.5D ． 1.5-第Ⅱ卷（非选择题共85分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上．16．已知圆22670x y x +-+=与抛物线22(0)y px p =>的准线相切，则p ＝． 17．正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有个（用数字作答）．18．tan 20tan 4020tan 40++的值是．19．如图，正方形A B C D 所在平面与正方形ABEF 所在平面成60°的二面角，则异面直线A D 与B F 所成角的余弦值是．ABDCFE三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．20．（本小题满分10分）解不等式1log (1)1a x ->．21．（本小题满分11分）已知△ABC 的三个内角A 、B 、C 满足：2A C B +=，11cos cos cos ACB+=-，求cos2A C -的值．22．（本小题满分12分）如图，在正三棱柱111ABC A B C -中，1E BB ∈，截面1A EC ⊥侧面1AC ．（1）求证：1BE EB =；（2）若111AA A B =，求平面1A EC 与平面111A B C 所成二面角（锐角）的度数．注意：在下面横线上填写适当内容，使之成为（1）的完整证明，交解答（2）．（右下图）（1）证明：在截面1A EC 内，过E 作1EG A C ⊥，G 是垂足． ①∵∴E G ⊥侧面1AC ，取A C 的中点F ，连结B F ，F G ，由A B B C =得BF AC ⊥， ②∵∴B F ⊥侧面1AC ，得B F ∥F G ，B F 、F G 确定一个平面，交侧面1AC 于F G ． ③∵ ∴B E ∥F G ，四边形B E G F 是平行四边形，B E F G =， ④∵ ∴F G ∥1A A ，△1AA C ∽△F G C ，⑤∵ ∴111122F G A A B B ==，即112B E B B =，故1BE EB =23．（本小题满分12分）某地现有耕地10000公顷，规划10年后粮食单产比现在增加22％，人A 1ACB1C 1EA 1 A CB B 1C 1EF G均粮食占有量比现在提高10％．如果人口年增长率为1％，那么耕地平均每年至多只能减少多少公顷（精确到1公顷）？（粮食单产＝总产量耕地面积，人均粮食占有量＝总产量总人口数24．（本小题满分12分）已知1l 、2l 是过点(0)P 的两条互相垂直的直线，且1l 、2l 与双曲线221y x -=各有两个交点，分别为1A 、1B 和2A 、2B ．（1）求1l 的斜率1k 的取值范围；（2）若1122|||A B A B =，求1l 、2l 的方程．25．（本小题满分12分）已知a 、b 、c 是实数，函数2()f x ax bx c =++，()g x ax b =+，当11x -≤≤时，|()|1f x ≤．（1）证明：||1c ≤；（2）证明：当11x -≤≤时，|()|2g x ≤；（3）设0a >，当11x -≤≤时，()g x 的最大值为2，求()f x ．数学试题参考答案一、选择题，本题考查基础知识，基本概念和基本运算能力13．14．15．16．三、解答题 17．1996年普通高等学校招生全国统一考试数学试题(理工农医类)参考解答及评分标准说明：一．本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误，就不再给分．三．解答右端所注分数，表示考生正确做到这一步应得的累加分数．四．只给整数分数．选择题和填空题不给中间分．一．选择题：本题考查基本知识和基本运算．第(1)－(10)题每小题4分，第(11)－(15)题每小题5分．满分65分．(1)C (2)A (3)D (4)B (5)A (6)D (7)B (8)A (9)D (10)B (11)C (12)C (13)A (14)D (15)B二．填空题：本题考查基本知识和基本运算．每小题4分，满分16分．（16）2 （17）32（18）3（19）42三．解答题(20)本小题考查对数函数性质，对数不等式的解法，分类讨论的方法和运算能力．满分11分．解：(Ⅰ)当a ＞1时，原不等式等价于不等式组：⎪⎪⎩⎪⎪⎨⎧>->-.11,011a x x——2分由此得xa 11>-．因为1－a <0，所以x <0，∴.011<<-x a——5分 (Ⅱ)当0<a <1⎪⎪⎩⎪⎪⎨⎧<->-.11,011a x x由①得，x >1或x <0，由②得，,110a x -<<∴ax -<<111 ——10分综上，当1>a 时，不等式的解集为⎭⎬⎫⎩⎨⎧<<-011x a x；当10<<a 时，不等式的解集为⎭⎬⎫⎩⎨⎧-<<a x x 111 ——11分(21)本小题考查三角函数基础知识，利用三角公式进行恒等变形和运算的能力．满分12分．解法一：由题设条件知B =60°，A +C =120°． ——2分 ∵,2260cos 2-=-∴22cos 1cos 1-=+CA将上式化为C A C A cos cos 22cos cos -=+ 利用和差化积及积化和差公式，上式可化为)]cos()[cos(22cos2cos2C A C A C A C A -++-=-+ ——6分将21)cos(,2160cos 2cos-=+==+C A C A代入上式得)cos(222)2cos(C A C A --=- 将1)2(cos 2)cos(2--=-C A C A 代入上式并整理得 023)2cos(2)2(cos 242=--+-CA C A ——9分,0)32cos22)(22cos2(=+---C A C A∵,032cos22≠+-C A ∴.022cos2=--C A 从而得.222cos=-C A ——12分解法二：由题设条件知B =60°，A +C =120°．设αα2,2=--=C A C A 则，可得α+= 60A ，α-=60C——3分所以)60cos(1)60cos(1cos 1cos 1αα-++=+CAααααs23c211s23c211++-=ααα22sin 43cos 41cos -=43cos cos 2-=αα ——7分依题设条件有Bcos 243cos cos 2-=-αα，∵21cos =B ∴2243cos cos 2-=-αα整理得,023cos 2cos 242=-+αα——9分,0)3cos 22)(2cos 2(=+-αα∵03cos 22≠+α，∴02cos 2=-α．从而得222cos=-C A ． ——12分(22)本小题考查空间线面关系，正三棱柱的性质，逻辑思维能力，空间想象能力及运算能力．满分12分．(Ⅰ) ①∵面A 1EC ⊥侧面AC 1， ——2分②∵面ABC ⊥侧面AC 1， ——3分 ③∵BE ∥侧面AC 1， ——4分 ④∵BE ∥AA 1， ——5分 ⑤∵AF =FC ， ——6分(Ⅱ)解：分别延长CE 、C 1B 1交于点D ，连结A 1D ．∵1EB ∥11112121,CC BB EB CC ==，∴,21111111B A C B DC DB ===∵∠B 1A 1C 1=∠B 1 C 1A 1=60°，∠DA 1B 1=∠A 1DB 1=21（180°－∠D B 1A 1）=30°，∴∠DA 1C 1=∠DA 1B 1+∠B 1A 1C 1=90°，即1DA ⊥11C A ——9分∵CC 1⊥面A 1C 1B 1，即A 1C 1是A 1C 在平面A 1C 1D 上的射影，根据三垂线定理得DA 1⊥A 1C ，所以∠CA 1C 1是所求二面角的平面角． ——11分∵CC 1=AA 1=A 1B 1=A 1C 1，∠A 1C 1C =90°，∴∠CA 1C 1=45°，即所求二面角为45° ——12分 (23)本小题主要考查运用数学知识和方法解决实际问题的能力，指数函数和二项式定理的应用，近似计算的方法和能力．满分10分．解：设耕地平均每年至多只能减少x 公顷，又设该地区现有人口为P 人，粮食单产为M 吨/公顷．依题意得不等式%)101(10%)11()1010(%)221(4104+⨯⨯≥+⨯-⨯+⨯PM P x M ——5分化简得]22.1)01.01(1.11[10103+⨯-⨯≤x——7分∵]22.1)01.01(1.11[10103+⨯-⨯)]01.001.01(22.11.11[1022101103+⨯+⨯+⨯-⨯=C C]1045.122.11.11[103⨯-⨯≈1.4≈ —— 9分∴x ≤4（公顷）．答：按规划该地区耕地平均每年至多只能减少4公顷． ——10分 (24)本小题主要考查直线与双曲线的性质，解析几何的基本思想，以及综合运用知识的能力．满分12分．解：（I ）依题设，l 1、l 2的斜率都存在，因为l 1过点P )0,2(-且与双曲线有两个交点，故方程组⎪⎩⎪⎨⎧=-≠+=1)0)(2(2211x y k x k y ① ——1分有两个不同的解．在方程组①中消去y ，整理得01222)1(2121221=-++-k x k x k ②若0121=-k ，则方程组①只有一个解，即l 1与双曲线只有一个交点，与题设矛盾，故0121≠-k ，即11≠k ，方程②的判别式为).13(4)12)(1(4)22(2121212211-=---=∆k k k k设2l 的斜率为2k ，因为2l 过点)0,2(-P 且与双曲线有两个交点，故方程组⎪⎩⎪⎨⎧=-≠+=.1),0)(2(2222x y k x k y ③ 有两个不同的解．在方程组③中消去y ，整理得01222)1(2222222=-++-k x k x k ④ 同理有)13(4,0122222-=∆≠-k k又因为l 1⊥l 2，所以有k 1·k 2=－1．——4分于是，l 1、l 2与双曲线各有两个交点，等价于⎪⎪⎩⎪⎪⎨⎧≠-=⋅>->-.1,1,013,0131212221k k k k k 解得⎪⎩⎪⎨⎧≠<<.1,33311k k ——6分∴)3,1()1,33()33,1()1,3(1 ----∈k ——7分(Ⅱ)设),(),,(221111y x B y x A 由方程②知112,122212121212121--=⋅--=+k k x x k k x x∴│A 1B 1│2=(x 1－x 2)2+(y 1－y 2)222121))(1(x x k -+=2212121)1()13)(1(4--+=kk k ⑤ ——9分同理，由方程④可求得222B A ，整理得2212121222)1()3)(1(4k k k B A --+=⑥由22115B A B A =，得2222115B A B A =将⑤、⑥代入上式得22121212212121)1()3)(1(45)1()13)(1(4k k k kk k --+⨯=--+解得21±=k取21=k 时，)2(22:),2(2:21+-=+=x y l x y l ；取21-=k 时，)2(22:),2(2:21+=+-=x y l x y l ．——12分(25)本小题主要考查函数的性质、含有绝对值的不等式的性质，以及综合运用数学知识分析问题与解决问题的能力．满分12分．(Ⅰ)证明：由条件当－1≤x ≤1时，│f (x )│≤1，取x =0得│c │=│f (0)│≤1，即│c │≤1． ——2分(Ⅱ)证法一：当a >0时，g (x )=ax +b 在[－1，1]上是增函数，∴g (－1)≤g (x )≤g (1)， ∵│f (x )│≤1 (－1≤x ≤1)，│c │≤1，∴g (1)=a +b =f (1)－c ≤│f (1)│+│c │≤2， g (－1)=－a +b =－f (－1)+c ≥－(│f (－1)│+│c │)≥－2，由此得│g (x )│≤2; ——5分当a <0时，g (x )=ax +b 在[－1，1]上是减函数，∴g (－1)≥g (x )≥g (1)， ∵│f (x )│≤1 (－1≤x ≤1)，│c │≤1，∴g (－1)=－a +b =－f (－1)+c ≤│f (－1)│+│c │≤2， g (1)=a +b =f (1)－c ≥－(│f (1)│+│c │)≥－2，由此得│g (x )│≤2; ——7分当a =0时，g (x )=b ，f (x )=bx +c ．∵－1≤x ≤1，∴│g (x )│=│f (1)－c │≤│f (1)│+│c │≤2．综上得│g (x )│≤2． ——8分证法二：由4)1()1(22--+=x x x ，可得b ax x g +=)()2121(])21()21[(22--++--+=x x b x x a])21()21([])21()21([22c x b x a c x b x a +-+--++++=),21()21(--+=x f x f ——6分当－1≤x ≤1时，有,0211,1210≤-≤-≤+≤x x根据含绝对值的不等式的性质，得2)21()21()21()21(≤-++≤--+x f x f x f x f即│g (x )│≤2． ——8分(Ⅲ)因为a >0，g (x )在[－1，1]上是增函数，当x =1时取得最大值2，即g (1)=a +b =f (1)－f (0)=2． ①∵－1≤f (0)=f (1)－2≤1－2=－1，∴c =f (0)=－1． ——10分因为当－1≤x ≤1时，f (x )≥－1，即f (x )≥f (0)，根据二次函数的性质，直线x =0为f (x )的图像的对称轴，由此得0,02==-b ab 即由① 得a =2．所以 f (x )=2x 2－1． ——12分。

数学排列组合

排列组合的体型总结与解题方法一、相临问题——捆绑法例1．7名学生站成一排，甲、乙必须站在一起有多少不同排法？解：两个元素排在一起的问题可用“捆绑”法解决，先将甲乙二人看作一个元素与其他五人进行排列，并考虑甲乙二人的顺序，所以共有种。

评注：一般地: 个人站成一排,其中某个人相邻,可用“捆绑”法解决，共有种排法。

二、不相临问题——选空插入法例2． 7名学生站成一排，甲乙互不相邻有多少不同排法？解：甲、乙二人不相邻的排法一般应用“插空”法，所以甲、乙二人不相邻的排法总数应为：种 .评注：若个人站成一排，其中个人不相邻，可用“插空”法解决，共有种排法。

三、复杂问题——总体排除法在直接法考虑比较难，或分类不清或多种时，可考虑用“排除法”，解决几何问题必须注意几何图形本身对其构成元素的限制。

例3.(1996年全国高考题)正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有多少个.解：从7个点中取3个点的取法有种，但其中正六边形的对角线所含的中心和顶点三点共线不能组成三角形，有3条，所以满足条件的三角形共有－3＝32个.四、特殊元素——优先考虑法对于含有限定条件的排列组合应用题，可以考虑优先安排特殊位置，然后再考虑其他位置的安排。

例4． (1995年上海高考题) 1名老师和4名获奖学生排成一排照像留念，若老师不排在两端，则共有不同的排法种．解：先考虑特殊元素（老师）的排法，因老师不排在两端，故可在中间三个位置上任选一个位置，有种，而其余学生的排法有种，所以共有＝72种不同的排法.例5．（2000年全国高考题）乒乓球队的10名队员中有3名主力队员，派5名队员参加比赛，3名主力队员要安排在第一、三、五位置，其余7名队员选2名安排在第二、四位置，那么不同的出场安排共有种.解：由于第一、三、五位置特殊，只能安排主力队员，有种排法，而其余7名队员选出2名安排在第二、四位置，有种排法，所以不同的出场安排共有＝252种.五、多元问题——分类讨论法对于元素多，选取情况多，可按要求进行分类讨论，最后总计。

(详细解析)1996年普通高等学校招生全国统一考试数学试题及答案(理)

1996年普通高等学校招生全国统一考试数学（理工农医类）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至2页．第Ⅱ卷3至8页．共150分．考试时间120分钟．第Ⅰ卷（选择题共65分）注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上． 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．3．考试结束，监考人将本试卷和答题卡一并收回．一．选择题：本大题共15小题，第1—10题每小题4分，第11—15题每小题5分，共65分．在每小题给出的四个选项中，只有一项是符合题目要求的1．已知全集I N =，集合{}{}2,,4,A x x n n N B x x n n N ==∈==∈||，则 A ．B A I = B ．B A I = C ．B A I = D ．B A I = 【答案】C【解析】由于B A Þ，所以AB I =．2．当1a >时，在同一坐标系中，函数xy a -=与log a y x =的图像【答案】A【解析】当1a >时，函数xy a -=是减函数，且过点(0,1)；而函数log a y x =为增函数，且过点(1,0)．3．若22sin cos x x >，则x 的取值范围是 A ．⎭⎬⎫⎩⎨⎧∈+<<-Z k k x k x ,412432ππππ B ．⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,452412ππππ C ．⎭⎬⎫⎩⎨⎧∈+<<-Z k k x k x ,4141ππππ D ．⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,4341ππππ 【答案】D【解析】2221sin cos sin sin 22x x x x >⇒>⇒>或sin 2x <-，解得24k x ππ+< 32()4k k Z ππ<+∈或322()44k x k k Z ππππ-<<-∈，即(21)(21)4k x k πππ-+<<- 3()4k Z π+∈，所以x 的取值范围是⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,4341ππππ．4．复数54)31()22(i i -+等于A ．i 31+B ．i 31+-C ．i 31-D ．i 31--【答案】B44425(2)12()i ω===-+-．5．如果直线,l m 与平面,,αβγ满足：,//,l l m βγαα=⊂和m γ⊥，那么必有A ．αγ⊥且l m ⊥B ．αγ⊥且//m βC ．//m β且l m ⊥D ．//αβ且αγ⊥ 【答案】A 【解析】略． 6．当22x ππ-≤≤时，函数()sin f x x x =+的A ．最大值是1，最小值是1-B ．最大值是1，最小值是12-C ．最大值是2，最小值是2-D ．最大值是2，最小值是1- 【答案】D【解析】因为()sin 2sin()3f x x x x π==+，由已知5636x πππ-≤+≤．故当 32x ππ+=，即6x π=时，()f x 有最大值是2；当36x ππ+=-，即2x π=-时，()f x 有最小值是1-． 7．椭圆⎩⎨⎧+-=+=ϕϕsin 51,cos 33y x 的两个焦点坐标是A ．(3,5),(3,3)---B ．(3,3),(3,5)-C ．(1,1),(7,1)-D ．(7,1),(1,1)--- 【答案】B【解析】消去参数可得直角坐标方程22(1)(3)1259y x +-+=，故焦点坐标是(3,3),(3,5)-．8．若02πα<<，则arcsin[cos()]arccos[sin()]2παπα+++等于A ．2πB ．2π-C ．22πα-D ．22πα--【答案】A【解析】解法一：由于已知sin 0,cos()02παα>+<，原式arcsin(sin )arccos(sin )arccos(sin )αααπααπ=-+-=-+-=-+arccos[cos()]()222πππααπα--=-+--=．解法二：当1x ≤时arcsin arccos 2x x π+=，而1sin 0α-<-<，∴原式arcsin(sin )arccos(sin )2παα=-+-=．9．将边长为a 的正方形ABCD 沿对角线AC 折起，使得BD a =，则三棱锥D ABC -的体积为A ．63aB ．123a C ．3123a D ．3122a 【答案】D【解析】取AC 的中点O ，连接,BO DO ，如图所示．,ABC ADC ∆∆均为等腰直角三角形，22AC BO DO ===， ∴2BOD π∠=，则DO ⊥面ABC ，DO 就是三棱锥D ABC -的高，所以231132212D ABC V a -=⋅⋅=．10．等比数列{}n a 的首项11a =-，前n 项和为n S ，若3231510=S S 则n n S ∞→lim 等于 A ．32 B ．23- C ．2 D ．2- 【答案】B【解析】显然1q ≠，由3231510=S S 得10151(1)31(1)32a q a q -=-，则105323110q q --=，解得 5132q =-，得12q =-，所以12lim 13n n a S q →∞==--．11．椭圆的极坐标方程为θρcos 23-=，则它在短轴上的两个顶点的极坐标是A ．(3,0),(1,)π B．3)22ππ C ．5(2,),(2,)33ππD ．（2arctg )22π- 【答案】C【解析】将极坐标方程为θρcos 23-=化为直角坐标方程22(1)143x y -+=，在短轴上的两个顶点的直角坐标是，所以极坐标是5(2,),(2,)33ππ．12．等差数列{}n a 的前m 项和为30，前2m 项和为100，则它的前3m 项和为A ．130B ．170C ．210D ．260 【答案】C【解析】由已知得230,100m m S S ==，则232,,m m m m m S S S S S --成等差数列，所以323()210m m m S S S =-=．13．设双曲线)0(12222b a by a x <<=-的半焦距为c ，直线l 过(,0),(0,)a b 两点．已知原点到直线l 的距离为c 43，则双曲线的离心率为 A ．2 B ．3 C ．2 D ．332 【答案】A【解析】直线l 的方程为0bx ay ab +-=，原点到直线l 4c =，则22222316a b c a b =+，即22222()316a c a c c -=，解得2e =或e =0a b <<，所以e ==>，所以3e =不合题意．14．母线长为1的圆锥体积最大时，其侧面展开图圆心角ϕ等于 A ．π322 B ．π332 C ．π2 D ．π362 【答案】D15．设()f x 是(,)-∞+∞上的奇函数，(2)()f x f x +=-，当01x ≤≤时，()f x x =，则(7.5)f 等于A ．0.5B ．0.5-C ．1.5D ． 1.5- 【答案】B【解析】(7.5)(5.52)(5.5)[(3.5)](3.5)(1.5)[(0.5)]f f f f f f f =+=-=--==-=---(0.5)0.5f =-=-．第Ⅱ卷（非选择题共85分）二．填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．16．已知圆07622=--+x y x 与抛物线)0(22>=p px y 的准线相切，则p = ．【答案】2【解析】圆的标准方程为22(3)16x y -+=，圆心和半径分别为(3,0),4，所以4312p=-=，则2p =．17．正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有个．（用数字作答）【答案】32【解析】从7个点中取3个点有37C 种取法，3个点共线的有3种，三角形共有37332C -=个．18．tg20tg403tg20tg40++的值是．【答案】3【解析】∵tg20tg40tg(2040)31tg20tg40++==-，∴tg20tg403(1-tg20tg40)+=，tg20tg403tg20tg403++=．19．如图，正方形ABCD 所在平面与正方形ABEF 所在平面成60的二面角，则异面直线AD与BF 所成角的余弦值是．【答案】42 【解析】由于//AD BC ，所以CBF ∠即为异面直线AD 与BF 所成角，设正方形边长为a ，在CBF ∆中，,,BF BC a FC =====，222cos 24BF BC FC CBF BF BC +-∠==⋅．三．解答题：本大题共6小题；共69分．解答应写出文字说明、证明过程或演算步骤． 20．（本小题满分11分）解不等式1)11(log >-xa ．【解】本小题考查对数函数性质，对数不等式的解法，分类讨论的方法和运算能力．满分11分．（Ⅰ）当1>a 时，原不等式等价于不等式组：⎪⎪⎩⎪⎪⎨⎧>->-.11,011a xx——2分由此得xa 11>-．因为10a -<，所以0x <，∴101x a<<-． ——5分（Ⅱ）当01a <<时，原不等式等价于不等式组：110,11.xa x⎧->⎪⎪⎨⎪-<⎪⎩——7分由①得，1x >或0x <，由②得，101x a <<-，∴ax -<<111． ——10分综上，当1>a 时，不等式的解集为⎭⎬⎫⎩⎨⎧<<-011x a x；当10<<a 时，不等式的解集为⎭⎬⎫⎩⎨⎧-<<a x x 111． ——11分 21．（本小题满分12分）已知ABC ∆的三个内角,,A B C 满足：BC A B C A cos 2cos 1cos 1,2-=+=+，求 2cosCA -的值．【解】本小题考查三角函数基础知识，利用三角公式进行恒等变形和运算的能力．满分12分．解法一：由题设条件知60,120B A C =+=． ——2分∵cos 60=-22cos 1cos 1-=+CA ．将上式化为C A C A cos cos 22cos cos -=+．利用和差化积及积化和差公式，上式可化为)]cos()[cos(22cos 2cos2C A C A CA C A -++-=-+． ——6分将21)cos(,2160cos 2cos-=+==+C A C A 代入上式得cos)22A C A C -=-．将1)2(cos 2)cos(2--=-CA C A 代入上式并整理得 023)2cos(2)2(cos 242=--+-CA C A ——9分(2cos3)022A C A C ---+=，∵302A C -+≠，∴2cos 02A C-=．从而得cos2A C -=． ——12分解法二：由题设条件知60,120B A C =+=．设2A Cα-=，则2A C α-=，可得60,60A C αα=+=-， ——3分所以)60cos(1)60cos(1cos 1cos 1αα-++=+ C A ααααsin 23cos 211sin 23cos 211++-=ααα22sin 43cos 41cos -=43cos cos 2-=αα． ——7分依题设条件有Bcos 243cos cos 2-=-αα， ∵21cos =B ，∴2243cos cos 2-=-αα．整理得22cos 0,αα+-= ——9分(2cos 3)0αα-+=，∵03cos 22≠+α，∴02cos 2=-α．从而得222cos=-C A ． ——12分22．（本小题满分12分）如图1，在正三棱柱111ABC A B C -中，1E BB ∈，截面1A EC ⊥侧面1AC ．（Ⅰ）求证：1BE EB =；（Ⅱ）若111AA A B =；求平面1A EC 与平面111A B C 所成二面角（锐角）的度数．注意：在下面横线上填写适当内容，使之成为（Ⅰ）的完整证明，并解答（Ⅱ）．（Ⅰ）证明：（如图2）在截面1A EC 内，过E 作1EG AC ⊥，G 是垂足．① ∵ ，∴EG ⊥侧面1AC ；取AC 的中点F ，连结,BF FG ，由AB BC = 得BF AC ⊥．② ∵ ，∴BF ⊥侧面1AC ；得//,,BF EG BF EG 确定一个平面，交侧面1AC 于FG ．③ ∵ ，∴//BE FG ，四边形BEGF 是平行四边形，BE FG =． ④ ∵ ，∴11//,FG AA AAC FGC ∆∆，⑤ ∵ ，∴112121BB AA FG ==，即112BE BB =，故1BE EB =．（Ⅱ）解：【解】本小题考查空间线面关系，正三棱柱的性质，逻辑思维能力，空间想象能力及运算能力．满分12分．（Ⅰ）①面1A EC ⊥侧面1AC ， ——2分②面ABC ⊥侧面1AC ， ——3分 ③//BE 侧面1AC ， ——4分 ④1//BE AA ， ——5分 ⑤//AF FC ， ——6分（Ⅱ）分别延长11,CE C B 交于点D ，连结1A D ．∵1111111//,22EB CC EB BB CC ==，∴,21111111B A C B DC DB ===∵11111160B AC C B A ∠=∠=︒，1111111(180)302DA B A DB DB A ∠=∠=︒-∠=︒，∴111111190DAC DA B B AC ∠=∠+∠=︒，即111DA AC ⊥． ——9分∵1CC ⊥面111AC B ，即11A C 是1A C 在平面11AC D 上的射影，根据三垂线定理得11DA A C ⊥，所以11CAC ∠是所求二面角的平面角． ——11分 ∵11111111,90CC AA A B AC AC C ===∠=︒，∴1145CA C ∠=，即所求二面角为45． ——12分 23．（本小题满分10分）某地现有耕地10000公顷，规划10年后粮食单产比现在增加22%，人均粮食占有量比现在提高10%．如果人口年增长率为1%，那么耕地平均每年至多只能减少多少公顷（精确到1公顷）?（粮食单产=耕地面积总产量，人均粮食占有量=总人口数总产量）【解】本小题主要考查运用数学知识和方法解决实际问题的能力，指数函数和二项式定理的应用，近似计算的方法和能力．满分10分．设耕地平均每年至多只能减少x 公顷，又设该地区现有人口为P 人，粮食单产为M 吨/公顷．依题意得不等式%)101(10%)11()1010(%)221(4104+⨯⨯≥+⨯-⨯+⨯P M P x M ．——5分化简得]22.1)01.01(1.11[10103+⨯-⨯≤x ． ——7分 ∵103312210101.1(10.01) 1.110[1]10[1(10.010.01)]1.22 1.22C C ⨯+⨯-=⨯-⨯+⨯+⨯+3 1.110[1 1.1045] 4.11.22≈⨯-⨯≈． —— 9分 ∴4x ≤（公顷）．答：按规划该地区耕地平均每年至多只能减少4公顷． ——10分 24．（本小题满分12分）已知12,l l 是过点)0,2(-P 的两条互相垂直的直线，且12,l l 与双曲线122=-x y 各有两个交点，分别为11,A B 和22,A B ．（Ⅰ）求1l 的斜率1k 的取值范围；（Ⅱ）若1122A B B =，求12,l l 的方程．【解】本小题主要考查直线与双曲线的性质，解析几何的基本思想，以及综合运用知识的能力．满分12分．（I ）依题设，12,l l 的斜率都存在，因为1l 过点)0,2(-P 且与双曲线有两个交点，故方程组⎪⎩⎪⎨⎧=-≠+=1)0)(2(2211x y k x k y ① ——1分有两个不同的解．在方程组①中消去y ，整理得01222)1(2121221=-++-k x k x k ． ②若0121=-k ，则方程组①只有一个解，即1l 与双曲线只有一个交点，与题设矛盾，故0121≠-k ，即11≠k ，方程②的判别式为2222211111)4(1)(21)4(31)k k k ∆=---=-．设2l 的斜率为2k ，因为2l 过点)0,2(-P 且与双曲线有两个交点，故方程组⎪⎩⎪⎨⎧=-≠+=.1),0)(2(2222x y k x k y ③ 有两个不同的解．在方程组③中消去y ，整理得01222)1(2222222=-++-k x k x k ． ④同理有)13(4,0122222-=∆≠-k k ．又因为12l l ⊥，所以有121l l ⋅=-． ——4分于是，12,l l 与双曲线各有两个交点，等价于⎪⎪⎩⎪⎪⎨⎧≠-=⋅>->-.1,1,013,0131212221k k k k k解得⎪⎩⎪⎨⎧≠<<.1,33311k k——6分∴)3,1()1,33()33,1()1,3(1 ----∈k ． ——7分（Ⅱ）设),(),,(221111y x B y x A ．由方程②知112,122212121212121--=⋅--=+k k x x k k x x ． ∴22222111212112()()(1)()A B x x y y k x x =-+-=+-22112214(1)(31)(1)k k k +-=-． ⑤ ——9分同理，由方程④可求得222B A ，整理得2212121222)1()3)(1(4k k k B A --+= ⑥ 由22115B A B A =，得2211225A B A B =将⑤、⑥代入上式得22121212212121)1()3)(1(45)1()13)(1(4k k k k k k --+⨯=--+，解得21±=k 取21=k 时，)2(22:),2(2:21+-=+=x y l x y l ；取21-=k 时，)2(22:),2(2:21+=+-=x y l x y l ． ——12分25．（本小题满分12分）已知,,a b c 是实数，函数2(),()f x ax bx c g x ax b =++=+，当11x -≤≤时，()1f x ≤．（Ⅰ）证明：1c ≤；（Ⅱ）证明：当11x -≤≤时，()2g x ≤；（Ⅲ）设0a >，当11x -≤≤时，()g x 的最大值为2，求()f x ．【解】本小题主要考查函数的性质、含有绝对值的不等式的性质，以及综合运用数学知识分析问题与解决问题的能力．满分12分．（Ⅰ）证明：由条件当11x -≤≤时，()1f x ≤，取0x =得(0)1c f =≤，即1c ≤．——2分（Ⅱ）证法一：当0a >时，()g x ax b =+在[1,1]-上是增函数，∴(1)(0)(1)g g g -≤≤，∵()1(11),1f x x c ≤-≤≤≤，∴(1)(1)(1)2g a b f c f c =+=-≤+≤，(1)(1)((1))2g a b f c f c -=-+=--+≥--+≥-，由此得()2g x ≤． ——5分当0a <时，()g x ax b =+在[1,1]-上是减函数，∴(1)(0)(1)g g g -≥≥， ∵()1(11),1f x x c ≤-≤≤≤，∴(1)(1)(1)2g a b f c f c -=-+=--+≤-+≤，(1)(1)((1))2g a b f c f c =+=-≥-+≥-，由此得()2g x ≤； ——7分当0a =时，(),()g x b f x bx c ==+．∵11x -≤≤，∴()(1)(1)2g x f c f c =-≤+≤．综上得()2g x ≤． ——8分证法二：由4)1()1(22--+=x x x ，可得221111()[()()]()2222x x x x g x ax b a b +-+-=+=-+- ])21()21([])21()21([22c x b x a c x b x a +-+--++++= 11()()22x x f f +-=-， ——6分当11x -≤≤时，有,0211,1210≤-≤-≤+≤x x 根据含绝对值的不等式的性质，得2)21()21()21()21(≤-++≤--+x f x f x f x f ，即()2g x ≤． ——8分（Ⅲ）因为0a >，()g x 在[1,1]-上是增函数，当1x =时取得最大值2，即(1)(1)(0)2g a b f f =+=-=． ①∵1(0)(1)2121f f -≤=-≤-=-，∴(0)1c f ==-． ——10分因为当11x -≤≤时，()1f x ≥-，即()(0)f x f ≥，根据二次函数的性质，直线0x =为()f x 的图像的对称轴，由此得02ba-=，即0b =．由①得2a =．所以 2()21f x x =-． ——12分。

1996年高考数学试题(全国文)及答案

1996年普通高等学校招生全国统一考试数学（文史类）一．选择题：本大题共15小题；第1—10题每小题4分，第11—15题每小题5分，共65分，在每小题给出的四个选项中，只有一项是符号题目要求的(1)设全集I ={1，2，3，4，5，6，7}，集合A ={1，3，5，7}，B ={3，5}．则()(A)I =A ∪B ；(B)I =A ∪B ；(C)I =A ∪B ；(D)A ∪B 。

(2)当a >1时，在同坐标系中．函数y =a －x与y =log a x 的图像是()(3)若sin 2x >cos 2x ，则x 的取值范围是()(A)⎭⎬⎫⎩⎨⎧∈+<<−Z k k x k x ,412432ππππ；(B)⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,452412ππππ；(C)⎭⎬⎫⎩⎨⎧∈+<<−Z k k x k x ,4141ππππ；(D)⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,4341ππππ。

(4)复数54)31()22i i −+（等于()(A)i 31+；(B)i 31+−；(C)i 31−；(D)i 31−−。

(5)6名同学排成一排，其中甲、乙两人必须排在一起的不同排法有()(A)720种；(B)360种；(C)240种；(D)120种。

(6)已知α是第三象限角sin α=－2524，则tg 2α=()(A)34；(B)43；(C)－43；(D)－34。

(7)如果直线l 、m 与平面α、β、γ满足：l =β∩γ，l ∥α，m =α，m ⊥γ，那么必有()(A)α⊥γ且l ⊥m (B)α⊥γ且m ∥β(C)m ∥β且l ⊥m (D)α∥β且α⊥γ(8)当－2π≤x ≤2π时，函数f (x )=sin x ＋3cos x 的()(A)最大值是1，最小值是－1；(B)最大值是1，最小值是－21；(C)最大值是2，最小值是－2；(D)最大值是2，最小值是－1。

五年高考数学真题分类解析-排列、组合、二项式定理和概率、统计

排列、组合、二项式定理和概率、统计一、选择题1.（2003京春理，9）某班新年联欢会原定的5个节目已排成节目单，开演前又增加了两个新节目.如果将这两个节目插入原节目单中，那么不同插法的种数为（）A.42B.30C.20D.122.（2003京春文，10）某班新年联欢会原定的5个节目已排成节目单，开演前又增加了两个新节目.如果将这两个新节目插入原节目单中，且两个新节目不相邻，那么不同插法的种数为（）A.6B.12C.15D.30 3.（2002京皖春理，6）从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同工作.若其中甲、乙两名志愿者都不能从事翻译工作，则选派方案共有（）A.280种B.240种C.180种D.96种4.（2002京皖春文，6）若从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同工作，则选派方案共有（）A.180种B.360种C.15种D.30种5.（2002京皖春理，10）对于二项式（x1+x 3）n（n ∈N *），四位同学作出了四种判断： ①存在n ∈N *，展开式中有常数项 ②对任意n ∈N *，展开式中没有常数项 ③对任意n ∈N *，展开式中没有x 的一次项 ④存在n ∈N *，展开式中有x 的一次项上述判断中正确的是（）A.①③B.②③C.②④D.①④6.（2002京皖春文，10）在（x1+x 2）6的展开式中，x 3的系数和常数项依次是（） A.20，20 B.15，20 C.20，15 D.15，157.（2002全国文，12、理，11）从正方体的6个面中选取3个面，其中有2个面不相邻的选法共有（）A.8种B.12种C.16种D.20种8.（2002北京文，9）5本不同的书，全部分给四个学生，每个学生至少1本，不同分法的种数为（）A.480B.240C.120D.969.（2002北京理，9）12名同学分别到三个不同的路口进行车流量的调查，若每个路口4人，则不同的分配方案共有（）A.4448412C C C 种B.34448412C C C 种C.3348412AC C种D.334448412A C C C 种10.（2001京皖春，3）1222C C lim ++∞→n n n nn 等于（）A.0B.2C.21D.41 11.（2001天津理，9）某赛季足球比赛的计分规则是：胜一场，得3分；平一场，得1分；负一场，得0分，一球队打完15场，积33分，若不考虑顺序，该队胜、负、平的情况共有（）A.3种B.4种C.5种D.6种12.（2000京皖春，8）从单词“equation ”中选取5个不同的字母排成一排，含有“qu ”（其中“ｑu ”相连且顺序不变）的不同排列共有（）A.120个B.480个C.720个D.840个D.554422A A A 种二、填空题23.（2003上海春，9）8名世界网球顶级选手在上海大师赛上分成两组，每组各4人，分别进行单循环赛，每组决出前两名，再由每组的第一名与另一组的第二名进行淘汰赛，获胜者角逐冠、亚军，败者角逐第3、4名，大师赛共有_____场比赛.24.（2002上海7）在某次花样滑冰比赛中，发生裁判受贿事件，竞赛委员会决定将裁判由原来的9名增至14名，但只任取其中7名裁判的评分作为有效分.若14名裁判中有2人受贿，则有效分中没有受贿裁判的评分的概率是_____.（结果用数值表示）25.（2002上海春，7）六位身高全不相同的同学拍照留念，摄影师要求前后两排各三人，则后排每人均比前排同学高的概率是_____.26.（2002上海春，5）若在（xx 15-）n的展开式中，第4项是常数项，则n = . 27.（2002全国理，16）（x 2+1）（x －2）7的展开式中x 3项的系数是 . 28.（2002上海文，9）某工程由下列工序组成，则工程总时数为天.29.（2002天津文，15）甲、乙两种冬小麦试验品种连续5年的平均单位面积产量如下（单位：t/hm 2）：其中产量比较稳定的小麦品种是_____.30.（2001上海，7）某餐厅供应客饭，每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种．现在餐厅准备了5种不同的荤菜，若要保证每位顾客有200种以上的不同选择，则餐厅至少还需准备不同的素菜品种种．（结果用数值表示）31.（2001全国，16）圆周上有2n 个等分点（n ＞1），以其中三个点为顶点的直角三角形的个数为 .32．（2001上海理，8）在代数式（4x 2－2x －5）（1＋21x）5的展开式中，常数项为． 33.（2001全国文，13）（21x ＋1）10的二项展开式中x 3的系数为 . 34.（2001上海春）在大小相同的6个球中，2个红球，4个白球.若从中任意选取3个，则所选的3个球中至少有1个红球的概率是_____.（结果用分数表示）35.（2001广东河南，13）已知甲、乙两组各有8人，现从每组抽取4人进行计算机知识竞赛，比赛人员的组成共有种可能（用数字作答）.36.（2001江西、山西、天津理）一个袋子里装有大小相同的3个红球和2个黄球，从中同时取出2个，则其中含红球个数的数学期望是_____.（用数字作答）37.（2001上海文）利用下列盈利表中的数据进行决策，应选择的方案是_____.38.（2000上海春，4）若（x +a ）5的展开式中的第四项是10a 2（a 为大于零的常数），则x =_____.39.（2000上海春，10）有n （n ∈N *）件不同的产品排成一排，若其中A 、B 两件产品排在一起的不同排法有48种，则n =_____.40.（2000京皖春理，17）103)1(xx 展开式中的常数项是_____. 41.（2000全国文、理，3）乒乓球队的10名队员中有3名主力队员，派5名参加比赛，3名主力队员要安排在第一、三、五位置，其余7名队员选2名安排在第二、四位置，那么不同的出场安排共有_____种（用数字作答）.42.（2000年上海，9）在二项式（x －1）11的展开式中，系数最小的项的系数为 .（结果用数值表示）43.（2000上海，10）有红、黄、蓝三种颜色的旗帜各3面，在每种颜色的3面旗帜上分别标上号码1、2和3.现任取3面，它们的颜色与号码均不相同的概率是 .44.（2000两省一市理，13）某厂生产电子元件，其产品的次品率为5%，现从一批产品中任意地连续取出2件，其中次品数以ξ的概率分布是三、解答题60.（2002天津文20，理19）某单位6个员工借助互联网开展工作，每个员工上网的概率都是0.5（相互独立）.（Ⅰ）求至少3人同时上网的概率；（Ⅱ）至少几人同时上网的概率小于0.3？61.（2001江西、山西、天津）如图10—1，用A 、B 、C 三类不同的元件连接成两个系统N 1，N 2.当元件A 、B 、C 都正常工作时，系统N 1正常工作；当元件A 正常工作且元件B 、C 至少有一个正常工作时，系统N 2正常工作.已知元件A 、B 、C 正常工作的概率依次为0．80、0．90、0．90.分别求系统N 1、N 2正常工作的概率P 1、P 2.62.（2001上海理）对任意一个非零复数z ，m z ={ω|ω=z 2n －1，n ∈N }（1）设α是方程x +21=x的一个根，试用列举法表示集合M α.若在M α中任取两个数，求其和为零的概率P .（2）设复数ω∈M z ，求证：M ω⊆M z .63.（2001全国理，20）已知i ，m ，n 是正整数，且1＜i ≤m ＜n . （1）证明n i i m A ＜m i i n A ；（2）证明（1＋m ）n ＞（1＋n ）m .64.（2000江西、山西、天津理，17）甲、乙二人参加普法知识竞答，共有10个不同的题目，其中选择题6个，判断题4个，甲、乙二人依次各抽一题.（1）甲抽到选择题、乙抽到判断题的概率是多少？（2）甲、乙二人中至少有一人抽到选择题的概率是多少？65.（2000上海，22）规定!)1()1(C m m x x x mx+-⋅⋅-⋅=，其中x ∈R ，m 是正整数，且0C x =1，这是组合数mn C （n 、m 是正整数，且m ≤n 的一种推广）.（1）（文）求315C -的值；（理）求515C -的值；（2）（文）设x ＞0，当x 为何值时，213)C (C x x 取最小值？（理，文2）组合数的两个性质： ①m n nmn-=C C . ②mn m n m n 11C C C +-=+. 是否都能推广到mx C （x ∈R ，m是正整数）的情形？若能推广，请写出推广的形式，并给出证明；若不能，则说明理由.（3）（理）已知组合数mn C 是正整数，证明：当x ∈Z ，m 是正整数时，mn C ∈Z . 66.（1996全国文24，理23）某地现有耕地10000公顷，规划10年后粮食单产比现在增加22%，人均粮食占有量比现在提高10%，如果人口年增长率为1%，那么耕地平均每年至多只能减少多少公顷（精确到1公顷）?●答案解析 1.答案：A解析：这是一个插空问题，应分两类：第一类，新增的两个节目连在一起；第二类，两个新增节目不连在一起，而原来的5个节目可看做分出6个空位.第一类则有2×16A 种不同的插法，第二类则有26A 种不同的插法.应用分类计数原理，共有12+30=42种不同的插法. 评述：该题是应用问题，内容贴近学生，有一定的综合性、灵活性、考查分析，解决问题及逻辑思维的能力.同时应有周密的思维习惯.2.答案：D解析：见第1题. 3.答案：B解析：因为甲、乙两名志愿者都不能从事翻译工作.因此，翻译工作从余下的四名志愿者选一人有14A 种，再从余下的5人中选3人从事导游、导购、保洁有35A 种.因此3514A A =240.4.答案：B 解析：46A =360.5.答案：D 解析：二项式（x 1+x 3）n 展开式的通项为T r +1=r n C (x1)n －r (x 3)r =r n C x r －n ·x 3r =r n C x 4r －n 当展开式中有常数项时，有4－n =0，即存在n 、r 使方程有解.当展开式中有x 的一次项时，有4r －n =1，即存在n 、r 使方程有解. 即分别存在n ，使展开式有常数项和一次项. 6.答案：C 解析：二项式（x1+x 2）6展开式的通项为： T r +1=636266C )()1(C --=r r r r rx x x∴当T r +1为x 3项时，r =3，∴T r +1=36C ·x 3=20·x 3 当T r +1为常数项时，r =2，∴T r +1=26C =157.答案：B解析：联想以空间模型，注意到“有2个面不相邻”，既可从相对平行的平面入手正面构造，即16C ·12C ；也可从反面入手剔除8个角上3个相邻平面，即：1836C C -. 8.答案：B解析：先把5本书中的两本捆起来（25C ），再分成四份（44A ），∴分法种数为25C ·44A =240（种）.9.答案：A解析：先分配4个人到第一个路口，再分配4个人到第二个路口，最后分配4个人到第三个路口，即：412C ·48C ·44C .10.答案：D解析：原式＝n n n n n n n n n n nn n n n n n n n n n n n n 2411)12(21)12)(22()1)(1(A A A A A A A A 122112111222++=++=++++=⋅⋅=++++++++∴41C C lim 1222=++∞→n n n nn 11.答案：A 解析：设该队胜x 场，平y 场，则负（15－x －y ）场，由题意得3x +y =33， ∴y =33－3x ≥0∴x ≤11，且x +y ≤15，（x ，y ∈N ）因此，有以下三种情况：⎩⎨⎧==⎩⎨⎧==⎩⎨⎧==69310011y x y x y x 或或评述：本题利用不定方程及穷举法解决排列、组合问题. 12.答案：B解析：4436A C ＝480．13.答案：A 14．答案：C解法一：由题意知，按买磁盘盒数多少可分三类：买4盒磁盘时，只有1种；买3盒磁盘时，有买3片或4片软件两种；买2盒磁盘时，可买3片、4片、5片或6片软件，有4种，故共有1＋2＋4＝7种不同的选购方式，答案为C.解法二：先买软件3片，磁盘2盒，共需320元，还有180元可用，按不再买磁盘、再买1盒磁盘、再买两盒磁盘三类，仿解法一可知选C.评述：本题主要考查分类计数原理、分类讨论思想.背景简单，但无现成模式可用，对分析解决问题的能力有较高要求.15.答案：D解析：设计让3所学校依次挑选，先由学校甲挑选，有2613C C 种，再由学校乙挑选，有2412C C 种，余下的到学校丙只有一种，于是不同的方法数共有13C ·26C ·2412C C ＝540种，答案为D.评述：设计一个程序是解答排列组合应用题的常见解法. 16.答案：D解法一：10个点任取4个点取法有410C 种，其中面ABC 内的6个点中任意4点都共面，从这6点中任取4点有46C 种，同理在其余3个面内也有46C 种，又每条棱与相对棱中点共面有6种，各棱中点中4点共面的有3种，故10个点中取4点，不共面的取法共有36C 4C 46410---＝141种.解法二：四面体记之为A —BCD ，设平面BCD 为α，那么从10个点中取4个不共面的点的情况共有四类：（1）恰有3个点在α上，有4（3C 36-）＝68种取法；（2）恰有2个点在α上，可分两种情况：该2个点在四面体的同一条棱上时有3)3C (C 2423-＝27种，该2个点不在同一条棱上，有（2326C 3C -）·（24C －1）＝30种；（3）恰有1个点在α上，可分两种情况，该点是棱的中点时有3×3＝9种，该点是棱的端点时有3×2＝6种；（4）4个点全不在α上，只有1种取法.根据分类计数原理得，不同的取法共有68＋27＋30＋9＋6＋1＝141种．评述：本题对空间想象能力要求较高，对观察能力和思维能力要求也高.在应用背景及其限制条件下合理分类是解题的关键.17.答案：B解析：四面体有4个顶点，6条棱有6个中点，每个面上的6个点共面，点A 所在的每个面中含A 的4点组合有35C 个，点A 在3个面内，共有335C 个组合，点A 在6条棱的三条棱上，每条棱上有3个点，这3点与对棱的中点共面，所以与点A 共面的四点组合共有335C +3=33（个）评述：本题考查组合的知识和空间想象能力.对考生的观察能力和思维能力有较高要求，考生失误的主要原因是没有把每条棱上的3点与它对棱上的中点共面的情况计算入内.18.答案：C解析：把甲、乙两人看作1个人，这样6个人看作5个人，5个人的全排列有55A 种，甲、乙两个人还有顺序问题，所以排法总数为55A ·22A =240（种）评述：这是一道有限制条件的排列题，考查排列的概念和排列数公式.“相邻问题”是一个常见的典型问题.19.答案：A解法一：其中2在个位的三位数有24A 个，4在个位的三位数有24A 个，故没有重复数字的三位偶数共有224A ＝24个，故选A.解法二：先排个位有12A 种，再排十位、百位有24A 种，于是合乎要求的三位偶数共有2412A A ＝24个.故选A. 评述：本题为有特殊要求的排列问题，考查排列基础知识和逻辑推理能力. 20.答案：D解析：∵原式=（1+x ）10－x 3（1+x ）10.∴欲求原展开式中x 5的系数，只需求出（1+x ）10展开式中x 5和x 2的系数.而（1+x ）10=1+…+210C x 2+…+510C x 5+….故（1－x 3）（1+x ）10展开式中，x 5的系数为510C －210C =207.21.答案：C解法一：从10人中选派4人有410C 种，进而对选出的4人具体分派任务，有1224C C 种，由分步计数原理得不同的选派方法为1224410C C C ＝2520种，答案为C.解法二：据分步计数原理，不同选法种数为210C ·18C ·17C ＝2520种.评述：本题主要考查组合和分步计数原理，答数较大，对组合数的计算要求较高.方法一用的是先选后派方法是处理排列组合应用题的基本方法.22.答案：D解析：先各看成整体，但水彩画不在两端，则为22A ，然后水彩画与国画各全排列，所以共有554422A A A ．23.答案：16解析：分两组比赛，每组有24C 场，每组的第一名与另一组的第二名比赛有2场，三、四名比赛，冠亚军比赛，共有224C +2+2=16（场）24.答案：133 解析：有效分应该是由没有受贿裁判的评分，因此，7名裁判应从12人中选712C ，则有效分中没有受贿裁判的评分的概率是133C C 714712 .25.答案：201 解析：因为后排每人均比前排人高，因此应将6人中最高的3个人放在后排，其余3人站前排.故所有排法有33A ·33A =36种.故后排每人均比前排同学高的概率为201A A A 663333=⋅ 26.答案：18 解析：∵5183333534)1(C )1()(C ---=-=n n n nx xx T 为常数项. ∴518-n =0，即n =18. 27.答案：1008解析：系数为：17C （－2）6+37C （－2）4=1008.28.答案：11解析：要完成某项工序，必须先完成它的紧前工序且在紧前工序完成的条件下，若干件工序可同时进行，因而工程总时数为：3+2+5+1=11（天）.29.答案：甲解析：根据题意，需要比较2*甲S 和2*乙S由于2*甲S =0.158，2*乙S =0.552 因此甲产量比较稳定. 30.答案：7解析：在5种不同的荤菜中取出2种的选择方式应有245C 25⨯=＝10（种）选择方式至少为200种，设素菜为x 种，∴252C C x ≥2002)1(-x x ≥20，x （x －1）≥40，x ≥7 ∴至少应为7种素菜. 31.答案：2n （n －1）解析：先在圆上找一点，2n 个点因为是等分点，所以过圆心的直径应有n ，减去过这点的直径，剩下的直径n －1个都可以与这个点形成直角三角形，∴一个点可以形成n －1个直角三角形，这样的点有2n 个.∴一共为2n （n －1）. 32.答案：15解析：15205)1(1C )4()1(1C 512415202505=+-=+-xx x . 33.答案：15 解析：15816891081C )21(C 3103310=⨯⨯⨯=⨯=34.答案：54 解析：所选3球中至少有一个红球的选法有12C ·2224C C +·14C =16（种）从6个球中任选3个球的选法有36C =20（种）. 故概率p =542016=. 评述：本题主要考查对可能事件的概率计算，以及考生分析问题解决问题的能力.古典概率是学习概率与统计的起点，而掌握古典概型的前提是能熟练地掌握排列组合的基本知识.35.答案：4900解析：完成这件事可分为两步：第一步：从甲组8人中抽取4个，有48C 种方法；第二步：从乙组8人中抽取4人，有48C 种方法. 因此，比赛人员的组成共有48C ·48C =4900种可能.评述：本题考查分步计数原理、组合的概念以及组合数的运算，考查分析问题、解决问题的能力.36.答案：1.2解析：设其中含红球个数为x ，则x =1或 x =2.而含一个红球的概率A 1=106C C C 251213=⋅含两个红球的概率为A 2=103C C 2523=∴含红球个数的数学期望为1×106+2×103=1.2 评述：本题考查数学期望的概念、概率的概念及它们的计算.37.答案：A 3解析：A 1的数学期望：1x E =0.25×50+0.30×65+0.45×26=43.7 A 2的数学期望：2x E =0.25×70+0.30×26+0.45×16=32.5 A 3的数学期望：3x E =0.25×（－20）+0.30×52+0.45×78=45.7A 4的数学期望：4x E =0.25×98+0.30×82+0.45×（－10）=44.6评述：本题考查概率与数学期望，考查学生识表的能力.对图表的识别能力，是近年高考突出考查的热点.图表语言与其数学语言的相互转换，应成为数学学习的一个重点，应引起高度重视.38.答案：a1 解析：∵x a a x T 33352135410)(C ==-，∴x ＝a1.39.答案：5解析：由11A 2--n n ＝48，得11A --n n ＝24，∵44A ＝24，∴n ＝5. 40.答案：210 解析：T r ＋1＝65301031102110)1(C )()(Cr rr rrr xx x ----=-⋅，令30－5r =0，得r =6.∴常数项T 7＝610C ·（－1）6＝210．41.答案：252解析：222733A C A ＝252．42.答案：－462解法一：因为在（x －1）11的展开式中，各项的二项式系数与系数相等或互为相反数，又展开式中二项式系数最大的项有两项，分别为第六项511C x 6（－1）5．第七项611C x 5（－1）6，所以得系数最小的项的系数为462C 511-=-．解法二：展开式中第r +1项为r rrx)1(C 1111--，要使项的系数最小，则r 为奇数，且使r11C 为最大，由此得r =5，所以项的最小系数为462)1(C 5511-=-．43.答案：141解析：从9面旗帜中任取3面，共有39C （种）取法. 现取3面，颜色与号码均不相同共有13C ·12C ·11C =6（种）因此，所求概率为141846C 639==. 44.答案：解析：设次品数为ξ，则ξ~（2，0.05），其中p =0.05为次品率，则q =0.95为正品率，于是由二项分布公式（列成表格）：即得所求结果.45.答案：12解析：先考虑A 种植在左边的情况，有三类：A 种植在最左边一垄上时，B 有三种不同的种植方法；A 种植在左边第二垄上时，B 有两种不同的种植方法；A 种植在左边第三垄上时，B 只有一种种植方法.又B 在左边种植的情况与A 时的相同，故共有2×（3＋2＋1）＝12种不同的选垄方法.评述：本题主要考查两个基本原理、分类讨论思想，对分析解决问题的能力有较高要求. 46.答案：40解析：由通项公式T r +1=r5C （x 3）5－r ·（22x ）r =r 5C ·2r ·x 15－5r由题意，令15－5r =5.得r =2. ∴含x 5项的系数为25C ·22=40. 47.答案：92 解析：掷两次骰子分别得到的总数m 、n 作为P 点的坐标共有16A ·16A =36（种）可能结果，其中落在圆内的点有8个：（1，1）、（2，2）、（1，2）、（2，1）、（1，3）、（3，1）、（2，3）、（3，2），则所求的概率为92368=. 评述：本题考查点与圆的位置关系，概率概念等基础知识以及运用数形结合的思想和分类讨论的思想解决实际问题的能力.48.答案： 179解析：展开式中x 10的系数与（x +2）10的展开式中x 10的系数和x 8的系数有关，由多项式运算法则知所求系数为010C ·（－1）＋210C ·22·1＝179.评述：本题考查在逻辑思维能力上的要求，兼考查分类讨论的思想.49. 答案：4 解析：T r ＋1＝r rn n x )(C ，令r =3得x 3的系数1611C 33=n n ，解得n =4. 50.答案： 4解析：T r ＋1＝929299292C )1()()2()1(C -+---⋅⋅⋅-=-r rr r r r r r rr xa xa x当392=-+r r ，即r =8时，492C )1(28898=⋅⋅--a ，解得a =4. 评述：本题考查二项式定理的基础知识，重点考查通项公式和项的系数的概念，兼考运算能力.60.解：（Ⅰ）至少3人同时上网的概率等于1减去至多2人同时上网的概率，即32216415611)5.0(C )5.0(C )5.0(C 1626616606=++-=---.（Ⅱ）至少4人同时上网的概率为3.03211)5.0(C )5.0(C )5.0(C 666656646>=++ 至少5人同时上网的概率为：3.0647)5.0)(C C (66656<=+. 因此，至少5人同时上网的概率小于0.3.61.解：分别记元件A 、B 、C 正常工作为事件A 、B 、C ，由已知条件 P （A ）＝0．80，P （B ）＝0．90，P （C ）＝0．90.（Ⅰ）因为事件A 、B 、C 是相互独立的，系统N 1正常工作的概率 P 1＝P （A ·B ·C ）＝P （A ）·P （B ）·P （C ）＝0．80×0．90×0．90＝0．648. 故系统N 1正常工作的概率为0．648．（Ⅱ）系统N 2正常工作的概率)]()(1[)()](1[)(2C P B P A P C B P A P P ⋅-⋅=⋅-⋅=.∵P （B ）＝1－P （B ）＝1－0．90＝0．10. P （C ）＝1－P （C ）＝1－0．90＝0．10.∴P 2＝0．80×［1－0．10×0．10］＝0．80×0．99＝0．792. 故系统N 2正常工作的概率为0．792. 62.解：（1）解方程x +21=x 得x =i 2222± 当α1=i 2222+时ω=α12n －1=112121])2222[()(ααααn nni i =+=由i n 的周期性知：ω有四个值. n =1时，ω=i i i 22222222+=+n =2时，ω=i i 222222221+-=+- n =3时，ω=i i i 22222222--=+- n =4时，ω=i i 222222221-=+ 当α2=2222-i 时，ω=α22n －1=2222)()(αααnni -=n =1时，ω=i i i 22222222-=-- n =2时，ω=i i 222222221--=-- n =3时，ω=i i i 22222222+-=- n =4时，ω=i i 222222221+=- ∴不管α=i 2222+还是α=i 2222- M α={i i i i 2222,2222,2222,2222--+--+ } P =3162C 224== （2）∵ω∈M z ，则ω=z 2m －1，m ∈N任取x ∈M ω，则x =ω2n －1，n ∈N而ω=z 2m －1 ∴x =（z 2m －1）2n －1=z (2m －1)(2n －1) ∵（2m －1）（2n －1）为正奇数∴x ∈M z ∴M ω⊆M z评述：复数的运算是复数的基础，本题考查复数的奇数次幂，由于i n 的周期性，因而 α2n －1只有四个值，题目以集合的形式给出复数ω，使复数与集合有机的结合在一起，不仅考查复数还考查集合的表示方法.而证明一个集合是另一个集合的子集在对集合的考查上又高了一个层次.证明尽管不繁，但思维层次较高.63.证明：（1）方法一：ii i m m i m m m m )1()1(A +-⋅⋅-⋅= ii i n ni n n n n )1()1(A +-⋅⋅-⋅= 对于m ＜n ，∴k ＝1，2，…，i －1有mkm n k n ->- ∴ii m i i n mn A A >即m i i n A ＞n ii m A 方法二：n i in A =个n n n n ⋅⋅·m ·（m －1）·（m －2）·…·（m －i +1） =mn ·（mn －n ）·（mn －2n ）·…·［mn －n （i －1）］①同理m i im A =mn ·（mn －m ）·（mn －2m ）·…·［mn －m （i －1）］ ②∵1＜i ≤m ＜n ，∴mn －n ＜mn －m ，mn －2n ＜mn －2m ，…， mn －n （i －1）＜mn －m （i －1） ③∴联系①、②、③可得n i im A ＜m i A i n . （2）由二项式定理：nn n n n nm m m m C C C )1(1100+++=+ mm m m m m nn n n C C C )1(1100+++=+ 又∵!A C i m m ii n ii n=而i n A m i ＞im A n i ∴2222C C n mmn > 3333C C n m m n >……m m m m m n n m C C >又∵11110000C C ,C C n m n mm n m n ==∴（1＋m ）n ＞（1＋n ）m评述：此题体现了命题指导思想上有加强离散数学分量的趋势.64.解：（1）甲从选择题中抽到一题的可能结果有16C 个，乙从判断题中抽到一题的可能结果有14C 个，故甲抽到选择题、乙抽到判断题的可能结果有16C ·14C 个；又甲、乙依次抽一题的可能结果有19110C C 个，所以甲抽到选择题、乙抽到判断题的概率为：1549024C C C C 191101416==⋅⋅. （2）甲、乙二人依次都抽到判断题的概率为：191101314C C C C ⋅⋅.故甲、乙二人中至少有一人抽到选择题的概率为：1－151390121C C C C 191101314=-=⋅ 或用以下解法：151315415431C C C C C C C C C C C C 191101614191101416191101516=++=⋅⋅+⋅⋅+⋅⋅. 评述：本题主要考查等可能事件的概率计算及分析和解决实际问题的能力. 65.（1）（文）解：680!3)17)(16)(15(C 315-=---=-.（理）解：11628C !5)19()16()15(C 519515=-=-⋅⋅-⋅-=- .（2）（文）解：)32(616)2)(1()C (C 2213-+=--=xx x x x x x x. ∵x ＞0，x +x2≥22. 当且仅当x =2时，等号成立.∴当x =2时，213)C (C x x 取得最小值.（理，文3）解：性质①不能推广.例如当x =2时，12C 有定义，但122C -无意义；性质②能推广，它的推广形式是m x m x mx11C C C +-=+，x ∈R ，m 是正整数，事实上当m =1时，有1101C 1C C +=+=+x x xx ，当m ≥2时，m x m xm x m x m x x x mm x m m x x x m m x x x m m x x x 11C !)1()2()1()11()!1()2()1()!1()2()1(!)1()1(C C +-=+⋅+-⋅⋅-⋅=++--+-⋅⋅-⋅=-+-⋅⋅-⋅++-⋅⋅-⋅=+ . （3）（理）证明：当x ≥m 时，组合数mx C ∈Z . 当0≤x ＜m 时，mx C =0∈Z . 当x ＜0时，∵－x +m －1＞0， ∴!)1()1(C m m x x x mx+-⋅⋅-⋅=m m x m mm x x m x 1C )1(!)()1()1()1(-+--=-⋅+-⋅⋅-+--= ∈Z .66.解：设耕地平均每年至多只能减少x 公顷，又设该地区现在人口为P 人，粮食单产为M 吨／公顷.依题意得不等式P M P x M 410410%)11()1010(%)221(≥+-⋅+⋅（1＋10％）化简得x ≤103［22.1)01.01(1.1110+⋅-］∵)]01.0C 01.0C 1(22.11.11[10]22.1)01.01(1.11[1022101103103+⋅++-=+- 1.4)1045.122.11.11(103≈⋅-≈ ∴x ≤4（公顷）答：按规划该地区耕地平均每年至多只能减少4公顷. ●命题趋向与应试策略1.本章内容在高考中所占比重不大，但试题都具有一定的灵活性、机敏性和综合性.在“倡导创新体系，提倡素质教育”的今天，本章的考题是最好的体现.一般有1～2道小题，且多为选择、填空题，应注意二项式定理在近似计算中的应用.2.高考对排列、组合内容的考查，一般以实际应用题形式出现，这是因为排列、组合的应用性概念强，并充满思辨性和解法多样性，符合高考选择题的特点，易于考查学生的能力，此类题大致可分两类.（1）有附加条件的排列问题，此类题多数只有一个附加条件，且以学生熟悉的数学问题或排队问题为主.（2）有附加条件的组合问题.此类题常以“至少取n个”或以几何为背景的分类组合问题为主.3.高考对二项式定理的考查，以二项式展开式及其通项公式内容为主，要有目标意识和构造意识，要注意展开式的通项公式正、反两方面的应用.此类题也可分两类.（1）直接运用通项公式求特定项的系数或与系数有关的问题.（2）需用转化思想化归为二项问题来处理的问题.4.高考对统计、概率内容的考查，往往以实际应用题出现.这既是这类问题的特点，也符合高考发展方向，考生要以课本概念和方法为主，以熟练技能，巩固概念为目标，查找知识缺漏，总结解题规律.5.本章试题的特点是：（1）综合性强.如排列、组合题大多能与集合、数列、立体几何等内容组合构成小型综合题，使每题涉及的知识点在两个以上.（2）应用性强，如统计问题及概率问题，都是以实际问题为背景.（3）对运用数学思想的要求高，如解排列、组合问题时，需分类讨论、分步讨论.以几何为背景的排列、组合题需用数形结合的思想，在解非二项问题时，需用转化思想化归为二项问题求解等，这种命题特点在以后的高考中仍会保持下去.6.根据高考试题的现状和发展趋势看，考生应：（1）立足基础知识和基本方法的复习.恰当选取典型例题，构建思维模式，造就思维依托和思维的合理定势，如对排列应用题可用①某元素排在某位上；②某元素不排在某位上；③某几个元素排在一起；④某几个元素不得相邻；⑤某几个元素顺序一定等基本问题，加强思维的规范训练.（2）抓好破势训练，为提高能力，运用变式题目，常规题向典型问题的转化，进行多种解法训练，从不同角度，不同侧面对题目进行全面分析，结合典型的错解分析，查找思维的缺陷，提高分析解决问题的能力.（3）抓好“操作”训练，就是面对问题，具体排一排、选一选，运用分类计数原理和分步计数原理为“完成这件事”设计合理的程序或分类标准，注意加强解题过程的展示与分析.（4）加强数学思想方法的训练.数学思想方法是高考的重要内容.分类讨论、转化思想、整体思想、正难则反等数学思想在本章试题中经常考查，如把（a＋b＋c）n常化为［（a＋b）＋c］n来处理，需要平时经常归纳总结.另外，在复习中要控制好训练题的难度.不做难题、偏题、怪题，一般两个以上附加条件的应用题可不考虑，文科复习在题型上应与理科相同，但题中数量关系可简单些，以降低题目的难度.（5）重点掌握随机事件、等可能事件，互斥事件、独立事件、独立重复试验中恰好发生n次等五种事件的概率，会用样本频率分布估计总体分布，会用样本平均数估计总体期望值，会用样本的方差估计总体方差.。

64高考数学易错题举例解析

k 2 或 k 3.
错解由已知得 y2=－4x2－16x－12，因此 x2+y2=－3x2－16x－12=－3(x+
8 2 28 )+ ， 3 3
8 28 28 ∴当 x=－3 时，x2+y2 有最大值 3 ，即 x2+y2 的取值范围是(－∞, 3 ]。分析没有注意 x 的取值范围要受已知条件的限制，丢掉了最小值。事实上，由于(x+2)2+ y2 y2 =1 (x+2)2=1－ ≤1 －3≤x≤－1， 4 4 x2+y2 的取值范围是[1, 28 ]。 3
1 ，显然，这两个条件是不能同时成立的。因此，8 不是最小值。 ab 1 1 1 1 1 1 2 事实上，原式= a2+b2+ 2 + 2 +4=( a2+b2)+( 2 + 2 )+4=[(a+b)2－2ab]+[( + )2－ ]+4 a b ab a b a b
第 2 页共 13 页
= (1－2ab)(1+ 由 ab≤(
从而当 x=－1 时 x2+y2 有最小值 1。∴
注意有界性：偶次方 x2≥0，三角函数－1≤sinx≤1，指数函数 ax>0，圆锥曲线有界性等。
●忽视不等式中等号成立的条件，导致结果错误。 1 1 【例 3】已知：a>0 , b>0 , a+b=1,求(a+ a )2+(b+ b )2 的最小值。错解 (a+
4 2
或 q 1。
错误分析在错解中，由
a1 (1 q 3 ) a1 (1 q 6 ) a (1 q 9 ) ， 2 1 1 q 1 q 1 q

4定积分的几何意义

[中国高考数学母题一千题](第0001号)定积分的几何意义定积分源自于求由连续曲线y=f(x)对应的曲边梯形面积,因此定积分具有较强的几何意义;充分利用定积分的几何意义可妙解一类定积分问题.[母题结构]:(Ⅰ)如果f(x)在区间[a,b]上满足f(x)≥0,则⎰b adx x f )(等于直线x= a,x=b(a<b),y=0和曲线y=f(x)所围成的曲边梯形的面积;(Ⅱ)如果f(x)在区间[a,b]上满足f(x)≤0,则⎰b adx x f )(等于直线x=a,x=b(a<b),y=0和曲线y=f(x)所围成的曲边梯形的面积的相反数; [解题程序]:根据定积分的几何意义可妙解圆形函数的定积分、定积分的大小比较、寻找定积分的面积等问题. 1.图形函数子题类型Ⅰ:(人教版.选修2-2.习题1.5(A 组)第4题)试用定积分的几何意义说明⎰-1021dx x 的大小.[解析]:根据定积分的几何意义,⎰-1021dx x 表示由直线x=0,x=1,y=0以及曲线y=21x -所围成的曲边梯形的面积;由y=21x -⇔x 2+y 2=1(y ≥0),即四分之一单位圆的面积⇒⎰-1021dx x =4π. [点评]:由定积分的几何意义,一般圆形函数f(x)=22)(a x r --的定积分可用圆或弓形的面积求出.2.大小比较子题类型Ⅱ:(2013年江西高考试题)若S 1=⎰212x dx,S 2=⎰211xdx,S 3=⎰21x e dx,则S 1,S 2,S 3的大小关系为( ) (A)S 1<S 2<S 3 (B)S 2<S 1<S 3 (C)S 2<S 3<S 1 (D)S 3<S 2<S 1[解析]:当x ∈[1,2]时,e x >x 2>x -1>0,根据定积分的几何意义⇒S 3>S 2>S 1.故选(B).[点评]:由定积分的几何意义知:若f(x)>g(x),则⎰b adx x f )(>⎰b a dx x g )(,这为定积分的大小比较提供了依据和方法. 3.面积意义子题类型Ⅲ:(2008年全国硕士研究生入学统一考试数学(二)试题)曲线方程为函数y=f(x)在区间[0,a]上有连续导数,则定积分⎰'a dx x f x 0)(=( ) (A)曲边梯形ABCD 面积 (B)梯形ABCD 面积 (C)曲边三角形ACD 面积 (D)三角形ACD 面积.[解析]:由[xf(x)]'=f(x)+x f '(x)⇒x f '(x)=[xf(x)]'-f(x)⇒⎰'a dx x f x 0)(=⎰-'a dx x f x xf 0)]}(])({[=⎰'a dx x xf 0])([-⎰a dx x f 0)(=xf(x)|a 0 -⎰a dx x f 0)(=af(a)-⎰a dx x f 0)(=矩形OBAC 面积-曲边梯形OBAD 的面积=曲边三角形ACD 面积.故选(C). [点评]:本题是定积分几何意义的典型题,解答本题的关键是构造xf '(x)=[xf(x)]'-f(x).4.子题系列: 1.(2000年全国硕士研究生入学统一考试数学(一)试题)⎰-1022dx x x = . 2.(1996年全国硕士研究生入学统一考试数学(二)试题)⎰-+-112)1(dx x x = . 3.(2012全国硕士研究生入学统一考试数学试题)⎰-2022dx x x x = .4.(2011年全国硕士研究生入学统一考试数学(一)试题)设I=⎰40sin ln πxdx ,J=⎰40cot ln πxdx ,K=⎰40cos ln πxdx ,则I,J,K 的大小关系是( ) (A)I<J<K (B)I<K<J (C)J<I<K (D)K<J<I5.(2003年全国硕士研究生入学统一考试数学(二)试题)设I 1=⎰40tan πdx x x ,I 2=⎰40tan πdx x x ,则( ) (A)I 1>I 2>1 (B)1>I 1>I 2 (C)I 2>I 1>1 (D)1>I 2>I 16.(2012年全国硕士研究生入学统一考试数学(二)试题)设I k =⎰πk x xdx e 0sin 2(k=1,2,3),则有( ) (A)I 1<I 2<I 3 (B)I 3<I 2<I 1 (C)I 2<I 3<I 1 (D)I 2<I 1<I 37.(2010年全国硕士研究生入学统一考试数学(二)试题)设函数y=f(x)在区间[-1,3]上的图形如图,则函数F(x)=⎰x dt t f 0)(的图形为( )(A) (B) (C) (D)8.(2007年全国硕士研究生入学统一考试数学(二)试题)如图,连续函数y=f(x)在区间[−3,−2],[2,3]上的图形分别是直径为1的上、下半圆周,在区间[−2,0],[0,2]的图形分别是直径为2的上、下半圆周,设F(x)=⎰x dt t f 0)(,则下列结论正确的是( ) (A)F(3)=-43F(-2) (B)F(3)=45F(2) (C)F(-3)=43F(2) (D)F(-3)=-45F(-2) 4.子题详解:1.解:由⎰-1022dx x x =圆(x-1)2+y 2=1的面积的41=4π.2.解:由⎰-+-112)1(dx x x =⎰--1121dx x =圆x 2+y 2=1的面积的21=2π. 3.解:令t=x-1,则dx=dt,t ∈[-1,1],⎰-2022dx x x x =⎰-+-1121)1(dt t t =⎰--1121dt t t (y=t 21t -为奇函数)+⎰--1121dt t =2π. 4.解:当x ∈(0,4π)时,0<sinx<cosx<cotx ⇒lnsinx<lncosx<lncotx.故选(B). 5.解:当x ∈(0,4π)时,tanx>x ⇒x x tan >1,x x tan <1⇒I 1>4π,I 2<4π.排除(A)(C)(D).故选(B).6.解:由I 1=⎰π0sin 2xdx e x ,I 2=⎰π20sin 2xdx e x =I 1+⎰ππ2sin 2xdx e x ,I 3=⎰π30sin 2xdx e x =I 2+⎰ππ32sin 2xdx e x ,⎰ππ2sin 2xdx e x <0,⎰ππ32sin 2xdx e x >0⇒I 1>I 2,I 3>I 2.故选(D).7.解:由y=f(x)的图形,其图像与x 轴及y 轴、x=x 0所围的图形的代数面积为所求函数F(x):①当x ∈[-1,0)时,F(x)为线性递增函数,且F(x)=⎰x dt t f 0)(=-⎰0)(x dt t f ≤0;②当x ∈[0,1)时,F(x)单调递减,且F(x)≤0;③当x ∈[1,2]时,F(x)单调递增,且F(x)≥0;④当x ∈(2,3]时,F(x)为常函数;⑤F(x)为连续函数.故选(D).8.解:由F(2)为半径是1的半圆面积=2π;F(3)=是两个半圆面积之差=2π-21⋅4π=83π=43F(2);由f(x)是奇函数⇒F(x)是偶函数⇒F(-3)=F(3)=43F(2).故选(C).。

30.向量旋转

杨老师高考数学丛书,给您一个智慧的人生！请尊重知识产权,不得翻印！高考数学母题[母题]Ⅰ(12-30):向量旋转(290) 731向量旋转 [母题]Ⅰ(12-30):(向量旋转公式)对任意平面向量AP =(x,y),把AP 绕其起点A 沿逆时针方向旋转θ角,得到向量AQ ,则向量AQ =(xcos θ-ysin θ,xsin θ+ycos θ). [解析]:如图,设AT 与x 轴的正向相同,<AP ,AT >=α,|AP |=r,则x=rcos α,y=rsin α;由∠QAP=θ⇒∠QAT=α+θ,又|AQ |=r ⇒AQ =(rcos(α+θ),rsin(α+θ))=(rcos αcos θ-rsin αsin θ,rsinαcos θ+rcos αsin θ)=(xcos θ-ysin θ,xsin θ+ycos θ). [点评]:在向量旋转公式中,旋转角θ也可为负角(顺时方向旋转),由向量旋转公式易得旋转点的坐标公式:若点A(x 0, y 0),把AP =(x,y)绕其起点A 沿逆时针方向旋转θ角后,得到向量AQ ,则点Q(xcos θ-ysin θ+x 0,xsin θ+ycos θ+y 0). [子题](1):(2012年安徽高考试题)在平面直角坐标系中,O(0,0),P(6,8),将向量OP 绕点O 按逆时针旋转43π后,得向量OQ ,则点Q 的坐标是( ) (A)(-72,-2) (B)(-72,2) (C)(-46,-2) (D)(-46,2)[解析]:由OP =(6,8),θ=43π⇒OQ =(6cos 43π-8sin 43π,6sin 43π+8cos 43π)=(-72,-2)⇒Q(-72,-2).故选(A). 注:由于向量旋转具有反映点与点对应关系的特征,因此,易解决:“求旋转后的点的坐标”的问题.[子题](2):(2014年全国高中数学联赛湖南初赛试题)给定平面向量a =(1,1),那么,平面向量b =(231-,231+)是向量a 经过( )(A)顺时针旋转600所得 (B)顺时针旋转1200所得 (C)逆时针旋转600所得 (D)逆时针旋转1200所得[解析]:设旋转角为θ,θ∈(-π,π],则向量b =(cos θ-sin θ,sin θ+cos θ)=(231-,231+)⇒cos θ-sin θ=231-且sin θ+cos θ=231+⇒cos θ=21,sin θ=23⇒θ=600.故选(C). 注:向量旋转公式将静态的角看成是由向量旋转而得的动态的角,因此,利用向量旋转公式可解决夹角的方向性问题. [子题](3):(1994年全国高考试题)已知直线l 过坐标原点,抛物线C 顶点在原点,焦点在x 轴正半轴上.若点A(-1,0)和点B(0,8)关于l 的对称点都在C 上,求直线l 和抛物线C 的方程.T x yAPQO[解析]:设抛物线C:y 2=2px(p>0),A,B 关于l 的对称点分别为A ',B ',直线l 的倾斜角为α,则∠AO A '=2α⇒A '(-cos2α,-sin2α);又由∠A 'O B '=900,|O B '|=|OB|=8⇒B '(8sin2α,-8cos2α)⇒sin 22α=-2pcos2α且64cos 22α=16psin2α⇒sin 32α=-8cos 32α⇒tan2α=-2⇒tan α=215+⇒p=552⇒直线l:y=215+x,抛物线C:y 2=554x. 注:平面向量的旋转具有代数与几何双重特征,因此,利用向量旋转公式易解决平面几何,尤其是平面解析几何问题. [子题系列]:1.(2005年全国高中数学联赛江苏初赛试题)设向量OA 绕点O 逆时针旋转2π得向量OB ,且2OA +OB =(7,9),则向量732 [母题]Ⅰ(12-30):向量旋转(290) OB = .2.(2008年四川高考试题)将直线y=3x 绕原点逆时针旋转900,再向右平移1个单位,所得到的直线为( )(A)y=-31x+31 (B)y=-31x+1 (C)y=3x-3 (D)y=31x+13.(1999年上海高考试题)直线y=33x 绕原点按逆时针方向旋转300后所得直线与圆(x-2)2+y 2=3的位置关系是( ) (A)直线过圆心 (B)直线与圆相交,但不过圆心 (C)直线与圆相切 (D)直线与圆没有公共点4.(2004年上海高考试题)若函数f(x)的图像可由函数y=lg(x+1)的图像绕坐标原点O 逆时针旋转2π得到,则f(x)=( ) (A)10-x -1 (B)10x -1 (C)1-10-x (D)1-10x5.(2008年全国高中数学联赛安徽预赛试题)若函数y=f(x)的图象绕原点顺时针旋转2π后,与函数y=g(x)的图象重合,则( ) (A)g(x)=f -1(-x) (B)g(x)=f -1(x) (C)g(x)=-f -1(-x) (D)g(x)=-f -1(x)6.(1987年全国高考试题)如图所示,正方形ABCD 在直角坐标平面内,已知其一条边AB 在直线y=x+4 上,C,D 在抛物线x=y 2上,求正方形ABCD 的面积.7.(1996年全国高中数学联赛上海初赛试题)连接椭圆4922y x +=1的右焦点F 2与椭圆上的动点A,作正方形F 2ABC(F 2、A 、B 、C 四顶点按顺时针方向排列),则当点A 沿椭圆运动一周后,动点C 的轨迹方程是 .8.(2006年上海交通大学保送生考试试题)A(0,1)是椭圆22a x +y 2=1(a>1)的一个顶点,是否存在以A 为直角顶点的内接于椭圆的等腰直角三角形？若存在,求出共有几个;若不存在,请说明理由. [子题详解]:1.解:设OA =(a,b),则OB =(-b,a),由2OA +OB =(7,9)⇒a=523,b=511⇒OB =(-511,523). 2.解:由直线y=3x 的法向量a =(3,-1)逆时针旋转900后得b =(1,3)⇒x+3y=0,再向右平移1个单位得:x-1+3y=0.故选(A).。

1996年高考试题

1996年全国普通高等学校招生统一考试（理工农医类）数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页.第Ⅱ卷3至8页.共150分.考试时间120分钟.第I卷（选择题共65分）注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.3.考试结束,监考人将本试卷和答题卡一并收回.一、选择题:本大题共15小题;第1—10题每小题4分,第11—15题每小题5分,共65分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知全集I=N,集合A={x│x=2n,n∈N},B={x│x=4n,n∈N},则(2)当a>1时,在同一坐标系中,函数y=a-x与y=log a x的图象是(3)若sin2x>cos2x,则x的取值范围是(A)α⊥γ且l⊥m(B)α⊥γ且m∥β(C)m∥β且l⊥m(D)α∥β且α⊥γ(A)(-3,5),(-3,-3) (B)( 3,3,),(3,-5)(C)(1,1,),(-7,1) (D)(7,-1,),(-1,-1)(9)将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥D-ABC的体积为(12)等差数列{a n的前m项和为30,前2m项和为100,则它的前3m项和为(A)130 (B)170(C)210 (D)260(14)母线长为1的圆锥体积最大时,其侧面展开图圆心角ψ等于(15)设f(x)是(-∞,+∞)上的奇函数,f(x+2)=f(x),当0≤x≤1时,f(x)=x,则f等于(A) (B)(C) (D)第Ⅱ卷(非选择题共85分)注意事项1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷中.2.答卷前将密封线内的项目填写清楚.二、填空题:本大题共4小题;每小题4分,共16分.把答案填在题中横线上.(16)已知圆x2+y2-6x-7=0与抛物线y2=2px(p>0)的准线相切.则P= .(17)正六边形的中心和顶点共7个点,以其中3个点为顶点的三角形共有个(用数字作答).(19)如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是 .三、解答题:本大题共6小题;共69分.解答应写出文字说明、证明过程或演算步骤.（20）（本小题满分11分）（21）（本小题满分12分）（22）（本小题满分12分）如图,在正三棱柱ABC-A1B1C1中,E∈BB1，截面A1EC⊥侧面AC1.(Ⅰ)求证:BE=EB1;(Ⅱ)若AA1=A1B1;求平面A1EC与平面A1B1C1所成二面角(锐角)的度数.注意:在下面横线上填写适当内容,使之成为(Ⅰ)的完整证明,并解答(Ⅱ).(Ⅰ)证明:在截面A1EC内,过E作EG⊥A1C,G是垂足.①∵∴EG⊥侧面AC1;取AC的中点F,连结BF,FG,由AB=BC得BF⊥AC,② ∵∴BF⊥侧面AC1;得BF∥EG,BF、EG确定一个平面,交侧面AC1于FG.③ ∵∴BE∥FG,四边形BEGF是平行四边形,BE=FG,④ ∵∴FG∥AA1,△AA1C∽△FGC,⑤ ∵(Ⅱ)解:（23）（本小题满分10分）某地现有耕地10000公顷,规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%.如果人口年增长率为1%,那么耕地平均每年至多只能减少多少公顷（精确到1公顷）?（24）（本小题满分12分）（25）（本小题满分12分）已知a、b、c是实数,函数f(x)=ax2+bx+c,g(x)=ax+b,当-1≤x≤1时,│f(x)│≤1.(Ⅰ)证明:│c│≤l;(Ⅱ)证明:当-1≤x≤1时,│g(x)│≤2;(Ⅲ)设a>0,当-1≤x≤1时,g(x)的最大值为2,求f(x).1996年全国普通高等学校招生统一考试（理工农医卷）数学参考答案说明:一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数.选择题和填空题不给中间分.一、选择题:本题考查基本知识和基本运算.第(1)-(10)题每小题4分,第(11)-(15)题每小题5分.满分65分.(1)C (2)A (3)D (4)B(5)A(6)D (7)B (8)A (9)D(10)B(11)C (12)C (13)A (14)D (15)B二、填空题:本题考查基本知识和基本运算.每小题4分,满分16分.(20)本小题考查对数函数性质,对数不等式的解法,分类讨论的方法和运算能力.满分11分.解:(Ⅰ)当a＞1时,原不等式等价于不等式组:因为1-a<0,所以x<0,(Ⅱ)当0<a<1时,原不等式等价于不等式组:由①得,x>1或x<0,(21)本小题考查三角函数基础知识,利用三角公式进行恒等变形和运算的能力.满分12分.解法一:由题设条件知B=60°,A+C=120°.2分利用和差化积及积化和差公式,上式可化为解法二:由题设条件知B=60°,A+C=120°.(22)本小题考查空间线面关系,正三棱柱的性质,逻辑思维能力,空间想象能力及运算能力.满分12分.(Ⅰ)①∵面A1EC⊥侧面AC1,2分②∵面ABC⊥侧面AC1,3分③∵BE∥侧面AC1,4分④∵BE∥AA1,5分⑤∵AF=FC,6分(Ⅱ)解:分别延长CE、C1B1交于点D,连结A1D.∵CC1⊥面A1C1B1,即A1C1是A1C在平面A1C1D上的射影,根据三垂线定理得DA1⊥A1C,所以∠CA1C1所求二面角的平面角.11分∵CC1=AA1=A1B1=A1C1,∠A1C1C=90°,∴∠CA1C1=45°,即所求二面角为45°. 1 2分(23)本小题主要考查运用数学知识和方法解决实际问题的能力,指数函数和二项式定理的应用,近似计算的方法和能力.满分10分.解:设耕地平均每年至多只能减少X公顷,又设该地区现有人口为P人,粮食单产为M吨/公顷.依题意得不等式答:按规划该地区耕地平均每年至多只能减少4公顷. 10分(24)本小题主要考查直线与双曲线的性质,解析几何的基本思想,以及综合运用知识的能力.满分12分.有两个不同的解.在方程组①中消去y,整理得有两个不同的解.在方程组③中消去y,整理得又因为l1⊥l2,所以有k1·k2=-1.4分于是,l1、l2与双曲线各有两个交点，等价于(Ⅱ)设A1(x1y1),B1(x2y2)1.由方程②知∴│A1B1│2=(x1-x2)2+(y1-y2)2将⑤、⑥代入上式得(25)本小题主要考查函数的性质、含有绝对值的不等式的性质，以及综合运用数学知识分析问题与解决问题的能力。

1996年全国高考数学试题

一九九六年全国高考数学试题理科试题一．选择题：本题共15个小题;第（1）-（10）题每小题4分，第（11）-（15）题每小题5分，共65分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知全集I=N ，集合},2|{N n n x x A ∈==，},4|{N n n x x B ∈==。

则（ C ）（A ）B A I ⋃= （B ）B A I ⋃= （C ）B A I ⋃= （D ）B A I ⋃=（2）当1>a 时，在同一坐标系中，函数x a y -=与x y a log =的图象是（ A ）（3）若x x 22cos sin >，则x 的取值范围是（ D ）（A ）},412432|{Z k k x k x ∈π+π<<π-π（B ）},452412|{Z k k x k x ∈π+π<<π+π（C ）},4141|{Z k k x k x ∈π+π<<π-π（D ）},4341|{Z k k x k x ∈π+π<<π+π（4）复数54)31()22(i i -+等于（ B ）（A ）i 31+ （B ）i 31+- （C ）i 31- （D ）i 31--（5）如果直线l 、m 与平面α、β、γ满足：α⊂αγ⋂β=m l l ,//,和γ⊥m ，那么必有（ A ）(A) y (B) y (C) y (D) yx（A ）γ⊥α且m l ⊥ （B ）γ⊥α且β//m （C ）β//m 且m l ⊥ （D ）βα//且γ⊥α（6）当22π≤≤π-x 时，函数x x x f cos 3sin )(+=的（ D ）（A ）最大值是1，最小值是-1 （B ）最大值是1，最小值是21- （C ）最大值是2，最小值是-2 （D ）最大值是2，最小值是-1 （7）椭圆⎩⎨⎧ϕ+-=ϕ+=.sin 51,cos 33y x 的两个焦点坐标是（ B ）（A ）（-3，5），（-3，-3）（B ）（3，3），（3，-5）（C ）（1，1），（-7，1）（D ）（7，-1），（-1，-1）（8）若20π<α<，则)](arccos[sin )]2(arcsin[cos α+π+α+π等于（ A ）（A ）2π （B ）2π- （C ）α-π22 （D ）α-π-22（9）将边长为a 的正方形ABCD 沿对角线AC 折起，使得BD=a ，则三棱锥D-ABC 的体积为（ D ）（A ）63a （B ）123a （C ）3123a （D ）3122a（10）等比数列}{n a 的首项11-=a ，前n 项和为n S ，若3231510=S S ，则nn S ∞→lim 等于（ B ）（A ）32 （B ）32- （C ）2 （D ）-2 （11）椭圆的极坐标方程为θ-=ρcos 23，则它在短轴上的两个顶点的极坐标是（ C ）（A ）（3，0），（1，π）（B ）（2,3π），（23,3π）（C ）（2，3π），（2，35π）（D ）（23,7arctg ），（232,7arctg -π）（12）等差数列}{n a 的前m 项和为30，前2m 项和为100，则它的前3m 项和为（ C ）（A ）130 （B ）170 （C ）210 （D ）260（13）设双曲线)0(12222b a by a x <<=-的半焦距为c ，直线l 过（a ，0），（0，b ）两点。

1996年全国高考数学(理科)试题

1996年全国统一高考数学试卷（理科数学）一、选择题：本大题共15小题:第1-10题每小题4分,第11-15题每小题5分,共65分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知全集I N =，集合{}2,A x x n n N ==∈，{}4,B x x n n N ==∈，则 A.I A B = B.()I I C A B = C.()I I A C B = D.()()I I I C A C B =2.当1a >时，在同一坐标系中，函数x y a -=与log a y x =的图象3．若22sin cos x x>，则x 的取值范围是A. 322,44x k x k k z ππππ⎧⎫-<<+∈⎨⎬⎩⎭ B. 522,44x k x k k z ππππ⎧⎫+<<+∈⎨⎬⎩⎭C. ,44x k x k k z ππππ⎧⎫-<<+∈⎨⎬⎩⎭D. 3,44x k x k k z ππππ⎧⎫+<<+∈⎨⎬⎩⎭44等于 A.1+ B. 1-+ C. 1- D. 1- 5．如果直线,l m 与平面,,αβγ满足：l βγ=，l ∥α，m α⊂和m γ⊥，那么必有A.αγ⊥且l m ⊥B.αγ⊥且m ∥βC.m ∥β且l m ⊥D.α∥β且αγ⊥ 6．当22x ππ-≤≤时，函数()sin f x x x =的A. 最大值是1,最小值是1-B. 最大值是1,最小值是12-C. 最大值是2,最小值是2-D. 最大值是2,最小值是1-7.椭圆33cos 15sin x y θθ=+⎧⎨=-+⎩（θ为参数）的两个焦点坐标是A.(3,5)-,(3,3)-B. (3,3),(3,5)-C. (1,1),(7,1)-D. (7,1),(1,1)-- 8.若02πα<<，则arcsin[cos()]arccos[sin()]2παπα+++等于 A.2πB. 2π-C. 22πα-D. 22πα--9．将边长为a 的正方形ABCD 沿对角线AC 折起，使得BD a =，则三棱锥D ABC -的体积为A.36aB. 312aC. 312D. 31210．等比数列{}n a 的首项11a =-，前n 项和为n S ，若1053132S S =,则lim n n S →∞等于A.23 B . 23- C. 2 D. 2- 11．椭圆的极坐标方程为32cos ρθ=-，则它在短轴上的两个顶点的极坐标是A.(3,0),(1,)πB.(3,)2π,3)2πC.(2,)3π,5(2,)3πD. )2,2arctan )2π- 12.等差数列{}n a 的前m 项和为30，前2m 项和为100，则它的前3m 项和为 A.130 B. 170 C. 210 D. 26013.设双曲线22221x y a b-=（0a b <<）的半焦距为c ，直线l 过(,0),(0,)a b 两点，已知原点到直线l的距离为4，则双曲线的离心率为 A.214.母线长为l 的圆锥体积最大时，其侧面展开图圆心角ϕ等于A.315.设()f x 是(,)-∞∞上的奇函数，(2)()f x f x +=-，当01x ≤≤时()f x x =，则(7.5)f 等于A. 0.5B. 0.5-C. 1.5D. 1.5- 二、填空题（共4小题，每小题4分，满分16分）16.已知圆22670x y x +--=与抛物线22(0)y px p =>的准线相切，则p =__ . 17.正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有个（用数字作答）．18.求值：tan 20tan 403tan 20tan 40++=_______ ．19.如图，正方形ABCD 所在平面与正方形ABEF 所在平面成60的二面角，则异面直线AD 与BF 所成角的余弦值是 ____ ．三、解答题：本大题共6小题,共65分.解答应写出文字说明、证明过程或推演步骤.20.（本小题满分11分）解不等式1log (1)1a x ->．21.（本小题满分12分）已知ABC ∆的三个内角,,A B C 满足：2A C B +=,11cos cos cos A C B+=-，求cos2A C-的值． 22．（本小题满分12分）如图，在正三棱柱111ABC A B C -中，E 在1BB 上，截面1A EC ⊥侧面11AAC C ．（1）求证：1BE EB =；注意：在下面横线上填写适当内容，使之成为（1）的完整证明，并解答（2）．（1）证明：在截面1A EC 内，过E 作1EG A C ⊥，G 是垂足． ①∵ _________ABCD E FABCEA 1B 1C 1∴EG ⊥侧面1AC ；取AC 的中点F ，连接,BF FG ，由AB BC =,得BF AC ⊥， ②∵ _________∴BF ⊥侧面1AC ；得BF ∥EG ，BF 、EG 确定一个平面，交侧面1AC 于FG ． ③∵ _________∴BE ∥FG ，四边形BEFG 是平行四边形，BE FG =， ④∵ _________∴FG ∥1AA ，1AA C ∆∽FGC ∆，⑤∵ _________∴111122FG AA BB ==，112BE BB =,故1BE EB =（2）若111AA A B =；求平面1A EC 与平面111A B C 所成二面角（锐角）的度数． 23.（本小题满分10分）某地现有耕地10000公顷，规划10年后粮食单产比现在增加22%，人均粮食占有量比现在提高10%．如果人口年增长率为1%，那么耕地平均每年至多只能减少多少公顷？（精确到1公顷）（粮食单产=总产量/耕地面积，人均粮食占有量=总产量/总人口数） 24.（本小题满分12分）已知1l ,2l 是过点(P 的两条互相垂直的直线，且1l ,2l 与双曲线221y x -=,各有两个交点，分别为1A ,1B 和2A ,2B ．（1）求1l 的斜率1k 的取值范围；（2）若1122A B B =，求1l ,2l 的方程． 25．（本小题满分12分）已知,,a b c R ∈，函数2()f x ax bx c =++，()g x ax b =+，当11x -≤≤时，()1f x ≤. （1）证明：1c ≤；（2）证明：当11x -≤≤时，()2g x ≤；（3）设0a >,当11x -≤≤时，()g x 的最大值为2，求()f x .。

1999年全国Ⅱ高考数学试题(文)

1999年普通高等数学招生全国统一考试（全国Ⅱ）文科数学参考公式：三角函数的积化和差公式：[]1sin cos sin()sin()2αβαβαβ=++- []1cos sin sin()sin()2αβαβαβ=+--[]1cos cos cos()cos()2αβαβαβ=++-[]1sin sin cos()cos()2αβαβαβ=-+--正棱台、圆台的侧面积公式1()2S c c l ='+台侧其中c '、c 分别表示上、下底面周长，l 表示斜高或母线长．球的体积公式：343V r π=球，其中R 表示球的半径．第Ⅰ卷（选择题共60分）一、选择题：本大题共14小题，第1－10题每小题4分，第11－14题每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．如图，I 是全集，M 、P 、S 是I 的子集，则阴影部分所表示的集合是A ．()M P SB ．()M P SC ．()M P SD ．()M P S2．已知映射:f A B →，其中，集合{}3,2,1,1,2,3,4A =---，集合B 中的元素都是A 中元素在的映射f 下的象，且对任意的a A ∈，在B 中和它对应的元素是||a ，则集合B 中元素的个数是A ．4B ．5C ．6D ．73．若函数()y f x =的反函数是()y g x =，()f a b =，0ab ≠，则()g b 等于A ．aB ．1a -C ．bD ．1b -4．函数()sin()(0)f x M x ωϕω=+>在区间[],a b 上是增函数，且()f a M =-，()f b M =，则函数()cos()g x M x ωϕ=+在[],a b 上A ．是增函数B ．是减函数C ．可以取得最大值MD ．可以取得最小值M -5．若()sin f x x 是周期为π的奇函数，则()f x 可以是I PMSABCDEFA ．sin xB ．cos xC ．sin 2xD ．cos 2x6．曲线220x y ++-=关于A．直线x =B ．直线y x =-轴对称C．点(-中心对称D．点()中心对称7．若干毫升水倒入底面半径为2cm 的圆柱形容器中，量得水面的高度为6cm ，若将这些水倒入轴截面是正三角形的倒圆锥形容器中，则水面的高度是A． B ．6cmC．D．8．若(32301232x a a x a x a x +=+++，则220213()()a a a a +-+的值为A ．1B ．－1C ．0D ．290y +-=截圆224x y +=得的劣弧所对的圆心角为A ．6π B ．4π C ．3π D ．2π 10．如图，在多面体ABCDEF 中，已知面ABCD 是边长为3的正方形，EF ∥AB ，32EF =，EF 与面AC 的距离为2，则该多面体的体积为 A ．92 B ．5C ．6D ．15211．若sin tan cot 22ππαααα⎛⎫>>-<< ⎪⎝⎭，则α的取值范围是A ．,24ππ⎛⎫-- ⎪⎝⎭B ．,04π⎛⎫-⎪⎝⎭C ．0,4π⎛⎫⎪⎝⎭D ．,42ππ⎛⎫⎪⎝⎭12．如果圆台的上底面半径为5，正底面半径为R ，中截面把圆台分为上、下两个圆台，它们的侧面积的比为1∶2，那么R ＝A ．10B ．15C ．20D ．2513．给出下列曲线方程：①4210x y +-=；②223x y +=；③2212x y +=；④2212x y -=其中与直线23y x =--有交点的所有曲线是A ．①③B ．②④C ．①②③D ．②③④14．某电脑用户计划使用不超过500元的奖金购买单位分别为60元、70元的单片软件和盒装磁盘，根据需要，软件至少买3片，磁盘至少买2盒，则不同的选购方式共有A ．5种B ．6种C ．7种D ．8种第Ⅱ卷（非选择题共90分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上．15．设椭圆22221(0)x y a b a b+=>>的右焦点为1F ，右准线为1l ，若过1F 且垂直于x 轴的弦长等于点1F 到1l 的距离，则椭圆的离心率是．16．在一块并排10龚的田地中，选择2龚分别种植A 、B 两种作物，每种作物种植一龚，为有利于作物生长，要求A 、B 两种作物的间隔不小于6龚，则不同的选龚方法共有种（用数字作答）．17．若正数a 、b 满足3ab a b =++，则ab 的取值范围是．18．α、β是两个不同的平面，m 、n 是平面α及β之外的两条不同直线，给出四个论断：①m n ⊥；②αβ⊥；③n β⊥；④m α⊥，以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题：．三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤．19．（本小题满分10分3lg 40x +=20．（本小题满分12分）数列{}n a 的前n 项和记为n S ，已知53()n n a S n N =-∈，求1221lim ()n n a a a -→∞+++ 的值．21．（本小题满分12分）设复数3cos 2sin z i θθ=+，求函数arg (0)2y z πθθ=-<<的最大值及对应的θ的值．22．（本小题满分12分）如图，已知正四棱柱1111ABCD A BC D -，点E 在棱1DD 上，截面EAC ∥1D B ，且面EAC 与底面ABCD 所成的角为45°，AB a =．（1）求截面EAC 的面积；（2）求异面直线11A B 与AC 之间的距离；（3）求三棱锥1B EAC -的体积．23．（本小题满分14分）如图为一台冷轧机的示意图．冷轧机由若干对轧辊组成，带钢从一端输入，经过各对轧辊逐步减薄后输出．（1）输入带钢的厚度为α，输出的带钢的厚度为β，若每对轧辊的减薄率不超过0r ．问冷轧机至少需要安装多少对轧辊？（一对轧辊减薄率＝输入该对的带钢厚度－从该对输出的带钢厚度输入该对的带钢厚度）（2）已知一台冷轧机共有4对减薄率为20％的轧辊，所有轧辊周长均为1600mm ．若第k 对轧辊有缺陷，每滚动一周在带钢上压出一个疵点，在冷轧机输出的带钢上，疵点的间距为k L ．为了便于检修，请计算1L 、2L 、3L 并填入下表（轧钢过程中，带钢宽度不变，且不考虑损耗）．24．（本小题满分14分）如图，给出定点(,0)(0)A a a >和直线:1l x =-．B 是直线l 上的动点，BOA ∠的角平分线交AB 于点C ．求点C 的轨迹方程，交讨论方程表示的曲线类型与a 值的关系．A B C D E A 1B 1C 1D 1…数学试题参考答案一、选择题，本题考查基础知识，基本概念和基本运算能力二、填空题．本题考查基础知识,基本概念和基本运算技巧 13． 14． 15． 16．三、解答题 17．1999年普通高等学校招生全国统一考试数学试题(文史类)参考解答及评分标准一．选择题：本题考查基本知识和基本运算．第(1)—(10)题每小题4分，第(11)—(14)题每小题5分．满分60分．(1) C (2) A (3) A (4) C (5) B (6) B (7) B (8) A (9) C (10) D (11) B (12) D (13) D (14) C二．填空题：本题考查基本知识和基本运算．每小题4分，满分16分．(15) 21(16) 12 (17) ；(18) m ⊥α，n ⊥β，α⊥β⇒m ⊥n 或m ⊥n ，m ⊥α，n ⊥β⇒α⊥β 三．解答题(19) 本小题主要考查对数方程、无理方程的解法和运算能力．满分10分．解：设y x =-2lg 3，原方程化为y －y 2+2=0 ——4分解得 y =－1，y =2． ——6分因为02lg 3≥-x ，所以将y =－1舍去．由2lg 3-x =2，得lg x =2，所以x =100． ——9分经检验，x =100为原方程的解． ——10分 (20) 本小题主要考查等比数列和数列极限等基础知识．满分12分．解：由 S n =a 1+a 2+…+a n 知a n =S n －S n －1(n ≥2)，a 1=S 1， ——2分由已知a n =5S n —3得 a n －1=5S n －1—3． ——4分于是 a n －a n －1=5(S n －S n －1)=5a n ，所以 a n =－41a n －1． ——6分由 a 1=5S 1—3，得 a 1=43．所以，数列{a n }是首项a 1=43，公比q =－41的等比数列． ——8分由此知数列 a 1，a 3，a 5，…，a 2n －1，…是首项为a 1=43，公比为241⎪⎭⎫⎝⎛-的等比数列．∴ ∞→n lim ( a 1+a 3+a 5+…+a 2n －1)=54411432=⎪⎭⎫ ⎝⎛--． ——12分 (21) 本小题主要考查复数的基本概念、三角公式和不等式等基础知识，考查综合运用所学数学知识解决问题的能力．满分12分．解：由20πθ<<得0tg >θ．由z =3cos θ+i sin θ得tg(arg z )=θθθtg 31cos 3sin =． ——3分故 y =tg(θ－arg z )θθθ2tg 311tg 31tg +-= θθtg tg 32+= ∵32tg tg 3≥+θθ，∴ 33tg tg 32≤+θθ． ——9分当且仅当θtg 3=tg θ(20πθ<<)时，即tg θ=3时，上式取等号．所以当θ=3π时，函数y 取得最大值33． ——12分 (22) 本小题主要考查空间线面关系、二面角和距离的概念，逻辑思维能力、空间想象能力及运算能力．满分12分．(Ⅰ) 解：如图，连结DB 交AC 于O ，连结EO ． ∵ 底面ABCD 是正方形，∴ DO ⊥AC ．又 ∵ ED ⊥底面AC ，∴ EO ⊥AC ．∴ ∠EOD 是面EAC 与底面AC 所成二面角的平面角， ——2分 ∴ ∠EOD =45º． DO =22a ，AC =2a ，EO =22a ·sec45º=a ．故 S △EAC =22a 2． ——4分 (Ⅱ) 解：由题设ABCD －A 1B 1C 1D 1是正四棱柱，得A 1A ⊥底面AC ，A 1A ⊥AC ．又 A 1A ⊥A 1B 1，∴ A 1A 是异面直线A 1B 1与AC 间的公垂线． ——6分 ∵ D 1B ∥面EAC ，且面D 1BD 与面EAC 交线为EO ，∴ D 1B ∥EO ．又O 是DB 的中点，∴ E 是D 1D 的中点，D 1B =2EO =2a ．∴ D 1D =221DB B D -=2a ．异面直线A 1B 1与AC 间的距离为2a ． ——8分 (Ⅲ) 解法一：如图，连结D 1B 1．∵ D 1D =DB =2a ，∴ BDD 1B 1是正方形．连结B 1D 交D 1B 于P ，交EO 于Q ． ∵ B 1D ⊥D 1B ，EO ∥D 1B ，∴ B 1D ⊥EO ．又 AC ⊥EO ，AC ⊥ED ．∴ AC ⊥面BDD 1B 1，∴ B 1D ⊥AC ，∴ B 1D ⊥面EAC ．∴ B 1Q 是三棱锥B 1－EAC 的高． ——10分由DQ =PQ ，得B 1Q =43B 1D =23a ． ∴ .42232231321a a a V EAC B =⋅⋅=- 所以三棱锥B 1－EAC 的体积是342a ． ——12分解法二：连结B 1O ，则EAC B V -1=21EOB A V -． ——10分∵ AO ⊥面BDD 1B 1，∴ AO 是三棱锥A －EOB 1的高，AO =22a ．在正方形BDD 1B 1中，E 、O 分别是D 1D 、DB 的中点(如右图)，则2431a S EOB =∆． ∴ 324222433121a a a V EAC B =⋅⋅⋅=-．所以三棱锥B 1－EAC 的体积是342a ． ——12分(23) 本小题主要考查等比数列、对数计算等基本知识，考查综合运用数学知识和方法解决实际问题的能力．满分14分．(Ⅰ) 解：厚度为α的带钢经过减薄率均为r 0的n 对轧辊后厚度为α(1－r 0)n ．为使输出带钢的厚度不超过β，冷轧机的轧辊数(以对为单位)应满足α(1－r 0)n ≤β，即 (1－r 0)n ≤αβ． ——4分由于(1－r 0)n >0，αβ>0，对上式两端取对数，得n lg(1－r 0)≤lg αβ．由于lg(1－r 0)<0，所以n ≥()01lg lg lg r --αβ．因此，至少需要安装不小于()01lg lg lg r --αβ的整数对轧辊． ——7分(Ⅱ)解法一：第k 对轧辊出口外疵点间距离为轧辊周长，在此处出口的两疵点间带钢的体积为1600·α(1－r )k ·宽度 (其中r =20%)，而在冷轧机出口处两疵点间带钢的体积为L k ·α(1－r )4·宽度．因宽度相等，且无损耗，由体积相等得1600·α(1－r )k =L k ·α(1－r )4 (r =20%)，即 L k =1600·0.8k －4． ——10分由此得L 3=2000(mm )，L 2=2500(mm )， L 1=3125(mm )．填表如下解法二：第3口处两疵点间带钢体积相等，因宽度不变，有1600=L 3·(1－0.2)，所以 L 3=8.01600=2000(mm )． ——10分同理 L 2=8.03L =2500(mm )． L 1=8.02L =3125(mm )．填表如下——14分 (24) 本小题主要考查曲线与方程，直线和圆锥曲线等基础知识，以及求动点轨迹的基本技能和综合运用数学知识解决问题的能力．满分14分．解法一：依题意，记B (－1，b ) (b ∈R )，则直线OA 和OB 的方程分别为y =0和y =－bx ．设点C (x ，y )，则有0≤x <a ，由OC 平分∠AOB ，知点C 到OA 、OB 距离相等．根据点到直线的距离公式得21bbx y y ++=． ① ——4分依题设，点C 在直线AB 上，故有()a x aby -+-=1． ——6分由 x －a ≠0，得 ()ax y a b -+-=1． ②将②式代入①代得()()()22222111⎥⎦⎤⎢⎣⎡-+-=⎥⎦⎤⎢⎣⎡-++a x xy a y a x y a y ，整理得y 2[(1－a )x 2－2ax +(1+a )y 2]=0． ——9分若y ≠0，则(1－a )x 2－2ax +(1+a )y 2=0 (0<x <a )；若y =0，则b =0，∠AOB =π，点C 的坐标为(0，0)，满足上式．综上得点C 的轨迹方程为(1－a )x 2－2ax +(1+a )y 2=0 (0≤x <a )． ——10分∵ a ≠1，∴ 111122222=-+⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛--a a y a a a a x (0≤x <a )． ③ ——12分由此知，当0<a <1时，方程③表示椭圆弧段；当a >1时，方程③表示双曲线一支的弧段． ——14分解法二：如图，设D 是l 与x 轴的交点，过点C 作CE ⊥x 轴，E 是垂足． (ⅰ)当|BD |≠0时，设点C (x ，y )，则0<x <a ，y ≠0．由CE ∥BD 得 ()a xa y EADA CE BD +-=⋅=1． ——3分∵ ∠COA =∠COB=∠COD －∠BOD=π－∠COA －∠BOD ， ∴ 2∠COA =π－∠BOD ．∵ ()()，，BOD BOD COACOACOA ∠-=∠-∠-∠=∠tg tg tg 1tg 22tg 2π ——6分 ()a xa y ODBD BOD xy COA +-==∠=∠1tg tg ，．∴()，a x a y xyx y+--=-⋅11222整理得(1－a )x 2－2ax +(1+a )y 2=0 (0<x <a )．——9分 (ⅱ) 当|BD |=0时，∠BOA =π，则点C 的坐标为 (0，0)，满足上式．综合(ⅰ)，(ⅱ)，得点C 的轨迹方程为 (1－a )x 2－2ax +(1+a )y 2=0 (0≤x <a )． ——10分以下同解法一．。

【高考数学试题】1996年普通高等学校招生全国统一考试.文科数学试题及答案

【高考数学试题】1996年普通高等学校招生全国统一考试数学(文史类)第Ⅰ卷(选择题共65分)注意事项:1.答案Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,在选涂其它答案,不能答在试题卷上.3.考试结束,监考人将本试卷和答题卡一并收回.一.选择题:本大题共15小题;第1—10题每小题4分,第11—15题每小题5分,共65分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设全集I=｛1,2,3,4,5,6,7｝,集合A=｛1,3,5,7｝,B=｛3,5｝.则(A)I=A∪B(B)I=∪B(C)I=A∪(D)I=∪(2)当a>1时,在同一坐标系中.函数y=a-x与y=logax的图象是(3)若sin2x>cos2x,则x的取值范围是(A){x|2kπ-3π/4<x<2kπ+π/4,k∈Z}(B){x|2kπ+π/4<x<2kπ+5π/4,k∈Z}(C){x|kπ-π/4<x<kπ+π/4,k∈Z}(D){x|kπ+3π/4<x<kπ+3π/4,k∈Z}(4)复数(2+2i)4/(1-i)5等于(A)1+i (B)-1+i (C)1-i (D)-1-i(5)6名同学排成一排,其中甲、乙两人必须排在一起的不同排法有(A)720种(B)360种(C)240种(D)120种(6)已知α是第三象限角且sinα=-24/25,则tgα=(A)4/3 (B)3/4 (C)-3/4 (D)-4/3(7)如果直线l、m 与平面α、β、γ满足l=β∩γ，l∥α，m =α，m⊥γ，那么必有(A)α⊥γ且l⊥m(B)α⊥γ且m∥β(C)m∥β且l⊥m (D)α∥β且α⊥γ(8)当-π/2≤x≤π/2时，函数f(x)＝sinx+cosx的(A)最大值是1,最小值是-1 (B)最大值是1,最小值是-1/2(C)最大值是2,最小值是-2 (D)最大值是2,最小值是-1(9)中心在原点，准线方程为x=±4，离心率为1/2的椭圆方程是(A)x2/4+y2/3=1 (B)x2/3+y2/4=1(C)x2/4+y2=1 (D)x2+y2/4=1(10)圆锥母线长为1,侧面展开图圆心角为240°,该圆锥的体积是(A)2π/81 (B)4π/81 (C)10π/81 (D)8π/81(11)椭圆25x2-150x+9y2+18y+9=0的两个焦点坐标是(A)(-3,5),(-3,-3) (B)(3,3),(3,-5)(C)(1,1),(-7,1) (D)(7,-1),(-1,-1)(12)将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥D-ABC 的体积为(A)a3/6 (B)a3/12 (C)a3/12 (D)a3/12(13)等差数列｛an｝的前m项和为30,前2m项和为100,则它的前3m项和为(A)130 (B)170 (C)210 (D)260(14)设双曲线x2/a2+y2/b2=1(0<a<b)的半焦距为c，直线l过(a,0),(0,b)两点.已知原点到直线的距离为c/4，则双曲线的离心率为(A)2 (B)(C)(D)2/3(15)设f(x)是(-∞,+∞)上的奇函数,f(x+2)=f(x),当0≤x≤1时,f(x)=x,则f(7,5)等于(A)0.5 (B)-0.5 (C)1.5 (D)-1.5第Ⅱ卷(非选择题共85分)注意事项:1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷中.2.答卷前将密封线内的项目填写清楚.二.填空题:本大题共4小题;每小题4分,共16分.把答案填在题中横线上.(16)已知点(-2,3)与抛物线y2=2px(p>0)的焦点的距离是5,则p=______.(17)正六边形的中心和顶点共7个点,以其中3个点为顶点的三角形共有______个.(用数字作答)(19)如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是______ .三.解答题:本大题共6小题;共69分.解答应写出文字说明、证明过程或演算步骤.(20)(本小题满分11分) 解不等式loga(x+1-a)>1.21)(本小题满分12分)设等比数列｛an ｝的前n项和为Sn.若S3+S6=2S9 ，求数列的公比q.(22)(本小题满分11分)已知三角形ABC的三个内角A,B,C满足A+C=2B,1/cosA+1/cosC=－/cosB,求cos{(A-C)/2}.(23)(本小题满分12分)【注意:本题的要求是,参照标号①的写法,在标号②、③、④、⑤的横线上填写适当步骤,完成(Ⅰ)证明的全过程;并解答(Ⅱ).】如图：在正三棱柱ABC－A1B1C1中,AB=AA1/3=a,E,F分别是BB1,CC1上的点,且BE=a,CF=2a.(Ⅰ)求证:面AEF⊥面ACF;(Ⅱ)求三棱锥A1-AEF的体积.(Ⅰ)证明:①∵BE=a,CF=2a,BE∥CF,延长FE与CB延长线交于D,连结AD.∴△DBE∽△DCF________________________________________________。

1996年全国统一高考数学试卷(文科)

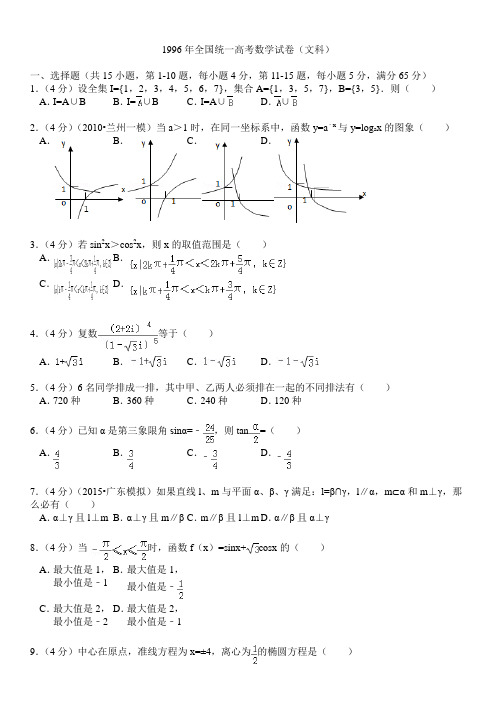
1996年全国统一高考数学试卷（文科）一、选择题（共15小题，第1-10题，每小题4分，第11-15题，每小题5分，满分65分）1．（4分）设全集I={1，2，3，4，5，6，7}，集合A={1，3，5，7}，B={3，5}．则（）A．I=A∪B B．I=∪B C．I=A∪D．∪2．（4分）（2010•兰州一模）当a＞1时，在同一坐标系中，函数y=a﹣x与y=log a x的图象（）A．B．C．D．3．（4分）若sin2x＞cos2x，则x的取值范围是（）A．B．C．D．4．（4分）复数等于（）A．B．C．D．5．（4分）6名同学排成一排，其中甲、乙两人必须排在一起的不同排法有（）A．720种B．360种C．240种D．120种6．（4分）已知α是第三象限角sinα=﹣，则tan=（）A．B．C．﹣D．﹣7．（4分）（2015•广东模拟）如果直线l、m与平面α、β、γ满足：l=β∩γ，l∥α，m⊂α和m⊥γ，那么必有（）A．α⊥γ且l⊥m B．α⊥γ且m∥βC．m∥β且l⊥m D．α∥β且α⊥γ8．（4分）当时，函数f（x）=sinx+cosx的（）A．最大值是1，最小值是﹣1 B．最大值是1，最小值是﹣C．最大值是2，最小值是﹣2 D．最大值是2，最小值是﹣19．（4分）中心在原点，准线方程为x=±4，离心为的椭圆方程是（）A ．=1B ．=1C ．+y 2=1D ．x 2+=110．（4分）圆锥母线长为1，侧面展开图圆心角为240°，该圆锥的体积（） A ． B ． C ．D ． 11．（5分）椭圆25x 2﹣150x+9y 2+18y+9=0的两个焦点坐标是（） A ．（﹣3，5），（﹣3，﹣3） B ．（3，3），（3，﹣5） C ．（1，1），（﹣7，1） D ．（7，﹣1），（﹣1，﹣1） 12．（5分）（2014•广西模拟）将边长为a 的正方形ABCD 沿对角线AC 折起，使得BD=a ，则三棱锥D ﹣ABC 的体积为（） A ． B ． C ． D ．13．（5分）等差数列{a n }的前m 项和为30，前2m 项和为100，则它的前3m 项和为（） A ． 130 B ． 170 C ． 210 D ． 26014．（5分）设双曲线=1（0＜a ＜b ）的半焦距为c ，直线l 过（a ，0）（0，b ）两点，已知原点到直线l 的距离为，则双曲线的离心率为（）A ．2 B ．C ．D ．15．（5分）设f （x ）是（﹣∞，+∞）上的奇函数，f （x+2）=﹣f （x ），当0≤x≤1时，f （x ）=x ，则f （7.5）等于（） A ． 0.5 B ． ﹣0.5 C ． 1.5 D ． ﹣1.5二、填空题（共4小题，每小题4分，满分16分） 16．（4分）已知点（﹣2，3）与抛物线y 2=2px （p ＞0）的焦点的距离是5，则p= _________ ． 17．（4分）正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有 _________ 个（用数字作答）．18．（4分）求值：tan20°+tan40°+tan20°tan40°= _________ ． 19．（4分）如图，正方形ABCD 所在平面与正方形ABEF 所在平面成60°的二面角，则异面直线AD 与BF 所成角的余弦值是 _________ ．三、解答题（共6小题，满分69分）20．（11分）解不等式log a（x+1﹣a）＞1．21．（12分）设等比数列{a n}的前n项和为S n．若S3+S6=2S9，求数列的公比q．22．（12分）已知△ABC的三个内角A，B，C满足：，求的值．23．（12分）如图：在正三棱柱ABC﹣A1 B1 C1中，AB==a，E，F分别是BB1，CC1上的点且BE=a，CF=2a．（Ⅰ）求证：面AEF⊥面ACF；（Ⅱ）求三棱锥A1﹣AEF的体积．24．（10分）某地现有耕地10000公顷，规划10年后粮食单产比现在增加22%，人均粮食占有量比现在提高10%．如果人口年增长率为1%，那么耕地平均每年至多只能减少多少公顷？（精确到1公顷）（粮食单产=，人均粮食占有量=）25．（12分）已知l1、l2是过点P（﹣，0）的两条互相垂直的直线，且l1、l2与双曲线y2﹣x2=1各有两个交点，分别为A1、B1和A2、B2．（1）求l1的斜率k1的取值范围；（2）若|A1B1|=|A2B2|，求l1、l2的方程．1996年全国统一高考数学试卷（文科）参考答案与试题解析一、选择题（共15小题，第1-10题，每小题4分，第11-15题，每小题5分，满分65分）1．（4分）设全集I={1，2，3，4，5，6，7}，集合A={1，3，5，7}，B={3，5}．则（）A．I=A∪B B．I=∪B C．I=A∪D．∪考点：并集及其运算．专题：综合题．分析：根据全集和集合B求出集合B的补集，然后求出A和B补集的并集，得到正确答案．解答：解：因为全集I={1，2，3，4，5，6，7}，B={3，5}，所以={1，2，4，6，7}，又A={1，3，5，7}，则A∪={1，2，3，4，5，6，7}=I．故选C点评：本题考查了并集及补集的运算，是一道基础题．2．（4分）（2010•兰州一模）当a＞1时，在同一坐标系中，函数y=a﹣x与y=log a x的图象（）A．B．C．D．考点：函数的图象与图象变化．专题：数形结合．分析：先将函数y=a﹣x化成指数函数的形式，再结合函数的单调性同时考虑这两个函数的单调性即可判断出结果．解答：解：∵函数y=a﹣x可化为函数y=，其底数小于1，是减函数，又y=log a x，当a＞1时是增函数，两个函数是一增一减，前减后增．故选A．点评：本题考查函数的图象，考查同学们对对数函数和指数函数基础知识的把握程度以及数形结合的思维能力．3．（4分）若sin2x＞cos2x，则x的取值范围是（）A．B．C．D．考点：余弦函数的单调性；二倍角的余弦．专题：计算题．分析：sin2x＞cos2x化为cos2x﹣sin2x＜0，就是cos2x＜0，然后求解不等式即可得到x的取值范围．解答：解：因为sin2x＞cos2x，所以cos2x﹣sin2x＜0，就是cos2x＜0解得：2kπ+＜2x＜2kπk∈Z所以x的取值范围是故选D．点评：本题考查余弦函数的单调性，二倍角的余弦，考查计算能力，是基础题．4．（4分）复数等于（）A．B．C．D．考点：复数代数形式的混合运算．分析：利用1的立方虚根的性质化简，然后求得答案．解答：解：复数==．故选B．点评：复数代数形式的混合运算，同时应用1的立方虚根的性质化简；本题是中档题．5．（4分）6名同学排成一排，其中甲、乙两人必须排在一起的不同排法有（）A．720种B．360种C．240种D．120种考点：排列、组合及简单计数问题．专题：计算题．分析：6名同学排成一排，其中甲、乙两人必须排在一起，对于相邻的问题，一般用捆绑法，首先把甲和乙看做一个元素，使得它与另外4个元素排列，再者甲和乙之间还有一个排列，根据分步计数原理得到结果．解答：解：∵6名同学排成一排，其中甲、乙两人必须排在一起，∴首先把甲和乙看做一个元素，使得它与另外4个元素排列，再者甲和乙之间还有一个排列，共有A55A22=240，故选C．点评：本题考查排列、组合及简单计数问题，考查相邻问题，是一个比较简单的题目，这种题目一般有限制条件，首先排列有限制条件的元素．6．（4分）已知α是第三象限角sinα=﹣，则tan=（）A．B．C．﹣D．﹣考点：弦切互化；象限角、轴线角．专题：综合题．分析：由α是第三象限角，得到cosα小于0，然后由sinα的值利用同角三角函数间的基本关系求出cosα的值，把所求的式子利用弦切互化公式化简后，把sinα和cosα的值代入即可求出值．解答：解：由α是第三象限角，得到cosα=﹣=﹣，则tan====﹣．故选D．点评：此题考查学生灵活运用同角三角函数间的基本关系及弦切互化公式化简求值，是一道中档题．7．（4分）（2015•广东模拟）如果直线l、m与平面α、β、γ满足：l=β∩γ，l∥α，m⊂α和m⊥γ，那么必有（）A．α⊥γ且l⊥m B．α⊥γ且m∥βC．m∥β且l⊥m D．α∥β且α⊥γ考点：空间中直线与平面之间的位置关系．分析：m⊂α和m⊥γ⇒α⊥γ，l=β∩γ，l⊂γ．然后推出l⊥m，得到结果．解答：解：∵m⊂α和m⊥γ⇒α⊥γ，∵l=β∩γ，l⊂γ．∴l⊥m，故选A．点评：本题考查空间直线与平面之间的位置关系，画出图形，帮助分析，考查逻辑思维能力和分析判断能力，基础题．8．（4分）当时，函数f（x）=sinx+cosx的（）A．最大值是1，最小值是﹣1 B．最大值是1，最小值是﹣C．最大值是2，最小值是﹣2 D．最大值是2，最小值是﹣1考点：三角函数中的恒等变换应用．分析：首先对三角函数式变形，提出2变为符合两角和的正弦公式形式，根据自变量的范围求出括号内角的范围，根据正弦曲线得到函数的值域．解答：解：∵f（x）=sinx+cosx=2（sinx+cosx）=2sin（x+），∵，∴f（x）∈[﹣1，2]，故选D点评：了解各公式间的内在联系，熟练地掌握这些公式的正用、逆用以及某些公式变形后的应用．掌握两角和与差的正弦、余弦、正切公式及其推导，本题主要是公式的逆用和对三角函数值域的考查．9．（4分）中心在原点，准线方程为x=±4，离心为的椭圆方程是（）A ．=1B ．=1C ．+y 2=1D ．x 2+=1考点：椭圆的标准方程．专题：综合题．分析：设出a ，b ，c 分别为椭圆的半长轴，半短轴及焦距的一半，根据椭圆的准线方程公式列出a 与c 的方程记作①，根据离心率列出a 与c 的方程记作②，联立①②即可求出a 与c 的值，根据a 2=b 2+c 2即可求出b 的值，由椭圆的中心在原点，利用a 与b 的值写出椭圆的标准方程即可．解答：解：设a 为半长轴，b 为半短轴，c 为焦距的一半，根据题意可知：±=±4即a 2=4c ①，=即a=2c ②，把②代入①解得：c=1，把c=1代入②解得a=2，所以b==，又椭圆的中心在原点，则所求椭圆的方程为：+=1．故选A ．点评：此题考查学生灵活运用椭圆的准线方程及离心率的公式化简求值，掌握椭圆的一些基本性质，是一道综合题．10．（4分）圆锥母线长为1，侧面展开图圆心角为240°，该圆锥的体积（） A ． B ． C ． D ．考点：棱柱、棱锥、棱台的体积．专题：计算题．分析：求出侧面展开图的弧长，就是圆锥的底面周长，求出底面半径，高，即可求出圆锥的体积．解答：解：侧面展开图的弧长，就是圆锥的底面周长：，底面半径为：，高：，圆锥的体积为：=故选C点评：本题是基础题，考查圆锥的侧面展开图与圆锥的关系，考查计算能力，注意弧长等于底面周长．11．（5分）椭圆25x 2﹣150x+9y 2+18y+9=0的两个焦点坐标是（） A ．（﹣3，5），（﹣3，﹣3） B ．（3，3），（3，﹣5） C ．（1，1），（﹣7，1） D ．（7，﹣1），（﹣1，﹣1）考点：椭圆的简单性质．专题：综合题．分析：把椭圆的方程化为标准方程后，找出a 与b ，根据a 2=b 2+c 2求出c 的值，然后根据椭圆的中心坐标即可得到两焦点的坐标．解答：解：把椭圆方程25x 2﹣150x+9y 2+18y+9=0化为标准方程为：+=1，所以a=5，b=3，则c==4，且椭圆的中心为（3，﹣1），则两焦点坐标分别为（3，3）和（3，﹣5）．故选B点评：此题考查学生灵活运用椭圆的简单性质化简求值，是一道中档题．12．（5分）（2014•广西模拟）将边长为a的正方形ABCD沿对角线AC折起，使得BD=a，则三棱锥D﹣ABC的体积为（）A．B．C．D．考点：棱柱、棱锥、棱台的体积．专题：计算题．分析：取AC的中点O，连接DO，BO，求出三角形DOB的面积，求出AC的长，即可求三棱锥D ﹣ABC的体积．解答：解：O是AC中点，连接DO，BO，如图，△ADC，△ABC都是等腰直角三角形，DO=B0==，BD=a，△BDO也是等腰直角三角形，DO⊥AC，DO⊥BO，DO⊥平面ABC，DO就是三棱锥D﹣ABC的高，S△ABC=a2三棱锥D﹣ABC的体积：，故选D．点评：本题考查棱锥的体积，是基础题．13．（5分）等差数列{a n}的前m项和为30，前2m项和为100，则它的前3m项和为（）A．130 B．170 C．210 D．260考点：等差数列的前n项和；等差数列的性质．专题：计算题．分析：利用等差数列的前n项和公式，结合已知条件列出关于a1，d的方程组，用m表示出a1、d，进而求出s3m；或利用等差数列的性质，s m，s2m﹣s m，s3m﹣s2m成等差数列进行求解．解答：解：解法1：设等差数列{a n}的首项为a1，公差为d，由题意得方程组，解得d=，a1=，∴s3m=3ma1+d=3m+=210．故选C．解法2：∵设{a n}为等差数列，∴s m，s2m﹣s m，s3m﹣s2m成等差数列，即30，70，s3m﹣100成等差数列，∴30+s3m﹣100=70×2，解得s3m=210．故选C．点评：解法1为基本量法，思路简单，但计算复杂；解法2使用了等差数列的一个重要性质，即等差数列的前n项和为s n，则s n，s2n﹣s n，s3n﹣s2n，…成等差数列．14．（5分）设双曲线=1（0＜a＜b）的半焦距为c，直线l过（a，0）（0，b）两点，已知原点到直线l的距离为，则双曲线的离心率为（）A．2B．C．D．考点：双曲线的简单性质．专题：计算题；压轴题．分析：直线l的方程为，原点到直线l的距离为，∴，据此求出a，b，c间的数量关系，从而求出双曲线的离心率．解答：解：∵直线l的方程为，c2=a2+b2∴原点到直线l的距离为，∴，∴16a2b2=3c4，∴16a2（c2﹣a2）=3c4，∴16a2c2﹣16a4=3c4，∴3e4﹣16e2+16=0，解得或e=2.0＜a＜b，∴e=2．故选A．点评：若，则有0＜b＜a．15．（5分）设f（x）是（﹣∞，+∞）上的奇函数，f（x+2）=﹣f（x），当0≤x≤1时，f（x）=x，则f（7.5）等于（）A．0.5 B．﹣0.5 C．1.5 D．﹣1.5考点：奇函数．专题：计算题；压轴题．分析：题目中条件：“f（x+2）=﹣f（x），”可得f（x+4）=f（x），故f（7.5）=f（﹣0.5）=﹣f（0.5）=﹣0.5．解答：解：∵f（x+2）=﹣f（x），∴可得f（x+4）=f（x），∵f（x）是（﹣∞，+∞）上的奇函数∴f（﹣x）=﹣f（x）．∴故f（7.5）=f（﹣0.5）=﹣f（0.5）=﹣0.5．故选B．点评：本题考查函数的奇偶性、周期性等，抽象函数是相对于给出具体解析式的函数来说的，它虽然没有具体的表达式，但是有一定的对应法则，满足一定的性质，这种对应法则及函数的相应的性质是解决问题的关键．二、填空题（共4小题，每小题4分，满分16分）16．（4分）已知点（﹣2，3）与抛物线y2=2px（p＞0）的焦点的距离是5，则p=4．考点：抛物线的简单性质．专题：计算题．分析：先根据抛物线的方程求得焦点的坐标，进而利用点到直线的距离建立方程求得p．解答：解：依题意可知抛物线的焦点为（，0）∴已知点到抛物线的焦点的距离为=5，求得p=4或﹣12（舍负），故答案为：4．点评：本题主要考查了抛物线的简单性质和两点间距离公式的应用．考查了学生基础知识的掌握和基本运算的能力．17．（4分）正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有32个（用数字作答）．考点：组合及组合数公式．专题：计算题．分析：正六边形的中心和顶点共7个点，选3个点的共有的方法减去在一条直线上的三点的个数即可．解答：解：正六边形的中心和顶点共7个点，选3个点的共有的方法是：C73=35在一条直线上的三点有3个符合题意的三角形有35﹣3=32个故答案为：32点评：本题考查组合及组合数公式，考查计算能力，逻辑思维能力，是基础题．18．（4分）求值：tan20°+tan40°+tan20°tan40°=．考点：两角和与差的正切函数．专题：计算题；压轴题．分析：利用60°=20°+40°，两角和的正切公式，进行变形，化为所求式子的值．解答：解：tan60°=tan（20°+40°）==tan20°+tan40°+tan20°tan40故答案为：点评：本题考查两角和的正切函数公式的应用，考查计算化简能力，观察能力，是基础题．19．（4分）如图，正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角，则异面直线AD与BF所成角的余弦值是．考点：异面直线及其所成的角．专题：计算题；作图题；压轴题．分析：由题意得，CB⊥AB，AB⊥BE．可得正方形ABCD所在平面与正方形ABEF的二面角即∠CBE=60°，同时也得AB⊥平面BCE，即AB⊥CE，即是EF⊥CE．进而求出CF、FB、BC，即可求出异面直线AD与BF所成角的余弦值．解答：解：由题意得，CB⊥AB，AB⊥BE．可得正方形ABCD所在平面与正方形ABEF的二面角即∠CBE=60°，同时也得AB⊥平面BCE，即AB⊥CE，即三角形CEF为直角三角形和三角形CBE为等边三角形；即是EF⊥CE．设AB=1，则CE=1，CF=，FB=，利用余弦定理，得．故异面直线AD与BF所成角的余弦值是．点评：此题主要考查异面直线的角度及余弦值计算．三、解答题（共6小题，满分69分）20．（11分）解不等式log a（x+1﹣a）＞1．考点：对数函数的单调性与特殊点；对数的运算性质．专题：计算题；分类讨论．分析：原不等式可转化为log a（x+1﹣a）＞log a a，分①a＞1②0＜a＜1两种情况讨论，结合对数函数的单调性解对数不等式可求．解答：解：①当a＞1时，原不等式等价于不等式组：解得x＞2a﹣1．②当0＜a＜1时，原不等式等价于不等式组：解得a﹣1＜x＜2a﹣1综上，当a＞1时，不等式的解集为{x|x＞2a﹣1}；当0＜a＜1时，不等式的解集为{x|a﹣1＜x＜2a﹣1}．点评：本小题考查对数函数的单调性性质的运用，对数不等式的解法，分类讨论的方法和运算能力．21．（12分）设等比数列{a n}的前n项和为S n．若S3+S6=2S9，求数列的公比q．考点：等比数列的性质．专题：综合题．分析：先假设q=1，分别利用首项表示出前3、6、及9项的和，得到已知的等式不成立，矛盾，所以得到q不等于1，然后利用等比数列的前n项和的公式化简S3+S6=2S9得到关于q的方程，根据q不等于0和1，求出方程的解，即可得到q的值．解答：解：若q=1，则有S3=3a1，S6=6a1，S9=9a1．但a1≠0，即得S3+S6≠2S9，与题设矛盾，q≠1．又依题意S3+S6=2S9可得整理得q3（2q6﹣q3﹣1）=0．由q≠0得方程2q6﹣q3﹣1=0．（2q3+1）（q3﹣1）=0，∵q≠1，q3﹣1≠0，∴2q3+1=0∴q=﹣．点评：本小题主要考查等比数列的基础知识，逻辑推理能力和运算能力，是一道综合题．22．（12分）已知△ABC的三个内角A，B，C满足：，求的值．考点：三角函数中的恒等变换应用；三角函数的积化和差公式．专题：计算题．分析：先根据A，B，C的关系求出B的值，再代入到中得到cosA，cosC的关系，根据和差化积及积化和差公式化简，再将cos，cos（A+C）的值代入整理后因式分解，即可求出的值．解答：解：由题设条件知B=60°，A+C=120°．∵，∴将上式化为利用和差化积及积化和差公式，上式可化为将代入上式得将代入上式并整理得，∵，∴从而得点评：本小题考查三角函数基础知识，利用三角公式进行恒等变形和运算的能力．23．（12分）如图：在正三棱柱ABC﹣A1 B1 C1中，AB==a，E，F分别是BB1，CC1上的点且BE=a，CF=2a．（Ⅰ）求证：面AEF⊥面ACF；（Ⅱ）求三棱锥A1﹣AEF的体积．考点：平面与平面垂直的判定；棱柱、棱锥、棱台的体积．专题：计算题；证明题．分析：（Ⅰ）欲证面ADF⊥面ACF，根据面面垂直的判定定理可知在平面ADF内一直线与平面ACF 垂直，根据题意易证CA⊥AD，而FC⊥面ACD，则CA是FA在面ACD上射影，FA∩AC=A，满足线面垂直的判定定理，则DA⊥面ACF，而DA⊂面ADF，满足面面垂直的判定定理．（Ⅱ）先根据将所求的体积进行转化，在面A1B1C1内作B1G⊥A1C1，垂足为G，求出B1G，然后利用体积公式进行求解即可．解答：解：（Ⅰ）∵BE：CF=1：2∴DC=2BD，∴DB=BC，∵△ABD是等腰三角形，且∠ABD=120°，∴∠BAD=30°，∴∠CAD=90°，∵FC⊥面ACD，∴CA是FA在面ACD上射影，且CA⊥AD，∵FA∩AC=A，DA⊥面ACF，DA⊂面ADF∴面ADF⊥面ACF．（Ⅱ）解：∵．在面A1B1C1内作B1G⊥A1C1，垂足为G．B1G=面A1B1C1⊥面A1C∵B1G⊥面A1C，∵E∈BB1，而BB1∥面A1C，∴三棱柱E﹣AA1F的高为B1G==AA1•=∴点评：本小题考查空间线面关系，正三棱柱的性质，逻辑思维能力，空间想象能力运算能力．24．（10分）某地现有耕地10000公顷，规划10年后粮食单产比现在增加22%，人均粮食占有量比现在提高10%．如果人口年增长率为1%，那么耕地平均每年至多只能减少多少公顷？（精确到1公顷）（粮食单产=，人均粮食占有量=）考点：二项式定理的应用；基本不等式在最值问题中的应用．专题：计算题；压轴题．分析：利用公式粮食单产=，人均粮食占有量=分别求出现在和10 年后的人均粮食占有量再利用已知条件人均粮食占有量比现在提高10%．列出不等式解得．解答：解：设耕地平均每年至多只能减少x公顷，又设该地区现有人口为P人，粮食单产为M吨/公顷．依题意得不等式化简得∵=≈4.1∴x≤4（公顷）．答：按规划该地区耕地平均每年至多只能减少4公顷．点评：本小题主要考查运用数学知识和方法解决实际问题的能力，指数函数和二项式定理的应用，近似计算的方法和能力．25．（12分）已知l1、l2是过点P（﹣，0）的两条互相垂直的直线，且l1、l2与双曲线y2﹣x2=1各有两个交点，分别为A1、B1和A2、B2．（1）求l1的斜率k1的取值范围；（2）若|A1B1|=|A2B2|，求l1、l2的方程．考点：直线与圆锥曲线的关系；直线的斜率；斜率的计算公式．专题：计算题；综合题；压轴题．分析：（1）显然l1、l2斜率都存在，设l1的斜率为k1，得到l1、l2的方程，将直线方程与双曲线方程联立方程组，消去y得到关于x的二次方程，再结合根的判别即可求得斜率k1的取值范围；（2）利用（1）中得到的关于x的二次方程，结合根与系数的关系，利用弦长公式列关于k的方程，解方程即可求得k值，从而求出l1、l2的方程．解答：解：（1）显然l1、l2斜率都存在，否则l1、l2与曲线不相交．设l1的斜率为k1，则l1的方程为y=k1（x+）．联立得y=k1（x+），y2﹣x2=1，消去y得（k12﹣1）x2+2k12x+2k12﹣1=0．①根据题意得k12﹣1≠0，②△1＞0，即有12k12﹣4＞0．③完全类似地有﹣1≠0，④△2＞0，即有12•﹣4＞0，⑤从而k1∈（﹣，﹣）∪（，）且k1≠±1．（2）由弦长公式得|A1B1|=．⑥完全类似地有|A2B2|=．⑦∵|A1B1|=|A2B2|，∴k1=±，k2=．从而l1：y=（x+），l2：y=﹣（x+）或l1：y=﹣（x+），l2：y=（x+）．点评：本题主要考查了直线与圆锥曲线的交点，直线和圆锥曲线的位置是解析几何中的一个重点内容，也是一个难点，在高考试题中占有一席之地，属于中档题．。

有关二项式定理的八篇论文

目提供的信息及各量之间的制约关系，巧妙构造方程，最终用方程理论求解．
例１（２００５年全国高考卷Ⅰ）的展开式中，常数项为．（用数字作答）
解：由．令，得．
故常数项为．故填６７２．
评注：凡涉及到展开式的项及其系数等问题时，常是先写出其通项公式，然后再
据题意进行求解，往往是结合方程思想加以解决．
例５（２００５年浙江卷）在的展开式中，含的项的系数是（）
Ａ．７４Ｂ．１２１Ｃ．Ｄ．
解法一：先求和，再求系数原式，求含的项的系数．等价于求中含的项的系数，
即为，故选Ｄ．
解法二：逐一求出，再相加
中的项的系数分别为，故所求的项的系数为，故选Ｄ．
三、表格化
求两个二项式积的展开式中某项的系数是二项式问题中的一个难点，既要考虑多
-2-
高考中二项式问题的处理策略ｐｒｔ
高考中二项式问题的处理策略
二项式定理的有关知识在高考中虽每年以小题的形式出现，但却是历年高考的必
考内容，由于其题型繁多，常使人感到扑朔迷离．本文提出了几种切实有效的处理方
法，旨在促进同学们解题能力的提高．
一、方程化
在求二项式中参数的值及特定项的系数等问题时，通常是利用展开式的通项与题
-6-
二项式系数的求和问题二项式系数的求和问题１．赋值求和问题例１设，求的值．解：令，得；令，得，两式相减得：．２．逆用定理求和问题例２已知等比数列的首项为，公比为，求和：．解：．３．倒序相加求和问题例３已知等差数列的首项为，公差为，求和：．解：令，则，两式相加，得．又在等差数列中，，所以，所以．４．建模求和问题例４求和：．解：此式为的展开式中项的系数，而从而转化为求展开式中项的系数，所以．５．裂项求和问题例５求和：．解：因为，所以．６．递推求和问题例６求和：．解：因为，所以．

(详细解析)1996年全国高考文科试题

1996年普通高等学校招生全国统一考试数学（文史类）第Ⅰ卷（选择题共65分）注意事项：1．答案Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上． 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，在选涂其它答案，不能答在试题卷上．3．考试结束，监考人将本试卷和答题卡一并收回．一．选择题：本大题共15小题；第1—10题每小题4分，第11—15题每小题5分，共65分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．设全集{}1,2,3,4,5,6,7I =，集合{}{}1,3,5,7,3,5A B ==．则 A ．I AB = B ．I A B =C ．I A B =D ．I A B =【答案】C【解析】显然C 正确．2．当1a >时，在同一坐标系中，函数xy a -=与log a y x =的图像【答案】A【解析】当1a >时，函数xy a -=是减函数，且过点(0,1)；而函数log a y x =为增函数，且过点(1,0)．3．若22sin cos x x >，则x 的取值范围是A ．⎭⎬⎫⎩⎨⎧∈+<<-Z k k x k x ,412432ππππ B ．⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,452412ππππ C ．⎭⎬⎫⎩⎨⎧∈+<<-Z k k x k x ,4141ππππ D ．⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,4341ππππ 【答案】D【解析】2221sin cos sin sin 22x x x x >⇒>⇒>或sin 2x <-，解得24k x ππ+< 32()4k k Z ππ<+∈或322()44k x k k Z ππππ-<<-∈，即(21)(21)4k x k πππ-+<<- 3()4k Z π+∈，所以x 的取值范围是⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,4341ππππ． 4．复数54)31()22(i i -+等于A ．i 31+B ．i 31+-C ．i 31-D ．i 31-- 【答案】B44425(2)12()i ω===--．5．6名同学排成一排，其中甲、乙两人必须排在一起的不同排法有 A ．720种 B ．360种 C ．240种 D ．120种【答案】C【解析】将甲、乙两人捆绑在一起，不同的排法有5252240A A =．6．已知α是第三象限角且24sin 25α=-，则tan 2α=A ．43 B ．34 C ．34- D ．43- 【答案】D【解析】由已知得7cos 25α=-，所以2sin 2sin 1cos 22tan 2sin cos2sincos222αααααααα-===71()42524325--==--．7．如果直线,l m 与平面,,αβγ满足：,//,l l m βγαα=⊂和m γ⊥，那么必有A ．αγ⊥且l m ⊥B ．αγ⊥且//m βC ．//m β且l m ⊥D ．//αβ且αγ⊥ 【答案】A 【解析】略． 8．当22x ππ-≤≤时，函数()sin f x x x =的A ．最大值是1，最小值是1-B ．最大值是1，最小值是12-C ．最大值是2，最小值是2-D ．最大值是2，最小值是1- 【答案】D【解析】因为()sin 2sin()3f x x x x π=+=+，由已知5636x πππ-≤+≤．故当 32x ππ+=，即6x π=时，()f x 有最大值是2；当36x ππ+=-，即2x π=-时，()f x 有最小值是1-．9．中心在原点，准线方程为4x =±，离心率为12的椭圆方程是 A ．22143x y += B ．22134x y += C ．2214x y += D ．2214y x += 【答案】A【解析】由题设可得214,2a c c a ==，解得2,1a c ==，所以椭圆方程是22143x y +=．10．圆锥母线长为1，侧面展开图圆心角为240︒，该圆锥的体积是A B ．881π C D ．1081π【答案】C【解析】设圆锥底面半径为r ，则224021360r ππ︒=⨯︒，得23r =，3=，圆锥的体积是212()33π=．11．椭圆222515091890x x y y -+++=的两个焦点坐标是A ．(3,5),(3,3)---B ．(3,3),(3,5)-C ．(1,1),(7,1)-D ．(7,1),(1,1)--- 【答案】B【解析】椭圆的标准方程为2222(1)(3)153y x +-+=，而2222153y x +=的焦点为(0,4)±，所以2222(1)(3)153y x +-+=的焦点坐标是(3,3),(3,5)-．12．将边长为a 的正方形ABCD 沿对角线AC 折起，使得BD a =，则三棱锥D ABC -的体积为A ．63aB ．123aC ．3123aD ．3122a【答案】D【解析】取AC 的中点O ，连接,BO DO ，如图所示．,ABC ADC ∆∆均为等腰直角三角形，2AC BO DO ===， ∴2BOD π∠=，则DO ⊥面ABC ，DO 就是三棱锥D ABC -的高，所以231132D ABC V a -=⋅=．13．等差数列{}n a 的前m 项和为30，前2m 项和为100，则它的前3m 项和为 A ．130 B ．170 C ．210 D ．260 【答案】C【解析】由已知得230,100m m S S ==，则232,,m m m m m S S S S S --成等差数列，所以323()210m m m S S S =-=．14．设双曲线)0(12222b a by a x <<=-的半焦距为c ，直线l 过(,0),(0,)a b 两点．已知原点到直线l 的距离为c 43，则双曲线的离心率为 A ．2 B ．3 C ．2 D ．332 【答案】A【解析】直线l 的方程为0bx ay ab +-=，原点到直线l 4=，则22222316a b c a b =+，即22222()316a c a c c -=，解得2e =或e =0a b <<，所以e ==>，所以e =15． ()f x 是(,)-∞+∞上的奇函数，(2)()f x f x +=-，当01x ≤≤时，()f x x =，则(7.5)f等于A ．0.5B ．0.5-C ．1.5D ． 1.5- 【答案】B【解析】(7.5)(5.52)(5.5)[(3.5)](3.5)(1.5)[(0.5)]f f f f f f f =+=-=--==-=---(0.5)0.5f =-=-．第Ⅱ卷（非选择题共85分）注意事项：1．第Ⅱ卷共6页，用钢笔或圆珠笔直接答在试题卷中． 2．答卷前将密封线内的项目填写清楚．二．填空题：本大题共4小题；每小题4分，共16分．把答案填在题中横线上．16．已知点(2,3)-与抛物线)0(22>=p px y 的焦点的距离是5，则p = ．【答案】45=，解得4p =．17．正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有个．（用数字作答）【答案】32【解析】从7个点中取3个点有37C 种取法，3个点共线的有3种，三角形共有37332C -=个．18．tg20tg403tg20tg40++的值是．【答案】3【解析】∵tg20tg40tg(2040)31tg20tg40++==-，∴tg20tg403(1-tg20tg40)+=，tg20tg403tg20tg403++=．19．如图，正方形ABCD 所在平面与正方形ABEF 所在平面成60的二面角，则异面直线AD 与BF 所成角的余弦值是．【答案】42 【解析】由于//AD BC ，所以CBF ∠即为异面直线AD 与BF所成角，设正方形边长为a ，在CBF ∆中，,,BF BC a FC =====，222cos 24BF BC FC CBF BF BC +-∠==⋅．三．解答题：本大题共6小题；共69分．解答应写出文字说明、证明过程或演算步骤．20．（本小题满分11分）解不等式log (1)1a x a +->．【解】本小题考查对数函数性质，对数不等式的解法，分类讨论的方法和运算能力，满分11分．（Ⅰ）1>a 时，原不等式等价于不等式组：10,1.x a x a a +->⎧⎨+->⎩ ——2分解得21x a >-． ——5分（Ⅱ）当01a <<时，原不等式等价于不等式组：10,1.x a x a a +->⎧⎨+-<⎩——7分解得121a x a -<<-． 10分综上，当1>a 时，不等式的解集为{}21x x a >-；当01a <<时，不等式的解集为{}121x a x a -<<-． ——11分21．（本小题满分12分）设等比数列{}n a 的前n 项和为n S ．若3692S S S +=，求数列的公比q ．【解】本小题主要考查等比数列的基础知识，逻辑推理能力和运算能力．满分12分．若1q =，则有3161913,6,9S a S a S a ===．但10a ≠，即得3692S S S +≠，与题设矛盾，故1q ≠． ——2分又依题意3692S S S +=可得369111(1)(1)2(1)111a q a q a q q q q---+=---．整理得363(21)0q q q --=．由0q ≠得方程63210q q --=．33(21)(1)0q q +-=， —— 9分∵ 31,1q q ≠≠，∴3210q +=，∴2q =-． ——12分22．（本小题满分11分）已知ABC ∆的三个内角,,A B C 满足：BC A B C A cos 2cos 1cos 1,2-=+=+，求 2cosCA -的值．解法一：由题设条件知60,120B AC =+=． ——2分=-22cos 1cos 1-=+C A ．将上式化为C A C A cos cos 22cos cos -=+．利用和差化积及积化和差公式，上式可化为)]cos()[cos(22cos 2cos2C A C A CA C A -++-=-+． ——6分将21)cos(,2160cos 2cos -=+==+C A C A 代入上式得cos)22A C A C -=-．将1)2(cos 2)cos(2--=-CA C A 代入上式并整理得 023)2cos(2)2(cos 242=--+-CA C A ——9分(2cos 3)022A C A C ---+=，∵302A C -+≠，∴2cos 02A C-=．从而得cos2A C -=——12分解法二：由题设条件知60,120B A C =+=．设2A Cα-=，则2A C α-=，可得60,60A C αα=+=-， ——3分所以)60cos(1)60cos(1cos 1cos 1αα-++=+ C A ααααsin 23cos 211sin 23cos 211++-=ααα22sin 43cos 41cos -=43cos cos 2-=αα． ——7分依题设条件有Bcos 243cos cos 2-=-αα， ∵21cos =B ，∴2243cos cos 2-=-αα．整理得22cos 0,αα+-= ——9分(2cos 3)0αα+=，∵03cos 22≠+α，∴02cos 2=-α．从而得222cos =-C A ． ——11分23．（本小题满分12分）【注意：本题的要求是，参照标号①的写法，在标号②、③、④、⑤的横线上填写适当步骤，完成（Ⅰ）证明的全过程；并解答（Ⅱ），如图2．】如图1，在正三棱柱111ABC A B C -中，13AA AB a ==，,E F 分别是11,BB CC 上的点，且,2BE a CF a ==．（Ⅰ）求证：面AEF ⊥面ACF ；（Ⅱ）求三棱锥1A AEF -的体积．（Ⅰ）证明： ①∵,2BE a CF a ==，//BE CF ，延长FE 与CB 延长线交于D ，连结AD ．∴DBEDCF ∆∆，∴DB BEDC CF=． ② ． ∴DB AB =．③ ． ∴DA AC ⊥．④ ． ∴FA AD ⊥．⑤ ． ∴AEF ⊥面ACF ．（Ⅱ）解：【解】本小题考查空间线面关系，正三棱柱的性质，逻辑思维能力，空间想象能力及运算能力．满分12分．（Ⅰ）②∵:1:2BE CF =，∴2DC DB =，∴DB BC =， ——1分③∵ABD ∆是等腰三角形，且120ABD ∠=︒，∴30BAD ∠=︒，∴90CAD ∠=︒， —— 3分 ④∵FC ⊥面ACD ，∴CA 是FA 在面ACD 上的射影，且CA AD ⊥， —— 5分 ⑤∵FA AC A =，DA ⊥面ACF ，DA ⊂面ADF ，∴面ADF ⊥面ACF ． 7分（Ⅱ）∵11A AEF E AA F V V --=，在面111A B C 内作111B G AC ⊥，垂足为G ．12B G =．面111A BC ⊥面1AC ，∴1B G ⊥面1AC ，∵1E BB ∈，而1//BB 面1AC ，∴三棱柱1E AA F -的高为2．——9分1112A FAS AA AC ∆=⋅= ——10分∴11A AEF E AA FV V --== ——12分24．（本小题满分10分）某地现有耕地10000公顷，规划10年后粮食单产比现在增加22%，人均粮食占有量比现在提高10%．如果人口年增长率为1%，那么耕地平均每年至多只能减少多少公顷（精确到1公顷）?（粮食单产=耕地面积总产量，人均粮食占有量=总人口数总产量）【解】本小题主要考查运用数学知识和方法解决实际问题的能力，指数函数和二项式定理的应用，近似计算的方法和能力．满分10分．设耕地平均每年至多只能减少x 公顷，又设该地区现有人口为P 人，粮食单产为M 吨/公顷．依题意得不等式%)101(10%)11()1010(%)221(4104+⨯⨯≥+⨯-⨯+⨯P M P x M ．——5分化简得]22.1)01.01(1.11[10103+⨯-⨯≤x ． ——7分 ∵103312210101.1(10.01) 1.110[1]10[1(10.010.01)]1.22 1.22C C ⨯+⨯-=⨯-⨯+⨯+⨯+3 1.110[1 1.1045] 4.11.22≈⨯-⨯≈． —— 9分 ∴4x ≤（公顷）．答：按规划该地区耕地平均每年至多只能减少4公顷． ——10分25．（本小题满分12分）已知12,l l 是过点)0,2(-P 的两条互相垂直的直线，且12,l l 与双曲线122=-x y 各有两个交点，分别为11,A B 和22,A B ．（Ⅰ）求1l 的斜率1k 的取值范围；（Ⅱ）若1A 恰是双曲线的一个顶点，求22A B 的值．【解】本小题主要考查直线与双曲线的性质，解析几何的基本思想，以及综合运用知识的能力．满分12分．（Ⅰ）依题设，12,l l 的斜率都存在，因为1l 过点)0,2(-P 且与双曲线有两个交点，故方程组1122(0),1.y k x k y x ⎧=+≠⎪⎨-=⎪⎩ ① ——1分有两个不同的解．在方程组①中消去y ，整理得01222)1(2121221=-++-k x k x k ． ② 若0121=-k ，则方程组①只有一个解，即1l 与双曲线只有一个交点，与题设矛盾，故 0121≠-k ，即11≠k ，方程②的判别式为2222211111)4(1)(21)4(31)k k k ∆=---=-．设2l 的斜率为2k ，因为2l 过点)0,2(-P 且与双曲线有两个交点，故方程组 ⎪⎩⎪⎨⎧=-≠+=.1),0)(2(2222x y k x k y ③ 有两个不同的解．在方程组③中消去y ，整理得01222)1(2222222=-++-k x k x k ． ④同理有)13(4,0122222-=∆≠-k k ．又因为12l l ⊥，所以有121l l ⋅=-． ——4分于是，12,l l 与双曲线各有两个交点，等价于⎪⎪⎩⎪⎪⎨⎧≠-=⋅>->-.1,1,013,0131212221k k k k k 解得⎪⎩⎪⎨⎧≠<<.1,33311k k——6分 ∴)3,1()1,33()33,1()1,3(1 ----∈k ． ——7分（Ⅱ）双曲线122=-x y 的顶点为(0,1),(0,1)-．取1(0,1)A时，有1(01k =，解得12k =．从而211k k =-= ——8分将2k =230x ++=． ⑤记2l 与双曲线的两交点为211222(,),(,)A x y B x y ，则2222222122121212()()3()3[()4]A B x x y y x x x x x x =-+-=-=+-．由⑤知1212)3x x x x +=-=．∴2222260,A B A B == ——11分当取1(0,1)A -时，由双曲线122=-x y 关于x 轴的对称性，知22A B =所以1l 过双曲线的一个顶点时，22A B = ——12分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1996年普通高等数学招生全国统一考试（全国Ⅱ）文科数学参考公式：三角函数的积化和差公式：[]1sin cos sin()sin()2αβαβαβ=++- []1cos sin sin()sin()2αβαβαβ=+--[]1cos cos cos()cos()2αβαβαβ=++-[]1sin sin cos()cos()2αβαβαβ=-+--正棱台、圆台的侧面积公式1()2S c c l ='+台侧其中c '、c 分别表示上、下底面周长，l 表示斜高或母线长．球的体积公式：343V r π=球，其中R 表示球的半径．第Ⅰ卷（选择题共65分）一、选择题：本大题共15小题，第1－10题第小题4分，第11－15题每小题5分，共65分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集{}1,2,3,4,5,6,7I =，集合{}1,3,5,7A =，{}3,5B =，则A ．I AB =B ．I A B =C ．I A B =D ．I A B =2．当1a >时，在同一坐标系中，函数xy a -=与logy x =的图像是3．若22sin cos x x >，则x 的取值范围是A ．322,44x k x k k Z ππππ⎧⎫-<<+∈⎨⎬⎩⎭B ．522,44x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭C ．22,44x k x k k Z ππππ⎧⎫-<<+∈⎨⎬⎩⎭D ．322,44x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭44等于A ．1B ．1-C ．1D ．1-5．6名同学排成一排，其中甲、乙两必须排在一起的不同排法有A ．720种B ．360种C ．240种D ．120种6．已知α是第三象限角，24sin 25α=-，则tan 2α＝ A ．43B ．34 C ．34- D ．43-7．如果直线,l m 与平面,,αβγ满足：l βγ= ，l ∥α，m α⊂和m γ⊥，那么必有A ．a γ⊥且l m ⊥B ．αγ⊥且m ∥βC ．m ∥β且l m ⊥D ．α∥β且αγ⊥8．当22x ππ-≤≤时，函数()sin f x x x =的A ．最大值是1，最小值是－1B ．最大值是1，最小值是12-C ．最大值是2，最小值是－2D ．最大值是2，最小值是－18．若02πα<<，则arcsin[cos()]arccos[sin()]2παπα+++等于A ．2π B ．2π-C ．22πα- D ．22πα--9．中心在原点，准线方程为4x =±，离心率为12的椭圆方程是 A ．22143x y += B ．22134x y += C ．2214x y += D ．2214y x += 10．圆锥母线长为1，侧面展开图圆心角为240°，该圆锥的体积A B ．881π C D ．1081π11．椭圆222515091890x x y y -+++=的两个焦点坐标是A ．(3,5)-，(3,3)--B ．(3,3)，(3,5)-C ．(1,1)，(7,1)-D ．(7,1)-，(1,1)--12．将边长为a 的正方形ABCD 沿对角线AC 折起，使得BD a =，则三棱锥D ABC -的体积为A ．36aB ．312aCD13．等差数列{}n a 的前m 项和为30，前2m 项和为100，则它的前3m 项和为A ．130B ．170C ．210D ．26014．设双曲线22221(0)x y a b a b-=<<的半焦距为c ，直线l 过(,0)a ，(0,)b 两点，已知原点到直线l，则双曲线的离心率为 A ．2BCD15．设()f x 是(,)-∞+∞上的奇函数，(2)()f x f x +=-，当01x ≤≤时，()f x x =，则(7.5)f 等于A ．0.5B ．0.5-C ．1.5D ． 1.5-第Ⅱ卷（非选择题共85分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上．16．已知点(2,3)-与抛物线22(0)y px p =>的焦点的距离是5，则p ＝．17．正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有个（用数字作答）．18．tan 20tan 4020tan 40+的值是． 19．如图，正方形ABCD 所在平面与正方形ABEF 所在平面成60°的二面角，则异面直线AD 与BF 所成角的余弦值是．三、解答题：本大题共6小题，共69分，解答应写出文字说明，证明过程或演算步骤．ABDCF EA 1AC BB 1C 1E F20．（本小题满分11分）解不等式log (1)1a x a +->．21．（本小题满分12分）设等比数列{}n a 的前n 项和为n S ．若3692S S S +=，求数列的公比q ． 22．（本小题满分11分）已知△ABC 的三个内角A、B 、C 满足：2A C B +=，11cos cos cos A C B+=-，求cos 2A C -的值． 23．（本小题满分12分）【注意：本题的要求是，参照标①的写法，在标号②、③、④、⑤的横线上填写适当步骤，完成（1）证明的全过程，并解答（2）．】如图，在正三棱柱111ABC A B C -中，13AA AB a ==，E ，F 分别是1BB ，1CC 上的点，且BE a =，2CF a =．（1）求证：面AEF ⊥面ACF ；（2）求三棱锥1A AEF -的体积．（1）证明：在截面1A EC 内，过E 作1EG AC ⊥，G 是垂足．①∵BE a =，2CF a =，BE ∥CF ，延长FE 与CB 延长线交于D ，连结AD ．∴△DBE ∽△DCF ∴DB BEDE CF= ② ∴DB AB =．③ ∴DA AC ⊥④ ∴FA AD ⊥⑤ ∴面AEF ⊥面ACF ．24．（本小题满分12分）某地现有耕地10000公顷，规划10年后粮食单产比现在增加22％，人均粮食占有量比现在提高10％．如果人口年增长率为1％，那么耕地平均每年至多只能减少多少公顷（精确到1公顷）？A 1AC BB 1C 1E FD（粮食单产＝总产量耕地面积，人均粮食占有量＝总产量总人口数25．（本小题满分12分）已知1l 、2l 是过点(P 的两条互相垂直的直线，且1l 、2l 与双曲线221y x -=各有两个交点，分别为1A 、1B 和2A 、2B ．（1）求1l 的斜率1k 的取值范围；（2）若1A 恰是双曲线的一个顶点，求22||A B 的值．数学试题参考答案一、选择题，本题考查基础知识，基本概念和基本运算能力二、填空题．本题考查基础知识,基本概念和基本运算技巧 13． 14． 15． 16．三、解答题 17．1996年普通高等学校招生全国统一考试数学试题(文史类)参考解答及评分标准说明：一．答指出了每题要考查主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准相应的评分细则．二．对计算题，当考生的解答某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答较错误，就不再给分．三．解答右端所注分数，表示考生正确做到这一步应得累加数．四．只给整数分数，选择题和填空题不给中间分．一．选择题：本题考查基本知识和基本运算，第(1)－(10)题每小题4分，第(11)－(15)题每小题5分．满分65分．(1)C (2)A (3)D (4)B (5)C (6)D (7)A (8)D (9)A (10)C (11)B (12)D (13)C (14)A (15)B二．填空题：本题考查基本知识和基本运算．每小题4分，满分16分．(16)4 (17)32 (18)3 (19)42 三．解答题(20)本小题考查对数函数性质，对数不等式的解法，分类讨论的方法和运算能力，满分11分．解：（Ⅰ）当a >1时，原不等式等价于不等式组：⎩⎨⎧>-+>-+.1,01a a x a x 解得 x >2a －1． (Ⅱ)当0<a <1时，原不等式等价于不等式组：⎩⎨⎧<-+>-+.101a a x a x 解得 a －1<x <2a －1综上，当a >1时，不等式的解集为{x |x >2a －1};当0<a <1时，不等式的解集为{x |a －1<x <2a －1}．(21)本小题主要考查等比数列的基础知识，逻辑推理能力和运算能力．满分12分．解：若q =1，则有S 3=3a 1，S 6=6a 1，S 9=9a 1．但a 1≠0，即得S 3＋S 6≠2S 9，与题设矛盾，q ≠1．又依题意S 3＋S 6=2S 9可得qq a q q a q q a --=--+--1)1(21)1(1)1(916131整理得q 3(2q 6－q 3－1)=0．由q ≠0得方程 2q 6－q 3－1=0．(2q 3＋1)(q 3－1)=0， ∵ q ≠1，q 3－1≠0，∴ 2q 3＋1=0∴ q =－243(22)本小题考查三角函数基础知识，利用三角公式进行恒等变形和运算能力．满分12分．解法一：由题设条件知B =60º，A ＋C =120º．∵ －︒60cos 2=－22∴ C A cos 1cos 1+=－22 将上式化为 cos A ＋cos C =－22 cos A cos C利用和差化积及积化和差公式，上式可化为2cos2C A +cos 2CA -=－2[cos(A ＋C)＋cos(A －C)] 将cos 2)(C A +=cos60º=21，cos(A +C )= 21代入上式得cos 2)(C A -=22－2cos(A －C)cos(A －C)=2cos 22)(C A -－1代入上式并整理得42cos 22)(C A -＋2cos 2)(C A -－32=0，(2cos2C A -－2)(22cos 2CA -＋3)=0． ∵ 22cos 2C A -＋3≠0，∴ 2cos 2C A -－2=0，∴ cos 2C A -=22．解法二：由题设条件知 B=60º，A ＋C =120º．设α=2C A - 则2C A -=2α，可得A=60º＋α，C=60º－α 所以)60cos(1)60cos(1cos 1cos 1o o αα-++=+C A =ααsin 23cos 211-＋ααsin 23cos 211+=ααα22sin 43cos 41cos -=43cos cos 2-αα依题得B cos 243cos cos 2-=-α，∵ cos B =21，∴ 2243cos cos 2-=-αα．整理得42cos 2α＋2cos α－32=0， (2cos α－2)(22cos α＋3)=0，∵ 22cos α＋3≠0，∴ 2cos α－2=0从而得cos 222=-C A ． (23)本小题考查空间线面关系，正三棱柱的性质，逻辑思维能力，空间想象能力运算能力．满分12分．(Ⅰ)②∵BE :CF =1:2 ∴ DC =2BD ，∴ DB =BC ，③∵△ABD 是等腰三角形，且∠ABD =120º，∴∠BAD =30º，∴∠CAD =90º， ④∵FC ⊥面ACD ， ∴CA 是F A 在面ACD 上射影，且CA ⊥AD ， ⑤∵F A ∩AC =A ，DA ⊥面ACF ，DA ⊂面ADF ⑥∴面ADF ⊥面ACF ． (Ⅱ)解： ∵ F AA E AEF A V V 11--=．在面A 1B 1C 1内作B 1G ⊥A 1C 1，垂足为G ．B 1G=23a 面A 1B 1C 1⊥面A 1 C ∵ B 1G ⊥面A 1 C ，∵ E ∈B B 1，而B B 1∥面A 1 C ，∴ 三棱柱E －AA 1F 的高为23a F AA S 1∆=AA 1·2AC =232a ∴43311a V V F AA E AEF A ==-- (24)本小题主要考查运用数学知识和方法解决实际问题的能力，指数函数和二项式定理的应用，近似计算的方法和能力．满分10分．解：设耕地平均每年至多只能减少x 公项，又设该地区现有人口为p 人，粮食单产为M 吨/公顷．依题意得不等式()()()()%10110%111010%2214104+⨯⨯≥+⨯-⨯+⨯PM P xM化简得x ≤103×[1－22.1)01.01(1.110+⨯]．∵ ()⎥⎦⎤⎢⎣⎡+⨯-⨯22.101.011.1110103=103×[1－22.11.1×(1＋110C ×0.01＋210C ×0.012＋…)] ≈103×[1－22.11.1×1.1045]≈4.1 9分∴ x ≤4(公顷)答：按规则该地区耕地平均每年至多只能减少4公顷．(25)本小题主要考查直线与双曲线的性质，解析几何的基本思想，以及综合运用知识的能力．满分12分．解：依题设：l 1、l 2都存在，因为l 1过点P ()02，-且与双曲线有两个交点，故方程组 y =k 1(x ＋2)(k 1≠0)，y 2－x 2=1 ①有两个不同的解，在方程组①中消去y ，整理得(21k －1)x 2＋2221k x ＋221k －1=0 ② 若(21k －1)=0，则方程①只有一个解，则l 1与以曲线只有一个交点，与题设矛盾．故(21k －1) ≠0，即|k 1|≠1．方程②的判别式为 △ 1=(2221k )2－4(21k －1)(221k －1)=4(321k －1)设l 2的斜率k 2，因为l 2过点P ()02，-且与双曲线有两个交点，故方程组 y =k 2(x ＋2)(k 2≠0)，y 2－x 2=1 ③有两个不同的解，在方程组③中消去y ，整理得(22k －1)x 2＋2222k x ＋222k －1=0 ④ 同理有(22k －1) ≠0，△2=4(322k －1) 又因为l 1⊥l 2，所以有k 1·k 2=－1 于是，l 1、l 2与双曲线各有两个交点，等价于 321k －1>0， 322k －1>0， k 1·k 2=－1， |k 1|≠1．解得3||331<<k ， |k 1| ≠1．∴ k 1∈(－3，－1) ∪(－1，－33)∪(33，1)∪(1，3) (Ⅱ)双曲线y 2－x 2=1的顶点(0，1)、(0，－1)．取A 1(0，1)时，有 k 1(0＋2)=1，解得k 1=22．从而k 2=11k -=－2．将k 2=－2代入方程④得 x 2＋42x ＋3=0 ⑤记l 2与双曲线的两交点为A 2(x 1，y 1)、B 2(x 2，y 2)，则|A2B2|2=(x1－x2)2+(y1－y2)2=3(x1－x2)2=3[(x1＋x2)2－4x1x2]．由⑤知x1＋x2=－42x1x2=3∴| A2 B2|2=60，| A2 B2|=215当取A1(0，－1)时，由双曲线y2－x2=1关于x轴的对称性，知| A2 B2|=215所以l1过双曲线的一个顶点时，|A2 B2|=215。