机构速度和加速度分析的一般图解法
合集下载
第三章 机构的运动分析--相对运动矢量方程图解法
（刚体的平面运动=随基点的平动+绕基点的转动） 若已知 VA、 和 aA、 B
VB VA VBA
大小
•
？ √ 方向 ？ √
LAB AB
n BA t BA
VA • aA
A V B
VBA
B
aB aA a a
大小
aB •
A
？ 方向 ？
√ 2LAB LAB √ BA AB
0
2 1 2 1
a a a
n
大小： 21 vB B 2 1 vB B Sin 90 2 1 vB B
2 1
方向：将 v B B 的方向顺着 1的转向转 900
aB B
2
K
1
大小： 21 vB B 2 1 vB B Sin 90 2 1 vB B
0
2 1 2 1
连接点p与任一点的矢量便代表该点在机构图中的同名点
的绝对速度，其指向是从p指向该点。如p→x代表 vX
连接其他任意两点的矢量便代表该两点在机构图中的同名
点间的相对速度，其指向适与速度的角标相反。如x→y代 表 vYX
速度影像的应用条件是同一构件内。
加速度影像（梅姆克第二定理）
– 一个刚体上三个点的加速度矢量末端在加速度平面图 中所构成的三角形与原始三角形同向相似。 π称为极点，代表所有构件上绝对加速度为零的点。 连接点π与任一点的矢量便代表该点在机构图中的同名点的 绝对加速度，其指向是从π指向该点。如π→x’代表示 aX 连接带有角标’的其他任意两点的矢量便代表该两点在机构 图中的同名点间的相对加速度，其指向适与加速度的角标相 反。如x’→y’代表 aYX 加速度分量一般用虚线表示。切向加速度用同名而不同上标 的两个字母表示，方向指向单撇(’)点。如y”→y’代表 atYX。而Y→X的向心加速度x’ → y”代表 anYX
VB VA VBA
大小
•
？ √ 方向 ？ √
LAB AB
n BA t BA
VA • aA
A V B
VBA
B
aB aA a a
大小
aB •
A
？ 方向 ？
√ 2LAB LAB √ BA AB
0
2 1 2 1
a a a
n
大小： 21 vB B 2 1 vB B Sin 90 2 1 vB B
2 1
方向：将 v B B 的方向顺着 1的转向转 900
aB B
2
K
1
大小： 21 vB B 2 1 vB B Sin 90 2 1 vB B
0
2 1 2 1
连接点p与任一点的矢量便代表该点在机构图中的同名点
的绝对速度，其指向是从p指向该点。如p→x代表 vX
连接其他任意两点的矢量便代表该两点在机构图中的同名
点间的相对速度，其指向适与速度的角标相反。如x→y代 表 vYX
速度影像的应用条件是同一构件内。
加速度影像（梅姆克第二定理）
– 一个刚体上三个点的加速度矢量末端在加速度平面图 中所构成的三角形与原始三角形同向相似。 π称为极点，代表所有构件上绝对加速度为零的点。 连接点π与任一点的矢量便代表该点在机构图中的同名点的 绝对加速度，其指向是从π指向该点。如π→x’代表示 aX 连接带有角标’的其他任意两点的矢量便代表该两点在机构 图中的同名点间的相对加速度，其指向适与加速度的角标相 反。如x’→y’代表 aYX 加速度分量一般用虚线表示。切向加速度用同名而不同上标 的两个字母表示，方向指向单撇(’)点。如y”→y’代表 atYX。而Y→X的向心加速度x’ → y”代表 anYX
《机械原理》
3lCB
?
方向： ? C→D
√ √
√ ⊥BC
图解上式得p’c’b’： aC =μ a p’c’ α 4= atC / lCD 方向：CCW α 3 = atCB/ lCB 方向：CCW 利用影象法求得p’c’e’ (d就是p) aE =μ a p’e’ 求构件6的加速度： aF = aE + anFE + atFE 大小： ? √ √ ? 方向： √ √ ‖FE ⊥FE 其中：anFE＝ω 25lFE 求得: aF =μ a p’f’ atFE =μ
A
α
B
I5
3
3
2 ω 3α b
ω4
4D
4
x4 Eα 5ω 5 5
F
6
x5
e x
③构件3、5上速度为零的点I3、I5
求作△bcp∽△BCI3 △efp∽△EFI5 得I3 得I5
f
c
p
I3
④构件3、5上加速度为零的 点Q3、Q5
求作△b’c’p’∽△BCQ3 △e’f’p’∽△EFQ5 得Q3 得Q5
ω 3 = μ vpb3 / lCB
b2
②加速度关系
2
A 1
ω1
B aB3 = anB3+ atB3 = aB2+ arB3B2 + akB3B2 3 21 2 l 3 αω 3 ? 2 VB3B2ω 3 大小： ? ω 3 BC ? l1ω C √ b3 方向： ? B→C ⊥CB B→A ∥BC 方向：VB3B2顺ω 3转过90°。 p ak B3B2
已知摆式运输机运动简图、各构件尺寸、ω 2，求： ①VF、aF、ω 3、ω 4、ω 5、α 3、α 4、α 5 ②构件3、4、5中任一速度为Vx的点X3、X4、X5的位置 ③构件3、5上速度为零的点I3、I5 ④构件3、5上加速度为零的点Q3、Q5 C 3 ⑤点I3、I5的加速度。 aI3、aI5 ω4 B 解：1)速度分析 ω2 E 2 ω3 4 VB＝LABω 2 ，pb ＝VB / μ V A D
?
方向： ? C→D
√ √
√ ⊥BC
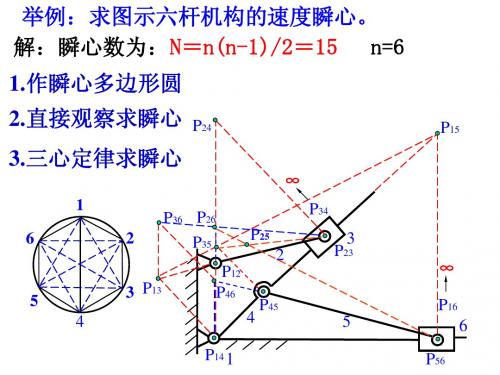
图解上式得p’c’b’： aC =μ a p’c’ α 4= atC / lCD 方向：CCW α 3 = atCB/ lCB 方向：CCW 利用影象法求得p’c’e’ (d就是p) aE =μ a p’e’ 求构件6的加速度： aF = aE + anFE + atFE 大小： ? √ √ ? 方向： √ √ ‖FE ⊥FE 其中：anFE＝ω 25lFE 求得: aF =μ a p’f’ atFE =μ
A
α
B
I5
3
3
2 ω 3α b
ω4
4D
4
x4 Eα 5ω 5 5
F
6
x5
e x
③构件3、5上速度为零的点I3、I5
求作△bcp∽△BCI3 △efp∽△EFI5 得I3 得I5
f
c
p
I3
④构件3、5上加速度为零的 点Q3、Q5
求作△b’c’p’∽△BCQ3 △e’f’p’∽△EFQ5 得Q3 得Q5
ω 3 = μ vpb3 / lCB
b2
②加速度关系
2
A 1
ω1
B aB3 = anB3+ atB3 = aB2+ arB3B2 + akB3B2 3 21 2 l 3 αω 3 ? 2 VB3B2ω 3 大小： ? ω 3 BC ? l1ω C √ b3 方向： ? B→C ⊥CB B→A ∥BC 方向：VB3B2顺ω 3转过90°。 p ak B3B2
已知摆式运输机运动简图、各构件尺寸、ω 2，求： ①VF、aF、ω 3、ω 4、ω 5、α 3、α 4、α 5 ②构件3、4、5中任一速度为Vx的点X3、X4、X5的位置 ③构件3、5上速度为零的点I3、I5 ④构件3、5上加速度为零的点Q3、Q5 C 3 ⑤点I3、I5的加速度。 aI3、aI5 ω4 B 解：1)速度分析 ω2 E 2 ω3 4 VB＝LABω 2 ，pb ＝VB / μ V A D
第3.3节 用矢量方程图解法作运动分析
c
速度多边形的用途 由两点的速度求构件上任意点的速度 C A 例如，求BC中间点E的速度VE 时，bc上 中间点e为E点的影像，连接pe就是VE a p ω E B
e b
c
2、同一构件上两点加速度之间的关系 设已知角速度ω ，A点加速度,求B点的加速度 A B两点间加速度之间的关系有： A
BA
C ω B aB
2 2 2
方向：顺时针
+ω +ω +ω
4 4 4
＝ μ aa’b’ ＝ μ a a’c’ ＝ μ a b’c’ A p’ ω α aA C
B
aB
得：a’b’/ lAB＝b’c’/ lBC＝ a’ c’/ lCA
∴△a’b’c’∽△ABC
p’a’b’c’－加速度多边形（或速度 图解）， p’－极点 加速度多边形的特性： ①联接p’点和任一点的向量代表该 点在机构图中同名点的绝对加速 度，指向为p’→该点。
VB B
2
VB B
2
1
1
VB
2
2
B（B1，B2）
vB2 vB1 vB2B1
VB
1
1
A
ω1
VB B
2
VB B
2
1
1
VB
：
aB2 aB1 a k B2B1 a r B2B1
2
2
B（B1，B2）
VB
aB1 a n B1 a t B1
等速
1
1
A
ω1
④极点p’代表机构中所有加速度为零的点。 用途：根据相似性原理由两点的加速度求任 意点的加速度。 例如，求BC中间点E的加速度aE 时，b’c’上中间
矢量方程图解法作速度加速度分析
2、作图方法
具体方法为图解矢量方程。
基础知识：一个矢量有大小和方向两个要素。
用图解的方法一个矢量方程可以求出两个未知要素（包括大小和
方向均可以）。
例题：
C B
A P
A BC
大小 ？ √ ？
方向 √ √ √
A BC
大小 √ √ ？
方向 √ √ ？
二、同一构件上两点之间的速度和加速度关系
8
8
B
3
P23 (P24)
2
4
C P34
1
A P12
（b） P13
8
P23 B 3 P34
2
A P12
1
4
P24 C P14
8
（d）
P13
3
A
M P23B
Vm
P24
2 A P12
1
C4
P14 P34
8
青岛滨海学院教师教案 §3-3 用矢量方程图解法作机构的速度及加速度分析
一、矢量方程图解法的基本原理及作图法
注意：速度影像只能应用于同一构件上的各点。 总结：
1） 一个矢量方程最多只能求解两个未知量； 2） P 称为极点，它代表机构中所有构件上绝对速度为零的点；
青岛滨海学院教师教案
（速度多边形中仅此一点，它可能对应机构中多个点：机架上的点或构件的绝 对瞬心点）
3）由 P 点指向速度多边形中任一点的矢量代表该点的绝对速度大小和方 向；
们可以得到：
(B1 B2 ) B
1 2
VB2 VB1 VB2B1
青岛滨海学院教师教案
aB2
a B1
aBr 2B1
机械原理第七版第三章
（二）、用解析法对平面连杆机构进行运动分析 用解析法对平面连杆机构进行运动分析又可分为：矢 量方程解析法、杆组法和矩阵法等。 矢量方程法是将机构中各种构件视为矢量，并构成封 闭矢量多边形，列出矢量方程，进而推导出未知量的表达 式。
复数矢量法 图示四杆机构，已知机构各构 件尺寸及原动件1的角位移θ 1和 角速度ω 1 ，现对机构进行位置、 速度、加速度分析 1、位置分析 矢量方程式：
第三章
平面机构的运动分析
§3-1 机构运动分析的任务、目的和方法 §3-2 用速度瞬心法作机构的速度分析
§3-3 用矢量方程图解法作机构的速度及 加速度分析
§3-4 综合运用瞬心法和矢量方程图解法 对复杂机构进行速度分析 §3-5 用解析法作机构的运动分析 返回
§3-1 机构运动分析的任务、目的和方法
i
2
l33e
i
3
l11 cos 1 l22 cos 2 l33 cos 3 l11 sin 1 l22 sin 2 l33 sin 3
3l3 sin( 3 2 ) 1l1 sin( 1 2 )
1L1 sin( 1 2 ) 3 L3 sin( 3 2 )
1L1 sin( 1 3 ) 2 L2 sin( 2 3 )
1L1 sin( 1 3 ) 2 L2 sin( 2 3 )
3、加速度分析
l11e i l22e i l33e i
1 2
3
2 i il1 1 e1
1
i l2 2e 2
1．任务 根据机构的尺寸及原动件已知运动规律，求构件中从动件上 某点的轨迹、位移、速度及加速度和构件的角位移、角速度及角 加速度。 2．目的 了解已有机构的运动性能，设计新的机械和研究机械动力性 能的必要前提。 3．方法 主要有图解法和解析法。图解法又有速度瞬心法和矢量方程 图解法（又称相对运动图解法）。 图解法： 形象、直观，用于平面机构简单方便，但精度 和求解效率较低。 解析法： 计算精度和求解效率高。可借助计算机计算。
考研机械原理第二讲 机构的运动分析
第二讲平面机构的运动分析一用速度瞬心法作机构的速度分析1 速度瞬心的定义：作平面相对运动两构件上任一瞬时其速度相等的点，称为这个瞬时的速度中心。
分类：相对瞬心－重合点绝对速度不为零绝对瞬心－重合点绝对速度为零2 瞬心数目 K＝N(N-1)/23 机构瞬心位置的确定直接观察法：适用于求通过运动副直接相联的两构件瞬心位置。
１）两构件组成转动副时，转动副中心即是它们的瞬心。
２）若两构件组成移动副时，其瞬心位于移动方向的垂直无穷远处。
３）若两构件形成纯滚动的高副时，其高副接触点就是它们的瞬心。
４）若两构件组成滚动兼滑动的高副时，其瞬心应位于过接触点的公法线上。
不直接形成运动副的两构件利用三心定理来确定其具体位置。
三心定理：三个彼此作平面平行运动的构件共有三个瞬心，且它们位于同一条直线上。
此法特别适用于两构件不直接相联的场合。
4传动比的计算ωi /ωj＝P1j P ij / P1i P ij两构件的角速度之比等于绝对瞬心至相对瞬心的距离之反比5.角速度方向的确定相对瞬心位于两绝对瞬心的同一侧，两构件转向相同相对瞬心位于两绝对瞬心之间，两构件转向相反。
常见题型：1.速度瞬心的求解（会用正多形法）2利用速度瞬心求解速度。
ωi /ωj ＝P 1j P ij / P 1i P ij例题：在图示四杆机构中，AB l =60mm ，CD l =90mm ，AD l =BC l =120mm ，2ω=10rad/s ，试用瞬心法求： (1)当ϕ=45°时，点C 的速度C v；(2)当ϕ=165°时，构件3的BC 线上(或其延长线上)速度最小的一点E 的位置及其速度大小；(3)当C v =0时，ϕ角之值(有两个解)。
P 13C(a)解：以选定的比例尺0.005/l m mm μ=作机构运动简图如图3-2所示。
（1）定瞬心P 13的位置，求v c 。
131331 6.07rad /AP DP l l s ωω==30.547/c l v CD m s μω==（2）如图（b ）所示，定出构件2的BC 线上速度最小的一点E 位置及速度的大小。
第3章机构的运动分析-1
E
an EB
C 3 4
ω3
aE e'
b'
ω2
A
2
aB
1
w4
D
a
t EB
a
n EB
(P12 )
以曲柄滑块机构为例，进一步说明用矢量方程图 解法作机构的速度分析和加速度分析的具体步骤。
例 : 已知曲柄滑块机构原动件 AB 的运动规律和各构件尺寸。求： (1)图示位置连杆BC的角速度和 其上各点速度。 (2)连杆BC的角加速度和其上C点 加速度。 ω2 2
极点
C
vEC
vCB vEB
b
bc 代表 vCB 。
e
3）在速度多边形中,极点p 代表机构中速 度为零的点。 4）已知某构件上两点的速度 ,可用速度影 像法求该构件上第三点的速度。
速度多边形
E B
A
C
vC x
p
极点
C
vEC e
vCB
vB
vEB
b
△bce ~ △BCE
已知连杆上两点的速度vB 、vC 用速度影像法可以确定vE 。
④确定点的轨迹（连杆曲线）。
V型发动机运动简图
D
E
C B
A
3-1
机构运动分析的任务、目的及方法
1.机构运动分析的任务与目的
（2）速度分析
5 4
①掌握从动件的度变化规律 是否满足工作要求。如牛 头刨床； ②为加速度分析作准备。
2
1 3
6
3-1 机构运动分析的任务、目的及方法
1.机构运动分析的任务与目的
用三心定理可以确定ω3、ω4 的大小。
平面铰链四杆机构
例2：用三心定理分析凸轮机构速度 (v3)。 1
an EB
C 3 4
ω3
aE e'
b'
ω2
A
2
aB
1
w4
D
a
t EB
a
n EB
(P12 )
以曲柄滑块机构为例，进一步说明用矢量方程图 解法作机构的速度分析和加速度分析的具体步骤。
例 : 已知曲柄滑块机构原动件 AB 的运动规律和各构件尺寸。求： (1)图示位置连杆BC的角速度和 其上各点速度。 (2)连杆BC的角加速度和其上C点 加速度。 ω2 2
极点
C
vEC
vCB vEB
b
bc 代表 vCB 。
e
3）在速度多边形中,极点p 代表机构中速 度为零的点。 4）已知某构件上两点的速度 ,可用速度影 像法求该构件上第三点的速度。
速度多边形
E B
A
C
vC x
p
极点
C
vEC e
vCB
vB
vEB
b
△bce ~ △BCE
已知连杆上两点的速度vB 、vC 用速度影像法可以确定vE 。
④确定点的轨迹（连杆曲线）。
V型发动机运动简图
D
E
C B
A
3-1
机构运动分析的任务、目的及方法
1.机构运动分析的任务与目的
（2）速度分析
5 4
①掌握从动件的度变化规律 是否满足工作要求。如牛 头刨床； ②为加速度分析作准备。
2
1 3
6
3-1 机构运动分析的任务、目的及方法
1.机构运动分析的任务与目的
用三心定理可以确定ω3、ω4 的大小。
平面铰链四杆机构
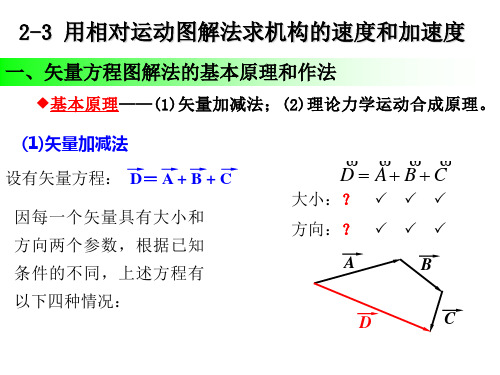
例2：用三心定理分析凸轮机构速度 (v3)。 1
机械原理 第二章-2相对运动图解、解析
1
3
aC1n c2 (c3) aC1t 4 D
A
4 P c1
一步减少未知数的个数。
n t k r aC2 aC3D aC3D aC1 aC2C1 aC2C1
2 3 l3
大小： 方向：
？ 3l3
√ √
21vC 2C 1 ？
√ ∥AB
C→D ⊥CD
2) 取速度比例尺a , 作 加速度多边形。
P
c1
( 顺时针 ）
2. 加速度分析：
1) 依据原理列矢量方程式 分析：
aC2 = aC1 + aC2C1
B
2 C akC2C1
当牵连点系（动参照系）为 转动时，存在科氏加速度。 3
D 4
ω1
1
1
c2 (c3)
r k aC2C1 aC2C1 aC2C1
科氏加速度
A
4 P c1
k r a 2 v
√
√
22lBC
C→B
？
⊥BC
b) 根据矢量方程式，取加速度比例尺
a
实际加速度
c´ 图示尺寸
m/
s2
p
mm
, 作矢量多边形。
c e b
p
极点
n
b
由加速度多边形得：
aC a pc m / s2
t 2 aCB l BC a nc l BC
同样，如果还需求出该构件上E 点的加速度 aE，则
pe 则代表 aE
由加速度多边形得：
p c´ n
aE pea
△b’c’e’ ~ △BCE , 叫 做
△BCE 的加速度影像，字 母的顺序方向一致。
机构速度和加速度分析的一般图解法
选已知参数较多的点一般为铰链点为此有时应将构件扩大至所选取的重合点1列矢量方程并分析各矢量2选取适当比例尺按方程作速度多边形及加速度多边形图3根据作图求解4科氏加速度存在的条件32用图解法作机构的运动分析用图解法作机构的运动分析23232323科氏加速度存在的条件科氏加速度存在的条件当两构件构成移动副若移动方向无转动分量即只作平动时无科氏加速度
§3-2 用图解法作机构的运动分析
1.矢量方程图解法
（1）矢量方程图解法的基本原理 理论力学中的运动合成原理 （2）矢量方程图解法的作法 在对机构进行速度和加速度分析时，首先根据运动合成原理 列出机构运动的矢量方程，然后再按方程作图求解 两构件以转动副相连时，在转动副中心处具有相同的速度和
加速度，两构件以移动副相连时，两构件具有相同的角速度和角
加速度
§3-2 用图解法作机构的运动分析
（3）矢量图的画法
D A B C
大小：？ √ √ 方向：？ √ √ √ √
D A B C
大小：√ 方向：√ ？ ？ √ √ √ √
B A
D
B
C
A
D
C
§3-2 用图解法作机构的运动分析
D A B C
加速度存在的条件
当两构件构成移动副，若移动方向无转动分量即只作平动时， 无科氏加速度； 当两构件构成移动副，若移动方向含有转动分量时，存在断
科氏加速度 3
2 2 3 2
2 3
3
大小：√ ？√√
方向：√ √ ？
？
方向：√ √ ？ √
B
B
A D
C
A D
C
§3-2 用图解法作机构的运动分析
2.利用同一构件上两点间的速度和加速度矢量方程作图求解
§3-2 用图解法作机构的运动分析
1.矢量方程图解法
（1）矢量方程图解法的基本原理 理论力学中的运动合成原理 （2）矢量方程图解法的作法 在对机构进行速度和加速度分析时，首先根据运动合成原理 列出机构运动的矢量方程，然后再按方程作图求解 两构件以转动副相连时，在转动副中心处具有相同的速度和
加速度，两构件以移动副相连时，两构件具有相同的角速度和角
加速度
§3-2 用图解法作机构的运动分析
（3）矢量图的画法
D A B C
大小：？ √ √ 方向：？ √ √ √ √
D A B C
大小：√ 方向：√ ？ ？ √ √ √ √
B A
D
B
C
A
D
C
§3-2 用图解法作机构的运动分析
D A B C
加速度存在的条件
当两构件构成移动副，若移动方向无转动分量即只作平动时， 无科氏加速度； 当两构件构成移动副，若移动方向含有转动分量时，存在断
科氏加速度 3
2 2 3 2
2 3
3
大小：√ ？√√
方向：√ √ ？
？
方向：√ √ ？ √
B
B
A D
C
A D
C
§3-2 用图解法作机构的运动分析
2.利用同一构件上两点间的速度和加速度矢量方程作图求解
第六章 平面机构的性能分析-2
（１）滑块与导杆相对移动时， 滑块同导杆角速度一致。
VB2B1
aKB2B1
（２）对于活动导路转动的移动副进行加速度分析时，除牵
连加速度和相对加速度之外，应添加：
科氏加速度aKB2B1 其大小为
aKB2B1 =21vB2B1
其方向为 相对速度vB2B1按牵连角速度1的顺、逆时针方向转过90的指向。
2
3、组成移动副的两个构件重合点间速度、加速度关系
①速度关系
VB3＝VB2+VB3B2
2
A 1 ω1 B
3 ω3 C
大小： ? √ 方向： √ √
VB3B2 的方向: b2 →b3
? ∥BC μ v= VB2 / pb2
p
ω 3 = μ vpb3 / lCB
b2
② 加速度关系 aB3 = anB3+ atB3 = aB2+ arB3B2 + akB3B2
v v v
VA A
C
√ ? √ ⊥CB pc 方向：p → c
ω
a a
VBA
B
ac 方向： a → c bc 方向： b → c
方向如图
AB杆的角速度ω ＝VBA/LBA＝（μ vab）/（μ l AB ） 同理：ω ＝（μ vca ） /（μ l CA） 得：ab/AB＝bc/ BC＝ca/CA
VCA VCB
图示机构中 连杆2上 B、C两点。 以运动参 数已知的B点为基点。
基点法研究的两点是同一 构件上不同位置的两个转 动副对应位置点。
②作平面运动的构件的两个基本运动副中，一个是转动副， 另一个是移动副，用重合点法建立两活动构件在该转动副中 心处的两重合点间的运动关系。
VB2B1
aKB2B1
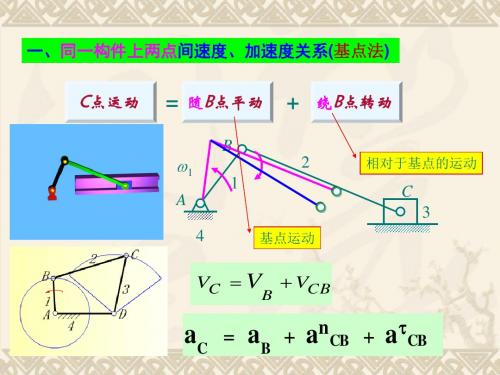
（２）对于活动导路转动的移动副进行加速度分析时，除牵
连加速度和相对加速度之外，应添加：
科氏加速度aKB2B1 其大小为
aKB2B1 =21vB2B1
其方向为 相对速度vB2B1按牵连角速度1的顺、逆时针方向转过90的指向。
2
3、组成移动副的两个构件重合点间速度、加速度关系
①速度关系
VB3＝VB2+VB3B2
2
A 1 ω1 B
3 ω3 C
大小： ? √ 方向： √ √
VB3B2 的方向: b2 →b3
? ∥BC μ v= VB2 / pb2
p
ω 3 = μ vpb3 / lCB
b2
② 加速度关系 aB3 = anB3+ atB3 = aB2+ arB3B2 + akB3B2
v v v
VA A
C
√ ? √ ⊥CB pc 方向：p → c
ω
a a
VBA
B
ac 方向： a → c bc 方向： b → c
方向如图
AB杆的角速度ω ＝VBA/LBA＝（μ vab）/（μ l AB ） 同理：ω ＝（μ vca ） /（μ l CA） 得：ab/AB＝bc/ BC＝ca/CA
VCA VCB
图示机构中 连杆2上 B、C两点。 以运动参 数已知的B点为基点。
基点法研究的两点是同一 构件上不同位置的两个转 动副对应位置点。
②作平面运动的构件的两个基本运动副中，一个是转动副， 另一个是移动副，用重合点法建立两活动构件在该转动副中 心处的两重合点间的运动关系。
机械原理-机构的运动分析
3、加速度分析
aC aB aCB
a C a C aB a CB a CB
n t n t
a B 12l AB
F
1
1 A B 2 E C
大小 lCD32
?
→A
lCB22 C→B
? ⊥CB
·
G
3
方向 C→D ⊥CD
取极点p’ ，按比例尺a作加速度图
1
4
D
' aC a p 'c ' aCB a b 'cc´
思考题：
P44 3-1
作业：
P44 3-3、3-6、3-8（b)
§3-3 用矢量方程图解法作机构的运动分析
一、矢量方程图解法的基本原理及作图法
1、基本原理 —— 相对运动原理 B（B1B2） 1
B
A
同一构件上两点间的运动关系
2
两构件重合点间的运动方程
vB v A vBA
aB a A aBA aA a
c´
aC a G e´
aCB
n2 ´ n2
p´
n3
aF
b´
加速度图分析小结： 1）p‘点代表所有构件上绝对加速度为零的影像点。 2）由p‘点指向图上任意点的矢量均代表机构图中对应点 的绝对加速度。 3）除 p′点之外，图中任意两个带“ ′”点间的连线 均代表机构图中对应两点间的相对加速度，其指向与加 速度的角标相反。 4）角加速度可用构件上任意两点之间的相对切向加速度 除于该两点之间的距离来求得，方向的判定采用矢量平 aCB b ' c ' 移法。 5）加速度影像原理：在加速度图上，同一构件上各点的 绝对加速度矢量终点构成的多边形与机构图中对应点构 成的多边形相似且角标字母绕行顺序相同。 6）加速度影像原理只能用于同一构件。
用矢量方程图解法作机构的速度及加速度分析
b2
ω3=v pb3/LBC，顺时针方向
加速度关系a ① 加速度关系
A
r B3B2
aB3 = a
大小 方向 ak
n B3
+a
t B3
= aB2 + a
+a
k B3B2
1 2 B
ω1
? ω23LBC ? ω21LAB ? 2vB3B2ω3 ? B→C ⊥CB B→A // //BC √ 转过90 沿ω3转过 °
方程不可解 方程可解 G C F E
D
vG = vB + vGB ＝ vC + vGC = vG 大小 ? √ ? ? √ ? 方向 ? √ √ √ √ ?
● 重合点应选已知参数较多的点(一般为铰链点) 。 重合点应选已知参数较多的点(一般为铰链点) 选C点为重合点 点为重合点 v C 3 = v C 4 + v C 3C 4 ? ? 大小 ? 方向 ? √ √
c b
p
角速度 ω=vBA/LBA=v ab/l AB，顺时针方向 / ， 同理 ω=v ca/l CA / ω=v cb/lCB / 因此 ab/AB=bc/BC=ca/CA / / / 于是 abc∽ABC
速度多边形 c b 速度极点 速度零点) (速度零点) C A
ω
a
B
p
●
●
●
●
速度多边形( 速度多边形(Velocity polygon)的性质 ) 联接p点和任一点的向量代表该点在 联接 点和任一点的向量代表该点在 机构图中同名点的绝对速度， 机构图中同名点的绝对速度 ， 指向 C 为p→该点。 →该点。 A 联接任意两点的向量代表该两点 ω 机构图中同名点的相对速度， 在 机构图中同名点的相对速度 ， 指向与速度的下标相反。 指向与速度的下标相反 。 如 bc代 代 a 表 vCB 而不是vBC 。 常用相对速度 而不是 来求构件的角速度。 来求构件的角速度。 abc∽ABC，称abc为ABC的速 ∽ ， 为 的速 c 度影像( ) 度影像(Velocity image)，两者相似 b 且字母顺序一致， 且字母顺序一致 ， 前者沿 ω方向转 过90。 速度极点 极点p代表机构中所有速度为 速度极点 代表机构中所有速度为 零的点的影像。 零的点的影像。
机械原理(2015春)矢量方程图解法 两构件上重合点间的速度和加速度分析
a = a + a + a 则
k
r
c1
c2
c1c2
c1c2
w a = 2 V k
c1c2
2 c1c2
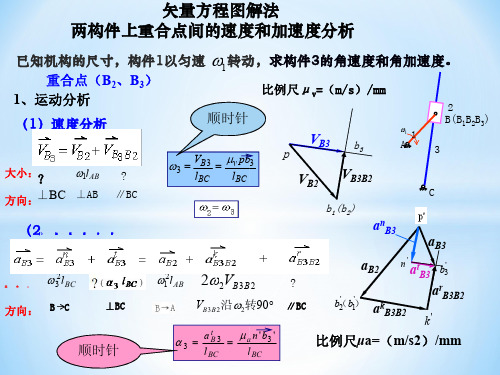
4 例题：已知构件1的运动，求： vC 、vD及 w2、w5和a5
（1）速度分析
v D = v B + v DB
大小 ? √
?
方向 ? √
√
v C = v B + v CB
?
√
?
√
√
√
vC = mv pc (m s) vCB = mv bc (m s)
.
p
VB3
b3
VB2
VB3B2
b1(b2)
w1 1
A
3
C
（2）
加
速
度
分
析
a n B3 a B3
大
小
：
w 32 l BC
方向： B C
⊥BC
顺时针
w12l AB
2w2VB 3 B 2
VB 3 B 2沿w 2转90°
a3
=
a
t B
3
l BC
=
m a n 'b3 ' l BC
?
∥BC
a B2
n ' atB3 b3'
当牵连运动为平动（ w1 = 0）则无科氏加速度。
v CB = w 2 l BC
p w 2
=
v CB l BC
=
m v bc l BC
（逆）
这里用速度影像求vD
选重合点：E(E4、E5)
VC
VD d
VB
b
矢量方程图解法作速度加速度分析
33用矢量方程图解法作机构的速度及加速度分析1掌握矢量方程图解法的基本原理及作图方法2熟练掌握相对运动图解法对机构进行速度加速度分析相对运动图解法矢量方程速度和加速度多边形教案编写日期讲解课后作业题33求作图示机构在所在位置时的全部的速度瞬心
青 岛 滨 海 学 院 教 师 教 案 课 题 教 学 目 的 要 求 教 学 重 点 教 学 难 点
C B A
A BC
大小 ？ √ ？ 方向 √ √ √
P
A BC
大小 √ √ ？ 方向 √ √ ？ 二、同一构件上两点之间的速度和加速度关系 已知：四杆机构 ABCDE 机构的位置如图所示，各个构件的长度已知，原 动件 1 的角速度 1 ，求： VC 、 VE 、 a C 、 a E 、 2 、 3 、 2 、 3 ？
青 岛 滨 海 学 院 教 师 教 案
解：1、求速度和角速度
VC VB VCB
大小 ？ lABω ？ 方向 ⊥CD ⊥AB ⊥BC → VC
VE VB VEB VC VEC
大小 方向 ？
1l AB ？
√
? → VE
？ √
⊥BE √ ⊥EC
2
VCB V , 方向：顺时针 3 C ,，逆时针 (方向判定采用矢量平移) l BC lCD
4
2
4 2 a EC l EC 2 2
∴ aCB : a EB : a EC lCB : l EB : l EC
∴ bc : be : ce BC : EB : EC 即 bce 和 BCE 相似， 称 bce 为
BCE 的加速度影像。 注意：只用于同一构件上。 小结：首先讲解上次作业中出现问题较多的部分；然后讲授矢量方程图解 法的基本原理和作图方法，接着用例题讲解了同一构件上两点之间的速度和加 速度关系的求解方法和步骤。 作业：P44 3-6 （利用 3-6 原题的已知条件，采用这节课讲解的矢量方
青 岛 滨 海 学 院 教 师 教 案 课 题 教 学 目 的 要 求 教 学 重 点 教 学 难 点
C B A
A BC
大小 ？ √ ？ 方向 √ √ √
P
A BC
大小 √ √ ？ 方向 √ √ ？ 二、同一构件上两点之间的速度和加速度关系 已知：四杆机构 ABCDE 机构的位置如图所示，各个构件的长度已知，原 动件 1 的角速度 1 ，求： VC 、 VE 、 a C 、 a E 、 2 、 3 、 2 、 3 ？
青 岛 滨 海 学 院 教 师 教 案
解：1、求速度和角速度
VC VB VCB
大小 ？ lABω ？ 方向 ⊥CD ⊥AB ⊥BC → VC
VE VB VEB VC VEC
大小 方向 ？
1l AB ？
√
? → VE
？ √
⊥BE √ ⊥EC
2
VCB V , 方向：顺时针 3 C ,，逆时针 (方向判定采用矢量平移) l BC lCD
4
2
4 2 a EC l EC 2 2
∴ aCB : a EB : a EC lCB : l EB : l EC
∴ bc : be : ce BC : EB : EC 即 bce 和 BCE 相似， 称 bce 为
BCE 的加速度影像。 注意：只用于同一构件上。 小结：首先讲解上次作业中出现问题较多的部分；然后讲授矢量方程图解 法的基本原理和作图方法，接着用例题讲解了同一构件上两点之间的速度和加 速度关系的求解方法和步骤。 作业：P44 3-6 （利用 3-6 原题的已知条件，采用这节课讲解的矢量方
机械原理——第3章 运动分析
机构的运动分析 3.2速度瞬心 1、直接观察法（两构件以运动副相联） 适用于求通过运动副直接相联的两构件瞬 法 心位置 瞬心定义
瞬心确定
1 P12 2 1 P12 2 ∞
1
2 P12 t
n 1 2 t
V12
n
机构的运动分析 3.2速度瞬心
法 瞬心定义 瞬心确定 2、三心定律（两构件间没有构成运动副） 三个彼此作平面运动的构件共有三个 瞬心，且它们位于同一条直线上。三心定 律特别适用于两构件不直接相联的场合。
VP24
P24
2 P12
ω2
1
ω4
VP24＝μ l(P24P12)· 2 ω
P14
VP24＝μ l(P24P14)· 4 ω ω 4 ＝ω 2·(P24P12)/ P24P14 方向: 顺时针, 与ω2相同
机构的运动分析 3.2速度瞬心 已知构件2的转速ω 2，求构件3的角速度ω 3 法 解: 用三心定律求出P23 nபைடு நூலகம்瞬心定义 2 求瞬心P23的速度 : 瞬心确定
P24 P12 1
P14 2 P23 3
4
P34
P13
机构的运动分析 3.2速度瞬心 举例：求曲柄滑块机构的速度瞬心
法 瞬心定义 瞬心确定 解：瞬心数为：K＝N(N-1)/2＝6 K=6
1.作瞬心多边形（圆）
2.直接观察求瞬心（以运动副相联） 3.三心定律求瞬心（构件间没有构成运动副） P13
1 ∞
2
P45
P23
3 ∞ P16
5
5 P56
6
机构的运动分析 3.2速度瞬心 1.求线速度 法 已知凸轮转速ω1，求推杆的速度 瞬心定义 解： 瞬心确定 ①直接观察求瞬心P13、 P23 应用 ②根据三心定律和公法线 3 P23 n－n求瞬心的位置P12 2 ③求瞬心P12的速度
机械原理矢量方程图解法
2。加速度分析
加速度分析必须在速度分析之后进行
p'b' aB
a aC a p'c' (m s2 )
b'n' 22lBC a
2
aCt B l BC
a n'c'
l BC
(逆)
aD
aB
a
n DB
a
t DB
大小 ？ 22l BD 2l BD
方向 ?
D B BD
加速度多边形的特点
1）由极点p’向外放射的矢量代表构 件相应点的绝对加速度。
' 5
l DF
方向：顺时针
重合点的选取:
重合点的选取应能使所列矢
量方程具有足够的已知要素并能
求解，为此可考虑将构件扩大， 包含所选的重合点。 如左图：
若取C(C2、C3)为重合点: 则：
VC2 VC3 VC2C3
ቤተ መጻሕፍቲ ባይዱ？0
？
？V
V
若取B(B2、B3)为重合点:
则：VB2 VB3 VB2B3
V?
?
3）速度影像：速度多边形上的三角形bcd与 机构简图上的三角形BCD相似，且三角 形bcd是三角形BCD沿构件2的角速度方 向转90度的相似三角形，字母的顺序也 一致。速度影像适用于求同一构件上其 它点的速度。
4）构件 2 角速度的确定
大小：
2
VCB lBC
V bc
lBC
方向： 将bc移到机构简图的C点，根据bc 绕 B点转动的方向确定。
选重合点：E(E4、E5)
vE5 vE4 vE5E4 大小 ？ ？ ？
选重合点：D(D4、D5) 方向 EF ?
// EF
机械原理 第3章 平面机构的运动分析
VD5 = VD4+ VD5D4 大小 ？ √ ？
方向 ⊥DF √ ∥移动方向
ω5= VD5/LDF
aD5
= aD5n +
a
t D5
=aD4
+
aD5D4k （哥氏加速度） +
aD5D4r
大小 ω52* LDF ？ √ 2ω4* VD5D4
？
方向
√ D→F ⊥DF
VD5D4方向沿ω4转过900
∥移动方向
二.实例分析
1、矢量方程图解法的基本原理和作法 原理：相对运动原理 方法：对矢量方程进行图解 1）同一构件上两点间速度和加速度的关系 同一构件上一点的运动可看成是随该构件上另 一点的平动和绕该点的转动的合成。
VB=VA+VBA aB=aA+aBAn+aBAt
1 同一构件两点间的和关系
构件2：已知B和B
1)去除局部自由度； 2)剔除虚约束；（D？）
3)正确确定运动副的数目； 4)构件编号； 5) 列式计算 • F=3×5－2×6－1×2
•用速度瞬心作机构的速度分析
•用矢量方程图解法作机构的速度分 析及加速度分析
第三章 平面机构的运动分析
3-1 平面机构运动分析的任务目的和方法 平面机构的运动分析是指 ：
已知原动件的运动规律、机构尺寸，求其 它构件上某点的运动（s、v、a）
方法：
1 、图解法 特点： 形象直观，精度低，用于求个别
位置的运动特性
VC = VB + VCB
大小 ？ √
？
方向∥X-X ⊥AB ⊥BC
设速度比例尺，作速度图，
设p（小写）为速度极点，
速度极点的速度为零。
机械原理 西工大第八版第3.2节 用矢量方程图解法作运动分析
a
k
B3B2
2vB3B22
无科氏加速度的四种情况 （1）1、3、4重合； （2）B处在最高、低点； （3）1、3垂直，
三、机构运动分析中应注意的若干问题
1.建立速度或加速度向量方程时，一定要从已知速度 或加速度的点开始列方程 重合点的选取原则 ——选已知参数较多的点 （一般为铰链点）
C A 1 2
n5 G 5 B ω1 A 6 1 D p c V E5E4 e5 e′ 5 c′ n2 k E 4 C 2 3 e 2 (e 4 ) e 2′ (e′ 4 ) n3 b′ b p′
解：1）取μL，画出机构图如图 2）计算F：F=3×5-2×7=1 等于原动件数，可解。 3）结构分析：机构由机架和原动件、Ⅱ级杆组2-3、Ⅱ级 杆组4-5组成。 4）Ⅱ级杆组2-3的运动分析： 速度分析： VC = VB + VCB 大小 ？ ω1LAB ？ 方向 ⊥CD ⊥AB ⊥CB
方向计量为正。
举例:已知四杆机构各杆长度和θ1，ω1，确定构件1在回转一周的过程中 每 隔30o 时构件2、3的方位角θ2、θ3 , 角速度ω2、ω3 , 角加速度α2、α3。
解：将封闭矢量方程式 :
i1
第三章
平面机构的运动分析
l1 l2 l3 l4 0 表示为复数形式，有
2．加速度分析：
B3 点 的 aB3 由 B2 的 牵 连 加 速 度 aB2 、 相 对 加 速 度 arB3B2 、 科 氏 加 速 度 akB3B2
=2ω2×VB3B2组成。即 anB3 + atB3 = anB2 + atB2 + arB3B2 + akB3B2 大小 ω32LBC ？ ω12LAB 0 ？ 2ω2VB3B2 方向 B→C ⊥BC B→A ∥BC VB3B2 沿ω3转90 取定极点Pˊ及比例尺μa。图解如图得： arB3B2 = μa· kb3ˊ m/s2 方向 k→b3ˊ atB3 =α3LBC =μa· n3b3ˊ m/s2 方向 n3→b3ˊ α3 = atB3/LBC 1/s2 转向 ccw（按atB确定）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§3-2 用图解法作机构的运动分析
1.矢量方程图解法
（1）矢量方程图解法的基本原理 理论力学中的运动合成原理 （2）矢量方程图解法的作法 在对机构进行速度和加速度分析时，首先根据运动合成原理 列出机构运动的矢量方程，然后再按方程作图求解 两构件以转动副相连时，在转动副中心处具有相同的速度和
加速度，两构件以移动副相连时，两构件具有相同的角速度和角
§3-2 用图解法作机构的运动分析
3.利用两构件重合点间的速度及加速度矢量方程作图求解 运动合成原理：构件i在重合点的运动可认为是随同构件j在重 合点的运动和构件i相对于构件j的相对运动的合成
重合点选取原则：选已知参数较多的点（一般为铰链点），
为此有时应将构件扩大至所选取的重合点 （1） 列矢量方程并分析各矢量 （2）选取适当比例尺按方程作速度多边形及加速度多边形图 （3）根据作图求解 （4）科氏加速度存在的条件
§3-2 用图解法作机构的运动分析
机构运动的图解法分析包括对机构的位置、速度和加速度的 分析。由于机构的位置图解分析实际上是按给定的机构尺寸及原 动件的位置作出其机构运动简图，在第2章已作介绍，所以本节 主要介绍机构的速度和加速度分析的图解法
一、机构速度及加速度分析的一般图解法
机构的速度及加速度分析的一般图解法为矢量方程图解法， 又称相对运动图解法
科氏加速度存在的条件
当两构件构成移动副，若移动方向无转动分量即只作平动时， 无科氏加速度； 当两构件构成移动副，若移动方向含有转动分量时，存在断
科氏加速度 3
2 2 3 2
2 3
3
大小：√ ？√√
方向：√ √ ？
？
方向：√ √ ？ √
B
B
A D
C
A D
C
§3-2 用图解法作机构的运动分析
2.利用同一构件上两点间的速度和加速度矢量方程作图求解
运动合成原理：同一构件上任意一点的运动可认为是随该构 件上基点作平动与绕基点作相对转动的合成 （1） 列矢量方程并分析各矢量 （2）选取适当比例尺按方程作速度多边形及加速度多边形图 （3）根据作图求解 （4）速度及加速度影像
加速度
§3-2 用图解法作机构的运动分析
（3）矢量图的画法
D A B C
大小：？ √ √ 方向：？ √ √ √ √
D A B C
大小：√ 方向：√ ？ ？ √ √ √ √
B A
D
B
CADC来自§3-2 用图解法作机构的运动分析
D A B C
大小：√ √ √ √
D A B C