初中数学青岛版八年级上册第5章 几何证明初步5.6 几何证明举例-章节测试习题(2)
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、如图,点在的延长线上,下列条件中能判断的是()A. B. C. D.2、如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是()A.不变B.一直变大C.先减小后增大D.先增大后减小3、如图,用尺规作出了BF∥OA,作图痕迹中,弧MN是()A.以B为圆心,OD长为半径的弧B.以C为圆心,CD长为半径的弧 C.以E为圆心,DC长为半径的弧 D.以E为圆心,OD长为半径的弧4、已知一个等腰三角形两个内角度数之比为1:4,则这个等腰三角形顶角度数为()A.75°B.90°C.105°D.120°或20°5、三角形的内角和等于()A. B. C. D.6、下列说法不能推出△ABC是直角三角形的是()A. B. C.∠A=∠B=∠C D.∠A=2∠B=2∠C7、下列命题中是真命题的是()A.相等的两个角是对顶角B.两条直线被第三条直线所截,同位角相等 C.在同一平面内,如a∥b,b∥c,则a∥c D.若a>b,则﹣a>﹣b8、如图,下列能判定AB∥CD的条件的个数()(1 )∠B=∠BCD;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A.1B.2C.3D.49、下列说法中正确的是A.过一点有且仅有一条直线与已知直线平行B.若,则点C是线段AB的中点C.两点之间的所有连线中,线段最短D.相等的角是对顶角10、如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A 与A′重合,若∠A=α,则∠1+∠2=()A.αB.2αC.180°﹣αD.180°﹣2α11、如图,ΔABC与ΔA’B’C’关于直线l对称,则∠B的度数为()A.30°B.50°C.90°D.100°12、如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为()A.70B.80C.90D.10013、如图,AB∥CD,则∠1.∠2.∠3.∠4的关系是( )A.∠1-∠2+∠3+∠4=180°B.∠1+∠2+∠3=∠4C.∠1+∠2-∠3+∠4=180°D.∠2+∠3+∠4 -∠1=180°14、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=2,BD=1,则AD的长是()A.1B.C.2D.415、下列条件中能得到互相平行的直线的是()A.互为邻补角的角平分线所在的直线B.对顶角的平分线所在的直线 C.两条平行线的一对内错角的平分线所在的直线 D.两条平行线的一对同旁内角的平分线所在的直线二、填空题(共10题,共计30分)16、如图,在△ABC中,∠ABC和∠ACB的角平分线交于点O,BO的延长线交于AC于点D,若∠DOC=40°,则∠A=________。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、已知,四边形ABCD中,AD∥BC,∠A=∠BCD=∠ABD,DE平分∠ADB,下列说法:①AB∥CD;②ED⊥CD;③S△EDF=S△BCF.其中错误的说法有()A.0个B.1个C.2个D.3个2、如图,下列条件中能判定直线l1∥l2的是()A.∠1=∠2B.∠1=∠5C.∠1+∠3=180°D.∠3=∠53、用反证法证明命题“在三角形中,至多有一个内角是钝角”时,应先假设( )A.至少有一个内角是钝角B.至少有两个内角是钝角C.至多有一个内角是钝角D.至多有两个内角是钝角4、如图,在△ABC中AC=BC,点D和E分别在AB和AC上,且AD=AE.连接DE,过点A的直线GH与DE平行,若∠C=40°,则∠GAD的度数为()A.40°B.45°C.55°D.70°5、将一直角三角板与两边平行的纸条按如图所示的方式放置,有下列结论:(1);(2);(3);(4).其中正确个数是()A.1个B.2个C.3个D.4个6、如图1,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于()A.30°B.40°C.60°D.70°7、如图,,,,则的度数为()A. B. C. D.8、把一张对边互相平行的纸条,折成如图所示,是折痕,若,则下列结论正确的有是( )( 1 );(2);(3);(4).A.1个B.2个C.3个D.4个9、下列说法错误的是()A.同角的余角相等B.内错角相等C.垂线段最短D.平行于同一条直线的两条直线平行10、下列条件能判定a∥b的是()A.∠1=∠4B.∠4=∠5C.∠3+∠5=180°D.∠2=∠411、如图、、三点共线,、、三点共线,且,,下列结论错误的是()A. B. C. D.12、如图,AC⊥BC,DE是AB的垂直平分线,∠CAE=30°,则∠B=()A.30°B.35°C.40°D.45°13、下列说法正确的有( )①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;③若线段AB 与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.A.1个B.2个C.3个D.4个14、如图,AB∥CD,DA⊥CE于点A.若∠EAB=55°,则∠D的度数为()A.25°B.35°C.45°D.55°15、学校体育室里有6个箱子,分别装有篮球和足球(不混装),数量分别是8,9,16,20,22,27,体育课上,某班体育委员拿走了一箱篮球,在剩下的五箱球中,足球的数量是篮球的2倍,则这六箱球中,篮球有()箱.A.2B.3C.4D.5二、填空题(共10题,共计30分)16、下面是“求作∠AOB的角平分线”的尺规作图过程.已知:如图,钝角∠AOB.求作:∠AOB的角平分线.作法:①在OA和OB上,分别截取OD、OE,使OD=OE;②分别以D、E为圆心,大于的长为半径作弧,在∠AOB内,两弧交于点C;③作射线OC.所以射线OC就是所求作的∠AOB的角平分线.在该作图中蕴含着几何的证明过程:由①可得:OD=OE由②可得:________由③可知:OC=OC∴________≌________(依据:________)∴可得∠COD=∠COE(全等三角形对应角相等)即OC就是所求作的∠AOB的角平分线.17、如图,△ABC中,AD平分∠BAC,EG⊥AD,分别交AB,AD,AC,BC的延长线于E,H,F,G已知四个式子:①∠1=(∠2+∠3);②∠1=(∠3-∠2);③∠4=(∠3-∠2);④∠4=∠1.其中正确的式子有________.(填写序号)18、如图,已知:,,,则________°.19、如图,已知a∥b,小亮把三角板的直角顶点放在直线b上.若∠1=35°,则∠2的度数为________.20、已知:△ABC≌△A′B′C′,∠A=∠A′=80°,∠B=∠B′=60°,则∠C′=________度.21、如图,已知AB∥CD,∠EAF = ∠EAB,∠ECF= ∠ECD,∠AFC=62°,则∠AEC度数是________22、如图,△ABC中∠B=60º,∠ACD=130º,则∠A=________º.23、已知,如图,点分别在和上,且,则________度.24、如图,将一张长方形纸条沿某条直线折叠,若,则∠2等于________.25、如图,直线a//b,将一直角三角形的直角顶点置于直线b上,若∠1=28°,则∠2的度数是________三、解答题(共5题,共计25分)26、如图,在. 是的平分线,是边上的高,,,求的度数.27、填空,完成下列证明过程.如图,△ABC和△FED中,AB=FE,BC=ED,点A,C,D,F在一条直线上,AD=FC.求证:AB∥EF.证明:∵AD=FC (已知),∴AD ▲= FC ▲,即▲=▲.在△ABC和△FED中,AB=FE (已知),BC=ED (已知),▲=▲(已证),∴△ABC≌△FED().∴∠A=∠F ().∴AB∥EF().28、如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE,求证:BD=DE.29、完成下列推理论证过程:如图,已知∠A=∠EDF,∠C=∠F,求证:BC∥EF证明:∵∠A=∠EDF(▲)∴▲∥▲(▲)∴∠C=∠BGD(▲)又∵∠C=∠F (已知)∴▲=∠F(等量代换)∴BC∥EF(▲)30、两块等腰直角三角尺与(不全等)如图(1)放置,则有结论:①②;若把三角尺绕着点逆时针旋转一定的角度后,如图(2)所示,判断结论:①②是否都还成立?若成立请给出证明,若不成立请说明理由.参考答案一、单选题(共15题,共计45分)1、A2、C3、B4、C5、D6、A7、B8、C9、B10、B11、D12、A13、B14、B15、B二、填空题(共10题,共计30分)16、17、18、19、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠EDF的度数为()A.50°B.40°C.80°D.60°2、如图,AB∥CD,若∠2是∠1的两倍,则∠2等于()A.60°B.90°C.120°D.150°3、如图,连接正十边形的对角线 AC 与 BD 交于点 E,则∠AED 的度数是()A.126°B.116°C.120°D.110°4、如图,在中,,,是的平分线,经过A,D两点的圆的圆心O恰好落在上,分别与、相交于点E、F.若圆半径为2.则阴影部分面积().A. B. C. D.5、如图,△ABC中,∠A=36°,∠B=60°,EF∥BC,FG平分∠AFE,则AFG的度数为()A.36°B.37°C.42°D.47°6、下列结论中,错误结论有();①三角形三条高(或高的延长线)的交点不在三角形的内部,就在三角形的外部;②一个多边形的边数每增加一条,这个多边形的内角和就增加360º;③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;④三角形的一个外角等于任意两个内角的和;⑤在中,若,则为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个A.6个B.5个C.4个D.3个7、△ABC中,∠A,∠B,∠C的对边分别为a,b,c,下列命题中的假命题是()A.若∠A=∠C-∠B,则∠C=90ºB.若∠C=90º,则C.若∠A=30º,∠B=60º,则AB=2BCD.若,则∠C=90º8、如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是()A.0B.C.D.19、若等腰中有一个内角为,则这个等腰三角形的一个底角的度数为()A. B. C. 或 D. 或10、如图,在中,,,则的度数是()A. B. C. D.11、如图,AE‖BD,∠1=120°,∠2=40°,则∠C的度数是()A.10°B.20°C.30°D.40°12、在△ABC中,∠B和∠C的平分线交于点I,边AB和AC的垂直平分线交于点O,若∠BIC=90°+ θ,则∠BOC=()A.90°﹣θB.2θC.180°﹣θD.以上答案都不对13、在如图,已知∠1=∠2,∠3=∠4,求证:AC∥DF,BC∥EF.证明过程如下:∵∠1=∠2(已知),∴AC∥DF(A.同位角相等,两直线平行),∴∠3=∠5(B.内错角相等,两直线平行).又∵∠3=∠4(已知)∴∠5=∠4(C.等量代换),∴BC∥EF(D.内错角相等,两直线平行).上述过程中判定依据错误的是()A.AB.BC.CD.D14、如图,在等边三角形的内部,作,两两相交于三点(三点不重合).设,则下列关系正确的是()A. B. C.D.15、如图,下列条件中能判定的是()A. B. C. D.二、填空题(共10题,共计30分)16、如图,这是生活中经常接触的小刀,刀片的外壳是四边形,而且刀片外壳与刀片合部分都是直角,刀片的上,下是平行的动刀片时会形成∠1和∠2,则∠1+∠2=________.17、如图,l∥m,∠1=120°,∠A=55°,则∠ACB的大小是________ .18、推理填空:如图,,,将说明成立的理由填写完整.解:因为(已知),所以(________)又因为(已知),所以(等量代换),所以________(同位角相等,两直线平行),所以(________)19、如图,在中,平分,的中垂线交于点,交于点,连接,.若,则的度数为________;20、已知,如图.AD∥BE,∠1=∠2,求证:∠A=∠E,请完成解答过程.证明:∵AD∥BE(已知)∴∠A=∠________(________)又∵∠1=∠2(已知)∴AC∥________(________)∴∠3=∠________(两直线平行,内错角相等)∴∠A=∠E(等量代换)21、如图,直线l∥m,点A在直线l上,点c在直线m上,且有AB⊥BC,∠1=40°,则∠2=________度.22、如图,直线、被直线所截,若,,则________.23、如图,已知,如果,那么的度数为________.24、如图,在△ABC中,AB、AC的垂直平分线l1、l2相交于点O,若∠BAC等于82°,则∠OBC=________°.25、如图所示,直线,直线分别与相交于点小宇同学利用尺规按以下步骤作图:①以点为圆心,以任意长为半径作弧交于点,交于点;②分别以为圆心,以大于长为半径作弧,两弧在内交于点;③作射线交于点.若,则的度数为________三、解答题(共5题,共计25分)26、如图在四边形ABCD中,∠B=∠D=90°,AE、CF分别平分∠BAD和∠BCD.试问直线AE、CF的位置关系如何?请说明你的理由.27、推理填空:如图,E点为DF上的点,B为AC上的点,,那么,请完成它成立的理由解:又)( ) ( ) ( )( )( )( )( )28、如图所示,直线 a 、 b 被 c 、 d 所截,且 c⊥a,c⊥b,∠1=70°,求∠2的度数.29、如图,△ABC中,∠A=90°,D为AC上一点,E为BC上一点,点A和点E关于BD对称,点B和点C关于DE对称.求∠ABC和∠C的度数.30、根据题意结合图形填空:已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.答:是,理由如下:∵AD⊥BC,EG⊥BC(▲_)∴∠4=∠5=90°(_▲)∴AD∥EG(▲_)∴∠1=∠E(▲)∠2=∠3(▲_)∵∠E=∠3(▲)∴▲(等量代换)∴AD是∠BAC的平分线(▲)参考答案一、单选题(共15题,共计45分)1、A2、C3、A4、C5、C6、C7、D8、D9、D10、B11、B12、B13、B14、B15、C二、填空题(共10题,共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、30、。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、如图,对于图中标记的各角,下列条件不能够推理得到a∥b的是( )A.∠1=∠2B.∠2=∠3C.∠1=∠3D.∠1+∠4=180°2、有理数数a,b在轴上的表示如图所示,则下列结论中:①ab<0,②a+b<0,③a﹣b<0,④a<,⑤﹣a>﹣b,正确的有()A.2个B.3个C.4个D.5个3、如图,直线m∥n,若∠1=30°,∠2=58°,则∠BAC的度数为()A.12°B.28°C.29°D.30°4、如图,直线a、b被直线c所截,下列说法正确的是()A. 当∠1=∠2时,一定有a∥bB. 当a∥b时,一定有∠1=∠2C. 当a∥b时,一定有∠1+∠2=180°D. 当a∥b时,一定有∠1+∠2=90°5、甲、乙、丙三位同学进行立定跳远比赛,每人轮流跳一次称为一轮,每轮按名次从高到低分别得3分、2分、1分(没有并列名次),他们一共进行了五轮比赛,结果甲共得14分;乙第一轮得3分,第二轮得1分,且总分最低.那么丙得到的分数是( )A.8分B.9分C.10分D.11分6、一副三角板按如图所示叠放在一起,则图中∠α的度数是()A.75°B.60°C.45°D.105°7、如图所示的图形中x的值是A.60B.40C.70D.808、如图,直线EF分别与直线AB,CD相交于点G、H,已知∠1=∠2=50°,GM平分∠HGB 交直线CD于点M.则∠3=()A.60°B.65°C.70°D.130°9、如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是()A.35°B.70°C.110°D.130°10、如图所示,在下列四组条件中,能判定AB∥CD的是()A.∠1=∠2B.∠ABD=∠BDCC.∠3=∠4D.∠BAD+∠ABC=180°11、如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC=()A.30°B.60°C.90°D.120°12、下列说法正确的个数()在同一平面内:①两条射线不相交就平行;②过一点有且只有一条直线与已知直线垂直;③有公共顶点且相等的角是对顶角;④直线外一点到已知直线的垂线段叫做这点到直线的距离;⑤过一点有且只有一条直线与已知直线平行.A.0个B.1个C.2个D.3个13、在△ABC中,若∠A=∠B=∠C,那么△ABC是( )A.直角三角形B.等边三角形C.锐角三角形D.钝角三角形14、如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于()A.50°B.80°C.65°D.115°15、如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=36°,则∠NFD′等于( )A.144°B.126°C.108°D.72°二、填空题(共10题,共计30分)16、如图,四边形ABCD内接于⊙O,BC是⊙O的直径,AD∥BC,AC与BD相交于点P,若∠APB=50°,则∠PBC=________.17、如果两条直线被第三条直线所截,一组同旁内角的度数之比为3∶2,差为36°,那么这两条直线的位置关系是________.18、如图,在平行四边形ABCD中,DE平分∠ADC,AD=7,BE=2,则平行四边形ABCD的周长是________.19、如图钢架中,焊上等长的7根钢条来加固钢架,若,则的度数是________.20、两条平行直线被第三条直线所截,则:①一对同位角的角平分线互相平行;②一对内错角的角平分线互相平行;③一对同旁内角的角平分线互相平行;④一对同旁内角的角平分线互相垂直.其中正确的结论是________ .(注:请把你认为所有正确的结论的序号都填上)21、如图,直角三角尺的直角顶点在直线b上,∠3 = 25°,转动直线a,当∠1=________,时,a∥b22、如图,△ABC≌△ADE,BC的延长线经过点E,交AD于F,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,则∠EAB= ________ °.23、已知长方形,点和点分别在和边上,如图将沿着折叠以后得到,与相交于点,与相交于点,则与的数量关系为________.24、如图,已知AF∥EC,AB∥CD,∠A=65°,则∠C=________度.25、如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,且∠A+∠ABC=90°,则∠PEF=________.三、解答题(共5题,共计25分)26、如图,已知∠ABC=52°,∠ACB=60°,BO,CO分别是∠ABC和∠ACB的平分线,EF过点O,且平行于BC,求∠BOC的度数.27、已知在中,是边上的一点,的角平分线交于点,且,求证:.28、如图Ⅰ,已知纸片中,,,将其折叠,如图Ⅱ,使点A与点B重合,折痕为,点D、E分别在、上,求的大小.29、如图,已知:∠DGA=∠FHC,∠A=∠F.求证:DF∥AC.(注:证明时要求写出每一步的依据)30、已知,射线分别和直线交于点,射线分别和直线交于点.点在上( 点与三点不重合).连接.请你根据题意画出图形并用等式直接写出、、之间的数量关系.参考答案一、单选题(共15题,共计45分)1、C2、B3、B4、C5、B6、D7、A8、B10、B11、B12、B13、A14、D15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、三、解答题(共5题,共计25分)26、27、29、30、。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、下列说法正确的是()A.“任意画一个三角形,其内角和为360°”是随机事件.B.某种彩票的中奖率是,说明每买100张彩票,一定有1张中奖.C.“篮球队员在罚球线上投篮一次,投中”为随机事件.D.投掷一枚质地均匀的硬币100次,正面向上的次数一定是50次.2、如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为()A.30°B.34°C.36°D.40°3、如图,已知AB∥CD,∠EBA=45°,∠E+∠D的度数为()A.30°B.60°C.90°D.45°4、如图,∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF等于()A.2B.3C.4D.55、如图所示,已知l1∥l2,直线l与l1、l2分别相交于C、D两点,把一块含有30°角的三角板按如图位置摆放.若∠1=130°,则∠2=()A.60°B.50°C.30°D.20°6、如图,AB∥CD,∠D=30°,∠E=35°,则∠B的度数为()A.60°B.65°C.70°D.75°7、如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是()A.①②③B.①②④C.①③④D.①②③④8、如图,将三角尺的直角顶点放在直尺的一边,∠1=30°,∠2=70°,则∠3等于()A.20°B.30°C.40°D.50°9、如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是()A.30°B.20°C.15°D.14°10、下列命题是真命题的是()A.内错角相等B.过一点有且只有一条直线与已知直线垂直C.同位角相等,两直线平行D.一个角的补角大于这个角11、如图,,,,则的度数为()A. B. C. D.12、下列命题为真命题的是()A.三角形的一个外角大于任何一个和它不相邻的内角B.两直线被第三条直线所截,同位角相等C.垂直于同一直线的两直线互相垂直D.三角形的外角和为13、如图,直线m∥n,若∠1=30°,∠2=58°,则∠BAC的度数为()A.12°B.28°C.29°D.30°14、将—副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )。
最新青岛版数学八年级上册5.6.1几何证明举例(同步练习)及答案.docx

5.6.1 几何证明举例1. 如图,玻璃三角板摔成三块,现在到玻璃店在配一块同样大小的三角板,最省事的方( )A. 带①去B. 带②去C. 带③去D.带①②③去2. 如图,已知∠1=∠2,则不一定能使△ABD ≌△ACD 的条件是( )A. AB=ACB. BD=CDC. ∠B=∠CD.∠BDA=∠CDA3. 如图,给出下列四组条件:①AB DE BC EF AC DF ===,,;②AB DE B E BC EF =∠=∠=,,;③B E BC EF C F ∠=∠=∠=∠,,;④AB DE AC DF B E ==∠=∠,,.其中,能使ABC DEF △≌△的条件共有( )A .1组B .2组C .3组D .4组4.如图,90E F ∠=∠=,B C ∠=∠,AE AF =,结论:①EM FN =;②CD DN =; ③FAN EAM ∠=∠; ④ACN ABM △≌△.其中正确的有( )A .1个B .2个C .3个D .4个第1题图 第2题图 第3题图5. 如图,在下列条件中,不能证明△ABD≌△ACD的是()A.BD=DC,AB=ACB.∠ADB=∠ADC,BD=DCC.∠B=∠C,∠BAD=∠CADD.∠B=∠C,BD=DC6. 如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是7.如图,△ABC中,BD=EC,∠ADB=∠AEC,∠B=∠C,则∠CAE= .8. 如图,点B、E、F、C在同一直线上,已知∠A =∠D,∠B =∠C,要使△ABF≌△DCE,以“AAS”需要补充的一个条件是(写出一个即可).9. 已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.求证:AB=DC AEFBCDMN10.如图,已知AD 是△ABC 的角平分线,在不添加任何辅助线的前提下,要使△AED ≌△AFD ,需添加一个条件是:_______________,并给予证明.参考答案1. C2. B3.C4.C5.D6.乙和丙7. ∠BAD8. AF=DE 或BF=CE 或BE=CF9. 证明:在△ABC 与△DCB 中(ABC DCB ACB DBCBC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩已知)(公共边) ∴△ABC ≌△DCB∴AB=DC10. 解法一:添加条件:AE =AF ,证明:在△AED 与△AFD 中,∵AE =AF ,∠EAD =∠FAD ,AD =AD ,∴△AED ≌△AFD (SAS ).解法二:添加条件:∠EDA =∠FDA ,证明:在△AED 与△AFD 中,∵∠EAD =∠FAD ,AD =AD ,∠EDA =∠FDA∴△AED ≌△AFD (ASA ).。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、如图,直线a、b被直线c所截,,若∠2=50º,则∠1等于( )A.120 ºB.130 ºC.140 ºD.150 º2、如图,将直尺与含角的直角三角板放在一起,若,则的度数是()A. B. C. D.3、甲、乙、丙三位同学进行立定跳远比赛,每人轮流跳一次称为一轮,每轮按名次从高到低分别得3分、2分、1分(没有并列名次),他们一共进行了五轮比赛,结果甲共得14分;乙第一轮得3分,第二轮得1分,且总分最低.那么丙得到的分数是( )A.8分B.9分C.10分D.11分4、如图,把矩形ABCD沿EF对折,若,则等于()A.115°B.130°C.120°D.65°5、小亮为宣传“两会”,设计了形状如图所示的彩旗,图中∠ACB=90°,∠D=15°,点A在CD上,AD=AB,BC=2dm,则AD的长为()A.3dmB.4dmC.5dmD.6dm6、在△ABC中,已知∠A=∠B= ∠C,则三角形是()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形7、如图,已知∠1 = 70º,如果CD∥BE,那么∠B的度数为()A.70ºB.100ºC.110ºD.120º8、如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数为()A.24°B.25°C.30°D.35°9、如图,直线,,,则的度数是()A. B. C. D.10、如图,在正方形的外侧,作等边三角形,则为()A.45°B.25°C.30°D.40°11、如图,直线,则的度数是().A.38°B.48°C.42°D.39°12、如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为()A.6B.7C.8D.913、如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为()A. B.1.5 C. D.214、下列说法:①有理数的绝对值一定是正数;②两点之间的所有连线中,线段最短;③相等的角是对顶角;④过一点有且仅有一条直线与已知直线垂直;⑤不相交的两条直线叫做平行线,其中正确的有()A.1个B.2个C.3个D.4个15、O是△ABC中∠ABC和∠ACB的平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E 点,若BC=10cm,那么△ODE的周长为()A.8cmB.9cmC.10cmD.11cm二、填空题(共10题,共计30分)16、如图,在与中,AB、EF相交于点D,点F在边BC上,,,.下列结论:①;②;③中,正确的是________.(填序号)17、如图,直线EF分别与直线AB、CD相交于点P和点Q,已知:AB∥CD,∠1=∠2,求证:PG∥QH。
初中数学青岛版八年级上册第5章 几何证明初步5.6 几何证明举例-章节测试习题(4)

章节测试题1.【题文】如图,在△ABC中,∠ABC>60°,∠BAC<60°,以AB为边作等边△ABD(点C、D在边AB的同侧),连接CD.(1)若∠ABC90°,∠BAC30°,求∠BDC的度数;(2)当∠BAC2∠BDC时,请判断△ABC的形状并说明理由;(3)当∠BCD等于多少度时,∠BAC2∠BDC恒成立.【答案】(1)30°;(2)(3)见解析【分析】(1)证明AC垂直平分BD,从而可得CD=BC,继而得∠BDC=30°;(2)设∠BDC=x,则∠BAC=2x,证明∠ACD=∠ADC,从而得AC=AD,再根据AB=AD可得AB=AC,从而得△ABC是等腰三角形;(3)如图,作等边△BCE,连接DE,证明△BCD≌△ECD后可得到∠BDE=2∠BDC,再通过证明△BDE≌△BAC得到∠BAC=∠BDE,从而得∠BAC=2∠BDC.【解答】解:(1)∵△ABD为等边三角形,∴∠BAD=∠ABD=60°,AB=AD,又∵∠BAC=30°,∴AC平分∠BAD,∴AC垂直平分BD,∴CD=BC,∴∠BDC=∠DBC=∠ABC-∠ABD=90°-60°=30°;(2)△ABC是等腰三角形,理由:设∠BDC=x,则∠BAC=2x,有∠CAD=60°-2x,∠ADC=60°+x,∴∠ACD=180°-∠CAD-∠ADC=60°+x,∴∠ACD=∠ADC,∴AC=AD,又∵AB=AD,∴AB=AC,即△ABC是等腰三角形;(3)当∠BCD=150°时,∠BAC=2∠BDC恒成立,如图,作等边△BCE,连接DE,∴BC=EC,∠BCE=60°.∵∠BCD=150°,∴∠ECD=360°-∠BCD-∠BCE=150°,∴∠DCE=∠DCB.又∵CD=CD,∴△BCD≌△ECD.∴∠BDC=∠EDC,即∠BDE=2∠BDC.又∵△ABD为等边三角形,∴AB=BD,∠ABD=∠CBE=60°,∴∠ABC=∠DBE=60°+∠DBC.又∵BC=BE,∴△BDE≌△BAC.∴∠BAC=∠BDE,2.【题文】如图,△ABC是等边三角形,D是AB上一点,以CD为一边向上作等边△ECD,连接AE.求证:(1)△AEC≌△BDC;(2)AE∥BC.【答案】(1)证明见解答;(2)证明见解答.【分析】(1)首先证明∠BCD=∠ACE,利用SAS即可证得△ACE≌△BCD;(2)根据SAS证△ACE≌△BCD,推出∠EAC=∠DBC=∠ACB,根据内错角相等,两直线平行即可证明结论.【解答】(1)∵△ABC是等边三角形∴ AC=BC,∠ACB=∠B =60°∵△ECD是等边三角形∴EC=DC,∠ECD=60°∴∠ACB-∠ACD=∠ECD-∠ACD∴△AEC≌△BDC.(2)∵△AEC≌△BDC∴∠EAC=∠B=60°∴∠EAC=∠ACB∴AE∥BC3.【题文】已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.【答案】(1)∠BAD=∠CAE;(2)∠DCE=60°,不发生变化.【分析】(1)由等边三角形的性质得出∠BAC=∠DAE,容易得出结论;(2)由△ABC和△ADE是等边三角形可以得出AB=BC=AC,AD=A E,∠ABC=∠ACB=∠BAC=∠DAE=60°,得出∠ABD=120°,再证明△ABD≌△ACE,得出∠ABD=∠ACE=120°,即可得出结论;【解答】解:(1)∠BAD=∠CAE;理由:∵△ABC和△ADE是等边三角形,∴∠BAC=∠DAE=60°,∴∠BAD=∠CAE;(2)∠DCE=60°,不发生变化;理由如下:∵△ABC是等边三角形,△ADE是等边三角形,∴∠DAE=∠BAC=∠ABC=∠ACB=60°,AB=AC,AD=AE.∴∠ABD=120°,∠BAC﹣∠BAE=∠DAE﹣∠BAE∴∠DAB=∠CAE.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴∠ACE=∠ABD=120°.∴∠DCE=∠ACE﹣∠ACB=120°﹣60°=60°.4.【题文】如图,在等边△ABC中,DE分别是AB,AC上的点,且AD=CE.(1)求证:BE=CD;(2)求∠1+∠2的度数.【答案】(1)见解析;(2)60°.【分析】(1)证这两条线段所在的两个三角形全等,即△ACD≌△CBE(SAS);(2)由△ACD≌△CBE可得∠1=∠ACD,结合等边三角形的性质即可. 【解答】解:(1)证明:∵△ABC是等边三角形,∴∠A=∠ACB=60°,AC=BC,在△ACD和△CBE中,AC=BC,∠A=∠BCE,AD=CE,∴△ACD≌△CBE(SAS),∴BE=CD;(2)解:∵△ACD≌△CBE,∴∠1=∠ACD,∴∠1+∠2=∠ACD+∠2=∠ACB=60°.5.【题文】如图,AD是等边三角形ABC的中线,E是AB上的点,且AE=AD,求∠EDB的度数.【答案】15°【分析】由AD是等边△ABC的中线,根据等边三角形中:三线合一的性质,即可求得又由根据等边对等角与三角形内角和定理,即可求得的度数,继而求得答案.【解答】解:∵AD是等边△ABC的中线,∴AD⊥BC,∠BAD=∠BAC=60°=30°,∴∠ADB=90°.∵AE=AD.∴∠ADE=∠AED==75°.∴∠EDB=∠ADB-∠ADE==15°.6.【题文】如图,等边三角形的边长为4,点是边上一动点(不与点重合),以为边在的下方作等边三角形,连接.(1)在运动的过程中,与有何数量关系?请说明理由.(2)当时,求的度数.【答案】(1) ,理由见解析;(2) .【分析】(1)AE=CD,证明△ABE≌△CBD,即可解决问题.(2)证明AE⊥BC;证明∠BDC=∠AEB,即可解决问题.【解答】解:(1)AE=CD;理由如下:∵△ABC和△BDE等边三角形∴AB=BC,BE=BD,∠ABC=∠EBD=60°;在△ABE与△CBD中,,∴△ABE≌△CBD(SAS),∴AE=CD.(2)∵BE=2,BC=4∴E为BC的中点;又∵等边三角形△ABC,∴AE⊥BC,由(1)知△ABE≌△CBD,∴∠BDC=∠AEB=90°.7.【题文】如图点D、E分别在等边ΔABC边BC、CA上,且CD=AE,联结AD、BE.(1)求证:BE=AD;(2)延长DA交BE于F,求∠BFD的度数.【答案】(1)证明见解析;(2)60°【分析】(1)根据等边三角形的性质可以得到∠BAC=∠ACB=60°,AC=AB,则∠EAB=∠ACD,根据SAS即可证得△ABE≌△CAD,然后根据全等三角形的对应边相等,即可证得:AD=BE.(2)易证∠AFE=∠ACD,从而∠BFA=∠ACB=60°.【解答】解:证明:∵△ABC是等边三角形,∴∠BAC=∠ACB=60°,AC=AB,∴∠EAB=∠ACD=120°,∵在△ABE和△CAD中,,∴△ABE≌△CAD(SAS),∴AD=BE.(2)如图,∵△ABE≌△CAD∴∠E=∠D∵∠EAF=∠DAC∴∠BFD=∠E+∠EAF=∠D+∠DAC=60°8.【题文】如图,等边△ABC中,点D在延长线上,CE平分∠ACD,且CE=BD.说明:△ADE是等边三角形.【答案】详见解析.【分析】要证△ADE为等边三角形,可以先证它为等腰三角形,再证该等腰三角形的一个内角为60°. 综合分析已知条件可知,可以利用△ABD和△ACE全等证明AD=AE. 根据已知条件和等边三角形的性质,不难证明∠B=∠ACE,进而利用SAS 证明△ABD和△ACE全等. 利用全等三角形的性质可以得到△ADE是等腰三角形. 利用全等三角形的性质,通过相关角之间的和差关系,不难证明∠DAE=∠BAC=60°,从而证明△ADE为等边三角形.【解答】证明:∵△ABC为等边三角形,∴∠B=∠ACB=∠BAC=60°,AB=AC.∵∠ACB=60°,∴∠ACD=180°-∠ACB=180°-60°=120°,∵CE平分∠ACD,∴.∴∠B=∠ACE.∵在△ABD和△ACE中,,∴△ABD≌△ACE (SAS),∴AD=AE,∠BAD=∠CAE.∵∠BAD=∠CAE,∴∠BAC+∠CAD=∠DAE+∠CAD,∴∠BAC=∠DAE=60°.∵∠DAE=60°,AD=AE,∴△ADE为等边三角形.9.【题文】如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.(1)当点E为AB的中点时(如图1),则有AE DB(填“>”“<”或“=”);(2)猜想AE与DB的数量关系,并证明你的猜想.【答案】(1)=;(2)AE=BD.【分析】(1)△BCE中可证,∠BCE=30°,又EB=EC,则∠D=∠ECB=30°,所以△BCE 是等腰三角形,结合AE=BE即可;(2)过E作EF∥BC交AC于F,用AAS证明△DEB≌△ECF.【解答】解:(1)∵△ABC是等边三角形,∴∠ABC=60°,AB=AC=BC.∵E为AB的中点,所以∠BCE=30°.∵ED=EC,∴∠D=∠BCE=30°,∴∠BED=30°,∴∠D=∠BED,∴BD=BE,∴BD=AE.(2)当点E为AB上任意一点时,AE与DB的大小关系不会改变.理由如下:过E作EF∥BC交AC于F,∵△ABC是等边三角形,∴∠ABC=∠ACB=∠A=60°,AB=AC=BC.∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,即∠AEF=∠AFE=∠A=60°.∴△AEF是等边三角形.∴AE=EF=AF.∵∠ABC=∠ACB=∠AFE=60°,∴∠DBE=∠EFC=120°,∠D+∠BED=∠FCE+∠ECD=60°.∵DE=EC,∴∠D=∠ECD.∴∠BED=∠ECF.在△DEB和△ECF中,∴△DEB≌△ECF(AAS).∴BD=EF=AE,即AE=BD.10.【题文】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,①求证:△BCE≌△ACD;②求证:CF=CH;③判断△CFH的形状并说明理由。
青岛版八年级数学上册同步练习附答案5.6 几何证明举例

5.6 几何证明举例1. 如图,在△ABC中,BC的垂直平分线交BC于点D,交AB的延长线于点E,连接CE. 求证:∠BCE=∠A +∠ACB .(第1题图)2. 如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D. 求证:∠CAB=∠AED.(第2题图)3. 如图,在△ABC中,分别作AB边,BC边的垂直平分线,两线相交于点P,分别交AB 边,BC边于点E,F.求证:AB,BC,AC的垂直平分线相交于点P.(第3题图)4. 如图,在△ABD中,∠BAC= 90°,AD⊥BC于点D,∠ABC的平分线BF交AD于点E,交AC于点F,FH⊥BC于点H. 求证:AE =FH.(第4题图)5. 如图,点D,E分别在△ABC的边AB,AC上,AB=AC.(1)如果DE∥BC,求证:AD=AE.(2)如果AD=AE,求证:DE∥BC.(第5题图)6. 如图,AB=AC,DB=DC. 求证:∠B=∠C.(第6题图)7. 如图,E,F是线段BC上两点,AB∥CD,AB=DC,CE=BF. 求证:AE=DF.(第7题图)8. 如图,DE∥BC,A是DE上一点,AD=AE,AB=AC. 求证:BE=CD.(第8题图)9. 如图,在△ABD中,AC⊥BD,垂足为C,AC=BC,点E在AC上,且CE=CD. 连接BE 并延长交AD于点F. 求证:BF⊥AD.(第9题图)10. 如图,AC与BD相交于点O,且AC=BD,AD=BC. 求证:OA=OB.(第10题图)答案1. 证明:∵BC 的垂直平分线交BC 于点D , ∴BE =CE , ∴∠BCE =∠CBE .∵∠CBE =∠A +∠ACB ,∴∠BCE =∠A +∠ACB .2. 证明:∵DE 是AB 的垂直平分线,∴EA =EB , ∴∠EAB =∠B .∵∠C =90°,∴∠CAB +∠B =90°.又∵∠AED +∠EAB =90°,∴∠CAB =∠AED .3.证明:∵P 是AB 边的垂直平分线上的一点, ∴P A = PB .同理可得,PB = PC .∴P A =PC .∴P 是AC 边的垂直平分线上的一点. ∴AB ,BC ,AC 的垂直平分线相交于点P .4. 证明:∵BF 平分∠ABC ,F A ⊥AB ,FH ⊥BC , ∴F A =FH ,∠ABF =∠EBD .又∵∠AFB +∠ABF = 90°,∠DEB +∠EBD = 90°, ∴∠AFB =∠DEB ,∴∠AFB =∠AEF .∴AF =AE .∴AE =FH .5. 证明:(1)∵AB =AC ,∴∠B =∠C .∵DE ∥BC ,∴∠B=∠ADE ,∠C=∠AED .∴∠ADE=∠AED ,∴AD =AE .(2)∵AD =AE ,∴∠ADE=∠AED=21(180°-∠A ). ∵AB =AC ,∴∠B =∠C=21(180°-∠A ). ∴∠B=∠ADE ,∴DE ∥BC .6. 证明:连接AD .在△ABD 和△ACD 中,⎪⎩⎪⎨⎧===,,,AD AD DC DB AC AB∴△ABD ≌△ACD (SSS ),∴∠B =∠C .7. 证明:∵CE =BF ,∴CE+EF =BF+EF ,即CF =BE .∵AB ∥CD ,∴∠B =∠C .在△ABE 和△DCF 中,⎪⎩⎪⎨⎧=∠=∠=,,,CF BE C B DC AB∴△ABE ≌△DCF (SSS ),∴AE =DF .8. 证明:∵AB =AC ,∴∠ABC =∠ACB .∵BC ∥DE ,∴∠DAB =∠ABC ,∠EAC =∠ACB , ∴∠DAB =∠EAC ,∴∠DAC =∠EAB .在△DAC 和△EAB 中,⎪⎩⎪⎨⎧=∠=∠=,,,AC AB EAC DAC AE AD∴△DAC ≌△EAB (SAS ),∴BE =CD .9. 证明:∵AC ⊥DB ,∴∠BCE =∠ACD = 90°.在△BCE 和△ACD 中,⎪⎩⎪⎨⎧=∠=∠=,,,AC BC BCE ACD CD CE∴△BCE ≌△ACD (SAS ),∴∠CBE=∠CAD . ∵在△ACD 中,∠CAD +∠ACD +∠D= 180°, 在△BDF 中,∠CBE +∠BFD +∠D= 180°,∴∠CAD +∠ACD +∠D=∠CBE +∠BFD +∠D= 180°, ∴∠ACD=∠BFD=90°,即BF ⊥AD .10. 证明:连接AB .在△ABD 和△BAC 中,⎪⎩⎪⎨⎧===,,,BA AB BC AD AC BD∴△ABD ≌△BAC (SSS ),∴∠BDA=∠ACB .在△AOD 和△BOC 中,⎪⎩⎪⎨⎧=∠=∠∠=∠,,,BC AD OCB ODA BOC AOD∴△AOD ≌△BOC (AAS ),∴OA=OB .。
八年级数学上册第五章几何证明初步5.6.2几何证明举例同步练习新版青岛版20180822142
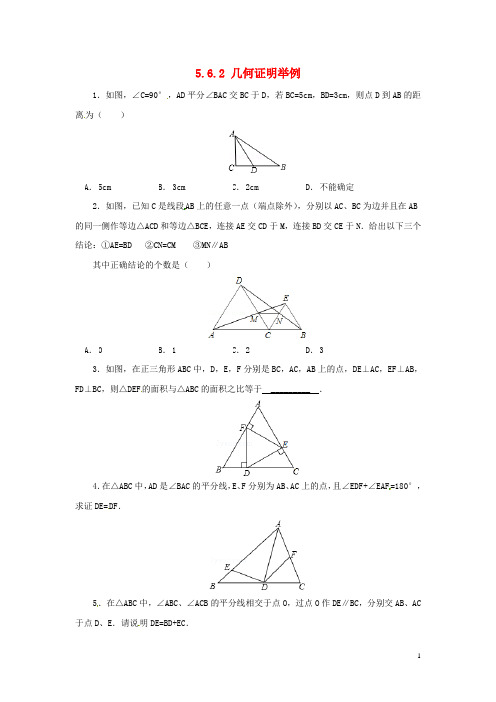
5.6.2 几何证明举例1.如图,∠C=90°,AD平分∠BAC交BC于D,若BC=5cm,BD=3cm,则点D到AB的距离为()3cm2.如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为边并且在AB 的同一侧作等边△ACD和等边△BCE,连接AE交CD于M,连接BD交CE于N.给出以下三个结论:①AE=BD②CN=CM③MN∥AB其中正确结论的个数是()3.如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于_________ .4.在△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,且∠EDF+∠EAF=180°,求证DE=DF.5.在△ABC中,∠ABC、∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB、AC 于点D、E.请说明DE=BD+EC.参考答案1. C2. D3. 1:34. 证明:过D作DM⊥AB,于M,DN⊥AC于N,即∠EMD=∠FND=90°,∵AD平分∠BAC,DM⊥AB,DN⊥AC,∴DM=DN(角平分线性质),∠DME=∠DNF=90°,∵∠EAF+∠EDF=180°,∴∠MED+∠AFD=360°﹣180°=180°,∵∠AFD+∠NFD=180°,∴∠MED=∠NFD,在△EM D和△FND中,∴△EMD≌△FND,∴DE=DF.5. 解:∵在△ABC中,OB和OC分别平分∠ABC和∠ACB,∴∠DBO=∠OBC,∠ECO=∠OCB,∵DE∥BC,∴∠DOB=∠OBC=∠DBO,∠EOC=∠OCB=∠ECO,∴DB=DO,OE=EC,∵DE=DO+OE,∴DE=BD+EC.百度文库是百度发布的供网友在线分享文档的平台。
百度文库的文档由百度用户上传,需要经过百度的审核才能发布,百度自身不编辑或修改用户上传的文档内容。
初中数学青岛版八年级上册第5章 几何证明初步5.6 几何证明举例-章节测试习题(1)

章节测试题1.【题文】如图,在中,,.(Ⅰ)过点作的平分线交于点(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);(Ⅱ)若,求点到的距离.【答案】(1)图形见解析(2)3【分析】(Ⅰ)根据角平分线的作法进行作图即可得;(Ⅱ)过点作,垂足为,由角平分线的性质可得DE=DC,求得DC 的长即可得.【解答】解:(Ⅰ)如图所示;(Ⅱ)过点作,垂足为由(Ⅰ)得,,又,∴,设,在中,,∴,在中,,∴,∴,∴,∴,∴,即点到的距离为.2.【题文】如图,在△ABC中,∠C=90°, AD平分∠BAC交BC于D,DE⊥AB 于E求证:(1)△ACD≌△AED;(2)若AB=6,求△DEB的周长。
【答案】(1)证明见解析;(2)6【分析】(1)根据角平分线性质求出CD=DE,根据HL定理求出两三角形全等即可;(2)根据全等三角形的性质得到AC=AE,CD=DE,由于AC=BC,等量代换得到BC=AE,于是得到△DEB的周长=DB+DE+EB=DB+CD+EB=CB+BE=AE+BE=6.【解答】解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90∘,∴CD=ED,∠DEA=∠C=90∘,在Rt△ACD和Rt△AED中,,∴Rt△ACD≌Rt△AED(HL);(2)∵△ACD≌△AED,∴AC=AE,CD=DE,∵AC=BC,∴BC=AE,∴△DEB的周长=DB+DE+EB=DB+CD+EB=CB+BE=AE+BE=AB=6.3.【题文】如图,已知△ABC中,AB=AC,BE平分∠ABC交AC于E,若∠A=90°,那么BC、BA、AE三者之间有何关系?并加以证明.【答案】见解析【分析】过点E作ED⊥BC交BC于点D,可得AE=DE,再通过证Rt△BAE≌Rt△BDE推出AB=BD,再求出CD=DE=AE,则可得出答案.【解答】解:BC、BA、AE三者之间的关系:BC=BA+AE,理由如下:如图,过E作ED⊥BC于点D,∵BE平分∠ABC,ED⊥BC,∠A=90°,∴AE=DE,∵在Rt△BAE和Rt△BDE中,BE=BE,AE=DE,∴Rt△BAE≌Rt△BDE(HL),∴BA=BD,∵AB=AC,∠A=90°,∴∠C=45°,∴∠CED=45°=∠C,∴DE=CD,∴AE=CD=DE,∴BC=BD+DC=BA+AE.4.【题文】如图所示,PA=PB,∠1+∠2=180°.求证:OP平分∠AOB.【答案】见解析【分析】过P作PE⊥OA于E,PF⊥OB于F,证△PEA≌△PFB,得出PE=PF,再根据角平分线判定即可得出.【解答】解:过点P作PE⊥AO,PF⊥BO,垂足分别为E,F,则∠AEP=∠BFP=90°.∵∠1+∠2=180°,∠2+∠PBF=180°,∴∠1=∠PBF.在△APE与△BPF中,∠1=∠PBF,∠AEP=∠BFP,PA=PB,∴△APE≌△BPF,∴PE=PF.∴点P在∠AOB的平分线上,即OP平分∠AOB.5.【题文】如图所示,∠1=∠2,AE⊥OB于点E,BD⊥OA于点D,AE与BD相交于点C.求证:AC=BC.【答案】见解答。
青岛版八上数学5.6几何证明举例(含答案)

三、解答题(共8小题;共54分)
23.如图, 中, .
(1)请以 所在的直线为对称轴,画出与 成轴对称的图形;
(2)所得图形与原图形组成的图形是等腰三角形吗?请说明理由.
24.如图所示,点 是 内一点, 于点 , 于点 ,且 ,点 在 上, , ,求 的度数.
25.已知: , , .求证: .
A.全部正确B.仅①和②正确C.仅①正确D.仅①和③正确
10.如图,已知: ,点 , , , 在射线 上,点 , , , 在射线 上, , , , 均为等边三角形,若 ,则 的边长为
A. B. C. D.
11.如图,在平面直角坐标系 中, , ,动点 在直线 上.若以 , , 三点为顶点的三角形是等腰三角形,则点 的个数是
A. B. C. D.
12.如图所示,在 中, , ,垂足分别为 , , , 交于点 ,已知 , ,则 的长是
二、填空题(共10小题;共30分)
13.如图,已知 , ,判定 的依据是“”.
14.如图所示,要在 区建一个工厂,位置选在到河流和公路的距离相等,并且到河流与公路交叉点 处的距离为 (指图上距离)处,则图中工厂的位置应建在,理由是.
24. (1) , , ,
平分 .
又 ,
.
,
.
25. (1)连接 .
, ,
.
在 和 中,
.
.
26. (1) 是 的中线,
,
, ,
.
在 和 中,
.
.
27. (1) (2)
28. (1) , 是等边三角形,
, , ,
,
.
在 与 中,
( ).
28. (2) ,
青岛版八年级上 第五章 《几何证明初步》单元检测题(含答案解析)

第5章几何证明初步检测题(时间:90分钟,满分:100分)一、选择题(每小题3分,共30分)1、下列语句中,不是命题的是()A.若两角之和为90°,则这两个角互补 B.同角的余角相等C.作线段的垂直平分线 D.相等的角是对顶角2、下列语句中属于定义的是()A.直角都相等 B.作已知角的平分线C.连接两点的线段的长度,叫做这两点间的距离。
D.两点之间,线段最短3、下面关于定理的说法不正确的是()A.定理是真命题 B.定理的正确性不需要证明C.定理可以作为推理论证的依据 D.定理的正确性需证明4、如图,在等边△中,,则等于()A 、B 、C 、D 、5、如图,已知,,,结论:①;②;③;④△≌△.其中正确的有()A、1个B、2个C、3个D、4个第6题图6、对于图中标记的各角,下列条件能够推理得到∥的是()A .∠1=∠2B 、∠2=∠4C 、∠3=∠4D .∠1+∠4=180° 7、如图,∥,,若,则等于( )A 、B 、C 、D 、8、 如图,在四边形ABCD 中,AC 垂直平分BD ,垂足为E ,下列结论不一定成立的是( )A 、AB =AD B 、CA 平分∠BCDC 、AB =BD D 、△BEC ≌△DEC 9、 如图,直线AB 、CD 交于点O ,OT ⊥AB 于O ,CE ∥AB 交CD 于点C ,若∠ECO =30°,则∠DOT 等于( )A .30°B .45°C .60°D .120°10、 图中有四条互相不平行的直线L 1、L 2、L 3、L 4所截出的七个角,关于这七个角的度数关系,下列选项正确的是( ) A .∠2=∠4+∠7 B .∠3=∠1+∠6C .∠1+∠4+∠6=180°D .∠2+∠3+∠5=360°二、填空题(每小题3分,共24分)11、写一个与直角三角形有关的定理 。
12、如图,一个直角三角形纸片,剪去直角后,得到一个四边形,第10题图第12题图第9题图则∠1+∠2= 度。
2019年精选初中数学八年级上册第5章 几何证明初步5.6 几何证明举例青岛版拔高训练【含答案解析】四十一

2019年精选初中数学八年级上册第5章几何证明初步5.6 几何证明举例青岛版拔高训练【含答案解析】四十一第1题【单选题】在期中考试中,同学甲、乙、丙、丁分别获得第一、第二、第三、第四名.在期末考试中,他们又是班上的前四名.如果他们当中只有一位的排名与期中考试中的排名相同,那么排名情况有( )种可能.A、5B、6C、7D、8【答案】:【解析】:第2题【单选题】如图所示,CD⊥AB,垂足为D,点F是BC上任意一点,FE⊥AB,垂足为E,且∠CDG=∠BFE,∠AGD=80°,∠ACB的度数为( ).A、50°B、55°C、80°D、60°【答案】:【解析】:第3题【单选题】某班有50人,其中35人参加文学社,45人参加书画社,38人参加音乐社,42人参加体育社,则四个社都去参加的学生至少是多少人?( )A、10B、121C、14D、16【答案】:【解析】:第4题【单选题】张大伯在中国银行存入10000元人民币,并在存单上留下了6位数的密码,每个数字都是0﹣9这十个数字中的一个,但由于年龄的缘故,张大伯忘记了密码中间的两个数字,那么张大伯最多可能实验多少次,才能正确输入密码( )A、1次B、50次C、100次D、200次【答案】:【解析】:第5题【单选题】一排有10个座位,其中某些座位已有人,若再来1人,他无论坐在何处,都与1人相邻,则原来最少就座的人有( )A、3个B、4个C、5个D、6个【答案】:【解析】:第6题【单选题】一座大楼有4部电梯,每部电梯可停靠六层(不一定是连续六层,也不一定停最底层).对大楼中任意的两层,至少有一部电梯可同时停靠,则这座大楼最多有( )层.A、11B、12C、13D、14【答案】:【解析】:第7题【填空题】甲、乙、丙、丁、戊与小强六位同学参加乒乓球比赛,每两人都要比赛一场,到现在为止,已知甲赛了5场,乙赛了4场,丙赛了3场,丁赛了2场,戊赛了1场,则小强赛了______场.【答案】:【解析】:第8题【填空题】【答案】:【解析】:第9题【填空题】在A、B、C三个盒子里分别放一些小球,小球数依次为a0 ,b0 ,c0 ,记为G0=(a0 ,b0 ,c0).游戏规则如下:若三个盒子中的小球数不完全相同,则从小球数最多的一个盒子中拿出两个,给另外两个盒子各放一个(若有两个盒子中的小球数相同,且都多于第三个盒子中的小球数,则从这两个盒子序在前的盒子中取小球),记为一次操作.若三个盒子中的小球数都相同,游戏结束,n次操作后的小球数记为Gn=(an ,bn ,cn).(1)若G0=(5,8,11),则第______次操作后游戏结束;(2)小明发现:若G0=(2,6,10),则游戏永远无法结束,那么G2014=______【答案】:【解析】:第10题【填空题】由红点与蓝点组成的16行与16列的正方形点阵中,相邻同色两点用与点同色的线段连接,相邻异色两点均用黄色的线段连接.已知共有133个红点,其中32个点在方阵的边界上,2个点在方阵的角上.若共有196条黄色线段,试问应有______条蓝色线段.【答案】:【解析】:第11题【解答题】某中学举行体育知识竞赛,红队、绿队进入决赛,每个队回答20道题,答对一道得10分,答错1题扣5分.不答扣3分,每个队的基础分均为0分,红队答对5道,答错6题,其余弃权,绿队答对7道,答错12题,弃权1道,你能判断哪个队得分高吗?【答案】:【解析】:第12题【解答题】S、J和R三人在火车上担任刹车员、司炉和司机(不一定依此顺序).今天火车上只有三位乘客,而且很凑巧,三位乘客的姓也是S、J和R.为了把工作人员和乘客区分开,让我们把乘客称为先生—S先生、J先生和R先生.此外,我们还知道:①R先生住在底特律市;②刹车员住在芝加哥和底特律之间的某地;③住在芝加哥的乘客和刹车员同姓;④刹车员的一位邻居也是一位乘客,他的年薪正好是刹车员的三倍(年薪为整数);⑤J先生一年恰好挣20000元,得靠政府救济过日子;⑥S的台球打得比司炉好;现在要问,谁是司机?【答案】:【解析】:第13题【解答题】小明早上起床,叠被用3分,刷牙洗脸用4分,烧开水用10分,吃早饭用7分,洗碗用1分,整理书包用2分,冲牛奶用1分,请帮小明安排一下如何才能最省时间?最短需用多长时间?【答案】:【解析】:。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、如图,AB∥CD,若∠2=135°,则∠1的度数是()A.30°B.45°C.60°D.75°2、下列命题中正确的有( ).①相等的角是对顶角;②若a//b,b//c,则a∥c;③同位角相等;④邻补角的平分线互相垂直.A.0个B.1个C.2个D.3个3、已知a∥b,将等腰直角三角形ABC按如图所示的方式放置,其中锐角顶点B,直角顶点C分别落在直线a,b上,若∠1=15°,则∠2的度数是()A.15°B.22.5°C.30°D.45°4、有理数数a,b在轴上的表示如图所示,则下列结论中:①ab<0,②a+b<0,③a﹣b<0,④a<,⑤﹣a>﹣b,正确的有()A.2个B.3个C.4个D.5个5、如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDB的度数等于()A.70°B.100°C.110°D.120°6、下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是()A.a=﹣2B.a=﹣1C.a=1D.a=27、下列说法正确是()A.相等的角是对顶角B.一个角的补角必是钝角C.同位角相等 D.一个角的补角比它的余角大90°8、一个三角形的两个内角分别为55°和65°,这个三角形的外角不可能是()A.115°B.120°C.125°D.130°9、如图,下列条件:∠1=∠2;∠3=∠4;∠2+∠3=∠5;∠2+∠3+∠A=180°;∠4+∠1=∠5,能判定AB∥DC有()A.3个B.4个C.5个D.6个10、在衣柜抽屉中杂乱无章地放着10只红色的袜子和10只蓝色的袜子.这20只袜子除颜色不同外,其他都一样.现在房间中一片漆黑,你想从抽屉中取出两只颜色相同的袜子.最少要从抽屉中取出()只袜子才能保证其中有两只配成颜色相同的一双.A.2只B.3只C.4只D.5只11、有下列四个命题:①相等的角是对顶角;②两条直线被第三条直线所截,同位角相等;③等角的邻补角相等;④垂直于同一条直线的两条直线互相平行.其中真命题的个数为()A.1B.2C.3D.412、把一块直尺与一块三角板放置,若∠1=50°,则∠2的度数为()A.115°B.120°C.130°D.140°13、举反例说明“一个角的余角大于这个角”是假命题,错误的是()A.设这个角是45°,它的余角是45°,但45°=45°B.设这个角是30°,它的余角是60°,但30°<60°C.设这个角是60°,它的余角是30°,但30°<60°D.设这个角是50°,它的余角是40°,但40°<50°14、能说明命题“对于任意实数a,a>-a”是假命题的一个反例是()A.a=B.a=1.5C.a=4D.a=-2215、如图,直线l1 ∥ l2 , CD⊥AB于点D ,∠1=50°,则∠BCD的度数为()A.40°B.45°C.50°D.30°二、填空题(共10题,共计30分)16、如图,直线,,,点在直线上,,若,则的度数为________.17、如图(右上),在△ABC中,∠ABC=24°,以AB为直径的⊙O交BC于点D,交CA 的延长线于点E,若点E在BD的垂直平分线上,则∠C的度数为________.18、等腰三角形的顶角为120°,则底角的度数为________.19、若∠1与∠2有一条边在同一直线上,且另一边互相平行,∠1=50°,则∠2=________.20、如图,在△ABC中,AC=BC=2,∠C=900, AD是△ABC的角平分线,DE⊥AB,垂足为E,AD的垂直平分线交AB于点F,则DF的长为________21、如图,已知直线AB∥CD,∠1=50°,则∠2=________.22、如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为________.23、如图,已知∠1=∠2,∠A=∠D,说明∠F与∠C相等的理由.解:∵∠1=∠2( 已知 ),∠2=∠4 (________),∴∠1=∠4( 等量代换 ),∴FB∥EC(________),∴∠3=∠C( 两直线平行,同位角相等).∵∠A=∠D(________),∴ED∥AC(________),∴∠F=∠3 (________),24、如图,EF∥AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,则∠FEC=________°.25、如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为________.三、解答题(共5题,共计25分)26、如图,∠1=70°,∠2=70°,∠3=105°,求∠4的度数.27、己知:如图,,CE平分ACD.求证:CE//AB.28、已知:如图,在四边形ABCD中,AB//CD,E、F为对角线AC上两点,且AE=CF,DF//BE.求证:四边形ABCD是平行四边形.29、如图,,,,,问直线与有怎样的位置关系,为什么?30、小红、小强、小华三名同学中有一个把教室打扫得干干净净,事后,老师问他们三人是谁做的好事.小红说:“是小强做的”;小强说:“不是我做的”;小华说:“不是我做的”如果他们三人中有两个说了假话,一人说了真话,那么老师能判定教室是哪个打扫的吗?(要有分析)参考答案一、单选题(共15题,共计45分)1、B2、C3、C4、B5、C6、A7、D8、D9、A10、B11、B12、D13、B15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、30、。
八年级数学上册第五章几何证明初步5.6.5几何证明举例同步练习新版青岛版

565几何证明举例1.两个直角三角形全等的条件是 ()A. 一锐角对应相等;B.两锐角对应相等;C. 一条边对应相等;D.两条边对应相等2.如图,/ B=Z D=90°, BC=CD / 1=30 °,则/ 2 的度数为()()A. AASB.SASC.HLD.SSS4. 已知在△ ABC^D ^ DEF 中,/ A=Z D=90° ,则下列条件中不能判定厶 ABC^D ^ DEF 全等 的是()A.AB=DE,AC=DFB.A C=EF,BC=DFC.AB=DE,BC=EFD. / C=Z F,BC=EF5. 如图,AB // EF// DC / ABC=90 ,AB=DC ,那么图中有全等三角形 ()A.5 对;B.4 对;C.3 对;D.2 对6. 女口图,已知 AC 丄BD 于点P , AP=CP ,请增加一个条件,使△ ABP B △ CDP (不 能添加辅助线),你增加的条件是7.如图,在 Rt △ ABC 和 Rt △ DCB 中,AB=DC,Z A=Z D=9 0°, AC 与 BD 交于点 8.如图,在厶ABC 中,AD 丄BC 于 D , BE 丄AC 于E , AD 与 BE 相交于点F ,若 BF=AC ,贝U / ABC=9.如图AB=AC, CD! AB 于D, BE 丄AC 于E , BE 与CD 相交于点 O.A. 30 °B. 60 °C. 30 和60。
之间D.以上都不对3.如果两个直角三角形的两条直角边对应相等,那么两个直角三角形全等的依据是,其判定依据是 ,还有△C0,则有△ 也△ 第7题图(1) 求证AD=AE(2) 连接OA BC,试判断直线OA BC的关系并说明理由.。
2022-2022学年度青岛版初中数学八年级上册第5章几何证明初步56几何证明举例知识点练习第九十三

2022-2022学年度青岛版初中数学八年级上册第5章几何证明初步56几何证明举例知识点练习第九十三篇 精品举例知识点练习第九十三篇第1题【单选题】如图所示,CD⊥AB,垂足为D,点F是BC上任意一点,FE⊥AB,垂足为E,且∠CDG=∠BFE,∠AGD=80°,∠ACB的度数为().A、50°B、55°C、80°D、60°【答案】:【解析】:第2题【单选题】下列推理正确的是()A、因为a∥d,b∥c,所以c∥d1、10B、因为a∥c,b∥d,所以c∥dC、因为a∥b,a∥c,所以b∥cD、因为a∥b,d∥c,所以a∥c【答案】:【解析】:第3题【单选题】如图游戏:人从格外只能进入第1格,在格中,每次可向前跳1格或2格,那么人从格外跳到第6格可以有()种方法.A、6B、7C、8D、9【答案】:【解析】:2、10第4题【单选题】一同学在n天假期中观察:(1)下了7次雨,在上午或下午(2)当下午下雨时,上午是晴天(3)一共有5个下午是晴天(4)一共有6个上午是晴天则n最小为()A、7B、9C、10D、11【答案】:【解析】:第5题【单选题】已知4个矿泉水空瓶可以换矿泉水一瓶,现有12个矿泉水空瓶,若不交钱,最多可以喝矿泉水瓶()A、2瓶B、3瓶C、4瓶D、5瓶3、10【答案】:【解析】:第6题【单选题】已知4个矿泉水空瓶可以换矿泉水一瓶,现有12个矿泉水空瓶,若不交钱,最多可以喝矿泉水瓶()A、2瓶B、3瓶C、4瓶D、5瓶【答案】:【解析】:第7题【单选题】世界杯足球赛小组赛,每个小组4个队进行单循环比赛,每场比赛胜队得3分,败队得0分,平局时两队各得1分,小组赛完以后,总积分最高的两个队出线进入下轮比赛,如果总积分相同,还要按净胜球排序,一个队要保证出线,这个队至少要积()A、6分B、7分C、8分D、9分【答案】:4、10【解析】:第8题【单选题】有8个小朋友围成一圈,按顺时针方向依次编为1﹣8号.现按如下方式发糖:给1号发1块;然后顺时针向隔过1人,给3号发1块;再顺时针向隔过2人给6号发1块;接着又顺时针向隔过1人后发1块糖;…;如此续行.问最先拿到10块糖的是()号小朋友?A、8B、5C、3D、2【答案】:【解析】:第9题【单选题】旅行团在一城市游览,有甲、乙、丙、丁四个景点,导游说:“①要游览甲,就得去乙;②乙、丙只能去一个;③丙、丁要么都去,要么都不去;”根据导游的说法,在下列选项中,该旅行团可能游览的景点是()A、甲、丙B、甲、丁C、乙、丁D、丙、丁5、10。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
章节测试题1.【题文】如图所示,△ABC中,AB,AC的垂直平分线分别交BC于点D,E,已知△ADE的周长为12 cm,求BC的长.【答案】BC=12 cm.【分析】由AB、AC的垂直平分线分别交BC于D、E,垂足分别是M、N,根据线段垂直平分线的性质,可得AD=BD,AE=EC,继而可得△ADE的周长等于BC 的长;【解答】解:因为AB,AC的垂直平分线分别交BC于点D,E,所以DA=DB,EA=EC,所以BC=BD+DE+EC=DA十DF+AE,即为△ADE的周长.又因为△ADE的周长为12 cm,所以BC=12 cm.2.【题文】如图所示,已知AB=AC=20 cm,DE垂直平分AB,垂足为E,DE 交AC 于点D,若△DBC的周长为35 cm,求BC的长.【答案】BC=15 cm.【分析】由DE垂直平分AB,根据线段垂直平分线的性质,即可求得AD=BD,又由△DBC的周长为35cm,易得BC+AC=35cm,继而求得BC长.【解答】解:∵DE垂直平分AB,∴AD=BD,∵△DBC的周长为35cm,∴BC+BD+CD=BC+AD+CD=BC+AC=35cm,∵AC=20cm,∴BC=15cm.3.【题文】如图所示,在△ABC中,∠A=90°,AC=8 cm,AB=6 cm,BC边的垂直平分线DE交BC于E,交AC于D,求△ABD的周长.【答案】△ABD的周长为14 cm.【分析】直接利用线段垂直平分线的性质得出BD=DC,进而得出答案;【解答】解:∵DF垂直平分BC,∴BD=DC,∴AC=AD+DC=AD+BD=8 cm.又∵AB=6 cm,∴AB+AD+DB=14 cm,即△ABD的周长为14 cm.4.【题文】如图,已知点P为∠MON内一点,点P与点A关于直线ON对称,点P与点B关于直线OM对称.连接AB,交ON于D点,交OM于C点,若AB长为15 cm,求△PCD的周长.【答案】15 cm.【分析】由点P与点A关于直线ON对称,点P与点B关于直线OM对称可得:ON垂直平分AP,OM垂直平分BP;根据垂直平分线的性质可得DA=DP,CP=CB,通过等量代换得到△PCD的周长与AB的数量关系,即可求解.【解答】解:∵点P与点A关于直线ON对称,点P与点B关于直线OM对称,∴ON垂直平分AP,OM垂直平分BP,∴DA=DP,CP=CB,∴△PCD的周长=PD+PC+CD=AD+DC+CB=AB=15cm.5.【题文】如图,已知直线l是AB的垂直平分线,M是直线l上的一点,D,E是AB上不同的点,则AM=BM吗?MD=ME吗?【答案】AM=BM,无法判断MD是否等于ME.【分析】由M在线段AB的垂直平分线l上,根据“线段的垂直平分线上任意一点,到线段两端点的距离相等”即可判断AM=BM成立;根据直线l不一定是DE的垂直平分线,则无法判断MD与ME的大小关系.【解答】解:∵l是AB的垂直平分线,∴AM=BM.由于D、E是AB上任意两点,所以MD不一定等于ME,只有当l经过DE的中点时,MD=ME.6.【题文】如图,△ABC中,D、E在AB上,且D、E分别是AC、BC的垂直平分线上一点.(1)若△CDE的周长为4,求AB的长;(2)若∠ACB=100°,求∠DCE的度数;(3)若∠ACB=a(90°<a<180°),则∠DCE=___________.【答案】(1)4;(2)20°;(3)2α-180°.【分析】(1)根据线段的垂直平分线的性质得到DC=DA,EC=EB,根据三角形的周长公式计算即可;(2)根据三角形内角和定理求出∠A+∠B的度数,根据等腰三角形的性质求出∠DCA+∠ECB,根据题意计算即可;(3)根据(2)的方法解答.【解答】解:(1)∵D、E分别是AC、BC的垂直平分线上一点,∴DC=DA,EC=EB,∵△CDE的周长=DC+DE+EC=4,∴DA+DE+EB=4,即AB的长为4;(2)∵∠ACB=100°,∴∠A+∠B=80°,∵DC=DA,∴∠DCA=∠A,∵EC=EB,∴∠ECB=∠B,∴∠DCA+∠ECB=80°,∴∠DCE=100°-80°=20°;(3)∵∠ACB=α,∴∠A+∠B=180°-α,∵DC=DA,∴∠DCA=∠A,∵EC=EB,∴∠ECB=∠B,∴∠DCA+∠ECB=180°-α,∴∠DCE=α-180°+α=2α-180°,故答案为:2α-180°.7.【题文】如图,已知在△ABC中,∠C=90°,AB的垂直平分线MN交BC于点D.(1)如果∠CAD=20°,求∠B的度数;(2)如果∠CAB=50°,求∠CAD的度数;(3)如果∠CAD:∠DAB=1:2,求∠CAB的度数.【答案】(1)∠B=35°;(2)∠CAD=10°;(3)∠CAB=54°.【分析】(1)根据直角三角形的性质求出∠ADC=70°,根据线段的垂直平分线的性质得到DA=DB,计算即可;(2)根据直角三角形的性质求出∠B的度数,根据线段的垂直平分线的性质得到DA=DB,计算即可;(3)设∠CAD=x,根据题意列出方程,解方程即可.【解答】解:(1)∵∠C=90°,∠CAD=20°,∴∠ADC=70°,∵DE是AB的垂直平分线,∴DA=DB,∴∠DAB=∠B=35°,答:∠B的度数是35°;(2)∵∠C=90°,∠CAB=50°,∴∠B=40°,∵DE是AB的垂直平分线,∴DA=DB,∴∠DAB=∠B=40°,∴∠CAD=10°;(3)设∠CAD=x,则∠DAB=∠B=2x,则x+2x+2x=90°,解得x=18,则∠CAB=54°.8.【题文】敌军基地在三条公路围成的三角区域内,我军一队战士在一条公路中点垂直射击,另一队战士在另一条公路中点垂直射击,均击中敌军基地,问第三队战士在公路何处垂直射击可击中目标?【答案】第三队战士在第三条公路中点处垂直射击可击中目标,理由见解析【分析】根据线段的垂直平分线的性质和判定定理进行解答即可.【解答】解:第三队战士在第三条公路中点处垂直射击可击中目标,∵一队战士在一条公路中点垂直射击,∴敌军基地到这条公路与另两条公路交点的距离相等,同理,敌军基地到第二条公路与另两条公路交点的距离相等,∴敌军基地在第三条公路与另两条公路交点之间公路的垂直平分线上,∴第三队战士在第三条公路中点处垂直射击可击中目标。
9.【题文】已知:如图, AB=AC,DE∥AC,求证:△BDE是等腰三角形.【答案】见解答。
【分析】根据等角对等边即可证明.【解答】证明:∵,∴,∵∥,∴,∴,∴△BDE为等腰三角形.10.【题文】如图,已知在△ABC中,∠ACB=90°,CD,CE三等分∠ACB,且CD⊥AB.求证:(1)AB=2BC;(2)CE=AE=EB.【答案】(1)证明见解析;(2)证明见解析【分析】(1)通过已知条件可以求得∠ACE=∠ECD=∠BCD=30°,∠ECB=60°,由CD⊥AB,求得∠B=60°,则由直角三角形的两个锐角互余的性质得到∠A=30°,然后根据30°角所对的直角边等于斜边的一半,可得BC=AB,即:AB=2BC;(2)由(1)可知:∠A=∠ACE=30°,∠ECB=∠B=60°,然后根据等角对等边即可得:CE=AE=EB.【解答】证明:(1)∵∠ACB=90°,CD,CE三等分∠ACB,∴∠ACE=∠ECD=∠BCD=30°,∠ECB=60°.∵CD⊥AB,∴∠B=60°,∴∠A=30°,∴BC=AB,即:AB=2BC;(2)由(1)可知:∠A=∠ACE=30°,∠ECB=∠B=60°,∴AE=CE,CE=BE,∴AE=CE=BE.11.【题文】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,连接BE、CE.(1)求证:BE=CE(2)如图2,若BE的延长线交AC于点F,且BF ⊥AC,垂足为F,原题设其它条件不变.求证:∠CAD=∠CBF(3)在(2)的条件下,若∠BAC=45,判断△CFE的形状,并说明理由.【答案】证明见解答。
【分析】(1)由条件证明△ABE≌△ACE即可;(2)利用垂直的定义可求得∠CAD+∠C=∠CBF+∠C=90°,可证得结论;(3)由条件可证明△AEF≌△BCF,可得AF=BF,可得出结论.【解答】解:(1)∵AB=AC,D是BC的中点∴∠BAE=∠CAE在△ABE和△ACE中,∴△ABE≌△ACE(SAS)∴BE=CE(2)∵AB=AC,点D是BC的中点∴AD⊥BC∴∠CAD+∠C=90°∵BF⊥AC∴∠CBF+∠C=90°∴∠CAD=∠CBF(3)∵∠BAC=45°,BF⊥AF∴△ABF为等腰直角三角形∴AF=BF在△AEF和△BCF中,∴△AEF≌△BCF(ASA).∴EF=CF∵∠CFE=90°∴△CFE为等腰直角三角形.12.【题文】已知在△ABC中,AB=AC。
(1)若D为AC的中点,BD把三角形的周长分为24cm和30cm两部分,求△ABC三边的长;(2)若D为AC上一点,试说明AC>(BD+DC)。
【答案】(1)三角形的三边长为16,16,22或20,20,14;(2)理由见解析【分析】(1)分两种情况讨论:当AB+AD=30,BC+DC=24或AB+AD=24,BC+DC=30,所以根据等腰三角形的两腰相等和中线的性质可求得,三边长为16,16,22或20,20,14;(2)根据三角形两边之和大于第三边即可得到AC>(BD+DC).【解答】解:(1)设三角形的腰AB=AC=x,若AB+AD=24cm,则:x+x=24∴x=16三角形的周长为24+30=54cm所以三边长分别为16,16,22;若AB+AD=30cm,则:x+x=30∴x=20∵三角形的周长为24+30=54cm∴三边长分别为20,20,14;因此,三角形的三边长为16,16,22或20,20,14。
(2)∵AC=AD+CD,AB=AC,∴2AC=AB+AD+CD>BD+DC,∴AC>(BD+DC)。
13.【题文】如果经过三角形某一个顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形的生成三角形,简称生成三角形.(1)如图,已知等腰直角三角形ABC,∠A=90°,试说明:△ABC是生成三角形;(2)若等腰三角形DEF有一个内角等于36°,请你画出简图说明△DEF是生成三角形.(要求画出直线,标注出图中等腰三角形的顶角、底角的度数)【答案】(1)见解析;(2)见解析.【分析】(1)根据等腰直角三角形的性质,可得△ABD、△ACD的形状,可得证明结论;(2)根据顶角是36°,可画底角的角平分线,可得答案,根据顶角是108°的等腰三角形,把顶角分成,可得答案.【解答】证明:过点A作AD⊥BC,垂足为D.∵AB=AC,∠BAC=90°,∴∠B=∠C=45°,∠BAD=∠CAD=∠BAC=45°,∴∠B=∠BAD,∠C=∠CAD,∴△ABD和△ACD是等腰三角形,∴△ABC是生成三角形;(2)如图:,△DEG与△EFG都是等腰三角形,△DEF是生成三角形.14.【题文】如图,在△ABC中,AB=AC,AD是BC边上的中线,E是AC边上的一点,且∠CBE=∠CAD.求证:BE⊥AC.【答案】证明见解析【分析】因为根据等腰三角形三线合一的性质可得:根据可得进而证明【解答】解:AD是BC边上的中线,又15.【题文】如图,在△ABC中,AB=AC,AD⊥BC于点D,AM是△ABC的外角∠CAE的平分线.(1)求证:AM∥BC;(2)若DN平分∠ADC交AM于点N,判断△ADN的形状并说明理由.【答案】(1)证明见解答;(2)△ADN是等腰直角三角形,理由见解答。
