材料力学I答案
孙训方材料力学(I)第五版课后习题答案完整版
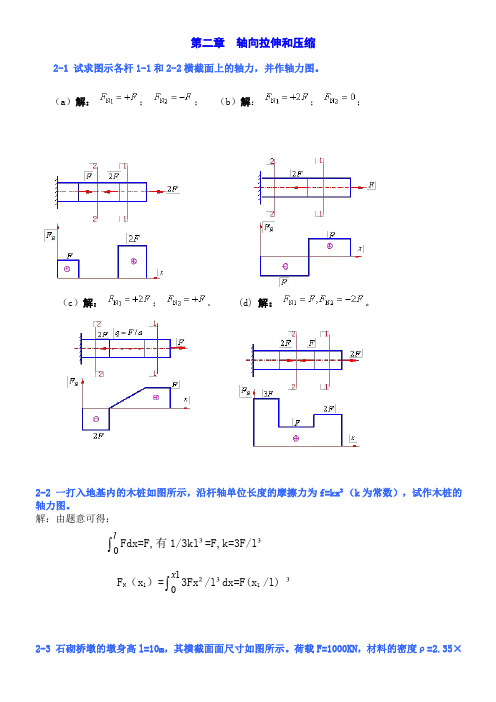
2-4
图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制成。下面的拉杆和中间竖向 的竖
撑杆用角钢构成,其截面均为两个 75mm×8mm 的等边角钢。已知屋面承受集度为 直均布荷载。试求拉杆 AE 和 EG 横截面上的应力。
解: 1) 求内力
=
取 I-I 分离体
得 取节点 E 为分离体
(拉)
,
故 2) 求应力
解: (1)求轴力 取节点 B 为研究对象,由其平衡条件得:
Y 0
N AB sin F 0 N AB F sin
X 0
N AB cos N BC 0
N BC N AB cos
(2)求工作应力
F cos F cot sin
2-11 图示结构中,AB 为水平放置的刚性杆,杆 1,2,3 材料相同,其弹性模量 E 210GPa ,已 知 l 1m , A1 A2 100mm 2 , A3 150mm 2 , F 20kN 。试求 C 点的水平位移和铅垂位移。
受力图 2-11 图 解: (1)求各杆的轴力 以 AB 杆为研究对象,其受力图如图所示。 因为 AB 平衡,所以
因此,
2
l
l
0
l F F l dx 2 Fl du dx ( 2 ) 0 0 EA( x) E A( x) E (d 1 d 2 ) u l
l 2 Fl 2 Fl 1 1 E (d1 d 2 ) u 0 E (d 1 d 2 ) d 2 d 1 x d 1 2l 2 0
2-13 图示 A 和 B 两点之间原有水平方向的一根直径 d 1mm 的钢丝, 在钢丝的中点 C 加一竖向荷 载 F。已知钢丝产生的线应变为 0.0035 ,其材料的弹性模量 E 210GPa , 钢丝的自重不计。试求: (1)钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律) ; (2)钢丝在 C 点下降的距75×8 等边角钢的面积 A=11.5 cm
完整版材料力学性能课后习题答案整理

完整版材料力学性能课后习题答案整理材料力学性能课后习题答案第一章单向静拉伸力学性能1、解释下列名词。
1弹性比功:金属材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
2.滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
3.循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
4.包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
5.解理刻面:这种大致以晶粒大小为单位的解理面称为解理刻面。
6.塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
脆性:指金属材料受力时没有发生塑性变形而直接断裂的能力韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。
7.解理台阶:当解理裂纹与螺型位错相遇时,便形成一个高度为b的台阶。
8.河流花样:解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。
是解理台阶的一种标志。
9.解理面:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似,故称此种晶体学平面为解理面。
10.穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
11.韧脆转变:具有一定韧性的金属材料当低于某一温度点时,冲击吸收功明显下降,断裂方式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变2、说明下列力学性能指标的意义。
答:E弹性模量G切变模量r规定残余伸长应力0.2屈服强度gt金属材料拉伸时最大应力下的总伸长率n应变硬化指数P153、金属的弹性模量主要取决于什么因素?为什么说它是一个对组织不敏感的力学性能指标?答:主要决定于原子本性和晶格类型。
合金化、热处理、冷塑性变形等能够改变金属材料的组织形态和晶粒大小,但是不改变金属原子的本性和晶格类型。
材料力学I期末考试题及答案

材料力学I期末考试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是基本假设?A. 均匀性假设B. 连续性假设C. 各向同性假设D. 各向异性假设答案:D2. 在拉伸试验中,材料的屈服强度是指:A. 弹性极限B. 屈服极限C. 强度极限D. 断裂强度答案:B3. 影响材料弹性模量的因素不包括:A. 材料种类B. 温度C. 材料的几何形状D. 加载速度答案:C4. 梁的弯曲应力公式为:A. σ = My/IB. σ = Mx/IC. σ = VQ/ID. σ = Vx/I答案:A5. 材料力学中,下列哪一项不是应力状态的描述?A. 正应力B. 剪应力C. 应力集中D. 应力梯度答案:D6. 材料的疲劳破坏通常发生在:A. 最大应力处B. 最小应力处C. 应力集中处D. 应力均匀处答案:C7. 根据材料力学理论,下列哪一项不是材料的强度理论?A. 最大正应力理论B. 最大剪应力理论C. 最大应变理论D. 能量理论答案:D8. 梁的弯曲变形公式为:A. v = (Mx/EI)(1 - x^2/L^2)B. v = (Mx/EI)(1 - x^3/L^3)C. v = (Mx/EI)(1 - x/L)D. v = (Mx/EI)(1 - x^2/L^3)答案:B9. 材料的塑性变形是指:A. 弹性变形B. 永久变形C. 可逆变形D. 弹性和塑性变形的总和答案:B10. 在拉伸试验中,材料的弹性模量可以通过下列哪一项来确定?A. 弹性阶段的斜率B. 屈服阶段的斜率C. 断裂阶段的斜率D. 塑性变形阶段的斜率答案:A二、填空题(每题2分,共20分)1. 材料力学中,__________是指材料在外力作用下发生形变,但当外力移除后,形变能够完全恢复的性质。
答案:弹性2. 当材料受到拉伸时,其内部产生的__________应力称为正应力。
答案:垂直3. 材料力学中,__________是指材料在外力作用下发生形变,但当外力移除后,形变不能完全恢复的性质。
东大14春学期《材料力学i》在线作业1答案

14春学期《材料力学Ⅰ》在线作业1一、单选题1.A. AB. BC. CD. D正确答案:D2.A. AB. BC. CD. D正确答案:B3.A. AB. BC. CD. D正确答案:C4. 7.4在下面关于梁、挠度和转角的讨论中,()是错误的A. A. 挠度的一阶导数等于转角B. 可以用简支梁的跨度中点的挠度代替最大的挠度C. 弯矩为零的一段梁上各界面的转角相等,挠度不一定相等D. 挠度最大的截面和转角不一定为零正确答案:B5. 12.2 对称循环的循环特性等于。
A.0;B. -1;C. 1;D. 0.5.A. AB. BC. CD. D正确答案:B6. 9.1 用叠加法计算组合变形杆件的内力和应力的限制条件是。
A.任何情况;B. 弹塑性变形;C. 弹性变形;D. 线弹性和小变形.A. AB. BC. CD. D正确答案:D7.A. AB. BC. CD. D正确答案:D8. 11.3、交变应力作用下的塑性材料破坏并不表现为脆性断裂A. 正确B. 错误C.D.正确答案:B9.A. AB. BC. CD. D正确答案:A10.A. AB. BC. CD. D正确答案:B11. 11.2研究冲击时的应力和应变已经不属于动载荷问题。
A. 正确B. 错误C.D.正确答案:B12.A. AB. BC. CD. D正确答案:A13.A. AB. BC. CD. D正确答案:C14. 12.1 交变应力是随时间作周期性变化。
A.正应力;B. 切应力;C. 应力;D. 载荷.A. AB. BC. CD. D正确答案:C15. 2.5 低碳钢的强度比合金钢的强度低。
A.对B. 错A. AB. BC. CD. D正确答案:A16. 4.4 平行移轴公式是求图形对与平行轴的。
A.形心轴、惯性矩和惯性积;B. 任意轴、惯性矩;C. 形心轴、惯性矩;D. 任意轴、惯性矩和惯性积.A. AB. BC. CD. D正确答案:A17.A. AB. BC. CD. D正确答案:D18.A. AB. BC. CD. D正确答案:B19. 6.4 弯曲切应力在横截面上沿高度的分布是。
《材料力学I》单元测试(四)

《材料力学I*》单元测试(四)一、 单选题1、 齿轮传动轴的变形形式为(D )。
A 、拉-压变形B 、扭转变形C 、拉-弯组合变形D 、弯-扭组合变形2、 处理组合变形的一般步骤是(D )。
A 、内力分析-外力分析-应力分析-强度计算B 、应力分析-强度计算-内力分析-外力分析C 、强度计算-外力分析-内力分析-应力分析D 、外力分析-内力分析-应力分析-强度计算3、 在拉-弯组合变形中,危险点的应力状态属于(A )。
A 、单向应力状态B 、二向应力状态C 、三向应力状态D 、应力状态不定4、 在弯-扭组合变形中,危险点的应力状态属于(A )。
A 、平面应力状态B 、空间应力状体C 、单向应力状态D 、都不对5、 两端铰链连接的压杆,其长度系数μ值是(A )。
A 、1.0 B 、0.7 C 、0.5 D 、26、 两端铰支的圆截面压杆,长1m ,直径50mm 。
其柔度为(C )。
A 、60 B 、66.7 C 、80 D 、50。
7、 图(a )杆件承受轴向拉力F ,若在杆上分别开一侧、两侧切口如图(b )、图(c )所示。
令杆(a )、(b )、(c )中的最大拉应力分别为、和,则下列结论中(C )是错误的。
A 、一定小于 B 、一定小于C 、一定大于 D 、可能小于8、 一方形横截面的压杆,若在其上钻一横向小孔(如图所示),则该杆与原来相比( B )。
A 稳定性降低,强度不变 B 稳定性不变,强度降低 C 稳定性和强度都降低 D 稳定性和强度都不变9、 若在强度计算和稳定性计算中取相同的安全系数,则在下列说法中,( B )是正确的。
A 、满足强度条件的压杆一定满足稳定性条件B 、满足稳定性条件的压杆一定满足强度条件 max 1σmax 2σmax 3σmax 1σmax 2σmax 1σmax 3σmax 3σmax 2σmax 3σmax 2σC 、满足稳定性条件的压杆不一定满足强度条D 、不满足稳定性条件的压杆不一定满足强度条件10、如图所示直杆,其材料相同,截面和长度相同,支承方式不同,在轴向压力作用下,哪个柔度最大,哪个柔度最小?有4种答案:正确答案是(B ) 。
中南大学材料力学练习题答案1

轴 向 拉 压 与 剪 切 (一)一、概念题1.C ;2.B ;3.B ;4. C ;5.B6.︒=0α的横截面;︒=90α的纵向截面;︒=45α的斜截面;︒=0α的横截面和︒=90α的纵向截面 7.230MPa ;325Mpa 8.0.47%;0.3%9.26.4%;65.2%;塑性材料10.杯口状;粒状;垂直;拉;成︒45左右的角;切 11.s σ;ssn σ;b σ;bbn σ二、计算题1.2.解:横截面上应力 M P a Pa A F N 10010100102010200643=⨯=⨯⨯==-σAB 斜截面(︒=50α):M P aM P aAB AB2.49100sin 21002sin 23.4150cos 100cos 22=︒===︒⨯==αστασσBC 斜截面(︒-=40α):MPaMPaBC BC2.49)80sin(21002sin 27.58)40(cos 100cos 22-=︒-===︒-⨯==αστασσ杆内最大正应力和最大切应力分别为:M P aM P a502100max max ====στσσ3.解:根据活塞杆的强度条件确定最大油压P 1:62112121013044)(⨯⨯=-d p d D ππ M P a p 1.181=根据螺栓的强度条件确定最大油压P 2:62221210110644)(⨯⨯⨯=-d p d D ππ M P a p 5.62=所以最大油压MPa p p 5.62==4.解: 研究A 轮,由静力平衡方程得 N A B AB F kN W F ===604 查型钢表得角钢的横截面面积 2410058.4m A -⨯=[]σσ<=*⨯⨯==-MPa AF NAB AB93.7310058.421060243所以斜杆AB 是安全的。
5.解:杆的轴力图为4923maxmax 105101004107.15-⨯=⨯⨯⨯===d AEF ENt t πσεmm d 20=6.解:(1)MPa Pa E 7351035.70035.01021089=⨯=⨯⨯==εσ(2)mmm ll l ll l 7.831037.810035.1)()(2222222=⨯=-=-+=-+∆=∆-ε(3)A F N σ=N F F N P 3.965.10037.834001.0107352sin 226=⨯⨯⨯⨯⨯==πθ轴 向 拉 压 与 剪 切 (二)一、概念题1. D ;2.A ;3.B ;4.D ;5.D ;6.D ;7.C 8.AP 25(压);)(27←EAPa9.[]τπ≤dhP;[]bs d D Pσπ≤-)(422;[]σπ≤24dP二、计算题1. 如图示,钢缆单位长度所受重力为γA q =,则x 截面上的轴力为 P x A P qx x F N +=+=γ)(。
材料力学网上作业题参考答案

东北农业大学网络教育学院材料力学网上作业题(2015更新版)绪论一、名词解释1.强度2. 刚度3. 稳定性4. 变形5. 杆件6.板或壳7.块体二、简答题1.构件有哪些分类?2. 材料力学的研究对象是什么?3. 材料力学的任务是什么?4. 可变形固体有哪些基本假设?5. 杆件变形有哪些基本形式?6. 杆件的几何基本特征?7.载荷的分类?8. 设计构件时首先应考虑什么问题?设计过程中存在哪些矛盾?第一章轴向拉伸和压缩一、名词解释1.内力2. 轴力3.应力4.应变5.正应力6.切应力7.伸长率8.断面收缩率9. 许用应力 10.轴向拉伸 11.冷作硬化二、简答题1.杆件轴向拉伸或压缩时,外力特点是什么?2.杆件轴向拉伸或压缩时,变形特点是什么?3. 截面法求解杆件内力时,有哪些步骤?4.内力与应力有什么区别?5.极限应力与许用应力有什么区别?6.变形与应变有什么区别?7.什么是名义屈服应力?8.低碳钢和铸铁在轴向拉伸时,有什么样的力学特性?9.强度计算时,一般有哪学步骤?10.什么是胡克定律?11.表示材料的强度指标有哪些?12.表示材料的刚度指标有哪些?13.什么是泊松比?14. 表示材料的塑性指标有哪些?15.拉压杆横截面正应力公式适用范围是什么?16.直杆轴向拉伸或压缩变形时,在推导横截面正应力公式时,进行什么假设?三、计算题1. 试用截面法求下列各杆指定截面的轴力。
2. 试用截面法求下列各杆指定截面的轴力。
3. 试用截面法求下列各杆指定截面的轴力。
4. 试用截面法求下列各杆指定截面的轴力。
5. 试用截面法求下列各杆指定截面的轴力。
6. 试用截面法求下列各杆指定截面的轴力。
7 高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的小径d = 175 mm。
已知作用于拉杆上的静拉力F=850 kN,试计算大钟拉杆横截面上的最大静应力。
8 一桅杆起重机如图所示,起重杆AB为一钢管,其外径D = 20 mm,内径d≈18 mm;钢绳CB的横截面面积为10 mm2。
(完整版)材料力学试题及答案
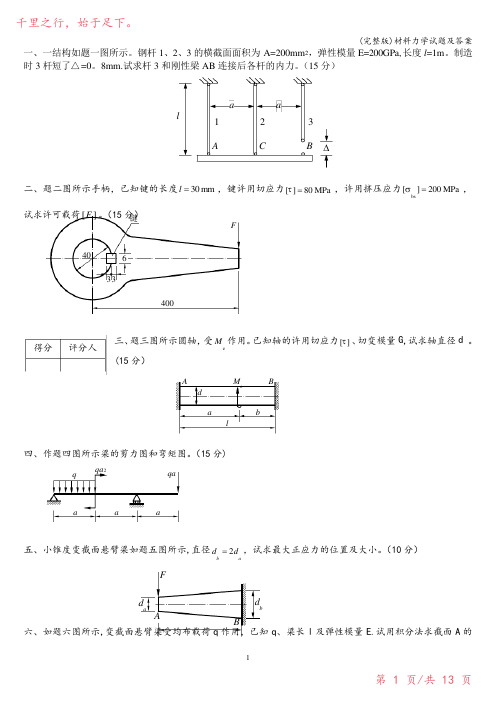
一、一结构如题一图所示。
钢杆1、2、3的横截面面积为A=200mm 2,弹性模量E=200GPa,长度l =1m 。
制造时3杆短了△=0。
8mm.试求杆3和刚性梁AB 连接后各杆的内力。
(15分)aalABC123∆二、题二图所示手柄,已知键的长度30 mm l =,键许用切应力[]80 MPa τ=,许用挤压应力bs[]200 MPa σ=,试求许可载荷][F 。
(15分)三、题三图所示圆轴,受eM 作用。
已知轴的许用切应力[]τ、切变模量G ,试求轴直径d 。
(15分)四、作题四图所示梁的剪力图和弯矩图。
(15分)五、小锥度变截面悬臂梁如题五图所示,直径2bad d =,试求最大正应力的位置及大小。
(10分)六、如题六图所示,变截面悬臂梁受均布载荷q 作用,已知q 、梁长l 及弹性模量E .试用积分法求截面A 的得分评分人F键40633400Aal bM eBd a a aqqaqa 2dbBda AF挠度w A 和截面C 的转角θC .(15分)七、如图所示工字形截面梁AB ,截面的惯性矩672.5610zI -=⨯m 4,求固定端截面翼缘和腹板交界处点a 的主应力和主方向。
(15分)一、(15分)(1)静力分析(如图(a))1N F2N F3N F图(a)∑=+=231,0N N N yF F F F(a)∑==31,0N N CF F M(b)(2)几何分析(如图(b))1l∆2l∆3l∆∆图(b)wql /3x lhb 0b (x )b (x )BAC 50kN AB0.75m303030140150zya∆=∆+∆+∆3212l l l(3)物理条件EA l F l N 11=∆,EA l F l N 22=∆,EAl F l N 33=∆ (4)补充方程∆=++EAlF EA l F EA l F N N N 3212 (c) (5)联立(a)、(b)、(c)式解得:kN FkN FF N N N 67.10,33.5231===二、(15分)以手柄和半个键为隔离体,S0, 204000OM F F ∑=⨯-⨯=取半个键为隔离体,bsS20F F F ==由剪切:S []s FA ττ=≤,720 N F = 由挤压:bs bs bs bs[][], 900N FF Aσσ=≤≤取[]720N F =.三、(15分)eABM M M +=0ABϕ=, A B M a M b ⋅=⋅得 e B a M M a b =+, e A b MM a b=+当a b >时 e316π ()[]M ad a b τ≥+;当b a >时 e316π ()[]M bd a b τ≥+。
材料力学习题与答案

韧脆转变温度:材料在低于某一温度tk时,会由韧性状态转变未脆性状态,tk称为韧脆转变温度。
什么是低温脆性、韧脆转变温度tk?产生低温脆性的原因是什么?体心立方和面心立方金属的低温脆性有和差异?为什么?
由于压痕较大,不宜于某些表面不允许有较大压痕的成品检验,也不宜于薄件试验。
不同材料需更换压头直径和改变试验力,压痕直径的测量也较麻烦。
2、洛氏硬度的测量原理
洛氏硬度是以压痕陷凹深度作为计量硬度值的指标。
洛氏硬度试验的优缺点
洛氏硬度试验避免了布氏硬度试验所存在的缺点。它的优点是:
1)因有硬质、软质两种压头,故适于各种不同硬质材料的检验,不存在压头变形问题;
热疲劳:机件在由温度循环变化时产生的循环热应力及热应力变形作用下发生的疲劳就叫热疲劳。
由于温度周期变化引起零件或构件的自由膨胀和收缩,而又因这种膨胀和收缩受到约束,产生了交变热应力,由这种交变热应力引起的破坏就叫热疲劳。
(1)渗碳层的硬度分布;(2)淬火钢;(3)灰铸铁;(4)鉴别钢中的隐晶马氏体和残余奥氏体;(5)仪表小黄铜齿轮;(6)龙门刨床导轨;(7)渗氮层;(8)高速钢刀具;(9)退火态低碳钢;(10)硬质合金。
(1)渗碳层的硬度分布----HK或-显微HV
(2)淬火钢-----HRC
(3)灰铸铁-----HB
根据σ/σ0.2的值,确定裂纹断裂韧度KIC是否休要修正
因为σ/σ0.2=900/1200=0.75>0.7,所以裂纹断裂韧度KI需要修正
对于无限板的中心穿透裂纹,修正后的KI为:
材料力学I期末考试题及答案

材料力学I期末考试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪个参数不是描述材料弹性性质的?A. 弹性模量B. 屈服强度C. 泊松比D. 剪切模量答案:B2. 在拉伸试验中,材料的屈服点是指:A. 应力达到最大值时对应的应变B. 应力达到最大值时对应的应力C. 材料开始发生塑性变形的应力D. 材料发生断裂的应力答案:C3. 根据胡克定律,下列哪个说法是正确的?A. 应力与应变成正比B. 应力与应变成反比C. 应力与应变成二次方关系D. 应力与应变成对数关系答案:A4. 在材料力学中,下列哪个参数是用来描述材料的韧性的?A. 弹性模量B. 屈服强度C. 硬度D. 冲击韧性答案:D5. 材料力学中,下列哪个参数是用来描述材料的塑性变形能力的?A. 弹性模量B. 屈服强度C. 硬度D. 延伸率答案:D6. 根据材料力学的基本原理,下列哪个说法是错误的?A. 应力是单位面积上的力B. 应变是单位长度的变化量C. 应力和应变都是标量D. 应力和应变之间存在线性关系答案:C7. 在材料力学中,下列哪个参数是用来描述材料的硬度的?A. 弹性模量B. 屈服强度C. 布氏硬度D. 冲击韧性答案:C8. 材料力学中,下列哪个参数是用来描述材料的疲劳强度的?A. 弹性模量B. 屈服强度C. 疲劳极限D. 冲击韧性答案:C9. 在材料力学中,下列哪个参数是用来描述材料的抗拉强度的?A. 弹性模量B. 屈服强度C. 抗拉强度D. 冲击韧性答案:C10. 材料力学中,下列哪个参数是用来描述材料的压缩强度的?A. 弹性模量B. 屈服强度C. 压缩强度D. 冲击韧性答案:C二、填空题(每题2分,共20分)1. 材料力学中,应力的定义是单位面积上的_______。
答案:力2. 材料力学中,应变的定义是单位长度上的_______。
答案:长度变化3. 材料力学中,弹性模量是描述材料_______性质的物理量。
答案:弹性4. 材料力学中,泊松比是描述材料在受到_______作用时,横向应变与纵向应变的比值。
材料力学第五课后题答案(孙训芳)

材料力学(I)第五版(孙训芳编)甘肃建筑职业技术学院长安大学土木工程材料力学温习材料材料力学第五版课后答案(孙训芳编)4-1试求图示各梁中指定截面上的剪力和弯矩 a (5)=h (4)001100110002222200022132241111223121140,222233RA RB S S q F F a q a q F q a a q aa M q a q a q aF M q a a q a a q a ----==⨯==-⨯==-⨯⨯⨯===⨯-⨯⨯⨯=b (5)=f (4)4-2试写出以下各梁的剪力方程和弯矩方程,并作剪力图和弯矩图 a (5)=a (4)b(5)=b(4)f(5)=f(4)4-3试利用载荷集度,剪力和弯矩间的微分关系做以下各梁的弯矩图和剪力e和f题)(e)(f)(h)4-4试做以下具有中间铰的梁的剪力图和弯矩图。
4-4 (b) 4-5 (b)4-5.依照弯矩、剪力与荷载集度之间的关系指出以下玩具和剪力图的错误的地方,并更正。
4-6.已知简支梁的剪力图如下图,试做梁的弯矩图和荷载图,梁上五集中力偶作用。
4-6(a) 4-7(a)4-7.依照图示梁的弯矩图做出剪力图和荷载图。
4-8用叠加法做梁的弯矩图。
4-8(b) 4-8(c)4-9.选择适合的方式,做弯矩图和剪力图。
4-9(b) 4-9(c)4-104-14.长度l=2m的均匀圆木,欲锯做Fa=的一段,为使锯口处两头面开裂最小,硬是锯口处弯矩为零,现将圆木放在两只锯木架上,一只锯木架放在圆木一段,试求另一只锯木架应放位置。
x=4-184-19M=30KN 4-214-234-254-284-294-334-364-355-25-35-75-155-225-23 选22a工字钢5-246-4 6/((233))A l Fl EA ∆=+6-127-3-55mpa 。
-55mpa7-4[习题7-3] 一拉杆由两段沿n m -面胶合而成。
第五版材料力学答案

第五版材料力学答案1. 什么是材料的弹性模量?材料的弹性模量是描述材料在受力作用下的变形能力的物理量,它是应力和应变之间的比值。
弹性模量越大,材料的刚度越大,变形能力越小;弹性模量越小,材料的刚度越小,变形能力越大。
常见的弹性模量有弹性模量、剪切模量和体积模量等。
2. 什么是材料的屈服强度?材料的屈服强度是指材料在受到外力作用下开始发生塑性变形的应力值。
超过屈服强度后,材料将发生不可逆的塑性变形。
屈服强度是材料的重要力学性能参数,对于材料的强度和使用性能有重要影响。
3. 什么是材料的断裂韧性?材料的断裂韧性是描述材料在受到外力作用下抵抗断裂的能力。
断裂韧性越大,材料在受到外力作用下越不容易发生断裂。
断裂韧性是衡量材料抗断裂能力的重要指标,对于材料的使用安全性具有重要意义。
4. 什么是材料的疲劳强度?材料的疲劳强度是指材料在交变应力作用下能够承受的最大应力值。
材料在长期交变应力作用下容易发生疲劳破坏,疲劳强度是描述材料抗疲劳破坏能力的重要参数,对于材料的使用寿命具有重要影响。
5. 什么是材料的弹性极限?材料的弹性极限是指材料在受到外力作用下发生弹性变形的极限应力值。
超过弹性极限后,材料将发生塑性变形。
弹性极限是描述材料在受力作用下的弹性变形能力的重要参数,对于材料的设计和使用具有重要意义。
6. 什么是材料的刚度?材料的刚度是描述材料在受力作用下的变形能力的物理量,它是应力和应变之间的比值。
刚度越大,材料在受力作用下的变形能力越小;刚度越小,材料在受力作用下的变形能力越大。
刚度是描述材料力学性能的重要参数,对于材料的设计和使用具有重要影响。
7. 什么是材料的蠕变强度?材料的蠕变强度是指材料在高温和持续应力作用下发生蠕变变形的能力。
蠕变强度是描述材料在高温条件下的稳定性能的重要参数,对于材料在高温环境下的使用具有重要影响。
总结,材料力学是工程学、材料学和力学的交叉学科,对于材料的性能分析和设计具有重要意义。
完整版材料力学性能课后习题答案整理

材料力学性能课后习题答案第一章单向静拉伸力学性能1、解释下列名词。
1弹性比功:金属材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
2.滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
3.循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
4.包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
5.解理刻面:这种大致以晶粒大小为单位的解理面称为解理刻面。
6.塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
脆性:指金属材料受力时没有发生塑性变形而直接断裂的能力韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。
7.解理台阶:当解理裂纹与螺型位错相遇时,便形成一个高度为b的台阶。
8.河流花样:解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。
是解理台阶的一种标志。
9.解理面:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似,故称此种晶体学平面为解理面。
10.穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
11.韧脆转变:具有一定韧性的金属材料当低于某一温度点时,冲击吸收功明显下降,断裂方式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变2、说明下列力学性能指标的意义。
答:E 弹性模量 G 切变模量 r σ规定残余伸长应力 2.0σ屈服强度 gt δ金属材料拉伸时最大应力下的总伸长率 n 应变硬化指数 P15 3、 金属的弹性模量主要取决于什么因素?为什么说它是一个对组织不敏感的力学性能指标?答:主要决定于原子本性和晶格类型。
合金化、热处理、冷塑性变形等能够改变金属材料的组织形态和晶粒大小,但是不改变金属原子的本性和晶格类型。
重庆大学材料力学答案 (1)

重庆大学材料力学答案题图所示中段开槽的杆件,两端受轴向载荷P 的作用,试计算截面1-1和2-2上的应力。
已知:P = 140kN ,b = 200mm ,b 0 = 100mm ,t = 4mm 。
题图解:(1) 计算杆的轴力 (2) 计算横截面的面积 (3) 计算正应力(注:本题的目的是说明在一段轴力相同的杆件内,横截面面积小的截面为该段的危险截面)横截面面积A=2cm 2的杆受轴向拉伸,力P=10kN ,求其法线与轴向成30°的及45°斜截面上的应力ασ及ατ,并问m ax τ发生在哪一个截面? 解:(1) 计算杆的轴力(2) 计算横截面上的正应力 (3) 计算斜截面上的应力(4) m ax τ发生的截面 ∵0)2cos(==ασαταd d 取得极值 ∴ 0)2cos(=α 因此:22πα=, ο454==πα故:m ax τ发生在其法线与轴向成45°的截面上。
(注:本题的结果告诉我们,如果拉压杆处横截面的正应力,就可以计算该处任意方向截面的正应力和剪应力。
对于拉压杆而言,最大剪应力发生在其法线与轴向成45°的截面上,最大正应力发生在横截面上,横截面上剪应力为零)题图所示阶梯直杆AC ,P =10kN ,l 1=l 2=400mm ,A 1=2A 2=100mm 2,E =200GPa 。
试计算杆AC 的轴向变形Δl 。
题图解:(1) 计算直杆各段的轴力及画轴力图 kN 101==P N (拉) kN 102-=-=P N (压)(2) 计算直杆各段的轴向变形mm 2.010010002004001000101111=⨯⨯⨯⨯==∆EA l N l (伸长)mm 4.05010002004001000102222-=⨯⨯⨯⨯-==∆EA l N l (缩短) (3) 直杆AC 的轴向变形m m 2.021-=∆+∆=∆l l l (缩短)(注:本题的结果告诉我们,直杆总的轴向变形等于各段轴向变形的代数和)题图所示结构,各杆抗拉(压)刚度EA 相同,试求节点A 的水平和垂直位移。
材料力学第五版(I)孙训方版课后习题答案

材料力学第五版(I)孙训方版课后习题答案材料力学第五版孙训方版课后习题答案材料力学第五版(一)孙迅芳对课后练习的回答[习题3-2]实心圆轴的直径d?100mm,长l?1m,其两端所受外力偶矩me?14kn?m,材料的切变模量g?80gpa。
试求:(1)最大剪应力和两端之间的相对旋转角;(2)图示截面上a、b、c三点处切应力的数值及方向;(3)c点处的切应变。
解:(1)计算最大切应力及两端面间的相对转角?max?mt?e。
wpwp11?d3??3.14159?1003?196349(mm3)。
3-21616式中,wp?故:?maxme14?106n?mm???71.302mpa3wp196349mm??t?l11,式中,ip??d4??3.14159?1004?9817469(mm4)。
故:gip3232t?l14000n?m?1m??0.0178254(rad)?1.02o92?124gip80?10n/m?9817469?10m??(2)求图示截面上a、b、c三点处切应力的数值及方向? A.B最大值?71.302 MPa,根据横截面上的剪应力分布规律:a、b、c三点的切应力方向如图所示。
?c??b?0.5?71.302?35.66mpa,(3)计算c点处的切应变?c?12?cg?35.66mpa?4?3?4.4575?10?0.446?10380?10mpa4-3试着利用荷载集中、剪力和弯矩之间的微分关系来绘制弯矩图和剪力E和F(以下梁的问题)1材料力学第五版孙迅芳版课后练习答案(e)(f)(h)4-8用叠加法绘制梁的弯矩图。
4-8(b)4-8(c)二材料力学第五版孙训方版课后习题答案三材料力学第五版孙训方版课后习题答案6-124材料力学第五版孙迅芳版课后练习答案[习题7-14]单元体各面上的应力如图所示。
试用应力圆的几何关系求主应力及最大切应力。
[习题7-15(a)]解:坐标平面应力:X(70,-40),y(30,-40),Z(50,0)单元体图应力圈由xy平面内应力值作a、b点,连接a、b交应力圆半径:C轴中心(50,0)[习题7-15(b)]解:坐标平面应力:X(60,40),y(50,0),Z(0,-40)单元体图应力圈轴于c点,oc=30,故应力圆圆心c(30,0)五由xz平面内应力作a、b点,连接a、b交。
材料力学 复习资料及答案

材料力学I 期末复习资料一、判断题1. 弹性体静力学的任务是尽可能的保证构件的安全工作。
(Y )2. 作用在刚体上的力偶可以任意平移,但作用在弹性体上的力偶一般不能平移。
(Y )3. 若构件上的某一点的任何方向都无应变,则该点无位移。
(N )4. 切应变是变形后构件后构件内任意两条微线段之间夹角的变化量。
(N )5. 胡克定律适用于弹性变形范围内。
(Y )6. 材料的延伸率与试件的尺寸有关。
(Y )7. 一般情况下,脆性材料的安全系数要比塑性材料的大些。
(Y )8. 受扭圆轴的最大切应力出现在横截面上。
(Y )9. 受扭圆轴的最大拉应力的值和最大剪应力的值相等。
(N )10.受扭杆件的扭矩,仅与杆件受到的外力偶矩有关,而与杆件的材料及横截面积的大小、形状无关。
(N )11.平面图形对某轴的静矩等于零,则该轴比为此图形的对称轴。
. (N )12.在一组平行轴中,平面图形对心轴的惯性矩最小。
(Y )13.两梁的跨度、承受的载荷以及支撑都相同,但材料和横截面积不同,则它们的剪力图和弯矩图不一定相同。
(N )14.最大弯矩必然发生在剪力为零的横截面上。
(N )15.若在结构对称的梁上,作用有反对称载荷,则该梁具有对称的剪力图和反对称的弯矩图。
(Y )16.控制梁弯曲强度的主要因素是最大弯矩值。
(N )17.在等截面梁中,正应力绝对值的最大值︱σ︱max比出现在弯矩值︱M︱max最大截面上。
(N )18.梁上弯矩最大的截面,挠度也最大;弯矩为零的截面,转角也为零。
(N )19.平面弯矩梁的挠曲线必定是一条与外力作用面重合或平行的平面曲线。
(Y )20.有正应力作用的方向上,必有线应变;没有正应力作用的方向上,必无线应变。
(N )21.脆性材料不会发生塑性屈服破坏,塑性材料不会发生脆性断裂破坏。
(N )22.纯剪切单元体属于单向应力状态。
(N )23.脆性材料的破坏形式一定是脆性断裂。
(N )24.材料的破坏形式由材料的种类和所处的应力状态而定。
材料力学习题册1-14概念答案

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( × ) 1.2 内力只作用在杆件截面的形心处。
( × ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( × ) 1.4 确定截面内力的截面法,适用于不管等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ∨ ) 1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ∨ ) 1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ∨ ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。
( ∨ ) 1.8 同一截面上各点的正应力σ必定大小相等,方向相同。
( × ) 1.9 同一截面上各点的切应力τ必相互平行。
( × ) 1.10 应变分为正应变ε和切应变γ。
( ∨ ) 1.11 应变为无量纲量。
( ∨ ) 1.12 假设物体各部分均无变形,则物体内各点的应变均为零。
( ∨ ) 1.13 假设物体内各点的应变均为零,则物体无位移。
( × ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( ∨ ) 1.15 题1.15图所示结构中,AD 杆发生的变形为弯曲与压缩的组合变形。
( ∨ )1.16 题1.16图所示结构中,AB 杆将发生弯曲与压缩的组合变形。
( × )二、填空题材料力学主要研究 受力后发生的,以及由此产生的 。
1.2 拉伸或压缩的受力特征是 ,变形特征是 。
1.3 剪切的受力特征是 ,变形特征B题5图题6图外力的合力作用线通过杆轴线 杆件 变形 应力,应变 沿杆轴线伸长或缩短 受一对等值,反向,作用线距离很近的力的作用 沿剪切面发生相对错动是 。
1.4 扭转的受力特征是 ,变形特征是 。
1.5 弯曲的受力特征是 ,变形特征是 。
1.6 组合受力与变形是指 。
材料力学答案

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( × ) 1.2 内力只作用在杆件截面的形心处。
( × ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( × )1.4 确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ∨ )1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ∨ ) 1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ∨ ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。
( ∨ ) 1.8 同一截面上各点的正应力σ必定大小相等,方向相同。
( × ) 1.9 同一截面上各点的切应力τ必相互平行。
( × ) 1.10 应变分为正应变ε和切应变γ。
( ∨ ) 1.11 应变为无量纲量。
( ∨ ) 1.12 若物体各部分均无变形,则物体内各点的应变均为零。
( ∨ ) 1.13 若物体内各点的应变均为零,则物体无位移。
( × ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( ∨ ) 1.15 题1.15图所示结构中,AD 杆发生的变形为弯曲与压缩的组合变形。
( ∨ )1.16 题1.16图所示结构中,AB 杆将发生弯曲与压缩的组合变形。
( × )二、填空题1.1 材料力学主要研究受力后发生的1.2 拉伸或压缩的受力特征是 ,变形特征是 。
1.3 剪切的受力特征是 ,变形特征是 。
1.4 扭转的受力特征是 ,变形特征是 。
1.5 弯曲的受力特征是 ,变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 , 和 三个方面。
1.8 所谓 ,是指材料或构件抵抗破坏的能力。
所谓 ,是指构件抵抗变形的能力。
所B题1.15图题1.16图外力的合力作用线通过杆轴线 杆件 沿杆轴线伸长或缩短 受一对等值,反向,作用线距离很近的力的作用 沿剪切面发生相对错动 外力偶作用面垂直杆轴线 任意二横截面发生绕杆轴线的相对转动外力作用线垂直杆轴线,外力偶作用面通过杆轴线梁轴线由直线变为曲线 包含两种或两种以上基本变形的组合 强度 刚度 稳定性 强度 刚度谓 ,是指材料或构件保持其原有平衡形式的能力。
材料力学内部习题集及答案

材料⼒学内部习题集及答案第⼆章轴向拉伸和压缩2-1⼀圆截⾯直杆,其直径d =20mm,长L =40m ,材料的弹性模量E =200GPa ,容重γ=80kN/m 3 ,杆的上端固定,下端作⽤有拉⼒F =4KN ,试求此杆的:⑴最⼤正应⼒;⑵最⼤线应变;⑶最⼤切应⼒;⑷下端处横截⾯的位移?。
解:⾸先作直杆的轴⼒图⑴最⼤的轴向拉⼒为232N,max 80100.024*********.8N 44d F V F L F ππγγ=+=+=+= 故最⼤正应⼒为:N,maxN,maxN,maxmax 222445004.8=15.94MPa 3.140.024F F F Addσππ?====?⑵最⼤线应变为:64maxmax915.94100.7971020010E σε-?===?? ⑶当α(α为杆内斜截⾯与横截⾯的夹⾓)为45?时,maxmax 7.97MPa 2ασττ===⑷取A 点为x 轴起点,2N (25.124000)N 4d F Vx F x F x πγγ=+=+=+故下端处横截⾯的位移为:240N 0025.1240001d d (12.564000)2.87mm LL F x x x x x EA EA EA+?===?+=?2-2试求垂直悬挂且仅受⾃重作⽤的等截⾯直杆的总伸长△L 。
已知杆横截⾯⾯积为A ,长度为L ,材料的容重为γ。
解:距离A 为x 处的轴⼒为所以总伸长2N 00()L d d 2LL F x Ax L x x EA EA Eγγ?===2-3图⽰结构,已知两杆的横截⾯⾯积均为A =200mm 2,材料的弹性模量E =200GPa 。
在结点A 处受荷载F 作⽤,今通过试验测得两杆的纵向线应变分别为ε1=4×10-4,ε2=2×10-4,试确定荷载P 及其⽅位⾓θ的⼤⼩。
解:由胡克定律得相应杆上的轴⼒为取A 节点为研究对象,由⼒的平衡⽅程得解上述⽅程组得2-4图⽰杆受轴向荷载F 1、F 2作⽤,且F 1=F 2=F ,已知杆的横截⾯⾯积为A ,材料的应⼒-应变关系为ε=c σn,其中c 、n 为由试验测定的常数。
材料力学 第五版 i 截面的几何性质+习题答案

附录I 截面的几何性质 习题解[习题I-1] 试求图示各截面的阴影线面积对x 轴的静积。
(a )解:)(24000)1020()2040(3mm y A S c x =+⨯⨯=⋅=(b )解:)(42250265)6520(3mm y A S c x =⨯⨯=⋅= (c )解:)(280000)10150()20100(3mm y A S c x =-⨯⨯=⋅=(d )解:)(520000)20150()40100(3mm y A S c x =-⨯⨯=⋅=[习题I-2] 试积分方法求图示半圆形截面对x 轴的静矩,并确定其形心的坐标。
解:用两条半径线和两个同心圆截出一微分面积如图所示。
dx xd dA ⋅=)(θ;微分面积的纵坐标:θsin x y =;微分面积对x 轴的静矩为: θθθθθdxd x x dx xd y dx xd y dA dS x ⋅=⋅⋅=⋅⋅=⋅=sin sin )(2半圆对x 轴的静矩为:32)]0cos (cos [3]cos []3[sin 33003002r r x d dx x S r rx =--⋅=-⋅=⋅=⎰⎰πθθθππ因为c x y A S ⋅=,所以c y r r ⋅⋅=232132π π34ry c = [习题I-3] 试确定图示各图形的形心位置。
(a ) 解:习题I-3(a): 求门形截面的形心位置矩形 Li Bi Ai Yci AiYci Yc 离顶边上 400 20 8000 160 1280000 左 150 20 3000 75 225000 右150 20 3000 75 225000140001730000Ai=Li*Bi Yc=∑AiYci/∑Ai(b)解:(c)解:[习题I-4]试求图示四分之一圆形截面对于x轴和y轴的惯性矩x I、y I和惯性积xy I。
解:用两条半径线和两个同心圆截出一微分面积如图所示。
dx xd dA ⋅=)(θ;微分面积的纵坐标:θsin x y =;微分面积对x 轴的惯性矩为: θθθθθdxd x dx xd x dx xd y dA y dI x ⋅=⋅⋅=⋅==232222sin sin )(四分之一圆对x 轴的惯性矩为: ⎰⎰⎰-⋅==2/0042/02322cos 1]4[sin ππθθθθd x d dx x I r rx)]2(2cos 21[2142/02/04θθθππd d r ⎰⎰-⋅= }]2[sin 212{82/04πθπ-=r 164r ⋅=π由圆的对称性可知,四分之一圆对y 轴的惯性矩为:164r I I x y ⋅==π微分面积对x 轴、y 轴的惯性积为:xydA dI xy =8)42(21]42[21)(21444042222022r r r x x r dx x r x ydx xdx I r rx r rxy =-=-=-==⎰⎰⎰- [习题I-5] 图示直径为mm d 200=的圆形截面,在其上、下对称地切去两个高为mm 20=δ的弓形,试用积分法求余下阴影部分对其对称轴x 的惯性矩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 轴向拉伸和压缩
§2-1 轴向拉伸和压缩的概念 §2-2 内力·截面法·及轴力图 §2-3 应力·拉(压)杆内的应力 §2-4 拉(压)杆的变形·胡克定律 §2-5 拉(压)杆内的应变能 §2-6 材料在拉伸和压缩时的力学性能 §2-7 强度条件·安全因数·许用应力 §2-8 应力集中的概念
1、若所挂重物的重量相同,哪根杆危险? 2、若C’的重量大于C的重量,哪根杆危险?
A
细 杆
A’
粗 杆
B
B’
C FN ? FN
C’
A A
材料力学Ⅰ电子教案
第二章 轴向拉伸和压缩
Ⅰ.应力的概念
受力杆件(物体)某一截面的M点附 近微面积ΔA上分布内力的平均集度 即平均应力, p F ,
m A
其方向和大小一般而言,随所取ΔA的大小而不同。
材料力学Ⅰ电子教案
Ⅱ. 截面法·轴力及轴力图
第二章 轴向拉伸和压缩
Fx 0
FN F 0
步骤:
FN F
(1)假想地截开指定截面; (2)用内力代替另一部分对所取分离体的作用力; (3)根据分离体的平衡求出内力值。
材料力学Ⅰ电子教案
横截面m-m上的内力FN其作用线与杆的轴线重合(垂直 于横截面并通过其形心)——轴力。无论取横截面m-m的左
材料力学Ⅰ电子教案
应力具有如下特征: (1)应力定义在受力物体的某一截面上的某一点处; (2)在某一截面上一点处的应力是矢量;
(3)应力量纲:ML-1T -2
应力单位:Pa(1 Pa = 1 N/m2,1 MPa = 106 Pa)。 (4)整个截面上各点处的应力与微面积之乘积的合成,即为
该截面上的内力。(静力等效)
FR
3
F
1
F 2
F F'=2ql
3 F
F
Fx 0 F 2F 2F FR 0
FR F
材料力学Ⅰ电子教案
FR = F
1
F2
1
F2
第二章 轴向拉伸和压缩
q
3
Fx
3
FR = F
FN1 = F
FN3 = F
F
FR = F FR = F
Fq
F N2
F
x1
F F Fx1 l
FN 2
计算简图:
桁架的示意图
(未考虑端部连接情况)
材料力学Ⅰ电子教案
第二章 轴向拉伸和压缩
§2-2 内力·截面法·及轴力图
Ⅰ. 内力
材料力学中所研究的内力——物体内各质点间原来相 互作用的力由于物体受外力作用而改变的量。
根据可变形固体的连续性假设,内力在物体内连续分布。 通常把物体内任一截面两侧相邻部分之间分布内力的 合力和合力偶简称为该截面上的内力(实质为分布内力系的 合成)。
材料力学Ⅰ电子教案
第二章 轴向拉伸和压缩
§2-1 轴向拉伸和压缩的概念
工程中有很多构件,例如屋架中的杆,是等直杆,作 用于杆上的外力的合力的作用线与杆的轴线重合。在这种 受力情况下,杆的主要变形形式是轴向伸长或缩短。
屋架结构简图
材料力学Ⅰ电子教案
第二章 轴向拉伸和压缩
受轴向外力作用的等截面直杆——拉杆和压杆
FN1=10 kN(拉力)
材料力学Ⅰ电子教案
第二章 轴向拉伸和压缩
(3)为方便,取横截面1-1左边 为分离体,假设轴力为拉力, 得: FN2=50 kN(拉力)
(4)为方便取截面3-3右边 为分离体,假设轴力为拉 力。
FN3=-5 kN (压力),同理,FN4=20 kN (拉力)
材料力学Ⅰ电子教案
第二章 轴向拉伸和压缩
为此: 1. 观察等直杆表面上相邻两条横向线在杆受拉(压)后
的相对位移:两横向线仍为直线,仍相互平行,且仍垂直 于杆的轴线。
2. 设想横向线为杆的横截面与杆的表面的交线。
平面假设——原为平面的横截面在杆变形后仍为平面,对 于拉(压)杆且仍相互平行,仍垂直于轴线。
材料力学Ⅰ电子教案
材料力学Ⅰ电子教案
第二章 轴向拉伸和压缩
该截面上M点处分布内力的集度为
p
lim F
A0 A
dF dA
,其
方向一般既不与截面垂直,也不与截面相切,称为总应力。
材料力学Ⅰ电子教案
第二章 轴向拉伸和压缩
总应力 p
法向分量 正应力s 切向分量 切应力t
某一截面上法向分 布内力在某一点处 的集度
某一截面上切向分 布内力在某一点处 的集度
第二章 轴向拉伸和压缩
3. 推论:拉(压)杆受力后任意两个横截面之间纵向线段的伸长(缩短)变 形是均匀的。 根据对材料的均匀、连续假设进一步推知,拉(压)杆横截
F
x1
Fx 0
FN2
2F
-
FR
-
Fx1 l
0
FN2
Fx1 l
F
材料力学Ⅰ电子教案
第二章 轴向拉伸和压缩
F q=F/l
F
l
2l
F l
F +
F
FN 图
F +
材料力学Ⅰ电子教案
第2章 拉伸、压缩与剪切
§2-3 应力·拉(压)杆内的应力
问题的提出: 杆AB与杆A’B’材料相同, 杆A’B’的截 面积大于杆AB的截面积。
边或右边为分离体均可。 轴力的正负规定: 按所对应的纵向变形为伸长或缩短 当轴力背离截面产生伸长变形为正;反之,当轴力指向
截面产生缩短变形为负。
轴力背离截面FN=+F
材料力学Ⅰ电子教案
第二章 轴向拉伸和压缩
Fx 0 FN F 0 FN F
轴力指向截面FN=-F
注意事项:用截面法求内力的过程中,在截取分离体 前,作用于物体上的外力(荷载)不能任意移动或用静力等 效的相当力系替代。
材料力学Ⅰ电子教案
Ⅱ.拉(压)杆横截面上的应力
第二章 轴向拉伸和压缩
分析:
FN
s dA
A
(1) 与轴力相应的只可能是正应力s,与切应力无关;
(2) 横截面上各点处s 相等时可组成通过横截面形心 的法向分布内力的合力——轴力FN;横截面上各点处s 不
相等时,特定条件下也可组成轴力FN。
材料力学Ⅰ电子教案
材料力学Ⅰ电子教案
第二章 轴向拉伸和压缩
F
F
(c)
(f)
轴力图(FN图)——显示横截面上轴力与横截面位置 的关系。
材料力学Ⅰ电子教案
例题2-1 试作此杆的轴力图。
第二章 轴向拉伸和压缩
(a)
等直杆的受力示意图
材料力学Ⅰ电子教案
解:
第二章 轴向拉伸和压缩
(1)为求轴力方便,先求出约束力 FR=10 kN (2)为方便,取横截面1-1左边 为分离体,假设轴力为拉力, 得
第二章 轴向拉伸和压缩
轴力图(FN图)显示了各段杆横截面上的轴力。 FN,max FN2 50 kN
思考:为何在F1,F2,F3作用着的B,C,D 截面处轴力图 发生突变?能否认为C 截面上的轴力为 55 kN?
材料力学Ⅰ电子教案
第二章 轴向拉伸和压缩
例题2-2:试作此杆的轴力图。
q
F
F
l
F
解: FR
