《画法几何及阴影透视第9章阴影》第1节阴影的基本知识

合集下载

《画法几何与阴影透视》第9章形体的阴和影复习思考题答案

第9章形体的阴和影复习思考题答案复习思考题9.1 阴和影有何区别？两者之间又有何关系？答：阴是指物体表面的背光部分，而影是指光线被物体阳面遮挡而在承影的阳面上所产生的阴暗部分。

物体的阴和影是随着光线的照射角度和方向而变化的，光源的位置不同，阴影的形状也不同。

9.2 什么是光线三角形法？答：由投射线和过点的空间光线及光线在平面上的投影构成的直角三角形称为光线三角形。

用光线三角形求解空间点在平面上落影的作图方法叫光线三角形法。

9.3 什么是端点虚影法？答：当承影面为投影面时，通过已知点的光与投影面的交点就是该点的落影。

如图9.6所示，为了作出通过空间点A的光线与投影面交点，可包含过A点的光线S作一铅垂面铅垂面F与投影面V和H的交线分别为fv、fH，过A点的光线S与交线fv的交点Av就是A点的真影。

假如没有V投影面，A点人形应落在(A H)处，故影点(A H)称为虚影。

虚影一般不画出，在以后的作影过程中，常常利用它来求直线的折影点。

这种求点落影的作图方法称为端点虚影法。

9.4 什么是光截面法？答：过空间点的空间光线，过空间点到投影面的投影线，以及空间光线在投影面上的投影组成铅垂光平面，利用光平面与立体之截交线求点落影的作图方法叫光截面法。

9.5 在正投影图中常用光线的方向是怎么规定的？用这种光线作影有何优点？为什么可以根据空间点对投影面的距离来作其落影？答：在正投影图中绘阴影，选用特定方向的平行光线，即当正立方体的各侧棱面平行于相应的投影面时，光线从正立方体的左、前、上角射向右、后、下角，即正立方体对角线的方向，常用光线的三个投影s、s′、s″与投影轴的夹角均为45°。

利用常用光线在正投影图中作阴影，可使物体各部分的落影宽度等于落影物伸出或凹进承影面的尺度，也正是每个正投影图所缺少的尺度，故作影后使物体的一个正投影图反映了长、宽、高三个方向的尺度，图形自然有立体感，其原因就是常用光线的各投影与投影轴之夹角为45°9.6 阐述直线落影的平行规律、相交规律、垂直规律。

第一节阴影的基本知识画法几何及阴影透视课件

光线阳面阴线阴面
影（或称落影）
影线
承影面
3
二、正投影图中加绘阴影的作用
（a）未画阴影的正投影图
（b）画出了阴影的正投影图
4
5
三、阴影在建筑表现图中的效果
(a) 未画阴影、图面单调呆板
(b) 加绘阴影、图面生动美观
6
四、常用光线
1
L l′ l" l' l"
45°
2 1
45°
1
45° 45°
57
1. 平行于投影面的多边形在该投影面上的落影
a' e'
b'
c' Bv
Av
d'
Ev
Dv
X
Cv
O
ab
c
de
58
59
2. 平面多边形在其平行平面上的落影
a' a'p e' e'p d'
b' b'p
c'
d'p
c'p
ab c PH ed
60
3. 平行于光线的平面图形的落影
a'
e' e'p
b'
c'
d'
第1节阴影的基本知识和点、直线、平面的阴影
§9-1 阴影的基本知识 §9-2 点的落影 §9-3 直线的落影 §9-4 平面的阴影
1
§9-1
阴影的基本知识
一、阴和影的形成二、正投影图中加绘阴影的作用三、阴影在建筑表现图中的效果四、光线和常用光线五、求常用光线的真实倾角
2
一、阴和影的形成

阴影的基本知识和点线面的阴影.ppt

O' Ov
O
56
水平圆在V面上的落影
O'
O'
O'
O'
Av
1v
Dv Av
6v 1ve
Dv Av 5v
1v 6v
Dv 5v
2v
Ov
4v 2v
Ov
4v 2v
Ov
4v
Bv
3v
Cv
7v Bv
8v 3v
Cv
7v Bv
8v 3v
Cv
a
1
d
(b)
(c)
(d)
2
O4
c
b
3
(a)
侧平圆在V面上的落影
Av
Dv
Ov
Bv
Cv
水平半圆在V面上的落影
1' 2'
Ⅰv
1
3'
4' 5Ⅴ' v
Ⅱv
Ⅳv
Ⅲv
5
2
4
3
• 水平圆在两个承影面上的落影
练习
求平面的落影
求落影
本章结束
A0
C0 C0 B0
c’ a0’
c0’
c0’ b0’
c
相交规律
直线与承影面相交，直线的落影必过交点
B L
B0
P A A0
两直线相交，落影也相交交点的影，就是两落影直线的交点
A A0
a’
a0 a
直线落在两相交承影面上落影为两段相交的折线
K A0
B0 K0
折影点
k’
a0 k
b0’ (b0) k0
平面多边形平行光线，其落影积聚为一条直线或折线

阴影透视透视图中的阴影PPT课件

• 1、水平线的落影
F
1
A
V2
Fx h
a
4B
N
―B
s°
Fy
V3 h
3 b2
E
―N
1
―
D ―E
AJ
14
第14页/共39页
三、直线的落影
V4
• 2、一般位置斜线的落影
F
A
B4
F V2
2
1
N
Fx h
― f2
Fy V1
V3
B
h
2E
b3
1
―N
a
― A
D J
―E
15
第15页/共39页
三、直线的落影
• 结论：画面平行光下，画面相交线的落影仍是画画相交线。其透视有灭点。 • 光平面灭线和承影面灭线的交点是两平面交线（即落影）的灭点。画面平行光下，光平面灭线是过该直线
灭点的光线平行线。
16
第16页/共39页
四、平面图形的阴影
• 1、平面图形的落影，是平面图形边线落影的集合。 • 2、平面的一侧为阴面，另一侧则为阳面。
17
第17页/共39页
四、平面图形的阴影
• 阴阳面的判别
18
第18页/共39页
四、平面图形的阴影
• 3、当平面与光线平行时，落影成直线段，平面的两侧均为阴面。
V3
V3
V2
V2
V2
V3 F1
Fx
C
D
B
A
Fy
V1
2、求作台阶的阴影。
22
第22页/共39页
五、建筑形体阴影作图示例
V3
V2
F1
ቤተ መጻሕፍቲ ባይዱ

阴影透视第一章建筑阴影的基本知识

阴影透视
第一章绪论
呈现阴影的三要素：光线、物体、承影面。呈现阴影的三要素：光线、物体、承影面。二习用光线为了作图简捷和度量方便，常采用一种特殊的平行光线，为了作图简捷和度量方便，常采用一种特殊的平行光线，称为习用光线。称为习用光线。习用光线在空间的方向为平行于各投影面的正立方体的体对角线的方向，它与三个投影面的倾角均相等，正立方体的体对角线的方向，它与三个投影面的倾角均相等， α=β=γ=35° α=β=γ=35°。
阴影透视
第一章绪论
§1-1 阴影的基本知识
在房屋建筑立面图上，准确的画出阴影，在房屋建筑立面图上，准确的画出阴影，可以使房屋凹凸、深浅、明暗的差异一目了然，屋凹凸、深浅、明暗的差异一目了然，从而使图面生动逼真，富于立体感，加强并丰富了立面图的表现力。逼真，富于立体感，加强并丰富了立面图的表现力。在立面图上画出阴影对研究建筑物造型是否优美，在立面图上画出阴影对研究建筑物造型是否优美，立面是否美观，比例是否恰当都有很大的帮助。立面是否美观，比例是否恰当都有很大的帮助。
a' l' 45° X 45° a l
Z
a'' l'' 45° YW
O
YH
阴影透视
§1-2 点的影
第一章绪论
一点在投影面上的落影 —— 光线迹点法 1.点在一个投影面上的落影 1.点在一个投影面上的落影如图所示，求点B的影，其实质是过点B作直线与习用光如图所示，求点的影，其实质是过点作直线与习用光的影线平行，然后求出该直线与承影面的交点．即为点B的影的影B 线平行，然后求出该直线与承影面的交点．即为点的影 O。在投影面上的点A，它的影A 与自身重合。在投影面上的点，它的影 0与自身重合。实质：点在承影面上实质：的影，的影，是过该点的光线延长后，线延长后，与承影面的交点。的交点。

画法几何与阴影透视教案-阴影透视

4、平面的阴影
三、与画面相交的平行光线下的阴影
1、竖直线在水平、垂直面上的落影
在水平面上的落影通过光线的基灭点。在倾斜面上的落影通过倾斜面的灭线和光平面灭线的交点。
2、与画面倾斜直线的落影
直线与承影面交点的落影就是它本身，这一点在作图中非常重要。与承影面平行的直线，在平行光线的照射下，其落影在空间平行于原直线，在透视图中与原直线有共同的灭点，图中MN直线平行于地面，在地面上的落影与MN直线具有相同的灭点。
1、阳面：面向光线照射方向的平面或曲面称为阳面，在透视图中比较明亮。
2、阴面：背向光线照射方向的平面或曲面称为阴面，在透视图中较暗。
3、承影面：物体被光线遮挡以后，在一些面上会出现阴影，这些面称为承影面。
二、画面平行光线下的阴影
1、画面平行光线的透视性质
2、点的落影
3、直线的落影将属于直线上的两点的落影求出，连线即为直线的落影。直线在承影面上的落影为过直线的光平面与承影面的交线。
教学基本内容纲要
一、阴影的基本概念
1、光平面：包含空间直线和光线的平面。
2、光线的种类
二、画面平行光线下的阴影
1、画面平行光线的透视性质
2、点的落影
3、直线的落影
4、平面的阴影
三、与画面相交的平行光线下的阴影
1、竖直线在水平、垂直面上的落影
2、与画面倾斜直线的落影
四、中心光线（辐射光线下）的阴影
教学重点
与难点
重点：绘制阴影图的基本方法；平行光线下的阴影。
难点：各种阴影图的画法；中心光线的阴影
教学过程
设计
一、阴影的基本概念
1、光平面：包含空间直线和光线的平面。
2、光线的种类
（1）、平行光线：平行光线包括与画面平行的行光线和与画面相交的平行光线。

阴影

求物体的阴影时，可按下列步骤进行：
(1) 根据常用光线的方向，找出物体的阳面与阴面，从而确定出阴线；
(2) 分别求出阴线上各端点在承影面(如墙面、门扇、窗扇等)上的影； (3) 连接阴线各端点的影柱的阴影
建筑立面细部的影子
门洞、雨篷、阳台及挑檐的阴影

门洞的影与窗洞的阴影求法类似；雨篷、挑檐的影与遮阳板的阴影求法相同。
房屋立面图上的阴影

画房屋立面图的阴影时，首先应了解各建筑细部在立面上的凹凸变化、
具体尺寸和相互位置关系，然后运用求阴影的基本方法，画出房屋立面图上的阴影。
阳台的阴影
房屋立面图上的阴影效果
直线的影
正垂线的影

正垂线在正平面上的影是一段通过该线段的积聚投影，且与水平线成
45°的斜直线。
正垂线在正平面上的影

侧垂线在正平面上的影与该侧垂线的V面投影平行且相等，二者之间的距离等于侧垂线与正平面之间的距离。铅垂线在正平面上的影是一段与该铅垂线的V面投影平行且相等的铅直线，二者之间的距离等于铅垂线与正平面之间的距离。

阴影的概念
2 、常用光线

特定方向的平行光线称为常用光线。
3、求阴影的基本方法

点的影——求点的影，就是求通过该点的光线(直线)与承
影面的交点。
点在墙面上的影
直线的影

直线在承影面上的影一般仍为直线，只有当直线平行于光线时，它的影
才是点。

若要作直线在某个承影面上的影，可先作出直线两端点的影并连接，即为该直线的影。
阴影
1、阴影的基本知识
阴影的概念

阴影形成的三个条件：光源、阻挡光线的物体、形成落影的表面。

《画法几何与阴影透视》教学课件—09形体的阴与影

5)、着色(受光区应着亮色)。
W
V
c〞
C
s〞
Cw
c
KH
AH
A
S B ﹙b﹚a
s
BH
H
画法几何与阴影透视
（4）雨蓬与隔板的阴影
作影思路：
1)、根据A点的落影Aw,
D
定出空间光线S及其投
C
影s、s′、s〞；
2)、由光线的方向定出雨蓬及隔板的阴线；
3)、依次作出上述阴线的影线；
5)、着色。
Dv
Cv
P
ap′
ap
PH
a
画法几何与阴影透视
点在一般位置平面上的落影
a′
s′
2′
P′
ap′
1′
2
sap
FH P
1
a
画法几何与阴影透视 a′
（3）当承影面为立体表面时，点的落影为含该点的光线与立体的交点。
t
C
D
a
画法几何与阴影透视
（3）圆柱的阴影
作阴影步骤：
1)、根据光线方向确定阴、阳面，从而定出阴线；
S
Ⅳ Ⅲ
Ⅴ
s
2)、逐段求出各段阴线的
落影；(即为圆柱落影的
Ⅱ
轮廓线)
3)、着色。
Ⅳo
Ⅴo
Ⅲo
Ⅰ
4
Ⅱo
3
5
Ⅰo
2
s
1
画法几何与阴影透视（4）圆筒内壁的阴影
S s
31
21 Ⅰ
41
51 Ⅵ
Ⅴ
Ⅴ0
Ⅳ
Ⅱ
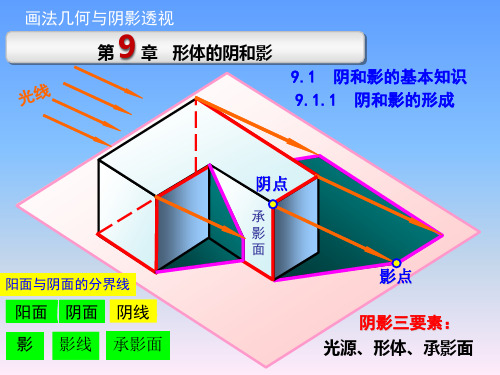
【例9.2】已知直线Aa为铅垂线；平面P为倾斜面，平面P在水平面上的投影为四边形DefG；光线方向为S，S在水平面上的投影为s，求直线Aa的落影。

阴影-美术类PPT课件

-
24
5. 雨蓬和门洞的阴影
从图7-32a看出，雨蓬的阴线段为ABGDE，其影落在墙面和门扇两个互相平行的承影面上。门洞边框的阴线段是FGI，其影落在门扇上，其中阴线段GI的影落在雨蓬的落影范围内，因此，作图时只需作出阴线FG的落影。
-
25
6. 台阶的阴影
从图7-36a中可以看出，台阶左栏板的阴线段ABC落影于地面、台阶的踢面和踏面以及墙面上。右栏板阴线段DEF则落影于地面和墙面上。阴影的作图如图7-36b所示。
45°，且通过DI的V投影d'(i')；
(4) 阴线段IE平行于V面，它在V面上的落影i'0e'0与
其V投影i'e'平行且长度相等；
(5) 阴线EF与CD类似，可按CD的落影作法作出EF
的落影。
-
23
4. 窗洞与窗台的阴影
从图中可以看出，窗洞边框的阴线段是EFG，其影分别落在窗台上、窗扇上。窗台的阴线段是IABCD，其影落在墙面上。根据点在承面上的落影与其在该面上的投影的水平、垂直距离等于空间点对该面的距离的性质，可以得出，落影宽度m反映了窗台出墙面的距离，落影宽度n反映了墙面凹入墙面的距离。
-
演示演示 14
-
返回
15
返回 -
下一页
16
8. 一直线同时落影于两承影面的作图
例2：求直线AB在P、Q面上的落影。空间分析：直线AB有一部分落影在P面上，另有一部分落影在Q面上，其落影的转折点必积聚在承影面P和Q的交线上。
-
17
三、平面多边形的落影
1. 平面多边形的落影作图
平面多边形落影的轮廓线--影线，就是多边形各边线的落影，影线所包围的区域就是该平面多边形在承影面上的落影。如图所示，平面多边形的落影的作图，为先作出它的顶点的落影，然后用直线依次连接而成．

阴影透视第一章建筑阴影的基本知识 - 副本

H H
c' c' d'
V
V
cd
阴影透视
第一章绪论
2.正垂线在V面上的落影与光线的V投影平行，即为与 OX轴成45°的直线；在H面上的落影与正垂线H面投影平行，即OX轴垂直。正垂线H面上的落影与正垂线的H投影的距离等于直线H面的距离。
第一章阴影的基本知识
一建筑阴影的基本概念与术语建筑物在光线照射下，一些表面向着光线，被照亮，称为阳面；另一些表面则背着光线，光线照射不到，显得阴暗，称为阴面。阳面和阴面的分界线称为阴线。照射在阳面上的光线，由于被建筑物挡住而形成了一些暗区。这些暗区与建筑物另一些表面或地面也交得黑暗的区域，这个区域称为影子或影，影的轮廓线称为影线，影所在的面称为承影面，阴面和影子合称为阴影。
d' c'
c
d
阴影透视
第一章绪论
2.特殊情况下，在投影面上作直线的落影时，可分别作出直线两端点的落影，如果两端点的落影不在同一承影面上时，则不能直接连接两端点的落影，而是要首先求出转折点，再相连。求转折点的方法：（1）求出一点在某一投影面上的虚影，把同一投影面上的真影与虚影相连，与OX轴的交点即为转折点。
V (A ) (a )
H H
a' X a a L
V
V
(a )
H
a
V
H
L
O
(a' ) O
H
阴影透视
第一章绪论
例1 求点B落在投影面上的影。
b' X O
b
分析：点B的V投影距投影轴的距离小于H投影距投影轴的距离，所以点B在H面上的落影为真影。
阴影透视
第一章绪论

第1章阴影基本知识及轴测图中的阴影

一、几何元素的落影
(一)、点的落影概念及求作 (二)、直线的落影及其落影规律 (三)、平面图形的阴影 1、平面图形落影的概念 ----通过该平面图形轮廓线上的光线所形成的光柱面与承影面的交线。 2、平面图形落影的求法 ----求平面图形轮廓线上各点同面落影的集合。 ①平面的落影：在一个承影面上的落影
2、棱锥的阴影：
S
S0
D E F A
C
B
二、基本几何体的阴影
3、圆柱的阴影：
D
S
s
O
B
Dh Oh
C
Bh
o
A
二、基本几何体的阴影
5、圆锥（正圆锥）
S
圆锥（倒圆锥）
S
s s
S
B
Sh
O
A
B
Bh
o
Oh
A
Ah
S
• 组合平面体的阴影
I
H
F M D
GKBiblioteka ECB L
A
D
F
E
K
L
B
G
C
H
I
M
A
§1-3 建筑细部的阴影
一、方帽圆柱的阴影(光线三角形法)
D
C
A Ⅲ
s
Ⅱ Ⅰ
E B
d0
a0
S
Ⅲ0
Ⅱ0 Ⅰ0
e0
E0 A0
D0
二、台阶的阴影(延棱扩面法)
C
B
A
b
3
B
G
F E
B2
A1
A
1 2
D
a
三、窗在室内的落影
V
C A
W
D
B
CW

01阴影基本知识及轴测图阴影

10
三、平面图形的阴影平面图形的阴影
V 1、平面图形落影的概念
A
三角形平面的落影
Av
B
(AH)
S s
X
BH
Ⅱo
av Ⅰo O
C CH c
2、平面图形落影的求作：通常平面图形落影的求作：平面图形落影的求作是用平面图形轮廓线上各点同是用平面图形轮廓线上各点同面落影连线来求作影线。面落影连线来求作影线。当各点的影不在同一平面上时，点的影不在同一平面上时，应利用假影求得折影点影求得折影点，利用假影求得折影点，再与其影相连。真影相连。
b a
H
四、基本几何体的阴影
1、棱柱的阴影棱柱的阴影阴线
C
D
阳面
B
A
s
s
S
阳阳面面
d c
S s
Do Co Bo
s
a
s
b
s
其余表面为阴面
12
2、棱锥的阴影
T
S
To (F) s E t C
D
13
§1-3
建筑细部的阴影
b′ s′ V F Ⅲ B
阴线
14

台阶的阴影
BH2
E
EH1 S s A
s′
第一章阴影
§1－1
一、阴影的形成
阴影的基本知识
二、图样中为何要加绘阴影
§1－2
一、点的落影及作法
轴测图中的阴影
二、直线的落影及作法四、基本体的落影及作法
三、平面的落影及作法
§1－3 建筑细部的阴影
2
§1－1 阴影的基础知识
一、阴影的形成
阳面

阴影图ppt(点、线)2011

３、交叉两条直线
(1)直线光线平面不平行空间交叉两直线的光线平面不平行，则他们的落影必然相交。
(2)投影光线平面平行空间交叉两直线的光线平面平行，则他们的落影必然也平行。
直线的影子投影小结一、直线在一个承影面上影子特性
１、直线与承影面相交
直线与承影面相交时，直线的影子通过交点，故影子的投影也通过交点的投影。
3、假影法——利用直线上点的假影
（1）点的假影落在V面上点的影子和H面上的假影及其作图
（2）假影法求直线一个端点的假点，确定直线在这个投影面上落影的方向，从而得到折点K，进而求得直线的落影。
4、光线返回法——利用两承影面的积聚性
直线与投影轴x交点的侧面投影就是原点，根据常用光线可得e”,反求可得折点eo,从而可以确定直线落影的方向，进而球的直线的落影。
(1)点落于平面图形内 (2)点落于平面图形外
点的影子投影小结
1、点的投影特性
空间点在某投影面上的落影，与其同面投影之间的水平距离和垂直距离，都正好等于空间点对该投影面之间的距离。
2、假影
假影不是真实存在的影子，假想投影面是透明的，点在另一投影面上产生的影子叫假影。
3、一般位置平面上的点
一般位置平面上的点的落影，采用画法几何中的辅助平面法求取。
２、垂直线的影子落在物体上
（1）垂直线落影的不变性垂直线在所垂直的方向落影，不管承影面如何，其落影均是与光线一致的450直线。
（2）垂直线落影的对称性 a、承影面为投影面垂直面垂直线在所垂直的投影面以外的两个投影面的投影，不管承影面如何，其另两个落影总是对称的。
b、承影面为一般位置面
三、投影面垂直线的影子的投影特性
（1）不变性：垂直线在所垂直投影面上，不管承影面如何，它的影子为一条450直线 (2) 落于另一投影面上的影子与直线本身的同名投影互相平行，且两投影间距离等于直线到承影面的距离。 (3) 落于两投影面上的影子是一条450直线和一条与直线本身平行直线组合的折线（4）对称性：垂直线在所垂直的投影面以外的两个投影面的投影，不管承影面如何，其另两个落影总是对称的。

阴影的基本知识

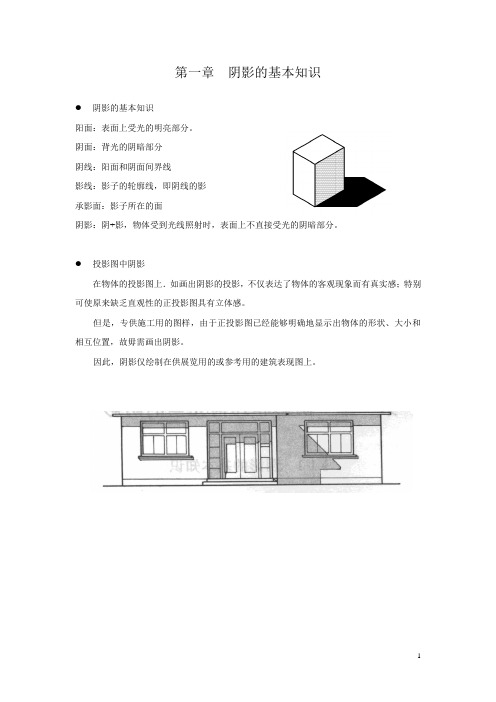
第一章阴影的基本知识
●阴影的基本知识
阳面：表面上受光的明亮部分。

阴面：背光的阴暗部分
阴线：阳面和阴面间界线
影线：影子的轮廓线，即阴线的影
承影面：影子所在的面
阴影：阴+影，物体受到光线照射时，表面上不直接受光的阴暗部分。

●投影图中阴影
在物体的投影图上．如画出阴影的投影，不仅表达了物体的客观现象而有真实感；特别可使原来缺乏直观性的正投影图具有立体感。

但是，专供施工用的图样，由于正投影图已经能够明确地显示出物体的形状、大小和相互位置，故毋需画出阴影。

因此，阴影仅绘制在供展览用的或参考用的建筑表现图上。

光线与常用光线
不同方向的光线，将产生不同形状的阴影。

在建筑图上加画阴影时，通常采用下述方向的平行光线，即光线L由左、前、上向右、后、下，并使光线L的三个投影l、l’、l’’对投影轴都成450的方向。

相当于由该正方体的前方左上角，射至后方右下角的对角线方向。

这种方向的平行光线，称为常用光线，常用光线与三个投影面的倾角均相等，
正投影图上使用常用光线作阴影，非但将使作图时方便和有统一的规律，且如以后所述，在某些情况下，可使阴影反映出有些形体的形状和相互间的距离关系而有量度性。

画法几何与阴影透视讲义

my
mx
fy
Fx
My
Mx
C°
Fy
g'
d1
B° A
D°
b1
B
L
画法几何与阴影透视讲义－透视篇
第九章
建筑透视图的基本画法
（2）用量点法求建筑形体的透视（a）
立面图
y
5 4 3 2 n2 6 mx
x
10
9 平面图
8 my n1
7
1
（a）已知条件
画法几何与阴影透视讲义－透视篇
第九章
建筑透视图的基本画法
用量点法求建筑形体的透视（b）
画法几何与阴影透视讲义－透视篇
第九章 b
建筑透视图的基本画法
（2）量点的作法
a a1 m b1
fm=fs
f
t
M B° A°
s
F
量点
b1
a1
T
Ta1=ta1
Tb1=tb1
画法几何与阴影透视讲义－透视篇
第九章
建筑透视图的基本画法
多方向时的量点
x y
fx
my
mx
fy
d1
b1
Y方向量点
Fx My
X方向量点
画法几何与阴影透视讲义透视篇第九章建筑透视图的基本画法二用量点法求建筑形体的透视用量点法求矩形的透视2用量点法求建筑形体的透视2用量点法求建筑形体的透视画法几何与阴影透视讲义透视篇第九章建筑透视图的基本画法1用量点法求矩形的透视1用量点法求矩形的透视画法几何与阴影透视讲义透视篇第九章建筑透视图的基本画法2用量点法求建筑形体的透视a2用量点法求建筑形体的透视a立面图平面图a已知条件画法几何与阴影透视讲义透视篇第九章建筑透视图的基本画法用量点法求建筑形体的透视用量点法求建筑形体的透视bb透视平面图画法几何与阴影透视讲义透视篇第九章建筑透视图的基本画法用量点法求建筑形体的透视用量点法求建筑形体的透视cc透视图画法几何与阴影透视讲义透视篇第九章建筑透视图的基本画法用距点法求形体的一点透视画法几何与阴影透视讲义透视篇第九章建筑透视图的基本画法1距点的概念空间图1距点的概念空间图454545454545aabb实际为量点的特例aa画法几何与阴影透视讲义透视篇第九章建筑透视图的基本画法距点的作法透视图距点的作法透视图4545画法几何与阴影透视讲义透视篇第九章建筑透视图的基本画法2用距点法求形体的一点透视a2用距点法求形体的一点透视a已知立面图平面图画法几何与阴影透视讲义透视篇第九章建筑透视图的基本画法用距点法求形体的一点透视b用距点法求形体的一点透视b求出距点d画法几何与阴影透视讲义透视篇第九章建筑透视图的基本画法用距点法求形体用距点法求形体的一点透视c透视平面图透视图画法几何与阴影透视讲义透视篇第九章建筑透视图的基本画法四距点法做室内透视

九阴影PPT课件

L A
A
l
1
B
例3 求直线在平面H 、P、Q上的落影
A
D
2
C
AP Q DpQ
B
CH 1
虚影
9.2 透视图中的阴影
一、画面平行光线下的阴影
1、画面平行光线的透视特性
（1）画面平行光线没有
L
V
灭点也称无灭光线。
l
S
（2）光线的透视与本身
O
平行。
X
s H
（3）光线的次透视是水
平线。
2、透视图上落影的基本画法
包含ＡＢ的光平面
灭线
二、画面相交光线下的阴影
1、画面相交光线的透视特性
L ML
l
X
V h
S
O s H
（1）画面相交光线有灭点也称有灭光线。
（2）光线的灭点在视平线的下方或上方，光线的透视汇交于光线的灭点。
Ml
（3）光线的次灭点在视平
线上，光线的次透视汇交于
光线的次灭点。
M1
M1
ML
Ml
常用光线
h
F
E
D
C 41 B
3A
E
D
42
B
Ld
1
l
a
A
例3：设定平行光线加绘台阶的阴影
L 绘制要点：利用阴线与承影面的交点求落影 C
2 6B
C0
A
8
7
B0 9
l
3
5
4
A0
1
F F0
10
L
lቤተ መጻሕፍቲ ባይዱ
B
C
6
c
C0
A2
8
3

阴影透视

二.阴影与光线
（一）阴影的分类
• 光有两种：阳光和日光。 • 阳光的光线是平行光，灯光的光线是放射光。 • 因此，阴影也分为两类：阳光阴影和灯光阴影。
（二）决定阴影形状的因素
1.受光物的形状：物体的大小，长短，高低，方圆等；
2.光源的种类：阳关或灯光；
3.光和物体的关系：光源处于不同的高度和方向；
作业：
习题集P85—P86页；
先从光足引经门底的直线与墙基线相交的点，过点向上作垂线；再从光点经门上端点引直线与点的垂线相交的B`点。先从光点经门上端A点引直线，从光足经门底C点引直线，两直线相交的 A`点；再过A`点作水平线与墙基线相交于E点， E点连接B`点，完成门在墙壁上的落影。
注意：落影的变化，取决于光源位置和光线角度，也取决于受影面的变化。
（一）立方体灯光阴影透视
确定光源高度，光足位置，分别过光源，光足作点ABCD和abcd连线并延长相交于 A1B1C1D1各点，连接各点完成透视图。
注意：与受影面垂直的直线，其影线消失于光足，如Aa与A1a；与受影面平行的直线，其影线和该直线透视方向一致，如AB与A1B1。
（二）室内灯光的光源是在有限的距离内，光足在基面上。灯光照
射通常处于室内，光线呈放射状，其产生的阴影效果与阳光阴影效果不同：一个灯光光源的环境中，可以有很多投影面，
如：地面，天花板，墙壁和桌面等，每个投影面上均有一个光足。物体的灯光阴影是有垂直，平行，倾斜于投影面的影线所构成，可归结为垂直直线和平行直线投影法则，即垂直于投影面的直线，其影线向投影面的光足集中；平行于投影面的直线，其影线与该直线平行，同一个消失点。当直线的影线在两个投影面出现时，按各个投影面与直线的关系确定。

画法几何与阴影透视9

• 空间直线上两线段的长度相等时，他们在承影面上的影子线段长度亦相等；又如空间直线上两线段长度之比，与他们的两影子线段长度之比亦相等。
如：ⅠⅡ=ⅡⅢ，则
Ⅰ0Ⅱ0=Ⅱ0Ⅲ0 ；
ⅠⅡ：ⅡⅤ= Ⅰ0Ⅱ0：Ⅱ0Ⅴ0
直线在一般位置平面上的落影
b‘
0
a‘
0
• 作出两个端点的影子的同名投影，相连即可得出直线的影子的同名投影。
L B A
B0 A0
b'
b' 0
a'
a’
d
a' 0
p'
a0 b0 P
a
b
b’ b’0
a’0
三、投影面垂直线的影子的投影特征
（1）投影面垂直线的影子在该投影面上投影
某投影面垂直线落于该投影面或平行投影面上影子，在该投影面必成一
直线，方向与光线在该投影面上45度投影方向一致。
影子在水平方向或垂直方向的宽度，等于直线本身长度。
A点影落在V面上 B点影落在H面上
C点影落在X轴上 D点影与自身重合
点在投影面上落影四种情况的投影图
影子的度量性：一点在某一投影面上的投影和影子间的水平和竖直距离，等于该点到该投影面的距离。
单面作图：应用点在投影面上的落影规律
l' d
d A0
a' 0 (c)
点在投影面上落影的求法
c’
b0’
K’’
K0’’
k0
o
作法三
（3）影子落于任何物体之上时
• 形成影子的直线为某一投影面垂直线时，则落于任一物体上的影子，在该投影面上的投影必定为一直线，且其方向与光线在该投影面上的投影方向（45°）一致。