语音信号采样和频谱分析
声音信号的频谱分析与频率测量方法

声音信号的频谱分析与频率测量方法声音是我们日常生活中不可或缺的一部分,我们通过声音来交流、表达情感,甚至通过声音来判断事物的性质。
然而,声音是如何产生的?我们如何对声音进行分析和测量呢?本文将介绍声音信号的频谱分析与频率测量方法。
声音信号是由空气中的振动引起的,当物体振动时,会产生压力波,通过空气传播出去,我们就能听到声音。
声音信号可以通过振动的频率和振幅来描述,其中频率是指振动的周期性,而振幅则是指振动的强度。
频谱分析是一种将声音信号分解成不同频率成分的方法。
它可以帮助我们了解声音信号的频率分布情况,从而更好地理解声音的特性。
频谱分析的基本原理是将声音信号转换为频域表示,即将信号从时域转换为频域。
这可以通过傅里叶变换来实现。
傅里叶变换是一种将时域信号转换为频域信号的数学方法。
它将信号分解成一系列正弦波的叠加,每个正弦波都有不同的频率和振幅。
通过傅里叶变换,我们可以得到声音信号的频谱图,从而了解声音信号中不同频率成分的贡献程度。
频谱图通常以频率为横轴,振幅或能量为纵轴,通过不同的颜色或灰度表示不同频率成分的强度。
频谱图可以直观地展示声音信号的频率分布情况,帮助我们分析声音的特性。
例如,在音乐领域,频谱分析可以用来研究音乐的音色特点,判断乐器的类型等。
除了频谱分析,频率测量是对声音信号进行定量分析的重要方法。
频率是声音信号中最基本的特征之一,它决定了声音的音调高低。
频率测量可以通过多种方法实现,其中一种常用的方法是自相关法。
自相关法是一种基于信号自身的周期性特点进行频率测量的方法。
它通过计算信号与自身的延迟版本之间的相似程度来确定信号的周期性。
具体而言,自相关法将信号与其自身进行延迟,然后计算它们之间的相关性。
通过寻找最大相关性的延迟值,我们可以得到信号的主要频率成分。
除了自相关法,还有一些其他的频率测量方法,如峰值检测法、零交叉法等。
这些方法在不同的应用场景下有着各自的优势和适用性。
例如,峰值检测法适用于测量周期性信号的频率,而零交叉法适用于测量非周期性信号的频率。
语音信号的采集与分析

南昌工程学院《语音信号的采集与分析》课程设计题目语音信号的采集与分析课程名称语音信号处理系院信息工程学院专业通信工程班级 10通信工程2班学生姓名刘敏学号 2010103362设计地点电子信息楼指导教师邹宝娟设计起止时间:2013年12月9日至2013年12月20日目录一、需求分析 (4)1.1选题背景及意义 (4)1.2设计要求 (4)二、系统总体设计 (4)2.1 系统设计思路 (4)2.2 功能结构图及功能说明 (4)2.3 工作原理 (6)三、系统详细设计 (6)3.1 语音信号的matlab仿真的数据分析 (6)3.2 程序代码分析 (12)四、调试与维护 (14)4.1 调试过程的问题与维护 (14)五、结束语 (15)六、参考文献 (16)七、指导教师评阅(手写) (17)一、需求分析1.1选题背景及意义该设计主要是介绍语音信号的采集与分析方法,通过PC机录制自己的一段声音,运用Matlab提供的函数进行仿真分析,并画出采样后语音信号的时域波形和频谱图,对所采集的语音信号加入干扰随机高斯噪声,对加入噪声的信号进行播放,并进行时域和频谱分析;对比加噪前后的时域图和频谱图,分析讨论采用什么样的滤波器进行滤除噪声。
1.2设计要求(1)通过PC机录制自己的一段声音“南昌工程学院刘敏”;(2)运用MATLAB中信号处理相关的函数对语音信号进行时域、频域上的分析,如短时能量,短时平均过零率,语谱图等;(3)运用MATLAB对语音信号进行综合与分析,包括语音信号的调制,叠加,和滤波等。
二、系统总体设计2.1 系统设计思路系统的整体设计思路包括语音信号的录制,语音信号的采集,语音信号的分析,其中语音信号的分析又包括了语音信号的时域分析和频域分析,语音信号的加噪处理和滤噪设计分析。
2.2 功能结构图及功能说明实际工作中,我们可以利用windows自带的录音机录制语音文件,声卡可以完成语音波形的A/D转换,获得WAVE文件,为后续的处理储备原材料。
语音信号的采集与频谱分析(附代码)

《信号与系统》大作业语音信号的采集与频谱分析——基于Matlab的语音信号处理学生姓名:学号:专业班级:电子工程学院卓越班指导老师:2015年6月22日摘要本设计用苹果手机自带的录音设备采集了原始语音,并导入了电脑转成wav格式,然后用MATLAB和Adobe audition对其进行时域分析。
接着利用傅里叶变换进行了频域分析,绘制频谱图,再录制一段加上歌曲的伴奏的语音与原唱进行了对比分析,得出了我与歌星在频域上的差别。
本设计给信号加了两种噪声并通过观察加噪后的频谱和试听回放效果比较加噪前后的差别,最后,设计了FIR数字低通滤波器和带通滤波器,分析滤波前后的频谱。
再次试听回放效果,得出结论。
关键词:语音、FFT、频谱图、噪声、滤波器AbstractThis design is based on the general function of Matlab and Adobe edition to deal with Audio signals. The original signals are collected by iPhone’s built-in recording equipment.First,I compare the file generated by myself with that of thesame song sang by a famous singer.The emphasis is generally laid on analysing the difference in frequncy domain,but time domain will be included too.After that,two noise signals are added to the original signal respectively and let them pass a filter to analyse it.In the two process mentioned before,I make comparison between the before and after frequency domain.Sampling Theorem is the base of my design.It is by sampling we can get discrete signals from the original one and draw the image in time domain.Also,fast fourier transform is employed(FFT)to get the signals in frequency domain.The ayalysis of frequency domain is the highlight of this design.Through this design,I can deepen my comprehension of principles of audio signals and I have learnt how to deal with it.Through met with much hindrance,I improved my skills finally.Keywords: audio signal、TTT、noise、filter1 绪论1.1课题的研究意义语音信号处理属于信息科学的一个重要分支,它是研究用数字信号处理技术对语音信号进行处理的一门新兴学科,同时又是综合性的多学科领域和涉及面很广的交叉学科,因此我们进行语言信号处理具有时代的意义。
专业的语音分析

专业的语音分析语音分析是一门专业领域,它研究和解析人类语音音频以获取信息并提供有关说话者、语言和语音的洞察。
这项技术在语音识别、情感识别、说话人认证等许多领域都有广泛的应用。
一、语音信号的基本分析方法1. 语音信号的采样和量化语音信号是通过麦克风等设备进行采样和量化得到的。
采样是指对连续的语音信号进行离散化处理,将其划分为若干个时间段,并记录在离散的时间点上。
量化是指对每个时间点上的采样值进行测量,将其表示为一个数字。
2. 语音信号的预加重预加重是为了弥补语音信号在传输过程中由于声音高频部分衰减较快而导致的信息损失。
预加重通过对语音信号进行高通滤波来增强高频部分的能量。
3. 语音信号的短时分析短时分析是将语音信号划分为若干个时间窗口,并在每个时间窗口内计算语音信号的能量、频谱等特征。
常用的方法有短时傅里叶变换、短时自相关函数等。
4. 语音信号的特征提取特征提取是从短时分析得到的语音信号中提取出有用的特征。
常用的特征包括梅尔频率倒谱系数(MFCC)、线性预测编码(LPC)系数等。
这些特征可以用来表示语音信号的声音特性和语音内容。
5. 语音信号的模型建立与识别建立语音信号的模型是为了将语音信号与特定的说话者、语言或语音内容关联起来。
常用的模型包括隐马尔科夫模型(HMM)、高斯混合模型(GMM)等。
识别是指通过比较语音信号的特征与模型之间的匹配度从而确定说话者、语言或语音内容。
二、语音分析的应用领域1. 语音识别语音识别是将语音信号转换为文本或命令的过程。
它在智能助理、语音输入、语音翻译等领域有广泛的应用。
通过语音识别技术,人们可以通过语音与计算机进行交互,提高工作效率和用户体验。
2. 情感识别语音信号中包含着说话者的情感信息。
通过语音分析技术,可以识别出语音信号中的情感类别,如愤怒、高兴、焦虑等。
情感识别在人机交互、心理健康评估等领域有着重要的应用价值。
3. 说话人认证说话人认证是通过语音信号判断说话者的身份。
声学信号处理技术在语音识别中的应用

声学信号处理技术在语音识别中的应用近年来,随着科技的不断进步,声学信号处理技术在语音识别领域中发挥着越来越重要的作用。
语音识别是一种能够将人类语音信息转化为数据的技术,它在人工智能、语音控制等领域有着广泛的应用。
本文将探讨声学信号处理技术在语音识别中的应用以及对其发展的影响。
首先,声学信号处理技术在语音识别中的重要作用体现在语音特征提取方面。
通过对语音信号进行采样和频谱分析,可以将其转化为数字信号,进而提取出一系列的特征参数。
这些特征参数包括音频频率、声强、音素等等,它们能够准确地描述语音信号的特点。
而声学信号处理技术能够对特征参数进行分析和处理,从而提高语音识别的精确度和准确性。
其次,声学信号处理技术在语音识别中的应用还表现在语音增强和噪声抑制方面。
在实际环境中,语音信号往往伴随着各种噪声,例如机器噪音、人声干扰等。
这些噪声会干扰语音信号的识别,降低语音识别的准确性。
声学信号处理技术可以通过信号降噪算法,对语音信号进行预处理,去除噪声干扰,从而有效提高语音识别的质量。
此外,声学信号处理技术还在语音信号编码和压缩方面发挥重要作用。
在语音通信和存储过程中,对语音信号进行编码和压缩可以减少数据的存储和传输成本。
声学信号处理技术可以对语音信号进行采样和量化,提取出较小的数据包络,从而实现高效的语音编码和压缩。
这不仅节省了存储空间和传输带宽,还提高了语音通信的效率。
此外,声学信号处理技术在语音识别中的应用还包括说话人识别和情感识别等方面。
通过分析语音信号中的特征参数,可以识别不同的说话人,并实现对其身份的验证和辨认。
这对一些需要身份验证的应用来说具有重要意义,例如银行电话客服、语音门禁系统等。
同时,声学信号处理技术还能够通过分析语音信号的音调、频率和音素等特征,进行情感识别,从而判断说话人的情绪和心理状态。
然而,声学信号处理技术在语音识别中的应用还存在一些挑战和不足之处。
首先,语音信号的多样性和复杂性对声学信号处理算法提出了更高的要求。
语音信号采集与时频域分析正文
第一章引言语音信号是一种非平稳的时变信号,它携带着各种信息。
在语音编码、语音合成、语音识别和语音增强等语音处理中无一例外需要提取语音中包含的各种信息。
语音信号分析的目的就在与方便有效的提取并表示语音信号所携带的信息。
语音信号分析可以分为时域和频域等处理方法。
语音信号可以认为在短时间内(一般认为在 10~30ms 的短时间内)近似不变,因而可以将其看作是一个准稳态过程, 即语音信号具有短时平稳性。
任何语音信号的分析和处理必须建立在“短时”的基础上, 即进行“短时分析”。
时域分析:直接对语音信号的时域波形进行分析,提取的特征参数有短时能量,短时平均过零率,短时自相关函数等。
频域分析:对语音信号采样,并进行傅里叶变换来进行频域分析。
主要分析的特征参数:短时谱、倒谱、语谱图等。
本文采集作者的声音信号为基本的原始信号。
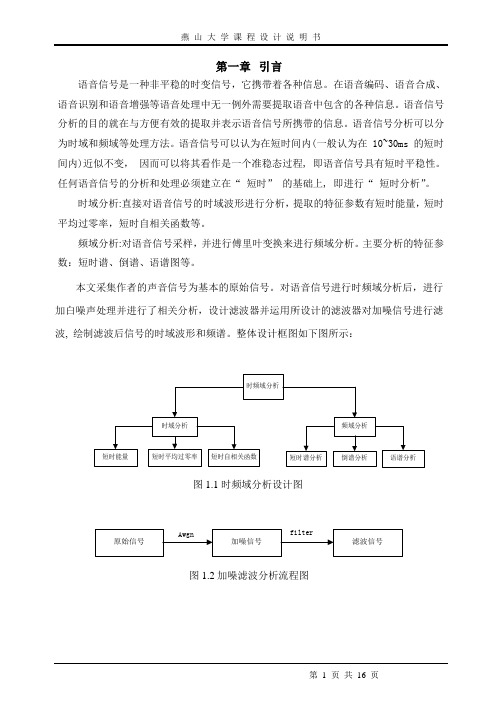
对语音信号进行时频域分析后,进行加白噪声处理并进行了相关分析,设计滤波器并运用所设计的滤波器对加噪信号进行滤波, 绘制滤波后信号的时域波形和频谱。
整体设计框图如下图所示:图1.1时频域分析设计图图1.2加噪滤波分析流程图第二章 语音信号时域分析语音信号的时域分析可直接对语音信号进行时域波形分析,在此只只针对语音信号的短时能量、短时平均过零率、短时自相关函数进行讨论。
2.1窗口选择由人类的发生机理可知,语音信号具有短时平稳性,因此在分析讨论中需要对语音信号进行加窗处理进而保证每个短时语音长度为10~30ms 。
通常选择矩形窗和哈明窗能得到较理想的“短时分析”设计要求。
两种窗函数的时域波形如下图2.1所示:samplew (n )samplew (n )图2.1 矩形窗和Hamming 窗的时域波形矩形窗的定义:一个N 点的矩形窗函数定义为如下{1,00,()n Nw n ≤<=其他(2.1)哈明窗的定义:一个N 点的哈明窗函数定义为如下0.540.46cos(2),010,()n n NN w n π-≤<-⎧⎨⎩其他= (2.2)这两种窗函数都有低通特性,通过分析这两种窗的频率响应幅度特性可以发现(如图2.2):矩形窗的主瓣宽度小(4*pi/N ),具有较高的频率分辨率,旁瓣峰值大(-13.3dB ),会导致泄漏现象;哈明窗的主瓣宽8*pi/N ,旁瓣峰值低(-42.7dB ),可以有效的克服泄漏现象,具有更平滑的低通特性。
《信号与系统》课程设计——数字语音信号的采样和重建

《信号与系统》课程设计——数字语⾳信号的采样和重建《信号与系统》课程设计——数字语⾳信号的采样和重建【设计题⽬】数字语⾳信号的采样和重建【设计⽬标】尝试对语⾳信号的时频域分析及采样和重建处理【设计⼯具】MATLAB【设计原理】通过MATLAB的函数wavread()可以读⼊⼀个.wav格式的⾳频⽂件,并将该⽂件保存到指定的数组中。
例如下⾯的语句(更详细的命令介绍可以⾃⼰查阅MATLAB的帮助)中,将.wav读⼊后存放到矩阵y中。
[y, Fs] = wavread('Q2.wav');对于单声道的⾳频⽂件,y只有⼀⾏,即⼀个向量;对于双声道的⾳频⽂件,y 有两⾏,分别对应了两个声道的向量。
我们这⾥仅对⼀个声道的⾳频进⾏分析和处理即可。
在获得信号向量y的同时,还可以获得该信号的采样频率,即Fs。
注意:.wav⽂件的采样频率为44.1KHz,采样后的量化精度是16位,不过我们不⽤关⼼其量化精度,因为在MATLAB读⼊后,已将其转换成double型的浮点数表⽰,范围在-1到+1之间。
因此,所有处理后的语⾳信号的幅度如果超过了1,在播放时会被⾃动处理为最⼤幅度,-1或者+1。
【设计内容】⼀、基本要求:1、语⾳信号的基本时频域分析:对语⾳信号进⾏时频域分析,绘制语⾳信号的时域波形图、频域频谱图。
其中,时域波形图的横轴要求为时间,频域频谱图的横轴要求为频率(注意,不是⾓频率)。
找到语⾳信号的主要频谱成分所在的带宽,验证为何电话可以对语⾳信号采⽤8KHz 的采样速率。
2、语⾳信号的降采样:对该语⾳信号进⾏五分之⼀的降采样,⽅法是对数组y中的数据,每间隔5个保留1个,这样得到的新的语⾳信号的采样频率为44.1/5KHz,即8.8KHz,通过wavpaly()播放降采样后的语⾳信号。
同时,对⽐降采样前后的语⾳信号的时域波形图、频域频谱图。
3、语⾳信号的先滤波再降采样:在MATLAB中先对数组y中的语⾳信号使⽤⼀个带宽为8.8KHz的理想低通滤波器进⾏滤波后,再对其进⾏五分之⼀的降采样,再次播放该语⾳信号,并与第2步的结果进⾏对⽐。
语音信号处理实验报告

通信与信息工程学院信息处理综合实验报告班级:电子信息工程1502班指导教师:设计时间:2018/10/22-2018/11/23评语:通信与信息工程学院二〇一八年实验题目:语音信号分析与处理一、实验内容1. 设计内容利用MATLAB对采集的原始语音信号及加入人为干扰后的信号进行频谱分析,使用窗函数法设计滤波器滤除噪声、并恢复信号。
2.设计任务与要求1. 基本部分(1)录制语音信号并对其进行采样;画出采样后语音信号的时域波形和频谱图。
(2)对所录制的语音信号加入干扰噪声,并对加入噪声的信号进行频谱分析;画出加噪后信号的时域波形和频谱图。
(3)分别利用矩形窗、三角形窗、Hanning窗、Hamming窗及Blackman 窗几种函数设计数字滤波器滤除噪声,并画出各种函数所设计的滤波器的频率响应。
(4)画出使用几种滤波器滤波后信号时域波形和频谱,对滤波前后的信号、几种滤波器滤波后的信号进行对比,分析信号处理前后及使用不同滤波器的变化;回放语音信号。
2. 提高部分(5)录制一段音乐信号并对其进行采样;画出采样后语音信号的时域波形和频谱图。
(6)利用MATLAB产生一个不同于以上频段的信号;画出信号频谱图。
(7)将上述两段信号叠加,并加入干扰噪声,尝试多次逐渐加大噪声功率,对加入噪声的信号进行频谱分析;画出加噪后信号的时域波形和频谱图。
(8)选用一种合适的窗函数设计数字滤波器,画出滤波后音乐信号时域波形和频谱,对滤波前后的信号进行对比,回放音乐信号。
二、实验原理1.设计原理分析本设计主要是对语音信号的时频进行分析,并对语音信号加噪后设计滤波器对其进行滤波处理,对语音信号加噪声前后的频谱进行比较分析,对合成语音信号滤波前后进行频谱的分析比较。
首先用PC机WINDOWS下的录音机录制一段语音信号,并保存入MATLAB软件的根目录下,再运行MATLAB仿真软件把录制好的语音信号用audioread函数加载入MATLAB仿真软件的工作环境中,输入命令对语音信号进行时域,频谱变换。
声学实验中的信号处理与分析

声学实验中的信号处理与分析声学实验是一项研究声音传播、声波振动特性以及声学现象的科学实践。
在声学实验中,信号处理与分析起着重要的作用,它可以帮助我们更好地理解声音的性质、捕捉声音的细节,并在各种应用领域中发挥重要作用。
一、信号处理在声学实验中的应用1. 声音采集与信号处理在声学实验中,首先需要采集声音信号。
传感器将声音信号转换成电信号,并通过采样与量化技术将连续的声音信号转换成数字信号。
然后,信号处理算法被应用于这些数字信号以提取和分析其中的音频特征。
2. 信号增强与滤波信号处理可以帮助我们对声音进行增强和滤波。
在声学实验中,我们可能面临各种环境噪声和杂音的干扰,这些噪声会对声音信号的质量和特征提供干扰。
通过应用信号处理技术,我们可以滤除这些噪声,以获得清晰的声音信号。
3. 频谱分析与谱估计频谱分析是声学实验中重要的信号处理任务之一。
它用于研究声音信号的频率成分和强度分布。
谱估计方法可以帮助我们分析声音信号的频谱特性,如频率成分、频谱泄露以及频谱斜率等。
4. 语音识别与语音合成信号处理在语音识别和语音合成中起着关键作用。
通过信号处理技术,我们可以将声音信号转换成文字或者根据文本生成自然流畅的语音。
二、声学实验中的信号分析1. 音频特征提取与识别在声学实验中,我们可以通过信号分析技术从声音信号中提取各种音频特征,如时域特征(如能量、过零率等)、频域特征(如频率、频谱特征等)以及时频域特征(如声谱图、梅尔频谱等)。
这些音频特征可以用于声音识别、语音指纹识别、音乐分类等应用中。
2. 噪声分析与环境监测声学实验中的噪声分析可以帮助我们了解各种环境下的噪声特征和强度。
通过分析噪声的频谱和时域特征,我们可以评估噪声对环境以及人体健康的影响,并采取相应的措施来减少噪声污染。
3. 振动分析与结构健康监测声学实验中的信号处理与分析也用于振动分析和结构健康监测。
通过对振动信号进行分析,我们可以评估结构的健康状态,检测结构的缺陷和损坏。
音乐信号频谱分析

利用双线性变换设 计IIR滤波器( 巴特 沃斯数字低通滤波 器的设计)",首先 要设计出满足指标
要求的模拟滤波器 的传递函数Ha(s), 然后由Ha(s)通过双 线性变换可得所要 设计的IIR滤波器的
系统函数H(z)
如果给定的指标为 数字滤波器的指标, 则首先要转换成模 拟滤波器的技术指 标,这里主要是边 界频率Wp和Ws的转 换,对ap和as指标
2.语音信号的采集
但过高的采样频率并不可取,对固定长 度(T)的信号,采集到过大的数据量 (N=T/△t),给计算机增加不必要的计算 工作量和存储空间
若数据量(N)限定,则采样时间过短,会 导致一些数据信息被排斥在外
采样频率过低,采样点间隔过远,则离 散信号不足以反映原有信号波形特征, 无法使信号复原,造成信号混淆
3.低通滤波器的设计
plot(x2)
subplot(2,1,2)
title('IIR低通滤波器 滤波后的时域波形')
%画出滤波前的时域图 plot(fl) sound(fl, 44100)
title('IIR低通滤波器 滤波前的时域波形')
%画出滤波后的时域图
%播放滤波后的信号
3.低通滤波器的设计
1 散的数字语音信号
采样也称抽样,是信号在时间上的离散化,即按照一定时间间隔△t在模拟信号x(t)上逐点采取其瞬时
2值
采样时必须要注意满足奈奎斯特定理,即采样频率fs必须以高于受测信号的最高频率两倍以上的速度进
3 行取样,才能正确地重建波它是通过采样脉冲和模拟信号相乘来实现的 4 在采样的过程中应注意采样间隔的选择和信号混淆:对模拟信号采样首先要确定采样间隔 5 如何合理选择△t涉及到许多需要考虑的技术因素 6 一般而言,采样频率越高,采样点数就越密,所得离散信号就越逼近于原信号
语音信号处理 实验报告

实验一、语音信号采集与分析一、实验目的:1)了解语音信号处理基本知识:语音信号的生成的数学模型。
2)在理论学习的基础上,进一步地理解和掌握语音信号的读入、回放、波形显示。
语音信号时域和频域分析方法。
二、实验原理一定时宽的语音信号,其能量的大小随时间有明显的变化。
其中清音段(以清音为主要成份的语音段),其能量比浊音段小得多。
短时过零数也可用于语音信号分析中,发浊音时,其语音能量约集中于3kHz以下,而发清音时,多数能量出现在较高频率上,可认为浊音时具有较低的平均过零数,而清音时具有较高的平均过零数,因而,对一短时语音段计算其短时平均能量及短时平均过零数,就可以较好地区分其中的清音段和浊音段,从而可判别句中清、浊音转变时刻,声母韵母的分界以及无声与有声的分界。
这在语音识别中有重要意义。
FFT在数字通信、语音信号处理、图像处理、匹配滤波以及功率谱估计、仿真、系统分析等各个领域都得到了广泛的应用。
本实验通过分析加噪的语音信号频谱,可以作为分离信号和噪声的理论基础。
三、实验内容:Matlab编程实验步骤:1.新建M文件,扩展名为“.m”,编写程序;2.选择File/Save命令,将文件保存在F盘中;3.在Command Window窗中输入文件名,运行程序;程序一、用MATLAB对原始语音信号进行时域分析,分析短时平均能量及短时平均过零数。
程序二、用MATLAB对原始语音信号进行频域分析,画出它的时域波形和频谱给原始的语音信号加上一个高频余弦噪声,频率为5kHz。
画出加噪后的语音信号时域和频谱图。
程序1.a=wavread(' D:\II.wav'); %读取语音信号的数据,赋给变量x1,这里的文件的全路径和文件名由个人设计n=length(a);N=320;subplot(3,1,1),plot(a);h=linspace(1,1,N);%形成一个矩形窗,长度为NEn=conv(h,a.*a);%求卷积得其短时能量函数Ensubplot(3,1,2),plot(En);for i=1:n-1if a(i)>=0b(i)= 1;elseb(i) = -1;endif a(i+1)>=0b(i+1)=1;elseb(i+1)=-1;endw(i)=abs(b(i+1)-b(i));end%求出每相邻两点符号的差值的绝对值k=1;j=0;while (k+N-1)<nZm(k)=0;for i=0:N-1;Zm(k)=Zm(k)+w(k+i);endj=j+1;k=k+160; %每次移动半个窗endfor w=1:jQ(w)=Zm(160*(w-1)+1)/640;%短时平均过零率endsubplot(3,1,3),plot(Q);实验结果打印粘贴到右侧:程序2:fs=22050; %语音信号采样频率为22050x1=wavread('D:\II.wav'); %读取语音信号的数据,赋给变量x1sound(x1,22050); %播放语音信号f=fs*(0:511)/1024;t=0:1/22050:(size(x1)-1)/22050; %将所加噪声信号的点数调整到与原始信号相同Au=0.03;d=[Au*cos(2*pi*5000*t)]'; %噪声为5kHz的余弦信号x2=x1+d;sound(x2,22050); %播放加噪声后的语音信号y2=fft(x2,1024); %对信号做1024点FFT变换figure(1)subplot(2,1,1);plot(x1) %做原始语音信号的时域图形title('原始语音信号');xlabel('time n');ylabel('幅值 n');subplot(2,1,2);plot(t,x2)title('加噪后的信号');xlabel('time n');ylabel('幅值 n');figure(2)subplot(2,1,1);plot(f,abs(x1(1:512)));title('原始语音信号频谱');xlabel('Hz');ylabel('幅值');subplot(2,1,2);plot(f,abs(y2(1:512)));title('加噪后的信号频谱');xlabel('Hz'); ylabel('幅值');实验结果打印粘贴到右侧:050010001500200025003000350040004500原始语音信号time n幅值 n加噪后的信号time n幅值 n020004000600080001000012000原始语音信号频谱Hz幅值加噪后的信号频谱Hz幅值四、实验分析加入噪声后音频文件可辨性下降,波形的平缓,频谱图上看,能量大部分集中在2000HZz到4000Hz之间。
语音的频率、频率分辨率、采样频率、采样点数、量化、增益

语⾳的频率、频率分辨率、采样频率、采样点数、量化、增益语⾳的频率、频率分辨率、采样频率、采样点数、量化、增益采样采样频率 每秒从连续信号中提取并组成离散信号的采样个数。
⽤Hz表⽰,采样频率的倒数是采样周期,即采样之间的时间间隔。
通俗的讲:采样频率是指计算机每秒钟采集的多少声⾳样本。
采样频率越⾼,即采样的间隔时间越短,则在单位时间内计算机得到的声⾳样本数据就越多,对声⾳波形的表⽰也越精确。
采样定理 也称作奈奎斯特采样定理,只有采样频率⾼于声⾳信号最⾼频率的两倍时,才能把数字信号表⽰的声⾳还原成为原来的声⾳。
所以采样定理确定了信号最⾼最⾼的频率上限,或能获取连续信号的所有信息的采样频率的下限。
举例:如果有⼀个20Hz的语⾳和⼀个20KHz的语⾳,我们以44.1KHz的采样率对语⾳进⾏采样,结果:20Hz语⾳每次振动被采样了40K20=200040K20=2000次;20KHz语⾳每次振动被采样了40K20K=240K20K=2次;所以在相同的采样率下,记录低频的信息远远⽐⾼频的详细。
上采样可以理解为信号的插值,下采样可以理解为信号的抽取。
带宽:采样频率的⼀半,最⾼频率等于采样频率的⼀半。
混叠 混叠也称为⽋采样,当采样频率⼩于最⼤截⽌频率两倍(奈奎斯特频率)的时候就会发⽣信号重叠,这⼀现象叫做混叠。
为了避免混叠现象,通常采⽤两种措施:1、提⾼采样频率,达到信号最⾼频率的两倍以上;2、输⼊信号通过抗混叠滤波器(低通滤波器)进⾏滤波处理,过滤掉频率⾼于采样率⼀半的信号。
语谱图和频谱图语⾳波形图 波形图表⽰语⾳信号的响度随时间变化的规律,横坐标表⽰时间,纵坐标表⽰声⾳响度,我们可以从时域波形图中观察语⾳信号随时间变化的过程以及语⾳能量的起伏频谱图 频谱图表⽰语⾳信号的功率随频率变化的规律,信号频率与能量的关系⽤频谱表⽰,频谱图的横轴为频率,变化为采样率的⼀半(奈奎斯特采样定理),纵轴为频率的强度(功率),以分贝(dB)为单位语谱图 横坐标是时间,纵坐标是频率,坐标点值为语⾳数据能量,能量值的⼤⼩是通过颜⾊来表⽰的,颜⾊越深表⽰该点的能量越强。
语音信号处理实验指导书

语音信号处理实验指导书实验一:语音信号的采集与播放实验目的:了解语音信号的采集与播放过程,掌握采集设备的使用方法。
实验器材:1. 电脑2. 麦克风3. 扬声器或者耳机实验步骤:1. 将麦克风插入电脑的麦克风插孔。
2. 打开电脑的录音软件(如Windows自带的录音机)。
3. 在录音软件中选择麦克风作为录音设备。
4. 点击录音按钮开始录音,讲话或者唱歌几秒钟。
5. 点击住手按钮住手录音。
6. 播放刚刚录制的语音,检查录音效果。
7. 将扬声器或者耳机插入电脑的音频输出插孔。
8. 打开电脑的音频播放软件(如Windows自带的媒体播放器)。
9. 选择要播放的语音文件,点击播放按钮。
10. 检查语音播放效果。
实验二:语音信号的分帧与加窗实验目的:了解语音信号的分帧和加窗过程,掌握分帧和加窗算法的实现方法。
实验器材:1. 电脑2. 麦克风3. 扬声器或者耳机实验步骤:1. 使用实验一中的步骤1-5录制一段语音。
2. 将录制的语音信号进行分帧处理。
选择合适的帧长和帧移参数。
3. 对每一帧的语音信号应用汉明窗。
4. 将处理后的语音帧进行播放,检查分帧和加窗效果。
实验三:语音信号的频谱分析实验目的:了解语音信号的频谱分析过程,掌握频谱分析算法的实现方法。
实验器材:1. 电脑2. 麦克风3. 扬声器或者耳机实验步骤:1. 使用实验一中的步骤1-5录制一段语音。
2. 将录制的语音信号进行分帧处理。
选择合适的帧长和帧移参数。
3. 对每一帧的语音信号应用汉明窗。
4. 对每一帧的语音信号进行快速傅里叶变换(FFT)得到频谱。
5. 将频谱绘制成图象,观察频谱的特征。
6. 对频谱进行谱减法处理,去除噪声。
7. 将处理后的语音帧进行播放,检查频谱分析效果。
实验四:语音信号的降噪处理实验目的:了解语音信号的降噪处理过程,掌握降噪算法的实现方法。
实验器材:1. 电脑2. 麦克风3. 扬声器或者耳机实验步骤:1. 使用实验一中的步骤1-5录制一段带噪声的语音。
MATLAB处理语音信号
MATLAB处理语⾳信号⼀、实验项⽬名称语⾳信号的处理⼆、实验⽬的综合运⽤数字信号处理课程的理论知识进⾏频谱分析以及滤波器设计,通过理论推导得出相应结论,并进⾏计算机仿真,从⽽复习巩固了课堂所学的理论知识,提⾼了对所学知识的综合应⽤能⼒。
三、实验内容1. 语⾳信号的采集2. 语⾳信号的频谱分析3. 设计数字滤波器和画出频率响应4. ⽤滤波器对信号进⾏滤波5. ⽐较滤波前后语⾳信号的波形及频谱6. 回放语⾳信号四、实验具体⽅案1.语⾳信号采集录制⼀段语⾳信号并保存为⽂件,长度控制在1秒,并对录制的信号进⾏采样;录制时使⽤Windows⾃带的录⾳机。
采样是将⼀个信号(即时间或空间上的连续函数)转换成⼀个数值序列(即时间或空间上的离散函数)。
采样定理指出,如果信号是带限的,并且采样频率⾼于信号带宽的两倍,那么,原来的连续信号可以从采样样本中完全重建出来。
如果信号带宽不到采样频率的⼀半(即奈奎斯特频率),那么此时这些离散的采样点能够完全表⽰原信号。
⾼于或处于奈奎斯特频率的频率分量会导致混叠现象。
⼤多数应⽤都要求避免混叠,混叠问题的严重程度与这些混叠频率分量的相对强度有关。
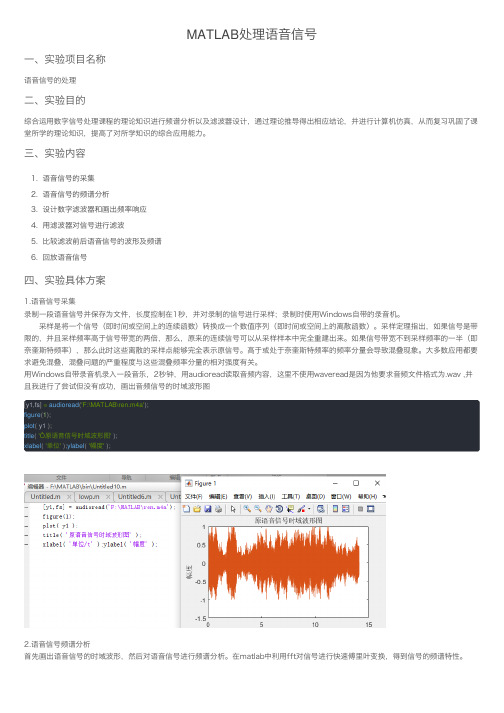
⽤Windows⾃带录⾳机录⼊⼀段⾳乐,2秒钟,⽤audioread读取⾳频内容,这⾥不使⽤waveread是因为他要求⾳频⽂件格式为.wav ,并且我进⾏了尝试但没有成功,画出⾳频信号的时域波形图[y1,fs]=audioread('F:\MATLAB\ren.m4a');figure(1);plot( y1 );title('Ô原语⾳信号时域波形图');xlabel('单位');ylabel('幅度');2.语⾳信号频谱分析⾸先画出语⾳信号的时域波形,然后对语⾳信号进⾏频谱分析。
在matlab中利⽤fft对信号进⾏快速傅⾥叶变换,得到信号的频谱特性。
Matlab的信号处理⼯具箱中的函数FFT可⽤于对序列的快速傅⾥叶变换分析,其调⽤格式是y=fft(x,N),其中,x是序列,y是序列的FFT变换结果,N为整数,代表做N点的FFT,若x为向量且长度⼩于N,则函数将x补零⾄长度N;若向量x长度⼤于N,则截断x使之长度为N。
语音信号_实验报告

一、实验目的1. 理解语音信号的基本特性及其在数字信号处理中的应用。
2. 掌握语音信号的采样、量化、编码等基本处理方法。
3. 学习语音信号的时域、频域分析技术。
4. 熟悉语音信号的增强、降噪等处理方法。
二、实验原理语音信号是一种非平稳信号,其特性随时间变化。
在数字信号处理中,我们通常采用采样、量化、编码等方法将语音信号转换为数字信号,以便于后续处理和分析。
三、实验内容1. 语音信号的采集与预处理- 使用麦克风采集一段语音信号。
- 对采集到的语音信号进行预加重处理,提高高频成分的幅度。
- 对预加重后的语音信号进行采样,采样频率为8kHz。
2. 语音信号的时域分析- 画出语音信号的时域波形图。
- 计算语音信号的短时能量和短时平均过零率,分析语音信号的时域特性。
3. 语音信号的频域分析- 对语音信号进行快速傅里叶变换(FFT)分析,得到其频谱图。
- 分析语音信号的频谱特性,提取关键频段。
4. 语音信号的增强与降噪- 在语音信号中加入噪声,模拟实际应用场景。
- 使用谱减法对加噪语音信号进行降噪处理。
- 对降噪后的语音信号进行主观评价,比较降噪效果。
5. 语音信号的回放与对比- 对原始语音信号和降噪后的语音信号进行回放。
- 对比分析两种语音信号的时域波形、频谱图和听觉效果。
四、实验步骤1. 采集语音信号- 使用麦克风采集一段时长为5秒的语音信号。
- 将采集到的语音信号保存为.wav格式。
2. 预处理- 使用Matlab中的preemphasis函数对采集到的语音信号进行预加重处理。
- 设置预加重系数为0.97。
3. 时域分析- 使用Matlab中的plot函数画出语音信号的时域波形图。
- 使用Matlab中的energy和zero crossing rate函数计算语音信号的短时能量和短时平均过零率。
4. 频域分析- 使用Matlab中的fft函数对语音信号进行FFT变换。
- 使用Matlab中的plot函数画出语音信号的频谱图。
浅析语音信号频谱分析方法

浅析语音信号频谱分析方法摘要:语音信号的频域分析就是分析语音信号的频域持征。
从广义上讲,语音信号的频域分析包括语音信号的频谱、功率谱、倒频谱、频谱包络分析等,而常用的频域分析方法有带通滤波器组法、傅里叶变换法、线件预测法等几种。
下面着重介绍前两种分析方法。
关键词:频谱分析、带通滤波器组法、傅里叶变换法傅里叶分析法因为语音波是一个非平稳过程,因此适用于周期、瞬变或平稳随机信号的标准傅里叶变换不能用来直接表示语音信号,而应该用短时傅里叶变换对语音信号的频谱进行分析,相应的频谱称为“短时谱”。
利用短时博里叶变换求语音的短时谱对第n 帧语音信号Xn(m)进行傅里叶变换(离散时域傅里叶变换,DTFT),可得到短时傅里叶变换,其定义如下:10()()N j w j w n n n m X e x m e --==∑(3-7)由定义可知,短时傅里叶变换实际就是窗选语音信号的标准傅里叶变换。
这里,窗w(n-m)是一个“滑动的”窗口,它随n 的变化而沿着序列X(n)滑动。
由于窗口是有限长度的,满足绝对可和条件,所以这个变换是存在的。
当然窗口函数不同,博里叶变换的结果也将不同。
设语音信号序列和窗口序列的标准傅早叶变换均存在。
当n 取固定值时,w(n-m)的傅里叶变换为:()()jw n jw n jw m w n m e e W e ∞---=-∞-=⋅∑(3-8)根据卷积定理,有:()()()jw jw jwn jw n X e X e e W e --⎡⎤=⋅⋅⎣⎦ (3-9) 因为上式右边两个卷积项均为关于角频率w 的以2π为周期的连续函数,所以也可将其写成以下的卷积积分形式:()-1()()()2jw j jn j w n X e W e e X e d θθθθ∏+∏⎡⎤⎡⎤=⋅⎣⎦⎣⎦∏⎰ (3-10) 即,假设x(m)的DTFT 是()jw X e ,且()w m 的DTFT 是()jw W e ,那么()jw n X e 是()jw X e 和()jw W e 的的周期卷积。
语音信号的分析与处理

语音信号的分析与处理在日常生活中,我们常常与语音信号打交道,如电话通讯、语音识别、音乐播放、影片配音等。
语音信号是人类声音的一种电信号表示形式,它的特性是非常复杂的,包括语音的声音频率、幅度大小、声音的拐角特征、信号的频率变化以及背景噪声等多方面因素。
因此,对语音信号正确分析和处理是现代通讯研究、智能语音识别和场景识别等领域的重要问题,也是一个迫切需要解决的问题。
一、语音信号的基本特征语音信号具有很多特征,如频率、能量、音色和韵律等。
频率是语音信号的基本特征之一,它是指语音信号中声音的高低频率。
音频信号的波形形状与频率息息相关。
一般组成语音的基元元音频率范围在250 Hz ~ 1000 Hz之间,辅音频率的范围在100 Hz ~ 4 kHz之间。
能量与音量相关,是指语音信号所含有的总能量。
音色是语音信号的另一个特征,它能够指示语音信号的来源。
最后,韵律则是指语音信号的节奏,其包含语音中音节、词语、句子和语气的信息。
二、语音信号的分析方法语音信号的分析方法可以分为时域分析和频域分析两种方式。
其中,时域分析是一种基于时间的分析,它通过观察信号的实时波形来分析语音信号的特征。
频域分析则是一种基于频率的分析,它通过观察信号的频谱特性来分析语音信号的频率、音量和音色。
1. 时域分析时域分析是一种非常基础的语音信号分析方法。
通常,时域分析方法通过分析语音信号的波形特征来判断语音信号的特点。
它能够检查信号在时间上的变化,比如分析语音信号中频率与振幅的变化。
这种方法主要通过时间和采样频率来确定语音信号的基本特征。
2. 频域分析频域分析则是一种付于注意的语音信号分析方法。
它主要通过傅里叶变换(Fourier transform)或小波变换(Wavelet transform)等频率分析方法来研究信号在不同频段上的特征。
通过频域分析可以获得信号在较高频段上的信息,该信息往往无法通过时域分析方法获得。
频域分析方法可以用于语音信号的分析、信号噪声抑制和语音信号质量改进等方面。
语音信号的频谱分析实验报告

综合设计实验语音信号的频谱分析一、实验内容录制一段个人自己的语音信号,并对录制的信号进行采样;画出采样后语音信号的时域波形和频谱图;在语音信号中增加正弦噪声信号(自己设置几个频率的正弦信号),对加入噪声信号后的语音信号进行频谱分析;给定滤波器的性能指标,采用窗函数法和双线性变换设计数字滤波器,并画出滤波器的频率响应;然后用自己设计的滤波器对采集的信号进行滤波,画出滤波后信号的时域波形和频谱,并对滤波前后的信号进行对比试听,分析信号的变化。
二、实现步骤1.语音信号的采集利用Windows下的录音机,录制一段自己的话音(“信号与系统”),时间在3s内。
然后在Matlab软件平台下,利用函数wavread对语音信号进行采样,采样频率设置为4kHz。
[y,fs,bits]=wavread('j.wav',[1024 63500]);sound(y,fs,bits);2.语音信号的频谱分析要求首先画出语音信号的时域波形;然后对语音号进行傅里叶变换,得到信号的频谱特性。
在采集得到的语音信号中加入正弦噪声信号(频率为10kHz),然后对加入噪声信号后的语音号进行傅里叶变换,得到信号的频谱特性。
并利用sound试听前后语音信号的不同。
3. 设计滤波器设计一个理想低通滤波器,滤除正弦噪声信号,得到信号的频谱特性。
要求采样卷积计算的方式滤除噪声,并利用sound试听滤波前后语音信号的不同。
1、语音信号的采集[y,fs,bits]=wavread('j.wav',[1024 63500]);sound(y,fs,bits);2、语音信号的频谱分析Y=fft(y,4096);figure(1);plot(y);title('语音信号的时域波形');figure(2);plot(abs(Y));title('语音信号的频谱特性');IIR 数字滤波器低通clear;close all;[y,fs,bits]=wavread('j.wav',[1024 63500]);Y=fft(y,4096);fb=1000;fc=1200;As=100;Ap=1;fs=22050;wc=2*fc/fs; wb=2*fb/fs;[n,wn]=ellipord(wc,wb,Ap,As);[b,a]=ellip(n,Ap,As,wn);figure(1);freqz(b,a,512,fs);x=filter(b,a,y);X=fft(x,4096);figure(2);subplot(2,2,1);plot(y);title('滤波前信号波形');subplot(2,2,2);plot(abs(Y));title('滤波前信号频谱');Subplot(2, 2 ,3);plot(x);title('滤波后信号波形');Subplot(2, 2 ,4);plot(abs(X));title('滤波后信号频谱');sound(x,fs,bits);IIR 高通wp=2*pi*4800/18000;wr=2*pi*5000/18000;Ap=1;Ar=15;T=1[N,wn]=buttord(wp/pi,wr/pi,Ap,Ar);[b,a]=butter(N,wn,'high');[db,mag,pha,grd,w]=freqz_m(b,a);subplot(211);plot(w/pi,mag);title('数字巴特沃茨高通滤波器幅度响应|Ha(J\Omega)|'); subplot(212);plot(w/pi,db);title('数字巴特沃茨高通滤波器幅度响应(db)');[y,Fs,nbite]=wavread('j.wav',[1024 63500]);Y=fft(y,4096);x=filter(b,a,y);X=fft(x,4096);figure(3)subplot(211);plot(y);title('原时域波形');subplot(212);plot(x);title('滤波后信号波形');figure(4)subplot(211);plot(abs(Y));title('原频谱频谱');subplot(212);plot(abs(X));title('滤波后信号频谱');sound(x,Fs);IIR 带通wp=[1200*pi*2/9000,3000*2*pi/9000];wr=[1000*2*pi/9000,3200*2*pi/9000];Ap=1;Ar=10 0;[N,wn]=buttord(wp/pi,wr/pi,Ap,Ar);[b,a]=butter(N,wn,'bandpass');[db,mag,pha,grd,w]=freqz_m(b,a);subplot(211);plot(w/pi,mag);title('数字巴特沃茨带通滤波器幅度响应|Ha(J\Omega)|');subplot(212);plot(w/pi,db);title('数字巴特沃茨带通滤波器幅度响应(db)');[y,Fs,nbite]=wavread('j.wav');Y=fft(y,4096);x=filter(b,a,y);X=fft(x,4096);figure(3)subplot(211);plot(y);title('原时域波形');subplot(212);plot(x);title('滤波后信号波形');figure(4)subplot(211);plot(abs(Y));title('原频谱频谱');subplot(212);plot(abs(X));title('滤波后信号频谱');sound(x,Fs);FIR 数字滤波器FIR 低通fsamp=8000;rp=1;rs=100;fcuts=[1000 1200];d1=(10^(rp/20)-1)/(10^(rp/20)+1);d2=10^(-rs/20);mags=[1 0];devs=[d1 d2];[n,wn,beta,ftype]=kaiserord(fcuts,mags,devs,fsamp); hh=fir1(n,wn,ftype,kaiser(n+1,beta),'noscale'); freqz(hh);[y,Fs,nbite]=wavread('j.wav');Y=fft(y,4096);x=fftfilt(hh,y);X=fft(x,4096);figure(2)subplot(211);plot(y);title('原时域波形');subplot(212);plot(x);title('滤波后信号波形'); figure(3)subplot(211);plot(abs(Y));title('原频谱频谱'); subplot(212);plot(abs(X));title('滤波后信号频谱'); sound(x,Fs);FIR 高通wc=2*pi*4800;wp=5000*2*pi/18000;f=[0.5333,0.5556]; m=[0,1];rp=1;rs=100;d1=(10^(rp/20)-1)/(10^(rp/20)+1);d2=10^(-rs/20); rip=[d2,d1];[N,fo,mo,w]=remezord(f,m,rip);N=N+2;hn=remez(N,fo,mo,w);[hw,w]=freqz(hn,1);plot(w/pi,20*log10(abs(hw)));[y,Fs,nbite]=wavread('j.wav');Y=fft(y,4096);x=fftfilt(hn,y);X=fft(x,4096);figure(2)subplot(211);plot(y);title('原时域波形');subplot(212);plot(x);title('滤波后信号波形');figure(3)subplot(211);plot(abs(Y));title('原频谱频谱');subplot(212);plot(abs(X));title('滤波后信号频谱');sound(x,Fs);FIR 带通wp1=2*pi*1200/8000;wp2=3000*2*pi/8000;wc1=2*pi*1000/8000;wc2=2*pi*3200*8000; f=[0.25,0.30,0.75,0.80][n,wn,bta,ftype]=kaiserord([0.25,0.30,0.75,0.80],[0 1 0],[0.01 0.1087 0.01]);h1=fir1(n,wn,ftype,kaiser(n+1,bta),'noscale');[hh1,w1]=freqz(h1,1,256);figure(1);plot(w1/pi,20*log10(abs(hh1)));grid;[y,Fs,nbite]=wavread('j.wav');Y=fft(y,4096);x=fftfilt(h1,y);X=fft(x,4096);figure(2)subplot(211);plot(y);title('原时域波形');subplot(212);plot(x);title('滤波后信号波形');figure(3)subplot(211);plot(abs(Y));title('原频谱频谱');subplot(212);plot(abs(X));title('滤波后信号频谱');sound(x,Fs);设计结果分析(1)语音分析图1图2Fs=22050; n=4096(2)IIR 低通图3滤波器在通带内平滑,通带截止频率为 1000hz,最大衰减 0dB;阻带起始频率为1200hz,最小衰减 100dB;相位不是线性变化, 基本满足性能要求.图4语音信号经过低通滤波器后,基本没发生变化(3) IIR 高通图5数字滤波器在通带内平滑,通带截止频率为0. 5π,最大衰减 0dB;阻带起始频率为 0. 48π,最小衰减 100dB;相位不是线性变化, 基本满足性能要求.语言信号经过高通滤波器后,低频分量基本被衰减。
语音信号实验报告

一、实验目的1. 理解语音信号的基本特性和处理方法。
2. 掌握语音信号的采样、量化、编码等基本过程。
3. 学习使用相关软件对语音信号进行时域和频域分析。
4. 了解语音信号的降噪、增强和合成技术。
二、实验原理语音信号是一种非平稳的、时变的信号,其频谱特性随时间变化。
语音信号处理的基本过程包括:信号采集、信号处理、信号分析和信号输出。
三、实验仪器与软件1. 仪器:计算机、麦克风、耳机。
2. 软件:Matlab、Audacity、Python。
四、实验步骤1. 信号采集使用麦克风采集一段语音信号,并将其存储为.wav格式。
2. 信号处理(1)使用Matlab读取.wav文件,提取语音信号的采样频率、采样长度和采样数据。
(2)将语音信号进行时域分析,包括绘制时域波形图、计算信号的能量和过零率等。
(3)将语音信号进行频域分析,包括绘制频谱图、计算信号的功率谱密度等。
3. 信号分析(1)观察时域波形图,分析语音信号的幅度、频率和相位特性。
(2)观察频谱图,分析语音信号的频谱分布和能量分布。
(3)计算语音信号的能量和过零率,分析语音信号的语音强度和语音质量。
4. 信号输出(1)使用Audacity软件对语音信号进行降噪处理,比较降噪前后的效果。
(2)使用Python软件对语音信号进行增强处理,比较增强前后的效果。
(3)使用Matlab软件对语音信号进行合成处理,比较合成前后的效果。
五、实验结果与分析1. 时域分析从时域波形图可以看出,语音信号的幅度、频率和相位特性随时间变化。
语音信号的幅度较大,频率范围一般在300Hz~3400Hz之间,相位变化较为复杂。
2. 频域分析从频谱图可以看出,语音信号的能量主要集中在300Hz~3400Hz范围内,频率成分较为丰富。
3. 信号处理(1)降噪处理:通过对比降噪前后的时域波形图和频谱图,可以看出降噪处理可以显著降低语音信号的噪声,提高语音质量。
(2)增强处理:通过对比增强前后的时域波形图和频谱图,可以看出增强处理可以显著提高语音信号的幅度和频率,改善语音清晰度。
MatLab对语音信号进行频谱分析及滤波

数字信号处理综合实验报告综合实验名称:应用Matlab对语音信号进行频谱分析及滤波系:学生姓名:班级:通信学号:11成绩:指导教师:开课时间:2011-2012学年上学期一.综合实验题目应用MatLab对语音信号进行频谱分析及滤波二.主要内容录制一段个人自己的语音信号,并对录制的信号进行采样;画出采样后语音信号的时域波形和频谱图;给定滤波器的性能指标,采用窗函数法和双线性变换设计滤波器,并画出滤波器的频率响应;然后用自己设计的滤波器对采集的信号进行滤波,画出滤波后信号的时域波形和频谱,并对滤波前后的信号进行对比,分析信号的变化;回放语音信号;课程设计应完成的工作:1、语音信号的采集;2、语音信号的频谱分析;3、数字滤波器的设计;4、对语音信号进行滤波处理;5、对滤波前后的语音信号频谱进行对比分析;三.具体要求1、学生能够根据设计内容积极主动查找相关资料;2、滤波器的性能指标可以根据实际情况作调整;3、对设计结果进行独立思考和分析;4、设计完成后,要提交相关的文档;1)课程设计报告书(纸质和电子版各一份,具体格式参照学校课程设计管理规定),报告内容要涵盖设计题目、设计任务、详细的设计过程、原理说明、、频谱图的分析、调试总结、心得体会、参考文献(在报告中参考文献要做标注,不少于5篇)。
2)可运行的源程序代码(电子版)在基本要求的基础上,学生可以根据个人对该课程设计的理解,添加一些新的内容;四.进度安排五.成绩评定(1)平时成绩:无故旷课一次,平时成绩减半;无故旷课两次平时成绩为0分,无故旷课三次总成绩为0分。
迟到15分钟按旷课处理(2)设计成绩:按照实际的设计过程及最终的实现结果给出相应的成绩。
(3)设计报告成绩:按照提交报告的质量给出相应的成绩。
课程设计成绩=平时成绩(30%)+设计成绩(30%)+设计报告成绩(40%)应用MatLab对语音信号进行频谱分析及滤波第一章实验任务录制一段个人自己的语音信号,并对录制的信号进行采样;画出采样后语音信号的时域波形和频谱图;给定滤波器的性能指标,采用窗函数法和双线性变换设计滤波器,并画出滤波器的频率响应;然后用自己设计的滤波器对采集的信号进行滤波,画出滤波后信号的时域波形和频谱,并对滤波前后的信号进行对比,分析信号的变化;回放语音信号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
语音信号采样和频谱分析
一.实验目的
(1)掌握傅里叶变换的物理意义,深刻理解傅里叶变换的内涵;
(2)了解MATLAB 对声音信号的处理指令;
(3)了解计算机存储信号的方式及语音信号的特点;
(4)加深对采样定理的理解;
(5)加深学生对信号分析工程应用的理解,拓展学生在信号分析领域的综合应用能力。
二.实验内容
本实验利用MATLAB 指令录制一段语音信号,观察其时域波形并进行傅里叶变换,观察其频域的频谱。
根据该信号的频谱构成,选择三种不同的采样频率重新录制该语音信号,并试听回放效果,进行比较,以验证采样定理,并了解MATLAB 对声音信号的处理指令,加深对采样定理的理解。
关键词:傅里叶变换 信号采样
三、实验原理
语音信号是一种连续变化的模拟信号,而计算机只能处理和记录二进制的数字信号,因此,由自然音而得的音频信号必须用计算机的声音编辑工具,先进行语音采样,然后利用了计算机上的A/D 转换器,将模拟的声音信号变成离散的量化了的数字信号量化和编码,变成二进制数据后才能送到计算机进行再编辑和存储。
语音信号输出时,量化了的数字信号又通过D/A 转换器,把保存起来的数字数据恢复成原来的模拟的语音信号。
(1)应用MATLAB 进行声音的录制 (2)应用MATLAB 进行声音的播放 (3)语音信号的频谱分析 。
傅里叶变换建立了信号频谱的概念。
所谓傅里叶分析即分析信号的频谱(频率构成)、频带宽度等。
对语音信号的分析也不例外,也必须采用傅里叶变换这一工具。
对于连续时间信号)(t f ,其傅里叶变换)(ωF 为:⎰∞
∞--=dt e t f F t j ωω)()(
四、实验任务
(1)应用MATLAB 进行声音的录制
在MATLAB 命令窗口中键入“y=wavrecord(8000,8000,1)”,并按回车键,此时刻以后的1(8000/8000)秒时段内的声音信号将以y 为文件名,以数字声音信号.wav 格式存储在MATLAB 的工作空间里。
纪录长度为80000,采样频率为8000Hz ,声道数为1。
图为录制的语音:“信号与系统”。
(2)应用MATLAB 进行声音的播放
在MATLAB 命令窗口中键入“sound(y,Fs)”,按下回车键就能听到回放的声音。
当Fs=8000时,听到的是原来未失真的声音;当Fs=6000时,听到的声音比较低沉;当Fs=10000时,听到的声音很尖锐。
(3)语音信号的频谱分析
在MATLAB 命令窗口中键入“p=fft(y);plot(abs(p))”按下回车键后出现如图所示图形:
从图中可以看出该音频的上限频率为4000Hz 。
(4)采样定理
一个频谱受限的信号f(t),如果频谱只占据m m ωω+-~的范围,则信号)(t f 可以用等间隔的抽样值唯一地表示。
而抽样间隔必须不大于m
f 21(其中m m f ⋅=πω2),或者说,最低抽样频率为m f 2。
低抽样频率为m f 2。
该实验中,音频的上限频率为4000Hz ,所以采用的抽样信号的频率为该频率的两倍8000Hz 。
当采用小于8000Hz 的频率抽样时,回放声音低沉;当采用大于8000Hz 的频率采样时,回放声音尖锐。
结论:
本次试验是进行语音信号的采集和频谱分析,实验纪录了长度为80000,采样频率为8000Hz 采样一段音频,并进行频谱分析,最终经过分析得只有以两倍上限频率回放音频时才会得到原音频信号,否则都会失真。
本次试验不仅学习到了新知识,而且复习到了抽样定理的许多内容,加深了对这些内容的理解,受益很多!!。
