立体几何与空间向量-浙江省台州市书生中学2020届高三数学复习专题练习(无答案)
立体几何与空间向量-浙江省台州市书生中学2020届高三数学复习专题练习(无答案)

立体几何例1.在三棱锥P ABC -中,PA ⊥底面ABC ,,6,8AB AC AB AC ⊥==,D 是线段AC 上一点,且3AD DC =.三棱锥P ABC -的各个顶点都在球O 表面上,过点D 作球O 的截面,若所得截面圆的面积的最大值与最小值之差为16π,则球O 的表面积为( )A .72πB .86πC .112πD .128π 2.三视图例2.某简单组合体的三视图如图所示,则该几何体的体积为( )A .164+πB .484π+C .4812π+D .4816π+3.常见几何体的体积计算公式例3.已知直角三角形 ABC 两直角边长之和为3,将ABC ∆绕其中一条直角边旋转一周,所形成旋转体体积的最大值为__________,此时该旋转体外接球的表面积为___________.例4.如图,三棱锥的顶点,,,都在同一球面上,过球心且,是边长为等边三角形,点、分别为线段,上的动点(不含端点),且,则三棱锥体积的最大值为__________.例5.如图,在几何体中,平面底面ABC , 四边形是正方形,,Q 是的中点,且,. 求证:平面; 求二面角的余弦值.例6.如图几何体中,底面ABCD 为正方形,PD ⊥平面ABCD ,//EC PD ,且22PD AD EC ===.(1)求证://BE 平面PDA ;(2)求PA 与平面PBD 所成角的大小.例7.已知三棱锥A BCD -的棱长均为6,其内有n 个小球,球1O 与三棱锥A BCD -的四个面都相切,球2O 与三棱锥A BCD -的三个面和球1O 都相切,如此类推,…,球n O 与三棱锥A BCD -的三个面和球1n O -都相切(2n ≥,且n *∈N ),则球1O 的体积等于__________,球n O 的表面积等于__________.例8.如图所示,在等腰梯形ABCD 中,,,E ,F 为AB 的三等分点,且将和分别沿DE 、CF 折起到A 、B 两点重合,记为点P . 证明:平面平面PEF ; 若,求PD 与平面PFC 所成角的正弦值.一、选择题1.(2020·福建高三月考(文))已知平面α⊥平面β,直线,m l ααβ⊂=I ,则“m l ⊥”是“m β⊥”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.(2020·湖北高三月考(文))某几何体的三视图如图所示,则该几何体的体积为( )A .4πB .2πC .πD .2π3.已知二面角l αβ--的大小为60°,b 和c 是两条异面直线,且,b c αβ⊥⊥,则b 与c 所成的角的大小为( )A .120°B .90°C .60°D .30°4.把正方形ABCD 沿对角线AC 折起,当以,,,A B C D 四点为顶点的棱锥体积最大时,直线BD 和平面ABC 所成的角的大小为( )A .90°B .60C .45°D .30°5.(2020·湖北高三月考(理))鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.从外观上看,是严丝合缝的十字立方体,其上下、左右、前后完全对称;六根等长的正四棱柱分成三组,经90°榫卯起来.如图所示,正四棱柱的高为8,底面正方形的边长为1,将这个鲁班锁放进一个球形容器内,则该球形容器半径的最小值为(容器壁的厚度忽略不计)( )A .65B .66C .69D .17.6.在三棱锥A-BCD 中,平面ABC 丄平面ADC, AD 丄AC,AD=AC, 3ABC π∠=,若此三棱锥的外接球表面积为28π,则三棱锥A-BCD 体积的最大值为( )A .7B .12C .6D .537.(2016·浙江高三学业考试)如图,在四面体ABCD 中,2AB CD ==,3AD BD ==,4AC BC ==,点E ,F ,G ,H 分别在棱AD ,BD ,BC ,AC 上,若直线AB ,CD 都平行于平面EFGH ,则四边形EFGH 面积的最大值是( )A .12B .22C .1D .28.(2020·浙江高三期末)斜三棱柱111ABC A B C -中,底面ABC 是正三角形,侧面11ABB A 是矩形,且123AA AB=,M 是AB 的中点,记直线1A M 与直线BC 所成的角为α,直线1A M 与平面ABC 所成的角为β,二面角1A AC B --的平面角为γ,则( )A .βγ<,αγ<B .βα<,βγ<C .βα<,γα<D .αβ<,γβ< 9.(2020·浙江高三学业考试)如图,在圆锥SO 中,A ,B 是O e 上的动点,BB '是O e 的直径,M ,N 是SB 的两个三等分点,()0AOB θθπ∠=<<,记二面角N OA B --,M AB B '--的平面角分别为α,β,若αβ≤,则θ的最大值是( )A .56π B .23π C .2π D .4π 10.设三棱锥V ABC -的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点),记直线PB 与直线AC 所成角为α,直线PB 与平面ABC 所成角为β,二面角P AC B --的平面角为γ,则( )A .,βγαγ<<B .,βαβγ<<C .,βαγα<<D .,αβγβ<<二、填空题11.已知平面αβ,和直线m ,给出条件:①m αP ;②m α⊥;③m α⊂;④αβ⊥;⑤αβP .(1)当满足条件____ 时,有m βP ;(2)当满足条件 ____ 时,有m β⊥.(填所选条件的序号)12.(2020·浙江高三期末)某几何体的三视图如图所示(单位:cm ),则该几何体的体积为______3cm ,表面积为______2cm .13.已知正三棱柱111ABC A B C -的六个顶点都在球O 的表面上,3AB =,异面直线1AC 与BC 所成角的余弦值为310,则1AA =_______,球O 的表面积为_______. 14.已知正三棱柱111ABC A B C -的六个顶点都在球O 的表面上,若这个三棱柱的体积为93,3AB =,则1AA =_______,球O 的表面积为_______.15.在三棱锥P ABC -中,PA ⊥底面ABC ,,6,8AB AC AB AC ⊥==,D 是线段AC 上一点,且3AD DC =.三棱锥P ABC -的各个顶点都在球O 表面上,过点D 作球O 的截面,则所得截面圆的面积的最小值为____.16.如图,在棱长为 1 的正方体1111ABCD A B C D -中,点M 是AD 的中点,动点P 在底面正方形ABCD 内(不包括边界),若1//B P 平面1A BM ,则1C P 长度的取值范围是_______.17.四棱锥S ABCD -中,底面ABCD 是边长为2的正方形,侧面SAD 是以AD 为斜边的等腰直角三角形,若π2π,33SAB ⎡⎤∠∈⎢⎥⎣⎦,则四棱锥S ABCD -的体积的取值范围为______.三、解答题18.(2020·浙江高三期末)已知斜三棱柱111ABC A B C -,2ABC π∠=,1AC BC ⊥,12BC BA ==,1BC =,123AC =.(1)求1AA 的长;(2)求1AA 与面ABC 所成的角的正切值.19.如图,在斜三棱柱111ABC A B C -中,平面ABC ⊥平面11A ACC ,12CC =,ABC V ,1ACC △,均为正三角形,E 为AB 的中点.(1)证明:1//AC 平面1B CE ,(2)求直线1AC 与平面11B BAA 所成角的正弦值.20.如图,三棱柱111ABC A B C -中,AB ⊥侧面11BB C C ,已知13BCC π∠=,1BC =,12AB C C ==,点E 是棱1C C 的中点.(1)求证:1C B ⊥平面ABC ;(2)在棱CA 上是否存在一点M ,使得EM与平面11A B E 所成角的正弦值为21111,若存在 ,求出CM CA的值;若不存在,请说明理由.21.如图,三棱柱1l l ABC A B C -中,11,,60AC BC AB AA BAA ==∠=︒.(1)求证:111AC B A ⊥; (2)若平面ABC ⊥平面11ABB A ,且AB BC =,求直线1CB 与平面1A BC 所成角的正弦值.22.如图,在四面体ABCD 中,E ,F 分别是线段AD ,BD 的中点,90ABD BCD ∠=∠=o ,2EC =2AB BD ==,直线EC 与平面ABC 所成的角等于30o .(1)证明:平面EFC ⊥平面BCD ;(2)求二面角A CE B --的余弦值.。
高考数学压轴专题台州备战高考《空间向量与立体几何》真题汇编含答案

【高中数学】数学《空间向量与立体几何》高考复习知识点一、选择题1.如图,在正方体1111ABCD A B C D - 中,,E F 分别为111,B C C D 的中点,点P 是底面1111D C B A 内一点,且//AP 平面EFDB ,则1tan APA ∠ 的最大值是( )A .2B .2C .22D .32【答案】C 【解析】分析:连结AC 、BD ,交于点O ,连结A 1C 1,交EF 于M ,连结OM ,则AO =P PM ,从而A 1P=C 1M ,由此能求出tan ∠APA 1的最大值.详解:连结AC 、BD ,交于点O ,连结A 1C 1,交EF 于M ,连结OM ,设正方形ABCD ﹣A 1B 1C 1D 1中棱长为1,∵在正方形ABCD ﹣A 1B 1C 1D 1中,E ,F 分别为B 1C 1,C 1D 1的中点, 点P 是底面A 1B 1C 1D 1内一点,且AP ∥平面EFDB , ∴AO =P PM ,∴A 1P=C 1M=244AC =, ∴tan ∠APA 1=11AA A P22. ∴tan ∠APA 1的最大值是2. 故选D .点睛:本题考查角的正切值的最大值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力,考查运算求解能力,是中档题.2.鲁班锁(也称孔明锁、难人木、六子联方)起源于古代中国建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.如图1,这是一种常见的鲁班锁玩具,图2是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁的表面积为( )A .8(6623)+B .6(8823)+C .8(632)+D .6(8832)+ 【答案】A 【解析】 【分析】该鲁班锁玩具可以看成是一个正方体截去了8个正三棱锥所余下来的几何体,然后按照表面积公式计算即可. 【详解】由题图可知,该鲁班锁玩具可以看成是一个棱长为222+的正方体截去了8个正三棱锥所余下来的几何体,且被截去的正三棱锥的底面边长为22,则该几何体的表面积为2116(222)42282322S ⎡=⨯+-⨯+⨯⨯⎢⎣8(623)=+.故选:A. 【点睛】本题考查数学文化与简单几何体的表面积,考查空间想象能力和运算求解能力.3.《乌鸦喝水》是《伊索寓言》中一个寓言故事,通过讲述已知乌鸦喝水的故事,告诉人们遇到困难要运用智慧,认真思考才能让问题迎刃而解的道理,如图2所示,乌鸦想喝水,发现有一个锥形瓶,上面部分是圆柱体,下面部分是圆台,瓶口直径为3厘米,瓶底直径为9厘米,瓶口距瓶颈为23332厘米,现将13鸦才能喝到水,则乌鸦共需要投入的石子数量至少是( )A .2颗B .3颗C .4颗D .5颗【答案】C 【解析】 【分析】利用图形中的数据,分别算出石子的体积和空瓶的体积即可. 【详解】如图,9,3,33AB cm EF GH cm LO cm ====所以60A ∠=︒,原水位线直径6CD cm =,投入石子后,水位线直径5IJ cm = 则由圆台的体积公式可得石子的体积为:()22319133MN CN IM CN IM ππ⋅⋅++⋅= 空瓶的体积为:()22213LN CN EL CN EL EL KL ππ⋅++⋅+⋅⋅633363993888πππ=+=()99329783,49191324ππ=∈ 所以至少需要4颗石子 故选:C 【点睛】本题考查的是圆台和圆柱体积的算法,掌握其公式是解题的关键.4.正方体1111ABCD A B C D -的棱长为1,动点M 在线段1CC 上,动点P 在平面..1111D C B A 上,且AP ⊥平面1MBD .线段AP 长度的取值范围为( )A .2⎡⎣B .3⎡⎣C .32⎣D .62⎣ 【答案】D 【解析】 【分析】以1,,DA DC DD 分别为,,x y z 建立空间直角坐标系,设(),,1P x y ,()0,1,M t ,由AP ⊥平面1MBD ,可得+11x t y t=⎧⎨=-⎩,然后用空间两点间的距离公式求解即可. 【详解】以1,,DA DC DD 分别为,,x y z 建立空间直角坐标系,则()()()()11,0,0,1,1,0,0,1,,0,0,1A B M t D ,(),,1P x y .()1,,1AP x y =-u u u r ,()11,1,1BD =--u u u u r ,()[]1,0,0,1,BM t t =-∈u u u u r由AP ⊥平面1MBD ,则0BM AP ⋅=u u u u r u u u r且01BD AP ⋅=u u u u r u u u r所以10x t -+=且110x y --+=得+1x t =,1y t =-.所以()2221311222AP x y t ⎛⎫=-++=-+ ⎪⎝⎭u u u r 当12t =时,min 6AP =u u u r ,当0t =或1t =时,max 2AP =u u u r , 62AP ≤≤u u ur 故选:D【点睛】本题考查空间动线段的长度的求法,考查线面垂直的应用,对于动点问题的处理用向量方法要简单些,属于中档题.5.若四面体的三视图如图所示,则该四面体的四个面中,直角三角形的面积和为( )A .2B .25C .425+D .4【答案】B 【解析】 【分析】根据四面体的三视图可知:一侧面垂直于底面,且底面是以该侧面与底面的交线为直角边的直角三角形,然后根据面面垂直的性质定理,得到与底面的另一直角边为交线的侧面为直角三角形求解. 【详解】由四面体的三视图可知:平面PAB ⊥平面ABC ,BC AB ⊥, 所以BC ⊥平面PAB ,所以BC PB ⊥, 所以,ABC PBC V V 是直角三角形, 如图所示:所以直角三角形的面积和为:11112252252222ABC PBC S S AB BC PB BC +=⨯⨯+⨯⨯=⨯⨯+⨯⨯=+V V . 故选:B 【点睛】本题主要考查三视图的应用以及线面垂直,面面垂直的关系,还考查了运算求解的能力,属于中档题.6.如图,直三棱柱ABC A B C '''-的侧棱长为3,AB BC ⊥,3AB BC ==,点E ,F 分别是棱AB ,BC 上的动点,且AE BF =,当三棱锥B EBF '-的体积取得最大值时,则异面直线A F '与AC 所成的角为( )A .2πB .3π C .4π D .6π 【答案】C 【解析】 【分析】设AE BF a ==,13B EBF EBF V S B B '-'=⨯⨯V ,利用基本不等式,确定点 E ,F 的位置,然后根据//EF AC ,得到A FE '∠即为异面直线A F '与AC 所成的角,再利用余弦定理求解. 【详解】设AE BF a ==,则()()23119333288B EBF a a V a a '-+-⎡⎤=⨯⨯⨯-⨯≤=⎢⎥⎣⎦,当且仅当3a a =-,即32a =时等号成立, 即当三棱锥B EBF '-的体积取得最大值时,点E ,F 分别是棱AB,BC 的中点, 方法一:连接A E ',AF ,则352A E '=,352AF =,2292A F AA AF ''=+=,13222EF AC ==, 因为//EF AC ,所以A FE '∠即为异面直线A F '与AC 所成的角,由余弦定理得222819452424cos 93222222A F EF A E A FE A F EF +-''+-'∠==='⋅⋅⨯⨯, ∴4A FE π'∠=.方法二:以B 为坐标原点,以BC 、BA 、BB '分别为x 轴、y 轴、z 轴建立空间直角坐标系,则()0,3,0A ,()3,0,0C ,()0,3,3A ',3,0,02F ⎛⎫⎪⎝⎭, ∴3,3,32A F ⎛⎫'=-- ⎪⎝⎭u u u u r ,()3,3,0AC =-u u u r ,所以9922cos ,9322A F AC A F AC A F AC +'⋅'==='⋅⨯u u u u r u u u r u u u u r u u u r u u u u r u u u r所以异面直线A F '与AC 所成的角为4π. 故选:C 【点睛】本题主要考查异面直线所成的角,余弦定理,基本不等式以及向量法求角,还考查了推理论证运算求解的能力,属于中档题.7.棱长为2的正方体被一个平面所截,得到几何体的三视图如图所示,则该截面的面积为( )A .92B .922C .32D .3【答案】A 【解析】 【分析】由已知的三视图可得:该几何体是一个正方体切去一个三棱台,其截面是一个梯形,分别求出上下底边的长和高,代入梯形面积公式可得答案. 【详解】由已知的三视图可得:该几何体是一个正方体切去一个三棱台ABC DEF -,所得的组合体,其截面是一个梯形BCFE , 22112+=22222+=222322()2+=故截面的面积1329(222)222S =⨯=, 故选:A . 【点睛】本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.8.在三棱锥P ABC -中,PA ⊥平面ABC ,且ABC ∆为等边三角形,2AP AB ==,则三棱锥P ABC -的外接球的表面积为( ) A .272π B .283πC .263π D .252π 【答案】B 【解析】 【分析】计算出ABC ∆的外接圆半径r ,利用公式222PA R r ⎛⎫=+ ⎪⎝⎭可得出外接球的半径,进而可得出三棱锥P ABC -的外接球的表面积. 【详解】ABC ∆的外接圆半径为232sin3AB r π==PA ⊥Q 底面ABC ,所以,三棱锥P ABC -的外接球半径为22222321123PA R r ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭, 因此,三棱锥P ABC -的外接球的表面积为222128443R πππ⎛⎫=⨯= ⎪ ⎪⎝⎭. 故选:B. 【点睛】本题考查三棱锥外接球表面积的计算,解题时要分析几何体的结构,选择合适的公式计算外接球的半径,考查计算能力,属于中等题.9.一个几何体的三视图如图所示,则该几何体的体积为A .383+B .823+C .283D .10【答案】A 【解析】【分析】根据三视图可知该几何体为一组合体,是一个棱长为2的正方体与三棱锥的组合体,根据体积公式分别计算即可. 【详解】几何体为正方体与三棱锥的组合体,由正视图、俯视图可得该几何体的体积为311232+232832V =⨯⨯⨯⨯=+, 故选A. 【点睛】本题主要考查了三视图,正方体与三棱锥的体积公式,属于中档题.10.已知四面体P ABC -的外接球的球心O 在AB 上,且PO ⊥平面ABC ,23AC AB =,若四面体P ABC -的体积为32,求球的表面积( ) A .8π B .12πC .83πD .123π【答案】B 【解析】 【分析】依据题意作出图形,设四面体P ABC -的外接球的半径为R ,由题可得:AB 为球的直径,即可求得:2AB R =,3AC R =, BC R =,利用四面体P ABC -的体积为32列方程即可求得3R =,再利用球的面积公式计算得解。
浙江省2020版高考数学专题8立体几何8.5空间向量及其应用检测

8.5 空间向量及其应用挖命题【考情探究】分析解读 1.空间角是立体几何中的一个突出的量化指标,是空间图形位置关系的具体体现,因此,空间角是高考的必考内容.2.考查空间角的计算,既可能以选择题、填空题的形式出现,也可能以解答题的形式出现.以探索题、最值问题考查空间角的计算,常以解答题的形式出现,空间角的计算主要是传统法和向量法.3.在立体几何解答题中,建立空间直角坐标系(或取基底向量),利用空间向量的数量积解决直线、平面间的位置关系、角度、长度等问题越来越受到青睐,特别是处理存在性问题、探索性问题、开放性问题等,比用传统方法简便快捷,一直是高考的重点和热点.4.预计2020年高考试题中,空间角的计算,空间向量在立体几何中的应用必是高考热点.复习时应高度重视.破考点【考点集训】考点一空间角1.(2018浙江嵊州高三期末质检,19,15分)如图,在菱形ABCD中,∠BAD=,ED⊥平面ABCD,EF∥DB,M是线段AE的中点,DE=EF=BD.(1)证明:DM∥平面CEF;(2)求直线DM与平面DEF所成角的正弦值.解析(1)证明:连接AC与BD交于点O,连接MO.因为DO∥EF,DO⊄平面CEF,EF⊂平面CEF,所以DO∥平面CEF.因为M是线段AE的中点,所以MO是△ACE的中位线,所以MO∥EC.又MO⊄平面CEF,EC⊂平面CEF,所以MO∥平面CEF,又MO∩DO=O,MO⊂平面MDO,DO⊂平面MDO,所以平面MDO∥平面CEF,又DM⊂平面MDO,所以DM∥平面CEF.(2)解法一:因为四边形ABCD是菱形,所以AC⊥BD.又因为ED⊥平面ABCD,AC⊂平面ABCD,所以ED⊥AC,又ED∩BD=D,所以AC⊥平面DEF.设BD=2,则点A到平面DEF的距离AO=.因为点M是线段AE的中点,所以点M到平面DEF的距离h=AO=.设直线DM与平面DEF所成的角为θ,则sin θ===.故直线DM与平面DEF所成角的正弦值为.解法二:设AB的中点为G,连接DG,则DG⊥DC.以D为坐标原点,DG,DC,DE所在直线分别为x轴,y轴,z轴建立空间直角坐标系.取BD=2,则D(0,0,0),M,E(0,0,1),F,所以=(0,0,1),=.设平面DEF的法向量为n=(x,y,z),则即可取法向量n=(1,-,0).又=,所以cos<,n>===,故直线DM与平面DEF所成角的正弦值为.2.(2017浙江高考模拟训练冲刺卷一,19)如图,在四棱锥A-BCDO中,DO⊥平面AOB,BO∥CD,OA=CD=2,OD=2,OB=4,∠AOB=120°.(1)求直线AC与平面ABD所成角的正弦值;(2)求二面角D-OA-C的余弦值.解析(1)如图,过点O在平面AOB内作OB的垂线OE,交AB于点E.∵DO⊥平面AOB,∴OD⊥OE,OD⊥OB,分别以OE,OB,OD所在的直线为x,y,z轴,建立空间直角坐标系,如图所示.则各点坐标为O(0,0,0),A(,-1,0),B(0,4,0),C(0,2,2),D(0,0,2),∴=(-,5,0),=(-,1,2).设平面ABD的法向量为n=(x,y,z),则由n·=0,n·=0,得取x=5,得n=(5,,2).设直线AC与平面ABD所成角为θ,又=(-,3,2),∴sin θ=|cos,n|==,故直线AC与平面ABD所成角的正弦值为.(2)设平面AOD的法向量为m1=(x,y,z),又=(,-1,0),=(0,0,2),∴由m1·=0,m1·=0,得取x=1,得m1=(1,,0).设平面AOC的法向量为m2=(a,b,c),又=(,-1,0),=(0,2,2),∴由m2·=0,m2·=0,得取b=,得m2=(1,,-1).∴cos m1,m2==,由图可知二面角D-OA-C的平面角为锐角,故二面角D-OA-C的余弦值为.考点二空间向量在立体几何中的应用1.(2017浙江台州4月调研卷(一模),17)如图,在棱长为2的正四面体A-BCD中,E、F分别为直线AB、CD上的动点,且|EF|=.若记EF的中点P的轨迹为L,则|L|等于.(注:|L|表示点P的轨迹的长度)答案π2.(2017浙江杭州二模(4月),19)如图,已知四边形ABCD是矩形,M,N分别为边AD,BC的中点,MN与AC交于点O,沿MN将矩形MNCD折起,设AB=2,BC=4,二面角B-MN-C的大小为θ.(1)当θ=90°时,求cos∠AOC的值;(2)当θ=60°时,点P是线段MD上一点,直线AP与平面AOC所成角为α.若sin α=,求线段MP的长.解析设E为AB的中点,连接OE,则OE⊥MN,以O为原点,OE,ON所在直线分别为x轴,y轴,建立空间直角坐标系(图略).(1)当θ=90°时,A(2,-1,0),C(0,1,2),∴=(2,-1,0),=(0,1,2),∴cos∠AOC==-.(2)由θ=60°得C(1,1,),D(1,-1,),M(0,-1,0),∴=(1,0,).设=λ(0≤λ≤1),则=+=(λ,-1,λ).∴=-=(λ-2,0,λ),设平面AOC的法向量为n=(x,y,z).∵n·=0,n·=0,=(2,-1,0),=(1,1,),∴取x=1,则y=2,z=-,故n=(1,2,-),由题意得,=,即3λ2-10λ+3=0,∴λ=或λ=3(舍去),∴在线段MD上存在点P符合题意,且MP=MD=.炼技法【方法集训】方法1 求直线与平面所成角的方法1.(2017浙江稽阳联谊学校联考(4月),19)如图(1)所示,四边形ABCD为梯形,AB∥CD,∠C=60°,点E在CD上,AB=CE=2,BF=BD=,BD⊥BC.现将△ADE沿AE翻折到图(2)中△APE的位置,使得二面角P-AE-C的大小为.(1)求PB的长度;(2)求证:PB⊥平面ABCE;(3)求直线AB与平面APE所成角的正弦值.解析(1)因为AB EC,所以四边形ABCE是平行四边形,所以BC∥AE,又因为BD⊥BC,所以BD⊥AE,所以AE⊥FB,AE⊥FP,所以∠PFB为二面角P-AE-C的平面角.(3分)由BF=,PF=2,得BP2=BF2+PF2-2BF·PFcos∠BFP=9,所以BP=3.(5分)(2)证明:由BF=,PF=2,BP=3知,PB2+BF2=PF2,所以BF⊥PB,①(7分)又因为BF⊥AE,PF⊥AE,BF∩PF=F,所以AE⊥平面PFB,所以AE⊥PB,②(9分)由①②可知,PB⊥平面ABCE.(10分)(3)解法一:作BN⊥PF于N点,连接AN.由(2)可知,AE⊥平面BFP,又AE⊂平面APE,∴平面BFP⊥平面APE.又平面BFP∩平面APE=PF,BN⊂平面BFP,所以BN⊥平面APE,(12分)所以∠BAN是直线AB与平面APE所成的角.(13分)易知BN=BFsin 60°=,则sin∠NAB===.故直线AB与平面APE所成角的正弦值为.(15分)解法二:易知BF,BP,BC两两互相垂直,建立如图所示的空间直角坐标系,则B(0,0,0),C(3,0,0),A(-1,,0),E(2,,0),P(0,0,3).(11分)设平面APE的法向量为n=(x,y,z).又=(3,0,0),=(1,-,3),所以由即得取z=1,得n=(0,,1).(13分)设直线AB与平面APE所成的角为θ,又=(1,-,0),所以sin θ=|cos<n,>|==,故直线AB与平面APE所成角的正弦值为.(15分)2.如图,△ABC是以C为直角的等腰直角三角形,直角边长为8,AE∶EC=5∶3,DE∥BC,沿DE 将三角形ADE折起,使得点A在平面BCED上的射影是点C,点M在AC上且MC=AC.(1)在BD上确定点N的位置,使得MN∥平面ADE;(2)在(1)的条件下,求CN与平面ABD所成角的正弦值.解析(1)由点A在平面BCED上的射影是点C,可知AC⊥平面BCED,而BC⊥CE,如图建立空间直角坐标系,可知各点的坐标为C(0,0,0),A(0,0,4),B(0,8,0),D(3,5,0),E(3,0,0).由MC=AC,可知点M的坐标为,设点N的坐标为(x,y,0),则由点N在BD上可得y=8-x,即点N的坐标为(x,8-x,0),则=.设平面ADE的法向量为n1=(x,y,z),则而=(0,-5,0),=(3,0,-4),所以取x=4,则z=3,可得n1=(4,0,3).MN∥平面ADE等价于n1·=0,即4x+0×(8-x)+3×=0.解之可得x=2,即点N的坐标为(2,6,0),所以点N为BD的靠近D点的三等分点.(2)由(1)可知=(2,6,0),设平面ABD的法向量为n2=(p,q,r),由题意可知而=(-3,3,0),=(0,8,-4),可得取p=1,则q=1,r=2.可得n2=(1,1,2).设CN与平面ABD所成角为θ,则sin θ==.方法2 求二面角的方法1.(2018浙江镇海中学期中,20)在多面体ABC-A1B1C1中,AA1∥BB1∥CC1,AA1=4,BB1=2,AB=4,CC1=3,AB⊥BB1,C1在平面ABB1A1上的射影E是线段A1B1的中点.(1)求证:平面ABC⊥平面ABB1A1;(2)若C1E=2,求二面角C1-AB1-C的余弦值.解析(1)证明:设线段AB的中点为O,连接OE,CO,则OE∥AA1,且OE==3,(2分)∵AA1∥CC1,∴OE∥CC1,又OE=CC1=3,∴四边形CC1EO为平行四边形,∴OC∥EC1.(4分)∵C1E⊥平面ABB1A1,∴OC⊥平面ABB1A1,(5分)∵OC⊂平面ABC,∴平面ABC⊥平面ABB1A1.(7分)(2)由(1)知OB,OE,OC两两互相垂直,分别以OB,OE,OC所在直线为x,y,z轴建立空间直角坐标系,则O(0,0,0),A(-2,0,0),B1(2,2,0),C(0,0,2),C1(0,3,2).(8分)设平面AB1C的法向量为m=(x,y,z),而=(4,2,0),=(2,0,2),由得取x=1,得m=(1,-2,-1).(10分)设平面AB1C1的法向量为n=(x1,y1,z1),而=(4,2,0),=(2,3,2),由得取x1=1,得n=(1,-2,2).(12分)∴cos<m,n>==,(14分)由图可知二面角C1-AB1-C的平面角为锐角,故二面角C1-AB1-C的余弦值为.(15分)2.(2017浙江名校(诸暨中学)交流卷四,19)如图,已知△ABC为等边三角形,M为AB的中点,AA1,BB1分别垂直平面ABC于点A,B,AA1=AB,BB1=AB,MN⊥A1B1,垂足为N.(1)求证:CN⊥A1B1;(2)求平面ABC与平面A1B1C所成的锐二面角的正切值.解析(1)证明:因为AA1,BB1分别垂直平面ABC于点A,B,所以平面AA1B1B⊥平面ABC,因为AC=BC,M为AB的中点,所以CM⊥AB,又平面AA1B1B∩平面ABC=AB,CM⊂平面AA1B1B,所以CM⊥平面A1ABB1,所以CM⊥A1B1,又因为MN⊥A1B1,所以A1B1⊥平面CMN,所以A1B1⊥CN.(2)解法一:如图,延长AB、A1B1相交于点D,连接CD,则CD为所求二面角的棱.因为BB1=AA1,BB1∥AA1,所以=,于是BD=BC=BA,于是∠ACD=90°,即CD⊥CA.又因为CD⊥AA1,所以CD⊥平面AA1C,所以CD⊥CA1.于是∠A1CA即为所求二面角的平面角. 在Rt△A1AC中,AA1=AB=AC,所以∠A1CA=45°,所以tan∠A1CA=1.所以平面ABC与平面A1B1C所成的锐二面角的正切值为1.解法二:如图,以M为原点,MA所在直线为x轴,MC所在直线为y轴建立空间直角坐标系,设AB=2.则C(0,,0),A1(1,0,2),B1(-1,0,1),=(1,-,2),=(-2,0,-1).设平面A1B1C的法向量为n1=(x,y,z).由·n1=0,·n1=0,得取x=1,则y=-,z=-2,故n1=(1,-,-2).设所求二面角的大小为θ,又平面ABC的一个法向量为n2=(0,0,1).所以cos θ===,所以tan θ=1.过专题【五年高考】A组自主命题·浙江卷题组考点一空间角1.(2018浙江,8,4分)已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点).设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S-AB-C的平面角为θ3,则( )A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1答案 D2.(2017浙江,9,4分)如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P,Q,R分别为AB,BC,CA上的点,AP=PB,==2.分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α,β,γ,则( )A.γ<α<βB.α<γ<βC.α<β<γD.β<γ<α答案 B3.(2016浙江文,14,4分)如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=,∠ADC=90°.沿直线AC将△ACD翻折成△ACD',直线AC与BD'所成角的余弦的最大值是.答案考点二空间向量在立体几何中的应用1.(2015浙江,15,6分)已知e1,e2是空间单位向量,e1·e2=.若空间向量b满足b·e1=2,b·e2=,且对于任意x,y∈R,|b-(xe1+ye2)|≥|b-(x0e1+y0e2)|=1(x0,y0∈R),则x0= ,y0= ,|b|= .答案1;2;22.(2018浙江,19,15分)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.(1)证明:AB1⊥平面A1B1C1;(2)求直线AC1与平面ABB1所成的角的正弦值.解析本题主要考查空间点、线、面位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力.解法一:(1)证明:由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB得AB1=A1B1=2,所以A1+A=A,故AB1⊥A1B1.由BC=2,BB1=2,CC1=1,BB1⊥BC,CC1⊥BC得B1C1=,由AB=BC=2,∠ABC=120°得AC=2,由CC1⊥AC,得AC1=,所以A+B1=A,故AB1⊥B1C1,因为A1B1,B1C1⊂平面A1B1C1,所以AB1⊥平面A1B1C1.(2)如图,过点C1作C1D⊥A1B1,交直线A1B1于点D,连接AD.由AB1⊥平面A1B1C1得平面A1B1C1⊥平面ABB1,由C1D⊥A1B1得C1D⊥平面ABB1,所以∠C1AD是AC1与平面ABB1所成的角.由B1C1=,A1B1=2,A1C1=得cos∠C1A1B1=,sin∠C1A1B1=,所以C1D=,故sin∠C1AD==.因此,直线AC1与平面ABB1所成的角的正弦值是.解法二:(1)证明:如图,以AC的中点O为原点,分别以射线OB,OC为x,y轴的正半轴,建立空间直角坐标系O-xyz.由题意知各点坐标如下:A(0,-,0),B(1,0,0),A1(0,-,4),B1(1,0,2),C1(0,,1).因此=(1,,2),=(1,,-2),=(0,2,-3).由·=0得AB1⊥A1B1.由·=0得AB1⊥A1C1.所以AB1⊥平面A1B1C1.(2)设直线AC1与平面ABB1所成的角为θ.由(1)可知=(0,2,1),=(1,,0),=(0,0,2).设平面ABB1的法向量n=(x,y,z).由即可取n=(-,1,0).所以sin θ=|cos<,n>|==.因此,直线AC1与平面ABB1所成的角的正弦值是.3.(2017浙江,19,15分)如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.(1)证明:CE∥平面PAB;(2)求直线CE与平面PBC所成角的正弦值.解析本题主要考查空间点、线、面的位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力.(1)证明:如图,设PA中点为F,连接EF,FB.因为E,F分别为PD,PA中点,所以EF∥AD且EF=AD. 又因为BC∥AD,BC=AD,所以EF∥BC且EF=BC,即四边形BCEF为平行四边形,所以CE∥BF,因此CE∥平面PAB.(2)分别取BC,AD的中点为M,N.连接PN交EF于点Q,连接MQ.因为E,F,N分别是PD,PA,AD的中点,所以Q为EF中点,在平行四边形BCEF中,MQ∥CE.由△PAD为等腰直角三角形得PN⊥AD.由DC⊥AD,N是AD的中点得BN⊥AD.所以AD⊥平面PBN,由BC∥AD得BC⊥平面PBN,那么平面PBC⊥平面PBN.过点Q作PB的垂线,垂足为H,连接MH.MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角.设CD=1.在△PCD中,由PC=2,CD=1,PD=得CE=,在△PBN中,由PN=BN=1,PB=得QH=,在Rt△MQH中,QH=,MQ=,所以sin∠QMH=.所以,直线CE与平面PBC所成角的正弦值是.一题多解(1)证明:设AD的中点为O,连接OB,OP.∵△PAD是以AD为斜边的等腰直角三角形,∴OP⊥AD.∵BC=AD=OD,且BC∥OD,∴四边形BCDO为平行四边形,又∵CD⊥AD,∴OB⊥AD,∵OP∩OB=O,∴AD⊥平面OPB.过点O在平面POB内作OB的垂线OM,交PB于M,以O为原点,OB所在直线为x轴,OD所在直线为y轴,OM所在直线为z轴,建立空间直角坐标系,如图.设CD=1,则有A(0,-1,0),B(1,0,0),C(1,1,0),D(0,1,0).设P(x,0,z)(z>0),由PC=2,OP=1,得得x=-,z=.即点P,而E为PD的中点,∴E.设平面PAB的法向量为n=(x1,y1,z1),∵=,=(1,1,0),∴⇒取y1=-1,得n=(1,-1,).而=,则·n=0,而CE⊄平面PAB,∴CE∥平面PAB.(2)设平面PBC的法向量为m=(x2,y2,z2),∵=(0,1,0),=,∴取x2=1,得m=(1,0,).设直线CE与平面PBC所成角为θ.则sin θ=|cos<m,>|==,故直线CE与平面PBC所成角的正弦值为.方法总结 1.证明直线与平面平行的方法.(例:求证:l∥α)①线面平行的判定定理:在平面α内找到一条与直线l平行的直线m,从而得到l∥α.②面面平行的性质:过直线l找到(或作出)一个平面β,使得β∥α,从而得l∥α.③向量法:(i)求出平面α的法向量n和直线l的方向向量l,证明n·l=0,得l∥α. (ii)证明直线l的方向向量l能被平面α内的两个基底向量所表示,得l∥α.2.求线面角的方法.①定义法:作出线面角,解三角形即可.②解斜线段、射影、垂线段构成的三角形.例:求AB与平面α所成角θ的正弦值,其中A∈α.只需求出点B到平面α的距离d(通常由等体积法求d),由sin θ=得结论.③向量法:求出平面α的法向量n,设直线AB与α所成角为θ,则sin θ=|cos<n,>|. 最好是画出图形,否则容易出错.B组统一命题、省(区、市)卷题组考点一空间角1.(2018课标全国Ⅰ理,12,5分)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )A. B. C. D.答案 A2.(2018课标全国Ⅱ理,16,5分)已知圆锥的顶点为S,母线SA,SB所成角的余弦值为,SA与圆锥底面所成角为45°.若△SAB的面积为5,则该圆锥的侧面积为.答案40π3.(2018课标全国Ⅱ理,20,12分)如图,在三棱锥P-ABC中,AB=BC=2,PA=PB=PC=AC=4,O为AC的中点.(1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.解析(1)证明:因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=2.连接OB.因为AB=BC=AC,所以△ABC为等腰直角三角形,且OB⊥AC,OB=AC=2.由OP2+OB2=PB2知PO⊥OB.由OP⊥OB,OP⊥AC知PO⊥平面ABC.(2)如图,以O为坐标原点,的方向为x轴正方向,建立空间直角坐标系O-xyz.由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,2),=(0,2,2).取平面PAC 的法向量=(2,0,0).设M(a,2-a,0)(0<a≤2),则=(a,4-a,0).设平面PAM的法向量为n=(x,y,z).由·n=0,·n=0得可取n=((a-4),a,-a),所以cos<,n>=.由已知可得|cos<,n>|=.所以=.解得a=-4(舍去)或a=.所以n=.又=(0,2,-2),所以cos<,n>=.所以PC与平面PAM所成角的正弦值为.4.(2018天津理,17,13分)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.(1)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;(2)求二面角E-BC-F的正弦值;(3)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.解析本小题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力. 依题意,可以建立以D为原点,分别以,,的方向为x轴,y轴,z轴的正方向的空间直角坐标系(如图),可得D(0,0,0),A(2,0,0),B(1,2,0),C(0,2,0),E(2,0,2),F(0,1,2),G(0,0,2),M,N(1,0,2) .(1)证明:依题意=(0,2,0),=(2,0,2).设n0=(x0,y0,z0)为平面CDE的法向量,则即不妨令z0=-1,可得n0=(1,0,-1).又=,可得·n0=0,又因为直线MN⊄平面CDE,所以MN∥平面CDE.(2)依题意,可得=(-1,0,0),=(1,-2,2),=(0,-1,2).设n=(x1,y1,z1)为平面BCE的法向量,则即不妨令z1=1,可得n=(0,1,1).设m=(x2,y2,z2)为平面BCF的法向量,则即不妨令z2=1,可得m=(0,2,1).因此有cos<m,n>==,于是sin<m,n>=.所以,二面角E-BC-F的正弦值为.(3)设线段DP的长为h(h∈[0,2]),则点P的坐标为(0,0,h),可得=(-1,-2,h).易知,=(0,2,0)为平面ADGE的一个法向量,故|cos<,>|==,由题意,可得=sin 60°=,解得h=∈[0,2].所以,线段DP的长为.方法归纳利用空间向量解决立体几何问题的一般步骤(1)审清题意并建系.利用条件分析问题,建立恰当的空间直角坐标系;(2)确定相关点的坐标.结合建系过程与图形,准确地写出相关点的坐标;(3)确定直线的方向向量和平面的法向量.利用点的坐标求出相关直线的方向向量和平面的法向量,若已知某直线垂直某平面,可直接取该直线的方向向量为该平面的法向量;(4)转化为向量运算.将空间位置关系转化为向量关系,空间角转化为向量的夹角问题去论证、求解;(5)问题还原.结合条件与图形,作出结论(注意角的范围).5.(2017课标全国Ⅰ理,18,12分)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.解析本题考查空间点、线、面的位置关系以及二面角的概念和计算,考查学生的空间想象能力、推理论证能力和运算求解能力.(1)证明:由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.由于AB∥CD,故AB⊥PD,又AP∩PD=P,AP、PD⊂平面PAD,所以AB⊥平面PAD.又AB⊂平面PAB,所以平面PAB⊥平面PAD.(2)解法一(综合法):根据题意可设AB=1,因为AB∥CD,∠APD=∠BAP=∠CDP=90°,PA=PD=AB=DC,所以四边形ABCD是平行四边形,且AD=PC=PB=CB=,取PB的中点为F,连接AF,CF,在等腰三角形PAB中,可得AF⊥PB,在等边三角形PBC中,可得CF⊥PB,所以∠AFC为二面角A-PB-C的平面角,由(1)知AB⊥平面PAD,又AD⊂平面PAD,所以AB⊥AD.所以平行四边形ABCD是矩形,连接AC,则AC=.在△AFC中,AC=,AF=,FC=,由余弦定理可得cos∠AFC==-,所以二面角A-PB-C的余弦值为-.解法二(向量法):在平面PAD内作PF⊥AD,垂足为F.由(1)可知,AB⊥平面PAD,故AB⊥PF,又AD∩AB=A,可得PF⊥平面ABCD.以 F为坐标原点,的方向为x轴正方向,||为单位长,建立如图所示的空间直角坐标系F-xyz.由(1)及已知可得A,P,B,C.所以=,=(,0,0),=,=(0,1,0).设n=(x1,y1,z1)是平面PCB的法向量,则即可取n=(0,-1,-).设m=(x2,y2,z2)是平面PAB的法向量,则即可取m=(1,0,1).则cos<n,m>==-.易知二面角A-PB-C为钝二面角,所以二面角A-PB-C的余弦值为-.方法总结面面垂直的证明及向量法求解二面角.(1)面面垂直的证明.证明两个平面互相垂直,可以在一个平面内找一条直线l,证明直线l垂直于另一平面. (2)利用空间向量求解几何体中的二面角的余弦值.建立空间直角坐标系,找到点的坐标,求出两个半平面的法向量n1,n2,设二面角的大小为θ,则|cos θ|=,再根据二面角的范围判断二面角余弦值的正负情况.6.(2017天津理,17,13分)如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.(1)求证:MN∥平面BDE;(2)求二面角C-EM-N的正弦值;(3)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为,求线段AH的长.解析本小题主要考查直线与平面平行、二面角、异面直线所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.如图,以A为原点,分别以,,方向为x轴、y轴、z轴正方向建立空间直角坐标系.依题意可得A(0,0,0),B(2,0,0),C(0,4,0),P(0,0,4),D(0,0,2),E(0,2,2),M(0,0,1),N(1,2,0).(1)证明:=(0,2,0),=(2,0,-2).设n=(x,y,z)为平面BDE的法向量,则即不妨设z=1,可得n=(1,0,1).又=(1,2,-1),可得·n=0.因为MN⊄平面BDE,所以MN∥平面BDE.(2)易知n1=(1,0,0)为平面CEM的一个法向量.设n2=(x,y,z)为平面EMN的法向量,则因为=(0,-2,-1),=(1,2,-1),所以不妨设y=1,可得n2=(-4,1,-2).因此有cos<n1,n2>==-,于是sin<n1,n2>=.所以,二面角C-EM-N的正弦值为.(3)依题意,设AH=h(0≤h≤4),则H(0,0,h),进而可得=(-1,-2,h),=(-2,2,2).由已知,得|cos<,>|===,整理得10h2-21h+8=0,解得h=或h=.所以,线段AH的长为或.方法总结利用空间向量法证明线面位置关系与计算空间角的步骤:(1)根据题目中的条件,充分利用垂直关系,建立适当的空间直角坐标系,尽量使相关点在坐标轴上,求出相关点的坐标;(2)求出相关直线的方向向量及相关平面的法向量,根据题目的要求,选择适当的公式,将相关的坐标代入进行求解或证明;(3)检验,得出最后结论.7.(2017课标全国Ⅱ理,19,12分)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°,E是PD的中点.(1)证明:直线CE∥平面PAB;(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.解析本题考查了线面平行的证明和线面角、二面角的计算.(1)取PA的中点F,连接EF,BF.因为E是PD的中点,所以EF∥AD,EF=AD.由∠BAD=∠ABC=90°得BC∥AD,又BC=AD,所以EF BC,四边形BCEF是平行四边形,CE∥BF,又BF⊂平面PAB,CE⊄平面PAB,故CE∥平面PAB.(2)由已知得BA⊥AD,以A为坐标原点,的方向为x轴正方向,||为单位长,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(1,0,0),C(1,1,0),P(0,1,),=(1,0,-),=(1,0,0).设M(x,y,z)(0<x<1),则=(x-1,y,z),=(x,y-1,z-).因为BM与底面ABCD所成的角为45°,而n=(0,0,1)是底面ABCD的法向量,所以|cos<,n>|=sin 45°,=,即(x-1)2+y2-z2=0.①又M在棱PC上,设=λ,则x=λ,y=1,z=-λ.②由①②解得(舍去),或所以M,从而=.设m=(x0,y0,z0)是平面ABM的法向量,则即所以可取m=(0,-,2).于是cos<m,n>==.易知所求二面角为锐角.因此二面角M-AB-D的余弦值为.方法总结本题涉及直线与平面所成的角和二面角,它们是高考热点和难点,解决此类题时常利用向量法,解题关键是求平面的法向量,再由向量的夹角公式求解.解题关键由线面角为45°求点M的坐标是解题的关键.考点二空间向量在立体几何中的应用1.(2018课标全国Ⅰ理,18,12分)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.解析(1)由已知可得,BF⊥EF,又BF⊥PF,且PF,EF⊂平面PEF,PF∩EF=F,所以BF⊥平面PEF,又BF⊂平面ABFD,所以平面PEF⊥平面ABFD.(2)作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD.以H为坐标原点,的方向为y轴正方向,||为单位长,建立如图所示的空间直角坐标系H-xyz.由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=,又PF=1,EF=2,故PE⊥PF,可得PH=,EH=,则H(0,0,0),P,D,=,=为平面ABFD的法向量.设DP与平面ABFD所成角为θ,则sin θ===.所以DP与平面ABFD所成角的正弦值为.易错警示利用空间向量求线面角的注意事项(1)先求出直线的方向向量与平面的法向量所夹的锐角(钝角时取其补角)的角度,再取其余角即为所求.(2)若求线面角的余弦值,要注意利用平方关系sin2θ+cos2θ=1求出其值,不要误以为直线的方向向量与平面的法向量所夹角的余弦值为所求.2.(2017山东理,17,12分)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB 边所在直线为旋转轴旋转120°得到的,G是的中点.(1)设P是上的一点,且AP⊥BE,求∠CBP的大小;(2)当AB=3,AD=2时,求二面角E-AG-C的大小.解析本题考查线面垂直的证明和二面角的计算.(1)因为AP⊥BE,AB⊥BE,AB,AP⊂平面ABP,AB∩AP=A,所以BE⊥平面ABP,又BP⊂平面ABP,所以BE⊥BP,又∠EBC=120°,因此∠CBP=30°.(2)解法一:取的中点H,连接EH,GH,CH.因为∠EBC=120°,所以四边形BEHC为菱形,所以AE=GE=AC=GC==.取AG中点M,连接EM,CM,EC,则EM⊥AG,CM⊥AG,所以∠EMC为所求二面角的平面角.又AM=1,所以EM=CM==2.在△BEC中,由于∠EBC=120°,由余弦定理得EC2=22+22-2×2×2×cos 120°=12,所以EC=2,因此△EMC为等边三角形,故所求的角为60°.解法二:以B为坐标原点,分别以BE,BP,BA所在的直线为x,y,z轴,建立如图所示的空间直角坐标系.由题意得A(0,0,3),E(2,0,0),G(1,,3),C(-1,,0),故=(2,0,-3),=(1,,0),=(2,0,3),设m=(x1,y1,z1)是平面AEG的法向量.由可得取z1=2,可得平面AEG的一个法向量m=(3,-,2).设n=(x2,y2,z2)是平面ACG的法向量.由可得取z2=-2,可得平面ACG的一个法向量n=(3,-,-2).所以cos<m,n>==.易知所求角为锐二面角,因此所求的角为60°.方法总结求二面角的常见方法有两种:一种是“找”,即根据二面角的面的特殊性(如等边三角形、等腰三角形、直角三角形、正方形、矩形、梯形等)找二面角的平面角的顶点,进而作出该平面角,再通过解三角形求解;另一种是“算”,即利用空间向量的坐标运算,由平面的法向量和夹角公式求解.利用空间向量的运算求二面角时,一定要注意二面角是锐二面角还是钝二面角.3.(2016天津,17,13分)如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.(1)求证:EG∥平面ADF;(2)求二面角O-EF-C的正弦值;(3)设H为线段AF上的点,且AH=HF,求直线BH和平面CEF所成角的正弦值.解析依题意,OF⊥平面ABCD,如图,以O为原点,分别以,,的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,依题意可得O(0,0,0),A(-1,1,0),B(-1,-1,0),C(1,-1,0),D(1,1,0),E(-1,-1,2),F(0,0,2),G(-1,0,0).(1)证明:依题意,=(2,0,0),=(1,-1,2).设n1=(x,y,z)为平面ADF的法向量,则即不妨设z=1,可得n1=(0,2,1),又=(0,1,-2),可得·n1=0,又因为直线EG⊄平面ADF,所以EG∥平面ADF.(2)易证=(-1,1,0)为平面OEF的一个法向量.依题意,=(1,1,0),=(-1,1,2).设n2=(x,y,z)为平面CEF的法向量,则即不妨设x=1,可得n2=(1,-1,1).因此有cos<,n2>==-,于是sin<,n2>=.所以,二面角O-EF-C的正弦值为.(3)由AH=HF,得AH=AF.因为=(1,-1,2),所以==,进而有H,从而=,因此cos<,n2>==-.所以,直线BH和平面CEF所成角的正弦值为.评析本题主要考查直线与平面平行和垂直、二面角、直线与平面所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.4.(2016北京,17,14分)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=.(1)求证:PD⊥平面PAB;(2)求直线PB与平面PCD所成角的正弦值;(3)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值;若不存在,说明理由.解析(1)证明:因为平面PAD⊥平面ABCD,AB⊥AD,所以AB⊥平面PAD.所以AB⊥PD.又因为PA⊥PD,PA∩AB=A,所以PD⊥平面PAB.(2)取AD的中点O,连接PO,CO.因为PA=PD,所以PO⊥AD.又因为PO⊂平面PAD,平面PAD⊥平面ABCD,所以PO⊥平面ABCD.因为CO⊂平面ABCD,所以PO⊥CO.因为AC=CD,所以CO⊥AD.如图建立空间直角坐标系O-xyz.由题意得,A(0,1,0),B(1,1,0),C(2,0,0),D(0,-1,0),P(0,0,1).设平面PCD的法向量为n=(x,y,z),则即令z=2,则x=1,y=-2.所以n=(1,-2,2).又=(1,1,-1),所以cos<n,>==-.所以直线PB与平面PCD所成角的正弦值为.(3)设M是棱PA上一点,则存在λ∈[0,1]使得=λ.因此点M(0,1-λ,λ),=(-1,-λ,λ).因为BM⊄平面PCD,所以BM∥平面PCD当且仅当·n=0,即(-1,-λ,λ)·(1,-2,2)=0.解得λ=.所以在棱PA上存在点M使得BM∥平面PCD,此时=.易错警示(1)证线面垂直时,要在“面”内找两条相交直线,分别与“线”垂直.(2)建立空间直角坐标系前,先明确备选坐标轴之间的两两垂直关系.(3)用向量法说明在某线段上存在满足某条件的点时,参数的取值范围易被忽视.评析本题考查线面垂直的证明,空间向量的应用等,对学生的空间想象能力、运算能力均有较高要求.C组教师专用题组考点一空间角1.(2014广东,5,5分)已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是( )A.(-1,1,0)B.(1,-1,0)C.(0,-1,1)D.(-1,0,1)答案 B2.(2014课标Ⅱ,11,5分)直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为( )A. B.C. D.答案 C3.(2015四川,14,5分)如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E,F分别为AB,BC的中点.设异面直线EM与AF所成的角为θ,则cos θ的最大值为.答案4.(2018天津文,17,13分)如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=2,∠BAD=90°.(1)求证:AD⊥BC;(2)求异面直线BC与MD所成角的余弦值;(3)求直线CD与平面ABD所成角的正弦值.解析本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识.考查空间想象能力、运算求解能力和推理论证能力.(1)证明:由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC.(2)取棱AC的中点N,连接MN,ND.又因为M为棱AB的中点,故MN∥BC.所以∠DMN(或其补角)为异面直线BC与MD所成的角. 在Rt△DAM中,AM=1,故DM==.因为AD⊥平面ABC,故AD⊥AC.在Rt△DAN中,AN=1,故DN==.在等腰三角形DMN中,MN=1,可得cos∠DMN==.所以,异面直线BC与MD所成角的余弦值为.(3)连接CM.因为△ABC为等边三角形,M为边AB的中点,故CM⊥AB,CM=.又因为平面ABC⊥平面ABD,而CM⊂平面ABC,故CM⊥平面ABD.所以,∠CDM为直线CD与平面ABD所成的角. 在Rt△CAD中,CD==4.在Rt△CMD中,sin∠CDM==.所以,直线CD与平面ABD所成角的正弦值为.5.(2017北京理,16,14分)如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=,AB=4.(1)求证:M为PB的中点;(2)求二面角B-PD-A的大小;(3)求直线MC与平面BDP所成角的正弦值.。
高考专题-- 立体几何与空间向量-浙江高三数学三轮复习---精校解析Word版

立体几何与空间向量1. 立体图形的截面问题高考对用一平面去截一立体图形所得平面图形的考查实质上对学生空间想象能力及对平面基本定理及线面平行与面面平行的性质定理的考查。
考生往往对这一类型的题感到吃力,实质上高中阶段对作截面的方法无非有如下两种:一种是利有平面的基本定理:一个就是一条直线上有两点在一平面内则这条直线上所在的点都在这平面内和两平面相交有且仅有一条通过该公共点的直线(即交线)(注意该定理地应用如证明诸线共点的方法:先证明其中两线相交,再证明此交点在第三条直线上即转化为此点为两平面的公共点而第三条直线是两平的交线则依据定理知交点在第三条直线;诸点共线:即证明此诸点都是某两平面的共公点即这此点转化为在两平的交线上)据这两种定理要做两平面的交线可在两平面内通过空间想象分别取两组直线分别相交,则其交点必为两平面的公共点,并且两交点的连线即为两平的交线.另一种方法就是依据线面平行及面面平行的性质定理,去寻找线面平行及面面平行关系,然后根据性质作出交线。
一般情况下这两种方法要结合应用.例1.已知正三棱柱111ABC A B C 的底面边长是10,高是12,过底面一边AB ,作与底面ABC 成060角的截面面积是___________________。
【答案】点评:判断截面的形状,应该将现有截面进行延伸,必须找出与整个几何体表面的截线.2.三视图高考对三视图的要求是:(1)理解简单空间图形 (柱、锥、台、球的简易组合) 的含义,了解中心投影的含义,掌握平行投影的含义;(2)理解三视图和直观图间的关系,掌握三视图所表示的空间几何体.会用斜二测法画出它们的直观图.从学生反馈情况看,主要错误是不能正确视图,还原几何体.突破这一瓶颈的有效途径,一是熟悉规则,二是多做一些练习.例2.【2017课标II ,理4】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )90πB.63πC.42πD.36π【答案】B【解析】点评:在由三视图还原为空间几何体的实际形状时,要从三个视图综合考虑,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线。
【精准解析】浙江省台州市书生中学2020届高三下学期模拟考试数学试题

2020年高考数学模拟试题一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}2A x x =<,{}230B x x x =-<,则A B =( )A. ()0,2B. ()0,3C. ()2,3D. ()2,3-【答案】A 【解析】 【分析】解不等式得到集合A 和集合B ,再求交集得到答案. 【详解】{}{}222A x x x x =<=-<<,{}{}23003B x x x x x =-<=<<,则()0,2A B =.故选:A.【点睛】本题考查了集合的交集运算,解不等式,属于简单题.2. 双曲线2214y x -=的渐近线方程是( )A. 52y x =±B. 5y x =C. 12y x =±D. 2y x =±【答案】D 【解析】 【分析】根据双曲线方程和渐近线方程直接求解.【详解】由双曲线方程可知1,2a b ==,并且焦点在x 轴,所以双曲线的渐近线方程2by x x a=±=±. 故选:D【点睛】本题考查双曲线方程和渐近线,重点考查基本公式,属于基础题型.3. 若实数x 、y 满足约束条件02200y x y x y ≥⎧⎪+-≤⎨⎪-≥⎩,则2z x y =-的最大值是( )A.23B.25C. 2D. 5【答案】C 【解析】 【分析】作出不等式组所表示的可行域,设2t x y =-,利用线性目标函数的几何意义求得t 的取值范围,再利用绝对值的性质可求得z 的最大值.【详解】作出不等式组02200y x y x y ≥⎧⎪+-≤⎨⎪-≥⎩所表示的可行域如下图所示:令2t x y =-,联立2200x y x y +-=⎧⎨-=⎩,解得23x y ==,可得点22,33A ⎛⎫⎪⎝⎭,同理可得点()2,0B ,平移直线2t x y =-,当直线2t x y =-经过可行域的顶点A 时,直线2t x y =-在x 轴上的截距最小,此时t 取最小值,即min 2222333t =-⨯=-; 当直线2t x y =-经过可行域顶点B 时,直线2t x y =-在x 轴上截距最大,此时t 取最大值,即max 2202t =-⨯=. 所以,2223x y -≤-≤,则022x y ≤-≤,因此,max 2z =. 故选:C.【点睛】本题考查线性目标函数绝对值的最值,考查数形结合思想的应用,属于基础题. 4. 某几何体的三视图如图所示,则该几何体的体积为( )A. 2B. 4C. 42D. 12【答案】B 【解析】 【分析】作出几何体的直观图,可知几何体为直三棱柱中截去一个三棱锥而形成,利用柱体和锥体的体积公式可计算出几何体的体积. 【详解】几何体的直观图如下图所示:可知几何体为直三棱柱111ABC A B C -中截去三棱锥111A A B C -所形成, 结合三视图中的数据可知,几何体的体积为2211123234232V =⨯⨯-⨯⨯⨯=. 故选:B.【点睛】本题考查利用三视图计算几何体的体积,解答的关键在于作出几何体的直观图,考查计算能力,属于基础题.5. 已知{}n a 是等差数列,111a =,n S 为数列{}n a 的前n 项和,且57S S =,则n S 的最大值为( ) A. 66 B. 56C. 46D. 36【答案】D 【解析】 【分析】由已知条件求得等差数列的公差,再运用等差数列的前n 项和公式和二次函数的最值可得选项.【详解】由已知57S S =,111a =得,115476++2572d d a a ⨯⨯=,所以2d =-, 所以()121++122n n n d n S na n ⨯-==-, 所以当6n =时,n S 有最大值为36, 故选:D.【点睛】本题考查等差数列的基本量的计算,二次函数的最值,属于基础题. 6. 在ABC 中,角A 、B 、C 所对的边分别是a 、b 、c ,则“sin sin sin a b cB C A+=+”是“ABC 为等腰三角形”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件【答案】A 【解析】 【分析】利用正弦定理边角互化思想结合充分条件、必要条件的定义判断即可. 【详解】充分性:sin sin sin a b c B C A +=+,得a b cb c a+=+,可得22a ac b bc +=+, 则220a b ac bc -+-=,即()()0a b a b c -++=,0a b c ++>,a b ∴=.所以,ABC 为等腰三角形,即充分性成立;必要性:若ABC 为等腰三角形,则a c =或b c =,那么等式sin sin sin a b cB C A+=+不一定成立,即必要性不成立.综上所述,“sin sin sin a b cB C A+=+”是“ABC 为等腰三角形”的充分不必要条件. 故选:A.【点睛】本题考查充分不必要条件的判断,涉及正弦定理边角互化思想的应用,考查推理能力,属于中等题.7. 已知随机变量ξ满足(0)1P p ξ==-,(1)P p ξ==,其中01p <<.令随机变量|()|E ηξξ=-,则( )A. ()()E E ηξ>B. ()()E E ηξ<C. ()()D D ηξ>D. ()()D D ηξ<【答案】D 【解析】 【分析】根据题意,列表求得随机变量ξ及η的分布列,可知均为两点分布.由两点分布的均值及方差表示出()(),E D ξξ和()E η()D η,根据01p <<比较大小即可得解. 【详解】随机变量ξ满足(0)1P p ξ==-,(1)P p ξ==,其中01p <<. 则随机变量ξ的分布列为:所以()()(),1E p D p p ξξ==- 随机变量|()|E ηξξ=-, 所以当0ξ=时,()E p ηξξ=-=,当1ξ=时,()1E p ηξξ=-=-所以随机变量|()|E ηξξ=-的分布列如下表所示(当0.5p =时,η只有一个情况,概率为1):ηp 1p -P1p -p则()()()()1121E p p p p p p η=-+-=-()()()()22211121D p p p p p p p p η=--⋅-+---⋅⎡⎤⎡⎤⎣⎦⎣⎦()()2121p p p =--当()()E E ξη=即()21p p p =-,解得12p =.所以A 、B 错误. ()()D D ξη-()()()21121p p p p p =----()22410p p =->恒成立.所以C 错误,D 正确 故选:D【点睛】本题考查了随机变量的分布列,两点分布的特征及均值和方差求法,属于中档题.8. 已知函数()()20xax bx cf x a e++=≠的部分图象如图所示,则( )A. 0a <B. 0a c ->C. 0b c -<D.320a b c -+<【答案】B 【解析】 【分析】求得函数()y f x =的导数()()22xax a b x b cf x e-+-+-'=,根据函数()y f x =的单调性可判断A 选项的正误,利用()1f '-、()1f '、()0f '的符号可分别判断D 、B 、C 选项的正误.【详解】()2x ax bx cf x e ++=,()()22xax a b x b c f x e-+-+-'∴=, 令()()22g x ax a b x b c =-+-+-,由图象可知,函数()y f x =先减后增再减,则0a -<,可得0a >,A 选项错误;()10f '-<,则()1320g a b c -=-+-<,则320a b c -+>,D 选项错误;()10f '>,则()10g a c =->,B 选项正确;()00f '>,则()00g b c =->,C 选项错误.故选:B.【点睛】本题考查利用函数的单调性判断不等式的正误,解答的关键在于利用导数符号与函数单调性之间的关系解题,考查分析问题和解决问题的能力,属于中等题.9. 已知椭圆22221(0)x y a b a b+=>>,1F ,2F 分别是椭圆的左、右焦点,A 是椭圆的下顶点,直线2AF 交椭圆于另一点P ,若1PF PA =,则椭圆的离心率为( )A.3B.13C.2D.12【答案】A 【解析】 【分析】由1PF PA =和12+2PFPF a =,用a 表示出1PF 和PA ,在1APF △中,求出11cos 3PAF ∠=,根据升幂公式可求1sin OAF ∠=,即为椭圆离心率.详解】解:如图,点P 在椭圆上,所以12+2PF PF a =,由1222,PF PA PF AF AF a ==+=,代入上式得,123,22a aPF PF == 在1APF △,222222111133122cos 32322a a a AF AP PF PAF a AF APa ⎛⎫⎛⎫+- ⎪ ⎪+-⎝⎭⎝⎭∠===⨯,又2111cos 12sin 3PAF OAF ∠=-∠=,所以13sin 3OAF ∠=, 即13sin 3c OAF e a ∠===, 故选:A .【点睛】考查利用椭圆的性质、解三角形的知识以及三角恒等变换求椭圆的离心率;基础题. 10. 如图,三棱锥V ABC -的侧棱长都相等,底面ABC 与侧面VAC 都是以AC 为斜边的等腰直角三角形,E 为线段AC 的中点,F 为直线AB 上的动点,若平面VEF 与平面VBC 所成锐二面角的平面角为θ,则cos θ的最大值是( )3B.2356【答案】D【解析】【分析】连接BE,以E为原点,EB为x轴,EC为y轴,EV为z轴,建立空间直角坐标系,求出平面VBC的一个法向量m,平面VEF的一个法向量n,利用cosm nm nθ⋅=即可求解. 【详解】底面ABC与侧面VAC都是以AC为斜边的等腰直角三角形,则Rt ABC Rt VAC≅,所以VA VC BA BC===设2VA VC BA BC VB=====,由E为线段AC的中点,则2VE BV==,由222VE BE VB+=,所以VE EB⊥,以E为原点,EB为x轴,EC为y轴,EV为z轴,建立空间直角坐标系,如图所示:则()2,0C,)2,0,0B,(2V,设(),2,0F x x,(0,2,2VC=-,(2,0,2VB=-,(2EV=,(,2,2VF x x=-,设平面VBC的一个法向量()111,,m x y z=,则m VCm VB⎧⋅=⎨⋅=⎩,即1111220220zx⎧+=⎪⎨-=⎪⎩,令11x=,则11y=,11z=,所以()1,1,1m=.设平面VEF 的一个法向量()222,,n x y z =,则00n EV n VF ⎧⋅=⎨⋅=⎩,即(222200x x x y =⋅+⋅+=⎪⎩,解得20z =,令21y =,则21x x=-, 所以21,1,0n x ⎛⎫=- ⎪⎪⎝⎭, 平面VEF 与平面VBC所成锐二面角的平面角为θ,则cos 3m n m n θ⋅==, 将分子、分母同除以1x,可得=令()2266632f x x x ⎛=-+=-+ ⎝⎭, 当x =时,()min 3f x=, 则cos θ3=. 故选:D【点睛】本题考查了空间向量法求二面角、考查了基本运算求解能力,解题的关键是建立恰当的空间直角坐标系,属于中档题.非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11. 我国古代数学名著《算法统宗》中有如下描述:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一.”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍.请问塔顶层有______盏灯,塔底层有_______盏灯.【答案】 (1). 3 (2). 192 【解析】 【分析】设塔的顶层共有1a 盏灯,则数列{}n a 是公比为2的等比数列,利用等比数列求和公式可求得1a 的值,进而可求得7a 的值,由此可得出结果.【详解】设塔的顶层共有1a 盏灯,则数列{}n a 是公比为2的等比数列,设其前n 项和为n S , 由题意可得()71711212738112a S a-===-,解得13a =,则6732192a =⨯=. 因此,塔顶层有3盏灯,塔底层有192盏灯. 故答案为:3;192.【点睛】本题考查等比数列中基本量的计算,考查等比数列前n 项和公式的应用,考查计算能力,属于基础题.12. 已知复数z 满足(1i)2+i z +=-(i 为虚数单位),则z 的虚部是_____,||z =______.【答案】 (1). 32【解析】 【分析】根据复数z 满足(1i)2+i z +=-,利用复数的除法化简得到1322z i =-+,再根据复数的概念和模的求法求解.【详解】因为复数z 满足(1i)2+i z +=-, 所以()()()()2121311122i i i z i i i i -+--+===-+++-所以z 的虚部是32,||z ==,故答案为:①32;②2【点睛】本题主要考查复数的运算以及复数的概念和模,还考查了运算求解的能力,属于基础题.13. 已知多项式25272701270127(1)(1)(2)(2)(2)x x a a x a x a x b b x b x b x +-=+++++++=++++,则0127a a a a ++++=_____,5b =______.【答案】 (1). 64- (2). 11 【解析】 【分析】第一空,赋值1x =-可得;第二空,利用5(1)x -展开式求3x 的系数与5x 的系数和即可. 【详解】取1x =-,501272(2)64a a a a ++++=⨯-=-5(1)x - 展开式的通项515(1)k k k kT C x ,则2200555(1)+(1)=11b C C =--故答案为:64-;11【点睛】本题主要考查展开式中的特定项系数及项的系数和.(1)利用赋值法求解项的系数和时,注意各项的系数是指某一项的字母前面的数值(包括符号);(2)求展开式中的特定项或其系数.可依据条件写出第1k +项,再由特定项的特点求出k 值即可.14. 已知圆224O x y +=:,过点)P作两条互相垂直的直线1l ,2l ,其中1l 交该圆于A ,B 两点,2l 交该圆于C ,D 两点,则AB 的最小值是_____,AB CD +的最大值是_____.【答案】 (1). 2 (2). 【解析】 【分析】将AB 用圆心到AB 的距离表示,再利用直角三角形中,直角边小于斜边,即可求得AB 的最小值;将AB CD +用圆心到两弦的弦心距表示,再利用基本不等式,即可求得AB CD +的最大值.【详解】过O 作OE AB ⊥,交AB 于点E ,过O 作OF CD ⊥,交CD 于点F , 连接OA ,OC ,设圆心O 到AB 的距离为1d ,圆心O 到CD 的距离为2d , 则22211224AB OA d d =-=- 又OE OP ≤∴圆心O 到AB 的距离1d 的最大值为3OP =, ∴AB 的最小值为min 2432AB =-=,2222221212222424AB CD OA d OC d d d +=--=--又222123d d OP +==,()22221212844831022d d d d -+-+--≤==当且仅当126d d ==时,等号成立, 所以221210242442102AB CD d d +=--≤⨯=, 所以AB 的最小值为2,AB CD +的最大值是10. 故答案为:2;10【点睛】本题主要考查的是圆的弦长的计算,其中涉及到基本不等式的应用,属于中档题.涉及直线被圆截得的弦长问题时,解法有以下两种:(1)几何法:利用半径长、弦心距、弦长的一半构成的直角三角形求解;(2)代数法:将直线方程与圆的方程组成方程组,设出交点坐标,若交点坐标简单易求,则直接利用两点间的距离公式进行求解;若交点坐标不易求,则将方程组消元后得一元二次方程,由一元二次方程中根与系数的关系可求弦长.15. 新型冠状病毒疫情期间,5位党员需要被安排到3个不同的路口执勤,每个路口至少安排一人,其中党员甲和乙不能被安排到同一个路口,那么总共有_______种不同安排方法.(用数字作答) 【答案】114 【解析】 【分析】先计算出没有限制条件下所有的排法种数,减去甲、乙两人安排在同一个路口时的排法种数,进而得解.【详解】先考虑没有限制条件下的排法种数,将5人分为三组,三组的人数分别为3、1、1或2、2、1,此时,所有的排法种数为2233535322150C C C A A ⎛⎫+= ⎪⎝⎭.其次考虑甲、乙两人安排在同一路口时的排法种数,此时有()12333336C C A +=种排法. 综上所述,共有15036114-=种. 故答案为:114.【点睛】本题考查人员安排问题,采用正难则反的思想求解,考查计算能力,属于中等题.16. 已知a R ∈,若函数()2x x e af x e=-在区间()1,2x ∈上存在最小值,则a 的取值范围是_______.【答案】42242222e e e e ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,, 【解析】 【分析】当0a >时,根据2x x e ay e=-的单调性,可知若存在极值点,则两端点处的函数值一正一负;当0a =时,由函数单调性知不合题意;当0a <时,结合对号函数的性质可确定最值点所满足的范围;综合三种情况可得最终结论.【详解】当0a >时,2x x e a y e =-在()1,2上单调递增,2max 22e ay e∴=-,min 2e a y e =-,若()f x 在()1,2上存在最小值,则220202e ae e a e⎧->⎪⎪⎨⎪-<⎪⎩,即()min 0f x =,解得:2422e ea <<;当0a =时,()22x xe ef x ==,在()1,2上单调递增,不存在最小值,不合题意; 当0a <时,()22x x x x e a e a f x e e=-=-, ()1,2x ∈,()2,x e e e ∴∈,又2x x e a e -≥2x x e ae -=时,即x e =, ∴若()f x 在()1,2上存在最小值,则2e e <<,解得:4222e e a -<<-;综上所述:a 的取值范围为42242222e e e e ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,,. 故答案为:42242222e e e e ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,,. 【点睛】本题考查根据函数在区间内有最值求解参数范围的问题;关键是能够通过分类讨论的方式,结合函数的单调性确定参数在不同范围内时,函数的最值点或区间端点值的符号,由此可构造不等式求得结果.17. 已知ABC ∆三边长分别为3P 是平面ABC 内任意一点,则PA PB PB PC PC PA ⋅+⋅+⋅的最小值是_______.【答案】163- 【解析】 【分析】 由()()()()PA PB PB PC PC PA PA PA AB PA AB PA AC PA AC PA⋅+⋅+⋅=⋅+++⋅+++⋅可得()232PA AB AC PA AB AC ++⋅+⋅,即()221333AB AC PA AB AC AB AC ⎛⎫++-++⋅ ⎪ ⎪⎝⎭,当03AB ACPA ++=,即P 是ABC 的重心时取等号,根据三角形中的条件可得出答案. 【详解】()()()()PA PB PB PC PC PA PA PA AB PA AB PA AC PA AC PA ⋅+⋅+⋅=⋅+++⋅+++⋅()232PA AB AC PA AB AC =++⋅+⋅()()222113333AB AC PA AB AC AB AC AB AC AB AC ⎛⎫+=+-++⋅≥-++⋅ ⎪ ⎪⎝⎭()221133AB AC AB AC =-++⋅ 当03AB ACPA ++=,即P 是ABC 的重心时取等号.ABC ∆三边长分别为3若BC =则1213362AB AC ⋅===,此时原式()11169136333=-++⨯=-若3BC =,则141372AB AC ⋅===,此时原式()111610137333=-++⨯=-若BC =,则6332AB AC ⋅===,此时原式()11161093333=-++⨯=- 所以PA PB PB PC PC PA ⋅+⋅+⋅的最小值是163- 故答案为: 163-【点睛】本题考查平面向量的线性运算,向量的数量积,考查运算求解能力,属于中档题. 三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 18. 已知函数()2sin cos cos 3f x x x x π⎡⎤⎛⎫=⋅-+ ⎪⎢⎥⎝⎭⎣⎦. (1)求()f x 的最小正周期; (2)求()f x 在0,2x π⎡⎤∈⎢⎥⎣⎦上的最大值,并求此时的x 值.【答案】(1)最小正周期为π;(2)最大值为2,此时3x π=.【解析】【分析】(1)利用三角恒等变换思想化简函数()y f x =的解析式为()33sin 262f x x π⎛⎫=-+ ⎪⎝⎭,利用正弦型函数的周期公式可求得函数()y f x =的最小正周期; (2)由0,2x π⎡⎤∈⎢⎥⎣⎦计算出26x π-的取值范围,利用正弦函数的基本性质可求得函数()y f x =的最大值,并可求出对应的x 值. 【详解】(1)()332sin cos cos 2sin cos sin 32f x x x x x x x π⎛⎫⎡⎤⎛⎫=⋅-+=+ ⎪ ⎪⎢⎥ ⎪⎝⎭⎣⎦⎝⎭233333sin cos 3sin sin 2cos 23sin 226x x x x x x π⎛⎫=+=-+=-+⎪⎝⎭, 因此,函数()y f x =的最小正周期为22T ππ==; (2)当0,2x π⎡⎤∈⎢⎥⎣⎦时,则52,666x πππ⎡⎤-∈-⎢⎥⎣⎦, 当226x ππ-=时,即当3x π=时,函数()y f x =取得最大值33. 【点睛】本题考查正弦型函数周期的计算,同时也考查了正弦型函数最值的求解,解答的关键在于利用三角恒等变换思想化简函数解析式,考查计算能力,属于中等题.19. 如图,已知三棱锥P ABC -中,平面PAC ⊥平面ABC ,2AB AC BC PA ====,120PAC ∠=,3PM MC =.(1)证明:BM PC ⊥;(2)求直线AB 和平面PBC 所成角的正弦值.【答案】(1)证明见解析;(2)39. 【解析】 【分析】(1)取AC 的中点E ,PC 的中点F ,连AF 、ME 、BE ,利用等腰三角形三线合一的性质得出BE AC ⊥,利用面面垂直的性质可得出BE ⊥平面PAC ,进而得出BE PC ⊥,再证明出ME PC ⊥,可得出PC ⊥平面MBE ,由此可得出BM PC ⊥;(2)过点E 作EH MB ⊥垂足为点H ,推导出EH ⊥平面PBC ,计算出EH ,可得出点A 到平面PBC 的距离为2EH ,由此可计算出直线AB 和平面PBC 所成角的正弦值为2EHAB,进而得解.【详解】(1)取AC 的中点E ,PC 的中点F ,连AF 、ME 、BE .PA AC =,F 为PC 的中点,AF PC ∴⊥,又3PM MC =,M ∴为CF 的中点,//ME AF ∴,ME PC ∴⊥,又 AB BC =,E 为BC 的中点,BE AC ∴⊥,又平面PAC ⊥平面ABC ,交线AC ,BE ⊂平面ABC ,BE ∴⊥平面PAC ,PC ⊂平面PAC ,BE PC ∴⊥,又MEBE E =,PC ∴⊥平面MBE ,BM ⊂平面MBE ,PC BM ∴⊥;(2)由(1)知PC ⊥平面MBE ,PC ⊂平面PBC ,∴平面MBE ⊥平面PBC ,过点E 作EH MB ⊥垂足为点H , 平面MBE平面PBC MB =,EH ⊂平面MBE ,EH ∴⊥平面PBC ,所以,EH 即是点E 到平面PBC 的距离,BE ⊥平面PAC ,ME ⊂平面PAC ,BE ME ∴⊥,2222213BE AB AE =-=-=cos601AF PA =⋅=,1122ME AF ∴==,MB∴===,113ME BEEHBM⋅∴===,又E是AC的中点,∴点A到面PBC的距离2Ah EH==,AB∴与面PBC所成角的正弦值为12AhAB==.【点睛】本题考查利用线面垂直证明线线垂直,同时也考查了线面角的正弦值的计算,考查推理能力与计算能力,属于中等题.20. 已知数列{}n a满足:11a=,221(21)(21)n nn a n a++=-*()n N∈. 正项数列{}n c满足:对每个*n N∈,21n nc a-=,且21nc-,2nc,21nc+成等比数列.(1)求数列{}n a,{}n c的通项公式;(2)当2n≥时,证明:1235111117314nn c c c c-≤++++<+.【答案】(1)2(21)na n=-,2221,*12nn n kc k Nn n k⎧=-=∈⎨=⎩-;(2)证明见解析;【解析】【分析】(1)由题意可得212(21)(21)nna na n++=-,由累乘法可得2(21)na n=-;由221(21)-n nc a n==-,得2nc n=(n为奇数),再根据21221,,-n n nc c c+是等比数列,可得到2-1nc n∴=(n是偶数),从而得出答案.(2)先验证2n=时,不等式成立,当3n≥时,不论n为奇数偶数都有()21111111nc n n n n n≥>=-++,2111111211nc n n n⎛⎫≤=-⎪--+⎝⎭,从而利用裂项相消法求和可证明结论.【详解】解:(1)解法一:由已知可得212(21)(21)nna na n++=-2n ∴≥时,13211221n n n n n a a a a a a a a a a ---∴=⋅⋯⋯⋅⋅ 22222222(21)(23)31(21)(23)(25)1n n n n n =⋅⋯⋯⋅=-----,又21(211)a =⨯-2(21)n a n ∴=-解法二:122(21)(21)n na a n n +=+-,即[]122(21)2(1)1n n a a n n +=+-- 2(21)n a n ∴-为常数列,122(21)(211)n a a n ∴=⨯--, 又21(211)a =⨯-2(21)n a n ∴=-又221(21)n n c a n ==-- 2n c n ∴=(n 为奇数)又21221,,n n n c c c +-是等比数列222221212121n n n c c c n n -+∴=⋅=-⋅+()()2(21)(21)n c n n ∴=-⋅+2(1)(1)n c n n n ∴=-⋅+=-1(n 是偶数)综上可得2(21)n a n =-,2221,*12n n n k c k N n n k ⎧=-=∈⎨=⎩- (2)先证123111174n c c c c ++++<…… 2n =时,12111471334c c +=+=<,显然成立. 3n ≥时,21n c n ≥- 3n ∴≥时,2111111211n c n n n ⎛⎫≤=- ⎪--+⎝⎭123n1111c c c c ∴+++⋯⋯+ 22111111111324354657(1)11n n ≤++++++⋯⋯++⋅⋅⋅⋅⋅---1111111111111123243546211n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+-++++⋯⋯++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥--+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦-----11117112214n n ⎛⎫=++< ⎪+⎝⎭--再证12351111131nn c c c c -≤+++++ ①2n =时,左边14133=+=,右边43=,成立;②3n ≥时,不论n 为奇数偶数都有()21111111n c n n n n n ≥>=-++ 222123111111111++334k c c c c n +++⋯⋯+≥+++ 11111++33445(1)n n ≥+++⨯⨯⨯+4111111+334451n n =+-+-+-+ 5131n =-+ 综上所述,当2n ≥时,不等式1235111117314n n c c c c -≤++++<+成立. 【点睛】本题考查利用数列的递推关系求数列的通项公式,考查数列不等式的证明,考查放缩法在证明不等式中的应用,考查裂项相消求和,将通项进行适当的放缩是解决本题的关键和难点,属于难题.21. 已知点F 是抛物线2:4C x y =的焦点,P 是其准线l 上任意一点,过点P 作直线PA ,PB 与抛物线C 相切,A ,B 为切点,PA ,PB 与x 轴分别交于Q ,R 两点.(1)求焦点F 的坐标,并证明直线AB 过点F ; (2)求四边形ABRQ 面积的最小值. 【答案】(1)(0,1)F ,证明见解析;(2)3 【解析】 【分析】(1)由点斜式设出直线,AP BP 的直线方程,再由P 在,PA PB 上,得出直线AB 的方程,从而证明直线AB 过点F ;(2)将直线AB 的方程与抛物线方程联立,结合韦达定理,抛物线的性质,点到直线的距离公式得出PAB S ∆,PQR S ∆,再由四边形ABRQ 的面积PAB PQR S S S ∆∆=-,结合导数得出四边形ABRQ 面积的最小值.【详解】(1)由题意可知(0,1)F设2212120,,,,(,1)44x x A x B x P x ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,则111:()2PA x l y y x x -=-即112x y x y =- 同理22:2PB x l y x y =-. 又P 在,PA PB 上,则1012021212x x y x x y ⎧-=-⎪⎪⎨⎪-=-⎪⎩,所以0:12AB x l y x =+所以直线AB 过焦点F. (2)由(1)知0:12AB x l y x =+,代入2:4C x y =得20240x x x --= 则1201224x x x x x +=⎧⎨=-⎩则22121212012()2244AB y y x x x x x ⎡⎤=++=+-+=+⎣⎦ P 到AB的距离d =所以201(2PAB S x ∆=+由(1)知12,0,,022x x Q R ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,则1212QR x x =-=所以PQR S ∆=令2t t =≥ 则四边形ABRQ 的面积311,(2)22PAB PQR S S S t t t ∆∆=-=-≥设311()22f t t t =-,231()22f t t '=-当2t ≥时,()0f t '>即函数()f t 在[2,)+∞上是增函数 则四边形ABRQ 面积的最小值为3【点睛】本题主要考查了抛物线中直线过定点问题,抛物线中的四边形的面积问题,属于中档题.22. 已知a R ∈,设函数2()(34)6ln 6f x ax a x x =-+++,()3g x ax =. (1)试讨论()f x 的单调性;(2)设函数()()()h x f x g x =+,是否存在实数a ,使得()h x 存在两个极值点1x ,2x ,且满足1212()()3ln 322h x h x x x ->--?若存在,求a 的取值范围;若不存在,请说明理由. 注:ln3 1.10≈.【答案】(1)答案不唯一,见解析;(2)存在,1143,⎛⎫⎪⎝⎭【解析】 【分析】(1)求出函数的定义域以及()(23)(-2)x ax f x x-'=,讨论a 的取值范围,即0a ≤,403a <<,43a =或43a >,利用导数与函数单调性的关系即可求解. (2)解法一:求出2246()ax x h x x'-+=,根据题意可得2230ax x -+=有两解两解12,x x ,从而可得124430,0,0a x x ∆=-⨯>>>,从而求得103a <<,由11221212126ln()()()4x h x h x x a x x x x x x -=+-+--,令121x t x =>,可得12212()()4ln 21h x h x t tx x t -=-+--,利用导数求出()24ln 21t m t tt -+=-的单调性,且根据(3)0,(1)0m m ==即可求解;解法二:根据函数有两个极值点可得103a <<,然后将不等式化为1212ln ln 304x x x x ->-,由方程2230ax x -+=,得1,21x a±=t =(0,1)t ∈,则213t a -=,将不等式化为关于t 的不等式,利用导数即可证出.【详解】解:(1)2()(34)6ln 6f x ax a x x =-+++的定义域为{|0}x x >6()2(34)f x ax a x '=-++=22(34)6ax a x x-++=(23)(-2)x ax x -,(i )若0a ≤,则20ax -<,所以()y f x =在3(0,)2递增,3(,)2+∞递减, (ii )若403a <<,则()y f x =在3(0,)2递增,32(,)2a 递减,在2(,)a+∞递增, (iii )若43a =,则()y f x =在(0,)+∞递增; (iv )若43a >,则()y f x =在2(0,)a 递增,在23(,)2a 递减,在3(,)2+∞递增.(2)解法一: 2()(34)6ln 6f x ax a x x =-+++,()3g x ax =2()()()46ln 6h x f x g x ax x x =+=-++26246()24ax x h x ax x x='-+=-+, 若()y h x =有两极值点, 则2230ax x -+=有两解两解12,x x ,121223,x x x x a a+==. 且124430,0,0a x x ∆=-⨯>>> 所以103a <<. 11221212126ln()()()4x h x h x x a x x x x x x -=+-+--令121x t x =>,则121212121221311331()()()()222x x a x x x x x x t x x x x ta+-=-⨯=-+⨯=- 12212()()4ln 21h x h x t tx x t -∴=-+--若1212()()3ln 32,2h x h x x x ->--则24ln 3ln 312t t t >-,28ln 3(1)ln 30t t t -->,令2()8ln 3(1)ln 3m t t t t =--(3)0,(1)0m m ==,()8ln 86ln 3m t t t '=+-(1)86ln30m '=->,(3)810ln30m '=-<46ln 3()886ln 33ln 3()6ln 3t t m t t tt⨯--''=-==所以()y m t '=在4(1,)3ln 3递增,在4(,)3ln 3+∞递减 又(1)86ln30m '=->,(3)810ln30m '=-< 则在区间4(,3)3ln 3内存在0t 使得0()0m t '=. 函数y =m (x )在0(1,)t 单调递增,在0(,3)t 单调递减, 由(3)0,(1)0m m ==,所以当(1,3)t ∈时满足1212()()3ln 32,2h x h x x x ->--2212124()14233x x a t x x ta a +=++==,所以411(,)1433(2)a t t=∈++即实数a 的取值范围为11(,)43解法二: 2()(34)6ln 6f x ax a x x =-+++,()3g x ax =2()()()46ln 6h x f x g x ax x x =+=-++26246()24ax x h x ax x x='-+=-+, 若()y h x =有两极值点,则2230ax x -+=有两解12,x x ,121223,x x x x a a+== 且124430,0,0a x x ∆=-⨯>>>,所以103a <<1212121212()()6(ln ln )()4h x h x x x a x x x x x x --=+-+--1212ln3ln 32622x x x x =-+>-+-即 1212lnln 304x x x x ->-由方程2230ax x -+=,得1,2x =令t =,(0,1)t ∈,则213ta -=,12212213ln2ln ln 3ln 3ln 311012441x t t x t t t x x t +----=-=>--令213()2lnln 311t tG t t t+=---,求导可得 222222222(1)21(2)4(1)3ln 3()3ln 31(1)(1)1(1)t t t t t G t t t t t t ----+'=⋅-⋅=-+---- 22222224(1)3ln 3(1)(43ln 3)(43ln 3)(1)(1)t t t t t --+--+==--.令()0G t '=,得到01t =,所以()y G t =在0(0,)t 上单调递增,在0(,1)t 单调递减.又(0)0G =,312()2ln 3ln 30324G =-=,所以由1()0,(0,)2G t t >∈得,1(0,)2,解得1143a <<. 故实数a 的取值范围是1143(,).【点睛】本题考查了利用导数研究函数的单调性、利用导数研究函数的极值、利用导数研究不等式恒成立问题,考查了分类讨论的思想,属于难题.。
2020版高考数学(浙江专用)一轮总复习检测:8.5 空间向量及其应用 Word版含解析
8.5空间向量及其应用挖命题【考情探究】分析解读 1.空间角是立体几何中的一个突出的量化指标,是空间图形位置关系的具体体现,因此,空间角是高考的必考内容.2.考查空间角的计算,既可能以选择题、填空题的形式出现,也可能以解答题的形式出现.以探索题、最值问题考查空间角的计算,常以解答题的形式出现,空间角的计算主要是传统法和向量法.3.在立体几何解答题中,建立空间直角坐标系(或取基底向量),利用空间向量的数量积解决直线、平面间的位置关系、角度、长度等问题越来越受到青睐,特别是处理存在性问题、探索性问题、开放性问题等,比用传统方法简便快捷,一直是高考的重点和热点.4.预计2020年高考试题中,空间角的计算,空间向量在立体几何中的应用必是高考热点.复习时应高度重视.破考点【考点集训】考点一空间角1.(2018浙江嵊州高三期末质检,19,15分)如图,在菱形ABCD中,∠BAD=,ED⊥平面ABCD,EF∥DB,M是线段AE的中点,DE=EF=BD.(1)证明:DM∥平面CEF;(2)求直线DM与平面DEF所成角的正弦值.解析(1)证明:连接AC与BD交于点O,连接MO.因为DO∥EF,DO⊄平面CEF,EF⊂平面CEF,所以DO∥平面CEF.因为M是线段AE的中点,所以MO是△ACE的中位线,所以MO∥EC.又MO⊄平面CEF,EC⊂平面CEF,所以MO∥平面CEF,又MO∩DO=O,MO⊂平面MDO,DO⊂平面MDO,所以平面MDO∥平面CEF,又DM⊂平面MDO,所以DM∥平面CEF.(2)解法一:因为四边形ABCD是菱形,所以AC⊥BD.又因为ED⊥平面ABCD,AC⊂平面ABCD,所以ED⊥AC,又ED∩BD=D,所以AC⊥平面DEF.设BD=2,则点A到平面DEF的距离AO=.因为点M是线段AE的中点,所以点M到平面DEF的距离h=AO=.设直线DM与平面DEF所成的角为θ,则sin θ===.故直线DM与平面DEF所成角的正弦值为.解法二:设AB的中点为G,连接DG,则DG⊥DC.以D为坐标原点,DG,DC,DE所在直线分别为x轴,y轴,z轴建立空间直角坐标系.取BD=2,则D(0,0,0),M,E(0,0,1),F,所以=(0,0,1),=.设平面DEF的法向量为n=(x,y,z),则即可取法向量n=(1,-,0).又=,所以cos<,n>===,故直线DM与平面DEF所成角的正弦值为.2.(2017浙江高考模拟训练冲刺卷一,19)如图,在四棱锥A-BCDO中,DO⊥平面AOB,BO∥CD,OA=CD=2,OD=2,OB=4,∠AOB=120°.(1)求直线AC与平面ABD所成角的正弦值;(2)求二面角D-OA-C的余弦值.解析(1)如图,过点O在平面AOB内作OB的垂线OE,交AB于点E.∵DO⊥平面AOB,∴OD⊥OE,OD⊥OB,分别以OE,OB,OD所在的直线为x,y,z轴,建立空间直角坐标系,如图所示.则各点坐标为O(0,0,0),A(,-1,0),B(0,4,0),C(0,2,2),D(0,0,2),∴=(-,5,0),=(-,1,2).设平面ABD的法向量为n=(x,y,z),则由n·=0,n·=0,得取x=5,得n=(5,,2).设直线AC与平面ABD所成角为θ,又=(-,3,2),∴sinθ=|cos,n|==,故直线AC与平面ABD所成角的正弦值为.(2)设平面AOD的法向量为m1=(x,y,z),又=(,-1,0),=(0,0,2),∴由m1·=0,m1·=0, 得取x=1,得m1=(1,,0).设平面AOC的法向量为m2=(a,b,c),又=(,-1,0),=(0,2,2),∴由m2·=0,m2·=0,得取b=,得m2=(1,,-1).∴cos m1,m2==,由图可知二面角D-OA-C的平面角为锐角,故二面角D-OA-C的余弦值为.考点二空间向量在立体几何中的应用1.(2017浙江台州4月调研卷(一模),17)如图,在棱长为2的正四面体A-BCD中,E、F分别为直线AB、CD上的动点,且|EF|=.若记EF的中点P的轨迹为L,则|L|等于.(注:|L|表示点P的轨迹的长度)答案π2.(2017浙江杭州二模(4月),19)如图,已知四边形ABCD是矩形,M,N分别为边AD,BC的中点,MN与AC交于点O,沿MN将矩形MNCD折起,设AB=2,BC=4,二面角B-MN-C的大小为θ.(1)当θ=90°时,求cos∠AOC的值;(2)当θ=60°时,点P是线段MD上一点,直线AP与平面AOC所成角为α.若sin α=,求线段MP的长.解析设E为AB的中点,连接OE,则OE⊥MN,以O为原点,OE,ON所在直线分别为x轴,y轴,建立空间直角坐标系(图略).(1)当θ=90°时,A(2,-1,0),C(0,1,2),∴=(2,-1,0),=(0,1,2),∴cos∠AOC==-.(2)由θ=60°得C(1,1,),D(1,-1,),M(0,-1,0),∴=(1,0,).设=λ(0≤λ≤1),则=+=(λ,-1,λ).∴=-=(λ-2,0,λ),设平面AOC的法向量为n=(x,y,z).∵n·=0,n·=0,=(2,-1,0),=(1,1,),∴取x=1,则y=2,z=-,故n=(1,2,-),由题意得,=,即3λ2-10λ+3=0,∴λ=或λ=3(舍去),∴在线段MD上存在点P符合题意,且MP=MD=.炼技法【方法集训】方法1 求直线与平面所成角的方法1.(2017浙江稽阳联谊学校联考(4月),19)如图(1)所示,四边形ABCD为梯形,AB∥CD,∠C=60°,点E在CD 上,AB=CE=2,BF=BD=,BD⊥BC.现将△ADE沿AE翻折到图(2)中△APE的位置,使得二面角P-AE-C的大小为.(1)求PB的长度;(2)求证:PB⊥平面ABCE;(3)求直线AB与平面APE所成角的正弦值.解析(1)因为AB EC,所以四边形ABCE是平行四边形,所以BC∥AE,又因为BD⊥BC,所以BD⊥AE,所以AE⊥FB,AE⊥FP,所以∠PFB为二面角P-AE-C的平面角.(3分)由BF=,PF=2,得BP2=BF2+PF2-2BF·PFcos∠BFP=9,所以BP=3.(5分)(2)证明:由BF=,PF=2,BP=3知,PB2+BF2=PF2,所以BF⊥PB,①(7分)又因为BF⊥AE,PF⊥AE,BF∩PF=F,所以AE⊥平面PFB,所以AE⊥PB,②(9分) 由①②可知,PB⊥平面ABCE.(10分)(3)解法一:作BN⊥PF于N点,连接AN.由(2)可知,AE⊥平面BFP,又AE⊂平面APE,∴平面BFP⊥平面APE.又平面BFP∩平面APE=PF,BN⊂平面BFP,所以BN⊥平面APE,(12分)所以∠BAN是直线AB与平面APE所成的角.(13分)易知BN=BFsin 60°=,则sin∠NAB===.故直线AB与平面APE所成角的正弦值为.(15分)解法二:易知BF,BP,BC两两互相垂直,建立如图所示的空间直角坐标系,则B(0,0,0),C(3,0,0),A(-1,,0),E(2,,0),P(0,0,3).(11分)设平面APE的法向量为n=(x,y,z).又=(3,0,0),=(1,-,3),所以由即得取z=1,得n=(0,,1).(13分)设直线AB与平面APE所成的角为θ,又=(1,-,0),所以sin θ=|cos<n,>|==,故直线AB与平面APE所成角的正弦值为.(15分)2.如图,△ABC是以C为直角的等腰直角三角形,直角边长为8,AE∶EC=5∶3,DE∥BC,沿DE将三角形ADE折起,使得点A在平面BCED上的射影是点C,点M在AC上且MC=AC.(1)在BD上确定点N的位置,使得MN∥平面ADE;(2)在(1)的条件下,求CN与平面ABD所成角的正弦值.解析(1)由点A在平面BCED上的射影是点C,可知AC⊥平面BCED,而BC⊥CE,如图建立空间直角坐标系,可知各点的坐标为C(0,0,0),A(0,0,4),B(0,8,0),D(3,5,0),E(3,0,0).由MC=AC,可知点M的坐标为,设点N的坐标为(x,y,0),则由点N在BD上可得y=8-x,即点N的坐标为(x,8-x,0),则=.设平面ADE的法向量为n1=(x,y,z),则而=(0,-5,0),=(3,0,-4),所以取x=4,则z=3,可得n1=(4,0,3).MN∥平面ADE等价于n1·=0,即4x+0×(8-x)+3×=0.解之可得x=2,即点N的坐标为(2,6,0),所以点N为BD的靠近D点的三等分点.(2)由(1)可知=(2,6,0),设平面ABD的法向量为n2=(p,q,r),由题意可知而=(-3,3,0),=(0,8,-4),可得取p=1,则q=1,r=2.可得n2=(1,1,2).设CN与平面ABD所成角为θ,则sin θ==.方法2 求二面角的方法1.(2018浙江镇海中学期中,20)在多面体ABC-A1B1C1中,AA1∥BB1∥CC1,AA1=4,BB1=2,AB=4,CC1=3,AB⊥BB1,C1在平面ABB1A1上的射影E是线段A1B1的中点.(1)求证:平面ABC⊥平面ABB1A1;(2)若C1E=2,求二面角C1-AB1-C的余弦值.解析(1)证明:设线段AB的中点为O,连接OE,CO,则OE∥AA1,且OE==3,(2分)∵AA1∥CC1,∴OE∥CC1,又OE=CC1=3,∴四边形CC1EO为平行四边形,∴OC∥EC1.(4分)∵C1E⊥平面ABB1A1,∴OC⊥平面ABB1A1,(5分)∵OC⊂平面ABC,∴平面ABC⊥平面ABB1A1.(7分)(2)由(1)知OB,OE,OC两两互相垂直,分别以OB,OE,OC所在直线为x,y,z轴建立空间直角坐标系,则O(0,0,0),A(-2,0,0),B1(2,2,0),C(0,0,2),C1(0,3,2).(8分)设平面AB1C的法向量为m=(x,y,z),而=(4,2,0),=(2,0,2),由得取x=1,得m=(1,-2,-1).(10分)设平面AB1C1的法向量为n=(x1,y1,z1),而=(4,2,0),=(2,3,2),由得取x1=1,得n=(1,-2,2).(12分)∴cos<m,n>==,(14分)由图可知二面角C1-AB1-C的平面角为锐角,故二面角C1-AB1-C的余弦值为.(15分)2.(2017浙江名校(诸暨中学)交流卷四,19)如图,已知△ABC为等边三角形,M为AB的中点,AA1,BB1分别垂直平面ABC于点A,B,AA1=AB,BB1=AB,MN⊥A1B1,垂足为N.(1)求证:CN⊥A1B1;(2)求平面ABC与平面A1B1C所成的锐二面角的正切值.解析(1)证明:因为AA1,BB1分别垂直平面ABC于点A,B,所以平面AA1B1B⊥平面ABC,因为AC=BC,M为AB的中点,所以CM⊥AB,又平面AA1B1B∩平面ABC=AB,CM⊂平面AA1B1B,所以CM⊥平面A1ABB1,所以CM⊥A1B1,又因为MN⊥A1B1,所以A1B1⊥平面CMN,所以A1B1⊥CN.(2)解法一:如图,延长AB、A1B1相交于点D,连接CD,则CD为所求二面角的棱.因为BB1=AA1,BB1∥AA1,所以=,于是BD=BC=BA,于是∠ACD=90°,即CD⊥CA.又因为CD⊥AA1,所以CD⊥平面AA1C,所以CD⊥CA1.于是∠A1CA即为所求二面角的平面角.在Rt△A1AC中,AA1=AB=AC,所以∠A1CA=45°,所以tan∠A1CA=1.所以平面ABC与平面A1B1C所成的锐二面角的正切值为1.解法二:如图,以M为原点,MA所在直线为x轴,MC所在直线为y轴建立空间直角坐标系,设AB=2.则C(0,,0),A1(1,0,2),B1(-1,0,1),=(1,-,2),=(-2,0,-1).设平面A1B1C的法向量为n1=(x,y,z).由·n1=0,·n1=0,得取x=1,则y=-,z=-2,故n1=(1,-,-2).设所求二面角的大小为θ,又平面ABC的一个法向量为n2=(0,0,1).所以cos θ===,所以tan θ=1.过专题【五年高考】A组自主命题·浙江卷题组考点一空间角1.(2018浙江,8,4分)已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点).设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S-AB-C的平面角为θ3,则()A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1答案D2.(2017浙江,9,4分)如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P,Q,R分别为AB,BC,CA上的点,AP=PB,==2.分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α,β,γ,则()A.γ<α<βB.α<γ<βC.α<β<γD.β<γ<α答案B3.(2016浙江文,14,4分)如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=,∠ADC=90°.沿直线AC将△ACD 翻折成△ACD',直线AC与BD'所成角的余弦的最大值是.答案考点二空间向量在立体几何中的应用1.(2015浙江,15,6分)已知e1,e2是空间单位向量,e1·e2=.若空间向量b满足b·e1=2,b·e2=,且对于任意x,y∈R,|b-(x e1+y e2)|≥|b-(x0e1+y0e2)|=1(x0,y0∈R),则x0=,y0=,|b|=.答案1;2;22.(2018浙江,19,15分)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.(1)证明:AB1⊥平面A1B1C1;(2)求直线AC1与平面ABB1所成的角的正弦值.解析本题主要考查空间点、线、面位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力.解法一:(1)证明:由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB得AB1=A1B1=2,所以A1+A=A,故AB1⊥A1B1.由BC=2,BB1=2,CC1=1,BB1⊥BC,CC1⊥BC得B1C1=,由AB=BC=2,∠ABC=120°得AC=2,由CC1⊥AC,得AC1=,所以A+B1=A,故AB1⊥B1C1,因为A1B1,B1C1⊂平面A1B1C1,所以AB1⊥平面A1B1C1.(2)如图,过点C1作C1D⊥A1B1,交直线A1B1于点D,连接AD.由AB1⊥平面A1B1C1得平面A1B1C1⊥平面ABB1,由C1D⊥A1B1得C1D⊥平面ABB1,所以∠C1AD是AC1与平面ABB1所成的角.由B1C1=,A1B1=2,A1C1=得cos∠C1A1B1=,sin∠C1A1B1=,所以C1D=,故sin∠C1AD==.因此,直线AC1与平面ABB1所成的角的正弦值是.解法二:(1)证明:如图,以AC的中点O为原点,分别以射线OB,OC为x,y轴的正半轴,建立空间直角坐标系O-xyz.由题意知各点坐标如下:A(0,-,0),B(1,0,0),A1(0,-,4),B1(1,0,2),C1(0,,1).因此=(1,,2),=(1,,-2),=(0,2,-3).由·=0得AB1⊥A1B1.由·=0得AB1⊥A1C1.所以AB1⊥平面A1B1C1.(2)设直线AC1与平面ABB1所成的角为θ.由(1)可知=(0,2,1),=(1,,0),=(0,0,2).设平面ABB1的法向量n=(x,y,z).由即可取n=(-,1,0).所以sin θ=|cos<,n>|==.因此,直线AC1与平面ABB1所成的角的正弦值是.3.(2017浙江,19,15分)如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.(1)证明:CE∥平面PAB;(2)求直线CE与平面PBC所成角的正弦值.解析本题主要考查空间点、线、面的位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力.(1)证明:如图,设PA中点为F,连接EF,FB.因为E,F分别为PD,PA中点,所以EF∥AD且EF=AD.又因为BC∥AD,BC=AD,所以EF∥BC且EF=BC,即四边形BCEF为平行四边形,所以CE∥BF,因此CE∥平面PAB.(2)分别取BC,AD的中点为M,N.连接PN交EF于点Q,连接MQ.因为E,F,N分别是PD,PA,AD的中点,所以Q为EF中点,在平行四边形BCEF中,MQ∥CE.由△PAD为等腰直角三角形得PN⊥AD.由DC⊥AD,N是AD的中点得BN⊥AD.所以AD⊥平面PBN,由BC∥AD得BC⊥平面PBN,那么平面PBC⊥平面PBN.过点Q作PB的垂线,垂足为H,连接MH.MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角.设CD=1.在△PCD中,由PC=2,CD=1,PD=得CE=,在△PBN中,由PN=BN=1,PB=得QH=,在Rt△MQH中,QH=,MQ=,所以sin∠QMH=.所以,直线CE与平面PBC所成角的正弦值是.一题多解(1)证明:设AD的中点为O,连接OB,OP.∵△PAD是以AD为斜边的等腰直角三角形,∴OP⊥AD.∵BC=AD=OD,且BC∥OD,∴四边形BCDO为平行四边形,又∵CD⊥AD,∴OB⊥AD,∵OP∩OB=O,∴AD⊥平面OPB.过点O在平面POB内作OB的垂线OM,交PB于M,以O为原点,OB所在直线为x轴,OD所在直线为y轴,OM所在直线为z轴,建立空间直角坐标系,如图.设CD=1,则有A(0,-1,0),B(1,0,0),C(1,1,0),D(0,1,0).设P(x,0,z)(z>0),由PC=2,OP=1,得得x=-,z=.即点P,而E为PD的中点,∴E.设平面PAB的法向量为n=(x1,y1,z1),∵=,=(1,1,0),∴⇒取y1=-1,得n=(1,-1,).而=,则·n=0,而CE⊄平面PAB,∴CE∥平面PAB.(2)设平面PBC的法向量为m=(x2,y2,z2),∵=(0,1,0),=,∴取x2=1,得m=(1,0,).设直线CE与平面PBC所成角为θ.则sin θ=|cos<m,>|==,故直线CE与平面PBC所成角的正弦值为.方法总结 1.证明直线与平面平行的方法.(例:求证:l∥α)①线面平行的判定定理:在平面α内找到一条与直线l平行的直线m,从而得到l∥α.②面面平行的性质:过直线l找到(或作出)一个平面β,使得β∥α,从而得l∥α.③向量法:(i)求出平面α的法向量n和直线l的方向向量l,证明n·l=0,得l∥α.(ii)证明直线l的方向向量l能被平面α内的两个基底向量所表示,得l∥α.2.求线面角的方法.①定义法:作出线面角,解三角形即可.②解斜线段、射影、垂线段构成的三角形.例:求AB与平面α所成角θ的正弦值,其中A∈α.只需求出点B到平面α的距离d(通常由等体积法求d),由sin θ=得结论.③向量法:求出平面α的法向量n,设直线AB与α所成角为θ,则sin θ=|cos<n,>|.最好是画出图形,否则容易出错.B组统一命题、省(区、市)卷题组考点一空间角1.(2018课标全国Ⅰ理,12,5分)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为()A. B. C. D.答案A2.(2018课标全国Ⅱ理,16,5分)已知圆锥的顶点为S,母线SA,SB所成角的余弦值为,SA与圆锥底面所成角为45°.若△SAB的面积为5,则该圆锥的侧面积为.答案40π3.(2018课标全国Ⅱ理,20,12分)如图,在三棱锥P-ABC中,AB=BC=2,PA=PB=PC=AC=4,O为AC的中点.(1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.解析(1)证明:因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=2.连接OB.因为AB=BC=AC,所以△ABC为等腰直角三角形,且OB⊥AC,OB=AC=2.由OP2+OB2=PB2知PO⊥OB.由OP⊥OB,OP⊥AC知PO⊥平面ABC.(2)如图,以O为坐标原点,的方向为x轴正方向,建立空间直角坐标系O-xyz.由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,2),=(0,2,2).取平面PAC的法向量=(2,0,0).设M(a,2-a,0)(0<a≤2),则=(a,4-a,0).设平面PAM的法向量为n=(x,y,z).由·n=0,·n=0得可取n=((a-4),a,-a),所以cos<,n>=.由已知可得|cos<,n>|=.所以=.解得a=-4(舍去)或a=.所以n=.又=(0,2,-2),所以cos<,n>=.所以PC与平面PAM所成角的正弦值为.4.(2018天津理,17,13分)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.(1)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;(2)求二面角E-BC-F的正弦值;(3)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.解析本小题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.依题意,可以建立以D为原点,分别以,,的方向为x轴,y轴,z轴的正方向的空间直角坐标系(如图),可得D(0,0,0),A(2,0,0),B(1,2,0),C(0,2,0),E(2,0,2),F(0,1,2),G(0,0,2),M,N(1,0,2).(1)证明:依题意=(0,2,0),=(2,0,2).设n0=(x0,y0,z0)为平面CDE的法向量,则即不妨令z0=-1,可得n0=(1,0,-1).又=,可得·n0=0,又因为直线MN⊄平面CDE,所以MN∥平面CDE.(2)依题意,可得=(-1,0,0),=(1,-2,2),=(0,-1,2).设n=(x1,y1,z1)为平面BCE的法向量,则即不妨令z1=1,可得n=(0,1,1).设m=(x2,y2,z2)为平面BCF的法向量,则即不妨令z2=1,可得m=(0,2,1).因此有cos<m,n>==,于是sin<m,n>=.所以,二面角E-BC-F的正弦值为.(3)设线段DP的长为h(h∈[0,2]),则点P的坐标为(0,0,h),可得=(-1,-2,h).易知,=(0,2,0)为平面ADGE的一个法向量,故|cos<,>|==,由题意,可得=sin 60°=,解得h=∈[0,2].所以,线段DP的长为.方法归纳利用空间向量解决立体几何问题的一般步骤(1)审清题意并建系.利用条件分析问题,建立恰当的空间直角坐标系;(2)确定相关点的坐标.结合建系过程与图形,准确地写出相关点的坐标;(3)确定直线的方向向量和平面的法向量.利用点的坐标求出相关直线的方向向量和平面的法向量,若已知某直线垂直某平面,可直接取该直线的方向向量为该平面的法向量;(4)转化为向量运算.将空间位置关系转化为向量关系,空间角转化为向量的夹角问题去论证、求解;(5)问题还原.结合条件与图形,作出结论(注意角的范围).5.(2017课标全国Ⅰ理,18,12分)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.解析本题考查空间点、线、面的位置关系以及二面角的概念和计算,考查学生的空间想象能力、推理论证能力和运算求解能力.(1)证明:由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.由于AB∥CD,故AB⊥PD,又AP∩PD=P,AP、PD⊂平面PAD,所以AB⊥平面PAD.又AB⊂平面PAB,所以平面PAB⊥平面PAD.(2)解法一(综合法):根据题意可设AB=1,因为AB∥CD,∠APD=∠BAP=∠CDP=90°,PA=PD=AB=DC,所以四边形ABCD是平行四边形,且AD=PC=PB=CB=,取PB的中点为F,连接AF,CF,在等腰三角形PAB中,可得AF⊥PB,在等边三角形PBC中,可得CF⊥PB,所以∠AFC为二面角A-PB-C的平面角,由(1)知AB⊥平面PAD,又AD⊂平面PAD,所以AB⊥AD.所以平行四边形ABCD是矩形,连接AC,则AC=.在△AFC中,AC=,AF=,FC=,由余弦定理可得cos∠AFC==-,所以二面角A-PB-C的余弦值为-.解法二(向量法):在平面PAD内作PF⊥AD,垂足为F.由(1)可知,AB⊥平面PAD,故AB⊥PF,又AD∩AB=A,可得PF⊥平面ABCD.以 F为坐标原点,的方向为x轴正方向,||为单位长,建立如图所示的空间直角坐标系F-xyz.由(1)及已知可得A,P,B,C.所以=,=(,0,0),=,=(0,1,0).设n=(x1,y1,z1)是平面PCB的法向量,则即可取n=(0,-1,-).设m=(x2,y2,z2)是平面PAB的法向量,则即可取m=(1,0,1).则cos<n,m>==-.易知二面角A-PB-C为钝二面角,所以二面角A-PB-C的余弦值为-.方法总结面面垂直的证明及向量法求解二面角.(1)面面垂直的证明.证明两个平面互相垂直,可以在一个平面内找一条直线l,证明直线l垂直于另一平面.(2)利用空间向量求解几何体中的二面角的余弦值.建立空间直角坐标系,找到点的坐标,求出两个半平面的法向量n1,n2,设二面角的大小为θ,则|cosθ|=,再根据二面角的范围判断二面角余弦值的正负情况.6.(2017天津理,17,13分)如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC 的中点,M是线段AD的中点,PA=AC=4,AB=2.(1)求证:MN∥平面BDE;(2)求二面角C-EM-N的正弦值;(3)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为,求线段AH的长.解析本小题主要考查直线与平面平行、二面角、异面直线所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.如图,以A为原点,分别以,,方向为x轴、y轴、z轴正方向建立空间直角坐标系.依题意可得A(0,0,0),B(2,0,0),C(0,4,0),P(0,0,4),D(0,0,2),E(0,2,2),M(0,0,1),N(1,2,0).(1)证明:=(0,2,0),=(2,0,-2).设n=(x,y,z)为平面BDE的法向量,则即不妨设z=1,可得n=(1,0,1).又=(1,2,-1),可得·n=0.因为MN⊄平面BDE,所以MN∥平面BDE.(2)易知n1=(1,0,0)为平面CEM的一个法向量.设n2=(x,y,z)为平面EMN的法向量,则因为=(0,-2,-1),=(1,2,-1),所以不妨设y=1,可得n2=(-4,1,-2).因此有cos<n1,n2>==-,于是sin<n1,n2>=.所以,二面角C-EM-N的正弦值为.(3)依题意,设AH=h(0≤h≤4),则H(0,0,h),进而可得=(-1,-2,h),=(-2,2,2).由已知,得|cos<,>|===,整理得10h2-21h+8=0,解得h=或h=.所以,线段AH的长为或.方法总结利用空间向量法证明线面位置关系与计算空间角的步骤:(1)根据题目中的条件,充分利用垂直关系,建立适当的空间直角坐标系,尽量使相关点在坐标轴上,求出相关点的坐标;(2)求出相关直线的方向向量及相关平面的法向量,根据题目的要求,选择适当的公式,将相关的坐标代入进行求解或证明;(3)检验,得出最后结论.7.(2017课标全国Ⅱ理,19,12分)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°,E是PD的中点.(1)证明:直线CE∥平面PAB;(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.解析本题考查了线面平行的证明和线面角、二面角的计算.(1)取PA的中点F,连接EF,BF.因为E是PD的中点,所以EF∥AD,EF=AD.由∠BAD=∠ABC=90°得BC∥AD,又BC=AD,所以EF BC,四边形BCEF是平行四边形,CE∥BF,又BF⊂平面PAB,CE⊄平面PAB,故CE∥平面PAB.(2)由已知得BA⊥AD,以A为坐标原点,的方向为x轴正方向,||为单位长,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(1,0,0),C(1,1,0),P(0,1,),=(1,0,-),=(1,0,0).设M(x,y,z)(0<x<1),则=(x-1,y,z),=(x,y-1,z-).因为BM与底面ABCD所成的角为45°,而n=(0,0,1)是底面ABCD的法向量,所以|cos<,n>|=sin 45°,=,即(x-1)2+y2-z2=0.①又M在棱PC上,设=λ,则x=λ,y=1,z=-λ.②由①②解得(舍去),或所以M,从而=.设m=(x0,y0,z0)是平面ABM的法向量,则即所以可取m=(0,-,2).于是cos<m,n>==.易知所求二面角为锐角.因此二面角M-AB-D的余弦值为.方法总结本题涉及直线与平面所成的角和二面角,它们是高考热点和难点,解决此类题时常利用向量法,解题关键是求平面的法向量,再由向量的夹角公式求解.解题关键由线面角为45°求点M的坐标是解题的关键.考点二空间向量在立体几何中的应用1.(2018课标全国Ⅰ理,18,12分)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC 折起,使点C到达点P的位置,且PF⊥BF.(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.解析(1)由已知可得,BF⊥EF,又BF⊥PF,且PF,EF⊂平面PEF,PF∩EF=F,所以BF⊥平面PEF,又BF⊂平面ABFD,所以平面PEF⊥平面ABFD.(2)作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD.以H为坐标原点,的方向为y轴正方向,||为单位长,建立如图所示的空间直角坐标系H-xyz.由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=,又PF=1,EF=2,故PE⊥PF,可得PH=,EH=,则H(0,0,0),P,D,=,=为平面ABFD的法向量.设DP与平面ABFD所成角为θ,则sin θ===.所以DP与平面ABFD所成角的正弦值为.易错警示利用空间向量求线面角的注意事项(1)先求出直线的方向向量与平面的法向量所夹的锐角(钝角时取其补角)的角度,再取其余角即为所求.(2)若求线面角的余弦值,要注意利用平方关系sin2θ+cos2θ=1求出其值,不要误以为直线的方向向量与平面的法向量所夹角的余弦值为所求.2.(2017山东理,17,12分)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是的中点.(1)设P是上的一点,且AP⊥BE,求∠CBP的大小;(2)当AB=3,AD=2时,求二面角E-AG-C的大小.解析本题考查线面垂直的证明和二面角的计算.(1)因为AP⊥BE,AB⊥BE,AB,AP⊂平面ABP,AB∩AP=A,所以BE⊥平面ABP,又BP⊂平面ABP,所以BE⊥BP,又∠EBC=120°,因此∠CBP=30°.(2)解法一:取的中点H,连接EH,GH,CH.因为∠EBC=120°,所以四边形BEHC为菱形,所以AE=GE=AC=GC==.取AG中点M,连接EM,CM,EC,则EM⊥AG,CM⊥AG,所以∠EMC为所求二面角的平面角.又AM=1,所以EM=CM==2.在△BEC中,由于∠EBC=120°,由余弦定理得EC2=22+22-2×2×2×cos120°=12,所以EC=2,因此△EMC为等边三角形,故所求的角为60°.解法二:以B为坐标原点,分别以BE,BP,BA所在的直线为x,y,z轴,建立如图所示的空间直角坐标系.由题意得A(0,0,3),E(2,0,0),G(1,,3),C(-1,,0),故=(2,0,-3),=(1,,0),=(2,0,3),设m=(x1,y1,z1)是平面AEG的法向量.由可得取z1=2,可得平面AEG的一个法向量m=(3,-,2).设n=(x2,y2,z2)是平面ACG的法向量.由可得取z2=-2,可得平面ACG的一个法向量n=(3,-,-2).所以cos<m,n>==.易知所求角为锐二面角,因此所求的角为60°.方法总结求二面角的常见方法有两种:一种是“找”,即根据二面角的面的特殊性(如等边三角形、等腰三角形、直角三角形、正方形、矩形、梯形等)找二面角的平面角的顶点,进而作出该平面角,再通过解三角形求解;另一种是“算”,即利用空间向量的坐标运算,由平面的法向量和夹角公式求解.利用空间向量的运算求二面角时,一定要注意二面角是锐二面角还是钝二面角.3.(2016天津,17,13分)如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.(1)求证:EG∥平面ADF;(2)求二面角O-EF-C的正弦值;(3)设H为线段AF上的点,且AH=HF,求直线BH和平面CEF所成角的正弦值.解析依题意,OF⊥平面ABCD,如图,以O为原点,分别以,,的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,依题意可得O(0,0,0),A(-1,1,0),B(-1,-1,0),C(1,-1,0),D(1,1,0),E(-1,-1,2),F(0,0,2),G(-1,0,0).(1)证明:依题意,=(2,0,0),=(1,-1,2).设n1=(x,y,z)为平面ADF的法向量,则即不妨设z=1,可得n1=(0,2,1),又=(0,1,-2),可得·n1=0,又因为直线EG⊄平面ADF,所以EG∥平面ADF.(2)易证=(-1,1,0)为平面OEF的一个法向量.依题意,=(1,1,0),=(-1,1,2).设n2=(x,y,z)为平面CEF的法向量,则即不妨设x=1,可得n2=(1,-1,1).因此有cos<,n2>==-,于是sin<,n2>=.所以,二面角O-EF-C的正弦值为.(3)由AH=HF,得AH=AF.因为=(1,-1,2),所以==,进而有H,从而=,因此cos<,n2>==-.所以,直线BH和平面CEF所成角的正弦值为.评析本题主要考查直线与平面平行和垂直、二面角、直线与平面所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.4.(2016北京,17,14分)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=.(1)求证:PD⊥平面PAB;(2)求直线PB与平面PCD所成角的正弦值;(3)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值;若不存在,说明理由.解析(1)证明:因为平面PAD⊥平面ABCD,AB⊥AD,所以AB⊥平面PAD.所以AB⊥PD.又因为PA⊥PD,PA∩AB=A,所以PD⊥平面PAB.(2)取AD的中点O,连接PO,CO.因为PA=PD,所以PO⊥AD.又因为PO⊂平面PAD,平面PAD⊥平面ABCD,所以PO⊥平面ABCD.因为CO⊂平面ABCD,所以PO⊥CO.因为AC=CD,所以CO⊥AD.如图建立空间直角坐标系O-xyz.由题意得,A(0,1,0),B(1,1,0),C(2,0,0),D(0,-1,0),P(0,0,1).设平面PCD的法向量为n=(x,y,z),则即令z=2,则x=1,y=-2.所以n=(1,-2,2).又=(1,1,-1),所以cos<n,>==-.所以直线PB与平面PCD所成角的正弦值为.(3)设M是棱PA上一点,则存在λ∈[0,1]使得=λ.因此点M(0,1-λ,λ),=(-1,-λ,λ).因为BM⊄平面PCD,所以BM∥平面PCD当且仅当·n=0,即(-1,-λ,λ)·(1,-2,2)=0.解得λ=.所以在棱PA上存在点M使得BM∥平面PCD,此时=.易错警示(1)证线面垂直时,要在“面”内找两条相交直线,分别与“线”垂直.(2)建立空间直角坐标系前,先明确备选坐标轴之间的两两垂直关系.(3)用向量法说明在某线段上存在满足某条件的点时,参数的取值范围易被忽视.评析本题考查线面垂直的证明,空间向量的应用等,对学生的空间想象能力、运算能力均有较高要求.C组教师专用题组考点一空间角1.(2014广东,5,5分)已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是()A.(-1,1,0)B.(1,-1,0)C.(0,-1,1)D.(-1,0,1)答案B2.(2014课标Ⅱ,11,5分)直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM 与AN所成角的余弦值为()A. B.C. D.答案C3.(2015四川,14,5分)如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ 上,E,F分别为AB,BC的中点.设异面直线EM与AF所成的角为θ,则cos θ的最大值为.答案4.(2018天津文,17,13分)如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB 的中点,AB=2,AD=2,∠BAD=90°.(1)求证:AD⊥BC;(2)求异面直线BC与MD所成角的余弦值;(3)求直线CD与平面ABD所成角的正弦值.解析本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识.考查空间想象能力、运算求解能力和推理论证能力.(1)证明:由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC.(2)取棱AC的中点N,连接MN,ND.又因为M为棱AB的中点,故MN∥BC.所以∠DMN(或其补角)为异面直线BC与MD所成的角.在Rt△DAM中,AM=1,故DM==.因为AD⊥平面ABC,故AD⊥AC.在Rt△DAN中,AN=1,故DN==.在等腰三角形DMN中,MN=1,可得cos∠DMN==.所以,异面直线BC与MD所成角的余弦值为.(3)连接CM.因为△ABC为等边三角形,M为边AB的中点,故CM⊥AB,CM=.又因为平面ABC⊥平面ABD,而CM⊂平面ABC,故CM⊥平面ABD.所以,∠CDM为直线CD与平面ABD所成的角.在Rt△CAD中,CD==4.在Rt△CMD中,sin∠CDM==.所以,直线CD与平面ABD所成角的正弦值为.5.(2017北京理,16,14分)如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=,AB=4.(1)求证:M为PB的中点;(2)求二面角B-PD-A的大小;(3)求直线MC与平面BDP所成角的正弦值.解析本题考查面面垂直的性质定理,线面平行的性质定理,二面角,直线与平面所成的角等知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力.(1)设AC,BD交点为E,连接ME.因为PD∥平面MAC,平面MAC∩平面PDB=ME,。
浙江省2020届高三数学一轮复习典型题专项训练:立体几何
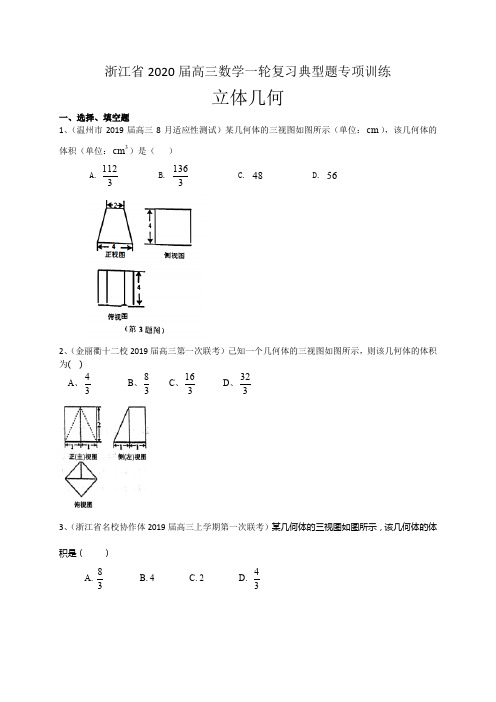
浙江省2020届高三数学一轮复习典型题专项训练立体几何一、选择、填空题 1、(温州市2019届高三8月适应性测试)某几何体的三视图如图所示(单位:cm ),该几何体的体积(单位:3cm )是( )A.3112 B. 3136C. 48D. 562、(金丽衢十二校2019届高三第一次联考)己知一个几何体的三视图如图所示,则该几何体的体积为( ) A 、43 B 、83 C 、163 D 、3233、(浙江省名校协作体2019届高三上学期第一次联考)某几何体的三视图如图所示,该几何体的体积是( )A.38 B. 4 C. 2 D. 344、(七彩阳光联盟2019届高三上学期期初联考)某几何体的三视图如图所示,其中俯视图是半径为1的半圆,则该几何体的体积为 ,表面积为 .5、(温州九校2019届高三第一次联考)已知m 为一条直线,βα,为两个不同的平面,则下列说法正确的是( )A.若,//,//βααm 则β//mB.若,,βαα⊥⊥m 则β//mC.若,//,βαα⊥m 则β⊥mD.若,,//βαα⊥m 则β⊥m6、(嘉兴市2019届高三上学期期末检测)某几何体的三视图如图所示(单位: cm ),则该几何体的体积(单位: cm 3)是A 、363B 、54C 、723D 、1087、(丽水、衢州、湖州三地市2019届高三上学期期末)如图,正四面体ABCD中,E,F分别是线段AC的三等分点,P是线段AB的中点,G是直线BD的动点,则()A.存在点G,使PG⊥EF成立B.存在点G,使FG⊥EP成立C.不存在点G,使平面EFG⊥平面ACD成立D.不存在点G,使平面EFG⊥平面ABD成立8、(宁波市2019届高三上学期期末考试)某几何体的三视图如图所示,则该几何体的体积为A. B. C. D.9、(台州市2019届高三上学期期末质量评估)如图,在矩形ABCD中,AB=2,AD=1,M为AB的中点,将△ADM沿DM翻折.在翻折过程中,当二面角A—BC—D的平面角最大时,其正切值为A.33B.12C.23D.1410、(浙南名校联盟(温州九校)2019届高三上学期期末联考)如图,在三棱柱111ABC A B C -中,点P 在平面111A B C 内运动,使得二面角P AB C --的平面角与二面角P BC A --的平面角互余,则点P 的轨迹是A .一段圆弧B .椭圆的一部分C .抛物线D .双曲线的一支11、(绍兴市2019届高三3月适应性考试)如图,在三棱柱111ABC A B C -中,1,,AB AC AA 两两互相垂直,1AB AC AA ==,M N ,是线段11,BB CC 上的点,平面AMN 与平面ABC 所成(锐)二面角为π6,当1||B M 最小时,AMB ∠= A .5π12B .π3C .π4D . π612、(杭州市2019届高三4月教学质量检测(二模))《九章算术》卷五商功中有如下问题:今有刍甍(音meng ,底面为矩形的屋脊状的几何体),下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.已知该刍甍的三视图如图所示,则此刍甍的体积等于( )A .3B .5C .6D . 12432113、(稽阳联谊学校2019届高三4月联考)在阿基米德的墓碑上刻着一副“圆柱容球”的几何图形,它的三视图如图所示,记球的体积为1V ,圆柱的体积为2V ,球的表面积为1S ,圆柱的全面积为2S ,则下列结论正确的是A.132V V 2=,132S S 2= B.123V V 2=,123S S 2=C.132V V 2=,123S S 2=D.123V V 2=,132S S 2=14、(绍兴市上虞区2019届高三第二次(5月)教学质量调测)已知棱长都为2的正三棱柱111ABC A B C -的直观图如图,若正三棱柱111ABC A B C -绕着它的一条侧棱1AA 所在直线旋转,则它的侧视图可以为15、(台州市2019届高三4月调研)一个几何体的三视图如图所示,则这个几何体的体积为 A.1 B.12 C.13 D.1616、(温州市2019届高三2月高考适应性测试)在正四面体 ABCD 中,P ,Q 分别是棱 AB ,CD 的中点,E ,F 分别是直线AB ,CD 上的动点,M 是EF 的中点,则能使点 M 的轨迹是圆的条件是(▲ )A 、PE +QF =2B 、PE •QF =2C 、PE =2QFD 、PE 2+QF 2=217、(温州市2019届高三8月适应性测试)设βα、是两个不同的平面,n m 、是两条不同的直线,下列说法正确的是( )A. 若m =⊥βαβα ,,n m ⊥,则β⊥nB. 若αβα//n ,⊥,则β⊥nC. 若α//m ,β//m 则βα//D. 若α⊥m ,β⊥m ,α⊥n ,则β⊥n参考答案:1、C2、B3、B4、3π,1522π++.提示:该几何体为圆锥的一半,且底面向上放置。
(浙江专版)2020届高考数学一轮复习单元检测八立体几何与空间向量单元检测(含解析)

单元检测八 立体几何与空间向量(时间:120分钟 满分:150分) 第Ⅰ卷(选择题 共40分)一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列命题中,错误的是( ) A .平行于同一平面的两个平面平行 B .平行于同一直线的两个平面平行C .一条直线与两个平行平面中的一个相交,那么这条直线必和另一个平面相交D .一条直线与两个平行平面所成的角相等 答案 B解析 选项A 正确,是面面平行的传递性.选项B 错误,比如正方体的两相邻侧面与一侧棱都平行,但两侧面所在平面相交.选项C 正确,由反证法,若直线与另一平面不相交,则直线在平面内或直线与平面平行,与直线与第一个平面相交矛盾.选项D 正确,由线面角定义可知正确.2.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( )A .25πB .50πC .125πD .都不对 答案 B解析 长方体的8个顶点都在同一球面上,则这个球是长方体的外接球,所以球的直径等于长方体的体对角线长,即R =32+42+522=522,所以球的表面积为4πR 2=4π·⎝ ⎛⎭⎪⎫5222=50π,故选B.3.如图,在多面体ABCDEF 中,已知底面ABCD 是边长为3的正方形,EF ∥AB ,EF =32,且EF与底面ABCD 的距离为2,则该多面体的体积为( )A.92B .5C .6D.152 答案 D解析 分别取AB ,CD 的中点G ,H ,连接EG ,GH ,EH ,把该多面体分割成一个四棱锥与一个三棱柱,可求得四棱锥的体积为3,三棱柱的体积为92,进而整个多面体的体积为152.4.如图,长方体ABCD —A 1B 1C 1D 1中,∠DAD 1=45°,∠CDC 1=30°,那么异面直线AD 1与DC 1所成角的余弦值是( )A.28 B.38 C.24D.34答案 C解析 由长方体∠DAD 1=45°,∠CDC 1=30°,设AD =DD 1=1,CD = 3.连接BC 1,BD . 由AD 1∥BC 1,所以异面直线AD 1与DC 1所成角,即∠BC 1D .在△BDC 1中,BC 1=2,BD =2,C 1D =2,由余弦定理可得cos∠BC 1D =C 1D 2+BC 21-BD22C 1D ·BC 1=22+2-222×2×2=24, 所以异面直线AD 1与DC 1所成角的余弦值是24. 5.(2018·嘉兴测试)已知两个不同的平面α,β和三条不同的直线m ,a ,b ,若α∩β=m ,a ⊂α且a ⊥m ,b ⊂β,设α和β所成的一个二面角的大小为θ1,直线a 与平面β所成的角的大小为θ2,直线a ,b 所成的角的大小为θ3,则( ) A .θ1=θ2≥θ3 B .θ3≥θ1=θ2 C .θ1≥θ3,θ2≥θ3 D .θ1≥θ2,θ3≥θ2答案 D解析 由题意可知θ1=θ2或θ1+θ2=π,因为线面角的范围为⎣⎢⎡⎦⎥⎤0,π2,二面角的范围为[0,π],所以θ1≥θ2;当b ⊥m 时,θ2=θ3,当b 不与m 垂直时,θ2<θ3,所以θ2≤θ3.故选D.6.若圆锥的侧面展开图是半径为2,圆心角为3π2的扇形,则由它的两条母线所确定的最大截面与底面所成二面角的余弦值为( ) A.24B.12C.22D.74答案 A解析 设圆锥底面圆的半径为r ,由2πr =3π2×2,得r =32,设轴截面顶角大小为2θ,则sin θ=34>22,所以2θ>π2,设两条母线所确定的截面最大时,两条母线的夹角为α, 则α≤2θ,最大截面所对应的三角形的面积S =12×2×2sin α,则α=π2,所以两条母线所确定的最大截面为等腰直角三角形,其斜边上的高为2,底面圆的圆心到最大截面斜边的距离为⎝ ⎛⎭⎪⎫322-(2)2=12,则两条母线所确定的最大截面与底面所成二面角的余弦值为122=24. 7.已知三棱锥S —ABC 的每个顶点都在球O 的表面上,SA ⊥底面ABC ,AB =AC =4,BC =215,且二面角S —BC —A 的正切值为4,则球O 的表面积为( ) A .240πB .248πC .252πD .272π 答案 D解析 设BC 的中点为D ,连接AD ,SD ,可得AD =1,则∠SDA 是二面角S —BC —A 的平面角,由于二面角S —BC —A 的正切值为4,∴SA =4,由余弦定理知,cos∠CAB =AB 2+AC 2-BC 22AB ×AC =16+16-602×4×4=-78,sin∠CAB =158, 由正弦定理知,△ABC 的外接圆直径 2r =BC sin∠CAB=215158=16,设三棱锥S —ABC 的外接球半径为R , 则⎝ ⎛⎭⎪⎫SA 22+r 2=R 2,得R 2=68, ∴球O 的表面积为4πR 2=272π,故选D.8.(2018·杭州质检)在三棱锥P -ABC 中,PA ⊥平面ABC ,∠BAC =90°,D ,E 分别是BC ,AB 的中点,AB ≠AC ,且AC >AD .设PC 与DE 所成角为α,PD 与平面ABC 所成角为β,二面角P-BC -A 为γ,则( )A .α<β<γB .α<γ<βC .β<α<γD .γ<β<α答案 A解析 由题图可知∠PCA =α<π2,∠PDA =β<π2,因为PA ⊥平面ABC ,所以tan α=PA AC ,tan β=PA AD. 又AC >AD ,故tan β>tan α,则β>α.过点A 作AQ ⊥BC ,垂足为Q ,连接PQ ,则∠PQA =γ, 同理可证得γ>β,所以α<β<γ,故选A.9.如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,侧棱AP ⊥平面ABCD ,AB =1,AP =3,点M 在线段BC 上,且AM ⊥MD ,则当△PMD 的面积最小时,线段BC 的长度为( )A.2B .2C.102 D.322答案 D解析 方法一 设BM =x ,MC =y ,则BC =AD =x +y , ∵PA ⊥平面ABCD ,MD ⊂平面ABCD ,∴PA ⊥MD , 又AM ⊥MD ,PA ∩AM =A ,PA ,AM ⊂平面PAM , ∴MD ⊥平面PAM ,又PM ⊂平面PAM ,∴MD ⊥PM , 易知AM =x 2+1,MD =y 2+1, 在Rt△AMD 中,AM 2+MD 2=AD 2,即x 2+1+y 2+1=(x +y )2,化简得xy =1.在Rt△PMD 中,PM =x 2+4,MD =y 2+1=1x 2+1,∴S △PMD =12PM ·MD =12·x 2+4·1x 2+1=12x 2+4x 2+5≥122x 2·4x 2+5=32,当且仅当x 2=4x 2,即x =2,y =22时取等号,此时BC =x +y =322.方法二 由题意知,AB ,AD ,AP 两两垂直.以A 为坐标原点,AB ,AD ,AP 所在直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,设BC =a ,M (1,x,0),x >0,则A (0,0,0),B (1,0,0),C (1,a,0),D (0,a,0),P (0,0,3).由AM ⊥MD ,得AM →·MD →=0,即(1,x,0)·(-1,a -x,0)=ax -x 2-1=0, 解得a =x +1x,而PM →·MD →=ax -x 2-1=0,∴PM ⊥MD ,∴S △PMD =12|PM →|·|MD →|=12x 2+4·(a -x )2+1=12x 2+4·1x 2+1=125+x 2+4x 2≥122x 2·4x 2+5=32,当且仅当⎩⎪⎨⎪⎧x 2=4x2,a =x +1x,即⎩⎨⎧x =2,a =2+12=322时等号成立,此时BC =322.10.(2018·温州市高考适应性考试)已知正四面体PABC ,Q 为△ABC 内的一点,记PQ 与平面PAB ,PAC ,PBC 所成的角分别为α,β,γ,则下列式子恒成立的是( )A .sin 2α+sin 2β+sin 2γ≥2 B .cos 2α+cos 2β+cos 2γ≥2 C .tan 2α+tan 2β+tan 2γ≤1 D.1tan 2α+1tan 2β+1tan 2γ≤1 答案 B解析 取点Q 为△ABC 的中心,设正面体的棱长为1,则sin α=sin β=sin γ=13×3232=13, 所以sin 2α+sin 2β+sin 2γ=13<2,排除A ;所以cos 2α=cos 2β=cos 2γ=1-⎝ ⎛⎭⎪⎫132=89,所以tan 2α=tan 2β=tan 2γ=18,所以1tan 2α+1tan 2β+1tan 2γ=24>1,排除D ;取BC 的中点D ,连接PD ,AD , 易知AP 与平面PBC 所成的角为∠APD , 且cos∠APD =12PA PD =1232=13,所以sin∠APD =23,所以tan∠APD =2>1,所以当点Q 靠近点A 时,QP 与平面PBC 所成的角的正切值大于1,所以tan 2α+tan 2β+tan 2γ>1,排除C.故选B.第Ⅱ卷(非选择题 共110分)二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.把答案填在题中横线上)11.某空间几何体的三视图(单位:cm)如图所示,则此几何体侧视图的面积为______cm 2,此几何体的体积为______cm 3.答案 27 67解析 此几何体的侧视图为直角三角形,高为4cm ,底为42-32=7,面积为12×4×7=27;该几何体是以正视图为底面的四棱锥,如图所示,其底面为直角梯形,面积是12(4+2)×6=18(cm 2),高为7,体积为13×18×7=67(cm 3).12.已知过球面上三点A ,B ,C 的截面到球心的距离等于球半径的一半,且AC =BC =6,AB =4,则球面面积为________. 答案 54π解析 如图,设球的半径为r ,O ′是△ABC 的外心,外接圆半径为R ,D 是AB 的中点, 则OO ′⊥平面ABC .在Rt△ACD 中,cos A =13,则sin A =223.在△ABC 中,由正弦定理得BC sin A =2R ,得R =924,即O ′C =924.在Rt△OCO ′中,r 2-14r 2=81×216,得r =362,S 球表=4π×544=54π.13.如图,在平行六面体ABCD -A 1B 1C 1D 1中,AB =1,AD =2,AA 1=3,∠BAD =90°,∠BAA 1=∠DAA 1=60°,则AC 1=________.答案23解析 ∵∠BAA 1=∠DAA 1=60°,∴A 1在平面ABCD 上的射影必落在直线AC 上, ∴平面ACC 1A 1⊥平面ABCD , ∵AB =1,AD =2,AA 1=3,AC 1→=AC →+CC 1→=AB →+AD →+AA 1→,∴|AC 1→|2=(AB →+AD →+AA 1→)2=|AB →|2+|AD →|2+|AA 1→|2+2AB →·AD →+2AB →·AA 1→+2AD →·AA 1→ =1+4+9+0+2×1×3×12+2×2×3×12=23,∴|AC 1→|=23,∴AC 1=23.14.(2018·浙江五校联考)在正三棱锥S -ABC 中,M 是SC 的中点,且AM ⊥SB ,底面边长AB =22,则正三棱锥S -ABC 的体积为________,其外接球的表面积为________. 答案 4312π解析 由正三棱锥的对棱互相垂直可得SB ⊥AC , 又SB ⊥AM ,AM ∩AC =A ,AM ,AC ⊂平面SAC ,所以SB ⊥平面SAC ,则SB ⊥SA ,SB ⊥SC .所以正三棱锥S -ABC 的三个侧面都是等腰直角三角形.又AB =22,所以SA =SB =SC =2,故正三棱锥S -ABC 是棱长为2的正方体的一个角,其体积为16SA ·SB ·SC =43,其外接球的直径2R =23,故外接球的表面积为4πR 2=12π.15.如图,在三棱锥S -ABC 中,若AC =23,SA =SB =SC =AB =BC =4,E 为棱SC 的中点,则直线AC 与BE 所成角的余弦值为__________,直线AC 与平面SAB 所成的角为__________.答案 1460°解析 取SA 的中点M ,连接ME ,BM ,则直线AC 与BE 所成的角等于直线ME 与BE 所成的角, 因为ME =3,BM =BE =23,cos∠MEB =ME 2+BE 2-MB 22ME ×BE=3+12-122×3×23=14,所以直线AC 与BE 所成角的余弦值为14.取SB 的中点N ,则AN ⊥SB ,CN ⊥SB , 又AN ∩CN =N ,AN ,CN ⊂平面ACN , 即SB ⊥平面ACN ,即平面SAB ⊥平面ACN , 因此直线AC 与平面SAB 所成的角为∠CAN , 因为AN =CN =AC =23,所以∠CAN =60°, 因此直线AC 与平面SAB 所成的角为60°.16.如图,已知四棱锥A -BCDE 中,AB =BC =2,BE =2CD =4,∠ABC =120°,∠EBC =30°,BE ∥CD ,M 为棱DE 的中点,三棱锥M -ABC 的体积为33,则点M 到平面ABC 的距离为________,二面角A -BC -D 的正弦值为________.答案 1 23解析 在△ABC 中,因为AB =BC =2,∠ABC =120°, 所以S △ABC =12×AB ×BC ×sin∠ABC = 3.设点M 到平面ABC 的距离为h ,则由题意得, 13×S △ABC ×h =13×3×h =33,所以h =1. 作MF ⊥BC 于点F ,MN ⊥平面ABC 于点N ,连接FN , 则BC ⊥平面MNF ,故NF ⊥BC ,故∠MFN 为二面角A -BC -D 的平面角或其补角.过点E 作ES ⊥BC 于点S ,过点D 作DT ⊥BC 的延长线于点T (图略),则ES =BE sin30°=2, 又BE ∥CD ,所以DT =CD sin30°=1, 所以MF =ES +DT 2=32,由(1)知MN =h =1,所以sin∠MFN =MN MF =23,设二面角A -BC -D 的平面角为θ,则sin θ=sin∠MFN =23.17.已知边长为1的正△A ′BC 的顶点A ′在平面α内,顶点B ,C 在平面α外的同一侧,点B ′,C ′分别为B ,C 在平面α内的射影,设BB ′≤CC ′,直线CB ′与平面A ′CC ′所成的角为φ.若△A ′B ′C ′是以角A ′为直角的直角三角形,则tan φ的最小值为________. 答案22解析 如图,以点A ′为坐标原点,A ′C ′,A ′B ′所在直线分别为x 轴,y 轴,建立空间直角坐标系.设B (0,b ,m ),C (c,0,n ),则⎩⎪⎨⎪⎧b 2+m 2=c 2+n 2=1,(0,b ,m )·(c ,0,n )=1·1·cos60°,0<m ≤n ,可得mn =12且0<m ≤n ,故0<m ≤22,又因为c 2+n 2=1,故n <1,又mn =12,故m >12,又因为tan φ=b =1-m 2,12<m ≤22,所以22≤tan φ<32,所以tan φ的最小值为22. 三、解答题(本大题共5小题,共74分.解答应写出文字说明,证明过程或演算步骤) 18.(14分)如图,在直三棱柱(侧棱垂直于底面)ABC -A 1B 1C 1中,AC =9,BC =12,AB =15,AA 1=12,点D 是AB 的中点.(1)求证:AC ⊥B 1C ; (2)求证:AC 1∥平面CDB 1.证明 (1)∵三棱柱ABC -A 1B 1C 1为直三棱柱, ∴CC 1⊥平面ABC ,又AC ⊂平面ABC ,∴CC 1⊥AC . 又∵AC =9,BC =12,AB =15, ∴AC 2+BC 2=AB 2,∴AC ⊥BC .∵CC 1,BC ⊂平面BB 1C 1C ,CC 1∩BC =C , ∴AC ⊥平面BB 1C 1C ,又B 1C ⊂平面BB 1C 1C ,∴AC ⊥B 1C .(2)取A 1B 1的中点D 1,连接C 1D 1,D 1D 和AD 1.∵AD ∥D 1B 1,且AD =D 1B 1, ∴四边形ADB 1D 1为平行四边形, ∴AD 1∥DB 1,又∵AD 1⊄平面CDB 1,DB 1⊂平面CDB 1, ∴AD 1∥平面CDB 1. ∵CC 1∥DD 1,且CC 1=DD 1,∴四边形CC 1D 1D 为平行四边形,∴C 1D 1∥CD , 又∵CD ⊂平面CDB 1,C 1D 1⊄平面CDB 1,∴C 1D 1∥平面CDB 1.∵AD 1∩C 1D 1=D 1,AD 1,C 1D 1⊂平面AC 1D 1, ∴平面AC 1D 1∥平面CDB 1,又AC 1⊂平面AC 1D 1,∴AC 1∥平面CDB 1.19.(15分)如图,在四棱锥P -ABCD 中,AD ⊥平面PDC ,AD ∥BC ,PD ⊥PB ,AD =1,BC =3,CD =4,PD =2.(1)求异面直线AP 与BC 所成角的余弦值; (2)求证:PD ⊥平面PBC ;(3)求直线AB 与平面PBC 所成角的正弦值.(1)解 由已知AD ∥BC ,得∠DAP 或其补角即为异面直线AP 与BC 所成的角.因为AD ⊥平面PDC ,所以AD ⊥PD .在Rt△PDA 中,由已知,得AP =AD 2+PD 2=5,故cos∠DAP =AD AP =55.所以异面直线AP 与BC 所成角的余弦值为55. (2)证明 因为AD ⊥平面PDC ,直线PD ⊂平面PDC ,所以AD ⊥PD . 又因为BC ∥AD ,所以PD ⊥BC ,又PD ⊥PB ,BC ,PB ⊂平面PBC ,BC ∩PB =B , 所以PD ⊥平面PBC .(3)解 过点D 作AB 的平行线交BC 于点F ,连接PF ,则DF 与平面PBC 所成的角等于AB 与平面PBC 所成的角.因为PD ⊥平面PBC ,故PF 为DF 在平面PBC 上的射影,所以∠DFP 为直线DF 和平面PBC 所成的角.由于AD ∥BC ,DF ∥AB ,故BF =AD =1,由已知,得CF =BC -BF =2.又AD ⊥DC ,故BC ⊥DC ,在Rt△DCF 中,可得DF =CD 2+CF 2=25,在Rt△DPF 中,可得sin∠DFP =PD DF =55. 所以,直线AB 与平面PBC 所成角的正弦值为55. 20.(15分)如图,在四棱锥P -ABCD 中,底面ABCD 为直角梯形,∠ADC =∠BCD =90°,BC=2,CD =3,PD =4,∠PDA =60°,且平面PAD ⊥平面ABCD .(1)求证:AD ⊥PB ;(2)在线段PA 上是否存在一点M ,使二面角M -BC -D 的大小为π6?若存在,求出PMPA 的值;若不存在,请说明理由.(1)证明过点B作BO∥CD,交AD于点O,连接PO,则AD⊥BO,在△PDO中,PD=4,DO=2,∠PDA=60°,则PO⊥AD,∵PO∩BO=O,PO,BO⊂平面POB,∴AD⊥平面POB,又∵PB⊂平面POB,∴AD⊥PB.(2)解假设存在点M,过点M作AD的平行线交PO于点N,连接BN,易知M,N,B,C四点共面,∵平面MBC∩平面BCD=BC,由(1)知,AD⊥平面POB,BC∥AD,则BC⊥平面POB,又BN⊂平面POB,∴BN⊥BC,又OB∥CD,则OB⊥BC,则∠NBO即为二面角M-BC-D的平面角,则tan∠NBO=33=NOOB,得NO=1,PN=PO-NO=23-1,∴PMPA=PNPO=23-123=1-36.21.(15分)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1,E ,F 分别是AB ,BC 的中点.(1)求A 1E 与B 1F 所成的角; (2)求A 1E 与平面BCC 1B 1所成的角. 解 (1)取AD 的中点H ,连接A 1H ,HE ,HF .由于H ,F 分别是AD ,BC 的中点,ABCD 为正方形, 所以HF ∥AB ,且HF =AB , 所以A 1B 1∥HF ,且A 1B 1=HF , 所以A 1B 1FH 为平行四边形, 所以B 1F ∥A 1H ,且B 1F =A 1H ,故A 1E 与B 1F 所成的角等于A 1E 与A 1H 所成的角,A 1E =2,HE =2,A 1H =2,故∠HA 1E =60°,故A 1E 与B 1F 所成的角为60°. (2)因为平面BCC 1B 1∥平面ADD 1A 1,所以直线A 1E 与平面BCC 1B 1所成的角即为直线A 1E 与平面ADD 1A 1所成的角, 所以∠EA 1A 即为所求角,而易知∠EA 1A =45°, 所以直线A 1E 与平面BCC 1B 1所成的角为45°.22.(15分)如图,四棱锥P —ABCD 中,底面ABCD 是矩形,平面PAD ⊥平面ABCD ,且△PAD 是边长为2的等边三角形,PC =13,点M 是PC 的中点.(1)求证:PA ∥平面MBD ;(2)点F 在PA 上,且满足AF FP =12,求直线DM 与平面FBD 所成角的正弦值.(1)证明 连接AC ,交BD 于点E ,连接ME . 因为四边形ABCD 是矩形, 所以点E 是AC 的中点, 又点M 是PC 的中点, 所以PA ∥ME ,又PA ⊄平面MBD ,EM ⊂平面MBD , 所以PA ∥平面MBD .(2)解 取AD 的中点O ,则PO ⊥AD ,又平面PAD ⊥底面ABCD ,平面PAD ∩底面ABCD =AD ,PO ⊂平面PAD ,故PO ⊥平面ABCD ,连接OC .在Rt△POC 中,OC =PC 2-PO 2=10, 所以在Rt△ODC 中,DC =OC 2-DO 2=3,以O 为坐标原点,OA ,OE ,OP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,则A (1,0,0),B (1,3,0),D (-1,0,0),C (-1,3,0), P (0,0,3),M ⎝ ⎛⎭⎪⎫-12,32,32, 则BD →=(-2,-3,0),设F (x 0,y 0,z 0),AF →=(x 0-1,y 0,z 0),AP →=(-1,0,3),BF →=(x 0-1,y 0-3,z 0). 则由AF →=13AP →得(x 0-1,y 0,z 0)=13(-1,0,3),即F ⎝ ⎛⎭⎪⎫23,0,33,则BF →=⎝ ⎛⎭⎪⎫-13,-3,33.设平面FBD 的法向量m =(x ,y ,z ),则⎩⎪⎨⎪⎧m ·BD →=0,m ·BF →=0,得⎩⎪⎨⎪⎧-2x -3y =0,-13x -3y +33z =0,令x =3,则y =-2,z =-53,故m =(3,-2,-53),又DM →=⎝ ⎛⎭⎪⎫12,32,32,设直线DM 与平面FBD 所成的角为θ,则 sin θ=|cos 〈m ,DM →〉|=|m ·DM →||m ||DM →|=9222·132=9286286,故直线DM 与平面FBD 所成角的正弦值为9286286.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何
例1.在三棱锥P ABC -中,PA ⊥底面ABC ,,6,8AB AC AB AC ⊥==,D 是线段AC 上一点,且
3AD DC =.三棱锥P ABC -的各个顶点都在球O 表面上,过点D 作球O 的截面,若所得截面圆的
面积的最大值与最小值之差为16π,则球O 的表面积为( ) A .72π B .86π C .112π D .128π
2.三视图
例2.某简单组合体的三视图如图所示,则该几何体的体积为( )
A .164+π
B .484π+
C .4812π+
D .4816π+ 3.常见几何体的体积计算公式
例3.已知直角三角形 ABC 两直角边长之和为3,将ABC ∆绕其中一条直角边旋转一周,所形成旋转体体积的最大值为__________,此时该旋转体外接球的表面积为___________.
例4.如图,三棱锥的顶点,,,都在同一球面上,
过球心且
,是边
长为
等边三角形,点、分别为线段,上的动点(不含端点),且
,则三棱锥
体积的最大值为__________.
例5.如图,在几何体中,平面底面ABC ,
四边形是正方形,,Q 是
的中点,且
,
.
求证:平面
; 求二面角的余弦值.
例6.如图几何体中,底面ABCD 为正方形,PD ⊥平面ABCD ,//EC PD ,且22PD AD EC ===.(1)求证://BE 平面PDA ; (2)求PA 与平面PBD 所成角的大小.
例7.已知三棱锥A BCD -的棱长均为6,其内有n 个小球,球1O 与三棱锥A BCD -的四个面都相切,球2O 与三棱锥A BCD -的三个面和球1O 都相切,如此类推,…,球n O 与三棱锥A BCD -的三个面和球1n O -都相切(2n ≥,且n *∈N ),则球1O 的体积等于__________,球n O 的表面积等于__________.
例8.如图所示,在等腰梯形ABCD 中,,
,E ,F 为AB 的三等分点,且
将
和
分别沿DE 、CF 折起到A 、B 两点重合,记为点P . 证明:平面平面PEF ;
若
,求PD 与平面PFC 所成角的正弦值.
一、选择题
1.(2020·福建高三月考(文))已知平面α⊥平面β,直线,m l ααβ⊂=,则“m l ⊥”是“m β⊥”
的( ) A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
2.(2020·湖北高三月考(文))某几何体的三视图如图所示, 则该几何体的体积为( )
A .4
π B .2π
C .π
D .2π
3.已知二面角l αβ--的大小为60°,b 和c 是两条异面直线,且,b c αβ⊥⊥,则b 与c 所成的角的大小为( )
A .120°
B .90°
C .60°
D .30°
4.把正方形ABCD 沿对角线AC 折起,当以,,,A B C D 四点为顶点的棱锥体积最大时,直线BD 和平面ABC 所成的角的大小为( ) A .90° B .60
C .45°
D .30°
5.(2020·湖北高三月考(理))鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.从外观上看,是严丝合缝的十字立方体,其上下、左右、前后完全对称;六根等长的正四棱柱分成三组,经90°榫卯起来.如图所示,正四棱柱的高为8,底面正方形的边长为1,将这个鲁班锁放进一个球形容器内,则该球形容器半径的最小值为(容器壁的厚度忽略不计)( ) A .
65
B .
66 C .69 D .17.
6.在三棱锥A-BCD 中,平面ABC 丄平面ADC, AD 丄AC,AD=AC, 3
ABC π
∠=,若此三棱锥的外接球
表面积为28π,则三棱锥A-BCD 体积的最大值为( )
A .7
B .12
C .6
D .
53
7.(2016·浙江高三学业考试)如图,在四面体ABCD 中,2AB CD ==,3AD BD ==,
4AC BC ==,点E ,F ,G ,H 分别在棱AD ,BD ,BC ,AC 上,若直线AB ,CD 都平
行于平面EFGH ,则四边形EFGH 面积的最大值是( ) A .12 B .2
2
C .1
D .2
8.(2020·浙江高三期末)斜三棱柱111ABC A B C -中,底面ABC 是正三角形,侧面11ABB A 是矩形,且123AA AB =,M 是AB 的中点,记直线1A M 与直线BC 所成的角为α,直线1A M 与平面ABC 所成的角为β,二面角1A AC B --的平面角为γ,则( ) A .βγ<,αγ< B .βα<,βγ< C .βα<,γ
α<
D .αβ<,γβ<
9.(2020·浙江高三学业考试)如图,在圆锥SO 中,A ,B 是O 上的动点,BB '是O 的直径,
M ,N 是SB 的两个三等分点,()0AOB θθπ∠=<<,记二面角N OA B --,M AB B '--的
平面角分别为α,β,若αβ≤,则θ的最大值是( ) A .56
π B .
23
π C .
2π
D .4
π 10.设三棱锥V ABC -的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点),记直线PB 与直线AC 所成角为α,直线PB 与平面ABC 所成角为β,二面角P AC B --的平面角为
γ,则( )
A .,βγαγ<<
B .,βαβγ<<
C .,βαγα<<
D .,αβγβ<<
二、填空题
11.已知平面αβ,和直线m ,给出条件: ①m α;②m α⊥;③m α⊂;④αβ⊥;⑤αβ.
(1)当满足条件____ 时,有m β;
(2)当满足条件 ____ 时,有m β⊥.(填所选条件的序号) 12.(2020·浙江高三期末)某几何体的三视图如图所 示(单位:cm ),则该几何体的 体积为______3cm ,表面积为______2cm .
13.已知正三棱柱111ABC A B C -的六个顶点都在球O 的表面上,3AB =,异面直线1AC 与BC 所成角的余弦值为
3
10
,则1AA =_______,球O 的表面积为_______. 14.已知正三棱柱111ABC A B C -的六个顶点都在球O 的表面上,若这个三棱柱的体积为93,3AB =,则1AA =_______,球O 的表面积为_______.
15.在三棱锥P ABC -中,PA ⊥底面ABC ,,6,8AB AC AB AC ⊥==,D 是线段AC 上一点,且
3AD DC =.三棱锥P ABC -的各个顶点都在球O 表面上,过点D 作球O 的截面,则所得截面圆的
面积的最小值为____.
16.如图,在棱长为 1 的正方体1111ABCD A B C D -中,点M 是AD 的中点,动点P 在底面正方形
ABCD 内(不包括边界),若1//B P 平面1A BM ,
则1C P 长度的取值范围是_______.
17.四棱锥S ABCD -中,底面ABCD 是边长为2的正方形,侧面SAD 是以AD 为斜边的等腰直角三角形,若π2π,33SAB ⎡⎤
∠∈⎢⎥⎣⎦
,则四棱锥S ABCD -的体积的取值范围为______.
三、解答题
18.(2020·浙江高三期末)已知斜三棱柱111ABC A B C -,
2
ABC π
∠=,1AC BC ⊥,12BC BA ==,
1BC =,123AC =.
(1)求1AA 的长;
(2)求1AA 与面ABC 所成的角的正切值.
19.如图,在斜三棱柱111ABC A B C -中,平面ABC ⊥平面11A ACC ,12CC =,ABC ,
1ACC △,均为正三角形,E 为AB 的中点. (1)证明:1//AC 平面1B CE ,
(2)求直线1AC 与平面11B BAA 所成角的正弦值.
20.如图,三棱柱111ABC A B C -中,AB ⊥侧面11BB C C ,已知13
BCC π
∠=,
1BC =,12AB C C ==,点E 是棱1C C 的中点. (1)求证:1C B ⊥平面ABC ;
(2)在棱CA 上是否存在一点M ,使得EM 与平面11A B E 所成角的正弦值为
211
11
,若存在 ,求出CM
CA
的值;若不存在,请说明理由.
21.如图,三棱柱1l l ABC A B C -中,11,,60AC BC AB AA BAA ==∠=︒.
(1)求证:1
11AC B A ⊥; (2)若平面ABC ⊥平面11ABB A ,且AB BC =, 求直线1CB 与平面1A BC 所成角的正弦值.
22.如图,在四面体ABCD 中,E ,F 分别是线段AD ,BD 的中点,90ABD BCD ∠=∠=,
2EC =2AB BD ==,直线EC 与平面ABC 所成的角等于30.
(1)证明:平面EFC ⊥平面BCD ; (2)求二面角A CE B --的余弦值.。
