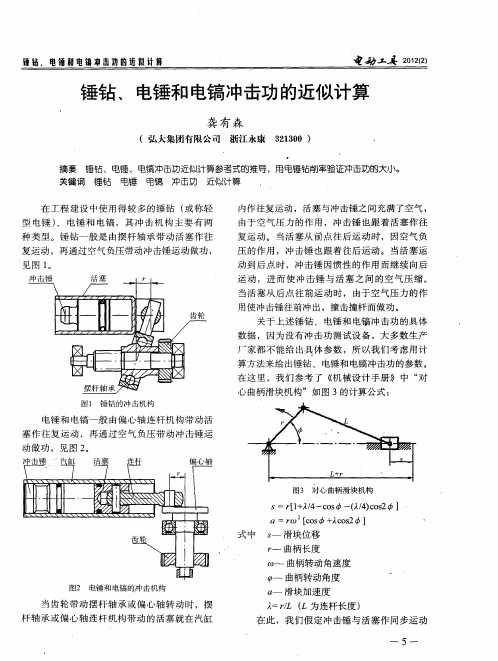
对心曲柄滑块机构计算
曲柄滑块机构的运动精度分析与计算

曲柄滑块机构的运动精度分析与计算宋亮;赵鹏兵【摘要】曲柄滑块机构是一种典型的四连杆机构,尽管设计时理论计算可以达到很高的精度,但是由于构件的制造误差及运动副的配合间隙等因素,会使机构在运动中产生输出误差,有时还会显著超出机构设计的允许误差.依据概率统计的相关理论进行机构设计,即考虑构件制造尺寸的随机误差,以保证机构运动的精度在允许的误差范围内.利用MATLAB进行仿真计算和实例研究,得出了理论设计和精度分析的计算结果.该方法准确、效率高、而且适合其它类型的机构设计,具有较大的工程实际应用价值.%Slider-crank mechanism is a typical four-bar linkage, in spite of the high precision when it' s calculated theoretically. The manufacturing error and kinematic pair clearance of the components will lead to the output error during the motion of the mechanism. Sometimes,it will significantly exceed the tolerance of the design. According to the probability and statistics theory, the mechanism is designed, that' s considering the random error of the component to make sure that the motion accuracy is in the allowed error range. Utilizing MATLAB to simulate and calculate based on case studies. and the theoretical design and accuracy analysis are obtained. This method is accurate and very efficiently, it also can be used in other kind of mechanism design, and it has much more practical value in engineering.【期刊名称】《科学技术与工程》【年(卷),期】2011(011)010【总页数】5页(P2201-2205)【关键词】曲柄滑块机构;运动学;概率设计;等影响法;精度分析【作者】宋亮;赵鹏兵【作者单位】海军装备部,西安,710043;西北工业大学现代设计与集成制造技术教育部重点实验室,西安,710072【正文语种】中文【中图分类】TH112.1曲柄滑块机构是一种单移动副的四连杆机构,如图1和图2所示,分别为对心和偏心曲柄滑块机构。
锤钻、电锤和电镐冲击功的近似计算
用使冲击锤往前冲 出,撞击撞杆而做功 。 关于上述锤 钻、 电锤 和 电镐冲击功 的具体
数 据 , 因为 没 有 冲 击 功 测 试 设 备 ,大 多 数 生 产 厂 家都 不 能 给 出具 体 参 数 ,所 以我 们 考 虑 用 计 算 方 法来 给 出锤钻 、 电锤 和 电镐 冲 击 功 的参 数 。 在 这 里 ,我 们 参 考 了 机 械 设 计 手 册 》 中 “ 对 心 曲柄 滑 块 机 构 ”如 图 3的计 算 公 式 :
锤钻、电锤和电镐冲击功的逝I计算 以
电劫 工其 2 2) 0 ( 12
锤钻 电锤和 电镐 冲击功 的近似计算
龚 有 森
(弘 大集 团有 限公 司 浙江 永 康 31 0 ) 2 30
●
摘要
关键词
锤 钻、电锤 、电镐冲击功近似计算参考式的推导 ,用电锤钻削率验证冲击功的大小。
锤钻 电锤 电镐 冲击功 近似计算 .
小。
正 比。但是偏心轴偏心距 r 、摆杆轴承 r 值和偏 心轴 、摆杆轴 承转 速 以及 冲击锤质量不 是越大 越好 ,它们 受到结构 、材料等条件 的限制 ,太 大还可 能引起零部件 损坏 、不冲击 等 问题 ,因
此这 三 个 参数 的合 理搭 配 才是 关键 。 按 上 式 计 算 的 冲 击 功 是 一 个 近 似 值 , 我 们 此 时 按 国 外 某 品牌 电锤 进 行 的计 算 结 果 与 其 冲
2/ F( n3 ) 1 7 2 r/ 0 (0 ) 7 7
一
钻 孑 直径 ,c L m
h 钻 孔 深度 ,c 一 m
f 钻 孔 所用 时 间 ,ri 一 an
从上 式可 以看 出冲击功 的大小 与偏心轴 偏 心距 r 或摆杆轴承 值 的平方成正 比, 与偏 心轴 、
机械原理试题及答案(试卷 答案)

2013年机械原理自测题(一)一.判断题(正确的填写“T”,错误的填写“F”)(20分)1、根据渐开线性质,基圆内无渐开线,所以渐开线齿轮的齿根圆必须设计比基圆大。
( F )2、对心的曲柄滑块机构,其行程速比系数K一定等于一。
( T )3、在平面机构中,一个高副引入二个约束。
( F )4、在直动从动件盘形凸轮机构中,若从动件运动规律不变,增大基圆半径,则压力角将减小( T )5、在铰链四杆机构中,只要满足杆长和条件,则该机构一定有曲柄存在。
( F )6、滚子从动件盘形凸轮的实际轮廓曲线是理论轮廓曲线的等距曲线。
( T )7、在机械运动中,总是有摩擦力存在,因此,机械功总有一部分消耗在克服摩擦力上。
( T )8、任何机构的从动件系统的自由度都等于零。
( T )9、一对直齿轮啮合传动,模数越大,重合度也越大。
( F )10、在铰链四杆机构中,若以曲柄为原动件时,机构会出现死点位置。
( F )二、填空题。
(10分)1、机器周期性速度波动采用(飞轮)调节,非周期性速度波动采用(调速器)调节。
2、对心曲柄滑块机构的极位夹角等于( 0 )所以(没有)急回特性。
3、渐开线直齿圆柱齿轮的连续传动条件是(重合度大于或等于1 )。
4、用标准齿条形刀具加工标准齿轮产生根切的原因是(齿条形刀具齿顶线超过极限啮合点N1 )。
5、三角螺纹比矩形螺纹摩擦(大),故三角螺纹多应用(联接),矩形螺纹多用于(传递运动和动力)。
三、选择题(10分)1、齿轮渐开线在()上的压力角最小。
A )齿根圆; B)齿顶圆; C)分度圆; D)基圆。
2、静平衡的转子(①)是动平衡的。
动平衡的转子(②)是静平衡的。
①A)一定; B)不一定; C)一定不。
②A)一定; B)不一定: C)一定不。
3、满足正确啮合传动的一对直齿圆柱齿轮,当传动比不等于一时,他们的渐开线齿形是( )。
A )相同的;B )不相同的。
4、对于转速很高的凸轮机构,为了减小冲击和振动,从动件运动规律最好采用( )的运动规律。
对心曲柄滑块机构原理

对心曲柄滑块机构原理
嘿,朋友们!今天咱来唠唠对心曲柄滑块机构原理。
你说这对心曲柄滑块机构啊,就像是一场奇妙的舞蹈。
曲柄就像是领舞的那个,带着滑块一块儿动起来。
想象一下,曲柄慢悠悠地转呀转,滑块呢,就跟着它在那轨道上滑来滑去,是不是挺有意思?
这机构里的各个部分那可都有它的用处。
曲柄呢,就负责提供动力,让整个动作能持续进行。
而滑块呢,就老老实实地顺着轨道跑,完成它该完成的任务。
这就好比是一个团队,每个人都有自己的角色,少了谁都不行啊!
咱平常生活里也有好多类似的例子呢。
就说骑自行车吧,脚踩踏板就像是曲柄在转动,带动链条,然后轮子就跟着转起来,这不就跟对心曲柄滑块机构差不多嘛。
还有啊,那钟摆,一摇一摆的,不也有点那个意思嘛。
你可别小瞧了这对心曲柄滑块机构,它在好多地方都大显身手呢!在机械制造里,那可是立下了汗马功劳。
一些机器的运作就得靠它来带动,没有它,好多东西都没法正常工作啦。
而且哦,这对心曲柄滑块机构还特别稳定。
它不会轻易出啥乱子,总是稳稳当当的工作着。
就像咱身边那些靠谱的朋友,啥时候都能靠得住。
再说说它的灵活性吧。
它能根据不同的需求进行调整和改变,多厉害呀!就好像一个武林高手,能随时变换招式来应对不同的情况。
哎呀呀,说了这么多,你们是不是对对心曲柄滑块机构有了更深的了解呢?这玩意儿真的是又有趣又实用啊!它就像一个隐藏在机械世界里的小魔法,默默地发挥着自己的作用。
所以啊,咱可得好好认识认识它,说不定啥时候就能派上大用场呢!总之,对心曲柄滑块机构,真是个了不起的存在呀!。
曲柄滑块机构分析

Fx
A
60
B Fy
求解过程:
第一步:以曲柄1为研究对象进行受力分析,如图 所示:
X方向:F21*cos(60)+Fx+F=0 Y方向:Fy+F21*sin(60)=0 转矩平衡方程:F*OA-F21*OB*sin(60)=0 三个未知量,三个方程,则可求解得到F21,即 曲柄对连杆的作用力。
7
F4 F’x
D.其他情况
13
扩展1:曲柄滑块机构
M B
A C
D
14
扩展2:当杆长发生变化时,弹簧力会发生什 么变化?
D
F
D
F
200 100 B
A
C
500 100 B
A
C
D
F
200 100 B
A
C
15
课后作业2:教材P77,课后习题4
图2-128所示为曲柄导杆机构。已知曲柄长为 a=100mm,曲柄回转中心A与导杆摆动中心C的 距离为b=200mm。曲柄以ω=36(°)/s的角速 度匀速转动。 (1)试建立该曲柄导杆机构的虚拟样机模型。 (2)仿真机构的虚拟样机模型,并测量获取导杆 角度、角速度和角加速度的变化规律; (3)试根据仿真分析结果,计算求取机构的行程 速比系数
16
课后作业1:教材P77,课后习题5
在图2-129所示的对心曲柄滑块机构,已知曲柄为 100cmx10cmx5cm的钢质杆,连杆为200cmx10cmx5cm的用在曲柄上的 驱动力矩为M1=20N.m。 (1)试建立该曲柄滑块机构的虚拟样机模型; (2)请仿真机构的虚拟样机模型,并测量获取滑块3在0s-20s运 动时间内的位移、速度和加速度的变化规律。
曲柄滑块机构分析
机械原理 第03章 连杆机构

平面四杆机构具有急回特性的条件: (1)原动件作等速整周转动;
(2)输出件作往复运动;
(3)
0
B2
2.曲柄滑块机构中,原动件AB以 1等速转动 B 2 b B 1 C2 C3 a b 2 1 1 1 a B1 C2 C 3 C1 B1 H A
A
C1
4
4
H
B2
偏置曲柄滑块机构
对心曲柄滑块机构 H=2a, 0 ,无急回特性。
一.平面四杆机构的功能及应用
1 .刚体导引功能 2.函数生成功能 3.轨迹生成功能 轨迹生成功能 是指连杆上某点通过某一 预先给定轨迹 的功能。 连杆
§2-4 平面四杆机构运动设计的基本问题与方法
一.平面四杆机构的功能及应用
1 .刚体导引功能 3.轨迹生成功能 2.函数生成功能 4.综合功能 O1 D1 上剪刀 D2 下剪刀
(b>c) (2b)
'
B
1
a
A
b
c
d
4
D r 3
C b 3 c
a-d
B2
r2
d c a b (2a )
d b a c (2b')
由(1)及(2a' )(2b')可得
d+a
d a , d b, d c
铰链四杆机构的类型与尺寸之间的关系:
在铰链四杆机构中: (1)如果最短杆与最长杆的长度之和小于或等于其它两杆 长度之和 ——满足杆长和条件 且: 1 以最短杆的相邻构件为机架,则此机构为以最短杆 为曲柄的曲柄摇杆机构; 2 以最短杆为机架,则此机构为双曲柄机构;
2 4
摆动导杆 机构
导杆:
C 3
曲柄滑块机构的运动分析及应用解读

机械原理课程机构设计实验报告题目:曲柄滑块机构的运动分析及应用小组成员与学号:刘泽陆(********)陈柯宇(11071177)熊宇飞(11071174)张保开(11071183)班级:1107172013年6月10日摘要 (3)曲柄滑块机构简介 (4)曲柄滑块机构定义 (4)曲柄滑块机构的特性及应用 (4)曲柄滑块机构的分类 (8)偏心轮机构简介 (9)曲柄滑块的动力学特性 (10)曲柄滑块的运动学特性 (11)曲柄滑块机构运行中的振动与平衡 (14)参考文献 (15)组员分工 (15)摘要本文着重介绍了曲柄滑块机构的结构,分类,用途,并进行了曲柄滑块机构的动力学和运动学分析,曲柄滑块机构的运动学特性分析,得出了机构压力表达式,曲柄滑块机构的运动特性分析,得出了滑块的位移、速度和加速度的运动表达式。
最后,对曲柄滑块机构运动中振动、平衡稳定性等进行了总结。
关键字:曲柄滑块动力与运动分析振动与平稳性ABSTRACTThe paper describes the composition of planar linkage, focusing on the structure, classification, use of a slider-crank mechanism and making the dynamic and kinematic analysis, kinematics characteristics of the crank slider mechanism analysis for a slider-crank mechanism, on one hand , we obtain the drive pressure of the slider-crank mechanism ,on the other hand,we obtain the expression of displacement, velocity and acceleration of movement. Finally, the movement of the vibration and balance stability of the crank slider mechanism are summarized.曲柄滑块机构简介曲柄滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
机械原理复习题(第3、4、5、8章)

第3章平面机构的运动分析第4章平面机构的力分析第5章机械的效率和自锁第8章平面连杆机构及其设计一、填空题:α=,则传动角γ=___________度,传动角越大,1、铰链四杆机构的压力角040传动效率越___________。
2、下图为一对心曲柄滑块机构,若以滑块3为机架,则该机构转化为机构;若以构件2为机架,则该机构转化为机构。
3、移动副的自锁条件是;转动副的自锁条件是。
4、曲柄摇杆机构中,当和共线时出现死点位置。
:5、曲柄摇杆机构中,只有取为主动件时,才有可能出现死点位置。
处于死点位置时,机构的传动角γ=__________度。
6、平行四边形机构的极位夹角θ=,它的行程速比系数K=。
7、曲柄滑块机构中,若增大曲柄长度,则滑块行程将。
8、如下图所示铰链四杆机构,70mm,150mm,110mm,90mm====。
若以a b c da杆为机架可获得机构,若以b杆为机架可获得机构。
9、如图所示铰链四杆机构中,若机构以AB杆为机架时,为机构;以CD 杆为机架时,为机构;以AD杆为机架时,为机构。
~10、在平面四杆机构中,和为反映机构传力性能的重要指标。
11、在曲柄摇杆机构中,如果将杆作为机架,则与机架相连的两杆都可以作运动,即得到双曲柄机构。
12、在摆动导杆机构中,若以曲柄为原动件,该机构的压力角为,其传动角为。
13、相对瞬心与绝对瞬心的相同点是,不同点是;在由N个构件组成的机构中,有个相对瞬心,有个绝对瞬心。
/二、判断题:1、对于铰链四杆机构,当机构运动时,传动角是不变的。
()2、在四杆机构中,若有曲柄存在,则曲柄必为最短杆。
()3、平面四杆机构的行程速度变化系数K 1,且K值越大,从动件急回越明显。
()4、曲柄摇杆机构中,若以摇杆为原动件,则当摇杆与连杆共线时,机构处于死点位置。
()5、曲柄的极位夹角θ越大,机构的急回特性也越显著。
()6、在实际生产中,机构的“死点”位置对工作都是不利的,处处都要考虑克服。
对心式曲柄滑块机构参考幻灯片

29
对心式曲柄滑块机构
偏心距e=0
左极限 位置
右极限 位置
30
对心式曲柄滑块机构
偏心距e=0
左极限 位置
右极限 位置
31
对心式曲柄滑块机构
偏心距e=0
左极限 位置
右极限 位置
32
对心式曲柄滑块机构
偏心距e=0
左极限 位置
右极限 位置
33
对心式曲柄滑块机构
偏心距e=0
左极限 位置
右极限 位置
19
对心式曲柄滑块机构
偏心距e=0
左极限 位置
右极限 位置
20
对心式曲柄滑块机构
偏心距e=0
左极限 位置
右极限 位置
21
对心式曲柄滑块机构
偏心距e=0
左极限 位置
右极限 位置
22
对心式曲柄滑块机构
偏心距e=0
左极限 位置
右极限 位置
23
对心式曲柄滑块机构
偏心距e=0
左极限 位置
右极限 位置
对心式曲柄滑块机构
偏心距e=0 右极限 位置
1
对心式曲柄滑块机构
偏心距e=0 右极限 位置
2
对心式曲柄滑块机构
偏心距e=0 右极限 位置
3
对心式曲柄滑块机构
偏心距e=0 右极限 位置
4
对心式曲柄滑块机构
偏心距e=0 右极限 位置
5
对心式曲柄滑块机构
偏心距e=0 右极限 位置
6
对心式曲柄滑块机构
13
对心式曲柄滑块机构
偏心距e=0 右极限 位置
14
对心式曲柄滑块机构
偏心距e=0 右极限 位置
机械原理期末考试测试题及答案详解

机械原理测试题一.判断题(正确的填写“ T”,错误的填写“ F”)1、依据渐开线性质,基圆内无渐开线,所以渐开线齿轮根圆一定设计比基圆大。
( F)2、对心的曲柄滑块机构,其行程速比系数K 必定等于一。
( T)3、在平面机构中,一个高副引入二个拘束。
( F)4、在直动从动件盘形凸轮机构中,若从动件运动规律不变,增大基圆半径,则压力角将减小( T)5、在铰链四杆机构中,只需知足杆长和条件,则该机构必定有曲柄存在。
( F)6、滚子从动件盘形凸轮的本质轮廓曲线是理论轮廓曲线的等距曲线。
( T )7、在机械运动中,总有摩擦力存在,所以,机械功总有一部分耗费在战胜摩擦力上。
( T)8、任何机构的从动件系统的自由度都等于零。
( T)9、一对直齿轮啮合传动,模数越大,重合度也越大。
( F)10、在铰链四杆机构中,若以曲柄为原动件时,机构会出现死点地点。
( F)11、一对相啮合的标准齿轮,小轮的齿根厚度比大轮的齿根厚度大。
( F)12、在曲柄滑块机构中,只需原动件是滑块,就必定有死点存在。
( T)13、两构件之间以点、线接触所构成的平面运动副称为高副,它产生两个拘束,而保存一个自由度。
( F)14、一对直齿轮啮合传动,模数越大,重合度也越大。
( F )15、平面四杆机构有无急回特征取决于极位夹角能否大于零。
( T)16、关于刚性转子,已知足动均衡者,也必知足静均衡。
( T)17、滚子从动件盘形凸轮的基圆半径和压力角应在凸轮的理论轮廓上胸怀。
( T )18、在考虑摩擦的转动副中,当匀速转动时,总反力作用线永久切于摩擦圆。
(T)19、当机构的自由度数大于零,且等于原动件数,则该机构拥有确立的相对运动。
(T)20、关于单个标准齿轮来说,节圆半径就等于分度圆半径。
( F )二、选择题1、为了减小机器运行中周期性速度颠簸的程度,应在机器中安装(B)。
A)调速器; B )飞轮; C )变速装置。
2、重合度εα = 1.6表示在本质啮合线上有( C )长度属于双齿啮合区。
《机械动力学答案》

A、急停阶段 B、启动阶段 C、稳定运转阶段 D、停车阶段 72、在动力分析中,主要涉及的力是( ) 。 A、驱动力 B、重力 C、摩擦力 D、生产阻力 73、以下选项中,与等效力有关的是( ) 。 A、外力 B、传动比 C、ωj/v D、vk/v 74、以下选项中,与等效力矩有关的是( ) 。 A、外力据 B、传动比 C、ωj/ω D、vk/ω 75、以下选项中,可归为阻尼的有( ) 。 A、物体的内力 B、物体表面间的摩擦力 C、周围介质的阻力 D、材料的内摩擦 四、填空题(每空 2 分,共 30 空,共 60 分) 76、从惯性载荷被平衡的程度看,平衡可分为 、 和 。 77、机械动力学的分析方法按功能分类可分为 和 。 78、动力学的分析方法按水平分类,可分为 、 、 和 。 79、用质量再分配实现摆动力的完全平衡,其分析方法主要有 、 、 和 。 80、机械系统运转的全过程可分为 、 和 这几个阶段。 81、机器人动力学是机器人 、 和 的基础。 82、工业机器人通常由 、 、 和 组成。 83、二自由度系统的等效转动惯量是系统的 、 、 和 的函数。 84、实现摆动力完全平衡的方法有 、 和 。 76、部分平衡、完全平衡、优化综合平衡 77、动力学反问题、动力学正问题 78、静力分析、动态静力分析、动态分析、弹性动态分析 79、广义质量代换法、线性独立矢量法、质量矩替代法、有限位置法 80、启动阶段、稳定运转阶段、停车阶段 81、操作机设计、控制器设计、动态性能分析 82、执行机构、驱动装置、控制系统、传感系统 83、时间、惯性参数、几何参数、广义坐标 84、加配重、合理布置机构、设置附加机构 五、计算题(第 85、86 题各 30 分,第 87 题 10 分,第 88 题 20 分,共 90 分) 85、如图所示为一对心曲柄滑块机构。曲柄以转速度 ω1 作等速回转运动,曲柄与水平方 向夹角为 θ1 ,曲柄长度为 r ,质心与其回转中心 A 重合。连杆长度 l ,连杆与水平方向夹 角为 θ 2 ,连杆质心 S2 到铰链 B 的距离 BS 2 = L ,连杆质量 m 2 ,对其质心的转动惯量 J 2 。 滑 块质量 m3 ,其质心与铰链 C 重合。1)画出曲柄、连杆和滑块的受力分析图;2)写出曲 柄、连杆和滑块的平衡方程。
机械原理考试试题及答案

试题1一、选择题(每空2分,共10分)1、平面机构中,从动件的运动规律取决于_D _____ 。
A、从动件的尺寸B 机构组成情况C 原动件运动规律D原动件运动规律和机构的组成情况2、一铰链四杆机构各杆长度分别为30mm, 60mm 80mm 100mm当以30mn!勺杆为机架时, 则该机构为 A 机构。
A、双摇杆B、双曲柄C、曲柄摇杆D不能构成四杆机构3、凸轮机构中,当推杆运动规律采用 C 时,既无柔性冲击也无刚性冲击。
A、一次多项式运动规律B、二次多项式运动规律C、正弦加速运动规律D余弦加速运动规律4、平面机构的平衡问题中,对“动不平衡”描述正确的是_B ________ 。
A、只要在一个平衡面内增加或出去一个平衡质量即可获得平衡B、动不平衡只有在转子运转的情况下才能表现出来C、静不平衡针对轴尺寸较小的转子(转子轴向宽度b与其直径D之比b/Dv0.2)D使动不平衡转子的质心与回转轴心重合可实现平衡5、渐开线齿轮齿廓形状决定于 D 。
A、模数B、分度圆上压力角C、齿数D前3项二、填空题(每空2分,共20分)1、两构件通过面接触而构成的运动副称为低副。
2、作相对运动的三个构件的三个瞬心必在同一条直线上。
3、转动副的自锁条件是驱动力臂w摩擦圆半径___________ 。
4、斜齿轮传动与直齿轮传动比较的主要优点:啮合性能好,重合度大,结构紧凑5、在周转轮系中,根据其自由度的数目进行分类:若其自由度为2,则称为差动轮系若其自由度为1,则称其为行星轮系。
6装有行星轮的构件称为行星架(转臂或系杆)。
7、棘轮机构的典型结构中的组成有:摇杆、棘爪、棘轮等。
三、简答题(15分)1、什么是构件?答:构件:机器中每一个独立的运动单元体称为一个构件;从运动角度讲是不可再分的单位体。
2、何谓四杆机构的“死点”?答:当机构运转时,若出现连杆与从动件共线时,此时丫=0,主动件通过连杆作用于从动件上的力将通过其回转中心,从而使驱动从动件的有效分力为零,从动件就不能运动,机构的这种传动角为零的位置称为死点。
偏置曲柄滑块机构与对心曲柄滑块机构的区别

偏置曲柄滑块机构与对心曲柄滑块机构的区别偏置曲柄滑块机构与对心曲柄滑块机构是机械设计中常见的两种机构,它们在工作原理、应用领域以及特点方面有很大的区别。
本文将对这两种机构进行全面评估,并从简到繁,由浅入深地探讨它们的差异,以便读者更深入地理解这两种机构的特点和应用。
1. 偏置曲柄滑块机构:偏置曲柄滑块机构是一种常见的转动-直线运动转换机构。
它由曲柄轴、曲柄、连杆和滑块组成。
其中,曲柄轴是固定的,曲柄则通过曲柄轴旋转,从而导致连杆和滑块产生直线运动。
- 工作原理:偏置曲柄滑块机构的工作原理非常简单。
当曲柄旋转时,连杆连接在曲柄和滑块之间,使得滑块随着曲柄的旋转而产生直线运动。
- 应用领域:由于偏置曲柄滑块机构结构简单、制造成本相对较低且运动传动效率较高,因此广泛应用于各种机械领域。
它常用于发动机中的活塞运动转换,或者用于工业生产中的压力和移动工作。
- 特点:相较于对心曲柄滑块机构,偏置曲柄滑块机构的特点如下:a) 运动传递方式不同:偏置曲柄滑块机构通过曲柄的旋转将转动运动转换为直线运动,而对心曲柄滑块机构则直接将转动运动转换为直线运动。
b) 运动轨迹不同:偏置曲柄滑块机构的滑块运动轨迹呈现椭圆形或近似椭圆形,而对心曲柄滑块机构的滑块运动轨迹为直线。
c) 可调性较强:由于偏置曲柄滑块机构的曲柄位置可以调整,因此可以通过改变曲柄的位置来调整滑块的运动速度和行程。
2. 对心曲柄滑块机构:对心曲柄滑块机构也是一种常见的转动-直线运动转换机构。
它由曲柄轴、曲柄、连杆和滑块组成。
与偏置曲柄滑块机构不同的是,对心曲柄滑块机构的曲柄轴与连杆的连接点处于同一轴线上。
- 工作原理:对心曲柄滑块机构的工作原理类似于偏置曲柄滑块机构。
当曲柄旋转时,连杆通过对心连接在曲柄上,并且滑块随着曲柄的旋转而实现直线运动。
- 应用领域:对心曲柄滑块机构由于其结构简单且运动平稳,常应用于精密机械、钟表、仪器仪表和自动化设备等领域。
- 特点:相较于偏置曲柄滑块机构,对心曲柄滑块机构的特点如下: a) 运动传递方式不同:对心曲柄滑块机构通过曲柄的旋转转换为连杆的直线运动,而偏置曲柄滑块机构则通过连杆的直线运动转换为滑块的直线运动。
偏置曲柄滑块机构与对心曲柄滑块机构的区别

偏置曲柄滑块机构与对心曲柄滑块机构的区别偏置曲柄滑块机构与对心曲柄滑块机构是机械工程中常见的两种运动转换机构,它们在工业生产和机械设计中都有着重要的应用。
两者之间的区别不仅仅在于结构形式上的差异,更在于其在实际应用中所具有的性能特点和适用范围。
在本文中,我们将深入探讨这两种曲柄滑块机构的区别,从结构原理、工作方式、性能特点等方面进行全面评估,以帮助读者更好地理解和应用这两种机构。
一、结构原理1. 偏置曲柄滑块机构偏置曲柄滑块机构由曲柄、连杆和滑块组成,其中曲柄的转动运动通过连杆传递给滑块,实现直线往复运动。
偏置曲柄滑块机构中的曲柄轴和滑块轨迹不在同一轴线上,因此称为偏置结构。
2. 对心曲柄滑块机构对心曲柄滑块机构同样由曲柄、连杆和滑块组成,不同之处在于曲柄轴和滑块轨迹在同一轴线上,因此称为对心结构。
这种结构在运动形式上与偏置曲柄滑块机构有所不同。
二、工作方式1. 偏置曲柄滑块机构偏置曲柄滑块机构在工作时,曲柄的旋转运动通过连杆传递给滑块,使得滑块做直线往复运动。
由于曲柄轴和滑块轨迹不在同一轴线上,滑块在往复运动过程中会受到一定的偏置影响,因此运动轨迹相对复杂。
2. 对心曲柄滑块机构对心曲柄滑块机构在工作时,曲柄轴和滑块轨迹在同一轴线上,因此滑块在往复运动过程中的轨迹相对简单,运动稳定。
三、性能特点1. 偏置曲柄滑块机构偏置曲柄滑块机构由于其曲柄轴和滑块轨迹不在同一轴线上,因此在运动过程中会受到一定的偏置影响,致使滑块运动不够稳定,因此适用于一些对运动要求不是特别高的场合。
2. 对心曲柄滑块机构对心曲柄滑块机构由于其滑块在往复运动过程中的轨迹相对简单,运动相对稳定,因此适用于对运动精度要求较高的场合。
个人观点和理解从以上对偏置曲柄滑块机构与对心曲柄滑块机构的比较可以看出,两者在结构原理、工作方式和性能特点上存在着明显的差异。
在实际工程设计中,我们需要根据具体的应用场合和要求,选择合适的曲柄滑块机构,以确保其性能和稳定性。
曲柄机构运动速度计算公式

曲柄机构运动速度计算公式
曲柄机构是一种常见的机械传动装置,它可以将旋转运动转换为直线运动,常见于内燃机的曲轴连杆机构、活塞泵等机械装置中。
在工程设计和分析中,计算曲柄机构的运动速度是非常重要的,可以帮助工程师们更好地理解和优化机构的运动特性。
本文将介绍曲柄机构运动速度的计算公式及其应用。
曲柄机构的基本结构包括曲柄、连杆和活塞。
曲柄是一个旋转的杆状零件,连杆连接曲柄和活塞,活塞则在直线轨道上做往复运动。
曲柄机构的运动速度可以通过曲柄的旋转速度和连杆的长度来计算。
下面将介绍曲柄机构运动速度的计算公式及其推导过程。
首先,我们需要了解曲柄机构的基本参数。
假设曲柄的长度为L,曲柄的角速度为ω,连杆的长度为r,活塞的速度为v。
根据几何关系,可以得到曲柄机构的运动速度计算公式如下:
v = ω r。
其中,v表示活塞的速度,ω表示曲柄的角速度,r表示连杆的长度。
这个公式表明,活塞的速度取决于曲柄的角速度和连杆的长度。
如果我们知道了曲柄的角速度和连杆的长度,就可以通过这个公式来计算活塞的速度。
接下来,我们来推导这个公式。
首先,考虑曲柄的运动,根据角速度的定义,曲柄的角速度ω可以表示为曲柄的角位移θ随时间t的变化率,即:ω = dθ / dt。
然后,考。
以曲柄为原动件的对心曲柄滑块机构的行程速比系数

以曲柄为原动件的对心曲柄滑块机构的行程速比系数对心曲柄滑块机构是一种常见的机械运动链,其原动件为曲柄,能够将旋转运动变为直线运动。
行程速比系数是对该机构运动特性的评估指标,它体现了曲柄的旋转行程与滑块的线性行程之间的比值关系。
行程速比系数的大小对于机构的运动性能和工作效率具有重要的影响。
本文将探讨以曲柄为原动件的对心曲柄滑块机构的行程速比系数,并深入剖析其特点和应用场景。
一、对心曲柄滑块机构的基本原理对心曲柄滑块机构由曲柄、连杆和滑块三个部分组成,其中曲柄是原动件,其通过旋转带动连杆以及滑块的运动。
曲柄的旋转行程称为转角,连杆的长度称为连杆长度,滑块的行程称为滑块位移。
对心曲柄滑块机构的运动特点决定了其行程速比系数的数值。
二、行程速比系数的定义和计算公式行程速比系数(Stroke Ratio)定义为曲柄的旋转角度与滑块的行程之间的比值关系,一般用符号Sr表示。
计算公式为:Sr = θ/ s其中,θ为曲柄的旋转角度,s为滑块的行程。
三、行程速比系数的特点1. 行程速比系数的值介于0和1之间。
当Sr为0时,表示滑块没有行程,即曲柄旋转一周,滑块不发生位移;当Sr为1时,表示滑块的行程与曲柄旋转角度相等。
2. 行程速比系数的大小决定了对心曲柄滑块机构的输出速度和力大小。
Sr较小时,滑块的行程较小,但输出速度较快;Sr较大时,滑块的行程较大,输出速度较慢但输出力较大。
3. 行程速比系数对于机构的平滑性和稳定性具有影响。
Sr较大时,曲柄的旋转角度变化较小,滑块的运动比较平稳;Sr较小时,曲柄的旋转角度变化较大,滑块的运动则较不平滑。
四、对心曲柄滑块机构的应用对心曲柄滑块机构广泛应用于各种工程和机械领域。
汽车发动机中的活塞连杆机构、冲压机中的液压裁切机构,以及造纸机中的切纸机构等。
在这些应用中,行程速比系数的选择需要根据具体的需求和工作条件进行。
个人观点和理解:对心曲柄滑块机构作为一种常见的机械运动链,其行程速比系数的选择和设计对于机构的性能和效率具有重要影响。
