静水中船舶大倾角横摇稳性的理论计算方法
船舶稳性核算—核算船舶动稳性

2. 最小倾覆力矩的概念
此时所得到的横倾力矩值称为极限横倾力矩。它表示船舶在 动平衡条件下能够承受的 外 加 横倾力矩的极限值。显然,当 船舶实际受到的外力矩大于横倾力矩的极限值时,船舶动平 衡遭到破坏,船舶就会倾覆,故这个横倾力矩的极限值又称 为最小倾覆力矩,即能使船舶倾覆的最小外力矩,以Mhmin表 示。 它是衡量船舶动稳性的重要指标。 最小倾覆力矩所对应的动倾角称为极限动倾角,以θdmax表示。
船舶的动平衡的条件目录 Nhomakorabea01
动稳性的概念
02 船舶运动过程的分析 03 船舶动平衡的条件与判断
1. 动稳性的概念
在稳性的分类中,我们就讲过按外力矩的性质有静稳性和动 稳性之分,而动稳性就是考虑船舶在倾斜过程中有角加速度 和惯性矩的稳性。
2. 船舶运动过程的分析
设船舶受到的合力矩M合=Mh-MR的作用,即合力矩等于外力矩减稳性 力矩。我们将船舶在合力矩作用下的运动情况进行分析,分一下几个阶段:
3. 船舶最小倾覆力矩的意义
从动稳性的要求考虑,保证船舶不至倾覆的条件是外力矩必 须不大于最小倾覆力矩,即Mh≤ Mhmin。
横倾角度θ 0 θS θd θS 0
外力矩Mh Mh Mh Mh Mh Mh
恢复力矩M 0 Mh 2Mh Mh 0
合力矩M Mh 0 -Mh 0 Mh
角加速度 最大(正) 0 最大(负) 0 最大(正)
角速度 0 最大 0 最大 0
2. 船舶运动过程的分析
1)θ=0时,外力矩最大,此时船舶的角加速度最大,角速度 为零,船舶向外力矩驱动的方向倾斜; 2 ) 在θ=θS时,外力矩等于稳性力矩,此时船舶的角加速度 为零,角速度最大,船舶继续向倾斜方向倾斜,角速度逐渐 减小; 3 ) 在θ=θd时,外力矩小于稳性力矩,此时船舶的角加速度 最大(负值),角速度为零,船舶向倾斜的反方向倾斜(即 回摇)。 4)再经过θS;再经过0;循环的过程。
船舶横摇运动,模型

船舶的横摇运动的数学模型为:e e e Dh N J Dh N J J αααφφφφφφφφ++∆=++∆+ 22)(1)求μ:若干模型试验资料表明,在线性范围内,无舭龙骨的船05.0~035.0=μ;有舭龙骨的船07.0~055.0=μ。
本次建模中取06.0=μ。
(2)求h :船舶初稳性高B h )05.0~04.0(=,规范要求集装箱船h 应大于0.3m ,其他船型可取小些,但也需大于0.15m 。
故:m h 72.01804.0=⨯=,满足规范要求。
(3)有效波倾φK 和重心高度g Z :根据若干客船资料表明,对于船型一般且重心位置适中的船舶,在谐摇附近的规则波中有效波倾系数可近似表示为: d Z K g 60.013.0+=φ式中:g Z 为由基线算起的重心高度;d 为船舶的吃水。
由于这个公式简单且具有一定的准确性,我国海船稳性规范中对一般民用船舶,在计算有效波倾时采用了这个公式。
为了使φK 不过分小又不能大于1,规范中对d Z g 加了附加的条件,即d Z g 的比值超过1.45时取1.45,小于0.917时取0.917. 所以,d Z g 取1,则有m d Z g 61=⨯=,73.060.013.060.013.0=+=+=d Z K gφ 惯性矩xx I :由杜埃尔公式:()g xx z B d D I 22412+= 将D ,B ,g Z 的值代入上式得:()())(10358.264188.91210926.54122722622s m kg z B d D I g xx ⋅⋅⨯=⨯+⨯⨯=+= 无因次衰减系数μ是表征横摇性能的重要参数,μ越大,自由横摇衰减越快,规则波中的频率响应函数就越小,特别对谐摇区的影响最为显著。
根据μ的定义可知: Dh I N xx =μ由上式可知:667106.072.010926.510358.206.0⨯=⨯⨯⨯⨯==Dh I N xx μ 式(2.21)可转化为: )()()(2)(2s s I Dh s s I N s s xxxx δφφφ=++ 令: ωξ22=xxI N 2ω=xxI Dh 则上式化为:)()()(2)(22s s s s s s δφωωξφφ=++进而得:2222)()(ωξωωδφ++=s s s s 将N 和xx I 的值代入式(2-32)、(2-33)得:⎪⎪⎩⎪⎪⎨⎧⨯⨯⨯=⨯⨯⨯=7627610358.272.010926.510358.2106.022ωωξ 解方程得⎩⎨⎧==43.006.0ωξ 综上所述,推导出“长征号”客货船在设计航速为17kn 时的横摇运动数学模型: 18.00516.018.0)()(2++=s s s s δφ。
浙江海洋学院船舶静水力性能及稳性计算

课程设计成果说明书题目:船舶静水力性能及稳性计算学生姓名:学号:学院:船舶与建筑工程学院班级:指导教师:浙江海洋学院教务处2012年 12月 25 日浙江海洋学院课程设计成绩评定表2012 —2013学年第一学期《船舶静力学》课程设计指导书一、设计目的《船舶静力学》是船舶与海洋工程专业的一门重要专业课,在课程中学习船体几何形体的表达方法;学习船舶安全漂浮水面保持一定稳性和浮态的基本原理和计算方法以及抗沉性能的研究。
根据教学大纲要求的重点内容,本课程设计包括两方面内容★:一是运用所学基本方法和知识完成某一条船的静水力性能计算并绘制出静水力曲线图,使学生在了解和掌握基本原理的前提下实践计算流程;二是采用变排水量法计算并完成某一条船的静、动稳性曲线绘制。
通过该课程设计环节达到对课程重点内容的消化和吸收,提高学生的工程技术素养,为后续课程学习和今后从事船舶设计、建造和开发等科研工作打下结实的理论基础。
注★:第一部分内容大部分学生完成,第二部分内容指定学生完成。
1班10,2班12二、内容1、静水力性能计算。
依据提供的船型图纸资料,完成以下设计任务:选取合适方法计算并绘制浮性和稳性曲线包括:(1) 型排水体积曲线(2) 排水量曲线(3) 浮心纵向坐标x B曲线(4) 浮心垂向坐标z B(或KB)曲线(5) 水线面面积Aw曲线(6) 漂心纵向坐标x F曲线(7) 每厘米吃水吨数TPC曲线(8) 横稳心半径BM曲线(9) 纵稳心半径BM L曲线(10) 每厘米纵倾力矩MTC曲线(11) 水线面系数C wP曲线(12) 中横剖面系数C M曲线(13) 方形系数C B曲线(14) 棱形系数C P曲线2、依据提供的船型图纸资料,完成以下设计任务:采用变排水量计算法计算并绘制设计排水量时对应的静、动稳性曲线,计算后得出稳性衡准数K值。
三、要求1.静水力性能采用excel 电子表格计算,静水力曲线图用AUTOCAD在计算机上完成。
船舶静稳性臂介绍及手动计算分析

船舶静稳性臂介绍及手动计算分析摘要:文章介绍了与船舶稳性息息相关的静稳性臂的定义,讲解了静稳性臂曲线的特征,并重点分析了在有一定的文件基础上手动计算静稳性臂并绘制静稳性曲线,进而根据此静稳性曲线来校核船舶的稳性。
标签:稳性回复力臂;静稳性臂;静稳性曲线;横倾角φ;复原力矩;自由液面船舶稳性系指船舶在外力矩(如风、浪等)的作用下发生倾斜,当外力矩消除后能自行恢复到原来平衡位置的能力,其大小取决于排水量、重心和浮心的相对位置等因素。
稳性是确保船舶及各种海上浮体安全航行及作业的主要性能指标之一,船舶稳性研究是船舶业中一个非常重要的课题。
在建造,航行等过程中时刻都应受到各方的关注,船舶在小倾角稳性主要考核的是初稳性GM值,大倾角稳性主要考核的静稳性臂GZ。
文章着重介绍大倾角稳性静稳性臂以及手动计算的方法。
如图1所示,船舶原浮于水线W0L0,在一外力矩的作用下产生一个较大的角度φ,此时浮于水线WφLφ,重心G位置不变,浮心B0移动到Bφ,于是重力Δ与浮力ω▽产生了一个复原力矩MR=Δ*GZ=Δ*L,L=GZ为重力作用线与浮力作用线之间的垂直距离,称为复原力臂或静稳性臂。
对于小倾角时,GZ=GM*sinφ。
对于大倾角时,GZ=B0R-B0E。
图2为一典型静稳性曲线图,横坐标为船舶的横倾角φ,纵坐标为静稳性臂的值L,如果得知一条船舶的静稳性曲线,则可根据此曲线的特征分析此船的稳性特点,并可校核在某一工况下是否有足够的稳性。
根据上图可以得出以下结论:(1)静稳性曲线在原点处的斜率等于初稳性高GM0。
(2)静稳性曲线下的面积等于船舶倾斜后所具有的位能,或者说等于倾斜力矩所做的功。
显然,静稳性曲线的面积越大,船舶的稳性越好。
因此,静稳性曲线下的面积也是表征船舶稳性的一个重要标志。
(3)静稳性曲线上的最高点表示船舶所能承受的最大静倾斜力矩,即船体本身所具有的最大复原力臂,其对应的横倾角为φmax。
(4)复原力矩MR为0即为静稳性曲线与横轴的交点,共有两个交点。
船舶静力学 第四章 大倾角稳性

第四章 大倾角稳性
4-1 概述 4-3 船舶静稳性曲线的等排水量计算法 4-2 船舶静稳性曲线的变排水量计算法 4-4 上层建筑及自由液面对静稳性曲线的影响 4-5 静稳性曲线的特征 4-6 动稳性 4-7 船舶在各种装载情况下的稳性校核计算 4-8 临界初稳性高曲线 4-9 船体几何要素等对稳性的影响及改进稳性的措施 4-10 移动式钻井平台稳性概述
计算得到相应船舶各种装载状态情况下的静稳 性曲线图。具体可列表进行计算:
表4-1 装载情况 排水体积= (m3) 重心高度KG= KG-KS= (m) (m)
横倾角()
l S(取自于横截曲线) sin (KG-KS) sin l = l S- (KG-KS) sin
10
20
30
40
a3
b1 a2 a3
40º 35º 30º
25º 20º 15º 10º
a2 a1 0º
5º
在每一等分角线(5º 、15º 、25º ……)处量取各横 剖面的入水和出水坐标值 a i和 b i 。 对于船形较复杂的船(如有隧道的内河船舶),量 取坐标值 a i和 b i要当心,具体说明如下:
N
+a
M2
则
"
L
2
L
2
0
1 3 b cos - ddx 3
2
Μ Μ 1 M 2
L
L
2
0
水线面WL对NN 轴线的面积惯性矩
1 3 a b 3 cos - ddx 3 (4-10)
1 L2 3 I L a b 3 dx 3 2
静水中船舶大倾角横摇稳性的理论计算方法

一步对其 在 大 风 浪 中 横 摇 运 动 的 非 线 性 进 行 研 究.
1 方法概述
1.1 现有方法综述 由于静水中船舶初稳性的静稳性力臂 lGZ =
ZGMSin! 是根据以下假定得出的[2]: (1)等体积的斜轴通过正浮水线面的漂心; (2)浮 心 移 动 曲 线 是 圆 弧 的 一 段,其 圆 心 为
第 i 个横剖面如图 (1 e)所示 . 本文首先假设 zh 为 已知(对于每个横剖面来说 zh 的值是相同的),纵 倾角!也为已知 . 当船舶发生横倾后,对于此横剖 面来说,图 (1 e)有
T' = T - zh
(3)
其中:每个横剖面在船舶发生纵倾后没有横倾时
的静吃水 T 满足
T = T0 -( L / 20)(11 - i)ta(n !) (4)
对静水中船舶大倾角横摇稳性的特点进行了介绍提出了一种新的计算船舶发生大倾角横摇时的静稳性力臂的计算方法在运用逐步逼近法计算每个横剖面的左右侧的浸深时考虑了在横摇过程中由于船舶首尾不对称造成的纵倾对每个横剖面浸深的影响然后根据重力与浮力平衡纵倾力矩之后为零这两个条件运用matlab数学工具语言的迭代算法求出了纵倾角以及水线面修正层厚度进而绘出了静稳性力臂曲线
精 度 大 小 要 求 来 确 定,则 每 一 等 分 为( dm T')/ I,其中 dm 为船舶的型深 . 把随船运动坐标 系 yOz 的 O 点移到 O' 点,则横倾后的水线在坐标
系 yO'z 中的方程为 z = y·ta(n "). 如图 (1 f),当
zx
=
T'
+
x·
dm
I
T'
时,y( zx)= T' / ta(n "),其中 x 是大于 0 小于 I 的 一个数,从 0 开始计数,依次加 1 . 从型值表中利用
第四章 大倾角稳性

dl B M cos 2 yB sin B M sin 2 z B cos KG cos d 原点处 0, M B0 M 0,z B KB0, 0, 1, B sin cos dl | 0 B0 M 0 KB0 KG GM。 d
dM 1
按
2 l 2
l
dm dx
L
2 l 2
l
l 1 3 1 a cos ddx M 1 l2 a 3 cos ddx 0 2 3 3
1 3 0 3 b cos ddx 2 L '' 1 2 M M 1 M 2 L 0 a 3 b 3 cos ddx 2 3 按照前一章的内容:水线面对NN轴线的面积惯性矩 M2
故M ' 0 OF 0 d 0 KB0 sin C cos
三、楔形(入水、出水)计算
V1 V2
1 2
2 L
L
2
a
0
2
b 2 ddx
V2
1 2
2 l 2
l
0
b 2 ddx
1 的计算
入水楔形取一微体积元d A dV1
Ld BO G cos y B sin (Z B KBO ) cos BO G
dy B dZB dLd BOG sin cos y b cos cos ( Z B KBO ) sin d d d dZ B dy B B M sin B M cos d d
第一篇第4章大倾角稳性

船舶静稳性曲线的变排水量计算法
三、稳性横截曲线 通常,按式( 4 一2)、(4 -4 )和(4 一7 )分别 计算4~5 根水线下不同横倾角时的排水体积▽ φ和ls (见图4 一6 )。然后以
ls为纵坐标,▽ φ为横坐标绘制 如图4 一7 所示对应不同横倾角 φ的ls=f (φ)曲线图,该图 称为稳性横截曲线图。
2 - 13
船舶静稳性曲线的变排水量计算法
沿整个船长 L积分得微楔形对 NN 轴线的体积静矩 整个入水楔形对 NN 轴线的体积静矩 同理,出水楔形对 NN 轴线的体积静矩 则 由于水线面 WφLφ对于NN 轴线的面积惯性矩
2 - 14
船舶静稳性曲线的变排水量计算法
将式(4 一6 )、(4 一8 )和(4一11 )代人式( 4 一 5 ) ,便可求得浮力作用线至 NN 轴线的距离 lφ,再将此 lφ代人式(4 - 7 ) ,即可求得浮力ω▽ φ,至假定重心 S 的距离ls。
2 - 16
船舶静稳性曲线的变排水量计算法
2 - 17
船舶静稳性曲线的变排水量计算法
有了上述稳性横截曲线图,可以根据船舶在各种装载情况 下的排水量及其重心高度,按下式( 4 一12 )可很方便 地求出船舶的静稳性曲线图.
式中ls可以从稳性横截曲线图上查得。 按式(4一12 )计算不同横倾角沪时的静稳性臂 ls,据此 即可绘制船舶在某一排水量时(即某一装载情况下)的静 稳性曲线。
第4章 大倾角稳性
4 一1 概述 4 一2 船舶静稳性曲线的变排水量计算法 4 一3 船舶静稳性曲线的等排水量计算法 4 一4 上层建筑及自由液面对静稳性曲线的影响 4 一5 静稳性曲线的特征 4 一6 动稳性 4 一7 船舶在各种装载情况下的稳性校核计算 4 一8 极限(许用)重心高度曲线 4 一2 -91 船体几何要素等对稳性的影响
船舶静力学大倾角稳性PPT课件

第18页/共31页
一般地增加船宽能有效的改善船舶稳性
问题六:对船舶整体性能而言,初稳性 高越大越好吗?为什么?
19
第19页/共31页
3、横剖面形状对稳性的影响
一般地V型剖面船的稳性比U型剖面船好
20
第20页/共31页
二、重心位置对稳性的影响
问题七:重量的垂向移动对船舶初稳性有什 么影响?
21
1、干舷高度对稳性的影响
问题五:干舷与吃水、型深之间有何关系?
15
第15页/共31页
增加干舷高度的影响:
1)在大倾角时,倾斜水线 面的惯性矩增大,稳性半 径增大,致使形状稳性臂 和静稳性臂也都增大,对 改善大倾角稳性有利。
2)甲板从A升到B,甲板边缘进水角增大,则最 大静倾角增大,消失角也相应增大,使静稳性 曲线下的面积增大,对改善大倾角稳性有利。 3)在干舷甲板A浸水之前,初稳性高度不变。
6
第6页/共31页
1、满足初稳性高度要求的极限重心高度的计算
式中
可根据排水量在船舶静水力曲
线图上查得。
7
第7页/共31页
因此,极限重心高度为:
(问题四:自由液面对船舶稳性的有什么影 响影响?怎样消除其影响?)
8
第8页/共31页
2、满足复原力臂和极限静倾角要求的极限 重心高度的计算
先假定几个重心高度,然后根据重心高度、
四、实际采用的极限重心高度曲线
对于不同的稳性要求,都有其对应的 极限重心高度曲线,实际上采用的极限重 心高度连成曲线应是船舶所需规范稳性要 求的各极限重心高度曲线的下包络线。
4
第4页/共31页
实际极限重心高度曲线的简便形式
5
第5页/共31页
第三章船舶横 摇

三、横摇微分方程解及频率响应函数
2。求解方程: 令其特解: 其中 为横摇角与波倾角的相位差 为波浪频率 将特解代入原方程:
三、横摇微分方程解及频率响应函数
求解方程: 由上可得横摇角:
定义
放大因数:
横摇幅值与有效波倾之比。
相位角:
三、横摇微分方程解及频率响应函数
三、横摇微分方程解及频率响应函数
不同种类船舶的固有周期
二、固有周期
5、横摇固有周期计算
计算横摇周期,主要是计算惯性矩。通常采用 近似公式估算。
0.7<∧θ<1.3
0.7 谐摇区 1.3
∧θ
设计横摇固有周期
海洋的波浪周期是有一定范围的,根据大量的统计资料可知, 波浪周期大于10s以上的比较罕见,短周期波浪出现较多。因此, 在船舶设计中,必须根据船舶航行海区的波浪情况,确定船舶的 固有周期。一般使船舶的固有周期尽量大些好,以避免共振横摇 的发生。大致取 ∧θ=(Tθ / TB )>1.3。
二、横摇受力分析
阻尼是影响船舶横摇最重要的因素,船舶横摇阻 尼与船型、舭龙骨、装载状况、横摇频率和横摇幅 值有关 ,精确地确定阻尼力矩是横摇研究中最困难 的问题。通常根据模型试验得到,在设计初期采用 经验公式估算。
二、横摇受力分析
二、横摇受力分析
3.惯性力矩
4. 波浪扰动力矩
二、横摇受力分析
(理论计算求频响)
船舶线性横摇 2。理论计算法求频率响应函数
其中:
放大因数
有限船宽的修正系数
有限吃水的修正系数 其值由下图查取。
船舶线性横摇
有限吃水的修正系数
船舶在不规则波中的线性横摇 3。可求横摇的位移、速度和加速度方差:
总结:以上是理论方法求频率响应函数和运动响应。
船舶静力学第4章 大倾角稳性(1)

§4-1 概述
一、研究方法 1、仍然是研究船舶倾斜后产生复原力矩以阻 止其倾覆的能力,而且着重研究复原力矩随横 倾角变化的能力; 2、假定船舶处于静水中,水线面为一水平平 面,并且不考虑横倾与纵倾之间的耦合作用。
1
二、关键问题
是确定复原力矩的大 小,而求复原力矩的 关键是确定船舶在横 倾后的浮心位置。有 两种方法: 1、利用倾斜水线计算 横倾后的浮心位置。 2、利用重心移动原理 计算倾斜后浮心位置 的移动距离。
60
横摇角的计算:
根据图形查得
61
62
2、最小风倾力矩(最小风倾力臂)的计算
63
二、初稳性高与静稳性曲线 三、船舶稳性横准的基本思想
稳性曲线只是表示了船舶本身所具有的抵抗 外力矩的能力,或者说,只表示了船舶本身 所具有的稳性能力。 至于船舶受到的力矩究竟有多大,以及是否 经受得住,这要看外力矩的作用情况而定。 外力矩主要来自风浪的作用,而风浪的大小 又与离岸距离以及水域开阔程度有关
式中 为 水线面对 N-N轴的面 积惯性矩 。
18
三、 稳性 插值 曲线
19
四、稳性横截曲线图
20
五、静稳性曲线
计算不同横倾角时的静稳性臂 l,据此可以绘制船舶在某一 排水量(即某一装载情况下) 时的静稳性曲线。
21
§4-3 静稳性曲线的等排水量法
• 一、基本原理 • 首先确定各倾角的等体积倾斜水线,然后分 别计算这些水线下的浮心位置,在计算各倾 角下的复原力臂并绘制该排水量时的静稳性 曲线。 • 二、具体计算方法 • 反复试算,以确定某一倾角下的等体积倾斜 水线。
43
三、静稳性和动稳性曲线的应用
1、动倾角的 确定
第一章船舶在静水中的摇荡 船舶运动学教学课件

Over damped
zo e ( b / 2 a ) t
No-Damping
t
Under damped Critically damped - Under Damped : samll damping, several oscillations - Critically Damped : important level of damping, overshoot once - Overdamped : large damping, no oscillation
四、阻尼系数的确定
2. 横摇的消灭曲线 纵坐标和横坐标的函数关系对应于阻尼力矩 和横摇角速度的函数关系:
船舶在静水中的有阻尼横摇
四、阻尼系数的确定
3. 阻尼系数与消灭系数之间的关系(能量法) 基本思想:在T/2内,幅值改变后势能减小 量等于阻尼消耗的能量。
能量相等
船舶在静水中的有阻力横摇
四、阻尼系数的确定
3. 阻尼系数与消灭系数之间的关系(能量法) 由上述方程可得:
结论:只要知道了消灭系数之后就可以确 定无因次衰减系数。其中消灭系数可以根据船 模试验求得。
船舶在静水中的有阻尼横摇
四、阻尼系数的确定
4. 经验公式(简单介绍) a)
b)
船舶在静水中的有阻尼横摇
四、阻尼系数的确定
4. 经验公式 c)
d)
简谐运动
Simple Harmonic Motion
弹簧-质量-阻尼系统 spring mass
damper
- Equation of motion (Free Oscillation) & Solution
The motion of the system is affected by the magnitude of damping.
第三章船舶横摇.

➢旋涡阻尼:船体弯曲部分附近形成旋涡,损失部分 能量而产生,与角速度平方成比例。
简谐运动 Simple Harmonic Motion
弹簧-质量-阻尼系统
Ship motion Roll
Friction
Eddy
Radiated wave
第三章 船舶横摇
重点:船舶在规则波中的线性横摇,. 难点:考虑非线性影响的共振横摇角计算
船舶横摇
线性横摇
波 横摇
表 浪 方程
观 扰 及解
重 力,
动 力 矩
有
‘放 大因 数概
效
念
波
倾
横摇水动力计算 非线性共
不规则播波
振横摇角 横摇临界状态
谱分析
惯 性 矩
固阻 有尼 周系 期数
一般 非线 性阻 尼共
规 范 横 摇 角
最大有义单元波:波长超过一定范 围的波,它在整个单元波中占有很 小的比例,所有波长大于最大有义 单元波的能量占总能量的5%
λ最大有义 ≈ 60 ζw/3
谐摇状态与临界状态
谱密度曲线的划分
船舶横摇及取决于波浪能量的大小,也取决于 谱密度曲线与放大因数曲线的关系
临界区域
超临界区域
例
第三章 船舶横摇
small GM ; tender ship less stable large period ; good sea keeping quality
二、固有周期
3. 阻尼对周期和振幅的影响(横摇周期) 定义:有阻尼横摇周期
二、固有周期
4、横摇固有周期的特点
两艘相近的船舶,横摇角近似与固有周期的平 方成反比:
船舶稳性知识点讲解(word)资料
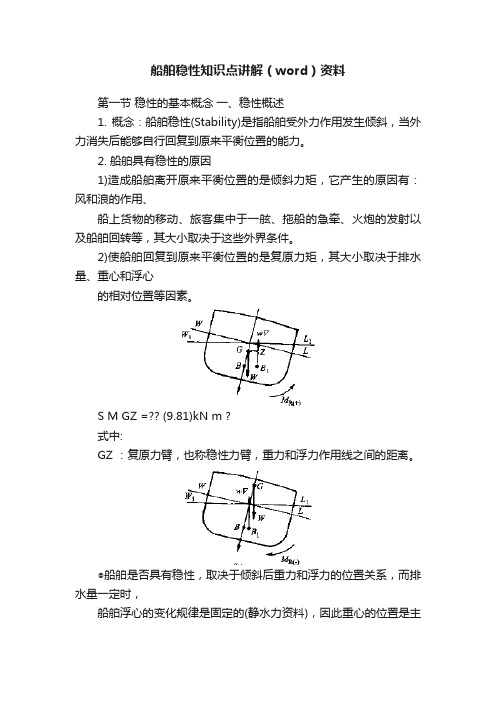
船舶稳性知识点讲解(word)资料第一节稳性的基本概念一、稳性概述1. 概念:船舶稳性(Stability)是指船舶受外力作用发生倾斜,当外力消失后能够自行回复到原来平衡位置的能力。
2. 船舶具有稳性的原因1)造成船舶离开原来平衡位置的是倾斜力矩,它产生的原因有:风和浪的作用、船上货物的移动、旅客集中于一舷、拖船的急牵、火炮的发射以及船舶回转等,其大小取决于这些外界条件。
2)使船舶回复到原来平衡位置的是复原力矩,其大小取决于排水量、重心和浮心的相对位置等因素。
S M GZ =?? (9.81)kN m ?式中:GZ :复原力臂,也称稳性力臂,重力和浮力作用线之间的距离。
◎船舶是否具有稳性,取决于倾斜后重力和浮力的位置关系,而排水量一定时,船舶浮心的变化规律是固定的(静水力资料),因此重心的位置是主观因素。
3. 横稳心(Metacenter)M :船舶微倾前后浮力作用线的交点,其距基线的高度KM 可从船舶资料中查取。
4. 船舶的平衡状态1)稳定平衡:G 在M 之下,倾斜后重力和浮力形成稳性力矩。
2)不稳定平衡:G 在M 之上,倾斜后重力和浮力形成倾覆力矩。
3)随遇平衡:G 与M 重合,倾斜后重力和浮力作用在同一垂线上,不产生力矩。
如下图所示例如:1)圆锥在桌面上的不同放置方法;2)悬挂的圆盘5. 船舶具有稳性的条件:初始状态为稳定平衡,这只是稳性的第一层含义;仅仅具有稳性是不够的,还应有足够大的回复能力,使船舶不致倾覆,这是稳性的另一层含义。
6. 稳性大小和船舶航行的关系1)稳性过大,船舶摇摆剧烈,造成人员不适、航海仪器使用不便、船体结构容易受损、舱内货物容易移位以致危及船舶安全。
2)稳性过小,船舶抗倾覆能力较差,容易出现较大的倾角,回复缓慢,船舶长时间斜置于水面,航行不力。
二、稳性的分类1. 按船舶倾斜方向分为:横稳性、纵稳性2. 按倾角大小分为:初稳性、大倾角稳性3. 按作用力矩的性质分为:静稳性、动稳性4. 按船舱是否进水分为:完整稳性、破舱稳性三、初稳性1. 初稳性假定条件:1)船舶微倾前后水线面的交线过原水线面的漂心F;2)浮心移动轨迹为圆弧段,圆心为定点M(稳心),半径为BM(稳心半径)。
船舶稳性—船舶大倾角静稳性

50 smax
60
70 θ v 80 θ °
静稳性曲线的基本特征
2)曲线上的反曲点 甲板浸水角θim 原点到最高点间的反曲点,θim后GZ增长减缓
3)静稳性曲线上的极值
Maximum Righting Arm (GZmax) 或Maximum Righting moment (Mrmax)
4)稳性消失角 (Capsizing angle )θv 静稳性曲线x横轴交点对应角
θv θf↗
三、静稳性曲线
3.影响静稳性曲线的因素:
2)船宽 B:↗GZmax ↗
θim、θf 、θsmax 、 θv↘
3.影响静稳性曲线的因素
3)重心高度 KG↗
GZ 、θv↘
GZ
KG3 KG2 KG1
KG1>KG2>KG3
θ
3.影响静稳性曲线的因素
4) Δ↗ KN↘ GZ↘ 但MR随Δ↗而增加 5)自由液面Ix:大倾角稳性的Ix随θ的增大而变大 6)初始横倾角θ
Z
G Z0
G0
B1
B0
N
KH
4)自由液面对大倾角稳性修正
复原力臂值减少:δGZ=δGMf sinθ(重量稳性力臂增加)
此法未考虑自由 液G面M对f横倾轴惯性(矩mi变x) 化。
三、静稳性曲线(Curve of Intact Statical Stability or Righting Arm Curve )
Δ一定时:GZ↗MR ↗
L1
W
Z
L
W1
θG
Δ B1
WN
H
K
图 静稳性力臂
二、静稳性力臂的求算 1. GZ表达式 1)基点法: GZ0=KN-KH
第四章大倾角稳性-PPT课件

重心修正后为:
' l' lS KG KS Sin
结论:上层建筑对静稳性曲线的影响是有利的。
注:影响是从一定角度开始的。
二、自由液面对静稳性曲线的影响
船内设有一定数量的燃油舱,淡水舱和压载水舱,具有自由液面,
舱内的液体重心,随船舶倾斜而移动,形成倾斜力矩 。
船舶正浮时,舱内液体的表面为ab,重心位于g。横倾φ 时,舱
1 L 3 3 2 I a b dx L 3 2
' ' M I cos d 0
四、稳性横截曲线
§4-3 静稳性曲线的等排水量计算法
一、基本计算公式
L GZ B R B E y cos Z KB sin B G si 0 0 B B 0 0
l 2 l 2
0
2 a d dx
' ' ( 2 ) M 的计算式
2 13 入水楔形 dm dA a cos a cos d 3 3
l 1 1 3 2 dM dm dx a cos d dx M a d d 1 l 0 cos 23 3 l 2 1 l 2 l 23 l 2
2 V' 1 Adx 2 2 M 1 m dx 2 1 1
。
设上层建筑入水部分的 横剖面面积为 A ,面积形心在 g处。
其中 l为上层建筑长度
' ls l C cos d KS Sin s 0
考虑上层建筑以后的浮 力作用线到假定重心 S 的距离
船舶最大横倾角的计算公式

船舶最大横倾角的计算公式
船舶的横倾角是指船体横向倾斜的角度,通常以船体的相对水平面为
参考。
计算船舶最大横倾角的公式有多种,下面将介绍两种常用的计算方法。
1.稳性曲线法(初步稳性计算法):
通过船舶的稳性曲线来计算最大横倾角。
稳性曲线是由船舶的形体参
数(如船长、船宽、船型等)、重心高度和抗倾力矩(饱和、部分载货等)等数据计算得出的曲线。
首先,需要计算船舶在不同仰角下的抗倾力矩,并绘制稳性曲线。
然后,选择最大的正常稳定角(通常为大于0度小于30度)所对应的仰角,即为船舶的最大横倾角。
2.回归法(回归分析法):
通过船舶的浮态试验数据来计算最大横倾角。
首先,需要进行浮态试验,记录船舶在不同横倾角下的浮力、配重和抗倾力矩等数据。
然后,将试验数据进行回归分析,建立船舶横倾角与浮力、配重和抗
倾力矩之间的数学模型。
利用该数学模型,可以计算出船舶在不同条件下
的最大横倾角。
需要注意的是,船舶最大横倾角的计算具有很高的复杂性,需要考虑
船舶的结构设计、货物分布和海况等因素。
所以,实际应用中,常常借助
计算机模拟或专业软件来进行计算和分析。
舰艇生命力_第5讲 舰船的大角稳性

课堂提问
5、 h 的计算方法有哪些? 1) 2)己知 T 查静水力曲线 →Zc, r, R →计算Zg →h, H; 3)用τ估算。
Ix r V
CB h
2
课堂提问
6、扶正力矩 m 的定义及组成 当舰船自平衡位置作无限小等容倾 斜时,重力与浮力构成的力矩叫扶正力 矩。 m=Phsinθ =Prsinθ - Pasinθ Prsinθ:船形稳度力矩,取决于船形,扶 正舰船。 Pasinθ:重量稳度力矩,取决于重心高度, 使船倾斜。
M
M
M
M(t)
0 (a)
t
0 (b)
t
0 (c)
t
瞬时
变值
图2-5-7
不变
①动倾力矩作用下的舰船运动
1
m 产生横倾角加速度ε,随着 m 当 时, kpD θ↑→角速度ω↑。 当 时, m ,将继续倾 kpD m ,ε=0,ω=ω 斜(惯性作用)。 当1 时,m ε<0,随 kpD m,产生负角加速度 着θ↑→角速度ω↓ m 当 时,ω=0, kpD m ,由于负加速度仍然 存在,舰船的倾斜将作回复运动。
mθ
l
h m—M < 0
θ
m
A
θ
A
θ 57.3
m
θ
V
m 30 ~ 45
θ
v 60 ~ 90
第五节 大角稳性
二、静稳度曲线及其特性
(1)几何特性:
②静稳度曲线在原点处切线的斜率,等于舰船在θ=0平衡 位置的稳定中心高h:
dl h cos 0 h d 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其中:L 为船长;Dg 为船舶质量;OG 即为船舶重 心在随船坐标系中的垂向位置 zG;# 为水的密度; g 为重力加速度 . 右式中第一项为环绕船体固定 坐标系原点 O 的形状复原力矩,它是绕船体周围 的水压力而引起的;第二项是由于船舶重量引起 的复原力矩,称为质量复原力矩 . 求解式(1)的关 键是求横剖面面积 A( x)和横剖面的中心在惯性
y z 中y 轴和z 轴方向的坐标值的计算可以像下文
所论述的那样来求解 . 在这 20 等份中取第 i 等份
内插法同样可以计算出 6( zx)的大小 . 紧接着计 算 6( zx)与 y( zx)的差,若其差值小于一个很小的 数,比如说 0 . 001,如若是,则此时的 x ·( dm T')/ I 即是需要求解的 zS 的大小;如若不成立,则 继续运 用 逐 步 逼 近 计 算 方 法 计 算 直 到 y( zx)-
" 收稿日期:2003-10-03. 基金项目:交通部跨世纪人才基金资助项目(95050531). 作者简介:李子富(1973-),男,四川大竹人,硕士研究生 .
10
大连海事大学学报
第 30 卷
性,而是以稳性力臂值 lGZ 直接反映船舶大倾角 稳性,大倾角稳性的大小仍然取决于恢复力矩 M 的大小[3]即 M = Dg· lGZ . 因此,计算 lGZ 值的大 小是关键 . 过去计算大横倾角稳性力臂值 lGZ 的 方法有:A·H·克雷洛夫方法、积分曲线法和求积 仪法[4],以及造船部门所用的假定重心法 . A·H· 克雷洛夫方法要求首先在透明蜡纸上画出船舶计 算水线的格子线和垂直格子线的垂线,然后,再沿 每一水线量取每个横剖面的入水纵坐标和出水纵 坐标的方法来计算;求积仪法也是要用到具体的 仪器才能进行计算,这些方法在当时科技不发达 的时代是适用的,它们都要借助一定的仪器或利 用作图法来求解,并且没有考虑在横摇过程当中 由于船舶首尾不对称造成的纵倾;假定重心法是 在已知 KN 曲线的基础上,根据船舶装载状态下 的排水体积查出此状态的 KN 值,然后,再根据此 装载状态的重心位置求出静稳性力臂值,此方法 对于船舶操纵来说是一种不错的方法,但是,这种 方法在开发六自由度的船舶操纵模拟器以及后续 讨论波浪中船舶的大倾角横摇稳性方面就显得不 那么适用了 . 本文提出新的计算方法可以在已知 船舶型线图以及船舶参数和装载情况下利用计算 机快速地计算出静稳性力臂,并且不用绘制等容 积水线或者作图 . 1.2 新的计算方法
由于船舶横摇运动是非对称运动,船舶的左 右吃水并不相同,所以不能再以简单的吃水来衡 量,由此引入一个概念 ——— 浸深 . 设 A( x)为船舶 瞬时横截面的浸水面积,A( x)与船舶的状态有 关[5],如图 (1 a)所示 . 设横倾水线与船型交点为 zp 和 zS,本文中称之为船舶左舷和右舷的浸深,它 们是纵倾角!、横摇角" 和瞬时吃水 T' 的函数 . 在 zp 和 zS 以及船舶姿态参数!、"和瞬时吃水 T' 已知 的情况下,复原力矩由下式提供:
图 l 船舶不同横倾角时的横剖面状态及其求解示意图
然而,在 求 解 zp 时 首 先 判 断 的 是 关 系 式:
T' / ta(n !)> 6(0)是否成立,其中 6(0)表示吃水 为 0 时的横剖面半宽,如果成立就利用图 (l a)或
的方法求得用 zh 和# 表 示 的 zp 和 zS,进 而 求 出 A( x),接着把 A( x)带入式(3). 然后运用 Matiab 中的 fSOive 函数迭代求解所编的 m 函数,这样就
关系式 T' / ta(n !)> 6(0)不成立时,再判断 zh 是 否大于 T,如若不大于则 zp 就等于 T[如图 (l c)所 示],反之则利用图 (l c)进行求解,对于这种情
况,首先是把 zh 分成 I 等分,在利用逐步逼近法求 解 zp 时,要注意:在坐标系 y 'z 中,当 z ! zh - T 时,T' ! 0,此时水线面半宽始终为零 . 求得 zp 和 zS 这两 个 值 以 后 就 可 以 把 它 们 带 入 式(2)求 出
初稳心 M,半径为初稳心半径 rBM; 然而,大倾角稳性是指船舶横倾角超过 10
~ 15 时的稳性,当横倾角增大时两浮力作用线 并不交在定点 M 上,而是离 M 点较远,并且船舶 横倾前后两水线面对于横倾轴的惯性矩数值发生 了变化,稳心半径也发生了变化,不同横倾角时横 稳心点 M 不再是固定不变的,这是由于水线上下 两部分船体形状所决定的 . 因此大倾角横倾时就 不能再运用小倾角横倾时的计算方法来计算了, 并且也不能用初稳性高度 ZGM 值来表示大倾角稳
文章编号:1006-773(6 2004)01-0009-05
静水中船舶大倾角横摇稳性的理论计算方法"
李子富,杨盐生,杜嘉立
(大连海事大学 航海学院,辽宁 大连 116026)
摘要:对静水中船舶大倾角横摇稳性的特点进行了介绍,提出了一种新的计算船舶发生大倾角横摇时的静
稳性力臂的计算方法,在运用逐步逼近法计算每个横剖面的左右侧的浸深时,考虑了在横摇过程中由于船舶 首尾不对称造成的纵倾对每个横剖面浸深的影响,然后,根据重力与浮力平衡、纵倾力矩之后为零这两个条 件,运用 Matlab 数学工具语言的迭代算法求出了纵倾角,以及水线面修正层厚度,进而绘出了静稳性力臂曲 线 . 最后,通过实例计算与分析验证了本文提出的方法是可行的 .
图 (l b)进行计算,否则用图 (l c)或图 (l c)进行 计算 . 在用图 (l a)或图 (l b)计算 zp 时,把 T' 分成 I 等分,其计算方法与上文论述的求解 zS 的过程 一样 . 在利用图 (l c)或图 (l c)进行计算时,如果 倾斜水线面与横剖面的左侧没有交点而是与横剖
变换的关系为:
y'B( x) = yB( x)cOS! - zB( x)Sin! (6) 由此可知为了能够求得 y'B(x)的值就要求出 yB(x) 和 zB( x)的值 . 为了能够求出 yB( x)和 zB( x)的值,如 图 (l f)所示,对于任意一横剖面,利用上文所述
的方法可以求得 zp 和 zS 的值,先利用梯形法则求
出吃水为 T' - zp 时的面积,设其为 A',这部分的
面积中心在坐标系 y z 中的坐标值为(0,- zp -
l( 2
T'
-
zp )-
zh),根据这两个的值将
zp 和 zS
之间
所夹横剖面部分分成 20 等分,则每一等分 z 轴方
向上的高度为( zp + zS)/ 20;当然也可以分成大于 20 等分,则 每 一 等 份 的 中 心 在 随 船 运 动 坐 标 系
(1 a)可以作为式(2)的图解,但是当横倾角较大
时应考虑图 (1 b)、图 (1 c)和图 (1 c)等三种情况 .
要解式(2)就必须求出 zp 和zS 的值,只要求出了 zp 和 zS 的解,y'B(x)的解也可以求出 .
在具体求解 A( x)时,按照通常做法把船体
分为 21 站位,每个站位对应着一个横剖面,其中
A( x)的值 . 因为横倾的船舶在静水中时,满足作
用在船体 浸 水 部 分 的 浮 力 和 船 体 的 质 量 必 须 平
衡,纵倾力矩必须为零 . 即满足
"
-
"g
xfA( x)c x
xa
+
Dg
=
0
"
xfxA( x)c x
xa
=
0
(5)
运用 Matiab 数学工具语言编一个 m 函数,这
第l期
李子富,等:静水中船舶大倾角横摇稳性的理论计算方法
ll
6( zx)小于既定的一个很小的数 . 当关系式 ! < arcta[n( dm - T')/ (6 dm)]不 成 立 时,利 用 图
(l a)、图 (l c)或图 (l c)计算 zS 时,从图上可以看 出无论是利用这三个图中的哪一个图来求解,都 可以用等式:zS = dm - T' 来求解 zS .
其中:T0 为没有发生纵倾和横倾时的平吃水 . 从 型值表中利用内插法可以计算出瞬时吃水为 T'
的水 线 面 半 宽 6( T'). 然 后 判 断 关 系 式 " < arcta[n( dm - T')/ 6( dm)]是否成立,如若成立则
用图 (1 a)来求解 zS,如若不成立则用图 (1 b)、图 (1 c)或图 (1 c)来求解,利用图 (1 a)求解 zS 时,把 dm - T' 分成 I 等分,I 的大小视所需求解的 zS 的
第 i 个横剖面如图 (1 e)所示 . 本文首先假设 zh 为 已知(对于每个横剖面来说 zh 的值是相同的),纵 倾角!也为已知 . 当船舶发生横倾后,对于此横剖 面来说,图 (1 e)有
T' = T - zh
(3)
其中:每个横剖面在船舶发生纵倾后没有横倾时
的静吃水 T 满足
T = T0 -( L / 20)(11 - i)ta(n !) (4)
坐标系下的坐标 y'B(x),其中 A( x)可以用下式来 计算[6]:
T
0
0
! ! ! A( x)= 26( z)cz + 6( z)cz + 6( z)cz +
0
zp
zS
(2 zS)]tan"
(2)
其中:6( z)是水线半宽,T 为考虑纵倾而没有考
虑横倾时的每个横截面的静吃水 . 一般情况下图
