热力学作业答案
热力学习题与答案(原件)

材料热力学习题1、阐述焓H 、内能U 、自由能F 以及吉布斯自由能G 之间的关系,并推导麦克斯韦方程之一:T P PST V )()(∂∂-=∂∂。
答: H=U+PV F=U-TS G=H-TS U=Q+W dU=δQ+δWdS=δQ/T, δW=-PdV dU=TdS-PdVdH=dU+PdV+VdP=TdS+VdP dG=VdP-SdTdG 是全微分,因此有:TP P TP ST V ,PT G T P G ,T V P G T P T G P ST G P T P G )()()()()()(2222∂∂-=∂∂∂∂∂=∂∂∂∂∂=∂∂∂∂=∂∂∂∂∂-=∂∂∂∂=∂∂∂因此有又而2、论述: 试绘出由吉布斯自由能—成分曲线建立匀晶相图的过程示意图,并加以说明。
(假设两固相具有相同的晶体结构)。
由吉布斯自由能曲线建立匀晶相图如上所示,在高温T 1时,对于所有成分,液相的自由能都是最低;在温度T 2时,α和L 两相的自由能曲线有公切线,切点成分为x1和x2,由温度T 2线和两个切点成分在相图上可以确定一个液相线点和一个固相线点。
根据不同温度下自由能成分曲线,可以确定多个液相线点和固相线点,这些点连接起来就成为了液相线和固相线。
在低温T 3,固相α的自由能总是比液相L 的低,因此意味着此时相图上进入了固相区间。
HPV UGTSTS FPV3、论述:通过吉布斯自由能成分曲线阐述脱溶分解中由母相析出第二相的过程。
第二相析出:从过饱和固溶体α中(x0)析出另一种结构的β相(xβ),母相的浓度变为xα. 即:α→β+ α1α→β+ α1 的相变驱动力ΔGm的计算为ΔGm=Gm(D)-Gm(C),即图b中的CD段。
图b中EF是指在母相中出现较大为xβ的成分起伏时,由母相α析出第二相的驱动力。
4、根据Boltzman方程S=kLnW,计算高熵合金FeCoNiCuCrAl和FeCoNiCuCrAlTi0.1(即FeCoNiCuCrAl各为1mol,Ti为0.1mol)的摩尔组态熵。
热力学习题(答案)

一、9选择题(共21分,每题3分)1、1.1mol理想气体从p-V图上初态a分别经历如图所示的(1)或(2)过程到达末态b.已知Ta<Tb,则这两过程中气体吸收的热量Q1和Q2的关系是[ A ](A) Q1>Q2>0; (B) Q2>Q1>0;(C) Q2<Q1<0; (D) Q1<Q2<0;(E) Q1=Q2>0.2、图(a),(b),(c)各表示连接在一起的两个循环过程,其中(c)图是两个半径相等的圆构成的两个循环过程, 图(a)和(b)则为半径不相等的两个圆.那么:[ C ](A) 图(a)总净功为负,图(b)总净功为正,图(c)总净功为零;(B) 图(a)总净功为负,图(b)总净功为负,图(c)总净功为正;(C) 图(a)总净功为负,图(b)总净功为负,图(c)总净功为零;(D) 图(a)总净功为正,图(b)总净功为正,图(c)总净功为负.3、如果卡诺热机的循环曲线所包围的面积从图中的abcda增大为ab’c’da,那么循环abcda与ab’c’da所做的净功和热机效率变化情况是:(A)净功增大,效率提高; [ D ](B)净功增大,效率降低;(C) 净功和效率都不变;(D) 净功增大,效率不变.4、一定量的理想气体分别由图中初态a经①过程ab和由初态a’经②过程初态a’cb到达相同的终态b, 如图所示,则两个过程中气体从外界吸收的热量Q1,Q2的关系为[ B ](A) Q1<0,Q1>Q2 ; (B) Q1>0, Q1>Q2 ;(C) Q1<0,Q1<Q2 ; (D) Q1>0, Q1<Q2 .5、根据热力学第二定律可知: [ D ](A) 功可以全部转换为热,但热不能全部转换为功;(B) 热可以从高温物体传到低温物体,但不能从低温物体传到高温物体;(C) 不可逆过程就是不能向相反方向进行的过程;(D) 一切自发过程都是不可逆的.6、对于理想气体来说,在下列过程中,哪个过程系统所吸收的热量、能的增量和对外做的功三者均为负值? [ D ](A) 等容降压过程; (B) 等温膨胀过程; (C) 绝热膨胀过程; (D) 等压压缩过程.7、在下列各种说法中,哪些是正确的? [ B ](1) 热平衡过程就是无摩擦的、平衡力作用的过程.(2) 热平衡过程一定是可逆过程.(3) 热平衡过程是无限多个连续变化的平衡态的连接.(4) 热平衡过程在p-V 图上可用一连续曲线表示. (A) (1),(2); (B) (3),(4); (C) (2),(3),(4); (D) (1),(2),(3),(4).8、对于室温下的双原子分子理想气体,在等压膨胀的情况下,系统对外所做的功与从外界吸收的热量之比A/Q 等于: [ D ] (A) 1/3; (B) 1/4; (C) 2/5; (D) 2/7.9、在温度分别为 327℃和27℃的高温热源和低温热源之间工作的热机,理论上的最大效率为 [ B ] (A) 25% (B) 50% (C) 75% (D) 91.74%10、一定量的理想气体,从p -V 图上初态a 经历(1)或(2)过程到达末态b ,已知a 、b 两态处于同一条绝热线上(图中虚线是绝热线),则气体在 [ B ](A) (1)过程中吸热,(2) 过程中放热. (B) (1)过程中放热,(2) 过程中吸热. (C) 两种过程中都吸热. (D) 两种过程中都放热.二、填空题pV1、有1mol刚性双原子分子理想气体,在等压膨胀过程中对外做功A,则其温度变化ΔT=___ A/R ___;从外界吸收的热量Q p=__7A/2 ___.2、一个作可逆卡诺循环的热机,其效率为η,它的逆过程的致冷机致冷系数w = T2/(T1-T2),则η与w的关系为_____11Wη=-_____.3.一热机由温度为727℃的高温热源吸热,向温度为527℃的低温热源放热.若热机在最大效率下工作,且每一循环吸热2000J,则此热机每一循环做功__400________J. 4.热力学第二定律的克劳修斯叙述是_热量不能自动地从低温物体传向高温物体开尔文叙述是_不可能把从单一热源吸收的热量在循环过程中全部转变为有用的功,而不引起任何其他物体为生变化_________________________.5、下面给出理想气体状态方程的几种微分形式,指出它们各表示什么过程.(1)pdV=(m/M)RdT表示___等压_________过程;(2)Vdp=(m/M)RdT表示_____等体_________过程;(3)pdV+Vdp=0表示_______等温_______过程.6、如图,温度为T0,2T0,3T0三条等温线与两条绝热线围成三个卡诺循环:(1)abcda;(2)dcefd;(3)abefa,则其效率分别为:η1=___33.3%___;η2=___50% ___;η3=____ 66.7%___.7. 理想气体在如图所示a-b-c 过程中,系统的能增量E =___0__8.已知一定量的理想气体经历p -T 图上所示的循环过程,图中过程1-2中,气体___吸热__(填吸热或放热)。
【精品】热力学作业题答案

【关键字】精品第二章2-1.使用下述方法计算1kmol 甲烷贮存在体积为0.1246m 3、温度为50℃的容器中产生的压力:(1)理想气体方程;(2)R-K 方程;(3)普遍化关系式。
解:甲烷的摩尔体积V =0.1246 m 3/1kmol=124.6 cm 3/mol查附录二得甲烷的临界参数:T c =190.6K P c =4.600MPa V c =99 cm 3/mol ω=0.008 (1) 理想气体方程P=RT/V=8.314×323.15/124.6×10-6=21.56MPa(2) R-K 方程 ∴()0.5RT aPV b T V V b =--+=19.04MPa (3) 普遍化关系式323.15190.6 1.695r c T T T === 124.6 1.259r c V V V ===<2∴利用普压法计算,01Z Z Z ω=+∵ c r ZRTP P P V == ∴c r PV Z P RT =迭代:令Z 0=1→P r0=4.687 又Tr=1.695,查附录三得:Z 0=0.8938 Z 1=0.462301Z Z Z ω=+=0.8938+0.008×0.4623=0.8975此时,P=P c P r =4.6×4.687=21.56MPa同理,取Z 1=0.8975 依上述过程计算,直至计算出的相邻的两个Z 值相差很小,迭代结束,得Z 和P 的值。
∴ P=19.22MPa2-4.将压力为2.03MPa 、温度为477K 条件下的2.83m 3NH 3压缩到0.142 m 3,若压缩后温度448.6K ,则其压力为若干?分别用下述方法计算:(1)Vander Waals 方程;(2)Redlich-Kwang 方程;(3)Peng-Robinson 方程;(4)普遍化关系式。
解:查附录二得NH 3的临界参数:T c =405.6K P c =11.28MPa V c =72.5 cm 3/mol ω=0.250 (1) 求取气体的摩尔体积对于状态Ⅰ:P=2.03 MPa 、T=447K 、V=2.83 m 3477405.6 1.176r c T T T === 2.0311.280.18r c P P P ===—普维法∴01.6 1.60.4220.4220.0830.0830.24261.176r BT =-=-=- 11c r c rBP PV BP P Z RT RT RT T =+==+→V=1.885×10-3m 3/mol∴n=2.83m 3/1.885×10-3m 3/mol=1501mol对于状态Ⅱ:摩尔体积V=0.142 m 3/1501mol=9.458×10-5m 3/mol T=448.6K (2) Vander Waals 方程 (3) Redlich-Kwang 方程 (4) Peng-Robinson 方程 ∵448.6405.6 1.106r c T T === ∴220.3746 1.542260.269920.3746 1.542260.250.269920.250.7433k ωω=+-=+⨯-⨯=∴()()()a T RTPV b V V b b V b =--++- (5) 普遍化关系式 ∵559.458107.2510 1.305r c V V V --==⨯⨯=<2 适用普压法,迭代进行计算,方法同1-1(3)2-7:答案: 3cm第三章3-3. 试求算1kmol 氮气在压力为10.13MPa 、温度为773K 下的内能、焓、熵、V C 、p C 和自由焓之值。
第一章热力学的基本规律课后作业及答案

第一章 热力学的基本规律1.1 试求理想气体的体胀系数α,压强系数β和等温压缩系数κT 。
解:已知理想气体的物态方程为nRT pV = 由此得到 体胀系数TpV nR T V V p 11==⎪⎭⎫ ⎝⎛∂∂=α, 压强系数TpV nR T P P V 11==⎪⎭⎫ ⎝⎛∂∂=β 等温压缩系数2111()T T V nRT V p V p pκ⎛⎫∂⎛⎫=-=-= ⎪ ⎪∂⎝⎭⎝⎭ 1.2试证明任何一种具有两个独立参量,T p 的物质,其物态方程可由实验测得的体胀系数α及等温压缩系数T k ,根据下述积分求得:ln (d d )T V T k p α=-⎰如果1Tα=,1T k p =,试求物态方程。
解 以,T p 为自变量,物质的物态方程为(,)V V T p =其全微分为d d d p TV V V T p T p ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭ (1) 全式除以V ,有d 11d d p TV V V T p V V T V p ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭根据体胀系数α和等温压缩系数T k 的定义,可将上式改写为d d d T VT k p Vα=- (2) 有ln (d d )T V T k p α=-⎰ (3)若1Tα=,1T k p =,式(3)可表示为11ln (d d )V T p T p=-⎰ (4)积分pV CT = (5)1.3测得一块铜块的体胀系数和等温压缩系数分别为514.8510K α--=⨯和71n 7.8*10p T κ--=,α和T κ可近似看作常量,今使铜块加热至10C ︒。
问(1压强要增加多少才能使铜块体积不变?(2若压强增加,铜块的体积改多少解:(1)有d d d T Vp p p V T V T ∂∂⎛⎫⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭知,当d 0V =时,有d 0d d d V Tp p T p T T T αβκ∂⎛⎫=+==⎪∂⎝⎭ 故 ()212121d T T TT p p T T T αακκ-==-⎰即 ()2121n 622p T p p p T T ακ∆=-=-= 分别设为V xp n ∆;,由定义得:4474.85810; 4.85101007.810T x V κ∆---=⨯=⨯-⨯⨯所以,44.0710V ∆-=⨯1.4 1mol 理想气体,在27C ︒的恒温下发生膨胀,其压强由n 20p 准静态地降到n 1p ,求气体所做的功和所吸取的热量。
北航工程热力学 作业答案参考

作业:思考题1-5,1-7;习题1-6。
S 1-5:何为平衡状态?平衡状态和均匀状态是否同一概念?平衡必须满足什么条件?系统不受外界影响的条件下,如果各部分的宏观状态参数不随时间变化,系统处于平衡状态。
平衡状态和均匀状态不是同一概念。
平衡状态强调不受外界影响+状态参数不随时间变化;均匀状态强调的是状态参数不随空间变化,空间分布均匀。
举例:封闭刚性容器内的水和水蒸汽混合物,处于平衡状态,但不处于均匀状态。
平衡条件:力平衡、温度平衡、化学平衡-无势差。
注意:要讲清楚二者的区别,而不是简单的判断和给出定义描述。
S 1-7:可逆过程与平衡过程(内平衡过程)有何区别?造成不可逆的因素有哪些?可逆过程一定是平衡过程,平衡过程不一定是可逆过程;无耗散(无摩擦)的平衡过程是可逆过程。
造成不可逆的因素:胀缩时有力不平衡、传热有温差,运动有摩擦。
注意:要讲清楚二者的区别,而不是简单的判断和给出定义描述。
X 1-6: 解:1760 1.03323 1.01325atm mmHg at bar === 19.829.82/1.033239.504p at atm atm === 2 4.24 4.24/1.01325 4.185p bar atm atm ===745745/7600.98B mmHg atm atm === 19.5040.9810.484A p p B atm =+=+= 2B A p p p +=210.484 4.185 6.299B A p p p atm =-=-= 注意:2B p p B =+是错误的;“真空度”:v p B p =-,B 一般特指地面标准大气压,1B atm =,所以1v p atm <。
S2-5:功是过程量,而推挤功pv 却只取决于状态,怎么理解?热力学力里的功是广义功,体系作功的大小与过程经历的路径和条件有关,不同的过程即使起止状态相同,做功大小也不同,因此,功是过程量。
热力学作业题答案复习课程

热力学作业题答案第二章2-1.使用下述方法计算1kmol 甲烷贮存在体积为0.1246m 3、温度为50℃的容器中产生的压力:(1)理想气体方程;(2)R-K 方程;(3)普遍化关系式。
解:甲烷的摩尔体积V =0.1246 m 3/1kmol=124.6 cm 3/mol查附录二得甲烷的临界参数:T c =190.6K P c =4.600MPa V c =99 cm 3/mol ω=0.008 (1) 理想气体方程P=RT/V=8.314×323.15/124.6×10-6=21.56MPa(2) R-K 方程2 2.52 2.560.5268.314190.60.427480.42748 3.2224.610c c R T a Pa m K mol P -⨯===⋅⋅⋅⨯ 53168.314190.60.086640.08664 2.985104.610c c RT b m mol P --⨯===⨯⋅⨯ ∴()0.5RT a P V b T V V b =--+()()50.5558.314323.15 3.22212.46 2.98510323.1512.461012.46 2.98510---⨯=--⨯⨯⨯+⨯=19.04MPa (3) 普遍化关系式 323.15190.6 1.695rc T T T === 124.6 1.259r c V V V ===<2∴利用普压法计算,01Z Z Z ω=+∵ c r ZRTPP P V == ∴ c r PVZ P RT=654.61012.46100.21338.314323.15cr r r PV Z P P P RT -⨯⨯⨯===⨯ 迭代:令Z 0=1→P r0=4.687 又Tr=1.695,查附录三得:Z 0=0.8938 Z 1=0.4623 01ZZ Z ω=+=0.8938+0.008×0.4623=0.8975此时,P=P c P r =4.6×4.687=21.56MPa同理,取Z 1=0.8975 依上述过程计算,直至计算出的相邻的两个Z 值相差很小,迭代结束,得Z 和P 的值。
中国石油大学远程教育化工热力学作业答案

化学热力学高升专答案第一次作业第 1 题水处于饱和蒸气状态,其自由度为您的答案:A题目分数:0.5此题得分:0.5批注:第 2 题如要查询水的饱和蒸气热力学性质表,则需要个独立状态参数的已知条件。
您的答案:A题目分数:0.5此题得分:0.5批注:第3题经历一个不可逆循环过程,体系工质的熵C您的答案:题目分数:0.5此题得分:0.5批注:第4题范德华方程与R- K方程均是常见的立方型方程,对于摩尔体积V 存在三个实根或者一个实根,当存在三个实根时,最大的V值是您的答案:B题目分数:0.5此题得分:0.5批注:第5题可以通过测量直接得到数值的状态参数是C您的答案:题目分数:0.5此题得分:0.5批注:第 6 题处于平衡的气体的摩尔体积vg 和液体的摩尔体积vL 的关系为您的答案:A题目分数:0.5批注:第7 题随着温度的增加,处于平衡的气体的摩尔体积vg和液体的摩尔体积vL的变化规律为您的答案:A题目分数:0.5此题得分:0.5批注:第8题您的答案:处于临界点的平衡的气体和液体B题目分数:0.5此题得分:0.5批注:第9题您的答案:超临界流体是下列条件下存在的物质A题目分数:0.5此题得分:0.5批注:第10 题对应态原理认为,在相同的对比态下,所有物质表现出相同的性质。
即您的答案:D题目分数:0.5此题得分:0.5批注:第11 题关于建立状态方程的作用,以下叙述不正确的是您的答案:C题目分数:0.5此题得分:0.5批注:第12 题纯流体在一定温度下,如压力低于该温度下的饱和蒸汽压,则此物质的状态为您的答案:D题目分数:0.5批注:第13 题利用麦克斯韦关系式,其目的是将难测的()与易测的()联系起来。
您的答案:C题目分数:0.5此题得分:0.5批注:第14 题真实气体在的条件下,其行为与理想气体相近。
您的答案:D题目分数:0.5此题得分:0.5批注:第15 题水的三相点的自由度数目为您的答案:A题目分数:0.5此题得分:0.5批注:第16 题二元系统气液平衡的自由度为2您的答案:错误题目分数:0.5此题得分:0.5批注:第17 题理想气体的熵仅仅是温度的函数您的答案:错误题目分数:0.5此题得分:0.5批注:第18 题某工质在封闭系统进行不可逆循环后,其熵必定增加您的答案:错误题目分数:0.5批注:第19 题理想气体经可逆绝热膨胀后,温度不变您的答案:错误题目分数:0.5 此题得分:0.5 批注:第20 题恒沸点和临界点时的气体和液体都是平衡的,而且两相的组成是相同的,其它的性质也相同您的答案:错误题目分数:0.5 此题得分:0.5 批注:第21题气体混合物的virial系数,如B, C…,只是温度和组分的物性的函数您的答案:错误题目分数:0.5 此题得分:0.5 批注:第22 题纯物质的三相点随着温度或压力的不同而改变您的答案:错误题目分数:0.5 此题得分:0.5 批注:第23题对于纯物质,当P> PC T> TC时,物质以液态存在您的答案:错误题目分数:0.5 此题得分:0.5 批注:第24题当压力大于临界压力时,纯物质就以液态存在您的答案:错误题目分数:0.5此题得分:0.5批注:第25 题温度和压力相同的两种理想气体(纯物质)等温等压混合后,则总体积为原来两气体体积之和,总熵为原来两气体熵之和您的答案:错误题目分数:0.5此题得分:0.5批注:第26 题由于分子间相互作用力的存在,实际气体的体积一定小于同温、同压下理想气体的体积,所以理想气体的压缩因子Z=1,实际气体的压缩因子Z< 1 您的答案:错误题目分数:0.5此题得分:0.5批注:第27 题纯物质的第二维里仅仅是温度的函数您的答案:正确题目分数:0.5此题得分:0.5批注:第28 题节流过程为等焓过程,所以节流后流体的温度不变您的答案:错误题目分数:0.5此题得分:0.5批注:第29 题对于一个绝热不可逆过程,其熵变可以设计一个可逆过程来计算您的答案:正确题目分数:0.5此题得分:0.5批注:第30 题吸热过程一定使系统熵增。
热学作业(附解答)

热学作业(附解答)热力学1.1mol理想气体(设γ=C p/C V为已知)的循环过程如T – V图所示,其中CA为绝热过程,A点状态参量(T1,V1)和B点状态参量(T2,V2)为已知。
试求C点的状态参量:则V c= ___________________ ,T c= ____________________,p c= ____________________,V2(V1/V2)γ-1T1(RT1/V2)(V1/V2)γ-12.所示的T – S(温熵)图表示热力学系统经历了一个ABCDA循环过程,该循环称为______________循环。
若图中矩形ABCD的面积是矩形ABEF的面积的1/3,则该循环的效率为__________________。
卡诺1/33.1 mol理想气体在气缸中进行无限缓慢的膨胀,其体积由V1变化到V2。
(1)当气缸处于绝热情况下时,理想气体熵的增量ΔS= _______________。
(2)当气缸处于等温情况下时,理想气体熵的增量ΔS= _______________。
1)02)R ln4.常温常压下,一定量的某种理想气体(其分子可视为刚性分子,自由度为i),在等压过程中吸热为Q,对外做功为W,内能增加为ΔE,则W/Q= ___________。
ΔE/Q= ___________。
5.一卡诺热机(可逆的),低温热源的温度为27℃,热机效率为40%,起高温热源温度为___________K。
今欲将该热机效率提高到50%,若低温热源保持不变,则高温热源的温度应增加____________K。
5001006.从统计的意义来解释,不可逆过程实质上是一个_________________的转变过程,一切实际过程都向着__________________的方向进行。
从几率较的状态到几率较大的状态状态的几率增大(或熵值增加)7.一个能透热的容器,盛有各为1mol的A、B两种理想气体,C为具有分子筛作用的活塞,能让A种气体自由通过,不让B种气体通过,如图所示。
西工大(冯青) 工程热力学作业答案 第一章

1-1体积为2L 的气瓶内盛有氧气2.858g,求氧气的比体积、密度和重度。
解:氧气的比体积为3310858.2102−−××==m V v =0.6998 m 3/kg 密度为vm V 110210858.233=××==−−ρ=1.429 kg/m 3重度80665.9429.1×==g ργ=14.01 N/m 31-2某容器被一刚性器壁分为两部分,在容器的不同部分安装了测压计,如图所示。
压力表A 的读数为0.125MPa,压力表B 的读数为0.190 MPa,如果大气压力为0.098 MPa,试确定容器两部分气体的绝对压力可各为多少?表C 是压力表还是真空表?表C的读数应是多少? 解:设表A、B、C 读出的绝对压力分别为A p 、B p 和C p 。
则根据题意,有容器左侧的绝对压力为=+=+==125.0098.0gA b A p p p p 左0.223 MPa 又∵容器左侧的绝对压力为gB C B p p p p +==左 ∴033.0190.0223.0gB C =−=−=p p p 左 MPa<b p∴表C 是真空表,其读数为033.0098.0C b vC −=−=p p p =0.065 MPa 则容器右侧的绝对压力为=−=−=065.0098.0vC b p p p 右0.033 MPa1-5水银温度计浸在冰水中时的水银柱长度为4.0cm,浸在沸水中时的水银柱长度为24.0cm。
试求:1)在室温为22℃时水银柱的长度为多少?2)温度计浸在某种沸腾的化学溶液中时,水银柱的长度为25.4cm,求溶液的温度。
解:假设水银柱长度随温度线性增加。
则1℃间隔的水银柱长度为424100−=ΔΔz t =5.00 ℃/cm 1) 在室温为22℃时水银柱的长度为=+=ΔΔ+5/224/0ztt z 8.4 cm2) 水银柱的长度为25.4cm时,溶液的温度为=×−=ΔΔ×−=5)44.25()(0ztz z t 107 ℃1-6如图所示,一垂直放置的汽缸内存有气体。
热力学课外习题(含答案)

判断题:√1.自然界发生的过程一定是不可逆过程。
×2.不可逆过程一定是自发过程。
(做了非体积功发生的过程不是自发过程)×3.熵增加的过程一定是自发过程。
(如自由膨胀过程)×4.绝热可逆过程的∆S = 0,绝热不可逆膨胀过程的∆S > 0,绝热不可逆压缩过程的∆S < 0。
×5.为了计算绝热不可逆过程的熵变,可以在始末态之间设计一条绝热可逆途径来计算。
(设计一条可逆非绝热可逆过程来计算熵变)×6.由于系统经循环过程后回到始态,∆S = 0,所以一定是一个可逆循环过程。
(环境可能提供负熵流)×7.平衡态熵最大。
(在隔离体系中是对的)×8.在任意一可逆过程中∆S = 0,不可逆过程中∆S > 0。
9.理想气体经等温膨胀后,由于∆U = 0,所以吸的热全部转化为功,这与热力学第二定律矛盾吗?(不矛盾,因为在热全部转化为功的同时,引起了气体的状态的变化)×10.当系统向环境传热时(Q < 0),系统的熵一定减少。
(熵变是可以过程的热温熵)√11.一切物质蒸发时,摩尔熵都增大。
(混乱度增大)×12.吉布斯函数减小的过程一定是自发过程。
(条件:等温等压,非体积功等于0)×13.在等温、等压下,吉布斯函数变化大于零的化学变化都不能进行。
(当有非体积功如电功时可以发生)×14.系统由V 1膨胀到V 2,其中经过可逆途径时做的功最多。
(等温条件下如对的)×15.因Q p =ΔH ,Q v =ΔU ,所以Q p 和Q v 都是状态函数。
(热是过程量,不是状态函数)×16.水溶液的蒸气压一定小于同温度下纯水的饱和蒸汽压。
(非挥发性溶质的稀溶液)×17.在等温等压不做非体积功的条件下,反应Δr G m <0时,若值越小,自发进行反应的趋势就越强,反应进行得越快。
华中科技大学热力学第四章课后作业答案
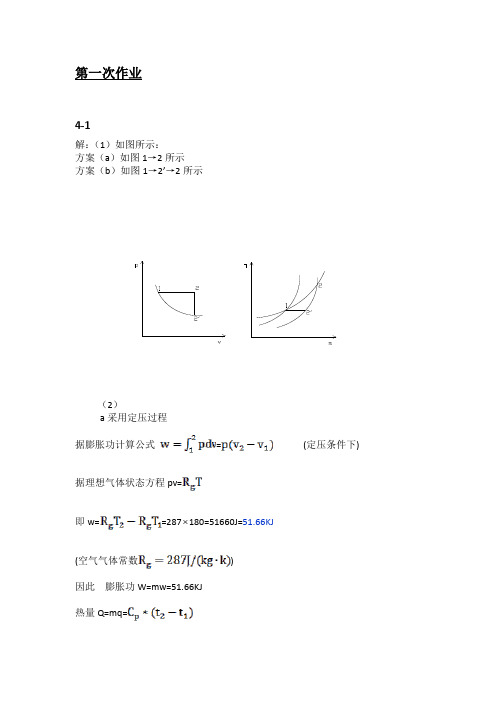
)
按平均热容表计算 =1.067kJ/(kg.K) 即热量 Q=1.067*180=192.06kJ 熵变 b 采用先定温后定容 为定温过程, =1.067*ln =0,501 kJ/(kg.K)
定容过成
,膨胀功为 0
即整个过程膨胀功 w=
=
=
=
据据理想气体状态方程 pv=
,且
即 ln
=ln =ln
(6)
4-5
Rg 377 J / ( Kg K ), k 1.25 的理想气体 1.36Kg, 从 P 1 551.6 KP a , t1 60℃ 经定容
过程达到 P 1 1655KP a ,过程中除了以搅拌器搅动气体外,还加入热量 105.5KJ, 求 (1) 终态温度 t2 (2) 经搅拌器输入的功量 (3)气体内能的变化 (4)气体熵的变化 解: (1) T2
T1 1655 P2 (273 60) 999.1K P 551.6 1
t2 726.1℃
(2) Cv
Rg k 1
1508KJ / ( Kg K )
U mcv (T2 T1) =1366.75KJ
Q U W 105.5 1366.75 1261.25KJ
∴w=300*287*ln ∴W=40.47kJ 热量 q= +
=40.47kJ
定温过程 ∴q=40.47+0.717*180=169.53 kJ 即 Q=169.53 kJ 熵变 +
定温过程熵变
=40.47/300=0.1349Kj/k
定容过程熵变
=
=0.717*0.47=0.337 Kj/k
Kj/k
T2 T1 (
工程热力学课后作业答案第五版(全)1

压送前储气罐中CO2的质量
p2v27?105?8.5
m2??kg
RT2287?288
压缩机每分钟充入空气量
pv1?105?3m??kg
RT287?288
ห้องสมุดไป่ตู้
所需时间
m1?
p1v1
RT1p2v2
RT2
t?
m2
?19.83min m
压送后储气罐中CO2的质量
(2)标准状态下N2的比容和密度
RT296.9?2733
v??=0.8m/kg
p101325
m?m1?m2?
=41.97kg
vp2p130099.3101.325
(?)?(?)?1000RT2T1287300273
??
(3)
13
=1.25kg/m v
2-2.已知N2的M=28,求(1)N2的气体常数;(2)标准状态下
T1?t1?273 T2?t2?273
压入的CO2的质量
(3) (4)
N2
的比容和密度;(3)
m?m1?m2?
p?0.1MPa,t?500℃时的摩尔容积Mv。
解:(1)N2的气体常数
2-6 空气压缩机每分钟自外界吸入温度为15℃、压力为0.1MPa的空气3 m3,充入容积8.5 m3的储气罐内。设开始时罐内的温度和压力与外界相同,问在多长时间内空气压缩机才能将气罐的表压力提高到0.7MPa?设充气过程中气罐内温度不变。
p?0.1MPa,t?500℃时的摩尔容积
Mv
RTMv =0
m=12.02kg
vp2p1
(?) RT2T1
热力学作业答案

循环过程系统的熵变是多少?
又因为
解:(1)对于可逆绝热过程,有 S1 0
等容过程,有
T1V1 1 T2V2 1
S2
dQ dE TT
1
CV
ln
V2 V1
CV
CP CV
T1 T2
dT T
CV
1 CV ln 2
3 (1) RT :
1mol 理想气体的内能;
2
(2) 3 R :
定容摩尔热容量
;
2
(3) 5 R : 定压摩尔热容量
;
2
10.绝热的容器被一隔板分为两半。设两边温度
相同。左边充满理想气体,其压强为P0,右边是 真空。当把隔板抽出时,左边的气体对真空作自
由膨胀,达到平衡后,气体的温度变化T_=__0
A
Q3’
Q2 地下水T2
Q
Q3
Q3'
T3 T1
Q1
T3 T2
T2 T3 T2
T1 T3 T1
Q1
(1
T1 T3
T3 T2
)
T3 T2
Q1
3H
5. 如图示,为1摩尔单原子分子理想气体的循环过程( ln2 = 0.69 )。求:(1)状态的状态参量;(2)求循环效率。
解:(1) PaVa RTa
7. 第二定律开尔文表述说明 热功转化过程 不可 逆,克劳修斯表述说明 热传递过程 不可逆。
8. 卡诺机从373K高温热源吸热,向273K低温热 源放热。若从高温热源吸收1000J热量,则该机
热力学习题答案

热力学基础一、选择题1、 在下列各种说法中,哪些是正确的? [ B ](1) 准静态过程就是无摩擦力作用的过程.(2) 准静态过程一定是可逆过程.(3) 准静态过程是无限多个连续变化的平衡态的连接.(4) 准静态过程在p -V 图上可用一连续曲线表示.A 、(1)、(2).B 、(3)、(4).C 、(2)、(3)、(4).D 、(1)、(2)、(3)、(4). [ D ]2、 根据热力学第二定律可知,下面说法正确的是A 、功可全部转换为热,但热不能全部转换为功。
B 、热可从高温物体传到低温物体,但不能从低温物体传到高温物体。
C 、不可逆过程就是不能向相反方向进行的过程。
D 、一切自发过程都是不可逆的。
3、 一绝热容器被隔板分成两半,一半是真空,另一半是理想气体.若把隔板抽出,气体将进行自由膨胀,达到平衡后 [ A ](A) 温度不变,熵增加. (B) 温度升高,熵增加.(C) 温度降低,熵增加. (D) 温度不变,熵不变.二、填空题4、 在p V 图上(1) 系统的某一平衡态用____一点_________来表示; (2) 系统的某一准静态过程用______一曲线__________来表示;(3) 系统的某一平衡循环过程用_____封闭曲线_____________来表示;5、 如图所示为一理想气体几种状态变化过程的P-V 图,其中MT 为等温线,MQ 为绝热线,在AM 、BM 、CM 三种准静态过程中:温度升高的是BM,CM____过程,气体吸热的是____CM_____过程。
温度降低的是____AM _____过程,气体放热的是___AM,BM______过程。
6、 理想气体经历绝热自由膨胀过程,达到平衡后,它的温度不变 ;它的熵 增加 。
(填“增加” 、“不变”或“减少”)。
7、一定量的某种气体在等压变化过程中对外作功200J ,若此气体为单原子分子气体,则过程中需吸热___500J__,若此气体分子为双原子分子气体,则需吸热700J 。
热力学基础习题、答案及解法(2011.1.6)

热力学基础习题、答案及解法一、选择题1. 如图一所示,一定量的理想气体,由平衡状态A 变到平衡状态B (b a P P =),则无论经过的是什么过程,系统必然 【B 】(A )对外做正功 (B )内能增加 (C )从外界吸热 (D )向外界吸热2. 对于室温下的单原子分子理想气体,在等压膨胀的情况下,系统对外所做的功与从外界吸收的热量之比Q W 等于 【C 】 (A )32 (B )21 (C )52 (D )72参考答案:T R MW p ∆=μT R i M Q p ∆⎪⎭⎫⎝⎛+=22μ522222=+=∆⎪⎭⎫ ⎝⎛+∆=i T R i M TR MQ W pp μμ3. 压强、体积、温度都相等的常温下的氧气和氦气,分别在等压过程中吸收了相等的热量,它们对外做的功之比为 【C 】 (A )1:1 (B )5:9 (C )5:7 (D )9:5参考答案:T R i M Q p ∆⎪⎭⎫ ⎝⎛+=22μ RT M pV μ=氦氧T T ∆⎪⎭⎫⎝⎛+=∆⎪⎭⎫ ⎝⎛+223225 P VA∙B∙O1图75=∆∆氦氧T T T R M W p ∆=μ 75=∆∆=氦氧氦氧T T W W p p 4. 在下列理想气体过程中,哪些过程可能发生? 【D 】 (A )等体积加热时,内能减少,同时压强升高 (B )等温压缩时,压强升高,同时吸收 (C )等压压缩时,内能增加,同时吸热 (D )绝热压缩时,压强升高,同时内能增加参考答案:0=dV 0=W T R i M E Q ∆⎪⎭⎫⎝⎛=∆=2μ 0=dT 0=∆E !11!2ln lnp p RT M V V RT MW Q μμ=== 0=dp T R i M Q ∆⎪⎭⎫ ⎝⎛+=22μ T R i M E ∆⎪⎭⎫ ⎝⎛=∆2μ T R MV p W ∆=∆=μ 0=dQ 0=Q ⎰⎪⎪⎭⎫⎝⎛--=-=∆⎪⎭⎫⎝⎛=-=∆--1011001112γγγγμV V V p pdV T R i M W E5. 分别在等温、等压、等容情况下,将400J 的热量传给标准状态下的2mol 氢气,关于3个过程热量和内能的变化说法正确的是【D 】 (A )等容过程做功最多,等压过程内能增加最多 (B )等压过程做功最多,等容过程内能增加最多 (C )等温过程做功最多,等压过程内能增加最多 (D )等温过程做功最多,等容过程内能增加最多参考答案:0=dV 0=W T R i M E Q ∆⎪⎭⎫⎝⎛=∆=2μ 0=dT 0=∆E !11!2ln lnp p RT M V V RT MW Q μμ===0=dp T R i M Q ∆⎪⎭⎫ ⎝⎛+=22μ T R i M E ∆⎪⎭⎫ ⎝⎛=∆2μ T R MV p W ∆=∆=μ 6. 如图所示,一定量的理想气体经历c b a →→过程,在此过程中气体从外界吸收热量Q ,系统内能变化ΔE ,则以下哪种说法是正确的? 【A 】 (A )系统从外界吸收热量,内能增大; (B )系统从外界吸收热量,内能减少; (C )系统向外界放出热量,内能增大; (D )系统向外界放出热量,内能减少。
工程热力学课后作业答案

p734-1 1kg 空气在可逆多变过程中吸热40kJ ,其容积增大为1102v v =,压力减少为8/12p p =,设比热为定值,求过程中内能旳变化、膨胀功、轴功以及焓和熵旳变化。
解:热力系是1kg 空气过程特性:多变过程)10/1ln()8/1ln()2/1ln()1/2ln(==v v p p n =0.9由于T c q n ∆=内能变化为R c v 25==717.5)/(K kg J •v p c R c 5727===1004.5)/(K kg J •=n c ==--v v c n kn c 51=3587.5)/(K kg J •n v v c qc T c u /=∆=∆=8×103J膨胀功:u q w ∆-==32 ×103J轴功:==nw w s 28.8 ×103J焓变:u k T c h p ∆=∆=∆=1.4×8=11.2 ×103J熵变:12ln 12lnp p c v v c s v p +=∆=0.82×103)/(K kg J •4-2 有1kg 空气、初始状态为MPa p 5.01=,1501=t ℃,进行下列过程:(1)可逆绝热膨胀到MPa p 1.02=;(2)不可逆绝热膨胀到MPa p 1.02=,K T 3002=;(3)可逆等温膨胀到MPa p 1.02=;(4)可逆多变膨胀到MPa p 1.02=,多变指数2=n ;试求上述各过程中旳膨胀功及熵旳变化,并将各过程旳相对位置画在同一张v p -图和s T -图上解:热力系1kg 空气(1) 膨胀功:])12(1[111k k p p k RT w ---==111.9×103J熵变为0(2))21(T T c u w v -=∆-==88.3×103J12ln 12ln p p R T T c s p -=∆=116.8)/(K kg J •(3)21ln1p p RT w ==195.4×103)/(K kg J • 21ln p p R s =∆=0.462×103)/(K kg J • (4)])12(1[111n n p p n RT w ---==67.1×103J n n p p T T 1)12(12-==189.2K 12ln 12ln p p R T T c s p -=∆=-346.4)/(K kg J •4-3 具有1kmol 空气旳闭口系统,其初始容积为1m 3,终态容积为10 m 3,当时态和终态温度均100℃时,试计算该闭口系统对外所作旳功及熵旳变化。
第八章 热力学作业(答案)

第八章 热力学基础一、选择题[ A ]1.(基础训练4)一定量理想气体从体积V 1,膨胀到体积V 2分别经历的过程是:A →B 等压过程,A →C 等温过程;A →D 绝热过程,其中吸热量最多的过程(A)是A →B. (B)是A →C. (C)是A →D.(D)既是A →B 也是A →C , 两过程吸热一样多。
【提示】功即过程曲线下的面积,由图可知AD AC AB A A A >>; 根据热力学第一定律:E A Q ∆+= AD 绝热过程:0=Q ; AC 等温过程:AC A Q =;AB 等压过程:AB AB E A Q ∆+=,且0>∆AB E[ B ]2.(基础训练6)如图所示,一绝热密闭的容器,用隔板分成相等的两部分,左边盛有一定量的理想气体,压强为p 0,右边为真空.今将隔板抽去,气体自由膨胀,当气体达到平衡时,气体的压强是(A) p 0. (B) p 0 / 2. (C) 2γp 0. (D) p 0 / 2γ. 【提示】该过程是绝热自由膨胀:Q=0,A=0;根据热力学第一定律Q A E =+∆得 0E ∆=,∴0T T =;根据状态方程pV RT ν=得00p V pV =;已知02V V =,∴0/2p p =.[ D ]3.(基础训练10)一定量的气体作绝热自由膨胀,设其热力学能增量为E ∆,熵增量为S ∆,则应有 (A) 0......0=∆<∆S E (B) 0......0>∆<∆S E . (C) 0......0=∆=∆S E . (D) 0......0>∆=∆S E【提示】由上题分析知:0=∆E ;而绝热自由膨胀过程是孤立系统中的不可逆过程,故熵增加。
[ D ]4.(自测提高1)质量一定的理想气体,从相同状态出发,分别经历等温过程、等压过程和绝热过程,使其体积增加1倍.那么气体温度的改变(绝对值)在 (A) 绝热过程中最大,等压过程中最小. (B) 绝热过程中最大,等温过程中最小. (C) 等压过程中最大,绝热过程中最小.(D) 等压过程中最大,等温过程中最小. 【提示】如图。
第五章 气体的热力性质(作业)

C p ,m 22.414 103
1.2978kJ/ m3 K
Q V0C p t2 t1 60000 1.2978 250 20 1.752 107 kJ/h
⑵用平均比热容计算
C p
20 0
20 250 Q V0 C p 250 C p 20 0 0 60000 1.312 2501.2976 20 1.812107 kJ/h
根据试算法,得
Z 0.99
pr 0.5202
p pr pC 0.5202 3.39 1.76MPa
h Cv t 2 t1 1.038 400 30 384.06kJ/kg
u Cv t2 t1 0.742 400 30 274.54kJ/kg
C p 1.038kJ/kg K
解:⑴用定值比热容计算
Cv 0.742kJ/kg K
S 120 1.004 ln 240.9 273 240.9 273 210 1.004 ln 400 273 150 273 32.495 41.041 8.546kJ/K h
上式不能应用于不同种类气体的混合。 上述绝热的混合过程是不可逆过程,空气的总熵必然增大。
对1kmol氧气有: H=6858.84KJ,U=4988.19KJ,S=-16.95KJ/k
(2)按能量平衡方程
Q n(HM Wt ) 1000 (6858.84 20000) 13141.16kJ
热力学习题参考答案
[5-12]两股压力相同的空气流,一股温度,t1=400℃,流量为qm1=120kg/h;另一 股t2=15℃,qm2=210kg/h,两股混合为相同压力的混合气流,若混合过程是绝热的, 求:⑴混合气流的温度;⑵混合过程空气的熵将增大还是减小,还是不变?⑶计算 熵变化量(用定值比热容计算)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 热力学基础一、选择题[ A ]1.(基础训练4)一定量理想气体从体积V 1,膨胀到体积V 2分别经历的过程是:A →B 等压过程,A →C 等温过程;A →D 绝热过程,其中吸热量最多的过程(A)是A →B. (B)是A →C. (C)是A →D. (D)既是A →B 也是A →C , 两过程吸热一样多。
【提示】功即过程曲线下的面积,由图可知AD AC AB A A A >>; 根据热力学第一定律:E A Q ∆+=AD 绝热过程:0=Q ;AC 等温过程:AC A Q =;AB 等压过程:AB AB E A Q ∆+=,且0>∆AB E[ B ]2.(基础训练6)如图所示,一绝热密闭的容器,用隔板分成相等的两部分,左边盛有一定量的理想气体,压强为p 0,右边为真空.今将隔板抽去,气体自由膨胀,当气体达到平衡时,气体的压强是(A) p 0. (B)p 0 / 2. (C) 2γp 0. (D) p 0 / 2γ.【提示】该过程是绝热自由膨胀:Q=0,A=0;根据热力学第一定律Q A E =+∆得 0E ∆=,∴0T T =;根据状态方程pV RT ν=得00p V pV =;已知02V V =,∴0/2p p =.[ D ]3.(基础训练10)一定量的气体作绝热自由膨胀,设其热力学能增量为E ∆,熵增量为S ∆,则应有(A) 0......0=∆<∆S E (B) 0......0>∆<∆S E . (C) 0......0=∆=∆S E . (D)0......0>∆=∆S E【提示】由上题分析知:0=∆E ;而绝热自由膨胀过程是孤立系统中的不可逆过程,故熵增加。
[ D ]4.(自测提高1)质量一定的理想气体,从相同状态出发,分别经历等温过程、等压过程和绝热过程,使其体积增加1倍.那么气体温度的改变(绝对值)在 (A) 绝热过程中最大,等压过程中最小. (B) 绝热过程中最大,等温过程中最小. (C) 等压过程中最大,绝热过程中最小.(D) 等压过程中最大,等温过程中最小.【提示】如图。
等温AC 过程:温度不变,0C A T T -=;等压过程:A B p p =,根据状态方程pV RT ν=,得:B AB AT T V V =,2B A T T ∴=,B A A T T T -=绝热过程:11A A D D T V T V γγ--=,1112A D A A D V T T T V γγ--⎛⎫⎛⎫== ⎪⎪⎝⎭⎝⎭,得:1112D A A A T T T T γ-⎡⎤⎛⎫-=-<⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,所以,选择(D )【或者】等压过程:()()p A B A B A A p V V R T T ν=-=-,pB A A T T Rν-=;绝热过程:()2D A i A E R T T ν=-∆=--,2D A AT T i R ν-=;∵2iR R νν<,由图可知p A A >, 所以 B A D A T T T T ->-[ A ]5.(自测提高3)一定量的理想气体,分别经历如图(1) 所示的abc 过程,(图中虚线ac 为等温线),和图(2)所示的def 过程(图中虚线df为绝热线).判断这两种过程是吸热还是放热. (A) abc 过程吸热,def 过程放热. (B) abc 过程放热,def 过程吸热. (C) abc 过程和def 过程都吸热.(D) abc 过程和def 过程都放热.【提示】(a ) , 0a c c a T T E E =∴-=Q ,()0abc abc c a abc Q A E E A =+-=>,吸热。
(b )df 是绝热过程,0df Q =,∴f d df E E A -=-,V()def def f d def df Q A E E A A =+-=-,“功”即为曲线下的面积,由图中可见,def df A A <,故0def Q <,放热。
[ B ]6.(自测提高6)理想气体卡诺循环过程的两条绝热线下的面积大小(图中阴影部分)分别为S 1和S 2,则二者的大小关系是:(A) S 1 > S 2. (B) S 1 = S 2.(C) S 1 < S 2. (D) 无法确定.【提示】两条绝热线下的面积大小即为“功的大小”。
绝热过程的功的大小为12()2iA E R T T ν=-∆=-,仅与高温和低温热源的温差有关,而两个绝热过程对应的温差相同,所以作功A 的数值相同,即过程曲线下的面积相同。
二、填空题1.(基础训练13)一定量的某种理想气体在等压过程中对外作功为 200 J .若此种气体为单原子分子气体,则该过程中需吸热 500 J ;若为双原子分子气体,则需吸热 700 J.【提示】据题意200()molMA pdV p V R T J M ==⋅∆=⋅∆=⎰ 22mol i M i E R T A M ⎛⎫∆=⋅∆=⎪⎝⎭,22i Q A E A +=+∆= 对于单原子分子:3i =,所以5500()2Q A J ==;对于双原子分子:5i =,所以7700()2Q A J == 2.(基础训练14)给定的理想气体(比热容比?为已知),从标准状态(p 0、V 0、T 0)开始,作绝热膨胀,体积增大到三倍,膨胀后的温度T =013T γ-,压强p =03p γ【提示】求温度的变化,可用绝热过程方程:1100T V TVγγ--=,100013V T T T V γγ--⎛⎫==⎪⎝⎭求压强的变化,可用绝热过程方程:00p V pV γγ=,得:0003V p p p V γγ⎛⎫== ⎪⎝⎭3.(自测提高11)有ν摩尔理想气体,作如图所示的循环过程acba ,其中acb 为半圆弧,b ?a 为等压线,p c =2p a .令气体进行a ?b 的等压过程时吸热Q ab ,则在此循环过程中气体净吸热量Q < Q ab . (填入:>,<或=)【提示】a-b 过程:2ab iQ A E S R T ν=+∆=+∆矩形而acba 循环过程的净吸热量Q A S '==半圆,∵p c =2p a ,由图可知:S S >矩形半圆,且0T ∆>,0E ∆>,所以 ab Q Q >4.(自测提高12)如图所示,绝热过程AB 、CD ,等温过程DEA , 和任意过程BEC ,组成一循环过程.若图中ECD 所包围的面积为70 J ,EAB 所包围的面积为30 J ,DEA 过程中系统放热100 J ,则:(1) 整个循环过程(ABCDEA )系统对外作功为 40J .(2) BEC 过程中系统从外界吸热为 140J .【提示】(1) 整个循环过程(ABCDEA )系统对外作功为p Vabp()307040J EABE ECDE A A A =+=-+=逆循(正循)()环环;(2)ABCDEA AB BEC CD DEA Q Q Q Q Q =+++00(100)BEC Q =+++-, 同时40()ABCDEA Q A J ==, 140()BEC Q J ∴=5.(自测提高13)如图示,温度为T 0,2 T 0,3 T 0三条等温线与两条绝热线围成三个卡诺循环:(1) abcda ,(2) dcefd ,(3) abefa ,其效率分别为η1:33.3% ,η2: 50% ,η3: 66.7%【提示】由121T T -=η (1T 对应高温热源的温度,2T 对应低温热源的温度),得:010211133cd ab T T T T η=-=-=,02011122ef cd T T T T η=-=-=,03021133ef ab T T T T η=-=-= 6.(自测提高15)1 mol 的单原子理想气体,从状态I (p 1,V 1)变化至状态II (p 2,V 2),如图所示,则此过程气体对外作的功为12211() 2p p V V +-(),吸收的热量为1221221113 ()() 22p p V V p V p V +-+-()【提示】①气体对外作的功 = 过程曲线下的梯形面积;②由热力学第一定律,得 21()2iQ A E A R T T ν=+∆=+-,其中3i =,1mol ν=,212211()R T T p V p V ν-=-,pOV3T 02TT 0fa db c eV2,V 2)三.计算题1.(基础训练18)温度为25℃、压强为1 atm 的1 mol 刚性双原子分子理想气体,经等温过程体积膨胀至原来的3倍.(1) 计算这个过程中气体对外所作的功. (2) 假若气体经绝热过程体积膨胀为原来的3倍,那么气体对外作的功又是多少?解:(1)等温膨胀:127325298T K =+=,213V V =,1mol ν=(2)绝热过程:21()2iA E R T T ν=-∆=--,其中5i =,1mol ν=,2T 可由绝热过程方程求得:112211T V TV γγ--=,111211211923V T T T K V γγ--⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭,2、(基础训练19)一定量的单原子分子理想气体,从初态A 出发,沿如图所示直线过程变到另一状态B ,又经过等容、等压两过程回到状态A .(1) 求A →B ,B →C ,C →A 各过程中系统对外所作的功W ,内能的增量?E 以及所吸收的热量Q .(2) 整个循环过程中系统对外所作的总功以及从外界吸收的总热量(过程吸热的代数和).解:3i =,(1) A B →:11()()2002B A B A A p p V V J =+-=C B →:20A =A C →:3()100A A C A p V V J =-=-33()()15022A C A A C C i E R T T p V p V J ν∆=-=-=-(2) 123100A A A A J =++=3.(基础训练22)一定量的理想气体经历如图所示的循环过程,A →B 和C →D 是等压过程,B →C 和D →A 是绝热过程.已知:T C =300 K ,T B =400 K .试求:此循环的效率.解: 211Q Q η=-)(1A B P T T C Q -=ν, 2()P C D Q C T T ν=-根据绝热过程方程得到:γγγγ----=D D AA T p T p 11, γγγγ----=C C B B T p T p 11 而 B A p p = , D C p p =所以有 C D B A T T T T //= ,21CBQ T Q T =故 %251112=-=-=BC T T Q Q η (此题不能直接由BCT T -=1η 式得出,因为不是卡诺循环。
