清华大学《运筹学教程》胡运权主编课后习题答案

合集下载

清华大学运筹学教程胡运权主编课后习题答案

8 10
x1 , x2 0
目标函数最优值（下界）为：6.4
17
第18页/共66页
l.7 分别用单纯形法中的大M法和两阶段法求解下列线性规划问题，并指出属哪—
类解。
max Z 3x1 x2 2x3
x1 x2 x3 6
(1)
st
2x1 2x2
x3 x3
0
2
x j 0（, j 1,,3）
所以最优解为X*=(1,3/2,0,0)T
第11页/共66页
0点
A1点 A2点
max Z 2x1 x2 3x1 5x2 15
(2) st.6x1 2x2 24 x1, x2 0
11
第12页/共66页
第13页/共66页
第14页/共66页
d
x
2
，
l.5 讨论c
,
上题(1)中，若目标函数变为max Z = d的值如何变化，使该问题可行域的每个
8
第9页/共66页
1.4 分别用图解法和单纯形法求解下述线性规划问题，并对照指出单纯形表中的各基可行解对应图解法中可行域的哪一顶点。
max Z 10x1 5x2
(1)
st.35xx11
4 x2 2 x2
9 8
x1, x2 0
9
第10页/共66页
cj
10
5 00
CB
xB
b
x1
x2
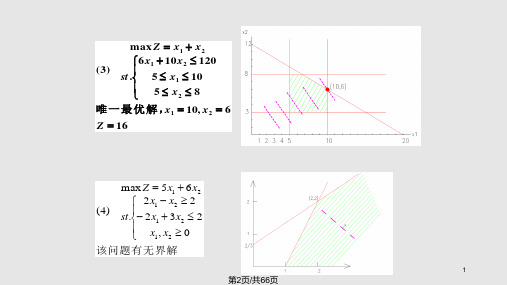
max Z x1 x2
(3)
st
6 .
x1 10x2 5 x1
120 10
5 x2 8
唯一最优解，x1 10, x2 6
Z 16
max Z 5x1 6x2 2x1 x2 2

运筹学教程（第二版）（胡运权）课后答案（清华大学出版社）

运筹学教程（第⼆版）（胡运权）课后答案（清华⼤学出版社）运筹学教程（第⼆版）习题解答第⼀章习题解答运筹学教程1.1 ⽤图解法求解下列线性规划问题。

并指出问题具有惟⼀最优解、⽆穷多最优解、⽆界解还是⽆可⾏解。

1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5 x 1 + 6 x 2≤ 82 5 ≤ x ? 1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3) 1 2 x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 21 2 ? ≥ 12 2 1 ? x , x ≥ 0 .? ?2 x 1 + x 2 ≤ 2st ?3x + 4 x (2) max Z = 3x 1 + 2 x 2x , x ≥ 0 1 2该问题⽆解≥ 12 2 1 ? ? 2 x 1 + x 2 ≤ 2st .?3 x +4 x ( 2 ) max Z = 3 x 1 + 2 x 2第⼀章习题解答3 2 1x = 1, x = 1, Z = 3是⼀个最优解⽆穷多最优解，1 2x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 2该问题有⽆界解1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5x 1 + 6 x 2第⼀章习题解答唯⼀最优解， x 1 = 10, x 2 = 6, Z = 16 ≤ 82 5 ≤ x ?1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3)第⼀章习题解答运筹学教程1.2 将下述线性规划问题化成标准形式。

运筹学清华大学出版社胡运权着课后答案

�12 x1 � 3 x2 � 6 x3 � 3 x4 � 9
(1)
st
��8 ��3
x1 x1
� �
x2 x6
� 4 x3 �0
�
2 x5
� 10
�� x j � 0�, j � 1,� ,6�
min Z � 5 x1 � 2 x2 � 3 x3 � 2 x4
� x1 � 2 x2 � 3 x3 � 4 x4 � 7
运筹学教程�第二版� 习题解答
运筹学教程
1.1 用图解法求解下列线性规划问题。并指出问题具有惟一最优解、无穷多最优解、无界解还是无可行解。
min Z � 2 x1 � 3 x2 � 4 x1 � 6 x2 � 6
(1) st .�� 2 x1 � 2 x2 � 4 �� x1 , x2 � 0
Z
0
0.5
2
0
5
0
0
1
1
5
2/5
0
11/5
0
43/5
page 10 6 January 2011
School of Management
运筹学教程
1.4 分别用图解法和单纯形法求解下述线性规划问题�并对照指出单纯形表中的各基可行解对应图解法中可行域的哪一顶点。
max Z � 10 x1 � 5 x2 �3 x1 � 4 x2 � 9
max Z � x1 � x2 �6 x1 � 10 x2 � 120 (3) st.�� 5 � x1 � 10 �� 5 � x2 � 8
max Z � 3x1 � 2 x2 �2 x1 � x2 � 2
(2) st.��3x1 � 4 x2 � 12 �� x1, x2 � 0

运筹学胡运权课后答案课件

m
a ij y i c j
i1
yi 0
y
无
i
约
束
( j 1,..., n1 )
( j n1 1,..., n ) (i 1,...m 1 ) (i m 1 1,...m )
运筹学胡运权课后答案
2.4
运筹学胡运权课后答案
运筹学胡运权课后答案
2.9
运筹学胡运权课后答案
（d）
对偶问题：
max w 2y1 3 y2 5 y3
y1 2y2 y3 2
3 y1
y2 4 y3 2
4 y1 3 y2 3 y3 4
y1 0, y2 0, y3取值无约束
对偶问题：
m
m i n w b i y i i1
m
a ij y i c j
i1
（1，2章）
运筹学胡运权课后答案
图解法：
当 x2 2 x 11 5z经过运筹点学胡（运1 权，课3 2 后）答案时， z最大。
单纯形法：添加松弛变量化为标准形式，
max z 10x1 5x2 0x3 0x4
3x1 5 x1
4x2 2x2
x3
x4
9 8

x
j
0
( j 1, 2, 3, 4)
运筹学胡运权课后答案
1.6（a）
运筹学胡运权课后答案
运筹学胡运权课后答案
1.7
运筹学胡运权课后答案
1.8
（P36公式）表1-24中，x1，x5为基变量，g=1， h=0，l=0。
运筹学胡运权课后答案
1.11
运筹学胡运权课后答案

二三版兼用《运筹学教程》胡运权主编课后习题答案(第三章)

表3-37
城市
电站
1
2
3
Ⅰ
15
18
22
Ⅱ
21
25
16
第三章习题解答
习题3.12的解答
城市城市
电站
1-1
城市 1-2
城市2
城市 3-1
城市 3-2
产量
Ⅰ
150 15
15 250 18
22
22 400
Ⅱ
140 21
第三章习题解答
表3-35
食品厂
面粉厂
1
2
3
产量
Ⅰ
3 10
2 20
Ⅱ
4 11
8 30
Ⅲ
8 11
4 20
销量
15 25 20
第三章习题解答
习题3.10的解答
食品厂面粉厂
Ⅰ Ⅱ Ⅲ 销量
1
3 15 4
8 15
2
10 5 11 20 11 25
3
20 2 8 4
20
4
0 10 0
0 10
产量
20 30 20
B3
B4 产量
A1 A2 A3 销量
3
7
6
45
2
4
3
22
4
3
8
56
3
3
2
2
第三章习题解答
习题3.9的解答
销地
产地
B1 B2 B3 B4 B5 产量A1源自33 7 6 24 0 5
A2
2 4 23 2 0 2
A3 销量
4 33 8 5 30 6 33223
第三章习题解答
3.10 某市有三个面粉厂，它们供给三个面食加工厂所需的面粉。各面粉厂的产量、各面食加工厂加工面粉的能力、各面食加工厂和各面粉厂之间的单位运价，均表示于表3-35中。假定在第1，2和3面食加工厂制作单位面粉食品的利润分别为12元、16元和11元，试确定使总效益最大的面粉分配计划(假定面粉厂和面食加工厂都属于同一个主管单位)。

运筹学胡运权部分课后习题答案

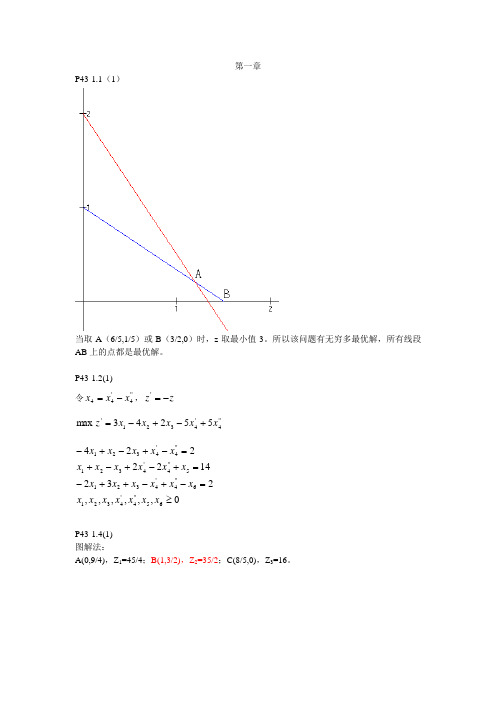
第一章P43-1.1（1）当取A （6/5,1/5）或B （3/2,0）时，z 取最小值3。

所以该问题有无穷多最优解，所有线段AB 上的点都是最优解。

P43-1.2(1)令''4'44x x x -=，z z -='''4'4321'55243max x x x x x z +-+-=,,,,,,232142222465''4'43216''4'43215''4'4321''4'4321≥=-+-++-=+-+-+=-+-+-x x x x x x x x x x x x x x x x x x x x x x x xP43-1.4(1) 图解法：A(0,9/4)，Z 1=45/4；B(1,3/2)，Z 2=35/2；C(8/5,0)，Z 3=16。

单纯形法：10 5 0 0C b X b b x1x2x3x4θ0 x39 3 4 1 0 30 x48 5 2 0 1 8/5δ10 5 0 00 x321/5 0 14/5 1 -3/5 3/210 x18/5 1 2/5 0 1/5 4δ0 1 0 -25 x23/2 0 1 5/14 -3/1410 x1 1 1 0 -1/7 2/7δ0 0 -5/14 -25/14依次相当于：原点；C；B。

P44-1.7(1)2 -1 2 0 0 0 -M -M -MC b X b b x1x2x3x4x5x6x7x8x9θ无界解。

两阶段法：阶段二：P45-1.10证明：CX (0)>=CX*，C*X*>=C*X (0) CX (0)-CX*+C*X*-C*X (0)>=0，即(C*-C)(X*-X (0))>=0。

P45-1.13设饲料i 使用x i （kg ），则543218.03.04.07.02.0m in x x x x x z ++++=s.t. 7001862354321≥++++x x x x x 305.022.05.054321≥++++x x x x x1008.022.05.054321≥++++x x x x x0,,,,54321≥x x x x x第二章P74-2.1(1)321532m ax y y y w ++=22321≤++y y y 243321≤++y y y 4334321=++y y y 无约束321,0,0y y y ≤≥P75-2.4(1),06353322232max 212121212121≥≥≤-≤+≤-≤++=y y y y y y y y y y y y w(2) (8/5,1/5)(3) 无穷多最优解。

16993-运筹学-习题答案选03_整数规划

运筹学教程（胡运权主编，清华第4版）部分习题答案（第五章）5.1设长度为a j的毛坯截取x j根，则min z = L - ∑j=1,2,...,n a j x js.t. ∑j=1,2,...,n a j x j≤ Lx j ≥ 0, integer, j = 1, 2, …, n即max z’ = ∑j=1,2,...,n a j x js.t. ∑j=1,2,...,n a j x j≤ Lx j ≥ 0, integer, j = 1, 2, …, n5.2设x j = 1, 当第j队员上场；x j = 0, 当第j队员不上场，则max z = 1.92x1 + 1.90x2 + 1.88x3 + 1.86x4 + 1.85x5 + 1.83x6 + 1.80x7 + 1.78x8s.t. x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8= 5x1 + x2 = 1x6 + x7 + x8 ≥ 1x6 ≤ 2 – (x1 + x4)x2 + x8 ≤ 1x j ={0 or 1}, j = 1, 2, …, 85.3max z = ∑i=1,2,...,m c i x is.t. ∑i=1,2,...,m a i x i≤ a∑i=1,2,...,m b i x i≤ bx i = 0 or 1, i = 1, 2, …, m5.4(1) x* = (3, 1); z* = 7(2) x* = (0, 9); z* = 95.5(1) 无可行解(2) x* = (1, 0, 0); z* = 25.6设x j = 1, 当消防站j不关闭；x j = 0, 当消防站j关闭min w = x1 + x2 + x3 + x4s.t. x1 + x2≥ 1 （区域1有消防站负责）x1 + x2≥ 1 （区域2有消防站负责）x1 ≥ 1 （区域3有消防站负责）x1 + x3≥ 1 （区域4有消防站负责）x3≥ 1 （区域5有消防站负责）x1 + x3 + x4≥ 1 （区域6有消防站负责）x1 + x4≥ 1 （区域7有消防站负责）x1 + x2 + x4≥ 1 （区域8有消防站负责）x2 + x4≥ 1 （区域9有消防站负责）x4≥ 1 （区域10有消防站负责）x3 + x4≥ 1 （区域11有消防站负责）x1, x2, x3, x4 = 0 或1最优解：x* = (1, 0, 1, 1); z* = 35.7设y i = 0，当条件i被选；y i = 1，当条件i不选∑j=1,2,…n a ij x j ≥ b i - My i, ( i = 1, 2, …, p)∑i=1,2,...,p y i = p - q5.11(1) 令x = 0x0 +1x1 + 4x2 + 6x3; x j = 0 or 1; x0 + x1 + x2 +x3 = 1(2) 令x = 0x0 +1x1 + 4x2 + 6x3; x j = 0 or 1; x0 + x1 + x2 +x3 = 1。

运筹学教程(第三版)清华大学出版社出版郭耀煌胡远权编著习题答案习题答案(第七章)

page 9 3 May 2011
决策（分配资金）决策（分配资金） 0 0 0 0 0 0 1 64 64 64 64 2 68 68 68 3 78 78 4 76
最优决策 0 1 2 3 3
最优决策的效益值 0 64 68 78 78
School of Management
运筹学教程
第七章习题解答
表7-20 项目 A B C 投资额 0 0 0 0 1 41 42 64 2 48 50 68 3 60 60 78 4 66 66 76 单位：万元单位：
page 8 3 May 2011
School of Management
运筹学教程
第七章习题解答
工厂3 工厂状态（状态（可能的投资数）投资数） 0 1 2 3 4
运筹学教程
第七章习题解答
最优解：购买1，购买1，购买3。最优解： Al购买， A2购买， A3购买。可靠性为0.042。。
page 13 3 May 2011
School of Management
运筹学教程
第七章习题解答
7.6 某工厂有 000台机器，可以在高、低两种不某工厂有l 台机器，台机器可以在高、同负荷下进行生产，假没在高负荷下生产时，同负荷下进行生产，假没在高负荷下生产时，产品的年产量s1和投入的机器数量y1的关系为s1=8y1，机器的年产量和投入的机器数量的关系为完好率为0.7；在低负荷下生产时，产品的年产量s 完好率为；在低负荷下生产时，产品的年产量 2 和投入的机器数量y 的关系为s 投入的机器数量 2 的关系为 2=5y2 ，机器的完好率为 0.9。现在要求制定一个年生产计划，问应如何安排年生产计划，。现在要求制定一个5年生产计划使在5年内的产品总产量最高年内的产品总产量最高。使在年内的产品总产量最高。表示低负荷，解：y=0表示低负荷，y=1表示高负荷表示低负荷表示高负荷 Y(1)=0 Y(2)=0 Y(3)=1 Y(4)=1 Y(5)=1 各月的产量如下：各月的产量如下： X(1)=5000，X(2)=4500，X(3)=64800，，，， X(4)=4536，X(5)=3175.2 ，

(完整word版)运筹学(胡运权)第五版课后答案,运筹作业

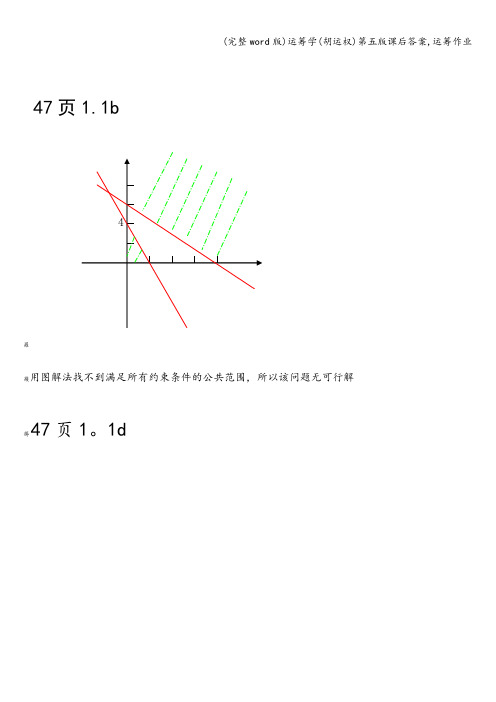
47页1.1b羅蕿用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解薅47页1。

1d蒂无界解（b）衿1.2蕿约束方程的系数矩阵A=1234莇2112蚄P1P2P3P4,运筹作业肀最优解A=（01/220）T和(0011）T页13题肆49膃设Xij为第i月租j个月的面积羄minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13+6000x23+7300x 14螁s.t.聿x11+x12+x13+x14≥15膃x12+x13+x14+x21+x22+x23≥10膀x13+x14+x22+x23+x31+x32≥20艿x14+x23+x32+x41≥12袇Xij≥0芃用excel求解为：薁用LINDO求解：羁LPOPTIMUMFOUNDATSTEP3薆OBJECTIVEFUNCTIONVALUE 蚇1)118400.0羂VARIABLEVALUEREDUCEDCOST 荿Z0.0000001。

000000虿X113.0000000。

000000螇X210。

0000002800。

000000莃X318。

0000000.000000肁X410.0000001100。

000000莈X120.0000001700.000000袆X220.0000001700。

000000螄X320.0000000。

000000蕿X130.000000400.000000膇X230。

0000001500。

000000袆X1412.0000000.000000袁ROWSLACKORSURPLUSDUALPRICES芁2)0。

000000—2800。

000000羆3）2.0000000.000000羆4)0。

000000—2800.000000节5）0。

000000-1700.000000蝿NO。

ITERATIONS=3罿答若使所费租借费用最小，需第一个月租一个月租期300平方米，租四个月租期1200平方米，第三个月租一个月租期800平方米,页14题肆50蚃设a1，a2，a3,a4,a5分别为在A1，A2，B1，B2，B3加工的Ⅰ产品数量，b1，b2，b3分别为在A1，A2，B1加工的Ⅱ产品数量,c1为在A2，B2上加工的Ⅲ产品数量。

习题答案选01_线性规划和单纯形法

习题答案选01_线性规划和单纯形法运筹学教程（胡运权主编，清华第三版）部分习题答案（第一章）1.1（1）无穷多解：α (6/5, 1/5) + (1- α) (3/2, 0)，α∈ [0,1]。

（2）无可行解；（3）x* = (10,6)，z* = 16；（4）最优解无界。

1.2（1）max z’ = 3x1 - 4x2 + 2x3 - 5x’4 + 5x’’4s.t. –4x1 + x2 –2x3 + x’4–x’’4 = 2x1 + x2 –x3 + 2x’4–2x’’4 + x5 = 14–2x1 + 3x2 + x3 –x’4+ x’’4– x6 = 2x1, x2, x3, x’4, x’’4, x5, x6 ≥ 0（2）max z’ = 2x’1 + 2x2 –3x’3 + 3x’’3s.t. x’1 + x2 + x’3 –x’’3 = 42x’1 + x2 –x’3 + x’’3 + x4 = 6x’1, x2, x’3, x’’3, x4, ≥ 01.3（1）基解：(0, 16/3, -7/6, 0, 0, 0)；(0, 10, 0, -7, 0, 0)；(0, 3, 0, 0, 7/2, 0)，是基可行解，z = 3，是最优解；(7/4, -4, 0, 0, 0, 21/4)；(0, 16/3, -7/6, 0, 0, 0)；(0, 0, -5/2, 8, 0, 0)；(1, 0, -1/2, 0, 0, 3)；(0, 0, 0, 3, 5, 0)，是基可行解，z = 0；(5/4, 0, 0, -2, 0, 15/4)；(3/4, 0, 0, 0, 2, 9/4)，是基可行解，z = 9/4；(0, 0, 3/2, 0, 8, 0)，是基可行解，z = 3，是最优解。

（2）基解：(-4, 11/2, 0, 0)；(2/5, 0, 11/5, 0)，是基可行解，z = 43/5；(-1/3, 0, 0, 11/6)；(0, 1/2, 2, 0)，是基可行解，z = 5，是最优解；(0, -1/2, 0, 2)；(0, 0, 1, 1)，是基可行解，z = 5，是最优解；最优解：α (0, 1/2, 2, 0) + (1- α) (0, 0, 1, 1)，α∈ [0,1]。

清华大学《运筹学教程》胡运权主编课后习题答案(第一章)

2)c=0
3)c>0
d<0 d=0 d>0
0
c 3 d 4
A1点 A1点 A3点
A2A3线段
3 c 5 4 d 2
c 5 d 2 c 5 d 2
c 3 d 4
A2点
A1A2线段 A1点
l.6 考虑下述线性规划问题：
max Z c1 x1 c2 x2 a11 x1 a12 x2 b1 st .a21 x1 a22 x2 b2 x1 , x2 0
-1
x2
0
x3
0
x4
-M
x5
-M
x6
CB
xB
x5
x6
x4
i
-M -M 0
3 6 4
[3] 4 1
1 3 2
0 -1 0
0 0 1
1 0 0
0 1 0 0
1 3/2 4 3 6/5 9/5
cj zj
7M-4
1 2 3 1 0 0 0
4M-1
1/3 [5/3] 5/3
5M/3+1/3
-M
0 -1 0 -M
0
0 0 1 0
0
1/3 -4/3 -1/3
-7M/3+4/3
-4 -M 0
x1
0
1 0 0
x6
x4
cj zj
cj
x6
是否基可行解
Z
(x1,x2,x3)
(x1,x2,x4) (x1,x2,x5) (x1,x2,x6)
0
0 0 7/4
61/3
10 3 -4
-7/6
0 0 0

《运筹学(胡运权)》第五版课后习题答案

1) 118400.0
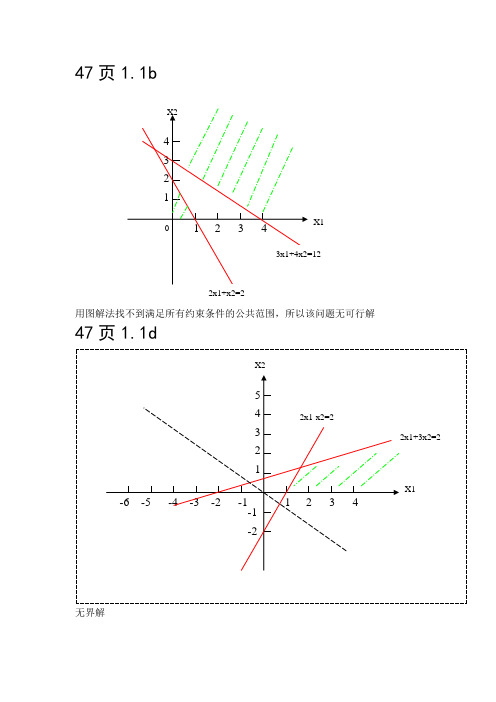
VARIABLE VALUE REDUCED COST
Z 0.000000 1.000000
X11 3.000000 0.000000
X21 0.000000 2800.000000
X31 8.000000 0.000000
X41 0.000000 1100.000000
X12 0.000000 1700.000000
程序法
6.4a
破圈法
避圈法
最小部分树16
6.4b
最小部分树32
172页6.11
红色曲线为使用一年卖出
蓝色曲线为使用两年卖出
绿色曲线为使用三年卖出
紫色曲线为使用四年卖出
最短路程为3.7万元，路径为v0-v1-v4或v0-v2-v4或v0-v1-v2-v4
三种方案分别为：第一年年初买新车，年末卖掉再买新车，一直用到第四年年末卖掉；
X2 1.000000 2.000000 INFINITY
X3 4.000000 1.000000 1.500000
X1,X2,X3 0.000000 0.000000 INFINITY
RIGHTHAND SIDE RANGES
ROW CURRENT ALLOWABLE ALLOWABLE
RHS INCREASE DECREASE
d)
maxz=3x1+x2+4x3-0.4y
s.t.
6x1+3x2+5x3≤45
3x1+4x2+5x3-y≤30
x1,x2,x3,y≥0
用lomdo求解为
LP OPTIMUM FOUND AT STEP 0
OBJECTIVE FUNCTION VALUE

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

运筹学教程
第一章习题解答
1.3 对下述线性规划问题找出所有基解，指出哪些是基可行解，并确定最优解。
max Z 3x1 x2 2x3
12x1 3x2 6x3 3x4 9
(1)
st
8 3
x1 x1
x2 x6
4x3 0
2 x5
10
x j 0（, j 1,,6）
min Z 5x1 2x2 3x3 2x4
第一章习题解答
max Z x1 x2 6x1 10x2 120 (3) st. 5 x1 10 5 x2 8
唯一最优解，x1 10, x2 6, Z 16
max Z 5x1 6x2
(4)
st.22xx11
x2 3x2
2
2
x1, x2 0
该问题有无界解
5
School of Management
X
0
对于任何0 a 1, 两点连线上的点X满足：
X aX (1) (1 a) X (2)也是可行解，且
CT X CT aX (1) CT (1 a) X (2)
C T aX (1) aCT X (2) C T X (2)
CT X (2) , 所以X也是最优解。
page 24 13 April 2021
(1)
st
x12x1x23xx23
2x4 x3
14 x4
. 2
x1, x2, x3 0, x4无约束
max Z 3x1 4x2 2x3 5x41 5x42
4x1 x2 2x3 x41 x42 2
st
x1 x2 x3 2x1 3x2
2x41 2x42 x3 x41 x42
运筹学教程
第一章习题解答
1.2 将下述线性规划问题化成标准形式。
min Z 3x1 4x2 2x3 5x4
4x1 x2 2x3 x4 2
(1)
st
x12x1x23xx23
2x4 x3
14 x4
. 2
x1, x2 , x3 0, x4无约束
min Z 2x1 2x2 3x3
X4 6 (b) (c) (d) 1 0
X5 1 -1 3 (e) 0 1
Cj－Zj
a -1 2 0 0
X1 (f) (g) 2 -1 1/2 0
X5 4 (h) (i) 1 1/2 1
b=2, cC=j4－, dZ=j -2, g=10, h=0,-7f=3, i=5j , e=2,kl=0, (l)
page 15 13 April 2021
15
School of Management
运筹学教程
第一章习题解答
l.6 考虑下述线性规划问题：
max Z c1x1 c2 x2
st.aa2111xx11
a12 x2 a22 x2
b1 b2
x1, x2 0
21上0≤界≤a。式1b22≤中≤5，1,481,试≤≤确bc11定≤≤目132, 标,42≤函≤c数a2≤2最1≤6优,5-值,14≤的≤a下a112≤界2≤3和6, ,
4 x2 2 x2
9 8
x1, x2 0
page 12 13 April 2021
12
School of Management
运筹学教程
第一章习题解答
max Z 2x1 x2
(2)
st.63xx11
5x2 2x2
15 24
x1, x2 0
page Z x1 2x2 x3 4x4
st.2x1
x2
x1 x2 x4 3x3 2x4
4 2 5 7
(i) (ii)
x1, x2 , x3, x4 0
模型中α，β为参数，要求：
(1) 组成两个新的约束 (i)’ ＝ (i)+(ii) ， (ii)’ ＝ (ii)一2(i)，根据(i)’，(ii)’以x1,x2为基变量，列出初始单纯形表；
17
School of Management
运筹学教程
第一章习题解答
解：下界对应的模型如下（ c,b取小，a取大）
max Z x1 4x2
st.43xx1165xx22
8 10
x1, x2 0
最优值（下界）为：6.4
page 18 13 April 2021
18
School of Management
(2)
st
x1 x2 x3 4 2x1 x2 x3 6
x1 0, x2 0, x3无约束
page 6 13 April 2021
6
School of Management
运筹学教程
第一章习题解答
min Z 3x1 4x2 2x3 5x4
4x1 x2 2x3 x4 2
X *是 max Z C* X的最优解，故
C* X * C* X 0 0;
(C* C)(X * X 0 )
C(X 0 X *) C*(X * X 0) 0
page 25 13 April 2021
25
School of Management
运筹学教程
第一章习题解答
1.11 考虑线性规划问题
6 x2 2 x2
6 4
x1, x2 0
无穷多最优解，
x1
1, x2
1,Z 3
3是一个最优解
max Z 3x1 2x2
(2)
st.32xx11
x2 2 4x2 12
x1, x2 0
该问题无解
4
School of Management
运筹学教程
page 5 13 April 2021
-3/4
2
c x1 1 1 0
page 14
j
13 April 2021
00
-2/14 -
10/35
3/14d- 14
School of Management
运筹学教程
第一章习题解答
当 c/d 在 3/10 到 5/2 之间时最优解为图中的A点；当c/d大于5/2且c大于等于0时最优解为图中的B点；当c/d小于3/10且d大于0时最优解为图中的C点；当c/d大于5/2且c小于等于0 时或当c/d小于3/10且d小于0时最优解为图中的原点。
page 16 13 April 2021
16
School of Management
运筹学教程
第一章习题解答
解：上界对应的模型如下（c,b取大，a取小）
max Z 3x1 6x2
st
.21xx1142xx22
12 14
x1, x2 0
最优值（上界）为：21
page 17 13 April 2021
运筹学教程
第一章习题解答
l.7 分别用单纯形法中的大M法和两阶
段法求解下列线性规划问题，并指出属哪—类
解。
max Z 3x1 x2 2x3
x1 x2 x3 6
(1)
st
2x1 2x2
x3 x3 0
2
x j 0（, j 1,,3）
该题是无界解。
page 19 13 April 2021
运筹学教程
同样适合第三版黄皮版
page 1 13 April 2021
1
School of Management
运筹学教程
运筹学教程（第二版）习题解答
安徽大学管理学院
洪文
page 2 13 April 2021
School of Management
运筹学教程
第一章习题解答
1.1 用图解法求解下列线性规划问题。并指出问题具有惟一最优解、无穷多最优解、无界解还是无可行解。
a=3, j=5, k= -1.5
page 23 13 April 2021
23
School of Management
运筹学教程
第一章习题解答
1.9 若X(1)、X(2)均为某线性规划问题的
最优解，证明在这两点连线上的所有点也是
该问题的最优解。 max Z CT X
设X (1)和X (2)满足： AX b
6x2 15x3 x2 x3 5
15
x j 0（, j 1,,3）
该题无可行解。
page 22 13 April 2021
22
School of Management
运筹学教程
第一章习题解答
1.8 已知某线性规划问题的初始单纯形
表和用单纯形法迭代后得到下面表格，试求括
弧中未知项数目a∼l值。X1 X2 X3 X4 X5
x2
x3
x4
0.5 2
0
0
1
1
0 11/5 0
Z 5 5 43/5
11
School of Management
运筹学教程
第一章习题解答
1.4 分别用图解法和单纯形法求解下述
线性规划问题，并对照指出单纯形表中的各基
可行解对应图解法中可行域的哪一顶点。
max Z 10x1 5x2
(1)
st.35xx11
(2)
st
2x1x1 22x2x23xx33
4 x4 2 x4
7 3
x j 0, ( j 1,4)
page 9 13 April 2021
9
School of Management
运筹学教程
第一章习题解答
max Z 3x1 x2 2x3
12x1 3x2 6x3 3x4 9
(1)
x5 x6
14 2
x1, x2 , x3 , x41, x42 , x6 0