三角形全等练习题

合集下载

全等三角形判定练习题

全等三角形判定练习题一、选择题1. 在三角形ABC和三角形DEF中，若AB=DE，AC=DF，BC=EF，那么这两个三角形：A. 相似B. 全等C. 不全等D. 无法确定2. 若三角形ABC的角A等于角D，且AB=DE，AC=DF，但BC不等于EF，这两个三角形：A. 相似B. 全等C. 不相似D. 不全等3. 已知三角形ABC与三角形DEF全等，根据SAS（边-角-边）判定，下列选项正确的是：A. AB=DE，BC=EF，角A=角DB. AB=DE，AC=DF，角B=角EA. AB=DE，角A=角D，角B=角ED. AB=DE，角A=角D，角C=角F二、填空题4. 如果三角形ABC与三角形DEF全等，且角A等于角D，角B等于角E，那么角C等于______。

5. 在三角形ABC中，若AB=AC，角A等于角B，根据______判定，三角形ABC是等腰三角形。

6. 如果三角形ABC的边AB等于三角形DEF的边DE，且角A等于角D，角B等于角E，但角C不等于角F，根据______判定，这两个三角形不全等。

三、解答题7. 已知三角形ABC与三角形DEF全等，且AB=DE，角B=角E，求证AC=DF。

8. 在三角形ABC中，已知AB=AC，角A=角B，求证三角形ABC是等腰三角形。

9. 根据SSS（边-边-边）判定，如果三角形ABC的边AB、AC、BC分别等于三角形DEF的边DE、DF、EF，那么这两个三角形是______。

10. 如果三角形ABC的边AB、AC等于三角形DEF的边DE、DF，但角A不等于角D，角B不等于角E，求证这两个三角形不全等。

四、证明题11. 证明：如果三角形ABC的角A等于角D，角B等于角E，且AB+AC=DE+DF，那么三角形ABC与三角形DEF全等。

12. 已知三角形ABC与三角形DEF全等，且角A等于角D，角B等于角E，证明：角C等于角F。

13. 在三角形ABC中，如果角A等于角B，且AB+BC=AC+BC，证明：三角形ABC是等腰三角形。

全等三角形经典题型50题(含答案)

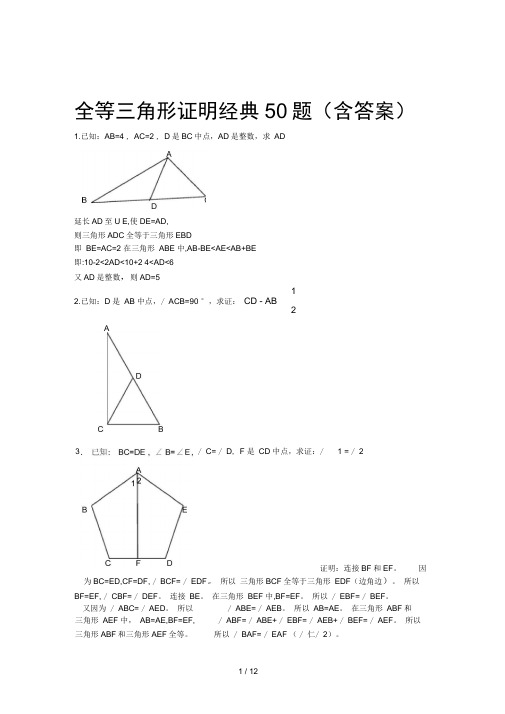
全等三角形证明经典50题（含答案）1.已知：AB=4 , AC=2 , D 是BC 中点，AD 是整数，求 AD延长AD 至U E,使DE=AD, 则三角形ADC 全等于三角形EBD即 BE=AC=2 在三角形 ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数，则AD=512.已知：D 是 AB 中点，/ ACB=90 °，求证： CD - AB2为BC=ED,CF=DF, / BCF= / EDF 。

所以三角形BCF 全等于三角形 EDF （边角边）。

所以BF=EF, / CBF= / DEF 。

连接 BE 。

在三角形 BEF 中,BF=EF 。

所以 / EBF= / BEF 。

/ ABE= / AEB 。

所以 AB=AE 。

在三角形 ABF 和 / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF 。

所以/ C= / D , F 是 CD 中点，求证：/ 1 = / 2证明：连接BF 和EF 。

因又因为 / ABC= / AED 。

所以三角形 AEF 中， AB=AE,BF=EF, 三角形ABF 和三角形AEF 全等。

所以 / BAF= / EAF （ / 仁/ 2）。

A3因为 EB = EF ,CE = CE ，所以△ CEBCEF 所以/ B = / CFE 因为/ B +/ D = 180° / CFE + / CFA = 180° 所以/ D = / CFA 因为 AC 平分/ BAD 所以/ DAC = / FAC 又因为 AC = AC 所以△ ADC 也厶AFC ( SAS ) 所以AD = AF 所以AE = AF + FE = AD + BE12.如图，四边形 ABCD 中，AB // DC ，BE 、CE 分别平分/ ABC 、/ BCD ，且点 E 在AD 上。

全等三角形练习题(很经典)

第十二章全等三角形第Ⅰ卷（选择题共30 分）一、选择题（每小题3分，共30分）1.下列说法正确的是（）A.形状相同的两个三角形全等B.面积相等的两个三角形全等C.完全重合的两个三角形全等D.所有的等边三角形全等2. 如图所示，a,b,c 分别表示△ABC 的三边长，则下面与△ABC 一定全等的三角形是（）3.如图所示，已知△ABE ≌△ACD ，∠1=∠2，∠B=∠C ，下列不正确的等式是（）A.AB=ACB.∠BAE=∠CADC.BE=DCD.AD=DE4. 在△ABC 和△A /B /C /中,AB=A /B /,∠B=∠B /,补充条件后仍不一定能保证△ABC ≌△A /B /C /,则补充的这个条件是( )A ．BC=B /C / B ．∠A=∠A /C ．AC=A /C /D ．∠C=∠C /5.如图所示，点B 、C 、E 在同一条直线上，△ABC 与△CDE 都是等边三角形，则下列结论不一定成立的是（）A.△ACE ≌△BCDB.△BGC ≌△AFCC.△DCG ≌△ECFD.△ADB ≌△CEA6. 要测量河两岸相对的两点A,B 的距离，先在AB 的垂线BF 上取两点C,D ，使CD=BC ，再作出BF 的垂线DE ，使A,C,E 在一条直线上（如图所示），可以说明△EDC ≌△ABC ，得ED=AB ，因此测得ED 的长就是AB的长，判定△EDC ≌△ABC 最恰当的理由是（）A.边角边B.角边角C.边边边D.边边角7.已知：如图所示，AC=CD ，∠B=∠E=90°，AC ⊥CD ，则不正确的结论是（）A ．∠A 与∠D 互为余角B ．∠A=∠2C ．△ABC ≌△CED D ．∠1=∠2第3题第5题第2题图第6题图AB C D第9题图ＣＯＢ，从而可以得到ＡＤ＝．，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一△≌△第19题图CF，求证：△ABC≌△DEF．。

三角形全等专题训练

三角形全等综合练习一1、如图（1）：AD ⊥BC ，垂足为D ，BD=CD 。

求证：△ABD ≌△ACD 。

2、如图（2）：AC ∥EF ，AC=EF ，AE=BD 。

求证：△ABC ≌△EDF 。

3、如图（3）：DF=CE ，AD=BC ，∠D=∠C 。

求证：△AED ≌△BFC 。

4、如图（4）：AB=AC ，AD=AE ，AB ⊥AC ，AD ⊥AE 。

求证：（1）∠B=∠C ，（2）BD=CE5、如图（5）：AB ⊥BD ，ED ⊥BD ，AB=CD ，BC=DE 。

求证：AC ⊥CE 。

6、如图（6）：CG=CF ，BC=DC ，AB=ED ，点A 、B 、C 、D 、E 在同一直线上。

求证：（1）AF=EG ，（2）BF ∥DG 。

（图1）DC B A F E （图2）D C B A FE （图3）D C B A E（图4）D C B A GF E （图6）D C B A E （图5）D B A7、如图（7）：AC ⊥BC ，BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN=BC 。

求证：（1）MN 平分∠AMB ，（2）∠A=∠CBM 。

8、如图（8）：A 、B 、C 、D 四点在同一直线上，AC=DB ，BE ∥CF ，AE ∥DF 。

求证：△ABE ≌△DCF 。

9、如图（9）AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。

求证：AM 是△ABC 的中线。

10、如图（10）∠BAC=∠DAE ，∠ABD=∠ACE ，BD=CE 。

求证：AB=AC 。

11、如图（11）∠1=∠2，∠3=∠4，P 是BC 上任一点。

求证：PA=PD 。

34、如图：AD 是△ABC 中∠BAC 的平分线，过AD 的中点E 作EF ⊥AD 交BC 的延长线于F ，连结AF 。

求证：∠B=∠CAF 。

图12N M （图7）C B A FE （图8）D C B A MF E （图9）C B A E （图10）D C B A P 4321（图11）D B A FE D C B A三角形全等综合练习二13、如图（13）△ABC ≌△EDC 。

全等三角形的判定练习题

全等三角形的判定练习题一、选择题1. 下列哪组条件可以判定两个三角形全等？A. 两边和其中一边的对角相等B. 两角和其中一角的对边相等C. 两边和它们的夹角相等D. 两角和其中一边相等A. ∠A=∠DB. ∠B=∠EC. ∠C=∠FA. SAS（边角边）B. ASA（角边角）C. AAS（角角边）D. SSS（三边）二、填空题1. 若两个三角形的______相等，且它们的夹角相等，则这两个三角形全等。

2. 在全等三角形中，对应边______相等，对应角______相等。

3. 要判定两个三角形全等，至少需要知道它们的______个元素相等。

三、判断题1. 若两个三角形的两边和它们的夹角分别相等，则这两个三角形一定全等。

（）2. 两个等腰三角形的底角相等，则这两个三角形全等。

（）3. 两个等边三角形的边长相等，则这两个三角形全等。

（）四、解答题1. 在△ABC中，AB=AC，∠B=∠C，求证：△ABC是等腰三角形。

2. 已知△ABC和△DEF，AB=DE，BC=EF，∠B=∠E，求证：△ABC≌△DEF。

3. 在△ABC中，AB=AC，∠A=40°，∠B=70°，求∠C的度数。

4. 已知△ABC和△DEF，AB=DE，BC=EF，AC=DF，求证：△ABC≌△DEF。

5. 在△ABC中，AB=8cm，AC=10cm，∠A=60°，求BC的长度。

五、作图题1. 请作出一个三角形，使其与给定三角形全等，已知条件是两边及其夹角。

2. 请作出一个三角形，使其与给定三角形全等，已知条件是两角及其夹边。

3. 请作出一个三角形，使其与给定三角形全等，已知条件是三边。

六、综合题1. 在平面直角坐标系中，点A(2, 3)，点B(6, 3)，点C和点D在x轴上，且△ABC≌△ABD，求点C和点D的坐标。

2. 在四边形ABCD中，AB=CD，AD=BC，且∠ABC=∠CDA=90°，证明：△ABC≌△CDA。

123456全等三角形练习题

全等三角形练习题A 卷姓名____________得分________________一．填空题(每空3分,共36分)1. 已知:如图,△ABC ≌△FED,且BC=DE.则∠A=__________,A D=_______．2. 如图,△ABD ≌△ACE,则AB 的对应边是_________,∠BAD 的对应角是______．3. 已知:如图,△ABE ≌△ACD,∠B=∠C,则∠AEB=_______,AE=________．4．已知：△ABC ≌△A ’B ’C ’， △A ’B ’C ’的周长为12cm ，则△ABC 的周长为 .5．如图, 已知：∠1=∠2 , ∠3=∠4 , 要证BD=CD , 需先证△AEB ≌△A EC , 根据是_________；再证△BDE ≌△______ , 根据是__________．4321EDCBA6．如图，∠1=∠2，由A.A.S 判定△ABD ≌△ACD ，则需添加的条件是____________.A B CD12AA'BCC'7．如图，在平面上将△ABC绕B点旋转到△A’BC’的位置时，AA’∥BC，∠ABC=70°，则∠CBC’为________度.二．选择题(每题4分,共24分)8、下列条件中，不能判定三角形全等的是（）A.三条边对应相等B.两边和一角对应相等C.两角和其中一角的对边对应相等D.两角和它们的夹边对应相等9. 如图,已知:△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是（）A.AB=ACB.∠BAE=∠CADC.BE=DCD.AD=DE10. 如图, AD=AE , AB=AC , BE、CD交于F , 则图中相等的角共有（除去∠DFE=∠BFC）（）A.5对B.4对C.3对D.2对11．如图,OA=OB,OC=OD, ∠O=60°, ∠C=25°则∠BED的度数是( )A.70°B. 85°C. 65°D. 以上都不对CDEABO12．如图, ∠A=∠D , OA=OD , ∠DOC=50°, 求∠DBC的度数为（）A.50°B.30°C.45°D.25°13. 如图, ∠ABC=∠DCB=70°, ∠ABD=40°, AB=DC , 则∠BAC= （）A.70°B.80°C.100°D.90°三．解答题(每题8分，共40分)14. 已知:如图 , 四边形ABCD中 , AB∥CD , AD∥BC．求证：△ABD≌△CDB.15. 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA.连结BC并延长到E,使EC=CB,连结DE,量出DE的长,就是A、B的距离.写出你的证明．16. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC ∥DF．17. 如图,已知: AD是BC上的中线,且DF=DE．求证:BE∥CF．18.如图, 已知：AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF．求证：AC=EF ．答案1.BC 和BC,CD 和CA,BD 和AB2.AB 和AC,AD 和AE,BD 和CE3. ∠F,CF4.AC, ∠CAE5. ∠ADC,AD6.57.128.ASA DEC SAS9. ∠B=∠C10.40℃ 11.B 12.C 13.D 14.D 15.D 16.B 17. A 18.C 19.D 20.B 21.由ASA 可证 22. 因为AC=CD EC=BC ∠ACB=∠ECD 所以 △ABC ≌△CED AB=ED 23.证△ABC ≌△FED 得∠ACB=∠F 所以AC ∥DF 24.证△BED ≌△CFD 得∠E=∠CFD 所以CF ∥BE 25.由AAS 证△ABC ≌△CED AC=EF.FGEDCB A全等三角形练习题 B卷一.填空题：(每空4分1.如图1，AD⊥BC，DB图1图32.如图2，若AB ＝DE ，BE ＝CF ，要证△ABF ≌△DEC ，需补充条件_______或_______.3.如图3，AB=DC ，AD=BC ，E.F 是DB 上两点且BE=DF ，若∠AEB=100°，∠ADB= 30，则∠BCF= .4.如图4，已知AB ∥CD ，AD ∥BC ，E.F 是BD 上两点，且BF ＝DE ，则图中共有对全等三角形.5.如图5，四边形ABCD 的对角线相交于O 点，且有AB ∥DC ，AD ∥BC ，则图中有＿＿＿对全等三角形.6.如图6，AE ＝AF ，AB ＝AC ，∠A ＝60°，∠B ＝24°，则∠BOC ＝__________.7.若△ABC ≌△A ′B ′C ′，AD 和A ′D ′分别是对应边BC 和B ′C ′的高，则△ABD ≌△A ′B ′D ′，理由是_______________.8.在Rt △ABC 中，∠C ＝90°，∠A.∠B 的平分线相交于O ，则∠AOB ＝_________.二.选择题：(每题4分,共16分)9.下列说法正确的是（）图4图5AEB O FC图6A.周长相等的两个三角形全等B.有两边和其中一边的对角对应相等的两个三角形全等C.面积相等的两个三角形全等D.有两角和其中一角的对边对应相等的两个三角形全等 10.下列条件中，能判定△ABC ≌△DEF 的是（） A.AB ＝DE ，BC ＝ED ，∠A ＝∠D B.∠A ＝∠D ，∠C ＝∠F ，AC ＝EF C.∠B ＝∠E ，∠A ＝∠D ，AC ＝EF D.∠B ＝∠E ，∠A ＝∠D ，AB ＝DE11.AD 是△ABC 中BC 边上的中线，若AB ＝4，AC ＝6，则AD 的取值范围是（） A.AD ＞1 B.AD ＜5 C.1＜AD ＜5 D.2＜AD ＜10 12. 在ABC ∆和C B A '''∆中，下列各组条件中，不能保证：C B A ABC '''∆≅∆的是（）① B A AB ''= ② C B BC ''= ③ C A AC ''= ④ A A '∠=∠ ⑤ B B '∠=∠ ⑥ C C '∠=∠ A. 具备①②③ B. 具备①②④ C. 具备③④⑤ D. 具备②③⑥ 三．解答题(共48分)13. 如图△ABN ≌△ACM,∠B 和∠C 是对应角,AB 与AC 是对应边,写出其他对应边和对应角.14. 如图, ∠AOB 是一个任意角,在边OA,OB 上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N 重合,过角尺顶点C 的射线OC 便是∠AOB 的平分线,为什么?15. 如图，已知AB ＝DC ，AC ＝DB ，BE ＝CE,求证：AE ＝DE.16. 如图，已知AC ⊥AB ，DB ⊥AB ，AC ＝BE ，AE ＝BD ，试猜想线段CE 与DE 的大小与位置关系，并证明你的结论.ABECDACEDB17.已知如图，E.F 在BD 上，且AB ＝CD ，BF ＝DE ，AE ＝CF,求证：AC 与BD 互相平分.18. 如图，∠ABC ＝90°，AB ＝BC ，D 为AC 上一点，分别过A.C 作BD 的垂线，垂足分别为E.F,求证：EF ＝CF －AE. 答案1.△ADC2. ∠B=∠C 或AF=DC3.704.27°5.36.37.两个三角形全等8.72°9.HL 10.135° 11.B 12.D 13.A 14.D 15.C 16.A 17.D 18.D 19. 对应边:AB AC,AN,AM,BN,CM 对应角:∠BAN=∠CAM, ∠ANB=∠AMC 20. △AMC ≌△CON 21.先证△ABC ≌△DBC 得∠ABC=∠DCB,再证△ABEABEO FDC≌△CED 22.垂直 23. 先证△ABE≌△DFC得∠B=∠D,再证△ABO≌△COD 24.证△ABF≌△BCF图 5全等三角形练习题 C 卷姓名____________得分________________一.填空题：(每题3分,共36分)1.如图1，若△ABC ≌△ADE ，∠EAC=35°，则∠BAD=_________度.2.如图2，沿AM 折叠，使D 点落在BC 上的N 点处，如果AD=7cm ，DM=5cm ，∠DAM=300，则NM= cm ，∠NAM= .3.如图3，△ABC ≌△AED ，∠C=85°，∠B=30°，则∠EAD= .4.已知：如图4，∠ABC ＝∠DEF ，AB ＝DE ，要说明△ABC ≌△DEF ，（1）若以“SAS ”为依据，还须添加的一个条件为________________. （2）若以“ASA ”为依据，还须添加的一个条件为________________. （3）若以“AAS ”为依据，还须添加的一个条件为________________.5.如图5，在△ABC 中，∠C ＝90°，AD 平分∠BAC ，DE ⊥AB 于E ，则△______≌△_______.ABCDE图1ABCDM N图2DBC= ，FO= .二.选择题(每题4分,共24分)9. 两个三角形只有以下元素对应相等，不能判定两个三角形全等的是（）A. 两角和一边B. 两边及夹角C. 三个角D. 三条边10. 如果两个三角形两边对应相等，且其中一边所对的角也相等，那么这两个三角形（）A. 一定全等B. 一定不全等C. 不一定全等D. 面积相等11. 如图9，已知AB＝DC，AD＝BC，E.F在DB上两点且BF＝DE，若∠AEB＝120°，∠ADB＝30°，则∠BCF= ( )A. 150°B.40°C.80°D. 90°图9 图10 图1112. 如图10，AB ⊥BC ，BE ⊥AC ，∠1=∠2，AD=AB ，则（）A. ∠1=∠EFDB. BE=ECC. BF=DF=CDD. FD ∥BC 13.下列说法正确是（）A . 三边对应平行的两个三角形是全等三角形B . 有一边相等，其余两边对应平行的两个三角形是全等三角形C . 有一边重合，其余两边对应平行的两个三角形是全等三角形 D. 有三个角对应相等的两个三角形是全等三角形14.如图11,已知在△ABC 中,AB=AC,D 为BC 上一点,BF=CD,CE=BD,那么∠EDF 等于( )A..90°－∠AB. 90°－21∠A C. 180°－∠A D. 45°－21∠A 三．解答题(共40分)15．如图，△ABC ≌△ADE ，∠E 和∠C 是对应角，AB 与AD 是对应边，写出另外两组对应边和对应角；ABCDEF12ADBCEF16．如图，A 、E 、F 、C 在一条直线上，△AED ≌△CFB ，你能得出哪些结论？17．如图，已知∠1=∠2，∠3=∠4，AB 与CD 相等吗？请你说明理由..3421DCBA18．如图，AB ∥CD ，AD ∥BC ，那么AD=BC ，AB=BC ，你能说明其中的道理吗？19．如图，已知：E 是∠AOB 的平分线上一点，EC ⊥OB ，ED ⊥OA ，C ，D 是垂足，连接CD ，说明:（1）∠ECD=∠EDC ；（2）OD=OC ；（3）OE 是CD 的中垂线.BFEDCBAC EDBAO答案1.35°2.7,5,30°3.504.BC=EF, ∠ACB=∠F, ∠A=∠D5.ACD,AED6.28°7.58.SAS9.60°,10 10.ED,EF,DF11.B 12.C 13.C 14.A 15.D 16.D 17.C 18.B 19.D 20.B 21.AE 和AC,ED 和BC, ∠B 和∠D, ∠BAC 和∠DAE 22.AD=BC,AE=CF,DE=BF,AD ∥BC, △ACD ≌△ACB,AB ∥CD 等 23.相等, △AOB ≌△DOC 24.连AC,证△ADC ≌△ABC25.(1)证DE=EC (2) 设BE 与CD 交于F,通过全等证DF=CF.。

全等三角形练习题

1/2
9、如图，如果将△ABC 向右平移 CF 的长度，则与△DEF 重合，那么图中相等的线段有 __________；若∠A＝46°，则∠D＝________.
10、已知△ABC≌△ A' B 'C ' ，若△ABC 的面积为 10 cm2 ，则△ A' B 'C ' 的面积为________ cm2 ，若△ A' B 'C ' 的周长为 16 cm ，则△ABC 的周长为________ cm ．
6. 将一张长方形纸片按如图所示的方式折叠，BC、BD 分别为折痕，则∠CBD 的度数为（）
A.60°
B.75°
C.90°
D.95°
二、填空题 7、如图，△ABC≌△AED，AB＝AE，∠1＝27°，则∠2＝___________.
8、已知△DEF≌△ABC，AB＝AC，且△ABC 的周长为 23 cm ， BC＝4 cm ，则△DEF 的边中必有一条边等于______.
C.2 个
D.3 个
4. 如图,△ABE≌△ACD,∠B＝50°,∠AEC＝120°,则∠DAC 的度数等于
（）
A.120° B.70°
C.60°
D.50°
5. 已知△ABC≌△DEF，BC＝EF＝6cm，△ABC 的面积为 18 平方厘米，EF 边上的高是（）
A.6cm
B.7cm
C.8cmD.9cm13、如图，点 B 在线段 AC 上，△ABD≌△EBC，AB=3cm，BC=4.5cm．
（1）求 DE 的长；
D
（2）判断 AC 与 BD 的位置关系，并说明理由．
E
A
B
C
2/2

全等三角形综合练习题含答案

全等三角形的判定（SSS）1、如图1，AB=AD，CB=CD，∠B=30°，∠BAD=46°，则∠ACD的度数是( )°°°°2、如图2，线段AD与BC交于点O，且AC=BD，AD=BC，•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBA =OC D.∠C=∠D3、在△ABC和△A1B1C1中，已知AB=A1B1，BC=B1C1，则补充条件____________，可得到△ABC≌△A1B1C1．4、如图3，AB=CD，BF=DE，E、F是AC上两点，且AE=CF．欲证∠B=∠D，可先运用等式的性质证明AF=________，再用“SSS”证明______≌_______得到结论．5、如图，AB=AC，BD=CD，求证：∠1=∠2．6、如图，已知AB=CD，AC=BD，求证：∠A=∠D．7、如图，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导下列结论：⑴∠D=∠B；⑵AE∥CF．8、已知如图，A、E、F、C四点共线，BF=DE，AB=CD.⑴请你添加一个条件，使△DEC≌△BFA；⑵在⑴的基础上，求证：DE∥BF.全等三角形的判定方法SAS专题练习1.如图，AB=AC，AD=AE，欲证△ABD≌△ACE，可补充条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD2.能判定△ABC≌△A′B′C′的条件是（）A．AB=A′B′，AC=A′C′，∠C=∠C′B. AB=A′B′，∠A=∠A′，BC=B′C′C. AC=A′C′，∠A=∠A′，BC=B′CD. AC=A′C′，∠C=∠C′，BC=B′C3.如图，AB与CD交于点O，OA=OC，OD=OB，∠AOD= ，根据_________可得到△AOD≌△COB，从而可以得到AD=_________．4.如图，已知BD=CD，要根据“SAS”判定△ABD≌△ACD，则还需添加的条件是。

全等三角形练习题含答案.docx

七年级全等测试一•选择题（共3小题）1. 如图，EB交AC于M ,交FC于D, AB交FC于N,∠ E=∠ F=90° ∠ B=∠ C, AE=AF给出下列结论：①∠ 1 = ∠2;②BE=CF③厶ACN^△ ABM:④CD=DN 其中正确的结论有（）£A. 4个B. 3个C. 2个D. 1个2. 如图，△ ABC为等边三角形，D、E分别是AC、BC上的点，且AD=CE AE与BD相交于点P，BF⊥AE于点F.若BP=4则PF的长（）A. 2B. 3C. 1D. 2 二3. 如图，OA=OC OB=OD且OA⊥OB, OC丄OD,下列结论：①△ AOD^△ COB②CD=AB③∠ CDA=Z ABC; 其中正确的结论是（）A.①②B.①②③C.①③D.②③.解答题（共11小题）4. 如图，四边形ABCD中，对角线AC BD交于点O, AB=AC点E是BD上点，且AE=AD ∠ EAD=Z BAC(1 求证：∠ ABD=Z ACD(2)若Z ACB=65,求Z BDC的度数.5. (1)如图①，在四边形ABCD中，AB// DC, E是BC的中点，若AE是Z BAD 的平分线，试探究AB, AD，DC之间的等量关系，证明你的结论；(2)如图②，在四边形ABCD中，AB// DC, AF与DC的延长线交于点F, E是BC的中点，若AE是Z BAF的平分线，试探究AB, AF, CF之间的等量关系，证明你的结论.6 .已知：在△ ABC中，AB=AC D为AC的中点，DE⊥ AB, DF⊥ BC,垂足分别为求证：△ ABC是等边三角形.7. 已知，在△ ABC中，Z A=90°, AB=AC点D为BC的中点.(1)如图①，若点E、F分别为AB、AC上的点，且DE⊥DF,求证：BE=AF(2)若点E、F分别为AB、CA延长线上的点，且DE⊥ DF,那么BE=AF吗？请利用图②说明理由.图①8.如图，在Rt A ABC,∠ ACB=90, AC=BC分别过A、B作直线I的垂线，垂足分别为M、N.(1)求证：△ AMC^A CNB(2)若AM=3, BN=5,求AB的长.9. 已知，如图，在等腰直角三角形中，∠ C=90o, D是AB的中点，DE⊥ DF,点E F 在AC BC上，求证：DE=DF10. 如图，OC是∠ MON内的一条射线，P为OC上一点，PAlOM，PB丄ON，垂足分别为A，B，PA=PB连接AB, AB与OP交于点E.(1)求证：△ OPA^A OPB11. 如图，△ ABC和厶ADE分别是以BC, DE为底边且顶角相等的等腰三角形, 点D 在线段BC上，AF平分DE交BC于点F,连接BE, EF.B(1)CD与BE 相等？若相等，请证明；若不相等，请说明理由;(2) 若∠ BAC=90,求证：BF2+CD^=FC2∙12. 如图，OC是∠ AoB的角平分线，P是OC上一点，PD丄0A, PEI0B,垂足分别为D，E. F是OC上另一点，连接DF，EF.13. 如图，OP平分∠ A0B, PEXOA于E，PF⊥OB于F,点M在OA上，点N在OB 上，且PM=PN.求证：EM=FN14. 如图，△ ABC中，D为BC边上一点，BE⊥AD的延长线于E, CF⊥AD于F, BE=CF求证：D为BC的中点.答案B•选择题（共3小题）1. 如图，EB交AC于M ,交FC于D, AB交FC于N,∠ E=∠ F=90° ∠ B=∠ C, AE=AF给出下列结论：①∠ 1 = ∠2;②BE=CF③厶ACN^△ ABM:④CD=DN 其中正确的结论有（）A. 4个B. 3个C 2个D. 1个【解答】解：τ∠E=∠ F=90o, ∠ B=∠ C, AE=AF •••△ ABE^△ ACF∙∙∙ BE=CF∠ BAE=/ CAF∠ BAE-∠ BAC=Z CAF-∠ BAC∙∙∙∠ 1=∠ 2△ABE^△ ACF∙∙∙∠ B=∠ C, AB=AC又∠ BAC=/ CAB△ACN^△ ABM.④CD=DN不能证明成立，3个结论对.故选：B.2. 如图，△ ABC为等边三角形，D、E分别是AC、BC上的点，且AD=CE AE与BD相交于点P, BF⊥AE于点F.若BP=4则PF的长（）A. 2B. 3 C 1 D. 2 二【解答】解：•••△ ABC是等边三角形,∙∙∙ AB=AC∙∙∙∠ BAC=/ C.在厶ABD和厶CAE中，f AB=AC* ZBAD=ZC,AD=CEI•••△ ABD^△ CAE (SAS .∙∙∙∠ABD=∠ CAE∙∙∙∠APD=Z ABP+∠ PABN BAC=60.∙∙∙∠ BPF=Z APD=60.∙∙∙∠ BFP=90, ∠BPF=60, ∙∙∙∠ PBF=30.∙∙∙ PF= K丄」-故选：A.3. 如图，OA=OC OB=OD且OA⊥OB, OC丄OD,下列结论：①△ AOD^△ COB②CD=AB③∠ CDA=Z ABC; 其中正确的结论是（）A.①②B.①②③C.①③D.②③【解答】解：I OA⊥ OB, OC⊥ OD,∙∠AOB=Z COD=9O.∙∠AOB∏∠ AOC=Z COc+∠ AOC即∠COB Z AOD.在厶AOB和厶COD中，'AO=COZAoB-ZCO D,BO^DOL•••△ AoB^△ COD ( SAS,∙∙∙ AB=CD ∠ ABO=∠ CDO.在厶AOD和厶COB中r AO=CO* ZACD=ZCOB,HO 二BO•••△ AOD^△ COB ( SAS∙∙∙∠ CBO=Z ADO,∙∙∙∠ ABO-∠ CBO=Z CDO-∠ ADO,即∠ ABC=/ CDA综上所述，①②③都是正确的.故选：B.二.解答题(共11小题)4. 如图，四边形ABCD中，对角线AC BD交于点O, AB=AC点E是BD上点，且AE=AD ∠ EAD=Z BAC(1)求证：∠ ABD=∠ ACD(2)若∠ ACB=65 ,求∠ BDC的度数.【解答】证明：(1)v∠ BAC=/ EAD∙∙∙∠BAC-∠ EAC∠ EAD-∠ EAC 即：∠ BAE=/ CADf AB=AC在厶ABE和厶ACD中* ZBAE=ZCADAE=ADI(2)τ∠ BOC是厶ABO和ADCO的外角∙∙∙∠BOC=/ ABD+∠ BAC, ∠ BOC=Z ACD+∠ BDC∙∙∙∠ ABcH-∠ BAC=Z ACcH-∠ BDCτ∠ ABD=∠ ACD∙∙∙∠ BAC=/ BDC∙∙∙∠ ACB=65, AB=AC∙∙∙∠ ABC=/ ACB=65∙∙∙∠BAC=180-∠ ABC-∠ ACB=180-65° - 65°=50°∙∙∙∠ BDC=/ BAC=50.5. (1)如图①，在四边形ABCD中，AB// DC, E是BC的中点，若AE是∠ BAD 的平分线，试探究AB, AD, DC之间的等量关系，证明你的结论；(2)如图②，在四边形ABCD中，AB// DC, AF与DC的延长线交于点F, E是BC的中点，若AE是∠ BAF的平分线，试探究AB, AF, CF之间的等量关系，证明你的结论.V E是BC的中点, ∙∙∙ CE=BEV AB// DC,【解答】解: (1)证明：延长AE交DC的延长线于点F,Br ZBAE=ZF在厶AEB和厶FEC中,ZMB二ZFEC,BE=CEI•••△ AEB^△ FEC∙∙∙ AB=FCV AE是∠ BAD的平分线，∙∙∙∠ BAE=/ EAD,V AB// CD,∙∙∙∠ BAE=/ F,∙∙∙∠ EAD=Z F,∙∙∙ AD=DF.∙. AD=DF=DCCF=D(+AB ,(2)如图②，延长AE交DF的延长线于点G , V E是BC的中点，.CE=BEV AB// DC,.∠ BAE=/ G,在厶AEB和厶GEC中，* Z规B=ZGEC,BE=CEI•••△ AEB^△ GEC.AB=GCV AE是∠ BAF的平分线,.∠ BAG=Z FAGV AB// CD,.∠ BAG=Z G ,图① 圏②∙∙∙∠ FAG=∠ G ,∙∙∙ FA=FG∙∙∙ AB=CG=A+CF,6 .已知：在△ ABC 中，AB=AC D 为AC 的中点，DE ⊥ AB, DF ⊥ BC,垂足分别为点E , F ,且DE=DF 求证：△ ABC 是等边三角形.【解答】证明：T DEXAB, DF ⊥ BC,垂足分别为点E , F ,∙∙∙∠ AED=Z CFD=90,V D 为AC 的中点，∙∙∙ AD=DC在 Rt A ADE 和 Rt A CDF 中，fAD=DCIDE=DF∙∙∙ Rt A ADE ^ Rt A CDF∙∙∙∠ A=∠ C,∙∙∙ BA=BC V AB=AC∙∙∙ AB=BC=AC•••△ ABC 是等边三角形.7. 已知,在厶ABC 中,∠ A=90o ° AB=AC 点D 为BC 的中点.(1) 如图①,若点E 、F 分别为AB 、AC 上的点,且DE ⊥DF ,求证：BE=AF(2) 若点E 、F 分别为AB 、CA 延长线上的点,且 DE ⊥ DF ,那么BE=AF 吗？请【解答】(1)证明：连接AD ,如图①所示.∙∙∙∠ A=90, AB=AC•••△ ABC为等腰直角三角形，∠ EBD=45.•••点D为BC的中点，∙∙∙ ADh BC=BD ∠ FAD=45.2∙∙∙∠BDE∏∠ EDA=90 , ∠ EDA+∠ ADF=90 ,∙∙∙∠ BDE=/ ADF.r ZEBD=ZFAD在△BDE和△ ADF 中,BD=AD ,ZBDE=ZADFL•••△ BDE^△ ADF (ASA ,∙∙∙ BE=AF(2) BE=AF证明如下：连接AD,如图②所示.∙∙∙∠ ABD=∠ BAD=45,∙∙∙∠ EBD=/ FAD=135.∙∙∙∠EDB∏∠ BDF=90, ∠ BDF+∠ FDA=90,∙∙∙∠ EDB=/ FDAr ZEBD=ZFAD在△ EDB和△ FDA 中,BD=AD ,ZEDB=ZFDAI•••△ EDB^△ FDA (ASA),B C图①8. 如图，在Rt A ABC,∠ ACB=90, AC=BC分别过A、B作直线I的垂线，垂足分别为M、N.(1)求证：△ AMC^A CNB(2)若AM=3, BN=5,求AB的长.【解答】解：(1)v AM丄I, BN丄l,∠ ACB=90,∙∙∙∠AMC=∠ ACB=Z BNC=90,∙∙∙∠MAC+∠MCA=90 ,∠MCA+∠NCB=180 - 90°=90°,∙∙∙∠MAC=∠ NCB,在厶AMC和厶CNB中，'Z AJIC=Z BNCZMAC=ZNCB,AC=BCL•••△ AMC^A CNB (AAS；(2)v^ AMC^A CNB,.∙. CM=BN=5∙∙∙Rt△ACM中,AC= 「=,_「=「;：，V Rt A ABC, ∠ACB=90, AC=BC=三,∙AB=I；'= 11 ;=2 ■'.B C9. 已知，如图，在等腰直角三角形中，∠ C=90o, D是AB的中点，DE⊥ DF,点E F 在AC BC上，求证：DE=DF【解答】证明：连接CD.T在等腰直角三角形ABC中，D是AB的中点.∙∙∙ CD为等腰直角三角形ABC斜边BC上的中线.∙∙∙ CD丄AB,∠ ACD=Z BCD=45, CD=BD=AD又V DEX DF∙∙∙∠ EDC∠ FDB在厶ECD^n△ FBD中'Z EDC=Z FDB，CD=BDZECD=ZFBD=45flL•••△ ECD^△ FDB (ASA10. 如图，OC是∠ MON内的一条射线，P为OC上一点，PAlOM, PB丄ON, 垂足分别为A，B，PA=PB连接AB, AB与OP交于点E.(1)求证：△ OPA^A OPB(2)若AB=6,求AE的长.【解答】解：(1)∙∙∙ PA⊥ OM, PB丄0N,∙∙∙∠PAO=∠ PBO=90,又V PA=PB PO=PO∙∙∙ Rt A AOP^ Rt A BoP(2)V A OPA^A OPB∙∙∙∠APE=/ BPE又V PA=PB∙∙∙ AE=BE∙∙∙ AE= AB=3.211. 如图,△ ABC和厶ADE分别是以BC, DE为底边且顶角相等的等腰三角形, 点D 在线段BC上,AF平分DE交BC于点F ,连接BE, EF.(1)CD与BE相等？若相等，请证明；若不相等，请说明理由；(2)若∠ BAC=90 ,求证：Bh+CD2=FD2∙【解答】解：（1）CD=BE理由如下:VA ABC和厶ADE为等腰三角形,∙∙∙ AB=AC AD=AEV∠ EAD=Z BAC∙∙∙∠EAD-∠ BAD=/ BAC-∠ BAD,即∠ EAB=∠ CAD,r AE=AD在厶EAB与厶CAD 中ZEAB=ZCAD,AB=ACI•••△ EAB^△ CAD,∙∙∙ BE=CD(2)τ∠BAC=90,•••△ ABC和厶ADE都是等腰直角三角形，∙∙∙∠ABF=Z C=45,•••△ EAB^△ CAD,∙∙∙∠EBA=/ C ,∙∙∙∠EBA=45 ,∙∙∙∠EBF=90,在Rt A BFE中,BF2+BE Z=ElF ,V AF平分DE ,∙∙∙ AF垂直平分DE,∙∙∙ EF=FD由(1)可知,BE=CD∙∙∙ BF2+CD2=FD212. 如图,OC是∠ AOB的角平分线,P是OC上一点,PD丄OA, PElOB,垂足分别为D , E. F是OC上另一点，连接DF, EF.求证：DF=EF【解答】证明：V OC是∠ AOB的角平分线,P是OC上一点,PD丄OA, PEl OB , ∙∙∙∠DOP=Z EOP PD=PE在 Rt A PoD 和 Rt A PoE 中，严二PE ,L OP=OP∙∙∙ Rt A POD ^ Rt A POE ( HL ),∙∙∙ OD=OEOD-OE在A ODF 和A OEF 中,ZmF=ZEOF ,L OF=OF•••△ ODF ^ A OEF (SAS ,∙∙∙ DF=EF13. 如图，OP 平分∠ AOB, PEXOA 于E , PF ⊥OB 于F ,点M 在OA 上，点N 在 OB 上，且 PM=PN .求证：EM=FN 【解答】证明： B•••点P 在∠ AOB 的平分线上，PE 丄0A 于E , PF 丄OB 于F ,∙∙∙ PF=PE在 Rt A PEM 和 Rt A PEN 中r PH-PN,(PE-PF ∙∙∙ Rt A PEM B Rt A PEN ( HL ), ∙∙∙ EM=FN14. 如图，△ ABC 中，D 为BC 边上一点，BE ⊥AD 的延长线于E, CF ⊥AD 于F , BE=CF 求证：D 为BC 的中点.【解答】证明：TBEIAD 的延长线于E , CFL AD 于F ,∙∙∙∠ CFD=∠ BED=90,r ZCFD=Z BED= 90β 在△BED和△ CFD中，ZCDF=ZBDEHE 二CF•••△ CDF^△ BDE (AAS∙∙∙ CD=BD∙∙∙ D为BC的中点.。

全等三角形综合练习题含答案

11.2 全等三角形的判定（SSS）1、如图1，AB=AD，CB=CD，∠B=30°，∠BAD=46°，则∠ACD的度数是( )A.120°B.125°C.127°D.104°2、如图2，线段AD与BC交于点O，且AC=BD，AD=BC，•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中，已知AB=A1B1，BC=B1C1，则补充条件____________，可得到△ABC≌△A1B1C1．4、如图3，AB=CD，BF=DE，E、F是AC上两点，且AE=CF．欲证∠B=∠D，可先运用等式的性质证明AF=________，再用“SSS”证明______≌_______得到结论．5、如图，AB=AC，BD=CD，求证：∠1=∠2．6、如图，已知AB=CD，AC=BD，求证：∠A=∠D．7、如图，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导下列结论：⑴∠D=∠B；⑵AE∥CF．8、已知如图，A、E、F、C四点共线，BF=DE，AB=CD.⑴请你添加一个条件，使△DEC≌△BFA；⑵在⑴的基础上，求证：DE∥BF.全等三角形的判定方法SAS 专题练习1.如图，AB=AC ，AD=AE ，欲证△ABD ≌△ACE ，可补充条件( ) A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD2.能判定△ABC ≌△A ′B ′C ′的条件是（） A ．AB=A ′B ′，AC=A ′C ′，∠C=∠C ′ B. AB=A ′B ′， ∠A=∠A ′，BC=B ′C ′ C. AC=A ′C ′， ∠A=∠A ′，BC=B ′C D. AC=A ′C ′， ∠C=∠C ′，BC=B ′C3.如图，AB 与CD 交于点O ，OA=OC ，OD=OB ，∠AOD= ，根据_________可得到△AOD ≌△COB ，从而可以得到AD=_________．4.如图，已知BD=CD ，要根据“SAS”判定△ABD ≌△ACD ，则还需添加的条件是。

全等三角形经典例题(含答案)

三角形全等典型例题集锦（含答案）一、选择题（本大题共13小题，共39.0分）1.如图，在△ABC中，∠C=90°，AD平分∠BAC交BC于点D，DE⊥AB于点E，如果BC=27，BD：CD=2：1，则DE的长是()A. 2B. 9C. 18D. 27【答案】B由“AAS”可证△ACD≌△AED，可得CD=DE=9．本题考查了全等三角形的判定和性质，角平分线的性质，证明△ACD≌△AED是本题的关键．解：∵BC=27，BD：CD=2：1，∴BD=18，CD=9，∵AD平分∠BAC，∴∠DAC=∠DAE，且AD=AD，∠DCA=∠DEA= 90°，∴△ACD≌△AED(AAS)∴CD=DE=9，故选B．2.如图，已知∠ABC=∠DCB，添加下列条件，不能使△ABC≌△DCB的是()A. AC=DBB. AB=DCC. ∠A=∠DD. ∠1=∠2【答案】A【解析】A.当添加AC=DB时，不能判定△ABC≌△DCB，故本选项符合题意;B.当添加AB=DC时，能判定△ABC≌△DCB，故本选项不符合题意;C.当添加∠A=∠D时，能判定△ABC≌△DCB，故本选项不符合题意;D.当添加∠2=∠1时，能判定△ABC≌△DCB，故本选项不符合题意，故选A．如图，下列三角形中，与△ABC全等的是()A. B. C. D.【答案】C3.如图，已知△ABC三条边、三个角，则甲、乙两个三角形中，与△ABC全等的图形是()A. 甲B. 乙C. 甲和乙D. 都不是【答案】C4.如图，∠ACB=90∘，AC=BC，BE⊥CE于E点，AD⊥CE于D点，AD=2.5cm，DE=1.7cm，则BE的长为()A. 0.8cmB. 1cmC. 1.5cmD. 4.2cm【答案】A【解析】∵BE⊥CE，AD⊥CE，∴∠E=∠ADC=90∘，∴∠EBC+∠BCE=90∘．∵∠BCE+∠DCA=∠ACB=90∘，∴∠EBC=∠DCA．在△CEB和△ADC中，{∠E=∠ADC,∠EBC=∠DCA, BC=CA,∴△CEB≌△ADC(AAS)，∴BE=DC，CE=AD=2.5cm．∵DC=CE−DE，DE=1.7cm，∴DC=2.5−1.7=0.8cm，∴BE=0.8cm，故选A．5.两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积为12AC⋅BD.其中正确的结论有()A. 0个B. 1个C. 2个D. 3个【答案】D如图，已知AB=AC，AD=AE，欲说明△ABD≌△ACE，需补充的条件是()A. ∠B=∠CB. ∠D=∠EC. ∠1=∠2D. ∠CAD=∠2【答案】C6.下列三角形中全等的两个是()A. ①②B. ②③C. ③④D. ①④【答案】A如图，D是AB上一点，DF交AC于点E，DE=FE，FC//AB.若AB=4，CF=3，则BD的长是()A. 0.5B. 1C. 1.5D. 2【答案】B7.如图，在△AOB和△COD中，OA=OB，OC=OD，OA<OC，∠AOB=∠COD=36°.连接AC，BD交于点M，连接OM.下列结论：①∠AMB=36°，②AC=BD，③OM 平分∠AOD，④MO平分∠AMD.其中正确的结论个数有()个．A. 4B. 3C. 2D. 1【答案】B【解析】解：∵∠AOB=∠COD=36°，∴∠AOB+∠BOC=∠COD+∠BOC，即∠AOC=∠BOD，在△AOC和△BOD中， {OA=OB∠AOC=∠BOD OC=OD∴△AOC≌△BOD(SAS)，∴∠OCA=∠ODB，AC=BD，故②正确；∵∠OCA=∠ODB，由三角形的外角性质得：∠CMD+∠OCA=∠COD+∠ODB，得出∠CMD=∠COD=36°，∠AMB=∠CMD=36°，故①正确；作OG⊥AM于G，OH⊥DM于H，如图所示则∠OGA=∠OHB=90°，在△OGA和△OHB中，∵{∠OGA=∠OHB=90°∠OAG=∠OBHOA=OB，∴△OGA≌△OHB(AAS)∴OG=OH，∴OM平分∠AMD，故④正确；假设OM平分∠AOD，则∠DOM=∠AOM，在△AMO与△DMO中，{∠AOM=∠DOMOM=OM∠AMD=∠DMO∴△AMO≌△OMD(ASA)，∴AO=OD，∵OC=OD，∴OA=OC，而OA<OC，故③错误；正确的个数有3个；故选：B．由SAS证明△AOC≌△BOD得出∠OCA=∠ODB，AC=BD，②正确；由全等三角形的性质得出∠OCA=∠ODB，由三角形的外角性质得：∠CMD+∠OCA=∠COD+∠ODB，得出∠CMD=∠COD=36°，∠AMB=∠CMD=36°，①正确；作OG⊥AM于G，OH⊥DM于H，如图所示：则∠OGA=∠OHB=90°，由AAS证明△OGA≌△OHB(AAS)，得出OG=OH，由角平分线的判定方法得出OM平分∠AMD，④正确；假设OM平分∠AOD，则∠DOM=∠AOM，由全等三角形的判定定理可得△AMO≌△OMD，得AO=OD，而OC=OD，所以OA=OC，而OA< OC，故③错误；即可得出结论．本题考查了全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识；证明三角形全等是解题的关键．8.尺规作图作角的平分线，作法步骤如下：9.①以点O为圆心，任意长为半径画弧，交OA、OB于C、D两点；②分别以C、D为圆心，大于12CD长为半径画弧，两弧交于点P；③过点P作射线OP，射线OP即为所求．则上述作法的依据是()．A. SSSB. SASC. AASD. ASA【答案】A本题考查了全等三角形的判定与性质、角平分线的尺规作图方法与作图原理，解题的关键是要理解作图过程中每一步的效果，即：OC=OD，CP=DP，OP=OP.连接CP、DP，由作图可证△OCP≌△ODP，则∠COP=∠DOP，而证明△OCP≌△ODP的条件就是作图的依据．【解答】解：如下图④所示：连接CP、DP在△OCP与△ODP中，由作图可知：{OC=ODCP=DPOP=OP∴△OCP≌△ODP(SSS)，∴∠COP=∠DOP，即OP是∠AOB的平分线．因此题中作法的依据是SSS．故选A．10.图中的小正方形边长都相等，若△MNP≌△MFQ，则点Q可能是图中的()A. 点DB. 点CC. 点BD. 点A【答案】A【解析】解：观察图象可知△MNP≌△MFD．故选：A．根据全等三角形的判定即可解决问题．本题考查全等三角形的判定，解题的关键是熟练掌握基本知识，属于中考常考题型．11.如图，AD//BC，点E是线段AB的中点，DE平分∠ADC，BC=AD+2，CD=7，则BC2−AD2的值等于()A. 14B. 9C. 8D. 5【答案】A延长CB和DE交于点F，∵AD//BC∴∠DAE=∠FBE∵点E是线段AB的中点，∴AE=BE∠AED=∠BEF∴△ADE≌△BFE(ASA∴∠ADE=∠BFE，AD =BF ∵DE 平分∠ADC ，∴∠ADE =∠CDE ∴∠CDE =∠BFE ∴CD =CF ∴BC +BF =BC +AD =CD =7∵BC =AD +2，∴解得BC =92，AD =52∴BC 2−AD 2=(92)2−(52)2=14．或者：∵BC +AD =7BC −AD =2∴BC 2−AD 2=(BC +AD)(BC −AD)=7×2=14．故选：A ．可以延长CB 和DE 交于点F ，证明△ADE≌△BFE(ASA)得∠ADE =∠BFE ，AD =BF ，再根据已知条件DE 平分∠ADC ，得∠ADE =∠CDE ，∠CDE =∠BFE ，得CD =CF ，进而得BC +BF =BC +AD =CD =7BC =AD +2，即可求解．本题考查了全等三角形的判定和性质，解决本题的关键是构造适当的辅助线．二、填空题（本大题共7小题，共21.0分）12. 如图，∠AOB 是任意一个角，在OA ，OB 边上分别取OM =ON ，移动角尺，使角尺两边相同的刻度分别与M ，N 重合，过角尺顶点C 的射线OC 便是∠AOB 平分线，此作法用的判定三角形全等的方法是 .(用字母表示即可)【答案】SSS【解析】略 13. 如图，在△ABC 中，AD ⊥BC ，CE ⊥AB ，垂足分别为D ，E ，AD ，CE 交于点H ，已知EH =EB =3，AE =4，则CH 的长是．14.【答案】1【解析】略15. 如图为6个边长相等的正方形的组合图形，则∠1−∠2+∠3= ．16.【答案】45°【解析】略17. 如图，△ABC 三个内角的平分线交于点O ，点D 在CA 的延长线上，且DC =BC.若∠D =20°，则∠ABC 的度数为．18.【答案】40°【解析】略19. 已知等边三角形的三条边，三个内角都相等．如图，△ABC 为等边三角形，点D ，E ，F 分别在边BC ，CA ，AB 上，且AE =CD =BF ，则△DEF 的形状按边分类为三角形． 20.【答案】等边【解析】略21. 如图，△ABC ，∠ABC =45°，∠ACB =30°，点D 在BC 上，点E 在△ABC 外，且AD =AE =CE ，AD ⊥AE ，则AB BD =______．【答案】√6+√22【解析】解：作DF ⊥AB 于点F ，作DG ⊥AC 于点G ，作EH ⊥AC 于点H ，∵∠ACB =30°，DG ⊥AC ，∴CD =2DG ，∵AE =CE ，EH ⊥AC ，∴AH =CH ，∴AC =2AH ，∵AD ⊥AE ，DG ⊥AC ，EH ⊥AC ，∴∠DAE =90°，∠DGA =∠AHE =90°，∴∠DAG +∠EAH =90°，∠EAH +∠AEH =90°，∴∠DAG =∠AEH ，在△DAG 和△AEH 中{∠DGA =∠AHE ∠DAG =∠AEH DA =AE∴△DAG≌△AEH(AAS)∴DG =AH ，∴AC =2DG ，∴AC =CD ，∴∠CAD =∠CDA ，∵∠ACB =30°，∵∠ABC=45°，∠ACB=30°，∴∠BAC=180°−∠ABC−∠ACB=105°，∴∠DAE=∠BAC−∠CAD=105°−75°=30°，∵DF⊥AB，∴∠DFA=∠DFB=90°，又∵∠B=45°，∠BAD=30°，∴AD=2DF，BF=DF，∴AF=√AD2−DF2=√3DF，BD=√BF2+DF2=√2DF，∴AB=AF+BF=√3DF+DF，∴ABBD =√3DF+DF√2DF=√6+√22，故答案为：√6+√22．作DF⊥AB于点F，作DG⊥AC于点G，作EH⊥AC于点H，然后根据直角三角形的性质和全等三角形的判定，利用勾股定理可以求得AB和BD与DF的关系，然后即可求得ABBD的值．本题考查全等三角形的判定与性质、等腰三角形的性质、勾股定理，解答本题的关键是明确题意，利用数形结合的思想解答．22.如图，AB=6cm，AC=BD=4cm，∠CAB=∠DAB=60°，点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动。

全等三角形练习题(含答案)

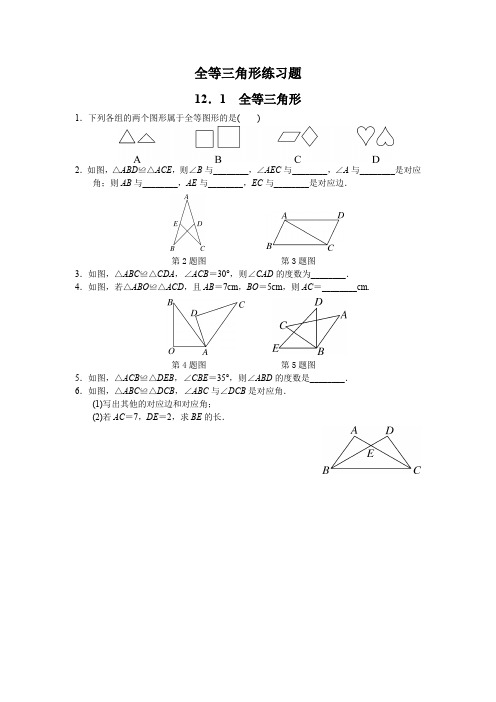
全等三角形练习题12．1全等三角形1．下列各组的两个图形属于全等图形的是()2．如图，△ABD≌△ACE，则∠B与________，∠AEC与________，∠A与________是对应角；则AB与________，AE与________，EC与________是对应边．第2题图第3题图3．如图，△ABC≌△CDA，∠ACB＝30°，则∠CAD的度数为________．4．如图，若△ABO≌△ACD，且AB＝7cm，BO＝5cm，则AC＝________cm.第4题图第5题图5．如图，△ACB≌△DEB，∠CBE＝35°，则∠ABD的度数是________．6．如图，△ABC≌△DCB，∠ABC与∠DCB是对应角．(1)写出其他的对应边和对应角；(2)若AC＝7，DE＝2，求BE的长．12．2三角形全等的判定第1课时“边边边”1．如图，下列三角形中，与△ABC全等的是()A．①B．②C．③D．④2．如图，已知AB＝AD，CB＝CD，∠B＝30°，则∠D的度数是()A．30° B．60° C．20° D．50°第2题图第3题图3．如图，AB＝DC，请补充一个条件：________，使其能由“SSS”判定△ABC≌△DCB. 4．如图，A，C，F，D在同一直线上，AF＝DC，AB＝DE，BC＝EF.求证：△ABC≌△DEF.5．如图，AB＝AC，AD＝AE，BD＝CE.求证：∠ADE＝∠AED.第2课时“边角边”1．如图，已知点F、E分别在AB、AC上，且AE＝AF，请你补充一个条件：________，使其能直接由“SAS”判定△ABE≌△ACF.第1题图第2题图2．如图，将两根钢条AA′、BB′的中点O连在一起，使AA′、BB′能绕着点O自由转动，就做成了一个测量工具，由三角形全等可知A′B′的长等于内槽宽AB，那么判定△OAB≌△OA′B′的理由是________．3．如图，AB＝AD，∠1＝∠2，AC＝AE. 求证：△ABC≌△ADE.4．如图，AE∥DF，AE＝DF，AB＝CD.求证：(1)△AEC≌△DFB；(2)CE∥BF.第3课时“角边角”“角角边”1．如图，已知∠1＝∠2，∠B＝∠C，若直接推得△ABD≌△ACD，则其根据是() A．SAS B．SSS C．ASA D．AAS第1题图第2题图2．如图，在△ABD与△ACD中，已知∠CAD＝∠BAD，在不添加任何辅助线的前提下，直接由“ASA”证明△ABD≌△ACD，需再添加一个条件，正确的是()A．∠B＝∠C B．∠CDA＝∠BDAC．AB＝AC D．BD＝CD3．如图，已知MA∥NC，MB∥ND，且MB＝ND.求证：△MAB≌△NCD.4．如图，在△ABC中，AD是BC边上的中线，E，F为直线AD上的两点，连接BE，CF，且BE∥CF.求证：(1)△CDF≌△BDE；(2)DE＝DF.第4课时“斜边、直角边”1．如图，∠BAD＝∠BCD＝90°，AB＝CB，可以证明△BAD≌△BCD的理由是() A．HL B．ASA C．SAS D．AAS第1题图第2题图2．如图，在Rt△ABC与Rt△DCB中，∠A＝∠D＝90°，请你添加一个条件(不添加字母和辅助线)，使Rt△ABC≌Rt△DCB，你添加的条件是________．3．如图，在△ABC中，AB＝CB，∠ABC＝90°，F为AB延长线上一点，点E在BC上，且AE＝CF.求证：∠AEB＝∠F.4．如图，点C，E，B，F在一条直线上，AB⊥CF于B，DE⊥CF于E，AC＝DF，AB＝DE.求证：CE＝BF.12．3 角的平分线的性质第1课时角平分线的性质1．如图，在Rt △ACB 中，∠C ＝90°，AD 平分∠BAC ，DE ⊥AB 于点E .若CD ＝6，则DE 的长为( )A ．9B ．8C ．7D ．6第1题图第2题图2．如图，在△ABC 中，∠C ＝90°，按以下步骤作图：①以点B 为圆心，以小于BC 的长为半径画弧，分别交AB ，BC 于点E ，F ；②分别以点E ，F 为圆心，以大于12EF 的长为半径画弧，两弧相交于点G ；③作射线BG ，交AC 边于点D .若CD ＝4，则点D 到斜边AB 的距离为________.3．如图，Rt △ABC 中，∠C ＝90°，AD 平分∠BAC ，交BC 于点D ，AB ＝10，S △ABD ＝15，求CD 的长．4．如图，CD ⊥AB 于点D ，BE ⊥AC 于点E ，BE ，CD 相交于点O ，且AO 平分∠BAC .求证：OB ＝OC .第2课时角平分线的判定1．如图，DE⊥AB于点E，DF⊥BC于点F，且DE＝DF.若∠DBC＝50°，则∠ABC的度数为()A．50° B．100° C．150° D．200°第1题图第3题图2．在三角形内部，到三角形的三边距离都相等的点是()A．三角形三条高的交点B．三角形三条角平分线的交点C．三角形三条中线的交点D．以上均不对3．如图，∠ABC＋∠BCD＝180°，点P到AB，BC，CD的距离都相等，则∠PBC＋∠PCB 的度数为________.4．如图，P是∠BAC内的一点，PE⊥AB，PF⊥AC，垂足分别为E，F，AE＝AF.求证：(1)PE＝PF；(2)AP平分∠BAC.5．如图，B是∠CAF内的一点，点D在AC上，点E在AF上，且DC＝EF，△BCD与△BEF的面积相等．求证：AB平分∠CAF.第十二章全等三角形 12．1 全等三角形1．D 2.∠C ∠ADB ∠A AC AD DB 3．30° 4.7 5.35°6．解：(1)对应边：AB 与DC ，AC 与DB ，BC 与CB .对应角：∠A 与∠D ，∠ACB 与∠DBC .(2)由(1)可知DB ＝AC ＝7，∴BE ＝BD －DE ＝7－2＝5.12．2 三角形全等的判定第1课时 “边边边”1．C 2.A 3.AC ＝BD4．证明：∵AF ＝DC ，∴AF －CF ＝DC －CF ，即AC ＝DF .在△ABC 和△DEF 中，⎩⎪⎨⎪⎧AC ＝DF ，AB ＝DE ，BC ＝EF ，∴△ABC ≌△DEF (SSS)．5．证明：在△ABD 与△ACE 中，⎩⎪⎨⎪⎧AB ＝AC ，AD ＝AE ，BD ＝CE ，∴△ABD ≌△ACE (SSS)，∴∠ADB ＝∠AEC .∵∠ADB ＋∠ADE ＝180°，∠AEC ＋∠AED ＝180°，∴∠ADE ＝∠AED .第2课时 “边角边”1．AB ＝AC 2.SAS3．证明：∵∠1＝∠2，∴∠BAC ＝∠DAE .在△ABC 与△ADE 中，∵⎩⎪⎨⎪⎧AB ＝AD ，∠BAC ＝∠DAE ，AC ＝AE ，∴△ABC ≌△ADE (SAS)．4．证明：(1)∵AE ∥DF ，∴∠A ＝∠D .∵AB ＝CD ，∴AC ＝DB .在△AEC 与△DFB 中，⎩⎪⎨⎪⎧AE ＝DF ，∠A ＝∠D ，AC ＝DB ，∴△AEC ≌△DFB (SAS)． (2)由(1)知△AEC ≌△DFB ，∴∠ECA ＝∠FBD ，∴CE ∥BF .第3课时 “角边角”“角角边”1．D 2.B3．证明：∵MB ∥ND ，∴∠MBA ＝∠D .∵MA ∥NC ，∴∠A ＝∠NCD .在△MAB 与△NCD 中，⎩⎪⎨⎪⎧∠MBA ＝∠D ，∠A ＝∠NCD ，MB ＝ND ，∴△MAB ≌△NCD (AAS)． 4．证明：(1)∵AD 是△ABC 的中线，∴BD ＝CD .∵BE ∥CF ，∴∠FCD ＝∠EBD .在△CDF 和△BDE 中，⎩⎪⎨⎪⎧ ∠FCD ＝∠EBD ，CD ＝BD ，∠CDF ＝∠BDE ，∴△CDF ≌△BDE (ASA)．(2)由(1)知△CDF ≌△BDE ，∴DF ＝DE .第4课时 “斜边、直角边”1．A 2.AB ＝DB (答案不唯一)3．证明：∵∠ABC ＝90°，∴∠CBF ＝90°.在Rt △ABE 和Rt △CBF 中， ∵⎩⎪⎨⎪⎧AE ＝CF ，AB ＝CB ，∴Rt △ABE ≌Rt △CBF (HL)．∴∠AEB ＝∠F .4．证明：∵AB ⊥CF ，DE ⊥CF ，∴∠ABC ＝∠DEF ＝90°.在Rt △ABC 和Rt △DEF 中，⎩⎪⎨⎪⎧AC ＝DF ，AB ＝DE ，∴Rt △ABC ≌Rt △DEF (HL)，∴BC ＝EF ，∴BC －BE ＝EF －BE ，即CE ＝BF . 12．3 角的平分线的性质第1课时角平分线的性质1．D 2.43．解：∵S △ABD ＝15，AB ＝10，∴点D 到AB 的距离h ＝2×1510＝3.∵AD 平分∠BAC ，∠C ＝90°，∴DC ＝h ＝3. 4．证明：∵CD ⊥AB ，BE ⊥AC ，AO 平分∠BAC ，∴OD ＝OE ，∠ODB ＝∠OEC ＝90°.在△DOB与△EOC 中，⎩⎪⎨⎪⎧∠DOB ＝∠EOC ，OD ＝OE ，∠ODB ＝∠OEC ，∴△DOB ≌△EOC (ASA)，∴OB ＝OC .第2课时角平分线的判定1．B 2.B 3.90°4．证明：(1)∵PE ⊥AB ，PF ⊥AC ，∴∠AEP ＝∠AFP ＝90°.在Rt △AEP 和Rt △AFP 中，⎩⎪⎨⎪⎧AP ＝AP ，AE ＝AF ，∴Rt △AEP ≌Rt △AFP (HL)，∴PE ＝PF .(2)∵PE⊥AB，PF⊥AC，PE＝PF，∴点P在∠BAC的平分线上，故AP平分∠BAC. 5．证明：∵DC＝EF，△DCB和△EFB的面积相等，∴点B到AC，AF的距离相等，∴AB 平分∠CAF.。

三角形全等aasasa练习题

三角形全等AAS/ASA练习题一．解答题（共14小题）1．如图，AC＝AE，∠C＝∠E，∠1＝∠2．求证：△ABC≌△ADE．2．已知，如图，AB＝AE，AB∥DE，∠ECB＝70°，∠D＝110°，求证：△ABC≌△EAD．3．如图，D是AB上一点，DF交AC于点E，DE＝FE，FC∥AB，求证：△ADE≌△CFE．4．如图，∠A＝∠B，AE＝BE，点D在AC 边上，∠1＝∠2，AE和BD相交于点O．求证：△AEC≌△BED．5．如图，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，垂足分别为D，E．求证：△ACD≌△CBE．6．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，过C点作直线l，点D，E在直线l上，连接AD，BE，∠ADC＝∠CEB ＝90°．求证：△ADC≌△CEB．7．已知：如图，点A、E、F、C在同一条直线上，AD∥CB，∠1＝∠2，AE＝CF．求证：△ADF≌△CBE．8．已知AB∥DE，BC∥EF，D，C在AF上，且AD＝CF，求证：△ABC≌△DEF．9．如图，AB＝AD，∠C＝∠E，∠1＝∠2，求证：△ABC≌△ADE．10．如图，AB＝AE，∠1＝∠2，∠C＝∠D．求证：△ABC≌△AED．12．如图（1），AB＝7cm，AC⊥AB，BD⊥AB垂足分别为A、B，AC＝5cm．点P在线段AB上以2cm/s的速度由点A向点B运动，同时，点Q在射线BD上运动．它们运动的时间为t（s）（当点P运动结束时，点Q运动随之结束）．（1）若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ是否全等，并判断此时线段PC和线段PQ的位置关系，请分别说明理由；（2）如图（2），若“AC⊥AB，BD⊥AB”改为“∠CAB＝∠DBA＝60°”，点Q的运动速度为xcm/s，其他条件不变，当点P、Q运动到某处时，有△ACP与△BPQ全等，求出相应的x、t的值．13．如图，△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，点P从A点出发沿A﹣C路径向终点C运动；点Q从B点出发沿B﹣C﹣A路径向终点A运动．点P和Q分别以每秒1cm和3cm的运动速度同时开始运动，其中一点到达终点时另一点也停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．则点P运动时间为多少时，△PEC与△QFC全等？14．如图1，在长方形ABCD中，AB＝CD＝6cm，BC＝10cm，点P从点B出发，以2cm/s 的速度沿BC向点C运动，设点P的运动时间为t秒，且t≤5．（1）PC＝cm（用含t的代数式表示）．（2）如图2，当点P从点B开始运动的同时，点Q从点C出发，以vcm/s的速度沿CD 向点D运动，是否存在这样的v值，使得以A、B、P为顶点的三角形与以P、Q、C为顶点的三角形全等？若存在，请求出v的值；若不存在，请说明理由．三角形全等AAS/ASA练习题参考答案一．解答题（共14小题）1．；2．；3．；4．；5．；6．；7．；8．；9．；10．；11．；12．；13．；14．（10﹣2t）；。

三角形全等的练习题

三角形全等的练习题一、选择题1. 在三角形ABC中，若AB=AC，且∠BAC=80°，则∠B的度数是：A. 50°B. 80°C. 100°D. 40°2. 已知两个三角形的三边对应相等，这两个三角形：A. 一定相似B. 一定全等C. 可能全等D. 可能相似3. 若三角形的两边及其夹角与另一个三角形的两边及其夹角相等，则这两个三角形：A. 一定全等B. 一定相似C. 不一定全等D. 不一定相似4. 根据SSS（边边边）全等条件，下列哪组三角形全等：A. △ABC和△DEF，AB=DE，BC=EF，AC=DFB. △ABC和△DEF，AB=DE，∠B=∠D，AC=DFC. △ABC和△DEF，AB=DE，∠A=∠D，BC=EFD. △ABC和△DEF，∠A=∠D，∠B=∠E，∠C=∠F5. 如果两个三角形的两组对应边分别相等，且它们的夹角不相等，那么这两个三角形：A. 全等B. 相似C. 不全等D. 不相似二、填空题6. 在三角形ABC中，如果AB=AC，BC=BD，且∠ABC=∠CBD=60°，则三角形ABC是________。

7. 根据AAS（角角边）全等条件，如果两个三角形的两个角和它们之间的一边对应相等，那么这两个三角形________。

8. 如果三角形ABC的边长分别为AB=5，AC=7，BC=6，那么三角形ABC 是________。

9. 在三角形ABC中，如果∠A=90°，AB=3，AC=4，那么BC的长度是________。

10. 如果两个三角形的对应角相等，且它们的对应边的比相等，那么这两个三角形________。

三、简答题11. 解释ASA（角边角）全等条件，并给出一个例子。

12. 如果两个三角形的一边和这条边的两个相邻角对应相等，这两个三角形是否全等？为什么？13. 描述SAS（边角边）全等条件，并给出一个应用场景。

全等三角形专项练习及答案

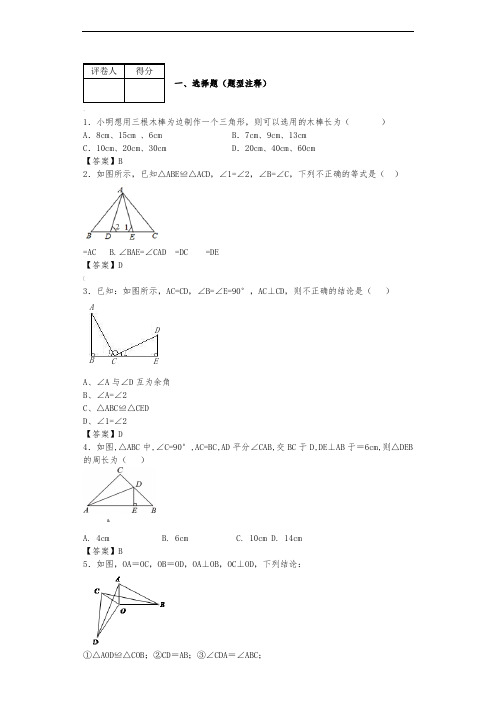
评卷人得分一、选择题（题型注释）、1．小明想用三根木棒为边制作一个三角形，则可以选用的木棒长为（）A．8cm、15cm 、6cm B．7cm、9cm、13cmC．10cm、20cm、30cm D．20cm、40cm、60cm【答案】B2．如图所示，已知△ABE≌△ACD，∠1=∠2，∠B=∠C，下列不正确的等式是（）=AC B.∠BAE=∠CAD =DC =DE【答案】D[3．已知：如图所示，AC=CD，∠B=∠E=90°，AC⊥CD，则不正确的结论是（）A、∠A与∠D互为余角B、∠A=∠2C、△ABC≌△CEDD、∠1=∠2【答案】D4．如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于＝6cm,则△DEB 的周长为（）A. 4cmB. 6cmC. 10cmD. 14cm【答案】B5．如图，OA＝OC，OB＝OD，OA⊥OB，OC⊥OD，下列结论：①△AOD≌△COB；②CD＝AB；③∠CDA＝∠ABC；&AB CDE1]其中正确的结论是( )A．①② B．①②③ C．①③ D．②③》【答案】B【解析】试题分析：因为OA＝OC，OB＝OD，OA⊥OB，OC⊥OD，可得△COD≌△AOB, ∠CDO＝∠ABO；∠DOC+∠AOC=∠AOB+∠AOC, OA＝OC，OB＝OD,所以△AOD≌△COB，所以CD＝AB,∠ADO=∠CBO；所以∠CDA＝∠ABC.故①②③都正确.故选B考点：三角形全等的判定和性质6．如图，△ABC中，∠B=∠C，BD=CF，BE=CD，∠EDF=α，则下列结论正确的是（）…A．2α+∠A=180° B．α+∠A=90° C．2α+∠A=90° D．α+∠A=180°【答案】A【解析】试题分析：根据已知条件可证明△BDE≌△CFD，则∠BED=∠CDF，由∠A+∠B+∠C=180°，得∠B=，因为∠BDE+∠EDF+∠CDF=180°，所以得出a与∠A的关系2a+∠A=180°．考点：全等三角形的判定和性质，三角形的内角和定理7．如图，AD是△ABC的中线，E、F分别在AB、AC上，且DE⊥DF，则（）~A．BE+CF＞EFB．BE+CF=EFC．BE+CF＜EFD．BE+CF与EF的大小关系不能确定．【答案】A．8．如图，△ABC中边AB的垂直平分线分别交BC，AB于点D，E，AE=3cm，△ADC的周长为9cm，则△ABC的周长是（）A．10cm B．12cm C．15cm D．17cm}【答案】C．【解析】试题分析：∵AB的垂直平分AB，∴AE=BE，BD=AD，∵AE=3cm，△ADC的周长为9cm，∴△ABC的周长是9cm+2×3cm=15cm，故选C．考点：线段垂直平分线的性质．9．如图所示，∠A+∠B+∠C+∠D+∠E的结果为（）A．90° B．1 80° C．360° D．无法确定【答案】?【解析】试题分析：延长BE交AC于F，∵∠A+∠B=∠2，∠D+∠E=∠1，∠1+∠2+∠C=180°，∴∠A+∠B+∠C+∠D+∠E=180°，考点：1．三角形内角和定理；2．三角形的外角性质．10．若△ABC中，2（∠A+∠C）=3∠B，则∠B的外角度数为何（）>A、36B、72C、108D、144【答案】C【解析】∵∠A+∠B+∠C=180°，∴2（∠A+∠B+∠C）=360°，∵2（∠A+∠C）=3∠B，∴∠B=72°，11．如图，AB∥CD，∠D =∠E =35°，则∠B的度数为（）.A．60° B．65° C．70° D．75°【答案】C.~12．如图，已知△ABC，O是△ABC内的一点，连接OB、OC，将∠ABO、∠ACO分别记为∠1、∠2，则∠1、∠2、∠A、∠O四个角之间的数量关系是（）A ．∠1+∠0=∠A+∠2B ．∠1+∠2+∠A+∠O=180°C ．∠1+∠2+∠A+∠O=360°D ．∠1+∠2+∠A=∠O【答案】D ．【解析】试题分析：连接AO 并延长，交BC 于点D ，》∵∠BOD 是△AOB 的外角，∠COD 是△AOC 的外角，∴∠BOD=∠BAD+∠1①，∠COD=∠CAD+∠2②，①+②得，∠BOC=（∠BAD+∠CAD ）+∠1+∠2，即∠BOC=∠BAC+∠1+∠2．故选D ．考点：1．三角形的外角性质；2．三角形内角和定理．13．如图，BD 是∠ABC 的角平分线，DE ⊥AB 于E ，DF ⊥BC 于F ，，，，△cm 12BC cm 18AB cm 362ABC ===S 则DE 的长是（）B.cm 512 D.cm 514 ￥【答案】B【解析】试题分析：∵BD 是∠ABC 的角平分线，DE ⊥AB ，DF ⊥BC,由角平分线的性质可得DE=DF ∴DCB S S ∆∆+=ADB ABC S △=DF DE ⋅⨯+⋅⨯12211821=9DE+6DF=15DE=36∴DE=cm 512 所以选B.考点：角平分线的性质？第II卷（非选择题）请点击修改第II卷的文字说明评卷人得分~二、填空题（题型注释）14．如图，△ABC中，∠A＝90°，DE是BC的垂直平分线，AD=DE，则∠C的度数是°．【答案】30°．【解析】试题分析：∵DE是BC的垂直平分线，∴DE⊥BC，∵∠A＝90°，AD=DE，∴BD平分∠AABC，∴∠ABD=∠DBC，∵DE是BC的垂直平分线，∴DC=BD，∴∠C=∠DBC，∴3∠C=90°，∴∠C=30°．故答案为：30°．考点：1．线段垂直平分线的性质；2．角平分线的性质．!15．如图，在△ABC中，∠ACB＝90°，AB的垂直平分线DE交AB于E，交AC于D，∠DBC＝30°，BD＝，则D到AB的距离为。

全等三角形练习题(打印版)

全等三角形练习题（打印版）### 全等三角形练习题#### 一、选择题1. 下列选项中，哪两个三角形是全等的？- A. △ABC与△DEF，因为AB=DE，AC=DF，BC=EF- B. △ABC与△DEF，因为∠A=∠D，∠B=∠E，∠C=∠F- C. △ABC与△DEF，因为AB=DE，∠A=∠D，∠B=∠E- D. △ABC与△DEF，因为AB=DE，BC=EF，∠A=∠D2. 根据SSS（边边边）全等条件，下列哪些条件能够判断两个三角形全等？- A. 三边长度相等- B. 两边及夹角相等- C. 一边及其对角相等- D. 两角及一边相等#### 二、填空题1. 如果△ABC与△DEF全等，且AB=DE，AC=DF，那么BC=______。

2. 根据AAS（角角边）全等条件，如果两个三角形的两个角和其中一角的对边相等，那么这两个三角形是______的。

#### 三、判断题1. 如果两个三角形的对应边成比例，那么这两个三角形一定是全等的。

（）2. SAS（边角边）全等条件是判定两个三角形全等的有效条件。

（）#### 四、简答题1. 解释什么是HL（直角三角形的斜边和一条直角边相等）全等条件，并给出一个例子。

2. 描述如何使用SAS全等条件来判断两个三角形是否全等。

#### 五、应用题1. 在△ABC中，已知AB=5cm，AC=4cm，BC=6cm。

在△DEF中，DE=7cm，DF=6cm，EF=5cm。

判断这两个三角形是否全等，并说明理由。

2. 如果△ABC与△DEF全等，且∠A=∠D=90°，AB=DE，AC=DF，求证BC=EF。

#### 六、证明题1. 已知△ABC与△DE F全等，且∠A=∠D，∠B=∠E，AB=DE。

证明AC=DF。

2. 证明：如果两个三角形的三边对应成比例，那么这两个三角形的对应角也相等。

注意：请在解答题目时，确保使用正确的数学符号和清晰的逻辑表达。

练习题的答案应简洁明了，避免冗长和不必要的解释。

全等三角形经典题型50题[含答案]

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

因为 BC=ED,CF=DF,∠BCF=∠EDF 。

所以三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF 。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2)。

ADBC4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ，所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC （SAS ）所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。