第六章 土力学 课后习题
土力学课后答案详解 第6章

2m 2m 2m
ϕ 1= 30 ° , γ 1= 18 κ Ν /m 3 ϕ 2= 26° , γ 1= 17κ Ν /m 3
ϕ 3= 26° , γ 3= 9κ Ν /m 3
6.21 题 6-1 图
解:
K a1
=
tan 2 (45o
−
ϕ1 2
)
=
tan 2 (45o
−
30o 2
)
压力。 6-3 朗肯土压力理论的基本假设是什么?
答:弹性半空间体内的应力状态,根据土的极限平衡条件而得出的土压力计算方法。在 弹性匀质的半空间体中,任一竖直面应都是对称面,其上的剪应力为零。 6-4 库仑土压力理论的基本假设是什么?
答:①墙后填土是理想的散粒体(粘聚力 c =0);②滑动破裂面为通过墙踵的平面。
第六章 思考题与习题
思考题
6-1 什么是主动土压力、被动土压力和静止土压力?三者的关系是什么? 答:(1)主动土压力:当挡土墙在外力作用下,向土体方向偏移至墙后土体达到极限平
衡状态时,作用在墙背上的土压力称为主动土压力,一般用 Ea 表示。
(2)被动土压力:当挡土墙在外力作用下,向土体方向偏移墙背土体达到极限平衡状
的状态。
当挡土墙离开土体向左移动时,墙后土体有伸张趋势。此时竖向应力σ z 不变,法向应 力σ x 减小,σ z 和σ x 仍为大、小主应力。当挡土墙位移使墙后土体达极限平衡状态时,σ x
达到最小值σ a ,其摩尔应力圆与抗剪强度包线相切。土体形成一系列滑裂面,面上各点都
处于极限平衡状态,称主动朗肯状态,此时墙背法向应力σ x 为最小主应力,即朗肯主动土
墙底:σ p1 = (q + γh)K p = (25 + 16 × 5) × 3.85 = 404.25kPa
土力学(河海大学第二版)第6章答案
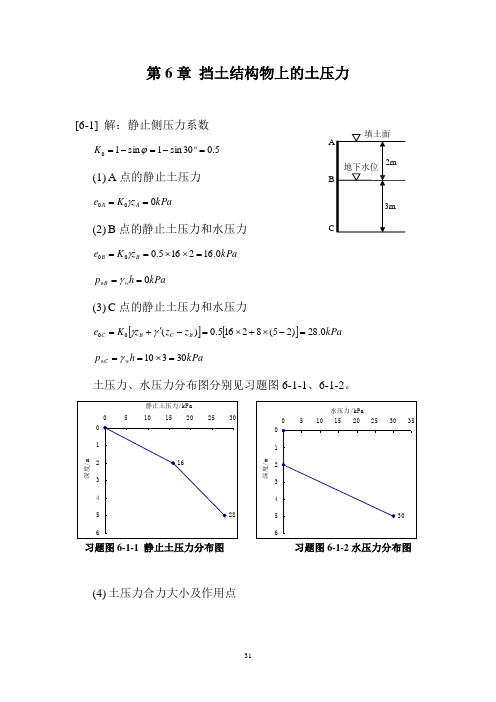
第6章 挡土结构物上的土压力[6-1] 解:静止侧压力系数5.030sin 1sin 10=-=-=ϕK(1) A 点的静止土压力kPa z K e A A 000==γ(2) B 点的静止土压力和水压力kPa z K e B B 0.162165.000=⨯⨯==γ kPa h p w wB 0==γ(3) C 点的静止土压力和水压力[][]kPa z z z K e B C B C 0.28)25(82165.0)(00=-⨯+⨯=-'+=γγ kPa h p w wC 30310=⨯==γ土压力、水压力分布图分别见习题图6-1-1、6-1-2。
习题图6-1-1 静止土压力分布图习题图6-1-2水压力分布图(4) 土压力合力大小及作用点()()()m kN z z e e z e E B C C B B B /82 0.30.280.16210.20.1621 21210000=⨯+⨯+⨯⨯=-++=静止土压力E 0的作用点离墙底的距离y 0为()()()()()()()()()()()()mz z z z e e z z z z e z z z z e E y B C B C B C B C B C B B C B B B 23.1 253125162821 2521251625231216210.821 3121 2131211000000=⎥⎦⎤⎢⎣⎡-⨯⨯-⨯-⨯+⎥⎦⎤⎢⎣⎡-⨯⨯-⨯+⎩⎨⎧⎥⎦⎤⎢⎣⎡-+⨯⨯⨯⨯=⎭⎬⎫⎥⎦⎤⎢⎣⎡---⎩⎨⎧+⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡-+=(5) 水压力合力大小及作用点()()m kN z z p P B C wC w /4525302121=-⨯⨯=-=水压力合力作用点距离墙底的距离为()()m z z y B C 0.13531310=-⨯=-='[6-2] 解:主动土压力系数:333.0245tan 121=⎪⎭⎫ ⎝⎛-=ϕ a K271.0245tan 222=⎪⎭⎫ ⎝⎛-=ϕ a K(1)各层面点的主动土压力 A 点:kPa qK e a aA 66.6333.0201=⨯==B 点上:()()kPa K q H e a aB 14.25333.02035.18111=⨯+⨯=+=γ上 B 点下:()()kPa K q H e a aB 46.20271.02035.18211=⨯+⨯=+=γ下C 点上:()()kPa K q H H e a aC 50.35271.02035.1835.1822211=⨯+⨯+⨯=++=γγ上 C 点下:kPa e e aC aC 50.35==上下D 点:()kPaK q H H H e a aD 72.44271.02045.835.1835.182322211=⨯+⨯+⨯+⨯=⎪⎭⎫ ⎝⎛+'++=γγγ土压力分布如习题图6-2-1。
《土力学》课后习题及详细解答

《土力学》课后习题答案第一章1-1:已知:V=72cm3m=129.1g m s=121.5g G s=2.70则:129.1121.56.3%121.5ssm mwm--===3333 129.1*1017.9/72121.5452.77245271.0*27121.5*1020.6/72sssV ssat w V ssat satmg g KN mvmV cmV V V cmm V mg g g KN mV Vγρρργρ========-=-=++=====3320.61010.6/121.5*1016.9/72sat wsdsat dKN mmg KN mVγγγγγγγγ'=-=-===='>>>则1-2:已知:G s=2.72 设V s=1cm3则33332.72/2.722.72*1016/1.72.720.7*1*1020.1/1.720.11010.1/75%1.0*0.7*75%0.5250.52519.3%2.720.525 2.721.sssd ds V wwrw w V rwsw sg cmm gmg g KN mVm Vg g KN mVKN mm V S gmwmm mg gVργρργργγγργρ======++===='=-=-========++===当S时,3*1019.1/7KN m=1-3:3477777331.70*10*8*1013.6*1013.6*10*20%2.72*1013.6*10 2.72*10850001.92*10s d w s s wm V kg m m w kg m m V m ρρ======++==挖1-4: 甲:33334025151* 2.72.7*30%0.81100%0.812.70.811.94/10.8119.4/2.71.48/1.8114.8/0.81p L P s s s s w r wV ws w s w s d s w d d vsI w w V m V g m g S m V m m g cm V V g KN m m g cm V V g KN m V e V ρρργρργρ=-=-=======∴==++===++=====+====设则又因为乙:3333381 2.682.68*22%0.47960.47962.680.47962.14/10.47962.14*1021.4/2.681.84/1.47961.84*1018.4/0.4796p L p s s s s w s V s w s V s d s w d d VsI w w V m V g m m w g V cm m m g cm V V g KN m m g cm V V g KN m V e V ρργρργρ=-========++===++======+=====设则则γγ∴<乙甲 d d γγ<乙甲 e e >乙甲 p p I I >乙甲则(1)、(4)正确1-5:1s w d G eρρ=+ 则2.7*1110.591.7022%*2.7185%0.59s wds r G e wG S e ρρ=-=-====>所以该料场的土料不适合筑坝,建议翻晒,使其含水率降低。
土力学 第六章 习题答案
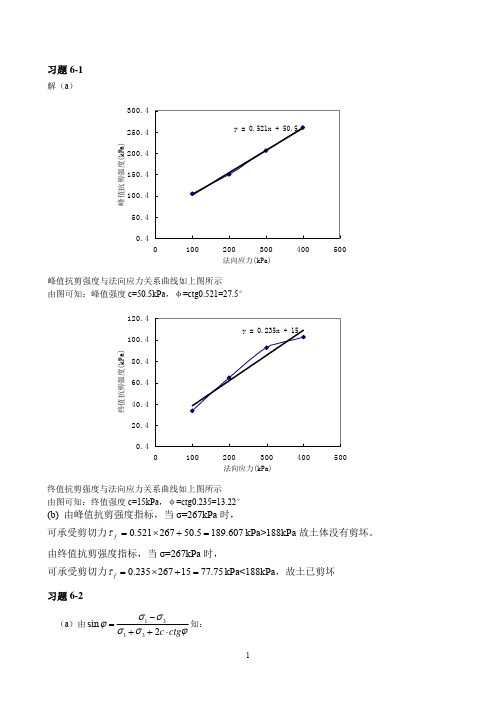
3 tg (45 破坏时, 1
2
) 100 tg 2 60 300 (kPa)
300 100 200 (kPa) ,已加 80 kPa,所以还需加 120 kPa。 1 1 3
(b) f 45
2
60 sin 2 f 200 sin120 86.8 (kPa) 2
tg 2 ( 45 ) 1 3
2
1 u1 u 2 ( 3 u1 u 2 )tg 2 (45 )
2
Af
u 2 1 3
u 2
1 3
1
u 2 Af
3 (1)
3
由 u1 3 70 44 26 , 3 70 , A f 0.2 得 1 26 u 2 ( 44 u 2 )tg 57.5
由 c tan 得:c=57.73kPa 习题 6-4
证 明: 由三轴固结不排水强度试验曲线可知, 半径 r cu ,sin
cu , 将上式化简得到: cu c c tan 3
cu ) cu sin (c c tan 3
cu
1 3
2
u2 45.54 (kPa) 2 Af
习题 6-7
应力路径的预备知识: 在二维应力问题中,应力的变化过程可以用若干个应力圆表示。但这种用若干个应力圆表示应力变化 过程的方法显然很不方便,特别是出现应力不是单调增加,而是有时增加,有时减小的情况,用应力圆表 示应力变化过程不但不方便,而且极易混乱。因此,应力变化过程较为简易的方法就是选择土体中某一个 特定的面上的应力变化来表示土单元体的应力变化。因为该面的应力在应力圆上表示为一个点,因此这个 面上的应力变化过程可用该点在应力坐标上的移动轨迹来表示,这个移动轨迹就称为应力路径。 通常选择与主应力面成 45º的斜面作为代表面最为方便,因为每个应力圆都可以用应力圆圆心的位置
土力学 课后习题与答案

土力学课后习题与答案土力学课后习题与答案第一章思考题11-1 什么叫土,土是怎样形成的,粗粒土和细粒土的组成有何不同, 1-2 什么叫残积土,什么叫运积土,他们各有什么特征,1-3 何谓土的级配,土的粒径分布曲线是怎样绘制的,为什么粒径分布曲线用半对数坐标, 1-4 何谓土的结构,土的结构有哪几种类型,它们各有什么特征, 1-5 土的粒径分布曲线的特征可以用哪两个系数来表示,它们定义又如何, 1-6如何利用土的粒径分布曲线来判断土的级配的好坏, 1-7 什么是吸着水,具有哪些特征,1-8 什么叫自由水,自由水可以分为哪两种, 1-9 什么叫重力水,它有哪些特征, 1-10 土中的气体以哪几种形式存在,它们对土的工程性质有何影响, 1-11 什么叫的物理性质指标是怎样定义的,其中哪三个是基本指标, 1-12 什么叫砂土的相对密实度,有何用途,1-13 何谓粘性土的稠度,粘性土随着含水率的不同可分为几种状态,各有何特性, 1-14 何谓塑性指数和液性指数,有何用途, 1-15 何谓土的压实性,土压实的目的是什么,1-16 土的压实性与哪些因素有关,何谓土的最大干密度和最优含水率, 1-17土的工程分类的目的是什么,1-18 什么是粗粒土,什么叫细粒土,习题11-1有A、B两个图样,通过室 1.土样A的密度比土样B的大; 2.土样A的干密度比土样B的大;?干密度3?湿密度…-?浮密度1-8 在图中,A土的液限为16.0%,塑限为13.0%;B土的液限为24.0%,塑限为14.0%,C土为无粘性土。
图中实线为粒径分布曲线,虚线为C土的粗粒频率曲线。
试按《土的分类标准》对这三种土进行分类。
1-9 某碾压土坝的土方量为20万方,设计填筑干密度为1.65限为20.0%,土粒比重为2.72。
问:?为满足填筑土坝需要,料场至少要有多少方土料,?如每日坝体的填筑量为3000?土坝填筑的饱和度是多少,g/cm3。
料的含水率为12.0%,天然密度为1.70 g/cm3,液限为32.0%,塑m3,该土的最优含水率为塑限的95%,为达到最佳碾压效果,每天共需要加多少水, 第二章思考题22-1 土中的应力按照其起因和传递方式分哪几种,怎么定义,2-2 何谓自重应力,何谓静孔隙水应力,计算自重应力应注意些什么,2-3 何谓附加应力,空间问题和平面问题各有几个附加应力分量,计算附加应力时对地基做了怎样的假定,2-4 什么叫柔性基础,什么叫刚性基础,这两种基础的基底压力有何不同,2-5 地基中竖向附加应力的分布有什么规律,相邻两基础下附加应力是否会彼此影响,2-6 附加应力的计算结果与地基中实际的附加应力能否一致,为什么,2-7 什么是有效应力,什么是孔隙应力,其中静孔隙应力如何计算,2-8 你能熟练掌握角度法和叠加原理的应用吗,会计算各种荷载条件下地基中任意点的竖向附加应力吗,习题22-1 如图所示为某地基剖面图,各土层的重度及地下水位如图,试求土的自重应力和静孔隙水应力,并绘出它们的分布图。
土力学习题及答案

《土力学》习题第一章 土的物理性质及工程分类选择题1.土颗粒的大小及其级配,通常是用颗粒级配曲线来表示的。
级配曲线越平缓表示: A .土颗粒大小较均匀,级配良好 B.土颗粒大小不均匀,级配不良 C. 土颗粒大小不均匀,级配良好2.作为填土工程的土料,压实效果与不均匀系数u C 的关系:A .u C 大比u C 小好 B. u C 小比u C 大好 C. u C 与压实效果无关3.有三个同一种类土样,它们的含水率w 都相同,但是饱和度r S 不同,饱和度r S 越大的土,其压缩性有何变化?A.压缩性越大B. 压缩性越小C. 压缩性不变4.有一非饱和土样,在荷载作用下,饱和度由80%增加至95%。
试问土样的重度γ和含水率w 怎样改变?A .γ增加,w 减小 B. γ不变,w 不变 C. γ增加,w 增加 5.土的液限是指土进入流动状态时的含水率,下述说法哪种是对的? A .天然土的含水率最大不超过液限 B. 液限一定是天然土的饱和含水率C. 天然土的含水率可以超过液限,所以液限不一定是天然土的饱和含水率 判断题6.甲土的饱和度大与乙土的饱和度,则甲土的含水率一定高于乙土的含水率7.粘性土的物理状态是用含水率表示的,现有甲、乙两种土,测得它们的含水率乙甲w w ,则可以断定甲土比乙土软8.土的液性指数L I 会出现L I >0或L I <0的情况 9.土的相对密实度r D 会出现r D >1或r D <1的情况 10.土的天然重度越大,则土的密实性越好 计算题11.击实试验,击实筒体积1000cm 2,测得湿土的质量为1.95kg ,取一质量为17.48kg 的湿土,烘干后质量为15.03kg ,计算含水率w 和干重度d r 。
12.已知某地基土试样有关数据如下:①天然重度r =18.4 kN/m 3,干密度d r =13.2 kN/m 3;②液限试验,取湿土14.5kg ,烘干后质量为10.3kg ;③搓条试验,取湿土条5.2kg ,烘干后质量为4.1kg ,求(1)土的天然含水率,塑性指数和液性指数;(2)土的名称和状态。
《土力学》课后习题答案

1-1 解:
(1)A试样
(1) B试样
1-2解:
已知: =15.3g =10.6g =2.70
饱和 =1
又知: 15.3-10.6=4.7g
(1) 含水量
= =0.443=44.3%
(2) 孔隙比
(3) 孔隙率
(4) 饱和密度及其重度
(5) 浮密度及其重度
(6) 干密度及其重度
1-3 解:
1-4 解:
20.58
(5) 确定压缩层厚度。
由表1可知,在第4计算点处 ,所以,取压缩层厚度为10.5m。
(6) 计算各分层的平均自重应力和平均附加应力(详见表2)。
(7) 由图4-29根据 和 分别查取初始孔隙比e1i和压缩稳定后的孔隙比e2i(结果见表2)。
表2 各分层的平均应力及其孔隙比
层号
层厚
(m)
平均自重应力
e2i
0-1
3.0
85.5
20.31
105.81
0.836
0.812
1-2
3.0
129.0
26.55
155.55
0.776
0.753
2-3
3.0
160.5
30.79
191.29
0.749
0.618
表4 基础侧边2下各分层的平均应力及其孔隙比
层号
层厚
(m)
平均自重应力
(kPa)
平均附加应力
(kPa)
加荷后的总应力
(1)甲基础在O点下2m处引起的竖向附加应力:
由于O点位于基础中心,荷载为梯形荷载,在O点的竖向附加应力和梯形荷载平均得的均布荷载相等,即可取 pn=(100+200)/2=150kPa
《土力学》课后习题答案解析

初始孔隙比
e1i
压缩稳定后的孔隙比
e2i
0-1
3.0
85.5
71.43
156.93
0.836
0.752
1-2
3.0
129.0
65.25
194.25
0.776
0.711
2-3
3.0
所以,地表面5-6处不会发生流土。
[3-5]已知: , , ,地下水位以上砂土层厚h1=1.5m,地下水位以下砂土层厚h2=1.5m,粘土层厚h3=3.0m。
解:由图可知,粘土层顶面测压管水位为 (以粘土层底面作为高程计算零点);
粘土层底面测压管水位为
(1)粘土层应力计算:
粘土层顶面应力:
总应力:
孔隙水应力:
13.50
0.250
30.00
43.50
(5)确定压缩层厚度。
对于基础侧边1,由表1可知,在第3计算点处 ,所以,取压缩层厚度为9.0m。
对于基础侧边2,由表2可知,在第5计算点处 ,所以,取压缩层厚度为15.0m。
(6)计算各分层的平均自重应力和平均附加应力(基础侧边1下的计算详见表3,基础侧边2下的计算详见表4)。
(3)求各分层点的自重应力(基础侧边1下的计算详见表1,基础侧边2下的计算详见表2)。
(4)求各分层点的竖向附加应力(基础侧边1下的计算详见表1,基础侧边2下的计算详见表2)。
表1基础侧边1下各分层点的自重应力和附加应力计算表
自
重应力
附
加
应
力
点
均
布
荷
载
三角
形荷载
附加
号
Hi
zi
zi/b
Kzs(查表2-6)
《土力学》第六章习题集及详细解答..

《土力学》第六章习题集及详细解答第6章土中应力一填空题1.分层总和法计算地基沉降量时,计算深度是根据应力和应力的比值确定的。
2.饱和土的有效应力原理为:总应力σ=有效应力σˊ+孔隙水压力u ,土的和只随有效应力而变。
地下水位上升则土中孔隙水压力有效应力。
3.地基土层在某一压力作用下,经历时间t所产生的固结变形量与最终固结变形量之比值称为。
二选择题1.对非压缩性土,分层总和法确定地基沉降计算深度的标准是( D )。
(A) ;(B) ;(C) ;(D)2.薄压缩层地基指的是基底下可压缩土层的厚度H与基底宽度b的关系满足( B )。
(A) ;(B) ;(C) ;(D)3.超固结比的土属于( B )。
(A) 正常固结土;(B) 超固结土;(C) 欠固结土;(D) 非正常土4.饱和黏性土层在单面排水情况下的固结时间为双面排水的( C )。
(A) 1倍;(B) 2倍;(C) 4倍;(D) 8倍5.某黏性土地基在固结度达到40%时的沉降量为100mm,则最终固结沉降量为( B )。
(A) 400mm ; (B) 250mm ; (C) .200mm ; (D) 140mm6.对高压缩性土,分层总和法确定地基沉降计算深度的标准是( C )。
(A) ;(B) ;(C) ;(D)7.计算时间因数时,若土层为单面排水,则式中的H取土层厚度的( B )。
(A)一半; (B) 1倍; (C) 2倍; (D) 4倍8.计算地基最终沉降量的规范公式对地基沉降计算深度的确定标准是( C )。
(A) ;(B) ;(C) ;(D)9.计算饱和黏性土地基的瞬时沉降常采用( C )。
(A) 分层总和法; (B) 规范公式; (C) 弹性力学公式;10.采用弹性力学公式计算地基最终沉降量时,式中的模量应取( A )(A) 变形模量; (B) 压缩模量; (C) 弹性模量; (D) 回弹模量11.采用弹性力学公式计算地基瞬时沉降时,式中的模量应取( C )。
《土力学》1-6章作业参考答案

第一章 土的物理性质及其工程分类P 60[2-2] 解:V=21.7cm 3,m=72.49-32.54=39.95g ,m S =61.28-32.54=28.74g ,m W =72.49-61.28=11.21g7.2195.39==V m ρ=1.84g/ cm 3,74.2821.11==sw m m w =39% 07.1184.1)39.01(174.21)1(=-+⨯⨯=-+=ρωρW S d eP 60[2-3] 解:963.0185.1)34.01(171.21)1(=-+⨯⨯=-+=ρωρWS d e 963.01963.071.21++=++=e e d s sat ρ=1.87 g/ cm 3,87.0187.1=-=-='W sat ρρρ g/ cm 3g ργ'='=0.87×10=8.7 kN/m 3P 60[2-4] 解:已知77.1=ρg/cm 3, w =9.8%,s d =2.67,461.0min =e ,943.0max =e∴656.0177.1)098.01(167.21)1(=-+⨯⨯=-+=ρωρW S d e ,∈=--=--=6.0461.0943.0656.0943.0min max max e e e e D r (0.33,0.67)∴该砂土处于中密状态。
P 60[2-5] 解:已知s d =2.73,w =30%,=L w 33%,=P w 17%土样完全饱和→1=r S ,sat ρρ=819.073.23.01=⨯=⇒==e e wd S S r ,819.01819.073.21++=++=e e d s sat ρ=1.95 g/ cm 3 3.0195.11+=+=w d ρρ=1.5 g/ cm 3,161733=-=-=P L p w w I 81.0161730=-=-=P P LI w w I 10<16=p I ≤17→该土为粉质粘土0.75<81.0=L I ≤1→该土处于软塑状态[附加1-1]证明下列换算公式:(1)w s d e d ρρ+=1;(2)γee S sw r ++=1γγ;(3)n n w S w s r γγ)1(-=(1)证明:设e V V V V V Ve V S V V SV S +=+===⇒=1,1w s s w s s s s d ed V V d V V V m ρρρρ+====1 (2)证明:设e V V V V V Ve V S V V SV S +=+===⇒=1,1V g V V V g m m V mg V G s s w w s w )()(ρργ+=+===ee S V V V S sw r s s w v r ++=+=1γγγγ (3)证明:设n V n V n VVV s v v -==⇒==1,,1∴nn w gV gV w V V w V V m m V m V V S w s v w s s v w s s ss v w s wv w w v w r γγρρρρρρρ)1(-====== [附加1-2]解:V=72cm 3,m=129.5g ,m S =121.5g ,m W =129.5-121.5=8g%6.65.1218===⇒S W m m ω 6.0172/5.129)066.01(17.21)1(=-+⨯⨯=-+=ρωρW S d e %7.296.07.2066.0=⨯==e d S S r ω 0.1872105.129=⨯===V mg V G γkN/m 36.20106.16.07.21=⨯+=++=W S sat e e d γγkN/m 36.10106.20=-=-='W sat γγγkN/m 39.16106.17.21=⨯=+=W S d e d γγkN/m 3∴γγγγ'>>>d sat[附加1-3]解:已知s d =2.68,w =32%,土样完全饱和→1=r S86.068.232.01=⨯=⇒==e ed S Sr ω02.1986.1)32.01(1068.286.01)1(=+⨯⨯=⇒=-+=γγωγW S d e kN/m 3[附加1-4]解:已知66.1=ρg/cm 3,s d =2.69,(1)干砂→w =0 ∴62.0166.1)01(169.21)1(=-+⨯⨯=-+=ρρw d e W S(2)置于雨中体积不变→e 不变∴%2.969.262.04.04.0=⨯=⇒==w e wd S S r [附加1-5]解:已知m=180g ,1w =18%,2w =25%,sss s s w m m m m m m m w -=-==18011=18%→s m =152.54g∴)(12w w m m s w -=∆=152.54×(0.25-0.18)=10.68g[附加1-6]实验室内对某土样实测的指标如下表所示,计算表土中空白部分指标。
清华大学土力学课后答案-第六章课后习题

6 4解: 36 , 20 cos 2 0.235 sin( ) sin 2 cos (1 ) cos 主动土压力: Ka 1.500m :ea1 1h1 K a 18*1.5*0.235 6.345kPa 5.0m处, ea 2 ( 1h1 ' h2 ) K a (18*1.5 11*3.5) *0.235 15.39kPa 水压力: 5.000米m处ew w h2 10* 3.5 35kPa 分布图略
' 总土压力:Ea Ea Ea 174.30 33.78 208.08kN / m ' Ea *3 Ea *2 2.162m Ea
总土压力作用点距离墙底:d
总土压力 Ea与水平面夹角: 33.69 30 69.69
2/5
6-6解:(1)0 3m主动土压力Ea1
1 3
1 1 Ea1 h12 K a1 *18*32 *0.482 39.04kN / m 2 2 Ea1与水平面夹角1 18.43 Ea1h Ea1 cos 1 37.14kN / m,Ea1v Ea1 sin 1 12.34kN / m (2)3 8m主动土压力Ea1和水压力 题目未说明填土性质,按照砂土处理. 将水位以上土折算成 ' 10kN / m3 , 和下部土性相同. 3*18 5.4m 10 3 2 arctan( ) 30.96 , 0, 30 , 0 5 cos 2 ( 2 ) Ka2 0.633, sin( ) *sin 2 2 cos 2 *cos( 2 )[1 ] cos( 2 ) *cos 2
1 h1
河海大学_土力学_课后习题答案

河海大学_土力学_课后习题答案思考题2 2-1土体的应力,按引起的原因分为自重应力和附加应力两种;按土体中土骨架和土中孔隙(水、气)的应力承担作用原理或应力传递方式可分为有效应力和孔隙应(压)力。
有效应力是指由土骨架传递(或承担)的应力。
孔隙应力是指由土中孔隙流体水和气体传递(或承担)的应力。
自重应力是指由土体自身重量所产生的应力。
附加应力是指由外荷(静的或动的)引起的土中应力。
2-2 自重应力是指由土体自身重量所产生的应力。
由静水位产生的孔隙水应力称为静孔隙水应力。
土体自重应力应由该点单位面积上土柱的有效重量来计算,如果存在地下水,且水位与地表齐平或高于地表,则自重应力计算时应采用浮重度,地下水位以下的土体中还存在静孔隙水应力。
2-3 附加应力是指由外荷(静的或动的)引起的土中应力。
空间问题有三个附加应力分量,平面问题有两个附加应力分量。
计算地基附加应力时,假定地基土是各向同性的、均匀的、线性变形体,而且在深度和水平方向上都是无限的。
2-4 实际工程中对于柔性较大(刚度较小)能适应地基变形的基础可以视为柔性基础。
对于一些刚度很大不能适应地基变形的基础可视为刚性基础。
柔性基础底面压力的分布和大小完全与其上的荷载分布于大小相同;刚性基础下的基底压力分布随上部荷载的大小、基础的埋深和土的性质而异。
2-5 基地中心下竖向附加应力最大,向边缘处附加应力将减小,在基底面积范围之外某点下依然有附加应力。
如果该基础相邻处有另外的荷载,也会对本基础下的地基产生附加应力。
2-6 在计算地基附加应力时,假定地基土是各向同性的、均质的、线性变形体,而且在深度的水平方向上都是无限的,这些条件不一定同时满足,因而会产生误差,所以计算结果会经常与地基中实际的附加应力不一致。
2-7 有效应力是指由土骨架传递(或承担)的应力。
孔隙应力是指由土中孔隙流体水和气体传递(或承担)的应力。
静孔隙水应力:习题22-1 解:根据图中所给资料,各土层交界面上的自重应力分别计算如下:cz0 0urhwwcz1 1h1 18.5'cz2 1h1 cz2 1h1 cz3 1h1 cz4 1h1 2-2解:23kPa7kPa55 (2 03h 37 1 8 122h 'h2' 55 222h 'h2 '2 'h3 221 0 )1kPa65 (1 946 5 10 )3kPa9 22kPa1 11h 'h2 '2 'h3 3'h 2249 2(1 9.5 10 )土的最大静孔隙水应力为:u0 rwhw 10 6 60kPa FV P G P GAd 2106基底压力:2 0 63 __ 3(1 62kN46 6pmpmaxinFvl b(16el)0.3178.k1Pa) 95.k9Pa6基底静压力:pn pmin r0d 95.9 17 1.0 78.9kPa pt pmaxpmin178.1 95. 98k2P.2 a只有前两章的,不过包括所有的思考题① 求O点处竖向附加应力由:m lzo12 n z 0 0 KS 0.250 0bb.5 4KSpn 4 0.25 78.9 78.9kPa b 1.5 0.5 n zb 0.5pt2由:m l0 Kt1 0 Kt2 0.2500 2 0.2582.2220.55kPazo2 2Kt1由:m lpt20 zo3 2Kt2bzo4 2KS4pt22 n z 2 0.25b82.22.50 KS4 0.250 020.55kPaz0 z01 z02 z03 z04 120kPa②求A点下4m处竖向附加应力由:m lzA16 4 n z 4 2.7 KS 0.103 6bb.52KSpn 2 0.1036 78.9 16.35kPa0.67 Kt 0.0695b662Ktpt 2 0.0695 82.2 11.4258kPa1.50.25 n z4由:m lzA2③zA zA1 zA2 16.35 11.4258 27.78kPa求B点下4m处竖向附加应力由:m l zB11.33 KS 0.1412b3b32KSpn 2 0.1412 78.9 22.28kPapt20.141282.225.80kPa3 1 n z 4zB2 KS由:m lzB3 Kt1pt2pt231 n z82.2282.221.33 Kt1 0.058 5Kt2 0.08260.0585 0.08262.39kPa3.39kPazB2 Kt2zB zB1 zB2 zB3 zB4 33.86kPa2-3 解:2-4 解:① 求自重应力zM 1h1 1'h2 19 4 (20 9.8) 1 86.19kPa zN zM 3'h3 86.19 (18.5 9.8) 3 112.26kPa 第三章思考题3 3-1水在土中的渗透速度与试样两端水平面间的水位差成正比,而与渗径长度成反比,即:v khLki 即为达西定律。
土力学课后题答案

土力学课后习题与答案思考题11-1 什么叫土?土是怎样形成的?粗粒土和细粒土的组成有何不同?1-2 什么叫残积土?什么叫运积土?他们各有什么特征?1-3 何谓土的级配?土的粒径分布曲线是怎样绘制的?为什么粒径分布曲线用半对数坐标?1-4 何谓土的结构?土的结构有哪几种类型?它们各有什么特征?1-5 土的粒径分布曲线的特征可以用哪两个系数来表示?它们定义又如何?1-6 如何利用土的粒径分布曲线来判断土的级配的好坏?1-7 什么是吸着水?具有哪些特征?1-8 什么叫自由水?自由水可以分为哪两种?1-9 什么叫重力水?它有哪些特征?1-10 土中的气体以哪几种形式存在?它们对土的工程性质有何影响?1-11 什么叫的物理性质指标 是怎样定义的?其中哪三个是基本指标?1-12 什么叫砂土的相对密实度?有何用途?1-13 何谓粘性土的稠度?粘性土随着含水率的不同可分为几种状态?各有何特性?1-14 何谓塑性指数和液性指数?有何用途?1-15 何谓土的压实性?土压实的目的是什么?1-16 土的压实性与哪些因素有关?何谓土的最大干密度和最优含水率?1-17 土的工程分类的目的是什么?1-18 什么是粗粒土?什么叫细粒土? 思考题22-1 土中的应力按照其起因和传递方式分哪几种?怎么定义?2-2 何谓自重应力,何谓静孔隙水应力?计算自重应力应注意些什么?2-3 何谓附加应力,空间问题和平面问题各有几个附加应力分量?计算附加应力时对地基做了怎样的假定?2-4 什么叫柔性基础?什么叫刚性基础?这两种基础的基底压力有何不同?2-5 地基中竖向附加应力的分布有什么规律?相邻两基础下附加应力是否会彼此影响?2-6 附加应力的计算结果与地基中实际的附加应力能否一致,为什么?2-7 什么是有效应力?什么是孔隙应力?其中静孔隙应力如何计算?2-8 你能熟练掌握角度法和叠加原理的应用吗?会计算各种荷载条件下地基中任意点的竖向附加应力吗?思考题33-1 何谓达西定律,达西定律成立的条件有哪些?3-2 实验室内测定渗透系数的方法有几种?它们之间又什么不同?3-3 流网有什么特征?3-4 渗透变形有几种形式?各有什么特征?3-5 什么是临界水力梯度?如何对其进行计算?3-6 孔隙水应力在静水条件下和在稳定渗流作用下有什么不同?如何利用流网确定渗流作用的孔隙水压力。
同济大学土力学第6章课后答案

) 2 300 300 2 0 0 18 3 tg (45 ) 2 10 tg (45 ) 6.45kPa 2 2 2
距离地面 3m 处下部:
pa 2上 1 h1tg 2 (450
1
) 2c1 tg (450
1
pa 2下 1 h1tg 2 (450 18 3 tg 2 (450
p0 2 1 h 1K 0 1 8 4 0 . 5 3 6 k P a
距离地面 6m 处:
p p 3 ( 1h1 2 h2 ) K p 2 2c2 K p 2 220.67kPa
p03 ( 1h1 2 h2 ) K0 (18 4 17.5 2) 0.5 53.50kPa
第 6 章 土压力计算 作业
【6-1】 按朗金土压力理论计算图 6-1 所示挡土墙上的主动土压力 Ea 及其分布图。
图 6-1
解: 距离地面 0m 处:
pa1 2c1tg (45
1
2
) 2 10 tg (45
30 ) 11.55kPa 2
距离地面 3m 处上部:
图 6-2 2
已知桥台台背宽度 B 5m ,桥台高度 H 6m 。填土性质为: 18kN/m ,
3
20 , c 13kPa ;地基土为黏土, 17.5kN/m 3 , 15 , c 15kPa ;土的侧压力
系数 K 0 0.5 。 解:
K p1 tg 2 (45
p p 2上 1h1K p1 2c1 K p1 18 4 2.040 2 13 2.040 146.88 37.14 184.02kPa
土力学 第六章 习题答案

sin c cos 3 1 sin
习题 6-5
(a)总应力法的图绘制如图 6-5-1 所示,由图中可知:Ccu=20.91kPa,φcu=16°
2
总应力法
16 °
20.91
0
100
200
300
400
主应力( kPa)
图 6-5-1 总应力法 (b)有效应力的计算如下表所示,如图 6-5-2 所示,由图可知,c/=2.71kPa,φ/=34° σ1 σ3 u σ1
/
145 60 31 114 29
228 100 55 173 45
310 150 92 218 58
401 200 126 275 74
σ3/
τf
有效应力法
Kf
29°
34°
2.71 2.24
0
100
200
300 有效主应力(kPa)
图 6-5-2 有效应力法 (c)Kf 如图 6-5-2 所示,由图可知,c/=2.24kPa,φ/=29° 习题 6-6 三轴试验中,总的孔压一般表达式为: u u0 u1 u2 对于饱和试样而言,B=1.0,初始孔压 u0 =0; u1 = 3 , u2 A( 1 3 ) ;
由 c tan 得:c=57.73kPa 习题 6-4
证 明: 由三轴固结不排水强度试验曲线可知, 半径 r cu ,sin
cu , 将上式化简得到: cu c c tan 3
cu ) cu sin (c c tan 3
120.4
y = 0.235x + 15
100.4
黄志全土力学课后习题答案第六章土压力理论

解:由题意知, 静止土压力系数为:0K 1sin =1sin 300.5土层中各点的静止土压力值为:0a 0b 01a0c 012a a e =0b e =K H =0.516216kPc e =K H +H =0.5162+189.8328.3kP 点:点:点:静止土压力的合力0E 为:00b 10b 0c 21111E e H +e +e H 162+16+28.3345.53kN m 2222静止土压力0E 的作用点距离墙底的距离0y 为:122200b120b 20c 0b 0H H H H 11y e H +H +e H +e e E 23223112322 162+3+163+28.31645.53232233.14m作用在墙上的静水压力合力w P 为:22w w 211P H 9.8344.1kN m 22静止土压力及水压力的分布如下图所示:e 0a =0e 0c =28.3kPa解:由题意知,墙背竖直且光滑,墙后填土表面水平,故使用朗肯土压力理论计算。
又知填土由两层无黏性土组成,故c 0 。
主动土压力系数:221a1222a230K tan 45tan 450.33332235K tan 45tan 450.271022墙背各点主动土压力强度为: a a1ab111a1a b211a2ac 1122a2d 1122ae =q K 200.3333 6.666kP b e =q+H K =20+18.530.333325.1642kP e =q+H K =20+18.530.271020.4605kP c e =q+H +H K 20+18.53+18.530.271035.501c e =q+H +H +kPa 点:点:点:点:33a2aH K 20+18.53+18.53+209.840.2710 46.5578kP 主动土压力的合力a E 为:a a b11b2c 2c d 3111E e +e H +e +e H +e +e H 22247.7453+83.9425+164.1176=295.8052kN m作用在墙上的静水压力合力w P 为:22w w 311P H 9.8478.4kN m 22总压力为:a w E E +P 78.4+295.8052=374.2052kN m 总压力E 的作用点距离墙踵的距离0y 为:1112a 0123b1a023b22303333322c b23c23d c2w 3H H H H e H +H +H +e e +H +H +e H +H 22321y E H H H H H H H +e e +H ++e H +e e +H 23223231169.983+221.9784+337.5983+112.8038+284374.2052.008+29.4848+104.53333.37m 主动土压力及水压力的分布如下图所示:习题6-3解:由题意得,填土为c 0的黏性土,填土受拉区的最大深度0qz主动土压力系数为:221a 15K tan 45tan 450.588822e a =6.666kPae d =46.5578kPa则0q 10z 0.89m 18主动土压力强度为:a a a e q+H K 10+1870.588821064.73kP 主动土压力a E 的作用点距离墙底的距离 0011y H z 70.89 2.04m 33被动土压力系数为:221p 15K tan 45+tan 45+ 1.698422p0p a e qK 10 1.6984+21043.0485kPp1p e q+H K 10+187 1.6984+210257.0469被动土压力的合力p E 为 p0p1pe +e 43.0485+257.0469E H 71050.3339kNm 22被动土压力p E 的作用点距离墙底的距离0y0p0p1p0p1H H H y e H +e e E 223177743.04857+257.046943.04851050.33392232.67m压力分布图如下图所示:q=10kpae a =64.73kPa习题6-4解:由题意知,墙背竖直且光滑,使用朗肯土压力理论计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
σczi+σ
比 e1i
比 e2i
zi(kpa)
Ⅰ
10
54
64
0.825 0.728
Ⅱ
32
54
86
0.787 0.717
Ⅲ 56.5
54
110.5 0.731 0.689
Ⅳ
94
54
148
0.718 0.673
因为,由题知粗砂土的沉降量可忽略不计,所以沉降量计算
为: S=Σ△S=Σ(e1i- e2i)*H/(1+ e1i) =[(0.825-0.728)/(1+0.825)]*1+[(0.731-0.689)/(1+0.731)]*2.5 +[(0.718-0.673)/(1+0.718)]*2.5=0.05315+0.06066+0.06548=17 9.29mm 所以,最终沉降量为 179.29mm
12. 某均质砂土地基剖面如图所示,地面上作用大面积均布 荷载 p 150kPa ,地下水位以上 l m 为毛细饱和区,土层孔 隙比 e0 0.75 ,比重 ds 2.7 ,试求 A 点、 B 点、C 处的垂 直总应力、有效应力和孔隙水压力,并分别画出沿土层 深度的分布曲线
解
:
sat= (Gs+e)/(1+e) w=10*(2.7+0.75)/(1+0.75)=19.7N/m^3
(3)将基底分为 4 个相等矩形 1、2、3、4,O 点为
每个矩形的角点,对应应力系数分别为 αc1、αc2、αc3、αc4
z=0.8 时 , 对 矩 形 1 有 m=l/b=2,n=z/b=0.8, 得
αc1=0.2176,同理 αc2=αc3=αc4=0.2176
则 σz 1=(αc1+αc2+αc3+αc4) p0=231.5kPa
z=1.6 时,得 αc1’=0.1482,同理 αc2=αc3=αc4=0.1482
σz 2=(αc1+αc2+αc3+αc4) p0=157.7kPa 如表下:
位置
Zi
Zi/b
L/b
Ks
σz =4Ksp0
ห้องสมุดไป่ตู้
1
0.0
0
2
0.2500
266
2
0.8
0.8
2
0.2176 231.5
3
1.6
1.6
2
0.1482 157.7
因 Tv=Cvt/H2 ,则 t=TvH2/Cv=0.25*0.82/(0.3*10-7)=40s
6-6. 某饱和软土地基厚 10 m,性能指标为:容重 17kN/m 3 , 含水量 W=50%,土粒比重 ds 2.7 ,孔隙比 e1 1.35 ,压缩 模量 Es 2MPa ,现在其上大面积堆载 80kPa,单面排水条 件下,固结度达到 80%所需时间为 2 年,求:
6-2. 现有两软粘土层(A、B)都受到 100kPa 的连续均匀荷 载,土层厚
度 H A : H B 2 :1,在 A 层内孔隙比从 1.060 减至 0.982;B 土层 内孔隙
比从 0.910 减至 0.850,已知当土的固结度达到 50%所需的 时间 tA : tB 5 :1,
问此二土层的渗透系数成何比例? 解:固结系数: Cv=k(1+e0)/rwav 又 Es = 1+ e0/av
面,此时粘土层的附加沉降量。
压力 p0 (kPa) 孔隙比 e
0 50 100 200 300 0.85 0.76 0.71 0.65 0.64
解:(1) a.填土土底压力为 p=r0h=18×3=54kPa
填土基底附加应力为
P0=p=54kPa b.求各层层面处的自重应力
σz0=0 σz1=18×1=18kPa σz2=18+(18-10) ×4=50kPa σz3=50+(20-10) ×5=100kPa c.求各分层面的竖向附加应力 σzi=p0=54kPa d.计算各分层的平均自重应力和平均附加应力 因为粗砂的压缩量不计,所以只用算黏土层的沉降即 可,即第三层,如下:
对 A 点有: A=P=150Kpa
'A=150Kpa
uA=0
对 B: uB=P+ sat*H1=150+19.7*1=169.7Kpa
'B=0 KPa
B= 'B+uB=169.7Kpa
对 C:uC=uB+ w*H2=169.7+10*3=199.7Kpa
C=P+ sat*4=150+19.4*4=228.8kpa
(3)由于土的固结度与性质相同,因而 Cv1=Cv2 ,T v1=Tv2 得 Cv1*t1/H2= Cv2*t2/(0.5H)2 t2=0.5 年
6-8. 在天然地表上作用有大面积均布荷载 p 54kPa ,资料如 图 a 所示,地下水位在地表下 1m 处,其上为毛细饱和带, 粘土层的压缩曲线如图 b,粗砂土的压缩量忽略不计,试 求在 p 作用下,地表的最终沉降量(要求采用分层总和法, 按图示分层计算)。
'C= C-uC=228.8-199.7=29.1Kpa
6-14. 在天然地面上大面积堆积厚 3m 填土,重度 0 18kN/m 3 , 不计粗砂的压缩量,地基条件及粘土层的压缩资料如图 和表所示,求:
(1) 原地面在大面积填土作用下的沉降量;
(2) 当上面的沉降稳定后,地下水位突然下降到粘土层顶
(3)计算各层竖向附加应力: 由题知,天然土表面作用大面积均布荷载,所以各层
附加应力均为 54 kPa 即 σzi=54 kPa
(4) 计算沉降量 由上右图可查相应的空隙比 e:
加荷后总
平均自重 平均附加
压缩稳定
层
应力 p2i= 初始孔隙
应力 p1i= 应力σ
后的孔隙
次 σczi(kpa)
zi(kpa)
p0 200 kPa 。求此建筑物在 A 、B 点引起的附加沉降量。 注:(1)电视塔的沉降可假定仅由软粘土层的压缩变形所
产生,且粘土层较薄,计算沉降量时可不分层; (2)应力变化范围不大, Es 或 a 可认为是常量, Es 3720kPa 。
解:将电视塔基础分为 4 个面积相等的小正方形 因为 a=5m,则 m=e/b=1,n=z/b=4 查得 αc1=0.027,同理 αc2=αc3=αc4=0.027 则 σz=(αc1+αc2+αc3+αc4)p0=4x0.027x150=16.2kPa 建筑物在电视塔中心下面黏土层的附加应力 σz’=(αc1’+αc2’+αc3+αc4’)p0
σczi+σzi 力σcz σzi+σcz
比 e1i
比 e2i
3
129
40
169
0.695 0.668
所以黏土层的附加沉降量为
S =( e1 增- e2 增)H/(1+ e1 增)=(0.695-0.668) ×5/ (1+0.695)=7.965cm
6-16 如图所示,己知电视塔的基底附加压力为均布荷载 p0 150 kPa ,建成后中心点最终沉降量为 4.1cm,如果在 该塔旁修建一建筑物,基底附加压力也为均布荷载
m1=45/10=1.5 n1=2
则 αc1’=αc2’=0.13565 又因 m2=15/10=1.5 n2 =z/b=2
则 αc3’=αc4’=0.10685 则 σz’=10.4kPa 又 s=PH/ES 则 s’/ s=σz’/ σz 代入数据,s’=2.73cm
18. 有一条形基础,埋深 2m,基底以下 5m 和 7m 处的附加 应力分别为 65kPa 和 43kPa ,若地下水位在地表处,土 的饱和重度sat=18kN/m3 ,该应力范围内的压缩模量 Es=1.8MPa , 试 问 5m ~ 7m 厚 土 层 压 缩 量 多 少 ? (w=10kN/m3)
)
/2=42kPa
P12=(50+64.4)/2=57.2kPa P21=(266+231.5 ) /2=248.75kPa
P22=(231.5+157.7 )
/2=194.6kPa
0-0.8m Δs1=ΔpH/Es=248.75*0.8/40000=4.975mm
0.8-1.6m 无解 (4)由 U-Tv 曲线图可知固结度为 60%的 Tv=0.25
(1) 此时沉降量为多少? (2) 此时软土的含水量为多少? (3) 若该层为两面排水,达到同样的固结度所需时间。 解:(1)由题意知软土层顶面的自重应力为 po =80kpa 所以软土层的最终沉降量为 S=po H/Es=80*10/2=400mm 当固结度达到 80%时,此时 St=U*S=400*80%=320mm (2)因为 St=(e1-e2)H/(1+e1) 即 320=(1.35-e2)*10000/(1+1.35) 解得 e2=1.2748 由 γw*ds(1+w1)/(1+ e2)= γ 得 w1=(1+ e2) γ/γw*ds-1=43.2%
(2) 水位下降后,位置 2 的自重应力增加了 σz2 增=10×4=40kPa
位置 3 的自重应力增加了 σz3 增=σz2 增=40kPa
所以平均自重应力增加量为 σcz=(σz2 增+σz3 增)/2=40kPa
孔隙比如下:
加荷后总 水位下降 总应力 压缩稳定 水位下降
层
应力 p2i= 增加的应 p2=σczi+ 后的孔隙 后的孔隙 次
由 Tv=Cv *t /H^2 知 t1/(H1/2)^2=t2(H2/2)^2 t1=(H^2/H^2)*t2=0.25t2 同一固结度下 a 土样比 b 土样先达到
