最新谢寿才版概率统计第四章习题及其解答

合集下载

概率论与数理统计第四章习题及答案

概率论与数理统计习题第四章随机变量的数字特征习题4-1 某产品的次品率为，检验员每天检验4次，每次随机地取10件产品进行检验，如发现其中的次品数多于1个，就去调整设备，以X 表示一天中调整设备的次数，试求)(X E （设诸产品是否为次品是相互独立的）.解：设表示一次抽检的10件产品的次品数为ξP =P （调整设备）=P (ξ>1)=1－P (ξ≤1)= 1－[P (ξ=0)+ P (ξ=1)]查二项分布表1－=.因此X 表示一天调整设备的次数时X ～B (4, . P (X =0)=⎪⎪⎭⎫ ⎝⎛04××=.P (X =1)=⎪⎪⎭⎫ ⎝⎛14××=, P (X =2)= ⎪⎪⎭⎫⎝⎛24××=.P (X =3)=⎪⎪⎭⎫ ⎝⎛34××=, P (X =4)= ⎪⎪⎭⎫ ⎝⎛44××=. 从而E (X )=np =4×=习题4-2 设随机变量X 的分布律为Λ,2,1,323)1(1==⎭⎬⎫⎩⎨⎧-=+j j X P jjj ,说明X的数学期望不存在.解：由于1111133322(1)((1))3j j j j j j j j j P X j j j j ∞∞∞++===-=-==∑∑∑，而级数112j j ∞=∑发散，故级数11133(1)((1))j jj j j P X j j∞++=-=-∑不绝对收敛，由数学期望的定义知，X 的数学期望不存在. 习题X-2 0 2 k p求)53(),(),(22+X E X E X E .解 E (X )=(-2)+0+2=由关于随机变量函数的数学期望的定理，知E (X 2)=(-2)2+02+22=E (3X 2+5)=[3 (-2)2+5]+[3 02+5]+[322+5]=如利用数学期望的性质，则有E (3X 2+5)=3E (X 2)+5=3+5=4.135)(3)53(,8.23.04.0)(,2.03.023.004.02)(222222)2(=+=+=⨯+⨯=-=⨯+⨯+⨯-=-X E X E X E X E习题4-4 设随机变量X 的概率密度为⎩⎨⎧≤>=-0,0,0,)(x x e x f x 求XeY X Y 2)2(;2)1(-==的数学期望.解22)(2)0(2)(2)2()()(00=-=+-=+⋅===∞-∞+-∞-+∞-∞-+∞∞-⎰⎰⎰⎰xx xx e dx e xe dx xe dx x dx x xf X E Y E I3131)()()(0303022=-==⋅==∞-∞+-∞+---⎰⎰xx x x X edx e dx e e e E Y E II 习题4-5 设),(Y X 的概率密度为⎩⎨⎧≤≤≤=其它,0,10,12),(2x y y y x f求)(),(),(),(22Y X E XY E Y E X E +.解各数学期望均可按照⎰⎰+∞∞-+∞∞-=dxdy y x f y x g Y X g E ),(),()],([计算。

概率论与数理统计第四章习题解

7.若连续型随机变量ξ的分布密度是：
⎧ax2 + bx + c , (0 < x < 1)
f (x) = ⎨ ⎩
0
， , (x ≤ 0, x ≥ 1)
已知 E(ξ ) ＝1/2， D(ξ ) =3/20,求系数 a 、 b 、 c .
解：应用密度函数的性质有：
∫1
(ax 2
+
bx
+
c)dx
=
(a
x3
解：(1). E(ξ ) ＝－2×0.4＋0×0.3＋2×0.3＝-0.2 .
(2). E(ξ 2 ) = 4 × 0.4 + 0 × 0.3 + 4 × 0.3 = 2.8，
则： E(3ξ 2 + 5) ＝ 3E(ξ 2 ) + 5 = 3 × 2.8 + 5 = 13.4 . (3).由(1),(2)解：
D(ξ ) = E(ξ 2 ) − E 2 (ξ ) = 2.8 − (−0.2)2 = 2.76 .
11.设随机变量
(ξ
,η)
具有概率密度：
f
( x,
y)
=
⎧1 ⎩⎨0
(| y |< x,0 < x < 1) (其它)
，试求：
-5-
E(ξ ) ， E(η) .
∫ ∫ ∫ ∫ ∫ 解：
E(ξ )
=
解：由连续型随机变量数学期望的定义式：
∫ ∫ ∫ +∞
1500
E(ξ ) = xf (x)dx =
1
x 2dx − 3000 x(x − 3000) dx
−∞
0 15002
1500 15002

谢寿才版概率统计第四章习题及其解答

谢寿才版概率统计第四章习题及其解答Revised at 2 pm on December 25, 2020.习题四1．设随机变量X 的分布律为-1 0 1 2求p 答案：4.0=p ，1)(=X E ，1)12(=-X E ； 2.设随机变量X 的分布律为-11且已知1.0)(=X E ,9.0)(2=X E ,求1p ，2p ，3p . 【解】因1231P P P ++=……①,又12331()(1)010.1E X P P P P P =-++=-=……②,222212313()(1)010.9E X P P P P P =-++=+=……③由①②③联立解得1230.4,0.1,0.5.P P P === 3.设随机变量X 的概率密度为求)(X E ，)(X D . 【解】1221()()d d (2)d E X xf x x x x x x x +∞-∞==+-⎰⎰⎰故 221()()[()].6D XE X E X =-=4.设随机变量X 的概率密度为求(1)c ；（2）)(X E ；（3）)(X D . 【解】(1) 由222()d e d 12k x c f x x cx x k+∞+∞--∞===⎰⎰得22c k =. (2) 2220()()d()2e d k x E X xf x x x k x x +∞+∞--∞==⎰⎰(3) 22222221()()d()2e .kxE X x f x x x k x k +∞+∞--∞==⎰⎰故222221π4π()()[()].4D X E X E X k k-=-=-=⎝⎭ 5. 过单位圆上一点P 作任意弦PA ，PA 与直径PB 的夹角θ服从区间⎪⎭⎫⎝⎛-2,2ππ上的均匀分布，求弦PA 的长度的数学期望.解：弦PA 的长为随机变量X ，由任意θ的密度函数为 6．设X 服从柯西分布，其密度函数为问)(X E 是否存在？解：因为所以EX 不存在。

概率论习题及解答-第四章特征函数

ξ = a min{Y, x} − bx.
从而平均利润
∫∞ E(ξ) = aE(min{Y, x}) − bx = a min{y, x}λe−λydy − bx
(∫ x
∫∞ 0
)
=a
yλe−λydy +
xλe−λydy − bx
(0
∫x x
)
= a − xe−λx + e−λydy + xe−λx − bx
∑ ∞
∑ ∞ ∑i
E(η) = iP(η = i) =
P(η = i)
i=1
i=1 k=1
∑ ∞ ∑ ∞
∑ ∞
=
P(η = i) = P(η k).
注意到
P(min{ξ1, ξ2, · · · , ξn}
k=1 i=k
k) = P(ξ1 k, ξ2
k=1
k, · · · , ξn
( ∑ )n
k) =
记 µk = p0 + p1 + · · · + pk−1, νk = 1 − µk, 试证明
∑ ∞ E(min{ξ1, ξ2, · · · , ξn}) = νkn,
k=1
∑ ∞ E(max(ξ1, ξ2, · · · , ξn)) = (1 − µnk ).
k=1
4
证明: 若 η 为取非负整值随机变量, 则
得
∑ ∞
∑ ∞
E(max{ξ1, ξ2, · · · , ξn}) = P(max{ξ1, ξ2, · · · , ξn} k) = (1 − µnk ).
k=1
k=1
练习4.1.11 设随机变量 ξ, η 独立同分布, ξ ∼ N (a, σ2), 试证明

概率论与数理统计》课后习题答案第四章

习题4.11．设10个零件中有3个不合格．现任取一个使用，若取到不合格品，则丢弃重新抽取一个，试求取到合格品之前取出的不合格品数X 的数学期望．解可得X 的概率分布为0123~77711030120120X ⎡⎤⎢⎥⎢⎥⎣⎦于是X 的数学期望为7771()012310301201204531208E X =⨯+⨯+⨯+⨯==2．.某人有n 把外形相似的钥匙，其中只有1把能打开房门，但他不知道是哪一把，只好逐把试开．求此人直至将门打开所需的试开次数X 的数学期望．解可得X 的概率分布为12~111n X nn n ⎡⎤⎢⎥⎢⎥⎣⎦于是X 的数学期望为111()121(1)122E X n n n nn n n n =⨯+⨯++⨯++==3．设5次重复独立试验中每次试验的成功率为0.9，若记失败次数为X ，求X 的数学期望。

解由题意~(5,0.1)X B ，则X 的数学期望为()50.10.5E X =⨯=4．设某地每年因交通事故死亡的人数服从泊松分布．据统计，在一年中因交通事故死亡一人的概率是死亡两人的概率的21，求该地每年因交通事故死亡的平均人数。

解设该地每年因交通事故死亡的人数为X ，由题意X 服从泊松分布() (0)P λλ>.因1{1}{2}2P X P X === 即121 41!22!ee λλλλλ--=⇒= 于是X 的数学期望为()4E X λ==所以地每年因交通事故死亡的平均人数为4人。

5．设随机变量X 在区间(1,7)上服从均匀分布，求2{()}P X E X <. 解因X 在区间(1,7)上服从均匀分布，故X 的数学期望为17()42E X +== 于是22{()}{4}1 {22}6P X E X P X P X <=<=<-<<=6．设连续型随机变量X 的概率密度为01() (,0)0 b ax x p x a b ⎧<<=>⎨⎩其它又知()0.75E X =,求,a b 的值解由密度函数的性质可得()1p x dx +∞-∞=⎰即1111b aax dx b =⇒=+⎰又由()0.75E X =，可得1()0.75b xp x dx x ax dx +∞-∞=⋅=⎰⎰即0.752ab =+ 求解110.752a b a b ⎧=⎪⎪+⎨⎪=⎪+⎩ 可得 3,2a b ==.7．设随机变量X 的概率密度为0<1()2 120 x x p x x x <⎧⎪=-≤<⎨⎪⎩其它求数学期望()E X解12013312201()() (2) ()133E X xp x dxx xdx x x dx x x x +∞-∞==⋅+⋅-=+-=⎰⎰⎰8.设随机变量X 的概率分布为 X -2 -1 0 1 P 0.2 0.3 0.1 0.4 求(1)(21)E X -；（2）2()E X .解 (1) (21)2()1E X E X -=- 其中()20.210.3010.40.3E X =-⨯-⨯++⨯=-则(21)2()12(0.3)1 1.6E X E X -=-=⨯--=-(2）22222()0.2(2)0.3(1)0.100.41 1.5E X =⨯-+⨯-+⨯+⨯=9．假设一部机器在一天内发生故障的概率为0.2，机器发生故障时全天停止工作。

概率论第四章习题解答(全)

(0.9)10 (0.9)9 3486 0.3874 0.7361
则需要调整设备的概率
P{Y 1} 1 P{Y } 1 0.7361 0.2639
（3）求一天中调整设备的次数 X 的分布律由于 X 取值为 0，1，2，3，4。 p 0.2369 ，则 X B (4, 0.2369) 于是
个随机变量，其概率密度为
1 x, 0 x 1500, 15002 1 f ( x) ( x 3000),1500 x 3000, 2 1500 0, 其它
求 E( X ) 解按连续型随机变量的数学期望的定义有
0 1500
E ( X ) xf ( x)dx xf ( x)dx
X p
2
3
4
9
1 8
5 8
1 8
1 8
所以
1 5 1 1 15 E( X ) 2 3 4 9 。 8 8 8 8 4
（2）因为 Y 的取值为 2,3，4，9 当 Y 2 时，包含的字母为“O”，“N”，故
P{Y 2}
1 C2 1 ； 30 15
当 Y 3 时，包含的 3 个字母的单词共有 5 个，故
P (Ck ) P ( Ak | A1 A2 Ak 1 ) P ( Ak 1 | A1 A2 Ak 2 ) P ( A2 | A1 ) P ( A1 )
而
P{ X 1} P ( A1 )
1 2
1 1 P{ X 2} P ( A1 A2 ) P ( A2 | A1 ) P ( A1 ) 3 2 1 2 1 1 1 P ( A2 | A1 A2 ) P ( A2 | A1 ) P ( A1 ) ， 4 3 2 4 3 一般地，若当 X k 时，盒中共有 k 1 只球，其中只有一只白球，故 P ( X k ) P ( A1 A2 Ak 1 Ak ) P ( Ak | A1 A2 Ak 1 ) P ( Ak 1 | A1 A2 Ak 2 ) P ( A2 | A1 ) P ( A1 ) 1 k 1 k 2 1 2 1 1 1 k 1 k k 1 4 3 2 k k

概率论与数理统计(第四版)习题答案全

概率论与数理统计习（第四版）题解答第一章随机事件及其概率·样本空间·事件的关系及运算一、任意抛掷一颗骰子，观察出现的点数。

设事件A 表示“出现偶数点”，事件B 表示“出现的点数能被3整除”．（1）写出试验的样本点及样本空间；（2）把事件A 及B 分别表示为样本点的集合；（3）事件B A AB B A B A ,,,,分别表示什么事件？并把它们表示为样本点的集合．解：设i ω表示“出现i 点”)6,,2,1( =i ，则（1）样本点为654321,,,,,ωωωωωω；样本空间为}.,,,,,{654321ωωωωωω=Ω （2）},,{642ωωωA =； }.,{63ωωB =（3）},,{531ωωωA =，表示“出现奇数点”；},,,{5421ωωωωB =，表示“出现的点数不能被3整除”；},,,{6432ωωωωB A =⋃，表示“出现的点数能被2或3整除”；}{6ωAB =，表示“出现的点数能被2整除且能被3整除”；},{B A 51ωω= ，表示“出现的点数既不能被2整除也不能被3整除”二、写出下列随机试验的样本空间及各个事件中的样本点：（1）同时掷三枚骰子，记录三枚骰子的点数之和．A —“点数之和大于10”，B —“点数之和小于15”．（2）一盒中有5只外形相同的电子元件，分别标有号码1，2，3，4，5．从中任取3只，A —“最小号码为1”．解：(1) 设i ω表示“点数之和等于i ”)18,,4,3( =i ，则},,,{1843ωωω =Ω；},,,{181211ωωωA =；}.,,,{1443ωωωB =(2) 设ijk ω表示“出现号码为k j i ,,”);5,,2,1,,(k j i k j i ≠≠= ，则},,,,,,,,,{345245235234145135134125124123ωωωωωωωωωω=Ω }.,,,,,{145135134125124123ωωωωωωA =三、设C B A ,,为三个事件，用事件之间的运算表示下列事件： (1) A 发生, B 与C 都不发生； (2) C B A ,,都发生；(3) C B A ,,中至少有两个发生； (4) C B A ,,中至多有两个发生．解：(1) C B A ；(2) ABC ；(3) ABC C AB C B A BC A ⋃⋃⋃或CA BC AB ⋃⋃(4) BC A C B A C AB C B A C B A C B A C B A ⋃⋃⋃⋃⋃⋃或C B A ⋃⋃或.ABC四、一个工人生产了n 个零件，以i A 表示他生产的第 i 个零件是合格品（n i ≤≤1）．用i A 表示下列事件：（1）没有一个零件是不合格品；（2）至少有一个零件是不合格品；（3）仅有一个零件是不合格品；（4）至少有一个零件不是不合格品．解：(1) n A A A 21；(2) n A A A 21或n A A A ⋃⋃⋃ 21； (3) n n n A A A A A A A A A 212121⋃⋃⋃ (4) n A A A ⋃⋃⋃ 21或.21n A A A第二章概率的古典定义·概率加法定理一、电话号码由七个数字组成，每个数字可以是0，1，2，…，9中的任一个数（但第一个数字不能为0），求电话号码是由完全不同的数字组成的概率．解：基本事件总数为611011011011011011019109⨯=C C C C C C C 有利事件总数为456789214151617181919⨯⨯⨯⨯⨯=C C C C C C C 设A 表示“电话号码是由完全不同的数字组成”，则0605.0109456789)(62≈⨯⨯⨯⨯⨯⨯=A P二、把十本书任意地放在书架上，求其中指定的三本书放在一起的概率．解：基本事件总数为!101010=A 指定的三本书按某确定顺序排在书架上的所有可能为!777=A 种；这三本书按确定的顺序放在书架上的所以可能的位置共818=C 种；这三本书的排列顺序数为!333=A ；故有利事件总数为!3!8!38!7⨯=⨯⨯(亦可理解为)3388P P 设A 表示“指定的三本书放在一起”，则067.0151!10!3!8)(≈=⨯=A P三、为了减少比赛场次，把二十个队任意分成两组（每组十队）进行比赛，求最强的两个队被分在不同组内的概率．解：20个队任意分成两组（每组10队）的所以排法，构成基本事件总数1020C ；两个最强的队不被分在一组的所有排法，构成有利事件总数91812C C 设A 表示“最强的两队被分在不同组”，则526.01910)(102091812≈==C C C A P四、某工厂生产的产品共有100个，其中有5个次品．从这批产品中任取一半来检查，求发现次品不多于1个的概率．解：设i A 表示“出现的次品为i 件”)5,4,3,2,1,0(=i ，A 表示“取出的产品中次品不多于 1个”，则 .10A A A ⋃=因为V A A =10，所以).()()(10A P A P A P +=而0281.0979942347)(5010050950≈⨯⨯⨯==C C A P 1529.09799447255)(501004995151≈⨯⨯⨯⨯==C C C A P 故 181.01529.00281.0)(=+≈A P五、一批产品共有200件, 其中有6件废品．求 (1) 任取3件产品恰有1件是废品的概率; (2) 任取3件产品没有废品的概率; (3) 任取3件产品中废品不少于2件的概率．解：设A 表示“取出的3件产品中恰有1件废品”；B 表示“取出的3件产品中没有废品”；C 表示“取出的3件产品中废品不少于2件”，则 (1) 0855.019819920019319418)(3200219416≈⨯⨯⨯⨯==C C C A P (2) 912.0198199200192193194)(32003194≈⨯⨯⨯⨯==C C B P(3) 00223.019819920012019490)(3200019436119426≈⨯⨯⨯⨯=+=C C C C C C P六、设41)( ,0 ,31)()()(======BC P P(AC)P(AB)C P B P A P ．求A , B , C 至少有一事件发生的概率．解：因为0==P(AC)P(AB)，所以V AC V AB ==,，从而V C AB =)(可推出0)(=ABC P设D 表示“A , B , C 至少有一事件发生”，则C B A D ⋃⋃=，于是有)()()()()()()()()(ABC P CA P BC P AB P C P B P A P C B A P D P +---++=⋃⋃= 75.04341313131==-++=第三章条件概率与概率乘法定理·全概率公式与贝叶斯公式一、设,6.0)|(,4.0)(,5.0)(===B A P B P A P 求)|(,)(B A A P AB P ．解：因为B A AB B B A A +=+=)(，所以)()()(B A P AB P A P +=，即14.06.0)4.01(5.0)()()()()()(=⨯--=-=-=B A P B P A P B A P A P AB P68.074.05.036.0)4.01(5.05.0)()()()()()]([)|(≈=--+=-+==B A P B P A P A P B A P B A A P B A A P二、某人忘记了电话号码的最后一个数字，因而他随意地拨号，求他拨号不超过两次而接通所需电话的概率．若已知最后一个数字是奇数，那么此概率是多少？解：设A 表示“第一次拨通”，B 表示“第二次拨通”，C 表示“拨号不超过两次而拨通”（1）2.0101101)()()(19111101911011=+=⋅+=+=C C C C C C A B P A P C P（2）4.05151)()()(2511141511=+=+=+=A A A A A A B P A P C P三、两台车床加工同样的零件，第一台出现废品的概率是0.03，第二台出现废品的概率是0.02．加工出来的零件放在一起，并且已知第一台加工的零件比第二台加工的零件多一倍．（1）求任意取出的零件是合格品的概率；（2）如果任意取出的零件是废品，求它是第二台车床加工的概率．解：设i A 表示“第i 台机床加工的零件”)2,1(=i ；B 表示“出现废品”；C 表示“出现合格品”（1）)()()()()()()()(22112121A C P A P A C P A P C A P C A P C A C A P C P +=+=+= 973.0)02.01(31)03.01(32≈-⨯+-⨯=（2）25.002.03103.03202.031)()()()()()()()()(22112222=⨯+⨯⨯=+==A B P A P A B P A P A B P A P B P B A P B A P四、猎人在距离100米处射击一动物，击中的概率为0.6；如果第一次未击中，则进行第二次射击，但由于动物逃跑而使距离变为150米；如果第二次又未击中，则进行第三次射击，这时距离变为200米．假定击中的概率与距离成反比，求猎人三次之内击中动物的概率．解：设i A 表示“第i 次击中”)3,2,1(=i ，则由题设，有1006.0)(1kA P ==，得60=k ，从而有4.015060150)(2===k A P ，.3.020060200)(3===k A P设A 表示“三次之内击中”，则321211A A A A A A A ++=，故有)()()()()()()(321211A P A P A P A P A P A P A P ++=832.03.0)4.01()6.01(4.0)6.01(6.0=⨯-⨯-+⨯-+= （另解）设B 表示“猎人三次均未击中”，则168.0)3.01)(4.01)(6.01()(=---=B P故所求为 832.0)(1)(=-=B P B P五、盒中放有12个乒乓球，其中有9个是新的．第一次比赛时从其中任取3个来用，比赛后仍放回盒中．第二次比赛时再从盒中任取3个，求第二次取出的都是新球的概率．解：设i A 表示“第一次取得i 个新球”)3,2,1,0(=i ，则2201)(312330==C C A P 22027)(31219231==C C C A P 220108)(31229132==C C C A P 22084)(31239033==C C C A P 设B 表示“第二次取出的都是新球”，则31236312373123831239322084220108220272201)()()(C C C C C C C C A B P A P B P i i i ⋅+⋅+⋅+⋅==∑=146.0532400776161112208444722010855142202755212201≈=⋅+⋅+⋅+⋅=第四章随机事件的独立性·独立试验序列一、一个工人看管三台车床，在一小时内车床不需要工人照管的概率：第一台等于0.9，第二台等于0.8，第三台等于0.7．求在一小时内三台车床中最多有一台需要工人照管的概率．解：设i A 表示“第i 台机床不需要照管”)3,2,1(=i ，则9.0)(1=A P 8.0)(2=A P 7.0)(3=A P再设B 表示“在一小时内三台车床中最多有一台需要工人照管”，则321321321321A A A A A A A A A A A A B +++=于是有)()()()()()()()()()()()()(321321321321A P A P A P A P A P A P A P A P A P A P A P A P B P +++=)7.01(8.09.07.0)8.01(9.07.08.0)9.01(7.08.09.0-⨯⨯+⨯-⨯+⨯⨯-+⨯⨯=902.0=．（另解）设i B 表示“有i 台机床需要照管”)1,0(=i ，B 表示“在一小时内三台车床中最多有一台需要工人照管”，则10B B B +=且0B 、1B 互斥，另外有504.07.08.09.0)(0=⨯⨯=B P398.0)7.01(8.09.07.0)8.01(9.07.08.0)9.01()(1=-⨯⨯+⨯-⨯+⨯⨯-=B P故902.0398.0504.0)()()()(1010=+=+=+=B P B P B B P B P ．二、电路由电池a 与两个并联的电池b 及c 串联而成．设电池c b a ,,损坏的概率分别是0.3、0.2、0.2，求电路发生间断的概率．解：设1A 表示“a 损坏”；2A 表示“b 损坏”；3A 表示“c 损坏”；则3.0)(1=A P 2.0)()(32==A P A P又设B 表示“电路发生间断”，则321A A A B +=于是有)()()()()(321321321A A A P A A P A P A A A P B P -+=+=)()()()()()(321321A P A P A P A P A P A P -+= 328.02.02.03.02.02.03.0=⨯⨯-⨯+=．三、三个人独立地去破译一个密码，他们能译出的概率分别为51、31、41，求能将此密码译出的概率．解：设A 表示“甲能译出”；B 表示“乙能译出”；C 表示“丙能译出”，则51)(=A P 31)(=B P 41)(=C P设D 表示“此密码能被译出”，则C B A D ⋃⋃=，从而有)()()()()()()()()(ABC P CA P BC P AB P C P B P A P C B A P D P +---++=⋃⋃= )()()()()()()()()()()()(C P B P A P A P C P C P B P B P A P C P B P A P +---++= 6.0413151415141513151413151=⨯⨯+⨯-⨯-⨯-++=．（另解）52)411)(311)(511()()()()()(=---===C P B P A P C B A P D P ，从而有6.053521)(1)(==-=-=D P D P四、甲、乙、丙三人同时对飞机进行射击，三人的命中概率分别为7.0,5.0,4.0．飞机被一人击中而被击落的概率为2.0，被两人击中而被击落的概率为6.0，若三人都击中，则飞机必被击落．求飞机被击落的概率．解：设1A 表示“甲命中”；2A 表示“乙命中”；3A 表示“丙命中”；则4.0)(1=A P5.0)(2=A P 7.0)(3=A P设i B 表示“i 人击中飞机” )3,2,1,0(=i ，则09.0)7.01)(5.01)(4.01()())(()()(3213210=---===A P A P A P A A A P B P )()(3213213211A A A A A A A A A P B P ++=)()()(321321321A A A P A A A P A A A P ++=)()()()()()()()()(321321321A P A P A P A P A P A P A P A P A P ++=36.07.0)5.01)(4.01()7.01(5.0)4.01()7.01)(5.01(4.0=⨯--+-⨯⨯-+--⨯=)()(3213213212A A A A A A A A A P B P ++=)()()(321321321A A A P A A A P A A A P ++=)()()()()()()()()(321321321A P A P A P A P A P A P A P A P A P ++=41.07.0)5.01)(4.01()7.01(5.0)4.01()7.01)(5.01(4.0=⨯--+-⨯⨯-+--⨯=14.07.05.04.0)()()()()(3213213=⨯⨯===A P A P A P A A A P B P设A 表示“飞机被击落”，则由题设有0)(0=B A P 2.0)(1=B A P 6.0)(2=B A P 1)(3=B A P故有458.0114.06.041.02.036.0009.0)()()(30=⨯+⨯+⨯+⨯==∑=i i i B A P B P A P ．五、某机构有一个9人组成的顾问小组，若每个顾问贡献正确意见的概率都是0.7，现在该机构内就某事可行与否个别征求每个顾问的意见，并按多数人意见作出决策，求作出正确决策的概率．解：设i A 表示“第i 人贡献正确意见”，则7.0)(=i A P )9,,2,1( =i ．又设m 为作出正确意见的人数，A 表示“作出正确决策”，则)9()8()7()6()5()5()(99999P P P P P m P A P ++++=≥=+⋅⋅+⋅⋅+⋅⋅=277936694559)3.0()7.0()3.0()7.0()3.0()7.0(C C C 9991889)7.0()3.0()7.0(⋅+⋅⋅+C C+⋅⋅+⋅⋅+⋅⋅=273645)3.0()7.0(36)3.0()7.0(84)3.0()7.0(126918)7.0()3.0()7.0(9+⋅⋅+0403.01556.02668.02668.01715.0++++=901.0=．六、每次试验中事件A 发生的概率为p ，为了使事件A 在独立试验序列中至少发生一次的概率不小于p ，问至少需要进行多少次试验？解：设做n 次试验，则n p A P A P )1(1}{1}{--=-=一次都不发生至少发生一次要p p n ≥--)1(1，即要p p n -≤-1)1(，从而有.1)1(log )1(=-≥-p n p 答：至少需要进行一次试验．第五章离散随机变量的概率分布·超几何分布·二项分布·泊松分布一、一批零件中有9个合格品与3个废品．安装机器时从这批零件中任取1个．如果每次取出的废品不再放回去，求在取得合格品以前已取出的废品数的概率分布．解：设X 表示“在取得合格品以前已取出的废品数”，则X 的概率分布为即亦即二、自动生产线在调整以后出现废品的概率为p ．生产过程中出现废品时立即进行调整．求在两次调整之间生产的合格品数的概率分布．解：设X 表示“在两次调整之间生产的合格品数”，且设p q -=1，则ξ的概率分布为三、已知一批产品共20个，其中有４个次品．（１）不放回抽样．抽取６个产品，求样品中次品数的概率分布；（２）放回抽样．抽取６个产品，求样品中次品数的概率分布．解：（1）设X 表示“取出的样本中的次品数”，则X 服从超几何分布，即X 的概率函数为)4,3,2,0()(6206164===-x C C C x X P xx从而X 的概率分布为即（2）设X 表示“取出的样本中的次品数”，则X 服从超几何分布，即X 的概率函数为)6,5,4,3,2,0()2.01()2.0()(66=-==-x C x X P xx x从而X 的概率分布为即四、电话总机为300个电话用户服务．在一小时内每一电话用户使用电话的概率等于0.01，求在一小时内有4个用户使用电话的概率（先用二项分布计算，再用泊松分布近似计算，并求相对误差）．解：（1）用二项分布计算)01.0(=p168877.0)01.01()01.0()1()4(2964430029644300≈-=-==C p p C ξP（2）用泊松分布计算)301.0300(=⨯==np λ168031355.0!43)4(34≈==-e ξP相对误差为.5168877.0168031355.0168877.0000≈-=δ五、设事件A 在每一次试验中发生的概率为0.3，当A 发生次数不少于3次时，指示灯发出信号．现进行了5次独立试验，求指示灯发出信号的概率．解：设X 表示“事件A 发生的次数”，则3.0)(==p A P ，5=n ，).3.0,5(~B X 于是有)5()4()3()3(=+=+==≥X P X P X P X P5554452335)1()1(p C p p C p p C +-+-=16308.000243.002835.01323.0≈++≈（另解） )2()1()0(1)3(1)3(=-=-=-=<-=≥X P X P X P X P X P322541155005)1()1()1(11p p C p p C p p C ------=16308.0≈六、设随机变量X 的概率分布为2, 1, ,0 , !)(===k k ak X P kλ；其中λ>0为常数，试确定常数a ．解：因为∑∞===01)(k k X P ，即∑∞==01!k kk λa ，亦即1=λae ，所以.λe a -=第六章随机变量的分布函数·连续随机变量的概率密度一、函数211x+可否是连续随机变量X 的分布函数？为什么？如果X 的可能值充满区间：（1）（∞+∞- ,）；（2）（0,∞-）．解：（1）设211)(x x F +=，则1)(0<<x F因为0)(lim =-∞→x F x ，0)(lim =+∞→x F x ，所以)(x F 不能是X 的分布函数．（2）设211)(x x F +=，则1)(0<<x F 且0)(lim =-∞→x F x ，1)(lim 0=-→x F x 因为)0( 0)1(2)('22<>+-=x x xx F ，所以)(x F 在（0,∞-）上单增．综上述，故)(x F 可作为X 的分布函数．二、函数x x f sin )(=可否是连续随机变量X 的概率密度？为什么？如果X 的可能值充满区间：（1）⎥⎦⎤⎢⎣⎡2,0π；（2）[]π,0；（3）⎥⎦⎤⎢⎣⎡23,0π．解：（1）因为⎥⎦⎤⎢⎣⎡∈2,0πx ，所以0sin )(≥=x x f ；又因为1cos )(2020=-=⎰ππx dx x f ，所以当⎥⎦⎤⎢⎣⎡∈2,0πx 时，函数x x f sin )(=可作为某随机变量X 的概率密度．（2）因为[]πx ,0∈，所以0sin )(≥=x x f ；但12cos )(00≠=-=⎰ππx dx x f ，所以当[]πx ,0∈时，函数x x f sin )(=不可能是某随机变量X 的概率密度．（3）因为⎥⎦⎤⎢⎣⎡∈23,0πx ，所以x x f sin )(=不是非负函数，从而它不可能是随机变量X 的概率密度．二、一批零件中有9个合格品与3个废品．安装机器时从这批零件中任取1个．如果每次取出的废品不再放回去，求在取得合格品以前已取出的废品数的分布函数，并作出分布函数的图形．解：设X 表示“取出的废品数”，则X 的分布律为于是，X 的分布函数为⎪⎪⎪⎩⎪⎪⎪⎨⎧>≤<≤<≤<≤=3,132,22021921,222110,430,0)(x x x x x x F 其图形见右：四、（柯西分布）设连续随机变量X 的分布函数为+∞<<∞-+=x x B A x F ,arctan )(．求：（1）系数A 及B ；（2）随机变量X 落在区间)1 ,1(-内的概率；(3) X 的概率密度．解：(1) 由0)2()(lim =-⋅+=-∞→πB A x F x ，12)(lim =⋅+=-∞→πB A x F x ，解得.1,21πB A ==即)( ,arctan 121)(+∞<<-∞+=x x πx F ． (2) .21)]1arctan(121[]1arctan 121[)1()1()11(=-+-+=--=<<-ππF F X P(3) X 的概率密度为)1(1)()(2x x F x f +='=π．五、（拉普拉斯分布）设随机变量X 的概率密度为+∞<<∞-=-x Ae x f x,)(．求：（1）系数A ；（2）随机变量X 落在区间)1,0(内的概率；（3）随机变量X 的分布函数．解：(1) 由1)(⎰+∞∞-=dx x f ，得1220⎰⎰+∞∞-+∞--===A dx e A dx Ae xx ，解得21=A ，即有).( ,21)(+∞<<-∞=-x e x f x(2) ).11(21)(2121)()10(101010ee dx e dx xf X P x x -=-===<<--⎰⎰(3) 随机变量X 的分布函数为⎪⎩⎪⎨⎧>-≤===-∞--∞-⎰⎰21102121)()(x e x e dx e dx x f x F x x x xx．第七章均匀分布·指数分布·随机变量函数的概率分布一、公共汽车站每隔5分钟有一辆汽车通过．乘客到达汽车站的任一时刻是等可能的．求乘客候车时间不超过3分钟的概率．解：设随机变量X 表示“乘客的候车时间”，则X 服从]5,0[上的均匀分布，其密度函数为⎩⎨⎧∉∈=]5,0[,0]5,0[,51)(x x x f 于是有.6.053)()30(3===≤≤⎰dx x f X P二、已知某种电子元件的使用寿命X (单位:h)服从指数分布，概率密度为⎪⎩⎪⎨⎧≤>=-.0,0;0,8001)(800x x e x f x任取３个这种电子元件，求至少有１个能使用1000h 以上的概率．解：设A 表示“至少有１个电子元件能使用1000h 以上”；321A 、A 、A 分别表示“元件甲、乙、丙能使用1000h 以上”．则287.08001)1000()()()(4510008001000800321≈=-==>===-∞+-∞+-⎰e e dx e X P A P A P A P xx)()()()()()()()()(321313221321321A A A P A A P A A P A A P A P A P A P A A A P A P +---++=⋃⋃=638.0287.0287.03287.0332≈+⨯-⨯=（另解）设A 表示“至少有１个电子元件能使用1000h 以上”．则287.08001)1000(4510008001000800≈=-==>-∞+-∞+-⎰e e dx e X P xx从而有713.01)1000(1)1000(45≈-=>-=≤-eX P X P ，进一步有638.0713.01)]1000([1)(33≈-≈≤-=X P A P三、(1) 设随机变量X 服从指数分布)(λe ．证明：对于任意非负实数s 及t ，有).()(t X P s X t s X P ≥=≥+≥这个性质叫做指数分布的无记忆性．(2) 设电视机的使用年数X 服从指数分布)10(．e ．某人买了一台旧电视机，求还能使用５年以上的概率．解：（１）因为)(~λe X ，所以R x ∈∀，有xex F λ--=1)(，其中)(x F 为X 的分布函数．设t s X A +≥=，t X B ≥=．因为s 及t 都是非负实数，所以B A ⊂，从而A AB =．根据条件概率公式，我们有)(1)(1)()()()()()()()(s X P t s X P s X P t s X P B P A P B P AB P B A P s X t s X P <-+<-=≥+≥====≥+≥tst s e e e λλλ--+-=----=]1[1]1[1)(．另一方面，我们有t t e e t F t X P t X P t X P λλ--=--=-=≤-=<-=≥)1(1)(1)(1)(1)(．综上所述，故有)()(t X P s X t s X P ≥=≥+≥．（２）由题设，知X 的概率密度为⎩⎨⎧≤>=-．，；，0001.0)(1.0x x e x f x 设某人购买的这台旧电视机已经使用了s 年，则根据上述证明的（１）的结论，该电视机还能使用5年以上的概率为6065.01.0)()5()5(5.051.051.05≈=-===≥=≥+≥-∞+-∞+-∞+⎰⎰e e dx e dx xf X P s X s X P xx ．答：该电视机还能使用5年以上的概率约为6065.0．四、设随机变量X 服从二项分布)4.0 ,3(B ，求下列随机变量函数的概率分布：（1）X Y 211-=；（2）2)3(2X X Y -=．解：X 的分布律为（1）X Y 211-=的分布律为（2）2)3(2X X Y -=的分布律为即五、设随机变量X 的概率密度为⎪⎩⎪⎨⎧≤>+=.0,0;0,)1(2)(2x x x x f π求随机变量函数X Y ln =的概率密度．解：因为)()()(ln )()(yX yY e F e X P y X P y Y P y F =<=<=<= 所以随机变量函数X Y ln =的概率密度为)( )1(2)()()()(2''+∞<<-∞+====y e e e e f e e F y F y f yyyyyyXYY π，即 )( )1(2)(2+∞<<-∞+=y e e y f yyY π．第八章二维随机变量的联合分布与边缘分布一、把一颗均匀的骰子随机地掷两次．设随机变量X 表示第一次出现的点数，随机变量Y 表示两次出现点数的最大值，求二维随机变量),(Y X 的联合概率分布及Y 的边缘概率分布．解：二维随机变量),(Y X 的联合概率分布为Y 的边缘概率分布为二、设二维随机变量（X ，Y ）的联合分布函数)3arctan )(2arctan (),(yC x B A y x F ++=．求：（1）系数A 、B 及C ；（2）（X ，Y ）的联合概率密度：（3）边缘分布函数及边缘概率密度．解：（1）由0)0,(,0),0(,1),(=-∞=∞-=∞+-∞F F F ，得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=--=++0)2(0)2)(0(1)2)(2(πB AC πC B A πC πB A 解得2πC B ==，.12πA =（2）因为)3arctan 2)(2arctan 2(1),(2yx y x F ++=πππ，所以（X ，Y ）的联合概率密度为.)9)(4(6),(),(222"y x y x F y x f xy ++==π （3）X 及Y 的边缘分布函数分别为 xxxX xdx x dy y x f dx x F ∞-∞-∞-+∞∞-=+==⎰⎰⎰2arctan1)4(2),()(2ππ2arctan 121x π+=yxyY ydy y dx y x f dy x F ∞-∞-∞-+∞∞-=+==⎰⎰⎰3arctan1)9(3),()(2ππ3arctan 121y π+=X 及Y 的边缘概率密度分别为⎰⎰⎰+∞+∞∞-+∞∞-++⋅=++==0222222)9(1)4(112)9)(4(6),()(dy y x dy y x dy y x f x f X ππ )4(2)3arctan 31()4(1122022x y x +=+⋅=∞+ππ ⎰⎰⎰+∞+∞∞-+∞∞-++=++==022222241)9(12)9)(4(6),()(dx x y dx y x dx y x f y f Y ππ)9(3)2arctan 21()9(122022y x y +=+=∞+ππ三、设),(Y X 的联合概率密度为⎩⎨⎧>>=+-.,00;0,,Ae ),(3y)(2x 其它y x y x f求：（1）系数A ；（2）),(Y X 的联合分布函数；（3）X 及Y 的边缘概率密度；（4）),(Y X落在区域R ：632 ,0 ,0<+>>y x y x 内的概率．解：（1）由1),(=⎰⎰+∞∞-+∞∞-dy dx y x f ，有16132==⎰⎰∞+∞+--A dy e dx e A y x ，解得.6=A （2）),(Y X 的联合分布函数为⎪⎩⎪⎨⎧>>==⎰⎰⎰⎰--∞-∞-其它0,06),(),(0032y x dy e dx e dy y x f dx y x F x yy x xy⎩⎨⎧>>--=--其它0,0)1)(1(32y x e e y x （3）X 及Y 的边缘概率密度分别为⎩⎨⎧≤>=⎪⎩⎪⎨⎧≤>==-+∞--∞+∞-⎰⎰00020006),()(2032x x ex x dy e e dy y x f x f x y x X⎩⎨⎧≤>=⎪⎩⎪⎨⎧≤>==-+∞--∞+∞-⎰⎰00030006),()(3032y y ex x dx e e dx y x f y f y y x Y（4）⎰⎰⎰⎰---==∈x y xRdy e dx edxdy y x f R Y X P 32203326),(}),{(6306271)(2---⎰-=-=e dx e e x四、设二维随机变量),(Y X 在抛物线2x y =与直线2+=x y 所围成的区域R 上服从均匀分布．求：(1) ),(Y X 的联合概率密度；(2) 概率)2(≥+Y X P ．解：(1) 设),(Y X 的联合概率密度为⎩⎨⎧∉∈=.),(, 0;),(,),(R y x R y x C y x f 则由129)322()2(21322122212==-+=-+==--+-⎰⎰⎰⎰⎰C x x x C dx x x C dy dx C Cdxdy x x R解得92=C ．故有⎪⎩⎪⎨⎧∉∈=.),(, 0;),(,92),(R y x R y x y x f(2) ⎰⎰⎰⎰⎰⎰++-≥++==≥+x x x x y x dy dx dy dx dxdy y x f Y X P 2212210229292),()2(⎰⎰-++=21210)2(92292dx x x xdx481.02713)322(92922132102≈=-++=x x x x ．第九章随机变量的独立性·二维随机变量函数的分布一、设X 与Y 是两个相互独立的随机变量，X 在]1,0[上服从均匀分布，Y 的概率密度为⎪⎩⎪⎨⎧≤>=-.0,0;0,21)(2y y e y f yY求 (1) ),(Y X 的联合概率密度; (2) 概率)(X Y P ≥．解: (1)X 的概率密度为⎩⎨⎧∉∈=)1,0(,0)1,0(,1)(x x x f X ，),(Y X 的联合概率密度为（注意Y X ,相互独立）⎪⎩⎪⎨⎧><<==-其它,00,10,21)()(),(2y x e y f x f y x f yY X（2）dx edx e dy e dx dxdy y x f X Y P x xyxy xy ⎰⎰⎰⎰⎰⎰-∞+-∞+-≥=-===≥1021022102)(21),()(7869.0)1(2221122≈-=-=--e ex二、设随机变量X 与Y 独立，并且都服从二项分布：.,,2 ,1 ,0 ,)(; ,,2 ,1 ,0 ,)(212211n j qp C j p n i q p C i p jn jjn Y in i i n X ====--证明它们的和Y X Z +=也服从二项分布．证明: 设j i k +=, 则ik n i k i k n ki i n i i n ki Y X Z q p C q p C i k P i P k Z P k P +---=-=∑∑=-===22110)()()()( ∑=-+=ki k n n k i n in q p C C2121)( 由knm ki ik nk m C C C +=-=∑, 有k n n ki in i n C C C21210+==∑. 于是有 ),,2,1,0( )(212121n n k q p C k P kn n k i n n Z +==-++ 由此知Y X Z +=也服从二项分布.三、设随机变量X 与Y 独立，并且X 在区间[0，1]内服从均匀分布，Y 在区间[0，2]内服从辛普森分布：⎪⎩⎪⎨⎧><≤<-≤≤=.20 0,; 2 1 ,2;10 ,)(y y y y y y y f Y 或求随机变量Y X Z +=的概率密度．解: X 的概率密度为 ⎩⎨⎧∉∈=]1,0[,0]1,0[,1)(x x y f ξ . 于是),(Y X 的联合概率密度为⎪⎩⎪⎨⎧≤<≤≤-≤≤≤≤=. 0, 2 1,10 ,210,10,),(其它当当y x y y x y y x fY X Z +=的联合分布函数为}),{(}{}{)(D y x P z Y X P z Z P z F Z ∈=≤+=≤=，其中D 是zy x ≤+与),(y x f 的定义域的公共部分.故有 ⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<+-≤<-+-≤≤><=3229321212331023,00)(222z z z z z z z z z z z F Z 从而随机变量Y X Z +=的概率密度为⎪⎪⎩⎪⎪⎨⎧≤<-≤<+-≤≤><=3232132103,00)(z z z z z z z z z f Z三、电子仪器由六个相互独立的部件ij L （3,2,1;2,1==j i ）组成，联接方式如右图所示．设各个部件的使用寿命ij X 服从相同的指数分布)(λe ，求仪器使用寿命的概率密度．解: 由题设，知ij X 的分布函数为⎩⎨⎧≤>-=-0,00,1x x e F x X ij λ 先求各个并联组的使用寿命)3,2,1( =i Y i 的分布函数.因为当并联的两个部件都损坏时,第i 个并联组才停止工作,所以有)3,2,1(),m ax (21==i Y i i i ξξ从而有)3,2,1( =i Y i 的分布函数为⎩⎨⎧≤>-==-0,00,)1()(221y y e F F y F y X X Y ii i λ 设Z "仪器使用寿命".因为当三个并联组中任一个损坏时,仪器停止工作.所以有),,min (321Y Y Y Z =.从而有Z 的分布函数为⎩⎨⎧≤>---=⎩⎨⎧≤>----=-0,00,])1(1[10,00)],(1)][(1)][(1[1)(32321z z e z z z F z F z F z F z Y Y Y Z λ故Z 的概率密度为⎩⎨⎧≤>--=---0,00,)2)(1(6)(23z z e e e z f z z z Z λλλλ第十章随机变量的数学期望与方差一、一批零件中有9个合格品与3个废品．安装机器时从这批零件中任取一个．如果取出的废品不再放回去，求在取得合格品以前已取出的废品数的数学期望、方差与标准差．解：设X 表示“在取得合格品以前已取出的废品数”，则X 的概率分布为即于是有1103322013220924491430=⨯+⨯+⨯+⨯=EX 即3.0004.03041.02205.0175.00≈⨯+⨯+⨯+⨯=EX2X 的分布为即于是有229220192209444914302=⨯+⨯+⨯+⨯=EX 即4091.0004.09041.04205.0175.002≈⨯+⨯+⨯+⨯=EX从而有3191.013310042471)11033(229)(222≈=-=-=EX EX DX 565.03191.0≈==DX X σ二、对某一目标进行射击，直至击中为止．如果每次射击命中率为p ，求射击次数的数学期望及方差．解：设X 表示“第i 次击中”),2,1( =i ，则X 的分布为于是有p q p q q p q p iqp ipqEX i i i i i i 1)1()1()(211111=-='-='===∑∑∑∞=∞=-∞=- 2X的分布为于是有p pp p q q p q p q q p pqi EX i i i ii i 122)1()1()(])([223111122-=-=-+='=''==∑∑∑∞=∞=∞=- 进一步有pp p p p EX EX DX 11)1(12)(22222-=--=-=三、设离散型随机变量X 的概率函数为,,2,1,21]2)1([ ==-=k k X P k k k问X 的数学期望是否存在？若存在，请计算)(X E ；若不存在，请解释为什么．解：因为∑∑∑∑∞=∞=∞=∞=-=⋅-=-=-==1111)1(212)1(]2)1([2)1()(k k k k k k k k k k ki i i k k k X P k x X P x 不绝对收敛，所以ξ没有数学期望．四、设随机变量X 的概率密度为⎪⎩⎪⎨⎧≥<-=.1, 0;1,11)(2x x xx f π 求数学期望)(X E 及方差)(X D ．解：011)()(112=-⋅==⎰⎰-+∞∞-dx xx dx x xf X E πdx x x dx x x dx x f x X D ⎰⎰⎰-=-⋅==-∞+∞-1022112221211)()(πππ21]arcsin 2112[2102=+--=x x x π五、（拉普拉斯分布）设随机变量X 的概率密度为 )( ,21)(+∞<<-∞=-x e x f x．求数学期望)(X E 及方差)(X D ．解：021)(===⎰⎰+∞∞--+∞∞-dx xe dx x xf EX x2!2)3(21)(0222==Γ====⎰⎰⎰+∞-+∞∞--+∞∞-dx e x dx e x dx x f x DX x x（分部积分亦可）第十一章随机变量函数的数学期望·关于数学期望与方差的定理一、设随机变量X 服从二项分布)4.0,3(B ，求2)3(X X Y -=的数学期望及方差．解：X 的概率分布为Y 的概率分布为2Y 的分布为于是有72.072.0128.00=⨯+⨯=EY72.072.0128.002=⨯+⨯=EY 2016.0)72.0(72.0)(222=-=-=EY EY DY二、过半径为R 的圆周上一点任意作这圆的弦，求所有这些弦的平均长度．解：在圆周上任取一点O ，并通过该点作圆得直径OA ．建立平面直角坐标系，以O 为原点，且让OA 在x 轴的正半轴上．通过O 任作圆的一条弦OB ，使OB 与x 轴的夹角为θ，则θ服从]2,2[ππ-上的均匀分布，其概率密度为⎪⎩⎪⎨⎧-∉-∈=]2,2[,0]2,2[,1)(ππθππθπθf ．弦OB 的长为 ]2,2[cos 2)(ππθθθ-∈=R L ，故所有弦的平均长度为⎰⎰-∞+∞-⋅==22cos 21)()()]([ππθθπθθθθd R d L f L EπθπθθπππRR d R4sin 4cos 4202===⎰．三、一工厂生产的某种设备的寿命X （以年计）服从指数分布，概率密度为⎪⎩⎪⎨⎧≤>=-. 0,0 ;0 ,41)(4x x e x f x工厂规定，出售的设备若在售出一年之内损坏可予以调换．若工厂售出一台设备赢利100元，调换一台设备厂方需花费300元．试求厂方出售一台设备的平均净赢利．解：由题设，有⎰⎰---∞--=-===<104110441141)()1(e e dx e dx x f X P x x 进而有 41)1(1)1(-=<-=≥eX P X P设Y 表示“厂方出售一台设备获得的净赢利”，则Y 的概率分布为从而有64.33200300100)1(200414141≈-⨯=⨯+-⨯-=---eee EY答：厂方出售一台设备获得的平均净赢利约为64.33元．四、设随机变量n X X X ,,21相互独立，并且服从同一分布，数学期望为μ，方差为2σ．求这些随机变量的算术平均值∑==ni i X n X 11的数学期望与方差．解：因为μ=)(i X E ，2)(σ=i X D ，且随机变量n X X X ,,21相互独立．所以有μμ=====∑∑∑∑====ni n i i ni i n i i n X E n X E n X n E X E 11111)(1)(1)1()(，nn X D n X D n X n D X D ni ni i n i i n i i 2122121211)(1)(1)1()(σσ=====∑∑∑∑====．五、一民航送客车载有20位旅客自机场开出，沿途有10个车站可以下车，到达一个车站时如没有旅客下车就不停车．假设每位旅客在各车站下车是等可能的，且各旅客是否下车相互独立．求该车停车次数的数学期望．解: 设i X 表示"第i 站的停车次数" (10,,2,1 =i ). 则i X 服从"10-"分布. 其中⎩⎨⎧=站有人下车若在第站无人下车若在第i i X i ,1,0于是iX 的概率分布为设∑==ni iXX 1, 则X 表示沿途停车次数, 故有]})10110(1[1)10110(0{10)(2020101101--⨯+-⨯===∑∑==i i i i EX X E EX748.8)9.01(1020≈-=即停车次数的数学期望为748.8.第十二章二维随机变量的数字特征·切比雪夫不等式与大数定律一、设二维随机变量),(Y X 的联合概率密度为()(). 1,222++=y xAy x f求：（1）系数A ；（2）数学期望)(X E 及)(Y E ，方差)(X D 及)(Y D ，协方差),cov(Y X ．解: (1) 由⎰⎰+∞∞-+∞∞-=1),(dxdy y x f . 有()()⎰⎰⎰⎰∞+∞-∞+∞-∞+==+=++1112022222A dr rrd A dxdy y xAπθπ解得, π1=A .(2) ()011),()(222⎰⎰⎰⎰∞+∞-∞+∞-∞+∞-∞+∞-=++==dx y xxdy dxdy y x xf X E π.由对称性, 知 0)(=Y E .⎰⎰+∞∞-+∞∞-==-=dxdy y x f x EX EX X E X D ),(])[()(222()⎰⎰∞+∞-∞+∞-++=dx y xx dy 222211π()()+∞=+++=+-+=+=∞+∞+∞+⎰⎰⎰22022220223]11)1ln([1)1(211rr dr rrr r dr rr d πθπ同理, 有 +∞=)(Y D .)()])([(),cov(XY E EY Y Ex X E Y X =--= ⎰⎰+∞∞-+∞∞-=dxdy y x xyf ),(()011),(222⎰⎰⎰⎰∞+∞-∞+∞-∞+∞-∞+∞-=++==dx y xxydy dxdy y x xyf π.二、设二维随机变量),(Y X 的联合概率密度为⎩⎨⎧<<<=其它．,0;10,,1),(x x y y x f求(1) ),cov(Y X ；(2) X 与Y 是否独立，是否相关，为什么？解: (1) 因为 ⎰⎰⎰⎰⎰====-∞+∞-∞+∞-10210322),(dx x dy xdx dxdy y x xf EX x x0),(10===⎰⎰⎰⎰-+∞∞-+∞∞-xx ydy dx dxdy y x yf EY0),()(1===⎰⎰⎰⎰-+∞∞-+∞∞-xxydy xdx dxdy y x xyf XY E所以有])32[()])([(),cov(Y X E EY Y EX X E Y X -=--=⎰⎰+∞∞-+∞∞-=dxdy y x xyf ),(010==⎰⎰-xxydy xdx ．(2) 当)1,0(∈x 时,有 ⎰⎰+∞∞--===x dy dy y x f x f xxX 2),()(; 当)1,0(∉x 时, 有0)(=x f X .即⎩⎨⎧∉∈=)1,0(0)1,0(2)(X x x x x f 同理有 ⎩⎨⎧∉+∈-=⎪⎩⎪⎨⎧∉∈=⎰⎰-)1,0(1)1,0(1)1,0()1,0()(11Y x y x y x dx x dx y f y y因为 ),()()(y x f y f x f Y X ≠, 所以X 与Y 不是独立的．又因为0),cov(=Y X , 所以X 与Y 是不相关的．三、利用切比雪夫不等式估计随机变量X 与其数学期望)(X E 的差的绝对值大于三倍标准差)(X σ的概率．解：91)3()3(2=≤>-ξξξξξD D D E P ．四、为了确定事件A 的概率，进行10000次重复独立试验．利用切比雪夫不等式估计：用事件A在10000次试验中发生的频率作为事件A 的概率的近似值时，误差小于0.01的概率．解：设ξ表示“在10000次试验中事件A 的次数”，则)5.0,10000(~B ξ且有50005.010000=⨯==np E ξ 2500)5.01(5.010000=-⨯⨯==npq D ξ于是有npqp npq p np m P p n m P 22)01.0(1)01.0(1)01.0()01.0(-=-≥<-=<- 75.025.011=-=-=pq五、样检查产品质量时，如果发现次品多于10个，则认为这批产品不能接受．应该检查多少个产品，可使次品率为10%的一批产品不被接受的概率达到0.9？解：设ξ表示“发现的次品件数”，则)1.0,(~n B ξ，现要求.nn ξE 1.0= n ξD 09.0=要使得9.0)10(=>ξP ，即9.0)10(=≤<n ξP ，因为9.0)10(=≤<n ξP ，所以 )3.01.03.01.03.01.010()10(nn n n n ξn n P ξD ξE n ξD ξE ξξD ξE P -≤-<-=-≤-<-)3.01.010()3()33.01.03.01.010(1,01,0nn n n n n ξn n P --≈≤-<-=ΦΦ1)3.0101.0()3(1,01,0--+nn n ΦΦ （德莫威尔—Laplace 定理）因为10>n ，所以53>n ，从而有1)3(1,0≈n Φ，故9.0)3.0101.0(1,0≈-nn Φ．查表有8997.0)28.1(1,0=Φ，故有28.13.0101.0≈-nn ，解得.146≈n答：应该检查约146个产品，方可使次品率为10%的一批产品不被接受的概率达到0.9．第十三章正态分布的概率密度、分布函数、数学期望与方差一、设随机变量X 服从正态分布)2,1(2N ，求（1）)8.56.1(<≤-X P ；（2）)56.4(≥X P ．解：(1) )4.2213.1()8.416.2()8.56.1(<-≤-=<-≤-=<≤-X P X P X P 8950.09032.019918.0)]3.1(1[)4.2()3.1()4.2(1,01,01,01,0=+-=--=--=ΦΦΦΦ(2) )78.12178.2(1)56.4(1)56.4(<-<--=<-=≥X P X P X P )]78.2(1)78.1(1)]78.2()78.1([11,01,01,01,0ΦΦΦΦ-+-=---=.0402.09973.09625.02=--二、已知某种机械零件的直径X （mm ）服从正态分布)6.0,100(2N ．规定直径在2.1100±（mm ）之间为合格品，求这种机械零件的不合格品率．解：设p 表示这种机械零件的不合格品率，则)2.1100(1)2.1100(≤--=>-=X P X P p ．而)26.01002()6.02.16.01006.02.1()2.1100(≤-≤-=≤-≤-=≤-X P X P X P 1)2(2)]2(1[)2()2()2(-Φ=Φ--Φ=-Φ-Φ=9544.019772.02=-⨯= 故0456.09544.01=-=p ．三、测量到某一目标的距离时发生的误差X (m)具有概率密度3200)20(22401)(--=x ex f π求在三次测量中至少有一次误差的绝对值不超过30m 的概率．解：三次测量中每次误差绝对值都超过30米可表为}30{}30{}30{>⋃>⋃>=ξξξD 第三次第二次第一次因为)40,20(~2N ξ，所以由事件的相互独立性，有31,01,033)]25.0(1)25.1([})3030{(})30{()(ΦΦ-+-=>+-<=>=ξξP ξP D P13025.05069.0)8944.05987.02(33≈=--=于是有86975.013025.01)(1}30{=-=-=<D P P 米至少有一次绝对值三次测量中ξ．四、设随机变量),(~2σμN X ，求随机变量函数Xe Y =的概率密度（所得的概率分布称为对数正态分布）．解：由题设，知X 的概率密度为)(21)(222)(+∞<<-∞=--x ex f x X σμσπ从而可得随机变量Y 的分布函数为)()()(y e P y Y P y F X Y ≤=≤=．当0≤y 时，有0)(=y F Y ；此时亦有0)(='y F Y ．当0>y 时，有dx ey X P y F yx Y ⎰∞---=≤=ln 2)(2221)ln ()(σμσπ．此时亦有222)(ln 21)(σμσπ--='y Y eyy F ．从而可得随机变量Y 的概率密度为⎪⎩⎪⎨⎧>≤=--.0,21;0,0)(222)(ln y e yy y f y Y σμσπ五、设随机变量X 与Y 独立，),(~211σμN X ，),(~222σμN Y ，求： (1) 随机变量函数bY aX Z +=1的数学期望与方差，其中a 及b 为常数； (2) 随机变量函数XY Z=2的数学期望与方差．解：由题设，有211)(,)(σμ==X D X E ；222)(,)(σμ==Y D Y E ．从而有(1)211)()()()()()(μμb a Y bE X aE bY E aX E bY aX E Z E +=+=+=+=； 222212221)()()()()()(σσb a Y D b X D a bY D aX D bY aX D Z D +=+=+=+=． (2)212)()()()(μμ===Y E X E XY E Z E ；)()()()()()()()(22222222Y E X E Y E X E XY E Y X E XY D Z D -=-== )()()]()()][()([2222Y E X E Y E Y D X E X D -++= )()()()()()(22X E Y D Y E X D Y D X D ++= 212222212221μσμσσσ++=．第十四章二维正态分布·正态随机变量线性函数的分布中心极限定理一、设二维随机变量),(Y X 服从二维正态分布，已知0)()(==Y E X E ，16)(=X D ，25)(=Y D ，并且12),cov(=Y X ，求),(Y X 的联合概率密度．。

概率论第四章习题解答

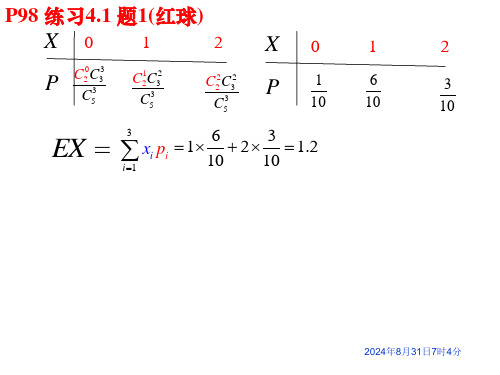
X9
EX 9
9
9
8 9
20
2024年8月31日7时4分
P104 练习4.2 题1 SD 1
1,1
f XY
x,
y
1 0
0 x 1, x y x 其它
yx
DZ D2X 1 4DX
EX xf x, ydxdy
0D
y x 1
1 0
x x
xdy
dx
1 2x2dx 2
P113 习题四一填空题 7 X与Y相互独立
f
X
x
2x
0
0
x 其它
1，fY
y
x y t
FT t PT t P X Y t fXY x, y dxdy
x yt
1当t 0时：FT t 0dxdy 0
0
x yt
2 当0 t时：FT
t
t
dx
tx 25e5x5 ydy
0
0
1 e5t 5te5t
t,0
x
FT
t
1
e5t
0
5te5t
t0 t0
33
2 EX 2
xi2 pij
i1 j1
20.1 30.3 30.1 2
33
3 EY 2
yi2 pij
12 0.212 0.112 0.1 22 0.1
22 0.132 0.332 0.1 4.8
i1 j1
12 0.2 12 0.1 12 0.1
12 0.1 12 0.1 0.6
2024年8月31日7时4分
P100 练习4.1 题12
2
f XY
x,
y
x

概率论与数理统计答案第四章习题

(x2
3000x)dx
1 1500 2
x3 3
1500 0
1 1500 2
(
x3 3
1500
x
2
)
3000 1500
500 4(500) (1000) 1500
X -2 0 2
6.设随机变量X的分布律为 pk 0.4 0.3 0.3 求E(X),E(X2),E(3X2+5).
3
解
E( X ) xk pk (2) 0.4 0 0.3 2 0.3 0.2
0),
2t ,
(a 1) a(a),
dx dt
2t
(1)
1,
(1
2)
.
E(X) 02tet
dt
2t
2 0t1 2etdt
2(3 2)
2 1 (1 2)
2
2
E(
X
2
)
0
3
(2t )3
2
2
et
2t
dt
2
2
0
te t
dt
2
2(2)
2
2
20. 设长方形的高(以m计)X~U(0,2),己知长方形的周长(以m计)为 20,求长方形面积A的数学期望和方差.
k 1
3
E( X 2 ) xk2 pk (2)2 0.4 02 0.3 22 0.3 2.8
k 1
3
E(3X2 5) (3xk2 5)pk [3(2)2 5]0.4[302 5]0.3[322 5]0.3 13.4
k1
或 E(3X2+5)= 3E(X2) + 5 = 32.8 + 5 =13.4

概率论与数理统计（I）第四章答案

第四章大数定律及中心极限定理导学——极限论在概率研究中的应用本章是承前启后的一章：明晰了“频率与概率的关系”，这是一个遗留问题。

并将《概率论》部分划上了一个句号，这是承前；说它启后，有定理设定：⋯⋯,21,,,n X X X 独立同分布，这一设定在《数理统计》部分一直沿用了下去。

全章由四节组成，§1节特征函数，§2节大数定律，讲了三个定理， §3节随机变量序列的两种收敛性，§4节中心极限定理。

三个定理。

“大数”及“极限”均要求+∞→n ，在实际问题中，n 充分大即可。

§2节主要研究对象为：算术平均值()n X X nX +⋯+=11；§4节的主要研究对象为： nni i X X X +⋯+=∑=11，比n X 1少了。

§2节的学习，不妨先从复习入手。

第二、三章已熟悉了()()⋅⋅D E 及,先推算出21)(,)(σμnX D X E =⋯==⋯=这是核心推导之一，后面学《数理统计》会反复使用，再由契比雪夫不等式及夹逼原理，可推出定理一，其中NX D 2)(σ=中的n1很宝贵。

定理二是由定理一推得的，关键点为：n A X X X n +⋯++=21及X X n n n ni i A ==∑=11，于是可用定理一了。

推导本身是一件很愉快的事。

§2节的三个定理可在比对中学习。

定理一（契）不要求⋯⋯,21,,,n X X X 一定为同分布，（贝）是由定理一（契）的特例。

定理二（马）不要求⋯⋯,21,,,n X X X 独立或同分布。

定理三（辛）不要求)(X D 一定存在，“契”“马”与“辛”的结论均为：μ−→−PX ,即算术平均值依概率收敛于数学期望。

“贝”的结论为：p nn PA −→−，即频率依概率收敛于概率。

这个结论很精致，十分简单了。

翻开§4节，一堆一堆的符号映入眼中，让人头大。

其实，若标准化方法娴熟，这一节并不难。

(完整版)概率论第四章答案

60解 E(Y) E(2X) 2E(X) 2 xe xdx 2,E(Z) E(e 2X ) e 2x e x dx 1.33. 游客乘电梯从底层到电视塔顶观光 , 电梯于每个整点的第 5 分钟、第 25 分钟和第 55分钟从底层起行 . 假设一游客在早八点的第 X 分钟到达底层侯梯处 , 且 X 在区间[0, 60] 上服从均匀分布 . 求该游客等候电梯时间的数学期望 . 解已知X 在[0,60] 上服从均匀分布 , 其概率密度为1X -20 2 P0.40.30.3E(X)；E(2－3 X); E(X 2)；2 E(3X 25).解由定义和数学期望的性质知E(X) ( 2) 0.4 0 0.3 2 0.30.2;E(2 3X) 2 3E(X ) 2 3 (0 2) 2.6; E(X 2) ( 2)2 0.4 0 20.3220 3 2.8 ;E(3X 2 5) 3E(X 2)53 2.8 5 13.4. 2. 设随机变量 X 的概率密度为xe, x 0, 1. 设随机变量 X 的分布律为习题 4-1f (x)2X求Y 2X 和Z e 2X的数学期望 .0,x ≤0.0,其它.记Y 为游客等候电梯的时间,则5 X, 0 X ≤5,25 X,5 X ≤25,Y g(X)55 X, 25 X ≤55,65 X,55 X ≤60.160 因此, E(Y) E[g(X)] g(x) f (x)dxg(x)dxf (x) 60, 0≤x≤60,60(A) 若 X ~ B(n, p),则E(X) np.c a ， Yc,X 1, X 0.于是 E(Y) (c a) P{ X 1} c P{X 0} ap c .据题意有 ap c a 10% , 因此应要求顾客角保费 c (0.1 p)a .习题 4-21. 选择题(1) 已知 E(X ) 1,D(X)3 则 E[3(X2 2)2] ().(A) 9.(B) 6.(C) 30.(D)36解 E[3(X 2)2] 3E(X24X 4)3[E(X 2)4E(X)4]3{D(X) [E(X)]2 4E(X) 4}3 (3 14 4) 36 .可见，应选 (D).(2) 设 X ~ B(n, p),E(X )6,D(X) 3.6 , 则有 ( ).(A) n 10, p 0.6 . (B) n 20, p 0.3 (C) n 15, p 0.4 .(D) n 12, p 0.5解因为 X ~ B(n, p), 所以 E(X)=np,D(X)=np(1-p), 得到 np=6, np(1-p)=3n=15 , p=0.4 . 可见，应选 (C).(3) 设 X 与 Y 相互独立，且都服从2N( , 2) , 则有 ( ).(A) E(X Y) E(X) E(Y). (B) E(X Y) 2 .(C) D(X Y) D(X)D(Y).(D) D(XY) 2 2.解注意到 E(X Y) E(X) E(Y) 0.由于 X 与Y 相互独立 ,所以D(X Y) D(X) D(Y) 222. 选 (D).(4) 在下列结论中 , 错误的是 ().6 . 解之 ,1 5 25(5 x)dx (25 x)dx600 5=11.67(分钟 )..14. 某保险公司规定 , 如果在一年内顾客的投保事件 A 发生 , 该公司就赔偿顾客 a 元. 若一年内事件 A 发生的概率为 p, 为使该公司受益的期望值等于 a 的 10％, 该公司应该要求顾客交多少保险费？解设保险公司要求顾客交保费 55(55 x)dx60 (65 x)dx55c 元. 1， 0, 则 P{X 1} p, P{X 0} p . 引入随机变量事件A 发生, 事件A 不发生. 保险公司的受益值(B) 若 X ~ U 1,1 ，则 D(X) 0 . (C) 若 X 服从泊松分布 , 则 D(X) E(X).(D) 若 X ~ N( , 1 2), 则 X~ N (0,1) .14.3 又 X 1, X 2 , X 3相互独立 , 所以D(Y) D(X 1 2X 2 3X 3) D(X 1) 4D(X 2) 9D(X 3)1 3 4 4 9 20.914. 设两个随机变量 X 和 Y 相互独立 , 且都服从均值为 0, 方差为的正态分布 , 求2 |X Y |的的期望和方差 .11 解记U X Y . 由于X ~ N(0, ),Y ~ N(0, ),所以22E(U) E(X) E(Y) 0, D(U) D(X) D(Y) 1. 由此 U ~ N (0,1) . 进而3203~ U( 1,1) , 则 D(X) (b a)122. 已知 X, Y 独立, E(X)= E(Y)=2, E(X 2)= E(Y 2)=5,解由数学期望和方差的性质有E(3X- 2Y)= 3E(X)-2 E (Y)=3×2-2×2=2,D(3X 2Y) 9D(X) 4D(Y)9 {E(X 2) [E(X)]2} 9 (5 4) 4 (5 4) X 2, X 3 相互独立 , 其中 2X 2解X221. 选(B).312求 E(3X-2Y),D(3X-2Y).3. 设随机变量 2X 2 ~ N (0, 22), X 3解由题设知X 1,~ P (3), 记 Y X 14 {E(Y 2) [E(Y)]2}13.X 1 服从区间[0, 6]上的均匀分布, 3X 3 ,求 E(Y)和 D(Y) .E(X 1) 3, D(X 1) E(X 3)(6 0)2 3,12 113,D(X 3)E(X 2) 0,D(X 2 ) 4,由期望的性质可得E(Y) E(X 12X 2 3X 3) E(X 1) 2E(X 2 ) 3E(X 3)5. 设随机变量X ~U[ 1,2], 随机变量1, X 0,Y 0, X 0,1, X 0. 求期望E(Y) 和方差D(Y) .解因为X的概率密度为1, 1≤x≤2,f X (x) 3于是Y的分布率为P{Y 1} P{XP{YP{Y 1} P{ X因此0, 其它.0110}-f X(x)dx dx-133 0}P{ X 0} 0 ,+2120}0 f X (x)dx dx0033 21 x22 E(|X Y|) E(|U |) |x| e 2dx 0 xe E(|U |2) E(U2) D(U ) [E(U)]22x2 dx02故而D(|X Y|) D(|U|) E(|U|2) [E(|U |)]22e1.2212故有6. 设随机变量U1,X1,求E(X+Y), D(X+Y).E(Y)E(Y2 ) (1)20212D(Y) E(Y2 )[E(Y)]2321.389.在区间[-2, 2]上服从均匀分布若U ≤1, 若U1.9, 随机变量1, 若U≤1, Y 1,若U 1.解(1) 随机变量(X, Y) 的可能取值为(-1,- 1),(- 1,1),(1,- 1),(1,1).-11 1P{X 1,Y 1}P{U ≤ 1,U ≤ 1} P{U ≤ 1}dx-24 4P{ X 1,Y 1}P{U ≤ 1,U1} 0,111 P{ X 1,Y1}P{U1,U ≤1}14dx , 221 1 P{X 1,Y1}P{U1,U1}dx .144 于是得 X 和Y 的联合密度分布X+Y-2 0 21 1 1 P{ X+Y =k}424(X+Y)24P{ (X+Y)2=k}1 1 22由此可见2 2 2 E(X Y) 0;D(X Y) E[( X Y)2] 2. 44习题 4-31. 选择题(1) 在下列结论中 , ( )不是随机变量 X 与 Y 不相关的充分必要条件(A) E(XY)=E(X)E(Y). (B) D(X+Y)=D(X)+D(Y).(C) Cov(X,Y)=0.(D) X 与 Y 相互独立 .解 X 与 Y 相互独立是随机变量 X 与 Y 不相关的充分条件 ,而非必要条件 . 选(D).(2) 设随机变量 X 和 Y 都服从正态分布 , 且它们不相关 , 则下列结论中不正确的是(C) X 与 Y 未必独立 . (D) 解对于正态分布不相关和独立是等价的 ).(A) X 与 Y 一定独立 . (B) (X, Y)服从二维正态分布 X+Y 服从一维正态分布 . 选 (A).(2) X(3) 设(X, Y)服从二元正态分布, 则下列说法中错误的是( ).(A) ( X, Y) 的边缘分布仍然是正态分布 . (B) X 与 Y 相互独立等价于 X 与 Y 不相关 . (C) (X, Y)是二维连续型随机变量 .(D)由(X, Y)的边缘分布可完全确定 (X, Y)的联合分布 .解仅仅由 (X, Y)的边缘分布不能完全确定 (X, Y)的联合分布 . 选 (D) 2 设 D(X)=4, D(Y)=6, ρXY =0.6, 求 D(3X-2Y) .解 D(3X 2Y) 9D(X) 4D(Y) 12Cov( X,Y)9 4 4 6 12 XY D(X) D(Y)36 24 12 0.6 2 6 24.727 .3. 设随机变量 X, Y 的相关系数为 0.5, E(X) E(Y) 0, E(X2) E(Y 2) 2,2求 E[(X Y)2] .2 2 2 解 E[(X Y)2] E(X 2) 2E(XY) E(Y 2)4 2[Cov( X,Y) E(X)E(Y)] 4 2 XY D(X) D(Y) 4 2 0.5 2 6.4. 设随机变量 (X, Y)的分布律为1 0 0.42 0 a 1 1 0.2 2 1 b 0.2 2b0.1. 由此可得边缘分布律5. 已知随机变量 ( X ,Y ) ~ N (0.5, 4; 0.1, 9; 0) , Z=2X- Y, 试求方差D(Z), 协方差X 1 2 Y 01P{X i} 0.6 0.4 P{Y j} 0.5 0.5E(Y) 0 0.5 1 0.5 0.5. 0.5 0.1. E(X) 1 0.6 2 0.4 1.4 , Cov( X,Y) E(XY) E(X)E(Y) 0.8 1.4 0.8 E(XY) 得 b 0.3. 进而 a于是故若 E(XY)=0.8, 求常数解首先由p ij 1 得 a b 0.4. 其次由i 1 j1Cov( X ,Z) , 相关系数 ρXZ .解由于 X,Y 的相关系数为零 , 所以 X 和 Y 相互独立(因X 和Y 服从正态分布 ). 因此D(Z) D(2X Y) 4D(X) D(Y) 4 4 9 25 ,Cov( X,Z) Cov( X,2X Y)2Cov(X,X) Cov( X,Y) .1 X Y关系数XY , Z . 求: (1) E(Z), D(Z)； (2) X 与 Z 的相关系数 ρXZ ; (3)问 XY2 3 2 X 与 Z 是否相互独立 ?为什么? 22 解 (1) 由于 X ~ N (1,32 ) , Y ~ N(0,42) , 所以(3) 由 XZ 0知X 与Z 不相关, 又 X 与Z 均服从正态分布 , 故知 X 与 Z 相互独立 .7．证明: 对随机变量 (X, Y), E(XY)=E(X)E(Y)或者 D(X Y)=D(X)+D(Y)的充要条件是 X 与 Y 不相关 .证首先我们来证明 E(XY) E(X)E(Y) 和D(X Y) D(X) D(Y)是等价的. 事实上, 注意到 D(X Y) D(X) D(Y) 2Cov( X,Y) . 因此D(X Y) D(X) D(Y) Cov( X,Y) 0 E(XY) E(X)E(Y).因此2D(X) Cov( X,Z) D(X) D(Z) 6. 设随机变量 (X, Y)服从二维正态分布 : XXZ0880.8 . 2522~ N(1,32), Y ~N(0, 42);X 与 Y 的相因此E(Z)D(Z) (2) 由于Cov( X,Z)所以XZXYD(X) D(Y) 12 346.Y 2) 1 13E(X)1E(Y) 2 1 3 11 2 0 1 3 Y 1 111Y 2) D(X) 9 D(Y) 42Cov( 3 X , 12Y) 1 16 1 Cov( X,Y) 1 4 1( 6) 3.4 33Y1 11 1) D(X) Cov( X,Y)9( 6)2 323 2E(X) 1,D(X) 9,E(Y) 0,D(Y) 16,Cov( X,Y)9 X Cov( X, 3 E(X 3D(X 3 1 9Cov( X,Z)D(X) D(Z)0.0,其次证明必要性 . 假设 E(XY)=E(X)E(Y), 则Cov( X,Y) E(XY) E(X)E(Y) 0 .最后证明充分性 . 假设 X 与 Y 不相关, 即 XY 0, 则Cov( X,Y)E(XY) E(X)E(Y) .总习题四1. 设 X 和 Y 是相互独立且服从同一分布的两个随机变量 , 已知 X 的分布律为 1 P{X i} ,i 1,2,3 . 又设U max{ X ,Y}, V min{ X,Y} .3(1) 写出二维随机变量 (U, V)的分布律 ;(2) 求 E(U ). 解 (1) 下面实际计算一下 P{U 1,V 3}.注意到U max{ X,Y}, V min{ X ,Y} , 因此P{U 1,V 3} P{X 1,Y 3}P{X 1}P{Y 1111(2) 由的分布律可得关于 U 的边缘分布律进而XYCov( X,Y)D(X) D(Y)0, 即 X 与 Y 不相关 .0 . 由此知P{X 3,Y 1} 3} P{X 3}P{Y 1} 21 3 5 22 所以 E(U) 112 33 5 22. 99 9 92. 从学校乘汽车到火车站的途中有 3 个交通岗 . 假设在各个交通岗遇到红灯的事件是2相互独立的 , 并且概率是 . 设 X 为途中遇到红灯的次数 , 求随机变量 X 的分布律、分布函5数和数学期望 .3. 设随机变量 (X,Y) 的概率密度为212y 2, 0≤ y ≤x ≤1, f(x,y) 0, 求E(X), E(Y), E(XY), E(X 2 Y 2).X0 1 2 3P2754 36 8125 125 125 1252754 36 8k} 0 1 2 3125125 125 125解令 X 表示途中遇到红灯的次数 , 由题设知 X ~ B(3,2) . 即 X 的分布律为53从而 E(X) kP{Xk16 5其它. 解 E(X) xf ( x, y)dxdy 1dx12y 2dy4x 4dxE(X) yf ( x, y)dxdy 0dx 0y12y 2dy 03x 4dxE(XY)xyf(x,y)dxdy1 dx 0x0 xy 12 y 2dy3x 5dxE(X 2 Y 2)(x 2 y 2) f (x,y)dxdy4. 设随机变量(4x5 12 x 5)dx 05 (X,Y)的概率密度为1sin( x f(x,y) 20,2 325 30 1 dx16 15 .(x 2y 2)35 3 612y 2dyy),π0≤x ≤ π, 0≤y ≤22 其它.求E(X),D(X),E(Y),D(Y),E(XY)和Cov(X,Y).于是有1. 22 所以协方差Cov( X,Y) E(XY) E(X)E(Y) 1.2 1615. 设随机变量 X 与 Y 独立, 同服从正态分布 N(0, ) , 求2(1) E(X Y); D( X Y)；(2) E (max{ X ,Y}); E(min{ X,Y}) .11解 (1) 记 X Y .由于 X ~ N(0, ),Y ~ N(0, ),所以E( ) E(X) E(Y) 0, D( ) D(X) D(Y) 1. 由此 ~ N(0,1).所以解 E(X)122xf(x,y)dxdy 2 2 x sin( x y)dxdy2E(X 2)2x f (x, y)dxdy2y)dxdy 2. 2 0 2 0x 2 sin(x x 2 E(| X Y |) E(| |)12|x| 2 e 2dx 2 0xe x 22 dx82D(X)2E(X 2)2[E(X)]22.16 22利用对称性 ,有E(Y) 4,D(Y) 16 2. 2 又E(XY)1 xyf ( x, y)dxdy22xy sin( x y)dxdy 1 2 1 2 02 xdx 02 xdx 02ysin(x y)dy 2 y[sin x cos y cos xsin y]dyE(XY) xyf (x, y)dxdy2e x 22E(| |2) 0E( 2) D( ) [E( )]21 故而D(| X Y|) D(| 22|) E(| |2) [E(| |)]2 1021.221 2所以 (2) 注意到max( X , Y) (X Y) |X Y | , min( X , Y)X Y |X Y|E[max( X , Y)] 112{E(X) E(Y) E[| X Y|]} 12 12 212,1 12{E(X) 6. 设随机变量 (X,Y) 的联合概率密度为 x y, 0≤ x ≤2,0≤y ≤2,f (x, y) 8E[min( X,Y)] E(Y) E[| X Y|]} 0, 求: E(X), E(Y), Cov( X,Y), ρXY , D (X+Y ). 解其它.注意到 f (x, y)只在区域 G:0≤x ≤2,0≤y ≤ 2上不为零,x x y dxdyG 82x(xE(X) xf(x,y)dxdy 因而所以E(X 2)2 dx 02dxD(X)21 0 x(x y)dy 42 x f (x,y)dxdy22 10x (x y)dy 4 22E(X 2) [E(X)]27 1)dx 7623(x 35 72 3 622x )dx11 3612 2 1 22 44 dx xy(x y)dy (x x)dx .8 0 0 4 0337 2 2 5 11E(X) , E(Y 2) E(X 2) , D(Y) D(X) . 6 3 364 491 Cov( X,Y) E(XY) E(X)E(Y) ,3 3636Cov( X,Y) 1XYD(X) D(Y) 11 5D(X Y) D(X) D(Y) 2Cov( X,Y) .917. 设A, B 为随机事件 , 且 P(A) ,P(B|A)41， A 发生 , XY 0， A 不发生 ,Y1P(AB)1111 解由P(B| A)得 P(AB)P(A) , 进而由3P(A)334 121P(AB)1P(A|B)得 P(B) 2P(AB). 在此基础上可以求得2P(B)6(1) P{ X1,Y 1} P(AB)112111P{X 0,Y 1}P(AB) P(B)P(AB)6 12 121 11P{ X 1,Y 0}P(AB)P(A) P(AB)412 6P{X 0,Y 0} P(AB)1 P(AUB) 1 [P(A)P(B) P(AB)]求: (1) 二维随机变量 (X, Y)的概率分布 ; (2) X 与Y 的相关系数XY111 21[111]2.4 6 12 3故(X, Y)的概率分布为由对称性知E(Y)这样，11,P(A|B) , 令 321， B 发生 , 0， B 不发生 .21312111612(2) 由(1)易得关于X 和Y的边缘分布律X0131P{X=k}44Y0151P{Y=k}66因此E(X)1,E(X2)1,4422113D(X) E(X 2)[E(X)]241616E(Y) 1,E(Y2) 1,D(Y) E(Y2)2[E(Y)]2 1 1 566 6 36 36又由(X, Y)的分布律可得21111 E(XY) 0 0 0 1 1 011.3121212 12故111E(XY) E(X)E(Y) 12 4615XY D(X) D(Y)3515.16 3601X。

概率论第4章习题参考解答

概率论第4章习题参考解答(总9页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--概率论第4章习题参考解答 1. 若每次射击中靶的概率为, 求射击10炮, 命中3炮的概率, 至少命中3炮的概率, 最可能命中几炮. 解: 设ξ为射击10炮命中的炮数, 则ξ~B (10,, 命中3炮的概率为 =⨯⨯==733103.07.0}3{C P ξ至少命中3炮的概率, 为1减去命中不到3炮的概率, 为=⨯⨯-=<-=≥∑=-2010103.07.01}3{1}3{i i i i C P P ξξ因np +p =10×+=不是整数, 因此最可能命中[]=7炮.2. 在一定条件下生产某种产品的废品率为, 求生产10件产品中废品数不超过2个的概率. 解: 设ξ为10件产品中的废品数, 则ξ~B (10,, 则废品数不超过2个的概率为=⨯⨯=≤∑=-20101099.001.0}2{i i i iC P ξ3. 某车间有20部同型号机床, 每部机床开动的概率为, 若假定各机床是否开动彼此独立, 每部机床开动时所消耗的电能为15个单位, 求这个车间消耗电能不少于270个单位的概率. 解: 设每时刻机床开动的数目为ξ, 则ξ~B (20,, 假设这个车间消耗的电能为η个单位, 则η=15ξ, 因此2061.02.08.0}18{}15270{}27015{}270{20182020=⨯⨯==≥=≥=≥=≥∑=-i i i iC P P P P ξξξη4. 从一批废品率为的产品中, 重复抽取20个进行检查, 求这20个产品中废品率不大于的概率. 解: 设这20个产品中的废品数为ξ, 则ξ~B (20,, 假设这20个产品中的废品率为η, 则η=ξ/20. 因此∑=-⨯⨯=≤=≤=≤320209.01.0}3{}15.020{}15.0{i i i iC P P P ξξη=5. 生产某种产品的废品率为, 抽取20件产品, 初步检查已发现有2件废品,问这20件中, 废品不少于3件的概率. 解: 设ξ为这20件产品中的废品数, 则ξ~B (20,, 又通过检查已经知道ξ定不少于2件的条件, 则要求的是条件概率 }2{}23{}2|3{≥≥⋂≥=≥≥ξξξξξP P P因事件}3{}2{≥⊃≥ξξ, 因此2}23{≥=≥⋂≥ξξξ因此5312.06083.02852.019.01.0209.019.01.01}{1}2{1}{}2{1}{}2{}{}{}{}2{}3{}2|3{192018222010202202202202203=-=⨯⨯--⨯⨯-==-=-===-===-=====≥≥=≥≥∑∑∑∑∑∑======C i P P i P P i P P i P i P i P P P P i i i i i i ξξξξξξξξξξξξξ6. 抛掷4颗骰子, ξ为出现1点的骰子数目, 求ξ的概率分布, 分布函数, 以及出现1点的骰子数目的最可能值. 解: 因掷一次骰子出现一点的概率为1/6, 则ξ~B (4,1/6), 因此有⎪⎪⎩⎪⎪⎨⎧≥<≤⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛<==⎪⎭⎫⎝⎛⨯⨯==∑≤--4140656100)(),4,3,2,1,0(6561}{4444x x C x x F k C k P x k kk k kk kξ或者算出具体的值如下所示：ξ0 1 23 4 P⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥<≤<≤<≤<≤<=41439992.0329838.0218681.0104823.000)(x x x x x x x F从分布表可以看出最可能值为0, 或者np +p =(4/6)+1/6=5/6小于1且不为整数, 因此最可能值为[5/6]=0. 7. 事件A 在每次试验中出现的概率为, 进行19次独立试验, 求(1)出现次数的平均值和标准差; (2)最可能出现的次数. 解: 设19次试验中事件A 出现次数为ξ, 则ξ~B (19,, 因此 (1)ξ的数学期望为E ξ=np =19×= 方差为Dξ=np (1-p )=19××=标准差为997.199.3===ξσξD(2)因np +p =+=6为整数, 因此最可能值为5和6. 8. 已知随机变量ξ服从二项分布, E ξ=12, D ξ=8, 求p 和n . 解: 由E ξ=np =12 (1) 和D ξ=np (1-p )=8 (2) 由(1)得n =12/p , 代入到(2)得 12(1-p )=8, 解出p =(12-8)/12=1/3= 代回到(1)式得n =12/p =12×3=36 9. 某柜台上有4个售货员, 并预备了两个台秤, 若每个售货员在一小时内平均有15分钟时间使用台秤, 求一天10小时内, 平均有多少时间台秤不够用. 解: 每个时刻构成一n =4的贝努里试验, 且p =15/60=, 因此, 设ξ为每个时刻要用秤的售货员数, 则ξ~B (4, , 当ξ>2时, 台秤不够用. 因此每时刻台秤不够用的概率为=+⨯⨯=>433425.075.025.0)2(C P ξ因此10个小时内平均有×10=个小时台秤不够用.10. 已知试验的成功率为p , 进行4重贝努里试验, 计算在没有全部失败的情况下, 试验成功不止一次的概率. 解: 设ξ为4次试验中的成功数, 则ξ~B (4,p ), 事件"没有全部失败"即事件{ξ>0}, 而事件"试验成功不止一次"即事件{ξ>1}, 因此要求的是条件概率P {ξ>1|ξ>0}, 又因事件{ξ>1}被事件{ξ>0}包含, 因此这两个事件的交仍然是{ξ>1}, 因此434141}0{1}1{}0{1}0{}1{}0|1{q pq q P P P P P P ---===-=-=-=>>=>>ξξξξξξξ其中q =1-p 11. ξ服从参数为2,p 的二项分布, 已知P (ξ≥1)=5/9, 那么成功率为p 的4重贝努里试验中至少有一次成功的概率是多少解: 因ξ~B (2,p ), 则必有9/5)1(1)0(1)1(2=--==-=≥p P P ξξ, 解得3/13/213/219/49/51)1(2=-==-=-=-p p p 则假设η为成功率为1/3的4重贝努里试验的成功次数, η~B (4,1/3), 则802.081161321)1(1)0(1)1(44=-=⎪⎭⎫⎝⎛-=--==-=≥p P P ηη12. 一批产品20个中有5个废品, 任意抽取4个, 求废品数不多于2个的概率解: 设ξ为抽取4个中的废品数, 则ξ服从超几何分布, 且有==≤∑=-24204155}2{i i i C C C P ξ 13. 如果产品是大批的, 从中抽取的数目不大时, 则废品数的分布可以近似用二项分布公式计算. 试将下例用两个公式计算, 并比较其结果. 产品的废品率为, 从1000个产品中任意抽取3个, 求废品数为1的概率. 解: 设任抽3个中的废品数为ξ, 则ξ服从超几何分布, 废品数为×1000=100 ===3100029001100}1{C C C P ξ 而如果用二项分布近似计算, n =3, p =, ξ~B (3,=⨯⨯≈=2139.01.0}1{C P ξ近似误差为, 是非常准确的.14. 从一副朴克牌(52张)中发出5张, 求其中黑桃张数的概率分布. 解: 设ξ为发出的5张中黑桃的张数, 则ξ服从超几何分布, 则)5,4,3,2,1,0(}{5525135213===--i C C C i P i i ξ则按上式计算出概率分布如下表所示:ξ0 1 2 34 5 P15. 从大批发芽率为的种子中, 任取10粒, 求发芽粒数不小于8粒的概率. 解: 设ξ为10粒种子中发芽的粒数, 则ξ服从超几何分布, 但可以用二项分布近似, 其中p =, n =10, 则∑=-⨯⨯=≥10810102.08.0}8{i i i iC P ξ=16. 一批产品的废品率为, 用普哇松分布公式求800件产品中废品为2件的概率, 以及不超过2件的概率. 解: 设ξ为800件产品中的废品数, 则ξ服从超几何分布, 可以用二项分布近似,则ξ~B (800, , 而因为试验次数很大废品率则很小, 可以用普阿松分布近似, 参数为 λ=np =800×=9526.0!8.0}2{1438.028.0}2{28.08.02=≈≤=≈=∑=--i i e i P e P ξξ17. 某种产品表面上的疵点数服从普哇松分布, 平均一件上有个疵点, 若规定疵点数不超过1个为一等品, 价值10元, 疵点数大于1不多于4为二等品, 价值8元, 4个以上为废品, 求产品为废品的概率以及产品的平均价值. 解: 设ξ为产品表面上的疵点数, 则ξ服从普哇松分布, λ=, 设η为产品的价值, 是ξ的函数. 则产品为废品的概率为0014.0!8.01}4{1}4{48.0=-=≤-=>∑=-i i e i P P ξξ==≤==∑=-108.0!8.0}1{}10{i i e i P P ξη==≤<==∑=-428.0!8.0}41{}8{i i e i P P ξη则产品的平均价值为 Eη = 10×P {η=10}+8×P {η=8}=10×+8×=(元) 18. 一个合订本共100页, 平均每页上有两个印刷错误, 假定每页上印刷错误的数目服从普哇松分布, 计算该合订本中各页的印刷错误都不超过4个的概率. 解: 设ξ为每页上的印刷错误数目, 则ξ服从普哇松分布, λ=2, 则1页印刷错误都不超过4个的概率为 ==≤∑=-402!2}4{i i e i P ξ而100页上的印刷错误都不超过4个的概率为[]=≤100}4{ξP19. 某型号电子管的“寿命”ξ服从指数分布, 如果它的平均寿命E ξ=1000小时, 写出ξ的概率密度, 并计算P (1000<ξ≤1200). 解: 因Eξ=1000=1/λ, 其概率密度为⎪⎩⎪⎨⎧≤>=-0010001)(1000x x ex xϕ 0667.0)12001000(2.111000120010001000=-=-=≤<----e e ee P ξ20. ξ~N (0,1), Φ0(x )是它的分布函数, φ0(x )是它的概率密度, Φ0(0), φ0(0), P (ξ=0)各是什么值解: 因有 20221)(x ex -=πϕ, ⎰∞--=Φxt dt ex 20221)(π, 因此φ0(x )为偶函数, 由对称性可知Φ0(0)=, 并有πϕ21)0(0=,因ξ为连续型随机变量, 取任何值的概率都为0, 即P (ξ=0)=0.21. 求出19题中的电子管在使用500小时没坏的条件下, 还可以继续使用100小时而不坏的概率解: 要求的概率为P (ξ>600|ξ>500), 因此905.0}500{}600{}500|600{1.010005001000600===>>=>>---e e eP P P ξξξξ22. 若ξ服从具有n 个自由度的χ2-分布, 证明ξ的概率密度为⎪⎪⎩⎪⎪⎨⎧<≥⎪⎭⎫ ⎝⎛Γ=---022)(21212x x e n x x x nn ϕ称此分为为具有n 个自由度的χ-分布证: 设ξη=, 则因ξ的概率密度函数为⎪⎪⎩⎪⎪⎨⎧≤>⎪⎭⎫ ⎝⎛Γ=--0221)(2122x x e x n x xn nξϕη的分布函数为)0()()()()()(22>=≤=≤=≤=x x F x P x P x P x F ξηξξη对两边求导得)0(22222)(2)(2121222222>⎪⎭⎫ ⎝⎛Γ=⎪⎭⎫ ⎝⎛Γ==-----x en xen xxx x x x n n x n n ξηϕϕ23. ξ~N (0,1), 求P {ξ≥0}, P {|ξ|<3}, P {0<ξ≤5}, P {ξ>3}, P {-1<ξ<3} 解: 根据ξ的对称性质及查表得: P {ξ≥0}=1-Φ0(0)=P {|ξ|<3}=2Φ0(3)-1=2×= P {0<ξ≤5}=Φ0(5)= P {ξ>3}=1-Φ0(3)==P {-1<ξ<3}=Φ0(3)-Φ0(-1)=Φ0(3)+Φ0(1)-1=+= 24. ξ~N (μ,σ2), 为什么说事件"|ξ-μ|<2σ"在一次试验中几乎必然出现解: 因为)1,0(~N σμξ- 19545.0197725.021)2(2}2{}2|{|0≈=-⨯=-Φ=<-=<-σμξσμξP P 因此在一次试验中几乎必然出现.25. ξ~N (10,22), 求P (10<ξ<13), P (ξ>13), P (|ξ-10|<2).解: 因为)1,0(~210N -ξ6826.018413.021)1(2}1210{}2|10{|0.0668193319.01)5.1(1}5.1210{}13{43319.05.093319.0)0()5.1(}5.12100{}1310{0000=-⨯=-Φ=<-=<-=-=Φ-=>-=>=-=Φ-Φ=<-<=<<ξξξξξξP P P P P P26. 若上题中已知P {|ξ-10|<c }=, P {ξ<d }=, 分别求c 和d .解: 因为)1,0(~210N -ξ, 则有 95.01)2(2}2210{}|10{|0=-Φ=<-=<-cc P c P ξξ 解得975.0295.01)2(0=+=Φc , 查表得,96.12=c得c = 再由5.00668.0)210(}210210{}{0<=-Φ=-<-=<d d P d P ξξ知,0210<-d 因此0668.0)210(1)210(00=-Φ-=-Φdd 即9332.00668.01)210(0=-=-Φd, 查表得5.1210=-d, 解得7310=-=d 27. 若ξ~N (μ,σ2), 对于P {μ-kσ<ξ<μ+kσ}=, 或, 或, 分别查表找出相应的k 值. 解: 先求P {μ-kσ<ξ<μ+kσ}=对应的k 值. 因)1,0(~N σμξ-, 因此 90.01)(2}{}{0=-Φ=<-=+<<-k k P k k P σμξσμξσμ即95.0290.01)(0=+=Φk , 查表得k = 同理, 由975.0295.01)(0=+=Φk , 查表得k = 由995.0299.01)(0=+=Φk , 查表得k = 28. 某批产品长度按N (50, 分布, 求产品长度在和之间的概率, 长度小于的概率.解: 设ξ为产品长度, 则ξ~N (50, , 且有)1,0(~25.050N -ξ, 则9545.0197725.021)2(2}225.050{}225.0502{}5.505.49{0=-⨯=-Φ=<-=<-<-=<<ξξξP P P0006871.09993129.01)2.3(1)2.3(}25.0502.4925.050{}2.49{00=-=Φ-=-Φ=-<-=<ξξP P29. ξi ~N (0,1)(i =1,2,3), 并且ξ1,ξ2,ξ3相互独立, ∑==3131i i ξξ,∑=-=312)(i i ξξη,求),cov(,),,cov(1ηξηξξE解: 此题要用到, 两个独立的服从正态分布的随机变量相加后得到的随机变量仍然服从正态分布. 因此, 因为3131,031=⎪⎭⎫ ⎝⎛==∑=i i D D E ξξξ, 则)31,0(~N ξ313131)()cov(2131111==⎪⎭⎫ ⎝⎛==∑=ξξξξξξξE E E i i32313121)cov(2)2()(22222=+⨯-=+-=+-=-ξξξξξξξξξξE E E E i i i i i因此2323)()(312312=⨯=-=⎪⎭⎫ ⎝⎛-=∑∑==i i i i E E E ξξξξη ξξ-i 也服从正态分布, 且有03131)]([),cov(2=-=-=-=-ξξξξξξξξξE E E i i i即ξ与ξξ-i 不相关, 而因为它们服从正态分布, 因此也就是ξ与ξξ-i 相互独立, 则ξ与2)(ξξ-i 也相互独立, 则ξ与η中的加和中的每一项相互独立, 当然也与η相互独立, 因此有0),cov(=ηξ, 因为相互独立的随机变量一定不相关.30. (ξ,η)有联合概率密度22)(21,2122ηξζπ+=+-y x e , 求ζ的概率密度.解: 由联合概率密度看出, ξ与η相互独立服从标准正态分布, 则有 ξ2与η2也相互独立且服从自由度为1的χ2-分布, 即ξ2~χ2(1), η2~χ2(1), 因此ζ=ξ2+η2~χ2(2), 即它的概率密度为 ⎪⎩⎪⎨⎧<>=-00212x x exζϕ 即ζ服从λ=1/2的指数分布.。

概率论与数理统计第四章随堂测验_详细答案

第四章随堂测验答案1.(,),2.4, 1.44,____,_____.X b n p EX DX n p ==== 则答：n =6, p =0.4因为(,)X b n p ，所以EX =np =2.4, DX =npq =np (1-p )=1.44.所以() 1.440.6,2.(1)41DX p p E n p np X -====-从而 2.40.4, 6.0.4EX p n p ==== 2.(),[(1)(2)]1____.,X P E X X λλ-=-= 则答：1,λ=解法同习题课例题1.23.1,()______.X X E X e -+=设服从参数为的指数分布则答：4/3.根据期望的性质可知，22()(),X X E X e EX E e --+=+其中因为X 服从参数为1的指数分布(1λ=)，所以,(,)000x x x e f x ->⎧=⎨≤⎩且EX =1，DX =1.另外，根据随机变量函数的期望的定义，可知2223300011().(3)3X x x x x x f x dx e d E e e e e dx e x +∞+∞+∞+∞-------∞====-=⎰⎰⎰ 故221()()1.334X X E X e EX E e --+=+=+=224.,0.5,0,2,X Y EX EY E EY X ====已知的相关系数为2[()]_____.E X Y +=则答：6.因为2220,,EX EY EX EY ====所以DX=DY=2.又22222[()]22()E X Y E X XY Y EX E XY EY ⎡⎤+=++=++⎣⎦，其中已知222E E Y X ==，而()Cov(,)XY E XY X Y EX E Y EY XE ρ=+=0.5001=⨯=，于是2[()]21.226E X Y ⨯++=+=2125.,,...,,(),(),n i i X X X E X a D X b ==设随机变量是相互独立的且1,2,...,,i n =1,()_____,()____1_.ni i X X X E D X n ====∑记则答：a, b 2/n.11222211111;11())1(.n n i i i i n n i i i i X na a n n n b D X nb n n E E X n EX D n X DX ====⎛⎫=== ⎪⎝⎭⨯==⨯⎛⎫=== ⎪⎝⎭∑∑∑∑6.,,,1,1,X Y Z EX EY EZ ===-已知三个随机变量中1,DX DY DZ === 0,0.5,0.5,XY XZ YZ ρρρ===-()_____,()_____.E X Y Z D X Y Z ++=++=则答：1, 3.()1111E X Y Z E X E Y E Z ++=++=+-=[][][]()()()2Cov(,)2Cov(,)2Cov(X,Z)Cov(Y,Z)2Cov(X,Y)+2Cov(X,Z)+2Cov(Y,Z)111201120.5112(0.5)12321.XZ YZ D X Y Z D X Y Z D X Y DZ X Y Z DX DY X Y DZ DX DY DZ DX DY DZ ρρρ++=++=++++=+++++=+++=+=+++⨯⨯⨯+⨯⨯⨯+⨯-⨯⨯=++7.(),[,,,]E XY EXEY C G H I =选择题：若则（可多选）(A)(),(B)()(C)(),(D),(E),,(F),(G),(H)0,(I)Cov(,)0.XY D XY DXDY D X Y DX DY D X Y DX DY X Y X Y X Y X Y X Y ρ=-=-+=+==独立不独立相关，不相关，。

概率统计第4章

+¥
10
E(Y ) = E(g(X )) =
+ò
40
-¥
ò
g(x ) f (x )dx =
ò
0
(10 - x ) dx 60
10
60 (70 - x ) (40 - x ) dx + ò dx = 15 40 60 60
14
2011-2012学年第2学期
定理设二元函数 g 分区连续，且 Z = g(X,Y ), 则 1）若 (X,Y )离散并有联合分布律
x
2011-2012学年第2学期
§4.1.3 数学期望的性质设以下所涉及的随机变量的数学期望均存在. 性质1 若对任意常数 a, b, c, 有线性性质
E(aX + bY + c ) = a E(X ) + b E(Y ) + c
提醒书上性质1, 2, 3均是以上性质1的特殊情形.
E(c ) = c E(aX ) = a E(X ) E(X + Y ) = E(X ) + E(Y ) E(X + c ) = E(X ) + c
E(Z ) = E(g (X,Y )) = y 30 y =x = D2
ò
+¥
-¥
ò
+¥
-¥
f (x, y )g (x, y )dxdy
òò òò
D2
D1
0.1y ´ 1 200 dxdy +
10
D1
10 20
x
é 0.1x + 0.05(y - x )ù 1 dxdy êë úû 200
o
= 1.7083(万元)
Z = g (X,Y ) = max{X ,Y }

《概率论与数理统计》习题及答案第四章

《概率论与数理统计》习题及答案第四章1．一个袋子中装有四个球，它们上面分别标有数字1,2,2,3，今从袋中任取一球后不放回，再从袋中任取一球，以,X Y 分别表示第一次，第二次取出的球上的标号，求(,)X Y 的分布列.解(,)X Y 的分布列为其中(1,1)(1)(1|1)0P X Y P X P Y X =======余者类推。

2．将一枚硬币连掷三次，以X 表示在三次中出现正面的次数，以Y 表示三次中出现正面次数与出现反面次数之差的绝对值，试写出(,)X Y 的分布列及边缘分布列。

解一枚硬币连掷三次相当于三重贝努里试验，故1~(3,).2X B 331()(),0,1,2,32k P X k C k ===，于是(,)X Y 的分布列和边缘分布为01013818i p ⋅其中(0,1)(0)(1|0)0P X Y P X P Y X =======，13313(1,1)(1)(1|1)()128P X Y P X P Y X C =======⨯=，余者类推。

3．设(,)X Y 的概率密度为又（1）{(,)|1,3}D x y x y =<<；（2）{(,)|3}D x y x y =+<。

求{(,)}P X Y D ∈ 解（1）1321{(,)}(6)8P x y D x y dxdxy ∈=--⎰=321(6)8x x y dxdy --- =)落在圆222()x y r r R +≤<内的概率. 解（1）22223201(R x y R CR dxdy C R C r drd ππθ+≤==-⎰⎰⎰⎰333233R R C R C πππ⎡⎤=-=⎢⎥⎣⎦， ∴33C R π=.（2）设222{(,)|}D x y x y r =+≤，所求概率为322323232133r r r Rr R R R πππ⎡⎤⎡⎤=-=-⎢⎥⎢⎥⎣⎦⎣⎦. 5．已知随机变量X 和Y 的联合概率密度为求X 和Y 的联合分布函数.解1设(,)X Y 的分布函数为(,)F x y ，则解2由联合密度可见，,X Y 独立，边缘密度分别为边缘分布函数分别为(),()X Y F x F y ，则设(,)X Y 的分布函数为(,)F x y ，则6．设二维随机变量(,)X Y 在区域:0D x <<求边缘概率密度。