最新1热力学的平衡态和状态方程汇总
物理-平衡态 温度 理想气体状态方程

统
开放(open)系统
—和外界既交换能量,又交换物质
绝热
密封 气体
密封 导热
热水
水和 密封 水蒸 导热 气
§1.1
平衡态 温度 理想气体状态方程
§1.1.1 平衡态 状态参量
平衡态:在不受外界影响的条件下,表征系统状态 的宏观参量取确定值,并且不随时间改变的状态。
“不受外界影响”指外界和系统 既不交换热,也不交换功,这一条 件必不可少。
状态描述 热
宏观参量描述
力
微观 —用描述微观粒子运动
学 系
状态的量描述
统
状态变化规律 —热力学第一、第二定律
热力学(Thermodynamics):在观察和实验 的基础上,通过归纳和推理研究热力学系统的 宏观状态变化规律。
统计物理学(Statistical Physics):以每个微 粒遵循的力学定律为基础,利用统计方法导 出系统的宏观热力学规律。
A
确定气体状态的参量可以是V ,T 或 P,T 或 P,V (状)态函数:其它可以表示为态参量函数的参量
§1.1.1 平衡态 状态参量
几何参量 —如:气体的体积
非热学 力学参量 —如:气体的压强
独有
状
化学参量 —如:各化学组分的质量
态
参
电磁参量 —如:电场和磁场强度
量
热学
独有
热学参量 —温度
§1.1.2 热力学第零定律 温度
§1.1.2 热力学第零定律 温度
137.04
A
B
137.04
A
B
137.04
A
B
热力学第零定律:如果系统A和系统B分别与 系统C的同一状态处于热平衡,那么A和B必 定处于热平衡。
第一章 平衡态及状态方程

关于α = κβp的推导
状态方程f(T,p,V)=0
推导:以 Vm, T 为状态参量,p 为态函数: p = p(Vm ,T )
dp
=
⎜⎛ ⎝
∂p ∂T
⎟⎞ dT ⎠V
+
⎜⎜⎝⎛
∂p ∂Vm
⎟⎟⎠⎞T dVm
=
pβdT
−
1 κVm
dVm
当 p = const 时,dp=0。 pβ = 1 ⎜⎛ ∂Vm ⎟⎞ = α κVm ⎝ ∂T ⎠ p κ
2. 物质的分子、原子处于永不停息的无规则的热运动状态。
无规则运动:分子完全随机的运动,该随机性包括速度大小和
速度方向。
各项同性
热运动: 分子运动的宏观整体表现。 平均效果等于零.
典型例子:布朗运动。 1827年
英国植物学家布朗(R. Brown)
微小颗粒的无规则运动称为布朗运动。
花粉、树脂、煤、烟灰、尘埃、化石、 玻璃、矿物等
• 按照状态参量的本身性质,可以分为几何参量、 力学参量、化学参量、电磁参量以及热学特有 的热学参量—温度。
Δp→0
1 V
(
ΔV Δp
)T
=
−
1 V
(
∂V ∂p
)T
α = κβp
•理想气体 pVm = RT
α = 1 , β = 1 ,κ = 1
T
Tp
⎧α = 10−4 K −1
液 体
⎪ ⎨β
= 101~2 K −1
⎪⎩κ = 10−6atm−1
H2O 1.8×10-4 K-1 46.3 K-1
3.9×10-6 atm-1 .
体膨胀 系数
大物热学第一章 热力学系统的平衡态及平衡方程PPT课件

vi v
pV vRT p pi
Dalton’s law of partial pressure: 混合气体的压强等于
-steady state 在外界影响下,系统的各部分宏观性质不随时间而
变化的状态。 例:
-Non-equilibrium state 系统的宏观性质随时间而变化的状态。
从非平衡态到平衡态的转变,称为驰豫过程。其时间
常数称为驰豫时间。
可编辑课件
8
-Quasi-static (quasi-stationary) state 从非平衡态到平衡态转变的热力学过程中,每一个
热学
Heat (and Thermodynamics)
什么是热学
研究热现象的规律及其应用的学科
热学包含的内容
1. 热学的基本参量——温度和热量的概念
2. 物质的热性质
状态方程 热膨胀 比热 热传递的规律
3. 热力学定律
第零、第一、第二、第三定律
4. 热现象的微观理论
气体分子运动论 统计物理
可编辑课件
强趋于零时的极限(稀薄气体)。(可以证明理想气体
的内能与压强无关)
理想气体在平衡态时满足
Charles law
pT
Gay-Lussac law V T Boyle-Marriotle law—一定质量的气体,当温度一定 时,P和V成反比
PV = const (T) 对于1 mole 理想气体
PVm = RT R为Universal gas constant
III.气体分子运动论的初步概念(1.1,1.6节)
可编辑课件
20
Ⅱ Equation of State 1. 什么是状态方程(状态方程的一般讨论)
热学1

组 成 成 分 均 匀 性 分
复相系统:多种物相组成的系统,或非均匀系统。 复相系统:多种物相组成的系统,或非均匀系统。
1. 热力学系统的平衡态及状态方程
• 热力学系统的状态参量
力学:物体的位置坐标 r,速度v等 热学体系的状态能否用一组 r 和v来描述? 热学系统所包含的分子数的数量级为1023,若用r和v 去描写,要解1023个牛顿方程,这是不可能的。
1bar =105 Pa 1atm =101325Pa = 760mmHg 1Torr =1mmHg 23 −1 1NA ≈ 6.0221367×10 mol
1. 热力学系统的平衡态及状态方程
1.3 平衡态的概念
• 在没有外界影响的情况下,系统各部分的宏观性质长时 在没有外界影响的情况下, 间不发生变化的状态称为平衡态 • 在外界的影响下,系统的宏观性质长时间不发生变化 在外界的影响下, 的状态称为稳定态 热动平衡态
-1/αp
0 p
100 t/oC
T0 = 273.15 C
o
p0
t = −T0 , p = 0
T0 + t p = p0 T0
绝对零度
T p = p0 T0
-1/αp -T0
0
100 t/oC
p T = T0 p0
1. 热力学系统的平衡态及状态方程
2)定压气体温度计 )
V =V0 (1+αV t)
形成固态 形成固态 当ε
>> EB 时,分子的平均动能远大于其间的势阱深度
分子尽可能地均匀充满占据的空间,形成气态 分子尽可能地均匀充满占据的空间,形成气态 当
ε ≈ EB
时,分子的动能与分子间的势阱相当
形成介于固态和气态之间的液态 形成介于固态和气态之间的液态
化工热力学公式总结

化工热力学公式总结1.热平衡公式:对于封闭系统,内能变化等于热变化和功变化之和。
即:ΔU=Q-W其中,ΔU表示内能变化,Q表示系统吸收或放出的热量,W表示系统对外做功。
2.热容公式:热容是单位质量物质温度变化1°C所吸收或放出的热量。
Q=mCΔT其中,Q表示吸收或放出的热量,m表示物质的质量,C表示热容,ΔT表示温度变化。
3.平衡常数(K)公式:对于化学反应:aA+bB↔cC+dD反应的平衡常数(K)定义为反应物浓度的乘积与生成物浓度的乘积之比:K=[C]^c[D]^d/[A]^a[B]^b其中,[A]、[B]、[C]、[D]表示反应物和生成物的摩尔浓度。
4.反应焓变(ΔH)公式:反应焓变是化学反应进行过程中吸热或放热的量。
根据焓守恒定律,反应焓变可以通过反应物和生成物焓变的差值表示:ΔH=ΣnΔHf(生成物)-ΣmΔHf(反应物)其中,n和m为反应物和生成物的系数,ΔHf表示物质的标准生成焓。
5.反应熵变(ΔS)公式:反应熵变是化学反应进行过程中熵的变化。
根据熵守恒定律,反应熵变可以通过反应物和生成物熵变的差值表示:ΔS=ΣnS(生成物)-ΣmS(反应物)其中,n和m为反应物和生成物的系数,S表示物质的熵。
6.反应自由能变(ΔG)公式:反应自由能变是化学反应进行过程中自由能的变化,可以通过反应物和生成物的自由能差值表示:ΔG=ΣnG(生成物)-ΣmG(反应物)其中,n和m为反应物和生成物的系数,G表示物质的自由能。
7.热力学平衡公式:对于可逆反应,根据吉布斯自由能变可以推导出热力学平衡公式:ΔG=ΔH-TΔS其中,ΔG为反应的吉布斯自由能变,ΔH为反应的焓变,ΔS为反应的熵变,T为温度。
以上是化工热力学中常用的公式总结,这些公式在研究和设计化工过程中起到了重要的作用。
通过应用这些公式,可以计算和预测系统的热力学性质和能量转化,从而优化化工过程的设计和操作。
同时,这些公式也为研究反应机理和确定过程条件提供了理论基础。
热力学方程
克斯韦关系式
❖10.2 麦克斯韦关系式
将上述导出结果用于热力学基本方程:
dU
TdS
pdV
T V
S
p S
V
dH
TdS
Vdp
T p
S
V S
p
dA
SdT
pdV
S V
T
பைடு நூலகம்
p T
V
dG
SdT
Vdp
S p
T
V T
p
这四个关系式统称 麦克斯韦关系式, 它们的重要意义在 于把不可直接测定 的量转化为可直接
测定量
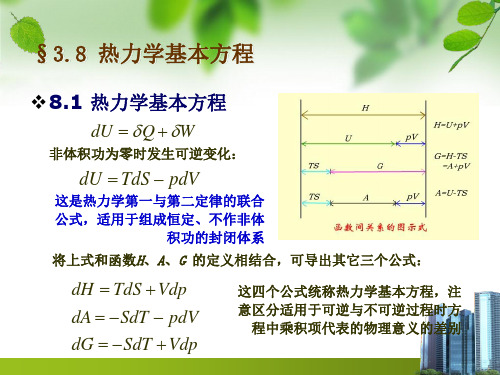
§3.8 热力学基本方程
❖8.1 热力学基本方程
dU Q W
非体积功为零时发生可逆变化:
dU TdS pdV
这是热力学第一与第二定律的联合 公式,适用于组成恒定、不作非体
积功的封闭体系
将上式和函数H、A、G 的定义相结合,可导出其它三个公式:
dH TdS Vdp dA SdT pdV dG SdT Vdp
这四个公式统称热力学基本方程,注 意区分适用于可逆与不可逆过程时方
程中乘积项代表的物理意义的差别
§3.8 热力学基本方程
❖8.2 热力学基本方程的应用
计算纯物质pVT变化过程的ΔA及ΔG
dA SdT pdV
dG SdT Vdp
★理想气体:
AT
nRT
ln V2 V1
GT
nRT
ln
p2 p1
dAT pdV dGT Vdp
★凝聚系统:
AT
V2 V1
pdV
0
GT
p2 Vdp V p
p1
§3.9 克拉佩龙方程
第1章 热力学系统的平衡态及状态方程

对于 mol理想气体
pV RT
V Vmol
理想气体的状态方程
M
:摩尔质量,分子量
2015/3/4
37
p
V
RT
R N Ak B
p n
N A
V
k BT nk BT
气体的分子数密度
N A
V
p nk BT
理想气体的状态方程
R kB 1.380658 1023 J K NA
2015/3/4
稳定平衡
11
理解:
分子被假设为半径为r0的刚性小球 分子的大小:0.1 nm = 10-10 m = 105 fm 分子不接触时,r>>r0,其间无相互作用; 分子接触时,rr0,分子间碰撞为弹性碰撞。 (r ) 12 6 r r
Lennard-Jones Potential Model
p p0 (1 a pT )
(4) 阿伏伽德罗定律 在相同的温度和压强下,摩尔数相同的 各种气体所占的体积相同。
T0 273.16 K, p0 1 atm V0 22.4144 L/mol
2015/3/4 34
标准状况下
3.理想气体的状态方程
由玻意耳定律
pV C(T )
由温度决定的常数
热 学
第1章 热力学系统的平衡态及状态方程 第2章 热平衡态的统计分布律 第3章 近平衡态中的输运过程
2015/3/4
1
绪言
热学:研究物质的热运动、热运动对物质 宏观性质的影响及其与物质的其他运动形 式之间转换规律的物理学分支。
▲ 研究对象: 宏观物体(大量分子原子系统) 或物体系 — 热力学系统 。 ▲ 研究内容:与热现象有关的性质和规律。
最新工程热力学复习总结

第一章基本概念、基本过程一、热力系统1、(热力)系统:系统:通常选取一定的工质或空间作为研究对象,称之为热力系统。
2、外界:与体系发生质、能交换的物系。
3、边界:系统与外界的分界面(线)。
边界可实可虚,可定可动。
二、系统的分类根据系统和外界之间物质、能量的交换情况分:1、闭口系统(控制质量):和外界没有物质交换。
2、开口系统(控制容积、控制体)和外界有物质交换。
3、绝热系统:和外界间没有热量交换。
4、孤立系统:和外界既无能量交换又无物质交换。
三、平■衡状态(一)定义:无外界影响(重力场除外)的条件下,系统保持状态参数不随时间而改变的状态。
1、热平衡:在无外界作用的条件下,系统内部、系统与外界之间无温差。
2、力平衡:在无外界作用的条件下,系统内部、系统与外界之间无压差。
3、化学平衡:在无外界作用的条件下,系统内部、系统与外界之间无化学势差。
平衡的充要条件:系统同时达到热平衡、力平衡、化学平衡。
(二)平衡状态的特点:1、在不受外界影响下,平衡不会自发的破坏;2、处于不平衡的系统,在不受外界影响时,会自发的趋于平衡;3、单相工质处于平衡状态时,在忽略重力的影响下,其内部性质均匀一致。
4、平衡必稳定,稳定未必平衡,平衡可以不均匀。
★对于气液两相并存的热力平衡系统,气相和液相密度不同,所以整个系统不是均匀的。
四、状态参数状态确定,状态参数的数值也确定,反之亦然。
非平衡状态系统内部存在不平衡势,因此不能用状态参数来描写。
(一)状态参数分类:1、基本状态参数:压力P、比体积v、温度T (可以直接测量)导出状态参数:内能U、粉H、痼S2、强度参数:参数与系统质量无关,且不可相加。
如:P、T广延参数:参数与系统质量成正比,且可相加。
如:m、V、U、H、S(二)基本状态参数1、温度摄氏温度t (C)与热力学温度T (K)关系:t=T-273.152、压力(绝对压力)p Pa、MPa(压强)单位面积上的垂直作用力。
绝对压力P;表压力p e;真空度p v;环境压力p bo,绝对压力的值不变,表压力或真空度会随着环境压力的变化而变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
孤立系
封闭系(闭系) 开放系(开系)
(isolated)
(closed)
(open)
例:以容器内水为研究对象(系统), 则其它均为外界
二、宏观量与微观量
1、宏观量(Macroscopic Quantity) 从整体上描述系统的状态量,一般可以直接测量。
广延量 可以累加的量 例如:质量M、体积V、 内能E 强度量 不可累加的量 例如:压强p、温度T 、 分子数密度n 2、微观量(Microscopic Quantity) 描述系统内微观粒子个体特征的物理量。
M
▪注意该状态方程的适用条件:
分子摩尔质量
温度足够高, 压强足够低(分子密度足够小)
三、描述物质状态变化性质的物理量
由状态方程 f(p,V,T)0 V V(T, p) 可定义:
1、体膨胀系数 在一定压强下,体积随温度增大的相对变化率
1 V
V T p
2、等温压缩系数
在一定温度下,体积随压强减小的相对变化率
1 p p T V
➢对于理想气体:
1 T
➢一般地,可以证明:p
作业: p39 1.1,1.3,1.10,1.14,1.21 1.28
§4 理想气体的压强与温度
一、气体分子运动论的基本观点
1、宏观的气体物质由大量微观粒子(分子、原子)组成, 分子之间有一定的间隙。 气体分子的密度(标准状态) ≈1019 个分子/cm3 气体分子的平均间距约为分子自身大小的10倍。
2、分子不停地作无规则热运动 ▪分子热运动的平均速度 v ≈ 102m/s 。
3、分子间有一定的作用力。 长程力 碰撞力
▪分子的平均碰撞次数:z ≈ 1010 次/秒 。
二、理想气体的微观模型
对单个分子的力学性质的假设(分子模型)
1、理想气体的分子之间的平均间隙远大于分子自身尺度,可 作为质点处理。
一、状态方程的一般概念
常常用p,V和T 这三个宏观量即可完备地描述热力学系 统的平衡态。
但实验证明,它们并非彼此独立,而是相互依赖的,且 总可满足一定的函数关系(具体由物质自身的性质决定):
f(p,V,T)0
——称为状态方程(或物态方程)。
二、理想气体的状态方程
pVRT
——其中ν为总质量为M的气体分子的摩尔数(mol)
2、分子间的长程力可忽略不计。
3、分子间的碰撞为完全弹性的,且分子运动可用牛顿定律 处理。
▪ 存在的问题: 分子数目十分巨大,如果对每一个分子列出其动力学方
是一种理想模型,也是本课程的主要研究内容。
2) 是动态平衡(Dynamic Equilibrium): 处在平衡态的大量分子仍在做热运动,而且因为碰撞, 每个分子的速度频繁改变,但系统的宏观量保持不变。
3) 存在涨落现象(Fluctuation): 处在平衡态的系统的宏观量,如压强、密度等量,总体 上不随时间改变, 但不能保证任何时刻大量分子分布与 运动的情况完全均匀一致。 例如:
如: 分子的质量m、直径 d 、速度 v、动量 p、能量 等。
3、微观量与宏观量有一定的内在联系。 例如,气体的压强是大量分子撞击器壁的平均效果; 物质的温度是大量分子作无规则热运动的剧烈程度的 宏观体现。
三、平衡态(Equilibrium State)
在不受外界影响的条件下,系统的宏观性质不随时间改 变的状态,称为平衡态。 说明: 1) 平衡态的基本特征:无宏观的物质流动和能量流动。
1热力学的平衡态和状态方程
第1章 热力学系统的平衡态及状态方程
§1 热力学系统及其状态参量 一、热力学系统(Thermodynamic System)
包含大量的分子、原子,其数量以阿伏加德罗常数 (Avgadro Constant)计
NA= 6.02×1023(mol-1)
热力学系统按照其与外界间的物质、能量交换关系,分为:
二、温度(Temperature)的宏观概念
温度: 处于热平衡态下的各个系统所共同具有的宏观性质。
思考:我们常常称温度为“物体冷热程度的量度”,这 种说法是否严格?
三、温标(Temperature Scale)
温度的定量表达。
在实践中,一般利用某种物质的某种热平衡状态(如:水 的三相点和沸点)作为温标的基准点,再借助物质的某种 宏观性质(如:体积、气压、电阻、光辐射强度……)随 温度的变化标定出温度的数值。
——此例中两侧粒子数不可能严格相同,这里的偏差 即称为涨落。
又如:布朗运动就是一种可观测的涨落现象。
分子数越多,涨落就越小,宏观态就越稳定。
§2 温度与温标 一、热力学第零定律(The Zeroth Law of Thermodyn接触的物体之间能够在某种情况下彼此 发生能量(热量)交换。
由此制成测量温度的仪器:温度计(Thermometer) 日常生活中常用的温标:摄氏(Celsius)温标 华氏(Fahrenheit)温标
❖理想气体温标与热力学温标
理想气体(Ideal Gas): 在同一温度下,体积与压强的乘积保持为常数的气体。
pV常量
根据理想气体这一性质确定的温标称为理想气体温标。
1 V
V p
T
➢对于理想气体: 1 T 1 p
三、描述物质状态变化性质的物理量
1、体膨胀系数 1 V
V T p
2、等温压缩系数
1 V
V p
T
➢对于理想气体:
1 T 1 p
由状态方程 f(p,V,T)0p p(V,T) 可定义:
3、等体压强系数 在一定体积下,压强随温度增大的相对变化率
从热平衡定律出发可以论证:存在一种不依赖于任何具 体物质特性的温标,称为热力学温标。
——在理想气体温标的有效范围内,热力学温标与理想气 体温标是完全相同的。
热力学温标下的温度又称为绝对温度,记为T。 温度的国际单位为: K(Kelvin)
✓热力学温度T与摄氏温度t的换算关系:Tt27.1(35K)
§3 状态方程
——热流(Heat Flow) 热平衡(Thermal Equilibrium):
发生热接触的两物体在不受外界影响时总会共同达到平衡态, 则说:这两个物体之间处于热平衡状态,或曰:达到了热平 衡。 且实验证明:
若两个物体均分别与第三个物体处于热平衡,则 这两个物体间亦必处于热平衡。
——热力学第零定律(热平衡定律)
