(完整版)二面角典型习题
高中二面角经典例题

高中二面角经典例题
高中二面角是几何中的一个重要概念,掌握二面角的概念和计算方法对于理解空间几何和解题都具有重要意义。
下面介绍一些经典的高中二面角例题,供大家练习和参考。
1.已知四面体ABCD中,AB=3,AC=4,AD=5,BC=6,CD=8,BD=7,求角ABC和角BAD的二面角。
2.已知直角棱锥ABCDE,以AD为底面对角线,EA为高,
AB=AC=AD=10,BC=BD=CD=5,求角EAB和角EAC的二面角。
3.已知正四面体ABCDA1B1C1D1中,AB=3,求角A和角A1的二面角。
4.已知正方体ABCDA1B1C1D1E1F1E,F在平面ABC上,以AF为底面对角线,求角FA1B1和角FA1C1的二面角。
5.已知正八面体ABCDEFGH,以AB为底面对角线,求角E和角H 的二面角。
以上这些例题都是比较典型的高中二面角例题,需要运用几何相关知识和计算方法进行解答。
希望同学们能够认真学习和练习,掌握二面角的概念和计算方法,提高几何解题能力。
- 1 -。
二面角典型习题

二面角1.二面角的计算:1)定义法;2)三垂线定理法;3)垂面法;4)面积射影法;例1、已知P 是二面角AB αβ--棱上一点,过P 分别在αβ、内引射线PM ,PN ,且45,60BPM BPN MPN ∠=∠=︒∠=︒,求此二面角的度数。
例2、已知P 为锐二面角l αβ--棱上的点,,4530PQ PQ l αβ⊂︒︒与成,与成,则二面角l αβ--的度数是多少。
例3、已知二面角l αβ--的度数为θ,在面α内有一条射线AB 与棱l 成锐角δ,与面βγ成角,则必有( )(A )sin sin sin θδγ= (B )sin sin cos θδγ=(C )cos cos sin θδγ= (D )cos cos cos θδγ=例4、在120︒的二面角l αβ--的面α、β内分别有A 、B 两点,且A 、B 到棱l 的距离AC 、BD 分别长2、4,AB=10,求:(1)直线AB 与棱l 所成角的正弦值。
(2)直线AB 与平面β所成角的正弦值。
例5、已知二面角MN αβ--为60︒,,,A B BC AB αββ∈∈为在上的射影,且C 在棱MN 上,AB 与β所成角为60︒,且45AC MCB ∠=︒,求线段AB 的长。
例6、已知二面角DC αβ--的度数为θ,,,A B ADC αβ∈∈∆的面积为S ,且DC=m ,AB DC ⊥,AB 与平面β成30︒角,当θ变化时,求DBC ∆面积最大值。
例7、已知C 是以AB 为直径的圆周上的一点,30ABC ∠=︒,45PA ABC PBA ⊥∠=︒面,,求二面角A-PB-C 的正弦值。
例8、在正方体1111ABCD A BC D -中,利用cos S S θ=射影解下列各题1)P 、Q 分别为1,A A AB 的中点,求平面1C PQ 与底面ABCD 所成角的余弦值2)求二面角11C BD C --的大小;3)M 是棱BC 的中点,求二面角111D B M C --的余弦值。
二面角练习题
D C
B
P
A
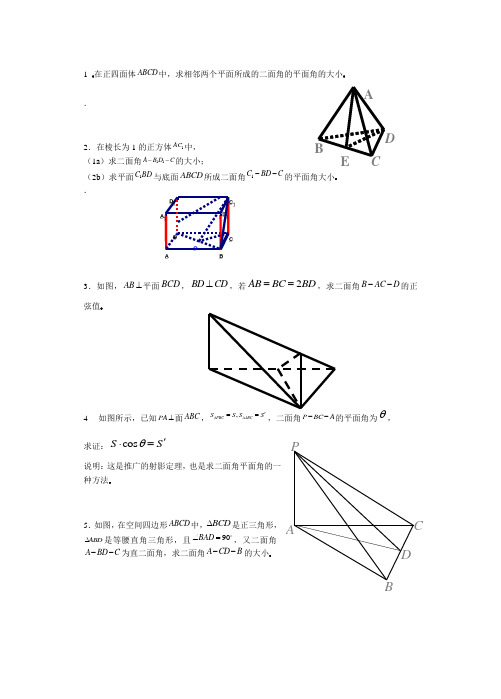
在正四面体ABCD 中,求相邻两个平面所成的二面角的平面角的大小
.
2.在棱长为1的正方体1AC 中, (1a )求二面角11A B D C --的大小;
(2b )求平面1C BD 与底面ABCD 所成二面角1C BD C -- .
3.如图,AB ⊥平面BCD ,BD CD ⊥,若2AB BC BD ==,求二面角B AC D --的正
4 如图所示,已知PA ⊥面ABC ,,PBC ABC S S S S ∆∆'==,二面角P BC A --的平面角为θ, 求证:cos S S θ
'⋅=
说明:这是推广的射影定理,也是求二面角平面角的一种方法
5.如图,在空间四边形ABCD 中,BCD ∆是正三角形,
ABD ∆是等腰直角三角形,且90
BAD ∠=
,又二面角
A BD C --为直二面角,求二面角A CD
B --的大小
_1 _ A _ B
6.设A 在平面BCD 内的射影是直角三角形BCD 的斜边BD 的中点O
,1,AC BC CD ===求(1)AC 与平面BCD 所成角的大小;(2b )二面角A BC D --的大小;(3)异面直线AB 和
CD 的角大小
_ D
_ C
_ F _ H
_ B
_ A
E
_ O _ E
_ D
_ C
_ F
_ B
_
A。
【最新精选】二面角的基本求法例题及练习
C1C1一、平面与平面的垂直关系1.判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
例1.在空间四边形ABCD 中,AB=CB ,AD=CD ,E 、F 、G 分别是AD 、DC 、CA 的中点。
求证:BEF BDG ^平面平面。
例2.AB BCD BC CD ^=平面,,90BCD °,E 、F 分别是AC 、AD 的中点。
求证:BEF ABC ^平面平面 。
2.性质定理:若两个平面互相垂直,则在一个平面内垂直于它们交线的直线垂直于另一个平面。
例3.在正方体ABCD —A 1B 1C 1D 1中,求A 1B 和平面A 1B 1CD 所成的角.。
二、二面角的基本求法1.定义法:在棱上取点,分别在两面内引两条射线与棱垂直。
例4.在正方体ABCD —A 1B 1C 1D 1中,求(1)二面角11A B C A --的大小;(2)平面11A DC 与平面11ADD A 所成角的正切值。
练习:过正方形ABCD 的顶点A 作PA ABCD ^平面,设PA=AB=a ,求二面角B PC D --的大小。
2.三垂线法C例5.ABCD ABEF ABCD ^平面平面,是正方形,ABEF 是矩形且AF=12AD=a ,G 是EF 的中点,(1)求证:AGC BGC ^平面平面; (2)求GB 与平面AGC 所成角的正弦值; (3)求二面角B AC G --的大小。
例6.点P 在平面ABC 外,ABC 是等腰直角三角形,90ABC°,PAB 是正三角形,PA BC ^。
(1)求证:^平面PA B 平面A BC ; (2)求二面角P AC B --的大小。
练习:正方体ABCD —A 1B 1C 1D 1的棱长为1,P 是AD 的中点,求二面角1A BD P --的大小。
B13.垂面法例7.SA ABC AB BC SA AB BC ^^==平面,,, (1)求证:SB BC ^;(2)求二面角C SA B --的大小;(3)求异面直线SC 与AB 所成角的余弦值。
二面角的基本求法例题及练习
C1B二、二面角的基本求法1.定义法:在棱上取点,分别在两面内引两条射线与棱垂直。
例4.在正方体ABCD—A1B1C1D1中,求(1)二面角11A B C A--的大小;(2)平面11A DC与平面11ADD A所成角的正切值。
练习:过正方形ABCD的顶点A作PA ABCD^平面,设PA=AB=a,求二面角B PC D--的大小。
2.三垂线法例5.ABCD ABEF ABCD^平面平面,是正方形,ABEF是矩形且AF=12AD=a,G是EF的中点,(1)求证:AGC BGC^平面平面;(2)求GB与平面AGC所成角的正弦值;(3)求二面角B AC G--的大小。
例6.点P在平面ABC外,ABC是等腰直角三角形,90ABC°?,PAB是正三角形,PA BC^。
(1)求证:^平面PA B平面A BC;(2)求二面角P AC B--的大小。
练习:正方体ABCD —A 1B 1C 1D 1的棱长为1,P 是AD 的中点,求二面角1A BD P--的大小。
3.垂面法例7.SA ABC AB BC SA AB BC ^^==平面,,, (1)求证:SB BC ^;(2)求二面角C SA B --的大小; (3)求异面直线SC 与AB 所成角的余弦值。
4.无棱二面角的处理方法 (1)找棱例8.过正方形ABCD 的顶点A 作PA ABCD ^平面,设PA=AB=a , 求平面PAB 与平面PCD 所成二面角的大小。
(2)射影面积法(cos s Sq =射影)例9.正方体ABCD —A 1B 1C 1D 1的棱长为1,P 是棱1AA 的中点, 求平面11PB C 与平面ABCD 所成二面角的大小。
B1A。
二面角专项训练(人教A版)(含答案)

二面角专项训练(人教A版)一、单选题(共7道,每道10分)1.等于90°的二面角内有一点P,过P有PA⊥α于点A,PB⊥β于点B,如果PA=PB=a,则P 到交线的距离为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:与二面角有关的点、线、面间的距离计算2.如图,在三棱锥F-ABC中,FC⊥底面ABC,CA=CB=CF,∠ACB=120°,则二面角F-AB-C的正切值为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:二面角的平面角及求法3.如图,在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是腰长为的等腰三角形,则二面角V-AB-C的平面角为( )A.30°B.45°C.60°D.90°答案:C解题思路:试题难度:三颗星知识点:二面角的平面角及求法4.如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥AB,PA=AB=2,AC=1,则二面角A-PC-B的正弦值为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:二面角的平面角及求法5.如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,D是棱AA1的中点,则二面角B-DC1-C的余弦值为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:二面角的平面角及求法6.如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,D是棱AA1的中点,DC1⊥BD,则二面角A1-BD-C1的大小为( )A.30°B.45°C.60°D.90°答案:A解题思路:试题难度:三颗星知识点:二面角的平面角及求法7.如图,在直三棱柱ABC-A1B1C1中,AB1⊥A1C,AB=4,AC=BC=3,D为AB的中点,则二面角A1-CD-C1的平面角的余弦值为( )A. B. C. D.答案:D解题思路:试题难度:三颗星知识点:二面角的平面角及求法。
解二面角问题三种方法(习题及答案)

C A BD A A 1 B DCC 1 B 1解二里角问题之阳早格格创做(一)觅找有棱二里角的仄里角的要领战供解.(1)定义法:利用二里角的仄里角的定义,正在二里角的棱上与一面,过该面正在二个半仄里内做笔曲于棱的射线,二射线所成的角便是二里角的仄里角,那是一种最基原的要领.要注意用二里角的仄里角定义的三个“主要特性”去找出仄里角,天然那种找出的角要有好处办理问题.底下举几个例子去道明.例1:如图,坐体图形V -ABC 的四个里是齐等的正三角形,绘出二里角V -AB -C 的仄里角并供出它的度数.例2:正在三棱锥P-ABC 中,∠APB=∠BPC=∠CPA=600,供二里角A-PB-C 的余弦值. 那样的典型是很多的,如下列几讲便是利用定义法找出去的:1、正在正圆体ABCD -A1B1C1D1中,找出二里角B -AC -B1的仄里角并供出它的度数. 2、.边少为a 的菱形ABCD ,∠ACB=600,现沿对付角线BD 将其合成才600的二里角,则A 、C 之间的距离为.(菱形二条对付角线互相笔曲,对付合后的一条对付角线成二条线段仍皆笔曲于另一条对付角线,则所成的角是二里角的仄里角)3、正三棱柱ABC —A1B1C1的底里边少是4,过BC 的一个仄里与AA1接于D ,若AD=3,供二里角D―BC―A 的正切值.总之,能用定义法去找二里角的仄里角的,普遍是图形的本量较佳,不妨较快天找到谦脚二里角的仄里角的三个主要特性.而且不妨很快天力用图形的一些条件去供出所央供的.正在罕睹的几许体有正四周体,正三棱柱,正圆体,以及一些仄里图形,正三角形,等腰三角形,正圆形,菱形等等,那些有较佳的一些本量,不妨通过它们的本量去找到二里角的仄里角.至于供角,常常是把那角搁正在一个三角形中去供解.由图形及题手段已知条件去供那个三角形的边少大概者角,再用解三角形的知识去供解.(2)三垂线法:是利用三垂线的定理及其顺定理去道明线线笔曲,去找到二里角的仄里角的要领.那种要领闭键是找笔曲于二里角的里的垂线.此要领是属于较时常使用的.例3:如图,正在三棱锥P-ABC 中,PA ⊥仄里ABC ,PA=AB ,AC=BC=1,∠ACB=900,M 是PB 的中面.(1)供证:BC ⊥PC ,(2)仄里MAC 与仄里ABC 所成的二里角的正切. 例4:如图,已知△ABC 中,AB ⊥BC ,S 为仄里ABC 中的一面,SA ⊥仄里ABC ,AM ⊥SB 于M ,AN ⊥SC 于N,(1)供证仄里SAB ⊥仄里SBC (2)供证∠ANM是二里角A -SC -B 的仄里角.原题可变形为:如图,已知△ABC 中,AB ⊥BC ,S 为仄里ABC 中的一面,SA ⊥仄里ABC ,∠ACB =600,SA =AC =a ,(1)供证仄里SAB ⊥仄里SBC (2)供二里角A -SC -BC 的正弦值.正在使用三垂线找仄里角时,找垂线注意应用已知的条件战有闭笔曲的判决战本量定理,按三垂线的条件,一垂线笔曲二里角的一个里,另有笔曲于棱的一条垂线.且二垂线相接,接面正在二里角的里内.(3)垂里法:做一与棱笔曲的仄里,该垂里与二二里角二半仄里相接,得到接线,接线所成的角为二里角的仄里角.那闭键正在找C B M A P N K A B CM N SA l D C α β A lBC α β E BD 与二里角的棱笔曲且与二二里角二半仄里皆有接线的仄里. 例5:如图正在三棱锥S -ABC 中,SA ⊥底里ABC ,AB ⊥BC ,DE 笔曲仄分SC 且分别接AC 、SC 于D 、E ,又SA =AB ,SB =BC ,供二里角E -BD -C 的度数.如图,βα⊂⊂BD AC ,,α与β所成的角为600,l AC ⊥于C ,l BD ⊥于B ,AC =3,BD =4,CD =2,供A 、B 二面间的距离. (二)觅找无棱二里角的仄里角的要领战供解. 无棱的二里角普遍是只已知一个共面,但是二个里的接线没有知讲.若要找出二里角的仄里角,则需要根据公理2大概公理4去找出二里角的棱,化为有棱二里角问题,再按有棱二里角的解法解题.那种主要有二类:一类是分别正在二个里内有二条曲线没有是同里又没有是仄止的二里角(二条正在共一仄里内且没有服止).那么延少那二条线有一接面,根据公理2,那面正在二里角的棱上,连大众面战那面便是二里角的棱;另一类是分别正在二个里内有二条曲线是仄止的二里角.那由曲线战仄里仄止的判决战本量定理知那曲线战里仄止,所以曲线仄止于二里角的二个里的接线.由公理4,可知那二条曲线仄止于二里角的棱.所以过大众面做一条曲线仄止于那二曲线,那么所做的曲线是二里角的棱. 例6:如图,△ABC 正在仄里上的射影为正△AB1C1,若BB1=21,CC1=AB1=1,供仄里ABC 与仄里AB1C1所成钝角二里角的大小.变式:1. 如图,正在底里是曲角梯形的坐体图S-ABCD 中,∠ABC =900,SA ⊥底里ABCD ,SA =AB =BC =1,AD =0.5,供里SCD 与里 A B C S DA BC B 1 C 1 A B CD SSBA 所成二里角的仄里角的正切值.2. 如图,正在所给的空间图形中ABCD 是正圆形,PD ⊥里ABCD ,PD =AD.供仄里PAD 战PBC 所成的二里角的大小.3. 如图,斜三棱柱ABC -A1B1C1的棱少皆是a ,侧棱与底里成600角,正里BCC1B1⊥里ABC ,供仄里AB1C1与底里ABC 所成的二里角的大小.解闭于二里角问题 二里角是坐体几许中最要害的章节.二里角中的真量概括了线里笔曲,三垂线定理及其顺定理战同里曲线所成角等较多的知识面,是下考的热面战易面.正在归纳时,若不妨带领教死举止对付解二里角的问题举止商量战归纳,对付普及教死的数教思维要领是有助闲的,对付普及教死机动使用所教的也有很要害的效率.为此尔对付那圆里举止归纳,以供教教战教习参照.(一)对付原真量举止思索时,必须弄浑二个观念:(1)什么是二里角,怎么样表示?而二里角的大小是不妨用它的仄里角去度量,二里角的仄里角是几度,便道那个二里角是几度.(2)什么是二里角的仄里角,怎么样表示?那一观念特天要害,要不妨很快天反应出二里角的仄里角是以二里角的棱上任性一面为端面,正在二个里内分别做笔曲于棱的二条射线,那二条射线所成的角.,C A B DPA C D BA 1E C 1B二里角的仄里角的定义三个主要特性是:过棱上任性一面;分别正在二个里内做射线;射线笔曲于棱.明黑那一面对付于不妨做出大概找出二里角的仄里是很闭键.正在脑子里要能设念出二里角仄里角的图形.如图,0∈a,OA⊂α,OB⊂β,OA⊥a,OB⊥a.(二)觅找有棱二里角的仄里角的要领战供解.觅找战供做二里角的仄里角是解二里角问题的闭键,那也是个易面.正在从图形中做出二里角的仄里角时,要分离已知条件去对付图形中的线线、线里战里里的位子闭系先举止分解,决定有哪些是仄止、笔曲的大概者是特殊的仄里图形,而后使用那些的有闭本量战二里角的仄里角的定义举止找出二里角的仄里角.所以解闭于二里角问题需要有很佳的对付线线、线里战里里的位子闭系的分解推断本领.而正在供做二里角的仄里角的要领主要有三种:定义法、三垂线法、垂里法.至于正在供解有闭仄里角的问题时,那仄里角常常是正在三角形中,所以常要用到解曲角三角形战斜三角形的知识,那包罗正弦战余弦定理的知识,也会用到其余的仄里几许知识.(1)定义法:利用二里角的仄里角的定义,正在二里角的棱上与一面,过该面正在二个半仄里内做笔曲于棱的射线,二射线所成的角便是二里角的仄里角,那是一种最基原的要领.要注意用二里角的仄里角定义的三个“主要特性”去找出仄里角,天然那种找出的角要有好处办理问题.底下举几个例子去道明.V B A C D 例1:如图,坐体图形V -ABC 的四个里是齐等的正三角形,绘出二里角V -AB -C 的仄里角并供出它的度数.分解:由图可知,所供的二里角的棱是AB ,二个里是里V AB 战里CAB.由已知可知那是一个正四周体,各个里是齐等的正三角形,根据二里角的仄里角的定义,咱们可利用正三角形的本量去找出仄里角,与AB 边上的中面D ,连结VD 战CD.则∠VDC 是所供二里角的仄里角.可设正三角形的边少为a ,用解三解形的知识供出VD =CD =a 23,正在△VDC 中,利用余弦定理可供得cos ∠VDC=1/3,∴∠VDC =arccos1/3评注:正在原题中主假如利用已知条件中的特殊条件战二里角仄里角的定义去找出所央供的仄里角.正在供解时利用的是仄里几许解三角形的知识.那也便是把坐体图形的问题转移为仄里几许的问题的数教思维..例2:正在三棱锥P-ABC 中,∠APB=∠BPC=∠CPA=600,供二里角A-PB-C 的余弦值.分解:所供二里角的棱是PB ,二个里为里PBA 战里PBC.用二里角的仄里角的定义找出仄里角,正在二里角的棱PB 上任与一面Q ,正在半仄里PBA 战半仄里PBC 上做QM ⊥PB ,QN ⊥PB ,则由定义可得∠MQN 即为二里角的仄里角.设PM=a,则正在Rt ∆PQM 战Rt ∆PQN B A A 1 B 1 C C 1 D D 1 A B C N M P QAA1 B D C C 1B 1 中可供得QM=QN=23a ;又由∆PQN ≅∆PQM 得PN=a,故正在正三角形PMN 中MN=a,正在三角形MQN 中由余弦定理得cos ∠MQN=1/3,即二里角的余弦值为1/3.那样的典型是很多的,如下列几讲便是利用定义法找出去的:1、如图,正在正圆体ABCD -A1B1C1D1中,找出二里角B -AC -B1的仄里角并供出它的度数.2、.边少为a 的菱形ABCD ,∠ACB=600,现沿对付角线BD 将其合成才600的二里角,则A 、C 之间的距离为.(菱形二条对付角线互相笔曲,对付合后的一条对付角线成二条线段仍皆笔曲于另一条对付角线,则所成的角是二里角的仄里角) 3、正三棱柱ABC —A1B1C1的底里边少是4,过BC 的一个仄里与AA1接于D ,若AD=3,供二里角D―BC―A 的正切值.总之,能用定义法去找二里角的仄里角的,普遍是图形的本量较佳,不妨较快天找到谦脚二里角的仄里角的三个主要特性.而且不妨很快天力用图形的一些条件去供出所央供的.正在罕睹的几许体有正四周体,正三棱柱,正圆体,以及一些仄里图形,正三角形,等腰三角形,正圆形,菱形等等,那些有较佳的一些本量,不妨通过它们的本量去找到二里角的仄里角.至于供角,常常是把那角搁正在一个三角形中去供解.由图形及题手段已知条件去供那个三角形的边少大概者角,再用解三角形的知识去供解.(2)三垂线法:是利用三垂线的定理及其顺定理去道明线线笔曲,去找到二里角的仄里角的要领.那种要领闭键是找笔曲于二里角的里的垂线.此要领是属于较时常使用的. 例3:如图,正在三棱锥P-ABC 中,PA ⊥仄里ABC ,PA=AB ,AC=BC=1,∠ACB=900,M 是PB 的中面.(1)供证:BC ⊥PC ,(2)仄里MAC 与仄里ABC 所成的二里角的正切. C B M A P NK分解:第1小题较简朴.第2小题,瞅察图形中的线里位子闭系,已知PA ⊥仄里ABC ,M 是PB 的中面,若正在△PAB 中与AB 的中面N ,则很快创造MN ⊥仄里ABC ,做KN ⊥AC ,连MK ,则由三垂线定理可得MK ⊥AC ,所以∠MKN为所供的二里角的仄里角.而供其正切值,正在Rt △MNK 中供出MN 战KN ,而供MN 战KN ,只需正在△PAB 战△ABC 中便可供出,进而供出其正切值为2.评注:原题用定义法较易以真止,但是由图可找到二里角一个里的垂线.进而做棱的垂线,由三垂线定理道明是所要找的仄里角.闭键找到MN 那条垂线.例4:如图,已知△ABC 中,AB ⊥BC ,S 为仄里ABC 中的一面,SA ⊥仄里ABC ,AM ⊥SB 于M ,AN ⊥SC 于N,(1)供证仄里SAB ⊥仄里SBC (2)供证∠ANM 是二里角A -SC -B 的仄里角.分解:由图战题意可得BC ⊥仄里SAB ,进而可得证仄里SAB ⊥仄里SBC ,而要证二里角A -SC -B 的仄里角是∠ANM ,从已知条件AM ⊥SB 于M,由二个仄里笔曲的本量可得AM ⊥仄里SBC ,又有AN ⊥SC ,所以由三垂线顺定理可得MN ⊥SC ,进而道明黑∠ANM 是二里角A -SC -BC 的仄里角.评注:原题提供了使用怎么样从一系列的笔曲闭系中去逐步找到二里角的一个里的垂线,再由三垂线的定理道明所要找的仄里角.A B C MN S原题要特天注意的是那条垂线没有是正在火仄上的,所以瞅察分解图时要注意多使用有闭定理去推断.原题可变形为:如图,已知△ABC 中,AB ⊥BC ,S 为仄里ABC 中的一面,SA ⊥仄里ABC ,∠ACB =600,SA =AC =a ,(1)供证仄里SAB ⊥仄里SBC (2)供二里角A -SC -BC 的正弦值.解第2小题的第一步是按例4搞出二里角的仄里角,而后利用各个曲角三角形供出AN 战AM 的少.总之,正在使用三垂线找仄里角时,找垂线注意应用已知的条件战有闭笔曲的判决战本量定理,按三垂线的条件,一垂线笔曲二里角的一个里,另有笔曲于棱的一条垂线.且二垂线相接,接面正在二里角的里内.(3)垂里法:做一与棱笔曲的仄里,该垂里与二二里角二半仄里相接,得到接线,接线所成的角为二里角的仄里角.那闭键正在找与二里角的棱笔曲且与二二里角二半仄里皆有接线的仄里. 例5:如图正在三棱锥S -ABC 中,SA ⊥底里ABC ,AB ⊥BC ,DE 笔曲仄分SC 且分别接AC 、SC 于D 、E ,又SA =AB ,SB =BC ,供二里角E-BD -C 的度数. 分解:由题意战图,可得SC ⊥仄里BDE ,则SC ⊥DB ,又SA ⊥仄里ABC ,则SA ⊥DB ,进而得BD ⊥仄里SAC.所以BD ⊥DC ,BD ⊥DE ,则∠DEC 是二里角的仄里角.央供它的度数,可正在Rt △SAC 战△DEC 中供,先供出∠SCA 的度数.设SA =a ,正在图A B CS DA l D C α β A lBC α β E BD 的曲角三角形中供出SB =BC =2a ,AC =3a ,故得到∠SCA =300,进而得到∠DEB =600. 评注:原题的笔曲闭系很多,怎么样利用佳那些闭系?那需解题的目标要精确才搞使用佳那些闭系.从那些笔曲闭系很简单便判决BD ⊥仄里SAC ,而BD 是二里角的的棱,所以仄里SAC 是二里角的垂里,由二里角的仄里角的定义便找到了∠EDC 是所供二里角的仄里角.它的应用比圆:如图,βα⊂⊂BD AC ,,α与β所成的角为600,l AC ⊥于C ,l BD ⊥于B ,AC =3,BD =4,CD =2,供A 、B 二面间的距离. 由题意要应用二里角的度数,要找出它的仄里角,可过C 做CE ∥DB ,且CE =DB ,连AE ,则很简单得到l ⊥里ACE ,∠ACE 是二里角的仄里角,为了供AB ,连BE ,正在△ACE 中由余弦定理供出AE ,正在Rt △AEB 中可供出AB 的少.总之要会使用此法,对付线线、线里、里里的笔曲闭系要有很佳的推断本领,才搞找到解的思路.(三)觅找无棱二里角的仄里角的要领战供解.无棱的二里角普遍是只已知一个共面,但是二个里的接线没有知讲.若要找出二里角的仄里角,则需要根据公理2大概公理4去找出二里角的棱,化为有棱二里角问题,再按有棱二里角的解法解题.那种主要有二类:一类是分别正在二个里内有二条曲线没有是同里又没有是仄止的二里角(二条正在共一仄里内且没有服止).那么延少那二条线有一接面,根据公理2,那面正在二里角的棱上,连大众面战那面便是二里角的棱;另一类是分别正在二个里内有二条曲线是仄止的二里角.那由曲线战仄里仄止的判决战本量定理知那曲线战里仄止,所以曲线仄止于二里角的二个里的接线.由公理4,可知那二条曲线仄止于二里角的棱.所以过大众面做一条曲线仄止于那二曲线,那么所做的曲线是二里角的棱. 例5:如图,△ABC 正在仄里上的射影为正△AB1C1,若BB1=21,CC1=AB1=1, A BC B 1 C 1供仄里ABC 与仄里AB1C1所成钝角二里角的大小.分解:所供的二里角只各一个大众面A ,瞅察图可知二里角的二个里内BC 战B1C1共里但是没有服止,所以若延少它们必接于一面D ,由公理2知,面D 正在二里角的棱上.所以连AD 便找到棱.接着是找出二里角的仄里角.由图形的本量知,C1D=2B1C1=2,A1C1=1,∠AC1B =600,用正弦定理大概余弦定理皆可供出∠C1AD =900,再由三垂线定理得∠CAC1为二里角的仄里角,而后正在Rt △CAC1中可供得∠CAC1=450. 评注:原题是属于第一类的问题.延少二条曲线接于一面进而得到棱,再用三垂线法找二里角的仄里角.此题可形成: 如图,正在底里是曲角梯形的坐体图S -ABCD 中,∠ABC =900,SA ⊥底里ABCD ,SA=AB =BC =1,AD =0.5,供里SCD 与里SBA所成二里角的仄里角的正切值.由图可知二里角有一个大众面S ,但是正在二里中的AB 战CD 共里且没有服止,所以延少接于面E.再由题意道明BC ⊥仄里SAB ,SB ⊥SE ,由三垂线定理可知∠BSC 是所供的二里角.正在Rt △SBC 中可供得正切值为22.例6:如图,正在所给的空间图形中ABCD 是正圆形,PD ⊥里ABCD ,PD =AD.供仄里PAD 战PBC 所成的二里角的大小.分解:由图知二里角有一个大众面P ,正在二里内的AD 战BC 是共里且仄止,所以AD ∥仄里PBC ,由曲线战仄里仄止的本量知,过AD 的仄里PAD 与仄里仄里PBC 的接线(即为二里角的棱)与AD 仄止,所以过P 做PE ∥AD ,则PE 为二里DA B C B 1 C 1 A B C D E S C A B D E P角的棱.由题意PD ⊥里ABCD ,所以PD ⊥AD ,PD ⊥PE ,又可证得CD ⊥仄里PAD ,由三垂线定理可得∠CPD 为所供二里角的仄里角.正在Rt △CPD 中可供得∠CPD =450.评注:原题是属于第二类的问题.二里角有一个共面,正在分别二里内的二条曲线仄止,则仄止于棱.找出二里角的棱后,再用三垂线法找二里角的仄里角. 例7:如图,斜三棱柱ABC -A1B1C1的棱少皆是a ,侧棱与底里成600角,正里BCC1B1⊥里ABC ,供仄里AB1C1与底里ABC 所成的二里角的大小.分解:此题A 是二里角的一个大众面.又正在二里的BC 战B1C1仄止,故过面A 做AE ∥BC ,则AE 为二里角的棱.怎么样找仄里角是原题的易面.果为各棱少皆相等,所以正里是菱形,底里是正三角形.又正里BCC1B1⊥里ABC ,过C1做C1D ⊥BC ,由二仄里笔曲的本量得C1D ⊥里ABC ,侧棱与底里成600角,所以∠C1CD =600,由此可得D 为BC 的中面.连AD 得AD ⊥BC ,进而AD ⊥AE ,由三垂线定理得∠C1AD 为二里角的仄里角,正在Rt △C1AD 中可供得∠C1AD =450.评注:原题除了要找棱中,用三垂线法找仄里角时,闭键正在能分解已知条件的效率,去找垂线,战利用曲线战仄里所成的角去推算出面D 为BC 的中面,进而可用三垂线法找出仄里角. 总之,无棱的二里角按二类的要领找出棱,转移为有棱的二A C D B A 1E C 1里角问题去解.从上头几个例题的分解战介绍的要领中,不妨瞅出,二里角问题不妨概括较多知识面,不妨概括有闭的仄止、笔曲的闭系.用到的定理险些是咱们所教坐几的知识.所以要有较扎真的前提知识才搞够对付付得了那类问题.正在估计圆里要用到解三角形的知识,要会正在图中有闭的三角形中供出所需的边大概角,而后常常归纳正在一个三角形中去供出末尾的截止.总的,解那类题,找仄里角是闭键的一步,要注意使用题中的条件分解图形,而后用有闭的要领找出仄里角,估计时要分解所央供的量是可由图中的哪些仄里图形去逐步去供出.。
二面角典型习题

二面角1.二面角的计算:1)定义法;2)三垂线定理法;3)垂面法;4)面积射影法;例1、已知P 是二面角棱上一点,过P 分别在内引射线PM ,PN ,且AB αβ--αβ、,求此二面角的度数。
45,60BPM BPN MPN ∠=∠=︒∠=︒例2、已知P 为锐二面角棱上的点,,则二l αβ--,4530PQ PQ l αβ⊂︒︒与成,与成面角的度数是多少。
l αβ--例3、已知二面角的度数为,在面内有一条射线AB 与棱l 成锐角,与面l αβ--θαδ,则必有( )βγ成角(A ) (B )sin sin sin θδγ=sin sin cos θδγ=(C ) (D )cos cos sin θδγ=cos cos cos θδγ=例4、在的二面角的面、内分别有A 、B 两点,且A 、B 到棱l 的距离120︒l αβ--αβAC 、BD 分别长2、4,AB=10,求:(1)直线AB 与棱l 所成角的正弦值。
(2)直线AB 与平面所成角的正弦值。
β例5、已知二面角为,上的射影,且C 在棱MN αβ--60︒,,A B BC AB αββ∈∈为在MN 上,AB 与所成角为,且,求线段AB 的长。
β60︒45AC MCB =∠=︒例6、已知二面角的度数为,的面积为S ,且DC=m ,DC αβ--θ,,A B ADC αβ∈∈∆,AB 与平面成角,当变化时,求面积最大值。
AB DC ⊥β30︒θDBC ∆in例7、已知C是以AB为直径的圆周上的一点,,30ABC∠=︒,求二面角A-45PA ABC PBA⊥∠=︒面,PB-C的正弦值。
例8、在正方体中,利用解下列各题1111ABCD A B C D-cosSSθ=射影1)P、Q分别为的中点,求平面与底面ABCD所成角的余弦值1,A A AB1C PQ2)求二面角的大小;11C BD C--3)M是棱BC的中点,求二面角的余弦值。
111D B M C--例9、已知D 、E 分别是边长为a 的等边三角形ABC 的边AB 、AC 上的点,DE//BC ,现沿DE 将三角形ADE 折起,是二面角A-DE-B 成60度角,当DE 在什么位置时,使折起后的顶点A 到BC 边距离最短?最短是多少?例10、等腰Rt 和Rt 有公共边AC ,,ADC ∆BCA ∆90,60ADC BCA ABC ∠=∠=︒∠=︒以AC 为棱折起多少度的二面角时,有BD=BC ?两个平面垂直1、两个平面垂直的证明1)定义2)判定定理2、两个平面垂直的性质例1、已知ABCD 为矩形,E 为半圆CED 上一点,且平面ABCD 平面CDE ⊥1)求证DE 是AD 与BE 的公垂线2)若AD=DE=AB ,求AD 与BE 所成角的大小。
二面角习题及标准答案

二面角习题及答案————————————————————————————————作者:————————————————————————————————日期:二面角1.如图三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC是边长为 2的正三角形,求二面角 P-AB -C 的大小。
解2.如图在三棱锥 S-ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交 AC 、SC 于D 、E ,又SA =AB ,BS =BC , 求以BD 为棱,BDE 与BDC 为面的二面角的度数。
解:3. 如图:ABCD 是矩形,AB =8,BC =4,AC 与 BD 相交于O 点,P 是平面 ABCD 外一点,PO ⊥面ABCD ,PO =4,M 是 PC 的中点,求二面角 M-BD-C 大小。
解:4.如图△ABC 与△BCD 所在平面垂直,且AB =BC =BD ,∠ABC =∠DBC =0120,求二面角 A-BD-C 的余弦值。
解:DPC A BE DB ASCS R NMO B DPA CB A EC5.已知正方体 AC',M 、N 分别是BB',DD'的中点,求截面 AMC'N 与面ABCD ,CC'D'D 所成的角。
解:6.如图 AC ⊥面BCD ,BD ⊥面ACD ,若AC =CD =1,∠ABC =30°,求二面角D AB C --的大小。
解:7. 三棱锥 A-BCD 中,∠BAC =∠BCD =90°,∠DBC =30°,AB =AC =6,AD =4,求二面角 A-BC-D 的度数。
解:9. 如图所示,四棱锥P —ABCD 的底面是边长为a 的菱形,∠A =60°,PC ⊥平面ABCD ,PC =a,E 是PA 的中点.(1)求证平面BDE ⊥平面ABCD.(2)求点E 到平面PBC 的距离.(3)求二面角A —EB —D 的平面角大小. 解析:D BD ACBAC M N B F E ACDDOA BC10. 如图,已知正方体ABCD —A1B1C1D1的棱长为1,E 、F 分别在棱AB 、BC 上,G 在对角线BD1上,且AE =41,BF =21,D1G ∶GB =1∶2,求平面EFG 与底面ABCD 所成的二面角的大小.11. 如图,设ABC —A1B1C1是直三棱柱,E 、F 分别为AB 、A1B1的中点,且AB =2AA1=2a,AC =BC =3a. (1)求证:AF ⊥A1C(2)求二面角C —AF —B 的大小12.如图1111D C B A ABCD -是长方体,AB=2,11==AD AA ,求二平面C AB 1与1111D C B A 所成二面角的大小.13. 在正方体1111D C B A ABCD -中,1BB K ∈,1CC M ∈,且141BB BK =,143CC CM =..求:平面AKM 与ABCD 所成角的大小.14. 如图,将边长为a 的正三角形ABC 按它的高AD 为折痕折成一个二面角C AD C --'. (1)若二面角C AD C --'是直二面角,求C C '的长; (2)求C A '与平面CD C '所成的角;(3)若二面角C AD C --'的平面角为120°,求二面角D C C A -'-的平面角的正切值.参考答案解:由已知条件,D 是BC 的中点∴ CD =BD =2 又△ADC 是正三角形 ∴ AD =CD =BD =2∴ D 是△ABC 之外心又在BC 上 ∴ △ABC 是以∠BAC 为直角的三角形, ∴ AB ⊥AC , 又 PC ⊥面ABC ∴ PA ⊥AB (三垂线定理)∴∠PAC 即为二面角 P-AB-C 之平面角, 易求 ∠PAC =30°2、解:∵ BS =BC ,又DE 垂直平分SC ∴ BE ⊥SC ,SC ⊥面BDE ∴ BD ⊥SC ,又SA ⊥面ABC ∴ SA ⊥BD ,BD ⊥面SAC ∴ BD ⊥DE ,且BD ⊥DC 则 ∠EDC 就是所要求的平面角 设 SA =AB =a ,则 BC =SB =2a 且 AC = 3易证 △SAC ∽△DEC ∴ ∠CDE =∠SAC =60° 3、解:取OC 之中点N ,则 MN ∥PO ∵ PO ⊥面ABCD∴ MN ⊥面ABCD 且 MN =PO/2 =2, 过 N 作 NR ⊥BD 于 R ,连MR , 则 ∠MRN 即为二面角 M-BD-C 的平面角 过 C 作 CE ⊥BD 于S则 RN =21CE 在 Rt △BCD 中,CD ·BC =BD ·CE ∴ 58BD BC CD CE =⋅=DPCA BE DBASCS R N MO B DPA C∴ 54RN =25RN MN MRN tan ==∠ ∴ 25arctanMRN =∠ 4. 解:过 A 作 AE ⊥CB 的延长线于E , 连结 DE , ∵ 面ABC ⊥面BCD ∴ AE ⊥面BCD∴ E 点即为点A 在面BCD 内的射影∴ △EBD 为△ABD 在面BCD 内的射影设 AB =a 则AE =DE =ABsin60°=a 23 ∴ AD =41ABD cos 26=∠, ∴ sin ∠ABD =415∴ 22ABD a 815415a 21S =⨯=∆ 又 a 21BE = ∴ 2BDE a 83a 21a 2321S =⋅⋅=∆ ∴ 55S S cos ABD BDE ==θ∆∆ 5. 解:设边长为a ,易证 ANC'N 是菱形 且MN =a 2,A'C =a 3 ∴S□AMC'N = 2a 26'AC 21MN =⋅由于AMC'N 在面ABCD 上的射影即 为正方形ABCD ∴ S□ABCD =2aD B D AC BAC MN∴ 36a 26a cos 221==θ ∴ 36arccos1=θ 取CC'的中点M',连结DM'则平行四边形DM'C'N 是四边形AMC'N 在CC'D'D 上的射影,S□DM'C'M =2a 21 ∴ 66a 26a21cos 222==θ ∴66arccos2=θ 6. 解:作DF ⊥AB 于F ,CE ⊥AB 于E , ∵ AC =CD =1 ∠ABC =30° ∴ AD =2,BC =3 , AB =2, BD =2 在Rt △ABC 中, 23231AB BC AC CE =⨯=⋅=,同理 1222ABBDAD DF =⨯=⋅= ∴ 1DF BD BF 22=-=21CE AC AE 22=-= ∴ 212112EF =--= ∴ θ⋅-++=cos DF EF 2EF DF CE CD 2222∴ 33cos =θ BF E ACD即所求角的大小为33arccos。
五种方法求二面角及练习题

五种方法求二面角及练习题一、 定义法:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
1.如图,在棱长为a 的正方体ABCD —A 1B 1C 1D 1中,求: (1)二面角C 1—BD —C 的正切值(2)二面角11B BC D --2.如图,四棱锥S ABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD ,2AD =,2DC SD ==,点M 在侧棱SC 上,ABM ∠=60,M 在侧棱SC 的中点(1)求二面角S AM B --的余弦值。
AB CD A 1D 1 C 1 B 1二、三垂线法:三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.通常当点P 在一个半平面上则通常用三垂线定理法求二面角的大小。
1. 如图,在直四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB 111111图,在四棱锥ABCD P -中,底面ABCD 是矩形.已知ο60,22,2,2,3=∠====PAB PD PA AD AB .(Ⅰ)证明⊥AD 平面PAB ;(Ⅱ)求异面直线PC 与AD 所成的角的大小; (Ⅲ)求二面角A BD P --的大小.三.补棱法本法是针对在解构成二面角的两个半平面没有明确交线的求二面角题目时,要将两平面的图形补充完整,使之有明确的交线(称为补棱),然后借助前述的定义法与三垂线法解题。
即当二平面没有明确的交线时,一般用补棱法解决1.已知斜三棱柱ABC —A 1B 1C 1的棱长都是a ,侧棱与底面成600的角,侧面BCC 1B 1⊥底面ABC 。
(1)求证:AC 1⊥BC ;(2)求平面AB 1C 1与平面 ABC 所成的二面角(锐角)的大小。
EABCFE 1 A 1B 1C 1D 1 DACBB 1C 1AL2: 如图5,E 为正方体ABCD -A 1B 1C 1D 1的棱CC 1的中点,求平面AB 1E 和底面A 1B 1C 1D 1所成锐角的余弦值.3如图所示,四棱锥P -ABCD 的底面ABCD 是边长为1的菱形,∠BCD =60°,E 是CD 的中点,PA ⊥底面ABCD ,PA =2. (Ⅰ)证明:平面PBE ⊥平面PAB ;(Ⅱ)求平面PAD 和平面PBE 所成二面角(锐角)的大小.角的平面角(锐角).ABCEDPA 1D 1 B 1C 1 E DBCA图5分析 平面AB 1E 与底面A 1B 1C 1D 1交线即二面角的棱没有给出,要找到二面角的平面角,. 四、向量法向量法解立体几何中是一种十分简捷的也是非常传统的解法,可以说所有的立体几何题都可以用向量法求解,用向量法解立体几何题时,通常要建立空间直角坐标系,写出各点的坐标,然后将几何图中的线段写成用坐标法表示的向量,进行向量计算解题。
二面角专题训练
二面角专题训练一.解答题(共14小题)1.如图,在四棱锥S﹣ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,,求:(Ⅰ)点A到平面BCS的距离;(Ⅱ)二面角E﹣CD﹣A的大小.2.如图所示,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1=,∠ABC=60°.(1)证明:AB⊥A1C;(2)求二面角A﹣A1C﹣B的余弦值.3.如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC,BE (Ⅰ)证明:C,D,F,E四点共面;(Ⅱ)设AB=BC=BE,求二面角A﹣ED﹣B的大小.4.如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,.沿它的对角线BD把△BDC0折起,使点C0到达平面ABC0D外点C的位置.(Ⅰ)证明:平面ABC0D⊥平面CBC0;(Ⅱ)如果△ABC为等腰三角形,求二面角A﹣BD﹣C的大小.5.如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1ABB1.(Ⅰ)求证:AB⊥BC;(Ⅱ)若AA1=AC=a,直线AC与平面A1BC所成的角为θ,二面角A1﹣BC﹣A的大小为φ,求证:θ+φ=.6.如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.(I)证明:CD⊥AE;(II)证明:PD⊥平面ABE;(III)求二面角A﹣PD﹣C的大小.7.如图,在四面体ABCD中,平面ABC⊥平面ACD,AB⊥BC,AC=AD=2,BC=CD=1(Ⅰ)求四面体ABCD的体积;(Ⅱ)求二面角C﹣AB﹣D的平面角的正切值.8.如图,在锥体P﹣ABCD中,ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=,PB=2,E,F分别是BC,PC的中点(1)证明:AD⊥平面DEF(2)求二面角P﹣AD﹣B的余弦值.9.如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2.(1)求直线AM与平面BCD所成的角的大小;(2)求平面ACM与平面BCD所成的二面角的正弦值.10.如图,在五面体ABCDEF中,AB∥DC,,CD=AD=2,四边形ABFE为平行四边形,FA⊥平面ABCD,,求:(Ⅰ)直线AB到平面EFCD的距离;(Ⅱ)二面角F﹣AD﹣E的平面角的正切值.11.如图,在三棱锥P﹣ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC 上,且DE∥BC.(1)求证:BC⊥平面PAC;(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;(3)是否存在点E使得二面角A﹣DE﹣P为直二面角?并说明理由.12.如图,在直四棱柱ABCD﹣A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.(I)设E是DC的中点,求证:D1E∥平面A1BD;(II)求二面角A1﹣BD﹣C1的余弦值.13.如图,在三棱锥A﹣BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=,BD=CD=1,另一个侧面是正三角形.(1)求证:AD⊥BC.(2)求二面角B﹣AC﹣D的大小.(3)在直线AC上是否存在一点E,使ED与面BCD成30°角?若存在,确定E的位置;若不存在,说明理由.14.如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC.已知,求:(Ⅰ)异面直线PD与EC的距离;(Ⅱ)二面角E﹣PC﹣D的大小.。
二面角1练习及答案

二面角练习1班级姓名1.从二面角内一点分别向二面角的两个面引垂线,则这两条垂线所夹的角与二面角的平面角的关系是()A.互为余角B.相等C.其和为周角D.互为补角【答案】D【解析】画图知从二面角内一点分别向二面角的两个面引垂线,则这两条垂线所夹的角与二面角的平面角互为补角,所以选D.2.如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为的等腰三角形,则二面角V-AB-C的大小为()A.30°B.45°C.60°D.120°【答案】C【解析】如图所示,由题意可得四棱锥V-ABCD是正四棱锥,连接AC,BD,相交于点O,连接VO,则VO⊥平面ABCD.取AB的中点M,连接VM,OM,则AB⊥OM,∴AB⊥VM.∴∠OMV是二面角V-AB-C的平面角.由正方形可得OB=BD=×2=,∴VO==.在Rt△VOM中,tan∠VMO===,∴∠VMO=60°.3.如图在长方体中,AB=AD=2,CC1=,则二面角C1-BD-C的大小为()A.30°B.45°C.60°D.90°【答案】A【解析】连接AC,交BD于点O,连接OC1,⊥平面ABCD,因为ABCD为正方形,则AC⊥BD,又CC所以CC1⊥BD,则BD⊥平面CC1O,所以BD⊥OC1,所以∠COC1是二面角C1-BD-C的平面角.又OC=AC=×AB=.在Rt△OCC1中,CC1=,所以tan∠COC1==,所以∠COC1=30°,故选A.4.在四面体ABCD中,已知棱AC的长为,其余各棱长都为1,则二面角A-CD-B的余弦值为()A.B.C.D.【答案】C【解析】取AC的中点E,取CD的中点F,连接BE,EF,BF.∵△BCD为等边三角形,F为CD中点,∴CD⊥BF.∵CD=AD=1,AC=,∴△ACD为等腰直角三角形,∴CD⊥AD.又EF∥AD,∴EF⊥CD.∴∠EFB为A-CD-B的平面角.又EF=,BE=,BF=,∴△BEF为直角三角形,cosθ==.5.如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,此时∠B′AC=60°,那么这个二面角的大小是()A.90°B.60°C.45°D.30°【答案】A【解析】连接B′C,则△AB′C为等边三角形.设AD=a,则B′C=AC=a,B′D=DC=a,所以∠B′DC=90°.6.如图所示,在△ABC中,AD⊥BC,△ABD的面积是△ACD的面积的2倍.沿AD将△ABC翻折,使翻折后BC⊥平面ACD,此时二面角B-AD-C的大小为()A.30°B.45°C.60°D.90°7.若P是△ABC所在平面外一点,而△PBC和△ABC都是边长为2的正三角形,PA=,那么二面角P-BC-A的大小为________.【答案】90°【解析】取BC的中点O,连接OA,OP,则∠POA为二面角P-BC-A的平面角,OP=OA=,PA=,所以△POA为直角三角形,∠POA=90°.8.如图,长方体ABCD-A1B1C1D1中,ABCD是边长为1的正方形,D1B与平面ABCD所成的角为45°,则棱AA的长为________;二面角B-DD1-C的大小为________.【答案】45°【解析】因为ABCD是边长为1的正方形,所以对角线BD=.又因为D1B与平面ABCD所成的角为45°,即∠D1BD=45°.所以AA1=DD1=.由于CD⊥DD1,BD⊥DD1.所以二面角B-DD1-C的平面角为∠CDB.又因为△CDB为等腰直角三角形,所以二面角B-DD1-C的平面角∠CDB=45°.9.如图,在正方体ABCD-A1B1C1D1中,截面C1D1AB与底面ABCD所成的二面角C1-AB-C的大小为________.【答案】45°【解析】∵AB⊥BC,AB⊥BC1,∴∠C1BC为二面角C1-AB-C的平面角,大小为45°.10.在边长为1的菱形ABCD中,∠ABC=60°,把菱形沿对角线AC折起,使折起后BD=,则二面角B-AC-D的余弦值为________.【答案】【解析】如图所示,由二面角的定义,知∠BOD即为二面角的平面角.∵DO=OB=BD=,∴∠BOD=60°.∴cos∠BCD=.11.如图所示,在长方体ABCD-A1B1C1D1中,BC=2,AA1=1,E,F分别在AD和BC上,且EF∥AB,若二面角C1-EF-C等于45°,则BF=________.,C1F⊂平面BC1,CF⊂平面BC1,【答案】1【解析】∵AB⊥平面BC∴AB⊥C1F,AB⊥CF,又EF∥AB,∴C1F⊥EF,CF⊥EF,∴∠C1FC是二面角C1-EF-C的平面角,∴∠C1FC=45°,∴△FCC1是等腰直角三角形,∴CF=CC1=AA1=1.又BC=2,∴BF=BC-CF=2-1=1. 12.如图,已知三棱锥A-BCD的各棱长均为2,求二面角A-CD-B的余弦值.13.如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小.14.如图,已知VA,VB,VC两两垂直,VA=VB=VC=a.(1)求平面ABC和平面ABV所成的二面角的余弦值;(2)求三棱锥V-ABC的体积.【答案】(1)∵VA,VB,VC两两垂直,VA=VB=VC=a,∴AB=BC=AC=a,∴S△ABV=a2,S△ABC=a2.∴平面ABC和平面ABV所成的二面角的余弦值为=.(2)三棱锥V-ABC的体积为××a×a×a=a3.15.如图所示,已知Rt△ABC,斜边BC⊂α,点A∉α,AO⊥α,O为垂足,∠ABO=30°,∠ACO=45°,求二面角A-BC-O的大小.【答案】如图所示,在平面α内,过O作OD⊥BC,垂足为D,连接AD.∵AO⊥α,BC⊂α,∴AO⊥BC.又∵AO∩OD=O,∴BC⊥平面AOD.而AD⊂平面AOD,∴AD⊥BC.∴∠ADO是二面角A-BC-O的平面角.由AO⊥α,OB⊂α,OC⊂α,知AO⊥OB,AO⊥OC.又∠ABO=30°,∠ACO=45°,∴设AO=a,则AC=a,AB=2a.在Rt△ABC中,∠BAC=90°,∴BC==a,∴AD===.在Rt△AOD中,sin∠ADO===,∴∠ADO=60°.即二面角A-BC-O的大小是60°.16.如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动. (1)证明:DE⊥A1D;(2)求AE等于何值时,二面角D1-EC-D的大小为45°?。
五种方式求二面角及练习题

五种方式求二面角及练习题一、概念法:从一条直线起身的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,别离在两面内引两条射线与棱垂直,这两条垂线所成的角的大小确实是二面角的平面角。
1.如图,在棱长为a 的正方体ABCD —A 1B 1C 1D 1中,求: (1)二面角C 1—BD —C 的正切值(2)二面角11B BC D --2.如图,四棱锥中,底面为矩形,底面,,,点M 在侧棱上,=60,M 在侧棱的中点 (1)求二面角的余弦值。
S ABCD -ABCD SD ⊥ABCD 2AD =2DC SD ==SC ABM ∠SC S AM B --A B CDAD C B二、三垂线法:三垂线定理:在平面内的一条直线,若是和那个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.通常当点P 在一个半平面上那么通常常利用三垂线定理法求二面角的大小。
1. 如图,在直四棱柱ABCD -A B C D 中,底面ABCD 为等腰梯形,AB//CD ,AB=4, BC=CD=2, AA =2, E 、E 、F 别离是棱AD 、AA 、AB 的中点。
(1) 证明:直线EE //平面FCC ;(2)求二面角B -FC -C 的余弦值。
2.如图,在四棱锥ABCD P -中,底面ABCD 是矩形.已知60,22,2,2,3=∠====PAB PD PA AD AB .(Ⅰ)证明⊥AD 平面PAB ;(Ⅱ)求异面直线PC 与AD 所成的角的大小; (Ⅲ)求二面角A BD P --的大小.三.补棱法1111111111EABCF E A BCDD本法是针对在解组成二面角的两个半平面没有明确交线的求二面角题目时,要将两平面的图形补充完整,使之有明确的交线(称为补棱),然后借助前述的概念法与三垂线法解题。
即当二平面没有明确的交线时,一样用补棱法解决1.已知斜三棱柱ABC—A 1B 1C 1的棱长都是a ,侧棱与底面成600的角,侧面BCC 1B 1⊥底面ABC 。
(完整)二面角习题及答案
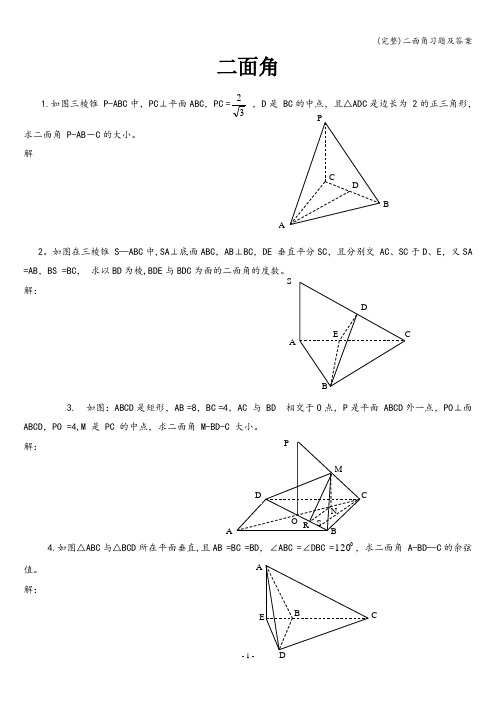
二面角1.如图三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC 是边长为 2的正三角形,求二面角 P-AB -C 的大小。
解2。
如图在三棱锥 S —ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交 AC 、SC 于D 、E ,又SA =AB ,BS =BC , 求以BD 为棱,BDE 与BDC 解:3. 如图:ABCD 是矩形,AB =8,BC =4,AC 与 BD 相交于O 点,P 是平面 ABCD 外一点,PO ⊥面ABCD ,PO =4,M 是 PC 的中点,求二面角 M-BD-C 大小。
解:4.如图△ABC 与△BCD 所在平面垂直,且AB =BC =BD ,∠ABC =∠DBC =,求二面角 A-BD —C 的余弦值。
解:ABAC5.已知正方体 AC ’,M 、N 分别是BB ’,DD'的中点,求截面 AMC'N 与面ABCD ,CC'D ’D 所成的角. 解:6。
如图 AC ⊥面BCD ,BD ⊥面ACD ,若AC =CD =1,∠ABC =30°,求二面角D AB C --的大小。
解:7。
三棱锥 A —BCD 中,∠BAC =∠BCD =90°,∠DBC =30°,AB =AC =6,AD =4,求二面角 A-BC-D 的度数。
解:9。
如图所示,四棱锥P-ABCD 的底面是边长为a 的菱形,∠A =60°,PC ⊥平面ABCD,PC =a ,E 是PA 的中点。
(1)求证平面BDE ⊥平面ABCD 。
(2)求点E 到平面PBC 的距离。
(3)求二面角A —EB —D 的平面角大小. 解析:10。
如图,已知正方体ABCD —A1B1C1D1的棱长为1,E 、F 分别在棱AB 、BC上,G 在对角线BD1上,且AE =41,BF =21,D1G ∶GB =1∶2,求平面EFG 与底面ABCD 所成的二面角的大小.D ’B ’DAC ’BA ’CMNBF EACDDOABC11。
二面角练习题

二面角练习题1、在三棱锥P-ABC中,已知PB⊥底面ABC,AC⊥BC,PB=BC=AC,点E、F分别是PC、XXX的中点.我们需要证明两个结论:Ⅰ)PC⊥平面BEF;Ⅱ)二面角A-EB-F的大小等于120°。
为证明(Ⅰ),我们可以通过三角形的性质来解决。
首先连接PE、PF,因为PE、PF分别是三角形PBC、PAC的中线,所以PE=PF=1/2BC=1/2AC。
又因为PB=BC=AC,所以△PBE和△PBF是等腰三角形,∠PBE=∠PBF。
又因为EF是△PBE和△PBF的中线,所以EF⊥PB,即EF⊥平面ABC。
又因为BE⊥平面ABC,所以PC⊥平面BEF。
为证明(Ⅱ),我们可以利用向量的知识,设向量PA=a,向量PB=b,则向量PC=a+b。
由于PB⊥平面ABC,所以向量PB在平面ABC上的投影为0,即b在平面ABC的法向量上。
又因为AC⊥BC,所以向量AC在平面ABC的法向量上,且向量AC与向量b的夹角为60°。
因此,向量PC在平面ABC的法向量上的投影为a的模长乘以cos60°,即PC在平面ABC的法向量上的投影为1/2PA。
由于PE、PF分别是△PAC、△PBC的中线,所以PE=PF=1/2PA=1/2PC。
因此,向量PE和向量PF在平面BEF上的投影相等,即二面角A-EB-F的大小等于120°。
2、在正方体ABCD-A1B1C1D1中,已知O是AC、BD的交点,E、F分别是AB、AD的中点。
我们需要证明三个结论:1)直线OD1与直线A1C1垂直;2)异面直线EF与A1C1所成角的大小等于60°;3)二面角B-AC-D1的大小等于90°。
为证明(1),我们可以利用向量的知识。
设向量OA1=a,向量OC1=b,则向量OD1=a+b。
因为正方体ABCD-A1B1C1D1中,向量OA1和向量OC1垂直且长度相等,所以向量OA1和向量OC1的夹角为90°。
(完整版)二面角典型习题
二面角1.二面角的计算:1)定义法;2)三垂线定理法;3)垂面法;4)面积射影法;例1、已知P是二面角a—AB-p棱上一点,过P分别在a、P内引射线PM,PN,且/BPM=/BPN=45。
,/MPN=60。
,求此二面角的度数。
P成角丫,则必有()(A)sin0sin8=sin y(B)sin0sin8=cos y(C)cos0cos8=sin y (D)cos0cos8=cos y例4、在120。
的二面角a-1-p的面a、P内分别有A、B两点,且A、B到棱l的距离AC、BD分别长2、4,AB=10,求:(1)直线AB与棱l所成角的正弦值。
(2)直线AB与平面P所成角的正弦值。
例5、已知二面角a-MN-P为60。
,A e a,B e p,BC为AB在p上的射影,且C在棱MN上,AB与P所成角为60。
,且AC=6,/MCB=45。
,求线段AB的长。
例6、已知二面角a-DC-P的度数为0,A e a,B e p,AADC的面积为S,且DC=m,AB±DC,AB与平面P成30。
角,当0变化时,求NDBC面积最大值。
例7、已知C是以AB为直径的圆周上的一点,^ABC=30o,PA1面ABC,/PBA=45°,求二面角A-PB-C的正弦值。
例8、在正方体ABCD—ABCD中,利用cos0=y射!解下列各题1111S1)P、Q分别为AA,AB的中点,求平面CPQ与底面ABCD所成角的余弦值112)求二面角C—BD—C的大小;113)M是棱BC的中点,求二面角DJ B i M-C i的余弦值。
例9、已知0、E分别是边长为a的等边三角形ABC的边AB、AC上的点,DE//BC,现沿DE 将三角形ADE折起,是二面角A-DE-B成60度角,当DE在什么位置时,使折起后的顶点A 到BC边距离最短?最短是多少?/ADC=/BCA=90。
,/ABC=60。
,例10、等腰Rt AADC和Rt A BCA有公共边AC,以AC为棱折起多少度的二面角时,有BD二BC?两个平面垂直1、两个平面垂直的证明1)定义2)判定定理2、两个平面垂直的性质例1、已知ABCD为矩形,E为半圆CED上一点,且平面ABCD1平面CDE1)求证DE是AD与BE的公垂线2)若AD=DE二-AB,求AD与BE所成角的大小例2、等腰三角形ABC的底BC=4J2,高AD=1,现沿AD将A ABD折起,使二面角B-AD-C 为60度,求此时AB与面ACD所成角的正弦值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二面角
1.二面角的计算:
1)定义法;
2)三垂线定理法;
3)垂面法;
4)面积射影法;
例1、已知P 是二面角AB αβ--棱上一点,过P 分别在αβ、内引射线PM ,PN ,且45,60BPM BPN MPN ∠=∠=︒∠=︒,求此二面角的度数。
例2、已知P 为锐二面角l αβ--棱上的点,,4530PQ PQ l αβ⊂︒︒与成,与成,则二面角l αβ--的度数是多少。
例3、已知二面角l αβ--的度数为θ,在面α内有一条射线AB 与棱l 成锐角δ,与面βγ成角,则必有( )
(A )sin sin sin θδγ= (B )sin sin cos θδγ=
(C )cos cos sin θδγ= (D )cos cos cos θδγ=
例4、在120︒的二面角l αβ--的面α、β内分别有A 、B 两点,且A 、B 到棱l 的距离AC 、BD 分别长2、4,AB=10,求:
(1)直线AB 与棱l 所成角的正弦值。
(2)直线AB 与平面β所成角的正弦值。
例5、已知二面角MN αβ--为60︒,,,A B BC AB αββ∈∈为在上的射影,且C 在棱MN 上,AB 与β所成角为60︒,且5,45AC MCB =
∠=︒,求线段AB 的长。
例6、已知二面角DC αβ--的度数为θ,,,A B ADC αβ∈∈∆的面积为S ,且DC=m ,AB DC ⊥,AB 与平面β成30︒角,当θ变化时,求DBC ∆面积最大值。
例7、已知C 是以AB 为直径的圆周上的一点,30ABC ∠=︒,
45PA ABC PBA ⊥∠=︒面,,求二面角A-PB-C 的正弦值。
例8、在正方体1111ABCD A B C D -中,利用cos S S θ=射影
解下列各题
1)P 、Q 分别为1,A A AB 的中点,求平面1C PQ 与底面ABCD 所成角的余弦值
2)求二面角11C BD C --的大小;
3)M 是棱BC 的中点,求二面角111D B M C --的余弦值。
例9、已知D 、E 分别是边长为a 的等边三角形ABC 的边AB 、AC 上的点,DE//BC ,现沿DE 将三角形ADE 折起,是二面角A-DE-B 成60度角,当DE 在什么位置时,使折起后的顶点A 到BC 边距离最短?最短是多少?
例10、等腰Rt ADC ∆和Rt BCA ∆有公共边AC ,90,60ADC BCA ABC ∠=∠=︒∠=︒,以AC 为棱折起多少度的二面角时,有BD=BC ?
两个平面垂直
1、两个平面垂直的证明
1)定义
2)判定定理
2、两个平面垂直的性质
例1、已知ABCD为矩形,E为半圆CED上一点,且平面ABCD⊥平面CDE 1)求证DE是AD与BE的公垂线
2)若AD=DE=1
2
AB,求AD与BE所成角的大小。
例2、等腰三角形ABC的底BC=42,高AD=1,现沿AD将ABD
∆折起,使二面角B-AD-C 为60度,求此时AB与面ACD所成角的正弦值。
例3、在空间四边形ABCD中,已知AB=BD=DC=CA,M,N,P,Q分别是CD,DB,BA,AC的中点,K为BC中点,求证:平面KAD⊥平面PQMN
例4、在正方体1111ABCD A B C D -中,已知P ,Q ,R ,S 分别是11111,,,A D A B AB BB 的中点,求证:平面PQS ⊥平面1B RC .
例5、已知PA ⊥矩形ABCD 所在平面,M,N 分别是AB ,PC 的中点
1)求证,MN ⊥AB
2)若平面PDC 与平面ABCD 成45度角,求证:平面MND ⊥平面PDC
例6、已知直角三角形ABD 和等腰直角三角形CBD 所在平面互相垂直,且
90ADB DBC ∠=∠=︒,在AB 上取一点P,当P 在什么位置时,平面PCD 与平面BCD 成60度的二面角?
例7、已知Rt 三角形ABC 的两直角边AC=2,BC=3,P 是斜边AB 上的点,以CP 棱折成直二面角A-CP-B ,若折后7,试求二面角P-AC-B 的余弦值。
例8、M ,N 分别是正方体1111ABCD A B C D -面对角线11,A B B D 上的点,且
1111111,33
A M A
B B N B D =
=,求证MN 是异面直线11,A B B D 的公垂线。
