曲面拟合原理与实例
多项式曲面拟合法程序

多项式曲面拟合法程序概述多项式曲面拟合法是一种数学方法,用于通过一组给定的数据点,拟合出一个多项式曲面。
该方法广泛应用于数据分析、图像处理、机器学习等领域。
本文将介绍多项式曲面拟合法的基本原理、算法步骤和实际应用。
基本原理多项式曲面拟合法的基本原理是通过最小二乘法来拟合数据点。
假设我们有一组数据点(x i,y i,z i),其中x i和y i是自变量,z i是因变量。
我们希望找到一个多项式曲面z=f(x,y),使得曲面上的点(x i,y i)与数据点(x i,y i,z i)之间的误差最小。
算法步骤多项式曲面拟合法的算法步骤如下:1.输入数据点(x i,y i,z i)。
2.选择多项式的阶数n。
3.构建系数矩阵A和常数向量B,其中A的第i行表示x i和y i的各次幂的系数,B的第i个元素表示z i。
4.求解线性方程组Ax=B,得到系数向量X=(x0,x1,x2,...,x n)。
5.根据系数向量X构建多项式曲面z=f(x,y),其中f(x,y)=x0+x1x+x2y+...+x n x n y n。
6.计算拟合误差,例如均方根误差(RMSE)或平均绝对误差(MAE)。
7.根据需要进行模型优化,例如调整多项式阶数n或采用正则化方法。
实际应用多项式曲面拟合法在许多领域都有广泛的应用。
以下是一些实际应用的例子:1. 数据分析在数据分析中,我们经常需要根据一组数据点来拟合出一个函数,以便进行数据预测或趋势分析。
多项式曲面拟合法可以用于拟合数据点,找到一个适合的函数模型。
2. 图像处理在图像处理中,我们经常需要对图像进行平滑处理或者边缘检测。
多项式曲面拟合法可以用于对图像中的像素点进行拟合,从而实现平滑或边缘检测的目的。
3. 机器学习在机器学习中,多项式曲面拟合法可以用于多项式回归问题。
通过拟合数据点,我们可以找到一个多项式模型,用于预测新的数据点。
总结多项式曲面拟合法是一种通过最小二乘法来拟合数据点的数学方法。
B样条曲面拟合

谢谢
这样的 节点矢量定义了一般非均匀B样条基.
分段贝齐尔曲线 其节点矢量中二端节点重复度与类型2相同, 为k+1。所不同的是,点数减1必 须等于次数的正整数倍,
二、曲面拟合的条件
待拟合曲面的控制点数 样条基次数 两个方向的节点向量
B样条曲面拟合
一、B样条曲线的种类及主要性质
均匀B样条曲线 均匀B样条曲线节点矢量中节点为沿参数轴 均匀或等距分布,所有节点区间长=Δi=ti+ti常数 >0(i=0,1,…,n+k)。这样的节点矢量定义了均匀 B样条基。 准均匀B样条曲线 其节点矢量中二端节点具有重复度k+1,即t0 =t1=…=tk,tn+1=tn+2=…=tn+k+1,所有内 节点均匀分布,重复度为1。
3、节点向量
节点向量是由数据点的参数化确定的,给定 曲面的数据点赋两个参数值,使位于拟和曲 面上的这些点与平面参数域内的点建立一一 对应的关系。 参数化的手段有:均与参数化、累加弦长参 数化、基面参数化。
得到数据点集的参数值后,就可以利用最小 二乘拟合反算曲面控制点
三、曲面拟合的实例
例1: 图1是一条三次B样条曲线与控制多 边形,符号“○”表示曲线初始控制点, “*”号表示曲线经一次4尺度加细后得到的 控制点,由图易见,加细后的控制点与曲线 更加接近。因此,可通过控制点的多尺度迭 代来生成B样条曲线增加了生成样条曲线的 速度。
例2 图2是利用第2节算法进行4尺度三层加细得 到的双三次B样条拟合曲面,0D为 (1+3)×(1+3)网格,经过三次4尺度加细 后3D为(64+3)×(64+3)网格,重建的B 样条曲面即有很好的光滑形状,又有很高的 逼近精度,同时,在上机实现时算法速度比 以前基于Binary细分多层加细算法的速度稍 快,主要由于减少了耗时的Step 2的次数。
20_数值分析5_6曲线拟合

0x, 1x, , nx, n m,
{jx} ( C[a,b] ) 在点集 {x0,x1, , xm} 上线性无关 . 问题 在曲线族 y ( x )
n j0
c j j ( x ) 中寻找一条曲线
y*(x),
使其能按照某种原则去拟合数据(5.92), 用 y*(x) 代替数据 (5.92) 反映的函数关系.
求血药浓度随时间的变化规律c(t).
10
2
c (t ) c 0 e
10
1
kt
c , k 为待定系数
10
0
0
2
4
6
8
半对数坐标系(semilogy)下的图形
曲线拟合问题的提法
已知一组(二维)数据,即平面上 m+1个点(xi,yi) i=0,1,…m, 寻求一个函数(曲线)y=f(x), 使 f(x)在某种准 则下与所有数据点最为接近,即曲线拟合得最好。 y + + +
(5.97)
* c0 ( f , 0 ) * c1 ( f , 1 ) * cn ( f , n )
证 (必要性) 记
F (C ) ( A C Y , A C Y )
m
i0
A ( C C *) 0
A (C
C *), A ( C C *) 0 .
F ( C ) F ( C *)
方程 ATAC* ATY 叫做最小二乘的法方程 或正规方程.
由 ATA 的正定性, 知法方程的解存在且唯一.
五、最小二乘法的精度
拟合曲线对数据的拟合精度, 可用误差平方和 来刻画.
曲面拟合及其在三维打印中的应用研究

曲面拟合及其在三维打印中的应用研究随着3D打印技术的发展和广泛应用,曲面拟合这一技术也逐渐被引入到3D打印领域中。
曲面拟合是一种数学方法,通过对曲面进行建模和参数化,实现对曲面的描述和几何操作。
在3D打印中,曲面拟合可以应用于模型的设计、优化和制造等方面,有效提高了3D打印的制造质量和效率。
一、曲面拟合的基本原理曲面拟合是一种数学方法,其基本原理是通过采集一定数量的曲面上的离散点,利用数学方法对这些点进行插值或拟合,得出一个连续的曲面模型。
常用的曲面拟合方法有贝塞尔曲面拟合、B样条曲面拟合、NURBS曲面拟合等。
这些方法主要通过对曲面的映射和变换进行操作,达到曲面的描述和拟合的效果。
二、曲面拟合在3D打印中的应用1.模型设计和优化曲面拟合可以应用于3D模型的设计和优化。
通过对曲面进行建模和参数化,可以实现对模型的优化和调整,达到更好的制造效果。
例如,在航空航天领域中,曲面拟合可以应用于飞机的机翼和机身等部件的设计和优化,实现更好的气动性能和稳定性。
2.模型制造曲面拟合也可以应用于3D模型的制造。
通过曲面拟合,可以将原始模型转换为一个可打印的曲面模型,提高制造效率和质量。
例如,在汽车制造中,曲面拟合可以应用于汽车外观件的制造,实现更好的表面光泽和质感。
3.模型修复曲面拟合可以应用于3D模型的修复和重建。
通过曲面拟合,可以将存在缺陷或损坏的模型进行修复和重建,达到复原原有的设计效果。
例如,在文物保护领域中,曲面拟合可以应用于古建筑和雕塑的修复和重建,实现更好的保存效果。
三、曲面拟合在3D打印中的局限性和挑战虽然曲面拟合在3D打印中具有广泛的应用前景,但是也存在一定的局限性和挑战。
首先,曲面拟合的精度和效率都与曲面的复杂程度有关。
当曲面较为复杂时,需要求解更多的参数和方程,导致计算量和时间成本较高,影响了打印效率和质量。
其次,曲面拟合的精度和鲁棒性也受到数据质量和噪声干扰的影响。
在应用过程中,需要对数据进行清洗和处理,避免噪声和异常值的影响。
曲面拟合是啥原理图的应用

曲面拟合是啥原理图的应用1. 曲面拟合的概念曲面拟合是一种数学建模技术,用于将一组离散点数据拟合成平滑的曲面。
它通过寻找最适合给定点集的曲面来实现数据的近似和拟合。
曲面拟合在计算机图形学、CAD/CAM、工程设计和地理信息系统等领域得到了广泛应用。
2. 曲面拟合的原理曲面拟合的原理基于数学最优化方法,旨在找到一个曲面模型,使其最接近给定的离散点数据。
常见的曲面拟合方法包括最小二乘法和样条曲面拟合等。
2.1 最小二乘法最小二乘法是曲面拟合中常用的一种方法。
它通过最小化数据点与曲面之间的距离来确定最佳拟合曲面。
最小二乘法可以分为线性最小二乘法和非线性最小二乘法。
2.1.1 线性最小二乘法线性最小二乘法适用于拟合线性模型的情况。
其基本原理是建立一个与数据点相匹配的线性模型,并通过最小化残差平方和来确定最佳拟合曲面。
线性最小二乘法的数学公式可以表示为:min E = Σ (yi - f(xi))^2其中,E为残差平方和,yi为实际观测值,f(xi)为线性模型的预测值。
2.1.2 非线性最小二乘法非线性最小二乘法适用于拟合非线性模型的情况。
其原理与线性最小二乘法类似,不过在计算残差平方和时,需要通过迭代的方式逼近最佳拟合结果。
非线性最小二乘法的数学公式可以表示为:min E = Σ (yi - f(xi;θ))^2其中,θ为模型参数,f(xi;θ)为非线性模型的预测值。
2.2 样条曲面拟合样条曲面拟合是一种使用控制点和插值方法构造曲面的技术。
它将拟合问题转化为一个插值问题,在给定的控制点上生成一个平滑的曲面。
样条曲面拟合的原理是通过插值方法将数据点与控制点相连,并在控制点上生成一个曲面模型,以实现数据的拟合。
3. 曲面拟合的应用曲面拟合在许多领域都有广泛的应用。
以下是一些常见的应用场景:•计算机图形学:曲面拟合可以用于生成光滑的曲线和曲面,用于渲染和动画效果的生成。
•CAD/CAM:曲面拟合可以用于设计和制造曲面形状的产品,例如汽车、飞机等。
vc多项式最小二乘法曲面拟合

vc多项式最小二乘法曲面拟合多项式最小二乘法曲面拟合是一种数据拟合方法,用于找到一个多项式函数来最好地拟合一组给定的数据点,从而能够得到一个具有最小均方误差的曲面模型。
在本文中,我们将讨论多项式最小二乘法曲面拟合的原理和应用。
首先,让我们来了解一下多项式最小二乘法的原理。
在数学上,最小二乘法是一种数学优化技术,其目标是通过最小化误差的平方和来找到一组参数,使得一个给定的数学模型能够最好地拟合一组数据点。
而在多项式最小二乘法中,我们使用多项式函数来对数据点进行拟合,通过最小化误差的平方和来找到最佳的多项式系数。
一般来说,一个n次多项式可以表示为:f(x) = a0 + a1x + a2x^2 + ... + anx^n其中,a0, a1, a2, ..., an为多项式的系数,x为自变量,f(x)为因变量。
对于给定的一组数据点(x1, y1), (x2, y2), ..., (xn, yn),我们可以建立一个包含n+1个未知数的方程组,通过最小二乘法来求解这些未知数,从而得到最佳的多项式系数。
接下来,让我们来看一下多项式最小二乘法曲面拟合的应用。
在实际应用中,多项式最小二乘法曲面拟合常常用于对实验数据进行分析和拟合,从而得到一个能够描述数据特征的多项式模型。
例如,在科学研究中,实验数据通常会包含一些误差和噪音。
通过多项式最小二乘法曲面拟合,我们可以将这些数据点平滑地连接起来,得到一个最佳的曲面模型,从而能够更清晰地展现数据的变化趋势。
而在工程领域中,多项式最小二乘法曲面拟合也可用于对物理现象进行建模和预测,从而帮助工程师更好地了解和分析实际问题。
除此之外,多项式最小二乘法曲面拟合还具有广泛的应用场景。
例如在金融领域,我们可以通过多项式最小二乘法曲面拟合来对股票价格进行预测和分析;在医学领域,我们可以利用多项式最小二乘法曲面拟合来研究生物医学数据的变化规律。
总的来说,多项式最小二乘法曲面拟合是一种非常有效的数据拟合方法,它能够对一组给定的数据点进行最佳的拟合,从而得到一个能够描述数据特征的多项式模型。
2、曲面拟合及其应用

故障 方法1 方法2 融合1 故障 方法1 方法2 融合1
H1 0.025 0.062 0.042 H6 0.022 0.025 0.020
H2 0.071 0.071 0.038 H7 0.035 0.022 0.105
H3 0.086 0.050 0.021 H8 0.017 0.038 0.016
3、在变压器短路故障在线监测中的应用
由二维坐标( Ui,Uti) 决定的Pi在一平面上,可利用二次曲面 拟合方程,即二维回归方程来描述:
P 0 1U 2U t 3U 2 4UU t 5U t2 1
同理,对于考虑了压力因素的温度参量,二维回归方程描述为:
5、总结及展望
1、
介绍了曲面拟合的背景及在各个领域 的应用情况
总 结
2、
分析了曲面拟合的基本原理及其实现 方法,着重介绍了最小二乘曲面拟合
3、
采用曲面拟合法进行变压器短路故障 在线监测中的信息融合,使传感器的 性能和精度得到了提高。
4、
采用曲面拟合法进行大型油浸式变压 器故障诊断中,能较好克服变压器故 障的误诊和漏诊,提高故障诊断水平 。
曲面拟合及其应用
主要内容
1、背景及应用
2、基本原理
3、在变压器短路故障在线监测中的应用
4、在大型油浸变压器故障诊断中的应用 5、总结及展望
1、背景及应用
在科学研究中,常常需要 根据实际实验测试数据分 析变量对目标函数的影响, 寻找目标函数与变量之间 的解析关系。
传统的插值法在使用时, 由于测量数据量大,导致 插值函数次数过高,计算 量大。同时,它无法识别 测试中的错误数据,容易 造成较大误差。
E [ Pk ( 0 1U 2U t 3U 2 4UU t 5U t2 )]2
最小二乘法拟合曲面

最小二乘法拟合曲面好嘞,今天我们聊聊一个有点“数学味”的话题——最小二乘法拟合曲面。
别紧张,虽然听起来像是要用大脑打怪,但其实它并没有那么复杂。
你可以把它想成是找一条最佳的“平衡线”,它帮助我们在一堆数据点中找到一个“最合适”的位置,就像你在百货商店里挑衣服,想要找到最合身、最舒服的一件。
假设你有一堆数据,这些数据可能有点乱七八糟,有高有低,不太规律,就像你在市场上看到的一堆蔬菜,有些西红柿红得发亮,有些却有点褐色,想找出一条合适的线,来把这些菜好好排列一下。
最小二乘法就是用来做这件事的,目的就是尽量让所有点都离拟合曲面“最近”。
怎么做到呢?就像是做个手术,把那些距离远的点“拉”回来,尽量让它们都处在一个比较“平滑”的状态下。
讲到这,你可能会想:那怎么知道“合适”呢?哈哈,别着急,最小二乘法有个“自我调节”的本领,就像老母鸡带小鸡一样,总能找到最合适的位置。
简单来说,它会去“最小化”那些“偏差”的平方。
啥意思呢?就是让每个数据点到拟合曲面(或者说“平衡线”)的距离尽可能小,越小越好。
你可以理解成,这个方法就是通过减少错误,来确保结果的准确性。
举个例子吧,假设你在一个大商场里走,眼前有一堆摊位,每个摊位上都有卖不同价格的商品。
你现在想挑一个摊位买东西,但你不能在每个摊位前都驻足,那样会浪费时间对吧?你干脆用一个小本子记下来,标记哪个摊位价格比较合适。
最小二乘法就像是这个本子,通过找到那些价格最符合你需求的摊位,最终帮你筛选出最合适的那几个。
说到这,可能有朋友会觉得,哎呀,这不就是个数学公式问题吗?确实,最小二乘法背后有个公式,原理看起来有点复杂,但其实也没那么恐怖。
你可以想象你拿着一根笔直的尺子,尝试把它摆放到数据点中间,目的是让它离所有点都尽量近,谁离得最远就把它“拉”回来。
尺子的位置就是最小二乘法为你找到的最佳拟合曲面。
好啦,别害怕。
这个过程其实并不是那么死板,操作起来也比较“人性化”。
就像你上大学时选择专业,总要做些权衡,有的选科成绩不错,但不喜欢;有的则刚好合适但成绩一般。
双曲线曲面拟合及在机械加工中的应用

双曲线曲面拟合及在机械加工中的应用在机械加工中,很多零部件需要进行表面的加工,以达到一定的精度和光洁度要求。
在表面加工的过程中,会用到各种各样的曲面拟合方法,而双曲线曲面拟合是其中的一种有效方法。
本文将着重介绍双曲线曲面拟合的原理及在机械加工中的应用。
一、双曲线曲面拟合的原理双曲线曲面是一种可以用双曲面方程表示的曲面,其数学表示形式为:1/x^2 + 1/y^2 = z^2/a^2其中,x和y是平面上的坐标,z是垂直于平面的坐标,a是常数。
这样的曲面具有很好的形状特点,例如双曲面切于自身轴线的所有平面都截得相同的彼此不相交的曲线,这些曲线被称为双曲线,因此称为双曲线曲面。
双曲线曲面拟合是指在有限点云数据上,利用双曲线曲面拟合算法,从点云数据中确定一条或多条双曲线曲面,使其最优化地逼近点云数据。
双曲线曲面的特点为双曲面方程的多项式阶级较低,计算复杂度较小,且能够准确地表现曲面的几何形状。
二、双曲线曲面拟合在机械加工中的应用在机械加工中,精度和表面光洁度是非常重要的,因此需要进行表面拟合。
双曲线曲面拟合因其计算简单、精度高而被广泛应用于机械加工领域中的模具、刀具、汽车零部件等领域。
例如,汽车工厂制造的车身模具等大型零部件往往具有曲面特征,必须使用双曲线曲面拟合算法对其进行表面拟合。
通过采集该模具的点云数据,在有限的数据范围内,使用双曲线曲面拟合算法为其确定一条或多条双曲线曲面,以取得最优化的表面数据描述。
然后,将计算出的曲面数据转化为机床语言,以进行加工。
另外,双曲线曲面拟合算法还在飞行器研究领域中具有广泛应用。
例如,在航空工业中,需要对机身表面的曲率进行拟合,以便确定飞机的空气动力学特性。
通过对机身进行三维扫描,获取点云数据,并使用双曲线曲面拟合算法,可以得到机身表面的精确曲率信息,从而有效地优化飞机的空气动力学性能。
总之,双曲线曲面拟合在机械加工中的应用领域广泛,具有较高的精度和可靠性,在加工行业中有着重要的地位。
matlab 曲面多项式拟合

Matlab曲面多项式拟合一、引言Matlab是一种非常强大的科学计算软件,广泛应用于工程、数学、统计学以及其他领域。
在工程和科学研究中,经常会遇到需要拟合数据的情况。
曲面多项式拟合是一种常见的拟合方法,可以用来近似描述数据所呈现的曲面形状。
本文将介绍在Matlab中如何进行曲面多项式拟合。
二、曲面多项式拟合的基本原理曲面多项式拟合是指利用多项式函数来逼近描述一个曲面的数据。
假设我们有一组实验数据,其中的每个数据点都包括两个自变量和一个因变量。
曲面多项式拟合的目标是找到一个多项式函数,使得该函数能够最好地拟合这些数据点,从而近似描述出数据所呈现的曲面形状。
一般来说,曲面多项式拟合的多项式阶数越高,拟合精度就越高,但也更容易受到数据噪声的影响。
三、在Matlab中进行曲面多项式拟合的步骤1. 准备数据在进行曲面多项式拟合之前,首先需要准备数据。
数据一般以矩阵的形式输入,其中每一行代表一个数据点,包括两个自变量和一个因变量。
在Matlab中,可以使用“meshgrid”函数生成自变量的网格数据,并利用这些网格数据计算因变量的数值,从而得到完整的数据集。
2. 进行拟合在准备好数据之后,可以使用Matlab中提供的“fit”函数进行拟合。
该函数可以指定需要拟合的自变量和因变量,以及拟合所采用的多项式阶数。
在拟合完成后,可以得到拟合的多项式函数以及拟合的曲面。
3. 可视化拟合结果拟合完成后,可以利用Matlab中的绘图函数将拟合的曲面可视化。
通过绘制原始数据点和拟合曲面,可以直观地观察拟合的效果,并进行进一步的分析和判断。
四、实例演示下面通过一个简单的实例演示在Matlab中进行曲面多项式拟合的步骤。
假设有如下的实验数据:X = [1, 2, 3, 4, 5];Y = [1, 2, 3, 4, 5];Z = [1, 4, 9, 16, 25];其中X和Y为自变量,Z为因变量。
我们希望利用这些数据进行曲面多项式拟合,并将拟合结果可视化。
CATIA软件曲面拟合方法

CATIA软件曲面拟合方法CATIA软件是一种常用的三维计算机辅助设计(CAD)软件,广泛应用于机械、航空航天、汽车等行业。
在CATIA软件中,曲面拟合是一项重要的工作步骤,用于将已有的散乱点云数据拟合成光滑的曲面。
本文将介绍CATIA软件的曲面拟合方法及其应用。
一、曲面拟合的基本原理曲面拟合是指通过已知的散乱点云,构建出一条或多条曲面,以最佳地逼近这些点云数据。
曲面拟合通常可以分为以下几个步骤:1. 数据准备:将需进行曲面拟合的散乱点云数据导入CATIA软件。
2. 点云处理:CATIA软件提供了多种点云处理工具,可以对导入的点云数据进行滤波、降噪等操作,以保证后续拟合的精度和准确性。
3. 曲面生成:在CATIA软件中,可以选择不同的曲面生成方法,如贝塞尔曲线、B样条曲线等,根据具体需求选择适合的曲面生成方法。
4. 曲面拟合:CATIA软件提供了多种曲面拟合工具,如最小二乘法拟合、最大似然法拟合等。
根据点云数据的特点和拟合需求,选择合适的拟合方法,并进行相应的参数设置。
5. 拟合评估:CATIA软件提供了拟合结果的可视化工具,可以对拟合结果进行评估和调整,以获得更好的拟合效果。
二、CATIA软件曲面拟合的应用领域CATIA软件的曲面拟合功能广泛应用于以下几个领域:1. 机械制造:在机械制造过程中,常常需要根据零件的草图或点云数据生成光滑曲面,以便进行后续的设计和加工。
CATIA软件的曲面拟合功能可以快速准确地生成满足要求的曲面,提高机械制造的效率和精度。
2. 航空航天:航空航天领域对于零件的表面精度要求非常高,常常需要将散乱点云数据拟合成光滑的曲面,以满足空气动力学和结构强度的要求。
CATIA软件的曲面拟合功能可以满足航空航天领域对曲面精度的要求。
3. 汽车设计:在汽车设计中,常常需要对车身、零件进行曲面设计和整形。
CATIA软件的曲面拟合功能可以快速生成符合造型要求的曲面,提高汽车设计的效率和外观质量。
曲面拟合原理与实例

多项式函数对所给的坐标进行拟合:构造关于系数 a ij 的多元函数:点( a 11 ,⋯, a pq )是多元函数 s(a 11,L , a pq )的极小点,其中 g 为权函数,默 认为 1,所以点( a 11 ,⋯, a pq )必须满足方程组saij在 g 1的情况下,有f (x, y) i 1 j a ij x yij1,11 aii1j1i 1 j 1 j x yf (x, y)a11a 12y 2 a 13yL q1a 1q ya 21x a 22xy2a 23xyLq1 a 2qxyMi1i1i 1 2Li 1 q 1a i1x i 1a i2x i 1ya i 3x i 1y 2a iq x i 1yq 1Mp1p1 p 1 2Lp 1 qa p1x a p2 x y a p 3x ya pq x yp,qpq即1给定一组坐标 (x g ,y g ,z g ) ,g 1,2,⋯,n , 表示有n 个点。
要求用以下二元 x2xx Mxp,y y2yMyq,Aa12L a1qa 22L a2q M O M a p2 L apq则函数又可表示为 f (x , y) x TAy ,拟合的目标就是求出系数矩阵 A 。
n 2s( a 11 ,L ,a pq ) g [ f (x g , y g )z g ]g1ng1pqi 1 j 1g (a ij x yi 1 j 1z g )2a11a21 M ap12[ f ( x g , y g) z g ] g1aija ij2[ f (x g , y g ) g1nz g ] aij [ f(x g ,y g )]2[f (x g ,y g ) i 1 j 1z g ]x g ygg1n2 g1因此可得 x ig 1y g j 1f(x g ,y g ) x g i 1y g j 1z gg1g1npq ni x g i1y g j11a x g y g1i 1 j x 1z gg111 g1 np,qni x g i1y g j1 1 1a x y i 1 j 1 x yzgg11,1g1p,qnna1 1 i 1 j ( x g y g x g y g1i 1 )x gy g j 1z g1,1g1g1u (i, j ) n(xg g11y g 1 i 1 xg y gj 1) ,v(i, j) ni 1 j 1 x g y g z g g1p,qa u (i, j) v(i, j) (i, j) (1,1),⋯,(p,q)上式实际共有 p q 个等式,可将这u 11(1,1) L u pq (1,1) a 11 M O MM u 11(p,q) L u pq ( p, q) a pq也就是 U*a=V 的形式,其中u 11 L u pq (1,1)U M O M ,u 11( p, q)L u pq ( p,q) p q 个等式写成矩阵的形式有: v(1,1)Mv( p,q)a 11 v(1,1) a M , V Ma pq v( p, q) nni 1 j 1 i 1 j 1 x g i 1y g j 1f(x g ,y g )U 为pq pq 阶矩阵,实现函数为function A=leftmatrix(x,p,y,q);V 为长pq 的列向量,实现函数为function B=rightmatrix(x,p,y,q,z)。
matlab曲面拟合并求面积

一、引言在工程和科学领域中,曲面拟合是一项重要的数学和计算技术,它可以帮助研究人员或工程师从实验或观测数据中找到最佳的曲面模型,以便进行进一步的分析和应用。
在众多的曲面拟合方法中,MATLAB 作为一种强大的数学建模和计算软件,具有丰富的曲面拟合工具箱,能够进行曲面拟合并求出面积,本文将介绍如何使用MATLAB进行曲面拟合并求面积的操作方法。
二、MATLAB曲面拟合的基本原理MATLAB中的曲面拟合通常通过拟合曲面上的数据点来实现。
曲面拟合的基本原理是在给定数据点的情况下,找到一个曲面模型来最好地拟合这些数据点。
常用的曲面拟合方法包括最小二乘法、样条插值、高阶多项式拟合等。
在MATLAB中,通过调用曲面拟合工具箱中的相应函数,可以很容易地实现曲面拟合操作。
三、MATLAB曲面拟合并求面积的步骤1. 数据准备在进行曲面拟合之前,首先需要准备好要拟合的数据。
这些数据可以是实验测量得到的点,也可以是由其他方法计算得出的点。
在MATLAB中,可以将这些数据点表示为一组(x, y, z)的坐标,其中x和y表示数据点的空间位置,z表示对应这些位置的数值。
2. 曲面拟合在准备好数据后,可以使用MATLAB中曲面拟合工具箱中的函数来进行曲面拟合。
可以使用“fit”函数来拟合一个曲面模型,比如二次曲面、三次曲面或其他自定义的曲面模型。
拟合的结果可以用于后续的分析和计算。
3. 计算面积在获得曲面拟合模型之后,可以利用该模型来计算曲面的面积。
MATLAB提供了丰富的数学计算函数,可以方便地进行曲面积分和面积计算。
通过调用这些函数,可以得到拟合曲面的面积,该面积反映了原始数据点所描述的曲面的实际面积。
四、MATLAB曲面拟合并求面积的实例下面以一个简单的实例来演示如何使用MATLAB进行曲面拟合并求面积。
假设有一组数据点如下所示:```x = [1, 2, 3, 4, 5];y = [1, 2, 3, 4, 5];z = [1, 4, 9, 16, 25];```我们可以利用这些数据点来进行曲面拟合,假设我们使用二次曲面模型来拟合这些数据点:```MATLABp = polyfitn([x', y'], z, 2); % 二次曲面拟合[X, Y] = meshgrid(1:0.1:5, 1:0.1:5);Zfit = polyvaln(p, [X(:), Y(:)]);Zfit = reshape(Zfit, size(X));```通过上述代码,我们可以得到拟合曲面Zfit。
曲面拟合算法的研究及应用

曲面拟合算法的研究及应用随着科学技术的日益发展,各行各业对于曲面拟合算法的需求也越来越高。
在许多应用场合下,如CAD(计算机辅助设计)、机器人技术、三维打印等,都需要通过数据点来对曲面进行拟合。
对于曲面拟合算法的研究和应用已经成为一个十分重要的研究方向。
一、曲面拟合算法介绍曲面拟合算法是利用函数拟合法对于曲面进行近似拟合的技术。
通过一组坐标点来描述一个三维曲面,而曲面拟合算法就是通过这组坐标点来搜索出一条接近点云的曲面,从而实现曲面的拟合。
目前常用的曲面拟合算法主要分为以下两类:一类是基于控制点(Control Point)的曲面拟合算法,此类算法需要事先选择一定数量的控制点,并且也常见于Bézier曲线或Bézier曲面的计算中;另一类是基于网格(Mesh)的曲面拟合算法,该类算法通常适用于后评估表面和基于几何约束的表面。
二、曲面拟合算法的应用1. CAD技术在CAD技术中,使用曲面拟合算法进行物体的建模是一个极其常见的方法。
由于CAD中需要对物体进行三维显示和模拟,在进行建模过程中,需要通过曲面拟合算法对于物体进行精确的处理,从而实现模型的高度精度和准确性。
2. 机器人技术在机器人技术领域中,曲面拟合算法多用于机器人视觉的处理中。
在一些需要高精度的机器人视觉系统中,需要对机器人的外形进行数学描述,而曲面拟合算法可以根据机器人表面的点云数据来推测出其外形,使得机器人视觉系统可以更加精确地执行任务。
3. 三维打印在三维打印领域中,曲面拟合算法的应用非常广泛。
当进行三维打印时,由于物体的三维形状复杂,因此需要对物体的表面进行精确的处理,使得打印结果符合预期。
在处理三维打印过程中,曲面拟合算法可以精确地恢复出物体的表面形状,从而减少可能的误差。
三、曲面拟合算法的研究在曲面拟合算法的研究领域中,目前主要的研究方向有以下两个方面:1. 算法优化在曲面拟合的算法应用中,算法的运行效率是非常重要的一个因素,这需要我们对算法进行优化。
双曲面拟合的数学原理与应用

双曲面拟合的数学原理与应用随着科技的进步,越来越多的业务需要使用到数学知识。
在工程领域中,由于存在各种各样的测量数据,因此需要进行数据的拟合,以更好地描述系统、预测未来。
而双曲面拟合正是其中的一种重要的方法。
一、什么是双曲面拟合双曲面(Hyperboloid)是一种非球形、非柱面的三维曲面,其数学表达式为:x²/a² + y²/b² - z²/c² = 1其中,a、b、c 分别为双曲面的三个轴向参数。
双曲面拟合是指通过寻找一组最佳参数 a、b、c,使得该双曲面能够与一组离散数据点最为接近。
这种方法被广泛应用于工程测量、光学、钟表、航天等领域。
二、双曲面拟合的数学原理双曲面拟合的数学原理主要依赖于最小二乘法(Least Square Method)。
最小二乘法是一种数学处理方法,其目的是通过寻求一个可接受的函数来对一系列数据点进行拟合。
在双曲面拟合中,最小二乘法被用来求解双曲面方程的未知参数 a、b、c。
这可以通过以下步骤实现:1. 假设是否存在一个符合条件的双曲面,一般假设为该双曲面与数据点的残差(即理论值与实际值之间的差)平方和最小。
2. 通过最小二乘法计算出残差平方和最小的三个轴向参数 a、b、c。
3. 将计算出的参数带入双曲面方程中,得到最终的双曲面拟合方程。
三、双曲面拟合的应用双曲面拟合的应用是非常广泛的,以下是其中的几个例子:1. 工程测量:斜面拟合、曲面拟合、磨损拟合等应用。
2. 光学:望远镜及显微镜物镜参数拟合、光滑曲面拟合等应用。
3. 钟表:钟表机芯摆调校、钟表壳体外形拟合等应用。
4. 航天:导弹鱼雷、卫星天线、火箭发动机喷口等应用。
通过以上例子,我们可以看到双曲面拟合在实际生产中的准确性和实用性。
但需要注意的是,双曲面拟合并非万能的方法,对于某些情况下,其他方法可能更为适合。
四、需要注意的事项1. 数据点的数量越多,其拟合效果越好。
MATALAB三维曲面拟合及其数学建模模型、案例参考

result=[ydata' yy' (yy-ydata)']
% a的值为拟合的目标函数的参数值利用lsqcurvefit进行拟合的它完整的语法形式是:
% [x,resnorm,residual,exitflag,output,lambda,jacobian] =lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)
二维曲线(非线性)拟合步骤
1.function F = myfun(x,xdata)
F = x(1)*xdata.^2 + x(2)*sin(xdata) + x(3)*xdata.^3; %可以是任意的
2.然后给出数据xdata和ydata
>>xdata = [3.6 7.7 9.3 4.1 8.6 2.8 1.3 7.9 10.0 5.4];
>>surfl(X,Y,Z);hold on;
>>surfl(XI,YI,ZZ+15)
>>axis([-3 3 -3 3 -5 20]);shading flat
>>hold off
例4
>>years = 1950:10:1990;
>>service = 10:10:30;
data=[x1;x2]; %类似于将x1 x2整合成一个2维数组。
a0= [-0.0014,0.07];
option=optimset('MaxFunEvals',5000);
曲面拟合算法在 CAD 中的应用研究

曲面拟合算法在 CAD 中的应用研究随着科技的不断进步,计算机辅助设计 (CAD) 工具的使用越来越广泛。
而曲线曲面设计作为一种非常常见的操作,它对于产品的美观性、机械性能等方面都有重要的作用。
然而,如何对复杂的曲面进行设计和编辑,是目前 CAD 工具需要解决的重要问题。
曲面拟合算法就是一种常用的技术来解决这个问题。
本文将介绍曲面拟合算法的原理、应用场景及其在 CAD 工具中的具体实现。
一、曲面拟合算法的原理曲面拟合算法主要是用于将给定的三维点云数据拟合成一个连续、平滑的曲面,以便于后续的 CAD 操作。
这里的“曲面”可以是二次曲面、三次曲面甚至更高次的曲面。
常见的曲面拟合算法包括最小二乘法曲面拟合、贝塞尔曲面拟合、B 样条曲面拟合等。
最小二乘法曲面拟合是一种基于最小化二次误差的曲面拟合方法。
它将曲面的表达式看作是一些特定参数的函数,并根据给定的点云数据,利用最小二乘法的原理求出合适的参数值,从而得到拟合的曲面。
最小二乘法曲面拟合的优点是求解简单,适用于数据量较小的情况。
贝塞尔曲面拟合是另一种常用的曲面拟合方法。
它利用贝塞尔多项式来表示曲面的形状,通过调整贝塞尔控制网格点的位置,来拟合给定的点云数据。
贝塞尔曲面拟合的优点是能够很好地拟合不规则形状的曲面。
B 样条曲面拟合是一种基于均匀拉格朗日多项式的曲面拟合方法。
它将曲面的控制点连接成网格点,再通过调整控制点的位置来达到拟合给定点云数据的目的。
B 样条曲面拟合的优点是能够很好地拟合规则形状的曲面。
二、曲面拟合算法的应用场景曲面拟合算法主要应用于以下场景:1. 工业设计。
在工业产品设计中,所涉及的曲面一般较为复杂,通过曲面拟合算法,可以实现对复杂曲面的快速建模和编辑。
2. 艺术设计。
在艺术品设计中,对于自然界中存在的非规则曲面,曲面拟合算法也可以用来进行建模,从而达到非常良好的效果。
3. 环境建模。
在三维场景建模中,需要对尽可能多的真实场景进行数字化建模,有时需要使用曲面拟合算法将其进行处理。
曲面拟合鼠标sensor算法应用

曲面拟合鼠标sensor算法应用近年来,随着计算机技术的不断发展和智能设备的普及,曲面拟合鼠标sensor算法的应用正在逐渐受到人们的关注。
曲面拟合算法是一种可以对鼠标sensor数据进行处理并进行曲面拟合的技术,它可以有效地改善鼠标sensor的精度和稳定性。
在本文中,我们将从深度和广度两个方面来探讨曲面拟合鼠标sensor算法的应用。
一、曲面拟合鼠标sensor算法的原理和方法曲面拟合鼠标sensor算法是基于数学模型的,它主要利用数学方法对鼠标sensor采集的数据进行曲面拟合。
在这个过程中,算法会通过对数据进行分析和处理,寻找出最符合实际情况的曲面,并将其应用到鼠标sensor的反馈中。
这样一来,鼠标就可以更准确地捕捉到用户的操作,并且可以对不同曲面进行适应,提高了其适用范围和可靠性。
曲面拟合鼠标sensor算法的方法主要可以分为以下几种:1. 多项式拟合:利用多项式函数对鼠标sensor数据进行拟合,通过选择不同的多项式次数和系数,可以得到不同精度和复杂度的曲面拟合结果。
2. 核方法拟合:核方法是一种通过对数据进行转换和处理,利用核函数来进行曲面拟合的方法,它可以克服数据的非线性问题,得到更加准确的拟合结果。
3. 曲面逼近:曲面逼近是一种利用局部的曲面来逼近整体曲面的方法,它可以减少计算量,并且更加适用于局部特征较为突出的曲面拟合。
二、曲面拟合鼠标sensor算法在实际应用中的意义及作用曲面拟合鼠标sensor算法的应用具有重要的意义和作用。
它可以提高鼠标的精度和稳定性,让用户在操作鼠标时更加方便和舒适。
曲面拟合算法还可以扩大鼠标sensor的适用范围,使其适用于更加复杂的工作环境和操作场景。
通过对鼠标sensor数据的曲面拟合,还可以提高鼠标的响应速度和准确度,提高用户的操作效率和体验。
三、个人观点与总结曲面拟合鼠标sensor算法的应用具有重要的意义和潜力。
它可以有效地改善鼠标的性能,提高用户的操作体验,并且可以适用于更加广泛的场景和需求。
曲面拟合
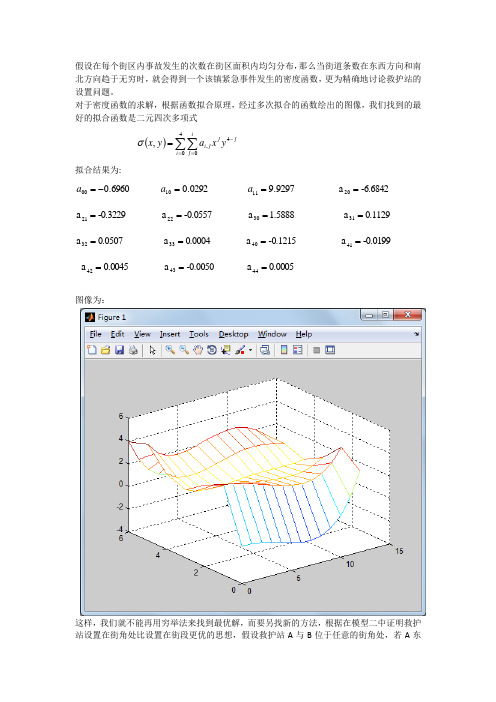
假设在每个街区内事故发生的次数在街区面积内均匀分布,那么当街道条数在东西方向和南北方向趋于无穷时,就会得到一个该镇紧急事件发生的密度函数,更为精确地讨论救护站的设置问题。
对于密度函数的求解,根据函数拟合原理,经过多次拟合的函数绘出的图像,我们找到的最好的拟合函数是二元四次多项式 ()jj i ij ji yx ay x -==∑∑=4400,,σ拟合结果为:6960.000-=a 0292.010=a 9297.911=a -6.6842a 20= -0.3229a 21= -0.0557a 22= 1.5888a 30= 0.1129 a 31= 0.0507 a 32= 0.0004a 33= -0.1215a 40= -0.0199a 41= 0.0045a 42= -0.0050a 43= 0.0005a 44=图像为:这样,我们就不能再用穷举法来找到最优解,而要另找新的方法,根据在模型二中证明救护站设置在街角处比设置在街段更优的思想,假设救护站A 与B 位于任意的街角处,若A东边紧急事件发生次数多于西边(在A 的负责范围内),则A 向东移动。
同样的讨论适用于南北方向。
当救护站两边发生的紧急事件次数相等时,救护站即处在最优位置。
问题转化为:已知一块质量分布不均匀的矩形木板的密度分布函数,求两个支撑点,使得只要木板在支撑点处受力即可保持平衡。
基本思想:任意选两个起始点,根据密度函数可以确定一条分界线,使在线两边的质量相等,然后再把每半边所在区域分成四个象限,若四个象限的质量满足条件:32414321A A A A A A A A +=++=+32414321B B B B B B B B +=++=+可推出:4231A A A A ==4132B B B B ==解方程可得A 与B 的最优位置。
而每个象限的质量可以通过 ),(y x σ乘以距离(y Y x X D -+-=1520,其中Y X ,为A 或B )在该象限积分⎰⎰dxdy D σ得到,但由于拟合得到的的四次函数很复杂,分界线可能不是直线,使难度大大增大,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多项式函数对所给的坐标进行拟合:构造关于系数a j 的多元函数:n2s( ai 1,L,apq)g[f(xg,yg )Z g]g 1点(311,…,a pq )是多元函数s (a 11,L ,a pq )的极小点,其中 g 为权函数,默认为1,所以点(811,…,a pq )必须满足方程组s3ijf(x,y)i 1 j 3j x yij 1,11ai i 1 j 1i 1 j 1 iX yf (x, y)a 11a 12y 2a 13yL q 1a 21x a 22xy2a 23xyLq 1a 2q xyM1i 1 i 12 Li 1 q 1a i1xy33Xya iqX y qMp 1p 1p 12Lp 1 qa p1X a p2X y a p3X ya pq X yp,qpq即1x 2x x M xp,yy2y M y q,A a 12La 1qa 22L a 2qM OMa p2La pqa iia 21Ma p1则函数又可表示为 f (x, y)x TAy ,拟合的目标就是求出系数矩阵 A 。
给定一组坐标(x g ’y g ’Z g ) , g 1,2,…,n ,表示有 n 个点。
要求用以下二元p q / i 1 j 1g ( a j X yi 1 j 1zg)2在g 1的情况下,有2[f (X g ,y g ) Z g ]g i2[f (X g ,y g )i 1 j 1Z g ]X g ygg in2g i因此可得nni 1 j 1 i 1 j 1 X g y gf(X g ,y g )X g y g Zgg 1g 1np qni X g1y g1 1 a X gy g 1i 1 jX gY g1Z gg 11 1g 1np,q ni X g1y g1 1 1aX g y gi 1 j 1X gy gz gg 11,1g 1p,qnnai 1 j(x gy g X g y g1、i 1Xy g1z g1,1g 1g 1p,qa u (i, j) v(i, j) (i, j)(1,1),…,(p,q)1,1上式实际共有p q 个等式,可将这比1(1,1) LU pq (1,1) anMO M MUn(p,q) L U pq (p,q) a pq也就是U*a=V 的形式,其中Un(1,1) L U pq (1,1)UM O MUn(P,q)LU pq (p,q)p q 个等式写成矩阵的形式有: v(1,1) M v( p, q)anv(1,1) a M ,V Ma pqv(p,q)2[f(X g ,y g ) 叩石If")]a ija ij x g 1y g 1f (xg ,y g ) x g+g zu (i, j)n(X g g 11yg1 i 1 X g y g 1), v(i,j)ni 1 j 1X g y gZ gg 1U为pq pq阶矩阵,实现函数为function A=leftmatrix(x,p,y,q);V为长pq的列向量,实现函数为function B=rightmatrix(x,p,y,q,z)。
这样就可以算出列矩阵a, 然后转化成A。
某地区有一煤矿,为估计其储量以便于开采,先在该地区进行勘探。
假设该地区是一长方形区域,长为4公里,宽为5公里。
经勘探得到如下数据: 煤矿勘探数据表请你估计出此地区内(2x4, 1 y 5 )煤的储量,单位用立方米表示,并用电脑画出该煤矿的三维图象。
如果直接画出三维曲面图形:clear;x=1:4;y=1:5;[X,Y]=meshgrid(x,y)Z=[13.72 25.80 8.47 25.27 22.32;15.47 21.33 14.49 24.83 26.19;23.28 26.48 29.14 12.04 14.58;19.95 23.73 15.35 18.01 16.29]'surf(X ,Y,Z);X =1 2 3 41 2 3 41 2 3 41 2 3 41 2 3 4Y =1 1 1 12 2 2 23 3 3 34 4 4 45 5 5 5Z =13.7200 15.4700 23.2800 19.950025.8000 21.3300 26.4800 23.73008.4700 14.4900 29.1400 15.350025.2700 24.8300 12.0400 18.010022.3200 26.1900 14.5800 16.2900粗略计算体积:底面积乘以平均高度。
p=sum(Z);q=P(:,[2,3,4]);h=sum(q')/15v=2000*4000*hh =20.0773v =1.6062e+008进行线性插值:xi=li nspace(1,4,31);yi=li nspace(1,5,41);[XI,YI]=meshgrid(xi,yi); ZI=i nterp2(X,Y,Z,XI,YI,'li near');surf(XI,YI,ZI);进行三次多项式插值:xi=li nspace(1,4, 31);yi=li nspace(1,5,Zl=interp2(X,Y,Z,XI,YI,' cubic ');surf(XI,YI,ZI);进行插值后计算体积:底面积乘以平均高度1 130、41);[XI,YI]=meshgrid(xi,yi);xi=li nspace(1,4,61);yi=linspace(1,5,81);[XI,YI]=meshgrid(xi,yi);Zl=i nterp2(X,Y,Z,XI,YI,'cubic');surf(XI,YI,ZI);H=0; n=0;for j=21:61for i=1:81H=H+ZI(i,j); n=n+1;endendnH=H/nS=2000*4000;V=S*H n =3321H =20.8222V =1.6658e+00830.上面是插值的方法解题,下面用拟合的方法解题。
为此编写了几个M函数:fun cti on U=leftmatrix(x,p,y,q)% U*a=V a 为系数列矩阵,长度为 p*q% U 为左边p*q 乘p*q 矩阵 % x,y 为长度一致的列矩阵,给定点的坐标 % p,q为拟合的函数中x,y 的幕的最高次数m=le ngth(x);if (nargin~=4) & (m~=le ngth(y))rightmatrix.mfun cti on V=rightmatrix(x,p,y,q,z)% U*a=V % V为一个列向量长为p*q% x y z 为点的坐标%p q 分别为xy 幕的最高次数 if n arg in~=5error( 'error check check! rightmatrix' endV=zeros(p*q,1); for i=1 : p*qx_z=quotie nt(i-1,q); y_z=mod(i-1,q);V(i,1)=qiuhe(x,x_z,y,y_z,z); endquuotie nt.mfun cti on sh=quotie nt(x,y) % sh 为x/y 的商sh=(x-mod(x,y))/y;error(end 'error check check!' );U_le ngth=p*q; U=zeros(U_le ngth,U_le ngth); for i=1 : p*q for j= 1 : p*qx_z=quotie nt(j-1,q)+quotie nt(i-1,q); y_z=mod(j_1,q)+mod(i_1,q); U(i,j)=qiuhe(x,x_z,y,y_z); end end% U 为p*q 阶方阵 %赋值0,目的是分配内存% x 的幕的次数,quotie nt %y 的幕的次数为求商qiuhe.mfun cti on he=qiuhe(x,p,y,q,z)% he x A p*y A q 从1 —>m 的和% x,y 向量长度相同% p,q分别为x,y的幕的次数m=le ngth(x);if (nargin<4 )&(m~=length(y))error( 'error check check!' );endif n arg in==4 %没有z , z=on es(m,1);end he=0;for i=1:mhe=he+x(i)Ap * y(i)Aq*z(i);% 1-->m 求和end先输入x=._、=••• z=. p=q=(注意x,y,z是向量); 拟合得到系数a,也就是得到了拟合的函数;根据拟合函数计算给定点(xx, yy)的函数值zz=f(xx, yy)并进行画图检验程序保存于M文件fit.m。
clear;[X,Y]=meshgrid(1:4,1:5);Z=[13.72 25.80 8.47 25.27 22.32;15.47 21.33 14.49 24.83 26.19;23.28 26.48 29.14 12.04 14.58;19.95 23.73 15.35 18.01 16.29]';x=reshape(X,20,1);y=reshape(Y,20,1);z=reshape(Z,20,1);p=4;q=5;U=leftmatrix(x,p,y,q); % U*a_ n=VV=rightmatrix(x,p,y,q,z);%a_n=i nv(U)*V;a_n=U\V;for i=1 : length(a_n) % 把长为p*q 的列向量a_n转换成p*q的矩阵aa ii=quotie nt(i-1,q)+1; % quotie nt %输入量至少为四,x,y行向量长度必需一样默认为元素全部为1的向量求商jj=mod(i-1,q)+1;aa(ii,jj)=a_n(i,1);endaa m=31;n=41; %m=4;n=5; [XI,YI]=meshgrid(linspace(1,4,m),linspace(1,5,n)); xx=reshape(XI,m*n,1); yy=reshape(YI,m*n,1);zz=zeros(m*n,1);xy=zeros(m*n,1);xt=zeros(m*n,1);yt=zeros(m*n,1);%zz=0; % zz for i=1 : p % for j=1 : q % aa xt=xx.A(i-1); yt=yy.A(j-1);xy=xt.*yt; zz=zz+aa(i,j).*xy;endendZI=reshape(zz,n,m); surf(XI,YI,ZI); %axis([1 4 1 5 0 30]) aa = 1.0e+003 *0.1465 -0.2678 0.2132 -0.0624 0.0058-0.7287 1.3972 -0.9275 0.2412 -0.02100.4416 -0.8415 0.5487 -0.1407 0.0122-0.0680 0.1295 -0.0839 0.0214 -0.0018是 xx,yy 代入所 拟 合的函数求出的函数 值函数为艺 aa(i,j)*x A i*y A j, (i=1...p,j=1...q) 为 pxq 的系数的矩 阵权函数在拟合的函数非常重要,不过她只能按你遇到的具体问题来取,我这里为1当p , q 越大时,拟合的函数与原数据的方差越小,但是有可能函数 本身抖动非常厉害,可以画图看出来。
