天大历年试题分类
天津大学考研试题及答案

天津大学考研试题及答案一、单项选择题(每题2分,共20分)1. 天津大学位于我国的哪个城市?A. 北京B. 上海C. 天津D. 广州答案:C2. 天津大学创建于哪一年?A. 1895年B. 1902年C. 1911年D. 1921年答案:A3. 天津大学是首批进入“211工程”的大学之一吗?A. 是B. 否答案:A4. 天津大学的校训是什么?A. 厚德博学,求是创新B. 厚德载物,自强不息C. 格物致知,明德至善D. 博学笃志,切问近思答案:A5. 天津大学在哪个学科领域具有显著优势?A. 工程学B. 医学C. 文学D. 法学答案:A6. 天津大学图书馆藏书量超过多少万册?A. 100万B. 200万C. 300万D. 400万答案:B7. 天津大学有多少个学院?A. 15个B. 20个C. 25个D. 30个答案:B8. 天津大学是教育部直属的高校吗?A. 是B. 否答案:A9. 天津大学在哪个区?A. 和平区B. 南开区C. 河西区D. 红桥区答案:B10. 天津大学校园内有多少个食堂?A. 3个B. 5个C. 7个D. 9个答案:B二、多项选择题(每题3分,共15分)1. 天津大学在哪些领域有国家重点学科?A. 化学工程与技术B. 材料科学与工程C. 机械工程D. 管理科学与工程答案:ABCD2. 天津大学有哪些国家级科研平台?A. 国家重点实验室B. 国家工程研究中心C. 国家工程技术研究中心D. 国家工程实验室答案:ABCD3. 天津大学提供哪些类型的研究生教育?A. 硕士研究生B. 博士研究生C. 专业学位研究生D. 非全日制研究生答案:ABCD三、简答题(每题5分,共20分)1. 请简述天津大学的历史沿革。
答案:天津大学前身为北洋大学,始建于1895年,是中国第一所现代大学,由清末洋务运动的代表人物盛宣怀创办。
后经过多次更名和迁址,于1951年正式更名为天津大学。
2. 天津大学在国际合作与交流方面有哪些举措?答案:天津大学积极开展国际合作与交流,与世界多所知名大学建立了合作关系,包括学生交换、联合培养、科研合作等多种形式。
天津大学最优化历年试题(精品资料).doc

【最新整理,下载后即可编辑】2003—2008《工程与科学计算》历届试题类型 1. 直解法例 1. 用列主元素Gauss 消去解下列线性方程组(结果保留5位小数)⎪⎩⎪⎨⎧=++=++=++0000.11000.12100.13310.18338.00000.10000.10000.16867.09000.08100.07290.0321321321x x x x x x x x x例2. 设线性方程组b Ax =,其中 11231112341113451A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦求)(A Cond ∞,并分析线性方程组是否病态 ? 2.迭代法例1. 设线性方程组b Ax =为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----221221122321x x x ααα , 0≠α写出求解线性方程组的Jacobi 迭代格式,并确定当α取何值时Jacobi 迭代格式收敛.例2. 写出求解线性方程组b Ax =的Seidel 迭代格式,并判断所写格式的收敛性,其中b Ax =为⎪⎩⎪⎨⎧=++-=+=-522826233213231x x xx x x x3.插值例 1. 已知,12144,11121,10100===(1)试用二次插值多项式计算115的近似值(数据保留至小数点后第5位)(2)估计所得结果的截断误差(数据保留至小数点后第5位) 例 2. 由下列插值条件4. Runge —Kutta 格式例 写出标准Kutta Runge -方法解初值问题⎩⎨⎧==+-=1)0(,1)0(sin 2'2'''y y xy xy y 的计算格式5. 代数精度例 1. 数值求积公式形如)1()0()1()0()()(321010f A f A f A f A x S dx x xf '+'++=≈⎰试确定其中参数,,,,4321A A A A 使其代数精度尽量高, 并确定代数精度.例 2. 验证数值求积公式20120()(1(1)(1f x dx A f A f A f ≈+++⎰是Gauss 型求积公式.6.Romberg 方法例 对积分⎰+1021dx x ,用Romberg 方法计算积分的近似值,误差不超过510-并将结果填入下表(结果保留至小数点后第五位).7(1)设)(x ϕ为],[b a 上关于权函数)(x ρ的n 次正交多项式,以)(x ϕ的零点为节点建立Lagrange 插值基函数)}({x l i , 证明:⎰⎰==ba ba i i ni dx x l x dx x l x ,,2,1,)]()[()()(2 ρρ证明: 设n 次正交多项式()x ϕ的零点为12,,n x x x ,则以这n 个零点为节点建立的Lagrange 插值基函数{()},1,2,i l x i n =是n-1次多项式,[]2()i l x 是2n-2次多项式. 故当()f x 取()i l x 和[]2()i l x 时Gauss 型求积公式1()()()nb k k ak x f x dx A f x ρ=≈∑⎰等号成立, 即 1()()()nb i k i k iak x l x dx A l x A ρ===∑⎰221()()()nbi k i k ia k x l x dx A l x A ρ===∑⎰则有 ⎰⎰==b abai i ni dx x l x dx x l x ,,2,1,)]()[()()(2 ρρ(2)对线性方程组b Ax =,若A 是n 阶非奇异阵,0≠b ,*x 是b Ax =的精确解,x 是b Ax =的近似解。
天津大学考试试题及答案

天津大学考试试题及答案一、单项选择题(每题2分,共20分)1. 天津大学位于我国的哪个直辖市?A. 北京B. 上海C. 天津D. 重庆答案:C2. 天津大学成立于哪一年?A. 1895年B. 1900年C. 1911年D. 1921年答案:A3. 下列哪项不是天津大学的主要学科领域?A. 工程学B. 文学C. 医学D. 法学答案:C4. 天津大学的校训是什么?A. 求实创新B. 厚德博学C. 自强不息D. 厚德载物答案:A5. 天津大学校园内著名的建筑是?A. 钟楼B. 鼓楼C. 塔楼D. 牌坊答案:A6. 天津大学的校徽颜色是什么?A. 蓝色B. 绿色C. 红色D. 黄色答案:A7. 天津大学图书馆藏书量超过多少册?A. 100万册B. 200万册C. 300万册D. 400万册答案:B8. 天津大学哪个学院是最早成立的?A. 机械工程学院B. 建筑学院C. 化工学院D. 材料科学与工程学院答案:A9. 天津大学在哪个国际大学排名中位列前茅?A. QS世界大学排名B. 泰晤士高等教育世界大学排名C. 世界大学学术排名D. 所有上述排名答案:D10. 天津大学每年举办的科技节是几月份?A. 3月B. 5月C. 9月D. 11月答案:B二、填空题(每题2分,共10分)1. 天津大学的校歌名称是______。
答案:《天津大学校歌》2. 天津大学校园内的著名景点之一是______湖。
答案:青年湖3. 天津大学在______年被确定为国家“211工程”重点建设大学。
答案:19954. 天津大学在______年成为“985工程”首批重点支持的大学。
答案:19995. 天津大学的校庆日是每年的______月______日。
答案:10月2日三、简答题(每题10分,共20分)1. 请简述天津大学的历史沿革。
答案:天津大学前身为北洋大学,始建于1895年,是中国第一所现代大学。
1951年,北洋大学与河北工学院合并,定名为天津大学。
天大历年试题分类

{
}
max {2cx Ax = bx ≥ 0}的最优解=
格= 。 (2004) 解:1. x* 2y*
,影子价
3. 某工程公司拟从 1、2、3、4 四个项目中选择若干项目。若令
⎧1,第i个项目被选中 …… 4 ,i = 1, xi = ⎨ ⎩0,第i个项目未选中
请用 xi 的线性表达式表示下列要求: (1)若项目 2 被选中,则项目 4 不能被选中: (2)只有项目 1 被选中,项目 3 才能被选中: 解:3. 。 (2004)
x4 − x5 ≥ 0, x1 + x4 ≤ 1.
1.某工程公司拟从四个项目中选择若干项目,若令 ⎧1, 第i个项目被选中 xi = ⎨ i = 1, 2,3, 4. ⎩0, 第i个项目末被选中 请用 xi 的线性表达式表示下列要求: (1)从 1,2,3 项目中至少选择一个: (2)只有项目 2 被选中,项目 4 才能被选中
σj
4) 5)
初表的出基变量为_____x4_____,进基变量为___x3______。 填完表 2,该表是否是终表?____是_____。若是,最优值 Z * = __-11______
⎡ 1 4 ⎤ 此线形规划对偶问题的最优解 Y * = ⎢ − , − ,0⎥ ⎣ 5 5 ⎦
(二)线性规划建模 二(20 分) 、某化学制药厂有 m 种有害副产品,它们的数量为 bi(i=1, …,m) 。按照规定, 必须经过处理,制成 n 种无害物后才能废弃。设 aij 为每制成一单位第 j(j=1, …,n)种无 害物可以处理掉第 i 种有害物的数量,cj 为制成一单位第 j 种无害物的费用。 1. 现欲求各无害物的产量 xj 以使总的处理费用为最小,请写出此问题的线性规划模型; 2. 写出此问题的对偶规划模型,并解释对偶规划模型的经济意义。 (2007) 解:1.
2023年天津大学城市规划原理历年真题

天津大学硕士院2023年招硕士生入学试题考试科目: 都市规划原理一、简答题(共10题, 每题4分, 本题40分)1.都市生态系统2.都市发展战略规划3.田园都市二、论述题1、古埃及旳都市规划成果和对后来都市规划旳影响意义, 古埃及旳都市建设特点2.控规和修规旳衔接3、都市总体艺术布局旳特点, 都市总体布局要点4.60年代都市规划学科获得旳成就5.都市绿地系统规划旳原则和措施6.都市历史文化遗产保护旳原则和措施7、都市整体环境保护天津大学硕士院2023年招硕士生入学试题考试科目: 都市规划原理一、简答题(共10题, 每题4分, 本题40分)1.都市生态系统2.规划管理3.一书两证4.城镇体系规划5.都市形态6.都市交通预测7、8、都市规划区9、都市管治10、交通量二、论述题1.17世纪巴洛克时期罗马改造以及绝对君权时期旳巴黎改建旳都市设计特性。
2.都市发展战略规划旳背景、作用及内容3.通过现代交通发展旳趋向和特点分析我国公交优先旳原则4.都市地段旳保护规定和内容与文物建筑保护旳规定和内容旳不一样。
5.都市设计旳含义和研究对象6.我国环境保护应重点处理旳问题7、居住区用地规划旳原则8、“田园都市”理论与80年代末流行旳“新都市主义”设计思潮旳异同。
9、举例一、两个经典都市, 试述西欧疏散于限制发展各大都市旳尝试。
10、60年代都市规划方面获得旳突出奉献和变化。
11.选择居住区用地旳重要原因天津大学硕士院2023年招硕士生入学试题考试科目: 都市规划原理一、简答题(共5题, 每题8分, 本题40分)1.雅典宪章和马丘比丘宪章2.田园都市与带行都市3.历史文化名城及历史文化名城保护规划4.都市生态规划5.都市发展战略规划二、简答题(共5题, 每题12分, 本题60分)1.都市规划实行管理旳重要内容2.现代交通发展旳趋向和特点及都市道路系统组织旳原则3.风景旅游都市布局旳特点4.都市历史地段旳保护规定和内容举例(不少于3个), 阐明文艺复兴与巴洛克时期广场建设旳成就三、论述题(共2题, 每题25分, 本题50分)1.试述20世纪50年代各国对古城、古建筑保护、对市中心和重要商业街区以及居住区旳规划构造等进行旳都市与建设旳探索。
天津大学结构力学考研试题2011-1996
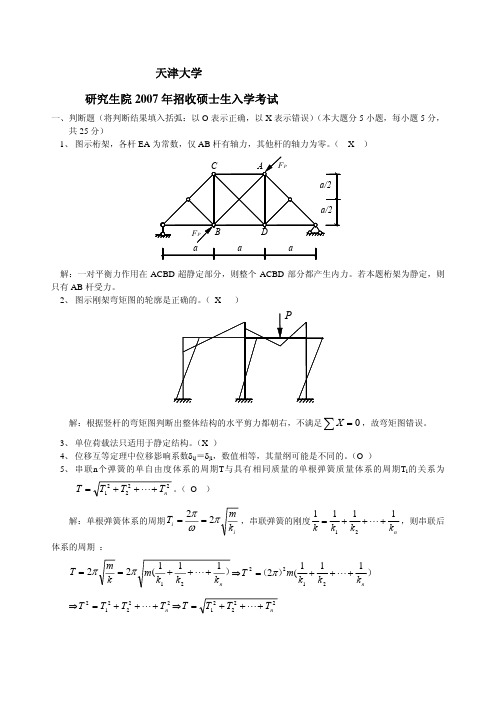
五、图示刚架,AB 杆及 CD 杆的线刚度为 i,BC 杆的线刚度为 2i,设固定端 D 向右移动Δ,试绘弯矩 图。(用位移法求解此题)(25 分)
l/2 l/2 l l
(a) 2i
B
i
(b) C
i
(c)
4i
3Δ i/2 l 3Δ i/2 l
3Δ i/2 l
3Δ i/2 l
i
A l
D Δ Δ/2
9Δ i/4l
。
(a)
M1
A
θΑ
(b)
M2 M1 θΒ B
EI l
EI
ϕΑ
l
解:图
a
中,由已知条件θ A
=
l 3EI
(M1
−
M2 2
) ,容易对比得出θ B
=
l 3EI
(M 2
−
M1 ) 2
当θB=B 0,即
M
=
2
M 2
1
时,a、b两图完全相同,带入θA可得θ A
=
l 3EI
(M1
−
M1 )= M1l 4 4EI
天津大学
研究生院 2007 年招收硕士生入学考试
一、判断题(将判断结果填入括弧:以 O 表示正确,以 X 表示错误)(本大题分 5 小题,每小题 5 分, 共 25 分)
1、 图示桁架,各杆 EA 为常数,仅 AB 杆有轴力,其他杆的轴力为零。( X )
C
A FP
a/2
a/2
FP B
D
a
a
a
解:一对平衡力作用在 ACBD 超静定部分,则整个 ACBD 部分都产生内力。若本题桁架为静定,则 只有 AB 杆受力。
天津大学《803机械原理与机械设计》历年考研真题汇编

目 录2011年天津大学机械原理与机械设计考研真题(回忆版)2009年天津大学803机械原理与机械设计考研真题2008年天津大学803机械原理与机械设计考研真题(部分)2007年天津大学403机械原理与机械设计考研真题2006年天津大学403机械原理与机械设计考研真题2005年天津大学423机械原理及机械设计考研真题2004年天津大学423机械原理及机械设计考研真题2003年天津大学423机械原理及机械零件考研真题版)f选择题较基础*较全ifh天大的资料、及历年真题中有部分喊题。
今年的选抒题.仙比较「aM图解法在F1处时,ABCD四杆机构处]•四点位置,DEF处「最小传动他.在F2时, A BCD四杆机构处于最小佳动角。
用图解法求DE、EF的长(12分)(图解法)一三、成粒仲劾类型.变位内轮,轮系*X=(17-Z)/I7,此题较简虬1叫、求凸轮反行程EI锁时.臭抡旋转角范围g图解法(1。
分)求自ih 度个虚:约束)。
还有几问比较难’H7分}六、求2、5的加 L 、A 4的年闻力,弯曲圈力的r匕求螺什最大迎切力.:较筒粘八、齿轮设计幽,.n接套聪中的公式,很简单兀、求制砌矩I.轴的改错,较筒单2009年天津大学803机械原理与机械设计考研真题考试甜旦代码:踱3试耕盲名称:机械原理与机械送衬W 入于伸修4U3十次二十・4朴I E 工八十为凶紊荃程必须与在答巍纸上,井写沱楚尊弓,答武哥在试卷K 无效,{C)不一定是一'单痕迷择^ 口。
小题,答小霆W 分,共4。
分) 圆枫破\.由对心曲松沿块挝拘的讯姑余杭通度国可做,吉潜坎姓P 极跟位置附,一_ 为■;; .(A)网精转速 (p 在杆加志坦 (C)清块上一点的域速度2机构自辕主妾是由于—的夺在漪产生的,有a 恭(A)驱幼力 (B)生产阻力 (C ;摩擦力 (D)攒性力2 .仅含一对噌舍齿抡的齿轮机梅临__Q 个速度瞬心,以相对瞬心的数目为(A)3: 2 '^?(B)2; 1 ■> (C)3: 1 JO) 2: 2 I 4一周转轮麝中.与某行星轮相啮合的齿皑_____ 牛心轮,至女(A) 一定是 (B)—定不是5.在选择凸艳机构的从泌运动狙律时,一段应根/工作要求若虑_.(A)运劫学 (B)动为陆性―—因吏舞"(C)运劾学和场方特姓 (D)舀轮瓣 , g .螺冶■平面刖尊辱引机曲时•位移西亲方程因―。
天津大学 结构力学 初试真题94到07年

天津大学研究生院1994年招收硕士生入学试题考试科目:结构力学(包含结构动力学) 题号:0901一.计算图1所示珩架指定杆的轴力()12,N N (10分)二.结构仅在ACB 部分温度升高t 度,并且在D 处作用外力偶M 。
试求图示刚架A,B 两点间水平向的相对位移。
已知:各杆的EI 为常值,α为线膨胀系数,h 为截面高度。
(20分)三.用力法分析图3所示结构,绘M 图。
计算时轴力和剪力对位移的影响略去不计。
各杆的EI 值相同。
(20分)半圆弧积分表:2211sin sin 2,cos sin 22424xx xdx x xdx x =-=+⎰⎰四.试用位移法求解图4所示刚架并绘M 图。
计算时不考虑轴力变形时对位移的影响。
(20分)杆端力公式:21,08f fABBA ql M M =-=,53,88f f AB BA ql ql Q Q ==- 一. 试用力矩分配法计算图5所示连续梁并绘M 图。
(10分)二. 求图示结构的自振频率和主振型,并作出振型图。
已知:122,,m m EI m m ===常数,忽略阻尼影响。
(20分)天津大学研究生院1995年招收硕士生入学试题考试科目:结构力学题号:0901一. 选择题:在正确答案处画“√”。
每题4分。
1.图示平面体系的几何组成性质是:A. 几何不变且无多余联系的B. 几何不变且有多余联系的C. 几何可变的D. 瞬变的2.图示结构A截面的剪力为:A. –PB. PC. P/2D. –P/23.图示珩架内力为零的杆为:A.3根B.6根C.8根D.7根3.图示结构的超静定次数为:A.6次B.4次C.5次D.7次4.图示梁当EI=常数时,B端的转角是:A. 3ql EI(顺时针)5/48B. 3ql EI(逆时针)5/48C. 3ql EI(逆时针)7/48D. 3ql EI(逆时针)9/48二.1.已知图示结构的M图,做Q.N图。
(10分)图(2.若P=1在梁AB上移动,试绘出M的影响线。
天津大学最优化历年试题

2003—2008《工程与科学计算》历届试题类型 1. 直解法例 1. 用列主元素Gauss 消去解下列线性方程组(结果保留5位小数)⎪⎩⎪⎨⎧=++=++=++0000.11000.12100.13310.18338.00000.10000.10000.16867.09000.08100.07290.0321321321x x x x x x x x x例2. 设线性方程组b Ax =,其中 11231112341113451A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦求)(A Cond ∞,并分析线性方程组是否病态 ? 2.迭代法例1. 设线性方程组b Ax =为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----221221122321x x x ααα , 0≠α写出求解线性方程组的Jacobi 迭代格式,并确定当α取何值时Jacobi 迭代格式收敛. 例 2. 写出求解线性方程组b Ax =的Seidel 迭代格式,并判断所写格式的收敛性,其中b Ax =为⎪⎩⎪⎨⎧=++-=+=-522826233213231x x xx x x x3.插值例 1. 已知,12144,11121,10100===(1)试用二次插值多项式计算115的近似值(数据保留至小数点后第5位) (2)估计所得结果的截断误差(数据保留至小数点后第5位) 例 2. 由下列插值条件4. Runge —Kutta 格式例 写出标准Kutta Runge -方法解初值问题⎩⎨⎧==+-=1)0(,1)0(sin 2'2'''y y x y xy y 的计算格式5. 代数精度例 1. 数值求积公式形如)1()0()1()0()()(321010f A f A f A f A x S dx x xf '+'++=≈⎰试确定其中参数,,,,4321A A A A 使其代数精度尽量高, 并确定代数精度. 例 2. 验证数值求积公式20120()(1(1)(1f x dx A f A f A f ≈++⎰是Gauss 型求积公式.6.Romberg 方法 例 对积分⎰+1021dx x ,用Romberg 方法计算积分的近似值,误差不超过510-并将结果填7.证明(1)设)(x ϕ为],[b a 上关于权函数)(x ρ的n 次正交多项式,以)(x ϕ的零点为节点建立Lagrange 插值基函数)}({x l i ,证明:⎰⎰==b abai i ni dx x l x dx x l x ,,2,1,)]()[()()(2Λρρ证明: 设n 次正交多项式()x ϕ的零点为12,,n x x x L ,则以这n 个零点为节点建立的Lagrange 插值基函数{()},1,2,i l x i n =L 是n-1次多项式,[]2()i l x 是2n-2次多项式. 故当()f x 取()i l x 和[]2()i l x 时Gauss 型求积公式1()()()nb k k ak x f x dx A f x ρ=≈∑⎰等号成立, 即1()()()nb i k i k iak x l x dx A l x A ρ===∑⎰221()()()nb i k i k iak x l x dx A l x A ρ===∑⎰则有 ⎰⎰==b abai i ni dx x l x dx x l x ,,2,1,)]()[()()(2Λρρ(2)对线性方程组b Ax =,若A 是n 阶非奇异阵,0≠b ,*x 是b Ax =的精确解,x 是b Ax =的近似解。
(整理)天津大学真题94-07.

天大考研相关信息2天津大学招收硕士研究生专业介绍专业代码:081303专业名称:城市规划与设计研究方向及硕士指导教师:指导教师研究方向运迎霞教授硕导 1.城市总体规划 2.城市土地开发与利用 3.控制性详细规划研究夏青教授硕导 1.住宅设计与居住区环境 2.高校校园规划 3.历史文化名城保护与规划姜耀明教授硕导 1.高校校园规划设计研究 2.居住小区规划设计研究3.城市中心区规划研究洪再生副教授硕导 1.城市更新与城市再开发 2.历史文化名城保护规划3.城市设计及理论陈天副教授硕导 1.城市设计及理论 2.城市环境与城市风貌规划3.人居环境设计4.城市形态与城市形象创造袁大昌副教授硕导 1.城市设计理论与实践 2.居住区规划龚清宇副教授硕导 1.生态的可持续性规划设计(ESDD)2.紧凑型城市结构与城市设计张晓宇副教授 1.城市总体规划2.计算机应用技术研究二、专业特点:本专业为国务院学位委员会批准的硕士学位授予单位。
师资力量雄厚。
教学设施有专用图书室、资料室、计算机绘图室、建筑造型室及模型室等。
城市规划与设计专业的研究方向主要是从事城市总体规划、详细规划、居住区环境及居住区规划设计、城市各类规划设计、旅游风景区规划设计、历史文化名城保护规划设计等课题的研究。
其他研究方向则侧重于城市环境、城市建筑群空间组合、现代城市建设理论以及中小城市和村镇规划、现代城市道路交通问题研究等课题。
本专业建于50年代中期,研究成果先后在《建筑学报》、《城市规划》、《建筑师》等刊物发表,获得国内外同行的好评。
出版了大量的专著,其中有些曾获国家科技进步奖、国家级或省部级奖,此外还从事了大量的实际规划设计项目,其中多项获省部级奖。
本专业于1962年开始招收研究生,对发展我国城市规划设计工作及培养理论研究人才肩负了重要任务。
三、硕士期间主要课程及论文要求:主要课程课程名称学时学分课程名称学时学分马克思主义理论课第一外国语(英、日、德、俄)数字化设计环境设计901204020 3521 城市规划设计(一)城市规划设计(二)建筑群与外部空间10010020 331论文要求:在学期间完成两篇读书报告,在正式刊物上发表一篇论文,毕业论文要求了解国内外学科动态,要有创新意识,写作时间满一年以上。
天津大学管理概论历年真题

学院专业班年级学号姓名共4 页第1 页
6、群体压力是指个体在群体中因与群体规范或其他多数成员意见时产生的
和焦虑心理。
7、网络图绘制中的冗余关系是指两道工序之间存在紧前或紧后关系。
四、简答题(5×4=20分)
1、系统管理原理应遵循的基本原则
2、简述管理发展史中“科学管理”理论的主要代表人及其主要贡献。
3、简述组织工作的特点
4、1933年梅奥在《工业文明的社会问题》一书中总结了霍桑实验的结果,得出了一些重要结论,这些结论有哪些?
5、控制工作的过程包括四个步骤,这四个步骤指的是什么?
五、是非题(5×2=10分)(判断下列各题的正确性。
正确的请在题后括号内打√,错误的请在题后括号内打×,错误的请加以改正。
)
1、以人为本的管理原理的思想基础认为人是“经济人”,应注重对其的物质奖励。
()
2、战略计划是为组织今后较短时间内设立目标的计划。
()
3、预算是计划的一种表现形式。
()
4、管理幅度是指一个管理者能够有效的管理下属的可能人数。
()
5、管理是动态的活动过程,其基本原理所包含的内容不是一成不变的。
()。
天津大学结构力学真题
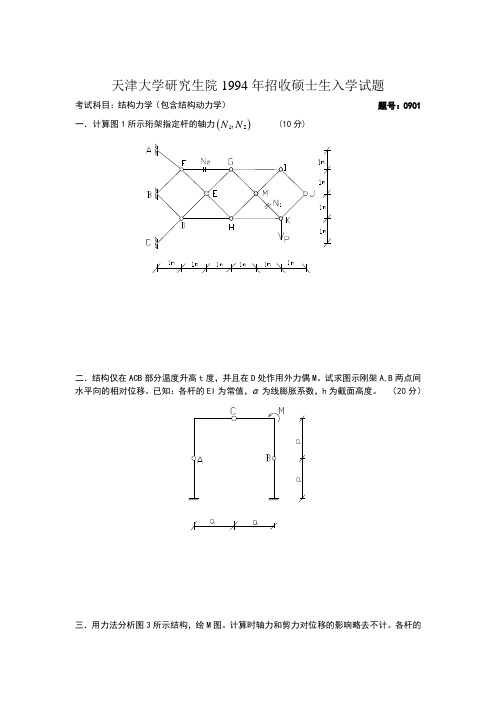
天津大学研究生院1994年招收硕士生入学试题考试科目:结构力学(包含结构动力学) 题号:0901 一.计算图1所示珩架指定杆的轴力()12,N N (10分)二.结构仅在ACB 部分温度升高t 度,并且在D 处作用外力偶M 。
试求图示刚架A,B 两点间水平向的相对位移。
已知:各杆的EI 为常值,α为线膨胀系数,h 为截面高度。
(20分)三.用力法分析图3所示结构,绘M 图。
计算时轴力和剪力对位移的影响略去不计。
各杆的EI 值相同。
(20分)半圆弧积分表:2211sin sin 2,cos sin 22424x x xdx x xdx x =-=+⎰⎰四.试用位移法求解图4所示刚架并绘M 图。
计算时不考虑轴力变形时对位移的影响。
(20分)杆端力公式:21,08f fABBA ql M M =-=,53,88ff AB BA ql ql Q Q ==-一.试用力矩分配法计算图5所示连续梁并绘M 图。
(10分)二.求图示结构的自振频率和主振型,并作出振型图。
已知:122,,m m EI m m ===常数,忽略阻尼影响。
(20分)天津大学研究生院1995年招收硕士生入学试题考试科目:结构力学题号:0901一.选择题:在正确答案处画“√”。
每题4分。
1.图示平面体系的几何组成性质是:A.几何不变且无多余联系的B.几何不变且有多余联系的C.几何可变的D.瞬变的2.图示结构A截面的剪力为:A. –PB. PC. P/2D. –P/23.图示珩架内力为零的杆为:A.3根B.6根C.8根D.7根3. 图示结构的超静定次数为:A . 6次B . 4次C . 5次D . 7次4. 图示梁当EI =常数时,B 端的转角是: A. 35/48ql EI (顺时针) B. 35/48ql EI (逆时针) C. 37/48ql EI (逆时针) D. 39/48ql EI (逆时针)二.计算题1.已知图示结构的M图,做图。
天津大学强基面试题目(3篇)

第1篇一、引言天津大学作为我国知名的高等学府,其强基计划旨在选拔一批有志向、有兴趣、有天赋的青年学生,进行专门培养,为国家重大战略领域输送后备人才。
面试作为强基计划选拔的重要环节,对考生的综合素质、创新能力、兴趣志向、科研潜质、科学精神等方面进行全面考察。
本文将结合天津大学强基计划的特点,对面试题目进行深入解析,帮助考生更好地备战面试。
二、面试题目类型天津大学强基计划面试题目主要分为以下几类:1. 学科素养类题目:考察考生对高中知识、大学专业知识和科学研究前沿内容的掌握程度。
2. 时事热点类题目:考察考生对社会热点问题的关注程度和思考能力。
3. 综合素质类题目:考察考生的思维能力、沟通能力、团队合作能力等。
4. 创新能力类题目:考察考生的创新思维、解决问题的能力等。
5. 科研潜质类题目:考察考生的科研兴趣、科研方法、科研实践等。
三、面试题目解析以下是一些典型的天津大学强基计划面试题目及其解析:(一)学科素养类题目1. 题目:你知道数学家张益唐的事迹么?朗道-西格尔零点猜想是什么?张益唐的工作有什么意义?解析:此题考察考生对数学家及其工作的了解程度。
张益唐是华裔数学家,他的研究成果对数学界产生了重要影响。
考生需要了解张益唐的事迹、朗道-西格尔零点猜想以及张益唐的工作意义。
2. 题目:讲一个你知道的数学定理,并谈谈它的证明。
解析:此题考察考生对数学定理的理解和掌握程度。
考生需要选择一个自己熟悉的数学定理,并对其证明过程进行阐述。
3. 题目:所有自然数之和是多少?解析:此题考察考生的数学思维能力和逻辑推理能力。
考生需要运用数学方法求解自然数之和。
4. 题目:不规则二维图形面积如何求解?解析:此题考察考生的几何知识和解决问题的能力。
考生需要运用几何知识求解不规则二维图形的面积。
5. 题目:导数有什么数学意义和物理意义?解析:此题考察考生对导数的理解程度。
考生需要从数学和物理两个方面阐述导数的意义。
(二)时事热点类题目1. 题目:同济大学强基计划考查到了新能源相关问题,你能谈谈你对新能源发展的看法吗?解析:此题考察考生对新能源发展的关注程度和思考能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、线性规划 二、运输问题 三、多目标规划 四、动态规划 五、图论六、网络计划技术 七、决策论 八、存储论 九、排队论 十、对策论 十一、模拟技术一、线性规划(一)选择填空题 (二)线性规划建模 (三)互补松弛应用 (四)灵敏度分析 (五)证明题(一)选择填空题型):(1)初表的出基变量为 ,进基变量为 。
[]=-1*)2(B最优基逆(3)填完终表。
=*)4(X 最优解=*)5(y 对偶问题最优解(6)若原问题增加一个新的非负变量,则对偶问题的最优目标值将(变大、不变、变小) 。
(2007)解:1.(1)出基变量为x 4;进基变量为x 3。
(2)*12105101305101112B -⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦。
(3)(4) *(4511)T X =(5) *14(0)55Y = (6) 变小1.用图解法解线性规划时,以下几种情况中不可能出现的是( )。
A .可行域(约束集合)有界,无有限最优解(或称无解界)B .可行域(约束集合)无界,有唯一最优解C .可行域(约束集合)是空集,无可行解D .可行域(约束集合)有界,有多重最优解 (2006)解:1. A2.根据线性规划的互补松弛定理,安排生产的产品机会成本一定( )利润。
A . 小于 B . 等于 C . 大于 D . 大于等于 (2006)解:2. B1.用大M 法求解Max 型线形规划时,人工变量在目标函数中的系数均为____________,若最优解的_______________中含有人工变量,则原问题无解。
(2005)解:1、-M 基变量1. 设线性规划问题}{0max ≥=bx Ax cx 有最优解*x 和影子价格*y ,则线性规划问题}{02max ≥=bx Ax cx 的最优解= ,影子价格= 。
(2004)解:1. x* 2y*3. 某工程公司拟从1、2、3、4四个项目中选择若干项目。
若令4101⋯⋯=⎩⎨⎧=,,个项目未选中,第个项目被选中,第i i i x i请用i x 的线性表达式表示下列要求:(1)若项目2被选中,则项目4不能被选中: (2)只有项目1被选中,项目3才能被选中: 。
(2004)解:3. 0,13142≤-≤+x x x x一、简答(18%)(1)请简述影子价格的定义。
(2)在使用单纯型表求解型线性规划时,资源的影子价格在单纯型表的什么位置上? (3)写出影子价格的数学表达式并用其定义加以验证 (4)试述运输问题中检验数的经济意义(2003)解:一、简答⑴当各资源增加一单位时引起的总收入的增量,影子价格大于零的资源一定没有剩余,有剩余一定为零。
⑵松弛变量检验数的负值,对偶问题的最优解。
⑶C B B -1B 是原问题{maxz=C X ∣AX ≤b,X ≥0}最优基 Z *= C B B -1b=Y *b Z *=y 1*b 1+y 2*b 2…y m *b m*z bδδ=y3* ⑷表明增加一个单位的运量会引起总运输费用的变化1. 线性规划原问题中约束的个数与其对偶问题中的 变量 个数相等。
若原问题第j 个约束为等式,则对偶问题第j 个 变量 自由。
(2002) 解:2. 设线性规划问题max:{cx|Ax ≤bx ≥0}有最优解,且最优解值z>0;如果c 和b 分别被v>1所乘,则改变后的问题 也有 (也有、不一定有)最优解;若有最优解,其最优解 大于 (大于、小于、等于)z 。
(2002)1.下列数学模型中 a 是线性规划模型。
(2001)⎭⎬⎫⎩⎨⎧++++=32954867min max )(321321x x x x x x Z b321324m ax )(x x x Z a ++=⎪⎩⎪⎨⎧≥≤++≤++0,,120544150637..321321321x x x x x x x x x t s ⎪⎩⎪⎨⎧≥≤++≤++0,,500896300355..321321321x x x x x x x x x t s 解:2.下列图形(阴影部分)中 b 是凸集。
(2001)(a ) (b ) (c ) 解:3.标准形式的线性规划问题,其可行解 b 是基本可行解,最优解 a 是可行解,最优解 a 能在可行域的某顶点达到。
(2001)(a )一定 (b )不一定 (c )一定不 解:4.目标函数取极小(min Z )的线性规划问题可以转化为目标函数取极大 b 的线性规划问题求解,原问题的目标函数值等于 c 。
(2001)(a )max Z (b )max (-Z ) (c )-max (-Z ) (d )-max Z (a )最小元素法 (b )比回路法 1. 线性规划单纯形算法的基本步骤是:(1) (2) (3) 每次迭代保持解的 ,改善解值的 。
对偶单纯形法每次迭代保持解的 ,改善解值的 。
(2000)解:确定一个初始基可行解;检验一个基可行解是否为最优解;寻找一个更好基可行解;可行性;最优性。
2. 设有线性规划问题[]{}0,|,m in ≥==∈=X b AX X R X CX f ,有一可行基B (为A 中的前m 列),记相应基变量为πX ,价格系数为C B ,相应于非基变量为X N ,价格系数为C N ,则相应于B 的基本可行解为X= ;用非基变量来表示基变量的表达式为X B = ;用非基变量表示目标函数的表达式为f= ,B 为最优基的条件是 。
(2000)解:111111,,(),00N B N B N N B B b B b B NX C B b C C B N X C C B N ------⎛⎫-+--≥ ⎪⎝⎭3. 线性规划(Min 型)问题有多重最优解时,其最优单纯形表上的特征为: (2000)解:0,0.j k j x σσ≥=所有检验数而某一个非基变量检验数 6. 某足球队要从1,2,3,4,5号五名队员中挑选若干名上场。
令⎩⎨⎧=54321i i 0i 1,,,,=号不上场,第号上场第i x 请用x i 的线性表达式表示下列要求:(1)从1,2,3中至多选2名: (2)如果2号和3号都上场,则5号不上场: (3)只有4号上场,1号才上场:(2000) 解:12345142,0, 1.x x x x x x x ++≥-≥+≤1.某工程公司拟从四个项目中选择若干项目,若令1,1,2,3,4.0,i i x i i ⎧==⎨⎩第个项目被选中第个项目末被选中请用x i 的线性表达式表示下列要求:(1)从1,2,3项目中至少选择一个: ,(2)只有项目2被选中,项目4才能被选中 。
(1999)解:1、x 1+x 2+x 3≥1x 2≥x 42.考虑线形规划问题123123123123max 512425..232,,0Z x x x x x x s t x x x x x x =++++≤⎧⎪-+=⎨⎪≥⎩45(1)上述模型的对偶模型为 , (2)对偶模型的最优解为 ,(3)当两种资源分别单独增加一个单位时,目标函数值分别增加 和 ,(4)最优基的逆矩阵1B -⎡⎤=⎢⎥⎣⎦(5)如果原问题增加一个变量,则对偶问题的可行域将可能变大还是变小?(1999)解:2.(1)1212121212min 5225212340,W y y y y y y y y y y =++≥⎧⎪-≥⎪⎨+≥⎪⎪≥⎩无符号限制(2)Y*=(295,-25)(3)295,-25(4)21551255⎛⎫- ⎪⎪ ⎪ ⎪⎝⎭(5)变小1.下面给出某线形规划的单纯形初表(表1)与某一中间表(表2)(Min 型):1) 初表的出基变量为__________,进基变量为_________。
2) 填完表2,该表是否是终表?_________。
若是,最优值=*Z ________ 3) 此线形规划对偶问题的最优解=*Y _______(1998)解:1.下面给出某线形规划的单纯形初表(表1)与某一中间表(表2)(Min 型):4) 初表的出基变量为_____x 4_____,进基变量为___x 3______。
5) 填完表2,该表是否是终表?____是_____。
若是,最优值=*Z __-11______此线形规划对偶问题的最优解=*Y ⎥⎦⎤⎢⎣⎡--,054,51 解: 解: 解: 解:解: 解:(二)线性规划建模 二(20分)、某化学制药厂有m 种有害副产品,它们的数量为b i (i=1,…,m )。
按照规定,必须经过处理,制成n 种无害物后才能废弃。
设aij 为每制成一单位第j (j=1,…,n )种无害物可以处理掉第i 种有害物的数量,cj 为制成一单位第j 种无害物的费用。
1. 现欲求各无害物的产量xj 以使总的处理费用为最小,请写出此问题的线性规划模型; 2. 写出此问题的对偶规划模型,并解释对偶规划模型的经济意义。
(2007) 解:1.11111221121122222112212min ..,,0nj jj n n n n m m mn n mn z c x a x a x a x b a x a x a x b s t a x a x a x bx x x ==∑++⋯+≥⎧⎪++⋯+≥⎪⎪⋯⋯⎨⎪++⋯+≥⎪⋯≥⎪⎩, 2.11112121112122222112212max ..,,0mi ii m m m m n n mn m nm z y b a y a y a y c a y a y a y c s t a y a y a y cy y y ==∑++⋯+≤⎧⎪++⋯+≤⎪⎪⋯⋯⎨⎪++⋯+≤⎪⋯≥⎪⎩, 经济意义:i y 为第i 种有害副产品不经处理直接废弃的费用。
二(10%)、某大型企业每年需要进行多种类型的员工培训。
假设共有需要培训的需求(如技术类、管理类)为6种,每种需求的最低培训人数为a i ,i=1,…,6, 可供选择的培训方式(如内部自行培训、外部与高校合作培训)有5种,每种的最高培训人数为bj, j=1,…,5。
又设若选择了第1种培训方式,则第3种培训方式也要选择。
记x ij 为第i 种需求由第j 方式培训的人员数量,z 为培训总费用。
费用的构成包括固定费用和可变费用,第j 种方式的固定费用为hj (与人数无关),与人数x ij 相应的可变费用为c ij (表示第j 方式培训第i 种需求类型的单位费用)。
如果以成本费用为优化目标,请建立该培训问题的结构优化模型(不解)。
(2006)解:二、ij x i j 设为第种需求由第种方式培训的人员数量,1j 0j y ⎧=⎨⎩选择培训方式否则565111min j j ij ij j i j z y h c x ====+∑∑∑615113(1,2,,5)(1,2,,6)00(1,6,1,2,,5)01(1,2,,5)ij j j i ij i j ijj x b y i x a i y y x i j y j ==⎧≤=∑⎪⎪⎪≥=∑⎪⎪-≤⎨⎪≥==⎪⎪==⎪⎪⎩L L L L L 或123约束依A,B 原料次序):(2)写出此问题的对偶规划模型(2003)解:⒈①maxz=30x 1+20x 2+35x 3-8x 1-5x 2-18x 3-5(x 1+0.4x 2+0.6x 3)-7(0.5x 1+0.6x 2+0.5x 3) 目标函数maxz=13.5x 1+8.8x 2+10.5x 3 约束条件 x 1+0.4x 2+0.6x 3≤350 0.5x 1+0.6x 2+0.5x 3≤460 x 1≥0,x 2≥0,x 3≥0②对偶规划模型目标函数 minw=350y 1+460y 2 约束条件y 1+0.5y 2≥13.5 0.4y 1+0.6y 2≥8.8 0.6y 1+0.5y 2≥10.5 y 1≥0,y 2≥0 三、(10%)某服装厂制造大、中、小三种尺寸的防寒服,所用资源有尼龙绸、尼龙棉、劳动力和缝纫设备。
