系统辨识作业1
系统辨识(1):辨识导引

后 , 多现 成 的控 制 系统 设 计 、 析 和综 合 方 法 都 可套 用 , 为实 际 许 分 因
系统 不是追 求一 个 新 的控 制 方 法 , 是 一个 比较成 熟 控 制 方 法 的可 而
靠应用 .
资 助项 目 国家 自然 科 学基 金 (0 70 3 694 4 ) 作 者 简 介 丁锋 , , 士 , 授 , 士生导师 , 男 博 教 博 主要 从 事 系 统 辨识 、 程 建 模 、 过 自适 应 控 制 方 面 的研
辨 识 得 到 了长 足 的 发 展 , 些 新 的 辨 识 一 方 法相 继 问 世 , 理 论 与 应 用 成 果 覆 盖 其
了 自然 科 学 和 社 会 科 学 的 各 个 领 域 , 包 括物理 学、 物学 、 生 地球 科 学 、 象 学 、 气 计 算机科 学、 经济学 、 心理 学、 政治 学等. 在 这 样 的 背 景 下 , 过 头 来 深 思 系统 辨 识 回 的 一 些 基 本 问题 , 系 统 辨 识 的 发 展 不 对 无 裨 益 . 为 系统 辨 识 的 导 引 论 文 , 单 作 简
()=G s ( ) u f f ( ) , ()=
次 的识 别 、 统参 系
数 的估计 , 以及 估计 方法 的收 敛性 等. 文简单 介绍 本 第 1 方程 是控 制 问题 , 2个 方 程 是 自校 正控 制 辨识 的定 义 、 学模 型与 辨识模 型 、 个 第 数 辨识 步骤 和辨识 问题 ( 自校 正解 决 跟 踪 问 题 , 程 中 的 Y t 一 般 改 方 法 的类 别. 后继 的系列文 章 中 , 依 次介绍 有关 方 () 在 将 为期 望的轨 迹 Y( ) , 3个方程 是辨 识 问题 . 只 ,t ) 第 这 是 简单说 明 了它们 的关 系 , 它们 各 形成 了一 门学科 , 有其各 自的研 究 目标和研 究 内容 .
系统辨识大作业.

系统辨识大作业
已知一系统为两输入单输出系统,观测数据受有色噪声污染,噪信比为N/S=0.1。
系统经2000次采样,存放于文件T3T.TXT中。
系统输入u1为7级M序列,u2为u1的63步移位序列。
模型类可选为:A(q-1)y(k)=B1(q)u1(k)+ B2(q)u2(k)+w(k)/C(q-1)。
要求编制程序,辨识出该模型的结构及参数。
作业文档要求:
描述问题;
选择辨识方法并简单说明所选方法中的结构辨识原理和参数估计原理;
程序流程图及程序清单;
说明程序中用到的一些技术,如数据标准化、UD分解、稳定性判断等;
结构搜索路线及各结构下的参数、残差;
给出最终结果:A(q-1)=
B1(q)=
B2(q)=
C(q-1)=
并给出选择此最终结果的理由;
用你的辨识结果来预报系统输出误差e(k)=y(k)-y(k),并画出e(101)-e(400)的曲线图。
系统辨识大作业1201张青

《系统辨识》大作业学号:********班级:自动化1班姓名:**信息与控制工程学院自动化系2015-07-11第一题模仿index2,搭建对象,由相关分析法,获得脉冲响应序列ˆ()g k,由ˆ()g k,参照讲义,获得系统的脉冲传递函数()G z和传递函数()G s;应用最小二乘辨识,获得脉冲响应序列ˆ()g k;同图显示两种方法的辨识效果图;应用相关最小二乘法,拟合对象的差分方程模型;构建时变对象,用最小二乘法和带遗忘因子的最小二乘法,(可以用辨识工具箱) 辨识模型的参数,比较两种方法的辨识效果差异;答:根据index2搭建结构框图:相关分析法:利用结构框图得到UY 和tout其中的U就是题目中要求得出的M序列,根据结构框图可知序列的周期是1512124=-=-=npN。
在command window中输入下列指令,既可以得到脉冲相应序列()g k:aa=5;NNPP=15;ts=2; RR=ones(15)+eye(15); for i=15:-1:1UU(16-i,:)=UY(16+i:30+i,1)'; endYY=[UY(31:45,2)];GG=RR*UU*YY/[aa*aa*(NNPP+1)*ts]; plot(0:2:29,GG) hold onstem(0:2:29,GG,'filled') Grid;title('脉冲序列g(τ)')最小二乘法建模的响应序列由于是二阶水箱系统,可以假设系统的传递函数为221101)(sa s a sb b s G +++=,已知)(τg ,求2110,,,a a b b已知G (s )的结构,用长除法求得G(s)的s 展开式,其系数等于从 )( g 求得的各阶矩,然后求G(s)的参数。
得到结果: a1 =-1.1561 a2 =0.4283 b0 =-0.0028 b1=0.2961在command window 中输入下列指令得到传递函数:最小二乘一次算法相关参数%最小二乘法一次完成算法 M=UY(:,1); z=UY(:,2); H=zeros(100,4); for i=1:100 H(i,1)=-z(i+1); H(i,2)=-z(i); H(i,3)=M(i+1); H(i,4)=M(i); endEstimate=inv(H'*H)*H'*(z(3:102)) %结束得到相关系数为:Estimate =-0.7866 0.1388 0.5707 0.3115带遗忘因子最小二乘法:%带遗忘因子最小二乘法程序M=UY(:,1);z=UY(:,2);P=1000*eye(5); %Theta=zeros(5,200); %Theta(:,1)=[0;0;0;0;0];K=zeros(4,400); %K=[10;10;10;10;10];lamda=0.99;%遗忘因数for i=3:201h=[-z(i-1);-z(i-2);M(i);M(i-1);M(i-2)];K=P*h*inv(h'*P*h+lamda);Theta(:,i-1)=Theta(:,i-2)+K*(z(i)-h'*Theta(:,i-2));P=(eye(5)-K*h')*P/lamda;endi=1:200;figure(1)plot(i,Theta(1,:),i,Theta(2,:),i,Theta(3,:),i,Theta(4,:),i,Theta(5,:) )title('带遗忘因子最小二乘法')grid%结束Estimate 可由仿真图得出,可知两种方法参数确定十分接近。
系统辨识大作业加学习心得

论文系统辨识姿态角控制1.系统辨识概述辨识、状态估计和控制理论是现代控制理论三个相互渗透的领域。
辨识和状态估计离不开控制理论的支持,控制理论的应用又几乎不能没有辨识和状态估计技术。
随着控制过程复杂性的提高,控制理论的应用日益广泛,但其实际应用不能脱离被控对象的数学模型。
然而在大多数情况下,被控对象的数学模型是不知道的,或者在正常运行期间模型的参数可能发生变化,因此利用控制理论去解决实际问题时,首先需要建立被控对象的数学模型。
系统辨识正是适应这一需要而形成的,他是现代控制理论中一个很活跃的分支。
社会科学和自然科学领域已经投入相当多的人力去观察、研究有关的系统辨识问题。
系统辨识是建模的一种方法,不同的学科领域,对应着不同的数学模型。
从某种意义上来说,不同学科的发展过程就是建立他的数学模型的过程。
辨识问题可以归结为用一个模型来表示可观系统(或将要改造的系统)本质特征的一种演算,并用这个模型吧对客观系统的理解表示成有用的形式。
当然可以刻有另外的描述,辨识有三个要素:数据,模型类和准则。
辨识就是按照一个准则在一组模型类中选择一个与数据拟合得最好的模型。
总而言之,辨识的实质就是从一组模型类中选择一个模型,按照某种准则,使之能最好地拟合所关心的实际过程的静态或动态特性。
通过辨识建立数学模型的目的是估计表征系统行为的重要参数,建立一个能模仿真实系统行为的模型,用当前可测量的系统的输入和输出预测系统输出的未来演变,以及设计控制器。
对系统进行分析的主要问题是根据输入时间函数和系统的特性来确定输出信号。
对系统进行控制的主要问题是根据系统的特性设计控制输入,使输出满足预先规定的要求。
而系统辨识所研究的问题恰好是这些问题的逆问题。
通常,预先给定一个模型类{}M(即给定一类已知结构的模型),一类输入信号u和等价准则(,)JLyyM(一般情况下,J是误差函数,是过程输出y和模型输出yM的一个泛函);然后选择是误差函数J达到最小的模型,作为辨识所要求的结果。
系统辨识作业

1.1讨论系统方程为:(信噪比)至少30%)()1()()1()(k e k u k b k ay k y +-=-+)(k e 为零均值白噪声, =)(k a =)(k b要求对系统参数辨识进行讨论(1) 定常系统 a=0.8,b=0.5参数递推估计 (2) 时变系统取不同值是的不同结果并讨论。
(1)取初值P (0)=I 、∧θ(0)=0选择方差为1的白噪声作为输入信号u (k ),L=300,采用RLS 算法进行参数估计,代码及仿真结果图如下:clear all ;close all ;a=[1 0.8]';b=[0.5]';d=1; %对象参数na=length(a)-1;nb=length(b)-1; %na 、nb 为A 、B 阶次L=300; %仿真长度uk=zeros(d+nb,1); %输入初值:uk(i)表示u(k-i) yk=zeros(na,1); %输出初值u=randn(L,1); %输入采用白噪声序列 xi=sqrt(0.1)*randn(L,1); %白噪声序列theta=[a(2:na+1);b]; %对象参数真值thetae_1=zeros(na+nb+1,1); %thetae 初值 P=10^6*eye(na+nb+1); for k=1:Lphi = [-yk;uk(d:d+nb)]; %´此处phi 为列向量 y(k)=phi'*theta + xi(k); %采集输出数据%递推最小二乘法K=P*phi/(1+phi'*P*phi);thetae( : ,k)=thetae_1 + K*(y(k)-phi'*thetae_1); P=(eye(na+nb+1)-K*phi')*P;%更新数据thetae_1 = thetae( : ,k);for i=d+nb:-1:2 uk(i)=uk(i-1); enduk(1)=u(k); for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);endplot([1:L],thetae); %line([1,L],[theta,theta]); xlabel('k');ylabel('参数估计a、b');legend('a_1','b_0');axis([0 L -2 2]);图1-1 递推最小二乘法的参数估计结果(2))取初值P(0)=I、∧θ(0)=0选择方差为1的白噪声作为输入信号u(k),取分别为0.91,0.95,0.98,1.00时,L=600,采用FFRLS算法进行参数估计,代码及仿真图如下所示:clear all;close all;a=[1 0.8]';b=[0.5]';d=1; %对象参数na=length(a)-1;nb=length(b)-1; %na、nb为A、B阶次L=600; %仿真长度uk=zeros(d+nb,1); %输入初值:uk(i)表示u(k-i)yk=zeros(na,1); %输出初值u=randn(L,1); %输入采用白噪声序列xi=sqrt(0.1)*randn(L,1); %白噪声序列thetae_1=zeros(na+nb+1,1); %thetae初值P=10^6*eye(na+nb+1);lambda=0.98; %遗忘因子范围[0.9 1]for k=1:Lif k==301a=[1 0.6]';b=[0.3]'; %对象参数突变endtheta( : ,k)=[a(2 : na+1);b]; %对象参数真值phi = [-yk;uk(d:d+nb)]; %´此处phi为列向量y(k)=phi'*theta( : ,k) + xi(k); %采集输出数据%遗忘因子递推最小二乘法·¨K=P*phi/(lambda+phi'*P*phi);thetae( : ,k)=thetae_1 + K*(y(k)-phi'*thetae_1);P=(eye(na+nb+1)-K*phi')*P/lambda;%更新数据thetae_1 = thetae( : ,k);for i=d+nb:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);endsubplot(1,2,1)plot([1:L],thetae(1:na,:));hold on;plot([1:L],theta(1:na,:),'k:'); xlabel('k');ylabel('参数估计a');legend('a_1');axis([0 L -2 2]);subplot(1,2,2)plot([1:L],thetae(na+1:na+nb+1,:));holdon;plot([1:L],theta(na+1:na+nb+1,:),'k:');xlabel('k');ylabel('参数估计b');legend('b_0');axis([0 L -0.5 2]);图1-2-1 遗忘因子递推最小二乘法的参数估计结果(λ=0.91)图1-2-2 遗忘因子递推最小二乘法的参数估计结果(λ=0.95)图1-2-3遗忘因子递推最小二乘法的参数估计结果( =0.98)图1-2-4 遗忘因子递推最小二乘法的参数估计结果(λ=1)由以上可以看出,技术对于参数突变的系统,采用FFRLS算法也能够有效地进行参数估计。
系统辩识作业题

系统辨识大作业
一.设SlSO系统差分方程为
y(k)=—α1y(k-1)-a2y(k-2)+bλu(k-1)+b2u(k-2)+ξ{k)
辨识参数向量为θ=[q a2b l b2]r,输入输出数据详见数据文件UyLtXt—uy3.txtoξ(k)为噪声方差各异的白噪声或有色噪声。
试求解:
1)用n元一次方程解析法,再求其平均值方法估计。
2)用最小二乘及递推最小二乘法估计。
;
3)用辅助变量法及其递推算法估计
4)用广义最小二乘法及其递推算法估计
5)用夏氏偏差修正法、夏氏改良法及其递推算法估计
6)用增广矩阵法估计
7)分析噪声父攵)特性;
二.用极大似然法估计6。
三.以上题的结果为例,进行:
1.分析比较各种方法估计的精度;
2.分析其计算量;
3.分析噪声方差的影响;
4.比较白噪声和有色噪声对辨识的影响。
四.系统模型阶次的辨识:
1.用三种方法确定系统的阶次并辨识;
2.分析噪声对定阶的影响;
3.比较所用三种方法的优劣及有效性;
五.给出由正弦输入求取系统开环频率响应特性曲线的辨识方法。
六.提出一种自己创造的辨识新方法,并用所给数据进行辨识验证。
注:闭卷考试时提交大作业报告。
系统辨识大作业

系 统 辨 识大 作 业系统辨识大作业1.考虑如下系统y() 1.5(1)0.7(2)(3)0.5(4)()k y k y k u k u k k ξ--+-=-+-+式中,()k ξ为白噪声。
取初值6(0)10P I =,ˆ(0)0θ=。
分别选择M 序列和方差为1的正态分布白噪声作为输入信号()u k ,采用递推最小二乘算法进行参数估计,迭代L=400步停止计算。
要求i) 给出基本迭代公式;ii) 画出程序流程框图;iii) 画出输入输出数据曲线、参数估计曲线、误差曲线;(提示:产生长度为L 方差为1的正态分布白噪声的MATLAB 命令为 randn (L,1)。
)答:选择如下形式的辨识模型)()4()3()2()1()(2121k k u b k u b k z a k z a k z ξ+-+-=-+-+设输入信号的取值是1.从1=k 到16=k 的M 序列,采用4位移位寄存器产生,幅度为0.03;2. 方差为1、长度为L 的正态分布白噪声,用randn(L,1)命令产生;i) 基本的迭代公式为1ˆˆˆ()(1)()[()()(1)]1()(1)()()(1)()()()[()()](1)T T T k k k z k k k k k k k k k k k I k k k θθθ-⎧=-+--⎪⎪⎡⎤=--+⎨⎢⎥Λ⎣⎦⎪⎪=--⎩K h K P h h P h P K h Pii) 程序流程框图iii)源代码与输入输出曲线、参数估计曲线、误差曲线%最小二乘递推算法辨识程序(输入信号采用M序列)clear %清理工作间变量L1=15; % M序列的周期L2=400; %迭代L2步后停止y1=1;y2=1;y3=1;y4=0; %四个移位寄存器的输出初始值%用4位移位寄存器生成M序列for i=1:L1; %开始循环,长度为L1x1=xor(y3,y4); %第一个移位寄存器的输入是第三个与第四个移位寄存器的输出的“或”x2=y1; %第二个移位寄存器的输入是第一个移位寄存器的输出x3=y2; %第三个移位寄存器的输入是第二个移位寄存器的输出x4=y3; %第四个移位寄存器的输入是第三个移位寄存器的输出y(i)=y4; %取出第四个移位寄存器的幅值为"0"和"1"的输出信号,即M序列if y(i)>0.5,u(i)=-0.03; %如果M序列的值为"1", 辨识的输入信号取“-0.03”else u(i)=0.03; %如果M序列的值为"0", 辨识的输入信号取“0.03”end %小循环结束y1=x1;y2=x2;y3=x3;y4=x4; %为下一次的输入信号做准备end %大循环结束,产生输入信号ufigure(1); %第1个图形stem(u),grid on %显示出输入信号径线图并给图形加上网格z(2)=0;z(1)=0; %设z的前两个初始值为零for k=3:15; %循环变量从3到15z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %输出采样信号endfigure(2); %第2个图形stem(z),grid on %显示出输出信号径线图并给图形加上网格%RLS递推最小二乘辨识c0=[0.001 0.001 0.001 0.001]'; %直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^6*eye(4,4); %直接给出初始状态P0,即一个充分大的实数单位矩阵E=0.000000005; %取相对误差E=0.000000005c=[c0,zeros(4,14)]; %被辨识参数矩阵的初始值及大小e=zeros(4,15); %相对误差的初始值及大小num=0; %迭代次数初始化for k=3:15; %开始求Kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1;x1=inv(x); %开始求K(k)k1=p0*h1*x1; %求出K的值d1=z(k)-h1'*c0; c1=c0+k1*d1; %求被辨识参数ce1=c1-c0; %求参数当前值与上一次的值的差值e2=e1./c0; %求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c0=c1; %新获得的参数作为下一次递推的旧参数c(:,k)=c1; %把辨识参数c 列向量加入辨识参数矩阵的最后一列p1=p0-k1*k1'*[h1'*p0*h1+1]; %求出p(k)的值p0=p1; %给下次用num=num+1; %迭代次数加1if num==L2break; %如果参数收敛情况满足要求,终止计算end %小循环结束end %大循环结束c,e %显示被辨识参数及其误差(收敛)情况%分离参数a1=c(1,:); a2=c(2,:);b1=c(3,:);b2=c(4,:);ea1=e(1,:); ea2=e(2,:);eb1=e(3,:);eb2=e(4,:);figure(3); %第3个图形i=1:15; %横坐标从1到15plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':') %画出a1,a2,b1,b2的各次辨识结果title('Parameter Identification with Recursive Least Squares Method') %图形标题figure(4); %第4个图形i=1:15; %横坐标从1到15plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:') %画出a1,a2,b1,b2的各次辨识结果的收敛情况title('Identification Precision') %图形标题输入输出曲线:参数估计曲线和误差曲线:%最小二乘递推算法辨识程序(输入信号采用正态白噪声)clear %清理工作间变量L2=400; %迭代L2步后停止%产生白噪声输入信号u=randn(L2,1); %产生长度为L2、方差为1的正态白噪声作为输入figure(1); %绘制输入信号图形stem(u),grid on %显示出输入信号径线图并给图形加上网格z(2)=0;z(1)=0; %设z的前两个初始值为零for k=3:15; %循环变量从3到15z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %输出采样信号endfigure(2); %绘制输出信号图形stem(z),grid on %显示出输出信号径线图并给图形加上网格%RLS递推最小二乘辨识c0=[0.001 0.001 0.001 0.001]'; %直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^6*eye(4,4); %直接给出初始状态P0,即一个充分大的实数单位矩阵E=0.000000005; %取相对误差E=0.000000005c=[c0,zeros(4,14)]; %被辨识参数矩阵的初始值及大小e=zeros(4,15); %相对误差的初始值及大小num=0; %迭代次数初始化for k=3:15; %开始求Kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1;x1=inv(x); %开始求K(k)k1=p0*h1*x1; %求出K的值d1=z(k)-h1'*c0; c1=c0+k1*d1; %求被辨识参数ce1=c1-c0; %求参数当前值与上一次的值的差值e2=e1./c0; %求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c0=c1; %新获得的参数作为下一次递推的旧参数c(:,k)=c1; %把辨识参数c 列向量加入辨识参数矩阵的最后一列p1=p0-k1*k1'*[h1'*p0*h1+1]; %求出p(k)的值p0=p1; %给下次用num=num+1; %迭代次数加1if num==L2break; %如果参数收敛情况满足要求,终止计算end %小循环结束end %大循环结束c,e %显示被辨识参数及其误差(收敛)情况%分离参数a1=c(1,:); a2=c(2,:);b1=c(3,:);b2=c(4,:);ea1=e(1,:); ea2=e(2,:);eb1=e(3,:);eb2=e(4,:);figure(3); %第3个图形i=1:15; %横坐标从1到15plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':') %画出a1,a2,b1,b2的各次辨识结果title('Parameter Identification with Recursive Least Squares Method') %图形标题figure(4); %第4个图形i=1:15; %横坐标从1到15plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:') %画出a1,a2,b1,b2的各次辨识结果的收敛情况title('Identification Precision') %图形标题输入输出曲线:参数估计曲线:2.考虑如下确定性系统() 1.5(1)0.7(2)(3)0.5(4)y k y k y k u k u k --+-=-+-采用梯度校正算法进行参数估计,通过相对误差准则停止计算。
系统辨识实验报告1

14
四.实验运行结果:
函数界面示意图: 6. 只显示结果界面: 7. 显示过程的参考界面:
15
心得体会
我很喜欢这个课程的期末考核方式,不用再拘泥于在题目当中对该课程的了 解,而是通过 4 个 C 语言设计的练习来达到学习的目的,而且对以后的学习还有 很大的帮助。
在编写 C 语言的过程中,也遇到了一些阻碍,特别是在编写第 3,4 个的时候。 比如:用的数组太多,并且未将其初始化,运行出来的结果经常是很长的一段随 机数;或者一模一样的程序有时候就可以正常运行,有时候就总是出现报错…… 这些都是让我心塞了两周的问题。在这些问题解决之后,运行出来的结果却与实 际模型参数的出入有点大,于是又重新查找第 2 个实验是否是 M 序列产生的方式 有问题。通过对初始化寄存器赋给不同的值,可以让结果与真实模型参数之间的 误差达到最小。
实验 4 ................................................ 错误!未定义书签。 一.实验内容及要求: ............................... 错误!未定义书签。 二.实验原理: ..................................... 错误!未定义书签。 三.数据递推关系图: ............................... 错误!未定义书签。
编写并调试动态离散时间模型 LS 成批算法程序。 要求:(1)原始数据由 DU 和 DY 读出。 (2)调用求逆及相乘子程序。 (3)显示参数辨识结果。
二.实验原理:
1.批次处理的方法就是把所有的数据采集到一次性进行处理,但前提是 白色噪声、及 M 序列所共同作用而产生的输出,才能使用最小二乘法。虽然 这种方法的计算量庞大,但经常用于处理时不变系统,方法简单。
系统辨识大作业

系统辨识大作业专业班级:自动化09-3学号:09051325姓名:吴恩作业一:设某物理量Y与X满足关系式2=++,实验获得一批数据Y aX bX c如下表,试辨识模型参数,,a b c。
(15分)解答:问题描述:由题意知,这是一个已知模型为Y=aX2+bX+c,给出了10组实验输入输出数据,要求对模型参数a,b,c进行辨识。
问题求解:这里对该模型参数辨识采用最小二乘法的一次算法(LS)求解。
2=++可以写成矩阵形式Y=AE+e;其中A=[X^2,X,1]构成, Y aX bX c利用matlab不难求解出结果。
运行结果:利用所求的的参数,求出给定的X对应的YE值,列表如下做出上表的图形如下12345678910xyy=ax 2+bx+c 参数求解结果分析:根据运行结果可以看出,拟合的曲线与真是观测的数据有误差,有出入,但是误差较小,可以接受。
出现误差的原因,一方面是由于给出的数据只有十个点,数据量太少,难以真正的充分的计算出其参数,另外,该问题求解采用的是LS 一次算法,因此计算方法本身也会造成相应的误差。
作业二:模仿实验二,搭建对象,由相关分析法,获得脉冲相应序列()g k,由()G z;和传递函数g k,参照讲义,获得系统的脉冲传递函数()G s及应用相关最小二乘法,拟合对象的差分方程模型;加阶跃()扰动,用最小二乘法和带遗忘因子的最小二乘法,辨识二阶差分方程的参数,比较两种方法的辨识差异;采用不少于两种定阶方法,确定对象的阶次。
对象模型如图:利用相关分析法,得到对象的脉冲相应序列。
如下图:(1).由脉冲相应序列,求解系统的脉冲传递函数G(z)Transfer function:0.006072 z^2 + 0.288 z + 0.1671-------------------------------z^2 + 0.1018 z - 0.7509Sampling time: 2(2).由脉冲相应序列求解系统的传递函数G(s)Transfer function:(0.04849+2.494e-018i)-----------------------s^2 + 0.1315 s + 0.6048(3).利用相关最小二乘法拟合系统的差分方程模型如下:(4).在t=100,加入一个0.5的阶跃扰动,,利用RLS求解差分方程模型:RLS加入遗忘因子之后与未加之前的曲线情况如下:未加遗忘因子之前参数以及残差的计算过程加入0.99的遗忘因子得到的参数辨识过程与残差的变化过程根据上面两种方法所得到的误差曲线和参数过渡过程曲线,我们可以看出来利用最小二乘法得到的参数最终趋于稳定,为利用带遗忘因子的最小二乘算法,曲线参数最终还是有小幅度震荡。
系统辨识大作业.

一、 问题描述考虑仿真对象:()0.9(1)0.15(2)0.02(3)0.7(1)0.15(2)()z k z k z k z k u k u k e k +-+-+-=---+ e() 1.0e(1)0.41e(2)(),~(0,1)k k k v k v N λ+-+-=式中,u(k)和z(k)是输入输出数据,v(k)是零均值、方差为1的不相关的随机噪声;u(k)采用与e(k)不相关的随机序列。
1. 设计实验,产生输入输出数据;2. 使用基本最小二乘法估计参数;3. 考虑其他适用于有色噪声的辨识方法估计参数;4. 模型验证。
二、 问题分析对于单输入单输出系统(Single Input Single Output, SISO ),如图 1所示,将待辨识的系统看作“灰箱”,它只考虑系统的输入输出特性,而不强调系统的内部机理。
图 1中,输入u(k)和输出z(k)是可以测量的,1()G z -是系统模型,用来描述系统的输入输出特性,y(k)是系统的实际输出。
1()N z -是噪声模型,v(k)是均值为零的不相关随机噪声,e(k)是有色噪声。
图 1 SISO 系统的“灰箱”结构对于SISO 随机系统,被辨识模型()G z 为:12121212()()()1n n nn b z b z b z y z G z u z a z a z a z ------+++==++++ 其相应的差分方程为11()()()n ni i i i y k a y k i b u k i ===--+-∑∑若考虑被辨识系统或观测信息中含有噪声,被辨识模型可改写为11()()()()n ni i i i z k a y k i b u k i v k ===--+-+∑∑式中,z(k)为系统输出量的第k 次观测值;y(k)为系统输出量的第k 次真值,y(k-1)为系统输出量的第k-1次真值,以此类推;u(k)为系统的第k 个输入值,u(k-1)为系统的第k-1个输入值;v(k)为均值为0的不相关随机噪声。
系统辨识(一)

系统辨识第一次作业杜国杰030130648一、阶跃响应(面积法)采用阶跃响应法辨识的一般步骤为:第一步,实际测取过程的阶跃响应;第二步,由阶跃响应求过程的传递函数。
常用方法有近似法、半对数法、切线法、两点法、面积法等,本次试验采用的是面积法,公式如下所示:(1-1)或者是:(1-2)原系统为2阶系统,传递函数为:辨识所得系统传递函数为:实验仿真程序为:clear;%传递函数num=[1];den=[1 0.5 1];T0=0.01; %采样时间t=0:T0:100;L=length(t); %数据长度h=(step(num,den,t)).';K=h(L);ht=h/K;dtjtthAdtitthAjtjjiii!)()](*1[)!1()()](*1[211--+---=⎰∑⎰∞-=---∞[]13111121111*1!)()!2()()!1()()(1dtjtAAitittyAAijjjijiiiii⎰∑∞-=------⎥⎦⎤⎢⎣⎡-+--+---=n=length(den)-1;m=length(num)-1; %求面积for i=1:n+mtemp1=0;for j=1:Ltemp1=temp1+(1-ht(j))*(-1*t(j))^(i-1)/factorial(i-1)*T0;endif i>1temp2=0;for ii=1:i-1temp=0;for j=1:Ltemp=temp+(1-ht(j))*(-1*t(j))^(ii-1)/factorial(ii-1)*T0;endtemp2=temp2+A(i-ii)*temp;endelsetemp2=0;endA(i)=temp1+temp2;endM1=[];for i=1:mM1=[M1;A(n+i-1:-1:n-m+i)];endM2=A(n+1:n+m).';b=-1*inv(M1)*M2;for i=1:nfor j=1:nif i<jM(i,j)=0;else if i==jM(i,j)=1;elseM(i,j)=A(i-j);endendendendB=zeros(n,1);for i=1:mB(i)=b(i);enda=M*B+A(1:n).';r_num=[flipud(b)' 1];r_den=[flipud(a)' 1];disp('原系统传递函数:');G1=tf(num,den)disp('辨识所得系统传递函数:');G2=tf(r_num,r_den)figure(1)step(G1,'b-',G2,'u-x')legend('原始响应曲线','辨识曲线')程序运行后得到的仿真结果如下图所示:图1-1 阶跃响应辨识结果由上图可以看出,由于系统为二阶,比较简单,辨识结果与原系统几乎完全相同,误差很小。
江南大学《系统辨识》试卷部分答案

江南大学《系统辨识》实体部分参考答案一、【每小题2分,其中10小题,共计20分】假设a ,b ,c ,d ,i θ是未知参数,υ 是噪声,写出下列系统的辨识模型(1) 12()t y t t e θθ=++解答:12()()()[1,][,]t T T Te y t t t t ϕθϕθθθ⎧-+=⎪=⎨⎪=⎩(2) 12()2cos()t y t t e t θθ=+++解答:122cos()()()()[1,][,]t T T T e t y t t t t ϕθϕθθθ⎧--+=⎪=⎨⎪=⎩(3) 21231()()y t t t t θθυθ=+++解答: 2123()()()()[1,,]1[,,]T T Ty t t t t t t ϕθυϕθθθθ⎧⎪=+⎪⎪=⎨⎪⎪=⎪⎩(4) 123()()t y t t e t θθθυ=++++解答:132()()()()[1,][,]t T T T y t e t t t t ϕθυϕθθθθ⎧-=+⎪=⎨⎪=+⎩(5) ()()()()()()()()1212......n n y t ax t bx t cx t dx t x t x t t υ=+++++ 解答:()()()()()()()1212()()()[,,...,,...][,,...,,]T T n n T y t t v t t x t x t x t x t x t x t a b c d ϕθϕθ⎧=+⎪=⎨⎪=⎩二、【每个2分,共计20分】假设i θ是未知参数,υ是噪声,写出下列系统辨识模型(1) 123()1t y t t e θθθ=+++解答: 1231()()()[1,,][,,]T T t T y t t t t e ϕθϕθθθθ⎧-+=⎪=⎨⎪=⎩(2) 212()()()...()()m m y t u t u t u t t θθθυ=++++解答:212()()()()[(),(),...,()][,,...,]T T m T m y t t t t u t u t u t ϕθυϕθθθθ⎧=+⎪=⎨⎪=⎩(3) 1234()()(1)(2)(1)(2)()y t t y t y t u t u t t θθθθυ+-+-=-+-+ 解答:()12341234()()(1)(2)(1)(2)()()()()[(1),(2),1,(2)][,,,]T T T y t t y t y t u t u t t t t t y t y t u t u t θθθθυϕθυϕθθθθθ⎧=----+-+-+=+⎪=------⎨⎪=⎩(4) 123()sin(/)(1)(1)cos()()y t t y t u t t t θπθθυ+-=-++解答:()123123()()s i n (/)(1)(1)c o s ()()()()()[s i n (/)(1),1,c o s ()][,,]T T T y t t t y t u t t t t t t t y t u t t θπθθυϕθυϕπθθθθ⎧=--+-++=+⎪=---⎨⎪=⎩ (5) 2()()()2s i n (/)y t a u t b u t c d t π=+++ 解答: 2()()()[(),(),2,sin(/)][,,,]T T T y t t t u t u t t a b c d ϕθϕπθ⎧=⎪=⎨⎪=⎩三、【10分】设三阶MA 模型为)3()2()1()()(321-+-+-+=t v d t v d t v d t v t y .其中,{})(t y 是已知观测序列,{})(t v 是零均值方差为2σ的随机白噪声序列,其便是模型为 )()()(t v t t y T +=θϕ● 写出信息向量)(t ϕ和参数向量θ的表达式● 写出θ的递推增广最小二乘(RELS)辨识算法.解答:)()()(t v t t y T +=θϕ)]3(),2(),1([)(---=t v t v t v t T θ其中,T d d d ],,[321=θ算法如下:的RELS R -θ)(ˆ)1()(ˆ1)(ˆ)1()(ˆ)()()]1(ˆ)(ˆ)()[()1(ˆ)(ˆt t p t t t p t t p t L t t t y t L t t T ϕϕϕϕθϕθθ-+-==--+-= )1()](ˆ)(1[)(--=t p t t L t p T ϕI p p 0)0(= T T T T d d d t t t t t v t v t v t v t ]ˆˆˆ[)(ˆ)(ˆ)(ˆ)()()]3(ˆ),2(ˆ),1(ˆ[)(ˆ321=-=---=θθϕϕϕ四、证明题【每小题2分,其中5题,计10分】设n T R t t t t t p t p ∈≥+-=--)(,0)(),()()1()(211ϕϕϕϕ格式阶单位矩阵,证明以下为n I I p n n ,)0(=(1))()(t t p ϕ )()1()(1)()1(t t p t t t p T ϕϕϕ-+-= (2)1)()()(≤t t p t T ϕϕ(3) )()()(1)()()()1(t t p t t t p t t p T ϕϕϕϕ-=-(4) )()1()()()()()(2t t p t p t t t p t T T ϕϕϕϕ-≤(5) 1()()(1)()T t t p t p t t ϕϕ∞=-∞∑(6) )()()(21t t p t t T ϕϕ∑∞=∞解答:(1)11()(1)()()T p t p t t t ϕϕ--=-+ ①对①式用矩阵求逆引理,则1()(1)(1)()[()(1)()]()(1)T T p t p t p t t I t p t t t p t ϕϕϕϕ-=---+-- 对上式两边乘)(t ϕ,可得)()1()(1)()1()()()1()()1()()(t t p t t t p t t t p t t p t t p T T ϕϕϕϕϕϕϕ-+----= )()1()(1)()1(t t p t t t p T ϕϕϕ-+-= (2)∵ )()1()(1)()1()()(t t p t t t p t t p T ϕϕϕϕ-+-=② 对②式左乘)(t Tϕ,可得)()1()(1)()1()()()()(t t p t t t p t t t p t T T T ϕϕϕϕϕϕ-+-= ∵0)1(≥-t p ∴1)()()(≤t t p t T ϕϕ (3)对①右乘p(t),可得)()()()()1(1t p t t t p t p IT ϕϕ+-=- ③ 面对③左乘)1(-t p ,右乘)(t ϕ,则有)()()()()1()()()()1(t t p t t t p t t p t t p T ϕϕϕϕϕ-+=- ④ 移向合并,可得)()()(1)()()()1(t t p t t t p t t p T ϕϕϕϕ-=-④对②式左乘(t)p(t) T ϕ,得)()1()(1)()1()()()()()(t t p t t t p t p t t t p t T T TT ϕϕϕϕϕϕ-+-= ∵0)1(≥-t p ∴0)()1()(≥-t t p t T ϕϕ∴)()1()()()()()(t t p t p t t t p t T T T ϕϕϕϕ-≤(1)()(1)()()()T p t p t p t t t p t ϕϕ-=+-∴11(1)()()()()(0)()T t i p t t t p t p t p p ϕϕ∞∞==-=∆=-∞∑∑ ⑤ ∵)()()1()(11t t t p t p T ϕϕ+-=--11(0)()()T t p t t ϕϕ∞-==+∑ ∴)0()(11--≥p t p∴when ∞→t ,则)()0(∞≥p p对⑤式两队取迹,得)]()1()()([)]()()()1([11t t p t p t tr t p t t t p tr i T i Tϕϕϕϕ-=-∑∑∞=∞= [(0)()]tr p p =-∞∞⑥∵)()1()()()()()(t t p t p t t t p t T T T ϕϕϕϕ-≤∴∞-≤∑∑∞=∞= )]()1()()()()()(11t t p t p t t t p t t T T t T ϕϕϕϕ。
系统辨识大作业

北京信息科技大学系统辨识大作业姓名:刘新菊班级:研1206学号:2012020176专业:模式识别与智能系统2012年—2013年第二学期大作业1.实验目的通过实验掌握辅助变量法辨识过程参数, AIC 准则和F 检验法辨识结构参数。
2.实验描述给出一个模型(图6.4),观测数据受有色噪声污染。
3.实验要求编制程序,辨识出该模型的结构参数及过程参数,噪声模型可以辨识也可以不辨识,对精度无要求。
4.实验原理AIC 准则定阶法来定阶,所用公式:n n n n Z H V θ=+[](1),(2),(3),...,()Tn Z z z z z L =1212,,...,,,...aTn n n a a a b b b θ⎡⎤=---⎣⎦(0)(1)...(1)(0)(1)...(1)(1)(0)...(2)(1)(0)...(2).........................(1)(2)...()(1)(2)...()n z z z n u u u n z z z n u u u n H z L z L z L n u L u L u L n ----⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥------⎣⎦其中模型参数n θ和 噪声()V k 方差的极大似然估计值为ML θ ,2v σ12()1()()MLML ML T T n n n nT v n n n n H H H Z Z H Z H L θσθθ-==--AIC 的定阶公式写成2()log 4v AIC n L n σ=+取1,2,3,4;n =分别计算()AIC n ,找到使()AIC n 最小的那个n 作为模型的阶次。
一般说来,这样得到的模型阶次都能比较接近实际过程的真实阶次。
5.实验内容仿真对象如图1传递函数()()120()8.31 6.21G ss s=++离散化为2118.07.110.2---+-zzz,故其仿真对象如下图1:U(k) 取6级M序列,幅度为1,v(k) 为服从N(0,1)分布的不相关随机噪声。
系统辨识答案
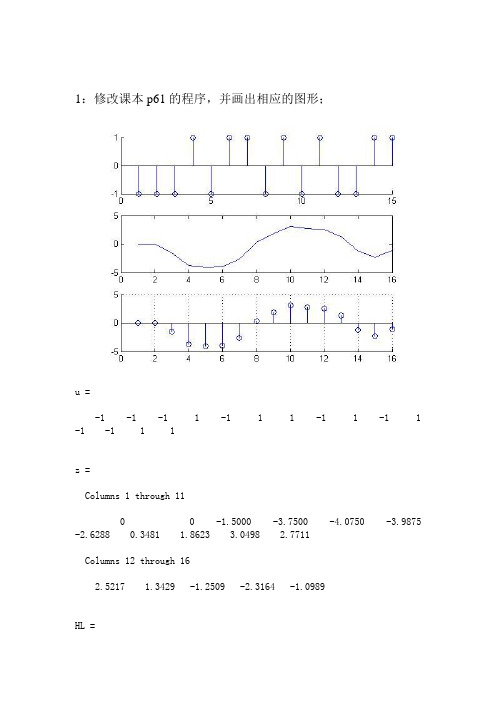
1:修改课本p61的程序,并画出相应的图形;u =-1 -1 -1 1 -1 1 1 -1 1 -1 1 -1 -1 1 1z =Columns 1 through 110 0 -1.5000 -3.7500 -4.0750 -3.9875 -2.6288 0.3481 1.8623 3.0498 2.7711Columns 12 through 162.5217 1.3429 -1.2509 -2.3164 -1.0989HL =0 0 -1.0000 -1.00001.5000 0 -1.0000 -1.00003.7500 1.5000 1.0000 -1.00004.0750 3.7500 -1.0000 1.0000 3.9875 4.0750 1.0000 -1.0000 2.6288 3.9875 1.0000 1.0000 -0.3481 2.6288 -1.0000 1.0000 -1.8623 -0.3481 1.0000 -1.0000 -3.0498 -1.8623 -1.0000 1.0000 -2.7711 -3.0498 1.0000 -1.0000 -2.5217 -2.7711 -1.0000 1.0000 -1.3429 -2.5217 -1.0000 -1.00001.2509 -1.3429 1.0000 -1.00002.3164 1.2509 1.0000 1.0000 ZL =-1.5000-3.7500-4.0750-3.9875-2.62880.34811.86233.04982.77112.52171.3429-1.2509-2.3164-1.0989c =-1.50000.70001.00000.5000a1 =-1.5000a2 =0.7000b1 =1b2 =0.50002:修改课本p63的程序,并画出相应的图形(V的取值范围为54-200);V = [54.3000, 61.8000, 72.4000, 88.7000, 118.6000, 194.0000]τP = [61.2000, 49.5000, 37.6000, 28.4000, 19.2000, 10.1000]τZL = [4.1141, 3.9020, 3.6270, 3.3464, 2.9549, 2.3125]τHL =-3.9945 1.0000-4.1239 1.0000-4.2822 1.0000-4.4853 1.0000-4.7758 1.0000-5.2679 1.0000c4 =1.40429.6786alpha = 1.4042beita = 1.5972e+0043:表1中是在不同温度下测量同一热敏电阻的阻值,根据测70时的电阻量值确定该电阻的数学模型,并求出当温度在C︒值。
系统辨识作业及答案解析

一. 问答题1. 介绍系统辨识的步骤。
答:(1)先验知识和建模目的的依据:(2)实验设计:(3)结构辨识:(4)参数估计;(5) 模型适用性检验。
2. 考虑单输入单输岀随机系统,状态空间模型yW = [1小•伙)+咻)转换成ARMA 模型。
答:ARMA 模型的特点是u(k)=O.1 0x(k + 1) =x 伙).2 0. y 伙)=[1 \]x(k) + v(k)3. 设有一个五级移位寄存器,反馈取自第2级和第3级输出的模2加法和匚试说明:(1)其输出序列是什么? (2)是否是M 序列? (3)它与反馈取自第4级与第3级输出模2加法和所得的序列有何不同? (4) 其逆M 序列是什么?答:(1)设设输入序列1 1111(1) 11111(9)01110 (17)00111(25)10011(2) 01111 (10)00111 (18)10011(26)01001(3) 00111 (11)10011 (19)01001(27)10100(4) 10011 (12)01001(20)10100(28)11010(5) 01001 (13)10100(21)11010(29)00111(6) 10100 (14)11010(22)11101(30)01110(7) 11010 (15)11101 (23)01110(31)00111(8) 11101 (16)01110(24)00111(32)10011其输出序列为:1 1 1 1 1 0 0 1 0 1(2) 不是M 序列⑶第4级与第3级模2相加结果(1) 11111(9)11001 (17)01111(25)01100皿+沪20 。
心)+ "伙)(2)01111 (10)01100(18)00111(26)10110(3)00111 (11)10110 (19)00011(27)01011(4)00011 (12)01011(20)10001(28)10101(5)10001 (13)10101(21)01000(29)11010(6)01000 (14)11010(22)00100(30)11101(7)00100 (15)11101 (23)10010(31)11110(8)10010 (16)11110(24)11001(32)01111不同点:第2级和第3级模二相加产生的序列,是从第4时刻开始,每隔7个时刻重复一次:第4级与第3级模2相加产生的,序列,是从第2时刻开始每隔15个时刻重复一次。
系统辨识期末作业

系统辨识期末作业一、系统辨识“系统辨识”是研究如何利用系统试验或运行的、含有噪声的输入输出数据来建立被研究对象数学模型的一种理论和方法。
系统辨识是建模的一种方法,不同的学科领域,对应着不同的数学模型。
从某种意义上来说,不同学科的发展过程就是建立他的数学模型的过程。
辨识问题可以归结为用一个模型来表示客观系统(或将要构造的系统)本质特征的一种演算,并用这个模型把对客观系统的理解表示成有用的形式。
当然也可以有另外的描述,辨识有三个要素:数据,模型类和准则。
辨识就是按照一个准则在一组模型类中选择一个与数据拟合得最好的模型。
总而言之,辨识的实质就是从一组模型类中选择一个模型,按照某种准则,使之能最好地拟合所关心的实际过程的静态或动态特性。
通过系统辨识建立对象数学模型的依据是:研究表明,从外部对一个系统的认识,是通过其输入输出数据来实现的,既然数学模型是表述一个系统动态特性的一种描述方式,而系统的动态特性的表现必然蕴含在它变化的输入输出数据中。
所以,通过记录系统在正常运行时系统的输入输出数据,或者通过测量系统在人为输入作用下的输出响应,然后对这些数据进行适当的系统处理、数学计算和归纳整理,提取数据中蕴含的系统信息,从而建立被控对象的数学描述,这就是系统辨识。
即系统辨识就是一种利用数学的方法从输入输出数据序列中提取对象数学模型的方法。
下面从三个方面来对系统辨识进行介绍:1、统辨识的方法(1)、经典的系统辨识办法在经典控制理论中,所分析研究的是单输入单输出系统,经常用到的系统模型是频率响应、权函数和传递函数。
所以早期系统辨识工作的主要内容也就是寻求描述单变量系统的频率特性、权函数和系统的传递函数。
早期的系统辨识所用的方法大多是在一定的连续时间性的输入信号下(非周期的或周期的),观测被识对象对这种输入作用的响应,例如频率响应或阶跃响应。
根据需要,再由这些响应特性求出系统的参数模型。
这些方法有阶跃响应法、频率特性法和相关分析法。
合工大系统辨识作业及答案

系统辨识作业一、 简答题1 系统辨识的实验设计应包含那些内容?答:系统辨识实验设计应包含选择实验信号、采样时间、辨识时间、输入输出数据长度等。
2 判断下列是否为一个正确周期的M 序列,并说明原因。
111100010011011 111100********* 答:不是M 序列,因为M 序列的周期为15,由M 序列的性质知序列中“1”的状态应为8个 而第一个中有9个 所以不是M 序列3证明加权最小二乘估计的无偏性。
证明:加权最小二乘估计的解为:()1ˆTT WLSW WY θ-=ΦΦΦ 其中Φ为输入矩阵 W 为加权矩阵 Y 为输出矩阵。
()()11ˆ()T T WLS T TE W W e E W We θθθ--⎡⎤⎡⎤=ΦΦΦΦ+⎣⎦⎢⎥⎣⎦⎡⎤=+ΦΦΦ⎢⎥⎣⎦由于Φ与e 统计独立,则()10T T E W We -⎡⎤ΦΦΦ=⎢⎥⎣⎦即ˆWLS E θθ⎡⎤=⎣⎦所以ˆWLSθ是无偏估计量,命题得证。
4比较最小二乘法、广义最小二乘法和辅助变量法的优缺点。
答:基本最小二乘对低噪声有效,参数估计值可很快收敛到真值,所需计算量相对较少,但对实际噪声估计有偏。
广义最小二乘法:计算量大,可能不收敛,可能是有偏估计。
但如果对噪声模型用随机逼近法,而对过程模型采取最小二乘法则获得较好形式的广义最小二乘法。
辅助变量法可以一次性完成计算,但是计算量也大,对初值选择很敏感。
5答:对于n 阶系统与n+1阶系统参数估计之间有如下的关系:对于n+1阶系统 ()()()11()()A z y k B z u k e k --=+设其待估参数为()011111...(1)(2)T T Tn n n n n b a b a b a b θθθ++⎡⎤⎡⎤+==⎣⎦⎣⎦ 则(1)()[()]T n A Y n θθθ=-Φ-Φ由题目知n=2时系统参数为准确值,则n=3时按照上式去计算,估算出的系数必远远偏离系统模型参数值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《系统辨识》作业 1题目最小二乘参数估计仿真学院信息科学与工程学院专业控制科学与工程姓名王瑞荣学号 030120694教师顾幸生2012年12月26日一:一般最小二乘法 考虑仿真系统:式中,)(k v 为方差为1的白噪声。
选用幅值为1的逆M 序列作为输入信号)(k u ,利用LS 算法进行参数估计,仿真结果如下表所示。
表1.1 批处理最小二乘法的参数估计结果仿真程序:%批处理最小二乘参数估计(LS ) clear all;a=[1 -1.5 0.7]'; b=[1 0.5]'; d=3; %对象参数na=length(a)-1; nb=length(b)-1; %na 、nb 为A 、B 阶次L=500; %数据长度uk=zeros(d+nb,1); %输入初值:uk(i)表示u(k-i) yk=zeros(na,1); %输出初值x1=1; x2=1; x3=1; x4=0; S=1; %移位寄存器初值、方波初值 xi=randn(L,1); %白噪声序列theta=[a(2:na+1);b]; %对象参数真值 for k=1:Lphi(k,:)=[-yk;uk(d:d+nb)]'; %此处phi(k,:)为行向量,便于组成phi 矩阵 y(k)=phi(k,:)*theta+xi(k); %采集输出数据IM=xor(S,x4); %产生逆M 序列 if IM==0 u(k)=-1; elseu(k)=1; endS=not(S); M=xor(x3,x4); %产生M 序列%更新数据)()4(5.0)3()2(7.0)1(5.1)(k v k u k u k y k y k y +-+-=-+--x4=x3; x3=x2; x2=x1; x1=M;for i=d+nb:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);endthetae=inv(phi'*phi)*phi'*y' %计算参数估计值thetae二:递推最小二乘算法 算法:已知:n a 、n b 和d 。
Step1 设置初值)0(P 和)0(∧θ,输入初始数据; Step2 采样当前输出)(k y 和输入)(k u ;Step3 利用递推公式,计算K(k)、)(k ∧θ和)(k P ; Step4 1+→k k ,返回Step2,继续循环。
考虑仿真系统:式中,)(k v 为方差为1的白噪声。
取初值I P 610)0(=、0)0(=∧θ。
选择方差为1的白噪声作为输入信号)(k u ,采用RLS 算法进行参数估计,仿真结果如图1.2所示。
5101520253035-2.5-2-1.5-1-0.500.511.52k参数估计a 、b图1.2 递推最小二乘法的参数估计结果当k=35时,参数估计值为0.48780.9276,0.6389,-1.4399,1021====∧∧∧∧b b a a 。
)()4(5.0)3()2(7.0)1(5.1)(k v k u k u k y k y k y +-+-=-+--仿真程序:%递推最小二乘参数估计(RLS)clear all; close all;a=[1 -1.5 0.7]'; b=[1 0.5]'; d=3; %对象参数na=length(a)-1; nb=length(b)-1; %na、nb为A、B阶次L=35; %仿真长度uk=zeros(d+nb,1); %输入初值:uk(i)表示u(k-i)yk=zeros(na,1); %输出初值u=randn(L,1); %输入采用白噪声序列xi=sqrt(0.1)*randn(L,1); %白噪声序列theta=[a(2:na+1);b]; %对象参数真值thetae_1=zeros(na+nb+1,1); %thetae初值P=10^6*eye(na+nb+1);for k=1:Lphi=[-yk;uk(d:d+nb)]; %此处phi为列向量y(k)=phi'*theta+xi(k); %采集输出数据%递推最小二乘法K=P*phi/(1+phi'*P*phi);thetae(:,k)=thetae_1+K*(y(k)-phi'*thetae_1);P=(eye(na+nb+1)-K*phi')*P;%更新数据thetae_1=thetae(:,k);for i=d+nb:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);endplot([1:L],thetae); %line([1,L],[theta,theta]);xlabel('k'); ylabel('参数估计a、b');legend('a_1','a_2','b_0','b_1');%axis([0 L -2 2]);三:遗忘因子递推最小二乘算法 算法:已知:n a 、n b 和d 。
Step1 设置初值)0(P 和)0(∧θ及遗忘因子λ,输入初始数据; Step2 采样当前输出)(k y 和输入)(k u ;Step3 利用遗忘因子递推公式,计算K(k)、)(k ∧θ和)(k P ; Step4 1+→k k ,返回Step2,继续循环。
考虑仿真系统:式中,)(k v 为方差为1的白噪声。
对象时变参数[]Tb b a a k 1021)(=θ为[]⎩⎨⎧-≤-=500,]2.05.14.01[500,5.017.05.1)( k k k TT θ 取初值I P 610)0(=、0)0(=∧θ。
选择方差为1的白噪声作为输入信号)(k u 。
遗忘因子最小二乘法、取遗忘因子λ=0.98,采用FFRLS 算法进行参数估计,仿真结果如图1.3(1)当[];)(时,参数估计值为T k 4835.00198.17103.05156.1500500-==∧θ 当[];)(时,参数估计值为T k 1026.05147.14609.00669.110001000-==∧θ可以看出,几十对于参数突变的系统,采用FFRLS 算法也能够有效地进行参数估计。
)()4()3()2()1()(1021k v k u b k b k y a k y a k y +-+-=-+-+5001000-2-1.5-1-0.500.511.52k参数估计a500100000.511.522.533.54k参数估计b图1.3(1) 遗忘因子递推最小二乘法的参数估计结果(λ=0.98)当取遗忘因子λ=1时,FFRLS 将退化为普通的RLS 算法,仿真结果如图1.3(2)所示。
5001000-2-1.5-1-0.500.511.52k参数估计a500100000.20.40.60.811.21.41.61.8k参数估计b图1.3(2) 递推最小二乘法的参数估计结果(λ=1)可以看出,RLS对于参数时变系统,即使增加数据长度,也不能有效的跟踪参数的变化(除非增加代数到30000代左右时才可较好跟踪(本例))。
仿真程序:%遗忘因子递推最小二乘参数估计(FFRLS)clear all; close all;a=[1 -1.5 0.7]'; b=[1 0.5]'; d=3; %对象参数na=length(a)-1; nb=length(b)-1; %na、nb为A、B阶次L=1000; %仿真长度uk=zeros(d+nb,1); %输入初值:uk(i)表示u(k-i)yk=zeros(na,1); %输出初值u=randn(L,1); %输入采用白噪声序列xi=sqrt(0.1)*randn(L,1); %白噪声序列thetae_1=zeros(na+nb+1,1); %thetae初值P=10^6*eye(na+nb+1);lambda=0.98; %遗忘因子范围[0.9 1]for k=1:Lif k==501a=[1 -1 0.4]';b=[1.5 0.2]'; %对象参数突变endtheta(:,k)=[a(2:na+1);b]; %对象参数真值phi=[-yk;uk(d:d+nb)];y(k)=phi'*theta(:,k)+xi(k); %采集输出数据%遗忘因子递推最小二乘法K=P*phi/(lambda+phi'*P*phi);thetae(:,k)=thetae_1+K*(y(k)-phi'*thetae_1);P=(eye(na+nb+1)-K*phi')*P/lambda;%更新数据thetae_1=thetae(:,k);for i=d+nb:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);endsubplot(1,2,1)plot([1:L],thetae(1:na,:)); hold on; plot([1:L],theta(1:na,:),'k:');xlabel('k'); ylabel('参数估计a');legend('a_1','a_2'); axis([0 L -2 2]);subplot(1,2,2)plot([1:L],thetae(na+1:na+nb+1,:)); hold on; plot([1:L],theta(na+1:na+nb+1,:),'k:'); xlabel('k'); ylabel('参数估计b');legend('b_0','b_1'); %axis([0 L -0.5 2]);。
