进制转换方法总结
进制转换方法总结

进制转换⽅法总结先讲⼀下定义吧,进制也就是进制位,对于接触过电脑的⼈来说应该都不陌⽣,我们常⽤的进制包括:⼆进制、⼋进制、⼗进制与⼗六进制,它们之间区别在于数运算时是逢⼏进⼀位。
⽐如⼆进制是逢2进⼀位,⼗进制也就是我们常⽤的0-9是逢10进⼀位。
其他的同理。
好的,接下来就是进制之间的互相转换了。
⼆进制与⼗进制之间的转换1.⼗进制转⼆进制⽅法为:⼗进制数除2取余法,即⼗进制数除2,余数为权位上的数,得到的商值继续除,直到商为0为⽌。
2.⼆进制转⼗进制⽅法为:把⼆进制数按权展开、相加即得⼗进制数。
⼆进制与⼋进制之间的转换1.⼋进制转⼆进制⽅法为:⼋进制数通过除2取余法,得到⼆进制数,对每个⼋进制为3个⼆进制,不⾜时在最左边补零。
2.⼆进制转⼋进制⽅法为:3位⼆进制数按权展开相加得到1位⼋进制数。
(注意事项,3位⼆进制转成⼋进制是从右到左开始转换,不⾜时补0)。
⼆进制与⼗六进制之间的转换1.⼗六进制转⼆进制⽅法为:⼗六进制数通过除2取余法,得到⼆进制数,对每个⼗六进制为4个⼆进制,不⾜时在最左边补零。
2.⼆进制转⼗六进制⽅法为:与⼆进制转⼋进制⽅法近似,⼋进制是取三合⼀,⼗六进制是取四合⼀。
(注意事项,4位⼆进制转成⼗六进制是从右到左开始转换,不⾜时补0)。
⼗进制与⼋进制与⼗六进制之间的转换1.⼗进制转⼋进制或者⼗六进制有两种⽅法第⼀:间接法—把⼗进制转成⼆进制,然后再由⼆进制转成⼋进制或者⼗六进制。
这⾥不再做图⽚⽤法解释。
第⼆:直接法—把⼗进制转⼋进制或者⼗六进制按照除8或者16取余,直到商为0为⽌。
(具体⽤法如下图)2.⼋进制或者⼗六进制转成⼗进制⽅法为:把⼋进制、⼗六进制数按权展开、相加即得⼗进制数。
(具体⽤法如下图)⼗六进制与⼋进制之间的转换⼋进制与⼗六进制之间的转换有两种⽅法第⼀种:他们之间的转换可以先转成⼆进制然后再相互转换。
第⼆种:他们之间的转换可以先转成⼗进制然后再相互转换。
这⾥就不再进⾏图⽚⽤法解释。
各种进制转换方法

一、二进制转十进制由二进制数转换成十进制数的基本做法是,把二进制数首先写成加权系数展开式,然后按十进制加法规则求和。
这种做法称为按权相加法。
二、十进制转二进制十进制数转换为二进制数时,由于整数和小数的转换方法不同,所以先将十进制数的整数部分和小数部分分别转换后,再加以合并。
1. 十进制整数转换为二进制整数十进制整数转换为二进制整数采用除2取余,逆序排列法。
具体做法是:用2去除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为零时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
2.十进制小数转换为二进制小数十进制小数转换成二进制小数采用乘2取整,顺序排列法。
具体做法是:用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来,先取的整数作为二进制小数的高位有效位,后取的整数作为低位有效位。
1.二进制与十进制的转换(1)二进制转十进制方法:按权展开求和例:(1011.01)2 =(1×23+0×22+1×21+1×20+0×2-1+1×2-2)10=(8+0+2+1+0+0.25)10=(11.25)10(2)十进制转二进制十进制整数转二进制数:除以2取余,逆序输出例:(89)10=(1011001)22 892 44 12 22 02 11 02 5 12 2 12 1 00 1十进制小数转二进制数:乘以2取整,顺序输出例:(0.625)10= (0.101)20.625 X 21.25 X 20.5 X 21.02.八进制与二进制的转换例:将八进制的37.416转换成二进制数:37 . 4 1 6011 111 .100 001 110即:(37.416)8 =(11111.10000111)2例:将二进制的10110.0011 转换成八进制:0 1 0 1 1 0 . 0 0 1 1 0 02 6 . 1 4即:(10110.011)2 =(26.14)83.十六进制与二进制的转换例:将十六进制数5DF.9 转换成二十进制转二进制:用2辗转相除至结果为1将余数和最后的1从下向上倒序写就是结果例如:302转化成二进制302/2 = 151 余0151/2 = 75 余175/2 = 37 余137/2 = 18 余118/2 = 9 余09/2 = 4 余14/2 = 2 余02/2 = 1 余0故二进制为100101110二进制转十进制从最后一位开始算,依次列为第0、1、2...位第n位的数(0或1)乘以2的n次方得到的结果相加就是答案例如:01101011.转十进制:第0位:1乘2的0次方=11乘2的1次方=20乘2的2次方=01乘2的3次方=80乘2的4次方=01乘2的5次方=321乘2的6次方=640乘2的7次方=0然后:1+2+0+8+0+32+64+0=107.二进制01101011=十进制107.。
常见的进制转换方法

一:简述:进位计数制:是人们利用符号来计数的方法。
一种进位计数制包含一组数码符号和两个基本因素。
(1)数码:用不同的数字符号来表示一种数制的数值,这些数字符号称为”数码”。
(2)基:数制所使用的数码个数称为”基”。
(3)权:某数制每一位所具有的值称为”权”。
二:进制转换的理论1、二进制数、十六进制数转换为十进制数:用按权展开法把一个任意R进制数a n a n-1 ...a1a0 . a-1a-2...a-m转换成十进制数,其十进制数值为每一位数字与其位权之积的和。
a n×R n+ a n-1×R n-1+…+ a1×R 1+ a0×R0+ a-1×R-1+ a-2×R-2 + …+ a-m×R-m2、十进制转化成R进制十进制数轮换成R进制数要分两个部分:整数部分:除R取余数,直到商为0,得到的余数即为二进数各位的数码,余数从右到左排列(反序排列)。
小数部分:乘R取整数,得到的整数即为二进数各位的数码,整数从左到右排列(顺序排列)。
3、十六进制转化成二进制每一位十六进制数对应二进制的四位,逐位展开。
4、二进制转化成十六进制将二进制数从小数点开始分别向左(对二进制整数)或向右(对二进制小数)每四位组成一组,不足四位补零。
三、具体实现1、二进制转换成十进制任何一个二进制数的值都用它的按位权展开式表示。
例如:将二进制数(10101.11)2转换成十进制数。
(10101.11)2=1*24+0*23+1*22+0*21+1*20+1*2-1+1*2-2=24+22+20+2-1+2-2=(21.75)102、十进制整理转换成二进制将十进制整数转换成二进制整数采用“除2取倒余法”。
即将十进制整数除以2,得到一个商和一个余数;再将商除以2,又得到一个商和一个余数;以此类推,直到商等于零为止。
每次得到的余数的倒排列,就是对应二进制数的各位数。
进制间的相互转化总结+例题

进制间的相互转化总结+例题进制转换:1. ⼗六进制与⼆进制相互转化 ⼗六进制的每⼀位占⼆进制中的四位,因此需要先定义⼗六进制从0~F的⼆进制值,即:string a[16] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110","0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};下标即⼗六进制数,再将每⼀个对应的⼆进制字符串拼起来就可以了。
如下例:2. ⼋进制与⼆进制相互转化 ⼆进制中的每三位对应⼋进制中的⼀位,因此也需要先对⼋进制中0~7定义其⼆进制值,即:string a[8] = {"000","001","010","011","100","101","110","111"};这样其下标就是⼋进制的值。
也可以⽤map定义,这样就可以直接根据字符串的值得到每⼀位⼋进制的值,再拼凑起来就可以了。
map<string,int> mp;mp["000"] = '0', mp["001"] = '1', mp["010"] = '2', mp["011"] = '3',mp["100"] = '4', mp["101"] = '5', mp["110"] = '6', mp["111"] = '7';3.⼆进制转⼗六进制 和⼆进制转⼋进制⼀样,只不过这⾥是每四位取⼀个⼗六进制,再拼起来就⾏了。
进制数的转换

进制数的转换在计算机科学中,进制数是十分重要的概念。
进制数是指使用一定的进位规则,将数字表示为不同进制下的数。
常见的进制有二进制、八进制、十进制和十六进制。
在计算机中,二进制是最常用的进制,因为计算机内部的所有数据都是以二进制形式存储的。
因此,我们需要掌握进制数的转换方法,以便在编程和计算机科学中应用。
一、二进制转八进制和十六进制将二进制数转换为八进制或十六进制,需要先将二进制数转换为十进制数,然后再将十进制数转换为八进制或十六进制。
下面是一个将二进制数转换为八进制和十六进制的示例:1. 将二进制数10110101转换为八进制数。
首先,将二进制数转换为十进制数:101101012 = 1 × 27 + 0 × 26 + 1 × 25 + 1 × 24 + 0 ×23 + 1 × 22 + 0 × 21 + 1 × 20= 18110然后,将十进制数181除以8,得到商22和余数5。
将余数5作为八进制数的第一位。
将商22再次除以8,得到商2和余数6。
将余数6作为八进制数的第二位。
最后,将商2作为八进制数的第三位。
因此,二进制数10110101转换为八进制数265。
2. 将二进制数10110101转换为十六进制数。
首先,将二进制数转换为十进制数:101101012 = 1 × 27 + 0 × 26 + 1 × 25 + 1 × 24 + 0 ×23 + 1 × 22 + 0 × 21 + 1 × 20= 18110然后,将十进制数181除以16,得到商11和余数5。
将余数5作为十六进制数的第一位。
将商11再次除以16,得到商0和余数11。
将余数11转换为十六进制中的B,作为十六进制数的第二位。
因为商为0,所以最后的十六进制数为5B。
二、八进制和十六进制转二进制将八进制或十六进制数转换为二进制数,需要将每个八进制或十六进制位转换为对应的三个或四个二进制位。
各种进制的相互转换

各种进制的相互转换进制是计算机科学中非常重要的概念。
在计算机中,所有的数字都是以二进制的形式存储的。
二进制是一种只有0和1两个数字的进制,也被称为基数为2的进制。
除了二进制,还有很多其他的进制,如八进制、十进制、十六进制等。
不同的进制在计算机中有着不同的应用,因此我们需要学会各种进制之间的相互转换。
一、十进制转二进制十进制是我们最为熟悉的进制,它是基数为10的进制。
在计算机中,我们需要将十进制转换为二进制,才能进行计算。
十进制转换为二进制的方法是不断地除以2,直到商为0为止,将每个余数从下往上排列起来就是二进制数。
例如,将十进制数13转换为二进制数:13 ÷ 2 = 6 (1)6 ÷ 2 = 3 03 ÷ 2 = 1 (1)1 ÷ 2 = 0 (1)因此,13的二进制数为1101。
二、二进制转十进制二进制转换为十进制的方法是将每个二进制位上的数字乘以2的n次方,其中n表示这个二进制位的位数。
然后将每个乘积相加起来就是十进制数。
例如,将二进制数1101转换为十进制数:1 × 2^3 + 1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 13因此,1101的十进制数为13。
三、十进制转八进制八进制是基数为8的进制。
将十进制数转换为八进制数的方法是不断地除以8,直到商为0为止,将每个余数从下往上排列起来就是八进制数。
例如,将十进制数125转换为八进制数:125 ÷ 8 = 15 (5)15 ÷ 8 = 1 (7)1 ÷ 8 = 0 (1)因此,125的八进制数为175。
四、八进制转十进制将八进制数转换为十进制数的方法是将每个八进制位上的数字乘以8的n次方,其中n表示这个八进制位的位数。
然后将每个乘积相加起来就是十进制数。
例如,将八进制数175转换为十进制数:1 × 8^2 + 7 × 8^1 + 5 × 8^0 = 125因此,175的十进制数为125。
进制转换方法

进制转换方法
进制转换方法是将一个数从一种进制表示转换为另一种进制表示的过程。
常见的进制包括二进制、八进制、十进制和十六进制。
以下是一些进制转换方法:
1. 二进制转十进制:将二进制数的每一位与相应的权值相乘,然后将结果相加即可得到十进制数。
2. 十进制转二进制:用除2取余法,将十进制数除以2得到商和余数,将余数从下往上排列即可得到二进制数。
3. 八进制转十进制:将八进制数的每一位与相应的权值(8的幂)相乘,然后将结果相加即可得到十进制数。
4. 十进制转八进制:用除8取余法,将十进制数除以8得到商和余数,将余数从下往上排列即可得到八进制数。
5. 十六进制转十进制:将每一位的十六进制数值与相应的权值(16的幂)相乘,然后将结果相加即可得到十进制数。
6. 十进制转十六进制:用除16取余法,将十进制数除以16得到商和余数,将余数从下往上排列即可得到十六进制数。
这些是常见的进制转换方法,掌握这些方法可以更方便地在不同进制之间进行转换。
所有进制互相转换的方法

所有进制互相转换的方法1.十-----二给你一个十进制,比如:6,如果将它转换成二进制数呢?10进制数转换成二进制数,这是一个连续除2的过程:把要转换的数,除以2,得到商和余数,将商继续除以2,直到商为0。
最后将所有余数倒序排列,得到数就是转换结果。
听起来有些糊涂1.十----->二给你一个十进制,比如说:6,如果将它转换成二进制数呢?10进制数转换成二进制数,这是一个连续除2的过程:把必须切换的数,除以2,获得商和余数,将商继续除以2,直到商为0。
最后将所有余数倒序排列,得到数就是转换结果。
听到出来有些迷糊?我们融合例子去表明。
比如说必须切换6为二进制数。
“把要转换的数,除以2,得到商和余数”。
必须切换的数是6,6÷2,获得商是3,余数就是0。
“将商继续除以2,直到商为0……”现在商是3,还不是0,所以稳步除以2。
那就:3÷2,得到商是1,余数是1。
“将商稳步除以2,直至万雅0……”现在商是1,还不是0,所以继续除以2。
那就:1÷2,获得商是0,余数就是1“将商继续除以2,直到商为0……最后将所有余数倒序排列”不好极!现在商已经就是0。
我们三次计算依次得到余数分别是:0、1、1,将所有余数倒序排列,那就是:110了! 6转换成二进制,结果就是110。
把上面的一段改成用表格来表示,则为:被除数排序过程商余数66/23033/21111/201(在计算机中,÷用/去则表示)2.二---->十二进制数切换为十进制数二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,建有一个二进制数:01100100,切换为10十进制为:01100100换算成十进制"^"为次方第0位0*2^0=0第1十一位0*2^1=0第2位1*2^2=4第3十一位0*2^3=0第4位0*2^4=0第5十一位1*2^5=32第6位1*2^6=64第7十一位0*2^7=0+公式:第n位10^(n-1)---------------------------用横式计算为:0*2^0+0*2^1+1*2^2+0*2^3+0*2^4+1*2^5+1*2^6+0*2^7=1000乘以多少都是0,所以我们也可以直接跳过值为0的位:1*2^2+1*2^5+1*2^6=1003.十---->八10十进制数转换成8十进制的方法,和切换为2十进制的方法相似,唯一变化:除数由2变为8。
进制转换方法总结

信息的编码再问学生计算机存储信息是不是都采用了二进制数?二进制也存在缺点,二进制都用0和1,而且位数太多,不易理解,也易出错。
为描述方便常用八、十进制,十六进制数表示二进制数在微机中,一般在数字的后面,用特定字母表示该数的进制。
十进制:日常生活中最常见的是十进制数,用十个不同的符号来表示:0、1、2、3、4、5、6、7、8、9。
基为:10运算规则:逢十进一,借一当十在十进制数的后面加大写字母D以示区别。
二进制:二进制数只有两个代码“0”和“1”,所有的数据都由它们的组合来实现。
基为:2运算规则:“逢二进一,借一当二”的原则。
在八进制数据后加英文字母“B”八进制:使用的符号:0、1、2、3、4、5、6、7;运算规则:逢八进一;基为:8在八进制数据后加英文字母“O”,十六进制:使用的符号:采用0~9和A、B、C、D、E、F六个英文字母一起共十六个代码。
运算规则:逢十六进一基为:16在十六进制数据后加英文字母“H”以示分别。
那么二进制数与八进制、十进制,十六进制数是怎么转换的呢?3、协作提高:用讲解法对二进制数与十进制数、十六进制数之间相互的转换的原理及方法(将二进制数字表示的位权值与十进制数字表示的位权值加以对比),叫几位学生到黑板上来做,其它同学在下面草稿纸上做。
观察在黑板上做的同学的对错情况,要知道错,错在那里。
由N进制数转换成十进制数的基本做法是,把N进制数首先写成加权系数展开式,然后按十进制加法规则求和。
这种做法称为"按权相加"法。
各数制的权如:十进制中,各位的权为10n-1二进制中,各位的权为2n-1十六进制中,各位的权为16n-1八进制中,各位的权为8n-11)、二进制转换为十进制各数制中整数部分不同位的权为“基的n-1次方(n为数值所在的位数,n的最小值取1)”,小数部分不同位的权值为“基的-n次方,从左向右,每移一位,幂次减1”。
二进制数的基数为2例(10110.011)2=()D作法:1×24+0×23+1×22+1×21+0×20+0×2-1+1×2-2+1×2-3 =(22.375)D八进制转换为十进制与二进制方法相同,只是八进制的基数为8(1011)8=1×83+0×82+1×81+1×80=(521)10十六进制转换为十进制二进制方法相同,只是十六进制的基数为16(1011)16=1×163+0×162+1×161+1×160=(4113)102.十进制转换成N进制:整数部分(除基取余法)不断除以N直到商为0,再把各次的余数倒排;小数部分(乘基取整法)不断乘以N直到小数部分为0,再把各次的整数顺排。
二进制、八进制、十进制、十六进制互相转换方法

二进制、八进制、十进制、十六进制互相转换方法有一个公式:二进制数、八进制数、十六进制数的各位数字分别乖以各自的基数的(N-1)次方,其和相加之和便是相应的十进制数。
个位,N=1;十位,N=2...举例:110B=1*2的2次方+1*2的1次方+0*2的0次方=0+4+2+0=6D110Q=1*8的2次方+1*8的1次方+0*8的0次方=64+8+0=72D110H=1*16的2次方+1*16的1次方+0*16的0次方=256+16+0=272D2、十进制数转二进制数、八进制数、十六进制数方法是相同的,即整数部分用除基取余的算法,小数部分用乘基取整的方法,然后将整数与小数部分拼接成一个数作为转换的最后结果。
3、二进制数转换成其它数据类型3-1二进制转八进制:从小数点位置开始,整数部分向左,小数部分向右,每三位二进制为一组用一位八进制的数字来表示,不足三位的用0补足,就是一个相应八进制数的表示。
010110.001100B=26.14Q八进制转二进制反之则可。
3-2二进制转十进制:见13-3二进制转十六进制:从小数点位置开始,整数部分向左,小数部分向右,每四位二进制为一组用一位十六进制的数字来表示,不足四位的用0补足,就是一个相应十六进制数的表示。
00100110.00010100B=26.14H十进制转各进制要将十进制转为各进制的方式,只需除以各进制的权值,取得其余数,第一次的余数当个位数,第二次余数当十位数,其余依此类推,直到被除数小于权值,最后的被除数当最高位数。
一、十进制转二进制如:55转为二进制2|5527――1 个位13――1 第二位6――1 第三位3――0 第四位1――1 第五位最后被除数1为第七位,即得110111二、十进制转八进制如:5621转为八进制8|5621702 ――5 第一位(个位)87 ――6 第二位10 ――7 第三位1 ――2 第四位最后得八进制数:127658三、十进制数十六进制如:76521转为十六进制16|765214726 ――5 第一位(个位)295 ――6 第二位18 ――6 第三位1 ――2 第四位最后得1276516二进制与十六进制的关系2进制0000 0001 0010 0011 0100 0101 0110 011116进制0 1 2 3 4 5 6 72进制1000 1001 1010 1011 1100 1101 1110 111116进制8 9 a(10) b(11) c(12) d(13) e(14) f(15)可以用四位数的二进制数来代表一个16进制,如3A16 转为二进制为:3为0011,A为1010,合并起来为00111010。
进制转换计算方法

进制转换计算方法【简单】
1.其他进制转成十进制
(1)整数
以二进制为例:100100
转成十进制从左到右乘以2的n-1次幂:1*2^5+0*2^4+0*2^3+1*2^2+0*2^1+0*2^0=36 (2)小数
以二进制为例:0.10010
转成十进制从左到右乘以2的n-1次幂:0*2^0+1*2^-1+0*2^-2+0*2^-3+1*2^-4+0*2^-5=0+0.5+0+0+0.0625+0=0.5625
其他进制数据转化方式等同
2.十进制转成其他进制
(1)整数
以二进制为例:36转成二进制
36/2=18 0
18/2=9 0
9/2=4 (1)
4/2=2 0
2/2=1 0
1/2=0 (1)
直到商为0为止,余数从右到左组合到一起即为2进制数值100100
(2)小数
以二进制为例:0.36转成二进制
0.36*2=0.72 0
0.72*2=1.44 (1)
0.44*2=0.88 0
0.88*2=1.76 (1)
0.76*2=1.52 (1)
0.52*2=1.04 (1)
直到十分位为0为止,整数位从右到左组合到一起即为2进制数值111010
其他进制数据转化方式等同。
3.其他进制之间转换要以十进制作为纽带进行转换
比如八进制转成二进制:要先把八进制转成十进制,再转成二进制。
进制之间的转换方法

进制之间的转换方法进制是计算机科学中非常重要的概念之一。
进制之间的转换方法是在计算机科学中非常基础、重要的技能,它是计算机编程和数据处理必备的知识之一。
在本文档中,将介绍如何在不同进制之间进行转换,包括二进制、八进制、十进制和十六进制,并提供相关的实例。
二进制(Binary)在计算机科学中,二进制是最常见的进制,因为计算机中的所有数据处理都是在二进制的基础上完成的。
二进制表示的是由 0 和 1 组成的数字系统。
在二进制中,每一位上的数字的权值都是 2 的幂次方,从右往左依次为1、2、4、8、16……如下表所示。
2^7 2^6 2^5 2^4 2^3 2^2 2^1 2^0128 64 32 16 8 4 2 1因此,一个八位的二进制数可以表示 0 ~ 255 的十进制数。
例如,二进制数 01100100 表示的是十进制数100 。
二进制转八进制将一个二进制数转换成八进制数,可以将二进制数每三位分为一组(从右往左),然后将每一组转换成相应的八进制数。
例如,将二进制数 11010 转换成八进制,可以按下面的方法进行:1. 将二进制数每三位分为一组:011 010 。
因为二进制数是从右往左数的,所以最后一组的位数不足三位,需要在最高位补 0 使其成为三个二进制位。
2. 将每组的二进制数转换成相应的八进制数。
011 对应的八进制数是 3,010 对应的八进制数是 2。
因此,11010 的八进制表示为 32。
二进制转十进制将一个二进制数转换成十进制数,可以将每一位上的数字乘以相应的权值,然后将所有的结果相加。
例如,将二进制数 101010 转换成十进制数,可以按下面的方法进行:1. 将每一位上的数字乘以相应的权值,从右往左依次为 1、2、4、8、16、32。
因此,101010 转换成十进制数为:0x20 + 2x16 + 0x8 + 1x4 + 0x2 + 1x1 = 42。
二进制转十六进制将一个二进制数转换成十六进制数,可以将二进制数每四位分为一组(从右往左),然后将每一组转换成相应的十六进制数。
各种进制之间的转换方法

各种进制之间的转换方法
首先,我们来讨论二进制和十进制之间的转换方法。
二进制是计算机中最常用的进制,而十进制则是我们日常生活中最常见的进制。
在二进制和十进制之间进行转换时,最简单的方法是将二进制数按权展开,然后相加即可得到其对应的十进制数。
例如,二进制数1011可以按权展开为12^3 + 02^2 + 12^1 + 12^0,计算后得到对应的十进制数为11。
接下来是八进制和十进制之间的转换方法。
八进制是以8为基数的进制,而十进制是以10为基数的进制。
在八进制和十进制之间进行转换时,我们可以将八进制数按权展开,然后相加得到其对应的十进制数,或者将十进制数除以8并取余数得到其对应的八进制数。
然后是十六进制和十进制之间的转换方法。
十六进制是以16为基数的进制,常用于表示颜色、内存地址等信息。
在十六进制和十进制之间进行转换时,我们可以将十六进制数按权展开,然后相加得到其对应的十进制数,或者将十进制数除以16并取余数得到其对应的十六进制数。
除了以上介绍的进制之间的转换方法,我们还可以通过进制之
间的转换来进行加减乘除运算。
例如,在二进制中进行加法运算时,我们可以按位相加,并注意进位的处理;在十六进制中进行乘法运
算时,我们可以将十六进制数转换为十进制数后进行乘法运算,再
将结果转换回十六进制数。
总之,掌握各种进制之间的转换方法对于理解计算机原理和进
行编程是非常重要的。
通过本文的介绍,希望读者能够更好地理解
和运用各种进制之间的转换方法,从而提高自己在计算机科学和数
学领域的能力。
所有进制互相转换的方法

进制转换1. 十 ----- 二给你一个十进制,比如:6,如果将它转换成二进制数呢? 10进制数转换成二进制数,这是一个连续除2的过程:把要转换的数,除以2,得到商和余数,将商继续除以2,直到商为0。
最后将所有余数倒序排列,得到数就是转换结果。
听起来有些糊涂1. 十 -----> 二给你一个十进制,比如:6,如果将它转换成二进制数呢?10进制数转换成二进制数,这是一个连续除2的过程:把要转换的数,除以2,得到商和余数,将商继续除以2,直到商为0。
最后将所有余数倒序排列,得到数就是转换结果。
听起来有些糊涂?我们结合例子来说明。
比如要转换6为二进制数。
“把要转换的数,除以2,得到商和余数”。
那么:十转二示意图要转换的数是6, 6 ÷ 2,得到商是3,余数是0。
“将商继续除以2,直到商为0……”现在商是3,还不是0,所以继续除以2。
那就: 3 ÷ 2, 得到商是1,余数是1。
“将商继续除以2,直到商为0……”现在商是1,还不是0,所以继续除以2。
那就: 1 ÷ 2, 得到商是0,余数是1“将商继续除以2,直到商为0……最后将所有余数倒序排列”好极!现在商已经是0。
我们三次计算依次得到余数分别是:0、1、1,将所有余数倒序排列,那就是:110了!6转换成二进制,结果是110。
把上面的一段改成用表格来表示,则为:被除数计算过程商余数6 6/2 3 03 3/2 1 11 1/2 0 1(在计算机中,÷用 / 来表示)2. 二 ----> 十二进制数转换为十进制数二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:0110 0100,转换为10进制为:下面是竖式:0110 0100 换算成十进制" ^ " 为次方第0位 0 * 2^0 = 0第1位 0 * 2^1 = 0第2位 1 * 2^2 = 4第3位 0 * 2^3 = 0第4位 0 * 2^4 = 0第5位 1 * 2^5 = 32第6位 1 * 2^6 = 64第7位 0 * 2^7 = 0 +公式:第N位10^(N-1)---------------------------100用横式计算为:0 * 2 ^ 0 + 0 * 2 ^ 1 + 1 * 2 ^ 2 + 0 * 2 ^ 3 + 0 * 2 ^ 4 + 1 * 2 ^ 5 + 1 * 2 ^ 6 + 0 * 2 ^ 7 = 1000乘以多少都是0,所以我们也可以直接跳过值为0的位:1 *2 ^ 2 + 1 * 2 ^ 5 + 1 * 2 ^ 6 = 1003. 十 ----> 八10进制数转换成8进制的方法,和转换为2进制的方法类似,唯一变化:除数由2变成8。
10进制转其他进制的方法

10进制转其他进制的方法在数字系统中,我们通常使用10个数字来表示所有的数字,从0到9、这种系统被称为十进制系统。
然而,有时我们需要将数字转换为其他进制,如二进制、八进制或十六进制。
下面是几种常见的将十进制转换为其他进制的方法:一、二进制转换方法:将十进制数字转换为二进制数字的方法是通过除2取余法。
以下是一个将十进制数字转换为二进制数字的例子:例子:将十进制数字27转换为二进制数字。
步骤1:用27除以2,并将商和余数记录下来。
27÷2=13 (1)步骤2:再用13除以2,并将商和余数记录下来。
13÷2=6 (1)步骤3:再用6除以2,并将商和余数记录下来。
6÷2=3 0步骤4:再用3除以2,并将商和余数记录下来。
3÷2=1 (1)步骤5:最后再用1除以2,并将商和余数记录下来。
1÷2=0 (1)二、八进制转换方法:将十进制数字转换为八进制数字的方法是通过除8取余法。
以下是一个将十进制数字转换为八进制数字的例子:例子:将十进制数字35转换为八进制数字。
步骤1:用35除以8,并将商和余数记录下来。
35÷8=4 (3)步骤2:再用4除以8,并将商和余数记录下来。
4÷8=0 (4)步骤3:将余数从最后一个到第一个,得到八进制数字:43所以,35的八进制表示为43三、十六进制转换方法:将十进制数字转换为十六进制数字的方法是通过除16取余法。
十六进制数字中,对于10到15分别用字母A到F表示。
以下是一个将十进制数字转换为十六进制数字的例子:例子:将十进制数字123转换为十六进制数字。
步骤1:用123除以16,并将商和余数记录下来。
123÷16=7...11(余数为11,对应十六进制中的B)步骤2:再用7除以16,并将商和余数记录下来。
7÷16=0...7(余数为7)步骤3:将余数从最后一个到第一个,得到十六进制数字:7B。
数的进制转换有哪些规律

数的进制转换有哪些规律一、引言数的进制是数学中的一个重要概念,它描述了数的表示方式。
在日常生活和计算机科学中,常用的进制有十进制、二进制、八进制和十六进制等。
本文将介绍数的进制转换的规律,帮助读者更好地理解和运用进制转换。
二、十进制与其他进制的转换1. 十进制转二进制十进制数转换为二进制数的方法是将十进制数不断除以2,直到商为0,然后将每一步的余数倒过来,即可得到对应的二进制数。
例如,十进制数13转换为二进制数的过程如下:13 ÷ 2 = 6 余 16 ÷ 2 = 3 余 03 ÷ 2 = 1 余 11 ÷2 = 0 余 1将每一步的余数倒过来,得到的二进制数为1101。
2. 十进制转八进制十进制数转换为八进制数的方法与转二进制类似,只需将十进制数不断除以8,直到商为0,然后将每一步的余数倒过来,即可得到对应的八进制数。
例如,十进制数37转换为八进制数的过程如下:37 ÷ 8 = 4 余 54 ÷ 8 = 0 余 4将每一步的余数倒过来,得到的八进制数为45。
3. 十进制转十六进制十进制数转换为十六进制数的方法与转二进制和八进制类似,只需将十进制数不断除以16,直到商为0,然后将每一步的余数倒过来,将10、11、12、13、14、15分别表示为A、B、C、D、E、F,即可得到对应的十六进制数。
例如,十进制数255转换为十六进制数的过程如下:255 ÷ 16 = 15 余 15(F)15 ÷ 16 = 0 余 15(F)将每一步的余数倒过来,得到的十六进制数为FF。
三、其他进制与十进制的转换1. 二进制转十进制二进制数转换为十进制数的方法是将二进制数从右往左依次乘以2的幂,再将结果相加。
例如,二进制数1101转换为十进制数的过程如下:1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰ = 8 + 4 + 0 + 1 = 132. 八进制转十进制八进制数转换为十进制数的方法与转二进制类似,只需将八进制数从右往左依次乘以8的幂,再将结果相加。
关于二进制、十进制、八进制、十六进制数据转换计算方法详细总结
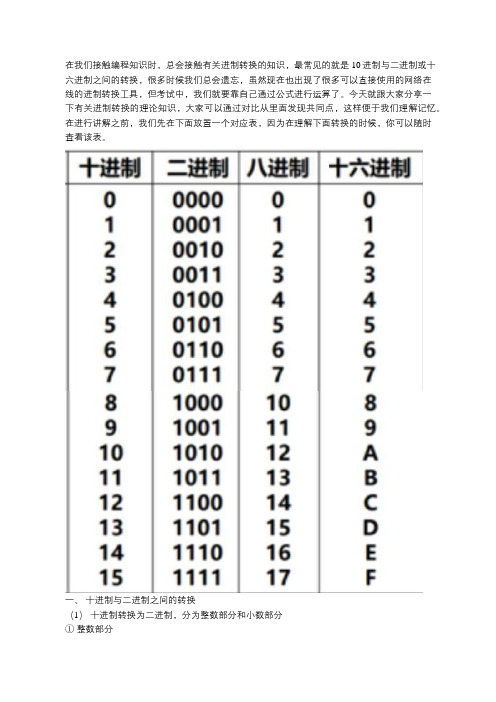
在我们接触编程知识时,总会接触有关进制转换的知识,最常见的就是10进制与二进制或十六进制之间的转换,很多时候我们总会遗忘,虽然现在也出现了很多可以直接使用的网络在线的进制转换工具,但考试中,我们就要靠自己通过公式进行运算了。
今天就跟大家分享一下有关进制转换的理论知识,大家可以通过对比从里面发现共同点,这样便于我们理解记忆。
在进行讲解之前,我们先在下面放置一个对应表,因为在理解下面转换的时候,你可以随时查看该表。
一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2商84余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000②小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25则整数部分为0小数部分为0.25;第二步将小数部分0.25乘以2得0.5则整数部分为0小数部分为0.5;第三步将小数部分0.5乘以2得1.0则整数部分为1小数部分为0.0;第四步读数从第一位读起读到最后一位即为0.001。
进制之间的转换

一、十进制与二进制之间的转换1、十进制转换为二进制(1)整数部分方法1(除2取余法):每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
举例:将十进制的10转换为二进制第一步,将商10除以2,商5余数为0;第二步,将商5除以2,商2余数为1;第三步,将商2除以2,商1余数为0;第四步,将商1除以2,商0余数为1;第五步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,得结果(1010)2;(2)小数部分(方法:乘2取整法)将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是0,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:将0.45转换为二进制(保留到小数点第四位)0.45*2=0.9取0;0.9*2=1.8取1;0.8*2=1.6取1;0.6*2=1.2取1;0.2*2=0.4取0;0.4*2=0.8取0;0.8*2=1.6取1;大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
这个也是计算机在转换中会产生误差,但是由于保留位数很多,精度很高,所以可以忽略不计。
那么,我们可以得出结果将0.45转换为二进制约等于 (0.0111)2。
注:整数的转换是精确的,小数的转换可能出现无穷小数或循环小数的情况。
总结进制数转换-二进制-八进制-十进制-十六进制--之间转换方法

*十进制数与二进制数间的转换
A. “十进制”转“二进 制”
2
19 余数 低位
2 91
2
41
2
20
2
10
0 1 高位
(19)10=(10011)2
B. “二进制”转“十进 制”
(10011)2
=1*2 4 +1*2 1
+1*2 0 =16+2+1 =19
注意:2 的0次方 等于1,
不是0
返回
*十进制数与八进制数间的转换
2
3、计算机中彩色图像的每一种颜色均可用红、 绿、蓝三原色调配出来,如果每种原色从浅到 深分为256个等级,一个原色需要用( )位二 进制数来表示。
A 24位 B 16位 C 8 位 D 256位
4、转换进制:
(11010)2 = ( )8 = ( )16 = ( )10
(0.010)2 = (
A. “十进制”转“八进 制”
8
19 余数 低位
8 23 02
高位
(19)10=(23)8
B. “八进制”转“十进 制”
(23)8
=2*8 1 +3*8 0
=16+3
=19
返回
*十进制数与十六进制数间的转换
A. “十进制”转“十六进 制”
16
27 余数 低位
16 1 11 01
写成(111)16
高位
0110 1110 0110. 1101 6 E 6. D
二进制数(11011100110.1101)2转换成十六进制 数是(6E6.D)16。
反之,将每位十六进制数分别用四位二进制数表 示,就可完成十六进制数和二进制数的转换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信息的编码
再问学生计算机存储信息是不是都采用了二进制数二进制也存在缺点,二进制都用0和1, 而且位数太多, 不易理解, 也易出错。
为描述方便常用八、十进制,十六进制数表示二进制数
在微机中,一般在数字的后面,用特定字母表示该数的进制。
十进制:日常生活中最常见的是十进制数,用十个不同的符号来表示:0、1、2、3、4、5、6、7、8、9。
基为:10
运算规则:逢十进一,借一当十
在十进制数的后面加大写字母D以示区别。
二进制:二进制数只有两个代码“0”和“1”,所有的数据都由它们的组合来实现。
基为:2
运算规则:“逢二进一,借一当二”的原则。
在八进制数据后加英文字母“B”
八进制:使用的符号:0、1、2、3、4、5、6、7;
运算规则:逢八进一;
基为:8
在八进制数据后加英文字母“O”,
十六进制:使用的符号:采用0~9和A、B、C、D、E、F六个英文字母一起共十六个代码。
运算规则:逢十六进一
基为:16
在十六进制数据后加英文字母“H”以示分别。
那么二进制数与八进制、十进制,十六进制数是怎么转换的呢
3、协作提高:用讲解法对二进制数与十进制数、十六进制数之间相互的转换的原理及方法(将二进制数字表示的位权值与十进制数字表示的位权值加以对比),叫几位学生到黑板上来做,其它同学在下面草稿纸上做。
观察在黑板上做的同学的对错情况,要知道错,错在那里。
由N进制数转换成十进制数的基本做法是,把N进制数首先写成加权系数展开式,然后按十进制加法规则求和。
这种做法称为"按权相加"法。
各数制的权
如:十进制中,各位的权为10n-1
二进制中,各位的权为2n-1
十六进制中,各位的权为16n-1
八进制中,各位的权为8n-1
1)、二进制转换为十进制
各数制中整数部分不同位的权为“基的n-1次方(n为数值所在的位数,n的最小值取1)”,小数部分不同位的权值为“基的-n次方,从左向右,每移一位,幂次减1”。
二进制数的基数为2
例()2=()D
作法:1×24+0×23+1×22+1×21+0×20+0×2-1 +1×2-2+1×2-3 =()D
八进制转换为十进制与二进制方法相同,只是八进制的基数为8(1011)8 = 1×83+0×82+1×81+1×80 = (521)10
十六进制转换为十进制二进制方法相同,只是十六进制的基数为16(1011)16 = 1×163+0×162+1×161+1×160 = (4113)10
2. 十进制转换成N进制:整数部分(除基取余法)不断除以N直到商为0,再把各次的余数倒排;小数部分(乘基取整法)不断乘以N 直到小数部分为0,再把各次的整数顺排。
十进制转换为二进制
十进制整数转换为二进制整数采用"除2取余,逆序排列"法。
具体做法是:用十进制整数去除2,可以得到一个商和余数;再用商去除2,又会得到一个商和余数,如此进行,直到商为0时为止,逆序排列余数
小数采用"乘2取整,顺序排列"法。
具体做法是:用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,此时0或1为二进制的最后一位。
或者达到所要求的精度为止。
【例1】将(236)D转换成二进制。
转换过程如图1所示。
如转成二进制的过程是:
×2= 得整数部分:1
×2= 得整数部分:1
×2= 得整数部分:0
×2= 得整数部分:1
所以=
十进制转换成8进制、16进制,与转成2进制的方法相同,但基数是8或16!
十进制转换成八进制有两种方法:
①整数部分
方法:除8取余法,即每次将整数部分除以8,余数为该位权上的数,而商继续除以8,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数起,一直到最前面的一个余数。
②小数部分
方法:乘8取整法,即将小数部分乘以8,然后取整数部分,剩下的小数部分继续乘以8,然后取整数部分,剩下的小数部分又乘以8,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,暂取个名字叫3舍4入。
例:将十进制数转换为八进制数
解:先将这个数字分为整数部分796和小数部分
转换八进制为
十进制小数转换成16进制
整数部分(除基取余法)不断除以16直到商为0,再把各次的余数倒排;小数部分(乘基取整法)不断乘以16直到小数部分为0或纯小数部分再把各次的整数顺排。
小数部分:
把十进制小数转换成16进制小数所采用的规则是“乘以16取整数”。
方法是用16乘以十进制纯小数,将其结果的整数部分记录,这就是对应的第n位小数;再用16乘以余下的纯小数部分,再去掉其结果的整数部分;如此类推,直到余下的纯小数为0或满足所要求的精度为止。
例:=H
*16= 记录11,并转换为16进制11D=BH
*16= 记录3,转换3D=3H,注:这里的被除数就是上一步的纯小数部分
*16= 循环了。
所以,=
二进制转换为八进制
转换方法:从小数点开始,将二进制数的整数和小数部分每三位分为一组,不足三位的分别在整数的最高位前和小数的最低位后加“0”补足,然后每组用等值的八进制码替代,即得八进制数。
例:(.0100111)2 = ()8
2.二进制数与十六进制数的相互转换
由于16=24,所以在将二进制数转换成十六进制数时,从小数点开始,将二进制数的整数和小数部分每四位分为一组,不足四位的分别在整数的最高位前和小数的最低位后加“0”补足,然后每组用等值的十六进制码替代,即得目的数。
十六进制数转换成二进制数时正好相反,一位十六进制数用四位二进制数来替换。
对于有小数的数,要分小数和整数部分处理。
例: 2=H
八进制转成十六进制可先转成二进制再转成十六进制
给出转换表让学生熟记
二进制的运算法则 算术运算:
加法:0+0=0 ,0+1=1,1+0=1,1+1=0 减法:0-0=0,1-0=1,1-1=0,0-1=1 乘法:0*0=0,0*1=0,1*0=0,1*1=1 除法:
0÷0=0
0÷1=0 1÷0 1÷1=1
二进制 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001
十进制 0 1 2 3 4 5 6 7 8 9
八进制 0 1 2 3 4 5 6 7 10 11
十六进制
0 1 2 3 4 5 6 7 8 9
与:0 and 0=0 , 0 and 1=0 , 1 and 0=0 , 1 and 1=1
或:0 or 0 =0 , 0 or 1=1 , 1 or 0=1 , 1 or 1=1
非:not 0=1 , not 1=0
异或:0 xor 0=0 , 0 xor 1=1 , 1 xor 0 =1 , 1 xor 1 =0
4、巩固提高:,用一定量的习题进行巩固,及时发现问题,及时纠正。
()10=()2
(10011)2=(19)10
(.11011)2=()8
()8=(.1)2
()2=()16
()16=(2
(73)8=(3B)16
(11010)2 = ( )8 = ( )16 = ( )10
2 = ( )10 = ( )8 = ( )16
( 43 )8 = ( )2 = ( )10
( a2 )16 = ( )8 = ( )2
5、比较下面最大的是:
A (110100)2
B (63)8
C (54)10
D (35)16
六、反思
1、对十进制转化为二进制数,求余数是正数,有的同学理解的不是
2、对二进制数、十六进制数转化为十进制数时,采用是按权展开相加法,但小学里的数学高中生会做错。
七、总结通过本节课的学习,让学生掌握二进制数、十进制数、十六进制数的相互转化。
记住方法:除二取余法,先余为低,后余为高。
按权展开相加法中,对权值的理解等,以后让学生多一些表现的机会。
