晶体的密堆积
金属晶体堆积方式分类

配位数 8 ,空钾 K 的 立方体心堆积
六方紧密堆积 —— IIIB,IVB 面心立方紧密堆积 —— IB,Ni,Pd, Pt 立方体心堆积 —— IA,VB,VIB
金属晶体堆积方式分类
金属晶体:晶胞在其内部有不同的排列方式, 一般可以分为三类。 ①面心立方堆积A 1类型:常见金属如:金、 银、铜、铝等 ②体心立方体堆积A2类型: 常见金属如:钠、 钾、铬、钼等。 ③六方堆积A3类型:常见金属如:镁、锌、 钛等。
例 金属晶体的密堆积结构
金属晶体中离子是以紧密堆积的形式存在的 。 用等径刚性球模型来讨论堆积方式。
在一个层中,最紧密的堆积方式,是一个球与 周围 6 个球相切,在中心的周围形成 6 个凹位,将 其算为第一层。
第二层对第一层来讲最紧密的堆积方式是将 球对准 1,3,5 位。 ( 或对准 2,4,6 位,其情 形是一样的 )
第三层,对第一、二层来说,第三层可以有两种 最紧密的堆积方式。
12
6
3
54
12
6
3
54
,
AB
第一种是将球对准第一层的球。 下图是此种六方 紧密堆积的前视图
12
A
6
3
54
B
A
每两层形成一个周期,即
B
AB AB 堆积方式,形成六方紧
A
密堆积。
配位数 12 。 ( 同层 6,上下层各 3 )
第三层的另一种排列 方式,是将球对准第一层 的 2,4,6 位,不同于 AB 两层的位置,这是 C 层。
12
6
3
54
12
金属晶体堆积方式
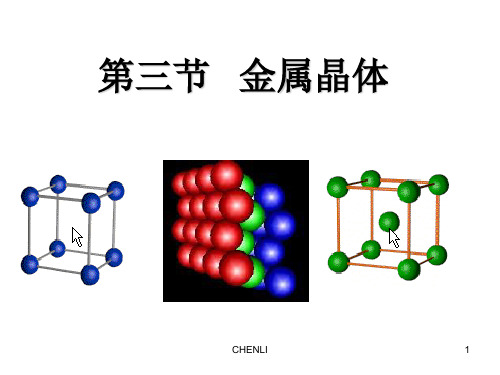
A B C A
重复ABC的堆积叫A1堆积,重复单位⃒ABC⃒。
CHENLI
5
A B A
重复AB的堆积叫A3堆积,重复单位⃒AB⃒方最密堆积 A3堆积: 抽出六方晶胞,又叫六方最密堆积(hexagonal
closest packing)简写为hcp 。
A B A
分数坐标: 配位数:12 空间利用率74% 晶胞内含有2个球。
chenli第三层球放在第二层球的空隙上有两种方式堆积重复单位abcaabbccaachenliaabbaa重复ab的堆积叫achenli抽出六方晶胞又叫六方最密堆积hexagonalclosestpacking简写为hcp堆积
第三节 金属晶体
CHENLI
1
1、简单立方堆积 -配位数:6
每个晶胞包含一个原子 空间利用率52%
1
4
2
3
6
1
4
2
3
5
CHENLI
2
2、钾型(体心立方堆积) -配位数:8
每个晶胞包含2个原子 空间利用率68%
5
6
8
7
1
2
4
3
CHENLI
3
密堆积原理:原子、离子、分子的排布总是 趋向于配位数高,空间利用率大的紧密堆 积结构方式,最紧密的堆积往往是最稳定 的结构。
CHENLI
4
密置堆:第三层球放在第二层球的空隙上有两种方式
CHENLI
7
4、面心立方最密堆积
A1堆积:
抽出立方面心晶胞,又叫面心立方最密堆积 (cubic closest packing)简写为ccp 。
z
A
B
C
y
x
金属晶体的密堆积

B
A
分数坐标:
密置层为(001)
(,,), ( , , ) or( , , )
y x
1200
晶胞内含有2个球。
14
§5-3 金属晶体和晶体结构的能带理论 2个球为二套等同点 结构基元:2个球 点阵型式: 六方简单 配位数: 12
B AA
B A
15
§5-3 金属晶体和晶体结构的能带理论
a 与r的关系: r a , r a
空间利用率
V球 %
V晶胞
(
a
a)
%
.%
总结:
பைடு நூலகம்
22
§5-3 金属晶体和晶体结构的能带理论
二、金属晶体的堆积型式和金属的原子半径
1、金属晶体的堆积型式(P524表5-3.2) 绝大多数金属单质都是A1,A2,A3型,少数金属单 质具有A4型(如:Si,Ge,Sn)或其它特殊结构型式(Mn--x)。 2、金属原子半径 定义:金属晶体中紧邻原子间距离的一半。
由此可推测该晶体是:
(B)
(A) 立方P (B) 立方I (C) 立方F (D) 立方C
习题:4 、已知某金属晶体的结构属A3型堆积,其原 子半径为r,则它的边长b,c等于:(A)
( A)b r, c r (B)b r , c r
(C)b c r
(D)b c r
33
§5-3 金属晶体和晶体结构的能带理论 例5、CuSn合金属NiAs型结构,六方晶胞参数 a=419.8pm,c=509.6pm ,晶胞中原子的分数坐标为: Cu(,,)(,, ) Sn( , , ), ( , , ) (1)计算Cu-Cu间的最短距离 (2)Sn原子按什么型式堆积? (3)Cu原子周围的原子围成什么多面体空隙?
金属晶体的三种密堆积方式

金属晶体的三种密堆积方式金属晶体的三种密堆积方式中,原子排列的密堆积方式是指原子在三维空间中紧密排列,以使得晶体的空间利用率达到最大。
密堆积方式可以有效影响金属的密度、强度、硬度等物理性质,因此在材料科学和固体物理中具有重要意义。
通常,金属晶体的密堆积方式主要分为以下三种:面心立方堆积(FCC)、六方最密堆积(HCP)和体心立方堆积(BCC)。
一、面心立方堆积(FCC)面心立方堆积(Face-Centered Cubic, FCC)是一种常见的密堆积方式,其中每个立方体的面上都有一个原子,且每个顶点上也有一个原子。
FCC结构可以看作是由许多面心立方单元重复堆积而成,其代表性金属包括铜(Cu)、铝(Al)、银(Ag)和金(Au)等。
1. 结构特点:在FCC结构中,每个原子都有12个最近邻原子,即配位数为12。
该结构单胞中包含4个原子(8个顶点上的原子分别与相邻单元共享,6个面的原子与邻近单元共享),堆积因子达到0.74,即约74%的空间被原子占据,属于最密堆积结构。
2. 性质:FCC结构由于其紧密的堆积方式,具有较高的塑性和延展性。
因此,FCC金属在室温下一般较易发生滑移,从而产生延展变形。
例如,铜和铝具有良好的延展性,易于加工成型。
3. 堆积方式:在面心立方堆积中,原子在平面上形成紧密的六边形排列,层间顺序为ABCABC 的排列模式。
这意味着每三层后结构重复,形成周期性排列。
4. 应用:FCC结构的金属由于其良好的延展性和抗冲击性,常用于制造电线、金属薄膜和结构材料等。
二、六方最密堆积(HCP)六方最密堆积(Hexagonal Close-Packed, HCP)是一种与面心立方相似的密堆积方式,但其晶体结构为六方柱体,且具有不同的堆积顺序。
HCP结构的代表性金属包括镁(Mg)、钛(Ti)、锌(Zn)和钴(Co)等。
1. 结构特点:在HCP结构中,原子的配位数同样为12,说明其紧密度与FCC相似。
晶体密堆积原理

密堆积:由无方向性的金属键、离子键和范德华 力等结合的晶体中,原子、离子或分子等微观 粒子总是趋向于相互配位数高,能充分利用空 间的堆积密度最大的那些结构。
密堆积方式因充分利用了空间,而使体系的势能 尽可能降低,而结构稳定。
常见的密堆积类型
常见密堆积型式
面心立方最密堆积(A1)
六方最密堆积(A3)
3
r 3a 4
r 3a 8
5.堆积方式与晶胞关系
A1—面心立方晶胞 A2—体心立方晶胞 A4—面心立方晶胞 A3—六方晶胞
六方晶胞中a=bc, ==90º, =120º
晶体类型
根据形成晶体的化合物的种类不同可以 将晶体分为:离子晶体、分子晶体、原 子晶体和金属晶体。
1. 离子晶体
离子键无方向性和饱和性,在离子晶体中 正、负离子尽可能地与异号离子接触,采 用最密堆积。 离子晶体可以看作大离子进行等径球密堆 积,小离子填充在相应空隙中形成的。 离子晶体多种多样,但主要可归结为6种 基本结构型式。
2
3
2a3 8 2r3
V球
2
4
3
r3
(晶胞中有2个球)
V球 V晶胞 100% 74.05%
A1型堆积方式的空间利用率计算
解:V晶胞
a3
32 2
r3
晶胞中含4个球 :
V球
4
4 3
r 3
空间利用率 V球 V晶胞 74.05%
2.体心立方密堆积(A2)
A2不是最密堆积。每个球有八个最近的配体 (处于边长为a的立方体的8个顶点)和6个稍远 的配体,分别处于和这个立方体晶胞相邻的六 个立方体中心。故其配体数可看成是14,空间 利用率为68.02%. 每个球与其8个相近的配体距离 d 3 a
第二章晶体结构(紧密堆积2)

0.123+0.172=0.295 0.277 0.018 0.715 NaCl NaCl 6
极化包括:主极化和被极化 在离子晶体中,一般阴离子半径较大,易于变形 而被极化,而主极化能力较低。阳离子半径相对较小, 当电价较高时其主极化作用大,而被极化程度较低。
五、鲍林规则
(1)在正离子的周围形成一负离子配位多面体, 正离子、负离子间的距离取决于半径之和,而配 位数取决于半径比。
正离子多面体之间倾向于不公用几何元素。
(5)晶体中,本质不同的结构组元的种类,倾向于 为数最少。(节省规则)
在一晶体结构中,晶体化学性质相似的不同离子,将尽 可能采取相同的配位方式。
总结:
鲍林规则由离子晶体结构中归纳出来的,符合于大多数离
子晶体结构。对理想晶体结构有用。但它不完全适用于过
渡金属化合物的离子晶体,更不适用非离子晶体,对于这 些晶体的结构,还需用晶体场和配位场理论说明。
1.6 晶体场理论和配位场理论
一、晶体场理论基础
所谓晶体场就是指晶格中由阳离子周围的配位体—与阳离 子成配位关系的阴离子或负离子指向中心阳离子的偶极分 子——所构成的一个静电场。
图1-五个d轨道的空间分布
二、d轨道的晶体场分裂
图1-正八面体络合的d轨道
t=4/9 o
四面体和八面体配位中过渡金属离子d轨道的相对
3+
影响因素:
1.正、负离子半径比 2.温度 3.压力 4.离子极化
四、 离子极化
在离子晶体中,通常把离子视作刚性的小球,这是 一种近似处理,这种近似仅在典型的离子晶体中误差较
小。实际上,在离子紧密堆积时,带电荷的离子所产生
的电场,必然要对另一个离子的电子云产生吸引或排斥 作用,使之发生变形,这种现象称为极化。
分子密堆积

分子密堆积密堆积:由无方向性的金属键、离子键和范德华力等结合的晶体中,原子、离子或分子等微观粒子总是趋向于相互配位数高,能充分利用空间的堆积密度最大的那些结构。
密堆积方式因充分利用了空间,而使体系的势能尽可能降低,而结构稳定。
密堆积原理是一个把中学化学的晶体结构内容联系起来的一个桥梁性的理论体。
常见的密堆积形式:1、面心立方最密堆积;2、六方最密堆积;3、体心立方米堆积。
1.分子晶体由分子构成,相邻分子靠分子间作用力相互吸引。
其中,分子间作用力包括范德华力和氢键。
特点:低熔点、硬度小、易升华。
2.分子晶体的分类(1)所有非金属氢化物(2)部分非金属单质(3)部分非金属氧化物(4)几乎所有的酸(5)绝大多数有机物3.分子晶体的结构特点(1)如果分子晶体中只有范德华力,绝大多数分子晶体为分子密堆积。
分子密堆积就是以一个分子为中心,其周围可以有12个紧邻的分子的特征,如碳六十。
(2)如果分子晶体中以氢键和范德华力结合,如冰的晶体,每个水分子周围有4个紧邻的水分子。
4.分子晶体熔沸点比较规律分子晶体中分子间作用力越大,熔沸点越高,而具有氢键的分子晶体熔沸点反常的高。
如熔沸点:(1)对于组成和结构相似的分子晶体,相对分子质量越大,分子间作用力越强,物质的熔沸点越高,如:(2)对于分子质量相近,但组成和结构不相似的物质,极性越大,其熔沸点就越高。
如:(3)在高级脂肪酸形成的油脂中,不饱和程度越大,熔沸点越低。
如:(4)烃、卤代烃、醇、醛、羧酸等有机物一般随着碳原子数的增加,熔沸点升高。
如:(5)同分异构体中,链烃的同分异构体随支链增多,沸点降低。
如:。
晶体密堆积

最紧密堆积方式
等径球的堆积
六方最紧密堆积
最紧密堆积中的空隙 不等径球的堆积
等径球质点堆积
等径球最紧密堆积时,在平面上每个球与6个球相接触, 形成第一层(球心位置标记为A),如图所示。此时, 每3个彼此相接触的球体之间形成1个弧线三角形空隙, 每个球周围有6个弧线三角形空隙,其中3个空隙的尖角 指向图的下方(其中心位置标记为B),另外3个空隙的 尖角指向图的上方(其中心位置标记为C),这两种空 隙相间分布。
两种最紧密堆积中,每个球体周围同种球体的个数均 为12。
A AA
B
A AC A A AAAAA
AAAA AAA
等径球质点堆积
A AA
B
A CA A A AAAAA
AAAA AAA
ABCABC……层序堆积 —面心立方密堆积A1
ABAB……的层序堆积 —六方密堆积A3
面心立方最紧密堆积
12
ห้องสมุดไป่ตู้
6
3
54
12
面的内容:
决定离子晶体结构的基本因素
一、内在因素对晶体结构的影响 1.质点的相对大小 2.晶体中质点的堆积 3.配位数与配位多面体 4.离子极化
二、外在因素对晶体结构的影响──同质多晶与类质 同晶及晶型转变
1.质点的相对大小—原子半径及离子半径
原子半径的大小与原子处于孤立状态还是处于结合 状态有关。
6
3
54
12
6
3
54
A B C
面心立方最紧密堆积
A C B A C B A
ABCABC……, 即每三层重复一次
面心立方最紧密堆积
12
6
3
54
面心立方最紧密堆积
2-密堆积
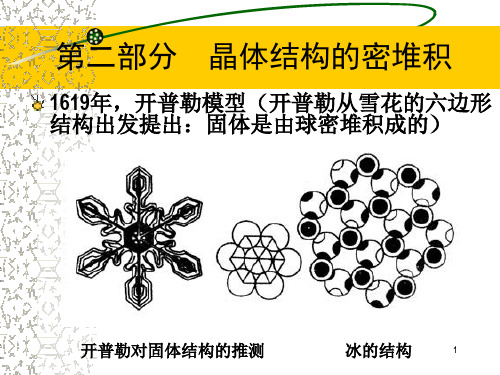
S a a sin 60 3 a2 2
平行六面体的高:
h 2边长为a的四面体高
2 6 a 2 6 a
3
3
20
V晶胞
3 a2 2 6 a
2
3
2a3 8 2r3
V球
2
4
3
r3
(晶胞中有2个球)
V球 V晶胞 100% 74.05%
21
22
23
隙上方,其排列方式与第一层相同,但与第
二层错开,形成ABAB…堆积。这种堆积方式
可以从中划出一个六方单位来,所以称为六
方最密堆积(A3)。
9
三维等径圆球的堆积(A3)
能量较低 密置层
A B A B A
B
A
10
A3最密堆积形成的六方晶胞
A3最密堆积形成后, 从中可以划分 出什么晶胞? 六方晶胞.
11
47
(4)六方ZnS晶胞图
48
六方ZnS
(1)六方晶系,简单六方晶胞 (2)Z=1 (3)Zn2+和S2- 六方最密堆积周期|AaBb|。 (4)配位数4:4。 (6)2s:0 0 0,2/3 1/3 1/2;
2Zn:0 0 5/8,2/3 1/3 1/8。
49
(5) CsCl型:
(1)立方晶系,简单立方晶胞。 (2)Z=1。 (3)Cs+,Cl-,离子键。 (4)配位数8:8。 (5) Cs+离子位于简单立方点阵的阵点上
3 30
A2型密堆积图片
31
金刚石型堆积(A4)
配位数为4,空间利用率为
34.01%,不是密堆积。这
种堆积方式的存在因为原
子间存在着有方向性的共
金属晶体中金属原子的相对最密堆积程度较低

金属晶体中金属原子的相对最密堆积程度较低全文共四篇示例,供读者参考第一篇示例:金属晶体是由金属原子通过一定的排列方式形成的固体结构。
在金属晶体中,金属原子之间存在着一定的间隙和相互作用,这些因素决定了金属晶体的性质和特点。
在金属晶体中,金属原子的相对最密堆积程度是一个重要的参数,它直接影响着金属晶体的密度、硬度、热导率等物理性质。
金属原子的最密堆积方式有两种,分别是六方最密堆积和面心立方最密堆积。
在六方最密堆积中,金属原子沿着六方向紧密堆积,形成了一个紧密排列的结构。
而在面心立方最密堆积中,金属原子沿着每个面心堆积,形成了一个更为密集的结构。
从理论上讲,面心立方最密堆积的金属晶体中金属原子的相对密度应该更高,因此更加紧密。
实际情况并非总是如此。
有些金属晶体中金属原子的相对最密堆积程度较低,即使采用面心立方最密堆积的方式排列,金属晶体的密度也不会很高。
这种现象通常出现在一些过渡金属和稀土金属中。
这些金属具有较大的原子半径和较为复杂的电子结构,导致金属原子之间的相互作用较弱,难以形成紧密的结构。
即使采用面心立方最密堆积的方式排列,金属原子之间仍然存在较大的间隙,使得金属晶体的密度较低。
这种现象在一些金属合金中尤为突出。
金属合金是由两种或多种金属原子混合组成的固体溶体,通常具有较高的强度和耐腐蚀性。
由于金属合金中金属原子种类的不同和比例的变化,金属原子之间的相互作用也会发生变化,导致金属合金中金属原子的相对最密堆积程度较低。
这种情况下,金属原子之间的间隙增大,使得金属合金的密度和硬度都会受到影响。
尽管金属晶体中金属原子的相对最密堆积程度较低可能会影响金属晶体的一些物理性质,但这并不意味着金属晶体就会失去其特有的优良性能。
事实上,低密度的金属晶体在一些方面还具有一定的优势。
低密度可以减小金属晶体的重量,使得金属材料更加轻便,适用于一些需要重量轻的领域。
低密度还可以降低金属晶体的硬度,使得金属材料更易加工,适用于一些需要易加工的领域。
晶体的密堆积讲诉

(要点二:晶体的密堆积方式)
同一层上等径圆球的最密堆积只有一种形式
两层等径圆球的 最密堆积也只有一种 形式, 如右图:
一、球数︰正八面体︰正四面体
一、球数︰正八面体︰正四面体 六方密堆积、A3 、hcp
立方面心密堆积、A1 、ccp
立方体心密堆积、A2 、bcp
二、原子坐标
三、四类堆积模型原子的空间占有率
2010年 5-4 A中的金属元素M可以形成不同形 式的羰基化合物或者羰基阴离子,按照18电子 规则画出Na2[M2(CO)10]的阴离子结构,指出M 的氧化态。
OC CO OC CO
2-
OC Cr
C位体提供给分子骨干的电子数目
配位体 配位形式 电子数目
H
μ1μ2μ3 1
文章还指出,All3和All4超原子都是具有40个价电子时最稳定。
⑴ 根据以上信息可预测Al13和Al14的稳定化合价态分别为 和 。
A114应具有元素周期表中 类化学元素的性质,理由
是:
。
⑵ 对Al13和A114的Al—Al键长的测定十分困难,而理论计算表明, Al13,和Al14中的Al—Al键长与金属铝的Al—Al键长相当,已知金 属铝的晶体结构采取面心立方最密堆积,密度约为2.7g/cm3,请估
3、奇数电子化合物
2005年第10题(10分)据世界卫生组织统计,全 球约有8000万妇女使用避孕环。常用避孕环都是 含金属铜的。据认为,金属铜的避孕机理之一是, 铜与子宫分泌物中的盐酸以及子宫内的空气反应, 生成两种产物,一种是白色难溶物S,另一种是酸 A。酸A含未成对电子,是一种自由基,具有极高 的活性,能杀死精子。 10-1写出铜环产生A的化学方程式。 10-2画出A分子的立体结构。
堆隙模型
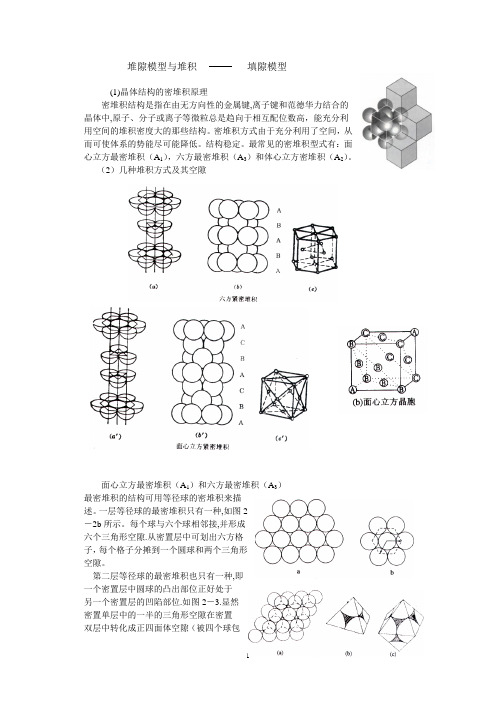
堆隙模型与堆积填隙模型(1)晶体结构的密堆积原理密堆积结构是指在由无方向性的金属键,离子键和范德华力结合的晶体中,原子、分子或离子等微粒总是趋向于相互配位数高,能充分利用空间的堆积密度大的那些结构。
密堆积方式由于充分利用了空间,从而可使体系的势能尽可能降低。
结构稳定。
最常见的密堆积型式有:面心立方最密堆积(A1),六方最密堆积(A3)和体心立方密堆积(A2)。
(2)几种堆积方式及其空隙面心立方最密堆积(A1)和六方最密堆积(A3)最密堆积的结构可用等径球的密堆积来描述。
一层等径球的最密堆积只有一种,如图2-2b所示。
每个球与六个球相邻接,并形成六个三角形空隙.从密置层中可划出六方格子,每个格子分摊到一个圆球和两个三角形空隙。
第二层等径球的最密堆积也只有一种,即一个密置层中圆球的凸出部位正好处于另一个密置层的凹陷部位.如图2-3.显然密置单层中的一半的三角形空隙在密置双层中转化成正四面体空隙(被四个球包围),另一半三角形空隙转化成正八面体空隙(被八个球包围)。
密置双层保持六重对称性。
由两层六方格子构成一个平行图2-3六面体,每个平行六面体分摊到一个圆球、两个正四体空隙和一个八面体空隙。
第三层等径中球的密堆积有两种方式:一种是第三层中球的位置落在密置双层的正四面体空隙之上,其投影位置与第二层球的位置错开但与第一层球的位置相同,即ABAB……堆积.这种堆积称六方紧堆积.它仍保持密置双层的对称性;另一种第三层中球的位置落在密置双层正八面体空隙之上,其投影位置既与第二层错开又与第一层错开,这种方式称为ABCABC……堆积.这种堆积称为面心紧密堆积.所谓A1堆积就是重复ABC堆积,记作︱ABC︱。
在密置层的垂直方向上有两种空隙相间分布,即以正四面体空隙、正八面体空隙、正四面体空隙为一个单位重复分布。
从A1堆积中可划出一个立方面心晶胞。
所谓A3堆积就是重复AB堆积,记作︱AB︱。
在密置层的垂直方向上空隙的分布要么始终是正四面体空隙, 要么始终是正八面体空隙.。
立方最密堆积配位数

立方最密堆积配位数
立方最密堆积是指在立方晶体结构中,原子的最密堆积方式。
它
是一种常见的结晶方式,也是我们日常生活中常见的晶体结构之一。
立方最密堆积的配位数是12,也就是说,每个原子周围有12个邻近的原子。
这种配位数是在三维空间中,原子之间排列最紧密的一种
方式。
在立方最密堆积中,每个原子都被六个邻近的原子所包围,它们
分层排列,呈现出六边形的堆积形状。
每一层的原子和相邻层的原子
交错排列,形成了稳定的结构。
立方最密堆积的结构密度相对较高,这是因为原子之间的接触面
积较大,使得原子之间的相互作用更为紧密。
这种紧密的结构使得立
方最密堆积晶体具有优异的物理性质,例如高熔点、高硬度和高密度等。
立方最密堆积的结构在许多金属和非金属中都有广泛应用。
例如,金属中的钠、银和铝等都采用立方最密堆积结构。
此外,一些非金属
材料,如硅和硫,也可以形成立方最密堆积结构。
了解立方最密堆积的配位数对我们研究晶体结构、探索材料性质
以及开发新型材料具有重要意义。
通过控制原子的排列方式和配位数,我们可以调控材料的物理性质,实现更多样化的应用。
总之,立方最密堆积配位数为12,它是一种常见的晶体结构,具有紧密排列、高密度和优异性能等特点。
了解和掌握立方最密堆积的配位数对于我们深入研究材料科学和应用具有重要的指导意义。
通过进一步的研究和探索,我们可以为材料科学的发展做出更大的贡献。
关于密堆积原理

关于密堆积原理高剑南﹙华东师范大学 200062﹚1. 从教材的一个改动说起某《化学》拓展型教材﹙试验本﹚p.48图2.17列了三种类型金属晶体的结构示意图﹙确切的表述是等径圆球的三种密堆积形式﹚,其中图⑴为体心立方堆积,图⑵为六方最密堆积,图⑶为立方最密堆积,文中第4行说“铝晶体中铝原子的堆积形式如图2.17⑵所示”。
在该教材试行本出版时,p.35图2.16除三种类型金属晶体的结构示意图由黑白图改为彩图,⑴⑵⑶分别改为﹙a ﹚﹙b ﹚﹙c ﹚外,重要的是p.34文中倒4行说“铝晶体中铝原子的堆积形式如图2.16﹙c ﹚所示”。
那么,铝晶体中铝原子的堆积形式究竟是六方最密堆积还是立方最密堆积?堆积形式与物质的性质又有什么关系?这些问题涉及到密堆积原理以及几种堆积方式。
2. 密堆积原理所谓密堆积原理是指由无方向性的金属键、离子键和范德华力等结合的晶体中,原子、离子和分子等微粒总是趋向于相互配位数高,堆积密度大,能充分利用空间,因而体系稳定的那些结构。
金属原子的电子云分布基本上是球对称的,可以把同一种金属晶体看成是由半径相等的圆球构成,因此金属晶体的结构可用等径圆球的密堆积模型来研究。
常见的堆积形式有:1A 、2A 、3A 和4A 等。
2.1 等径球的密置层和密置双层1A 和3A 堆积是等径球的密置层以两种不同方式堆积而成的最密堆积。
密置层的结构如图1所示,每个球与6个球紧密接触,形成6个三角形空隙,其中1、3、5三角形空隙的底边在下、顶点在上,2、4、6三角形空隙的底边在上、顶点在下。
图1 等径球的密置层在堆积第二层等径球时,这个密置层中圆球的凸出部位正好处于第一密置层的凹陷部位,也就是一个球同时与第一密置层的三个球接触,它可以占据1、3、5空隙,也可占据2、4、6空隙,但不会两者都占,也不会混合占据。
如果占据1、3、5空隙,第一密置层中的1、3、5三角形空隙转化成密置双层中的底面在下、顶点在上的正四面体空隙T +,见图2-(a )。
金属晶体(llx)

密置双层
红、蓝球是同种 原子, 原子,使用两种 色球只是为了看 清两层的关系 。
密置双层
密置双层中间形成两种空隙: 密置双层中间形成两种空隙 正八面体空隙(由 构成) 正八面体空隙 由3A+3B构成 构成 正四面体空隙(由 构成) 正四面体空隙 由3A+1B或1A+3B构成 或 构成
第三层叠加到第二层B上时, 第三层叠加到第二层B上时,可以填在正八面体空隙上 ,也可以填在正四面体空隙上。 也可以填在正四面体空隙上。
A3型最密堆积: ABAB…… 型最密堆积:
第3层球堆在正四面体空隙上 A3型 六方堆积 型
金属晶体 中原子的 堆积方式
立方堆积
体心立方堆积
六方堆积
面心立方堆积
钋 型
钾 型
镁 型
铜 型
4个▲ 四面体空隙 3个● 八面体空隙
第三层球放在第二层球的正八面体空隙空隙上形成ABC 第三层球放在第二层球的正八面体空隙空隙上形成ABC 正八面体空隙空隙上形成 堆积(A 堆积) 堆积(A1堆积)
A B C A
重复ABC的堆积叫A 堆积,重复单位ABC ABC。 重复ABC的堆积叫A1堆积,重复单位ABC。 ABC的堆积叫
A 1型 (局部 放大)Байду номын сангаас放大)
ABCABC…
垂直于密置层观察(俯视图 垂直于密置层观察 俯视图) 俯视图
平行于密置层观察(侧视图 平行于密置层观察 侧视图) 侧视图
A 1型
面心 立方堆积
第3层球堆在正八面 体空隙上
ABC ABC 形式的堆积, 形式的堆积, 为什么是面心立方堆积? 为什么是面心立方堆积?
C B A
A 3型 : 第 3 层球堆在正 四面体空隙 上(局部放 大)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
晶体的密堆积
摘要:新课程、新教材、新高考,研究新教材,研究新高考,对于广大教师来说时不我待,新教材中存在很多疑难问题,仁者见仁智者见智。
化学选修三《物质结构与性质》第三章,是本模块较难的内容,对学生要求较低,教师授课时要把握好尺度。
关键词:新课程晶体结构密堆积晶胞空间利用率
学生在学习化学教材《选修三》第三章时,因为前面教材对这方面的知识涉及很少,对于晶体的堆积方式感到十分困惑,所以笔者针对这个问题进行分析。
由于金属键、离子键、范德华力等没有方向性和饱和性,所以在金属晶体,离子晶体,和一些分子型晶体中,组成晶体的微粒总是趋向于相互配位数高,能充分利用空间的密度大的紧密堆积结构,密堆积方式因充分利用了空间,而使体系的势能尽可能降低,而结构稳定。
为了研究方便,将晶体中的原子,离子等视为具有一定体积的圆球。
空间利用率:单位体积中圆球所占体积的百分数
配位数:一个圆球周围的圆球数目
一、等径圆球的密堆积
把组成金属单质晶体的原子看作是等经圆球。
单层密堆积中只有一种方式,(见人教版教材中图3-22)这种堆积方式中,每个球的配位数为6,在第一层上堆积第二层时,要形成最密堆积,必须把球放在第二层的空隙上。
这样,仅有半数的三角形空隙放进了球,而另一半空隙上方是第二层的空隙。
第一层上放了球的一半三角形空隙,被4个球包围,形成四面体空隙;另一半其上方是第二层球的空隙,被6个球包围,形成八面体空隙。
第二层堆积时形成了两种空隙:四面体空隙和八面体空隙。
那么,在堆积第三层时就会产生两种方式:
①六方密堆积(A3密堆积)
在等径圆球密置双层之上再放一层,有两种方式,其中之一是和三层中球的位置在密置双层的正四面体空隙之上,即第三层与第一层重复,即采用A BAB…方式堆积(如图a)从中可以抽出六方晶胞,所以称为六方密堆积,(亦叫A3密堆积)配位数为12,空间利用率
为74.05%,金属Zn、Mg、Be等属于这种结构。
晶胞为六棱柱的三分之一,平行六面体,截面为平行四边形
每个晶胞中含有原子数=1+4x1/12+4x1/6=2
A3型堆积方式的空间利用率计算
在A3型堆积中取出六方晶胞,平行六面体的底是平行四边形,各边长a=2r,则平行四边形的面积:
平行六面体的高
②面心立方密堆积(A1型密堆积)
放置第三层时,球的位置落在密置双层正八面体空隙之上投影位置即与第二层球错开又与第二层球错开,即采用ABCABC方式堆积(如图b)从中可以抽出立方面心晶胞,所以称为面心立方堆积(也称A1型密堆积)每个晶胞中含4个圆球配位数为12,空间利用率为74.05%。
金属Cu、Al、Au等的结构属于这种结构。
分子晶体干冰也属于这种堆积。
每个晶胞中含有原子数=8x1/8+6x1/2=4
A1型堆积方式的空间利用率计算
除了以上两种密堆积方式外,还有两种常见的密堆积方式(但不是最密堆积)
③体心立方密堆积(A2型密堆积)
A2密堆积不是最密堆积,其结构见人教版教材图3-24从这种堆积方式中可抽取出立方体心晶胞,所以称为体心立方密堆积(也称A2型密堆积)每个晶胞中有两个球,配位数为8,空间利用率为68.02%
④金刚石型密堆积(A4型密堆积)
A4型密堆积也不是最密堆积,其结构见教材中图3-14,在这种密堆积中,配位数为4,空间利用率为34.01%。
二、非等径球体做紧密堆积时
非等径球体做紧密堆积时,可以看作较大的球体成等大球的堆积方式,较小的球体按其本身的大小来填充八面体或者四面体空隙,这多见于离子晶体中,比如氯化钠、氯化铯等。
参考文献:
[1]《物质结构》高等教育出版社ISBN-04=002115-3/0.757
[2]《无机化学》第二版高等教育出版社13010-01189。
