上海大学611数学分析初试大纲

合集下载

上海大学2018年学术型硕士研究生初试科目及参考书目

上海大学 2018 年学术型硕士研究生初试科目及参考书目
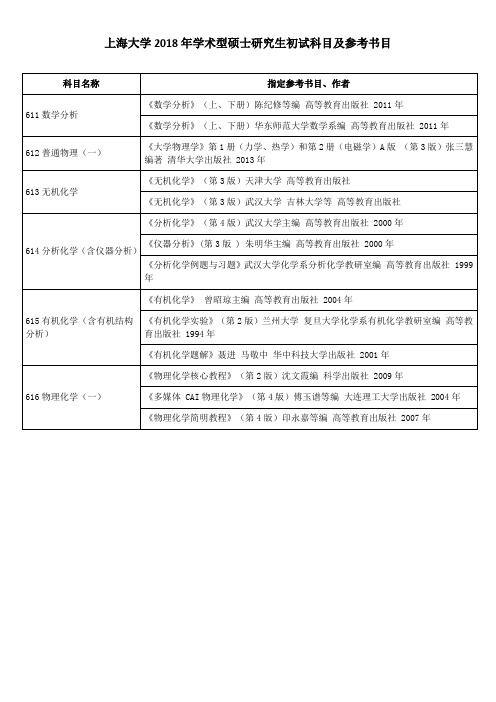
科目名称 611 数学分析《数学分析》（上、下册）华东师范大学数学系编高等教育出版社 2011 年 612 普通物理（一）《大学物理学》第 1 册（力学、热学）和第 2 册（电磁学）A 版（第 3 版）张三慧编著清华大学出版社 2013 年《无机化学》（第 3 版）天津大学高等教育出版社 613 无机化学《无机化学》（第 3 版）武汉大学吉林大学等高等教育出版社《分析化学》（第 4 版）武汉大学主编高等教育出版社 2000 年 614 分析化学（含仪器分析）《仪器分析》(第 3 版 ) 朱明华主编高等教育出版社 2000 年《分析化学例题与习题》武汉大学化学系分析化学教研室编高等教育出版社 1999 年《有机化学》曾昭琼主编高等教育出版社 2004 年 615 有机化学（含有机结构分析）《有机化学实验》（第 2 版）兰州大学复旦大学化学系有机化学教研室编高等教育出版社 1994 年《有机化学题解》聂进马敬中华中科技大学出版社 2001 年《物理化学核心教程》（第 2 版）沈文霞编科学出版社 2009 年 616 物理化学（一）《多媒体 CAI 物理化学》（第 4 版）傅玉谱等编大连理工大学出版社 2004 年《物理化学简明教程》（第 4 版）印永嘉等编高等教育出版社 2007 年指定参考书目、作者《数学分析》（上、下册）陈纪修等编高等教育出版社 2011 年
《表征》霍尔编徐亮陆兴华译商务印书馆 2003 年《文化理论与大众文化导论》（第 5 版）斯道雷著常江译北京大学出版社 2010 年《文化理论关键词》卡瓦拉罗张卫东等译江苏人民出版社 2006 年《西方都市文化研究读本》薛毅(主编) 广西师范大学出版社 2008 年《漫长的革命》雷蒙德威廉斯倪伟译上海人民出版社 2012 年 618 文化研究《知识分子论》萨义德著单德兴译三联书店 2005 年《中文世界的文化研究》王晓明（编）上海书店 2012 年《社会学的想象力》米尔斯著李康译北京师范大学出版社 2017 年《关键概念：传播与文化研究辞典》费斯克著许静译新华出版社 2004 年《媒体文化》凯尔纳著丁宁译商务印书馆 2004 年《末日船票：日常生活中的文化分析》罗小茗上海人民出版社 2015 年《中国古代史》朱绍侯等主编福建人民出版社《中国近代史》（第 4 版）李侃等著中华书局 619 中国史综合《中国现代史》王桧林主编北京师范大学出版社《国史纲要》陈勇主编上海大学出版社 620 世界史综合《世界史》（六卷本）吴于廑齐世荣主编高等教育出版社《全球化：全球治理》俞可平社科文献出版社 2003 年《全球化：文化冲突与共生》苏国勋等社科文献出版社 2006 年《全球化：西方理论前沿》杨雪冬社科文献出版社 2002 年《全球问题与新兴政治》蔡拓天津人民出版社 2011 年《全球化背景下的宗教与政治》刘义上海大学出版社 2011 年 621 全球学与全球化理论《全球主义批评与当代中国意识形态建设》申小翠光明日报出版社 2011 年《全球学评论》（第一卷）郭长刚商务印书馆 2012 年《全球史评论》（第 1-6 卷）刘新成《环境生态学导论》（第 2 版）盛连喜主编北京：高等教育出版社 2006 年 6 月《总体设计》（第 1 版）【美】凯文·林奇中国建筑工业

上海市考研数学复习资料数学分析重点解析

上海市考研数学复习资料数学分析重点解析数学分析是考研数学科目中的一大难点，也是考生们普遍感到困惑的一门课程。

为了帮助广大考生高效备考，本文将对上海市考研数学复习资料中的数学分析重点进行深入解析。

在文章中，将对数学分析的基础概念、重点知识点以及解题技巧进行详细剖析，以期帮助考生们更加全面地掌握数学分析的内容。

一、基础概念解析在数学分析的学习过程中，理解和运用基础概念是非常重要的。

本节将重点解析一些基础概念，包括极限、连续性和导数等。

1. 极限极限是数学分析中的基础概念，也是数学思维的核心。

在学习和理解极限概念时，有一些重要的定理和性质需要掌握。

例如夹逼准则、无穷小与无穷大的关系以及函数极限的运算法则等。

2. 连续性连续性是数学分析中的另一个重要概念。

通过理解连续函数的定义和性质，可以帮助考生更好地解决与连续性相关的问题。

例如连续函数在闭区间上的性质、连续函数的中值定理等。

3. 导数导数是微积分学中的重要概念，也是数学分析中的重点内容。

理解导数的定义和性质，能够帮助考生解决与导数相关的应用问题。

例如函数的导数定义、连续函数可导的条件、导数的四则运算法则等。

二、重点知识点解析在上海市考研数学复习资料中，数学分析中的一些重点知识点需要重点关注。

本节将对这些重点知识点进行解析，并给出相应的例题。

1. 函数极值和最值掌握函数极值和最值的求解方法，对于解决与函数的极值和最值相关的问题具有重要意义。

需要熟悉区间的开闭性质以及极值和最值存在的条件。

同时，还要注意极大极小值和最大最小值的区别。

2. 泰勒展开泰勒展开是将一个函数在某一点附近用多项式逼近的方法，通过掌握泰勒展开的定义和应用，能够解决与函数逼近相关的问题。

重点掌握泰勒展开的公式和使用方法，以及误差估计。

3. 积分计算积分是数学分析中的难点之一，熟练掌握积分的计算方法对于解决与面积、曲线长度、体积等相关问题非常重要。

需要重点掌握不定积分和定积分的计算方法，以及常见的积分公式与性质。

考试大纲_611数学分析

硕士研究生入学考试大纲考试科目名称：数学分析一、考试要求：本数学分析考试大纲适用于报考沈阳工业大学应用数学专业的硕士研究生入学考试。

要求考生熟悉数学分析的基本概念、掌握基本理论和基本方法，会用数学分析的基本技巧，要求考生具有抽象思维能力、逻辑推理能力、空间想象能力、一定的计算能力、运用所学知识综合分析和解决问题的能力。

二、考试内容：第二章数列极限1数列极限概念，会用ε—N，ε—δ语言证明极限存在。

2收敛数列的性质3 数列极限存在的条件第三章函数极限1 函数极限概念2 函数极限的性质3 函数极限存在的条件4 两个重要极限5 无穷小量与无穷大量，无穷小量的阶，等价无穷小。

第四章函数的连续性1 连续性概念，断间断点及类型。

2 连续函数的性质，一致连续的概念。

3 初等函数的连续性，闭区间上连续函数的性质第五章导数和微分1 导数的概念，左、右导数。

2 求导法则3 参变量函数的导数4 高阶导数5 微分，导数与微分之间的关系。

第六章微分中值定理及其应用1 罗尔定理、拉格朗日中值定理、柯西中值定理2 L’Hospital法则求极限。

3 函数的单调性、泰勒公式4 函数的极值与最大（小）值5 函数的凸性与拐点第七章实数的完备性1 实数完备性的基本定理：单调有界数列必有极限，确界原理，区间套定理，有界数列必有收敛的子列，有限覆盖定理，cauchy收敛准则。

2 闭区间上连续函数性质的证明。

第八章不定积分1 不定积分概念与基本积分公式2 换元积分法与分部积分法3 有理函数和可化为有理函数的不定积第九章定积分1 定积分的概念与性质2 变限函数及性质，牛顿—莱布尼茨公式3 定积分存在的充要条件，函数的可积性。

4 微积分学的基本定理及定积分的计算。

第十章定积分的应用1平面图形的面积。

2由平行截面面积求体积。

3曲线的弧长与曲率。

4旋转曲面的面积。

第十一章反常积分1反常积分的概念。

2无穷积分的性质与收敛判别。

3瑕积分的性质与收敛判别。

《数学分析》考试大纲

《数学分析》考试大纲1．实数集与函数（1）掌握集合的概念与运算，区间与邻域。

理解映射与一一对应概念。

了解几个重要不等式。

理解确界原理。

（2）掌握函数概念。

掌握复合函数方法。

了解反函数存在定理。

理解初等函数。

（3）掌握函数的几种特性（单调性、有界性、奇偶性、周期性等）2. 数列极限（1）理解数列极限概念。

（2）掌握收敛数列的性质。

理解数列极限存在的条件。

3. 函数极限（1）理解函数极限概念，掌握ε-δ论证方法。

（2）掌握函数极限的性质。

理解函数极限存在的条件。

（3）掌握两个重要极限的应用。

（4）掌握无穷小与无穷大概念。

4. 函数的连续性（1）理解函数的连续与间断概念。

（2）了解连续函数的性质。

了解复合函数与反函数的连续性。

理解闭区间上连续函数的性质。

（3）理解函数的一致连续性。

理解初等函数的连续性。

5. 导数和微分（1）掌握导数概念。

（2）掌握求导法则与导数计算。

（3）理解微分概念。

（4）理解高阶导数与高阶微分6. 微分中值定理及其应用（1）理解Rolle中值定理，Lagrange中值定理，Cauchy中值定理。

（2）掌握Taylor公式和L’Hospital法则。

（3）理解函数的凸性及其性质。

（4）掌握利用导数研究函数的性态及函数作图。

7. 实数的完备性（1）理解子列概念。

理解致密性定理，区间套定理，有限覆盖定理。

理解实数连续性定理的等价性。

（2）了解上、下极限概念。

8．不定积分（1）理解原函数与不定积分概念。

掌握基本积分公式和不定积分的运算法则。

（2）掌握换元积分法与分部积分法。

（3）掌握有理函数的不定积分，三角函数的不定积分和某些无理函数的不定积分。

9. 定积分（1）理解定积分概念。

掌握Newton-Leibniz公式。

（2）了解Darboux上、下和与Darboux上、下积分。

理解可积充要条件和可积函数类。

（3）理解定积分性质。

掌握变限积分及其性质。

理解积分中值定理。

10. 定积分的应用（1）理解微元法的基本思想。

《数学分析》考试大纲 .doc

《数学分析》考试大纲一、考试的性质数学分析是大学数学系本科学生的最基本课程之一，也是大多数理工科专业学生的必修基础课。

为帮助考生明确考试范围和有关要求，特制订出本考试大纲。

本考试大纲主要根据北京林业大学数学与应用数学本科《数学分析》教学大纲编制而成，适用于报考北京林业大学数学学科各专业（基础数学、概率论与数理统计、计算数学、应用数学）硕士学位研究生的考生。

二、考试内容和基本要求1．实数集与函数（1）确界概念，确界原理（2）函数概念与运算，初等函数要求：理解确界概念与确界原理，并能运用于有关命题的运算与证明。

深刻理解函数的意义，掌握函数的四则运算。

2．数列极限（1）数列极限的ε一N定义（2）收敛数列的性质（3）数列的单调有界法则，柯西收敛准则，重要极限要求：深刻理解数列极限的ε一N定义，并会运用它验证给定数列的极限；掌握数列极限的性质，并会运用它证明或计算给定数列的极限；掌握数列极限存在的充要条件与充分条件，并能运用这些条件证明或判断数列极限的存在性；掌握重要极限并能运用它计算某些数列极限。

3．函数极限(1) 函数极限的ε一M定义和ε一δ定义，单侧极限(2) 函数极限的性质(3) 海涅定理（归结原则），柯西收敛准则，两个重要极限(4) 无穷小量与无穷大量的定义、性质，无穷小（大）量阶的比较要求:理解各类函数极限的定义，并能按定义验证给定的函数极限；掌握函数极限的性质，并能用它证明或计算给定的函数极限。

掌握函数极限的归结原则，并能用它来判断函数极限的存在性和计算某些数列极限。

掌握函数极限的柯西准则，了解单侧极限的单调有界定理；熟练掌握两个重要极限，并运用它们进行有关函数极限的计算；掌握各类无穷小量与无穷大量的定义与性质，理解无穷小（大）量的阶的概念。

4．函数的连续性(1) 函数在一点连续，单侧连续和在区间上连续的定义，间断点的类型(2) 连续函数的局部性质。

复合函数的连续性，反函数的连续性。

闭区间上连续函数的性质。

811(数学分析)考试大纲

2010年硕士研究生入学考试《数学分析》考试大纲Ⅰ考试内容和考试要求一．函数、极限、连续与一致连续考试内容：实数的概述，函数的概念，具有某些特殊性质的函数。

复合函数、反函数、分段函数的概念。

基本初等函数的性质及其图形，初等函数及函数关系的建立。

函数（数列）的定义和性质，极限的四则运算法则，极限存在的条件，两个重要的极限，连续和一致连续的定义，连续函数的运算，初等函数的连续性，闭区间上连续函数的性质。

考试要求：1. 理解函数的概念，掌握函数的表示法，会建立应用问题的函数关系。

2. 理解数集的确界原理，会求一个实数集的上、下确界。

3. 了解函数的有界性、单调性、周期性和奇偶性。

4. 理解复合函数及分段函数的概念，理解反函数的概念。

5. 掌握基本初等函数的性质及其图形，了解初等函数的概念。

6. 理解极限的概念，理解函数左极限与右极限的概念以及函数极限存在与左右极限之间的关系，掌握极限的性质及四则运算法则。

7. 掌握极限存在的几个准则（单调有界原理，柯西准则，夹逼准则，归结原则），并会利用它们判定极限的存在性，掌握利用两个重要的极限求极限的方法。

8. 理解无穷小量、无穷大量的概念，掌握无穷小量的比较方法，会应用等价无穷小量求极限。

9. 理解函数连续性的概念（含左连续、右连续），会判别函数间断点的类型，理解一致连续性的概念。

10. 了解连续函数的性质和初等函数的连续性，理解闭区间上连续函数的性质（有界性，最大值和最小值定理，介值定理，一致连续性定理），并会应用这些性质。

二．一元函数的微分学考试内容：导数的定义及几何意义，导数的四则运算法则，反函数求导法则，复合函数求导法则，初等函数的导数、隐函数及其由参数方程式表示的函数的导数。

函数的微分的定义及运算，高阶导数及高阶微分。

微分中值定理，洛必达法则，函数单调性的判别，函数的极值，函数图形的凸凹性、拐点及渐近线，函数图形的描绘，函数的最大值、最小值。

泰勒中值定理。

硕士研究生入学考试大纲-601数学分析

全国硕士研究生入学统一考试数学专业《数学分析》考试大纲I 考查目标全国硕士研究生入学统一考试数学专业《数学分析》考试是为我校招收数学硕士生设置的具有选拔性质的考试科目。

其目的是科学、公平、有效地测试考生是否具备攻读数学专业硕士所必须的基本素质、一般能力和培养潜能，以利于选拔具有发展潜力的优秀人才入学，为数学学科及社会的发展培养具有良好职业道德、法制观念和国际视野、具有较强分析与解决问题能力的高层次、应用型、复合型的数学专业人才。

考试要求是测试考生掌握分析、表达与解决问题的一些基本能力和技能。

具体来说就是：要求考生理解数学分析的基本概念和基本理论，掌握数学分析的基本思想和方法具有抽象思维能力、逻辑推理能力、运算能力和综合运用所学的知识分析问题和解决问题的能力。

II 考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分，考试时间180分钟。

二、答题方式答题方式为闭卷、笔试。

不得使用带有公式和文本存储功能的计算器。

三、试卷内容与题型结构一元函数微积分约占 60%，多元函数微积分约占 25%，无穷级数约占 20有以下三种题型：填空题或选择题（20%）、计算题（30%）、综合题（50%）III 考查内容1、极限和函数的连续性（1）熟练掌握数列极限与函数极限的概念；理解无穷小量、无穷大量的概念及基本性质。

（2）掌握极限的性质及四则运算法则，能够熟练运用迫敛性定理和两个重要极限。

（3）熟练掌握：区间套定理，确界存在定理，单调有界原理，聚点定理，有限覆盖定理，Cauchy收敛准则；并理解其相互关系。

（4）熟练掌握函数连续性的概念及相关的不连续点类型。

能够熟练地运用函数连续的四则运算与复合运算性质。

（5）熟练掌握闭区间上连续函数的基本性质：有界性定理、最值定理、介值定理，一致连续性。

（6）熟练掌握实数基本理论和性质，会用实数理论及性质表达和证明相关命题。

2、一元函数微分学（1）理解导数和微分的概念及其相互关系，理解导数的几何意义，理解函数可导性与连续性之间的关系。

上海大学611数学分析考研精编资料目录大纲

上海大学611数学分析考研精品资料目录大纲
一、上海大学611数学分析考研真题汇编及考研大纲
1．上海大学611数学分析2000-2007、2009、2013年考研真题，暂无答案。

2上海大学611数学分析考研大纲
①2018年上海大学611数学分析考研大纲
二、上海大学611数学分析考研资料
3．陈纪修《数学分析》考研相关资料
①上海大学611数学分析之陈纪修《数学分析》考研复习笔记。

②上海大学611数学分析之陈纪修《数学分析》本科生课件。

③上海大学611数学分析之陈纪修《数学分析》复习提纲。

4．上海大学611数学分析考研核心题库（含答案）
①上海大学611数学分析考研核心题库之计算题精编。

5．上海大学611数学分析考研模拟题[仿真+强化+冲刺]
①上海大学611数学分析考研专业课六套仿真模拟题。

②上海大学611数学分析考研强化六套模拟题及详细答案解析。

③上海大学611数学分析考研冲刺六套模拟题及详细答案解析。

三、资料获取VX：ky21985
四、研究生入学考试指定/推荐参考书目（资料不包括教材）
7．上海大学611数学分析考研初试参考书
《数学分析》（上、下册）陈纪修等编高等教育出版社2011年
《数学分析》（上、下册）华东师范大学数学系编高等教育出版社2011年
五、研究生入学适用院系/专业
8．上海大学611数学分析适用院系/专业
力学所；理学院。

上海大学数学系研究生考试大纲

考核重点包括
1.数学分析课程的基本概念。
2.实数的基本性质相关的几个公理的等价性以及它们的应用。
3.极限的各种计算方法与理论证明。
4.连续与间断、一致连续以及闭区间上连续函数性质的证明与应用。
5.中值定理包括微分、积分中值定理的理论推导及应用，特别是用来证明各种不等式。
6.微积分基本定理的内容和理论，定积分可积性的判定以及各种广义积分收敛性的判定。
考试科目：611数学分析
一、复习要求：
要求学生掌握数学分析课程的基本概念、基本结论与算法，能够运用数学分析的理论求解和证明相关命题。
二、主要复习内容：
本课程考核内容包括实数的基本理论与极限、单变量微积分学，级数论，多变量微积分学、广义积分五大部分组成.
实数的基本理论和极限理论部分包括变量与函数，极限与连续，连续函数以及闭区间上的连续函数的性质；单变量微积分包括导数与微分，几个中值定理，微积分学的基本定理及其应用，不定积分，定积分及其应用。级数论中含数项级数，函数项级数（含幂级数、泰勒级数），富里埃级数和富里埃变换。多变量微积分学中含多元函数的极限与连续，偏导数和全微分，极值和条件极值，隐函数定理与函数相关性；多重积分及其应用，曲线积分，曲面积分以及场论初步。广义积分部分包括含参变量的积分和广义积分。
11.二重和三重积分以及一些特殊的及相互关系。
7.级数(各种级数)的收敛性(含绝对、条件以及一致收敛性)判定，函数的幂级数展开和富里埃级数展开以及收敛范围的确定，各种级数的特定求和办法。
8.平面点集的性质，多元函数极限值的计算以及连续性、可微性的讨论和几何应用，。
9.一元函数和多元函数极值的计算及应用。
10.隐函数定理与函数相关性的结论与证明和应用。

数学分析610研究生入学考试大纲

《数学分析》（610）研究生入学考试大纲一、参考书目：1．《数学分析》第四版（上、下册）华东师范大学数学系编（高等教育出版社）。

2．《数学分析》（上、下册）盛炎平等编（机械工业出版社）。

二、考试大纲：（第一章～第二十二章，所有带*号的部分不用看）第一章实数集与函数数集的确界，确界原理.第二章数列极限极限定义，收敛数列性质，单调有界原理，重要极限.第三章函数极限函数极限定义，函数极限性质，两个重要极限，无穷大量与无穷小量，渐近线.第四章函数连续性函数连续概念，间断点分类，连续函数的性质，一致连续的概念.第五章导数与微分导数概念，导数几何意义，求导法则，基本求导公式，参变量函数求导，高阶导数，微分的概念，几何意义.第六章微分中值定理及其应用罗尔定理，拉格朗日定理，函数单调性的判定，柯西中值定理，不定式极限的罗必达法则，泰勒公式,，函数极值的判定，最值问题，函数凹凸性的判定.第七章实数的完备性了解刻画实数完备性定理的内容.第八章不定积分原函数与不定积分概念，基本积分公式，换元法与分部积分法.第九章定积分定积分概念，定积分性质，牛顿-莱布尼兹公式，变限积分和原函数存在定理，积分中值定理，计算积分的换元法与分部积分法.第十章定积分应用计算平面图形面积，立体体积，曲线弧长，旋转曲面面积.第十一章反常积分无穷积分和瑕积分的概念和性质，非负无穷积分和瑕积分的比较判别法，一般无穷积分和瑕积分的狄立克莱判别法和阿贝尔判别法.第十二章数项级数级数收敛的定义，级数的性质，正项级数的比较、根值、比值判别法，一般项级数的阿贝尔判别法和狄立克雷判别法.第十三章函数列与函数项级数函数列的一致收敛性，一致收敛的柯西准则及充要条件，一致收敛函数列的极限函数的性质，函数项级数一致收敛概念，判别法，一致收敛函数项级数的性质.第十四章幂级数幂级数的收敛半径、收敛区间、收敛域，收敛半径的计算，幂级数的性质，泰勒级数，初等函数的幂级数展开.第十五章傅立叶级数三角级数，正交系，收敛定理，周期函数的傅里叶展开，偶函数与奇函数的傅里叶级数与展开.第十六章多元函数的极限与连续二元函数的极限与连续.第十七章多元函数微分学偏导数的概念，全微分的概念，偏导数的几何意义，复合函数的求导法则，方向导数与梯度的概念，多元函数的极值问题.第十八章隐函数定理及其应用了解隐函数定理，会隐函数求导，曲线的切线，曲面的切平面与法线，条件极值问题.第十九章含参积分该章不考察.第二十章曲线积分第一型曲线积分定义与计算，第二型曲线积分的定义与计算，两类积分的联系.第二十一章重积分二重积分的概念、性质，直角坐标计算，极坐标计算，格林公式，曲线积分与路径的无关性，三重积分的定义，性质，利用直角坐标计算，柱坐标计算，球坐标计算.第二十二章曲面积分第一型曲面积分定义与计算，第二型曲面积分的定义与计算，高斯公式与斯托克斯公式三、试卷结构：1.概念简答题；2.计算题；3.证明题.。

611数学考试大纲

数学考试大纲[考试科目] 微积分、线性代数、概率论微积分一、函数、极限、连续考试内容函数的概念及其表示法函数的有界性、单调性、周期性和奇偶性反函数、复合函数、隐函数、分段函数基本初等函数的性质及其图形初等函数数列极限与函数极限的概念保号性函数的左极限和右极限无穷小和无穷大的概念及其关系无穷小的基本性质及阶的比较极限四则运算两个重要极限函数连续与间断的概念初等函数的连续性闭区间上连续函数的性质考试要求．理解函数的概念，掌握函数的表示法。

．了解函数的有界性、单调性、周期性和奇偶性。

．掌握复合函数、反函数、隐函数和分段函数的概念。

．理解基本初等函数的性质及其图形，理解初等函数的概念。

．会建立简单应用问题中的函数关系式。

．了解数列极限和函数极限（包括左、右极限）的概念。

. 理解数列极限和函数极限的保号性，掌握保号性的简单应用。

．了解无穷小的概念和其基本性质，掌握无穷小的阶的比较方法，了解无穷大的概念及其与无穷小的关系。

．了解极限的性质与极限存在的两个准则（单调有界数列有极限、夹逼定理），掌握极限四则运算法则，会应用两个重要极限。

．理解函数连续性的概念（含左连续与右连续）。

．了解连续函数的性质和初等函数的连续性。

了解闭区间连续函数的性质（有界性、最大值和最小值定理、介值定理）及其简单应用。

二、一元函数微分学考试内容导数的概念函数的可导性与连续性之间的关系导数的四则运算基本初等函数的导数复合函数、反函数和隐函数的导数高阶导数微分的概念和运算法则罗尔（）定理和拉格朗日（）中值定理及其洛必达（'）法则函数单调性函数的极值函数图形的凹凸性、拐点及渐近线、函数的最大值和最小值考试要求．理解导数的概念及可导性与连续性之间的关系，了解导数的几何意义与经济意义（含边际和弹性的概念）。

．掌握基本初等函数的导数公式、导数的四则运算法则及复函数的求导法则；掌握反函数与隐函数求导法，了解对数求导方法。

．了解高阶导数的概念，会求二阶导数以及较简单函数的阶导数。

2018上海大学：各院系考研专业课复习资料

2018上海大学：各院系考研专业课复习资料
2018考研已开始，为方便上海大学考研学子更好地复习，聚英考研网特意为大家分享上海大学各学院的专业考研真题等资料，希望更多考生能够在专业课上赢得高分，升入理想的院校。

以上内容由聚英考研网整理发布，此外，我们会为广大考生持续更新最新的考研报考信息及考研辅导班！我们还提供更多关于上海大学考研最新研讯、考研经验、考研真题等一手资讯。

或者可以加入我们的2018考研qq群和众多考研学子一起备战考研！。

601数学分析考研大纲

7．含参变量的积分和广义积分
理解含参变量的积分及由含参变量积分所确定的函数的性质（连续性，可微性，可积性），了解含参变量广义积分的定义，掌握一致收敛的定义，一致收敛积分的判别法（魏尔斯特拉斯判别法），及一致收敛积分的性质（连续性定理，积分顺序交换定理，积分号下求导定理），了解欧拉积分。
积分的定义及性质，掌握不定积分的基本公式与运算法则，会计算不定积分（“凑”微分法、换元积分法、分部积分法、有理函数积分法），会求简单的有理函数的积分，掌握其他类型的积分法。掌握定积分存在的充分必要条件（第一充要条件、第二充要条件），了解可积函数类，掌握定积分的计算――基本公式（牛顿－莱布尼兹公式）、换元公式、分部积分公式，会利用定积分来求和式的极限。了解椭圆积分（第一类、第二类、第三类）。掌握定积分的应用和近似计算，会计算平面图形的面积，曲线的弧长，体积，旋转曲面的面积，质心，平均值，功。知道广义积分分为无限区间上的广义积分和无界函数的积分两种，了解无穷限广义积分和无界函数广义积分的概念，会利用定义来求这两类广义积分。了解无穷限广义积分和级数之间的关系，掌握这两类积分收敛的判别法（比较判别发、柯希判别法及其极限形式），会证明广义积分的敛散性，了解什么是柯西主值，会求广义积分的柯西主值。
5．多元函数的极限论
掌握平面点集上的有关定义（邻域，点列的极限，开集，闭集，区域，内点，外点、聚点），了解平面点集的几个基本定理（矩形套定理、致密性定理、有限覆盖定理、收敛原理），理解多元函数的概念（二元函数），理解二元函数极限和连续性的定义，了解有界闭区域上连续函数的性质（有界性定理、一致连续性定理、最大值最小值定理、零点存在定理），掌握二重极限和二次极限的定义，并会求二元函数的二重极限和二次极限，了解二重极限和二次极限之间的关系。
掌握二重积分、三重积分、第一类曲线积分、第一类曲面积分、第二类曲线积分、第二类曲面积分的概念及其积分的性质。掌握二重积分与三重积分的计算及应用（化二重积分为二次积分，用极坐标计算二重积分，二重积分的一般变量替换，化三重积分为三次积分，三重积分的变量替换）。了解积分在物理上的应用（质心，矩，引力）。了解广义重积分的定义。掌握第一、二类曲线积分和第一、二类曲面积分的计算，会计算曲面的面积，会化第一类曲面积分为二重积分。了解两类曲线积分之间和两类曲面积分之间的联系，掌握各种积分间的联系（格林公式、高斯公式、斯托克司公式），会利用这些公式计算曲线的积分。会使用平面曲线积分与路径无关的条件，了解场及向量场的散度与旋度的概念。会用重积分、曲线积分及曲面积分求一些几何量与物理量（如体积、曲面面积、弧长、质量、重心、转动惯量、引力、功等）。

硕士《数学分析》考试大纲 .doc

硕士《数学分析》考试大纲课程名称：数学分析科目代码：661适用专业：数学与应用数学专业参考书目：1、《数学分析》（上下册）第一版，陈纪修，於崇华，金路；高等教育出版社1999.92、《数学分析》（上下册）第二版，陈纪修，於崇华，金路；高等教育出版社2004.103、《数学分析》（上下册），卓里奇；高等教育出版社2006.124、《数学分析》（上下册），华东师范大学，高等教育出版社2010.7一、数列极限1、充分认识实数系的连续性；理解并掌握确界存在定理及相关知识。

2、充分理解数列极限的定义，熟练掌握用数列极限的定义证明有关极限问题，以及数列极限的各种性质及其运算。

3、掌握无穷大量的概念及其相关知识；熟练掌握Stolz定理的内容及其结论及应用。

4、理解单调有界数列收敛定理的内容及其结论，并能熟练解决相关的极限问题。

5、充分理解区间套定理、致密性定理、完备性定理各自的内容和结论；进一步认识实数系的连续性与实数系的完备性的关系；明确有关收敛准则中的各定理之间逻辑关系。

二、函数极限与连续函数1、充分理解函数极限的定义，熟练掌握用函数极限的定义证明有关极限问题；以及函数极限的各种性质及其运算。

2、明确数列极限与函数极限的关系；熟练掌握单侧极限以及各种极限过程的极限。

3、充分理解连续函数的概念，熟练掌握用连续函数的定义和运算解决有关函数连续性问题。

明确不连续点的类型；掌握反函数、复合函数的连续性。

4、熟练掌握无穷小（大）量的概念以及自身的比较，并能熟练应用于极限问题当中。

5、充分掌握闭区间上连续函数的各种性质；充分理解函数的一致连续性及相关定理。

三、微分1、充分理解微分的概念、导数的概念，以及可微、可导、连续三者的关系。

2、熟练掌握导数的运算、反函数、复合函数的求导法则，做到得心应手。

3、理解高阶导数和高阶微分的概念，熟练掌握高阶导数的运算法则。

四、微分中值定理及其应用1、充分理解以Lagrange中值定理为核心的各微分中值定理的内容和结论；掌握应用微分中值定理揭示函数自身的特征和函数之间的关系。

上海大学2016年研究生参考书目范文

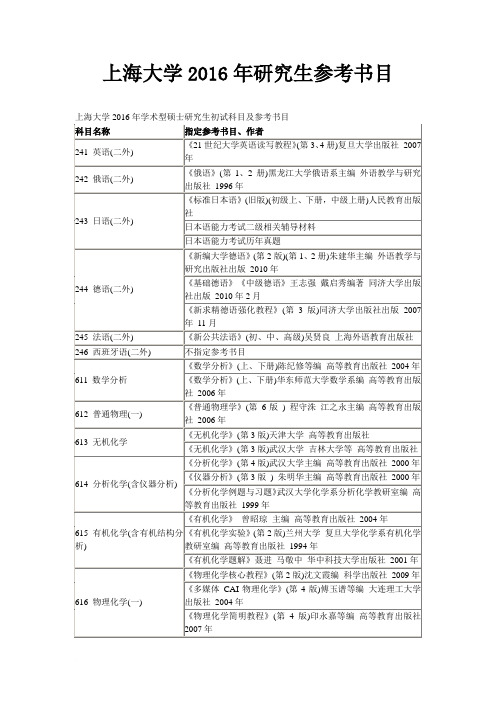
上海大学2016年研究生参考书目上海大学2016年学术型硕士研究生初试科目及参考书目科目名称指定参考书目、作者241 英语(二外) 《21世纪大学英语读写教程》(第3、4册)复旦大学出版社2007年242 俄语(二外) 《俄语》(第1、2册)黑龙江大学俄语系主编外语教学与研究出版社1996年243 日语(二外) 《标准日本语》(旧版)(初级上、下册，中级上册)人民教育出版社日本语能力考试二级相关辅导材料日本语能力考试历年真题244 德语(二外) 《新编大学德语》(第2版)(第1、2册)朱建华主编外语教学与研究出版社出版2010年《基础德语》《中级德语》王志强戴启秀编著同济大学出版社出版2010年2月《新求精德语强化教程》(第3版)同济大学出版社出版2007年11月245 法语(二外) 《新公共法语》(初、中、高级)吴贤良上海外语教育出版社246 西班牙语(二外) 不指定参考书目611 数学分析《数学分析》(上、下册)陈纪修等编高等教育出版社2004年《数学分析》(上、下册)华东师范大学数学系编高等教育出版社2006年612 普通物理(一) 《普通物理学》(第6版) 程守洙江之永主编高等教育出版社2006年613 无机化学《无机化学》(第3版)天津大学高等教育出版社《无机化学》(第3版)武汉大学吉林大学等高等教育出版社614 分析化学(含仪器分析) 《分析化学》(第4版)武汉大学主编高等教育出版社2000年《仪器分析》(第3版) 朱明华主编高等教育出版社2000年《分析化学例题与习题》武汉大学化学系分析化学教研室编高等教育出版社1999年615 有机化学(含有机结构分析) 《有机化学》曾昭琼主编高等教育出版社2004年《有机化学实验》(第2版)兰州大学复旦大学化学系有机化学教研室编高等教育出版社1994年《有机化学题解》聂进马敬中华中科技大学出版社2001年616 物理化学(一) 《物理化学核心教程》(第2版)沈文霞编科学出版社2009年《多媒体CAI物理化学》(第4版)傅玉谱等编大连理工大学出版社2004年《物理化学简明教程》(第4版)印永嘉等编高等教育出版社2007年618 文化研究《表征》霍尔编徐亮陆兴华译商务印书馆2003年《文化理论与大众文化导论》(第5版)斯道雷著常江译北京大学出版社2010年《文化理论关键词》卡瓦拉罗张卫东等译江苏人民出版社2006年《城市文化》芒福德宋俊岭等译建筑工业出版社2009年《漫长的革命》雷蒙德威廉斯倪伟译上海人民出版社2012年《巨大灵魂的战栗》毛尖(编) 上海书店出版社2013年《知识分子论》萨义德著单德兴译三联书店2005年《公共社会学》布洛维著社会科学文献出版社2007年《中文世界的文化研究》王晓明(编) 上海书店2012年《社会学的想象力》米尔斯著陈强张永强译三联书店2005年《传播与社会：政治经济与文化分析》赵月枝著中国传媒大学出版社2011年619 历史学综合《中国古代史》朱绍侯等主编福建人民出版社《中国近代史》(第4版) 李侃等著中华书局《中国现代史》王桧林主编北京师范大学出版社《国史纲要》陈勇主编上海大学出版社《世界史》(六卷本)吴于廑齐世荣主编高等教育出版社620 全球学与全球化理论《全球化：全球治理》俞可平社科文献出版社2003年《全球化：文化冲突与共生》苏国勋等社科文献出版社2006年《全球化：西方理论前沿》杨雪冬社科文献出版社2002年《全球问题与新兴政治》蔡拓天津人民出版社2011年《全球化背景下的宗教与政治》刘义上海大学出版社2011年《全球主义批评与当代中国意识形态建设》申小翠光明日报出版社2011年《全球学评论》(第一卷)郭长刚商务印书馆2012年《全球史评论》(第1-6卷)刘新成621 英美文学史《美国文学选读》(第3版)陶洁北京：高等教育出版社2011年《美国文学史》童明编著南京译林出版社2002年《英国文学选读》(第2版)王守仁编著高等教育出版社 2005年5月《简明英国文学史》(高等学校英语专业系列教材)(第1版)刘意青刘炅编著外语教学与研究出版社2008年10月622 综合日语(语言能力、文学、文化等) 《日语综合教程》(第7、8册)季林根《日语概说》皮细庚上海外语教学出版社《现代日语语言学概论》(日文版)崔崟凯程考研集训营，为学生引路，为学员服务！第 3 页共 21 页《新编日本文学史》市古贞次《日本古典文学读本》刘瑞芝《日本文化概论》韩立红《菊与刀》露丝·本尼迪克特623 英语语言学《The Study of Language (语言研究)》 George Yule 外语教学与研究出版社剑桥大学出版社 2004年《新编语言学教程》(第1版)刘润清文旭编著外语教学与研究出版社 2006年3月624 法理学及民法学《法理学》李清伟主编上海人民出版社 2013年《法理学》(第3版)沈宗灵主编北京大学出版社 2009年《民法》(第 5版)王利明主编中国人民大学出版社 2010年 7月625 细胞生物学《细胞生物学》王金发 21世纪高等院校教材国家理科基地教材科学出版社 2011年《细胞生物学》面向 21世纪课程教材翟中和王喜忠丁明孝高等教育出版社 2011年626 生态学《生态学》李博主编北京：高等教育出版社 2000年《基础生态学》孙濡泳主编北京：高等教育出版社 2002年《动物生态学原理》(第3版)孙儒泳编著北京师范大学出版社2001年《环境生态学导论》(第2版) 盛连喜主编北京：高等教育出版社 2006年 6月627 艺术学理论《艺术学概论》彭吉象高等教育出版社 2002年或旧版《比较文化与艺术哲学》金丹元上海文艺出版社 2002年 632 美术理论《中国画论辑要》周积寅编著江苏美术出版社 1985/2005年《西方美术理论简史》李宏编著西南师范大学出版社 2008年634 环境艺术设计理论《室内设计资料集》张绮曼郑曙阳编著中国建筑工业出版社《中国建筑史》潘西谷主编中国建筑工业出版社《外国建筑史(十九世纪末叶以前)》陈志华著中国建筑工业出版社《外国近现代建筑史》罗小未主编中国建筑工业出版社《建筑设计基础》田云庆胡新辉程雪松编著上海人民美术出版社《室内设计原理》陈易主编中国建筑工业出版社大学本科相关教材637 展示设计相关的设计基础及会展艺术设计书籍，相关的展示技术及国际展示业的图书638 城市艺术体验原理《城市形态》【美】凯文·林奇华夏出版社《城市意象》别名：《城市印象》【美】凯文·林奇华夏出版社《总体设计》(第1版)【美】凯文·林奇中国建筑工业639 中外建筑史《中国建筑史》潘谷西编中国建筑工业出版社2009年8月《外国建筑史》( 19世纪末叶以前)陈志华编中国建筑工业出版社2010年1月《外国近现代建筑史》罗小未编中国建筑工业出版社2004年8月640 城乡规划原理《城市规划原理》(第4版)吴志强李德华主编中国建筑工业出版社2010年9月641 设计艺术理论《艺术设计概论》李砚祖湖北美术出版社2002年《艺术设计学十五讲》凌继尧北京大学出版社2006年《设计学概论》尹定邦湖南科技出版社2001年其他相关艺术设计理论书籍642 新闻传播理论与方法(模块一：新闻传播理论+定量研究方法) 《理论新闻传播学导论》童兵中国人民大学出版社2011年《传播学通论》戴元光金冠军主编上海交通大学出版社2007年《传播研究方法》陈国明彭文正等复旦大学出版社2011年《新闻学引论》郝雨上海交通大学出版社2008年《中外传播学名著导读》郭建斌吴飞主编浙江大学出版社2005年注：上述论著如果重印，可以用新版。

【实用文档】上海大学数学分析[1]21.doc

每年的题目基本上都是15题，每题十分，总150分。

祝你们考研成功！！！上海大学2000年度研究生入学考试试题数学分析 1、设122(1)n n x x nx y n n +++=+，若lim n n x a →∞=，证明：（1）当a 为有限数时，lim 2n n ay →∞=；（2）当a =+∞时，lim n n y →∞=+∞.2、设()f x 在[]0,1上有二阶导数（端点分别指左、右导数），(0)(1)0f f ==，且[]0,1min ()1f x =-证明：[]0,1max ()8f x ''≥3、证明：黎曼函数[]1, x= (0,,)()0,10,p q p q q q R x ⎧>⎪=⎨⎪⎩当为互质整数在上可积当x 为无理数.4、证明：12210()lim (0),t tf x dx f t x π+-→=+⎰其中()f x 在[]1,1-上连续.5、设()1ln 11n n p a n ⎛⎫=+- ⎪⎝⎭，讨论级数2n n a +∞=∑的收敛性.6、设()f x dx +∞⎰收敛且()f x 在[]0,+∞上单调，证明：01lim ()()h n h f nh f x dx ++∞+∞→==∑⎰.7、计算曲面2222x y z a ++=包含在曲面22221(0)x y b a a b+=<≤内的那部分的面积.8、将函数()f x x =在[]0,2π上展成Fourier 级数,并计算级数1sin k kk +∞=∑的值. 上海大学2001年度研究生入学考试试题数学分析1、计算下列极限、导数和积分:(1) 计算极限1lim ();xx x +→ (2) 计算2()()x x f t dt ϕ=⎰的导数()x ϕ',其中()f x 2,(1).1,(1)t t t t ≤⎧=⎨+>⎩(3) 已知)211sin x x'⎤=⎥+⎦,求积分2011sin I dx x π=+⎰.(4) 计算()()22222()0x y z t f t xyz dxdydz t ++≤=>⎰⎰⎰的导数()f t '(只需写出()f t '的积分表达式).2、设()f x 在[],a b 上连续，在(),a b 上可导，若()()0f a f b >且()02a bf +=，试证明必存在(),a b ξ∈使得()0f ξ'=. 3、令(),1y F x y y xe =+-(1)、证明:111311,0,,;,0,,.2121221212F x x F x x ⎛⎫⎛⎫⎛⎫⎡⎤<∈->∈- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦(2)、证明:对任意的11,1212x ⎛⎫∈- ⎪⎝⎭,方程(),0F x y >在13,22y ⎛⎫∈ ⎪⎝⎭中存在唯一的解()y x . (3)、计算(0)y '和(0)y ''. 4、一致连续和一致收敛性(1)、函数2()f x x =在[]0,1上是一致连续的,对210ε-=,试确定0δ>,使得当1201x x ≤<≤,且12x x δ-<时有3321210x x --<.(2)、设[]2231(),0,1,1,2,,2n n x f x x n n x+=∈=+证明: ()n f x 在[]0,1上是内闭一致收敛的,但不是一致收敛的.5、曲线积分、格林公式和原函数. (1)计算第二型曲线积分()221,2L xdy ydxI x y π-=+⎰其中L 是逐段光滑的简单闭曲线,原点属于L 围成的内部区域,(L)的定向是逆时针方向.(2) 设(),p x y ,(),q x y 除原点外是连续的,且有连续的偏导数,若<a>()(),,0,0p qx y y x∂∂=≠∂∂ <b>()0,L pdy qdx c +=≠⎰其中(L)的参数方程cos ,(02)sin x tt y t π=⎧≤≤⎨=⎩证明：存在连续可微函数()()(),,,0,0F x y x y ≠，使得()()2222,,,22F c y F c xp x y q x y x x y y x y ππ∂∂=+=-∂+∂+.上海大学2002年度研究生入学考试题数学分析1、求α和β使得当x →+∞等价于无穷小量x βα.2、求椭圆2221Ax Bxy Cy ++=所围成的面积S ,其中20,0,,,A AC B A B C >->均为常数.3、试给出三角级数01(cos sin )2n n n a a nx b nx ∞=++∑中系数的计算公式(不必求出具体值),使得该级数在[]0,1上一致收敛到2x ,并说明理论依据。