全等三角形判定-专题复习50题(含答案)
初中全等三角形经典题型50题(含答案)

所以:AB=AC;
三角形ABD全等于三角形ACD;
∠BAD=∠CAD;AD是等腰三角形的顶角平分线所以:AD垂直BC
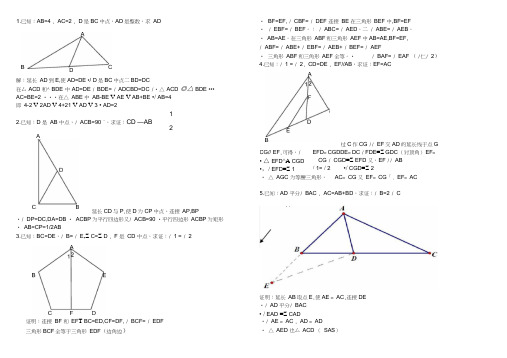
19.(5分)如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.
求证:∠OAB=∠OBA
因为AOM与MOB都为直角三角形、共用OM,且∠MOA=∠MOB
又∵,AE,BE均为∠PAB和∠CBA的角平分线∴∠EAB+∠EBA=90°∴∠AEB=90°,EAB为直角三角形在三角形ABF中,AE⊥BF,且AE为∠FAB的角平分线
∴三角形FAB为等腰三角形,AB=AF,BE=EF在三角形DEF与三角形BEC中,∠EBC=∠DFE,且BE=EF,∠DEF=∠CEB,∴三角形DEF与三角形BEC为全等三角形,∴DF=BC∴AB=AF=AD+DF=AD+BC
初中全等三角形证明经典50题(含答案)
1.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD
延长AD到E,使DE=AD,
则三角形ADC全等于三角形EBD
即BE=AC=2在三角形ABE中,AB-BE<AE<AB+BE
即:10-2<2AD<10+2 4<AD<6
又AD是整数,则AD=5
2.已知:D是AB中点,∠ACB=90°,求证:
证明:在AC上截取AE=AB,连接ED∵AD平分∠BAC∴∠EAD=∠BAD又∵AE=AB,AD=AD∴⊿AED≌⊿ABD(SAS)∴∠AED=∠B,DE=DB∵AC=AB+BD AC=AE+CE∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C
全等三角形经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=ACAD BC BACDF21E5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠ C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD8. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB AD BC A9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF。
∵BC=ED,CF=DF,∠BCF=∠EDF。
∴三角形BCF全等于三角形EDF(边角边)。
∴BF=EF,∠CBF=∠DEF。
连接BE。
在三角形BEF中,BF=EF。
∴ ∠EBF=∠BEF 。
又∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
10. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CG∠CGD =∠EFD又EF ∥AB∴∠EFD =∠1∠1=∠2∴∠CGD =∠2∴△AGC 为等腰三角形,AC =CG又 EF =CG∴EF =AC11. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CB ACDF21 E证明:延长AB 取点E ,使AE =AC ,连接DE∵AD 平分∠BAC∴∠EAD =∠CAD∵AE =AC ,AD =AD∴△AED ≌△ACD (SAS )∴∠E =∠C∵AC =AB+BD∴AE =AB+BD∵AE =AB+BE∴BD =BE∴∠BDE =∠E∵∠ABC =∠E+∠BDE∴∠ABC =2∠E∴∠ABC =2∠C12. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC又∵AC =AC∴△ADC ≌△AFC (SAS )CD B A∴AD =AF∴AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含答案)
全等三角形证明经典50题(含答案)1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 AD延长AD 至U E,使DE=AD, 则三角形ADC 全等于三角形EBD即 BE=AC=2 在三角形 ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=512.已知:D 是 AB 中点,/ ACB=90 °,求证: CD - AB2为BC=ED,CF=DF, / BCF= / EDF 。
所以 三角形BCF 全等于三角形 EDF (边角边)。
所以BF=EF, / CBF= / DEF 。
连接 BE 。
在三角形 BEF 中,BF=EF 。
所以 / EBF= / BEF 。
/ ABE= / AEB 。
所以 AB=AE 。
在三角形 ABF 和 / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF 。
所以/ C= / D , F 是 CD 中点,求证:/ 1 = / 2证明:连接BF 和EF 。
因又因为 / ABC= / AED 。
所以 三角形 AEF 中, AB=AE,BF=EF, 三角形ABF 和三角形AEF 全等。
所以 / BAF= / EAF ( / 仁/ 2)。
A3因为 EB = EF ,CE = CE , 所以△ CEBCEF 所以/ B = / CFE 因为/ B +/ D = 180° / CFE + / CFA = 180° 所以/ D = / CFA 因为 AC 平分/ BAD 所以/ DAC = / FAC 又因为 AC = AC 所以△ ADC 也厶AFC ( SAS ) 所以AD = AF 所以AE = AF + FE = AD + BE12.如图,四边形 ABCD 中,AB // DC ,BE 、CE 分别平分/ ABC 、/ BCD ,且点 E 在AD 上。
三角形全等的判定证明题-(含答案)
三角形全等的判定一、(SSS)1.如图,AD=AC ,BD=BC ,QA 求证:△ABC≌△ABD .证明:在△ABC 和ABD 中,⎩⎨⎧ AD =ACBD =BCAB =AB ,∴△ABC≌△ABD(SSS )2.如图,AB=AD ,CB=CD ,求证:△ABC≌△AD C .证明:∵在△ABC 和△ADC 中⎩⎨⎧ AB =ADBC =CDAC =AC,∴△ABC≌△ADC(SSS ).3.如图,A 、D 、B 、E 在同一直线上,AC=EF ,AD=BE ,BC=DF ,求证:∠C=∠F.证明:∵AD=BE∴AD+DB=BE+DB,即:AB=DE ,在△ABC 和△DEF 中,⎩⎨⎧ AC =EFAB =DEBC =DF ,∴△ABC≌△DEF(SSS ),∴∠C=∠F.4.如图,已知线段AB 、CD 相交于点O,AD 、CB 的延长线交于点E,OA=OC,EA=EC,请说明∠A=∠C.解:连结OE 在△EAC 和△EBC 中OA OC EA EC OE OE ⎧⎪⎨⎪⎩===(已知)(已知)(公共边)∴△EAC ≌△EBC (SSS )∴∠A =∠C (全等三角形的对应角相等)二、(SAS )5.已知:如图,点A 、B 、C 、D 在同一条直线上,EA ⊥AD ,FD ⊥AD ,AE =DF ,AB =DC .求证:∠ACE =∠DBF .证明:∵AB =DC∴AC =DB∵EA ⊥AD ,FD ⊥AD∴∠A =∠D =90°在△EAC 与△FDB 中⎪⎩⎪⎨⎧=∠=∠=DBAC D A FDEA∴△EAC ≌△FDB (SAS )∴∠ACE =∠DBF .6.如图CE=CB ,CD=CA ,∠DCA=∠ECB ,求证:DE=AB .证明:∵∠DCA=∠ECB ,∴∠DCA+∠ACE=∠BCE+∠ACE ,∴∠DCE=∠ACB ,∵在△DCE 和△ACB 中,∴△DCE ≌△ACB (SAS )∴DE=AB .7. 已知:如图,点A 、B 、C 、D 在同一条直线上,EA ⊥AD ,FD ⊥AD ,AE =DF ,AB =DC .求证:∠ACE =∠DBF .证明:∵AB =DC∴AC =DB∵EA ⊥AD ,FD ⊥AD∴∠A =∠D =90°在△EAC 与△FDB 中⎪⎩⎪⎨⎧=∠=∠=DBAC D A FDEA∴△EAC ≌△FDB (SAS )∴∠ACE =∠DBF .8. 如图CE=CB ,CD=CA ,∠DCA=∠ECB ,求证:DE=AB .证明:∵∠DCA=∠ECB,∴∠DCA+∠ACE=∠BCE+∠ACE,∴∠DCE=∠ACB,∵在△DCE和△ACB中,∴△DCE≌△ACB(SAS)∴DE=AB.三、(ASA)(AAS)9.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AC=DF.证明:∵FB=CE,∴BC=EF.∵AB∥ED,∴∠B=∠E∵AC∥EF,∴∠ACB=∠DFE.在△ABC和△DEF中{∠B=∠EBC=EF∠ACB=∠DFE∴△ABC≌△DEF(ASA).∴AC=DF.10. 如图,在△AEC和△DFB中,∠E=∠F,点A,B,C,D在同一直线上,AE∥DF,AB=CD,求证:CE=BF。
(完整版)全等三角形经典题型50题(含答案),推荐文档
E
∵∠ABD+∠ADB=90°,∠ACF+∠CDE=90°
又∵∠ADB=∠CDE
D
∴∠ABD=∠ACF 在△ABD 和△ACF 中 ∠ABD=∠ACF, AB=AC,
∠BAD=∠CAF=90° ∴△ABD≌△ACF(ASA) ∴BD=CF ∴BD=2CE
B
C
25、(10 分)如图:DF=CE,AD=BC,∠D=∠C。求证:△AED≌△
BFC。
D
EF
C
A
26、(10 分)如图:AE、BC 交于点 M,F 点在 AM 上, BE∥CF,BE=CF。 求证:AM 是△ABC 的中线。 证明: ∵BE‖CF ∴∠E=∠CFM,∠EBM=∠FCM ∵BE=CF
B
ቤተ መጻሕፍቲ ባይዱB A
F
M
C
E
∴△BEM≌△CFM
∴BM=CM ∴AM 是△ABC 的中线.
C
B
D
2. 已知:AC 平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE
6. 如图,四边形 ABCD 中,AB∥DC,BE、CE 分别平分∠ABC、∠BCD,且点 E 在 AD 上。求证:BC=AB+DC。
.
7.已知:AB//ED,∠EAB=∠BDE,AF=CD,EF=BC,求证:∠F=∠C
D
AC 是公共边,所以 AAS==>三角形 ADC 全等于三角形
ABC. 所以 BC 等于 DC,角 3 等于角 4,EC=EC 三角形
A
1 2
5 E6
3 4
C
DEC 全等于三角形 BEC 所以∠5=∠6
13.已知:如图,DC∥AB,且 DC=AE,E 为 AB 的中点,
人教版初中数学全等三角形证明题(经典50题)

人教版初中数学全等三角形证明题(经典50题)(含答案)1.已知:A B=4,A C=2,D 是B C 中点,A D 是整数,求A D?AB CD解析:延长A D 到E,使DE=A D,则三角形A D C 全等于三角形E B D即BE=A C=2 在三角形A B E 中,AB-BE<A E<A B+B E即:10-2<2A D<10+2 4<A D<6又A D 是整数,则A D=512.已知:D 是A B 中点,∠AC B=90°,求证:C D AB2ADC B3.已知:BC=D E,∠B=∠E,∠C=∠D,F 是C D 中点,求证:∠1=∠2A 12BEC F D证明:连接 BF 和 EF 。
因为 BC=E D,CF=D F,∠BCF=∠ED F 。
所以 三角形 B CF 全等于三角形 E DF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接 BE 。
在三角形 BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠A B C=∠A E D 。
所以 ∠A BE=∠AE B 。
所以 A B=A E 。
在三角形 A BF 和三角形 AEF 中, A B =A E,BF=EF, ∠ABF=∠A B E+∠EBF=∠A E B+∠BEF=∠A EF 。
所以 三角 形 A BF 和三角形 AEF 全等。
所以 ∠B AF=∠E AF (∠1=∠2)。
A 4. 已知:∠1=∠2,C D=D E ,EF//AB ,求证:EF=A C证明: 过 E 点,作 E G//AC ,交 A D 延长线于 G 则2 1 FCD∠DE G=∠D C A ∵C D=D E ∴⊿A D C ≌⊿G D E , ∠D G E=∠2A A S又 E( ) B∴E G=A C ∵EF//AB ∴∠DFE=∠1 ∵∠1=∠2 ∴∠DFE=∠D G E ∴EF=E G ∴EF=A C5. 已知:A D 平分∠B A C ,A C=A B+B D ,求证:∠B=2∠CACB D证明: 在 A C 上截取 AE=A B ,连接 E D ∵AD 平分∠B A C ∴∠E A D=∠BA D 又 ∵AE=A B , A D=A D ∴⊿AE D ≌⊿A B D ( S AS ) ∴∠AE D=∠B , D E=D B ∵A C =A B+B DA C =A E+CE ∴CE=D E ∴∠C=∠E D C ∵∠AE D=∠C+∠E D C=2∠C ∴∠B= 2∠C6. 已知:A C 平分∠B A D ,C E ⊥A B ,∠B+∠D=180°,求证:AE=A D +B E证明:在B C上截取BF=B A,连接EF.∠A BE=∠FBE,BE=BE,则⊿A BE≌ΔFBE(SAS),∠EFB=∠A;A B平行于C D,则:∠A+∠D=180°;又∠EFB+∠EFC=180°,则∠EFC=∠D;又∠FCE=∠D C E,CE=CE,故⊿FCE≌ΔDCE(AAS),FC=CD. 所以,BC=BF+FC=A B+C D.13.已知:A B//E D,∠E A B=∠B D E,E DA F=CCFA B证明:A B//ED,A E//BD推出AE=B D,又有AF=C D,EF=B CA D则:△AE D 是等腰三角形。
(完整版)全等三角形证明经典50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C14. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB15. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BED C B A FE PD A CB16. 已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC18.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .19.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA20.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .21.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B22.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.F AEDCB P E D CB A DC B A23.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC . (2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .证明:25、如图:DF=CE ,AD=BC ,∠D=∠C 。
八年级全等三角形证明经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+2 1<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
全等三角形判定专题复习题含答案

全等三角形判定一、选择题:1.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A.SSS B.SAS C.AAS D.ASA2.方格纸中,每个小格顶点叫做一个格点,以格点连线为边的三角形叫做格点三角形.如图,在4×4的方格纸中,有两个格点三角形△ABC、△DEF,下列说法中成立的是()A.∠BCA=∠EDF B.∠BCA=∠EFDC.∠BAC=∠EFD D.这两个三角形中,没有相等的角3.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是()A.△ABD和△C DB的面积相等B.△ABD和△CDB的周长相等C.∠A+∠ABD=∠C+∠CBD D.AD∥BC,且AD=BC4.下列判断中错误..的是()A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等5.使两个直角三角形全等的条件是()A.一个锐角对应相等B.两个锐角对应相等C.一条边对应相等 D.两条边对应相等6.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于()A.∠EDB B.∠BED C.∠AFB D.2∠ABF7.在△ABC和△A/B/C/中,已知∠A=∠A/,AB=A/B/,在下面判断中错误的是( )A.若添加条件AC=A/C/,则△ABC≌△△A/B/C/B.若添加条件BC=B/C/,则△ABC≌△△A/B/C/C.若添加条件∠B=∠B/,则△ABC≌△△A/B/C/D.若添加条件∠C=∠C/,则△ABC≌△△A/B/C/8.如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF()A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F9.如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是()A.4cm B.6cm C.8cm D.9cm在如图所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),则与△ABC有一条公共边且全等的所有格点三角形个数是()A.1 B.2 C.3 D.411.如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为()A. a2B. a2C. a2D. a212.在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是()A.B.C.D.二、填空题:13.如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上块,其理由是.14.如图示,点B在AE上,∠CBE=∠DBE,要使ΔABC≌ΔABD, 还需添加一个条件是__________.(填上你认为适当的一个条件即可)15.如图,已知∠1=∠2,AC=AD,请增加一个条件,使△ABC≌△AED,你添加的条件是.16.如图,∠1=∠2,要使△ABD≌△ACD,需添加的一个条件是(只添一个条件即可).17.如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形对.18.如图,△ABD≌△BAC,若AD=BC,则∠BAD的对应角是.19.如图,已知AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,则∠ACE= 度.如图,如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三边所对的角的关系是.三、解答题:21.如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A.B.试说明AD+AB=BE.22.如图,E、A.C三点共线,AB∥CD,∠B=∠E,,AC=CD。
全等三角形经典题型50题(含答案解析)
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF和三ADBC角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DG E ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠E DC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
(完整版)全等三角形证明经典50题(含答案)
证明:连接 BF 和 EF T BC=ED,CF=DF, / BCF= / EDF 三角形BCF 全等于三角形 EDF (边角边)1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 ADD • BF=EF, / CBF= / DEF 连接 BE 在三角形 BEF 中,BF=EF • / EBF= / BEF 。
: / ABC= / AED 。
二 / ABE= / AEB 。
• AB=AE 。
在三角形 ABF 和三角形 AEF 中AB=AE,BF=EF, / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF • 三角形 ABF 和三角形 AEF 全等。
•/ BAF= / EAF ( /仁/ 2)4.已知:/ 1 = / 2, CD=DE , EF//AB ,求证:EF=AC解:延长 AD 到E,使AD=DE •/ D 是BC 中点二BD=DC 在厶 ACD 和^ BDE 中 AD=DE / BDE= / ADCBD=DC /•△ ACD ◎△ BDE ••• AC=BE=2 •••在△ ABE 中 AB-BE V AE V AB+BE •/ AB=4 即 4-2 V 2AD V 4+21 V AD V 3 • AD=21 2.已知:D 是 AB 中点,/ ACB=90 °,求证:CD —AB 2A CG// EF ,可得,/• △ EFD ^A CGD•,/ EFD =Z 1过C 作CG // EF 交AD 的延长线于点GEFD = CGDDE = DC / FDE =Z GDC (对顶角) EF = CG / CGD =Z EFD 又,EF // AB / 1= / 2 •/ CGD =Z 2 • △ AGC 为等腰三角形, AC = CG 又 EF = CG 「. EF = AC 延长CD 与P ,使D 为CP 中点。
连接 AP,BP •/ DP=DC,DA=DB • ACBP 为平行四边形又/ ACB=90 •平行四边形 ACBP 为矩形 • AB=CP=1/2AB 3.已知:BC=DE ,/ B= / E ,Z C=Z D , F 是 CD 中点,求证:/ 1 = / 2 5.已知:AD 平分/ BAC , AC=AB+BD ,求证:/ B=2 / C证明:延长 AB 取点E ,使AE = AC ,连接DE •/ AD 平分/ BAC• / EAD =Z CAD•/ AE = AC , AD = AD • △ AED 也厶 ACD ( SAS )•••/ E = Z C•/ AC = AB+BD •AE = AB+BD•/ AE = AB+BE •BD = BE •••/ BDE =Z E •••/ ABC =Z E+ / BDE •••/ ABC = 2 / E •••/ ABC = 2 / C ••• AE = AF + FE = AD + BE12.如图,四边形ABCD中,AB 在AD上。
全等三角形证明50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=2ADBC2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP ,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ,可得,∠EFD =CGD DE =DC∠FDE =∠GDC (对顶角)BA CDF2 1 EEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF ∵CE ⊥AB∴∠CEB =∠CEF =90° ∵EB =EF ,CE =CE , ∴△CEB ≌△CEF ∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC∴△ADC ≌△AFC (SAS ) ∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DEADB C∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=28. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=29.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF。
(完整版)全等三角形证明经典50题(含答案)
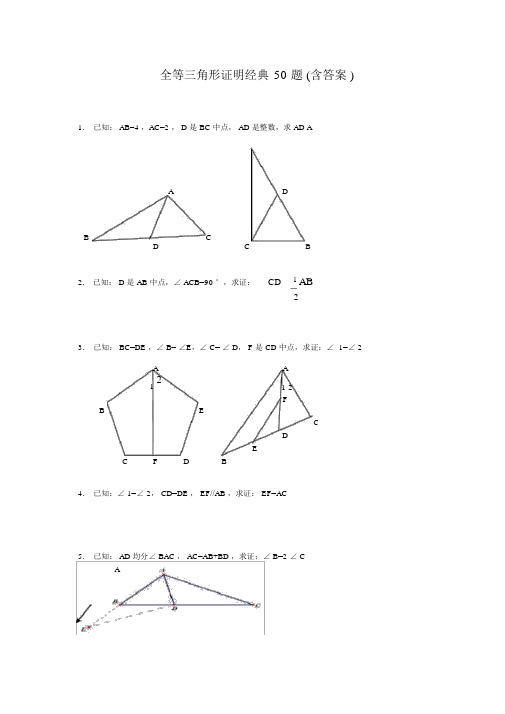
全等三角形证明经典50 题 (含答案 )1.已知: AB=4 ,AC=2 , D 是 BC 中点, AD 是整数,求 AD AA DB CD C B2. 已知: D 是 AB 中点,∠ ACB=90 °,求证:CD 1 AB23.已知: BC=DE ,∠ B= ∠E,∠ C= ∠ D, F 是 CD 中点,求证:∠ 1=∠ 2A A1 21 2BFECDEC FD B4.已知:∠ 1=∠ 2, CD=DE , EF//AB ,求证: EF=AC5.已知: AD 均分∠ BAC , AC=AB+BD ,求证:∠ B=2 ∠ CA6.已知: AC 均分∠ BAD , CE⊥ AB ,∠ B+ ∠D=180 °,求证: AE=AD+BE12.如图,四边形 ABCD 中, AB ∥ DC ,BE、 CE 分别均分∠ ABC 、∠ BCD ,且点 E 在 AD上。
求证: BC=AB+DC 。
E DCFA B13.已知: AB//ED ,∠ EAB= ∠ BDE , AF=CD , EF=BC ,求证:∠ F=∠ C14.P 是∠ BAC 均分线 AD 上一点, AC>AB ,求证: PC-PB<AC-AB CAP DB15. 已知∠ ABC=3 ∠ C,∠ 1=∠2, BE⊥ AE ,求证: AC-AB=2BE16.已知, E 是 AB 中点, AF=BD , BD=5 , AC=7 ,求 DCDF A CE B18.如图,在△ABC 中, BD =DC ,∠ 1=∠ 2,求证: AD⊥BC .19.如图, OM 均分∠ POQ ,MA ⊥ OP,MB⊥ OQ , A、 B 为垂足, AB 交 OM 于点 N.求证:∠ OAB=∠OBA20.( 5 分)如图,已知 AD ∥BC,∠ PAB 的均分线与∠ CBA 的均分线订交于 E, CE 的连线交AP 于 D .求证: AD +BC =AB.PACEDCD BA B21.如图,△ ABC 中, AD 是∠ CAB 的均分线,且AB=AC+CD,求证:∠ C=2∠ B22.( 6 分)如图①, E、F 分别为线段AC 上的两个动点,且DE ⊥AC 于 E, BF⊥AC 于 F ,若 AB=CD , AF=CE, BD 交 AC 于点 M.(1)求证: MB=MD , ME =MF(2)当 E、F 两点挪动到如图②的地点时,其他条件不变,上述结论可否建立?若建立请赐予证明;若不建立请说明原因.23.已知:如图,DC∥ AB,且 DC =AE, E 为 AB 的中点,( 1)求证:△ AED≌△ EBC.( 2)观看图前,在不添协助线的状况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):AE ODB C24.( 7 分)如图,△ ABC 中,∠ BAC=90 线垂直于过 C 点的直线于 E,直线 CE 交求证: BD =2CE.度, AB=AC, BD 是∠ ABC 的均分线, BD 的延伸BA 的延伸线于 F.FAED证明:B C25、如图: DF=CE, AD=BC,∠ D=∠ C。
(完整word版)八年级全等三角形证明经典50题(含答案).doc

1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求ADA 解:延长AD 至IJE,使AD=DE・・・D 是BC 中点BD=DC在厶ACD 和厶BDE 中AD=DEZBDE= ZADC BD=DCAA ACD A BDE•*. AC=BE=2・・•在△ ABE 中AB-BE < AE<AB+BE・・・AB=4即 4・2 <2AD < 4+21 < AD < 3・・・AD=2延长CD 与P,使D 为CP 中点。
连接VDP=DC,DA=DBA AC BP 为平行四边形又 Z ACB=90・・・平行四边形ACBP 为矩形AAB=CP=1/2AB 2.已知:D 是AB 中点,Z ACB=90 0,求证:CD [AB 2AAP,BP3.已知:BC=DE , Z B= ZE, Z C= ZD , F 是CD 中点,求证:Z 1= Z2证明:连接BF和EF・・・ BC=ED,CF=DF, Z BCF= Z EDF・・・三角形BCF全等于三角形EDF(边角边)・・・ BF=EF, ZCBF=Z DEF连接BE在三角形BEF中,BF=EF/. Z EBF=Z BEFo・・・ Z ABC= Z AED o・・・ Z ABE= Z AEBo/. AB=AE o在三角形ABF和三角形AEF屮AB=AE,BF=EF,ZABF= Z ABE+ Z EBF= ZAEB+ Z BEF= Z AEF・・・三角形ABF和三角形AEF全等。
・・・ Z BAF= Z EAF(Z 1= Z 2)o4. 己知:Z 1= Z 2 , CD=DE , EF//AB ,求证:EF=AC过C作CG〃EF交AD的延长线于点GCG// EF,可得,Z EFD= CGDDE= DCZFDE= Z GDC (对顶角)AA EFD^A CGDEF= CGZCGD = Z EFD又,EF// AB・・・,Z EFD= Z 1Z1= Z 2・・・Z CGD= Z 2・・・△ AGC为等腰三角形,AC= CG又EF=CG・・・EF= AC5.已知:AD 平分Z BAC, AC=AB+BD ,求证:Z B=2 Z C证明:延长AB取点E,使AE=AC,连接DEVAD 平分Z BACAZ EAD=Z CAD・・・AE=AC, AD = ADA A AED^A ACD ( SAS)AZ E=Z CVAC = AB+BD・・・AE= AB+BD・・・AE= AB+BEABD = BE・・・Z BDE=Z EVZ ABC=Z E+ Z BDEAZ ABC = 2 ZEAZ ABC = 2 ZC6.己知:AC 平分Z BAD , CE丄AB , Z B+ Z D=180 ° ,求证:AE=AD+BE・・・CE丄AB ・・・Z CEB=Z CEF= 90° ・・・EB=EF, CE = CE, AACEB^ACEF ・・・Z B=Z CFEVZ B+Z D= 180 ° , ZCFE+Z CFA= 180 0AZ D = Z CFAVAC 平分Z BAD・・・Z DAC = Z FACVAC = AC・・・△ ADC 竺△ AFC ( SAS)/.AD = AF ・・・AE= AF+ FE= AD + BE解:延长AD至IJE,使AD=DE・・・D是BC中点・・・BD=DC在厶ACD和厶BDE中AD=DEZBDE= Z ADCBD=DC7.已知:AB=4 , AC=2 , D是BC屮点, AD是整数,求ADA 证明:在AE上取F,使EF= EB,连接CFAAACD^ABDE•*. AC=BE=2・・•在△ ABE中AB-BE < AE<AB+BE・・・AB=4即4・2 < 2AD < 4+21 < AD < 3・・・AD=218.已知:D 是AB 中点,Z ACB=90 0,求证:CD -AB2解:延长AD到E,使AD=DE・・・D是BC屮点・・・BD=DC在厶ACD和厶BDE中AD=DEZBDE= Z ADCBD=DCAA ACD A BDE•*. AC=BE=2•・•在A ABE中9.已知:BC=DE , Z B= ZE, Z C= ZD , F 是CD 中点,求证:Z 1= Z2A证明:连接BF和EF。
全等三角形判定-专题复习50题(含答案)

A.一个锐角对应相等C.一条边对应相等B.两个锐角对应相等全等三角形判定、选择题:1-如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全样的三角形,那么这两个三角形完全一样的依据是()A.SSSB.SASC.AASD.ASA2•方格纸中,每个小格顶点叫做一个格点,以格点连线为边的三角形叫做格点三角形。
如图,在4X4的方格纸中,有两个格点三角形△ABC、ADEF,下列说法中成立的是()A.ZBCA=ZEDF CoZBAC=ZEFDB.ZBCA=ZEFDD.这两个三角形中,没有相等的角3•如图所示,△ABD9ACDB,下面四个结论中,不正确的是()A.△ABD和厶CDB的面积相等B.AABD和厶CDB的周长相等C.ZA+ZABD=ZC+ZCBDD.AD〃BC,且AD=BC4.下列判断中错误的是()A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等5-使两个直角三角形全等的条件是()6•如图,在AABC和厶BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则Z AACB等于(B.ZBEDC.寺ZAFBD.2ZABFA.ZEDBBA B C DB.ZA=ZDC.AC=DD.ZACB=ZF7.在AABC 和厶A /B /C /中,已知ZA=ZA /,AB=A /B /,在下面判断中错误的是()A. 若添加条件AC=A /C /,则厶ABC^^^A /B /C /B. 若添加条件BC=B /C /,则厶ABC^^^A /B /C /C 。
若添加条件ZB=ZB /,则△ABC^^^A /B /C /D 。
若添加条件ZC=ZC /,则△ABC^^^A /B /C /8•如图,AABC 和厶DEF 中,AB=DE 、ZB=ZDEF,添加下列哪一个条件无法证明厶ABC^^DEF ()9•如图,在△ABC 中,ZABC=45°,AC=8cm,F 是高AD 和BE 的交点,则BF 的长是()A.4cmB.6cmC.8cmD.9cm1°.在如图所示的5X5方格中,每个小方格都是边长为1的正方形,AABC 是格点三角形(即顶点恰好是正方形的顶点),则与△ABC 有一条公共边且全等的所有格点三角形个数是()11.如图,点E 在正方形ABCD 的对角线AC 上,且EC=2AE ,直角三角形FEG 的两直角边EF 、EG 分别交BC 、DC 于点M 、N.若正方形ABCD 的边长为a,则重叠部分四边形EMCN 的面积为( A.AC 〃DF12-在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A 地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是(C、填空题:I3•如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上—块,其理由是.14.如图示,点B在AE上,ZCBE=ZDBE,要使AABC^AABD,还需添加一个条件是,(填上你认为适当的一个条件即可)15•如图,已知Z1=Z2,AC=AD,请增加一个条件,使△ABC9AAED,你添加的条件是16-如图,Z1=Z2,要使△ABD9AACD,需添加的一个条件是(只添一个条件即可).17•如图,在△ABC中,AB=AC,AD丄BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形对.18•如图,△ABD9ABAC,若AD=BC,则ZBAD的对应角是.19-如图,已知AB丄BD,垂足为B,ED丄BD,垂足为D,AB=CD,BC=DE,则ZACE=_度.2°・如图,如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三边所对的角的关系是.三、解答题:21•如图,ZDCE=90°,CD=CE,AD丄AC,BE丄AC,垂足分别为A.B.试说明AD+AB=BE.22.如图,E、A.C三点共线,AB〃CD,ZB=ZE,,AC=CD。
全等三角形经典题型50题(含答案)
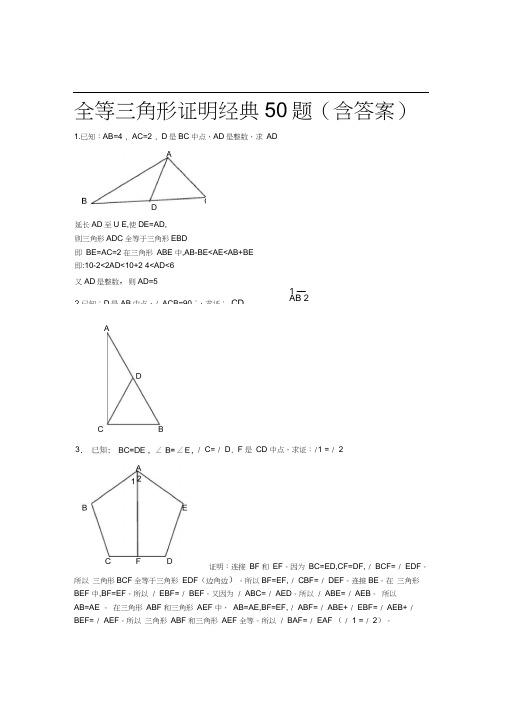
全等三角形证明经典50题(含答案)1.已知:AB=4 , AC=2 , D是BC中点,AD是整数,求AD/ C= / D, F 是CD 中点,求证:/ 1 = / 2证明:连接BF 和EF。
因为BC=ED,CF=DF, / BCF= / EDF。
所以三角形BCF全等于三角形EDF(边角边)。
所以BF=EF, / CBF= / DEF。
连接BE。
在三角形BEF 中,BF=EF。
所以 / EBF= / BEF。
又因为 / ABC= / AED。
所以 / ABE= / AEB。
所以AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF, / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF。
所以三角形ABF 和三角形AEF 全等。
所以 / BAF= / EAF (/ 1 = / 2)。
延长AD至U E,使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD是整数,则AD=52.已知:D是AB中点,/ ACB=90 °,求证:CD1 —AB 2A34. 已知:/ 仁/2, CD=DE , EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于 G 则/ DEG= / DCA , / DGE= / 2 又 •/ CD=DE U ADC 也"GDE ( AAS )••• EG=AC •/ EF//AB /-Z DFE= / 1 v/ 1 = / 2:丄 DFE= / DGE ••• EF=EG •: EF=AC5. 已知:AD 平分Z BAC , AC=AB+BD ,求证:Z B=2 / C证明:在 AC 上截取 AE=AB ,连接 ED •/ AD 平分Z BAC :•/ EAD= Z BAD 又 v AE=AB ,AD=AD :•" AED 6 ABD (SAS )•:Z AED= Z B ,DE=DB v AC=AB+BDAC=AE+CE •: CE=DE :-Z C=Z EDC vZ AED= Z C+ Z EDC=2 Z C -Z B=2 Z C 6. 已知:AC 平分Z BAD , CE 丄 AB , Z B+ Z D=180 °,求证: AE=AD+BE证明:在AE 上取F ,使EF = EB , 连接CF 因为CE 丄AB 所以Z CEB=Z CEF = 90° 因为 EB = EF , CE = CE , 所以△CEBCEF 所以Z B = Z CFE 因为Z B+ Z D = 180°, Z CFE +Z CFA = 180° 所以Z D = Z CFA 因为 AC 平分Z BAD 所以Z DAC=Z FAC 又因为 AC = AC 所以△ ADC AFC (SAS ) 所以 AD = AF 所以 AE = AF + FE=AD + BE12.如图,四边形 ABCD 中,AB // DC , BE 、CE 分别平分Z ABC 、Z BCD ,且点 E 在AD 上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形判定一、选择题:1.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A.SSS B.SAS C.AAS D.ASA2.方格纸中,每个小格顶点叫做一个格点,以格点连线为边的三角形叫做格点三角形.如图,在4×4的方格纸中,有两个格点三角形△ABC、△DEF,下列说法中成立的是()A.∠BCA=∠EDF B.∠BCA=∠EFDC.∠BAC=∠EFD D.这两个三角形中,没有相等的角3.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是()A.△ABD和△C DB的面积相等B.△ABD和△CDB的周长相等C.∠A+∠ABD=∠C+∠CBD D.AD∥BC,且AD=BC4.下列判断中错误..的是()A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等5.使两个直角三角形全等的条件是()A.一个锐角对应相等B.两个锐角对应相等C.一条边对应相等 D.两条边对应相等6.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于()A.∠EDB B.∠BED C.∠AFB D.2∠ABF7.在△ABC和△A/B/C/中,已知∠A=∠A/,AB=A/B/,在下面判断中错误的是( )A.若添加条件AC=A/C/,则△ABC≌△△A/B/C/B.若添加条件BC=B/C/,则△ABC≌△△A/B/C/C.若添加条件∠B=∠B/,则△ABC≌△△A/B/C/D.若添加条件∠C=∠C/,则△ABC≌△△A/B/C/8.如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF()A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F9.如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是()A.4cm B.6cm C.8cm D.9cm10.在如图所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),则与△ABC有一条公共边且全等的所有格点三角形个数是()A.1 B.2 C.3 D.411.如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为()A. a2B. a2C. a2D. a212.在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A 地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是()A.B.C.D.二、填空题:13.如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上块,其理由是.14.如图示,点B在AE上,∠CBE=∠DBE,要使ΔABC≌ΔABD, 还需添加一个条件是__________.(填上你认为适当的一个条件即可)15.如图,已知∠1=∠2,AC=AD,请增加一个条件,使△ABC≌△AED,你添加的条件是.16.如图,∠1=∠2,要使△ABD≌△ACD,需添加的一个条件是(只添一个条件即可).17.如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形对.18.如图,△ABD≌△BAC,若AD=BC,则∠BAD的对应角是.19.如图,已知AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,则∠ACE= 度.20.如图,如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三边所对的角的关系是.三、解答题:21.如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A.B.试说明AD+AB=BE.22.如图,E、A.C三点共线,AB∥CD,∠B=∠E,,AC=CD。
求证:BC=ED。
23.如图:AD是△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD。
求证:BE⊥AC。
24.如图,已知△ABC中,∠1=∠2,AE=AD,求证:DF=EF.25.如图所示,已知AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.26.如图,点A,B,C,D在一条直线上,△ABF≌△DCE.你能得出哪些结论?(请写出三个以上的结论)27.已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.28.如图,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:BC=AE.29.已知:如图AC,BD相交于点O,∠A=∠D,AB=CD,求证:△AOB≌△DOC.30.如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.求证:AD=AE.31.如图,已知点B、E、C、F在同一条直线上,BE=CF,AB∥DE,∠A=∠D.求证:AB=DE.32.如图,已知AD=BC,AC=BD.(1)求证:△ADB≌△BCA;(2)OA与OB相等吗?若相等,请说明理由.33.如图,已知在四边形ABCD中,E是AC上一点,∠1=∠2,∠3=∠4.求证:∠5=∠6.34.已知:BE⊥CD,BE=DE,BC=DA,求证:①△BEC≌△DEA;②DF⊥BC.35.如图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB,(1)试证明:DE=BF;(2)连接DF、BE,猜想DF与BE的关系?并证明你的猜想的正确性.36.如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.求证:AE=CE.37.如图,已知:正方形ABCD,由顶点A引两条射线分别交BC、CD于E、F,且∠EAF=45°,求证:BE+DF=EF.38.如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于点F,且BE=CF.求证:AD平分∠BAC.39.如图,点A.C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF.求证:DE=CF.40.如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于 D.求证:AD+BC=AB.41.如图,在△ABC中,点D、E分别在AB、AC上,AB=AC,BD=CE,BE与CD交于O.求证:△ABE≌△ACD.42.如图,AB=DC,AC=DB,求证:AB∥CD.43.如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.44.如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.(1)求证:CF=DG;(2)求出∠FHG的度数.45.已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.46.如图,点D,E分别在AB,AC上,且AD=AE,∠BDC=∠CEB.求证:BD=CE.47.如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.(1)求证:△ABE≌DCE;(2)当∠AEB=50°,求∠EBC的度数?48.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.49.如图,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.50.如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.求证:BD=CE.参考答案1.D2.B3.A4.B5.D6.C7.B8.C.9.C.10.C11.D12.【解答】解:A.延长AC、BE交于S,∵∠CAB=∠EDB=45°,∴AS∥ED,则SC∥DE.同理SE∥CD,∴四边形SCDE是平行四边形,∴SE=CD,DE=CS,即走的路线长是:AC+CD+DE+EB=AC+CS+SE+EB=AS+BS;B、延长AF、BH交于S1,作FK∥GH与BH的延长线交于点K,∵∠SAB=∠S1AB=45°,∠SBA=∠S1BA=70°,AB=AB,∴△SAB≌△S1AB,∴AS=AS1,BS=BS1,∵∠FGH=180°﹣70°﹣43°=67°=∠GHB,∴FG∥KH,∵FK∥GH,∴四边形FGHK是平行四边形,∴FK=GH,FG=KH,∴AF+FG+GH+HB=AF+FK+KH+HB,∵FS1+S1K>FK,∴AS+BS>AF+FK+KH+HB,即AC+CD+DE+EB>AF+FG+GH+HB,13.答案为:第1,利用SAS得出全等三角形,即可配成与原来同样大小的一块.14.答案为:BC=BD;15.答案为:AE=AB.16.答案为:CD=BD.17.答案为:418.答案为:∠ABC.19.答案为:90°.20.答案为:相等或互补.21.解:∵∠DCE=90°(已知),∴∠ECB+∠ACD=90°,∵EB⊥AC,∴∠E+∠ECB=90°(直角三角形两锐角互余).∴∠ACD=∠E(同角的余角相等).∵AD⊥AC,BE⊥AC(已知),∴∠A=∠EBC=90°(垂直的定义)在Rt△ACD和Rt△BEC中,,∴Rt△ACD≌Rt△BEC(AAS).∴AD=BC,AC=BE(全等三角形的对应边相等),∴AD+AB=BC+AB=AC.∴AD+AB=BE.22.证明:∵AB∥CD,∴∠BAC=∠ECD,在△ABC和△CED中,∠BAC=∠ECD,∠B=∠E,AC=CD.∴△ACB≌△CED(AAS),∴BC=ED.23.证明:(1) AD为△ABC上的高,∴BDA=ADC =90.∵BF=AC,FD=CD.∴Rt△BDF≌Rt△ADC.(2)由①知∠C=∠BFD,∠CAD=∠DBF.∠BFD= ∠AFE,又∠CBE=∠CAD,∴∠AEF=∠BDF.∠BDF= 90,∴BE⊥AC.24.证明:在△ABE和△ACD中,,∴△ABE≌△ACD(AAS),∴AB=AC,∵AE=AD,∴AB﹣AD=AC﹣AE,即BD=CE,在△BDF和△CEF中,,∴△BDF≌△CEF(AAS),∴DF=EF.25.证明:连接AD,在△ACD和△ABD中,,∴△ACD≌△ABD(SSS),∴∠EAD=∠FAD,即AD平分∠EAF,∵DE⊥AE,DF⊥AF,∴DE=DF.26.解:∵△ABF≌△DCE∴∠BAF=∠CDE,∠AFB=∠DEC,∠ABF=∠DCE,AB=DC,BF=CE,AF=DE;∴AF∥ED,AC=BD,BF∥CE.27.解:(1)在△ABC中,∠BAC=90°,∴∠BAD=90°-∠EAC。
