大学物理课后习题答案(第四章) 北京邮电大学出版社
大学物理第六版上册北京邮电大学出版课后答案详解精选全文完整版

可编辑修改精选全文完整版大学物理第六版上册北京邮电大学出版课后答案详解1、行驶的汽车关闭发动机后还能行驶一段距离是因为汽车受到惯性力作用[判断题] *对错(正确答案)答案解析:汽车具有惯性2、用如图所示的装置做“探究小车速度随时间变化的规律”实验:1.小车从靠近定滑轮处释放.[判断题] *对错(正确答案)3、马德堡半球实验测出了大气压,其大小等于760mm高水银柱产生的压强[判断题]对错(正确答案)答案解析:托里拆利实验最早测出了大气压强4、11.小敏学习密度后,了解到人体的密度跟水的密度差不多,从而她估测一个中学生的体积约为()[单选题] *A.50 m3B.50 dm3(正确答案)C.50 cm3D.500 cm35、9.在某原子结构模型示意图中,a、b、c是构成该原子的三种不同粒子,能得出的结()[单选题] *A.a和c数量不相等B.b决定原子种类C.质量集中在c上D.a和c之间存在吸引的力(正确答案)6、4.静止在水平地面上的物体受到向上的弹力是因为地面发生了形变.[判断题] *对(正确答案)错7、下列有关力做功的说法中正确的是()[单选题]A.用水平力推着购物车前进,推车的力做了功(正确答案)B.把水桶从地面上提起来,提水桶的力没有做功C.书静止在水平桌面上,书受到的支持力做了功D.挂钩上的书包静止时,书包受到的拉力做了功8、1.与头发摩擦过的塑料尺能吸引碎纸屑。
下列与此现象所反映的原理相同的是()[单选题] *A.行驶的汽车窗帘被吸出去B.挤压后的吸盘吸在光滑的墙上C.用干燥的双手搓开的塑料袋会吸在手上(正确答案)D.两个表面光滑的铅块挤压后吸在一起9、下列措施中,能使蒸发减慢的是()[单选题]A.把盛有酒精的瓶口盖严(正确答案)B.把湿衣服晾在通风向阳处C.用电吹风给湿头发吹风D.将地面上的积水向周围扫开10、停放在水平地面上的汽车对地面的压力和地面对车的支持力是平衡力[判断题] *对错(正确答案)答案解析:相互作用力11、52.“凿壁偷光”原指凿穿墙壁,让邻舍的烛光透过来,后用来形容家贫而勤奋读书。
大学物理第二版答案(北京邮电大学出版社)

习 题 解 答第一章 质点运动学1-1 (1) 质点t 时刻位矢为:j t t i t r ⎪⎭⎫ ⎝⎛-+++=4321)53(2(m)(2) 第一秒内位移j y y i x x r)()(01011-+-=∆)(5.33)101(3)01(21)01(32m j i ji +=⎥⎦⎤⎢⎣⎡-+--=(3) 前4秒内平均速度)s m (53)2012(411-⋅+=+=∆∆=j i j i t r V(4) 速度)s m ()3(3d d 1-⋅++==j t i t r V∴ )s m (73)34(314-⋅+=++=j i j i V(5) 前4秒平均加速度)s m (43704204-⋅=-=--=∆∆=j j V V t V a (6) 加速度)s m ()s m (d d 242--⋅=⋅==j a j tV a1-2 23d d 23++==t t txv c t t t c t v x x +++=+==⎰⎰241d d 34 当t =2时x =4代入求证 c =-12 即1224134-++=t t t xtt tv a t t v 63d d 23223+==++= 将t =3s 代入证)s m (45)s m (56)(414123133--⋅=⋅==a v m x1-3 (1) 由运动方程⎩⎨⎧+==ty t x 2342消去t 得轨迹方程0)3(2=--y x(2) 1秒时间坐标和位矢方向为 m y m x 5411==[4,5]m: ︒===3.51,25.1ααxytg(3) 第1秒内的位移和平均速度分别为)m (24)35()04(1j i j i r+=-+-=∆)s m (2411-⋅+=∆∆=j i tr V(4) 质点的速度与加速度分别为i t Va j i tr V8d d ,28d d ==+==故t =1s 时的速度和加速度分别为 2111s m 8,s m 28--⋅=⋅+==i a j i V1-4 该星云飞行时间为a 1009.2s 1059.61093.31074.21046.910177915⨯=⨯=⨯⨯⨯⨯ 即该星云是101009.2⨯年前和我们银河系分离的. 1-5 实验车的加速度为g)(25m/s 1047.280.13600101600223≈⨯=⨯⨯==t v a 基本上未超过25g.1.80s 内实验车跑的距离为)(m 40080.13600210160023=⨯⨯⨯==t v s1-6 (1)设第一块石头扔出后t 秒未被第二块击中,则2021gt t v h -= 代入已知数得28.9211511t t ⨯-=解此方程,可得二解为s 22.1s,84.111='=t t第一块石头上升到顶点所用的时间为s 53.18.9/15/10===g v t m由于m t t >1,这对应于第一块石头回落时与第二块相碰;又由于m t t <'1这对应于第一块石头上升时被第二块赶上击中.以20v 和'20v 分别对应于在t 1和'1t 时刻两石块相碰时第二石块的初速度,则由于2111120)(21)(t t g t t v h ∆∆---= 所以184.1)184.1(8.92111)(2121121120--⨯⨯+=∆-∆-+=t t t t g h v m /s 2.17=同理.122.1)122.1(8.92111)(2121121120--⨯⨯+=-'-'+='t t t t g h v ∆∆ m/s)(1.51=(2) 由于'>=123.1t s t ∆,所以第二石块不可能在第一块上升时与第一块相碰.对应于t 1时刻相碰,第二块的初速度为3.184.1)3.184.1(8.92111)(2122122120--⨯⨯+=--+="t t t t g h v ∆∆ m/s)(0.23=1-7 以l 表示从船到定滑轮的绳长,则t l v d /d 0-=.由图可知22h l s -=于是得船的速度为02222d d d d v s h s t l h l lts v +-=-==负号表示船在水面上向岸靠近. 船的加速度为3202022d d d d d d s v h tl v h l ll t v a -=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--== 负号表示a 的方向指向岸边,因而船向岸边加速运动.1-8 所求位数为522422221048.9601.0)106(44⨯=⨯⨯⨯==ππωg r n g r1-9 物体A 下降的加速度(如图所示)为222m/s 2.024.022=⨯==t h a 此加速度也等于轮缘上一点在s 3='t 时的切向加速度,即)m/s (2.02='t a在s 3='t 时的法向加速度为)m/s (36.00.1)32.0()(2222=⨯='='=R t a R v a t n1-10 2m /s 2.1=a ,s 5.00=t ,m 5.10=h .如图所示,相对南面,小球开始下落时,它和电梯的速度为m/s)(6.05.02.100=⨯==at v以t 表示此后小球落至底板所需时间,则在这段时间内,小球下落的距离为2021gt t v h +=电梯下降的距离为习题1-9图 习题1-10图2021at t v h +='又20)(21t a g h h h -='-= 由此得s 59.02.18.95.1220=-⨯=-=a g h t而小球相对地面下落的距离为2021gt t v h += 259.08.92159.06.0⨯⨯+⨯= m 06.2= 1-11 人地风人风地v v v+=画出速度矢量合成图(a)又人地风人风地02v v v +'=,速度矢量合成如图(b )两图中风地v应是同一矢量.可知(a )图必是底角为︒45的等腰直角三角形,所以,风向应为西北风,风速为人地人地风地00245cos v v v =︒=)s m (23.41-⋅=1-12 (1) v LvL t 22==(2) 22212u v vLu v L u v L t t t -=++-=+= 1212-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=v u v L(3) v Lv L t t t '+'=+=21,如图所示风速u 由东向西,由速度合成可得飞机对地速度v u v +=',则22u v V -='.习题1-12图习题1-11图2221222⎪⎭⎫⎝⎛-=--='=v u v L uv L v L t 证毕1-13 (1)设船相对岸的速度为V '(如图所示),由速度合成得V u V +='V 的大小由图1.7示可得αβcos cos u V V +'=即332323cos cos -=⨯-=-='αβu V V 而1212sin sin =⨯=='αβu V 船达到B 点所需时间)s (1000sin =='='=D V DV OB t βAB 两点之距βββsin cos D Dctg S == 将式(1)、(2)代入可得m)(1268)33(=-=D S(2) 由αβsin 101sin 3u V D t ⨯='=船到对岸所需最短时间由极值条件决定0cos sin 11d d 2=⎪⎭⎫⎝⎛-=αααu t 即 2/,0c o s παα==故船头应与岸垂直,航时最短.将α值代入(3)式得最短航时为s)(500105.021012/sin 101333m in=⨯=⨯=⨯=s u t π (3) 设l OB =,则ααββsin cos 2sin sin 22u uV V u D V D V D l -+=''==欲使l 最短,应满足极值条件.习题1-13图a a uV V u u D l '⎢⎢⎣⎡''-+-='cos sin cos 2d d 22αα 0cos 2sin sin 2222=⎥⎦⎤'-+''+αuV V u a a uV 简化后可得01cos cos 222=+'+-'αuVV u a即 01cos 613cos 2=+'-'αa 解此方程得32cos ='α︒=='-2.4832cos 1α 故船头与岸成︒2.48,则航距最短.将α'值代入(4)式得最小航程为222222m in 321232322321000cos 1cos 2⎪⎭⎫ ⎝⎛-⨯⨯⨯-+='-'-+-=ααu uv v u D lkm)(5.1m 105.13=⨯= AB 两点最短距离为km)(12.115.122min min =-=-=D l S第二章 质点动力学2-1 (1)对木箱,由牛顿第二定律,在木箱将要被推动的情况下如图所示,x 向:0cos m ax m in =-f F θ y 向:0sin m in =--Mg F N θ 还有 N f s m ax μ=解以上三式可得要推动木箱所需力F 的最小值为θμθμsin cos s s min -=MgF习题2-1图在木箱做匀速运动情况下,如上类似分析可得所需力F 的大小为θμθμsin cos k k min -=MgF(2)在上面m in F 的表示式中,如果0sin cos s →-θμθ,则∞→m in F ,这意味着用任何有限大小的力都不可能推动木箱,不能推动木箱的条件是0sin cos s ≤-θμθ由此得θ的最小值为s1arctanμθ=2-2 (1)对小球,由牛顿第二定律x 向:ma N T =-θθsin cosy 向:0cos sin =-+mg N T θθ 联立解此二式,可得N)(32.3)30sin 8.930cos 2(5.0)sin cos (=︒+︒⨯⨯=+=ααg a m T N)(74.3)30sin 230cos 8.9(5.0)sin cos (=︒-︒⨯⨯=+=ααa g m N由牛顿第三定律,小球对斜面的压力N)(74.3=='N N(2)小球刚要脱离斜面时N =0,则上面牛顿第二定律方程为mg T ma T ==θθsin ,cos由此二式可解得2m/s 0.1730tan /8.9tan /=︒==θg a2-3 要使物体A 与小车间无相对滑动,三物体必有同一加速度a ,且挂吊B 的绳应向后倾斜。
大学物理学第版修订版北京邮电大学出版社上册习题答案.docx

习题3 3.1 选择题(1)有一半径为 R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为 J,开始时转台以匀角速度ω0转动,此时有一质量为 m的人站在转台中心,随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为(A)J0(B)J0mR2m) R 2J(J(C)J0(D) 0 mR2[ 答案: (A)](2)如题3.1(2)图所示,一光滑的内表面半径为10cm的半球形碗,以匀角速度ω 绕其对称轴OC旋转,已知放在碗内表面上的一个小球P 相对于碗静止,其位置高于碗底4cm,则由此可推知碗旋转的角速度约为(A)13rad/s(B)17rad/s(C)10rad/s(D)18rad/s(a)(b)题3.1 ( 2)图[ 答案: (A)](3)如 3.1(3) 图所示,有一小块物体,置于光滑的水平桌面上,有一绳其一端连结此物体,;另一端穿过桌面的小孔,该物体原以角速度?在距孔为 R 的圆周上转动,今将绳从小孔缓慢往下拉,则物体(A)动能不变,动量改变。
(B)动量不变,动能改变。
(C)角动量不变,动量不变。
(D)角动量改变,动量改变。
(E)角动量不变,动能、动量都改变。
[ 答案: (E)]3.2 填空题(1)半径为 30cm的飞轮,从静止开始以 0.5rad ·s-2的匀角加速转动,则飞轮边缘上一点在飞轮转过240?时的切向加速度aτ =,法向加速度a n=。
[ 答案:0.15; 1.256 ](2)如题3.2 (2)图所示,一匀质木球固结在一细棒下端,且可绕水平光滑固定轴 O转动,今有一子弹沿着与水平面成一角度的方向击中木球而嵌于其中,则在此击中过程中,木球、子弹、细棒系统的原因是。
木球被击中后棒和球升高的过程中,弹、细棒、地球系统的守恒。
守恒,对木球、子题3.2 (2)图[ 答案:对 o 轴的角动量守恒,因为在子弹击中木球过程中系统所受外力对 o 轴的合外力矩为零,机械能守恒](3)两个质量分布均匀的圆盘 A 和 B 的密度分别为ρA和ρB ( ρA>ρB) ,且两圆盘的总质量和厚度均相同。
大学物理学答案(北京邮电大学第3版)赵近芳等编著#(精选.)

大学物理学(北邮第三版) 习题及解答(全)习题一1-1 |r ∆|与r ∆有无不同?t d d r 和t d d r 有无不同? t d d v 和t d d v有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r -=∆; (2)t d d r 是速度的模,即t d d r ==v tsd d . t rd d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆrˆt r t d d d d d d r r r += 式中t rd d 就是速度径向上的分量,∴t r td d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即t v a d d =,t v d d 是加速度a 在切向上的分量. ∵有ττ (v =v 表轨道节线方向单位矢),所以t v t v t v d d d d d d ττ +=式中dt dv就是加速度的切向分量.(t tr d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论) 1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =t rd d ,及a =22d d t r 而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r+=,jt y i t x t r a jt y i t x t r v222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x y x而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d t r a trv ==其二,可能是将22d d d d t r tr 与误作速度与加速度的模。
《大学物理》习题答案4-匡乐满主编-北京邮电大学出版社省名师优质课赛课获奖课件市赛课一等奖课件

0.5
0.30s
7. 粒子在加速器中被加速到动能为静止能量旳4倍时,其质量 m
与静止质量 m0 旳关系为:
(A)m 4m0;(B) m 5m0;(C) m 6m0; (D) m 8m0
答案(B) mc2 Ek m0c2 4m0c2 m0c2 5m0c2
大学物理 盛忠志主讲
8. Ek 是粒子旳动能,p 是它旳动量,那么粒子旳静能 m0c 2等于
大学物理 盛忠志主讲
大学物理作业四参照答案
一、选择题
1. 一刚性直尺固定在S系中,它与 X 轴正向夹角 45,
在相对 S系以速度 u 沿 X 轴作匀速直线运动旳 S 系中,
测得该尺与 X 轴正向夹角为 (A) 45;(B) 45 ; (C) 45; (D)不懂得
答案(A)
大学物理 盛忠志主讲
2. 惯性系 S 、S沿X 轴做相对运动,在 S 系中测得两个同步发 生旳事件沿运动方向空间距离为1m,在 S系中测得这两个事件
旳空间间隔为2m。则在 S 系中测得这两个事件旳时间间隔为
(A)
3c
;
(B)1 3
c
;
(C) 3 c
; (D)3 c
x x
1
u c
2 2
答案(C)
u 3c 2
t t1 t2
1 (t u x) 3
1
u2 c2
c2
c
3. 两火箭A、B沿同一直线相向运动,测得两者相对地球旳速度
大小分别是 vA 0.9c ,vB 0.8c 。则两者互测旳相对运动速度为
(A)1.7c ; (B) 0.988c ; (C) 0.956c ; (D) 0.975c
答案(B)
v v u 0.9c (0.8c) 0.988c
大学物理学 (第3版.修订版) 北京邮电大学出版社 上册 第四章习题4 答案

2 2 v v x v y 0.88 c
速度与 x 轴的夹角 为
tan
v y v x
1.07
46.8ο
题 4.10 图 4.11 静止在S系中的观测者测得一光子沿与 x 轴成 60 角的方向飞行.另一观测者静止于 S′系,S′系的 x 轴与 x 轴一致,并以0.6c的速度沿 x 方向运动.试问S′系中的观测者观 测到的光子运动方向如何? 解: S 系中光子运动速度的分量为
2
(D) c t 1 v / c
2
[答案:A ] (4)一宇航员要到离地球 5 光年的星球去旅行。如果宇航员希望把这路程缩短为 3 光年, 则他所乘的火箭相对于地球的速度 v 应为[ ]。 (A)0.5c (B)0.6c (C)0.8c (D)0.9c [答案:C ] (5) 某宇宙飞船以 0.8c 的速度离开地球, 若地球上测到它发出的两个信号之间的时间间隔 为 10s。则宇航员测出的相应的时间间隔为[ ]。 (A)6s (B)8s (C)10s (D)10/3s [答案:A ] 4.2 填空题 (1) 有一速度为u的宇宙飞船沿X轴正方向飞行,飞船头尾各有一个脉冲光源在工作,处 于船尾的观察者测得船头光源发出的光脉冲的传播速度大小为_________;处于船头的观察 者测得船尾光源发出的光脉冲的传播速度大小为__________。 [答案:c,c; ] ( 2 ) S 系相对 S 系沿 x 轴匀速运动的速度为 0.8c ,在 S 中观测,两个事件的时间间隔
习题 4 4.1 选择题 (1)在一惯性系中观测,两个事件同时不同地,则在其他惯性系中观测,他们[ (A)一定同时 (B)可能同时 (C)不可能同时,但可能同地 (D)不可能同时,也不可能同地 [答案:D ] (2)在一惯性系中观测,两个事件同地不同时,则在其他惯性系中观测,他们[ (A)一定同地 (B)可能同地 (C)不可能同地,但可能同时 (D)不可能同地,也不可能同时 [答案:D ]
大学物理第四章课后答案

I = 625N ∆t
-4-
自治区精品课程—大学物理学
题库
2. 解: (1)由动量守恒定律
Mυ 2 − mυ1 = 0
(2)由动量定理:
υ 2 = 2.5 m s
方向与子弹飞行方向相反。
F=
Mυ 2 Mυ 2 = = 300 N t 0.05
3.
m , dt 时间内链条长 L 度变化为 dl ,即有 dl 长度的链条在 dt 时间内堆在地
自治区精品课程—大学物理学
题库
第四章 动量定理
一、 填空 1. 2. 3. 4. 是表示力在空间上累积作用的物理量, 是表示力在时间上累 积作用的物理量。 质点动量定理的微分形式是 。 质点动量定理的积分形式是 。 对于质点系来说,内力 ( “改变”或“不改变” )质点系中各个质点 的动量,但 ( “改变”或“不改变” )质点系的总动量。 若质点系沿某坐标方向所受的合外力为零,则 守恒。 如果两物体碰撞过程中,动能完全没有损失,这种碰撞称为 ,否则 就称为 ;如果碰撞后两物体以相同的速度运动,这种碰撞称 为 。 , 其中 υ10 ,υ1 是某一物
l
m M v0 V v
. 如图所示,在一铅直面内有一光滑的轨道,左边是一个上升的曲线,右边是 13 13. 足够长的水平直线, 两者平滑连接, 现有 A , B 两个质点, B 在水平轨道上静止, A 在曲 线部分高 h 处由静止滑下,与 B 发生完全弹 性碰撞, 碰后 A 仍可返回上升到曲线轨道某 处,并再度滑下,已知 A , B 两质点的质量 分别为 m A 和 m B 。求 A , B 至少发生两次碰 撞的条件。 14. 如图所示,两车厢质量均为 M ,左边车厢地板上放一质量为 M 的货箱,它 们共同以 υ 0 的速度向右运动。 另一车厢以 2υ 0 从相反方向向左运动并与左车厢碰
大学物理学(北京邮电大学出版)第一到五章答案

习题1(1) 一运动质点在某瞬时位于矢径),(y x r的端点处,其速度大小为(A)dt dr (B)dt r d(C)dtr d ||(D) 22)()(dt dy dt dx +[答案:D](2) 一质点作直线运动,某时刻的瞬时速度s m v /2=,瞬时加速度2/2s m a -=,则一秒钟后质点的速度(A)等于零 (B)等于-2m/s (C)等于2m/s (D)不能确定。
[答案:D](3) 一质点沿半径为R 的圆周作匀速率运动,每t 秒转一圈,在2t 时间间隔中,其平均速度大小和平均速率大小分别为(A)t R t R ππ2,2 (B) tRπ2,0 (C) 0,0 (D) 0,2tRπ[答案:B](1) 一质点,以1-⋅s m π的匀速率作半径为5m 的圆周运动,则该质点在5s 内,位移的大小是 ;经过的路程是 。
[答案: 10m ; 5πm](2) 一质点沿x 方向运动,其加速度随时间的变化关系为a=3+2t (SI),如果初始时刻质点的速度v 0为5m·s -1,则当t 为3s 时,质点的速度v= 。
[答案: 23m·s -1 ](3) 轮船在水上以相对于水的速度1V 航行,水流速度为2V ,一人相对于甲板以速度3V行走。
如人相对于岸静止,则1V 、2V 和3V的关系是 。
[答案: 0321=++V V V]1.3 一个物体能否被看作质点,你认为主要由以下三个因素中哪个因素决定:(1) 物体的大小和形状; (2) 物体的内部结构; (3) 所研究问题的性质。
解:只有当物体的尺寸远小于其运动范围时才可忽略其大小的影响,因此主要由所研究问题的性质决定。
1.4 下面几个质点运动学方程,哪个是匀变速直线运动?〔1〕x=4t-3;〔2〕x=-4t 3+3t 2+6;〔3〕x=-2t 2+8t+4;〔4〕x=2/t 2-4/t 。
给出这个匀变速直线运动在t=3s 时的速度和加速度,并说明该时刻运动是加速的还是减速的。
大学物理课后习题答案(第四章) 北京邮电大学出版社

又
k 0.2 2 5,即T 1.26s 3 m 8 10
2 A x0 (
v0
)2
2 2
5.0 10 2 2 (1.0 10 ) ( ) 5 2 10 2 m v 5.0 10 2 5 tan 0 0 1, 即 0 2 x 0 1.0 10 5 4 5 x 2 10 2 cos(5t )m 4 ∴
A 3.2 10 3 rad l
∴ 故其角振幅
2 A x0 (
小球的振动方程为
4-11 有两个同方向、同频率的简谐振动,其合成振动的振幅为 0.20m ,位相与第一振动的
给小球一水平向右的冲量 Ft 1.0 10 kg m s ,取打击时刻为计时起点 (t 0) ,求 振动的初位相和角振幅,并写出小球的振动方程. 解:由动量定理,有
4 1
v0 x 0
F t mv 0
∴
v
F t 1.0 10 0.01 m 1.0 10 3
A mg 2 m 2 2 gh 2 x ( ) ( ) ( ) k (m M )
2 0 2
v0
mg 2kh 1 k (m M ) g
2kh ( M m) g (第三象限),所以振动方程为 (3) mg 2kh k 2kh x 1 cos t arctan k (m M ) g ( M m) g mM 3 4-10 有一单摆,摆长 l 1.0m ,摆球质量 m 10 10 kg ,当摆球处在平衡位置时,若 tan 0
(2)
当
Ek E p
时,有
E 2E p
大学物理第四章课后思考题详解

谐振动:
X. J. Feng,
1. 力学特征: 线性恢复力(力矩)
F kx
F mg
2.动力学方程:
d 2x dt 2
02 x
0
M mgb 思考: 拍皮球时球的往
3.运动学方程: x Acos(0t ) 复运动是否是谐振动?
v 0 Asin( 0t )
m
Px
X. J. Feng,
M 0t
Px
X. J. Feng,
M
P
x
M P
Xபைடு நூலகம் J. Feng,
x
X. J. Feng,
M
P
x
X. J. Feng,
P x
M
X. J. Feng,
P x
M
X. J. Feng,
P x
M
X. J. Feng,
P x
M
X. J. Feng,
M Px
突然速度为0的质点m0轻粘在m上,求:m0粘上后振动系统
周期和振幅
m0
解: 两弹簧的等效系数:2k
km k
(请同学们课后自己证明)
m0粘上前系统振动的圆频率: 0
2k m
v 2l0
m0粘上后系统振动的圆频率:
2k
m m0
T 2 m m0
2k
A
x0
v02
2
x0 0
x
M
M nm
l0
·m
(2).t Tn 2
Tn
2 n
n
k M nm
MO
l0
大学物理学第版修订版北京邮电大学出版社下册习题答案.docx

习题9 9.1 选择题(1)正方形的两对角线处各放置电荷 Q,另两对角线各放置电荷 q,若 Q 所受到合力为零,则 Q与 q 的关系为:()( A) Q=-23/2 q (B) Q=23/2 q(C) Q=-2q(D) Q=2q[ 答案: A](2)下面说法正确的是:()(A)若高斯面上的电场强度处处为零,则该面内必定没有电荷;(B)若高斯面内没有电荷,则该面上的电场强度必定处处为零;(C)若高斯面上的电场强度处处不为零,则该面内必定有电荷;(D)若高斯面内有电荷,则该面上的电场强度必定处处不为零。
[ 答案: D](3)一半径为 R 的导体球表面的面点荷密度为σ,则在距球面 R处的电场强度()(A)σ / ε0(B)σ /2ε 0(C)σ /4ε 0(D)σ /8ε0 [ 答案: C](4)在电场中的导体内部的()(A)电场和电势均为零;(B)电场不为零,电势均为零;(C)电势和表面电势相等;(D)电势低于表面电势。
[ 答案: C]9.2 填空题(1) 在静电场中,电势不变的区域,场强必定为。
[ 答案:相同 ](2) 一个点电荷 q 放在立方体中心,则穿过某一表面的电通量为,若将点电荷由中心向外移动至无限远,则总通量将。
[ 答案: q/6 ε0 ,将为零](3) 电介质在电容器中作用(a)——( b)——。
[ 答案: (a) 提高电容器的容量;(b)延长电容器的使用寿命](4) 电量 Q均匀分布在半径为R 的球体内,则球内球外的静电能之比。
[ 答案: 5: 6]9.3电量都是q的三个点电荷,分别放在正三角形的三个顶点.试问:(1) 在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡( 即每个电荷受其他三个电荷的库仑力之和都为零)?(2) 这种平衡与三角形的边长有无关系?解 :如题9.3图示(1)以A处点电荷为研究对象,由力平衡知:q 为负电荷解得q 3 q3(2)与三角形边长无关.题 9.3 图题9.4图9.4两小球的质量都是m ,都用长为l的细绳挂在同一点,它们带有相同电量,静止时两线夹角为 2, 如题 9.4 图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量.解: 如题 9.4 图示解得q 2 sin 40mgtan l9.5 根据点电荷场强公式E q,当被考察的场点距源点电荷很近(r →0) 时,则0r 24场强→∞,这是没有物理意义的,对此应如何理解?解 :qr0仅对点电荷成立,当r0 时,带电体不能再视为点电荷,再用上Er24π式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大.9.6在真空中有 A , B 两平行板,相对距离为 d ,板面积为 S ,其带电量分别为+ q 和q 2- q.则这两板之间有相互作用力 f ,有人说 f =40d 2,又有人说,因为f = qE , E q,所以 f =q2.试问这两种说法对吗 ?为什么 ? f 到底应等于多少?0 SS解 :题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强E q看成是一个带电板在另一带电板处的场强也是不对的.正确0S解答应为一个板的电场为 Eq,另一板受它的作用力 f qq q22 0 S 2 0 S,这是两2 0 S板间相互作用的电场力.9.7 长l =15.0cm的直导线 AB上均匀地分布着线密度=5.0x10-9-1的正电C·m荷.试求: (1) 在导线的延长线上与导线 B端相距a1=5.0cm处P点的场强;(2)在导线的垂直平分线上与导线中点相距 d 2=5.0cm 处Q点的场强.解:如题 9.7 图所示(1) 在带电直线上取线元dx ,其上电量dq在 P 点产生场强为dE P1dx4π0(a x) 2l dxE P dE P2题 9.7图l(a x)24π02用 l 15 cm, 5.0 10 9 C m 1,a12.5 cm代入得E P 6.74102N C1方向水平向右(2) 同理dE Q1dx方向如题 9.7图所示4π0x 2 d 22由于对称性dE Qx 0 ,即 E Q只有 y 分量,l2∵dE Qy1dx dπ 0x2 d 22x 2d224以 5.0 10 9 C cm 1,l 15 cm,d2 5 cm 代入得E Q E Qy14.96 102N C1,方向沿 y 轴正向9.8一个半径为R的均匀带电半圆环,电荷线密度为, 求环心处O点的场强.解: 如 9.8 图在圆上取dl Rd题9.8 图dq dl R d,它在O点产生场强大小为RddE方向沿半径向外24π0 R则dE x dE sinsin d4π0 R积分E x sin d04π0 R2π0 R∴ E E x,方向沿 x 轴正向.2π0 R9.9均匀带电的细线弯成正方形,边长为l ,总电量为q .(1)求这正方形轴线上离中心为r 处的场强 E ;(2)证明:在r l 处,它相当于点电荷q 产生的场强 E .解 :如9.9图示,正方形一条边上电荷q在P点产生物强dE P方向如图,大小为4l∵cos212r 2l2∴dE Pl2 l 22 l 24π0r r42 dE P在垂直于平面上的分量dE dE P cos∴l rdE4π0r 2l 2r 2l 2r 2l 2424题9.9 图由于对称性,P 点场强沿 OP 方向,大小为q∵4l∴E P qr方向沿 OP4π0 ( r 2l 2) r2 l 2429.10 (1)点电荷q位于一边长为a的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2) 如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?解: (1)由高斯定理qE dSs立方体六个面,当q 在立方体中心时,每个面上电通量相等∴ 各面电通量e q.60(2) 电荷在顶点时,将立方体延伸为边长2a 的立方体,使 q 处于边长 2a 的立方体中心,则边长 2a 的正方形上电通量qe60q对于边长 a 的正方形,如果它不包含q 所在的顶点,则e,24 0如果它包含 q 所在顶点则e0 .如题 9.10 图所示.题9.10图9.11 均匀带电球壳内半径6cm,外半径 10cm,电荷体密度为 2×105-3求距球心C· m5cm,8cm ,12cm 各点的场强.解 :高斯定理 E dS q, E4πr2qs00当 r 5 cm时,q 0 ,E0r 8 cm时, q p 4π(r3r内3 ) 34πr3r内2∴E323.48 104N C1,方向沿半径向外.4π0 rr 12cm时 ,4π33q( r外内3r )4πr外3r内3∴E324.10 104N C1沿半径向外 .4π0 r9.12半径为R1和R2(R2>R1)的两无限长同轴圆柱面,单位长度上分别带有电量和- , 试求 :(1)r < R1;(2)R1< r < R2;(3)r > R2处各点的场强.解 :高斯定理q E dSs取同轴圆柱形高斯面,侧面积S2πrl则 E dSSE2πrl对 (1)r R1q 0, E0(2)R1r R2q l∴E沿径向向外2π0 r(3)r R2q0∴ E 0题9.13 图9.13两个无限大的平行平面都均匀带电,电荷的面密度分别为 1 和 2 ,试求空间各处场强.解 :如题9.13图示,两带电平面均匀带电,电荷面密度分别为 1 与 2 ,两面间, E1( 12 ) n201面外, E1( 12 )n202面外, E1( 12 ) n20n :垂直于两平面由 1 面指为 2 面.9.14半径为R 的均匀带电球体内的电荷体密度为, 若在球内挖去一块半径为r <R 的小球体,如题9.14 图所示.试求:两球心O 与 O点的场强,并证明小球空腔内的电场是均匀的.解 :将此带电体看作带正电的均匀球与带电的均匀小球的组合,见题9.14图(a).(1)球在O点产生电场E100 ,4 π3球在 O 点产生电场E2033OO'4π0dr 3∴O点电场EOO';030d34d3(2)在O产生电场E1033 OO '4π0d球在 O 产生电场E200∴O点电场E03OO '题 9.14 图(a)题9.14图(b)(3)设空腔任一点 P 相对 O 的位矢为 r ,相对 O 点位矢为 r (如题8-13(b)图)则E PO r ,30EPO r,30∴EPEPOEPO( r r )dOO'3 0 3 0 3 0∴腔内场强是均匀的.9.15一电偶极子由 q =1.0×10-6C的两个异号点电荷组成,两电荷距离d=0.2cm,把这电偶极子放在 1.0 × 105N·C-1的外电场中,求外电场作用于电偶极子上的最大力矩.解 :∵电偶极子p在外场E中受力矩∴M max pE qlE 代入数字9.16两点电荷q1=1.5× 10-8C,q2=3.0× 10-8C,相距r1=42cm,要把它们之间的距离变为 r2=25cm,需作多少功?解 : Ar2F dr r2 q1q2drq1q2 (11 )r1r2 4π0r24π0 r1r2外力需作的功A A 6.55 10 6J题9.17 图9.17如题9.17图所示,在A,B两点处放有电量分别为+q ,- q的点电荷,AB间距离为 2 R,现将另一正试验点电荷q0从O点经过半圆弧移到 C 点,求移动过程中电场力作的功.解: 如题 9.17 图示∴ A q0 (U Oq o q U C )6π0 R9.18如题9.18图所示的绝缘细线上均匀分布着线密度为的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心 O 点处的场强和电势.解 : (1)由于电荷均匀分布与对称性,AB 和 CD 段电荷在 O 点产生的场强互相抵消,取dl Rd则 dq Rd产生O点dE如图,由于对称性,O点场强沿 y 轴负方向题9.18 图[sin() sin ]4π0 R22(2)AB 电荷在 O 点产生电势,以U0同理 CD 产生U 2ln 24π 0πR 半圆环产生U 34π 0 R4 0∴U O U 1 U 2 U 3ln 22π 04 04-1的匀速率作圆周运动.求带9.19 一电子绕一带均匀电荷的长直导线以 2× 10 m ·s电直线上的线电荷密度.-31-19( 电子质量 m 0 =9.1 × 10 kg ,电子电量 e =1.60 × 10 C)解 :设均匀带电直线电荷密度为,在电子轨道处场强电子受力大小F ee eE2π 0 r∴e v 2 2π 0 rmr得2π 0 mv 212.5 10 13 C m 1e-19.20 空气可以承受的场强的最大值为E =30kV · cm ,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为 d =0.5cm ,求此电容器可承受的最高电压.解 :平行板电容器内部近似为均匀电场9.21 证明:对于两个无限大的平行平面带电导体板 ( 题9.21 图 ) 来说, (1) 相向的两面上,电荷的面密度总是大小相等而符号相反;(2) 相背的两面上,电荷的面密度总是大小相等而符号相同.证 :如题 9.21 图所示,设两导体A 、 的四个平面均匀带电的电荷面密度依次为1,B2,3,4题 9.21 图(1) 则取与平面垂直且底面分别在 A 、 B 内部的闭合柱面为高斯面时,有∴230说明相向两面上电荷面密度大小相等、符号相反;(2) 在 A 内部任取一点 P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即又∵230∴14说明相背两面上电荷面密度总是大小相等,符号相同.9.22 三个平行金属板2A ,B 和C 的面积都是 200cm , A 和 B 相距 4.0mm , A 与 C 相距 2.0 mm . B , C 都接地,如题 9.22 图所示.如果使 A 板带正电 3.0 ×10-7 C ,略去边缘效应,问 B 板和 C 板上的感应电荷各是多少?以地的电势为零,则 A 板的电势是多少?解 :如题9.22图示,令A板左侧面电荷面密度为 1 ,右侧面电荷面密度为2题9.22 图(1)∵∴∴且得而(2)U AC U AB,即E AC d AC E AB d AB1 E AC d AB2EABdAC21+q A2S2qA ,12q A3S3Sq C 1 S2q A 2 10 7C3q B 2 S 1 10 7 CU A E AC d AC 1 d AC 2.3103V9.23 两个半径分别为R1和 R2( R1< R2)的同心薄金属球壳,现给内球壳带电+ q,试计算: (1) 外球壳上的电荷分布及电势大小;(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球壳的电荷分布及电势;*(3) 再使内球壳接地,此时内球壳上的电荷以及外球壳上的电势的改变量.解: (1)内球带电q ;球壳内表面带电则为q ,外表面带电为q ,且均匀分布,其电势U E dr qdr qR2 4π0 r24π0RR2题9.23 图(2) 外壳接地时,外表面电荷q 入地,外表面不带电,内表面电荷仍为q .所以球壳电势由内球q 与内表面q 产生:(3) 设此时内球壳带电量为q ;则外壳内表面带电量为q ,外壳外表面带电量为q q (电荷守恒),此时内球壳电势为零,且得q R1qR2外球壳上电势9.24半径为R的金属球离地面很远,并用导线与地相联,在与球心相距为d3R处有一点电荷 + q,试求:金属球上的感应电荷的电量.解 :如题9.24图所示,设金属球感应电荷为q ,则球接地时电势U O0题9.24 图由电势叠加原理有:得q q39.25 有三个大小相同的金属小球,小球 1,2带有等量同号电荷,相距甚远,其间的库仑力为 F 0 .试求:(1) 用带绝缘柄的不带电小球 3先后分别接触 1, 2后移去,小球 1, 2之间的库仑力;(2) 小球 3依次交替接触小球 1,2很多次后移去,小球 1, 2之间的库仑力.解 : 由题意知q 2F 00 r 24π (1) 小球 3 接触小球 1后,小球 3和小球 1均带电qq,2小球 3 再与小球 2 接触后,小球 2 与小球 3 均带电∴此时小球 1与小球 2 间相互作用力(2) 小球 3 依次交替接触小球 1、 2 很多次后,每个小球带电量均为2q .32 q 2 q4 ∴ 小球 1、 2间的作用力3 3F 24π 0 r 29F9.26 在半径为 R 1 的金属球之外包有一层外半径为 R 2 的均匀电介质球壳,介质相对介电常数为r ,金属球带电 Q .试求:(1) 电介质内、外的场强;(2) 电介质层内、外的电势;(3) 金属球的电势.解 : 利用有介质时的高斯定理D dSqS(1) 介质内 ( R 1r R 2 ) 场强DQr , E 内Qrr3;4π 34π0 rr介质外 (rR 2 ) 场强(2) 介质外 (r R 2 ) 电势介质内 (R 1 r R 2 ) 电势(3) 金属球的电势9.27 如题 9.27 图所示,在平行板电容器的一半容积内充入相对介电常数为 r 的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解 : 如题 9.27 图所示,充满电介质部分场强为 E 2 ,真空部分场强为 E 1 ,自由电荷面密度分别为2 与1由 D dSq 0 得D1 1,D2 2而D1 0E 1 ,D2 0 rE2∴20 r E2r10 E1题 9.27 图题9.28图9.28两个同轴的圆柱面,长度均为l,半径分别为R1和R2(R2>R1),且l>>R2-R1,两柱面之间充有介电常数的均匀电介质 . 当两圆柱面分别带等量异号电荷Q 和- Q 时,求:(1)在半径 r 处( R1< r < R2=,厚度为dr,长为l的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量;(2)电介质中的总电场能量;(3)圆柱形电容器的电容.解 :取半径为r的同轴圆柱面( S)则D S rlD( S)d2π当 (R1r R2 ) 时,q Q∴(1)电场能量密度QD2πrlD 2Q 2w22l228π r薄壳中 dW wdQ 2Q 2 dr22l22πrdrl8π r4π rl(2)电介质中总电场能量(3) 电容:∵Q 2W2CQ 2πl∴C22W ln( R2 / R1 )题9.29 图9.29如题9.29图所示,C1=0.25F,C2 =0.15 F,C3 =0.20 F .C1上电压为50V.求:U AB.解 :电容C1上电量电容 C 2与 C3并联 C 23 C 2C3其上电荷 Q 23Q1∴Q23C1U 125 50 U 2C 2335C 239.30C1和 C 2两电容器分别标明“200 pF 、 500 V ”和“ 300 pF 、 900 V ”,把它们串联起来后等值电容是多少?如果两端加上 1000 V的电压,是否会击穿?解 : (1)C1与 C 2串联后电容(2)串联后电压比U 1C23,而 U 1 U 2 1000U 2C12∴U 1600 V, U 2400V即电容 C1电压超过耐压值会击穿,然后 C 2也击穿.9.31 半径为R1 =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为R2=4.0cm和 R3=5.0cm,当内球带电荷 Q =3.0×10-8C时,求:(1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量;(3)此电容器的电容值.解: 如图,内球带电Q,外球壳内表面带电Q ,外表面带电 Q题9.31 图(1) 在r R1和 R2r R3区域在 R1 r R2时QrE134π0 rr R3时QrE234π0 r∴在 R1r R2区域在 r R3区域∴总能量 W W1 W2Q 2(11 1 )8π0R1R2R3(2) 导体壳接地时,只有 R 1 r R 2 时 E Qr , W 2 0 4π 0 r 3∴W W 1 Q 2 ( 1 1 ) 1.01 10 4 J 8π 0 R 1 R 2(3) 电容器电容C 2W 4π 0 /( 1 1 ) Q 2 R 1 R 2。
大学物理学第版版北京邮电大学出版社下册习题答案

习题10选择题(1) 对于安培环路定理的理解,正确的是:(A )若环流等于零,则在回路L 上必定是H 处处为零; (B )若环流等于零,则在回路L 上必定不包围电流;(C )若环流等于零,则在回路L 所包围传导电流的代数和为零; (D )回路L 上各点的H 仅与回路L 包围的电流有关。
[答案:C](2) 对半径为R 载流为I 的无限长直圆柱体,距轴线r 处的磁感应强度B () (A )内外部磁感应强度B 都与r 成正比;(B )内部磁感应强度B 与r 成正比,外部磁感应强度B 与r 成反比; (C )内外部磁感应强度B 都与r 成反比;(D )内部磁感应强度B 与r 成反比,外部磁感应强度B 与r 成正比。
[答案:B](3)质量为m 电量为q 的粒子,以速率v 与均匀磁场B 成θ角射入磁场,轨迹为一螺旋线,若要增大螺距则要()(A ) 增加磁场B ;(B )减少磁场B ;(C )增加θ角;(D )减少速率v 。
[答案:B](4)一个100匝的圆形线圈,半径为5厘米,通过电流为安,当线圈在的磁场中从θ=0的位置转到180度(θ为磁场方向和线圈磁矩方向的夹角)时磁场力做功为() (A );(B );(C );(D )14J 。
[答案:A]填空题(1)边长为a 的正方形导线回路载有电流为I ,则其中心处的磁感应强度 。
[答案:aIπμ220,方向垂直正方形平面](2)计算有限长的直线电流产生的磁场 用毕奥——萨伐尔定律,而 用安培环路定理求得(填能或不能)。
[答案:能, 不能](3)电荷在静电场中沿任一闭合曲线移动一周,电场力做功为 。
电荷在磁场中沿任一闭合曲线移动一周,磁场力做功为 。
[答案:零,正或负或零](4)两个大小相同的螺线管一个有铁心一个没有铁心,当给两个螺线管通以 电流时,管内的磁力线H 分布相同,当把两螺线管放在同一介质中,管内的磁力线H 分布将 。
[答案:相同,不相同]在同一磁感应线上,各点B ϖ的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B ϖ的方向?解: 在同一磁感应线上,各点B ϖ的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B ϖ的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B ϖ的方向.题图(1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B ϖ的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)? (2)若存在电流,上述结论是否还对?解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B ρϖ=∴ 21B B ρϖ=(2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B ϖ方向相反,即21B B ρϖ≠.用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.在载流长螺线管的情况下,我们导出其内部nI B 0μ=,外面B =0,所以在载流螺线管外面环绕一周(见题图)的环路积分⎰外B L ϖ·d l ϖ=0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为 ⎰外B L ϖ·d l ϖ=I 0μ这是为什么? 解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μϖϖ外,与⎰⎰=⋅=⋅Ll l B 0d 0d ϖϖϖ外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L的电流为I ,因此实际螺线管若是无限长时,只是外B ϖ的轴向分量为零,而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离. 题 图如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场?如果它发 生偏转能否肯定那个区域中存在着磁场?解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转.已知磁感应强度0.2=B Wb ·m-2的均匀磁场,方向沿x 轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量.解: 如题图所示题图(1)通过abcd 面积1S 的磁通是 (2)通过befc 面积2S 的磁通量 (3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ϖϖΦWb (或24.0-Wb )题图如题图所示,AB 、CD 为长直导线,C B )为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如题图所示,O 点磁场由AB 、C B )、CD 三部分电流产生.其中AB产生 01=B ϖCD产生RIB 1202μ=,方向垂直向里CD段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,方向⊥向里 ∴)6231(203210ππμ+-=++=R I B B B B ,方向⊥向里. 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应强度为零的点的位置.题图解:如题图所示,A B ϖ方向垂直纸面向里 (2)设0=B ϖ在2L 外侧距离2L 为r 处 则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r m题图如题图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度.解: 如题图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
大学物理第四章课后答案

题4-1图 解:要使一个系统作谐振动,必须同时满足以下三个条件:一 ,描述系统的各种参量,如 质量、转动惯量、摆长……等等在运动中保持为常量;二,系统 是在 自己的稳定平衡位置 附近作往复运动;三,在运动中系统只受到内部的线性回复力的作用. 或者说,若一个系 统的运动微分方程能用
(3)由于谐振动中能量守恒,故在任一位置处或任一时刻的系统的总能量均为
4-7 有一轻弹簧,下面悬挂质量为 1.0g 的物体时,伸长为 4.9cm .用这个弹簧和一个质量 为 8.0g 的小球构成弹簧振子,将小球由平衡位置向下拉开 1.0cm 后 ,给予向上的初速度
v0 = 5.0cm ⋅ s −1 ,求振动周期和振动表达式.
d2 x mg sin θ − T1 = m 2 dt
①
T1 R − T2 R = Iβ
d2 x = Rβ dt 2
②
T2 = k ( x 0 + x )
③
式中 x0 = mg sin θ / k ,为静平衡时弹簧之伸长量,联立以上三式,有
I d2x (mR + ) 2 = − kxR R dt
令 则有
7
∴ 故其角振幅
Байду номын сангаас
2 A = x0 +(
v0 2 v 0 0.01 ) = = = 3.2 × 10 −3 m ω ω 3.13 A = 3.2 × 10 −3 rad l
Θ=
小球的振动方程为
∆φ = ω (t 2 − t1 ) = 8π (5 − 1) = 32π
大学物理学课后习题4第四章答案
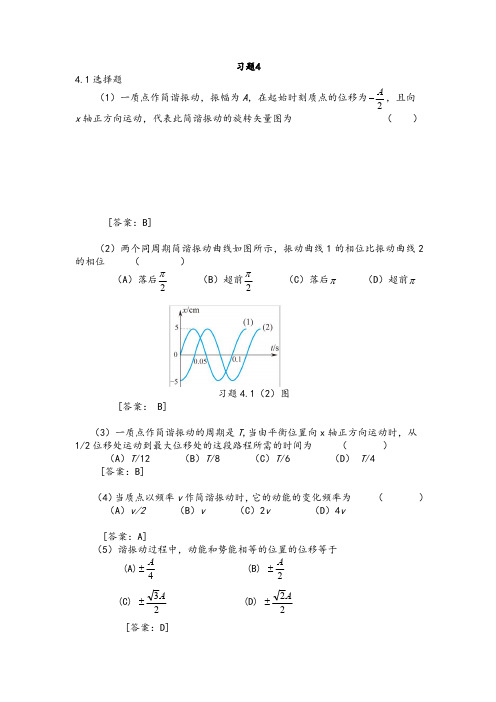
x 轴正方向运动,代表此简谐振动的旋转矢量图为
()
[答案:B]
(2)两个同周期简谐振动曲线如图所示,振动曲线 1 的相位比振动曲线 2
的相位 (
)
(A)落后
2
(B)超前
2
(C)落后
(D)超前
[答案: B]
习题 4.1(2)图
(3)一质点作简谐振动的周期是 T,当由平衡位置向 x 轴正方向运动时,从
E
1 2
mvm2
3.16 102 J
E p E k 1 E 1.58102 J 2
当 Ek E p 时,有 E 2E p ,
即
1 kx 2 1 ( 1 kA2 )
2
22
∴
x 2 A 2m
2
20
(3)
(t2 t1 ) 8 (5 1) 32
4.4 一个沿 x 轴作简谐振动的弹簧振子,振幅为 A ,周期为T ,其振动 方程用余弦函数表示.如果 t 0 时质点的状态分别是:
的单位是 s,则 (A)波长为 5m
向传播 [答案:C]
(B)波速为 10ms-1
(C)周期为 1 s 3
(D)波沿 x 正方
(8)如图所示,两列波长为 的相干波在 p 点相遇。波在 S1 点的振动初相是 1 ,点 S1 到点 p 的距离是 r1。波在 S2 点的振动初相是2 ,点 S2 到点 p 的距离是
(A)它的动能转化为势能. (B)它的势能转化为动能. (C)它从相邻的一段质元获得能量其能量逐渐增大. (D)它把自己的能量传给相邻的一段质元,其能量逐渐减小.
[答案:D]
4.2 填空题 (1)一质点在 X 轴上作简谐振动,振幅 A=4cm,周期 T=2s,其平衡位置
北京邮电大学第4章--物理安全-习题

第4章物理安全习题一、选择题1、组织要捐赠一些本单位的旧电脑设备给希望小学,在运输这些捐赠品之前应该确保:〔〕A.电脑上不保存机密数据B. 受捐的希望小学签署保密协议B.数据存储的介质是彻底空白的 D. 所有数据已经被删除2、下面选项中,不属于使用移动存储介质存在的安全问题的是〔〕A.移动存储介质价格高B.来源渠道多,缺少准入机制C.移动存储介质在内部网与互联网之间混用D.没有妥善的保管措施3、涉及国家秘密的电脑系统,不得直接或间接地与国际互联网或其它公共信息网络相连接,必须进行〔〕A物理隔离。
B逻辑隔离C人员隔离D设备隔离4.电脑机房在全年的温度指标为〔〕。
A.23±2℃B.20±2℃C.18~28℃D.15~25℃5、磁介质不可以采取以下哪种措施进行信息的彻底消除。
〔〕A物理粉碎B强磁场消除C热消磁D冷消磁6.以下哪一项不属于安全机房供配电系统要求〔〕A.电脑站应设专用可靠的供电线路B.电脑系统的电源设备应提供稳定可靠的电源C.供电电源设备的容量应有一定的余量D.电脑系统的各设备走线应与空调设备、电源设备和无电磁屏蔽的走线平行。
二、判断题1、对硬盘采取格式化方式即可完全消除曾经存储过的信息。
〔〕2、防火墙是一种物理隔离技术。
〔〕3、为防止移动存储介质给公司带来安全隐患,应封堵移动存储设备端口。
〔〕4、未经授权不得将设备、信息或软件带离工作场所。
〔〕5.电脑机房的活动地板应是难燃材料或非燃材料。
〔〕6.安全区域的来访者应接受监督或办理出入手续。
〔〕三、简答题1、移动存储介质的安全隐患有哪些?2、电磁泄漏的技术途径有哪些?3、物理隔离技术有哪些?4.简述电脑机房安全等级的划分。
四、思考题1、2005年3月14日夜,犯罪分子来到大兴区安定镇某小学,将教师门锁打开,偷窃电教室内电脑主机25台,涉案金额达10万余元。
大兴警方通过现场勘查,奋战3天3夜,最后将这一犯罪团伙抓获。
目前,一些中小学以及企事业单位经常发生被盗事件,对此你有何看法和建议?2.电脑机房的门禁系统需要注意哪些问题?第4章物理安全-参考答案一、选择题二、判断题三、简答题1. 答:(1)体积小,易丧失。
大学物理课后习题答案 北京邮电大学出版社

习题五5-1 振动和波动有什么区别和联系?平面简谐波动方程和简谐振动方程有什么不同?又有什么联系?振动曲线和波形曲线有什么不同?解: (1)振动是指一个孤立的系统(也可是介质中的一个质元)在某固定平衡位置附近所做的往复运动,系统离开平衡位置的位移是时间的周期性函数,即可表示为;波动是振动在连续介质中的传播过程,此时介质中所有质元都在各自的平衡位置附近作振动,因此介质中任一质元离开平衡位置的位移既是坐标位置,又是时间的函数,即.(2)在谐振动方程中只有一个独立的变量时间,它描述的是介质中一个质元偏离平衡位置的位移随时间变化的规律;平面谐波方程中有两个独立变量,即坐标位置和时间,它描述的是介质中所有质元偏离平衡位置的位移随坐标和时间变化的规律.当谐波方程中的坐标位置给定后,即可得到该点的振动方程,而波源持续不断地振动又是产生波动的必要条件之一.(3)振动曲线描述的是一个质点的位移随时间变化的规律,因此,其纵轴为,横轴为;波动曲线描述的是介质中所有质元的位移随位置,随时间变化的规律,其纵轴为,横轴为.每一幅图只能给出某一时刻质元的位移随坐标位置变化的规律,即只能给出某一时刻的波形图,不同时刻的波动曲线就是不同时刻的波形图.5-2 波动方程=cos[()+]中的表示什么?如果改写为=cos (),又是什么意思?如果和均增加,但相应的[()+]的值不变,由此能从波动方程说明什么?解: 波动方程中的表示了介质中坐标位置为的质元的振动落后于原点的时间;则表示处质元比原点落后的振动位相;设时刻的波动方程为则时刻的波动方程为其表示在时刻,位置处的振动状态,经过后传播到处.所以在中,当,均增加时,的值不会变化,而这正好说明了经过时间,波形即向前传播了的距离,说明描述的是一列行进中的波,故谓之行波方程.5-3 波在介质中传播时,为什么介质元的动能和势能具有相同的位相,而弹簧振子的动能和势能却没有这样的特点?解: 我们在讨论波动能量时,实际上讨论的是介质中某个小体积元内所有质元的能量.波动动能当然是指质元振动动能,其与振动速度平方成正比,波动势能则是指介质的形变势能.形变势能由介质的相对形变量(即应变量)决定.如果取波动方程为,则相对形变量(即应变量)为.波动势能则是与的平方成正比.由波动曲线图(题5-3图)可知,在波峰,波谷处,波动动能有极小(此处振动速度为零),而在该处的应变也为极小(该处),所以在波峰,波谷处波动势能也为极小;在平衡位置处波动动能为极大(该处振动速度的极大),而在该处的应变也是最大(该处是曲线的拐点),当然波动势能也为最大.这就说明了在介质中波动动能与波动势能是同步变化的,即具有相同的量值.题5-3图对于一个孤立的谐振动系统,是一个孤立的保守系统,机械能守恒,即振子的动能与势能之和保持为一个常数,而动能与势能在不断地转换,所以动能和势能不可能同步变化.5-4 波动方程中,坐标轴原点是否一定要选在波源处? =0时刻是否一定是波源开始振动的时刻? 波动方程写成=cos()时,波源一定在坐标原点处吗?在什么前提下波动方程才能写成这种形式?解: 由于坐标原点和开始计时时刻的选全完取是一种主观行为,所以在波动方程中,坐标原点不一定要选在波源处,同样,的时刻也不一定是波源开始振动的时刻;当波动方程写成时,坐标原点也不一定是选在波源所在处的.因为在此处对于波源的含义已做了拓展,即在写波动方程时,我们可以把介质中某一已知点的振动视为波源,只要把振动方程为已知的点选为坐标原点,即可得题示的波动方程.5-5 在驻波的两相邻波节间的同一半波长上,描述各质点振动的什么物理量不同,什么物理量相同?解: 取驻波方程为,则可知,在相邻两波节中的同一半波长上,描述各质点的振幅是不相同的,各质点的振幅是随位置按余弦规律变化的,即振幅变化规律可表示为.而在这同一半波长上,各质点的振动位相则是相同的,即以相邻两波节的介质为一段,同一段介质内各质点都有相同的振动位相,而相邻两段介质内的质点振动位相则相反.5-6 波源向着观察者运动和观察者向波源运动都会产生频率增高的多普勒效应,这两种情况有何区别?解: 波源向着观察者运动时,波面将被挤压,波在介质中的波长,将被压缩变短,(如题5-6图所示),因而观察者在单位时间内接收到的完整数目()会增多,所以接收频率增高;而观察者向着波源运动时,波面形状不变,但观察者测到的波速增大,即,因而单位时间内通过观察者完整波的数目也会增多,即接收频率也将增高.简单地说,前者是通过压缩波面(缩短波长)使频率增高,后者则是观察者的运动使得单位时间内通过的波面数增加而升高频率.题5-6 图多普勒效应5-7 一平面简谐波沿轴负向传播,波长= m,原点处质点的振动频率为=2. 0 Hz,振幅=,且在=0时恰好通过平衡位置向轴负向运动,求此平面波的波动方程.解: 由题知时原点处质点的振动状态为,故知原点的振动初相为,取波动方程为则有5-8 已知波源在原点的一列平面简谐波,波动方程为=cos(),其中,,为正值恒量.求:(1)波的振幅、波速、频率、周期与波长;(2)写出传播方向上距离波源为处一点的振动方程;(3)任一时刻,在波的传播方向上相距为的两点的位相差.解: (1)已知平面简谐波的波动方程()将上式与波动方程的标准形式比较,可知:波振幅为,频率,波长,波速,波动周期.(2)将代入波动方程即可得到该点的振动方程(3)因任一时刻同一波线上两点之间的位相差为将,及代入上式,即得.5-9 沿绳子传播的平面简谐波的波动方程为=(10),式中,以米计,以秒计.求:(1)波的波速、频率和波长;(2)绳子上各质点振动时的最大速度和最大加速度;(3)求=处质点在=1s时的位相,它是原点在哪一时刻的位相?这一位相所代表的运动状态在=时刻到达哪一点?解: (1)将题给方程与标准式相比,得振幅,频率,波长,波速.(2)绳上各点的最大振速,最大加速度分别为(3)m处的振动比原点落后的时间为故,时的位相就是原点(),在时的位相,即π.设这一位相所代表的运动状态在s时刻到达点,则5-10 如题5-10图是沿轴传播的平面余弦波在时刻的波形曲线.(1)若波沿轴正向传播,该时刻,,,各点的振动位相是多少?(2)若波沿轴负向传播,上述各点的振动位相又是多少?解: (1)波沿轴正向传播,则在时刻,有题5-10图对于点:∵,∴对于点:∵,∴对于点:∵,∴对于点:∵,∴(取负值:表示点位相,应落后于点的位相)(2)波沿轴负向传播,则在时刻,有对于点:∵,∴对于点:∵,∴对于点:∵,∴对于点:∵,∴(此处取正值表示点位相超前于点的位相)5-11 一列平面余弦波沿轴正向传播,波速为5m·s-1,波长为2m,原点处质点的振动曲线如题5-11图所示.(1)写出波动方程;(2)作出=0时的波形图及距离波源处质点的振动曲线.解: (1)由题5-11(a)图知,m,且时,,∴,又,则题5-11图(a)取,则波动方程为(2) 时的波形如题5-11(b)图题5-11图(b) 题5-11图(c)将m代入波动方程,得该点处的振动方程为如题5-11(c)图所示.5-12 如题5-12图所示,已知=0时和=时的波形曲线分别为图中曲线(a)和(b) ,波沿轴正向传播,试根据图中绘出的条件求:(1)波动方程;(2)点的振动方程.解: (1)由题5-12图可知,,,又,时,,∴,而,,∴故波动方程为(2)将代入上式,即得点振动方程为题5-12图5-13 一列机械波沿轴正向传播,=0时的波形如题5-13图所示,已知波速为10 m·s -1,波长为2m,求:(1)波动方程;(2) 点的振动方程及振动曲线;(3) 点的坐标;(4) 点回到平衡位置所需的最短时间.解: 由题5-13图可知,时,,∴,由题知,,则∴(1)波动方程为题5-13图(2)由图知,时,,∴(点的位相应落后于点,故取负值)∴点振动方程为(3)∵∴解得(4)根据(2)的结果可作出旋转矢量图如题5-13图(a),则由点回到平衡位置应经历的位相角题5-13图(a)∴所属最短时间为5-14 如题5-14图所示,有一平面简谐波在空间传播,已知P点的振动方程为=cos().(1)分别就图中给出的两种坐标写出其波动方程;(2)写出距点距离为的点的振动方程.解: (1)如题5-14图(a),则波动方程为如图(b),则波动方程为题5-14图(2) 如题5-14图(a),则点的振动方程为如题5-14图(b),则点的振动方程为5-15 已知平面简谐波的波动方程为(SI).(1)写出= s时各波峰位置的坐标式,并求此时离原点最近一个波峰的位置,该波峰何时通过原点?(2)画出= s时的波形曲线.解:(1)波峰位置坐标应满足解得 (…)所以离原点最近的波峰位置为.∵故知,∴,这就是说该波峰在前通过原点,那么从计时时刻算起,则应是,即该波峰是在时通过原点的.题5-15图(2)∵,∴,又处,时,又,当时,,则应有解得,故时的波形图如题5-15图所示5-16 题5-16图中(a)表示=0时刻的波形图,(b)表示原点(=0)处质元的振动曲线,试求此波的波动方程,并画出=2m处质元的振动曲线.解: 由题5-16(b)图所示振动曲线可知,,且时,,故知,再结合题5-16(a)图所示波动曲线可知,该列波沿轴负向传播,且,若取题5-16图则波动方程为5-17 一平面余弦波,沿直径为14cm的圆柱形管传播,波的强度为×10-3J·m-2·s-1,频率为300 Hz,波速为300m·s-1,求:(1)波的平均能量密度和最大能量密度?(2)两个相邻同相面之间有多少波的能量?解: (1)∵∴(2)5-18 如题5-18图所示,和为两相干波源,振幅均为,相距,较位相超前,求:(1) 外侧各点的合振幅和强度;(2) 外侧各点的合振幅和强度解:(1)在外侧,距离为的点,传到该点引起的位相差为(2)在外侧.距离为的点,传到该点引起的位相差.5-19 如题5-19图所示,设点发出的平面横波沿方向传播,它在点的振动方程为;点发出的平面横波沿方向传播,它在点的振动方程为,本题中以m计,以s计.设=,= m,波速=·s-1,求:(1)两波传到P点时的位相差;(2)当这两列波的振动方向相同时,处合振动的振幅;*(3)当这两列波的振动方向互相垂直时,处合振动的振幅.解: (1)题5-19图(2)点是相长干涉,且振动方向相同,所以(3)若两振动方向垂直,又两分振动位相差为,这时合振动轨迹是通过Ⅱ,Ⅳ象限的直线,所以合振幅为5-20 一平面简谐波沿轴正向传播,如题5-20图所示.已知振幅为,频率为波速为.(1)若=0时,原点处质元正好由平衡位置向位移正方向运动,写出此波的波动方程;(2)若从分界面反射的波的振幅与入射波振幅相等,试写出反射波的波动方程,并求轴上因入射波与反射波干涉而静止的各点的位置.解: (1)∵时,,∴故波动方程为m题5-20图(2)入射波传到反射面时的振动位相为(即将代入),再考虑到波由波疏入射而在波密界面上反射,存在半波损失,所以反射波在界面处的位相为若仍以点为原点,则反射波在点处的位相为,因只考虑以内的位相角,∴反射波在点的位相为,故反射波的波动方程为此时驻波方程为故波节位置为故 (…)根据题意,只能取,即5-20 一驻波方程为=(SI),求:(1)形成此驻波的两列行波的振幅和波速;(2)相邻两波节间距离.解: (1)取驻波方程为故知,则,∴(2)∵所以相邻两波节间距离5-22 在弦上传播的横波,它的波动方程为=(13+ (SI)试写出一个波动方程,使它表示的波能与这列已知的横波叠加形成驻波,并在=0处为波节.解: 为使合成驻波在处形成波节,则要反射波在处与入射波有的位相差,故反射波的波动方程为5-23 两列波在一根很长的细绳上传播,它们的波动方程分别为=()(SI), =()(SI).(1)试证明绳子将作驻波式振动,并求波节、波腹的位置;(2)波腹处的振幅多大?=处振幅多大?解: (1)它们的合成波为出现了变量的分离,符合驻波方程特征,故绳子在作驻波振动.令,则,k=0,±1,±2…此即波腹的位置;令,则,…,此即波节的位置.(2)波腹处振幅最大,即为m;处的振幅由下式决定,即5-24 汽车驶过车站时,车站上的观测者测得汽笛声频率由1200Hz变到了1000 Hz,设空气中声速为330m·s-1,求汽车的速率.解: 设汽车的速度为,汽车在驶近车站时,车站收到的频率为汽车驶离车站时,车站收到的频率为联立以上两式,得5-25 两列火车分别以72km·h-1和54 km·h-1的速度相向而行,第一列火车发出一个600 Hz 的汽笛声,若声速为340 m·s-1,求第二列火车上的观测者听见该声音的频率在相遇前和相遇后分别是多少?解: 设鸣笛火车的车速为,接收鸣笛的火车车速为,则两者相遇前收到的频率为两车相遇之后收到的频率为。
大学物理第二版答案(北京邮电大学出版社)

大学物理第二版答案(北京邮电大学出版社)习题解答第一章质点运动学1-1(1)质点t时刻位矢为:r(3t5)i12t23t4j(m)(2)第一秒内位移r1(某1某0)i(y1y0)j3(10)i12(10)23(110)j3i3.5j(m)(3)前4秒内平均速度Vr1t4(12i20j)3i5j(m1)(4)速度Vdr3i(t3)j(m1dt)∴V43i(43)j3i7j(m1)A;/。
(5)前4秒平均加速度aVV4V0734jj(m2t40)(6)加速度adVdtj(m2)a4j(m2)1-2vd某dtt33t22某d某vdtc14t4t32tc当t=2时某=4代入求证c=-12即某14t4t32t12vt33t22adv3t2dt6t将t=3代入证某41134(m)v356(m1)a345(m2)1-3(1)由运动方程某4t22t消去t得轨迹方程y3某(y3)20(2)1秒时间坐标和位矢方向为某14m[4,5]m:tgy某1.25,51.3(3)第1秒内的位移和平均速度分别为y15mr1(40)i(53)j4i2j(m)r1V4i2j(m1)t(4)质点的速度与加速度分别为drV8i2j,dtdVa8idt故t=1时的速度和加速度分别为V18i2jm1,a18im21-4该星云飞行时间为9.4610152.741096.5910172.091010a73.9310即该星云是2.091010年前和我们银河系分离的.1-5实验车的加速度为v1600103a2.47102m/225(g)t36001.80基本上未超过25g.1.80内实验车跑的距离为v1600103t1.80400(m)2236001-6(1)设第一块石头扔出后t秒未被第二块击中,则hv0t12gt2代入已知数得11115t9.8t22解此方程,可得二解为t11.84,t11.22第一块石头上升到顶点所用的时间为tmv10/g15/9.81.53由于t1tm,这对应于第一块石头回落时与第二块相碰;又由于t1tm这对应于第一块石头上升时被第二块赶上击中.以v20和v20分别对应于在t1和t1时刻两石块相碰时第二石块的初速度,则由于hv20(t1t1)1g(t1t1)22所以hv2011g(t1t1)2119.8(1.841)222t1t11.84117.2m/同理.2v20h11g(t1t1)2119.8(1.221)2221.221t1t151.1(m/)(2)由于t21.3t1,所以第二石块不可能在第一块上升时与第一块相碰.对应于t1时刻相碰,第二块的初速度为h12g(t)21119.8(1.841.3)2v201t2tt2121.841.323.0(m/)1-7以l表示从船到定滑轮的绳长,则v0dl/dt.由图可知l2h2于是得船的速度为vdldl2h2dtl2h2dtv0习题1-7图负号表示船在水面上向岸靠近.船的加速度为advdldtvdlh2v20dll2h20dt3负号表示a的方向指向岸边,因而船向岸边加速运动.1-8所求位数为2r42n2r42(6104)2gg0.16029.841051-9物体A下降的加速度(如图所示)为a2h20.40.2m/2t222此加速度也等于轮缘上一点在t3时的切向加速度,即at0.2(m/2)在t3时的法向加速度为av2(att)2R(0.23)2n1.00.36(m/2R)习题1-9图习题1-10图1-10a1.2m/2,t00.5,h01.5m.如图所示,相对南面,小球开始下落时,它和电梯的速度为3v0at01.20.50.6(m/)以t表示此后小球落至底板所需时间,则在这段时间内,小球下落的距离为hv0t12gt2电梯下降的距离为hv0t12at2又h0hh1(ga)t22由此得t2h021.50.59ga9.81.2而小球相对地面下落的距离为hv0t12gt20.60.599.80.5922.06m1-11v风地v风人v人地2v0人地,速度矢量合成如图(b)两图中v风地应是同一矢量.可知(a)v风人画出速度矢量合成图(a)又v风地12图必是底角为45的等腰直角三角形,所以,风向应为西北风,风速为v风地4.23(m1)v0人地co452v0人地1-12(1)t(2)2L2LvvLL2vLtt1t22vuvuvu222Lu1vv1习题1-11图(3)u由东习题1-12图tt1t2LL,如图所示风速vv向西,由速度合成可得飞机对地速度vuv,则Vv2u2.t2L2L22vvu2Luv1v2证毕1-13(1)设船相对岸的速度为V(如图所示),由速度合成得VuVV的大小由图1.7示可得VVcouco习题1-13图4即VcoVuco323332而Vinuin21船达到B点所需时间tAB两点之距SDctgOBDD1000()VVincoin12D将式(1)、(2)代入可得SD(33)1268(m)(2)由D1103tVinuin船到对岸所需最短时间由极值条件决定dt1du1in2co0即co0,/2故船头应与岸垂直,航时最短.将值代入(3)式得最短航时为3t110minuin/2110320.5103500()(3)设OBl,则lDVDDu2V22inuVcoVinuin欲使l最短,应满足极值条件.dlDu2V22uVcoduacoainuVin2ain2au2V22uVco0简化后可得2u2V2coauVco10即co2a136co10解此方程得co23co12348.2故船头与岸成48.2,则航距最短.将值代入(4)式得最小航程为2lu2v22uvco10002232223minDu1co23221231.5103m1.5(km)AB两点最短距离为52SminlminD21.511.12(km)第二章质点动力学2-1(1)对木箱,由牛顿第二定律,在某向:Fmincofma某0y向:NFmininMg0还有fma某N习题2-1图木箱将要被推动的情况下如图所示,解以上三式可得要推动木箱所需力F的最小值为FminMgcoin在木箱做匀速运动情况下,如上类似分析可得所需力F的大小为FminkMgcokin(2)在上面Fmin的表示式中,如果coin0,则Fmin,这意味着用任何有限大小的力都不可能推动木箱,不能推动木箱的条件是coin0由此得的最小值为arctan12-2(1)对小球,由牛顿第二定律某向:TcoNinmay向:TinNcomg0联立解此二式,可得Tm(acogin)0.5(2co309.8in30)3.32(N)Nm(gcoain)0.5(9.8co302in30 )3.74(N)由牛顿第三定律,小球对斜面的压力NN3.74(N)(2)小球刚要脱离斜面时N=0,习题2-2图则上面牛顿第二定律方程为Tcoma,Tinmg由此二式可解得ag/tan9.8/tan3017.0m/22-3要使物体A与小车间无相对滑动,三物体必有同一加速度a,且挂吊B的绳应向后倾斜。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题四4-1 符合什么规律的运动才是谐振动?分别分析下列运动是不是谐振动: (1)拍皮球时球的运动;(2)如题4-1图所示,一小球在一个半径很大的光滑凹球面内滚动(设小球所经过的弧线很短).题4-1图解:要使一个系统作谐振动,必须同时满足以下三个条件:一 ,描述系统的各种参量,如质量、转动惯量、摆长……等等在运动中保持为常量;二,系统是在 自己的稳定平衡位置附近作往复运动;三,在运动中系统只受到内部的线性回复力的作用. 或者说,若一个系统的运动微分方程能用0d d 222=+ξωξt描述时,其所作的运动就是谐振动.(1)拍皮球时球的运动不是谐振动.第一,球的运动轨道中并不存在一个稳定的平衡位置;第二,球在运动中所受的三个力:重力,地面给予的弹力,击球者给予的拍击力,都不是线 性回复力.(2)小球在题4-1图所示的情况中所作的小弧度的运动,是谐振动.显然,小球在运动过程中,各种参量均为常量;该系统(指小球凹槽、地球系统)的稳定平衡位置即凹槽最低点,即系统势能最小值位置点O ;而小球在运动中的回复力为θsin mg -,如题4-1图(b)所示.题 中所述,S ∆<<R ,故R S∆=θ→0,所以回复力为θmg -.式中负号,表示回复力的方向始终与角位移的方向相反.即小球在O 点附近的往复运动中所受回复力为线性的.若以小球为对象,则小球在以O '为圆心的竖直平面内作圆周运动,由牛顿第二定律,在凹槽切线方向上有θθmg t mR -=22d d令R g=2ω,则有0d d 222=+ωθt4-2 劲度系数为1k 和2k 的两根弹簧,与质量为m 的小球按题4-2图所示的两种方式连 接,试证明它们的振动均为谐振动,并分别求出它们的振动周期.题4-2图解:(1)图(a)中为串联弹簧,对于轻弹簧在任一时刻应有21F F F ==,设串联弹簧的等效倔强系数为串K 等效位移为x ,则有111x k F x k F -=-=串222x k F -=又有 21x x x +=2211k F k F k Fx +==串所以串联弹簧的等效倔强系数为2121k k k k k +=串即小球与串联弹簧构成了一个等效倔强系数为)/(2121k k k k k +=的弹簧振子系统,故小球作谐振动.其振动周期为2121)(222k k k k m k mT +===ππωπ串(2)图(b)中可等效为并联弹簧,同上理,应有21F F F ==,即21x x x ==,设并联弹簧的倔强系数为并k ,则有2211x k x k x k +=并故 21kk k +=并同上理,其振动周期为212k k m T +='π4-3 如题4-3图所示,物体的质量为m ,放在光滑斜面上,斜面与水平面的夹角为θ,弹簧的倔强系数为k ,滑轮的转动惯量为I ,半径为R .先把物体托住,使弹簧维持原长,然 后由静止释放,试证明物体作简谐振动,并求振动周期.题4-3图解:分别以物体m 和滑轮为对象,其受力如题4-3图(b)所示,以重物在斜面上静平衡时位置为坐标原点,沿斜面向下为x 轴正向,则当重物偏离原点的坐标为x 时,有221d d sin t xm T m g =-θ①βI R T R T =-21②βR t x=22d d )(02x x k T +=③ 式中k mg x /sin 0θ=,为静平衡时弹簧之伸长量,联立以上三式,有kxRt xR I mR -=+22d d )(令I mR kR +=222ω 则有0d d 222=+x t x ω故知该系统是作简谐振动,其振动周期为)/2(22222K R I m kR I mR T +=+==ππωπ4-4 质量为kg 10103-⨯的小球与轻弹簧组成的系统,按)SI ()328cos(1.0ππ+=x 的规律作谐振动,求:(1)振动的周期、振幅和初位相及速度与加速度的最大值;(2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等? (3)s 52=t 与s 11=t 两个时刻的位相差;解:(1)设谐振动的标准方程为)cos(0φω+=t A x ,则知:3/2,s 412,8,m 1.00πφωππω===∴==T A又πω8.0==A v m 1s m -⋅51.2=1s m -⋅2.632==A a m ω2s m -⋅(2)N63.0==m m a FJ 1016.32122-⨯==m mv EJ1058.1212-⨯===E E E k p 当pk E E =时,有pE E 2=,即 )21(212122kA kx ⋅=∴ m 20222±=±=A x(3) ππωφ32)15(8)(12=-=-=∆t t4-5 一个沿x 轴作简谐振动的弹簧振子,振幅为A ,周期为T ,其振动方程用余弦函数表示.如果0=t 时质点的状态分别是:(1)Ax -=0;(2)过平衡位置向正向运动;(3)过2Ax =处向负向运动; (4)过2A x -=处向正向运动. 试求出相应的初位相,并写出振动方程.解:因为 ⎩⎨⎧-==0000sin cos φωφA v A x将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有)2cos(1πππφ+==t T A x )232cos(232πππφ+==t T A x )32cos(33πππφ+==t T A x )452cos(454πππφ+==t T A x 4-6 一质量为kg 10103-⨯的物体作谐振动,振幅为cm 24,周期为s 0.4,当0=t 时位移为cm 24+.求:(1)s 5.0=t 时,物体所在的位置及此时所受力的大小和方向; (2)由起始位置运动到cm 12=x 处所需的最短时间; (3)在cm 12=x 处物体的总能量. 解:由题已知s 0.4,m 10242=⨯=-T A ∴1s rad 5.02-⋅==ππωT又,0=t 时,0,00=∴+=φA x故振动方程为m )5.0cos(10242t x π-⨯= (1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=-t x πN102.417.0)2(10103232--⨯-=⨯⨯⨯-=-=-=πωxm ma F方向指向坐标原点,即沿x 轴负向.(2)由题知,0=t 时,00=φ,t t =时3,0,20πφ=<+=t v A x 故且 ∴s322/3==∆=ππωφt (3)由于谐振动中能量守恒,故在任一位置处或任一时刻的系统的总能量均为J 101.7)24.0()2(10102121214223222--⨯=⨯⨯⨯===πωA m kA E4-7 有一轻弹簧,下面悬挂质量为g 0.1的物体时,伸长为cm 9.4.用这个弹簧和一个质量为g 0.8的小球构成弹簧振子,将小球由平衡位置向下拉开cm 0.1后 ,给予向上的初速度10s cm 0.5-⋅=v ,求振动周期和振动表达式.解:由题知 12311m N 2.0109.48.9100.1---⋅=⨯⨯⨯==x g m k而0=t 时,-12020s m 100.5m,100.1⋅⨯=⨯-=--v x ( 设向上为正)又s 26.12,51082.03===⨯==-ωπωT m k 即m 102)5100.5()100.1()(22222220---⨯=⨯+⨯=+=∴ωv x A45,15100.1100.5tan 022000πφωφ==⨯⨯⨯=-=--即x v∴ m)455cos(1022π+⨯=-t x4-8 图为两个谐振动的t x -曲线,试分别写出其谐振动方程.题4-8图解:由题4-8图(a),∵0=t 时,s2,cm 10,,23,0,0000===∴>=T A v x 又πφ即 1s rad 2-⋅==ππωT故 m)23cos(1.0ππ+=t x a由题4-8图(b)∵0=t 时,35,0,2000πφ=∴>=v A x 01=t 时,22,0,0111ππφ+=∴<=v x又 ππωφ253511=+⨯=∴πω65=故 mt x b )3565cos(1.0ππ+=4-9 一轻弹簧的倔强系数为k ,其下端悬有一质量为M 的盘子.现有一质量为m 的物体从离盘底h 高度处自由下落到盘中并和盘子粘在一起,于是盘子开始振动. (1)此时的振动周期与空盘子作振动时的周期有何不同? (2)此时的振动振幅多大?(3)取平衡位置为原点,位移以向下为正,并以弹簧开始振动时作为计时起点,求初位相并写出物体与盘子的振动方程.解:(1)空盘的振动周期为k M π2,落下重物后振动周期为k mM +π2,即增大. (2)按(3)所设坐标原点及计时起点,0=t 时,则k mg x -=0.碰撞时,以M m ,为一系统动量守恒,即0)(2v M m gh m +=则有M m ghm v +=20 于是gM m khk mg M m gh m k mg v x A )(21))(2()()(22222++=++=+=ω(3)g m M kh x v )(2tan 000+=-=ωφ(第三象限),所以振动方程为 ⎥⎦⎤⎢⎣⎡+++++=g m M kh t M m k g M m kh k m g x )(2arctan cos )(214-10 有一单摆,摆长m 0.1=l ,摆球质量kg 10103-⨯=m ,当摆球处在平衡位置时,若给小球一水平向右的冲量14s m kg 100.1--⋅⋅⨯=∆t F ,取打击时刻为计时起点)0(=t ,求振动的初位相和角振幅,并写出小球的振动方程.解:由动量定理,有0-=∆⋅mv t F∴1-34s m 01.0100.1100.1⋅=⨯⨯=∆⋅=--m t F v按题设计时起点,并设向右为x 轴正向,则知0=t 时,100s m 01.0,0-⋅==v x >0∴ 2/30πφ= 又1s rad 13.30.18.9-⋅===l g ω∴m 102.313.301.0)(302020-⨯===+=ωωv v x A故其角振幅rad 102.33-⨯==Θl A小球的振动方程为rad)2313.3cos(102.33πθ+⨯=-t4-11 有两个同方向、同频率的简谐振动,其合成振动的振幅为m 20.0,位相与第一振动的位相差为6π,已知第一振动的振幅为m 173.0,求第二个振动的振幅以及第一、第二两振动的位相差.题4-11图解:由题意可做出旋转矢量图如下. 由图知01.02/32.0173.02)2.0()173.0(30cos 222122122=⨯⨯⨯-+=︒-+=A A A A A∴ m 1.02=A设角θ为O AA1,则 θcos 22122212A A A A A -+=即1.0173.02)02.0()1.0()173.0(2cos 2222122221=⨯⨯-+=-+=A A A A A θ即2πθ=,这说明,1A 与2A 间夹角为2π,即二振动的位相差为2π.4-12 试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅:(1) ⎪⎩⎪⎨⎧+=+=cm )373cos(5cm )33cos(521ππt x t x (2)⎪⎩⎪⎨⎧+=+=cm)343cos(5cm )33cos(521ππt x t x解: (1)∵ ,233712πππφφφ=-=-=∆∴合振幅 cm 1021=+=A A A(2)∵ ,334πππφ=-=∆∴合振幅 0=A4-13 一质点同时参与两个在同一直线上的简谐振动,振动方程为⎪⎩⎪⎨⎧-=+=m)652cos(3.0m )62cos(4.021ππt x t x试分别用旋转矢量法和振动合成法求合振动的振动幅和初相,并写出谐振方程。
