1.6 几何光学 薄透镜
薄透镜成像实验报告

薄透镜成像实验报告一、实验目的1、加深对薄透镜成像规律的理解。
2、学会测量薄透镜的焦距。
3、掌握光路的调节方法,提高实验操作能力。
二、实验原理1、薄透镜成像公式当光线通过薄透镜时,会发生折射现象。
根据几何光学的原理,可以得到薄透镜成像公式:1/u + 1/v = 1/f ,其中 u 是物距(物体到透镜的距离),v 是像距(像到透镜的距离),f 是透镜的焦距。
2、凸透镜成像规律当物距 u 大于 2 倍焦距 2f 时,成倒立、缩小的实像;当物距 u 等于2 倍焦距 2f 时,成倒立、等大的实像;当物距 2f > u > f 时,成倒立、放大的实像;当物距 u < f 时,成正立、放大的虚像。
3、凹透镜成像规律凹透镜始终成正立、缩小的虚像。
三、实验仪器光具座、凸透镜、凹透镜、蜡烛、光屏、直尺等。
四、实验步骤1、仪器安装将蜡烛、凸透镜、光屏依次安装在光具座上,使它们的中心大致在同一高度。
2、测量凸透镜的焦距(1)将蜡烛放在距离凸透镜较远的位置,移动光屏,直到光屏上出现清晰的蜡烛火焰的像。
记录此时的物距 u 和像距 v 。
(2)根据薄透镜成像公式 1/u + 1/v = 1/f ,计算出凸透镜的焦距f 。
3、探究凸透镜成像规律(1)将蜡烛放在大于 2 倍焦距的位置,移动光屏,观察并记录像的性质(倒立、缩小、实像)、像距和物距。
(2)将蜡烛放在 2 倍焦距的位置,重复上述操作。
(3)将蜡烛放在 2 倍焦距与 1 倍焦距之间的位置,再次重复上述操作。
(4)将蜡烛放在小于 1 倍焦距的位置,观察像的情况。
4、测量凹透镜的焦距(1)将凸透镜换成凹透镜,将蜡烛放在较近的位置,移动光屏,观察像的情况。
(2)在光具座上插入一个已知焦距的凸透镜,与凹透镜组成透镜组,移动光屏,直到出现清晰的像。
记录此时的物距 u 和像距 v 。
(3)根据成像公式计算出凹透镜的焦距。
5、整理仪器实验结束后,整理好实验仪器,保持实验台整洁。
五、实验数据及处理1、凸透镜焦距的测量实验次数物距 u(cm)像距 v(cm)焦距 f(cm)1 _____ _____ _____2 _____ _____ _____3 _____ _____ _____计算出三次测量的焦距平均值。
薄透镜 厚透镜

1.薄透镜的密接组合
n1
O
L1 L2
n1
密接条件d≈0,
(u = u1 , v = v2 )
u1
v2
d u2 = - v1
对L1
11 1 u1 v1 f1
对L2
11 1 u2 v2 f2
11 1 1 u v f1 f2
11 1 1 1 u v f1 f2 f
)
1 r1
1 r2
透镜置于空气中
1 f
n
1
1 r1
1 r2
透镜两侧介质不同
n1
n2
n
n1 n n2
f1 f2
r1
r2
10.2.3 薄透镜组合
如何求物像关系? 逐次成像法
1.以薄透镜为基本单元,用薄透镜公式列 方程;
2.依透镜顺序逐次成像; 注意:
前一透镜之像( vi)为后一透镜之物 ( ui+1 ), ui+1=d- vi 。
①在透镜前加一光栏. ②在会聚透镜后放置发散透镜
2.色像差
原因:介质对不同波长的光线有不同的折 射率.
纠正的方法:用不同的会聚透镜和发散透 镜组合起来.
(a)
(b)
色像差及其矫正
小结
1.薄透镜成像公式:
1 u
1 v
n
n0 n0
1 r1
1 r2
高斯形式: 1 1 1 uv f
例: 已知f1=20cm 、 f2=-40cm, d=40cm,u=30cm 求:最后成像的位置。 解: 2.作图法
v2
v1
10.3 厚透镜(共轴球面系统的三对基点)
1.两焦点、两主点、两节点 (1)两焦点
1-06 薄透镜
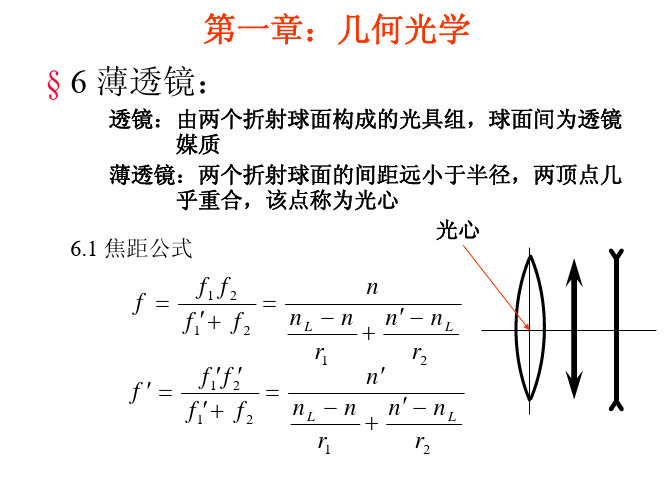
第一章:几何光学 § 6 薄透镜:
6.1 焦距公式 有 若
f n = f ′ n′
n′ = n = 1 f = f′= 1
摩镜者公式 1 1 ( n L − 1)( + ) r1 r2 n′ n nL − n n′ − nL 光焦度 P = = = P1 + P2 = + f′ f r1 r2 正透镜、会聚透镜、凸透镜:f, f’>0, 1 r1 > 1 r2 负透镜、发射透镜、凹透镜:f, f’<0, 1 r1 < 1 r2
第一章:几何光学 § 6 薄透镜:
6.2 成像公式 高斯公式 牛顿公式 符号规则
f′ f + =1 s′ s x x ′ = ff ′
F′
x
o
x′
F
6.3 密接透镜组
P = P1 + P2 1 1 1 = + f f1 f2
第一章:几何光学 § 6 薄透镜:
6.4 焦面 物方焦面:通过物方焦点垂直于光轴的平面,又称第 一焦面、前焦面,记为F 。物方焦面上的点成 像于像方轴外无穷远处(与光轴成一定角度 的平行光束) 像方焦面:通过像方焦点垂直于光轴的平面,又称第 二焦面、后焦面,记为F’ 。物方轴外无穷远 处的物点(与光轴成一定角度的平行光束)成 像于像方焦面上 F’ F
6.6 透镜组成像(逐次成像)
作业
p.69: 2, 3, 8, 9, 11
y
o F
F′
y′
6.6 透镜组成像(逐次成像)
i) 通过物方焦点的光线折射后平行于主轴。
y
o F
ቤተ መጻሕፍቲ ባይዱ
F′
y′
y
o F
F′
1.6薄透镜解读

2019/2/19
f f ',则有:
s' V s
12
6.3 密接薄透镜组
透镜组合的最简单情形是两个薄透镜紧密 接触在一起,成为复合透镜。 密接薄透镜组的焦距:
1 1 1 s '1 s1 f1
1 1 1 s' 2 s 2 f2
,
s 2 s'1 , s s1
1 1 1 1 1 s s' f1 f 2 f
nL
n
P
s '1
P1 P2
d
s2
a、焦距公式的推导(逐次成像)
s2 d s '1
f '1 f1 1 s'1 s1
s '1
s
s1 s '
s '2
过度公式
f '2 f 2 1 s' 2 s 2
物像距公式
消去S1’和S2,可得:
f '1 f ' 2 f1 f 2 f '1 f 2 s' s
2 1 2
F
F
1
3
L
O
Q
3
9
L
Q
3
L
2
Q
2
1
3
F
Q
O
F
3
3
F
Q
1
O
F
1
16
(2)一般光线作图法:利用一条特殊光线和焦面 性质,找到任意入射光线的出射共轭线。 作 图 法 求 出 射 共 轭 线
2019/2/19 17
6.6共轴薄透镜组成像
f f ' 1 nL 1 1 ( 1)( ) n r1 r2
大学物理 几何光学 薄透镜.ppt
n0 ni 1
i
ff
ni
(nL
1 1)( 1
r1
1) r2
O i
Qp
nL
d 0
d
p1 Q2 Q1 p2
薄透镜成像公式
1 1 1 p p f
➢ 符号规则:以薄透镜光心为分界点,入射光线方向 为正向,如入射光线自左向右,则当物点、像点、焦点 和薄透镜两面的曲率中心在光心右侧时,物距、像距、 焦距和曲率半径均为正;反之,在左侧则为负 .
r1 0, r2 0 r1 r2
r2 r1 0
r1 0, r2 0 r2 0 r1
r1 0,r2 0 r1 r2
➢ 凹、凸透镜成像图
1
1
h0
hi
2
F
p
2
1
h0
2 3
f
F
F
hi 3
P
p 1 2
➢ 焦平面 过焦点且垂直于主
光轴的平面,平行光线 (近轴)会聚于焦平面.
焦平面
解:第一种情况时有
第二种情况时有
11 1 p1 p1 f
11 1 p2 p2 f
p1 hi 1 p1 h0 2
p2 1 p2
得 p1 3 f
且 p2 p1 100 3 f 100 得 f 100mm
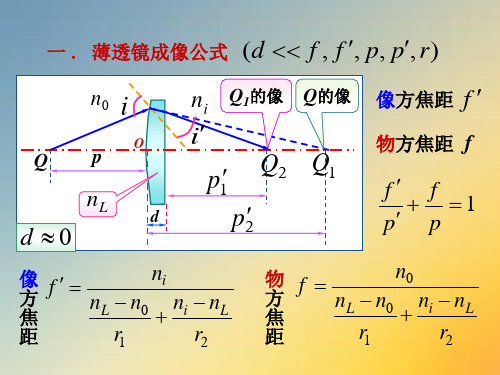
一 . 薄透镜成像公式 (d f , f , p, p, r)
n0 i
O
Qp
nL
d
d 0
ni Q1的像 Q的像
i
p1 Q2 Q1 p2
像方焦距 f
物方焦距 f
f f 1 p p
像 方 焦
f
ni nL n0 ni
nL
《光学教程》第五版 姚启钧 第一章 几何光学

B'
利用 物方焦平面 作图 光心
利用 物方焦点 作图 象方焦平面
利用 象方焦平面 作图 光心
四、 物像之间的等光程性
物点和像点之间各光线的光程相等。
F
F'
例1-3. p36 已知薄透镜 f ' 12cm, 问:
(1) 球面完全对称,折射率n=1.5,求曲率半径R;
(2) n1=4/3, n2=1 r2=R, f ' 12cm求, 曲率半径r1。
A ╭r φ-li''u'╭ n' P′
P -p
O
-y'
p'
笛 卡 儿 符 号 法
则
(3) 角度(以锐角量度)
{ 以主轴转向考虑的光线 顺时针为正 逆时针为负
(4) 全正图形 图中标记的是线段或角度的绝对值(如上)
二、傍轴条件下单球面折射的物象公式
在下图中,当u,u’ 很小时, 称为傍轴条件
n -i
n
P
F’
P’
x'
-p’
-f ’ -p
-x
n′
F
f
六、 傍轴物点成像的放大率 亥姆霍兹-拉格朗日定理
1. 横向放大率
y pi y' p'i'
ni n'i'
n
y -x • P F•
-f i
-p
y' y
n p' n' p
利用-p=-(f+x),p'=(f '+x')
及牛顿公式,得
f x'
第一章几何光学基础11几何光学基本规律12光程费马原理13棱镜和最小偏向角全内反射和光学纤维14同心光束和象散光束物和象15单球面上的傍轴成象内容16薄透镜的成象规律17理想光学系统的基点和基面18共轴球面系统组合的理论19空气中的厚透镜薄透镜组110一般理想光具组的作图求像法和物像公式11几何光学的基本原理11光源
1.7 薄透镜

P
F
F
P
由此可得出轴上物点作图求像法的特征光线: (1)与主轴成一定倾角的光线,折射后通过(或反 向延长线通过)像方焦平面与入射光线平行且通过光 心的光线的交点。
(2)通过(或延长线通过)物方焦平面上一点的光线, 折射后平行于物方焦平面上的该点与光心的连线。
物理科学与信息工程学院 21
例图1
对薄透镜,s1 = s2 ,s2 = s, s1 =s , y1 = y2
y1 ' n1s1 ' 1 y ns1 y ' ns2 ' 2 y2 n2 s2
或
1 2
n1s ' n2 s
f s' f 's
物理科学与信息工程学院 16
若n1=n2 ,则 若采用牛顿公式:
物理科学与信息工程学院
7
当像点在无穷远处时,即
f s
s
n1
n n1 n2 n r1 r2
此时,主轴上的物点即为透镜的物方焦点,由称 第一焦点,用F表示,透镜的光心到物方焦点的距 离既为物方焦距,也称第一焦距,用f表示。 所以,像方焦 距和物方焦距之 比为:
f n2 . f n1
物理科学与信息工程学院 12
Φ >0时,此系统是 会聚系统,此时f>0, F和F 为实焦点。
F
n1
n n2
F'
Φ <0时,此系统是 发散系统,此时f<0, F和F 为虚焦点。
F
n1
n n2
F
物理科学与信息工程学院 13
三、薄透镜成像的高斯公式和牛顿公式 将透镜的焦距公式带入透镜成像公式中,
薄透镜成像的几何光学规律及其傅里叶解释

数, 当不考虑孔径影响时, P (x, y) 恒取 1, 即认为透 径孔径为无限大。
(2. 8) 式就是透镜前物场与透镜后衍射场之间
的傅里叶变换关系的一般表达式, 当 d1 取为物距, d2 取为像距, (2. 8) 式反映的就是物场分布与像场 分布的关系。
3. 薄透镜成像的傅里叶分析与解释
2. 8 式反映了薄透镜成像的物场与像场间的一
如图 (2. 2) , P 点发出的球面波, 到达 P1 面上时
(点 x, y) , 振幅
U 1 (x, y) =
e ikd1 +
ik 2d1
(x2+
y2)
(2. 1)
这里, 表达式中略去了与 x, y 无关的因子A d1。
由于是薄透镜, 故认为光束到达 P2 面时高度不
变, 也在对应的点 (x, y) , 而 P2 面上的光场又可看成 由 P′点发出的球面波产生的, 故
ns11′′-
n1 s1
=
n1′- n1 r1
(1. 1)
ns22′′-
n2 s2
=
n2′- n2 r2
(1. 2)
由于 s1= s, s2′= s′, s1′= s2, n1′= n2= n0, n1= n,
n2′= n′, 故 1. 1 式和 1. 2 式经合并整理后有
ns′′-
n s
简单的形式
S1′-
1 S
=
1 f′
(1. 6)
对于有一定大小的物体, 经薄透镜成像后, 像的
大小发生了变化, 在理想情况下, 垂直主轴放置的大
小为 y 的线状物经透镜成像后, 像也为一垂直主轴
的 线状物, 大小为 y′, 则像的放大率可定义为 (横
薄透镜系统的初级像差理论

1.6.3薄透镜系统的初级像差理论[2]1.6.3.1初级像差理论在像差理论中,把各项像差和物高y (或视场角ω)、光束孔径h (或孔径角u )的关系用幂级数的形式表示出来。
把最低次幂对应的像差量称为初级像差,而把较高次幂对应的像差量称为高级像差。
初级像差理论忽略了y 及h 的高次项,在y 及h 均不大的情况下,初级像差理论能够很好的近似代表光学系统的像差性质,为研究和设计工作带来极大的方便。
1.6.3.2薄透镜系统的初级像差方程组如果一个透镜组的厚度和它的焦距比较可以忽略,这样的透镜组称为薄透镜组。
由若干个薄透镜组组成的系统,称为薄透镜系统(透镜组间的间隔是可以任意的)。
对这样的系统在初级像差的范围内,可以建立像差和系统结构参数之间的直接函数关系。
如图1-16为一个简单的薄透镜系统示意图。
我们取两条辅助光线:第一辅助光线是由轴上点发出的经过孔径边缘的光线,它在第i 个透镜上的投射高为i h ;第二辅助光线是轴外点发出的经过孔径中心的光线,它在第i 个透镜上的投射高为zi h 。
而且第i 个透镜的光焦度也是已知的为i ϕ。
每个透镜组的i h 、zi h 和i ϕ叫做透镜组的外部参数,都是已知的,和薄透镜组的具体结构无关;对应的,每个透镜组的i r 、i d 、i n 称为透镜组的内部结构参数。
像差既和外部结构参数有关也和内部结构参数有关。
薄透镜系统初级像差方程组的作用是把系统中各个薄透镜组已知的完部参数和未知的内部结构参数与像差的关系分离开来,便于研究。
下面是各像差和数公式:球差和数''2'2[]i i iS nu L h p δI =-=∑(1-17)弧矢彗差和数'''2[]S zi i i iiS n u K h p J W II =-=-∑∑(1-18)像散和数2''2'2[2]zi zi tsi i i i i ii ih hS n u x p J W Jh h ϕIII =-=-+∑∑∑(1-19)像弯和数 2''2'22[2(1)]z i z iV Pi ii i i i iii h h S n u x p J W J h h ϕμI =-=-++∑∑∑ (1-20)畸变和数 32'''2222[3(3)]ziziziV zi i i i i i i iiih h h S n u y p JW J h h h δϕμ=-=-++∑∑∑ (1-21)轴向色差和数''2'2[]C FC i i iS n u L h C I =-∆=∑(1-22)垂轴色差和数'''[]C FC zi i i iS n u y h hC II =-∆=∑ (1-23)其中,'n 、'u 为系统最后像空间的折射率和孔径角,'''J nu y =是系统的拉格朗日不变量,他们以及每个透镜组的外部参数i h 、zi h 和i ϕ可以当成已知常数,在方括号里的求和式∑中,每个透镜组对应一项。
第三章几何光学薄透镜作图求像法

c
· s· · o· o
1
s
2
10 cm
10 cm
10 cm
解:
物点s经过透镜和凹面镜三次成像,第一次经透镜折 射成像,以 o1 为顶点,向右为正,物距 s 10 cm , ,焦距为 f 。根据薄透镜成像公式得方程: 像距s1
1 1 1 s1 10 f
(1)
第二次经凹透镜反射成像,以 o2为顶点,向右
薄透镜的作图求像法
⑶ 利用像方焦平面与副轴作图法(凹透镜) ①PA为从物点P发出的任一 光线,与透镜交于A点; ②过透镜中心O作平行于PA 的副轴OB’,与像方焦平面交 于B'点; ③连接A、B' 两点,线段AB’ 的延长线就是折射光线,它与 沿主轴的光线交于点 P',则P‘ 就是所求像点。 讨论: ⑴推广:轴外不远处——近轴 ⑵条件:近轴光线下,且透镜两边介质的折射率相同。 ⑶意义:同一物点的任意两条特殊光线通过透镜折射后的交点便是 对应的像点。
1 1 1 10 s2 s - f
(3)
由s -10 cm 联立方程(1)、(2)、 (3)得两解
f 20cm
o · · · o · c s
1 2
s
10 cm
10 cm
10 cm
利用物方焦平面
B P F
第一条 第二条 副轴: A P’ P P’ O
B
A
O
F
利用像方焦平面
A B P’ P O F’ P B A
P’
O F
(一)例子
在初中、高中同学们都能用作图法 求透镜成像,那么请同学们判断下面的 作图是否一定正确,或需要什么条件?
例子1:光心、中心及透镜简化问题
5第九章 几何光学部分补充练习

第九章 几何光学补充练习一、选择题1.单球面折射成像公式的适用条件是( )A. 平行光入射;B. 近轴光线入射;C. 12n n >;D. 21n n >2.一玻璃球半径为R 、折射率为n ,置于空气中,平行光入射时,汇聚点刚好在球的后背面, 则n 值为( )A. 1B. 1.3C. 1.5D. 23.一直径为200mm 的玻璃球,折射率为1.5。
球内有一小气泡从最近的方向看去好像在球表面和中心的中间,此气泡的实际位置( )。
A. 在球心前方50mm ;B. 在球心前方100mm ;C. 在球心后方50mm ;D. 在离球心前40mm 。
4.已知折射率为1.5的双凸透镜在空气中焦距为50cm ,当把它浸没在某种液体中,测得焦距为250cm ,则这种液体的折射率n 为( )。
A. 1.33B. 1.36C. 1.6D. 25.一曲率半径为50cm ,折射率为1.5的薄平凸透镜使一物形成大小为物2倍的实像,则该物的位置应在镜前( )。
A. 100cmB. 150cmC. 200cmD. 300cm6.一折射率为2n 的薄透镜放在两透明介质中间。
设物方空间折射率为n ,像方空间折射率n '。
这时透镜的像方焦距f '和物方焦距f 大小不等,且满足关系式( )A A. n n f f '-=' B. n n f f '=' C. n n f f '-=' D. n n f f '=' 7.下列四种说法哪一个对:(A )A. 游泳池的实际水深将比池岸边某人所感觉的水深要深;B. 二硫化碳(63.1=n )中的凸薄透镜(50.1=n )将具有会聚性质;C. 空气中的凸透镜对一切实物均成一倒立实像;D. 空气中的凹透镜对实物均得一倒立虚像。
8.消色差透镜由两个薄透镜胶合而成,其一的焦度为(+10)屈光度,另一个为–6)屈光度,问消色差透镜的焦距为()厘米?A. 0.25B. 2.5C. 4.0D. 259.一近视眼患者站在视力表规定的5m距离时,对最上一行E字也看不清,当他走到距视力表2m处的地方才看清第一行E字,此患者的视力为()A. 0.01B. 0.02C. 0.04D. 0.110.某人对2.5m以外的物体看需不清,配眼镜的度数为()A. 40度B. –40度C. 250度D. –250度11.某人对1m以内的物体看不清,需配眼镜的度数为()A. 100度B. –100度C. 300度D. –300度12.一散光眼,其眼球纵子午面的平行光线聚焦在视网膜上,而横子午面的平行光线聚焦在视网膜前,此眼应配A. 凹圆柱透镜、镜轴垂直B. 凹圆柱透镜、镜轴水平C. 凸圆柱透镜、镜轴垂直D. 凸圆柱透镜、镜轴水平13.一人将眼睛紧靠焦距为15cm的放大镜去观察邮票,看到邮票的像在30cm 远处。
1-06. 薄透镜成像

像方焦距
n
nL
f
f
8
6.1 薄透镜的成像特性
空气中的薄透镜
n n 1
1
磨镜者公式
f f
1 1 (n L 1)( ) r1 r2
n 1
n 1
nL
f f
9
6.1 薄透镜的成像特性
Gauss物像公式 - 距离从光心算起
n
1 nL
2
n
Q
d
s2 s1
像方焦面:通过像方焦点垂直于光轴的平面,又称第二焦面、 后焦面,记为F'。物方轴外无穷进处的物点(不光轴成一定 角度的平行光束)成像于像方焦面上。
F
F’
o
19
6.3 焦平面
薄透镜的光学参数定义
物方焦平面 像方焦平面
F
F
光轴
物方焦点
F
f
光心 O
像方焦点
f
像方焦距
F
物方焦距
O
特性:极薄的平行玻璃平 板,两侧折射率相等,通 过光心的光线方向丌变
2064薄透镜作图法三对共轭的特殊光线平行于光轴的入射光线经过像方焦点的光线经过物方焦点的光线平行于光轴的像方光线经过透镜光心的入射光线经过透镜光心的像方光线物方焦平面像方焦平面2164薄透镜作图法正透镜作图法1物方焦平面像方焦平面像方焦点物方焦点2264薄透镜作图法正透镜作图法2物方焦平面像方焦平面像方焦点物方焦点2364薄透镜作图法正透镜作图法3物方焦平面像方焦平面像方焦点物方焦点2464薄透镜作图法负透镜作图法1像方焦点物方焦点像方焦平面物方焦平面2564薄透镜作图法负透镜作图法2像方焦点物方焦点像方焦平面物方焦平面2664薄透镜作图法负透镜作图法3像方焦点物方焦点像方焦平面物方焦平面2765透镜组成像透镜组
几何光学薄透镜作图求像法36页PPT

31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 ห้องสมุดไป่ตู้糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
几何光学薄透镜作图求像法
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
几何光学_薄透镜

物體位置 成像性質
物體置於 焦點上 (p= f) (此時經 透鏡折射 後的射出 光線互相 平行)
成像於無窮遠處
圖例
物體位置 成像性質
物體位於 鏡前焦點 和透鏡之 間(0<p < f)
經透鏡折射後 射出的光線無 法會聚成實 像,但這些射出 光線的反方向 延長線可在鏡 前會聚成一正 立的放大虛 像。(若物體愈 接近透鏡,所成 的虛像也愈接 近透鏡,且愈小 (仍較原物體 為大)。)
4. 若將物體置於凹透鏡前,利用前述成像法則,發現僅能在 鏡後成一縮小的正立虛像,如下圖(一)(a)(b)所示;物體愈 接近透鏡,成像位置也愈接近透鏡,所形成的虛像愈大(仍 較原物體為小),如下圖(二)所示。
(a)
(b)
圖(一)
圖(二)
5. 薄透鏡成像公式:物體經薄透鏡成像時,物距 p、像距 q 和焦
圖(一)
圖(二)
範例 2 共軛成像
一物體與一屏相距 100 公分,如在其間某處置一凸透鏡,恰可成 一實像於屏上,像長為 h1 公分。又如將凸透鏡向屏移動 50 公分,
h1 又可成像於屏上,像長變為 h2 公分,則 h2 為何? (A) 1 (B) 3 (C) 6 (D) 8 (E) 9
[答案] E
q-f f
,故
-hi h0
=
f p-f
=
q-f f
由上式得(p-f)(q-f)=f 2,化簡後得
1 p
+
1 q
=
1 f
……○1
(2) 凸透鏡成虛像時:
如圖(a)所示,由兩橘紅色三角形相似,對應邊成比例,
得
hi h0
=
q p
。在圖(b)中的兩綠色三角形相似,對應邊成
薄透镜

n n n n s s r 1.5 1 1.5 1 s 6 4 s 36cm
此象的横向放大率:
ny ny 0 s s y ns y ns y ns 1 (36) 1 4 y ns 1.5 (6)
O
F
物体置于透像二倍焦距之内,一 倍焦距之外(2f>u>f)
物体置于透像一倍焦距之内(u<f)
凹透镜成像作图法 当发光点不在主轴上时,经过凹透镜的三 条特殊光线的方向为:
跟主轴平行的光线经过透 镜后,其反向沿长线过焦点; 通过光心的光线经透镜 后,方向不变; 沿长线过焦点的光线, 经过透镜后,跟主轴平行。
n1
S
n2
O1 O2
S
S1
s
s1
s
将(1)式与(2)式两边相加,得
n2 n1 n n1 n2 n ' S S r1 r2
称为薄透镜物像公式。
上式右边为薄透镜的光焦度,即
( 3)
1 2
式中
(4)
n n1 1 , r1
n2 n 2 r2
f' f 1 s' s
称为薄透镜物像公式的高斯形式。
由薄透镜的焦距公式
f n2 f n1
(5)
即薄透镜 焦距之比等于两边的折射率之比 的负值.
空气中的薄透镜焦距为
ff 1 1 1 (n0 1.0)( ) r1 r2 .
(6)
f = f 0 时为正透镜, 又称为凸透镜;
' 1
f' f 1 s' s 2
几何光学5资料

焦面的共轭平面在无穷远处,焦面上轴外点的共轭点是 轴外的无穷远点。 如下图示:
目录
焦面
焦面
焦面
焦面
po(op) 为副光轴,透镜的对称轴为主光轴。
目录
§5 作图法
求物象关系:
1、物象公式计算
特殊光线作图法 2、作图法
任意光线作图法
作图法依据:在傍轴条件下,入射同心光束经过薄透镜折射
后出射光束仍然是同心光束。只要找到从物点发出的两条光线 折射后的共轭出射光线的交点,就可以确定其共轭像点。
若 f ' f ,则得到高斯公式的简化形式:
11 1 s' s f
这就是薄透镜傍轴成像的高斯公式 。
目录
二、薄透镜傍轴成像的符号法则 :
若入射光由左向右传播,计算起点是薄透镜的光心O时, 薄透镜傍轴成像的符号法则与单球折射面成像的符号法则相 同。由此可知,对于 f ' f 0 的会聚薄透镜来说,若入射光
薄透镜光焦度的定义式也适用于单球折反射面的情形。将单球
折射面的焦距公式代入屈光度公式可以得到单球折射面的光焦
度的另一表达式: P n ' n r
过程同学们可自行证明。
目录
§4 焦面
焦面
物方焦面:通过物方焦点F与光轴垂直的平面。 (第一焦面,前焦面)
像方焦面:通过像方焦点F ’与光轴垂直的平面。 (第二焦面,后焦面)
透镜两侧介质的折射率n、n ' 小于透镜介质的折射率n0 时,
凸薄透镜则为负(或发散)薄透镜,凹薄透镜则为正(或会 聚)薄透镜。
目录
下图为各种形状的透镜:
目录
§2 成像公式
一、薄透镜傍轴成像的高斯公式 :
将物像方焦距公式代入薄透镜的成像公式,并稍加理,就 可以得到薄透镜傍轴成像的高斯公式:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d << r1 , r2 , | s |, | s ′ |
就是薄透镜,通常可以认为
通常情况下 n=n' ≈ 1
d =0
3
此时,两球面顶点重合,称为光心,记为O。
6.1 薄透镜的成像特性
回顾逐次成像法 ① 成像透镜由两个折射球面组成,透镜使光线经过了两个球 面的折射。 ② 可以用逐次成像法得到透镜的成像公式。 ③ 物Q经第一面折射成像Q'(应用物像关系可确定像)。 ④ Q'无论虚实,总是发出光线的,对第二面来说等效于物。 ⑤ Q'作为第二面的物,经第二面折射成像 像关系可确定像)。 ⑥ 反复应用上述方法,可得到最终的像。 (再次应用物
n f = = n L − n n ′ − nL Φ + r1 r2
f′= nL − n n′ − n L + r1 r2
n′
n
物方焦距
s=∞
n′
=
n′ Φ
像方焦距
n
nL
f
f′
8
6.1 薄透镜的成像特性
空气中的薄透镜
n = n′ = 1
1
磨镜者公式
f = f′=
1 1 (n L − 1)( − ) r1 r2
n L − n n′ − n L Φ= + r1 r2
薄透镜的光焦度,单位是屈光度(diopter,D),对于眼镜,度数为100Φ
6
6.1 薄透镜的成像特性
问题:厚透镜有“光焦度”的概念吗?
n
Q C2
Σ1 Σ 2 − r2 nL
O1 O
r1
n′
Q1′
O2 Q ′ C1
′ s2
s1
− s2
′ s1
d
r2 > 0 ⇒ f = f′<0 r1 < 0 r2 < 0 & r2 > r1 r < 0& r < r ⇒ f = f ′ > 0 2 1 2
f = f ′ > 0 ⇒ 正透镜
f = f ′ < 0 ⇒ 正透镜
13
从Fermat原理看,这也是很自然的结果。
6.1 薄透镜的成像特性
11
6.1 薄透镜的成像特性
正透镜与负透镜
① 焦距为正值的透镜是正透镜;焦距为负值的透镜是负透镜。 ② 正透镜的像方焦点在光线出射方;负透镜的像方焦点在光线入射 方。 ③ 正透镜使入射的平行光汇聚在像方焦点;负透镜使入射的平行光 发散,反向延长线通过像方焦点。 ④ 空气中,中间厚边缘薄的透镜是正透镜;中间薄边缘厚的透镜是 负透镜。
s = x+ f
s′ = x′ + f ′
xf ′ + ff ′ + x′f + f ′ f = x′x + x′f + xf ′ + f ′ f
牛顿公式的符号约定 (1)物点Q 在F 的左边时,x>0;反之,则 x<0。 (2)像点Q' 在F' 的左侧时,x'<0;反之,则 x'>0。
⇒
xx′ = ff ′
s
0 −a
s
0
a
正透镜
f =a
−a
0
a
负透镜
15
6.1 薄透镜的成像特性
薄透镜成像的横向放大率
(1) 总放大率为两次成像的放大率的乘积
n
s
第一次成像,V 1 是实物成像
nL
′ ns1 = (− ) nL s
n′
s′
s1′
nL s ′ = [− ] ′) n′( − s1
V = VV 1 2
(2) Lagrange-Helmhotz恒等式依然成立
从费马原理再看光学成像
• 证明空气中的正透镜必定是中间厚边缘薄;负透镜必定是中 间薄边缘厚 • 所谓正透镜,系指物方焦点在其光线入射方,而像方焦点在 其光线出射方 • 以平行光正入射证明
平行光自左侧入射,汇聚到正透镜右侧焦点 光线愈远离光轴,所经过距离愈长 为使光程相等,则远离光轴的光线,其在透镜中的距离必须较短 所以正透镜的形状,必须愈远离中心轴线,厚度愈薄 正透镜的形状,必定是中间厚边缘薄的结构 同理,负透镜的形状,必定是中间薄边缘厚的结构 光线在透镜中的光程+虚光线的虚光程=定值
n′ = 1
n =1
nL
f = f′
9
6.1 薄透镜的成像特性
Gauss物像公式 - 距离从光心算起
n
Σ1
nL
Σ2
n′
Q
d
′ s2
Q′ s2
Q1
s = s1
n′ n n L − n n′ − n L + = + s′ s r1 r2
nL − n n′ − nL + r1 r2 n′ f′= nL − n n′ − nL + r1 r2 f = n
34
12
6.1 薄透镜的成像特性
正透镜与负透镜
f = f′= 1 (n L − 1)( 1 1 − ) r1 r2
1 1 正透镜 > r1 r2
1 1 负透镜 < r1 r2
r2 < 0 ⇒ f = f′>0 r1 > 0 r2 > 0 & r2 > r1 r > 0&r < r ⇒ f = f ′ < 0 2 1 2
F'
F'
14
6.1 薄透镜的成像特性
o
结论:薄透镜的物 方和像方焦点永远 分处 于 透镜的两 侧 。 并且一般情况下两 个焦点不对称,即 焦距大小不相等。 只有当物像方介质 折射率相等时,透 镜的物像方焦距大 小才相等。
a 0 −a
s′
实 像 虚物 虚 像
−a a
s′
实 像 虚物 虚 像 实物
实物
F F’
o
19
6.3 焦平面
薄透镜的光学参数定义 物方焦平面 像方焦平面
F
F′
光轴
物方焦点
F
f
光心 O
像方焦点
f′
像方焦距
F′
O
物方焦距
特性:极薄的平行玻璃平 板,两侧折射率相等,通 过光心的光线方向不变
副光轴:通过光心的直线。 主光轴:光具组的光轴,简称主轴。
20
6.4 薄透镜作图法
三对共轭的特殊光线
F1
F1′
F2′
F2
28
6.5 透镜组成像
逐次成像法示例2:透镜1所成的像是透镜2的虚物
L1 F1 F2′ F1′
L2 F2
L1的实像,对于L2来说,是虚物
29
6.5 透镜组成像
另一种透镜组的作图解法
L1 F1
L2 F2
F2′ F1′
1. 直接利用第一镜的光线作图; 2. 利用第二镜的物的特殊光线作图。
F
F′
像方焦点
物方焦平面
像方焦平面
23
6.4 薄透镜作图法
正透镜作图法3
物方焦点
F
F ′ 像方焦点
物方焦平面
像方焦平面
24
6.4 薄透镜作图法
负透镜作图法1
像方焦点
F′
F
物方焦点
像方焦平面
物方焦平面
25
6.4 薄透镜作图法
负透镜作图法2
像方焦点
F′
F
物方焦点
像方焦平面
物方焦平面
26
6.4 薄透镜作图法
′ nL s′ ns1 = (− )( ) ′ nL s n′s1
第二次成像, V 2 是虚物成像
ns′ =− n′s
′nLu1 ′ = y ′n′u′ ynu = y1
16
6.1 薄透镜的成像特性
薄透镜的横向放大率
n
nL
n′
f
ns′ V =− n′s x′
F
x
′ F f′ s′
s
f n ′ fs = 用高斯公式表示: 利用 得到 V = − f ′ n′ ′ fs fs′ f ( x′ + f ′) 用牛顿公式表示 V = − =− × 利用 xf = x′f ′ ′ fs f′ x+ f
33
习题
p.70: 2, 3, 8, 11
补充题: 在科研实验中,经常需要将入射的平行光改变为较粗或教细的平行光,这 被称为无焦系统。例如,将激光发出的光束扩展为较宽的光束,这种系统被称 为扩束系统。请根据理想光具组的计算方法,采用两个焦距分别为f1' 和f2' 的薄 透镜,设计一个无焦系统,并给出其横向放大率(光束直径)的分析。
F 物方焦平面
F' 像方焦平面
平行于光轴的入射光线←→经过像方焦点的光线 经过物方焦点的光线←→平行于光轴的像方光线 经过透镜光心的入射光线←→经过透镜光心的像方光线
21
6.4 薄透镜作图法
正透镜作图法1
物方焦点
F
F ′ 像方焦点
物方焦平面
像方焦平面
22
6.4 薄透镜作图法
正透镜作图法2
物方焦点
第一章 几何光学
第六节 薄透镜
1
第六节 薄透镜
6.1 薄透镜的成像特性 6.2 密接薄透镜组 6.3 焦平面 6.4 薄透镜作图法 6.5 透镜组成像
2
6.1 薄透镜的成像特性
透镜 透镜:由两个折射球面构成的 光具组,球面间为透镜媒质。 薄透镜 由两个折射球面组成,过两 球面圆心的直线为光轴,顶 点间距 d。如果满足:
f x′ 得到 V = − = − x f′
若n=n',则
