广东省佛山市2013年中考数学试卷(含解析)
2013年广东省中考数学试卷及答案解析
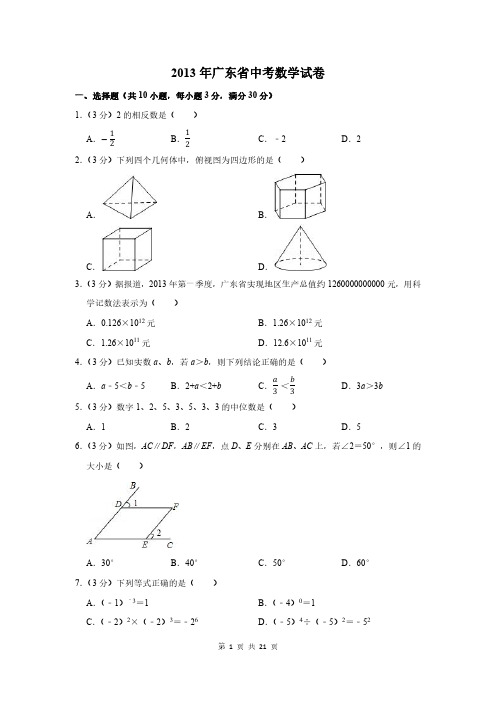
B、六棱柱的俯视图是六边形,故此选项错误;
C、正方体俯视图是正方形,故此选项正确;
D、圆锥的俯视图是有圆心的圆,故此选项错误,
故选:C.
3.(3 分)据报道,2013 年第一季度,广东省实现地区生产总值约 1260000000000 元,用科
学记数法表示为( )
A.0.126×1012 元
B.1.26×1012 元
6% 28%
20% 16% 100%
21.(8 分)雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐 款活动.第一天收到捐款 10000 元,第三天收到捐款 12100 元. (1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率; (2)按照(1)中收到捐款的增长率速度,第四天该单位能收到多少捐款?
大小是( )
A.30°
B.40°
C.50°
D.60°
【解答】解:∵AB∥EF,
∴∠A=∠2=50°,
∵AC∥DF,
∴∠1=∠A=50°.
故选:C.
7.(3 分)下列等式正确的是( )
A.(﹣1)﹣3=1
B.(﹣4)0=1
C.(﹣2)2×(﹣2)3=﹣26
D.(﹣5)4÷(﹣5)2=﹣52
【解答】解:A、(﹣1)﹣3=﹣1,故此选项错误;
卡相应位置上. 11.(4 分)分解因式:x2﹣9= (x+3)(x﹣3) .
【解答】解:x2﹣9=(x+3)(x﹣3).
故答案为:(x+3)(x﹣3).
12.(4 分)若实数 a、b 满足|a+2|
ኃ ,则
1.
【解答】解:根据题意得:
,
ኃ
解得:
, ኃ
2013年广东省中考数学试题及答案

2013年广东省中考数 学说明:1. 全卷共4页,考试用时100 分钟.满分为 120 分.2.答题前,考生务必用黑色字迹的签字笔或钢笔在答题卡上填写自己准考证号、姓名、试室号、座位号,用2B 铅笔把对应号码的标号涂黑.3.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案,答案不能答在试题上. 4.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.5.考生务必保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑. 1. 2的相反数是A.21-B. 21C.-2D.2 2.下列几何体中,俯视图为四边形的是3.据报道,2013年第一季度,广东省实现地区生产总值约1 260 000 000 000元,用科学记数法表示为A. 0.126×1012元 B. 1.26×1012元 C. 1.26×1011元 D. 12.6×1011元 4.已知实数a 、b ,若a >b ,则下列结论正确的是 A.55-<-b a B.b a +<+22 C.33ba < D.b a 33>5.数据1、2、5、3、5、3、3的中位数是 A.1 B.2 C.3 D.56.如题6图,AC ∥DF,AB ∥EF,点D 、E 分别在AB 、AC 上,若∠2=50°, 则∠1的大小是A.30°B.40°C.50°D.60°7.下列等式正确的是 A.1)1(3=-- B. 1)4(0=- C. 6322)2()2(-=-⨯- D. 2245)5()5(-=-÷-8.不等式5215+>-x x 的解集在数轴上表示正确的是9.下列图形中,不是..轴对称图形的是10.已知210k k <<,则是函数11-=x k y 和xk y 2=的图象大致是二、填空题(本大题6小题,每小题4分,共24分)请将下列各题的正确答案填写在答题卡相应的位置上.11.分解因式:92-x =________________.12.若实数a 、b 满足042=-++b a ,则=ba 2________.13.一个六边形的内角和是__________.14.在R t △ABC 中,∠ABC=90°,AB=3,BC=4,则sinA=________.15.如题15图,将一张直角三角板纸片ABC 沿中位线DE 剪开后,在平面上将△BDE 绕着CB 的中点D 逆时针旋转180°,点E 到了点E ′位置, 则四边形ACE ′E 的形状是________________.16.如题16图,三个小正方形的边长都为1,则图中阴影部分面积的和是__________(结果保留π).三、解答题(一)(本大题3小题,每小题5分,共15分) 17.解方程组⎩⎨⎧=++=821y x y x18.从三个代数式:①222b ab a +-,②b a 33-,③22b a -中任意选择两个代数式构造成分式,然后进行化简,并求当3,6==b a 时该分式的值. ① ②19.如题19图,已知□ABCD.(1)作图延长BC,并在BC的延长线上截取线段CE,使得CE=BC(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,不连结AE,交CD于点F,求证△AFD≌△EFC.四、解答题(二)(本大题3小题,每小题8分,共24分)20.某校教导处为了解该校七年级同学对排球、乒乓球、羽毛球、篮球和足球五种球类运动项目的喜爱情况(每位同学必须且只能选择最喜爱的一项运动项目),进行了随机抽样调查,并将调查结果统计后绘制成了如【表1】和题20图所示的不完整统计图表.(1)请你补全下列样本人数分布表(【表1】)和条形统计图(题20图);(2)若七年级学生总人数为920人,请你估计七年级学生喜爱羽毛球运动项目的人数.21.雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?22.如题22图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.(1)设R t△CBD的面积为S1, R t△BFC的面积为S2, R t△DCE的面积为S3 ,则S1______ S2+ S3(用“>”、“=”、“<”填空);(2)写出题22图中的三对相似三角形,并选择其中一对进行证明.五、解答题(三)(本大题3小题,每小题9分,共27分) 23. 已知二次函数1222-+-=m mx x y .(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式; (2)如题23图,当2=m 时,该抛物线与y 轴交于点C,顶点为D, 求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P,使得PC+PD 最短?若P 点 存在,求出P 点的坐标;若P 点不存在,请说明理由.24.如题24图,⊙O 是Rt △ABC 的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5, BE ⊥DC 交DC 的延长线于点E. (1)求证:∠BCA=∠BAD; (2)求DE 的长;(3)求证BE 是⊙O 的切线.25.有一副直角三角板,在三角板ABC 中,∠BAC=90°,AB=AC=6,在三角板DEF 中,∠FDE=90°,DF=4,DE=34.将这副直角三角板按如题25图(1)所示位置摆放,点B 与点F 重合,直角边BA 与FD 在同一条直线上.现固定三角板ABC,将三角板DEF 沿射线BA 方向平行移动,当点F 运动到点A 时停止运动.(1)如题25图(2),当三角板DEF 运动到点D 与点A 重合时,设EF 与BC 交于点M, 则∠EMC=______度;(2)如题25图(3),在三角板DEF 运动过程中,当EF 经过点C 时,求FC 的长;(3)在三角板DEF 运动过程中,设BF=x ,两块三角板重叠部分面积为y ,求y 与x 的函数解析式,并求出对应的x 取值范围.2013年广东省中考 数学参考答案1、答案:C解析:2的相反数为-2,选C ,本题较简单。
2013年广东省佛山市高中阶段招生考试数学试题(解析版)

2013年广东省佛山市高中阶段招生考试数学试题一、选择题(每小题3分,共30分) 1.2-的相反数是( )A .2B .2-C .21D .21- 2.下列计算正确的是( )A .1243a a a =⋅ B .743)(a a = C .3632)(b a b a = D .)0( 43≠=÷a a a a 3.并排放置的等底等高的圆锥和圆柱(如图)的主视图是( )4.分解因式a a -3的结果是( )A .)1(2-a aB .2)1(-a aC .)1)(1(-+a a aD .)1)((2-+a a a 5.化简)12(2-÷的结果是( )A .122-B .22-C .21-D .22+6.掷一枚有正反面的均匀硬币,正确的说法是( ) A .正面一定朝上 B .反面一定朝上C .正面比反面朝上的概率大D .正面和反面朝上的概率都是0.5 7.如图,若∠A =60°,AC =20m ,则BC 大约是(结果精确到0.1m)( ) A .34.64m B .34.6m C .28.3m D .17.3m 9.多项式2321xy xy -+的次数及最高次项的系数分别是( )A .3 3-,B .3 2-,C .3 5-,D .3 2, 10.某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y 与时间x 的关系的大致图象是( )二、填空题(每小题3分,共15分)11.数字9 600 000用科学记数法表示为________________.A .B .C .D .ACB第7题图12.方程0222=--x x 的解是_________________. 15.命题“对顶角相等”的条件是______________.三、解答题(第16~20每小题6分,第21~23每小题8分,第24小题10分,第25小题11分,共75分) 16.计算:[])24()2(5213-÷----+⨯.17.网格图中每个方格都是边长为1的正方形.若A ,B ,C ,D ,E ,F 都是格点, 试说明△ABC ∽△DEF .18.按要求化简:21312aa a -++-. 要求:见答题卡.19.已知两个语句:①式子12-x 的值在1(含1)与3(含3)之间; ②式子12-x 的值不小于1且不大于3. 请回答以下问题:AB C DE F 第17题图(1) 两个语句表达的意思是否一样(不用说明理由)? (2) 把两个语句分别用数学式子表示出来.22.课本指出:公认的真命题称为公理,除了公理外,其他的真命题(如推论、定理等)的正确性都需要通过推理的方法证实.(1) 叙述三角形全等的判定方法中的推论AAS ; (2) 证明推论AAS .要求:叙述推论用文字表达;用图形中的符号表达已知、 求证,并证明,证明对各步骤要注明依据.23.在一次考试中,从全体参加考试的1000名学生中随机抽取了120名学生的答题卷进行统计分析.其中,某个单项选择题答题情况如下表(没有多选和不选):(1) 根据统计表画出扇形统计图;要求:画图前先求角;画图可借助任何工具,其中一个角的作图 用尺规作图(保留痕迹,不写作法和证明);统计图中标注角度. (2) 如果这个选择题满分是3分,正确的选项是C ,则估计全体学生该题的平均得分是多少?25.我们知道,矩形是特殊的平行四边形,所以矩形除了具备平行四边形的一切性质还有其特殊的性质;同样,ABCDEF第22题图第23题图黄金矩形是特殊的矩形,因此黄金矩形有与一般矩形不一样的知识. 已知平行四边形ABCD ,∠A =60°,AB =2a ,AD =a . (1) 把所给的平行四边形ABCD 用两种方式分割并作说明 (见题答卡表格里的示例);要求:用直线段分割,分割成的图形是学习过的特殊图形且不超出四个. (2) 图中关于边、角和对角线会有若干关系或问题.现在请计算两条对角线的长度.要求:计算对角线BD 长的过程中要有必要的论证;直接写出对角线AC 的长. 解:在表格中作答(2)第25题图第25题图第25题图2013年广东省佛山市高中阶段招生考试数学试题(解析版)一、选择题(每小题3分,共30分)1.(2013年佛山市)2-的相反数是( ) A .2 B .2- C .21 D .21- 分析:根据相反数的定义:只有符号不同的两个数叫做互为相反数即可得到答案解:﹣2的相反数是2,故选:A .点评:此题主要考查了相反数,关键是掌握相反数的定义 2.(2013年佛山市)下列计算正确的是( )A .1243a a a =⋅ B .743)(a a = C .3632)(b a b a = D .)0( 43≠=÷a a a a 分析:根据同底数幂乘法、幂的乘方、积的乘方的运算性质,利用排除法求解解:A 、应为a 3•a 4=a 7,故本选项错误;B 、应为(a 3)4=a 12,故本选项错误; C 、每个因式都分别乘方,正确;D 、应为a 3÷a 4=(a ≠0),故本选项错误.故选C .点评:本题考查了同底数幂的乘法,积的乘方和幂的乘方,需熟练掌握且区分清楚,才不容易出错 3.(2013年佛山市)并排放置的等底等高的圆锥和圆柱(如图)的主视图是( )分析:找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中 解:圆锥的左视图是三角形,圆柱的左视图是长方形, 故选:B .点评:本题考查了三视图的知识,主视图是从物体的正面看得到的视图 4.(2013年佛山市)分解因式a a -3的结果是( )A .)1(2-a a B .2)1(-a a C .)1)(1(-+a a a D .)1)((2-+a a a分析:首先提取公因式a ,再利用平方差公式进行二次分解即可解:a 3﹣a=a (a 2﹣1)=a (a+1)(a ﹣1), 故选:C .点评:此题主要考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止 5.(2013年佛山市)化简)12(2-÷的结果是( )A .122-B .22-C .21-D .22+分析:分子、分母同时乘以(+1)即可解:原式===2+.A .B .C .D .故选D .点评:本题考查了分母有理化,正确选择两个二次根式,使它们的积符合平方差公式是解答问题的关键 6.(2013年佛山市)掷一枚有正反面的均匀硬币,正确的说法是( ) A .正面一定朝上 B .反面一定朝上C .正面比反面朝上的概率大D .正面和反面朝上的概率都是0.5 分析:根据掷一枚有正反面的均匀硬币,则得到正反两面的概率相等,即可得出答案 解:∵掷一枚有正反面的均匀硬币,∴正面和反面朝上的概率都是0.5.故选:D . 点评:此题主要考查了概率的意义,根据正反面出现的机会均等是解题关键7.(2013年佛山市)如图,若∠A =60°,AC =20m ,则BC 大约是(结果精确到0.1m)( ) A .34.64m B .34.6m C .28.3m D .17.3m分析:首先计算出∠B 的度数,再根据直角三角形的性质可得AB=40m ,再利用勾股定理计算出BC 长即可 解:∵∠A=60°,∠C=90°,∴∠B=30°,∴AB=2AC ,∵AC=20m ,∴AB=40m , ∴BC====20≈34.6(m ),故选:B . 点评:此题主要考查了勾股定理,以及直角三角形的性质,关键是掌握在直角三角形中,30°角所对的直角边等于斜边的一半.在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方 8.(2013年佛山)半径为3的圆中,一条弦长为4,则圆心到这条弦的距离是()A.3B.4C.5D.7分析:过点O 作OD ⊥AB 于点D ,由垂径定理可求出BD 的长,在Rt △BOD 中,利用勾股定理即可得出OD 的长.解:如图所示:过点O 作OD ⊥AB 于点D , ∵OB=3,AB=3,OD ⊥AB , ∴BD=AB=×4=2, 在Rt △BOD 中,OD===.故选C .点评:本题考查的是垂径定理,根据题意画出图形,利用勾股定理求出OD 的长是解答此题的关键 9.(2013年佛山市)多项式2321xy xy -+的次数及最高次项的系数分别是( )A .3 3-,B .3 2-,C .3 5-,D .3 2, 分析:根据多项式中次数最高的项的次数叫做多项式的次数可得此多项式为3次,最高次项是﹣3xy 2,系数是数字因数,故为﹣3.解:多项式1+2xy ﹣3xy 2的次数是3,最高次项是﹣3xy 2,系数是﹣3; 故选:A .点评:此题主要考查了多项式,关键是掌握多项式次数的计算方法与单项式的区别10.(2013年佛山市)某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y 与时间x的关系的大致图象是( )分析:根据在每段中,离家的距离随时间的变化情况即可进行判断ACB第7题图x y O A . xyO B .x yO C . xyOD .解:图象应分三个阶段,第一阶段:匀速跑步到公园,在这个阶段,离家的距离随时间的增大而增大; 第二阶段:在公园停留了一段时间,这一阶段离家的距离不随时间的变化而改变.故D 错误;第三阶段:沿原路匀速步行回家,这一阶段,离家的距离随时间的增大而减小,故A 错误,并且这段的速度小于于第一阶段的速度,则C 错误. 故选B .点评:本题考查了函数的图象,理解每阶段中,离家的距离与时间的关系,根据图象的斜率判断运动的速度是解决本题的关键.二、填空题(每小题3分,共15分)11.(2013年佛山市)数字9 600 000用科学记数法表示为________________.分析:科学记数法的表示形式为a ×10n的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.解:将9 600 000用科学记数法表示为:9.6×106.故答案为:9.6×106.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a ×10n的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.12.(2013年佛山市)方程0222=--x x 的解是_________________.分析:首先把常数﹣2移到等号右边,再两边同时加上一次项系数一半的平方,把左边配成完全平方公式,再开方,解方程即可.解:x 2﹣2x ﹣2=0,移项得:x 2﹣2x=2,配方得:x 2﹣2x+1=2+1,(x ﹣1)2=3,两边直接开平方得:x ﹣1=,则x 1=+1,x 2=﹣+1. 点评:此题主要考查了配方法解一元二次方程,配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数. 13.(2013•佛山)在1,2,3,4四个数字中随机选两个不同的数字组成两位数,则组成的两位数大于40的概率是 .分析:画出树状图,然后根据概率公式列式计算即可得解 解:根据题意画出树状图如下:一共有12种情况,组成的两位数大于40的情况有3种, 所以,P (组成的两位数大于40)==.故答案为:.点评:本题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比 14.(2013•佛山)图中圆心角∠AOB=30°,弦CA ∥OB ,延长CO 与圆交于点D ,则∠BOD= .分析:根据平行线的性质由CA ∥OB 得到∠CAO=∠AOB=30°,利用半径相等得到∠C=∠OAC=30°,然后根据圆周角定理得到∠AOD=2∠C=60°,则∠BOD=60°﹣30°=30°. 解:解:∵CA ∥OB ,∴∠CAO=∠AOB=30°,∵OA=OC ,∴∠C=∠OAC=30°,∴∠AOD=2∠C=60°,∴∠BOD=60°﹣30°=30°.故答案为30°.点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.也考查了平行线的性质.15.(2013年佛山市)命题“对顶角相等”的条件是______________.分析:根据命题由题设与结论组成可得到对顶角相等”的“条件”是若两个角是对顶角,结论是这两个角相等 解:“对顶角相等”的“条件”是两个角是对顶角. 故答案为:两个角是对顶角.点评:本题考查了命题:判断事物的语句叫命题;正确的命题称为真命题;错误的命题称为假命题;命题由题设与结论组成,两个互换题设与结论的命题称为互逆命题.三、解答题(第16~20每小题6分,第21~23每小题8分,第24小题10分,第25小题11分,共75分) 16.(2013年佛山市)计算:[])24()2(5213-÷----+⨯.分析:根据负整数指数幂以及绝对值、乘方运算法则等性质,先算乘方,再算乘除,最后算加法得出即可 解:2×[5+(﹣2)3]﹣(﹣|﹣4|÷2﹣1=2×(5﹣8)﹣(﹣4÷)=﹣6﹣(﹣8)=2. 点评:此题主要考查了实数运算,本题需注意的知识点是:负整数指数幂时,a ﹣p=17.(2013年佛山市)网格图中每个方格都是边长为1的正方形. 若A ,B ,C ,D ,E ,F 都是格点,试说明△ABC ∽△DEF .分析:利用图形与勾股定理可以推知图中两个三角形的三条对应边成比例,由此可以证得△ABC ∽△DEF . 解:证明:∵AC=,BC==,AB=4,DF==2,EF==2,ED=8, ∴===2,∴△ABC ∽△DEF .点评:本题考查了相似三角形的判定、勾股定理.相似三角形相似的判定方法有:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;这是判定三角形相似的一种基本方法.相似的基本图形可分别记为“A ”型和“X ”型,如图所示在应用时要善于从复杂的图形中抽象出这些基本图形;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似; (4)两角法:有两组角对应相等的两个三角形相似. 18.(2013年佛山市)按要求化简:21312aa a -++-. 要求:见答题卡. AB C D EF 第17题图意最后结果要化简. 解:原式=﹣= ==.点评:此题主要考查了分式的加减,关键是掌握异分母分式加减法法则:把分母不相同的几个分式化成分母相同的分式,叫做通分,经过通分,异分母分式的加减就转化为同分母分式的加减.19.(2013年佛山市)已知两个语句:①式子12-x 的值在1(含1)与3(含3)之间; ②式子12-x 的值不小于1且不大于3. 请回答以下问题:(3) 两个语句表达的意思是否一样(不用说明理由)? (4) 把两个语句分别用数学式子表示出来.分析:(1)注意分析“在1(含1)与3(含3)之间”及“不小于1且不大于3”的意思即可; (2)根据题意可得不等式组.解:(1)一样;(2)①式子2x ﹣1的值在1(含1)与3(含3)之间可得1≤2x ﹣1≤3; ②式子2x ﹣1的值不小于1且不大于3可得.点评:此题主要考查了由实际问题抽象出一元一次不等式组,关键是正确理解题意,抓住题干中体现不等关系的词语. 20.(6分)(2013•佛山)如图,圆锥的侧面展开图是一个半圆,求母线AB 与高AO 的夹角.参考公式:圆锥的侧面积S=πrl ,其中r 为底面半径,l 为母线长.分析:设出圆锥的半径与母线长,利用圆锥的底面周长等于侧面展开图的弧长得到圆锥的半径与母线长,进而表示出母线与高的夹角的正弦值,也就求出了夹角的度数.解:设圆锥的母线长为l,底面半径为r,则:πl=2πr,∴l=2r,∴母线与高的夹角的正弦值==,∴母线AB与高AO的夹角30°.点评:此题主要考查了圆锥的侧面展开图的弧长等于圆锥的底面周长;注意利用一个角相应的三角函数值求得角的度数.21 21.(8分)(2013•佛山)已知正比例函数y=ax与反比例函数的图象有一个公共点A(1,2).(1)求这两个函数的表达式;(2)画出草图,根据图象写出正比例函数值大于反比例函数值时x的取值范围.分析:(1)分别把A点坐标代入正比例函数解析式和反比例函数解析式,求出a与b的值,从而确定两函数解析式;(2)先画出y=和y=2x的图象,根据对称性得到两函数的另一个交点B与点A关于原点对称,则B点坐标为(﹣1,﹣2),然后观察图象得到当﹣1<x<0或x>2时,正比例函数图象都在反比例函数图象上方,即正比例函数值大于反比例函数值.解:(1)把A(1,2)代入y=ax得a=2,所以正比例函数解析式为y=2x;把A(1,2)代入y=得b=1×2=2,所以反比例函数解析式为y=;(2)如图,当﹣1<x<0或x>1时,正比例函数值大于反比例函数值.点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.22.(2013年佛山市)课本指出:公认的真命题称为公理,除了公理外,其他的真命题(如推论、定理等)的正确性都需要通过推理的方法证实.(3)叙述三角形全等的判定方法中的推论AAS;(4)证明推论AAS.要求:叙述推论用文字表达;用图形中的符号表达已知、求证,并证明,证明对各步骤要注明依据.分析:(1)两边及其夹角分别对应相等的两个三角形全等.(2)根据三角形内角和定理和全等三角形的判断定理ASA来证明.解:(1)三角形全等的判定方法中的推论AAS指的是:两边及其夹角分别对应相等的两个三角形全等.(2)已知:在△ABC与△DEF中,∠A=∠D,∠C=∠F,BC=EF.求证:△ABC≌△DEF.证明:如图,在△ABC与△DEF中,∠A=∠D,∠C=∠F(已知),∴∠A+∠C=∠D+∠F(等量代换).又∵∠A+∠B+∠C=180°,∠D+∠E+∠F=180°(三角形内角和定理),∴∠B=∠E.∴在△ABC与△DEF 中,,∴△ABC≌△DEF(ASA).点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.23.(2013年佛山市)在一次考试中,从全体参加考试的1000名学生中随机抽取了120名学生的答题卷进行统计分析.其中,某个单项选择题答题情况如下表(没有多选和不选):选项 A B C D选择人数15 5 9010(3)根据统计表画出扇形统计图;要求:画图前先求角;画图可借助任何工具,其中一个角的作图用尺规作图(保留痕迹,不写作法和证明);统计图中标注角度.(4)如果这个选择题满分是3分,正确的选项是C,则估计全体学生该题的平均得分是多少?分析:(1)根据用每个选项的人数除以总数即可得出扇形图中所占比例,进而求出各角的度数;(2)根据统计表求出总得分,进而得出平均分即可.解:(1)根据图表数据得出:选A的所占圆心角为:×360°=45°;选B的所占圆心角为:×360°=15°;选C的所占圆心角为:×360°=270°;选D的所占圆心角为:×360°=30°.如图所示:(2)∵选择题满分是3分,正确的选项是C,∴全体学生该题的平均得分为:=2.25(分),答:全体学生该题的平均得分是2.25分.AB CDE F第22题图第23题图点评:本题考查的是扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.24.(10分)(2013•佛山)如图①,已知抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3).(1)求抛物线的函数表达式;(2)求抛物线的顶点坐标和对称轴;(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).分析:(1)把点A、B、C代入抛物线解析式y=ax2+bx+c利用待定系数法求解即可;(2)把抛物线解析式整理成顶点式形式,然后写出顶点坐标与对称轴即可;(3)根据顶点坐标求出向上平移的距离,再根据阴影部分的面积等于平行四边形的面积,列式进行计算即可得解.解:(1)∵抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3),∴,解得,所以抛物线的函数表达式为y=x2﹣4x+3;(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的顶点坐标为(2,﹣1),对称轴为直线x=2;(3)如图,∵抛物线的顶点坐标为(2,﹣1),∴PP′=1,阴影部分的面积等于平行四边形A′APP′的面积,平行四边形A′APP′的面积=1×2=2,∴阴影部分的面积=2.点评:本题考查了待定系数法求二次函数解析式,二次函数的性质,二次函数图象与几何变换,(3)根据平移的性质,把阴影部分的面积转化为平行四边形的面积是解题的关键.25.(2013年佛山市)我们知道,矩形是特殊的平行四边形,所以矩形除了具备平行四边形的一切性质还有其特殊的性质;同样,黄金矩形是特殊的矩形,因此黄金矩形有与一般矩形不一样的知识.已知平行四边形ABCD ,∠A =60°,AB =2a ,AD =a . (3) 把所给的平行四边形ABCD 用两种方式分割并作说明 (见题答卡表格里的示例);要求:用直线段分割,分割成的图形是学习过的特殊图形且不超出四个. (4) 图中关于边、角和对角线会有若干关系或问题.现在请计算两条对角线的长度.要求:计算对角线BD 长的过程中要有必要的论证;直接写出对角线AC 的长. 解:在表格中作答(2)分析:(1)方案一:分割成两个等腰梯形;方案二:分割成一个等边三角形、一个等腰三角形和一个直角三角形;(2)利用平行四边形的性质、等边三角形的性质、勾股定理作答,认真计算即可.上底长都为,下底长都为 a ∵AB=2a ,E 为AB 中点, ∴AE=BE=a ,∵AD=AE=a ,∠A=60°,∴△ADE 为等边三角形,∠ADE=∠DEA=60°,DE=AE=a ,第25题图又∵∠BED+∠DEA=180°,∴∠BED=180°﹣∠DEA=180°﹣60°=120°,又∵DE=BE=a,∠BED=120°,∴∠BDE=∠DBE=(180°﹣120°)=30°,∴∠ADB=∠ADE+∠BDE=60°+30°=90°∴Rt△ADB中,∠ADB=90°,由勾股定理得:BD2+AD2=AB2,即BD2+a2=(2a)2,解得BD=a.如右图②所示,AC=2OC=2=2=2•a=a.∴BD=a,AC=a.点评:本题是几何综合题,考查了四边形(平行四边形、等腰梯形、菱形、矩形)、三角形(等边三角形、等腰三角形、直角三角形)的图形与性质.第(1)问侧重考查了几何图形的分割、剪拼、动手操作能力和空间想象能力;第(2)问侧重考查了几何计算能力.本题考查知识点全面,对学生的几何综合能力要求较高,是一道好题。
广东省数学中考试卷和详细答案和考点分析(2013--2015)

2013年广东省中考数学试卷一、选择题(共10小题,每小题3分,满分30分)1.(3分)2的相反数是()A.B.C.﹣2D.22.(3分)下列四个几何体中,俯视图为四边形的是()3.(3分)据报道,2013年第一季度,广东省实现地区生产总值约1260 000 000 000元,用科学记数法表示为()A.0.126×1012元B.1.26×1012元C.1.26×1011元D.12.6×1011元4.(3分)已知实数a、b,若a>b,则下列结论正确的是()A.a﹣5<b﹣5B.2+a<2+b C.D.3a>3b5.(3分)数字1、2、5、3、5、3、3的中位数是()A.1B.2C.3D.56.(3分)如图,AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是()A.30°B.40°C.50°D.60°7.(3分)下列等式正确的是()A.(﹣1)﹣3=1B.(﹣4)0=1C.(﹣2)2×(﹣2)3=﹣26D.(﹣5)4÷(﹣5)2=﹣528.(3分)不等式5x﹣1>2x+5的解集在数轴上表示正确的是()A.B.C.D.9.(3分)下列图形中,不是轴对称图形的是()10.(3分)已知k1<0<k2,则函数y=k1x﹣1和y=的图象大致是()A.B.C.D.二、填空题(本大题6小题,每小题4分,共24分)请将下列各题的正确答案填写在答题卡相应位置上.11.(4分)分解因式:x2﹣9=.12.(4分)若实数a、b满足|a+2|,则=.13.(4分)一个六边形的内角和是.14.(4分)在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则sinA=.15.(4分)如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE 绕着CB的中点D逆时针旋转180°,点E到了点E′位置,则四边形ACE′E的形状是.16.(4分)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是(结果保留π).三、解答题(一)(本大题3小题,每小题5分,共15分)17.(5分)解方程组.18.(5分)从三个代数式:①a2﹣2ab+b2,②3a﹣3b,③a2﹣b2中任意选两个代数式构造分式,然后进行化简,并求出当a=6,b=3时该分式的值.19.(5分)如图,已知▱ABCD.(1)作图:延长BC,并在BC的延长线上截取线段CE,使得CE=BC(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,连结AE,交CD于点F,求证:△AFD≌△EFC.四、解答题(二)(本大题3小题,每小题8分,共24分)20.(8分)某校教导处为了解该校七年级同学对排球、乒乓球、羽毛球、篮球和足球五种球类运动项目的喜爱情况(每位同学必须且只能选择最喜爱的一项运动项目),进行了随机抽样调查,并将调查结果统计后绘制成了如图和所示的不完整统计图表.(1)请你补全下列样本人数分布表和条形统计图(如图);(2)若七年级学生总人数为920人,请你估计七年级学生喜爱羽毛球运动项目的人数.样本人数分布表类别人数百分比排球36%乒乓球1428%羽毛球15篮球20%足球816%合计100%21.(8分)雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)按照(1)中收到捐款的增长率速度,第四天该单位能收到多少捐款?22.(8分)如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1S2+S3(用“>”、“=”、“<”填空);(2)写出如图中的三对相似三角形,并选择其中一对进行证明.四、解答题(三)(本大题3小题,每小题9分,共27分)23.(9分)已知二次函数y=x2﹣2mx+m2﹣1.(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P 点的坐标;若P点不存在,请说明理由.24.(9分)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.25.(9分)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=.将这副直角三角板按如图1所示位置摆放,点B 与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.(1)如图2,当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC=度;(2)如图3,在三角板DEF运动过程中,当EF经过点C时,求FC的长;(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.2013年广东省中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)1.(3分)(2016•德州)2的相反数是()A.B.C.﹣2D.2【考点】相反数.【分析】根据相反数的概念解答即可.【解答】解:2的相反数是﹣2,故选:C.【点评】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号;一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.2.(3分)(2013•广东)下列四个几何体中,俯视图为四边形的是()【考点】简单几何体的三视图.【分析】俯视图是从物体上面看,所得到的图形.【解答】解:A、三棱锥的俯视图是,故此选项错误;B、六棱柱的俯视图是六边形,故此选项错误;C、正方体俯视图是正方形,故此选项正确;D、圆锥的俯视图是有圆心的圆,故此选项错误,故选:C.【点评】本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.3.(3分)(2013•东莞市)据报道,2013年第一季度,广东省实现地区生产总值约1260 000 000 000元,用科学记数法表示为()A.0.126×1012元B.1.26×1012元C.1.26×1011元D.12.6×1011元【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于1260 000 000 000有13位,所以可以确定n=13﹣1=12.【解答】解:1260 000 000 000=1.26×1012.故选B.【点评】此题考查科学记数法表示较大的数的方法,准确确定a与n值是关键.4.(3分)(2013•东莞市)已知实数a、b,若a>b,则下列结论正确的是()A.a﹣5<b﹣5B.2+a<2+b C.D.3a>3b【考点】不等式的性质.【分析】以及等式的基本性质即可作出判断.【解答】解:A、a>b,则a﹣5>b﹣5,选项错误;B、a>b,则2+a>2+b,选项错误;C、a>b,则>,选项错误;D、正确.故选D.【点评】主要考查了不等式的基本性质.“0”是很特殊的一个数,因此,解答不等式的问题时,应密切关注“0”存在与否,以防掉进“0”的陷阱.不等式的基本性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.5.(3分)(2013•东莞市)数字1、2、5、3、5、3、3的中位数是()A.1B.2C.3D.5【考点】中位数.【分析】将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.【解答】解:将数据从大到小排列为:1,2,3,3,3,5,5,则中位数是3.故选:C.【点评】本题考查了中位数的知识,属于基础题,掌握中位数的定义及计算方法是关键.6.(3分)(2013•东莞市)如图,AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是()A.30°B.40°C.50°D.60°【考点】平行线的性质.【分析】由AC∥DF,AB∥EF,根据两直线平行,同位角相等,即可求得∠1=∠A=∠2=50°.【解答】解:∵AB∥EF,∴∠A=∠2=50°,∵AC∥DF,∴∠1=∠A=50°.故选C.【点评】此题考查了平行线的性质.此题比较简单,注意掌握两直线平行,同位角相等定理的应用,注意掌握数形结合思想的应用.7.(3分)(2013•东莞市)下列等式正确的是()A.(﹣1)﹣3=1B.(﹣4)0=1C.(﹣2)2×(﹣2)3=﹣26D.(﹣5)4÷(﹣5)2=﹣52【考点】负整数指数幂;同底数幂的乘法;同底数幂的除法;零指数幂.【分析】根据负整数指数幂:a﹣p=(a≠0,p为正整数),零指数幂:a0=1(a≠0),同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.同底数幂的除法法则:底数不变,指数相减分别进行计算,可得答案.【解答】解:A、(﹣1)﹣3=﹣1,故此选项错误;B、(﹣4)0=1,故此选项正确;C、(﹣2)2×(﹣2)3=﹣25,故此选项错误;D、(﹣5)4÷(﹣5)2=52,故此选项错误;故选:B.【点评】此题主要考查了负整数指数幂、零指数幂、同底数幂的乘除法,关键是熟练掌握各运算的计算法则,不要混淆.8.(3分)(2013•东莞市)不等式5x﹣1>2x+5的解集在数轴上表示正确的是()A.B.C.D.【考点】在数轴上表示不等式的解集;解一元一次不等式.【专题】存在型.【分析】先求出不等式的解集,再在数轴上表示出来即可.【解答】解:移项得,5x﹣2x>5+1,合并同类项得,3x>6,系数化为1得,x>2,在数轴上表示为:故选A.【点评】本题考查了在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.9.(3分)(2013•广东)下列图形中,不是轴对称图形的是()【考点】轴对称图形.【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.【解答】解:A是中心对称图形,不是轴对称图形,B、C、D都是轴对称图形,故选:A.【点评】此题主要考查了轴对称图形,关键是正确找出对称轴.10.(3分)(2013•东莞市)已知k1<0<k2,则函数y=k1x﹣1和y=的图象大致是()A.B.C.D.【考点】反比例函数的图象;一次函数的图象.【专题】压轴题.【分析】根据反比例函数的图象性质及正比例函数的图象性质可作出判断.【解答】解:∵k1<0<k2,b=﹣1<0∴直线过二、三、四象限;双曲线位于一、三象限.故选:A.【点评】本题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.二、填空题(本大题6小题,每小题4分,共24分)请将下列各题的正确答案填写在答题卡相应位置上.11.(4分)(2016•镇江)分解因式:x2﹣9=(x+3)(x﹣3).【考点】因式分解-运用公式法.【分析】本题中两个平方项的符号相反,直接运用平方差公式分解因式.【解答】解:x2﹣9=(x+3)(x﹣3).故答案为:(x+3)(x﹣3).【点评】主要考查平方差公式分解因式,熟记能用平方差公式分解因式的多项式的特征,即“两项、异号、平方形式”是避免错用平方差公式的有效方法.12.(4分)(2013•东莞市)若实数a、b满足|a+2|,则=1.【考点】非负数的性质:算术平方根;非负数的性质:绝对值.【分析】根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.【解答】解:根据题意得:,解得:,则原式==1.故答案是:1.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.13.(4分)(2013•东莞市)一个六边形的内角和是720°.【考点】多边形内角与外角.【分析】根据多边形内角和公式进行计算即可.【解答】解:由内角和公式可得:(6﹣2)×180°=720°.故答案为:720°.【点评】此题主要考查了多边形内角和公式,关键是熟练掌握计算公式:(n﹣2).180°(n ≥3)且n为整数).14.(4分)(2013•东莞市)在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则sinA=.【考点】锐角三角函数的定义;勾股定理.【分析】首先由勾股定理求得斜边AC=5;然后由锐角三角函数的定义知sinA=,然后将相关线段的长度代入计算即可.【解答】解:∵在Rt△ABC中,∠ABC=90°,AB=3,BC=4,∴AC==5(勾股定理).∴sinA==.故答案是:.【点评】本题考查了锐角三角函数定义,勾股定理.本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.15.(4分)(2013•东莞市)如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,则四边形ACE′E的形状是平行四边形.【考点】图形的剪拼.【分析】四边形ACE′E的形状是平行四边形;首先根据三角形中位线的性质可得DE∥AC,DE=AC,再根据旋转可得DE=DE′,然后可根据一组对边平行且相等的四边形是平行四边形进行判定即可.【解答】解:四边形ACE′E的形状是平行四边形;∵DE是△ABC的中线,∴DE∥AC,DE=AC,∵将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,∴DE=DE′,∴EE′=2DE=AC,∴四边形ACE′E的形状是平行四边形,故答案为:平行四边形.【点评】此题主要考查了图形的剪拼,以及平行四边形的判定,关键是掌握一组对边平行且相等的四边形是平行四边形.16.(4分)(2015•青海)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是(结果保留π).【考点】扇形面积的计算.【专题】压轴题.【分析】阴影部分可看成是圆心角为135°,半径为1是扇形.【解答】解:根据图示知,∠1+∠2=180°﹣90°﹣45°=45°,∵∠ABC+∠ADC=180°,∴图中阴影部分的圆心角的和是90°+90°﹣∠1﹣∠2=135°,∴阴影部分的面积应为:S==.故答案是:.【点评】本题考查学生的观察能力及计算能力.求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.三、解答题(一)(本大题3小题,每小题5分,共15分)17.(5分)(2013•东莞市)解方程组.【考点】解二元一次方程组.【专题】计算题.【分析】将方程组中的第一个方程代入第二个方程消去x求出y的值,进而求出x的值,即可得到方程组的解.【解答】解:,将①代入②得:2(y+1)+y=8,去括号得:2y+2+y=8,解得:y=2,将y=2代入①得:x=2+1=3,则方程组的解为.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.18.(5分)(2013•广东)从三个代数式:①a2﹣2ab+b2,②3a﹣3b,③a2﹣b2中任意选两个代数式构造分式,然后进行化简,并求出当a=6,b=3时该分式的值.【考点】分式的化简求值.【专题】开放型.【分析】选②与③构造出分式,再根据分式混合运算的法则把原式进行化简,把a、b的值代入进行计算即可.【解答】解:选②与③构造出分式,,原式==,当a=6,b=3时,原式==.【点评】本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.19.(5分)(2013•东莞市)如图,已知▱ABCD.(1)作图:延长BC,并在BC的延长线上截取线段CE,使得CE=BC(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,连结AE,交CD于点F,求证:△AFD≌△EFC.【考点】作图—复杂作图;全等三角形的判定;平行四边形的性质.【分析】(1)根据题目要求画出图形即可;(2)首先根据平行四边形的性质可得AD∥BC,AD=BC,进而得到AD=CE,∠DAF=∠CEF,进而可利用AAS证明△AFD≌△EFC.【解答】(1)解:如图所示:(2)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵BC=CE,∴AD=CE,∵AD∥BC,∴∠DAF=∠CEF,∵在△AFD和△EFC中,,∴△AFD≌△EFC(AAS).【点评】此题主要考查了平行四边形的性质,以及全等三角形的判定,关键是正确画出图形,掌握平行四边形的性质.四、解答题(二)(本大题3小题,每小题8分,共24分)20.(8分)(2013•东莞市)某校教导处为了解该校七年级同学对排球、乒乓球、羽毛球、篮球和足球五种球类运动项目的喜爱情况(每位同学必须且只能选择最喜爱的一项运动项目),进行了随机抽样调查,并将调查结果统计后绘制成了如图和所示的不完整统计图表.(1)请你补全下列样本人数分布表和条形统计图(如图);(2)若七年级学生总人数为920人,请你估计七年级学生喜爱羽毛球运动项目的人数.样本人数分布表类别人数百分比排球36%乒乓球1428%羽毛球15篮球20%足球816%合计100%【考点】条形统计图;用样本估计总体;统计表.【专题】计算题.【分析】(1)由排球的人数除以所占的百分比求出总人数,乘以篮球所占的百分比即可求出篮球的人数,补全条形统计图,如图所示,求出羽毛球所占的百分比,补全人数分布图,如图所示;(2)用人数乘以羽毛球所占的百分比即可求出人数.【解答】解:(1)3÷6%=50人,则篮球的人数为50×20%=10人,则补全条形统计图如下:羽毛球占总数的百分比为:15÷50=30%,补全人数分布表为:类别人数百分比排球36%乒乓球1428%羽毛球1530%篮球1020%足球816%合计50100%(2)920×30%=276人.则七年级学生喜爱羽毛球运动项目的人数为276人.【点评】此题考查了条形统计图,扇形统计图,中位数,以及众数,弄清题意是解本题的关键.21.(8分)(2013•东莞市)雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)按照(1)中收到捐款的增长率速度,第四天该单位能收到多少捐款?【考点】一元二次方程的应用.【专题】增长率问题.【分析】(1)解答此题利用的数量关系是:第一天收到捐款钱数×(1+每次增长的百分率)2=第三天收到捐款钱数,设出未知数,列方程解答即可;(2)第三天收到捐款钱数×(1+每次增长的百分率)=第四天收到捐款钱数,依此列式子解答即可.【解答】解:(1)设捐款增长率为x,根据题意列方程得,10000×(1+x)2=12100,解得x1=0.1,x2=﹣2.1(不合题意,舍去);答:捐款增长率为10%.(2)12100×(1+10%)=13310元.答:第四天该单位能收到13310元捐款.【点评】本题考查了一元二次方程的应用,列方程的依据是:第一天收到捐款钱数×(1+每次降价的百分率)2=第三天收到捐款钱数.22.(8分)(2013•东莞市)如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1= S2+S3(用“>”、“=”、“<”填空);(2)写出如图中的三对相似三角形,并选择其中一对进行证明.【考点】相似三角形的判定;矩形的性质.【分析】(1)根据S1=S矩形BDEF,S2+S3=S矩形BDEF,即可得出答案.(2)根据矩形的性质,结合图形可得:△BCD∽△CFB∽△DEC,选择一对进行证明即可.【解答】(1)解:∵S1=BD×ED,S矩形BDEF=BD×ED,∴S1=S矩形BDEF,∴S2+S3=S矩形BDEF,∴S1=S2+S3.(2)答:△BCD∽△CFB∽△DEC.证明△BCD∽△DEC;证明:∵∠EDC+∠BDC=90°,∠CBD+∠BDC=90°,∴∠EDC=∠CBD,又∵∠BCD=∠DEC=90°,∴△BCD∽△DEC.【点评】本题考查了相似三角形的判定,注意掌握相似三角形的判定定理,最经常用的就是两角法,此题难度一般.四、解答题(三)(本大题3小题,每小题9分,共27分)23.(9分)(2013•东莞市)已知二次函数y=x2﹣2mx+m2﹣1.(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P 点的坐标;若P点不存在,请说明理由.【考点】二次函数综合题.【分析】(1)根据二次函数的图象经过坐标原点O(0,0),直接代入求出m的值即可;(2)根据m=2,代入求出二次函数解析式,进而利用配方法求出顶点坐标以及图象与y 轴交点即可;(3)根据当P、C、D共线时PC+PD最短,利用平行线分线段成比例定理得出PO的长即可得出答案.【解答】解:(1)∵二次函数的图象经过坐标原点O(0,0),∴代入二次函数y=x2﹣2mx+m2﹣1,得出:m2﹣1=0,解得:m=±1,∴二次函数的解析式为:y=x2﹣2x或y=x2+2x;(2)∵m=2,∴二次函数y=x2﹣2mx+m2﹣1得:y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的顶点为:D(2,﹣1),当x=0时,y=3,∴C点坐标为:(0,3),∴C(0,3)、D(2,﹣1);(3)当P、C、D共线时PC+PD最短,过点D作DE⊥y轴于点E,∵PO∥DE,∴=,∴=,解得:PO=,∴PC+PD最短时,P点的坐标为:P(,0).【点评】此题主要考查了二次函数的综合应用以及配方法求二次函数顶点坐标以及最短路线问题等知识,根据数形结合得出是解题关键.24.(9分)(2013•东莞市)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.【考点】切线的判定;圆周角定理;相似三角形的判定与性质.【专题】压轴题.【分析】(1)根据BD=BA得出∠BDA=∠BAD,再由∠BCA=∠BDA即可得出结论;(2)判断△BED∽△CBA,利用对应边成比例的性质可求出DE的长度.(3)连接OB,OD,证明△ABO≌△DBO,推出OB∥DE,继而判断BE⊥OB,可得出结论.【解答】(1)证明:∵BD=BA,∴∠BDA=∠BAD,∵∠BCA=∠BDA(圆周角定理),∴∠BCA=∠BAD.(2)解:∵∠BDE=∠CAB(圆周角定理)且∠BED=∠CBA=90°,∴△BED∽△CBA,∴=,即=,解得:DE=.(3)证明:连结OB,OD,在△ABO和△DBO中,,∴△ABO≌△DBO(SSS),∴∠DBO=∠ABO,∵∠ABO=∠OAB=∠BDC,∴∠DBO=∠BDC,∴OB∥ED,∵BE⊥ED,∴EB⊥BO,∴BE是⊙O的切线.【点评】本题考查了切线的判定及圆周角定理的知识,综合考查的知识点较多,解答本题要求同学们熟练掌握一些定理的内容.25.(9分)(2013•东莞市)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.(1)如图2,当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC=15度;(2)如图3,在三角板DEF运动过程中,当EF经过点C时,求FC的长;(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.【考点】相似形综合题.【专题】压轴题.【分析】(1)如题图2所示,由三角形的外角性质可得;(2)如题图3所示,在Rt△ACF中,解直角三角形即可;(3)认真分析三角板的运动过程,明确不同时段重叠图形的变化情况:(I)当0≤x≤2时,如答图1所示;(II)当2<x≤6﹣时,如答图2所示;(III)当6﹣<x≤6时,如答图3所示.【解答】解:(1)如题图2所示,∵在三角板DEF中,∠FDE=90°,DF=4,DE=,∴tan∠DFE==,∴∠DFE=60°,∴∠EMC=∠FMB=∠DFE﹣∠ABC=60°﹣45°=15°;(2)如题图3所示,当EF经过点C时,FC====;(3)在三角板DEF运动过程中,(I)当0≤x≤2时,如答图1所示:设DE交BC于点G.过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN.又∵NF==MN,BN=NF+BF,∴NF+BF=MN,即MN+x=MN,解得:MN=x.y=S△BDG﹣S△BFM=BD•DG﹣BF•MN=(x+4)2﹣x•x=x2+4x+8;(II)当2<x≤6﹣时,如答图2所示:过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN.又∵NF==MN,BN=NF+BF,∴NF+BF=MN,即MN+x=MN,解得:MN=x.y=S△ABC﹣S△BFM=AB•AC﹣BF•MN=×62﹣x•x=x2+18;(III)当6﹣<x≤6时,如答图3所示:由BF=x,则AF=AB﹣BF=6﹣x,设AC与EF交于点M,则AM=AF•tan60°=(6﹣x).y=S△AFM=AF•AM=(6﹣x)•(6﹣x)=x2﹣x+.综上所述,y与x的函数解析式为:y=.【点评】本题是运动型综合题,解题关键是认真分析三角板的运动过程,明确不同时段重叠图形形状的变化情况.在解题计算过程中,除利用三角函数进行计算外,也可以利用三角形相似,殊途同归.参与本试卷答题和审题的老师有:sd2011;wdzyzlhx;星期八;zhjh;caicl;zcx;CJX;sjzx;HLing;wdxwwzy;HJJ;dbz1018;sks;ZJX;gbl210;未来(排名不分先后)菁优网2016年12月20日考点卡片1.相反数(1)相反数的概念:只有符号不同的两个数叫做互为相反数.(2)相反数的意义:掌握相反数是成对出现的,不能单独存在,从数轴上看,除0外,互为相反数的两个数,它们分别在原点两旁且到原点距离相等.(3)多重符号的化简:与“+”个数无关,有奇数个“﹣”号结果为负,有偶数个“﹣”号,结果为正.(4)规律方法总结:求一个数的相反数的方法就是在这个数的前边添加“﹣”,如a的相反数是﹣a,m+n的相反数是﹣(m+n),这时m+n是一个整体,在整体前面添负号时,要用小括号.2.非负数的性质:绝对值任意一个数的绝对值都是非负数,当几个数或式的绝对值相加和为0时,则其中的每一项都必须等于0.根据上述的性质可列出方程求出未知数的值.3.科学记数法—表示较大的数(1)科学记数法:把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,n是正整数,这种记数法叫做科学记数法.【科学记数法形式:a×10n,其中1≤a<10,n为正整数.】(2)规律方法总结:①科学记数法中a的要求和10的指数n的表示规律为关键,由于10的指数比原来的整数位数少1;按此规律,先数一下原数的整数位数,即可求出10的指数n.②记数法要求是大于10的数可用科学记数法表示,实质上绝对值大于10的负数同样可用此法表示,只是前面多一个负号.4.非负数的性质:算术平方根(1)非负数的性质:算术平方根具有非负性.(2)利用算术平方根的非负性求值的问题,主要是根据被开方数是非负数,开方的结果也是非负数列出不等式求解.非负数之和等于0时,各项都等于0利用此性质列方程解决求值问题.5.同底数幂的乘法(1)同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.a m•a n=a m+n(m,n是正整数)(2)推广:a m•a n•a p=a m+n+p(m,n,p都是正整数)在应用同底数幂的乘法法则时,应注意:①底数必须相同,如23与25,(a2b2)3与(a2b2)4,(x﹣y)2与(x﹣y)3等;②a可以是单项式,也可以是多项式;③按照运算性质,只有相乘时才是底数不变,指数相加.(3)概括整合:同底数幂的乘法,是学校整式乘除运算的基础,是学好整式运算的关键.在运用时要抓住“同底数)这一关键点,同时注意,有的底数可能并不相同,这时可以适当变形为同底数幂.6.同底数幂的除法同底数幂的除法法则:底数不变,指数相减.a m÷a n=a m﹣n(a≠0,m,n是正整数,m>n)①底数a≠0,因为0不能做除数;②单独的一个字母,其指数是1,而不是0;③应用同底数幂除法的法则时,底数a可是单项式,也可以是多项式,但必须明确底数是什么,指数是什么.7.因式分解-运用公式法1、如果把乘法公式反过来,就可以把某些多项式分解因式,这种方法叫公式法.平方差公式:a2﹣b2=(a+b)(a﹣b);完全平方公式:a2±2ab+b2=(a±b)2;2、概括整合:①能够运用平方差公式分解因式的多项式必须是二项式,两项都能写成平方的形式,且符号相反.②能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.3、要注意公式的综合应用,分解到每一个因式都不能再分解为止.8.分式的化简求值先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.【规律方法】分式化简求值时需注意的问题1.化简求值,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤,代入求值的模式一般为“当…时,原式=…”.2.代入求值时,有直接代入法,整体代入法等常用方法.解题时可根据题目的具体条件选择合适的方法.当未知数的值没有明确给出时,所选取的未知数的值必须使原式中的各分式都有意义,且除数不能为0.9.零指数幂零指数幂:a0=1(a≠0)由a m÷a m=1,a m÷a m=a m﹣m=a0可推出a0=1(a≠0)注意:00≠1.10.负整数指数幂负整数指数幂:a﹣p=1ap(a≠0,p为正整数)注意:①a≠0;②计算负整数指数幂时,一定要根据负整数指数幂的意义计算,避免出现(﹣3)﹣2=(﹣3)×(﹣2)的错误.③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.④在混合运算中,始终要注意运算的顺序.。
广东省佛山市中考数学试卷及答案

2013年广东省佛山市中考数学试卷参考答案与试题解析ACBCD DBCAB二、填空题11.(3分)(2013•佛山)数字9 600 000用科学记数法表示为9.6×106.解答:解:将9 600 000用科学记数法表示为:9.6×106.故答案为:9.6×106.12.(3分)(2013•佛山)方程x2﹣2x﹣2=0的解是x1=+1,x2=﹣+1.解答:解:x2﹣2x﹣2=0,移项得:x2﹣2x=2,配方得:x2﹣2x+1=2+1,(x﹣1)2=3,两边直接开平方得:x﹣1=,则x1=+1,x2=﹣+1.13.(3分)(2013•佛山)在1,2,3,4四个数字中随机选两个不同的数字组成两位数,则组成的两位数大于40的概率是.解答:解:根据题意画出树状图如下:一共有12种情况,组成的两位数大于40的情况有3种,所以,P(组成的两位数大于40)==.故答案为:.14.(3分)(2013•佛山)图中圆心角∠AOB=30°,弦CA∥OB,延长CO与圆交于点D,则∠BOD=30°.解答:解:∵CA∥OB,∴∠CAO=∠AOB=30°,∵OA=OC,∴∠C=∠OAC=30°,∴∠AOD=2∠C=60°,∴∠BOD=60°﹣30°=30°.故答案为30°.15.(3分)(2013•佛山)命题“对顶角相等”的“条件”是两个角是对顶角.三、解答题16.解答:解:2×[5+(﹣2)3]﹣(﹣|﹣4|÷2﹣1=2×(5﹣8)﹣(﹣4÷)=﹣6﹣(﹣8)=2.17.解答:证明:∵AC=,BC==,AB=4,DF==2,EF==2,ED=8,∴===2,∴△ABC∽△DEF.18.解答:解:原式=﹣===.19.解答:解:(1)一样;(2)①式子2x﹣1的值在1(含1)与3(含3)之间可得1≤2x﹣1≤3;②式子2x﹣1的值不小于1且不大于3可得.20.解答:解:设圆锥的母线长为l,底面半径为r,则:πl=2πr,∴l=2r,∴母线与高的夹角的正弦值==,∴母线AB与高AO的夹角30°.21.解答:解:(1)把A(1,2)代入y=ax得a=2,所以正比例函数解析式为y=2x;把A(1,2)代入y=得b=1×2=2,所以反比例函数解析式为y=;(2)如图,当﹣1<x<0或x>1时,正比例函数值大于反比例函数值.22.解答:解:(1)三角形全等的判定方法中的推论AAS指的是:两边及其夹角分别对应相等的两个三角形全等.(2)已知:在△ABC与△DEF中,∠A=∠D,∠C=∠F,BC=EF.求证:△ABC≌△DEF.证明:如图,在△ABC与△DEF中,∠A=∠D,∠C=∠F(已知),∴∠A+∠C=∠D+∠F(等量代换).又∵∠A+∠B+∠C=180°,∠D+∠E+∠F=180°(三角形内角和定理),∴∠B=∠E.∴在△ABC与△DEF中,,∴△ABC≌△DEF(ASA).23.解答:解:(1)根据图表数据得出:选A的所占圆心角为:×360°=45°;选B的所占圆心角为:×360°=15°;选C的所占圆心角为:×360°=270°;选D的所占圆心角为:×360°=30°.如图所示:(2)∵选择题满分是3分,正确的选项是C,∴全体学生该题的平均得分为:=2.25(分),答:全体学生该题的平均得分是2.25分.24.解答:解:(1)∵抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3),∴,解得,所以抛物线的函数表达式为y=x2﹣4x+3;(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的顶点坐标为(2,﹣1),对称轴为直线x=2;(3)如图,∵抛物线的顶点坐标为(2,﹣1),∴PP′=1,阴影部分的面积等于平行四边形A′APP′的面积,平行四边形A′APP′的面积=1×2=2,∴阴影部分的面积=2.25.解答:解:(1)在表格中作答:分割图形分割或图形说明示例:示例:①分割成两个菱形.②两个菱形的边长都为a,锐角都为60°.①分割成两两个等腰梯形.②两个等腰梯形的腰长都为a,上底长都为,下底长都为a,上底角都为120°,下底角都为60°.①分割成一个等边三角形、一个等腰三角形、一个直角三角形.②等边三角形的边长为a,等腰三角形的腰长为a,顶角为120°.直角三角形两锐角为30°、60°,三边为a 、a、2a.。
2013年广东省中考数学试卷-答案

(2)见解析
【解析】(1)如图所示:
(2)证明:∵四边形 是平行四边形,
∴ , ,
∵ ,
∴ ,
∵ ,
∴ ,
∵在 和 中, ,
∴ .
【提示】(1)根据题目要求画出图形即可;
(2)首先根据平行四边形的性质可得 , ,进而得到 , ,进而可利用AAS证明 .
【考点】复杂作图,全等三角形的判定,平行四边形的性质
【提示】(1)由排球的人数除以所占的百分比求出总人数,乘以篮球所占的百分比即可求出篮球的人数,补全条形统计图,如图所示,求出羽毛球所占的百分比,补全人数分布图,如图所示;
(2)用人数乘以羽毛球所占的百分比即可求出人数.
【考点】条形统计图,用样本估计总体,统计表
21.【答案】(1)
(2)
【解析】(1)设捐款增长率为x,根据题意列方程得, ,解得 (不合题意,舍去);
故选:D.
【提示】俯视图是从物体上面看,所得到的图形.
【考点】简单几何体的三视图
3.【答案】B
【解析】 .
故选B
【提示】科学记数法的表示形式为 的形式,其中 ,n为整数.确定n的值是易错点,由于 有13位,所以可以确定 .
【考点】科学记数法—表示较大的数
4.【答案】D
【解析】A. ,则 ,选项错误;
B. ,则 ,选项错误;
C. ,则 ,选项错误;
D.正确.
故选D.
【提示】以及等式的基本性质即可作出判断.
【考点】不等式的性质
5.【答案】C
【解析】将数据从大到小排列为:1,2,3,3,3,5,5,则中位数是3.
故选C.
【提示】将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
2013年广东省佛山市中考数学试卷及答案解析

=
.
第 2 页 共 19 页
15.(3 分)命题“对顶角相等”的“条件”是
.
三、解答题(第 16~20 每小题 6 分,第 21~23 每小题 6 分,第 24 小题 10 分,第 25 小题
11 分,共 75 分) 16.(6 分)计算:2×[5+(﹣2)3]﹣(﹣|﹣4|÷2﹣1).
17.(6 分)网格图中每个方格都是边长为 1 的正方形.若 A,B,C,D,E,F 都是格点,
试说明△ABC∽△DEF.
th
18.(6 分)按要求化简: t
.
19.(6 分)已知两个语句: ①式子 2x﹣1 的值在 1(含 1)与 3(含 3)之间; ②式子 2x﹣1 的值不小于 1 且不大于 3. 请回答以下问题:
(1)两个语句表达的意思是否一样(不用说明理由)? (2)把两个语句分别用数学式子表示出来. 20.(6 分)如图,圆锥的侧面展开图是一个半圆,求母线 AB 与高 AO 的夹角.参考公式: 圆锥的侧面积 S=πrl,其中 r 为底面半径,l 为母线长.
23.(8 分)在一次考试中,从全体参加考试的 1000 名学生中随机抽取了 120 名学生的答题 卷进行统计分析.其中,某个单项选择题答题情况如下表(没有多选和不选):
选项
A
B
C
D
选择人数
15
5
90
10
(1)根据统计表画出扇形统计图;
第 4 页 共 19 页
要求:画图前先求角;画图可借助任何工具,其中一个角的作图用尺规作图(保留痕迹, 不写作法和证明);统计图中标注角度. (2)如果这个选择题满分是 3 分,正确的选项是 C,则估计全体学生该题的平均得分是 多少?
2013年广东省中考数学试卷及答案

2013年广东省初中毕业生学业考试数学说明:1. 全卷共4页,考试用时100 分钟.满分为120 分.2.答题前,考生务必用黑色字迹的签字笔或钢笔在答题卡上填写自己准考证号、姓名、试室号、座位号,用2B铅笔把对应号码的标号涂黑.3.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案,答案不能答在试题上.4.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.5.考生务必保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑.1. 2的相反数是A. B. C.-2 D.2答案:C解析:2的相反数为-2,选C,本题较简单。
2.下列几何体中,俯视图为四边形的是答案:D解析:A、B、C的俯视图分别为五边形、三角形、圆,只有D符合。
3.据报道,2013年第一季度,广东省实现地区生产总值约1 260 000 000 000元,用科学记数法表示为A. 0.126×1012元B. 1.26×1012元C. 1.26×1011元D. 12.6×1011元答案:B解析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.1 260 000 000 000=1.26×1012元4.已知实数、,若>,则下列结论正确的是A. B. C. D.答案:D解析:不等式的两边同时加上或减去一个数,不等号的方向不变,不等式的两边同时除以或乘以一个正数,不等号的方向也不变,所以A、B、C错误,选D。
中考数学-2013年广东省中考数学试卷及答案(word解析版)

2013年广东省初中毕业生学业考试数学说明:1. 全卷共4页,考试用时100 分钟.满分为120 分.2.答题前,考生务必用黑色字迹的签字笔或钢笔在答题卡上填写自己准考证号、姓名、试室号、座位号,用2B 铅笔把对应号码的标号涂黑.3.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案,答案不能答在试题上.4.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.5.考生务必保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑.1. 2的相反数是A.21 B.21 C.-2 D.2答案:C解析:2的相反数为-2,选C ,本题较简单。
2.下列几何体中,俯视图为四边形的是答案:D解析:A 、B 、C 的俯视图分别为五边形、三角形、圆,只有D 符合。
3.据报道,2013年第一季度,广东省实现地区生产总值约 1 260 000 000 000元,用科学记数法表示为A. 0.126×1012元 B. 1.26×1012元 C.1.26×1011元 D. 12.6×1011元答案:B解析:科学记数法的表示形式为a ×10n的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.1 260 000 000 000=1.26×1012元4.已知实数a 、b ,若a >b ,则下列结论正确的是A.55b a B.b a22 C.33b a D.ba 33答案:D解析:不等式的两边同时加上或减去一个数,不等号的方向不变,不等式的两边同时除以或乘以一个正数,不等号的方向也不变,所以A 、B 、C 错误,选D 。
2013年广东省中考数学试卷及答案(Word解析版)

12.若实数a 、b 满足042=-++b a ,则=ba 2________. 16.如题16图,三个小正方形的边长都为1,则图中阴影部分面积的和是83π__________(结果保留π).五、解答题(三)(本大题3小题,每小题9分,共27分)23. 已知二次函数1222-+-=m mx x y .(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;(2)如题23图,当2=m 时,该抛物线与y 轴交于点C,顶点为D,求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P,使得PC+PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.解析:(1)m=±1,二次函数关系式为x x y x x y 2222-=+=或;(2)当m=2时,1)2(3422--=+-=x x x y ,∴D(2,-1);当0=x 时,3=y ,∴C(0,3).(3)存在.连结C 、D 交x 轴于点P,则点P 为所求,由C(0,3)、D(2,-1)求得直线CD 为32+-=x y当0=y 时,23=x ,∴P(23,0).25.有一副直角三角板,在三角板ABC 中,∠BAC=90°,AB=AC=6,在三角板DEF 中,∠FDE=90°,DF=4,DE=34.将这副直角三角板按如题25图(1)所示位置摆放,点B 与点F 重合,直角边BA 与FD 在同一条直线上.现固定三角板ABC,将三角板DEF 沿射线BA 方向平行移动,当点F 运动到点A 时停止运动.(1)如题25图(2),当三角板DEF 运动到点D 与点A 重合时,设EF 与BC 交于点M, 则∠EMC=______度;(2)如题25图(3),在三角板DEF 运动过程中,当EF 经过点C 时,求FC 的长;(3)在三角板DEF 运动过程中,设BF=x ,两块三角板重叠部分面积为y ,求y与x 的函数解析式,并求出对应的x 取值范围.解析。
2013年广东省中考数学试卷及答案

2013年广东省中考数学试卷一、选择题(共10小题,每小题3分,满分30分) B B3.(3分)(2013•广东)据报道,2013年第一季度,广东省实现地区生产总值约1260 000 0006.(3分)(2013•广东)如图,AC ∥DF ,AB ∥EF,点D 、E 分别在AB 、AC 上,若∠2=50°,则∠1的大小是( ). . . .9.(3分)(2013•广东)下列图形中,不是轴对称图形的是( )...10.(3分)(2013•广东)已知k1<0<k2,则函数y=k1x﹣1和y=的图象大致是()B二、填空题(本大题6小题,每小题4分,共24分)请将下列各题的正确答案填写在答题卡相应位置上.11.(4分)(2013•平凉)分解因式:x2﹣9=_________.12.(4分)(2013•广东)若实数a、b满足|a+2|,则=_________.13.(4分)(2013•广东)一个六边形的内角和是_________.14.(4分)(2013•广东)在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则sinA=_________.15.(4分)(2013•广东)如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,则四边形ACE′E的形状是_________.16.(4分)(2013•广东)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是_________(结果保留π).三、解答题(一)(本大题3小题,每小题5分,共15分)17.(5分)(2013•广东)解方程组.18.(5分)(2013•广东)从三个代数式:①a2﹣2ab+b2,②3a﹣3b,③a2﹣b2中任意选两个代数式构造分式,然后进行化简,并求出当a=6,b=3时该分式的值.19.(5分)(2013•广东)如图,已知▱ABCD.(1)作图:延长BC,并在BC的延长线上截取线段CE,使得CE=BC(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,连结AE,交CD于点F,求证:△AFD≌△EFC.四、解答题(二)(本大题3小题,每小题8分,共24分)20.(8分)(2013•广东)某校教导处为了解该校七年级同学对排球、乒乓球、羽毛球、篮球和足球五种球类运动项目的喜爱情况(每位同学必须且只能选择最喜爱的一项运动项目),进行了随机抽样调查,并将调查结果统计后绘制成了如图和所示的不完整统计图表.(1)请你补全下列样本人数分布表和条形统计图(如图);(2)若七年级学生总人数为920人,请你估计七年级学生喜爱羽毛球运动项目的人数.21.(8分)(2013•广东)雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)按照(1)中收到捐款的增长率速度,第四天该单位能收到多少捐款?22.(8分)(2013•广东)如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1_________ S2+S3(用“>”、“=”、“<”填空);(2)写出如图中的三对相似三角形,并选择其中一对进行证明.四、解答题(三)(本大题3小题,每小题9分,共27分)23.(9分)(2013•广东)已知二次函数y=x2﹣2mx+m2﹣1.(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P 点的坐标;若P点不存在,请说明理由.24.(9分)(2013•广东)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.25.(9分)(2013•广东)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.(1)如图2,当三角板DEF运动到点D到点A重合时,设EF与BC交于点M,则∠EMC= _________度;(2)如图3,当三角板DEF运动过程中,当EF经过点C时,求FC的长;(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.。
2013年广东省各市中考数学分类解析专题1实数

A a 2.5B 2.5 aC a 2.5D a 2.5广东各市2山3年中考数学试题分类解析汇编专题实数一、选择题1. (2013年广东佛山3分) 2的相反数是【】C. 12【答案】A. 1考点】相反数口【分析】相反数的定义杲!如果两个数只有苻号不同,我们称苴中一个数为另一千数的相反数,特别地・o e 数还是0.囲!K-2的相反数是二故选亠 2. (2013年广东佛山3分)化简22[的结果是【 】A . 2 2 1 B- 2 2 C . 1 2 D . 2 23. (2013年广东广州3分)比0大的数是【 】1 A -1 B C 0 D 12【答案】D.【考点】实数的大小比簽,【分析】根据实数的夫小比较法顽 正数大于0*于负数,两个负数相比,绝对直走的反而小口因1匕T-Z-lcW 二比。
大的数是1・故选D ・23分)实数a 在数轴上的位置如图所示,则 |a 2.5 =【A . 2D .【分析】分子、分母同时乗以血+1即可:4. (2013年广东广州T^iTS+ii| — L11 + 11【看亞】绝对值和数轴.【分析】由数轴可知.a< 2.5 * §Pa- 2.5< 0 .'. a-2 5 =-*a-2 51= 2 5-a -故选弓-5. (2013年广东茂名3分)下列实数中,最小的数是【】A .—3B . 3 C. 1 D . 03【答案】2・【若点】冥数的大『卜比较.【分祈】很据实数的大小比较法駅正数大于E Q大于员航两牛负歎相比絶对值大的反而小.因此,-3<0<1<3,贵卜的数是7A・36. (2013年广东茂名3分)PM2.5是指大气中直径小于或等于 2.5 叩(0.0000025m)的颗粒物,含有大量有毒、有害物质,也称可入肺颗粒物.将0.0000025用科学记数法表示为【】A . 25 X10「7B . 2.5 X0「6C. 0.25 X0「5 D . 2.5 氷06【答案】缶【萼亘】科学记敎法x匕分析】根抿斜学谨t法的走义,科学记数法的袁示册式为凶仇其中1WKW・n为整甑表示时关键里确定请的值限矗11的值.在确定口的值时.看该数是大于或等干1还是T于1-当删犬于或等干I时•口城数位元薮减h当该敕小于1时,一口为它第一个有效数字前C的个数(剖盼前的1牛0)■ 0.0000025虽有JS数字前育行个3冶小数点前的1个①,从而0.0000025= 25xl0_\故选弐7. (2013年广东梅州3分)四个数-1 , 0, 1, 2中为无理数的是【】2A . —1B . 0 C. 1 D . . 22【答案】)【考点】无理数•【分折】无理颈就是无限不循环小驗有理数是整数与分数的统称.即有限小赦和无隈循环小数是苞理数,而不循环小数是无理裁.由此@卩可判定选择项;-h o是整^ 是有理轨丄是分熱是有理驗无理数孫JT •故选口28. (2013年广东深圳3分)—3的绝对值是【】A.3B. 一3 C・〔D・[3 3【答案】瓜【者点】相反数.【分析】相反数的走义杲;如果两个数貝有符号不同,我们称其中一^対另一个数的相長数,持别地「洱数还是丄因此一3的相反教是3.故选A.鼻<2013 3分)臬活动中,共募得捐款32000000元■将第血罠00用科学记数注表卞两【]A.032xlp3 C3.2X1C D32X1Q'【答案】G【专点】科学记数袪口【分析】根据科学记数法的定义科学记敌法的表示形式为护1”具中Ka<lC, zi为整紀表示时关键理确宦a的值以圧昭的值.在确宦n的值时,看臓是大于或等于1还是可于1.当该数尢于或等于1时心曲数位元数减1;当该較小于1时,-11沖它第一个肓舱数孚前0的个敎(舍卜数点前的1个P •耳曲口贺一共从而32000000=3,2^ 10\ 故选C・10. (2013年广东省3分)2的相反数是【】A. 1B. 1C—2 D.22 2【甞案】C・【肴点】相反数.【分析】相反频的定义是’如果两个数只有符号不1司,我们称其中一6数为另一个馥的相反数.特别地,D的数还是h 因此:的相反数是一h抜选U11. (2013年广东省3分)据报导,2013年第一季度,广东省实现地区生产总值约 1 260 000 000000元,用科学记数法表示为【】A. 0.126 X121 元B. 1.26 X ft元C. 1.26 X 10元D. 12.6 X 10元【答案】玄【苕盘】科学记数法.【分析】根摇科学记数法的定义,科学记数法的表示形式为旳只其中iwxia 口为整如表示时关蘿轟定盘的值以及"的值.衽确定n的值时,看该数是大于或等于1还是4吁L当该数大于或等于1时小尙数位元数减b当该数小于1时.一宜为它第一个有效数字前:〕的个数(含小薮点前的1个汨・1⑷:烦j 一共W 位,从而1 260 OOO OOaOOO=L26«1012H 故选B・12. (2013年广东省3分)下列等式正确的是【】A. ( 1) 3 1B. ( 4)0 1C. 26D. 52【答案】氏【考点】负整数指数嶽同底数幕的乘法和险法,零簸鼠【分折】棍捉负整数指数黑同底数幕的秉法和除法,零扌旨数黑运算法刚逐一作出判断:A. Jl)T=-h故此遥项错误;Bs (-4)°=1,故此选项正關:C* | -2 F x 4 -2』=卜-2 P = -2’,故Lt选项错误$Ds 1-5/ -r<-5(2= »-513= 52> 故此选匝错i吴口故选B P13. (2013年广东湛江4分)下列各数中,最小的数是【】A. 1B. 1 C .0 D. 1【答案】Do【澹点】实数的大小上肉t,【分析】根据实数田大小比靈法则,正敎大于h。
2013年广东省中考数学试卷及答案

2013年广东省中考数学试卷一、选择题(共10小题,每小题3分,满分30分)1.(3分)(2013•广东)2的相反数是()A.B.C.﹣2 D.22.(3分)(2013•广东)下列四个几何体中,俯视图为四边形的是()A.B.C.D.3.(3分)(2013•广东)据报道,2013年第一季度,广东省实现地区生产总值约1260 000 000 000元,用科学记数法表示为()A.0.126×1012元B.1.26×1012元C.1.26×1011元D.12.6×1011元4.(3分)(2013•广东)已知实数a、b,若a>b,则下列结论正确的是()A.a﹣5<b﹣5 B.2+a<2+b C.D.3a>3b5.(3分)(2013•广东)数学1、2、5、3、5、3、3的中位数是()A.1B.2C.3D.56.(3分)(2013•广东)如图,AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是()A.30°B.40°C.50°D.60°7.(3分)(2013•广东)下列等式正确的是()A.(﹣1)﹣3=1 B.(﹣4)0=1 C.(﹣2)2×(﹣2)3=﹣26D.(﹣5)4÷(﹣5)2=﹣528.(3分)(2013•广东)不等式5x﹣1>2x+5的解集在数轴上表示正确的是()A.B.C.D.9.(3分)(2013•广东)下列图形中,不是轴对称图形的是()A.B.C.D.10.(3分)(2013•广东)已知k1<0<k2,则函数y=k1x﹣1和y=的图象大致是()A.B.C.D.二、填空题(本大题6小题,每小题4分,共24分)请将下列各题的正确答案填写在答题卡相应位置上.11.(4分)(2013•平凉)分解因式:x2﹣9=_________.12.(4分)(2013•广东)若实数a、b满足|a+2|,则=_________.13.(4分)(2013•广东)一个六边形的内角和是_________.14.(4分)(2013•广东)在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则sinA=_________.15.(4分)(2013•广东)如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,则四边形ACE′E的形状是_________.16.(4分)(2013•广东)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是_________(结果保留π).三、解答题(一)(本大题3小题,每小题5分,共15分)17.(5分)(2013•广东)解方程组.18.(5分)(2013•广东)从三个代数式:①a2﹣2ab+b2,②3a﹣3b,③a2﹣b2中任意选两个代数式构造分式,然后进行化简,并求出当a=6,b=3时该分式的值.19.(5分)(2013•广东)如图,已知▱ABCD.(1)作图:延长BC,并在BC的延长线上截取线段CE,使得CE=BC(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,连结AE,交CD于点F,求证:△AFD≌△EFC.四、解答题(二)(本大题3小题,每小题8分,共24分)20.(8分)(2013•广东)某校教导处为了解该校七年级同学对排球、乒乓球、羽毛球、篮球和足球五种球类运动项目的喜爱情况(每位同学必须且只能选择最喜爱的一项运动项目),进行了随机抽样调查,并将调查结果统计后绘制成了如图和所示的不完整统计图表.(1)请你补全下列样本人数分布表和条形统计图(如图);(2)若七年级学生总人数为920人,请你估计七年级学生喜爱羽毛球运动项目的人数.样本人数分布表类别人数百分比排球 3 6%乒乓球14 28%羽毛球15篮球20%足球8 16%合计100%21.(8分)(2013•广东)雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)按照(1)中收到捐款的增长率速度,第四天该单位能收到多少捐款?22.(8分)(2013•广东)如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1_________ S2+S3(用“>”、“=”、“<”填空);(2)写出如图中的三对相似三角形,并选择其中一对进行证明.四、解答题(三)(本大题3小题,每小题9分,共27分)23.(9分)(2013•广东)已知二次函数y=x2﹣2mx+m2﹣1.(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P 点的坐标;若P点不存在,请说明理由.24.(9分)(2013•广东)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.25.(9分)(2013•广东)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.(1)如图2,当三角板DEF运动到点D到点A重合时,设EF与BC交于点M,则∠EMC= _________度;(2)如图3,当三角板DEF运动过程中,当EF经过点C时,求FC的长;(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.2013年广东省中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)1.(3分)(2013•广东)2的相反数是()A.B.C.﹣2 D.2考点:相反数.分析:根据相反数的概念解答即可.解答:解:2的相反数是﹣2,故选:C.点评:本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号;一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.2.(3分)(2013•广东)下列四个几何体中,俯视图为四边形的是()A.B.C.D.考点:简单几何体的三视图.分析:俯视图是从物体上面看,所得到的图形.解答:解:A、五棱柱的俯视图是五边形,故此选项错误;B 、三棱锥的俯视图是,故此选项错误;C、球的俯视图是圆,故此选项错误;D、正方体俯视图是正方形,故此选项正确;故选:D.点评:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.3.(3分)(2013•广东)据报道,2013年第一季度,广东省实现地区生产总值约1260 000 000 000元,用科学记数法表示为()A.0.126×1012元B.1.26×1012元C.1.26×1011元D.12.6×1011元考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于1260 000 000 000有13位,所以可以确定n=13﹣1=12.解答:解:1260 000 000 000=1.26×1012.故选B.点评:此题考查科学记数法表示较大的数的方法,准确确定a与n值是关键.4.(3分)(2013•广东)已知实数a、b,若a>b,则下列结论正确的是()A.a﹣5<b﹣5 B.2+a<2+b C.D.3a>3b考点:不等式的性质.分析:以及等式的基本性质即可作出判断.解答:解:A、a>b,则a﹣5>b﹣5,选项错误;B、a>b,则2+a>2+b,选项错误;C、a>b,则>,选项错误;D、正确.故选D.点评:主要考查了不等式的基本性质.“0”是很特殊的一个数,因此,解答不等式的问题时,应密切关注“0”存在与否,以防掉进“0”的陷阱.不等式的基本性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.5.(3分)(2013•广东)数学1、2、5、3、5、3、3的中位数是()A.1B.2C.3D.5考点:中位数.分析:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.解答:解:将数据从大到小排列为:1,2,3,3,3,5,5,则中位数是3.故选C.点评:本题考查了中位数的知识,属于基础题,掌握中位数的定义及计算方法是关键.6.(3分)(2013•广东)如图,AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是()A.30°B.40°C.50°D.60°考点:平行线的性质.分析:由AC∥DF,AB∥EF,根据两直线平行,同位角相等,即可求得∠1=∠A=∠2=50°.解答:解:∵AB∥EF,∴∠A=∠2=50°,∵AC∥DF,∴∠1=∠A=50°.故选C.点评:此题考查了平行线的性质.此题比较简单,注意掌握两直线平行,同位角相等订立的应用,注意掌握数形结合思想的应用.7.(3分)(2013•广东)下列等式正确的是()A.(﹣1)﹣3=1 B.(﹣4)0=1 C.(﹣2)2×(﹣2)3=﹣26D.(﹣5)4÷(﹣5)2=﹣52考点:负整数指数幂;同底数幂的乘法;同底数幂的除法;零指数幂.分析:根据负整数指数幂:a﹣p=(a≠0,p为正整数),零指数幂:a0=1(a≠0),同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.同底数幂的除法法则:底数不变,指数相减分别进行计算,可得答案.解答:解:A、(﹣1)﹣3=﹣1,故此选项错误;B、(﹣4)0=1,故此选项正确;C、(﹣2)2×(﹣2)3=﹣25,故此选项错误;D、(﹣5)4÷(﹣5)2=52,故此选项错误;故选:B.点评:此题主要考查了负整数指数幂、零指数幂、同底数幂的乘除法,关键是熟练掌握各运算的计算法则,不要混淆.8.(3分)(2013•广东)不等式5x﹣1>2x+5的解集在数轴上表示正确的是()A.B.C.D.考点:在数轴上表示不等式的解集;解一元一次不等式.专题:存在型.分析:先求出不等式的解集,再在数轴上表示出来即可.解答:解:移项得,5x﹣2x>5+1,合并同类项得,3x>6,系数化为1得,x>2,在数轴上表示为:故选A.点评:本题考查了在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.9.(3分)(2013•广东)下列图形中,不是轴对称图形的是()A.B.C.D.考点:轴对称图形.分析:根据轴对称图形的概念对各选项分析判断即可得出答案.解答:解:A、是轴对称图形,故本选项错误;B、是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项正确;D、是轴对称图形,故本选项错误.故选C.点评:本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.10.(3分)(2013•广东)已知k1<0<k2,则函数y=k1x﹣1和y=的图象大致是()A.B.C.D.考点:反比例函数的图象;一次函数的图象.分析:根据反比例函数的图象性质及正比例函数的图象性质可作出判断.解答:解:∵k1<0<k2,b=﹣1<0∴直线过二、三、四象限;双曲线位于一、三象限.故选A.点评:本题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.二、填空题(本大题6小题,每小题4分,共24分)请将下列各题的正确答案填写在答题卡相应位置上.11.(4分)(2013•平凉)分解因式:x2﹣9=(x+3)(x﹣3).考点:因式分解-运用公式法.分析:本题中两个平方项的符号相反,直接运用平方差公式分解因式.解答:解:x2﹣9=(x+3)(x﹣3).点评:主要考查平方差公式分解因式,熟记能用平方差公式分解因式的多项式的特征,即“两项、异号、平方形式”是避免错用平方差公式的有效方法.12.(4分)(2013•广东)若实数a、b满足|a+2|,则=1.考点:非负数的性质:算术平方根;非负数的性质:绝对值.分析:根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.解答:解:根据题意得:,解得:,则原式==1.故答案是:1.点评:本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.13.(4分)(2013•广东)一个六边形的内角和是720°.考点:多边形内角与外角.分析:根据多边形内角和公式进行计算即可.解答:解:由内角和公式可得:(6﹣2)×180°=720°.故答案为:720°.点评:此题主要考查了多边形内角和公式,关键是熟练掌握计算公式:(n﹣2).180°(n≥3)且n为整数).14.(4分)(2013•广东)在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则sinA=.考点:锐角三角函数的定义;勾股定理.分析:首先由勾股定理求得斜边AC=5;然后由锐角三角函数的定义知sinA=,然后将相关线段的长度代入计算即可.解答:解:∵在Rt△ABC中,∠ABC=90°,AB=3,BC=4,∴AC==5(勾股定理).∴sinA==.故答案是:.点评:本题考查了锐角三角函数定义,勾股定理.本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.15.(4分)(2013•广东)如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,则四边形ACE′E的形状是平行四边形.考点:图形的剪拼.分析:四边形ACE′E的形状是平行四边形;首先根据三角形中位线的性质可得DE∥AC,DE=AC,再根据旋转可得DE=DE′,然后可根据一组对边平行且相等的四边形是平行四边形进行判定即可.解答:解:四边形ACE′E的形状是平行四边形;∵DE是△ABC的中线,∴DE∥AC,DE=AC,∵将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,∴DE=DE′,∴EE′=2DE=AC,∴四边形ACE′E的形状是平行四边形,故答案为:平行四边形.点评:此题主要考查了图形的剪拼,以及平行四边形的判定,关键是掌握一组对边平行且相等的四边形是平行四边形.16.(4分)(2013•广东)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是(结果保留π).考点:扇形面积的计算.分析:阴影部分可看成是圆心角为135°,半径为1是扇形.解答:解:根据图示知,∠1+∠2=180°﹣90°﹣45°=45°,∴图中阴影部分的圆心角的和是90°+90°﹣∠1﹣∠2=135°,∴阴影部分的面积应为:S==.故答案是:.点评:本题考查学生的观察能力及计算能力.求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.三、解答题(一)(本大题3小题,每小题5分,共15分)17.(5分)(2013•广东)解方程组.考点:解二元一次方程组.专题:计算题.分析:将方程组中的第一个方程代入第二个方程消去x求出y的值,进而求出x的值,即可得到方程组的解.解答:解:,将①代入②得:2(y+1)+y=8,去括号得:2y+2+y=8,解得:y=2,将y=2代入①得:x=2+1=3,则方程组的解为.点评:此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.18.(5分)(2013•广东)从三个代数式:①a2﹣2ab+b2,②3a﹣3b,③a2﹣b2中任意选两个代数式构造分式,然后进行化简,并求出当a=6,b=3时该分式的值.考点:分式的化简求值.专题:开放型.分析:选②与③构造出分式,再根据分式混合运算的法则把原式进行化简,把a、b的值代入进行计算即可.解答:解:选②与③构造出分式,,原式==,当a=6,b=3时,原式==.点评:本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.19.(5分)(2013•广东)如图,已知▱ABCD.(1)作图:延长BC,并在BC的延长线上截取线段CE,使得CE=BC(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,连结AE,交CD于点F,求证:△AFD≌△EFC.考点:作图—复杂作图;全等三角形的判定;平行四边形的性质.分析:(1)根据题目要求画出图形即可;(2)首先根据平行四边形的性质可得AD∥BC,AD=BC,进而得到AD=CE,∠DAF=∠CEF,进而可利用AAS证明△AFD≌△EFC.解答:(1)解:如图所示:(2)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵BC=CE,∴AD=CE,∵AD∥BC,∴∠DAF=∠CEF,∵在△ADF和△ECF中,,∴△ADF≌△ECF(AAS).点评:此题主要考查了平行四边形的性质,以及全等三角形的判定,关键是正确画出图形,掌握平行四边形的性质.四、解答题(二)(本大题3小题,每小题8分,共24分)20.(8分)(2013•广东)某校教导处为了解该校七年级同学对排球、乒乓球、羽毛球、篮球和足球五种球类运动项目的喜爱情况(每位同学必须且只能选择最喜爱的一项运动项目),进行了随机抽样调查,并将调查结果统计后绘制成了如图和所示的不完整统计图表.(1)请你补全下列样本人数分布表和条形统计图(如图);(2)若七年级学生总人数为920人,请你估计七年级学生喜爱羽毛球运动项目的人数.样本人数分布表类别人数百分比排球 3 6%乒乓球14 28%羽毛球15篮球20%足球8 16%合计100%考点:条形统计图;用样本估计总体;统计表.专题:计算题.分析:(1)由排球的人数除以所占的百分比求出总人数,乘以篮球所占的百分比即可求出篮球的人数,补全条形统计图,如图所示,求出羽毛球所占的百分比,补全人数分布图,如图所示;(2)用人数乘以羽毛球所占的百分比即可求出人数.解答:解:(1)3÷6%=50人,则篮球的人数为50×20%=10人,则补全条形统计图如下:羽毛球占总数的百分比为:15÷50=30%,补全人数分布表为:类别人数百分比排球 3 6%乒乓球14 28%羽毛球15 30%篮球10 20%足球8 16%合计50 100%(2)920×30%=276人.则七年级学生喜爱羽毛球运动项目的人数为276人.点评:此题考查了条形统计图,扇形统计图,中位数,以及众数,弄清题意是解本题的关键.21.(8分)(2013•广东)雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)按照(1)中收到捐款的增长率速度,第四天该单位能收到多少捐款?考点:一元二次方程的应用.专题:增长率问题.分析:(1)解答此题利用的数量关系是:第一天收到捐款钱数×(1+每次降价的百分率)2=第三天收到捐款钱数,设出未知数,列方程解答即可;(2)第三天收到捐款钱数×(1+每次降价的百分率)=第四天收到捐款钱数,依此列式子解答即可.解答:解:(1)设捐款增长率为x,根据题意列方程得,10000×(1+x)2=12100,解得x1=0.1,x2=﹣2.1(不合题意,舍去);答:捐款增长率为10%.(2)12100×(1+10%)=13310元.答:第四天该单位能收到13310元捐款.点评:本题考查了一元二次方程的应用,列方程的依据是:第一天收到捐款钱数×(1+每次降价的百分率)2=第三天收到捐款钱数.22.(8分)(2013•广东)如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1=S2+S3(用“>”、“=”、“<”填空);(2)写出如图中的三对相似三角形,并选择其中一对进行证明.考点:相似三角形的判定;矩形的性质.分析:(1)根据S1=S矩形BDEF,S2+S3=S矩形BDEF,即可得出答案.(2)根据矩形的性质,结合图形可得:△BCD∽△CFB∽△DEC,选择一对进行证明即可.解答:(1)解:∵S1=BD×ED,S矩形BDEF=BD×ED,∴S1=S矩形BDEF,∴S2+S3=S矩形BDEF,∴S1=S2+S3.(2)答:△BCD∽△CFB∽△DEC.证明△BCD∽△DEC;证明:∵∠EDC+∠BDC=90°,∠CBD+∠BDC=90°,∴∠EDC=∠CBD,又∵∠BCD=∠DEC=90°,∴△BCD∽△DEC.点评:本题考查了相似三角形的判定,注意掌握相似三角形的判定定理,最经常用的就是两角法,此题难度一般.四、解答题(三)(本大题3小题,每小题9分,共27分)23.(9分)(2013•广东)已知二次函数y=x2﹣2mx+m2﹣1.(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P 点的坐标;若P点不存在,请说明理由.考点:二次函数综合题.分析:(1)根据二次函数的图象经过坐标原点O(0,0),直接代入求出m的值即可;(2)根据m=2,代入求出二次函数解析式,进而利用配方法求出顶点坐标以及图象与y轴交点即可;(3)根据当P、C、D共线时PC+PD最短,利用平行线分线段成比例定理得出PO 的长即可得出答案.解答:解:(1)∵二次函数的图象经过坐标原点O(0,0),∴代入二次函数y=x2﹣2mx+m2﹣1,得出:m2﹣1=0,解得:m=±1,∴二次函数的解析式为:y=x2﹣2x或y=x2+2x;(2)∵m=2,∴二次函数y=x2﹣2mx+m2﹣1得:y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的顶点为:D(2,﹣1),当x=0时,y=3,∴C点坐标为:(0,3);(3)当P、C、D共线时PC+PD最短,过点D作DE⊥y轴于点E,∵PO∥DE,∴=,∴=,解得:PO=,∴PC+PD最短时,P点的坐标为:P(,0).点评:此题主要考查了二次函数的综合应用以及配方法求二次函数顶点坐标以及最短路线问题等知识,根据数形结合得出是解题关键.24.(9分)(2013•广东)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.考点:切线的判定;圆周角定理;相似三角形的判定与性质.分析:(1)根据BD=BA得出∠BDA=∠BAD,再由∠BCA=∠BDA即可得出结论;(2)判断△BED∽△CBA,利用对应边成比例的性质可求出DE的长度.(3)连接OB,OD,证明△ABO≌△DBO,推出OB∥DE,继而判断OB⊥DE,可得出结论.解答:(1)证明:∵BD=BA,∴∠BDA=∠BAD,∵∠BCA=∠BDA(圆周角定理),∴∠BCA=∠BAD.(2)解:∵∠BDE=∠CAB(圆周角定理),∠BED=∠CBA=90°,∴△BED∽△CBA,∴=,即=,解得:DE=.(3)证明:连结OB,OD,在△ABO和△DBO中,∵,∴△ABO≌△DBO,∴∠DBO=∠ABO,∵∠ABO=∠OAB=∠BDC,∴∠DBO=∠BDC,∴OB∥ED,∵BE⊥ED,∴EB⊥BO,∴OB⊥BE,∴BE是⊙O的切线.点评:本题考查了切线的判定及圆周角定理的知识,综合考查的知识点较多,解答本题要求同学们熟练掌握一些定理的内容.25.(9分)(2013•广东)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.(1)如图2,当三角板DEF运动到点D到点A重合时,设EF与BC交于点M,则∠EMC= 15度;(2)如图3,当三角板DEF运动过程中,当EF经过点C时,求FC的长;(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.考点:相似形综合题.分析:(1)如题图2所示,由三角形的外角性质可得;(2)如题图3所示,在Rt△ACF中,解直角三角形即可;(3)认真分析三角板的运动过程,明确不同时段重叠图形的变化情况:(I)当0≤x≤2时,如答图1所示;(II)当2<x≤6﹣时,如答图2所示;(III)当6﹣<x≤6时,如答图3所示.解答:解:(1)如题图2所示,∵在三角板DEF中,∠FDE=90°,DF=4,DE=,∴tan∠DFE==,∴∠DFE=60°,∴∠EMC=∠FMB=∠DFE﹣∠ABC=60°﹣45°=15°;(2)如题图3所示,当EF经过点C时,FC====;(3)在三角板DEF运动过程中,(I)当0≤x≤2时,如答图1所示:设DE交BC于点G.过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN.又∵NF==MN,BN=NF+BF,∴NF+BF=MN,即MN+x=MN,解得:MN=x.y=S△BDG﹣S△BFM=BD•DG﹣BF•MN=(x+4)2﹣x•x=x2+4x+8;(II)当2<x≤6﹣时,如答图2所示:过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN.又∵NF==MN,BN=NF+BF,∴NF+BF=MN ,即MN+x=MN,解得:MN=x.y=S△ABC﹣S△BFM=AB•AC ﹣BF•MN=×62﹣x •x=x2+18;(III)当6﹣<x≤6时,如答图3所示:由BF=x,则AF=AB﹣BF=6﹣x,设AC与EF交于点M,则AM=AF•tan60°=(6﹣x).y=S△AFM =AF•AM=(6﹣x)•(6﹣x)=x2﹣x+.综上所述,y与x的函数解析式为:y=.点评:本题是运动型综合题,解题关键是认真分析三角板的运动过程,明确不同时段重叠图形形状的变化情况.在解题计算过程中,除利用三角函数进行计算外,也可以利用三角形相似,殊途同归.21。
2013年广东省佛山市高中阶段招生考试数学试题

2013年广东省佛山市高中阶段招生考试数学试题一、选择题(每小题3分,共30分)1.(2013年佛山市)2-的相反数是( ) A .2 B .2- C .21 D .21- 2.(2013年佛山市)下列计算正确的是( )A .1243a a a =⋅ B .743)(a a = C .3632)(b a b a = D .)0( 43≠=÷a a a a3.(2013年佛山市)并排放置的等底等高的圆锥和圆柱(如图)的主视图是( )4.(2013年佛山市)分解因式a a -3的结果是( )A .)1(2-a a B .2)1(-a a C .)1)(1(-+a a a D .)1)((2-+a a a 5.(2013年佛山市)化简)12(2-÷的结果是( ) A .122- B .22-C .21-D .22+6.(2013年佛山市)掷一枚有正反面的均匀硬币,正确的说法是( ) A .正面一定朝上 B .反面一定朝上C .正面比反面朝上的概率大D .正面和反面朝上的概率都是0.5 7.(2013年佛山市)如图,若∠A =60°,AC =20 m ,则BC 大约是(结果精确到0.1 m)( ) A .34.64 m B .34.6 m C .28.3 m D .17.3 m 8.(2013年佛山)半径为3的圆中,一条弦长为4,则圆心到这条弦的距离是( ) A .3 B .4 C .5 D .79.(2013年佛山市)多项式2321xy xy -+的次数及最高次项的系数分别是( ) A .3 3-, B .3 2-, C .3 5-, D .3 2,A .B .C .D .ACB第7题图第3题图10.(2013年佛山市)某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y 与时间x 的关系的大致图象是( )二、填空题(每小题3分,共15分)11.(2013年佛山市)数字9 600 000用科学记数法表示为________________. 12.(2013年佛山市)方程0222=--x x 的解是_________________. 13.(2013•佛山)在1,2,3,4四个数字中随机选两个不同的数字组成两位数,则组成的两位数大于40的概率是 .14.(2013•佛山)图中圆心角∠AOB=30°,弦CA ∥OB ,延长CO 与圆交于点D ,则∠BOD= .15.(2013年佛山市)命题“对顶角相等”的条件是______________.三、解答题(第16~20每小题6分,第21~23每小题8分,第24小题10分,第25小题11分,共75分)16.(2013年佛山市)计算:[])24()2(5213-÷----+⨯.17.(2013年佛山市)网格图中每个方格都是边长为1的正方形.若A ,B ,C ,D ,E ,F 都是格点,试说明 △ABC ∽△DEF .18.(2013年佛山市)按要求化简:21312a a a -++-. xy O A .xyOB .xyOC .xyOD .AB C D EF 第17题图第14题图要求:见答题卡. 解答过程解答步骤 说明 解题依据(用文字或符号填写知识的名称和具体内容,每空一个) 21312a a a -++- 此处不填 此处不填=)1)(1()3(22-++-+a a a a示例:通分示例:分式的基本性质:分式的分子和分母都乘以同一个不等于零的整式,分式的值不变(或者“同分母分式相加减法则:acb ac a b ±=±”) =)1)(1(322-+--+a a a a 去括号① =)1)(1(1-+-a a a合并同类项 此处不填= ②③④19.(2013年佛山市)已知两个语句:①式子12-x 的值在1(含1)与3(含3)之间; ②式子12-x 的值不小于1且不大于3. 请回答以下问题:(1) 两个语句表达的意思是否一样(不用说明理由)? (2) 把两个语句分别用数学式子表示出来.20.(2013年佛山市)如图,圆锥的侧面展开图是一个半圆,求母线AB 与高AO 的夹角.参考公式:圆锥的侧面积S=πrl ,其中r 为底面半径,l 为母线长.21.(8分)(2013年佛山市)已知正比例函数y=ax 与反比例函数的图象有一个公共点A (1,2).(1)求这两个函数的表达式;(2)画出草图,根据图象写出正比例函数值大于反比例函数值时x 的取值范围.22.(2013年佛山市)课本指出:公认的真命题称为公理,除了公理外,其他的真命题(如推论、定理等)的正确性都需要通过推理的方法证实.(1) 叙述三角形全等的判定方法中的推论AAS ; (2) 证明推论AAS .要求:叙述推论用文字表达;用图形中的符号表达已知、 求证,并证明,证明对各步骤要注明依据.23.(2013年佛山市)在一次考试中,从全体参加考试的1000名学生中随机抽取了120名学生的答题卷进行统计分析.其中,某个单项选择题答题情况如下表(没有多选和不选):选项 A BC D 选择人数1559010(1) 根据统计表画出扇形统计图;要求:画图前先求角;画图可借助任何工具,其中一个角的作图用尺规作图(保留痕迹,不写作法和证A B C DEF第22题图第23题图第21题图明);统计图中标注角度.(2) 如果这个选择题满分是3分,正确的选项是C ,则估计全体学生该题的平均得分是多少?24.(10分)(2013年佛山市)如图①,已知抛物线y=ax 2+bx+c 经过点A (0,3),B (3,0),C (4,3). (1)求抛物线的函数表达式; (2)求抛物线的顶点坐标和对称轴;(3)把抛物线向上平移,使得顶点落在x 轴上,直接写出两条抛物线、对称轴和y 轴围成的图形的面积S (图②中阴影部分).25.(2013年佛山市)我们知道,矩形是特殊的平行四边形,所以矩形除了具备平行四边形的一切性质还有其特殊的性质;同样,黄金矩形是特殊的矩形,因此黄金矩形有与一般矩形不一样的知识.已知平行四边形ABCD ,∠A =60°,AB =2a ,AD =a .(1) 把所给的平行四边形ABCD 用两种方式分割并作说明A BCD第25题图第24题图(见答题卡表格里的示例);要求:用直线段分割,分割成的图形是学习过的特殊图形且不超出四个.(2)图中关于边、角和对角线会有若干关系或问题.现在请计算两条对角线的长度.要求:计算对角线BD长的过程中要有必要的论证;直接写出对角线AC的长.解:在表格中作答2013年广东省佛山市高中阶段招生考试数学试题参考答案一、1.A分析:根据相反数的定义:只有符号不同的两个数叫做互为相反数即可得到答案.解:﹣2的相反数是2,故选A.点评:此题主要考查了相反数,关键是掌握相反数的定义.2.C分析:根据同底数幂乘法、幂的乘方、积的乘方的运算性质,利用排除法求解解:A、应为a3•a4=a7,故本选项错误;B、应为(a3)4=a12,故本选项错误;C、每个因式都分别乘方,正确;D、应为a3÷a4=(a≠0),故本选项错误.故选C.点评:本题考查了同底数幂的乘除法,积的乘方和幂的乘方,需熟练掌握且区分清楚,才不容易出错.3.B分析:找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.解:圆锥的左视图是三角形,圆柱的左视图是长方形,故选B.点评:本题考查了三视图的知识,主视图是从物体的正面看得到的视图.4.C分析:首先提取公因式a,再利用平方差公式进行二次分解即可.解:a3﹣a=a(a2﹣1)=a(a+1)(a﹣1),故选C.点评:此题主要考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能再分解为止.5.D分析:分子、分母同时乘以(+1)即可.解:原式===2+.故选D.点评:本题考查了分母有理化,正确选择一个二次根式,使它们的积符合平方差公式是解答问题的关键.6.D分析:根据掷一枚有正反面的均匀硬币,则得到正反两面的概率相等,即可得出答案.解:因为掷一枚有正反面的均匀硬币,所以正面和反面朝上的概率都是0.5.故选D.点评:此题主要考查了概率的意义,根据正反面出现的机会均等是解题关键.7.B分析:首先计算出∠B的度数,再根据直角三角形的性质可得AB=40 m,再利用勾股定理计算出BC长即可.解:因为∠A=60°,∠C=90°,所以∠B=30°,所以AB=2AC.因为AC=20 m,所以AB=40 m.所以BC====20≈34.6(m).故选B.点评:此题主要考查了勾股定理,以及直角三角形的性质,关键是掌握在直角三角形中,30°角所对的直角边等于斜边的一半.在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.8.C分析:过点O作OD⊥AB于点D,由垂径定理可求出BD的长,在Rt△BOD中,利用勾股定理即可得出OD的长.解:如图所示,过点O作OD⊥AB于点D.第8题解析图因为OB=3,AB=4,OD⊥AB,所以BD=AB=×4=2.在Rt△BOD中,OD===.故选C.点评:本题考查的是垂径定理,根据题意画出图形,利用勾股定理求出OD的长是解答此题的关键.9.A分析:根据多项式中次数最高的项的次数叫做多项式的次数可得此多项式为3次,最高次项是﹣3xy2,系数是数字因数,故为﹣3.解:多项式1+2xy﹣3xy2的次数是3,最高次项是﹣3xy2,系数是﹣3;故选A.点评:此题主要考查了多项式,关键是掌握多项式次数的计算方法与单项式的区别.10.B分析:根据在每阶段中,离家的距离随时间的变化情况即可进行判断.解:图象应分三个阶段,第一阶段:匀速跑步到公园,在这个阶段,离家的距离随时间的增大而增大;第二阶段:在公园停留了一段时间,这一阶段离家的距离不随时间的变化而改变,故D错误;第三阶段:沿原路匀速步行回家,这一阶段,离家的距离随时间的增大而减小,故A错误;并且这段的速度小于第一阶段的速度,则C错误.故选B.点评:本题考查了函数的图象,理解每阶段中,离家的距离与时间的关系,根据图象的斜率判断运动的速度是解决本题的关键.二、11.9.6×106分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a 时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解:将9 600 000用科学记数法表示为:9.6×106.故答案为9.6×106.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.12.x1=+1,x2=﹣+1分析:首先把常数﹣2移到等号右边,再两边同时加上一次项系数一半的平方,把左边配成完全平方公式,再开方,解方程即可.解:x2﹣2x﹣2=0,移项,得x2﹣2x=2,配方,得x2﹣2x+1=2+1,即(x﹣1)2=3,两边开平方,得x﹣1=,则x1=+1,x2=﹣+1.点评:此题主要考查了配方法解一元二次方程,配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.13.分析:画出树状图,然后根据概率公式列式计算即可得解.解:根据题意画出树状图如下:一共有12种情况,组成的两位数大于40的情况有3种,所以P(组成的两位数大于40)==.故答案为.点评:本题考查了列表法与树状图法,用到的知识点为概率=所求情况数与总情况数之比.14.30°分析:根据平行线的性质由CA∥OB得到∠CAO=∠AOB=30°,利用半径相等得到∠C=∠OAC=30°,然后根据圆周角定理得到∠AOD=2∠C=60°,则∠BOD=60°﹣30°=30°.解:因为CA∥OB,所以∠CAO=∠AOB=30°.因为OA=OC,所以∠C=∠OAC=30°,所以∠AOD=2∠C=60°,所以∠BOD=60°﹣30°=30°.故答案为30°.点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.也考查了平行线的性质.15.两个角是对顶角分析:根据命题由题设与结论组成,可得到“对顶角相等”的条件是若两个角是对顶角,结论是这两个角相等.解:“对顶角相等”的条件是两个角是对顶角.故答案为两个角是对顶角.点评:本题考查了命题:判断事物的语句叫命题;正确的命题称为真命题;错误的命题称为假命题;命题由题设与结论组成,两个互换题设与结论的命题称为互逆命题.三、16.分析:根据负整数指数幂以及绝对值、乘方运算法则等性质,先算乘方,再算乘除,最后算加法得出即可.解:2×[5+(﹣2)3]﹣(﹣|﹣4|÷2-1=2×(5﹣8)﹣(﹣4÷)=﹣6﹣(﹣8)=2.点评:此题主要考查了实数运算,本题需注意的知识点是:负整数指数幂时,a -p =.17.分析:利用图形与勾股定理可以推知图中两个三角形的三条对应边成比例,由此可以证得△ABC ∽ △DEF . 解:因为AC=,BC==,AB=4,DF==2,EF==2,ED=8,所以===21,所以△ABC ∽△DEF . 点评:本题考查了相似三角形的判定、勾股定理.三角形相似的判定方法有:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;这是判定三角形相似的一种基本方法.相似的基本图形可分别记为“A ”型和“X ”型,如图所示在应用时要善于从复杂的图形中抽象出这些基本图形;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.18.分析:首先通分,把分母化为(a+1)(a ﹣1),再根据同分母分数相加减,分母不变,分子相加减进行计算,注意最后结果要化简. 解:原式=﹣===.点评:此题主要考查了分式的加减,关键是掌握异分母分式加减法法则:把分母不相同的几个分式化成分母相同的分式,叫做通分,经过通分,异分母分式的加减就转化为同分母分式的加减.19.分析:(1)注意分析“在1(含1)与3(含3)之间”及“不小于1且不大于3”的意思即可; (2)根据题意可得不等式组.解:(1)一样;(2)①式子2x ﹣1的值在1(含1)与3(含3)之间可得1≤2x ﹣1≤3; ②式子2x ﹣1的值不小于1且不大于3可得.点评:此题主要考查了由实际问题抽象出一元一次不等式组,关键是正确理解题意,抓住题干中体现不等关系的词语.20.分析:设出圆锥的半径与母线长,利用圆锥的底面周长等于侧面展开图的弧长得到圆锥的半径与母线长,进而表示出母线与高的夹角的正弦值,也就求出了夹角的度数. 解:设圆锥的母线长为l ,底面半径为r ,则πl =2πr ,所以l =2r . 所以母线与高的夹角的正弦值==,所以母线AB 与高AO 的夹角30°.点评:此题主要考查了圆锥的侧面展开图的弧长等于圆锥的底面周长;注意利用一个角相应的三角函数值求得角的度数.21.分析:(1)分别把A点坐标代入正比例函数解析式和反比例函数解析式,求出a与b的值,从而确定两函数解析式;(2)先画出y=和y=2x的图象,根据对称性得到两函数的另一个交点B与点A关于原点对称,则B点坐标为(﹣1,﹣2),然后观察图象得到当﹣1<x<0或x>1时,正比例函数图象都在反比例函数图象上方,即正比例函数值大于反比例函数值.解:(1)把A(1,2)代入y=ax,得a=2,所以正比例函数解析式为y=2x;把A(1,2)代入y=,得b=1×2=2,所以反比例函数解析式为y=.第21题解析图(2)如图,当﹣1<x<0或x>1时,正比例函数值大于反比例函数值.点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.22.分析:(1)两角及其中一角的对边分别对应相等的两个三角形全等.(2)根据三角形内角和定理和全等三角形的判断定理ASA来证明.解:(1)三角形全等的判定方法中的推论AAS指的是:两角及其中一角的对边分别对应相等的两个三角形全等.(2)已知:在△ABC与△DEF中,∠A=∠D,∠C=∠F,BC=EF.求证:△ABC≌△DEF.证明:如图,在△ABC与△DEF中,∠A=∠D,∠C=∠F(已知),所以∠A+∠C=∠D+∠F(等量代换).又因为∠A+∠B+∠C=180°,∠D+∠E+∠F=180°(三角形内角和定理),所以∠B=∠E.所以在△ABC与△DEF 中,,所以△ABC≌△DEF(ASA).点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.23.分析:(1)根据用每个选项的人数除以总数即可得出扇形图中所占比例,进而求出各角的度数;(2)根据统计表求出总得分,进而得出平均分即可.解:(1)根据图表数据得出:选A 的所占圆心角为:×360°=45°;选B 的所占圆心角为:×360°=15°;选C 的所占圆心角为:×360°=270°;选D 的所占圆心角为:×360°=30°.如图所示:(2)因为选择题满分是3分,正确的选项是C ,所以全体学生该题的平均得分为:=2.25(分).点评:本题考查的是扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.24.分析:(1)把点A、B、C代入抛物线解析式y=ax2+bx+c利用待定系数法求解即可;(2)把抛物线解析式整理成顶点式形式,然后写出顶点坐标与对称轴即可;(3)根据顶点坐标求出向上平移的距离,再根据阴影部分的面积等于平行四边形的面积,列式进行计算即可.解:(1)因为抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3),所以,解得,所以抛物线的函数表达式为y=x2﹣4x+3;(2)因为y=x2﹣4x+3=(x﹣2)2﹣1,所以抛物线的顶点坐标为(2,﹣1),对称轴为直线x=2;(3)如图,因为抛物线的顶点坐标为(2,﹣1),所以PP′=1,阴影部分的面积等于平行四边形A′APP′的面积,平行四边形A′APP′的面积=1×2=2,所以阴影部分的面积=2.点评:本题考查了待定系数法求二次函数解析式,二次函数的性质,二次函数图象与几何变换,第(3)小题根据平移的性质,把阴影部分的面积转化为平行四边形的面积是解题的关键.25.分析:(1)方案一:分割成两个等腰梯形;方案二:分割成一个等边三角形、一个等腰三角形和一个直角三角形;(2)利用平行四边形的性质、等边三角形的性质、勾股定理作答,认真计算即可.第24题解析图第23题解析图解:(1)在表格中作答:分割图形分割或图形说明示例:示例:①分割成两个菱形.②两个菱形的边长都为a,锐角都为60°.①分割成两个等腰梯形.②两个等腰梯形的腰长都为a,上底长都为,下底长都为a,上底角都为120°,下底角都为60°.①分割成一个等边三角形、一个等腰三角形、一个直角三角形.②等边三角形的边长为a ,等腰三角形的腰长为a,顶角为120°.直角三角形两锐角为30°、60°,三边为a、a、2a.因为AB=2a,E为AB中点,所以AE=BE=a.因为AD=AE=a,∠A=60°,所以△ADE为等边三角形,∠ADE=∠DEA=60°,DE=AE=a.又因为∠BED+∠DEA=180°,所以∠BED=180°﹣∠DEA=180°﹣60°=120°.又因为DE=BE=a,∠BED=120°,所以∠BDE=∠DBE=(180°﹣120°)=30°.所以∠ADB=∠ADE+∠BDE=60°+30°=90°.所以Rt△ADB中,∠ADB=90°,由勾股定理,得BD2+AD2=AB2,即BD2+a2=(2a)2,解得BD=a.如下图②所示,AC=2OC=2=2=2•a=a.所以BD=a,AC=a.点评:本题是几何综合题,考查了四边形(平行四边形、等腰梯形、菱形、矩形)、三角形(等边三角形、等腰三角形、直角三角形)的图形与性质.第(1)问侧重考查了几何图形的分割、剪拼、动手操作能力和空间想象能力;第(2)问侧重考查了几何计算能力.本题考查知识点全面,对学生的几何综合能力要求较高,是一道好题.第25题解析图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省佛山市2013年中考数学试卷一、选择题(每小题3分,共30分)1.(3分)(2013•佛山)﹣2的相反数是( )A . 2B . ﹣2C .D .考点:相反数.分析: 根据相反数的定义:只有符号不同的两个数叫做互为相反数即可得到答案.解答:解:﹣2的相反数是2,故选:A . 点评:此题主要考查了相反数,关键是掌握相反数的定义.2.(3分)(2001•东城区)下列计算正确的是( ) A . a 3•a 4=a 12 B . (a 3)4=a 7 C . (a 2b )3=a 6b 3 D . a 3÷a 4=a(a ≠0)考点:幂的乘方与积的乘方;同底数幂的乘法. 分析: 根据同底数幂乘法、幂的乘方、积的乘方的运算性质,利用排除法求解.解答: 解:A 、应为a 3•a 4=a 7,故本选项错误;B 、应为(a 3)4=a 12,故本选项错误;C 、每个因式都分别乘方,正确;D 、应为a 3÷a 4=(a ≠0),故本选项错误.故选C .点评: 本题考查了同底数幂的乘法,积的乘方和幂的乘方,需熟练掌握且区分清楚,才不容易出错.3.(3分)(2013•佛山)并排放置的等底等高的圆锥和圆柱(如图)的主视图是( )A .B .C .D .考点:简单组合体的三视图.分析: 找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.解答:解:圆锥的左视图是三角形,圆柱的左视图是长方形,故选:B . 点本题考查了三视图的知识,主视图是从物体的正面看评: 得到的视图.4.(3分)(2013•佛山)分解因式a 3﹣a 的结果是( ) A . a (a 2﹣1) B . a (a ﹣1)2 C . a (a+1)(a ﹣1) D . (a 2+a )(a ﹣1)考点:提公因式法与公式法的综合运用.分析: 首先提取公因式a ,再利用平方差公式进行二次分解即可.解答:解:a 3﹣a=a (a 2﹣1)=a (a+1)(a ﹣1), 故选:C . 点评:此题主要考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.5.(3分)(2013•佛山)化简的结果是( )A .B .C .D .考点:分母有理化.分析: 分子、分母同时乘以(+1)即可.解答: 解:原式===2+.故选D . 点评: 本题考查了分母有理化,正确选择两个二次根式,使它们的积符合平方差公式是解答问题的关键.6.(3分)(2013•佛山)掷一枚有正反面的均匀硬币,正确的说法是( )A . 正面一定朝上B . 反面一定朝上C . 正面比反面朝上的概率大D . 正面和反面朝上的概率都是0.5考点:概率的意义.分析: 根据掷一枚有正反面的均匀硬币,则得到正反两面的概率相等,即可得出答案.解答:解:∵掷一枚有正反面的均匀硬币,∴正面和反面朝上的概率都是0.5. 故选:D .点评: 此题主要考查了概率的意义,根据正反面出现的机会均等是解题关键.7.(3分)(2013•佛山)如图,若∠A=60°,AC=20m ,则BC 大约是(结果精确到0.1m ) ( )A . 34.64mB . 34.6mC . 28.3mD . 17.3m考点:勾股定理;含30度角的直角三角形.分析:首先计算出∠B 的度数,再根据直角三角形的性质可得AB=40m ,再利用勾股定理计算出BC 长即可. 解答: 解:∵∠A=60°,∠C=90°,∴∠B=30°,∴AB=2AC ,∵AC=20m ,∴AB=40m ,∴BC====20≈34.6(m ),故选:B .点评:此题主要考查了勾股定理,以及直角三角形的性质,关键是掌握在直角三角形中,30°角所对的直角边等于斜边的一半.在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.8.(3分)(2013•佛山)半径为3的圆中,一条弦长为4,则圆心到这条弦的距离是( )A . 3B . 4C .D .考点:垂径定理;勾股定理.专题:探究型.分析:过点O 作OD ⊥AB 于点D ,由垂径定理可求出BD的长,在Rt △BOD 中,利用勾股定理即可得出OD 的长.解答:解:如图所示:过点O 作OD ⊥AB 于点D , ∵OB=3,AB=3,OD ⊥AB ,∴BD=AB=×4=2,在Rt △BOD 中,OD===.故选C .点评:本题考查的是垂径定理,根据题意画出图形,利用勾股定理求出OD 的长是解答此题的关键.9.(3分)(2013•佛山)多项式1+2xy ﹣3xy 2的次数及最高次项的系数分别是( )A . 3,﹣3B . 2,﹣3C . 5,﹣3D . 2,3考点:多项式.分析:根据多项式中次数最高的项的次数叫做多项式的次数可得此多项式为3次,最高次项是﹣3xy 2,系数是数字因数,故为﹣3.解答:解:多项式1+2xy ﹣3xy 2的次数是3,最高次项是﹣3xy 2,系数是﹣3; 故选:A .点评: 此题主要考查了多项式,关键是掌握多项式次数的计算方法与单项式的区别.10.(3分)(2013•佛山)某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y 与时间x 的关系的大致图象是( ) A . B . C . D .考函数的图象.点:分析: 根据在每段中,离家的距离随时间的变化情况即可进行判断.解答: 解:图象应分三个阶段,第一阶段:匀速跑步到公园,在这个阶段,离家的距离随时间的增大而增大;第二阶段:在公园停留了一段时间,这一阶段离家的距离不随时间的变化而改变.故D 错误;第三阶段:沿原路匀速步行回家,这一阶段,离家的距离随时间的增大而减小,故A 错误,并且这段的速度小于于第一阶段的速度,则C 错误.故选B .点评:本题考查了函数的图象,理解每阶段中,离家的距离与时间的关系,根据图象的斜率判断运动的速度是解决本题的关键.二、填空题(每小题3分,共15分)11.(3分)(2013•佛山)数字9 600 000用科学记数法表示为 9.6×106.考点:科学记数法—表示较大的数.分析: 科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.解答:解:将9 600 000用科学记数法表示为:9.6×106. 故答案为:9.6×106. 点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.12.(3分)(2013•佛山)方程x 2﹣2x ﹣2=0的解是 x 1=+1,x 2=﹣+1 .考点:解一元二次方程-配方法.分析:首先把常数﹣2移到等号右边,再两边同时加上一次项系数一半的平方,把左边配成完全平方公式,再开方,解方程即可.解答:解:x 2﹣2x ﹣2=0,移项得:x 2﹣2x=2, 配方得:x 2﹣2x+1=2+1,(x ﹣1)2=3,两边直接开平方得:x ﹣1=,则x 1=+1,x 2=﹣+1.点评: 此题主要考查了配方法解一元二次方程,配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.13.(3分)(2013•佛山)在1,2,3,4四个数字中随机选两个不同的数字组成两位数,则组成的两位数大于40的概率是.考点:列表法与树状图法.专题:图表型.分析:画出树状图,然后根据概率公式列式计算即可得解. 解答:解:根据题意画出树状图如下:一共有12种情况,组成的两位数大于40的情况有3种,所以,P (组成的两位数大于40)==.故答案为:.点评: 本题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.14.(3分)(2013•佛山)图中圆心角∠AOB=30°,弦CA ∥OB ,延长CO 与圆交于点D ,则∠BOD= 30° .考点:圆周角定理;平行线的性质.专题:计算题.分析: 根据平行线的性质由CA ∥OB 得到∠CAO=∠AOB=30°,利用半径相等得到∠C=∠OAC=30°,然后根据圆周角定理得到∠AOD=2∠C=60°,则∠BOD=60°﹣30°=30°. 解答: 解:∵CA ∥OB ,∴∠CAO=∠AOB=30°,∵OA=OC ,∴∠C=∠OAC=30°,∴∠AOD=2∠C=60°,∴∠BOD=60°﹣30°=30°.故答案为30°.点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.也考查了平行线的性质.15.(3分)(2013•佛山)命题“对顶角相等”的“条件”是 两个角是对顶角 .考点:命题与定理.分析: 根据命题由题设与结论组成可得到对顶角相等”的“条件”是若两个角是对顶角,结论是这两个角相等. 解答: 解:“对顶角相等”的“条件”是两个角是对顶角. 故答案为:两个角是对顶角.点评:本题考查了命题:判断事物的语句叫命题;正确的命题称为真命题;错误的命题称为假命题;命题由题设与结论组成,两个互换题设与结论的命题称为互逆命题.三、解答题(第16~20每小题6分,第21~23每小题6分,第24小题10分,第25小题11分,共75分)16.(6分)(2013•佛山)计算:2×[5+(﹣2)3]﹣(﹣|﹣4|÷2﹣1).考点:实数的运算;负整数指数幂.分析: 根据负整数指数幂以及绝对值、乘方运算法则等性质,先算乘方,再算乘除,最后算加法得出即可. 解答: 解:2×[5+(﹣2)3]﹣(﹣|﹣4|÷2﹣1=2×(5﹣8)﹣(﹣4÷)=﹣6﹣(﹣8)=2.点评: 此题主要考查了实数运算,本题需注意的知识点是:负整数指数幂时,a ﹣p =.17.(6分)(2013•佛山)网格图中每个方格都是边长为1的正方形.若A ,B ,C ,D ,E ,F 都是格点,试说明△ABC ∽△DEF .考点:相似三角形的判定;勾股定理.专题:证明题;网格型.分析:利用图形与勾股定理可以推知图中两个三角形的三条对应边成比例,由此可以证得△ABC ∽△DEF . 解答: 证明:∵AC=,BC==,AB=4,DF==2,EF==2,ED=8, ∴===2,∴△ABC ∽△DEF .点评: 本题考查了相似三角形的判定、勾股定理.相似三角形相似的判定方法有:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;这是判定三角形相似的一种基本方法.相似的基本图形可分别记为“A ”型和“X ”型,如图所示在应用时要善于从复杂的图形中抽象出这些基本图形;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.18.(6分)(2013•佛山)按要求化简:.考点:分式的加减法.分析:首先通分,把分母化为(a+1)(a ﹣1),再根据同分母分数相加减,分母不变,分子相加减进行计算,注意最后结果要化简.解答:解:原式=﹣ ===. 点评:此题主要考查了分式的加减,关键是掌握异分母分式加减法法则:把分母不相同的几个分式化成分母相同的分式,叫做通分,经过通分,异分母分式的加减就转化为同分母分式的加减.19.(6分)(2013•佛山)已知两个语句:①式子2x ﹣1的值在1(含1)与3(含3)之间; ②式子2x ﹣1的值不小于1且不大于3.请回答以下问题:(1)两个语句表达的意思是否一样(不用说明理由)?(2)把两个语句分别用数学式子表示出来.考点:由实际问题抽象出一元一次不等式组.分析: (1)注意分析“在1(含1)与3(含3)之间”及“不小于1且不大于3”的意思即可;(2)根据题意可得不等式组. 解答: 解:(1)一样; (2)①式子2x ﹣1的值在1(含1)与3(含3)之间可得1≤2x ﹣1≤3;②式子2x ﹣1的值不小于1且不大于3可得.点评:此题主要考查了由实际问题抽象出一元一次不等式组,关键是正确理解题意,抓住题干中体现不等关系的词语.20.(6分)(2013•佛山)如图,圆锥的侧面展开图是一个半圆,求母线AB 与高AO 的夹角.参考公式:圆锥的侧面积S=πrl ,其中r 为底面半径,l 为母线长.考点:圆锥的计算.分析:设出圆锥的半径与母线长,利用圆锥的底面周长等于侧面展开图的弧长得到圆锥的半径与母线长,进而表示出母线与高的夹角的正弦值,也就求出了夹角的度数.解答: 解:设圆锥的母线长为l ,底面半径为r ,则:πl=2πr ,∴l=2r ,∴母线与高的夹角的正弦值==,∴母线AB 与高AO 的夹角30°.点评:此题主要考查了圆锥的侧面展开图的弧长等于圆锥的底面周长;注意利用一个角相应的三角函数值求得角的度数.21.(8分)(2013•佛山)已知正比例函数y=ax 与反比例函数的图象有一个公共点A (1,2).(1)求这两个函数的表达式;(2)画出草图,根据图象写出正比例函数值大于反比例函数值时x 的取值范围.考点:反比例函数与一次函数的交点问题.专题:数形结合.分析: (1)分别把A 点坐标代入正比例函数解析式和反比例函数解析式,求出a 与b 的值,从而确定两函数解析式;(2)先画出y=和y=2x 的图象,根据对称性得到两函数的另一个交点B 与点A 关于原点对称,则B 点坐标为(﹣1,﹣2),然后观察图象得到当﹣1<x <0或x >2时,正比例函数图象都在反比例函数图象上方,即正比例函数值大于反比例函数值.解答:解:(1)把A (1,2)代入y=ax 得a=2, 所以正比例函数解析式为y=2x ;把A (1,2)代入y=得b=1×2=2,所以反比例函数解析式为y=;(2)如图,当﹣1<x <0或x >1时,正比例函数值大于反比例函数值.点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.22.(8分)(2013•佛山)课本指出:公认的真命题称为公理,除了公理外,其他的真命题(如推论、定理等)的正确性都需要通过推理的方法证实.(1)叙述三角形全等的判定方法中的推论AAS ;(2)证明推论AAS .要求:叙述推论用文字表达;用图形中的符号表达已知、求证,并证明,证明对各步骤要注明依据.考点:全等三角形的判定;命题与定理.分析: (1)两边及其夹角分别对应相等的两个三角形全等.(2)根据三角形内角和定理和全等三角形的判断定理ASA 来证明.解答: 解:(1)三角形全等的判定方法中的推论AAS 指的是:两边及其夹角分别对应相等的两个三角形全等.(2)已知:在△ABC 与△DEF 中,∠A=∠D ,∠C=∠F ,BC=EF .求证:△ABC ≌△DEF .证明:如图,在△ABC 与△DEF 中,∠A=∠D ,∠C=∠F (已知),∴∠A+∠C=∠D+∠F (等量代换).又∵∠A+∠B+∠C=180°,∠D+∠E+∠F=180°(三角形内角和定理),∴∠B=∠E .∴在△ABC 与△DEF 中,, ∴△ABC ≌△DEF (ASA ).点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL . 注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.23.(8分)(2013•佛山)在一次考试中,从全体参加考试的1000名学生中随机抽取了120名学生的答题卷进行统计分析.其中,某个单项选择题答题情况如下表(没有多选和不选):选项 A BC D 选择人数 155 90 10 (1)根据统计表画出扇形统计图;要求:画图前先求角;画图可借助任何工具,其中一个角的作图用尺规作图(保留痕迹,不写作法和证明);统计图中标注角度.(2)如果这个选择题满分是3分,正确的选项是C ,则估计全体学生该题的平均得分是多少?考点:扇形统计图;用样本估计总体;统计表.分析: (1)根据用每个选项的人数除以总数即可得出扇形图中所占比例,进而求出各角的度数;(2)根据统计表求出总得分,进而得出平均分即可.解答:解:(1)根据图表数据得出: 选A 的所占圆心角为:×360°=45°; 选B 的所占圆心角为:×360°=15°; 选C 的所占圆心角为:×360°=270°; 选D 的所占圆心角为:×360°=30°.如图所示:(2)∵选择题满分是3分,正确的选项是C , ∴全体学生该题的平均得分为:=2.25(分), 答:全体学生该题的平均得分是2.25分.点评:本题考查的是扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.24.(10分)(2013•佛山)如图①,已知抛物线y=ax 2+bx+c 经过点A (0,3),B (3,0),C (4,3).(1)求抛物线的函数表达式;(2)求抛物线的顶点坐标和对称轴;(3)把抛物线向上平移,使得顶点落在x 轴上,直接写出两条抛物线、对称轴和y 轴围成的图形的面积S (图②中阴影部分).考点: 待定系数法求二次函数解析式;二次函数的性质;二次函数图象与几何变换.分析: (1)把点A 、B 、C 代入抛物线解析式y=ax 2+bx+c 利用待定系数法求解即可;(2)把抛物线解析式整理成顶点式形式,然后写出顶点坐标与对称轴即可;(3)根据顶点坐标求出向上平移的距离,再根据阴影部分的面积等于平行四边形的面积,列式进行计算即可得解.解答: 解:(1)∵抛物线y=ax 2+bx+c 经过点A (0,3),B (3,0),C (4,3), ∴, 解得,所以抛物线的函数表达式为y=x 2﹣4x+3;(2)∵y=x 2﹣4x+3=(x ﹣2)2﹣1,∴抛物线的顶点坐标为(2,﹣1),对称轴为直线x=2;(3)如图,∵抛物线的顶点坐标为(2,﹣1), ∴PP ′=1,阴影部分的面积等于平行四边形A ′APP ′的面积, 平行四边形A ′APP ′的面积=1×2=2,∴阴影部分的面积=2.点评: 本题考查了待定系数法求二次函数解析式,二次函数的性质,二次函数图象与几何变换,(3)根据平移的性质,把阴影部分的面积转化为平行四边形的面积是解题的关键.25.(11分)(2013•佛山)我们知道,矩形是特殊的平行四边形,所以矩形除了具备平行四边形的一切性质还有其特殊的性质;同样,黄金矩形是特殊的矩形,因此黄金矩形有与一般矩形不一样的知识.已知平行四边形ABCD ,∠A=60°,AB=2a ,AD=a .(1)把所给的平行四边形ABCD 用两种方式分割并作说明(见题答卡表格里的示例);要求:用直线段分割,分割成的图形是学习过的特殊图形且不超出四个.分割图形分割或图形说明 示例: 示例:①分割成两个菱形.②两个菱形的边长都为a ,锐角都为60°.(2)图中关于边、角和对角线会有若干关系或问题.现在请计算两条对角线的长度.要求:计算对角线BD 长的过程中要有必要的论证;直接写出对角线AC 的长.考点:四边形综合题.分析:(1)方案一:分割成两个等腰梯形;方案二:分割成一个等边三角形、一个等腰三角形和一个直角三角形;(2)利用平行四边形的性质、等边三角形的性质、勾股定理作答,认真计算即可.解答: 解:(1)在表格中作答: 分割图形 分割或图形说明 示例:示例:①分割成两个菱形.②两个菱形的边长都为a ,锐角都为60°.①分割成两两个等腰梯形.②两个等腰梯形的腰长都为a ,上底长都为,下底长都为a ,上底角都为120°,下底角都为60°.①分割成一个等边三角形、一个等腰三角形、一个直角三角形.②等边三角形的边长为a ,等腰三角形的腰长为a ,顶角为120°.直角三角形两锐角为30°、60°,三边为a 、a 、2a .(2)如右图①,连接BD,取AB中点E,连接DE.∵AB=2a,E为AB中点,∴AE=BE=a,∵AD=AE=a,∠A=60°,∴△ADE为等边三角形,∠ADE=∠DEA=60°,DE=AE=a,又∵∠BED+∠DEA=180°,∴∠BED=180°﹣∠DEA=180°﹣60°=120°,又∵DE=BE=a,∠BED=120°,∴∠BDE=∠DBE=(180°﹣120°)=30°,∴∠ADB=∠ADE+∠BDE=60°+30°=90°∴Rt△ADB中,∠ADB=90°,由勾股定理得:BD2+AD2=AB2,即BD2+a2=(2a)2,解得BD=a.如右图②所示,AC=2OC=2=2=2•a=a.∴BD=a,AC=a.点评: 本题是几何综合题,考查了四边形(平行四边形、等腰梯形、菱形、矩形)、三角形(等边三角形、等腰三角形、直角三角形)的图形与性质.第(1)问侧重考查了几何图形的分割、剪拼、动手操作能力和空间想象能力;第(2)问侧重考查了几何计算能力.本题考查知识点全面,对学生的几何综合能力要求较高,是一道好题.。
