模型参考自适应控制建大资料精品PPT课件
合集下载
《自适应控制》课件

软件实现
01
02
03
控制算法选择
根据被控对象的特性和控 制要求,选择合适的控制 算法,如PID控制、模糊 控制等。
软件开发环境
选择合适的软件开发环境 ,如MATLAB、Simulink 等,进行控制算法的实现 和仿真。
软件集成与调试
将各个软件模块集成在一 起,进行系统调试,确保 软件能够正常工作并满足 控制要求。
直接优化目标函数的自适应系统是一种通过直接优化系统目标函数,对系统参数 进行调整的自适应控制系统。
详细描述
直接优化目标函数的自适应系统根据系统目标函数和约束条件,通过优化算法寻 找最优的系统参数,以实现系统性能的最优。这种系统广泛应用于控制工程、航 空航天等领域。
自校正调节器
总结词
自校正调节器是一种通过实时校正系统参数,实现系统性能提升的自适应控制系统。
要点二
详细描述
在进行自适应控制系统设计时,首先需要对系统进行建模 ,即通过数学模型来描述系统的动态行为。这个模型可以 是线性或非线性的,取决于系统的复杂性和特性。在建立 模型后,需要对模型参数进行估计,这通常涉及到使用各 种算法和优化技术来不断调整和更新系统参数,以使系统 能够更好地适应外界环境的变化。
详细描述
最小均方误差算法基于最小化预测误差的平方和来调整控制参数,通过不断迭代计算,逐渐减小误差 ,使系统输出逐渐接近目标值。该算法具有较好的跟踪性能和鲁棒性,广泛应用于各种自适应控制系 统。
极点配置算法
总结词
极点配置算法是一种自适应控制算法,通过 调整系统参数使系统的极点配置在期望的位 置上,以达到系统稳定和性能优化的目的。
特点
自适应控制具有适应性、实时性和智 能性等特点,能够自动调整控制参数 和策略,以适应不同环境和条件下的 变化。
自适应控制课件

ɺ x m = Am x m + Bm u, x m (0) = x m 0
(2.1)
m维分段连续的输入向量 维分段连续的输入向量 n维状态向量 n维状态向量 相应维数常数矩阵 参考模型为稳定的,并且是完全可控和完全可观测的。 参考模型为稳定的,并且是完全可控和完全可观测的。 在可调参数模型参考自适应系统中,可调系统 可调参数模型参考自适应系统中, 模型参考自适应系统中
w(k )
u (k )
y (k )
自校正控制系统结构图
2.2 模型参考自适应控制
2.2.1 模型参考自适应控制的数学描述
模型参考自适应控制系统由参考模型、可调系统和自适应机构三部分组成. 模型参考自适应控制系统由参考模型、可调系统和自适应机构三部分组成 参考模型 三部分组成
参考模型 可调机构 自适应机构 根据系统广义误差 e (t ) , 按照 一定的规律改变可调系统的结构或参数。 一定的规律改变可调系统的结构或参数。 理想模型
ɺ x m = Am x m + Bm u, x m (0) = x m 0
(2.1)
在可调参数模型参考自适应系统中,可调系统 在可调参数模型参考自适应系统中, 参数模型参考自适应系统中
ɺ x = A(e, t ) x + B (e, t )u x (0) = x 0 , A(0) = A0 , B (0) = B0
模型参考自适应控制系统结构图
2.2.1 模型参考自适应控制的数学描述
2.2.1.1 并联模型参考自适应系统的数学模型 并联模型参考自适应系统可以用状态方程和输入-输出方程进行描述。 并联模型参考自适应系统可以用状态方程和输入-输出方程进行描述。 状态方程 进行描述 一、用状态方程描述的模型参考自适应系统 对于连续模型参考自适应控制系统 对于连续模型参考自适应控制系统 连续模型 参考模型: 参考模型:
(2.1)
m维分段连续的输入向量 维分段连续的输入向量 n维状态向量 n维状态向量 相应维数常数矩阵 参考模型为稳定的,并且是完全可控和完全可观测的。 参考模型为稳定的,并且是完全可控和完全可观测的。 在可调参数模型参考自适应系统中,可调系统 可调参数模型参考自适应系统中, 模型参考自适应系统中
w(k )
u (k )
y (k )
自校正控制系统结构图
2.2 模型参考自适应控制
2.2.1 模型参考自适应控制的数学描述
模型参考自适应控制系统由参考模型、可调系统和自适应机构三部分组成. 模型参考自适应控制系统由参考模型、可调系统和自适应机构三部分组成 参考模型 三部分组成
参考模型 可调机构 自适应机构 根据系统广义误差 e (t ) , 按照 一定的规律改变可调系统的结构或参数。 一定的规律改变可调系统的结构或参数。 理想模型
ɺ x m = Am x m + Bm u, x m (0) = x m 0
(2.1)
在可调参数模型参考自适应系统中,可调系统 在可调参数模型参考自适应系统中, 参数模型参考自适应系统中
ɺ x = A(e, t ) x + B (e, t )u x (0) = x 0 , A(0) = A0 , B (0) = B0
模型参考自适应控制系统结构图
2.2.1 模型参考自适应控制的数学描述
2.2.1.1 并联模型参考自适应系统的数学模型 并联模型参考自适应系统可以用状态方程和输入-输出方程进行描述。 并联模型参考自适应系统可以用状态方程和输入-输出方程进行描述。 状态方程 进行描述 一、用状态方程描述的模型参考自适应系统 对于连续模型参考自适应控制系统 对于连续模型参考自适应控制系统 连续模型 参考模型: 参考模型:
模型参考自适应控制建大资料精品PPT课件

p( s )
p( s )
其中: p(s) sn a1sn-1 an-1s an
q(s) b1sn-1 b2sn-2 bn
– Km为常数,根据系统希望的动态响应事先确定 – p(s)、q(s)已知
R
—kpm(—qs()—s)
ym +e
Kc
Kp
-pq-((-ss-))- -
yp
适应律
R
- 麻省理工学院于1958年提出的,因此也叫MIT方法 - 最早提出、最早应用的一种方法 - 理论简单,实施方便,可用模拟元件实现 - 实质是一个可调增益的系统
一. 单个参数的MIT方法
第三章模型参考自适应控制 §2 局部参数最优化设计方法
工作背景
设参考模型为 Kmq( s) ,对象模型为 K p(t)q(s)
一般来说,自适应控制系统在反馈控制的 基本回路上加上自适应机构构成。具有三 方面的功能:
(1)在线辨识。 (2)决策控制。 (3)在线修正。
自适应控制系统主要分为两大类: (1)模型参考自适应控制系统。 (2)自校正自适应控制系统
模型参考自适应控制
(Model Reference Adaptive Control) MRAC
(2.3)
Kc
p( D)
欲消去 q(D) / p(D),
ym Km q( D)
R
p( D)
即:
q( D) p( D)
ym R Km
Байду номын сангаас
代入(2.3)式,
e Kc
-
Kp Km
ym
(2.4)
e
Kp
Kc - Km ym
Kc
-
B2e
模型参考自适应控制ppt课件

kpDp (s)
(1)
kmNm (s)
又
P( s)
Yp (s) R(s)
a*(s)
(s)
1
Dm (s) kmNm (s)
b* (s)
Dm (s) (s)
kma*(s)
0 (s)Dm (s) kmb*(s)
(2)
即
kp
N p (s) Dp (s)
kma*(s)
0 (s)Dm (s) kmb*(s)
23
2、假定
被辨识对象:
P(s) Yp (s) kpN p (s) R(s) Dp (s)
参考模型: 参考输入:
M (s) Ym (s) km Nm (s) U (s) Dm (s)
设r(t)是t的分段连续函数,且有界。 辨识的目的:根据可量测的r(t)和yp (t) 决定k p , N p (s), Dp (s)的系数。
设置参数可调的控制器,与模型一起组成参数可调系统
16
前馈可调增益 反馈可调增益
u
t
使ymt
完全跟踪
ypt
p(s)
r(t)
kp
y p (t )
s ap
- e1(t)
a0(t)
前馈
M (s)
+ u(t) km
-
s am
+
ym (t )
反馈 b0(t) 可调系统
17
其中:
模型的输入控制u t 为
过程位置互换。
基本思想:同MARC设计思想,即通过自适应控制器
来调整模型使e(t)0,这样的模型就是我
们要辨识的结果。
“对偶性质”设计MRAC的方法用于辨识; 将模型参考辨识方法用于设计MARC。
第十七部分模型参考自适应控制教学课件

再进一步探讨当et 0时,在什么条件下能同时达到参数误差的 渐近稳定,即同时能满足 AtAM,BtBM的问题。由状态广义 误差方程(17-45)可得,当 et 0 时
A M A t x s B M B t r 0
(17-51)
以上恒等式成立说明有三种可能情况:
⑴ x s 和 r 线性相关,并有 A M A t及 B M B t;
KoB12e1tK KM o yMt
(17-11) (17-12) (17-13)
(17-14)
令
B
2 B1
Ks KM
,则得
K oB e1tyM t
(17-15)
这就是可调整参数K o 的自适应律。于是M.I.T.自适应控制系统的 数学模型可归结为
输出误差: D s e 1 s K M K o K s N s r s 模型输出: D s y M s K M N s r s
数的充要条件是存在正定矩阵 P、Q ,并满足式(17-36)、式(17-37)。
下面来讨论受控对象全部状态可直接获取的情况下,基于李雅普 诺夫稳定性理论进行自适应控制系统设计的方法。
设可调系统数学模型为
给定参考模型为
x s A tx s B tr
x M A M x M B M r
(17-42) (17-43)
线性时不变系统的稳定性定理
线性时不变自治系统xA x在平衡点 x 0 是渐近稳定的,当且仅 当对任意给定的正定对称矩阵Q ,都存在一个正定对称矩阵 P ,并 满足如下李雅普诺夫方程:
ATPPAQ
(17-33)
则标量函数VxxTPx即为该系统的李雅谱诺夫函数。
函数的正实性
凡满足以下两个条件的实有理函数W s ,称为正实函数: ⑴ W s 只能含有s 左半平面的极点及虚轴上的其留数为正的一
自适应控制课件

模型参考自适应控制系统结构图
2.2.1 模型参考自适应控制的数学描述
2.2.1.1 并联模型参考自适应系统的数学模型 并联模型参考自适应系统可以用状态方程和输入-输出方程进行描述。 并联模型参考自适应系统可以用状态方程和输入-输出方程进行描述。 状态方程 进行描述 一、用状态方程描述的模型参考自适应系统 对于连续模型参考自适应控制系统 对于连续模型参考自适应控制系统 连续模型 参考模型: 参考模型:
i
由广义误差 e = y m − y s 通过自适应规律进行自适 应调整
Ds (t , p) = N s (t , p) =
i =0 m
∑ a si (e, t ) p ∑ bsi (e, t ) p
n
(2.11) (2.12)
i
i =0
2.2.1.1 并联模型参考自适应系统的数学模型 二、用输入-输出方程描述的模型参考自适应系统 用输入- 信号综合自适应方案中 在信号综合自适应方案中,可调系统的输入输出方程为
2.2 模型参考自适应控制
2.2.1 模型参考自适应控制的数学描述
不为0 广义误差向量 e 不为0时,自适应机构按照一定规律改变可调机构的结构或参 数或直接改变被控对象的输入信号, 数或直接改变被控对象的输入信号,以使得系统的性能指标达到或接近希望的性能 指标。 指标。 参数自适应方案:通过更新可调机构的参数来实现的模型参考自适应控制。 参数自适应方案:通过更新可调机构的参数来实现的模型参考自适应控制。 可调机构的参数来实现的模型参考自适应控制 信号综合自适应方案:通过改变施加到系统的输入端信号来实现的模型参考自适应 信号综合自适应方案:通过改变施加到系统的输入端信号来实现的模型参考自适应 系统的输入端信号 控制。 控制。
自适应控制-PPT精品文档
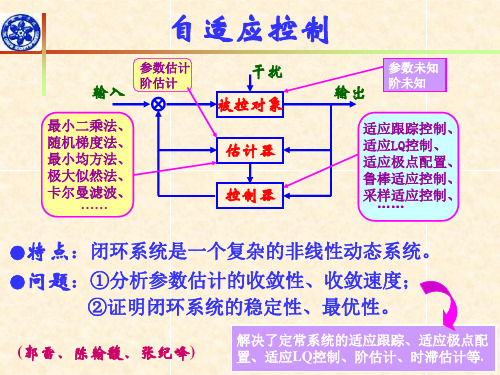
②证明闭环系统的稳定性、最优性。
(郭雷、陈翰馥、张纪峰)
解决了定常系统的适应跟踪、适应极点配 置、适应LQ控制、阶估计、时滞估计等.
随机混杂系统控制
输入
突变参数 离散参数
X
dx A ( x B ( u t t) tdt t) tdt C ( u t) tdw t
输出
采样 数据 采样控 制器
t
F ( b ) { f ( ) :f ( x ) O (| x | ), as x }
b
Question: Can we stabilize the uncertain system corresponding to f( ) F ( b ) for any b ?
Theorem:
The Capability of Feedback
Theorem : The maximum uncertainty that can be
dealt with by feedback is a ball with radius
in the normed function space (F,|| ||) , centered at zero .
●
L 为不确定性的度量
3 L 2 2
是反馈能镇定的临界值。
(郭雷、谢亮亮)
有限信息系统控制
●
双值传感器控制系统
y
设计控制或参 数辨识时唯一 可利用的信息
符号传感器
系统的 输出是 不可量 测量。
Sign (y C )
先验知识 客观条件 模 型 类 参数辨识
建模
控制指标
控 制 器
可量测量
输出
被控系统
ut ukh
自适应控制课件——多模型自适应控制

3.5046 0.0148 d 1 1.6729 7 . 7000 0.1543
0.0096 6.8978 B1 0.2652 0.0131 0.0556
,
0.0193 0.3138 0.1649 18.7269 1.4760
A2 B2 r r
三、多模型自适应飞行控制律重构
假设操纵面故障只影响系统的控制矩阵B,而正常模态和故障模态下的
A, d都相同。事实上,操纵面故障主要影响操纵效率. 当飞机发生故障时采用相应的重构控制律, 是一种典型的多模态切换控制。 采用多模型自适应控制可以自动监测 飞机状态的变化,并选择相应的控制律 飞行高度为3000米、速度0.5马赫 双引擎喷气式飞机线性化模型
1 q M Iy
令 f ( X ) q f q ( X ) 得到扩展线性化方程:
f ( X ) A f q ( X ) f ( X ) f ( X ) U q B f q ( X ) f q ( X ) q U
三、多模型自适应飞行控制律重构
对线性化系统采用线性反馈
u u K ( x x ) G(w w)
通过选择合适的K使系统具有与平衡点无关的常值稳定闭环极点, 通过选择合适的G可以使系统跟踪期望指令w
三、多模型自适应飞行控制律重构
纵向运动的控制
纵向短周期运动的状态变量 简化的速度方程: V
X [ q]T
u u1
重构控制器1
。 。 。
固定模型N
。 。 。
yN
eN
固定模型1
y1 y
e1
飞机
0.0096 6.8978 B1 0.2652 0.0131 0.0556
,
0.0193 0.3138 0.1649 18.7269 1.4760
A2 B2 r r
三、多模型自适应飞行控制律重构
假设操纵面故障只影响系统的控制矩阵B,而正常模态和故障模态下的
A, d都相同。事实上,操纵面故障主要影响操纵效率. 当飞机发生故障时采用相应的重构控制律, 是一种典型的多模态切换控制。 采用多模型自适应控制可以自动监测 飞机状态的变化,并选择相应的控制律 飞行高度为3000米、速度0.5马赫 双引擎喷气式飞机线性化模型
1 q M Iy
令 f ( X ) q f q ( X ) 得到扩展线性化方程:
f ( X ) A f q ( X ) f ( X ) f ( X ) U q B f q ( X ) f q ( X ) q U
三、多模型自适应飞行控制律重构
对线性化系统采用线性反馈
u u K ( x x ) G(w w)
通过选择合适的K使系统具有与平衡点无关的常值稳定闭环极点, 通过选择合适的G可以使系统跟踪期望指令w
三、多模型自适应飞行控制律重构
纵向运动的控制
纵向短周期运动的状态变量 简化的速度方程: V
X [ q]T
u u1
重构控制器1
。 。 。
固定模型N
。 。 。
yN
eN
固定模型1
y1 y
e1
飞机
模型参考自适应控制

调整策略
针对不同的被控对象和工况,需要设计相应的调整策略,以快速响应系统变化并保持控制性能。这需 要对被控系统的特性和动态行为有深入了解。
模型参考自适应控制在复杂系统中的应用拓展
复杂系统控制
模型参考自适应控制适用于具有非线性、时变和不确定性的复杂系统。通过设计合适的 自适应律和控制器,可以实现对复杂系统的有效控制。
2
在模型参考自适应控制中,滑模控制可以用于设 计自适应控制器,使得被控系统的状态跟踪误差 收敛到零。
3
滑模控制具有鲁棒性强、对系统参数变化不敏感 等优点,因此在模型参考自适应控制中具有广泛 的应用前景。
基于模糊逻辑的模型参考自适应控制
模糊逻辑是一种处理不确定性和模糊信息的智能控制方法,通过将模糊集合和模糊推理规则应用于控 制系统,可以实现模型参考自适应控制。
系统稳定性
系统稳定性是确保控制过程平稳、可靠的关键因素。在模型参考自适应控制中,需要权衡控制精度和系统稳定在线优化
模型参考自适应控制需要在线优化控制参数,以适应系统状态的变化和外部扰动。优化算法的选择和 应用对于提高控制性能和系统适应性至关重要。
化工过程控制
在化工生产过程中,模型参考自适应控制用于实现反应过程的优化 和稳定控制,提高生产效率和产品质量。
智能制造系统
在智能制造领域,模型参考自适应控制用于自动化流水线和智能机 器人的精确控制,提高生产效率和降低能耗。
机器人领域的应用
移动机器人导航
模型参考自适应控制用于移动机器人的路径规划和避障,提高机 器人在复杂环境下的自主导航能力。
应用领域
模型参考自适应控制的应用领域广泛,包括航空航天、机器人、电力系统和化工过程等。 随着技术的不断发展,其在智能制造、新能源和生物医学等领域的应用前景也日益广阔。
针对不同的被控对象和工况,需要设计相应的调整策略,以快速响应系统变化并保持控制性能。这需 要对被控系统的特性和动态行为有深入了解。
模型参考自适应控制在复杂系统中的应用拓展
复杂系统控制
模型参考自适应控制适用于具有非线性、时变和不确定性的复杂系统。通过设计合适的 自适应律和控制器,可以实现对复杂系统的有效控制。
2
在模型参考自适应控制中,滑模控制可以用于设 计自适应控制器,使得被控系统的状态跟踪误差 收敛到零。
3
滑模控制具有鲁棒性强、对系统参数变化不敏感 等优点,因此在模型参考自适应控制中具有广泛 的应用前景。
基于模糊逻辑的模型参考自适应控制
模糊逻辑是一种处理不确定性和模糊信息的智能控制方法,通过将模糊集合和模糊推理规则应用于控 制系统,可以实现模型参考自适应控制。
系统稳定性
系统稳定性是确保控制过程平稳、可靠的关键因素。在模型参考自适应控制中,需要权衡控制精度和系统稳定在线优化
模型参考自适应控制需要在线优化控制参数,以适应系统状态的变化和外部扰动。优化算法的选择和 应用对于提高控制性能和系统适应性至关重要。
化工过程控制
在化工生产过程中,模型参考自适应控制用于实现反应过程的优化 和稳定控制,提高生产效率和产品质量。
智能制造系统
在智能制造领域,模型参考自适应控制用于自动化流水线和智能机 器人的精确控制,提高生产效率和降低能耗。
机器人领域的应用
移动机器人导航
模型参考自适应控制用于移动机器人的路径规划和避障,提高机 器人在复杂环境下的自主导航能力。
应用领域
模型参考自适应控制的应用领域广泛,包括航空航天、机器人、电力系统和化工过程等。 随着技术的不断发展,其在智能制造、新能源和生物医学等领域的应用前景也日益广阔。
模型参考自适应控制.ppt
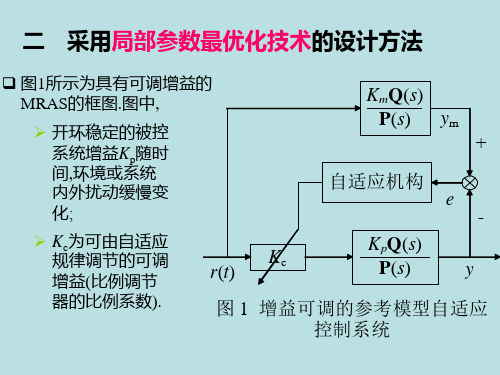
e -
y
图 1 增益可调的参考模型自适应 控制系统
即e(t)所满足的微分方程为:P(D)e (Km KcK p )Q(D)r
微分算子:D
d dt
,
D
2
d2 dt 2
....
两边对Kc求导: P(D) e Kc
K pQ(D)r
ym
KmQ(s) P(s)
r
P(D) ym KmQ(D)r
比较可得:e Kc
• 由图4,参考模型和参数可调被控系统的s域表达式分别为
Ym (s)
KmN (s) D(s)
r(s)
(1)
Y (s) KcKpN (s) r(s)
(2)
D(s)
其中D(s)和N(s)分别为如下已知的n阶的稳定首一多项式和n-1阶
多项式
n-1
D(s) sn aisi
n-1
N (s) bisi
iT -eP ri ,i 1,2,, m
则 V -eTQe为负定,从而广义误差系统为渐近稳定。
这种方法要求所有状态可测,这对许多实际对象往往不 现实,为此可采用按对象输入输出来直接设计自适应控制系 统。其中一种为直接法,它根据对象的输入输出来设计自适 应控制器,从而来调节可调参数,使可调系统与给定参考模 型匹配,另一种为间接法,利用对象的输入输出设计一个自 适应观测器,实时地给出对象未知参数和状态的估计,然后 利用这些估计值再来设计自适应控制器,使对象输出能跟踪 模型输出,或使其某一性能指标最优。
a2 s 2
Kp a1s
1
参考模型:Gm
(s)
a2 s 2
Km a1s
1
这时闭环自适应控制系统为:
P(D)e (Km Kc K p )Q(D)r
模型参考自适应PPT文档67页

42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联模 Nhomakorabea参考自适应
51、山气日夕佳,飞鸟相与还。 52、木欣欣以向荣,泉涓涓而始流。
53、富贵非吾愿,帝乡不可期。 54、雄发指危冠,猛气冲长缨。 55、土地平旷,屋舍俨然,有良田美 池桑竹 之属, 阡陌交 通,鸡 犬相闻 。
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联模 Nhomakorabea参考自适应
51、山气日夕佳,飞鸟相与还。 52、木欣欣以向荣,泉涓涓而始流。
53、富贵非吾愿,帝乡不可期。 54、雄发指危冠,猛气冲长缨。 55、土地平旷,屋舍俨然,有良田美 池桑竹 之属, 阡陌交 通,鸡 犬相闻 。
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一般来说,自适应控制系统在反馈控制的 基本回路上加上自适应机构构成。具有三 方面的功能:
(1)在线辨识。 (2)决策控制。 (3)在线修正。
自适应控制系统主要分为两大类: (1)模型参考自适应控制系统。 (2)自校正自适应控制系统
模型参考自适应控制
(Model Reference Adaptive Control) MRAC
- 麻省理工学院于1958年提出的,因此也叫MIT方法 - 最早提出、最早应用的一种方法 - 理论简单,实施方便,可用模拟元件实现 - 实质是一个可调增益的系统
一. 单个参数的MIT方法
第三章模型参考自适应控制 §2 局部参数最优化设计方法
工作背景
ห้องสมุดไป่ตู้
设参考模型为 Kmq( s) ,对象模型为 K p(t)q(s)
回顾
自适应控制的基本思想是:在控制系统设 计时,不断地测量受控对象的状态,性能 或者参数,从而认识或掌握系统当前的运 行状况,并将系统当前的性能指标与期望 的指标进行比较,从而根据比较结果作出 决策,来改变控制器的结构、参数或根据 自适应的规律来改变控制作用,以保证系 统运行在某种意义下最优或次优。
R
调节器
被控对象
+
可调系统
Yp
适应机构
二 工作原理 分类 – 并联型
– 串联型
– 串并联型
技术难点 — 设计自适应机构,确定自适应律 – 局部参数最优化方法 – 利用李雅普诺夫稳定性理论的设计方法 – 利用波波夫超稳定性理论的设计方法
§2 局部参数最优化设计方法
第三章 模型参考自适应控制
一 单个参数的MIT方法 简介(以调节器的增益Kc作为可调参数的MIT方法)
p( s )
p( s )
其中: p(s) sn a1sn-1 an-1s an
q(s) b1sn-1 b2sn-2 bn
– Km为常数,根据系统希望的动态响应事先确定 – p(s)、q(s)已知
R
—kpm(—qs()—s)
ym +e
Kc
Kp
-pq-((-ss-))- -
yp
适应律
R
关键是求出
J J
,
。
T
二 具有多个可调参数的MIT的设计
第三章模型参考自适应控制 §2 局部参数最优化设计方法
假设:可调系统的参数已位于参考模型参数的某个邻域内。
设参考模型为:
可调系统为:
m
Gm (s)
ym( s ) R( s )
i si
i0
n
1 isi
i 1
m
G p ( s)
y p( s ) R( s)
Kc
K
p
q(s) ]R
p(s)
(Km
-
Kc
K
p
)
q(s) p(s)
R
引入微分算子D,即: D d D2 d 2
dt
dt2
—kpm(—qs()—s)
Kp
-pq-((-ss-))-
适应律
ym +e -
yp
e的微分方程:
e (Km - KcKp) q(D) R p( D)
(2.2)
e - Kp q(D) R
i si
i0 n
1 isi
i 1
广义输出误差为:
e(t)=ym(t)-yp(t),目标函数为:J
1 2
t1e2 ( t0
)d
设计目标是寻求 i (e,t), i (e,t) 的调节规律,以使J 最小。
按照单参数的调节规律,可导出下列适应律:
—kpm(—qs()—s)
ym +e
Kc
Kp
-pq-((-ss-))- -
yp
适应律
- 被控对象受扰,Kp(t)产生漂移,改变系统的动态性能
- Kp(t)的变化是不可测的,其动态漂移将反映在过程输出Yp上
- 为了克服Kp的漂移而产生的影响,增加了一个可调增益Kc的 调节器,补偿Kp漂移而产生的影响。
(2.3)
Kc
p( D)
欲消去 q(D) / p(D),
ym Km q( D)
R
p( D)
即:
q( D) p( D)
ym R Km
代入(2.3)式,
e Kc
-
Kp Km
ym
(2.4)
e
Kp
Kc - Km ym
Kc
-
B2e
e Kc
(2.1)
第三章模型参考自适应控制 §2 局部参数最优化设计方法
§1 简介
一类重要的自适应控制系统 - 模型参考自适应控制系统
一 组成
R
参考模型
调节器
被控对象
+
可调系统
Ym
e+ _
Yp
适应机构
1. 可调系统 — 可变调节器 + 被控对象 2. 参考模型(代表系统希望的输出响应) 3. 比较器 — 广义误差信号 4. 自适应机构 — 自适应律
参考模型
Ym
e+ _
代入(2.1)式: Kc B e ym (2.5)
其中 B
B2
Kp Km
为一系数。
自适应律为一积分适应律:Kc(t )
Kc(0)
t
B0
e
ymd
(2.6)
系统构成框图:
Kmq(s)
ym
R
P(s)
+e
-*
Kc
Kp
q(s)
p(s)
yp
*B
+
Kc(0)
需要两个乘法器和一个积分器,可用模拟元件构成。
当其它参数,如T、τ发生变化时,也可仿效这种方法设计,
参考模型
Ym
_e
+ _
R
调节器
被控对象
+
可调系统
Yp
§1 简介
适应机构
R
自适应辨识
- 把对象放在参考模型的位置 - 适应机构根据e 改变可调系统的参数
被控过程 可调系统
ym
+e _ yp
适应机构
- 当e趋近于零时,可调系统模型收敛于被控对象的模型
参考模型
Ym
_e
+ _
第三章模型参考自适应控制 §1 简介
t
控制目标是: J e2( )d 为最小。
0
一. 单个参数的MIT方法 R 设计问题 (最优化方法) 工作原理
—kpm(—qs()—s)
ym +e
Kc
Kp
-pq-((-ss-))- -
yp
适应律
t
广义误差 e=Ym-Yp,目标: J e2( )d 为最小。
0
按照最优化中的梯度法,
Kc Kc(0) - B1 J Kc
R
调节器
被控对象
+
可调系统
Yp
适应机构
二 工作原理
自适应控制(模型跟随) - 参考模型输出Ym(k)是可调系统的参考轨迹 - 希望对象的动态输出跟踪参考模型的输出 - 适应机构比较两者之差,确定自适应规律 - 改变调节器参数(参数自适应型),或产生一辅助输入信 号(信号综合型)
第三章模型参考自适应控制
B1为常数
J
t
2e
e
d
Kc 0 Kc
代入上式,
Kc
Kc(0)
-
B2
t 0
e
e Kc
d
,
B2 2 B1
即:
Kc
-
B2e
e Kc
(2.1)
e : 灵敏度函数,反映参数变化 Kc 对误差e变化的大小,求解关键。
求 e : Kc
e ym - yp
R Kc
[
Kmq(s) p(s)
-
