光的折射定律的证明
光的折射和反射定律

光的折射和反射定律光的折射和反射定律是光学研究中的基本原理,它们描述了光线在两种不同介质之间传播时的行为。
在本文中,我将详细介绍光的折射和反射定律的概念、原理和应用。
一、折射定律1. 概念光的折射是指光线从一种介质传播到另一种介质时,由于两种介质的光速不同,光线的传播方向会发生改变的现象。
2. 折射定律折射定律是描述光在界面上折射现象的基本规律,可以用下式表示:n₁sinθ₁ = n₂sinθ₂其中,n₁和n₂分别表示两个介质的折射率,θ₁和θ₂分别表示入射角和折射角。
3. 原理折射定律的原理基于光的波动性和光速在介质中的差异。
当光从一种介质传播到另一种介质时,由于介质的不同,光在两种介质中传播的速度不同,导致光线传播方向发生改变。
4. 应用折射定律在科学研究和实际应用中有着广泛的应用。
例如,它可以解释为何水中的物体看起来会偏移、杆子在水中看起来弯曲等现象。
二、反射定律1. 概念光的反射是指光线遇到界面时,一部分光线从界面上反射回来的现象。
2. 反射定律反射定律是描述光在界面上反射现象的基本规律,可以用下式表示:θ₁ = θ₂其中,θ₁和θ₂分别表示入射角和反射角。
3. 原理反射定律的原理基于光的波动性和光在界面上的反射规律。
当光线遇到界面时,它会发生反射,反射角等于入射角。
4. 应用反射定律广泛应用于光学仪器、镜面反射、光线的偏转等领域。
例如,平面镜、凸透镜等光学仪器都是基于反射定律设计和工作的。
三、折射和反射的区别和联系1. 区别折射和反射的主要区别在于光线传播的方向和角度变化。
折射是光线从一种介质传播到另一种介质中,光线的传播方向发生改变;而反射是光线遇到界面时从界面上反射回来。
2. 联系折射和反射都是光传播过程中常见的现象,它们遵循一定的定律。
折射定律和反射定律在描述和解释折射和反射现象时提供了准确的数学关系。
结语光的折射和反射定律是光学研究中的重要基础,正确理解和应用这些定律对于解释和分析光的传播行为具有关键作用。
第4章 第1节 光的折射定律

第4章第1节光的折射定律第1节光的折射定律光的折射定律和折射率1.光的折射光从一种介质斜射入另一种介质时,传播方向会改变,这种现象叫做光的折射.图4-1-12.入射角与折射角的定性关系入射角:入射光线与法线间的夹角,一般用i表示.折射角:折射光线与法线间的夹角,一般用r表示.实验表明:当入射角变化时折射角随着改变.3.斯涅耳定律(折射定律)入射角的正弦与折射角的正弦之比是一个常数.即sin isin r=n.4.折射率(1)定义光从真空射入某种介质发生折射时,入射角i的正弦与折射角r的正弦之比.用n表示.(2)定义式n=sin i sin r.(3)意义:介质的折射率反映了光在介质中的偏折度.(4)折射率与光速的关系光在不同介质中的传播速度不同,且都小于光在真空中的传播速度;某种介质的折射率,等于光在真空中的速度与光在这种介质中的速度之比,即n=c/v.[再判断]1.入射角变化,折射角也随之变化,但入射角一定大于折射角.(×)2.光的折射率随入射角的增大而增大.(×)3.介质的折射率越大,光在这种介质中的传播速度越小.(√)[后思考]B.此介质折射率为 3C.光在介质中速度比在空气中小D.光在介质中速度比在空气中大E.当入射角增大时,折射角也增大,但折射率不变【解析】由折射定律n=sin θ2sin θ1=3,A错误,B正确;又由n=c v知光在介质中速度比在空气中小,C正确,D错误.根据折射率的物理意义,E正确.【答案】BCE2.利用半圆柱形玻璃,可减小激光光束的发散程度.在如图4-1-3所示的光路中,A为激光的出射点,O为半圆柱形玻璃横截面的圆心,AO过半圆顶点.若某条从A点发出的与AO成α角的光线,以入射角i入射到半圆弧上,出射光线平行于AO,求此玻璃的折射率.图4-1-3【解析】根据光路图,由折射定律得n=sin isin r,由几何关系得r=i-α故n=sin isin (i-α)【答案】sin isin (i-α)折射问题的四点注意1.根据题意画出正确的光路图;2.利用几何关系确定光路中的边、角关系,要注意入射角、折射角的确定;3.利用反射定律、折射定律求解;4.注意光路可逆性、对称性的应用.实验: 测量介质的折射率玻璃砖、白纸三张、木板、大头针四枚、图钉四枚、量角器、刻度尺、铅笔.2.实验步骤(1)如图4-1-4所示,将白纸用图钉钉在平木板上;图4-1-4(2)在白纸上画出一条直线aa′作为界面(线),过aa′上的一点O画出界面的法线NN′,并画一条线段AO作为入射光线;(3)把长方形玻璃砖放在白纸上,使它的长边跟aa′对齐,画出玻璃砖的另一边bb′;(4)在直线AO上竖直插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线方向直到P2的像挡住P1的象.再在观察者一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3及P1、P2的像,记下P3、P4的位置;(5)移去大头针和玻璃砖,过P3、P4所在处作直线O′B与bb′交于O′,直线O′B就代表了沿AO方向入射的光线通过玻璃砖后的传播方向;(6)连接OO′,入射角i=∠AON,折射角r=∠O′ON′,用量角器量出入射角和折射角,从三角函数表中查出它们的正弦值,把这些数据记录在自己设计的表格中;(7)用上述方法分别求出入射角分别为30°、45°、60°时的折射角,查出它们的正弦值,填入表格中.3.数据处理方法一:平均值法求出在几次实验中所测sin isin r的平均值,即为玻璃砖的折射率.图4-1-5方法二:图象法在几次改变入射角、对应的入射角和折射角正弦值的基础上,以sin i值为横坐标、以sin r值为纵坐标,建立直角坐标系,如图4-1-5所示.描数据点,过数据点连线得一条过原点的直线.求解图线斜率k,则k=sin rsin i=1n,故玻璃砖折射率n=1k.图4-1-6方法三:作图法在找到入射光线和折射光线以后,以入射点O为圆心,以任意长为半径画圆,分别与AO交于C点,与OE(或OE的延长线)交于D点,过C、D两点分别向N′N作垂线,交NN′于C′、D′,用直尺量出CC′和DD′的长,如图4-1-6所示.由于sin i=CC′CO,sin r=DD′DO,而CO=DO,所以折射率n1=sin isin r=CC′DD′.3.如图4-1-7所示,关于“测定玻璃的折射率”的实验,回答以下问题.图4-1-7(1)请证明图中的入射光线和射出玻璃砖的光线是平行的.(2)为减小实验误差,入射角大一些好还是小一些好?【解析】(1)如图所示,证明:n=sin i1sin r1=sin r2sin i2而r1=i2所以i1=r2,所以入射光线平行于出射光线.(2)大一些好.这样测量的误差会小些,可以减小实验误差.【答案】见解析4.在“测定玻璃折射率”的实验中,某同学经正确操作插好了4枚大头针,如图4-1-8甲所示.(1)在图4-1-8乙中画出完整的光路图;(2)对你画出的光路图进行测量和计算,求得该玻璃砖的折射率n=______(保留3位有效数字);【解析】(1)分别连接玻璃砖两侧的大头针所在的点,并延长与玻璃砖边分别相交,标出传播方向,然后连接玻璃砖边界的两交点,即为光线在玻璃砖中传播的方向.光路如图所示.(2)设方格纸上正方形的边长为1,光线的入射角为i,折射角为r,则sin i= 5.35.32+42=0.798,sin r= 2.22.22+3.62=0.521所以玻璃的折射率n =sin i sin r =0.7980.521=1.53. 【答案】 (1)见解析 (2)1.53(说明:±0.03范围内都可)实验时应注意的三点1.实验时,尽可能将大头针竖直插在纸上,且P 1和P 2之间,P 2与O 点之间,P 3与P 4之间,P 3与E 之间距离要稍大一些. 2.入射角i 应适当大一些,以减小测量角度的误差,但入射角不宜太大,也不宜太小.3.玻璃砖应选用宽度较大的,宜在5 cm 以上.若宽度太小,则测量误差较大.对 折 射 现 象 的 解 释1.水中的物体看起来比实际的要浅,这是因为水的折射率大于空气的折射率,光从水中射入空气时,折射角大于入射角.2.一束白光射入三棱镜时会发生色散现象,这是因为不同颜色的光在同一介质中的传播速度不同,折射率不同,其中红光的传播速度最大,折射率最小,经三棱镜后偏折程度最小,紫光的传播速度最小,折射率最大,经三棱镜后偏折程度最大.平常我们所说的某介质的折射率是指七种色光的平均折射率.[再判断]1.当光从水中射入空气中时,折射角大于入射角.(√)2.不同颜色的光在同一种介质中的折射率不同.(√)3.当一束白光射入三棱镜时,红光偏折程度最大,紫光偏折程度最小.(×)[后思考]棱镜对不同单色光的折射率相同吗?对哪种单色光的折射率最大?【提示】 不相同,对紫光的折射率最大.[核心点击]1.同一介质对不同色光的折射率不同,对红光的折射率最小,对紫光的折射率最大.2.由n=cv可知,各种色光在同一介质中的光速不同,红光速度最大,紫光速度最小.3.同一频率的色光在不同介质中传播时,频率不变,光速改变(v=cn=λf),波长亦随之改变.5.如图4-1-9所示,从点光源S发出的一细束白光以一定的角度入射到三棱镜的表面,经过三棱镜的折射后发生色散现象,在光屏的ab间形成一条彩色光带.下面的说法中正确的是()【导学号:78510042】图4-1-9A.a侧是红光,b侧是紫光B.在真空中a侧光的波长小于b侧光的波长C.三棱镜对a侧光的折射率大于对b侧光的折射率D.在三棱镜中a侧光的速率比b侧光小E.在三棱镜中a、b两侧光的速率相同【解析】由题图可以看出,a侧光偏折得较厉害,三棱镜对a侧光的折射率较大.所以a侧光是紫光,波长较短,b侧光是红光,波长较长,因此A错,B、C正确;又v=cn,所以三棱镜中a侧光的传播速率小于b侧光的传播速率,D正确,E错误.【答案】BCD6.如图4-1-10所示,有一截面是直角三角形的棱镜ABC,∠A=30°,它对红光的折射率为n1,对紫光的折射率为n2,在距AC边d处有一与AC平行的光屏,现有由以上两种色光组成的很细的光束垂直AB边射入棱镜.①红光和紫光在棱镜中的传播速度之比为多少?②若两种色光都能从AC面射出,求在光屏MN上两光点的距离.图4-1-10【解析】 ①v 红=c n 1,v 紫=c n 2所以v 红v 紫=n 2n 1②画出两种色光通过棱镜的光路图,如图所示,由图得sin r 1sin 30°=n 1sin r 2sin 30°=n 2x =d (tan r 2-tan r 1)=d (n 24-n 22-n 14-n 21) 【答案】 ①n 2n 1 ②d (n 24-n 22-n 14-n 21) 复色光通过三棱镜发生色散的规律如图4-1-11所示,复色光经过棱镜折射后分散开来,是因为复色光中包含多种颜色的光,同一种介质对不同色光的折射率不同.图4-1-111.折射率越大,偏折角也越大,经棱镜折射后,越靠近棱镜的底部.2.折射率大的,在介质中传播速度小,复色光经三棱镜折射后,靠近顶端的色光的传播速度大,靠近棱镜底端的色光的传播速度小.。
光的折射定律

光的折射定律1.定义:折射定律是几何光学的基本定律之一.是在光的折射过程中,确定折射光线与入射光线之间关系的定律.公元二世纪,希腊人托勒密(90—168)通过实验研究了光的折射现象.1.实验设计:托勒密的实验设计如图所示:在一个圆盘上装上两把能绕盘中心S旋转的中间可以活动的尺子.将圆盘面垂直立于水中,水面到达圆心处.2.实验方法:实验时转动两把尺子使之分别与入射光线和折射光线重合.然后把圆盘取出,分别按照尺的位置测出入射角和折射角.3.实验结果:托勒密通过上述的方法测得从空气中射入水中的光线折射时的一系列对应值为:4.数据分析:托勒密通过分析以上数据,得出结论:折射角和入射角是成正比关系.今天我们知道这个结论是不正确的,它只有在入射角很小的情况下才近似成立.5.留给我们的沉思:从托勒密的实验设计实验方法到实验数据的收集可以说是完全正确的.他的实验结果也是相当精确的,与现代值几乎没有多大的差别.但是托勒密可惜的是未能从正确的数据中发现正确的规律,从这里可看出对实验数据正确处理,加上正确理论的指导在发现规律中的重要性.托勒密是第一个用实验方法测定入射角和折射角的人,他曾求出具有单位半径的圆中弧与所对应的弦长数字,并巧妙地用数学方法编制了表(相当于现代的正弦三角函数表),他当时对折射角和入射角的测量是相当精确的,如果他当时把关于光折射的实验数据与他所编制的这份表作一比较的话,他就会不难发现入射角的正弦与折射角的正弦之比对给定的两种介质来说是一个常数,这样他就会发现折射定律,然而他却没有这样做,以致错过了一次发现的机会.3.开普勒对折射规律的修正德国人开普勒在汇集前人光学知识的基础上,断定托勒密关于折射规律的结论是不正确的.于是他开始便想通过实验发现折射定律,但实验最后没有成功.他便转向从理论上加以探索.他得出的折射定律是:折射角由两部分组成,一部分正比于入射角,另一部分正比于入射角的正割;只有在入射角小于30°时,入射角和折射角成正比的关系才成立,显然,开普勒关于折射定律的研究和修正比托勒密前进了一步.但还没能给出正确荷兰数学家斯涅耳(1591—1626)于1620年前后,通过实验确立了开普勒想发现而没有能够发现的折射定律.他注意研究了水中的物体看起来象飘浮的现象,做了如下实验:当在空气中的0点观察水中的A点时,犹如在B点一样,如图(A)所示.斯涅耳发现,对于任意入射角存在以下关系(B)图所示.斯涅耳没有用理论推导,而是用实验又验证了它.斯涅耳对折射定律作了如下表述:在不相同的介质里,入射角和折射角的余割之比总是保持相同的值.法国人笛卡儿,他以媒质中球的运动作类比,试图说明折射定律.如图所示,假设球在媒质Ⅰ中运动,当进入媒质Ⅱ时,球速的水平分量不变,垂直部分增大,Ⅱ中的光速变成Ⅰ中光速的u倍.其结果球在媒质Ⅱ内部偏转,而所需时间仅为通过媒质Ⅰ中所需时间的1/u.因此根据几何关系,可得在这段时间内,球在水平方向前进的距离BE等于CB/u.所以式中i为入射角,r为折射角.法国人费马(1601—1665)从理论上得到费马原理,并用演绎方法从费马原理中推导出折射定律.1.费马从理论上得到费马原理.费马从理论上推导出:光沿着光程为极值的路径传播.设某空间介质的折射率连续变化,光由A点传播到B点就必循一曲线,如图所示它的总光程为根据变分法原理,光程为极值的条件为此式即为费马原理的数学表达式.由费马原理可以推导出反射定律和折射定律,并可证明它们的光程为极值.2.费马用演绎方法导出折射定律费马在前人发现折射定律的基础上对光的折射定律又有了新的发展.费马认为,导出折射定律可以采取另一种截然不同的思考方法.他假定不同媒质对光的传播表现出不同的阻力,他首先指出,光在不同媒质中传播时,所走路程取极值,即遵从费马原理.即是说,光从空间的一点到另一点,是沿着光程为极值(最小、最大或常量)的路程传播的.借助于光程这个概念可将光在媒质中所走过的路程折算为光在真空中通过的路程,这样便于比较光在不同媒质中所走路程的长短.1661年费马运用费马原理成功地导出了折射定律.六、光的折射定律的现代表述当光从一种介质射向另一种介质的平滑界面时,一部分光被界面反射,另一部分光透过界面在另一种介质中折射,折射光线服从折射定律:折射光线AB位于入射光线SA和法线AN所决定的平面(称为入射面)内,折射光和入射光分别在法线的两侧,入射角i与折射角r有如下关系式:式中n21是一个与角度大小无关的常数,称为第二介质对第一介质的相对折射率.但由于光是电磁波,所以该定律可从惠更斯原理导出,并得:该式进一步给出了折射率n21与两边介质中的光速V1和V2之间的关系.该定律同样适用于声波和无线电波.。
光的折射定律与介质

光的折射定律与介质光是我们生活中非常重要的一种现象,它对我们的生活和科学研究都具有重要的影响。
而光的折射定律是光学中一个非常基础的定律,用来描述光在介质中传播时的行为。
在本文中,我们将详细介绍光的折射定律和介质对光的影响。
一、光的折射定律光的折射是指光线由一种介质进入另一种介质时改变传播方向的现象。
根据实验观察,我们可以得出光的折射定律:"当光从一种介质入射到另一种介质中时,入射光线与折射光线的入射角和折射角的正弦之比,等于两种介质的折射率的比值。
"这个定律可以用下面的公式来表示:n1sinθ1 = n2sinθ2其中,n1和n2分别是两种介质的折射率,θ1是入射角,θ2是折射角。
利用光的折射定律,我们可以解释和预测光线在介质中的传播路径和行为。
同时,我们也可以根据这个定律设计和改进各种光学器件,如透镜、棱镜等。
二、介质对光的折射的影响介质是指光在其中传播的物质,可以是固体、液体或气体。
不同的介质对光的传播和折射有不同的影响,下面我们将介绍一些常见的介质对光的折射的影响。
1. 固体介质固体介质中的原子和分子紧密排列,光在其中传播时会遇到晶格结构的阻碍,因此光的速度会比在真空中慢。
这导致了光在固体中的折射角度会比在空气或真空中的折射角度小。
2. 液体介质液体介质中的分子之间的距离比固体介质大,因此光的速度会比在固体中快一些。
相比之下,光在液体中的折射角度会比在固体中的折射角度大一些。
3. 气体介质气体介质是光速度最快的介质,光在其中的传播速度远远大于在固体或液体中的传播速度。
因此,光在气体中的折射角度会比在固体或液体中的折射角度更大。
除了介质的物理性质外,介质的折射率也会对光的折射产生影响。
折射率反映了光在介质中传播时受阻力的大小。
折射率越大,光的传播速度越慢,同时折射角度也会变大。
总结:光的折射定律和介质对光的折射有着密切的关系。
通过光的折射定律,我们可以预测和解释光在不同介质中传播时的行为。
第1讲 光的折射、全反射

第1讲光的折射、全反射知识点光的折射定律Ⅱ折射率Ⅰ1.折射现象01改变的现象。
2.折射定律(1)02同一平面内,折射光线与入射03两侧;入射角的正弦与折射角的正弦04成正比。
(2)05sinθ1sinθ2=n12,式中n12是比例常数。
(3)06可逆的。
3.折射率(1)定义:光从真空射入某种介质发生折射时,07入射角的正弦与08折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率,用符号n表示。
(2)09光学特性,折射率大,说明光从真空斜射入该介质时偏折的角度大,反之偏折的角度小。
(3)定义式:n=sinθ1sinθ2,不能说n与sinθ1成正比、与sinθ2成反比,对于确定的某种介质而言,入射角的正弦与折射角的正弦成正比。
折射率由介质本身的光学10频率决定。
(4)光在不同介质中的速度不同,某种介质的折射率,等于光在真空中的传播速度c与光在这种介质中的传播速度v之比,即n=cv,因v<c,故任何介质的折11大于(填“大于”或“小于”)1。
(5)相对折射率:光从介质1射入介质2时,入射角θ1与折射角θ2的正弦之比叫做介质2对介质1的相对折射率。
4.光密介质与光疏介质(1)光密介质:折射率12较大的介质。
(2)光疏介质:折射率13较小的介质。
(3)光密介质和光疏介质是14相对的。
某种介质相对其他不同介质可能是光密介质,也可能是光疏介质。
知识点全反射、光导纤维Ⅰ1.全反射(1)条件:①光从光密介质射入01光疏介质。
②入射角02大于或等于临界角。
(2)现象:折射光完全消失,只剩下03反射光。
(3)临界角:折射角等于90°时的入射角,用C表示,sin C=041 n 。
(4)应用:①光导纤维;②全反射棱镜。
2.光的色散(1)光的色散现象:含有多种颜色的光被分解为05单色光的现象。
(2)色散规律:白光是由红、橙、黄、绿、青、蓝、紫七种色光组成的,折射率依次增大,红光的最小,紫光的最大,当一束白光入射到棱镜界面时,七种色光以相同的入射角射到棱镜界面,各种色光的折射角不同,红光偏折得最小,紫06紫光的偏折最大,07红光的偏折最小。
折射定律定义

折射定律定义
折射定律(Snell's Law)是描述光在两种介质之间传播时会发生折射的现象的物理定律。
它表明,当光线从一种介质进入另一种介质时,光线的入射角和折射角满足以下关系:
n₁sinθ₁ = n₂sinθ₂
其中,n₁和n₂分别是两种介质的折射率,θ₁为光线与法线的入射角,θ₂为光线与法线的折射角。
折射定律描述了光线传播时光的速度和方向发生变化的规律。
当光线从光密介质进入光疏介质时,折射角大于入射角,光线向法线倾斜;当光线从光疏介质进入光密介质时,折射角小于入射角,光线远离法线。
折射定律在光的折射、透视等现象的解释和应用上有重要意义。
光的反射与折射定律

光的反射与折射定律光是一种电磁波,在空气、水、玻璃等介质中传播时,会发生反射和折射现象。
光的反射和折射定律是描述光在界面上的传播规律。
本文将详细介绍光的反射和折射定律及其背后的原理。
一、光的反射定律光的反射是指光线从一种介质射入另一种介质后,沿原来的方向返回第一种介质的现象。
根据光的反射定律,我们可以得到以下结论:1. 入射角等于反射角:当光线从一种介质垂直射入另一种介质时,光线遇到界面时会发生反射。
根据光的反射定律,入射角等于反射角。
这意味着光线与法线的夹角相等,即入射角θi等于反射角θr。
2. 反射角位于反射平面内:反射角θr位于反射平面内,反射平面是入射光线和法线所在的平面。
二、光的折射定律光的折射是指光线从一种介质射入另一种介质后改变传播方向的现象。
根据光的折射定律,我们可以得到以下结论:1. 斯涅尔定律:斯涅尔定律描述了光线在界面上的折射规律。
它表明入射角、折射角和两种介质的折射率之间存在一个简单的关系,即n₁sinθ₁ = n₂sinθ₂,其中n₁和n₂分别是两种介质的折射率,θ₁和θ₂分别是入射角和折射角。
2. 光从光密介质向光疏介质的折射规律:当光线从一个折射率较大的介质射入折射率较小的介质时,入射角变大,同时折射角也变大。
当入射角达到临界角时,光线将不再折射,而是发生全反射。
3. 光的全反射:当入射角大于临界角时,光线无法从光密介质中射入光疏介质,此时发生全反射。
全反射是光的一种特殊折射现象,它在光纤通信等领域得到广泛应用。
三、光的反射和折射定律的应用光的反射和折射定律在日常生活和科学研究中有着广泛的应用。
以下是其中的一些例子:1. 平面镜和曲面镜:根据光的反射定律,我们可以解释镜面的成像原理。
平面镜和曲面镜都利用了光线的反射来实现成像功能。
2. 显微镜和望远镜:显微镜和望远镜利用多次反射和折射来放大物体,并使其对人眼可见。
3. 光纤通信:光纤通信是一种基于光的反射和折射原理的通信技术,通过光纤传输信号,具有高速、大带宽和抗干扰等优势。
光的折射总结归纳

光的折射总结归纳光线在不同介质中传播时会发生折射现象,这是由于光速在不同介质中的传播速度不同引起的。
本文将对光的折射进行总结归纳,包括折射定律、光的折射角和入射角之间的关系、光的折射现象以及光的折射的应用等方面。
1. 折射定律折射定律是描述光线在两种介质交界面上的折射关系的定律。
它由斯涅尔(Snell)在17世纪提出,并经验性地总结为如下公式:n1sinθ1 = n2sinθ2其中,n1和n2分别为两种介质的折射率,θ1为入射角,θ2为折射角。
该定律表明入射角和折射角的正弦值在两种介质中的折射率之比保持不变。
2. 光的折射角和入射角之间的关系根据折射定律,可以得出光的折射角和入射角之间的关系。
当光从光疏介质(折射率较小)射向光密介质(折射率较大)时,入射角较大的光线向交界面法线弯曲,折射角较小;而入射角较小时则相反,折射角较大。
这一关系可以用来解释折射现象的变化规律。
3. 光的折射现象光的折射现象包括了光从一种介质射向另一种介质时的折射、反射和全反射等现象。
当光从光疏介质射向光密介质,并且入射角大于临界角时,光线会发生全反射,完全沿原介质传播方向反射回去。
这在光纤通信中得到了广泛应用。
4. 光的折射的应用光的折射在生活和科技中有着广泛的应用。
其中,光学器件如透镜、棱镜、光纤等都利用了光的折射特性进行设计和制造。
透镜的折射原理使得我们能够通过调整透镜的形状来实现对光线的聚焦和散焦,从而实现放大或缩小的效果。
而棱镜则能够通过折射和反射使得光线发生不同的偏转,实现光谱分析和光学仪器的设计。
此外,光纤通信是利用光的折射和全反射原理进行信息传输的重要技术。
光纤作为一种传输介质,能够将光信号传输得更远,并且信号传输的速度更快,抗干扰性能更强。
总结归纳:光的折射定律是描述光线在两种介质交界面上折射关系的定律。
光的折射角和入射角之间的关系符合折射定律,入射角和折射角的正弦值在两种介质折射率之间的比保持不变。
光的折射现象包括折射、反射和全反射等,在光学器件和光纤通信等领域得到了广泛应用。
光折射定律

猜想:光的折射现象也是因为光在不同介质中传播速 度不同引起的.且规律同上.
材料展示:
• 光在不同介质中的传播速度: 真空:3.0 x 10*8 m/s 空气:2.99 x 10*8 m/s 水: 2.25 x 10*8 m/s 玻璃: 2.00 x 10*8 m/s
几种常见物质的折射率 物质 折射率 物质 折射率
sin i n sin r
N
i
O
空气
玻璃
r B
N'
折射率
光从真空射入某种介质时,虽入射角的正弦跟
折射角的正弦之比为一常数n,但是对不同的介质来 说,这个常数n是不同的,它是一个反应介质光学性
质的物理量,物理学中把光从真空射入某种介质发
生折射时,入射角与折射角的正弦之比n,叫做这种
介质的折射率: n sin i
同种介质对不同频率的光的偏折角度不同;
同种介质对不同频率的光的折射率不同.
光的色散
色散
A、复色光在介质中由于折射率不同而分解成 单色光的现象叫做光的色散。
B、色散的原因: 同一介质对不同色光的折射率不同。 C、光谱:色散时产生的(按一定顺序排列的)
彩色光带叫做光谱。
色光 物理量 频率 f 偏向角θ 绝对折射率 n 同一介质中的 速度 v 同一介质中的 波长 真空中的速度 真空中的波长
所以,光路是可逆的.
i
空气
水
r
思考:为什么光从真空(空气)进入某种介质时,传播方 向会发生改变?是什么因素导致了这种方向的变化?
类比1:机械波从一种介质进入另一种介质时传播方向
也发生了改变,这是因为机械波在不同介质中的传
播速度不同引起的,规律:
sin i v1 sin r v2
光的折射定律 课件(共17张PPT)

入射角
折射角
i/r
Sini/sinr
100
6.70
1.49
1.49
200
13.30
1.50
1.49
300
19.60
1.53
1.49
400
25.20
1.59
1.51
500
30.70
1.63
1.50
600 700
35.10 38.60
1.71 1.81
1.51 1.50
800
40.60
1.97
1.51
⑥入射角的正弦和折射 角的正弦成正比
在折射时光路是可逆的.
例一
如图一个储油桶的底面直径与高均为d.当
桶内没有油时,从某点A恰能看到桶底边
缘的某点B。当桶内油的深度等于桶高的
一半时,仍沿AB方向看去,恰好看到桶
低上的点C,CB两点距离d/4.求油的折
射率和光在油中传播的速度。
AF
A
B
C
O dG
B CD
解: 因底面直径和桶高相等,由此可知
介质 折射率
金刚石 2.42
二氧化碳 1.63
玻璃
1.5-1.8
水晶
1.55
介质 岩盐 酒精
水
空气
折射率
1.55 1.36 1.33
1.00028
4、真空本身的折射率 n =1,所有介质的折射率大于1
三、光的折射的一般规律
光从空气斜射入水中或其他介质 中时,折射光线与入射光线、法线在 同一平面内;折射光线和入射光线分 居法线两侧;折射角小于入射角;当 光线垂直射向介质表面时,传播方向 不改变.
∠AOF= ∠ABG=450
(参考资料)反射定律和折射定律的证明
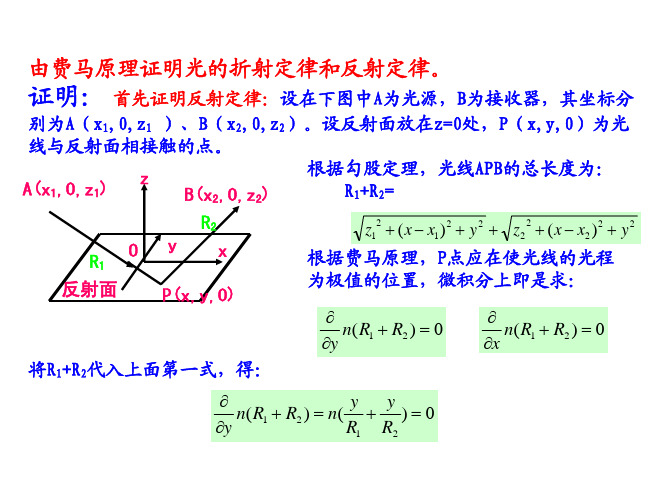
R1
R2
而同时 sin i = x − x1 R1
z A
sin i' = x2 − x R2
综合上三式 ,有:
i R1
n
O
n’
x-x1
i P
x2-x x
i’ R2 B
sin i' = n sin i n'
此即为折射定律第二条,折射角 的正弦与入射角的正弦之比与入 射角的大小无关,仅由两种介质 的折射率决定。
根据勾股定理,光线AP和PB的几何长度为:
R1 =
z12 + (x − x1)2 + y2 , R2 =
z
2 2
+
(x
−
x2 )2
+
y2
光线APB的光程为:
S = nR1 + n' R2
根据费马原理,P点应在使光线APB的光程为极值的位置,即求:
z A(x1,0,z1)
∂ ∂y
(nR1
+
n'
R2
)
=
0
n 由前一式,得:
∂ ∂x
(nR1
+
n'
R2
)
=
0
R1
O
折射面
yx n’
P(x,y,0)
R2
B(x2,0,z2)
n y + n' y = 0
R1
R2
y=0
上式意味着折射发生在垂直于折射面的平面 内,入射线、法线、折射线在同一平面内。 再设入射角为i、折射角为i’,则由后一式, 可得:
n x − x1 + n' x − x2 = 0
11.3 光的反射和折射

课 堂 练 习4
光在某种介质中的传播,介质的折射率为2,若要使光从此介质射 向真空时发生全反射,则入射角不可能的值是:[ A ] A. 150 B. 300 C. 450 D. 600 某介质的折射率为1.414,一束光从介质射向空气,入射角为60°, 如图所示的哪个光路图是正确的? D
劣质的玻璃中往往含有气泡.这些空气泡看上去比较亮,对这一现象 有下列不同的解释,其中正确的是( D ) 荷叶上的露珠 A空气泡对光线有聚集作用,因而较亮. 夏天马路上的蜃景现象 B.空气泡对光线有发散作用.因而较亮. C.从空气泡到达玻璃的界面处的光一部分发生全反射,因而较亮. D.从玻璃到达空气泡的界面处的光一部分发生全反射,因而较亮.
由折射定律sinθ=nsinr,代入上式中,得:
L
dn cos 1 1 2 sin 2 n
二、全反射和临界角 1、定义:当入射角增大到某一角度,使折射角达到90°时,折 射光完全消失,只剩下反射光;当入射光再增大时,入射光仍被全 部返回。 这种现象叫做全反射。
【观 察】随着入射角的增大,反 射光线和折射光线的亮度如何变化? 为什么?怎样解释该现象?
C
空气
玻璃 (D) (C) (A) (B) 3.理论和实验证明: 某种介质的折射率,等于光在真空中的速度跟光在这种 介质中的速度之比。
c 决定式: n v
介质的折射率是由介质本身 性质决定的.它取决于光在 介质中传播的速度.
c v n 1 sin i sin r i r
课 堂 练 习6
1.(03全国)一束单色光从空气射入玻璃中,则其 ( C ) A.频率不变,波长变长 B 频率变大,波长不变 C 频率不变,波长变短 D 频率变小,波长不变 2.(04全国春季)对于单色光,玻璃的折射率比水大, 则此光在玻璃中传播时( C ) A、其速度比在水中的大,其波长比在水中的长 B、其速度比在水中的大,其波长比在水中的短 C、其速度比在水中的小,其波长比在水中的短 D、其速度比在水中的小,其波长比在水中的长 3.紫光由折射率为n的棱镜进入空气,则下列说法中正确的是 B A.频率为原来的n倍,波长为原来的1/n B.波长为原来的n倍,波速为原来的n倍 C.频率为原来的n倍,波长为原来的n倍 D.频率为原来的1/n,波长为原来的n倍
光的折射

总结出光的折射规律 (1)三线关系:折射光线与入射光线、法 线在同一平面内(三线共面);折射光 线和入射光线分居法线的两侧(法线居 中)。 (2)因果关系:折射角随入射角同方向变 化。
光的折射现象: 光从一种介质斜射入另一种介质时传播 方向发生偏折的现象
我编写的程序原理:
入 n1 射 (x,y) 线 1
法 线 设入射线上一点(x,y),坐标原点 (m,n),折射线上一点(a,b).
反射线
sin 1
m
2
o(m,n) n2 2 (a,b) 折射线
sin 2
am (a m )
2
(b n )
2
由斯涅尔定理知
n1 sin 1 n 2 sin 2
光的折射
光的折射定律(斯涅尔定律):光入射到 不同介质的界面上会发生反射和折射。 其中入射光和折射光位于同一个平面上, 并且与界面法线的夹角满足如下关系: n1sinθ1 = n2sinθ2
其中,n1和n2分别是两个介质的折 射率,θ1和θ2分别是入射光(或折射光) 与界面法线的夹角,叫做入射角和折射 角。以上公式又叫斯涅尔公式
2
n1 ( m x )
2
2
m
我设计程序的目的:
通过改变入射角的位置和改变n1 n2的值,能 直观的演示下面两种现象之间的变化情况: (1)同一入射光线从一种介质分别斜射入另一 种不同介质时,折射角也随之改变;(2)入射光 线从一种介质斜射入另一种介质时,随着入射 角的改变,折射角也改变。
n1
2
(m x) (n y )
2
2 2
(m x)
n2
2
(a m ) (a m )
2
费马原理证明光的折射定律的一种方法

雏仿 教 育 学 院 学 报 ( 自然 科 学 版
一 九 八 八 年 第一 期 ( 总 第
期
建
费 马 原 理 证 明光 的 折 射
定律 的 一 种方法
王
由费 马 原 理 推 导 光 的 折 射 定律 的 问题
式: 设 两 个 均 匀 介质 的分 界 面 是 平
,
权
在 现 行 的 几 本 教 科 书① 中 都是这 样 的证 明 形
的学 生这 样 想 象
这 一 结论 在 推 导过 程 电没 有 证 明 甚 至 有 把 折射 点 C 画 在 A ` B ` 之 外 ( 图 2 ) , 再将 光 程 月 己 B 对 苏 求一 阶 导 数
n
Z
等于 零 而 得 出
n a s 卫几 忿工 二 一
s l
。
忿名
的结论
这 是 否 也可 以 认为 是 折射 定律 呢 ? , , 从数 学 上 分析 这 个 结 论 是证 明了 入 射 光 线与 折射光线弓 害法线 酶 两厕{ 但给 学 生 匆
“
:
对 于 上 述 的 证 明方 式
,
推 导 过 程无 可 非 议
’
。
但在 教 学 当 中 广 有不 少 的学 生 提 出 这 样
’ `
。
为 什 么折 射 点 C 在 A B 之 间 时
:
`
,
光 程 必 小 子 亡点 在通 丑 之 外 的 相 应 光 程
”
`
也
入 射 光 线 与 折射 光线 分 居 法 线 的 两 侧
万
.
面
,
:
,
。
它 们 的 绝对 折 射 率分 别 为
玲:
折射定律的两种证明方法(详细)

折射定律的两种证明⽅法(详细)//3700//3.7 ⼏何中的⼀些极值问题折射定律质点花时间最短运动轨迹选址问题实验演⽰⼏何中⼀些求极值问题,可以⽤微分法求解,也可借助⼏何或物理概念寻求特殊的技巧解法。
下⾯举⼏个例⼦。
问题⼀:(折射定律)设有⼀质点从点A ()11,y x 运动到点B ()22,y x ()0,021<>y y ,该质点的运动速度在上半平⾯为常数v 1,下半平⾯为常数v 2.此质点应沿什么路径运动才能使花费时间最短?问题⼆:(质点花时间最短运动轨迹)设⼀质点从点A(x 1,y 1)运动到点B(x 2,y 2), 其运动速度是纵坐标的可微函数v(y).若要求所花时间最短,求它的运动轨迹。
问题三:(选址问题)设有m 个村庄m A A A ,,,21 各有⼩学⽣m n n n ,,,21 ⼈,今要合建⼀所⼩学校,使全部学⽣所⾛的总路程最短,问应如何选择校址? //3710 ⼀. 折射定律设有⼀质点从点A ()11,y x 运动到点B ()22,y x ()0,021<>y y ,该质点的运动速度在上半平⾯为常数v 1,下半平⾯为常数v 2.此质点应沿什么路径运动才能使花费时间最短?显然该质点在上半平⾯和下半平⾯都应是直线。
故从A 到B 应为折线,只需求出折点C 即可。
设AC 、 BC 与y 轴的夹⾓分别为i 1, i 2, 我们来证明当21证明:⽅法⼀(⽤⼏何⽅法)⽅法⼆(⽤微分⽅法) //sm3711 ⽤⼏何⽅法证明:任取另⼀路径AC 1B, 质点经路径ACB 所花时间为21v BCv AC +经AC 1B 所花时间为2111v BC v AC +只需证当 (*) 成⽴时,211121v BC v AC v BC v AC +≤+. 过C 1分别向AC 延长线和CB 作垂线C 1D 1和C 1D 2,则 11CD AD AC -=, 22CD BD BC += )v CD v CD (v BD v AD )v CD v BD ()v CD v AD (v BC v AC 112222112222111121-++=++-=+∴(**) 212111221111i sin CC CD ,i sin CC CD i D CC i D CC ==∴=∠=∠,, 011112211211211v BC v AC v BD v AD v BC v AC ,BC BD ,AC AD (**)+≤+=+∴≤≤//sm3712 ⽤微分⽅法证明:设折点C 的坐标为()0,x 则质点经ACB 所花时间()()2222212121v y x x v y x x t +-++-=()()2211222222121211v i sin v i sin v y x x /)x x (v y x x /)x x (dx dt -=+--++--= ∴0=dx dt等价于2211sin sin v i v i =. 这与(*)等价.这就是光的折射定律:当光从⼀种介质进⼊另⼀种介质时⼊射⾓的正弦与折射⾓的正弦之⽐等于光在两种介质中的速度⽐.//sm3720⼆、质点花时间最短的运动轨迹问题:设⼀质点从点A(x 1,y 1)运动到点B(x 2,y 2), 其运动速度是纵坐标的可微函数v(y).若要求所花时间最短,求它的运动轨迹。
第四章 第1节 光的折射定律

答案:
6 2
33×10-8
[课堂双基落实]
1.[多选]关于光的折射现象下列说法正确的是
()
A.当入射角发生变化时,反射角和折射角都会发生变化
B.折射角总小于入射角
C.折射光线一定在法线和入射光线所确定的平面内
D.在光的反射中光路是可逆的,但在折射中光路是不可逆的
解析:由光的反射定律和折射定律可知 A、C 是正确的;当
C.如果光线从 Q 的下表面射出,出射光线与下表面所夹的 锐角一定大于 θ
D.如果光线从 Q 的下表面射出,出射光线与下表面所夹的 锐角一定小于 θ
[思路点拨] 解答本题可按以下思路分析:
作光路图
→
确定入射角、折射角
→
根据折射 定律判断
解析:作出光路图,如图所示。
由题意可知,光线垂直射入 Q,根据折射定律,则有: nP=ssiinn αβ,nQ=ssiinn γi,因为 nP<nQ,β=γ,所以 α<i, 所以 D 对。 答案:D
视深问题的求解
[典题例析] 3.有人在游泳池边“竖直”向下观察池水的深度,池水的视 深为 h,已知水的折射率为43,那么池水的实际深度为多少? [思路点拨] 解答该题可按如下思路分析:
画光路图 → 寻找几何关系 → 应用折射定律 → 求水深
解析:由池底某点 P 发出的光线,在水中和空气中的光路如
________,光进入液体后经过_______s 到达底面。
解析:因为入射角 θ1=90°-30°=60°,
折射角
θ2=90°-45°=45°所以
n=ssiinn
θθ12=ssiinn
6405°°=
6 2
光在液体中传播时:位移
用惠更斯原理证明折射定律

用惠更斯原理证明折射定律惠更斯原理,听起来高深莫测,其实有点像生活中的小道理。
想象一下,咱们在一个大池塘边,扔进一颗石子,哇,水面上波纹四散开来,形成一圈一圈的涟漪。
这些涟漪,就像光波的传播一样,都是从石子落水的那个点开始的。
每个波纹的每个点,都是一个新的波源,这就是惠更斯的基本思想。
惠更斯原理就是告诉我们,每个光波的点都能成为新波的源头,光就这样在空间里欢快地跳跃,像在开party。
说到折射定律,我们得想象一下光从一个地方跑到另一个地方,像个小调皮,一会儿在水里,一会儿又跑到空气里。
你看看,光在空气中的速度是299,792公里每秒,而在水里,它就慢了下来,大概是225,000公里每秒。
你能想象吗?这就像小朋友在操场上疯玩,跑得飞快,一到教室里就乖乖坐下来了。
光在不同介质里的速度差异,就是折射的秘密所在。
要用惠更斯原理解释折射,我们就得好好描绘一下。
当光线进入水中,嘿,情况就变了。
你可以想象一下,一只小船在水中航行,突然进入了泥泞的地方,船速一下子慢下来了。
光线在不同介质中也是这样的道理。
当光线从空气进入水中,前面的部分率先减速,后面的部分还在飞速前进,这样一来,光线的方向就变了,形成了折射。
像是打篮球,球在空中飞得好好的,突然接触到地面,反弹的角度就会变,光线也是如此。
再来看看惠更斯原理如何巧妙地帮助我们解释折射。
假设你把一个激光笔从空气中照进水里,光线入水的一瞬间,前面的小波源慢了下来,而后面的光线仍在快速奔跑。
这样,光线的路径就会发生偏折,形成一个新的方向。
就像在高速公路上,前面的车子突然减速,后面的车子不得不调整方向一样。
惠更斯原理在这里就像是一个聪明的导航仪,指引着光线如何优雅地转弯。
这时候我们用到的就是折射定律了,简单来说就是:入射角和折射角的比值等于两种介质中光速的比值。
用一个简单的公式表示出来就是:sin(入射角) / sin(折射角) = v1 / v2。
咱们不说公式多复杂,实际上它就是在告诉你,光线在不同介质中的“转身”是有规律可循的。
光的折射定律的证明

别为介质I,II,其折射率分别为七,n。
由A点发出一束细平行光射向X轴与X轴交点为C(x,0)最终经过B点。
设气< x < x2。
作MN 1 x轴于C点,MN为法线。
入射角i = ZACM,折射角r = /BCN。
光程△ = n i \A^ + n2 \BC\=n <(x- x )2 + j2 + n <(x - x)2 + j21 1 1 2、2 2 又光在折射率为n的介质中的传播时间_s_ s _ns _ At ====v c c c (1)(2)n由费马定理:光总是沿着光程最短的路径传播由(2)式又可知光总是沿着通过介质时间最短的路径传播。
n、:'(x—x)2 + j2 + n J(x—x)2 + j2t = ------- 1 -- -1 ------ 4―2------- 」(3)c要使'取极值则需使武°计算得:dt 2 n (x一x ) n (x一x)dx c J(x - x )2 + j2 J(x - x)2 + j2、」n (x - x ) n (x - x )=°即n (x - x ) = n (x - x)(x -x )2+ j2j(x - x)2+ j21 1 "2 1(5)x - x而sin i = . 1 ----寸(x -气)2+ j2sin r (6)折射定律的证明如图建立直角坐标系,给定平面内两点A(x , j)B(x , j)分居x轴两侧,x轴两侧分 1 1 2 2x -将(5)式带入(4)式可得:n sin i = n sin r折射定律的一般表达式:sin i = n2isin r⑻式中n2i为介质II相对于介质I的折射率nn = t2i ni特殊情况:当光从真空(折射率为1)射入折射率为n的介质中折射定律可表达为:sin i = n sin r (7)(8)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
折射定律的证明
如图建立直角坐标系,给定平面内两点11(,)A x y 22(,)B x y 分居x 轴两侧,x
轴两侧分
别为介质I ,II ,其折射率分别为12,n n 。
由A 点发出一束细平行光射向x 轴与x 轴交点为(,0)C x 最终经过B 点。
设12x x x <<。
作MN ⊥x 轴于C 点,MN 为法线。
入射角i ACM =∠,折射角r BCN =∠。
光程12n AC n BC ∆=+
n n = (1)
又 光在折射率为 n 的介质中的传播时间
s s ns t c v c c
n
∆==== (2) 由费马定理:光总是沿着光程最短的路径传播由(2)式又可知光总是沿着通过介质时间最短的路径传播。
t = (3) 要使t 取极值则需使
0dt dx
= 计算得:
2dt dx c ⎡⎤=
(4) 0=
= (5)
而sin i
sin r (6)
将(5)式带入(4)式可得:
12sin sin n i n r = (7)
折射定律的一般表达式:21sin sin i n r = (8)
(8)式中21n 为介质II 相对于介质I 的折射率
2211
n n n = 特殊情况:当光从真空(折射率为1)射入折射率为n 的介质中折射定律可表达为:
sin sin i n r =。
