在计算机中数学函数的表达含义和符号
计算机公式与函数知识

计算机公式与函数知识一、计算机公式的概念与特点1.常量:常量是固定不变的数值,如整数、浮点数、布尔值等。
在计算机程序中,常量用于表示具体的数值或逻辑状态。
2.变量:变量是在程序运行过程中可以改变数值的符号。
通过给变量赋值,可以在程序中保存和处理不同的数值。
变量常用于存储中间结果和用户输入等数据。
3.运算符:运算符是用于进行数学运算和逻辑判断的符号。
常见的数学运算符包括加减乘除、取余、幂等等。
逻辑运算符包括与、或、非等。
运算符能够对常量和变量进行操作,生成新的数值或逻辑结果。
4.函数:函数是一种特殊的公式,它接受输入参数,经过特定的计算逻辑,返回一个结果。
函数可以封装常用的数学运算,实现函数的复用和模块化。
1.精确性:计算机公式能够精确表示数学运算和逻辑关系。
它能够处理大量的数据,并返回确切的数值或逻辑结果。
2.灵活性:计算机公式可以根据实际需求进行扩展和修改。
通过改变公式中的常量、变量以及运算符,可以实现不同的计算逻辑。
3.可重用性:计算机公式可以在多个程序中重复使用。
通过定义函数,可以将公式进行封装,方便在不同的程序中调用和调试。
二、计算机函数的概念与应用计算机函数是计算机程序中的一种特殊结构,它包含了一系列执行特定任务的语句。
函数将输入参数映射为输出结果,用于实现特定的计算逻辑。
1. 函数的概念:函数是一段独立的代码,它接受输入参数并返回一个结果。
函数由函数名、参数列表、函数体和返回值组成。
函数可以接受任意数量的参数,执行一系列语句,并通过return语句返回结果。
2.函数的应用:(1)数学建模:函数在数学建模中起到关键作用。
通过将实际问题转化为数学模型,定义合适的函数,可以实现对问题的建模和求解。
数学建模常用的函数包括线性函数、指数函数、对数函数等。
(2)数据分析:函数在数据分析中用于处理和分析大量的数据。
例如,通过编写统计函数可以计算数据的平均值、方差、标准差等统计指标。
通过编写机器学习算法,可以实现对数据的分类、回归、聚类等分析。
(完整word版)高数符号大全

高等数学常用符号大全及符号的含义acsc xy,余割函数反函数在x处的值,即 x = csc y θ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a•ba、b向量的点积(a•b)a、b向量的点积|v|向量v的模|x|数x的绝对值表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在Σ其上部。
如j从1到100 的和可以表示成:。
这表示 1+ 2 + … + nM表示一个矩阵或数列或其它|v>列向量,即元素被写成列或可被看成k×1阶矩阵的向量<v|被写成行或可被看成从1×k阶矩阵的向量dx变量x的一个无穷小变化,dy, dz, dr等类似ds长度的微小变化ρ变量 (x2+ y2+ z2)1/2或球面坐标系中到原点的距离r 变量 (x2+ y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值,为一个面积、体积或超体积d2f/dx2f关于x的二阶导数f(2)(x)同样也是f关于x的二阶导数f(k)(x)f关于x的第k阶导数,f(k-1)(x)的导数T 曲线切线方向上的单位向量,如果曲线可以描述成 r(t), 则T =(dr/dt)/|dr/dt|ds沿曲线方向距离的导数κ曲线的曲率,单位切线向量相对曲线距离的导数的值:|dT/ds|NdT/ds投影方向单位向量,垂直于TB平面T和N的单位法向量,即曲率的平面τ曲线的扭率: |dB/ds|g重力常数F力学中力的标准符号k弹簧的弹簧常数pi第i个物体的动量H物理系统的哈密尔敦函数,即位置和动量表示的能量{Q, H}Q, H的泊松括号以一个关于x的函数的形式表达的f(x)的积分函数f 从a到b的定积分。
数学的语言如何理解和运用数学符号

数学的语言如何理解和运用数学符号数学是一门使用特定的符号和语言描述和解决问题的学科。
它通过使用数学符号来代表数学概念、关系和操作,从而提供了一种精确的工具来研究问题、推导定理和解决实际应用。
本文将探讨数学的语言,即使用数学符号的方式,以及如何理解和运用这些符号。
一、数学符号的基本组成数学符号是数学语言的基本组成部分,它们可以用来表示数学对象、运算符号和关系等。
下面是一些常见的数学符号及其含义:1. 数字:0、1、2、3、4、5、6、7、8、9等表示具体数值的符号;2. 数学运算符号:+、-、×、÷等表示加减乘除等运算的符号;3. 方括号、圆括号、花括号等:用于分组、表示区间等;4. 希腊字母:如α、β、γ等表示特定的数学对象或变量;5. 英文字母:表示变量、未知数、常数等;6. 等于号:= 表示两个表达式相等;7. 不等号:≠ 表示两个表达式不等;8. 大于号、小于号等:>、<表示大小关系;9. 数学函数符号:如sin、cos、log等表示特定的数学函数。
以上只是一部分常见的数学符号,实际上数学符号的种类非常丰富。
了解这些符号的含义和用法是理解数学语言的基础。
二、数学符号的语法和用法数学符号的语法和用法遵循一定的规则和约定,掌握这些规则对于正确理解和运用数学符号非常重要。
1. 表达式与方程:数学符号常常用于表示数学表达式和方程。
表达式由数和运算符号组成,例如:2+5=7。
方程是等式的一种特殊形式,其中包含一个或多个未知数,例如:x+3=8。
2. 关系符号的运用:大于号、小于号等关系符号表示大小关系。
例如:2 < 5表示2小于5。
等于号表示相等关系,例如:x = 3表示x等于3。
3. 函数符号的使用:数学函数常用符号表示,如sin表示正弦函数,cos表示余弦函数。
在函数符号后面通常用括号表示自变量,例如sin(x)表示以x为自变量的正弦函数。
4. 运算的优先级:不同的运算符号具有不同的优先级,通常按照乘除法优先于加减法的原则进行计算。
探索数学符号认识数学符号的意义和用法

探索数学符号认识数学符号的意义和用法探索数学符号:认识数学符号的意义和用法数学作为一门抽象的学科,借助符号来表达各种数学概念和关系。
数学符号的使用不仅能够简化数学表达,还可以提高数学思维的逻辑性和精确性。
本文将探索数学符号的意义和用法,帮助读者更好地理解数学符号的实质。
一、数学符号的基本意义数学符号是数学语言的重要组成部分,其基本意义在于用一种简练的形式来表示某种数学概念或操作。
通过符号的使用,可以将复杂的数学问题简化为简单的表达式,从而提高数学计算的效率。
例如,用“+”来表示加法运算,用“=”来表示等号关系,这些符号的简洁性使得数学的表达更加凝练和明确。
二、数学符号的分类数学符号根据其所代表的概念和用途分为多个类别,下面将介绍几种常见的数学符号。
1.基本运算符号基本运算符号是最常见的数学符号之一,包括加法“+”、减法“-”、乘法“×”、“⋅”或“*”、除法“÷”、“/”和等号“=”。
这些符号用于基本的算术运算和方程等式的表达,是数学中最为基础的符号。
2.代数符号代数符号用于表示未知数或变量,常见的代数符号包括字母“x”、“y”、“z”等。
代数符号的使用使得数学问题的表达更加灵活,能够处理更加复杂的数学关系。
通过代数符号,我们可以推导和解决各种代数方程,并求得未知数的数值。
3.函数符号函数符号用于表示数学中的函数关系,较为常见的函数符号包括“f”、“g”和“h”等。
函数符号在数学分析和微积分中起到重要的作用,用于描述各种数学函数的定义和性质,以及函数之间的关联。
4.集合符号集合符号用于表示数学中的集合关系,包括并集“∪”、交集“∩”、包含关系“⊆”、“⊇”等。
集合符号的使用方便了对集合运算的表达,可以描述集合之间的各种关联和属性。
5.几何符号几何符号用于表示几何中的各种图形和关系,例如平行符号“||”、垂直符号“⊥”、相似符号“∼”等。
几何符号的使用可以简洁地表达几何形状和关系,帮助我们研究几何问题。
数学的语言学习数学中的专业术语和符号

数学的语言学习数学中的专业术语和符号数学是一门理性而精确的学科,其中运用了许多专业术语和符号来表达数学思想和解决问题。
掌握这些术语和符号对于学习和理解数学概念至关重要。
本文将探讨数学中的专业术语和符号,重点介绍其使用方法和意义。
一、数学专业术语的学习数学专业术语是数学领域内的特定词汇,用于描述概念、定理和推理过程等。
学习数学专业术语有助于准确理解和表达数学思想。
以下是一些常见的数学专业术语:1. 函数(Function):函数是数学中常见的概念,表示一种特定的对应关系。
函数通常用符号 f(x) 或 g(x) 表示,其中 x 为自变量,f(x)为关于 x 的函数值。
2. 导数(Derivative):导数是描述函数变化率的概念,表示函数在某一点的瞬时变化速率。
导数常用符号 f'(x) 或 dy/dx 表示,其中 f'(x)表示函数 f(x) 的导数。
3. 积分(Integral):积分是求函数面积或曲线长度的方法,也是导数的逆运算。
积分常用符号∫f(x)dx 表示,其中∫表示积分运算符。
4. 矩阵(Matrix):矩阵是由数字排列成的矩形数表,用于表示线性方程组或进行线性变换。
矩阵通常用方括号 [] 表示,例如 A = [a_ij],其中 a_ij 表示矩阵 A 中的元素。
5. 向量(Vector):向量是表示大小和方向的量,常用于描述物理力学和几何概念。
向量通常用有方向的箭头表示,例如向量 v。
学习数学专业术语时,可以通过阅读教材、参考词典以及专业论文等渠道进行学习。
同时,积极解决数学问题,参与数学讨论和实践操作,也能够加深对数学术语理解和运用的熟练程度。
二、数学符号的学习除了专业术语外,数学领域中还广泛使用各种符号来简化表达和表示数学关系。
掌握数学符号对于理解和解决数学问题非常重要。
以下是一些常见的数学符号:1. 加号(+)和减号(-):加号表示两数之和,减号表示两数之差。
例如,a + b 表示 a 和 b 的和,a - b 表示 a 和 b 的差。
如何在Excel中使用函数进行数值计算

如何在Excel中使用函数进行数值计算Excel是一款强大的电子表格软件,广泛应用于数据处理和数值计算。
它提供了丰富的内置函数,可以帮助用户进行各种数值计算。
本文将介绍如何在Excel中使用函数进行数值计算。
一、基本数学函数的使用使用基本数学函数可以进行简单的数值计算,如加减乘除等。
以下是一些常用的基本数学函数及其使用方法:1. 加法:使用“+”符号,例如:=A1+B1,表示将A1单元格和B1单元格的值相加。
2. 减法:使用“-”符号,例如:=A1-B1,表示将B1的值从A1的值中减去。
3. 乘法:使用“*”符号,例如:=A1*B1,表示将A1单元格的值和B1单元格的值相乘。
4. 除法:使用“/”符号,例如:=A1/B1,表示将A1单元格的值除以B1单元格的值。
在使用基本数学函数时,可以通过引用单元格的方式来获取数值,也可以直接输入数值。
二、常用函数的使用除了基本数学函数外,Excel还提供了许多常用的函数,可以进行更复杂的数值计算。
以下是一些常用函数的使用方法:1. SUM函数:用于求和。
例如:=SUM(A1:A5),表示求A1到A5单元格的和。
2. AVERAGE函数:用于求平均值。
例如:=AVERAGE(A1:A5),表示求A1到A5单元格的平均值。
3. MAX函数:用于求最大值。
例如:=MAX(A1:A5),表示求A1到A5单元格中的最大值。
4. MIN函数:用于求最小值。
例如:=MIN(A1:A5),表示求A1到A5单元格中的最小值。
5. COUNT函数:用于计数。
例如:=COUNT(A1:A5),表示计算A1到A5单元格中非空单元格的个数。
6. IF函数:用于条件判断。
例如:=IF(A1>B1, "大于", "小于等于"),表示如果A1大于B1,则结果为"大于",否则结果为"小于等于"。
除了上述函数,Excel还提供了许多其他函数,如平方根函数、对数函数、幂函数等,可以根据具体的数值计算需求选择合适的函数进行使用。
数学符号的使用和理解

数学符号的使用和理解数学符号作为数学的一种特殊语言,对于数学的表达和推理起到了至关重要的作用。
正确理解和运用数学符号,不仅可以提高数学问题的解决效率,还能够帮助我们更深入地理解数学的本质。
本文将探讨数学符号的使用方法和其所代表的数学概念。
一、基本数学符号的使用1. 加减乘除:在数学中,加法符号"+"表示两个数的和,减法符号"-"表示两个数的差,乘法符号"×"或"*"表示两个数的积,除法符号"÷"或"/"表示两个数的商。
这些基本符号在日常的数学计算中经常用到,我们要确保使用正确并注意运算的顺序。
2. 等于号:等于号"="用于表示左右两边的表达式或数值相等。
要注意区分等于号和不等号"≠"的使用,避免混淆。
3. 大于、小于和等于:大于号">"表示左边的数值比右边的大,小于号"<"表示左边的数值比右边的小,大于等于号"≥"表示左边的数值大于或等于右边的数值,小于等于号"≤"表示左边的数值小于或等于右边的数值。
这些符号在数学不等式和方程组的解表示中经常使用。
4. 括号和方括号:括号"()"和方括号"[]"常用来表示运算的优先级和表示范围。
在进行数学计算时,我们要遵循括号内优先的原则,并正确理解方括号所表示的区间和集合。
二、高级数学符号的理解1. Σ符号:Σ是希腊字母Sigma的大写形式,表示求和。
如果有数列a₁,a₂,a₃,...,aₙ,要求它们的和,可以用Σ符号表示为Σaᵢ。
其中i是从1到n的变量,表示求和的范围。
Σ符号的应用使得复杂的求和问题变得简洁明了。
2. ∫符号:∫是对数学积分的符号表示,表示求函数的不定积分。
高中数学符号读法大全及意义

高中数学符号读法大全及意义一、基本数学符号1. +:加号,表示加法运算。
2. -:减号,表示减法运算。
3. ×:乘号,表示乘法运算。
4. ÷:除号,表示除法运算。
5. =:等于号,表示相等关系。
6. ≠:不等号,表示不相等关系。
7. <:小于号,表示小于关系。
8. >:大于号,表示大于关系。
9. ≤:小于等于号,表示小于等于关系。
10. ≥:大于等于号,表示大于等于关系。
二、集合符号1. ∈:属于,表示一个元素属于某个集合。
2. ∉:不属于,表示一个元素不属于某个集合。
3. ∪:并集,表示所有在某一个以上的集合中出现的元素的新集合。
4. ∩:交集,表示属于所有给定集合的元素的新集合。
5. ⊆:包含关系(子集),表示一个集合包含于另一个集合。
6. ⊇:包含关系(超集),表示一个集合包含另一个集合。
7. ∅:空集,表示没有任何元素的集合。
三、数学函数符号1. f(x):函数符号,表示自变量为x时,函数的值。
2. g(x):函数符号,表示自变量为x时,函数的值。
3. h(x):函数符号,表示自变量为x时,函数的值。
4. lim:极限符号,表示函数在逼近某个数值时的极限。
5. sin:正弦函数符号,表示角度的正弦值。
6. cos:余弦函数符号,表示角度的余弦值。
7. tan:正切函数符号,表示角度的正切值。
8. log:对数函数符号,表示以某个底数为底的对数函数。
四、微积分符号1. dy/dx:导数符号,表示某个函数在某点的导数。
2. ∫:积分符号,表示函数在某个区间上的积分值。
3. dx:微分符号,表示微分变量。
4. Δx:增量符号,表示微分变量的增量。
五、几何图形符号1. ∆ABC:三角形符号,表示三条边分别为AB、BC和CA的三角形。
2. △DEF:三角形符号,表示三条边分别为DE、EF和FD的三角形。
3. ∠:角符号,表示两条射线之间的角度。
4. ⊥:垂直符号,表示两条直线垂直。
特殊符号名称

特殊符号名称概述在我们日常的书写和文字表达中,特殊符号扮演着重要的角色。
特殊符号是指那些不属于字母、数字或汉字等常见字符的符号。
它们可能具有特定的含义,用途广泛,被广泛应用于各个领域,特别是在计算机科学、数学和代码编写中。
本文档将介绍一些常见的特殊符号及其名称。
通过了解这些符号的名称和用途,我们可以更好地理解它们在不同领域中的应用,提高我们的书写和交流能力。
一、常见数学符号1. “+” (加号)加号是最基本的数学符号之一,用于表示两个数的相加。
2. “-” (减号)减号用于表示两个数的相减。
3. “x” (乘号)乘号用于表示两个数的相乘。
4. “÷” (除号)除号用于表示两个数的相除。
5. “=” (等号)等号用于表示两个数或表达式的相等关系。
6. “<” (小于号)小于号用于表示一个数小于另一个数的关系。
7. “>” (大于号)大于号用于表示一个数大于另一个数的关系。
8. “≤” (小于或等于号)小于或等于号表示一个数小于或等于另一个数的关系。
9. “≥” (大于或等于号)大于或等于号表示一个数大于或等于另一个数的关系。
二、计算机科学符号1. “<” (尖括号)尖括号用于表示代码中的标签,通常与其他符号结合使用。
2. “>” (尖括号)与尖括号相对应,它也用于表示代码中的标签。
3. “/” (斜杠)斜杠用于表示文件路径或网址。
4. “\\” (反斜杠)反斜杠通常用于表示转义字符,在代码编写中具有特殊的意义。
5. “{ }” (花括号)花括号用于标识代码块。
6. “( )” (圆括号)圆括号用于表示函数参数、优先级、数学表达式等。
7. “[ ]” (方括号)方括号在计算机科学中具有多种用途,例如表示数组、索引或注释等。
8. “|” (管道符号)管道符号用于连接命令和程序,并将一个程序的输出作为另一个程序的输入。
9. “%” (百分号)百分号用于表示百分数。
10. “!” (感叹号)感叹号用于表示逻辑非运算或表示强调。
数学函数关系表达

数学函数关系表达数学函数是数学中的一种基本概念,它描述了数值之间的关系。
函数关系的表达方式有多种,每种方式都有其独特的特点和应用场景。
本文将探讨几种常见的数学函数关系表达方式,并分析其优缺点。
一、函数关系的符号表示在数学中,函数关系可以用符号表示。
常见的符号表示方式有:1. 函数关系的显式表达式函数关系的显式表达式是最常见的表达方式。
它通过一个公式明确地表示出函数关系。
例如,函数y = f(x)可以用显式表达式y = 2x + 3来表示。
这种表达方式简洁明了,适用于简单的函数关系。
然而,对于复杂的函数关系,显式表达式可能变得冗长和难以理解。
2. 函数关系的隐式表达式函数关系的隐式表达式是通过方程或条件来表示的。
例如,函数关系x^2 +y^2 = 1可以用隐式表达式表示。
这种表达方式适用于无法用显式表达式表示的函数关系,但求解和分析隐式表达式的函数关系可能会更加困难。
3. 函数关系的级数展开函数关系的级数展开是将函数关系表示为级数的形式。
级数展开可以用于近似计算和函数逼近。
例如,函数关系e^x = 1 + x + x^2/2! + x^3/3! + ...可以用级数展开表示。
级数展开的优点是可以用有限项来近似计算函数值,但在某些情况下,级数展开的收敛性可能需要额外的条件。
二、函数关系的图像表示除了符号表示外,函数关系还可以通过图像表示。
图像表示是一种直观且易于理解的方式,它可以帮助我们更好地理解函数关系的性质和特点。
1. 函数关系的曲线图函数关系的曲线图是函数关系在坐标系中的图形表示。
通过绘制函数关系的曲线图,我们可以直观地看到函数的增减性、极值点、拐点等性质。
曲线图的优点是可以清晰地展示函数关系的特点,但在某些情况下,函数关系的曲线图可能会很复杂,需要使用计算机绘图工具进行绘制。
2. 函数关系的散点图函数关系的散点图是将函数关系的离散点在坐标系中表示出来。
散点图可以用于观察函数关系的离散性质和分布规律。
下角标函数-概述说明以及解释

下角标函数-概述说明以及解释1.引言1.1 概述下角标函数是一种在数学和计算机科学领域中广泛使用的函数类型,它在表示数值、字符或其他数据时起到非常重要的作用。
具体来说,下角标函数是一种通过使用下标符号来表示元素或对象的函数。
下角标通常用于指示元素的位置、顺序或标识,并提供了一种简洁、清晰的方式来访问和处理数据。
它在许多领域中都有广泛的应用,包括数学、物理、计算机科学等。
在数学中,下角标函数常用于表示系列中的第n个元素。
例如,在表示向量或矩阵中的元素时,可以使用下角标函数来指定其位置。
同时,下角标函数也常被用于表示数列中的元素,可以通过下标来获取特定位置处的数值。
这种方式简化了数学表达式的书写和理解,使得数学推导和计算过程更加直观和方便。
在计算机科学中,下角标函数同样具有重要的意义。
在编程中,下角标函数常常用于表示数组和列表中的元素。
通过使用下角标来访问和修改特定位置的数据,程序可以更加灵活地操作和处理数据。
此外,下角标函数还可以用来表示字符串中的字符,允许我们通过下标来访问和操作字符串的各个部分。
这种表达方式在字符串处理和文本分析中非常常见。
总之,下角标函数作为一种常见的数学和计算机科学概念,具有广泛的应用和重要的作用。
它通过使用下标符号来表示元素或对象,提供了一种简洁、清晰的方式来访问和处理数据。
无论在数学推导、编程实现还是数据处理过程中,下角标函数都是一个不可或缺的工具,为我们的工作和研究带来了很大的便利。
在接下来的文章中,我们将更详细地探讨下角标函数的定义、应用和特性,希望能够深入理解和学习这一重要概念。
文章结构部分的内容如下:1.2 文章结构本文将按照以下结构来进行论述下角标函数的概述、定义、应用和特性,最后总结下角标函数的优势,并展望其未来发展。
首先,引言部分将从概述、文章结构、目的以及总结等方面介绍本文的主要内容和意义。
接着,正文部分将深入探讨下角标函数的定义、其在实际应用中的使用场景以及相关特性。
数学符号的使用和理解

数学符号的使用和理解数学符号是数学语言中的重要组成部分,它们起到了一种简洁、精确地表达数学概念和关系的作用。
在数学领域中,掌握和理解数学符号的使用对于学习和应用数学至关重要。
本文将介绍数学符号的分类、常见符号的含义以及使用数学符号的注意事项。
一、数学符号的分类数学符号可以分为几个不同的类别,如下所示:1.运算符号:用于表示加减乘除、开方、求和、积分等数学运算,如"+"表示加法,"-"表示减法,"×"表示乘法,"÷"表示除法。
2.比较符号:用于表示大小关系,如">"表示大于,"<"表示小于,"="表示等于,">="表示大于等于,"<="表示小于等于。
3.集合符号:用于表示集合之间的关系和操作,如"∈"表示属于,"∪"表示并集,"∩"表示交集,"∖"表示差集,"⊆"表示子集。
4.数学函数符号:用于表示数学函数,如"sin"表示正弦函数,"cos"表示余弦函数,"log"表示对数函数,"exp"表示指数函数。
5.矩阵和向量符号:用于表示矩阵和向量,如"A"表示矩阵,"x"表示向量,"ϵ"表示空集。
二、常见符号的含义和用法1.π(pi):表示圆周率,约等于3.14159,常用于计算圆的周长和面积。
2.√(根号):表示开方,如√9=3,√25=5,√x表示对x进行开方。
3.Σ(求和符号):表示对一系列数进行求和,如Σn表示1到n的所有整数相加。
4.∫(积分符号):表示求函数的极限和,如∫f(x)dx表示对函数f(x)进行积分。
函数的表示法ppt

根据函数解析式,在坐标系上描出对应的点。
画出坐标系
在平面直角坐标系中,以横轴表示自变量,纵轴表示因变 量。
连接点
按照自变量从小到大的顺序,用平滑的曲线将各点连接起 来。
图像法的优缺点
• 优点 • 可视化直观:函数图像能够直观地展现函数的变化趋势和特征。 • 信息丰富:图像上可以获得函数的重要信息,如极值点、单调性等。 • 便于比较:多个函数图像在同一坐标系下可以直观地进行比较。 • 缺点 • 精度受限:图像法只能近似地表达函数,无法提供精确值。 • 作图繁琐:绘制函数图像需要一定时间和精力。 • 适用范围有限:对于复杂函数或超越函数,图像法可能无法准确表达。
数据可视化中应用图像法可以将大量数据信息 直观呈现,提表格法:通过列出表格的方式来表示函数关系,如 线性回归模型参数的表格形式表示。
应用案例:医学研究中的生存分析,通过表格列出 患者的年龄、性别、生存时间等信息。
统计分析中应用表格法可以简洁明了地呈现数据 信息,方便进行数据分析和挖掘。
程序法在算法模拟中的应用
程序法:通过编写程序的方式来实现一个函数关系,如使用某种编程语言实现一个排序算法。 应用案例:计算机模拟导弹轨迹、预测人口增长等。 算法模拟中应用程序法可以更加灵活地实现各种算法,进行更为复杂和精细的模拟和分析。
THANKS
谢谢您的观看
根据函数的对应关系,可以将函数 分为线性函数、二次函数、幂函数 、对数函数、三角函数等。
函数表示方法的分类
解析式表示法
图象表示法
表格表示法
程序表示法
通过数学符号来表示函数,如 y = f(x)。
通过绘制函数的图象来表示函数 。
通过列出函数的自变量和因变量 的对应值来表示函数。
微积分领域使用的数学符号

微积分领域使用的数学符号在数学中有许多不同的符号,它们有助于数学家们快速地表达复杂的概念以及表示思考过程。
其中最常用的符号是来自微积分领域的数学符号,这些符号不仅用于表达数学概念,而且用于计算机程序,以便对数学运算进行模拟。
常用符号在微积分领域,常见的符号有负号、数字、字母、加号、减号、乘号、除号、等号、函数符号和括号等。
负号“-”用于表示负数,加号“+”用于表示正数,减号“-”表示减法运算,乘号“*”用于表示乘法运算,除号“/”表示除法运算,等号“=”表示等式,函数符号“f(x)”用于表示函数等。
常见符号在微积分中,求导符号为“’”,即“”,表示求导运算。
另外,还有三角函数的常用符号,如正弦函数的符号为“sin(x)”,余弦函数的符号为“cos(x)”,正切函数的符号为“tan(x)”等。
另外,还有指数函数的符号,如幂函数的符号为“a^b”,表示a 的b次幂;b幂函数的符号为“b^a”,表示以b为底a次幂;以及对数函数的符号为“log a”,表示以a为底的对数等。
还有一些常用的微积分符号,如积分符号为“∫”,表示定积分;积分常数为“C”,表示积分常数;符为“d/dx”,表示求;平方根符为“√”,表示开平方;立方根符为“”,表示开立方等。
在使用符号的时候,需要注意的是,有些符号的使用有一定的规则,因此在使用符号时需要注意遵守。
此外,在使用符号时,还需要根据实际情况添加注释,以便更好地理解数学内容。
结论从上述内容可以看出,微积分领域使用的数学符号有许多,它们不仅用于表达数学概念,而且用于计算机编程模拟数学运算。
因此,在使用微积分领域使用的数学符号时,我们需要加以注意,既要掌握符号的正确使用,又要注释清楚,以便更好地理解数学内容。
如何编写函数公式

如何编写函数公式一、前言在数学和计算机科学领域,函数公式是一种非常重要的表达方式。
编写函数公式不仅可以帮助我们更好地理解和描述问题,还可以方便我们进行计算和分析。
本文将介绍如何编写函数公式,希望能够对读者有所帮助。
二、数学函数公式的编写1. 函数的定义在数学中,函数是一种将一个集合中的元素映射到另一个集合中的元素的规则。
函数通常用符号 f(x) 表示,其中 x 是输入,f(x) 是输出。
函数的定义通常包括定义域、值域和函数表达式三个部分。
例如,定义一个函数 f(x) = x^2,其中 x 的定义域为实数集,值域为非负实数集。
这个函数的表达式表示输入 x 的平方是输出 f(x)。
2. 常见函数公式在数学中,有许多常见的函数公式,例如:- 线性函数:f(x) = kx + b,其中 k 和 b 是常数。
- 幂函数:f(x) = x^n,其中 n 是正整数。
- 指数函数:f(x) = a^x,其中 a 是正实数。
- 对数函数:f(x) = log_a(x),其中 a 是正实数。
- 三角函数:sin(x)、cos(x)、tan(x) 等。
3. 函数公式的表示方法在数学中,函数公式可以用多种方式表示,例如:- 代数式:f(x) = x^2。
- 函数图像:可以用图像表示函数的变化趋势。
- 函数表格:可以用表格列出函数的输入和输出值。
- 函数符号:可以用符号表示函数的特定性质,例如 f(x) 是偶函数或奇函数。
三、计算机函数公式的编写1. 函数的定义在计算机科学中,函数是一种可重复使用的代码块,用于执行特定的任务。
函数通常包括函数名、参数和返回值三个部分。
例如,定义一个函数square(x),用于计算输入x 的平方,并返回结果。
这个函数的定义可以写成:```def square(x):return x ** 2```2. 常见函数公式在计算机科学中,有许多常见的函数公式,例如:- 数学函数:可以用 Python 的 math 模块调用常见的数学函数,例如sin(x)、cos(x)、tan(x) 等。
常用数学符号读法大全以及主要数学符号含义

常用数学符号读法大全以及主要数学符号含义大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita 西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omi kron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽数学符号:(1)数量符号:如:i,2+i,a,x,自然对数底e,圆周率π.(2)运算符号:如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(∪),交集(∩),根号(√),对数(log,lg,ln),比(:),微分(dx),积分(∫)等.(3)关系符号:如“=”是等号,“≈”是近似符号,“≠”是不等号,“>”是大于符号,“<”是小于符号,“→”表示变量变化的趋势,“∽”是相似符号,“≌”是全等号,“∥”是平行符号,“⊥”是垂直符号,“∝”是反比例符号,“∈”是属于符号,“C”或“C下面加一横”是“包含”符号等.(4)结合符号:如圆括号“()”方括号“[]”,花括号“{}”括线“—”(5)性质符号:如正号“+”,负号“-”,绝对值符号“‖”(6)省略符号:如三角形(△),正弦(sin),余弦(cos),x的函数(f(x)),极限(lim),因为(∵),所以(∴),总和(∑),连乘(∏),从n个元素中每次取出r个元素所有不同的组合数(C(r)(n) ),幂(A,Ac,Aq,x^n),阶乘(!)等.数学符号的意义符号意义∞无穷大π圆周率|x|绝对值∪并集∩交集≥大于等于≤小于等于≡恒等于或同余ln(x)以e为底的对数lg(x)以10为底的对数floor(x)上取整函数ceil(x)下取整函数x mod y求余数x - floor(x) 小数部分∫f(x)dx不定积分∫[a:b]f(x)dx a到b的定积分→等价于趋向于数学符号的应用P为真等于1否则等于0∑[1≤k≤n]f(k) 对n进行求和,可以拓广至很多情况如:∑[n is prime][n < 10]f(n)∑∑[1≤i≤j≤n]n^2lim f(x) (x->?) 求极限f(z) f关于z的m阶导函数C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除nm⊥n m与n互质a ∈A a属于集合A#A 集合A 中的元素个数“∑”数学里的连加符号,叫西格马,求和的意思要给出上下界限(比如k是自然数∑k(上界限至n,下界限从k=0开始) ∑k=0+1+2+……+n {大括号(bracket)是用来规定运算次序的符号。
运算符、布尔运算、表达式、标准函数
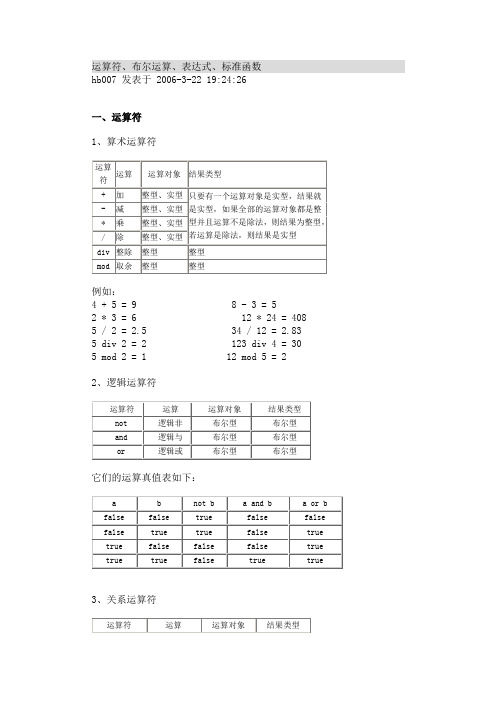
运算符、布尔运算、表达式、标准函数hb007 发表于 2006-3-22 19:24:26一、运算符1、算术运算符例如:4 +5 = 9 8 - 3 = 52 *3 = 6 12 * 24 = 4085 / 2 = 2.5 34 / 12 = 2.83 5 div 2 = 2 123 div 4 = 30 5 mod 2 = 1 12 mod 5 = 22、逻辑运算符它们的运算真值表如下:3、关系运算符例如:设a,b为标准数据类型的变量,则:a=b 如果a等于b结果为真,否则为假。
a<>b 如果a不等于b结果为真,否则为假。
a<b 如果a小于b结果为真,否则为假。
a>b 如果a大于b结果为真,否则为假。
a<=b 如果a小于等于b结果为真,否则为假。
a>=b 如果a在于等于b结果为真,否则为假。
例如:5=5 结果为真。
5=10 结果为假。
false<true 结果为真。
false>true 结果为假。
'A'<'C' 结果为真。
12.5>-8 结果为真。
24>=21 结果为真。
10.3<10 结果为假。
二、运算符的优先级三、布尔运算要判断“X>Y”是否成立,其结果不是一个算术量(即数值),而是“成立”或“不成立”,也可以用“真”表示“成立”,用“假”表示“不成立”,也就是说,它的结果是一个逻辑值(“真”或者“假”)。
逻辑运算又叫布尔运算。
布尔(Bool)是英国数学家的名字,他首先提出对二值变量进行逻辑运算的代数,称为布尔代数。
1、布尔常量Pascal语言中“真”用true表示,“假”用False表示。
所以布尔类型只有true与false两个常量。
2、布尔型符号常量(boolean)在程序的说明部分,可以定义布尔符号常量。
如:constt=true;f=false;执行部分就可以用t代表true,用f 代表false。
复杂运算符号的认识与运用

复杂运算符号的认识与运用现代数学是构建在复杂运算符号之上的,这些符号在数学表达和问题求解中起着至关重要的作用。
掌握复杂运算符号的含义和运用方法,对于提高数学能力和解决实际问题都具有重要意义。
本文将重点介绍一些常见的复杂运算符号,包括等于号、不等于号、约等于号、箭头符号和逻辑与或非符号。
等于号(=)是数学中最基本的符号之一,表示两个数或两个表达式相等。
例如,若a = b,则a和b代表相同的数或表达式。
等于号在数学证明中也起着重要作用,通过使用等于号,我们可以推导出各种数学结论。
不等于号(≠)表示两个数或两个表达式不相等。
它的作用是排除相等的情况,指出两者之间存在差异。
例如,若a ≠ b,则a和b代表不同的数或表达式。
不等于号在比较大小、判断关系和解决方程等问题中经常使用。
约等于号(≈)用来表示两个数或两个表达式在某种程度上接近或相似。
它并不表示绝对的相等,而是一种近似关系。
在实际测量和计算中,我们无法得到完全精确的结果,这时可以使用约等于号来表示结果的近似值。
箭头符号(→)常用于表示数列、函数和映射等对象之间的关系。
例如,若数列a1, a2, a3, ...按照某种规律演算,其中an表示第n个数,则可以使用箭头符号表示为a1 → a2 → a3 → ...。
箭头符号也可以用于表示极限、趋势和推导等数学概念。
逻辑与(∧)、或(∨)和非(¬)是数学逻辑中常见的复杂运算符号。
逻辑与符号表示同时满足两个或多个条件的关系,逻辑或符号表示满足其中一个或多个条件的关系,逻辑非符号表示否定某个条件。
这些运算符号在逻辑推理和证明中起着核心作用,也是计算机科学中的基础。
掌握复杂运算符号的认识和运用,可以帮助我们更加准确地表达数学思想和解决数学问题。
然而,只是简单地背诵符号的定义是远远不够的,更重要的是要理解它们背后的数学概念和思维方式。
只有通过深入学习和实践,才能真正掌握这些符号的用法。
总结起来,等于号、不等于号、约等于号、箭头符号和逻辑与或非符号是复杂运算中常见的符号。
数学函数的定义与运算

第二次课实验二数学函数的定义与运算,绘制函数图形【实验要求】:1. 掌握变量赋值;2. 掌握常用数学函数及函数值运算;3. 自定义函数(含分段函数);4. 掌握一般一元函数与参数方程函数作图;5. 了解二元函数作图。
2.1 实验指导知识(1)变量命名Mathematica中的变量名必须是以字母开头的并由字母或数字组成的字符串(长度不限),但是不能含有空格或标点符号,大写与小写字母用于表示不同的变量。
例如x,a1,b12,Tc都是合法的变量名,2a是不合法的变量名, a1与A1是不同的变量。
(2)变量赋值一个变量可以表示各种类型的数或字符串,也可以表示一个算式。
与C语言不同,不必事先声明变量的类型,Mathematica 会根据用户给变量所赋的值自动处理。
在Mathematica中,使用赋值表达式不仅可以将数值存入变量,还可以将含有变量的表达式存入另一变量,这样就能建立起来变量之间的函数关系。
使用等号给变量赋值,具体格式如下:【变量名=赋值(可含表达式)】x =Value 给x 赋值。
x = y =Value 同时给x ,y 赋相同的值。
{x ,y ,…}={Value1,Value2,…} 同时给x ,y ,…赋不同的值。
例1 当t=2.5时,计算221t e 的值In[1]:=t=2.5Out[1]=2.5In[2]:=(1/Sqrt[Pi])*Exp[t^2/2]Out[2]=12.8409例2 观察下面给x 、a 、b 、c 等变量的赋值方法和输出效果。
In[1]:=x=2Out[1]=2In[2]:=a1=s+tOut[2]=s+tIn[3]:=a=b=c=1Out[3]=1In[4]:={u ,v}={1,2}Out[4]={1,2}In[5]:=x=aOut[5]=1In[6]:=xOut[6]=1In[7]:=s=1Out[7]=1In[8]:=a1Out=1+t说明:上例分成两部分:In[1]--In[4]是4个赋值式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a c o t h ( x ) 求c o t h-1x= 0 . 5 l n ( (x+ 1 ) / (x-1 ) )。
s e c h ( x ) 求双曲正割x,即1 / ( c o s hx)。
s p h 2 c a r t ( a l p h a , t h e t a , r )
在M AT L A B中也有更高级的预定义数学函数。
命令集1 3 特殊的数学函数
l e g e n d r e ( n,x ) 返回一个n +1长度的向量,代表与n次l e g e n d r e函数相
[ t,n ] = r a t ( x,t o l ) 与上相同,但相对误差小于t o l。
r a t ( x ) 求x的连续的分数表达式。
r a t ( x,t o l ) 求带相对误差t o l的x的连续的分数表达式。
命令集11 有关复数的函数
r e a l ( z ) 求z的实部。
c s c h ( x ) 求双曲余割x,即1 / ( s i n hx)。
a s e c h ( x ) 求s e c h-1x= l n 。
a c s c h ( x ) 求c s c h-1x= l n ((1+ 1 + x
命令集1 0 取整命令和有关命令
r o u n d ( x ) 求最接近x的整数。如果x是一个向量,则适用于所有元素。
i m a g ( z ) 求z的虚部。
a b s ( z ) 求z的绝对值,即|z|。
c o n j ( z ) 求z的复数共扼,即z。
a n g l e ( z ) 求z的相角,即z=x+i y=rei 中的。
u n w r a p ( v ) 求与v相同长度的向量。这里,两个相邻元素间的相角差已经改变,
g a m m a l n ( x ) 求g函数的自然对数。用l o g ( g a m m a ( x ) )可以避免
上下溢出。
b e t a ( x,y ) 求?函数,即:
自变量x必须在[ 0,1 ]间隔内,如果由三个自变量
调用此函数,可以使用下面的命令b e t a i n c。
b e t a i n c ( x,a,b ) 求不完全b函数,类似地定义不完全g函数。
a c o t ( x ) 求反余切x=四象限反正切( 1 /x)。
s e c ( x ) 求正割x,即1 / ( c o sx)。
c s c ( x ) 求余割x,即1 / ( s i nx)。
a s e c ( x ) 求s e c-1x= a r c c o s ( 1 /x)。
a c s c ( x ) 求c s c-1x= a r c s i n ( 1 /x)。
命令集9 数学函数
a b s ( x ) 求x的绝对值,即|x|。
s i g n ( x ) 求x的符号,如果是正的得1;负的得- 1;零得0。
s q r t ( x ) 求x的平方根,即。
pow2(x, f) 求x×2 f。把f 加到x的浮点格式下的指数上计算是一种十分有效的运算。
e x p ( x ) 求x的指数函数,即ex。
一个错误信息。
Hale Waihona Puke 命令集1 2 坐标转换 [theta, r]= 将笛卡尔坐标转换为极坐标,极坐标t h e t a和r是由卡笛尔x
cart2pol(x, y) 和y得到。
第2章M AT L A B启动2 3
下载
■
[ x,y ]=p o l 2 c a r t 将极坐标转换为笛卡尔坐标,笛卡尔坐标x和y是从极坐标
e r f c x ( x ) 求成比例的互补误差函数。键入help e r f c x可
得到更多信息。
[ k,e ] = e l l i p k e ( m ) 求第1和第2类0 <m< 1的完全椭圆函数
[ j 1,j 2,j 3 ] = e l l i p j ( x,m )求J a c o b i椭圆函数。
(theta, r) theta和r得到。
[ a l p h a,t h e t a,r ]= 将卡笛尔坐标转换为球坐标,角a l p h a、t h e t a和长度r是从
cart2sph(x, y, z)笛卡尔坐标x、y和z得到。
[x, y, z]= 将球坐标转换为笛卡尔坐标x、y和z。
help dir 给出目录d i r的内容。
h t h e l p 对一个超链接数据库打开一个M ATLAB GUI 。这个命令用
h e l p d e s k替换,也可能在今后的版本中删除。
h t p p 是链接到h t h e l p中的帮助文件的一个预处理器。
l o a d h t m l 通过h t h e l p和h t t p用于加载、中断和显示H T M L文件。
c o t ( x ) 求余切x,即1 / ( t a nx),x为弧度。
a s i n ( x ) 求反正弦,即s i n-1x。
a c o s ( x ) 求反余弦,即c o s-1x。
a t a n ( x ) 求反正切,即t a n-1x。
a t a n 2 ( x , y ) 求四象限反正切(x/y),其结果在[- , ]区间内。
f i x ( x ) 求0方向最接近x的整数。即负x向上四舍五入,正x向下四舍五入。
f l o o r ( x ) 求小于或等于x的最接近的整数。
c e i l ( x ) 求大于或等于x的最接近的整数。
rem(x, y) 求整除x/y的余数。
gcd(x, y) 求整数x和y的最大公因子。
帮助命令和示范
帮助总是可以通过使用下列命令中的任何一条获得。
命令集1 8 帮助命令
h e l p 给出大约2 0个主题的列表,每个主题给出了基本信息。这些主
题以目录给出,有关每个主题的信息通过help dir给出,这里
的d i r是目录。
help command 对指定的命令给出帮助。
b e t a l n ( x,y ) 求b函数的自然对数。
e x p i n t ( x ) 求
2 4 M ATLAB 5 手册
下载
e r f ( x ) 求误差函数,即积分:
e r f i n v ( y ) 求逆误差函数。
e r f c ( x ) 求互补误差函数1-e r f ( x )。
是否是复型而调用不同的程序,但这些程序能被直
接调用。输入help bessel可以得到更多的信息。
bessely(n, x) 求与b e s s e l有相同自变量的第2类贝塞尔函数。
g a m m a ( x ) 求g函数,即对正x:
要获得负x的定义,键入help gamma。
g a m m a i n c ( x,a ) 求不完全g函数
■
h e l p d e s k 在M AT L A B帮助桌面上启动一个带索引页的We b浏览器。
doc command 在M AT L A B帮助桌面上得到命令c o m m a n d的帮助页。
web URL 将浏览器指向U R L,如果需要则打开一个浏览器。参见h e l p
w e b可以得到更多信息。
lookfor text 在所有的M文件的第1行中查找字符串t e x t。
d e m o 给出一个M AT L A B的不同命令、函数和应用领域的示范。命令
d e m o运行M ATLAB Expo,它显示选择不同示范实例的一个菜单。
也可以找到几个简单的游戏。
e x p o 运行M ATLAB Expo;也可参见d e m o。
[g, c, d]=gcd(,xy ) 求g,c,d,满足g=x c+y d。
l c m ( x,y ) 求正整数x和y的最小公倍数,也能用于决定最小公因子。
[ t,n ] = r a t ( x ) 由有理数t / n求x的近似值,这里的t和n是整数,相对误差小
于1 0-6。也可参见r a t s (第5 . 1 . 2节),它给出了对应的字符串。
i n f o 给出有关M AT L A B的信息。例如,什么种类的计算机能够运行
M AT L A B,如何得到更多的有关M AT L A B最近的进展和新版的
信息等等。
w h a t s n e w 给出新版本中新命令的有关信息。
s u b s c r i b e 使之变成一个M AT L A B的预约用户。
关的值和对x的0到n次计算的值。如果x=x是一个向
量,则这个命令返回一个矩阵,列是为x的每一个元
素计算的L e g e n d r e函数值。x的每个元素都必须在[-
1,1]范围内。
bessel(n, x) 求第1类贝塞尔函数, n和x可以是向量,但n必须是
步长为1的递增,范围为[ 0,1 0 0 0 ]。这个命令根据x
因此,差最大为
unwrap(v, k)求出如上的一个向量,但用转移偏差k代替
c p l x p a i r ( v ) 给出一个v中各元素按实部递增排序,并使其复数组合成复数共扼
对的一个向量。在一个共扼对中,负虚部在前,实元素排在向量
的后部。如果v的一个元素在v中没有它自己的复数共扼,则显示
w h y 解释为什么一些事情会出错。
