假设检验(全)
考研概率论与数理统计公式大全

考研概率论与数理统计公式大全一、概率论部分:1.概率公式:-事件的概率:P(A)=n(A)/n(S),其中n(A)表示事件A发生的可能性,n(S)表示样本空间S中的样本个数。
-互斥事件的概率:P(A∪B)=P(A)+P(B)。
-非互斥事件的概率:P(A∪B)=P(A)+P(B)-P(A∩B)。
2.条件概率公式:-事件A在事件B发生的条件下发生的概率:P(A,B)=P(A∩B)/P(B)。
3.乘法公式:-事件A、B同时发生的概率:P(A∩B)=P(A)*P(B,A)=P(B)*P(A,B)。
4.全概率公式:-事件A可以由一系列互斥且构成样本空间的事件B1、B2、..、Bn发生的概率:P(A)=P(A∩B1)+P(A∩B2)+...+P(A∩Bn)=ΣP(A∩Bi)。
5.贝叶斯公式:-已知事件A发生的条件下事件B发生的概率:P(B,A)=P(A∩B)/P(A)=P(A,B)*P(B)/P(A)。
6.重要的离散概率分布:-二项分布:P(X=k)=C(n,k)*p^k*(1-p)^(n-k),其中n为试验次数,k为成功次数,p为每次成功的概率。
-泊松分布:P(X=k)=(λ^k*e^(-λ))/k!,其中λ为单位时间(或单位面积)内随机事件发生的平均次数。
7.重要的连续概率分布:-均匀分布:f(x)=1/(b-a),其中a为最小值,b为最大值。
-正态分布:f(x)=(1/(σ*√(2π)))*e^(-(x-μ)^2/(2σ^2)),其中μ为均值,σ为标准差。
二、数理统计部分:1.基本概念:-总体:研究对象的全体。
-样本:从总体中抽取的一部分个体。
-参数:总体的特征数值。
-统计量:样本的特征数值。
2.基本统计量:- 样本均值:x̄ = (x1 + x2 + ... + xn) / n,其中x1、x2、..、xn为样本数据,n为样本容量。
- 样本方差:s^2 = ((x1-x̄)^2 + (x2-x̄)^2 + ... + (xn-x̄)^2) / (n-1)。
单样本的假设检验全英文版PPTOne Sample test of Hypothesis

What is a Hypothesis?
A Hypothesis is a statement about the value of a population parameter developed for the purpose of testing.
Examples of hypotheses made about a population parameter are:
Step 5: Take a sample, arrive at a decision
Do not reject null
Reject null and accept alternate
Байду номын сангаас
Definitions
Null Hypothesis H0: A statement about the value of a population parameter.
One-Sample Tests of Hypothesis
GOALS When you have completed this chapter, you will be able to:
FIVE Conduct a test of hypothesis about a population proportion. SIX Define Type I and Type II errors. SEVEN Compute the probability of a Type II error.
Hypothesis Testing
Step 1: State null and alternate hypotheses
Step 2: Select a level of significance
minitab教程-假设检验

b
12
2P检验P均大于0.05,无显 著性差异
b
13
7、双方差检验
一位保健顾问想比较患者对两家医院的 满意度评分。这位顾问收集了 20 名患者 对这两家医院的评分。这位顾问执行了 双方差检验,以确定患者对两家医院的 评分的标准差是否存在差异。
原假设声明标准差之间的比值为 1。由于两个 p 值
都大于显著性水平(用 α 或 alpha 表示)0.05,因
此顾问无法否定原假设。顾问的证据不足,无法
b
得14 出两家医院的标准差不同的结论。
8、等方差检验
一位保健顾问想比较患者对两家医院的 满意度评分。这位顾问收集了 20 名患者 对这两家医院的评分。这位顾问执行了 双方差检验,以确定患者对两家医院的 评分的标准差是否存在差异。
MINITAB教程假设检验源自全海军b1
1、单样本Z检验
某汽车租赁公司老板怀疑公司汽车的年公里数大于 全国12000公里的平均水平。他从公司中随机选取了 225辆汽车,并且测量的结果均值为12375公里,s为 2415公里。试检验该公司汽车年公里数的总体均值 是否高于全国的平均水平。
b
2
P值<0.05,否定假设,即表明数据有显著性证据表明 不等于假设均值。
b
3
2、单样本t检验
某种电子元件的平均寿命x(单位:小时)服从正态 分布,现测得16只元件的平均寿命为240.9±102.2小 时,问有否理由认为元件的平均寿命大于225小时 (α=0.05)。
b
4
P>0.05,无显著性差异
b
5
3、双样本t检验
为了解内毒素对肌酐的影响,将20只雄性中年大鼠 随机分为甲组和乙组。甲组中每只大鼠不给予内毒 素,乙组中的每只大鼠则给予3mg/kg的内毒素。分 别测得两组大鼠的肌酐结果的均值和标准差为:甲 组(5.360±1.669mg/L)、乙组(8.150±1.597 mg/L)。问:内毒素是否对肌酐有影响?
minitab教程-假设检验

检验
一位保健顾问想比较患者对两家医院的满 意度评分。这位顾问收集了 20 名患者对 这两家医院的评分。这位顾问执行了双方 差检验,以确定患者对两家医院的评分的 标准差是否存在差异。
原假设声明标准差之间的比值为 1。由于两个 p 值 都大于显著性水平(用 α 或 alpha 表示)0.05,因 此顾问无法否定原假设。顾问的证据不足,无法 得出两家医院的标准差不同的结论。
P<0.05,两组数据有显著性差异
双样本T检验要在假定两总体方差相等的条件下才能进行。
4、配对t检验
一位生理学家想要确定某个特定的赛跑项目是否对 静息心率有影响。对随机选择的20个人测量了心率。 然后让这些人参与该赛跑项目,并在一年后再次测 量心率。对每个人前后进行的两次测量构成一个观 测值对,得出如下汇总数据,20人训练后与训练前 静息心率的平均差为-2.200±3.254,问赛跑项目是否 对静息心率有影响。
P<0.05,有显著性差异
5、单比率检验(1P检验)
在全国调查中有75%的人经常使用安全带,现随机拦 截100辆汽车,共发现70人使用安全带,试比分析本 次调查是否与全国水平相同。
P>0.05,无显著性差异
6、双样本比率(2P检验)
为考察在常规治疗的同时辅以心理治疗的效果,某 医院将同种疾病的患者随机分成“常规治疗组”和 “常规与同时辅以心理治疗组”。经一个疗程治疗 后,以相同的标准衡量,常规组80名中,有效者48 名;联合组75名中,有效者55名。试判断就总体而 言,两种疗法的有效率是否确有差异?
2、单样本t检验
某种电子元件的平均寿命x(单位:小时)服从正态 分布,现测得16只元件的平均寿命为240.9±102.2小 时,问有否理由认为元件的平均寿命大于225小时 (α=0.05)。
《统计学》第5章 假设检验

假设不成立时,即拒绝原假设时备以选择的假设,通常用H1 表示。备择
假设和原假设互斥,如在例5.1中,原假设是“2022 年全国城市平均
PM2.5 浓度与2018 年相比没有显著差异”,那么备择假设就是“2022
年全国城市平均PM2.5 浓度与2018 年相比存在显著差异”。相应的统计
小越好。但是,在一定的样本容量下,减少犯第I类错误的概率,就会
使犯第II类错误的概率增大;减少犯第II类错误的概率,会使犯第I类
错误的概率增大。增加样本容量可以使犯第I类错误的概率和犯第II类
错误的概率同时减小,然而现实中资源总是有限的,样本量不可能没有
限制。因此,在给定的样本容量下,必须考虑两类可能的错误之间的权
易被否定,若检验结果否定了原假设,则说明否定的理由是充分的。
第四章 参数估计
《统计学》
16
5.1 假设检验的基本原理
(四) P值法
假设检验的另一种常用方法是利用P值(P-value) 来确定检验决策。P值
指在原假设0 为真时,得到等于样本观测结果或更极端结果的检验统计
量的概率,也被称为实测显著性水平。P值法的决策规则为:如果P值大
1.96) 中。这里−1.96和1.96 称为临界值,区间(−1.96, 1.96) 两侧的
区域则被称为拒绝域。基于样本信息,可以计算得到相应的z检验统计量
值,已知ҧ = 46,0 = 53, = 14 , n = 100 = −5
14/10
第四章 参数估计
《统计学》
14
5.1 假设检验的基本原理
犯第I 类(弃真) 错误的概率 也称为显著性水平(Significance level),
logistic回归模型的假设检验方法 -回复

logistic回归模型的假设检验方法-回复Logistic回归模型是一种经典的统计学习方法,用于解决二分类问题。
它基于一组假设,这些假设在进行模型的参数估计和推断时起到了重要作用。
本文将详细介绍Logistic回归模型的假设及其假设检验方法。
一、Logistic回归模型的假设Logistic回归模型的假设主要包括以下几个方面:1. 二分类假设:Logistic回归模型假设数据是二分类的,即样本数据只具有两个类别,用0和1表示。
2. 线性关系假设:Logistic回归模型假设自变量和因变量之间存在一个线性关系。
这个假设是建立在一个重要的推论上,即在自变量和因变量之间不存在非线性关系。
3. 独立性假设:Logistic回归模型假设不同样本之间是独立的。
这意味着各个样本之间的观测结果相互独立,不会相互影响。
4. 同方差性假设:Logistic回归模型假设不同样本之间的方差相等。
这意味着模型的预测误差的方差是恒定的,不会随着自变量的变化而变化。
二、Logistic回归模型的假设检验方法为了对Logistic回归模型的假设进行检验,我们需要进行一系列的统计推断。
下面将介绍三种常用的假设检验方法。
1. Wald检验Wald检验是一种常用的假设检验方法,它基于Logistic回归模型中的参数估计值和标准误差。
Wald检验的原假设和备择假设分别是H0: β=0和H1: β≠0。
具体步骤如下:(1)计算参数的估计值β_hat以及标准误差SE_beta;(2)计算检验统计量Wald statistic,即Wald = (β_hat - 0) / SE_beta;(3)根据Wald统计量的分布情况,计算p值;(4)根据p值和事先设定的显著性水平进行决策,如果p值小于显著性水平,则拒绝原假设。
2. 似然比检验似然比检验是一种用来比较两个模型拟合优度的统计检验方法。
在Logistic回归模型中,我们比较的是全模型和约简模型的拟合优度。
统计假设检验的思想(最全版)PTT文档

引言
前一章中我们讨论了如何根据样本去得到总体分布中所含参数的 最优(优良)估计。
用参数估计方法得到的总体参数的优良估计值,去代替总体分 布的未知参数而得到的“总体”,与真的总体作比较,就要考察它
们 之间是否在统计意义上相拟合,尽管这种比较也只能在样本的基础 上进行。那么,怎样在样本的基础上做出一个有较大把握的结论, 就是统计假设检验问题。事实上,实际中很多统计问题都可以作为 统计假设检验问题予以解决。
53、、统显计著假性设假检要设验检对中验的:判是断只作性考出错虑误假犯有第设两一即类类:可错误。的概率的最简单的统计假设检验。
那么,临界域
简单地说• ,统计假这设种检验仅问涉题,及就到是要总在体原假分设布的备未选假知设参数中作的出统拒绝计哪假一个设接受称哪为一个:的参判数断。假设。
这样就可以做出等价的判断:当
•
这种不同于参数假设的统计假设称为:非参数假设。
– 例如:设某种蔬菜的农药残留量X 的分布函数为 F(x),
– H 0 : F(x) {对数正态分布族} ; H1 : F(x) { 正态分布族} 都是 非参数假设。
• 从上面我们看到,一个统计假设是对总体分布状态的一种陈述。如果一个统计假设可完全 确定总体的分布,则称这种假设为:简单统计假设 或 简单假设。否则,称为:复合统计 假设 或 简称 复合假设。
是拒H绝1 的判断。 那么我们的检验“法则”是什么呢?
• 它应该是以定义在样本空间上的一个样本函数为依据所构成的一个“准则”。一
那第么二, 类为错什误么:能受做假旦出、样拒受绝伪本错观误测。的值决定确呢定?后,我们就可以根据这个“准则”作出:“拒H绝0 ”,还是 H 1
简单地说,统计假“设拒检验绝问题,的就”是判要在断原。假设 备选假设 中作出拒绝哪一个接受哪一个的判断。
假设检验 全

1
信号检测与估计
假设检验
问题如何提出:雷达需要从回波信号中判断有 无目标存在,通信需要判断接收到的究竟是几 个可能的发射信号中的哪一个○1 。
由于接收机热噪声、信道畸变或目标起伏,使 得我们观测到的信号具有不确定性○2 ,因此有必 要运用统计的方法来指导我们进行选择。
统计假设检验就是根据观测样本对几种可能
型,并按照某种最优准则设计接收机,最后对
接收机的性能进行评估。本章重点讨论最后两
点○4 。
3
信号检测与估计
假设检验
5.1 引言-introduction
4
信号检测与估计
假设检验
5.2 简单检测问题-A Simple Detection Problem
假定消息取值为 m0 (比如 0)或 m1 (比如 1), 由于事先并不知道传递的是什么消息,所以将 其视作取值为 m0 或 m1 的随机变量 m ,各自出现的 概率分别为 P0 和 P1 :
(7)
其中可将参数α 或它的函数定义为“信噪比”
(SNR)。
图 5.2 给出了以(7)式中信噪比 SNR 为参量
时, P(D1 | H0 ) 和 P(D1 | H1) = 1− P(D0 | H1) 的关系曲线。 图 5.2 也是接收机工作特性(Receiver operating
characteristic, ROC)的一种形式。
p0 ( y)P(H0 )
py (y)
所以判决规则成为,若
λ(y) =
p0 ( y) p1( y)
>
P(H0 )
P(H1)
(3)
则选择 H1,即 m = m1 。 p0 ( y) 和 p1( y) 都称为似然函数 (likelihood function),λ(y) 称为似然比(likelihood
假设检验大全

两个总体
2-Sample t . Paired t(成对非独立样本)
三个以上总体
One way ANOVA
一个总体
卡方(χ2)检验
两个总体 三个以上总体
2- Variance 等方差检验
一个总体
1-Proportion
两个总体
2-Proportion
三个以上总体 离散数据
P-Chart, ANOM 列联表. 拟合优度检验
连续数据
相关关系, 回归分析
一个总体
符号检验(1-Sample Sign), 符号秩检验(1-Sample wilcoxon)
两个总体 三个以上总体
MW检验(Mann-whitney Test), 符号秩检验(1-Sample wilcoxon) MM检验(Mood's Median), KW检验(Kruskal Wallis)
分类 均值检验
参数检验
方差检验
比例检验
系数检验或 关系检验
非参数检验或分布Байду номын сангаас验
常用假设检验大全参考
Hypothesis Test (Parametric Test & Non-Parametric Test) 假设检验大验大全(参数检验和非参数检)
前提
举例
一个总体
1-Sample Z(总体σ已知,n>30) 1-Sample t(总体σ未知,n<30)
关于假设检验如何选择备择假设和原假设

关于假设检验如何选择备择假设和原假设1. 单侧检验原假设的选择疑问 就以往的概括性理论而言,在单侧检验中一般将研究者想收集证据予以支持的假设作为备择假设H1。
这就是说一个研究者想证明自己的研究结论是正确的,备择假设的方向就要与想要证明其正确性的方向一致;同时将研究者想收集证据证明其不正确的假设作为原假设H0。
例1:一项研究表明,采用新技术生产后,将会使产品的使用寿命明显延长到1500小时以上。
检验这一结论是否成立。
按照前面的理论,研究者是想证明自己的研究结论(寿命延长)是正确的,于是备择假设的方向为“>”(寿命延长),即建立的原假设与备择假设应为: 例2,一项研究表明,改进生产工艺后,会使产品的废品率降低到2%以下。
检验这一结论是否成立。
根据研究者总是想证明自己的研究结论(废品率降低)是正确的,选择备择假设的方向为“<”(废品率降低)。
建立的原假设与备择假设应为 但在实际的操作中,这种以将自己想要证明的结论放在备择假设中的办法却会带来疑问。
例3:某灯泡制造商声称,该企业所生产的灯泡的平均使用寿命在1000小时以上。
如果准备进一批货,怎样进行检验。
根据上面的理论,一种认为是:检验权在销售商一方。
作为销售商,总是想收集证据证明生产商的说法(寿命在1000小时以上)是不是正确的。
于是选取备择假设的方向为“<”(寿命不足1000小时),建立的原假设与备择假设应为 但是这种看法会带来疑问,我为什么一定要证明生产商的说法是错误的呢?如果是一个关系稳定,长期合作的供货商,这种“找茬”的理念肯定会有破坏两家厂商合作的可能。
并且这种方式有一个严重的隐患,即使确实是小于1000的,但如果幅度较小,假设检验会认为这个小于1000是不显著的,接受原假设。
厂商还可能受损失。
但如果将检验方式颠倒: 即使μ确实是大于1000的,但如果幅度较小,假设检验会认为这个大于1000是不显著的,接受原假设。
厂商就可能“冤枉好人”。
临界值假设检验的基本步骤

临界值假设检验的基本步骤嘿,咱今儿个就来聊聊临界值假设检验的那些事儿哈!你说这临界值假设检验,就像是一个神秘的侦探游戏。
首先呢,你得提出个假设,这就好比你锁定了一个嫌疑人。
可别小看这一步哦,要是假设错了,那后面可就全跑偏啦!这就好像你本来要找个小偷,结果却认定是个好人,那还咋找真相呀!然后呢,就是根据这个假设去收集证据啦!这证据就像是一个个小线索,得仔细找,认真分析。
比如说,统计数据呀,各种实验结果呀,都得好好琢磨。
接下来,就是计算啦!这计算可不能马虎,得像个细心的账房先生一样,一笔一笔算清楚。
算啥呢?算那个关键的统计量。
再然后呀,就是要和那个临界值去比一比啦!这就像是一场比赛,看看咱算出来的这个统计量能不能超过或者低于那个临界值。
如果超过了或者低于了,嘿嘿,那就有戏啦!这时候就该下结论啦!如果统计量在临界值范围内,那就说明咱一开始的假设可能是对的;要是超出了范围,那咱就得推翻假设,重新再来。
这就好比侦探找到了确凿的证据,是抓还是放,就得果断决定。
你想想,要是没有这些步骤,那岂不是乱套啦?就像没头苍蝇一样瞎撞。
咱再打个比方,临界值假设检验就像是走迷宫。
你得先选个入口,这就是假设;然后沿着路走,收集线索,就是计算和分析;到了关键路口,看看能不能过去,就是和临界值比较;最后决定走哪条路,就是下结论。
总之啊,临界值假设检验可不是随随便便就能搞定的,每一步都得认真对待,不能有一丝马虎。
不然得出个错误的结论,那可就麻烦大啦!你说是不是这个理儿呀?所以呀,咱可得好好把这些步骤都记牢咯,这样在遇到问题的时候才能游刃有余呀!咱可不能在这上面栽跟头呀,对吧?。
统计学名词大全

统计学名词大全统计学名词大全统计学是一门研究数据收集、处理、分析和解释的学科。
它广泛应用于各个领域,包括经济学、社会科学、医学和自然科学等。
以下是一些常见的统计学名词,供参考:1. 总体(Population):指研究对象的全体。
在统计学中,总体是指研究对象的全部个体或观测值的集合。
2. 样本(Sample):指从总体中抽取的一部分个体或观测值的集合。
样本是总体的一种代表性子集,用来进行统计分析。
3. 参数(Parameter):指总体的特征量。
参数是用来描述总体的数值,如总体的均值、方差等。
4. 统计量(Statistic):指样本的特征量。
统计量是用来描述样本的数值,如样本的均值、方差等。
5. 随机变量(Random Variable):指在随机试验中可能取不同数值的变量。
随机变量可以是离散的,也可以是连续的。
6. 概率(Probability):指某一事件发生的可能性。
概率是一个介于0和1之间的数,表示事件发生的程度。
7. 频数(Frequency):指数据中某个数值出现的次数。
频数用来描述数据的分布情况。
8. 频率(Frequency):指频数与总体或样本大小之比,表示某个数值出现的频繁程度。
9. 经验分布函数(Empirical Distribution Function):指样本中小于或等于某一数值的观测值的比例。
经验分布函数用来描述样本数据的累计分布情况。
10. 中心极限定理(Central Limit Theorem):指在一定条件下,大样本的样本均值近似服从正态分布。
中心极限定理是统计学中重要的定理,用于推断总体参数。
11. 置信区间(Confidence Interval):指对总体参数的估计范围。
置信区间是一个区间,包含真实参数的概率较高。
12. 假设检验(Hypothesis Testing):指对总体参数的假设进行推断。
假设检验包括建立原假设和备择假设,以及通过样本数据来判断何种假设是合理的。
2023考研概率统计全考点精讲-第八讲 假设检验(仅数一)

第八讲 假设检验(仅数一)【考试要求】1.(仅数一)理解显著性检验的基本思想,掌握假设检验的基本步骤.了解假设检验可能产生的两类错误.2.(仅数一)掌握单个及两个正态总体的均值和方差的假设检验.考点:假设检验1.假设检验关于总体分布中未知参数取值所提出的假设称为原假设,记为0H ;对立于原假设的假设称为备择假设,记为1H .假设检验就是根据样本,按照某种检验法则,决定在0H 与1H 之中接受其一. 对总体分布中未知参数提出的假设进行检验的问题,叫做参数假设检验. 【注】理论依据:小概率事件原理. 2.两类错误在0H 为真的情况下,而作出拒绝0H 的选择,称此类错误为第一类错误(弃真错误).在0H 为假(本来就不成立)的情况下,而作出接受0H 的选择,称此类错误为第二类错误(取伪错误).把犯第一类错误和第二类错误的概率分别记为α和β,则00{|}P H H α=拒绝为真,00{|}P H H β=接受不真.3.显著性检验在给定样本容量的情况下,我们总是控制第一类错误的概率,使它不大于α,而不考虑犯第二类错误的概率,这种检验称为显著性检验. 数α称为显著性水平.由样本对原假设进行判断总是通过一个统计量完成的,称该统计量为检验统计量.当检验统计量在某个区域W 上取值时,我们拒绝原假设0H ,称区域W 为拒绝域,拒绝域的边界点称为临界点.4. 双边检验与单边检验设总体X 的分布中有某一未知参数θ.形如00:H θθ=,10:H θθ≠的假设检验称为双边检验;形如00:H θθ≤(或者0θθ=),10:H θθ>的假设检验称为右边检验; 形如00:H θθ≥(或者0θθ=),10:H θθ<的假设检验称为左边检验,右边检验和左边检验统称为单边检验.5. 假设检验的一般步骤(1)根据实际问题的要求,提出原假设0H 和备择假设1H . (2)给出显著性水平α以及样本容量n . (3)确定检验统计量K 及拒绝域的形式;(4)按犯第一类错误的概率等于α求出拒绝域W ;(5)根据样本值计算K 的观察值k ,当k W ∈时,拒绝原假设0H ;否则,接受0H .6. 正态总体均值、方差的假设检验(1)单个正态总体的假设检验法(2)两个正态总体的假设检验法【例1】 某厂生产某种产品,正常生产时,该产品的某项指标服从正态分布2(5038)N ,.,在生产过程中为检验机器生产是否正常,随机抽取50件产品,其平均指标为26.51=x (设生产过程中方差不改变),在显著性水平为05.0=α下,检验生产过程是否正常.【例2】(1998-1)(课后作业)设某次考试的学生成绩服从正态分布,从中随机地抽取36位考生的成绩,算得平均成绩为66.5分,标准差为15分. 问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70分?给出检验过程.附表:t 分布表 ()(){}p P t n t n p ≤=,。
假设检验中的原假设和备择假设
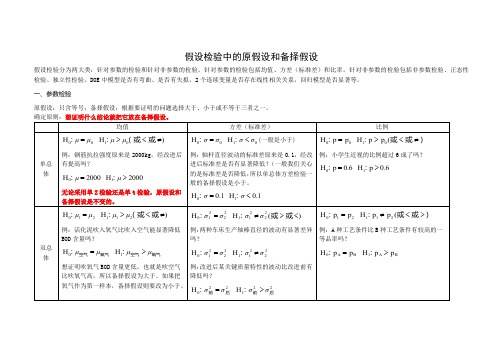
假设检验中的原假设和备择假设假设检验分为两大类:针对参数的检验和针对非参数的检验。
针对参数的检验包括均值、方差(标准差)和比率。
针对非参数的检验包括非参数检验、正态性检验、独立性检验、DOE中模型是否有弯曲、是否有失拟,2个连续变量是否存在线性相关关系,回归模型是否显著等。
一、参数检验原假设:只含等号;备择假设:根据要证明的问题选择大于、小于或不等于三者之一。
确定原则:想证明什么结论就把它放在备择假设。
二、非参数检验针对中位数的检验,包括单总体非参数检验的单样本符号、单样本Wilcoxon 符号秩检验;双总体非参数检验中的Mann-Whitney 检验和多总体非参数检验中的Kruskal-Wallis 、Mood 中位数检验,虽然针对的是中位数的检验,但仍然是解决均值问题(如面粉生产是否正常的例子,当数据服从正态分布时,可以针对均值采用单样本Z 检验或单样本t 检验,也可以针对中位数采取单样本Wilcoxon 符号秩检验,结论都是面粉生产不正常,也就是说面粉的均值与20有显著差别),所以只需要把参数检验中的均值μ换成中位数m 即可,原假设和备择假设的写法相同。
三、其他非参数检验其他非参数检验种类很多,但一般是把常见的形态作为原假设,少见的形态作为备择假设。
类似于民事诉讼中的原假设和备择假设。
如甲起诉乙欠自己30000元,由于任何人之间不欠钱是常见的形态,所以法庭在审理时,应该做出如下假设:元乙欠甲元乙不欠甲30000:30000:10H H如果没有证据证明乙欠甲30000元,也就不能拒绝原假设,判决的结果应该是乙无需向甲支付30000元;当有足够的证据证明乙欠甲30000元时,才能拒绝原假设,判定乙需要向甲支付欠款30000元。
这也是“无罪推定”立法原则的具体体现。
而南京彭宇案之所以引起极大争议,首先在于法官的逻辑错误或采取了“有罪推定”的原则,彭宇没有证据证明自己没有过失,就说明有过失,需要承担民事责任,也就是说当时法官的假设是:彭宇有过失彭宇无过失::10H H在双方都没有足够证据的情况下,当然是不能拒绝原假设,判定彭宇有过失,需要承担民事责任,所有当时的主审法官还是需要好好学习一下假设检验的。
(全英文版)六西格玛黑带6个sigma系列十六:假设检验(附有案例和数据源)Hypothesis Testing

5. Robust Design (Static)
6. Control Phase 7. Error-proofing
VSM
8. Summary
Project Presentations
Week Five: Review Projects through Improve Phase
2
W3-3 Hypothesis Testing_Inst.ppt
In this module, we continue learning how to perform proper statistical inference that will lead to valid conclusions.
4
W3-3 Hypothesis Testing_Inst.ppt
Hypothesis Testing
Instructor File Week Three – Module Three
Black Belt Training
Week One 5 Self-taught Modules
✓ 1. Six Sigma Overview ✓ 2. Recognizing Improvement Opportunities ✓ 3. Defining Opportunities in Sigma TRAC ✓ 4. Meet Minitab® ✓ 5. Data Collection and Analysis
– Hypothesis Testing is used to verify that a suspected X truly impacts the Y.
▪ After solutions are implemented: – Hypothesis Testing is used to verify that the Y did change.
假设检验的基本方法

假设检验的基本方法假设检验是统计学中常用的一种方法,用于判断样本数据对于某个假设的支持程度。
在进行假设检验时,我们通常会先提出一个原假设(null hypothesis),然后收集样本数据,利用统计方法来判断这些数据对原假设的支持程度。
如果样本数据与原假设相悖,我们就会拒绝原假设,否则我们就会接受原假设。
接下来,我将介绍假设检验的基本方法。
首先,我们需要明确原假设和备择假设。
原假设通常是我们想要进行检验的假设,而备择假设则是与原假设相对立的假设。
在进行假设检验时,我们通常会利用样本数据来判断原假设是否成立,从而间接地判断备择假设的成立情况。
其次,我们需要选择适当的假设检验方法。
常见的假设检验方法包括Z检验、T检验、卡方检验等。
在选择假设检验方法时,我们需要根据样本数据的类型和假设的具体情况来进行选择,以确保检验结果的准确性和可靠性。
接着,我们需要确定显著性水平。
显著性水平通常用α表示,它代表了我们在进行假设检验时所允许的错误率。
一般情况下,我们会将显著性水平设定为0.05,这意味着我们允许在5%的情况下犯错,接受备择假设而拒绝原假设,或者接受原假设而拒绝备择假设。
最后,我们进行假设检验的计算。
在进行计算时,我们需要利用样本数据的统计量(如均值、标准差等)来计算检验统计量,然后将其与相应的分布进行比较,从而得出检验的结论。
在进行计算时,我们需要注意选择适当的检验统计量和分布,以确保检验结果的准确性和可靠性。
总之,假设检验是统计学中一种重要的推断方法,它能够帮助我们判断样本数据对于某个假设的支持程度。
在进行假设检验时,我们需要明确原假设和备择假设,选择适当的假设检验方法,确定显著性水平,并进行相应的计算。
通过合理地进行假设检验,我们能够更加准确地判断假设的成立情况,为科学研究和决策提供可靠的依据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
21
信号检测与估计
假设检验
P(H 0 )(C10 − C00 ) p0 ( y) − P(H1 )(C01 − C11) p1( y) < 0
时选择 H1,或等价地,当 λ( y) = p1( y) / p0 ( y) > P(H 0 )(C10 − C00 ) / P(H1 )(C01 − C11) = λt (5) 时选择 H1。
18
信号检测与估计
假设检验
5.3 贝叶斯准则-Bayes’ Criterion
根据判决策略的各种后果的代价,可以建立评 判策略优劣的实用和普遍的标准。一旦指定了 代价,就可对所使用的特定判决方法的平均代 价进行计算,并选择使平均代价最小的方法。
设作出的判决是 Di ,即数据产生时认定 Hi 假设 为真,而事实上此时 H j 假设才是正确决策。如 果i = j ,则作出的决策是正确的,而当i ≠ j 时则 作出了错误的判决。
时选择 H1。因为
P(H1 | y ≤ Y ≤ y + dy)
=
P( y
≤ Y ≤ y + dy | H1)P(H1) P( y ≤ Y ≤ y + dy)
=
p1( y)dyP(H1)
py (y)dy
=
p1( y)P(H1)
py (y)
类似的,
8
信号检测与估计
假设检验
P(H 0
|
y ≤Y
≤
y + dy) =
m1
2 n
)
2
dy
∫=
(1/α ) ln(P0 −∞
/ P1 )−α
/ 2 (2π
) −1/ 2
exp
−u2 2
du
(6)
13
信号检测与估计
其中
假设检验
α = (m1 − m0 ) /σ n
如果 m1 < m0 ,(6)式保持不变,但α = (m0 − m1) /σ n 。 所以定义
α =| m1 − m0 | /σ n
型,并按照某种最优准则设计接收机,最后对
接收机的性能进行评估。本章重点讨论最后两
点○4 。
3
信号检测与估计
假设检验
5.1 引言-introduction
4
信号检测与估计
假设检验
5.2 简单检测问题-A Simple Detection Problem
假定消息取值为 m0 (比如 0)或 m1 (比如 1), 由于事先并不知道传递的是什么消息,所以将 其视作取值为 m0 或 m1 的随机变量 m ,各自出现的 概率分别为 P0 和 P1 :
是选择 H1为真,相应的错误概率为 P(H0 ) 。由(6)
16
信号检测与估计
假设检验
式可知,此时 P(D1 | H0 ) = 1, P(D0 | H1) = 0
反之,如果 P(H0 ) > P(H1) ,则总是选择 H0 为真,相 应 的 错 误 概 率 为 P(H1) 。 对 于 特 殊 情 况 P(H0 ) = P(H1) = 1/ 2 ,由式(6)与(8)可得
y
>
yt
=
[σ
2 n
/(m1
− m0 )]ln(P0
/ P1) + (m1
+
m0 ) / 2
(5)
则选择 H1,反之选择 H0 。也就是说,可将接收信 号的 y 值与某一门限比较。该例子中,数据 y 称为
检验统计量(test statistic),即接收机要计算的量。
10
信号检测与估计
假设检验
图 5.1 是针对 m0 = 0, m1 = 1,σ n = 1 的特例。
设噪声方差为
σ
2 n
,则所关心的两种情况
m0
和
m1
,
分别对应于接收数据 y 的两种不同概率密度。在
这两种情况中,
y
都是方差为
σ
2 n
的高斯变量,但
均值分别为 m0 或 m1 ,即
6
信号检测与估计
假设检验
p0
(
y)
=
(2πσ
2 n
) −1 /
2
exp[−(
y
−
m0
)2
/
2σ
2 n
]
或
p1 (
y)
=
(2πσ
(7)
其中可将参数α 或它的函数定义为“信噪比”
(SNR)。
图 5.2 给出了以(7)式中信噪比 SNR 为参量
时, P(D1 | H0 ) 和 P(D1 | H1) = 1− P(D0 | H1) 的关系曲线。 图 5.2 也是接收机工作特性(Receiver operating
characteristic, ROC)的一种形式。
Criterion
在二元通信系统中,两类错误的代价是相同 的。因此合理的代价是,
, , C00 = C11 = 0 C01 = C10 = c 并使平均代价式最小:
C = c [P(H0 )P(D1 | H0 ) + P(H1 )P(D0 | H1)] = cPe (1) 其中 Pe 为错误概率。由于 c 是常数,所以使平均代 价最小化等价于使 Pe 最小化。因此对于接收数据
假设检验
第五章 假设检验-Hypothesis Testing
本 章 研 究 的 问 题 : 统 计 假 设 检 验 ( statistical hypothesis testing )。给定观测样本和几种可能 的概率分布,最优地确定出当前数据服从那一 种分布。统计假设检验在数学上属于决策论 (decision theory)的范畴。在工程上,通常称 为检测理论(detection theory)。
ratio),不等式右边为门限(threshold)。上述判
决规则称为似然比检验(likelihood ratio test)。对
数似然比定义为:
9
信号检测与估计
假设检验
ln[λ(y)] =
ln
p0 ( y) p1( y)
与似然比成单调关系。
(4)
将(1)式中两种假定的高斯密度代入(4),
并假定 m1 > m0 ,则得到下面的法则。若
14
信号检测与估计
假设检验
图 5.2 (5.6) 式与(5.7) 式中的二元检测的接收机工作特性曲线, P0 = P1 , SNR 为 a .
15
信号检测与估计
假设检验
在通信系统中,通常对于如(6)式和(7)式那样单
独考虑两类错误概率不感兴趣,而是关注总的
平均错误概率。由于事件 m = m0 与 m = m1 是互斥
(2)
∫ P(D1 | H 0 ) = R1 p0 ( y)dy
20
信号检测与估计
假设检验
并且
∫ P(D1 | H1) = R1 p1( y)dy
(3)
P(D0 | H 0 ) = 1− P(D1 | H 0 ) , P(D0 | H1) = 1− P(D1 | H1) , 则得到如下形式的平均代价:
C = P(H 0 )C00 + P(H1 )C01
∫+ R1 [P(H 0 )(C10 − C00 ) p0 ( y) −P(H1 )(C01 − C11) p1( y)]dy (4)
最终目的是按照使平均代价(4)式最小的原则来
选择 R1 。因此,应使被积函数中为负的所有点都 归入 R1 中,因为这样可以使平均代价最小。即当
19
信号检测与估计
假设检验
令 Cij 为当 H j 为真时选择 Hi 的代价,错误决策的代
价大于正确决策的代价:
Ci≠ j, j − C jj > 0
对所有 i, j
(1)
本节先假定问题是二元的。决策的平均代价为
由于
C = P(H 0 )[C00 P(D0 | H 0 ) + C10 P(D1 | H 0 )] + P(H1 )[C01P(D0 | H1) + C11P(D1 | H1)]
使风险最小的贝叶斯准则又一次用到了似然
比检验。与前面的最大后验概率准则以及后面
的纽曼—皮尔逊准则相比,除了所用门限不同 外,其余形式是一样的。事实上,如果选择代
价使得 C10 − C00 = C01 − C11 ,那么最大后验概率准则 就是贝叶斯准则的一个特例。
22
信号检测与估计
假设检验
5.4 最小错误概率准则-Minimum Error Probability
P(H0 ) = P(m = m0 ) = P0 P(H1) = P(m = m1 ) = P1 这里, P(H0 ) 和 P(H1) 称为先验概率。
5
信号检测与估计
假设检验
传输信道将零均值高斯随机噪声 n 附加到消息 上,使得所呈现的数据成为随机变量 y = m + n 。 通过对接收数据 y 的处理,根据一定的规则判断 所发送的消息是 m0 还是 m1 ,同时在平均的意义上 评估此判决策略的优劣。
1
信号检测与估计
假设检验
问题如何提出:雷达需要从回波信号中判断有 无目标存在,通信需要判断接收到的究竟是几 个可能的发射信号中的哪一个○1 。
由于接收机热噪声、信道畸变或目标起伏,使 得我们观测到的信号具有不确定性○2 ,因此有必 要运用统计的方法来指导我们进行选择。
统计假设检验就是根据观测样本对几种可能
的,所以平均错误概率为
Pe = P(D1 | H 0 )P(H 0 ) + P(D0 | H1)P(H1)
(8)
图 5.3 中以 P(H0 )为参数画出了信噪比(7)式和平
