实验五 抽样分布于区间估计之用Excel进行假设检验
使用EXCEL进行区间估计及确定样本容量

区间估计
一、区间估计的Excel实现
1、总体方差已知,在某显著性水平下,均值区间估计。
某药材生产商需要对某仓库中的1000箱药材的平均重量进行估计。
已知药材重量的总体标准差为5千克,在随机抽取40箱样本称重后计算出每箱的平均值为52千克,求该仓库中每箱药材平均重量的区间估计(置信水平95%)
2.总体方差未知,大样本(n>=30)时的均值区间估计。
某药材生产商需要对其仓库中的1000箱药材的平均重量进行估计,药材重量的总体方差未知。
随机抽取50箱样本称重后
结果如下表所示。
求该仓库中每箱药材平均
重量在95%置信水平下的区间估计。
3.总体方差未知,小样本(n<30)下的均值区间估计。
T分布
tinv( )——求某自由度水平下,某显著性水平(注意录入的是a,而不是a/2!)下的t临界值。
某药材生产商需要对其仓库中的1000项药材的平均重量进行估计,药材重量的总体方差未知,随机抽取16箱样本称重后结果如下表所示,求该仓库中每箱药材平均重量在95%置信水平下的区间估计。
二、样本容量估计
已知样本方差、抽样误差,求样本容量。
教材55页,第5题
课堂练习:某市场调查公司接受客户委托,调查学生每月上网的时间,由于市场调查公司没做过此类调查,在正式调查前首先进行了一次预调查,抽取了20名学生进行访谈,结果如下表所示。
而客户要求偏差不超过0.5小时,试分别求在1%和5%的显著性水平下需要调查的学生的数量。
表1 20名学生每月上网时间(小时)
参考答案:a=0.01时,n=572人;a=0.05时, n=331人。
利用EXCEL进行区间估计概要

②选择单元格D1,在“插入”菜单中选择“函数” 选 项,打开“粘贴函数”对话框如图所示。
③在“函数分类”列表中选择“统计”,在“函数名” 列表中选 择计数函数COUNT。单击“确定”按钮,打开计数函 数 对话框如图所示。
④在value1中输入数据范围。单击A列列头,或输 入“A:A”,这相当于选择整个列,包括标题和
操作步骤如下: ①打开“参数估计.xls“工作薄,选择“均值”工 作表。 ②选择单元格A1:A11,即“灯泡平均耐用小时” 数据,拖动鼠标将其移到将G列。 ③在单元格 A1 中输入“行人数”,从单元格 A2 起输入例题的调查数据。 ④当数据输入完毕后,结果如下页图所示。
从图中可以看出,在95%的置信度下,行人数位于306人
值为20。
计算结果如图所示:
案例研究: 市场研究中使用区间估计
例 张先生是台湾某集团的企划部经理,在今年的规划中, 集团准备在某地新建一家新的零售商店。张先生目前正 在做这方面的准备工作。其中有一项便是进行市场调查。 在众多信息中,经过该地行人数量是要考虑的一个很重 要的方面。张先生委托他人进行了两个星期的观察,得 到每天经过该地人数如下: • 544,468,399,759,526,212,256,456,553,259, 469,366,197,178 • 将此数据作为样本,商店开张后经过该地的人数作为总 体。样本均值为 403人,在 95% 的置信度下,能否知道 每天经过此地的人数吗?
①打开“参数估计.xls”工作簿,选择“比例估计”工 作表如图所示 :
②在单元格B2中输入n值为350。 ③在单元格B3中键入公式“=112/350”,用Excel来计 算抽样比例Pi值为0.32。 ④在单元格B4中键入公式 “=SQRT(B3*(1-B3)/B2)” 计 算比例标准误差。其显示值为0.024934。
利用EXCEL进行区间估计ppt课件

值为20。
计算结果如图所示:
案例研究: 市场研究中使用区间估计
例 张先生是台湾某集团的企划部经理,在今年的规划中, 集团准备在某地新建一家新的零售商店。张先生目前正 在做这方面的准备工作。其中有一项便是进行市场调查。 在众多信息中,经过该地行人数量是要考虑的一个很重 要的方面。张先生委托他人进行了两个星期的观察,得 到每天经过该地人数如下: • 544,468,399,759,526,212,256,456,553,259, 469,366,197,178 • 将此数据作为样本,商店开张后经过该地的人数作为总 体。样本均值为 403人,在 95% 的置信度下,能否知道 每天经过此地的人数吗?
④在单元格B3中输入公式“=NORMSINV(B2)”, 计算与B2的置信度相应的左侧Z值。显示对 应于96%的置信度的Z值为1.750686。 ⑤在B5单元格中根据上面样本容量的计算公式, 输入公式“=(B3^2*B4^2)/B1^2” 计算样本容 量,显示值为19.15564。 ⑥在B6单元格输入“=CEILING(B5,2)”,显示
⑧在“Probability”中输入“1-D5”,所显示的值是0.05。 ;在“Deg_freedom"中输入自由度的表达式,即“D1- 1”,所显示值是9,单击“确定”按钮,单元格D6中显示 值为2.262159。
⑨在单元格 D7 中输入计算抽样极限误差 t 的公式,它 是t值和标准误差的乘积,公式为“=D6*D4”,显示 值为36.04255。 ⑩在单元格 D8 和 D9 中输入计算置信区间上限和下限 的公式,下限为样本均值减抽样极限误差,上限为 样本均值加抽样极限误差。其公式分别为“ =D2D7”和“=D2+D7”,显示值为1285.057和1357.143。 这样,总体均值的95%的置信区间为:
使用EXCEL进行区间估计及确定样本容量

使用EXCEL进行区间估计及确定样本容量区间估计和确定样本容量是统计学中非常重要的概念。
在进行统计分析时,我们通常有一个总体参数需要估计,但是通常我们无法获得整个总体的数据,而只能获得样本数据。
因此,我们需要使用区间估计来估计参数的范围,并且需要确定样本容量来保证估计的准确性和可靠性。
区间估计是通过样本数据来对总体参数进行估计,并给出一个范围区间来表达不确定性。
常用的区间估计方法有置信区间和预测区间。
在Excel中,我们可以使用函数来进行区间估计。
首先,我们需要计算样本的均值和标准差。
假设有一个包含样本数据的列A,我们可以使用AVERAGE函数来计算样本均值,使用STDEV函数来计算样本标准差。
例如,我们有一个含有100个观测值的样本,可以使用以下公式计算样本均值和样本标准差:样本均值:=AVERAGE(A1:A100)样本标准差:=STDEV(A1:A100)接下来,我们可以使用Excel的统计函数来计算置信区间的上限和下限。
假设我们要计算一个95%的置信区间,我们可以使用以下公式:置信区间下限:=CONFIDENCE.NORM(0.05,STDEV(A1:A100),COUNT(A1:A100))置信区间上限:=CONFIDENCE.NORM(0.05,STDEV(A1:A100),COUNT(A1:A100))其中,0.05为置信水平,STDEV(A1:A100)为样本标准差,COUNT(A1:A100)为样本容量。
另外,我们也可以使用Excel的数据分析工具来进行区间估计。
首先,我们需要安装数据分析工具包(如果未安装),然后找到"数据"选项卡,点击"数据分析",选择"t检验:配对两样本"或者"z检验:两样本或一个样本平均值"。
在打开的对话框中,填入相应的参数,例如选择样本数据的范围,设置置信水平等。
点击"确定"后,Excel会自动计算出区间估计的结果。
如何利用Excel进行数据的假设检验

如何利用Excel进行数据的假设检验在Excel中进行数据的假设检验是一种常用且有效的分析方法。
本文将为您介绍如何利用Excel进行数据的假设检验,以帮助您更好地理解和运用这一分析工具。
一、什么是假设检验假设检验是统计学中常用的一种方法,用于判断某个统计推断是否成立。
在研究中,我们常常需要对某个假设进行验证,而假设检验正是这样一种方法。
它基于样本数据,通过计算得到的统计量与理论值之间的差异,来评估假设的合理性。
二、使用Excel进行假设检验的步骤下面将以一个实际案例来介绍如何利用Excel进行数据的假设检验。
假设场景:某公司想要验证其新推出的产品广告对销售量是否有显著影响。
为了进行假设检验,他们随机抽取了100个销售记录,并记录了广告投入金额和对应的销售量。
现在需要对广告对销售量的影响进行假设检验。
步骤一:准备数据首先,在Excel中准备好需要进行分析的数据。
假设我们将广告投入金额放在A列,销售量放在B列。
在C列,计算广告投入金额与销售量的相关性。
在D列,计算广告投入金额的平均值。
在E列,计算销售量的平均值。
步骤二:计算相关统计量在Excel中,可以使用函数来计算相关统计量。
在C列输入函数"=CORREL(A2:A101,B2:B101)",即可计算出广告投入金额与销售量之间的相关系数。
步骤三:设置假设根据具体问题,设置原假设和备择假设。
在本例中,原假设为“广告投入金额对销售量没有显著影响”,备择假设为“广告投入金额对销售量有显著影响”。
步骤四:计算检验统计量在Excel中,可以使用函数来计算检验统计量。
在F列输入函数"=TTEST(A2:A101,B2:B101,2,1)",即可计算出两个样本之间的T值。
步骤五:判断是否拒绝原假设根据检验统计量的计算结果,利用Excel的函数可以得到拒绝原假设的概率。
在本例中,我们可以在H列输入函数"=T.DIST.2T(ABS(F2),99)",即可得到拒绝原假设的概率。
Excel在假设检验和方差分析中的应用实验指导

Excel 在假设检验和方差分析中的应用
一、Excel 在假设检验中的应用
例1:某机械厂生产某型号螺栓,正常生产螺栓口径如从与平均数x ,方差2σ=36mm 的正态分布。
现在从新批量的螺栓中抽取10只实测计算样本方差为42mm ,试以显著性水平α=0.05检验总体方差是否显著提高了。
分析:此题是对总体方差进行假设检验,已知总体服从正态分布,且总体方差和样本方差均已知,因此我们选择2χ统计量。
Excel 进行分析:
1、录入相关指标及数据。
2、计算检验统计量2χ。
在B5单元格输入公式“=B2*B4/B3”。
3、计算临界值()12-n αχ。
在B6单元格输入公式“=CHIINV(0.05,9)”。
4、计算P-值。
在B7单元格输入公式“=CHIDIST(10.5,9)”。
5、根据以上结果由检验统计量2χ<临界值()12-n αχ,或者P-值>显著性水平α,得出检验统计量的观测值落在接受域,因而接受原假设,认为总体方差没有显著提高。
二、Excel 在方差分析中的应用
具体操作见课本。
利用EXCEL进行区间估计讲解
②在单元格B1中输入极限误差2,在单元格B2中输 入置信度0.96(或96%)。
③在单元格B4中输入标准差5。单元格B3中需要输 入与B2中置信度相对应的Z值。使用NORNSINV 函数,可以把左侧概率转换成Z值。
④在单元格B3中输入公式“=NORMSINV(B2)”, 计算与B2的置信度相应的左侧Z值。显示对 应于96%的置信度的Z值为1.750686。
⑩在单元格D8和D9中输入计算置信区间上限和下限 的公式,下限为样本均值减抽样极限误差,上限为 样本均值加抽样极限误差。其公式分别为“=D2D7”和“=D2+D7”,显示值为1285.057和1357.143。
这样,总体均值的95%的置信区间为:
1285.057 1357.143
总体均值区间估计结果如图所示:
• 544,468,399,759,526,212,256,456,553,259, 469,366,197,178
• 将此数据作为样本,商店开张后经过该地的人数作为总 体。样本均值为403人,在95%的置信度下,能否知道 每天经过此地的人数吗?
操作步骤如下:
①打开“参数估计.xls“工作薄,选择“均值”工 作表。
①打开“参数估计.xls”工作簿,选择“比例估计”工 作表如图所示 :
②在单元格B2中输入n值为350。
③在单元格B3中键入公式“=112/350”,用Excel来计 算抽样比例Pi值为0.32。
④在单元格B4中键入公式 “=SQRT(B3*(1-B3)/B2)” 计 算比例标准误差。其显示值为0.024934。
在单元格D5中输入置信度95%,注意加上百分号。 在单元格D6中使用TINV函数计算在95%置信度和 自由度下的t值。
⑥选择单元格D6,在“插入”菜单中选择“函数” 选项,打开“粘贴函数”对话框。
用Excel进行参数的假设检验
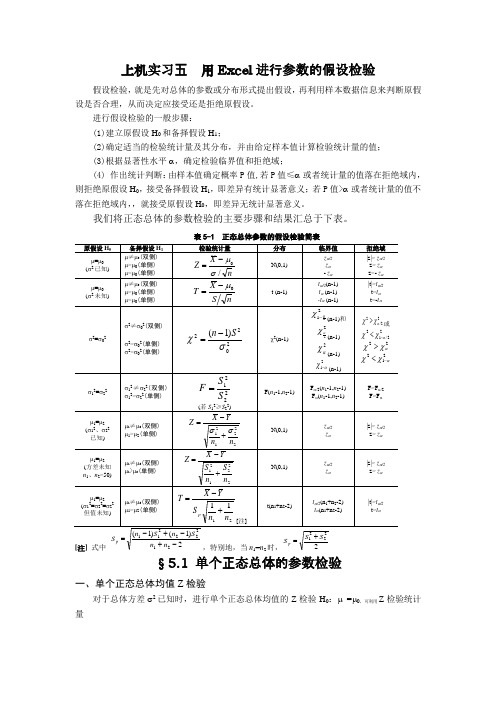
上机实习五用Excel进行参数的假设检验假设检验,就是先对总体的参数或分布形式提出假设,再利用样本数据信息来判断原假设是否合理,从而决定应接受还是拒绝原假设。
进行假设检验的一般步骤:(1)建立原假设H0和备择假设H1;(2)确定适当的检验统计量及其分布,并由给定样本值计算检验统计量的值;(3)根据显著性水平α,确定检验临界值和拒绝域;(4) 作出统计判断:由样本值确定概率P值,若P值≤α或者统计量的值落在拒绝域内,则拒绝原假设H0,接受备择假设H1,即差异有统计显著意义;若P值>α或者统计量的值不落在拒绝域内,,就接受原假设H0,即差异无统计显著意义。
我们将正态总体的参数检验的主要步骤和结果汇总于下表。
表5-1 正态总体参数的假设检验简表§5.1 单个正态总体的参数检验一、单个正态总体均值Z检验对于总体方差σ2已知时,进行单个正态总体均值的Z检验H0:μ=μ0,可利用Z检验统计量n X Z /0σμ-=来进行。
在Excel 中,可利用函数ZTEST 进行,其格式为ZTEST (array, a , sigma) 返回Z 检验的双侧概率P 值P{|Z|>z},n aX Z /σ-=其中 Array 为用来检验的数组或数据区域;a 为被检验的已知均值,即μ0;Sigma 为已知的总体标准差σ,如果省略,则使用样本标准差S 。
例如,要检验样本数据3, 6, 7, 8, 6, 5, 4, 2, 1, 9的总体均值是否等于4,如果已知其总体标准差为2,则只需计算ZTEST({3, 6, 7, 8, 6, 5, 4, 2, 1, 9}, 4,2),其概率值P=0.0409951<0.05,认为在显著性水平α=0.05下,总体均值与4有显著差异。
如果总体标准差未知,而用样本标准差S 替代时,计算ZTEST({3, 6, 7, 8, 6, 5, 4, 2, 1, 9}, 4),得到其概率值P =0.090574>0.05,认为在显著性水平α=0.05下,总体均值与4无显著差异。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验五抽样分布于区间估计之用EXCEL进行假设检验一、实验目的及要求
熟练使用Excel进行参数的假设检验
二、实验内容
本章介绍的假设检验包括一个正态总体的参数检验和两个正态总体的参数检验。
对于一个正态总体参数的检验,可利用函数工具和自己输入公式的方法计算统计量,并进行检验。
1)一个正态总体的参数检验
❶一个正态总体均值的假设检验:方差已知
【例1】假设某批矿砂10个样品中的镍含量,经测定为3.28,3.27,3.25,3.25,3.27,3.24,3.26,3.24,3.24,3.25(单位:%)。
设总体服从正态分布,且方差为,
问:在下能否认为这批矿砂的平均镍含量为3.25。
解根据题意,提出检验的原假设和备择假设是
:;:
这是一个双侧检验问题,具体步骤如下:
步骤一:输入数据。
打开Excel工作簿,将样本观测值输入到A1:A10单元格中。
步骤二:假设检验。
1. 在B2中输入“=AVERAGE(A1:A10)”,回车后得到样本平均值3.255;
2. 在B3中输入总体标准差0.01;
3. 在B4中输入样本容量10;
4. 在B5中输入显著性水平0.01;
5. 在B6中输入“”,即输入“”,回车后得标准正态分布的的双侧分位数;
“”,
6.在B7中输入检验统计量的计算公式:
回车后得统计量的值:。
步骤三:结果分析。
由于,未落入否定域内,所以接受原假设,即这批矿砂的平均镍含量为3.25 %。
❷一个正态总体均值的假设检验:方差未知
【例2】某一引擎生产商声称其生产的引擎的平均速度每小时高于公里。
现将生产的20台引擎装入汽车内进行速度测试,得到行驶速度(单位:公里/小时)如下:
250 236 245 261 256
258 242 262 249 251
254 250 247 245 256
256 258 254 262 263
试问:样本数据在显著性水平为0.025时是否支持引擎生产商的说法。
解根据题意,提出检验的原假设和备择假设是
:;:
这是一个右侧检验问题,具体步骤如下:
步骤一:输入数据。
打开Excel工作簿,将样本观测值输入到B3:F6单元格中,如下图所示:
步骤二:假设检验。
1. 计算样本平均速度,在单元格D8中输入公式:“”,回车后得到样本平均速度为25
2.75;
2. 计算样本标准差,在单元格D9中输入公式:“”,回车后得到样本标准差为7.31167;
3. 在单元格D10中输入样本容量20;
4. 在单元格D11中输入检验统计量的计算公式:“”,回车后得统计量的值:。
5. 在单元格D12中输入公式:“=TINV(2*0.025,D10-1)”,回车后得到自
由度为的分布的双侧分位数。
步骤三:结果分析。
原假设:的否定域为,由于,
没有落在否定域内,故接受原假设,样本数据并不支持该制造商的说法。
一个正态总体方差的假设检验:均值未知
【例3】假设原材料抗拉强度的方差不超过5时为合格品。
现取出25件原材料组成随机样本,测得样本方差为7,试问该批原材料是否合格。
假设原材料的抗拉强度近似服从正态分布。
解根据题意,提出检验的原假设和备择假设是
:;:
这是一个右侧检验问题,具体步骤如下:
1. 打开Excel工作簿。
2. 在B3中输入总体方差5。
3. 在B4中输入样本方差7。
4. 在B5中输入样本容量25。
5. 在B6中输入显著性水平0.05。
6.在B7中输入公式:“”,即输入“”,回车后得自由度为的分布的
的上侧分位数。
7.在单元格B8中输入检验统计量的计算公式:“”,回
车后得统计量的值:。
由于,所以不否定,认为该批原材料合格。
2)两个正态总体的假设检验
两个正态总体均值相等的假设检验:已知
【例4】装配一个部件可以采用不同的方法,我们关心的问题是哪一种方法的效率更高。
劳动效率可以用平均装配时间反映。
现从采用不同的方法装配的部件中各随机抽取12件产品,记录各自的装配时间(单位:分钟)如下:
甲方法:31 34 29 32 35 38 34 30 29 32 31 26 乙方法:26 24 28 29 30 29 32 26 31 29 32 28 假设两总体为正态总体,且方差相同。
问两种方法的装配时间有无显著不同。
解根据题意,提出检验的原假设和备择假设是
:;:
这是一个双侧检验问题,具体步骤如下:
步骤一:输入数据。
打开Excel工作簿,将样本观测值输入到A2:B13单元格中。
步骤二:假设检验。
1. 选择“工具”下拉菜单。
2. 选择“数据分析”选项。
3. 在分析工具中选择“t检验:平均值的成对二样本分析”。
4. 当出现对话框后,
⑴在“变量1的区域”方框内键入A2:A13;
⑵在“变量2的区域”方框内键入B2:B13;
⑶在“假设平均差”方框内键入0;
⑷在“”方框内键入0.05;
⑸在“输出选项”中选择“输出区域”,并在“输出区域”方框内键入C1;
⑹选择“确定”。
输出结果如下:
由于,拒绝,表明两种方法的装配时间有显著不同。
两个正态总体方差相等的假设检验:未知
【例5】检验例4中两个总体的方差是否相等。
解根据题意,提出检验的原假设和备择假设是
:;:
这是一个双侧检验问题,具体步骤如下:
步骤一:输入数据。
打开Excel工作簿,将样本观测值输入到A2:B13单元格中。
步骤二:假设检验。
1. 选择“工具”下拉菜单。
2. 选择“数据分析”选项。
3. 在分析工具中选择“F检验:双样本方差”。
4. 当出现对话框后,
⑴在“变量1的区域”方框内键入A2:A13;
⑵在“变量2的区域”方框内键入B2:B13;
⑶在“”方框内键入0.05;
⑷在“输出选项”中选择“输出区域”,并在“输出区域”方框内键入C1;
⑸选择“确定”。
输出结果如下:
由于,故不能否定原假设,表明两种方法装配时间的方差没有显著差异。
【思考题1】某城镇去年居民家庭平均每人每月生活费收入275元。
根据抽样调
367 322 294 273 237 398 327 298 276 246
311 355 240 275 296 324 382 229 264 288
235 271 291 319 360 226 262 286 309 352
337 222 260 284 304 343 217 259 283 303
200 253 281 301 329 212 257 281 303 332
高(α=0.05)?
【思考题2】为了评价两个学校的教学质量,分别在两个学校抽取样本。
在A学校抽取30名学生,在B学校抽取40名学生,对两个学校的学生同时进行一次英语标准化考试,成绩如下表所示。
假设学校A考试成绩的方差为64,学校B考试成绩的方差为100。
检验两个学校的教学质量是否有显著差异。
