实验3 假设检验
假设检验的基本原理与一般步骤

解 因为 X ~ N ( , 2 ), 0.15,
要检验假设 H0 : 10.5, H1 : 10.5,
n 15, x 10.48, 0.05, 则 x 0 10.48 10.5 0.516,
/ n 0.15 / 15
查表得 z0.05 1.645,
~
N (0,1),
由标准正态分布分位点的定义得 k z / 2 ,
当 x μ0 σ/ n
zα/2 时,拒绝H
0
, x μ0 σ/ n
zα/2 时, 接受H
0.
假设检验过程如下:
在实例中若取定 0.05, 则 k z / 2 z0.025 1.96, 又已知 n 9, 0.015, 由样本算得 x 0.511, 即有 x 0 2.2 1.96,
作出接受还是拒绝H0的判断。由于样本具有随机 性,因而假设检验所作出的结论有可能是错误的. 这种错误有两类:
(1) 当原假设H0为真, 观察值却落入拒绝域, 而 作出了拒绝H0的判断, 称做第Ⅰ类错误, 又叫
‘弃真’. 犯第一类错误的概率是显著性水. 平
(2) 当原假设H0不真, 而观察值却落入接受域, 而作出了接受H0的判断, 称做第Ⅱ类错误, 又叫 ‘取伪’. 当样本容量 n 一定时, 若减少犯第Ⅰ类错误的概 率, 则犯第Ⅱ类错误的概率往往增大.若要使犯 两类错误的概率都减小, 除非增加样本容量.
分析: 用μ和σ分别表示这一天袋装糖重 总体X 的均值和标准差,
由长期实践可知, 标准差较稳定, 设 0.015,
则 X ~ N ( , 0.0152 ), 其中 未知.
问题: 根据样本值判断 0.5 还是 0.5 . 提出两个对立假设H0 : 0 0.5 和 H1 : 0 .
实验三 用EXCEL进行参数估计和假设检验
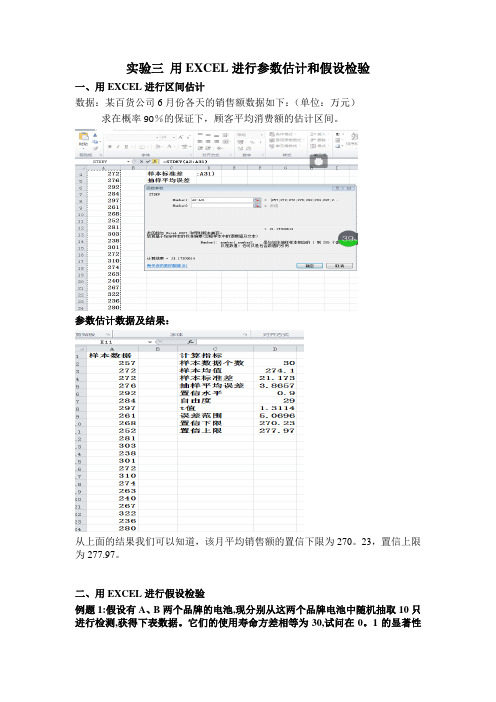
实验三用EXCEL进行参数估计和假设检验一、用EXCEL进行区间估计数据:某百货公司6月份各天的销售额数据如下:(单位:万元)求在概率90%的保证下,顾客平均消费额的估计区间。
参数估计数据及结果:从上面的结果我们可以知道,该月平均销售额的置信下限为270。
23,置信上限为277.97。
二、用EXCEL进行假设检验例题1:假设有A、B两个品牌的电池,现分别从这两个品牌电池中随机抽取10只进行检测,获得下表数据。
它们的使用寿命方差相等为30,试问在0。
1的显著性水平下,可否认为两个品牌的平均使用寿命存在显著差异?据上,提出原假设:A、B两个品牌的电池使用寿命不存在显著差异,备择假设:A、B两个品牌的电池使用寿命存在显著差异。
进行Z检验—双样本平均差检验:得如下所示结果:此次检验属于双尾检验,P=01101282872 > 显著性水平0.1,所以在0。
1的显著性水平下不能拒绝原假设,即可以认为两个品牌的平均使用寿命不存在显著性差异。
例题2:用某种药物治疗9例再生障碍性贫血患者,治疗前后患者血红蛋白变化的数据如下表所示。
问在0。
05的显著性水平下,能否认为这种药物至少可以使血红蛋白数量增加15个单位?提出原假设:这种药物不能使患者血红蛋白至少增加15个单位;备择假设:这种药物可以使患者的血红蛋白至少增加15个单位。
由于总体平均差已知,选用t-检验:平均值的成对二样本分析:得结果如下:由于显著性水平为0.05大于P值0.00037558,因此要拒绝原假设,即可以认为这种药物至少能使血红蛋白数量增加15个单位。
例题3:某研究所试验出一批新品种,想知道新品种产量是否比老品种产量有显著提高,随机抽取新老品种产量各9个,数据如下(单位:千克).试问,在0.05的显著性水平下,可否认为新品种比老品种的产量有显著提高?据条件,提出原假设:新品种比老品种产量没有显著提高;备择假设:新品种比老品种产量显著提高。
得出t检验:双样本异方差分析结果如下:在显著性水平为0.05的单侧检验下,P值为0。
实验三参数估计及假设检验

实验三参数估计与假设检验实验四(1)CONFIDENCE函数求置信区间公式:CONFIDENCE(显著水平Alpha,数据区域的总体标准偏差假设为已知Standard_dev,样本容量size )实验内容及步骤1.利用“描述统计”分析工具,可以计算正态分布下方差未知的样本均值极限误差,从而实现单个正态总体均值的区间估计。
2.直接调用函数CONFIDENCE,输入参数值计算置信区间。
3.在Excel中直接输入命令CONFIDENCE和相应参数计算置信区间。
实验四(2) 总体方差已知均值的假设检验实验目的及要求掌握利用Excel 的正态分布函数NORMSDIST、判断函数IF 等,构造一张能够实现在总体方差已知情况下进行总体均值假设检验的Excel工作表。
实验内容及步骤例1-6:利用Excel 的正态分布函数NORMSDIST、判断函数IF 等,构造一张能够实现在总体方差已知情况下进行总体均值假设检验的Excel 工作表。
操作步骤:STEP1:构造工作表。
如图1-16 所示,首先在各个单元格输入以下的内容,其中左边是变量名,右边是相应的计算公式。
STEP2:为表格右边的公式计算结果定义左边的变量名。
选定A3:B4,A6:B8,A10:A11,A13:A15 和A17:B19 单元格,选择“插入”菜单的“名称”子菜单的“指定”选项,用鼠标点击“最左列”选项,然后点击“确定”按扭即可。
图1-16STEP3:输入样本数据,以及总体标准差、总体均值假设、置信水平数据。
如图1-17所示。
STEP4:为样本数据命名。
选定C1:C11 单元格,选择“插入”菜单的“名称”子菜单的“指定”选项,用鼠标点击“首行”选项,然后点击“确定”按扭,得到如图1-17中所示的计算结果。
图1-17结果说明:如图1-17所示,该例子的检验结果不论是单侧还是双侧均为拒绝Ho 假设。
所以,根据样本的计算结果,在5%的显著水平之下,拒绝总体均值为35 的假设。
实验设计中的假设检验方法

实验设计中的假设检验方法实验设计是科学研究中不可或缺的一个部分。
在实验设计中,我们需要根据研究问题设计出合适的实验方案,并进行数据收集和分析。
其中,假设检验是一个非常重要的统计方法,用于对实验结果的可靠性进行验证和判断。
一、假设检验的基本概念假设检验是指根据样本数据对总体参数进行推断的一种统计方法。
在假设检验中,我们通常会根据研究问题和样本数据,提出一个关于总体参数的假设,然后根据一定的统计方法进行检验,以确定该假设是否成立。
举个例子,假设我们想研究某种药物对癌症治疗的效果。
我们可以将患者随机地分成两组,一组使用药物治疗,另一组使用安慰剂进行对比。
然后我们可以根据两组患者的数据,比如生存时间、癌症复发率等指标,来检验使用药物是否对治疗效果产生了显著的影响。
在假设检验中,我们需要根据研究问题和样本数据,提出两种假设:原假设(H0)和备择假设(H1)。
原假设是指我们最初的假设,通常是一个默认或常规假设,比如“两组数据没有显著差异”或“药物对治疗没有显著影响”。
备择假设是指我们希望证实的假设,通常是对原假设的否定或替代假设,比如“两组数据有显著差异”或“药物对治疗有显著影响”。
假设检验的过程主要包括以下几个步骤:1. 建立原假设和备择假设。
2. 确定显著性水平,一般设置为0.05或0.01等。
3. 根据样本数据计算统计量的值。
4. 计算统计量的p值,即原假设成立的概率。
5. 判断p值是否小于显著性水平,如果小于,则拒绝原假设,接受备择假设;如果大于,则接受原假设,拒绝备择假设。
二、假设检验的类型在假设检验中,主要有以下几种类型:1. 单样本假设检验。
这种假设检验适用于只有一个样本的情况,比如我们想比较某种产品的销售额是否达到预期水平。
在这种假设检验中,原假设通常是“产品销售额在预期水平以下”。
2. 独立样本假设检验。
这种假设检验适用于存在两个或多个独立样本的情况,比如我们想比较男性和女性在某项指标上的差异。
作业三 假设检验

作业三假设检验一、为了研究两种教学方法的效果。
选择了6对智商、年龄、阅读能问:能否认为新教学方法优于原教学方法?问:(1)男性的身高与女性的身高是否相等?(2)学生的体重是否等于45公斤?三、双样本T检验(Independent-Samples T Test过程)分别测得14例老年性慢性支气管炎病人及11例健康人的尿中17酮类固醇实验步骤:1.建立数据文件。
定义变量名:把实际观察值定义为x,再定义一个变量group来区分病人与健康人。
输入原始数据,在变量group中,病人输入1,健康人输入2。
2. 选择菜单“Analyz e→Compare Means→Independent-samples T Test”项,弹出“Independent- samples T Test”对话框。
从对话框左侧的变量列表中选x,进入“Test Variable(s)”框,选择变量“group”,进入“Grouping Variable”框,点击“Define Groups”钮弹出“Define Groups”定义框,在Group 1中输入1,在Group 2中输入2。
3.单击“OK”按钮,得到输出结果。
四.成对样本T检验(Paired-Samples T Test过程)某单位研究饲料中缺乏维生素E与肝中维生素A含量的关系,将大白鼠按性别、体重等配为8对,每对中两只大白鼠分别喂给正常饲料和维生素E缺乏饲料,一段时期后将之宰杀,测定其肝中维生素A含量(μmol/L)如下,问饲料中缺乏维生素E对鼠肝中维生素A含量有无影响?实验步骤:1.建立数据文件。
定义变量名:正常饲料组测定值为x1,维生素E缺乏饲料组测定值为x2,输入原始数据。
2.选择菜单“Analyz e→Compare Means→Paired-samples T Test”项,弹出“Paired - samples T Test”对话框。
从对话框左侧的变量列表中选择变量x1、x2进入Variables框。
概率论与数理统计实验实验3参数估计假设检验

概率论与数理统计实验实验3 参数估计假设检验实验目的实验内容直观了解统计描述的基本内容。
2、假设检验1、参数估计3、实例4、作业一、参数估计参数估计问题的一般提法X1, X2,…, Xn要依据该样本对参数作出估计,或估计的某个已知函数.现从该总体抽样,得样本设有一个统计总体,总体的分布函数向量). 为F(x, ),其中为未知参数( 可以是参数估计点估计区间估计点估计——估计未知参数的值区间估计——根据样本构造出适当的区间,使他以一定的概率包含未知参数或未知参数的已知函数的真?(一)、点估计的求法1、矩估计法基本思想是用样本矩估计总体矩.令设总体分布含有个m未知参数??1 ,…,??m解此方程组得其根为分别估计参数??i ,i=1,...,m,并称其为??i 的矩估计。
2、最大似然估计法(二)、区间估计的求法反复抽取容量为n的样本,都可得到一个区间,这个区间可能包含未知参数的真值,也可能不包含未知参数的真值,包含真值的区间占置信区间的意义1、数学期望的置信区间设样本来自正态母体X(1) 方差?? 2已知, ?? 的置信区间(2) 方差?? 2 未知, ?? 的置信区间2、方差的区间估计未知时, 方差?? 2 的置信区间为(三)参数估计的命令1、正态总体的参数估计设总体服从正态分布,则其点估计和区间估计可同时由以下命令获得:[muhat,sigmahat,muci,sigmaci] = normfit(X,alpha)此命令以alpha 为显著性水平,在数据X下,对参数进行估计。
(alpha缺省时设定为0.05),返回值muhat是X的均值的点估计值,sigmahat是标准差的点估计值, muci是均值的区间估计,sigmaci是标准差的区间估计.例1、给出两列参数?? =10, ??=2正态分布随机数,并以此为样本值,给出?? 和?? 的点估计和区间估计命令:r=normrnd(10,2,100,2);[mu,sigm,muci,sigmci]=normfit(r);[mu1,sigm1,muci1,si gmci1]=normfit(r,0.01);mu=9.8437 9.9803sigm=1.91381.9955muci=9.4639 9.584310.2234 10.3762sigmci=1.68031.75202.2232 2.3181mu1=9.8437 9.9803sigm1=1.91381.9955muci1=9.3410 9.456210.3463 10.5043sigmci1=1.6152 1.68412.3349 2.4346例2、产生正态分布随机数作为样本值,计算区间估计的覆盖率。
实验三用EXCEL进行参数估计和假设检验

实验三用EXCEL进行参数估计和假设检验摘要:本实验使用EXCEL软件进行参数估计和假设检验。
参数估计是指通过样本数据推断总体参数的值,常用的参数估计方法有点估计和区间估计。
假设检验是用来检验一些统计假设是否为真,常用的假设检验方法有单样本t检验、双样本t检验等。
实验通过实际数据的计算和分析,演示了如何使用EXCEL进行参数估计和假设检验。
关键词:参数估计、假设检验、EXCEL一、引言参数估计和假设检验是统计学中常用的数据分析方法。
参数估计是指通过样本数据推断总体参数的值,主要用于描述统计量的位置和离散程度,常用的参数估计方法有点估计和区间估计。
假设检验则是用来检验一些统计假设是否为真,常用的假设检验方法有单样本t检验、双样本t检验等。
EXCEL是常用的电子表格软件,其强大的数据分析功能可以方便地进行参数估计和假设检验。
本实验将使用EXCEL软件进行参数估计和假设检验,通过实际数据的计算和分析,演示如何使用EXCEL进行参数估计和假设检验。
二、方法本实验所用到的数据地区100例成人男性的身高数据,我们将使用该数据进行参数估计和假设检验。
1.参数估计(1)点估计根据样本数据,可以通过计算样本平均数、样本方差等统计量来估计总体参数的值。
在EXCEL中,可以使用以下函数来进行点估计的计算:-平均数函数:AVERAGE-方差函数:VAR.S(2)区间估计区间估计是对总体参数进行估计的一种方法,可以通过计算置信区间来估计总体参数的值。
在EXCEL中,可以使用以下函数来进行区间估计的计算:-置信区间函数:CONFIDENCE.T2.假设检验假设检验是用来检验一些统计假设是否为真的方法,可以通过计算检验统计量的值和p值来进行假设检验的判断。
在EXCEL中,可以使用以下函数来进行假设检验的计算:-单样本t检验:T.TEST-双样本t检验:T.TEST三、结果与分析根据实际数据的计算和分析,我们得到如下结果:1.参数估计(1)点估计通过样本数据的计算,我们得到了身高的平均数为175.8cm,方差为42.24cm。
假设检验

假设检验是数理统计学中根据一定假设条件由样本推断总体的一种方法。
具体作法是:根据问题的需要对所研究的总体作某种假设,记作H0;选取合适的统计量,这个统计量的选取要使得在假设H0成立时,其分布为已知;由实测的样本,计算出统计量的值,并根据预先给定的显著性水平进行检验,作出拒绝或接受假设H0的判断。
常用的假设检验方法有u—检验法、t—检验法、X2检验法、F—检验法,秩和检验等。
目录简介假设检验亦称“显著性检验(Test of statistical significance)”,是假设检验用来判断样本与样本,样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。
其基本原理是先对总体的特征作出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受作出推断。
生物现象的个体差异是客观存在,以致抽样误差不可避免,所以我们不能仅凭个别样本的值来下结论。
当遇到两个或几个样本均数(或率)、样本均数(率)与已知总体均数(率)有大有小时,应当考虑到造成这种差别的原因有两种可能:一是这两个或几个样本均数(或率)来自同一总体,其差别仅仅由于抽样误差即偶然性所造成;二是这两个或几个样本均数(或率)来自不同的总体,即其差别不仅由抽样误差造成,而主要是由实验因素不同所引起的。
假设检验的目的就在于排除抽样误差的影响,区分差别在统计上是否成立,并了解事件发生的概率。
在质量管理工作中经常遇到两者进行比较的情况,如采购原材料的验证,我们抽样所得到的数据在目标值两边波动,有时波动很大,这时你如何进行判定这些原料是否达到了我们规定的要求呢?再例如,你先后做了两批实验,得到两组数据,你想知道在这两试实验中合格率有无显著变化,那怎么做呢?这时你可以使用假设检验这种统计方法,来比较你的数据,它可以告诉你两者是否相等,同时也可以告诉你,在你做出这样的结论时,你所承担的风险。
假设检验的思想是,先假设两者相等,即:µ=µ0,然后用统计的方法来计算验证你的假设是否正确。
3总体均值的假设检验

• 第3步:在分析工具中选择“t检验:平均值的成对二样 本分析”
• 第4步:当出现对话框后
•
在“变量1的区域”方框内键入数据区域
•
在“变量2的区域”方框内键入数据区域
• 为0)
在“假设平均差”方框内键入假设的差值(这里
•
在“”框内键入给定的显著性水平
1 - 29
质量管理 学实验
匹配样本
(数据形式)
质量管理
实验三
学实验 总体均值的假设检验
1 一个(单)总体均值的检验 2 两个(双)总体均值之差的检验
1 -1
质量管σ2理已知时,样本均值的抽样分布 学实验
总体是否正态分布
否
是
样本容量n
大
小
正态分布
x
~N
(, 1 2 )
n
或Z x ~ N (0,1) / n
1 -2
正态分布 非正态分布
x
~N
•第1步:将原始数据输入到Excel工作表格中
•第2步:选择“工具”下拉菜单并选择“数据分析”选项
•第3步:在“数据分析”对话框中选择 “t-检验:双样本异方 差假设”
•第4步:当对话框出现后
•
在“变量1的区域”方框中输入第1个样本的数据区域
•
在“变量2的区域”方框中输入第2个样本的数据区域
•
在“假设平均差”方框中输入假定的总体均值之差
•
在“”方框中输入给定的显著性水平(本例为0.05)
•
在“输出选项”选择计算结果的输出位置,然后“确
定”
1 - 25
质量管理 学实验
两个总体均值之差的 检验
(匹配样本)
1 - 26
质量管理 两个总体均值之差的检验
假设检验的步骤和用途

假设检验的步骤和用途假设检验是统计学中一种常用的推断方法,用于判断样本数据是否支持某个假设。
它可以帮助我们做出关于总体参数的推断,从而对研究问题进行验证和决策。
本文将介绍假设检验的步骤和用途。
一、假设检验的步骤假设检验的步骤通常包括以下几个步骤:1. 确定原假设和备择假设:原假设(H0)是我们要进行检验的假设,通常是我们希望证伪的假设;备择假设(H1)是与原假设相对立的假设,通常是我们希望支持的假设。
2. 选择适当的检验统计量:根据研究问题和数据类型,选择适当的检验统计量。
常见的检验统计量有t检验、F检验、卡方检验等。
3. 确定显著性水平:显著性水平(α)是我们在进行假设检验时事先设定的一个阈值,用于判断样本数据是否支持原假设。
常见的显著性水平有0.05和0.01。
4. 计算检验统计量的观察值:根据样本数据计算出检验统计量的观察值。
5. 确定拒绝域:拒绝域是在给定显著性水平下,检验统计量观察值落在其中时,我们拒绝原假设的区域。
6. 做出决策:根据检验统计量的观察值是否落在拒绝域内,做出接受或拒绝原假设的决策。
二、假设检验的用途假设检验在实际应用中有着广泛的用途,主要包括以下几个方面: 1. 参数估计:假设检验可以帮助我们对总体参数进行估计。
通过对样本数据进行假设检验,我们可以得到对总体参数的点估计和置信区间估计。
2. 假设验证:假设检验可以帮助我们验证研究问题中的假设。
通过对样本数据进行假设检验,我们可以判断样本数据是否支持原假设,从而对研究问题进行验证。
3. 决策制定:假设检验可以帮助我们做出决策。
通过对样本数据进行假设检验,我们可以根据检验结果做出接受或拒绝原假设的决策,从而对实际问题进行决策制定。
4. 质量控制:假设检验可以帮助我们进行质量控制。
通过对生产过程中的样本数据进行假设检验,我们可以判断生产过程是否正常,从而进行质量控制和改进。
5. 科学研究:假设检验在科学研究中有着重要的应用。
统计分析实验3 假设检验 (2)

实验三假设检验
一、实验目的
通过本次实验,了解如何进行各种类型参数检验和非参数检验。
二、实验性质
必修,基础层次
三、主要仪器及试材
计算机及SPSS软件
四、实验内容
1.单一样本T检验
2.独立样本T检验
3.配对样本T检验
4.非参数卡方检验
五、实验学时
4学时
六、上机作业
(2)学生的体重是否等于45公斤?
2.双样本T 检验(Independent-Samples T Test 过程)
分别测得14例老年性慢性支气管炎病人及11例健康人的尿中17酮类固醇
某单位研究饲料中缺乏维生素E 与肝中维生素A 含量的关系,将大白鼠按性别、体重等配为8对,每对中两只大白鼠分别喂给正常饲料和维生素E 缺乏饲料,一段时期后将之宰杀,测定其肝中维生素A 含量(μmol/L )如下,问饲料
4.如下表
5.某工厂生产一批产品,质量检查规定:其次品率05.00≤p ,则这批产品可以出厂,否则不能出厂. 现从这批产品中抽查50件产品,发现有4件次品,试问这批产品能否出厂?(提示:用非参数的二项分布检验05.00≤p 是否可接受)。
假设检验的步骤和用途

假设检验的步骤和用途假设检验是统计学中一种重要的推断方法,用于判断样本数据与总体参数之间是否存在显著差异。
在进行假设检验时,需要经过一系列步骤来完成检验过程,同时也需要清楚地了解假设检验的具体用途。
本文将详细介绍假设检验的步骤和用途,帮助读者更好地理解和应用这一统计方法。
### 假设检验的步骤假设检验通常包括以下几个步骤:1. **建立假设**:在进行假设检验之前,首先需要明确研究的问题,并建立原假设(H0)和备择假设(H1)。
原假设通常是研究者想要进行推翻的假设,备择假设则是与原假设相对立的假设。
2. **选择显著性水平**:显著性水平(α)是在假设检验中设定的一个阈值,用于判断样本数据是否足够显著以拒绝原假设。
通常情况下,显著性水平取0.05或0.01。
3. **选择检验统计量**:根据研究问题的特点和数据类型,选择适当的检验统计量,如t检验、F检验、卡方检验等。
4. **计算检验统计量的取值**:根据样本数据计算出检验统计量的具体数值。
5. **确定拒绝域**:根据显著性水平和自由度确定拒绝域的临界值,如果计算得到的检验统计量落在拒绝域内,则拒绝原假设。
6. **做出决策**:比较计算得到的检验统计量与拒绝域的临界值,根据判断结果做出接受或拒绝原假设的决策。
7. **得出结论**:根据决策结果,得出对研究问题的结论,判断样本数据是否支持备择假设。
### 假设检验的用途假设检验在统计学中具有广泛的应用,主要用途包括:1. **判断总体参数**:通过假设检验可以判断样本数据与总体参数之间是否存在显著差异,从而对总体参数进行推断。
2. **比较实验组与对照组**:在实验设计和医学研究中,假设检验常用于比较实验组与对照组之间的差异,判断实验处理是否有效。
3. **验证研究假设**:研究者在进行科学研究时,通常会提出研究假设,通过假设检验来验证研究假设的成立与否。
4. **质量控制**:在生产过程中,假设检验可以用于质量控制,判断产品是否符合标准要求。
假设检验的基本概念及其应用

假设检验的基本概念及其应用假设检验是统计学中重要的推断方法之一,用于对统计推断的结果进行判断。
它通过对样本数据进行分析,进行统计推断,并对研究假设进行验证。
本文将介绍假设检验的基本概念,并探讨其在实际应用中的重要性。
一、基本概念1.1 假设检验的定义假设检验是通过对样本数据进行统计分析,对研究假设进行评估的一种方法。
它的基本思想是通过对比样本数据和假设的理论值之间的差异,判断这种差异是否达到了显著水平,从而对研究假设的真实性进行推断。
1.2 假设检验的步骤假设检验通常包括以下步骤:(1)提出假设:根据研究问题和目标,提出原假设(H0)和备择假设(H1);(2)选择检验统计量:根据假设的具体内容,选择适当的检验统计量;(3)确定显著水平:根据研究的具体要求,确定显著水平α;(4)计算检验统计量的值:根据样本数据和所选择的检验统计量,计算出检验统计量的值;(5)做出决策:根据检验统计量的值与临界值或拒绝域的比较结果,对原假设进行接受或拒绝的决策;(6)得出结论:根据所做出的决策,对研究问题进行结论的推断。
二、应用案例为了更好地理解假设检验的应用,我们以医学领域为例进行说明。
2.1 研究背景假设有一种新型药物声称可以显著降低患者的血压水平。
为了验证这一假设,我们进行了一项实验,将患者随机分为两组,一组接受新药治疗,另一组接受安慰剂治疗。
我们希望通过假设检验来判断新药物是否真的具有降低血压的效果。
2.2 假设的建立在这个案例中,我们可以建立以下假设:原假设(H0):新药物对血压水平没有显著影响;备择假设(H1):新药物对血压水平有显著影响。
2.3 检验统计量的选择针对这个案例,我们可以选择相关的检验统计量,如t检验、F检验等。
根据实验设计的不同,选择合适的检验统计量进行分析。
2.4 显著水平的确定在进行假设检验时,我们需要确定显著水平α的大小。
一般情况下,我们选择显著水平为0.05,即α=0.05。
2.5 计算检验统计量的值根据实验数据和所选择的检验统计量,计算出检验统计量的值。
假设检验的定义和步骤

假设检验的定义和步骤假设检验是一种统计推断方法,用于判断某种假设是否成立。
它可以帮助我们从样本数据中推断总体的特征,并且在决策和判断中起到重要的作用。
下面将介绍假设检验的定义和步骤。
一、定义假设检验是基于样本数据对总体参数进行推断的方法。
它基于一个原假设(H0)和一个备择假设(H1),通过对样本数据进行统计分析,得出关于总体参数的结论。
二、步骤假设检验的步骤一般包括以下几个阶段:1. 建立假设:在进行假设检验之前,需要明确原假设和备择假设。
原假设通常是我们要进行推断的对象是否符合某种特定的条件,备择假设则是原假设的补集。
2. 选择显著性水平:显著性水平是用来判断原假设是否成立的标准。
一般情况下,我们会选择一个显著性水平(通常用α表示),如0.05或0.01,来作为判断的标准。
3. 选择统计检验方法:根据数据类型和假设条件的不同,选择适当的统计检验方法。
常见的统计检验方法包括t检验、F检验、卡方检验等。
4. 计算统计量:根据选定的统计检验方法,计算得到相应的统计量。
统计量的计算方法根据具体的检验方法而定。
5. 确定拒绝域:根据显著性水平和统计量的分布,确定拒绝域。
拒绝域是在原假设成立的条件下,观察到的统计量取值落在其中的区域。
6. 判断结论:将计算得到的统计量与拒绝域进行比较,若统计量的取值落在拒绝域内,则拒绝原假设,接受备择假设;若统计量的取值落在拒绝域外,则接受原假设。
7. 给出推断:根据判断的结论,给出对总体的推断。
若拒绝原假设,则说明总体不符合假设条件;若接受原假设,则说明总体符合假设条件。
假设检验是一种重要的统计分析方法,可以帮助我们从样本数据中推断总体的特征。
通过明确假设、选择显著性水平、选择适当的统计检验方法、计算统计量、确定拒绝域、判断结论和给出推断,我们可以得出对总体的结论。
这种方法在科学研究、医学实验、市场调查等领域都有广泛的应用。
sas实验三参数检验与假设检验指导书

实验三参数检验与假设检验(2学时)一、实验目的(1)、掌握假设检验基本步骤;(2)、会用SAS软件进行假设检验;(3)、能够用SAS软件解决实际问题。
二、实验学时:2学时三、实验要求(1)掌握Ttest过程、Means过程和Univariate过程的应用;(2)对上述过程输出的结果会分析。
四、实验原理1、两组比较的方法:2、两组比较的语句:五、实验举例从10例腹泻病患者服用某种新药前和后1天的粪便中测得大肠杆菌(Baci)的数据如下,试分析服药前后该新药对Baci含量有无显著影响(此为自身配解:程序如下:data ttest4_8;input baci1 baci2 @@;diff=baci1-baci2;cards;33.0 23.3 35.8 21.7 28.8 19.4 31.4 26.8 42.6 32.025.8 23.1 31.6 25.3 29.0 23.7 22.4 21.8 30.2 17.6;run;proc univariate normal plot;var diff;run;主要输出结果如下:结果分析:(1) 差量的正态性检验.W=0.970391,P=0.8944,大于0.05,故差量是服从正态分布。
(2)用关于差量的总体均数为零的t检验的结果:t=5.47,P=0.0004,拒绝Ho:差量均数为零的假设。
(3) 结论为:服这种亲朋药前后对病人体内的Baci含量有显著影响,这种药对治疗腹泻有较好的效果。
(注意:如果差量不服从正态分布,则应该用符号秩(Sgn Rank)检验的结果,即参照Sign M Pr>=|M| 一行的结论。
)六、实验内容为了提高员工的工作质量,某公司对员工进行了一个月的集中培训。
下表是其(1)两次考核的成绩是否服从正态?(2)经过培训是否提高了员工的考核成绩?这两个问题中均取显著性水平 =0.1。
六、思考练习教材p116/3。
实验三 假设检验的SPSS实现

实验三假设检验的SPSS实现一、实验目的与要求1.掌握单样本t检验的基本原理和spss实现方法。
2.掌握两样本t检验的基本原理和spss实现方法。
3.熟悉配对样本t检验的基本原理和spss实现方法。
二、实验内容提要1.从一批木头里抽取5根,测得直径如下(单位:cm):12.3 12.8 12.4 12.1 12.7(1) 求总体直径95%的置信区间。
(2)是否能认为这批木头的平均直径是12.3cm ?2.比较两批电子器材的电阻,随机抽取的样本测量电阻如题表2所示,试比较两批电子器材的电阻是否相同?A批0.140 0.138 0.143 0.142 0.144 0.148 0.137 B批0.135 0.140 0.142 0.136 0.138 0.140 0.1413. 配对t检验的实质就是对差值进行单样本t检验,要求按此思路对上题进行重新分析,比较其结果和配对t检验的结果有什么异同。
三、实验步骤为完成实验提要1.可进行如下步骤1.在变量视图中新建一个数据,在数据视图中录入数据,在分析中选择比较均值,单样本t检验,将直径添加到检验变量,点击确定。
單一樣本統計資料N 平均數標準偏差標準錯誤平均值直径 5 12.4600 .28810 .12884單一樣本檢定檢定值= 12.3T df 顯著性(雙尾)平均差異95% 差異數的信賴區間下限上限直径 1.242 4 .282 .16000 -.1977 .5177为完成实验提要2.可进行如下步骤2.1 新建一个数据,在变量视图中输入电阻和批次,然后再数据视图中录入数据,分析——比较均值——独立样本T检验(分组选批次,输入1,2)确定群組統計資料批次 N平均數 標準偏差 標準錯誤平均值电阻1 7 .14171 .003773 .001426 27.13886.002610.000986会根据方差齐性检验结果选择T 检验中结果中有用的信息。
为完成内容提要3.需进行如下步骤:3.1. 方法一:在变量视图中添加差值,选择转换的计算变量,在目标变量智能光添加差值,数字表达式为A 组 – B 组,点击确定。
假设检验实验报告

假设检验实验报告摘要:本实验旨在通过假设检验研究新药对患者的治疗效果。
实验组和对照组的患者分别接受新药和安慰剂治疗,记录两组患者的疗效指标,并使用合适的假设检验方法对结果进行分析。
结果表明,新药组的治疗效果明显优于对照组,具有显著统计学意义。
关键词:假设检验,新药,安慰剂,治疗效果,统计学意义引言:假设检验是现代统计学中应用广泛的一种方法,被广泛用于医学、生物学等研究领域。
本实验旨在通过假设检验方法评估新药对患者的治疗效果,为研究提供可靠的统计学依据。
材料与方法:1.参与者招募:从一家医院的患者中随机筛选50名患者作为实验组,选取另外50名患者作为对照组。
2.分组治疗:实验组的患者接受新药治疗,每天服用一次;对照组的患者接受安慰剂治疗,服用方式与实验组相同。
3.记录指标:记录两组患者的疗效指标,包括治疗前后的症状评分和身体指标变化等。
4.数据处理:使用合适的统计学软件进行数据整理和分析,采用适当的假设检验方法对结果进行统计分析。
结果:1.样本特征:实验组和对照组的患者在年龄、性别等方面无显著差异。
2.症状评分:在治疗后的症状评分上,实验组的平均得分为4.5,对照组的平均得分为6.83.变化幅度:实验组患者的症状指标变化平均为-2.1,对照组患者的症状指标变化平均为-0.9讨论:本实验通过假设检验方法对新药治疗和安慰剂治疗的疗效进行了比较。
结果显示,新药组的治疗效果明显优于对照组,并具有显著统计学意义(p<0.05)。
在症状评分和指标变化上,新药组的结果均表现出更好的疗效。
这说明该新药在治疗相关疾病方面具有显著效果,值得进一步开展临床研究。
结论:本实验使用假设检验方法对新药治疗和安慰剂治疗的疗效进行了比较。
结果显示,新药在治疗相关疾病方面表现出显著优势,具有显著统计学意义。
这一结果为该新药的进一步应用提供了可靠的统计学依据,并对相关疾病的治疗提供了新的选择。
致谢:感谢本实验中参与的患者对本研究的支持,感谢实验组和对照组的医护人员的协助和配合,以及导师对本实验的指导和帮助。
假设检验的步骤和用途

假设检验的步骤和用途假设检验是统计学中一种重要的方法,广泛应用于不同领域的数据分析中。
它通过对样本数据的分析,来推断总体特征,从而为科学研究、政策制定和决策提供依据。
本文将详细介绍假设检验的步骤以及它的实际用途。
一、假设检验的基本概念在进行假设检验之前,我们需要明确几个基本概念:假设:在统计分析中,有两种主要的假设,即“零假设”(H0)和“备择假设”(H1或Ha)。
零假设通常表示没有效应或没有差异,而备择假设则表示存在效应或存在差异。
显著性水平(α):显著性水平是研究者预先设定的一个阈值,常用的值有0.05、0.01等。
它代表了拒绝零假设时可能犯错误的概率。
P值:P值是观察到的数据与零假设一致性的一种衡量指标。
当P 值小于显著性水平时,我们就拒绝零假设。
类型I错误与类型II错误:类型I错误是指在零假设为真时错误地拒绝零假设;而类型II错误则是在零假设为假时未能拒绝零假设。
了解了这些基本概念后,我们接下来将讨论假设检验的具体步骤。
二、假设检验的步骤1. 确定研究问题和提出假设在任何研究中,首要任务是明确研究目的,并针对研究问题提出相应的假设。
例如,在药物效果研究中,可以提出以下假设:零假设(H0):该药物对疾病没有显著效果。
备择假设(H1):该药物对疾病有显著效果。
2. 选择合适的统计检验方法根据数据类型与样本特点选择合适的统计检验方法。
常见的方法包括:t检验:用于负离子小组之间均值比较。
方差分析(ANOVA):用于比较三个及以上组均值。
卡方检验:用于分类变量间关系的检验。
3. 收集数据并计算统计量收集所需的数据,依据选定的统计方法计算出相应的统计量。
例如,如果选择t检验,则需计算样本均值、标准差及样本容量等。
4. 确定显著性水平和计算P值在进行统计检验之前,需确定显著性水平(α),然后利用统计软件或手动计算的方法得出对应的P值,判断结果是否显著。
5. 做出决策并解释结果根据计算得到的P值与事先定义的显著性水平进行比较:如果P值≤ α,则拒绝零假设,认为结果是显著的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告
课程名称试验设计与数据分析姓名邵建智
学号3110100122
专业生物系统工程
实验名称假设检验
浙江大学生物系统工程与食品科学学院
二O一三年八月制
实验三:假设检验
实验类型:上机操作
实验地点:农生环D-414
指导老师:傅霞萍
实验日期:2013 年10 月8 日
一、实验目的和要求
(1)熟练使用SPSS进行假设检验(工具/Analyze/Compare means)
二、实验内容和原理
2.1实验原理
假设检验是一种由样本的差异去推断样本所在总体是否存在差异的统计方法。
常用于解决两种工艺方法的比较、一种新添加剂与对照两处理的比较、两种食品内含物测定方法的比较、检验某产品是否达到某项质量标准、检验某项有害物指标是否超标等问题。
根据涉及的统计量不同,选择进行u检验、t检验、F检验等显著性检验。
2.2 实验内容(显著性水平α=5%)
(1)单样本t检验
问题1:某公司经理宣称他的雇员英语水平很高,如果按照英语六级考试,一般平均得分为75分,现从雇员中随机选出11人参加考试,得分如下:
80,81,72,60,78,65,56,79,77,87,76
问:该经理的宣称是否可信?
(2)两独立样本t检验
问题2:分别在10个食品厂各自测定了大米饴糖和玉米饴糖的还原糖含量,结果见下表,试比较两种饴糖的还原糖含量有无显著差异?
(3)成对样本(两配对样本)t检验
目的:利用来自两个总体的配对样本数据,推断两个总体的均值是否存在显著差异。
问题3:以下是对促销人员进行培训前后的促销数据,试问该培训是否产生了显著效果。
三、主要仪器设备/实验环境(使用的软件等)
IBM SPSS 19.0等
四、操作方法与实验步骤(必填,上机操作过程,可以插图)
a)提出原假设H0
b)选择检验统计量
c)计算检验统计量观测值和概率P值
d)给定显著性水平α并作出决策
(1)单样本t检验
选择“分析”-“比较均值”-“单样本T检验”
检验变量选择“成绩”,检验值设为75,单击“确定”
(2)两独立样本t检验
选择“分析”-“比较均值”-“独立样本T检验”
使用指定值,组1为:1,组2为:2,单击“继续”
检验变量选择“含糖量”,分组变量选择“品种”,单击“确定”
(3)成对样本(两配对样本)t检验
选择“分析”-“比较均值”-“配对样本T检验”
成对变量选择“培训前”和“培训后”为一对,单击“确定”
五、实验数据记录和处理(必填,图表数据、计算结果、对图表的处理)(1)单样本t检验
(3)成对样本(两配对样本)t检验
六、实验结果与分析(必填)
(1)单样本t检验
1)11个样本的均值,标准差,均值的标准误分别为73.73,9,51,2,880。
2)原假设H0:μ=75,自由度df=10,对均值进行t检验,在显著性水平α=5%时,双侧检验的概率值P=0.668>0.5,差异不显著,所以不能拒绝原假设,所以该经理的话正确。
1)大米饴糖和玉米饴糖的样本数均为10个,均值分别为37.840,35.930,标准差分别为0.6433,0.6865,均值的标准误分别为0.2034,0.2171。
2)先对方差进行F检验,在显著性水平α=5%时,双侧检验的概率值P=0.703>0.05,差异不显著,所以认为大米饴糖和玉米饴糖的两组样本的方差相等。
3)再大米饴糖和玉米饴糖的均值进行t检验,原假设H0:大米饴糖和玉米饴糖的含糖量无显著差异,由表知:P=0,所以拒绝原假设,即认为大米饴糖和玉米饴糖的含糖量有显著差异。
(3)成对样本(两配对样本)t检验
1)培训前与培训后的均值分别为485.83,560.00,标准差分别为81.180,61.938,均值的标准误分别为23.435,17,880
2)原假设H0:培训前后数据无明显差异,对培训前后的均值进行t检验,在显著性水平α=5%时,双侧检验的概率值P=0.04<0.05,差异显著,所以拒绝原假设,即认为培训产生了显著效果。
七、讨论、心得
1. 在进行单样本t检验时,若将原假设改为:H0:μ>=75,则接下来的t检验不再是双侧
检验,而变成单侧检验,得到的概率值也是不相同的;若能明显看出成绩的平均值不小于75时设原假设为:H0:μ=75,则得到的概率值又是不同的。
2. 在进行两独立样本t检验时,需要先对方差进行F检验,在对均值进行t检验,若得到
F检验的P值大于0.05,则认为方差相等,依表中第一行再进行t检验,若得到F检验的P值小于0.05,则认为方差不相等,应依表中第二行进行t检验。
3. 检验时,若取的置信区间不同,可能得到不同的结果,如在90%的置信度下,接受原
假设,可能在95%的置信度下,就会拒绝原假设。
4. 检验时,使用t值和P值效果是相同的,但在SPSS能直接给出P值的情况下使用P
值直接判断其与0。
05或0.01之间的关系更简便些。
