《人工神经网络建模》PPT课件
合集下载
《人工神经网络》课件

添加项标题
动量法:在梯度下降法的基础上,引入动量项,加速收敛速 度
添加项标题
RMSProp:在AdaGrad的基础上,引入指数加权移动平 均,提高了算法的稳定性和收敛速度
添加项标题
随机梯度下降法:在梯度下降法的基础上,每次只使用一个 样本进行更新,提高了训练速度
添加项标题
AdaGrad:自适应学习率算法,根据历史梯度的平方和来 调整学习率,解决了学习率衰减的问题
情感分析:分析文本中的情感 倾向,如正面评价、负面评价 等
推荐系统
推荐系统是一种基于用户历史行为 和偏好的个性化推荐服务
推荐算法:协同过滤、深度学习、 矩阵分解等
添加标题
添加标题
添加标题
添加标题
应用场景:电商、社交媒体、视频 网站等
应用效果:提高用户满意度、增加 用户粘性、提高转化率等
Part Six
类型:Sigmoid、 Tanh、ReLU等
特点:非线性、可 微分
应用:深度学习、 机器学习等领域
权重调整
权重调整的目的:优化神经网络的性能 权重调整的方法:梯度下降法、随机梯度下降法等 权重调整的步骤:计算损失函数、计算梯度、更新权重 权重调整的影响因素:学习率、批次大小、优化器等
Part Four
《人工神经网络》PPT 课件
,
汇报人:
目录
01 添 加 目 录 项 标 题 03 神 经 网 络 基 础 知 识 05 神 经 网 络 应 用 案 例 07 未 来 发 展 趋 势 与 挑 战
02 人 工 神 经 网 络 概 述 04 人 工 神 经 网 络 算 法 06 神 经 网 络 优 化 与 改 进
深度学习算法
卷积神经网络(CNN):用于图像处理和识别 循环神经网络(RNN):用于处理序列数据,如语音识别和自然语言处理 长短期记忆网络(LSTM):改进的RNN,用于处理长序列数据 生成对抗网络(GAN):用于生成新数据,如图像生成和文本生成
动量法:在梯度下降法的基础上,引入动量项,加速收敛速 度
添加项标题
RMSProp:在AdaGrad的基础上,引入指数加权移动平 均,提高了算法的稳定性和收敛速度
添加项标题
随机梯度下降法:在梯度下降法的基础上,每次只使用一个 样本进行更新,提高了训练速度
添加项标题
AdaGrad:自适应学习率算法,根据历史梯度的平方和来 调整学习率,解决了学习率衰减的问题
情感分析:分析文本中的情感 倾向,如正面评价、负面评价 等
推荐系统
推荐系统是一种基于用户历史行为 和偏好的个性化推荐服务
推荐算法:协同过滤、深度学习、 矩阵分解等
添加标题
添加标题
添加标题
添加标题
应用场景:电商、社交媒体、视频 网站等
应用效果:提高用户满意度、增加 用户粘性、提高转化率等
Part Six
类型:Sigmoid、 Tanh、ReLU等
特点:非线性、可 微分
应用:深度学习、 机器学习等领域
权重调整
权重调整的目的:优化神经网络的性能 权重调整的方法:梯度下降法、随机梯度下降法等 权重调整的步骤:计算损失函数、计算梯度、更新权重 权重调整的影响因素:学习率、批次大小、优化器等
Part Four
《人工神经网络》PPT 课件
,
汇报人:
目录
01 添 加 目 录 项 标 题 03 神 经 网 络 基 础 知 识 05 神 经 网 络 应 用 案 例 07 未 来 发 展 趋 势 与 挑 战
02 人 工 神 经 网 络 概 述 04 人 工 神 经 网 络 算 法 06 神 经 网 络 优 化 与 改 进
深度学习算法
卷积神经网络(CNN):用于图像处理和识别 循环神经网络(RNN):用于处理序列数据,如语音识别和自然语言处理 长短期记忆网络(LSTM):改进的RNN,用于处理长序列数据 生成对抗网络(GAN):用于生成新数据,如图像生成和文本生成
人工神经网络教学课件

2006年
Hinton等人提出了深度学习的概念,使得神经网络的层次和参数数量大大增加,提高了模型的表示能力和泛化能力。
1997年
Bengio等人提出了卷积神经网络(CNN),用于图像识别和处理。
感知机模型:由输入层、隐藏层和输出层组成,通过权重和激活函数实现非线性映射,完成分类或识别任务。
人工神经网络的基本结构
人工神经网络教学课件
目录
CONTENTS
人工神经网络简介人工神经网络的基本结构常见的人工神经网络模型人工神经网络的训练与优化人工神经网络的应用场景人工神经网络的未来展望
人工神经网络简介
人工神经网络是一种模拟生物神经网络结构和功能的计算模型,由多个神经元相互连接而成,通过训练和学习来处理和识别数据。
适用于小样本数据集和高维数据集
支持向量机在小样本数据集和高维数据集上表现良好,因为它主要基于数据的内积运算,而不是计算输入空间中的距离。这使得它在文本分类、生物信息学等领域得到广泛应用。
核函数的选择对模型性能影响较大
支持向量机通过核函数将输入空间映射到高维特征空间,然后在这个空间中找到最优决策边界。不同的核函数会导致不同的决策边界,因此选择合适的核函数对模型性能至关重要。
总结词
自然语言处理是人工神经网络的另一个应用领域,通过训练神经网络理解和生成自然语言文本,实现文本分类、情感分析、机器翻译等功能。
自然语言处理是利用人工神经网络对自然语言文本进行分析、理解和生成,广泛应用于搜索引擎、智能问答、新闻推荐等领域。通过训练神经网络理解和生成自然语言文本,可以实现文本分类、情感分析、机器翻译等功能,提高自然语言处理的准确性和效率。
人工神经网络具有自适应性、非线性、并行处理和鲁棒性等特点,能够处理复杂的模式识别和预测问题。
Hinton等人提出了深度学习的概念,使得神经网络的层次和参数数量大大增加,提高了模型的表示能力和泛化能力。
1997年
Bengio等人提出了卷积神经网络(CNN),用于图像识别和处理。
感知机模型:由输入层、隐藏层和输出层组成,通过权重和激活函数实现非线性映射,完成分类或识别任务。
人工神经网络的基本结构
人工神经网络教学课件
目录
CONTENTS
人工神经网络简介人工神经网络的基本结构常见的人工神经网络模型人工神经网络的训练与优化人工神经网络的应用场景人工神经网络的未来展望
人工神经网络简介
人工神经网络是一种模拟生物神经网络结构和功能的计算模型,由多个神经元相互连接而成,通过训练和学习来处理和识别数据。
适用于小样本数据集和高维数据集
支持向量机在小样本数据集和高维数据集上表现良好,因为它主要基于数据的内积运算,而不是计算输入空间中的距离。这使得它在文本分类、生物信息学等领域得到广泛应用。
核函数的选择对模型性能影响较大
支持向量机通过核函数将输入空间映射到高维特征空间,然后在这个空间中找到最优决策边界。不同的核函数会导致不同的决策边界,因此选择合适的核函数对模型性能至关重要。
总结词
自然语言处理是人工神经网络的另一个应用领域,通过训练神经网络理解和生成自然语言文本,实现文本分类、情感分析、机器翻译等功能。
自然语言处理是利用人工神经网络对自然语言文本进行分析、理解和生成,广泛应用于搜索引擎、智能问答、新闻推荐等领域。通过训练神经网络理解和生成自然语言文本,可以实现文本分类、情感分析、机器翻译等功能,提高自然语言处理的准确性和效率。
人工神经网络具有自适应性、非线性、并行处理和鲁棒性等特点,能够处理复杂的模式识别和预测问题。
《人工神经网络》课件

拟牛顿法
改进牛顿法的不足,使用正定矩阵近 似Hessian矩阵,提高优化效率。
共轭梯度法
结合梯度下降法和共轭方向的思想, 在每一步迭代中选择合适的共轭方向 进行搜索。
遗传算法
模拟生物进化过程的优化算法,通过 选择、交叉、变异等操作寻找最优解 。
正则化技术
L1正则化
对权重参数的绝对值进行惩罚总结词
自然语言处理是利用人工神经网络对自然语言文本进行分析和处理的技术。
详细描述
自然语言处理是实现人机文本交互的关键技术之一,通过训练神经网络对大量文本数据进 行学习,可以实现对文本的自动分类、情感分析、机器翻译等功能。
具体应用
在社交媒体领域,自然语言处理技术可以用于情感分析和舆情监控;在新闻媒体领域,可 以用于新闻分类和摘要生成;在机器翻译领域,可以用于实现多语言之间的自动翻译。
06
人工神经网络的未 来展望
新型神经网络模型的研究
持续探索新型神经网络模型
随着技术的不断发展,新型神经网络模型的研究将不断涌现,以解决传统模型无法处理 的复杂问题。这些新型模型可能包括更复杂的拓扑结构、更高效的参数优化方法等。
结合领域知识进行模型设计
未来的神经网络模型将更加注重与领域知识的结合,以提高模型的针对性和实用性。例 如,在医疗领域,结合医学影像和病理学知识的神经网络模型能够更准确地辅助医生进
THANKS
感谢您的观看
文字、人脸等目标的技术。
02 03
详细描述
图像识别是人工神经网络应用的重要领域之一,通过训练神经网络对大 量图像数据进行学习,可以实现对图像的自动分类、目标检测、人脸识 别等功能。
具体应用
在安防领域,图像识别技术可以用于人脸识别和视频监控;在医疗领域 ,可以用于医学影像分析;在电商领域,可以用于商品图片的自动分类 和检索。
人工神经网络ppt课件
LOGO
人工神经网络ppt课件
感知器
• 一种类型的ANN系统是以感知器为基础
• 感知器以一个实数值向量作为输入,计 算这些输入的线性组合,如果结果大于 某个阈值,就输出1,否则输出-1
o(x1,..xn .), 11w 0w 1o x1 t.h..ew nrxnw 0ise
其 值 率中,。每用特个来别w决地i是定 ,一输-w个入0是实xi阈对数值感常。知量器,输或出叫的做贡权献
• 算法的一种常用改进方法是随着梯度下降步数 的增加逐渐减小学习速率
2019.12.18
机器学习-人工神经网络 作者:Mitchell 译者:曾华军等 讲者:陶晓鹏
26
梯度下降的随机近似
• 梯度下降是一种重要的通用学习范型,它是搜 索庞大假设空间或无限假设空间一种策略
• 梯度下降应用于满足以下条件的任何情况
2019.12.18
机器学习-人工神经网络 作者:Mitchell 译者:曾华军等 讲者:陶晓鹏
33
可微阈值单元
• 使用什么类型的单元来构建多层网络?
• 多个线性单元的连接仍产生线性函数,而我们 希望构建表征非线性函数的网络
Байду номын сангаас
• 感知器单元可以构建非线性函数,但它的不连 续阈值使它不可微,不适合梯度下降算法
2019.12.18
机器学习-人工神经网络 作者:Mitchell 译者:曾华军等 讲者:陶晓鹏
25
梯度下降法则的推导(4)
• 梯度下降算法如下
– 选取一个初始的随机权向量 – 应用线性单元到所有的训练样例,根据公式4.7计算
每个权值的w 更新权值
• 因为误差曲面仅包含一个全局的最小值,所以 无论训练样例是否线性可分,算法都会收敛到 具有最小误差的权向量,条件是使用足够小的 学习速率
人工神经网络ppt课件
感知器
• 一种类型的ANN系统是以感知器为基础
• 感知器以一个实数值向量作为输入,计 算这些输入的线性组合,如果结果大于 某个阈值,就输出1,否则输出-1
o(x1,..xn .), 11w 0w 1o x1 t.h..ew nrxnw 0ise
其 值 率中,。每用特个来别w决地i是定 ,一输-w个入0是实xi阈对数值感常。知量器,输或出叫的做贡权献
• 算法的一种常用改进方法是随着梯度下降步数 的增加逐渐减小学习速率
2019.12.18
机器学习-人工神经网络 作者:Mitchell 译者:曾华军等 讲者:陶晓鹏
26
梯度下降的随机近似
• 梯度下降是一种重要的通用学习范型,它是搜 索庞大假设空间或无限假设空间一种策略
• 梯度下降应用于满足以下条件的任何情况
2019.12.18
机器学习-人工神经网络 作者:Mitchell 译者:曾华军等 讲者:陶晓鹏
33
可微阈值单元
• 使用什么类型的单元来构建多层网络?
• 多个线性单元的连接仍产生线性函数,而我们 希望构建表征非线性函数的网络
Байду номын сангаас
• 感知器单元可以构建非线性函数,但它的不连 续阈值使它不可微,不适合梯度下降算法
2019.12.18
机器学习-人工神经网络 作者:Mitchell 译者:曾华军等 讲者:陶晓鹏
25
梯度下降法则的推导(4)
• 梯度下降算法如下
– 选取一个初始的随机权向量 – 应用线性单元到所有的训练样例,根据公式4.7计算
每个权值的w 更新权值
• 因为误差曲面仅包含一个全局的最小值,所以 无论训练样例是否线性可分,算法都会收敛到 具有最小误差的权向量,条件是使用足够小的 学习速率
人工神经网络PPT演示课件

感知器的学习算法
采用感知器学习规则进行训练。训练步骤为:
① 对各初始权值w0j(0),w1j(0),w2j(0),…,wnj(0),j=1,2,…,m(m为计算层的节点数) 赋予较小的非零随机数;
② 输入样本对{Xp,dp},其中Xp=(-1, x1p , x2p ,…, xnp ),dp为期望的输出向量(教师信 号),上标p代表样本对的模式序号,设样本集中的样本总数为P,则p=1,2,…,P;
③
计算各节点的实际输出
o
p j
(t
)
sgn[X
T j
(t)
X
],
j 1,2,, m
;
④
调整各节点对应的权值,Wj
(t
1)
Wj
(t)
[dLeabharlann p jop j
]X
p
,
j 1,2,, m
,其中η
为学习率,用于控制调整速度,太大会影响训练的稳定性,太小则使训练的收敛
速度变慢,一般取0<η ≤1;
x1
oj Wj
x2 ······ xi ······xn
由方程 w1 j x1 w2 j x2 Tj 0 确定的直线成为二维输入样本空间上的一条分界线。
② 设输入向量X=(x1,x2,x3)T,则三个输入分量在几何上构成一个三维空间。节点j的
输出为
1, o j 1,
w1 j x1 w2 j x2 w3 j x3 Tj 0 w1 j x1 w2 j x2 w3 j x3 Tj 0
智能信息处理技术
华北电力大学
1
第5章 人工神经网络
1 人工神经网络基础知识 2 前馈神经网络 3 自组织神经网络 4 反馈神经网络
《人工神经网络讲》课件

应用场景
常用于模式分类、预测等静态数据处理任务。
循环神经网络
定义
循环神经网络是一种能够处理序列数据的神经网络,通过记忆单 元实现信息的循环传递。
特点
循环神经网络能够捕捉序列数据中的长期依赖关系,但训练过程 中容易陷入梯度消失或梯度爆炸问题。
应用场景
广泛应用于自然语言处理、语音识别、机器翻译等领域。
03
智能控制
强化学习与神经网络的结合在智能控制领域具有广泛的应用前景,例如
机器人控制、自动驾驶等。通过训练神经网络代理在模拟环境中进行学
习,可以实现高效、安全的智能控制。
深度学习与人工神经网络的结合
深度生成模型
生成模型如变分自编码器(VAE)和生成对抗网络(GAN)可以学习从噪声生成数据的分布,并生成全新的数据样本 。通过结合深度学习和神经网络,可以创建更强大、更灵活的生成模型,用于图像生成、文本生成等领域。
深度神经网络
1 2 3
定义
深度神经网络是指神经网络中包含多个隐藏层的 结构,能够提取更抽象的特征表示。
特点
深度神经网络具有强大的特征学习和分类能力, 但需要大量的训练数据和计算资源,且容易过拟 合。
应用场景
广泛应用于图像识别、语音识别、自然语言处理 等领域。
自组织映射网络
定义
自组织映射网络是一种无监督学 习的神经网络,通过自组织的方 式对输入数据进行降维或聚类。
人工神经网络讲
BIG DATA EMPOWERS TO CREATE A NEW
ERA
• 人工神经网络简介 • 常见的人工神经网络模型 • 人工神经网络的训练方法 • 人工神经网络的应用场景 • 人工神经网络的未来展望
目录
CONTENTS
常用于模式分类、预测等静态数据处理任务。
循环神经网络
定义
循环神经网络是一种能够处理序列数据的神经网络,通过记忆单 元实现信息的循环传递。
特点
循环神经网络能够捕捉序列数据中的长期依赖关系,但训练过程 中容易陷入梯度消失或梯度爆炸问题。
应用场景
广泛应用于自然语言处理、语音识别、机器翻译等领域。
03
智能控制
强化学习与神经网络的结合在智能控制领域具有广泛的应用前景,例如
机器人控制、自动驾驶等。通过训练神经网络代理在模拟环境中进行学
习,可以实现高效、安全的智能控制。
深度学习与人工神经网络的结合
深度生成模型
生成模型如变分自编码器(VAE)和生成对抗网络(GAN)可以学习从噪声生成数据的分布,并生成全新的数据样本 。通过结合深度学习和神经网络,可以创建更强大、更灵活的生成模型,用于图像生成、文本生成等领域。
深度神经网络
1 2 3
定义
深度神经网络是指神经网络中包含多个隐藏层的 结构,能够提取更抽象的特征表示。
特点
深度神经网络具有强大的特征学习和分类能力, 但需要大量的训练数据和计算资源,且容易过拟 合。
应用场景
广泛应用于图像识别、语音识别、自然语言处理 等领域。
自组织映射网络
定义
自组织映射网络是一种无监督学 习的神经网络,通过自组织的方 式对输入数据进行降维或聚类。
人工神经网络讲
BIG DATA EMPOWERS TO CREATE A NEW
ERA
• 人工神经网络简介 • 常见的人工神经网络模型 • 人工神经网络的训练方法 • 人工神经网络的应用场景 • 人工神经网络的未来展望
目录
CONTENTS
机器学习与应用第02讲人工神经网络ppt课件
1
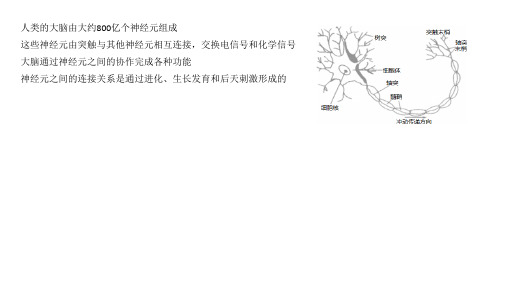
w(2) 21
y1
w222
y2
w223
y3
w224
y4
b22
神经网络每一层完成的变换
ul Wlxl1 bl
xl f ul
权重矩阵的每一行为本层神经元与上一层所有神经 元的连接权重
激活函数分别作用于每个神经元的输出值,即向量 的每个分量,且使用了相同的函数
内积 加偏置
激活函数
w11l
以下面的3层网络为例:
输入层
隐含层
输出层
激活函数选用sigmoid:
f
x
1
1 exp
x
隐含层完成的变换:
y1 1 exp
1
w(1) 11
x1
w112 x2
w113 x3
b11
1
y2 1 exp
w(1) 21
x1
w212 x2
w213 x3
b21
y3 1 exp
1
w(1) 31
分类问题-手写数字图像识别
28 28
输入层有784个神经元
隐含层的神经元数量根据需要设定
0 1 2 3 4 5 6 7 8 9
输出层有10个神经元
回归问题-预测人脸关键点 神经网络直接为输入图像预测出关键点的坐标(x, y)
反向传播算法简介 解决神经网络参数求导问题 源自微积分中多元函数求导的链式法则 与梯度下降法配合,完成网络的训练
y1
w122
y2
w132
y3
w142
y4
b12
z2 1 exp
1
w(2) 21
y1
w222
y2
w223
y3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学模型
• 分类结果:(1.24,1.80),(1.28,1.84)属于Af类;(1.40, 2.04)属于 Apf类.
图2 分类直线图
数学模型
•缺陷:根据什么原则确定分类直线?
• 若取A=(1.46,2.10), B=(1.1,1.6)不变,则分类直线 变为 y=1.39x+0.071
分类结果变为: (1.24,1.80), (1.40,2.04) 属于Apf类; (1.28,1.84)属于Af类
• 1.82 1.54 Af
数
• 2.08 1.56 Af
学
模
型
• 问:如果抓到三只新的蚊子,它们的触角长和 翼长分别为(l.24,1.80); (l.28,1.84);(1.40, 2.04).问它们应分别属于哪一个种类?
解法一:
• 把翼长作纵坐标,触角长作横坐标;那么每个 蚊子的翼长和触角决定了坐标平面的一个点.其 中 6个蚊子属于 APf类;用黑点“·”表示;9个 蚊子属 Af类;用小圆圈“。”表示.
神经网络研究的两个方面 • 从生理上、解剖学上进行研究 • 从工程技术上、算法上进行研究
数学模型
三、人工神经网络 (Artificial Neuron Nets, 简称ANN)
• 神经元的数学模型
图4神经元的数学模型
数学模型
• 其中x=(x1,…xm)T 输入向量,y为输出,wi 是权系数;输入与输出具有如下关系:
(2)并行结构.对神经网络中的每一个神经元来说;其 运算都是同样的.这样的结构最便于计算机并行处理.
(3)具有学习和记忆能力.一个神经网络可以通过训练 学习判别事物;学习某一种规律或规则.神经网络可以 用于联想记忆.
(4)对数据的可容性大.在神经网络中可以同时使用量化 数据和质量数据(如好、中、差、及格、不及格等).
• 大脑可视作为1000多亿神经元组成的神经网络
• 图3 神经元的解剖图
数学模型
• 神经元的信息传递和处理是一种电化学活 动.树突由于电化学作用接受外界的刺激;通 过胞体内的活动体现为轴突电位,当轴突电位 达到一定的值则形成神经脉冲或动作电位;再 通过轴突末梢传递给其它的神经元.从控制论 的观点来看;这一过程可以看作一个多输入单 输出非线性系统的动态过程
触角长 类别 1.14 Apf 1.18 Apf 1.20 Apf 1.24 Af 1.26 Apf 1.28 Apf 1.30 Apf 1.36 Af
• 翼长 触角长 类别
• 1.64 1.38 Af
• 1.82 1.38 Af
• 1.90 1.38 Af
• 1.70 1.40 Af
• 1.82 1.48 Af
一、引例
人工神经网络建模 (Artificial Neuron Nets)
• 1981年生物学家格若根(W. Grogan)和维什(W.Wirth)发现了两类蚊子 (或飞蠓midges).他们测量了这两类蚊子每个个体的翼长和触角长,数据如下:
• 翼长 • 1.78 • 1.96 • 1.86 • 1.72 • 2.00 • 2.00 • 1.96 • 1.74
学 模
型
2、神经网络的数学模型
• 众多神经元之间组合形成神经网络,例如下图 的含有中间层(隐层)的B-P网络
数
学
图5 带中间层的B-P网络
模经网络的作用
(1)蚂蚁群
一个蚂蚁有50个神经元,单独的一个蚂蚁不能做太多 的事;甚至于不能很好活下去.但是一窝蚂蚁;设有 10万 个体,那么这个群体相当于500万个神经元(当然不是简单 相加,这里只为说明方便而言);那么它们可以觅食、搬 家、围攻敌人等等.
• 得到的结果见图1
数 学 模 型
• 图1飞蠓的触角长和翼长
• 思路:作一直线将两类飞蠓分开
• 例如;取A=(1.44,2.10)和 B=(1.10,1.16), 过A B两点作一条直线:
•
y= 1.47x - 0.017
• 其中X表示触角长;y表示翼长.
• 分类规则:设一个蚊子的数据为(x, y) • 如果y≥1.47x - 0.017,则判断蚊子属Apf类; • 如果y<1.47x - 0.017;则判断蚊子属Af类.
(2)网络说话
人们把一本教科书用网络把它读出来(当然需要通过光 电,电声的信号转换);开始网络说的话像婴儿学语那样发 出“巴、巴、巴”的声响;但经过B-P算法长时间的训练竟 能正确读出英语课本中 90%的词汇. 从此用神经网络来识别语言和图象形成一个新的热潮. 数学模型
4、人工神经网络的基本特点
(1)可处理非线性
(5)神经网络可以用大规模集成电路来实现.如美国用 256 个神经元组成的神经网络组成硬件用于识别手写体的邮政编 码.
数学模型
四、反向传播算法(B-P算法) Back propagation algorithm
算法的目的:根据实际的输入与输出数据,计算模型的参 数(权系数)
1.简单网络的B-P算法
图6 简单网络
数学模型
• 假设有P个训练样本,即有P个输入输出对 • (Ip, Tp),p=1,…,P, 其中
• 哪一分类直线才是正确的呢?
• 因此如何来确定这个判别直线是一个值得研究的 问题.一般地讲,应该充分利用已知的数据信息 来确定判别直线.
数学模型
• 再如,如下的情形已经不能用分类直线的办法:
• 新思路:将问题看作一个系统,飞蠓的数据作为
输入,飞蠓的类型作为输出,研究输入与输出的
关系。
数学模型
二、神经元与神经网络
m
y f ( wi xi ) i 1
• θ为阈值,f(X)是激发函数;它可以是线性
函数,也可以是非线性函数.
数学模型
例如,若记
m
z
wi xi
i 1
取激发函数为符号函数
1, x 0, sgn(x) 0, x 0.
则
y
f (z)
1,
m
wi xi ,
i 1 m
0,
wi xi ,
i 1
S型激发函数:
数
f (x) 1 , 1 ex
0 f (x) 1;
学 模
型
或
f
(x)
ex ex
ex ex
,
1 f (x) 1.
• 注:若将阈值看作是一个权系数,-1是一个固定的 输入,另有m-1个正常的输入,则(1)式也可表 示为:
m
y f ( wi xi ) i1
(1)
数
• 参数识别:假设函数形式已知,则可以从已有的 输入输出数据确定出权系数及阈值。
• 分类结果:(1.24,1.80),(1.28,1.84)属于Af类;(1.40, 2.04)属于 Apf类.
图2 分类直线图
数学模型
•缺陷:根据什么原则确定分类直线?
• 若取A=(1.46,2.10), B=(1.1,1.6)不变,则分类直线 变为 y=1.39x+0.071
分类结果变为: (1.24,1.80), (1.40,2.04) 属于Apf类; (1.28,1.84)属于Af类
• 1.82 1.54 Af
数
• 2.08 1.56 Af
学
模
型
• 问:如果抓到三只新的蚊子,它们的触角长和 翼长分别为(l.24,1.80); (l.28,1.84);(1.40, 2.04).问它们应分别属于哪一个种类?
解法一:
• 把翼长作纵坐标,触角长作横坐标;那么每个 蚊子的翼长和触角决定了坐标平面的一个点.其 中 6个蚊子属于 APf类;用黑点“·”表示;9个 蚊子属 Af类;用小圆圈“。”表示.
神经网络研究的两个方面 • 从生理上、解剖学上进行研究 • 从工程技术上、算法上进行研究
数学模型
三、人工神经网络 (Artificial Neuron Nets, 简称ANN)
• 神经元的数学模型
图4神经元的数学模型
数学模型
• 其中x=(x1,…xm)T 输入向量,y为输出,wi 是权系数;输入与输出具有如下关系:
(2)并行结构.对神经网络中的每一个神经元来说;其 运算都是同样的.这样的结构最便于计算机并行处理.
(3)具有学习和记忆能力.一个神经网络可以通过训练 学习判别事物;学习某一种规律或规则.神经网络可以 用于联想记忆.
(4)对数据的可容性大.在神经网络中可以同时使用量化 数据和质量数据(如好、中、差、及格、不及格等).
• 大脑可视作为1000多亿神经元组成的神经网络
• 图3 神经元的解剖图
数学模型
• 神经元的信息传递和处理是一种电化学活 动.树突由于电化学作用接受外界的刺激;通 过胞体内的活动体现为轴突电位,当轴突电位 达到一定的值则形成神经脉冲或动作电位;再 通过轴突末梢传递给其它的神经元.从控制论 的观点来看;这一过程可以看作一个多输入单 输出非线性系统的动态过程
触角长 类别 1.14 Apf 1.18 Apf 1.20 Apf 1.24 Af 1.26 Apf 1.28 Apf 1.30 Apf 1.36 Af
• 翼长 触角长 类别
• 1.64 1.38 Af
• 1.82 1.38 Af
• 1.90 1.38 Af
• 1.70 1.40 Af
• 1.82 1.48 Af
一、引例
人工神经网络建模 (Artificial Neuron Nets)
• 1981年生物学家格若根(W. Grogan)和维什(W.Wirth)发现了两类蚊子 (或飞蠓midges).他们测量了这两类蚊子每个个体的翼长和触角长,数据如下:
• 翼长 • 1.78 • 1.96 • 1.86 • 1.72 • 2.00 • 2.00 • 1.96 • 1.74
学 模
型
2、神经网络的数学模型
• 众多神经元之间组合形成神经网络,例如下图 的含有中间层(隐层)的B-P网络
数
学
图5 带中间层的B-P网络
模经网络的作用
(1)蚂蚁群
一个蚂蚁有50个神经元,单独的一个蚂蚁不能做太多 的事;甚至于不能很好活下去.但是一窝蚂蚁;设有 10万 个体,那么这个群体相当于500万个神经元(当然不是简单 相加,这里只为说明方便而言);那么它们可以觅食、搬 家、围攻敌人等等.
• 得到的结果见图1
数 学 模 型
• 图1飞蠓的触角长和翼长
• 思路:作一直线将两类飞蠓分开
• 例如;取A=(1.44,2.10)和 B=(1.10,1.16), 过A B两点作一条直线:
•
y= 1.47x - 0.017
• 其中X表示触角长;y表示翼长.
• 分类规则:设一个蚊子的数据为(x, y) • 如果y≥1.47x - 0.017,则判断蚊子属Apf类; • 如果y<1.47x - 0.017;则判断蚊子属Af类.
(2)网络说话
人们把一本教科书用网络把它读出来(当然需要通过光 电,电声的信号转换);开始网络说的话像婴儿学语那样发 出“巴、巴、巴”的声响;但经过B-P算法长时间的训练竟 能正确读出英语课本中 90%的词汇. 从此用神经网络来识别语言和图象形成一个新的热潮. 数学模型
4、人工神经网络的基本特点
(1)可处理非线性
(5)神经网络可以用大规模集成电路来实现.如美国用 256 个神经元组成的神经网络组成硬件用于识别手写体的邮政编 码.
数学模型
四、反向传播算法(B-P算法) Back propagation algorithm
算法的目的:根据实际的输入与输出数据,计算模型的参 数(权系数)
1.简单网络的B-P算法
图6 简单网络
数学模型
• 假设有P个训练样本,即有P个输入输出对 • (Ip, Tp),p=1,…,P, 其中
• 哪一分类直线才是正确的呢?
• 因此如何来确定这个判别直线是一个值得研究的 问题.一般地讲,应该充分利用已知的数据信息 来确定判别直线.
数学模型
• 再如,如下的情形已经不能用分类直线的办法:
• 新思路:将问题看作一个系统,飞蠓的数据作为
输入,飞蠓的类型作为输出,研究输入与输出的
关系。
数学模型
二、神经元与神经网络
m
y f ( wi xi ) i 1
• θ为阈值,f(X)是激发函数;它可以是线性
函数,也可以是非线性函数.
数学模型
例如,若记
m
z
wi xi
i 1
取激发函数为符号函数
1, x 0, sgn(x) 0, x 0.
则
y
f (z)
1,
m
wi xi ,
i 1 m
0,
wi xi ,
i 1
S型激发函数:
数
f (x) 1 , 1 ex
0 f (x) 1;
学 模
型
或
f
(x)
ex ex
ex ex
,
1 f (x) 1.
• 注:若将阈值看作是一个权系数,-1是一个固定的 输入,另有m-1个正常的输入,则(1)式也可表 示为:
m
y f ( wi xi ) i1
(1)
数
• 参数识别:假设函数形式已知,则可以从已有的 输入输出数据确定出权系数及阈值。
