libsvm的原理及使用方法介绍
最新LibSVM分类的实用指南

L i b S V M分类的实用指南LibSVM分类的实用指南摘要SVM(support vector machine)是一项流行的分类技术。
然而,初学者由于不熟悉SVM,常常得不到满意的结果,原因在于丢失了一些简单但是非常必要的步骤。
在这篇文档中,我们给出了一个简单的操作流程,得到合理的结果。
(译者注:本文中大部分SVM实际指的是LibSVM)1入门知识SVM是一项非常实用的数据分类技术。
虽然SVM比起神经网络(Neural Networks)要相对容易一些,但对于不熟悉该方法的用户而言,开始阶段通常很难得到满意的结果。
这里,我们给出了一份指南,根据它可以得到合理结果。
需要注意,此指南不适用SVM的研究者,并且也不保证一定能够获得最高精度结果。
同时,我们也没有打算要解决有挑战性的或者非常复杂的问题。
我们的目的,仅在于给初学者提供快速获得可接受结果的秘诀。
虽然用户不是一定要深入理解SVM背后的理论,但为了后文解释操作过程,我们还是先给出必要的基础的介绍。
一项分类任务通常将数据划分成训练集和测试集。
训练集的每个实例,包含一个"目标值(target value)"(例如,分类标注)和一些"属性(attribute)"(例如,特征或者观测变量)。
SVM的目标是基于训练数据产出一个模型(model),用来预测只给出属性的测试数据的目标值。
给定一个训练集,"实例-标注"对,,支持向量机需要解决如下的优化问题:在这里,训练向量xi通过函数Φ被映射到一个更高维(甚至有可能无穷维)空间。
SVM在这个高维空间里寻找一个线性的最大间隔的超平面。
C 0是分错项的惩罚因子(penalty parameter of the error term)。
被称之为核函数(kernel function)。
新的核函数还在研究中,初学者可以在SVM书中找到如下四个最基本的核函数:(线性、多项式、径向基函数、S型)1.1实例表1是一些现实生活中的实例。
SVM模式识别与回归软件包(LibSVM)详解
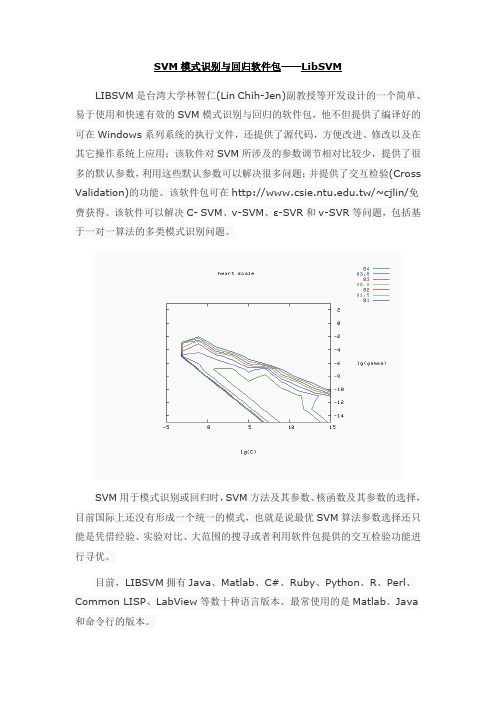
SVM模式识别与回归软件包——LibSVMLIBSVM是台湾大学林智仁(Lin Chih-Jen)副教授等开发设计的一个简单、易于使用和快速有效的SVM模式识别与回归的软件包,他不但提供了编译好的可在Windows系列系统的执行文件,还提供了源代码,方便改进、修改以及在其它操作系统上应用;该软件对SVM所涉及的参数调节相对比较少,提供了很多的默认参数,利用这些默认参数可以解决很多问题;并提供了交互检验(Cross Validation)的功能。
该软件包可在.tw/~cjlin/免费获得。
该软件可以解决C- SVM、ν-SVM、ε-SVR和ν-SVR等问题,包括基于一对一算法的多类模式识别问题。
SVM用于模式识别或回归时,SVM方法及其参数、核函数及其参数的选择,目前国际上还没有形成一个统一的模式,也就是说最优SVM算法参数选择还只能是凭借经验、实验对比、大范围的搜寻或者利用软件包提供的交互检验功能进行寻优。
目前,LIBSVM拥有Java、Matlab、C#、Ruby、Python、R、Perl、Common LISP、LabView等数十种语言版本。
最常使用的是Matlab、Java 和命令行的版本。
就要做有关SVM的报告了!由于SVM里面的有关二次优化的不是那么容易计算得到的,最起码凭借我现在的理论知识和编程能力是不能达到!幸好,现在又不少的SVM工具,他可以帮助你得到支持向量(SV),甚至可以帮助你得到预测结果,归一化数据等等。
其中SVM-light,LibSVM是比较常用的!SVM-light我们实验室有这方面的代码,而我自己就学习了下怎么使用LIBSVM(来自台湾大学林智仁)。
实验步骤如下:1:首先安装LIBSVM,这个不用多说,直接去他的官网上看:.tw/~cjlin/libsvm/index.html2:处理数据,把数据制作成LIBSVM的格式,其每行格式为:label index1:value1 index2:value2 ...其中我用了复旦的分类语料库,当然我先做了分词,去停用词,归一化等处理了3:使用svm-train.exe训练,得到****.model文件。
libsvm参数说明

libsvm参数说明(实用版)目录1.引言2.LIBSVM 简介3.LIBSVM 参数说明4.使用 LIBSVM 需要注意的问题5.结束语正文1.引言支持向量机(Support Vector Machine, SVM)是一种非常强大和灵活的监督学习算法,它可以用于分类和回归任务。
在 SVM 的研究和应用中,LIBSVM 是一个非常重要的工具,它为 SVM 的实现和应用提供了强大的支持。
本文将对 LIBSVM 的参数进行详细的说明,以帮助读者更好地理解和使用这个工具。
2.LIBSVM 简介LIBSVM 是一个开源的 SVM 实现库,它提供了丰富的功能和接口,可以支持多种操作系统,包括 Windows、Linux 和 Mac OS 等。
LIBSVM 主要包括三个部分:svm-train、svm-predict 和 svm-plot。
svm-train 用于训练 SVM 模型,svm-predict 用于预测新数据,svm-plot 用于绘制各种图表,以便于观察和分析模型性能。
3.LIBSVM 参数说明LIBSVM 的参数设置对于模型的性能至关重要。
以下是一些常用的参数及其说明:- -train:用于指定训练数据的文件名。
- -test:用于指定测试数据的文件名。
- -model:用于指定模型文件的名称。
- -参数:用于设置 SVM 模型的参数,例如 C、核函数等。
- -cache-size:用于设置缓存大小,以加速训练过程。
- -tolerance:用于设置收敛阈值,控制训练过程的终止条件。
- -shrinking:用于设置是否使用启发式方法进行训练。
- -probability:用于设置是否计算预测概率。
4.使用 LIBSVM 需要注意的问题在使用 LIBSVM 时,需要注意以下问题:- 设置合适的参数:LIBSVM 的参数设置对模型性能有很大影响,需要根据具体问题和数据集进行调整。
- 特征选择:在实际应用中,特征选择对于模型性能至关重要。
LIBSVM使用方法

LIBSVM1 LIBSVM简介LIBSVM是台湾大学林智仁(Lin Chih-Jen)副教授等开发设计的一个简单、易于使用和快速有效的SVM模式识别与回归的软件包,他不但提供了编译好的可在Windows 系列系统的执行文件,还提供了源代码,方便改进、修改以及在其它操作系统上应用;该软件还有一个特点,就是对SVM所涉及的参数调节相对比较少,提供了很多的默认参数,利用这些默认参数就可以解决很多问题;并且提供了交互检验(Cross -SVM回归等问题,包括基于一对一算法的多类模式识别问题。
SVM用于模式识别或回归时,SVM方法及其参数、核函数及其参数的选择,目前国际上还没有形成一个统一的模式,也就是说最优SVM算法参数选择还只能是凭借经验、实验对比、大范围的搜寻或者利用软件包提供的交互检验功能进行寻优。
ν-SVM回归和ε-SVM分类、νValidation)的功能。
该软件包可以在.tw/~cjlin/免费获得。
该软件可以解决C-SVM分类、-SVM回归等问题,包括基于一对一算法的多类模式识别问题。
SVM用于模式识别或回归时,SVM方法及其参数、核函数及其参数的选择,目前国际上还没有形成一个统一的模式,也就是说最优SVM算法参数选择还只能是凭借经验、实验对比、大范围的搜寻或者利用软件包提供的交互检验功能进行寻优。
2 LIBSVM使用方法LibSVM是以源代码和可执行文件两种方式给出的。
如果是Windows系列操作系统,可以直接使用软件包提供的程序,也可以进行修改编译;如果是Unix类系统,必须自己编译,软件包中提供了编译格式文件,我们在SGI工作站(操作系统IRIX6.5)上,使用免费编译器GNU C++3.3编译通过。
2.1 LIBSVM 使用的一般步骤:1) 按照LIBSVM软件包所要求的格式准备数据集;2) 对数据进行简单的缩放操作;3) 考虑选用RBF 核函数;4) 采用交叉验证选择最佳参数C与g;5) 采用最佳参数C与g 对整个训练集进行训练获取支持向量机模型;6) 利用获取的模型进行测试与预测。
libsvm参数说明

libsvm参数说明摘要:一、libsvm 简介- 什么是libsvm- libsvm 的作用二、libsvm 参数说明- 参数分类- 参数详细说明- 核函数参数- 松弛参数- 惩罚参数- 迭代次数参数- 其他参数三、libsvm 参数调整- 参数调整的重要性- 参数调整的方法正文:【libsvm 简介】libsvm 是一款广泛应用于机器学习领域的开源软件,全称是“LIBSVM”,它提供了支持向量机(SVM)的完整实现,可以用于分类和回归等多种任务。
libsvm 不仅支持常见的数据集格式,还提供了丰富的API 接口,方便用户进行二次开发和应用。
libsvm 的主要作用是帮助用户解决高维数据分类和回归问题。
在面对高维数据时,传统的分类算法可能会遇到“维数灾难”,导致分类效果不佳。
而libsvm 通过使用核函数技术,将高维数据映射到低维空间,从而有效地解决了这个问题。
【libsvm 参数说明】libsvm 提供了丰富的参数供用户调整,以达到最佳分类效果。
这些参数主要分为以下几类:1.核函数参数:包括核函数类型(如线性核、多项式核、径向基函数核等)和核函数参数(如径向基函数核的核径宽)。
2.松弛参数:用于控制分类间隔的大小,对最终分类结果有一定影响。
3.惩罚参数:控制模型对误分类的惩罚力度,对分类效果有重要影响。
4.迭代次数参数:控制支持向量机算法的迭代次数,影响模型的收敛速度。
5.其他参数:如学习率、最小化目标函数的迭代次数等。
【libsvm 参数调整】参数调整是libsvm 使用过程中非常重要的一环,合适的参数设置可以使模型达到更好的分类效果。
参数调整的方法主要有以下几种:1.网格搜索法:通过遍历参数空间的各个点,找到最佳参数组合。
这种方法适用于参数空间较小的情况。
2.随机搜索法:在参数空间中随机选取一定数量的点进行遍历,找到最佳参数组合。
这种方法适用于参数空间较大,且网格搜索法效果不佳的情况。
3.贝叶斯优化法:利用贝叶斯理论,对参数进行加权调整,以提高搜索效率。
libsvm参数说明

libsvm参数说明【原创版】目录1.概述2.安装与配置3.参数说明4.应用实例5.总结正文1.概述LIBSVM 是一个开源的支持向量机(SVM)算法库,它可以在多种平台上运行,包括 Windows、Linux 和 Mac OS。
LIBSVM 提供了一系列用于解决分类和回归问题的工具和算法,它的核心是基于序列最小化算法的支持向量机。
2.安装与配置在使用 LIBSVM 之前,需要先安装它。
在 Windows 平台上,可以直接下载LIBSVM 的二进制文件,然后设置环境变量。
对于 Linux 和 Mac OS 平台,需要先安装相应的依赖库,然后编译并安装 LIBSVM。
在安装完成后,需要配置 LIBSVM 的参数,包括选择核函数、设置惩罚参数等。
这些参数对于支持向量机的性能至关重要,需要根据实际问题进行调整。
3.参数说明LIBSVM 的参数主要包括以下几个方面:- 核函数:LIBSVM 支持多种核函数,包括线性核、多项式核、径向基函数(RBF)核和 Sigmoid 核。
核函数的选择取决于问题的性质,需要根据实际问题进行选择。
- 惩罚参数:惩罚参数用于控制模型的复杂度,避免过拟合。
惩罚参数的取值范围是 0 到 1,取值越小,模型的复杂度越高,过拟合的风险也越高。
- 迭代次数:迭代次数用于控制算法的收敛速度,取值越大,收敛速度越快,但可能会影响模型的精度。
- 随机种子:随机种子用于生成随机数,影响模型的初始化和迭代过程。
在实际应用中,建议设置随机种子,以保证模型的可重复性。
4.应用实例LIBSVM 在实际应用中可以用于多种问题,包括分类、回归和排序等。
例如,在人脸检测、车牌识别和文本分类等问题中,可以使用 LIBSVM 来实现支持向量机算法。
5.总结LIBSVM 是一个功能强大的支持向量机库,它提供了多种核函数和参数设置,可以用于解决多种实际问题。
第1页共1页。
LIBSVM使用方法

LIBSVM使用方法1libsvm简介2libsvm使用方法libsvm就是以源代码和可执行文件两种方式得出的。
如果就是windows系列操作系统,可以轻易采用软件包提供更多的程序,也可以展开修正编程;如果就是unix类系统,必须自己编程,软件包中提供更多了编程格式文件,我们在sgi工作站(操作系统irix6.5)上,采用免费编译器gnuc++3.3编程通过。
2.1libsvm使用的一般步骤:1)2)3)4)5)6)按照libsvm软件包所建议的格式准备工作数据集;对数据展开直观的翻转操作方式;考量采用rbf核函数;使用交叉检验挑选最佳参数c与g;使用最佳参数c与g对整个训练集展开训练以获取积极支持向量机模型;利用以获取的模型展开测试与预测。
2.2libsvm使用的数据格式该软件采用的训练数据和检验数据文件格式如下:::...其中就是训练数据集的目标值,对于分类,它就是标识某类的整数(积极支持多个类);对于重回,就是任一实数。
就是以1已经开始的整数,可以就是不已连续的;为实数,也就是我们常说道的自变量。
检验数据文件中的label只用作排序准确度或误差,如果它就是未明的,只需用一个数核对这一栏,也可以空着不填上。
在程序包中,还包括存有一个训练数据实例:heart_scale,便利参照数据文件格式以及练采用软件。
可以撰写大程序,将自己常用的数据格式转换成这种格式。
2.3svmtrain和svmpredict的用法svmtrain(训练建模)的用法:svmtrain[options]training_set_file[model_file]options:需用的选项即为则表示的涵义如下-ssvm类型:svm设置类型(默认0)0--c-svc1--v-svc2–一类svm3--e-svr4--v-svr-t核函数类型:核函数设置类型(默认2)0–线性:u'v1–多项式:(r*u'v+coef0)^degree2–rbf函数:exp(-r|u-v|^2)3–sigmoid:tanh(r*u'v+coef0)-ddegree:核函数中的degree设置(预设3)-gr(gama):核函数中的?函数设置(默认1/k)-rcoef0:核函数中的coef0设置(预设0)-ccost:设置c-svc,?-svr和?-svr的参数(默认1)-nnu:设置?-svc,一类svm和?-svr的参数(预设0.5)-pe:设置?-svr中损失函数?的值(默认0.1)-mcachesize:设置cache内存大小,以mb为单位(预设40)-eε:设置允许的终止判据(默认0.001)-hshrinking:与否采用启发式,0或1(预设1)-wiweight:设置第几类的参数c为weight?c(c-svc中的c)(默认1)-vn:n-fold可视化检验模式其中-g选项中的k是指输入数据中的属性数。
libsvm使用说明

libSVM的使用文档11. 程序介绍和环境设置windows下的libsvm是在命令行运行的Console Program。
所以其运行都是在windows的命令行提示符窗口运行(运行,输入cmd)。
运行主要用到的程序,由如下内容组成:libsvm-2.9/windows/文件夹中的:svm-train.exesvm-predict.exesvm-scale.exelibsvm-2.9/windows/文件夹中的:checkdata.pysubset.pyeasy.pygrid.py另外有:svm-toy.exe,我暂时知道的是用于演示svm分类。
其中的load按钮的功能,是否能直接载入数据并进行分类还不清楚,尝试没有成功;python文件夹及其中的svmc.pyd,暂时不清楚功能。
因为程序运行要用到python脚本用来寻找参数,使用gnuplot来绘制图形。
所以,需要安装python和Gnuplot。
(Python v3.1 Final可从此下载:/detail/33/320958.shtml)(gnuplot可从其官网下载:)为了方便,将gnuplot的bin、libsvm-2.9/windows/加入到系统的path中,如下:gnuplot.JPGlibsvm.JPG这样,可以方便的从命令行的任何位置调用gnuplot和libsvm的可执行程序,如下调用svm-train.exe:pathtest.JPG出现svm-train程序中的帮助提示,说明path配置成功。
至此,libsvm运行的环境配置完成。
下面将通过实例讲解如何使用libsvm进行分类。
2. 使用libsvm进行分类预测我们所使用的数据为UCI的iris数据集,将其类别标识换为1、2、3。
然后,取3/5作为训练样本,2/5作为测试样本。
使用论坛中“将UCI数据转变为LIBSVM使用数据格式的程序”一文将其转换为libsvm所用格式,如下:训练文件tra_iris.txt1 1:5.4 2:3.4 3:1.7 4:0.21 1:5.1 2:3.7 3:1.5 4:0.41 1:4.6 2:3.6 3:1 4:0.21 1:5.1 2:3.3 3:1.7 4:0.51 1:4.8 2:3.4 3:1.9 4:0.2……2 1:5.9 2:3.2 3:4.8 4:1.82 1:6.1 2:2.8 3:4 4:1.32 1:6.3 2:2.5 3:4.9 4:1.52 1:6.1 2:2.8 3:4.7 4:1.22 1:6.4 2:2.9 3:4.3 4:1.3……3 1:6.9 2:3.2 3:5.7 4:2.33 1:5.6 2:2.8 3:4.9 4:23 1:7.7 2:2.8 3:6.7 4:23 1:6.3 2:2.7 3:4.9 4:1.83 1:6.7 2:3.3 3:5.7 4:2.13 1:7.2 2:3.2 3:6 4:1.8……测试文件tes_iris.txt1 1:5.1 2:3.5 3:1.4 4:0.21 1:4.9 2:3 3:1.4 4:0.21 1:4.7 2:3.2 3:1.3 4:0.21 1:4.6 2:3.1 3:1.5 4:0.21 1:5 2:3.6 3:1.4 4:0.21 1:5.4 2:3.9 3:1.7 4:0.4……2 1:7 2:3.2 3:4.7 4:1.42 1:6.4 2:3.2 3:4.5 4:1.52 1:6.9 2:3.1 3:4.9 4:1.52 1:5.5 2:2.3 3:4 4:1.32 1:6.5 2:2.8 3:4.6 4:1.5……3 1:6.3 2:3.3 3:6 4:2.53 1:5.8 2:2.7 3:5.1 4:1.93 1:7.1 2:3 3:5.9 4:2.13 1:6.3 2:2.9 3:5.6 4:1.83 1:6.5 2:3 3:5.8 4:2.2……libsvm的参数选择一直是令人头痛的问题。
【个人总结系列-52】SVM支持向量机基本原理及LIBSVM介绍

3.1 支持向量机基本原理数据分类是数据挖掘中的一个重要内容,数据分类是指在已有分类的训练数据的基础上,根据某种原理,经过训练形成一个分类器;然后使用分类器判断没有分类的数据的类别。
注意,数据都是以向量形式出现的,如<0.4, 0.123, 0.323,…>。
支持向量机是一种基于分类边界的方法。
其基本原理是(以二维数据为例):如果训练数据分布在二维平面上的点,它们按照其分类聚集在不同的区域。
基于分类边界的分类算法的目标是,通过训练,找到这些分类之间的边界(直线的――称为线性划分,曲线的――称为非线性划分)。
首先给出一个非常简单的分类问题(线性可分),我们要用一条直线,将下图中黑色的点和白色的点分开,很显然,下图的这条直线就是我们要求的直线之一(可以有无数条这样的直线)。
图3-1 SVM示例假如说,我们令黑色的点 = -1,白色的点 = +1,直线f(x) = w.x + b,这儿的x、w是向量,其实写成这种形式也是等价的f(x) = w1x1 + w2x2 … + wnxn + b, 当向量x的维度=2的时候,f(x) 表示二维空间中的一条直线,当x的维度=3的时候,f(x) 表示3维空间中的一个平面,当x的维度=n > 3的时候,表示n维空间中的n-1维超平面。
我们令黑色白色两类的点分别为+1, -1,所以当有一个新的点x需要预测属于哪个分类的时候,我们用sgn(f(x)),就可以预测了,sgn表示符号函数,当f(x) > 0的时候,sgn(f(x)) = +1, 当f(x) < 0的时候sgn(f(x)) = –1。
但是我们怎样才能取得一个最优的划分直线f(x)呢?下图的直线表示几条可能的f(x)图3-2 线性可分的多种情况一个很直观的感受是,让这条直线到给定样本中最近的点最远,下面给出两张图,来说明该问题:图3-3 两种线性可分情形分析比较这两种分法哪种更好,从直观上来说,就是分割的间隙越大越好,把两个类别的点分得越开越好。
LIBSVM使用介绍

附录1:LIBSVM的简单介绍1. LIBSVM软件包简介LIBSVM是台湾大学林智仁(Chih-Jen Lin)博士等开发设计的一个操作简单、易于使用、快速有效的通用SVM软件包,可以解决分类问题(包括C SVC−、SVCν−)、回归问题(包括SVRε−、SVRν−)以及分布估计(on e class SVM−−)等问题,提供了线性、多项式、径向基和S形函数四种常用的核函数供选择,可以有效地解决多类问题、交叉验证选择参数、对不平衡样本加权、多类问题的概率估计等。
LIBSVM是一个开源的软件包,需要者都可以免费的从作者的个人主页.tw/~cjlin/处获得。
他不仅提供了LIBSVM的C++语言的算法源代码,还提供了Python、Java、R、MA TLAB、Perl、Ruby、LabVIEW 以及C#.net等各种语言的接口,可以方便的在Windows或UNIX平台下使用,也便于科研工作者根据自己的需要进行改进(譬如设计使用符合自己特定问题需要的核函数等)。
另外还提供了WINDOWS平台下的可视化操作工具SVM-toy,并且在进行模型参数选择时可以绘制出交叉验证精度的等高线图。
2. LIBSVM使用方法简介LIBSVM在给出源代码的同时还提供了Windows操作系统下的可执行文件,包括:进行支持向量机训练的svmtrain.exe;根据已获得的支持向量机模型对数据集进行预测的svmpredict.exe;以及对训练数据与测试数据进行简单缩放操作的svmscale.exe。
它们都可以直接在DOS环境中使用。
如果下载的包中只有C++的源代码,则也可以自己在VC等软件上编译生成可执行文件。
LIBSVM使用的一般步骤是:1)按照LIBSVM软件包所要求的格式准备数据集;2)对数据进行简单的缩放操作;3)考虑选用RBF核函数2 (,)x yK x y eγ−−=;4)采用交叉验证选择最佳参数C与γ;5)采用最佳参数C与γ对整个训练集进行训练获取支持向量机模型;6)利用获取的模型进行测试与预测。
LibSVM使用的简单介绍

LIBSVM使用的详细说明一、基本介绍LIBSVM是台湾大学林智仁教授2001年开发的一套支持向量机的库,运算速度快,可以很方便的对数据做分类或回归。
由于LIBSVM程序小,运用灵活,输入参数少,并且是开源的,易于扩展,因此成为目前国内应用最多的SVM的库。
这套库目前已经发展到2.9版。
主要有5个文件夹和一些c++源码文件。
Java主要是应用于java平台;Python是用来参数优选的工具,稍后介绍;svm-toy是一个可视化的工具,用来展示训练数据和分类界面,里面是源码,其编译后的程序在windows文件夹下;tools—主要包含四个python文件,用来数据集抽样(subset),参数优选(grid),集成测试(easy), 数据检查(check data);windows包含libSVM四个exe程序包,我们所用的库就是他们。
其中svm-scale.exe是用来对原始样本进行缩放的;svm-train.exe主要实现对训练数据集的训练,并可以获得SVM模型;svmpredict 是根据训练获得的模型,对数据集合进行预测。
还有一个svm-toy.exe之前已经交待过,是一个可视化工具。
里面还有个heart_scale,是一个样本文件,可以用记事本打开,用来测试用的。
二、LIBSVM的使用规范1. libSVM的数据格式Label 1:value 2:value …Label是类别的标识,比如上节train.model中提到的1 -1,你可以自己随意定,比如-10,0,15。
如果是回归,这是目标值,就要实事求是了。
Value就是要训练的数据,从分类的角度来说就是特征值,数据之间用空格隔开,比如:-15 1:0.708 2:1056 3:-0.3333需要注意的是,如果特征值为0,特征冒号前面的(姑且称做序号)可以不连续。
如:-15 1:0.708 3:-0.3333表明第2个特征值为0,从编程的角度来说,这样做可以减少内存的使用,并提高做矩阵内积时的运算速度。
1-6 lib-svm 经典使用 理论和介绍 工具用法 grid.py easy.py等

1/flydreamGG/archive/2009/08.aspx/flydreamGG/archive/2009/08.aspxLibSVM学习(一)——初识LibSVM 收藏LibSVM是台湾林智仁(Chih-Jen Lin) 教授2001年开发的一套支持向量机的库,这套库运算速度还是挺快的,可以很方便的对数据做分类或回归。
由于libSVM程序小,运用灵活,输入参数少,并且是开源的,易于扩展,因此成为目前国内应用最多的SVM的库。
这套库可以从.tw/~cjlin/免费获得,目前已经发展到2.89版。
下载.zip格式的版本,解压后可以看到,主要有5个文件夹和一些c++源码文件。
Java ——主要是应用于java平台;Python ——是用来参数优选的工具,稍后介绍;svm-toy ——一个可视化的工具,用来展示训练数据和分类界面,里面是源码,其编译后的程序在windows文件夹下;tools ——主要包含四个python文件,用来数据集抽样(subset),参数优选(grid),集成测试(easy), 数据检查(checkdata);windows ——包含libSVM四个exe程序包,我们所用的库就是他们,里面还有个heart_scale,是一个样本文件,可以用记事本打开,用来测试用的。
其他.h和.cpp文件都是程序的源码,可以编译出相应的.exe文件。
其中,最重要的是svm.h和svm.cpp文件,svm-predict.c、svm-scale.c和svm-train.c(还有一个svm-toy.c在svm-toy文件夹中)都是调用的这个文件中的接口函数,编译后就是windows下相应的四个exe程序。
另外,里面的README 跟FAQ 也是很好的文件,对于初学者如果E文过得去,可以看一下。
下面以svm-train为例,简单的介绍下,怎么编译:(这步很简单,也没必要,对于仅仅使用libsvm库的人来说,windows下的4个exe包已经足够了,之所以加这步,是为了那些做深入研究的人,可以按照自己的思路改变一下svm.cpp,然后编译验证)我用的是VC 6.0,新建一个控制台(win32 console application)程序,程序名叫svm-train(这个可以随意),点击OK后,选择empty。
使用libsvm对MNIST数据集进行实验---浅显易懂!

使⽤libsvm对MNIST数据集进⾏实验---浅显易懂!在学SVM中的实验环节,⽼师介绍了libsvm的使⽤。
当时看完之后感觉简单的说不出话来。
1. libsvm介绍虽然原理要求很⾼的数学知识等,但是libsvm中,完全就是⼀个⼯具包,拿来就能⽤。
当时问了好⼏遍⽼师,公司⾥做svm就是这么简单的?敲⼏个命令⾏就可以了。
貌似是这样的。
当然,在⼤数据化的背景下,还会有⽐如:并⾏SVM、多核函数SVM等情况的研究和应⽤。
实验环节⽼师给的数据很简单,也就1000个数据点,使⽤svm进⾏分类。
没有太多好说的。
于是⾃⼰想要试试做⼿写字体分类检测,类似于⾏车违章拍照后的车牌识别。
从⽹上搜到了数据集为MNIST数据集,是⼀个⼊门的基本数据集。
关于libsvm的介绍和使⽤参考:。
不过,svm-toy是最多⽀持三分类的,⽽不是只是⼆分类。
使⽤windows⽂件夹下的svm-train.exe,svm-predict.exe命令可以来进⾏建模和预测,具体参数看⽂档。
svm-train的主要可选参数有:-s 选择SVM类型。
⼀般选的是C-SVM-c 选择松弛变量的权重系数。
C越⼤,对松弛变量的惩罚越⼤,两个⽀持向量直线之间的间隔就越⼩,模型就越精确苛刻,对噪声数据点容忍⼩,越容易过拟合;C越⼩,两个⽀持向量直线之间的距离越⼤,对噪声的容忍能⼒就越⼤,最终效果越好。
但是,模型分错的数据点就越多,容易⽋拟合。
-t 选择核函数。
⼀般是线性和RBF做对⽐,线性速度更快,但要求数据可分;RBF更通⽤,默认选择RBF。
-g garma系数。
是exp(-gamma*|u-v|^2),相当于gamma=1/(2τ^2)。
τ表⽰⾼斯函数中的宽度,g与τ成反⽐。
g越⼤,τ越⼩,则⾼斯函数越窄,覆盖⾯积⼩,这样需要的⽀持向量越多,模型越复杂,容易过拟合。
-wi 对样本分类的权重分配。
因为,在分类中,某些分类可能更加重要。
-v 交叉验证的参数。
libsvm参数说明

libsvm参数说明摘要:一、libsvm 简介1.libsvm 的作用2.libsvm 的安装和使用二、libsvm 参数说明1.核函数选择2.C 参数调整3.罚参数选择4.迭代次数选择5.其他参数三、libsvm 参数调整策略1.交叉验证2.网格搜索3.启发式方法四、libsvm 在实际应用中的案例分析1.情感分析2.文本分类3.图像分类正文:一、libsvm 简介libsvm 是一款常用的支持向量机(SVM)开源实现库,它提供了C、Python、Java 等语言的接口,方便用户在不同平台上进行使用。
libsvm 具有较高的效率和准确性,被广泛应用于数据挖掘、机器学习、模式识别等领域。
1.libsvm 的作用libsvm 主要作用是实现支持向量机算法,它可以解决分类和回归问题,包括线性分类和非线性分类。
此外,libsvm 还提供了核函数,使得它可以处理高维数据和复杂数据的分类问题。
2.libsvm 的安装和使用libsvm 的安装过程比较简单,只需要按照官方文档的指导进行操作即可。
安装完成后,可以通过调用libsvm 提供的API 进行模型的训练和预测。
二、libsvm 参数说明libsvm 提供了丰富的参数供用户调整,以达到最佳的效果。
1.核函数选择核函数是libsvm 的重要组成部分,它决定了libsvm 如何处理输入数据。
libsvm 提供了多种核函数,如线性核、多项式核、径向基函数核等。
用户可以根据问题的特点选择合适的核函数。
2.C 参数调整C 参数是libsvm 中的一个重要参数,它控制了模型的软约束程度。
较小的C 值会使得模型更加灵活,可能导致过拟合;较大的C 值会使得模型更加严格,可能导致欠拟合。
因此,合理调整C 参数对于模型的性能至关重要。
3.罚参数选择罚参数是libsvm 中的另一个重要参数,它控制了模型对训练数据的惩罚程度。
较小的罚参数会导致模型对训练数据的拟合程度过高,可能会导致过拟合;较大的罚参数会使得模型对训练数据的拟合程度降低,可能会导致欠拟合。
libsvm的原理及使用方法介绍

LibSVM学习目录LibSVM学习 (1)初识LibSVM (1)第一次体验libSvm (3)LibSVM使用规范 (5)1. libSVM的数据格式 (5)2. svmscale的用法 (5)3. svmtrain的用法 (6)4. svmpredict 的用法 (7)逐步深入LibSVM (7)分界线的输出 (11)easy.py和grid.py的使用 (13)1. grid.py使用方法 (13)2. easy.py使用方法 (14)参考 (16)LibSVM学习初识LibSVMLibSVM是台湾林智仁(Chih-Jen Lin's) 教授2001年开发的一套支持向量机的库,这套库运算速度还是挺快的,可以很方便的对数据做分类或回归。
由于libSVM程序小,运用灵活,输入参数少,并且是开源的,易于扩展,因此成为目前国内应用最多的SVM的库。
这套库可以从林智仁的home page上免费获得,目前已经发展到3.0版。
下载.zip格式的版本,解压后可以看到,主要有5个文件夹和一些c++源码文件。
Java ——主要是应用于java平台的源码和libsvm.jar包;Python ——是用来参数优选的工具,稍后介绍;svm-toy ——一个可视化的工具,用来展示训练数据和分类界面,里面是源码,其编译后的程序在windows文件夹下;tools ——主要包含四个python文件,用来数据集抽样(subset.py),参数优选(grid.py),集成测试(easy.py), 数据检查(checkdata.py);windows ——包含libSVM四个exe程序包,我们所用的库和程序就是它们。
其他.h和.cpp文件都是程序的源码,可以编译出相应的.exe文件。
其中,最重要的是svm.h 和svm.cpp文件,svm-predict.c、svm-scale.c和svm-train.c(还有一个svm-toy.cpp在svm-toy\qt 文件夹中)都是调用的这个文件中的接口函数,编译后就是windows下相应的四个exe程序。
高光谱 libsvm 分类

高光谱libsvm 分类全文共四篇示例,供读者参考第一篇示例:高光谱图像是一种具有连续且密集的光谱信息的遥感影像类型,具有丰富的光谱特征,可以提供大量反映地物表面特征的信息。
在高光谱图像应用中,分类和识别是一个重要的研究内容,而支持向量机(Support Vector Machine,简称SVM)是一种常用的分类方法之一。
本文将介绍高光谱图像分类中使用libsvm工具进行分类的方法及其应用。
一、高光谱图像分类概述高光谱图像是通过遥感技术获取的一种具有丰富光谱信息的影像,其可以捕捉地物表面的特定光谱特征,有助于对地物进行精准分类和识别。
高光谱数据拥有数百个波段,使得在分类过程中可以更加精细地区分不同的地物类型。
在高光谱图像分类中,传统的分类方法通常会面临维度灾难和过拟合等问题,而支持向量机能够有效应对这些问题,是一种被广泛应用的分类方法之一。
二、支持向量机分类算法介绍支持向量机是一种基于统计学习理论的二元分类方法,其核心思想是通过建立一个最优的超平面来完成分类任务。
在支持向量机分类中,训练数据被映射到高维空间中,找到能够最大化间隔的超平面,并通过支持向量来确定分类决策边界。
支持向量机具有良好的泛化能力和鲁棒性,在分类问题中表现出色,特别适用于高维数据和小样本数据的分类任务。
三、libsvm工具介绍libsvm是一种快速且高效的支持向量机库,由台湾国立大学林智仁博士团队开发,支持向量机的分类和回归等任务。
libsvm具有简洁的代码结构和友好的接口,使得用户可以方便地进行模型训练和预测。
libsvm还提供了多种核函数的选择,可以根据不同任务需求进行灵活的设置。
在高光谱图像分类任务中,libsvm可以帮助研究者高效地进行地物分类和识别。
四、高光谱图像分类中libsvm的应用在高光谱图像分类中,libsvm可以用于对高光谱数据进行地物分类和识别。
需要将高光谱数据进行预处理,包括数据校正、特征提取等步骤。
然后,将处理后的数据输入到libsvm中进行模型训练,通过调整参数和选择合适的核函数对模型进行优化。
libsvm参数说明

libsvm参数说明摘要:1.LIBSVM 简介2.LIBSVM 参数说明3.LIBSVM 的使用方法4.LIBSVM 的应用场景5.总结正文:1.LIBSVM 简介LIBSVM 是一个开源的支持向量机(Support Vector Machine,简称SVM)算法库,它可以在各种平台上运行,包括Windows、Linux 和MacOS 等。
LIBSVM 提供了一系列的机器学习算法,如线性SVM、多项式SVM、径向基函数SVM 等,这些算法可以广泛应用于各种数据挖掘和机器学习任务中,如分类、回归和排序等。
2.LIBSVM 参数说明在使用LIBSVM 时,需要对数据进行预处理,主要包括数据格式转换、特征选择和样本划分等。
此外,还需要对SVM 算法的参数进行设置,以优化模型的性能。
LIBSVM 中常用的参数包括:(1)核函数(Kernel):LIBSVM 支持多种核函数,如线性核、多项式核、径向基函数核和Sigmoid 核等。
核函数的选择会影响到模型的复杂度和分类性能。
(2)惩罚参数(C):惩罚参数用于控制模型对训练数据的拟合程度。
较小的C 值会导致模型过于复杂,容易出现过拟合现象;较大的C 值则会使模型过于简单,容易出现欠拟合现象。
(3)度量函数(Metric):LIBSVM 支持多种度量函数,如欧氏距离、汉明距离和马氏距离等。
度量函数的选择会影响到模型的性能。
(4)迭代次数(Max_iter):迭代次数用于控制模型的训练过程,较小的迭代次数会导致模型训练不充分,较大的迭代次数则会使模型训练时间过长。
(5)终止条件(Epsilon):终止条件用于控制模型的训练过程,当模型的误差小于指定的Epsilon 时,训练过程将终止。
3.LIBSVM 的使用方法使用LIBSVM 时,需要先下载并安装LIBSVM 库,然后按照以下步骤进行操作:(1)准备数据集:将数据集转换为LIBSVM 所支持的格式,通常为文本格式或ARFF 格式。
使用libsvm

支持向量机(SVM,Support Vector Machine)是一种基于统计学习理论的模式识别方法,在解决小样本、高维度及非线性的分类问题中应用非常广泛。
LIBSVM是一个由台湾大学林智仁(Lin Chih-Jen)教授等开发的SVM模式识别与回归的软件包,使用简单,功能强大,本文主要介绍其在Matlab中的使用。
4. 添加路径为了以后使用的方便,建议把LIBSVM的编译好的文件所在路径(如C:\libsvm-3.17\matlab)添加到Matlab的搜索路径中。
具体操作为:(中文版Matlab对应进行)HOME -> Set Path -> Add Folder -> 加入编译好的文件所在的路径(如C:\libsvm-3.17\ma tlab)当然也可以把那4个编译好的文件复制到想要的地方,然后再把该路径添加到Matlab的搜索路径中。
LIBSVM软件包中自带有测试数据,为软件包根目录下的heart_scale文件,可以用来测试L IBSVM是否安装成功。
这里的heart_scale文件不能用Matlab的load进行读取,需要使用l ibsvmread读取。
进入LIBSVM的根目录运行以下代码(因为heart_scale文件没有被添加进搜索路径中,其他路径下无法访问这个文件):如果LIBSVM安装正确的话,会出现以下的运行结果,显示正确率为86.6667%。
使用SVM前首先得了解SVM的工作原理,简单介绍如下。
SVM(Support Vector Machine,支持向量机)是一种有监督的机器学习方法,可以学习不同类别的已知样本的特点,进而对未知的样本进行预测。
SVM本质上是一个二分类的算法,对于n维空间的输入样本,它寻找一个最优的分类超平面,使得两类样本在这个超平面下可以获得最好的分类效果。
这个最优可以用两类样本中与这个超平面距离最近的点的距离来衡量,称为边缘距离,边缘距离越大,两类样本分得越开,SVM就是寻找最大边缘距离的超平面,这个可以通过求解一个以超平面参数为求解变量的优化问题获得解决。
matlab下的LIBSVM的使用

相关参数
-c(默认1,范围(0,+ ))
-n(默认0.5,范围(0,1]) -n(默认0.5,范围(0,1])
-c(默认1,(0, + )) -p(默认0.1,(0, + ))
-c(默认1,(0, + ))
-n(默认0.5,(0,1])
Company Logo
主要参数设置
-t(默认2)——选择核函数
Company Logo
测试数据及格式
测试数据集
– libsvm官方提供的测试数据格式是C++版本使用 的,需要使用libsvmread进行格式转换
– UCI数ቤተ መጻሕፍቲ ባይዱ集 –等
格式
– 标签 属性编号1:属性值1 属性编号2: 属性值2 – 如:+1 1:0.78 2:1 3:1 ........
如如modelsvmtrainlabeldatac1w12w105companylogo标签1的样本惩罚参数为2标签为1的样本惩罚参数为05主要参数设置?v一般选择5或10交叉检验参数必须大于2当使用此参数时返回的结果不再是一个结构体model分类问题返回的是交叉检验下的平均分类准且率回归问题回归问题返回的是交叉检验下的平均均方差误差返回的是交叉检验下的平均均方差误差companylogo测试数据及格式?测试数据集libsvm官方提供的测试数据格式是c版本使用的需要使用libsvmread进行格式转换uci数据集等companylogo?格式标签属性编号1
Company Logo
编译
make 命令
– 编译后文件夹中会出现多个svmtrain.mexw32、 svmpredict.mexw32等文件。
– .mexw32文件是加密文件,打开为乱码。 – 运行help对这些函数无效
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LibSVM学习目录LibSVM学习 (1)初识LibSVM (1)第一次体验libSvm (3)LibSVM使用规范 (5)1. libSVM的数据格式 (5)2. svmscale的用法 (5)3. svmtrain的用法 (6)4. svmpredict 的用法 (7)逐步深入LibSVM (7)分界线的输出 (11)easy.py和grid.py的使用 (13)1. grid.py使用方法 (13)2. easy.py使用方法 (14)参考 (16)LibSVM学习初识LibSVMLibSVM是台湾林智仁(Chih-Jen Lin's) 教授2001年开发的一套支持向量机的库,这套库运算速度还是挺快的,可以很方便的对数据做分类或回归。
由于libSVM程序小,运用灵活,输入参数少,并且是开源的,易于扩展,因此成为目前国内应用最多的SVM的库。
这套库可以从林智仁的home page上免费获得,目前已经发展到3.0版。
下载.zip格式的版本,解压后可以看到,主要有5个文件夹和一些c++源码文件。
Java ——主要是应用于java平台的源码和libsvm.jar包;Python ——是用来参数优选的工具,稍后介绍;svm-toy ——一个可视化的工具,用来展示训练数据和分类界面,里面是源码,其编译后的程序在windows文件夹下;tools ——主要包含四个python文件,用来数据集抽样(subset.py),参数优选(grid.py),集成测试(easy.py), 数据检查(checkdata.py);windows ——包含libSVM四个exe程序包,我们所用的库和程序就是它们。
其他.h和.cpp文件都是程序的源码,可以编译出相应的.exe文件。
其中,最重要的是svm.h 和svm.cpp文件,svm-predict.c、svm-scale.c和svm-train.c(还有一个svm-toy.cpp在svm-toy\qt 文件夹中)都是调用的这个文件中的接口函数,编译后就是windows下相应的四个exe程序。
另外,里面的README 跟FAQ 也是很好的文件,对于初学者如果E文过得去,可以看一下。
下面以svm-train为例,简单的介绍下,怎么编译:(这步很简单,也没必要,对于仅仅使用libsvm库的人来说,windows下的4个exe包已经足够了,之所以加这步,是为了那些做深入研究的人,可以按照自己的思路改变一下svm.cpp,然后编译验证)我用的是VC 6.0,新建一个控制台(win32 console application)程序,程序名叫svmtrain (这个可以随意),点击OK后,选择empty。
进入程序框架后,里面什么都没有,然后找到你的程序目录,把svm-train.c、svm.h和svm.cpp拷贝过去(.c文件是c语言的,要是你习惯了c++,你尽可以改成.cpp),然后把这3个文件添加到工程,编译。
如果没错误,到debug下面看看,是不是有个svm-train.exe。
其实windows下的svm-train.exe就是这样编译出来的。
哈哈,怎么样是不是很简单。
但是,这样的程序直接运行没意义,他要在dos下运行,接收参数才行。
下面开始我们的libsvm的体验之旅。
第一次体验libSvm1. 把LibSVM包解压到相应的目录(因为我只需要里面windows文件夹中的东东,我们也可以只把windows文件夹拷到相应的目录),比如D:\libsvm。
2. 在电脑“开始”的“运行”中输入cmd,进入DOS环境。
定位到D:\libsvm\windows目录下,具体命令如下:(上面第一行是先定位到盘符d,第二行cd 是定位到相应盘符下的目录)3. 进行libsvm训练,输入命令:(这里要注意文件的名字,2.89以前版本都是svmtrain.exe) svm-train heart_scale train.modelPS:heart_scale ——是目录下的已经存在的样本文件(此处将下载的压缩文件中的heart_scale放置入D:\libsvm\windows下即可),要换成自己的文件,只需改成自己的文件名就可以了。
PS:train.model ——是创建的结果文件,保存了训练后的结果。
#iter为迭代次数;nu 是你选择的核函数类型的参数;obj为SVM文件转换为的二次规划求解得到的最小值,rho为判决函数的偏置项b;nSV 为标准支持向量个数(0<a[i]<c),nBSV为边界上的支持向量个数(a[i]=c);Total nSV为支持向量总个数(对于两类来说,因为只有一个分类模型Total nSV = nSV,但是对于多类,这个是各个分类模型的nSV之和)。
在目录下,还可以看到产生了一个train.model文件,可以用记事本打开,记录了训练后的结果。
svm_type c_svc //所选择的svm类型,默认为c_svckernel_type rbf //训练采用的核函数类型,此处为RBF核gamma 0.0769231 //RBF核的参数γnr_class 2 //类别数,此处为两分类问题total_sv 132 //支持向量总个数rho 0.424462 //判决函数的偏置项blabel 1 -1 //原始文件中的类别标识nr_sv 64 68 //每个类的支持向量机的个数SV //以下为各个类的权系数及相应的支持向量到现在,第一次体验libsvm到这就基本结束了,其他的两个(svm-predict、svm-scale)的使用过程类似。
怎么样,挺爽的吧。
对于个别参数你还不理解,没关系,下面我们会具体讲到。
LibSVM使用规范其实,这部分写也是多余,google一下“libsvm使用”,就会N多的资源,但是,为了让你少费点心,在这里就简单的介绍一下,有不清楚的只有动动你的mouse了。
需要说明的是,2.89版本以前,都是svmscale、svmtrain和svmpredict,最新的是svm-scale、svm-train 和svm-predict,要是用不习惯,只需要把那四个exe文件名去掉中间的短横线,改成svmscale、svmtrain和svmpredict就可以了,我们还是按原来函数名的讲。
1. libSVM的数据格式Label 1:value 2:value ….Label:是类别的标识,比如上节train.model中提到的1 -1,你可以自己随意定,比如-10,0,15。
当然,如果是回归,这是目标值,就要实事求是了。
Value:就是要训练的数据,从分类的角度来说就是特征值,数据之间用空格隔开;比如: -15 1:0.708 2:1056 3:-0.3333需要注意的是,如果特征值为0,特征冒号前面的(姑且称做序号)可以不连续。
如:-15 1:0.708 3:-0.3333表明第2个特征值为0,从编程的角度来说,这样做可以减少内存的使用,并提高做矩阵内积时的运算速度。
我们平时在matlab中产生的数据都是没有序号的常规矩阵,所以为了方便最好编一个程序进行转化。
2. svmscale的用法svmscale是用来对原始样本进行缩放的,范围可以自己定,一般是[0,1]或[-1,1]。
缩放的目的主要是:1)防止某个特征过大或过小,从而在训练中起的作用不平衡;2)为了计算速度。
因为在核计算中,会用到内积运算或exp运算,不平衡的数据可能造成计算困难。
用法:svmscale [-l lower] [-u upper][-y y_lower y_upper] [-s save_filename] [-r restore_filename] filename其中,[]中都是可选项:-l:设定数据下限;lower:设定的数据下限值,缺省为-1-u:设定数据上限;upper:设定的数据上限值,缺省为1-y:是否对目标值同时进行缩放;y_lower为下限值,y_upper为上限值;-s save_filename:表示将缩放的规则保存为文件save_filename;-r restore_filename:表示将按照已经存在的规则文件restore_filename进行缩放;filename:待缩放的数据文件,文件格式按照libsvm格式。
默认情况下,只需要输入要缩放的文件名就可以了:比如(已经存在的文件为test.txt) svmscale test.txt这时,test.txt中的数据已经变成[-1,1]之间的数据了。
但是,这样原来的数据就被覆盖了,为了让规划好的数据另存为其他的文件,我们用一个dos的重定向符> 来另存为(假设为out.txt):svmscale test.txt > out.txt运行后,我们就可以看到目录下多了一个out.txt文件,那就是规范后的数据。
假如,我们想设定数据范围[0,1],并把规则保存为test.range文件:svmscale –l 0 –u 1 –s test.range test.txt > out.txt这时,目录下又多了一个test.range文件,可以用记事本打开,下次就可以用-r test.range来载入了。
3. svmtrain的用法svmtrain我们在前面已经接触过,他主要实现对训练数据集的训练,并可以获得SVM 模型。
用法:svmtrain [options] training_set_file [model_file]其中,options为操作参数,可用的选项即表示的涵义如下所示:-s 设置svm类型:0 – C-SVC1 – v-SVC2 – one-class-SVM3 –ε-SVR4 – n - SVR-t 设置核函数类型,默认值为20 -- 线性核:u'*v1 -- 多项式核:(g*u'*v+ coef 0)degree2 -- RBF 核:exp(-γ*||u-v||2)3 -- sigmoid 核:tanh(γ*u'*v+ coef 0)-d degree: 设置多项式核中degree的值,默认为3-gγ: 设置核函数中γ的值,默认为1/k,k为特征(或者说是属性)数;-r coef 0:设置核函数中的coef 0,默认值为0;-c cost:设置C-SVC、ε-SVR、n - SVR中从惩罚系数C,默认值为1;-n v :设置v-SVC、one-class-SVM 与n - SVR 中参数n ,默认值0.5;-p ε:设置v-SVR的损失函数中的e ,默认值为0.1;-m cachesize:设置cache内存大小,以MB为单位,默认值为40;-e ε:设置终止准则中的可容忍偏差,默认值为0.001;-h shrinking:是否使用启发式,可选值为0 或1,默认值为1;-b 概率估计:是否计算SVC或SVR的概率估计,可选值0 或1,默认0;-wi weight:对各类样本的惩罚系数C加权,默认值为1;-v n:n折交叉验证模式;model_file:可选项,为要保存的结果文件,称为模型文件,以便在预测时使用。
