郑州大学随机信号处理大作业
随机信号分析大作业

随机信号分析大作业2016.12.6希尔伯特变换及其应用一、背景及意义在通信系统中,经常需要对一个信号进行正交分解,即分解为同相分量和正交分量。
由于希尔伯特变换可以提供90度的相位变化而不影响频谱分量的幅度,即对信号进行希尔伯特变换就相当于对该信号进行正交移相,使它成为自身的正交对。
因此,希尔伯特在通信领域获得了广泛应用。
对HHT采样频率、终止准则、曲线拟合、边界处理以及模态混叠等问题进行了分析,并基于HHT的时间特征尺度概念,提出了一种新的边界处理方法:边界局部特征尺度延拓法,较好地改善了边界效应对EMD分解的影响。
将HHT用于电力系统的信号处理,并根据HHT的信号突变检测性能,提出了一种超高压输电线路的EMD故障测距方法。
仿真实验表明,该方法能很好地实现故障定位及测距。
物理意义:希尔伯特可看成一种滤波,其本质上是对所有输入信号的90度相移器;对于稳定的实因果信号,其傅立叶变换的实部和虚部满足希尔伯特变换关系,同时其对数幅度谱和相位谱之间也满足此关系,前提是该信号为最小相位信号。
工程意义:对于自由度为一维的条信号,比如PAM,其等效基带信号是实的,这意味着对应的基带频谱是共轭对称的,即一半的频谱是冗余的,那么就可以将频谱滤除一半再进行传输,这就形成了所谓的单边带调制(SSB)。
而理论上,一个信号和其Hilbert 变化后的值相加,就可以得到所谓解析信号,该信号只保留原信号的正频谱。
而单边带调制虽然节省传输频率,但为了进行边带滤波,必须进行复杂的频谱成形,发送和接收的复杂度都比较高,相干载波的相位误差所造成的影响大。
所以,选择PAM信号进行频谱滤除的滤波器具有一定的滚降,即保留部分PAM信号中的冗余频谱,这样就成为VSB调制。
二、希尔伯特变换的发展现状近年来,随着现代信号的向前发展,人们从不同的研究领域和应用角度出发,提出了拓展经典Hilbert变换,提出了分数阶Hilbert变换,拓展了它的应用范围。
《随机信号分析》大作业概述.

大连民族学院《随机信号分析》大作业9.3.2随机变量及其数字特征运算的MATLAB实现班级:学号:姓名:指导老师:二零一五年一月《随机信号分析》大作业摘要编制一通用程序,实现产生两个任意指定区间[a,b]和[c,d]上的均匀分布的随机变量。
分别计算这两个随机变量的均值和方差以及两个随机变量的协方差和相关系数,并根据计算结果分析这两个随机变量的相关性(两个随机数的长度要相等)。
关键词:均值;方差;协方差;相关系数目录摘要 (II)第1章要求 (1)1.1预习内容 (1)1.2任务 (1)1.3思考题 (1)第2章随机变量及其数字特征运算 (2)2.1连续型随机变量的数学期望(均值) (2)2.1.1连续型随机变量的数学期望 (2)2.1.2数学期望的性质 (2)2.2随机变量的方差 (2)2.2.1定义 (2)2.2.2性质 (3)2.3协方差和相关系数 (3)2.3.1定义 (3)2.3.2协方差的性质 (3)2.3.3相关系数的性质 (3)第3章程序实现及代码 (4)3.1任务 (4)3.1.1 代码 (4)3.1.2 结果 (5)3.1.3 结果分析 (6)3.2思考题 (7)3.2.1 代码 (7)3.2.2 结果 (8)参考文献 (11)B 卷 (12)第1章要求1.1 预习内容计算随机变量数字特性的部分MATLAB函数见表9.2,这些函数的调用方法及使用举例参见9.1节的相关内容。
1.2 任务编制一通用程序,实现产生两个任意指定区间[a,b]和[c,d]上的均匀分布的随机变量。
分别计算这两个随机变量的均值和方差以及两个随机变量的协方差和相关系数,并根据计算结果分析这两个随机变量的相关性(两个随机数的长度要相等)。
1.3 思考题利用MATLAB的在线帮助功能,自学与指数分布有关的MATLAB函数的使用方法。
编制一通用程序,实现产生任意指定参数λ1和λ2的两个指数分布随机变量(随机元素为30个)。
随机信号处理作业南理工(有程序)

《随机信号处理》上机实验仿真报告学院:电子工程与光电技术学院指导老师:顾红日期:2014年11月10日题目1:<问题>线性调频脉冲信号,时宽10us ,带宽543MHz ,对该信号进行匹配滤波后,即脉压处理,处理增益为多少?脉压后的脉冲宽度为多少?并用图说明脉压后的脉冲宽度,内差点看3dB 带宽,以该带宽说明距离分辨率与带宽的对应关系。
建议补充:比较矩形视频脉冲信号、矩形包络单个中频脉冲信号、线性调频矩形脉冲信号匹配滤波,说明脉压后的脉冲3dB 宽度变化,与原脉冲的宽度比较得出压缩比即增益。
另外,通过仿真加噪声0dB 信噪比来看脉压后信噪比有没有提升。
<理论分析>:(1)线性调频信号(LFM )是雷达中常用的信号,其数学表达式为:212()2()()c j f t kt t s t rect eTπ+= 式中c f 为载波频率,t rect T ⎛⎫⎪⎝⎭为矩形信号: 11()0,t t rect TT elsewise⎧ , ≤⎪=⎨⎪ ⎩当TB>1时,LFM 信号特征表达式如下:(2)在输入为确知加白噪声的情况下,所得输出信噪比最大的线性滤波器就是匹配滤波器。
线性调频信号叠加上噪声其表达式为:2()j kt t t S rect e Tπ=()(,10)t S t awgn S =白噪声条件下,匹配滤波器的脉冲响应:*()()o h t ks t t =-<仿真程序>:B=543e6; %带宽(这里设置带宽为学号后三位),程序段①从这行开始 fs=10*B; %采样频率 ts=1/fs;T=10e-6; %脉宽10μs N=T/ts; %采样点数 t=linspace(-T/2,T/2,N); K=B/T;a=1; %这里调频信号幅值假设为1 %% 线性调频信号si=a*exp(j*pi*K*t.^2); figure(1)plot(t*1e6,si);xlabel('t/μs');ylabel('si');title('线性调频信号时域波形图');grid on; sfft=fft(si);f=(0:length(sfft)-1)*fs/length(sfft)-fs/2;%f=linspace(-fs/2,fs/2,N); figure(2)plot(f*1e-6,fftshift(abs(sfft)));xlabel('f/MHz');ylabel('sfft');title('线性调频信号频域波形图');grid on; axis([-300,300,-inf,inf]); %程序段①到这行结束 %% 叠加高斯白噪声 ni=rand(1,N);disp('输入信噪比为:');SNRi=10*log10(a^2/var(ni)/2) xi=ni+si; figure(3)plot(t*1e6,real(xi));xlabel('t/us');ylabel('xi');title('叠加噪声后实际信号时域波形图'); x1fft=fft(xi); %输入信号频谱f=(0:length(x1fft)-1)*fs/length(x1fft)-fs/2; figure(4)plot(f*1e-6,fftshift(abs(x1fft)));xlabel('f/MHz');ylabel('x1fft');title('叠加噪声后实际信号频谱图');grid on; %% 匹配滤波器ht=exp(-j*pi*K*t.^2);x2=conv(ht,xi);L=2*N-1;ti=linspace(-T,T,L);ti=ti*B; %换算为B的倍数X2=abs(x2)/max(abs(x2));figure(5)plot(ti,20*log10(X2+1e-6));xlabel('t/B');ylabel('匹配滤波幅度');title('匹配滤波结果图');grid on; axis([-3,3,-4,inf]);%% 计算信噪比X22=abs(x2);%实际信号n2=conv(ht,ni);%噪声n22=abs(n2);s2=conv(ht,si);%信号s22=abs(s2);SNRo=(max(s22)^2)/(var(n2))/2;disp('输出信噪比为:');SNRo=10*log10(SNRo)disp('信噪比增益为:');disp(SNRo-SNRi)%% 匹配滤波器的幅频特性hw=fft(ht);f2=(0:length(hw)-1)*fs/length(hw)-fs/2;f2=f2/B;hw1=abs(hw);hw1=hw1./max(hw1);plot(f2,fftshift(20*log(hw1+1e-6)));xlabel('f/B');ylabel('幅度');title('匹配滤波器的幅频特性图');%% 匹配滤波器处理后的信号Sot=conv(si,ht);subplot(211)L=2*N-1;t1=linspace(-T,T,L);Z=abs(Sot);Z=Z/max(Z);Z=20*log10(Z+1e-6);Z1=abs(sinc(B.*t1));Z1=20*log10(Z1+1e-6);t1=t1*B;plot(t1,Z,t1,Z1,'r.');axis([-15,15,-50,inf]);grid on;legend('emulational','sinc');xlabel('Time in sec \times\itB');ylabel('Amplitude,dB');title('匹配滤波器处理后信号');subplot(212)N0=3*fs/B;t2=-N0*ts:ts:N0*ts; t2=B*t2;plot(t2,Z(N-N0:N+N0),t2,Z1(N-N0:N+N0),'r.'); axis([-inf,inf,-50,inf]);grid on;set(gca,'Ytick',[-13.4,-4,0],'Xtick',[-3,-2,-1,-0.5,0,0.5,1,2,3]); xlabel('Time in sec \times\itB'); ylabel('Amplitude,dB');title('匹配滤波器处理后信号(放大)'); %% 输出频谱 xfft=fft(x2);f3=(0:length(xfft)-1)*fs/length(xfft)-fs/2; xfft1=abs(xfft);xfft1=xfft1./max(xfft1); figure(7)plot(f3/B,fftshift(20*log(xfft1+1e-6)));xlabel('f/B');ylabel('幅度');title('输出信号频谱图');<仿真结果与分析>:对于一个理想的脉冲压缩系统,要求发射信号具有非线性的相位谱,并使其包络接近矩形;其中)(t S 就是信号s(t)的复包络。
随机信号大作业

随机信号大作业随机信号大作业第一章上机题:设有随机初相信号X(t)=5cos(t+),其中相位是在区间(0,2)上均匀分布的随机变量。
(1)试用Matlab编程产生其三个样本函数。
(2)产生t=0时的10000个样本,并画出直方图估计P(x)画出图形。
解:(1)由Matlab产生的三个样本函数如下图所示:程序源代码:clcclearm=unifrnd(0,2*pi,1,10);fork=1:3t=1:0.1:10;X=5*cos(t+m(k));plo t(t,X);holdonendxlabel('t');ylabel('X(t)');gridon;axistight;(2)产生t=0时的10000个样本,并画出直方图估计P(x)的概率密度并画出图形。
源程序代码:clear;clc;=2*pi*rand(10000,1);x=5*cos();figure(2),hist(x,20);holdon;第二章上机题:利用Matlab程序设计一正弦型信号加高斯白噪声的复合信号。
(1)分析复合信号的功率谱密度,幅度分布的特性;(2)分析复合信号通过RC积分电路后的功率谱密度和相应的幅度分布特性;(3)分析复合信号通过理想低通系统后的功率谱密度和相应的幅度分布特性。
解:设正弦信号的频率为10HZ,抽样频率为100HZx=sin(2*pi*fc*t)正弦曲线图:程序块代码:clearall;fs=100;fc=10;n=201;t=0:1/fs:2;x=sin(2*pi*fc*t);y=awgn(x,10);m=50;i=-0.49:1/fs:0.49;forj=1:mR(j)=sum(y(1:n-j-1).*y(j:199),2)/(n-j);Ry(49+j)=R(j);Ry(51-j)=R(j);endsubplot(5,2,1);plot(t,x,'r');title('正弦信号曲线');ylabel('x');xlabel('t/20pi');grid;(1)正弦信号加上高斯白噪声产生复合信号y:y=awgn(x,10)对复合信号进行傅里叶变换得到傅里叶变换:Y(jw)=fft(y)复合信号的功率谱密度函数为:G(w)=Y(jw).*conj(Y(jw)/length(Y(jw)))复合信号的曲线图,频谱图和功率谱图:程序块代码:plot(t,y,'r');title('复合信号曲线');ylabel('y');xlabel('t/20pi');grid;程序块代码:FY=fft(y);FY1=fftshift(FY);f=(0:200)*fs/n-fs/2;plot(f,abs(FY1),'r');title('复合信号频谱图');ylabel('F(jw)');xlabel('w');grid;程序块代码:P=FY1.*conj(FY1)/length(FY1);plot(f,P,'r');title('复合信号功率谱密度图');ylabel('G(w)');xlabel('w');grid;(2)正弦曲线的复合信号通过RC积分电路后得到信号为:通过卷积计算可以得到y2即:y2=conv2(y,b*pi^-b*t)y2的幅度分布特性可以通过傅里叶变换得到Y2(jw)=fft(y2)y2的功率谱密度G2(w)=Y2(jw).*conj(Y2(jw)/length(Y2(jw)))复合信号通过RC积分电路后的曲线频谱图和功率谱图:程序块代码:b=10;y2=conv2(y,b*pi^-b*t);Fy2=fftshift(fft(y2));f=(0:400)*fs/n-fs/2;plot(f,abs(Fy2),'r');title('复合信号通过RC系统后频谱图');ylabel('Fy2(jw)');xlabel('w');grid;程序代码:P2=Fy2.*conj(Fy2)/length(Fy2);plot(f,P2,'r');title('复合信号通过RC系统后功率密度图');ylabel('Gy2(w)');xlabel('w');grid;(3)复合信号y通过理想滤波器电路后得到信号y3通过卷积计算可以得到y3即:y3=conv2(y,sin(10*t)/(pi*t))y3的幅度分布特性可以通过傅里叶变换得到Y3(jw)=fft(y3),y3的功率谱密度G3(w)=Y3(jw).*conj(Y3(jw)/length(Y3(jw)))复合信号通过理想滤波器后的频谱图和功率密度图:程序块代码:y3=conv2(y,sin(10*t)/(pi*t));Fy3=fftshift(fft(y3));f3=(0:200)*fs/n-fs/2;plot(f3,abs(Fy3),'r');title('复合信号通过理想滤波器频谱图');ylabel('Fy3(jw)');xlabel('w');grid;程序块代码:P3=Fy3.*conj(Fy3)/length(Fy3);plot(f3,P3,'r');title('理想信号通过理想滤波器功率密度图');ylabel('Gy3(w)');xlabel('w');grid;。
郑州大学随机信号处理大作业

2.2
傅里叶变换
傅立叶变换(DFT)认为:有限长的数据段可看作无限长的取样序列进行加窗 截断后的结果。不论是数据加窗还是自相关函数加窗,在频率域都会发生“泄 露”现象,即功率谱主瓣的能量泄露到旁瓣中去,这样,弱信号的主瓣很容易 被强信号的旁瓣淹没或畸变,造成谱的模糊与失真。为了降低旁瓣,很多学者 在选择窗口函数的形式上和窗口处理函数方法上想办法,但是所有的旁瓣抑制
4 / 20
2.3.3 Levinson-Durbin 快速递推法 用线性方程组的常用算法(例如高斯消元法)求解(2. 3. 9)式, 需要的运算量数 量级为 p 3 。 但若利用系数矩阵的对称性和 Toeplitz 性质, 则可构成一些高效算法, Levinson-Durbin 算法是其中最著名、应用最广泛的一种。这种算法的运算量量 级为 p 2 。这是一种按阶次进行递推的算法,即首先以 AR (0)和 AR (1)模型参数作
2 / 20
技术都是以损失谱分辨率为代价的。谱分析应用中,谱分辨率和低旁瓣是同样 重要的指标,在作 DFT 时,人们常在有效数据后面补一些零,使得补零后的数 据 N 为 2 的整数次幂以便于快速傅立叶变换,而那些认为在傅立叶变换之前对 数据段补零可以改善周期图的谱分辨率是一种模糊的错误概念,因为补零后, 虽然谱线能够增密,但因为补零没有增加任何新的信息,因此不可能提高分辨 率。谱分辨率的极限只能由取样数据段的长度决定。 2.3 AR 模型
1 / 20
第2章 谱估计理论基础
2.1 几种主要的谱估计方法 信号处理的核心,说到底就是如何保证在信号受到干扰产生失真的情况下, 正确恢复原有信号,提取有用信息。而功率谱(简称谱)估计就是信号处理的一个 重要分支,它应用范围很广,日益受到各学科和应用领域的极大重视。它是在 频率域研究随机信号的统计规律,其中心目的为了估计出随机干扰信号并将其 去除,提取有用信号,对语音、声纳、雷达等信号处理,有着重要的意义,广 泛应用于通信、控制、地球物理,它的研究对象主要是零均值平稳高斯过程。 以傅立叶变换为基础谱估计一般称为的传统(或经典)谱估计方法,传统谱估计法 又可以分为直接法和间接法, 后来由于 FFT 的出现, 直接法和间接法往往被结合 起来使用。在信号分析方法中,傅立叶变换是较常用的数学工具。时间信号经 过傅立叶变换后,可得到它的频谱,平稳随机过程的相关函数和它的功率谱密 度是一对傅立叶变换对。 近几年,在信号功率谱密度估计方面出现了许多新的算法,其中应用最广 泛的算法是 1967 年由 Burg 提出的最大嫡谱估计, 这些新方法连同演变出来的各 种算法不下几十种,统称为现代谱估计。它是相对经典谱估计方法而言的。其 比较有名的是:Levinson-Durbin 算法自回归模型、Burg 算法的最大嫡分析、正反 向线性预测的最小二乘算法、自回归模型、滑动平均模型、自回归一滑动平均 模型 Pisarenko 谐波分解法、Prony 提取极点法、Prony 谱线分解法以及 Capon 最大似然估计法。根据算法的基本属性,把这些算法归纳在图 2. l
随机信号大作业

随机信号⼤作业随机信号⼤作业02111465 冯英旺1.⽤matlab编程产⽣随机初相信号X(t)=5cos(t+a)(其中a是区间(0,2π)上均匀分布的随机变量)的三个样本函数。
解:程序如下:a=unifrnd(0,2*pi,1,10);t=0:0.1:10;for j=1:3x=5*cos(t+a(j));plot(t,x);hold onendxlabel('t');ylabel('x(t)');gridon;axis tight;运⾏结果:2.利⽤matlab程序设计⼀正弦型信号加⾼斯⽩噪声的复合信号。
分析复合信号通过理想低通系统后的功率谱密度和相应的幅度分布特性。
解:设正弦信号为x=sin(2*pi*10*t)先画出复合信号曲线程序如下:clear all;fs=100;fc=10;n=201;t=0:1/fs:2;x=sin(2*pi*fc*t);y=awgn(x,10);plot(t,y,'r');title('复合信号曲线');ylabel('y');xlabel('t/20pi');grid;通过理想低通系统后的曲线和频谱图,程序如下:y1=conv2(y,sin(10*t)/(pi*t)); plot(t,y1,'r');title('通过低通系统复合信号曲线');ylabel('y1');xlabel('t/20pi');grid;Fy=fftshift(fft(y1));f1=(0:200)*fs/n-fs/2;plot(f1,abs(Fy),'r');title('复合信号通过理想低通系统频谱图'); ylabel('Fy(jw)');xlabel('w');grid;功率谱,源程序如下:P=Fy.*conj(Fy)/length(Fy);plot(f1,P,'r');title('复合信号通过理想低通系统功率谱'); ylabel('Gy(w)');xlabel('w');grid;3.利⽤matlab程序分别设计⼀正弦型信号,⾼斯⽩噪声信号。
随机信号分析与处理习题解答_罗鹏飞

n
n
∑ ∑ E( X ) = mP{X = m} = mCnm pm (1− p)n−m
m=0
m=0
∑n
=m
n!
pm (1− p)n−m
m=0 m!(n − m)!
∑ = n m n(n −1)(n − 2) (n − m +1) pm (1− p)n−m
1,后 m 个取 0)的概率为 pm (1− p)n−m 。而 X 取 m 的两两互不相容的方式有 Cnm 种可能,
故有
P{X = m} = Cnm p m (1 − p)n−m , m = 0,1, 2,....n
n
∑ 所以 X = Xi 服从参数为 n,p 的二项分布。 i =1
且有 E( Xi ) = 1⋅ P{Xi = 1}+ 0 ⋅ P{Xi = 0} = p ,
1.1 设有两个随机变量 X 和 Y,证明
fY|X ( y | x) =
f (x, y) f X (x)
,
f X |Y
(x
|
y)
=
f (x, y) fY (y)
y x+Δx
∫ ∫ f (x, y)dxdy
提示:首先证明 F ( y | x < X ≤ x + Δx) = −∞ x
,然后对 y 求导得,
i =1
i =1
n
n
D( X ) = D(∑ Xi ) = ∑ D( Xi ) = np(1− p)
i =1
i =1
1.3 设随机变量 Y 与 X 满足如下函数关系
Y = g( X ) = sin( X + θ)
随机信号分析仿真

随机信号分析原理大作业报告专业:水声工程姓名: xxx学号:xxxxxxxxxx题目要求:给定一个白噪声信号,它的均值和方差自定。
1.设计一个线性滤波器,使该滤波器的输出为一个窄带信号。
并给出该窄带信号在不同的3个典型中心频率和带宽时的波形。
2.对该滤波器输出的上述窄带信号,用莱斯表示法对其进行建模,画出)(t a和)(t b的波形。
3.计算上述3种窄带信号对应的瞬时频率和瞬时相位,并进行包络检测。
)整个频率区间,即图6 滤波器2输出信号的时域波形附件一滤波器1输出信号仿真程序clear allclose allclc%产生高斯白噪声N=25000; %序列长度my_var = 2;noise = sqrt(my_var)*randn(1,N);%均值为0,方差为2 figure(1)plot(noise)title('均值为0方差为2的高斯白噪声')grid onfs = 25000;%采样频率f0 = 1000;%中心频率%滤波器f_pass = [900 1100];omega_pass = 2*f_pass/fs;b = fir1(192,omega_pass);figure(2)freqz(b,1,1024)%滤波器幅度和相位图像grid on%噪声通过窄带滤波器filter_outpu = filter(b,1,noise);figure(3)plot(filter_outpu)title('窄带信号在时域的波形')grid on%做fft变换Nfft = fs;fft_x = fft(filter_outpu,Nfft);ff = 0:fs/Nfft:fs-fs/Nfft;figure(4)plot(ff,20*log10(abs(fft_x)))%窄带信号的频谱title('窄带信号的频谱')xlabel('频率 Hz')ylabel('幅度 dB')grid on%窄带信号在时域的波形X_t = filter_outpu;t = 0:1/fs:1-1/fs;figure(5)plot(t,X_t)title('窄带信号在时域的波形')xlabel('t / s')grid on%莱斯表示法h_X = hilbert(X_t,Nfft) ;%希尔伯特变换omega0 = 2*pi*f0;A_t = X_t.*cos(omega0*t)+h_X.*sin(omega0*t);B_t = -1*X_t.*sin(omega0*t)+h_X.*cos(omega0*t); figure(6)subplot(2,1,1);plot(t,A_t)grid onhold onsubplot(2,1,2);plot(t,B_t)grid on%瞬时频率瞬时相位theta_t = atan(h_X./X_t); xh1=unwrap(angle(h_X)); omega_t=fs*diff(xh1)/(2*pi); figure(7)plot(omega_t);title('瞬时频率')omega_t = diff(theta_t); figure(8)plot(t,theta_t)title('瞬时相位')grid on%包络检测am = abs(h_X);figure(9)plot(t,X_t,t,am,'r') %包络title('窄带信号的包络')grid on。
数字信号处理教程之大作业

数字信号处理教程之大作业郭航(2014212596)1)解:参考书p3862)解:参考书p3961.数字滤波器通带截止频率π/5rad 通带最大衰减3dB 阻带截止频率3*π/5rad 阻带最小衰减20dB2.频率预畸变(T=2)047121.37638192tan tan6232910.32491969tan tan1032s 102p p===Ω===Ωπωπωs793.159398.0456.23854.23*8187.0*331*9512.0*3311111211231231231311221131231131213121a 3132221112.031105.031123112131112121)(1.0))(()()())(()()()()(2,,,)2()(--s )(21s 2)21122(312521)(+-----------=----=---==-=-=+=+===-==⇒-=-==-====⇒--+=-=+-+=+-+=++=--------------∑∑∑z z z z z z z z z z e zez e z e k z e A nT nT a t t tt Nk t s k a k kk a T T T k s Kk z H sT e en u nT h n h e e t u t u e e t u e A t h s s A A s s s A s H s s s s s s H 则有:部分分式形式:3.设计其系统函数(p355-(7.5.24))593154531.125392584.1997697634.1) 6232910.32491969 047121.37638192lg(2/)110110(lg )lg(2/)110110(lg 3.021.01.0==⎥⎦⎤⎢⎣⎡--=⎥⎥⎦⎤⎢⎢⎣⎡ΩΩ--≥p s R A s s N所以 N=2 查表7.4得14142136.11)(2a ++=s s s H4.求数字滤波器的系统函数4363449349.0463.15434211047121.37638192110*21.0c ==-Ω=ΩNA ss1903969022.0436*******.0*4142136.11903969022.04142136.1)()s (2222++=Ω+Ω+Ω==Ωs s s s H H cc c sa lp c16170849412.01903969022.0001903969022.0210210======e e e d d d根据 表7.9 得807481843.1)(3171882269.0/)(8958353866.0/)22(1053382101.0/)(2106764203.0/)22(1053382101.0/)(221022102220122102220122100=++==+-=-=-==+-==-==++=c e c e e R R c e c e e B R c e e B R c d c d d A R c d d A R c d c d d A21212211221103171882269.08958353866.011053382101.021********.010********.01)(--------+-++=++++=zz z z z B z B zA z A A z HT=2; %设置采样周期为2fs=1/T; %采样频率为周期倒数Wp=0.2*pi/T;Ws=0.6*pi/T; %设置归一化通带和阻带截止频率Ap=3;As=20; %设置通带最大和最小衰减[N,Wc]=buttord(Wp,Ws,Ap,As,'s'); %调用butter函数确定巴特沃斯滤波器阶数[B,A]=butter(N,Wc,'s'); %调用butter函数设计巴特沃斯滤波器W=linspace(0,pi,400*pi); %指定一段频率值hf=freqs(B,A,W); %计算模拟滤波器的幅频响应subplot(2,1,1);plot(W/pi,abs(hf)/abs(hf(1))); %绘出巴特沃斯模拟滤波器的幅频特性曲线grid on;title('巴特沃斯模拟滤波器');xlabel('Frequency/Hz');ylabel('Magnitude');[D,C]= bilinear (B,A,fs); %调用双线性变换法Hz=freqz(D,C,W); %返回频率响应subplot(2,1,2);plot(W/pi,abs(Hz)/abs(Hz(1))); %绘出巴特沃斯数字低通滤波器的幅频特性曲线grid on; title('巴特沃斯数字滤波器');xlabel('Frequency/Hz');ylabel('Magnitude');wp=0.2*pi;ws=0.6*pi;Rp=3;As=20;ripple=10^(-Rp/20);Attn=10^(-As/20);Fs=0.5;T=1/Fs;Omgp=(2/T)*tan(wp/2);Omgs=(2/T)*tan(ws/2);[n,Omgc]=buttord(Omgp,Omgs,Rp,As,'s')[ba1,aa1]=butter(n,Omgc,'s');[bd,ad]=bilinear(ba1,aa1,Fs)[sos,g]=tf2sos(bd,ad)[H,w]=freqz(bd,ad);dbH=20*log10((abs(H)+eps)/max(abs(H)));subplot(2,2,1),plot(w/pi,abs(H));ylabel('|H|');title('幅度响应');axis([0,1,0,1.1]);set(gca,'XTickMode','manual','XTick',[0,0.25,0.4,1]); set(gca,'YTickMode','manual','YTick',[0,Attn,ripple,1]); gridsubplot(2,2,2),plot(w/pi,angle(H)/pi);ylabel('\phi');title('相位响应');axis([0,1,-1,1]);set(gca,'XTickMode','manual','XTick',[0,0.25,0.4,1]); set(gca,'YTickMode','manual','YTick',[-1,0,1]);gridsubplot(2,2,3),plot(w/pi,dbH);title('幅度响应(dB)');ylabel('dB');xlabel('频率(\pi)');axis([0,1,-40,5]);set(gca,'XTickMode','manual','XTick',[0,0.25,0.4,1]); set(gca,'YTickMode','manual','YTick',[-50,-15,-1,0]); gridsubplot(2,2,4),zplane(bd,ad);axis([-1.1,1.1,-1.1,1.1]);title('零极图');n =2Omgc =0.4363bd =0.1053 0.2107 0.1053ad =1.0000 -0.8958 0.3172sos =1.00002.0000 1.0000 1.0000 -0.8958 0.3172g =0.1053。
郑州大学 电气工程信号分析与处理实验一

郑州大学 电气工程学院实 验 报 告学生姓名 学号20090220 成绩 批阅人 专业 自动化 同组实验人 实验名称 离散时间序列的卷积 所属课程 信号分析与处理 实验室(房间号) 3207 实验时间11年12月 日 时-- 时 一 实验目的学会用MATLAB 实现对离散时间序列的卷积,掌握利用h(n)与输入x(n)卷积来求系统零状态响应的方法。
二 实验设备(名称,型号或规格,数量)或软件名称MATLAB 软件使用MATLAB 中求卷积函数的conv(),并对结果分析总结。
三 实验内容(接线图或实验程序等)和步骤实验内容:设线性时不变系统的单位脉冲响应为h(t)=)()9.0(t n ε,输入序列分别为()=n x )(t ε-)10(-t ε,求系统的输出y(n)。
实验程序:nx=-4:40;x=zeros(1,length(nx));x(1,5:14)=1;nh=0:40;h=(0.9).^nh;[y,ny]=conv_m(x,nx,h,nh);subplot(3,1,1);stem(nx,x,'filled');axis([-4,40,0,1]);titl e('x[n]');subplot(3,1,2);stem(nh,h,'filled');axis([-4,40,0,1]);titl e('h[n]');subplot(3,1,3);stem(ny,y,'filled');axis([-4,40,0,8]);titl e('y[n]');四实验数据记录实验结果:x[n]0.51h[n]05101520253035405y[n]改变参数以后的程序:nx=-4:40;x=zeros(1,length(nx)); x(1,5:24)=1; nh=0:40;h=(0.9).^nh;[y,ny]=conv_m(x,nx,h,nh);subplot(3,1,1);stem(nx,x,'filled');axis([-4,40,0,1]);titl e('x[n]');subplot(3,1,2);stem(nh,h,'filled');axis([-4,40,0,1]);titl e('h[n]');subplot(3,1,3);stem(ny,y,'filled');axis([-4,40,0,10]);tit le('y[n]');输出结果:x[n]00.51h[n]0510152025303540510y[n]五 实验结果分析从上图可以看出,输出序列的峰值在输入序列值从1变为0时出现。
随机振动与信号分析(研究生大作业)试验报告

课程:《随机振动与信号分析》作业题目:动力特性测试报告小组成员:专业方向:结构工程学院名称:土木工程学院指导老师:****** 教授2014 年7月目录第一章实验目的 (3)第二章实验原理 (3)第三章实验仪器及操作步骤 (7)3.1 实验仪器 (7)3.2 实验步骤 (9)第四章实验数据处理及分析..................................................... 错误!未定义书签。
4.1振动信号的预处理 ............................................................ 错误!未定义书签。
4.1.1快速傅里叶变换(FFT).................. 错误!未定义书签。
4.2.2消除趋势项 ............................. 错误!未定义书签。
4.2.3平滑处理 ............................... 错误!未定义书签。
4.2振动信号的频域分析........................................................ 错误!未定义书签。
4.2.1平均周期图方法 ......................... 错误!未定义书签。
4.2.2自功率谱密度函数 ....................... 错误!未定义书签。
4.2.3互功率谱密度函数 ....................... 错误!未定义书签。
4.2.4频响函数 ............................... 错误!未定义书签。
4.2.5相干函数 ............................... 错误!未定义书签。
4.3振动信号的模态分析 (20)第五章数据统计分析 ................................................................. 错误!未定义书签。
随机信号大作业

随机信号大作业
大作业建议如下:
1. 随机信号的统计分析:选择一个随机信号,对其进行统计分析。
可以计算平均值、
方差、自相关函数、互相关函数等指标,了解信号的基本统计特性。
2. 随机信号的功率谱密度估计:选择一个随机信号,通过频谱估计方法(如傅里叶变换、周期图法、自相关法等),对其功率谱密度进行估计。
比较不同方法的估计结果,并讨论其优缺点。
3. 高斯白噪声的产生及检测:了解高斯白噪声的定义及特性,编程实现高斯白噪声的
产生,并通过相关统计检验(如卡方检验、Kolmogorov-Smirnov检验),对生成的噪声进行检测。
4. 随机过程的模拟及识别:选择一种随机过程(如马尔可夫过程、线性时不变过程等),编程实现其模拟,并通过识别方法(如自回归模型、卡尔曼滤波器等),对实
际观察到的随机过程进行识别和模型拟合。
5. 随机信号的滤波:选择一个随机信号,设计一个滤波器,对信号进行滤波处理。
可
以比较不同滤波器设计方法(如IIR滤波器、FIR滤波器等)的效果并进行评估。
6. 随机信号的压缩与重构:选择一个随机信号,使用信号压缩算法(如小波变换、奇
异值分解等),对信号进行压缩,并通过信号重构方法,将压缩后的信号进行恢复。
比较不同压缩和重构方法的效果及开销。
以上是一些建议的大作业题目,你可以根据自己的兴趣和能力选择其中一个或结合多
个进行深入研究。
希望对你有帮助!。
随机信号处理计算机作业

计算机作业1题目要求设有AR(2)模型X(n)=-0.3X(n-1)-0.5X(n-2)+W(n),W(n)是零均值正态白噪声,方差为4。
(1)用MATLAB模拟产生X(n)的500观测点的样本函数,并绘出波形;(2)用产生的500个观测点估计X(n)的均值和方差;(3)画出理论的功率谱;(4)估计X(n)的相关函数和功率谱。
实验目的通过本实验,加深对信号均值,方差,相关函数和功率谱估计的理解。
实验程序代码(在matlab的环境下)%%%AR(2)模型%%产生样本函数wn=2.*randn(1,500);n=1:500;xn(1)=1;xn(2)=2;for i=3:500xn(i)=-0.3*xn(i-1)-0.5*xn(i-2)+wn(i);endfigure;plot(xn);title('离散信号样本函数原始波形');%%%估计x(n)的均值和方差m_xn=mean(xn);m_xnvar_xn=var(xn);var_xn%%%画出理论的功率谱figure;Rxx=xcorr(xn)/25000;Pww=fft(Rxx);f=(0:length(Pww)-1)*1000/length(Pww); plot(f,10*log10(abs(Pww)));title('信号理论功率谱');%%%画出估计的相关函数和功率谱figure;subplot(211);R=xcorr(xn);plot(R);title('信号估计相关函数');[P,w]=periodogram(xn,(hamming(500))'); subplot(212);plot(P);title('信号估计功率谱');实验结果1.离散信号原始样本函数波形2.估计xn的均值(m_xn)和方差(var_xn)m_xn = -0.0933var_xn =5.71413.信号的理论功率谱4.信号估计的相关函数和功率谱计算机作业2题目要求1、模拟一个均匀分布的白噪声通过一个低通滤波器,观测输出信号的概率密度。
通信信号处理仿真大作业
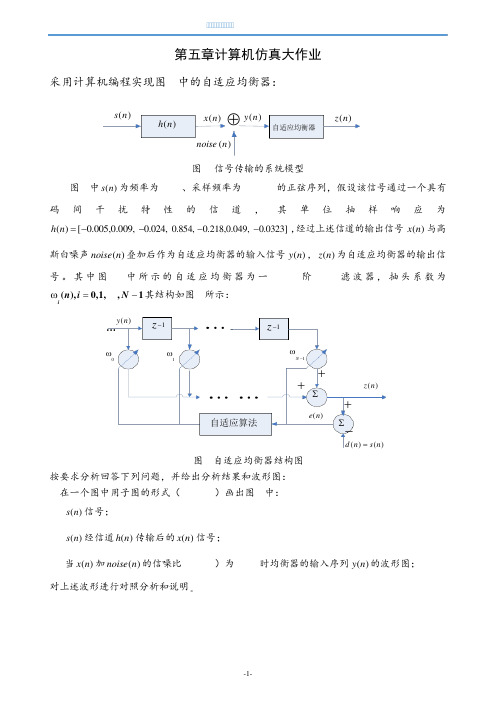
第五章计算机仿真大作业采用计算机编程实现图1中的自适应均衡器:()h n ()s n ()x n ⊕()noise n ()y n 自适应均衡器()z n图1 信号传输的系统模型图1中()s n 为频率为10Hz 、采样频率为1000Hz 的正弦序列,假设该信号通过一个具有码间干扰特性的信道,其单位抽样响应为()[0.005,0.009,0.024,h n =--0.854,0.218,0.049,0.0323]--,经过上述信道的输出信号()x n 与高斯白噪声()noise n 叠加后作为自适应均衡器的输入信号()y n ,()z n 为自适应均衡器的输出信号。
其中图1中所示的自适应均衡器为一N=31阶FIR 滤波器,抽头系数为(),0,1,,1in i N ω=-其结构如图2所示: 1z -()y n 0ω1ω∑∑++()()d n s n =+-()z n ()e n 1z -1N ω-自适应算法图2自适应均衡器结构图按要求分析回答下列问题,并给出分析结果和波形图: 1.在一个图中用子图的形式(subplot )画出图1中: (1)()s n 信号;(2)()s n 经信道()h n 传输后的()x n 信号;(3)当()x n 加()noise n 的信噪比SNR(dB )为20dB 时均衡器的输入序列()y n 的波形图; 对上述波形进行对照分析和说明。
01002003004005006007008009001000-101正弦信号s(n)01002003004005006007008009001000-101x(n)序列1002003004005006007008009001000-101y(n)序列分析说明:s(n)通过具有码间干扰特性的信道h(n),由于信道存在一定的误差和码间干扰使系统的性能下降,x(n)的波形密度减小了,但整体波形没有发生变化。
加入噪声后,y (n )的幅值没有变化,但整个波形由于受到噪声干扰浮现“毛刺”现象,波形不在平滑。
信号分析处理大作业报告+程序

1.设计方案如下①利用MATLAB中的wavread命令来读入语音信号,将它赋值给某一向量。
再将该向量看作一个普通的信号,对其进行FFT变换实现频谱分析,再依据实际情况对它进行滤波。
对于波形图与频谱图(包括滤波前后的对比图)都可以用MATLAB画出。
②由于音频信号是连续且长度未知,故可以采用N阶低通滤波器。
滤掉低频部分的噪音,剩下的就是原信号了。
③将去噪后的信号写成wav格式的文件可以使用wavwrite函数。
2. 步骤①录制一段歌曲,采用Matlab工具对此音频信号用FFT作谱分析。
②录制一段音频信号并命名为信xinhao1.wav存放在文件夹中。
③使用wavread函数读出此信号。
④用函数FFT进行傅里叶变换,得到波形图,幅值图,频谱图。
⑤加入一个随机高斯噪声,将原始信号与噪声叠加产生加噪之后的声音文件,得到xinhao2.wav文件。
⑥通过N阶低通滤波器对噪声语音滤波,在Matlab中,FIR 滤波器利用函数filter对信号进行滤波,得到xinhao3.wav文件。
首先通过MATLAB工具编程获取音频文件的原始信号波形,原信号幅值和原始信号频谱图如下:然后通过加一个高斯噪声对其分析可得加噪声后信号波形,加噪声后幅值和加噪声后信号频谱图如下:最后再通过N阶低通滤波器对噪声信号滤波,在Matlab中,FIR 滤波器利用函数filter对信号进行滤波,从而得到滤波后信号波形,滤波后幅值和滤波后信号频谱图:程序[x]=wavread('C:\Users\h\Desktop\xinhao1.wav');X=fft(x,2048);figure(1)fs=abs(X);plot(fs);xlabel('HZ');ylabel('|Y(d)|');subplot(2,2,1);plot(x);xlabel('HZ');ylabel('|Y(d)|');title('原始信号波形');subplot(2,2,2);plot(X);xlabel('HZ');ylabel('|Y(d)|');title('原始信号幅值');subplot(2,2,3);plot(fs);xlabel('HZ');ylabel('|Y(d)|');title('原始信号频谱');figure(2)N=length(x); %计算原始语音信号的长度y1=0.05*randn(N,1); %加上一个高斯随机噪声x1=x+y1;x2=fft(x1,2048);mt=abs(x1);plot(mt);xlabel('HZ');ylabel('|Y(d)|');subplot(2,2,1);plot(x1);xlabel('HZ');ylabel('|Y(d)|');title('加噪声后的波形');subplot(2,2,2);plot(x2);xlabel('HZ');ylabel('|Y(d)|');title('加噪声后的幅值');subplot(2,2,3);plot(mt);xlabel('HZ');ylabel('|Y(d)|');title('加噪声后的频谱');ht=43000;bits=16;wavwrite(x1,ht,bits,'C:\Users\wentao\h\xinhao2.wav');%将加噪声的信号保存figure(3)N=15;wc=0.3;[b,a]=butter(N,wc);x3=fft(x);fp=abs(x3);y2=filter(b,a,x);Y1=fft(y2);subplot(2,2,1);plot(y2);xlabel('HZ');ylabel('|Y(d)|');title('滤波后信号的波形');subplot(2,2,2);plot(Y1);xlabel('HZ');ylabel('|Y(d)|');title('滤波后信号的幅值');subplot(2,2,3);plot(fp);xlabel('HZ');ylabel('|Y(d)|');title('滤波后信号的频谱');wavwrite(y2,ht,bits,'C:\Users\h\Desktop\xinhao3.wav');%将滤波之后保存。
(完整版)随机信号处理考题答案

(完整版)随机信号处理考题答案填空:1.假设连续随机变量的概率分布函数为F(x)则F(-∞)=0, F (+∞)=12.随机过程可以看成是样本函数的集合,也可以看成是随机变量的集合3.如果随机过程X(t)满足任意维概率密度不随时间起点的变化而变化,则称X(t)为严平稳随机过程,如果随机过程X(t)满足均值为常数,自相关函数只与时间差相关则称X(t)为广义平稳随机过程4.如果一零均值随机过程的功率谱,在整个频率轴上为一常数,则称该随机过程为白噪声,该过程的任意两个不同时刻的状态是不相关5. 宽带随机过程通过窄带线性系统,其输出近似服从正态分布,窄带正态噪声的包络服从瑞利分布,而相位服从均匀分布6.分析平稳随机信号通过线性系统的两种常用的方法是冲激响应法,频谱法7.若实平稳随机过程相关函数为Rx(τ)=25+4/(1+6τ),则其均值为5或-5,方差为4 7.匹配滤波器是输出信噪比最大作为准则的最佳线性滤波器。
1.广义各态历经过称的信号一定是广义平稳随机信号,反之,广义平稳的随机信号不一定是广义各态历经的随机信号2.具有高斯分布的噪声称为高斯噪声,具有均匀分布的噪声叫均匀噪声,而如果一个随机过程的概率谱密度是常数,则称它为白噪声3.白噪声通过都是带宽的线性系统,输出过程为高斯过程4.平稳高斯过程与确定的信号之和是高斯过程,确定的信号可以认为是该过程的数学期望5.平稳正态随机过程的任意概率密度只由均值和协方差阵确定1.白噪声是指功率谱密度在整个频域内均匀分布的噪声。
3.对于严格平稳的随机过程,它的均值与方差是与时间无关的函数,即自相关函数与时间间隔有关,与时间起点无关。
4.冲激响应满足分析线性输出,其均值为_____________________。
5.偶函数的希尔伯特变换是奇函数。
6.窄带随机过程的互相关函数公式为P138。
1.按照时间和状态是连续还是离散的,随机过程可分为四类,这四类是连续时间随机过程,离散型随机过程、随机序列、离散随机序列。
随机信号处理上机答案
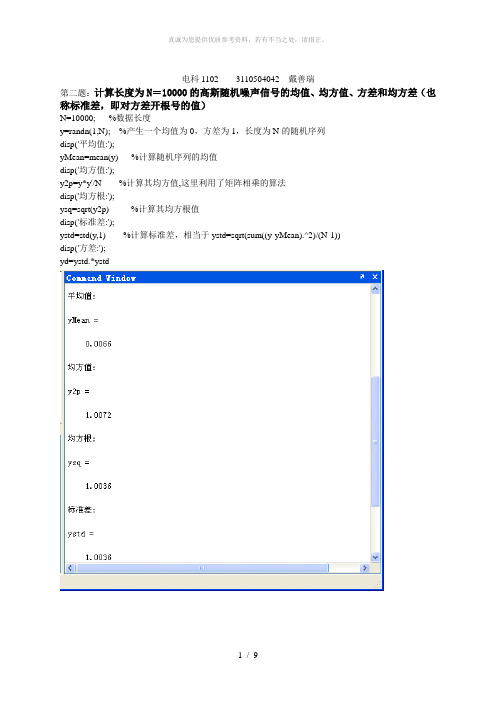
电科1102 3110504042 戴善瑞第二题:计算长度为N=10000的高斯随机噪声信号的均值、均方值、方差和均方差(也称标准差,即对方差开根号的值)N=10000; %数据长度y=randn(1,N); %产生一个均值为0,方差为1,长度为N的随机序列disp('平均值:');yMean=mean(y) %计算随机序列的均值disp('均方值:');y2p=y*y'/N %计算其均方值,这里利用了矩阵相乘的算法disp('均方根:');ysq=sqrt(y2p) %计算其均方根值disp('标准差:');ystd=std(y,1) %计算标准差,相当于ystd=sqrt(sum((y-yMean).^2)/(N-1))disp('方差:');yd=ystd.*ystd第三题:求一白噪声加正弦信号以及白噪声的自相关函数,并进行分析比较。
(显示出信号及相关函数的波形)clf;N=1000; Fs=500; %数据长度和采样频率n=0:N-1;t=n/Fs; %时间序列Lag=100; %延迟样点数?x=sin(2*pi*20*t)+0.6*randn(1,length(t)); %白噪声加正弦信号[c,lags]=xcorr(x,Lag,'unbiased'); %估计原始信号x的无偏自相关subplot(2,2,1),plot(t,x);xlabel('时间/s');ylabel('x(t)');title('带噪声周期信号');grid on;subplot(2,2,2),plot(lags/Fs,c); %绘x信号的自相关,lags/Fs为时间序列xlabel('时间/s');ylabel('Rx(t)');title('带噪声周期信号的自相关');grid on;x1=randn(1,length(x)); %产生一与x长度一致的随机信号x1[c,lags]=xcorr(x1,Lag,'unbiased'); %求随机信号x1的无偏自相关subplot(2,2,3),plot(t,x1); %绘制随机信号x1xlabel('时间/s');ylabel('x1(t)');title('噪声信号');grid on;subplot(2,2,4);plot(lags/Fs,c); %绘制随机信号x1的无偏自相关xlabel('时间/s');ylabel('Rx1(t)');title('噪声信号的自相关');grid on第四题:已知两个周期信号)2sin()(ft t x π=,)602sin(2.0)(0+=ft t y π,其中f=20Hz ,求互相关函数)(τxy R ,并将这2个周期信号以及互相关的图形显示出来。
随机信号处理原理与实践 题目整理

解: ,由Levinson关系式 可得
可见,极点为0.2和0.6,都在z平面单位圆内,所以该AR(2)模型是因果稳定的。
第六题
1.我们希望从观察矢量 和 中估计序列 。确定最优滤波系数、误差矢量 。
(2)解上述Yule-Walker方程可得:
(3)因为 均值为0,所以 的均值为零(1分),其方差等于平均功率(1分),即
第四章
1.证明由下式(1)和(2)给出的前向和后向AR过程具有相同的功率谱密度。
证明:对(1)式 ,
对(2)式
由上述可知,前向和后向AR过程具有相同的功率谱密度。
2.已知随机序列的观测值 ,试用快速相关算法求其功率密度谱。
解:给定序列补零后序列的长度为 ,那么 ,则:
又因为 ,按自相关函数是偶函数的性质,所以 是偶序列,所以
; ;
故得: ; ; ;
相关图法:求得 后,代入 ,再利用IDFT最后求功率谱密度的估计
周期图法:用直接法计算序列 的功率谱
解:求 得DFT: ;
;;Βιβλιοθήκη 故:第五章1.有一个自相关序列为 的信号s(n),被均值为零、噪声方差为1的加性白噪声v(n)干扰,白噪声与信号不相关。用维纳滤波器从被污染的信号x(n)=s(n)+v(n)中尽可能恢复s(n),求出一阶FIR滤波器的系数和最小均方误差。(14分)
(2)输出随机信号 的功率谱
解:(1)功率谱密度定义为其自相关序列的DTFT:
复功率谱密度定义为其自相关序列的z变换:
(2)功率谱
5.已知随机过程 ,其中 为均匀分布于 中的随机变量。试求:(1)均值(2)自相关函数.
多种功率谱估计郑州大学随机信号处理大作业

随机信号处理大作业多种功率谱估计的算法实现及性能比较一、引言频谱分析是信号处理的基石,为我们提供了时域以外的另一种信号研究手段——频域,使得很多在时域看起来很复杂的问题,用频域来分析就变得十分简单。
对于随机信号而言,由于不存在傅里叶变换,我们通过对其功率谱的分析来研究其频域特性。
功率谱估计问题就是根据一组有限观测值来估计该过程谱的内容,对于平稳随机过程而言,所有的功率谱估计方法都是根据有限的观测值来逼近真实值,估计结果的好坏与估计方法密切相关。
功率谱估计的方法可分为古典法和现代法,古典法基于傅里叶变换,包括直接法和间接法,现代谱估计包括直接解Yule-Walker 方程法、Levinson-Durbin 快速递推法、Burg 算法、MUSIC 算法、本文将对上述功率谱估计的方法进行分析。
二、原理及过程1 、古典法这里采用古典法中的直接法(周期图法)进行功率谱估计,其具体步骤如下。
第一步:由获得的N 点数据构成的有限长序列直接求傅里叶变换,得频谱(1.1)第二步:取频谱幅度的平方,并处以N,以此作为对真实功率谱的估计,即(1.2)2、Yule-Walker 方程法①假定所研究的随机过程是由一白噪声序列激励一因果稳定的可逆线性系统的输出②由观测获得的数据记录估计的参数③由的参数估计的功率谱由上可知,可以将平稳随机信号的功率谱表示为2.1)其中, 是白噪声 的功率谱(为常数), 是系统 的频谱。
这样谱估计问题就转化为模型参数的估计问题,在 AR 、MA 和 ARMA 三种模型中,求 AR 模型 的参数是解线性方程,易于求解,并且 MA 模型和 ARMA 模型都可以用高阶的 AR 模型近似, 所以这里我们采用 AR 模型来进行功率谱估计。
阶 AR 模型的系统函数为(2.2)阶 AR 模型有 +1 个待定参数: , ,⋯, 和系统增益 G 。
(2.4)可表示成下面的矩阵形式:上式用到了自相关函数的偶对称性质,由这 个方程,可以求出 个参数 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ep ( N p 1) 。这意味着,已知数据 x(n)( 0 x(n) N 1)是通过对无穷长数据序
7 / 20
列 x(n)( n ) 加窗得到的。将 e p (n) a pi x(n i ) 代入式(3.1.1)得
i 0
p
构成的 N 阶取样自相关矩阵。因此,用时间平均最小化准则同样可以导出 Yule-Walker 方程组,不过方程组中的 R 要用反取代。取样自相关矩阵左是正定 的,因而能够保证所得到的预测误差滤波器是最小相位的,因而也能保证反射 系数的模值都小于 1,这是使滤波器稳定的充分条件。 用 Yule-Walker 算法估计 AR 模型参数的具体步骤为 (1)根据式(3. 1. 3)计算自相关函数。 (2)用 Levinson-Durbin 算法求解 Yule-Walker 方程组
故最后求得的观测数据的功率谱为
由此可见,基于模型的现代谱估计过程一般可以分为三个步骤进行: (1)为被估计的随机过程确定或选择一个合理的模型。这有赖于对随机过程进行 理论分析和实验研究。 (2)根据已知观测数据 x(n),0 n N 1 , 估计模型的参数{ ak }和{{ bk )。 这涉及到 对各种算法的研究。通常,模型参数的数据量比观测数据的数据量少很多,因 此,为数据压缩创造了条件。 (3)用估计得到的模型参数代入式(2. 3. 4)计算功率谱的估值。 由式(2. 3. 1)可见,产生随机序列的模型其系统函数是有理函数,具有 q 个零点 和 p 个极点称为自回归滑动平均模型,用 ARMA (p, q)表示。若 q=0, b0 1 ,系 统函数 H (z) =1/A (z)只有极点称为自回归((AR)模型,用 AR (p)表示。若 A (z) =1, 则系统函数 H(z)=B(z)只有零点称为滑动平均(MA)模型,用 MA (q)表示。在这三 种模型中,AR 模型得到普遍应用,其原因是 AR 模型的参数计算是线性方程比 较简单,它与建立在外推自相关函数时保持原概论空间的嫡最大的最大嫡法是 等价的。同时很适于表示很窄的频谱,在谱估计时,由于递推特性所以所需的 数据很短,而 MA 模型表示窄谱时一般需要数量很多的参数,ARMA 模型虽然所 需的参数数量最少,但参数估计的算法是非线性方程组,其运算远比 AR 模型复 杂。况且根据 Wold 证明,任意 ARMA 或 MA 信号模型可以用无限阶或阶数足够 大的 AR 模型来表示的.所以本论文对现代谱估计方法着重介绍利用 AR 模型进行 功率谱估计的理论和算法。 2.3.2 AR 模型的 Yule-walker 方程 以 AR 模型为基础的谱估计可由式(2. 3. 4)计算, 只是这里的 q=0, b0 0 m 。 这就需要知道模型的阶数 P 和 P 个 AR 系数,以及模型激励源的方差 2 。为此, 必须把这些参数和己知(或估计得到)的自相关函数联系起来,这就是著 Yule-walker 方程。
基于 AR 模型的功率谱估计
摘要
频域分析又称谱分析,主要研究信号在中的各种特征。功率谱密度函数描 述随机过程的功率随频率的平均分布。功率谱估计问题就是根据一组有限观测 值来确定该过程谱的内容。对于平稳随机过程来说,功率谱理论上的数值不可 能实现,只能用有限的观测值来估计或者逼近真实值,从而叫真实的反应问题 的本质。当然估计结果的好坏,与采用的处理方法有很大关系。 本文概要介绍了古典谱估计方法以及其基本原理,详细介绍了基于 AR 模型 的功率谱估计的原理、算法。古典谱估计主要基于离散傅里叶变换(DFT) ,包 括周期图法和相关函数法及在此基础上改进的方法; 基于 AR 模型的功率谱估计, 是参数法做功率谱估计的一种,简而言之,就是通过计算模型的参数而不是做 FFT 来做功率谱估,本文主要介绍的基于 AR 模型的功率谱估计的方法,主要有 Levinson-Durbin 快速算法和 Burg 算法。本文通过 MATLAB 编程分别利用古典法 和基于 AR 模型的功率谱估计法对信号加噪声进行功率谱估计,并通过不同的点 数以及不同的频率间隔的比较来分析古典法和基于 AR 模型的功率谱估计法做出 相应的分析。 关键词:AR 模型 功率谱估计 Levinson-Durbin 快速算法 Burg 算法
4 / 20
2.3.3 Levinson-Durbin 快速递推法 用线性方程组的常用算法(例如高斯消元法)求解(2. 3. 9)式, 需要的运算量数 量级为 p 3 。 但若利用系数矩阵的对称性和 Toeplitz 性质, 则可构成一些高效算法, Levinson-Durbin 算法是其中最著名、应用最广泛的一种。这种算法的运算量量 级为 p 2 。这是一种按阶次进行递推的算法,即首先以 AR (0)和 AR (1)模型参数作
相应的差分方程为
在功率谱估计中,若观测的数据 x (n)是平稳随机过程,则该系统的输入 u (n) 也可以认为是平稳的,因而观测数据的功率谱为
一般信号的模型的输入数据是不能观测到的,在已知模型参数或频响| H (e jw ) |
3 / 0
的条件下,为了求得模型输出功率谱的估值,最简单的方法就是假设输入 u (n) 为零均值的白噪序列。离散时间白噪声自相关函数与功率谱分别为
为 m 阶时的前向预测的最小误差功率(此处省去了 “min", 且 m m 2 )。 由(2. 3. 9)式,当 m =1 时,有
6 / 20
第3章 AR 模型参数提取方法
3.1.1 Yule-Walker 算法 用最小平方时间平均准则代替集合平均准则,有
式中, e p (n) 可由长度为 P+1 的预测误差滤波器冲激响应序列 ( 1, a p1 , a p 2, , a pp )与长度为 N 的数据序列((x(0), x(1) ,...}x(N-1))进行卷积得到。因 而 e p (n) 序列的长度为 N+P,这就决定了式(3. 1. 1)中求和的项数。显然,在计 算卷积时, 在数据段 xN (n) 的两端, 实际上添加了若干零取样值。 实际上,e p (n) 是由 xN (n) 经过冲激响应为 api (i 0,1,, p; a p0 1) 的滤波器得到的。只要 xN (n) 的 第 一 个 数 据 x (0) 进 入 滤 波 器 , 滤 波 器 便 输 出 第 一 个 误 差 信 号 取 样 值
2.2
傅里叶变换
傅立叶变换(DFT)认为:有限长的数据段可看作无限长的取样序列进行加窗 截断后的结果。不论是数据加窗还是自相关函数加窗,在频率域都会发生“泄 露”现象,即功率谱主瓣的能量泄露到旁瓣中去,这样,弱信号的主瓣很容易 被强信号的旁瓣淹没或畸变,造成谱的模糊与失真。为了降低旁瓣,很多学者 在选择窗口函数的形式上和窗口处理函数方法上想办法,但是所有的旁瓣抑制
(3)用 AR 参数的估计值,可以计算功率谱
3.1.2 Burg 算法 为了克服 L-D 算法中因估计相关函数给功率谱带来的影响,Burg (1968)提出 一种新的算法,其基本思想是直接从观测的数据利用线性预测器得前向和后向 预测的总均方误差之和为最小的准则来估计预测系数, 进而通过 L-D 算法的递推 公式求出 AR 模型优化的参数。 前、后向预测误差的定义式分别为
第1章 引言
谱估计在信号处理方法中有很重要的作用,它不仅是分析、了解信号所含 有用信息的工具,也是信号内在本质的一种表现形式。古典谱估计方法存在着 分辨率低和方差性能不好的问题。现代谱分析是针对经典谱估计的不足,近几 年提出的谱估计新方法,其基本思路是:在进行谱估计过程中,对有限数据以外 的数据不做任何确定性假设,利用己知数据,采用外推或预测方法,由观测数 据推求 m N 以后的数据。在这种情况下,首先必须寻找一个产生随机信号的模 型,通过观测的数据把模型的参数估计出来,进而求得所需的功率谱。基于模 型的功率谱估计方法,不作自相关函数 Rxx (m) 0 , m > n 的假设,从而避免了功 率泄漏,提高了分辨率。 功率谱估计应用范围很广,日益受到各学科和应用领域的极大重视。以傅 立叶变换为基础的传统(或经典)谱估计方法,虽然具有计算效率高的优点,但 却有着频率分辨率低和旁瓣泄漏严重的固有缺点。这就迫使人们大力研究现代 谱估计方法。现代谱估计方法是以参数模型为基础的方法。
2.3.1 引言 为了克服经典谱估计的缺点,近年来在实现高分辨率谱估计技术方面取得 了很大的进展,提出了许多功率谱估计的参数方法,也就是现代谱估计的基本 方法。其基本思想是在进行谱估计过程对所观测的有限数据以外的数据不作任 何确定性假设。在对这些数据如何产生具有一定先验知识的基础上,采取外推 或预测的方法,从观测的数据推求 m 大于等于 N 以后的数据。显然,在这种情 况下,首先必须寻求一个产生随机信号的模型。通过观测数据把模型的参数估 计出来,进而求得所需的功率谱。所以参数法是基于模型(信号参数模型)的功率 谱估计方法。 这种方法既不需要加窗、 又不对相关函数做 R xx (m) 0, m N 的假设, 从而避免功率泄漏,提高了分辨率。 本节所讨论的信号模型,认为所观测的数据 x (n)是由某输入序列 u (n)激励 线性离散物理可实现系统的相应输出,如图 2. 2 所示,按离散系统的系统函数 其通式可写成为
2 / 20
技术都是以损失谱分辨率为代价的。谱分析应用中,谱分辨率和低旁瓣是同样 重要的指标,在作 DFT 时,人们常在有效数据后面补一些零,使得补零后的数 据 N 为 2 的整数次幂以便于快速傅立叶变换,而那些认为在傅立叶变换之前对 数据段补零可以改善周期图的谱分辨率是一种模糊的错误概念,因为补零后, 虽然谱线能够增密,但因为补零没有增加任何新的信息,因此不可能提高分辨 率。谱分辨率的极限只能由取样数据段的长度决定。 2.3 AR 模型
5 / 20
为初始条件,计算 AR (2)模型参数;然后根据这些参数计算 AR (3)模型的参数,等 等,一直到计算出 AR (p)模型参数为止。这样,当整个迭代计算结束后,不仅求 得了所需要的 p 阶 AR 模型的参数,而且还得到了所有各低阶模型的参数。定义
