1:MATLAB及基本运算
第二讲 MATLAB基本运算

矩阵下标的用途
访问超出矩阵范围时,产生 Index exceeds matrix dimentions 存储超出矩阵范围时,矩阵自动调节 大小,将指定位置元素置入,其他没 指定数的位置默认为零。
2010-12-25
21
矩阵下标的用途
(2)矩阵连接 例:a=[1 2;3 4] b=[a a+5; a-5 zeros(size(a)] 将小矩阵嵌套入大矩阵,实现矩阵连接。
将矩阵按创建原则写入一个M文件, 在MATLAB的命令窗口或程序中直接执 行该M文件,即将矩阵调入工组空间。
2010-12-25
15
利用MATLAB函数创建矩阵 利用MATLAB函数创建矩阵 MATLAB
ones( m, n) - m行n列的1阵产生 zeros(m, n) -产生m行n列的全0阵 rand(m, n) -产生m行n列均匀分布全列的在 [0,1]区间的随机阵 randn(m, n) -产生m行n列的正态分布矩阵 eye(n) -产生n维单位阵
2010-12-25 18
2.2.3 矩阵的下标 .2.3
子矩阵提取A(v1, v2)
v1表示子矩阵包含的行标构成的向量 v2表示子矩阵包含的列标构成的向量 B1=A(:, [1, 3]) 为:时表示要提取所有行(列) B2=A(1:2:end, :) end表示最后一行(列) B3=A([3,2,1],[2,3,4]) 例: B4=A(:, end:-1:1) 提取A矩阵所有行、1,3列 提取A矩阵 3,2,1 行、2,3,4 列构成子矩阵 提取A矩阵全部奇数行,所有列 将A矩阵左右翻转
2010-12-25
13
直接输入法创建矩阵
例:创建矩阵
实验一 MATLAB运算基础

实验一MATLAB运算基础一、实验目的1.熟悉启动和退出MATLAB的方法。
2.熟悉MATLAB命令窗口的组成。
3.掌握建立矩阵的方法。
4.掌握MATLAB各种表达式的书写规则以及常用函数的使用。
二、实验内容1.先求下列表达式的值,然后显示MATLAB工作空间的使用情况并保存全部变量。
(1)z1=2sin85°1+e2(2)z2=12ln(x+1+x2),其中x=21+2i−0.455(3)z3=e0.3a−e−0.3a2sin(a+0.3)+ln0.3+a2,a=−3.0,−2.9,…,,2.9,3.0(4)z4=t2,t2-1,t2-2t+1,0≤t<11≤t<22≤t<3,其中t=0:0.5:2.5解:(1)z1=2*sin(85*pi/180)/(1+exp(1)*exp(1));(2)x=[2,1+2i;-0.45,5];z2=0.5*log(x+sqrt(1+x*x));(3)a=-3.0:0.1:3.0;z3=(exp(0.3*a)-exp(-0.3*a))/2.*sin(a+0.3)+log((0.3+a)/2); (4)t=0:0.5:2.5;z4=t.^2-(1-2.*t).*(t<3&t>=2)-(t<2&t>=1);运行结果:z1 =0.2375z2 =0.7114 - 0.0253i 0.8968 + 0.3658i0.2139 + 0.9343i 1.1541 - 0.0044iz3=Columns 1 through 270.7388 + 3.1416i 0.7696 + 3.1416i 0.7871 + 3.1416i0.7913 + 3.1416i 0.7822 + 3.1416i 0.7602 + 3.1416i0.7254 + 3.1416i 0.6784 + 3.1416i 0.6196 + 3.1416i0.5496 + 3.1416i 0.4688 + 3.1416i 0.3780 + 3.1416i0.2775 + 3.1416i 0.1680 + 3.1416i 0.0497 + 3.1416i-0.0771 + 3.1416i-0.2124 + 3.1416i -0.3566 + 3.1416i-0.5104 + 3.1416i -0.6752 + 3.1416i -0.8536 + 3.1416i-1.0497 + 3.1416i -1.2701 + 3.1416i -1.5271 + 3.1416i-1.8436 + 3.1416i -2.2727 + 3.1416i -2.9837 + 3.1416iColumns 28 through 61-37.0245 -3.0017 -2.3085 -1.8971-1.5978 -1.3575 -1.1531 -0.9723 -0.8083 -0.6567 -0.5151 -0.3819-0.2561 -0.1374 -0.02550.07920.1766 0.2663 0.3478 0.42060.4841 0.5379 0.5815 0.61450.6366 0.6474 0.6470 0.63510.6119 0.5777 0.5327 0.47740.4126 0.3388z4 =Columns 1 through 60 0.2500 0 1.2500 7.0000 10.2500 使用情况:a 1x61 488 doublet 1x6 48 doublex 2x2 64 double complexz1 1x1 8 doublez2 2x2 64 double complexz3 1x61 976 double complexz4 1x6 48 double2.已知:A=1234−4347873657,B=13−12033−27求下列表达式的值:(1)A+6*B和A−B+I(其中I为单位矩阵)(2)A*B和A.*B(3)A^3和A.^3(4)A/B及A\B(5)[A,B]和[A([1,3],:);B^2]解:A=[12,34,-4;34,7,87;3,65,7];B=[1,3,-1;2,0,3;3,-2,7];I=eye(3);(1)A+6*B;A-B+I;(2)A*B;A.*B(3)A^3;A.^3;(4)A/B;A\B(5)[A,B];[A([1,3],:);B^2];运行结果:(1)ans =18 52 -1046 7 10521 53 49ans =12 31 -332 8 840 67 1(2)ans =68 44 62309 -72 596154 -5 241ans =12 102 468 0 2619 -130 49(3)ans =37226 233824 48604247370 149188 60076678688 454142 118820ans =1728 39304 -6439304 343 65850327 274625 343(4)ans =16.4000 -13.6000 7.600035.8000 -76.2000 50.200067.0000 -134.0000 68.0000ans =-0.0313 0.3029 -0.33240.0442 -0.0323 0.10630.0317 -0.1158 0.1558(5)ans =12 34 -4 1 3 -134 7 87 2 0 33 65 7 3 -2 7ans =12 34 -43 65 74 5 111 0 1920 -5 403.设有矩阵A和BA=12367811121349145101516171819202122232425, B=301617−699423713−411(1)求它们的乘积C。
MATLAB数据及其运算

补:两个多维数组的 点运算。
3. MATLAB常用数学函数
函数使用说明:
(1) 三角函数以弧度为单位计算。 (2) abs函数可以求实数的绝对值、复数的 模、字符串的ASCII码值。 (3) 用于取整的函数有fix、floor、ceil、 round,要注意它们的区别。 (4) rem与mod函数的区别。rem(x,y)和 mod(x,y)要求x,y必须为相同大小的实矩阵 或为标量。
p25
A=[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ]
[1 3 5 11 13 15 ]
A( [1,3],[1 3 5] )
可以利用 一般向量 和 end 运算符来表示矩阵下标, 从而获得子矩阵。end表示某一维的末尾元素下标。
A( [1,end-பைடு நூலகம்],[1 :2:end] ) ?
例2.3 建立5阶方阵A,判断A的元素是否能被3整 除。
A =[24,35,13,22,63;23,39,47,80,80; ... 90,41,80,29,10;45,57,85,62,21;37,19,31,88,76]
P = rem(A,3)==0
其中,rem(A,3)是矩阵A的每个元素除以3的余数 矩阵。此时,0被扩展为与A同维数的零矩阵,P 是进行等于(==)比较的结果矩阵。
A(3,2)=200
采用矩阵元素的序号(Index)来引用矩阵元素。
1 矩阵元素的序号就是相应元素在内存中的排列顺序。在
4
MATLAB中,矩阵元素按列存储,先第一列,再第二列,依 次类推。例如
2 A=[1,2,3 ;
Matlab基本运算

2.1 变量和数据操作2.1.1 变量与赋值1.变量命名在MA TLA B 6.5中,变量名是以字母开头,后接字母、数字或下划线的字符序列,最多63个字符。
在MA TLA B中,变量名区分字母的大小写。
2.赋值语句(1) 变量=表达式(2) 表达式其中表达式是用运算符将有关运算量连接起来的式子,其结果是一个矩阵。
2.1.2 预定义变量在MA TLA B工作空间中,还驻留几个由系统本身定义的变量。
例如,用pi表示圆周率π的近似值,用i,j表示虚数单位。
预定义变量有特定的含义,在使用时,应尽量避免对这些变量重新赋值。
2.1.3 内存变量的管理1.内存变量的删除与修改MATLAB工作空间窗口专门用于内存变量的管理。
在工作空间窗口中可以显示所有内存变量的属性。
当选中某些变量后,再单击Delete 按钮,就能删除这些变量。
当选中某些变量后,再单击Ope n按钮,将进入变量编辑器。
通过变量编辑器可以直接观察变量中的具体元素,也可修改变量中的具体元素。
clear命令用于删除M A TLA B工作空间中的变量。
w ho和wh os这两个命令用于显示在MAT LAB工作空间中已经驻留的变量名清单。
who 命令只显示出驻留变量的名称,whos在给出变量名的同时,还给出它们的大小、所占字节数及数据类型等信息。
2.内存变量文件利用MA T文件可以把当前MA TL AB工作空间中的一些有用变量长久地保留下来,扩展名是.mat。
MA T文件的生成和装入由save和load 命令来完成。
常用格式为:save 文件名[变量名表] [-append][-ascii]load 文件名[变量名表] [-ascii]其中,文件名可以带路径,但不需带扩展名.mat,命令隐含一定对.mat文件进行操作。
MATLAB 常用知识1 向量运算

MATLAB 常用知识1-向量运算
By D. J. Liu
向量定义
向量只有一行(行向量) 或一列(列向量)
1等差向量生成方法
(1) 冒号生成法
X=X0:D: Xn
X0: 第一个元素
D: 公差
Xn: 最后一个元素
(2) linspace函数生成法
X=linspace(X0, Xn, n)
X0: 第一个元素
Xn: 最后一个元素
n: 元素个数
2 n维向量定义
a = [a1, a2, … , an] (n维行向量)
a(1)=a1, a(1)=a1, …, a(n)=an
b = [b1, b2, … , bn]’(n维列向量)
b(1)=b1, b(1)=b1, …, b(n)=bn
3向量书写规则
(1)元素之间用逗号或空格分开生成行向量。
X = [1, 2, 3] 或X = [1 2 3]
(2)元素之间用分号隔开生成列向量。
X = [1; 2; 3] 或X = [1 2 3]’
向量运算函数
1 min(X)
求向量X所有元素的最小值
2 max(X)
求向量X所有元素的最大值
3 mean(X)
求向量X所有元素的平均值
4 sum(X)
求向量X所有元素的和
5 std(X)
求向量X所有元素的标准差
6 length(X)
求向量X元素的个数
7 sort(X)
将向量X所有元素按升序排列
8 cumsum(X)
将向量X所有元素进行累加
9 cumprod(X)
将向量X所有元素进行累乘
10 range(X)
求向量X中最大元素与最小元素的差值。
MATLAB教程

sqrt(x):开平方
real(z):复数z的实部
imag(z):复数z的虚部
conj(z):复数z的共轭复数
round(x):四舍五入至最近整数
fix(x):无论正负,舍去小数至最近整数
floor(x):地板函数,即舍去正小数至最近整数
ceil(x):天花板函数,即加入正小数至最近整数
y = sin(10)*exp(-0.3*4^2);
若要显示变数y的值,直接键入y即可:
>>y
y =-0.0045
在上例中,sin是正弦函数,exp是指数函数,这些都是MATLAB常用到的数学函数。
下表即为MATLAB常用的基本数学函数及三角函数:
小整理:MATLAB常用的基本数学函数
abs(x):纯量的绝对值或向量的长度
举例来说,下列命令会产生一个长度为6的调和数列(Harmonic sequence):
x = zeros(1,6); % x是一个16的零矩阵
for i = 1:6,
x(i) = 1/i;
end
在上例中,矩阵x最初是一个16的零矩阵,在for圈中,变数i的值依次是1到6,因此矩阵x的第i个元素的值依次被设为1/i。我们可用分数来显示此数列:
MATLAB可在同时执行数个命令,只要以逗号或分号将命令隔开:
x = sin(pi/3); y = x^2; z = y*10,
z =
7.5000
若一个数学运算是太长,可用三个句点将其延伸到下一行:
z = 10*sin(pi/3)* ...
sin(pi/3);
若要检视现存於工作空间(Workspace)的变数,可键入who:
(完整word)MATLAB常用

背出来,Matlab就无敌了一 matlab常用函数1、特殊变量与常数ans 计算结果的变量名computer 确定运行的计算机eps 浮点相对精度Inf 无穷大I 虚数单位inputname 输入参数名NaN 非数nargin 输入参数个数nargout 输出参数的数目pi 圆周率nargoutchk 有效的输出参数数目realmax 最大正浮点数realmin 最小正浮点数varargin 实际输入的参量varargout 实际返回的参量操作符与特殊字符+ 加 - 减*矩阵乘法 .* 数组乘(对应元素相乘)^ 矩阵幂 .^ 数组幂(各个元素求幂)\ 左除或反斜杠 / 右除或斜面杠。
/ 数组除(对应元素除)kron Kronecker张量积:冒号 () 圆括[] 方括。
小数点.。
父目录 .。
继续,逗号(分割多条命令) ; 分号(禁止结果显示)% 注释!感叹号 ' 转置或引用 = 赋值== 相等〈〉不等于& 逻辑与|逻辑或~逻辑非 xor 逻辑异或2、基本数学函数abs 绝对值和复数模长acos,acodh 反余弦,反双曲余弦acot,acoth 反余切,反双曲余切 acsc,acsch 反余割,反双曲余割 angle 相角asec,asech 反正割,反双曲正割secant 正切asin,asinh 反正弦,反双曲正弦 atan,atanh 反正切,双曲正切tangent 正切atan2 四象限反正切ceil 向着无穷大舍入complex 建立一个复数conj 复数配对cos,cosh 余弦,双曲余弦csc,csch 余切,双曲余切cot,coth 余切,双曲余切exp 指数fix 朝0方向取整floor 朝负无穷取整*** 最大公因数imag 复数值的虚部lcm 最小公倍数log 自然对数log2 以2为底的对数log10 常用对数mod 有符号的求余nchoosek 二项式系数和全部组合数real 复数的实部rem 相除后求余round 取整为最近的整数sec,sech 正割,双曲正割sign 符号数sin,sinh 正弦,双曲正弦sqrt 平方根 tan,tanh 正切,双曲正切3、基本矩阵和矩阵操作blkding 从输入参量建立块对角矩阵eye 单位矩阵linespace 产生线性间隔的向量logspace 产生对数间隔的向量numel 元素个数ones 产生全为1的数组rand 均匀颁随机数和数组randn 正态分布随机数和数组zeros 建立一个全0矩阵 colon) 等间隔向量cat 连接数组diag 对角矩阵和矩阵对角线fliplr 从左自右翻转矩阵flipud 从上到下翻转矩阵repmat 复制一个数组(完整word)MATLAB常用 reshape 改造矩阵roy90 矩阵翻转90度tril 矩阵的下三角triu 矩阵的上三角dot 向量点集cross 向量叉集ismember 检测一个集合的元素intersect 向量的交集 setxor 向量异或集 setdiff 向是的差集 union 向量的并集数值分析和傅立叶变换 cumprod 累积 cumsum 累加 cumtrapz 累计梯形法计算数值微分 factor 质因子 inpolygon 删除多边形区域内的点 max 最大值 mean 数组的均值 mediam 中值 min 最小值 perms 所有可能的转换 polyarea 多边形区域 primes 生成质数列表 prod 数组元素的乘积 rectint 矩形交集区域 sort 按升序排列矩阵元素 sortrows 按升序排列行 std 标准偏差 sum 求和 trapz 梯形数值积分 var 方差 del2 离散拉普拉斯 diff 差值和微分估计 gradient 数值梯度 cov 协方差矩阵 corrcoef 相关系数 conv2 二维卷积 conv 卷积和多项式乘法 filter IIR或FIR滤波器 deconv 反卷积和多项式除法 filter2 二维数字滤波器 cplxpair 将复数值分类为共轭对 fft 一维的快速傅立叶变换 fft2 二维快速傅立叶变换 fftshift 将FFT的DC分量移到频谱中心 ifft 一维快速反傅立叶变换 ifft2 二维傅立叶反变换 ifftn 多维快速傅立叶变换 ifftshift 反FFT偏移 nextpow2 最靠近的2的幂次 unwrap 校正相位角多项式与插值 conv 卷积和多项式乘法 roots 多项式的根 poly 具有设定根的多项式 polyder 多项式微分 polyeig 多项式的特征根 polyfit 多项式拟合 polyint 解析多项式积分 polyval 多项式求值 polyvalm 矩阵变量多项式求值 residue 部分分式展开 interp1 一维插值 interp2 二维插值 interp3 三维插值 interpft 使用FFT的一维插值 interpn 多维插值 meshgrid 为3维点生成x和y的网格 ndgrid 生成多维函数和插值的数组 pchip 分段3次Hermite插值多项式 ppval 分段多项式的值 spline 3次样条数据插值绘图函数 bar 竖直条图 barh 水平条图 hist 直方图 histc 直方图计数 hold 保持当前图形 loglog x,y对数坐标图 pie 饼状图 plot 绘二维图 polar 极坐标图 semilogy y轴对数坐标图 semilogx x轴对数坐标 subplot 绘制子图 bar3 数值3D竖条图 bar3h 水平3D条形图 comet3 3D慧星图 cylinder 圆柱体 fill3 填充的3D多边形 plot3 3维空间绘图 quiver3 3D震动(速度)图 slice 体积薄片图 sphere 球 stem3 绘制离散表面数据 wate***ll 绘制瀑布 trisurf 三角表面 clabel 增加轮廓标签到等高线图中 datetick 数据格式标记 grid 加网格线 gtext 用鼠标将文本放在2D图中 legend 图注 plotyy 左右边都绘Y轴 title 标题 xlabel X轴标签 ylabel Y轴标签 zlabel Z轴标签 contour 等高线图 contourc 等高线计算 contourf 填充的等高线图 hidden 网格线消影 meshc 连接网格/等高线 mesh 具有参考轴的3D网格 peaks 具有两个变量的采样函数 surf 3D阴影表面图 su***ce 建立表面低层对象 surfc 海浪和等高线的结合 surfl 具有光照的3D阴影表面 trimesh 三角网格图二 Matlab常用指令1、通用信息查询(General information)demo 演示程序 help 在线帮助指令 helpbrowser 超文本文档帮助信息 helpdesk 超文本文档帮助信息 helpwin 打开在线帮助窗 info MATLAB 和MathWorks 公司的信息 subscribe MATLAB 用户注册 ver MATLAB 和TOOLBOX 的版本信息 version MATLAB 版本 whatsnew 显示版本新特征2、工作空间管理(Managing the workspace)clear 从内存中清除变量和函数 exit 关闭MATLAB load 从磁盘中调入数据变量 pack 合并工作内存中的碎块 quit 退出MATLAB save 把内存变量存入磁盘 who 列出工作内存中的变量名 whos 列出工作内存中的变量细节 workspace 工作内存浏览器3 、管理指令和函数(Managing commands and functions)edit 矩阵编辑器 edit 打开M 文件 inmem 查看内存中的P 码文件 mex 创建MEX 文件 open 打开文件 pcode 生成P 码文件 type 显示文件内容 what 列出当前目录上的M、MAT、MEX 文件 which 确定指定函数和文件的位置4 、搜索路径的管理(Managing the seach patli)addpath 添加搜索路径 rmpath 从搜索路径中删除目录 path 控制MATLAB 的搜索路径 pathtool 修改搜索路径5、指令窗控制(Controlling the command window)beep 产生beep 声 echo 显示命令文件指令的切换开关 diary 储存MATLAB 指令窗操作内容 format 设置数据输出格式 more 命令窗口分页输出的控制开关6、操作系统指令(Operating system commands)cd 改变当前工作目录 computer 计算机类型 copyfile 文件拷贝 delete 删除文件 dir 列出的文件 dos 执行dos 指令并返还结果 getenv 给出环境值 ispc MATLAB 为PC(Windows)版本则为真 isunix MATLAB 为Unix 版本则为真 mkdir 创建目录 pwd 改变当前工作目录 unix 执行unix 指令并返还结果 vms 执行vms dcl 指令并返还结果 web 打开web 浏览器 ! 执行外部应用程序三 Matlab运算符和特殊算符1、算术运算符(Arithmetic operators)+ 加—减 * 矩阵乘 .*数组乘 ^ 矩阵乘方 .^ 数组乘方 \ 反斜杠或左除 / 斜杠或右除。
第二讲 Matlab的基本计算

>>a3=mat2str( a,2 ) %一行字符
字符串的应用:作出函数图形,并标注最大值点。 字符串的应用:作出函数图形,并标注最大值点。
y = e 2t sin(3t ) 0 ≤ t ≤ 10
clear %清除内存变量 t = 0 : 0.01 : 10; %时间 t 从 0 到 10 每隔 0.01 均匀采样 y = exp( -2*t ) .* sin( 3*t ); %对应每一个 t 求 y 值 %求最大值 y_max 及其下标 i_max [ y_max, i_max ] = max( y ); %横坐标字符串 t_text = [ 't = ', num2str( t(i_max) ) ]; %纵坐标字符串 y_text = [ 'y = ', num2str( y_max ) ]; %三行字符来标识最大值点 max_text = char( 'Maxium', t_text, y_text ); %图名称字符串 Title = [ 'y = exp( -2*t ) .* sin( 3*t )' ]; %新建一个图形窗 figure %画一条黑色的水平线 plot( t,zeros( size(t) ), 'k' ) %保持图形不被清除 hold on %蓝色实线画曲线 y(t) plot( t, y, 'b' ) %大小为 20 的红圆点标记最大值点 plot( t(i_max), y_max, 'r.', 'MarkerSize', 20 ) %在最大值点附近显示注释字符 text( t(i_max)+0.3, y_max+0.05, max_text ) %显示图名、横坐标名、纵坐标名 title( Title ); %取消图形保持 xlabel( 't' ) ylabel( 'y' ) hold off
matlab实验一

实验一、MATLAB基本操作一、基本操作1、命令窗口的简单使用(1)简单矩阵的输入(2)求[12+2×(7-4)]÷32的算术运算结果2、有关向量、矩阵或数组的一些运算(1)设A=15;B=20;求C=A+B与c=a+b?(2)设A=[1 2 3;4 5 6;7 8 9],B=[9 8 7;6 5 4;3 2 1];求A*B与A.*B?说明*与.*的运算特点A=[1 2 3;4 5 6;7 8 9],B=[9 8 7;6 5 4;3 2 1](3)设a=10,b=20;求i=a/b与j=a\b?a=10,b=20(4)设a=[1 -2 3;4 5 -4;5 -6 7];请设计出程序,分别找出小于0的矩阵元素及其位置。
(5)在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8];看结果如何?如果改成运行A=[1,2;3,4]+i[5,6;7,8],结果又如何?(6)请写出完成下列计算的指令:a=[1 2 3;3 4 2;5 2 3],求a^2=?,a.^2=?(7)有一段指令如下,请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X(:)矩阵变为一维矩阵使用三元组方法,创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0(8)写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A >> D = A.^B C =3 9 27 D =1 32 7293、 已知⎪⎭⎫ ⎝⎛+⋅=-334sin 234πt e y t 若需要计算t ∈[-1,1],取间隔为0.01,试计算出相对应的y 值。
二、运算基础1、 设有矩阵A 和B ,A=[1 2 3 4 5;6 7 8 9 10;11 12 13 14 15;1617 18 19 20;21 22 23 24 25],B=[3 0 16;17 -6 9;0 23 -4;9 7 0;4 13 11]; 1) 求它们的乘积C2)将矩阵C的右下角3x2子矩阵赋给D2、完成下列操作1)求[100,999]之间能被61整除的数及其个数(提示:先利用冒号表达式,再利用find和length函数。
上机实验1:熟悉matlab基本操作

上机实验1:熟悉matlab基本操作实验目的:熟悉matlab的基本操作,掌握一些常用命令的用法。
实验内容:1.编写matlab命令(函数),可以完成以下任务:(1)matlab中的PI?(=Pi)大约等于?(2)如何使用sum命令?(3)函数max的作用?举例说明。
(4)命令help,lookfor,demo的用法?102? 5.Sin6(5)计算7.Tan62。
回答以下问题:(1)matlab是什么意思?(2)matlab命令who与whos有什么区别?(3)matlab命令clear与clc有什么区别?(4)命令:与linspace,logspace的区别?计算机实验2:矩阵运算与matlab命令实验目的:熟悉matlab矩阵运算命令。
实验内容:1.请直接在Matlab下输入以下常数,查看它们的值:(1)I,J,EPS(2)inf,Nan,PI(3)realmax(4)realmin2、使用lookfor指令,找出具有下列功能的matlab指令。
(1)求矩阵的大小(即行维度和列维度)(2)找出矩阵每一直行的最大值(3)对矩阵的每一直行进行排序(4)逆矩阵(inversematrix)的计算(5)求矩阵的rank几个常见的matlab命令:*zerooneseyelinspaceranddiag\\/detinveigrank计算机实验3:MATLAB程序设计实验目的:熟悉matlab程序控制结构,掌握用m文件或函数的编写方法。
实验内容:x2x6,x0且x??4?1、f(x)的定义如下:f(x)??x2?5x?6,0?x?10,x?2且x?3,写一个matlab函x2?十、1.其他人?数字func1实现该函数,并在区间[?10,15]内绘制该函数的图像。
2.编写一个matlab函数myfun M来计算以下方程式:y=0.5*exp(x/3)-x*x*sin(x)其中x是函数的输入,Y是函数的输出。
MATLAB编程及应用 李辉 PPT课件 第2章 MATLAB基本计算和基础知识

2.2.2 系统预定义变量
MATLAB系统提供了一些用户不能清除的特殊变量,
即系统预定义变量。
MATALB系统预定义变量及其含义
预定义变量名
含义
ans pi eps nan或NAN inf i或j
运算结果默认变量名 圆周率 浮点数的精度,也是系统运算时确定的极小值 非数,如0/0 无穷大,如1/0 虚数标志,i=j=sqrt(-1)
1.0000 + 2.0000i >> b=3+4*j b=
3.0000 + 4.0000i
2.3.2 逻辑类型
MATLAB本身并没有专门提供逻辑类型,而借用整型来描
述逻辑类型数据。MATLAB规定,逻辑数据真(true)为1、
逻辑数据假(false)为0。
>> 2<3 ans =
logical 1 >> 2>3 ans = logical 0
>> sin(pi/3) ans =
0.8660
➢ 复数的计算:MATLAB还具有超越计算器的功能, 它认识复数,能够进行复数的计算。
>> (2+3i)+(4+5i) ans =
6.0000 + 8.0000i
Байду номын сангаас
2.2 变量
变量是指在程序执行过程中其值可以变化的量。
变量
用户自定义变量 系统预定义变量
2.3 数据类型
MATLAB数据类型
数值类型 逻辑类型 字符串类型 单元类型 结构类型
2.3.1 数值类型
数值类型分类方法
根据数据存 储空间和方 式分类
根据数据结 构分类
实验一 常用基本信号的MATLAB表示和运算
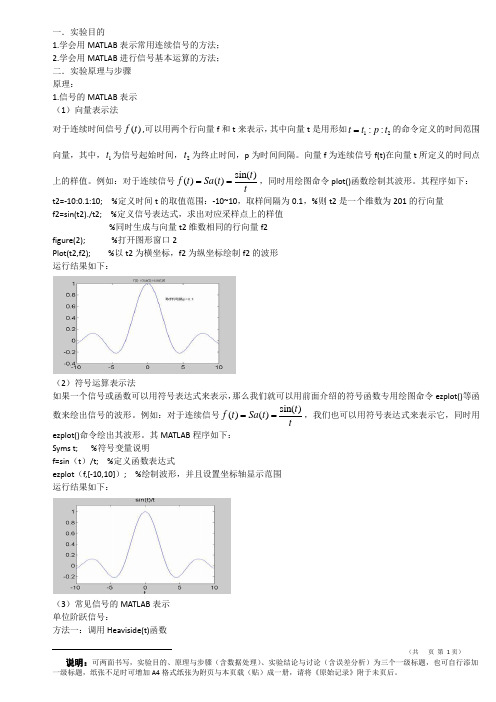
一.实验目的1.学会用MATLAB 表示常用连续信号的方法;2.学会用MATLAB 进行信号基本运算的方法; 二.实验原理与步骤 原理:1.信号的MATLAB 表示 (1)向量表示法对于连续时间信号()f t ,可以用两个行向量f 和t 来表示,其中向量t 是用形如12::t t p t =的命令定义的时间范围向量,其中,1t 为信号起始时间,2t 为终止时间,p 为时间间隔。
向量f 为连续信号f(t)在向量t 所定义的时间点上的样值。
例如:对于连续信号sin()()()t f t Sa t t==,同时用绘图命令plot()函数绘制其波形。
其程序如下: t2=-10:0.1:10; %定义时间t 的取值范围:-10~10,取样间隔为0.1,%则t2是一个维数为201的行向量 f2=sin(t2)./t2; %定义信号表达式,求出对应采样点上的样值 %同时生成与向量t2维数相同的行向量f2 figure(2); %打开图形窗口2Plot(t2,f2); %以t2为横坐标,f2为纵坐标绘制f2的波形 运行结果如下:(2)符号运算表示法如果一个信号或函数可以用符号表达式来表示,那么我们就可以用前面介绍的符号函数专用绘图命令ezplot()等函数来绘出信号的波形。
例如:对于连续信号sin()()()t f t Sa t t==,我们也可以用符号表达式来表示它,同时用ezplot()命令绘出其波形。
其MATLAB 程序如下: Syms t; %符号变量说明f=sin (t )/t; %定义函数表达式ezplot (f,[-10,10]); %绘制波形,并且设置坐标轴显示范围 运行结果如下:(3)常见信号的MATLAB 表示 单位阶跃信号:方法一:调用Heaviside(t)函数首先定义函数Heaviside(t)的m函数文件,该文件名应与函数名同名即Heaviside.m。
%定义函数文件,函数名为Heaviside,输入变量为x,输出变量为yfunction y=Heaviside(t)y=(t>0);%定义函数体,即函数所执行指令%此处定义t>0时y=1,t<=0时y=0,注意与实际的阶跃信号定义的区别。
MATLAB应用 MATLAB数据及运算
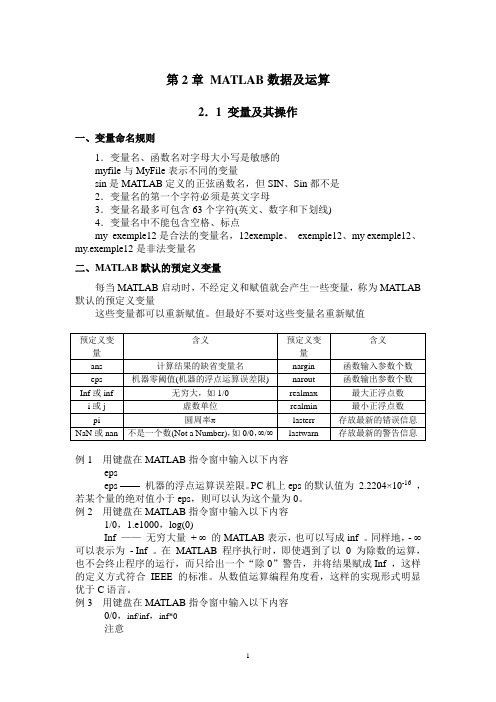
第2章MATLAB数据及运算2.1 变量及其操作一、变量命名规则1.变量名、函数名对字母大小写是敏感的myfile与MyFile表示不同的变量sin是MATLAB定义的正弦函数名,但SIN、Sin都不是2.变量名的第一个字符必须是英文字母3.变量名最多可包含63个字符(英文、数字和下划线)4.变量名中不能包含空格、标点my_exemple12是合法的变量名,12exemple、_exemple12、my exemple12、my.exemple12是非法变量名二、MATLAB默认的预定义变量每当MATLAB启动时,不经定义和赋值就会产生一些变量,称为MATLAB 默认的预定义变量这些变量都可以重新赋值。
但最好不要对这些变量名重新赋值例1 用键盘在MATLAB指令窗中输入以下内容epseps ——机器的浮点运算误差限。
PC机上eps的默认值为2.2204×10-16,若某个量的绝对值小于eps,则可以认为这个量为0。
例2 用键盘在MATLAB指令窗中输入以下内容1/0,1.e1000,log(0)Inf ——无穷大量+ ∞的MATLAB表示,也可以写成inf 。
同样地,- ∞可以表示为- Inf 。
在MATLAB 程序执行时,即使遇到了以0 为除数的运算,也不会终止程序的运行,而只给出一个“除0”警告,并将结果赋成Inf ,这样的定义方式符合IEEE 的标准。
从数值运算编程角度看,这样的实现形式明显优于C语言。
例3 用键盘在MATLAB指令窗中输入以下内容0/0,inf/inf,inf*0注意在MATLAB 中,即使遇到以0为除数的运算,程序也不会终止运行。
这时只给出一个警告,并将结果赋给inf 或NaNNaN —— 不定式( not a number ) ,通常由 0 / 0 运算、Inf / Inf 及其他可能的运算得出。
NaN 是一个很奇特的量,如 NaN 与Inf 的乘积仍为 NaN 。
MATLAB及基本运算

矩阵运算
矩阵加法
执行矩阵加法运算,要求两个矩阵的 维度必须相同。
矩阵减法
执行矩阵减法运算,要求两个矩阵的 维度必须相同。
矩阵乘法
通过使用"*"运算符执行矩阵乘法运 算,要求第一个矩阵的列数必须与第 二个矩阵的行数相等。
矩阵转置
通过使用"'"运算符执行矩阵转置运算, 将矩阵的行转换为列,将列转换为行。
图像增强
使用Matlab的图像处理工具箱进行图像的 对比度增强、直方图均衡化等增强操作。
图像变换
使用Matlab的图像处理工具箱进行图像的 缩放、旋转、剪切等几何变换。
图像分割和识别
使用Matlab的图像处理工具箱进行图像分 割、边缘检测、特征提取和识别等操作。
THANKS
感谢观看
数值分析
数值积分
使用Matlab的`integral`函数进行数值积 分。
最优化问题求解
使用Matlab的`fminbnd`函数求解无约束 最优化问题,使用`fmincon`函数求解约束
最优化问题。
微分方程求解
使用Matlab的`ode45`函数求解常微分方 程。
插值和拟合
使用Matlab的`polyfit`函数进行多项式插 值,使用`lsqcurvefit`函数进行非线性曲 线拟合。
03
02
1984年
Matlab 1.0版本发布,标志着 Matlab的诞生。
2000年代至今
Matlab不断更新迭代,功能日益强 大。
04
Matlab的主要特点
数值计算
Matlab以数值计算为核心,提 供了大量的数学函数库,方便
用户进行各种数值计算。
MATLAB入门教程)1.MATLAB的基本知识

1-1、基本运算与函数在MATLAB下进行基本数学运算,只需将运算式直接打入提示号(>>)之後,并按入Enter 键即可。
例如:>> (5*2+1.3-0.8)*10/25ans =4.2000MATLAB会将运算结果直接存入一变数ans,代表MATLAB运算後的答案(Answer)并显示其数值於萤幕上。
小提示:">>"是MATLAB的提示符号(Prompt),但在PC中文视窗系统下,由於编码方式不同,此提示符号常会消失不见,但这并不会影响到MATLAB的运算结果。
我们也可将上述运算式的结果设定给另一个变数x:x = (5*2+1.3-0.8)*10^2/25x = 42此时MATLAB会直接显示x的值。
由上例可知,MATLAB认识所有一般常用到的加(+)、减(-)、乘(*)、除(/)的数学运算符号,以及幂次运算(^)。
小提示:MATLAB将所有变数均存成double的形式,所以不需经过变数宣告(Variable declaration)。
MATLAB同时也会自动进行记忆体的使用和回收,而不必像C语言,必须由使用者一一指定.这些功能使的MATLAB易学易用,使用者可专心致力於撰写程式,而不必被软体枝节问题所干扰。
若不想让MATLAB每次都显示运算结果,只需在运算式最後加上分号(;)即可,如下例:y = sin(10)*exp(-0.3*4^2);若要显示变数y的值,直接键入y即可:>>yy =-0.0045在上例中,sin是正弦函数,exp是指数函数,这些都是MATLAB常用到的数学函数。
下表即为MATLAB常用的基本数学函数及三角函数:小整理:MATLAB常用的基本数学函数abs(x):纯量的绝对值或向量的长度angle(z):复数z的相角(Phase angle)sqrt(x):开平方real(z):复数z的实部imag(z):复数z的虚部conj(z):复数z的共轭复数round(x):四舍五入至最近整数fix(x):无论正负,舍去小数至最近整数floor(x):地板函数,即舍去正小数至最近整数ceil(x):天花板函数,即加入正小数至最近整数rat(x):将实数x化为分数表示rats(x):将实数x化为多项分数展开sign(x):符号函数(Signum function)。
如何在MATLAB中进行数值计算

如何在MATLAB中进行数值计算1.基本数学操作:-加法、减法、乘法、除法:使用+、-、*、/操作符进行基本算术运算。
-幂运算:使用^或.^(点乘)操作符进行幂运算。
- 开平方/立方:可以使用sqrt(或power(函数进行开平方和立方运算。
2.矩阵操作:- 创建矩阵:可以使用矩阵构造函数如zeros(、ones(、rand(等创建矩阵。
- 矩阵运算:使用*操作符进行矩阵相乘,使用transpose(函数进行矩阵转置。
- 矩阵求逆和求解线性方程组:使用inv(函数求矩阵的逆,使用\操作符求解线性方程组。
3.数值积分和微分:- 数值积分:使用integral(函数进行数值积分。
可以指定积分函数、积分上下限和积分方法。
- 数值微分:使用diff(函数进行数值微分。
可以指定微分函数和微分变量。
4.解方程:- 一元方程:使用solve(函数可以解一元方程。
该函数会尝试找到方程的精确解。
- 非线性方程组:使用fsolve(函数可以求解非线性方程组。
需要提供初始值来开始求解过程。
-数值方法:可以使用牛顿法、二分法等数学方法来求解方程。
可以自定义函数来实现这些方法。
5.统计分析:- 统计函数:MATLAB提供了丰富的统计分析函数,如mean(、std(、var(等用于计算均值、标准差、方差等统计量。
- 直方图和密度估计:使用histogram(函数可以绘制直方图,并使用ksdensity(函数进行核密度估计。
- 假设检验:使用ttest(或anova(函数可以进行假设检验,用于比较多组数据之间的差异。
6.数值优化:- 非线性最小化:使用fminunc(函数可以进行非线性最小化。
需要提供目标函数和初始点。
- 线性规划:使用linprog(函数可以进行线性规划。
需要提供目标函数和限制条件。
- 整数规划:使用intlinprog(函数可以进行整数规划。
需要提供目标函数和整数约束。
7.拟合曲线:- 线性拟合:使用polyfit(函数进行线性拟合。
matlab实验:运算基础并且附有答案 (1)

实验二、MATLAB运算基础一、实验目的掌握MATLAB各种表达式的书写规则及常用函数的使用。
掌握MATLAB中字符串、元胞数组和结构的常用函数的使用。
二、实验内容及步骤1、设有矩阵A和B,A=[1 2 3 4 5;6 7 8 9 10;11 12 13 14 15;16 1718 19 20;21 22 23 24 25],B=[3 0 16;17 -6 9;0 23 -4;9 7 0;4 1311]1)求它们的乘积C >>C=A*B2)将矩阵C的右下角3x2子矩阵赋给D >>I=[3 4 5];J=[2 3];D=C(I,J)也可以用>>D=C([3 4 5],[2 3])D =520 397705 557890 7172、完成下列操作1)求[100,999]之间能被61整除的数及其个数(提示:先利用冒号表达式,再利用find和length函数。
)>> a=100:999;find(rem(a,61)==0)ans =23 84 145 206 267 328 389 450 511572 633 694 755 816 877>> b=a(ans)b =122 183 244 305 366 427 488 549 610 671 732 793 854 915 976>> length(b)ans =152)建立一个字符串向量,删除其中的大写字母(提示:利用find函数和空矩阵。
)a=’I am maying’;a( find(a>’A’&a<’Z’))=[]3、已知A=[23 10 -78 0;41 -45 65 5;32 5 0 32;6 -54 92 14],取出其前3行构成矩阵B,其前两列构成矩阵C,其左下角3x2子矩阵构成矩阵D,B与C的乘积构成矩阵E,分别求E<D、E&D、E|D、~E|~D。
实验1 MATLAB基本操作

一、实验目的1.熟悉MATLAB 的使用方法及特点;学会建立MATLAB 搜索路径;熟悉MATLAB 工作空间、MATLAB 集成环境、命令窗口;掌握MATLAB 的通用命令、管理命令和函数、管理变量和工作空间的使用方法;2.掌握MATLAB 基本操作及矩阵基础知识,包括:输入矩阵、矩阵的转置、矩阵元素求和、矩阵下际、矩阵连接、矩阵行列删除、矩阵产生和操作、逻辑和关系运算、操作符和特殊字符、基本矩阵和矩阵操作、基本矩阵和阵列;掌握特殊变量和常数;掌握基本数学函数。
二、实验内容1.利用基本矩阵产生 3x3 和15x8 的单位阵,全1 阵,全0 阵,均匀分布的随机阵([-1,1]之间),正态分布随机阵(方差4,均值1)eye(3),eye(15,8)ones(3),ones(15,8)zeros(3),zeros(15,8)1-2*rand(3),1-2*rand(15,8)2*randn(3)+1, 2*randn(15,8)+12.利用diag()函数和rot90()产生下列矩阵:0 0 8 2 0 4a= 0 -7 5 b= 0 5 02 3 0 7 0 8然后求解a 阵的逆矩阵aa 及b 阵的特征值和对应特征向量,并利用reshape 将aa 阵变换成行向量。
X=diag([2 -7 8]),Y=diag([3 5],-1),a=rot90(X+Y)M=diag([2 5 8]),N=diag([7 0 4]),b=M+rot90(N)aa=inv(a) reshape(aa,1,9) d=eig(b) [V,D]=eig(b)aa =-0.1339 0.2143 0.50000.0893 -0.1429 00.1250 0 0ans = -0.1339 0.0893 0.1250 0.2143 -0.1429 0 0.5000 0 0d =-1.082811.08285.0000V = -0.7921 -0.4030 00 0 1.00000.6104 -0.9152 0D = -1.0828 0 00 11.0828 00 0 5.00003产生一均匀分布在(-5,5)随机阵(50x2),精确到小数点后一位x=5-round(100*rand(50,2))/104.编程实现当α∈[-π,π],间隔为1o 时,求解正弦和余弦的值,并利用plot()函数绘制正弦,余弦曲线。
实验一Matlab运算基础

利用不同的方法对 =z
x2 − y2 16 9
在(-3,3)上的二维插值效果
进行比较。
三、实验总结
结合平时生活、学习经验,体会本次实验各种 方法的用处和重要性。
实验六 Matlab的基本应用3: 常微分方程求解
一、实验目的
1、学会用Matlab进行常微分方程的求解、 随机试验和统计作图
2、掌握相关数据分析函数库的内容
quit或exit
关闭/推出MATALB
二、实验内容
矩阵创建
直接输入 用语句生成 矩阵连接 创建矩阵函数 矩阵操作 复数
矩阵运算 元素群运算
P86, 4.1,4.2, 4.3,4.10
三、实验分析
1 2 3
4 6 8
矩阵A= 4 5 6 ,B= 5 5 6
7 8 9
3 2 2
(1)计算A*B, A.*B, 并比较两者的区别? (2)expm,sqrtm,logm与exp,sqrt,log的区别?
二、实验内容
(1)已知矩阵A=
5 9
2 1
,B=
1 9
2 2
,
做简单的关系运算A>B, A==B, A<B, 并做逻辑 运算(A==B)&(A<B), (A==B)&(A>B)。
(2)编写程序(分别用for 和while),实现:
用公式 π =1− 1 + 1 − 1 +…… 求π 的近似值,
4 357
直到某一项的绝对值小于10-6 为止。
三、实验分析与总结
对流程控制语句和结构进行分析和总结。
实验三 Matlab绘图
一、实验目的
1、了解并掌握matlab的基本绘图
MATLAB入门教程.pdf

MATLAB 入门教程
1.MATLAB 的基本知识
1-1、基本运算与函数
在 MATLAB 下进行基本数学运算,只需将运算式直接打入提示号(>>)之後, 并按入 Enter 键即可。例如: >> (5*2+1.3-0.8)*10/25 ans =4.2000 MATLAB 会将运算结果直接存入一变数 ans,代表 MATLAB 运算後的答案 (Answer)并显示其数值於萤幕上。 小提示: ">>"是 MATLAB 的提示符号(Prompt),但在 PC 中文视窗系统下, 由於编码方式不同,此提示符号常会消失不见,但这并不会影响到 MATLAB 的 运算结果。 我们也可将上述运算式的结果设定给另一个变数 x: x = (5*2+1.3-0.8)*10^2/25 x = 42 此时 MATLAB 会直接显示 x 的值。由上例可知,MATLAB 认识所有一般常用到 的加(+)、减(-)、乘(*)、除(/)的数学运算符号,以及幂次运算(^)。 小提示: MATLAB 将所有变数均存成 double 的形式,所以不需经过变数宣告 (Variable declaration)。MATLAB 同时也会自动进行记忆体的使用和回收,而不 必像 C 语言,必须由使用者一一指定.这些功能使的 MATLAB 易学易用,使用者 可专心致力於撰写程式,而不必被软体枝节问题所干扰。 若不想让 MATLAB 每次都显示运算结果,只需在运算式最後加上分号(;)即 可,如下例: y = sin(10)*exp(-0.3*4^2); 若要显示变数 y 的值,直接键入 y 即可: >>y y =-0.0045 在上例中,sin 是正弦函数,exp 是指数函数,这些都是 MATLAB 常用到的数学 函数。 下表即为 MATLAB 常用的基本数学函数及三角函数: 小整理:MATLAB 常用的基本数学函数 abs(x):纯量的绝对值或向量的长度 angle(z):复 数 z 的相角(Phase angle) sqrt(x):开平方 real(z):复数 z 的实部 imag(z):复数 z 的虚 部 conj(z):复数 z 的共轭复数 round(x):四舍五入至最近整数 fix(x):无论正负,舍去小数至最近整数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.对数等分生成向量 函数logspace用来生成对数等分向量: LOGSPACE Logarithmically spaced vector. LOGSPACE(d1, d2) generates a row vector of 50 logarithmically equally spaced points between decades 10^d1 and 10^d2. If d2 is pi, then the points are between 10^d1 and pi. LOGSPACE(d1, d2, N) generates N points. logspace(0,5,6) , 此处log以10为底数。
特殊矩阵的生成
[ ] 空阵; zeros 全0阵;eye 单位阵;ones 全1阵; rand随机阵;magic魔方矩阵;company伴随矩阵; pascal Pascal矩阵;gallery Higham测试阵; rosser 经典对称特征值测试矩阵; hadamard Hadamard矩阵; toeplitz Toeplitz矩阵; hankel Hankel矩阵;vander 范得蒙矩阵; hilb Hilbert矩阵; wilkinson Wilkinson’s特征值测试矩阵; invhilb 反Filbert矩阵。
-0.2706 0.4824 -0.0353 0.0471
-0.9412 0.7647 -0.4706 0.2941
矩阵的行列式运算
det(A) 表示计算矩阵A的行列式。 例:对于上面的a,有: det(a)= -85 det(inv(a)) = -0.0118
矩阵的幂运算:
^ Matrix power. Z = X^y is X to the y power if y is a scalar and X is square. If y is an integer greater than one, the power is computed by repeated multiplication. For other values of y the calculation involves eigenvalues and eigenvectors. Z = X^Y is X to the Y power, if Y is a square matrix and X is a scalar, computed using eigenvalues and eigenvectors.
在欧美高校,MATLAB已经成为线性代 数、自动控制理论、数理统计、数字信号 处理、时间序列分析、动态系统仿真等高 级课程的基本教学工具;成为攻读学位的 本科生、硕士生、博士生必须掌握的基本 技能。在国内,目前各个高校也正在逐步 开设相关课程,为广大学生学习和使用 MATLAB提供方便。
§1.2 MATLAB的语言特点 优点:简洁、紧凑,使用方便灵活, 库函数丰富、可靠;运算符丰富,提供了 几乎和C语言一样多的运算符;具有结构 化的控制语句,面向对象编程的特性;语 法限制不严格,程序设计自由度大;程序 的可移植性很好;图形功能强大;具有功 能强劲的工具箱;源程序具有开放性。 缺点:程序的执行速度较慢。
a=[1 2 3 4 5678 3 4 5 6] a= 1 2 3 5 6 7 3 4 5
4 8 6
几个重要的Matlab矩阵命令
• • • • • • • • zeros ones eye linspace rand diag \ /
• • • • • • • det inv eig rank rref orth null
关于SUM的用法,有: SUM Sum of elements. For vectors, SUM(X) is the sum of the elements of X. For matrices, SUM(X) is a row vector with the sum over each column. For N-D arrays, SUM(X) operates along the first non-singleton dimension. SUM(X,DIM) sums along the dimension DIM.
MATLAB及基本运算
第一章 MATLAB概述 第二章 数值计算功能
第一章 MATLAB概述
§1.1 发展历史 1970s,创始人:Cleve Moler博士; 1984年,Cleve Moler和John Little成立了 MathWorks公司,将MATLAB推上市场; 1993年推出MATLAB4.0版; 1997年推出5.0版; 1998年推出5.2版; 目前我们可以看到的最新版本为7.x版。
矩阵与常数间的运算
矩阵与常数间的运算为矩阵的每一个元素 之间的运算。需要注意的是作除法运算时,常 数只能作除数。 矩阵的逆运算 inv(A) :表示求矩阵A的逆矩阵。 例如:a=[2 1 -3 -1;3 1 0 7;-1 2 4 -2;1 0 -1 5]
a= 2 1 -3 -1 3 1 0 7 -1 2 4 -2 1 0 -1 5 inv(a) ans = -0.0471 0.5882 0.3882 -0.3529 -0.2235 0.2941 -0.0353 -0.0588
理论复习:解的理论
• 若秩(A) = 秩(A,b) = n, 存在唯一解; • 若秩(A) = 秩(A,b) < n, 存在无穷多解,其 通解可表示为Ax=0的一个基础解系与Ax=b 的一个特解的叠加; • 若秩(A) 秩(A,b),则无解,寻求最小二乘 近似解
逆
• 方阵A称为可逆的,如果存在方阵B,使 AB=BA=E 则称B为A的逆矩阵,记 为B = A -1。 • 方阵A可逆的充要条件是A0。 A -1 =
intro : 介绍界面
who : 查 询
whos: 查 询
clear: 清 除
第二章 数值计算功能
§2.1 数字及其运算
Matlab的基本运算单元是以数字为元素 的矩阵,而将数字看成 1×1 矩阵作统一处 理,当我们使用数的运算功能时,我们可以 如同平时用手在纸上写字一样,直接写出 要计算的表达式后,按回车键即可得到结 果。
Example: If X = [0 1 2 3 4 5] then sum(X,1) is [3 5 7] and sum(X,2) is [ 3 12];
叉积 实现函数:cross C=cross(A,B) A与B必须为3维向量; 混合积: a=[1 2 3]; b=[3 4 5]; c=cross(a,b) c= -2 4 -2 dot(a,cross(b,c)) ans = 24
矩阵的基本运算
矩阵的四则运算 : 加 + A+B (同维矩阵) 矩阵相加 减 - A-B (同维矩阵 ) 矩阵相减 乘 * A*B (A的列数=B的行数 ) 矩阵相乘 左除 \ A\B (=INV(A)*B) 用于求方程组的解 右除/ A/B (=A*INV(B)) 用于求方程组的解 点乘.* A.*B 同维矩阵或其中一个为数 对应元素相乘 点除./ A./B 同维矩阵或其中一个为数 对应元素相除
主要工具箱
• 数学类:最优化,统计,神经网络,符 号数学,偏微分方程,样条函数,数据 拟合、结构动力学,虚拟现实等 • 数据库类 • 信号处理类 • 控制工程类 • 金融经济类 • 系统仿真类(Simulink)
几个有用的命令
Help : 包括help,help+函数名, helpwin 和helpdesk。 demo : 演示界面
1 A* A
特征值与特征向量
• 对于方阵A,若存在数和非零向量x使 Ax=x
则称为A一个特征值,x为A的一个 对应于特征值的特征向量。 • 特征值计算归结为特征多项式的求根。
• 对应于特征值的特征向量是齐次线性 方程组(A - E) x = 0 的所有非零解。
正交矩阵
• 正交向量 x’x=0
输入输出格式用format命令来控制: FORMAT SHORT 5位 FORMAT LONG 15位 FORMAT RAT 有理数表达 注:具体可用 help format 查看
常住变量: pi, i 或 j, inf, NaN
§2.2 向量及其运算
输入向量的方法: 1. 直接输入法
A=[1 2 3 4], B=[1,2,3,4], C=[1;2;3;4],元素用[ ]括起来,元素之间 用空格或逗号分隔表示行向量, 用分号分隔就表示列向量。
例如:>>23*23 ans = 529 这里 ans 是系统规定的存放计算结果的变量, 也可以自己定义,如: >>x=230 x= 230
>>y=450 y= 450 >>z=x*y z= 103500 这 里 , 将 x 定 义 为 230 , y 定 义为复杂的时 候。
例如:分别计算水在温度为0、20、40、60和 80度时的黏度。已知水的黏度随温度的变化 公式为:
,,
其中:
0
1 at bt
3
2
0 1.785e
a 0.03368
b 0.000221
用Matlab计算的命令为: muw0=1.785e-3; % 定义零度时的黏度 a=0.03368; b=0.000221; t=0:20:80; % 定义温度变量 muw=muw0./(1+a*t+b*t.^2) muw = 0.0018 0.0010 0.0007 0.0005 0.0003
• 单位向量 x’x=1 • 正交矩阵A’A=E • 正交矩阵的各列向量两两正交,且均为单 位向量
矩阵及其运算
MatLab的所有数值计算功能都是以(复) 矩阵为基本单元进行的,因此MatLab 对矩阵的运算功能是最全、最强的。
