【精品】高中物理竞赛选拔综合经典习题(Word版含详细答案)

合集下载

高中物理竞赛十年预赛真题热学纯手打word版含答案

十年真题－热学（预赛）1．（34届预赛2）系统1和系统2质量相等，比热容分别为C 1和C 2，两系统接触后达到够达到共同的温度T ，整个过程中与外界（两系统之外）无热交换．两系统初始温度T 1和T 2的关系为A ．T 1＝C 2C 1(T －T 2)－TB ．T 1＝C 1C 2(T －T 2)－T C ．T 1＝C 1C 2(T －T 2)＋T D ．T 1＝C 2C 1(T －T 2)＋T 2．（31届预赛1）一线膨胀系数为α的正立方体物块，当膨胀量较小时，其体膨胀系数等于A ．αB ．α1/3C ．α3D ．3α3．（29届预赛1）下列说法中正确的是A ．水在0℃时密度最大B ．一个绝热容器中盛有气体，假设把气体中分子速率很大的如大于v A 的分子全部取走，则气体的温度会下降，此后气体中不再存在速率大于v A 的分子C ．杜瓦瓶的器壁是由两层玻璃制成的，两层玻璃之间抽成真空，抽成真空的主要作用是既可降低热传导，又可降低热辐射D ．图示为一绝热容器，中间有一隔板，隔板左边盛有温度为T 的理想气体，右边为真空．现抽掉隔板，则气体的最终温度仍为T4．(28届预赛2)下面列出的一些说法中正确的是A ．在温度为20ºC 和压强为1个大气压时，一定量的水蒸发为同温度的水蒸气，在此过程中，它所吸收的热量等于其内能的增量．B ．有人用水银和酒精制成两种温度计，他都把水的冰点定为0度，水的沸点定为100度，并都把0刻度与100刻度之间均匀等分成同数量的刻度，若用这两种温度计去测量同一环境的温度（大于0度小于100度）时，两者测得的温度数值必定相同．C ．一定量的理想气体分别经过不同的过程后，压强都减小了，体积都增大了，则从每个过程中气体与外界交换的总热量看，在有的过程中气体可能是吸收了热量，在有的过程中气体可能是放出了热量，在有的过程中气体与外界交换的热量为零.D ．地球表面一平方米所受的大气的压力，其大小等于这一平方米表面单位时间内受上方作热运动的空气分子对它碰撞的冲量，加上这一平方米以上的大气的重量．5．（27届预赛2）烧杯内盛有0℃的水，一块0℃的冰浮在水面上，水面正好在杯口处．最后冰全部融化成0℃的水．在这过程中A ．无水溢出杯口，但最后水面下降了B ．有水溢出杯口，但最后水面仍在杯口处C ．无水溢出杯口，水面始终在杯口处D ．有水溢出杯口，但最后水面低于杯口6．（27届预赛3）如图所示，a和b是绝热气缸中的两个活塞，它们把气缸分成甲和乙两部分，两部分中都封有等量的理想气体．a是导热的，其热容量可不计，与气缸壁固连．b 是绝热的，可在气缸内无摩擦滑动，但不漏气，其右方为大气．图中k为加热用的电炉丝．开始时，系统处于平衡状态，两部分中气体的温度和压强皆相同．现接通电源，缓慢加热一段时间后停止加热，系统又达到新的平衡，则A．甲、乙中气体的温度有可能不变B．甲、乙中气体的压强都增加了C．甲、乙中气体的内能的增加量相等D．电炉丝放出的总热量等于甲、乙中气体增加内能的总和7．（27届预赛4）一杯水放在炉上加热烧开后，水面上方有“白色气”；夏天一块冰放在桌面上，冰的上方也有“白色气”．A．前者主要是由杯中水变来的“水的气态物质”B．前者主要是由杯中水变来的“水的液态物质”C．后者主要是由冰变来的“水的气态物质”D．后者主要是由冰变来的“水的液态物质”8．（26届预赛3）一根内径均匀、两端开中的细长玻璃管，竖直插在水中，管的一部分在水面上．现用手指封住管的上端，把一定量的空气密封在玻璃管中，以V0表示其体积；然后把玻璃管沿竖直方向提出水面，设此时封在玻璃管中的气体体积为V1；最后把玻璃管在竖直平面内转过900，让玻璃管处于水平位置，设此时封在玻璃管中的气体体积为V2．则有A．V1＞V0≥V2B．V1＞V0＞V2C．V1=V2＞V0D．V1＞V0，V2＞V09．（25届预赛4）如图所示，放置在升降机地板上的盛有水的容器中，插有两根相对容器的位置是固定的玻璃管a和b，管的上端都是封闭的，下端都是开口的．管内被水各封有一定质量的气体．平衡时，a管内的水面比管外低，b管内的水面比管外高．现令升降机从静止开始加速下降，已知在此过程中管内气体仍被封闭在管内，且经历的过程可视为绝热过程，则在此过程中A．a中气体内能将增加，b中气体内能将减少B．a中气体内能将减少，b中气体内能将增加C．a、b中气体内能都将增加D．a、b中气体内能都将减少10．（25届预赛5）图示为由粗细均匀的细玻璃管弯曲成的“双U形管”，a、b、c、d 为其四段竖直的部分，其中a、d上端是开口的，处在大气中．管中的水银把一段气体柱密封在b、c内，达到平衡时，管内水银面的位置如图所示．现缓慢地降低气柱中气体的温度，若c中的水银面上升了一小段高度Δh，则A．b中的水银面也上升ΔhB．b中的水银面也上升，但上升的高度小于ΔhC ．气柱中气体压强的减少量等于高为Δh 的水银柱所产生的压强D ．气柱中气体压强的减少量等于高为2Δh 的水银柱所产生的压强11．（31届预赛9）图中所示的气缸壁是绝热的．缸内隔板A 是导热的，它固定在缸壁上．活塞B 是绝热的，它与缸壁的接触是光滑的，但不漏气.B 的上方为大气.A 与B 之间以及A 与缸底之间都盛有n mol 的同种理想气体．系统在开始时处于平衡状态，现通过电炉丝E 对气体缓慢加热．在加热过程中，A 、B 之间的气体经历_________过程，A 以下气体经历________过程；气体温度每上升1K ，A 、B 之间的气体吸收的热量与A 以下气体净吸收的热量之差等于_____________．已知普适气体常量为R ．答案：等压、等容、nR解析：在加热过程中，AB 之间的气体的压强始终等于大气压强与B 活塞的重力产生的压强之和，故进行的是等压变化，由于隔板A 是固定在气缸内的，所以，A 以下的气体进行的是等容变化，当气体温度升高1K 时，AB 之间的气体吸收的热量为Q 1＝P ΔV +ΔU ，A以下的气体吸收的热量为Q 2＝ΔU ，又根据克拉伯龙方程p ΔV ＝nR ΔT ，所以Q 1－Q 2＝p ΔV＝nR .12．（28届预赛6）在大气中，将一容积为0.50m 3的一端封闭一端开口的圆筒筒底朝上筒口朝下竖直插人水池中，然后放手，平衡时，筒内空气的体积为0.40m 3.设大气的压强与10.0m 高的水柱产生的压强相同，则筒内外水面的高度差为．答案：2.5m13．（34届预赛13）横截面积为S 和2S 的两圆柱形容器按图示方式连接成一气缸，每隔圆筒中各置有一活塞，两活塞间的距离为l ，用硬杆相连，形成“工”字形活塞，它把整个气缸分隔成三个气室，其中Ⅰ、Ⅲ室密闭摩尔数分别为ν和2ν的同种理想气体，两个气室内都有电加热器；Ⅱ室的缸壁上开有一个小孔，与大气相通；1mol 该种气体内能为CT（C 是气体摩尔热容量，T 是气体的绝对温度）．当三个气室中气体的温度均为T 1时，“工”字形活塞在气缸中恰好在图所示的位置处于平衡状态，这时Ⅰ室内空气柱长亦为l ，Ⅱ室内空气的摩尔数为32ν．已知大气压不变，气缸壁和活塞都是绝热的，不计活塞与气缸之间的摩擦．现通过电热器对Ⅰ、Ⅲ两室中的气体缓慢加热，直至Ⅰ室内气体的温度升为其初始状态温度的2倍，活塞左移距离d ．已知理想气体常量为R ，求：（1）Ⅲ室内气体初态气柱的长度；（2）Ⅲ室内气体末态的温度；（3）此过程中ⅠⅢ室密闭气体吸收的总热量．解析：（1）设大气压强为p 0．初态：Ⅰ室内气体压强为p 1；Ⅲ室内气体压强为p 1′，气柱的长度为l ′．末态：Ⅰ室内气体压强为p 2；Ⅲ室内气体压强为p 2′．由初态到末态：活塞左移距离为d ．对初态应用气体状态方程，对Ⅰ室气体有：p 1lS ＝νRT 1 ①对Ⅱ室内气体有：p 0(l 2×S ＋l 2×2S )＝32ν0RT 1②对Ⅲ室内气体有：p1′l′(2S)＝(2ν)RT1③由力学平衡条件有：p1′(2S)＝p1S＋p0(2S－S) ④由题给条件和①②③④式得：l′＝ν2ν1+ν0l＝2νν+ν0l⑤（2）对末态应用气体状态方程，对Ⅰ室内气体有：p2(l－d)S＝νRT2＝νR·2T1⑥对Ⅲ室内气体有：p2′(l′＋d)(2S)＝(2ν)RT2′⑦由力学平衡条件有：p2′(2S)＝p2S＋p0(2S－S) ⑧联立②⑤⑥⑦⑧和题给条件得：T2′＝2νl+(ν+ν0)d(l－d)(ν+ν0)⎝⎛⎭⎫1＋ν02νl－dl T1⑨（3）大气对密闭气体系统做的功为W＝p0(2S－S)(－d)＝－p0Sd＝－dlν0RT1⑩已利用②式．系统密闭气体内能增加量为：ΔU＝νC(T2－T1)＋(2ν)C(T2′－T1)＝νC(2T2′－T1) ⑪由⑨⑩式得：ΔU＝2νl+(ν+ν0)d(l－d)(ν+ν0)⎝⎛⎭⎫2ν＋l－dlν0CT1－νCT1⑫系统吸收的热量为：Q＝ΔU－W＝2νl+(ν+ν0)d(l－d)(ν+ν0)⎝⎛⎭⎫2ν＋l－dlν0CT1－νCT1＋dlν0RT1⑬参考评分：第（1）问9分，①②③④式各2分，⑤式1分．第（2）问4分，⑥⑦⑧⑨式各1分．第（3）问7分，⑩⑪式各2分，⑫式1分，⑬式2分．14．（33届预赛16）充有水的连通软管常常用来检验建筑物的水平度．但软管中气泡会使得该软管两边管口水面不在同一水平面上．为了说明这一现象的物理原理，考虑如图所示的连通水管（由三段内径相同的U形管密接而成），其中封有一段空气（可视为理想气体），与空气接触的四段水管均在竖直方向；且两个有水的U形管两边水面分别等高．此时被封闭的空气柱的长度为L a ．已知大气压强P 0、水的密度ρ、重力加速度大小为g ，L 0≡P 0/(ρg)．现由左管口添加体积为ΔV ＝xS 的水，S 为水管的横截面积，在稳定后：（1）求两个有水的U 形管两边水面的高度的变化和左管添水后封闭的空气柱的长度；（2）当x <<L 0、L a<<L 0时，求两个有水的U 形管两边水面的高度的变化（用x 表出）以及空气柱的长度．已知1+z ≈1+12z ，当z <<1．解析：解法（一）（1）设在左管添加水之前左右两个U 形管两边水面的高度分贝为h 1和h 2，添加水之后左右两个U 形管两边水面的高度分别为h 1L 和h 1R 、h 2L 和h 2R ．如图所示，设被封闭的空气的压强为p ，空气柱的长度为L b ．水在常温常压下可视为不可被压缩的流体，故：2h 1＋x ＝h 1L ＋h 1R ①2h 2＝h 2L ＋h 2R ②由力学平衡条件有：p 0＋ρgh 1L ＝p ＋ρgh 1R ③p 0＋ρgh 2R ＝p ＋ρgh 2L④由于连通管中间高度不变，有：h 1＋h 2＋L a ＝h 1R ＋h 2L ＋L b ⑤由玻意耳定律得：p 0L a ＝pL b ⑥联立①②③④⑤⑥式得p 满足的方程：L 0p 0p 2＋⎝⎛⎭⎫L a －L 0－x 2p －p 0L a ＝0 解得：p ＝p 02L 0⎣⎡⎦⎤L 0－L a ＋x 2＋⎝⎛⎭⎫L a －L 0－x 22+4L a L 0 ⑦ 将⑦式带入⑥式得：L b ＝12⎣⎡⎦⎤L a －L 0－x 2＋⎝⎛⎭⎫L a －L 0－x 22+4L a L 0 ⑧ 由①②③④⑦式得：Δh 1L ≡h 1L －h 1＝x －Δh 1R＝x －L 02＋14[L 0－L a ＋x 2＋⎝⎛⎭⎫L a －L 0－x 22+4L a L 0] ⑨ ＝5x －2L a －2L 08＋14⎝⎛⎭⎫L a －L 0－x 22+4L a L 0 Δh 1R ≡h 1R －h 1＝L 0+x 2－p 2ρg＝L 0+x 2－14⎣⎡⎦⎤L 0－L a ＋x 2＋⎝⎛⎭⎫L a －L 0－x 22+4L a L 0 ⑩＝3x +2L a +2L 08－14⎝⎛⎭⎫L a －L 0－x 22+4L a L 0 Δh 2L ≡h 2L －h 2＝L 02－p 2ρg ＝L 02－14⎣⎡⎦⎤L 0－L a ＋x 2＋⎝⎛⎭⎫L a －L 0－x 22+4L a L 0 ⑪ ＝2L a +2L 0－x 8－14⎝⎛⎭⎫L a －L 0－x 22+4L a L 0 Δh 2R ≡h 2R －h 2＝－Δh 2L＝x －2L a －2L 08＋14⎝⎛⎭⎫L a －L 0－x 22+4L a L 0 ⑫ （2）在x <<L 0和L a <<L 0的情形下，由⑧式得：L b ≈L a ⑬⑦式成为：p ≈p 0(1＋x 2L 0) ⑭ 由⑨⑩⑪⑫⑬⑭式得：Δh 1L ≈34x ⑮ Δh 1R ≈－Δh 2L ＝Δh 2R ≈14x ⑯ 参考评分：第（1）问14分，①②③④⑤⑥⑦⑧式各1分，⑨⑩式各2分，⑪⑫式各1分；第（2）问6分，⑬⑭式各1分，⑮⑯式各2分．解法（二）（1）设U 形管1左侧末态水面比初态上升x 2＋y ，右侧末态水面比初态上升x 2－y ，U 形管2左侧末态水面比初态下降y ，右侧末态水面比初态上升y ．由玻意耳定律得： L a L 0＝L b (L 0＋2y ) ①由几何关系有：L a －x 2＋2y ＝L b ②将②式带入①式得：L a L 0＝(L a －x 2＋2y ) (L 0＋2y ) ③解得： y ＝x 8－L 04－L a 4＋14⎝⎛⎭⎫L 0＋L a －x 22＋2xL 0 ④ 此即U 形管2左侧末态比初态水面下降值，也是右侧末态比初态水面上升值（负根y＝x 8－L 04－L a 4－14⎝⎛⎭⎫L 0＋L a －x 22＋2xL 0不符合题意，已舍去）．U 形管1左侧末态比初态水面上升：x 2＋y ＝5x －2L a －2L 08＋14⎝⎛⎭⎫L a ＋L 0－x 22＋2xL 0 ⑤ 右侧末态比初态水面上升：x 2－y ＝3x ＋2L a ＋2L 08－14⎝⎛⎭⎫L a ＋L 0－x 2 2＋2xL 0 ⑥ 将④式带入②式得：L b ＝L a －x 2＋2y ＝2L a －2L 0－x 4＋12⎝⎛⎭⎫L a ＋L 0－x 22＋2xL 0 ⑦ （2）在x <<L 0和L a <<L 0的情形下，④⑤⑥⑦式中的根号部分⎝⎛⎭⎫L a ＋L 0－x 22＋2xL 0＝L a 2＋L 02＋x 24＋2L 0L a －xL 0－xL a ＋2xL 0 ＝L 01+L a 2L 02＋x 24L 02＋2L a L 0－xL a 2L 02＋x L 0≈L 0⎣⎡⎦⎤1＋12（L a 2L 02＋x 24L 02＋2L a L 0－xL a L 02＋x L 0 ＝L 0＋12⎣⎡⎦⎤L a 2L 0＋x 24L 0＋2L a －xL a L 0＋x ⑧ ≈L 0＋12(2L a ＋x ) ＝L a ＋L 0＋x 2⑧式在推导过程中用到了1+z ≈1+12z ，当z <<1．将⑧式带入④⑤⑥⑦式中分别得到：y ≈x 8－L 04－L a 4＋14⎝⎛⎭⎫L 0＋L a ＋x 2＝x 4⑨ x 2＋y ≈x 2＋x 4＝3x 4⑩ x 2－y ≈x 2－x 4＝x 4⑪ L b ≈L a 2－L 02－x 4＋12⎝⎛⎭⎫L 0＋L a ＋x 2＝L a ⑫参考评分：第（1）问14分，①式4分，②③式各1分，④式3分，⑤式2分，⑥式1分．第（2）问6分，⑨⑩式各2分，⑪⑫式各1分．15．(32届预赛15)如图，导热性能良好的气缸A 和B 高度均为h （已除开活塞的厚度），横截面积不同，竖直浸没在温度为T 0的恒温槽内，它们的底部由一细管连通（细管容积可忽略）．两气缸内各有一个活塞，质量分别为m A ＝2m 和m B ＝m ，活塞与气缸之间无摩擦，两活塞的下方为理想气体，上方为真空．当两活塞下方气体处于平衡状态时，两活塞底面相对于气缸底的高度均为h /2．现保持恒温槽温度不变，在两活塞上面同时各缓慢加上同样大小的压力，让压力从零缓慢增加，直至其大小等于2m g （g 为重力加速度）为止，并一直保持两活塞上的压力不变；系统再次达到平衡后，缓慢升高恒温槽的温度，对气体加热，直至气缸B 中活塞底面恰好回到高度为h /2处．求：（1）两个活塞的横截面积之比S A ∶S B ．（2）气缸内气体的最后的温度．（3）在加热气体的过程中，气体对活塞所做的总功．解析：（1）平衡时气缸A 、B 内气体的压强相等，故：m A g S A ＝m B g S B① 由①式和题给条件得： S A ∶S B ＝2∶1 ②（2）两活塞上各放一质量为2m 的质点前，气体的压强p 1和体积V 1分别为：p 1＝2mg S A ＝mg S B③ V 1＝32S B h ④ 两活塞上各放一质量为2m 的质点后，B 中活塞所受到的气体压力小于它和质点所受重力之和，B 中活塞将一直下降至气缸底部为之，B 中气体全部进入气缸A ．假设此时气缸A 中活塞并未上升到气缸顶部，气体的压强p 2＝4mg S A ＝2mg S B⑤ 设平衡时气体体积为V 2，由于初态末态都是平衡态，由理想气体状态方程有：p 1V 1T 0＝p 2V 2T 0⑥ 由③④⑤⑥式得： V 2＝34S 0h ＝38S A h ⑦ 这时气体的体积小于气缸A 的体积，与活塞未上升到气缸顶部的假设一致．缓慢加热时，气体先等压膨胀，B 中活塞不动，A 中活塞上升；A 中活塞上升至顶部后，气体等容升压；压强升至3mg S B时，B 中活塞开始上升，气体等压膨胀．设当温度升至T 时，该活塞恰好位于h 2处．此时气体的体积变为V 3＝52S B h ⑧ 气体压强 p 3＝3mg S B⑨ 设此时气缸内气体的温度为T ，由状态方程有：p 2V 2T 0＝p 3V 3T⑩ 由⑤⑦⑧⑨⑩式得： T ＝5T 0 ⑪（3）升高恒温槽的温度后，加热过程中，A 活塞上升量为h －38h ＝58h ⑫ 气体对活塞所做的总功为W ＝4mg ·58h ＋3mg ·h 2＝4mgh ⑬ 参考评分：第（1）问3分，①式2分，②式1分；第（2）问13分，③④⑤⑥式各2分，⑦⑧⑨⑩⑪式各1分；第（3）问4分，⑫⑬式各2分．16．（31届预赛14）1mol 的理想气体经历一循环过程1-2-3-1，如p -T 图示所示，过程1-2是等压过程，过程3-1是通过p -T 图原点的直线上的一段，描述过程2-3的方程为c 1p 2+c 2p =T ，式中c 1和c 2都是待定的常量，p 和T 分别是气体的压强和绝对温度．已知，气体在状态1的压强、绝对温度分别为P 1和T 1，气体在状态2的绝对温度以及在状态3的压强和绝对温度分别为T 2以及p 3和T 3．气体常量R 也是已知的．(1)求常量c 1和c 2的值；(2)将过程1-2 -3 -1在p -v 图示上表示出来；(3)求该气体在一次循环过程中对外做的总功．解析：（1）设气体在状态i （i ＝1、2、3）下的压强、体积和温度分别为p i 、V i 和T i ，由题设条件有：c 1p 22＋c 2p 2＝T 2 ①c 1p 32＋c 2p 3＝T 3 ②由此解得：c 1＝T 2p 3－T 3p 2p 22p 3－p 32p 2＝T 2p 3－T 3p 1p 12p 3－p 32p 1③ c 2＝T 2p 32－T 3p 22p 2p 32－p 22p 3＝T 2p 32－T 3p 12p 1p 32－p 12p 3④ （2）利用气体状态方程pV ＝RT 以及V 1＝R T 1p 1、V 2＝R T 2p 2、V 3＝R T 3p 3⑤ 可将过程2—3的方程写为p V 2－V 3p 2－p 3＝V ＋V 2p 3－V 3p 2p 2－p 3⑥ 可见，在p －V 图上过程2－3是以（p 2，V 2）和（p 3，V 3）为状态端点的直线，过程3－1是通过原点直线上的一段，因而描述其过程的方程为：p T ＝c 3 ⑦ 式中c 3是一常量，利用气体状态方程pV ＝RT ，可将过程3－1的方程改写为：V ＝R c 3＝V 3＝V 1 ⑧ 这是以（p 3，V 1）和（p 1，V 1）为状态端点的等容降压过程．综上所述，过程1－2－3－1在p －V 图上是一直角三角形，如图所示．（3）气体在一次循环过程中对外做的总功为：W ＝－12(p 3－p 1)(V 2－V 1) ⑨ 利用气体状态方程pV ＝RT 和⑤式，上式即：W ＝－12R (T 2－T 1)⎝⎛⎭⎫p 3p 1－1 ⑩ 参考评分：第（1）问8分，①②③④式各2分；第（2）问10分，⑤⑥式各2分，过程1－2－3－1在p －V 上的图示正确得6分；第（3）问2分，⑩式2分．17．(30届预赛14)如图所示，1摩尔理想气体，由压强与体积关系的p-V 图中的状态A 出发，经过一缓慢的直线过程到达状态B ，已知状态B 的压强与状态A 的压强之比为12，若要使整个过程的最终结果是气体从外界吸收了热量，则状态B 与状态A 的体积之比应满足什么条件？已知此理想气体每摩尔的内能为32RT ，R 为普适气体常量，T 为热力学温度．解析：令ΔU 表示系统内能的增量，Q 和W 分别表示系统吸收的热量和外界对系统所做的功，由热力学第一定律有：ΔU ＝Q ＋W ①令T 1和T 2分别表示状态A 和状态B 的温度，有：ΔU ＝32R (T 2－T 1) ②令p 1、p 2和V 1、V 2分别表示状态A 、B 的压强和体积，由②式和状态方程可得： ΔU＝32(p 2V 2－p 1V 1) ③由状态图可知，做功等于图线下所围面积，即：W ＝－12(p 1＋p 2)(V 2－V 1) ④要系统吸热，即Q ＞0，由以上格式可得：32(p 2V 2－p 1V 1)＋12(p 1＋p 2)(V 2－V 1)＞0⑤按题意，p 2p 1＝12，带入上式，可得：V 2V 1＞32 ⑥参考评分：①②③式各3分，④式4分，⑤式3分，⑥式2分．18．(29届预赛14)由双原子分子构成的气体，当温度升高时，一部分双原子分子会分解成两个单原子分子，温度越高，被分解的双原子分子的比例越大，于是整个气体可视为由单原子分子构成的气体与由双原子分子构成的气体的混合气体．这种混合气体的每一种成分气体都可视作理想气体．在体积V ＝0.045m 3的坚固的容器中，盛有一定质量的碘蒸气，现于不同温度下测得容器中蒸气的压强如下：试求温度分别为1073K 和1473K 时该碘蒸气中单原子分子碘蒸气的质量与碘的总质量之比值．已知碘蒸气的总质量与一个摩尔的双原子碘分子的质量相同，普适气体常量R ＝8.31J·mol －1·K －1解析：以m 表示碘蒸气的总之，m 1表示蒸气的温度为T 时单原子分子的碘蒸气的质量，μ1、μ2分别表示单原子分子碘蒸气和双原子分子碘蒸气的摩尔质量，p 1、p 2分别表示容器中单原子分子碘蒸气和双原子分子碘蒸气的分压强，则由理想气体的状态方程有：p 1V ＝m 1μ1RT ① p 2V＝m －m 1μ2RT②其中，R 为理想气体常量．根据道尔顿分压定律，容器中碘蒸气的总压强p 满足：p ＝p 1＋p 2 ③设α＝m 1m 为单原子分子碘蒸气的质量与碘蒸气的总质量的比值，注意到μ1＝12μ2 ④ 由以上各式解得：α＝μ2V mR ·p T－1 ⑤ 带入有关数据可得，当温度为1073K 时，α＝0.06 ⑥ 当温度为1473K 时，α＝0051 ⑦ 参考评分：①②③⑤式各4分，⑥⑦式各2分．19．（26届预赛15）图中M 1和M 2是绝热气缸中的两个活塞，用轻质刚性细杆连结，活塞与气缸壁的接触是光滑的、不漏气的，M 1是导热的，M 2是绝热的，且M 2的横截面积是M 1的2倍．M 1把一定质量的气体封闭在气缸为L 1部分，M 1和M 2把一定质量的气体封闭在气缸的L 2部分，M 2的右侧为大气，大气的压强p 0是恒定的．K 是加热L 2中气体用的电热丝．初始时，两个活塞和气体都处在平衡状态，分别以V 10和V 20表示L 1和L 2中气体的体积．现通过K 对气体缓慢加热一段时间后停止加热，让气体重新达到平衡太，这时，活塞未被气缸壁挡住．加热后与加热前比，L 1和L 2中气体的压强是增大了、减小还是未变？要求进行定量论证．解析：解法（一）用n 1和n 2分别表示L 1和L 2中气体的摩尔数，p 1、p 2和V 1、V 2分别表示L 1和L 2中气体处在平衡状态时的压强和体积，T 表示气体的温度（因为M 1是导热的，两部分气体的温度相等），由理想气体状态方程有：p 1V 1＝n 1RT ①p 2V 2＝n 2RT ②式中R 为普适气体常量．若以两个活塞和轻杆构成的系统为研究对象，处在平衡状态时有：p 1S 1－p 2S 1＋p 2S 2－p 0S 2＝0 ③已知S 2＝2S 1 ④有③④式得：p 1＋p 2＝2p 0 ⑤由①②⑤三式得：p 1＝2n 1n 2p 0V 2V 1＋n 1n 2V 2 ⑥若⑥式中的V 1、V 2是加热后L 1和L 2中气体的体积，则p 1就是加热后L 1中气体的压强．加热前L 1中气体的压强则为p 10＝2n 1n 2p 0V 20V 10＋n 1n 2V 2 ⑦ 设加热后L 1中气体体积的增加量为ΔV 1，L 2中气体体积的增加量为ΔV 2，因连接两活塞的杆是刚性的，活塞M 2的横截面积是M 1的2倍，故有：ΔV 1＝ΔV 2＝ΔV ⑧加热后L 1和L 2中气体的体积都是增大的，即ΔV ＞0．（若ΔV ＜0，即加热后活塞是向左移动的，则大气将对封闭在气缸中的气体做功，电热丝又对气体加热，根据热力学第一定律，气体的内能增加，温度将上升，而体积是减小的，故L 1和L 2中气体的压强p 1和p 2都将增大，这违反力学平衡条件⑤式）于是有V 1＝V 10＋ΔV ⑨V 2＝V 20＋ΔV ⑩由⑥⑦⑨⑩四式得：p 1－p 10＝2n 1n 2p 0(V 10－V 20)ΔV ⎣⎡⎦⎤V 10＋ΔV ＋n 1n 2(V 20＋ΔV )⎝⎛⎭⎫V 10＋n 1n 2V 20 ⑪由⑪式可知：若加热前V 10＝V 20，则p 1＝p 10，即加热后p 1不变，由⑤式知p 2亦不变；若加热前V 10＜V 20，则p 1＜p 10，即加热后p 1必减小，由⑤式知p 2必增大；若加热前V 10＞V 20，则p 1＞p 10，即加热后p 1必增大，由⑤式知p 2必减小．参考评分：得到⑤式3分，得到⑧式3分，得到⑪式8分，最后结论6分．解法（二）设加热前L 1和L 2中气体的压强和体积分别为p 10、p 20和V 10、V 20，以p 1、p 2和V 1、V 2分别表示加热后L 1和L 2中气体的压强和体积，由于M 1是导热的，加热前L 1和L 2中气体的温度是相等的，设为T 0，加热后L 1和L 2中气体的温度也相等，设为T ．因为加热前、后两个活塞和轻杆构成的系统都处在力学平衡状态，注意到S 2＝2S 1，力学平衡条件分别为：p 10＋p 20＝2p 0 ①p 1＋p 2＝2p 0 ②由①②两式得：p 1－p 10＝－(p 2－p 20) ③根据理想气体状态方程，对L 1中的气体有：p 1V 1p 10V 10＝T T 0④ 对L 2中气体有：p 2V 2p 20V 20＝T T 0⑤ 由④⑤两式得：p 1V 1p 10V 10＝p 2V 2p 20V 20⑥ ⑥式可改写成：⎝⎛⎭⎫1＋p 1－p 10p 10⎝⎛⎭⎫1＋V 1－V 10V 10＝⎝⎛⎭⎫1＋p 2－p 20p 20⎝⎛⎭⎫1＋V 2－V 20V 20 ⑦ 因连接两活塞的杆是刚性的，活塞M 2的横截面积是M 1的2倍，故有：V 1－V 10＝V 2－V 20 ⑧把③⑧式带入⑦式得：⎝⎛⎭⎫1＋p 1－p 10p 10⎝⎛⎭⎫1＋V 1－V 10V 10＝⎝⎛⎭⎫1－p 1－p 10p 20⎝⎛⎭⎫1＋V 1－V 10V 20 ⑨ 若V 10＝V 20，则由⑨式得p 1＝p 10，若加热前L 1中气体的体积等于L 2中气体的体积，则加热后L 1中气体的压强不变，由②式可知加热后L 2中气体的压强亦不变；若V 10＜V 20，则由⑨式得p 1＜p 10，若加热前L 1中气体的体积小于L 2中气体的体积，则加热后L 1中气体的压强必减小，由②式可知加热后L 2中气体的压强必增大；若V 10＞V 20，则由⑨式得p 1＞p 10，若加热前L 1中气体的体积大于L 2中气体的体积，则加热后L 1中气体的压强必增大，由②式可知加热后L 2中气体的压强必减小；参考评分：得到①式和②式或得到③式得3分，得到⑧式得3分，得到⑨式得8分，最后结论得6分．。

高一物理竞赛选拔试题及答案

高一物理竞赛选拔试题及答案一、选择题（每题3分，共30分）1. 一个物体从静止开始做匀加速直线运动，第1s内、第2s内、第3s内位移之比为：A. 1:3:5B. 1:2:3C. 1:3:6D. 1:4:9答案：B2. 一个质量为m的物体从高度为h的斜面顶端无初速度滑下，斜面与水平面的夹角为θ，物体与斜面间的动摩擦因数为μ，则物体滑到斜面底端时的速度大小为：A. √(2gh(1-μ))B. √(2gh(1+μ))C. √(2gh(1-μ/2))D. √(2gh(1+μ/2))答案：C3. 一个质量为m的物体以初速度v0沿水平方向抛出，不计空气阻力，经过时间t后，其速度方向与水平方向的夹角θ为：A. θ = arctan(2gt/v0)B. θ = arctan(gt/v0)C. θ = arctan(v0/gt)D. θ = arctan(2v0/gt)答案：B4. 一个质量为m的物体从高度为h的光滑斜面顶端无初速度滑下，斜面与水平面的夹角为θ，物体滑到斜面底端时的动能为：A. mghB. mg(h-1/2h)C. mg(h-1/2hcosθ)D. mg(h-1/2hcos²θ)5. 一个质量为m的物体以初速度v0沿水平方向抛出，不计空气阻力，经过时间t后，其速度大小为：A. v = v0 + gtB. v = v0 - gtC. v = √(v0² + (gt)²)D. v = √(v0² - (gt)²)答案：C6. 一个质量为m的物体从高度为h的光滑斜面顶端无初速度滑下，斜面与水平面的夹角为θ，物体滑到斜面底端时的重力势能变化量为：A. -mghB. -mg(h-1/2h)C. -mg(h-1/2hcosθ)D. -mg(h-1/2hcos²θ)7. 一个质量为m的物体以初速度v0沿水平方向抛出，不计空气阻力，经过时间t后，其水平位移为：A. x = v0tB. x = v0t - 1/2gt²C. x = v0t + 1/2gt²D. x = v0t - gt²答案：A8. 一个质量为m的物体从高度为h的光滑斜面顶端无初速度滑下，斜面与水平面的夹角为θ，物体滑到斜面底端时的重力势能变化量为：A. -mghB. -mg(h-1/2h)C. -mg(h-1/2hcosθ)D. -mg(h-1/2hcos²θ)9. 一个质量为m的物体以初速度v0沿水平方向抛出，不计空气阻力，经过时间t后，其竖直位移为：A. y = 1/2gt²B. y = v0t - 1/2gt²C. y = v0t + 1/2gt²D. y = v0t - gt²答案：A10. 一个质量为m的物体从高度为h的光滑斜面顶端无初速度滑下，斜面与水平面的夹角为θ，物体滑到斜面底端时的动能为：A. mghB. mg(h-1/2h)C. mg(h-1/2hcosθ)D. mg(h-1/2hcos²θ)答案：D二、填空题（每题4分，共20分）11. 一个物体从静止开始做匀加速直线运动，第1s内、第2s内、第3s内位移之比为1:3:5，那么第4s内、第5s内、第6s内位移之比为________。

高二物理竞赛选拔考试试题(附答案)

高二物理竞赛选拔考试试题一、单项选择题：（3×10＝30分）1、有一辆用链条传动的变速自行车，中轴(踏脚转轴)有两个齿轮盘，其齿数各为48、38，后轴飞轮上有三个齿轮盘，其齿数分别为14、17、24，若人以相同的转速带动踏脚，则用不同的齿轮盘组合，能使白行车得到的最大行进速度与最小行进速度比值约为:（）A、2.27B、2.17C、1.36D、1.262、如图所示，F 1、F2为有一定夹角的两个力，L为过O点的一条直线，当L取什么方向时，F1、F2在L上分力之和为最大: （）A、F1、F2合力的方向B、F1、F2中较大力的方向C、F1、F2中较小力的方向D、以上说法都不止确3、如图所示，物体A、B与水平桌面间动摩擦因数相等，用轻弹簧连接当用水平力F 拉A使A、B共同做匀加速直线运动，则将力F突然撒去的瞬间:（）A、A、B加速度均变为零B、A做减速运动，B做加速运动C、A做减速运动，B加速度为零D、A、B均做减速运动4、图A-D是表示电量q与电势差U的关系图。

哪一张图正确表示出使一定质量的油滴静止在水平放置的两平行板之间，油滴所带的电量q与两平行板的电势差U之间的关系：（）5、有一直角V形长槽，固定地放在水平面上，槽的两侧壁与水平面夹角均为45º，有一质量为M的正方形木块与槽二侧璧面间的最大静摩擦系数分别为μ1、μ2（μ1>μ2）。

现水平推动木块使之沿槽运动，则木块所受摩擦力为：（）A、mgμ1B、mgμ2C、（μ1+μ2）mg/2D、（μ1+μ2）mg/26、一台用非铁磁性物质制成的天平(包括天平盘)，可认为它不受磁力影响。

左盘中央放一铁块A；其上方不远处有一固定在支架上的电磁铁B(支架也放在左盘上)。

未通电时，天平平衡；给B通电后，在铁块A被吸起离开天平盘但未碰到B的上升过程中，天平的状态为: （）A、右盘下降B、仍保持平衡C、左盘下降D、无法判断7、如图所示，两只相同的白炽灯L1和L2串联接在电压恒定的电路中，若L1的灯丝断了，经搭丝后与L 2串联，重新接在原电路中，则此时L l的亮度与灯丝末断时比较：（）A、不变B、变亮C、变暗D、条件不足，无法判断8、如图所示，条形磁铁沿闭合螺线管的轴线方向穿过螺线管，水平地面光滑，条形磁铁的重力和空气阻力不计，则整个运动过程中:（）A、条形磁铁一定作匀速直线运动B、上述系统动能和动量都不守恒C、上述系统动能不守恒，动量守恒D、条形磁铁，螺线管及小车组成的系统动能、动量都守恒9、如图所示，两端封闭的均匀细玻璃管，管内有两部分相同的理想气体A和B，中间用一小段水银柱隔开。

高一物理奥赛选拔考试精选全文

可编辑修改精选全文完整版高一物理测试题一．选择题（每小题至少有一个选项符合要求，每题6分，共30分，选对部分答案得3分，有错选或多选不得分）1. 如图所示，平行四边形ABCD 的两条对角线的交点为G 。

在平行四边形内任取一点O ，作矢量OA 、OB 、OC 、OD ，则这四个矢量所代表的四个共点力的合力等于（）A. 4OGB. 2ABC. 4GBD. 2CB解析：如图2所示，延长OG 至P ，使GP ＝OG ，连结PA 、PB 、PC 、PD ，得平行四边形AODP 和平行四边形COBP 。

由力的平行四边形定则知道，矢量OA 、OD 所代表的两个共点力的合力可用矢量OP 表示，即。

同理，矢量OB 、OC 所代表的两个共点力的合力也可用矢量OP 表示，即。

从而，四个共点力的合力。

所以A 项正确。

2.汽车刹车后做匀减速直线运动,直到停下来,汽车在刹车后的运动过程中,前一半位移和后一半位移中的平均速度为1v 和2v ,前一半时间和后一半时间中的平均速度为a v 和b v ,则下面说法正确的是() A.3:1v :v ,1:)12(v :v b a 21=+= B.()1:3v :v,13:1v :v b a21=-=C.1:3v :v ,1:2v :v b a 21==D.1:)12(v :v ,1:3v :v b a 21+==答案:A(点拨:由运动的可逆性,将此减速运动看作初速度为0的匀加速直线运动,则前半位移与后半位移所用时间之比为()1:12-,所以()1:12v :v 21+=;前半时间与后半时间的位移之比为3:1,所以1:3v :v b a =)v /m ·s －1t /s24 6 8 2 4 6 8 10 12 14 16 O3. 一只兔子向着相距为S 的大白菜走去。

若它每秒所走的距离，总是从嘴到白菜剩余距离的一半。

试分析兔子是否可以吃到大白菜？兔子平均速度的极限值是多少？A. 能、无穷大B. 能、0C. 不能、0D. 不能、S/24. 甲车由静止开始做匀加速直线运动,通过位移s 后速度达到v,然后做匀减速直线运动直至静止,乙车由静止开始做匀加速直线运动,通过位移2s 后速度也达到v.然后做匀减速直线运动直至静止,甲、乙两车在整个运动中的平均速度分别为v 1和v 2,v 1与v 2的关系是( ) A.v 1＞v 2 B.v 1=v 2 C.v 1＜v 2 D.无法确定答案:B(点拨:此题用图象法解极为简单,分别作甲、乙两车的s-t 图象(如右图),因为s-t 图中面积表示位移则:v 21t v t 21t s v OAB 1=⨯==∆甲甲甲,v 21t vt 21t s v OCD 2=⨯==∆乙乙乙)5.物体以速度v 匀速通过直线上的A 、B 两点，所用时间为t ；现在物体从A 点由静止出发，先匀加速直线运动(加速度为a 1)到某一最大速度v m 后立即做匀减速直线运动(加速度大小为a 2)至B 点速度恰好减为0，所用时间仍为t ．则物体的（ AD ）A ．v m 只能为2v ，与a 1、a 2的大小无关B ．v m 可为许多值，与a 1、a 2的大小有关C ．a 1、a 2须是一定的D ．a 1、a 2必须满足12112ta a v+=解答：122m m s vt v t v v ==→= 而12121222112m m v v v v t t a a a a a a v =+=+→+=三、计算题（每题12分，共60分）9.在水平地面上有一质量为2kg 的物体，物体在水平拉力F 的作用下由静止开始运动，10s 后拉力大小减为3F，该物体的运动速度随时间变化的图像如图所示，求：（1）物体受到的拉力F 的大小；（2）物体与地面之间的动摩擦因数（g 取10m/s 2）．7. 一质点自原点出发沿x 轴做一维运动，其速度v 与时间t 之关系如右图所示，其中连续两次速度为0之间的关系曲线均为折线。

高中物理奥林匹克竞赛专题重点习题(有答案)-word

等于 R ．试求环中心 O 点处的场强和电势．
的正电荷 , 两直导线的长度和半圆环的半径都
解: (1) 由于电荷均匀分布与对称性， AB 和 CD 段电荷在 O 点产生的场强互相抵消，取 dl Rd
则 dq
Rd 产生 O 点 dE 如图，由于对称性， O 点场强沿 y 轴负方向
题 8-17 图
(2) AB 电荷在 O 点产生电势，以 U
解：如题 9-7 图所示， O 点磁场由 AB 、 B C 、 CD 三部分电流产生．其中
AB 产生 B1 0
CD 产生 B2
0 I ，方向垂直向里 12R
第3 页
CD 段产生
B3
0I R
(sin
90
4
sin 60 )
0I (1
2R
3 ) ，方向
2
向里
2
∴ B0 B1 B2 B3
0I (1 3
) ，方向向里．
r 8 cm时，
4π
q
p 3
(r 3
r内3 )
4π r 3 r内2
∴
E
3 4π 0 r 2
3.48
10 4 N
C
1
，
方向沿半径向外．
q r 12 cm时,
4π
3
(
r
3 外
r内3）
E
∴
4π 3 r外
r内3
3
4π0r 2
4.10 10 4 N C 1 沿半径向外 .
8-11 半径为 R1 和 R2 ( R2 ＞ R1 ) 的两无限长同轴圆柱面，单位长度上分别带有电量
8-24 图由电势叠加原理有：
q
得
q
3

高中物理竞赛题(含答案)

高中物理竞赛题(含答案)一、单项选择题1. 在自由落体过程中，物体的势能增加，动能减小。

A. 正确B. 错误2. 一列火车以$v$速度行驶，它的长度为$L$，宁静的人听到车头发出声音后$T$秒后听到车尾发出的声音。

则$v$为：A. $\frac{L}{2T}$B. $\frac{2L}{T}$C. $\frac{L}{T}$D. $\frac{T}{L}$3. 两个均质、半径相等、长度不同的均匀圆筒A、B，均可在竖直平面内以固定点O为转轴转动，轴线分别与定点OA、OB平行。

当它们同时从静止转动起来时，轮毂周向速度$V_1$比$V_2$：A. $V_1=V_2$B. $V_1>V_2$C. $V_1<V_2$D. 不确定4. 一个长为$L$的导线，施加电流$I$，沿任意方向在匀强磁场中运动，做完一周回路时，会发生电流改变的原因是：A. 因为改变导线的长度B. 因为导线被磁场力拉直了C. 因为导线切割磁力线D. 不确定5. 一根长度为$l$，截面积为$S$，长度均匀分布电荷$q$的细长直线，经过小球$O$（$O$到直线距离为$r$）的电场强度$E$是：A. $\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}$B. $\frac{1}{4\pi\epsilon_0}\frac{q}{\sqrt{l^2+r^2}}$C. $\frac{1}{4\pi\epsilon_0}\frac{ql}{\sqrt{l^2+r^2}}$D. $\frac{1}{4\pi\epsilon_0}\frac{q}{l^2+r^2}$答案：1.A 2.B 3.C 4.C 5.A二、填空题1. 一个直导线，垂直于均匀磁场B，长度为$l$，电流为$I$，受到的磁感应强度$B_1$是$______$2. 单色光的波长为500nm，折射率为1.5，其在空气和该介质交界面的发射角是$______°$3. 质量为$m$，长度为$l$，弹性系数为$k$的弹簧在自由状态下的振动周期是$______$4. 质量为$m$的物体在竖直向下的重力作用下自由下落的过程中，重力势能不断$______$，动能不断$______$5. 一列火车以$v$速度行驶，铁轨相对静止。

高中物理竞赛试题及答案

高中物理竞赛试题及答案【篇一：第32届全国中学生物理竞赛预赛试卷及答案(标准word版)】=txt>本卷共16题，满分200分．一、选择题．本题共5小题，每小题6分．在每小题给出的4个选项中，有的小题只有一项符合题意，有的小题有多项符合题意。

把符合题意的选项前面的英文字母写在每小题后面的方括号内．全部选对的得6分，选对但不全的得3分，有选错或不答的得0分．1.2014年3月8日凌晨2点40分，马来西亚航空公司一架波音777-200飞机与管制中心失去联系．2014年3月24日晚，初步确定失事地点位于南纬31o52′、东经115 o 52′的澳大利亚西南城市珀斯附近的海域．有一颗绕地球做匀速圆周运动的卫星，每天上午同一时刻在该区域正上方对海面拍照，则 a.该卫星一定是地球同步卫星 b.该卫星轨道平面与南纬31 o 52′所确定的平面共面 c.该卫星运行周期一定是地球自转周期的整数倍 d.地球自转周期一定是该卫星运行周期的整数倍2.23892u（铀核）衰变为22288rn（氡核）要经过3．如图，一半径为r的固定的光滑绝缘圆环，位于竖直平面内；环上有两个相同的带电小球a和b(可视为质点)，只能在环上移动，静止时两小球之间的距离为r。

现用外力缓慢推左球a使其到达圆环最低点c，然后撤除外力．下列说法正确的是a.在左球a到达c点的过程中，圆环对b球的支持力变大 b．在左球a到达c点的过程中，外力做正功，电势能增加。

c.在左球a到达c点的过程中，a、b两球的重力势能之和不变 d.撤除外力后，a、b两球在轨道上运动过程中系统的能量守恒4．如图，o点是小球平抛运动抛出点；在o点有一个频闪点光源，闪光频率为30hz；在抛出点的正前方，竖直放置一块毛玻璃，小球初速度与毛玻璃平面垂直．在小球抛出时点光源开始闪光．当点光源闪光时，在毛玻璃上有小球的一个投影点．已知图中o点与毛玻璃水平距离l=1．20 m，测得第一、二个投影点之间的距离为0.05 m．取重力加速度g=10m/s2．下列说法正确的是a.小球平抛运动的初速度为4m/sb．小球平抛运动过程中，在相等时间内的动量变化不相等 c．小球投影点的速度在相等时间内的变化量越来越大 d.小球第二、三个投影点之间的距离0．15m5．某同学用电荷量计(能测出一段时间内通过导体横截面的电荷量)测量地磁场强度，完成了如下实验：如图，将面积为s，电阻为的矩形导线框abcd沿图示方位水平放置于地面上某处，将其从图示位置绕东西轴转180o，测得通过线框的电荷量为q1；将其从图示位置绕东西轴转90 o ，测得通过线框的电荷量为q2.该处地磁场的磁感应强度大小应为rrrq12rq12222221?q2 c. q12?q1q2?q2a. d. ?q2 b. ?q1q2?q2sss4s2二、填空题．把答案填在题中的横线上．只要给出结果，不需写出求得结果的过程．6．(10分)水平力f方向确定，大小随时间的变化如图a所示；用力f拉静止在水平桌面上的小物块，在f从0开始逐渐增大的过程中，物块的加速度a随时间变化的图象如图b所示．重力加速度大小为10m/s2。

高一物理竞赛试题(含答案)+物理竞赛预赛试卷及答案

高一物理竞赛试题(含答案)+物理竞赛预赛试卷及答案高一物理竞赛试题一、单项选择题（共6小题，每题3分，共18分）1．如图，滑块A 置于水平地面上，滑块B 在一水平力作用下紧靠滑块A （A 、B 接触面竖直），此时A 恰好不滑动，B 刚好不下滑．已知A 与B 间的动摩擦因数为µ1，A 与地面间的动摩擦因数为µ2，最大静摩擦力等于滑动摩擦力．A 与B 的质量之比为（）A ． 211μμ B ．2121-1μμμμC ． 21211μμμμ+D ．21212μμμμ+ 2．如图所示，轻杆BC 的一端铰接于C ，另一端悬挂重物G ，并用细绳绕过定滑轮用力拉住．开始时，∠BCA ＞90°，现用拉力F 使∠BCA 缓慢减小，直到BC 接近竖直位置的过程中，杆BC 所受的压力（）A ．保持不变B ．逐渐增大C ．逐渐减小D ．先增大后减小3、如图，用橡皮筋将一小球悬挂在小车的架子上，系统处于平衡状态。

现使小车从静止开始向左加速，加速度从零开始逐渐增大到某一值，然后保持此值，小球稳定偏离竖直方向某一角度（橡皮筋在弹性限度内）。

与稳定在竖直位置时相比，小球高度A 一定升高B 一定降低C 保持不变D 升高或降低由橡皮筋的劲度系数决定4、一带有乒乓球发射机的乒乓球台如图所示。

水平台面的长和宽分别为L 1和L 2，中间球网高度为h 。

发射机安装于台面左侧边缘的中点，能以不同速率向右侧不同方向水平发射乒乓球，发射点距台面高度为3h 。

不计空气的作用，重力加速度大小为g 。

若乒乓球的发射速率为v 在某范围内，通过选择合适的方向，就能使乒乓球落到球网右侧台面上，则v 的最大取值范围是 A ．12266g g v h h LL << B ．22112(4)46gg v h hLL L +<<C ．22112(4)12626g g v h h L L L +<<D ．22112(4)1426g g v h h LL L +<<5．在街头的理发店门口常可以看到这样的标志：一个转动的圆筒，外表有螺旋斜条纹。

高中物理竞赛含答案(很经典)

一、1. 操作方案：将保温瓶中90.0t =℃的热水分若干次倒出来。

第一次先倒出一部分，与温度为010.0t =℃的构件充分接触，并达到热平衡，构件温度已升高到1t ，将这部分温度为1t 的水倒掉。

再从保温瓶倒出一部分热水，再次与温度为1t 的构件充分接触，并达到热平衡，此时构件温度已升高到2t ，再将这些温度为2t 的水倒掉。

然后再从保温瓶中倒出一部分热水来使温度为2t 的构件升温……直到最后一次，将剩余的热水全部倒出来与构件接触，达到热平衡。

只要每部分水的质量足够小，最终就可使构件的温度达到所要求的值。

2. 验证计算：例如，将1.200kg 热水分5次倒出来，每次倒出0m ＝0.240kg ，在第一次使热水与构件达到热平衡的过程中，水放热为1001()Q c m t t =- （1）构件吸热为110()Q cm t t '=- （2）由11Q Q '=及题给的数据，可得1t ＝27.1℃ （3）同理，第二次倒出0.240kg 热水后，可使构件升温到2t ＝40.6℃ （4）依次计算出1t ～的数值，分别列在下表中。

可见＝66.0℃时，符合要求。

附：若将1.200kg 热水分4次倒，每次倒出0.300kg ，依次算出1t ～4t 的值，如下表中的数据：由于4t ＝65.2℃＜66.0℃，所以如果将热水等分后倒到构件上，则倒出次数不能少于5次。

5t 5t v zv ⊥vθv二、设计的磁场为沿z 轴方向的匀强磁场，O 点和M 点都处于这个磁场中。

下面我们根据题意求出这种磁场的磁感应强度的大小。

粒子由O 点射出就进入了磁场，可将与z 轴成θ角的速度分解成沿磁场方向的分速度Z v 和垂直于磁场方向的分速度v ⊥（见图预解20-4-1），注意到θ很小，得cos Z v v v θ=≈ （1） sin v v v θθ⊥=≈ （2）粒子因具有垂直磁场方向的分速度，在洛仑兹力作用下作圆周运动，以R 表示圆周的半径，有2v qBv m R⊥⊥=圆周运动的周期2RT v π⊥=由此得2mT qBπ=（3）可见周期与速度分量v ⊥无关。

高中物理竞赛练习题与答案

高中物理竞赛练习题与答案高中物理竞赛练习题与答案物理学起始于伽利略和牛顿的年代，它已经成为一门有众多分支的基础科学。

物理学是一门实验科学，也是一门崇尚理性、重视逻辑推理的科学。

物理学充分用数学作为自己的工作语言，它是当今最精密的一门自然科学学科。

以下是店铺帮大家整理的高中物理竞赛练习题与答案，欢迎大家借鉴与参考，希望对大家有所帮助！1.天然放射现象的发现揭示了A.原子还可再分B.原子的核式结构C.原子核还可再分D.原子核由质子和中子组成2.下列说法中正确的是A.质子与中子的质量不等，但质量数相等B.两个质子间，不管距离如何，核力总是大于库仑力C.同一种元素的两个原子核可能有相同的质量数和不同的中子数D.除万有引力外，两个中子之间不存在其它相互作用力3.在氢原子中，电子绕核在各个可能轨道上运动的能量，包括电势能和动能两部分，当电子从离核较近的轨道向离核较远的轨道跃迁过程中A.电势能增大，动能减小，原子能量不变B.电势能增大，动能减小，原子能量减小C.电势能增大，动能减小，原子能量增大D.电势能增大，动能增大，原子能量增大n E/eV-0.28 4.氢原子能级图如右，用光子能量E=12.3eV的一束光照射一群处于基-0.38 态的氢原子，受光照后的氢原子可能发生跃迁的情况应是 -0.54-0.85 A.电子轨道量子数由n=1跃迁到n=3-1.51 B.电子轨道量子数由n=1跃迁到n=4-3.40 C.电子轨道量子数由n=1跃迁到n=2D.电子不可能发生轨道跃迁，氢原子仍处于基态2075.从23592U 衰变为82Pb，共经历的α衰变和β衰变的次数依次是 1 -13.60A.14次和10次B.7次和4次C.7次和5次D.7次和10次6.下面关于原子核衰变的说法中正确的是：①发生α衰变时，原子核在周期表中的位置向前移两位；②发生β衰变时，原子核在周期表中的位置向后移一位；③一个原子核不可能同时发生α、β衰变，④发生β衰变时原子核的质量数不变A．只有①② B．只有①②③ C．只有②④ D．①②③④7.以下几个原子核反应中，X代表α粒子的反应式是A.2He+4Be→126C+XC.1H+1H→10n+X 2349 234234B.90Th→91Pa+X 30D.15P→14Si+X 308.重核裂变和轻核聚变是人们利用原子能的两种主要途径，关于它们的说法中正确的是A.裂变过程质量增大，聚变过程质量亏损B.聚变过程质量增大，裂变过程质量亏损C.聚变和裂变过程都有质量亏损D.聚变和裂变过程都有质量增加9.下列说法正确的是A. α射线与γ射线都是电磁波B. β射线为原子的核外电子电离后形成的电子流C.用加温、加压或改变其化学状态的'方法都不能改变原子核衰变的半衰期D.原子核经过衰变生成新核，反应前后总质量不变10.若元素A的半衰期为4天，元素B的半衰期为5天，相同质量的A和B，经过20天后剩下的质量之比mA∶mB。

高中物理竞赛题(含答案)

高中物理竞赛题(含答案)高中物理竞赛题(含答案)一、选择题1. 以下哪个量纲与能量相同？A. 动量B. 功C. 功率D. 力答案：B. 功2. 以下哪个力不属于保守力？A. 弹簧力B. 重力C. 摩擦力D. 电场力答案：C. 摩擦力3. 一块物体在重力作用下自由下落，下列哪个物理量不随时间变化？A. 动能B. 动量C. 速度D. 位移答案：B. 动量4. 在以下哪个条件下，物体落地时速度为零？A. 重力作用下自由下落B. 匀加速直线运动C. 抛体运动D. 飞机减速降落答案：B. 匀加速直线运动5. 下列哪个现象可以说明动量守恒定律？A. 质点在外力作用下保持做直线运动B. 物体上升时速度减小C. 原地旋转的溜冰运动员脚迅速收回臂伸直D. 跳板跳高运动员下降时肌肉突然放松答案：C. 原地旋转的溜冰运动员脚迅速收回臂伸直二、填空题1. 单个质点的能量守恒定律表达式为________。

答案：E1 + K1 + U1 = E2 + K2 + U22. 一个质量为2.0 kg的物体从静止开始下滑，下滑的最后速度为4.0 m/s，物体下滑的高度为5.0 m，重力加速度为9.8 m/s²，摩擦力大小为2.0 N，那么物体所受到的摩擦力的摩擦因数为________。

答案：0.53. 在太阳系中，地球和太阳之间的引力为F，地球和月球之间的引力为f。

已知太阳质量为地球质量的300000倍，月球质量为地球质量的0.012倍。

下列哪个关系式成立？A. F = 300,000fB. F = 0.012fC. F = 300,000²fD. F = 0.012²f答案：A. F = 300,000f4. 一个质点从A点沿一固定的能量守恒定律表达式为E1 + K1 + U1 = E2 + K2 + U2路径运动到B点，以下哪个表达式正确？A. E1 + K1 + U1 = E2 + K2 + U2 + WB. E1 + K1 + U1 = E2 + K2 + U2 - WC. K1 + U1 = K2 + U2D. E1 - E2 = U2 - U1答案：D. E1 - E2 = U2 - U1三、解答题1. 一个木块沿水平面内的光滑竖直墙壁从静止开始下滑，当木块下滑一段距离后，由于摩擦力的作用，木块的速度减小。

(完整word版)高二物理竞赛及答案

A、滑块从M到N的过程中，速度可能一直增大
B、滑块从位置1到2的过程中，电场力做的功比从位置3到4的小
C、在M、N之间的范围内，可能存在滑块速度相同的两个位置
D、在M、N之间可能存在只由电场力确定滑块加速度大小的三个位置
9．如图9所示，平行板电容器的两极板A、B接于电池两极，一带正电的小球悬挂在电容器内部，闭合S，电容器充电，这时悬线偏离竖直方向的夹角为θ，则下列说法正确的是（）
B．0.15A，方向向左
C．0.2 A，方向向左
D．0.3A，方向向右
第Ⅱ卷
一．选择题答题处。（40分）
题号
1
2
3
4
5
6
7
8
9
10
选项
二．填空题。（2小题，共20分）
11．（10分）某同学和你一起探究弹力和弹簧伸长的关系，并测弹簧的劲度系数k。做法是先将待测弹簧的一端固定在铁架台上，然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧，并使弹簧另一端的指针恰好靠近刻度尺。当弹簧自然下垂时，指针指示的刻度数值记作L0，弹簧下端挂一个50g的砝码时，指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时，指针指示的刻度数值记作L2，……，挂七个50g的砝码时，指针指示的刻度数值记作L7。
A．当水平面光滑时，aaB．当水平面光滑时，a= a
C．当水平面粗糙时，aaD．当水平面粗糙时，a= a
3.如图3所示，质量为m的物体放在水平放置的钢板c上，与钢板间的动摩因数为。由于光滑导轨槽a、b控制，物体只能沿水平导轨槽运动。现使钢板以速度v1向右运动，同时用力F沿导轨槽的方向拉动物体使物体以速度v2沿槽运动，则F的大小为：()
高二物理竞赛试卷
一、选择题。
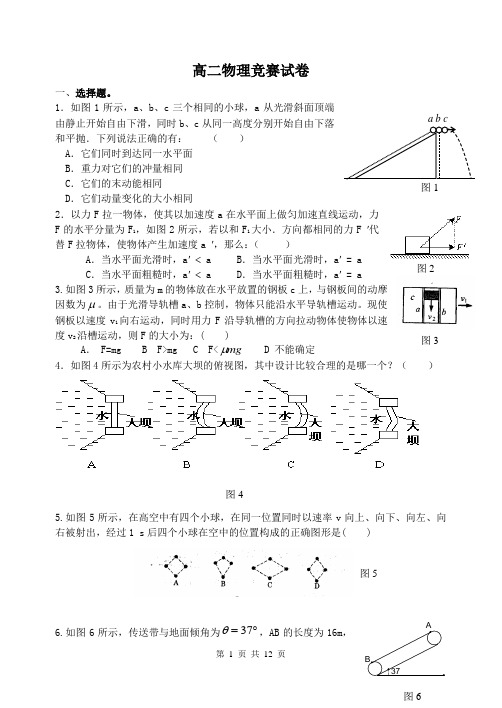
1．如图1所示，a、b、c三个相同的小球，a从光滑斜面顶端由静止开始自由下滑，同时b、c从同一高度分别开始自由下落和平抛．下列说法正确的有：（）

全国高中物理竞赛初赛试题及标准答案(全word版)

2014第31届全国中学生物理竞赛预赛试题及参考答案与评分标准一、选择题．本题共5小题，每小题6分，在每小题给出的4个选项中，有的小题只有一项符合题意，有的小题有多项符合题意．把符合题意的选项前面的英文字母写在每小题后面的方括号内，全部选对的得6分，选对但不全的得3分，有选错或不答的得0分．1．一线膨胀系数为α的正立方体物块，当膨胀量较小时，其体膨胀系数等于A．αB．α1/3C．α3D．3α2．按如下原理制作一杆可直接测量液体密度的秤，称为密度秤，其外形和普通的杆秤差不多，装秤钩的地方吊着一体积为lcm3的较重的合金块，杆上有表示液体密度数值的刻度．当秤砣放在Q点处时秤杆恰好平衡，如图所示，当合金块完全浸没在待测密度的液体中时，移动秤砣的悬挂点，直至秤杆恰好重新平衡，便可直接在杆秤上读出液体的密度．下列说法中错误的是A．密度秤的零点刻度在Q点B．秤杆上密度读数较大的刻度在较小的刻度的左边C．密度秤的刻度都在Q点的右侧D．密度秤的刻度都在Q点的左侧3．一列简谐横波在均匀的介质中沿z轴正向传播，两质点P1和P2的平衡位置在x轴上，它们相距60cm，当P1质点在平衡位置处向上运动时，P2质点处在波谷位置，若波的传播速度为24 m/s，则该波的频率可能为A．50Hz B．60HzC．400Hz D．410Hz4．电磁驱动是与炮弹发射、航空母舰上飞机弹射起飞有关的一种新型驱动方式，电磁驱动的原理如图所示，当直流电流突然加到一固定线圈上，可以将置于线圈上的环弹射出去．现在同一个固定线圈上，先后置有分别用钢、铝和硅制成的形状、大小和横截面积均相同的三种环；当电流突然接通时，它们所受到的推力分别为F1、F2和F3．若环的重力可忽略，下列说法正确的是A．F1>F2>F3B．F2>F3>F1C．F3>F2> F1D．F1=F2=F35．质量为m A的A球，以某一速度沿光滑水平面向静止的B球运动，并与B球发生弹性正碰．假设B球的质量m B可选取为不同的值，则A．当m B=m A时，碰后B球的速度最大B．当m B=m A时，碰后B球的动能最大C．在保持m B>m A的条件下，m B越小，碰后B球的速度越大D．在保持m B<m A的条件下，m B越大，碰后B球的动量越大二、填空题．把答案填在题中的横线上，只要给出结果，不需写出求得结果的过程．6．（10分）用国家标准一级螺旋测微器（直标度尺最小分度为0.5mm，丝杆螺距为0.5mm，套管上分为50格刻度）测量小球直径．测微器的初读数如图(a)所示，其值为_____mm，测量时如图(b)所示，其值为_____mm，测得小球直径d=___________mm．7．（10分）为了缓解城市交通拥问题，杭州交通部门在禁止行人步行的十字路口增设“直行待区”（行人可从天桥或地下过道过马路），如图所示．当其他车道的车辆右拐时，直行道上的车辆可以提前进入“直行待行区”；当直行绿灯亮起时，可从“直行待行区”直行通过十字路口．假设某十字路口限速50km/h，“直行待行区”的长度为12m，从提示进入“直行待行区”到直行绿灯亮起的时间为4s.如果某汽车司机看到上述提示时立即从停车线由静止开始匀加速直线运动，运动到“直行待行区”的前端虚线处正好直行绿灯亮起，汽车总质量为1.5t，汽车运动中受到的阻力恒为车重的0.1倍，则该汽车的行驶加速度为_________；在这4s内汽车发动机所做的功为_____________（取g=10m/s2）8．（10分）如图所示，两个薄透镜L1和L2共轴放置，已知L1的焦距f1=f，L2的焦距f2=―f，两透镜间的距离也是f，小物体位于物面P 上，物距u1=3f．(1)小物体经过这两个透镜成的像在L2的_____边，到L2的距离为________，是______像（填“实”或“虚”）、_______像（填“正”或“倒”），放大率为___________．(2)现把两个透镜位置调换，若还要使给定的原物体在原像处成像，两透镜作为整体应沿光轴向______边移动距离_________．这个新的像是______（填“实”或“虚”）、______像（填“正”或“倒”），放大率为__________．9．(10分)图中所示的气缸壁是绝热的．缸内隔板A是导热的，它固定在缸壁上．活塞B是绝热的，它与缸壁的接触是光滑的，但不漏气．B 的上方为大气．A与Ｂ之间以及A与缸底之间都盛有n mol的同种理想气体，系统在开始时处于平衡状态．现通过电炉丝E对气体缓慢加热，在加热过程中，A、B之间的气体经历____过程．A以下气体经历____过程；气体温度每上升１K，A、B之间的气体吸收的热量与A 以下气体净吸收的热量之差等于＿＿＿＿＿．已知普适气体常量为Ｒ．10.（10分）字宙空间某区域有一磁感应强度大小为B=1.0×10-9T的均匀磁场，现有一电子绕磁力线做螺旋运动．该电子绕磁力线旋转一圈所需的时间间隔为_____s；若该电子沿磁场方向的运动速度为1.0×10-2c（c为真空中光速的大小），则它在沿磁场方向前进1.0×10-3光年的过程中，绕磁力线转了_____圈. 已知电子电荷量为1.60×10-19C，电子质量为9.11×10-31kg．三、计算题，计算题的解答应写出必要的文字说明、方程式和重要的演算步骤，只写出最后结果的不能得分．有数值计算的，答案中必须明确写出数值和单位．11．（15分）如图所示，一水平放置的厚度为t折射率为n的平行玻璃砖，下表面镀银（成反射镜）．一物点A位于玻璃砖的上方距玻璃砖的上表面为h处．观察者在A点附近看到了A点的像．A点的像到A点的距离等于多少？不考虑光经玻璃砖上表面的反射．12.（20分）通常电容器两极板间有多层电介质，并有漏电现象．为了探究其规律性，采用如图所示的简单模型，电容器的两极板面积均为A．其间充有两层电介质l和2，第1层电介质的介电常数、电导率（即电阻率的倒数）和厚度分别为ε1、σ1和d1，第2层电介质的则为ε2、σ2和d2．现在两极板加一直流电压U，，电容器处于稳定状态．(1)画出等效电路图；(2)计算两层电介质所损耗的功率；(3)计算两介质交界面处的净电荷量；提示：充满漏电电介质的电容器可视为一不漏电电介质的理想电容和一纯电阻的并联电路．13. (20分)如图所示，一绝缘容器内部为长方体空胶，其长和宽分别为a和b，厚度为d，其两侧等高处装有两根与大气相通的玻璃管（可用来测量液体两侧的压强差）．容器内装满密度为ρ的导电液体，容器上下两端装有铂电极A和C，这样就构成了一个液体电阻，该液体电阻置于一方向与容器的厚度方向平行的均匀恒定的磁感应强度为B的磁场中，并通过开关K接在一电动势为ε、内阻为r的电池的两端，闭合开关．若稳定时两侧玻璃管中液面的高度差为h，求导电液体的电导率σ．重力加速度大小为g．14.（20分）lmol的理想气体经历一循环过程l—2—3—1，如p—T 图示所示．过程l—2是等压过程，过程3—1是通过p—T图原点的直线上的一段，描述过程2—3的方程为c1p2+ c2p =T，式中c1和c2都是待定的常量，p和T分别是气体的压强和绝对温度．已知，气体在状态l的压强、绝对温度分别为p1和T1．气体在状态2的绝对温度以及在状态3的压强和绝对湿度分别为T2以及p3和T3．气体常量R也是已知的．(1)求常量c1和c2的值；(2)将过程l—2—3—1在p—V图示上表示出来；(3)求该气体在一次循环过程中对外做的总功．15. (20分)一个ω介子飞行时衰变成静止质量均为m的三个π介子，这三个π介子的动量共面．已知：衰变前后介子运动的速度都远小于光在真空中的速度c；衰变后的三个π介子的动能分别为T1、T2和T3，且第一、二个π介子飞行方向之间的夹角为θl，第二、三个π介子飞行方向之间的夹角为θ2（如图所示）；介子的动能等于介子的能量与其静止时的能量（即其静止质量与c2的乘积）之差．求ω介子在衰变前的辨阀的飞行方向（用其飞行方向与衰变后的第二个介子的飞行方向的夹角即图中的φ角表示）及其静止质量．16. (25分)一圈盘沿顺时针方向绕过圆盘中心O并与盘面垂直的固定水平转轴以匀角速度ω=4.43rad/s转动．圆盘半径r=1.00m，圆盘正上方有一水平天花板．设圆盘边缘各处始终有水滴被甩出．现发现天花板上只有一点处有水．取重力加速度大小g=9. 80m/s2．求(1)天花板相对于圆盘中心轴O点的高度；(2)天花板上有水的那一点的位置坐标，参考答案与评分标准一、1. (D) 2. (C) 3. (AD) 4. (A) 5. (BCD)二、6. 0.022～0.024mm (3分)；3.772～3.774mm(3分)；3.748～3.752mm(4分)(若有效位数错，无分)7. 1.5m/s 2(5分)；4.5×104J(5分)8.(1)右，f ，实，倒，1 (每空1分)(2)左，2f ，实，倒，1 (每空1分)9. 等压(2分)；等容(2分)；nR(6分)10. 3.6×10-2(5分)；8.8×107(5分)三、11.(15分) 由折射定律得：sin θi =sin θd …①由几何关系得：x 1=htan θi …②，x 2=htan θd …③，H=2(x 1+x 2)tan(900―θi )…④，H 为物A 到像A /的距离，在小角度近似下有：tan θi ≈sin θi ，tan θd ≈sin θd ，tan(900―θi )≈1sinθi…⑤，联立以上各式得：H=2(h+t n) …⑥ 评分标准：①式3分，②③④式各2分，⑤⑥各3分12.(20分)(1)等效电路如图所示 (2)等效电容C 1和C 2为：C 1=ε1A d1，C 2=ε2A d2…①等效电阻R 1和R 2为： R 1=d1σ1A ，R 2=d2σ2A…② 两层电介质所消粍的功率为：P=U2R1+R2=U2Aσ1σ2d1σ2+d2σ1…③ (3)没两层介质各自上下界面之间的电压分别为U 1和U 2，上层介质界面上的电荷为：Q 1=CU 1=ε1A d1·UR1R1+R2=ε1σ2AU d1σ2+d2σ1…④，下层介质界面上的电荷为：Q 2=ε2σ1AU d1σ2+d2σ1…⑤ 两层介质交界面处的净电荷量为：Q=Q 1―Q 2=(ε1σ2―ε2σ1)AU d1σ2+d2σ1…⑥ 评分标准：第(1)问4分(可不标字母、箭头)，第(2)问9分，①②③式各3分，第(3)问7分，④⑤式各2分，⑥式3分13.(20分)沿着电流I 的方向液柱长度为a ，该液柱受到的安培力大小为：F 安=BIa …①液柱两侧面受到的由压强差产生的压力大小为：F P =ρghad …②水平方向上二力平衡，有：F 安=F P …③，由欧姆定律得：ε=I(R+r)…④，式中R=a σbd…⑤ 由以上各式解得：σ=ρgha b(Bε―rρghd )…⑥评分标准：①式4分，②③④⑤式各3分，⑥式4分14.(20分)(1)设气体在状态i(i=1、2和3)下的压强、体积和绝对温度分别为p i 、V i 和T i ，由题设条件有： c 1p 22 + c 2p 2 =T 2…①，c 1p 32 + c 2p 3 =T 3…②由此解得：c 1=T2p3―T3p2p22p3―p32p2=T2p3―T3p1p12p3―p32p1…③，c 1=T2p32―T3p22p2p32―p22p3=T2p32―T3p12p1p33―p12p3…④ (2)利用气体状态方程pV=RT ，以及V 1=R T1p1，V 2=R T2p2，V 3=R T3p3…⑤可将过程2―3的方程为：p V2―V3p2―p3=V+V2p3―V3p2p2―p3…⑥可见，在p ―V 图上过程2―3是以(p 2，V 2)和(p 3，V 3)为状态端点的直线段，过程3―1是通过原点直线上的一段，因而描述其过程的方程为：pT =c 3…⑦，式中c 3是一常量，利用气体状态方程pV=RT ，可将过程3—1的方程改写为：V=Rc3=V 3=V 1…⑧，这是以(p 3，V 1)和(p 1，V 1)为状态端点的等容降压过程.综上所述，过程1―2―3―1在p ―V 图上是一直角三角形，如图所示.(3)气体在一次循环过程中对外做的总功为：W=―12(p 3―p 1)(V 2―V 1)…⑨利用气体状态方程pV=RT 和⑤式，上式即W=―12R(T 2―T 1)(p3p1―1)…⑩评分标准：第(1)问8分，①②③④式各2分；第(2)问10分，⑤⑥式各2分，过程1―2―3―1在p ―V 上的图示正确得6分；第(3)问2分，⑩式2分.15.(20分)以第二个π介子的飞行方向为x 轴，以事件平面为x ―y 平面，设衰变前ω介子和衰变后三个π介子的动量大小分别为P ω、P 1、P 2和P 3，衰变前后粒子在x 和y 方向的动量分别守恒，有：P ωcos φ=P 1cos θ1+P 2+P 3cos θ2…⑴，―P ωsin φ=―P 1sin θ1+P 3sin θ2 …⑵ 衰变前后粒子的总能量守恒，有：m ωc 2+T ω=(mc 2+T 1)+(mc 2+T 2)+(mc 2+T 3)…⑶，式中左端和右端三个括号内的分别是衰变前ω介子的总能量(静能和动能之和)和衰变后三个π介子的总能量，动能可由动量和静质量表示：T ω=pω22mω…⑷，T 1=p122m …⑸，T 2=p222m …⑹，T 3=p322m…⑺ 分别由⑤⑥⑦式得p 1=2mT1…⑻，p 2=2mT2…⑼，p 3=2mT3…⑽ 联立①②⑧⑨⑩式得：φ=arctan T1sin θ1―T3sin θ2T1cos θ1+T2+T3cos θ2…⑾P ω2=2m(T 1+T 2+T 3)+4m T1T3cos(θ1+θ2)+T1T2cos θ1+T2T3cos θ2]…⑿ 由③④式得：2m ω2c 2―2m ω(3mc 2+T 1+T 2+T 3)+2m(T 1+T 2+T 3)+4m[T1T3cos(θ1+θ2)+T1T2cos θ1+T2T3cos θ2]=0 …⒀ 其解为m ω=32m+12c2(T 1+T 2+T 3)+[32m+12c2(T 1+T 2+T 3)]2―Pω22c2…⒁ 式中p ω2由⑿式给出。

高中物理奥赛综合训练题(参考解答或答案)

高中物理奥赛综合训练题1、长方形风筝如图1所示，其宽度a = 40cm ，长度b = 50cm ，质量M = 200g（其中包括以轻绳吊挂的纸球“尾巴”的质量M′= 20g ，纸球可当作质点）。

AO 、BO 、CO 为三根绑绳，AO=BO，C为底边中点；绑绳及放风筝的牵绳均不可伸缩，质量不计。

放风筝时，设风速为零，牵绳保持水平拉紧状态。

当放风筝者以速度v持牵绳奔跑时，风筝单位面积所受的空气作用力垂直于风筝表面，量值为P = Kvsinα，K = 8N s/m3，α为风筝表面与水平面的夹角。

风筝表面为光滑平面，各处所受空气作用力近似相等，g取10m/s2。

试求：（1）放风筝者至少应以多大速度持牵绳奔跑，风筝才能做水平飞行?（2）这时风筝面与水平面的夹角应为何值?假设通过调整绑绳长度可使风筝面与水平面成任意角度α。

2、如图2是一个直径为D的圆柱体，其侧面刻有螺距为h的螺旋形凹槽，槽内有一小球，为使小球能自由落下，必须要以多大的加速度来拉缠在圆柱体侧面的绳子?3、（前苏联奥林匹克竞赛题）快艇系在湖边，湖岸是直线，系绳突然松脱，风吹着快艇以恒定速度v0 = 2.5km/h沿与湖岸成15°角的方向飘去，一人能在岸上以v1 = 4km/h行走或在水中以v2 = 2km/h游泳。

试问：（1）他能否赶上快艇；（2）当快艇速度多大时，他总可以赶上快艇。

4、（北京市高中物理竞赛题）一辆汽车沿水平公路以速度v无滑动地运动，如果车轮半径为R ，试求车轮抛出的水滴上升的最大高度和抛出点的位置。

5、（全国中学生物理竞赛题）图3中，AOB是一内表面光滑的楔形槽，固定在水平桌面(图中纸面)上，夹角α = 15°，现将一质点在BOA面内从C处以速度v = 3m/s射出，其方向与AO间的夹角为β = 30°，OC= 1m ，设质点与桌面的摩擦可忽略不计，质点与OB 面及OA面的碰撞都是弹性碰撞，且每次碰撞时间极短，可忽略不计。

【精品】高中物理竞赛选拔综合经典习题(Word版含详细答案)

高中物理竞赛复赛经典练习题1. （本题6分）一长度为l 的轻质细杆，两端各固结一个小球A 、B （见图），它们平放在光滑水平面上。

另有一小球D ，以垂直于杆身的初速度v 0与杆端的Α球作弹性碰撞．设三球质量同为m ，求：碰后（球Α和Β）以及D 球的运动情况．2. （本题6分）质量m =10 kg 、长l =40 cm 的链条，放在光滑的水平桌面上，其一端系一细绳，通过滑轮悬挂着质量为m 1 =10 kg 的物体，如图所示．t = 0时,系统从静止开始运动, 这时l 1 = l 2 =20 cm< l 3．设绳不伸长，轮、绳的质量和轮轴及桌沿的摩擦不计，求当链条刚刚全部滑到桌面上时，物体m 1速度和加速度的大小．3. （本题6分）长为l 的匀质细杆，可绕过杆的一端O 点的水平光滑固定轴转动，开始时静止于竖直位置．紧挨O 点悬一单摆，轻质摆线的长度也是l ，摆球质量为m ．若单摆从水平位置由静止开始自由摆下，且摆球与细杆作完全弹性碰撞，碰撞后摆球正好静止．求： (1) 细杆的质量．(2) 细杆摆起的最大角度θ．4. （本题6分）质量和材料都相同的两个固态物体，其热容量为C ．开始时两物体的温度分别为T 1和T 2（T 1 > T 2）．今有一热机以这两个物体为高温和低温热源，经若干次循环后，两个物体达到相同的温度，求热机能输出的最大功A max ．5. （本题6分）如图所示，123415641 为某种一定量的理想气体进行的一个循环过程，它是由一个卡诺正循环12341 和一个卡诺逆循环15641 组成．已知等温线温度比T 1 / T 2 = 4，卡诺正逆循环曲线所包围面积大小之比为S 1 / S 2 = 2．求循环123415641的效率η．6. （本题6分）将热机与热泵组合在一起的暖气设备称为动力暖气设备，其中带动热泵的动力由热机燃烧燃料对外界做功来提供.热泵从天然蓄水池或从地下水取出热量，向温度较高的暖气系统的水供热.同时，暖气系统的水又作为热机的冷却水.若燃烧1kg 燃料，锅炉能获得的热量为H ，锅炉、地下水、暖气系统的水的温度分别为210℃，15℃，60℃.设热机及热泵均是可逆卡诺机.试问每燃烧1kg 燃料，暖气系统所获得热量的理想数值（不考虑各种实际损失）是多少？7. （本题5分）如图所示，原点O 是波源，振动方向垂直于纸面，波长是λ ．AB 为波的反射平面，反射时无相位突变π．O 点位于A 点的正上方，h AO =．Ox 轴平行于AB ．求Ox 轴上干涉加强点的坐标（限于x ≥ 0）．8. （本题6分）一弦线的左端系于音叉的一臂的A 点上，右端固定在B 点，并用T = 7.20 N 的水平拉力将弦线拉直，音叉在垂直于弦线长度的方向上作每秒50次的简谐振动（如图）．这样，在弦线上产生了入射波和反射波，并形成了驻波．弦的线密度η = 2.0 g/m ，弦线上的质点离开其平衡位置的最大位移为4 cm ．在t = 0时，O 点处的质点经过其平衡位置向下运动，O 、B 之间的距离为L = 2.1 m ．试求：12T 1 6543 VpOT 2A(1) 入射波和反射波的表达式； (2) 驻波的表达式．9. （本题6分）用每毫米300条刻痕的衍射光栅来检验仅含有属于红和蓝的两种单色成分的光谱．已知红谱线波长λR 在 0.63─0.76μm 范围内，蓝谱线波长λB 在0.43─0.49 μm 范围内．当光垂直入射到光栅时，发现在衍射角为24.46°处，红蓝两谱线同时出现． (1) 在什么角度下红蓝两谱线还会同时出现？(2) 在什么角度下只有红谱线出现？10. （本题6分）如图所示，用波长为λ= 632.8 nm (1 nm = 10-9 m)的单色点光源S 照射厚度为e = 1.00×10-5 m 、折射率为n 2 = 1.50、半径为R = 10.0 cm 的圆形薄膜F ，点光源S 与薄膜F 的垂直距离为d = 10.0 cm ，薄膜放在空气（折射率n 1 = 1.00）中，观察透射光的等倾干涉条纹．问最多能看到几个亮纹？（注：亮斑和亮环都是亮纹）．11. （本题6分）507⨯双筒望远镜的放大倍数为7，物镜直径为50mm .据瑞利判据，这种望远镜的角分辨率多大？设入射光波长为nm 550.已知眼睛瞳孔的最大直径为7.0mm .求出眼睛对上述入射光的分辨率.用得数除以7，和望远镜的角分辨率对比，然后判断用这种望远镜观察时实际起分辨作用的是眼睛还是望远镜.12. （本题6分）一种利用电容器控制绝缘油液面的装置示意如图. 平行板电容器的极板插入油中，极板与电源以及测量用电子仪器相连，当液面高度变化时，电容器的电容值发生改变，使电容器产生充放电，从而控制电路工作. 已知极板的高度为a ，油的相对电容率为εr ，试求此电容器等效相对电容率与液面高度h 的关系.13. （本题6分）在平面螺旋线中，流过一强度为I 的电流，求在螺旋线中点的磁感强度的大小．螺旋线被限制在半径为R 1和R 2的两圆之间，共n 圈．[提示：螺旋线的极坐标方程为b a r +=θ，其中a ，b 为待定系数]14. （本题6分）一边长为a 的正方形线圈，在t = 0 时正好从如图所示的均匀磁场的区域上方由静止开始下落，设磁场的磁感强度为B ϖ(如图)，线圈的自感为L ，质量为m ，电阻可忽略．求线圈的上边进入磁场前，线圈的速度与时间的关系．15. （本题6分）如图所示，有一圆形平行板空气电容器，板间距为b ，极板间放一与板绝缘的矩形线圈．线圈高为h ，长为l ，线圈平面与极板垂直，一边与极板中心轴重合，另一边沿极板半径放置．若电容器极板电压为U 12 = U m cos ω t ，求线圈电压U 的大小．Bϖ16. （本题6分）在实验室中测得电子的速度是0.8c ，c 为真空中的光速．假设一观察者相对实验室以0.6c 的速率运动，其方向与电子运动方向相同，试求该观察者测出的电子的动能和动量是多少？（电子的静止质量m e ＝9.11×10-31kg ）17. （本题6分）已知垂直射到地球表面每单位面积的日光功率（称太阳常数）等于1.37×103 W/m 2．(1) 求太阳辐射的总功率． (2) 把太阳看作黑体，试计算太阳表面的温度．（地球与太阳的平均距离为1.5×108 km ，太阳的半径为6.76×105 km ，σ = 5.67×10-8 W/(m 2·K 4)）18. （本题6分））已知氢原子的核外电子在1s 态时其定态波函数为 a r a /3100e π1-=ψ，式中 220em h a e π=ε ．试求沿径向找到电子的概率为最大时的位置坐标值．( ε0 = 8.85×10-12 C 2·N -1·m -2 ，h = 6.626×10-34 J ·s ， m e = 9.11×10-31 kg ， e = 1.6 ×10-19 C )参考答案1. （本题6分）解：设碰后刚体质心的速度为v C ，刚体绕通过质心的轴的转动的角速度为ω，球D 碰后的速度为v '，设它们的方向如图所示．因水平无外力，系统动量守恒：C m m m v v v )2(0+'= 得：(1)20C v v v ='- 1分弹性碰撞，没有能量损耗，系统动能不变；222220])2(2[21)2(212121ωl m m m m C ++'=v v v ，得 (2)22222220l C ω+='-v v v 2分系统对任一定点的角动量守恒,选择与A 球位置重合的定点计算．A 和D 碰撞前后角动量均为零，B 球只有碰后有角动量，有])2([0C B l ml ml v v -==ω，得(3)2lC ω=v 2分(1)、(2)、(3)各式联立解出 lC 00;2;0vv v v ==='ω。

高中物理奥林匹克竞赛专题重点习题(有答案)-精选文档

8-6 长=15.0cm的直导线AB 上均匀地分布着线密度=5.0x10-9C ·m-1的正电荷．试求：(1)在导线的延长线上与导线B 端相距=5.0cm 处点的场强；(2)在导线的垂直平分线上与导线中点相距=5.0cm处点的场强．解：如题8-6图所示(1)在带电直线上取线元，其上电量在点产生场强为用，, 代入得方向水平向右(2)同理方向如题8-6图所示由于对称性，即只有分量，以, ,代入得，方向沿轴正向8-7 一个半径为的均匀带电半圆环，电荷线密度为,求环心处点的场强．解: 如8-7图在圆上取题8-7图，它在点产生场强大小为方向沿半径向外则积分∴，方向沿轴正向．8-9 (1)点电荷位于一边长为a 的立方体中心，试求在该点电荷电场中穿过立方体的一个面的电通量；(2)如果该场源点电荷移动到该立方体的一个顶点上，这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示，在点电荷的电场中取半径为R 的圆平面．在该平面轴线上的点处，求：通过圆平面的电通量．() 解: (1)由高斯定理立方体六个面，当在立方体中心时，每个面上电通量相等∴ 各面电通量．(2)电荷在顶点时，将立方体延伸为边长的立方体，使处于边长的立方体中心，则边长的正方形上电通量l λ1a P 2d Qx d q d P 15=l cm 9100.5-⨯=λ1m C -⋅5.12=a cm 21074.6⨯=P E 1C N -⋅2220d d π41d +=x x E Q λε⎰=lQxEd QEy 9100.5-⨯=λ1cm C -⋅15=l cm 5d 2=cm 21096.14⨯==Qy Q E E 1C N -⋅y R λO ϕRd dl =ϕλλd d d R l q ==O 20π4d d R R E εϕλ=ϕϕελϕd sin π4sin d d 0RE E x ==RR E x 000π2d sin π4ελϕϕελπ==⎰R E E x 0π2ελ==x q q q A x Rarctan=α0d εq S E s ⎰=⋅ q 06εqe =Φa 2q a 2a 206εq e =Φ对于边长的正方形，如果它不包含所在的顶点，则，如果它包含所在顶点则．如题8-9(a)图所示．题8-9(3)图题8-9(a)图题8-9(b)图题8-9(c)图 (3)∵通过半径为的圆平面的电通量等于通过半径为的球冠面的电通量，球冠面积**关于球冠面积的计算：见题8-9(c)图8-10 均匀带电球壳内半径6cm ，外半径10cm ，电荷体密度为2×C ·m -3求距球心5cm ，8cm ,12cm 各点的场强．解: 高斯定理,当时，,时， ∴，方向沿半径向外． cm 时,∴沿半径向外.8-11 半径为和(＞)的两无限长同轴圆柱面，单位长度上分别带有电量和-,试求:(1)＜；(2) ＜＜；(3) ＞处各点的场强．解: 高斯定理取同轴圆柱形高斯面，侧面积则对(1)(2)∴沿径向向外(3)8-16 如题8-16图所示，在，两点处放有电量分别为+,-的点电荷，间距离为2，现a q 024εqe =Φq0=Φe R 22x R +510-0d ε∑⎰=⋅q S E s2π4ε∑=qr E 5=r cm 0=∑q 0=E 8=r cm ∑q 3π4p =3(r )3内r -()2023π43π4r r r E ερ内-=41048.3⨯≈1C N -⋅12=r 3π4∑=ρq -3(外r ）内3r ()420331010.4π43π4⨯≈-=r r r E ερ内外1C N -⋅1R 2R 2R 1R λλr 1R 1R r 2R r 2R 0d ε∑⎰=⋅q S E srl S π2=rlE S E Sπ2d =⋅⎰1R r <0,0==∑E q 21R r R <<λl q =∑rE 0π2ελ=2R r >0=∑q A B q q AB R将另一正试验点电荷从点经过半圆弧移到点，求移动过程中电场力作的功．解: 如题8-16图示8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为的正电荷,两直导线的长度和半圆环的半径都等于．试求环中心点处的场强和电势．解: (1)由于电荷均匀分布与对称性，和段电荷在点产生的场强互相抵消，取则产生点如图，由于对称性，点场强沿轴负方向题8-17图(2)电荷在点产生电势，以同理产生半圆环产生8-24 半径为的金属球离地面很远，并用导线与地相联，在与球心相距为处有一点电荷+，试求：金属球上的感应电荷的电量．解: 如题8-24图所示，设金属球感应电荷为，则球接地时电势8-24图由电势叠加原理有：得9-6 已知磁感应强度Wb ·m-2的均匀磁场，方向沿轴正方向，如题9-6图所示．试求：(1)通过图中面的磁通量；(2)通过图中面的磁通量；(3)通过图中面的磁通量．解：如题9-6图所示题9-6图(1)通过面积的磁通是(2)通过面积的磁通量 (3)通过面积的磁通量(或曰)题9-7图9-7 如题9-7图所示，、为长直导线，为圆心在点的一段圆弧形导线，其半径为．若通以电流，求点的磁感应强度．解：如题9-7图所示，点磁场由、、三部分电流产生．其中产生产生，方向垂直向里q O C λR O AB CD O θd d R l =θλd d R q =O Ed O y AB O 0=∞U CD 2ln π402ελ=U 0034π4πελελ==R R U R R d 3=q q '0=O U -='q 3q0.2=B x abcd befc aefd abcd 1S befc 2S aefd 3S 24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ΦWb 24.0-Wb AB CD C BO R I O O AB C BCD AB 01=B CD RIB 1202μ=段产生，方向向里 ∴，方向向里．9图9-9 如题9-9图所示，两根导线沿半径方向引向铁环上的，两点，并在很远处与电源相连．已知圆环的粗细均匀，求环中心的磁感应强度．解：如题9-9图所示，圆心点磁场由直电流和及两段圆弧上电流与所产生，但和在点产生的磁场为零。

高中物理竞赛题含答案

高中物理竞赛题含答案一、选择题1. 以下哪个物理量是标量？（A）A. 功B. 力C. 速度D. 位移答案：A2. 下列哪个图示了一个物体的加速度随时间的变化呈现为匀加速的情况？（D）A.B.C.D.答案：D3. 光速在真空和介质中的大小关系为：（B）A. 光速在真空与介质中大小相等B. 光速在真空中大于介质中C. 光速在介质中大于真空中D. 光速在介质中与真空中无关答案：B4. 两个球分别从10米和20米的高度落下，它们同时落地。

它们落地时哪个球的速度更大？（A）A. 速度相同B. 10米高度的球速度更大C. 20米高度的球速度更大D. 无法确定答案：A5. 如下图，取自然长度为l、未受拉伸前横截面面积为S的弹性绳，悬挂一质量为m的物体，当物体静止时，绳的长度为l0。

如果物体做振动，振动小于一定范围时，弹性绳对物体做的回复力F正比于振动小的幅度x，弹性系数k即为它的比例系数。

当振动进一步扩大超过一定范围时，弹性绳不能完全回复原状态，即绳有一定的塑性。

当振动到达最大时，弹性绳的长度变为l'，则l'与l的变化关系正确的是：（D）A. l' = l(1+x)B. l' = l(1-x)C. l' = l(1+x^2)D. l' = l(1+x)^2答案：D6. 有一小车运动，其初始速度为12米/秒，加速度为8米/秒²，运动的时间为5秒，则小车所运动的距离是（B）A. 180米B. 1800米C. 2800米D. 3520米答案：B二、填空题1. 一个在半径为R的圆形轨道上做匀速圆周运动的质点，速率为v，则此质点的向心加速度为______，受到的向心力为______。

答案：v²/R，mv²/R2. 一个在平面直角坐标系中做匀加速直线运动的物体，其速度可以表示为v=at，物体在t=1时的位移为2米，则它在t=2时的位移为______米。

高中物理竞赛(详细答案)

高中物理竞赛试题卷考生须知：● 本卷分卷Ⅰ和卷Ⅱ，卷Ⅰ卷Ⅱ均做在答题卷上,满分140分，竞赛时间2小时。

● 姓名、报名号和所属学校必须写在首页左侧指定位置，写在其他地方者按废卷论。

●本卷g=10m/s 2卷Ⅰ一、单项选择题（每题8分，共48分）1、如图，O 是一固定的点电荷，另一点电荷P 从很远处以初速度0v 射入点电荷O 的电场，在电场力作用下的运动轨迹是曲线MN 。

a 、b 、c 是以O 为中心，c b a R R R 、、为半径画出的三个圆，a b b c R R R R -=-。

1、2、3、4为轨迹MN 与三个圆的一些交点。

以12W 表示点电荷P 由1到2的过程中电场力做的功的大小，34W 表示由3到4的过程中电场力做的功的大小，则1、2、 3A ．34122W W =B ．34122W W >C ．P 、Q 两电荷可能同号，也可能异号D ．P 的初速度方向的延长线与O 之间的距离可能为零2．如图，在00>>y x 、的空间中有恒定的匀强磁场，磁感强度的方向垂直于oxy 平面向里，大小为B 。

现有一质量为m 电量为q 的带电粒子，在x 轴上到原点的距离为0x 的P 点，以平行于y 轴的初速度射入此磁场，在磁场作用下沿垂直于y 轴的方向射出此磁场。

不计重力的影响。

由这些条件可知，A ．不能确定粒子通过y 轴时的位置B ．不能确定粒子速度的大小C ．不能确定粒子在磁场中运动所经历的时间D ．以上三个判断都不对3、如图，在正六边形的a 、c 两个顶点上各放一带正电的点电荷，电量的大小都是1q ，在b 、d 两个顶点上，各放一带负电的点电荷，电量的大小都是2q ，21q q >。

已知六边形中心O点处的场强可用图中的四条有向线段中的一条来表示，它是哪一条？A ．1EB ．2EC ．3ED ．4E4、如图所示，竖直放置在匀强磁场中的固定光滑长直导轨，自身的电阻不计。

磁场方向垂直于纸面向里，磁感应强度B =0.5T 。

高中物理竞赛试题库附详细答案

高中物理竞赛试题库附详细答案一、选择题1. 下图是一台垂直面上的运动物体的加速度-时间图象，物体的初始速度为零。

根据图象可知，该物体的速度-时间图象为：A) 直线斜率为正的一条直线B) 曲线C) 直线斜率为负的一条直线D) 无法确定答案：A) 直线斜率为正的一条直线解析：根据加速度-时间图象的性质，直线斜率为正的一条直线表示物体在做匀加速运动。

2. 一个物体垂直抛掷，竖直上抛的速度和竖直下落的速度分别为v0和v1，则该物体上抛的时间与下落的时间比值为：A) v1/v0B) √(v1/v0)C) v0/v1D) √(v0/v1)答案：D) √(v0/v1)解析：根据物体竖直抛掷运动的性质，上抛和下落的时间比值为：上抛的时间/下落的时间= √(v0/v1)。

3. 将物体1质量为m1=2kg的铁块放在静止的光滑桌面上，物体2质量为m2=3kg的物体1上，两物体间没有任何摩擦力。

物体1与物体2在竖直方向上的加速度为：A) 7/5m/s²B) 6/5m/s²C) 5/7m/s²D) 5/6m/s²答案：A) 7/5m/s²解析：根据牛顿第二定律和叠加力的原理：F = (m1 + m2) * am1 * g - m2 * g = (m1 + m2) * a2 * 9.8 -3 * 9.8 = (2 + 3) * a19.6 - 29.4 = 5a-9.8 = 5aa = -9.8 / 5a = -1.96 m/s²因为加速度的方向与重力方向相反，所以取绝对值：|a| = 1.96 m/s²所以物体1与物体2在竖直方向上的加速度为1.96 m/s²，即7/5m/s²。

二、填空题1. 物体从A点自由下落到B点，高度差为10m，重力加速度为10m/s²，则到达B点时的速度为___m/s。

答案：14 m/s解析：根据加速度公式：v² = u² + 2as其中，v是最终速度，u是初始速度，a是加速度，s是位移。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高中物理竞赛复赛经典练习题1. （本题6分）一长度为l 的轻质细杆，两端各固结一个小球A 、B （见图），它们平放在光滑水平面上。

1分即碰后，D 球静止，刚体（球A 、B 及细杆）以速度v C 平移并绕通过质心的轴以角速度ω 转动．2. （本题6分）解：分别取m 1和链条m 为研究对象，坐标如图．设链条在桌边悬挂部分为x ， a m T g m 11=-， ma l xgm T =-/，解出)/1(21l x g a -= 2分当链条刚刚全部滑到桌面时x = 0，a ==g 21 4.9 m/s 2xt x x t a d d d d d d d d vvv v -=⋅== x l x g x a d )/1(21d d --=-=v v 2分两边积分 ⎰⎰--=002d )1(d 2l x l xg v v v22222)4/3(/21gl l gl gl =-=v==2321gl v 1.21 m/s 2分3.（本题6分）解：(1) 设摆球与细杆碰撞时速度为v 0，碰后细杆角速度为ω，系统角动量守恒得： J ω = m v 0l 1分由于是弹性碰撞，所以单摆的动能变为细杆的转动动能2202121ωJ m =v 1分代入J ＝231Ml ，由上述两式可得 M ＝3m 1分 (2) 由机械能守恒式mgl m =2021v 及 ()θωcos 121212-=Mgl J 2分并利用(1) 中所求得的关系可得 31arccos=θ 1分4. （本题6分）解：设两物体达到的相同温度为T ，由热力学第一定律知 )()(||2121T T C T T C Q Q A ---=-=CT T T C 2)(21-+= 1分由熵的计算有 21221lnln ln T T T C T T C T T C S =+=∆ 2分由熵增加原理知 ∆S ≥ 0 1分 ∴ T ≥21T T 1分将上式代入A 的式子中得 A ≤21212)(T T C T T C -+∴2121max 2)(T T C T T C A -+= 1分5. （本题6分）解： 21211Q Q Q Q '++'-=η 1分 Q 1与Q 2分别为12341 循环中系统吸的热与放的热（绝对值），1Q ' 与 2Q '分别为15641 循环中系统放的热与吸的热（绝对值）．又知4//2121==Q Q T T 1分 21212S S Q Q ==- 1分4//2121=''=Q Q T T 1分 221S Q Q ='-' 1分于是得 21)3/8(S Q = 22)3/2(S Q =21)3/4(S Q =' 22)3/1(S Q =' ∴ 3/1=η 1分6. （本题6分）解：设锅炉、地下水以及暖气系统的温度分别以T 1，T 2，T 3，表示.显然工作于锅炉和暖气系统之间的可逆卡诺热机的效率为311T T η=-热（1） 1分按照热机效率的定义1W W Q Hη''==热（2） 1分联立（1）式与（2）式，可以得到()131T T HW H T η-'==热（3）设可逆卡诺热机对暖气系统输送的热量为Q 3，由热机效率公式可知331Q T H T = （4） 1分工作于地下水和暖气系统之间的热泵也是可逆卡诺机，同样有223232Q T Q Q T T '=''--即 3332Q T W T T '=- （5） 1分上式中的W 为外界对热泵输入的功，它全部由（3）式表示的可逆卡诺热机做的功提供，即W W ='，将（3）式代入（5）式，可得3313332132T T T TQ W H T T T T T -'==⋅-- （6） 1分暖气系统从热机与热泵组合在一超的暖气设备得到的总热量为（4）式与（6）式之和3313331132333333150348348345T T T T Q Q Q H H H T T T T ⎛⎫-⎛⎫'=+=+⋅=+⨯≈ ⎪ ⎪-⎝⎭⎝⎭ 1分可见这一将热机与热泵组合在一起的暖气设备称为动力暖气设备的供热是由锅炉直接供热的3倍.7.（本题6分）解：沿Ox 轴传播的波与从AB 面上P 点反射来的波在坐标x 处相遇，两波的波程差为x h x -+=22)2/(2δ 2分代入干涉加强的条件，有：λk x h x =-+22)2/(2， k = 1，2，… 1分λλxk k x h x 2422222++=+22242λλkh xk -=λλk k h x 24222-= ． 2分k = 1，2，3，…，< 2 h /λ．（当 x = 0时，由2224λk h -可得k = 2 h /λ．）1分8.（本题6分）解：按题意，弦线上行波的频率ν = 50 Hz ，波速u = (T/η)1/2 = 60 m/s ，波长λ = u /ν = 1.2m. 取O 点为x 轴和y 轴的原点．x 轴向右，y 轴向上．令入射波在B 点的初相为π-21B φ，则其表达式为 ]2)(22cos[1π-+-π-π=B L x t A y φλν ① B 点为固定点，则反射波的表达式为]2)(22cos[2π++-π+π=B L x t A y φλν ② 2分弦线上驻波表式为 21y y y +=]2cos[]2)(2cos[2B t L x A φνλ+ππ+-π= ③据此，O 点振动方程为 ]2cos[]22cos[20B t L A y φνλ+ππ+π-=由4/7/=λL 有 )2cos(20B vt A y φ+π-=)2cos(2π-+π=B vt A φ ④ 1分由③式可知弦线上质点的最大位移为2A ，即 2A = 4 cm再由题给条件可得④式中 π=π-21B φ，即π=23B φ 1分由此可得： (1) 入射波 ]26.0100cos[100.221π+π-π⨯=-x t y (SI) 反射波 ]26.0100cos[100.222π+π+π⨯=-x t y (SI) 1分驻波 )2100cos(6.0cos100.42π+ππ⨯=-t x y (SI) 1分9.（本题6分）解： ∵ a +b = (1 / 300) mm = 3.33 μm (1) (a + b ) sin ψ =k λ ∴ k λ= (a + b ) sin24.46°= 1.38 μm ∵ λR =0.63─0.76 μm ； λB ＝0.43─0.49 μm对于红光，取k =2 , 则 λR =0.69 μm 1分对于蓝光，取k =3, λB =0.46 μm 1分红光最大级次 k max = (a + b ) / λR =4.8, 1分取k max =4则红光的第4级与蓝光的第6级还会重合．设重合处的衍射角为ψ' , 则()828.0/4sin =+='b a R λψ∴ ψ'=55.9° 1分 (2) 红光的第二、四级与蓝光重合，且最多只能看到四级，所以纯红光谱的第一、三级将出现． ()207.0/sin 1=+=b a R λψ ψ1 = 11.9° 1分 ()621.0/3sin 3=+=b a R λψ ψ3 = 38.4° 1分10. （本题6分）解：对于透射光等倾条纹的第k 级明纹有：λk r e n =cos 22 2分中心亮斑的干涉级最高，为k max ，其r = 0，有： =⨯⨯⨯⨯==--752max 10328.61000.150.122λen k 47.4 应取较小的整数，k max = 47（能看到的最高干涉级为第47级亮斑）． 2分最外面的亮纹干涉级最低，为k min ，相应的入射角为 i m = 45︒(因R =d ),相应的折射角为r m ，据折射定律有 m m r n i n sin sin 21=∴ 50.145sin 00.1sin )sin (sin 1211︒==--m m i n n r = 28.13° 由 λmin 2cos 2k r e n m = 得：752min 10328.613.28cos 1000.150.12cos 2--⨯︒⨯⨯⨯==λmr e n k = 41.8应取较大的整数，k min = 42（能看到的最低干涉级为第42级亮斑）． 2分 ∴最多能看到6个亮斑（第42，43，44，45，46，47级亮斑）．11. （本题6分）解：通过此题可以对望远镜的分辨本领和人眼的分辨本领有一比较.望远镜的角分辨率为 95c 31.22 1.2255010rad 1.34105010D λθ---⨯⨯===⨯⨯ rad 2分瞳孔的角分辨率为 95c 31.22 1.2255010rad 9.610710D λθ---⨯⨯'===⨯'⨯ rad 2分得 5c 1.37107θ-'=⨯rad由于c c 7θθ'>，所以用此望远镜时，角分辨率实际为人眼所限制，实际起分辨作用的还是眼睛. 2分12. （本题6分）解：设极板面积为S ，间距为d ，浸入油的下部分的电容为 S ahdC r εε01=；露在上面的部分的电容为 S aha dC -=02ε. 代入并联电容公式，有 ]1)1[(021+-=+=ahd SC C C r εε. 2分令等效相对电容率为*r ε，有 ]1)1[(0*0+-=ah d S d S rr εεεε， 2分因此等效相对电容率为 1)1(*+-=ah r r εε.由上式看出，等效相对电容率随着液面的升高而线性增大，亦即电容器的电容将随液面的升高而线性增大；油本身的相对电容率εr 愈大，对液面高度变化的反应愈为灵敏. 2分13.（本题6分）解：螺旋线上电流元l I ϖd 在中心O 处产生的磁场为30d 4d rrl I B ϖϖϖ⨯π=μ 其数值为 20sin d 4d rl I B αμπ= 2分由图可见 θαd sin d r l = 由螺线方程 b a r +=θ θd d a r = ∴ ar rI B d 4d 0π=μ ⎰π=21d 40R R ar r I B μ120ln 4R R a I π=μ 2分螺线共n 匝当 0=θ 时， b b a R r =+===01][θθ当 π=n 2θ 时， b a n b a R r n +π=+==π=2][22θθ ∴ π-=n R R a 212 12120ln 2R R R R nIB -=μ 2分14.（本题6分）解：电动势v Ba =E 且 IR tIL=-d d E ∵ R =0 ， ∴ =tILd d v Ba =E 1分在重力与磁力作用下线圈的运动BaI mg tm -=d d v1分两边同时对t 微分： =22d d tm v t IBa d d -0d d 222=+v v ωt , mL a B 222=ω 1分)sin(ϕω+=t A v 1分∵ t = 0 时，v = 0 g t=d d v∴ ω/g A = 0=ϕ 1分∴ t mL Bagωsin =v 1分d θ15.（本题6分）解：由关于H ϖ的全电流定律 ⎰⋅⎰⋅∂∂=S L S t D l H ϖϖϖϖd d 1分在板间半径为r ，圆心在轴线上与板面平行的圆周上有t D r r H d /d 22π=π 1分 )cos (d d 2)(d d 201202t U t b r b U t r r H m ωεε=ππ=t U br m ωωεsin 20-= 1分穿过矩形线圈的磁通量为⎰⋅=SS B ϖϖd Φ⎰=l r Bh 0d ⎰-=l m r h U b r 000d )(sin 2ωωεμt b hl U m ωωμεsin 4200-= 1分矩形线圈中的感生电动势 td d Φ-=E t b hl U m ωωμεcos 42200= 1分线圈电压为 t bhl U U m ωωμεcos 42200==E （∵开路 ∴ = U ） 1分16.（本题6分）解：设实验室为K 系，观察者在K ′系中，电子为运动物体．则K ′对K 系的速度为u = 0.6c ，电子对K 系速度为v x = 0.8c ．电子对K ′系的速度c c u u x x x 385.0)/(12=--='v v v 2分观察者测得电子动能为 J 1085.6)1)/(11(15220-⨯=-'-=c c m E x K v 2分动量 x m p v '=2)/(1c m x x v v '-'=＝1.14×10-22 kg ·m/s 2分17.（本题5分）解： (1) 太阳在单位时间内辐射的总能量E = 1.37×103×4π(R SE )2 = 3.87×1026 W 2分(2) 太阳的辐射出射度=π=204Sr E E 0.674×108 W/m 2 1分由斯特藩－玻尔兹曼定律 40T E σ=可得 5872/40==σE T K 2分18.（本题5分）解：氢原子1s 态的定态波函数为球对称的，在径向r →r + d r 区间找到电子的概率为r r w d 422100π=ψ即 a r r w /22e -∝ 2分沿径向对w 求极大， )e (d d d d /22a r r rr w -=0e )22(/22=-=-a r a r r 得 ===220eπe m h a r ε0.529×10-10 m 3分。