Fe-Al-Si三元扩散偶中合金元素扩散行为的动力学计算
第八章 扩散

2 2
在给定条件下Cm,D, l 皆为定值。只有当 t 时 C / C m 0 才完全均匀化,可见所谓均匀化只有相 对意义。一般来说,只有偏析衰减到一定程度(如
1 1 0 ),即可认为均匀化了。凝固过程细化晶粒,及通
过锻造、轧制、热处理使组织充分细化都可以大大缩短 均匀化退火时间
a.同素异晶转变的金属中,D随晶体结构改变, 910℃,Dα-Fe/Dγ-Fe=280, α-Fe致密度低, 且易形成空位。 b.晶体各向异性使D有各向异性。 铋扩散的各向异性,菱方系Bi沿C轴的自扩 散为垂直C轴方向的1/106 六方系的Zn:平行底面的自扩散系数大于 垂直底面的,因底面原子排列紧密,穿过底面 困难。
Cs C0 2 Dt
C0为原始浓度;Cs为渗碳气氛浓度Cx为距表 x erf 面x处的浓度; ( 2 D t ) erf ( z ) 为误差函数
Fick第二定律的解无限大物体中扩散应用
2.扩散方程在扩散退火过程的应用
显微偏析是合金在结晶过程中形成的,在铸件,锻件中 普遍存在。扩散退火时将零件在高温下长时间保温可促 使成分的均匀化。 具有显微偏析的合金其组元分布大多呈周期性变化。 在研究扩散退火过程时,可以近似为 Dt /t
8.3.3.晶体结构 晶体结构对扩散有影响,有些金属存在同 素异构转变,当它们的晶体结构改变后, 扩散系数也随之发生较大的变化。例如铁 在912℃时发生-Fe-Fe转变,-Fe的自 扩散系数大约是-Fe的240倍。所有元素在 -Fe中的扩散系数都比在-Fe中大,其原 因是体心立方结构的致密度比面心立方结 构的致密度小,原子较易迁移。
空位扩散机制--- 3.交换机制 相邻两原子交换位臵而实现 F10-14:扩散的交换机 制
第四章_金属和合金中的扩散

根据上式,热力学力之间并非是完全独立的。n元系中,只有n-1个 力是独立的。对于浓度梯度,因为有 xi = 1 和 Ci = C 的关系,所 以n元系中,也只有n-1个是独立的。
扩散的菲克定律
菲克定律是在1855年由菲克给出的扩散流量和浓度梯度的关系。
ln B = 1+ ln xB 称它为热力学因子,以表示,即 ln B ln A =1+ =1+ lnxB lnxA
DB和DA可简写成 DB = M B RT DA = M A RT 对于B在A中的极稀固溶液,因为活度系数近似为常数,所以热力
ln A 1+ ln xA
J i = Ci vi
对于不同的参考坐标架,组元运动速度不同,从而流量也不同。 两种坐标系 : 实验参考系 —相对于观察者是不动的,相应的扩散流量记为J0。
点阵参考系 —把坐标固定在晶体点阵的原子面上,通常在晶体内 插入惰性标志物以作标记,相应的扩散流量记为J。
若在某处点阵参考系相对于实验参考系的运动速度为v,则在该处 第i组元(“组元”应包括空位)相对于两种参考坐标架的流量之间 的关系为:
扩散机制
①间隙机制 (a)从一个间隙到近 邻另一个间隙 (b)间隙原子把相邻 的一个原子挤入相 邻的间隙 (c)挤列机制 (d)“哑铃结构”的 跳动 ②空位机理 ③换位机制 (e)直接换位 (f)回旋换位
②
(a)
(f)
(b)
(e) (c)
扩散的宏观理论
参考系 流量和力之间的关系 扩散的菲克定律—第一定律,第二定律 二元系的扩散—固溶体中溶质原子的扩散; 臵换固溶体的扩散 —两种坐标架下组元扩散流量间的关系 禀性扩散系数和互扩散系数 Smigelkas和Kirkendall 的实验 禀性扩散系数与热力学函数间的关系 自扩散系数。 扩散方程的解(以二元系为例) 稳态扩散 扩散系数和浓度有关时扩散方程的积分解, 扩散系数为常数时:半无限长扩散偶扩散方程的解,用扩散 偶方法求扩散系数,扩散系数为常数时用分离变量获得的扩散方 程解,扩散系数为常数时的高斯解,平方根关系。 数值解方法
fe的扩散激活能和参考扩散系数

主题:fe的扩散激活能和参考扩散系数一、概述1.1 fe的扩散激活能是指在固态材料中,铁原子在晶格中扩散所需的能量。
1.2 参考扩散系数是描述固态材料中各种原子扩散能力大小的参数。
二、fe的扩散激活能2.1 fe的扩散激活能与材料的晶体结构及温度密切相关。
2.1.1 在相同晶体结构下,不同温度下fe的扩散激活能会有所差异。
2.1.2 在相同温度下,不同晶体结构下fe的扩散激活能也会有所差异。
2.2 fe的扩散激活能对材料的扩散速率影响很大。
2.2.1 fe的扩散激活能越低,材料的扩散速率越快。
2.2.2 通过改变材料的晶体结构或温度,可以间接调控fe的扩散激活能。
三、参考扩散系数3.1 参考扩散系数是通过实验测量得到的参数。
3.2 参考扩散系数与温度呈正相关关系。
3.2.1 随着温度的升高,参考扩散系数会增加。
3.2.2 不同材料的参考扩散系数随温度升高的速率可能不同。
3.3 参考扩散系数可用于计算材料中各种原子的扩散速率。
3.3.1 一些计算模型中采用了参考扩散系数的概念,通过该系数可以预测材料中各种原子的扩散行为。
四、fe的扩散激活能和参考扩散系数的相关性4.1 fe的扩散激活能与参考扩散系数之间存在一定关联。
4.1.1 在一些模型中,fe的扩散激活能与参考扩散系数相关联。
4.1.2 通过实验或理论计算,可以得到fe的扩散激活能和参考扩散系数的关系。
五、应用5.1 fe的扩散激活能和参考扩散系数在材料热处理、表面涂层等领域具有重要意义。
5.2 通过调控fe的扩散激活能和参考扩散系数,可以改善材料的性能。
六、结论6.1 fe的扩散激活能和参考扩散系数是研究材料扩散行为的重要参数。
6.2 进一步研究fe的扩散激活能和参考扩散系数的相关性,对于材料科学领域具有重要意义。
七、深入研究fe的扩散激活能和参考扩散系数的相关性Fe的扩散激活能和参考扩散系数对固体材料中的铁原子扩散行为具有重要影响,因此深入研究它们之间的相关性是非常重要的。
关于影响金属材料固态扩散的因素与控制

影响金属材料固态扩散的因素与控制摘要:由扩散第一定律可知,在浓度梯度一定时,原子扩散仅取决于扩散系数D。
对于典型的原子扩散过程,D符合Arrhenius公式,。
因此,D仅取决于D0、Q和T,凡是能改变这三个参数的因素都将影响扩散过程。
关键词:温度,因素,扩散,组元,系数一,温度由扩散系数表达式看出,温度越高,原子动能越大,扩散系数呈指数增加。
以C 在γ-Fe中扩散为例,已知D0=2.0×10-5m2/s,Q=140×103J/mol,计算出927℃和1027℃时C的扩散系数分别为1.76×10-11m2/s,5.15×10-11m2/s。
温度升高100℃,扩散系数增加三倍多。
这说明对于在高温下发生的与扩散有关的过程,温度是最重要的影响因素。
应该注意,有些材料在不同温度范围内的扩散机制可能不同,那么每种机制对应的D和Q不同,D便不同。
在这种情况下,~并不是一条直线,而是由若干条直线组成的折线。
例如,许多卤化物和氧化物等离子化合物的扩散系数在某一温度会发生突变,反映了在这一温度以上和以下受到两种不同的机制控制。
图3.15表示出Na+离子在NaCl晶体中扩散系数的实验值。
其中,高温区发生的是以点缺陷扩散为主的本征扩散,低温区发生的是以夹杂产生或控制的缺陷扩散为主的非本征扩散。
二,成分1,组元性质原子在晶体结构中跳动时必须要挣脱其周围原子对它的束缚才能实现跃迁,这就要部分地破坏原子结合键,因此扩散激活能Q和扩散系数D必然与表征原子结合键大小的宏观或者微观参量有关。
无论是在纯金属还是在合金中,原子结合键越弱,Q越小,D越大。
合金中的情况也一样。
考虑A、B组成的二元合金,若B组元的加入能使合金的熔点降低,则合金的互扩散系数增加;反之,若能使合金的熔点升高,则合金的互扩散系数减小,在微观参量上,凡是能使固溶体溶解度减小的因素,都会降低溶质原子的扩散激活能,扩散系数增大。
金属学与热处理8.2扩散定律

当t 0时,C
x 0
, C
x 0
0
当t 0时, C x 0
Q x2 c( x, t ) exp( ) 4 Dt 2 Dt
13
8.3 影响扩散的因素
扩散是一个基本的动力学过程,对材料制备、加 工中的性能变化及显微结构形成以及材料使用过程中 性能衰减起着决定性的作用,对相应过程的控制,往 往从影响扩散速度的因素入手来控制,因此,掌握影 响扩散的因素对深入理解扩散理论以及应用扩散理论 解决实际问题具有重要意义。
000000???????????xxxctcct时当时当扩散是一个基本的动力学过程对材料制备加工中的性能变化及显微结构形成以及材料使用过程中性能衰减起着决定性的作用对相应过程的控制往往从影响扩散速度的因素入手来控制因此掌握影往从影响扩散速度的因素入手来控制因此掌握影响扩散的因素对深入理解扩散理论以及应用扩散理论解决实际问题具有重要意义
基本概念
固体中原子的运动有两种不同的方式:一种为大量原子集 体的协同运动,或称机械运动;另一种为无规则的热运动, 其中包括热振动和跳跃迁移。
扩散:热激活的原子通过自身的热振动克服束缚而迁移 它处的过程。 本质:原子无序跃迁的统计结果。(不是原子的定向移 动)。
1
扩散的分类
根据有无浓度变化
15
(1)温度
无论是间隙机制,还是空位机制,都遵循热激活规律,温 度提高,能超过能垒的几率越大,同时晶体的平衡空位浓度也
越高,这些都是提高扩散系数的原因。扩散系数与温度 T 成指 数 关系。对固体中扩散型相
变、晶粒长大,化学热处 理有重要影响。例如:工 业渗碳:1027℃比927℃时, D增加三倍,即渗碳速度加 快三倍。
北京科技大学材料学院材科基考研章节考点分析

北京科技大学材料学院材科基考研章节考点分析结构与缺陷2002年一.名词解释(1)点阵畸变(2)柏氏矢量(5分)二.画立方(111)面、(435)面。
写出立方晶系空间点阵特征。
(10分)四.画图并简述形变过程中位错增殖的机制。
(10分)十二、简述金属晶体中缺陷的类型(单考生做)。
(10分)2003年一、名词解释(1)刃型位错和螺形位错模型(2)晶界与界面能(10分)三、点阵参数?正方和立方的空间点阵特征是?画出立方(12-3)面(12分)十一、什么是固溶体?影响固溶体的原因有哪些?固溶体与其纯溶剂组元相比,其结构、力学性能和物理性能发生了哪些变化?(12分)十五、根据缺陷相对于晶体尺寸和其影响范围的大小,缺陷可以分为哪几类?简述这几类缺的特征。
(12分)2004年一、简述 2金属键 3中间相 4布喇菲点阵 7位错(12分)二、单相金属或合金各晶粒间的界面一般称之为晶界,通常晶界又分为小角度晶界和大角度晶界两大类,试问:划分为两类晶界的依据是什么?并讨论构成小角度晶界的结构模型。
(10分)三、分别画出立方的(110)、(112)晶面和[110]、[111]晶向。
(10分)四、讨论晶体结构和空间点阵之间的关系。
(10分)五、什么是固溶体?讨论影响固溶体溶解度的主要因素。
(10分)十四、叙述常见的金属晶体中的内外界面。
(10分)2005年一、什么是晶面族?{111}晶面族包含哪些晶面?二、面心立方结构金属的[110]和[111]晶向间的夹角是多少?{100}面间距是多少?三、面心立方结构和密排六方结构金属中的原子堆垛方式和致密度是否有差异?请加以说明。
(20分)四、解释间隙固溶体和间隙相的含义,并加以比较。
五、为什么固溶体的强度比金属高?(15分)六、晶体内若有较多的线缺陷(位错)或面缺陷(晶界、孪晶界等),其强度会明显升高,这些现象称为什么?强度提高的原因是什么?上述两类缺陷是怎样进入晶体的?举例说明如何提高这些缺陷的数目?(15分)2006年一、(以面心立方晶胞为例)描述晶体结构(晶胞)特征的常用参数有哪些?二、在体心立方晶胞中画出一个最密排方向并标明晶向指数;再画出过该方向的两个不同的低指数(简单)晶面,写出对应的晶面指数。
第三章固体中的扩散课堂课资

d lnCi
当 (1 d ln i ) 0 时, D 0 ,发生下坡扩散。
d lnCi
章节内容
22
3-2 扩散热力学
在下述情况下会发生上坡扩散: (1)存在弹性应力梯度。 (2)晶界的内吸附。 (3)施加大的电场或温度场。
章节内容
32
3-3 扩散机制和扩散激活能
三、扩散激活能
(一)间隙扩散激活能
间隙原子处于位置1和3时,
其自由能最低(等于G1),当 间隙原子从位置1跳跃至位置3
时,必须经过位置2,把A原子 适当挤开,使点阵产生瞬时畸
间隙原子的位置与自由能的关系
变,相应的畸变能即是间隙原子跳跃时所需克服的能垒。
章节内容
短路扩散:通过缺陷(如表面、晶界、位错等)进行的
扩散。
章节内容
25
3-3 扩散机制和扩散激活能
一、扩散机制
(一)间隙扩散机制
原子从一个晶格间隙位置跳跃到相
邻的晶格间隙位置,从而引起原子的扩
散。
间隙扩散机制
间隙固溶体中溶质原子的扩散即是通过间隙机制进行的。
章节内容
26
3-3 扩散机制和扩散激活能
(二)空位扩散机制
注意: erf(0) 0
erf() 1
erf( ) erf( )
章节内容
10
3-1 扩散第一定律和第二定律
(二)两端成分不受扩散影响的扩散偶
边界条件:t 0
x
x
,则C ,则C
C1 C2
初始条件:t = 0
x
x
0, 则C 0, 则C
C1 C2
第4章 金属中的扩散

柯肯达尔效应机制
(a)
(b)
(c)
(f)
(e)
(d)
Zn原子的扩散速率大于铜原子的扩散速率,导致纯铜一 遍不断的产生空位,当Zn原子越过标记面后,空位朝相反的 方向越过标记面进入黄铜一侧,并在黄铜一侧聚集,形成孔 洞,导致黄铜体积缩小。
柯肯达尔效应的意义:否定了置换固溶体的置换扩散机 制,支持了空位扩散机制。
间隙扩散:原子从一个晶格间隙位置迁移到另一个间隙位 置的扩散方式。
这种方式进行扩散的可能性很大,因为溶质原子只占据 少量间隙位置,即每个间隙原子周围都有较多的间隙位置是 空着的,故供其跃迁的位置很多。
3.2 置换机制
交换机理:相邻原子相互交换位置、进行迁移。 ——引起的点阵畸变大。
轮换机理:相邻三个原子或四个原子同时进行旋转式的交 换位置。 ——引起点阵畸变较小。
1.2 扩散概念与本质 扩散:由构成物质的微粒(离子、原子、分子)的热 运动而产生的物质迁移现象。
原子在点阵平衡位置进行无规则的热振动,某些原子的 能量超过了势垒,将离开原位置而跃迁到新的位置即发生了 原子的迁移。原子跃迁不是定向的,原子向四面八方都可以 跳跃。
要想实现宏观扩散效果,就要求晶体周期场的势能曲线 是倾斜的。这样由平衡态A到平衡态B的跃迁几率较大,这样 才能实现宏观的原子扩散。
即第二个面的扩散通量为第一个面注入的溶质与在这一段距 离内溶质浓度变化引起的扩散通量之和;
稳态扩散时,J1=J2 ,
J x
0
非稳态扩散时,J1≠J2
J 0 x
微小体积内物质的积存率=
J1
J2
J x
dx
(5)
微小体积内的物质积存速率还可用体积浓度C的变化率来表
《Al-Si-Mg三元近共晶合金定向凝固组织与形成》范文

《Al-Si-Mg三元近共晶合金定向凝固组织与形成》篇一一、引言随着现代工业的快速发展,轻质合金材料在众多领域中得到了广泛的应用。
其中,Al-Si-Mg三元近共晶合金以其优良的物理性能和机械性能,在汽车、航空航天、电子封装等领域具有重要地位。
本文将重点研究Al-Si-Mg三元近共晶合金的定向凝固组织及其形成的高质量特征,探讨其内在机理和应用前景。
二、Al-Si-Mg三元近共晶合金的基本特性Al-Si-Mg三元近共晶合金主要由铝、硅和镁等元素组成,其近共晶成分的微观组织主要由初生相、共晶相和少量其他杂质相组成。
这种合金具有优良的铸造性能、热稳定性和抗腐蚀性,同时具有较高的强度和良好的延展性。
三、定向凝固组织的形成过程定向凝固是一种通过控制合金的冷却速度和温度梯度,使合金在凝固过程中按照一定的方向生长的技术。
在Al-Si-Mg三元近共晶合金的定向凝固过程中,由于温度梯度和冷却速度的控制,合金中的各组分元素将按照一定的顺序和方向进行结晶,形成具有特定形态和结构的凝固组织。
四、定向凝固组织的形态与结构Al-Si-Mg三元近共晶合金的定向凝固组织主要由初生相、共晶相和其他杂质相组成。
初生相通常为铝基固溶体或铝硅化合物,具有特定的晶体形态和取向。
共晶相则是由铝、硅和镁元素共同形成的复杂化合物,具有特定的相结构和相分布。
这些相在定向凝固过程中按照一定的方向生长,形成了具有特定形态和结构的凝固组织。
五、高质量的形成与特性通过定向凝固技术,Al-Si-Mg三元近共晶合金可以形成高质量的组织结构。
这种高质量的组织结构具有优异的力学性能、热稳定性和抗腐蚀性。
首先,其高强度和高硬度使其在承受重载和冲击时具有良好的表现。
其次,其优异的热稳定性使其在高温环境下仍能保持较好的性能。
此外,其良好的抗腐蚀性使其在恶劣的环境中具有较长的使用寿命。
六、应用前景Al-Si-Mg三元近共晶合金的定向凝固组织和高质量特性使其在众多领域具有广泛的应用前景。
【国家自然科学基金】_fe-al合金_基金支持热词逐年推荐_【万方软件创新助手】_20140801
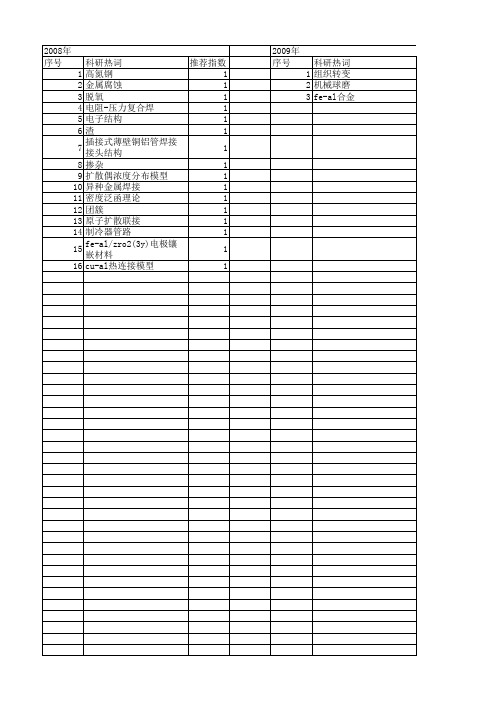
2013年 科研热词 镀层组织 结构空位 热空位 热浸镀 内耗 zn-15 si含量 fe-al合金 长程序参数 金属间化合物 超精细相互作用 缺陷 穆斯堡尔谱 磨损 磁致伸缩 电阻率 生长动力学 正电子湮没寿命谱 机械合金化 有序畴界 摩擦 微观组织 微观相场 形核孕育期 弥散强化 固溶 光谱 体心立方 低合金高强钢 二进制 ti)合金 si(≤0.1 b2fe-al合金 b2-feal金属间化合物 b2 fe-al合金 al镀层 al-zn-1.6 a1镀层 3d电子 推荐指数 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 55 1 1
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
科研热词 推荐指数 高氮钢 1 金属腐蚀 1 脱氧 1 电阻-压力复合焊 1 电子结构 1 渣 1 插接式薄壁铜铝管焊接接头结构 1 掺杂 1 扩散偶浓度分布模型 1 异种金属焊接 1 密度泛函理论 1 团簇 1 原子扩散联接 1 制冷器管路 1 fe-al/zro2(3y)电极镶嵌材料 1 cu-al热连接模型 1
科研热词 界面反应 热浸镀锌铝 扩散通道 扩散偶 zn-fe-al体系 zn-fe-al system interface reaction hot-dipping zn-al diffusion path diffusion couple
推荐指数 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
《材料科学基础》第四章 固体中的扩散

第四章固体中的扩散物质传输的方式:1、对流--由内部压力或密度差引起的2、扩散--由原子性运动引起的固体中物质传输的方式是扩散扩散:物质中的原子或分子由于热运动而进行的迁移过程本章主要内容:扩散的宏观规律:扩散物质的浓度分布与时间的关系扩散的微观机制:扩散过程中原子或分子迁移的机制一、扩散现象原子除在其点阵的平衡位置作不断的振动外,某些具有高能量的单个原子可以通过无规则的跳动而脱离其周围的约束,在一定条件下,按大量原子运动的统计规律,有可能形成原子定向迁移的扩散流。
将两根含有不同溶质浓度的固溶体合金棒对焊起来,形成扩散偶,扩散偶沿长度方向存在浓度梯度时,将其加热并长时间保温,溶质原子必然从左端向右端迁移→扩散。
沿长度方向浓度梯时逐渐减少,最后整个园棒溶质原子浓度趋于一致二、扩散第一定律(Fick第一定律)Fick在1855年指出:在单位时间内通过垂直于扩散方向某一单位截面积的扩散物质流量(扩散通量)与该处的浓度梯度成正比。
数学表达式(扩散第一方程)式中 J:扩散通量:物质流通过单位截面积的速度,常用量钢kg·m-2·s-1D:扩散系数,反映扩散能力,m2/S:扩散物质沿x轴方向的浓度梯度负号:扩散方向与浓度梯度方向相反可见:1), 就会有扩散2)扩散方向通常与浓度方向相反,但并非完全如此。
适用:扩散第一定律没有考虑时间因素对扩散的影响,即J和dc/dx不随时间变化。
故Fick第一定律仅适用于dc/dt=0时稳态扩散。
实际中的扩散大多数属于非稳态扩散。
三、扩散第二定律(Fick第二定律)扩散第二定律的数学表达式表示浓度-位置-时间的相互关系推导:在具有一定溶质浓度梯度时固溶体合金棒中(截面积为A)沿扩散方向的X轴垂截取一个微体积元A·dx,J1,J2分别表示流入和流出该微体积元的扩散通量,根据扩散物质的质量平衡关系,流经微体积的质量变化为:流入的物质量—流出的物质量=积存的物质量物质量用单位时间扩散物质的流动速度表示,则流入速率为,流出速率为∴积存率为积存速度也可以用体质C的变化率表示为比较上述两式,得将Fick第一定律代入得=(D) ——扩散第二方程若扩散系统D与浓度无关,则对三维扩散,扩散第二方程为:(D与浓度,方向无关)1、晶体中原子的跳动与扩散晶体中的扩散是大量原子无规则跳动的宏观统计结果。
【材料科学基础】必考知识点第六章

2020届材料科学基础期末必考知识点总结第六章固体中的扩散第一节概述1 扩散的现象与本质(1)扩散:热激活的原子通过自身的热振动克服束缚而迁移它处的过程。
(2)现象:柯肯达尔效应。
(3)本质:原子无序跃迁的统计结果。
(不是原子的定向移动)。
2 扩散的分类(1)根据有无浓度变化自扩散:原子经由自己元素的晶体点阵而迁移的扩散。
(如纯金属或固溶体的晶粒长大。
无浓度变化。
)互扩散:原子通过进入对方元素晶体点阵而导致的扩散。
(有浓度变化)(2)根据扩散方向下坡扩散:原子由高浓度处向低浓度处进行的扩散。
上坡扩散:原子由低浓度处向高浓度处进行的扩散。
(3)根据是否出现新相原子扩散:扩散过程中不出现新相。
反应扩散:由之导致形成一种新相的扩散。
3 固态扩散的条件(1)温度足够高;(2)时间足够长;(3)扩散原子能固溶;(4)具有驱动力:化学位梯度。
第二节扩散定律1 菲克第一定律(1)第一定律描述:单位时间内通过垂直于扩散方向的某一单位面积截面的扩散物质流量(扩散通量J)与浓度梯度成正比。
(2)表达式:J=-D(dc/dx)。
(C-溶质原子浓度;D-扩散系数。
)(3)适用条件:稳态扩散,dc/dt=0。
浓度及浓度梯度不随时间改变。
2 菲克第二定律一般:∂C/∂t=∂(D∂C/∂x)/ ∂x二维:(1)表达式特殊:∂C/∂t=D∂2C/∂x2三维:∂C/∂t=D(∂2/∂x2+∂2/∂y2+∂2/∂z2)C稳态扩散:∂C/∂t=0,∂J/∂x=0。
(2)适用条件:非稳态扩散:∂C/∂t≠0,∂J/∂x≠0(∂C/∂t=-∂J/∂x)。
3 扩散第二定律的应用(1)误差函数解适用条件:无限长棒和半无限长棒。
表达式:C=C1-(C1-C2)erf(x/2√Dt) (半无限长棒)。
在渗碳条件下:C:x,t处的浓度;C1:表面含碳量;C2:钢的原始含碳量。
(2)正弦解C x=Cp-A0sin(πx/λ)Cp:平均成分;A0:振幅Cmax- Cp;λ:枝晶间距的一半。
Al-Cu二元系在540℃时的扩散行为研究

Al-Cu二元系在540℃时的扩散行为研究OUYANG Yifang;LIU Ke;CAO Yu;CHEN Hongmei;TAO Xiaoma【摘要】[目的]研究Al-Cu二元系在540℃的扩散行为,为Al-Cu双金属复合结构实用化提供参考依据.[方法]利用电子探针显微分析仪(EPMA)对不同退火温度下二元扩散偶的形貌和成分进行分析研究.[结果]将Al-Cu二元扩散偶在540℃的真空退火炉中分别退火36 h、48 h和60 h后,在扩散区可以观察到4种金属间化合物(IMCs)θ(Al2 Cu)、η2(Al0.939 Cu0.987)、ζ2(Al9 Cu11.5)和γ1(Al4 Cu9).中间化合物扩散层的厚度与时间的平方根呈现线性关系,符合抛物线生长规律.同时,为了进一步研究Al-Cu之间的扩散行为,对互扩散系数进行计算,并对该方法做详细的介绍.[结论]随着温度的升高,金属间化合物的生长常数和互扩散系数也随之增加,其中Al4 Cu9的生长常数和扩散系数在4个IMCs最大.金属间化合物的生长主要受到体扩散的控制.【期刊名称】《广西科学》【年(卷),期】2018(025)006【总页数】5页(P654-657,662)【关键词】扩散偶;生长常数;互扩散系数;中间化合物【作者】OUYANG Yifang;LIU Ke;CAO Yu;CHEN Hongmei;TAO Xiaoma 【作者单位】;;;;【正文语种】中文【中图分类】TG111.60 引言【研究意义】Cu作为铝合金中常见的合金元素,对铝合金的强度,耐热性以及加工性能起到了良好的强化作用,在航空航天结构件、微电子、焊接、机械加工、粉末冶金等领域有着广泛的应用[1-4]。
由于Al和Cu在性能方面差别显著,并且Al-Cu接头的焊接问题是Al-Cu双金属复合结构实用化的关键[5]。
因此研究二者之间的扩散行为具有十分重要的意义。
【前人研究进展】由Al-Cu二元相图(图1)[6-7]可知,不同的实验方法和处理条件,得到的中间化合物的数量有所不同。
10材料科学基础课件-第六章扩散

• 若渗 件是低碳钢,成分为C0,则解为: 若渗C件是低碳钢,成分为 则解为: 件是低碳钢
x C(x, t) = Cs − (Cs −C0 )erf ( ) 2 Dt
返回
x C(x, t) = Cs − (Cs − C0 )erf ( ) 2 Dt
例2:含C量0.20%的低碳钢在927℃进行气体渗碳。假定 0.20%的低碳钢在927℃进行气体渗碳。 的低碳钢在927℃进行气体渗碳 表面C含量增加到0.9%,试求距表面0.5mm处 表面C含量增加到0.9%,试求距表面0.5mm处,C含 0.9% 0.5mm 量达0.4%所需的时间。已知D =1.28× 量达0.4%所需的时间。已知D927=1.28×10 0.4%所需的时间 解:已知C0 、Cs、C( x, t )、x、D代入式得: 代入式得: 已知 代入式得
返回
3、扩散偶问题
如图扩散偶,经时间t 如图扩散偶,经时间t 高温扩散后, 处的溶质浓 高温扩散后,x处的溶质浓 度为: 度为:
C1 + C2 C1 −C2 x C(x, t) = erf ( + ) 2 2 2 Dt
0 C C2 C2 J C2 > C1 C1
C1
x
返回
4、脱碳问题
C C0
含碳量为C0的碳钢在空气 量为C 中加热,经时间t 中加热,经时间t脱C浓度为: 浓度为:
61扩散的宏观规律及其应用62扩散的微观规律63上坡扩散与反应扩散64影响扩散的因素61扩散的宏观规律及其应用扩散偶实例其加热至高温并长时间保温后高浓度一端必然向低浓度端方向迁移沿长度方向浓度逐渐变缓最后趋于一致
第六章
扩散
物质中原子、分子的迁移现象 固体中物质传输的唯一方式
返回
扩散激活能

答:由于原子近似刚性球体,所以两原子对换位置时,它们近邻的原子必须后退,以让出适当的空间。 当对调完毕后,这些原子或多或少地恢复到原来的位置。这样的过程势必使交换原子对附近的晶格 产生强烈的畸变,这对直接换位机制来说是不利的。因此,这种扩散机制实际上是不大可能实现的。
面缺陷:本身所处于较高的能量状态,相应扩散激活能也就较低。
Ds Dg Dg 0.4 0.8 1.2 1.6 2.0 2.4 3.0 Ag的自扩散系数Db,晶界扩散系数Dg和表面扩散系数Ds
(5)材料的成分
原子之间的结合键力越强,通常对应材料的熔点也越高,激活能较大,扩散系数较小。材料的 成分不同,即组成材料的元素和比例不同,不同原子之间结合键能不一样,成分的变化也影响不同 类型结合键的相对数量,所以材料的成分变化带来的影响有: 结合键能不同,影响到激活能进而影响扩散系数; 结合键能的不同,一种元素的数量(成分比例)可能改变自己或其他元素的化学位,从而影响扩散 的速度,甚至方向; 空位扩散(置换原子)通量决定于互扩散系数,互扩散系数本身就是各组元成分的函数。
菲克第二定律菲克第二定律表象理论表象理论lnnlnrt热力学分析热力学分析扩散系数热力学因子低浓度扩散属正扩散即从高浓度此时lnnln从一个间隙到近邻另一个间隙空位机理空位机理间隙原子把相间隙原子把相邻的一个原子挤入邻的一个原子挤入相邻的间隙相邻的间隙换位机制换位机制直接换位直接换位回旋换位回旋换位原子跳动与扩散距原子跳动与扩散距菲克第一定律和菲克第二定律及其在各种条件下的解反映了原子扩散的宏观规律
1/T 扩散系数与温度的关系
例题:在773K所做的扩散实验指出,在1010个原子中有一个原子具有足够的激活能跳出其点阵位 置而进入间隙位置,在873K此比例会增加到10-9。 (1)求此跳跃所需要的激活能; (2)973K具有足够能量的原子所占的比例是多少?
8 金属的固态扩散

7
= 1× 1019 原子 / m3
位置
X
(3) 正弦解
边界条件:C ( x = 0, t ) = C p dC λ (x = , t) = 0 dx 2 求解Fick第二定律 ∂C = ∂ ( D ∂C ) ∂t ∂x ∂x 2 解为 C ( x, t ) = C p + A0 sin( π x ) exp(− π Dt ) λ λ2 πx π 2 Dt 即 C ( x, t ) − C p = A0 sin( ) exp(− 2 ) λ λ
J1 A − J 2 A = −
∂C ∂J =− ∂t ∂x
∂J Adx ∂x
∂ (CAdx) ∂C = Adx ∂t ∂t J = −D dC dx
∂C ∂ ∂C = (D ) ∂t ∂x ∂x
∂C ∂C =D 2 ∂t ∂x
2
(1) 误差函数解
适用条件:无限长棒或半无限长棒的扩散 问题。
1) 无限长扩散偶的扩散
扩散对于材料的加工过程具有重要影响。
Furnace for heat treating steel using the carburization process
8.1.1 固态扩散的分类
(1) 根据扩散方向是否与浓度的方向相同进 行分类 1) 上坡扩散:原子由低浓度处向高浓度处进 行的扩散。(如液态合金的共晶转变、固 溶体的共析转变;固溶体中新相析出及新 相长大)
8.3.2 扩散激活能
(3) 空位扩散的激活能 D=D0exp[-(∆Ev+∆E)/kT] 空位扩散激活能包括原子迁移能和空位形 成能。 Q空位>Q间隙 lnD=lnD0-Q/kT,lnD与1/T呈直线关系。
8.3.3 柯肯达尔效应与扩散驱动力
元素扩散的动力学

元素扩散的动力学元素扩散是物质传输的一种重要形式,它广泛存在于工业生产、材料加工、医学等领域。
元素扩散的动力学是研究元素在晶体内部扩散过程的机理、规律和影响因素的学科。
一、元素扩散的基本原理元素扩散是指物质从高浓度区向低浓度区传输的过程,这是一个自发的热力学过程。
其实质是原子在热力学势能梯度下的运动,始终趋向平衡态。
一个体系中,热力学势能越高的区域原子越多,趋向势能低的区域。
在晶体内,原子是周期性排列的,晶体通过晶格缺陷来实现元素扩散。
元素扩散的本质是原子在热力学势能梯度下的运动,具有以下三个特征:1. 沿着浓度梯度方向发生。
2. 向热力势能降低的方向进行。
3. 必须具有合适的传输通道或缺陷,例如晶格缺陷。
元素扩散的机理主要包括空位扩散机制和间隙原子扩散机制两种。
1. 空位扩散机制空位扩散是指晶体中原子位置发生变化时,空位穴始终被占据,成为该点的新位置所在的原子的空位,产生了新的空位和缺陷。
空位扩散机制是在高温下,分子热运动的作用下,空位穴扩散到相邻的位置,把一个元素原子运到空位的位置上。
空位扩散主要发生在晶体中间性设计的晶界和薄膜中。
2. 间隙原子扩散机制间隙原子扩散是指晶格中的原子在晶体结构中与原本原子占位位置不匹配的位置中,如四面体空洞、六面体空洞等。
当空位扩散不起作用时,间隙原子扩散会变成晶体中唯一的原子扩散机制。
通过这一机制,原子从一个空位跳到在晶体结构中空余的间隙中,然后继续跳。
间隙原子扩散主要发生在低温和截然不同的非晶状态中(例如玻璃)。
三、元素扩散的影响因素1. 温度随着温度的升高,元素扩散速率也会增加,因为热运动的平均速率增加,原子的扩散能量也会增加,扩散距离将增加。
2. 扩散剂扩散剂是促进扩散的物质。
它们的选择受到研究目的的限制。
扩散剂能够降低活化能,增加扩散系数,提高扩散速率。
例如,在铜和锌的混合相中,铜是扩散剂。
3. 晶体结构和缺陷晶体的结构和确定缺陷类型和浓度也会影响元素扩散的速率。
第四章 晶态固体中的扩散

对于立方点阵,所有跳动都有相同的长度,此时
R r nr 2 2 2
n
n
(4.14)
R 2 r n n
(4.15)
式4.15表明,原子迁移的平均距离与跳动次数n 的平方根成正比。若原子跳动n次所需的时间为t, 则n=Гt(Г原子的跳动频率),所以,原子迁移 的平均距离又与时间的平方根成正比。
(4.21)
根据热力学 G H TS E TS 凝聚态体系 H E
固态时⊿S随温度变化不大,可视为常数, 故式4.21可写为
D [2PZ exp(S / k)]exp(E / kT) (4.22)
rn之和即rrinin???1完全无规则行走每次跳动方向均与前次的跳动方向无关对任意的点积???????212rrinin??????????????????rrrrjiiinjniinin1112122因而41141241002111???????????rrjiiinjni大多数情况下由于晶体中存在着点缺陷空位间隙原子及在合金中存在着异类原子因此在两次跳跃方向之间总是不可避免地存在着相关效应此时02111???????????rrjiiinjni当存在相关效应时可用一种简便的方法定量表示这些相关即求实际的r2实际和完全无规行走的r2无规行走之比
t
x
C J t x
将菲克第一定律代入上式,可得
C (D C ) t x x
(4.2)
该方程为菲克第二定律定律。如果假定D与 浓度无关,则上式可简化为
(4.3)
菲克第二定律表达了扩散元素浓度与时间及 位置的一般关系。根据初始条件和边界条件处理 具体问题,便可获得相应的解。
三、扩散方程的解
对于非稳态扩散,则需对菲克第二定律按 所研究问题的初始条件和边界条件求解。
扩散偶制备技术发展及其应用

扩散偶制备技术发展及其应用毕亚男; 吴先月; 陈松; 谢明; 方继恒; 刘曦【期刊名称】《《贵金属》》【年(卷),期】2019(040)0z1【总页数】11页(P62-72)【关键词】扩散偶; 制备方法; 应用; 高通量; 贵金属【作者】毕亚男; 吴先月; 陈松; 谢明; 方继恒; 刘曦【作者单位】昆明贵金属研究所稀贵金属综合利用新技术国家重点实验室昆明650106【正文语种】中文【中图分类】TG146.3扩散偶最早出现于材料、冶金科学的研究中。
一般扩散偶是指两个材料通过扩散后冶金结合在一起的试样,并在垂直于冶金结合面方向发生了扩散,形成了具有一定厚度的由材料1到材料2的成分连续过渡,或形成了相界面,过渡层厚度可以满足用电子探针测定成分分布的需要。
这个过渡层或相界面虽然在宏观上是一个二维的面,一般基于局部平衡原理认为界面两侧是处于局域平衡状态。
早期的扩散偶多是二元,后期随着相图测试技术的发展出现了三元、四元扩散偶,特别是2012年来随着材料基因组工程中高通量制备技术的快速发展,出现了扩散多元节、薄膜掩膜法等基于扩散偶思想的大量新技术和新方法,而目前对于该技术的发展和特征还没有系统的总结和归纳,基于此本文进行了相应的研究和总结。
扩散偶法最早见于碳原子在钢铁中的扩散特性的研究,首先提出这一概念的是Girchner。
20世纪40年代出现了扩散偶法应用到二元系相关测定的报告[1]。
该方法主要用于测定扩散系数或者研究二元系中相关系研究,而且由于当时测试技术比较落后,主要采用光学、硬度法和常规化学分析方法进行研究,所以该技术的发展比较缓慢。
从上世纪80年代开始,中南大学金展鹏院士[2]首先根据扩散偶局部平衡原理,针对三元扩散偶,采用电子探针微区成分分析手段,进行三元相图的测定,并在国际上产生重要影响,该方法也被称为Changshang-Jin方法。
并逐渐在国内外推广开来,成为测量多元合金相图和扩散动力学的高效方法。
材料科学基础 西安交大 石德珂 第七章 材料中的原子扩散
后退 下页
二、烧结
烧结过程如下:将压实的粉末加 热到高温,在初期,相互接触的 颗粒开始逐渐形成颈的连接(图 7-15)烧结初期主要是表面扩散, 后期主要是晶界扩散。烧结速率 主要取决于两个因素:①粉末原 材料的颗粒粗细;②原子的扩散 速率,这决定于温度。
后退 下页
后退
返回
下页
第五节 固态相变中的形核
后退 下页
说明
(1)可确定不同时间t和距界面厚度不同处x的浓度 C=f(x,t); (2)当距离界面x处的浓度为一不确定值时,则扩 散所需时间t将与层深x2成正比关系;
C1 C 2 (3)当x=0时, 0, C 即在扩散过程中界面 2
上的浓度恒定不变;
(4)如扩散偶之一不存在原子浓度时,C1=0,则:
二、Fick第二定律
质量平衡关系: (在微小体积中积存的物质) =(留入的物质量)J1(留出的物质量)J2
dJ J 2 J1 dx dx x dc dJ D dx dx x dx x
dc J 1 J 2 dt dx
C2 x C 1 erf 2 2 Dt
后退 下页
2.半无限长棒的扩散方程解
初始条件:t=0,C=C2 x=∞, 则C=C1 0 边界条件:t≥0, x =0, 则C=C2
后退 下页
C2 x
x 其解: C C1 (C1 C 2)erf 2 Dt
900℃时,Ni在 Fe中的扩散系数比 r Fe 中 扩散系数约大1400倍。 527 ℃时,N在 Fe中的扩散系数比 r Fe 中 扩散系数约大1500倍。
原因:
Fe bcc 致密度K小
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
偶 中的成 分分 布进 行 测 定 ; 同时结 合 F _ l i 系的热 力 学与动 力 学性 质 , 用 T em . a eA — 体 s 采 hr oC l c& DC R I T A软 件 中的 移动 界 面模 型 , F 、 l s 元 素 随 温度 与 时间的 浓度 变化 情 况进 行 了模 拟 对 eA 和 i 计 算 , 算结 果与 实验 测 定的 成分 分布 数据 吻合 得 较好 , 而验 证 了计 算 中所 采 用 热 力 学与 动 计 从 力 学参数 的有 效性 , 并可 为模 拟相 关合 金体 系中相 组 成 的演 变行 为提供 计 算依据 。
【 e Wod 】 F —1 i y e Df s nC u l , hroC l &D C R ow r Ky rs e . s m, iui op s T e .a A SS t f o e m c IT A Sf a t e
相 变 诱 发 塑 性 钢 ( rnfr a o n u e T a s m t n Id cd o i
He Ya ln He Zho g i g L i n i n p n iL n
( c ol f t i sSinea dE gn eig S a ga U i ri ) S h o o Ma r l c c n n ier , h n h i nv sy ea e n e t
tn . Th i lto e u t r n g o g e me twih t e me s r d c n e tai n prfls, wh c e e smu ain r s ls we e i o d a r e n t h a u e o c n rto o e i ih
第3 2卷
第 6期
上
海
金
属
Vo . 1 32, No 6 .
21 0 0年 1 1月
S HANGHAI ME TAL S
No e e ,2 1 v mb r扩 散 偶 中 合 金 元 素 扩 散 行 为 的 动 力 学 计 算 eA — 三 S
0 e.M n ia o n t e e c u ls we e me s rd b fF a d S tmsi h s o p e r a u e y EPMA.Ai e y Th r - l & DI TRA d d b e mo Cac C s fwae p c a e,a s h o c n r to r f e fFe,M nd S n e tb ih d d f i n c u l swe e ot r a k g lo t e c n e tain p o l so i a ii sa ls e i uso o p e r f
c c ltd b v n o n a y mo e o p i g t emo y a c a d k n t r p r e fF — — i s s l a u a e y mo i g b u d r d l c u l h r d n mi n i e i p o e t s o e A1 y - n c i - - S -
【 关键 词 】 F .1 i 系 扩散 偶 eA. 体 S
T em .a hr oCl DC R c& IT A软件
KI NETI CALCULATI C oN oN AToM I DI C FFUS oN I BEHAVI oR I Fe A1S N . . iTERNARY FFUS oN DI I Co UPLES
何燕 霖 何忠平 李 麟
( 海 大 学 材料 科 学 与 工 程 学 院 , 海 2 07 ) 上 上 0 0 2
【 要 】 建 立 了 F 一 . %A —. %S/ e和 F 一. % A -. %S/ e两组 扩散 偶 , 摘 e6 8 1 O iF 1 e6 3 I 9 iF O 分别 对 其
【 bt c】 Df s ncul f e . %A..%S F n e6 3 1 .%S F e A s at r iui ope o F . 8 1 0 i eadF一.%A— 9 i ewr f o s 6 1 / 0 / e
p e a e n n e ld fr3 h a 5 ℃ a d 6 t 0 ℃ r s e t ey h o c nr t n p o l s r p rd a d a n a e o t 0 0 1 n 4 h a 0 0 1 e p c i l .T ec n e t i rf e v ao i
s o d t e v ld t fte o y a c a d k n t a a t r fFe M — is se h we h ai iy o h r d n mi n i e i p rmee s o - S y tm. I c u d p o ie t e m c t o l r vd h p r mee sf rsmu ai n o h c o tucu a v l to e a iro ee a ta ly s se a a t r i l t ft e mir sr t r le ou in b h v o fr l v n l y t m. o o o
