11-特征值法概率统计最优化问题
考研数学面试题目(3篇)

第1篇一、面试题目1. 请简述数学分析中极限的定义和性质。
解析:数学分析中,极限是指当自变量x趋向于某一点a时,函数f(x)的值趋向于某一点L。
具体来说,如果对于任意给定的正数ε,都存在一个正数δ,使得当0<|x-a|<δ时,有|f(x)-L|<ε,则称函数f(x)当x趋向于a时极限为L,记作lim(x→a)f(x)=L。
2. 请解释数学中的导数的概念及其几何意义。
解析:导数是描述函数在某一点处的局部变化率。
对于函数y=f(x),在点x0处的导数表示为f'(x0)。
几何意义上,导数表示曲线在该点的切线斜率。
3. 请简述多元函数偏导数的概念及其几何意义。
解析:多元函数偏导数是指多元函数在某一点处,仅考虑一个变量变化时,函数的导数。
对于多元函数z=f(x,y),在点(x0,y0)处的偏导数表示为f_x'(x0,y0)和f_y'(x0,y0)。
几何意义上,偏导数表示曲线在该点的切线斜率。
4. 请解释定积分的概念及其物理意义。
解析:定积分是指将一个函数在一个区间上的无穷小分割,然后求和并取极限的过程。
物理意义上,定积分可以表示曲线下方的面积、物理量在某段时间内的累积量等。
5. 请简述多元函数的积分概念及其物理意义。
解析:多元函数的积分是指将一个多元函数在一个区域上的无穷小分割,然后求和并取极限的过程。
物理意义上,多元函数的积分可以表示空间曲面的面积、物理量在某区域内的累积量等。
6. 请解释数学中的级数收敛的概念。
解析:级数收敛是指一个无穷级数的各项之和趋向于某个确定的值。
如果对于任意给定的正数ε,都存在一个正整数N,使得当n>N时,级数的部分和S_n与该确定值L之差的绝对值小于ε,则称该级数收敛。
7. 请简述线性代数中矩阵的概念及其运算。
解析:矩阵是一种由数字组成的矩形阵列,表示线性变换、线性方程组等。
矩阵的运算包括加法、数乘、乘法等。
8. 请解释线性代数中行列式的概念及其性质。
十大数学算法

十大数学算法数学算法是应用数学的重要组成部分,它们是解决数学问题的有效工具。
在计算机科学中,数学算法被广泛应用于图像处理、数据分析、机器学习等领域。
下面将介绍十大经典数学算法,它们涵盖了数值计算、图论、概率统计等多个数学领域的核心算法。
一、牛顿法牛顿法是一种用于求解方程的迭代数值方法。
它通过不断逼近函数的根,实现方程的求解。
牛顿法的核心思想是利用函数的局部线性近似来逼近根的位置,通过迭代求解函数的根。
牛顿法在优化问题中有广泛应用,如求解最优化问题和非线性方程组。
二、高斯消元法高斯消元法是一种用于求解线性方程组的经典方法。
通过不断进行行变换,将线性方程组转化为上三角矩阵,进而直接求解出线性方程组的解。
高斯消元法在线性代数和计算机图形学中有广泛的应用。
三、快速傅里叶变换快速傅里叶变换(FFT)是一种高效的离散傅里叶变换计算方法。
它通过分治法将离散傅里叶变换的计算复杂度降低到O(n log n)的时间复杂度。
FFT在信号处理、图像处理等领域有广泛应用。
四、Prim算法Prim算法是一种用于求解最小生成树的贪心算法。
通过不断选取与当前最小生成树连接的最小权重边,逐步构建最小生成树。
Prim算法在图论和网络优化中有重要应用。
五、Dijkstra算法Dijkstra算法是一种用于求解单源最短路径问题的贪心算法。
通过使用优先队列来存储节点,不断选择当前最短路径长度的节点,逐步求解最短路径。
Dijkstra算法在路由器和网络优化中有广泛应用。
六、最小二乘法最小二乘法是一种用于求解参数估计问题的优化方法。
通过最小化观测值与估计值之间的差异平方和,得到参数的最优估计。
最小二乘法在回归分析和数据拟合中广泛应用。
七、蒙特卡洛方法蒙特卡洛方法是一种通过随机抽样和统计模拟,来解决复杂问题的数值方法。
它通过随机抽样来估计问题的概率或者数值解,适用于各种复杂的概率和统计计算问题。
八、梯度下降法梯度下降法是一种常用的优化算法,主要用于求解无约束最优化问题。
数学建模基础知识

数学建模基础知识引言:数学建模是一门以数学为工具、以实际问题为研究对象、以模型为核心的学科。
它通过将实际问题抽象为数学模型,并利用数学方法对模型进行分析和求解,从而得到问题的解决方案。
在数学建模中,有一些基础知识是必不可少的,本文将介绍数学建模的基础知识,包括概率与统计、线性代数、微积分和优化算法。
一、概率与统计概率与统计是数学建模的基础。
概率论用于描述随机现象的规律性,统计学则用于从观测数据中推断总体的特征。
在数学建模中,需要根据实际问题的特点选择合适的概率模型,并利用统计方法对模型进行参数估计。
1.1 概率模型概率模型是概率论的基础,在数学建模中常用的概率模型包括离散型随机变量模型和连续型随机变量模型。
离散型随机变量模型适用于描述离散型随机事件,如投硬币的结果、掷骰子的点数等;连续型随机变量模型适用于描述连续型随机事件,如身高、体重等。
在选择概率模型时,需要根据实际问题的特点进行合理选择。
1.2 统计方法统计方法用于从观测数据中推断总体的特征。
在数学建模中,经常需要根据样本数据对总体参数进行估计。
常用的统计方法包括点估计和区间估计。
点估计用于估计总体参数的具体值,如均值、方差等;区间估计则用于给出总体参数的估计范围。
另外,假设检验和方差分析也是数学建模中常用的统计方法。
二、线性代数线性代数是数学建模的重要工具之一。
它研究线性方程组的解法、向量空间与线性变换等概念。
在线性方程组的求解过程中,常用的方法包括高斯消元法、矩阵的逆和特征值分解等。
线性代数还广泛应用于图论、网络分析等领域。
2.1 线性方程组线性方程组是线性代数的基础,它可以用矩阵和向量的形式来表示。
求解线性方程组的常用方法有高斯消元法、矩阵的逆矩阵和克拉默法则等。
高斯消元法通过矩阵的初等行变换将线性方程组转化为简化行阶梯形式,从而求得方程组的解。
2.2 向量空间与线性变换向量空间是线性代数的核心概念,它由若干个向量组成,并满足一定的运算规则。
数学建模常用知识点总结

数学建模常用知识点总结1.1 矩阵及其运算矩阵是一个矩形的数组,由行和列组成。
可以进行加法、减法和数乘运算。
1.2 矩阵的转置对矩阵进行转置就是把矩阵的行和列互换得到的新矩阵。
1.3 矩阵乘法矩阵A和矩阵B相乘得到矩阵C,要求A的列数等于B的行数,C的行数是A的行数,列数是B的列数。
1.4 矩阵的逆只有方阵才有逆矩阵,对于矩阵A,如果存在矩阵B,使得AB=BA=I,那么B就是A的逆矩阵。
1.5 行列式行列式是一个标量,是一个方阵所表示的几何体积的无向量。
1.6 特征值和特征向量对于矩阵A,如果存在标量λ和非零向量x,使得Ax=λx,那么λ就是A的特征值,x就是对应的特征向量。
1.7 线性相关和线性无关对于一组向量,如果存在一组不全为零的系数,使得它们的线性组合等于零向量,那么这组向量就是线性相关的。
1.8 空间与子空间空间是向量的集合,子空间是一个向量空间的子集,并且本身也是一个向量空间。
1.9 线性变换对于向量空间V和W,如果满足T(v+u)=T(v)+T(u)和T(kv)=kT(v),那么T就是一个线性变换。
1.10 最小二乘法对于一个线性方程组,如果方程个数大于未知数个数,可以使用最小二乘法来求得最优解。
1.11 奇异值分解矩阵分解的方法之一,将一个任意的矩阵分解为三个矩阵的乘积。
1.12 特征分解对于一个对称矩阵,可以将其分解为特征向量和特征值的乘积。
1.13 线性代数在建模中的应用在数学建模中,线性代数是非常重要的基础知识,它可以用来表示和分析问题中的数据,解决矩阵方程组、优化问题、回归分析等。
二、微积分2.1 极限和连续性极限是指一个函数在某一点上的局部性质,连续性则是函数在某一点上的全局性质。
2.2 导数和微分对于一个函数y=f(x),它的导数可以表示为f’(x),其微分可以表示为dy=f’(x)dx。
2.3 泰勒级数泰勒级数是一种用多项式逼近函数的方法,在建模中可以用来进行函数的近似计算。
正定矩阵的判定方法

正定矩阵的判定方法概述正定矩阵是线性代数中一个重要的概念,它在许多数学和科学领域中都有广泛的应用。
在解决优化问题、最小二乘法、概率统计和信号处理等领域中,正定矩阵的判定方法是关键的操作。
本文将介绍什么是正定矩阵,并详细讨论几种判定正定矩阵的方法。
正定矩阵的定义在开始讨论正定矩阵的判定方法之前,我们首先来了解正定矩阵的定义。
一个n × n 的实对称矩阵 A 称为正定矩阵,如果对于任意的非零向量 x,都有 x^TAx > 0。
其中,x^T 表示 x 的转置,x^TAx 表示向量 x 与矩阵 A 的乘积。
根据这个定义,我们可以得出正定矩阵的一些基本特征:1. 正定矩阵的特征值均为正数。
2. 正定矩阵的所有主子式(即从左上角到右下角的任意一组连续的对角线元素)均为正数。
3. 正定矩阵的所有奇异值均为正数。
接下来,我们将详细讨论几种常见的判定正定矩阵的方法。
1. 全主子式判定法全主子式判定法是最常用的判定正定矩阵的方法之一。
根据正定矩阵的定义,我们知道所有的主子式都应该是正数。
因此,我们可以通过计算矩阵的所有主子式,并检查它们是否都大于零来判断矩阵是否为正定矩阵。
具体的步骤如下:1) 对于一个n × n 的矩阵 A,计算所有的k × k 的主子式 D1,D2, ..., Dn,其中 k = 1, 2, ..., n。
2) 检查所有的主子式是否都大于零。
如果是,则矩阵 A 是正定矩阵;否则,矩阵 A 不是正定矩阵。
这种方法的时间复杂度为 O(n^3),其中 n 是矩阵的维度。
2. 特征值判定法特征值判定法是另一种常用的判定正定矩阵的方法。
根据正定矩阵的定义,我们知道矩阵的特征值都应该是正数。
因此,我们可以通过计算矩阵的特征值,并检查它们是否都大于零来判断矩阵是否为正定矩阵。
具体的步骤如下:1) 对于一个n × n 的矩阵 A,求解其特征值λ1, λ2, ..., λn。
特征值和标准值

特征值和标准值在数学和统计学中,特征值和标准值是两个重要的概念,它们在矩阵、线性代数、概率论等领域都有广泛的应用。
特征值和标准值的概念及其性质对于理解和解决实际问题具有重要意义。
本文将对特征值和标准值进行详细的介绍和解释,希望能够帮助读者更好地理解和运用这两个概念。
特征值和特征向量是矩阵的重要性质,它们在矩阵对角化、线性变换、特征分解等方面具有重要作用。
对于一个n阶方阵A,如果存在一个非零向量v和一个标量λ,使得Av=λv成立,则称λ为矩阵A的特征值,v为对应于特征值λ的特征向量。
特征值和特征向量的求解可以通过解线性方程组(A-λI)v=0来实现,其中I为单位矩阵。
特征值和特征向量的性质包括,矩阵的特征值之和等于矩阵的迹,矩阵的特征值之积等于矩阵的行列式,特征向量线性无关等。
标准值是统计学中常用的概念,它用来衡量一个数值相对于平均值的偏离程度。
标准值通常用标准差来表示,标准差是一组数据的离散程度的度量,它的大小决定了数据的波动程度。
标准值的计算方法是将一个数值减去平均值,再除以标准差,得到的结果即为标准值。
标准值的性质包括,68%的数据落在一个标准差范围内,95%的数据落在两个标准差范围内,99.7%的数据落在三个标准差范围内。
特征值和标准值在实际问题中有着广泛的应用。
在工程领域,特征值和特征向量可以用来描述振动系统的固有频率和振动模态,对于结构的稳定性和安全性具有重要意义。
在金融领域,标准值可以用来衡量资产价格的波动程度,帮助投资者进行风险管理和资产配置。
在生物学和医学领域,标准值可以用来评估人群的健康状况,帮助医生进行疾病诊断和治疗。
总之,特征值和标准值是数学和统计学中重要的概念,它们在理论研究和实际应用中都具有重要的作用。
通过对特征值和标准值的深入理解和运用,可以帮助我们更好地理解和解决实际问题,提高工作和研究的效率和质量。
希望本文对读者有所帮助,谢谢阅读!。
概率统计实验12多准则决策问题

实验十二 多准则决策问题一 实验目的通过用层次分析法解决一个多准则决策问题, 学习层次分析法的基本原理与方法; 掌握用层次分析法建立数学模型的基本步骤;学会用Mathematica 解决层次分析法中的数学问题.二 学习Mathematica 命令有时在计算中只需求出实数解, 而省略复数解, 则可以输入调用只求实数解的软件包. 输入<<Miscellaneous\RealOnly.m即可.三 实验的基本原理与方法层次分析法是一种简便、灵活而实用的多准则决策方法. 它特别适用于难以完全定量进行分析的,又相互关联、相互制约的众多因素构成的复杂问题. 它把人的思维过程层次化、数量化, 是系统分析的一个新型的数学方法.运用层次分析法建模,大体上可分四个基本步骤进行:1. 建立层次结构首先对所面临的问题要掌握足够的信息. 搞清楚问题的范围、因素、各因素之间的相互关系,及所要解决问题的目标. 把问题条理化、层次化,构造出一个有层次的结构模型. 在这个模型下,复杂问题被分解为元素的组成部分. 这些元素又按其属性及关系形成若干层次. 层次结构一般分三类:第一类为最高层,它是分析问题的预定目标和结果,也称目标层;第二类为中间层,它是为了实现目标所涉及的中间环节,如:准则、子准则,也称准则层;第三类为最低层,它包括了为实现目标可供选择的各种措施、决策方案等,也称方案层. OO 的影响之比,全部比较的结果可用矩阵表示,n n ij==⨯矩阵称为判断矩阵. 定义1 若判断矩阵满足下列条件:则称判断矩阵A 为正互反矩阵.怎样确定判断矩阵A 的元素ij a 取值?当某层的元素n C C C ,,,21 对于上一层某元素O 的影响可直接定量表示时(如利润多少),i C 与j C 对O 的影响之比可以直接确定,ij a 的值也易得到.但对于大多数社会经济问题,特别是比较复杂的问题,元素i C 和j C 对O的重要性不容易直接获得,需要通过适当的方法解决.通常取数字1-9及其倒数作为ij a 的取值范围.这是因为在进行定性的成对比较时,人们头脑中通常有5个明显的等级:因素太多,将超出人们的判断比较能力,降低精确. 实践证明,成对比较的尺度以72±为宜. 故ij a 的取值范围是1,2,9, 及其倒数1,.91,,21 3. 计算层次单排序并做一致性检验层次单排序是指同一层次各个元素对于上一层次中的某个元素的相对重要性进行排序. 具体做法是:根据同一层n 个元素n C C C ,,,21 ,对上一层某元素O 的判断矩阵A 求出它们对于元素O 的相对排序权重,记为:n w w w ,,,21 .写成向量形式:()T n w w w w ,,,21 = ,称为A 的排序权重向量. 其中i w 表示第i 个元素对上一层中某元素O 所占的比重. 从而得到层次单排序.层次单排序权重向量可有几种方法求解,常用的方法是利用判断矩阵A 的特征值与特征向量来计算排序权重向量w .为此引出矩阵的特征值与特征向量的有关理论.定义2 如果一个正互反矩阵().,,2,1,,n j i a A nn ij ==⨯满足 ),,2,1,,(n k j i a a a ik jk ij ==⨯,则称矩阵A 具有一致性,称元素k j i c c c ,,的成对比较是一致的; 并且称A 为一致矩阵.根据矩阵理论,可以得到如下几个定理.定理1 n 阶正互反矩阵A 的最大特征根m ax λn ≥,当n =λ时,A 是一致的.定理2 n 阶正互反矩阵是一致矩阵的充分必要条件是最大特征值m ax λn =.计算排序权重向量方法和步骤:设()T n w w w w ,,,21 =是n 阶判断矩阵的排序权重向量,当A 为一致矩阵时,根据n 阶判断矩阵构成的意义,显然有⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n n n n n n w w w w w w w w w w w w w w w w w w A 212221212111 (1) 因而满足 nw Aw =. 这里n 是矩阵A 的最大特征根,w 是相应的特征向量;当A 为一般的判断矩阵时w Aw max λ=. 其中m ax λ是A 的最大特征值(也称主特征根),w 是相应的特征向量(也称主特征向量). 经归一化后(即:∑==n i i w11),可近似作为排序权重向量,这种方法称为特征根法.一致性检验:在判断矩阵的构造中,并没有要求判断矩阵具有一致性的特点. 这是由于客观事物的复杂性与人的认识的多样性所决定.特别是在规模大、因素多的情况下,对于判断矩阵的每个元素来说,不可能求出精确的ji w w .但要求判断矩阵大体上应该是一致的. 一个经不起推敲的判断矩阵有可能导致决策的失误. 利用上述方法计算排序权向量,当判断矩阵过于偏离一致性时,其可靠程度也出现问题. 因此需要对判断矩阵的一致性进行检验. 其步骤如下:(1)计算一致性指标..I C1..max --=n nI C λ (2)当0..=I C 时,即n =max λ时,判断矩阵A 是一致的.当..I C 值越大,判断矩阵A 的不一致的程度越严重.(2)查找相应的平均随机一致性指标..I R下表给出了n (从1—11)阶正互反矩阵,用了100—150个随机样本矩阵A 算出的随机一致性指标..I R......I R I C R C = (3) 当10.0..<R C 时,认为判断矩阵的一致性是可以接受的,否则应对判断矩阵作适当修正.4. 计算层次总排序权重并做一致性检验在得到了某层元素对其上一层中某元素的排序权重向量后,还需要得到各层元素,特别是最低层中各方案对于目标层的排序权重,即层次总排序权重向量,从而进行方案选择. 层次总排序权重要自上而下地将层次单排序的权重进行合成得到.考虑3个层次的决策问题. 若第一层只有1个元素,第二层有n 个元素,第三层有m 个元素,设第二层对第一层的层次单排序的权重向量为:第三层对第二层的层次单排序的权重为:以)3(k w 为列向量构成矩阵 ()nm nm m m n n n w w w w w w w w w w w w W ⨯⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==)3()3(2)3(1)3(2)3(22)3(12)3(1)3(21)3(11)3()3(2)3(1)3(,,,(4) 则第三层对第一层的层次总排序权重向量为)2()3()3(w W w = (5)一般地,若有s 层,则第k 层对第一层的总排序权重向量为s k w W w k k k ,,4,3,)1()()( ==- (6)其中)(k W 是以第k 层对第k-1层的排序权向量为列向量组成的矩阵,)1(-k w 是第k-1层对第一层的总排序权重向量. 按照上述递推公式,可得到最下层(第s 层)对第一层的总排序权重向量为 )2()3()1()()(w W W W w s s s -= (7)层次总排序权重向量也要进行一致性检验. 具体方法是从最高层到最低层逐层进行. 定义3:若考虑的决策问题共有s 层. 设第l (s l ≤≤3)层的一致性指标为)1(.,,.,.)()(2)(1层元素的数目是第-l n I C I C I C l n l l ; 第l 层的随机一致性指标为 )()(2)(1.,,.,.l n l l I R I R I R ,令)1()(1)(1)(].,,.[.-=l l l l w I C I C I C (8))1()(1)(1)(].,,.[.-=l l l l w I R I R I R (9)则第l 层对第一层的总排序权向量的一致性比率为s l I R I C R C RC l l l l ,,4,3,....)()()1()( =+=-. (10) 其中)2(.R C 为由(3)式计算的第二层对第一层的排序权向量的一致性比率. 当最下层对第一层的总排序权向量的一致性比率1.0.)(<s RC 时,认为整个层次结构的比较判断可通过一致性检验.。
课程大纲-西安建筑科技大学研究生院

课程大纲课程编号(理学院)课程名称随机规划学时40基本预备知识 1. 概率统计2. 最优化理论与算法3. 随机过程授课方式讲授、研讨基本要求掌握随机规划模型的类型。
(3TKH 主要类型),了解分布问题中参数LP 及其最优值得表达式,了解Z(3 )的可测性及其概率分布,掌握简单分布问题的计算方法,了解逼近方法和最优值的数学期望的估计,掌握有补偿的二阶段问题和二阶段问题的数值解法,了解概率约束规划和随机拟次梯度法,了解上图收敛性。
教材及参考书《随机规划》,王全德编著,南京大学出版社,1990 年。
《随机线性规划》,Kall 著,王金德译,南京大学出版社。
讲授的主要内容:(每章后附学时数)1.随机规划的模型(6 学时)1.1分布问题,二阶段有补偿问题,概率约束问题;1.2多阶段有补偿问题和多阶段概率约束计划;1.3各类问题的统一形式与相互关系。
2.分布问题:(6 学时)2.1参数LP;2.2Z(3)的可测性;2.3最优化Z(3 )的概率分布;2.4简单分布问题的计算方法;2.5逼近方法与最优值的数学期望的估计。
3.有补偿二阶段问题(8 学时)3.1一般有补偿二阶段的问题;3.2具有固定补偿矩阵的情形;3.3具有完备和简单补偿矩阵的二阶段问题。
4.二阶段问题的数值解法(8 学时)4.1具有离散随机变量的二阶段问题的解法;4.2简单补偿问题的解法。
5.概率约束规划(6 学时)可行解集合的特性,约束函数的分析性质,数值解法,逼近方法。
6.随机拟次梯度法(* )(2 学时)7. 应用举例(2 学时)8. 上图收敛性(2 学时)注:(*)只做了解课程名称学时基本预备知识值代数601. 数学分析2. 线性代数3. 矩阵论4. 计算方法授课方式讲授基本要求1. 知道矩阵计算的基本工具,熟悉Vandermonde、Toeplitz 等方程组的解法及某些迭代法的收敛性,了解多项式加速技巧。
2.掌握不完全分解预先共轭梯度法,广义共轭剩余法,Lanczos 方法,求解特征值问题的同伦方法和分而治之法以及求解Jacobi 矩阵特征值反问题的正交约化法。
正定二次型判定方法

正定二次型判定方法正定二次型是数学中重要的概念之一,它在很多领域中都有着广泛的应用。
在线性代数中,正定二次型是指对于任意非零向量,其二次型值都大于零。
本文将介绍正定二次型的判定方法。
我们需要了解什么是二次型。
二次型是指一个关于n个变量的二次齐次多项式,通常表示为Q(x)=x^TAx,其中x是一个n维列向量,A是一个对称矩阵。
二次型在很多问题中起到了至关重要的作用,比如在优化问题、概率统计和物理学中。
对于一个二次型,我们希望能够判断它是否是正定的。
如果一个二次型是正定的,那么它具有以下性质:1. 二次型的所有特征值都大于零;2. 对于任意非零向量x,有x^TAx>0。
那么如何判断一个二次型是否正定呢?有以下几种方法:1. 特征值判定法:计算对称矩阵A的所有特征值,如果所有特征值都大于零,则二次型是正定的。
这是一种常用的判定方法,但需要计算所有的特征值,计算复杂度较高。
2. Sylvester判准则:根据A的主子式的符号判断。
一个n阶矩阵A的主子式是A的前k行和前k列所组成的子矩阵的行列式,记作Dk。
如果A的所有主子式Dk的符号交替,即D1>0,D2<0,D3>0,...,(-1)^(n-1)Dn>0,则二次型是正定的。
这种方法通过计算主子式的符号来判断二次型的正定性,计算复杂度较低。
3. 正定矩阵的定义:如果一个矩阵A满足对任意非零向量x,都有x^TAx>0,则A是正定矩阵,对应的二次型是正定的。
这种方法直接使用正定矩阵的定义进行判断,判断过程较为直观。
总结起来,判断二次型是否是正定的方法有特征值判定法、Sylvester判准则和正定矩阵的定义。
这些方法各有优缺点,我们可以根据具体情况选择合适的方法。
在实际应用中,正定二次型的判定方法可以帮助我们解决很多问题。
比如在优化问题中,我们希望找到一个使目标函数取得最小值的向量,可以通过判断二次型的正定性来确定是否存在最小值。
考研复试数学面试题目(3篇)

第1篇一、数学分析1. 请解释实数的完备性及其意义。
2. 证明:若数列{an}单调有界,则{an}收敛。
3. 设函数f(x)在[a, b]上连续,在(a, b)内可导,且f'(x)≠0,证明:存在一点ξ∈(a, b),使得f'(ξ)=f(b)-f(a)/(b-a)。
4. 证明:若函数f(x)在[a, b]上连续,在(a, b)内可导,且f'(x)≤0,则f(x)在[a, b]上单调递减。
5. 设函数f(x)在[a, b]上连续,在(a, b)内可导,且f'(x)≠0,证明:存在一点ξ∈(a, b),使得f'(ξ)=f(b)-f(a)/(b-a)。
6. 证明:若函数f(x)在[a, b]上连续,在(a, b)内可导,且f'(x)≤0,则f(x)在[a, b]上单调递减。
7. 设函数f(x)在[a, b]上连续,在(a, b)内可导,且f'(x)≠0,证明:存在一点ξ∈(a, b),使得f'(ξ)=f(b)-f(a)/(b-a)。
8. 证明:若函数f(x)在[a, b]上连续,在(a, b)内可导,且f'(x)≤0,则f(x)在[a, b]上单调递减。
9. 设函数f(x)在[a, b]上连续,在(a, b)内可导,且f'(x)≠0,证明:存在一点ξ∈(a, b),使得f'(ξ)=f(b)-f(a)/(b-a)。
10. 证明:若函数f(x)在[a, b]上连续,在(a, b)内可导,且f'(x)≤0,则f(x)在[a, b]上单调递减。
二、高等代数1. 请解释行列式的定义及其性质。
2. 证明:若矩阵A可逆,则|A|≠0。
3. 设矩阵A为n阶方阵,求证:A的行列式|A|等于其特征值的乘积。
4. 证明:若矩阵A为n阶方阵,且|A|=0,则A不可逆。
5. 设矩阵A为n阶方阵,求证:A的行列式|A|等于其特征值的乘积。
统计学原理随堂练习-华工

第一章绪论1.(判断题) 统计数据的分析是统计学的核心内容,它是通过统计描述和统计推断的方法探索数据内在规律的过程。
答案:√2.(判断题) 描述统计学是研究如何根据样本数据去推断通体数量特征的方法。
答案:×3.(判断题) 描述统计学是整个统计学的根底,推断统计学是现代统计学的主要内容。
答案:√4.(判断题) 推断统计学在现代统计学中的地位和作用越来越重要,已成为统计学的核心内容。
答案:√5.(判断题) 统计数据的计量尺度分为定类尺度、定序尺度、定距尺度和定比尺度。
答案:√6.(判断题) 定量数据说明的是现象的数量特征,是能够用数值来表现。
答案:√7.(判断题) 定性数据说明的是现象的品质特征,是不能用数值来表现。
答案:√8.(判断题) 统计指标表现为绝对数、相对数和平均数三种形式。
答案:√9.(判断题) 产品产量是时期数。
答案:√10.(判断题) 股票价格是时点数。
答案:√11.(判断题) 考试成绩分为优、良、中、及格、不及格,这是按定类尺度划分的。
答案:×12.(判断题) 考试成绩用"百分制〞度量,这是按定比尺度划分的。
答案:×13.(判断题) 将全部人口分为男女两局部,男性所占比重就是比率相对数。
答案:×14.(判断题) 动态数列就是将*同时期的各指标数值按照组别进展排序得到的数列。
答案:×15.(判断题) "企业数〞、"年龄〞都是离散变量。
答案:×16.(判断题) "性别〞、"产品等级〞属于数量变量。
答案:×17.(判断题) 数据的加工处理方法、数据分布特征的概括与分析方法等属于描述统计学的内容。
答案:√18.(判断题) 人的身高、体重、机器设备台数等都是连续变量。
答案:×19.(判断题) 离散变量的变量值只能按整数计算,不可能有小数。
答案:×20.(判断题) 价值单位是以货币形式对现象进展度量,如国民生产总值、商品销售额等。
高中数学:掌握高级代数和概率统计

高中数学:掌握高级代数和概率统计1. 引言1.1 概述高中数学是我们学习数学的重要阶段,它为我们打下了坚实的数学基础,并起到了培养我们逻辑思维和解决问题能力的作用。
在高中数学中,高级代数和概率统计是两个重要而又有挑战性的领域。
掌握这两个领域的知识和技巧将帮助我们更好地理解和应用数学,为未来的学术和职业发展奠定扎实的基础。
1.2 文章结构本文将围绕高级代数和概率统计展开讨论。
首先,我们将介绍高级代数方面的内容,包括多项式和因式分解、方程与不等式以及线性代数与矩阵等核心概念。
然后,我们会转向概率统计领域,并介绍概率基础知识、随机变量与概率分布以及统计推断与假设检验等主题。
最后,在解题技巧与策略部分,我们将分享一些有关解题思路指导、高级代数问题解决方法论以及概率统计问题求解技巧的经验和建议。
通过全面深入地了解这些内容,我们将能够更加自信和有效地应对高中数学中的各种问题。
1.3 目的本文的目的是帮助读者全面了解和掌握高级代数和概率统计这两个重要领域,在数学学习中取得更好的成绩。
我们希望通过对关键知识点的介绍、对解题方法和策略的分享,使读者在面对高级代数和概率统计题目时能够有条不紊地思考和解决问题。
同时,通过本文的阅读,读者也将获得一些关于数学思维和推理能力培养的启示,从而提升自己在数学领域以及其他相关领域的表现。
以上就是文章“1. 引言”部分内容,请问还有其他方面需要补充吗?2. 高级代数:2.1 多项式和因式分解:在高级代数中,多项式是一个重要的概念。
多项式可以包含一个或多个变量,并由常数系数和各个变量的幂次组成。
因式分解是将一个多项式拆解为不可再分解的乘积形式的过程。
多项式的因式分解可以通过以下几种常见方法实现:- 提取公因子:如果一个多项式中的每一项都有一个相同的公因子,那么可以使用提取公因子法进行因式分解。
- 使用特定公式:例如,平方差、立方差、差平方等特殊公式可以帮助我们更容易地进行因式分解。
数学建模常用算法

数学建模常用算法数学建模是指将实际问题转化为数学模型,并通过数学方法进行求解的过程。
在数学建模中,常用的算法有很多种,下面将介绍一些常见的数学建模算法。
1.最优化算法:-线性规划算法:如单纯形法、内点法等,用于求解线性规划问题。
-非线性规划算法:如最速下降法、牛顿法等,用于求解非线性规划问题。
-整数规划算法:如分支定界法、割平面法等,用于求解整数规划问题。
2.概率统计算法:-蒙特卡洛模拟:通过模拟随机事件的方式,得出问题的概率分布。
-贝叶斯统计:利用先验概率和条件概率,通过数据更新后验概率。
-马尔可夫链蒙特卡洛:用马尔可夫链的方法求解复杂的概率问题。
3.图论算法:-最短路径算法:如迪杰斯特拉算法、弗洛伊德算法等,用于求解两点之间的最短路径。
-最小生成树算法:如普里姆算法、克鲁斯卡尔算法等,用于求解图中的最小生成树。
- 最大流最小割算法: 如Edmonds-Karp算法、Dinic算法等,用于求解网络流问题。
4.插值和拟合算法:-多项式插值:如拉格朗日插值、牛顿插值等,用于通过已知数据点拟合出多项式模型。
-最小二乘法拟合:通过最小化实际数据与拟合模型之间的差异来确定模型参数。
-样条插值:通过使用多段低次多项式逼近实际数据,构造连续的插值函数。
5.遗传算法和模拟退火算法:-遗传算法:通过模拟自然选择、遗传变异和交叉等过程,优化问题的解。
-模拟退火算法:模拟固体退火过程,通过随机策略进行,逐步靠近全局最优解。
6.数据挖掘算法:- 聚类算法: 如K-means算法、DBSCAN算法等,用于将数据分为不同的类别。
-分类算法:如朴素贝叶斯算法、决策树算法等,用于通过已知数据的类别预测新数据的类别。
- 关联分析算法: 如Apriori算法、FP-growth算法等,用于发现数据集中的关联规则。
以上只是数学建模中常用的一些算法,实际上还有很多其他算法也可以应用于数学建模中,具体使用哪种算法取决于问题的性质和要求。
工程数学“概率论与数理统计”测试题参考答案

工程数学期末复习要点邹斌现在主要讨论工程数学这门课程的考核要求,08秋工程数学考试形式为半开卷,行考比例占30%,我们将分章节复习。
本课程分线性代数和概率统计两部分共7章内容。
分别是行列式、矩阵、线性方程组、矩阵的特征值及二次型、随机事件与概率、随机变量的分布和数字特征、数理统计基础。
第一部分线性代数一、行列式复习要求(1)知道n阶行列式的递归定义;(2)掌握利用性质计算行列式的方法;(3)知道克莱姆法则。
考核要求:行列式性质的计算(选择或填空)二、矩阵复习要求(1)理解矩阵的概念,了解零矩阵、单位矩阵、数量矩阵、对角矩阵、上(下)三角矩阵、对称矩阵的定义,了解初等矩阵的定义;(2)熟练掌握矩阵的加法、数乘矩阵、乘法、转置等运算;(3)掌握方阵乘积行列式定理;(4)理解可逆矩阵和逆矩阵的概念及性质,掌握矩阵可逆的充分必要条件;(5)熟练掌握求逆矩阵的初等行变换法,会用伴随矩阵法求逆矩阵,掌握求解简单的矩阵方程的方法;(6)理解矩阵秩的概念,掌握矩阵秩的求法;(7)会分块矩阵的运算。
考核要求:(1)矩阵乘法(选择或填空)(2)求逆矩阵(3阶)初等行变换法(计算题)(3)求矩阵的秩(等于阶梯形矩阵的非零行数)三、线性方程组复习要求(1)掌握向量的线性组合与线性表出的方法,了解向量组线性相关与线性无关的概念,会判别向量组的线性相关性;(2)会求向量组的极大线性无关组,了解向量组和矩阵的秩的概念,掌握求向量组的秩和矩阵的秩的方法;(3)理解线性方程组的相容性定理,理解齐次线性方程组有非零解的充分必要条件。
熟练掌握用矩阵初等行变换方法判断齐次与非齐次线性方程组解的存在性和惟一性;(4)熟练掌握齐次线性方程组基础解系和通解的求法;(5)了解非齐次线性方程组解的结构,掌握求非齐次线性方程组通解的方法。
考核要求:(1)线性相关性(选择或填空)(2)会求向量组的极大线性无关组(计算题)(3)线性方程组的判定定理(选择或填空)(4)熟练掌握齐次和非齐次方程组的基础解系和通解的求法(计算题)四、矩阵的特征值及二次型复习要求(1)理解矩阵特征值、特征多项式及特征向量的定义,掌握特征值与特征向量的求法;(2)了解矩阵相似的定义,相似矩阵的性质;(3)知道正交矩阵的定义和性质;(4)理解二次型定义、二次型的矩阵表示、二次型的标准形,掌握用配方法化二次型为标准形的方法;(5)了解正定矩阵的概念,会判定矩阵的正定性。
线性代数与概率统计及答案

线性代数部分第一章 行列式一、单项选择题1.=0001001001001000 .A 0B 1-C 1D 22.=0001100000100100 .A 0B 1-C 1D 2 3.若a a a a a =22211211,则=21112212ka a ka a .A kaB ka -C a k 2D a k 2-4. 已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-, 则=x .A 0B 3-C 3D 25. k 等于下列选项中哪个值时,齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x kx x kx x kx x x 有非零解.A 1-B 2-C 3-D 06.设行列式na a a a =22211211,m a a a a =21231113,则行列式232221131211--a a a a a a 等于A. m n -B.)(-n m +C. n m +D.n m -二、填空题1. 行列式=0100111010100111.2.行列式010...0002...0.........000 (10)0 0n n =-.3.如果M a a a a a a a a a D ==333231232221131211,则=---=323233312222232112121311133333 3a a a a a a a a a a a a D .4.行列式=--+---+---1111111111111111x x x x .5.已知三阶行列式中第二列元素依次为1,2,3, 其对应的余子式依次为3,2,1,则该行列式的值为.6.齐次线性方程组⎪⎩⎪⎨⎧=+-=+=++0020232121321x x x kx x x x kx 仅有零解的充要条件是.7.若齐次线性方程组⎪⎩⎪⎨⎧=+--=+=++0230520232132321kx x x x x x x x 有非零解,则k =.三、计算题2.yxyx x y x y y x y x+++;3.解方程0011011101110=x x xx ;6. 111...1311...1112 (1).........111...(1)b b n b----7. 11111222123111...1..................nb a a a b b a a b b b a ; 8.121212123.....................n nn x a a a a x a a a a x a a a a x;四、证明题1.设1=abcd ,证明:011111111111122222222=++++dddd c c c c b b b b a a a a .2.3332221112333332222211111)1(c b a c b a c b a x c b x a x b a c b x a x b a c b x a xb a -=++++++.3.))()()()()()((111144442222d c b a c d b d b c a d a c a b d c b a dcbad c b a +++------=.第二章 矩阵一、单项选择题1. A 、B 为n 阶方阵,则下列各式中成立的是 ;a 22A A =b ))((22B A B A B A +-=- c AB A A B A -=-2)( d T T T B A AB =)( 2.设方阵A 、B 、C 满足AB=AC,当A 满足 时,B=C;a AB =BAb 0≠Ac 方程组AX=0有非零解d B 、C 可逆 3.若A 为n 阶方阵,k 为非零常数,则=kA ;a A kb A kc A k nd A k n4.设A 为n 阶方阵,且0=A ,则 ;a A 中两行列对应元素成比例b A 中任意一行为其它行的线性组合c A 中至少有一行元素全为零d A 中必有一行为其它行的线性组合 5.设A 为n 阶方阵,*A 为A 的伴随矩阵,则 ; (a) a 1*-=A A b A A =* c 1*+=n AA d 1*-=n AA6. 设A ,B 为n 阶方矩阵,22B A =,则下列各式成立的是 ; a B A = b B A -= c B A = d 22B A = 7.设A 为n 阶可逆矩阵,则下面各式恒正确的是 ; a T A A 22= b 112)2(--=A Ac 111])[(])[(---=T T T A Ad T T T T A A ])[(])[(11--=8.已知⎪⎪⎪⎭⎫ ⎝⎛=113022131A ,则 ;a A A T =b *1A A =-c ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛113202311010100001Ad ⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛113202311010100001A9.设I C B A ,,,为同阶方阵,I 为单位矩阵,若I ABC =,则 ;a I ACB =b I CAB =c I CBA =d I BAC = 10.n 阶矩阵A 可逆的充要条件是 ; a A 的每个行向量都是非零向量 b A 中任意两个行向量都不成比例c A 的行向量中有一个向量可由其它向量线性表示d 对任何n 维非零向量X ,均有0≠AX 11. 设矩阵A=1,2,B=⎪⎪⎭⎫ ⎝⎛4321,C⎪⎪⎭⎫⎝⎛=654321则下列矩阵运算中有意义的是A .ACB B .ABC C .BACD .CBA 12.设矩阵A,B 均为可逆方阵,则以下结论正确的是DA .⎪⎪⎭⎫ ⎝⎛B A 可逆,且其逆为⎪⎪⎭⎫ ⎝⎛--11B AB .⎪⎪⎭⎫ ⎝⎛B A 不可逆 C .⎪⎪⎭⎫ ⎝⎛B A 可逆,且其逆为⎪⎪⎭⎫ ⎝⎛--11A BD .⎪⎪⎭⎫ ⎝⎛B A 可逆,且其逆为⎪⎪⎭⎫ ⎝⎛--11B A13.已知向量TT )0,3,4,1(23,)1,2,2,1(2--=β+α---=β+α,则β+α=AA .T)1,1,2,0(-- B.T)1,1,0,2(-- C .T)0,2,1,1(-- D .T)1,5,6,2(---14.设A 和B 为n 阶方阵,下列说法正确的是CA. 若AB AC =,则B C =B. 若0AB =,则0A =或0B =C. 若0AB =,则0A =或0B =D. 若0A E -=,则A E =6、设两事件A二、填空题1.设A 为n 阶方阵,I 为n 阶单位阵,且I A =2,则行列式=A _______2.行列式=---000c b c a ba_______3.设A 为5阶方阵,*A 是其伴随矩阵,且3=A ,则=*A _______4.设4阶方阵A 的秩为2,则其伴随矩阵*A 的秩为_______ 三、计算题1.解下列矩阵方程X 为未知矩阵.1 223221103212102X ⎛⎫⎛⎫ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭ ;2 0101320100211100110X ⎛⎫⎛⎫⎛⎫ ⎪ ⎪=- ⎪ ⎪ ⎪-⎝⎭ ⎪ ⎪⎝⎭⎝⎭ ; 3 2AX A X =+,其中423110123A ⎛⎫⎪= ⎪⎪-⎝⎭;2.设A 为n 阶对称阵,且20A =,求A .3.设11201A ⎛⎫= ⎪⎝⎭,23423A ⎛⎫= ⎪⎝⎭,30000A ⎛⎫= ⎪⎝⎭,41201A ⎛⎫= ⎪⎝⎭,求1234A A A A ⎛⎫⎪⎝⎭.4.设211011101,121110110A B ⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,求非奇异矩阵C ,使T A C BC =.四、证明题1. 设A 、B 均为n 阶非奇异阵,求证AB 可逆.2. 设0k A =k 为整数, 求证I A -可逆.4. 设n 阶方阵A 与B 中有一个是非奇异的,求证矩阵AB 相似于BA .5. 证明可逆的对称矩阵的逆也是对称矩阵.第三章 向量一、单项选择题1. 321,,ααα, 21,ββ都是四维列向量,且四阶行列式m =1321βααα,n =2321ααβα,则行列式)(21321=+ββαααn m a +)( n m b -)( n m c +-)( n m d --)(2. 设A 为n 阶方阵,且0=A ,则 ;成比例中两行(列)对应元素A a )( 线性组合中任意一行为其它行的A )b ( 零中至少有一行元素全为A c )( 线性组合中必有一行为其它行的A )d (3. 设A 为n 阶方阵,n r A r <=)(,则在A 的n 个行向量中 ;个行向量线性无关必有r a )(个行向量线性无关任意r )b (性无关组个行向量都构成极大线任意r c )(个行向量线性表示其它任意一个行向量都能被r )d (4. n 阶方阵A 可逆的充分必要条件是n r A r a <=)()( n A b 的列秩为)(零向量的每一个行向量都是非)(A c 的伴随矩阵存在)(A d5. n 维向量组12,,...,s ααα线性无关的充分条件是)(a 12,,...,s ααα都不是零向量)(b 12,,...,s ααα中任一向量均不能由其它向量线性表示 )(c 12,,...,s ααα中任意两个向量都不成比例 )(d 12,,...,s ααα中有一个部分组线性无关二、填空题1. 若T )1,1,1(1=α,T )3,2,1(2=α,T t ),3,1(3=α线性相关,则t=▁▁▁▁;2. n 维零向量一定线性▁▁▁▁关;3. 向量α线性无关的充要条件是▁▁▁▁;4. 若321,,ααα线性相关,则12,,...,s ααα)3(>s 线性▁▁▁▁关;5. n 维单位向量组一定线性▁▁▁▁;三、计算题 1. 设T )1,1,1(1λα+=,T )1,1,1(2λα+=,T )1,1,1(3λα+=,T),,0(2λλβ=,问1λ为何值时,β能由321,,ααα唯一地线性表示2λ为何值时,β能由321,,ααα线性表示,但表达式不唯一 3λ为何值时,β不能由321,,ααα线性表示 2. 设T )3,2,0,1(1=α,T )5,3,1,1(2=α,T a )1,2,1,1(3+=α,T a )8,4,2,1(4+=α,T b )5,3,1,1(+=β问: 1b a ,为何值时,β不能表示为4321,,,αααα的线性组合 2b a ,为何值时,β能唯一地表示为4321,,,αααα的线性组合 3. 求向量组T )4,0,1,1(1-=α,T )6,5,1,2(2=α,T )2,5,2,1(3=α,T )0,2,1,1(4--=α,T )14,7,0,3(5=α的一个极大线性无关组,并将其余向量用该极大无关组线性表示; 四、证明题1. 设2131222112,3,ααβααβααβ-=-=+=,试证321,,βββ线性相关;2. 设12,,...,n ααα线性无关,证明12231,,...,n αααααα+++在n 为奇数时线性无关;在n 为偶数时线性相关;第四章 线性方程组一、单项选择题1.设n 元齐次线性方程组0AX =的系数矩阵的秩为r ,则0AX =有非零解的充分必要条件是A r n =B r n <C r n ≥D r n >2.设A 是m n ⨯矩阵,则线性方程组AX b =有无穷解的充要条件是A ()r A m <B ()r A n <C ()()r Ab r A m =<D ()()r Ab r A n =<3.设A 是m n ⨯矩阵,非齐次线性方程组AX b =的导出组为0AX =,若m n <,则A AX b =必有无穷多解B AX b =必有唯一解C 0AX =必有非零解D 0AX =必有唯一解4.方程组1232332422(2)(3)(4)(1)x x x x x x λλλλ+-=⎧⎪+=⎨⎪-=----⎩无解的充分条件是λ=A 1B 2C 3D 45.方程组12323331224(1)(3))(1))x x x x x x x λλλλλλ++=-⎧⎪-=-⎪⎨=-⎪⎪-=---⎩有唯一解的充分条件是λ=A 1B 2C 3D 4 二、填空题1. 设A 为100阶矩阵,且对任意100维的非零列向量X ,均有0AX ≠,则A 的秩为 .2. 线性方程组1231212320200kx x x x kx x x x ++=⎧⎪+=⎨⎪-+=⎩仅有零解的充分必要条件是 .3. 设12,,s X X X 和1122s s c X c X c X +++均为非齐次线性方程组AX b =的解12,,s c c c 为常数,则12s c c c +++= .4. 若线性方程组AX b =的导出组与0(())BX r B r ==有相同的基础解系,则()r A = .5. 若线性方程组m n A X b ⨯=的系数矩阵的秩为m ,则其增广矩阵的秩为 .三、计算题1. 已知123,,ααα是齐次线性方程组0AX =的一个基础解系,问122331,,αααααα+++是否是该方程组的一个基础解系 为什么2. 设54331012263211311111A -⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦,12010560011210012320B --⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥--⎣⎦,已知B 的行向量都是线性方程组0AX =的解,试问B 的四个行向量能否构成该方程组的基础解系 为什么3. 设四元齐次线性方程组为 Ι:122400x x x x +=⎧⎨-=⎩1求Ι的一个基础解系2如果12(0,1,1,0)(1,2,2,1)T T k k +-是某齐次线性方程组II 的通解,问方程组Ι和II 是否有非零的公共解 若有,求出其全部非零公共解;若无,说明理由;第五章 特征值与特征向量一、单项选择题1. 设001010100A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则A 的特征值是 ;a -1,1,1b 0,1,1c -1,1,2d 1,1,22. 设110101011A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则A 的特征值是 ;a 0,1,1b 1,1,2c -1,1,2d -1,1,1 3. 设A 为n 阶方阵, 2A I =,则 ;a ||1A =b A 的特征根都是1c ()r A n =d A 一定是对称阵4. 若12,x x 分别是方阵A 的两个不同的特征值对应的特征向量,则1122k x k x +也是A 的特征向量的充分条件是 ;a 1200k k ==且b 1200k k ≠≠且c 120k k =d 1200k k ≠=且 5. 若n 阶方阵,A B 的特征值相同,则 ;a A B =b ||||A B =c A 与B 相似d A 与B 合同二、填空题1. n 阶零矩阵的全部特征值为_______;2. 设A 为n 阶方阵,且I A =2,则A 的全部特征值为_______;3. 设A 为n 阶方阵,且0=m A m 是自然数,则A 的特征值为_______;4. 若A A =2,则A 的全部特征值为_______;5. 若方阵A 与I 4相似,则=A _______;三、计算题1. 若n 阶方阵A 的每一行元素之和都等于a ,试求A 的一个特征值及该特征值对应的一个特征向量.2. 求非奇异矩阵P ,使1P AP -为对角阵.1 2112A ⎛⎫= ⎪⎝⎭2 112131201A -⎛⎫⎪=-- ⎪ ⎪--⎝⎭四、证明题1. 设A 是非奇异阵, λ是A 的任一特征根,求证1λ是1A -的一个特征根,并且A 关于λ的特征向量也是1A -关于1λ的特征向量. 2. 设2A E =,求证A 的特征根只能是1±.3. 设n 阶方阵A 与B 中有一个是非奇异的,求证矩阵AB 相似于BA .4. 证明:相似矩阵具有相同的特征值.5. 设n 阶矩阵A E ≠,如果()()r A E r A E n ++-=,证明:-1是A 的特征值;6. 设A B ,证明kk A B ;7. 设12,αα是n 阶矩阵A 分别属于12,λλ的特征向量,且12λλ≠,证明12αα+不是A 的特征向量;概率论部分一、填空:每题3分,共15分1. 假设,A B 是两独立的事件,()0.7,()0.3P A B P A ⋃==,则()P B =_________; 2. 设A,B 是两事件,(|)1/4,()1/3P A B P B ==,则()P AB =__________; 3. 若二维随机变量(X,Y)满足()()()E XY E X E Y =,则X Y 与________; 4. 随机变量~(0,1),23,~X N Y X Y =+则_________; 5. 设总体)1,0(~N X ,1210,,,X X X 是来自总体X 的样本,则X 服从_________分布;二、选择:每题3分,共15分1. 如果成立,则事件,A B 互为对立事件....()()1A AB B AB C AB A B D P A P B =Φ=Ω=Φ⋃=Ω+=且2. 若X 的概率密度为02()4240x x f x xx ≤≤⎧⎪=-≤≤⎨⎪⎩其它,则{3}P X ≤= .3/2A .5/2B .7/2C .4D3. 设随机变量),(~p n B X ,则方差var()X =.A np .(1)B n p - 2.C np .(1)D np p -4. 下列结论正确的是A .X 与Y 相互独立,则X 与Y 不相关B .X 与Y 不独立,则X 与Y 相关C .X 与Y 不相关,则X 与Y 相互独立D .X 与Y 相关,则X 与Y 相互独立5. 设n X X X ,,,21 为来自正态总体2~(,)X N μσ的一个样本,其中μ已知,2σ未知,则下面不是统计量的是 ()A 1X ()B 221()ni i X μσ=-∑()C 211()n i i X n μ=-∑ ()D 211()1n i i X X n =--∑ 三、计算:共70分1.15分甲乙两袋,甲袋中有两白球一个黑球,乙袋中有一个白球两个黑球;先从甲袋中取一球放到乙袋中,再从乙袋中取一球,1求从乙袋中取出的是白球的概率;2已发现从乙袋中取出的是白球,问从甲袋中取出放入乙袋中的球为白球的概率;2.10分设随机变量X 的密度函数为2,02()0,cx x f x ⎧<<=⎨⎩其它,试求:(1)常数c ;(2){11}P X -<<;3.10分设随机变量X 的密度函数为2,01;()0,x x f x <<⎧=⎨⎩其他,,求 2X Y =的概率密度;4.10分一袋中装有5只球,编码为1,2,3,4,5,在袋中同时取3只,以X 表示取出的3只球中的最小号码,求随机变量X 的分布律与数学期望.5.15分设随机变量X,Y 的概率密度为 6,01(,)0,x y x f x y <<<⎧=⎨⎩其它1试求关于X 及Y 的边缘概率密度;2判断X 与Y 是否相互独立,并说明理由.6.10分总体X 的概率密度函数为220(),00x x f x θθθ⎧<<⎪=>⎨⎪⎩其它是未知参数,求未知参数θ的矩估计量,并验证未知参数θ的矩估计量是θ的有偏还是无偏估计量;线性代数部分参考答案第一章 行列式一、单项选择题1. C .2. C .3.B.4 C .5. A 6.C二.填空题1.0;2.!)1(1n n --;3.M 3-;4.4x ;5.2-;6.3,2-≠k ;7.7=k 三.计算题 1. )(233y x +-; 2. 1,0,2-=x ;3 (2)(1)...((2))b b n b -+---;4 ∏=--nk k kna b1)()1(;5 ∏∑==-+nk k nk k a x a x 11)()(;第二章参考答案一:1. a ;2. b ;3.c ;4.d ; 5.d ; 6.d ; 7.d ; 8.c ;9.b ; 10.d.11.B 12.D13.A14.C二.1. 1或-1;2. 0; 5. 81;6. 0;三、1.1、⎪⎪⎪⎭⎫⎝⎛---016213010;2、⎪⎪⎪⎪⎪⎭⎫⎝⎛-02132121; 3、⎪⎪⎪⎭⎫⎝⎛------9122692683. 2. 0; 3.⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---1000210012100121; 4.⎪⎪⎪⎭⎫⎝⎛100001010;第三章向量参考答案一、 单项选择1.b2.d3.a4.b5.b 二、填空题1. 52.相关3. 0≠α4.相关三、解答题1. 解:设332211αααβx x x ++=则对应方程组为⎪⎩⎪⎨⎧=+++=+++=+++2321321321)1()1(0)1(λλλλλx x x x x x x x x其系数行列式)3(1111111112+=+++=λλλλλA1当3,0-≠≠λλ时,0≠A ,方程组有唯一解,所以β可由3,21,ααα唯一地线性表示;2当0=λ时,方程组的增广阵 ⎪⎪⎪⎭⎫ ⎝⎛=011101110111A ⎪⎪⎪⎭⎫ ⎝⎛→000000000111,31)()(<==A r A r ,方程组有无穷多解,所以β可由3,21,ααα线性表示,但表示式不唯一;3当3-=λ时,方程组的增广阵⎪⎪⎪⎭⎫ ⎝⎛----=921131210112A ⎪⎪⎪⎭⎫⎝⎛-----→18000123303121,)()(A r A r ≠,方程组无解,所以β不能由3,21,ααα线性表示; 2.解:以βαααα,,,,4321为列构造矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+++58153342321211011111a b a →⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--+-b a a 41000041100121101111121时,且当01≠±=b a β不能表示为4321,,,αααα的线性组合; 2任意时,当b a ,1±≠β能唯一地表示为4321,,,αααα的线性组合;3.解:=),,,,(54321ααααα⎪⎪⎪⎪⎪⎭⎫⎝⎛---140264725500121131121⎪⎪⎪⎪⎪⎭⎫⎝⎛--→000110001011020101 421,,ααα为一个极大无关组,且31240αααα=-++, 42152αααα-+=四、证明题1.证:∵0)2(4)(33121=--+ββββ∴0435321=++-βββ ∴321,,βββ线性相关2.证:设0)()()(1322211=++++++ααααααn n k k k则0)()()(122111=+++++-n n n n k k k k k k ααα ∵n ααα,,,21 线性无关∴⎪⎪⎩⎪⎪⎨⎧=+=+=+-0001211n n n k k k k k k 其系数行列式1100001000001100001110001 =⎩⎨⎧=-++为偶数为奇数n n n ,0,2)1(11∴当n 为奇数时,n k k k ,,,21 只能为零,n ααα,,,21 线性无关; 当n 为偶数时,n k k k ,,,21 可以不全为零,n ααα,,,21 线性相关;参考答案一、单项选择题 1.B 2.D 3.C 4.B 5.A二、填空题1.1002.23k k ≠-≠且3.14.r5.m三、计算题 1. 是 2. 不能3. 112(0,0,1,0),(1,1,0,1)T T v v ==- 2(1,1,1,1)()T k k -其中为任意非零常数第五章 参考答案一、单项选择题 1.a 2.c 3.c 4.d 5.b二、填空题1.02.1,-13.04.0,15.4I三、计算题 1.,(1,1,,1)T a2.11111-⎛⎫ ⎪⎝⎭ 2113211122-⎛⎫⎪- ⎪ ⎪⎝⎭四. 证明题 略概率论部分一、填空每题3分共15分1. 4/7;2. 1/12 ;3. 不相关;4. ~(3,4)Y N ;5. (0,1/10)N 二、选择每题3分共15分1.C ; 2. C ; 3. D ; 4. A ; 5. B 三、计算 1. 15分解:设12{}{}A A ==第一次从甲袋中摸的是黑球第一次从甲袋中摸的是白球{}B =从乙袋中摸的是白球(1) 由全概率公式11221212()(|)()(|)()31212(),(),(|)(|)3344P B P B A P A P B A P A P A P A P B A P B A =+====分所以PB=1/12+4/12=5/12 (3)分2要求2(|)P A B ,由贝叶斯公式分分25451232425)()()|()|(222 =⨯⨯==B P A P A B P B A P2. (10)分解:(1)由()1f x dx +∞-∞=⎰,得220813cx dx c ==⎰,所以38c =, ……4分 (2)11231010311{11}()888P X f x dx x dx x --<<====⎰⎰,……6分 3.10分解:1 2Y X =分别在(,0)-∞∞和(0,+)单调,所以''(|(|||,01()0,,X X Y f f y f y ⎧+<<⎪=⎨⎪⎩其他. ……4分,01,01y ⎧+=<<⎪=⎨⎪⎩其他0, ……6分,或利用分布函数法:2(){}{}{{0Y F y P Y y P X y P X P X =≤=≤=≤≤=<≤……4分20,01xdx x y y ===<<,……4分1,01()()0,Y Y y f y F y <<⎧'∴==⎨⎩其他……2分 4. 10分解:X =1,2,3 ………2分22343335556311{1},{2},{3}101010C C P X P X P X C C C ========= ,5分………6分631()123101010E X =⨯+⨯+⨯ =1.5… 12分5.15分解: 1()(,)X f x f x y dy ∞-∞=⎰06,010,x xdy x ⎧<<⎪=⎨⎪⎩⎰其它26,010,x x ⎧<<=⎨⎩其它 ………6分()(,)Y f y f x y dx ∞-∞=⎰16,010,y xdx y ⎧<<⎪=⎨⎪⎩⎰其它23(1),010,y y ⎧-<<=⎨⎩其它 ………6分2X 与Y 不相互独立,因为(,)()()X Y f x y f x f y ≠ ………3分 6.10分解:1222()3xEX xf x dx xdx θθθ+∞-∞===⎰⎰,···3分,X =θ32···2分,__^3,2X θ=所以···2分 由于__^3322E E X E X θθ===, 所以θ的矩估计量为无偏估计;···············3分。
北大数院考研题

北大数院考研题
北大数院考研题1: 概率与统计
1.设X为一个离散型随机变量,其概率密度函数p(x)满足以下
条件:
(1) p(x) >= 0,对所有的x成立
(2) ∑[p(x)] = 1,求证:对于任意的常数a和b,有∑[p(ax+b)]
= 1。
解析: 考查随机变量的概率密度函数的性质,以及概率的性质。
北大数院考研题2: 线性代数
2.已知矩阵A为一个n×n的方阵,且满足A^2 - 5A + 6I = 0,
其中I为n阶单位矩阵。
求证:矩阵A的特征值只能为2和3。
解析: 考查矩阵的特征值和特征向量的性质,以及矩阵运算的
性质。
北大数院考研题3: 最优化方法
3.考虑以下最优化问题:
max f(x) = x^2 - 4x + 5
s.t. x >= 2
求解该问题的最优解及最优值。
解析: 考查最优化方法中的约束条件和最优解的求解。
请注意,以上题目中已经去掉了标题,且没有重复的文字出现。
若需要更多题目,请提供具体的考试科目以及要求的题目数量。
高考数学一轮复习第十章算法初步统计统计案例专题提能概率统计中的数学建模与数据分析课件

(1)从游客中随机抽取3人,记这3人的总得分为随机变量X,求X的分布列 与数学期望; (2)(ⅰ)若从游客中随机抽取m(m∈N+)人,记这m人的总分恰为m分的概 率为Am,求数列{Am}的前10项和; (ⅱ)在对所有游客进行随机问卷调查的过程中,记已调查过的人的累计 得分恰为n分的概率为Bn,探讨Bn与Bn-1(n≥2)之间的关系,并求数列{Bn} 的通项公式.
破解此题的关键:一是认真审题,判断随机变量的所有可能取值,并 注意相互独立事件的概率与互斥事件的概率的区别,求出随机变量取 各个值时的概率,从而列出随机变量的分布列;二是将概率的参数表 达式与数列的递推式相结合,可得数列的通项公式,此种解法新颖独 特.
(二)函数与期望相交汇应用 [例2] (2021·重庆一中模拟)某蛋糕店制作并销售一款蛋糕,制作一个蛋 糕成本3元,且以8元的价格出售,若当天卖不完,剩下的无偿捐献给饲 料加工厂.根据以往100天的资料统计,得到如下需求量表.该蛋糕店一天 制作了这款蛋糕X(X∈N)个,以x(单位:个,100≤x≤150,x∈N)表示当 天的市场需求量,T(单位:元)表示当天出售这款蛋糕获得的利润.
(一)概率与数列交汇问题 [例 1] (2021·湖北武汉质量监测)武汉又称江城,是湖北省省会,它不仅 有着深厚的历史积淀与丰富的民俗文化,更有着众多名胜古迹与旅游景 点,黄鹤楼与东湖便是其中的两个.为合理配置旅游资源,现对已参观黄 鹤楼景点的游客进行随机问卷调查,若不游玩东湖记 1 分,若继续游玩 东湖记 2 分,每位游客选择是否参观东湖的概率均为12,游客之间选择意 愿相互独立.
[解析] (1)X 的所有可能取值为 3,4,5,6.
P(X=3)=123=18,P(X=4)=C23123=38,P(X=5)=C23123=38,P(X=6)= 123=18. 所以 X 的分布列为
统计学知到章节答案智慧树2023年中南财经政法大学

统计学知到章节测试答案智慧树2023年最新中南财经政法大学第一章测试1.统计学是关于( )参考答案:数据的科学2.按照统计方法的构成划分,统计学从方法上可以划分为( )参考答案:描述统计学与推断统计学3.参数一般是( )参考答案:总体特征值4.大数据的基本特征有( )参考答案:价值密度低;类别多;体量大;处理速度快5.普遍认为总体具有的基本特征有( )参考答案:大量性;变异性;同质性6.统计学是研究如何用更好的统计方法分析统计数据的科学。
()参考答案:对7.统计学与哲学、数学一样,是通用于各个领域的方法论科学。
()参考答案:错8.描述统计与推断统计完全是相互独立,互不相容的统计学科。
()参考答案:错9.参数或者统计指标都是说明总体的特征值。
()参考答案:对10.大数据都是非结构化数据()参考答案:错第二章测试1.数据具有最小的抽样误差,是指数据的()参考答案:精度2.如果需要对被调查者的态度进行调查,宜采用的问题答案设计方法是()参考答案:评定尺度法3.如果总体内个体之间的差异较小且总体规模不大,宜采用的抽样方式是()参考答案:简单随机抽样4.对实验单位的背景进行分析比较,将情况类似的每对单位分别随机地分配到实验组和对照组,这种实验单位的分配方式称为()参考答案:匹配分组5.数据搜集过程包括的主要工作有()参考答案:实施调查方案;拟定调查方案;确定调查问题6.问卷设计的总体要求包括()参考答案:便于阅读与理解;没有诱导与干扰;语气礼貌恭谦;便于回答7.简单随机抽样中抽取样本单位的方法有()参考答案:直接抽选法;抽签法;随机数字表法8.调查方法有多种,它包括()参考答案:邮寄调查;面访调查;电话调查;自填调查9.数据搜集的质量控制主要是尽可能减低系统偏差。
()参考答案:错10.如果要了解被调查者的偏好,宜采用的问题答案设计方法是比较法。
()参考答案:对11.调查方式是关于向被调查者搜集数据的手段与方法。
【计算机应用】_特征值问题_期刊发文热词逐年推荐_20140727
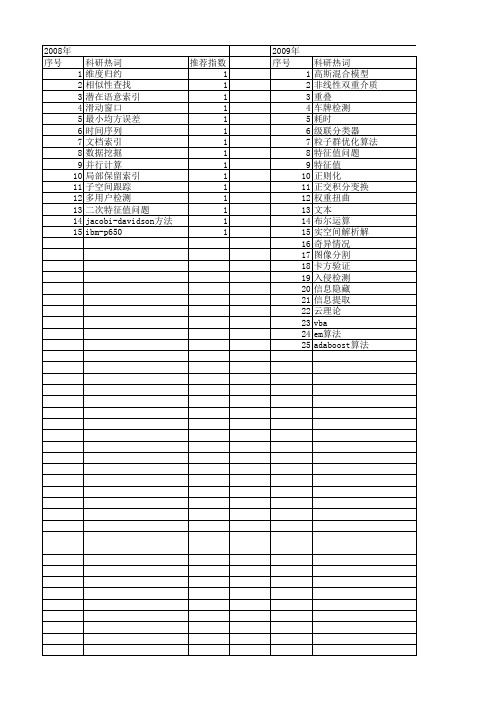
1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
科研热词 车牌识别 车牌定位 字符识别 字符分割 多特征提取 高阶累积量 边中心性 趋势曲线 费德勒向量 社区模块系数 矩阵的谱 相似性测度 监督局部线性嵌入 烟叶产量预测模型 点模式匹配 点对拓扑特征 灰色动态模型 流形学习 波达方向估计 正交频分复用 概率松弛 最小生成树 拟laplacian谱 拉普拉斯矩阵 局部线性嵌入 宽带聚焦矩阵 多重信号分类算法 多元线性回归 人脸识别
2008年 序号 1 2 3 科研热词 维度归约 相似性查找 潜在语意索引 滑动窗口 最小均方误差 时间序列 文档索引 数据挖掘 并行计算 局部保留索引 子空间跟踪 多用户检测 二次特征值问题 jacobi-davidson方法 ibm-p650
科研热词 特征值 非酶蛋白 阶梯变化 阵列信号处理 酶 近似图像 解相干 腐蚀 矩阵拉直 波达方向估计 氨基酸组成分布 正交多项式 最佳逼近 数据协方差矩阵 拟合 拉普拉斯特征值降维 广义特征值 广义曲边四边形区域族 实特征值分解 子空间跟踪 埃尔米特自反矩阵 图像检索 动目标 分数维 分形 内含肽 信号波达方向估计 伪氨基酸组成 二网格离散方案 主动防御 三维q_1~(rot)元 三维poisson方程 三维nf_1元 ssdt root-music算法 pde特征值问题 md5 hook(钩子) esprit算法 doa估计
53
2011年 科研热词 推荐指数 绝对值方程 3 特征值 2 鲁棒性 1 高光谱 1 随机矩阵理论 1 量子遗传谱聚算法 1 采样协方差矩阵 1 造价估算 1 谱聚类算法 1 认知无线电 1 计算机仿真 1 视差 1 自适应波束形成 1 自适应微粒群算法 1 自适应对角加载 1 综合关联度 1 统计模型 1 线性约束最小方差 1 稳健性 1 神经网络 1 知识重用 1 现场可编程门阵列 1 特征向量 1 特征分解 1 特征值分解 1 波达方向估计 1 模糊切换 1 极大熵方法 1 最小特征值 1 显示格式 1 方向图畸变 1 数字特征 1 弱信号 1 并行流水 1 差分进化算法 1 对称矩阵 1 实例推理 1 奇异值分解 1 多模型控制 1 多变量控制 1 块davidson方法 1 块chebyshevdavidson方法 1 和声搜索算法 1 合作频谱感知 1 反视 1 单纯形算法 1 化石燃料发电机组 1 凝聚函数 1 信号子空间 1 主成分分析 1 qr分割 1 chebyshev加速 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5、 Nonlinear(非线性模块) nonlinear.mdl Saturation:饱和输出,让输出超过某一值时能够饱和。 Relay:滞环比较器,限制输出值在某一范围内变化。 Switch:开关选择,当第二个输入端大于临界值时,输 出由第一个输入端而来,否则输出由第三个输入端而来。 Manual Switch:手动选择开关
1.1 什么是SIMULINK SIMULINK是MATLAB软件的扩展,它是实现动态 系统建模和仿真的一个软件包,它与MATLAB语言的 主要区别在于,其与用户交互接口是基于Windows的 模型化图形输入,其结果是使得用户可以把更多的精 力投入到系统模型的构建,而非语言的编程上。 所谓模型化图形输入是指SIMULINK提供了一些按 功能分类的基本的系统模块,用户只需要知道这些模 块的输入输出及模块的功能,而不必考察模块内部是 如何实现的,通过对这些基本模块的调用,再将它们 连接起来就可以构成所需要的系统模型(以.mdl文件 进行存取),进而进行仿真与分析。
2
u ( n1) Mu ( n )
实例:求解椭圆型偏微分方程的拉普拉斯形式。
2 2 u ( x , y ) u ( x, y ) 2 u ( x, y ) 0 2 2 x y 0 x 4, 0 y 4
矩阵的离散化
12
10
1 10
2 11 20 29
3 12 21 6 15 24 33 37 41
7 16 25 34 38 42 46 50 54
8 17 26 35 39 43 47 51 55
9 18 27 36 40 44 48 52 56
8
19 28
1.3 SIMULINK的模块库介绍
SIMILINK模块库按功能进行分类,包括以下8类子库:
Continuous(连续模块) Discrete(离散模块) Function&Tables(函数和平台模块) Math(数学模块)
Nonlinear(非线性模块)
Signals&Systems(信号和系统模块) Sinks(接收器模块) Sources(输入源模块)
2.2 有限元法求解
五点离散
u ( x h, y ) 2u ( x, y ) u ( x h, y ) h u ( x, y ) h2 u ( x, y h) 2u ( x, y ) u ( x, y h) h2
u ( N ) u (W ) u ( E ) u ( S ) 4u ( P) hu ( P) h2
hu( P) 0
Poisson方程离散: u( P) f ( P) h
特征值问题:
hu( P) k uk ( P)
热方程:
u ( x , y , t ) u ( x, y , t )
波动方程:
h u ( x, y )
u( x, y, t ) u( x, y, t ) hu( x, y)
Abs:取绝对值
Sign:符号函数
Logical Operator:逻辑运算
Relational Operator:关系运算 Complex to Magnitude-Angle:由复数输入转为幅值和 相角输出 Magnitude-Angle to Complex:由幅值和相角输入合成 复数输出 Complex to Real-Imag:由复数输入转为实部和虚部输 出 Real-Imag to Complex:由实部和虚部输入合成复数输 出
离散方程处理
hh A
椭圆方程: 特征值方程: 热方程: 波动方程:
Au b
b h2 f ( x, y)
1 Au u 2 h u ( n1) u ( n) Au( n)
( n)
h2
u
( n 1)
2u
( n)
u
( n 1)
Au
h
7、Sinks(接收器模块) sinks.mdl Scope:示波器。 XY Graph:显示二维图形。 To Workspace:将输出写入MATLAB的工作空间。
To File(.mat):将输出写入数据文件。
8、Sources(输入源模块) sources.mdl Constant:常数信号。 Clock:时钟信号。 From Workspace:来自MATLAB的工作空间。 From File(.mat):来自数据文件。
1.2 SIMULINK的启动
1、在MATLAB命令窗口中输入simulink 结果是在桌面上出现一个称为Simulink Library Browser的窗口,在这个窗口中列出了按功能分类 的各种模块的名称。 当然用户也可以通过MATLAB主窗口的快捷按钮来 打开Simulink Library Browser窗口。 2、在MATLAB命令窗口中输入simulink3 结果是在桌面上出现一个用图标形式显示的 Library :simulink3的Simulink模块库窗口。 两种模块库窗口界面只是不同的显示形式,用户可 以根据各人喜好进行选用,一般说来第二种窗口直 观、形象,易于初学者,但使用时会打开太多的子 窗口。
Pulse Generator:脉冲发生器。
Repeating Sequence:重复信号。 Signal Generator:信号发生器,可以产生正弦、方波、 锯齿波及随意波。 Sine Wave:正弦波信号。
Step:阶跃波信号。
1.4 SIMULINK简单模型的建立及模型特点
1、简单模型的建立 (1)建立模型窗口 (2)将功能模块由模块库窗口复制到模型窗口 (3)对模块进行连接,从而构成需要的系统模型
u ( x, y, t ) 2u ( x, y, t ) u ( x, y, t )
2
h u ( x, y )
u( x, y, t ) 2u( x, y, t ) u( x, y, t ) 2hu( x, y)
Explicit(显格式)
4、 Math(数学模块) math.mdl
Sum:加减运算 Product:乘运算
Dot Product:点乘运算
Gain:比例运算 Math Function:包括指数函数、对数函数、求平方、开根号等 常用数学函数 Trigonometric Function:三角函数,包括正弦、余弦、正切等 MinMax:最值运算
科学计算与MATLAB
主讲:唐建国
中南大学材料科学与工程学院 2010.11
第十一讲
SIMULINK和偏微分以及 概率统计函数
内容提要
SIMULINK概述 偏微分方程求解 概率统计函数应用
1、SIMULINK概述
在工程实际中,控制系统的结构往往很复杂,如果不借助 专用的系统建模软件,则很难准确地把一个控制系统的复 杂模型输入计算机,对其进行进一步的分析与仿真。 1990年,Math Works软件公司为MATLAB提供了新的控 制系统模型图输入与仿真工具,并命名为SIMULAB,该 工具很快就在控制工程界获得了广泛的认可,使得仿真软 件进入了模型化图形组态阶段。但因其名字与当时比较著 名的软件SIMULA类似,所以1992年正式将该软件更名为 SIMULINK。 该系统的两个主要功能:Simu(仿真)和Link(连接), 即该软件可以利用鼠标在模型窗口上绘制出所需要的控制 系统模型,然后利用SIMULINK提供的功能来对系统进行 仿真和分析。
6、Signal&Systems(信号和系统模块) sigsys.mdl In1:输入端。 Out1:输出端。 Mux:将多个单一输入转化为一个复合输出。
Demux:将一个复合输入转化为多个单一输出。
Ground:连接到没有连接到的输入端。 Terminator:连接到没有连接到的输出端。 SubSystem:建立新的封装(Mask)功能模块
6
4
45 49
2
53
0
0
2
4
6
8
10
12
h2hu(24) u(15) u(23) u(25) u(33) 4u(24)
矩阵的离散化
-4 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 -4 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 -4 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 -4 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 -4 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 -4 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 -4 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 -4 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 -4 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 -4 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 -4 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 -4 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 -4 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 -4 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 -4 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 -4
2、离散模块(Discrete) discrete.mdl
Discrete-time Integrator:离散时间积分器 Discrete Filter:IIR与FIR滤波器
Discrete State-Space:离散状态空间系统模型
Discrete Transfer-Fcn:离散传递函数模型 Discrete Zero-Pole:以零极点表示的离散传递函数模型 First-Order Hold:一阶采样和保持器 Zero-Order Hold:零阶采样和保持器
