补水不等于保湿 角质层含水量达10%肌肤最健康
聚四氟乙烯材料力学性能参数表
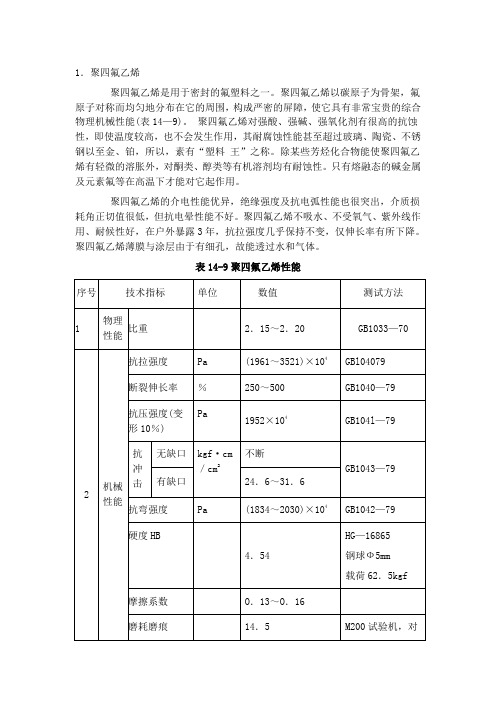
1.聚四氟乙烯聚四氟乙烯是用于密封的氟塑料之一。
聚四氟乙烯以碳原子为骨架,氟原子对称而均匀地分布在它的周围,构成严密的屏障,使它具有非常宝贵的综合物理机械性能(表14—9)。
聚四氟乙烯对强酸、强碱、强氧化剂有很高的抗蚀性,即使温度较高,也不会发生作用,其耐腐蚀性能甚至超过玻璃、陶瓷、不锈钢以至金、铂,所以,素有“塑料王”之称。
除某些芳烃化合物能使聚四氟乙烯有轻微的溶胀外,对酮类、醇类等有机溶剂均有耐蚀性。
只有熔融态的碱金属及元素氟等在高温下才能对它起作用。
聚四氟乙烯的介电性能优异,绝缘强度及抗电弧性能也很突出,介质损耗角正切值很低,但抗电晕性能不好。
聚四氟乙烯不吸水、不受氧气、紫外线作用、耐候性好,在户外暴露3年,抗拉强度几乎保持不变,仅伸长率有所下降。
聚四氟乙烯薄膜与涂层由于有细孔,故能透过水和气体。
表14-9聚四氟乙烯性能聚四氟乙烯在200℃以上,开始极微量的裂解,即使升温到结晶体熔点327℃,仍裂解很少,每小时失重为万分之二。
但加热至400℃以上热裂解速度逐渐加快,产生有毒气体,因此,聚四氟乙烯烧结温度一般控制在375~380℃。
聚四氟乙烯分子间的范德华引力小,容易产生键间滑动,故聚四氟乙烯具有很低的摩擦系数及不粘性,摩擦系数在已知固体材料中是最低的。
聚四氟乙烯的导热系数小,该性能对其成型工艺及应用影响较大。
其不但导热性差,且线膨胀系数较大,加入填充剂可适当降低线膨胀系数。
在负荷下会发生蠕变现象,亦称作“冷流”,加入填充剂可减轻蠕变程度。
聚四氟乙烯可以添加不同的填充剂,选择的填充剂应基本满足下述要求:能耐380℃高温即四氟制品的烧结温度;与接触的介质不发生反应;与四氟树脂有良好的混入性;能改善四氟制品的耐磨性、冷流性、导热性及线膨胀系数等。
常用的填充剂有无碱无蜡玻璃纤维、石墨、碳纤维、MoS2、A123、CaF2、焦炭粉及各种金属粉。
如填充玻璃纤维或石墨,可提高四氟制品的耐磨、耐冷流性,填充MoS2可提高其润滑性,填充青铜、钼、镍、铝、银、钨、铁等,可改善导热性,填充聚酰亚胺或聚苯酯,可提高耐磨性,填充聚苯硫醚后能提高抗蠕变能力,保证尺寸稳定等。
安徽省县中联盟2023-2024学年高二上学期10月联考数学试卷及答案

函蜘郎长芒邻茶栩2023"-'2024学年安徽县中联盟高二10月联考数学试题考生注意:l.满分150分,考试时间120分钟。
2.考生作答时,请将答案答在答题卡上。
选择题每小题选出答案后,用2B铅笔把答超卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效。
3.本卷命题范困:人教版必修第一册、第二册,选择性必修笫一册2.2结束。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的.L已知i是虚数单位,-a+bi=2b-i,a,bER,则la一如=A.我B.戎 C.22.已知直线l的一个方向向批为(烈,-3),则直线l的倾斜角a=A. 30•B. so· c. 120° o. 1so03.在棱长为2的正方体ABCD-A心C1D1中,E、F,G、H分别为AIBl、B心、A1D1、BB1的中.盲盲点,则IGF+GH+2EGI=A../6B.2屈D../5C.月D.2我l4.已知直线l1y=-工+1与y轴交千点P,将l绕点P逆时针旋转45°后与工轴交千点Q,要使2直线l平移后经过点Q,则应将直线l1A.向左平移一个单位长度 16B.向右平移一个单位长度65C.向左平移一个单位长度 53 D.向右平移一个单位长度3一酝• 盲• • 5.巳知向批OA=(0,1,2),0B=(一1,0,l),0C=(2,1,入),若O,A,B,C共而,则0C在OB上的投影向址的桢为A.q B.我c.孚过6.光线通过点A(2,3),在直线l,工+y+l=O上反射,反射光线经过点B(2,2),则反射光线所.(f: ·1'[线方程为A. 6:r-5y-2=0C. 5:r-6y+2=0认6.1·+Sy-22=0D.釭+6y-22=0[抖二J O丿l联打·数学卷第1页(共4页)RJ】4048B7.已知向俅a=(2,1),b= (0,2),c=(一1,1),集合A={,m m=a+入b},B={nl n=b+入2c},其中入1山ER,则A.AnB=0B.An B={2,0}C.若d EAn B,则(a,心为钝角D.若dEA nB,则l b=d2&已知a=/1了一』了,b=6斗,c=logs3-¾log克则9A.a<b<cB. b<c<aC. b<a<cD. c<a<b二、选择题:本题共4小题,每小题5分,共20分。
2021年高考英语重点词汇分类记忆:e+辅音开头词汇

e-/ex:向外1.edit [ˈedɪt] v.【拆记】e:向外,dit=don,给予,向外给出给出好文章,需要好好edit。
【变】edition [ɪˈdɪʃ(ə)n]n.editor [ˈedɪtə(r)] n.【例】I used to edit the college paper in the old days.The second edition was published only in America.cate [ˈedjʊkeɪt] vt.【拆记】e:向外,duc:引,ate:动词后缀,educate一个人就是把他的内心向外引。
【变】educator ['edju:keitə(r)] n.education [edjʊˈkeɪʃ(ə)n] n.【例】It takes patience to educate children.2.effort [ˈefət]n.【拆记】e:向外,fort=forc,力量,向外给出力量就是在作出effort。
【例】She took a deep breath and sat up slowly and with great effort.3.elect [ɪˈlekt] vt.【拆记】e:向外,lect 选择,选你出来当领导人这是在elect。
【例】The people of the Philippines have voted to elect a new president.4.evaluate [ɪˈvæljʊeɪt] v.【拆记】e:向外,valu:价值,ate:动词后缀,向外给出价格,就是evaluate。
【例】The market situation is difficult to evaluate.5.exact [ɪɡˈzækt] a.【拆记】ex:向外,act:行动,一个特工外出行动凡事得力求exact。
江苏省常州市联盟学校2024届高三上学期10月学情调研数学试卷及答案

常州市联盟学校2023—2024学年度第一学期学情调研高三年级数学试卷出卷老师审卷老师考试时间120分钟本试卷共22大题满分150分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1 已知集合A={-2,-1,l, 2}, B={x I 3, <l},则A B= ()A.{-2,-1}8.{1,2}C.{-2,-1,1}D .{-2,-1,2}2."x<O"是“ln(x+1) <0"的()A.充分不必要条件8.必要不充分条件C.充要条件D.既不充分也不必要条件3设m,n, I是三条不同的直线,a,/J ,y是三个不同的平面,有下列命题中,真命题为()A.若m..ln,l..ln,则m..llC.若,m//n,则B 若a.L fJ 'fJ .L y,则a .L rD若m//n,ml/a,则nlla4已知圆台的上下底面半径分别为1和2,侧面积为3石.兀,则该圆台的体积为()竺3A归_38 C.5兀血3D 5 “幸福感指数”是指某个人主观地评价他对自己目前生活状态满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示幸福感指数越高.已知甲、乙、丙、丁4人的幸福感指数分别为:4五万万+言:((lg 2)2 + lg 2-lg 50+ lg 25) + log 5 8x log 2 25:Iog 2150: (石)邱则这4人的幸福感指数最高的是(A.甲B.乙C.丙D.丁6如图,该图象是下列四个函数中的某个函数的大致图象,则该函数是(v-.,\:3 +3xA .y =x 2 +l3 X 一X 2B.y =.:.:..,-C. y= XCOSX 人:2+ I . -·.,x 2 +1 D .)2sinxI=2x'+l第6题7已知直线2ax-2y-a=O 与曲线y = l n(2x-l)相切,则实数u 为()2一eA 五3B C.2e五2Dx 2 -2x+4,x <28已知函数肛)={3l ,设aeR,若关千x 的不等式f(x)之1X-a1在R上恒成立,则a -x+-x 之22X的取值范围是(A .[-¾,¥]B[气节]C. [-¾号]二、多选题,本题共8小题,每小题5分,共40分.9下列命题正确的是(12A.若随机变矗X的方差为—,则D(5X+2)=1425D .[-;,号]B.对千随机事件A与B,若P(B)= 0.3, P(B I A )=0.7,则事件A与B独立C.设随机变量引服从正态分布N(O ,l),若P(乒>1)= p'则P(一I<;<0)=�-p2D.根据分类变矗X与Y的成对样本数据,计算得到z 2=3.112,根据a=0.05的独立性检验(P(z 2>3.841) = 0.05),有95%的把握认为X与Y有关10下列命题中正确的是()A 若踞函数f (x )的图像过点A(3,上),则f(x)=x -327 B 若函数f(x)={ x,x<ax 2,x2:a在R上单调递增,则a的取值范围是[l ,位))I3c.已知x>O ,y >O,且-+-=I,则x+2y的最小值为7+2✓6X yD .已知函数t.(x)满足八-x)+ j (x) =I, g ( e x g(x )=—阳(x )与g (x)的图象的交点坐标依次为e x -1 (x ,, Y ,),(屯),2),··,(xs ,Y s ),则L (.,\'.;+),,) =8;:1II.已知函数八)x 2+3x+lx) =,其中xER,则()e'A不等式f(x)�-e 2对VxER恒成立B若关于x的方程f(x)=k有且只有两个实根,则k的取值范围(-式o]C 方程八f(x))=0恰有3个实根11 5 D若关千x的不等式f(x)乙釭恰有1个正整数解,则a的取值范围为(了';]l2已知函数y=f(x)满足:对于任意实数x,yER ,都有2f(x)f(y)= f (x + y ) + f(x -y),且f(l) = -1,则()A.f(x)是奇函数C (扣)是曲线y =f(x)的一对称中心B.f(x)是低函数D .f(2022) = 1三、填空题:本题共4小题,每小题5分,共20分.13牛顿曾经提出了常温环境下的温度冷却模型:0=(Ol-O。
专题复习数形结合(含答案)

专题复习三数形结合I、专题精讲:数学家华罗庚说得好:“数形结合百般好,隔离分家万事休,几何代数统一体,永远联系莫分离".几何图形的形象直观,便于理解,代数方法的一般性,解题过程的机械化,可操作性强,便于把握,因此数形结合思想是数学中重要的思想方法.所谓数形结合就是根据数学问题的题设和结论之间的在联系,既分析其数量关系,又揭示其几何意义使数量关系和几何图形巧妙地结合起来,并充分地利用这种结合,探求解决问题的思路,使问题得以解决的思考方法.II、典型例题剖析例1.某公司推销一种产品,设X(件)是推销产品的数量,y (元)是推销费,图3—3—1巳表示了公司每月付给推销员推销费的两种方案,看图解答下列问题:(1)求Y1与Y2的函数解析式;(2)解释图中表示的两种方案是如何付推销费的?(3)如果你是推销员,应如何选择付费方案?Y<兀)Y1 Y2-。
2。
」600500400300200100解:(1) y1=20x,y2=10x+300. 图3-3-1(2) Y1是不推销产品没有推销费,每推销10件产品得推销费200元,Y2是保底工资300元,每推销10件产品再提成100元.(3)若业务能力强,平均每月保证推销多于30件时,就选择Yi的付费方案;否则,选择Y2的付费方案.点拨:图象在上方的说明它的函数值较大,反之较小,当然,两图象相交时,说明在交点处的函数值是相等的.例2.某农场种植一种蔬菜,销售员平根据往年的销售t每于克销售价(元)情况,对今年这种蔬菜的销售价格进行了预测,预测 5情况如图3—3—2,图中的抛物线(部分)表示这种蔬菜销售价与月份之间的关系,观察图象,你能得到关于这种蔬菜销售情况的哪些信息?答题要求:(1)请提供四条信息;(2)不必求函数的解析.解:(1) 2月份每千克销售价是3.5元;7对月份每千克销售价是0.5元;(3) 1月到7月的销售价逐月下降;(4) 7月到12月的销售价逐月上升;4321o I 1 2 3 4 5 6 7 s 9 10 11 12月份图3-3-2(5) 2月与7月的销售差价是每千克3元;(6) 7月份销售价最低,1月份销售价最高;(7) 6月与8月、5月与9月、4月与10月、3月与11月,2月与12月的销售价分别相同.点拨:可以运用二次函数的性质:增减性、对称性.最大(小)值等,得出多个结论.例3.某报社为了解读者对本社一种报纸四个版面的喜欢情况,对读者作了一次问卷调查,要求读者选出自己最喜欢的一个版面,将所得数据整理后绘制成了如图3—3—3所示的条形统计图:个单位:人2000(1)请写出从条形统计图中获得的一条信息;(2)请根据条形统计图中的数据补全如图3—3—4所示的扇形统计图(要求:第二版与第三版相邻,并说明这两福统计图各有什么特点?图3-3-3(3)请你根据上述数据,对该报社提出一条合理的建议。
新人教版初中英语八年级英语下册重点句型短语归纳整理全册整理名校资料

-新人教版初中英语八年级英语下册要点句型·短语概括整理全册整理-名校资料————————————————————————————————作者:————————————————————————————————日期: ?新人教版初中英语八年级英语下册要点句型·短语概括整理全册撰稿:立宏教育Unit1What’sthematter?37.falldown跌倒38.feelsick感觉恶心一、要点短语39.haveanosebleed流鼻血1.haveafever发热40.cuthisknee割伤他的膝盖2.haveacough咳嗽41.putherheadback把她的头向3.have atoothache牙疼后仰4.talk toomuch说得太多42.haveproblemsbreathing 5.drinkenoughwater喝足够的呼吸困难水43.mountainclimbing爬山运动6.haveacold受凉;感冒44.beused todoingsth.习7.haveastomachache胃疼惯做某事8.haveasoreback背疼45.runout(of)用完;用尽9.havea sorethroat喉咙痛46.sothat以便10.liedownandrest躺下来休47.so...that这样以致息于11.hotteawithhoney加蜂蜜的热48.beincontrolof掌管;管理茶49.in adifficultsituation在闲境屮12.seeadentist看牙医50.keepondoingsth.持续或坚持做13.getanX-ray拍X光片某事14.takeone’s temperature量51.makeadecision做出决定体温52.takerisks冒险15.putsomemedicineonsth.53.giveup放弃在上边敷药16.feelveryhot感觉很热17.soundlike听起来像allweekend整个周末inthesameway以相同的方式gotoadoctor看医生goalong沿着走22.onthesideoftheroad在马路边二、要点句型1.What’sthematter?hat’sthematterwithyou?=What’sthetroublewithyou?What’swrongwithyou?你怎么了?2.Whatshouldshedo?她该怎么办呢?ShouldItakemytemperature?23.shoutforhelp高声呼救我应当量一下体温吗?24.without thinkingtwice没主语+should/shouldn’t+动词原有多想形...25.getoff下车①Youshouldliedownandre26.haveaheartproblem有st.心脏病你应当躺下歇息一会儿。
辅音前后连缀(中文)

前缀A-1 a- 加在单词或词根前面, 表示不,无,非2 a- 加在单词前, 表示在..., ...的3 ab-, abs- 加在词根前,表示相反,变坏,离去等4 ab-, ac-, ad-, af-, ag-, an-, ap-, ar-, as-, at- 等加在同辅音字母词根前,表示一再等加强意5 ad- 加在单词或词根前, 表示做....., 加强......6 amphi- 表示两个、两种7 an- 在词根前, 表示不,无8 ana- 表示错误,在旁边,分开9 ante- 表示前面,先10 anti- 表示反对,相反11 apo- 表示离开,远离12 auto- 表示自动、自已B-13 be- 构成动词,表示使......成为14 be- 构成一些介词15 bene- 表示善, 好16 bi- 表示二个, 两17 by- 表示在旁边,副的C-18 cata- 表示向下,相反,离开19 circum- 表示环绕,周围20 co- 表示共同,通常放元音词根前21 col-, cor- 在同辅音词根前, 表示共同22 com-, con- 表示共同23 contra - 表示反对,相反24 counter - 表示反对,相反D-25 de- 表示去掉,变坏,离开,变慢,向下等26 de- 表示使....成为,加强等27 deca- 表示十28 deci- 表示十分之一29 demi- 表示半30 di- 表示二个,双31 di- 表示使...变成,分开,离开32 dia- 表示穿过,二者之间33 dif- 和辅音重复表示不,否定,分开34 dis- 表示不,消失掉35 dis- 表示分开,分离36 dys- 表示坏,不良E37 e-, ef- 表示出,出来,38 em-, en-, 表示进入... 之中,包围39 em-,en-, 表示使..... 进入状态40 endo- 表示内部41 epi- 表示在...上,在...周围,在...后面42 eu- 表示好,优秀43 ex- 表示出,出去44 ex- 表示前面的,前任的45 exo- 表示外部的,外面46 extra- 表示以外的,超过的F47 fore- 表示前面,预先H48 hecto- 表示百,许多49 hemi- 表示半50 hepta- 表示七51 hetero- 表示异类,异种52 hexa- 表示六53 holo- 表示全部'54 homo- 表示同类的55 hyper- 表示超过,太多56 hypo- 表示下面,次等I57 il-, ir- 辅音重复表示不,无58 il-,ir- 表示使.....成为,进入59 im-, in- 表示不,无,非60 im-,in- 表示向内,进入61 inter- 表示在..... 之间,相互62 intra- 表示在内,内部63 intro- 表示向内,入内64 iso- 表示等, 同K65 kilo- 表示一千M66 macro- 表示宏传,大67 mal-; male 表示坏,恶68 meta- 表示超过, 改变69 micro- 表示微,小70 milli- 表示千,千分之一71 mini- 表示小72 mis- 表示错误,坏73 mono- 表示单个,一个74 multi- 表示多,很多N75 neo- 表示新的76 non- 表示不,非O77 ob- 表示逆,倒,加强意义78 octa- 表示八 ; 亦作octo79 omni- 表示全部,到处80 out- 示超过,过度81 out- 表示出去,过时82 over- 表示过度,过份83 over- 表示翻转84 over- 表示在... 之上P85 paleo- 表示古,旧86 pan- 表示广泛的87 para- 表示半,类似,辅助88 para- 表示旁边89 para- 表示降落伞90 pen- 表示近似,差不多91 penta- 表示五92 per- 表示贯穿,自始至终93 per- 表示假,坏94 peri- 表示周围,靠近95 poly- 表示多96 post- 表示在后面97 post- 表示邮件,邮政98 pre- 表示 ...前的,预先99 pro- 表示赞同,亲...100 pro- 表示向前,在前101 pro- 表示很多...102 proto- 表示原始...103 pseudo- 表示假,伪Q104 quadri-,quadru- 表示四105 quasi- 表示类似,准R106 re- 表示向后,相反107 re- 表示一再,重新108 retro- 表示向后,倒退S109 se- 表示分开,离开,区别开110 semi- 表示半111 sept-,septi- 表示七112 sex-, sexi- 表示六113 step- 表示后,继或前夫(妻)所生114 stereo- 表示立体115 sub- 表示在下面,次一等,副手116 sub- 表示接近,靠近117 suc-, suf-, sup-, sur- 等辅音重复表示在...下面118 super- 表示在...上面119 super- 表示超级,超过,过度120 supra- 表示超...121 sur- 辅音不重复表示超过,在上面122 sus- 表示在... 下面123 sym-, syn- 表示共同,相同T124 tetra- 表示四125 trans- 表示横过,越过126 trans- 表示变换,改变';转移127 tri- 表示三128 twi- 表示二、两U129 ultra- 表示极端130 ultra- 表示超出,超过131 un- 表示不,无,非,没有132 un- 表示打开,解开,弄出133 under- 表示在...下,在...之内134 under- 表示不足,不够135 under- 表示副手 3136 uni- 表示一个、单一V137 vice- 表示副W138 with- 表示向后,相反后缀A139 -ability 表名词,能...;性质140 -able 表形容词,可...的,能...141 -ably 表副词,能...地142 -aceous 表形容词,具有...特征的143 -acious 表形容词,有特征的,多...的144 -acity 表名词,有...倾向145 -acle 表名词, ... 物品,状态146 -acy 表名词, ...性质,状态147 -ad 表名词, ...东西,状态148 -ade 表名词, 表示状态,物品149 -ade 表示个人或集体150 -age 表示:费用151 -age 表示场所,物品152 -age 名词后缀,表示状态,总称153 -ain 表名词, ...人154 -air 表名词,人、物155 -aire 表名词, ...人156 -al 表形容词, ...的157 -al 表名词,人,物,状态158 -ality 表名词,状态,性质159 -ally 表副词,由al+ly 构成, ...地160 -an 表名词和形容词, ...地方,...人161 -ance 表名词,性质,状况162 -aneity 表名词,表示性质,状态163 -aneous 表形容词, ...有; ...特征的164 -ant 表形容词, ...的165 -ant 表名词, ...人166 -ant 表名词, ...剂167 -ar 表形容词, ...的168 -ard 表名词,不好的人169 -arian, 表形容词或名词, ...的(人)170 -arium 表名词,地点,场所171 -ary 表名词,人,场所,物172 -ary 表形容词, ...的173 -ast 表名词, ...人,物174 -aster 表名词,不怎么样的人175 -ate 表动词,做,造成176 -ate 表形容词,具有...的177 -ate 表名词,人或地位178 -atic 表形容词,有...性质的179 -ation 表名词,行为,过程,结果180 -ative 表形容词,有...倾向(性质)的181 -ator 表名词,通常由ate结尾的动词而来,做事的人或物182 -atory 表名词场所,地点183 -atory 表形容词,有...性质的184 -cy 表名词,也作-acy, 性质,状态D185 -dom 表名词,状态或领域E186 -ee 表名词,被动或主动的人187 -eer 表名词, ... 人员188 -el 表名词,人或物189 -en 表动词,变成190 -en 表形容词,由...制成的,通常加在名词后面191 -en 表名词,人或物192 -ence 表名词,性质,状态193 -ency 表名词,ence 的变体194 -enne 表名词,女性195 -ent 表形容词, ...的196 -ent 表名词, ...药剂197 -ent 表名词, ...人198 -eous 表形容词,有...的199 -er 表动词,反复做200 -er 表名词,物品,机器201 -er 表名词, ...人202 -ern 表形容词, ...方向的203 -ern 表名词, ...场所204 -ery 表名词,场所,地点205 -ery 表名词,行为,情况206 -esque 表形容词,如...的207 -ess 表名词,女性,雌性208 -et 表名词,小东西209 -etic 表形容词,属于...的210 -ette 表名词,小的东西或状态211 -ety 表名词,状态212 -eur 表名词, ...人F213 -faction 表名词,达到的状态,由-fy转化而来214 -fic 表形容词,产生...的215 -fication 表名词,由fic变化而来216 -fier 表名词,人或物,由-ify转化而来217 -fold 表形容词或副词,倍,双重218 -form 表形容词,有...形状的219 -ful 表形容词, 有...的220 -ful 表名词, 满,量221 -fy 表动词, ...化,成为... ,更多时候作 -ifyH222 -hood 表名词, 时期,性质等I223 -ia 表名词, 某种病224 -ia 表名词, 总称,状态225 -ial 表形容词,有...的226 -ian 表名词,某种人227 -ian 表形容词, ...国家的228 -ibility 表名词,具备...性质的229 -ible 形容词能...的230 -ic 表形容词, ....的,有时作-tic231 -ic 表名词,某种药232 -ic 表名词,人或学科233 -ical 表形容词, ...的234 -ice 表名词,行为,状态235 -ics 表名词,学科,学术236 -id 表形容词,如...的237 -ie 表名词,小东西或人238 -ier 表名词,人或物239 -ile 表形容词, ...的240 -ile 表名词,物体241 -ine 表形容词, ...的242 -ine 表名词,人或女人243 -ine 表名词,状态, 药物等244 -ing 表形容词,正...的,令人...的245 -ing 表名词,行业246 -ing 表名词,物品247 -ing 表名词,状态248 -ion 表名词,动作或状态分为 --sion和--tion两种249 -ion 表示某种物,用品250 -ior 表形容词,较...的251 -ious 表形容词, ....的252 -ise 表动词后缀,和 -ize 相同,是 -ize 的变体, ...化253 -ise 表名词,物品,状态254 -ish 表形容词,象...一样,有的... ,通常放在一具体名词后255 -ish 表动词,造成...256 -ish 表示国家的或语言257 -ism 表示学术或学术流派258 -ism 表示行为, 现象,状态259 -ism 表示疾病260 -ism 表示具备某种性质261 -ism 名词,表示各种主义,宗教262 -ist 表名词,表示信仰者,专家或从事人263 -ist 以-ist 结尾的单词,不少同时可做名词和形容词用。
江西省部分学校2024-2025学年高三上学期10月联考试题 数学 含解析

高三数学试卷注意事项:1答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效3考试结束后,将本试卷和答题卡一井交回.4本试卷主要考试内容:集合与常用逻辑用语,不等式,函数与导数,三角函数,解三角形.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.I 已知全集U=AvB={0,1,2,3,4,5},A^(见B)= {1,3,5},则集合B =()A.{1,3,5}B.{0,2,4}C.0D.{0,1,2,3,4,5}25兀25冗2.sin" �-cos —= ()1212 1-2A 五2B1-2c石D.-—3已知函数f(x)的定义域为R,且f(x+y)-f(x -y)=2f(y),则/(0)=()A.0B.IC.2D.-14已知x>O,y>O,且-+2y =l.则2x +一的最小值为()yA.2B.4C.6 D .85设函数f(x)=ln 伬+l)+sin.x+1,则曲线y =f(x)在点(0,1)处的切线与两坐标轴所围成的三角形的面积为()A -B . -C .-D22 3636把某种物体放在空气中,若该物体原来的温度是0“C ,空气的温度是0。
'C,则mun 后该物体的温度0°C 满足0=0。
+(O '飞)e 了若O 。
,0'不变,在t 1m i n ,t 2min 后该物体的温度分别为O1°C,02°C ,且O.>仇,则下列结论正确的是()22t t >< l l t t A BC若0'>0。
,则t.>片若0'<0。
,则t1< t2D若0'>0o,则t.<片若0'<0o,则t1> t27已知log.,m> l(m, n > 0且m*l,n* l),m+n= e2,则()A.(m-n,十l)e<lB.(m-n+l)">lC.lm-nl e<lD.lm-nl e>I8在c,.ABC中,AB=4,BC=6,乙ABC=90°,点P在c,.AB C内部,且乙BPC=90°,AP =2,记乙ABP=a,则tan2a=()3 24 3A.2B.3C.3D.4二多选题:本题共3小题,每小题6分,共18分在每小题给出的选项中,有多项符合题目要求全部选对的得6分,部分选对的得部分分,有选错的得0分9已知命题p玉eR,x-l xl>x2,命题q如aE(沪),cos(¾-a)=s in(千叶,则()A.P是真命题B勹D是真命题c.q是真命题 D ---q是真命题10已知函数f(x)=c o s(x+:),则()A.f(x)为偶函数B.f(x)的最大值为cos2c.J(x)在(1,2)上单调递减D.f(x)在(1,20)上有6个零点11已知函数f(x)=�x, +bx'+ex,下列结论正确的是()A若x=X。
英语字母密码记忆法

记部全要但不你�……d C s o F c a M Y Q P X b C m W B�母字列下了出写你给人某�如比
? 9O :U 8 ? & w . B # D : X : c !t en.iliyij.ww w
。写小是还写大是母字个每住记的确准能要还且而�序顺其及母字些这住
。法方演表记记种一的写小是还�写大是母
d 7E /H : L 6l ) | $u 0E .x (o :。 台平动互 流交 的型大业 专域 领术学等 发开 脑右法忆 记词 单语英,读速, 读阅速快,词单 背,教 早, 图导维 思,法方忆 记是�业
专最 力忆 记高提� 构机 威权的训 培忆 记内国是 司公训培忆 记马海
。了事件那起想就疤伤着看�命的我了要乎几�头木小块一了进扎中眼脐肚�m、72
。写小、大的母字
�衣大的脚到裹头从种那是”衣大 “如 �些一张夸得象想以可程编的写小大于对 �时用应想联在
r ) J 3 J $ w (y *t en.iliyij.w ww
土尘种那是”路小“�路马油柏的净干敞宽成想可”路大“�服衣小的袖进伸能只中那是”衣小“
文英出说确准能便以�象形程编的母字写小、写大中脑大化强要之总�等道小肠羊的扬飞
于小
F 9 a $b 5 e ,^ 0~ $r 2Y ,网练 训力忆记国中
于大 u
吃小 鸡小 �度�幅小 衣小 弟小
�题大 t
k 0 K 9p . W 0G 8F !t en.iliyij.w ww
事小 儿小
事大 s 口大 q
�度�幅大 f 衣大 e 地大 d
H 6y 9x 'y #^ , M$H 9
字写小、大个干若出写地意随是而�序顺常正的母字文英个 62 按不是就序排母字文英谓所 序排母字文英
广东省2025届高三上学期毕业班调研考试(一) 数学试卷(含解析)

2025届广东省高三毕业班调研考试(一)数学试卷及答案一、单选题(本大题共8小题)1.已知集合2{|8150},{|5}A x x x B x x =∈-+≤=<Z ,则A B ⋂=()A.{}3B.{}3,4C.{}4,5D.{}3,4,52.已知1z ,2z 是两个虚数,则“1z ,2z 均为纯虚数”是“12z z 为实数”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.已知a和b 的夹角为150︒,且2,a b == ()2a b b +⋅= ()A.9-B.3-C.3D.94.已知π2sin sin 33αα⎛⎫+-= ⎪⎝⎭,则πcos 23α⎛⎫+= ⎪⎝⎭()A.59-B.19-C.19D.595.已知等比数列{}n a 为递增数列,n nnb a=.记,n n S T 分别为数列{}{},n n a b 的前n 项和,若2133312a a a S T =+=,,则n S =()A.141n --B.()11414n --C.()14112n-D.24n -6.已知体积为的球O 与正四棱锥的底面和4个侧面均相切,已知正四棱锥的底面边长为则该正四棱锥体积值是()A.B.C.D.7.斐波那契数列因数学家斐波那契以兔子繁殖为例而引入,又称“兔子数列”.这一数列如下定义:设{}n a 为斐波那契数列,()*12121,1,3,N n n n a a a a a n n --===+≥∈,其通项公式为n n n a ⎡⎤⎛=-⎥ ⎥⎝⎭⎝⎭⎦,设n是2log 1(14(x x x ⎡⎤⎣⎦+-<+的正整数解,则n 的最大值为()A.5B.6C.7D.88.函数()ln f x x =与函数()212g x mx =+有两个不同的交点,则m 的取值范围是()A.21,e ⎛⎫-∞ ⎪⎝⎭B.21,2e ⎛⎫-∞ ⎪⎝⎭C.210,e ⎛⎫⎪⎝⎭D.210,2e ⎛⎫ ⎪⎝⎭二、多选题(本大题共3小题)9.现有十个点的坐标为()()()121000,x x x ,,,,,,它们分别与()()()1210101010y y y ,,,,,,关于点(3,5)对称已知1210,,,x x x 的平均数为a ,中位数为b ,方差为c ,极差为d ,则1210,,,y y y 这组数满足()A.平均数为6a -B.中位数为6b -C.方差为cD.极差为d10.设123,,z z z 是非零复数,则下列选项正确的是()A. 2211z z =B.1212z z z z +=+C.若122i 2z --=,则116i z +-的最小值为3D.若22i i 4z z ++-=,则2z的最小值为11.已知定义在R 上的函数()f x 的图象连续不间断,当()()0e e e 0x f x f x ≥+--=,,且当>0时,()()e e 0f x f x ''++->,则下列说法正确的是()A.()e 0f =B.()f x 在(),e -∞上单调递增,在()e,+∞上单调递减C.若()()1212,x x f x f x <>,则212ex x +<D.若12,x x 是()()()2e 2g xf x x =+--在()0,2e 内的两个零点,且12x x <,则()()211ef x f x <<三、填空题(本大题共3小题)12.已知等差数列{}n a 的首项12a =,公差3d =,求第10项10a 的值为.13.若()554325432102x a x a x a x a x a x a +=+++++,则531420a a a a a a ++=++.14.如图,在矩形ABCD 中,8,6,,,,,AB BC E F G H ==分别是矩形四条边的中点,点Q 在直线HF 上,点N 在直线BC 上,,,OQ kOH CN kCF k ==∈R,直线EQ 与直线GN 相交于点R ,则点R 的轨迹方程为.四、解答题(本大题共5小题)15.在ABC 中,角A B C ,,的对边分别为a b c ,,,已知2cos2cos22sin 2sin sin B A C B C-=-(1)求A ;(2)若23b c P Q ==,,,分别为边a b ,上的中点,G 为ABC 的重心,求PGQ ∠的余弦值.16.设A B ,两点的坐标分别为())3,0,3,0.直线AH BH ,相交于点H ,且它们的斜率之积是13-.设点H 的轨迹方程为C .(1)求C ;(2)不经过点A 的直线l 与曲线C 相交于E 、F 两点,且直线AE 与直线AF 的斜率之积是13-,求证:直线l 恒过定点.17.如图所示,四边形ABCD 是圆柱底面的内接四边形,AC 是圆柱的底面直径,PC 是圆柱的母线,E 是AC 与B 的交点,608AB AD BAD AC ∠=== ,,.(1)记圆柱的体积为1V ,四棱锥P ABCD -的体积为2V ,求12V V ;(2)设点F 在线段AP 上,且存在一个正整数k ,使得PA kPF PC kCE ==,,若已知平面FCD 与平面PCD 的夹角的正弦值为1313,求k 的值.18.已知函数()()1ln f x x x =-,(1)已知函数()()1ln f x x x =-的图象与函数()g x 的图象关于直线=−1对称,试求()g x ;(2)证明()0f x ≥;(3)设0x 是()1f x x =+的根,则证明:曲线ln y x =在点()00,ln A x x 处的切线也是曲线e x y =的切线.19.如果函数()F x 的导数为()()F x f x '=,可记为()()d f x x F x =⎰,若()0f x ≥,则()()()baf x dx F b F a =-⎰表示曲线()y f x =,直线x a x b ==,()a b <以及x 轴围成的“曲边梯形”的面积.如:22d x x x C =+⎰,其中C 为常数;()()222204xdx C C =+-+=⎰,则表0,1,2x x y x C ===+及x 轴围成图形面积为4.(1)若()()()e1d 02xf x x f =+=⎰,,求()f x 的表达式;(2)求曲线2y x =与直线6y x =-+所围成图形的面积;(3)若()[)e 120,x f x mx x =--∈+∞,,其中m ∈R ,对[)0,a b ∀∈+∞,,若a b >,都满足()()0d d a b f x x f x x >⎰⎰,求m 的取值范围.参考答案1.【答案】B【分析】先解不等式求得集合A ,进而求得A B ⋂.【详解】集合()(){}2{|8150}{|350}3,4,5A x x x x x x =∈-+≤=∈--≤=Z Z .而{|5}B x x =<,故{}3,4A B ⋂=.故选B.2.【答案】A【分析】设12i,i(,R z b z c b c ==∈且,0)b c ≠,可得12z z ∈R ,如121i 12+2i 2z z +==,可得结论.【详解】若12,z z 均为纯虚数,设12i,i(,z b z c b c ==∈R 且,0)b c ≠,则12i i z b b z c c ==∈R ,所以“12,z z 均为纯虚数”是12zz 是实数的充分条件,当121i,22i z z =+=+,121i 12+2i 2z z +==,所以“12,z z 均为纯虚数”是12z z 是实数的不必要条件,综上所述:“12,z z 均为纯虚数”是12z z 是实数的充分不必要条件.故选A.3.【答案】C【分析】根据向量数量积运算求得正确答案.【详解】()222a b b a b b+⋅=⋅+ 2cos1502a b b=⋅⋅︒+2223⎛=+⋅= ⎝⎭.故选C.4.【答案】B【分析】利用两角和差公式以及倍角公式化简求值可得答案.【详解】由题干得2π1sin sin sin cos sin 332ααααα⎛⎫=+-=- ⎪⎝⎭1πsin cos 26ααα⎛⎫-=+ ⎪⎝⎭所以22ππ21cos 22cos 1213639αα⎛⎫⎛⎫⎛⎫+=+-=⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故选B.5.【答案】C【分析】利用等比数列的通项公式及前n 项和公式求解q 的值,再由数列的单调性进一步判断即可.【详解】2131133141122312a a a a q a S T q q q=⇒=⇒=+=⇒++=,则()()2121294214042q q q q q q -+=--=⇒==,.由于{}n a 为递增数列,则1144q a ==,,所以{}n a 的通项公式为24n n a -=所以()()11414411412nn n S -==--.故选C.6.【答案】A【分析】设正四棱锥P ABCD -的内切球的半径为R ,H 为底面中心,取CD 的中点F ,设O 点在侧面PCD 上的投影为Q 点,则Q 点在PF 上,利用∽ POQ PFH 求出球心到四棱锥顶点的距离h ,再由棱锥的体积公式计算可得答案.【详解】设正四棱锥P ABCD -的内切球的半径为R ,H 为底面中心,由体积为34π3R得R =,连接PH ,PH ⊥平面ABCD ,球心O 在PH 上,OH R =,取CD 的中点F ,连接,HF PF ,设O 点在侧面PCD 上的投影为Q 点,则Q 点在PF 上,且OQ PF ⊥,∽ POQ PFH ,球心到四棱锥顶点的距离为h ,所以=PQ PH OQ FH,h ,所以1181283333==ABCD V S PH .故选A.7.【答案】A【分析】利用给定条件结合对数的性质构造42n a <,两侧同时平方求最值即可.【详解】由题知n是2log 1(14(xx x ⎡⎤⎣⎦-<+的正整数解,故2log (1(14n nn ⎡⎤⎣⎦-<+,取指数得((4112n n n +--<,同除2n得,42n n -<⎝⎭⎝⎭,故42n n ⎡⎤⎫-⨯⎥⎪⎪⎥⎝⎭⎝⎭⎦,即42n a <,根据{}n a 是递增数列可以得到{}2n a 也是递增数列,于是原不等式转化为2812525n a <⨯<.而565,8a a ==可以得到满足要求的n 的最大值为5,故A 正确.故选A.8.【答案】D【分析】利用参变分离将函数图象有两个交点问题转化为y m =和()21ln 2x h x x -=的图象有两个交点,由导数求得ℎ的单调性并求得最大值即可得出结论.【详解】由()21ln 02mx x x +=>得22ln 1m x x -=,则问题转化为y m =和()21ln 2x h x x-=的图象有两个交点,而()()()2232112ln 21ln 2x x x x x h x x x ⎛⎫⋅-- ⎪-'⎝⎭==,令ℎ'>0,解得0e x <<,令ℎ'<0,解得e x >,故ℎ在()0,e 上单调递增,在()e,+∞单调递减,则()()2max 1e 2e h x h ==,ℎ大致图象如下所示:结合图象可知,m 的取值范围是210,2e ⎛⎫ ⎪⎝⎭故选D.9.【答案】ABCD【分析】根据对称知识可得()6110i i y x i i =-∈≤≤Z ,,结合平均数、中位数、方差、极差的性质,即可判断出答案.【详解】由于()()()121,0,,0,,,0x x x ,它们分别与()()()1210,10,,10,,,10y y y 关于点(3,5)对称,则有()6110i i x y i i +=∈≤≤Z ,,即有()6110i i y x i i =-∈≤≤Z ,.则由平均数的性质可得1210,,,y y y 这组数的平均数为6a -,结合中位数性质可知中位数为6b -,结合方差性质可得方差为c ,极差非负,所以极差为d .故选ABCD.10.【答案】CD【分析】利用共轭复数的概念和加减运算性质判断A,举反例判断B,利用复数模的性质得到轨迹方程,结合圆的性质判断C,利用复数模的性质得到轨迹方程,结合椭圆的性质判断D 即可.【详解】对于A.,设1i z a b =+,则1i z a b =-,所以22221(i)2i z a b a b ab =+=-+,2221(i)2i z a b a b ab =-=--,当,a b 有1个为0或全为0时, 2211z z =,当,a b 均不为0时,2211,z z 无法比较大小,故A 错误,对于B,当1i z =,2i z =-时,120z z +=,此时120z z +=,122z z +=,故1212z z z z +=+不成立,故B 错误,对于C,设1i z a b =+,因为122i 2z --=,所以i 22i 2a b +--=,故有2(2)i 2a b -+-=,可得22(2)(2)4a b -+-=,所以1z 的轨迹是以()2,2为圆心,2为半径的圆,而116i i 16i 1(6)i z a b a b +-=++-=++-=,故116i z +-表示点(),a b 到定点()1,6-的距离,由圆的性质可知,1min 16i 23z +-==,故C 正确,对于D,设2z a bi =+,所以2i i i (1)i z a b a b +=++=++=,2i i i (1)i z a b a b -=+-=+-=,而22i i 4z z ++-=,故4,所以得到点(),a b 到两定点()0,1-,()0,1的距离之和为4,故2z 的轨迹是以()0,1-,()0,1为焦点的椭圆,故轨迹方程为22143y x +=,而2z 表示(),a b 到原点的距离,由椭圆的几何性质可得当点B 在椭圆的左右顶点时,2z 取得最小值,此时2z =2min z =D 正确.故选CD .11.【答案】ACD【分析】A 选项,令=0,可求()e f ;B 选项,对()()e e e 0f x f x +--=两边求导,结合()()e e 0f x f x ''++->得()e 0f x '-<,()e 0f x '+>,可判断()f x 单调性;C 选项,12e x x ,,的大小关系进行分类讨论,利用函数单调性,证明不等式;D 选项,证明212e x x +<,利用函数单调性,证明()()12f x f x <且()()21e f x f x <,可得结论.【详解】A 选项,令=0,则有()()()()e e e 1e e 0f f f -=-=,所以()e 0f =,故A 正确.B 选项,对()()e e e 0f x f x +--=两边求导,得()()e e e 0f x f x '++-=',所以()()e e e f x f x +=-'-',代入()()e e 0f x f x ''++->,得当>0时,()()1e e 0f x '-->,所以()e 0f x '-<.又因为()()e e 0f x f x ''++->,所以,()e 0f x '+>.因此,当e x <时,()0f x '<,()f x 在(),e -∞上单调递减;当e x >时,()0f x '>,()f x 在()e,+∞上单调递增.故B 错误.C 选项,对12e x x ,,的大小关系进行分类讨论:①当12e x x <≤时,()f x 在(),e -∞上单调递减,所以()()12f x f x >,显然有212e x x +<;②当12e x x ≤<时,()f x 在()e,+∞上单调递增,不符合题意;③当12e x x <<时,当0x ≥时,()()e e e f x f x +=-.令()()()()()()122e e,e 2e e 2e t x f t f t f x f x f x ∞=+∈+=->=-,,,又因为()()e 0f x f ≥=,所以()22e 0f x ->,因此()()()()1222e 2e 2e f x f x f x f x >=->-.因为12e 2e e x x <-<,,由()f x 的单调性得,212e x x +<.故C 正确.D 选项,因为()()()()()()2200e 202e 2e e 20e e 220g f g f g f =+->=+->=-=-<,,,所以120e 2e x x <<<<.先证212e x x +<,即证122e x x ->,即()12e 0g x ->,只需证()2112e (2e e)20f x x -+--->,即证()211e (e )20f x x +-->.事实上,()()()()()2211111e e 2e 20f x x f x x g x +-->+--==,因此212e x x +<得证.此时有1210e 2e 2e x x x <<<<-<.因为()()()()()22211122e 22e e 2e 2f x x x x f x =--+=---+<--+=,又()10f x ≠,所以()()211f x f x <,因为()()()2112e e f x f x f x <-=,又()10f x ≠,所以()()21e f x f x <.综上,()()211e f x f x <<,故D 正确.故选ACD.【方法总结】导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.证明不等式,构造一个适当的函数,利用它的单调性进行解题,是一种常用技巧.许多问题,如果运用这种思想去解决,往往能获得简洁明快的思路,有着非凡的功效.12.【答案】29【分析】根据等差数列的通项公式求得正确答案.【详解】依题意101922729a a d =+=+=.故答案为:29.13.【答案】121122【分析】利用赋值法令1x =,1x =-,联立方程组求解即可.【详解】令1x =,得()554321012243a a a a a a +==+++++,令1x =-,得()5543210121a a a a a a -+==-+-+-+,则()()543210543210531243112122a a a a a a a a a a a a a a a +++++--+-+-+-++===,且()()543210543210420243112222a a a a a a a a a a a a a a a ++++++-+-+-++++===,故531420121122a a a a a a ++=++.故答案为:121122.14.【答案】()221,3916y x y -=≠-【分析】以HF 所在直线为x 轴,GE 所在直线为y 轴建立平面直角坐标系,求出直线EQ 的方程与直线GN 的方程,联立求解即可.【详解】以HF 所在直线为x 轴,GE 所在直线为y 轴建立平面直角坐标系.因为8,6AB BC ==,所以()()()()()()0,0,4,0,4,0,0,3,0,3,4,3O H F E G C --,所以()4,0OH =- ()()0,3,4,3CF OC =-= ,又因为,OQ kOH CN kCF == ,所以()()4,0,0,3OQ k CN k =-=-,所以()()4,0,4,33Q k N k --.因为()()0,3,4,0E Q k --,所以直线EQ 的方程为334y x k=--①,因为()()0,3,4,33G N k -,所以直线GN 的方程为334ky x =-+②.由①可得()()3043xk x y =-≠+,代入②化简可得()2210916y x x -=≠,,结合图象易知点R 可到达()0,3G ,但不可到达()0,3E -,所以点R 的轨迹方程为()221,3916y x y -=≠-,故答案为:()221,3916y x y -=≠-.15.【答案】(1)π3;(2)133266-.【分析】(1)根据二倍角公式将已知条件变形转化,再根据正弦定理边角互化,带入到余弦定理即可求得;(2)根据已知设AB c AC b ==,,表达出AP BQ ,,再根据余弦定理可求得结果.【详解】(1)因为2cos2cos22sin 2sin sin B A C B C -=-,所以()()22212sin 12sin 2sin 2sin sin B A C B C ---=-,即222sin sin sin sin sin A B C B C =+-,由正弦定理得222a c b bc =+-,由余弦定理得1cos 2A =,因为()π0π3A A ∈=,,;(2)设AB c AC b== ,,1cos 2332b c b c A ⋅=⋅=⨯⨯= ,依题意可得()1122AP b c BC b c BQ b c =+=-=- ,,,所以AP===,BQ===()221111143917224424424AP BQ b c b c b b c c⎛⎫⋅=+-=-⋅-=--=-⎪⎝⎭,所以cosAP BQPGQAP BQ⋅∠==-⋅.16.【答案】(1)(2213x y x+=≠;(2)证明见解析.【分析】(1)设点H的坐标为(),x y,然后表示出直线,AH BH的斜率,再由它们的斜率之积是13-,列方程化简可得点H的轨迹方程;(2)设()()1122,,,E x yF x y,当直线l斜率不存在时,求得直线l为x=0,当直线l 斜率存在时,设直线:l y kx b=+,由13AE AFk k⋅=-得2213=-,将直线方程代入椭圆方程化简利用根与系数的关系,代入上式化简可得20b=,从而可求得直线恒过的定点.【详解】(1)设点H的坐标为(),x y,因为点A的坐标是(),所以直线AH的斜率AHk x=≠,同理,直线BH的斜率BHk x=,由已知,有(13x-≠±,化简,得点H的轨迹方程为(2213x y x+=≠,即点H的轨迹是除去()),两点的椭圆.(2)证明:设()()1122,,,E x yF x y①当直线l斜率不存在时,可知1221,x x y y==-,且有22111313AE AFx yk k⎧+=⎪⎪⎨⎪⋅=-⎪⎩,解得1101x y==±,,此时直线l为x=0,②当直线l斜率存在时,设直线:l y kxb=+,则此时有:2213AE AFk k+++++⋅==-联立直线方程与椭圆方程2213y kx b x y =+⎧⎪⎨+=⎪⎩,消去y 可得:()222316310kx kbx b +++-=,根据韦达定理可得:122631kb x x k -+=+,21223331b x x k -=+,所以2222222233613131336333131b kbk kb b k k b kb k k --⋅+⋅+++=---++++,所以222222(33)63113k b k b b k --++=-,所以221=-所以20b =,则0b =或b=,当b=时,则直线(:l y k x =+恒过A 点与题意不符,舍去,故0b =,直线l 恒过原点()0,0,结合①,②可知,直线l 恒过原点()0,0,原命题得证.【关键点拨】此题考查椭圆的轨迹方程,考查直线与椭圆的位置关系,考查椭圆中直线过定点问题,解题的关键是设出直线方程代入椭圆方程化简,利用根与系数的关系结合已知条件求解,考查计算能力.17;(2)4k =.【分析】(1)利用圆柱以及棱锥的体积公式,即可求得答案.(2)建立空间直角坐标系,求出相关点坐标,利用空间角的向量求法,结合平面FCD 与平面PCD 的夹角的正弦值,即可求得答案.【详解】(1)在底面ABCD 中,因为AC 是底面直径,所以90ABC ADC ∠=∠=,又AB AD =,故ACB ≌ACD,所以13042BAC DAC BAD BC CD AB AD ∠∠∠=======,,因为PC 是圆柱的母线,所以PC ⊥面ABCD ,所以211π()16π2V AC PC PC ==⨯,211112243232V AB BC PC PC=⨯⨯⨯⋅⋅=⨯⨯⨯⨯=,因此12VV=;(2)以C为坐标原点,以,CA CP为,x z轴正方向,在底面ABCD内过点C作平面PAC的垂直线为y轴,建立如图所示的空间直角坐标系.因为30BAC DAC AB AD∠∠===,,所以ABE≌ADEV,故90AEB AED∠∠== ,所以1622BE DE AB AE CE AC AE=====-=,,2PC kCE k==,因此()()()()()() 0,0,0,8,0,0,2,,0,0,2,2,,0,0,2C AD P k CD CP k==,()8,0,2PA k=-,因为PA kPF=,所以18,0,2PF PAk k⎛⎫==-⎪⎝⎭,则88,0,22,,0,22F k CF kk k⎛⎫⎛⎫-=-⎪ ⎪⎝⎭⎝⎭设平面FCD和平面PCD的法向量分别为()()111222,,,,,n x y z m x y z==,则有:()1111822020n CF x k zkn CD x⎧⋅=+-=⎪⎨⎪⋅=+=⎩,2222020m CP kzm CD x⎧⋅==⎪⎨⋅=+=⎪⎩,取())()221,,1,3,4n k k k k m⎛⎫=----=-⎪⎪⎝⎭,设平面FCD与平面PCD的夹角为θ,则sinθ=所以有:2cos cos,13m nθ==,整理得2120k k--=,2120k k-+=(无解,舍),由于k为正整数,解得4k=.18.【答案】(1)()()()3ln2,(2)g x x x x=----<-;(2)证明见解析;(3)证明见解析.【分析】(1)由()()11f x g x --=-+,得()()()12ln 1g x x x -+=----,再利用换元法求()g x ;(2)分区间讨论各因式的符号或利用导数证明;(3)取曲线e x y =上的一点()11e ,xB x ,设()ln g x x =在A 处的切线即是()ex h x =在B 处的切线,证明直线AB 的斜率等于()ln g x x =在A 处的切线斜率和()e xh x =在B 处的切线斜率即可.【详解】(1)因为()f x 的图象与()g x 的图象关于直线=−1对称,所以()()11f x g x --=-+.又因为()()()()()111ln 12ln 1f x x x x x ⎡⎤--=-----=----⎣⎦,所以()()()12ln 1g x x x -+=----,令1t x =-+,则1x t =+,所以()()][()()()21ln 113ln 2g t t t t t ⎡⎤=--+--+=----⎣⎦,因此()()()3ln 2,(2)g x x x x =----<-.(2)证明:解法1:当1x ≥时,10x -≥且ln 0x ≥,此时()()1ln 0f x x x =-≥;当01x <<时,10x -<且ln 0x <,此时()()1ln 0f x x x =->,故综上()0f x ≥.解法2:()1ln 1f x x x +'=-,令()1ln 1x x xϕ=+-,()2110x x x ϕ'=+>在()0,+∞上恒成立,故()x ϕ在()0,+∞上单调递增,即()f x '在()0,+∞上单调递增,因此当01x <<时,()()10f x f ''<=;当()()110x f x f ''≥≥=,;因此()f x 在()0,1上单调递减,在[)1,+∞上单调递增,故()()10f x f ≥=.(3)证明:不妨取曲线e x y =上的一点()11e ,xB x ,设()ln g x x =在A 处的切线即是()e xh x =在B 处的切线,则()()10101e x g x h x x ''===,得101ln x x =,则B 的坐标0011ln x x ⎛⎫ ⎪⎝⎭,,由于()0001ln 1x x x -=+,所以0001ln 1x xx +=-,则有()()2000000000002000000000011111ln ln 111111ln ln 11ABx x x x x x x x x x k g x x x x x x x x x x x ++-----======++--'++-,综上可知,直线AB 的斜率等于()ln g x x =在A 处的切线斜率和()e xh x =在B 处的切线斜率,所以直线AB 既是曲线ln y x =在点()00n ,l A x x 处的切线也是曲线e x y =的切线.19.【答案】(1)()e 1xf x x =++;(2)1256;(3)12m ≤.【分析】(1)根据新定义及()02f =计算得解;(2)根据新定义,构造函数()26g x x x =-+-即可得出面积;(3)根据所给条件可得()()d F x f x x =⎰在[)0,+∞上单调递增,转化为()0f x ≥在[)0,+∞恒成立,分离参数后利用导数求出函数最值即可得解.【详解】(1)()()e 1d e x xf x x x C =+=++⎰,其中C 为常数.而()02f =,即102C ++=,所以1=C ,所以()e 1xf x x =++.(2)联立26y x y x ⎧=⎨=-+⎩,解得123,2x x =-=,当32x -<<时,26x x -+>,令()26,g x x x =-+-()()2311d 623F x g x x x x x C ==-+-+⎰,则围成的面积()()()2389125d 23212189326S g x x F F -⎛⎫⎛⎫==--=-+----+= ⎪⎪⎝⎭⎝⎭⎰.(3)令()()d F x f x x =⎰,由题意可知,[)0,a b a b ∀∈+∞>,,,满足()()()()00F a F F b F ->-,即()()F a F b >,即()()d F x f x x =⎰在[)0,+∞上单调递增,进而()0f x ≥在[)0,+∞恒成立,e 120x mx --≥在()0,+∞恒成立.由于>0,即e 12x m x -≥,令()e 12x g x x-=,则()22e 2e 24x x x g x x -+'=,令()()2e 2e 22e 0x x xh x x h x x '=-+=≥,,所以ℎ在[)0,+∞上单调递增,所以()()00h x h ≥=,即()0g x '≥,进而()g x 在()0,+∞单调递增,而()000e 1e 1lim lim lim 222x x x x x g x x →+→+→+-===,所以()12g x ≥,所以12m ≤.【关键点拨】本题第三步关键在于利用a b >,都满足()()0d d abf x x f x x >⎰⎰,得出函数()()d F x f x x =⎰在[)0,+∞上单调递增,再转化为()0f x ≥在[)0,+∞恒成立,分离参数求解.。
高中数学必修第一册 《一元二次函数、方程和不等式》期末复习专项训练(学生版+解析版)

高中数学必修第一册《一元二次函数、方程和不等式》期末复习专项训练一、单选题l. (2022·四川绵阳·高一期末〉下列结论正确的是(〉A.若的b,则。
c>bc c.若。
>b,则。
+c>b+cl I B.若α>b,则-〉-a D D.着。
>b,则。
2> b22.(2022·辽宁·新民市第一高级中学高一期末〉已知α<b<O,则(〉A.a2 <abB.ab<b2C.a1 <b1D.a2 >b i3.(2022·陕西汉中·高一期末〉若关于工的不等式,咐2+2x+m>O的解集是R,则m的取值范围是(〉A.(I, +oo)B.(0, I〕C.( -J, I)D.(J, +oo)4.(2022·广东珠海高一期末〉不等式。
+l)(x+3)<0的解集是(〉A.RB.②c.{对-3<x<-I} D.{xi x<-3,或x>-l}5. (2022·四川甘孜·高一期末〉若不等式似2+bx-2<0的解集为{xl-2<x<I},则。
÷b=( )A.-2B.OC.ID.26. (2022·湖北黄石·商一期末〉若关于X的不等式x2-ax’+7>。
在(2,7)上有实数解,则α的取值范围是(〉A.(唱,8)B.(叫8] c.(叫2./7) D.(斗)7.(2022·新疆乌市一中高一期末〉已知y=(x-m)(x-n)+2022(n> m),且α,β(α〈别是方程y=O的两实数根,则α,β,111,n的大小关系是(〉A.α<m<n<βC.m<α〈β<nB.m<α<n<βD.α<m<β<n8.(2022·浙江·杭州四中高一期末〉已失11函数y=κ-4+...2....(x>-1),当x=a时,y取得最小值b,则。
2024年苏科版高二数学上册月考试卷515

2024年苏科版高二数学上册月考试卷515考试试卷考试范围:全部知识点;考试时间:120分钟学校:______ 姓名:______ 班级:______ 考号:______总分栏题号一二三四五六总分得分评卷人得分一、选择题(共6题,共12分)1、的二项展开式中,项的系数是()A. 45B. 90C. 135D. 2702、【题文】为了得到函数的图象,只需把函数图象上的所有点()A. 纵坐标伸长到原来的2倍,横坐标不变B. 横坐标伸长到原来的2倍,纵坐标不变C. 纵坐标缩短到原来的倍,横坐标不变D. 横坐标缩短到原来的倍,纵坐标不变3、若b<0<a,d<c<0,则下列不等式中必成立的是()A. ac>bdB.C. a+c>b+dD. a﹣c>b﹣d4、已知函数f(x0在R上连续可导,则等于()A.B.C.D.5、如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等边三角形,则直线PC与平面ABCD所成角的正切值为()A.B.C.D.6、复数z=5+3i的共轭复数对应的点所在的象限是()A. 第一象限B. 第二象限C. 第三象限D. 第四象限评卷人得分二、填空题(共9题,共18分)7、【题文】已知ΔABC中,∠A,∠B,∠C的对边分别为a,b,c,若a=1,2cosC+c=2b,则ΔABC的周长的取值范围是__________.8、【题文】高二某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:,.左上图是按上述分组方法得到的频率分布直方图. 则成绩大于等于 14秒且小于16秒的学生人数为____.9、【题文】_________10、【题文】如图给出的是求的值的一个程序框图;其中判断框内应填入的条件是_____________11、“存在x∈(0,+∞)使不等式mx2+2x+m>0成立”为假命题,则m的取值范围为____.12、已知F1、F2分别是椭圆C:=1(a>b>0)的左、右焦点,点P在椭圆C上,线段PF1的中点在y 轴上,若2∠PF1F2=∠F1PF2,那么椭圆的离心率为____.13、如果随机变量ξ~N(-1,σ2),且P(-3≤ξ≤-1)=0.4,则P(ξ≥1)= ______ .14、已知向量a鈫�=(2,鈭�1),b鈫�=(0,1)则|a鈫�+2b鈫�|= ______ .15、在3名男教师和3名女教师中选取3人参加义务献血,要求男、女教师都有,则有 ______ 种不同的选取方法(用数字作答).评卷人得分三、作图题(共5题,共10分)16、著名的“将军饮马”问题:有一位将军骑着马要从A地走到B地;但途中要到水边喂马喝一次水,则将军怎样走最近?17、A是锐角MON内部任意一点,在∠MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小.(如图所示)18、著名的“将军饮马”问题:有一位将军骑着马要从A地走到B地;但途中要到水边喂马喝一次水,则将军怎样走最近?19、A是锐角MON内部任意一点,在∠MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小.(如图所示)20、已知,A,B在直线l的两侧,在l上求一点,使得PA+PB最小.(如图所示)评卷人得分四、解答题(共4题,共20分)21、(本题满分12分)已知命题方程表示圆;命题双曲线的离心率若命题“”为假命题,“”为真命题,求实数的取值范围.22、某工厂有工人1000名;其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).(Ⅰ)A类工人中和B类工人各抽查多少工人?(Ⅱ)从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2表1:。
安徽省合肥市瑶海区2022-2023学年八年级下学期期末数学试卷(含解析)

安徽省合肥市瑶海区2022-2023学年八年级下学期期末数学试卷〈解析版〉一、选择题.〈本大题共10小题,每小题4分,满分40分〉每小题都给出A、B、C、D四个选项,其中只有一个是符合题目要求的.1.(4分〉下列式子中,是二次根式的是(A. '1/7 B飞/2 C.'\j-3 D. "Ix2.(4分〉若关于x的方程。
n+2):x2 -3x+ l =O是一元二次方程,则m的取值范剧是〈c.m丐丘·立 D.m>OA.m寻i:QB.111> -23.(4分)如图,在Rt6ABC中,L'.ACB=90。
,CD是AB J2l上的高,若AC=3,AB=5,则CD=(A. 2B.2.4 c.3 D.�4.(4分)如图,在口AMCN中,对角线AC、MN交子点。
,点B和点D分别在E OM、ON的延长线上.添加以下条件,不能说明四边形ABCD是平行四边形的是(�A.AB=ADB.ADI/BCC.BM=DND.LMAB=LNCD5.(4分)如图,为了了解某校学生的课外阅读情况,小明同学在全校随机抽取40名学生进行调查,并将统计数据汇总,整理绘制成学生每周课外阅读时间频数分布茧,方图,(每组含前一个边界倍,不含后一个边界值〉如图所示,若该校有学生2338入,估计阅读时民;不低于6小时的人数约有()人.4事j数斗17105 。
A.351982 4 6 8 10时'f1可(小时)8.818 C.1052 D. 15206.(4分)如图,在0ABCD中,对角线AC、BD交子点o.若AB=2,AC=8, BD=川,AD=n. 则化简:�+占�的结果为(B DA.n+m -118.n-m-9 C.m-n+9 D.11-m-n7.(4分)菜商店对一利1商品进行库存消理,第一次降价30%,销量不佳;第二次又降价10%,销售大增,很快就清理了库存设两次降价的平均降价率为λ’,下面所列方程正确的是(A. 300+10% - -x28.(l -30%) (1 -10%) = (I -2x)C.(1-30%) (1-10%) =2 (1-x)D.(! -30%) (J -10%) = (! -x) 28.(4分)在矩形ABCD中,E是AD的中点,将l:::.ABE沿BE折叠后待J1JL:::.GB£,延长BG 交直线CD于点F,若CF=I,FD=2,则BC的长为〈〉A.纣飞8.3 c.'N6或纠言 D. '2:1/2成39.(4分〉如图,在l:::.ABC中,D是AC边上的中点,E在BC上,且£C=2町,y!I]且=〈FEA.2B.3 c.4 D.5JO. (4分)若关于x的一元二次方程x2-2.x牛。
高中数学必修第一册 《集合与常用逻辑用语》期末复习专项训练(学生版+解析版)

高中数学必修第-册《集合与常用逻辑用语》期末复习专项训练一、单选题I.(2022·北京清华附中高一朔和已知命题p:\fa e (O,+oo),。
」>2,则『p是(〉A.3αε(0,+oo),α+->2α C.3ae(O,+oo),α+-三2B.3a岳(0,+oo),。
+->2。
D.3a 1c (0,+oo),a +-� 2。
2.(2022·江苏盐城·高一期末〉设综合P=\斗x是正四棱校),Q= {斗x是长方休),M=\xlx是正方体},则〈〉A.M 罕Q罕PB.M罕P罕QC.P罕Q罕MD.Q罕M罕P3.(2022·浙江省义乌中学高一期末〉己知集合A={.�i x=3n+l, neN},集合B={3.4,5忌,7,8,10},贝l]A nB 中元索的个数为(〉A.I8. 2 c.3 D. 44.(2022湖南·高一期末〉设综合M={xix=缸,neZ},N={xlx=2n+l,neZ}, P={xlx=制,neZ},则(〉A.MVPB.POMC.NnP*②D.Mr,N°*②5.(2022湖南岳阳·高一期末〉下列元素与集合的关系中,正确的是(〉A.-J eN8.O e N"6.(2022·浙江·杭州四中高一期末〉咱<x<2A.必要而不充分条件C充要条件C .../3 e Q8.充分而不必要条件D._3:o:R5 D.既不充分也不必要条件7.(2022·贵州六盘水·高一期末〉己知集合M={xl(x-3)(x+1)=0},N={-1,0,2,4,5},贝l]MnN=( )A.{2,-1}B.{-1}C.(0,1,4)D. {-1,0,3,5)8.(2022洞商安阳高一期末〉集合A=仰,1,认8},B={xl2'eA},将综合A,B分别用如闺中的两个困表示,则因t i二l阴影部分表示的集合中元素个数恰好为2的是〈〉A.A BB.A Bc.A B D.A B9. (2022湖北·华中师大一附中高一期末〉已知综合M={0,1斗,N={-1,0,1,2},则“aeM”是“aeN”的(〉A.充分不必要条件C充姿条件B.必要不充分条件D.既不充分也不必要条件IO. (2叫西附中高一期末〉己贵阳M={xix午二k e z},集合N忖=号-�,k 斗则MnN=( )A.②B.儿fC. ND.Z11. (2022湖南湘西·高一期末〉己知P:xy>O, q, x>O, y>O,则P是q的(〉A.充分不必要条件B.必要不充分条件C充要条件 D.既不充分也不必要条件12. (2022浙江嘉兴高一期末〉飞>b >叫宁;啪(〉A.充分不必要条件C充要条件二、多选题B. 必要不充分条件D. 既不充分又不必要条件13. (2022·河南·永城市酋桥乡重点中学高一期末〉使x-..!..,,0成立的一个充分条件可以是(〉A.x<-1B.O<x<lC. -段生ID..x;, 114. (2022·甘肃张掖·高一期末〉下列关系武错误的是〈)A. 0e{O}B.{2) s; {1,2)C. Ji �QD. OeZ15. (2022·福建厦门·高一期末〉已知。
2024年广东省中考数学真题(学生版+解析版)

2024年广东省中考数学真题满分120分考试用时120分钟注意事项:1. 答题前,考生务必用黑色字迹的签字笔或钢笔将自己的准考证号、姓名、考场号和座位号填写在答题卡上.用2B 铅笔在“考场号”和“座位号”栏相应位置填涂自己的考场号和座位号,将条形码粘贴在答题卡“条形码粘贴处"2. 作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3. 非选择题必须用黑色字迹的签字笔或钢笔作答,答案必须写在答题卡各题目指定区域内相应位置上:如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4. 考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 计算—5+3的结果是()A. 2B. —2C. 82. 下列几何图形中,既是中心对称图形也是轴对称图形的是()A 6B二c .QD. —8D.3. 2024年6月6日,嫦娥六号在距离地球约384000千米外上演“太空牵手”,完成月球轨道的交会对接.数据384000用科学记数法表示为()A. 3.84xl04B. 3.84xl05C. 3.84xl06D. 38.4xl054. 如图,一把直尺、两个含30°的三角尺拼接在一起,则乙ACE 的度数为()11/三l0三�:'I'IA. 120°B . 90° 5. 下列计算正确的是()A. a 2 . a s= a 10B. a s -;-Q 2 = a 4C . 60°D . 30°C. —2a +5a =7a25D. (a ) = a 106.长江是中华民族的母亲河,长江流域孕育出藏羌文化、巴蜀文化、荆楚文化、吴越文化等区域文化.若从上述四种区域文化中随机选一种文化开展专题学习,则选中“巴蜀文化”的概率是()1 1 3A.—B.—C.—D. —4 3 47.完全相同的4个正方形面积之和是100,则正方形的边长是()A.2B.5C.10D.208.若点(0,Y1),(1, Y2),(2,Y3)都在二次函数y=x2的图象上,则()A.Y3 > Y2 > Y1B.Y2 > Y1 > Y3C.Y1 > Y3> Y2D.Y3 > Y1 > Y22 39.方程=-的解为()X—3 XA.x=3B.X=-9C.x=9D.X=—310.已知不等式kx+b<O的解集是x<2,则一次函数y= kx+b的图象大致是()y,321A.B.I 2 3 xy,321霆3 ,y3,y-2-3D.3.x -3-2-10-1-2-3_、填空题:本大题共5小题,每小题3分,共15分.11.数据2,3, 5, 5, 4的众数是12.关千x的不等式组中,两个不等式的解集如图所示,则这个不等式组的解集是2 -1 fl I13.若关千X的一元二次方程x2+2x+c=O有两个相等的实数根,则c=a 314.计算:- =a-3 a-315.如图,菱形A BCD的面积为24,点E是AB的中点,点F是BC上的动点若D BEF的面积为4,则图中阴影部分的面积为I三、解答题(一):本大题共3小题,每小题7分,共21分.1 16. 计算:2°X-—+✓4-3-13 17. 如图,在AB C 中,乙C=90°.(1)实践与操作:用尺规作图法作乙A的平分线AD交BC 千点D (保留作图痕迹,不要求写作法)(2)应用与证明:在(1)条件下,以点D 为圆心,DC 长为半径作D . 求证:AB 与D 相切.18. 中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQ MN 充电站的平面示意图,矩形A BCD 是其中一个停车位.经测量,缰Q =60°,AB=5.4m , CE=l.6m , GH _l_CD, GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.,(`,I l,r ·1-` .tI凡根据以上信息回答下列问题:(结果精确到O .lm,参考数据✓3:::::1.73)(1)求PQ 的长;(2)该充电站有20个停车位,求P N 的长.四、解答题(二):本大题共3小题,每小题9分,共27分.19. 端午假期,王先生计划与家人一同前往景区游玩,为了选择一个最合适的景区,王先生对A、B 、C三个景区进行了调查与评估.他依据特色美食、自然风光、乡村民宿及科普基地四个方面,为每个景区评分(10分制).三个景区的得分如下表所示:景区特色美食自然风光乡村民宿科普基地A687 9B 7 7 87C886 6(1)若四项所占百分比如图所示,通过计算回答:王先生会选择哪个景区去游玩?(2)如果王先生认为四项同等重要,通过计算回答:王先生将会选择哪个景区去游玩?(3)如果你是王先生,请按你认为各项“重要程度”设计四项得分的百分比,选择最合适的景区,并说明理由.20. 广东省全力实施“百县千镇万村高质量发展工程", 2023年农产品进出口总额居全国首位,其中荔枝鲜果远销欧美.某果商以每吨2万元价格收购早熟荔枝,销往国外.若按每吨5万元出售,平均每天可售出100吨.市场调查反映:如果每吨降价1万元,每天销售量相应增加50吨.该果商如何定价才能使每天的“利润”或“销售收入“最大?并求出其最大值.(题中“元”为人民币)21. 综合与实践【主题】滤纸与漏斗【素材】如图1所示:少一张直径为10cm的圆形滤纸;@一只漏斗口直径与母线均为7cm的圆锥形过滤漏斗.�7cm叶图l【实践操作】步骤1:取一张滤纸;步骤2:按如图2所示步骤折叠好滤纸;步骤3:将其中一层撑开,围成圆锥形;步骤4:将围成圆锥形滤纸放入如图1所示漏斗中.气_芍c 厂。
广东省惠州市2024-2025学年高三上学期第二次调研考试 数学 含解析

惠州市2025届高三第二次调研考试试题数学全卷满分150分,时间120分钟.2024.10注意事项:1答题前,考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写在答题卡上.2.作答单项及多项选择题时,选出每个小题答案后,用2B铅笔把答题卡上对应题目的答案信息点涂黑如需改动,用橡皮擦干净后,再选涂其它答案,写在本试卷上无效.3非选择题必须用黑色字迹签字笔作答,答案必须写在答题卡各题指定的位置上,写在本试卷上无效一、单项选择题:本题共8小题,每小题满分5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求,选对得5分,选错得0分l已知集合A={�2�x<5},集合B={xl x2-4x<O},则A^B=( )A.(o,s)B.[2,4) c.(4,5) o.(-00,O)u[2,+oo)2已知复数z满足z2+l = 0,则lz+ll=( )A.3B.2C.l D.五3已知等差数列{a,,}前9项的和为27,如=8,则a.oo= ()A.100B.99C.98 0.974在正方体ABCD-'4iB1Cp1中,棱BC,A戊的中点分别为E,F,则直线E F与平面ABBA所成角的正弦值为()石 B. 森2石 D. 痀5已知向凳a,b满足:a=(✓3,1),叫=石,(兹-b )·6=3,则向豐6在向榄五上的投影向榄为()A胃气)B[竿i)C[告)叶亨订6已知函数f(x)=log2厅-2ax),aeR,则“a:s;O"是“函数f(x)在(1,七吩上单调递增"的()A充分不必要条件B必要不充分条件C充要条件D既不充分也不必要条件7已知“水滴"的表面是一个由圆锥的侧面和部分球面(常称为“球冠”)所围成的几何体如图所示,将“水滴"的轴截面看成由线段AB,AC 和优弧BC所围成的平面图形,其中点B,C 所在直线与水平面平行,AB和AC与圆弧相切已知“水滴"的“竖直高度”与“水平宽度”(“水平宽度”指的是平行千水4平面的直线截轴截面所得线段的长度的最大值)的比值为-,则sin乙BAC=<A3416 24A.-B .- C.—D .—55252538在统计某学校所有选择理科和文科的学生数据中,发现理科生多千文科生,女生多千男生,则关千本次学生样本的数据中,结论一定成立的是()A理科男生多千文科女生B文科女生多千文科男生C理科女生多干文科男生D理科女生多于理科男生二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求全部选对的得6分,部分选对的得部分分,有选错的得0分9某公司为保证产品生产质量,连续10天监测某种新产品生产线的次品件数,得到关千每天出现的次品的件数的一组样本数据:3,4, 3, 1,5, 3, 2,5, 1, 3则关千这组数据的结论正确的是()A极经是4B众数小千平均数c .方差是2D数据的第80百分位数为4.510函数f (x) =A sin (cvx+ <p)(A> O,a> > 0树<§)的部分图象如图所示,现将f(x )的图象向左平移巴6个单位长度,得到函数g(x)的图象,则下列结论正确的是(2亡7兀X12兀A.<p =-一6B.(i)=2c .函数)1= xf (x +王)是奇函数12 D.g (x )=2c os (2x -¾)II 如图,心形曲线L:x 2+(y -|入扩=1与Y 轴交于A ,B 两点,点P 是L 上的一个动点,则()ypXBA点[孚叩11(-1,1.)均在L 上B.IO月的最大值和最小值之和为3C 点P 的纵坐标的最大值为J5D.I PAl+IPB 怍2石三、填空题:本题共3小题,每小题5分,共15分.12.在(x+1)5的二项展开式中,各项的系数和为13椭圆于fi =l (a >b>O )的左、右顶点分别是A 、B ,左、右焦点分别是R 、F2,若I A F.I ,I F.Fzl,IF.纠成等比数列,则此椭圆的离心率e=.14若关千X的方程ln(ax4)=[二了有实根,则a江护的最小值为四、解答题:本题共5小题,共77分解答应写出必要的文字说明、证明过程或演算步骤15(本题满分13分)已知函数f(x)=�X 2一x-2ln x(l)求曲线y=f(x)在点(l,f(1))处的切线方程:(2)求函数f(x)在区间[1,e]上的晟小值16(木题满分15分)如图,四棱锥P-ABCD中,PA J_底面ABCD,AB II CD,AD=CD=l.乙BAD=120',乙ACB=90°.D C(l)求证:BC上平面PAC:(2)若PA=石,求平面PCD与平面PCA夹角的余弦值l7 (本题满分15分)已知双曲线C:x2-y2=l及直线l:y=虹-1(])若l与C有两个不同的交点,求实数K的取值范围:(2)若l与C交千A,B两点,O是坐标原点,且t:.OAB的面积为J5,求实数K的值18(本题满分17分)记t:,.ABC的内角A,B,C的对边分别为a,b,c,已知a<b<c且tanA,tanB, t anC均为整数(I)求tanA,tanB, t anC的值,(2)设AC的中点为D,求乙CDB的余弦值19(本题满分17分)若数列{a,,}(1 s n s k, n E N*, k EN*)满足a,,叶0,1},则称数列{a,,}为K项0-1数列,由所有k项0-1数列组成集合M ks4)时,a,,=0,求数列{(-l)飞,}的所有(])若伈}是12项0-1数列,当且仅当n=3p(p E N*,p项的和;(2)从梊合M人.中仔意取出两个数列{动,{丸},记X=区|a,-b/|i=I@求随机变量X的分布列,并证明:E(X)>一:k2@若用某软件产生k(k2'.:2)项0-1数列,记事件A =“第一次产生数字1"'B=“第二次产生数字l"'且0<P(A ) <1,0<P (B) <l若P(BIA)<P(B区),比较P(Al B)与P(AI B )的大小惠州市2025届高三第二次调研考试试题高三数学参考答案与评分细则一、单项选择题:本题共8小题,每小题满分5分,共40分.题号2345 678答案BDc BAADcl 【解析】因为B ={xl O < x <4},所以A nB={xl 2�x<4}故选:B 2【解析】因为z 2+l=O,即z 2= -1,所以z =土,所以卜+11=11士11=f言75了=J5故选:D.的公妇为d,由已知得:{9a, +36d =273【解析】设等劳数列{a ,,},解得a,= -1, cl = 1,a, +9d =8所以a 100=a , + 99d = -1 + 99 = 98故选:C.4【解析】连接FB ,在正方体ABCD -f\B ,C 1D 1中,BC..l 平面A BB A ,棱BC 的中点为E,则BE..l 平面A BB I A ,而BFc 平面A BB A ,故BE..l BF,则乙EFB 即为迎线EF 与平面A BB I A 所成角,设正方体棱长为2,则BE=l,BF=.JB I F 2+B阻=j了I =心,BE1✓6则EF =✓BF 2+BE 2=拆,故sin乙E FB =--=--=一-故选:BEF拆6A lni ,DI L ,“K ,','…,'} ,夕,j A5【解析】由例=石,(2ii-b)·b =3,得2li·b -lbi 2=2li·b -2=3,即a 6=-525由已知得la:1=2,所以向摄6在向量a上的投影向量为彗向=\卢=`石,l)=厂产,i)故选:A .as l6【解析】若函数f(x)在(l,切)上单调递增,则{,解得a5-,Il-2a之02所以“a�O"是"函数f(x)在(1.冲~)上单调递增”的充分不必要条件.故选:A7【解析】设优弧BC 所在圆的圆心为O,半径为R,连接OA ,OB ,OC 易知“水滴"的"竖直商度”为OA +R, OA +R 45 “水平宽度”为2R,由题意知=一,解得OA=-R 因为AB 与圆弧相切千点B ,2R 3 3OB R 3 所以B 在Rt 心ABO 中,sin乙BAO =—=—=-冗OA 5 :::...R5,又乙BAO e l 0,一,(』4所以COS乙BAO=.Jl-sm 汔BAO =一,由对称性知,5乙BAO =乙CA O,则乙BAC=2乙BAO,3 4 24所以sin 乙BAC=2sin 乙BAOcos 乙BA0=2x-=-x-=—故选:D.5 5 258【解析】根据已知条件设理科女生有x 1人,理科男生有X 2人:文科女生有)'1人,文科男生有)5人;根据题意可知:X 1 + X 2 > Y i + Y 2'X i +Y i > X 2 + Y 2'根据同向不等式可加的性质有:X 1 + X 2 + X 1 + Y 1 > Y 1 + Y 2 + X 2 + Y 2'即X 1> Y 2,所以理科女生多千文科男生,C正确其他选项没有足够证据论证故选:C .二、多项选择题:本题共3小题,每小题满分6分,共18分.在每小题给出的四个选项中,有多项符合题目要求全部选对得6分,部分选对得部分分,有选错的得0分.题号I 9 I 10 I 11全部正确选项I A D I ABO I ACD9【解析】数据从小到大排列为:1,1, 2, 3, 3, 3, 3, 4, 5, 5对千A,该组数据的极差为5-1=4,故A正确:对于B,众数为3,平均数为lx2+2+3x4+4+5x210=3,两者相等,故B错误;对干C,方差为而伈-3)2x2+(2-3)2xl+(3-3)2x4+(4-3)2xl+(S-3)2x2] = 1.8,故C错误,对千D,10x80%=8,这组数据的第80百分位数为第8个数和第9个数的平均数4.5,故D正确故选:AD.10【解析】由图像可知:f(x)ma x = 2, A= 2:又f(0)=2s叩=-l,故sinrp=一L,又lrp|<巴,所以rp=-巴,所以A项正确,2 2 6已知f(气=2sin(五0-勹=0,由五点作图法可知:卫坛-巴=亢,解得:OJ=2'所以B项正l2 12 6 l2 6确;故f(x) =2sin(三)则xj.(咕)=2xsin2x设h(x)=xf.(咕)=2xsin2x则h(-x)= 2(-x)sin(-2x) =2.xsin2x= h(x),所以函数y=.-1;小号)是偶函数,故C项错误g(x)=f(x十艺)=2s i n[2(x+:)-去]=2s i n(2x+艺)=2c o s[�-(2x+艺)]=2cos甘-2x)=2cos(三),所以D项正确故选:ABD.五II【解析】A选项,经验算,点(—,0和(-1,1)的坐标满足曲线L的方程x2 +(y-lxl)2 =L所以` o)和(-l,l)均在L上故2A项:确B 选项,I OP l =心三了,因为曲线L:x江(y-I 入扩=l 关千Y 轴对称,当x 以0时,x 2 +(y-x)2 =l,设x=cos0, y-x= s in0,0e[-豆],2 2.l+co s20 所以IOPl 2=.,\,:2+y 2=cos 20+(cos0+sin0)2 =l+�+sin20 23 1 3森l =-+sin20+-cos20=-+—sin (20 + rp ),其中tanrp =一,2 22 22 所以OP l min =[工石-�,10P 1m ax =[工石+12 2 2 2 2 2,所以10月的最大值和最小值之和为石,故B项错误;C 选项,因为曲线L:x 2+(y -l x 忙=1关千Y 轴对称,当x习0时,x 2+(y-x)2 =I ,则(y-x)2 =1-.,\,,2,所以y =x 土』7了因求,占P 的纵坐标的最大值,故取y =x+.[i':了,2又y 2=(x +石二了)=1+2x../I 二了=1+2[x.了7平1+.,\,;2+(l -入"2)=2(当且仅当x 2=上时等号2成立),所以y�.,fi ,故C项正确;x -D 选项,IPA I +I P B� 2✓3等价千点P 在椭圆上-+—=1内(包含椭圆),由B 项可知,即满足:322(cos0+sin0)2 +3cos 20 � 6,即2(l+sin20)+3(1+cos20)�6,整理得:23 4sin20 + 3cos20 � 5,即5sin(20+/3)�5'其中其中tan/3=-,即sin(20+/3)�l 恒成立,则故D4项正确故选:A BD .三、填空题:本题共3小题,每小题5分,共15分.12.32五5314.e i12.【解析】当x =l 时,二项式展升式各项的系数和为25=32故答案为:3213【解析】由题意知I Mi l =a-c,I F;Fz l =2c,IF;科=c+a,且三者成等比数列,则IFiFi l 2= IAF;I .I F;BIl石石即4c 2= (c-a )(c +a )= c 2 -a 2,所以e 2=-,所以e =—故答案为:—-55514【解析】设方程ln (釭+勹=k的实根为X。
深入分析IT4IT框架,构建最佳的企业数字化运营架构体系,并持续支持企业实施数字化转型

%;9'<
=*")*"+4
(>"+/2
?!"+#+
("+.-
&''(
8
&''& &''/
/
&
(
&
(
-
(
,
,
2
-
//
- !.
0
A0 &''0
/ & /& 0
.
"+)$3 @572
P
>)4&DJE*9A8M#1. '4&<:C / # N:4&JE3QC ?;JE@-L0!KA =, (5G+'O"79A4&<:F$ 'I%(5B2<:C H 6JEA
!"#"$%&'()*%+$', -.%)"/#'012$1.3%02'452"/122'$6'$6)6..672
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如对您有帮助,可购买打赏,谢谢
补水不等于保湿角质层含水量达10%肌肤最健康
导语:冬季肌肤普遍容易干燥皲裂,因此补水和保湿成为冬季肌肤护理的重点。
如何正确补充肌肤水分,而单纯的补水是不是就能满足肌肤的需要?
“为什么我的脸一到冬天就变态?在夏天秋天时还光溜溜油滑滑的皮肤,最近却变得干干涩涩?”每年冬天,就会有无数个女生提出这样的疑问。
为什么冬季肌肤会比其他季节更容易出现状况呢?而这样的情况应该加强哪个护肤步骤来加以改善呢?
角质层变化让肌肤容易脱皮
角质层是皮肤的最外层,对于皮肤屏障功能的完整起着很重要的作用。
角质层中的皮脂膜可以起到锁水的功效,能防止肌肤水分的丢失。
在炎热季节肌肤为抵抗紫外线而角质变厚,但到了秋天因紫外线渐弱,使得已肥厚的角质会逐渐还原至原来的厚度,因而在冬季会感觉到皮肤有明显粉状脱屑现象,皮肤也会有沙沙的特别粗糙的感觉。
肌肤含水量多少最佳?
皮肤水分含量的多少直接决定了皮肤的外观,而角质层是位于皮肤的最外层,因此角质层的含水量也在很大程度上影响着皮肤的外观。
在正常情况下,角质层的含水量应该在10%左右,低于这个水平就是缺水的皮肤了。
补水不等于保湿冬季肌肤如何保湿
补水保湿常常被放在一起讲,因此很多消费者会误认为补水等同于保湿,但是在具体的护肤程序中,补水和保湿是完全不同的两项护肤程序。
补水相当于补充肌肤缺失的水分,而保湿更多的是起到锁住水分不让其流失的作用。
冬季肌肤补水的重点在于及时将肌肤的水分锁住,因此乳液和乳霜
生活中的小知识分享,对您有帮助可购买打赏。
