用MATLAB实现语音信号的时域分析
如何在MATLAB中进行语音信号处理

如何在MATLAB中进行语音信号处理一、引言语音信号处理是一门充满挑战的学科,它涉及到声音的产生、捕捉、转换和处理等一系列过程。
在现代科技的支持下,MATLAB作为一种强大的工具,被广泛应用于语音信号处理领域。
本文将介绍如何使用MATLAB进行语音信号处理,包括信号预处理、语音分析和语音合成等方面。
二、信号预处理在进行语音信号处理之前,我们通常需要对信号进行预处理。
信号预处理的目标是将原始信号进行降噪、滤波和归一化等处理,以便后续的分析和处理。
在MATLAB中,我们可以使用一系列函数来实现信号预处理的过程。
首先,我们可以使用MATLAB提供的降噪算法对信号进行降噪处理。
常用的降噪算法有加性白噪声降噪算法、小波降噪算法等。
通过对原始信号进行降噪处理,可以有效提取出语音信号的有效信息。
其次,我们可以使用滤波技术对信号进行滤波处理。
滤波的目的是去除信号中的不必要成分,保留感兴趣的频率成分。
在MATLAB中,我们可以使用卷积和滤波函数来实现滤波过程。
最后,我们还可以对信号进行归一化处理。
归一化可以使信号的幅值范围在一个确定的范围内,方便后续的处理和比较。
在MATLAB中,我们可以使用归一化函数对信号进行归一化处理。
三、语音分析语音信号的分析是语音信号处理的关键步骤,它可以帮助我们了解信号的基本特征和结构。
在MATLAB中,我们可以使用一系列函数来实现语音信号的分析。
首先,我们可以使用MATLAB提供的时域分析函数对语音信号进行时域分析。
时域分析可以帮助我们了解信号的振幅、频率和相位等特征。
通过时域分析,我们可以得到语音信号的波形图、能谱图和自相关函数等。
其次,我们还可以使用频域分析函数对语音信号进行频域分析。
频域分析可以帮助我们了解信号的频率成分和频率分布等特征。
通过频域分析,我们可以得到语音信号的频谱图、功率谱密度图和谱线图等。
最后,我们还可以使用梅尔频率倒谱系数( MFCC)来提取语音信号的特征。
MFCC是一种广泛应用于语音识别领域的特征提取方法。
实验二 语音信号的时域分析

实验二 语音信号的时域分析1 实验目的通过Matlab 编程实现语音信号的时域波形图,并观察清音、浊音信号的时域特点。
掌握语音信号的时域分析技术,如短时平均能量、短时平均幅度、短时平均过零率分析、短时平均自相关、短时平均幅度差。
2 实验原理语音信号的时域分析就是分析和提取语音信号的时域参数。
时域分析通常用于最基本的参数分析及应用,此方法表示语音信号比较直观,物理意义明确,实现起来比较简单,运算量少。
3 实验过程1)观察浊音信号波形图2)观察清音信号波形图3)计算语音信号的短时能量、短时平均幅度并画图120()N n n m E x m -==∑10|()|N n n m M x m -==∑4)计算信号的短时平均过零率并画图 11{|sgn[()]sgn[(1)]|}2N n n m Zn x m x m -==--∑ 5)计算语音信号的短时自相关函数并画图10()()()N k n n n m R k x m x m k --==+∑6)计算语音信号的短时平均幅度差函数并画图10()|()()|N k n n nm F k x m x m k --==-+∑一.短时能量[x,fs,bits]=wavread('c:\WINDOWS\Media\chimes.wav') x=x(:,1);c=x;x=x';N=256;M=N/2;k=1:N;w=0.54-0.46*cos(2*pi/N*k);Fn=fix((L-N)/M)+1;y=[];for i=1:Fnbeg=(i-1)*M+1;ed=beg+N-1;temp=x(beg:ed);temp=temp.*w;y=[y;temp];endEn=[];k=0;for i=1:Fnx=y(i,:);temp=sum(x.*x,2);En=[En,temp];endEn=sum(y.*y,2);subplot(211);plot(c);subplot(212);plot(En);xlabel('time');ylabel('amplitude');title('picture');二.短时自相关函数[x,fs,bits]=wavread('c:\WINDOWS\Media\chimes.wav') x=x(:,1);x=x';N=256;M=N/2;k=1:N;w=0.54-0.46*cos(2*pi/N*k);Fn=fix((L-N)/M)+1;y=[];for i=1:Fnbeg=(i-1)*M+1;ed=beg+N-1;temp=x(beg:ed);temp=temp.*w;y=[y;temp];endZn=sum(abs(sign(y(2:N))-sign(y(1:N-1))),2)*0.5N=256;K=128;for i=1:Fnr=[];x=y(i,:);for k=1:Kr(k)=sum(x(1:N-k).*x(k+1:N),2);endendplot(r);三.短时平均过零率[x,fs,bits]=wavread('c:\WINDOWS\Media\chimes.wav') x=x(:,1);c=x;x=x';N=256;M=N/2;k=1:N;w=0.54-0.46*cos(2*pi/N*k);Fn=fix((L-N)/M)+1;y=[];for i=1:Fnbeg=(i-1)*M+1;ed=beg+N-1;temp=x(beg:ed);temp=temp.*w;y=[y;temp];endfor i=1:Fnx=y(i,:);Zn1=[0];for k=2:NZ=0.5*abs(sign(x(k))-sign(x(k-1)));Zn1=Zn1+Z;endZn=[Zn,Zn1];endsubplot(211);plot(c);subplot(212);plot(Zn);xlabel('time');ylabel('amplitude');title('picture');四.短时平均幅度[x,fs,bits]=wavread('c:\WINDOWS\Media\chimes.wav') x=x(:,1);c=x;x=x';N=256;M=N/2;w=0.54-0.46*cos(2*pi/N*k); Fn=fix((L-N)/M)+1;y=[];for i=1:Fnbeg=(i-1)*M+1;ed=beg+N-1;temp=x(beg:ed);temp=temp.*w;y=[y;temp];endEn=[];k=0;for i=1:Fnx=y(i,:);temp=sum(abs(x),2);En=[En,temp];endEn=sum(y.*y,2);subplot(211);plot(c);subplot(212);plot(En);xlabel('time');ylabel('amplitude');title('picture');五.短时平均幅度差函数[x,fs,bits]=wavread('c:\WINDOWS\Media\chimes.wav') x=x(:,1);x=x';N=256;M=N/2;k=1:N;w=0.54-0.46*cos(2*pi/N*k);Fn=fix((L-N)/M)+1;y=[];for i=1:Fnbeg=(i-1)*M+1;ed=beg+N-1;temp=x(beg:ed);temp=temp.*w;y=[y;temp];endZn=sum(abs(sign(y(2:N))-sign(y(1:N-1))),2)*0.5N=256;K=128;for i=1:Fnr=[];x=y(i,:);for k=1:KF1(k)=abs(x(M)-x(M+k));endendplot(F1);。
实验二基于MATLAB分析语音信号频域特征

实验二 基于MATLAB 分析语音信号频域特征一、实验目的信号的傅立叶表示在信号的分析与处理中起着重要的作用。
因为对于线性系统来说,可以很方便地确定其对正弦或复指数和的响应,所以傅立叶分析方法能完善地解决许多信号分析和处理问题。
另外,傅立叶表示使信号的某些特性变得更明显,因此,它能更深入地说明信号的各项物理现象。
由于语音信号是随着时间变化的,通常认为,语音是一个受准周期脉冲或随机噪声源激励的线性系统的输出。
输出频谱是声道系统频率响应与激励源频谱的乘积。
声道系统的频率响应及激励源都是随时间变化的,因此一般标准的傅立叶表示虽然适用于周期及平稳随机信号的表示,但不能直接用于语音信号。
由于语音信号可以认为在短时间内,近似不变,因而可以采用短时分析法。
本实验要求掌握傅里叶分析原理,会利用已学的知识,编写程序估计短时谱、倒谱,画出语谱图,并分析实验结果,在此基础上,借助频域分析方法所求得的参数分析语音信号的基音周期或共振峰。
二、实验原理1、短时傅立叶变换由于语音信号是短时平稳的随机信号,某一语音信号帧的短时傅立叶变换的定义为:()()()jwjwmn m X e x m w n m e∞-=-∞=-∑ (1.1)其中w(n-m)是实窗口函数序列,n 表示某一语音信号帧。
令n-m=k',则得到(')'()(')(')jwjw n k n k X e w k x n k e∞--=-∞=-∑ (1.2)于是可以得到()()()jw jwnjwkn k X e ew k x n k e∞-=-∞=-∑ (1.3)假定()()()jwjwkn k X e w k x n k e∞=-∞=-∑ (1.4)则可以得到()()jw jwn jw n n X e e X e -= (1.5)同样,不同的窗口函数,将得到不同的傅立叶变换式的结果。
由上式可见,短时傅立叶变换有两个变量:n 和ω,所以它既是时序n 的离散函数,又是角频率ω的连续函数。
MATLAB语音信号的时域分析

语音信号的时域与频域分析一、用MATLAB实现语音信号的时域分析1.MATLAB程序代码(1)由麦克风采集语音数据,将采集的数据存成WAV文件(采样率为8000Hz),存在本人的文件夹中。
所用程序代码为:clear;close all;Fs=8000;y=wavrecord(5*Fs,Fs,'double');wavwrite(y,'f:\\a');soundview(y,Fs,'name')(2)读取WAV文件,显示语音信号的波形。
所用程序代码为:x=wavread('f:\\a.wav');figure;plot(x);axis([0,size(x,1),-0.35,0.3]);%坐标轴范围title('语音信号时域波形');xlabel('样点数');ylabel('幅度');(3)读取WAV文件,计算并显示语音的短时能量(窗函数为矩形窗,帧长为20)。
所用程序代码为:x=wavread('f:\\a.wav');x=double(x);f=enframe(x,20,100);energy=sum(abs(f),2);subplot(2,2,1);plot(x);axis([0,size(x,1),-0.7,0.9]);title('语音信号时域波形');xlabel('样点数');ylabel('幅度');subplot(2,2,2);plot(energy);title('语音信号的短时能量');legend('帧长LEN=20');f=enframe(x,20,200);energy=sum(abs(f),2);subplot(2,2,3);plot(energy);title('语音信号的短时能量');legend('帧长LEN=100');f=enframe(x,20,400);energy=sum(abs(f),2); subplot(2,2,4);plot(energy);title('语音信号的短时能量');legend('帧长LEN=200');(4)读取WAV文件,计算并显示语音的短时过零率(窗函数为矩形窗,帧长为256,帧移为128),所用程序代码为:x=wavread('f:\\a.wav');x=double(x);LEN=100;INC=100;f=enframe(x,LEN,INC);%分帧%计算短时过零率z=zeros(size(f,1),1);difs=0.01;for i=1:size(f,1)s=f(i,:);for j=1:(length(s)-1)if s(j)*s(j+1)<0&abs(s(j)-s(j+1))>difs;z(i)=z(i)+1;end end endsubplot(2,1,1);plot(x);axis([0,size(x,1),-0.35,0.3]);title('语音信号时域波形');xlabel('样点数');ylabel('幅度');subplot(2,1,2);plot(z); title('语音信号的短时过零率');xlabel('帧数');ylabel('短时过零率');(5)读取WAV文件,当窗函数为矩形窗、帧长为20时,计算一帧浊音的短时自相关函数所用的程序代码为:x=wavread('f:\\a.wav');x=double(x);LEN=100;INC=100;f=enframe(x,LEN,INC);ff=f(72,:);%选取一帧浊音信号ff=ff'.*rectwin(length(ff));%计算短时自相关N=LEN;R=zeros(1,N);for k=1:NR(k)=sum(ff(k:N).*ff(1:N-k+1));endfor k=1:NR1(k)=R(k)/R(1);Endsubplot(2,1,1);plot(ff);axis([0,N,-0.5,0.5])title('加矩形窗的语音帧');xlabel('样点数');ylabel('幅度');subplot(2,1,2);plot(R1);axis([0,N,-1,1])title('加矩形窗的短时自相关函数');xlabel('k');ylabel('R(k)');2.图像及结论(1)利用8000Hz的采样频率对输入的语音信号进行采样,采样点数为40000个,持续时间为4秒,存储格式为double。
基于MATLAB的语音信号时域特性分析_语音信号处理实验报告

南京信息工程大学 实验(实习)报告实验(实习)名称 基于MATLAB 的语音信号时域特性分析 实验(实习)日期 2013.4.18 得分 ___指导教师院电子与信息工程专业电子信息工程年级 班次 姓名 学号一、实验目的语音信号是一种非平稳的时变信号,它携带着各种信息。
在语音编码、语音合成、语音识别和语音增强等语音处理中无一例外需要提取语音中包含的各种信息。
语音信号分析的目的就在与方便有效的提取并表示语音信号所携带的信息。
语音信号分析可以分为时域和变换域等处理方法,其中时域分析是最简单的方法,直接对语音信号的时域波形进行分析,提取的特征参数主要有语音的短时能量,短时平均过零率,短时自相关函数等。
本实验要求掌握时域特征分析原理,并利用已学知识,编写程序求解语音信号的短时过零率、短时能量、短时自相关特征,分析实验结果,并能掌握借助时域分析方法所求得的参数分析语音信号的基音周期及共振峰。
二、实验原理及实验结果1.窗口的选择通过对发声机理的认识,语音信号可以认为是短时平稳的。
在5~50ms 的范围内,语音频谱特性和一些物理特性参数基本保持不变。
我们将每个短时的语音称为一个分析帧。
一般帧长取10~30ms 。
我们采用一个长度有限的窗函数来截取语音信号形成分析帧。
通常会采用矩形窗和汉明窗。
图1.1给出了这两种窗函数在帧长N=50时的时域波形。
0.20.40.60.811.21.41.61.82矩形窗samplew (n )0.10.20.30.40.50.60.70.80.91hanming 窗samplew (n )图1.1 矩形窗和Hamming 窗的时域波形矩形窗的定义:一个N 点的矩形窗函数定义为如下{1,00,()n Nw n ≤<=其他hamming 窗的定义:一个N 点的hamming 窗函数定义为如下0.540.46cos(2),010,()n n NN w n π-≤<-⎧⎨⎩其他=这两种窗函数都有低通特性,通过分析这两种窗的频率响应幅度特性可以发现(如图1.2):矩形窗的主瓣宽度小(4*pi/N ),具有较高的频率分辨率,旁瓣峰值大(-13.3dB ),会导致泄漏现象;汉明窗的主瓣宽8*pi/N ,旁瓣峰值低(-42.7dB ),可以有效的克服泄漏现象,具有更平滑的低通特性。
基于MATLAB的语音信号时域特征分析(

基于MATLAB 的语音信号时域特征分析研究背景及意义:语音信号是一种非平稳的时变信号,它携带着各种信息。
在语音编码、语音合成、语音识别和语音增强等语音处理中无一例外需要提取语音中包含的各种信息。
语音信号分析的目的就在与方便有效的提取并表示语音信号所携带的信息。
语音信号分析可以分为时域和变换域等处理方法,其中时域分析是最简单的方法,直接对语音信号的时域波形进行分析,提取的特征参数主要有语音的短时能量,短时平均过零率, 短视自相关函数。
短时自相关函数自相关函数用于衡量信号自身时间波形的相似性。
清音和浊音的发声机理不同,因而在波形上也存在着较大的差异。
浊音的时间波形呈现出一定的周期性,波形之间相似性较好;清音的时间波形呈现出随机噪声的特性,样点间的相似性较差。
因此,我们用短时自相关函数来测定语音的相似特性。
短时自相关函数定义为:()()()()()n m R k x m w n m x m k w n m k ∞=-∞=-+--∑令'm n m =+´,并且'()()w m w m -=,可以得到:1''''()[()()][()()][()()][()()]N k n m m R k x n m w m x n m k w m k x n m w m x n m k w m k ∞--=-∞==++++=++++∑∑ 图1给出了清音的短时自相关函数波形,图7给出了不同矩形窗长条件下(窗长分别为N=70,N=140,N=210,N=280)浊音的短时自相关函数波形。
由图1.1、图1.2短时自相关函数波形分析可知:清音接近于随机噪声,清音的短时自相关函数不具有周期性,也没有明显突起的峰值,且随着延时k 的增大迅速减小;浊音是周期信号,浊音的短时自相关函数呈现明显的周期性,自相关函数的周期就是浊音信号的周期,根据这个性质可以判断一个语音信号是清音还是浊音,还可以判断浊音的基音周期。
基于MATLAB的语音信号的时、频域分析课程设计

摘要用MATLAB对于语音信号进行分析和处理,采集语音信号后,在MATLAB软件平台进行频谱分析;并对所采集的语音信号加入干扰噪声,对加入噪声的信号进行频谱分析,设计合适的滤波器滤除噪声,恢复原信号。
本次设计介绍了基于MATLAB的对语音信号的采集,处理及滤波器的设计,并使之实现的过程。
关键词:MATLAB;语音信号;滤波器;加噪;除噪目录摘要 (1)1 设计原理 (1)1.1 理论原理 (1)1.1.1采样频率 (1)1.1.2采样位数 (1)1.1.3采样定理 (1)1.1.4时域信号的FFT分析 (2)1.1.5数字信号的滤波器原理和方法 (2)1.1.6 各种不同类型滤波器的性能比较 (3)1.1.7离散傅立叶变换 (3)2 信号采集及读取 (4)3 构造受干扰信号并对其进行FFT频谱分析 (6)4 数字滤波器设计 (8)4.1 用窗函数法设计IIR带通滤波器 (8)4.2 用窗函数法设计FIR低通滤波器 (10)5信号处理 (12)5.1 IIR带通滤波 (12)5.2 FIR低通滤波 (14)6心得体会 (16)7 参考文献: (16)1设计原理1.1 理论原理1.1.1 采样频率也称为采样速度或者采样率,定义了每秒从连续信号中提取并组成离散信号的采样个数,它用赫兹(Hz)来表示。
采样频率只能用于周期性采样的采样器,对于非周期性采样的采样器没有规则限制。
通俗的讲采样频率是指计算机每秒钟采集多少个声音样本,是描述声音文件的音质、音调,衡量声卡、声音文件的质量标准。
采样频率越高,即采样的间隔时间越短,则在单位时间内计算机得到的声音样本数据就越多,对声音波形的表示也越精确。
1.1.2采样位数即采样值或取样值,用来衡量声音波动变化的参数,是指声卡在采集和播放声音文件时所使用数字声音信号的二进制位数。
1.1.3采样定理在进行模拟/数字信号的转换过程中,当采样频率fs.max 大于信号中最高频率fmax的2倍时(fs.max>=2fmax),采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的5~10倍;采样定理又称奈奎斯特定理。
如何使用MATLAB进行语音信号处理与识别

如何使用MATLAB进行语音信号处理与识别引言:语音信号处理与识别是一项应用广泛的领域,它在语音通信、语音识别、音频压缩等方面发挥着重要作用。
在本文中,我们将介绍如何使用MATLAB进行语音信号处理与识别。
首先,我们将讨论语音信号的特征提取,然后介绍常用的语音信号处理方法,最后简要概述语音信号的识别技术。
一、语音信号的特征提取语音信号的特征提取是语音信号处理与识别的重要一环。
在MATLAB中,我们可以通过计算音频信号的频谱特征、时域特征以及声学特征等方式来进行特征提取。
其中,最常见的特征提取方法是基于傅里叶变换的频谱分析方法,比如短时傅里叶变换(STFT)和梅尔频谱倒谱系数(MFCC)。
1. 频谱特征:频谱特征主要包括功率谱密度(PSD)、频谱包络、谱熵等。
在MATLAB中,我们可以使用fft函数来计算信号的频谱,使用pwelch函数来计算功率谱密度,使用spectrogram函数来绘制语谱图等。
2. 时域特征:时域特征主要包括幅度特征、能量特征、过零率等。
在MATLAB中,我们可以使用abs函数来计算信号的幅度谱,使用energy函数来计算信号的能量,使用zcr函数来计算信号的过零率等。
3. 声学特征:声学特征主要包括基频、共振频率等。
在MATLAB中,我们可以通过自相关函数和Cepstral分析等方法来计算声学特征。
二、语音信号处理方法语音信号处理方法主要包括降噪、去除回声、语音增强等。
在MATLAB中,我们可以通过滤波器设计、自适应噪声抑制和频谱减法等方法来实现这些功能。
1. 降噪:降噪通常包括噪声估计和降噪滤波两个步骤。
在MATLAB中,我们可以使用统计模型来估计噪声,然后使用Wiener滤波器或者小波阈值法来降噪。
2. 去除回声:回声是语音通信中的常见问题,我们可以使用自适应滤波器来抑制回声。
在MATLAB中,我们可以使用LMS算法或者NLMS算法来实现自适应滤波。
3. 语音增强:语音增强通常包括增加语音信号的声音清晰度和提高语音的信噪比。
课程设计基于MATLAB的语音信号录制采集和分析的程序设计

MA TLAB课程设计说明书摘要语音信号的采集与分析技术是一门涉及面很广的交叉科学,它的应用和发展与语音学、声音测量学、电子测量技术以及数字信号处理等学科紧密联系。
该设计主要介绍语音信号的采集与分析方法,通过PC机录制自己的一段声音,运用Matlab提供的函数进行仿真分析,并画出采样后语音信号的时域波形和频谱图,对所采集的语音信号加入干扰随机高斯噪声,对加入噪声的信号进行播放,并进行时域和频谱分析;对比加噪前后的时域图和频谱图,分析讨论采用什么样的滤波器进行滤除噪声。
关键词:语音信号;采集与分析;Matlab目录摘要 (I)1 语音信号的录制 (1)2 语音信号的采集 (3)3 语音信号的分析 (4)3.1语音信号时域分析 (4)3.2语音信号频域分析 (5)4 语音信号的加噪处理 (7)5 滤噪设计分析 (11)6 设计总结 (12)参考文献 (13)附录 (14)1 语音信号的录制为了将原始模拟语音信号变为数字信号,必须经过采样和量化两个步骤,从而得到时间和幅度上均为离散的数字语音信号。
语音信号经过预滤波和采样后,由A/D变换器变换为二址制数字码。
这种防混叠滤波通常与模数转换器做在一个集成块内,因此目前来说,语音信号的数字化的质量还是有保证的。
市面上购买到的普通声卡在这方面做的都很好,语音声波通过话筒输入到声卡后直接获得的是经过防混叠滤波、A/D变换、量化处理的离散的数字信号。
将声卡作为对象处理采集语音信号Matlab将声卡作为对象处理,其后的一切操作都不与硬件直接相关,而是通过对该对象的操作来作用于硬件设备(声卡)。
操作时首先要对声卡产生一个模拟输入对象(ai),给ai对象添加一个通道设置采样频率后,就可以启动设备对象,开始采集数据,采集完成后停止对象并删除对象。
实际工作中,我们可以利用windows自带的录音机录制语音文件,图1是基于PC机的语音信号录制过程,声卡可以完成语音波形的A/D转换,获得WAVE文件,为后续的处理储备原材料。
基于Matlab的语音信号分析与处理

集和播放声音文件时所使用数字声音信号的二进制位数。采样频率是指录音设备 在一秒钟内对声音信号的采样次数于音频接口来说是最为重要的两个指标,也是选择音频 接口的两个重要标准。无论采样频率如何,理论上来说采样的位数决定了音频数 据最大的力度范围。每增加一个采样位数相当于力度范围增加了 6dB。采样位数 越多则捕捉到的信号越精确。对于采样率来说你可以想象它类似于一个照相机, 44.1kHz 意味着音频流进入计算机时计算机每秒会对其拍照达 441000 次。显然 采样率越高,计算机摄取的图片越多,对于原始音频的还原也越加精确。
关键字:清浊语音信号采集;傅里叶变换;滤波器设计;信号处理
目录
前 言............................................................................................................................1 一 语音信号特性介绍与采集......................................................................................2
在设计中要用到数字滤波器, 它是数字信号处理中及其重要的一部分。随着 信息时代和数字技术的发展,受到人们越来越多的重视。数字滤波器可以通过数 值运算实现滤波,所以数字滤波器处理精度高、稳定、体积小、重量轻、灵活不 存在阻抗匹配问题,可以实现模拟滤波器无法实现的特殊功能。数字滤波器种类 很多,根据其实现的网络结构或者其冲激响应函数的时域特性,可分为两种,即 有限冲激响应( FIR,Finite Impulse Response)滤波器和无限冲激响应( IIR,Infinite Impulse Response)滤波器。
(完整word版)基于MATLAB对语音信号进行分析和处理

基于MATLAB对语音信号进行分析和处理一、设计目的1.学会MATLAB的使用,掌握MA TLAB的程序设计方法;2.掌握在Windows环境下语音信号采集的方法;3.掌握数字信号处理的基本概念、基本理论和基本方法;4.掌握MATLAB设计FIR和IIR数字滤波器的方法;5.学会用MA TLAB对信号进行分析和处理。
二、设计过程1、语音信号采集与分析运用windows下的录音机,录制一段自己的话音,时间为两秒。
然后在MATLAB 软件平台下,利用函数wavread对语音信号进行采样,再运用plot函数画出语音信号的时域波形,最后在语音信号频谱分析时运用fft对信号进行快速傅里叶变换,得到频谱特性图形。
人为设计一个固定频率5500Hz的噪声干扰信号。
噪声信号通常为随机序列,在本设计中用正弦序列代替,干扰信号构建命令函数为d=[Au*sin(2*pi*5500*t)]',给出的干扰信号为一个正弦信号,针对上面的语音信号 ,采集了其中一段。
再对噪音信号进行频谱变换得到其频谱图。
2、滤波器设计和运用滤波器进行滤波1 )窗函数和等波纹逼近法设计FIR滤波器及滤波首先根据阻带最小衰减选定窗口类型,然后调用fir1函数设计线性相位FIR数字滤波器,再用freqz函数画出其频谱图形,最后运用fftfilt函数对信号进行滤波。
而等波纹逼近法中则运用remez和remezord直接设计FIR滤波器,然后运用fftfilt函数对信号进行滤波。
2 )双线性变换法社设计IIR数字滤波器及滤波首先将数字滤波器的技术指标运用预畸校正法转换成模拟滤波器的设计指标:Ωph=2/T*tan(wp/2),然后用butter、cheby1设计各种模拟滤波器,再用bilinear函数进行模拟滤波器和数字滤波器之间的转换,最后用filter函数对语音信号进行滤波,并运用函数sound播放滤波后语音。
三、结果及分析1、用MATLAB对原始语音信号进行分析,画出它的时域波形和频谱时域波形和频谱:图1 原始语音信号图2 语音信号频率响应图图3 原始语音信号FFT与信号频谱2、给原始的语音信号加上一个高频余弦噪声,频率为5500hz。
基于MATLAB语音信号检测分析及处理

第一章绪论Matlab是矩阵实验室(Matrix Laboratory)的简称,是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括Matlab和Simulink两大部分。
1.1 Matlab简介MATLAB是英文MATrix LABoratory(矩阵实验室)的缩写。
早期的MATLAB 是用FORTRAN语言编写的,尽管功能十分简单,但作为免费软件,还是吸引了大批使用者。
经过几年的校际流传,在John Little。
Cleve Moler和Steve Banger 合作,于1984年成立MathWorks公司,并正式推出MATLAB第一版版。
从这时起,MATLAB的核心采用C语言编写,功能越来越强大,除原有的数值计算功能外,还新增了图形处理功能。
MathWorks公司于1992年推出了具有划时代意义的4.0版;1994年推出了4.2版扩充了4.0版的功能,尤其在图形界面设计方面提供了新方法;1997年春5.0版问世,5.0版支持了更多的数据结构,使其成为一种更方便、更完善的编程语言;1999年初推出的MATLAB5.3版在很多方面又进一步改进了MATLAB语言的功能,随之推出的全新版本的最优化工具箱和Simulink3.0达到了很高水平;2000年10月,MATLAB6.0版问世,在操作页面上有了很大改观,为用户的使用提供了很大方便,在计算机性能方面,速度变的更快,性能也更好,在图形界面设计上更趋合理,与C语言接口及转换的兼容性更强,与之配套的Simulink4.0版的新功能也特别引人注目;2001年6月推出的MATLAB6.1版及Simulink4.1版,功能已经十分强大;2002年6月推出的MATLAB6.5版及Simulink5.0版,在计算方法、图形功能、用户界面设计、编程手段和工具等方面都有了重大改进;2004年,MathWorks公司推出了最新的MA TLAB7.0版,其中集成了最新的MATLAB7编译器、Simumlink6.0仿真软件以及很多工具箱。
基于MATLAB实现对语音信号分析

基于MATLAB实现对语音信号分析语音信号分析是一种研究语音产生、处理和识别的技术,它在语音识别、音频处理和语音合成等领域都有广泛的应用。
MATLAB提供了丰富的工具箱和函数,使得语音信号分析变得简单高效。
在本文中,我们将介绍如何使用MATLAB对语音信号进行分析。
首先,我们需要将语音信号加载到MATLAB中。
MATLAB提供了`audioread`函数用于读取音频文件,返回音频数据和采样率。
音频数据是一个一维向量,表示音频信号的振幅。
采样率则表示每秒采样的样本数。
```matlab[audio, fs] = audioread('speech.wav');```接下来,我们可以对音频信号进行一系列的分析。
以下是一些常见的分析方法:1. 时域分析:时域分析是研究音频信号在时间上的变化。
MATLAB提供了`plot`函数用于绘制音频信号的波形图。
```matlabxlabel('Time (s)');ylabel('Amplitude');title('Speech Waveform');```2. 频谱分析:频谱分析是研究音频信号在频率上的成分。
MATLAB提供了`fft`函数用于计算音频信号的傅里叶变换,返回频谱数据。
频谱数据是一个复数向量,表示音频信号在不同频率上的幅度和相位。
```matlabN = length(audio);frequencies = (0:N-1) / N * fs;spectrum = abs(fft(audio));plot(frequencies, spectrum);xlabel('Frequency (Hz)');ylabel('Magnitude');title('Speech Spectrum');```3. 短时能量和过零率:短时能量和过零率可以反映音频信号的能量和频率特性。
用Matlab编程实现语音信号的短时分析

end
figure(2)
subplot(4,1,2)
jj=[1:240];
plot(jj, Yn1,'b');
grid
%%%%%%清音,取12120--12360个点
%短时自相关函数
temp=Y(12121:12360);
%% %temp2=reshape(temp,1,240);
%temp=temp2.*B;
Mn(ii)=sum(abs(temp))/N;
end
figure(1)
subplot(4,1,2)
jj=[1:(LL-1)*240];
plot(jj, Mn,'b');
grid
% axis([12000,16000,0,0.015])
%短时过零率
Zn=zeros(1,(LL-1)*240);
for ii=2:(LL-1)*240,
for ii=[1:240-nn],
Yn1(nn) =Yn1(nn)+ abs(temp(ii)-temp(nn+ii));
end
end
figure(2)
subplot(4,1,2)
jj=[1:240];
plot(jj, Yn1,'b');
grid
%%%%%%清音,取12120--12360个点
%短时自相关函数
六、附录
源程序:
%没有加窗nowindow.wav
N=240
Y=WAVREAD('nowindow',[1 18000]);
L=length(Y)%30秒,每秒8000个点,一共240000个点
LL=length(Y)/N %一共1000帧
MATLAB技术语音信号处理

MATLAB技术语音信号处理一、引言语音信号处理是一门重要的学科,广泛应用于通信、语音识别、音频处理等领域。
而MATLAB作为一种强大的科学计算软件,为语音信号处理提供了丰富的工具包和函数库。
本文将介绍MATLAB在语音信号处理中的应用和技术。
二、语音信号的获取语音信号是由声音波动产生的振动信号。
在MATLAB中,可以通过调用麦克风设备或读取音频文件的方式获取语音信号。
通过内置函数和工具箱,可以对语音信号进行实时处理或离线处理。
三、语音信号预处理在进行语音信号处理之前,需要对语音信号进行预处理,以滤除噪声和提取关键信息。
MATLAB提供了丰富的预处理函数和工具,如加窗、提取谱特征、语音分割等。
四、语音信号分析语音信号分析是语音信号处理的核心环节之一。
在MATLAB中,可以使用时域分析、频域分析、短时傅里叶变换等方法对语音信号进行分析。
此外,还可以通过小波分析、线性预测分析等技术提取语音信号的特征。
五、语音信号合成通过分析得到的语音信号特征,可以进行语音信号的合成。
MATLAB提供了多种合成算法和函数,如基频周期法、线性预测编码法等。
通过合成技术,可以实现对语音信号的合成和转换。
六、语音信号增强语音信号往往受到环境噪声的影响,降低了语音信号的质量和可理解性。
为了提高语音信号的清晰度和鲁棒性,需要进行语音信号增强。
MATLAB提供了多种经典的语音增强算法,如谱减法、最小均方差法等。
七、语音识别语音识别是将语音信号转化为文本或命令的过程。
MATLAB提供了强大的语音识别工具箱,包括模型训练、特征提取、分类和评估等功能。
通过使用这些工具,可以实现自动语音识别和语音命令控制。
八、语音合成语音合成是通过计算机生成语音信号。
MATLAB提供了多种语音合成算法和工具,如文本到语音转换、语音合成模型等。
通过使用这些工具,可以生成自然流畅的语音信号。
九、语音信号处理应用领域语音信号处理在许多领域都有广泛的应用。
例如,通信领域中的语音编解码、降噪和增强;医学领域中的心脏音频分析和语音识别用于医疗记录;音频处理领域中的音频编辑和转换等。
MATLAB语音信号分析和处理

Computer Knowledge and Technology 电脑知识与技术计算机工程应用技术本栏目责任编辑:梁书第7卷第13期(2011年5月)MATLAB 语音信号分析和处理冯玉亮,孙祥娥(长江大学电子信息信学院,湖北荆州434023)摘要:MATLAB 作为一款具备强大科学计算能力和图形显示功能的软件在科学研究以及实际应用的各个领域得到了广泛的应用。
文章介绍了FFT 频谱分析原理及其显示,MATLAB 中相关函数的功能,滤波器的设计和使用。
在此基础上对实际采集的一段含噪声语音信号进行了相关分析处理,试验证明MATLAB 对语音信号的处理十分简单方便,易于实现。
关键词:语音信号处理;MATLAB ;滤波器;频谱分析中图分类号:TN912文献标识码:A 文章编号:1009-3044(2011)13-3145-03Analysis and Processing Speech Signal Based on MATLABFENG Yu-liang,SUN Xiang-e(Electronic and Information Institute of Yangtze University,Jingzhou 434102,China)Abstract:As a scientific software with the characteristic of powerful computing capability and strong graphical display,Matlab has been widely used in scientific research and practical applications in various fields.This paper introduces the principle of FFT firstly,Matlab fuc -tions about display,filter designing are discribed too.And then,an actual speech signal is analysed and processed by matlab.Though analysis the frequency character of noise and raw speech,the proper filter is designed and the noise is surpressed.Matlab can execute those analysis and peocessing simplely and conveniently.Key words:the speech signal proseccing;matlab;filter;frequency character analysis数字信号处理是一门发展迅速、应用广泛的前沿性学科,加上现在科技的迅速发展,数字信号处理也在逐步向着数字化、可视化、软件化的方向发展。
基于MATLAB的语音信号时域特征分析
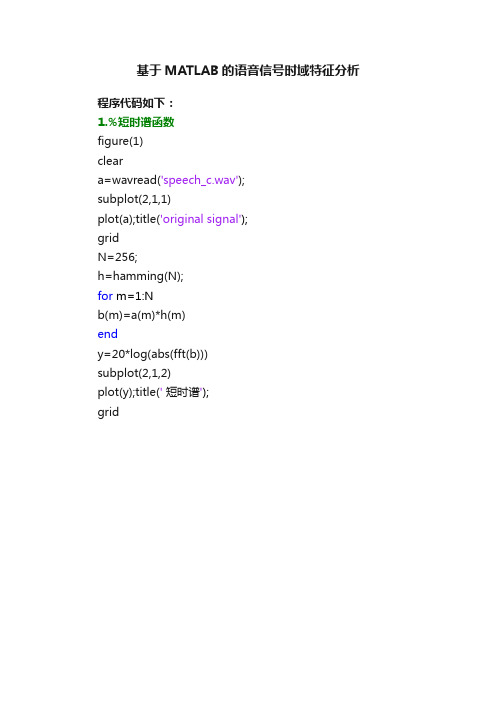
基于MATLAB的语音信号时域特征分析程序代码如下:1.%短时谱函数figure(1)cleara=wavread('speech_c.wav');subplot(2,1,1)plot(a);title('original signal');gridN=256;h=hamming(N);for m=1:Nb(m)=a(m)*h(m)endy=20*log(abs(fft(b)))subplot(2,1,2)plot(y);title(' 短时谱');grid2.%语谱图figure(2)[x,fs,nbits]=wavread('speech_c.wav') specgram(x,512,fs,100);xlabel('时间(s)');ylabel('频率(Hz)');title('语谱图');3.%短时能量figure(3);a=wavread('speech_c.wav');sound(a);subplot(6,1,1),plot(a);N=32;for i=2:6h=linspace(1,1,2.^(i-2)*N); %形成一个矩形窗,长度为2.^(i-2)*NEn=conv(h,a.*a); % 求短时能量函数Ensubplot(6,1,i),plot(En);if(i==2) legend('N=32');elseif(i==3) legend('N=64');elseif(i==4) legend('N=128');elseif(i==5) legend('N=256');elseif(i==6) legend('N=512');endendfigure(4);a=wavread('bird.wav');subplot(6,1,1),plot(a);N=32;for i=2:6h=hanning(2.^(i-2)*N); %形成一个汉明窗,长度为2.^(i-2)*N En=conv(h,a.*a); % 求短时能量函数Ensubplot(6,1,i),plot(En);if(i==2) legend('N=32');elseif(i==3) legend('N=64');elseif(i==4) legend('N=128');elseif(i==5) legend('N=256');elseif(i==6) legend('N=512');endend4 %短时平均过零率figure(5);a=wavread('speech_c.wav');n=length(a);N=320;subplot(3,1,1),plot(a);h=linspace(1,1,N);En=conv(h,a.*a); %求卷积得其短时能量函数En subplot(3,1,2),plot(En);for i=1:n-1if a(i)>=0b(i)= 1;elseb(i) = -1;endif a(i+1)>=0b(i+1)=1;elseb(i+1)= -1;endw(i)=abs(b(i+1)-b(i)); %求出每相邻两点符号的差值的绝对值endk=1;j=0;while (k+N-1)<nZm(k)=0;for i=0:N-1;Zm(k)=Zm(k)+w(k+i);endj=j+1;k=k+N/2; %每次移动半个窗endfor w=1:jQ(w)=Zm(160*(w-1)+1)/(2*N); %短时平均过零率endsubplot(3,1,3),plot(Q);5.%短时自相关函数figure(6)N=240a=wavread('speech_c.wav'); x=a(85001:85240);x=x.*rectwin(240);R=zeros(1,240);for k=1:240for n=1:240-kR(k)=R(k)+x(n)*x(n+k); endendj=1:240;plot(j,R);grid;6.%短时平均幅度figure(7)N=240;L=length(a)LL=length(a)/Na=wavread('speech_c.wav');sound(a);Mn=sum(abs(a))/NMn=zeros(1,(LL-1)*240);for ii=1:(LL-1)*240;temp=a(ii:ii+240);Mn(ii)=sum(abs(temp))/N;endjj=[1:(LL-1)*240];plot(jj, Mn,'b');grid一.实验要求1 以波形和短时频谱的形式表示一个语音片段2 用matlab 产生一个声谱图,然后将它和matlab中的specgram.m文件进行比较以保证正确性3对语音信号的时域波形进行分析,提取的特征参数主要有语音的短时能量,短时平均过零率,短时平均幅度,短时自相关函数等。
语音信号的短时时域分析数字语音处理及MATLAB仿真教学课件

对于随机信号,R(0)对应于平均功率
36
数字语音处理及MATLAB仿真 张雪英编著
3.6.2 语音信号的短时自相关函数
采用短时分析方法,定义语音信号短时自相关函数为
Rn k x mw n m x m k w n k m
每 10ms 内的过零数
过零率概率分布
33
数字语音处理及MATLAB仿真 张雪英编著
端点检测
端点检测目的:从包含语音的一段信号中确 定出语音的起点及结束点。
有效的端点检测不仅能使处理时间减到最少, 而且能抑制无声段的噪声干扰,提高语音处理的 质量。
34
数字语音处理及MATLAB仿真 张雪英编著
3.6 短时自相关分析
3.2.1 语音信号的预加重处理
预加重目的:为了对语音的高频部分进行加重, 去除口唇辐射的影响,增加语音的高频分辨率。 可通过一阶FIR高通数字滤波器来实现:
H (z) 1 z1
设n时刻的语音采样值为x(n) ,经过预加重处理后 的结果为
y(n) x(n) x(n 1)
5
数字语音处理及MATLAB仿真 张雪英编著
几种常见的短时处理方法是: 1. T[x(m)] x2 (m),h(n) w2 (n) Qn 对应于能量; 2. T[x(m)] sgn[x(m,)]sgn[x(m1)],h(n) w(n)
Qn 对应于平均过零率;
3. T[x(m)] x(m)x(mk),hn wnwn k
Qn 对应于自相关函数 ;
3.6.1 短时自相关函数
时域离散确定信号的自相关函数定义为:
R(k)
∑ ∞
xm
xm
利用MATLAB进行时域分析

利用MATLAB进行时域分析时域分析是信号处理中的重要一环,它可以帮助我们了解信号的时域特性和动态行为。
MATLAB是一个功能强大的数学软件,其中的信号处理工具箱可以方便地进行时域分析。
首先,我们需要将信号载入到MATLAB中。
MATLAB支持多种载入信号的方式,如读取文件、生成随机信号或者使用MATLAB中的内置信号。
如果有信号文件,我们可以使用`audioread`函数将音频文件加载到MATLAB中。
如下所示的代码将导入名为`audio.wav`的文件并存储为`y`变量:```matlab[y, Fs] = audioread('audio.wav');```其中,`y`是一个包含音频数据的向量,`Fs`是采样率。
第二步是绘制信号波形。
通过使用`plot`函数,我们可以可视化信号的时域波形。
以下代码将绘制信号`y`的波形:```matlabt = (0:length(y)-1)/Fs; % 计算时间轴plot(t, y);xlabel('Time (s)');ylabel('Amplitude');title('Time Domain Analysis');```这将绘制信号`y`的时间波形,其中x轴表示时间,y轴表示信号的幅度。
接下来,我们可以计算信号的功率谱密度(PSD)。
功率谱密度是用于描述信号频谱特性的一种方法。
MATLAB提供了`pwelch`函数用于计算功率谱密度。
以下代码计算信号`y`的功率谱密度:```matlab[p,f] = pwelch(y,[],[],[],Fs); % 计算功率谱密度plot(f, 10*log10(p));xlabel('Frequency (Hz)');ylabel('Power Spectral Density (dB/Hz)');title('Power Spectral Density');```这将绘制信号`y`的功率谱密度图,其中x轴表示频率,y轴表示功率谱密度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一、用MATLAB实现语音信号的时域分析1.实验目的观察并验证语音信号的时域特性,理解并掌握典型的语音信号时域分析方法和时域特征,为深入学习语音信号处理的各种应用奠定基础。
2.MATLAB程序代码(1)由麦克风采集语音数据,将采集的数据存成WA V文件(采样率为8000Hz),存在本人的文件夹中。
所用程序代码为:clear;close all;Fs=8000;y=wavrecord(5*Fs,Fs,'double');wavwrite(y,'f:\\a');soundview(y,Fs,'name')(2)读取WA V文件,显示语音信号的波形。
所用程序代码为:x = wavread('f:\\a.wav');figure;plot(x);axis([0,size(x,1),-0.35,0.3]); %坐标轴范围title('语音信号时域波形');xlabel('样点数'); ylabel('幅度');(3)读取WA V文件,计算并显示语音的短时能量(窗函数为矩形窗,帧长为20)。
所用程序代码为:x = wavread('f:\\a.wav');x = double(x);f = enframe(x,20, 100);energy = sum(abs(f), 2);subplot(2,2,1);plot(x);axis([0,size(x,1),-0.7,0.9]);title('语音信号时域波形');xlabel('样点数'); ylabel('幅度');subplot(2,2,2);plot(energy);title('语音信号的短时能量');legend('帧长LEN = 20');f = enframe(x,20, 200);energy = sum(abs(f), 2);subplot(2,2,3);plot(energy);title('语音信号的短时能量');legend('帧长LEN = 100');f = enframe(x,20, 400);energy = sum(abs(f), 2);subplot(2,2,4);plot(energy);title('语音信号的短时能量');legend('帧长LEN = 200');(4)读取WA V文件,计算并显示语音的短时过零率(窗函数为矩形窗,帧长为256,帧移为128),所用程序代码为:x = wavread('f:\\a.wav');x = double(x);LEN =100;INC=100;f = enframe(x, LEN, INC); %分帧% 计算短时过零率z = zeros(size(f,1),1);difs =0.01;for i=1:size(f,1)s=f(i,:);for j=1:(length(s)-1)if s(j)* s(j+1)<0&abs(s(j)-s(j+1))>difs;z(i)= z(i)+1;endendendsubplot(2,1,1); plot(x);axis([0,size(x,1),-0.35,0.3]);title('语音信号时域波形'); xlabel('样点数'); ylabel('幅度');subplot(2,1,2);plot(z);title('语音信号的短时过零率');xlabel('帧数'); ylabel('短时过零率');(5)读取WA V文件,当窗函数为矩形窗、帧长为20时,计算一帧浊音的短时自相关函数所用的程序代码为:x = wavread('f:\\a.wav');x = double(x);LEN = 100;INC= 100;f = enframe(x, LEN, INC);ff=f(72,:); %选取一帧浊音信号ff=ff'.*rectwin(length(ff));% 计算短时自相关N=LEN;R=zeros(1,N);for k=1:NR(k)= sum(ff(k:N).*ff(1:N-k+1));endfor k=1:NR1(k)= R(k)/R(1);endsubplot(2,1,1);plot(ff);axis([0,N,-0.5,0.5])title('加矩形窗的语音帧'); xlabel('样点数'); ylabel('幅度');subplot(2,1,2); plot(R1);axis([0,N,-1,1])title('加矩形窗的短时自相关函数'); xlabel('k'); ylabel('R(k)');3.实验结果及其分析(1)本实验利用8000Hz的采样频率对输入的语音信号进行采样,采样点数为40000个,持续时间为4秒,存储格式为double。
之后将数字语音数据写入F盘的a.wav 文件,这段波形是读音为’ke’的波形,并通过放音设备进行回放。
回放的GUI界面如图1所示,通过该界面可以观察采集的语音信号。
图1 用soundview函数显示的语音信号(2)本实验将L盘的a.wav文件读取出来,并显示文件中的语音信号波形,显示的波形如图2所示。
该波形是汉语拼音“ke”的时域波形。
从图2可以看出,[K]是清音,它的波形峰值较低;[e]是浊音,它的波形峰值较高。
0.511.52 2.533.54x 104语音信号时域波形样点数幅度图2 语音“ke ”的时域波形(3)本实验将L 盘的a.wav 文件读取出来,当帧长取不同值时计算语音信号的短时能量,如图3所示。
从图3可以看出,浊音短时能量大,短时平均幅度大,短时过零率低,浊音具有较强的能量值,音段内隐藏信息的能力高。
清音短时能量小,短时平均幅度小,能量值较低,音段内隐藏信息的能力较低;1234x 104-0.50.5语音信号时域波形样点数幅度100200300400051015语音信号的短时能量501001502000510语音信号的短时能量501000510语音信号的短时能量图3 不同帧长对应的短时能量(4)本实验首先读取a.wav 中的语音数据,之后计算每一帧的短时过零率,最后将原始语音信号和短时过零率显示出来,如图4所示。
从图4可以看出,清音的过零率较高,浊音的过零率较低。
0.511.52 2.533.54x 104语音信号时域波形样点数幅度50100150200250300350020406080语音信号的短时过零率帧数短时过零率图4 短时过零率(5)本实验首先读取a.wav 中的语音数据,之后对数据进行分帧加窗处理,帧长为256,帧移为128。
选取其中的一帧浊音(第*帧)并计算这帧的短时自相关函数。
当窗函数分别为矩形窗和汉明窗时,截取的语音信号和短时自相关函数如图5和图6所示。
从图5和图6可以看出,矩形窗能够比汉明窗更明显的显示出第一个峰值。
当窗函数为矩形窗,不同帧长(帧移=帧长)的一帧浊音对应的短时自相关函数如图7和图8所示。
从图7和图8可以看出,帧长越长,越容易区分其最大值。
当窗函数为矩形窗,帧长为256,帧移为128,选取一帧清音,获得的短时自相关函数如图9所示。
从图5和图9可以看出,浊音具有明显的周期性,清音无明显周期。
02468101214161820-0.50.5加矩形窗的语音帧样点数幅度2468101214161820-1-0.500.51加矩形窗的短时自相关函数kR (k )图5 加矩形窗的短时自相关函数050100150200250-0.50.5加汉明窗的语音帧样点数幅度50100150200250-1-0.500.51加矩形窗的短时自相关函数kR (k )图6 加汉明窗的短时自相关函数-0.50.5加矩形窗的语音帧样点数幅度-1-0.500.51加矩形窗的短时自相关函数kR (k )图7 帧长为50时的短时自相关函数0102030405060708090100-0.50.5加矩形窗的语音帧样点数幅度102030405060708090100-1-0.500.51加矩形窗的短时自相关函数kR (k )图8 帧长为100时的短时自相关函数0102030405060708090100-0.50.5一帧清音样点数幅度102030405060708090100-1-0.500.51短时自相关函数kR (k )图9 清音的短时自相关函数4. 思考题短时能量的主要用途有哪些?答:可以区分清音段与浊音段,可以用来区分,有声与无声的分界,生母和韵母的分界等,也可以用于语音识别中。
