七年级(下)数学培优试题(一)含答案
(完整版)初一数学下册相交线与平行线试题(带答案) (一)培优试卷
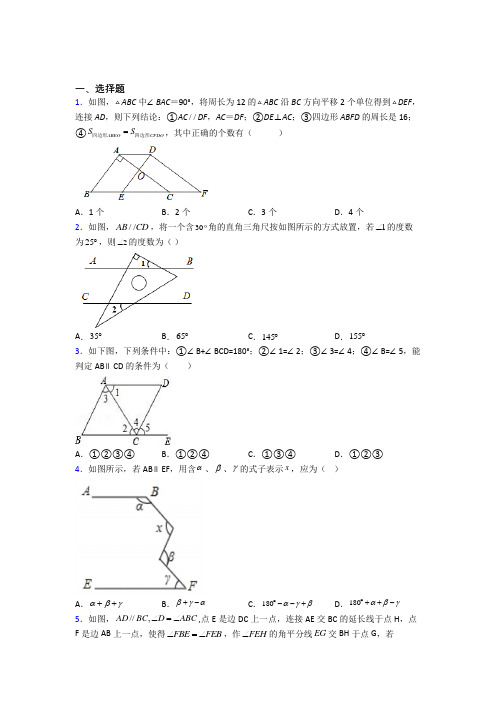
一、选择题1.如图,ABC 中∠BAC =90°,将周长为12的ABC 沿BC 方向平移2个单位得到DEF ,连接AD ,则下列结论:①AC //DF ,AC =DF ;②DE ⊥AC ;③四边形 ABFD 的周长是16;④ABEO CFDO S S =四边形四边形,其中正确的个数有( )A .1个B .2个C .3个D .4个2.如图,//AB CD ,将一个含30角的直角三角尺按如图所示的方式放置,若1∠的度数为25︒,则2∠的度数为( )A .35︒B .65︒C .145︒D .155︒3.如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB ∥CD 的条件为( )A .①②③④B .①②④C .①③④D .①②③ 4.如图所示,若AB ∥EF ,用含α、β、γ的式子表示x ,应为( )A .αβγ++B .βγα+-C .180αγβ︒--+D .180αβγ︒++- 5.如图,//,AD BC D ABC ∠=∠,点E 是边DC 上一点,连接AE 交BC 的延长线于点H ,点F 是边AB 上一点,使得FBE FEB ∠=∠,作FEH ∠的角平分线EG 交BH 于点G ,若100DEH ︒∠=,则BEG ∠的度数是( )A .30︒B .40︒C .50︒D .60︒6.如图,//AB CD ,PF CD ⊥于F ,40AEP ∠=︒,则EPF ∠的度数是( )A .120︒B .130︒C .140︒D .150︒7.如图,已知直线AB ,CD 被直线AC 所截,AB ∥CD ,E 是平面内CD 上方的一点(点E 不在直线AB ,CD ,AC 上),设∠BAE =α,∠DCE =β.下列各式:①α+β,②α﹣β,③β﹣α,④180°﹣α﹣β,⑤360°﹣α﹣β中,∠AEC 的度数可能是( )A .①②③B .①②④⑤C .①②③⑤D .①②③④⑤ 8.如图,从①12∠=∠,②C D ∠=∠,③//DF AC 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )A .0B .1C .2D .39.如图,直线a ,b 被直线c ,d 所截,若12∠=∠,3125∠=︒,则4∠的度数是( )A .65︒B .60︒C .55︒D .75︒ 10.如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( )A .50°、130°B .都是10°C .50°、130°或10°、10°D .以上都不对 二、填空题11.如图,已知//AB CD ,CE 、BE 的交点为E ,现作如下操作:第一次操作,分别作ABE ∠和DCE ∠的平分线,交点为1E ,第二次操作,分别作1ABE ∠和1DCE ∠的平分线,交点为2E ,第三次操作,分别作2ABE ∠和2DCE ∠的平分线,交点为3E ,…,第n 次操作,分别作1n ABE -∠和1n DCE -∠的平分线,交点为n E .若BEC α∠=,则n E ∠的度数是__________.12.如图,已知AB ∥CD ,点E ,F 分别在直线AB ,CD 上点P 在AB ,CD 之间且在EF 的左侧.若将射线EA 沿EP 折叠,射线FC 沿FP 折叠,折叠后的两条射线互相垂直,则∠EPF 的度数为 _____.13.如图,在平面内,两条直线1l ,2l 相交于点O ,对于平面内任意一点M ,若p ,q 分别是点M 到直线1l ,2l 的距离,则称(,)p q 为点M 的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有________个.14.某段铁路两旁安置了两座可旋转探照灯,主道路是平行,即PQ ∥MN . 如图所示,灯A 射线从AM 开始顺时针旋转至AN 便立即回转,灯B 射线从BP 开始顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视.若灯A 转动的速度是每秒2度,灯B 转动的速度是每秒1度. 若灯B 射线先转动30秒,灯A 射线才开始转动,在灯B 射线到达BQ 之前,A 灯转动_________秒,两灯的光束互相平行.15.如图,AB ∥CD ,点P 为CD 上一点,∠EBA 、∠EPC 的角平分线于点F ,已知∠F =40°,则∠E =_____度.16.如图,已知∠A =(60﹣x )°,∠ADC =(120+x )°,∠CDB =∠CBD ,BE 平分∠CBF ,若∠DBE =59°,则∠DFB =___.17.如图,已知//AB CD ,BF 平分ABE ∠,//BF DE ,且40D ∠=︒,则BED ∠的度数为______.18.如图,//AB DE ,AD AB ⊥,AE 平分BAC ∠交BC 于点F .如果24CAD ∠=︒,则=E ∠__︒.19.如图,在长方形ABCD 中,4AB =,6BC =,将长方形ABCD 沿着BC 方向平移得到长方形A B C D ''''.若ABB A ''是正方形,则四边形ABC D ''的周长是______.20.如图,直线//MN PQ ,MN 与直线AB ,AC 分别交于D ,E ,PQ 与直线AB ,AC 分别交于F ,G ,若75C ∠=︒,26BGF ∠=︒,则AEN ∠=_________度.三、解答题21.如图,直线//PQ MN ,点C 是PQ 、MN 之间(不在直线PQ ,MN 上)的一个动点.(1)如图1,若1∠与2∠都是锐角,请写出C ∠与1∠,2∠之间的数量关系并说明理由; (2)把直角三角形ABC 如图2摆放,直角顶点C 在两条平行线之间,CB 与PQ 交于点D ,CA 与MN 交于点E ,BA 与PQ 交于点F ,点G 在线段CE 上,连接DG ,有BDF GDF ∠=∠,求AEN CDG∠∠的值; (3)如图3,若点D 是MN 下方一点,BC 平分PBD ∠, AM 平分CAD ∠,已知25PBC ∠=︒,求ACB ADB ∠+∠的度数.22.如图,//MN PQ ,直线AD 与MN 、PQ 分别交于点A 、D ,点B 在直线PQ 上,过点B 作BG AD ⊥,垂足为点G .(1)如图1,求证:90MAG PBG ∠+∠=︒;(2)若点C 在线段AD 上(不与A 、D 、G 重合),连接BC ,MAG ∠和PBC ∠的平分线交于点H 请在图2中补全图形,猜想并证明CBG ∠与AHB ∠的数量关系;23.已知,如图:射线PE 分别与直线AB 、CD 相交于E 、F 两点,PFD ∠的角平分线与直线AB 相交于点M ,射线PM 交CD 于点N ,设PFM α∠=︒,EMF β∠=︒且()2350αβα-+-=.(1)α=________,β=________;直线AB 与CD 的位置关系是______;(2)如图,若点G 是射线MA 上任意一点,且MGH PNF ∠=∠,试找出FMN ∠与GHF ∠之间存在一个什么确定的数量关系?并证明你的结论.(3)若将图中的射线PM 绕着端点P 逆时针方向旋转(如图)分别与AB 、CD 相交于点1M 和点1N 时,作1PM B ∠的角平分线1M Q 与射线FM 相交于点Q ,问在旋转的过程中1FPN Q∠∠的值变不变?若不变,请求出其值;若变化,请说明理由.24.如图1,点E 在直线AB 、DC 之间,且180DEB ABE CDE ∠+∠-∠=︒.(1)求证://AB DC ;(2)若点F 是直线BA 上的一点,且BEF BFE ∠=∠,EG 平分DEB ∠交直线AB 于点G ,若20D ∠=︒,求FEG ∠的度数;(3)如图3,点N 是直线AB 、DC 外一点,且满足14CDM CDE ∠=∠,14ABN ABE ∠=∠,ND 与BE 交于点M .已知()012CDM αα∠=︒<<︒,且//BN DE ,则NMB ∠的度数为______(请直接写出答案,用含α的式子表示).25.如图,已知直线12//l l ,点A B 、在直线1l 上,点C D 、在直线2l 上,点C 在点D 的右侧,()80,2,ADC ABC n BE ∠=︒∠=︒平分,ABC DE ∠平分ADC ∠,直线BE DE 、交于点E .(1)若20n =时,则BED ∠=___________;(2)试求出BED ∠的度数(用含n 的代数式表示);(3)将线段BC 向右平行移动,其他条件不变,请画出相应图形,并直接写出BED ∠的度数.(用含n 的代数式表示)【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据平移的性质逐一判定即可.【详解】解:∵将ABC 沿BC 向右平移2个单位得到DEF ,∴AC //DF ,AC =DF ,AB =DE ,BC =EF ,AD =BE =CF =2,∠BAC =∠EDF =90°, ∴ED ⊥DF ,四边形ABFD 的周长=AB +BC +CF +DF +AD =12+2+2=16.∵S △ABC =S △DEF ,∴S △ABC ﹣S △OEC =S △DEF ﹣S △OEC ,∴S 四边形ABEO =S 四边形CFDO ,即结论正确的有4个.故选:D.【点睛】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.也考查了平移的距离以及图形的面积.2.A解析:A【分析】过三角板60°角的顶点作直线EF∥AB,则EF∥CD,利用平行线的性质,得到∠3+∠4=∠1+∠2=60°,代入计算即可.【详解】如图,过三角板60°角的顶点作直线EF∥AB,∵AB∥CD,∴EF∥CD,∴∠3=∠1,∠4=∠2,∵∠3+∠4=60°,∴∠1+∠2=60°,∵∠1=25°,∴∠2=35°,故选A.【点睛】本题考查了平行线的辅助线构造,平行线的判定与性质,三角板的意义,熟练掌握平行线的判定与性质是解题的关键.3.C解析:C【详解】解:①∵∠B+∠BCD=180°,∴AB∥CD;②∵∠1=∠2,∴AD∥BC;③∵∠3=∠4,∴AB∥CD;④∵∠B=∠5,∴AB∥CD;∴能得到AB∥CD的条件是①③④.故选C.【点睛】此题主要考查了平行线的判定,解题关键是合理利用平行线的判定,确定同位角、内错角、同旁内角. 平行线的判定:同旁内角互补,两直线平行;内错角相等,两直线平行;同位角相等,两直线平行.4.C解析:C【分析】过C作CD∥AB,过M作MN∥EF,推出AB∥CD∥MN∥EF,根据平行线的性质得出α+∠BCD=180°,∠DCM=∠CMN,∠NMF=γ,求出∠BCD=180°-α,∠DCM=∠CMN=β-γ,即可得出答案.【详解】过C作CD∥AB,过M作MN∥EF,∵AB∥EF,∴AB∥CD∥MN∥EF,∴α+∠BCD=180°,∠DCM=∠CMN,∠NMF=γ,∴∠BCD=180°-α,∠DCM=∠CMN=β-γ,∴x=∠BCD+∠DCM=180αγβ︒--+,故选:C.【点睛】本题考查了平行线的性质的应用,主要考查了学生的推理能力.5.B解析:B【分析】AD∥BC,∠D=∠ABC,则AB∥CD,则∠AEF=180°-∠AED-∠BEG=180°-2β,在△AEF中,100°+2α+180°-2β=180°,故β-α=40°,即可求解.【详解】解:设FBE=∠FEB=α,则∠AFE=2α,∠FEH的角平分线为EG,设∠GEH=∠GEF=β,AD∥BC,∴∠ABC+∠BAD=180°,而∠D=∠ABC,∴∠D+∠BAD=180°,∴AB∥CD,∠DEH=100°,则∠CEH=∠FAE=80°,∠AEF=180°-∠FEG-∠BEG=180°-2β,在△AEF中,在△AEF中,80°+2α+180-2β=180°故β-α=40°,而∠BEG=∠FEG-∠FEB=β-α=40°,故选:B.【点睛】此题考查平行线的性质,解题关键是落脚于△AEF内角和为180°,即100°+2α+180°-2β=180°,题目难度较大.6.B解析:B【分析】过点P作MN∥AB,结合垂直的定义和平行线的性质求∠EPF的度数.【详解】解:如图,过点P作MN∥AB,∵∠AEP=40°,∴∠EPN=∠AEP=40°∵AB∥CD,PF⊥CD于F,∴PF⊥MN,∴∠NPF=90∴∠EPF=∠EPN+∠NPF=40°+90°=130°故答案为B【点睛】本题考查了平行线的判定定理和性质,作出辅助线构造平行线是解答本题的关键.7.C解析:C【分析】根据点E有6种可能位置,分情况进行讨论,依据平行线的性质以及三角形外角性质进行计算求解即可.【详解】解:(1)如图1,由AB∥CD,可得∠AOC=∠DCE1=β,∵∠AOC=∠BAE1+∠AE1C,∴∠AE1C=β﹣α.(2)如图2,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,∴∠AE2C=α+β.(3)如图3,由AB∥CD,可得∠BOE3=∠DCE3=β,∵∠BAE3=∠BOE3+∠AE3C,∴∠AE3C=α﹣β.(4)如图4,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,∴∠AE4C=360°﹣α﹣β.综上所述,∠AEC的度数可能是β﹣α,α+β,α﹣β,360°﹣α﹣β.故选:C.【点睛】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同位角相等;两直线平行,内错角相等.8.D解析:D【分析】分别任选其中两个条件作为已知,然后结合平行线的判定与性质,证明剩余一个条件是否成立即可.【详解】解:如图所示:(1)当①∠1=∠2,则∠3=∠2,故DB∥EC,则∠D=∠4;当②∠C=∠D,故∠4=∠C,则DF∥AC,可得:∠A=∠F,即①②可证得③;(2)当①∠1=∠2,则∠3=∠2,故DB∥EC,则∠D=∠4,当③∠A=∠F,故DF∥AC,则∠4=∠C,故可得:∠C=∠D,即①③可证得②;(3)当③∠A=∠F,故DF∥AC,则∠4=∠C,当②∠C=∠D,则∠4=∠D,故DB∥EC,则∠2=∠3,可得:∠1=∠2,即②③可证得①.故正确的有3个.故选:D.【点睛】本题主要考查了平行线的判定和性质,正确掌握并熟练运用平行线的判定与性质是解题关键.9.C解析:C【分析】首先证明a∥b,推出∠4=∠5,求出∠5即可.【详解】解:∵∠1=∠2,∴a∥b,∴∠4=∠5,∵∠5=180°﹣∠3=55°,∴∠4=55°,故选:C.【点睛】本题考查平行线的判定和性质,解题的关键是熟练掌握基本知识,属于中考常考题型.10.C解析:C【分析】首先由两个角的两边分别平行,可得这两个角相等或互补.然后设其中一角为x°,由其中一个角比另一个角的3倍少20°,然后分别从两个角相等与互补去分析,即可求得答案,注意别漏解.【详解】解:∵两个角的两边分别平行,∴这两个角相等或互补.设其中一角为x°,若这两个角相等,则x=3x﹣20,解得:x=10,∴这两个角的度数是10°和10°;若这两个角互补,则180﹣x=3x﹣20,解得:x=50,∴这两个角的度数是50°和130°.∴这两个角的度数是50°、130°或10°、10°.故选:C.【点睛】此题考查了平行线的性质与一元一次方程的解法.此题难度适中,解题的关键是掌握如果两个角的两边分别平行,则这两个角相等或互补,注意方程思想的应用.二、填空题11.【分析】先过E作EF∥AB,根据AB∥CD,得出AB∥EF∥CD,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE;根据∠ABE和∠DCE的平分线交点为E1,解析:12n α⎛⎫⎪⎝⎭【分析】先过E作EF∥AB,根据AB∥CD,得出AB∥EF∥CD,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE;根据∠ABE和∠DCE的平分线交点为E1,则可得出∠CE1B=∠ABE1+∠DCE1=12∠ABE+12∠DCE=12∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2=12∠ABE1+12∠DCE1=12∠CE1B=14∠BEC;根据∠ABE2和∠DCE2的平分线,交点为E3,得出∠BE3C=18∠BEC;…据此得到规律∠E n=n12∠BEC,最后求得度数.【详解】如图1,过E作EF∥AB.∵AB∥CD,∴AB∥EF∥CD,∴∠B=∠1,∠C=∠2.∵∠BEC=∠1+∠2,∴∠BEC=∠ABE+∠DCE;如图2:∵∠ABE 和∠DCE 的平分线交点为E 1,∴∠CE 1B =∠ABE 1+∠DCE 1=12∠ABE +12∠DCE =12∠BEC .∵∠ABE 1和∠DCE 1的平分线交点为E 2,∴∠BE 2C =∠ABE 2+∠DCE 2=12∠ABE 1+12∠DCE 1=12∠CE 1B =14∠BEC ; ∵∠ABE 2和∠DCE 2的平分线,交点为E 3,∴∠BE 3C =∠ABE 3+∠DCE 3=12∠ABE 2+12∠DCE 2=12∠CE 2B =18∠BEC ; …以此类推,∠E n =n12∠BEC , ∵BEC α∠=, ∴n E ∠的度数是12n⎛⎫ ⎪⎝⎭α. 故答案为:12n ⎛⎫ ⎪⎝⎭α. 【点睛】本题考查了角平分线的定义以及平行线性质:两直线平行,内错角相等的运用.解决问题的关键是作平行线构造内错角,解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线. 12.45°或135°【分析】根据题意画出图形,然后利用平行线的性质得出∠EMF 与∠AEM 和∠CFM 的关系,然后可得答案.【详解】解:如图1,过作,,,,,,,同理可得,由折叠可解析:45°或135°【分析】根据题意画出图形,然后利用平行线的性质得出∠EMF 与∠AEM 和∠CFM 的关系,然后可得答案.【详解】解:如图1,过M 作//MN AB ,//AB CD ,////AB CD NM ∴,AEM EMN ∴∠=∠,NMF MFC ∠=∠,90EMF ∠=︒,90AEM CFM ∴∠+∠=︒,同理可得P AEP CFP ∠=∠+∠, 由折叠可得:12AEP PEM AEM ∠=∠=∠,12PFC PFM CFM ∠=∠=∠, 1()452P AEM CFM ∴∠=∠+∠=︒, 如图2,过M 作//MN AB ,//AB CD ,////AB CD NM ∴,180AEM EMN ∴∠+∠=︒,180NMF MFC ∠+∠=︒,360AEM EMF CFM ∴∠+∠+∠=︒,90EMF ∠=︒,36090270AEM CFM ∴∠+∠=︒-︒=︒, 由折叠可得:12AEP PEM AEM ∠=∠=∠,12PFC PFM CFM ∠=∠=∠, 12701352P ∴∠=︒⨯=︒, 综上所述:EPF ∠的度数为45︒或135︒,故答案为:45°或135°.【点睛】本题主要考查了平行线的性质,关键是正确画出图形,分两种情况分别计算出∠EPF 的度数.13.4【分析】到的距离是2的点,在与平行且与的距离是2的两条直线上;同理,点在与的距离是1的点,在与平行,且到的距离是1的两直线上,四条直线的距离有四个交点.因而满足条件的点有四个.【详解】解:解析:4【分析】到1l 的距离是2的点,在与1l 平行且与1l 的距离是2的两条直线上;同理,点M 在与2l 的距离是1的点,在与2l 平行,且到2l 的距离是1的两直线上,四条直线的距离有四个交点.因而满足条件的点有四个.【详解】解:到1l 的距离是2的点,在与1l 平行且与1l 的距离是2的两条直线上;到2l 的距离是1的点,在与2l 平行且与2l 的距离是1的两条直线上;以上四条直线有四个交点,故“距离坐标”是(2,1)的点共有4个.故答案为:4.【点睛】本题主要考查了到直线的距离等于定长的点的集合.14.30或110【分析】分两种情况讨论:两束光平行;两束光重合之后(在灯B射线到达BQ之前)平行,然后利用平行线的性质求解即可.【详解】解:设灯转动t秒,两灯的光束互相平行,即AC∥BD,①当解析:30或110【分析】分两种情况讨论:两束光平行;两束光重合之后(在灯B射线到达BQ之前)平行,然后利用平行线的性质求解即可.【详解】解:设灯转动t秒,两灯的光束互相平行,即AC∥BD,①当0<t≤90时,如图1所示:∵PQ∥MN,则∠PBD=∠BDA,∵AC∥BD,则∠CAM=∠BDA,∴∠PBD=∠CAM有题意可知:2t=30+t解得:t=30,②当90<t<150时,如图2所示:∵PQ∥MN,则∠PBD+∠BDA=180°,∵AC∥BD,则∠CAN=∠BDA,∴∠PBD+∠CAN=180°,∴30+t+(2t-180)=180解得:t=110综上所述,当t=30秒或t=110秒时,两灯的光束互相平行.故答案为:30或110【点睛】本题主要考查补角、角的运算、平行线的性质的应用,解题的关键是熟练掌握平行线的性质,注意分两种情况谈论.15.80【详解】如图,根据角平分线的性质和平行线的性质,可知∠FMA=∠CPE=∠F+∠1,∠ANE=∠E+2∠1=∠CPE=2∠FMA,即∠E=2∠F=2×40°=80°.故答案为80.解析:80【详解】如图,根据角平分线的性质和平行线的性质,可知∠FMA=12∠CPE=∠F+∠1,∠ANE=∠E+2∠1=∠CPE=2∠FMA,即∠E=2∠F=2×40°=80°.故答案为80.16.【分析】根据题意可得,设,分别表示出,进而根据平行线的性质可得∠DFB.【详解】∠A=(60﹣x)°,∠ADC=(120+x)°,,,,,,BE 平分∠CBF ,,设,∠DB解析:62︒【分析】根据题意可得//AB CD ,设EBF EBC α∠=∠=,分别表示出,ABD DBF ∠∠,进而根据平行线的性质可得∠DFB .【详解】∠A =(60﹣x )°,∠ADC =(120+x )°,180A ADC ∴∠+∠=︒,//AB CD ∴,CDB ABD ∴∠=∠,CDB CBD ∠=∠,ABD CBD ∴∠=∠,BE 平分∠CBF ,EBF EBC ∴∠=∠,设EBF EBC α∠=∠=,∠DBE =59°,∴59DBF α∠=︒-,59ABD DBC α∴∠=∠=︒+,5959118ABF ABD DBF αα∴∠=∠+∠=︒++︒-=︒,//AB CD ,180********DFB ABF ∴∠=︒-∠=︒-︒=︒.故答案为:62︒.【点睛】本题考查了平行线的判定与性质,角平分线的定义,证明//AB CD 是解题的关键. 17.140°【分析】延长DE 交AB 的延长线于G ,根据两直线平行,内错角相等可得∠D =∠AGD ,再根据两直线平行,同位角相等可得∠AGD =∠ABF ,然后根据角平分线的定义得∠EBF =∠ABF ,再根据平解析:140°【分析】延长DE 交AB 的延长线于G ,根据两直线平行,内错角相等可得∠D =∠AGD ,再根据两直线平行,同位角相等可得∠AGD =∠ABF ,然后根据角平分线的定义得∠EBF =∠ABF ,再根据平行线的性质解答.【详解】解:如图,延长DE 交AB 的延长线于G ,∵//AB CD ,∴∠D =∠AGD =40°,∵BF //DE ,∴∠AGD =∠ABF =40°,∵BF 平分∠ABE ,∴∠EBF =∠ABF =40°,∵BF //DE ,∴∠BED =180°﹣∠EBF =140°.故答案为:140°.【点睛】本题考查了平行线的性质,角平分线的定义,熟记性质并作辅助线是解题的关键. 18.33【分析】根据求出∠C=90°,再求出∠BAD=66°,根据角平分线性质得∠DAE=33°,由三角形的外角性质得∠ADE=114°,最后由三角形内角和定理可得结论.【详解】解:∵,,∴∠解析:33【分析】根据//AB DE 求出∠C=90°,再求出∠BAD=66°,根据角平分线性质得∠DAE=33°,由三角形的外角性质得∠ADE=114°,最后由三角形内角和定理可得结论.【详解】解:∵//AB DE ,AD AB ⊥,∴∠180BAD D ∠+∠=︒,且90BAD ∠=︒∴90D ∠=︒∵∠CAD =24°∴∠BAC =90°-∠CAD =90°-24°=66°,∵AE 是∠BAC 的平分线∴∠EAB =11663322BAC ∠=⨯︒=︒ ∵//AB DE ,∴33E EAB ∠=∠=︒故答案为:33【点睛】此题主要考查了平行线的性质,角平分线的定义,准确识图,灵活运用相关知识是解题的关键.19.28【分析】根据平移的性质求出,再由长方形的周长公式求解即可.【详解】解:由题意可知,四边形是正方形,∴,,又∵长方形由长方形平移得到,∴∵∴四边形的周长为:故答案为:28【点解析:28【分析】根据平移的性质求出10BC '=,再由长方形的周长公式求解即可.【详解】解:由题意可知,四边形ABB A ''是正方形,∴4BB AB '==,642B C BC '==-=,又∵长方形A B C D ''''由长方形ABCD 平移得到,∴6B C BC ''==∵4610BC BB B C ''''=+=+=∴四边形ABC D '的周长为:(104)228+⨯=故答案为:28【点睛】此题主要考查了平移的性质,求出10BC '=是解答此题的关键.20.131【分析】过点C 作CH ∥MN ,根据平行线的性质求出∠NEC 即可.【详解】解:过点C 作CH ∥MN ,∵,∴CH ∥PQ ,∴,∵,∴,∵CH ∥MN ,∴,∴故答案为:131.解析:131【分析】过点C 作CH ∥MN ,根据平行线的性质求出∠NEC 即可.【详解】解:过点C 作CH ∥MN ,∵//MN PQ ,∴CH ∥PQ ,∴26HCB BGF ∠=∠=︒,∵75ACB ∠=︒,∴49ACH ∠=︒,∵CH ∥MN ,∴49CEN ACH ∠=∠=︒,∴131180CEN AEN ∠︒∠==︒-故答案为:131.【点睛】本题考查了平行线的性质与判定,解题关键是恰当作平行线,根据平行线的性质进行推理计算.三、解答题21.(1)见解析;(2)12;(3)75°【分析】(1)根据平行线的性质、余角和补角的性质即可求解.(2)根据平行线的性质、对顶角的性质和平角的定义解答即可.(3)根据平行线的性质和角平分线的定义以及三角形内角和解答即可.【详解】解:(1)∠C=∠1+∠2,证明:过C作l∥MN,如下图所示,∵l∥MN,∴∠4=∠2(两直线平行,内错角相等),∵l∥MN,PQ∥MN,∴l∥PQ,∴∠3=∠1(两直线平行,内错角相等),∴∠3+∠4=∠1+∠2,∴∠C=∠1+∠2;(2)∵∠BDF=∠GDF,∵∠BDF=∠PDC,∴∠GDF=∠PDC,∵∠PDC+∠CDG+∠GDF=180°,∴∠CDG+2∠PDC=180°,∴∠PDC=90°-12∠CDG,由(1)可得,∠PDC+∠CEM=∠C=90°,∴∠AEN=∠CEM,∴190(90)90122CDGAEN CEM PDCCDG CDG CDG CDG︒-︒-∠∠∠︒-∠====∠∠∠∠,(3)设BD交MN于J.∵BC平分∠PBD,AM平分∠CAD,∠PBC=25°,∴∠PBD=2∠PBC=50°,∠CAM=∠MAD,∵PQ∥MN,∴∠BJA=∠PBD=50°,∴∠ADB=∠AJB-∠JAD=50°-∠JAD=50°-∠CAM,由(1)可得,∠ACB=∠PBC+∠CAM,∴∠ACB+∠ADB=∠PBC+∠CAM+50°-∠CAM=25°+50°=75°.【点睛】本题考查了平行线的性质、余角和补角的性质,解题的关键是根据平行找出角度之间的关系.22.(1)证明见解析;(2)补图见解析;当点C 在AG 上时,290AHB CBG ∠-∠=︒;当点C 在DG 上时,290AHB CBG ∠+∠=︒.【分析】(1)过点G 作//GE MN ,根据平行线的性质即可求解;(2)分两种情况:当点C 在AG 上,当点C 在DG 上,再过点H 作//HF MN 即可求解.【详解】(1)证明:如图,过点G 作//GE MN ,∴MAG AGE ∠=∠,∵//MN PQ ,∴//GE PQ .∴PBG BGE ∠=∠.∵BG AD ⊥,∴90AGB ∠=︒,∴90MAG PBG AGE BGE AGB ∠+∠=∠+∠=∠=︒.(2)补全图形如图2、图3,猜想:290AHB CBG ∠-∠=︒或290AHB CBG ∠+∠=︒.证明:过点H 作//HF MN .∴1AHF ∠=∠.∵//MN PQ ,∴//HF PQ∴2BHF ∠=∠,∴12AHB AHF BHF ∠=∠+∠=∠+∠.∵AH 平分MAG ∠,∴21MAG ∠=∠.如图3,当点C 在AG 上时,∵BH 平分PBC ∠,∴22PBC PBG CBG ∠=∠+∠=∠,∵//MN PQ ,∴MAG GDB ∠=∠,2212290AHB MAG PBG CBGGDB PBG CBG CBG∴∠=∠+∠=∠+∠+∠=∠+∠+∠=︒+∠即290AHB CBG ∠-∠=︒.如图2,当点C 在DG 上时,∵BH 平分PBC ∠,∴22PBC PBG CBG ∠=∠-∠=∠.∴2212290AHB MAG PBG CBG CBG ∠=∠+∠=∠+∠-∠=︒-∠.即290AHB CBG ∠+∠=︒.【点睛】本题考查了平行线的基本性质、角平分线的基本性质及角的运算,解题的关键是准确作出平行线,找出角与角之间的数量关系.23.(1)35,35,平行;(2)∠FMN +∠GHF =180°,证明见解析;(3)不变,2【分析】(1)根据(α-35)2+|β-α|=0,即可计算α和β的值,再根据内错角相等可证AB ∥CD ; (2)先根据内错角相等证GH ∥PN ,再根据同旁内角互补和等量代换得出∠FMN +∠GHF =180°;(3)作∠PEM 1的平分线交M 1Q 的延长线于R ,先根据同位角相等证ER ∥FQ ,得∠FQM 1=∠R ,设∠PER =∠REB =x ,∠PM 1R =∠RM 1B =y ,得出∠EPM 1=2∠R ,即可得1FPN Q∠∠=2. 【详解】解:(1)∵(α-35)2+|β-α|=0,∴α=β=35,∴∠PFM =∠MFN =35°,∠EMF =35°,∴∠EMF =∠MFN ,∴AB ∥CD ;(2)∠FMN +∠GHF =180°;理由:由(1)得AB ∥CD ,∴∠MNF =∠PME ,∵∠MGH =∠MNF ,∴∠PME =∠MGH ,∴GH ∥PN ,∴∠GHM =∠FMN ,∵∠GHF +∠GHM =180°,∴∠FMN +∠GHF =180°;(3)1FPN Q∠∠的值不变,为2, 理由:如图3中,作∠PEM 1的平分线交M 1Q 的延长线于R ,∵AB ∥CD ,∴∠PEM 1=∠PFN ,∵∠PER =12∠PEM 1,∠PFQ =12∠PFN ,∴∠PER =∠PFQ ,∴ER ∥FQ ,∴∠FQM 1=∠R ,设∠PER =∠REB =x ,∠PM 1R =∠RM 1B =y ,则有:122y x Ry x EPM ⎧⎨⎩=+∠=+∠, 可得∠EPM 1=2∠R ,∴∠EPM 1=2∠FQM 1,∴11EPM FQM ∠∠=1FPN Q∠∠=2. 【点睛】本题主要考查平行线的判定与性质,熟练掌握内错角相等证平行,平行线同旁内角互补等知识是解题的关键.24.(1)见解析;(2)10°;(3)18015α︒-【分析】(1)过点E 作EF ∥CD ,根据平行线的性质,两直线平行,内错角相等,得出,CDE DEF ∠=∠结合已知条件180DEB ABE CDE ∠+∠-∠=︒,得出180,FEB ABE ∠+∠=︒即可证明;(2)过点E 作HE ∥CD ,设,,GEF x FEB EFB y ∠=∠=∠= 由(1)得AB ∥CD ,则AB ∥CD ∥HE ,由平行线的性质,得出20,DEF D EFB y ∠=∠+∠=︒+再由EG 平分DEB ∠,得出,DEG GEB GEF FEB x y ∠=∠=∠+∠=+则2DEF DEG GEF x y ∠=∠+∠=+,则可列出关于x 和y 的方程,即可求得x ,即GEF ∠的度数;(3)过点N 作NP ∥CD ,过点M 作QM ∥CD ,由(1)得AB ∥CD ,则NP ∥CD ∥AB ∥QM ,根据14CDM CDE ∠=∠和CDM α∠=,得出3,MDE α∠=根据CD ∥PN ∥QM ,DE ∥NB ,得出,PND CDM DMQ α∠=∠=∠=3,EDM BNM α∠=∠=即4,BNP α∠=根据NP ∥AB ,得出4,PNB ABN α∠=∠=再由14ABN ABE ∠=∠,得出16,ABM α∠=由AB ∥QM ,得出18016,QMB α∠=︒-因为NMB NMQ QMB ∠=∠+∠,代入α的式子即可求出BMN ∠.【详解】(1)过点E 作EF ∥CD ,如图,∵EF ∥CD ,∴,CDE DEF ∠=∠∴,DEB CDE DEB DEF FEB ∠-∠=∠-∠=∠∵180DEB ABE CDE ∠+∠-∠=︒,∴180,FEB ABE ∠+∠=︒∴EF ∥AB ,∴CD ∥AB ;(2)过点E 作HE ∥CD ,如图,设,,GEF x FEB EFB y ∠=∠=∠=由(1)得AB ∥CD ,则AB ∥CD ∥HE ,∴20,,D DEH HEF EFB y ∠=∠=︒∠=∠=∴20,DEF DEH HEF D EFB y ∠=∠+∠=∠+∠=︒+又∵EG 平分DEB ∠,∴,DEG GEB GEF FEB x y ∠=∠=∠+∠=+∴2,DEF DEG GEF x y x x y ∠=∠+∠=++=+即220,x y y +=︒+解得:10,x =︒即10GEF ∠=︒;(3)过点N 作NP ∥CD ,过点M 作QM ∥CD ,如图,由(1)得AB ∥CD ,则NP ∥CD ∥AB ∥QM ,∵NP ∥CD ,CD ∥QM ,,CDM α∠=∴PND CDM DMQ α∠=∠=∠=,又∵14CDM CDE ∠=∠, ∴33,MDE CDM α∠=∠=∵//BN DE ,∴3,MDE BNM α∠=∠=∴34,PNB PND BNM ααα∠=∠+∠=+=又∵PN ∥AB ,∴4,PNB NBA α∠=∠= ∵14ABN ABE ∠=∠, ∴44416,ABM ABN αα∠=∠=⨯=又∵AB ∥QM ,∴180,ABM QMB ∠+∠=︒∴18018016,QMB ABM α∠=︒-∠=︒-∴1801618015NMB NMQ QMB ααα∠=∠+∠=+︒-=-.【点睛】本题考查平行线的性质,角平分线的定义,解决问题的关键是作平行线构造相等的角,利用两直线平行,内错角相等,同位角相等来计算和推导角之间的关系.25.(1)60°;(2)n °+40°;(3)n °+40°或n °-40°或220°-n °【分析】(1)过点E 作EF ∥AB ,然后根据两直线平行内错角相等,即可求∠BED 的度数; (2)同(1)中方法求解即可;(3)分当点B 在点A 左侧和当点B 在点A 右侧,再分三种情况,讨论,分别过点E 作EF ∥AB ,由角平分线的定义,平行线的性质,以及角的和差计算即可.【详解】解:(1)当n =20时,∠ABC =40°,过E 作EF ∥AB ,则EF ∥CD ,∴∠BEF =∠ABE ,∠DEF =∠CDE ,∵BE 平分∠ABC ,DE 平分∠ADC ,∴∠BEF =∠ABE =20°,∠DEF =∠CDE =40°,∴∠BED =∠BEF +∠DEF =60°;(2)同(1)可知:∠BEF=∠ABE=n°,∠DEF=∠CDE=40°,∴∠BED=∠BEF+∠DEF=n°+40°;(3)当点B在点A左侧时,由(2)可知:∠BED=n°+40°;当点B在点A右侧时,如图所示,过点E作EF∥AB,∵BE平分∠ABC,DE平分∠ADC,∠ABC=2n°,∠ADC=80°,∴∠ABE=12∠ABC=n°,∠CDG=12∠ADC=40°,∵AB∥CD∥EF,∴∠BEF=∠ABE=n°,∠CDG=∠DEF=40°,∴∠BED=∠BEF-∠DEF=n°-40°;如图所示,过点E作EF∥AB,∵BE平分∠ABC,DE平分∠ADC,∠ABC=2n°,∠ADC=80°,∴∠ABE=12∠ABC=n°,∠CDG=12∠ADC=40°,∵AB∥CD∥EF,∴∠BEF=180°-∠ABE=180°-n°,∠CDE=∠DEF=40°,∴∠BED=∠BEF+∠DEF=180°-n°+40°=220°-n°;如图所示,过点E作EF∥AB,∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,∴∠ABG=12∠ABC=n°,∠CDE=12∠ADC=40°,∵AB∥CD∥EF,∴∠BEF=∠ABG=n°,∠CDE=∠DEF=40°,∴∠BED=∠BEF-∠DEF=n°-40°;综上所述,∠BED的度数为n°+40°或n°-40°或220°-n°.【点睛】此题考查了平行线的判定与性质,以及角平分线的定义,正确应用平行线的性质得出各角之间关系是解题关键.。
(必考题)初中数学七年级下期末经典题(提高培优)(1)

一、选择题1.如图,将△ABC 沿BC 方向平移3cm 得到△DEF,若△ABC 的周长为20cm ,则四边形ABFD 的周长为( )A .20cmB .22cmC .24cmD .26cm2.已知实数a ,b ,若a >b ,则下列结论错误的是 A .a-7>b-7B .6+a >b+6C .55a b >D .-3a >-3b3.不等式组213312x x +⎧⎨+≥-⎩<的解集在数轴上表示正确的是( )A .B .C .D .4116( ) A .±12B .±14C .14D .125.下面不等式一定成立的是( ) A .2a a < B .a a -<C .若a b >,c d =,则ac bd >D .若1a b >>,则22a b >6.下列方程中,是二元一次方程的是( ) A .x ﹣y 2=1B .2x ﹣y =1C .11y x+= D .xy ﹣1=07.16的平方根为( ) A .±4 B .±2 C .+4 D .28.已知关于x 的不等式组321123x x x a --⎧≤-⎪⎨⎪-<⎩恰有3个整数解,则a 的取值范围为( ) A .12a <≤B .12a <<C .12a ≤<D .12a ≤≤9.如图,已知两直线1l 与2l 被第三条直线3l 所截,下列等式一定成立的是( )A .12∠∠=B .23∠∠=C .24∠∠+=180°D .14∠∠+=180°10.如图,下列能判断AB ∥CD 的条件有 ( )①∠B +∠BCD =180° ②∠1 = ∠2 ③∠3 =∠4 ④∠B = ∠5 A .1B .2C .3D .411.下列说法正确的是( ) A .两点之间,直线最短;B .过一点有一条直线平行于已知直线;C .和已知直线垂直的直线有且只有一条;D .在平面内过一点有且只有一条直线垂直于已知直线. 12.已知m=4+3,则以下对m 的估算正确的( ) A .2<m <3B .3<m <4C .4<m <5D .5<m <613.在平面直角坐标系中,点A 的坐标()0,1,点B 的坐标()3,3,将线段AB 平移,使得A 到达点()4,2C ,点B 到达点D ,则点D 的坐标是( )A .()7,3B .()6,4C .()7,4 D .()8,414.不等式组2201x x +>⎧⎨-≥-⎩的解在数轴上表示为( )A .B .C .D .15.已知a ,b 为两个连续整数,且191<b,则这两个整数是( )A .1和2B .2和3C .3和4D .4和5二、填空题16.一棵树高h (m )与生长时间n (年)之间有一定关系,请你根据下表中数据,写出h (m )与n (年)之间的关系式:_____. n/年 2 4 6 8 … h/m2.63.23.84.4…17.已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N (下面是推理过程,请你填空).解:∵∠BAE+∠AED=180°(已知)∴ AB ∥ ( ) ∴∠BAE= ( 两直线平行,内错角相等 ) 又∵∠1=∠2∴∠BAE ﹣∠1= ﹣∠2即∠MAE= ∴ ∥NE ( ) ∴∠M=∠N ( ) 18.如果点p(3,2)m m +-在x 轴上,那么点P 的坐标为(____,____).19.如图,已知直线,AB CD 相交于点O ,如果40BOD ∠=︒,OA 平分COE ∠,那么DOE ∠=________度.20.如果方程组23759x y x y +=⎧⎨-=⎩,的解是方程716x my +=的一个解,则m 的值为____________.21.《孙子算经》是中国古代重要的数学著作,现在的传本共三卷,卷上叙述算筹记数的纵横相间制度和筹算乘除法;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法,其中记载:“今有木、不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺,木长几何?”译文:“用一根绳子量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还到余1尺,问木长多少尺?”设绳长x 尺,木长y 尺.可列方程组为__________. 22.已知方程1(2)(3)5m n m xn y --+-=是二元一次方程,则mn =_________;23.若2(2)9x m x +-+是一个完全平方式,则m 的值是_______.24.两条直线相交所成的四个角中,有两个角分别是(2x -10)°和(110-x)°,则x =_____. 25.如图,将△ABC 沿BC 方向平移1个单位得到△DEF ,若△ABC 的周长等于8,则四边形ABFD 的周长等于_______.三、解答题26.解不等式组523(1)13222x x x x +>-⎧⎪⎨≤-⎪⎩,并求出它的所有整数解的和. 27.如图,12180∠+∠=︒,B DEF ∠=∠,55BAC ∠=︒,求DEC ∠的度数.28.一个正数x 的两个平方根是2a -3与5-a ,求x 的值.29.如图1,在平面直角坐标系中,A (a ,0)是x 轴正半轴上一点,C 是第四象限内一点,CB ⊥y 轴交y 轴负半轴于B (0,b ),且|a ﹣3|+(b +4)2=0,S 四边形AOBC =16.(1)求点C 的坐标.(2)如图2,设D 为线段OB 上一动点,当AD ⊥AC 时,∠ODA 的角平分线与∠CAE 的角平分线的反向延长线交于点P ,求∠APD 的度数;(点E 在x 轴的正半轴). (3)如图3,当点D 在线段OB 上运动时,作DM ⊥AD 交BC 于M 点,∠BMD 、∠DAO 的平分线交于N 点,则点D 在运动过程中,∠N 的大小是否会发生变化?若不变化,求出其值;若变化,请说明理由.30.已知:方程组713x y ax y a+=--⎧⎨-=+⎩的解x为非正数,y为负数.(1)求a的取值范围;(2)化简|a-3|+|a+2|;(3)在a的取值范围中,当a为何整数时,不等式2ax+x>2a+1的解为x<1.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1.D2.D3.A4.A5.D6.B7.A8.A9.D10.C11.D12.B13.C14.D15.C二、填空题16.h=03n+2【解析】【分析】本题主要考查了用待定系数法求一次函数的解析式可先设出通式然后将已知的条件代入式子中求出未知数的值进而求出函数的解析式【详解】设该函数的解析式为h=kn+b将n=2h=217.见解析【解析】【分析】由已知易得AB∥CD则∠BAE=∠AEC又∠1=∠2所以∠MAE=∠A EN则AM∥EN故∠M=∠N【详解】∵∠BAE+∠AED=180°(已知)∴AB∥CD(同旁内角互补两直线18.0【解析】【分析】根据x轴上的点的纵坐标为0可得m-2=0即可求得m=2由此求得点P的坐标【详解】∵点在x轴上∴m-2=0即m=2∴P(50)故答案为:50【点睛】本题考查了x轴上的点的坐标的特点熟19.100【解析】【分析】根据对顶角相等求出∠AOC再根据角平分线和邻补角的定义解答【详解】解:∵∠BOD=40°∴∠AOC=∠BOD=40°∵OA平分∠COE∴∠AOE=∠AOC=40°∴∠CO E=820.2【解析】分析:求出方程组的解得到x与y的值代入方程计算即可求出m的值详解:①+②×3得:17x=34即x=2把x=2代入①得:y=1把x=2y=1代入方程7x+my=16得:14+m=16解得:m21.【解析】【分析】本题的等量关系是:绳长-木长=45;木长-绳长=1据此可列方程组求解【详解】设绳长x尺长木为y尺依题意得故答案为:【点睛】此题考查由实际问题抽象出二元一次方程组解题关键在于列出方程22.-2【解析】【分析】二元一次方程满足的条件:含有2个未知数未知数的项的次数是1的整式方程列出方程组求出mn的值然后代入代数式进行计算即可得解【详解】∵方程是二元一次方程∴且m-2≠0n=1∴m=-223.8或﹣4【解析】解:∵x2+(m-2)x+9是一个完全平方式∴x2+(m-2)x+9=(x±3)2而(x±3)2=x2±6x+9∴m-2=±6∴m=8或m=-4故答案为8或-424.40或80【解析】当这两个角是对顶角时(2x-10)=(110-x)解之得x=40;当这两个角是邻补角时(2x-10)+(110-x)=180解之得x=80;∴x的值是40或80点睛:本题考查了两条25.10【解析】【分析】根据平移的性质可得AD=CF=1AC=DF然后根据四边形的周长的定义列式计算即可得解【详解】∵△ABC沿BC方向平移2个单位得到△DEF∴AD=CF=1AC=DF∴四边形ABFD三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1.D解析:D【解析】平移不改变图形的形状和大小,对应线段平行且相等,平移的距离等于对应点的连线段的长,则有AD=BE=3,DF=AC,DE=AB,EF=BC,所以:四边形ABFD的周长为:AB+BF+FD+DA=AB+BE+EF+DF+AD=AB+BC+CA+2AD=20+2×3=26.故选D.点睛:本题考查了平移的性质,理解平移不改变图形的形状和大小,只改变图形的位置,对应线段平行(或在同一条直线上)且相等,平移的距离即是对应点的连线段的长度是解题的关键,将四边形的周长作相应的转化即可求解.2.D解析:D【解析】A.∵a>b,∴a-7>b-7,∴选项A正确;B.∵a>b,∴6+a>b+6,∴选项B正确;C.∵a >b ,∴55a b >,∴选项C 正确; D.∵a >b ,∴-3a <-3b ,∴选项D 错误. 故选D.3.A解析:A 【解析】 【分析】先求出不等式组的解集,再在数轴上表示出来即可. 【详解】213312x x +⎧⎨+≥-⎩<①② ∵解不等式①得:x <1, 解不等式②得:x≥-1, ∴不等式组的解集为-1≤x <1, 在数轴上表示为:,故选A . 【点睛】本题考查了解一元一次不等式组和在数轴上表示不等式组的解集,能根据不等式的解集求出不等式组的解集是解此题的关键.4.A解析:A 【解析】 【分析】根据平方根的性质:一个正数的平方根有两个,它们互为相反数计算即可. 【详解】 11614,14的平方根是12± , 11612±, 故选A. 【点睛】本题考查平方根的性质,一个正数的平方根有两个,它们互为相反数,0的平方根还是0,熟练掌握相关知识是解题关键.5.D解析:D 【解析】 【分析】根据不等式两边加(或减)同一个数(或式子),不等号的方向不变,不等式两边乘(或除以)同一个正数,不等号的方向不变,不等式两边乘(或除以)同一个负数,不等号的方向改变,可得答案. 【详解】A. 当0a ≤时,2aa ≥,故A 不一定成立,故本选项错误; B. 当0a ≤时,a a -≥,故B 不一定成立,故本选项错误;C. 若a b >,当0c d =≤时,则ac bd ≤,故C 不一定成立,故本选项错误;D. 若1a b >>,则必有22a b >,正确; 故选D . 【点睛】主要考查了不等式的基本性质.“0”是很特殊的数,因此,解答不等式的问题时,应密切关注“0”存在与否,以防掉进“0”的陷阱.不等式的基本性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.6.B解析:B 【解析】 【分析】根据二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1,像这样的整式方程叫做二元一次方程.据此逐一判断即可得. 【详解】解:A .x-y 2=1不是二元一次方程; B .2x-y=1是二元一次方程;C .1x+y =1不是二元一次方程; D .xy-1=0不是二元一次方程; 故选B . 【点睛】本题考查二元一次方程的定义,解题的关键是掌握含有两个未知数,并且含有未知数的项的次数都是1,像这样的整式方程叫做二元一次方程.7.A解析:A 【解析】 【分析】根据平方根的概念即可求出答案. 【详解】∵(±4)2=16,∴16的平方根是±4. 故选A .【点睛】本题考查了平方根的概念,属于基础题型.8.A解析:A 【解析】 【分析】先根据一元一次不等式组解出x 的取值范围,再根据不等式组只有三个整数解,求出实数a 的取值范围即可. 【详解】3211230x x x a --⎧≤-⎪⎨⎪-<⎩①②, 解不等式①得:x≥-1, 解不等式②得:x<a ,∵不等式组321123x x x a --⎧≤-⎪⎨⎪-<⎩有解, ∴-1≤x<a ,∵不等式组只有三个整数解, ∴不等式的整数解为:-1、0、1, ∴1<a≤2, 故选:A 【点睛】本题考查一元一次不等式组的整数解,解答此题要先求出不等式组的解集,求不等式组的解集要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.9.D解析:D 【解析】 【分析】由三线八角以及平行线的性质可知,A ,B ,C 成立的条件题目并没有提供,而D 选项中邻补角的和为180°一定正确. 【详解】1∠与2∠是同为角,2∠与3∠是内错角,2∠与4∠是同旁内角,由平行线的性质可知,选项A ,B ,C 成立的条件为12l l //时,故A 、B 、C 选项不一定成立, ∵1∠与4∠是邻补角, ∴∠1+∠4=180°,故D 正确. 故选D . 【点睛】本题考查三线八角的识别及平行线的性质和邻补角的概念.本题属于基础题,难度不大.10.C解析:C【解析】【分析】判断平行的条件有:同位角相等、内错角相等、同旁内角互补,依次判断各选项是否符合.【详解】①∠B+∠BCD=180°,则同旁内角互补,可判断AB∥CD;②∠1 = ∠2,内错角相等,可判断AD∥BC,不可判断AB∥CD;③∠3 =∠4,内错角相等,可判断AB∥CD;④∠B = ∠5,同位角相等,可判断AB∥CD故选:C【点睛】本题考查平行的证明,注意②中,∠1和∠2虽然是内错角关系,但对应的不是AB与CD 这两条直线,故是错误的.11.D解析:D【解析】解:A.应为两点之间线段最短,故本选项错误;B.应为过直线外一点有且只有一条一条直线平行于已知直线,故本选项错误;C.应为在同一平面内,和已知直线垂直的直线有且只有一条,故本选项错误;D.在平面内过一点有且只有一条直线垂直于已知直线正确,故本选项正确.故选D.12.B解析:B【解析】【分析】【详解】∵12,∴3<m<4,故选B.【点睛】的取值范围是解题关键.13.C解析:C【解析】根据A 和C 的坐标可得点A 向右平移4个单位,向上平移1个单位,点B 的平移方法与A 的平移方法相同,再根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得点D 的坐标.【详解】解:∵点A (0,1)的对应点C 的坐标为(4,2),即(0+4,1+1),∴点B (3,3)的对应点D 的坐标为(3+4,3+1),即D (7,4);故选:C.【点睛】此题主要考查了坐标与图形的变化——平移,关键正确得到点的平移方法.14.D解析:D【解析】【分析】解不等式组求得不等式组的解集,再把其表示在数轴上即可解答.【详解】2201x x ①②+>⎧⎨-≥-⎩, 解不等式①得,x >-1;解不等式②得,x ≤1;∴不等式组的解集是﹣1<x ≤1.不等式组的解集在数轴上表示为:故选D.【点睛】本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解决问题的关键.15.C解析:C【解析】试题解析:∵4195,∴319<4,∴这两个连续整数是3和4,故选C .16.h =03n+2【解析】【分析】本题主要考查了用待定系数法求一次函数的解析式可先设出通式然后将已知的条件代入式子中求出未知数的值进而求出函数的解析式【详解】设该函数的解析式为h =kn+b 将n =2h =2解析:h =0.3n+2【解析】【分析】本题主要考查了用待定系数法求一次函数的解析式,可先设出通式,然后将已知的条件代入式子中求出未知数的值,进而求出函数的解析式.【详解】设该函数的解析式为h =kn+b ,将n =2,h =2.6以及n =4,h =3.2代入后可得2 2.64 3.2k b k b +=⎧⎨+=⎩, 解得0.32k b =⎧⎨=⎩, ∴h =0.3n+2,验证:将n =6,h =3.8代入所求的函数式中,符合解析式;将n =8,h =4.4代入所求的函数式中,符合解析式;因此h (m )与n (年)之间的关系式为h =0.3n+2.故答案为:h =0.3n+2.【点睛】本题主要考查用待定系数法求一次函数关系式的方法.用来表示函数关系的等式叫做函数解析式,也称为函数关系式.17.见解析【解析】【分析】由已知易得AB∥CD 则∠BAE=∠AEC 又∠1=∠2所以∠MAE=∠AEN 则AM∥EN 故∠M=∠N【详解】∵∠BAE+∠AED=180°(已知)∴AB∥CD(同旁内角互补两直线解析:见解析【解析】【分析】由已知易得AB ∥CD ,则∠BAE=∠AEC ,又∠1=∠2,所以∠MAE=∠AEN ,则AM ∥EN ,故∠M=∠N .【详解】∵∠BAE +∠AED =180°(已知) ∴AB ∥CD (同旁内角互补,两直线平行)∠BAE =∠AEC (两直线平行,内错角相等)又∵∠1=∠2,∴∠BAE −∠1=∠AEC −∠2,即∠MAE =∠NEA ,∴AM ∥EN ,(内错角相等,两直线平行)∴∠M =∠N (两直线平行,内错角相等)【点睛】考查平行线的判定与性质,熟练掌握平行线的判定定理与性质定理是解题的关键. 18.0【解析】【分析】根据x 轴上的点的纵坐标为0可得m-2=0即可求得m=2由此求得点P 的坐标【详解】∵点在x 轴上∴m-2=0即m=2∴P (50)故答案为:50【点睛】本题考查了x 轴上的点的坐标的特点熟解析:0【解析】【分析】根据x 轴上的点的纵坐标为0可得m-2=0,即可求得m=2,由此求得点P 的坐标.【详解】∵点p(3,2)m m +-在x 轴上, ∴m-2=0,即m=2, ∴P (5,0).故答案为:5,0.【点睛】本题考查了x 轴上的点的坐标的特点,熟知x 轴上的点的纵坐标为0是解决问题的关键. 19.100【解析】【分析】根据对顶角相等求出∠AOC 再根据角平分线和邻补角的定义解答【详解】解:∵∠BOD=40°∴∠AOC=∠BOD=40°∵OA 平分∠COE ∴∠AOE=∠AOC=40°∴∠COE=8解析:100【解析】【分析】根据对顶角相等求出∠AOC ,再根据角平分线和邻补角的定义解答.【详解】解:∵∠BOD=40°,∴∠AOC=∠BOD=40°,∵OA 平分∠COE ,∴∠AOE=∠AOC=40°,∴∠COE=80°.∴∠DOE=180°-80°=100°故答案为:100.【点睛】本题考查了对顶角相等的性质,角平分线、邻补角的定义,是基础题,熟记性质并准确识图是解题的关键.20.2【解析】分析:求出方程组的解得到x与y的值代入方程计算即可求出m 的值详解:①+②×3得:17x=34即x=2把x=2代入①得:y=1把x=2y=1代入方程7x+my=16得:14+m=16解得:m解析:2【解析】分析:求出方程组的解得到x与y的值,代入方程计算即可求出m的值.详解:23759x yx y+=⎧⎨-=⎩①②,①+②×3得:17x=34,即x=2,把x=2代入①得:y=1,把x=2,y=1代入方程7x+my=16得:14+m=16,解得:m=2,故答案为:2.点睛:此题考查了解二元一次方程组和二元一次方程解的概念,解出二元一次方程组的解代入另一个方程是解决此题的关键.21.【解析】【分析】本题的等量关系是:绳长-木长=45;木长-绳长=1据此可列方程组求解【详解】设绳长x尺长木为y尺依题意得故答案为:【点睛】此题考查由实际问题抽象出二元一次方程组解题关键在于列出方程解析:4.5 11 2x yx y-=⎧⎪⎨=-⎪⎩【解析】【分析】本题的等量关系是:绳长-木长=4.5;木长-12绳长=1,据此可列方程组求解.【详解】设绳长x尺,长木为y尺,依题意得4.5 11 2x yx y-=⎧⎪⎨=-⎪⎩,故答案为:4.5 11 2x yx y-=⎧⎪⎨=-⎪⎩.【点睛】此题考查由实际问题抽象出二元一次方程组,解题关键在于列出方程.22.-2【解析】【分析】二元一次方程满足的条件:含有2个未知数未知数的项的次数是1的整式方程列出方程组求出mn 的值然后代入代数式进行计算即可得解【详解】∵方程是二元一次方程∴且m-2≠0n=1∴m=-2解析:-2【解析】【分析】二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程,列出方程组求出m 、n 的值,然后代入代数式进行计算即可得解.【详解】 ∵方程1(2)(3)5m n m x n y --+-=是二元一次方程, ∴11m -=且m-2≠0,n=1,∴m=-2,n=1,∴mn =-2.故答案为:-2.【点睛】本题主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.23.8或﹣4【解析】解:∵x2+(m-2)x+9是一个完全平方式∴x2+(m-2)x+9=(x±3)2而(x±3)2=x2±6x+9∴m -2=±6∴m=8或m=-4故答案为8或-4 解析:8或﹣4【解析】解:∵x 2+(m -2)x +9是一个完全平方式,∴x 2+(m -2)x +9=(x ±3)2. 而(x ±3)2=x 2±6x +9,∴m -2=±6,∴m =8或m =-4.故答案为8或-4. 24.40或80【解析】当这两个角是对顶角时(2x-10)=(110-x)解之得x=40;当这两个角是邻补角时(2x-10)+(110-x)=180解之得x=80;∴x 的值是40或80点睛:本题考查了两条解析:40或80【解析】当这两个角是对顶角时,(2x -10) =(110-x ),解之得x =40;当这两个角是邻补角时,(2x -10) +(110-x ) =180,解之得x =80;∴x 的值是40或80.点睛:本题考查了两条直线相交所成的四个角之间的关系及分类讨论的数学思想,两条直线相交所成的四个角或者是对顶角的关系,或者是邻补角的关系,明确这两种关系是解答本题的关键.25.10【解析】【分析】根据平移的性质可得AD=CF=1AC=DF 然后根据四边形的周长的定义列式计算即可得解【详解】∵△ABC 沿BC 方向平移2个单位得到△DEF∴AD=CF=1AC=DF∴四边形ABFD解析:10【解析】【分析】根据平移的性质可得AD=CF=1,AC=DF ,然后根据四边形的周长的定义列式计算即可得解.【详解】∵△ABC 沿BC 方向平移2个单位得到△DEF ,∴AD=CF=1,AC=DF ,∴四边形ABFD 的周长=AB+(BC+CF )+DF+AD=AB+BC+AC+AD+CF ,∵△ABC 的周长=8,∴AB+BC+AC=8,∴四边形ABFD 的周长=8+1+1=10.故答案为10.【点睛】本题考查了平移的性质,熟记性质得到相等的线段是解题的关键.三、解答题26.512x -<,-2 【解析】【分析】先求出两个不等式的解集,再求其公共解,然后求出整数解的和即可.【详解】 解:523(1)13222x x x x +>-⎧⎪⎨-⎪⎩①② 解不等式①得52x >-, 解不等式②得1x ≤,∴512x -<,x 为整数,可取-2,-1,0,1.则所有整数解的和为21012--++=-.【点睛】 此题考查一元一次不等式组解集,解题关键在于掌握简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解). 27.55︒【解析】【分析】只要证明AB ∥DE ,利用平行线的性质即可解决问题.【详解】解:∵1180CDF ∠+∠=︒,12180∠+∠=︒,∴2CDF ∠=∠,∴//EF BC ,∴DEF CDE ∠=∠,∵B DEF ∠=∠,∴B CDE ∠=∠,∴//DE AB ,∴55DEC BAC ∠=∠=︒.【点睛】此题考查平行线的判定和性质,解题的关键是熟练掌握基本知识.28.x=49【解析】试题分析:根据一个正数的平方根有两个,它们是互为相反数可得: 2a -3+5-a =0,可求出a =2-,即可求出这个正数的两个平方根是-7和7,根据平方根的意义可求出x .试题解析: 因为一个正数x 的两个平方根是2a -3与5-a ,所以2a -3+5-a =0,解得a =2-,所以2a -3=7-,所以49x =.29.(1) C (5,﹣4);(2)90°;(3)见解析.【解析】分析:(1)利用非负数的和为零,各项分别为零,求出a ,b 即可;(2)用同角的余角相等和角平分线的意义即可;(3)利用角平分线的意义和互余两角的关系简单计算证明即可.详解:(1)∵(a ﹣3)2+|b+4|=0,∴a ﹣3=0,b+4=0,∴a=3,b=﹣4,∴A (3,0),B (0,﹣4),∴OA=3,OB=4,∵S 四边形AOBC =16.∴0.5(OA+BC )×OB=16, ∴0.5(3+BC )×4=16, ∴BC=5,∵C 是第四象限一点,CB ⊥y 轴,∴C (5,﹣4);(2)如图,延长CA,∵AF是∠CAE的角平分线,∴∠CAF=0.5∠CAE,∵∠CAE=∠OAG,∴∠CAF=0.5∠OAG,∵AD⊥AC,∴∠DAO+∠OAG=∠PAD+∠PAG=90°,∵∠AOD=90°,∴∠DAO+∠ADO=90°,∴∠ADO=∠OAG,∴∠CAF=0.5∠ADO,∵DP是∠ODA的角平分线,∴∠ADO=2∠ADP,∴∠CAF=∠ADP,∵∠CAF=∠PAG,∴∠PAG=∠ADP,∴∠APD=180°﹣(∠ADP+∠PAD)=180°﹣(∠PAG+∠PAD)=180°﹣90°=90°即:∠APD=90°(3)不变,∠ANM=45°理由:如图,∵∠AOD=90°,∴∠ADO+∠DAO=90°,∵DM⊥AD,∴∠ADO+∠BDM=90°,∴∠DAO=∠BDM,∵NA是∠OAD的平分线,∴∠DAN=0.5∠DAO=0.5∠BDM,∵CB⊥y轴,∴∠BDM+∠BMD=90°,∴∠DAN=0.5(90°﹣∠BMD),∵MN是∠BMD的角平分线,∴∠DMN=0.5∠BMD,∴∠DAN+∠DMN=0.5(90°﹣∠BMD)+0.5∠BMD=45°在△DAM中,∠ADM=90°,∴∠DAM+∠DMA=90°,在△AMN中,∠ANM=180°﹣(∠NAM+∠NMA)=180°﹣(∠DAN+∠DAM+∠DMN+∠DMA)=180°﹣[(∠DAN+DMN)+(∠DAM+∠DMA)] =180°﹣(45°+90°)=45°,∴D点在运动过程中,∠N的大小不变,求出其值为45°点睛:此题是四边形综合题,主要考查了非负数的性质,四边形面积的计算方法,角平分线的意义,解本题的关键是用整体的思想解决问题,也是本题的难点.30.(1)-2<a≤3.(2)5;(3)a=-1.【解析】【分析】(1)求出不等式组的解集即可得出关于a的不等式组,求出不等式组的解集即可;(2)根据a的范围去掉绝对值符号,即可得出答案;(3)求出a<-12,根据a的范围即可得出答案.【详解】解:(1)713x y ax y a+=-⎧⎨-=+⎩①②∵①+②得:2x=-6+2a,x=-3+a,①-②得:2y=-8-4a,y=-4-2a,∵方程组713x y ax y a+=-⎧⎨-=+⎩的解x为非正数,y为负数,∴-3+a≤0且-4-2a<0,解得:-2<a≤3;(2)∵-2<a≤3,∴|a-3|+|a+2|=3-a+a+2=5;(3)2ax+x>2a+1,(2a+1)x>2a+1,∵不等式的解为x<1∴2a+1<0,∴a<-12,∵-2<a≤3,∴a的值是-1,∴当a为-1时,不等式2ax+x>2a+1的解为x<1.【点睛】本题考查了解方程组和解不等式组的应用,主要考查学生的理解能力和计算能力,题目比较好.。
人教版2020七年级数学下册期中综合复习培优训练题1(附答案详解)

人教版2020七年级数学下册期中综合复习培优训练题1(附答案详解)1.和数轴上的点一一对应的是( )A .整数B .实数C .有理数D .无理数2.如图,已知直线AB ∥CD ,直线l 与直线AB 、CD 相交于点,E 、F ,将l 绕点E 逆时针旋转40°后,与直线AB 相交于点G ,若∠GEC=80°,那么∠GFE=( )A .60°B .50°C .40°D .30°3.如图,在平面直角坐标系上有个点()1,0P ,点P 第1次向上跳运1个单位至点()11,1P 紧接着第2次向左跳动2个单位至点()21,1P-,第3次向上跳动1个单位,第4次向右跳运3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位, ⋯,依此规律跳动下去,点P 第2016次跳动至点2016P 的坐标是( )A .()505,1008B .()505,1008-C .()504,1007D .()504.1007- 4.下列命题正确的个数是( )①等腰三角形的腰长大于底边长;②三条线段a 、b 、c ,如果a b c +>,那么这三条线段一定可以组成三角形;③等腰三角形是轴对称图形,它的对称轴是底边上的高;④面积相等的两个三角形全等.A .0个B .1个C .2个D .3个5.下列各数是无理数的是( )A .4B .2.2020020002C .39D .﹣16.一个运算程序输入后,得到的结果是221x -,则这个运算程序是( )A.先乘2,然后平方,再减去1 B.先平方,然后减去1,再乘2C.先平方,然后乘2,再减去1 D.先减去1,然后平方,再乘27.如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2017的横坐标为()A.1010B.2C.1D.﹣10068.下列计算结果正确的是:( )A.B.C.D.9.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形的边在轴上,的中点是坐标原点固定点,,把正方形沿箭头方向推,使点落在轴正半轴上点处,则点的对应点的坐标为()A.B.C.D.10.若点A到直线l的距离为7cm,点B到直线l的距离为3cm,则线段AB的长度为()A.10cm B.4cm C.10cm或4cm D.至少4cm11.关于x轴、y轴或远点对称的点的坐标的特征点P与点p′关于x轴对称⇔_____坐标相等,_____坐标互为相反数点P与点p′关于y轴对称⇔______坐标相等,_____坐标互为相反数点P与点p′关于原点对称⇔___________坐标均互为相反数12.在平面直角坐标系中,点P(﹣2,6)在第____象限.13.已知点A(-2,0),B(3,0),则S∆ABC=_______.14.如图,在一次军棋比赛中,如果团长所在的位置的坐标为(2,-5),司令所在的位置的坐标为(4,-2),那么工兵所在的位置的坐标为_________.15.若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3=45°,则∠1的度数为______. 16.已知31x 0216+=,则x=_______ 17.借助于计算器计算,可求2243+;224433+;22444333+…… 仔细观察上面几题的计算结果,试猜想2220092009444333⋅⋅⋅+⋅⋅⋅n n 的结果为_________. 18.已知|x ﹣y+2|+2x y +-=0,则x 2﹣y 2的值为______.19.在平面坐标系中,正方形ABCD 的位置如图所示,点A 的坐标为(1,0),点D 的坐标为(0,2),延长CB 交x 轴于点A 1,作正方形A 1B 1C 1C ,延长C 1B 1交x 轴于点A 2,作正方形A 2B 2C 2C 1,…按这样的规律进行下去,第2017个正方形的面积为__________。
(完整版)七年级数学下册名校课堂训练:实数测试(一)培优试题

一、选择题1.求1+2+22+23+…+22020的值,可令S =1+2+22+23+…+22020,则2S =2+22+23+24+…+22021,因此2S -S =22021-1.仿照以上推理,计算出1+2020+20202+20203+…+20202020的值为( ) A .2020202012020-B .2021202012020-C .2021202012019-D .2020202012019-2.已知: []x 表示不超过x 的最大整数,例: ][3.93, 1.82⎡⎤=-=-⎣⎦,令关于k 的函数()][1k 44k k f +⎡⎤=-⎢⎥⎣⎦ (k 是正整数),例:()][313344f +⎡⎤=-⎢⎥⎣⎦=1,则下列结论错误..的是( ) A .()10f = B .()()4f k f k += C .()()1f k f k +≥D .()0f k =或13.对一组数(),x y 的一次操作变换记为()1,P x y ,定义其变换法则如下:()()1,,P x y x y x y =+-,且规定()()()11,,n n Px y P P x y -=(n 为大于1的整数), 如,()()11,23,1P =-,()()()()()21111,21,23,12,4P P P P ==-=,()()()()()31211,21,22,46,2P P P P ===-,则()20171,1P -=( ). A .()10080,2B .()10080,2- C .()10090,2- D .()10090,24.若29x =,|y |=7,且0x y ->,则x +y 的值为( ) A .﹣4或10B .﹣4或﹣10C .4或10D .4或﹣105.下列命题是真命题的有( )个 ①两个无理数的和可能是无理数;②两条直线被第三条直线所截,同位角相等;③同一平面内,垂直于同一条直线的两条直线互相平行; ④过一点有且只有一条直线与已知直线平行; ⑤无理数都是无限小数. A .2B .3C .4D .56.数轴上A ,B ,C ,D 四点中,两点之间的距离最接近于6的是( )A .点C 和点DB .点B 和点CC .点A 和点CD .点A 和点B7.将尺寸如图的4块完全相同的长方形薄木块(厚度忽略不计)进行拼摆,恰好可以不重叠地摆放在如图的甲、乙两个方框内.已知小木块的宽为2,图甲中阴影部分面积为19,则图乙中AD 的长为( )A .2192+B .194+C .2194+D .192+8.若1a >,则a ,a -,1a的大小关系正确的是( ) A .1a a a>->B .1a a a>-> C .1a a a>>- D .1a a a->>9.下列说法中,正确的个数是( ).(1)64-的立方根是4-;(2)49的算术平方根是7±;(3)2的立方根为32;(4)7是7的平方根.A .1B .2C .3D .410.已知f(1)=2 (取12⨯的末位数字),f(2)=6 (取2?3的末位数字),f(3)=2 (取34⨯的末位数字),…, 则()()()()f 1f 2f 3f 2021++++的值为( )A .4036B .4038C .4042D .4044二、填空题11.在数轴上,点M ,N 分别表示数m ,n ,则点M ,N 之间的距离为|m ﹣n |. (1)若数轴上的点M ,N 分别对应的数为2﹣2和﹣2,则M ,N 间的距离为 ___,MN 中点表示的数是 ___.(2)已知点A ,B ,C ,D 在数轴上分别表示数a ,b ,c ,d ,且|a ﹣c |=|b ﹣c |=23|d ﹣a |=1(a ≠b ),则线段BD 的长度为 ___.12.若(a ﹣1)2与1b +互为相反数,则a 2018+b 2019=_____.13.观察下列等式:1﹣12=12,2﹣25=85,3﹣310=2710,4﹣417=6417,…,根据你发现的规律,则第20个等式为_____.14.若|x |=3,y 2=4,且x >y ,则x ﹣y =_____.15.对于有理数a ,b ,规定一种新运算:a ※b=ab+b ,如2※3=2×3+3=9.下列结论:①(﹣3)※4=﹣8;②若a ※b=b ※a ,则a=b ;③方程(x ﹣4)※3=6的解为x=5;④(a ※b )※c=a ※(b ※c ).其中正确的是_____(把所有正确的序号都填上). 16.在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①, 然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②, ②-①得,3S-S=39-1,即2S=39-1, 所以S=.得出答案后,爱动脑筋的张红想:如果把“3”换成字母m (m ≠0且m ≠1),能否求出1+m +m 2+m 3+m 4+…+m 2016的值?如能求出,其正确答案是 ______ .17.定义一种新运算a b ※,其规则是:当a b >时,2a b a b =-※,当a b =时,a b a b =+※,当a b <时,2a b b a =-※,若()21x -=※,则x =____________. 18.20b a -=,则2+a b 的值是__________; 19.(y +1)2=0,则(x +y )3=_____.20.规定:用符号[x ]表示一个不大于实数x 的最大整数,例如:[3.69]=3,=2,[﹣2.56]=﹣3,[=﹣2.按这个规定,[1]=_____.三、解答题21.对于有理数a 、b ,定义了一种新运算“※”为:()()223a b a b a b a b a b ⎧-≥⎪=⎨-<⎪⎩※如:532537=⨯-=※,2131313=-⨯=-※. (1)计算:①()21-=※______;②()()43--=※______;(2)若313m x =-+※是关于x 的一元一次方程,且方程的解为2x =,求m 的值; (3)若3241A x x x =-+-+,3262B x x x =-+-+,且3A B =-※,求322x x +的值. 22.阅读材料:求2320192020122222++++++的值.解:设2320192020122222S =++++++①,将等式①的两边同乘以2, 得234202020212222222S =++++++②,用②-①得,2021221S S -=-即202121S =-. 即2320192020202112222221++++++=-.请仿照此法计算:(1)请直接填写231222+++的值为______; (2)求231015555+++++值;(3)请直接写出20212345201920201011010101010101011-+-+-+-+-的值. 23.阅读材料,回答问题:(1)对于任意实数x ,符号[]x 表示“不超过x 的最大整数”,在数轴上,当x 是整数,[]x 就是x ,当x 不是整数时,[]x 是点x 左侧的第一个整数点,如[]33=,[]22-=-,[]2.52=,[]1.52-=-,则[]3.4=________,[]5.7-=________.(2)2015年11月24日,杭州地铁1号线下沙延伸段开通运营,极大的方便了下沙江滨居住区居民的出行,杭州地铁收费采用里程分段计价,起步价为2元/人次,最高价为8元/人次,不足1元按1元计算,具体权费标准如下:①若从下沙江滨站到文海南路站的里程是3.07公里,车费________元,下沙江滨站到金沙湖站里程是7.93公里,车费________元,下沙江滨站到杭州火东站里程是19.17公里,车费________元;②若某人乘地铁花了7元,则他乘地铁行驶的路程范围(不考虑实际站点下车里程情况)?24.阅读下面文字:对于5231591736342⎛⎫⎛⎫⎛⎫-+-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭可以如下计算:原式()()()5231591736342⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+++-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦()()()5231591736342⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-+-+-++-⎡⎤ ⎪ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭⎝⎭⎣⎦ 1014⎛⎫=+- ⎪⎝⎭114=-上面这种方法叫拆项法,你看懂了吗? 仿照上面的方法,计算: (1)115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭(2)235120192018201720163462⎛⎫⎛⎫-++-+ ⎪ ⎪⎝⎭⎝⎭25.(概念学习)规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”,一般地,把n 个a (a ≠0)记作a ⓝ,读作“a 的圈n 次方”. (初步探究)(1)直接写出计算结果:2③= ,(﹣12)⑤= ;(深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?(1)试一试:仿照上面的算式,将下列运算结果直接写成乘方的形式.(﹣3)④= ;5⑥= ;(﹣12)⑩= .(2)想一想:将一个非零有理数a 的圈n 次方写成乘方的形式等于 ; 26.阅读材料,回答问题:(1)对于任意实数x ,符号[]x 表示“不超过x 的最大整数”,在数轴上,当x 是整数,[]x 就是x ,当x 不是整数时,[]x 是点x 左侧的第一个整数点,如[]33=,[]22-=-,[]2.52=,[]1.52-=-,则[]3.4=________,[]5.7-=________.(2)2015年11月24日,杭州地铁1号线下沙延伸段开通运营,极大的方便了下沙江滨居住区居民的出行,杭州地铁收费采用里程分段计价,起步价为2元/人次,最高价为8元/人次,不足1元按1元计算,具体权费标准如下:①若从下沙江滨站到文海南路站的里程是3.07公里,车费________元,下沙江滨站到金沙湖站里程是7.93公里,车费________元,下沙江滨站到杭州火东站里程是19.17公里,车费________元;②若某人乘地铁花了7元,则他乘地铁行驶的路程范围(不考虑实际站点下车里程情况)?27.观察下列各式,并用所得出的规律解决问题:(11.414≈14.14141.4,……0.1732 1.732≈17.32,……由此可见,被开方数的小数点每向右移动______位,其算术平方根的小数点向______移动______位.(2 3.873 1.225≈≈_____≈______.(31=10=100=,…… 小数点的变化规律是_______________________.(4 2.154≈0.2154≈-,则y =______. 28.先阅读然后解答提出的问题:设a 、b 是有理数,且满足3=-a b a 的值.解:由题意得(3)(0-++=a b ,因为a 、b 都是有理数,所以a ﹣3,b+2也是有理数,a-3=0,b+2=0, 所以a=3,b=﹣2, 所以3(2)8=-=-a b .问题:设x 、y 都是有理数,且满足2210x y -=+x+y 的值.29.规定:求若干个相同的有理数(均不等于 0)的除法运算叫做除方,如 2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等,类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈 3 次方,”(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作:“(﹣3)的圈 4 次方”.一般地,把个记作 a ⓝ,读作 “a 的圈 n 次方” (初步探究)(1)直接写出计算结果:2③,(﹣12)③. (深入思考) 2④21111112222222⎛⎫=⨯⨯⨯=⨯= ⎪⎝⎭我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?(2)试一试,仿照上面的算式,将下列运算结果直接写成幂的形式.5⑥;(﹣12)⑩. (3)猜想:有理数 a (a≠0)的圈n (n≥3)次方写成幂的形式等于多少. (4)应用:求(-3)8×(-3)⑨-(﹣12)9×(﹣12)⑧ 30.a 是不为1的有理数,我们把11a-称为a 的差倒数.如:2的差倒数是1112=--,现已知a 1=12,a 2是a 1的差倒数,a 3是a 2的差倒数,a 4是a 3的差倒数,… (1)求a 2,a 3,a 4的值;(2)根据(1)的计算结果,请猜想并写出a 2016•a 2017•a 2018的值; (3)计算:a 33+a 66+a 99+…+a 9999的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】由题意可知S = 1+2020+20202+20203+…+20202020①,可得到2020S =2020+20202+20203+…+20202020+20202021②,然后由②-①,就可求出S 的值. 【详解】解:设S = 1+2020+20202+20203+…+20202020① 则2020S =2020+20202+20203+…+20202020+20202021② 由②-①得: 2019S =20202021-1 ∴2021202012019S -=.故答案为:C . 【点晴】本题主要考查探索数与式的规律,有理数的加减混合运算.2.C解析:C 【分析】根据新定义的运算逐项进行计算即可做出判断. 【详解】A. ()f 1=][11144+⎡⎤-⎢⎥⎣⎦=0-0=0,故A 选项正确,不符合题意; B. ()f k 4+=][k 41k 444+++⎡⎤-⎢⎥⎣⎦=][k 1k 1144+⎡⎤+-+⎢⎥⎣⎦=][k 1k 44+⎡⎤-⎢⎥⎣⎦,()f k =][k 1k 44+⎡⎤-⎢⎥⎣⎦, 所以()()f k 4f k +=,故B 选项正确,不符合题意;C. ()f k 1+=k 11k 1k 2k 14444+++++⎡⎤⎡⎤⎡⎤⎡⎤-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦,()f k = ][k 1k 44+⎡⎤-⎢⎥⎣⎦, 当k=3时,()f 31+=323144++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=0,()f 3= ][31344+⎡⎤-⎢⎥⎣⎦=1, 此时()()f k 1f k +<,故C 选项错误,符合题意; D.设n 为正整数,当k=4n 时,()f k =4n 14n 44+⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=n-n=0, 当k=4n+1时,()f k =4n 24n 144++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=n-n=0, 当k=4n+2时,()f k =4n 34n 244++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=n-n=0, 当k=4n+3时,()f k =4n 44n 344++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=n+1-n=1, 所以()f k 0=或1,故D 选项正确,不符合题意, 故选C. 【点睛】本题考查了新定义运算,明确运算的法则,运用分类讨论思想是解题的关键.3.D解析:D 【详解】因为()()11,10,2P -=,()()()()()21111,11,10,2=2,2P P P P -=-=-,()()()()()31211,11,22,20,4P P P P -=-=-=,()()41,14,4P -=-,()()51,10,8P -= ()()61,18,8P -=-,所以()()211,10,2n n P --=,()()21,12,2n n n P -=-,所以 ()()100920171,10,2P -=,故选D.4.B解析:B 【分析】先根据平方根、绝对值运算求出,x y 的值,再代入求值即可得. 【详解】解:由29x =得:3x =±, 由7y =得:7y =±,0x y ->, x y ∴>,37x y =-⎧∴⎨=-⎩或37x y =⎧⎨=-⎩, 则3(7)10x y +=-+-=-或3(7)4x y +=+-=-, 故选:B . 【点睛】本题考查了平方根、绝对值等知识点,熟练掌握各运算法则是解题关键.5.B解析:B 【分析】分别根据无理数的定义、同位角的定义、平行线的判定逐个判断即可. 【详解】解:①两个无理数的和可能是无理数,比如:π+π=2π,故①是真命题; ②两条直线被第三条直线所截,同位角不一定相等,故②是假命题; ③同一平面内,垂直于同一条直线的两条直线互相平行,故③是真命题; ④在同一平面内,过一点有且只有一条直线与已知直线平行,故④是假命题; ⑤无理数是无限不循环小数,都是无限小数,故⑤是真命题. 故选:B 【点睛】本题考查了命题与定理的知识,解题的关键是了解平行线的性质及判定、无理数的定义,难度不大.6.A解析:A 【分析】的范围,结合数轴可得答案. 【详解】 解:∵4<6<9, ∴2<3,∴的是点C 和点D .故选:A .【点睛】本题考查的是实数与数轴,熟知实数与数轴上各点是一一对应关系是解答此题的关键.7.C解析:C【分析】设木块的长为x,结合图形知阴影部分的边长为x-2,根据其面积为19得出(x-2)2=19,利用平方根的定义求出符合题意的x的值,由AD=2x可得答案.【详解】解:设木块的长为x,根据题意,知:(x-2)2=19,则2x-=∴2x=22x=(舍去)则24BC x==,故选:C.【点睛】本题主要考查算术平方根,解题的关键是结合图形得出木块长、宽与阴影部分面积间的关系.8.C解析:C【分析】可以用取特殊值的方法,因为a>1,所以可设a=2,然后分别计算|a|,-a,1a,再比较即可求得它们的关系.【详解】解:设a=2,则|a|=2,-a=-2,112a=,∵2>12>-2,∴|a|>1a>-a;故选:C.【点睛】此类问题运用取特殊值的方法做比较简单.9.C解析:C【详解】4-,故(1)对;根据算术平方根的性质,可知49的算术平方根是7,故(2)错;根据立方根的意义,可知23)对;7的平方根.故(4)对; 故选C.10.C解析:C 【分析】先计算部分数的乘积,观察运算结果,发相规律,每运算5次后结果重复出现,求出f(1)+f(2)+f(3)+f(4)+f(5)和,再求2021次运算重复的次数,用除数5,商和余数表示2021=5×404+1,说明重复404次和f(2021)=2的结果,(f(1)+f(2)+f(3)+f(4)+f(5))×10+2计算结果即可. 【详解】解:f(1)=2, f(2)=6,f(3)=2,f(4)=0,f(5)=0,f(6)=2,f(7)=6,f(8)=2,f(9)=0,f(10)=0,f(11)=2, 每5次运算一循环,f(1)+f(2)+f(3)+f(4)+f(5)=2+6+2+0+0=10, 2021=5×404+1,()()()()f 1f 2f 3f 2021++++=10×404+2=4040+2=4042.故选:C . 【点睛】本题考查新定义运算,读懂题目的含义与要求,掌握运算的方法,观察部分运算结果,从中找出规律,用规律解决问题是解题关键.二、填空题 11.2 【分析】(1)直接根据定义,代入数字求解即可得到两点间的距离;根据两点之间的距离得出其一半的长度,然后结合其中一个端点表示的数求解即可得中点表示的数;(2)先根据|a ﹣c|=|b ﹣c|与a≠解析:2 【分析】(1)直接根据定义,代入数字求解即可得到两点间的距离;根据两点之间的距离得出其一半的长度,然后结合其中一个端点表示的数求解即可得中点表示的数;(2)先根据|a ﹣c |=|b ﹣c |与a ≠b 推出C 为AB 的中点,然后根据题意分类讨论求解即可. 【详解】解:(1)由题意,M ,N 间的距离为(222==;∵2MN =, ∴112MN =, 由题意知,在数轴上,M 点在N 点右侧, ∴MN 的中点表示的数为21-+;(2)∵1a c b c -=-=且a b ,∴数轴上点A 、B 与点C 不重合,且到点C 的距离相等,都为1,∴点C 为AB 的中点,2AB =,∵213d a -=, ∴32d a -=, 即:数轴上点A 和点D 的距离为32,讨论如下: 1>若点A 位于点B 左边:①若点D 在点A 左边,如图所示:此时,37222BD AD AB =+=+=; ②若点D 在点A 右边,如图所示:此时,31222BD AB AD =-=-=; 2>若点A 位于点B 右边:①若点D 在点A 左边,如图所示:此时,31222BD AB AD =-=-=; ②若点D 在点A 右边,如图所示:此时,37222BD AD AB =+=+=; 综上,线段BD 的长度为12或72, 故答案为:2;21;12或72. 【点睛】本题考查数轴上两点间的距离,以及与线段中点相关的计算问题,理解数轴上点的特征以及两点间的距离表示方法,灵活根据题意分类讨论是解题关键.12.0【分析】根据相反数的概念和非负数的性质列出方程,求出a、b的值,最后代入所求代数式计算即可.【详解】解:由题意得,(a﹣1)2+=0,则a﹣1=0,b+1=0,解得,a=1,b=﹣1,解析:0【分析】根据相反数的概念和非负数的性质列出方程,求出a、b的值,最后代入所求代数式计算即可.【详解】解:由题意得,(a﹣1)20,则a﹣1=0,b+1=0,解得,a=1,b=﹣1,则a2018+b2019=12018+(﹣1)2019=1+(﹣1)=0,故答案为:0.【点睛】本题考查了相反数的性质和算术平方根非负性的性质,正确运用算术平方根非负性的性质是解答本题的关键.13.20﹣.【分析】观察已知等式,找出等式左边和右边的规律,再归纳总结出一般规律,由此即可得出答案.【详解】观察已知等式,等式左边的第一个数的规律为,第二个数的规律为:分子为,分母为等式右边的解析:20﹣208000= 401401.【分析】观察已知等式,找出等式左边和右边的规律,再归纳总结出一般规律,由此即可得出答案.【详解】观察已知等式,等式左边的第一个数的规律为1,2,3,,第二个数的规律为:分子为1,2,3,,分母为222112,215,3110,+=+=+=等式右边的规律为:分子为3331,2,3,,分母为222112,215,3110,+=+=+= 归纳类推得:第n 个等式为32211n n n n n -=++(n 为正整数) 当20n =时,这个等式为322202020201201-=++,即20800020401401-= 故答案为:20800020401401-=. 【点睛】 本题考查了实数运算的规律型问题,从已知等式中归纳类推出一般规律是解题关键. 14.1或5.【分析】根据题意,利用绝对值的代数意义及平方根定义求出x 与y 的值,代入原式计算即可得到结果.【详解】解:根据题意得:x =3,y =2或x =3,y =﹣2,则x ﹣y =1或5.故答案为1解析:1或5.【分析】根据题意,利用绝对值的代数意义及平方根定义求出x 与y 的值,代入原式计算即可得到结果.【详解】解:根据题意得:x =3,y =2或x =3,y =﹣2,则x ﹣y =1或5.故答案为1或5.【点睛】此题考查了代数式求值,熟练掌握运算法则是解本题的关键.15.①③【分析】题目中各式利用已知的新定义公式计算得到结果,即可做出判断.【详解】(−3)※4=−3×4+4=−8,所以①正确;a ※b=ab+b ,b ※a=ab+a ,若 a=b ,两式相等,若解析:①③【分析】题目中各式利用已知的新定义公式计算得到结果,即可做出判断.(−3)※4=−3×4+4=−8,所以①正确;a※b=ab+b,b※a=ab+a,若 a=b ,两式相等,若a≠b,则两式不相等,所以②错误;方程(x−4) )※3=6化为3(x−4)+3=6,解得x=5,所以③正确;左边=(a※b) ※c=(a×b+b) )※c=(a×b+b)·c+c=abc+bc+c右边=a※(b※c)=a※(b×c+c)=a(b×c+c) +(b×c+c)=abc+ac+bc+c2两式不相等,所以④错误.综上所述,正确的说法有①③.故答案为①③.【点睛】有理数的混合运算, 解一元一次方程,属于定义新运算专题,解决本题的关键突破口是准确理解新定义.本题主要考查学生综合分析能力、运算能力.16..【解析】试题分析:设S=1+m+m2+m3+m4+…+m2016…………………①,在①式的两边都乘以m,得:mS=m+m2+m3+m4+…+m2016+m2017…………………②②一①得:解析:.【解析】试题分析:设S=1+m+m2+m3+m4+…+m2016…………………①,在①式的两边都乘以m,得:mS=m+m2+m3+m4+…+m2016+m2017…………………②②一①得:mS―S=m2017-1.∴S=.考点:阅读理解题;规律探究题.17.或﹣5【分析】根据新定义运算法则,分情况讨论求解即可.【详解】解:当x>﹣2时,则有,解得:,成立;当x=﹣2时,则有,解得:x=3,矛盾,舍去;当x<﹣2时,则有,解得:x=﹣5,成立解析:12或﹣5【分析】根据新定义运算法则,分情况讨论求解即可.解:当x >﹣2时,则有()22(2)1x x -=--=※,解得:12x =-,成立;当x =﹣2时,则有()2(2)1x x -=+-=※,解得:x =3,矛盾,舍去;当x <﹣2时,则有()22(2)1x x -=⨯--=※,解得:x =﹣5,成立,综上,x =12-或﹣5, 故答案为:12-或﹣5. 【点睛】本题考查新定义下的实数运算、解一元一次方程,理解新定义运算法则,运用分类讨论思想正确列出方程是解答的关键.18.10【分析】根据二次根式的性质和绝对值的性质求出a ,b 计算即可;【详解】∵,∴,∴,∴.故答案是10.【点睛】本题主要考查了代数式求值,结合二次根式的性质和绝对值的性质计算即可. 解析:10【分析】根据二次根式的性质和绝对值的性质求出a ,b 计算即可;【详解】∵20b a -=,∴2020a b a -=⎧⎨-=⎩, ∴24a b =⎧⎨=⎩, ∴22810a b +=+=.故答案是10.【点睛】本题主要考查了代数式求值,结合二次根式的性质和绝对值的性质计算即可.19.0根据非负数的性质列式求出x、y,然后代入代数式进行计算即可得解.【详解】解:∵+(y+1)2=0∴x﹣1=0,y+1=0,解得x=1,y=﹣1,所以,(x+y)3=(1﹣1)解析:0【分析】根据非负数的性质列式求出x、y,然后代入代数式进行计算即可得解.【详解】解:∵(y+1)2=0∴x﹣1=0,y+1=0,解得x=1,y=﹣1,所以,(x+y)3=(1﹣1)3=0.故答案为:0.【点睛】本题考查了非负数的性质.解题的关键是掌握非负数的性质:几个非负数的和为0时,这几个非负数都为0.20.-5【详解】∵3<<4,∴−4<−<−3,∴−5<−−1<−4,∴[−−1]=−5.故答案为−5.点睛:本题考查了估算无理数的大小的应用,解决此题的关键是求出的范围. 解析:-5【详解】∵,∴,∴,∴故答案为−5..三、解答题21.(1)①5;②2-;(2)1;(3)16.【分析】(1)根据题中定义代入即可得出;(2)根据2x =,讨论3和 m 的两种大小关系,进行计算;(3)先判定A 、B 的大小关系,再进行求解.【详解】(1)根据题意:∵21>-,∴()()212215-=⨯--=※,∵43-<-,∴()()()243434223--=--⨯-=-+=-※. (2)∵2x =,∴31325m =-+⨯=※,① 若3m >,则235m ⨯-=,解得1m =,②若3m <, 则2353m -⨯=,解得3m =-(不符合题意), ∴1m =.(3)∵()()323224162210A B x x x x x x x -=-+-+--+-+=--<,∴A B <, ∴()3232224162333A B A B x x x x x x =-=-+-+--+-+=-※, 得380x x +-=,∴3222816x x +=⨯=.【点睛】本题考查了一种新运算,读懂题意掌握新运算并能正确化简是解题的关键.22.(1)15;(2)11514-;(3)111. 【分析】(1)先计算乘方,即可求出答案;(2)根据题目中的运算法则进行计算,即可求出答案;(3)根据题目中的运算法则进行计算,即可求出答案;【详解】解:(1)231248125122=++++=++;故答案为:15;(2)设231015555T =+++++①,把等式①两边同时乘以5,得 112310555555T =+++++②,由②-①,得:11451T =-, ∴11514T -=, ∴31121015551455++=+++-; (3)设234520192020110101010101010M =-+-+-+-+①, 把等式①乘以10,得:3456222019020202110101010101010101010M =-+-+-+-++②,把①+②,得:202111110M =+, ∴202110111M +=, ∴232452019200022111010101010110010111-+-+-+-++=, ∴20212345201920201011010101010101011-+-+-+-+- 20212021101101111+=- 111=. 【点睛】本题考查了数字的变化规律,熟练掌握运算法则,熟练运用有理数乘法,以及运用消项的思想是解题的关键.23.(1)3;6-;(2)①2;3;6.②这个乘客花费7元乘坐的地铁行驶的路程范围为:大于24公里小于等于32公里.【分析】(1)根据题意,确定实数左侧第一个整数点所对应的数即得;(2)①根据表格确定乘坐里程的对应段,然后将乘坐里程分段计费并累加即得; ②根据表格将每段的费用从左至右依次累加直至费用为7元,进而确定7元乘坐的具体里程即得.【详解】(1)∵3 3.44<<∴[]3.43=∵6 5.75-<-<-∴[]5.76-=-故答案为:3;6-.(2)①∵3.074<∴3.07公里需要2元∵47.9312<<∴7.93公里所需费用分为两段即:前4公里2元 ,后3.93公里1元∴7.93公里所需费用为:2+1=3(元)∵19.212174<<∴19.17公里所需费用分为三段计费即: 前4公里2元,4至12公里2元,12公里至19.17公里2元;∴19.17公里所需费用为:2226++=(元)故答案为:2;3;6.②由题意得:乘坐24公里所需费用分为三段:前4公里2元,4至12公里2元,12公里至24公里2元;∴乘坐24公里所需费用为:2226++=(元)∵由表格可知:乘坐24公里以上的部分,每一元可以坐8公里∴7元可以乘坐的地铁最大里程为:24+8=32(公里)∴这个乘客花费7元乘坐的地铁行驶的路程范围为:大于24公里小于等于32公里 答:这个乘客花费7元乘坐的地铁行驶的路程范围为:大于24公里小于等于32公里.【点睛】本题是阅读材料题,考查了实数的实际应用,根据材料中的新定义举一反三并挖掘材料中深层次含义是解题关键.24.(1)14-(2)124- 【分析】(1)根据例子将每项的整数部分相加,分数部分相加即可解答;(2)根据例子将每项的整数部分相加,分数部分相加即可解答.【详解】(1)115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭()115112744362⎛⎫=--+-+--+- ⎪⎝⎭ 104⎛⎫=+- ⎪⎝⎭ 14=- (2)原式()235120192018201720163462⎛⎫=-+-++-+-+ ⎪⎝⎭ 124⎛⎫=-+- ⎪⎝⎭ 124=- 【点睛】此题考察新计算方法,正确理解题意是解题的关键,根据例子即可仿照计算.25.初步探究:(1)12,-8;深入思考:(1)(−13)2,(15)4,82;(2)21n a -⎛⎫ ⎪⎝⎭【分析】初步探究:(1)分别按公式进行计算即可;深入思考:(1)把除法化为乘法,第一个数不变,从第二个数开始依次变为倒数,由此分别得出结果;(2)结果前两个数相除为1,第三个数及后面的数变为1a ,则11n a a a -⎛⎫=⨯ ⎪⎝⎭ⓝ;【详解】 解:初步探究:(1)2③=2÷2÷2=12, 111111-=-----222222⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫÷÷÷÷ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⑤111=1---222⎛⎫⎛⎫⎛⎫÷÷÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ()11-2--22⎛⎫⎛⎫÷÷ ⎪ ⎪⎝⎭⎝⎭=-8; 深入思考:(1)(-3)④=(-3)÷(-3)÷(-3)÷(-3)=1×(−13)2=(−13)2; 5⑥=5÷5÷5÷5÷5÷5=(15)4; 同理可得:(﹣12)⑩=82; (2)21n a a -⎛⎫= ⎪⎝⎭ⓝ【点睛】本题是有理数的混合运算,也是一个新定义的理解与运用;一方面考查了有理数的乘除法及乘方运算,另一方面也考查了学生的阅读理解能力;注意:负数的奇数次方为负数,负数的偶数次方为正数,同时也要注意分数的乘方要加括号,对新定义,其实就是多个数的除法运算,要注意运算顺序.26.(1)3;6-;(2)①2;3;6.②这个乘客花费7元乘坐的地铁行驶的路程范围为:大于24公里小于等于32公里.【分析】(1)根据题意,确定实数左侧第一个整数点所对应的数即得;(2)①根据表格确定乘坐里程的对应段,然后将乘坐里程分段计费并累加即得; ②根据表格将每段的费用从左至右依次累加直至费用为7元,进而确定7元乘坐的具体里程即得.【详解】(1)∵3 3.44<<∴[]3.43=∵6 5.75-<-<-∴[]5.76-=-故答案为:3;6-.(2)①∵3.074<∴3.07公里需要2元∵47.9312<<∴7.93公里所需费用分为两段即:前4公里2元 ,后3.93公里1元∴7.93公里所需费用为:2+1=3(元)∵19.212174<<∴19.17公里所需费用分为三段计费即: 前4公里2元,4至12公里2元,12公里至19.17公里2元;∴19.17公里所需费用为:2226++=(元)故答案为:2;3;6.②由题意得:乘坐24公里所需费用分为三段:前4公里2元,4至12公里2元,12公里至24公里2元;∴乘坐24公里所需费用为:2226++=(元)∵由表格可知:乘坐24公里以上的部分,每一元可以坐8公里∴7元可以乘坐的地铁最大里程为:24+8=32(公里)∴这个乘客花费7元乘坐的地铁行驶的路程范围为:大于24公里小于等于32公里 答:这个乘客花费7元乘坐的地铁行驶的路程范围为:大于24公里小于等于32公里.【点睛】本题是阅读材料题,考查了实数的实际应用,根据材料中的新定义举一反三并挖掘材料中深层次含义是解题关键.27.(1)两;右;一;(2)12.25;0.3873;(3)被开方数的小数点向右(左)移三位,其立方根的小数点向右(左)移动一位;(4)-0.01【分析】(1)观察已知等式,得到一般性规律,写出即可;(2)利用得出的规律计算即可得到结果;(3)归纳总结得到规律,写出即可;(4)利用得出的规律计算即可得到结果.【详解】解:(11.41414.14≈141.4≈,……0.1732 1.732≈17.32,……由此可见,被开方数的小数点每向右移动两位,其算术平方根的小数点向右移动一位. 故答案为:两;右;一;(2 3.873 1.225≈12.25≈0.3873;故答案为:12.25;0.3873;(31=10=100=,……小数点的变化规律是:被开方数的小数点向右(左)移三位,其立方根的小数点向右(左)移动一位;(4)∵ 2.154≈0.2154≈-,∴0.2154≈,∴0.2154≈-,∴y=-0.01.【点睛】此题考查了立方根,以及算术平方根,弄清题中的规律是解本题的关键.28.7或-1.【分析】根据题目中给出的方法,对所求式子进行变形,求出x、y的值,进而可求x+y的值.【详解】解:∵2210x y-=+∴()22100x y--+-=,∴2210x y--=0-=0∴x=±4,y=3当x=4时,x+y=4+3=7当x=-4时,x+y=-4+3=-1∴x+y的值是7或-1.【点睛】本题考查实数的运算,解题的关键是弄清题中给出的解答方法,然后运用类比的思想进行解答.29.(1)12,-2;(2)(15)4,(﹣2)8;(3)n-21a⎛⎫⎪⎝⎭;(4)7-28.【分析】(1)分别按公式进行计算即可;(2)把除法化为乘法,第一个数不变,从第二个数开始依次变为倒数,由此分别得出结果;(3)结果前两个数相除为1,第三个数及后面的数变为1a ,则aⓝ=a×(1a)n-1;(4)将第二问的规律代入计算,注意运算顺序.【详解】解:(1)2③=2÷2÷2=12,(﹣12)③=﹣12÷(﹣12)÷(﹣12)=﹣2;(2)5⑥=5×15×15×15×15×15=(15)4,同理得;(﹣12)⑩=(﹣2)8;(3)aⓝ=a×1a×1a×…×n-211a a⎛⎫= ⎪⎝⎭;(4)(-3)8×(-3)⑨-(﹣12)9×(﹣12)⑧=(-3)8×(1-3)7 -(﹣12)9×(-2)6=-3-(-12)3=-3+1 8=7 -28.【点睛】本题是有理数的混合运算,也是一个新定义的理解与运用;一方面考查了有理数的乘除法及乘方运算,另一方面也考查了学生的阅读理解能力;注意:负数的奇数次方为负数,负数的偶数次方为正数,同时也要注意分数的乘方要加括号,对新定义,其实就是多个数的除法运算,要注意运算顺序.30.(1)a2=2,a3=-1,a4=1 2(2)a2016•a2017•a2018= -1(3)a33+a66+a99+…+a9999=-1【分析】(1)将a1=12代入11a-中即可求出a2,再将a2代入求出a3,同样求出a4即可.(2)从(1)的计算结果可以看出,从a1开始,每三个数一循环,而2016÷3=672,则a2016=-1,a2017=12,a2018=2然后计算a2016•a2017•a2018的值;(3)观察可得a3、a6、a9、…a99,都等于-1,将-1代入,即可求出结果.【详解】(1)将a1=12,代入11a-,得21=211-2a=;将a2=2,代入11a-,得31=-11-2a=;将a3=-1,代入11a-,得411=1--12a=().(2)根据(1)的计算结果,从a1开始,每三个数一循环,而2016÷3=672,则a2016=-1,a2017=12,a2018=2所以,a2016•a2017•a2018=(-1)×12×2= -1(3)观察可得a3、a6、a9、…a99,都等于-1,将-1代入,a33+a66+a99+…+a9999=(-1)3+(-1)6+(-1)9+…+(-1)99=(-1)+1+(-1)+…(-1)=-1【点睛】此类问题考查了数字类的变化规律,解题的关键是要严格根据定义进行解答,同时注意分析循环的规律.。
(必考题)初中数学七年级下期末经典练习(提高培优)(1)

一、选择题1.如图,已知∠1=∠2,∠3=30°,则∠B 的度数是( )A .20B .30C .40D .602.如图,将一张长方形纸条折叠,如果∠1=130°,则,∠2=( )A .100°B .130°C .150°D .80°3.已知关于x 的不等式组{x >1x <m的解中有3个整数解,则m 的取值范围是( ) A .3<m≤4B .4≤m<5C .4<m≤5D .4≤m≤54.已知实数a ,b ,若a >b ,则下列结论错误的是A .a-7>b-7B .6+a >b+6C .55ab > D .-3a >-3b5.下面不等式一定成立的是( )A .2a a <B .a a -<C .若a b >,c d =,则ac bd >D .若1a b >>,则22a b > 6.10+1的值应在( )A .3和4之间B .4和5之间C .5和6之间D .6和7之间7.在平面直角坐标系中,若点A(a ,-b)在第一象限内,则点B(a ,b)所在的象限是( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限8.若不等式组20{210x a x b +---><的解集为0<x <1,则a ,b 的值分别为( ) A .a =2,b =1 B .a =2,b =3 C .a =-2,b =3 D .a =-2,b =19.小明要从甲地到乙地,两地相距1.8千米.已知他步行的平均速度为90米/分,跑步的平均速度为210米/分,若他要在不超过15分钟的时间内从甲地到达乙地,至少需要跑步多少分钟?设他需要跑步x 分钟,则列出的不等式为( )A .210x +90(15﹣x )≥1.8B .90x +210(15﹣x )≤1800C .210x +90(15﹣x )≥1800D .90x +210(15﹣x )≤1.8 10.如图,将△ABE 向右平移2cm 得到△DCF ,如果△ABE 的周长是16cm ,那么四边形ABFD 的周长是( )A .16cmB .18cmC .20cmD .21cm 11.关于x 的不等式x-b>0恰有两个负整数解,则b 的取值范围是A .32b -≤<-B .32b -<≤-C .32b -≤≤-D .-3<b<-2 12.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A (﹣2,1)和B (﹣2,﹣3),那么第一架轰炸机C 的平面坐标是( )A .(2,﹣1)B .(4,﹣2)C .(4,2)D .(2,0)13.在平面直角坐标系中,点A 的坐标()0,1,点B 的坐标()3,3,将线段AB 平移,使得A 到达点()4,2C ,点B 到达点D ,则点D 的坐标是( )A .()7,3B .()6,4C .()7,4D .()8,4 14.若点(),1P a a -在x 轴上,则点()2,1Q a a -+在第( )象限. A .一 B .二 C .三 D .四15.如图,直线l 1∥l 2,被直线l 3、l 4所截,并且l 3⊥l 4,∠1=44°,则∠2等于( )A .56°B .36°C .44°D .46°二、填空题16.如图,在平面直角坐标系中,点A 的坐标为(2,0),点B 的坐标为(0,1),将线段AB 平移,使其一个端点到C (3,2),则平移后另一端点的坐标为______________.17.某小区地下停车场入口门栏杆的平面示意图如图所示,BA 垂直地面AE 于点A ,CD 平行于地面AE ,若∠BCD =120° ,则∠ABC = ________.18.已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N (下面是推理过程,请你填空).解:∵∠BAE+∠AED=180°(已知) ∴ AB ∥ ( )∴∠BAE= ( 两直线平行,内错角相等 )又∵∠1=∠2∴∠BAE ﹣∠1= ﹣∠2即∠MAE=∴ ∥NE ( )∴∠M=∠N ( )19.如图8中图①,两个等边△ABD ,△CBD 的边长均为1,将△ABD 沿AC 方向向 右平移到△A′B′D′的位置得到图②,则阴影部分的周长为_________.20.若二元一次方程组3354x y x y +=⎧⎨-=⎩的解为x a y b=⎧⎨=⎩,则a ﹣b=______. 21.二项方程32540x +=在实数范围内的解是_______________22.如图,已知AB 、CD 相交于点O,OE ⊥AB 于O ,∠EOC=28°,则∠AOD=_____度;23.关于x 的不等式组352223x x x a-≤-⎧⎨+>⎩有且仅有4个整数解,则a 的整数值是______________.24.如图,点A ,B ,C 在直线l 上,PB ⊥l ,PA=6cm ,PB=5cm ,PC=7cm ,则点P 到直线l 的距离是_____cm.25.如图,直线1l ∥2l ,αβ∠∠=,1∠=35°,则2∠=____°.三、解答题26.为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:(1)被抽样调查的学生有______人,并补全条形统计图;(2)每天户外活动时间的中位数是______(小时);(3)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?27.某工厂现有甲种原料3600kg ,乙种原料2410kg ,计划利用这两种原料生产A ,B 两种产品共500件,产品每月均能全部售出.已知生产一件A 产品需要甲原料9kg 和乙原料3kg ;生产一件B 种产品需甲种原料4kg 和乙种原料8kg .(1)设生产x 件A 种产品,写出x 应满足的不等式组.(2)问一共有几种符合要求的生产方案?并列举出来.(3)若有两种销售定价方案,第一种定价方案可使A 产品每件获得利润1.15万元,B 产品每件获得利润1.25万元;第二种定价方案可使A 和B 产品每件都获得利润1.2万元;在上述生产方案中哪种定价方案盈利最多?(请用数据说明)28.已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.29.某商场计划从厂家购进甲、乙两种不同型号的电视机,已知进价分别为:甲种每台1500元,乙种每台2100元.(1)若商场同时购进这两种不同型号的电视机50台,金额不超过76000元,商场有几种进货方案,并写出具体的进货方案.(2)在(1)的条件下,若商场销售一台甲、乙型号的电视机的销售价分别为1650元、2300元,以上进货方案中,哪种进货方案获利最多?最多为多少元?30.为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:(1)该班总人数是;(2)根据计算,请你补全两个统计图;(3)观察补全后的统计图,写出一条你发现的结论.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1.B2.A3.C4.D5.D6.B7.D8.A9.C10.C11.A12.A13.C14.B15.D二、填空题16.(13)或(51)【解析】【分析】平移中点的变化规律是:横坐标右移加左移减;纵坐标上移加下移减【详解】解:①如图1当A平移到点C时∵C(32)A的坐标为(20)点B的坐标为(01)∴点A的横坐标增大17.150°【解析】【分析】先过点B作BF∥CD由CD∥AE可得CD∥BF∥AE继而证得∠1+∠BCD=180°∠2+∠BAE=180°又由BA垂直于地面AE于A∠BCD=120°求得答案【详解】如图过18.见解析【解析】【分析】由已知易得AB∥CD则∠BAE=∠AEC又∠1=∠2所以∠MAE=∠AEN则AM∥EN故∠M=∠N【详解】∵∠BAE+∠AED=180°(已知)∴AB∥CD(同旁内角互补两直线19.2【解析】【分析】根据两个等边△ABD△CBD的边长均为1将△ABD沿AC方向向右平移到△ABD的位置得出线段之间的相等关系进而得出OM+MN+NR+GR+EG+OE=A′D′+CD=1+1=2即可20.【解析】【分析】把xy的值代入方程组再将两式相加即可求出a﹣b的值【详解】将代入方程组得:①+②得:4a﹣4b=7则a﹣b=故答案为【点睛】本题考查二元一次方程组的解解题的关键是观察两方程的系数从而21.x=-3【解析】【分析】由2x3+54=0得x3=-27解出x值即可【详解】由2x3+54=0得x3=-27∴x=-3故答案为:x=-3【点睛】本题考查了立方根正确理解立方根的意义是解题的关键22.62【解析】【分析】【详解】∵∴∠BOC=90°-28°=62°∵∠BOC=∠AOD∴∠AOD=62°23.12【解析】【分析】求出每个不等式的解集根据已知得出不等式组的解集根据不等式组的整数解即可得出关于a的不等式组求出即可【详解】解不等式3x-5≤2x-2得:x≤3解不能等式2x+3>a得:x>∵不等24.【解析】【分析】根据点到直线的距离是直线外的点到这条直线的垂线段的长度可得答案【详解】解:∵PB⊥lPB=5cm∴P到l的距离是垂线段PB的长度5cm故答案为:5【点睛】本题考查了点到直线的距离的定25.145【解析】【分析】如图:延长AB交l2于E根据平行线的性质可得∠AED=∠1根据可得AE//CD根据平行线的性质可得∠AED+∠2=180°即可求出∠2的度数【详解】如图:延长AB交l2于E∵l三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1.B解析:B【解析】【分析】根据内错角相等,两直线平行,得AB∥CE,再根据性质得∠B=∠3.【详解】因为∠1=∠2,所以AB∥CE所以∠B=∠3=30故选B【点睛】熟练运用平行线的判定和性质.2.A解析:A【解析】∠︒∴∠︒∴∠∠︒ .故选A.1=1303=502=23=1003.C解析:C【解析】【分析】表示出不等式组的解集,由解集中有3个整数解,确定出m的范围即可.【详解】不等式组解集为1<x<m,由不等式组有3个整数解,且为2,3,4,得到4<m≤5,故选C.【点睛】此题考查了一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.4.D解析:D【解析】A.∵a >b ,∴a-7>b-7,∴选项A 正确;B.∵a >b ,∴6+a >b+6,∴选项B 正确;C.∵a >b ,∴55a b >,∴选项C 正确;D.∵a >b ,∴-3a <-3b ,∴选项D 错误.故选D. 5.D解析:D【解析】【分析】根据不等式两边加(或减)同一个数(或式子),不等号的方向不变,不等式两边乘(或除以)同一个正数,不等号的方向不变,不等式两边乘(或除以)同一个负数,不等号的方向改变,可得答案.【详解】A. 当0a ≤时,2a a ≥,故A 不一定成立,故本选项错误; B. 当0a ≤时,a a -≥,故B 不一定成立,故本选项错误; C. 若ab >,当0cd =≤时,则ac bd ≤,故C 不一定成立,故本选项错误;D. 若1a b >>,则必有22a b >,正确;故选D .【点睛】主要考查了不等式的基本性质.“0”是很特殊的数,因此,解答不等式的问题时,应密切关注“0”存在与否,以防掉进“0”的陷阱.不等式的基本性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.6.B解析:B【解析】解:∵34<<,∴415<<.故选B .的取值范围是解题关键.7.D解析:D【解析】【分析】先根据第一象限内的点的坐标特征判断出a、b的符号,进而判断点B所在的象限即可.【详解】∵点A(a,-b)在第一象限内,∴a>0,-b>0,∴b<0,∴点B((a,b)在第四象限,故选D.【点睛】本题考查了点的坐标,解决本题的关键是牢记平面直角坐标系中各个象限内点的符号特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负.8.A解析:A【解析】试题分析:先把a、b当作已知条件求出不等式组的解集,再与已知解集相比较即可求出a、b的值.解:20210x ax b+->⎧⎨--<⎩①②,由①得,x>2﹣a,由②得,x<12b+,故不等式组的解集为;2﹣a<x<12b +,∵原不等式组的解集为0<x<1,∴2﹣a=0,12b+=1,解得a=2,b=1.故选A.9.C解析:C【解析】【分析】根据题意,利用要在不超过15分钟的时间内从甲地到达乙地建立不等式即可解题.【详解】解:由题可知只需要小明在15分钟之内走过的路程大于1800即可,即210x+90(15﹣x)≥1800故选C.【点睛】本题考查了一次不等式的实际应用,属于简单题,建立不等关系是解题关键.10.C解析:C【解析】试题分析:已知,△ABE向右平移2cm得到△DCF,根据平移的性质得到EF=AD=2cm,AE=DF ,又因△ABE 的周长为16cm ,所以AB+BC+AC=16cm ,则四边形ABFD 的周长=AB+BC+CF+DF+AD=16cm+2cm+2cm=20cm .故答案选C .考点:平移的性质.11.A解析:A【解析】【分析】根据题意可得不等式恰好有两个负整数解,即-1和-2,再结合不等式计算即可.【详解】根据x 的不等式x -b >0恰有两个负整数解,可得x 的负整数解为-1和-20x b ->x b ∴>综合上述可得32b -≤<-故选A.【点睛】本题主要考查不等式的非整数解,关键在于非整数解的确定.12.A解析:A【解析】【分析】根据A (﹣2,1)和B (﹣2,﹣3)的坐标以及与C 的关系进行解答即可.【详解】解:因为A (﹣2,1)和B (﹣2,﹣3),所以建立如图所示的坐标系,可得点C 的坐标为(2,﹣1).故选:A .【点睛】考查坐标问题,关键是根据A (﹣2,1)和B (﹣2,﹣3)的坐标以及与C 的关系解答.13.C解析:C【解析】【分析】根据A和C的坐标可得点A向右平移4个单位,向上平移1个单位,点B的平移方法与A 的平移方法相同,再根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得点D的坐标.【详解】解:∵点A(0,1)的对应点C的坐标为(4,2),即(0+4,1+1),∴点B(3,3)的对应点D的坐标为(3+4,3+1),即D(7,4);故选:C.【点睛】此题主要考查了坐标与图形的变化——平移,关键正确得到点的平移方法.14.B解析:B【解析】【分析】由点P在x轴上求出a的值,从而得出点Q的坐标,继而得出答案.【详解】∵点P(a,a-1)在x轴上,∴a-1=0,即a=1,则点Q坐标为(-1,2),∴点Q在第二象限,故选:B.【点睛】此题考查点的坐标,解题的关键是掌握各象限及坐标轴上点的横纵坐标特点.15.D解析:D【解析】解:∵直线l1∥l2,∴∠3=∠1=44°.∵l3⊥l4,∠2=90°-∠3=90°-44°=46°.故选D.二、填空题16.(13)或(51)【解析】【分析】平移中点的变化规律是:横坐标右移加左移减;纵坐标上移加下移减【详解】解:①如图1当A平移到点C时∵C(32)A的坐标为(20)点B的坐标为(01)∴点A的横坐标增大解析:(1,3)或(5,1)【解析】【分析】平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.【详解】解:①如图1,当A平移到点C时,∵C(3,2),A的坐标为(2,0),点B的坐标为(0,1),∴点A的横坐标增大了1,纵坐标增大了2,平移后的B坐标为(1,3),②如图2,当B平移到点C时,∵C(3,2),A的坐标为(2,0),点B的坐标为(0,1),∴点B的横坐标增大了3,纵坐标增大2,∴平移后的A坐标为(5,1),故答案为:(1,3)或(5,1)【点睛】本题考查坐标系中点、线段的平移规律,关键要理解在平面直角坐标系中,图形的平移与图形上某点的平移相同,从而通过某点的变化情况来解决问题.17.150°【解析】【分析】先过点B作BF∥CD由CD∥AE可得CD∥BF∥AE继而证得∠1+∠BCD=180°∠2+∠BAE=180°又由BA垂直于地面AE于A∠BCD=120°求得答案【详解】如图过解析:150°【解析】【分析】先过点B作BF∥CD,由CD∥AE,可得CD∥BF∥AE,继而证得∠1+∠BCD=180°,∠2+∠BAE=180°,又由BA垂直于地面AE于A,∠BCD=120°,求得答案.如图,过点B作BF∥CD,∵CD∥AE,∴CD∥BF∥AE,∴∠1+∠BCD=180°,∠2+∠BAE=180°,∵∠BCD=120°,∠BAE=90°,∴∠1=60°,∠2=90°,∴∠ABC=∠1+∠2=150°.故答案是:150o.【点睛】考查了平行线的性质.注意掌握辅助线的作法,注意数形结合思想的应用.18.见解析【解析】【分析】由已知易得AB∥CD则∠BAE=∠AEC又∠1=∠2所以∠MAE=∠AEN则AM∥EN故∠M=∠N【详解】∵∠BAE+∠AED=180°(已知)∴AB∥CD(同旁内角互补两直线解析:见解析【解析】【分析】由已知易得AB∥CD,则∠BAE=∠AEC,又∠1=∠2,所以∠MAE=∠AEN,则AM∥EN,故∠M=∠N.【详解】∵∠BAE+∠AED=180°(已知)∴AB∥CD(同旁内角互补,两直线平行)∠BAE=∠AEC(两直线平行,内错角相等)又∵∠1=∠2,∴∠BAE−∠1=∠AEC−∠2,即∠MAE=∠NEA,∴AM∥EN,(内错角相等,两直线平行)∴∠M=∠N(两直线平行,内错角相等)【点睛】考查平行线的判定与性质,熟练掌握平行线的判定定理与性质定理是解题的关键.19.2【解析】【分析】根据两个等边△ABD△CBD的边长均为1将△ABD沿AC方向向右平移到△ABD的位置得出线段之间的相等关系进而得出OM+MN+NR+GR+E G+OE=A′D′+CD=1+1=2即可【解析】【分析】根据两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A’B’D’的位置,得出线段之间的相等关系,进而得出OM+MN+NR+GR+EG+OE=A′D′+CD=1+1=2,即可得出答案.【详解】解:∵两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B′D′的位置,∴A′M=A′N=MN,MO=DM=DO,OD′=D′E=OE,EG=EC=GC,B′G=RG=RB′,∴OM+MN+NR+GR+EG+OE=A′D′+CD=1+1=2;故答案为2.20.【解析】【分析】把xy的值代入方程组再将两式相加即可求出a﹣b的值【详解】将代入方程组得:①+②得:4a﹣4b=7则a﹣b=故答案为【点睛】本题考查二元一次方程组的解解题的关键是观察两方程的系数从而解析:7 4【解析】【分析】把x、y的值代入方程组,再将两式相加即可求出a﹣b的值.【详解】将x ay b=⎧⎨=⎩代入方程组3354x yx y+=⎧⎨-=⎩,得:3354a ba b+=⎧⎨-=⎩①②,①+②,得:4a﹣4b=7,则a﹣b=74,故答案为74.【点睛】本题考查二元一次方程组的解,解题的关键是观察两方程的系数,从而求出a﹣b的值.21.x=-3【解析】【分析】由2x3+54=0得x3=-27解出x值即可【详解】由2x3+54=0得x3=-27∴x=-3故答案为:x=-3【点睛】本题考查了立方根正确理解立方根的意义是解题的关键【解析】【分析】由2x 3+54=0,得x 3=-27,解出x 值即可.【详解】由2x 3+54=0,得x 3=-27,∴x=-3,故答案为:x=-3.【点睛】本题考查了立方根,正确理解立方根的意义是解题的关键.22.62【解析】【分析】【详解】∵∴∠BOC=90°-28°=62°∵∠BOC=∠AOD∴∠AOD=62°解析:62【解析】【分析】【详解】∵OE AB ⊥,28EOC ∠=,∴∠BOC=90°-28°=62°∵∠BOC=∠AOD∴∠AOD=62°. 23.12【解析】【分析】求出每个不等式的解集根据已知得出不等式组的解集根据不等式组的整数解即可得出关于a 的不等式组求出即可【详解】解不等式3x -5≤2x -2得:x≤3解不能等式2x+3>a 得:x >∵不等解析:1,2【解析】【分析】求出每个不等式的解集,根据已知得出不等式组的解集,根据不等式组的整数解即可得出关于a 的不等式组,求出即可.【详解】解不等式3x-5≤2x -2,得:x≤3,解不能等式2x+3>a ,得:x >32a -, ∵不等式组有且仅有4个整数解,∴-1≤32a -<0, 解得:1≤a <3,∴整数a 的值为1和2,故答案为:1,2.【点睛】本题考查了一元一次不等式组的整数解,解答本题的关键应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.24.【解析】【分析】根据点到直线的距离是直线外的点到这条直线的垂线段的长度可得答案【详解】解:∵PB⊥lPB=5cm∴P 到l 的距离是垂线段PB 的长度5cm 故答案为:5【点睛】本题考查了点到直线的距离的定解析:【解析】【分析】根据点到直线的距离是直线外的点到这条直线的垂线段的长度,可得答案.【详解】解:∵PB ⊥l ,PB=5cm ,∴P 到l 的距离是垂线段PB 的长度5cm ,故答案为:5.【点睛】本题考查了点到直线的距离的定义,熟练掌握是解题的关键.25.145【解析】【分析】如图:延长AB 交l2于E 根据平行线的性质可得∠AED=∠1根据可得AE//CD 根据平行线的性质可得∠AED+∠2=180°即可求出∠2的度数【详解】如图:延长AB 交l2于E ∵l解析:145【解析】【分析】如图:延长AB 交l 2于E ,根据平行线的性质可得∠AED=∠1,根据αβ∠∠=可得AE//CD ,根据平行线的性质可得∠AED+∠2=180°,即可求出∠2的度数.【详解】如图:延长AB 交l 2于E ,∵l 1//l 2,∴∠AED=∠1=35°,∵αβ∠∠=,∴AE//CD ,∴∠AED+∠2=180°,∴∠2=180°-∠AED=180°-35°=145°,故答案为145【点睛】本题考查了平行线的判定和性质,通过内错角相等证得AE//CD 是解题关键.三、解答题26.(1)500;(2)1;(3)该校每天户外活动时间超过1小时的学生有800人.【解析】【分析】(1)根据条形统计图和扇形统计图可以求得被调查学生总数和1.5小时的学生数,从而可以将条形统计图补充完整;(2)根据条形统计图可以得到这组数据的中位数;(3)根据条形统计图可以求得校共有1850名学生,该校每天户外活动时间超过1小时的学生有多少人.【详解】(1)0.5小时的有100人占被调查总人数的20%,∴被调查的人数有:10020%500÷=,27.(1)94(500)360038(500)2410x x x x +-≤⎧⎨+-≤⎩;(2)符合的生产方案为①生产A 产品318件,B 产品182件;②生产A 产品319件,B 产品181件;③生产A 产品320件,B 产品180件;(3)第二种定价方案的利润比较多.【解析】分析:(1)关系式为:A 种产品需要甲种原料数量+B 种产品需要甲种原料数量≤3600;A 种产品需要乙种原料数量+B 种产品需要乙种原料数量≤2410,把相关数值代入即可;(2)解(1)得到的不等式,得到关于x 的范围,根据整数解可得相应方案;(3)分别求出两种情形下的利润即可判断;详解:(1)由题意()94(500)3600385002410x x x x +-≤⎧⎨+-≤⎩. (2)解第一个不等式得:x≤320,解第二个不等式得:x≥318,∴318≤x≤320,∵x 为正整数,∴x=318、319、320,500﹣318=182,500﹣319=181,500﹣320=180,∴符合的生产方案为①生产A 产品318件,B 产品182件;②生产A产品319件,B产品181件;③生产A产品320件,B产品180件;(3)第一种定价方案下:①的利润为318×1.15+182×1.25=593.2(万元),②的利润为:319×1.15+181×1.25=593.1(万元)③的利润为320×1.15+180×1.25=593(万元)第二种定价方案下:①②③的利润均为500×1.2=600(万元),综上所述,第二种定价方案的利润比较多.点睛:本题考查理解题意能力,生产不同产品所用的原料不同,关键是在原料范围内求得生产的产品,从而求解.找出题目中的不等量关系列出不等式组是解答本题的关键.28.证明见解析.【解析】【分析】由∠1=∠2,得BD∥CE,所以∠4=∠E,又∠3=∠E,所以∠3=∠4,可得AD∥BE.【详解】证明:∵∠1=∠2,又∵∠3=∠E,∴BD∥CE,∴∠3=∠4,∴∠4=∠E,∴AD∥BE.【点睛】本题考核知识点:平行线的判定.解题关键点:理解平行线的判定.29.(1)有2种进货方案:方案一:是购进甲种型号的电视机49台,乙种型号的电视机1台;方案二:是甲种型号的电视机50台,乙种型号的电视机0台;(2)方案一的利润大,最多为7550元.【解析】【分析】(1)设购进甲种型号的电视机x台,则乙种型号的电视机y台.数量关系为:两种不同型号的电视机50台,金额不超过76000元;(2)根据利润=数量×(售价-进价),列出式子进行计算,即可得到答案.【详解】解:(1)设购进甲种型号的电视机x台,则乙种型号的电视机(50-x)台.则1500x+2100(50-x)≤76000,解得:x≥4813.则50≥x≥4813.∵x是整数,∴x=49或x=50.故有2种进货方案:方案一:是购进甲种型号的电视机49台,乙种型号的电视机1台;方案二:是甲种型号的电视机50台,乙种型号的电视机0台;(2)方案一的利润为:49×(1650-1500)+(2300-2100)=7550(元)方案二的利润为:50×(1650-1500)=7500(元).∵7550>7500∴方案一的利润大,最多为7550元.【点睛】本题考查了一元一次不等式的应用.解决问题的关键是读懂题意,依题意列出不等式进行求解.30.(1)40;(2)答案见解析;(3)答案不唯一,如优秀人数逐渐增多,增大的幅度逐渐减小等.【解析】【分析】(1)由两个统计图可以发现第一次22名优秀的同学占55%,故该班总人数为2255%=40÷;(2)第四次优秀人数为:4085%=34⨯,第三次优秀率为3240×100%=80%,据此可以补全统计图;(3)根据图像可以写出优秀人数逐渐增多,增大的幅度逐渐减小等信息.【详解】解:(1)由题意可得:该班总人数是:22÷55%=40(人);故答案为:40;(2)由(1)得,第四次优秀的人数为:40×85%=34(人),第三次优秀率为:3240×100%=80%;如图所示:;(3)答案不唯一,如优秀人数逐渐增多,增大的幅度逐渐减小等.【点睛】此题主要考查了条形统计图以及折线统计图,利用图形获取正确信息是解题关键.。
(必考题)初中数学七年级下期末经典习题(提高培优)(1)

一、选择题1.已知二元一次方程组m 2n 42m n 3-=⎧⎨-=⎩,则m+n 的值是( ) A .1 B .0C .-2D .-1 2.不等式组213312x x +⎧⎨+≥-⎩<的解集在数轴上表示正确的是( ) A .B .C .D .3.如图,数轴上表示2、5的对应点分别为点C ,B ,点C 是AB 的中点,则点A 表示的数是( )A .5-B .25-C .45-D .52-4.如图,直线a ∥b ,直线c 与直线a 、b 分别交于点A 、点B ,AC ⊥AB 于点A ,交直线b 于点C .如果∠1=34°,那么∠2的度数为( )A .34°B .56°C .66°D .146°5.将一副三角板和一张对边平行的纸条按如图摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )A .15°B .22.5°C .30°D .45°6.某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打( )A .6折B .7折C .8折D .9折7.如图,在平面直角坐标系xOy 中,点P(1,0).点P 第1次向上跳动1个单位至点P 1(1,1),紧接着第2次向左跳动2个单位至点P 2(﹣1,1),第3次向上跳动1个单位至点P 3,第4次向右跳动3个单位至点P 4,第5次又向上跳动1个单位至点P 5,第6次向左跳动4个单位至点P 6,….照此规律,点P 第100次跳动至点P 100的坐标是( )A .(﹣26,50)B .(﹣25,50)C .(26,50)D .(25,50)8.为了绿化校园,30名学生共种78棵树苗,其中男生每人种3棵,女生每人种2棵,设男生有x 人,女生有y 人,根据题意,所列方程组正确的是( )A .783230x y x y +=⎧⎨+=⎩B .782330x y x y +=⎧⎨+=⎩C .302378x y x y +=⎧⎨+=⎩D .303278x y x y +=⎧⎨+=⎩ 9.已知{x =1y =2 是关于x ,y 的二元一次方程x-ay=3的一个解,则a 的值为( ) A .1B .-1C .2D .-2 10.方程组23x y a x y +=⎧⎨-=⎩的解为5x y b=⎧⎨=⎩,则a 、b 分别为( ) A .a=8,b=﹣2B .a=8,b=2C .a=12,b=2D .a=18,b=8 11.已知4<m <5,则关于x 的不等式组0420x m x -<⎧⎨-<⎩的整数解共有( ) A .1个 B .2个 C .3个 D .4个12.已知32x y =-⎧⎨=-⎩是方程组12ax cy cx by +=⎧⎨-=⎩的解,则a 、b 间的关系是( ) A .491b a -= B .321a b += C .491b a -=- D .941a b +=13.下列四个说法:①两点之间,线段最短;②连接两点之间的线段叫做这两点间的距离;③经过直线外一点,有且只有一条直线与这条直线平行;④直线外一点与这条直线上各点连接的所有线段中,垂线段最短.其中正确的个数有( )A .1个B .2个C .3个D .4个14.已知x 、y 满足方程组2827x y x y +=⎧⎨+=⎩,则x +y 的值是( ) A .3 B .5C .7D .9 15.若0a <,则下列不等式不成立的是( )A .56a a +<+B .56a a -<-C .56a a <D .65a a < 二、填空题16.若关于x 、y 的二元一次方程组2133x y m x y -=+⎧⎨+=⎩的解满足x +y >0,则m 的取值范围是____.17.如图,在平面直角坐标系中,点A 的坐标为(2,0),点B 的坐标为(0,1),将线段AB 平移,使其一个端点到C (3,2),则平移后另一端点的坐标为______________.18.某小区地下停车场入口门栏杆的平面示意图如图所示,BA 垂直地面AE 于点A ,CD 平行于地面AE ,若∠BCD =120° ,则∠ABC = ________.19.如果a 的平方根是3±,则a =_________20.若将点A (1,3)向左平移2个单位,再向下平移4个单位得到点B , 则点B 的坐标为_______.21.已知21x y =⎧⎨=⎩是方程组ax 5{1by bx ay +=+=的解,则a ﹣b 的值是___________ 22.如图,将周长为8的△ABC 沿BC 方向向右平移1个单位得到△DEF ,则四边形ABFD 的周长为 .23.如图,直线//a b ,点B 在直线上b 上,且AB ⊥BC ,∠1=55°,则∠2的度数为______.24.已知方程组236x yx y+=⎧⎨-=⎩的解满足方程x+2y=k,则k的值是__________.25.关于x的不等式111x-<-的非负整数解为________.三、解答题26.某运输公司现将一批152吨的货物运往A,B两地,若用大小货车15辆,则恰好能一次性运完这批货.已知这两种大小货车的载货能力分别为12吨/辆和8吨/辆,其运往A,B 两地的运费如下表所示:目的地(车型)A地(元/辆)B地(元/辆)大货车800900小货车400600(1)求这15辆车中大小货车各多少辆.(用二元一次方程组解答)(2)现安排其中的10辆货车前往A地,其余货车前往B地,设前往A地的大货车为x辆,前往A,B两地总费用为w元,试求w与x的函数解析式.27.如图,直线AB与CD相交于点O,∠BOE=∠DOF=90°.(1)写出图中与∠COE互补的所有的角(不用说明理由).(2)问:∠COE与∠AOF相等吗?请说明理由;(3)如果∠AOC=15∠EOF,求∠AOC的度数.28.已知:用3辆A型车和2辆B型车载满货物一次可运货17吨;用2辆A型车和3辆B型车载满货物一次可运货l8吨,某物流公刊现有35吨货物,计划同时租用A型车a 辆,B型车b辆,一次运完,且恰好每辆车都载满货物.根据以上信息,解答下列问题:(1)l辆A型车和l辆B型车都载满货物一次可分别运货多少吨?(2)请你帮该物流公司设计租车方案;(3)若A型车每辆需租金200元/次,B型车每辆需租金240元/次,请选出最省钱的租车方案,并求出最少租车费.29.问题情境在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.操作发现(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;结论应用(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG =α,则∠CFG 等于______(用含α的式子表示).30.解不等式-3+3+121-3-18-xxx x⎧≥⎪⎨⎪<⎩()【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1.D2.A3.C4.B5.A6.B7.C8.A9.B10.C11.B12.D13.C14.B15.C二、填空题16.m>-2【解析】【分析】首先解关于x和y的方程组利用m表示出x+y代入x+y>0即可得到关于m的不等式求得m的范围【详解】解:①+②得2x+2y=2m+4则x+y=m+2根据题意得m+2>0解得m>17.(13)或(51)【解析】【分析】平移中点的变化规律是:横坐标右移加左移减;纵坐标上移加下移减【详解】解:①如图1当A平移到点C时∵C(32)A的坐标为(20)点B的坐标为(01)∴点A的横坐标增大18.150°【解析】【分析】先过点B作BF∥CD由CD∥AE可得CD∥BF∥AE继而证得∠1+∠BCD=180°∠2+∠BAE=180°又由BA垂直于地面AE于A∠BCD=120°求得答案【详解】如图过19.81【解析】【分析】根据平方根的定义即可求解【详解】∵9的平方根为∴=9所以a=81【点睛】此题主要考查平方根的性质解题的关键是熟知平方根的定义20.(﹣1﹣1)【解析】试题解析:点B的横坐标为1-2=-1纵坐标为3-4=-1所以点B的坐标是(-1-1)【点睛】本题考查点的平移规律;用到的知识点为:点的平移左右平移只改变点的横坐标左减右加;上下平21.4;【解析】试题解析:把代入方程组得:①×2-②得:3a=9即a=3把a=3代入②得:b=-1则a-b=3+1=422.【解析】试题解析:根据题意将周长为8的△ABC沿边BC向右平移1个单位得到△DEF则AD=1BF=BC+CF=BC+1DF=AC又∵AB+BC+AC=10∴四边形ABFD的周长=AD+AB+BF+D23.【解析】【分析】先根据∠1=55°AB⊥BC求出∠3的度数再由平行线的性质即可得出结论【详解】解:∵AB⊥BC∠1=55°∴∠3=90°-55°=35°∵a∥b∴∠2=∠3=35°故答案为:35°【24.-3【解析】分析:解出已知方程组中xy的值代入方程x+2y=k即可详解:解方程组得代入方程x+2y=k得k=-3故本题答案为:-3点睛:本题的实质是考查三元一次方程组的解法需要对三元一次方程组的定义25.012【解析】【分析】先解不等式确定不等式的解集然后再确定其非负整数解即可得到答案【详解】解:解不等式得:∵∴∴的非负整数解为:012故答案为:012【点睛】本题主要考查了二次根式的应用及一元一次不三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1.D解析:D【解析】分析:根据二元一次方程组的特点,用第二个方程减去第一个方程即可求解.详解:24 23m nm n-=⎧⎨-=⎩①②②-①得m+n=-1.故选:D.点睛:此题主要考查了二元一次方程组的特殊解法,关键是利用加减法对方程变形,得到m+n这个整体式子的值.2.A解析:A【解析】【分析】先求出不等式组的解集,再在数轴上表示出来即可.【详解】213312x x +⎧⎨+≥-⎩<①②∵解不等式①得:x <1,解不等式②得:x≥-1,∴不等式组的解集为-1≤x <1, 在数轴上表示为:,故选A .【点睛】本题考查了解一元一次不等式组和在数轴上表示不等式组的解集,能根据不等式的解集求出不等式组的解集是解此题的关键. 3.C解析:C【解析】【分析】首先可以求出线段BC 的长度,然后利用中点的性质即可解答.【详解】∵表示25C ,B , 5,∵点C 是AB 的中点,则设点A 的坐标是x ,则5∴点A 表示的数是5故选C .【点睛】本题主要考查了数轴上两点之间x 1,x 2的中点的计算方法.4.B解析:B【解析】分析:先根据平行线的性质得出∠2+∠BAD =180°,再根据垂直的定义求出∠2的度数. 详解:∵直线a ∥b ,∴∠2+∠BAD =180°.∵AC ⊥AB 于点A ,∠1=34°,∴∠2=180°﹣90°﹣34°=56°.故选B .点睛:本题主要考查了平行线的性质,解题的关键是掌握两直线平行,同旁内角互补,此题难度不大.5.A解析:A【解析】试题分析:如图,过A 点作AB ∥a ,∴∠1=∠2,∵a ∥b ,∴AB ∥b ,∴∠3=∠4=30°,而∠2+∠3=45°,∴∠2=15°,∴∠1=15°.故选A .考点:平行线的性质.6.B解析:B【解析】【详解】设可打x 折,则有1200×10x -800≥800×5%, 解得x≥7.即最多打7折.故选B .【点睛】本题考查的是一元一次不等式的应用,解此类题目时注意利润和折数,计算折数时注意要除以10.解答本题的关键是读懂题意,求出打折之后的利润,根据利润率不低于5%,列不等式求解. 7.C解析:C【解析】【分析】解决本题的关键是分析出题目的规律,以奇数开头的相邻两个坐标的纵坐标是相同的,所以第100次跳动后,纵坐标为100250÷=,其中4的倍数的跳动都在y 轴的右侧,那么第100次跳动得到的横坐标也在y 轴的右侧.1P 横坐标为1,4P 横坐标为2,8P 横坐标为3,以此类推可得到100P 的横坐标.【详解】解:经过观察可得:1P 和2P 的纵坐标均为1,3P 和4P 的纵坐标均为2,5P 和6P 的纵坐标均为3,因此可以推知99P 和100P 的纵坐标均为100250÷=;其中4的倍数的跳动都在y 轴的右侧,那么第100次跳动得到的横坐标也在y 轴的右侧.1P 横坐标为1,4P 横坐标为2,8P 横坐标为3,以此类推可得到:n P 的横坐标为41n ÷+(n 是4的倍数). 故点100P 的横坐标为:1004126÷+=,纵坐标为:100250÷=,点P 第100次跳动至点100P 的坐标为()26,50.故选:C .【点睛】本题考查规律型:点的坐标,解题的关键是分析出题目的规律,找出题目中点的坐标的规律,属于中考常考题型.8.A解析:A【解析】【分析】【详解】该班男生有x 人,女生有y 人.根据题意得:303278x y x y +=⎧⎨+=⎩, 故选D .考点:由实际问题抽象出二元一次方程组. 9.B解析:B【解析】【分析】把{x =1y =2代入x-ay=3,解一元一次方程求出a 值即可. 【详解】∵{x =1y =2是关于x ,y 的二元一次方程x-ay=3的一个解, ∴1-2a=3解得:a=-1故选B.【点睛】本题考查二元一次方程的解,使方程左右两边相等的未知数的值,叫做方程的解;一组数是方程的解,那么它一定满足这个方程.10.C解析:C【解析】试题解析:将x=5,y=b代入方程组得:10{53b ab+=-=,解得:a=12,b=2,故选C.考点:二元一次方程组的解.11.B解析:B【解析】【分析】先求解不等式组得到关于m的不等式解集,再根据m的取值范围即可判定整数解.【详解】不等式组0 420 x mx-<⎧⎨-<⎩①②由①得x<m;由②得x>2;∵m的取值范围是4<m<5,∴不等式组420x mx-<⎧⎨-<⎩的整数解有:3,4两个.故选B.【点睛】本题考查了一元一次不等式组的整数解,用到的知识点是一元一次不等式组的解法,m的取值范围是本题的关键.12.D解析:D【解析】【分析】把3{2xy=-=-,代入1{2ax cycx by+=-=,即可得到关于,,a b c的方程组,从而得到结果.【详解】由题意得,321322a cc b--=⎧⎨-+=⎩①②,3,2⨯⨯①②得,963 644a cc b--=⎧⎨-+=⎩③④-④③得941a b+=,故选:D.13.C解析:C【分析】根据线段公理,两点之间的距离的概念,平行公理,垂线段最短等知识一一判断即可.【详解】解:①两点之间,线段最短,正确.②连接两点之间的线段叫做这两点间的距离,错误,应该是连接两点之间的线段的距离叫做这两点间的距离.③经过直线外一点,有且只有一条直线与这条直线平行,正确.④直线外一点与这条直线上各点连接的所有线段中,垂线段最短.正确.故选C .【点睛】本题考查线段公理,两点之间的距离的概念,平行公理,垂线段最短等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.14.B解析:B【解析】【分析】把两个方程相加可得3x+3y=15,进而可得答案.【详解】两个方程相加,得3x+3y=15,∴x+y=5,故选B.【点睛】本题主要考查解二元一次方程组,灵活运用整体思想是解题关键.15.C解析:C【解析】【分析】直接根据不等式的性质进行分析判断即可得到答案.【详解】A .0a <,则a 是负数,56a a +<+可以看成是5<6两边同时加上a ,故A 选项成立,不符合题意;B .56a a -<-是不等式5<6两边同时减去a ,不等号不变,故B 选项成立,不符合题意;C .5<6两边同时乘以负数a ,不等号的方向应改变,应为:56a a >,故选项C 不成立,符合题意;D .65a a<是不等式5<6两边同时除以a ,不等号改变,故D 选项成立,不符合题意. 故选C .本题考查的实际上就是不等式的基本性质:不等式的两边都加上(或减去)同一个数(或式子)不等号的方向不变;不等式两边同乘以(或除以)同一个正数,不等号的方向不变;不等式两边同乘以(或除以)同一个负数,不等号的方向改变.二、填空题16.m>-2【解析】【分析】首先解关于x和y的方程组利用m表示出x+y代入x+y>0即可得到关于m的不等式求得m的范围【详解】解:①+②得2x+2y=2m+4则x+y=m+2根据题意得m+2>0解得m>解析:m>-2【解析】【分析】首先解关于x和y的方程组,利用m表示出x+y,代入x+y>0即可得到关于m的不等式,求得m的范围.【详解】解:2133x y mx y-=+⎧⎨+=⎩①②,①+②得2x+2y=2m+4,则x+y=m+2,根据题意得m+2>0,解得m>﹣2.故答案是:m>﹣2.【点睛】本题考查的是解二元一次方程组和解一元一次不等式,解答此题的关键是把m当作已知数表示出x+y的值,再得到关于m的不等式.17.(13)或(51)【解析】【分析】平移中点的变化规律是:横坐标右移加左移减;纵坐标上移加下移减【详解】解:①如图1当A平移到点C时∵C (32)A的坐标为(20)点B的坐标为(01)∴点A的横坐标增大解析:(1,3)或(5,1)【解析】【分析】平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.【详解】解:①如图1,当A平移到点C时,∵C(3,2),A的坐标为(2,0),点B的坐标为(0,1),∴点A的横坐标增大了1,纵坐标增大了2,平移后的B坐标为(1,3),②如图2,当B平移到点C时,∵C(3,2),A的坐标为(2,0),点B的坐标为(0,1),∴点B的横坐标增大了3,纵坐标增大2,∴平移后的A坐标为(5,1),故答案为:(1,3)或(5,1)【点睛】本题考查坐标系中点、线段的平移规律,关键要理解在平面直角坐标系中,图形的平移与图形上某点的平移相同,从而通过某点的变化情况来解决问题.18.150°【解析】【分析】先过点B作BF∥CD由CD∥AE可得CD∥BF∥AE继而证得∠1+∠BCD=180°∠2+∠BAE=180°又由BA垂直于地面AE于A∠BCD=120°求得答案【详解】如图过解析:150°【解析】【分析】先过点B作BF∥CD,由CD∥AE,可得CD∥BF∥AE,继而证得∠1+∠BCD=180°,∠2+∠BAE=180°,又由BA垂直于地面AE于A,∠BCD=120°,求得答案.【详解】如图,过点B作BF∥CD,∵CD∥AE,∴CD∥BF∥AE,∴∠1+∠BCD=180°,∠2+∠BAE=180°,∵∠BCD=120°,∠BAE=90°,∴∠1=60°,∠2=90°,∴∠ABC=∠1+∠2=150°.故答案是:150o.【点睛】考查了平行线的性质.注意掌握辅助线的作法,注意数形结合思想的应用.19.81【解析】【分析】根据平方根的定义即可求解【详解】∵9的平方根为∴=9所以a=81【点睛】此题主要考查平方根的性质解题的关键是熟知平方根的定义解析:81【解析】【分析】根据平方根的定义即可求解.【详解】∵9的平方根为3±,,所以a=81【点睛】此题主要考查平方根的性质,解题的关键是熟知平方根的定义.20.(﹣1﹣1)【解析】试题解析:点B的横坐标为1-2=-1纵坐标为3-4=-1所以点B的坐标是(-1-1)【点睛】本题考查点的平移规律;用到的知识点为:点的平移左右平移只改变点的横坐标左减右加;上下平解析:(﹣1,﹣1)【解析】试题解析:点B的横坐标为1-2=-1,纵坐标为3-4=-1,所以点B的坐标是(-1,-1).【点睛】本题考查点的平移规律;用到的知识点为:点的平移,左右平移只改变点的横坐标,左减右加;上下平移只改变点的纵坐标,上加下减.21.4;【解析】试题解析:把代入方程组得:①×2-②得:3a=9即a=3把a=3代入②得:b=-1则a-b=3+1=4解析:4;【解析】试题解析:把21xy=⎧⎨=⎩代入方程组得:25{21a bb a++=①=②,①×2-②得:3a=9,即a=3,把a=3代入②得:b=-1,则a-b=3+1=4,22.【解析】试题解析:根据题意将周长为8的△ABC沿边BC向右平移1个单位得到△DEF则AD=1BF=BC+CF=BC+1DF=AC又∵AB+BC+AC=10∴四边形ABFD的周长=AD+AB+BF+D解析:【解析】试题解析:根据题意,将周长为8的△ABC沿边BC向右平移1个单位得到△DEF,则AD=1,BF=BC+CF=BC+1,DF=AC,又∵AB+BC+AC=10,∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10.考点:平移的性质.23.【解析】【分析】先根据∠1=55°AB⊥BC求出∠3的度数再由平行线的性质即可得出结论【详解】解:∵AB⊥BC∠1=55°∴∠3=90°-55°=35°∵a∥b∴∠2=∠3=35°故答案为:35°【解析:【解析】【分析】先根据∠1=55°,AB⊥BC求出∠3的度数,再由平行线的性质即可得出结论【详解】解:∵AB⊥BC,∠1=55°,∴∠3=90°-55°=35°.∵a∥b,∴∠2=∠3=35°.故答案为:35°.【点睛】本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等。
(完整版)初中七年级下册实数数学附答案(一)培优试卷

一、选择题1.下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,依此类推,则第⑦个图形中五角星的个数是( )A .98B .94C .90D .862.设记号*表示求a 、b 算术平均数的运算,即*2a ba b +=,则下列等式中对于任意实数a ,b ,c 都成立的是( ).①(*)()*()a b c a b a c +=++;②*()()*a b c a b c +=+; ③*()(*)(*)a b c a b a c +=+;④()()**22aa b c b c +=+. A .①②③B .①②④C .①③④D .②④ 3.若9﹣13的整数部分为a ,小数部分为b ,则2a +b 等于( ) A .12﹣13B .13﹣13C .14﹣13D .15﹣134.如示意图,小宇利用两个面积为1 dm 2的正方形拼成了一个面积为2 dm 2的大正方形,并通过测量大正方形的边长感受了2dm 的大小. 为了感知更多无理数的大小,小宇利用类似拼正方形的方法进行了很多尝试,下列做法不能实现的是( )A .利用两个边长为2dm 8的大小B .利用四个直角边为3dm 18的大小C 2的正方形以及一个直角边为2dm 6dm 的大小D .利用四个直角边分别为1 dm 和3 dm 的直角三角形以及一个边长为2 dm 的正方形感知10的大小5.已知a ,b 为两个连续的整数,且18a b <<a b + ) A .4B .3C .5D 106.下列说法:①所有无理数都能用数轴上的点表示;②若一个数的平方根等于它本身,则这个数是0或1;③任何实数都有立方根;164±,其中正确的个数有( ) A .0个B .1个C .2个D .3个7.如图,四个有理数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+p=0,则m,n,p,q四个有理数中,绝对值最大的一个是()A.p B.q C.m D.n8.对于任意不相等的两个实数a,b,定义运算:a※b=a2﹣b2+1,例如3※2=32﹣22+1=6,那么(﹣5)※4的值为()A.﹣40 B.﹣32 C.18 D.109.设n为正整数,且n<65<n+1,则n的值为()A.5 B.6 C.7 D.810.任何一个正整数n都可以进行这样的分解:n=p×q(p,q都是正整数,且p≤q),如果p×q在n的所有分解中两个因数之差的绝对值最小,我们就称p×q是n的黄金分解,并规定:F(n)=pq,例如:18可以分解为1×18;2×9;3×6这三种,这时F(18)=3162=,现给出下列关于F(n)的说法:①F(2) =12;② F(24)=38;③F(27)=3;④若n是一个完全平方数,则F(n)=1,其中说法正确的个数有()A.1个B.2个C.3个D.4个二、填空题11.观察下列等式:1﹣12=12,2﹣25=85,3﹣310=2710,4﹣417=6417,…,根据你发现的规律,则第20个等式为_____.12.对于这样的等式:若(x+1)5=a0x5+a1x4+a2x3+a3x2+a4x+a5,则﹣32a0+16a1﹣8a2+4a3﹣2a4+a5的值为_____.13.在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,②-①得,3S-S=39-1,即2S=39-1,所以S=.得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 ______ .14.若[x]表示不超过x的最大整数.如[π]=3,[4]=4,[﹣2.4]=﹣3.则下列结论:①[﹣x]=﹣[x];②若[x]=n,则x的取值范围是n≤x<n+1;③x=﹣2.75是方程4x﹣[x]+5=0的一个解;④当﹣1<x<1时,[1+x]+[1﹣x]的值为1或2.其中正确的结论有 ___(写出所有正确结论的序号).15.将1236按如图方式排列.若规定m,n表示第m排从左向右第n个数,则()7,3所表示的数是___________.16.对两数a ,b 规定一种新运算:2a b ab ⊗=,例如:2422416⊗=⨯⨯=,若不论x 取何值时,总有a x x ⊗=,则a =______.17.若[)x 表示大于x 的最小整数,如[)56=,[)1.81-=-,则下列结论中正确的有______(填写所有正确结论的序号).①[)01=;②33055⎡⎫-=⎪⎢⎣⎭;③[)0x x -<;④[)1x x x <≤+;⑤存在有理数x 使[)0.2x x -=成立.18.已知有理数1a ≠,我们把11a-称为a 的差倒数,如:2的差倒数是1112=--,1-的差倒数是()11112=--,如果13a =-,2a 是1a 的差倒数,4a 是3a 的差倒数,4a 是5a 的差倒数…依此类推,那么的12342017201820192020a a a a a a a a -+-⋅⋅⋅+-+-值是______. 19.定义运算“@”的运算法则为:xy 4+2@6 =____.20.在平面直角坐标系xOy 中,对于点P(x ,y),如果点Q(x ,'y )的纵坐标满足()()x y x y y y x x y -≥⎧=⎨-<'⎩当时当时,那么称点Q 为点P 的“关联点”.请写出点(3,5)的“关联点”的坐标_______;如果点P(x ,y)的关联点Q 坐标为(-2,3),则点P 的坐标为________.三、解答题21.规定:求若千个相同的有理数(均不等于0)的除法运算叫做除方,如()()()()2223333÷÷-÷-÷-÷-,等,类比有理数的乘方,我们把222÷÷记作()32,读作“2的圈3次方”,()()()()3333-÷-÷-÷-记作()()43-,读作“3-的圈4次方”,一般地,把n aa a a a↑÷÷÷⋯⋯÷记作()n a ,读作“a ”的圈n 次方.(初步探究)(1)直接写出计算结果:()()32=- ;()()42=- ; (2)关于除方,下列说法错误的是( )A .任何非零数的圈2次方都等于1B .对于任何正整数(),1=1n nC .()()433=4D .负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数 (深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢? (3)试一试:()()()2446113=5=35⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,,依照前面的算式,将()93,()1012⎛⎫- ⎪⎝⎭的运算结果直接写成幂的形式是()93= ,()101=2⎛⎫- ⎪⎝⎭;(4)想一想:将一个非零有理数a 的圆n 次方写成幂的形式是:()n a = ;(5)算一算:()()()()4652311122333⎛⎫⎛⎫÷-⨯---÷ ⎪ ⎪⎝⎭⎝⎭.22.在已有运算的基础上定义一种新运算⊗:x y x y y ⊗=-+,⊗的运算级别高于加减乘除运算,即⊗的运算顺序要优先于+-⨯÷、、、运算,试根据条件回答下列问题. (1)计算:()53⊗-= ;(2)若35x ⊗=,则x = ;(3)在数轴上,数x y 、的位置如下图所示,试化简:1x y x ⊗-⊗;(4)如图所示,在数轴上,点AB 、分别以1个单位每秒的速度从表示数-1和3的点开始运动,点A 向正方向运动,点B 向负方向运动,t 秒后点AB 、分别运动到表示数a 和b 的点所在的位置,当2a b ⊗=时,求t 的值.23.阅读下列解题过程:为了求23501222...2+++++的值,可设23501222...2S =+++++,则2345122222...2S =+++++,所以得51221S S -=-,所以5123505121:1222...221S =-+++++=-,即; 仿照以上方法计算:(1)2320191222...2+++++= . (2)计算:2320191333...3+++++ (3)计算:101102103200555...5++++ 24.阅读型综合题对于实数x y ,我们定义一种新运算(),L x y ax by =+(其中a b ,均为非零常数),等式右边是通常的 四则运算,由这种运算得到的数我们称之为线性数,记为(),L x y ,其中x y ,叫做线性数的一个数对.若实数 x y ,都取正整数,我们称这样的线性数为正格线性数,这时的x y ,叫做正格线性数的正格数对.(1)若(),3L x y x y =+,则()2,1L = ,31,22L ⎛⎫= ⎪⎝⎭;(2)已知(),3L x y x by =+,31,222L ⎛⎫= ⎪⎝⎭.若正格线性数(),18L x kx =,(其中k 为整数),问是否有满足这样条件的正格数对?若有,请找出;若没有,请说明理由. 25.阅读下面的文字,解答问题22的小数部分我们不可能全部地写出来,于是小明用2﹣1来表示2的小数部分,你同意小明的表示方法吗? 事实上,小明的表示方法是有道理的,因为2的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:4<7<9,即2<7<3, ∴7的整数部分为2,小数部分为(7﹣2)请解答:(1)57整数部分是 ,小数部分是 .(2)如果11的小数部分为a ,7的整数部分为b ,求|a ﹣b |+11的值. (3)已知:9+5=x +y ,其中x 是整数,且0<y <1,求x ﹣y 的相反数. 26.先阅读然后解答提出的问题:设a 、b 是有理数,且满足2322+=-a b ,求b a 的值. 解:由题意得(3)(2)20-++=a b ,因为a 、b 都是有理数,所以a ﹣3,b+2也是有理数, 由于2是无理数,所以a-3=0,b+2=0, 所以a=3,b=﹣2, 所以3(2)8=-=-a b .问题:设x 、y 都是有理数,且满足225y 1035x y -+=+,求x+y 的值.27.如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法. (1)图2中A 、B 两点表示的数分别为___________,____________;(2)请你参照上面的方法:①把图3中51⨯的长方形进行剪裁,并拼成一个大正方形.在图3中画出裁剪线,并在图4的正方形网格中画出拼成的大正方形,该正方形的边长a =___________.(注:小正方形边长都为1,拼接不重叠也无空隙)②在①的基础上,参照图2的画法,在数轴上分别用点M 、N 表示数a 以及3a -.(图中标出必要线段的长)28.规定:求若千个相同的有理数(均不等于0)的除法运算叫做除方,如()()()()2223333÷÷-÷-÷-÷-,等,类比有理数的乘方,我们把222÷÷记作()32,读作“2的圈3次方”,()()()()3333-÷-÷-÷-记作()()43-,读作“3-的圈4次方”,一般地,把n aa a a a↑÷÷÷⋯⋯÷记作()n a ,读作“a ”的圈n 次方.(初步探究)(1)直接写出计算结果:()()32=- ;()()42=- ; (2)关于除方,下列说法错误的是( )A .任何非零数的圈2次方都等于1B .对于任何正整数(),1=1n nC .()()433=4D .负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数 (深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢? (3)试一试:()()()2446113=5=35⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,,依照前面的算式,将()93,()1012⎛⎫- ⎪⎝⎭的运算结果直接写成幂的形式是()93= ,()101=2⎛⎫- ⎪⎝⎭;(4)想一想:将一个非零有理数a 的圆n 次方写成幂的形式是:()n a = ;(5)算一算:()()()()4652311122333⎛⎫⎛⎫÷-⨯---÷ ⎪ ⎪⎝⎭⎝⎭.29.阅读理解:一个多位数,如果根据它的位数,可以从左到右分成左、中、右三个数位相同的整数,其中a 代表这个整数分出来的左边数,b 代表的这个整数分出来的中间数,c 代表这个整数分出来的右边数,其中a ,b ,c 数位相同,若b ﹣a =c ﹣b ,我们称这个多位数为等差数. 例如:357分成了三个数3,5,7,并且满足:5﹣3=7﹣5; 413223分成三个数41,32,23,并且满足:32﹣41=23﹣32; 所以:357和413223都是等差数.(1)判断:148 等差数,514335 等差数;(用“是”或“不是”填空) (2)若一个三位数是等差数,试说明它一定能被3整除; (3)若一个三位数T 是等差数,且T 是24的倍数,求该等差数T .30.规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(-3)÷(-3)÷(-3)÷(-3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(-3)÷(-3)÷(-3)÷(-3)记作(-3)④,读作“-3的圈4次方”,一般地,把n aa a a a÷÷÷⋯÷个 (a≠0)记作a ⓝ,读作“a 的圈 n 次方”.(初步探究)(1)直接写出计算结果:2③=___,(12)⑤=___; (2)关于除方,下列说法错误的是___A .任何非零数的圈2次方都等于1;B .对于任何正整数n ,1ⓝ=1;C .3④=4③;D .负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数. (深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?(1)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式. (-3)④=___; 5⑥=___;(-12)⑩=___.(2)想一想:将一个非零有理数a 的圈n 次方写成幂的形式等于___; (3)算一算:212÷(−13)④×(−2)⑤−(−13)⑥÷33【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】学会寻找规律,第①个图2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,那么第n 个图呢,能求出这个即可解得本题。
北师大版七年级数学下册 第1—3章 综合培优、拔高练习(含答案)
北师大版七年级数学下册第1—3章综合培优、拔高练习一、填空题:1.以下三种沿AB折叠的方法:(1)如图①,展开后测得∠1=∠2;(2)如图②,展开后测得∠1=∠2且∠3=∠4;(3)如图③,测得∠1=∠2.其中能判定纸带两条边线a,b互相平行的是________(填序号).答案:(1)(2)2.如图,一个长方形花园ABCD,AB=a,AD=b,该花园中建有一条长方形小路LMPQ和一条平行四边形小路RSTK,若LM=RS=c,则该花园中可绿化部分(即除去小路后剩余部分)的面积为________________.答案:ab-ac-bc+c23.用如图所示的正方形和长方形卡片若干张,拼成一个长为(3a+b),宽为(a+b)的长方形(要求:所拼图形中,卡片之间不能重叠,不能有空隙),则需要A类卡片、B类卡片、C类卡片的张数分别为________.答案:3张,4张,1张点拨:由(3a+b)(a+b)=3a2+4ab+b2可知,需A类卡片3张、B类卡片4张、C类卡片1张.4.如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F=________.答案:5°点拨:过点F向左作FH∥BA,则AB∥CD∥HF,所以∠BED=∠CDE,∠AGF+∠GFH=180°,∠BEF=∠EFH,所以∠GFH=180°-∠AGF=50°.因为EF平分∠BED,所以∠BEF=12∠BED=12∠CDE=59.5°,所以∠EFH=59.5°,所以∠EFG=∠EFH-∠GFH=9.5°.5.按一定规律排列的一列数:21,22,23,25,28,213,….若x,y,z表示这列数中的连续三个数,猜想x,y,z满足的关系式是 .答案:xy=z6.《数书九章》中的秦九韶算法是我国南宋时期的数学家秦九韶提出的一种多项式简化算法.在现代,利用计算机解决多项式的求值问题时,秦九韶算法依然是最优的算法.例如,计算“当x=8时,多项式3x3-4x2-35x+8的值”,按照秦九韶算法,可先将多项式3x3-4x2-35x+8一步步地进行改写:3x3-4x2-35x+8=x(3x2-4x-35)+8=x[x(3x-4)-35]+8.按改写后的方式计算,它一共做了3次乘法,3次加法,与直接计算相比节省了乘法次数,使计算量减少.计算当x=8时,多项式的值为1 008.请参考上述方法,将多项式x3+2x2+x-1改写为_________________________;当x=8时,多项式的值为________.答案:x[x(x+2)+1]-1;6477.如图,已知A1B∥A n C,则∠A1+∠A2+…+∠A n等于答案:如图,过点A2作A2D∥A1B,过点A3作A3E∥A1B,……因为A1B∥A n C,所以A3E∥A2D∥…∥A1B∥A n C.所以∠A1+∠A1A2D=180°,∠DA2A3+∠A2A3E=180°……所以∠A1+∠A1A2A3+…+∠A n-1A n C=(n-1)·180°.8.小明早晨从家骑车到学校,先上坡,后下坡,行驶情况如图所示,如果返回时上、下坡的速度与去学校时上、下坡的速度相同,那么小明从学校骑车回家用的时间是________.答案:37.2 min 点拨:由题图可知,去学校时上坡速度为3 600÷18=200(m/min),下坡速度为(9 600-3 600)÷(30-18)=500(m/min),返回途中,上、下坡的路程与去时刚好相反,所用时间为3 600÷500+(9 600-3 600)÷200=37.2(min).9.如图①,在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.在这个变化过程中,变量x表示点R运动的路程,变量y表示△MNR的面积,图②表示变量y随x 的变化情况,则当y=9时,点R所在的边是____________.答案:PN边或QM边10. 将杨辉三角中的每一个数都换成分数,得到一个如图所示的分数三角形,称为莱布尼茨三角形.若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数112,则(9,2)表示的分数是________.答案:172点拨:观察题图可得以下规律:是第几行就有几个分数;每行每个分数的分子都是1;每行第一个分数的分母为行数,第n (n 为大于1的整数)行的第二个分数的分母为n (n -1).故(9,2)表示的分数为19×8=172. 11.如图,直线AB 与直线CD 交于点O ,OE ⊥AB ,∠DOF =90°,OB 平分∠DOG ,有下列结论:①当∠AOF =60°时,∠DOE =60°;②OD 为∠EOG 的平分线;③与∠BOD 相等的角有三个;④∠COG =∠AOB -2∠EOF .其中正确的结论是________(填序号).答案:①③④ 12.观察下列运算并填空.1×2×3×4+1=24+1=25=52;2×3×4×5+1=120+1=121=112;3×4×5×6+1=360+1=361=192;4×5×6×7+1=840+1=841=292;7×8×9×10+1=5040+1=5041=712;……试猜想:(n +1)(n +2)(n +3)(n +4)+1=________.答案:()2215++n n二、解答题13.如图,在四边形ABCD中,AB∥CD,点P为BC上一点(点P与B,C不重合),设∠CDP=∠α,∠CPD=∠β,你能不能说明,不论点P在BC上怎样运动,总有∠α+∠β=∠B?答案:解:能.过点P作PE∥CD交AD于E,则∠DPE=∠α.因为AB∥CD,所以PE∥AB.所以∠CPE=∠B,即∠DPE+∠β=∠α+∠β=∠B.故不论点P在BC上怎样运动,总有∠α+∠β=∠B.14.弹簧挂上物体后会伸长.已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:所挂物体的质量/kg 0 1 2 3 4 5 6 7弹簧的长度/cm 12 12.5 13 13.5 14 14.5 15 15.5(1)当所挂物体的质量为3 kg时,弹簧的长度是________;(2)在弹性限度内如果所挂物体的质量为x kg,弹簧的长度为y cm,根据上表写出y与x的关系式;(3)当所挂物体的质量为5.5 kg时,请求出弹簧的长度;(4)如果弹簧的最大长度为20 cm,那么该弹簧最多能挂质量为多少的物体?答案:解:(1)13.5 cm(2)由表格可知,y与x之间的关系式为y=12+0.5x.(3)当x=5.5时,y=12+0.5×5.5=14.75,即弹簧的长度为14.75 cm.(4)当y=20时,20=12+0.5x,解得x=16,故该弹簧最多能挂16 kg的物体.15.利用我们学过的知识,可以导出下面这个形式优美的等式:a2+b2+c2-ab-bc-ac=12[(a-b)2+(b-c)2+(c-a)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐美、简洁美.(1)请你检验这个等式的正确性;(2)若a=2 020,b=2 021,c=2 022,你能很快求出a2+b2+c2-ab-bc-ac的值吗?答案:解:(1)等式右边=12(a2-2ab+b2+b2-2bc+c2+a2-2ac+c2)=12(2a2+2b2+2c2-2ab-2bc-2ac)=a2+b2+c2-ab-bc-ac=等式左边,所以等式是成立的.(2)原式=12×[(2 020-2 021)2+(2 021-2 022)2+(2 022-2 020)2]=3.16.先计算,再找出规律,然后根据规律填空.(1)计算:①(a-1)(a+1)=________;②(a-1)(a2+a+1)=________;③(a-1)(a3+a2+a+1)=________.(2)根据(1)中的计算,用字母表示出你发现的规律.(3)根据(2)中的结论,直接写出结果:①(a-1)(a9+a8+a7+a6+a5+a4+a3+a2+a+1)=__________;②若(a-1)·M=a15-1,则M=______________________________________;③(a-b)(a5+a4b+a3b2+a2b3+ab4+b5)=__________;④(2x-1)(16x4+8x3+4x2+2x+1)=__________.答案:解:(1)①a2-1②a3-1③a4-1(2)规律:(a-1)(a n+a n-1+a n-2+…+a3+a2+a+1)=a n+1-1(n为正整数).(3)①a10-1②a14+a13+a12+a11+…+a3+a2+a+1③a6-b6④32x5-117.如图,MN∥EF,C为两直线之间一点.(1)如图①,∠CAM与∠CBE的平分线相交于点D,若∠ACB=100°,求∠ADB的度数.(2)如图②,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并证明你的结论.(3)如图③,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请写出∠ACB与∠ADB的数量关系,并证明你的结论.答案:解:(1)如图①,过点C作CG∥MN,过点D作DH∥MN,因为MN∥EF,所以MN∥CG∥DH∥EF,所以∠1=∠ADH,∠2=∠BDH,∠MAC=∠ACG,∠EBC =∠BCG .因为∠MAC 与∠EBC 的平分线相交于点D ,所以∠1=12∠MAC =12∠ACG ,∠2=12∠EBC =12∠BCG , 所以∠ADB =12(∠ACG +∠BCG )=12∠ACB . 因为∠ACB =100°,所以∠ADB =50°.(2)∠ADB =180°-12∠ACB . 证明:如图②,过点C 作CG ∥MN ,过点D 作DH ∥MN ,因为MN ∥EF ,所以MN ∥CG ∥DH ∥EF ,所以∠1=∠ADH ,∠2=∠BDH ,∠NAC =∠ACG ,∠FBC =∠BCG .因为∠MAC 与∠EBC 的平分线相交于点D ,所以∠1=12∠MAC ,∠2=12∠EBC , 所以∠ADB =∠1+∠2=12(∠MAC +∠EBC )=12(180°-∠ACG +180°-∠BCG )=12(360°-∠ACB ),所以∠ADB =180°-12∠ACB . (3)∠ADB =90°-12∠ACB . 证明:如图③,过点C 作CG ∥MN ,过点D 作DH ∥MN ,因为MN ∥EF ,所以MN ∥CG ∥DH ∥EF ,所以∠DBE =∠BDH ,∠NAC =∠ACG ,∠FBC =∠BCG .因为∠MAC 的平分线与∠FBC 的平分线所在的直线相交于点D ,所以∠CAD =12∠MAC ,∠DBE =12∠CBF ,所以∠ADB =180°-∠CAD -∠CAN -∠BDH=180°-12∠MAC -∠ACG -12∠CBF =180°-12∠MAC -∠ACG -12∠BCG =180°-12(180°-∠ACG )-∠ACG -12∠BCG =180°-90°+12∠ACG -∠ACG -12∠BCG =90°-12∠ACG -12∠BCG =90°-12(∠ACG +∠BCG ) =90°-12∠ACB . 点拨:解答本题的关键是过“拐点”(折线中两条线段的公共端点)作直线的平行线,利用平行线的判定和性质求角的度数或探究角的数量关系;由于条件类似,因此其解题过程也可以类比完成,所不同的是结论虽类似但也有些变化.18.小明用的练习本可以到甲超市购买,也可以到乙超市购买.已知两超市的标价都是每本1元,但甲超市的优惠条件是购买10本以上,从第11本开始按标价的70%卖;乙超市的优惠条件是每本都按标价的85%卖.(1)当小明要买20本时,到哪家超市购买较省钱?(2)写出在甲超市购买,总价y 甲(元)与购买本数x (本)(x >10)的关系式.(3)小明现有24元,最多可以买多少本练习本?答案:解:(1)买20本时,在甲超市购买需用10×1+10×1×70%=17(元),在乙超市购买需用20×1×85%=17(元),所以买20本到两家超市买价钱一样.(2)y 甲=10×1+(x -10)×1×70%=0.7x +3(x >10).(3)由题知在乙超市购买,总价y 乙(元)与购买本数x (本)的关系式为y 乙=x ×1×85%=1720x . 所以当y 甲=24时,24=0.7x +3,x =30;当y 乙=24时,24=1720x ,x ≈28. 所以拿24元最多可以买30本练习本(在甲超市购买).19. 如图,AB ∥CD ,直线EF 分别交AB ,CD 于点G ,H ,GM ,HN 分别为 ∠BGE 和∠DHG 的平分线.(1)试判断GM 和HN 的位置关系.(2)如果GM 是∠AGH 的平分线,(1)中的结论还成立吗?请说明理由.(3)如果GM 是∠BGH 的平分线,(1)中的结论还成立吗?如果不成立,你能得到什么结论?请说明理由.答案:解:(1)∵AB ∥CD ,∴∠BGE =∠DHG .∵GM ,HN 分别为∠BGE 和∠DHG 的平分线,∴∠MGE =12∠BGE ,。
(最新)北师大七年级下册数学 整式乘法综合培优 练习题【精编 含解析】

七下整式乘法综合培优1.若(x 2+mx-8) (x 2-3x+n)的展开式中不含x 2和x 3项,求m 和n 的值2.化简求值:2223[()()6](2)a b a b a b ab +--+÷-,其中a=11()2--,b=01.3.化简求值:[34322223111()()3]()262x y xy xy xy -+-⋅÷-,其中x =﹣1,y =1.4.先化简,再求值:(1)()()()()3123654a a a a +----,其中2a =.(2)()()()2221331x x x x x x +---+-,其中15x =.5.下面是小颖化简整式的过程,仔细阅读后解答所提出的问题.解:x (x+2y )﹣(x+1)2+2x=x 2+2xy ﹣x 2+2x+1+2x 第一步=2xy+4x+1 第二步(1)小颖的化简过程从第 步开始出现错误;(2)对此整式进行化简.6.王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部份铺上地砖.(1)木地板和地砖分别需要多少平方米?(2)如果地砖的价格为每平方米x 元,木地板的价格为每平方米3x 元,那么王老师需要花多少钱?7.将多项式(x-2)(x2+ax-b)展开后不含x2项和x项.求2a2-b的值.8.学习整式的乘法时可以发现:用两种不同的方法表示同一个图形的面积,可以得到一个等式,进而可以利用得到的等式解决问题.图1图2(1)如图1是由边长分别为a,b的正方形和长为a、宽为b的长方形拼成的大长方形,由图1,可得等式:(a+2b)(a+b)=;(2)①如图2是由几个小正方形和小长方形拼成的一个边长为a+b+c的大正方形,用不同的方法表示这个大正方形的面积,得到的等式为;②已知a +b +c =11,ab +bc +ac =38,利用①中所得到的等式,求代数式a 2+b 2+c 2的值.9.先阅读,再填空解题:(x +5)(x +6)=x 2+11x +30;(x -5)(x -6)=x 2-11x +30;(x -5)(x +6)=x 2+x -30;(x +5)(x -6)=x 2-x -30.观察积中的一次项系数、常数项与两因式中的常数项有何关系?答:_________________________________________________________________________________根据以上的规律,用公式表示出来:____________________________________根据规律,直接写出下列各式的结果:(a +99)(a -100)=________;(y -80)(y -81)=________.10.(知识生成)我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到222)2a b a ab b +=++(,基于此,请解答下列问题:(1)根据图2,写出一个代数恒等式:.(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,222++= .a b c(3) 小明同学用图中x 张边长为a 的正方形,y张边长为b 的正方形,z 张宽、长分别为a、b 的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z=(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:.11.小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)⑴请用代数式表示装饰物的面积:________,用代数式表示窗户能射进阳光的面积是______(结果保留π)⑵当a=32,b=1时,求窗户能射进阳光的面积是多少?(取π≈3 )⑶小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?12.(1)填空:)(a b a b-+=()______ ;22)(a b a ab b-++=()______ ;3223)(a b a a b ab b-+++=()______ ;(2)猜想:(a-b)(a n-1+a n-2b+a n-3b2+…+ab n-2+b n-1)= ______ (其中n为正整数,且n≥2);(3)利用(2)猜想的结论计算:①29+28+27+…+22+2+1②210-29+28-…-23+22-2.13.将一张如图①所示的长方形铁皮四个角都剪去边长为30cm 的正方形,再四周折起,做成一个有底无盖的铁盒,如图②.铁盒底面长方形的长是4acm ,宽是3acm.(1)请用含有a 的代数式表示图①中原长方形铁皮的面积;(2)若要在铁盒的外表面涂上某种油漆,每1元钱可涂油漆的面积为50a cm 2,则在这个铁盒的外表面涂上油漆需要多少钱(用含有a 的代数式表示)?14.若()222833x px x x q ⎛⎫++-+ ⎪⎝⎭的积中不含2x 与3x 项. (1)求p 、q 的值;(2)求代数式()()3122016201823p qpq p q --++的值.15.若2x+3·3x+3=36x-2,则x 的值是多少?16.阅读:已知x2y=3,求2xy(x5y2-3x3y-4x)的值.分析:考虑到x,y的可能值较多,不能逐一代入求解,故考虑整体思想,将x2y=3整体代入. 解:2xy(x5y2-3x3y-4x)=2x6y3-6x4y2-8x2y=2(x2y)3-6(x2y)2-8x2y=2×33-6×32-8×3=-24.你能用上述方法解决以下问题吗?试一试!(1)已知ab=3,求(2a3b2-3a2b+4a)·(-2b)的值;(2)已知a2+a-1=0,求代数式a3+2a2+2018的值.17.欢欢和乐乐两人共同计算一道整式乘法题:(2x+a)(3x+b),由于欢欢抄错了第一个多项式中a的符号,得到的结果为6x2-13x+6;乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为2x2-x-6.(1)你能否知道式子中的a,b的值各是多少?(2)请你计算出这道整式乘法题的正确结果.18.(1)你发现了吗?2222()333=⨯,22211133()222322()333-==⨯=⨯,由上述计算,我们发现2223()___()32--; (2)请你通过计算,判断35()4与34()5-之间的关系; (3)我们可以发现:()m b a -____()m ab(0)ab ≠ (4)利用以上的发现计算:3477()()155-⨯.参考答案1.解:原式=x 4+(m-3)x 3+(n-3m-8)x 2+(mn+24)x-8n , 根据展开式中不含x 2和x 3项得:30380m n m -=⎧⎨--=⎩, 解得:317m n =⎧⎨=⎩. 2.解:原式=222223[226](2)a ab b a ab b a b ab ++-+-+÷-=(4ab +6a 2b 3)÷(﹣2ab )=﹣2﹣3ab 2当a =112-⎛⎫- ⎪⎝⎭=﹣2,b =01=1时,原式=﹣2﹣3×(﹣2)×12=﹣2+6=4. 3.解:[34322223111()()3]()262x y xy xy xy -+-⋅÷- =[(﹣91218x y )+2421336x y xy ⋅]361()8x y ÷- =(91218x y -+36112x y )361()8x y ÷- =x 6y 6﹣23, 当x =﹣1,y =1时,原式=(﹣1)6×16﹣23=1﹣23=13. 4.解:(1)()()()()3123654a a a a +----22673629202223a a a a a =---+-=- 将2a =代入得值为21;(2)()()()2221331x x x x x x +---+-3322333323x x x x x x x =+-+--+=-+ 将15x =代入得值为1355.解:(1)括号前面是负号,去掉括号应变号,故第一步出错,故答案为一;(2)x (x+2y )﹣(x+1)2+2x=x 2+2xy ﹣x 2﹣2x ﹣1+2x =2xy ﹣1.6.解:(1)卧室的面积是2b (4a -2a )=4ab (平方米),厨房、卫生间、客厅的面积和是b ·(4a -2a -a )+a ·(4b -2b )+2a ·4b =ab +2ab +8ab =11ab (平方米), 即木地板需要4ab 平方米,地砖需要11ab 平方米;(2)11ab ·x +4ab ·3x =11abx +12abx =23abx (元), 即王老师需要花23abx 元.7.解:原式=3x +ax²−bx −2x²−2ax +2b=3x +(a −2)x²−(2a +b )x +2b ,由展开后不含x 2项和x 项,则有a −2=0,−(2a +b )=0,∴a =2,b =−4,∴2a²−b =2×2²+4=12.8.解:(1)a 2+3ab +2b 2;(2)① (a +b +c )2=a 2+b 2+c 2+2ab +2bc +2ac ;②解:由①,得(a +b +c )2=a 2+b 2+c 2+2(ab +bc +ac ).因为a +b +c =11,ab +bc +ac =38.所以112=a 2+b 2+c 2+2×38. 所以a 2+b 2+c 2=45.故答案为:(1)a 2+3ab +2b 2;(2)① (a +b +c )2=a 2+b 2+c 2+2ab +2bc +2ac ;②45.9. 解:(1)观察积中的一次项系数、常数项与两因式中的常数项有何关系是:一次项系数是两因式中的常数项的和,常数项是两因式中的常数项的积;(2)根据以上的规律,用公式表示出来:(a+b )(a+c )=a 2+(b+c )a+bc ;(3)根据(2)中得出的公式得:(a+99)(a-100)=a 2-a-9900; (y-80)(y-81)=y 2-161y+6480.故填:一次项系数是两因式中的常数项的和,常数项是两因式中的常数项的积; (a+b )(a+c )=a 2+(b+c )a+bc ; a 2-a-9900,y 2-161y+6480.10.解:(1)(a +b +c )2=a 2+b 2+c 2+2ab +2ac +2bc ;(2)∵a +b +c =10,ab +bc +ac =35,∴a 2+b 2+c 2=(a +b +c )2﹣2(ab +ac +bc )=100﹣70=30; (3)根据题意得:(2a +b )(a +2b )=22252a ab b ++,∴x =2,y =5,z =2,∴x +y +z =9;(4)第一个图形的体积=3x x -,第二个图形的体积为:(1)(1)x x x +-.∵两个图形的体积相等,∴3x x -=(1)(1)x x x +-.11.解:试题解析:(1)12π(2b -)2=8πb 2, ab -8πb 2. (2)ab -8πb 2=32×1-8π×1 =32-38=98.(3)更大了,窗帘的面积:π(4b )2=16πb 2 , ( ab -16πb 2)-(ab -8πb 2)=8πb 2-16πb 2=16πb 2.故答案为: (1). 8πb 2, ab -8πb 2 (2). 98, (3). 更大了,16πb 2. 12.解:(1)(a -b )(a +b )=a 2-b 2;;;(2)由(1)可得,(a -b )(a n -1+a n -2b +a n -3b 2+…+ab n -2+b n -1)=a n -b n ;(3)①29+28+27+…+23+22+2+1=(2-1)×(29+28×1+27×12+…+23·16+22·17+2·18+19)=210-110=210-1=1023.②210-29+28-…-23+22-2=13×[2-(-1)]×[210+29×(-1)1+28×(-1)2+…+23×(-1)7+22×(-1)8+2×(-1)9+(-1)10-1]=13×[211-(-1)11]-13×3×1=682.13.解:(1)原长方形铁皮的面积是(4a +60)(3a +60)=(12a 2+420a +3600)(cm 2).(2)这个铁盒的表面积是12a 2+420a +3600-4×30×30=(12a 2+420a)(cm 2),则在这个铁盒的外表面涂上油漆需要的钱数是(12a 2+420a)÷50a =(600a +21000)(元). 14.解:(1)()222833x px x x q ⎛⎫++-+ ⎪⎝⎭ =x 4-3x 3+qx 2+px 3-3px 2+pqx+283x 2-28x+283q=x 4+(p-3)x 3+(q-3p+283)x 2+(pq-28)x+283q , 因为它的积中不含有x 2与x 3项,则有,p-3=0,q-3p+283=0 解得,p=3,q=13-; (2)()()3122016201823p q pq p q --++ =632016218()3p q pq q pq-++⋅ =332016218()()3p pq pq q pq -⋅++⋅ =-8×332016211113[3()][3()]()133333()3⋅⨯-++⨯-⨯-⨯⨯- =-8×1127(1)39⨯--+ =2161139-+ =72159. 15.解:因为36x-2=(62)x-2=62(x-2),所以2x+3·3x+3=(2×3)x+3=6x+3, 所以x+3=2(x-2),解得x=7.16.解:(1)(2a 3b 2-3a 2b+4a)·(-2b)=-4a 3b 3+6a 2b 2-8ab=-4(ab)3+6(ab)2-8ab将ab=3代入上式,得−4×33+6×32−8×3=-78所以(2a 3b 2-3a 2b+4a)·(-2b)=−78 (2)∵a 2+a=1,∴a 3+2a 2+2018=a 3+a 2+a 2+2018=a(a 2+a)+a 2+2018=a +a 2+2018=1+2018=2019.17.解:(1)根据题意可知(2x -a)(3x +b)=6x 2+2bx -3ax -ab =6x 2-13x +6 可得2b -3a =-13①.可知(2x +a)(x +b)=2x 2-x -6,即2x 2+2bx +ax +ab =2x 2-x -6 可得2b +a =-1②,由①②可得a =3,b =-2.(2)(2x +3)(3x -2)=6x 2+5x -6.18.解:(1)我们发现223() = (23)2- (2)计算得35125464⎛⎫= ⎪⎝⎭, -34125564⎛⎫= ⎪⎝⎭ ∴3-35445⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭(3)我们可以发现:mba-⎛⎫⎪⎝⎭=mab⎛⎫⎪⎝⎭(0ab≠).(4)利用以上的发现计算:-3477155⎛⎫⎛⎫⨯⎪ ⎪⎝⎭⎝⎭=3415775⎛⎫⎛⎫⨯=⎪ ⎪⎝⎭⎝⎭3315771897555⎛⎫⎛⎫⎛⎫⨯⨯=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭。
人教版七年级下册数学期末解答题培优题(含答案)

人教版七年级下册数学期末解答题培优题(含答案)一、解答题1.(1)如图1,分别把两个边长为1cm的小正方形沿一条对角线裁成4个小三角形拼成一个大正方形,则大正方形的边长为______cm;(2)若一个圆的面积与一个正方形的面积都是22πcm,设圆的周长为C圆.正方形的周长为C正,则C圆______C正(填“=”,或“<”,或“>”)(3)如图2,若正方形的面积为2900cm,李明同学想沿这块正方形边的方向裁出一块面积为2740cm的长方形纸片,使它的长和宽之比为5:4,他能裁出吗?请说明理由?2.如图,用两个面积为28cm的小正方形纸片剪拼成一个大的正方形.(1)大正方形的边长是________cm;(2)请你探究是否能将此大正方形纸片沿着边的方向裁出一个面积为214cm的长方形纸片,使它的长宽之比为2:1,若能,求出这个长方形纸片的长和宽,若不能,请说明理由.3.如图,用两个边长为103的小正方形拼成一个大的正方形.(1)求大正方形的边长?(2)若沿此大正方形边的方向出一个长方形,能否使裁出的长方形的长宽之比为3:2,且面积为480cm2?4.小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁处一块面积为300cm2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案;(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案,若不能,请简要说明理由.5.某市在招商引资期间,把已倒闭的油泵厂出租给外地某投资商,该投资商为减少固定资产投资,将原来的400m2的正方形场地改建成300m2的长方形场地,且其长、宽的比为5:3.(1)求原来正方形场地的周长;(2)如果把原来的正方形场地的铁栅栏围墙全部利用,围成新场地的长方形围墙,那么这些铁栅栏是否够用?试利用所学知识说明理由.二、解答题6.已知,AB ∥CD ,点E 在CD 上,点G ,F 在AB 上,点H 在AB ,CD 之间,连接FE ,EH ,HG ,∠AGH =∠FED ,FE ⊥HE ,垂足为E . (1)如图1,求证:HG ⊥HE ;(2)如图2,GM 平分∠HGB ,EM 平分∠HED ,GM ,EM 交于点M ,求证:∠GHE =2∠GME ;(3)如图3,在(2)的条件下,FK 平分∠AFE 交CD 于点K ,若∠KFE :∠MGH =13:5,求∠HED 的度数.7.如图,已知直线//AB 射线CD ,100CEB ∠=︒.P 是射线EB 上一动点,过点P 作PQ //EC 交射线CD 于点Q ,连接CP .作PCF PCQ ∠=∠,交直线AB 于点F ,CG 平分ECF ∠.(1)若点P ,F ,G 都在点E 的右侧,求PCG ∠的度数;(2)若点P ,F ,G 都在点E 的右侧,30EGC ECG ∠-∠=︒,求CPQ ∠的度数; (3)在点P 的运动过程中,是否存在这样的情形,使:4:3EGC EFC ∠∠=?若存在,求出CPQ ∠的度数;若不存在,请说明理由.8.已知AB ∥CD ,线段EF 分别与AB ,CD 相交于点E ,F .(1)请在横线上填上合适的内容,完成下面的解答:如图1,当点P 在线段EF 上时,已知∠A =35°,∠C =62°,求∠APC 的度数; 解:过点P 作直线PH ∥AB , 所以∠A =∠APH ,依据是 ; 因为AB ∥CD ,PH ∥AB , 所以PH ∥CD ,依据是 ; 所以∠C =( ),所以∠APC =( )+( )=∠A +∠C =97°. (2)当点P ,Q 在线段EF 上移动时(不包括E ,F 两点): ①如图2,∠APQ +∠PQC =∠A +∠C +180°成立吗?请说明理由;②如图3,∠APM =2∠MPQ ,∠CQM =2∠MQP ,∠M +∠MPQ +∠PQM =180°,请直接写出∠M ,∠A 与∠C 的数量关系. 9.已知//AB CD ,点E 在AB 与CD 之间. (1)图1中,试说明:BED ABE CDE ∠=∠+∠;(2)图2中,ABE ∠的平分线与CDE ∠的平分线相交于点F ,请利用(1)的结论说明:2BED BFD ∠=∠.(3)图3中,ABE ∠的平分线与CDE ∠的平分线相交于点F ,请直接写出BED ∠与BFD ∠之间的数量关系.10.已知//AM CN ,点B 为平面内一点,AB BC ⊥于B .(1)如图1,求证:90A C ∠+∠=︒;(2)如图2,过点B 作BD MA ⊥的延长线于点D ,求证:ABD C ∠=∠;(3)如图3,在(2)问的条件下,点E 、F 在DM 上,连接BE 、BF 、CF ,且BF 平分DBC ∠,BE 平分ABD ∠,若AFC BCF ∠=∠,3BFC DBE ∠=∠,求EBC ∠的度数.三、解答题11.为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A 射线从AM 开始顺时针旋转至AN 便立即回转,灯B 射线从BP 开始顺时针旋转至BQ 便立即回转,两灯不停交又照射巡视.若灯A 转动的速度是每秒2度,灯B 转动的速度是每秒1度.假定主道路是平行的,即//PQ MN ,且:3:2BAM BAN ∠∠=.(1)填空:BAN ∠=_________;(2)若灯B 射线先转动30秒,灯A 射线才开始转动,在灯B 射线到达BQ 之前,A 灯转动几秒,两灯的光束互相平行?(3)如图2,若两灯同时转动,在灯A 射线到达AN 之前.若射出的光束交于点C ,过C 作ACD ∠交PQ 于点D ,且126ACD ∠=︒,则在转动过程中,请探究BAC ∠与BCD ∠的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.12.将两块三角板按如图置,其中三角板边AB AE =,90BAC EAD ∠=∠=︒,45C ∠=︒,30D ∠=︒.(1)下列结论:正确的是_______. ①如果60BFD ∠=︒,则有//BC AD ; ②180BAE CAD ∠+∠=︒;③如果//BC AD ,则AB 平分EAD ∠.(2)如果150CAD ∠=︒,判断BFD ∠与C ∠是否相等,请说明理由.(3)将三角板ABC 绕点A 顺时针转动,直到边AC 与AD 重合即停止,转动的过程中当两块三角板恰有两边平行时,请直接写出EAB ∠所有可能的度数.13.已知:三角形ABC 和三角形DEF 位于直线MN 的两侧中,直线MN 经过点C ,且BC MN ⊥,其中A ABC CB =∠∠,DEF DFE ∠=∠,90∠+∠=︒ABC DFE ,点E 、F 均落在直线MN 上.(1)如图1,当点C 与点E 重合时,求证://DF AB ;聪明的小丽过点C 作//CG DF ,并利用这条辅助线解决了问题.请你根据小丽的思考,写出解决这一问题的过程. (2)将三角形DEF 沿着NM 的方向平移,如图2,求证://DE AC ;(3)将三角形DEF 沿着NM 的方向平移,使得点E 移动到点E ',画出平移后的三角形DEF ,并回答问题,若DFE α∠=,则∠=CAB ________.(用含α的代数式表示) 14.如图1所示:点E 为BC 上一点,∠A =∠D ,AB ∥CD (1)直接写出∠ACB 与∠BED 的数量关系;(2)如图2,AB ∥CD ,BG 平分∠ABE ,BG 的反向延长线与∠EDF 的平分线交于H 点,若∠DEB 比∠GHD 大60°,求∠DEB 的度数;(3)保持(2)中所求的∠DEB 的度数不变,如图3,BM 平分∠EBK ,DN 平分∠CDE ,作BP ∥DN ,则∠PBM 的度数是否改变?若不发生变化,请求它的度数,若发生改变,请说明理由.(本题中的角均为大于0°且小于180°的角).15.已知AB ∥CD ,点M 在直线AB 上,点N 、Q 在直线CD 上,点P 在直线AB 、CD 之间,∠AMP =∠PQN =α,PQ 平分∠MPN .(1)如图①,求∠MPQ 的度数(用含α的式子表示);(2)如图②,过点Q 作QE ∥PN 交PM 的延长线于点E ,过E 作EF 平分∠PEQ 交PQ 于点F .请你判断EF 与PQ 的位置关系,并说明理由;(3)如图③,在(2)的条件下,连接EN ,若NE 平分∠PNQ ,请你判断∠NEF 与∠AMP 的数量关系,并说明理由.四、解答题16.如图①,AD 平分BAC ∠,AE ⊥BC ,∠B=450,∠C=730. (1) 求DAE ∠的度数;(2) 如图②,若把“AE ⊥BC ”变成“点F 在DA 的延长线上,FE BC ⊥”,其它条件不变,求DFE ∠ 的度数;(3) 如图③,若把“AE ⊥BC ”变成“AE 平分BEC ∠”,其它条件不变,DAE ∠的大小是否变化,并请说明理由.17.操作示例:如图1,在△ABC 中,AD 为BC 边上的中线,△ABD 的面积记为S 1,△ADC 的面积记为S 2.则S 1=S 2.解决问题:在图2中,点D 、E 分别是边AB 、BC 的中点,若△BDE 的面积为2,则四边形ADEC 的面积为 . 拓展延伸:(1)如图3,在△ABC 中,点D 在边BC 上,且BD =2CD ,△ABD 的面积记为S 1,△ADC 的面积记为S 2.则S 1与S 2之间的数量关系为 .(2)如图4,在△ABC 中,点D 、E 分别在边AB 、AC 上,连接BE 、CD 交于点O ,且BO =2EO ,CO =DO ,若△BOC 的面积为3,则四边形ADOE 的面积为 . 18.如图,△ABC 中,∠ABC 的角平分线与∠ACB 的外角∠ACD 的平分线交于A 1.(1)当∠A为70°时,∵∠ACD-∠ABD=∠______∴∠ACD-∠ABD=______°∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线∴∠A1CD-∠A1BD=12(∠ACD-∠ABD)∴∠A1=______°;(2)∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、A n,请写出∠A与∠A n的数量关系______;(3)如图2,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F=______.(4)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E 滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q-∠A1的值为定值.其中有且只有一个是正确的,请写出正确的结论,并求出其值.19.直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B在射线OM上运动,A、B不与点O重合,如图1,已知AC、BC分别是∠BAP和∠ABM角的平分线,(1)点A、B在运动的过程中,∠ACB的大小是否发生变化?若发生变化,请说明理由;若不发生变化,试求出∠ACB的大小.(2)如图2,将△ABC沿直线AB折叠,若点C落在直线PQ上,则∠ABO=________,如图3,将△ABC沿直线AB折叠,若点C落在直线MN上,则∠ABO=________(3)如图4,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其反向延长线交于E、F,则∠EAF=;在△AEF中,如果有一个角是另一个角的32倍,求∠ABO的度数.20.如图,//MN GH ,点A 、B 分别在直线MN 、GH 上,点O 在直线MN 、GH 之间,若116NAO ∠=︒,144OBH ∠=︒.(1)AOB ∠= ︒;(2)如图2,点C 、D 是NAO ∠、GBO ∠角平分线上的两点,且35CDB ∠=︒,求ACD ∠ 的度数;(3)如图3,点F 是平面上的一点,连结FA 、FB ,E 是射线FA 上的一点,若MAE ∠=n OAE ∠,HBF n OBF ∠=∠,且60AFB ∠=︒,求n 的值.【参考答案】一、解答题1.(1);(2)<;(3)不能,理由见解析 【分析】(1)根据所拼成的大正方形的面积为2即可求得大正方形的边长;(2)由圆和正方形的面积公式可分别求的圆的半径及正方形的边长,进而可求得圆和正方形的解析:(122)<;(3)不能,理由见解析 【分析】(1)根据所拼成的大正方形的面积为2即可求得大正方形的边长;(2)由圆和正方形的面积公式可分别求的圆的半径及正方形的边长,进而可求得圆和正方形的周长,利用作商法比较这两数大小即可;(3)利用方程思想求出长方形的长边,与正方形边长比较大小即可;【详解】解:(1)∵小正方形的边长为1cm , ∴小正方形的面积为1cm 2, ∴两个小正方形的面积之和为2cm 2, 即所拼成的大正方形的面积为2 cm 2, 设大正方形的边长为x cm , ∴22x = , ∴x∴; (2)设圆的半径为r , ∴由题意得22r ππ=, ∴r = ∴=22C r π=圆 设正方形的边长为a ∵22a π=, ∴a∴=4C a =正∴1C C ===<圆正 故答案为:<;(3)解:不能裁剪出,理由如下: ∵正方形的面积为900cm 2, ∴正方形的边长为30cm∵长方形纸片的长和宽之比为5:4, ∴设长方形纸片的长为5x ,宽为4x , 则54740x x ⋅=, 整理得:237x =,∴22(5)252537925900x x ==⨯=>, ∴22(5)30x >, ∴530x >,∴长方形纸片的长大于正方形的边长, ∴不能裁出这样的长方形纸片. 【点睛】本题通过圆和正方形的面积考查了对算术平方根的应用,主要是对学生无理数运算及比较大小进行了考查.2.(1)4;(2)不能,理由见解析. 【分析】(1)根据已知正方形的面积求出大正方形的边长即可;(2)先设未知数根据面积=14(cm2)列方程,求出长方形的边长,将长方形的长与正方形边长比较大小再解析:(1)4;(2)不能,理由见解析.【分析】(1)根据已知正方形的面积求出大正方形的边长即可;(2)先设未知数根据面积=14(cm2)列方程,求出长方形的边长,将长方形的长与正方形边长比较大小再判断即可.【详解】解:(1)两个正方形面积之和为:2×8=16(cm2),∴拼成的大正方形的面积=16(cm2),∴大正方形的边长是4cm;故答案为:4;(2)设长方形纸片的长为2xcm,宽为xcm,则2x•x=14,解得:x=2x,∴不存在长宽之比为2:1且面积为214cm的长方形纸片.【点睛】本题考查了算术平方根,能够根据题意列出算式是解此题的关键.3.(1)大正方形的边长是;(2)不能【分析】(1)根据已知正方形的面积求出大正方形的面积,即可求出边长;(2)先求出长方形的边长,再判断即可.【详解】(1)大正方形的边长是(2)设长方形纸解析:(1)大正方形的边长是2)不能【分析】(1)根据已知正方形的面积求出大正方形的面积,即可求出边长;(2)先求出长方形的边长,再判断即可.【详解】(1)大正方形的边长是(2)设长方形纸片的长为3xcm,宽为2xcm,则3x•2x=480,解得:因为片的长宽之比为2:3,且面积为480cm2.【点睛】本题考查算术平方根,解题的关键是能根据题意列出算式.4.(1)可以以正方形一边为长方形的长,在其邻边上截取长为15cm的线段作为宽即可裁出符合要求的长方形;(2)不能,理由见解析.【解析】(1)解:设面积为400cm2的正方形纸片的边长为a cm∴解析:(1)可以以正方形一边为长方形的长,在其邻边上截取长为15cm的线段作为宽即可裁出符合要求的长方形;(2)不能,理由见解析.【解析】(1)解:设面积为400cm2的正方形纸片的边长为a cm∴a2=400又∵a>0∴a=20又∵要裁出的长方形面积为300cm2∴若以原正方形纸片的边长为长方形的长,则长方形的宽为:300÷20=15(cm)∴可以以正方形一边为长方形的长,在其邻边上截取长为15cm的线段作为宽即可裁出符合要求的长方形(2)∵长方形纸片的长宽之比为3:2∴设长方形纸片的长为3x cm,则宽为2x cm∴6x 2=300∴x 2=50又∵x>0∴x=∴长方形纸片的长为又∵(2=450>202即:>20∴小丽不能用这块纸片裁出符合要求的纸片5.(1)原来正方形场地的周长为80m;(2)这些铁栅栏够用.【分析】(1)正方形边长=面积的算术平方根,周长=边长×4,由此解答即可;(2)长、宽的比为5:3,设这个长方形场地宽为3am,则长为解析:(1)原来正方形场地的周长为80m;(2)这些铁栅栏够用.【分析】(1)正方形边长=面积的算术平方根,周长=边长×4,由此解答即可;(2)长、宽的比为5:3,设这个长方形场地宽为3am,则长为5am,计算出长方形的长与宽可知长方形周长,同理可得正方形的周长,比较大小可知是否够用.【详解】解:(1(m),4×20=80(m),答:原来正方形场地的周长为80m;(2)设这个长方形场地宽为3am,则长为5am.由题意有:3a×5a=300,解得:a,∵3a表示长度,∴a>0,∴a∴这个长方形场地的周长为 2(3a+5a)=16a(m),∵∴这些铁栅栏够用.【点睛】本题考查了算术平方根的实际应用,解答本题的关键是明确题意,求出长方形和正方形的周长.二、解答题6.(1)见解析;(2)见解析;(3)40°【分析】(1)根据平行线的性质和判定解答即可;(2)过点H作HP∥AB,根据平行线的性质解答即可;(3)过点H作HP∥AB,根据平行线的性质解答即可.解析:(1)见解析;(2)见解析;(3)40°【分析】(1)根据平行线的性质和判定解答即可;(2)过点H作HP∥AB,根据平行线的性质解答即可;(3)过点H作HP∥AB,根据平行线的性质解答即可.【详解】证明:(1)∵AB∥CD,∴∠AFE=∠FED,∵∠AGH=∠FED,∴∠AFE=∠AGH,∴EF∥GH,∴∠FEH+∠H=180°,∵FE⊥HE,∴∠FEH=90°,∴∠H=180°﹣∠FEH=90°,∴HG⊥HE;(2)过点M作MQ∥AB,∵AB∥CD,∴MQ∥CD,过点H作HP∥AB,∵AB∥CD,∴HP∥CD,∵GM平分∠HGB,∠BGH,∴∠BGM=∠HGM=12∵EM平分∠HED,∠HED,∴∠HEM=∠DEM=12∵MQ∥AB,∴∠BGM=∠GMQ,∵MQ∥CD,∴∠QME=∠MED,∴∠GME=∠GMQ+∠QME=∠BGM+∠MED,∵HP∥AB,∴∠BGH=∠GHP=2∠BGM,∵HP∥CD,∴∠PHE=∠HED=2∠MED,∴∠GHE=∠GHP+∠PHE=2∠BGM+2∠MED=2(∠BGM+∠MED),∴∠GHE=∠2GME;(3)过点M作MQ∥AB,过点H作HP∥AB,由∠KFE:∠MGH=13:5,设∠KFE=13x,∠MGH=5x,由(2)可知:∠BGH=2∠MGH=10x,∵∠AFE+∠BFE=180°,∴∠AFE=180°﹣10x,∵FK平分∠AFE,∴∠AFK=∠KFE=12∠AFE,即1(18010)132x x︒-=,解得:x=5°,∴∠BGH=10x=50°,∵HP∥AB,HP∥CD,∴∠BGH=∠GHP=50°,∠PHE=∠HED,∵∠GHE=90°,∴∠PHE=∠GHE﹣∠GHP=90°﹣50°=40°,∴∠HED=40°.【点睛】本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质定理以及灵活构造平行线是解题的关键.7.(1)40°;(2)65°;(3)存在,56°或20°【分析】(1)依据平行线的性质以及角平分线的定义,即可得到∠PCG的度数;(2)依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠G解析:(1)40°;(2)65°;(3)存在,56°或20°【分析】(1)依据平行线的性质以及角平分线的定义,即可得到∠PCG的度数;(2)依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠GCF=25°,再根据PQ∥CE,即可得出∠CPQ=∠ECP=65°;(3)设∠EGC=4x,∠EFC=3x,则∠GCF=4x-3x=x,分两种情况讨论:①当点G、F在点E 的右侧时,②当点G、F在点E的左侧时,依据等量关系列方程求解即可.【详解】解:(1)∵∠CEB=100°,AB∥CD,∴∠ECQ=80°,∵∠PCF=∠PCQ,CG平分∠ECF,∴∠PCG=∠PCF+∠FCG=12∠QCF+12∠FCE=12∠ECQ=40°;(2)∵AB∥CD∴∠QCG=∠EGC,∠QCG+∠ECG=∠ECQ=80°,∴∠EGC+∠ECG=80°,又∵∠EGC-∠ECG=30°,∴∠EGC=55°,∠ECG=25°,∴∠ECG=∠GCF=25°,∠PCF=∠PCQ=12(80°-50°)=15°,∵PQ∥CE,∴∠CPQ=∠ECP=65°;(3)设∠EGC=4x,∠EFC=3x,则∠GCF=∠FCD=4x-3x=x,①当点G、F在点E的右侧时,则∠ECG=x,∠PCF=∠PCD=32 x,∵∠ECD=80°,∴x+x+32x+32x=80°,解得x=16°,∴∠CPQ=∠ECP=x+x+32x=56°;②当点G、F在点E的左侧时,则∠ECG=∠GCF=x,∵∠CGF=180°-4x,∠GCQ=80°+x,∴180°-4x=80°+x,解得x=20°,∴∠FCQ=∠ECF+∠ECQ=40°+80°=120°,∴∠PCQ=12∠FCQ=60°,∴∠CPQ=∠ECP=80°-60°=20°.【点睛】本题主要考查了平行线的性质,解题时注意:两直线平行,同旁内角互补;两直线平行,内错角相等.8.(1)两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH;∠APH,∠CPH;(2)①∠APQ+∠PQC=∠A+∠C+180°成立,理由见解答过程;②3∠PMQ+∠A+∠C=360°.解析:(1)两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH;∠APH,∠CPH;(2)①∠APQ+∠PQC=∠A+∠C+180°成立,理由见解答过程;②3∠PMQ+∠A+∠C=360°.【分析】(1)根据平行线的判定与性质即可完成填空;(2)结合(1)的辅助线方法即可完成证明;(3)结合(1)(2)的方法,根据∠APM=2∠MPQ,∠CQM=2∠MQP,∠PMQ+∠MPQ+∠PQM=180°,即可证明∠PMQ,∠A与∠C的数量关系.【详解】解:过点P作直线PH∥AB,所以∠A=∠APH,依据是两直线平行,内错角相等;因为AB∥CD,PH∥AB,所以PH∥CD,依据是平行于同一条直线的两条直线平行;所以∠C=(∠CPH),所以∠APC=(∠APH)+(∠CPH)=∠A+∠C=97°.故答案为:两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH;∠APH,∠CPH;(2)①如图2,∠APQ+∠PQC=∠A+∠C+180°成立,理由如下:过点P作直线PH∥AB,QG∥AB,∵AB∥CD,∴AB∥CD∥PH∥QG,∴∠A=∠APH,∠C=∠CQG,∠HPQ+∠GQP=180°,∴∠APQ+∠PQC=∠APH+∠HPQ+∠GQP+∠CQG=∠A+∠C+180°.∴∠APQ+∠PQC=∠A+∠C+180°成立;②如图3,过点P作直线PH∥AB,QG∥AB,MN∥AB,∵AB∥CD,∴AB∥CD∥PH∥QG∥MN,∴∠A=∠APH,∠C=∠CQG,∠HPQ+∠GQP=180°,∠HPM=∠PMN,∠GQM=∠QMN,∴∠PMQ=∠HPM+∠GQM,∵∠APM=2∠MPQ,∠CQM=2∠MQP,∠PMQ+∠MPQ+∠PQM=180°,∴∠APM+∠CQM=∠A+∠C+∠PMQ=2∠MPQ+2∠MQP=2(180°﹣∠PMQ),∴3∠PMQ+∠A+∠C=360°.【点睛】考核知识点:平行线的判定和性质.熟练运用平行线性质和判定,添加适当辅助线是关键.9.(1)说明过程请看解答;(2)说明过程请看解答;(3)∠BED=360°-2∠BFD.【分析】(1)图1中,过点E作EG∥AB,则∠BEG=∠ABE,根据AB∥CD,EG∥AB,所以CD∥EG,解析:(1)说明过程请看解答;(2)说明过程请看解答;(3)∠BED=360°-2∠BFD.【分析】(1)图1中,过点E作EG∥AB,则∠BEG=∠ABE,根据AB∥CD,EG∥AB,所以CD∥EG,所以∠DEG=∠CDE,进而可得∠BED=∠ABE+∠CDE;(2)图2中,根据∠ABE的平分线与∠CDE的平分线相交于点F,结合(1)的结论即可说明:∠BED=2∠BFD;(3)图3中,根据∠ABE的平分线与∠CDE的平分线相交于点F,过点E作EG∥AB,则∠BEG+∠ABE=180°,因为AB∥CD,EG∥AB,所以CD∥EG,所以∠DEG+∠CDE=180°,再结合(1)的结论即可说明∠BED与∠BFD之间的数量关系.【详解】解:(1)如图1中,过点E作EG∥AB,则∠BEG=∠ABE,因为AB∥CD,EG∥AB,所以CD∥EG,所以∠DEG=∠CDE,所以∠BEG+∠DEG=∠ABE+∠CDE,即∠BED=∠ABE+∠CDE;(2)图2中,因为BF平分∠ABE,所以∠ABE=2∠ABF,因为DF平分∠CDE,所以∠CDE=2∠CDF,所以∠ABE +∠CDE =2∠ABF +2∠CDF =2(∠ABF +∠CDF ),由(1)得:因为AB ∥CD ,所以∠BED =∠ABE +∠CDE ,∠BFD =∠ABF +∠CDF ,所以∠BED =2∠BFD .(3)∠BED =360°-2∠BFD .图3中,过点E 作EG ∥AB ,则∠BEG +∠ABE =180°,因为AB ∥CD ,EG ∥AB ,所以CD ∥EG ,所以∠DEG +∠CDE =180°,所以∠BEG +∠DEG =360°-(∠ABE +∠CDE ),即∠BED =360°-(∠ABE +∠CDE ),因为BF 平分∠ABE ,所以∠ABE =2∠ABF ,因为DF 平分∠CDE ,所以∠CDE =2∠CDF ,∠BED =360°-2(∠ABF +∠CDF ),由(1)得:因为AB ∥CD ,所以∠BFD =∠ABF +∠CDF ,所以∠BED =360°-2∠BFD .【点睛】本题考查了平行线的性质,解决本题的关键是掌握平行线的性质.10.(1)见解析;(2)见解析;(3).【分析】(1)先根据平行线的性质得到,然后结合即可证明;(2)过作,先说明,然后再说明得到,最后运用等量代换解答即可; (3)设∠DBE=a ,则∠BFC=3解析:(1)见解析;(2)见解析;(3)︒=∠105EBC .【分析】(1)先根据平行线的性质得到C BDA ∠=∠,然后结合AB BC ⊥即可证明;(2)过B 作//BH DM ,先说明ABD CBH ∠=∠,然后再说明//BH NC 得到CBH C ∠=∠,最后运用等量代换解答即可;(3)设∠DBE =a ,则∠BFC =3a ,根据角平分线的定义可得∠ABD =∠C =2a ,∠FBC =12∠DBC =a +45°,根据三角形内角和可得∠BFC +∠FBC +∠BCF =180°,可得∠AFC =∠BCF 的度数表达式,再根据平行的性质可得∠AFC +∠NCF =180°,代入即可算出a 的度数,进而完成解答.【详解】(1)证明:∵//AM CN ,∴C BDA ∠=∠,∵AB BC ⊥于B , ∴90B ∠=︒,∴90A BDA ∠+∠=︒,∴90A C ∠+∠=︒;(2)证明:过B 作//BH DM ,∵BD MA ⊥,∴90ABD ABH ∠+∠=︒,又∵AB BC ⊥,∴90ABH CBH ∠+∠=︒,∴ABD CBH ∠=∠,∵//BH DM ,//AM CN∴//BH NC ,∴CBH C ∠=∠,∴ABD C ∠=∠;(3)设∠DBE =a ,则∠BFC =3a ,∵BE 平分∠ABD ,∴∠ABD =∠C =2a ,又∵AB ⊥BC ,BF 平分∠DBC ,∴∠DBC =∠ABD +∠ABC =2a +90,即:∠FBC =12∠DBC =a +45°又∵∠BFC +∠FBC +∠BCF =180°,即:3a +a +45°+∠BCF =180°∴∠BCF =135°-4a ,∴∠AFC=∠BCF=135°-4a,又∵AM//CN,∴∠AFC+∠NCF=180°,即:∠AFC+∠BCN+∠BCF=180°,∴135°-4a+135°-4a+2a=180,解得a=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.【点睛】本题主要考查了平行线的性质、角平分线的性质及角的计算,熟练应用平行线的性质、角平分线的性质是解答本题的关键.三、解答题11.(1)72°;(2)30秒或110秒;(3)不变,∠BAC=2∠BCD【分析】(1)根据∠BAM+∠BAN=180°,∠BAM:∠BAN=3:2,即可得到∠BAN的度数;(2)设A灯转动t秒,解析:(1)72°;(2)30秒或110秒;(3)不变,∠BAC=2∠BCD【分析】(1)根据∠BAM+∠BAN=180°,∠BAM:∠BAN=3:2,即可得到∠BAN的度数;(2)设A灯转动t秒,两灯的光束互相平行,分两种情况进行讨论:当0<t<90时,根据2t=1•(30+t),可得t=30;当90<t<150时,根据1•(30+t)+(2t-180)=180,可得t=110;(3)设灯A射线转动时间为t秒,根据∠BAC=2t-108°,∠BCD=126°-∠BCA=t-54°,即可得出∠BAC:∠BCD=2:1,据此可得∠BAC和∠BCD关系不会变化.【详解】解:(1)∵∠BAM+∠BAN=180°,∠BAM:∠BAN=3:2,∴∠BAN=180°×2=72°,5故答案为:72;(2)设A灯转动t秒,两灯的光束互相平行,①当0<t<90时,如图1,∵PQ∥MN,∴∠PBD=∠BDA,∵AC∥BD,∴∠CAM=∠BDA,∴∠CAM=∠PBD∴2t=1•(30+t),解得t=30;②当90<t<150时,如图2,∵PQ∥MN,∴∠PBD+∠BDA=180°,∵AC∥BD,∴∠CAN=∠BDA∴∠PBD+∠CAN=180°∴1•(30+t)+(2t-180)=180,解得t=110,综上所述,当t=30秒或110秒时,两灯的光束互相平行;(3)∠BAC和∠BCD关系不会变化.理由:设灯A射线转动时间为t秒,∵∠CAN=180°-2t,∴∠BAC=72°-(180°-2t)=2t-108°,又∵∠ABC=108°-t,∴∠BCA=180°-∠ABC-∠BAC=180°-t,而∠ACD=126°,∴∠BCD=126°-∠BCA=126°-(180°-t)=t-54°,∴∠BAC:∠BCD=2:1,即∠BAC=2∠BCD,∴∠BAC和∠BCD关系不会变化.【点睛】本题主要考查了平行线的性质以及角的和差关系的运用,解决问题的关键是运用分类思想进行求解,解题时注意:两直线平行,内错角相等;两直线平行,同旁内角互补.12.(1)②③;(2)相等,理由见解析;(3)30°或45°或75°或120°或135°【分析】(1)根据平行线的判定和性质分别判定即可;(2)利用角的和差,结合∠CAB=∠DAE=90°进行判断解析:(1)②③;(2)相等,理由见解析;(3)30°或45°或75°或120°或135°【分析】(1)根据平行线的判定和性质分别判定即可;(2)利用角的和差,结合∠CAB=∠DAE=90°进行判断;(3)依据这两块三角尺各有一条边互相平行,分五种情况讨论,即可得到∠EAB角度所有可能的值.【详解】解:(1)①∵∠BFD=60°,∠B=45°,∴∠BAD+∠D=∠BFD+∠B=105°,∴∠BAD=105°-30°=75°,∴∠BAD≠∠B,∴BC和AD不平行,故①错误;②∵∠BAC+∠DAE=180°,∴∠BAE+∠CAD=∠BAE+∠CAE+∠DAE=180°,故②正确;③若BC∥AD,则∠BAD=∠B=45°,∴∠BAE=45°,即AB平分∠EAD,故③正确;故答案为:②③;(2)相等,理由是:∵∠CAD=150°,∴∠BAE=180°-150°=30°,∴∠BAD=60°,∵∠BAD+∠D=∠BFD+∠B,∴∠BFD=60°+30°-45°=45°=∠C;(3)若AC∥DE,则∠CAE=∠E=60°,∴∠EAB=90°-60°=30°;若BC∥AD,则∠B=∠BAD=45°,∴∠EAB=45°;若BC∥DE,则∠E=∠AFB=60°,∴∠EAB=180°-60°-45°=75°;若AB∥DE,则∠D=∠DAB=30°,∴∠EAB=30°+90°=120°;若AE∥BC,则∠C=∠CAE=45°,∴∠EAB=45°+90°=135°;综上:∠EAB 的度数可能为30°或45°或75°或120°或135°.【点睛】本题考查了平行线的判定和性质,角平分线的定义,解题的关键是理解题意,分情况画出图形,学会用分类讨论的思想思考问题.13.(1)见解析;(2)见解析;(3)见解析;.【分析】(1)过点C 作,得到,再根据,,得到,进而得到,最后证明;(2)先证明,再证明,得到,问题得证;(3)根据题意得到,根据(2)结论得到∠D解析:(1)见解析;(2)见解析;(3)见解析;2α.【分析】(1)过点C 作//CG DF ,得到DFE FCG ∠=∠,再根据90BCF ∠=︒,90∠+∠=︒ABC DFE ,得到ABC BCG ∠=∠,进而得到//CG AB ,最后证明//DF AB ; (2)先证明90ACB DEF ∠+∠=︒,再证明90ACB ACE ∠+∠=︒,得到DEF ACE ∠=∠,问题得证;(3)根据题意得到DFE DEF α∠=∠=,根据(2)结论得到∠DEF =∠ECA =α,进而得到=90BC AC A B α=∠︒-∠,根据三角形内角和即可求解.【详解】解:(1)过点C 作//CG DF ,DFE FCG ∴∠=∠,BC MN ⊥,90BCF ∴∠=︒,90BCG FCG ∴∠+∠=︒,90BCG DFE ∴∠+∠=︒,90ABC DFE ∠+∠=︒,ABC BCG ∴∠=∠,//CG AB ∴,//DF AB ∴;(2)解:ABC ACB ∠=∠,DEF DFE ∠=∠,又90ABC DFE ∠+∠=︒,90ACB DEF ∴∠+∠=︒,BC MN ⊥,90BCM ∴∠=︒,90ACB ACE ∴∠+∠=︒,DEF ACE ∴∠=∠,//DE AC ∴;(3)如图三角形DEF 即为所求作三角形.∵DFE α∠=,∴DFE DEF α∠=∠=,由(2)得,DE ∥AC ,∴∠DEF =∠ECA =α,∵90ACB ACE ∠+∠=︒,∴∠ACB =90α︒-,∴ =90BC AC A B α=∠︒-∠,∴∠A =180°-A ABC CB -∠∠=2α.故答案为为:2α.【点睛】本题考查了平行线的判定,三角形的内角和等知识,综合性较强,熟练掌握相关知识,根据题意画出图形是解题关键.14.(1) ;(2) ;(3)不发生变化,理由见解析【分析】(1)如图1,延长DE 交AB 于点F ,根据平行线的性质推出;(2)如图2,过点E 作ES ∥AB ,过点H 作HT ∥AB ,根据AB ∥CD ,AB ∥E 解析:(1) +180ACB BED ∠∠=︒;(2) 100︒;(3)不发生变化,理由见解析【分析】(1)如图1,延长DE 交AB 于点F ,根据平行线的性质推出+180ACB BED ∠∠=︒;(2)如图2,过点E 作ES ∥AB ,过点H 作HT ∥AB ,根据AB ∥CD ,AB ∥ES 推出BED ABE CDE ∠=∠+∠,再根据AB ∥TH ,AB ∥CD 推出GHD THD THB ∠=∠-∠,最后根据BED ∠比BHD ∠大60︒得出BED ∠的度数;(3)如图3,过点E 作EQ ∥DN ,根据DEB CDE ABE ∠=∠+∠得出βα-的度数,根据条件再逐步求出PBM ∠的度数.【详解】(1)如答图1所示,延长DE 交AB 于点F .AB ∥CD ,所以D EFB ∠=∠,又因为A D ∠=∠,所以A EFB ∠=∠,所以AC ∥DF ,所以ACB CED ∠=∠.因为+180CED BED ∠∠=︒,所以+180ACB BED ∠∠=︒.(2)如答图2所示,过点E 作ES ∥AB ,过点H 作HT ∥AB .设ABG EBG α∠=∠=,FDH EDH β∠=∠=,因为AB ∥CD ,AB ∥ES ,所以ABE BES ∠=∠,SED CED ∠=∠,所以21802BED BES SED ABE CDE αβ∠=∠+∠=∠+∠=+︒-,因为AB ∥TH ,AB ∥CD ,所以ABG THB ∠=∠,FDH DHT ∠=∠,所以GHD THD THB βα∠=∠-∠=-,因为BED ∠比BHD ∠大60︒,所以2+1802()60αββα︒---=︒,所以40βα-=︒,所以40BHD ∠=︒,所以100BED ∠=︒(3)不发生变化如答图3所示,过点E 作EQ ∥DN .设CDN EDN α∠=∠=,EBM KBM β∠=∠=,由(2)易知DEB CDE ABE ∠=∠+∠,所以2+1802100αβ︒-=︒,所以40βα-=︒, 所以180()180DEB CDE EDN EBM PBM PBM αβ∠=∠+∠+︒-∠+∠=+︒--∠, 所以80()40PBM βα∠=︒--=︒.【点睛】本题考查了平行线的性质,求角的度数,正确作出相关的辅助线,根据条件逐步求出角度的度数是解题的关键.15.(1)2α;(2)EF ⊥PQ ,见解析;(3)∠NEF =∠AMP ,见解析【分析】1)如图①,过点P 作PR ∥AB ,可得AB ∥CD ∥PR ,进而可得结论;(2)根据已知条件可得2∠EPQ+2∠PEF =解析:(1)2α;(2)EF ⊥PQ ,见解析;(3)∠NEF =12∠AMP ,见解析【分析】1)如图①,过点P 作PR ∥AB ,可得AB ∥CD ∥PR ,进而可得结论;(2)根据已知条件可得2∠EPQ+2∠PEF =180°,进而可得EF 与PQ 的位置关系; (3)结合(2)和已知条件可得∠QNE =∠QEN ,根据三角形内角和定理可得∠QNE =12(180°﹣∠NQE)=1(180°﹣3α),可得∠NEF=180°﹣∠QEF﹣∠NQE﹣∠QNE,进而可2得结论.【详解】解:(1)如图①,过点P作PR∥AB,∵AB∥CD,∴AB∥CD∥PR,∴∠AMP=∠MPR=α,∠PQN=∠RPQ=α,∴∠MPQ=∠MPR+∠RPQ=2α;(2)如图②,EF⊥PQ,理由如下:∵PQ平分∠MPN.∴∠MPQ=∠NPQ=2α,∵QE∥PN,∴∠EQP=∠NPQ=2α,∴∠EPQ=∠EQP=2α,∵EF平分∠PEQ,∴∠PEQ=2∠PEF=2∠QEF,∵∠EPQ+∠EQP+∠PEQ=180°,∴2∠EPQ+2∠PEF=180°,∴∠EPQ+∠PEF=90°,∴∠PFE=180°﹣90°=90°,∴EF⊥PQ;∠AMP,理由如下:(3)如图③,∠NEF=12由(2)可知:∠EQP=2α,∠EFQ=90°,∴∠QEF=90°﹣2α,∵∠PQN=α,∴∠NQE=∠PQN+∠EQP=3α,∵NE平分∠PNQ,∴∠PNE=∠QNE,∵QE∥PN,∴∠QEN=∠PNE,∴∠QNE=∠QEN,∵∠NQE=3α,∴∠QNE=12(180°﹣∠NQE)=12(180°﹣3α),∴∠NEF=180°﹣∠QEF﹣∠NQE﹣∠QNE=180°﹣(90°﹣2α)﹣3α﹣12(180°﹣3α)=180°﹣90°+2α﹣3α﹣90°+3 2α=12α=12∠AMP.∴∠NEF=12∠AMP.【点睛】本题考查了平行线的性质,角平分线的性质,熟悉相关性质是解题的关键.四、解答题16.(1)∠DAE =14°;(2)∠DFE =14°;(3)∠DAE 的大小不变,∠DAE=14°,证明详见解析.【分析】(1)求出∠ADE的度数,利用∠DAE=90°-∠ADE即可求出∠DAE解析:(1)∠DAE =14°;(2)∠DFE =14°;(3)∠DAE 的大小不变,∠DAE =14°,证明详见解析.【分析】(1)求出∠ADE的度数,利用∠DAE=90°-∠ADE即可求出∠DAE的度数.(2)求出∠ADE的度数,利用∠DFE=90°-∠ADE即可求出∠DAE的度数.(3)利用AE平分∠BEC,AD平分∠BAC,求出∠DFE=15°即是最好的证明.【详解】(1)∵∠B=45°,∠C=73°,∴∠BAC=62°,∵AD平分∠BAC,∴∠BAD=∠CAD=31°,∴∠ADE=∠B+∠BAD=45°+31°=76°,∵AE⊥BC,∴∠AEB=90°,∴∠DAE=90°-∠ADE=14°.(2)同(1),可得,∠ADE=76°,∵FE⊥BC,∴∠FEB=90°,∴∠DFE=90°-∠ADE=14°.(3)DAE∠=14°∠的大小不变.DAE理由:∵ AD平分∠ BAC,AE平分∠BEC∴∠BAC=2∠BAD,∠BEC=2∠AEB∵∠BAC+∠B+∠BEC+∠C =360°∴2∠BAD+2∠AEB=360°-∠B-∠C=242°∴∠BAD+∠AEB=121°∵∠ADE=∠B+∠BAD∴∠ADE=45°+∠BAD∴∠DAE=180°-∠AEB-∠ADE=180°-∠AEB-45°-∠BAD=135°-(∠AEB+∠BAD)=135°-121°=14°【点睛】本题考查了三角形内角和定理和三角形外角的性质,熟练掌握性质是解题的关键. 17.解决问题:6;拓展延伸:(1)S1=2S2 (2)10.5【解析】试题分析:解决问题:连接AE,根据操作示例得到S△ADE=S△BDE,S△ABE=S△AEC,从而得到结论;拓展延伸:(1)解析:解决问题:6;拓展延伸:(1)S1=2S2(2)10.5【解析】试题分析:解决问题:连接AE,根据操作示例得到S△ADE=S△BDE,S△ABE=S△AEC,从而得到结论;拓展延伸:(1)作△ABD的中线AE,则有BE=ED=DC,从而得到△ABE的面积=△AED的面积=△ADC的面积,由此即可得到结论;(2)连接AO.则可得到△BOD的面积=△BOC的面积,△AOC的面积=△AOD的面积,△EOC的面积=△BOC的面积的一半,△AOB的面积=2△AOE的面积.设△AOD的面积=a,△AOE的面积=b,则a+3=2b,a=b+1.5,求出a、b的值,即可得到结论.。
【解析版】安庆市初中数学七年级下期末知识点(培优提高)(1)

一、选择题1.同学们喜欢足球吗?足球一般是用黑白两种颜色的皮块缝制而成的,如图所示,黑色皮块是正五边形,白色皮块是正六边形.若一个球上共有黑白皮块32块,请你计算一下,黑色皮块和白色皮块的块数依次为()A.16块,16块B.8块,24块C.20块,12块D.12块,20块2.某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打()A.6折B.7折C.8折D.9折3.已知平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )A.﹣3B.﹣5C.1或﹣3D.1或﹣54.已知{x=1y=2是关于x,y的二元一次方程x-ay=3的一个解,则a的值为()A.1B.-1C.2D.-25.已知关于x,y的二元一次方程组231ax byax by+=⎧⎨-=⎩的解为11xy=⎧⎨=-⎩,则a﹣2b的值是()A.﹣2B.2C.3D.﹣36.方程组23x y ax y+=⎧⎨-=⎩的解为5xy b=⎧⎨=⎩,则a、b分别为()A.a=8,b=﹣2B.a=8,b=2C.a=12,b=2D.a=18,b=8 7.16的平方根为()A.±4B.±2C.+4D.28.在实数0,-π34中,最小的数是()A.0B.-πC3D.-49.如图,如果AB∥CD,那么下面说法错误的是()A .∠3=∠7B .∠2=∠6C .∠3+∠4+∠5+∠6=180°D .∠4=∠810.在平面直角坐标系内,线段CD 是由线段AB 平移得到的,点A (-2,3)的对应点为C (2,5),则点B (-4,-1)的对应点D 的坐标为()A .()8,3--B .()4,2C .()0,1D .()1,811.如图,下列能判断AB ∥CD 的条件有 ( )①∠B +∠BCD =180°②∠1 = ∠2 ③∠3 =∠4 ④∠B = ∠5 A .1B .2C .3D .4 12.在直角坐标系中,若点P(2x -6,x -5)在第四象限,则x 的取值范围是( )A .3<x <5B .-5<x <3C .-3<x <5D .-5<x <-3 13.用反证法证明命题“在三角形中,至多有一个内角是直角”时,应先假设( ) A .至少有一个内角是直角B .至少有两个内角是直角C .至多有一个内角是直角D .至多有两个内角是直角 14.不等式组2201x x +>⎧⎨-≥-⎩的解在数轴上表示为( ) A .B .C .D .15.关于x ,y 的方程组2,226x y a x y a +=⎧⎨+=-⎩的解满足0x y +=,则a 的值为( ) A .8 B .6C .4D .2 二、填空题16.已21x y =⎧⎨=-⎩是关于x 、y 的二次元方程39ax y +=的解,则a 的值为___________ 17.若关于x ,y 的二元一次方程组3133x y a x y +=+⎧⎨+=⎩的解满足x +y <2,则a 的取值范围为_____.18.如图8中图①,两个等边△ABD ,△CBD 的边长均为1,将△ABD 沿AC 方向向右平移到△A′B′D′的位置得到图②,则阴影部分的周长为_________.19.若3的整数部分是a ,小数部分是b ,则3a b -=______.20.用适当的符号表示a 是非负数:_______________.21.若a ,b 均为正整数,且a >7,b <32,则a +b 的最小值是_______________.22.线段CD 是由线段AB 平移得到的,其中点A (﹣1,4)平移到点C (﹣3,2),点B (5,﹣8)平移到点D ,则D 点的坐标是________.23.结合下面图形列出关于未知数x ,y 的方程组为_____.24.两条直线相交所成的四个角中,有两个角分别是(2x -10)°和(110-x)°,则x =_____.25.比较大小:23________13.三、解答题26.某校八年级举行英语演讲比赛,准备用1200元钱(全部用完)购买A ,B 两种笔记本作为奖品,已知A ,B 两种每本分别为12元和20元,设购入A 种x 本,B 种y 本. (1)求y 关于x 的函数表达式.(2)若购进A 种的数量不少于B 种的数量.①求至少购进A 种多少本?②根据①的购买,发现B 种太多,在费用不变的情况下把一部分B 种调换成另一种C ,调换后C 种的数量多于B 种的数量,已知C 种每本8元,则调换后C 种至少有______本(直接写出答案)27.已知//AB CD ,点M 为平面内一点.(1)如图1,ABM ∠和DCM ∠互余,小明说过M 作//MP AB ,很容易说明BM CM ⊥。
(完整版)人教版七年级数学下册二元一次方程组试题(带答案) (一)培优试题

一、选择题1.现有如图(1)的小长方形纸片若干块,已知小长方形的长为a,宽为b.用3个如图(2)的全等图形和8个如图(1)的小长方形,拼成如图(3)的大长方形,若大长方形的宽为30cm,则图(3)中阴影部分面积与整个图形的面积之比为()A.15B.16C.17D.182.小兰:“小红,你上周买的笔和笔记本的价格是多少啊?”小红:“哦,…,我忘了!只记得先后买了两次,第一次买了 5 支笔和 10 本笔记本共花了 42 元钱,第二次买了 10 文笔和5 本笔记本共花了 30 元钱.”请根据小红与小兰的对话,求得小红所买的笔和笔记本的价格分别是( )A.0.8 元/支,2.6 元/本B.0.8 元/支,3.6 元/本C.1.2 元/支,2.6 元/本D.1.2 元/支,3.6 元/本3.甲、乙两人共同解关于x,y的方程组532ax byx cy+=⎧⎨+=⎩①②,甲正确地解得21xy=⎧⎨=-⎩乙看错了方程②中的系数c,解得31xy=⎧⎨=⎩,则2()a b c++的值为()A.16 B.25 C.36 D.494.巴广高速公路在5月10日正式通车,从巴中到广元全长约为126km.一辆小汽车,一辆货车同时从巴中,广元两地相向开出,经过45分钟相遇,相遇时小汽车比货车多行6km,设小汽车和货车的速度分别为xkm/h,ykm/h,则下列方程组正确的是()A.()()45126456x yx y⎧+=⎪⎨-=⎪⎩B.()312646x yx y⎧+=⎪⎨⎪-=⎩C.()()31264456x yx y⎧+=⎪⎨⎪-=⎩D.()()31264364x yx y⎧+=⎪⎪⎨⎪-=⎪⎩5.已知方程组5354x yax y+=⎧⎨+=⎩和2551x yx by-=⎧⎨+=⎩有相同的解,则2a b-的值为()A.15B.14C.10D.86.已知方程组2106x ybx ay+=⎧⎨+=⎩和10312ax y bx y-=⎧⎨-=⎩有相同的解,则-a b的值为()A.1 B.1-C.2 D.2-7.已知关于x ,y 的方程组35225x y ax y a -=⎧⎨-=-⎩,则下列结论中正确的有( )个①当5a =时,方程组的解是1020x y =⎧⎨=⎩;②当x ,y 的值互为相反数时,20a =③不存在一个实数a 使得x y =; ④若23722a y -=,则2a =. A .1B .2C .3D .48.已知11x y =⎧⎨=-⎩是二元一次方程组2123ax by ax by +=⎧⎨-=⎩的解,则3a b -的值为( )A .-2B .2C .-4D .49.若关于x ,y 的方程组48ax by ax by -=-⎧⎨+=⎩的解是23x y =⎧⎨=⎩,则方程组(3)(1)4(3)(1)8a x b y a x b y +--=-⎧⎨++-=⎩的解是( )A .14x y =-⎧⎨=⎩B .23x y =⎧⎨=⎩C .14x y =⎧⎨=-⎩D .52x y =⎧⎨=⎩10.如果32x y =⎧⎨=-⎩是方程组15ax by ax by +=⎧⎨-=⎩的解,则a 2008+2b 2008的值为( )A .1B .2C .3D .4二、填空题11.小红买了80分、120分的两种邮票,共花掉16元钱(两种邮票都买),则购买方案共有 种.12.一个两位数的数字和为14,若调换个位数字与十位数字,新数比原数小36,则这个两位数是_____.13.若方程组1122a x y c a x y c +=⎧⎨+=⎩的解是12x y =⎧⎨=⎩,则方程组111222a x y c a a x y c a +=-⎧⎨+=-⎩的解是______.14.已知21x y =⎧⎨=⎩是二元一次方程组81mx ny nx my +=⎧⎨-=⎩________.15.在平面直角坐标系中,将点P 向左平移2个单位长度,再向上平移3个单位长度,得到P '(﹣1,3),则点P 坐标为___.16.关于x ,y 的二元一次方程2x +3y =12的非负整数解有______组.17.某商场地下停车场有5个出口,5个入口,每天早晨7点开始对外停车且此时车位空置率为80%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个入口和2个出口,8小时车库恰好停满;如果开放4个入口和2个出口,1.6小时车库恰好停满.2021年五一节期间,由于商场人数增多,早晨7点时的车位空置率变为60%,又因为车库改造,只能开放3个入口和2个出口,则从早晨7点开始经过______小时车库恰好停满.18.已知关于x ,y 的二元一次方程()()12120m x my m +++=﹣﹣,无论实数m 取何值,此二元一次方程都有一个相同的解,则这个相同的解是______.19.小明、小红和小光共解出了100道数学题目,每人都解出了其中的60道题目,如果将其中只有1人解出的题目叫做难题,2人解出的题目叫做中档题,3人都解出的题目叫做容易题,那么难题比容易题多________道. 20.某出租车起步价所包含的路程为02km ,超过2km 的部分按每千米另收费.小江乘坐这种出租车走了7km ,付了16元;小北乘坐这种出租车走了13km ,付了28元.设这种出租车的起步价为x 元,超过2km 后每千米收费y 元.根据题意,可列方程组为_________.三、解答题21.在平面直角坐标系xOy 中,把线段AB 先向右平移h 个单位,再向下平移1个单位得到线段CD (点A 对应点C ),其中()(),,,A a b B m n 分别是第三象限与第二象限内的点.(1)若|3|10,2a b h ++=,求C 点的坐标; (2)若1b n =-,连接AD ,过点B 作AD 的垂线l ①判断直线l 与x 轴的位置关系,并说明理由;②已知E 是直线l 上一点,连接DE ,且DE 的最小值为1,若点B ,D 及点(),s t 都是关于x ,y 的二元一次方程(0)px qy k pq +=≠的解(),x y 为坐标的点,试判断()()s m t n -+-是正数、负数还是0?并说明理由.22.在平面直角坐标系中,若点P (x ,y )的坐标满足x ﹣2y +3=0,则我们称点P 为“健康点”:若点Q (x ,y )的坐标满足x +y ﹣6=0,则我们称点Q 为“快乐点”. (1)若点A 既是“健康点”又是“快乐点”,则点A 的坐标为 ;(2)在(1)的条件下,若B 是x 轴上的“健康点”,C 是y 轴上的“快乐点”,求△ABC 的面积;(3)在(2)的条件下,若P 为x 轴上一点,且△BPC 与△ABC 面积相等,直接写出点P 的坐标.23.在平面直角坐标系xOy 中,点()4,0A -,点()0,3B ,点()3,0C .(1)ABC 的面积为______;(2)已知点()1,2D -,()2,3E --,那么四边形ACDE 的面积为______.(3)奥地利数学家皮克发现了一类快速求解格点多边形的方法,被称为皮克定理:如果用m 表示格点多边形内的格点数,n 表示格点多边形边上的格点数,那么格点多边形的面积S 和m 与n 之间满足一种数量关系.例如刚刚求解的几个多边形面积中,我们可以得到如表中信息:形内格点数m 边界格点数n格点多边形面积SABC6 11 四边形ACDE 8 11 五边形ABCDE208②中六边形FGHIJK 的面积为______(本大题无需写出解题过程,写出正确答案即可).24.七年(1)(2)两班各40人参加垃圾分类知识竞赛,规则如图.比赛中,所有同学均按要求一对一连线,无多连、少连.(1)分数5,10,15,20中,每人得分不可能是________分.(2)七年(1)班有4人全错,其余成员中,满分人数是未满分人数的2倍;七年(2)班所有人都得分,最低分人数的2倍与其他未满分人数之和等于满分人数. ①问(1)班有多少人得满分?②若(1)班除0分外,最低得分人数与其他未满分人数相等,问哪个班的总分高?25.对于不为0的一位数m 和一个两位数n ,将数m 放置于两位数之前,或者将数m 放置于两位数的十位数字与个位数字之间就可以得到两个新的三位数,将较大三位数减去较小三位数的差与15的商记为(),F m n .例如:当1m =,68n =时,可以得到168,618.较大三位数减去较小三位数的差为618168450-=,而4501530÷=,所以()1,6830F =. (1)计算:()2,17F .(2)若a 是一位数,b 是两位数,b 的十位数字为x (18x ≤≤,x 为自然数),个位数字为8,当()()11,509,862F a F b +=时,求出所有可能的a ,b 的值.26.为鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市居民“一户一表”生活用水阶梯式计费价格表的部分信息,请解答: 自来水销售价格 每户每月用水量 单位:元/吨15吨及以下a超过15吨但不超过25吨的部分 b超过25吨的部分5(1)小王家今年3月份用水20吨,要交水费___________元;(用a ,b 的代数式表示) (2)小王家今年4月份用水21吨,交水费48元;邻居小李家4月份用水27吨,交水费70元,求a ,b 的值.(3)在第(2)题的条件下,若交水费76.5元,求本月用水量.(4)在第(2)题的条件下,小王家5月份用水量与4月份用水量相同,却发现要比4月份多交9.6元钱水费,小李告诉小王说:“水价调整了,表中表示单位的a ,b 的值分别上调了整数角钱(没超过1元),其他都没变.”到底上调了多少角钱呢?请你帮小王求出符合条件的所有可能情况. 27.阅读下面资料:小明遇到这样一个问题:如图1,对面积为a 的△ABC 逐次进行以下操作:分别延长AB 、BC 、CA 至A 1、B 1、C1,使得A 1B =2AB ,B 1C =2BC ,C1A =2CA ,顺次连接A 1、B 1、C 1,得到△A 1B 1C 1,记其面积为S 1,求S 1的值.小明是这样思考和解决这个问题的:如图2,连接A 1C 、B 1A 、C 1B ,因为A 1B =2AB ,B 1C =2BC ,C 1A =2CA ,根据等高两三角形的面积比等于底之比,所以11∆∆=A BC B CA S S =11∆∆=A BC C AB S S =2S △ABC =2a ,由此继续推理,从而解决了这个问题.(1)直接写出S 1= (用含字母a 的式子表示). 请参考小明同学思考问题的方法,解决下列问题:(2)如图3,P 为△ABC 内一点,连接AP 、BP 、CP 并延长分别交边BC 、AC 、AB 于点D 、E 、F ,则把△ABC 分成六个小三角形,其中四个小三角形面积已在图上标明,求△ABC 的面积.(3)如图4,若点P 为△ABC 的边AB 上的中线CF 的中点,求S △APE 与S △BPF 的比值. 28.为了加强公民的节水意识,合理利用水资源,某城市规定用水收费标准如下:每户每月用水量不超过6米3时,水费按a 元/米3收费;每户每月用水量超过6米3时,不超过的部分每立方米仍按a 元收费,超过的部分按c 元/米3收费,该市某用户今年3、4月份的用水量和水费如下表所示:月份 用水量(m 3)收费(元) 3 5 7.5 4927系式;(2)已知某户5月份的用水量为8米3,求该用户5月份的水费. 29.阅读下列材料,解答下面的问题:我们知道方程2312x y +=有无数个解,但在实际生活中我们往往只需求出其 正整数解.例:由2312x y +=,得:1222433x xy -==-,(x 、y 为正整数) ∴01220x x >⎧⎨->⎩,则有06x <<.又243x y =-为正整数,则23x为正整数.由2与3互质,可知:x 为3的倍数,从而x=3,代入2423xy =-=∴2x+3y=12的正整数解为32x y =⎧⎨=⎩问题:(1)请你写出方程25x y +=的一组正整数解: . (2)若62x -为自然数,则满足条件的x 值为 . (3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?30.五一节前,某商店拟购进A 、B 两种品牌的电风扇进行销售,已知购进3台A 种品牌电风扇所需费用与购进2台B 种品牌电风扇所需费用相同,购进1台A 种品牌电风扇与2台B 种品牌电风扇共需费用400元.(1)求A 、B 两种品牌电风扇每台的进价分别是多少元?(2)销售时,该商店将A 种品牌电风扇定价为180元/台,B 种品牌电风扇定价为250元/台,商店拟用1000元购进这两种风扇(1000元刚好全部用完),为能在销售完这两种电风扇后获得最大的利润,该商店应采用哪种进货方案?【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】观察图③可知3个小长方形的宽与1个小长方形的长的和等于大长方形的宽,小长方形的4个长等于小长方形的3个长与3个宽的和,可列出关于a ,b 的方程组,解方程组得出a ,b 的值;利用a ,b 的值分别求得阴影部分面积与整个图形的面积,即可求得影部分面积与整个图形的面积之比. 【详解】解:根据题意、结合图形可得:330433a b a a b+=⎧⎨=+⎩, 解得:155a b =⎧⎨=⎩,∴阴影部分面积223()310300=-=⨯=a b , 整个图形的面积304304151800=⨯=⨯⨯=a , ∴阴影部分面积与整个图形的面积之比300118006==, 故选B . 【点睛】本题考查了二元一次方程组的应用,理解题意并利用大长方形的长与宽和小长方形的关系建立二元一次方程组是解题的关键.2.D解析:D 【分析】首先设小红所买的笔的价格是x 元/支,笔记本的价格是y 元/本,根据关键语句“第一次买了5支笔和10本笔记本共花了42元钱,”可得方程5x+10y=42,“第二次买了10支笔和5本笔记本共花了30元钱”可得方程10x+5y=30,联立两个方程,再解方程组即可. 【详解】解:设小红所买的笔的价格是x 元/支,笔记本的价格是y 元/本,由题意得:5104210530x y x y +=⎧⎨+=⎩ 解得: 1.23.6x y =⎧⎨=⎩ 故答案为D. 【点睛】本题主要考查了二元一次方程组的应用,关键是弄懂题意,找出题目中的等量关系,再列出方程组即可.3.B解析:B 【分析】将x =2,y =﹣1代入方程组中,得到关于a 与b 的二元一次方程与c 的值,将x =3,y =1代入方程组中的第一个方程中得到关于a 与b 的二元一次方程,联立组成关于a 与b 的方程组,求出方程组的解得到a 与b 的值,即可确定出a ,b 及c 的值. 【详解】把21x y =⎧⎨=-⎩代入得:2562a b c -=⎧⎨-=⎩,解得:c =4,把31x y =⎧⎨=⎩代入得:3a +b =5,联立得:2535a b a b -=⎧⎨+=⎩,解得:21a b =⎧⎨=-⎩,则(a +b +c )2=(2﹣1+4)2=25. 故选B . 【点睛】本题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.4.D解析:D 【详解】设小汽车的速度为xkm/h ,则45分钟小汽车行进的路程为34xkm ;设货车的速度为ykm/h ,则45分钟货车行进的路程为34ykm .由两车起初相距126km ,则可得出34(x+y )=126;又由相遇时小汽车比货车多行6km ,则可得出34(x-y )=6.可得出方程组31264364x y x y ⎧+=⎪⎪⎨⎪-=⎪⎩()(). 故选:D .点睛:学生在分析解答此题时需注意弄清题意,明白所要考查的要点.另外,还需注意单位的换算,避免粗心造成失误.5.C解析:C 【分析】联立不含a 与b 的方程组成方程组,求出方程组的解得到x 与y 的值,进而求出a 与b 的值,代入原式计算即可求出值. 【详解】 解:根据题意,则5325x y x y +=⎧⎨-=⎩①②, 由①×2+②得:11x =11, 解得:x =1,把x =1代入①得:5+y =3, 解得:y =-2;把x =1,y =-2代入5451ax y x by +=⎧⎨+=⎩,则104521a b -=⎧⎨-=⎩,解得:142a b =⎧⎨=⎩,∴2142210a b -=-⨯=. 故选:C . 【点睛】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.6.A解析:A 【分析】根据两个方程组解相同,解方程组210312x y x y +=⎧⎨-=⎩,把求得的x 、y 的值分别两个方程组中的另一个方程即可得到关于a 、b 的方程组,解方程组即可求得a 、b 的值,从而可求得结果的值. 【详解】∵方程组2106x y bx ay +=⎧⎨+=⎩和10312ax y bx y -=⎧⎨-=⎩有相同的解∴方程组210312x y x y +=⎧⎨-=⎩①②与106ax y bbx ay -=⎧⎨+=⎩有相同的解由①×3+②得:7x =42 解得:x =6把x =6代入①得:12+y =10 解得:y =-2∴62x y =⎧⎨=-⎩是方程组210312x y x y +=⎧⎨-=⎩①②与106ax y b bx ay -=⎧⎨+=⎩的解把62x y =⎧⎨=-⎩代入106ax y b bx ay -=⎧⎨+=⎩中,得:6210626a b b a +=⎧⎨-=⎩化简得:35133a b a b -=-⎧⎨-+=⎩③④③+④×3得:4b =8 解得:b =2把b =2代入④得:-a +6=3 解得:a =3故方程组解为32a b =⎧⎨=⎩∴a -b =3-2=1 故选:A . 【点睛】本题主要考查了二元一次方程组的解法、二元一次方程组的解,理解二元一次方程组的解是本题的关键.7.B解析:B 【分析】①把a =5代入方程组求出解,即可作出判断;②由题意得x +y =0,变形后代入方程组求出a 的值,即可作出判断;③若x =y ,代入方程组,变形得关于a 的方程,即可作出判断;④根据题中等式得2a ﹣3y =7,代入方程组求出a 的值,即可作出判断.【详解】解:①把a =5代入方程组得:3510(1)20(2)x y x y -=⎧⎨-=⎩, 由(2)得x =2y ,将x =2y 代入(1)得:y =10,将y =10代入x =2y 得:x =20,解得:2010x y =⎧⎨=⎩,故①错误; ②当x ,y 的值互为相反数时,x +y =0,即:y =﹣x代入方程组得:35225x x a x x a +=⎧⎨+=-⎩, 整理,得82(3)35(4)x a x a =⎧⎨=-⎩, 由(3)得:14x a =, 将14x a =代入(4),得:354a a =-, 解得:a =20,故②正确;③若x =y ,则有225x a x a -=⎧⎨-=-⎩, 可得:a =a ﹣5,矛盾,∴不存在一个实数a 使得x =y ,故③正确;④352(5)25(6)x y a x y a -=⎧⎨-=-⎩, (5)-(6)×3,得:15y a =-,将15y a =-代入(6),得:25x a =-,∴原方程组的解为2515x a y a =-⎧⎨=-⎩, ∵23722a y -=,∴2a ﹣3y =7,把y =15﹣a 代入得:2a ﹣45+3a =7,解得:a =525,故④错误; ∴正确的选项有②③两个.【点睛】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.本题属于基础题型,难度不大.8.A解析:A【分析】把11x y =⎧⎨=-⎩代入二元一次方程组2123ax by ax by +=⎧⎨-=⎩并解方程组,再把a,b 代入3a b -. 【详解】把11x y =⎧⎨=-⎩代入二元一次方程组2123ax by ax by +=⎧⎨-=⎩,得 2123a b a b -=⎧⎨+=⎩ 解得11a b =⎧⎨=⎩所以3a b -=-2故选:A【点睛】本题考查了二元一次方程组的解,以及二元一次方程组的解法,其基本思路是消元,消元的方法有:加减消元法和代入消元法两种,灵活选择合适的方法是解答本题的关键. 9.A解析:A【分析】通过观察所给方程组的关系可得3213x y +=⎧⎨-=⎩,求出x 、y 即可. 【详解】解:∵关于x ,y 的方程组48ax by ax by -=-⎧⎨+=⎩的解是23x y =⎧⎨=⎩, ∴234238a b a b -=-⎧⎨+=⎩, 又∵(3)(1)4(3)(1)8a xb y a x b y +--=-⎧⎨++-=⎩, ∴3213x y +=⎧⎨-=⎩, 解得14x y =-⎧⎨=⎩, ∴方程组(3)(1)4(3)(1)8a x b y a x b y +--=-⎧⎨++-=⎩的解为14x y =-⎧⎨=⎩,【点睛】本题考查二元一次方程组的解,解题的关键是要知道两个方程组之间的关系. 10.C解析:C【分析】将方程组的解代入方程组可得关于a 、b 的二元一次方程组321325a b a b -=⎧⎨+=⎩,再求解方程组即可求解.【详解】解:∵32x y =⎧⎨=-⎩是方程组15ax by ax by +=⎧⎨-=⎩的解, ∴321325a b a b -=⎧⎨+=⎩①②, ①+②得,a =1,将a =1代入①得,b =1,∴a 2008+2b 2008=1+2=3,故选:C .【点睛】本题考查了二元一次方程组的解,熟练掌握加减消元法和代入消元法解二元一次方程组是解题的关键.二、填空题11.6【分析】设80分的邮票购买x 张,120分的邮票购买y 张,根据题意列方程0.8x+1.2y=16,用含y 的代数式表示x 得,根据x 、y 都是整数取出x 与y 的对应值,得到购买方案.【详解】解:设8解析:6【分析】设80分的邮票购买x 张,120分的邮票购买y 张,根据题意列方程0.8x+1.2y=16,用含y 的代数式表示x 得3202x y =-,根据x 、y 都是整数取出x 与y 的对应值,得到购买方案. 【详解】解:设80分的邮票购买x 张,120分的邮票购买y 张,0.8x+1.2y=16,解得3202x y =-, ∵x 、y 都是正整数,∴当y=2、4、6、8、10、12时,x=17、14、11、8、5、2,∴共有6种购买方案,故答案为:6.【点睛】此题考查一元二次方程的实际应用,根据题意只得到一个方程时,可将方程变形为用一个未知数表示另一个未知数的形式,然后根据未知数的要求得到对应值即可解决实际问题. 12.95【详解】设十位数字为x ,个位数字为y ,根据题意所述的等量关系可得出方程组,求解即可得,即这个两位数为95.故答案为95.【点睛】本题考查了二元一次方程组的应用,解答本题的关键是设出未知解析:95【详解】设十位数字为x ,个位数字为y ,根据题意所述的等量关系可得出方程组14101036x y x y y x +=⎧⎨+--=⎩,求解即可得95x y =⎧⎨=⎩,即这个两位数为95. 故答案为95.【点睛】本题考查了二元一次方程组的应用,解答本题的关键是设出未知数,注意掌握二位数的表示方法.13.【分析】先将方程组的解代入方程组得到c1−a1=2,c2−a2=2,再将所求方程组用加减消元法求解即可.【详解】解:∵方程组的解是,∴,∴c1−a1=2,c2−a2=2,∴可化为,①解析:02x y =⎧⎨=⎩先将方程组的解代入方程组得到c 1−a 1=2,c 2−a 2=2,再将所求方程组用加减消元法求解即可.【详解】解:∵方程组1122a x y c a x y c +=⎧⎨+=⎩的解是12x y =⎧⎨=⎩, ∴112222a c a c +=⎧⎨+=⎩, ∴c 1−a 1=2,c 2−a 2=2,∴111222a x y c a a x y c a +=-⎧⎨+=-⎩可化为1222a x y a x y +=⎧⎨+=⎩①②, ①−②,得(a 1−a 2)x =0,∴x =0,将x =0代入①中,得y =2,∴方程组的解为02x y =⎧⎨=⎩, 故答案为02x y =⎧⎨=⎩. 【点睛】本题考查二元一次方程组的解,会用加减消元法解方程组,并能灵活将方程组变形是解题的关键.14.2【分析】根据题意,将代入二元一次方程组,得到关于m 、n 的二元一次方程组,求出后代入即可.【详解】将代入二元一次方程组,得,解得,,,,,故答案为:2.【点睛】本题主要考查解析:2根据题意,将21x y =⎧⎨=⎩代入二元一次方程组81mx ny nx my +=⎧⎨-=⎩,得到关于m 、n 的二元一次方程组,求出后代入即可.【详解】将21x y =⎧⎨=⎩代入二元一次方程组81mx ny nx my +=⎧⎨-=⎩, 得2821m n n m +=⎧⎨-=⎩, 解得32m n =⎧⎨=⎩,=2,故答案为:2.【点睛】本题主要考查了解二元一次方程组,算术平方根,解题关键是熟练掌握二元一次方程组的解法.15.(1,0)【分析】根据向左平移,横坐标减,向上平移,纵坐标加的性质进行分析,通过列二元一次方程组并求解,即可得到答案.【详解】设点P 坐标为(x ,y ).将点P 向左平移2个单位长度,再解析:(1,0)【分析】根据向左平移,横坐标减,向上平移,纵坐标加的性质进行分析,通过列二元一次方程组并求解,即可得到答案.【详解】设点P 坐标为(x ,y ).将点P 向左平移2个单位长度,再向上平移3个单位长度,得:()2,3x y -+∴2133x y -=-⎧⎨+=⎩∴10x y =⎧⎨=⎩∴点P 坐标为(1,0).故答案为:(1,0).【点睛】本题考查了坐标、平移、二元一次方程组的知识;解题的关键是熟练掌握坐标、平移的性质,从而完成求解.16.3【分析】把x 看做已知数表示出y ,确定出非负整数x 与y 的值即.【详解】解:方程2x+3y=12,解得:y=-x+4,当x=0时,方程变形为3y=12,解得y=4;当x=3时,方程变形为解析:3【分析】把x 看做已知数表示出y ,确定出非负整数x 与y 的值即.【详解】解:方程2x +3y =12,解得:y =-23x +4, 当x =0时,方程变形为3y =12,解得y =4;当x =3时,方程变形为6+3y =12,解得y =2;当x =6时,方程变形为12+3y =12,解得y =0;∴关于x ,y 的二元一次方程2x +3y =12的非负整数解有3组:04x y ==⎧⎨⎩、32x y ⎧⎨⎩==和60x y ⎧⎨⎩==. 故答案为3【点睛】此题考查了二元一次方程的解,用x 表示出y 是解本题的关键.17.2【分析】设1个进口1小时开进辆车,1个出口1小时开出辆,根据题意列出方程组求得、,进一步代入求得答案即可.【详解】设1个进口1小时开进辆车,1个出口1小时开出辆,车位总数为,由题意得,解解析:2【分析】设1个进口1小时开进x 辆车,1个出口1小时开出y 辆,根据题意列出方程组求得x 、y ,进一步代入求得答案即可.【详解】设1个进口1小时开进x 辆车,1个出口1小时开出y 辆,车位总数为a ,由题意得()8(22)80%1.64280%x y a x y a -=⎧⎨-=⎩, 解得:5320a x a y ⎧=⎪⎪⎨⎪=⎪⎩, 则360%322520a a a ⎛⎫÷⨯-⨯= ⎪⎝⎭小时, 答:从早晨7点开始经过2小时车库恰好停满.故答案为:2.【点睛】此题考查二元一次方程组的实际运用,找出题目蕴含的数量关系是解决问题的关键. 18.【分析】将方程整理成关于m 的一元一次方程,若无论实数m 取何值,此二元一次方程都有一个相同的解,则与m 无关,从而令m 的系数为0,从而得关于x 和y 的二元一次方程组,求解即可.【详解】将(m+1)解析:11x y =-⎧⎨=⎩ 【分析】将方程整理成关于m 的一元一次方程,若无论实数m 取何值,此二元一次方程都有一个相同的解,则与m 无关,从而令m 的系数为0,从而得关于x 和y 的二元一次方程组,求解即可.【详解】将(m+1)x+(2m-1)y+2-m=0整理得:mx+x+2my-y+2-m=0,即m (x+2y-1)+x-y+2=0, 因为无论实数m 取何值,此二元一次方程都有一个相同的解,所以21020x y x y +-=⎧⎨-+=⎩, 解得:11x y =-⎧⎨=⎩. 故答案为:11x y =-⎧⎨=⎩. 【点睛】考查了含参数的二元一次方程有相同解问题,解题关键是利用转化思想.19.【分析】本题可设x 道难题,y 道中档题,z 道容易题,因为小明、小林和小颖共解出100道数学题,所以x+y+z=100①,又因每人都解出了其中的60道,只有1人解出的题叫做难题,2人解出的题叫做中档解析:【分析】本题可设x 道难题,y 道中档题,z 道容易题,因为小明、小林和小颖共解出100道数学题,所以x+y+z =100①,又因每人都解出了其中的60道,只有1人解出的题叫做难题,2人解出的题叫做中档题,3人都解出的题叫做容易题,所以有x+2y+3z =180②,①×2-②,得x-z =20,所以难题比容易题多20道.【详解】设x 道难题,y 道中档题,z 道容易题。
(完整版)初一数学下册不等式试卷(含答案) 培优试题

一、选择题1.如图,在数轴上,已知点A ,B 分别表示数1,23x -+,那么数轴上表示数2x -+的点应落在( )A .点A 的左边B .线段AB 上C .点B 的右边D .数轴的任意位置 2.小兰:“小红,你上周买的笔和笔记本的价格是多少啊?”小红:“哦,…,我忘了!只记得先后买了两次,第一次买了 5 支笔和 10 本笔记本共花了 42 元钱,第二次买了 10 文笔和 5 本笔记本共花了 30 元钱.”请根据小红与小兰的对话,求得小红所买的笔和笔 记本的价格分别是( )A .0.8 元/支,2.6 元/本B .0.8 元/支,3.6 元/本C .1.2 元/支,2.6 元/本D .1.2 元/支,3.6 元/本 3.若a b >,则下列不等式一定成立的是( ) A .ac bc < B .21a b ->- C .11a b -<- D .||||a b > 4.若关于x 的不等式0ax b ->的解集是12x <,则关于x 的不等式bx a <的解集是( ) A .2x <-B .2x <C .2x >-D .2x > 5.若关于x 的不等式31x m 的正整数解是1,2,3,则整数m 的最大值是( )A .10B .11C .12D .13 6.喜迎建党100周年,某校举行党史知识竞赛,共30道题,每道题都给出4个答案,其中只有一个答案正确,选对得4分,不选或选错扣2分,得分不低于80分得奖,那么得奖至少应选对的题数是( )A .23B .24C .25D .267.设[x )表示大于x 的最小整数,如[3)=4,[-1.2)=-1,下列结论:①[0)=0;②[x )-x 的最小值是0;③[x )-x 的最大值是1;④存在实数x ,使[x )-x =0.5成立,其中正确的是( )A .①②B .③④C .①②③D .②③④8.若不等式组5231x a x x >⎧⎨+<+⎩的解集为x >4,则a 的取值范围是( ) A .a >4 B .a <4 C .a ≤4 D .a ≥49.某次知识竞赛共有20道题,答对一题得10分,答错或不答均扣5分,小玉得分超过95分,他至多可以答错的试题道数为( )A .5B .6C .7D .810.已知关于x 的不等式组100x x a ->⎧⎨-≤⎩,有以下说法: ①如果它的解集是1<x ≤4,那么a =4;②当a =1时,它无解;③如果它的整数解只有2,3,4,那么4≤a <5;④如果它有解,那么a ≥2.其中说法正确的个数为( )A .1个B .2个C .3个D .4个二、填空题11.某校七年级有4个班,共180人,(1)班至(4)班的人数分别a ,b ,c ,d ()a b c d <<<.已知(1)班的人数不少于41人,且b c a d +>+,则(4)班人数为______.12.已知实数a ,b ,满足14a b ≤+≤,01a b ≤-≤且2a b -有最大值,则82021a b +的值是__________.13.对非负实数x “四舍五入”到个位的值记为x <>,即:当n 为非负整数时,如果1122n x n -<+,则x n <>=.如:0.480<>=, 3.54<>=.如果43x x <>=,则x =___________.14.若不等式组01x a x a -⎧⎨-⎩-的解集中的任何一个x 的值均不在2≤x ≤5的范围内,则a 的取值范围为________.15.不等式组29611x x x k +>+⎧⎨-<⎩的解集为2x <,则k 的取值范围为_____. 16.若关于x 的不等式组{2x 713x a 12-≤->的整数解共有6个,则a 的取值范围是______. 17.在关于x 、y 的方程组2728x y m x y m+=+⎧⎨+=-⎩中,未知数满足x≥0,y >0,那么m 的取值范围是_________________.18.对于任意实数m 、n ,定义一种运算m ※n =mn ﹣m ﹣n +3,例如:3※5=3×5﹣3﹣5+3=10.请根据上述定义解决问题:若a <4※x <7,且解集中有三个整数解,则整数a 的取值可以是_________.19.若不等式组220x a b x ->⎧⎨->⎩的解集为11x -<<,则()a b +的立方根是______. 20.已知不等式组()32215233x a x x x ⎧+<+⎪⎨-<+⎪⎩的整数解有3个,则a 的取值范围为______. 三、解答题21.如图,数轴上两点A 、B 对应的数分别是﹣1,1,点P 是线段AB 上一动点,给出如下定义:如果在数轴上存在动点Q ,满足|PQ |=2,那么我们把这样的点Q 表示的数称为连动数,特别地,当点Q 表示的数是整数时我们称为连动整数.(1)﹣3,0,2.5是连动数的是 ;(2)关于x 的方程2x ﹣m =x +1的解满足是连动数,求m 的取值范围 ; (3)当不等式组11212()3x x a +⎧>-⎪⎨⎪+-⎩的解集中恰好有4个解是连动整数时,求a 的取值范围. 22.某电器超市销售每台进价分别为200元、170元的A 、B 两种型号的电风扇,下表是近两周的销售情况:(进价、售价均保持不变,利润 = 销售收入-进货成本)(1)求A 、B 两种型号的电风扇的销售单价;(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A 种型号的电风扇最多能采购多少台?(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.23.请阅读求绝对值不等式3x <和3x >的解的过程.对于绝对值不等式3x <,从图1的数轴上看:大于3-而小于3的数的绝对值小于3,所以3x <的解为33x -<<;对于绝对值不等式3x >,从图2的数轴上看:小于3-或大于3的数的绝对值大于3,所以3x >的解为3x <-或3x >.(1)求绝对值不等式32x ->的解(2)已知绝对值不等式21x a -<的解为3b x <<,求2a b -的值(3)已知关于x ,y 的二元一次方程组234461x y m x y m -=-⎧⎨+=-+⎩的解满足2x y +≤,其中m 是负整数,求m 的值.24.阅读材料:如果x 是一个有理数,我们把不超过x 的最大整数记作[]x .例如,[]3.23=,[]55=,[]2.13-=-,那么,[]x x a =+,其中01a ≤<.例如,[]3.2 3.20.2=+,[]550=+,[]2.1 2.10.9-=-+.请你解决下列问题:(1)[]4.8=__________,[]6.5-=__________;(2)如果[]5x =,那么x 的取值范围是__________;(3)如果[]5231x x -=+,那么x 的值是__________;(4)如果[]x x a =+,其中01a ≤<,且[]41a x =+,求x 的值.25.如图所示,在平面直角坐标系xOy 中,点A ,B ,C 的坐标为()0,a ,(),0b ,(),b c ,其中a ,b ,c 满足()23210a b a b -+-+=,40c -≤.(1)求a ,b ,c 的值;(2)若M 在x 轴上,且12COM ABC S S =△△,求M 点坐标; (3)如果在第二象限内有一点()1,1P m -,m 在什么取值范围时,AOP 的面积不大于ABC 的面积?求出在符合条件下,AOP 面积最大值时点P 的坐标.26.若关于x 的方程ax +b =0(a ≠0)的解与关于y 的方程cy +d =0(c ≠0)的解满足﹣1≤x ﹣y ≤1,则称方程ax +b =0(a ≠0)与方程cy +d =0(c ≠0)是“友好方程”.例如:方程2x ﹣1=0的解是x =0.5,方程y ﹣1=0的解是y =1,因为﹣1≤x ﹣y ≤1,方程2x ﹣1=0与方程y ﹣1=0是“友好方程”.(1)请通过计算判断方程2x ﹣9=5x ﹣2与方程5(y ﹣1)﹣2(1﹣y )=﹣34﹣2y 是不是“友好方程”.(2)若关于x 的方程3x ﹣3+4(x ﹣1)=0与关于y 的方程32y k ++y =2k +1是“友好方程”,请你求出k 的最大值和最小值.27.使方程(组)与不等式(组)同时成立的末知数的值称为此方程(组)和不等式(组)的“理想解”.例:已知方程2x ﹣3=1与不等式x +3>0,当x =2时,2x ﹣3=2×2﹣3=1,x +3=2+3=5>0同时成立,则称x =2是方程2x ﹣3=1与不等式x +3>0的“理想解”.(1)已知①1322x ->,②2(x +3)<4,③12x -<3,试判断方程2x +3=1的解是否是它们中某个不等式的“理想解”,写出过程;(2)若00x x y y =⎧⎨=⎩是方程x ﹣2y =4与不等式31x y >⎧⎨<⎩的“理想解”,求x 0+2y 0的取值范围. 28.小语爸爸开了一家茶叶专卖店,包装设计专业毕业的小语为爸爸设计了一款纸质长方体茶叶包包装盒(纸片厚度不计).如图,阴影部分是裁剪掉的部分,沿图中实线折叠做成的长方体纸盒的上下底面是正方形,有三处长方形形状的“接口”用来折叠后粘贴或封盖.(1)若小语用长40cm ,宽34cm 的长方形纸片,恰好能做成一个符合要求的包装盒,盒高是盒底边长的2.5倍,三处“接口”的宽度相等.则该茶叶盒的容积是多少?(2)小语爸爸的茶叶专卖店以每盒200元购进一批茶叶,按进价增加18%作为售价,第一个月由于包装粗糙,只售出不到一半但超过三分之一的量;第二个月采用了小语的包装后,马上售完了余下的茶叶,但每盒成本增加了6元,售价仍不变,已知在整个买卖过程中共盈利1800元,求这批茶叶共进了多少盒?29.材料1:我们把形如ax by c +=(a 、b 、c 为常数)的方程叫二元一次方程.若a 、b 、c 为整数,则称二元一次方程ax by c +=为整系数方程.若c 是a ,b 的最大公约数的整倍数,则方程有整数解.例如方程342,735,426x y x y x y +=-=+=都有整数解;反过来也成立.方程6310421x y x y +=-=和都没有整数解,因为6,3的最大公约数是3,而10不是3的整倍数;4,2的最大公约数是2,而1不是2的整倍数.材料2:求方程56100x y +=的正整数解. 解:由已知得:1006100520555y y y y x y ---===--……① 设5y k =(k 为整数),则5y k =……② 把②代入①得:206x k =-.所以方程组的解为2065x k y k=-⎧⎨=⎩ , 根据题意得:206050k k ->⎧⎨>⎩. 解不等式组得0<k <103.所以k 的整数解是1,2,3. 所以方程56100x y +=的正整数解是:145x y =⎧⎨=⎩,810x y =⎧⎨=⎩,215x y =⎧⎨=⎩. 根据以上材料回答下列问题:(1)下列方程中:① 3911x y +=,② 15570x y -=,③ 63111x y +=,④ 27999x y -=,⑤ 9126169x -=,⑥ 22121324x y +=.没有整数解的方程是 (填方程前面的编号);(2)仿照上面的方法,求方程3438x y +=的正整数解;(3)若要把一根长30m 的钢丝截成2m 长和3m 长两种规格的钢丝(两种规格都要有),问怎样截才不浪费材料?你有几种不同的截法?(直接写出截法,不要求解题过程) 30.阅读材料:如果x 是一个有理数,我们把不超过x 的最大整数记作[x ] .例如,[3.2]=3,[5]=5,[-2.1]=-3.那么,x =[x ]+a ,其中0≤a <1.例如,3.2=[3.2]+0.2,5=[5]+0,-2.1=[-2.1]+0.9.请你解决下列问题:(1)[4.8]= ,[-6.5]= ;(2)如果[x ]=3,那么x 的取值范围是 ;(3)如果[5x -2]=3x +1,那么x 的值是 ;(4)如果x =[x ]+a ,其中0≤a <1,且4a = [x ]+1,求x 的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】根据数轴上的点表示的数右边的总比左边的大,可得不等式,根据解不等式,可得答案;根据不等式的性质,可得点在A 点的右边,根据作差法,可得点在B 点的左边.【详解】解:由数轴上的点表示的数右边的总比左边的大,得:-2x +3>1,解得x <1;-x >-1.-x +2>-1+2,解得-x +2>1.所以数轴上表示数-x +2的点在A 点的右边;作差,得:-2x +3-(-x +2)=-x +1,由x <1,得:-x >-1,-x +1>0,-2x +3-(-x +2)>0,∴-2x +3>-x +2,所以数轴上表示数-x +2的点在B 点的左边,点A 的右边.故选B .【点睛】本题考查了一元一次不等式,解题的关键是利用数轴上的点表示的数右边的总比左边的大得出不等式.2.D解析:D【分析】首先设小红所买的笔的价格是x 元/支,笔记本的价格是y 元/本,根据关键语句“第一次买了5支笔和10本笔记本共花了42元钱,”可得方程5x+10y=42,“第二次买了10支笔和5本笔记本共花了30元钱”可得方程10x+5y=30,联立两个方程,再解方程组即可.【详解】解:设小红所买的笔的价格是x 元/支,笔记本的价格是y 元/本,由题意得:5104210530x y x y +=⎧⎨+=⎩ 解得: 1.23.6x y =⎧⎨=⎩ 故答案为D.【点睛】本题主要考查了二元一次方程组的应用,关键是弄懂题意,找出题目中的等量关系,再列出方程组即可.3.C解析:C【分析】根据不等式的性质逐项判断即可;【详解】解:A .a b >,当0c 时,ac bc =,所以A 选项不符合题意;B .当0a =,1b =-,21a b -=-,所以B 选项不符合题意;C .a b >,则a b -<-,11a b -<-,所以C 选项符合题意;D .0a =,1b =-,则||||a b <,所以D 选项不符合题意.故选:C .【点睛】本题主要考查了不等式的基本性质,准确分析判断是解题的关键.4.D解析:D【分析】由题意可知,a 、b 均为负数,且可得a =2b ,把a =2b 代入bx <a 中,则可求得bx <a 的解集.【详解】由0ax b ->得:ax b >∵不等式0ax b ->的解集为12x <∴a <0∴12b x a <= ∴a =2b∴b <0由bx a <,得2bx b <∵b <0∴x >2故选:D .【点睛】本题考查了解一元一次不等式,关键是由条件确定字母a 的符号,从而确定a 与b 的关系,易出现错误的地方是求bx <a 的解集时,忽略b 的符号,从而导致结果错误. 5.D解析:D【分析】先解不等式得到x <()113m -,再根据正整数解是1,2,3得到3<()113m -≤4时,然后从不等式的解集中找出适合条件的最大整数即可.【详解】解不等式31x m 得x <()113m -, 关于x 的不等式31x m 的正整数解是1,2,3,∴ 3<()113m -≤4,解得10 < m ≤ 13, ∴整数m 的最大值为13.故选:D .【点睛】本题考查了一元一次不等式的整数解,解决此类问题的关键在于正确解得不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式的最大整数解.6.B解析:B【分析】设选对x 道题,则不选或选错(30﹣x )道题,根据得分=4×选对题目数-2×不选或选错题目数结合得分不低于80分,即可得出关于x 的一次不等式,解之取得最小值即可得出结论.【详解】解:设选对x 道题,则不选或选错(30﹣x )道题,依题意,得:4x ﹣2(30﹣x )≥80,解得:x ≥703. ∵x 为正整数,∴要得奖至少应选对24道题,故选:B .【点睛】本题考查了一元一次不等式的应用,根据各数量间的关系,正确的列出一元一次不等式是解题的关键.7.B解析:B【分析】利用题中的新定义计算即可求出值.【详解】解:由题意可知:∵[x )表示大于x 的最小整数,∴设[x )=n ,则n -1≤x <n ,∴[x )-1≤x <[x ),∴0<[x )-x ≤1,∴①[0)1=,故①错误;②[)x x -可无限接近0,但取不到0,无最小值,故②错误;③[)x x -的最大值是1,当x 为整数时,故③正确;④存在实数x ,使[)0.5x x -=成立,比如x =1.5,故④正确,故选:B .【点睛】此题考查了解一元一次不等式,读懂新定义,并熟练掌握运算法则是解本题的关键. 8.C解析:C【分析】分别解两个不等式,根据不等式组的解集即可求解.【详解】5231x a x x ⎧⎨++⎩>①<②, 解不等式①得,x a >,解不等式②得,4x >,∵不等式组的解集是4x >,∴a ≤4.故选:C .【点睛】本题考查不等式组的解集,掌握“同大取大,同小取小,大小小大取中间,大大小小无解了”取解集是解题的关键.9.B解析:B【分析】-道,根据题意列出一元一次不设小玉答对了x道题目,则答错或不答的题目一共为(20)x等式求解即可;【详解】-道,解:设小玉答对了x道题目,则答错或不答的题目一共为(20)x由题意可得,x x-->,105(20)95x>,解得13∴小玉至少要答对14道题目,至多答错20146-=(道),故选:B.【点睛】本题主要考查了一元一次不等式的应用,准确列式计算是解题的关键.10.C解析:C【分析】分别求出每个不等式的解集,再根据各结论中a的取值情况逐一判断即可.【详解】解:由x﹣1>0得x>1,由x﹣a≤0得x≤a,①如果它的解集是1<x≤4,那么a=4,此结论正确;②当a=1时,它无解,此结论正确;③如果它的整数解只有2,3,4,那么4≤a<5,此结论正确;④如果它有解,那么a>1,此结论错误;故选:C.【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.二、填空题11.47或48人【分析】根据题意令,满足,由于,得,又根据,得,可得,当①时,,枚举出所有情况;同理当②时,,同理,,,,,,枚举出所有的情况,选出满足条件的情况即可.【详解】解:,令(),解析:47或48人【分析】根据题意令41,41,41,41a b c d a m b m c m d m =+=+=+=+,满足0a b c d m m m m ≤<<<,由于180a b c d +++=,得+16a b c d m m m m ++=,又根据b c a d +>+,得b c a d m m m m +>+,可得1682a d m m +<=,当①7a d m m +=时,9bc m m +=,枚举出所有情况;同理当②6ad m m +=时,10b c m m +=,同理,5a d m m +=,4a d m m +=,3a d m m +=,2a d m m +=,1a d m m +=,枚举出所有的情况,选出满足条件的情况即可.【详解】解:41,a a b c d ≥<<<,∴令41,41,41,41a b c d a m b m c m d m =+=+=+=+(0a b c d m m m m ≤<<<),由于180a b c d +++=,故有414++180a b c d m m m m ⨯++=,得+16a b c d m m m m ++=,又b c a d +>+,故41+4141+41+b c a d m m m m ++>+,b c a d m m m m ∴+>+,而+16a b c d m m m m ++=,1682a d m m ∴+<=, 当①7a d m m +=时,9bc m m +=,根据0a b c d m m m m ≤<<<,枚举一下,只有下列情况满足,141,44,47,48a b c d ︒====,241,45,46,48a b c d ︒====,342,45,46,47a b c d ︒====,②6a d m m +=时,10b c m m +=,根据0a b c d m m m m ≤<<<,即使0,6a d m m ==,由于0a b c d m m m m ≤<<<,c m ∴最大取5,而此时1055b m =-=,有c b m m =,不符合要求,故此时没有情况满足,同理,5a d m m +=,4a d m m +=,3a d m m +=,2a d m m +=,1a d m m +=,均没有情况满足,综上所述,(4)班的人数为47或48人,故答案是:47或48人.【点睛】本题考查了不等式在生活中的应用,解题的关键是掌握不等式的性质,进行分类讨论,也体现了同学的枚举能力.12.8【分析】把变形得,故可求出有最大值时,a ,b 的值,代入故可求解.【详解】设=∴a-2b=(m+n )a+(m-n)b∴,解得∴=∵,∴,∴∴有最大值1此时,解得a=1,b=解析:8【分析】把2a b -变形得()()1322a b a b -++-,故可求出2a b -有最大值时,a ,b 的值,代入82021a b +故可求解.【详解】设2a b -=()()m a b n a b ++-∴a -2b =(m +n )a +(m -n )b∴12m n m n +=⎧⎨-=⎩,解得1232m n ⎧=-⎪⎪⎨⎪=⎪⎩∴2a b -=()()1322a b a b -++- ∵14a b ≤+≤,01a b ≤-≤ ∴()11222a b -≤-+≤-,()33022a b ≤-≤ ∴221a b -≤-≤∴2a b -有最大值1 此时()1122a b -+=-,()3322a b -= 解得a =1,b =0∴82021a b +=8故答案为:8.【点睛】此题主要考查不等式组的应用与求解,解二元一次方程组,解题的关键是根据题意把把2a b -变形得()()1322a b a b -++-,从而求解. 13.0或或【分析】根据的定义可得一个关于的一元一次不等式组,解不等式组、结合为非负整数即可得.【详解】解:由题意得:,即,解不等式①得:,解不等式②得:,则不等式组的解集为,为非负实数解析:0或34或32 【分析】根据x <>的定义可得一个关于x 的一元一次不等式组,解不等式组、结合43x 为非负整数即可得.【详解】解:由题意得:41413232x x x -<+≤, 即41324132x x x x ⎧-≤⎪⎪⎨⎪<+⎪⎩①②, 解不等式①得:32x ≤, 解不等式②得:32x >-, 则不等式组的解集为3322x -<≤, x 为非负实数, 302x ∴≤≤, 4023x ∴≤≤, 43x 为非负整数, 403x ∴=或413x =或423x =, 解得0x =或34x =或32x =, 故答案为:0或34或32. 【点睛】本题考查了一元一次不等式组的应用,理解x <>的定义是解题关键.14.a≤1或a≥5【分析】解不等式组,求出x 的范围,根据任何一个x 的值均不在2≤x≤5范围内列出不等式,解不等式得到答案.【详解】解:不等式组的解集为:a <x <a+1,∵任何一个x 的值均不在2解析:a ≤1或a ≥5【分析】解不等式组01x a x a ->⎧⎨-<⎩,求出x 的范围,根据任何一个x 的值均不在2≤x≤5范围内列出不等式,解不等式得到答案.【详解】解:不等式组01x a x a ->⎧⎨-<⎩的解集为:a <x <a+1, ∵任何一个x 的值均不在2≤x≤5范围内,∴x <2或x >5,∴a+1≤2或a≥5,解得,a≤1或a≥5,∴a 的取值范围是:a≤1或a≥5,故答案为:a≤1或a≥5.【点睛】本题考查的是不等式的解集的确定,根据不等式的解法正确解出不等式是解题的关键,根据题意列出新的不等式是本题的重点.15.k≥1【详解】解不等式2x+9>6x+1可得x <2,解不等式x-k <1,可得x <k+1,由于x <2,可知k+1≥2,解得k≥1.故答案为k≥1.解析:k≥1【详解】解不等式2x+9>6x+1可得x <2,解不等式x-k <1,可得x <k+1,由于x <2,可知k+1≥2,解得k≥1.故答案为k≥1.16.-18≤a<-15【分析】首先确定不等式组的解集,先利用含a 的式子表示,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于a 的不等式组,从而得出a 的范围.【详解】解不等式,得:解析:-18≤a<-15【分析】首先确定不等式组的解集,先利用含a 的式子表示,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于a 的不等式组,从而得出a 的范围.【详解】解不等式271x -≤,得:4x ≤,解不等式312x a ->,得:123a x +>, 因为不等式组的整数解有6个,所以12213a +-≤<-, 解得:1815a -≤<-,故答案为1815a -≤<-.【点睛】本题主要考查了一元一次不等式组的整数解.利用不等式组的整数解个数来列出关于a 的不等式组是解题的关键.17.-2≤m <3【解析】【分析】先解方程组求出方程组的解,然后根据x≥0,y >0列出关于m 的不等式组,解不等式组即可得.【详解】解方程组,得,由x≥0,y >0则有,解得:-2≤m <3,故答案解析:-2≤m <3【解析】【分析】先解方程组求出方程组的解,然后根据x≥0,y >0列出关于m 的不等式组,解不等式组即可得.【详解】解方程组2728x y m x y m +=+⎧⎨+=-⎩,得23x m y m =+⎧⎨=-⎩, 由x≥0,y >0则有2030m m +≥⎧⎨->⎩, 解得:-2≤m <3,故答案为:-2≤m <3.【点睛】本题考查了一元一次不等式组,二元一次方程组的解,熟练掌握解法是关键. 18.【分析】利用题中的新定义列出不等式组,求出解集即可确定出a 的范围.【详解】根据题中的新定义化简得:a≤4x -4−x +3<7,整理得: ,即<x <,由不等式组有3个整数解,即为2,1,解析:4,3,2---【分析】利用题中的新定义列出不等式组,求出解集即可确定出a 的范围.【详解】根据题中的新定义化简得:a ≤4x -4−x +3<7,整理得:31731x x a -<⎧⎨->⎩, 即13a +<x <83, 由不等式组有3个整数解,即为2,1,0, 所以1103a +-≤< 解得-4<a <-1所以a 可取的正数解有:-4,-3,-2故答案为:-4,-3,-2【点睛】此题考查了一元一次不等式组的整数解,实数的运算,以及一元一次不等式的整数解,熟练掌握运算法则是解本题的关键.19.-1【分析】先求出两个不等式的解集,再结合不等式组的解集列出关于a 、b 的方程,求出a 、b 的值,继而代入再求解立方根即可.【详解】解:解不等式,得:,解不等式,得:,∵不等式组的解集为,解析:-1【分析】先求出两个不等式的解集,再结合不等式组的解集列出关于a 、b 的方程,求出a 、b 的值,继而代入再求解立方根即可.【详解】解:解不等式2x a ->,得:2x a +>,解不等式20b x ->,得:2x b <, ∵不等式组的解集为11x -<<,∴21a +=-,12b =, 解得3a =-,2b =,∴()a b +1-,故答案为:-1.【点睛】本题主要考查解一元一次不等式组,解题的关键是掌握解一元一次不等式的步骤和依据及实数的运算.20.【分析】先求出不等式组的解集,然后根据不等式组的整数解有3个,可得到关于 的不等式组,即可求解.【详解】解不等式①,得: ,解不等式②,得: ,∵不等式组的整数解有3个,∴,解得:解析:12a ≤<【分析】先求出不等式组的解集,然后根据不等式组的整数解有3个,可得到关于a 的不等式组,即可求解.【详解】()32215233①②⎧+<+⎪⎨-<+⎪⎩x a x x x 解不等式①,得:4x a <-+ ,解不等式②,得:1x >- ,∵不等式组的整数解有3个,∴243a <-+≤,解得: 12a ≤<.故答案为:12a ≤<.【点睛】本题主要考查了一元一次不等式组的整数解,熟练掌握解求不等式组解集的口诀:同大取大,同小取小大小小大中间找,大大小小找不到(无解)是解题的关键.三、解答题21.(1)﹣3,2.5;(2)﹣4<m <﹣2或0<m <2;(3)1≤a <2.【分析】(1)根据连动数的定义逐一判断即得答案;(2)先求得方程的解,再根据连动数的定义得出相应的不等式组,解不等式组即可求出结果;(3)先解不等式组中的每个不等式,再根据连动整数的概念得到关于a 的不等式组,解不等式组即可求得答案.解:(1)设点P 表示的数是x ,则11x -≤≤,若点Q 表示的数是﹣3,由2PQ =可得()32x --=,解得:x =﹣1或﹣5,所以﹣3是连动数;若点Q 表示的数是0,由2PQ =可得02x -=,解得:x =2或﹣2,所以0不是连动数; 若点Q 表示的数是2.5,由2PQ =可得 2.52x -=,解得:x =﹣0.5或4.5,所以2.5是连动数;所以﹣3,0,2.5是连动数的是﹣3,2.5,故答案为:﹣3,2.5;(2)解关于x 的方程2x ﹣m =x +1得:x =m +1,∵关于x 的方程2x ﹣m =x +1的解满足是连动数,∴112112m m ---<⎧⎨-->⎩或112112m m +-<⎧⎨++>⎩, 解得:﹣4<m <﹣2或0<m <2;故答案为:﹣4<m <﹣2或0<m <2;(3)()112123x x a +⎧>-⎪⎨⎪+-≤⎩①②, 解不等式①,得x >﹣3,解不等式②,得x ≤1+a ,∵不等式组()112123x x a +⎧>-⎪⎨⎪+-≤⎩的解集中恰好有4个解是连动整数, ∴四个连动整数解为﹣2,﹣1,1,2,∴2≤1+a <3,解得:1≤a <2,∴a 的取值范围是1≤a <2.【点睛】本题是新定义试题,以数轴为载体,主要考查了一元一次不等式组,正确理解连动数与连动整数、列出相应的不等式组是解题的关键.22.(1)A 、B 两种型号电风扇的销售单价分别为250元、210元;(2)超市最多采购A 种型号电风扇10台时,采购金额不多于5400元;(3)超市不能实现利润1400元的目标;【分析】(1)根据第一周和第二周的销售量和销售收入,可列写2个等式方程,再求解二元一次方程组即可;(2)利用不多于5400元这个量,列写不等式,得到A 型电风扇a 台的一个取值范围,从而得出a 的最大值;(3)将B 型电风扇用(30-a)表示出来,列写A 、B 两型电风扇利润为1400的等式方程,可求得a 的值,最后在判断求解的值是否满足(2)中a 的取值范围即可解:(1)设A 、B 两种型号电风扇的销售单价分别为x 元、y 元,依题意得:3518004103100x y x y +=⎧⎨+=⎩,解得:250210x y =⎧⎨=⎩, 答:A 、B 两种型号电风扇的销售单价分别为250元、210元.(2)设采购A 种型号电风扇a 台,则采购B 种型号电风扇(30-a )台.依题意得:200a+170(30-a )≤5400,解得:a≤10.答:超市最多采购A 种型号电风扇10台时,采购金额不多于5400元;(3)依题意有:(250-200)a+(210-170)(30-a )=1400,解得:a=20,∵a≤10,∴在(2)的条件下超市不能实现利润1400元的目标.【点睛】本题是二元一次方程和一元一次不等式应用题的综合考查,解题关键是依据题意,找出等量关系式(不等关系式),然后按照题目要求相应求解23.(1)x >5或x <1;(2)9;(3)m =-3或m =-2或m =-1【分析】(1)由绝对值的几何意义即可得出答案;(2)由|21|x a -<知21a x a -<-<,据此得出1122a a x -+<<,再结合3b x <<可得出关于a 、b 的方程组,解之即可求出a 、b 的值,从而得出答案;(3)两个方程相加化简得出1x y m +=--,由||2x y +知22x y -+,据此得出212m ---,解之求出m 的取值范围,继而可得答案.【详解】解:(1)根据绝对值的定义得:32x ->或32x -<-,解得5x >或1x <;(2)|21|x a -<,21a x a ∴-<-<, 解得1122a a x -+<<, 解集为3b x <<, ∴12132a b a -⎧=⎪⎪⎨+⎪=⎪⎩, 解得52a b =⎧⎨=-⎩, 则2549a b -=+=;(3)两个方程相加,得:3333x y m +=--,1x y m ∴+=--,||2x y +,22x y ∴-+,212m ∴---,解得31m -,又m 是负整数,3m ∴=-或2m =-或1m =-.【点睛】本题主要考查解一元一次不等式,解题的关键是掌握绝对值的几何意义及解一元一次不等式和不等式组的能力.24.(1)4,-7;(2)56x ≤<;(3)53;(4)1x =-或14或112或324 【分析】(1)根据[]x 表示不超过x 的最大整数的定义及例子直接求解即可;(2)根据[]x 表示不超过x 的最大整数的定义及例子直接求解即可;(3)由材料中“[]x x a =+,其中01a ≤<”得出315232x x x +-<+,解不等式,再根据3x +1为整数,即可计算出具体的值;(4)由材料中的条件[]41a x =+可得[]14x a +=,由01a <,可求得[]x 的范围,根据[]x 为整数,分情况讨论即可求得x 的值.【详解】(1)[]4.84=,[]6.57-=-.故答案为:4,-7.(2)如果[]5x =. 那么x 的取值范围是56x <.故答案为:56x <.(3)如果[]5231x x -=+,那么315232x x x +-<+. 解得:322x < ∵31x +是整数. ∴53x =. 故答案为:53. (4)∵[]x x a =+,其中01a <,∴[]x x a =-,∵[]41a x =+,∴[]14x a +=.∵01a <,∴[]1014x +<,∴[]13x -<,∴[]1x =-,0,1,2.当[]1x =-时,0a =,1x =-;当[]0x =时,14a =,14x =; 当[]1x =时,12a =,112x =; 当[]2x =时,34a =,324x =; ∴1x =-或14或112或324. 【点睛】本题考查了新定义下的不等式的应用,关键是理解题中[]x 的意义,列出不等式求解;最后一问要注意不要漏了情况.25.(1)2a =,3b =,4c =;(2)3,02⎛⎫- ⎪⎝⎭或3,02⎛⎫ ⎪⎝⎭;(3)m 的范围51m -≤<;P 的坐标是()6,1-.【分析】(1)根据乘方、算术平方根的性质,通过列二元一次方程组并求解,得a 和b 的值;根据绝对值的性质,列一元一次方程并求解,从而得到答案;(2)设(),0M t ,根据题意列方程,结合绝对值的性质求解,得t 的值;再根据坐标的性质分析,即可得到答案(3)P 在第二象限以及AOP 的面积不大于ABC 的面积,通过列一元一次不等式并求解,即可得到m 的范围,再根据1APO S m =-△的变化规律计算,即可得到答案.【详解】(1)∵()2320a b -=, ∴10320a b a b -+=⎧⎨-=⎩ 解得:23a b =⎧⎨=⎩ ∵40c -≤∴40c -=∴4c =;(2)根据题意,设(),0M t ∵14362ABC S ∆=⨯⨯= ∴1422CMO S t t =⨯=△∴23t = ∴32t =±∴M 点坐标为3,02⎛⎫- ⎪⎝⎭或3,02⎛⎫ ⎪⎝⎭; (3)11121122APO S AO m m m =-=⨯-=-△ ∵P 在第二象限 ∴10m -<∴1APO S m =-△∵B 、C 的横坐标相同,∴//BC y 轴1143622ABC S BC OB =⋅=⨯⨯=△ ∵AOP ABC S S ≤∴16m -≤5m ≥-∵P 点在第二象限∴10m -<∴1m <∴m 的范围为51m -≤<∵当1m <时,APO S △随m 的增大而减小;∴当5m =-时,AOP S 的最大值为6∴P 的坐标是()6,1-.【点睛】本题考查了算术平方根、乘方、二元一次方程组、一元一次方程、一元一次不等式、直角坐标系、绝对值的知识;解题的关键是熟练以上知识,从而完成求解.26.(1)是;(2)k 的最小值为﹣23,最大值为83 【分析】(1)分别解出两个方程,得到x ﹣y 的值,即可确定两个方程是“友好方程”;(2)分别解两个方程为x =1,325k y +=,再由已知可得﹣1≤3215k +-≤1,求出k 的取值范围为即可求解.【详解】解:(1)由2x ﹣9=5x ﹣2,解得x =73-, 由5(y ﹣1)﹣2(1﹣y )=﹣34﹣2y ,解得y =﹣3,∴x ﹣y =23,∴﹣1≤x ﹣y ≤1,∴方程2x ﹣9=5x ﹣2与方程5(y ﹣1)﹣2(1﹣y )=﹣34﹣2y 是“友好方程”; (2)由3x ﹣3+4(x ﹣1)=0,解得x =1, 由3212y k y k ++=+,解得325k y +=, ∵两个方程是“友好方程”,∴﹣1≤x ﹣y ≤1,∴﹣1≤3215k +-≤1, ∴2833k -≤≤ ∴k 的最小值为﹣23,最大值为83. 【点睛】本题主要考查了解一元一次方程和解一元一次不等式组,解题的关键在于能够熟练掌握相关知识进行求解.27.(1)2x +3=1的解是不等式12x -<3的理想解,过程见解析;(2)2<x 0+2y 0<8 【分析】(1)解方程2x +3=1的解为x =﹣1,分别代入三个不等式检验即可得到答案; (2)由方程x ﹣2y =4得x 0=2y 0+4,代入不等式解得﹣12<y 0<1,再结合x 0=2y 0+4,通过计算即可得到答案.【详解】(1)∵2x +3=1∴x =﹣1, ∵x ﹣12=﹣1﹣12=﹣32<32∴方程2x +3=1的解不是不等式1322x ->的理想解; ∵2(x +3)=2(﹣1+3)=4,∴2x +3=1的解不是不等式2(x +3)<4的理想解; ∵12x -=112--=﹣1<3, ∴2x +3=1的解是不等式12x -<3的理想解; (2)由方程x ﹣2y =4得x 0=2y 0+4,代入不等式组31x y >⎧⎨<⎩,得002431y y +>⎧⎨<⎩; ∴﹣12<y 0<1,∴﹣2<4y 0<4,∵00000422244x y y y y =+=+++。
最新成都七年级下期末数学B卷(三角全等)几何压轴题汇编一(含答案)培优

最新成都七年级下期末数学B卷(三角全等)几何压轴题汇编一培优一.解答题(共30小题)1.如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.(1)如图1,当点E在边BC上时,求证DE=EB;(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.2.探究等边三角形“手拉手”问题.(1)如图1,已知△ABC,△ADE均为等边三角形,点D在线段BC上,且不与点B、点C重合,连接CE,试判断CE与BA的位置关系,并说明理由;(2)如图2,已知△ABC、△ADE均为等边三角形,连接CE、BD,若∠DEC=60°,试说明点B,点D,点E在同一直线上;(3)如图3,已知点E在等边△ABC外,并且与点B位于线段AC的异侧,连接BE、CE.若∠BEC=60°,猜测线段BE、AE、CE三者之间的数量关系,并说明理由.3.如图,△ABC中,AB=AC,∠EAF═∠BAC,BF⊥AE于E交AF于点F,连接CF.(1)如图1所示,当∠EAF在∠BAC内部时,求证:EF=BE+CF.(2)如图2所示,当∠EAF的边AE、AF分别在∠BAC外部、内部时,求证:CF=BF+2BE.4.如图1,AB∥CD,G为AB、CD之间一点.(1)若GE平分∠AEF,GF平分∠EFC.求证:EG⊥FG;(2)如图2,若∠AEP=∠AEF,∠CFP=∠EFC,且FP的延长线交∠AEP的角平分线于点M,EP的延长线交∠CFP的角平分线于点N,猜想∠M+∠N的结果并且证明你的结论;(3)如图3,若点H是射线EB之间一动点,FG平分∠EFH,MF平分∠EFC,过点G作GQ⊥FM于点Q,请猜想∠EHF与∠FGQ的关系,并证明你的结论.5.现给出一个结论:“直角三角形斜边上的中线等于斜边的一半”.该结论是正确的,用图形语言可表示为:如图1,在Rt△ABC中,∠C=90°,若点D为AB中点,则CD=AB.请结合上述结论解决如下问题:已知,点P是射线BA上一动点(不与A,B合)分别过点A,B向直线CP作垂线,垂足分别为E,F,其中Q为AB边的中点.(1)如图2,当点P与点Q重合时,AE与BF的位置关系是,QE与QF的数量关系是.(2)如图3,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明.(3)如图4,当点P在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路.6.如图,在△ABC中,AB=AC,∠BAC=90°,AE是过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E.(1)求证:△ABD≌△CAE;(2)若DE=3,CE=2,求BD.7.如图1,在△ABC中,∠BAC=90°,点D为AC边上一点,连接BD,点E为BD上一点,连接CE,使得∠CED=∠ABD,过点A作AG⊥CE,垂足为G,AG交ED于点F.(1)判断AF与AD的数量关系,并说明理由;(2)如图2,若AC=CE,点D为AC的中点,AB与AC相等吗?为什么?(3)在(2)的条件下,如图3,若DF=5,求△DEC的面积.8.在△ABC中,∠B=60°,D是BC上一点,且AD=AC.(1)如图1,延长BC至E,使CE=BD,连接AE.求证:AB=AE;(2)如图2,在AB边上取一点F,使DF=DB,求证:AF=BC;(3)如图3,在(2)的条件下,P为BC延长线上一点,连接P A,PF,若P A=PF,猜想PC与BD的数量关系并证明.9.(1)如图1,△ABC和△DCE都是等边三角形,且B,C,D三点在一条直线上,连接AD,BE相交于点P,求证:BE=AD.(2)如图2,在△BCD中,若∠BCD<120°,分别以BC,CD和BD为边在△BCD外部作等边△ABC,等边△CDE,等边△BDF,连接AD、BE、CF恰交于点P.①求证:AD=BE=CF;②如图2,在(2)的条件下,试猜想PB,PC,PD与BE存在怎样的数量关系,并说明理由.10.如图,在△ABC中,AB=AC=3,∠B=∠C=50°,点D在线段BC上运动(点D不与点B,C重合),连接AD,作∠ADE=50°,DE交线段AC于点E.(1)当∠BDA=110°时,∠EDC=°,∠AED=°,∠DAE=°;(2)当DC等于多少时?△ABD≌△DCE,请说明理由.(3)在点D的运动过程中,请直接写出当△ADE是等腰三角形时∠BDA的度数.11.已知:△ABC为等边三角形.(1)如图1,点D、E分别为边BC、AC上的点,且BD=CE.i)求证:△ABD≌△BCE;ii)求∠AFE的度数;(2)如图2,点D为△ABC外一点,BA、CD的延长线交于点E,连接AD,已知∠BDC=60°,且AD =2,CD=5,求BD的长;(3)如图3,线段DB的长为3,线段DC的长为2,连接BC,以BC为边作等边△ABC,连接AD,直接写出当线段AD取最大值与最小值时∠BDC的度数.12.如图,△ABC和△DEF是两个等腰直角三角形,∠BAC=∠DFE=90°,AB=AC,FD=FE,△DEF 的顶点E在边BC上移动,在移动过程中,线段DE与线段AB相交于点P,线段EF与线段CA相交于点Q.(1)如图1,当E为BC中点,且BP=CQ时,求证:△BPE≌△CQE;(2)如图2,当ED经过点A,且BE=CQ时,求∠EAQ的度数;(3)如图3,当E为BC中点,连接AE、PQ,若AP=3,AQ=4,PQ=5,求AC的长.13.(1)如图1,在等腰△ABC中,AC=BC,在底边上任取一点D,连接CD,将△ACD沿CD翻折得到△A′CD,A′C与AB相交于点O.求证:∠A′DB=∠A′CB;(2)如图2,Rt△ABC中,AC=BC,过点C作直线l平行于AB,在点C的右侧取一点E,作∠BEF=90°,射线EF交边AC于点F,请证明BE=EF;(3)如图3,△ABC中,AC=BC,过点C作直线l平行于AB,在点C的左侧任取一点E,作∠BEF=∠ACB,射线EF交射线CA于点F,请证明BE=EF.14.(1)如图(1),在△ABC中,∠A<45°,点D在AB边上,且CD=CB,∠ABC=2∠A,求证:AD =CD.(2)如图(2),在△ABC中,∠A=45°,点D在AB边上,且CD=CB,过点B作BE⊥CD,垂足为E,延长BE交AC于点F.①求证:BC=BF;②作FH⊥AB,垂足为H,若△BDE的面积为m,四边形DEFH的面积为n,求△BCE的面积(用含m,n的代数式表示).15.如图1,在△ABC中,∠ABC=90°,AB=BC,l是过点B的一条直线,过点A作AD⊥l于D,过点C 作CG⊥l于G.(1)求证:BD=CG;(2)如图(2)延长CG至E,连接BE,以BE为直角边作等腰直角三角形EBF,∠EBF=90°,连接AF交l于M.试探究CE与BM的数量关系,并说明理由.(3)在(2)的条件下,若S△BFM=45,BG=12.直接写出CE的长.16.已知,△ABC和△DEC都是等腰直角三角形,且∠BAC=∠DEC=90°,将△DEC绕点C在平面内进行旋转,连接AE,点M为线段AE的中点.(1)如图1,当点D在BC边上时.连接DM并延长交AC于G,求证:AG=CE;(2)如图2,若点D在△ABC的内部,过点A作AG∥DE,交DM的延长线于点G,连接BG,求证:BG=AE,且BG⊥AE;(3)如图3,点D在△ABC的外部,仍过点A作AG∥DE,交DM的延长线于点G,(2)中的两个结论是否仍然成立.若成立;请证明,若不成立,请说明理由.17.(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点且∠EAF=60°,直接写出图中线段BE、EF、FD之间的数量关系,不必证明.(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由.(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以45海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以60海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两舰艇分别到站E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.18.已知:如图,△ABC中,AB=BC,∠ABC=90°,过点A作射线AD,使AD∥BC,点E在AC上,连接BE,过点E作BE的垂线交AD于点F.(1)求证:∠DFE=∠ABE;(2)求证:EF=BE;(3)延长FE到G,使EG=EF,连接CG,求证:CG∥AB.19.已知:在四边形ABCD中,AC,BD相交于点E,且点E是AC的中点,AC⊥BD,过点B作BF⊥CD,垂足为点F,BF与AC交于点G.(1)如图1,求证:∠BGE=∠ADE;(2)如图2,若∠ABC=90°;①求证:DE=EG;②若AC=8,△BCG的面积为4,求四边形ABCD的面积.20.(1)如图1,在△ABC中,AB=4,AC=6,AD是BC边上的中线,延长AD到点E使DE=AD,连接CE,把AB,AC,2AD集中在△ACE中,利用三角形三边关系可得AD的取值范围是;(2)如图2,在△ABC中,AD是BC边上的中线,点E,F分别在AB,AC上,且DE⊥DF,求证:BE+CF >EF;(3)如图3,在四边形ABCD中,∠A为钝角,∠C为锐角,∠B+∠ADC=180°,DA=DC,点E,F 分别在BC,AB上,且∠EDF=∠ADC,连接EF,试探索线段AF,EF,CE之间的数量关系,并加以证明.21.(1)如图1,在四边形ABCD中,AB=AD,∠BAD=100°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=50°.探究图中线段EF,BE,FD之间的数量关系.小明同学探究的方法是:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF ≌△AGF,可得出结论,他的结论是(直接写结论,不需证明);(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且2∠EAF=∠BAD,上述结论是否仍然成立,若成立,请证明,若不成立,请说明理由;(3)如图3,四边形ABCD是边长为7的正方形,∠EBF=45°,直接写出△DEF的周长.22.如图1,∠FBD=90°,EB=EF,CB=CD.(1)求证:EF∥CD;(2)如图2所示,若将△EBF沿射线BF平移,即EG∥BC,∠FBD=90°,EG=EF,CB=CD,请问(1)中的结论是否仍成立?请证明.23.如图,AC平分∠BAD,CB⊥AB于点B,CD⊥AD于点D.(1)如图1,求证:CB=CD;(2)如图2,点E,F分别是线段AD,AB上的动点,连接EF,交AC于点G,且满足DE+BF=EF.(ⅰ)试探究∠AFE与∠ACE之间满足的数量关系,并说明理由;(ⅱ)若DE=1,BF=n,且S△AEF=S△CED,请直接写出的值(用含n的代数式表示),不必写出求解过程.24.如图,在正方形ABCD中,点F是直线BC上一动点,连接AF,将线段AF绕点F顺时针旋转90°,得到线段FH,连接AH交直线DC于点E,连接EF和CH,设正方形ABCD的边长为x.(1)如图1,当点F在线段BC上移动时,求△CEF的周长(用含x的代数式表示);(2)如图1,当点F在线段BC上移动时,猜想∠EFC和∠EHC的关系,并证明你的结论;(3)如图2,当点F在边BC的延长线上移动时,请直接写出∠EFC和∠EHC的关系(不需要证明).25.已知:△ABC中,∠ACB=90°,AC=BC,过点A作AD⊥AE,且AE=AD.(1)如图1,当点D在线段BC上时,过点E作EH⊥AC于H,连接DE.求证:EH=AC;(2)如图2,当点D在CB延长线上时,连接BE交AC的延长线于点M.求证:BM=EM;(3)在(2)的条件下,若AC=7CM,请直接写出的值(不需要计算过程).26.如图1,四边形ABCD中,AD∥BC,∠BDC=90°,BD=CD,DM是BC边上的中线.过点C作CE ⊥AB,垂足为E,CE交线段BD于点F,交DM于点N,连接AF.(1)求证:△ABD≌△NCD;(2)试探索线段AF,AB和CF之间数量关系,并证明你的结论;(3)当∠BAD等于多少度时,点E恰好为AB的中点?27.已知在四边形ABCD中,∠BAD+∠BCD=180°,AB=BC.(1)如图1,连接BD,若∠ABD=∠CBD,则AB与AD有什么位置关系,请说明理由?(2)如图2,若P,Q两点分别在线段AD,DC上,且满足PQ=AP+CQ,请猜想∠PBQ与∠ABP+∠QBC是否相等,并说明理由.(3)如图3,若点Q在DC的延长线上,点P在DA的延长线上,且仍然满足PQ=AP+CQ,请写出∠PBQ与∠ADC的数量关系,并加以说明.28.在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.(1)如图1,连接EC,求证:△EBC是等边三角形;(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.29.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)求证:△ABC≌△ADE;(2)求∠F AE的度数;(3)求证:CD=2BF+DE.30.如图1,在正方形ABCD中,∠GAH=45°,∠GAH的两边分别与线段BC,CD相交于E,F(点E 不与B,C重合;点F不与C,D重合).(1)填空:线段BE,EF,DF的数量关系是;(2)如图2,点P是EF的中点,连接AP,作点E关于直线AB的对称点E',作点F关于直线AD的对称点F′,连接E′F′,求证:E′F′=2AP;(3)如图3,若E,F是BC,CD上的定点,利用(1),(2)的结论探究:当AP=m,BE+DF=n时,在线段AB,AD上是否分别存在M,N,使四边形MEFN的周长有最小值,若存在,请求出最小值;若不存在,请说明理由.(用m,n的代数式表示)参考答案一.解答题(共30小题)1.如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.(1)如图1,当点E在边BC上时,求证DE=EB;(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.【解答】(1)证明:∵△CDE是等边三角形,∴∠CED=60°,∴∠EDB=60°﹣∠B=30°,∴∠EDB=∠B,∴DE=EB;(2)解:ED=EB,理由如下:取AB的中点O,连接CO、EO,∵∠ACB=90°,∠ABC=30°,∴∠A=60°,OC=OA,∴△ACO为等边三角形,∴CA=CO,∵△CDE是等边三角形,∴∠ACD=∠OCE,在△ACD和△OCE中,,∴△ACD≌△OCE,∴∠COE=∠A=60°,∴∠BOE=60°,在△COE和△BOE中,,∴△COE≌△BOE,∴EC=EB,∴ED=EB;(3)取AB的中点O,连接CO、EO、EB,由(2)得△ACD≌△OCE,∴∠COE=∠A=60°,∴∠BOE=60°,△COE≌△BOE,∴EC=EB,∴ED=EB,∵EH⊥AB,∴DH=BH=3,∵GE∥AB,∴∠G=180°﹣∠A=120°,∵∠GCD=∠GCE+60°=∠CDA+60°,∴∠GCE=∠CDA,在△CEG和△DCO中,,∴△CEG≌△DCO,∴CG=OD,设CG=a,则AG=5a,OD=a,∴AC=OC=4a,∵OC=OB,∴4a=a+3+3,解得,a=2,2.探究等边三角形“手拉手”问题.(1)如图1,已知△ABC,△ADE均为等边三角形,点D在线段BC上,且不与点B、点C重合,连接CE,试判断CE与BA的位置关系,并说明理由;(2)如图2,已知△ABC、△ADE均为等边三角形,连接CE、BD,若∠DEC=60°,试说明点B,点D,点E在同一直线上;(3)如图3,已知点E在等边△ABC外,并且与点B位于线段AC的异侧,连接BE、CE.若∠BEC=60°,猜测线段BE、AE、CE三者之间的数量关系,并说明理由.【解答】(1)解:结论:CE∥AB.理由:如图1中,∵△ABC,△ADE都是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=∠B=60°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴∠B=∠ACE=60°,∴∠BAC=∠ACE=60°,(2)证明:如图2中,由(1)可知,△ABD≌△ACE,∴∠ADB=∠AEC,∵△ADE是等边三角形,∴∠AED=∠ADE=60°,∵∠BEC=60°,∴∠AEC=∠AED+∠BEC=120°,∴∠ADB=∠AEC=120°,∴∠ADB+∠ADE=120°+60°=180°,∴B,D,E共线.(3)解:结论:BE=AE+EC.理由:在线段BE上取一点H,使得BH=CE,设AC交BE于点O.∵△ABC是等边三角形,∴AB=BC,∠BAC=60°,∵∠BEC=60°,∴∠BAO=∠OEC=60°,∵∠AOB=∠EOC,∵BA=CA,BH=CE,∴△ABH≌△ACE(SAS),∴∠BAH=∠CAE,AH=AE,∴∠HAE=∠BAC=60°,∴△AEH是等边三角形,∴AE=EH,∴BE=BH+EH=EC+AE,即BE=AE+EC.3.如图,△ABC中,AB=AC,∠EAF═∠BAC,BF⊥AE于E交AF于点F,连接CF.(1)如图1所示,当∠EAF在∠BAC内部时,求证:EF=BE+CF.(2)如图2所示,当∠EAF的边AE、AF分别在∠BAC外部、内部时,求证:CF=BF+2BE.【解答】证明:(1)如图,在EF上截取EH=BE,连接AH,∵EB=EH,AE⊥BF,∴AB=AH,∵AB=AH,AE⊥BH,∵AB=AC,∴AC=AH,∵∠EAF═∠BAC∴∠BAE+∠CAF=∠EAF,∴∠BAE+∠CAF=∠EAH+∠F AH,∴∠CAF=∠HAF,在△ACF和△AHF中,,∴△ACF≌△AHF(SAS),∴CF=HF,∴EF=EH+HF=BE+CF;(2)如图,在BE的延长线上截取EN=BE,连接AN,∵AE⊥BF,BE=EN,AB=AC,∴AN=AB=AC,∵AN=AB,AE⊥BN,∴∠BAE=∠NAE,∵∠EAF═∠BAC∴∠EAF+∠NAE=(∠BAC+2∠NAE)∴∠F AN=∠CAN,∴∠F AN=∠CAF,在△ACF和△ANF中,,∴△ACF≌△ANF(SAS),∴CF=NF,∴CF=BF+2BE.4.如图1,AB∥CD,G为AB、CD之间一点.(1)若GE平分∠AEF,GF平分∠EFC.求证:EG⊥FG;(2)如图2,若∠AEP=∠AEF,∠CFP=∠EFC,且FP的延长线交∠AEP的角平分线于点M,EP的延长线交∠CFP的角平分线于点N,猜想∠M+∠N的结果并且证明你的结论;(3)如图3,若点H是射线EB之间一动点,FG平分∠EFH,MF平分∠EFC,过点G作GQ⊥FM于点Q,请猜想∠EHF与∠FGQ的关系,并证明你的结论.【解答】解:(1)∵AB∥CD,∴∠AEF+∠CFE=180°,∵GE平分∠AEF,GF平分∠EFC,∴∠AEG=∠FEG=∠AEF,∠CFG=∠GFE=∠CFE,∴∠FEG+∠GFE=90°,即EG⊥FG;(2)∵分别过M,N作MG∥AB,NH∥AB,∵AB∥CD,∴AB∥MG∥NH∥CD,∴∠AEM=∠EMG,∠GMF=∠MFC,∠AEN=∠ENH,∠HNF=∠NFC,∴∠EMF=∠AEM+∠MFC,∠ENF=∠AEN+∠NFC,同理:∠EPF=∠AEP+∠PFC,∴∠EMF+∠ENF=∠AEM+∠MFC+∠AEN+∠NFC,∵EM平分∠AEN,FN平分∠MFC,∴∠AEM=∠AEN,∠NFC=∠MFC,∴∠EMF+∠ENF=∠AEN+∠MFC+∠MFC+∠AEN=(∠MFC+∠AEN),∵∠AEP=∠AEF,∠CFP=∠EFC,∴∠MFC+∠AEN=(∠AEF+∠EFC)=×180°=72°,∴∠EMF+∠ENF=(∠MFC+∠AEN)=×72°=108°;(3)∠FGQ=∠EHF.证明:∵AB∥CD,∴∠EHF+∠CFH=180°,∵GQ⊥MF,∴∠FGQ=90°﹣∠GFQ,∵FG平分∠EFH,MF平分∠EFC,∴∠GFE=∠EFH,∠QFE=∠CFE,∴∠GFQ=∠CFH=(180°﹣∠EHF)=90°﹣∠EHF,∴∠FGQ=90°﹣(90°﹣∠EHF)=∠EHF.5.现给出一个结论:“直角三角形斜边上的中线等于斜边的一半”.该结论是正确的,用图形语言可表示为:如图1,在Rt△ABC中,∠C=90°,若点D为AB中点,则CD=AB.请结合上述结论解决如下问题:已知,点P是射线BA上一动点(不与A,B合)分别过点A,B向直线CP作垂线,垂足分别为E,F,其中Q为AB边的中点.(1)如图2,当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是QE =QF.(2)如图3,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明.(3)如图4,当点P在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路.【解答】解:(1)如图1,当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是QE=QF,理由:∵Q为AB的中点,∴AQ=BQ,∵AE⊥CQ,BF⊥CQ,∴AE∥BF,∠AEQ=∠BFQ=90°,在△AEQ和△BFQ中,,∴△AEQ≌△BFQ(AAS),∴QE=QF,故答案为:AE∥BF,QE=QF.(2)结论:QE=QF,理由:如图2,延长EQ交BF于D,∵由(1)知:AE∥BF,∴∠AEQ=∠BDQ,在△AEQ和△BDQ中,,∴△AEQ≌△BDQ(AAS),∴EQ=DQ,∵∠BFE=90°,∴QE=QF.(3)当点P在线段BA(或AB)的延长线上时,此时(2)中的结论成立,理由:延长EQ交FB于D,如图3,∵由(1)知:AE∥BF,∴∠AEQ=∠BDQ,在△AEQ和△BDQ中,,∴△AEQ≌△BDQ(AAS),∴EQ=DQ,∵∠BFE=90°,∴QE=QF.6.如图,在△ABC中,AB=AC,∠BAC=90°,AE是过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E.(1)求证:△ABD≌△CAE;(2)若DE=3,CE=2,求BD.【解答】(1)证明:∵BD⊥AE于D,CE⊥AE于E,∠BAC=90°,∴∠BDA=∠AEC=90°,∠DBA+∠BAD=90°,∠BAD+∠EAC=90°,∴∠DBA=∠EAC,在△ABD和△CAE中,,∴△ABD≌△CAE(AAS);(2)解:由(1)知,△ABD≌△CAE,则BD=AE,AD=CE.∵DE=3,CE=2∴AE=AD+DE=CE+DE=5.∴BD=AE=5.7.如图1,在△ABC中,∠BAC=90°,点D为AC边上一点,连接BD,点E为BD上一点,连接CE,使得∠CED=∠ABD,过点A作AG⊥CE,垂足为G,AG交ED于点F.(1)判断AF与AD的数量关系,并说明理由;(2)如图2,若AC=CE,点D为AC的中点,AB与AC相等吗?为什么?(3)在(2)的条件下,如图3,若DF=5,求△DEC的面积.【解答】解:(1)结论:AF=AD.理由:如图1中,∵∠BAC=90°,∴∠ADB=90°﹣∠ABD,∵AG⊥CE,∴∠FGE=90°,∴∠EFG=∠AFD=90°﹣∠CED,∵∠CED=∠ABD,∴∠AFD=∠ADF,∴AF=AD.(2)结论:AB=AC.理由:如图2中,∵∠AFD=90°﹣∠CED,∠ADB=90°﹣∠ABD,∠CED=∠ABD,∴∠AFD=∠ADF,∴AF=AD,∠BF A=180°﹣∠AFD=180°﹣∠ADF=∠CDE,∵D为AC的中点,∴AD=CD=AF,∴△ABF≌△CED(AAS),∴AB=CE,∵CE=AC,∴AB=AC.(3)连接AE,过点A作AH⊥AE交BD延长线于点H,连接CH.∵∠BAC=90°,∴∠BAE=∠CAH,设∠ABD=∠CED=α,则∠F AD=2α,∠ACG=90°﹣2α,∵CA=CE,∴∠AEC=∠EAC=45°+α,∴∠AED=45°,∴∠AHE=45°,∴AE=AH,∵AB=AC,∴△ABE≌△ACH(SAS),∴∠AEB=∠AHC=135°,∴∠CHD=90°,过点A作AK⊥ED于H,∴∠AKD=∠CHD=90°,∵AD=CD,∠ADK=∠CDH,∴△AKD≌△CHD(AAS)∴DK=DH,∵AK⊥DF,AF=AD,AE=AH,∴FK=DK,EK=HK,∴DH=DK=KF=EF=,∴DE=,EH=10,∵△AEH是等腰直角三角形,AK⊥EH,∴AK=EK=KH=5,∴S△EDC=•DE•CH=××5=.8.在△ABC中,∠B=60°,D是BC上一点,且AD=AC.(1)如图1,延长BC至E,使CE=BD,连接AE.求证:AB=AE;(2)如图2,在AB边上取一点F,使DF=DB,求证:AF=BC;(3)如图3,在(2)的条件下,P为BC延长线上一点,连接P A,PF,若P A=PF,猜想PC与BD的数量关系并证明.【解答】(1)证明:∵AC=AD,∴∠ADC=∠ACD,∴180°﹣∠ADC=180°﹣∠ACD,即∠ADB=∠ACE,在△ABD和△AEC中,,∴△ABD≌△AEC(SAS),∴AB=AE;(2)延长CE到E,使CE=BD,由(1)知,AB=AE,∴∠E=∠B=60°,∴∠EAB=180°﹣∠E﹣∠B=60°,∴△ABE是等边三角形,同理,△DBF是等边三角形,∴AB=BE.BF=BD=CE,∴AB﹣BF=BE﹣CE,即AF=BC;(3)猜想:PC=2BD,理由如下:在CP上取点E,使CE=BD,连接AE,由(1)可知:AB=AE,∴∠AEB=∠B=60°,∴∠AEP=180°﹣∠AEB=120°,∵DF=DB,∠DFB=∠B=60°,∴∠PDF=∠DFB+∠B=120°,∴∠AEP=∠PDF,又∵P A=PF,∴∠P AF=∠PF A,∵∠APE=180°﹣∠B﹣∠P AF=120°﹣∠P AF,∠PFD=180°﹣∠DFB﹣∠PF A=120°﹣∠PF A,∴∠APE=∠PFD,在△APE和△PFD中,,∴△APE≌△PFD(AAS),∴PE=DF,又∵DF=DB,∴PE=DB,又∵PC=PE+CE,∴PC=2BD.9.(1)如图1,△ABC和△DCE都是等边三角形,且B,C,D三点在一条直线上,连接AD,BE相交于点P,求证:BE=AD.(2)如图2,在△BCD中,若∠BCD<120°,分别以BC,CD和BD为边在△BCD外部作等边△ABC,等边△CDE,等边△BDF,连接AD、BE、CF恰交于点P.①求证:AD=BE=CF;②如图2,在(2)的条件下,试猜想PB,PC,PD与BE存在怎样的数量关系,并说明理由.【解答】(1)证明:∵△ABC和△DCE都是等边三角形,∴BC=AC,CE=CD,∠ACB=∠DCE=60°,∴∠ABC+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,∴∠BCE≌△ACD(SAS),∴BE=AD;(2)①证明:∵△ABC和△CDE是等边三角形,∴AB=BC,CD=BE,∠ACB=∠DCE=60°,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴AD=BE,同理:△ABD≌△CBF(SAS),∴AD=CF,即AD=BE=CF;②解:结论:PB+PC+PD=BE,理由:如图2,AD与BC的交点记作点Q,则∠AQC=∠BQP,由①知,△ACD≌△BCE,∴∠CAD=∠CBE,在△ACQ中,∠CAD+∠AQC=180°﹣∠ACB=120°,∴∠CBE+∠BQP=120°,在△BPQ中,∠APB=180°﹣(∠CBE+∠BQP)=60°,∴∠DPE=60°,同理:∠APC=60°,∴∠CPD=120°,在PE上取一点M,使PM=PC,∴△CPM是等边三角形,∴CP=CM,∠PCM=∠CMP=60°,∴∠CME=120°=∠CPD,∵△CDE是等边三角形,∴CD=CE,∠DCE=60°=∠PCM,∴∠PCD=∠MCE,∴△PCD≌△MCE(SAS),∴PD=ME,∴BE=PB+PM+ME=PB+PC+PD.10.如图,在△ABC中,AB=AC=3,∠B=∠C=50°,点D在线段BC上运动(点D不与点B,C重合),连接AD,作∠ADE=50°,DE交线段AC于点E.(1)当∠BDA=110°时,∠EDC=20°,∠AED=70°,∠DAE=60°;(2)当DC等于多少时?△ABD≌△DCE,请说明理由.(3)在点D的运动过程中,请直接写出当△ADE是等腰三角形时∠BDA的度数.【解答】解:(1)∵∠BDA=110°,∠ADE=50°,∴∠CDE=180°﹣∠BDA﹣∠ADE=180°﹣110°﹣50°=20°,∵∠C=50°,∴∠AED=∠CDE+∠C=20°+50°=70°,在△ADE中,∠DAE=180°﹣∠ADE﹣∠AED=180°﹣50°﹣70°=60°,故答案为:20,70,60;(2)当DC=3时,△ABD≌△DCE,理由:在△ABD中,∠BAD+∠BDA=180°﹣∠B=130°,∵∠BDA+∠EDC=180°﹣∠ADE=130°,∴∠BAD=∠CDE,∵∠B=∠C,△ABD≌△DCE,∴CD=AB=3;(3)∵△ADE是等腰三角形,∴①当AD=AE时,∠AED=∠ADE=50°,∵∠C=50°,∴点E与点C重合,不符合题意,舍去,当AD=ED时,∠AED=(180°﹣∠ADE)=65°,∴∠CDE=∠AED﹣∠C=15°,∴∠BDA=180°﹣∠ADE﹣∠CDE=115°,当AE=DE时,∠AED=180°﹣2∠ADE=80°,∴∠CDE=∠AED﹣∠C=30°,∴∠BDA=180°﹣∠ADE﹣∠CDE=100°,即当△ADE是等腰三角形时∠BDA的度数为115°或100°.11.已知:△ABC为等边三角形.(1)如图1,点D、E分别为边BC、AC上的点,且BD=CE.i)求证:△ABD≌△BCE;ii)求∠AFE的度数;(2)如图2,点D为△ABC外一点,BA、CD的延长线交于点E,连接AD,已知∠BDC=60°,且AD =2,CD=5,求BD的长;(3)如图3,线段DB的长为3,线段DC的长为2,连接BC,以BC为边作等边△ABC,连接AD,直接写出当线段AD取最大值与最小值时∠BDC的度数.【解答】(1)i)证明:如图1中,∵△ABC是等边三角形,∴AB=BC,∠ABD=∠C=60°,∵BD=CE,∴△ABD≌△BCE(SAS).ii)解:如图1中,∵△ABD≌△BCE,∴∠BAD=∠CBE,∴∠AFE=∠FBA+∠BAD=∠FBA+∠CBE=∠CBA=60°.(2)解:如图2中,在DB上取一点J,使得CJ=CD,∵∠CDJ=60°,CJ=CD,∴△CDJ是等边三角形,∴∠JCD=∠ACB=60°,DJ=DC=CJ,∴∠BCJ=∠ACD,∵CB=CA,∴△BCJ≌△ACD(SAS),∴BJ=AD,∴BD=BJ+DJ=AD+DC=2+5=7.(3)解:如图3中,以CD为边向外作等边△CDT,连接BT.∵CT=CD,CB=CA,∠TCD=∠BCA=60°,∴∠TCB=∠DCA,∴△TCB≌△DCA(SAS),∴BT=AD,∵CT=CD=2,BD=3,∴3﹣2≤BT≤3+2,∴1≤BT≤5,∴1≤AD≤5.∴AD的最小值为1,最大值为5.当AD取最小值时,点T落在线段BD上,∠BDC=60°,当AD取最大值时,点T落在BD的延长线上,∠BDC=120°.12.如图,△ABC和△DEF是两个等腰直角三角形,∠BAC=∠DFE=90°,AB=AC,FD=FE,△DEF 的顶点E在边BC上移动,在移动过程中,线段DE与线段AB相交于点P,线段EF与线段CA相交于点Q.(1)如图1,当E为BC中点,且BP=CQ时,求证:△BPE≌△CQE;(2)如图2,当ED经过点A,且BE=CQ时,求∠EAQ的度数;(3)如图3,当E为BC中点,连接AE、PQ,若AP=3,AQ=4,PQ=5,求AC的长.【解答】(1)证明:∵△ABC是等腰直角三角形,∴∠B=∠C=45°,AB=AC,∵E是BC的中点,∴BE=CE,在△BPE和△CQE中,∵,∴△BPE≌△CQE(SAS);(2)解:∵∠AEQ=45°,∠B=45°,∴∠AEB+∠QEC=135°,∠AEB+∠BAE=135°,∴∠QEC=∠BAE,又∵∠B=∠C,BE=CQ,∴△ABE≌△ECQ(AAS),∴AE=EQ,∴∠EAQ=∠EQA=.(3)在CQ上截取CH,使得CH=AP,连接EH,由(1)知AE=CE,∠C=∠EAP=45°,∵在△CHE与△APE中:,∴△CHE≌△APE(SAS),∴HE=PE,∠CEH=∠AEP,∴∠HEQ=∠AEC﹣∠CEH﹣∠AEQ=∠AEC﹣∠AEP﹣∠AEQ=∠AEC﹣∠PEF=90°﹣45°=45°,∴∠HEQ=∠PEQ=45°,∵在△HEQ与△PEQ中:,∴△HEQ≌△PEQ(SAS),∴HQ=PQ,∴AC=AQ+QH+CH=AQ+PQ+AP=4+5+3=12.13.(1)如图1,在等腰△ABC中,AC=BC,在底边上任取一点D,连接CD,将△ACD沿CD翻折得到△A′CD,A′C与AB相交于点O.求证:∠A′DB=∠A′CB;(2)如图2,Rt△ABC中,AC=BC,过点C作直线l平行于AB,在点C的右侧取一点E,作∠BEF=90°,射线EF交边AC于点F,请证明BE=EF;(3)如图3,△ABC中,AC=BC,过点C作直线l平行于AB,在点C的左侧任取一点E,作∠BEF=∠ACB,射线EF交射线CA于点F,请证明BE=EF.【解答】证明:(1)∵AC=BC,∴∠A=∠B,由折叠的性质得:∠A'=∠A,∴∠A'=∠B,∵∠A'DB+∠A'+∠A'OD=180°,∠A'CB+∠B+∠BOC=180°,∠A'OD=∠BOC,∴∠A′DB=∠A′CB;(2)过点E作EG⊥CE交BC于点G,如图2所示:则∠GEC=90°,∵∠ACB=90°,AC=BC,∴∠CAB=∠CBA=45°,∵CE∥AB,∴∠ECB=∠CBA=45°,∴△CEG是等腰直角三角形,∴EC=EG,∠ECF=∠EGB=135°,∵∠BEF=∠GEC=90°,∴∠CEF=∠GEB,在△CEF和△GEB中,,∴△CEF≌△GEB(ASA),∴BE=EF;(3)在CF上取一点G,使∠EGC=∠ECG,如图3所示:则EG=EC,同(1)得:∠EFG=∠EBC,∵AC=BC,∴∠CAB=∠CBA,∵CE∥AB,∴∠ECG=∠CAB,∠HCB=∠CBA,∴∠EGC=∠ECG=∠CAB=∠CBA=∠HCB,∴∠EGF=∠ECB,在△CEB和△GEF中,,∴△CEB≌△GEF(AAS),∴BE=EF.14.(1)如图(1),在△ABC中,∠A<45°,点D在AB边上,且CD=CB,∠ABC=2∠A,求证:AD =CD.(2)如图(2),在△ABC中,∠A=45°,点D在AB边上,且CD=CB,过点B作BE⊥CD,垂足为E,延长BE交AC于点F.①求证:BC=BF;②作FH⊥AB,垂足为H,若△BDE的面积为m,四边形DEFH的面积为n,求△BCE的面积(用含m,n的代数式表示).【解答】(1)证明:如图1中,∵CB=CD,∴∠B=∠CDB,∵∠B=2∠A,∴∠BDC=2∠A,∵∠BDC=∠A+∠DCA,∴∠A=∠DCA,∴AD=CD.(2)①证明:如图2中,过点C作CM⊥BD于M.∵CM⊥BD,BE⊥CD,∴∠BED=∠CMD=90°,∴∠EBD+∠CDB=90°,∠MCD+∠CDB=90°,∴∠DBE=∠MCD,∵CB=CD,CM⊥BD,∴∠BCM=∠DCM=∠ABF,∵∠AMC=90°,∠A=45°,∴∠ACM=45°,∴∠BCF=∠BCM+∠ACM=∠BCM+45°,∠BFC=∠ABF+∠A=∠ABF+45°,∴∠BCF=∠BFC,∴BC=BF.②解:∵FH⊥AB,CM⊥BD∴∠FHB=∠CMD=90°,∵∠FBH=∠MCD,CD=CB=BF,∴△CMD≌△BHF(AAS),∴S△MCD=S△BFH=m+n,∵BM=MD,∴S△BCD=2S△MCD=2m+2n,∴S△BCE=S△BCD﹣S△BDE=2m+2n﹣m=m+2n.15.如图1,在△ABC中,∠ABC=90°,AB=BC,l是过点B的一条直线,过点A作AD⊥l于D,过点C 作CG⊥l于G.(1)求证:BD=CG;(2)如图(2)延长CG至E,连接BE,以BE为直角边作等腰直角三角形EBF,∠EBF=90°,连接AF交l于M.试探究CE与BM的数量关系,并说明理由.(3)在(2)的条件下,若S△BFM=45,BG=12.直接写出CE的长.【解答】(1)证明:∵AD⊥l,CG⊥l,∴∠ADB=∠BGC=∠ABC=90°,∵∠DAB+∠DBA=∠GBC+∠DBA=90°,∴∠DAB=∠GBC,在△ABD和△BCG中,,∴△ABD≌△BCG(AAS),∴BD=CG;(2)解:CE=2BM,理由如下:作FN⊥l于N,如图2所示:则FN∥AD,∴∠ADM=∠FNM,由(1)得:△ABD≌△BCG(AAS),∴AD=BG,S△ABD=S△BCG,同理:△FBN≌△BEG(AAS),∴S△FBN=S△BEG,FN=BG,∴AD=FN,在△ADM和△FNM中,,∴△ADM≌△FNM(AAS),∴S△ADM=S△FNM,AM=FM,∴S△ABF=2S△ABM=2S△BFM=S△ABD+S△FBN=S△BCG+S△BEG,即S△BCE=2S△ABM,∴CE×BG=2×BM×AD,∴CE=2BM;(3)解:由(2)得:S△BCE=2S△BFM=90,∴CE×BG=90,即CE×12=90,∴CE=15.16.已知,△ABC和△DEC都是等腰直角三角形,且∠BAC=∠DEC=90°,将△DEC绕点C在平面内进行旋转,连接AE,点M为线段AE的中点.(1)如图1,当点D在BC边上时.连接DM并延长交AC于G,求证:AG=CE;(2)如图2,若点D在△ABC的内部,过点A作AG∥DE,交DM的延长线于点G,连接BG,求证:BG=AE,且BG⊥AE;(3)如图3,点D在△ABC的外部,仍过点A作AG∥DE,交DM的延长线于点G,(2)中的两个结论是否仍然成立.若成立;请证明,若不成立,请说明理由.【解答】(1)证明:如图1中,∵△ABC和△DEC都是等腰直角三角形,且∠BAC=∠DEC=90°,∴∠ACB=∠CDE=45°,∴AC∥DE,∴∠GAM=∠DEM,∵∠AMG=∠EMD,AM=EM,∴△AGM≌△EDM(ASA),∴AG=DE,∵DE=EC,∴AG=CE.(2)证明:如图2中,延长ED交AB于T,设AE交BG于点O.∴AG∥DE,∴∠GAM=∠DEM,∵∠AMG=∠EMD,AM=EM,∴△AGM≌△EDM(ASA),∴AG=DE,∵DE=EC,∴AG=CE,∵∠CET=∠CAT=90°,∴∠ACE+∠ATE=180°,∵∠BTD+∠ATE=180°,∴∠ACE=∠BTD,∵ET∥AG,∴∠BTD=∠BAG,∴∠ACE=∠BAG,∴CA=AB,CE=AG,∴△ACE≌△BAG(SAS),∴AE=BG,∠EAC=∠ABG,∵∠EAC+∠BAE=90°,∴∠ABG+∠BAE=90°,∴∠AOB=90°,∴AE⊥BG.(3)解:如图3中,结论成立.理由:如图2中,延长ED交AB于T,设AE交BG于点O.∴AG∥DE,∴∠GAM=∠DEM,∵∠AMG=∠EMD,AM=EM,∴△AGM≌△EDM(ASA),∴AG=DE,∵DE=EC,∴AG=CE,∵∠CET=∠CAT=90°,∴∠ACE+∠ATE=180°,∵ET∥AG,∴∠ATE+∠BAG=180°,∴∠ACE=∠BAG,∴CA=AB,CE=AG,∴△ACE≌△BAG(SAS),∴AE=BG,∠EAC=∠ABG,∵∠EAC+∠BAE=90°,∴∠ABG+∠BAE=90°,∴∠AOB=90°,∴AE⊥BG.17.(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点且∠EAF=60°,直接写出图中线段BE、EF、FD之间的数量关系,不必证明.(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由.(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以45海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以60海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两舰艇分别到站E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.【解答】解:(1)EF=BE+DF,如图1,理由如下:在△ABE和△ADG中,,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,∴∠EAF=∠GAF,在△AEF和△AGF中,,∴△AEF≌△AGF(SAS),∴EF=FG,∵FG=DG+DF=BE+DF,∴EF=BE+DF;(2)结论EF=BE+DF仍然成立;理由如下:延长FD到点G.使DG=BE.连接AG,如图2,在△ABE和△ADG中,,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,∴∠EAF=∠GAF,在△AEF和△AGF中,,∴△AEF≌△AGF(SAS),∴EF=FG,∵FG=DG+DF=BE+DF,∴EF=BE+DF;(3)如图3,连接EF,延长AE、BF相交于点C,∵∠AOB=30°+90°+(90°﹣70°)=140°,∠EOF=70°,∴∠EOF=∠AOB,又∵OA=OB,∠OAC+∠OBC=(90°﹣30°)+(70°+50°)=180°,∴符合(2)中的条件,∴结论EF=AE+BF成立,即EF=2×(45+60)=210(海里).∴两舰艇之间的距离为210海里.18.已知:如图,△ABC中,AB=BC,∠ABC=90°,过点A作射线AD,使AD∥BC,点E在AC上,连接BE,过点E作BE的垂线交AD于点F.(1)求证:∠DFE=∠ABE;(2)求证:EF=BE;(3)延长FE到G,使EG=EF,连接CG,求证:CG∥AB.【解答】解:(1)证明:如图,∵AD∥BC,∴∠DFE=∠FHB,∵BE⊥EF,∴∠FHB+∠EBH=90°,∵∠ABC=90°,∴∠ABE+∠EBH=90°,∴∠FHB=∠ABE,∴∠DFE=∠ABE;(2)证明:如图,过点E作EM⊥AD于点M,EN⊥AB于点N,∵AB=BC,∠ABC=90°,∴∠BAC=∠BCA=45°,∵AD∥BC,∴∠DAC=∠ACB=45°,∵EM⊥AD,EN⊥AB,∴EM=EN,∠EMF=∠ENB=90°,∵∠DFE=∠ABE,∴△EFM≌△EBN(AAS),∴EF=BE;(3)证明:∵BE⊥EG,EF=BE=EG,∴BF=BG,∠FBG=90°,∵∠ABC=90°,∴∠ABF=∠CBG,∵AB=BC,∴△ABF≌△CBG(SAS),∴∠BCG=∠BAF=90°,∴∠BCG=∠ABC=90°,∴CG∥AB.19.已知:在四边形ABCD中,AC,BD相交于点E,且点E是AC的中点,AC⊥BD,过点B作BF⊥CD,垂足为点F,BF与AC交于点G.(1)如图1,求证:∠BGE=∠ADE;(2)如图2,若∠ABC=90°;①求证:DE=EG;②若AC=8,△BCG的面积为4,求四边形ABCD的面积.【解答】(1)证明:∵点E是AC的中点,AC⊥BD,∴AD=CD,△ADC是等腰三角形,∴∠DAC=∠DCA,∵AC⊥BD,BF⊥CD,∴∠BEG=∠CFG=90°,∵∠BGE=∠FGC,∴∠EBG=∠FCG,∴∠EBG=∠DAE,∵∠BEG=∠AED,∴∠BGE=∠ADE;(2)①证明:∵点E是AC的中点,AC⊥BD,∴△ABC是等腰三角形,∵∠ABC=90°,∴∠BAE=∠ABE=45°,∴AE=BE,在△AED和△BEG中,,∴△AED≌△BEG(ASA),∴DE=EG;②解:∵∠ABC=90°,点E是AC的中点,∴AE=CE=BE=AC=×8=4,∵S△BCG=CG•BE=×CG×4=2CG,∴2CG=4,∴CG=2,∴DE=EG=CE﹣CG=4﹣2=2,∴S四边形ABCD=S△ABC+S△ADC=AC•BE+AC•DE=×8×4+×8×2=24.20.(1)如图1,在△ABC中,AB=4,AC=6,AD是BC边上的中线,延长AD到点E使DE=AD,连接CE,把AB,AC,2AD集中在△ACE中,利用三角形三边关系可得AD的取值范围是1<AD<5;(2)如图2,在△ABC中,AD是BC边上的中线,点E,F分别在AB,AC上,且DE⊥DF,求证:BE+CF >EF;(3)如图3,在四边形ABCD中,∠A为钝角,∠C为锐角,∠B+∠ADC=180°,DA=DC,点E,F 分别在BC,AB上,且∠EDF=∠ADC,连接EF,试探索线段AF,EF,CE之间的数量关系,并加以证明.【解答】(1)解:如图1中,∵CD=BD,AD=DE,∠CDE=∠ADB,∴△CDE≌△BDA(SAS),∴EC=AB=4,∵6﹣4<AE<6+4,∴2<2AD<10,∴1<AD<5,故答案为1<AD<5.(2)证明:如图2中,延长ED到H,使得DH=DE,连接DH,FH.∵BD=DC,∠BDE=∠CDH,DE=DH,∴△BDE≌△CDH(SAS),∴BE=CH,∵FD⊥EH.DE=DH,∴EF=FH,在△CFH中,CH+CF>FH,∵CH=BE,FH=EF,∴BE+CF>EF.。
人教版中学七年级数学下册期末解答题培优题及答案

人教版中学七年级数学下册期末解答题培优题及答案一、解答题1.(1)如图1,分别把两个边长为1cm的小正方形沿一条对角线裁成4个小三角形拼成一个大正方形,则大正方形的边长为______cm;(2)若一个圆的面积与一个正方形的面积都是22πcm,设圆的周长为C圆.正方形的周长为C正,则C圆______C正(填“=”,或“<”,或“>”)(3)如图2,若正方形的面积为2900cm,李明同学想沿这块正方形边的方向裁出一块面积为2740cm的长方形纸片,使它的长和宽之比为5:4,他能裁出吗?请说明理由?2.如图1,用两个边长相同的小正方形拼成一个大的正方形.(1)如图2,若正方形纸片的面积为12dm,则此正方形的对角线AC的长为 dm.(2)如图3,若正方形的面积为162cm,李明同学想沿这块正方形边的方向裁出一块面积为122cm的长方形纸片,使它的长和宽之比为3∶2,他能裁出吗?请说明理由.3.教材中的探究:如图,把两个边长为1的小正方形沿对角线剪开,用所得到的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法(数轴的单位长度为1).(1)阅读理解:图1中大正方形的边长为________,图2中点A表示的数为________;(2)迁移应用:请你参照上面的方法,把5个小正方形按图3位置摆放,并将其进行裁剪,拼成一个大正方形.①请在图3中画出裁剪线,并在图3中画出所拼得的大正方形的示意图.②利用①中的成果,在图4的数轴上分别标出表示数-0.5以及35-的点,并比较它们的大小.4.如图,用两个面积为2200cm的小正方形拼成一个大的正方形.(1)则大正方形的边长是___________;(2)若沿着大正方形边的方向裁出一个长方形,能否使裁出的长方形纸片的长宽之比为5:4,且面积为2360cm?5.如图用两个边长为18cm的小正方形纸片拼成一个大的正方形纸片,沿着大正方形纸片的边的方向截出一个长方形纸片,能否使截得的长方形纸片长宽之比为3:2,且面积为30cm2?请说明理由.二、解答题6.已知,AB∥DE,点C在AB上方,连接BC、CD.(1)如图1,求证:∠BCD+∠CDE=∠ABC;(2)如图2,过点C作CF⊥BC交ED的延长线于点F,探究∠ABC和∠F之间的数量关系;(3)如图3,在(2)的条件下,∠CFD的平分线交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.7.已知直线AB//CD,点P、Q分别在AB、CD上,如图所示,射线PB按逆时针方向以每秒12°的速度旋转至PA便立即回转,并不断往返旋转;射线QC按逆时针方向每秒3°旋转至QD停止,此时射线PB也停止旋转.(1)若射线PB、QC同时开始旋转,当旋转时间10秒时,PB'与QC'的位置关系为;(2)若射线QC先转15秒,射线PB才开始转动,当射线PB旋转的时间为多少秒时,PB′//QC′.8.已知:直线AB∥CD,M,N分别在直线AB,CD上,H为平面内一点,连HM,HN.(1)如图1,延长HN至G,∠BMH和∠GND的角平分线相交于点E.求证:2∠MEN﹣∠MHN=180°;(2)如图2,∠BMH和∠HND的角平分线相交于点E.①请直接写出∠MEN与∠MHN的数量关系:;②作MP平分∠AMH,NQ∥MP交ME的延长线于点Q,若∠H=140°,求∠ENQ的度数.(可直接运用①中的结论)9.汛期即将来临,防汛指挥部在某水域一危险地带两岸各安置了一探照灯,便于夜间查看河水及两岸河堤的情况.如图1,灯A射出的光束自AM顺时针旋转至AN便立即回转,灯B射出的光束自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A射出的光束转动的速度是a︒/秒,灯B射出的光束转动的速度是b︒/秒,且a、b满足20a b a b(-++-=.假定这一带水域两岸河堤是平行的,即//34)PQ MN,且∠=︒.45BAN(1)求a、b的值;(2)如图2,两灯同时转动,在灯A射出的光束到达AN之前,若两灯射出的光束交于点C ,过C 作CD AC ⊥交PQ 于点D ,若20BCD ∠=︒,求BAC ∠的度数;(3)若灯B 射线先转动30秒,灯A 射出的光束才开始转动,在灯B 射出的光束到达BQ 之前,A 灯转动几秒,两灯的光束互相平行?10.如图,已知直线//AB 射线CD ,110CEB ∠=︒.P 是射线EB 上一动点,过点P 作//PQ EC 交射线CD 于点Q ,连接CP .作PCF PCQ ∠=∠,交直线AB 于点F ,CG 平分ECF ∠.(1)若点P ,F ,G 都在点E 的右侧. ①求PCG ∠的度数;②若30EGC ECG ∠-∠=︒,求CPQ ∠的度数.(不能使用“三角形的内角和是180︒”直接解题)(2)在点P 的运动过程中,是否存在这样的偕形,使:3:2EGC EFC ∠∠=?若存在,直接写出CPQ ∠的度数;若不存在.请说明理由.三、解答题11.如图1,由线段,,,AB AM CM CD 组成的图形像英文字母M ,称为“M 形BAMCD ”.(1)如图1,M 形BAMCD 中,若//,50AB CD A C ∠+∠=︒,则M ∠=______; (2)如图2,连接M 形BAMCD 中,B D 两点,若150,B D AMC α∠+∠=︒∠=,试探求A ∠与C ∠的数量关系,并说明理由;(3)如图3,在(2)的条件下,且AC 的延长线与BD 的延长线有交点,当点M 在线段BD 的延长线上从左向右移动的过程中,直接写出A ∠与C ∠所有可能的数量关系.12.已知:直线1l ∥2l ,A 为直线1l 上的一个定点,过点A 的直线交 2l 于点B ,点C 在线段BA 的延长线上.D ,E 为直线2l 上的两个动点,点D 在点E 的左侧,连接AD ,AE ,满足∠AED =∠DAE .点M 在2l 上,且在点B 的左侧.(1)如图1,若∠BAD =25°,∠AED =50°,直接写出∠ABM 的度数 ;(2)射线AF 为∠CAD 的角平分线.① 如图2,当点D 在点B 右侧时,用等式表示∠EAF 与∠ABD 之间的数量关系,并证明; ② 当点D 与点B 不重合,且∠ABM +∠EAF =150°时,直接写出∠EAF 的度数 .13.综合与探究(问题情境)王老师组织同学们开展了探究三角之间数量关系的数学活动.(1)如图1,EF ∥MN ,点A 、B 分别为直线EF 、MN 上的一点,点P 为平行线间一点,请直接写出∠PAF 、∠PBN 和∠APB 之间的数量关系; (问题迁移)(2)如图2,射线OM 与射线ON 交于点O ,直线m ∥n ,直线m 分别交OM 、ON 于点A 、D ,直线n 分别交OM 、ON 于点B 、C ,点P 在射线OM 上运动.①当点P 在A 、B (不与A 、B 重合)两点之间运动时,设∠ADP =∠α,∠BCP =∠β.则∠CPD ,∠α,∠β之间有何数量关系?请说明理由;②若点P 不在线段AB 上运动时(点P 与点A 、B 、O 三点都不重合),请你画出满足条件的所有图形并直接写出∠CPD ,∠α,∠β之间的数量关系.14.已知射线//AB 射线CD ,P 为一动点,AE 平分PAB ∠,CE 平分PCD ∠,且AE 与CE 相交于点E .(注意:此题不允许使用三角形,四边形内角和进行解答)(1)在图1中,当点P 运动到线段AC 上时,180APC ∠=︒.直接写出AEC ∠的度数; (2)当点P 运动到图2的位置时,猜想AEC ∠与APC ∠之间的关系,并加以说明; (3)当点P 运动到图3的位置时,(2)中的结论是否还成立?若成立,请说明理由:若不成立,请写出AEC ∠与APC ∠之间的关系,并加以证明.15.已知//a b ,直角ABC 的边与直线a 分别相交于O 、G 两点,与直线b 分别交于E 、F 点,90ACB ∠=.(1)将直角ABC 如图1位置摆放,如果46AOG ∠=,则CEF ∠=______; (2)将直角ABC 如图2位置摆放,N 为AC 上一点,180NEF CEF ︒∠+∠=,请写出NEF ∠与AOG ∠之间的等量关系,并说明理由.(3)将直角ABC 如图3位置摆放,若140GOC ∠=,延长AC 交直线b 于点Q ,点P 是射线GF 上一动点,探究POQ ∠,OPQ ∠与PQF ∠的数量关系,请直接写出结论.四、解答题16.在△ABC 中,射线AG 平分∠BAC 交BC 于点G ,点D 在BC 边上运动(不与点G 重合),过点D 作DE ∥AC 交AB 于点E .(1)如图1,点D 在线段CG 上运动时,DF 平分∠EDB①若∠BAC =100°,∠C =30°,则∠AFD = ;若∠B =40°,则∠AFD = ; ②试探究∠AFD 与∠B 之间的数量关系?请说明理由;(2)点D 在线段BG 上运动时,∠BDE 的角平分线所在直线与射线AG 交于点F 试探究∠AFD 与∠B 之间的数量关系,并说明理由17.如图①,将一副直角三角板放在同一条直线AB 上,其中∠ONM =30°,∠OCD =45°.(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;(2)将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN 与CD相交于点E,求∠CEN的度数;(3)将图①中的三角板OMN绕点O按每秒30°的速度按逆时针方向旋转一周,在旋转的过程中,在第____________秒时,直线MN恰好与直线CD垂直.(直接写出结果)18.(生活常识)射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等.如图 1,MN 是平面镜,若入射光线AO 与水平镜面夹角为∠1,反射光线OB 与水平镜面夹角为∠2,则∠1=∠2 .(现象解释)如图 2,有两块平面镜OM,ON,且OM⊥ON,入射光线AB 经过两次反射,得到反射光线CD.求证AB∥CD.(尝试探究)如图 3,有两块平面镜OM,ON,且∠MON =55︒,入射光线AB 经过两次反射,得到反射光线CD,光线AB 与CD 相交于点E,求∠BEC 的大小.(深入思考)如图 4,有两块平面镜OM,ON,且∠MON =α ,入射光线AB 经过两次反射,得到反射光线CD,光线AB 与CD 所在的直线相交于点E,∠BED=β , α 与β 之间满足的等量关系是 .(直接写出结果)19.如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.(1)当∠A为70°时,∵∠ACD-∠ABD=∠______∴∠ACD-∠ABD=______°∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线∴∠A1CD-∠A1BD=1(∠ACD-∠ABD)2∴∠A1=______°;(2)∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、A n,请写出∠A与∠A n的数量关系______;(3)如图2,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F=______.(4)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E 滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q-∠A1的值为定值.其中有且只有一个是正确的,请写出正确的结论,并求出其值.20.如图,△ABC和△ADE有公共顶点A,∠ACB=∠AED=90°,∠BAC=45°,∠DAE=30°.(1)若DE//AB,则∠EAC=;(2)如图1,过AC上一点O作OG⊥AC,分别交A B、A D、AE于点G、H、F.①若AO=2,S△AGH=4,S△AHF=1,求线段OF的长;②如图2,∠AFO的平分线和∠AOF的平分线交于点M,∠FHD的平分线和∠OGB的平分线交于点N,∠N+∠M的度数是否发生变化?若不变,求出其度数;若改变,请说明理由.【参考答案】一、解答题1.(1);(2)<;(3)不能,理由见解析 【分析】(1)根据所拼成的大正方形的面积为2即可求得大正方形的边长;(2)由圆和正方形的面积公式可分别求的圆的半径及正方形的边长,进而可求得圆和正方形的解析:(12)<;(3)不能,理由见解析 【分析】(1)根据所拼成的大正方形的面积为2即可求得大正方形的边长;(2)由圆和正方形的面积公式可分别求的圆的半径及正方形的边长,进而可求得圆和正方形的周长,利用作商法比较这两数大小即可;(3)利用方程思想求出长方形的长边,与正方形边长比较大小即可; 【详解】解:(1)∵小正方形的边长为1cm , ∴小正方形的面积为1cm 2, ∴两个小正方形的面积之和为2cm 2, 即所拼成的大正方形的面积为2 cm 2, 设大正方形的边长为x cm , ∴22x = , ∴x∴; (2)设圆的半径为r , ∴由题意得22r ππ=, ∴r =∴=22C r π=圆 设正方形的边长为a ∵22a π=, ∴a∴=4C a =正∴1C C ===<圆正 故答案为:<;(3)解:不能裁剪出,理由如下: ∵正方形的面积为900cm 2, ∴正方形的边长为30cm∵长方形纸片的长和宽之比为5:4, ∴设长方形纸片的长为5x ,宽为4x , 则54740x x ⋅=, 整理得:237x =,∴22(5)252537925900x x ==⨯=>, ∴22(5)30x >, ∴530x >,∴长方形纸片的长大于正方形的边长, ∴不能裁出这样的长方形纸片. 【点睛】本题通过圆和正方形的面积考查了对算术平方根的应用,主要是对学生无理数运算及比较大小进行了考查.2.(1);(2)不能,理由见解析 【分析】(1)由正方形面积,可求得正方形边长,然后利用勾股定理即可求出对角线长;(2)利用方程思想求出长方形的长边,然后与正方形边长比较大小即可. 【详解】 解:解析:(1)2)不能,理由见解析 【分析】(1)由正方形面积,可求得正方形边长,然后利用勾股定理即可求出对角线长; (2)利用方程思想求出长方形的长边,然后与正方形边长比较大小即可. 【详解】解:(1)∵正方形纸片的面积为21dm , ∴正方形的边长1AB BC dm ==, ∴AC =.(2)不能;根据题意设长方形的长和宽分别为3xcm 和2xcm . ∴长方形面积为:2?312x x =,解得:x =∴长方形的长边为.∵4, ∴他不能裁出. 【点睛】本题考查了算术平方根在长方形和正方形面积中的应用,灵活的进行算术平方根计算及无理数大小比较是解题的关键.3.(1);(2)①见解析;②见解析, 【分析】(1)设正方形边长为a ,根据正方形面积公式,结合平方根的运算求出a 值,则知结果;(2)① 根据面积相等,利用割补法裁剪后拼得如图所示的正方形;②解析:(1)2,2-;(2)①见解析;②见解析,350.5-+<-【分析】(1)设正方形边长为a,根据正方形面积公式,结合平方根的运算求出a值,则知结果;(2)① 根据面积相等,利用割补法裁剪后拼得如图所示的正方形;②由题(1)的原理得出大正方形的边长为5,然后在数轴上以-3为圆心,以大正方形的边长为半径画弧交数轴的右方与一点M,再把N点表示出来,即可比较它们的大小.【详解】解:设正方形边长为a,∵a2=2,∴a=2±,故答案为:2,2-;(2)解:①裁剪后拼得的大正方形如图所示:②设拼成的大正方形的边长为b,∴b2=5,∴b=±5,在数轴上以-3为圆心,以大正方形的边长为半径画弧交数轴的右方与一点M,则M表示的数为-3+5,看图可知,表示-0.5的N点在M点的右方,∴比较大小:350.5-+<-.【点睛】本题主要考查平方根与算术平方根的应用及实数的大小比较,熟练掌握平方根与算术平方根的意义及实数的大小比较是解题的关键.4.(1);(2)不能剪出长宽之比为5:4,且面积为的大长方形,理由详见解析【分析】(1)根据已知得到大正方形的面积为400,求出算术平方根即为大正方形的边长;(2)设长方形纸片的长为,宽为,根据解析:(1)20cm ;(2)不能剪出长宽之比为5:4,且面积为2360cm 的大长方形,理由详见解析【分析】(1)根据已知得到大正方形的面积为4002cm ,求出算术平方根即为大正方形的边长;(2)设长方形纸片的长为5xcm ,宽为4xcm ,根据面积列得54360x x ⋅=,求出x =得到520x =>,由此判断不能裁出符合条件的大正方形.【详解】(1)∵用两个面积为2200cm 的小正方形拼成一个大的正方形,∴大正方形的面积为4002cm ,∴20cm =故答案为:20cm ;(2)设长方形纸片的长为5xcm ,宽为4xcm ,54360x x ⋅=,解得:x520x =,答:不能剪出长宽之比为5:4,且面积为2360cm 的大长方形.【点睛】此题考查利用算术平方根解决实际问题,利用平方根解方程,正确理解题意是解题的关键. 5.不能截得长宽之比为,且面积为cm2的长方形纸片,见解析【分析】根据拼图求出大正方形的边长,再根据长方形的长、宽之比为3:2,计算长方形的长与宽进行验证即可.【详解】解:不能,因为大正方形纸解析:不能截得长宽之比为3:2,且面积为30cm 2的长方形纸片,见解析【分析】根据拼图求出大正方形的边长,再根据长方形的长、宽之比为3:2,计算长方形的长与宽进行验证即可.【详解】解:不能,2+2=36(cm 2),所以大正方形的边长为6cm ,设截出的长方形的长为3b cm ,宽为2b cm ,则6b 2=30,所以b =5(取正值), 所以3b =35=45>36,所以不能截得长宽之比为3:2,且面积为30cm 2的长方形纸片.【点睛】本题考查了算术平方根,理解算术平方根的意义是正确解答的关键.二、解答题6.(1)证明见解析;(2);(3).【分析】(1)过点作,先根据平行线的性质可得,再根据平行公理推论可得,然后根据平行线的性质可得,由此即可得证;(2)过点作,同(1)的方法,先根据平行线的性质解析:(1)证明见解析;(2)90ABC F ∠-∠=︒;(3)45︒.【分析】(1)过点C 作CF AB ∥,先根据平行线的性质可得180ABC BCF ∠+∠=︒,再根据平行公理推论可得CFDE ,然后根据平行线的性质可得180CDE BCF BCD ∠+∠+∠=︒,由此即可得证;(2)过点C 作CG AB ∥,同(1)的方法,先根据平行线的性质得出180ABC BCG ∠+∠=︒,180F BCG BCF ∠+∠+∠=︒,从而可得ABC F BCF ∠-∠=∠,再根据垂直的定义可得90BCF ∠=︒,由此即可得出结论;(3)过点G 作GM AB ,延长FG 至点N ,先根据平行线的性质可得ABH MGH ∠=∠,MGN DFG ∠=∠,从而可得MGH MGN ABH DFG ∠-∠=∠-∠,再根据角平分线的定义、结合(2)的结论可得45MGH MGN ∠=-∠︒,然后根据角的和差、对顶角相等可得BGD CG MGH MGN F ∠-∠=∠-∠,由此即可得出答案.【详解】证明:(1)如图,过点C 作CF AB ∥,180ABC BCF ∴∠+∠=︒,AB DE ,CF DE ∴,180CDE DCF ∴∠+∠=︒,即180CDE BCF BCD ∠+∠+∠=︒,CDE BCF BCD ABC BCF ∴∠+∠+∠=∠+∠,BCD CDE ABC ∴∠+∠=∠;(2)如图,过点C 作CG AB ∥,180ABC BCG ∴∠+∠=︒,AB DE ,CG DE ∴,180F FCG ∴∠+∠=︒,即180F BCG BCF ∠+∠+∠=︒,F BCG BCF ABC BCG ∴∠+∠+∠=∠+∠,ABC F BCF ∴∠-∠=∠,CF BC ⊥,90BCF ∴∠=︒,90ABC F ∴∠-∠=︒;(3)如图,过点G 作GM AB ,延长FG 至点N ,ABH MGH ∴∠=∠,AB DE ,GM DE ∴,MGN DFG ∴∠=∠, BH 平分ABC ∠,FN 平分CFD ∠,11,22ABH AB D C CF DFG ∴∠=∠∠∠=, 由(2)可知,90ABC CFD ∠-∠=︒,411225MGH MGN ABH DFG CF B D A C ∠-∠=∠-∠∠∠-==∴︒, 又BGD MGH MGD CGF DGN MGN MGD ∠=∠+∠⎧⎨∠=∠=∠+∠⎩, 45MGH BGD GF MGN C ∠-∠∴-==∠∠︒.【点睛】本题考查了平行线的性质、对顶角相等、角平分线的定义等知识点,熟练掌握平行线的性质是解题关键.7.(1)PB′⊥QC′;(2)当射线PB旋转的时间为5秒或25秒或45秒时,PB′∥QC′【分析】(1)求出旋转10秒时,∠BPB′和∠CQC′的度数,设PB′与QC′交于O,过O作OE∥AB,根解析:(1)PB′⊥QC′;(2)当射线PB旋转的时间为5秒或25秒或45秒时,PB′∥QC′【分析】(1)求出旋转10秒时,∠BPB′和∠CQC′的度数,设PB′与QC′交于O,过O作OE∥AB,根据平行线的性质求得∠POE和∠QOE的度数,进而得结论;(2)分三种情况:①当0<t≤15时,②当15<t≤30时,③当30<t<45时,根据平行线的性质,得出角的关系,列出t的方程便可求得旋转时间.【详解】解:(1)如图1,当旋转时间30秒时,由已知得∠BPB′=10°×12=120°,∠CQC′=3°×10=30°,过O作OE∥AB,∵AB∥CD,∴AB∥OE∥CD,∴∠POE=180°﹣∠BPB′=60°,∠QOE=∠CQC′=30°,∴∠POQ=90°,∴PB′⊥QC′,故答案为:PB′⊥QC′;(2)①当0<t≤15时,如图,则∠BPB′=12t°,∠CQC′=45°+3t°,∵AB∥CD,PB′∥QC′,∴∠BPB′=∠PEC=∠CQC′,即12t=45+3t,解得,t=5;②当15<t≤30时,如图,则∠APB′=12t﹣180°,∠CQC'=3t+45°,∵AB∥CD,PB′∥QC′,∴∠BPB′=∠BEQ=∠CQC′,即12t﹣180=45+3t,解得,t=25;③当30<t≤45时,如图,则∠BPB′=12t﹣360°,∠CQC′=3t+45°,∵AB∥CD,PB′∥QC′,∴∠BPB′=∠BEQ=∠CQC′,即12t﹣360=45+3t,解得,t=45;综上,当射线PB旋转的时间为5秒或25秒或45秒时,PB′∥QC′.【点睛】本题主要考查了平行线的性质,第(1)题关键是作平行线,第(2)题关键是分情况讨论,运用方程思想解决几何问题.8.(1)见解析;(2)①2∠MEN+∠MHN=360°;②20°【分析】(1)过点E作EP∥AB交MH于点Q,利用平行线的性质、角平分线性质、邻补角和为180°,角与角之间的基本运算、等量代换等即解析:(1)见解析;(2)①2∠MEN+∠MHN=360°;②20°【分析】(1)过点E作EP∥AB交MH于点Q,利用平行线的性质、角平分线性质、邻补角和为180°,角与角之间的基本运算、等量代换等即可得证.(2)①过点H作GI∥AB,利用(1)中结论2∠MEN﹣∠MHN=180°,利用平行线的性质、角平分线性质、邻补角和为180°,角与角之间的基本运算、等量代换等得出∠AMH+∠HNC=360°﹣(∠BMH+∠HND),进而用等量代换得出2∠MEN+∠MHN=360°.②过点H作HT∥MP,由①的结论得2∠MEN+∠MHN=360°,∠H=140°,∠MEN=110°.利用平行线性质得∠ENQ+∠ENH+∠NHT=180°,由角平分线性质及邻补角可得∠ENQ+∠ENH+140°﹣12(180°﹣∠BMH)=180°.继续使用等量代换可得∠ENQ度数.【详解】解:(1)证明:过点E作EP∥AB交MH于点Q.如答图1∵EP∥AB且ME平分∠BMH,∴∠MEQ=∠BME=12∠BMH.∵EP∥AB,AB∥CD,∴EP∥CD,又NE平分∠GND,∴∠QEN=∠DNE=12∠GND.(两直线平行,内错角相等)∴∠MEN=∠MEQ+∠QEN=12∠BMH+12∠GND=12(∠BMH+∠GND).∴2∠MEN=∠BMH+∠GND.∵∠GND+∠DNH=180°,∠DNH+∠MHN=∠MON=∠BMH.∴∠DHN=∠BMH﹣∠MHN.∴∠GND+∠BMH﹣∠MHN=180°,即2∠MEN﹣∠MHN=180°.(2)①:过点H作GI∥AB.如答图2由(1)可得∠MEN=12(∠BMH+∠HND),由图可知∠MHN=∠MHI+∠NHI,∵GI∥AB,∴∠AMH=∠MHI=180°﹣∠BMH,∵GI∥AB,AB∥CD,∴GI∥CD.∴∠HNC=∠NHI=180°﹣∠HND.∴∠AMH+∠HNC=180°﹣∠BMH+180°﹣∠HND=360°﹣(∠BMH+∠HND).又∵∠AMH+∠HNC=∠MHI+∠NHI=∠MHN,∴∠BMH+∠HND=360°﹣∠MHN.即2∠MEN+∠MHN=360°.故答案为:2∠MEN+∠MHN=360°.②:由①的结论得2∠MEN+∠MHN=360°,∵∠H=∠MHN=140°,∴2∠MEN=360°﹣140°=220°.∴∠MEN=110°.过点H作HT∥MP.如答图2∵MP∥NQ,∴HT∥NQ.∴∠ENQ+∠ENH+∠NHT=180°(两直线平行,同旁内角互补).∵MP平分∠AMH,∴∠PMH=12∠AMH=12(180°﹣∠BMH).∵∠NHT=∠MHN﹣∠MHT=140°﹣∠PMH.∴∠ENQ+∠ENH+140°﹣12(180°﹣∠BMH)=180°.∵∠ENH=12∠HND.∴∠ENQ+12∠HND+140°﹣90°+12∠BMH=180°.∴∠ENQ+12(HND+∠BMH)=130°.∴∠ENQ+12∠MEN=130°.∴∠ENQ=130°﹣110°=20°.【点睛】本题考查了平行线的性质,角平分线的性质,邻补角,等量代换,角之间的数量关系运算,辅助线的作法,正确作出辅助线是解题的关键,本题综合性较强.9.(1),;(2)30°;(3)15秒或82.5秒【分析】(1)解出式子即可;(2)根据,用含t 的式子表示出,根据(2)中给出的条件得出方程式 ,求出 t 的值,进而求出的度数;(3)根据灯B 的解析:(1)3a =,1b =;(2)30°;(3)15秒或82.5秒【分析】(1)解出式子()2340a b a b -++-=即可;(2)根据//PQ MN ,用含t 的式子表示出BCA ∠,根据(2)中给出的条件得出方程式 ()()9090180229020⎡⎤∠=︒-∠=︒-︒-︒=︒-︒=︒⎣⎦BCD BCA t t ,求出 t 的值,进而求出BAC ∠的度数;(3)根据灯B 的要求,t <150,在这个时间段内A 可以转3次,分情况讨论.【详解】解:(1)2|3|(4)0a b a b -++-=.又|3|0a b -≥,2(4)0a b +-≥.3a ∴=,1b =;(2)设A 灯转动时间为t 秒,如图,作//CE PQ ,而//,PQ MN////,PQ CE MN ∴1803ACE CAN t ∴∠=∠=︒-︒,BCE CBD t ∠=∠=︒,()()18031802∴∠=∠+∠=︒+︒-︒=︒-︒BCA CBD CAN t t t ,90ACD ∠=︒,[]9090180(2)(2)9020∴∠=︒-∠=︒-︒-︒=︒-︒=︒BCD BCA t t ,55∴=t()1803∠=︒-︒CAN t ,()()451803313516513530∴∠=︒-︒-︒=︒-︒=︒-︒=︒⎡⎤⎣⎦BAC t t(3)设A 灯转动t 秒,两灯的光束互相平行.依题意得0150t <<①当060t <<时,两河岸平行,所以()233t ∠=∠=︒ 两光线平行,所以2130t ∠=∠=+︒所以,13∠=∠即:330=+t t ,解得15t =;②当60120t <<时,两光束平行,所以()2330t ∠=∠=+︒两河岸平行,所以12180∠+∠=︒13180t ∠=-︒所以,318030180-++=t t ,解得82.5t =;③当120150t <<时,图大概如①所示336030t t -=+,解得195150t =>(不合题意)综上所述,当15t =秒或82.5秒时,两灯的光束互相平行.【点睛】这道题考察的是平行线的性质和一元一次方程的应用.根据平行线的性质找到对应角列出方程是解题的关键.10.(1)①35°;(2)55°;(2)存在,或【分析】(1)①依据平行线的性质以及角平分线的定义,即可得到∠PCG 的度数; ②依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠GCF=20° 解析:(1)①35°;(2)55°;(2)存在,52.5︒或7.5︒【分析】(1)①依据平行线的性质以及角平分线的定义,即可得到∠PCG 的度数;②依据平行线的性质以及角平分线的定义,即可得到∠ECG =∠GCF =20°,再根据PQ ∥CE ,即可得出∠CPQ=∠ECP=60°;(2)设∠EGC=3x,∠EFC=2x,则∠GCF=3x-2x=x,分两种情况讨论:①当点G、F在点E 的右侧时,②当点G、F在点E的左侧时,依据等量关系列方程求解即可.【详解】解:(1)①∵AB∥CD,∴∠CEB+∠ECQ=180°,∵∠CEB=110°,∴∠ECQ=70°,∵∠PCF=∠PCQ,CG平分∠ECF,∴∠PCG=∠PCF+∠FCG=12∠QCF+12∠FCE=12∠ECQ=35°;②∵AB∥CD,∴∠QCG=∠EGC,∵∠QCG+∠ECG=∠ECQ=70°,∴∠EGC+∠ECG=70°,又∵∠EGC-∠ECG=30°,∴∠EGC=50°,∠ECG=20°,∴∠ECG=∠GCF=20°,∠PCF=∠PCQ=12(70°−40°)=15°,∵PQ∥CE,∴∠CPQ=∠ECP=∠ECQ-∠PCQ=70°-15°=55°.(2)52.5°或7.5°,设∠EGC=3x°,∠EFC=2x°,①当点G、F在点E的右侧时,∵AB∥CD,∴∠QCG=∠EGC=3x°,∠QCF=∠EFC=2x°,则∠GCF=∠QCG-∠QCF=3x°-2x°=x°,∴∠PCF=∠PCQ=12∠FCQ=12∠EFC=x°,则∠ECG=∠GCF=∠PCF=∠PCD=x°,∵∠ECD=70°,∴4x=70°,解得x=17.5°,∴∠CPQ=3x=52.5°;②当点G、F在点E的左侧时,反向延长CD到H,∵∠EGC=3x°,∠EFC=2x°,∴∠GCH=∠EGC=3x°,∠FCH=∠EFC=2x°,∴∠ECG=∠GCF=∠GCH-∠FCH=x°,∵∠CGF=180°-3x°,∠GCQ=70°+x°,∴180-3x=70+x,解得x=27.5,∴∠FCQ=∠ECF+∠ECQ=27.5°×2+70°=125°,∠FCQ=62.5°,∴∠PCQ=12∴∠CPQ=∠ECP=62.5°-55°=7.5°,【点睛】本题主要考查了平行线的性质,掌握两直线平行,同旁内角互补;两直线平行,内错角相等是解题的关键.三、解答题11.(1)50°;(2)∠A+∠C=30°+α,理由见解析;(3)∠A-∠DCM=30°+α或30°-α【分析】(1)过M作MN∥AB,由平行线的性质即可求得∠M的值.(2)延长BA,DC交于E,解析:(1)50°;(2)∠A+∠C=30°+α,理由见解析;(3)∠A-∠DCM=30°+α或30°-α【分析】(1)过M作MN∥AB,由平行线的性质即可求得∠M的值.(2)延长BA,DC交于E,应用四边形的内角和定理与平角的定义即可解决问题.(3)分两种情形分别求解即可;【详解】解:(1)过M作MN∥AB,∵AB∥CD,∴AB∥MN∥CD,∴∠1=∠A,∠2=∠C,∴∠AMC=∠1+∠2=∠A+∠C=50°;故答案为:50°;(2)∠A+∠C=30°+α,延长BA,DC交于E,∵∠B+∠D=150°,∴∠E=30°,∵∠BAM+∠DCM=360°-(∠EAM+∠ECM)=360°-(360°-∠E-∠M)=30°+α;即∠A+∠C=30°+α;(3)①如下图所示:延长BA、DC使之相交于点E,延长MC与BA的延长线相交于点F,∵∠B+∠D=150°,∠AMC=α,∴∠E=30°由三角形的内外角之间的关系得:∠1=30°+∠2∠2=∠3+α∴∠1=30°+∠3+α∴∠1-∠3=30°+α即:∠A-∠C=30°+α.②如图所示,210-∠A=(180°-∠D CM)+α,即∠A-∠DCM=30°-α.综上所述,∠A -∠DCM =30°+α或30°-α.【点睛】本题考查了平行线的性质.解答该题时,通过作辅助线准确作出辅助线l ∥AB ,利用平行线的性质(两直线平行内错角相等)将所求的角∠M 与已知角∠A 、∠C 的数量关系联系起来,从而求得∠M 的度数.12.(1);(2)①,见解析;②或【分析】(1)由平行线的性质可得到:,,再利用角的等量代换换算即可;(2)①设,,利用角平分线的定义和角的等量代换表示出对比即可;②分类讨论点在的左右两侧的情况,解析:(1)125︒;(2)①2ABD EAF ∠=∠,见解析;②30或110︒【分析】(1)由平行线的性质可得到:DEA EAN =∠∠,MBA BAN =∠∠,再利用角的等量代换换算即可;(2)①设EAF α∠=,AED=DAE=β∠∠,利用角平分线的定义和角的等量代换表示出ABD ∠对比即可;②分类讨论点D 在B 的左右两侧的情况,运用角的等量代换换算即可.【详解】.解:(1)设在1l 上有一点N 在点A 的右侧,如图所示:∵12//l l∴DEA EAN =∠∠,MBA BAN =∠∠∴50AED DAE EAN ==︒∠=∠∠∴255050125BAN BAD DAE EAN =++=︒+︒+︒=︒∠∠∠∠125BAM =︒∠(2)①2ABD=EAF ∠∠.证明:设EAF α∠=,AED=DAE=β∠∠.∴+=+FAD EAF DAE αβ=∠∠∠.∵AF 为CAD ∠的角平分线,∴22+2CAD FAD αβ==∠∠.∵12l l ,∴EAN=AED=β∠∠.∴2+22CAN CAD DAE EAN αβββα=--=--=∠∠∠∠.∴=22ABD CAN EAF α∠∠==∠.②当点D 在点B 右侧时,如图:由①得:2ABD EAF ∠=∠又∵180ABD ABM +=︒∠∠∴2180ABM EAF +=︒∠∠∵150ABM EAF ∠+∠︒=∴18015030EAF =︒-︒=︒∠当点D 在点B 左侧,E 在B 右侧时,如图:∵AF 为CAD ∠的角平分线 ∴12DAF CAD =∠∠∵12l l∴AED NAE =∠∠,CAN ABE =∠∠∵DAE AED NAE ==∠∠∠ ∴11()22DAE DAE NAE DAN =+=∠∠∠∠ ∴11()(360)22EAF DAF DAE CAD DAN CAN =+=+=︒-∠∠∠∠∠∠ 11802ABE =︒-∠ ∵180ABE ABM +=︒∠∠∴11180(180)9022EAF ABM ABM =︒-︒-=︒+∠∠∠ 又∵150EAF ABM +=︒∠∠∴1190(150)16522EAF EAF EAF =︒+⨯︒-=︒-∠∠∠ ∴110EAF =︒∠当点D 和F 在点B 左侧时,设在2l 上有一点G 在点B 的右侧如图:此时仍有12DAE DAN =∠∠,12DAF CAD =∠∠ ∴11(360)1802211180(180)9022EAF DAE DAF CAN ABG ABM ABM =+=︒-=︒-=︒-︒-=︒+∠∠∠∠∠∠∠ ∴110EAF =︒∠综合所述:30EAF ∠=︒或110︒【点睛】本题主要考查了平行线的性质,角平分线的定义,角的等量代换等,灵活运用平行线的性质和角平分线定义等量代换出角的关系是解题的关键.13.(1)∠PAF +∠PBN +∠APB =360°;(2)①,见解析;②或【分析】(1)作PC ∥EF ,如图1,由PC ∥EF ,EF ∥MN 得到PC ∥MN ,根据平行线的性质得∠PAF +∠APC =180°,∠解析:(1)∠PAF +∠PBN +∠APB =360°;(2)①CPD αβ∠=∠+∠,见解析;②CPD βα∠=∠-∠或CPD αβ∠=∠-∠【分析】(1)作PC ∥EF ,如图1,由PC ∥EF ,EF ∥MN 得到PC ∥MN ,根据平行线的性质得∠PAF +∠APC =180°,∠PBN +∠CPB =180°,即有∠PAF +∠PBN +∠APB =360°;(2)①过P 作PE ∥AD 交ON 于E ,根据平行线的性质,可得到EPD α∠=∠,CPE β∠=∠,于是CPD αβ∠=∠+∠;②分两种情况:当P 在OB 之间时;当P 在OA 的延长线上时,仿照①的方法即可解答.【详解】解:(1)∠PAF +∠PBN +∠APB =360°,理由如下:作PC ∥EF ,如图1,∵PC ∥EF ,EF ∥MN ,∴PC ∥MN ,∴∠PAF +∠APC =180°,∠PBN +∠CPB =180°,∴∠PAF +∠APC +∠PBN +∠CPB =360°,∴∠PAF +∠PBN +∠APB =360°;(2)①CPD αβ∠=∠+∠,理由如下:如答图,过P 作PE ∥AD 交ON 于E ,∵AD ∥BC ,∴PE ∥BC ,∴EPD α∠=∠,CPE β∠=∠,∴CPD αβ∠=∠+∠②当P 在OB 之间时,CPD αβ∠=∠-∠,理由如下:如备用图1,过P 作PE ∥AD 交ON 于E ,∵AD ∥BC ,∴PE ∥BC ,∴EPD α∠=∠,CPE β∠=∠,∴CPD αβ∠=∠-∠;当P 在OA 的延长线上时,CPD βα∠=∠-∠,理由如下:如备用图2,过P 作PE ∥AD 交ON 于E ,∵AD ∥BC ,∴PE ∥BC ,∴EPD α∠=∠,CPE β∠=∠,∴CPD βα∠=∠-∠;综上所述,∠CPD ,∠α,∠β之间的数量关系是CPD βα∠=∠-∠或CPD αβ∠=∠-∠.【点睛】本题考查了平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.难点是分类讨论作平行辅助线.14.(1);(2),证明见解析;(3),证明见解析.【分析】(1)过点作,先根据平行线的性质、平行公理推论可得,从而可得,再根据平行线的性质可得,然后根据角平分线的定义可得,最后根据角的和差即可得; 解析:(1)90︒;(2)2APC AEC ∠=∠,证明见解析;(3)2360APC AEC ∠+∠=︒,证明见解析.【分析】(1)过点E 作//EF AB ,先根据平行线的性质、平行公理推论可得,AEF BAE CEF DCE ∠=∠∠=∠,从而可得AEC BAE DCE ∠=∠+∠,再根据平行线的性质可得180PAB PCD ∠+∠=︒,然后根据角平分线的定义可得11,22BAE PAB DCE PCD ∠=∠∠=∠,最后根据角的和差即可得; (2)过点E 作//EF AB ,过点P 作//PQ AB ,先根据(1)可得1()2AEC BAE DCE PAB PCD ∠=∠+∠=∠+∠,再根据(1)同样的方法可得APC PAB PCD ∠=∠+∠,由此即可得出结论;(3)过点E 作//EF AB ,过点P 作//PQ AB ,先根据(1)可得2PAB PCD AEC ∠+∠=∠,再根据平行线的性质、平行公理推论可得180,180APQ PAB CPQ PCD ∠=︒-∠∠=︒-∠,然后根据角的和差、等量代换即可得出结论.【详解】解:(1)如图,过点E 作//EF AB ,AEF BAE ∴∠=∠,//AB CD ,//EF CD ∴,CEF DCE ∴∠=∠,AEC AEF CEF BAE DCE ∴∠=∠+∠=∠+∠,又//AB CD ,且点P 运动到线段AC 上,180PAB PCD ∴∠+∠=︒,AE ∵平分PAB ∠,CE 平分PCD ∠, 11,22BAE PAB DCE PCD ∴∠=∠∠=∠, 111()90222AEC PAB PCD PAB PCD ∴∠=∠+∠=∠+∠=︒; (2)猜想2APC AEC ∠=∠,证明如下:如图,过点E 作//EF AB ,过点P 作//PQ AB ,由(1)已得:1()2AEC BAE DCE PAB PCD ∠=∠+∠=∠+∠, 同理可得:APC PAB PCD ∠=∠+∠,2APC AEC ∴∠=∠;(3)2360APC AEC ∠+∠=︒,证明如下:如图,过点E 作//EF AB ,过点P 作//PQ AB ,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级(下)数学培优试题(一)含答案
一.选择题(共10小题,每小题3分,计30分.每小题只有一个选项符合题意)
1.下列各式计算正确的是( )
A.3332x x x ⋅= B .235()x x = C .358x x x += D .444()xy x y =
2.下列能用平方差公式计算的是( )
A.)y x )(y x (-+- B .)x 1)(1x (--- C.)x y 2)(y x 2(-+ D.)1x )(2x (+-
3.如图1,已知∠1=110°,∠2=70°,∠4=115°,则∠3的度数为( ) A .65º B .70º C .97º D .115º
4.2011世界园艺博览会在西安浐灞生态区举办,这次会园占地
面积为418万平方米,这个数据用科学记数法可表示为(保留
两个有效数字)( ) 图1
A.4.18×106平方米
B. 4.1×106平方米 C . 4.2×106平方米 D.
4.18×104平方米
5.某校组织的联欢会上有一个闯关游戏:将四张画有含30°的直角三
角形、正方形、等腰三角形、平行四边形这四种图形的卡片任意摆放,
将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称
图形就可以过关,那么翻一次就过关的概率是( )
A.1/4
B. 1/2 C . 1/3 D.1
6.如图2,一块实验田的形状是三角形(设其为△ABC ),管理员从
BC 边上的一点D 出发,沿DC →CA →AB →BD 的方向走了一圈回
到D 处,则管理员从出发到回到原处在途中身体( )
A.转过90° B .转过180° C.转过270° D.转过
a b c d
2 4 1
360°
7. 如图3所示,在△ABC 和△DEF 中,BC ∥EF ,∠BAC =∠D ,
且AB =DE =4,BC =5,AC =6,则EF 的长为( ).
A 4
B .5
C .6 D.不能确定
8.地表以下的岩层温度y 随着所处深度x 的变化而变化,在某个地点 y 与x 的关系可以由公式2035+=x y 来表示,则y 随x 的增大而
( ) 图3
A 、增大
B 、减小
C 、不变
D 、以上答案
都不对
9. 如图4,图象描述了某汽车在行驶过程中速度与时
间的关系,下列说法中错误的是
( ) .
A.第3分时汽车的速度是40千米/时
B.第12分时汽车的速度是0千米/时
C .从第3分到第6分,汽车行驶了120千米
D.从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
10. 下列交通标志中,轴对称图形的个数是( )
A.4个
B.3个
C.2个
D.1个
二.填空题:(每空3分,共36分)
11.代数式3234155a x a x x -+是___ ____项式,次数是
__ ___次 图4
124︒
78︒E
D C
B A
12.计算:2
--+-=___________
x x x
(1)(23)(23)
13. 如图5,DAE是一条直线,DE∥BC,则∠BAC=_____.
图5
14.北冰洋的面积是1475.0万平方千米,精确到___ __位,有
___ _个有效数字
15.某七年级(2)班举行“建党九十周年”演讲比赛,共有甲、
乙、丙三位选手,班主任让三位选手抽签决定演讲先后顺序,
从先到后恰好是甲、乙、丙的概率是.图6
16. 如图6,⊿ABC中,∠A=40°,∠B=72°,CE平分∠ACB,
CD⊥AB于D,DF⊥CE,则∠CDF =
17. 如图7,AB∥EF∥DC,∠ABC=90°,AB=DC,则
图中有全等三角形对.
18.一根弹簧原长13厘米,挂物体质量不得超过16千克,并且
图7
每挂1千克就伸长0.5厘米,则当挂物体质量为10千克,弹簧
长度为________厘米,挂物体X(千克)与弹簧长度y(厘米)
的关系式为_______.(不考虑x的取值范围)
19.如图8,D,E为AB,AC的中点,DE//BC,将△ABC沿线段DE 折叠,使点A落在点F处,若∠B=50°,则∠BDF=______.
图8
三.解答题(共54分)
20. 计算:(每小题5分,共10分)
①3b-2a2-(-4a+a2+3b)+a2②(4m3n-6 m2n2+12mn3)÷2mn
21.(7分)先化简,再求值:22
+---÷,其中10
xy xy x y xy
[(2)(2)2(2)]()
x=,
1
y=-.
25
22.(8分)小明家的阳台地面,水平铺设着仅颜色不同的18块黑色方砖(如图10所示),他从房间里向阳台抛小皮球,小皮球最终随机
停留在某块方砖上.
(1)分别求出小皮球停在黑色方砖和白色方砖上的概率;
(2)要使这两个概率相等,可以改变第几行第即列的哪块方砖颜色?怎样改变?
23.(9分)公园里有一条“Z ”字型道路ABCD ,如图,其中AB ∥CD ,在AB 、BC 、CD 三段路旁各有一只石凳E 、M 、F ,M 恰为BC 的中点,且E 、F 、M 在同一直线上,在BE 道路中停放着一排小汽车,从而无法直接测量B 、E 之间的距离,你能想出解决的方法吗?请说明其中的道理.
图
10
24. (10分)小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校. 以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题: (1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
0 2 4 6 8 10 12 14 时间(分
家
25.(10分)两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B C E
,,在同一条直线上,连结CD,AB AC
∴=,AE AD
=.请找出图②中的全等三角形,并说明理由(说明:结论中不得含有未标识的字母);
C
图图
七年级(下)数学期末试题评分标准及参考答案2011.6 命题:李丹(教研室) 检测:史晓锋(龙泉中学)
一、单项选择题(每小题3分,计30分)
1.D
2.B
3.D
4.C
5.B
6.B
7.B
8.A
9.C 10.B
二、填空题(每空3分,计36分)
11. 三,五 12.-3x 2-2x +10 13. 46° 14. 千,五 15. 6
1 16. 74° 17.3
18. 18,y=13+0.5x 19. 80°
三、解答题(共54分)
20. ①解:原式=3b -2a 2+4a -a 2-3b +a
2 (3分) =-2a 2+4a (5分)
②解:原式=4m 3n÷2mn -6m 2n 2÷2mn +12mn 3÷2mn (2分) =2m 2-3mn +6n 2
(5分)
21. 解:原式2222(424)()x y x y xy =--+÷22()x y xy xy =-÷=-.(5分) 当10x =,125y =-时,原式1210255
⎛⎫=-⨯-= ⎪⎝⎭.(7分) 22. 解:(1)P (黑色方砖)=95,P (白色方砖)=9
4;(6分)
(2)要使这两个概率相等,可将其中的一块黑色方砖换为白色方砖,所改变的黑色方砖所在的行、列数答案不唯一,只要写准确即可得分.(8分)
23.解:能.在图中连结E 、M 、F .(1分)
理由:AB ∥CD →⎪⎭
⎪⎬⎫=∠=∠∠=∠CM BM C B FMC EMB (4分)
∴△EBM ≌△FCM (ASA )(7分)
∴BE=CF .因此测量C 、F 之间的距离就是B 、E 之间的距离.(9分)
24. 解:(1)1500米; (2分)
(2)12-14分钟最快,速度为450米/分. (5分)
(3)小明在书店停留了4分钟. (7分)
(4)小明共行驶了2700米,共用了14分钟. (10分)
25. 解:图2中ABE ACD △≌△.(2分)
理由如下: ABC △与AED △都是直角三角形
∴90BAC EAD ∠=∠= (4分)
BAC CAE EAD CAE ∴∠+∠=∠+∠
即BAE CAD ∠=∠ (6分)
又∵AB=AC,AE=AD
ABE ACD ∴△≌△ (10分。
