计算方法实验一
实验一常用计算方法及描述统计量分析

实验一常用计算方法及描述统计量分析1.引言描述统计量是统计学中常用的数据分析方法。
通过统计样本数据的各种特征指标,可以对总体数据的一些性质进行分析和描述。
本实验主要介绍几种常用的计算方法及描述统计量分析。
2.均值均值是描述数据集中趋势的一个重要统计量。
一组数据的均值可以通过将所有观察值相加,然后除以观察值的总数来计算。
均值可以用来描述一个数据集的集中趋势,通常用符号μ来表示。
3.中位数中位数是将一组有序数据划分为较小和较大两部分的值,位于中间位置的值。
对于一个有序的数据集,中位数就是位于中间位置的数值。
如果数据集的观察值个数是奇数,则中位数是排在中间的值;如果数据集的观察值个数是偶数,中位数是排在中间两个值的平均值。
4.众数众数是数据集中出现频率最高的数值。
一个数据集可以有一个或多个众数。
众数可以用来描述数据集中出现频率最高的数值,通常用符号Mo 表示。
5.极差极差是描述数据集分散程度的一个统计量。
它是数据集中最大值与最小值的差别。
极差可以用来描述数据集的波动性,如果极差较大,说明数据分散程度较大。
6.方差方差是描述数据集分散程度的一个统计量。
方差是数据与其均值之间差异的平均平方值。
方差可以用来描述数据集的波动性,如果方差较大,说明数据分散程度较大。
7.标准差标准差是描述数据集分散程度的一个统计量。
标准差是方差的平方根,用符号σ来表示。
标准差可以用来描述数据集的波动性,如果标准差较大,说明数据分散程度较大。
8.相关系数相关系数是描述两个变量之间关系强度的一个统计量。
相关系数的取值范围在-1到1之间,当相关系数为正时,表示两个变量正相关,当相关系数为负时,表示两个变量负相关。
相关系数可以用来描述两个变量之间的关联程度。
9.回归分析回归分析是一种描述和预测变量之间关系的方法。
回归分析可以用来研究因变量与自变量之间的关系,并通过建立回归方程对因变量进行预测和解释。
10.结论通过实验一的学习,我们了解了常用的计算方法及描述统计量分析。
计算方法_实验报告

一、实验目的1. 理解并掌握计算方法的基本概念和原理;2. 学会使用计算方法解决实际问题;3. 提高编程能力和算法设计能力。
二、实验内容本次实验主要涉及以下内容:1. 线性方程组的求解;2. 多项式插值;3. 牛顿法求函数零点;4. 矩阵的特征值和特征向量求解。
三、实验环境1. 操作系统:Windows 102. 编程语言:Python3.83. 科学计算库:NumPy、SciPy四、实验步骤及结果分析1. 线性方程组的求解(1)实验步骤a. 导入NumPy库;b. 定义系数矩阵A和增广矩阵b;c. 使用NumPy的linalg.solve()函数求解线性方程组。
(2)实验结果设系数矩阵A和增广矩阵b如下:A = [[2, 1], [1, 2]]b = [3, 2]解得:x = [1, 1]2. 多项式插值(1)实验步骤a. 导入NumPy库;b. 定义插值点x和对应的函数值y;c. 使用NumPy的polyfit()函数进行多项式拟合;d. 使用poly1d()函数创建多项式对象;e. 使用多项式对象计算插值点对应的函数值。
(2)实验结果设插值点x和对应的函数值y如下:x = [1, 2, 3, 4, 5]y = [1, 4, 9, 16, 25]拟合得到的二次多项式为:f(x) = x^2 + 1在x = 3时,插值得到的函数值为f(3) = 10。
3. 牛顿法求函数零点(1)实验步骤a. 导入NumPy库;b. 定义函数f(x)和导数f'(x);c. 设置初始值x0;d. 使用牛顿迭代公式进行迭代计算;e. 判断迭代结果是否满足精度要求。
(2)实验结果设函数f(x) = x^2 - 2x - 3,初始值x0 = 1。
经过6次迭代,得到函数零点x ≈ 3。
4. 矩阵的特征值和特征向量求解(1)实验步骤a. 导入NumPy库;b. 定义系数矩阵A;c. 使用NumPy的linalg.eig()函数求解特征值和特征向量。
计算方法 实验一 方程求根

实验一方程求根(1)二分法
1、实验程序
实现二分法的MATLAB函数文件agui_bisect.m
2. 在MATLAB命令窗口输入及实验结果及操作界面
(2)迭代法
1、实验程序
实现二分法的MATLAB函数文件agui_iterative.m
2、在MATLAB命令窗口输入及实验结果及操作界面
(3)牛顿法
1、实验程序
实现二分法的MATLAB函数文件agui_newton.m
2、在MATLAB命令窗口输入及实验结果及操作界面
结果分析:
由上面的对二分法、迭代法、牛顿法三种方法的三次实验结果,我们可以得出这样的结论:
二分法要循环k=10次,迭代法要迭代k=4次,牛顿法要迭代k=2次才能达到精度为0.5*10^-3的要求,而且方程0210=-+x e x
的精确解经计算,为0.0905250,由此可知,牛顿法和迭代法的精确度要优越于二分法。
而这三种方法中,牛顿法不仅计算量少,而且精确度高。
从而可知牛顿迭代法收敛速度明显加快,但由所学的内容可知,其收敛性与初值有关,它是局部收敛的。
二分法收敛虽然是速度最慢,但也常用于求精度不高的近似根。
而迭代法是逐次逼近的方法,原理简单,但存在收敛性和收敛速度的问题。
总之各种方法都各有优劣,适用于不同的情况中,须具体情况具体分析。
计算方法实验报告

班级:地信11102班序号: 20姓名:任亮目录计算方法实验报告(一) (3)计算方法实验报告(二) (6)计算方法实验报告(三) (9)计算方法实验报告(四) (13)计算方法实验报告(五) (18)计算方法实验报告(六) (22)计算方法实验报告(七) (26)计算方法实验报告(八) (28)计算方法实验报告(一)一、实验题目:Gauss消去法解方程组二、实验学时: 2学时三、实验目的和要求1、掌握高斯消去法基础原理2、掌握高斯消去法法解方程组的步骤3、能用程序语言对Gauss消去法进行编程实现四、实验过程代码及结果1、实验算法及其代码模块设计(1)、建立工程,建立Gauss.h头文件,在头文件中建类,如下:class CGauss{public:CGauss();virtual ~CGauss();public:float **a; //二元数组float *x;int n;public:void OutPutX();void OutputA();void Init();void Input();void CalcuA();void CalcuX();void Calcu();};(2)、建立Gauss.cpp文件,在其中对个函数模块进行设计2-1:构造函数和析构函数设计CGauss::CGauss()//构造函数{a=NULL;x=NULL;cout<<"CGauss类的建立"<<endl;}CGauss::~CGauss()//析构函数{cout<<"CGauss类撤销"<<endl;if(a){for(int i=1;i<=n;i++)delete a[i];delete []a;}delete []x;}2-2:函数变量初始化模块void CGauss::Init()//变量的初始化{cout<<"请输入方程组的阶数n=";cin>>n;a=new float*[n+1];//二元数组初始化,表示行数for(int i=1;i<=n;i++){a[i]=new float[n+2];//表示列数}x=new float[n+1];}2-3:数据输入及输出验证函数模块void CGauss::Input()//数据的输入{cout<<"--------------start A--------------"<<endl;cout<<"A="<<endl;for(int i=1;i<=n;i++)//i表示行,j表示列{for(int j=1;j<=n+1;j++){cin>>a[i][j];}}cout<<"--------------- end --------------"<<endl;}void CGauss::OutputA()//对输入的输出验证{cout<<"-----------输出A的验证-----------"<<endl;for(int i=1;i<=n;i++){for(int j=1;j<=n+1;j++){cout<<a[i][j]<<" ";}cout<<endl;}cout<<"---------------END--------------"<<endl;}2-4:消元算法设计及实现void CGauss::CalcuA()//消元函数for(int k=1 ;k<n;k++){for(int i=k+1;i<=n;i++){double lik=a[i][k]/a[k][k];for(int j=k;j<=n+1;j++){a[i][j]-=lik*a[k][j];}a[i][k]=0; //显示消元的效果}}}2-5:回代计算算法设计及函数实现void CGauss::CalcuX()//回带函数{for(int i=n;i>=1;i--){double s=0;for(int j=i+1;j<=n;j++){s+=a[i][j]*x[j];}x[i]=(a[i][n+1]-s)/a[i][i];}}2-6:结果输出函数模块void CGauss::OutPutX()//结果输出函数{cout<<"----------------X---------------"<<endl;for(int i=1 ;i<=n;i++){cout<<"x["<<i<<"]="<<x[i]<<endl;}}(3)、“GAUSS消元法”主函数设计int main(int argc, char* argv[]){CGauss obj;obj.Init();obj.Input();obj.OutputA();obj.CalcuA();obj.OutputA();obj.CalcuX();obj.OutPutX();//obj.Calcu();return 0;2、实验运行结果计算方法实验报告(二)一、实验题目:Gauss列主元消去法解方程组二、实验学时: 2学时三、实验目的和要求1、掌握高斯列主元消去法基础原理(1)、主元素的选取(2)、代码对主元素的寻找及交换2、掌握高斯列主元消去法解方程组的步骤3、能用程序语言对Gauss列主元消去法进行编程实现四、实验过程代码及结果1、实验算法及其代码模块设计(1)、新建头文件CGuassCol.h,在实验一的基础上建立类CGauss的派生类CGuassCol公有继承类CGauss,如下:#include "Gauss.h"//包含类CGauss的头文件class CGaussCol:public CGauss{public:CGaussCol();//构造函数virtual ~CGaussCol();//析构函数public:void CalcuA();//列主元的消元函数int FindMaxIk(int k);//寻找列主元函数void Exchange(int k,int ik);//交换函数void Calcu();};(2)、建立CGaussCol.cpp文件,在其中对个函数模块进行设计2-1:头文件的声明#include "stdafx.h"#include "CGuassCol.h"#include "math.h"#include "iostream.h"2-2:派生类CGaussCol的构造函数和析构函数CGaussCol::CGaussCol()//CGaussCol类构造函数{cout<<"CGaussCol类被建立"<<endl;}CGaussCol::~CGaussCol()//CGaussCol类析构函数{cout<<"~CGaussCol类被撤销"<<endl;}2-3:高斯列主元消元函数设计及代码实现void CGaussCol::CalcuA()//{for(int k=1 ;k<n;k++){int ik=this->FindMaxIk(k);if(ik!=k)this->Exchange(k,ik);for(int i=k+1;i<=n;i++){float lik=a[i][k]/a[k][k];for(int j=k;j<=n+1;j++){a[i][j]-=lik*a[k][j];}}}}2-4:列主元寻找的代码实现int CGaussCol::FindMaxIk(int k)//寻找列主元{float max=fabs(a[k][k]);int ik=k;for(int i=k+1;i<=n;i++){if(max<fabs(a[i][k])){ik=i;max=fabs(a[i][k]);}}return ik;}2-5:主元交换的函数模块代码实现void CGaussCol::Exchange(int k,int ik)//做交换{for(int j=k;j<=n+1;j++){float t=a[k][j];a[k][j]=a[ik][j];a[ik][j]=t;}}(3)、建立主函数main.cpp文件,设计“Gauss列主元消去法”主函数模块3-1:所包含头文件声明#include "stdafx.h"#include "Gauss.h"#include "CGuassCol.h"3-2:主函数设计int main(int argc, char* argv[]){CGaussCol obj;obj.Init();//调用类Gauss的成员函数obj.Input();//调用类Gauss的成员函数obj.OutputA();//调用类Gauss的成员函数obj.CalcuA();obj.OutputA();obj.CalcuX();obj.OutPutX();return 0;}2、实验结果计算方法实验报告(三)一、实验题目:Gauss完全主元消去法解方程组二、实验学时: 2学时三、实验目的和要求1、掌握高斯完全主元消去法基础原理;2、掌握高斯完全主元消去法法解方程组的步骤;3、能用程序语言对Gauss完全主元消去法进行编程(C++)实现。
东南大学计算方法实验报告

计算方法与实习实验报告学院:电气工程学院指导老师:***班级:160093******学号:********实习题一实验1 拉格朗日插值法一、方法原理n次拉格朗日插值多项式为:L n(x)=y0l0(x)+y1l1(x)+y2l2(x)+…+y n l n(x)n=1时,称为线性插值,L1(x)=y0(x-x1)/(x0-x1)+ y1(x-x0)/(x1-x0)=y0+(y1-x0)(x-x0)/(x1-x0)n=2时,称为二次插值或抛物线插值,精度相对高些L2(x)=y0(x-x1)(x-x2)/(x0-x1)/(x0-x2)+y1(x-x0)(x-x2)/(x1-x0)/(x1-x2)+y2(x-x0)(x-x1)/(x2-x0)/(x2-x1)二、主要思路使用线性方程组求系数构造插值公式相对复杂,可改用构造方法来插值。
对节点x i(i=0,1,…,n)中任一点x k(0<=k<=n)作一n 次多项式l k(x k),使它在该点上取值为1,而在其余点x i(i=0,1,…,k-1,k+1,…,n)上为0,则插值多项式为L n(x)=y0l0(x)+y1l1(x)+y2l2(x)+…+y n l n(x) 上式表明:n 个点x i(i=0,1,…,k-1,k+1,…,n)都是l k(x)的零点。
可求得l k三.计算方法及过程:1.输入节点的个数n2.输入各个节点的横纵坐标3.输入插值点4.调用函数,返回z函数语句与形参说明程序源代码如下:#include<iostream>#include<math.h>using namespace std;#define N 100double fun(double *x,double *y, int n,double p);void main(){int i,n;cout<<"输入节点的个数n:";cin>>n;double x[N], y[N],p;cout<<"please input xiangliang x= "<<endl;for(i=0;i<n;i++)cin>>x[i];cout<<"please input xiangliang y= "<<endl;for(i=0;i<n;i++)cin>>y[i];cout<<"please input LagelangrichazhiJieDian p= "<<endl;cin>>p;cout<<"The Answer= "<<fun(x,y,n,p)<<endl;system("pause") ;}double fun(double x[],double y[], int n,double p){double z=0,s=1.0;int k=0,i=0;double L[N];while(k<n){ if(k==0){ for(i=1;i<n;i++)s=s*(p-x[i])/(x[0]-x[i]);L[0]=s*y[0];k=k+1;}else{s=1.0;for(i=0;i<=k-1;i++)s=s*((p-x[i])/(x[k]-x[i]));for(i=k+1;i<n;i++) s=s*((p-x[i])/(x[k]-x[i]));L[k]=s*y[k];k++;}}for(i=0;i<n;i++)z=z+L[i];return z;}五.实验分析n=2时,为一次插值,即线性插值n=3时,为二次插值,即抛物线插值n=1,此时只有一个节点,插值点的值就是该节点的函数值n<1时,结果都是返回0的;这里做了n=0和n=-7两种情况3<n<100时,也都有相应的答案常用的是线性插值和抛物线插值,显然,抛物线精度相对高些n次插值多项式Ln(x)通常是次数为n的多项式,特殊情况可能次数小于n.例如:通过三点的二次插值多项式L2(x),如果三点共线,则y=L2(x)就是一条直线,而不是抛物线,这时L2(x)是一次式。
计算方法与计算 实验一误差分析

% 输出的量--每次迭代次数k和迭代值xk,
%
--每次迭代的绝对误差juecha和相对误差xiangcha,
误差分析
误差问题是数值分析的基础,又是数值分析中一个困难的课题。在实际计算 中,如果选用了不同的算法,由于舍入误差的影响,将会得到截然不同的结果。 因此,选取算法时注重分析舍入误差的影响,在实际计算中是十分重要的。同时, 由于在数值求解过程中用有限的过程代替无限的过程会产生截断误差,因此算法 的好坏会影响到数值结果的精度。 一、实验目的
因为运行后输出结果为: y 1.370 762 168 154 49, yˆ =1.370 744 664 189
38, R 1.750 396 510 491 47e-005, WU= 1.782 679 830 970 664e-005 104 . 所
以, yˆ 的绝对误差为 10 4 ,故 y
③ 运行后输出计算结果列入表 1–1 和表 1-2 中。
④ 将算法 2 的 MATLAB 调用函数程序的函数分别用 y1=15-2*x^2 和
y1=x-(2*x^2+x-15)/(4*x+1)代替,得到算法 1 和算法 3 的调用函数程序,将其保
存,运行后将三种算法的前 8 个迭代值 x1, x2 ,, x8 列在一起(见表 1-1),进行
的精确解 x* 2.5 比较,观察误差的传播.
算法 1 将已知方程化为同解方程 x 15 2x2 .取初值 x0 2 ,按迭代公式
xk1 15 2xk2
计算方法实验一-二分法

学院 长望学院 专业 大气科学实验班 年级 班次 1 姓名 仙女 学号1. 引言-问题重述问题一要求对方程3()250f x x x =--=,用二分法,至少找到一个根,并展示一下信息:(a )近似根(b )初始猜测(区间)(c )迭代次数(d )停止准则(3)收敛速度 问题二要求用二分法求出以下两个方程的近似根:(a )5()10f x x x =--=,(b )22520x e x -+=.2. 数学公式-数值方法和参数定义二分法求根原理为:若[,]f C a b ∈,严格单调,且()()0f a f b <g ,则f 在(,)a b 上有一实根。
其基本思想为:逐步将区间分半,计算中点处的函数值,根据介值定理选择比原区间缩小一半的有根区间,如此继续下去,直到得到满足精度要求,从而求出满足给定精度的根的近似值。
针对问题一,本文根据方程,定义函数f(x)=a*x*x*x+b*x*x+c*x+d=0,其中,,,a b c d 为各项系数;精度16eps e =-;,m n 分别为求根区间的左右端点,即收敛区间[,]m n ;i 为近似根;v 为收敛速度,count 为当前迭代次数。
其中,count 为单精度int 类型,其余均为双精度double 类型。
基于以上参数定义,设置收敛准则为:当根和函数值的精度小于所设置精度时,结束循环,并输出收敛区间、迭代次数、近似根以及收敛速度。
具体表现为:每进行一次循环视近似根i 的相对位置对收敛区间进行修正,同时对迭代次数+1;收敛速度可通过下式计算:11n n n n x x v x x +--=-. 针对问题二(a )在问题一的基础上,更改方程f(x)=a*x*x*x+b*x*x+c*x+d=0的系数以及相关项即可求得相应结果。
对于(b )将方程改为:exp(2*x)-5*x*x+20=。
3. 数值实验-讨论和分析数值结果针对方程3()250f x x x =--=,首先对其求导,判断单调性,再进行需略估算,发现(2)(3)0f f <g ,于是设置初始收敛区间为[2,3],进而通过二分法求得结果如图1。
计算方法实验一

计算方法实验一1.迭代函数对收敛性的影响实验目的:初步了解非线性方程的简单迭代法及其收敛性,体会迭代函数对收敛性的影响,知道当迭代函数满足什么条件时,迭代法收敛。
实验内容:用简单迭代法求方程 012)(3=--=x x x f 的根。
方案一: 化012)(3=--=x x x f 为等价方程 )(213x x x φ==∆+= 方案二: 化012)(3=--=x x x f 为等价方程 )(123x x x φ==∆-=实验要求:(1)分别对方案一、方案二取初值00=x ,迭代10次,观察其计算值,并加以分析。
(2)用MATLAB 内部函数solve 直接求出方程的所有根,并与(1)的结果进行比较。
2. 初值的选取对迭代法的影响实验目的:通过具体的数值实验,体会选取不同的初值对同一迭代法的影响。
实验内容:用牛顿迭代法求方程 013=--x x 在x =1.5附近的根。
实验要求:(1)对牛顿迭代公式: 131231----=+k k k k k x x x x x ,编写程序进行实验,分别取00=x ,5.10=x 迭代10次,观察比较其计算值,并分析原因。
(2)用MATLAB 内部函数solve 直接求出方程的所有根,并与(1)的结果进行比较。
1. 收敛性与收敛速度的比较实验目的:通过用不同迭代法解同一非线性方程,比较各种方法的收敛性与收敛速度。
实验内容:求解非线性方程 0232=-+-x e x x 的根,准确到106-。
实验要求:(1) 用你自己设计的一种线性收敛的迭代法求方程的根,然后用斯蒂芬森加速迭代计算。
输出迭代初值、各次迭代值及迭代次数。
(2)用牛顿迭代法求方程的根,输出迭代初值、各次迭代值及迭代次数,并与(1)的结果比较。
(3)用MATLAB内部函数solve直接求出方程的所有根,并与(1)、(2)的结果进行比较。
相关MATLAB函数提示:参考程序function [p0,err,k,y]=newton(f,df,p0,delta,epsilon,max1)%Input - f is the object function% - df is the derivative of f% - p0 is the initial approximation to a zero of f% - delta is the tolerance for p0% - epsilon is the tolerance for the function values y% - max1 is the maximum number of iterations%Output - p0 is the Newton-Raphson approximation to the zero% - err is the error estimate for p0% - k is the number of iterations% - y is the function value f(p0)%If f and df are defined as M-file functions use the @ notation% call [p0,err,k,y]=newton(@f,@df,p0,delta,epsilon,max1).%If f and df are defined as anonymous functions use the% call [p0,err,k,y]=newton(f,df,p0,delta,epsilon,max1).% NUMERICAL METHODS: Matlab Programs% (c) 2004 by John H. Mathews and Kurtis D. Fink% Complementary Software to accompany the textbook:% NUMERICAL METHODS: Using Matlab, Fourth Edition% ISBN: 0-13-065248-2% Prentice-Hall Pub. Inc.% One Lake Street% Upper Saddle River, NJ 07458for k=1:max1p1=p0-f(p0)/df(p0);err=abs(p1-p0);relerr=2*err/(abs(p1)+delta);p0=p1;y=f(p0);if (err<delta)|(relerr<delta)|(abs(y)<epsilon),break,end end。
数值计算方法实验1
学院(系)名称:)()()()(0101112x x x f x f x f x x ---=附录(源程序及运行结果):一.二分法#include<stdio.h>#include<math.h>double f(double x){return x*x-x-1;}void main(){float a=0,b=0,x=1,m,e;int k;while(f(a)*f(b)>0){printf("请输入区间a,b的值。
以及精度e\n");scanf("%f,%f,%f",&a,&b,&e);}k=0;if(f(a)*f(b)==0){if(f(a)==0)printf("使用二分法输出:a=%f,k=%d\n",a,k);elseprintf("使用二分法输出:b=%f,k=%d\n",b,k);}else{while(f(a)*f(b)!=0){m=(a+b)/2;if(fabs(a-b)/2<e){printf("使用二分法输出:m=%f,k=%d\n",m,k);break;}else {if(f(a)*f(m)>0)a=m;else b=m;k=k+1;}}}}运行结果:二.迭代法与牛顿迭代法#include<stdio.h>#include<math.h>double f(double x){return exp(-x);}double f1(double x){return (x*exp(x)-1);}double ff(double x){return (exp(x)+x*exp(x));}void diedaifa(double x0,double e,int N){double x1;int k=1;while(k!=N){x1=f(x0);if(fabs(x1-x0)>=e){k++;if(k==N)printf("迭代失败!\n");x0=x1;}else{printf("使用迭代法输出结果:%lf\n",x1);break;}}}void NDdiedaifa(double x0,double e,int N){int k=1;double x1;while(k!=N){if(ff(x0)==0)printf("公式f(x)奇异!\n");else{x1=x0-f1(x0)/ff(x0);if(fabs(x1-x0)>=e){k++;if(k==N)printf("迭代失败!\n");x0=x1;}else{printf("使用牛顿迭代法输出结果:%lf\n",x1);break;}}}}void main(){double x0,e;int N;printf("请输入初值:");scanf("%lf",&x0);printf("精度:");scanf("%lf",&e);printf("以及判定迭代失败的最大次数N:");scanf("%d",&N);diedaifa(x0,e,N);NDdiedaifa(x0,e,N);}运行结果:四.双点弦截法#include<stdio.h>#include<math.h>double f(double x){return (x*x*x+3*x*x-x-9);}void main(){double x0,x1,x2,e;int N;int k=1;printf("请输入初值x0和x1:");scanf("%lf,%lf",&x0,&x1);printf("精度:");scanf("%lf",&e);printf("以及判定迭代失败的最大次数N:");scanf("%d",&N);while(k!=N){x2=x1-f(x1)*(x1-x0)/(f(x1)-f(x0));if(fabs(f(x2))>=e){k++;if(k==N)printf("迭代失败!\n");x0=x1;x1=x2;}else{printf("使用双点弦截法输出结果:%lf\n",x2);break;}}}运行结果:。
计算方法实验报告(附代码)

实验一 牛顿下山法实验说明:求非线性方程组的解是科学计算常遇到的问题,有很多实际背景.各种算法层出不穷,其中迭代是主流算法。
只有建立有效的迭代格式,迭代数列才可以收敛于所求的根。
因此设计算法之前,对于一般迭代进行收敛性的判断是至关重要的。
牛顿法也叫切线法,是迭代算法中典型方法,只要初值选取适当,在单根附近,牛顿法收敛速度很快,初值对于牛顿迭代 至关重要。
当初值选取不当可以采用牛顿下山算法进行纠正。
牛顿下山公式:)()(1k k k k x f x f x x '-=+λ下山因子 ,,,,322121211=λ下山条件|)(||)(|1k k x f x f <+实验代码:#include<iostream> #include<iomanip> #include<cmath>using namespace std;double newton_downhill(double x0,double x1); //牛顿下山法函数,返回下山成功后的修正初值double Y; //定义下山因子Y double k; //k为下山因子Y允许的最小值double dfun(double x){return 3*x*x-1;} //dfun()计算f(x)的导数值double fun1(double x){return x*x*x-x-1;} //fun1()计算f(x)的函数值double fun2(double x) {return x-fun1(x)/dfun(x);} //fun2()计算迭代值int N; //N记录迭代次数double e; //e表示要求的精度int main(){double x0,x1;cout<<"请输入初值x0:";cin>>x0;cout<<"请输入要求的精度:";cin>>e;N=1;if(dfun(x0)==0){cout<<"f'(x0)=0,无法进行牛顿迭代!"<<endl;}x1=fun2(x0);cout<<"x0"<<setw(18)<<"x1"<<setw(18)<<"e"<<setw(25)<<"f(x1)-f(x0)"<<endl;cout<<setiosflags(ios::fixed)<<setprecision(6)<<x0<<" "<<x1<<" "<<fabs(x1-x0)<<" "<<fabs(fun1(x1))-fabs(fun1(x0))<<endl;if(fabs(fun1(x1))>=fabs(fun1(x0))){ //初值不满足要求时,转入牛顿下山法x1=newton_downhill(x0,x1);} //牛顿下山法结束后,转入牛顿迭代法进行计算while(fabs(x1-x0)>=e){ //当精度不满足要求时N=N+1;x0=x1;if(dfun(x0)==0){cout<<"迭代途中f'(x0)=0,无法进行牛顿迭代!"<<endl;} x1=fun2(x0);cout<<setiosflags(ios::fixed)<<setprecision(6)<<x0<<" "<<x1<<" "<<fabs(x1-x0)<<endl;}cout<<"迭代值为:"<<setiosflags(ios::fixed)<<setprecision(6)<<x1<<'\n';cout<<"迭代次数为:"<<N<<endl;return 0;}double newton_downhill(double x0,double x1){Y=1;cout<<"转入牛顿下山法,请输入下山因子允许的最小值:";cin>>k;while(fabs(fun1(x1))>=fabs(fun1(x0))){if(Y>k){Y=Y/2;}else {cout<<"下山失败!";exit(0);}x1=x0-Y*fun1(x0)/dfun(x0);}//下山成功则cout<<"下山成功!Y="<<Y<<",转入牛顿迭代法计算!"<<endl;return x1;}实验结果:图4.1G-S 迭代算法流程图实验二 高斯-塞德尔迭代法实验说明:线性方程组大致分迭代法和直接法。
计算方法实验报告

实验一:误差传播与算法稳定性实验目的:体会稳定性在选择算法中的地位。
实验内容:考虑一个简单的由积分定义的序列10I ,0,1,10nn x dx n a x==+⎰其中a 为参数,分别对0.05a =及15a =按下列两种方法计算。
方案1:用递推公式11,1,2,,10n n I aI n n-=-+= 递推初值可由积分直接得01lna I a+= 方案2:用递推公式111(),,1,,1n n I I n N N a n-=-+=-根据估计式当1n a n ≥+时,11(1)(1)(1)n I a n a n <<+++或当01n a n ≤<+时,11(1)(1)n I a n n<≤++ 取递推初值 当1n a n ≥+时, 11121()2(1)(1)(1)2(1)(1)N N a I I a N a N a a N +≈+=+++++ 当01n a n ≤<+时,111()2(1)(1)N N I I a N N≈+++ 实验要求:列出结果,并对其稳定性进行分析比较,说明原因。
实验二:非线性方程数值解法实验目的:探讨不同方法的计算效果和各自特点 实验内容:应用算法(1)牛顿法;(2)割线法 实验要求:(1)用上述各种方法,分别计算下面的两个例子。
在达到精度相同的前提下,比较其迭代次数。
(I )31080x x +-=,取00x =;(II) 2281(0.1)sin 1.060x x x -+++=,取00x =;(2) 取其它的初值0x ,结果如何?反复选取不同的初值,比较其结果; (3) 总结归纳你的实验结果,试说明各种方法的特点。
实验三:选主元高斯消去法----主元的选取与算法的稳定性问题提出:Gauss 消去法是我们在线性代数中已经熟悉的。
但由于计算机的数值运算是在一个有限的浮点数集合上进行的,如何才能确保Gauss 消去法作为数值算法的稳定性呢?Gauss 消去法从理论算法到数值算法,其关键是主元的选择。
《数值计算方法》实验 (1)

电子科技大学《数值计算方法》
实
验
报
告
输入6,1;0,1,21i i n a b i i n ===+=−" 结果得f=1.718263
输入10,1;0,1,21i i n a b i i n ===+=−" 结果得f=1.718282
输入100,1;0,1,21i i n a b i i n ===+=−" 结果得f=1.718282
从中计算结果看随n 增大迭代计算结果逐渐稳定,可认为出现此现象有两种情况一是对该输入序列a,b 用此迭代公式随序列増长会逐渐逼近一个稳定值,二是在迭代计算过程中产生大数“吃掉”小数现象且计算结果只取7为有效数字。
3. 实验结论
在计算机内做加法运算时,首先要对加数作对阶处理,加之计算机字长有限,因尽量避免出现大数吃小数现象,计算时要注意运算次序,否则会影响结果的可靠性。
报告评分:
指导教师签字:。
计算方法实验报告

1. 熟悉并掌握常用的计算方法,包括数值积分、数值微分、线性方程组求解等。
2. 培养运用计算机进行数值计算的能力。
3. 增强对数值计算误差的分析和判断能力。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.83. 库:NumPy、SciPy、Matplotlib三、实验内容1. 数值积分(1)函数:f(x) = x^2(2)区间:[0, 1](3)方法:梯形法、辛普森法、复合梯形法2. 数值微分(1)函数:f(x) = e^x(2)点:x = 1(3)方法:有限差分法、中点法、牛顿法3. 线性方程组求解(1)方程组:2x + 3y - z = 8-x + 2y + 2z = -3x - y + 3z = 5(2)方法:高斯消元法、LU分解法1. 数值积分(1)编写函数f(x) = x^2(2)定义积分区间[0, 1](3)实现梯形法、辛普森法、复合梯形法(4)计算积分结果2. 数值微分(1)编写函数f(x) = e^x(2)定义点x = 1(3)实现有限差分法、中点法、牛顿法(4)计算导数结果3. 线性方程组求解(1)定义方程组系数矩阵A和常数向量b(2)实现高斯消元法、LU分解法(3)求解方程组(4)输出解向量x五、实验结果与分析1. 数值积分(1)梯形法:积分结果约为1.6667(2)辛普森法:积分结果约为1.6447(3)复合梯形法:积分结果约为1.6458分析:三种方法计算结果接近,但辛普森法误差最小。
2. 数值微分(1)有限差分法:导数结果约为2.7183(2)中点法:导数结果约为2.7183(3)牛顿法:导数结果约为2.7183分析:三种方法计算结果一致,误差较小。
3. 线性方程组求解(1)高斯消元法:解向量x = [2, 1, 1](2)LU分解法:解向量x = [2, 1, 1]分析:两种方法求解结果一致,且解向量正确。
六、实验总结本次实验通过Python编程,实现了数值积分、数值微分和线性方程组求解。
计算方法实验报告01

y13=polyval(p3,t)
y14=polyval(p4,t)
r1=sum((y1-y11).^2)
r2=sum((y2-y12).^2)
r3=sum((y1-y13).^2)
r4=sum((y2-y14).^2)
plot(t,y11,'r',t,y12,'b')
plot(t,y13,'r',t,y14,'b')
4. 程序运行结果及分析(输出计算结果,结果分析)
分别画出t与浓度c的散点图(上图代表甲,下图代表乙):
分别画出t与浓度的对数y(t)=ln c(t)的散点图(上图代表甲,下图代表乙)
进行一次多项式拟合得:
y1(t)=−0.2319t+2.9795
y2(t)=−0.1278t+2.9829
进行二次多项式拟合得:
y1(t)=−0.2322t+2.9798
y2(t)=−0.1278t+2.9830
进行一次多项式拟合得到拟合曲线如图(下方代表甲,上方代表乙):
进行二次多项式拟合得到拟合曲线如图(下方代表甲,上方代表乙):
对数值结果进行分析:
进行一次多项式拟合误差平方和分别为:
r1=0.0137
r2=0.0063
进行一次多项式拟合误差平方和分别为:
r1=0.0137
r2=0.0063
经分析:
本次实验一次多项式拟合和二次多项式拟合相差不大;。
《计算方法》实验报告材料

double Newton(double x,vector<double>&X,vector<double>&Y);
int main(){
char a='n';
do{
int n;
cout<<"请输入插值点个数:"<<endl;
for(int i=0;i<N;i++){
X[i]=p;
Y[i]=1/(1+p*p);
p=p+c;
}
cout<<"请输入要求值x的值:"<<endl;
double x;
cin>>x;
double result=fenduan(N,X,Y,x,c);
cout<<"由分段线性插值法得出结果: "<<result<<endl;
cin>>n;
vector<double>X(n,0);
vector<double>Y(n,0);
cout<<"请输入插值点对应的值及函数值(Xi,Yi):"<<endl;
for(int i=0;i<n;i++){
cin>>X[i]>>Y[i];
}
cout<<"请输入要求值x的值:"<<endl;
计算方法数值实验报告

计算方法数值实验报告(一)班级:0902 学生:苗卓芳 倪慧强 岳婧实验名称: 解线性方程组的列主元素高斯消去法和LU 分解法实验目的: 通过数值实验,从中体会解线性方程组选主元的必要性和LU 分解法的优点,以及方程组系数矩阵和右端向量的微小变化对解向量的影响。
实验内容:解下列两个线性方程组(1) ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--11134.981.4987.023.116.427.199.103.601.3321x x x (2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----15900001.582012151526099999.23107104321x x x x 解:(1) 用熟悉的算法语言编写程序用列主元高斯消去法和LU 分解求解上述两个方程组,输出Ax=b 中矩阵A 及向量b, A=LU 分解的L 及U ,detA 及解向量。
①先求解第一个线性方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--11134.981.4987.023.116.427.199.103.601.3321x x x在命令窗口中运行A=[3.01,6.03,1.99;1.27,4.16,-1.23;0.987,-4.81,9.34] 可得A =3.0100 6.0300 1.99001.2700 4.1600 -1.23000.9870 -4.8100 9.3400b=[1,1,1]可得b =1 1 1H =det(A)可得 H =-0.0305列主元高斯消去法:在命令窗口中运行function x=Gauss_pivot(A,b)、A=[3.01,6.03,1.99;1.27,4.16,-1.23;0.987,-4.81,9.34];b=[1,1,1];n=length(b);x=zeros(n,1);c=zeros(1,n);dl=0;for i=1:n-1max=abs(A(i,i));m=i;for j=i+1:nif max<abs(A(j,i))max=abs(A(j,i));m=j;endendif(m~=i)for k=i:nc(k)=A(i,k);A(i,k)=A(m,k);A(m,k)=c(k);enddl=b(i);b(i)=b(m);b(m)=dl;endfor k=i+1:nfor j=i+1:nA(k,j)=A(k,j)-A(i,j)*A(k,i)/A(i,i);endb(k)=b(k)-b(i)*A(k,i)/A(i,i);A(k,i)=0;endendx(n)=b(n)/A(n,n);for i=n-1:-1:1sum=0;for j=i+1:nsum =sum+A(i,j)*x(j);endx(i)=(b(i)-sum)/A(i,i);end经程序可得实验结果ans =1.0e+003 *1.5926-0.6319-0.4936LU分解法:在命令窗口中运行function x=lu_decompose(A,b)A=[3.01,6.03,1.99;1.27,4.16,-1.23;0.987,-4.81,9.34];b=[1,1,1];L=eye(n);U=zeros(n,n);x=zeros(n,1);c=zeros(1,n);for i=1:nU(1,i)=A(1,i);if i==1;L(i,1)=1;elseL(i,1)=A(i,1)/U(1,1);endendfor i=2:nfor j=i:nsum=0;for k=1:i-1sum =sum+L(i,k)*U(k,j);endU(i,j)=A(i,j)-sum;Ifj~=nsum=0;for k=1:i-1sum=sum+L(j+1,k)*U(k,i);endL(j+1,i)=(A(j+1,i)-sum)/U(I,i);endendendy(1)=b(1);for k=2:nsum=0;forj=1:k-1sum=sum+L(k,j)*y (j);endy(k)=b(k)-sum;endx(n)=y(n)/U(n,n);260页最后一行c(k)=A(i,k);A(i,k)=A(m,k);A(m,k)=c(k);enddl=b(i);b(i)=b(m);b(m)=dl;endfor k=i+1:nfor j=i+1:nA(k,j)=A(k,j)-A(i,j)*A(k,i)/A(i,i);endb(k)=b(k)-b(i)*A(k,i)/A(i,i);A(k,i)=0;endendx(n)=b(n)/A(n,n);for i=n-1:-1:1sum=0;for j=i+1:nsum =sum+A(i,j)*x(j);endx(i)=(b(i)-sum)/A(i,i);end经程序可得结果ans =1.0e+003 *1.5926-0.6319-0.4936②再求解第二个线性方程组⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----15900001.582012151526099999.23107104321x x x x 即A=[10,-7,0,1;-3,2.099999,6,2;5,-1,5,-1;2,1,0,2];b=[8,5.900001,5,1];重复上述步骤可的结果为ans =0.0000-1.00001.00001.0000(2)将方程组(1)中系数3.01改为3.00,0.987改为0.990,用列主元高斯消去法求解变换后的方程组,输出列主元行交换次序,解向量x 及detA ,并与(1)中结果比较。
计算方法实验报告一
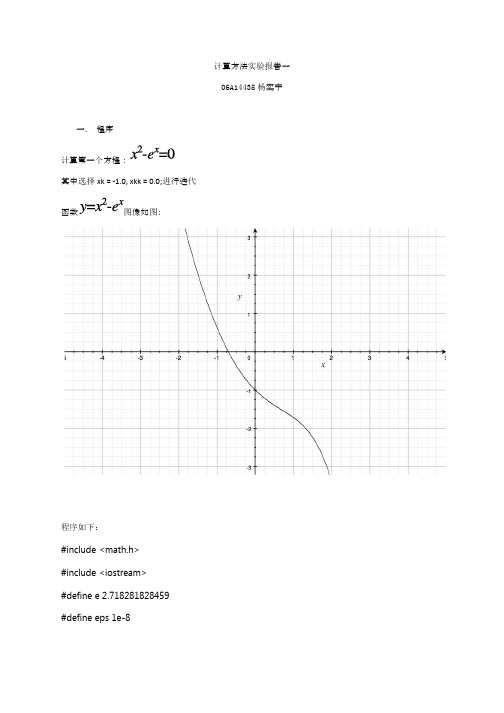
计算方法实验报告一06A14435杨奕宁一.程序计算第一个方程:其中选择xk = -1.0, xkk = 0.0;进行迭代函数图像如图:程序如下:#include <math.h>#include <iostream>#define e 2.718281828459#define eps 1e-8usingnamespace std;double f1(double x){double y;y = pow(x,2.0) - pow(e , x ) ;return y;}int main(int argc, constchar * argv[]) {// insert code here...double result = 0.0;double xk,xkk;xk =-1.0;xkk = 0.0;while (fabs(xk - xkk) > eps){result = xk - f3(xk) / (f3(xk) - f3(xkk))*(xk - xkk); xkk = xk;xk = result;}cout<<xk<<endl;return0;}计算结果得:x = -0.703467;计算第二个方程:其中选择xk = 0.0;xkk = 1.0;进行迭代函数图像如图:程序如下:#include <math.h>#include <iostream>#define e 2.718281828459#define eps 1e-8 usingnamespace std;double f2(double x){double y;y = x * pow(e, x) - 1;return y;}int main(int argc, constchar * argv[]) {// insert code here...double result = 0.0;double xk,xkk;xk =0.0;xkk = 1.0;while (fabs(xk - xkk) > eps){result = xk - f3(xk) / (f3(xk) - f3(xkk))*(xk - xkk); xkk = xk;xk = result;cout<<xk<<endl;}cout<<xk<<endl;return0;}计算结果得:x = 0.567143;计算第三个方程:其中选择xk = 1.0;xkk = 2.0;进行迭代函数图像如图:程序如下:#include <math.h>#include <iostream>#define e 2.718281828459#define eps 1e-8 usingnamespace std;double f3(double x){double y;y = log(x) + x - 2;return y;}int main(int argc, constchar * argv[]) {// insert code here...double result = 0.0;double xk,xkk;xk =1.0;xkk = 2.0;while (fabs(xk - xkk) > eps){result = xk - f3(xk) / (f3(xk) - f3(xkk))*(xk - xkk);xkk = xk;xk = result;cout<<xk<<endl;}cout<<xk<<endl;return0;}计算结果得:x = 1.55715;二.学习心得割线法是通过不断迭代,逐渐逼近正确结果的方式。
计算方法实验

1、实验内容
试用最小二乘法分别求一次和二次多项式,使其与下列数据按拟
合,并比较两曲线的优劣。
xi
1.36 1.49 1.73 1.81 1.95
yi
14.094 15.069 16.844 17.378 18.435
2.实验原理
曲线拟合的最小二乘法:设通过点(������������,������������ )的规律为 y=f(x),即
cout << "Input the "<< num <<" of x:"; cin >> data_x[num-1]; cout << "Input the "<< num <<" of y:"; cin >> data_y[num-1];
num--; } double A =0.0; double B =0.0; double C =0.0; double D =0.0; A = (data_x*data_x).sum(); B = data_x.sum(); C = (data_x*data_y).sum(); D = data_y.sum(); double k,b,tmp =0; if(tmp=(A*data_x.size()-B*B)) {
double h=(b-a)/n; double T=0; for(int i=1;i<n;i++) {
T=T+Function(a+i*h); } T*=2; T=(Function(a)+Function(b)+T)*h/2; return T; } //复化辛普森公式 double MulripleSimpson(double a,double b,int n) { double h=(b-a)/n; double T=0; for(int i=0;i<n;i++) {
《计算方法实验》课件

计算方法实验 PPT 课件
实验介绍
实验安排
详细介绍了实验进行的时间安排和实验室要求。
实验目的
阐述了学习计算方法实验的重要目标和价值。
实验内容概述
概括性地介绍了实验涉及的主要内容和操作。
计算方法基础知识回顾
数值计算方法概述
概括了数值计算方法的定义和应用领域。
插值法简介
解释了插值法在数值计算中的作用和原理。
1 实验步骤
具体描述了进行插值法实验的步骤和操作流程。
2 实验要求
列举了完成实验所需的前置条件和要求。
3 实验结果和分析
总结了实验结果并给出了相关数据的分析和解释。
实验三:数值微积分实验
1 实验步骤
具体说明了进行数值微 积分实验的步骤和具体 操作。
2 实验要求
概述了完成实验所需的 前提条件和技术要求。
其他资料
介绍了一些其他有关计算方法实验的相关资料和参考。
3 实验结果和分析
总结了实验的结果,并 进行了相应数据分析和 解读。
实验总结
实验心得
分享了在完成实验过程中 的感悟和收获。
实验成果展示
展示了实验中获得的数据 和图表等成果知识和技能。
参考资料
书籍
推荐了一些计算方法方面的经典教材和参考书籍。
网络资源
提供了一些在线学习计算方法实验的优质网站和资源。
矩阵运算基础
介绍了矩阵的基本运算规则和重要性。
数值微积分概述
回顾了数值微积分的基本概念和计算方法。
实验一:矩阵运算实验
1 实验步骤
详细说明了进行矩阵运 算实验的步骤和操作。
2 实验要求
列出了完成实验所需的 前提条件和要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏科技大学
电子信息学院
实验报告
实验名称:插值方法
学号:姓名:班级:
完成日期:2014年10月20日
实验一 插值方法
一、实验目的及意义
[1] 了解插值的基本原理
[2] 了解拉格朗日插值、线性插值、样条插值的基本思想; [3] 了解三种网格节点数据的插值方法的基本思想;
[4] 掌握用MATLAB 计算三种一维插值和两种二维插值的方法; [5] 通过范例展现求解实际问题的初步建模过程;
通过自己动手作实验学习如何用插值方法解决实际问题,提高探索和解决问题的能力。
通过撰写实验报告,促使自己提炼思想,按逻辑顺序进行整理,并以他人能领会的方式表达自己思想形成的过程和理由。
提高写作、文字处理、排版等方面的能力。
二、实验内容
1.用MATLAB 或Visual C++实现拉格朗日插值方法;2.用三种插值方法对已知函数进行插值计算,通过数值和图形输出,比较它们的效果;3.针对实际问题,试建立数学模型,
并求解。
三、实验步骤
1.开启软件平台——MATLAB 或Visual C++,开启其编辑窗口; 2.根据各种数值解法步骤编写成代码文件; 3.保存文件并运行;
4.观察运行结果(数值或图形);
5.写出实验报告,并浅谈学习心得体会。
四、实验要求与任务
根据实验内容和步骤,完成以下具体实验,要求写出实验报告(实验目的→问题→数学模型→算法与编程→计算结果→分析、检验和结论→心得体会)
基础实验
1. 一维插值 利用以下一些具体函数,考察分段线性插值、三次样条插值和拉格朗日多项式插值等三种插值方法的差异。
1)
2
11
x
+,x ∈[-5,5]; 2)sin x , x ∈[0,2π]; 3)cos 10
x , x ∈[0,2π].
注意:适当选取节点及插值点的个数;比较时可以采用插值点的函数值与真实函数值的
差异,或采用两个函数之间的某种距离。
附上你的源代码和比较结果。
应用实验(附上代码和实验结果)
2.火车行驶的路程、速度数据如表7.2,计算从静止开始20 分钟内走过的路程。
(提示:路程是速度对时间的积分,可以先对速度与时间的关系进行插值,然后再用辛普森公式求积分)
表7.2
3.确定地球与金星之间的距离
天文学家在1914年8月份的7次观测中,测得地球与金星之间距离(单位:米),并取其常用对数值,与日期的一组历史数据如表7.3。
由此推断何时金星与地球的距离(米)的对数值为9.9351799?。
