如何用excel数据表计算卡方检验的p值
Excel的chitest函数

Excel的chitest函数
Excel的chitest函数是用于计算卡方检验的函数。
卡方检验是一种统计学方法,用于确定两个分类变量之间是否具有显著差异。
通过计算卡方值和自由度,可以确定p值,进而判断两个变量是否相关。
在Excel中,chitest函数的语法如下:
CHITEST(actual_range, expected_range)
其中actual_range是实际观测值的数据区域,expected_range 是期望值的数据区域。
通常情况下,期望值是通过计算得到的,可以使用Excel的其他函数如COUNT、SUM等函数来计算。
使用chitest函数进行卡方检验的步骤如下:
1. 收集实际观测值和期望值的数据。
2. 将实际观测值和期望值输入到Excel中,并分别选中它们的数据区域。
3. 在Excel的函数库中找到chitest函数,并使用它进行计算。
4. 根据计算结果,判断两个变量之间是否具有显著差异。
需要注意的是,在进行卡方检验时,样本数量应该足够大,并且各个类别的样本数量不应该过小,否则会影响结果的可靠性。
此外,卡方检验仅对离散变量适用,对于连续变量,需要使用其他的统计方法进行分析。
- 1 -。
卡方检验excel操作步骤

卡方检验excel操作步骤
嘿,朋友们!今天咱就来唠唠卡方检验在 Excel 里咋操作。
咱先打开 Excel 表格,就像打开一扇通往知识宝库的门一样。
然后呢,把咱要分析的数据整整齐齐地填进去,这就好比给宝库里面摆上
宝贝。
接下来,咱得找到那个专门算卡方的工具。
这就好像在宝库里面找
一件特别趁手的兵器。
找到了,就可以开始大显身手啦!
咱把该填的数据都填进去,就跟给兵器装上弹药似的。
然后轻轻一点,嘿,结果就出来啦!这感觉,就像魔术师突然变出了神奇的东西。
你说这卡方检验有啥用啊?那用处可大了去了!它能帮咱看看两组
数据之间是不是有啥关联呀。
比如说,咱想知道男生和女生对某个东
西的喜好是不是不一样,卡方检验就能给出答案。
这就好像有个小侦
探在帮咱找线索一样。
咱再想想,要是没有 Excel 这么方便的工具,那得费多大劲去算这
个卡方啊!咱得一个数一个数地去摆弄,那多麻烦!现在可好啦,Excel 就像个智能小助手,几下就帮咱搞定了。
操作卡方检验的时候,可别粗心大意哦,就像走钢丝一样,得小心
翼翼的。
一个数据错了,那结果可能就全错啦!那可不行,咱得认真
对待,就像对待宝贝一样。
你说这 Excel 是不是很厉害?它能帮咱干好多事儿呢!卡方检验只
是其中之一。
咱学会了这个,以后再遇到类似的问题,就可以轻松解
决啦,就像有了一把万能钥匙。
总之呢,卡方检验在 Excel 里的操作其实不难,只要咱用心去学,
去练,肯定能掌握得牢牢的。
到时候,咱就能用它来解决各种问题啦,那感觉多棒啊!还等啥,赶紧去试试吧!。
利用Excel计算p值的方法-最新版

利用Excel 计算p 值的方法一、Excel 中计算各种分布的概率的函数:),,(}{),(),(}{)(0);2,,(}|{|);1,,(}{)(t t );(}{22n m x fdist x F P n m F F n x chidist x P n x n x tdist x T P n x tdist x T P n x normsdist x Z P =>=>>=>=>=≤—分布—卡方分布!函数中参数必须—分布—标准正态分布χχ注意:函数tdist(x , n, 1)中第一个参数x 的值必须大于0!如果实际计算}{x T P >时, 遇到x < 0的情况,则要进行适当转化!根据t 分布的对称性有:(1) 当x < 0时,)1,|,(|1|}|{}{n x tdist x T P x T P -=<=>;(2) 当x < 0时,)1,|,(||}|{}{n x tdist x T P x T P =>=<。
另外,函数chidist(x , n)和fdist(x , m, n)中的第一个参数x 也都必须大于0!下页还有内容!二、p 值就是根据一个具体样本拒绝原假设时,实际所犯的第一类错误的概率。
计算p 值的公式中不等号的方向和备择假设的不等号的方向 (即拒绝域不等号的方向) 一致。
)]2,1,(1),2,1,([2}){},{min(2)2,1,(1}{)2,1,(}{F )),(1),(min(2}){},{min(2),(1}{),(}{);2,,(|}|{2)1,,||(}{)1,,||(1}{)2,,(|}|{2)1,,(1}{)1,,(}{)p t (t |)|(2|}|{2)(}{)(1}{Z 111222212212212111111010101自由度自由度自由度自由度值不等:自由度自由度值小于:自由度自由度值大于:检验:自由度,自由度值不等:自由度值小于:自由度值大于:检验:仍不变自由度值不等:自由度值小于:自由度值大于:自由度值不等:自由度值小于:自由度值大于:值时,按以下公式计算的值检验统计量检验:值:值:值:检验:f Fdist f Fdist f F P f F P p H f Fdist f F P p H f Fdist f F P p H chidist chidist X P X P p H chidist X P p H chidist X P p H t tdist t T P p H t tdist t T P p H t tdist t T P p H t tdist t T P p H t tdist t T P p H t tdist t T P p H z normsdist z Z P p H z normsdist z Z P p H z normsdist z Z P p H -=≤≥=⇒-=≤=⇒=≥=⇒-=≤≥=⇒-=≤=⇒=≥=⇒=≥=⇒=≤=⇒-=≥=⇒<=≥=⇒-=≤=⇒=≥=⇒-=-≤=⇒≠=≤=⇒<-=≥=⇒>χχχχχχχχχμμμμμμ值则按下面的公式计算0,如果大于0p t。
用excel求卡方检验的p值之欧阳育创编

创作:欧阳育
率或构成比之间差别的显著性分析,用以说明两类属性现象之间是否存在一定的关系。
比较的A、B两组数据分别用a、b、c、d表示,a为A组的阳性例数,b为A组的阴性例数,c为B组的阳性例数,d为B组的阴性例数。
按实际值和理论值分别输入四个单元格,如图5-4-18所示。
d表示。
a=52,为A组的阳性例数;b=19,为A组的阴性例数;c=39,为B组的阳性例数;d=3,为B组的阴性例数。
根据公式计算理论-19)。
结果,将鼠标器移至工具栏的“ fx”处,鼠标器左键点击工具栏的“ fx”快捷键,打开函数选择框。
计”项,然后在“函数名”栏内选择“CHITEST”函数,用鼠标器点击“确定”按钮,打开数据输入框(图5-4-20)。
际值(a、b、c、d)的起始单元格和结束单元格的行列号,在“Expected_range”项的输入框内输入理论值(T11、T12、T21、T22)的图5-4-20)。
用鼠标器点击“确定”按钮,观察计算结果。
值计算结果
值的计算结果。
在“编辑”栏处显示χ2检验的函数“CHITEST”及两组比较数据的起始与结束单元格的行列号(图5-4-21)。
时间:2021.02.04 创作:欧阳育。
用EXCEL进行卡方检验(χ2)

用EXCEL进行卡方检验(χ2)卡方(χ2)常用以检验两个或两个以上样本率或构成比之间差别的显著性分析,用以说明两类属性现象之间是否存在一定的关系。
卡方检验常采用四格表,如图 5-4-18所示,比较的A、B两组数据分别用a、b、c、d表示,a为A组的阳性例数,b为A组的阴性例数,c为B组的阳性例数,d为B组的阴性例数。
用EXCEL进行卡方检验时,数据的输入方式按实际值和理论值分别输入四个单元格,如图5-4-18所示。
(1)比较的A、B两组数据分别用a、b、c、d表示。
a=52,为A组的阳性例数;b=19,为A组的阴性例数;c=39,为B组的阳性例数;d=3,为B组的阴性例数。
根据公式计算理论值T11、T12、、T21和T22。
将实际值和理论值分别输入如图所示的四个单元格(图5-4-19)。
选择表的一空白单元格,存放概率p值的计算结果,将鼠标器移至工具栏的“ fx”处,鼠标器左键点击工具栏的“ fx”快捷键,打开函数选择框。
(2)在函数选择框的“函数分类”栏选择“统计”项,然后在“函数名”栏内选择“CHITEST”函数,用鼠标器点击“确定”按钮,打开数据输入框(图5-4-20)。
(3)在“Actual_range”项的输入框内输入实际值(a、b、c、d)的起始单元格和结束单元格的行列号,在“Expected_range”项的输入框内输入理论值(T11、T12、T21、T22)的起始单元格和结束单元格的行列号,起始单元格和结束单元格的行列号之间用“:”分隔(图5-4-20)。
在数据输入完毕后,p值的计算结果立即显示。
用鼠标器点击“确定”按钮,观察计算结果。
图5-4-18四格表图5-4-19四格表数据输入图5-4-20计算选择框图5-4-21 p值计算结果(4)在表存放概率p值的空白单元格处显示p值的计算结果。
在“编辑”栏处显示χ2检验的函数“CHITEST”及两组比较数据的起始与结束单元格的行列号(图5-4-21)。
卡方检验医学统计EXCEL模板

卡方检验医学统计EXCEL模板卡方检验是一种用来判断两个分类变量之间是否存在显著关联的统计方法,常应用于医学研究中,比如判断其中一种疾病是否与其中一种风险因素相关等。
在进行卡方检验时,我们需要计算一个卡方值,并根据卡方分布表得到相应的P值,进而判断两个变量之间的关联性。
下面我们介绍如何使用Excel来进行卡方检验,并给出一个模板供参考。
首先,我们需要准备两个分类变量的数据,假设我们研究其中一种疾病与性别的关系,将性别分为男和女两个分类。
假设我们有100个样本数据,其中男性有60人,女性有40人。
我们想要判断性别是否与患该种疾病的风险相关。
接下来,我们使用Excel来计算卡方值。
首先,将数据按照以下表格形式输入到Excel中:```疾病男性女性患病ab未患病cd```在Excel中,我们可以将上述数据输入到A1:D3单元格范围中。
然后,我们需要计算每个单元格的期望频数。
期望频数是指根据两个变量的边际分布计算得到的理论上的预期频数。
在E1单元格中输入以下公式:"=SUM($B$2:$B$3)*SUM($C$2:$D$2)/SUM($B$2:$D$3)",在F1单元格中输入公式:"=SUM($B$2:$B$3)*SUM($D$2:$D$3)/SUM($B$2:$D$3)",在E2单元格中输入公式:"=SUM($C$2:$D$3)*SUM($C$2:$D$2)/SUM($B$2:$D$3)",在F2单元格中输入公式:"=SUM($C$2:$D$3)*SUM($D$2:$D$3)/SUM($B$2:$D$3)"。
然后,我们需要计算每个单元格的卡方值。
在G2单元格中输入公式:"=((B2-E2)^2)/E2",在H2单元格中输入公式:"=((B2-F2)^2)/F2",在G3单元格中输入公式:"=((C3-E3)^2)/E3",在H3单元格中输入公式:"=((C3-F3)^2)/F3"。
excel数据表计算卡方检验的p值

(二)用EXCEL的统计函数进行统计卡方检验(χ2)卡方(χ2)常用以检验两个或两个以上样本率或构成比之间差别的显著性分析,用以说明两类属性现象之间是否存在一定的关系。
卡方检验常采用四格表,如图5—4-18所示,比较的A、B两组数据分别用a、b、c、d表示,a为A组的阳性例数,b 为A组的阴性例数,c为B组的阳性例数,d为B组的阴性例数。
用EXCEL进行卡方检验时,数据的输入方式按实际值和理论值分别输入四个单元格,如图5-4—18所示。
(1)比较的A、B两组数据分别用a、b、c、d表示.a=52,为A组的阳性例数;b=19,为A组的阴性例数;c=39,为B组的阳性例数;d=3,为B组的阴性例数.根据公式计算理论值T11、T12、、T21和T22。
将实际值和理论值分别输入如图所示的四个单元格(图5-4—19)。
选择表的一空白单元格,存放概率p值的计算结果,将鼠标器移至工具栏的“fx”处,鼠标器左键点击工具栏的“fx”快捷键,打开函数选择框。
(2)在函数选择框的“函数分类”栏选择“统计"项,然后在“函数名”栏内选择“CHITEST”函数,用鼠标器点击“确定”按钮,打开数据输入框(图5-4—20)。
(3)在“Actual_range”项的输入框内输入实际值(a、b、c、d)的起始单元格和结束单元格的行列号,在“Expected_range”项的输入框内输入理论值(T11、T12、T21、T22)的起始单元格和结束单元格的行列号,起始单元格和结束单元格的行列号之间用“:”分隔(图5—4-20)。
在数据输入完毕后,p值的计算结果立即显示。
用鼠标器点击“确定"按钮,观察计算结果.图5—4—18四格表图5—4—19 四格表数据输入图5—4-20 计算选择框图5-4-21 p值计算结果4.在表存放概率p 值的空白单元格处显示p 值的计算结果。
在“编辑"栏处显示χ2检验的函数“CHITEST”及两组比较数据的起始与结束单元格的行列号(图5-4—21)。
excel卡方检验函数

excel卡方检验函数卡方检验是统计学中常用的方法之一,可以用来比较观察数据和理论数据之间的偏差情况。
在Excel软件中,我们可以使用CHISQ.TEST函数来进行卡方检验。
下面将介绍CHISQ.TEST函数的具体使用方法。
一、 CHISQ.TEST函数语法及参数=CHISQ.TEST(实际值范围,理论值范围)其中实际值范围和理论值范围可以是单个区域,也可以是多个区域。
下面通过实例来说明CHISQ.TEST函数的使用方法。
实例:假设有一家公司想要比较其两个销售团队的销售额是否存在显著差异。
公司随机抽取了100个客户,其中50个客户由销售团队A负责,另外50个客户由销售团队B负责。
这些客户的销售额数据如下:销售团队A 销售额销售团队B 销售额客户1 10 客户51 12客户2 15 客户52 14客户3 20 客户53 11客户4 8 客户54 13客户5 18 客户55 10客户6 22 客户56 17客户7 14 客户57 19...... ...... ...... ......客户50 16 客户100 24现在,我们需要使用CHISQ.TEST函数来检验销售团队A和销售团队B的销售额是否存在显著差异。
以下是具体步骤:1. 首先,打开Excel软件并新建一个工作表。
在该工作表中,输入如上表所示的销售额数据。
2. 接着,我们需要计算实际值和理论值。
实际值是指销售团队A和销售团队B的销售额在每个区间出现的次数,理论值是指销售团队A和销售团队B的销售额在每个区间出现的次数的期望值。
为方便计算,我们可以将销售额分成几个区间,例如0-5,5-10,10-15,15-20,20-25等。
根据实际数据,可以得到每个区间A团队和B团队的销售额在该区间出现的次数,以及该区间的期望频数。
如下表所示:销售额区间观察到的A销售额的次数观察到的B销售额的次数期望频数0-5 0 0 15-10 3 3 1010-15 21 14 2515-20 18 18 2020-25 8 15 10其中,期望频数可以使用以下公式计算:期望频数 = (该区间的总销售额/总客户数) × 该团队客户数例如,对于区间10-15,其中的期望频数为:期望频数= (10+11+12+13+14+15)/100 × 50 = 25在Excel中,可以在任意单元格中输入以下公式:=CHISQ.TEST(B2:B6,D2:D6)其中,B2:B6和D2:D6分别表示实际值和理论值所在的区域。
用excel求卡方检验的p值

(二)用EXCEL的统计函数进行统计4.卡方检验(χ2)卡方(χ2)常用以检验两个或两个以上样本率或构成比之间差别的显著性分析,用以说明两类属性现象之间是否存在一定的关系。
卡方检验常采用四格表,如图5-4-18所示,比较的A、B两组数据分别用a、b、c、d表示,a 为A组的阳性例数,b为A组的阴性例数,c为B组的阳性例数,d为B组的阴性例数。
用EXCEL进行卡方检验时,数据的输入方式按实际值和理论值分别输入四个单元格,如图5-4-18所示。
(1)比较的A、B两组数据分别用a、b、c、d表示。
a=52,为A组的阳性例数;b=19,为A 组的阴性例数;c=39,为B组的阳性例数;d=3,为B组的阴性例数。
根据公式计算理论值T11、T12、、T21和T22。
将实际值和理论值分别输入如图所示的四个单元格(图5-4-19)。
选择表的一空白单元格,存放概率p值的计算结果,将鼠标器移至工具栏的“fx”处,鼠标器左键点击工具栏的“fx”快捷键,打开函数选择框。
(2)在函数选择框的“函数分类”栏选择“统计”项,然后在“函数名”栏内选择“CHITEST”函数,用鼠标器点击“确定”按钮,打开数据输入框(图5-4-20)。
(3)在“Actual_rang e”项的输入框内输入实际值(a、b、c、d)的起始单元格和结束单元格的行列号,在“Expected_ra nge”项的输入框内输入理论值(T11、T12、T21、T22)的起始单元格和结束单元格的行列号,起始单元格和结束单元格的行列号之间用“:”分隔(图5-4-20)。
在数据输入完毕后,p值的计算结果立即显示。
用鼠标器点击“确定”按钮,观察计算结果。
图5-4-18 四格表图5-4-19 四格表数据输入图5-4-20 计算选择框图5-4-21 p值计算结果4.在表存放概率p 值的空白单元格处显示 p值的计算结果。
excel中p值函数

excel中p值函数
Excel中的p值函数是一种用于统计分析的功能,可以帮助用户计算出数据集中的概率值。
通常在数据分析中,我们需要确定某些事件的概率,比如样本均值是否与总体均值相等、两个样本的方差是否相等等等。
这些问题都可以通过p值函数来计算得出。
在Excel中,我们可以使用STDEV.P、T.TEST、CHISQ.TEST等函数来计算p值。
其中,STDEV.P函数用于计算样本的标准偏差,T.TEST函数用于计算t 分布的概率值,CHISQ.TEST函数用于计算卡方分布的概率值等等。
对于某些特定的问题,我们还可以使用F.TEST、Z.TEST等函数来计算p值。
总之,Excel中的p值函数可以帮助我们快速、准确地进行统计分析,从而更好地理解数据集的特征和规律。
- 1 -。
excel卡方检验的函数

在Excel中,进行卡方检验的函数是`CHISQ.TEST`。
使用方法如下:
1. 打开Excel文件,在任意一个单元格中输入“=CHISQ.TEST”。
2. 在括号中输入你想要进行卡方检验的数据。
CHISQ.TEST函数接受两个参数,第一个参数是实际值,第二个参数是理论值。
这两个参数可以是5×1的矩阵。
3. 点击回车键,Excel会返回一个P值。
这个P值是指,通过卡方检验得到的观测到的统计量,比卡方分布图中的左边界还要小的概率。
通常来说,如果P值小于0.05,我们将拒绝原假设,认为两个销售团队的销售额在这些区间内存在显著差异。
如果P值大于或等于0.05,那么我们接受原假设,认为两个销售团队的销售额在这些区间内不存在显著差异。
需要注意的是,在使用CHISQ.TEST函数时,我们需要正确计算实际值和理论值,并正确指定函数的参数。
用excel求卡方检验的p值之欧阳歌谷创编
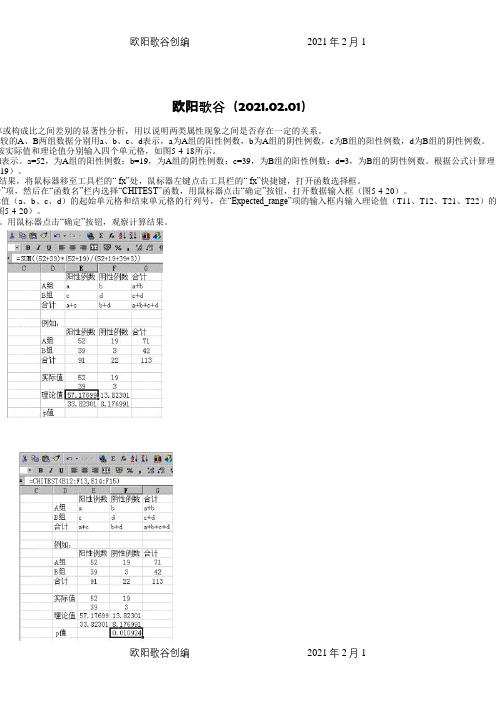
欧阳歌谷(2021.02.01)
率或构成比之间差别的显著性分析,用以说明两类属性现象之间是否存在一定的关系。
比较的A、B两组数据分别用a、b、c、d表示,a为A组的阳性例数,b为A组的阴性例数,c为B组的阳性例数,d为B组的阴性例数。
按实际值和理论值分别输入四个单元格,如图5-4-18所示。
d表示。
a=52,为A组的阳性例数;b=19,为A组的阴性例数;c=39,为B组的阳性例数;d=3,为B组的阴性例数。
根据公式计算理论-19)。
结果,将鼠标器移至工具栏的“ fx”处,鼠标器左键点击工具栏的“ fx”快捷键,打开函数选择框。
计”项,然后在“函数名”栏内选择“CHITEST”函数,用鼠标器点击“确定”按钮,打开数据输入框(图5-4-20)。
际值(a、b、c、d)的起始单元格和结束单元格的行列号,在“Expected_range”项的输入框内输入理论值(T11、T12、T21、T22)的图5-4-20)。
用鼠标器点击“确定”按钮,观察计算结果。
值计算结果
值的计算结果。
在“编辑”栏处显示χ2检验的函数“CHITEST”及两组比较数据的起始与结束单元格的行列号(图5-4-21)。
用EXCEL进行卡方检验(χ2)

用EXCEL进行卡方检验(χ2)卡方(χ2)常用以检验两个或两个以上样本率或构成比之间差别的显著性分析,用以说明两类属性现象之间是否存在一定的关系。
卡方检验常采用四格表,如图 5-4-18所示,比较的A、B两组数据分别用a、b、c、d表示,a为A组的阳性例数,b为A组的阴性例数,c为B组的阳性例数,d为B组的阴性例数。
用EXCEL进行卡方检验时,数据的输入方式按实际值和理论值分别输入四个单元格,如图5-4-18所示。
(1)比较的A、B两组数据分别用a、b、c、d表示。
a=52,为A组的阳性例数;b=19,为A组的阴性例数;c=39,为B组的阳性例数;d=3,为B组的阴性例数。
根据公式计算理论值T11、T12、、T21和T22。
将实际值和理论值分别输入如图所示的四个单元格(图5-4-19)。
选择表的一空白单元格,存放概率p值的计算结果,将鼠标器移至工具栏的“ fx”处,鼠标器左键点击工具栏的“ fx”快捷键,打开函数选择框。
(2)在函数选择框的“函数分类”栏选择“统计”项,然后在“函数名”栏内选择“CHITEST”函数,用鼠标器点击“确定”按钮,打开数据输入框(图5-4-20)。
(3)在“Actual_range”项的输入框内输入实际值(a、b、c、d)的起始单元格和结束单元格的行列号,在“Expected_range”项的输入框内输入理论值(T11、T12、T21、T22)的起始单元格和结束单元格的行列号,起始单元格和结束单元格的行列号之间用“:”分隔(图5-4-20)。
在数据输入完毕后,p值的计算结果立即显示。
用鼠标器点击“确定”按钮,观察计算结果。
图5-4-18四格表图5-4-19四格表数据输入图5-4-20计算选择框图5-4-21 p值计算结果(4)在表存放概率p值的空白单元格处显示p值的计算结果。
在“编辑”栏处显示χ2检验的函数“CHITEST”及两组比较数据的起始与结束单元格的行列号(图5-4-21)。
卡方检验的简单计算方法

1、把数据整理成四格表
发生数未发生数合计
方法1 a b a+b
方法2 c d c+d
合计a+c b+d n(总统计量)
2、利用卡方检验计算器V1.61(网络下载,据说需注册,但不注册也能用)
把四格表数值带入卡方计算器,计算出X2值。
3、利用Excel表格
打开Excel,随意选择一个单元格,点击菜单栏插入—函数,默认在CHIDIST,点击确定,出现如下输入框:
在第一行中X中输入X2值,第二行即自由度,四格表为1,输入后自动出现计算结果即为P值。
4、如果多个结果比较时是分别计算卡方值的,要把表中的数据分别和总数据列成四格表.
例如
就要列四格表分别比较每种病与总量n之间的卡方值。
如自身溶贫:。
利用Excel计算p值的方法-最新版

利用Excel 计算p 值的方法一、Excel 中计算各种分布的概率的函数:),,(}{),(),(}{)(0);2,,(}|{|);1,,(}{)(t t );(}{22n m x fdist x F P n m F F n x chidist x P n x n x tdist x T P n x tdist x T P n x normsdist x Z P =>=>>=>=>=≤—分布—卡方分布!函数中参数必须—分布—标准正态分布χχ注意:函数tdist(x , n, 1)中第一个参数x 的值必须大于0!如果实际计算}{x T P >时, 遇到x < 0的情况,则要进行适当转化!根据t 分布的对称性有:(1) 当x < 0时,)1,|,(|1|}|{}{n x tdist x T P x T P -=<=>;(2) 当x < 0时,)1,|,(||}|{}{n x tdist x T P x T P =>=<。
另外,函数chidist(x , n)和fdist(x , m, n)中的第一个参数x 也都必须大于0!下页还有内容!二、p 值就是根据一个具体样本拒绝原假设时,实际所犯的第一类错误的概率。
计算p 值的公式中不等号的方向和备择假设的不等号的方向 (即拒绝域不等号的方向) 一致。
)]2,1,(1),2,1,([2}){},{min(2)2,1,(1}{)2,1,(}{F )),(1),(min(2}){},{min(2),(1}{),(}{);2,,(|}|{2)1,,||(}{)1,,||(1}{)2,,(|}|{2)1,,(1}{)1,,(}{)p t (t |)|(2|}|{2)(}{)(1}{Z 111222212212212111111010101自由度自由度自由度自由度值不等:自由度自由度值小于:自由度自由度值大于:检验:自由度,自由度值不等:自由度值小于:自由度值大于:检验:仍不变自由度值不等:自由度值小于:自由度值大于:自由度值不等:自由度值小于:自由度值大于:值时,按以下公式计算的值检验统计量检验:值:值:值:检验:f Fdist f Fdist f F P f F P p H f Fdist f F P p H f Fdist f F P p H chidist chidist X P X P p H chidist X P p H chidist X P p H t tdist t T P p H t tdist t T P p H t tdist t T P p H t tdist t T P p H t tdist t T P p H t tdist t T P p H z normsdist z Z P p H z normsdist z Z P p H z normsdist z Z P p H -=≤≥=⇒-=≤=⇒=≥=⇒-=≤≥=⇒-=≤=⇒=≥=⇒=≥=⇒=≤=⇒-=≥=⇒<=≥=⇒-=≤=⇒=≥=⇒-=-≤=⇒≠=≤=⇒<-=≥=⇒>χχχχχχχχχμμμμμμ值则按下面的公式计算0,如果大于0p t。
统计学p值excel计算

统计学p值excel计算引言:统计学是一个广泛的学科,与数学和算法密不可分。
其目的是从数据中获得有意义的信息,并帮助我们做出正确的决策。
在统计学中,p值是一个重要的参数,用于判断实验结果的显著性。
现在,让我们来学习如何在Excel中计算p值。
统计学概述:统计学是一门旨在从数据中获取有用信息,并将这些信息应用于各种领域的学科。
在实验研究中,统计学可以帮助我们评估研究发现的可信度。
其中,p值是一项重要的统计学概念,它代表了实验结果的显著性。
通俗来讲,p值简单地描述了用实验得到的数据,有多少是我们科学突破的重要信息。
P值计算方法:Excel是一款功能强大的电子表格软件,可以通过内置的功能轻松计算p值。
在Excel中,借助STUDENT函数(t分布函数)根据样本数据计算出t值,从而得到p值。
具体的Excel公式如下:「=TDIST(x, degrees of freedom, tails)」或「=T.INV(probability, degrees of freedom)」,其中x代表t值,自由度代表样本数减一,tails代表单双尾,单尾为1,双尾为2。
示例:为了更好地理解在Excel中如何计算p值,这里以一个示例为例。
假设有两个数据集,样本数分别为10和15,样本均值分别为20和25,标准差分别为5和7. 我们需要比较这两个数据集,以确定它们之间的差异是否显著。
我们可以采用如下步骤计算p值:1. 在Excel中输入数据集和相关统计信息;2. 使用Excel公式= TTEST(Range 1,Range 2,2,3)计算t值;3. 再使用Excel公式=TDIST(t,df,2)计算p值。
其中,df是自由度,等于两个样本数之和减2;4. 按下回车键,即可在Excel中获得p值。
总结:统计学是一门非常重要的学科,它可以帮助我们判断实验结果的可靠性。
在统计学中,p值是一项必须要了解的概念。
借助Excel的强大功能,我们可以轻松计算出实验数据的p值,用以判断实验结果的显著性。
利用Excel计算p值的方法-最新版

利用Excel 计算p 值的方法一、Excel 中计算各种分布的概率的函数:),,(}{),(),(}{)(0);2,,(}|{|);1,,(}{)(t t );(}{22n m x fdist x F P n m F F n x chidist x P n x n x tdist x T P n x tdist x T P n x normsdist x Z P =>=>>=>=>=≤—分布—卡方分布!函数中参数必须—分布—标准正态分布χχ注意:函数tdist(x , n, 1)中第一个参数x 的值必须大于0!如果实际计算}{x T P >时, 遇到x < 0的情况,则要进行适当转化!根据t 分布的对称性有:(1) 当x < 0时,)1,|,(|1|}|{}{n x tdist x T P x T P -=<=>;(2) 当x < 0时,)1,|,(||}|{}{n x tdist x T P x T P =>=<。
另外,函数chidist(x , n)和fdist(x , m, n)中的第一个参数x 也都必须大于0!下页还有内容!二、p 值就是根据一个具体样本拒绝原假设时,实际所犯的第一类错误的概率。
计算p 值的公式中不等号的方向和备择假设的不等号的方向 (即拒绝域不等号的方向) 一致。
)]2,1,(1),2,1,([2}){},{min(2)2,1,(1}{)2,1,(}{F )),(1),(min(2}){},{min(2),(1}{),(}{);2,,(|}|{2)1,,||(}{)1,,||(1}{)2,,(|}|{2)1,,(1}{)1,,(}{)p t (t |)|(2|}|{2)(}{)(1}{Z 111222212212212111111010101自由度自由度自由度自由度值不等:自由度自由度值小于:自由度自由度值大于:检验:自由度,自由度值不等:自由度值小于:自由度值大于:检验:仍不变自由度值不等:自由度值小于:自由度值大于:自由度值不等:自由度值小于:自由度值大于:值时,按以下公式计算的值检验统计量检验:值:值:值:检验:f Fdist f Fdist f F P f F P p H f Fdist f F P p H f Fdist f F P p H chidist chidist X P X P p H chidist X P p H chidist X P p H t tdist t T P p H t tdist t T P p H t tdist t T P p H t tdist t T P p H t tdist t T P p H t tdist t T P p H z normsdist z Z P p H z normsdist z Z P p H z normsdist z Z P p H -=≤≥=⇒-=≤=⇒=≥=⇒-=≤≥=⇒-=≤=⇒=≥=⇒=≥=⇒=≤=⇒-=≥=⇒<=≥=⇒-=≤=⇒=≥=⇒-=-≤=⇒≠=≤=⇒<-=≥=⇒>χχχχχχχχχμμμμμμ值则按下面的公式计算0,如果大于0p t。
excelt统计量检验的p值

主题:Excel统计量检验的p值内容:1. 介绍统计量检验的概念统计量检验是统计学中常用的一种假设检验方法,用于判断样本数据与总体数据之间是否存在显著差异。
在实际应用中,经常需要使用Excel进行统计量检验,并获取相应的p值来判断检验的结果是否显著。
2. Excel中统计量检验的功能Excel提供了丰富的统计分析功能,包括各种假设检验方法。
在数据分析工具包中,可以找到各种常见的统计量检验方法,如t检验、F检验、卡方检验等。
通过这些功能,用户可以方便地进行统计量检验,并获取相应的p值。
3. 如何使用Excel进行统计量检验在Excel中进行统计量检验通常需要遵循以下步骤:a. 准备数据:首先需要准备待分析的数据,数据可以直接输入到Excel 的工作表中,也可以导入外部数据文件。
b. 选择统计分析工具:在Excel的“数据”选项卡中,可以找到“数据分析”功能,通过这个功能可以选择相应的统计量检验方法。
c. 输入参数:在弹出的对话框中,需要输入所需的参数,如样本数据的范围、假设检验的类型、显著性水平等。
d. 获取结果:完成参数输入后,Excel会给出统计量检验的结果,包括检验统计量的数值和p值等。
4. 解读p值的意义在统计量检验中,p值是一个非常重要的指标,它代表了在原假设成立的条件下,观察到样本数据或更特殊情况的概率。
通常情况下,如果p值小于显著性水平(通常取0.05),就可以拒绝原假设,认为样本数据与总体数据之间存在显著差异;反之,如果p值大于显著性水平,则接受原假设,认为样本数据与总体数据之间没有显著差异。
5. p值的计算方法Excel可以直接给出统计量检验的p值,但对于想要了解p值的计算方法的用户,也可以自行利用Excel进行计算。
在t检验、F检验等参数的计算中,p值通常通过查找t分布表或F分布表来获得相应的概率。
对于卡方检验等非参数检验,p值的计算会采用不同的方法,但都可以通过Excel进行实现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何用EXCEL的统计函数进行统计卡方检验(χ2)
卡方(χ2)常用以检验两个或两个以上样本率或构成比之间差别的显著性分析,用以说明两类属性现象之间是否存在一定的关系。
卡方检验常采用四格表,如图5-4-18所示,比较的A、B两组数据分别用a、b、c、d表示,a为A组的阳性例数,b 为A组的阴性例数,c为B组的阳性例数,d为B组的阴性例数。
用EXCEL进行卡方检验时,数据的输入方式按实际值和理论值分别输入四个单元格,如图5-4-18所示。
(1)比较的A、B两组数据分别用a、b、c、d表示。
a=52,为A组的阳性例数;b=19,为A组的阴性例数;c=39,为B组的阳性例数;d=3,为B组的阴性例数。
根据公式计算理论值T11、T12、、T21和T22。
将实际值和理论值分别输入如图所示的四个单元格(图5-4-19)。
选择表的一空白单元格,存放概率p值的计算结果,将鼠标器移至工具栏的“fx”处,鼠标器左键点击工具栏的“fx”快捷键,打开函数选择框。
(2)在函数选择框的“函数分类”栏选择“统计”项,然后在“函数名”栏内选择“CHITEST”函数,用鼠标器点击“确定”按钮,打开数据输入框(图5-4-20)。
(3)在“Actual_range”项的输入框内输入实际值(a、b、c、d)的起始单元格和结束单元格的行列号,在“Expected_range”项的输入框内输入理论值(T11、T12、T21、T22)的起始单元格和结束单元格的行列号,起始单元格和结束单元格的行列号之间用“:”分隔(图5-4-20)。
在数据输入完毕后,p值的计算结果立即显示。
用鼠标器点击“确定”按钮,观察计算结果。
图5-4-18 四格表图5-4-19 四格表数据输入
图5-4-20 计算选择框图5-4-21 p值计算结果
4.在表存放概率p 值的空白单元格处显示p 值的计算结果。
在“编辑”栏处显示χ2检验的函数“CHITEST”及两组比较数据的起始与结束单元格的行列号(图5-4-21)。
