实验一用递推公式计算定积分
定积分运算法则

• 通过定积分求解经济学中的边际产量、边际消费等边际问题
求解经济学中的总量问题
• 通过定积分求解经济学中的总产量、总消费等总量问题
求解经济学中的平均问题
• 通过定积分求解经济学中的平均产量、平均消费等平均问题
谢谢观看.
Thank you for watching.
Docs
⌛️
06
定积分的数值计算方法
数值积分的基本原理与方法
数值积分的定义
数值积分的方法
• 通过数值方法近似求解定积分的值
• 辛普森法
• 龙贝格法
• 高斯积分法
数值积分的误差分析与控制
误差分析
误差控制
• 分析数值积分方法的误差来源
• 选择合适的数值积分方法
• 估计数值积分方法的误差范围
• 控制积分区间的长度
求解物体的速度
• 通过定积分求解物体在变力作用下的速度
求解物体的加速度
• 通过定积分求解物体在变力作用下的加速度
定积分在工程学中的应用
求解工程问题的面积
求解工程问题的体积
求解工程问题的质心位置
• 通过定积分求解曲线围成的面积
• 通过定积分求解曲面围成的体积
• 通过定积分求解物体的质心位置
定积分在经济学中的应用
积分问题
换元积分法的原理
• 利用换元公式将原积分变量变换为新变量,从而简化积分过程
换元积分法的常见类型与方法
01
幂函数换元法
• 将复杂的幂函数积分问题转化为简单的指数函数积分问
题
02
三角函数换元法
• 将复杂的三角函数积分问题转化为简单的指数函数积分
问题
03
《数学实验》实验报告——定积分的近似求解
3
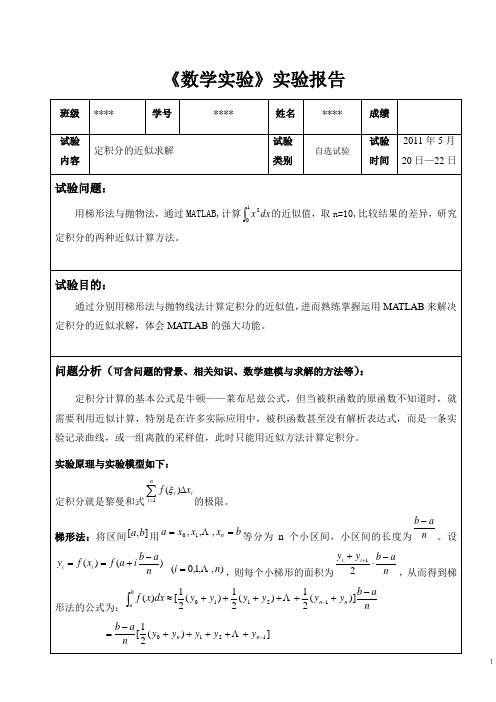
2 梯形法程序如下: f=input('请输入被积函数 f(x)='); qujian=input('请输入积分区间[a,b]='); n=input('请输入子区间个数 n='); s=0; for i=1:n-1 x=qujian(1)+(qujian(2)-qujian(1))/n*i; y=eval(f); s=s+y; end x=qujian(1); y=eval(f); s=s+y/2; x=qujian(2); y=eval(f); s=s+y/2; disp('定积分的近似值是:'); s=s*(qujian(2)-qujian(1))/n
《数学实验》实验报告
班级 试验 内容 **** 学号 **** 姓名 试验 类别
自选试验
****
成绩 试验 时间 2011 年 5 月 20 日—22 日
定积分的近似求解
试验问题:
用梯形法与抛物法,通过 MATLAB,计算 x 2 dx 的近似值,取 n=10,比较结果的差异,研究
0 1
定积分的两种近似计算方法。
1 1 1 2 ph 3 6rh h(2 ph 2 6r ) h( y 0 4 y1 y 2 ) 3 3 3 。 ba n ,则上面所求的 S 等于区间 [ x0 , x2 ] 上以抛物线为曲边的曲边梯形的面积。同理可
取
以得到区间 [ xi 1 , xi 1 ] 上以抛物线为曲边的曲边梯形的面积:
试验目的:
通过分别用梯形法与抛物线法计算定积分的近似值, 进而熟练掌握运用 MATLAB 来解决 定积分的近似求解,体会 MATLAB 的强大功能。
数学实验报告定积分计算(3篇)

第1篇一、实验目的1. 理解定积分的概念和意义。
2. 掌握定积分的计算方法。
3. 通过实验,加深对定积分理论知识的理解和应用。
二、实验原理定积分是微积分学中的一个基本概念,它表示某一曲线与x轴及两条垂直于x轴的直线所围成的平面图形的面积。
定积分的计算方法主要有直接积分法、分部积分法、换元积分法等。
三、实验仪器与材料1. 计算机2. 计算软件(如MATLAB、Mathematica等)3. 数学教材和参考书籍四、实验内容1. 理论学习(1)复习定积分的定义、性质和计算方法。
(2)了解定积分在物理学、工程学、经济学等领域的应用。
2. 实验操作(1)计算以下定积分:∫(0到1)x^2 dx(2)使用MATLAB软件进行定积分计算,并比较与手工计算的结果。
3. 结果分析(1)分析手工计算与MATLAB计算的结果差异,找出原因。
(2)总结定积分计算方法在实际应用中的优缺点。
五、实验步骤1. 理论学习(1)阅读数学教材,了解定积分的定义、性质和计算方法。
(2)查阅相关资料,了解定积分在各个领域的应用。
2. 实验操作(1)使用计算器或手工计算定积分∫(0到1)x^2 dx,得到结果。
(2)打开MATLAB软件,编写以下代码进行定积分计算:```matlabsyms x;I = int(x^2, 0, 1);```运行代码,得到结果。
3. 结果分析(1)比较手工计算和MATLAB计算的结果,发现两者基本一致。
(2)分析定积分计算方法在实际应用中的优缺点,总结如下:优点:- 定积分计算方法可以处理各种复杂函数,具有广泛的适用性。
- 定积分在物理学、工程学、经济学等领域的应用非常广泛。
缺点:- 对于某些复杂函数,计算过程较为繁琐,需要花费较多时间。
- 在实际应用中,可能需要根据具体情况选择合适的计算方法。
六、实验总结通过本次实验,我们了解了定积分的概念、性质和计算方法,并掌握了使用MATLAB软件进行定积分计算的方法。
积分计算超强总结(循环递推法)

【解】
.
【注】本例中没有出现循环递推的形式,所以放在这里是为了提醒大家当出现 减 的时候,不能将它们完全抵消,而要留下一个任意常数.
上述问题也可以改作为用循环递推法计算定积分的例子,这意义就不大了.下面举几个原函数不是初等函数的定积分计算例子,注意到定积分值与积分变量名称无关,可以考虑使用换元法.为了与原积分 可以做比较,必须保持积分区间 不变,翻折变换 可以达到此目的.所谓翻折变换是以区间 的中点为不动点的翻折.
【例5】求 .
【解】在翻折变换 下,有
,
所以,有 .
【例6】求 .
【解】在翻折变换 下,有
,
所以,有 .
利用循环递推法计算不定积分时,因为不定积分的计算结果与积分变量的名称有关,所以比较适合用分部积分法,而这时换元积分法恐怕是没有用的.
【例1】求 .
【解】
.
所以 ,即 .
【例2】求 .
【解】
,
所以 .
【例3】求 .
【解】
.
所以,有 .
【注】本题用换元 的方法,一样可以得到结果,但还要用到三角倍角公式和回代的过程,略显麻烦.
循环递推法
循环递推法是积分计算的一种重要的辅助方法.对于某些积分问题,在通过换元积分法或分部积了原积分的表达式
.
这样,实际上也就得到了需要的结果了,这种方法称为循环递推法.
这里需要注意的是:若 表示的是不定积分,等式另一边的 虽然表示的是同一个函数的不定积分,但是应该有一个常数的差别.所以在移项合并时,必须留下一个常数.
定积分的计算

则 有 a f ( x )dx f [ ( t )] ( t )dt .
b
证
设F ( x ) 是 f ( x ) 的一个原函数,
a f ( x )dx F (b) F (a ),
b
( t ) F [( t )],
dF dx f ( x ) ( t ) f [( t )]( t ), ( t ) dx dt
第四节 定积分的计算
一、直接利用牛顿-莱布尼兹公式 二、换元积分法 定理 假设 (1)f ( x ) 在[a , b] 上连续;
(2)函数 x (t ) 在[ , ] 上是单值的且有连续 导数; (3)当t 在区间[ , ] 上变化时, x (t ) 的值
在[a , b]上变化,且 ( ) a 、 ( ) b ,
1 1 4 4 x tan x 0 tan xdx 2 0 2 1 ln 2 4 ln sec x 0 . 8 2 8 4 4
例3 解
计算
1
0
ln(1 x ) dx . 2 (2 x )
0
1
1 ln(1 x ) 1 dx 0 ln(1 x )d 2 (2 x ) 2 x
1 2
xdx 1 x2
练习:
xdx 0 1 cos 2 x .
4
1
0
ln(1 x ) dx . 2 (2 x )
xdx . 例2 计算 0 1 cos 2 x
解
4
1 cos 2 x 2 cos x ,
2
xdx xdx 4 4 x d tan x 2 0 1 cos 2 x 0 2 cos x 0 2
-例谈定积分的计算方法和技巧
-----------------------------------Docin Choose -----------------------------------豆 丁 推 荐↓精 品 文 档The Best Literature----------------------------------The Best Literature例谈定积分的计算方法和技巧韦兰英(南宁师范高等专科学校数学与计算机科学系,广西龙州532400)摘要:文章通过举例,主要从五个方面探讨了简化定积分计算所采用的方法和技巧,这些方法和技巧既可减少计算量,提高效率,又可以开拓解题思路,提高学生定积分的计算能力。
关键词:定积分;计算;方法;技巧中图分类号:O13文献标识码:A文章编号:1008-696X(2008)04-0112-03On Methods and Techniques of Calculation on Definite IntegralWei Lanying(Dept.of Maths and Computer Science,Nanning Teachers College,Longzhou,Guangxi532400,China) Abstract:The methods and techniques on simplified calculation on definite integral are discussed with examples from five aspects,which helps reduce the amount of calculation and improve the efficency and performance in students'exercises.Key words:definite integral;calculation;method;technique定积分是积分学的一个基本问题,是高等数学的重要概念之一。
计算方法与计算 实验一误差分析

% 输出的量--每次迭代次数k和迭代值xk,
%
--每次迭代的绝对误差juecha和相对误差xiangcha,
误差分析
误差问题是数值分析的基础,又是数值分析中一个困难的课题。在实际计算 中,如果选用了不同的算法,由于舍入误差的影响,将会得到截然不同的结果。 因此,选取算法时注重分析舍入误差的影响,在实际计算中是十分重要的。同时, 由于在数值求解过程中用有限的过程代替无限的过程会产生截断误差,因此算法 的好坏会影响到数值结果的精度。 一、实验目的
因为运行后输出结果为: y 1.370 762 168 154 49, yˆ =1.370 744 664 189
38, R 1.750 396 510 491 47e-005, WU= 1.782 679 830 970 664e-005 104 . 所
以, yˆ 的绝对误差为 10 4 ,故 y
③ 运行后输出计算结果列入表 1–1 和表 1-2 中。
④ 将算法 2 的 MATLAB 调用函数程序的函数分别用 y1=15-2*x^2 和
y1=x-(2*x^2+x-15)/(4*x+1)代替,得到算法 1 和算法 3 的调用函数程序,将其保
存,运行后将三种算法的前 8 个迭代值 x1, x2 ,, x8 列在一起(见表 1-1),进行
的精确解 x* 2.5 比较,观察误差的传播.
算法 1 将已知方程化为同解方程 x 15 2x2 .取初值 x0 2 ,按迭代公式
xk1 15 2xk2
定积分基本计算公式

令 xa
a
F ( a ) ( a ) C ,
(a ) a f ( t )dt 0 F (a ) C ,
F ( x ) a f ( t )dt C ,
x
a
x
f ( t )dt F ( x ) F (a ),
令x b
a f ( x )dx F (b) F (a ).
0
b( x )
证:
F ( x)
0
a( x )
f (t )dt
a( x ) 0
0
b( x )
f ( t )dt
f ( t )dt ,
F ( x ) f b( x )b( x ) f a( x )a( x )
例1
e 求 lim cos x
x 0
例3
设 f ( x ) 在[0,1]上连续,且 f ( x ) 1.证明
2 x 0 f ( t )dt 1在[0,1]上只有一个解.
证 令 F ( x ) 2 x f ( t )dt 1,
0 x
x
f ( x ) 1,
F ( x ) 2 f ( x ) 0,
y
x
f ( t )dt ,
由积分中值定理得
( x )
f ( )x,
f ( ), x
在x与x x之间.
lim lim f ( ) x 0 x x 0
( x ) f ( x ).
o
a
x x x b x
x 0, x
F ( x ) 在[0,1]上为单调增加函数. F (0) 1 0,
实验一 用递推公式计算定积分

实验一 用递推公式计算定积分09信息 符文飞 09211210071、实验目的:由于一个算法是否稳定,十分重要。
如果算法不稳定,则数值计算的结果就会严重背离数学模型的真实结果,因此,在选择数值计算公式来进行近似计算时,我们应特别注意选用那些在数值计算过程中不会导致误差迅速增长的公式。
体会稳定性在选择算法中的地位.误差扩张的算法是不稳定的,是我们所不期望的;误差衰竭的算法是稳定的.是我们努力寻求的,这是贯穿本课程的目标.通过上机计算,了解舍入误差所引起的数值不稳定性。
2、实验题目:对n =0,1,2,…,20,计算定积分dx x x y n n ⎰+=1053、实验原理由于y(n)= = – 在计算时有两种迭代方法,如下:方法一: y(n)= – 5*y(n-1),n=1,2,3, (20)取y(0)= = ln6-ln5 ≈ 0.182322方法二:利用递推公式:y(n-1)=-*y(n),n=20,19, (1)而且,由 = * ≤≤* = 可取:y(20)≈*()≈0.008730.4、实验内容:算法1的程序:y0=log(6.0)-log(5.0);y1=0;n=1;while n<=30y1=1/n-5*y0;fprintf('y[%d]=%-20f',n,y1);y0=y1;n=n+1;if mod(n,1)==0;fprintf('\n')endend算法2的程序:y0=(1/105+1/126)/2;y1=0;n=1;while n<=30y1=1/(5*n)-y0/5;fprintf('y[%d]=%-20f',n,y1)y0=y1;n=n+1;if mod(n,1)==0fprintf('\n')endend5、实验结果对于算法1:y[1]=0.088392y[2]=0.058039y[3]=0.043139y[4]=0.034306y[5]=0.028468y[6]=0.024325y[7]=0.021233y[8]=0.018837y[9]=0.016926y[10]=0.015368y[11]=0.014071y[12]=0.012977y[13]=0.012040y[14]=0.011229y[15]=0.010519y[16]=0.009904y[17]=0.009304y[18]=0.009035y[19]=0.007457y[20]=0.012713y[21]=-0.015946y[22]=0.125183y[23]=-0.582439y[24]=2.953862y[25]=-14.729311 y[26]=73.685015y[27]=-368.388036 y[28]=1841.975892 y[29]=-9209.844979y[30]=46049.258229 对于算法2:y[1]=0.198254y[2]=0.060349y[3]=0.054597y[4]=0.039081y[5]=0.032184y[6]=0.026897y[7]=0.023192y[8]=0.020362y[9]=0.018150y[10]=0.016370y[11]=0.014908y[12]=0.013685y[13]=0.012648y[14]=0.011756y[15]=0.010982y[16]=0.010304y[17]=0.009704y[18]=0.009170y[19]=0.008692y[20]=0.008262y[21]=0.007871y[22]=0.007517y[23]=0.007192y[24]=0.006895y[25]=0.006621y[26]=0.006368y[27]=0.006134y[28]=0.005916y[29]=0.005713y[30]=0.0055246、实验结果分析:由实验结果可以看到,算法1在计算过程中误差会增长,所以算法1不稳定。
定积分递推公式例题

定积分递推公式例题0到PI/2上sin^n(x)的定积分,在n大于等于2的时候有递推公式。
你不妨用n表示来推一下。
第一步,拆出来一个sinx写作-d(cosx),分部积分,一次分部积分以后变成了sinx的n-2次方和cosx的平方的乘积,cosx平方写成1-sin^2(x)的形式。
拆开两项,又变成了这个递推公式。
令n阶的积分值用I{n}表示的话,递推公式是,I{n}=[n/(n-1)]I{n-2}。
最后的结果,n分为奇偶两种情况。
像你这道题,前面那个n=2,后面那个n=4。
分别等于小于等于n的偶数的乘积做分母,小于n的奇数的乘积做分子,最后乘以PI/2。
如果n是奇数,那么分母是奇数的乘积,分子是偶数,最后不乘PI/2。
你可以自己算一下。
这种式子写出来也没有什么可读性。
在定积分的计算中,有一种题型是积分中含有正整数,当我们碰到这种题型时一般会使用分部积分法推导出递推公式然后计算。
设在[a,b]上连续,在(a,b)上二阶可导且二阶导有界,证明:证明:(1):若在端点处取得最值,则不等式显然成立:(2):若不在端点处取得最值,则在极值点处取得,则有根据Taylor公式在最大值处展开设在[a,b]上连续,在[0,1]上可积。
证明:证明:令两式相减,得将区间分为,模仿7.1的例题这个没有留言功能,如果有错误请私信指出(2)n n n n n→∞+++.分析将这类问题转化为定积分主要是确定被积函数和积分上下限.若对题目中被积函数难以想到,可采取如下方法:先对区间[0,1]n等分写出积分和,再与所求极限相比较来找出被积函数与积分上下限.解将区间[0,1]n等分,则每个小区间长为1i x n?=,然后把2111n n n =?的一个因子1n乘入和式中各项.于是将所求极限转化为求定积分.即33322。
数值实验

(1)用列主元消元法求解
(2)用列主元消元法求 的行列式。
实验题目
分别用列主元消元法与不选主元消元法求解,分析对结果的影响。
(1) ,
(2) ,
2.LU分解法的优点
实验题目
给定矩阵A与向量b
,
(1)(1)求A的LU分解;
(2)(2)利用A的LU分解求解下列方程组:
① ② ③
对③,若先求 ,再解 有何缺点?
确定系数,求解方程
它是严重病态的。取不同的n,并在 区间上取n个等分点,计算上述系数距阵A的条件数,画出 曲线。
数值实验六
1.1.拟合多项式实验
实验题目
给定数据点 及 如表 所示。
表
0
0.5
0.6
0.7
0.8
0.9
1.0
1
1.75
1.96
2.19
2.44
2.71
3.00
.
用最小二乘法求拟合数据的多项式,并求平方误差,做出离散函数 和拟合函数的图形。
用迭代法求解
(1)(1)选取不同初值 和不同的b,给定迭代误差用两种迭代法计算,观测得到的迭代向量并分析计算结果给出结论。
(2)(2)取定 及b,将A的主对角线元素成倍放大,其他不变,用简单迭代法计算多次,比较收敛速度,分析计算结果并给出结论。
实验题目
① , ,
② ,
数值实验四
1.1.求特征值与特征向量(各种方法的使用与比较)
数值实验
数值实验一
1 .递推计算的稳定性
实验题目
n=0,1,…10
其中a为参数,分别对a=0.05及a=15按下列两种方法计算,列出结果,并对其可靠性进行分析比较,说明原因。
计算方法实验报告

实验一:误差传播与算法稳定性实验目的:体会稳定性在选择算法中的地位。
实验内容:考虑一个简单的由积分定义的序列10I ,0,1,10nn x dx n a x==+⎰其中a 为参数,分别对0.05a =及15a =按下列两种方法计算。
方案1:用递推公式11,1,2,,10n n I aI n n-=-+= 递推初值可由积分直接得01lna I a+= 方案2:用递推公式111(),,1,,1n n I I n N N a n-=-+=-根据估计式当1n a n ≥+时,11(1)(1)(1)n I a n a n <<+++或当01n a n ≤<+时,11(1)(1)n I a n n<≤++ 取递推初值 当1n a n ≥+时, 11121()2(1)(1)(1)2(1)(1)N N a I I a N a N a a N +≈+=+++++ 当01n a n ≤<+时,111()2(1)(1)N N I I a N N≈+++ 实验要求:列出结果,并对其稳定性进行分析比较,说明原因。
实验二:非线性方程数值解法实验目的:探讨不同方法的计算效果和各自特点 实验内容:应用算法(1)牛顿法;(2)割线法 实验要求:(1)用上述各种方法,分别计算下面的两个例子。
在达到精度相同的前提下,比较其迭代次数。
(I )31080x x +-=,取00x =;(II) 2281(0.1)sin 1.060x x x -+++=,取00x =;(2) 取其它的初值0x ,结果如何?反复选取不同的初值,比较其结果; (3) 总结归纳你的实验结果,试说明各种方法的特点。
实验三:选主元高斯消去法----主元的选取与算法的稳定性问题提出:Gauss 消去法是我们在线性代数中已经熟悉的。
但由于计算机的数值运算是在一个有限的浮点数集合上进行的,如何才能确保Gauss 消去法作为数值算法的稳定性呢?Gauss 消去法从理论算法到数值算法,其关键是主元的选择。
0到2πsin的n次方的定积分

0到2πsin的n次方的定积分引言定积分是微积分中的重要概念,用于计算函数在给定区间上的面积或曲线下的面积。
本文将探讨如何计算函数sin的n次方在区间[0,2π]上的定积分,从而深入了解定积分的计算方法和应用。
定积分的基本概念定积分是微积分中的一个基本概念,表示函数在某一区间上的面积。
对于一个函数f(x),在区间[a,b]上的定积分表示为:∫[a,b] f(x) dx其中,∫表示积分符号,a和b分别是积分的下限和上限,f(x)是被积函数,dx表示对自变量x的积分。
定积分的几何意义定积分的几何意义是函数曲线与x轴之间的面积。
当被积函数f(x)大于等于0时,定积分表示曲线上方与x轴之间的面积,当被积函数f(x)小于等于0时,定积分表示曲线下方与x轴之间的面积。
定积分的计算方法定积分的计算有多种方法,常见的方法包括几何法、代数法和微积分法。
下面将介绍几种常用的计算方法。
几何法几何法是通过图形的面积来计算定积分。
对于简单的几何图形,如矩形、三角形和梯形等,可以直接计算出面积。
对于复杂的曲线,可以使用近似的方法来计算面积,如分割区间、计算小矩形面积的和等。
代数法代数法是通过对被积函数进行求导和积分运算,将定积分转化为求导和积分的基本运算。
对于一些简单的函数,可以直接进行求导和积分运算得到定积分的结果。
对于复杂的函数,可以利用一些基本的积分公式和性质进行计算。
微积分法微积分法是通过微积分的基本定理来计算定积分。
微积分的基本定理包括牛顿-莱布尼茨公式和微积分基本定理。
牛顿-莱布尼茨公式表示定积分可以通过原函数的差值来计算,微积分基本定理则表示定积分可以通过原函数的导数来计算。
计算0到2πsin的n次方的定积分现在我们来计算函数sin的n次方在区间[0,2π]上的定积分。
首先,我们需要确定被积函数和积分的区间。
被积函数:f(x) = sin^n(x) 积分区间:[0,2π]根据定积分的计算方法,我们可以选择合适的方法来计算定积分。
定积分的递推公式法

定积分的递推公式法定积分是微积分中的一个重要分支,通过对函数曲线下面的面积进行计算,可以求解出很多实际问题的结果。
在定积分的求解中,递推公式法是一种基础的求解方式,本文将详细介绍它的方法和应用。
一、递推公式法的基本思路递推公式法是一种基于积分学基本定理,以及分部积分的思路来逐步递推求解定积分的方法。
基本定理告诉我们,对于一个函数f(x),它的一个定积分可以转化为求取它的一个原函数F(x)在区间[x0,x]上的差值F(x)−F(x0)。
这就为我们提供了一个新的计算思路:将定积分分解成为两个不同区间上的积分,通过求解这两个积分来逐步得到定积分的结果。
接下来,我们可以用分部积分来处理这个新的积分式,对于一个函数f(x)g(x),由积分学的公式得到:∫f(x)g'(x)dx=f(x)g(x)-∫g(x)f'(x)dx因此,我们可以对新的积分式进行分部积分,得到下面的递推公式:∫[a,b]f(x)dx=F(b)-F(a)=∫[a,c]f(x)dx+∫[c,b]f(x)dx=F(c)-F(a)+F(b)-F(c)其中,F(x)表示f(x)的一个原函数,在第二步中将式子拆成了两个区间的积分来处理。
这个递推式子实现了将原来的一个积分拆成了两个积分的思路。
二、递推公式法的具体应用递推公式法通过分解积分式子,并结合分部积分的方式,将定积分的求解分解成了逐步递推的方式。
接下来我们将通过具体的例子来介绍这个方法的应用。
例一:求解积分∫[0,1]x^2dx对于这个积分,我们可以用递推公式法逐步求解。
首先,我们将定积分分解成为两个不同区间上的积分:∫[0,1]x^2dx=∫[0,1/2]x^2dx+∫[1/2,1]x^2dx。
接下来,我们进行分部积分,对于第一个积分得到:∫[0,1/2]x^2dx=[x^3/3]0 1/2=1/24对于第二个积分,我们同样进行分部积分,得到:∫[1/2,1]x^2dx=[x^3/3]1/2 1=7/24因此,将两个积分的结果进行叠加,即可得到原来定积分的值:∫[0,1]x^2dx=1/24+7/24=1/4例二:求解积分∫[0,1]e^xdx对于这个积分,我们同样可以将定积分分解成为两个不同区间上的积分:∫[0,1]e^xdx=∫[0,1/2]e^xdx+∫[1/2,1]e^xdx。
用递推公式计算定积分(matlab版)上课讲义

0.1823 -0.4116 2.3914 -11.7069 58.7346 -293.5063
仅供学习与交流,如有侵权请联系网站删除 谢谢4
精品资料
%再显示 y(7)—y(11) ans =
1.0e+005 * 0.0147
的公式。
仅供学习与交流,如有侵权请联系网站删除 谢谢8
利用递推公式:y(n-1)= - *y(n),n=20,19,…,1.
而且,由 = *
≤
≤*
=
可取:y(20)≈ *(
)≈0.008730.
仅供学习与交流,如有侵权请联系网站删除 谢谢2
精品资料
实验内容: 对算法一,程序代码如下: function [y,n]=funa() syms k n t; t=0.182322; n=0; y=zeros(1,20); y(1)=t; for k=2:20 y(k)=1/k-5*y(k-1); n=n+1; end y(1:6) y(7:11) 对算法二,程序代码如下: %计算定积分; %n--表示迭代次数; %y 用来存储结果; function [y,n]=f(); syms k y_20; y=zeros(21,1); n=1;
Columns 12 through 20 -0.0000 0.0000 -0.0001 0.0006 -0.0029 0.0143 -0.0717 0.3583 -1.7916
n = 19
算法二结果: >> [y,b]=f
仅供学习与交流,如有侵权请联系网站删除 谢谢6
精品资料
y= 0.1823 0.0884 0.0580 0.0431 0.0343 0.0285 0.0243 0.0212 0.0188 0.0169 0.0154 0.0141 0.0130 0.0120 0.0112 0.0105 0.0099 0.0093 0.0089 0.0083 0.0087
用递推公式计算定积分(matlab版)

用递推公式计算定积分实验目的:1.充分理解不稳定的计算方法会造成误差的积累,在计算过程中会导致误差的迅速增加,从而使结果产生较大的误差.2.在选择数值计算公式来进行近似计算时,应学会选用那些在计算过程中不会导致误差迅速增长的计算公式.3.理解不稳定的计算公式造成误差积累的来源与具体过程;4.掌握简单的matlab语言进行数值计算的方法.实验题目:对n=0,1,2,…,20,计算定积分:实验原理:由于y<n>= = –在计算时有两种迭代方法,如下:方法一:y<n>=– 5*y<n-1>,n=1,2,3, (20)取y<0>= = ln6-ln5 ≈ 0.182322方法二:利用递推公式:y<n-1>=-*y<n>,n=20,19, (1)而且,由 = * ≤≤* =可取:y<20>≈*<>≈0.008730.实验内容:对算法一,程序代码如下:function [y,n]=funa<>syms k n t;t=0.182322;n=0;y=zeros<1,20>;y<1>=t;for k=2:20y<k>=1/k-5*y<k-1>;n=n+1;endy<1:6>y<7:11>对算法二,程序代码如下:%计算定积分;%n--表示迭代次数;%y用来存储结果;function [y,n]=f<>;syms k y_20;y=zeros<21,1>;n=1;y_20=<1/105+1/126>/2;y<21>=y_20;for k=21:-1:2y<k-1>=1/<5*<k-1>>-y<k>/5;n=n+1;end实验结果:由于计算过程中,前11个数字太小,后9个数字比较大,造成前面几个数字只显示0.0000的现象,所以先输出前6个,再输出7—11个,这样就能全部显示出来了.算法一结果:[y,n]=funa%先显示一y<1>—y<6>ans =0.1823-0.41162.3914-11.706958.7346-293.5063%再显示y<7>—y<11>ans =1.0e+005 *0.0147-0.07340.3669-1.83469.1728y =1.0e+012 *Columns 1 through 11 0.0000-0.00000.0000-0.00000.0000-0.00000.0000-0.00000.0000-0.00000.0000Columns 12 through 20 -0.00000.0000-0.00010.0006-0.00290.0143-0.07170.3583-1.7916n = 19算法二结果:>> [y,b]=fy =0.18230.08840.05800.04310.03430.02850.02430.02120.01880.01690.01540.01410.01300.01200.01120.01050.00990.00930.00890.00830.0087b =21实验分析:从两题的计算结果可以看出来,算法一是不稳定的,而算法二是稳定的.对算法一:由于y<1>本身具有一定的误差 ,设为a_1,则由于y<n>=1/n-5y<n-1>=1/n-5<1/<n-1>-5y<n-1>>=……=1/n-5/<n-1>-5^2/<n-2>-…-<5^n>*y<0>所以经过多次迭代后会使误差增大很多倍.由此可知:在实际应用过程中应尽量避免使用数值不稳定的公式.。
数值分析实验

数值分析实验3(总5页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--贵州师范大学数学与计算机科学学院学生实验报告课程名称: 数值分析 班级: 信本班 实验日期: 2013 年 9 月 3日学 号: 姓名: 孙泽香 指导教师: 实验成绩:一、实验名称实验一:递推法的稳定性,秦九韶算法二、实验目的及要求1. 熟悉数值稳定的概念, 通过上机计算,了解舍入误差所引起的数值不稳定性.2. 培养Matlab 编程与上机调试能力.三、实验环境每人一台计算机,要求安装Windows XP 操作系统,Microsoft office2003、(或。
四、实验内容1.教材例中,取16位数字计算,并分析、比较计算结果.2.设100999832()101100994321f x x x x x x x =+++++++,用秦九韶算法编程计算()f x 在1,2,3,4x =上的值.五、算法描述及实验步骤1. 设(1)从0I 尽可能精确的近似值出发,利用递推公式:115(1,2,,14)n n I I n n -=-+=, 计算从1I 到14I 的近似值;(2)从15I 较粗糙的估计值出发,用递推公式:111(15,14,,3,2)55n n I I n n -=-+=计算从1I 到14I 的近似 .2. 秦九韶算法给定n 次多项式Pn (x )=a(n)x^n+a(n-1)x^(n-1)+…+a(1)x+a(0).要计算Pn(x)在x 处的值。
今考虑n 次多项式Pn (x ),用V(k)表示第k 层的值(从里面数起),依次计算 V (1)=a(n)x+a(n-1) V(2)=V(1)x+a(n-2) … V(n)=V(n-1)x+a(0). 显然V (n )=Pn (x ).记a(n)=V(0),上述计算过程可写成:V(0)=a(n)V(k)=V(k-1)*x+a(n-k),(k=1,2,…,n).六、调试过程及实验结果算法一:>> format long e>> syms x;>> fun=inline('1./(x+5)');>> I(1)=quad(fun,0,1);>> for n=1:14I(n+1)=1/n-5*I(n);end>> II =Columns 1 through 3Columns 4 through 6Columns 7 through 9Columns 10 through 12Columns 13 through 15算法二:>> format long e>> syms x;>> fun=inline('x.^14./(x+5)');>> I(15)=quad(fun,0,1);>> for n=14:-1:1I(n)=1/(5*n)-I(n+1)/5;end>> II =Columns 1 through 3Columns 4 through 6Columns 7 through 9Columns 10 through 12Columns 13 through 15设f(x)=101x^100+100x^99+…+3x^2+2x+1,用秦九韶算法编程计算f(x)在x=1,2,3,4上的值。
定积分的计算方法

本科毕业论文定积分的计算方法专业数学与应用数学作者姓名班级2007级1班学号2007011105 指导教师提交日期2011年5月10日陇东学院数学与统计学院2011年5月定积分的计算方法(陇东学院数学与统计学院,甘肃 庆阳 745000)摘 要:本文从定义法,几何意义计算法,公式法以及特殊计算法和近似计算方法讨论了定积分的计算.关键词: 定积分; 计算方法; 二重积分; 近似计算一 引言在数学分析的学习以及科学研究中,到处都会遇到微分、积分的计算问题,微分的计算比较容易,积分的计算难度就要大多了.正因为如此,人们对积分的计算从理论到实践进行了大量的研究,总结了许多种方法.在此,着重对定积分的计算方法和技巧做归类简析.二 正文1根据定义计算定积分定积分的定义]1[:一般地,设函数()f x 在区间[,]a b 上连续,用分点0121i i n a x x x x x x b -=<<<<<<<=将区间[,]a b 任意分成n 个小区间,每个小区间长度为x ∆(b ax n-∆=),在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ= ,作和式:11()()nnn i i i i b aS f x f n ξξ==-=∆=∑∑如果x ∆无限接近于0(亦即n →+∞)时,上述和式n S 无限趋近于常数S ,那么称该常数S 为函数()f x 在区间[,]a b 上的定积分.记为:()baS f x dx =⎰其中()f x 称为被积函数,x 叫做积分变量,[,]a b 为积分区间,b 积分上限,a 积分下限.计算定积分可以通过计算极限ini io x x f ∆∑=→∆1)(lim ξ 来实现.例1]4[ 用定积分的定义求.dx e bax ⎰解 因为xe xf =)(为],[b a 上的连续函数,所以对于任意分割T 和任意点集},{i ξ有i ni i T x f ∆∑=→1)(lim ξ都存在且相等,即dx e bax ⎰存在,所以,把],[b a 平均分成n 等份,因此每个子区间的长度.nab x i -=∆ 取每一子区间的右端点为i ξ,即,i n ab a i -+=ξ于是ni a b a i ef )()(-+=ξ,这样=∆∑=i ni i x f 1)(ξna b a ni ni a b a e nab e-+=-+=-⋅∑(1)(na b a e)(2-++++ nab ena b n a --+))( na b ee nab ee eab na b a na b n nab na b a -⋅-=-⋅-=--+---+)1(]1)[(/),1(--na b e因此dx e bax⎰i ni i n x f ∆=∑=∞→1)(lim ξ∞→=n lim /)1(na b eeab na b a -⋅---+)1(--na b e.)1(a b ab a e e ee -=-=-小结: 用定积分的定义计算定积分,能解决的定积分其被积函数一般是比较简单的情形,主要因为和式x f ni i∆∑=1)(ξ 的极限一般不容易求.2 利用定积分的几何意义计算一般情况下,定积分()baf x dx ⎰的几何意义是介于x 轴、函数()f x 的图形以及直线,x a x b==之间各部分面积的代数和,在x 轴上方的面积取正号,在x 轴下方的面积取负号. 例2 根据定积分的几何意义求下列定积分的值:(1)⎰-x x d 11, (2)⎰--x x R R R d 22, (3)⎰x x d cos 02π, (4)⎰-x x d 11. 解(1)由下图(1)所示,0)(d 1111=+-=⎰-A A x x .- 11 11A A O xyRy2A(2)由上图(2)所示,2d 2222R A x x R RRπ==-⎰-.(3)由上图(3)所示,0)()(d c o s 5353543π20=--++=+-+=⎰A A A A A A A x x .(4)由上图(4)所示,1112122d 611=⋅⋅⋅==⎰-A x x . 3 公式法凡运用不定积分的基本公式和牛顿——菜不尼玆公式计算定积分的方法,称为公式法.公式法适用于解决能用不定积分求出被积函数的原函数的这类函数积分的问题.而用不定积分求原函数时有直接积分、还原积分、分部积分,因此相应地也有定积分的直接积分、还原积分、分部积分法等.牛顿—莱布尼兹公式]1[ 设)(x f 在],[b a 上连续,且)(x F 是)(x f 的一 个原函数,则)()()(a F b F dx x f ba-=⎰. (1)公式(1)是著名的牛顿—莱布尼兹公式.牛顿—莱布尼兹公式把定积分的计算问题归结为求被积函数的原函数在上、下限处函数值之差的问题,从而巧妙地避开了求和式极限的艰难道路,为运用定积分计算普遍存在的总量问题另辟坦途.例如1cos 42]cos [)11sin 2(1212++=+-=+++⎰πarctgx x x dx x x x . O x y1 - 13A 4 A 5 A 2 π π( 3 )1-1- 11 O xy6A 6A (4)4 特殊计算方法 4.1方程式求解在计算过程中,通过解方程(组)的方式求定积分.例3 求xdx e I x sin 20⎰=π.解 xdx e I xsin 20⎰=π=02sin πxe x-xdx e x cos 20⎰π=x xde e cos 202⎰-ππ=⎥⎥⎦⎤⎢⎢⎣⎡+-⎰xdx e xe e x x sin cos 20022πππI e xdx e e x-+=-+=⎰1sin 12202πππ解方程:)1(21122+=⇒-+=ππe I I e I .4.2消项法对某些不便计算的积分,经过一定的变化,将其中某些部分积分相互抵消而得其值.作为一种方法只能尝试着使用. 例4]4[ 求dx x x I ⎰++=1021)1ln(.解 ⎰⎰⎰=-=+=+=404040c o s )4c o s (2ln cos cos sin ln)1ln(ππππdt t t dt t t t dt tgt I tgtx ⎰⎰⎰--+=404040.cos ln )4cos(ln 2ln ππππtdt dt t dt而⎰⎰⎰==--=404044.cos ln cos ln )4cos(ln πππππtdt udu dt t tu.2ln 82ln 40ππ==⎰dt I4.3 利用导数计算定积分例5]5[ ⎰π203.sin xdx x 求解 令,0)(,6)(''',6)('',3)(')()4(23====⇒=x f x f x x f x x f x x f)]2('')0(''[)]2()0([sin )]()([20)4(πππf f f f xdx x f x f ---=-⎰即].120[]80[sin )0(3203πππ---=-⎰xdx x.812sin 2203πππ-=⎰xdx x4.4 利用递推公式例6]5[ 计算xdx e x I xn n sin 20⎰=π.c o s 20x d x e x J x n n ⎰=π解 x d x e x x d x e xn x e x I x n xn xn n c o s s i n s i n2020102⎰⎰--=-πππn n xnJ nI e --=-12)2(π. (2)同理:n n n I nJ J +-=-1. (3)由(2),(3)得:⎪⎪⎩⎪⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡--⎪⎭⎫ ⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡+-⎪⎭⎫ ⎝⎛=---=112112221221n n n n n n n n nJnI e J nJ nI e I ππππ ,,2,1 =n 其中 2121sin 220+==⎰ππe xdx e I x ,.2121cos 2200-==⎰ππe xdx e J x4.5 利用二重积分计算定积分先将定积分设法化为二重积分,再用二重积分的性质进行计算. 例7]1[ 计算dx xxx I ⎰-=13ln 解,2l n l i m ,0l n l i m 1,0l n 31303=-=--→→-x xx x x x xx x x x )内连续,且在( 故 dx x x x ⎰-13ln 有意义,又 ,ln 313dy x xxx y ⎰=-.2l n 11131103131=+===∴⎰⎰⎰⎰⎰dy y dx x dy dy x dx I y y 4.6 利用带参变量的积分计算定积分 例8 计算dx xxx I ⎰-=13ln (即例7) 解 令dx xxx b I b ⎰-=10ln )( )0(≥b ,显然,0)(=b IC b b I bdx x b I b ++=⇒+==⎰)1ln()(11)('10)1(=I 21ln 2ln )1ln()(2ln +=-+=⇒-=∴b b b I C .2ln 213ln)3(=+==∴I I 4.7]3[ 利用留数计算积分这是将实积分转变为复变函数积分,再利用复变函数中留数理论进行计算. 例9 计算.1cos 2dx x x ⎰+∞∞-+解 211)(xx R +=为分母2次,分子0次的有理函数,故上述积分存在.且R(z)在上 半平面只有一个一级极点i ,在实轴上无孤立奇点,又i e z e i z i e z R s iz i iz21)(lim ],)([Re 120-→=+∙-=.221sin 1cos 11222ei e i dx x x i dx x x dx x e ix ππ=∙=+++=+∴-∞+∞-∞+∞-∞+∞-⎰⎰⎰ .)(1cos 2ee R dx x x I e ππ==+=∴⎰+∞∞-5 近似计算法]2[根据定积分的几何意义:dx x f ba⎰)(表示的是以)(x f 为曲边,以x 轴上的区间],[b a 为低的曲边梯形面积的代数和.我们可以用x 轴上的分点b x x x x x n ==,,,,210 ,将曲边梯形的低],[b a 平均分成N 个小区间,每个小区间的长度为,Nab x -=∆过分点作平行于y 轴的线段将整个曲边梯形分成N 个小的曲边梯形,每个小的曲边梯形面积都用已知图形的面积来近似代替.根据已知图形的形状可以分为以下近似计算法:5.1矩形法以第i 个小区间左或右端点对应的函数值x x f x f i i ∆-以为高或,)()1(为低作一个小 矩形,用这个小矩形面积x x f x x f i i ∆∆-)()1(或来近似代替第i 个小曲边梯形的面积(n i ,,2,1 =), 于是Na b x f dx x f Na b x f x x f dx x f ni i bani i n i i ba-≈--=∆-≈∑⎰∑∑⎰===111)()()1()1()(或上式称为矩形法公式.5.2梯形法以第i 个小区间左右端点i i x x ,1-对应的函数值)(),1(i i x f x f -为上下低,以x ∆为高作一个梯形,其面积为2)]()1([xx f x f i i ∆+-,将其作为第i 个小的曲边梯形面积的近似值),,2,1(n i =,于是 xx f x f x x f x f x x f x f dx x f n n ba∆+++∆++∆+≈-⎰)]()([21)]()([21)]()([21)(12110=)]()()(21)(21[10n n x f x f x f x f n a b ++++- 上式称为梯形公式.5.3辛普森法当分点N=2n 时,每个小区间的长度h=nab 2-,过每个分点作平行于Y 轴的直线,它们与曲线 310222111000,,,).,(,),,(),,()(M M M y x M y x M y x M x f y n n n 过点分别交于点= 可确定一条抛物线,以此抛物线为曲边,以区间[20,x x ]为底边的曲边梯形的面积432210,,);4(3M M M y y y h同理以过点++所确定的抛物线为曲边,以区间],[42x x 为底的曲边梯形面积为n n n M M M y y y h21222432,,)4(3--++过点 确定的抛物线为曲边,以区间],[222n n x x -为低的小曲边梯形面积为)4(321222n n n y y y h++--.于是)](4)(2)[(6)(123122422--+++++++++-≈⎰n n n o bay y y y y y y y Nab dx x f上式成为辛普森公式.例10 分别用矩形法,梯形法,辛普森法计算定积分⎰+1021x dx的近似值.解 将区间[0,1]十等分,个基点上被积函数的值列表如下.(取七位有效数字)i x 0 0.1 0.2 0.3 0.4 0.5 i y10.99009900.96153850.91743120.86206900.8000000i x 0.6 0.7 0.8 0.9 1 i y0.73529410.67114090.60975610.55248620.5① 用矩形法公式去计算(取四位有效数字)8099.0)(1011910102=+++≈+⎰y y y dx x dx(或7600.0)(1011021=+++y y y ) ② 用矩形法公式去计算(取四位有效数字)7850.0)22(1011109210102=++++≈+⎰y y y y y x dx ③ 用辛普森法去计算去计算(取七为有效数字)7853982.0)](2)(4[301184********02=+++++++++≈+⎰y y y y y y y y x dx . 准确值:78539816.04112===⎰πarctg dx x与上述值比较,普森法计算结果有六位有效数字是准确的,更接近于真实值.参考文献:[1]华东师范大学数学系.数学分析(第三版).高等教育出版社,2001 [2]首都师范大学数学系.数值分析 科学出版社,2000[3]同济大学数学教研组.高等数学(第三版).高等教育出版社,1988 [4]邓乐斌.数学分析的理论,方法与技巧.华中科技大学出版社. [5]姚允龙.高等数学与数学分析—方法导引.复旦大学出版社,1992。
定积分计算实验报告(3篇)

第1篇一、实验目的1. 理解定积分的概念,掌握定积分的计算方法。
2. 熟悉数值积分的方法,提高数值计算能力。
3. 通过实验,验证定积分的计算结果,加深对定积分理论的理解。
二、实验原理定积分是数学分析中的一个基本概念,它表示函数在某一区间上的累积效果。
对于给定的函数f(x),在区间[a, b]上的定积分可以表示为:∫[a, b] f(x) dx其中,dx表示无穷小的区间宽度。
在实际计算中,定积分往往采用数值积分的方法进行近似计算。
三、实验仪器与软件1. 仪器:计算机2. 软件:MATLAB四、实验步骤1. 输入函数表达式:在MATLAB中输入待积分函数的表达式,例如f(x) = x^2。
2. 设置积分区间:设定积分的上下限a和b。
3. 选择数值积分方法:MATLAB提供了多种数值积分方法,如梯形法、辛普森法、高斯法等。
根据需要选择合适的方法。
4. 进行数值积分计算:调用MATLAB的数值积分函数,如quad函数,进行积分计算。
5. 结果分析:观察计算结果,与理论值进行对比,分析误差来源。
五、实验数据及结果1. 函数表达式:f(x) = x^22. 积分区间:[0, 1]3. 数值积分方法:辛普森法4. 计算结果:I ≈ 1.1666666667六、误差分析1. 理论值:∫[0, 1] x^2 dx = [x^3/3] |[0, 1] = 1/32. 误差来源:a. 数值积分方法的误差:由于数值积分方法是一种近似计算方法,其计算结果与真实值存在一定的误差。
b. 计算过程中的舍入误差:在计算过程中,由于计算机的浮点数表示,可能导致舍入误差。
3. 误差分析:计算结果与理论值相差较大,说明数值积分方法的误差较大。
在实际应用中,可以根据需要选择合适的数值积分方法,以减小误差。
七、实验结论1. 通过本次实验,掌握了定积分的计算方法,了解了数值积分的方法及其优缺点。
2. 了解了数值积分方法在计算过程中的误差来源,为实际应用提供了参考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 用递推公式计算定积分
09信息 符文飞 07
1、实验目的:
由于一个算法是否稳定,十分重要。
如果算法不稳定,则数值计算的结果就会严重背离数学模型的真实结果,因此,在选择数值计算公式来进行近似计算时,我们应特别注意选用那些在数值计算过程中不会导致误差迅速增长的公式。
体会稳定性在选择算法中的地位.误差扩张的算法是不稳定的,是我们所不期望的;误差衰竭的算法是稳定的.是我们努力寻求的,这是贯穿本课程的目标.通过上机计算,了解舍入误差所引起的数值不稳定性。
2、实验题目:
对n =0,1,2,…,20,计算定积分dx x x y n n ⎰+=10
5
3、实验原理
由于y(n)= = –
在计算时有两种迭代方法,如下:
方法一: y(n)= – 5*y(n-1),n=1,2,3, (20)
取y(0)= = ln6-ln5 ≈ 0.182322
方法二:
利用递推公式:y(n-1)=-*y(n),n=20,19, (1)
而且,由 = * ≤≤* =
可取:y(20)≈*()≈0.008730.
4、实验内容:
算法1的程序:
y0=log(6.0)-log(5.0);
y1=0;
n=1;
while n<=30
y1=1/n-5*y0;
fprintf('y[%d]=%-20f',n,y1);
y0=y1;
n=n+1;
if mod(n,1)==0;
fprintf('\n')
end
end
算法2的程序:
y0=(1/105+1/126)/2;
y1=0;
n=1;
while n<=30
y1=1/(5*n)-y0/5;
fprintf('y[%d]=%-20f',n,y1)
y0=y1;
n=n+1;
if mod(n,1)==0
fprintf('\n')
end
end
5、实验结果
对于算法1:
y[1]=0.088392
y[2]=0.058039
y[3]=0.043139
y[4]=0.034306
y[5]=0.028468
y[6]=0.024325
y[7]=0.021233
y[8]=0.018837
y[9]=0.016926。
