三余弦定理与三正弦定理
6.4.3正弦定理余弦定理(第1课时)课件高一下学期数学人教A版

2ab
应用:已知三条边求角度.
变形二
a2 (b c)2 2bc(1 cos A)
b2 (a c)2 2a(c 1- cos B)
c2 (a b)2 2a(b 1- cos C)
应用:配方法的使用
想一想: 余弦定理在直角三角 形中是否
仍然成立?
cosC=
例 2 在△ABC 中,已知 a= 3,b= 2,B=45°,解此三角形.
解析 由余弦定理知 b2=a2+c2-2accos B.
∴2=3+c2-2 3·22c.即 c2- 6c+1=0.
6+ 2
6- 2
6+ 2
解得 c= 2 或 c= 2 ,当 c= 2 时,由余弦定理得
cos A=b2+2cb2c-a2=2+
一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.已知 三角形的几个元素求其他元素的过程叫做解三角形.
在 ABC中,三个内角A、B、C的对边长分别记作a,b,c
二、余弦定理
在三角形ABC中,三个角A,B,C所对的边分别
为a,b,c,怎样用a,b和C表示c?
如图,设CB a,CA b, AB c,那么
3 2.
2.解析 ∵a∶b∶c=2∶ 6∶( 3+1), 令 a=2k,b= 6k,c=( 3+1)k(k>0). 由余弦定理的变形得,
又∵0°<B<180°, ∴B=150°.
cos
b2+c2-a2 6k2+ 3+12k2-4k2 A= 2bc = 2× 6k× 3+1k =
22.
∴A=45°.
题型二 已知两边及一角解三角形
和减去这两边与它们夹角的余弦的积的两倍.
高考数学立体几何中与角有关的四大定理及其证明
则 cosθ = cos2β + cos2γ - 2cosαcosβcosγ sinα
证明:设 ∠HAC = θ1,∠HAB = θ2 ⇒ α = θ1 + θ2,
由三余弦定理得:
cos β cosγ
= =
cosθ cosθ
cosθ1 cosθ2
① ②
由①和②得 cosθ = cosβ = cosγ ③ cosθ1 cosθ2
α
Aβ
γ
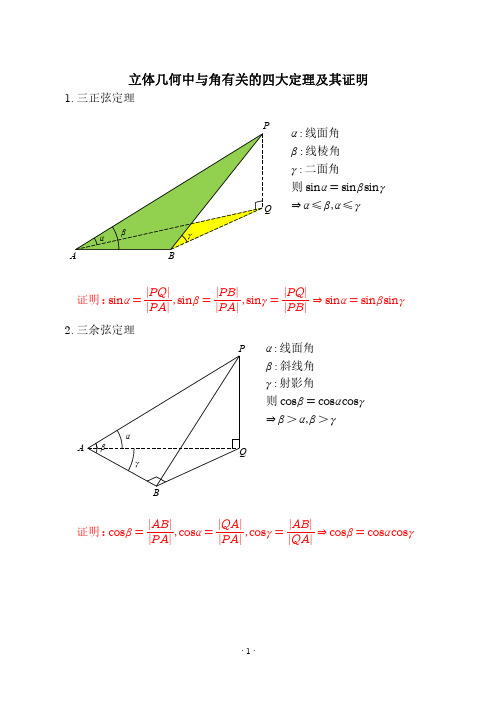
P α : 线面角 β : 斜线角 γ : 射影角 则 cosβ = cosαcosγ ⇒ β > α,β > γ
Q
B
证明:cosβ =
AB PA
,cosα =
QA PA
,cosγ =
AB QA
⇒ cosβ = cosαcosγ
·1·
3. 三夹角公式
P
θ
Aβ
γ
α
C H
B
若 θ 为 PA 与平面 ABC 的夹角
⋅
HO BO
AH AO
⋅
BH BO
= cosθ - cosθ1cosθ2 sinθ1sinθ2
注:若 φ =
π 2
,
则该定理退化为三余弦定理
·3·
立体几何中与角有关的四大定理及其证明
1. 三正弦定理
β α
A
γ
B
P
α : 线面角 β : 线棱角 γ : 二面角 则 sinα = sinβsinγ Q ⇒ α ≤ β,α ≤ γ
证明:sinα =
PQ PA
,sinβ =
PB PA
,sinγ =
PQ PB
⇒ sinα = sinβsinγ
三余弦定理·三垂线定理·三正弦定理

三余弦定理·三垂线定理·三正弦定理三余弦定理(最小角定理或爪子定理)设A 为面上一点,过A 的直线AO 在面上的射影为AB ,AC 为面上的一条直线,那么∠OAC,∠BAC,∠OAB 三角的余弦关系为: cos ∠OAC=cos ∠BAC ×cos ∠OAB(cos ∠BAC 和cos ∠OAB 只能是锐角)斜线与平面内一条直线夹角的余弦值=斜线与平面所成角的余弦值射影与平面内直线夹角的余弦值. 证明:如上图,自点O 作OB ⊥AB 于点B ,过B 作BC ⊥AC 于C ,连OC ,则易知△ABC 、△AOC 、△ABO 均为直角三角形.OA AC AB AC OA AB ===θθθcos ,cos ,cos 21∴ 21cos cos cos θθθ⨯=辅助记忆:这三个角中,角θ是最大的,其余弦值最小,等于另外两个角的余弦值之积。
斜线与平面所成角1θ是斜线与平面内所有直线所成的角中最小的角。
三垂线定理(三余弦定理的特殊情况)平面内的一条直线,如果与穿过这个平面的一条斜线在这个平面上的射影垂直,那么它也和这条斜线垂直。
逆定理:如果平面内一条直线和穿过该平面的一条斜线垂直,那么这条直线也垂直于这条斜线在平面内的射影。
三正弦定理设二面角M -AB -N 的度数为α,在平面M 上有一条射线AC ,它和棱AB 所成角为β,和平面N所成的角为γ,则 sin γ=sin α·sin β(如图)证明:如上图,过C 作CO ⊥平面N 于点O ,过O 作直线OB ⊥二面角的棱于点B ,连OA ,CB ,则易知△CAO ,△CBO ,△ABC 均为直角三角形.于是,sin=AC CO,sin=BC CO ,sin β=AC BC∴ sin γ=sin α·sin β附:β。
三角函数中的正弦定理与余弦定理

三角函数中的正弦定理与余弦定理三角函数是数学中常用的一种函数,在几何学中也起着重要的作用。
本文将探讨三角函数中的两个关键定理:正弦定理和余弦定理。
这两个定理在解决各种三角形问题时非常有用,通过它们可以计算出未知的边长和角度。
一、正弦定理正弦定理是一个关于三角形边长和角度之间关系的定理,它适用于所有的三角形。
正弦定理表达的是三角形中一个角的正弦值与其对边的比例关系。
设三角形的三边分别为a、b、c,相应的角为A、B、C,那么正弦定理可以表示为:a/sinA = b/sinB = c/sinC这个定理的一种形式是:a/sinA = 2R其中,R是三角形外接圆的半径。
正弦定理的应用非常广泛,例如可以通过已知两边和一个角度,求解未知边长或者角度。
同时,它也常用于解决三角形的面积问题。
二、余弦定理余弦定理是另一个与三角形边长和角度之间关系的定理,与正弦定理相比,余弦定理更加灵活,适用于各种类型的三角形。
余弦定理表达的是三角形中一个角的余弦值与其对边的平方和其他两边的乘积之间的关系。
设三角形的三边分别为a、b、c,相应的角为A、B、C,那么余弦定理可以表示为:a^2 = b^2 + c^2 - 2bc*cosAb^2 = a^2 + c^2 - 2ac*cosBc^2 = a^2 + b^2 - 2ab*cosC余弦定理的应用非常广泛,可以通过已知三边求解未知角度或者通过已知两边和一个夹角求解未知边长。
三、正弦定理与余弦定理的关系正弦定理和余弦定理在解决三角形问题时可以互相补充使用。
根据正弦定理,我们可以求解任意一个角的正弦值,通过求解余弦,我们可以得知其他两个角的余弦值。
进而,我们可以通过余弦定理求解三角形的边长。
例如,在解决三角形的边长问题时,我们可以首先使用正弦定理求解一个角的正弦值,然后使用余弦定理求解其他两个角的余弦值。
通过已知角度的余弦值,我们可以应用余弦定理求解未知边长。
在实际应用中,我们常常需要通过这两个定理来解决与三角形相关的问题。
三余弦定理

三余弦定理 内容:若平面的一条斜线与这个平面所成角为α,平面内的一条直线与这条斜线及其射影所成的锐角(或直角)分别为γβ,,则有γαβcos cos cos ⋅=。
α定理概述设A 为面上一点,过A 的直线AO 在面上的射影为AB,AC 为面上的一条直线,那么∠OAC,∠BAC,∠OAB 三角的余弦关系为:cos∠OAC=cos∠BAC×cos∠OAB (∠BAC 与∠OAB 只能就是锐角)通俗点说就就是,cos 平面斜线与平面直线夹角(OAC)=cos 斜线射影与平面直线夹角(BAC)xcos 平面斜线与斜线射影夹角(OAB).又叫最小角定理或爪子定理,可以用于求平面斜线与平面内直线成的最小角.定理证明如上图,自点O 作OB⊥AB 于点B,过B 作BC⊥AC 于C,连OC,则由线线垂直,线面垂直,面面垂直易知△ABC、△AOC、△ABO 均为直角三角形.cos θ1=AB∶OA,cos θ2=AC∶AB,cos θ=AC∶OA,不难验证:cos θ=cos θ1×cos θ2.三正弦定理该定理从老版高中教材人教版《数学》必修第二册(下A),P35的例1:“河堤斜面与水平面所成的二面角为60°,堤面上有一条直道CD,它与堤脚水平线AB 的夹角为30°,沿这条直道从堤脚向上行走10m 时人升高了多少?”抽象出来的一般结论.定理概述设二面角M -AB -N 的度数为α,在平面M 上有一条射线AC,它与棱AB 所成角为β,与平面N 所成的角为γ,则sin γ=sin α·sin β(如图)三正弦定理示意图定理证明如上图,过C作CO⊥平面N于点O,过O作直线OB⊥二面角的棱于点B,连OA,CB,则易知△CAO,△CBO,△ABC均为直角三角形.于就是,sinγ=CO︰AC,sinα=sin∠CBO=CO︰BC,sinβ=sin∠BAC=BC︰AC.由此容易推得sinγ=sinα·sinβ定理应用编辑如果将三正弦定理与三余弦定理联合起来,用于解答立体几何综合题,您会发现出乎意料地简单,甚至不用作任何辅助线!例1如图,已知A1B1C1-ABC就是正三棱柱,D就是AC中点,若AB1⊥BC1,求以BC1为棱,DBC1与CBC1为面的二面角α的度数、(1994年全国高考理科数学23题)三正弦定理应用之例1题图三正弦定理应用之例1解答例2已知Rt△ABC的两直角边AC=2,BC=3.P为斜边AB上一点,现沿CP将此直角三角形折成直二面角A-CP-B(如下图),当AB=√7时,求二面角P-AC-B大小.(上海市1986年高考试题,难度系数0、28)三正弦定理应用之例2题图三正弦定理应用之例2解答三余弦定理定理应用如果将三余弦定理与三正弦定理联合起来使用,用于解答立体几何综合题,您会发现出乎意料地简单,甚至不用作任何辅助线!例1 如图,已知A1B1C1-ABC就是正三棱柱,D就是AC中点,若AB1⊥BC1,求以BC1为棱,DBC1与CBC1为面的二面角α的度数、(1994年全国高考理科数学23题)三余弦定理应用例题1三余弦定理应用例题1解答例2 已知Rt△ABC的两直角边AC=2,BC=3.P为斜边AB上一点,现沿CP将此直角三角形折成直二面角A-CP-B(如下图),当AB=√7时,求二面角P-AC-B大小.(上海市1986年高考试题,难度系数0、28)三余弦定理应用例题2三余弦定理应用例题2解答例3.已知菱形ABCD的边长为1,∠BAD=60°,现沿对角线BD将此菱形折成直二面角 A-BD-C(如图6).( 1)求异面直线AC与BD所成的角;( 2)求二面角A-CD-B的大小.三余弦定理应用例题3。
证明三角形的方法

证明三角形的方法证明三角形的方法有很多,以下将介绍其中几种常见的证明三角形的方法。
方法一:正弦定理三角形的正弦定理是指,在任意一个三角形ABC中,有以下等式成立:a/sinA = b/sinB = c/sinC其中a、b、c分别是三角形ABC的边长,A、B、C分别是三角形ABC的内角。
通过正弦定理,我们可以通过已知的两个角和一个边长,求得另外两个边长,或者通过已知的两个边长和一个角,求得另外一个边长。
这样,我们就可以确定了三角形ABC的三个边长。
方法二:余弦定理三角形的余弦定理是指,在任意一个三角形ABC中,有以下等式成立:c²= a²+ b²- 2abcosC其中a、b、c分别是三角形ABC的边长,C是三角形ABC的对应内角。
通过余弦定理,我们可以通过已知的两个边长和一个内角,求得另外一个边长,或者通过已知的三个边长,求得一个内角。
这样,我们就可以确定了三角形ABC的三个边长或三个内角。
方法三:勾股定理三角形的勾股定理是指,如果一个三角形的两个边长和斜边的关系满足a²+ b²= c²,则这个三角形是一个直角三角形。
勾股定理是三角形中最常用的定理之一,通过勾股定理,我们可以判断一个三角形是否为直角三角形。
方法四:相似三角形的性质如果两个三角形的对应角度相等,则这两个三角形是相似的。
相似三角形的性质可以帮助我们求解未知的三角形边长或者角度。
如果两个三角形相似,那么它们的对应边长之间存在着等比关系。
通过相似三角形的性质,我们可以利用已知的三角形边长和角度来求解未知的三角形边长或者角度。
方法五:共线性质三角形的三个顶点可以看作是三个向量,在平面直角坐标系下,可以使用向量的共线性质来证明三角形。
如果三个顶点的向量满足向量共线的性质,则可以证明这三个点是一个三角形。
共线性质可以通过向量的线性组合来表示,如果一个向量可以表示为另外两个向量的线性组合,则这三个向量是共线的。
正弦定理与余弦定理的使用

正弦定理与余弦定理的使用三角函数是数学中的重要概念,其中正弦定理与余弦定理是常用的三角函数定理。
本文将对正弦定理与余弦定理的使用进行探讨。
1. 正弦定理的使用正弦定理是指在任意三角形ABC中,三条边a、b、c与其对应的角A、B、C之间的关系。
其数学表达式为:a/sinA = b/sinB = c/sinC正弦定理可以用于求解三角形内部元素的相关问题。
例如,已知三角形两边长度和夹角时,可以利用正弦定理求解第三边的长度。
又或者已知两边长度和夹角时,可以通过正弦定理求解夹角的大小。
2. 余弦定理的使用余弦定理是指在任意三角形ABC中,三条边a、b、c与其对应的角A、B、C之间的关系。
其数学表达式为:c² = a² + b² - 2abcosC余弦定理也常用于求解三角形内部元素的相关问题。
例如,已知三边长度时,可以通过余弦定理求解夹角的大小。
又或者已知两边长度和夹角时,可以利用余弦定理求解第三边的长度。
3. 使用示例现假设有一个三角形ABC,已知边长a=5,边长b=7,夹角C=60度。
我们可以通过正弦定理和余弦定理来求解其他未知量。
首先应用正弦定理,根据a/sinA = b/sinB = c/sinC,我们可以得到c/sinC = a/sinA,带入已知条件可得:c/sin60 = 5/sinA进一步化简可得:c = 5*sin60 / sinA对于未知角A,我们可以通过求反正弦函数来得到其大小。
接下来,我们可以应用余弦定理来求解角C的大小。
根据c² = a² +b² - 2abcosC,带入已知条件可得:5² = 7² + c² - 2*7*c*cos60进一步化简可得:c² - 7c + 21 = 0通过解一元二次方程,我们可以求解得到c的值。
通过以上的例子,我们可以看到正弦定理与余弦定理在解决三角形相关问题时的重要性。
任意三角形三角函数公式

任意三角形三角函数公式一、正弦定理正弦定理是三角形中的重要定理之一,它描述了三角形的边长和角度之间的关系。
在任意三角形ABC中,我们可以用正弦定理来表示三角形的边长和角度之间的关系。
正弦定理的数学表达式为:a/sinA = b/sinB = c/sinC其中a、b、c分别表示三角形ABC的三边的长度,A、B、C表示对应的角度。
通过正弦定理,我们可以计算出三角形中任意一个角的正弦值,从而进一步计算出三角形的边长。
二、余弦定理余弦定理是三角形中的另一个重要定理,它描述了三角形的边长和角度之间的关系。
在任意三角形ABC中,我们可以用余弦定理来表示三角形的边长和角度之间的关系。
余弦定理的数学表达式为:c^2 = a^2 + b^2 - 2abcosC其中a、b、c分别表示三角形ABC的三边的长度,C表示对应的角度。
通过余弦定理,我们可以计算出三角形中任意一个角的余弦值,从而进一步计算出三角形的边长。
三、正切定理正切定理是三角形中的另一个重要定理,它描述了三角形的边长和角度之间的关系。
在任意三角形ABC中,我们可以用正切定理来表示三角形的边长和角度之间的关系。
正切定理的数学表达式为:tanA = a/b其中a、b分别表示三角形ABC的两边的长度,A表示对应的角度。
通过正切定理,我们可以计算出三角形中任意一个角的正切值,从而进一步计算出三角形的边长。
正弦定理、余弦定理和正切定理是三角形中常用的三角函数公式。
它们描述了三角形中边长和角度之间的关系,可以方便地计算三角形的边长和角度。
在实际应用中,这些三角函数公式被广泛运用于测量、导航、建筑等领域。
通过测量三角形的边长和角度,我们可以确定物体的位置、测量距离、计算高度等。
这些三角函数公式为我们提供了一个强大的工具,帮助我们解决实际问题。
正弦定理、余弦定理和正切定理是解决三角形问题的重要工具。
它们通过三角函数的关系,将三角形的边长和角度联系起来,为我们提供了便捷的计算方法。
三余弦定理和三正弦定理

Ⅰ.三余弦定理
设A为面上一点,过A的直线AO在面上的射影为AB,AC为面上的一条直线,那么∠OAC,∠BAC,∠OAB三角的余弦关系为:
cos∠OAC=cos∠BAC×cos∠OAB (cos∠BAC和cos∠OAB只能是锐角)
定理证明:如上图,自点O作OB⊥AB于点B,过B作BC⊥AC于C,连OC,则易知△ABC、△AOC、△ABO均为直角三角形.cosθ1=AB∶OA,cosθ2=AC∶AB,cosθ=AC∶OA,不难验证:cosθ=cosθ1×cosθ2.
Ⅱ三正弦定理.
设二面角M-AB-N的度数为α,在平面M上有一条射线AC,它和棱AB所成角为β,和平面N所成的角为γ,则sinγ=sinα·sinβ(如图)
定理证明:如上图,过C作CO⊥平面N于点O,过O作直线OB⊥二面角的棱于点B,连OA,CB,则易知△CAO,△CBO,△ABC均为直角三角形.于是,sinγ=CO︰AC,sinα=sin∠CBO=CO︰BC,
sinβ=sin∠BAC=BC︰AC.
由此容易推得sinγ=sinα·sinβ
定理应用:如果将三余弦定理和三正弦定理联合起来使用,用于解答立体几何综合题,你会发现出乎意料地简单,甚至不用作任何辅助线!
地址:
/view/2208745.htm
/view/3267172.htm。
三余弦与三正弦定理课件-高一数学人教A版(2019)必修第二册

A
则 BK AC (三垂线定理),
BKH 即为二面角 A DC B 的平面角,
设 BC 1,则 BK 3 , BH 2 ,sin BKH BH 2 ;
2
2
BK 3
AC / /DF , DF 与平面 DBC 所成角即为 AC 与平面 DBC 所成角,设为 ,
则由三正弦定理得: sin sin ACD sin BKH 2 2 3 。
SO OF
tan 3
1
3
B
C
三、定理应用:
例 3、2017 浙江高考第 15 题)如图,某人在垂直于水平地面 ABC
的墙面前的点 A 处进行射击训练。易知点 A 到墙面的距离为 AB ,
某目标点 P 沿墙面上的射击线 CM 移动,此人为了准确瞄准目标点 P ,
需计算由点 A 观察点 P 的仰角 的大小。
5
5
E M
A
H
D
N
C
三、定理应用:
例 5:(2020 年浙江高考 19 题)如图,三棱台 DEF ABC 中, 面 ADFC 面 ABC , ACB ACD 45 , DC 2BC.
(1)证明: EF DB ;
(2)求 DF 与面 DBC 所成角的正弦值。
解:(1)由平面 ADFC 平面 ABC 可知,
B
O
M
C
的余弦值等于斜线与平面所成的
角 的余弦值乘以射影与平面内
的直线的夹角 的余弦值,
即 cos cos cos 。
为便于记忆,我们约定:
为斜线角, 为线面角, 为射影角。
2、定理证明:
cos cos ABO OB
AB
cos cos ABC BC
第六章6.4.3余弦定理、正弦定理PPT课件(人教版)

训练题
1.[2019·江西九江一中高一检测]若三角形的三边长之比是1∶ 3 ∶2,
则其所对角之比是( A ) A.1∶2∶3 B.1∶ 3 ∶2 C.1∶ 2 ∶ 3 D. 2 ∶ 3 ∶2
2. [2019·江西赣州五校高一联考]已知△ABC中,a∶b∶c=2∶ 6 ∶
( 3 +1),求△ABC中各角的度数.
训练题
1. 2019·江西九江一中高一检测]设△ABC的内角A,B,C的对边分别为
a,b,c,且cos A= 3 ,cos B= 5 ,b=3,则c=
5
13
14 5
.
2. [2019·北京东城区高三二模]在△ABC中,A= ,a2+b2-c2=ab, 4
c=3,则C=
3 ,a=
6.
3.已知两边及一边的对角解三角形 例5在△ABC中,a= 3 ,b= 2 ,B=45°,求A,C,c.
【解】 ∵ A=45°,C=30°,∴ B=180°-(A+C)=105°.
由 a = c 得a= csinA =10 sin45 =10 2 .
sinA sinC
sinC
sin30
由 b = c 得b= csinB =10 sin105 =20sin 75°.
sinB sinC
sinC
sin30
∵ sin 75°=sin (30°+45°)=sin 30°cos 45°+cos 30°sin 45°=
【解】 由正弦定理及已知条件,有 3 = 2 ,得sin A= 3 .
sinA sin45
2
∵ a>b,∴ A>B=45°.∴ A=60°或120°.
当A=60°时,C=180°-45°-60°=75°,
三角形的余弦定理与正弦定理

三角形的余弦定理与正弦定理三角形是几何学中最基本的形状之一。
在研究三角形的性质和特征时,余弦定理和正弦定理起到了重要的作用。
它们是利用三角形的边长和角度之间的关系来解决各种三角形问题的工具。
本文将详细介绍三角形的余弦定理与正弦定理的定义、公式推导和应用。
一、余弦定理余弦定理是描述三角形边长与角度关系的定理。
对于任意三角形ABC,假设a、b、c分别表示BC、AC和AB的边长,而∠A、∠B和∠C分别表示三角形的内角A、B和C,则余弦定理可以表示为以下公式:c² = a² + b² - 2ab·cosCb² = a² + c² - 2ac·cosBa² = b² + c² - 2bc·cosA其中,cosA、cosB和cosC分别表示角A、B和C的余弦值。
推导过程:我们可以通过向三角形ABC引入高,再利用勾股定理和直角三角形的性质推导余弦定理。
设三角形ABC的高为h,起点为顶点A,终点为D,连接BD和CD,如图所示。
[图示]由于三角形ADC为直角三角形,根据勾股定理,我们可以得到:AC² = AD² + CD² ------ (1)在三角形ABD中,我们可以应用勾股定理得到:AB² = AD² + BD² ------ (2)注意到BD = BC - CD,将其代入式(2),我们可以得到:AB² = AD² + (BC - CD)²= AD² + BC² + CD² - 2BC·CD ------ (3)由于三角形ABC为平面图形,AD ⊥ BC,所以∠ADC = ∠C。
根据余弦定理,我们可以得到:CD² = AC² + AD² - 2AC·AD·cosC ------ (4)将式(1)代入式(4),我们可以得到:CD² = (AD² + CD²) + AD² - 2√(AD² + CD²)√AD·cosC= 2AD² + CD² - 2AD·CD·cosC将式(4)代入式(3),我们可以得到:AB² = 2AD² + BC² - 2BC·CD + 2AD² - 2√(AD² + CD²)√AD·cosC= 4AD² + BC² - 2BC·CD - 2√(AD² + CD²)√AD·cosC= 4AD² + BC² - 2BC·CD - 2AC·AD·cosC由于三角形为平面图形,所以CD = BC·cosA,代入上式得:AB² = 4AD² + BC² - 2BC²·cosA - 2AC·AD·cosC= 4AD² + BC² - 2BC²·cosA - 2AC²·cosC= 4AD² + BC² - 2AC²·cosC - 2BC²·cosA由几何性质可知,4AD² = c²,所以:c² = a² + b² - 2ab·cosC ------ (5)同理,可以推导出余弦定理的其他两个公式。
高中体育-三余弦定理(最小角定理)与三正弦定理

高中体育-三余弦定理(最小角定理)与三正
弦定理
三角形是几何学中一个重要的概念,而三余弦定理(最小角定理)和三正弦定理则是解决三角形相关问题时经常使用的重要工具。
本文将介绍这两个定理的概念和应用。
三余弦定理(最小角定理)
三余弦定理(最小角定理)是指一个三角形中的任意一条边的
平方等于其他两条边的平方和减去这两条边的乘积与这两条边的夹
角的余弦的乘积。
即:
ab^2 = ac^2 + bc^2 - 2ac * bc * cosA
其中,a、b、c为三角形的边长,A为边a对应的夹角。
根据
这个定理,我们可以通过已知两边和它们的夹角来推导出第三条边
的长度,或者通过已知三条边的长度来计算夹角的大小。
这个定理常用于解决关于三角形边长和夹角的问题,例如求解三角形的面积、判断三角形的形状等。
三正弦定理
三正弦定理是指在一个任意三角形中,三条边的长度与它们所对应的角的正弦之间的关系。
即:
a / sinA =
b / sinB =
c / sinC
这个定理可以帮助我们在已知一个三角形的两个角度和边长的情况下,求解出第三个角度或边长的数值。
三正弦定理常常用于求解不直角三角形的边长和角度,尤其是当我们只知道两个角度和一个边长时,可以通过这个定理计算出其他未知量。
总结:三余弦定理和三正弦定理是高中数学中与三角形相关的重要定理。
通过运用这两个定理,我们可以解决关于三角形的边长和夹角的各种问题,在几何学的学习中具有重要的应用价值。
三角函数中线定理公式

三角函数中线定理公式一、正弦定理正弦定理描述了一个三角形中,每条边的长度与对应角的正弦值之间的关系。
设一个三角形的三个顶点分别为A、B、C,它们对应的边长分别为a、b、c,以及对应的角度分别为α、β、γ,则正弦定理可以表达为:a/sinα = b/sinβ = c/sinγ该定理可以简化为以下形式:sinα/a = sinβ/b = sinγ/c正弦定理可以用来计算未知角度或边长的具体数值,只要知道其他已知量即可。
例如,已知一个三角形的两个角和边长,可以利用正弦定理求解第三个角或边长。
二、余弦定理余弦定理描述了一个三角形中,每条边的长度与对应角的余弦值之间的关系。
设一个三角形的三个顶点分别为A、B、C,它们对应的边长分别为a、b、c,以及对应的角度分别为α、β、γ,则余弦定理可以表达为:a² = b² + c² - 2bc cos αb² = a² + c² - 2ac cos βc² = a² + b² - 2ab cos γ余弦定理可以用来计算未知角度或边长的具体数值,只要知道其他已知量即可。
例如,已知一个三角形的两个角和边长,可以利用余弦定理求解第三个角或边长。
三、正切定理正切定理描述了一个三角形中,每条边的长度与对应角的正切值之间的关系。
设一个三角形的三个顶点分别为A、B、C,它们对应的边长分别为a、b、c,以及对应的角度分别为α、β、γ,则正切定理可以表达为:tan α = a/btan β = b/atan γ = a/b正切定理可以用来计算未知角度或边长的具体数值,只要知道其他已知量即可。
例如,已知一个三角形的两个角和边长,可以利用正切定理求解第三个角或边长。
综上所述,三角函数中的线定理是非常重要的概念,帮助我们研究和理解三角形的性质和关系。
通过正弦定理、余弦定理和正切定理,我们可以计算未知角度或边长的具体数值,解决各类三角形的相关问题。
正弦定理和余弦定理的关系

正弦定理和余弦定理的关系
正弦定理和余弦定理都是解决三角形中任意一角的大小和三角形中的边之间的关系的定理,但它们的公式和使用方法略有不同。
正弦定理是指在一个三角形中,任意一条边与这条边相对的角的正弦值成比例。
具体而言,以三角形的三个内角为A、B 和C 分别对应三条边a、b 和c,正弦定理公式为:a/ sinA = b/ sinB = c/ sinC。
余弦定理则是以三角形余弦公式为基础,用于计算任意一条边的平方与其余两条边平方之差的差。
具体而言,以三角形的三个内角为A、B 和C 分别对应三条边a、b 和c,余弦定理公式为:a^2 = b^2 + c^2 - 2bc*cosA (同理,还可以得到b^2 和c^2的计算公式)。
两者之间有什么关系呢?实际上,它们之间存在着互相转化的关系。
以正弦定理为例,当已知三角形的两个角度和一个对边时,可以利用正弦定理计算出第三条边。
接着,再利用余弦定理计算出剩下的两个角度,即可完整的求出整个三角形。
反之,如果已知三条边长度,可以先用余弦定理求出一个角度,再根据正弦定理求出剩下的两个角度。
综上所述,正弦定理和余弦定理是求解三角形问题时经常用到的常用公式,它们可以互相转化,同时可以结合其他几何学知识,进一步帮助我们解决各种四边形、
多边形等几何图形的问题。
三角形正玄余玄正切定理公式

三角形正玄余玄正切定理公式
三角形的正弦、余弦和正切定理公式如下:
1. 正弦定理:在任意三角形ABC中,角A、B、C所对的边长分别为a、b、c,三角形外接圆的半径为R,直径为D。
则有:
a/sinA=b/sinB=c/sinC=2r=D(r为外接圆半径,D为直径)。
2. 余弦定理:对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
对于边长为a、b、c而相应角为A、B、C的三角形则有:
a²=b²+c²-2bc·cosA;
b²=a²+c²-2ac·cosB;
c²=a²+b²-2ab·cosC。
也可表示为:
cosC=(a²+b²-c²)/2ab;
cosB=(a²+c²-b²)/2ac;
cosA=(c²+b²-a²)/2bc。
3. 正切定理:在三角形中,任意两条边的和除以第一条边减第二条边的差所得的商,等于这两条边对角的和的一半的正切除以第一条边对角减第二条边对角的差的一半的正切所得的商。
对于边长为a,b和c而相应角为A,B
和C的三角形,有:
(a-b)/(a+b)=[tan(A-B)/2]/[tan(A+B)/2];
(b-c)/(b+c)=[tan(B-C)/2]/[tan(B+C)/2];
(c-a)/(c+a)=[tan(C-A)/2]/[tan(C+A)/2]。
以上信息仅供参考,如果您还有疑问,建议咨询数学领域专业人士或查阅数学书籍。
三角形中的正弦与余弦定理

三角形中的正弦与余弦定理三角形是几何学中非常重要的概念,它的性质和定理有助于解决各种与三角形相关的问题。
在本篇文章中,我们将讨论三角形中的两个重要定理,即正弦定理与余弦定理。
正弦定理是指在任意三角形ABC中,有一个关系式可以成立:三角形的任意一条边的长度和与该边对应的角的正弦值之间存在一个比例关系。
假设三角形ABC的三边分别为a、b和c,并分别对应的内角为A、B和C。
根据正弦定理,我们可以得到以下的关系式:a/sinA = b/sinB = c/sinC这个定理的一个很有用的推论是:如果一个三角形的两个角的正弦值相等,那么这两个角也相等。
正弦定理在解决涉及到角度和边长的问题时非常有用。
接下来,让我们来讨论余弦定理。
余弦定理描述了任意三角形ABC 中的一条边的平方等于另外两条边的平方和减去这两条边的乘积与该边对应的角的余弦值的乘积。
以三角形ABC为例,设三边分别为a、b和c,而对应的内角为A、B和C。
根据余弦定理,我们可以得到以下的关系式:a^2 = b^2 + c^2 - 2bc cosAb^2 = a^2 + c^2 - 2ac cosBc^2 = a^2 + b^2 - 2ab cosC余弦定理经常被用于计算一个三角形的边长或角度,特别是当我们只知道两边的长度和它们之间的夹角时。
正弦定理和余弦定理是解决三角形相关问题的重要工具。
它们可以帮助我们计算三角形的边长、角度、以及其他相关的属性。
在实际应用中,我们可以利用这两个定理解决建筑、航海、天文学等领域的问题。
总结起来,正弦定理和余弦定理是求解三角形问题时非常有用的工具。
通过理解和运用这两个定理,我们可以更好地理解和解决与三角形相关的各种问题。
无论是在学术研究还是实际应用中,它们都扮演着重要的角色。
三角形正余弦定理

三角形正余弦定理三角形是我们初中数学学习的重点内容之一,而正余弦定理是三角形的重要定理之一。
正余弦定理是通过三角形的边长和角度之间的关系来描述三角形的定理。
下面我们来详细介绍一下正余弦定理。
正余弦定理是用来求解三角形的边长或角度的定理。
它可以帮助我们在已知一些边长和角度的情况下,求解其他未知的边长和角度。
正余弦定理的表达式如下:正弦定理:在一个三角形ABC中,边长a、b、c与对应的角A、B、C之间满足以下关系:a/sinA = b/sinB = c/sinC余弦定理:在一个三角形ABC中,边长a、b、c与对应的角A、B、C之间满足以下关系:a² = b² + c² - 2bc*cosAb² = a² + c² - 2ac*cosBc² = a² + b² - 2ab*cosC正余弦定理的应用非常广泛,下面我们来看一些实际问题的例子。
例一:已知一个三角形的两个边长和夹角,求解第三边长。
假设在一个三角形ABC中,已知边长a=5,边长b=7,夹角C=60°,我们可以通过正弦定理来求解边长c。
根据正弦定理:a/sinA = b/sinB = c/sinC代入已知条件:5/sinA = 7/sinB = c/sin60°通过计算,我们可以求得sinA=0.866和sinB=0.5然后,我们可以通过sinA=0.866求得角A的近似值为60°,然后再代入边长a和角A的值来求解边长c。
通过计算,我们可以求得边长c≈9.17例二:已知一个三角形的两个边长和一个角度,求解另外两个角度。
假设在一个三角形ABC中,已知边长a=4,边长b=6,角C=45°,我们可以通过余弦定理来求解角A和角B。
根据余弦定理:a² = b² + c² - 2bc*cosA代入已知条件:4² = 6² + c² - 2*6*c*cos45°通过计算,我们可以求得c² - 12c + 20 = 0解方程得到c≈2.53然后,我们可以通过cosA = (b² + c² - a²) / (2bc)来求解角A。
