一维抛物线型方程数值解法(1)(附图及matlab程序)
一维抛物型偏微分方程初边值问题求解

一维抛物型偏微分方程初边值问题求解摘要:一、引言二、一维抛物型偏微分方程1.定义与性质2.初边值问题三、求解方法1.紧差分格式2.追赶法3.有限元算法四、Matlab程序实现1.紧差分格式程序2.追赶法程序五、结论与展望正文:一、引言在数学、物理等领域,偏微分方程是一类重要的方程。
其中,一维抛物型偏微分方程在科学研究和实际应用中具有广泛的意义。
本文将探讨一维抛物型偏微分方程的初边值问题的求解方法,并介绍相应的Matlab程序实现。
二、一维抛物型偏微分方程1.定义与性质一维抛物型偏微分方程是指具有如下形式的方程:u_t = a * u_xx其中,u(x, t) 表示未知函数,t 表示时间,x 表示空间坐标,a 为常数。
2.初边值问题初边值问题是指在给定的初始条件和边界条件下求解偏微分方程的问题。
在一维抛物型偏微分方程中,初边值问题可以表示为:u(x, 0) = u_0(x)u(x, t) = u_t(x, t) 在边界x=0,x=L上三、求解方法1.紧差分格式紧差分格式是一种求解偏微分方程的方法,其精度为O(h^(1/2) * Δt),无条件稳定。
在这种方法中,我们首先需要建立离散的网格系统,然后通过数值积分求解离散化的偏微分方程。
2.追赶法追赶法是一种求解线性方程组的方法,也可以用于求解初边值问题。
在这种方法中,我们首先需要将偏微分方程转化为线性方程组,然后使用追赶法求解线性方程组。
3.有限元算法有限元算法是一种基于变分原理的求解方法,可以将偏微分方程问题转化为求解有限元空间的线性方程组。
这种方法在求解一维抛物型偏微分方程时具有较高的精度和可靠性。
一维波动方程加权差分格式求数值解matlab程序

一维波动方程是描述波动传播的数学模型,在工程和物理学等领域有着重要的应用。
求解一维波动方程的数值解是一项具有挑战性的任务,对于大多数情况而言,解析解并不容易得到,因此数值方法是一种有效的求解途径。
本文将以加权差分格式为例,探讨如何使用Matlab程序求解一维波动方程的数值解。
一、一维波动方程的数学模型一维波动方程描述了空间维度和时间维度上的波动传播规律,在无阻尼情况下可以用如下的偏微分方程表示:∂^2u/∂t^2 = c^2∂^2u/∂x^2其中u(x, t)是波动的位移,c是波速,x和t分别是空间和时间的变量。
这是一个典型的双变量偏微分方程,求解这样的方程通常需要借助数值方法。
二、加权差分格式加权差分格式是求解偏微分方程数值解的一种方法,它将偏微分方程的微分算子用离散化的差分算子来逼近,得到一个离散的代数方程组,再利用数值计算方法来求解这个代数方程组。
对于一维波动方程,我们可以采用加权差分格式来进行求解。
1. 空间上的离散化对于空间上的离散化,我们可以采用有限差分法来逼近微分算子,通常采用中心差分格式。
假设在空间上我们将取n个离散点,空间步长为Δx,则可以得到以下近似:∂^2u/∂x^2 ≈ (u(x+Δx) - 2u(x) + u(x-Δx))/Δx^2将这个近似代入原方程,就可以得到离散化后的代数方程组。
2. 时间上的离散化对于时间上的离散化,我们可以采用显式或隐式的时间离散化方法。
在这里我们以显式的欧拉方法为例,假设在时间上我们将取m个离散点,时间步长为Δt,则可以得到以下近似:∂^2u/∂t^2 ≈ (u(x, t+Δt) - 2u(x, t) + u(x, t-Δt))/Δt^2将这个近似代入原方程,就可以得到离散化后的代数方程组。
3. 加权差分格式的权重选择加权差分格式需要指定一个权重参数来对离散化的方程进行求解,典型的有中心差分格式、向前差分格式和向后差分格式等。
选择合适的差分格式能够提高数值解的稳定性和精度。
matlab绘图(一维、二维、三维)

>> t=[0:0.1:20];
>> x=t;
>> y=sin(t); >> z=cos(t); >> plot3(x,y,z)
第25页,共42页。
数学实验
数学实验
先画点 (x,y,z),后连线,构成曲面网格图
点: ( xij , yij , zij ) i 1,,m, j 1,,n
x11 x12
第13页,共42页。
同时绘制多个函数图像
数学实验
plot(x1,y1,s1,x2,y2,s2, ... ,xn,yn,sn)
等价于:
hold on
plot(x1,y1,s1) plot(x2,y2,s2) ...
plot(xn,yn,sn)
属性选项 可以省略
第14页,共42页。
图形的其他属性
数学实验
Property: linewidth, markersize, fontsize, fontweight, fontname, …
第9页,共42页。
图形的其他属性
坐标轴标注 xlabel(’text’) 或 ylabel(’text’)
例:
数学实验
第10页,共42页。
图形的其他属性
添加图例 legend(string1,string2, ...) >> legend('cos(x)');
Matlab 绘图
数学实验
如何画出 y=sin(x) 在 [0, 2*pi] 上的图像?
第1页,共42页。
Matlab 绘图
数学实验
手工作图
找点: x=0, pi/3, pi/2, 2*pi/3, pi, …
一维抛物型偏微分方程初边值问题求解

一维抛物型偏微分方程初边值问题求解标题:深度剖析一维抛物型偏微分方程初边值问题求解在数学和物理领域中,偏微分方程是一种重要的数学工具,被广泛应用于描述自然界中的各种现象和规律。
一维抛物型偏微分方程初边值问题求解是其中的一个重要领域,对于理解热传导、扩散和波动等问题具有重要意义。
本文将深入探讨一维抛物型偏微分方程初边值问题的求解方法,并以此为基础,展开对这一领域的全面评估。
1. 引言一维抛物型偏微分方程是描述时间和空间变化的物理量之间的关系的数学方程。
它具有广泛的应用,包括热传导、扩散、波动等诸多领域。
在实际问题中,我们经常需要求解一维抛物型偏微分方程的初边值问题,这就是本文要探讨的重点。
2. 理论基础在讨论一维抛物型偏微分方程初边值问题的求解之前,我们首先需要了解其理论基础。
一维抛物型偏微分方程通常具有形式:\[ \frac{\partial u}{\partial t} = c^2 \frac{\partial^2 u}{\partialx^2} + f(x, t) \]其中,\( u(x, t) \) 是待求函数,\( c \) 是常数,\( f(x, t) \) 是已知函数。
对于这类方程,我们需要给定初始条件 \( u(x, 0) = \phi(x) \) 和边界条件 \( u(0, t) = g(t) \) 以及 \( u(l, t) =h(t) \)。
3. 求解方法在实际问题中,我们可以采用分离变量法、变量替换法、差分法等多种方法来求解一维抛物型偏微分方程的初边值问题。
这里我们以分离变量法为例进行讨论。
我们可以假设解具有形式:\[ u(x, t) = X(x)T(t) \]将其代入原方程,得到两个关于 \( X \) 和 \( T \) 的常微分方程,分别为:\[ \frac{1}{c^2}\frac{X''(x)}{X(x)} = \frac{T'(t)}{T(t)} = -\lambda \]解出 \( X(x) \) 和 \( T(t) \) 后,再利用边界条件和初始条件,我们就可以得到一维抛物型偏微分方程初边值问题的解。
【MATLAB与机械设计】一维优化之二次插值法(抛物线法)

【MATLAB与机械设计】⼀维优化之⼆次插值法(抛物线法)⼆次插值法⼜称抛物线法,它是利⽤函数在极值点附近具有⼆次函数的性质建⽴起来的⼀种多项式逼近⽅法。
利⽤⽬标函数在若⼲点的信息(函数值、导数值等),构造⼀个与⽬标函数值相接近的插值多项式,⽤该多项式的最优解作为函数的近似最优解,随着搜索区间的逐次缩短,多项式的最优点与原函数最优点的距离逐渐减⼩,直⾄满⾜精度要求。
1.⼆次插值的程序框图:2. MATLAB可执⾏程序function [x,f_x]=Quadratic_interpolation(f,x1,x2,x3,exp)%% 函数说明%{本函数应⽤于⼆次插值其中f表⽰输⼊函数x1,x2,x3表⽰要进⾏插值的三个点exp精度x:为输出的极⼩值点f_x:为输出的极⼩值调⽤⽅法:clc;clear;f=@(x)(x+1/x);[x,f]=n_d(f,0,10,30,0.01);xf%}%% 函数主题f1=f(x1);f2=f(x2);f3=f(x3);%{sov_f=[f1,f2,f3]';sov_x=[1,x1,x1^21,x2,x2^21,x3,x3^2];sov_a=sov_x\sov_f;a=sov_a;a0=a(1);a1=a(2);a2=a(3);%x_m=-a1/(2*a2);%}while 1A=2*(f1*(x2-x3)+f2*(x2-x1)+f3*(x1-x2));B=(f1*(x2^2-x3^2)+f2*(x2^2-x1^2)+f3*(x1^2-x2^2));if A==0disp('run is lost!!')elsex_m=B/A;if abs(x2-x_m)<expif f(x_m)<=f2x=x_m;f_x=f(x_m);breakelsex=x2;f_x=f2;breakendelseif (x_m-x1)*(x_m-x2)<0if f(x_m)<=f2x3=x2;x2=x_m;f3=f2;f2=f(x_m);elsex1=x_m;f1=f(x_m);endelseif f(x_m)<=f2x1=x2;x2=x_m;f1=f2;f2=f(x_m);elsex3=x_m;f3=f(x_m);end end endendendend。
抛物线法matlab

d3=(d2-d1)/(t(3)-t(1));
B=d2+d3*(t(3)-t(2));%计算算法中的B
root=t(3)-2*f3/(B+sign(B)*sqrt(B^2-4*f3*d3));
tol=abs(root-t(3));
end
end
f1=subs(sym(f),findsym(sym(f)),t(1)); %计算3个点的函数值
f2=subs(sym(f),findsym(sym(f)),t(2));
f3=subs(sym(f),findsym(sym(f)),t(3));
d1=(f2-f1)/(t(2)-t(1));%计算3个差分
d3=(f2-f1)/(x-a);
B=d2+d3*(x-b);
root=x-2*fx/(B+sign(B)*sqrt(B^2-4*fx*d3));
t=zeros(3);
t(1)=a;
t(2)=b;
t(3)=x;
while(tol>eps)
t(1)=t(2); %保存3个点
t(2)=t(3);
t(3)=root;
return;
else
tol=1;
fa=subs(sym(f),findsym(sym(f)),a);
fb=subs(sym(f),findsym(sym(f)),a);
fx=subs(sym(f),findsym(sym(f)),x);
d1=(fb-fa)/(b-a);
d2=(fx-fb)/(x-b);
批注本地保存成功开通会员云端永久保存去开通
抛物线法的MATLAB程序代码如下:
matlab曲率半径 (1)

matlab曲率半径 (1)Matlab曲率半径曲率半径是在数学和物理学中用于描述曲线弯曲程度的一个重要概念。
在Matlab中,我们可以使用不同的方法来计算曲线的曲率半径,包括数值解法和符号解法。
本文将介绍如何使用Matlab计算曲率半径,并提供一些实例来展示其应用。
1. 数值解法数值解法是使用数值逼近的方法计算曲线的曲率半径。
在Matlab中,我们可以通过以下步骤来实现:步骤一:导入曲线数据首先,我们需要导入曲线的数据点。
假设我们有一条曲线,其中包含n个数据点,每个数据点的坐标为(xi, yi)。
在Matlab中,我们可以使用如下代码导入数据:```x = [x1, x2, ..., xn];y = [y1, y2, ..., yn];```步骤二:计算曲线切线向量接下来,我们需要计算曲线上每个数据点的切线向量。
切线向量可以通过计算相邻两个数据点之间的差分来获得。
在Matlab中,我们可以使用如下代码计算切线向量:```dx = diff(x);dy = diff(y);```步骤三:计算切线向量的长度计算切线向量的长度,即切线的长度。
在Matlab中,我们可以使用如下代码计算切线长度:```tangent_length = sqrt(dx.^2 + dy.^2);```步骤四:计算曲率半径通过计算切线长度和切线向量之间的关系,我们可以得到曲线的曲率半径。
在Matlab中,我们可以使用如下代码计算曲率半径:```curvature_radius = tangent_length.^2./(dx.*dy - dy.*dx);```2. 符号解法符号解法是使用符号计算方法来计算曲线的曲率半径。
在Matlab中,我们可以使用符号函数来代表曲线,并利用符号运算来求解曲率半径。
下面是一个示例:假设我们有一个二次曲线,其方程为y = ax^2 + bx + c。
我们可以使用符号计算的方法求解其曲率半径。
步骤一:定义符号变量和函数首先,我们需要定义符号变量和符号函数。
matlab实现Newton法-割线法-抛物线法

matlab实现Newton法-割线法-抛物线法(一)实验目的:熟悉和掌握Newton法,割线法,抛物线法的方法思路,并能够在matlab上编程实现(二)问题描述:问题一. 方程求根(1).给定一个三次方程,分别用Newton法,割线法,抛物线法求解. 方程的构造方法:(a)根:方程的根为学号的后三位乘以倒数第二位加1再除以1000. 假设你的学号为B06060141,则根为141*(4+1)/1000=0.564(b)方程:以你的学号的后三位数分别作为方程的三次项,二次项,一次项的系数,根据所给的根以及三个系数确定常数项.例如:你的学号是B06060141,则你的方程是x3+4x2+x+a0=0的形式.方程的根为0.564,因此有0.5643+4*0.5642+0.564+a0=0,于是a0=-2.015790144你的方程为x3+4x2+x-2.015790144=0.(2)假设方程是sinx+4x2+x+a0=0的形式(三个系数分别是学号中的数字),重新解决类似的问题(3)构造一个五次方程完成上面的工作.四次方程的构造:将三次多项式再乘以(x-p*)2得到对应的五次多项式(p*为已经确定的方程的根,显然,得到的五次方程有重根). (4)将(2)中的方程同样乘以(x-p*)得到一个新的方程来求解(三)算法介绍在本文题中,我们用到了newton法,割线法,抛物线法。
1.Newton法迭代格式为:x k+1=x k−f(x k)f′(x k+1)当初值x0与真解足够靠近,newton迭代法收敛,对于单根,newton收敛速度很快,对于重根,收敛较慢。
2.割线法:为了回避导数值f′(x k)的计算,使用x k,x k−1上的差商代替f′(x k),得到割线法迭代公式:x k+1=x k−x k−x k−1f(x k)−f(x k−1)f(x k)割线法的收敛阶虽然低于newton法,但迭代以此只需计算一次f(x k)函数值,不需计算其导数,所以效率高,实际问题中经常应用。
MATLAB_微分方程问题的解法

• 描述函数:
function dx=apolloeq(t,x) mu=1/82.45; mu1=1-mu; r1=sqrt((x(1)+mu)^2+x(3)^2); r2=sqrt((x(1)-mu1)^2+x(3)^2); dx=[x(2); 2*x(4)+x(1)-mu1*(x(1)+mu)/r1^3-mu*(x(1)-mu1)/r2^3; x(4); -2*x(2)+x(3)-mu1*x(3)/r1^3-mu*x(3)/r2^3];
• 可采用comet3( )函数绘制动画式的轨迹。 >> comet3(x(:,1),x(:,2),x(:,3))
• 描述微分方程是常微分方程初值问题数值求解 的关键。
>> f1=inline(['[-8/3*x(1)+x(2)*x(3); -10*x(2)+10*x(3);',... '-x(1)*x(2)+28*x(2)-x(3)]'],'t','x'); >> t_final=100; x0=[0;0;1e-10]; >> [t,x]=ode45(f1,[0,t_final],x0); >> plot(t,x), figure; >> plot3(x(:,1),x(:,2),x(:,3)); axis([10 42 -20 20 -20 25]); 得出完全一致的结果。
6.2.3 一阶微分方程组的数值解
6.2.3.1 四阶五级Runge-Kutta-Felhberg算法
通过误差向量调节步长,此为自动变步长方法。 四阶五级RKF算法有参量系数表。
matlab微分方程常用数值解法

一、概述Matlab作为一种常用的科学计算软件,在微分方程的数值解法领域具有广泛的应用。
微分方程是描述自然现象中变化规律的数学工具,而数值解法则是指使用计算机进行近似求解微分方程的方法。
在Matlab 中,有多种常用的数值解法可以用来求解微分方程,例如欧拉法、改进的欧拉法、四阶龙格-库塔法等。
本文将对这些数值解法进行介绍和比较,以帮助读者更好地理解和应用微分方程求解数值方法。
二、欧拉法欧拉法是微分方程的最简单的数值解法之一,它通过离散化微分方程进行近似求解。
具体而言,对于一阶常微分方程dy/dx=f(x,y),可以利用欧拉法进行数值解。
欧拉法的基本思想是将自变量x的增量Δx分成n个小区间,然后根据微分方程的数值近似公式y(x+Δx)=y(x)+f(x,y)Δx对每个小区间进行迭代计算。
欧拉法的优点是简单易实现,但由于它是一阶的数值方法,因此对于某些微分方程求解效果可能不够准确。
三、改进的欧拉法改进的欧拉法是对欧拉法的一种改进,它通过在每个小区间内使用平均斜率来提高求解的精度。
具体而言,对于微分方程dy/dx=f(x,y),改进的欧拉法可以通过以下迭代公式进行数值求解:y(x+Δx)=y(x)+Δx/2[f(x,y)+f(x+Δx,y+Δx*f(x,y))]改进的欧拉法相比于欧拉法具有更高的数值精度,但计算量也相对增加。
四、四阶龙格-库塔法四阶龙格-库塔法是一种常用的数值微分方程求解方法,它通过四次迭代计算来获得微分方程的数值解。
具体而言,对于微分方程dy/dx=f(x,y),四阶龙格-库塔法可以用以下公式进行数值求解:k1=f(x,y)k2=f(x+Δx/2,y+Δx/2*k1)k3=f(x+Δx/2,y+Δx/2*k2)k4=f(x+Δx,y+Δx*k3)y(x+Δx)=y(x)+Δx/6*(k1+2*k2+2*k3+k4)四阶龙格-库塔法相比于欧拉法和改进的欧拉法具有更高的数值精度和稳定性,但计算量也相对较大。
抛物线法求方程
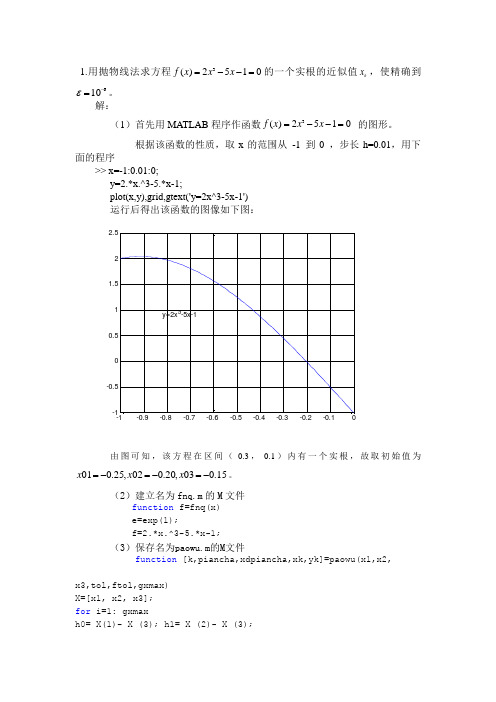
x,使精确到1.用抛物线法求方程0=xxf的一个实根的近似值x--125)(3=kε。
6=10-解:(1)首先用MATLAB程序作函数0=xxf的图形。
-x(3=1-52)根据该函数的性质,取x的范围从-1 到0 ,步长h=0.01,用下面的程序>> x=-1:0.01:0;y=2.*x.^3-5.*x-1;plot(x,y),grid,gtext('y=2x^3-5x-1')运行后得出该函数的图像如下图:由图可知,该方程在区间(-0.3,-0.1)内有一个实根,故取初始值为-01-=xx。
.0=x-=03.015,20,02.025(2)建立名为fnq.m的M文件function f=fnq(x)e=exp(1);f=2.*x.^3-5.*x-1;(3)保存名为paowu.m的M文件function [k,piancha,xdpiancha,xk,yk]=paowu(x1,x2,x3,tol,ftol,gxmax)X=[x1, x2, x3];for i=1: gxmaxh0= X(1)- X (3); h1= X (2)- X (3);u0= fnq (X (1))- fnq (X (3) );u1= fnq (X (2))- fnq (X (3));c= fnq (X (3));fenmu= h0^2* h1- h1^2* h0; afenzi= u0* h1- u1* h0;bfenzi= u1*h0^2-u0*h1^2;a= afenzi/ fenmu; b= bfenzi/ fenmu;deta=b^2-4*a*c;cha=[abs(X(3)-X(1)),abs(X(3)-X(2)),abs(X(2)- X(1))];piancha =min(cha); xdpiancha= piancha/( abs (X(3))+eps);if deta<0disp('提示:根的判别式值为负数.'),detakf=sqrt(deta);elseif deta<=0disp('提示:根的判别式值为零.'),detakf=0;elsedisp('提示:根的判别式值为正数.'),detakf=sqrt(deta);endif b<0detakf=- detakf;endz=-2*c/(b+ detakf);xk= X(3)+ z;q1= xk - X (1); q2= xk - X (2);q3= xk - X (3);if abs(q2)< abs(q1)X1=[X(2), X(1), X(3)]; X= X1;Y= fnq(X);endif abs(q3)< abs(q1)X2=[X(1), X(3), X(2)]; X= X2;Y= fnq(X);endX(3)= xk; Y(3)=fnq(X(3));yk= Y(3); [i piancha xdpiancha xk yk]if (abs(yk)<ftol)&(( piancha <tol)|(xdpiancha< tol))k=i; X(3)= xk; Y(3)=fnq(X(3));yk= Y(3);return;endendif i>gxmaxdisp('请注意:迭代次数超过给定的最大值gxmax,请重新输入初始值x1,x2,x3') return;endP=[i,piancha,xdpiancha,xk,yk]';(4)在MATLAB工作窗口输入程序[k,piancha,xdpiancha,xk,yk]=paowu(-0.25,-0.20,-0.15,1e-6,1e-6,50) (5)运行后输出的结果提示:根的判别式值为正数.ans =1.0000 0.0500 0.3333 -0.2034 0.0000 提示:根的判别式值为正数.ans =2.0000 0.0034 0.0166 -0.2034 -0.0000 提示:根的判别式值为正数.ans =3.0000 0.0000 0.0000 -0.2034 0 提示:根的判别式值为正数.ans =4.0000 0.0000 0.0000 -0.2034 0 k =4piancha =2.3295e-010xdpiancha =1.1455e-009xk =-0.2034yk =10 的根的近似值xk =-0.2034,其函数值为yk =0,即,迭代k=4 次,得到精度为6xk的相邻最小偏差为piancha =2.3295e-010 ,其相对误差为xdpiancha =1.1455e-009。
(完整word版)matlab数值分析例题

1、 在MATLAB 中用Jacobi 迭代法讨论线性方程组,1231231234748212515x x x x x x x x x -+=⎧⎪-+=-⎨⎪-++=⎩(1)给出Jacobi 迭代法的迭代方程,并判定Jacobi 迭代法求解此方程组是否收敛。
(2)若收敛,编程求解该线性方程组.解(1):A=[4 -1 1;4 —8 1;-2 1 5] %线性方程组系数矩阵A =4 -1 1 4 -8 1 —2 1 5>> D=diag(diag(A))D =4 0 0 0 —8 0 0 0 5〉〉 L=—tril (A,-1) % A 的下三角矩阵L =0 0 0 —4 0 0 2 —1 0〉〉U=-triu(A,1)% A的上三角矩阵U =0 1 —10 0 —10 0 0B=inv(D)*(L+U)% B为雅可比迭代矩阵B =0 0.2500 —0。
25000.5000 0 0.12500。
4000 —0.2000 0〉〉r=eigs(B,1)%B的谱半径r =0。
3347 〈1Jacobi迭代法收敛。
(2)在matlab上编写程序如下:A=[4 —1 1;4 -8 1;—2 1 5];〉〉b=[7 —21 15]';>〉x0=[0 0 0]’;〉〉[x,k]=jacobi(A,b,x0,1e—7)x =2。
00004.00003。
0000k =17附jacobi迭代法的matlab程序如下:function [x,k]=jacobi(A,b,x0,eps)% 采用Jacobi迭代法求Ax=b的解%A为系数矩阵%b为常数向量%x0为迭代初始向量%eps为解的精度控制max1= 300; %默认最多迭代300,超过300次给出警告D=diag(diag(A));%求A的对角矩阵L=-tril(A,—1); %求A的下三角阵U=—triu(A,1); %求A的上三角阵B=D\(L+U);f=D\b;x=B*x0+f;k=1;%迭代次数while norm(x-x0)>=epsx0=x;x=B*x0+f;k=k+1;if(k〉=max1)disp(’迭代超过300次,方程组可能不收敛’);return;endend2、设有某实验数据如下:(1)在MATLAB中作图观察离散点的结构,用多项式拟合的方法拟合一个合适的多项式函数;(2)在MATLAB中作出离散点和拟合曲线图。
一维抛物线偏微分方程数值解法

一维抛物线偏微分方程数值解法(2)上一篇文章请参看一维抛物线偏微分方程数值解法(1)解一维抛物线型方程(理论书籍可以参看孙志忠:偏微分方程数值解法)Ut-Uxx=0, 0<x<1,0<t<=1(Ut-aUxx=f(x,t),a>0)U(x,0)=e^x, 0<=x<=1,U(0,t)=e^t,U(1,t)=e^(1+t), 0<t<=1精确解为:U(x,t)=e^(x+t);Matlab程序:(此为向后差分法)function [u p e x t]=pwxywxh(h1,h2,m,n)%欧拉向后差分法解一维抛物线型偏微分方程%此程序用的是追赶法解线性方程组%h1为空间步长,h2为时间步长%m,n分别为空间,时间网格数%p为精确解,u为数值解,e为误差x=(0:m)*h1+0;t=(0:n)*h2+0;for(i=1:n+1)for(j=1:m+1)f(i,j)=0;endendfor(i=1:n+1)u(i,1)=exp(t(i));u(i,m+1)=exp(1+t(i));endfor(i=1:m+1)u(1,i)=exp(x(i));endr=h2/(h1*h1);for(i=2:n+1) %外循环,先固定每一时间层,每一时间层上解一线性方程组%a(1)=0;b(1)=1+2*r;c(1)=-r;d(1)=u(i-1,2)+h2*f(i,2)+r*u(i,1);for(k=2:m-2)a(k)=-r;b(k)=1+2*r;c(k)=-r;d(k)=u(i-1,k+1)+h2*f(i,k+1);%输入部分系数矩阵,为0的矩阵元素不输入%enda(m-1)=-r;b(m-1)=1+2*r;d(m-1)=u(i-1,m)+h2*f(i,m)+r*u(i,m+1);for(k=1:m-2) %开始解线性方程组消元过程a(k+1)=-a(k+1)/b(k);b(k+1)=b(k+1)+a(k+1)*c(k);d(k+1)=d(k+1)+a(k+1)*d(k);endu(i,m)=d(m-1)/b(m-1); %回代过程%for(k=m-2:-1:1)u(i,k+1)=(d(k)-c(k)*u(i,k+2))/b(k);endendfor(i=1:n+1)for(j=1:m+1)p(i,j)=exp(x(j)+t(i)); %p为精确解e(i,j)=abs(u(i,j)-p(i,j));%e为误差endend[u p e x t]=pwxywxh(0.1,0.005,10,200);surf(x,t,e);xlabel('x');ylabel('t');zlabel('e');>> title('误差曲面');plot(t,e)误差较之前的欧拉向前差分格式增长了两倍[u p e x t]=pwxywxh(0.1,0.05,10,20); plot(t,e)[u p e x t]=pwxywxh(0.01,0.05,100,20); plot(t,e)[u p e x t]=pwxywxh(0.01,0.005,100,200);plot(x,e)[u p e x t]=pwxywxh(0.005,0.005,200,200); plot(x,e)X=1时,出现了误差??? 不是边界条件吗?不能理解这方法还是比前一种方法误差大呀不过可以随便改变时间、空间步长。
Matlab方程的求解

Matlab方程的求解Matlab是一个广泛使用的数学编程环境,它提供了许多强大的数值计算功能,包括求解各种数学方程。
以下是一些关于如何在Matlab中求解方程的基本步骤。
步骤1:启动Matlab首先,你需要打开Matlab。
你可以在Windows、macOS或Linux等操作系统上安装和使用Matlab。
步骤2:创建方程在Matlab中求解方程的第一步是创建方程。
例如,如果你想求解以下线性方程:2x + 3y = 104x - y = 14你可以在Matlab中输入这些方程如下:eq1 = 2x + 3y == 10;eq2 = 4*x - y == 14;步骤3:使用solve函数求解方程接下来,你可以使用Matlab中的solve函数来求解这些方程。
solve函数可以找到使方程为零的变量值。
你可以输入以下命令来求解上述方程:sol = solve([eq1, eq2], [x, y]);在这个例子中,sol是一个包含解的对象,x和y是未知数,eq1和eq2是包含已知数的方程列表。
这个命令会找到满足这两个方程的x和y的值。
步骤4:显示解你可以使用以下命令来查看解:disp(sol)这将显示包含解的对象sol的属性。
例如,它可能会显示以下内容:x = 1.0000 + 2.0000i y = 3.0000 + 2.0000i这表明x的值为1+2i,y的值为3+2i。
如果你需要的是实数解,可以通过以下方法获得:x_real = real(sol.x); y_real = real(sol.y);disp([x_real, y_real])以上就是在Matlab中求解方程的基本步骤。
需要注意的是,对于一些更复杂的方程或者非线性方程,可能需要使用其他的Matlab函数或者额外的工具箱来求解。
在处理复杂的数学问题时,Matlab的文档和帮助功能可以提供更多的信息和帮助。
教你用MATLAB快速作一维、二维、三维图

subplot(2,2,3);
• ct=cos(x)./(sin(x)+eps);
plot(x,t);
title('tangent(x)');
• subplot(2,2,1); 分成2×2区域且指定1号为活动区 axis ([0 2*pi -40 40]);
• plot(x,y);
subplot(2,2,4);
• 下述程序段绘制一正方形并以黄色填充:
精选可编辑ppt
20
• x=[0 1 1 0 0]; 正方形顶点坐标向量
• y=[0 0 1 1 0]; • fill(x,y,'y');绘制并以黄色填充正方形图
• 再如:
• x=[0:0.025:2*pi];
• y=sin(3*x);
• fill(x,y,[0.5 0.3 0.4]); 颜色向量
24
2、多条曲线
plot3(x,y,z)
其中x,y,z都是m*n矩阵,其对应的每一列表示一条曲线.
例 画多条曲线观察函数Z=(X+Y).^2.
解 x=-3:0.1:3;y=1:0.1:5; [X,Y]=meshgrid(x,y); Z=(X+Y).^2; plot3(X,Y,Z)
列程序段将绘制条形图形
x=[-2.5:0.25:2.5];
y=exp(-x.*x); bar(x,y); 绘制条形图命令
精选可编辑ppt
19
• 6.3 填充图形
• fill(x,y,’c’)函数用来绘制并填充二维多
边图形,x和y为二维多边形顶点坐标向 量。字符 ’c’ 规定填充颜色,其取值前 已叙述。
-0.6
精选可编辑ppt
一维抛物线型方程数值解法附图及matlab程序

一维抛物线偏微分方程数值解法(1)解一维抛物线型方程(理论书籍可以参看孙志忠:偏微分方程数值解法)Ut-Uxx=0, 0<x<1,0<t<=1(Ut-aUxx=f(x,t),a>0)U(x,0)=e^x, 0<=x<=1,U(0,t)=e^t,U(1,t)=e^(1+t), 0<t<=1精确解为:U(x,t)=e^(x+t);下面给出两个matlab程序,实质一样(用的是向前欧拉格式)第二个程序由之前解线性方程组的G-S迭代法得到,迭代次数k=2(固定)function [p u e x t]=pwxywxq(h1,h2,m,n)% 解抛物线型一维方程向前欧拉格式(Ut-aUxx=f(x,t),a>0)%不用解线性方程组,由下一层(时间层)的值就直接得到上一层的值%m,n为x,t方向的网格数,例如(2-0)/0.01=200;%e为误差,p为精确解u=zeros(n+1,m+1);x=0+(0:m)*h1;t=0+(0:n)*h2;for(i=1:n+1)u(i,1)=exp(t(i));u(i,m+1)=exp(1+t(i));endfor(i=1:m+1)u(1,i)=exp(x(i));endfor(i=1:n+1)for(j=1:m+1)f(i,j)=0;endendr=h2/(h1*h1); %此处r=a*h2/(h1*h1);a=1 要求r<=1/2差分格式才稳定for(i=1:n)for(j=2:m)u(i+1,j)=(1-2*r)*u(i,j)+r*(u(i,j-1)+u(i,j+1))+h2*f(i,j);endendfor(i=1:n+1)for(j=1:m+1)p(i,j)=exp(x(j)+t(i));e(i,j)=abs(u(i,j)-p(i,j));endend或者:function [u e p x t k]=paowuxianyiweixq(h1,h2,m,n,kmax,ep)% 解抛物线型一维方程向前欧拉格式(Ut-aUxx=f(x,t),a>0)%kmax为最大迭代次数%m,n为x,t方向的网格数,例如(2-0)/0.01=200;%e为误差,p为精确解syms temp;u=zeros(n+1,m+1);x=0+(0:m)*h1;t=0+(0:n)*h2;for(i=1:n+1)u(i,1)=exp(t(i));u(i,m+1)=exp(1+t(i));endfor(i=1:m+1)u(1,i)=exp(x(i));endfor(i=1:n+1)for(j=1:m+1)f(i,j)=0;endenda=zeros(n,m-1);r=h2/(h1*h1);%此处r=a*h2/(h1*h1);a=1 要求r<=1/2差分格式才稳定for(k=1:kmax)for(i=1:n)for(j=2:m)temp=(1-2*r)*u(i,j)+r*(u(i,j-1)+u(i,j+1))+h2*f(i,j); a(i+1,j)=(temp-u(i+1,j))*(temp-u(i+1,j));u(i+1,j)=temp;endenda(i,j)=sqrt(a(i,j));if(k>kmax)break;endif(max(max(a))<ep)break;endendfor(i=1:n+1)for(j=1:m+1)p(i,j)=exp(x(j)+t(i));e(i,j)=abs(u(i,j)-p(i,j));endend在命令窗口中输入:[p u e x t]=pwxywxq(0.1,0.005,10,200);>> surf(x,t,u)>> shading interp;>> xlabel('x');ylabel('t');zlabel('u');>> title('一维抛物线方程向前欧拉法数值解');surf(x,t,p)>> shading interp;xlabel('x');ylabel('t');zlabel('p');>> title('一维抛物线方程向前欧拉法精确解')同理:plot(x,u)>> xlabel('x');ylabel('u');>> title('固定时间改变x u与x 的关系数值解')[p u e x t]=pwxywxq(0.1,0.01,10,100);surf(x,t,u)Warning: Axis limits outside float precision, use ZBuffer or Painters instead. Not renderingWarning: Axis limits outside float precision, use ZBuffer or Painters instead. Not renderingWarning: Axis limits outside float precision, use ZBuffer or Painters instead. Not renderingWarning: Axis limits outside float precision, use ZBuffer or Painters instead. Not rendering>> surf(x,t,e)Warning: Axis limits outside float precision, use ZBuffer or Painters instead. Not renderingWarning: Axis limits outside float precision, use ZBuffer or Painters instead. Not renderingWarning: Axis limits outside float precision, use ZBuffer or Painters instead. Not rendering>>所以空间步长与时间步长需要满足上面所说的关系继续减小时间步长[p u e x t]=pwxywxq(0.1,0.001,10,1000)此为欧拉向前差分法,向后差分法请参看下一篇文章:一维抛物线偏微分方程数值解法(2)(附matlab程序及图片)我近期在做这个,有兴趣可以一起学习百度账号:草随风逝。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一维抛物线偏微分方程数值解法(1)
解一维抛物线型方程(理论书籍可以参看孙志忠:偏微分方程数值解法)
Ut-Uxx=0, 0<x<1,0<t<=1(Ut-aUxx=f(x,t),a>0)
U(x,0)=e^x, 0<=x<=1,
U(0,t)=e^t,U(1,t)=e^(1+t), 0<t<=1
精确解为:U(x,t)=e^(x+t);
下面给出两个matlab程序,实质一样(用的是向前欧拉格式)
第二个程序由之前解线性方程组的G-S迭代法得到,迭代次数k=2(固定)
function [p u e x t]=pwxywxq(h1,h2,m,n)
% 解抛物线型一维方程向前欧拉格式(Ut-aUxx=f(x,t),a>0)
%不用解线性方程组,由下一层(时间层)的值就直接得到上一层的值
%m,n为x,t方向的网格数,例如(2-0)/0.01=200;
%e为误差,p为精确解
u=zeros(n+1,m+1);
x=0+(0:m)*h1;
t=0+(0:n)*h2;
for(i=1:n+1)
u(i,1)=exp(t(i));
u(i,m+1)=exp(1+t(i));
end
for(i=1:m+1)
u(1,i)=exp(x(i));
end
for(i=1:n+1)
for(j=1:m+1)
f(i,j)=0;
end
end
r=h2/(h1*h1); %此处r=a*h2/(h1*h1);a=1 要求r<=1/2差分格式才稳定for(i=1:n)
for(j=2:m)
u(i+1,j)=(1-2*r)*u(i,j)+r*(u(i,j-1)+u(i,j+1))+h2*f(i,j);
end
end
for(i=1:n+1)
for(j=1:m+1)
p(i,j)=exp(x(j)+t(i));
e(i,j)=abs(u(i,j)-p(i,j));
end
end
或者:
function [u e p x t k]=paowuxianyiweixq(h1,h2,m,n,kmax,ep)
% 解抛物线型一维方程向前欧拉格式(Ut-aUxx=f(x,t),a>0)
%kmax为最大迭代次数
%m,n为x,t方向的网格数,例如(2-0)/0.01=200;
%e为误差,p为精确解
syms temp;
u=zeros(n+1,m+1);
x=0+(0:m)*h1;
t=0+(0:n)*h2;
for(i=1:n+1)
u(i,1)=exp(t(i));
u(i,m+1)=exp(1+t(i));
end
for(i=1:m+1)
u(1,i)=exp(x(i));
end
for(i=1:n+1)
for(j=1:m+1)
f(i,j)=0;
end
end
a=zeros(n,m-1);
r=h2/(h1*h1);%此处r=a*h2/(h1*h1);a=1 要求r<=1/2差分格式才稳定
for(k=1:kmax)
for(i=1:n)
for(j=2:m)
temp=(1-2*r)*u(i,j)+r*(u(i,j-1)+u(i,j+1))+h2*f(i,j); a(i+1,j)=(temp-u(i+1,j))*(temp-u(i+1,j));
u(i+1,j)=temp;
end
end
a(i,j)=sqrt(a(i,j));
if(k>kmax)
break;
end
if(max(max(a))<ep)
break;
end
end
for(i=1:n+1)
for(j=1:m+1)
p(i,j)=exp(x(j)+t(i));
e(i,j)=abs(u(i,j)-p(i,j));
end
end
在命令窗口中输入:
[p u e x t]=pwxywxq(0.1,0.005,10,200);
>> surf(x,t,u)
>> shading interp;
>> xlabel('x');ylabel('t');zlabel('u');
>> title('一维抛物线方程向前欧拉法数值解');
surf(x,t,p)
>> shading interp;
xlabel('x');ylabel('t');zlabel('p');
>> title('一维抛物线方程向前欧拉法精确解')
同理:
plot(x,u)
>> xlabel('x');ylabel('u');
>> title('固定时间改变x u与x 的关系数值解')
[p u e x t]=pwxywxq(0.1,0.01,10,100);
surf(x,t,u)
Warning: Axis limits outside float precision, use ZBuffer or Painters instead. Not rendering
Warning: Axis limits outside float precision, use ZBuffer or Painters instead. Not rendering
Warning: Axis limits outside float precision, use ZBuffer or Painters instead. Not rendering
Warning: Axis limits outside float precision, use ZBuffer or Painters instead. Not rendering
>> surf(x,t,e)
Warning: Axis limits outside float precision, use ZBuffer or Painters instead. Not rendering
Warning: Axis limits outside float precision, use ZBuffer or Painters instead. Not rendering
Warning: Axis limits outside float precision, use ZBuffer or Painters instead. Not rendering
>>
所以空间步长与时间步长需要满足上面所说的关系
继续减小时间步长
[p u e x t]=pwxywxq(0.1,0.001,10,1000)
此为欧拉向前差分法,向后差分法请参看下一篇文章
:一维抛物线偏微分方程数值解法(2)(附matlab程序及图片)
我近期在做这个,有兴趣可以一起学习
百度账号:草随风逝。
