自适应MATLABlms程序

合集下载

LMS算法自适应滤波器的MATLAB仿真与DSP实现

据存储器，６４ｋ字的程序存储器．具有高度并行性．用ＤＳＰ特有的汇编语言实现以上３种ＬＭＳ算法自适应滤波器．在ＴＭＳ３２０Ｃ５４Ｘ的指令系统中，单周期乘／累加指令ＭＡＣ和循环寻址方式可使滤波器在一个周期内完成每个样值的计算．在实现ＬＭＳ自适应算法时，由于要计算两组数对应项乘积的累加和，还有要采用循环寻址方式，因此，本文滤波器程序中采用ＤＳＰ指令中的ＲＰＴＺ和ＭＡＣ结合循环寻址方式实现两累加和的运算．ＲＰＴＺＡ，＃Ｆ１ＬＴＥＲＭＡＣ℃ＯＦＦ＿ＤＰ＋０％，＊ＤＡＴＡ＿ＤＰ＋０％，Ａ其中，ＲＰＴＺ指令用于将累加器Ａ清零，将立即数１０（本实验中滤波器阶数取１１）装入到重复计数器，使下条ＭＡＣ指令重复执行１０＋１次．ＭＡＣ指令实现将两存储区数据的乘积累加到累加器Ａ，使存储器的指针以循环寻址的方式指向下一个存储区．其中，ＦＩＬＴＥＲ，ＣＯＦＦ＿ＤＰ，ＤＡＴＡ—ＤＰ分别为自适应滤波器的阶数，自适应滤波器系数缓冲区指针和输入样值缓冲区指针．为了提高算法效率，程序中使用了ＴＭＳ３２０Ｃ５４Ｘ特有的ＬＭＳ指令，来快速实现本文的几种自适应滤波器．设计中，采用１５００Ｈｚ的期望信号与３１２Ｈｚ的噪声信号叠加作为１１个系数的自适应滤波器的一个输入信号，对于每一个时刻ｒ／，，计算自适应滤波器的输出，误差信号是输出信号与期望信号的差值．固定步长ＬＭＳ算法，变步长ＬＭＳ算法和归一化ＬＭＳ算法在ＳＺ—ＥＰＰ５４１６评估板上实现的结果如图３所示．７０（ｄ）归一化ＬＭＳ算法滤波结果图３ＤＳＰ实现结果Ｆｉｇ．３ＴｈｅｒｅａｌｉｚａｔｉｏｎＤＳＰ图３中，横坐标为仿真时间，竖坐标为波形幅值，图３（ａ）为输入含噪声的叠加信号，图３（ｂ）为固定步长ＬＭＳ算法滤波器实现结果，从图３（ｂ）中可以看出，在滤波初始阶段，滤波结果不明显，输入的叠加信号经过自适应滤波器后在初始阶段噪声没有得到明显抑制，存在较大稳态误差，收敛速度比较慢，收敛速度和稳态误差都有待改善．图３（ｃ）为变步长ＬＭＳ算法滤波结果，从图３（ｃ）中可以看出，在滤波初始阶段，稳态误差已得到改善，但仍有较小稳态误差浮动，初始收敛速度有所加快，输入的叠加信号经过自适应滤波器后噪声得到较明显抑制，滤波性能优于固定步长ＬＭＳ算法．图３（ａ）为归一化ＬＭＳ算法滤波结果，从图３（ｄ）中可以看出，在滤波初始阶段，稳态误差已经得到明显改善，稳态误差浮动已经得到改善，输入的叠加信号经过自适应滤波器后噪声得到更明显抑制，更好的克服了固定步长存在的矛盾．可见，此滤波器滤波效果最为明显．４结论初始收敛速度与稳态误差是衡量自适应滤波算法性能优劣的两个重要技术指标，本文通过对固定步长，变步长ＬＭＳ算法和归一化ＬＭＳ算法自适应滤波器进行ＭＡＴＬＡＢ仿真与ＤＳＰ实现，比较滤波结果，证明了归一化ＬＭＳ算法能够保证具有更快的收敛速度与更小的稳态误差，能有效去除不相关的独立噪声的干扰，克服了固定步长在增大初始收敛速度与减小稳态误差之间存在的矛盾，优化了自适应滤波器的性能，滤波效果明显．参考文献：【ｌ】１ＳｈｉｒｅｅｎＷ，ＬｉＴ．ＡＤＳＰ－Ｎｍｅｄａｃｔｉｖｅｐｏｗｅｒｆｉｌｔｅｒｆｏｒｌｏｗｖｏｌｔａｇｅｄｉｓｔｒｉｂｕｔｉｏｎｓｙｓｔｅｍｓ田．Ｆ＿如２ｔｒｉｃＰｏｗｅｒｓｙＢｔｅｌ璐Ｒｅｓｅａｒｃｈ，２００８，７８：１５６１—１５６７．【２】吕振肃，熊景松．一种改进的变步长ＬＭＳ自适应算法【刀．信号处理，２００８，２４（１）：１４４－１４６．ＬｖｚＳ，ＸｉｏｎｇＪＳ．Ａｎｏｖｄｉ呻ｒ－－ｏｖｅｄｖａｒｉａｂｌｅｓｔｅｐ－ｓｉｚｅＬＭＳ妇ｒｉⅡ姗田．ＳｉｇｌｌａｌＰｒｏｃｅｓｓｉｎｇ，２００８，２４（１）：１４４一１４６．【３】ＫｕｋｒｅｒＯ．№ｃａｎｉＩＩＡ．Ｆｒｅｑｕｅｎｃｙ－ｒｅｓｐｏｎｓｅ－ｓｈａｐｅｄＬＭＳａｄａｐｔｉｖｅｆｉｌｔｅｒ田．Ｄｉｇｉｔａｌｓｉｌ｝ＩａｌＰｒｏ∞ｓ＊ｉｎｇ，２００６，１６：８５５—８６９．【４】叶永生，余容桂．一种新的自适应最小均方算法及其应用研究【刀．电测与仪表，２００８，４５（７）：１９—２２．ＹｅＹＳ。

Matlab中的自适应控制设计方法

Matlab中的自适应控制设计方法自适应控制是一种广泛应用于工程领域的控制策略，它通过实时地调整控制器参数，以适应系统动态特性的变化。

Matlab是一个功能强大的工具，提供了丰富的工具箱和函数，使得自适应控制的设计和实现变得更加便捷。

本文将介绍几种常见的自适应控制设计方法，并说明在Matlab中的实现。

1. 最小均方（LMS）算法最小均方算法是一种基于误差信号的单参数自适应调整方法。

通过最小化误差信号的均方值，实时更新参数以使系统逐渐趋于稳定。

Matlab中可使用函数"lms"来实现LMS算法的设计。

该函数可以根据输入信号和期望输出信号的数据进行参数的自适应调整。

2. 递归最小二乘（RLS）算法递归最小二乘算法是一种多参数自适应调整方法，它通过将参数更新与误差信号相关联，实现对参数的在线更新。

相较于LMS算法，RLS算法具有更好的收敛性能和稳定性。

Matlab中的函数"rls"可以实现递归最小二乘算法的设计，用户可以根据系统的要求自定义相关参数。

3. 自适应模型预测控制（MPC）算法自适应模型预测控制算法中，控制器利用系统的模型对未来的输出进行预测，并根据预测结果进行参数调整。

通过不断更新模型中的参数和系统输出的观测值，实现了对动态特性的自适应调整。

Matlab提供了函数"mpc"用于实现自适应模型预测控制的设计。

用户可以通过设定模型和目标函数等参数，实现对系统的自适应控制。

4. 遗传算法（GA）优化方法遗传算法是一种基于自然进化原理的优化方法，通过模拟自然选择、交叉和变异等过程，寻找最优的参数组合。

Matlab中的函数"ga"可以实现遗传算法的设计，用户可以根据系统的需求和约束，设定适应度函数以及参数的取值范围，实现对系统参数的自适应优化。

自适应控制在实际的工程中有着广泛的应用，例如航空、汽车、机器人等领域。

通过Matlab中提供的强大工具和函数，工程师可以轻松地实现自适应控制的设计和实现。

使用Matlab技术进行自适应控制的基本步骤

使用Matlab技术进行自适应控制的基本步骤自适应控制是一种能够根据外界环境或系统变化自动调整控制策略的控制方法。

Matlab作为一种强大的数值计算软件，提供了丰富的工具和函数库，可用于实现自适应控制算法。

本文将介绍使用Matlab技术进行自适应控制的基本步骤。

1. 确定系统模型自适应控制首先需要对控制对象进行建模和描述。

在Matlab中，可以使用系统工具箱或函数库来创建系统模型。

对于连续系统，可以使用tf函数或ss函数来创建传递函数或状态空间模型。

对于离散系统，可以使用tf函数或zpk函数来创建传递函数或零极点模型。

2. 设计控制器在自适应控制中，控制器通常分为两部分：一个固定的基准控制器和一个自适应参数调整器。

基准控制器可以是一个PID控制器或其他控制算法，而自适应参数调整器通过不断更新参数来适应系统变化。

在Matlab中，可以使用控制系统工具箱提供的函数来设计基准控制器。

例如，可以使用pid函数来设计PID控制器，或者使用rltool函数进行更复杂的控制器设计。

3. 确定自适应参数确定自适应参数是自适应控制的关键步骤。

在Matlab中，可以使用自适应控制工具箱提供的函数来确定自适应参数。

例如，可以使用adapt函数来实现参数自适应。

4. 确定参考模型参考模型是指期望系统输出的理想轨迹。

在自适应控制中，参考模型可以帮助我们评估自适应控制的性能。

在Matlab中，可以使用step函数来生成理想的参考模型。

5. 实时参数估计和调整自适应控制中的一个关键任务是实时参数估计和调整。

在Matlab中，可以使用lms函数来实现最小均方算法，用于实时参数估计和调整。

此外，Matlab还提供了其他自适应滤波算法和函数，可根据具体需求进行选择和应用。

6. 仿真和验证完成上述步骤后，可以使用Matlab进行仿真和验证。

可以通过建模仿真来评估自适应控制的性能和稳定性。

在Matlab中，可以使用sim函数来实现系统仿真，并通过绘图和分析结果来验证控制效果。

LMS算法MatLab实现

LMS算法MatLab实现LMS算法MatLab实现LMS⾃适应滤波器是使滤波器的输出信号与期望响应之间的误差的均⽅值为最⼩，因此称为最⼩均⽅（LMS）⾃适应滤波器。

其原理及推导见function [yn,W,en]=LMS(xn,dn,M,mu,itr)% LMS(Least Mean Squre)算法% 输⼊参数:% xn 输⼊的信号序列 (列向量)% dn 所期望的响应序列 (列向量)% M 滤波器的阶数 (标量)% mu 收敛因⼦(步长) (标量) 要求⼤于0,⼩于xn的相关矩阵最⼤特征值的倒数% itr 迭代次数 (标量) 默认为xn的长度,M<itr<length(xn)% 输出参数:% W 滤波器的权值矩阵 (矩阵)% ⼤⼩为M x itr,% en 误差序列(itr x 1) (列向量)% yn 实际输出序列 (列向量)% 参数个数必须为4个或5个if nargin == 4 % 4个时递归迭代的次数为xn的长度itr = length(xn);elseif nargin == 5 % 5个时满⾜M<itr<length(xn)if itr>length(xn) | itr<Merror('迭代次数过⼤或过⼩!');endelseerror('请检查输⼊参数的个数!');end% 初始化参数en = zeros(itr,1); % 误差序列,en(k)表⽰第k次迭代时预期输出与实际输⼊的误差W = zeros(M,itr); % 每⼀⾏代表⼀个加权参量,每⼀列代表-次迭代,初始为0% 迭代计算for k = M:itr % 第k次迭代x = xn(k:-1:k-M+1); % 滤波器M个抽头的输⼊y = W(:,k-1).' * x; % 滤波器的输出en(k) = dn(k) - y ; % 第k次迭代的误差% 滤波器权值计算的迭代式W(:,k) = W(:,k-1) + 2*mu*en(k)*x;end% 求最优时滤波器的输出序列yn = inf * ones(size(xn));for k = M:length(xn)x = xn(k:-1:k-M+1);yn(k) = W(:,end).'* x;endLMS函数的⼀个实例：%function main()close all% 周期信号的产⽣t=0:99;xs=10*sin(0.5*t);figure;subplot(2,1,1);plot(t,xs);grid;ylabel('幅值');title('it{输⼊周期性信号}');% 噪声信号的产⽣randn('state',sum(100*clock));xn=randn(1,100);subplot(2,1,2);plot(t,xn);grid;ylabel('幅值');xlabel('时间');title('it{随机噪声信号}');% 信号滤波xn = xs+xn;xn = xn.' ; % 输⼊信号序列dn = xs.' ; % 预期结果序列M = 20 ; % 滤波器的阶数rho_max = max(eig(xn*xn.')); % 输⼊信号相关矩阵的最⼤特征值mu = rand()*(1/rho_max) ; % 收敛因⼦ 0 < mu < 1/rho[yn,W,en] = LMS(xn,dn,M,mu);% 绘制滤波器输⼊信号figure;subplot(2,1,1);plot(t,xn);grid;ylabel('幅值');xlabel('时间');title('it{滤波器输⼊信号}');% 绘制⾃适应滤波器输出信号subplot(2,1,2);plot(t,yn);grid;ylabel('幅值');xlabel('时间');title('it{⾃适应滤波器输出信号}');% 绘制⾃适应滤波器输出信号,预期输出信号和两者的误差figureplot(t,yn,'b',t,dn,'g',t,dn-yn,'r');grid;legend('⾃适应滤波器输出','预期输出','误差');ylabel('幅值');xlabel('时间');title('it{⾃适应滤波器}');运⾏后的结果如下：。

自适应噪声抵消LMS算法Matlab仿真

自适应噪声抵消LMS 算法Matlab 仿真传统的宽带信号中抑制正弦干扰的方法是采用陷波器(notch filter),为此我们需要精确知道干扰正弦的频率.然而当干扰正弦频率是缓慢变化时,且选频率特性要求十分尖锐时,则最好采用自适应噪声抵消的方法.下图是用一个二阶FIR 的LMS 自适应滤波器消除正弦干扰的一个方案。

1）借助MATLAB 画出误差性能曲面和误差性能曲面的等值曲线； 2）写出最陡下降法， LMS 算法的计算公式（δ=0.4）；3）用MATLAB 产生方差为0.05,均值为0白噪音S(n)，并画出其中一次实现的波形据2）中的公式，并利用3）中产生的S(n)，在1）中的误差性能曲面的等值曲n 的值曲线上叠加画出LMS 法时100情况确定，一般选取足够大以使算法达到基)(n y 宽带信号+正弦干扰0()()()y n S n N n =+图；4）根线上叠加画出采用最陡下降法， LMS 法时H(n)的在叠代过程中的轨迹曲线。

5）用MATLAB 计算并画出LMS 法时随时间变化曲线（对应S(n)的某一次的一次实现）和e(n)波形；某一次实现的结果并不能从统计的角度反映实验的结果的正确性，为得到具有统计特性的实验结果，可用足够多次的实验结果的平均值作为实验的结果。

用MATLAB 计算并画出LMS 法时J(n)的100次实验结果的平均值随时间n 的变化曲线。

6）用MATLAB 计算并在1）中的误差性能曲面的等次实验中的H(n)的平均值的轨迹曲线；（在实验中n=1,,…..N,N 的取值根据实验本收敛）01(),(0)0.052()sin(16102()sin()16ss S n r N n n N n n πππ==+是均匀分布的白噪音不相关和)(),()(10n N n N n S)(n x x 1()())(n e n N n =1、用Matlab画误差性能曲面和误差性能曲面的等值曲线的程序如下：[h0,h1] = meshgrid(-2:0.1:4 , -4:0.1:2);J=0.55+h0.*h0+h1.*h1+2*cos(pi/8)*h1.*h0-sqrt(2)*h0*cos(pi/10)-sqrt(2)*h1*cos(9*pi/40);echo on;v=0:0.1:2;%axis([-4 4 -4 4 0 100]);figure(1);%误差曲面surf(h0,h1,J);xlabel('h0');ylabel('h1');title('误差性能曲面');figure(2);contour(h0,h1,J,v); %等值曲线xlabel('h0');ylabel('h1');title('误差性能曲面等值曲线');运行结果如下图示：2、①最陡下降法计算公式：）（n 21)()1(H G V n H n δ−=+ 其中δ取0.4，H(0)=[3 -4]，T ⎟⎠⎞⎜⎝⎛+=⎟⎠⎞⎜⎝⎛−⎥⎦⎤⎢⎣⎡⎟⎠⎞⎜⎝⎛+==⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛=⎥⎦⎤⎢⎣⎡−⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=−=∑∑==1016k 2cos 2116)(2sin 210162sin 2161)(r 16k2cos 16)(2sin 2162sin 2161)(r )1()0(2)()()0()1()1()0(22)(2)(V 15015010G ππππππππi yx i xx yx yx xx xx xx xx yxxx k i i k k i i k r r n h n h r r r r r n H R n 而故⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡−⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=5320.37362.2)0(5377.06725.02)()(19239.09239.012)(10G G V n h n h n V②LMS 算法计算公式：,...2,1,0),1()1()()1()1()()1()1(e =+++=++−+=+n n X n e n H n H n X n H n y n T δ其中δ取0.4。

基于LMS算法的自适应对消器的MATLAB实现

基于LMS算法的自适应对消器的MATLAB实现LMS（Least Mean Squares）算法是一种常用于自适应信号处理领域的算法，用于实现自适应滤波器或者自适应对消器。

本文将介绍基于LMS 算法的自适应对消器的MATLAB实现。

自适应对消器是一种用于消除信号中的干扰或噪声的滤波器，它的系数会随着输入信号的变化而自适应地调整。

LMS算法是一种广泛使用的自适应算法，它通过最小化预测误差的平方来更新滤波器的权值。

该算法适用于非线性系统、时变系统以及参数不确定的系统。

在MATLAB中，我们可以使用以下步骤来实现基于LMS算法的自适应对消器：1.定义输入信号和期望输出信号：```matlabinput_signal = ... % 输入信号desired_output = ... % 期望输出信号```2.初始化自适应对消器的滤波器系数和步长：```matlabfilter_order = ... % 滤波器阶数filter_coefficients = zeros(filter_order, 1); % 滤波器系数初始化为零step_size = ... % 步长```3.对于每个输入样本，计算预测输出和误差，并更新滤波器的系数：```matlabfor k = 1:length(input_signal)%根据当前输入样本计算预测输出predicted_output = filter_coefficients' * input_signal(k,:);%计算当前误差error = desired_output(k) - predicted_output;%更新滤波器系数filter_coefficients = filter_coefficients + step_size * error * input_signal(k,:);end```4.最后```matlabfiltered_signal = filter_coefficients' * new_input_signal;```需要注意的是，LMS算法的性能和收敛速度与步长的选择有很大关系。

自适应LMS算法及其应用

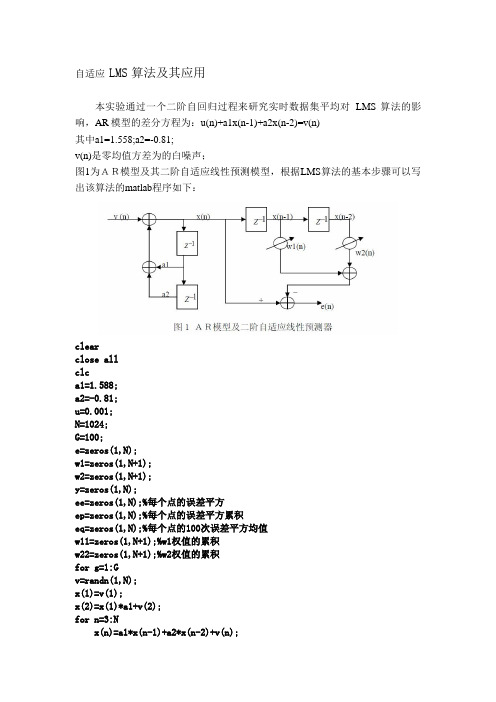
自适应LMS算法及其应用本实验通过一个二阶自回归过程来研究实时数据集平均对LMS算法的影响，AR模型的差分方程为：u(n)+a1x(n-1)+a2x(n-2)=v(n)其中a1=1.558;a2=-0.81;v(n)是零均值方差为的白噪声；图1为ＡＲ模型及其二阶自适应线性预测模型，根据LMS算法的基本步骤可以写出该算法的matlab程序如下：clearclose allclca1=1.588;a2=-0.81;u=0.001;N=1024;G=100;e=zeros(1,N);w1=zeros(1,N+1);w2=zeros(1,N+1);y=zeros(1,N);ee=zeros(1,N);%每个点的误差平方ep=zeros(1,N);%每个点的误差平方累积eq=zeros(1,N);%每个点的100次误差平方均值w11=zeros(1,N+1);%w1权值的累积w22=zeros(1,N+1);%w2权值的累积for g=1:Gv=randn(1,N);x(1)=v(1);x(2)=x(1)*a1+v(2);for n=3:Nx(n)=a1*x(n-1)+a2*x(n-2)+v(n);endfigure(1)plot(x)title('输入信号x')for n=3:Ny(n)=w1(n)*x(n-1)+w2(n)*x(n-2);e(n)=x(n)-y(n);w1(n+1)=w1(n)+2*u*e(n)*x(n-1);w2(n+1)=w2(n)+2*u*e(n)*x(n-2);ee(n)=e(n)^2;endw11=w1+w11;w22=w2+w22;ep=ep+ee;endeq=ep/G;W1=w11/G;W2=w22/G;figure(2)subplot(2,1,1)plot(w1)hold onsubplot(2,1,2)plot(W1)hold onsubplot(2,1,1)plot(w2,'r')title('w1与w2的收敛曲线,u=0.004')hold onsubplot(2,1,2)plot(W2,'r');title('100次平均后w1与w2的收敛曲线,u=0.004')figure(3)subplot(2,1,1)plot(e)title('误差曲线（学习曲线）u=0.004')subplot(2,1,2)plot(eq)title('100次平均误差曲线（学习曲线）u=0.004')下面对结果进行分析：图3为w1与w2的收敛曲线，比较平滑的为100次平均求得的收敛曲线，而另外一种起伏较大的为单次实现的收敛曲线，权初值为0。

matlab的lms算法

matlab的lms算法"matlab的lms算法"一、介绍matlab是一种强大的数值计算和科学编程工具，可以用于各种信号处理和机器学习应用。

其中，最小均方（LMS）算法是一种自适应滤波算法，常用于信号降噪和系统辨识等领域。

本文将详细介绍matlab中的LMS 算法的实现步骤和应用。

二、LMS算法原理LMS算法是基于梯度下降的一种自适应滤波算法，用于根据输入信号和期望输出信号来估计系统的权重。

其基本原理是通过调整权重，使得算法输出的估计信号与期望输出信号之间的均方误差最小化。

LMS算法的迭代公式如下：w(n+1) = w(n) + μ* e(n) * x(n)其中，w(n)表示第n次迭代的权重，μ是步长（学习速率），e(n)表示估计信号与期望输出信号之间的误差，x(n)表示输入信号。

三、matlab中的LMS算法实现步骤1. 定义输入信号和期望输出信号在matlab中，首先需要定义输入信号和期望输出信号。

输入信号一般为一个信号向量，期望输出信号为一个与输入信号长度相同的向量。

2. 初始化权重和步长LMS算法需要初始化权重和步长。

权重可以初始化为全零向量，步长可以根据实际应用进行选择，常用的有固定步长和自适应步长。

3. 迭代更新权重使用迭代公式进行权重更新，更新的次数可以根据实际情况进行选择。

每次迭代时，根据输入信号和当前权重估计输出信号，计算误差，并根据误差和步长更新权重。

4. 输出估计信号使用更新后的权重和输入信号计算估计输出信号，并将其作为最终的LMS 算法输出。

四、案例应用：噪声消除为了更好地理解LMS算法的应用，我们将通过一个噪声消除的案例来演示其使用方法。

假设我们有一个含有噪声的信号，并且我们希望通过LMS 算法来滤除噪声。

1. 定义输入信号和期望输出信号首先，我们生成一个长度为N的纯净信号，并向其添加一定程度的高斯噪声，生成含有噪声的输入信号。

我们还定义一个与输入信号长度相同的期望输出信号，该信号为纯净信号。

基于LMS的自适应滤波器典型应用的MATLAB实现

LM S 算法一般包括滤波过程和自适应过程, 这两个过程一起工作组成一个反馈环。图 1 中, x ( n) 为输入信号, y ( n ) 为输出信号, d ( n ) 为参考信号或期望信号 , e( n) 是 d ( n) 与 y ( n) 的误差信号。自适应滤波器的滤波系数受误差信号 e( n) 控制 , 根据 e( n) 的值和自适应算法自动调整。推导如下: 假设 x ( n) 是一长度为 M 的序列, 由图 1 有:
e2 ( n ) =
n= 0
[ d( n) k= 0
h( k ) x ( n
- k ) ] 这个平方误差的和是这个滤波器系数的二次函数。因此 , 对于滤波器系数 { h ( k) } 的最小化就会产生一组线性方程。为了求解这组方程组, 有很多种算法, L MS 算法是其中的一种。 1. 2 LM S 算法的具体步骤 LM S 算法基本上是一种递推算法, 它用任意
2
选择的{ h( k ) } 的初始值作为开始 , 然后将每一新的输入样本{ x ( n ) } 输入到这个自适应 FIR 滤波器, 计算相应的输出 { y ( n ) } , 形成误差信号 e( n) = d ( n) - y ( n ) , 并按方程 h n ( k ) = h n- 1 ( k ) + ! N- 1 更新滤波器系数, 这里称为步长参数, x ( n - k ) 是输入信号在时间 n 位于滤波器的第 k 个样本, 而 e( n ) x ( n- k) 是对第 k 个滤波器系数的一个梯度负值的近似( 估计 ) 。 2 MAT LAB 实现 M AT L AB 有专门的函数 ADAPT L MS 实现自适应滤波 , ADAP T LM S 函数的用法为 : [ y , e, s ] = ADAPT LM S( x , d , s) 其中 y 为滤波器的输出信号 , x 为滤波器的输入信号 , d 为期望信号, e 为误差信号, s 为包含构体 [ y, e, S] = adaptlms( x , d, S) ; % 自适应滤波 st em ( [ b. ∀ , S. coeffs. ∀ ] ) ; % 画出识别的系统和未知系统的参数。 e( n) x ( n - k ) , 0 ! k

MATLAB做LMS算法（最小均方误差算法）

MATLAB做LMS算法（最⼩均⽅误差算法）⽬录背景知识⾃适应滤波的4种不同应⽤是：预测、辨识、反建模和⼲扰抵消LMS算法(最⼩均⽅误差算法)是⾃适应滤波算法的⼀种，主要⼲的事情是：基于最⼩均⽅误差准则，使滤波器的输出信号与期望输出信号之间的均⽅误差最⼩。

LMS算法简单有效，计算量⼩，鲁棒性好，易于实现。

代码LMS.m 代码来⾃这本书,本⼈改了2个句⼦这份代码是真的强，0.05π⾓频率的单频信号叠上3dB且0均值的加性⾼斯⽩噪声，很快被“纠正回”期望的0.05π⾓频率的单频信号。

%⽤MATLAB实现LMS算法，将输⼊和输出信号进⾏对⽐，并给出均⽅误差曲线。

%假设滤波器抽头个数为k，数据长度为Ng=100; %统计仿真次数为gN=1024; %输⼊信号抽样点数为Nk=128; %时域抽头LMS算法滤波器阶数pp=zeros(g,N-k);%将每次独⽴循环的误差结果存于矩阵pp中，以便后⾯取平均u=0.0002;%步长因⼦ufor q=1:1:gt=1:1:N;a=1;s=a*sin(0.05*pi*t); %输⼊单频信号sfigure(1);subplot(311);plot(t,real(s) ); %信号s时域波形title('信号s时域波形');xlabel('n');ylabel('s');axis([0,N,-a-1,a+1]);xn=awgn(s,5);%加⼊均值为0的⾼斯⽩噪声，信噪⽐为3dB%设置初值y=zeros(1,N);%输出信号yy(1:k)=xn(1:k);%将输⼊信号xn的前k个值赋值给y的前k个值w=zeros(1,k); %设置抽头加权初值e=zeros(1,N); %误差信号%⽤LMS算法迭代滤波for i=(k+1):1:NXN=xn((i-k+1):(i));y(i)=w*XN';e(i)=s(i)-y(i);w=w+u*e(i)*XN;endpp(q, : )=( e(k+1:N ) ).^2;endsubplot(312);plot(t,real(xn)); %信号s时域波形title('信号s加噪声后的时域波形');subplot(313);plot(t,real(y));%信号s时域波形title('⾃适应滤波后的输出时域波形');bi=mean(pp,1); %对第⼀维度求平均%⼈⽣苦短，对某⼀维度求平均这么写不是更好写吗figure(2);t=1:1:N-k;plot(t,bi,'r');title('均⽅误差-时间曲线') %太蠢了这⾥为什么会写hold on参考1. 《⽆线通信的MATLAB和FPGA实现》 3.5.3 LMS算法的MATLAB实现2.Processing math: 100%。

基于matlab的LMS自适应滤波器仿真

线性预测器与噪声对消器对比仿真最小均方准则求滤波器系数

通过正则方程求出维纳解输入与期望信号不一定联合平稳
在实际应用必须找到递推算法更新系数
最速下降法与正则方程配合得递推式
参考资料：/nk/qlxy/
线性预测器

噪声对消器

滤波器输出逼近信号源
滤波器输出逼近噪声源

参考信号为信号源

参考信号为噪声源
误差信号为系统输出

滤波器输出即为系统输出

灰度图像去噪处理
景甜原始图
景甜加噪图
1.用噪声对消器去噪处理
S.H.E原始图
2.讨论步长μ影响
(1)收敛速度 (2)去噪质量
S.H.E加噪图
μ=0.001
μ=0.00012
S.H.E复原图(1)
基于基于matlabmatlab的的lmslms自适应滤自适应滤波器仿真波器仿真线性预测器与噪声对消器对比仿真lmslms自适应滤波器原理简述自适应滤波器原理简述11输入与期望信号不一定联合平稳lmslms自适应滤波器原理简述自适应滤波器原理简述2在实际应用必须找到递推算法更新系数最速下降法与正则方程配合得递推式参考资料
S.H.E复原图(2)
景甜复原图(1)
景甜误差图片(1)
景甜复原图(2)
景甜误差图片(2)
收敛速度：步长大，速度快，步长小，收敛速度慢去噪质量：步长大，质量差，步长小，稳态成像质量高
源程序
clear all; clc; delta = 1/1000; t = 0:delta:10; t = t'; % 转换成列向量 s = sin(2*pi*t); sigma_n0 =1; n0 = sigma_n0*randn(size(t)); x = s + n0; % 原始输入端的输入信号,为被噪声污染的正弦信号 d = x; % 对于自适应对消器，用x作为期望信号 n1 = n0; % 参考输入端的输入信号，为与n0相关的噪声 % 设计自适应滤波器 N = 5; % 滤波器阶数 w = ones(N,1); % 初始化滤波器权值 wn=zeros(N,length(t)-N+1); u = 0.0001; % 步长因子 y = zeros(length(t),1); for k = N:length(t) wn(:,k-N+1)=w; y(k) = n1(k-N+1:k)'*w; e(k) = d(k) - y(k); w = w + 2*u*e(k).*n1(k-N+1:k); % 跟新权值 end % 图像化仿真效果 subplot(211),plot(t,x);title('被噪声污染的正弦信号'); subplot(212),plot(t,s,'r',t,e,'g'); % 对消噪声后，误差信号即为对原始信号的估计 legend('原始正弦信号','自适应滤波后的信号'); title('滤波效果'); %figure(2) %clf; %plot(t(1:length(wn(1,:))),wn(1,:),'r',t(1:length(wn(1,:))),wn(3,:),'g');

基于MATLAB的自适应滤波器设计

基于MATLAB的自适应滤波器设计自适应滤波器是一种能够根据输入信号的特性自动调整滤波参数的滤波器。

它的核心思想是根据输入信号与期望输出信号之间的误差来更新滤波器的权值，从而实现对输入信号的准确滤波。

在MATLAB中，可以使用自适应滤波器工具箱来设计和实现自适应滤波器。

自适应滤波器工具箱提供了多种自适应滤波器算法的函数和工具，例如LMS（最小均方误差）算法、RLS（递归最小二乘）算法等。

下面以LMS算法为例，介绍如何基于MATLAB进行自适应滤波器设计。

首先，需要准备好输入信号和期望输出信号。

可以使用MATLAB的信号处理工具箱来生成具有特定频率和幅度的输入信号，或者使用已有的实验数据。

期望输出信号可以根据输入信号进行一定的处理得到，或者使用已有的实验数据。

然后，需要选择自适应滤波器的结构和算法。

在MATLAB中，可以使用`dsp.LMSFilter`类来实现LMS算法。

可以根据输入信号和期望输出信号的特性，选择自适应滤波器的阶数、步长等参数。

接下来，可以使用`dsp.LMSFilter`类的对象来进行自适应滤波器的初始化和更新。

可以通过调用`step`方法来实时更新滤波器的权值，并获取输出信号。

具体步骤如下：1. 创建`dsp.LMSFilter`对象，并指定滤波器的阶数和步长。

```matlablmsFilter = dsp.LMSFilter('Length', filterOrder, 'StepSize', stepSize);```2.初始化滤波器的权值。

```matlablmsFilter.Weights = initialWeights;```3.使用循环结构，依次读取输入信号的每个样本，并根据期望输出信号计算滤波器的权值，同时获取输出信号。

```matlabfor i = 1:length(inputSignal)[outputSignal, lmsFilter] = step(lmsFilter, inputSignal(i), desiredOutput(i));end```4.完成滤波器的更新后，可以获取最终的输出信号。

LMS算法自适应滤波器MATLAB仿真作业

LMS 自适应滤波器仿真作业工程1班220150820 王子豪1. 步骤1)给定滤波器的长度M，步长µ和滤波器初始值h0；2)求数据向量X(n)=[x(n),x(n-1),...,x(n-M-1)]T，其中x(n)为输入信号，M为滤波器抽头系数；3)求输出y(n)=X(n)*h；4)计算误差值e(n)=d(n)-y(n)；5)更新滤波器系数h(n+1)=h(n)+µe(n)X(n)；6)重复以上步骤，知道h收敛到最优的滤波器系数h opt2. 仿真结果产生均值为0，方差为1的高斯白噪声e(n)，经过系统H(z)后输出的x(n) 通过LMS滤波器进行自适应滤波，迭代次数为500次，总共做了100次求平均均方误差e(n)^2。

当u分别取0.002、0.005、0.008、0.01时，LMS自适应滤波器的性能曲线如图1所示：图1 不同u的取值下自适应滤波器的性能曲线对应的滤波器系数a1、a2学习曲线如图2、图3所示：图2 不同u的取值下自适应滤波器系数a1的学习曲线图3 不同u的取值下自适应滤波器系数a2的学习曲线3. 结果分析1.仿真结果得出：步长因子μ与收敛时间成反比，图形的收敛时间随着步长因子μ的增大而减小，这决定了LMS算法学习过程的快慢。

2.当步长因子μ增大时虽然收敛时间减少，但会导致失调增大，例如当μ等于0.01时，图形失调已经很严重，不符合预期要求了。

3.控制失调与加快收敛速度不能兼得。

4. Matlab程序代码clear;clc;N=2048; %信号的取样点数M=2; %滤波器抽头的个数iter=499; %迭代次数%初始化X_A=zeros(M,1); %X数据向量y=zeros(1,N); %预测输出en=zeros(1,iter); %误差向量enp=zeros(1,iter); %平均误差W=zeros(iter,M); %每一行代表一次迭代滤波器的M个抽头参数% 迭代计算u=0.002; %固定步长for j=1:100 %做100次实验取平均ex=randn(1,N); %噪声信号e(n)x=filter(1,[1,-1.6,0.8],ex); %经过系统H(Z)之后输出xd=x; %参考信号for k=M+1:iter %第k次迭代X_A=x(k-1:-1:k-M)';y(k)=W(k,:)* X_A; %滤波器的输出en(k)=d(k)-y(k) ; %第k次迭代的误差W(k+1,:)=W(k,:) + u*en(k)*X_A'; %滤波器权值计算的迭代式endenp=enp+en.^2;endenp=enp/100; %取平均误差figure(1);plot(enp);xlabel('迭代次数');ylabel('均方误差e(n)^2');title('当u=0.008时，连续做100次平均所得到的性能曲线');learn1=W(:,1);learn2=W(:,2);figure(2);subplot(2,1,1);plot(learn1);title('当u=0.008时的学习曲线');xlabel('迭代次数');ylabel('a1的学习曲线');subplot(2,1,2);plot(learn2);xlabel('迭代次数');ylabel('a2的学习曲线');。

matlab 自适应滤波

matlab 自适应滤波自适应滤波是一种信号处理技术，它能够根据输入信号的统计特性自动调整滤波器的参数，从而适应不同的环境和噪声条件。

在MATLAB中，我们可以利用信号处理工具箱中的函数实现自适应滤波，例如`nlms`和`rls`函数。

自适应滤波的基本原理是根据输入信号和误差信号的统计特性，通过不断调整滤波器的系数来最小化误差信号的方差。

根据滤波器的更新策略的不同，自适应滤波可以分为最小均方（LMS）算法和递归最小二乘（RLS）算法。

LMS算法是一种迭代算法，每一次迭代都会根据当前输入信号和误差信号来更新滤波器的系数。

MATLAB中的`nlms`函数可以实现LMS算法的自适应滤波。

在使用`nlms`函数时，需要指定输入信号、期望信号（即原始信号），以及滤波器的初始系数。

然后，`nlms`函数会根据输入信号的样本数据和期望信号来计算滤波器的输出信号，并根据差错信号的信息来更新滤波器的系数。

通过多次迭代，滤波器的系数逐渐趋于收敛，从而得到去噪后的信号。

RLS算法是一种基于递归估计的算法，它能够根据过去的输入信号和误差信号的历史数据来计算滤波器的系数。

MATLAB中的`rls`函数可以实现RLS算法的自适应滤波。

在使用`rls`函数时，需要指定输入信号、期望信号（即原始信号），以及滤波器的初始系数。

然后，`rls`函数会根据输入信号和期望信号的历史数据来计算滤波器的系数，并根据当前输入信号和期望信号来计算滤波器的输出信号。

通过递归计算和数据更新，滤波器的系数会不断调整，从而得到去噪后的信号。

自适应滤波在信号处理中具有广泛的应用。

例如，在通信系统中，自适应滤波可以用于抑制信道噪声和多路径干扰，提高信号的质量和可靠性。

在医学影像处理中，自适应滤波可以用于去除图像中的噪声，提高图像的清晰度和对比度。

此外，自适应滤波还可以用于语音信号处理、雷达信号处理、机器视觉等领域。

总结来说，MATLAB中的自适应滤波函数`nlms`和`rls`可以实现信号的去噪和滤波。

在Matlab中实现自适应滤波算法的实践指南

在Matlab中实现自适应滤波算法的实践指南引言：自适应滤波算法是一种重要的信号处理技术，在许多领域都得到了广泛的应用。

它通过实时调整滤波器参数来适应信号的变化，从而提高信号去噪和信号恢复的效果。

本文将介绍如何使用Matlab实现自适应滤波算法，并给出一些实践指导。

一、自适应滤波的原理自适应滤波算法的核心思想是根据信号的统计特性来调整滤波器的参数。

常见的自适应滤波算法包括LMS（最小均方）算法和RLS（递推最小二乘）算法。

LMS算法通过不断地调整滤波器的权值来使预测误差最小化；RLS算法则通过递推最小化滤波器的误差代价函数来更新权值。

这两种算法都可以实现自适应滤波的目的，但是在不同的应用场景中可能有差异。

二、Matlab中的自适应滤波函数在Matlab中，提供了一些方便实现自适应滤波算法的函数。

其中最常用的是`nlms`函数和`rls`函数。

`nlms`函数实现了LMS算法，可以用于实时的自适应滤波；`rls`函数实现了RLS算法，适用于更复杂的信号恢复任务。

三、使用`nlms`函数实现自适应滤波下面以一个简单的例子来说明如何使用`nlms`函数实现自适应滤波。

假设我们有一个带噪声的正弦信号，我们可以通过自适应滤波来去除噪声。

首先，我们生成一个1000个采样点的正弦信号，并添加高斯白噪声。

```matlabt = 0:0.1:100;x = sin(t);noise = 0.5*randn(size(t));y = x + noise;```接下来，我们使用`nlms`函数进行自适应滤波。

首先，我们需要初始化滤波器权重。

通常可以将初始权重设置为0或者一个很小的值。

然后，我们使用一个循环来逐步更新滤波器权重，直到达到滤波的要求。

```matlaborder = 10; % 滤波器阶数mu = 0.1; % 步长参数w = zeros(order+1, 1); % 初始化滤波器权重for i = order+1:length(y)input = y(i:-1:i-order); % 输入信号output = input' * w; % 滤波输出error = x(i) - output; % 预测误差w = w + mu * input * error; % 权重更新end```最后，我们可以将滤波器的输出与原始信号进行对比，评估滤波效果。

lms自适应滤波算法matlab

lms自适应滤波算法matlab
自适应滤波算法matlab
自适应滤波是指根据信号的变化情况来调整滤波器的参数，使滤波器适应不同信号环境，以最佳的抑制信号中噪声和其他干扰的能力。

自适应滤波在现实中有着广泛的应用，其中最常用的就是LMS(Least Mean Square, 最小均方误差)算法，它是一种收敛算法，可以快速、稳定地收敛，目前已经被广泛应用在信号处理、智能控制等领域。

LMS算法包含的组件有信号贡献函数、模型函数、误差更新函数和滤波函数。

信号贡献函数是用来计算信号当前帧和计算当前帧的贡献值的
函数，也就是当前信号的权重，这个参数的计算方法是通过积分或者是求和的方法来计算的。

模型函数是计算模型参数的函数，这个函数的输入是信号贡献函数的输出，也就是贡献值，输出就是系数矩阵，我们就是根据系数矩阵来计算出最优的参数，也就是滤波器的参数。

误差更新函数是计算模型误差的函数，也就是根据当前模型的输出和实际数据的误差来更新模型参数的函数，一般来说我们计算本次误差则可以估计新的模型参数和新的数据矩阵。

滤波函数就是使用模型参数来实现数据的滤波处理，它的目的是为了抑制信号的噪声，达到更好的信号质量。

- 1 -。