工程力学专业英语翻译
工程力学专业英语翻译

The intensity of force, that is, the force per unit area, is called the stress and is commonly denoted by the Greek letter σ. Assuming that the stress has a uniform distribution over the cross section [see Fig.1(b)], we can readily see that its resultant is equal to the intensity σ times the cross-sectional area A of the bar. Furthermore, from the equilibrium of the body shown in Fig.1(b), we can also see that this resultant must be equal in magnitude and opposite in direction to the force P. Hence, we obtain σ = P/A. (1)
当一种材料的应力与应变表现出线性关系时,我们称这种材 料为线弹性材料。这是许多固体材料的一个极其重要的性质,这 些材料包括大多数金属,塑料,木材,混凝土和陶瓷。对于被拉 伸的梁来说,这种应力与应变之间的线性关系可以用简单方程(3) σ= Eε 来表示,这里E是一个已知的比例常数,即该材料的弹性模 量。
英语专业名称翻译

专业名称翻译哲学Philosophy马克思主义哲学Philosophy of Marxism中国哲学Chinese Philosophy外国哲学Foreign Philosophies逻辑学Logic伦理学Ethics美学Aesthetics宗教学Science of Religion科学技术哲学Philosophy of Science and Technology经济学Economics理论经济学Theoretical Economics政治经济学Political Economy经济思想史History of Economic Thought经济史History of Economic西方经济学Western Economics世界经济World Economics人口、资源与环境经济学Population, Resources and Environmental Economics应用经济学Applied Economics国民经济学National Economics区域经济学Regional Economics财政学(含税收学)Public Finance (including Taxation)金融学(含保险学)Finance (including Insurance)产业经济学Industrial Economics国际贸易学International Trade劳动经济学Labor Economics统计学Statistics数量经济学Quantitative Economics中文学科、专业名称英文学科、专业名称国防经济学National Defense Economics法学Law法学Science of Law法学理论Jurisprudence法律史Legal History宪法学与行政法学Constitutional Law and Administrative Law刑法学Criminal Jurisprudence民商法学(含劳动法学、社会保障法学) Civil Law and Commercial Law (including Science of Labour Law and Science of Social Security Law )诉讼法学Science of Procedure Laws经济法学Science of Economic Law环境与资源保护法学Science of Environment and Natural Resources Protection Law国际法学(含国际公法学、国际私法学、国际经济法学、) International law (including International Public law, International Private Law and International Economic Law)军事法学Science of Military Law政治学Political Science政治学理论Political Theory中外政治制度Chinese and Foreign Political Institution科学社会主义与国际共产主义运动Scientific Socialism and InternationalCommunist Movement中共党史(含党的学说与党的建设) History of the Communist Party of China(including the Doctrine of China Party and Party Building)马克思主义理论与思想政治教育Education of Marxist Theory and Education in Ideology and Politics国际政治学International Politics国际关系学International Relations外交学Diplomacy社会学Sociology社会学Sociology人口学Demography人类学Anthropology民俗学(含中国民间文学) Folklore (including Chinese Folk Literature)民族学Ethnology民族学Ethnology马克思主义民族理论与政策Marxist Ethnic Theory and Policy中国少数民族经济Chinese Ethnic Economics中国少数民族史Chinese Ethnic History中国少数民族艺术Chinese Ethnic Art教育学Education教育学Education Science教育学原理Educational Principle课程与教学论Curriculum and Teaching Methodology教育史History of Education比较教育学Comparative Education学前教育学Pre-school Education高等教育学Higher Education成人教育学Adult Education职业技术教育学V ocational and Technical Education特殊教育学Special Education教育技术学Education Technology心理学Psychology基础心理学Basic Psychology发展与心理学Developmental and Educational Psychology应用心理学Applied Psychology体育学Science of Physical Culture and Sports体育人文社会学Humane and Sociological Science of Sports运动人体科学Human Movement Science体育教育训练学Theory of Sports Pedagogy and Training民族传统体育学Science of Ethnic Traditional Sports文学Literature中国语言文学Chinese Literature文艺学Theory of Literature and Art语言学及应用语言学Linguistics and Applied Linguistics汉语言文字学Chinese Philology中国古典文献学Study of Chinese Classical Text中国古代文学Ancient Chinese Literature中国现当代文学Modern and Contemporary Chinese Literature中国少数民族语言文学Chinese Ethnic Language andLiterature比较文学与世界文学Comparative Literature and World Literature外国语言文学Foreign Languages and Literatures英语语言文学English Language and Literature俄语语言文学Russian Language and Literature法语语言文学French Language and Literature德语语言文学German Language and Literature日语语言文学Japanese Language and Literature印度语言文学Indian Language and Literature西班牙语语言文学Spanish Language and Literature阿拉伯语语言文学Arabic Language and Literature欧洲语言文学European Language and Literature亚非语言文学Asian-African Language and Literature外国语言学及应用语言学Linguistics and Applied Linguistics inForeign Languages新闻传播学Journalism and Communication新闻学Journalism传播学Communication艺术学Art艺术学Art Theory音乐学Music美术学Fine Arts设计艺术学Artistic Design戏剧戏曲学Theater and Chinese Traditional Opera电影学Film广播电视艺术学Radio and television Art舞蹈学Dance历史学History历史学History史学理论及史学史Historical Theories and History of Historical Science考古学及博物馆学Archaeology and Museology历史地理学Historical Geography历史文献学(含敦煌学、古文字学) Studies of Historical Literature (includingPaleography and Studies of Dunhuang)专门史History of Particular Subjects中国古代史Ancient Chinese History中国近现代史Modern and Contemporary Chinese History世界史World History理学Natural Science数学Mathematics基础数学Fundamental Mathematics计算数学Computational Mathematics概率论与数理统计Probability and Mathematical Statistics应用数学Applied mathematics运筹学与控制论Operational Research and Cybernetics物理学Physics理论物理Theoretical Physics粒子物理与原子核物理Particle Physics and Nuclear Physics原子与分子物理Atomic and Molecular Physics等离子体物理Plasma Physics凝聚态物理Condensed Matter Physics声学Acoustics光学Optics无线电物理Radio Physics化学Chemistry无机化学Inorganic Chemistry分析化学Analytical Chemistry有机化学Organic Chemistry物理化学(含化学物理)Physical Chemistry (including Chemical Physics) 高分子化学与物理Chemistry and Physics of Polymers天文学Astronomy天体物理Astrophysics天体测量与天体力学Astrometry and Celestial Mechanics地理学Geography自然地理学Physical Geography人文地理学Human Geography地图学与地理信息系统Cartography and Geography Information System大气科学Atmospheric Sciences气象学Meteorology大气物理学与大气环境Atmospheric Physics and Atmospheric Environment 海洋科学Marine Sciences物理海洋学Physical Oceanography海洋化学Marine Chemistry海洋生理学Marine Biology海洋地质学Marine Geology地球物理学Geophysics固体地球物理学Solid Earth Physics空间物理学Space Physics地质学Geology矿物学、岩石学、矿床学Mineralogy, Petrology, Mineral Deposit Geology 地球化学Geochemistry古生物学与地层学(含古人类学)Paleontology and Stratigraphy (including Paleoanthropology)构造地质学Structural Geology第四纪地质学Quaternary Geology生物学Biology植物学Botany动物学Zoology生理学Physiology水生生物学Hydrobiology微生物学Microbiology神经生物学Neurobiology遗传学Genetics发育生物学Developmental Biology细胞生物学Cell Biology生物化学与分子生物学Biochemistry and Molecular Biology生物物理学Biophysics生态学Ecology系统科学Systems Science系统理论Systems Theory系统分析与集成Systems Analysis and Integration科学技术史History of Science and Technology工学Engineering力学Mechanics一般力学与力学基础General and Fundamental Mechanics固体力学Solid Mechanics流体力学Fluid Mechanics工程力学Engineering Mechanics机械工程Mechanical Engineering机械制造及其自动化Mechanical Manufacture and Automation机械电子工程Mechatronic Engineering机械设计与理论Mechanical Design and Theory车辆工程Vehicle Engineering光学工程Optical Engineering仪器科学与技术Instrument Science and Technology精密仪器及机械Precision Instrument and Machinery测试计量技术及仪器Measuring and Testing Technologies and Instruments材料科学与工程Materials Science and Engineering材料物理与化学Materials Physics and Chemistry材料学Materialogy材料加工工程Materials Processing Engineering冶金物理化学Physical Chemistry of Metallurgy钢铁冶金Ferrous Metallurgy有色金属冶金Non-ferrous Metallurgy动力工程及工程热物理Power Engineering and Engineering Thermophysics工程热物理Engineering Thermophysics热能工程Thermal Power Engineering动力机械及工程Power Machinery and Engineering流体机械及工程Fluid Machinery and Engineering制冷及低温工程Refrigeration and Cryogenic Engineering化工过程机械Chemical Process Equipment电气工程Electrical Engineering电机与电器Electric Machines and Electric Apparatus电力系统及其自动化Power System and its Automation高电压与绝缘技术High V oltage and Insulation Technology电力电子与电力传动Power Electronics and Power Drives电工理论与新技术Theory and New Technology of Electrical Engineering电子科学与技术Electronics Science and Technology物理电子学Physical Electronics电路与系统Circuits and Systems微电子学与固体电子学Microelectronics and Solid State Electronics电磁场与微波技术Electromagnetic Field and Microwave Technology信息与通信工程Information and Communication Engineering通信与信息系统Communication and Information Systems信号与信息处理Signal and Information Processing控制科学与工程Control Science and Engineering控制理论与控制工程Control Theory and Control Engineering检测技术与自动化装置Detection Technology and Automatic Equipment系统工程Systems Engineering模式识别与智能系统Pattern Recognition and Intelligent Systems导航、制导与控制Navigation, Guidance and Control计算机科学与技术Computer Science and Technology计算机软件与理论Computer Software and Theory计算机系统结构Computer Systems Organization计算机应用技术Computer Applied Technology建筑学Architecture建筑历史与理论Architectural History and Theory建筑设计及其理论Architectural Design and Theory城市规划与设计(含风景园林规划与设计)Urban Planning and Design (including Landscape Planning and Design)建筑技术科学Building Technology Science土木工程Civil Engineering岩土工程Geotechnical Engineering结构工程Structural Engineering供热、供燃气、通风及空调工程Heating, Gas Supply, Ventilating and Air Conditioning Engineering防灾减灾工程及防护工程Disaster Prevention and Reduction Engineering and Protective Engineering桥梁与隧道工程Bridge and Tunnel Engineering水利工程Hydraulic Engineering水文学及水资源Hydrology and Water Resources水力学及河流动力学Hydraulics and River Dynamics水工结构工程Hydraulic Structure Engineering水利水电工程Hydraulic and Hydro-Power Engineering港口、海岸及近海工程Harbor, Coastal and Offshore Engineering测绘科学与技术Surveying and Mapping大地测量学与测量工程Geodesy and Survey Engineering摄影测量与遥感Photogrammetry and Remote Sensing地图制图学与地理信息工程Cartography and Geographic Information Engineering化学工程与技术Chemical Engineering and Technology化学工程Chemical Engineering化学工艺Chemical Technology生物化工Biochemical Engineering应用化学Applied Chemistry工业催化Industrial Catalysis地质资源与地质工程Geological Resources and Geological Engineering矿产普查与勘探Mineral Resource Prospecting and Exploration地球探测与信息技术Geodetection and Information Technology地质工程Geological Engineering矿业工程Mineral Engineering采矿工程Mining Engineering矿物加工工程Mineral Processing Engineering安全技术及工程Safety Technology and Engineering石油与天然气工程Oil and Natural Gas Engineering油气井工程Oil-Gas Well Engineering油气田开发工程Oil-Gas Field Development Engineering油气储运工程Oil-Gas Storage and Transportation Engineering纺织科学与工程Textile Science and Engineering纺织工程Textile Engineering纺织材料与纺织品设计Textile Material and Textiles Design纺织化学与染整工程Textile Chemistry and Dyeing and Finishing Engineering服装设计与工程Clothing Design and Engineering轻工技术与工程The Light Industry Technology and Engineering制浆造纸工程Pulp and Paper Engineering制糖工程Sugar Engineering发酵工程Fermentation Engineering皮革化学与工程Leather Chemistry and Engineering交通运输工程Communication and Transportation Engineering道路与铁道工程Highway and Railway Engineering交通信息工程及控制Traffic Information Engineering & Control交通运输规划与管理Transportation Planning and Management载运工具运用工程Vehicle Operation Engineering船舶与海洋工程Naval Architecture and Ocean Engineering船舶与海洋结构物设计制造Design and Construction of Naval Architecture and Ocean Structure轮机工程Marine Engine Engineering水声工程Underwater Acoustics Engineering航空宇航科学与技术Aeronautical and Astronautical Science and Technology飞行器设计Flight Vehicle Design航空宇航推进理论与工程Aerospace Propulsion Theory and Engineering航空宇航器制造工程Manufacturing Engineering of Aerospace Vehicle人机与环境工程Man-Machine and Environmental Engineering兵器科学与技术Armament Science and Technology武器系统与运用工程Weapon Systems and Utilization Engineering兵器发射理论与技术Armament Launch Theory and Technology火炮、自动武器与弹药工程Artillery, Automatic Gun and Ammunition Engineering军事化学与烟火技术Military Chemistry and Pyrotechnics核科学与技术Nuclear Science and Technology核能科学与工程Nuclear Energy Science and Engineering核燃料循环与材料Nuclear Fuel Cycle and Materials核技术及应用Nuclear Technology and Applications辐射防护及环境保护Radiation and Environmental Protection农业工程Agricultural Engineering农业机械化工程Agricultural Mechanization Engineering农业水土工程Agricultural Water-Soil Engineering农业生物环境与能源工程Agricultural Biological Environmental and Energy Engineering农业电气化与自动化Agricultural Electrification and Automation林业工程Forestry Engineering森林工程Forest Engineering木材科学与技术Wood Science and Technology林产化学加工工程Chemical Processing Engineering of Forest Products环境科学与工程Environmental Science and Engineering环境科学Environmental Science环境工程Environmental Engineering生物医学工程Biomedical Engineering食品科学与工程Food Science and Engineering食品科学Food Science粮食、油脂及植物蛋白工程Cereals, Oils and Vegetable Protein Engineering农产品加工及贮藏工程Processing and Storage of Agriculture Products水产品加工及贮藏工程Processing and Storage of Aquatic Products农学Agriculture作物学Crop Science作物栽培学与耕作学Crop Cultivation and Farming System作物遗传育种学Crop Genetics and Breeding园艺学Horticulture果树学Pomology蔬菜学Olericulture茶学Tea Science农业资源利用学Utilization Science of Agricultural Resources土壤学Soil Science植物营养学Plant Nutrition植物保护学Plant Protection植物病理学Plant Pathology农业昆虫与害虫防治Agricultural Entomology and Pest Control农药学Pesticide Science畜牧学Animal Science动物遗传育种与繁殖Animal Genetics, Breeding and ReproductionScience动物营养与饲料科学Animal Nutrition and Feed Science草业科学Practaculture Science特种经济动物饲养学(含蚕、蜂等)The Rearing of Special-type Economic Animals (including Silkworm, Honeybees, etc.)兽医学Veterinary Medicine基础兽医学Basic Veterinary Medicine预防兽医学Preventive Veterinary Medicine临床兽医学Clinical Veterinary Medicine林学Forestry林木遗传育种学Forest Tree Genetics and Breeding森林培育学Silviculture森林保护学Forest Protection森林经理学Forest Management野生动植物保护与利用Wildlife Conservation and Utilization园林植物与观赏园艺Ornamental Plants and Horticulture水土保持与荒漠化防治Soil and Water Conservation and Desertification Combating 水产学Fisheries Science水产养殖学Aquaculture Science捕捞学Fishing Science渔业资源学Science of Fisheries Resources医学Medicine医学Medicine基础医学Basic Medicine人体解剖与组织胚胎学Human Anatomy, Histology and Embryology免疫学Immunology病原生物学Pathogenic Organisms病理学与病理生理学Pathology and Pathophysiology法医学Forensic Medicine放射医学Radiation Medicine航空航天与航海医学Aerospace and Nautical medicine临床医学Clinical Medicine内科学(含心血管病学、血液病学、呼吸系病学、消化系病学、内分泌与代谢病学、肾脏病学、风湿病学、传染病学)Internal medicine (including Cardiology, Hematology, Respiratory, Gastroenterology, Endocrinology and Metabolism, Nephrology, Rheuma-tology, Infectious Diseases)儿科学Pediatrics老年医学Geriatrics神经病学Neurology精神病与精神卫生学Psychiatry and Mental Health皮肤病与性病学Dermatology and Venereology影像医学与核医学Imaging and Nuclear Medicine临床检验诊断学Clinical Laboratory Diagnostics护理学Nursing外科学(含普通外科学、骨外科学、泌尿外科学、胸心血管外科学、神经外科学、整形外科学、烧伤外科学、野战外科学)Surgery (General Surgery, Orthopedics, Urology, Cardiothoracic Surgery, Neurosurgery, Plastic Surgery, Burn Surgery, Field Surgery)妇产科学Obstetrics and Gynecology眼科学Ophthalmic Specialty耳鼻咽喉科学Otolaryngology肿瘤学Oncology康复医学与理疗学Rehabilitation Medicine & Physical Therapy运动医学Sports Medicine麻醉学Anesthesiology急诊医学Emergency Medicine口腔医学Stomatology口腔基础医学Basic Science of Stomatology口腔临床医学Clinical Science of Stomatology公共卫生与预防医学Public Health and Preventive Medicine流行病与卫生统计学Epidemiology and Health Statistics劳动卫生与环境卫生学Occupational and Environmental Health营养与食品卫生学Nutrition and Food Hygiene儿少卫生与妇幼保健学Maternal, Child and Adolescent Health卫生毒理学Hygiene Toxicology军事预防医学Military Preventive Medicine中医学Chinese Medicine中医基础理论Basic Theories of Chinese Medicine中医临床基础Clinical Foundation of Chinese Medicine中医医史文献History and Literature of Chinese Medicine方剂学Formulas of Chinese Medicine中医诊断学Diagnostics of Chinese Medicine中医内科学Chinese Internal Medicine中医外科学Surgery of Chinese Medicine中医骨伤科学Orthopedics of Chinese Medicine中医妇科学Gynecology of Chinese Medicine中医儿科学Pediatrics of Chinese Medicine中医五官科学Ophthalmology and Otolaryngoloy of Chinese Medicine针灸推拿学Acupuncture and Moxibustion and Tuina of Chinese medicine民族医学Ethnomedicine中西医结合医学Chinese and Western Integrative Medicine中西医结合基础医学Basic Discipline of Chinese and Western Integrative中西医结合临床医学Clinical Discipline of Chinese and Western Integrative Medicine药学Pharmaceutical Science药物化学Medicinal Chemistry药剂学Pharmaceutics生药学Pharmacognosy药物分析学Pharmaceutical Analysis微生物与生化药学Microbial and Biochemical Pharmacy药理学Pharmacology中药学Science of Chinese Pharmacology军事学Military Science军事思想学及军事历史学Military Thought and Military History军事思想学Military Thought军事历史学Military History战略学Science of Strategy军事战略学Military Strategy战争动员学War Mobilization战役学Science of Operations联合战役学Joint Operation军种战役学(含第二炮兵战役学)Armed Service Operation (including Operation of Strategic Missile Force)战术学Science of Tactics合同战术学Combined-Arms Tactics兵种战术学Branch Tactics军队指挥学Science of Command作战指挥学Combat Command军事运筹学Military Operation Research军事通信学Military Communication军事情报学Military Intelligence密码学Cryptography军事教育训练学(含军事体育学)Military Education and Training (including Military Physical Training)军制学Science of Military System军事组织编制学Military Organizational System军队管理学Military Management军队政治工作学Science of Military Political Work军事后勤学与军事装备学Science of Military Logistics and Military Equipment军事后勤学Military Logistics后方专业勤务Rear Special Service军事装备学Military Equipment管理学Management Science管理科学与工程Management Science and Engineering工商管理学Science of Business Administration会计学Accounting企业管理学(含财务管理、市场营销学、人力资源管理学)Corporate Management (including Financial Management, Marketing, and Human Resources Management)旅游管理学Tourist Management技术经济及管理学Technology Economy and Management农林经济管理学Agricultural and Forestry Economics & Management农业经济管理学Agricultural Economics & Management林业经济管理学Forestry Economics & Management公共管理学Science of Public Management行政管理学Administration Management社会医学与卫生事业管理学Social Medicine and Health Management教育经济与管理学Educational Economy and Management社会保障学Social Security土地资源管理学Land Resource Management图书馆、情报与档案学Science of Library, Information and Archival图书馆学Library Science情报学Information Science档案学Archival Science。
本科研究生各专业名称英文翻译

果树学 Pomology
蔬菜学 Olericulture
茶学 Tea Science
农业资源利用学 Utilization Science of Agricultural Resources
土壤学 Soil Science
植物营养学 Plant Nutrition
儿科学 Pediatrics
老年医学 Geriatrics
神经病学 Neurology
精神病与精神卫生学 Psychiatry and Mental Health
皮肤病与性病学 Dermatology and Venereology
影像医学与核医学 Imaging and Nuclear Medicine
森林培育学 Silviculture
森林保护学 Forest Protection
森林经理学 Forest Management
野生动植物保护与利用 Wildlife Conservation and Utilization
园林植物与观赏园艺 Ornamental Plants and Horticulture
生物化学与分子生物学 Biochemistry and Molecular Biology
生物物理学 Biophysics
生态学 Ecology
系统科学 Systems Science
系统理论 Systems Theory
系统分析与集成 Systems Analysis and Integration
中医医史文献 History and Literature of Chinese Medicine
方剂学 Formulas of Chinese Medicine
2014专业课程中英文对照表
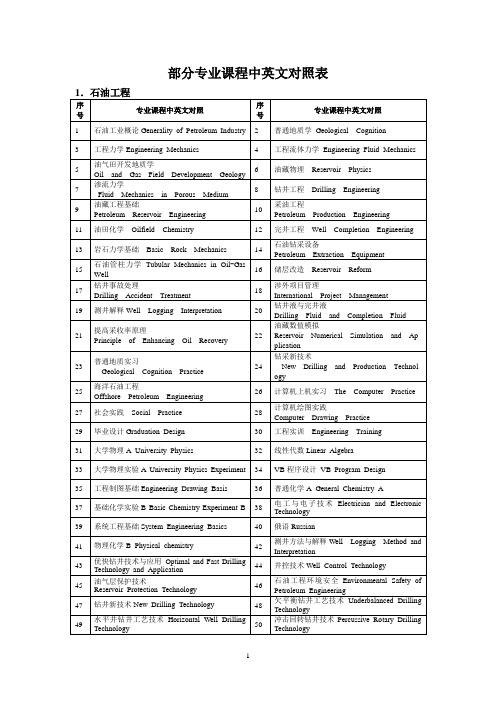
1.石油工程
序号
专业课程中英文对照
序号
专业课程中英文对照
1
石油工业概论GeneralityofPetroleumIndustry
2
普通地质学GeologicalCognition
3
工程力学EngineeringMechanics
4
工程流体力学EngineeringFluidMechanics
5
油气田开发地质学
OilandGasFieldDevelopmentGeology
6
油藏物理ReservoirPhysics
7
渗流力学
FluidMechanicsinPorousMedium
8
钻井工程DrillingEngineering
9
油藏工程基础
PetroleumReservoirEngineering
29
毕业设计GraduationDesign
30
工程实训EngineeringTraining
31
大学物理AUniversityPhysics
32
线性代数LinearAlgebra
33
大学物理实验AUniversityPhysicsExperiment
34
VB程序设计VBProgramDesign
35
49
水平井钻井工艺技术HorizontalWellDrillingTechnology
50
冲击回转钻井技术PercussiveRotaryDrillingTechnology
51
现代试井解释方法TheModernWellLoggingInterpretationMethod
工程力学外文翻译范文工程力学英文什么说

工程力学外文翻译范文工程力学英文什么说工程力学,英文是:engineering mechanics。
例句:并基于工程力学对充填体强度及其安全性进行了分析研究。
An analysis study was conducted on the strength and safety of the backfill materialbased on the engineering mechanics.详细解释:engineering英[?end???n??r??] 美[?end???n?r??]n. 工程(学),工程师行业; 操纵,管理; 土木工程,工事; 开车技术;[例句]He has not studied mechanics or engineering.他没有学习过力学和工程学。
mechanics 英[m?'k?n?ks] 美[m??k?n?ks]n. 力学; 机械学; 构成法; 技术;[例句]He has not studied mechanics or engineering.他没有学习过力学和工程学。
机械学院工程力学专业的英文是Engineering Mechanics major in Mechanical Engineering。
工程力学专业本专业培养具备力学基础理论知识、计算和试验能力,能在各种工程(如机械、土建、材料、能源、交通、航空、船舶、水利、化工等)中从事与力学有关的科研、技术开发、工程设计和力学教学工作的高级工程科学技术人才。
本专业主要学习力学、数学基本理论和知识,受到必要的工程技能训练,具有应用计算机和现代实验技术手段解决与力学有关的工程问题的基本能力。
《工程力学》是土木工程专业主要的技术基础课,而且也是学生公认的一门比较难学的课程。
该课程不但要求学生能正确理解基本概念,而且要求学生要学会用所学内容求解各种工程和生活中的各种力学问题。
所以该课程要求学生具有较好的高等数学基础。
(完整word版)所有学科英文翻译

哲学Philosophy马克思主义哲学 Philosophy of Marxism中国哲学 Chinese Philosophy外国哲学 Foreign Philosophies逻辑学 Logic伦理学 Ethics美学 Aesthetics宗教学 Science of Religion科学技术哲学 Philosophy of Science and Technology经济学 Economics理论经济学 Theoretical Economics政治经济学 Political Economy经济思想史 History of Economic Thought经济史 History of Economic西方经济学 Western Economics世界经济 World Economics人口、资源与环境经济学 Population, Resources and Environmental Economics应用经济学 Applied Economics国民经济学 National Economics区域经济学 Regional Economics法学 LawCommunist Movement中共党史(含党的学说与党的建设) History of the Communist Party of China(including the Doctrine of China Party and Party Building)马克思主义理论与思想政治教育 Education of Marxist Theory and Education in Ideology and Politi cs国际政治学 International Politics国际关系学 International Relations外交学 Diplomacy社会学 Sociology社会学 Sociology人口学 Demography人类学 Anthropology民俗学(含中国民间文学) Folklore (including Chinese Folk Literature)民族学 Ethnology民族学 Ethnology马克思主义民族理论与政策 Marxist Ethnic Theory and Policy 中国少数民族经济 Chinese Ethnic Economics中国少数民族史 Chinese Ethnic History中国少数民族艺术 Chinese Ethnic Art教育学 Education教育学 Education Science教育学原理 Educational Principle课程与教学论 Curriculum and Teaching Methodology教育史 History of Education比较教育学 Comparative Education学前教育学 Pre-school Education高等教育学 Higher Education成人教育学 Adult Education职业技术教育学 Vocational and Technical Education特殊教育学 Special Education教育技术学 Education Technology心理学 Psychology基础心理学 Basic Psychology发展与心理学 Developmental and Educational Psychology应用心理学 Applied Psychology体育学 Science of Physical Culture and Sports体育人文社会学 Humane and Sociological Science of Sports 运动人体科学 Human Movement Science体育教育训练学 Theory of Sports Pedagogy and Training民族传统体育学 Science of Ethnic Traditional Sports文学 Literature中国语言文学 Chinese Literature文艺学 Theory of Literature and Art语言学及应用语言学 Linguistics and Applied Linguistics汉语言文字学 Chinese Philology中国古典文献学 Study of Chinese Classical Text中国古代文学 Ancient Chinese Literature中国现当代文学 Modern and Contemporary Chinese Literature中国少数民族语言文学 Chinese Ethnic Language andLiterature比较文学与世界文学 Comparative Literature and World Literature外国语言文学 Foreign Languages and Literatures英语语言文学 English Language and Literature俄语语言文学 Russian Language and Literature法语语言文学 French Language and Literature德语语言文学 German Language and Literature日语语言文学 Japanese Language and Literature印度语言文学 Indian Language and Literature西班牙语语言文学 Spanish Language and Literature阿拉伯语语言文学 Arabic Language and Literature欧洲语言文学 European Language and Literature亚非语言文学 Asian—African Language and Literature外国语言学及应用语言学 Linguistics and Applied Linguistics inForeign Languages新闻传播学 Journalism and Communication新闻学 Journalism传播学 Communication艺术学 Art艺术学 Art Theory音乐学 Music美术学 Fine Arts设计艺术学 Artistic Design戏剧戏曲学 Theater and Chinese Traditional Opera电影学 Film广播电视艺术学 Radio and television Art舞蹈学 Dance历史学 History历史学 History史学理论及史学史 Historical Theories and History of Historical Science 考古学及博物馆学 Archaeology and Museology历史地理学 Historical Geography历史文献学(含敦煌学、古文字学) Studies of Historical Literature (including Paleography and Studies of Dunhuang)专门史 History of Particular Subjects中国古代史 Ancient Chinese History中国近现代史 Modern and Contemporary Chinese History世界史 World History理学 Natural Science数学 Mathematics基础数学 Fundamental Mathematics计算数学 Computational Mathematics概率论与数理统计 Probability and Mathematical Statistics应用数学 Applied mathematics运筹学与控制论 Operational Research and Cybernetics物理学 Physics理论物理 Theoretical Physics粒子物理与原子核物理 Particle Physics and Nuclear Physics原子与分子物理 Atomic and Molecular Physics等离子体物理 Plasma Physics凝聚态物理 Condensed Matter Physics声学 Acoustics光学 Optics无线电物理 Radio Physics化学 Chemistry无机化学 Inorganic Chemistry分析化学 Analytical Chemistry有机化学 Organic Chemistry物理化学(含化学物理) Physical Chemistry (including Chemical Physics)高分子化学与物理 Chemistry and Physics of Polymers天文学 Astronomy天体物理 Astrophysics天体测量与天体力学 Astrometry and Celestial Mechanics地理学 Geography自然地理学 Physical Geography人文地理学 Human Geography地图学与地理信息系统 Cartography and Geography Information System大气科学 Atmospheric Sciences气象学 Meteorology大气物理学与大气环境 Atmospheric Physics and Atmospheric Environment海洋科学 Marine Sciences物理海洋学 Physical Oceanography海洋化学 Marine Chemistry海洋生理学 Marine Biology海洋地质学 Marine Geology地球物理学 Geophysics固体地球物理学 Solid Earth Physics空间物理学 Space Physics地质学 Geology矿物学、岩石学、矿床学 Mineralogy, Petrology, Mineral Deposit Geology 地球化学 Geochemistry古生物学与地层学(含古人类学) Paleontology and Stratigraphy (including Paleoanthropology)构造地质学 Structural Geology第四纪地质学 Quaternary Geology生物学 Biology植物学 Botany动物学 Zoology生理学 Physiology水生生物学 Hydrobiology微生物学 Microbiology神经生物学 Neurobiology遗传学 Genetics发育生物学 Developmental Biology细胞生物学 Cell Biology生物化学与分子生物学 Biochemistry and Molecular Biology生物物理学 Biophysics生态学 Ecology系统科学 Systems Science系统理论 Systems Theory系统分析与集成 Systems Analysis and Integration科学技术史 History of Science and Technology工学 Engineering力学 Mechanics一般力学与力学基础 General and Fundamental Mechanics固体力学 Solid Mechanics流体力学 Fluid Mechanics工程力学 Engineering Mechanics机械工程 Mechanical Engineering机械制造及其自动化 Mechanical Manufacture and Automation机械电子工程 Mechatronic Engineering机械设计与理论 Mechanical Design and Theory车辆工程 Vehicle Engineering光学工程 Optical Engineering仪器科学与技术 Instrument Science and Technology精密仪器及机械 Precision Instrument and Machinery测试计量技术及仪器 Measuring and Testing Technologies and Instruments 材料科学与工程 Materials Science and Engineering材料物理与化学 Materials Physics and Chemistry材料学 Materialogy材料加工工程 Materials Processing Engineering冶金工程 Metallurgical Engineering冶金物理化学 Physical Chemistry of Metallurgy钢铁冶金 Ferrous Metallurgy有色金属冶金 Non—ferrous Metallurgy动力工程及工程热物理 Power Engineering and Engineering Thermophysics 工程热物理 Engineering Thermophysics热能工程 Thermal Power Engineering动力机械及工程 Power Machinery and Engineering流体机械及工程 Fluid Machinery and Engineering制冷及低温工程 Refrigeration and Cryogenic Engineering化工过程机械 Chemical Process Equipment电气工程 Electrical Engineering电机与电器 Electric Machines and Electric Apparatus电力系统及其自动化 Power System and its Automation高电压与绝缘技术 High Voltage and Insulation Technology电力电子与电力传动 Power Electronics and Power Drives电工理论与新技术 Theory and New Technology of Electrical Engineering电子科学与技术 Electronics Science and Technology物理电子学 Physical Electronics电路与系统 Circuits and Systems微电子学与固体电子学 Microelectronics and Solid State Electronics电磁场与微波技术 Electromagnetic Field and Microwave Technology信息与通信工程 Information and Communication Engineering通信与信息系统 Communication and Information Systems信号与信息处理 Signal and Information Processing控制科学与工程 Control Science and Engineering控制理论与控制工程 Control Theory and Control Engineering检测技术与自动化装置 Detection Technology and Automatic Equipment系统工程 Systems Engineering模式识别与智能系统 Pattern Recognition and Intelligent Systems导航、制导与控制 Navigation, Guidance and Control计算机科学与技术 Computer Science and Technology计算机软件与理论 Computer Software and Theory计算机系统结构 Computer Systems Organization计算机应用技术 Computer Applied Technology建筑学 Architecture建筑历史与理论 Architectural History and Theory建筑设计及其理论 Architectural Design and Theory城市规划与设计(含风景园林规划与设计) Urban Planning and Design (including Landscape Plannin g and Design)建筑技术科学 Building Technology Science土木工程 Civil Engineering岩土工程 Geotechnical Engineering结构工程 Structural Engineering市政工程 Municipal Engineering供热、供燃气、通风及空调工程 Heating, Gas Supply, Ventilating and Air Conditioning Engineering防灾减灾工程及防护工程 Disaster Prevention and Reduction Engineering and Protective Engineeri ng桥梁与隧道工程 Bridge and Tunnel Engineering水利工程 Hydraulic Engineering水文学及水资源 Hydrology and Water Resources水力学及河流动力学 Hydraulics and River Dynamics水工结构工程 Hydraulic Structure Engineering水利水电工程 Hydraulic and Hydro-Power Engineering港口、海岸及近海工程 Harbor, Coastal and Offshore Engineering测绘科学与技术 Surveying and Mapping大地测量学与测量工程 Geodesy and Survey Engineering摄影测量与遥感 Photogrammetry and Remote Sensing地图制图学与地理信息工程 Cartography and Geographic Information Engineering化学工程与技术 Chemical Engineering and Technology化学工程 Chemical Engineering化学工艺 Chemical Technology生物化工 Biochemical Engineering应用化学 Applied Chemistry工业催化 Industrial Catalysis地质资源与地质工程 Geological Resources and Geological Engineering矿产普查与勘探 Mineral Resource Prospecting and Exploration地球探测与信息技术 Geodetection and Information Technology地质工程 Geological Engineering矿业工程 Mineral Engineering采矿工程 Mining Engineering矿物加工工程 Mineral Processing Engineering安全技术及工程 Safety Technology and Engineering石油与天然气工程 Oil and Natural Gas Engineering油气井工程 Oil-Gas Well Engineering油气田开发工程 Oil-Gas Field Development Engineering油气储运工程 Oil-Gas Storage and Transportation Engineering纺织科学与工程 Textile Science and Engineering纺织工程 Textile Engineering纺织材料与纺织品设计 Textile Material and Textiles Design纺织化学与染整工程 Textile Chemistry and Dyeing and Finishing Engineering服装设计与工程 Clothing Design and Engineering轻工技术与工程 The Light Industry Technology and Engineering制浆造纸工程 Pulp and Paper Engineering制糖工程 Sugar Engineering发酵工程 Fermentation Engineering皮革化学与工程 Leather Chemistry and Engineering交通运输工程 Communication and Transportation Engineering道路与铁道工程 Highway and Railway Engineering交通信息工程及控制 Traffic Information Engineering & Control交通运输规划与管理 Transportation Planning and Management载运工具运用工程 Vehicle Operation Engineering船舶与海洋工程 Naval Architecture and Ocean Engineering船舶与海洋结构物设计制造 Design and Construction of Naval Architecture and Ocean Structure 轮机工程 Marine Engine Engineering水声工程 Underwater Acoustics Engineering航空宇航科学与技术 Aeronautical and Astronautical Science and Technology飞行器设计 Flight Vehicle Design航空宇航推进理论与工程 Aerospace Propulsion Theory and Engineering航空宇航器制造工程 Manufacturing Engineering of Aerospace Vehicle人机与环境工程 Man—Machine and Environmental Engineering兵器科学与技术 Armament Science and Technology武器系统与运用工程 Weapon Systems and Utilization Engineering兵器发射理论与技术 Armament Launch Theory and Technology火炮、自动武器与弹药工程 Artillery, Automatic Gun and Ammunition Engineering军事化学与烟火技术 Military Chemistry and Pyrotechnics核科学与技术 Nuclear Science and Technology核能科学与工程 Nuclear Energy Science and Engineering核燃料循环与材料 Nuclear Fuel Cycle and Materials核技术及应用 Nuclear Technology and Applications辐射防护及环境保护 Radiation and Environmental Protection农业工程 Agricultural Engineering农业机械化工程 Agricultural Mechanization Engineering农业水土工程 Agricultural Water—Soil Engineering农业生物环境与能源工程 Agricultural Biological Environmental and Energy Engineering 农业电气化与自动化 Agricultural Electrification and Automation林业工程 Forestry Engineering森林工程 Forest Engineering木材科学与技术 Wood Science and Technology林产化学加工工程 Chemical Processing Engineering of Forest Products环境科学与工程 Environmental Science and Engineering环境科学 Environmental Science环境工程 Environmental Engineering生物医学工程 Biomedical Engineering食品科学与工程 Food Science and Engineering食品科学 Food Science粮食、油脂及植物蛋白工程 Cereals, Oils and Vegetable Protein Engineering农产品加工及贮藏工程 Processing and Storage of Agriculture Products水产品加工及贮藏工程 Processing and Storage of Aquatic Products农学 Agriculture作物学 Crop Science作物栽培学与耕作学 Crop Cultivation and Farming System作物遗传育种学 Crop Genetics and Breeding园艺学 Horticulture果树学 Pomology蔬菜学 Olericulture茶学 Tea Science农业资源利用学 Utilization Science of Agricultural Resources土壤学 Soil Science植物营养学 Plant Nutrition植物保护学 Plant Protection植物病理学 Plant Pathology农业昆虫与害虫防治 Agricultural Entomology and Pest Control农药学 Pesticide Science畜牧学 Animal Science动物遗传育种与繁殖 Animal Genetics, Breeding and ReproductionScience动物营养与饲料科学 Animal Nutrition and Feed Science草业科学 Practaculture Science特种经济动物饲养学(含蚕、蜂等) The Rearing of Special-type EconomicAnimals (including Silkworm, Honeybees, etc.)兽医学 Veterinary Medicine基础兽医学 Basic Veterinary Medicine预防兽医学 Preventive Veterinary Medicine临床兽医学 Clinical Veterinary Medicine林学 Forestry林木遗传育种学 Forest Tree Genetics and Breeding森林培育学 Silviculture森林保护学 Forest Protection森林经理学 Forest Management野生动植物保护与利用 Wildlife Conservation and Utilization园林植物与观赏园艺 Ornamental Plants and Horticulture水土保持与荒漠化防治 Soil and Water Conservation and Desertification Combating水产学 Fisheries Science水产养殖学 Aquaculture Science捕捞学 Fishing Science渔业资源学 Science of Fisheries Resources医学 Medicine基础医学 Basic Medicine人体解剖与组织胚胎学 Human Anatomy, Histology and Embryology免疫学 Immunology病原生物学 Pathogenic Organisms病理学与病理生理学 Pathology and Pathophysiology法医学 Forensic Medicine放射医学 Radiation Medicine航空航天与航海医学 Aerospace and Nautical medicine临床医学 Clinical Medicine内科学(含心血管病学、血液病学、呼吸系病学、消化系病学、内分泌与代谢病学、肾脏病学、风湿病学、传染病学) Internal medicine (including Cardiology, Hematology, Respiratory, Gastroenterolog y, Endocrinology and Metabolism, Nephrology, Rheuma-tology, Infectious Diseases)儿科学 Pediatrics老年医学 Geriatrics神经病学 Neurology精神病与精神卫生学 Psychiatry and Mental Health皮肤病与性病学 Dermatology and Venereology影像医学与核医学 Imaging and Nuclear Medicine临床检验诊断学 Clinical Laboratory Diagnostics护理学 Nursing外科学(含普通外科学、骨外科学、泌尿外科学、胸心血管外科学、神经外科学、整形外科学、烧伤外科学、野战外科学) Surgery (General Surgery, Orthopedics, Urology, Cardiothoracic Surgery, Neuros urgery, Plastic Surgery, Burn Surgery, Field Surgery)妇产科学 Obstetrics and Gynecology眼科学 Ophthalmic Specialty耳鼻咽喉科学 Otolaryngology肿瘤学 Oncology康复医学与理疗学 Rehabilitation Medicine & Physical Therapy运动医学 Sports Medicine麻醉学 Anesthesiology急诊医学 Emergency Medicine口腔医学 Stomatology口腔基础医学 Basic Science of Stomatology口腔临床医学 Clinical Science of Stomatology公共卫生与预防医学 Public Health and Preventive Medicine流行病与卫生统计学 Epidemiology and Health Statistics劳动卫生与环境卫生学 Occupational and Environmental Health营养与食品卫生学 Nutrition and Food Hygiene儿少卫生与妇幼保健学 Maternal, Child and Adolescent Health卫生毒理学 Hygiene Toxicology军事预防医学 Military Preventive Medicine中医学 Chinese Medicine中医基础理论 Basic Theories of Chinese Medicine中医临床基础 Clinical Foundation of Chinese Medicine中医医史文献 History and Literature of Chinese Medicine方剂学 Formulas of Chinese Medicine中医诊断学 Diagnostics of Chinese Medicine中医内科学 Chinese Internal Medicine中医外科学 Surgery of Chinese Medicine中医骨伤科学 Orthopedics of Chinese Medicine中医妇科学 Gynecology of Chinese Medicine中医儿科学 Pediatrics of Chinese Medicine中医五官科学 Ophthalmology and Otolaryngoloy of Chinese Medicine针灸推拿学 Acupuncture and Moxibustion and Tuina of Chinese medicine民族医学 Ethnomedicine中西医结合医学 Chinese and Western Integrative Medicine中西医结合基础医学 Basic Discipline of Chinese and Western Integrative中西医结合临床医学 Clinical Discipline of Chinese and Western Integrative Medicine药学 Pharmaceutical Science药物化学 Medicinal Chemistry药剂学 Pharmaceutics生药学 Pharmacognosy药物分析学 Pharmaceutical Analysis微生物与生化药学 Microbial and Biochemical Pharmacy药理学 Pharmacology中药学 Science of Chinese Pharmacology军事学 Military Science军事思想学及军事历史学 Military Thought and Military History军事思想学 Military Thought军事历史学 Military History战略学 Science of Strategy军事战略学 Military Strategy战争动员学 War Mobilization战役学 Science of Operations联合战役学 Joint Operation军种战役学(含第二炮兵战役学) Armed Service Operation (including Operation of Strategic Miss ile Force)战术学 Science of Tactics合同战术学 Combined—Arms Tactics兵种战术学 Branch Tactics军队指挥学 Science of Command作战指挥学 Combat Command军事运筹学 Military Operation Research军事通信学 Military Communication军事情报学 Military Intelligence密码学 Cryptography军事教育训练学(含军事体育学) Military Education and Training (including Military Physical Training)管理学 Management Science管理科学与工程 Management Science and Engineering工商管理学 Science of Business Administration会计学 Accounting企业管理学(含财务管理、市场营销学、人力资源管理学) Corporate Management (including Financia l Management, Marketing, and Human Resources Management)旅游管理学 Tourist Management技术经济及管理学 Technology Economy and Management农林经济管理学 Agricultural and Forestry Economics & Management农业经济管理学 Agricultural Economics & Management林业经济管理学 Forestry Economics & Management公共管理学 Science of Public Management。
力学名词英文翻译

力学通类名词力学 mechanics牛顿力学 Newtonian mechanics经典力学 classical mechanics静力学 statics运动学 kinematics动力学 dynamics动理学 kinetics宏观力学 macroscopic mechanics,macromechanics 细观力学 mesomechanics微观力学 microscopic mechanics,micromechanics 一般力学 general mechanics固体力学 solid mechanics流体力学 fluid mechanics理论力学 theoretical mechanics应用力学 applied mechanics工程力学 engineering mechanics实验力学 experimental mechanics计算力学 computational mechanics理性力学 rational mechanics物理力学 physical mechanics地球动力学 geodynamics力 force作用点 point of action作用线 line of action力系 system of forces力系的简化 reduction of force system 等效力系 equivalent force system刚体 rigid body力的可传性 transmissibility of force 平行四边形定则 parallelogram rule力三角形 force triangle力多边形 force polygon零力系 null-force system平衡 equilibrium力的平衡 equilibrium of forces平衡条件 equilibrium condition平衡位置 equilibrium position平衡态 equilibrium state分析力学 analytical mechanics拉格朗日乘子 Lagrange multiplier拉格朗日[量] Lagrangian拉格朗日括号 Lagrange bracket循环坐标 cyclic coordinate循环积分 cyclic integral哈密顿[量] Hamiltonian哈密顿函数 Hamiltonian function正则方程 canonical equation正则摄动 canonical perturbation正则变换 canonical transformation正则变量 canonical variable哈密顿原理 Hamilton principle作用量积分 action integral哈密顿--雅可比方程 Hamilton-Jacobi equation 作用--角度变量 action-angle variables阿佩尔方程 Appell equation劳斯方程 Routh equation拉格朗日函数 Lagrangian function诺特定理 Noether theorem泊松括号 poisson bracket边界积分法 boundary integral method并矢 dyad运动稳定性 stability of motion轨道稳定性 orbital stability李雅普诺夫函数 Lyapunov function渐近稳定性 asymptotic stability结构稳定性 structural stability久期不稳定性 secular instability弗洛凯定理 Floquet theorem倾覆力矩 capsizing moment自由振动 free vibration固有振动 natural vibration暂态 transient state环境振动 ambient vibration反共振 anti-resonance衰减 attenuation库仑阻尼 Coulomb damping同相分量 in-phase component非同相分量 out-of-phase component超调量 overshoot参量[激励]振动 parametric vibration模糊振动 fuzzy vibration临界转速 critical speed of rotation阻尼器 damper半峰宽度 half-peak width集总参量系统 lumped parameter system相平面法 phase plane method相轨迹 phase trajectory等倾线法 isocline method跳跃现象 jump phenomenon负阻尼 negative damping达芬方程 Duffing equation希尔方程 Hill equationKBM方法 KBM method, Krylov-Bogoliu-bov-Mitropol'skii method 马蒂厄方程 Mathieu equation平均法 averaging method组合音调 combination tone解谐 detuning耗散函数 dissipative function硬激励 hard excitation硬弹簧 hard spring, hardening spring谐波平衡法 harmonic balance method久期项 secular term自激振动 self-excited vibration分界线 separatrix亚谐波 subharmonic软弹簧 soft spring ,softening spring软激励 soft excitation邓克利公式 Dunkerley formula瑞利定理 Rayleigh theorem分布参量系统 distributed parameter system 优势频率 dominant frequency模态分析 modal analysis固有模态 natural mode of vibration同步 synchronization超谐波 ultraharmonic范德波尔方程 van der pol equation频谱 frequency spectrum基频 fundamental frequencyWKB方法 WKB method, Wentzel-Kramers-Brillouin method 缓冲器 buffer风激振动 aeolian vibration嗡鸣 buzz倒谱 cepstrum颤动 chatter蛇行 hunting阻抗匹配 impedance matching机械导纳 mechanical admittance机械效率 mechanical efficiency机械阻抗 mechanical impedance随机振动 stochastic vibration, random vibration隔振 vibration isolation减振 vibration reduction应力过冲 stress overshoot喘振 surge摆振 shimmy起伏运动 phugoid motion起伏振荡 phugoid oscillation驰振 galloping陀螺动力学 gyrodynamics陀螺摆 gyropendulum陀螺平台 gyroplatform陀螺力矩 gyroscoopic torque陀螺稳定器 gyrostabilizer陀螺体 gyrostat惯性导航 inertial guidance姿态角 attitude angle方位角 azimuthal angle舒勒周期 Schuler period机器人动力学 robot dynamics多体系统 multibody system多刚体系统 multi-rigid-body system机动性 maneuverability凯恩方法 Kane method转子[系统]动力学 rotor dynamics转子[一支承一基础]系统 rotor-support-foundation system 静平衡 static balancing动平衡 dynamic balancing静不平衡 static unbalance动不平衡 dynamic unbalance现场平衡 field balancing不平衡 unbalance不平衡量 unbalance互耦力 cross force挠性转子 flexible rotor分频进动 fractional frequency precession半频进动 half frequency precession油膜振荡 oil whip转子临界转速 rotor critical speed自动定心 self-alignment亚临界转速 subcritical speed涡动 whirl连续过程 continuous process碰撞截面 collision cross section通用气体常数 conventional gas constant 燃烧不稳定性 combustion instability稀释度 dilution完全离解 complete dissociation火焰传播 flame propagation组份 constituent碰撞反应速率 collision reaction rate 燃烧理论 combustion theory浓度梯度 concentration gradient阴极腐蚀 cathodic corrosion火焰速度 flame speed火焰驻定 flame stabilization火焰结构 flame structure着火 ignition湍流火焰 turbulent flame层流火焰 laminar flame燃烧带 burning zone渗流 flow in porous media, seepage达西定律 Darcy law赫尔-肖流 Hele-Shaw flow毛[细]管流 capillary flow过滤 filtration爪进 fingering不互溶驱替 immiscible displacement不互溶流体 immiscible fluid互溶驱替 miscible displacement互溶流体 miscible fluid迁移率 mobility流度比 mobility ratio渗透率 permeability孔隙度 porosity多孔介质 porous medium比面 specific surface迂曲度 tortuosity空隙 void空隙分数 void fraction注水 water flooding可湿性 wettability地球物理流体动力学 geophysical fluid dynamics 物理海洋学 physical oceanography大气环流 atmospheric circulation海洋环流 ocean circulation海洋流 ocean current旋转流 rotating flow平流 advection埃克曼流 Ekman flow埃克曼边界层 Ekman boundary layer大气边界层 atmospheric boundary layer大气-海洋相互作用 atmosphere-ocean interaction 埃克曼数 Ekman number罗斯贝数 Rossby unmber罗斯贝波 Rossby wave斜压性 baroclinicity正压性 barotropy内磨擦 internal friction海洋波 ocean wave盐度 salinity环境流体力学 environmental fluid mechanics斯托克斯流 Stokes flow羽流 plume理查森数 Richardson number污染源 pollutant source污染物扩散 pollutant diffusion噪声 noise噪声级 noise level噪声污染 noise pollution排放物 effulent工业流体力学 industrical fluid mechanics流控技术 fluidics轴向流 axial flow并向流 co-current flow对向流 counter current flow横向流 cross flow螺旋流 spiral flow旋拧流 swirling flow滞后流 after flow混合层 mixing layer抖振 buffeting风压 wind pressure附壁效应 wall attachment effect, Coanda effect简约频率 reduced frequency爆炸力学 mechanics of explosion终点弹道学 terminal ballistics动态超高压技术 dynamic ultrahigh pressure technique 流体弹塑性体 hydro-elastoplastic medium热塑不稳定性 thermoplastic instability空中爆炸 explosion in air地下爆炸 underground explosion水下爆炸 underwater explosion电爆炸 discharge-induced explosion激光爆炸 laser-induced explosion核爆炸 nuclear explosion点爆炸 point-source explosion殉爆 sympathatic detonation强爆炸 intense explosion粒子束爆炸 explosion by beam radiation 聚爆 implosion起爆 initiation of explosion爆破 blasting霍普金森杆 Hopkinson bar电炮 electric gun电磁炮 electromagnetic gun爆炸洞 explosion chamber轻气炮 light gas gun马赫反射 Mach reflection基浪 base surge成坑 cratering能量沉积 energy deposition爆心 explosion center爆炸当量 explosion equivalent火球 fire ball爆高 height of burst蘑菇云 mushroom侵彻 penetration规则反射 regular reflection崩落 spallation应变率史 strain rate history流变学 rheology聚合物减阻 drag reduction by polymers挤出[物]胀大 extrusion swell, die swell 无管虹吸 tubeless siphon剪胀效应 dilatancy effect孔压[误差]效应 hole-pressure[error]effect 剪切致稠 shear thickening剪切致稀 shear thinning触变性 thixotropy反触变性 anti-thixotropy超塑性 superplasticity粘弹塑性材料 viscoelasto-plastic material 滞弹性材料 anelastic material本构关系 constitutive relation麦克斯韦模型 Maxwell model沃伊特-开尔文模型 Voigt-Kelvin model宾厄姆模型 Bingham model奥伊洛特模型 Oldroyd model幂律模型 power law model应力松驰 stress relaxation应变史 strain history应力史 stress history记忆函数 memory function衰退记忆 fading memory应力增长 stress growing粘度函数 voscosity function相对粘度 relative viscosity复态粘度 complex viscosity拉伸粘度 elongational viscosity拉伸流动 elongational flow第一法向应力差 first normal-stress difference 第二法向应力差 second normal-stress difference 德博拉数 Deborah number魏森贝格数 Weissenberg number动态模量 dynamic modulus振荡剪切流 oscillatory shear flow宇宙气体动力学 cosmic gas dynamics等离[子]体动力学 plasma dynamics电离气体 ionized gas行星边界层 planetary boundary layer阿尔文波 Alfven wave泊肃叶-哈特曼流] Poiseuille-Hartman flow哈特曼数 Hartman number生物流变学 biorheology生物流体 biofluid生物屈服点 bioyield point生物屈服应力 bioyield stress电气体力学 electro-gas dynamics铁流体力学 ferro-hydrodynamics血液流变学 hemorheology, blood rheology血液动力学 hemodynamics磁流体力学 magneto fluid mechanics磁流体动力学 magnetohydrodynamics, MHD磁流体动力波 magnetohydrodynamic wave磁流体流 magnetohydrodynamic flow磁流体动力稳定性 magnetohydrodynamic stability 生物力学 biomechanics生物流体力学 biological fluid mechanics生物固体力学 biological solid mechanics宾厄姆塑性流 Bingham plastic flow开尔文体 Kelvin body沃伊特体 Voigt body可贴变形 applicable deformation可贴曲面 applicable surface边界润滑 boundary lubrication液膜润滑 fluid film lubrication向心收缩功 concentric work离心收缩功 eccentric work关节反作用力 joint reaction force微循环力学 microcyclic mechanics微纤维 microfibril渗透性 permeability生理横截面积 physiological cross-sectional area 农业生物力学 agrobiomechanics纤维度 fibrousness硬皮度 rustiness胶粘度 gumminess粘稠度 stickiness嫩度 tenderness渗透流 osmotic flow易位流 translocation flow蒸腾流 transpirational flow过滤阻力 filtration resistance压扁 wafering风雪流 snow-driving wind停滞堆积 accretion遇阻堆积 encroachment沙漠地面 desert floor流沙固定 fixation of shifting sand流动阈值 fluid threshold固体力学弹性力学 elasticity弹性理论 theory of elasticity均匀应力状态 homogeneous state of stress应力不变量 stress invariant应变不变量 strain invariant应变椭球 strain ellipsoid均匀应变状态 homogeneous state of strain应变协调方程 equation of strain compatibility拉梅常量 Lame constants各向同性弹性 isotropic elasticity旋转圆盘 rotating circular disk楔 wedge开尔文问题 Kelvin problem布西内斯克问题 Boussinesq problem艾里应力函数 Airy stress function克罗索夫--穆斯赫利什维利法 Kolosoff-Muskhelishvili method 基尔霍夫假设 Kirchhoff hypothesis板 Plate矩形板 Rectangular plate圆板 Circular plate环板 Annular plate波纹板 Corrugated plate加劲板 Stiffened plate,reinforced Plate中厚板 Plate of moderate thickness弯[曲]应力函数 Stress function of bending 壳 Shell扁壳 Shallow shell旋转壳 Revolutionary shell球壳 Spherical shell[圆]柱壳 Cylindrical shell锥壳 Conical shell环壳 Toroidal shell封闭壳 Closed shell波纹壳 Corrugated shell扭[转]应力函数 Stress function of torsion 翘曲函数 Warping function半逆解法 semi-inverse method瑞利--里茨法 Rayleigh-Ritz method松弛法 Relaxation method莱维法 Levy method松弛 Relaxation量纲分析 Dimensional analysis自相似[性] self-similarity影响面 Influence surface接触应力 Contact stress赫兹理论 Hertz theory协调接触 Conforming contact滑动接触 Sliding contact滚动接触 Rolling contact压入 Indentation各向异性弹性 Anisotropic elasticity颗粒材料 Granular material散体力学 Mechanics of granular media热弹性 Thermoelasticity超弹性 Hyperelasticity粘弹性 Viscoelasticity对应原理 Correspondence principle褶皱 Wrinkle塑性全量理论 Total theory of plasticity 滑动 Sliding微滑 Microslip粗糙度 Roughness非线性弹性 Nonlinear elasticity大挠度 Large deflection突弹跳变 snap-through有限变形 Finite deformation格林应变 Green strain阿尔曼西应变 Almansi strain弹性动力学 Dynamic elasticity运动方程 Equation of motion准静态的 Quasi-static气动弹性 Aeroelasticity水弹性 Hydroelasticity颤振 Flutter弹性波 Elastic wave简单波 Simple wave柱面波 Cylindrical wave水平剪切波 Horizontal shear wave竖直剪切波 Vertical shear wave体波 body wave无旋波 Irrotational wave畸变波 Distortion wave膨胀波 Dilatation wave瑞利波 Rayleigh wave等容波 Equivoluminal wave勒夫波 Love wave界面波 Interfacial wave边缘效应 edge effect塑性力学 Plasticity可成形性 Formability金属成形 Metal forming耐撞性 Crashworthiness结构抗撞毁性 Structural crashworthiness 拉拔 Drawing破坏机构 Collapse mechanism回弹 Springback挤压 Extrusion冲压 Stamping穿透 Perforation层裂 Spalling塑性理论 Theory of plasticity安定[性]理论 Shake-down theory运动安定定理 kinematic shake-down theorem 静力安定定理 Static shake-down theorem率相关理论 rate dependent theorem载荷因子 load factor加载准则 Loading criterion加载函数 Loading function加载面 Loading surface塑性加载 Plastic loading塑性加载波 Plastic loading wave简单加载 Simple loading比例加载 Proportional loading卸载 Unloading卸载波 Unloading wave冲击载荷 Impulsive load阶跃载荷 step load脉冲载荷 pulse load极限载荷 limit load中性变载 nentral loading拉抻失稳 instability in tension加速度波 acceleration wave本构方程 constitutive equation完全解 complete solution名义应力 nominal stress过应力 over-stress真应力 true stress等效应力 equivalent stress流动应力 flow stress应力间断 stress discontinuity应力空间 stress space主应力空间 principal stress space静水应力状态 hydrostatic state of stress 对数应变 logarithmic strain工程应变 engineering strain等效应变 equivalent strain应变局部化 strain localization应变率 strain rate应变率敏感性 strain rate sensitivity应变空间 strain space有限应变 finite strain塑性应变增量 plastic strain increment累积塑性应变 accumulated plastic strain 永久变形 permanent deformation内变量 internal variable应变软化 strain-softening理想刚塑性材料 rigid-perfectly plastic Material 刚塑性材料 rigid-plastic material理想塑性材料 perfectl plastic material材料稳定性 stability of material应变偏张量 deviatoric tensor of strain应力偏张量 deviatori tensor of stress应变球张量 spherical tensor of strain应力球张量 spherical tensor of stress路径相关性 path-dependency线性强化 linear strain-hardening应变强化 strain-hardening随动强化 kinematic hardening各向同性强化 isotropic hardening强化模量 strain-hardening modulus幂强化 power hardening塑性极限弯矩 plastic limit bending Moment塑性极限扭矩 plastic limit torque弹塑性弯曲 elastic-plastic bending弹塑性交界面 elastic-plastic interface弹塑性扭转 elastic-plastic torsion粘塑性 Viscoplasticity非弹性 Inelasticity理想弹塑性材料 elastic-perfectly plastic Material 极限分析 limit analysis极限设计 limit design极限面 limit surface上限定理 upper bound theorem上屈服点 upper yield point下限定理 lower bound theorem下屈服点 lower yield point界限定理 bound theorem初始屈服面 initial yield surface后继屈服面 subsequent yield surface屈服面[的]外凸性 convexity of yield surface截面形状因子 shape factor of cross-section沙堆比拟 sand heap analogy屈服 Yield屈服条件 yield condition屈服准则 yield criterion屈服函数 yield function屈服面 yield surface塑性势 plastic potential能量吸收装置 energy absorbing device能量耗散率 energy absorbing device塑性动力学 dynamic plasticity塑性动力屈曲 dynamic plastic buckling塑性动力响应 dynamic plastic response塑性波 plastic wave运动容许场 kinematically admissible Field静力容许场 statically admissible Field流动法则 flow rule速度间断 velocity discontinuity滑移线 slip-lines滑移线场 slip-lines field移行塑性铰 travelling plastic hinge塑性增量理论 incremental theory of Plasticity米泽斯屈服准则 Mises yield criterion普朗特--罗伊斯关系 prandtl- Reuss relation特雷斯卡屈服准则 Tresca yield criterion洛德应力参数 Lode stress parameter莱维--米泽斯关系 Levy-Mises relation亨基应力方程 Hencky stress equation赫艾--韦斯特加德应力空间 Haigh-Westergaard stress space 洛德应变参数 Lode strain parameter德鲁克公设 Drucker postulate盖林格速度方程 Geiringer velocity Equation结构力学 structural mechanics结构分析 structural analysis结构动力学 structural dynamics拱 Arch三铰拱 three-hinged arch抛物线拱 parabolic arch圆拱 circular arch穹顶 Dome空间结构 space structure空间桁架 space truss雪载[荷] snow load风载[荷] wind load土压力 earth pressure地震载荷 earthquake loading弹簧支座 spring support支座位移 support displacement支座沉降 support settlement超静定次数 degree of indeterminacy 机动分析 kinematic analysis结点法 method of joints截面法 method of sections结点力 joint forces共轭位移 conjugate displacement影响线 influence line三弯矩方程 three-moment equation 单位虚力 unit virtual force刚度系数 stiffness coefficient柔度系数 flexibility coefficient力矩分配 moment distribution力矩分配法 moment distribution method力矩再分配 moment redistribution分配系数 distribution factor矩阵位移法 matri displacement method单元刚度矩阵 element stiffness matrix单元应变矩阵 element strain matrix总体坐标 global coordinates贝蒂定理 Betti theorem高斯--若尔当消去法 Gauss-Jordan elimination Method 屈曲模态 buckling mode复合材料力学 mechanics of composites复合材料 composite material纤维复合材料 fibrous composite单向复合材料 unidirectional composite泡沫复合材料 foamed composite颗粒复合材料 particulate composite层板 Laminate夹层板 sandwich panel正交层板 cross-ply laminate斜交层板 angle-ply laminate层片 Ply多胞固体 cellular solid膨胀 Expansion压实 Debulk劣化 Degradation脱层 Delamination脱粘 Debond纤维应力 fiber stress层应力 ply stress层应变 ply strain层间应力 interlaminar stress比强度 specific strength强度折减系数 strength reduction factor 强度应力比 strength -stress ratio横向剪切模量 transverse shear modulus 横观各向同性 transverse isotropy正交各向异 Orthotropy剪滞分析 shear lag analysis短纤维 chopped fiber长纤维 continuous fiber纤维方向 fiber direction纤维断裂 fiber break纤维拔脱 fiber pull-out纤维增强 fiber reinforcement致密化 Densification最小重量设计 optimum weight design网格分析法 netting analysis混合律 rule of mixture失效准则 failure criterion蔡--吴失效准则 Tsai-W u failure criterion达格代尔模型 Dugdale model断裂力学 fracture mechanics概率断裂力学 probabilistic fracture Mechanics格里菲思理论 Griffith theory线弹性断裂力学 linear elastic fracture mechanics, LEFM 弹塑性断裂力学 elastic-plastic fracture mecha-nics, EPFM 断裂 Fracture脆性断裂 brittle fracture解理断裂 cleavage fracture蠕变断裂 creep fracture延性断裂 ductile fracture晶间断裂 inter-granular fracture准解理断裂 quasi-cleavage fracture穿晶断裂 trans-granular fracture裂纹 Crack裂缝 Flaw缺陷 Defect割缝 Slit微裂纹 Microcrack折裂 Kink椭圆裂纹 elliptical crack深埋裂纹 embedded crack[钱]币状裂纹 penny-shape crack预制裂纹 Precrack短裂纹 short crack表面裂纹 surface crack裂纹钝化 crack blunting裂纹分叉 crack branching裂纹闭合 crack closure裂纹前缘 crack front裂纹嘴 crack mouth裂纹张开角 crack opening angle,COA裂纹张开位移 crack opening displacement, COD裂纹阻力 crack resistance裂纹面 crack surface裂纹尖端 crack tip裂尖张角 crack tip opening angle, CTOA裂尖张开位移 crack tip opening displacement, CTOD 裂尖奇异场 crack tip singularity Field裂纹扩展速率 crack growth rate稳定裂纹扩展 stable crack growth定常裂纹扩展 steady crack growth亚临界裂纹扩展 subcritical crack growth裂纹[扩展]减速 crack retardation止裂 crack arrest止裂韧度 arrest toughness断裂类型 fracture mode滑开型 sliding mode张开型 opening mode撕开型 tearing mode复合型 mixed mode撕裂 Tearing撕裂模量 tearing modulus断裂准则 fracture criterionJ积分 J-integralJ阻力曲线 J-resistance curve断裂韧度 fracture toughness应力强度因子 stress intensity factorHRR场 Hutchinson-Rice-Rosengren Field守恒积分 conservation integral有效应力张量 effective stress tensor应变能密度 strain energy density能量释放率 energy release rate内聚区 cohesive zone塑性区 plastic zone张拉区 stretched zone热影响区 heat affected zone, HAZ延脆转变温度 brittle-ductile transition temperature 剪切带 shear band剪切唇 shear lip无损检测 non-destructive inspection双边缺口试件 double edge notched specimen, DEN specimen单边缺口试件 single edge notched specimen, SEN specimen三点弯曲试件 three point bending specimen, TPB specimen中心裂纹拉伸试件 center cracked tension specimen, CCT specimen 中心裂纹板试件 center cracked panel specimen, CCP specimen紧凑拉伸试件 compact tension specimen, CT specimen大范围屈服 large scale yielding小范围攻屈服 small scale yielding韦布尔分布 Weibull distribution帕里斯公式 paris formula空穴化 Cavitation应力腐蚀 stress corrosion概率风险判定 probabilistic risk assessment, PRA损伤力学 damage mechanics损伤 Damage连续介质损伤力学 continuum damage mechanics细观损伤力学 microscopic damage mechanics累积损伤 accumulated damage脆性损伤 brittle damage延性损伤 ductile damage宏观损伤 macroscopic damage细观损伤 microscopic damage微观损伤 microscopic damage损伤准则 damage criterion损伤演化方程 damage evolution equation 损伤软化 damage softening损伤强化 damage strengthening损伤张量 damage tensor损伤阈值 damage threshold损伤变量 damage variable损伤矢量 damage vector损伤区 damage zone疲劳 Fatigue低周疲劳 low cycle fatigue应力疲劳 stress fatigue随机疲劳 random fatigue蠕变疲劳 creep fatigue腐蚀疲劳 corrosion fatigue疲劳损伤 fatigue damage疲劳失效 fatigue failure疲劳断裂 fatigue fracture疲劳裂纹 fatigue crack疲劳寿命 fatigue life疲劳破坏 fatigue rupture疲劳强度 fatigue strength疲劳辉纹 fatigue striations疲劳阈值 fatigue threshold交变载荷 alternating load交变应力 alternating stress应力幅值 stress amplitude应变疲劳 strain fatigue应力循环 stress cycle应力比 stress ratio安全寿命 safe life过载效应 overloading effect循环硬化 cyclic hardening循环软化 cyclic softening环境效应 environmental effect裂纹片 crack gage裂纹扩展 crack growth, crack Propagation 裂纹萌生 crack initiation循环比 cycle ratio实验应力分析 experimental stress Analysis 工作[应变]片 active[strain] gage基底材料 backing material应力计 stress gage零[点]飘移 zero shift, zero drift应变测量 strain measurement应变计 strain gage应变指示器 strain indicator应变花 strain rosette应变灵敏度 strain sensitivity机械式应变仪 mechanical strain gage直角应变花 rectangular rosette引伸仪 Extensometer应变遥测 telemetering of strain横向灵敏系数 transverse gage factor横向灵敏度 transverse sensitivity焊接式应变计 weldable strain gage平衡电桥 balanced bridge粘贴式应变计 bonded strain gage粘贴箔式应变计 bonded foiled gage粘贴丝式应变计 bonded wire gage桥路平衡 bridge balancing电容应变计 capacitance strain gage补偿片 compensation technique补偿技术 compensation technique基准电桥 reference bridge电阻应变计 resistance strain gage温度自补偿应变计 self-temperature compensating gage 半导体应变计 semiconductor strain Gage集流器 slip ring应变放大镜 strain amplifier疲劳寿命计 fatigue life gage电感应变计 inductance [strain] gage光[测]力学 Photomechanics光弹性 Photoelasticity光塑性 Photoplasticity杨氏条纹 Young fringe双折射效应 birefrigent effect等位移线 contour of equal Displacement暗条纹 dark fringe条纹倍增 fringe multiplication干涉条纹 interference fringe等差线 Isochromatic等倾线 Isoclinic等和线 isopachic应力光学定律 stress- optic law主应力迹线 Isostatic亮条纹 light fringe光程差 optical path difference热光弹性 photo-thermo -elasticity光弹性贴片法 photoelastic coating Method 光弹性夹片法 photoelastic sandwich Method 动态光弹性 dynamic photo-elasticity空间滤波 spatial filtering空间频率 spatial frequency起偏镜 Polarizer反射式光弹性仪 reflection polariscope残余双折射效应 residual birefringent Effect应变条纹值 strain fringe value应变光学灵敏度 strain-optic sensitivity应力冻结效应 stress freezing effect应力条纹值 stress fringe value应力光图 stress-optic pattern暂时双折射效应 temporary birefringent Effect脉冲全息法 pulsed holography透射式光弹性仪 transmission polariscope实时全息干涉法 real-time holographic interferometry网格法 grid method全息光弹性法 holo-photoelasticity全息图 Hologram全息照相 Holograph全息干涉法 holographic interferometry全息云纹法 holographic moire technique全息术 Holography全场分析法 whole-field analysis散斑干涉法 speckle interferometry散斑 Speckle错位散斑干涉法 speckle-shearing interferometry, shearography 散斑图 Specklegram白光散斑法 white-light speckle method云纹干涉法 moire interferometry[叠栅]云纹 moire fringe[叠栅]云纹法 moire method云纹图 moire pattern离面云纹法 off-plane moire method参考栅 reference grating试件栅 specimen grating分析栅 analyzer grating面内云纹法 in-plane moire method脆性涂层法 brittle-coating method条带法 strip coating method坐标变换 transformation of Coordinates计算结构力学 computational structural mechanics 加权残量法 weighted residual method有限差分法 finite difference method有限[单]元法 finite element method配点法 point collocation里茨法 Ritz method广义变分原理 generalized variational Principle 最小二乘法 least square method胡[海昌]一鹫津原理 Hu-Washizu principle赫林格-赖斯纳原理 Hellinger-Reissner Principle 修正变分原理 modified variational Principle约束变分原理 constrained variational Principle混合法 mixed method杂交法 hybrid method边界解法 boundary solution method有限条法 finite strip method半解析法 semi-analytical method协调元 conforming element非协调元 non-conforming element混合元 mixed element杂交元 hybrid element边界元 boundary element强迫边界条件 forced boundary condition 自然边界条件 natural boundary condition 离散化 Discretization离散系统 discrete system连续问题 continuous problem广义位移 generalized displacement广义载荷 generalized load广义应变 generalized strain广义应力 generalized stress界面变量 interface variable节点 node, nodal point[单]元 Element角节点 corner node边节点 mid-side node内节点 internal node无节点变量 nodeless variable杆元 bar element桁架杆元 truss element梁元 beam element二维元 two-dimensional element一维元 one-dimensional element三维元 three-dimensional element轴对称元 axisymmetric element板元 plate element壳元 shell element厚板元 thick plate element三角形元 triangular element四边形元 quadrilateral element四面体元 tetrahedral element曲线元 curved element二次元 quadratic element线性元 linear element三次元 cubic element四次元 quartic element等参[数]元 isoparametric element超参数元 super-parametric element亚参数元 sub-parametric element节点数可变元 variable-number-node element拉格朗日元 Lagrange element拉格朗日族 Lagrange family巧凑边点元 serendipity element巧凑边点族 serendipity family无限元 infinite element单元分析 element analysis单元特性 element characteristics刚度矩阵 stiffness matrix几何矩阵 geometric matrix等效节点力 equivalent nodal force节点位移 nodal displacement节点载荷 nodal load位移矢量 displacement vector载荷矢量 load vector质量矩阵 mass matrix集总质量矩阵 lumped mass matrix相容质量矩阵 consistent mass matrix阻尼矩阵 damping matrix瑞利阻尼 Rayleigh damping刚度矩阵的组集 assembly of stiffness Matrices 载荷矢量的组集 consistent mass matrix质量矩阵的组集 assembly of mass matrices单元的组集 assembly of elements局部坐标系 local coordinate system局部坐标 local coordinate面积坐标 area coordinates体积坐标 volume coordinates曲线坐标 curvilinear coordinates静凝聚 static condensation合同变换 contragradient transformation 形状函数 shape function试探函数 trial function检验函数 test function权函数 weight function样条函数 spline function代用函数 substitute function降阶积分 reduced integration零能模式 zero-energy modeP收敛 p-convergenceH收敛 h-convergence掺混插值 blended interpolation等参数映射 isoparametric mapping双线性插值 bilinear interpolation小块检验 patch test非协调模式 incompatible mode节点号 node number单元号 element number带宽 band width带状矩阵 banded matrix变带状矩阵 profile matrix带宽最小化 minimization of band width波前法 frontal method子空间迭代法 subspace iteration method 行列式搜索法 determinant search method 逐步法 step-by-step method纽马克法 Newmark威尔逊法 Wilson拟牛顿法 quasi-Newton method牛顿-拉弗森法 Newton-Raphson method增量法 incremental method初应变 initial strain初应力 initial stress切线刚度矩阵 tangent stiffness matrix割线刚度矩阵 secant stiffness matrix模态叠加法 mode superposition method平衡迭代 equilibrium iteration子结构 Substructure子结构法 substructure technique超单元 super-element网格生成 mesh generation结构分析程序 structural analysis program 前处理 pre-processing后处理 post-processing网格细化 mesh refinement应力光顺 stress smoothing组合结构 composite structure流体力学流体动力学 fluid dynamics连续介质力学 mechanics of continuous media介质 medium流体质点 fluid particle无粘性流体 nonviscous fluid, inviscid fluid连续介质假设 continuous medium hypothesis流体运动学 fluid kinematics水静力学 hydrostatics液体静力学 hydrostatics支配方程 governing equation伯努利方程 Bernoulli equation伯努利定理 Bernonlli theorem毕奥-萨伐尔定律 Biot-Savart law欧拉方程 Euler equation亥姆霍兹定理 Helmholtz theorem开尔文定理 Kelvin theorem涡片 vortex sheet库塔-茹可夫斯基条件 Kutta-Zhoukowski condition布拉休斯解 Blasius solution达朗贝尔佯廖 d'Alembert paradox 雷诺数 Reynolds number施特鲁哈尔数 Strouhal number随体导数 material derivative不可压缩流体 incompressible fluid 质量守恒 conservation of mass动量守恒 conservation of momentum 能量守恒 conservation of energy 动量方程 momentum equation能量方程 energy equation控制体积 control volume液体静压 hydrostatic pressure涡量拟能 enstrophy压差 differential pressure流[动] flow流线 stream line流面 stream surface流管 stream tube迹线 path, path line流场 flow field流态 flow regime流动参量 flow parameter流量 flow rate, flow discharge。
合肥工业大学各学院、专业名称及其英文翻译

计算机与信息学院 School of Computer and Information
17、计算机科学与技术 Computer Science & Technology
18、电子信息工程 Electronic Information Engineering
机械与汽车工程学院 School of Machinery and Automobile Engineering
3、车辆工程 Vehicles Engineering
4、工业工程 Industrial Engineering
5、工业设计 Industry Design
22、高分子材料与工程 Macromolecule Material and Engineering
23、化学工程与工艺 Chemical Engineering and Technics
24、制药工程 Pharmacy Engineering
25、应用化学 Applied Chemistry
55、英语 English
56、法学 Law
57、社会工作 Social Work
生物与食品工程学院 School of Biotechnology and Food Engineering
58、生物工程 Bioengineering
仪器科学与光电工程学院 School of Instrument Science and Opto-electronic Engineering
1、测控技术与仪器 Measurement & Control Technology and Instrument
2、光信息科学与技术 Optic Information Science & Technology
大学各个专业英语翻译压缩版

1哲学 Philosophy马克思主义哲学Philosophy of Marxism中国哲学 Chinese Philosophy外国哲学 Foreign Philosophies逻辑学 Logic伦理学Ethics美学 Aesthetics宗教学Science of Religion科学技术哲学Philosophy of Science and Technology 经济学 Economics理论经济学 Theoretical Economics政治经济学 Political Economy经济思想史History of Economic Thought经济史History of Economic西方经济学 Western Economics世界经济 World Economics人口、资源与环境经济学Population, Resources and Environmen tal Economics应用经济学 Applied Economics国民经济学National Economics2区域经济学 Regional Economics财政学(含税收学)Public Finance (including Taxation)金融学(含保险学)Finance (including Insurance)产业经济学 Industrial Economics国际贸易学 International Trade劳动经济学 Labor Economics统计学 Statistics数量经济学 Quantitative Economics 国防经济学National Defense Economics法学 Law法学 Science of Law法学理论 Jurisprudence法律史 Legal History宪法学与行政法学Constitutional Law and Administrative L aw刑法学 Criminal Jurisprudence民商法学(含劳动法学、社会保障法学) Civil Law and Commercial Law (includin g Science of Labour Law and Science of Social Security Law )诉讼法学 Science of Procedure Laws3经济法学 Science of Economic Law环境与资源保护法学Science of Environment and Natural Resources Protection Law国际法学(含国际公法学、国际私法学、国际经济法学、)International law (including International Public law, International Private Law and International Economic Law)军事法学 Science of Military Law政治学 Political Science政治学理论 Political Theory中外政治制度Chinese and Foreign Political Institution科学社会主义与国际共产主义运动Scientific Socialism and International Communist Movement中国共产党历史(含党的学说与党的建设)History of the Communist Party of China (including the Doctrine of China Partyand Party Building)马克思主义理论与思想政治教育4Education of Marxist Theory and Education in Ideology and Politics国际政治学 International Politics国际关系学 International Relations外交学 Diplomacy社会学 Sociology社会学 Sociology人口学 Demography人类学 Anthropology民俗学(含中国民间文学)Folklore (including Chinese Folk Literature)民族学 Ethnology民族学 Ethnology马克思主义民族理论与政策Marxist Ethnic Theory and Policy中国少数民族经济Chinese Ethnic Economics中国少数民族史Chinese Ethnic History中国少数民族艺术 Chinese Ethnic Art教育学 Education教育学 Education Science教育学原理 Educational Principle课程与教学论5Curriculum and Teaching Methodology教育史 History of Education比较教育学Comparative Education学前教育学Pre-school Education高等教育学 Higher Education成人教育学Adult Education职业技术教育学Vocational and Technical Education特殊教育学 Special Education教育技术学Education Technology心理学 Psychology基础心理学 Basic Psychology发展与心理学Developmental and Educational Psychology应用心理学 Applied Psychology体育学Science of Physical Culture and Sports体育人文社会学Humane and Sociological Science of Sports运动人体科学Human Movement Science6体育教育训练学Theory of Sports Pedagogy and Training民族传统体育学Science of Ethnic Traditional Sports文学 Literature中国语言文学 Chinese Literature文艺学 Theory of Literature and Art语言学及应用语言学Linguistics and Applied Linguistics汉语言文字学Chinese Philology中国古典文献学Study of Chinese Classical Text中国古代文学Ancient Chinese Literature中国现当代文学Modern and Contemporary Chinese Literature中国少数民族语言文学Chinese Ethnic Language and Literature比较文学与世界文学Comparative Literature and World Literature外国语言文学Foreign Languages and Literatures英语语言文学English Language and Literature俄语语言文学Russian Language and Literature法语语言文学French Language and Literature德语语言文学German Language and Literature日语语言文学Japanese Language and Literature印度语言文学Indian Language and Literature西班牙语语言文学Spanish Language and Literature阿拉伯语语言文学Arabic Language and Literature欧洲语言文学European Language and Literature亚非语言文学Asian-African Language and Literature 外国语言学及应用语言学Linguistics and Applied Linguistics in Fo reign Languages新闻传播学Journalism and Communication8新闻学 Journalism传播学 Communication艺术学 Art艺术学 Art Theory音乐学Music美术学 Fine Arts设计艺术学 Artistic Design戏剧戏曲学Theater and Chinese Traditional Opera 电影学 Film广播电视艺术学Radio and television Art舞蹈学 Dance历史学 History史学理论及史学史Historical Theories and History of Histo rical Science考古学及博物馆学Archaeology and Museology历史地理学 Historical Geography历史文献学(含敦煌学、古文字学) Studies of Historical Literature (includin g Paleography and Studies of Dunhuan g)专门史 History of Particular Subjects 中国古代史 Ancient Chinese History中国近现代史Modern and Contemporary Chinese History世界史 World History理学 Natural Science数学 Mathematics基础数学 Fundamental Mathematics计算数学 Computational Mathematics概率论与数理统计Probability and Mathematical Statistics应用数学 Applied mathematics运筹学与控制论Operational Research and Cybernetics物理学 Physics理论物理 Theoretical Physics粒子物理与原子核物理Particle Physics and Nuclear Physics原子与分子物理Atomic and Molecular Physics等离子体物理 Plasma Physics凝聚态物理Condensed Matter Physics声学 Acoustics10光学 Optics无线电物理Radio Physics化学Chemistry无机化学 Inorganic Chemistry分析化学 Analytical Chemistry有机化学 Organic Chemistry物理化学(含化学物理)Physical Chemistry (including ChemicalPhysics)高分子化学与物理Chemistry and Physics of Polymers天文学 Astronomy天体物理 Astrophysics天体测量与天体力学Astrometry and Celestial Mechanics地理学 Geography自然地理学 Physical Geography人文地理学Human Geography地图学与地理信息系统Cartography and Geography Information System大气科学 Atmospheric Sciences气象学 Meteorology大气物理学与大气环境Atmospheric Physics and AtmosphericEnvironment海洋科学 Marine Sciences物理海洋学 Physical Oceanography海洋化学 Marine Chemistry海洋生理学 Marine Biology海洋地质学 Marine Geology地球物理学 Geophysics固体地球物理学 Solid Earth Physics空间物理学 Space Physics地质学 Geology矿物学、岩石学、矿床学Mineralogy, Petrology, Mineral DepositGeology地球化学 Geochemistry古生物学与地层学(含古人类学)Paleontology and Stratigraphy (including Paleoanthropology)构造地质学 Structural Geology第四纪地质学 Quaternary Geology生物学 Biology植物学 Botany动物学 Zoology生理学 Physiology水生生物学 Hydrobiology12微生物学 Microbiology神经生物学 Neurobiology遗传学 Genetics发育生物学 Developmental Biology细胞生物学 Cell Biology生物化学与分子生物学Biochemistry and Molecular Biology生物物理学 Biophysics生态学 Ecology系统科学 Systems Science系统理论 Systems Theory系统分析与集成Systems Analysis and Integration科学技术史History of Science and Technology工学 Engineering力学 Mechanics一般力学与力学基础General and Fundamental Mechanics固体力学 Solid Mechanics流体力学 Fluid Mechanics工程力学 Engineering Mechanics机械工程 Mechanical Engineering机械制造及其自动化Mechanical Manufacture and Automation机械电子工程Mechatronic Engineering机械设计与理论Mechanical Design and Theory车辆工程Vehicle Engineering光学工程 Optical Engineering仪器科学与技术Instrument Science and Technology精密仪器及机械Precision Instrument and Machinery 测试计量技术及仪器Measuring and Testing Technologies an d Instruments材料科学与工程Materials Science and Engineering材料物理与化学Materials Physics and Chemistry材料学 Materialogy材料加工工程Materials Processing Engineering冶金工程Metallurgical Engineering 冶金物理化学of Metallurgy钢铁冶金 Ferrous Metallurgy14有色金属冶金 Non-ferrous Metallurgy 动力工程及工程热物理Power Engineering and Engineering Th ermophysics工程热物理Engineering Thermophysics热能工程Thermal Power Engineering 动力机械及工程Power Machinery and Engineering流体机械及工程Fluid Machinery and Engineering制冷及低温工程Refrigeration and Cryogenic Engineering 化工过程机械Chemical Process Equipment电气工程 Electrical Engineering电机与电器Electric Machines and Electric Apparatu s电力系统及其自动化Power System and its Automation高电压与绝缘技术High Voltage and Insulation Technology 电力电子与电力传动Power Electronics and Power Drives 电工理论与新技术Theory and New Technology of Electrical Engineering电子科学与技术Electronics Science and Technology物理电子学Physical Electronics电路与系统Circuits and Systems微电子学与固体电子学Microelectronics and Solid State Electronics电磁场与微波技术Electromagnetic Field and Microwave Technology信息与通信工程Information and Communication Engineering通信与信息系统Communication and Information Systems信号与信息处理Signal and Information Processing控制科学与工程Control Science and Engineering16控制理论与控制工程Control Theory and Control Engineering检测技术与自动化装置Detection Technology and Automatic Equipment系统工程 Systems Engineering模式识别与智能系统Pattern Recognition and Intelligent Systems导航、制导与控制Navigation, Guidance and Control计算机科学与技术Computer Science and Technology计算机软件与理论Computer Software and Theory计算机系统结构Computer Systems Organization计算机应用技术Computer Applied Technology建筑学 Architecture建筑历史与理论Architectural History and Theory建筑设计及其理论Architectural Design and Theory城市规划与设计(含风景园林规划与设计)Urban Planning and Design (including Landscape Planning and Design)建筑技术科学Building Technology Science土木工程 Civil Engineering岩土工程 Geotechnical Engineering结构工程Structural Engineering市政工程 Municipal Engineering供热、供燃气、通风及空调工程Heating, Gas Supply, Ventilating and AirConditioning Engineering防灾减灾工程及防护工程Disaster Prevention and Reduction Engineering and Protective Engineering桥梁与隧道工程Bridge and Tunnel Engineering水利工程 Hydraulic Engineering水文学及水资源Hydrology and Water Resources水力学及河流动力学Hydraulics and River Dynamics水工结构工程Hydraulic Structure Engineering18水利水电工程Hydraulic and Hydro-Power Engineering港口、海岸及近海工程Harbor, Coastal and Offshore Engineering测绘科学与技术Surveying and Mapping大地测量学与测量工程Geodesy and Survey Engineering摄影测量与遥感Photogrammetry and Remote Sensing地图制图学与地理信息工程Cartography and Geographic Information Engineering化学工程与技术Chemical Engineering and Technology化学工程 Chemical Engineering化学工艺 Chemical Technology生物化工 Biochemical Engineering应用化学 Applied Chemistry工业催化 Industrial Catalysis地质资源与地质工程Geological Resources and Geological Engineering矿产普查与勘探Mineral Resource Prospecting and Explo ration地球探测与信息技术Geodetection and Information Technolo gy地质工程 Geological Engineering矿业工程 Mineral Engineering采矿工程 Mining Engineering矿物加工工程Mineral Processing Engineering安全技术及工程Safety Technology and Engineering石油与天然气工程Oil and Natural Gas Engineering油气井工程Oil-Gas Well Engineering油气田开发工程Oil-Gas Field Development Engineering 油气储运工程Oil-Gas Storage and Transportation Engi neering纺织科学与工程Textile Science and Engineering纺织工程 Textile Engineering20纺织材料与纺织品设计Textile Material and Textiles Design纺织化学与染整工程Textile Chemistry and Dyeing and Finishi ng Engineering服装设计与工程Clothing Design and Engineering轻工技术与工程The Light Industry Technology and Engi neering制浆造纸工程Pulp and Paper Engineering制糖工程Sugar Engineering发酵工程Fermentation Engineering 皮革化学与工程Leather Chemistry and Engineering道路与铁道工程Highway and Railway Engineering交通信息工程及控制Traffic Information Engineering & Contr ol交通运输规划与管理Transportation Planning and Manageme nt载运工具运用工程Vehicle Operation Engineering船舶与海洋工程Naval Architecture and Ocean Engineering船舶与海洋结构物设计制造Design and Construction of Naval Architecture and Ocean Structure轮机工程 Marine Engine Engineering水声工程Underwater Acoustics Engineering航空宇航科学与技术Aeronautical and Astronautical Scienceand Technology飞行器设计 Flight Vehicle Design航空宇航推进理论与工程Aerospace Propulsion Theory and Engineering航空宇航器制造工程Manufacturing Engineering of Aerospace Vehicle人机与环境工程Man-Machine and Environmental Engineering22兵器科学与技术Armament Science and Technology武器系统与运用工程Weapon Systems and Utilization Engineering兵器发射理论与技术Armament Launch Theory and Technology火炮、自动武器与弹药工程Artillery, Automatic Gun and Ammunition Engineering军事化学与烟火技术Military Chemistry and Pyrotechnics核科学与技术Nuclear Science and Technology核能科学与工程Nuclear Energy Science and Engineering核燃料循环与材料Nuclear Fuel Cycle and Materials核技术及应用Nuclear Technology and Applications辐射防护及环境保护Radiation and Environmental Protection农业工程Agricultural Engineering农业机械化工程Agricultural Mechanization Engineering农业水土工程Agricultural Water-Soil Engineering农业生物环境与能源工程Agricultural Biological Environmental and Energy Engineering农业电气化与自动化Agricultural Electrification and Automation林业工程Forestry Engineering森林工程 Forest Engineering木材科学与技术Wood Science and Technology林产化学加工工程Chemical Processing Engineering of Forest Products环境科学与工程Environmental Science and Engineering环境科学Environmental Science环境工程Environmental Engineering生物医学工程Biomedical Engineering食品科学与工程Food Science and Engineering24食品科学 Food Science粮食、油脂及植物蛋白工程Cereals, Oils and Vegetable Protein Engineering农产品加工及贮藏工程Processing and Storage of Agriculture Products水产品加工及贮藏工程Processing and Storage of Aquatic Products农学 Agriculture交通运输工程Communication and Transportation Engineering作物学 Crop Science作物栽培学与耕作学Crop Cultivation and Farming System作物遗传育种学Crop Genetics and Breeding园艺学 Horticulture果树学 Pomology蔬菜学 Olericulture茶学 Tea Science农业资源利用学Utilization Science of Agricultural Resources土壤学 Soil Science植物营养学 Plant Nutrition植物保护学 Plant Protection植物病理学 Plant Pathology农业昆虫与害虫防治Agricultural Entomology and Pest Contr ol农药学 Pesticide Science畜牧学 Animal Science动物遗传育种与繁殖Animal Genetics, Breeding and Reprodu ction Science动物营养与饲料科学Animal Nutrition and Feed Science草业科学 Practaculture Science特种经济动物饲养学(含蚕、蜂等)The Rearing of Special-type Economic A nimals (including Silkworm, Honeybees, etc.) 兽医学 Veterinary Medicine基础兽医学Basic Veterinary Medicine 预防兽医学Preventive Veterinary Medicine临床兽医学26Clinical Veterinary Medicine林学 Forestry林木遗传育种学Forest Tree Genetics and Breeding森林培育学 Silviculture森林保护学Forest Protection森林经理学 Forest Management野生动植物保护与利用Wildlife Conservation and Utilization 园林植物与观赏园艺Ornamental Plants and Horticulture水土保持与荒漠化防治Soil and Water Conservation and Deser tification Combating水产学 Fisheries Science水产养殖学 Aquaculture Science捕捞学 Fishing Science渔业资源学Science of Fisheries Resources医学Medicine基础医学 Basic Medicine人体解剖与组织胚胎学Human Anatomy, Histology and Embry ology免疫学 Immunology 病原生物学 Pathogenic Organisms病理学与病理生理学Pathology and Pathophysiology法医学 Forensic Medicine放射医学Radiation Medicine航空航天与航海医学Aerospace and Nautical medicine临床医学 Clinical Medicine内科学(含心血管病学、血液病学、呼吸系病学、消化系病学、内分泌与代谢病学、肾脏病学、风湿病学、传染病学)Internal medicine (including Cardiology,Hematology, Respiratory, Gastroenterology, Endocrinology and Metabolism, Nephrology, Rheuma-tology, Infectious Diseases)儿科学 Pediatrics老年医学 Geriatrics神经病学 Neurology精神病与精神卫生学Psychiatry and Mental Health皮肤病与性病学Dermatology and Venereology28影像医学与核医学Imaging and Nuclear Medicine临床检验诊断学Clinical Laboratory Diagnostics护理学 Nursing外科学(含普通外科学、骨外科学、泌尿外科学、胸心血管外科学、神经外科学、整形外科学、烧伤外科学、野战外科学)Surgery (General Surgery, Orthopedics,Urology, Cardiothoracic Surgery, Neurosurgery, Plastic Surgery, Burn Surgery, Field Surgery)妇产科学 Obstetrics and Gynecology眼科学 Ophthalmic Specialty耳鼻咽喉科学 Otolaryngology肿瘤学 Oncology康复医学与理疗学Rehabilitation Medicine & Physical Therapy运动医学Sports Medicine麻醉学 Anesthesiology急诊医学 Emergency Medicine口腔医学 Stomatology口腔基础医学Basic Science of Stomatology口腔临床医学Clinical Science of Stomatology公共卫生与预防医学Public Health and Preventive Medicine流行病与卫生统计学Epidemiology and Health Statistics劳动卫生与环境卫生学Occupational and Environmental Health营养与食品卫生学Nutrition and Food Hygiene儿少卫生与妇幼保健学Maternal, Child and Adolescent Health卫生毒理学 Hygiene Toxicology军事预防医学Military Preventive Medicine中医学Chinese Medicine中医基础理论Basic Theories of Chinese Medicine中医临床基础Clinical Foundation of Chinese Medicine中医医史文献30History and Literature of Chinese Medicine方剂学 Formulas of Chinese Medicine中医诊断学Diagnostics of Chinese Medicine中医内科学 Chinese Internal Medicine中医外科学Surgery of Chinese Medicine中医骨伤科学Orthopedics of Chinese Medicine中医妇科学Gynecology of Chinese Medicine中医儿科学Pediatrics of Chinese Medicine中医五官科学Ophthalmology and Otolaryngoloy of Chinese Medicine针灸推拿学Acupuncture and Moxibustion and Tuina of Chinese medicine民族医学 Ethnomedicine中西医结合医学Chinese and Western Integrative Medicine中西医结合基础医学31Basic Discipline of Chinese and Western Integrative中西医结合临床医学Clinical Discipline of Chinese and Weste rn Integrative Medicine药学 Pharmaceutical Science药物化学 Medicinal Chemistry药剂学 Pharmaceutics生药学 Pharmacognosy药物分析学 Pharmaceutical Analysis 微生物与生化药学Microbial and Biochemical Pharmacy 药理学 Pharmacology中药学Science of Chinese Pharmacology军事学 Military Science军事思想学及军事历史学Military Thought and Military History 军事思想学 Military Thought军事历史学 Military History战略学 Science of Strategy军事战略学Military Strategy战争动员学 War Mobilization战役学Science of Operations32联合战役学 Joint Operation军种战役学(含第二炮兵战役学)Armed Service Operation (including Op eration of Strategic Missile Force)战术学 Science of Tactics合同战术学Combined-Arms Tactics 兵种战术学 Branch Tactics军队指挥学Science of Command作战指挥学 Combat Command军事运筹学Military Operation Research军事通信学Military Communication军事情报学Military Intelligence密码学 Cryptography军事教育训练学(含军事体育学) Military Education and Training (includi ng Military Physical Training)军制学Science of Military System军事组织编制学Military Organizational System军队管理学 Military Management军队政治工作学Science of Military Political Work33军事后勤学与军事装备学Science of Military Logistics and Military Equipment军事后勤学 Military Logistics后方专业勤务 Rear Special Service军事装备学 Military Equipment管理学 Management Science管理科学与工程Management Science and Engineering 工商管理学Science of Business Administration会计学 Accounting 企业管理学(含财务管理、市场营销学、人力资源管理学)Corporate Management (including Fina ncial Management, Marketing, and Hu man Resources Management)旅游管理学 Tourist Management技术经济及管理学Technology Economy and Management 农林经济管理学Agricultural and Forestry Economics & Management农业经济管理学34Agricultural Economics & Management 林业经济管理学Forestry Economics & Management公共管理学Science of Public Management行政管理学Administration Management社会医学与卫生事业管理学Social Medicine and Health Manageme nt教育经济与管理学Educational Economy and Management 社会保障学 Social Security土地资源管理学Land Resource Management图书馆、情报与档案学Science of Library, Information and Arch ival图书馆学Library Science情报学 Information Science档案学 Archival Science。
机械工程力学专业英语翻译

4 Overview of Engineering Mechanics(工程力学概况)(1) Ideally, however, every such item has been designed according to some set of “functional requirements” as perceived by the designers-that is, it has been designed so as to answer the question, “E xactly what function should it perform?” In the world of engineering, the major function frequently is to support some type of loading due to weight, inertia, pressure, etc. From the beams in our homes to the wings of an airplane, there must be an appropriate melding of materials, dimensions, and fastenings to produce structures that will perform their functions reliably for a reasonable cost over a reasonable lifetime.然而,在理想的情况下,每一件产品都是设计人员根据对某些“功能要求”的理解而设计出来的,也就是说,在设计过程中,应该回答这样的问题,即“它应该具有哪种确切的功能?”在工程领域,主要功能通常是承受由于重力,惯性力,压力等作用的一些类型的载荷。
从我们居住房屋的梁到飞机机翼,都必须有一个适当的材料,尺寸,在较合理地寿命基础上具有较合理地成本,并能可靠地完成其功能的产品结构连接的组合。
大学各个专业名称的英文翻译

中文学科、专业名称英文学科、专业名称哲学 Philosophy哲学 Philosophy马克思主义哲学 Philosophy of Marxism中国哲学 Chinese Philosophy外国哲学 Foreign Philosophies逻辑学 Logic伦理学 Ethics美学 Aesthetics宗教学 Science of Religion科学技术哲学 Philosophy of Science and Technology经济学 Economics理论经济学 Theoretical Economics政治经济学 Political Economy经济思想史 History of Economic Thought经济史 History of Economic西方经济学 Western Economics世界经济 World Economics人口、资源与环境经济学 Population, Resources and Environmental Economics应用经济学 Applied Economics国民经济学 National Economics区域经济学 Regional Economics财政学(含税收学) Public Finance (including Taxation)金融学(含保险学) Finance (including Insurance)产业经济学 Industrial Economics国际贸易学 International Trade劳动经济学 Labor Economics统计学 Statistics数量经济学 Quantitative Economics中文学科、专业名称英文学科、专业名称国防经济学 National Defense Economics法学 Law法学 Science of Law法学理论 Jurisprudence法律史 Legal History宪法学与行政法学 Constitutional Law and Administrative Law刑法学 Criminal Jurisprudence民商法学(含劳动法学、社会保障法学) Civil Law and Commercial Law (including Science of Labour Law and Science of Social Security Law )诉讼法学 Science of Procedure Laws经济法学 Science of Economic Law环境与资源保护法学 Science of Environment and Natural Resources Protection Law 国际法学(含国际公法学、国际私法学、国际经济法学、) International law (including International Public law, International Private Law and International Economic Law)军事法学 Science of Military Law政治学 Political Science政治学理论 Political Theory中外政治制度 Chinese and Foreign Political Institution科学社会主义与国际共产主义运动 Scientific Socialism and International Communist Movement中*史(含党的学说与党的建设) History of the Communist Party of China(including the Doctrine of China Party and Party Building)马克思主义理论与思想政治教育 Education of Marxist Theory and Education in Ideology and Politics国际政治学 International Politics国际关系学 International Relations外交学 Diplomacy社会学 Sociology社会学 Sociology人口学 Demography人类学 Anthropology民俗学(含中国民间文学) Folklore (including Chinese Folk Literature)民族学 Ethnology民族学 Ethnology马克思主义民族理论与政策 Marxist Ethnic Theory and Policy中国少数民族经济 Chinese Ethnic Economics中国少数民族史 Chinese Ethnic History中国少数民族艺术 Chinese Ethnic Art教育学 Education教育学 Education Science教育学原理 Educational Principle课程与教学论 Curriculum and Teaching Methodology教育史 History of Education比较教育学 Comparative Education学前教育学 Pre-school Education高等教育学 Higher Education成人教育学 Adult Education职业技术教育学 Vocational and Technical Education特殊教育学 Special Education教育技术学 Education Technology心理学 Psychology基础心理学 Basic Psychology发展与心理学 Developmental and Educational Psychology应用心理学 Applied Psychology体育学 Science of Physical Culture and Sports体育人文社会学 Humane and Sociological Science of Sports运动人体科学 Human Movement Science体育教育训练学 Theory of Sports Pedagogy and Training民族传统体育学 Science of Ethnic Traditional Sports文学 Literature中国语言文学 Chinese Literature文艺学 Theory of Literature and Art语言学及应用语言学 Linguistics and Applied Linguistics汉语言文字学 Chinese Philology中国古典文献学 Study of Chinese Classical Text中国古代文学 Ancient Chinese Literature中国现当代文学 Modern and Contemporary Chinese Literature中国少数民族语言文学 Chinese Ethnic Language andLiterature比较文学与世界文学 Comparative Literature and World Literature外国语言文学 Foreign Languages and Literatures英语语言文学 English Language and Literature俄语语言文学 Russian Language and Literature法语语言文学 French Language and Literature德语语言文学 German Language and Literature日语语言文学 Japanese Language and Literature印度语言文学 Indian Language and Literature西班牙语语言文学 Spanish Language and Literature阿拉伯语语言文学 Arabic Language and Literature欧洲语言文学 European Language and Literature亚非语言文学 Asian-African Language and Literature外国语言学及应用语言学 Linguistics and Applied Linguistics inForeign Languages新闻传播学 Journalism and Communication新闻学 Journalism传播学 Communication艺术学 Art艺术学 Art Theory音乐学 Music美术学 Fine Arts设计艺术学 Artistic Design戏剧戏曲学 Theater and Chinese Traditional Opera电影学 Film广播电视艺术学 Radio and television Art舞蹈学 Dance历史学 History历史学 History史学理论及史学史 Historical Theories and History of Historical Science考古学及博物馆学 Archaeology and Museology历史地理学 Historical Geography历史文献学(含敦煌学、古文字学) Studies of Historical Literature (including Paleography and Studies of Dunhuang)专门史 History of Particular Subjects中国古代史 Ancient Chinese History中国近现代史 Modern and Contemporary Chinese History世界史 World History理学 Natural Science数学 Mathematics基础数学 Fundamental Mathematics计算数学 Computational Mathematics概率论与数理统计 Probability and Mathematical Statistics应用数学 Applied mathematics运筹学与控制论 Operational Research and Cybernetics物理学 Physics理论物理 Theoretical Physics粒子物理与原子核物理 Particle Physics and Nuclear Physics原子与分子物理 Atomic and Molecular Physics等离子体物理 Plasma Physics凝聚态物理 Condensed Matter Physics声学 Acoustics光学 Optics无线电物理 Radio Physics化学 Chemistry无机化学 Inorganic Chemistry分析化学 Analytical Chemistry有机化学 Organic Chemistry物理化学(含化学物理) Physical Chemistry (including Chemical Physics) 高分子化学与物理 Chemistry and Physics of Polymers天文学 Astronomy天体物理 Astrophysics天体测量与天体力学 Astrometry and Celestial Mechanics地理学 Geography自然地理学 Physical Geography人文地理学 Human Geography地图学与地理信息系统 Cartography and Geography Information System大气科学 Atmospheric Sciences气象学 Meteorology大气物理学与大气环境 Atmospheric Physics and Atmospheric Environment 海洋科学 Marine Sciences物理海洋学 Physical Oceanography海洋化学 Marine Chemistry海洋生理学 Marine Biology海洋地质学 Marine Geology地球物理学 Geophysics固体地球物理学 Solid Earth Physics空间物理学 Space Physics地质学 Geology矿物学、岩石学、矿床学 Mineralogy, Petrology, Mineral Deposit Geology 地球化学 Geochemistry古生物学与地层学(含古人类学) Paleontology and Stratigraphy (including Paleoanthropology)构造地质学 Structural Geology第四纪地质学 Quaternary Geology生物学 Biology植物学 Botany动物学 Zoology生理学 Physiology水生生物学 Hydrobiology微生物学 Microbiology神经生物学 Neurobiology遗传学 Genetics发育生物学 Developmental Biology细胞生物学 Cell Biology生物化学与分子生物学 Biochemistry and Molecular Biology生物物理学 Biophysics生态学 Ecology系统科学 Systems Science系统理论 Systems Theory系统分析与集成 Systems Analysis and Integration科学技术史 History of Science and Technology工学 Engineering力学 Mechanics一般力学与力学基础 General and Fundamental Mechanics固体力学 Solid Mechanics流体力学 Fluid Mechanics工程力学 Engineering Mechanics机械工程 Mechanical Engineering机械制造及其自动化 Mechanical Manufacture and Automation机械电子工程 Mechatronic Engineering机械设计与理论 Mechanical Design and Theory车辆工程 Vehicle Engineering光学工程 Optical Engineering仪器科学与技术 Instrument Science and Technology精密仪器及机械 Precision Instrument and Machinery测试计量技术及仪器 Measuring and Testing Technologies and Instruments 材料科学与工程 Materials Science and Engineering材料物理与化学 Materials Physics and Chemistry材料学 Materialogy材料加工工程 Materials Processing Engineering冶金工程 Metallurgical Engineering冶金物理化学 Physical Chemistry of Metallurgy钢铁冶金 Ferrous Metallurgy有色金属冶金 Non-ferrous Metallurgy动力工程及工程热物理 Power Engineering and Engineering Thermophysics工程热物理 Engineering Thermophysics热能工程 Thermal Power Engineering动力机械及工程 Power Machinery and Engineering流体机械及工程 Fluid Machinery and Engineering制冷及低温工程 Refrigeration and Cryogenic Engineering化工过程机械 Chemical Process Equipment电气工程 Electrical Engineering电机与电器 Electric Machines and Electric Apparatus电力系统及其自动化 Power System and its Automation高电压与绝缘技术 High Voltage and Insulation Technology电力电子与电力传动 Power Electronics and Power Drives电工理论与新技术 Theory and New Technology of Electrical Engineering电子科学与技术 Electronics Science and Technology物理电子学 Physical Electronics电路与系统 Circuits and Systems微电子学与固体电子学 Microelectronics and Solid State Electronics电磁场与微波技术 Electromagnetic Field and Microwave Technology信息与通信工程 Information and Communication Engineering通信与信息系统 Communication and Information Systems信号与信息处理 Signal and Information Processing控制科学与工程 Control Science and Engineering控制理论与控制工程 Control Theory and Control Engineering检测技术与自动化装置 Detection Technology and Automatic Equipment系统工程 Systems Engineering模式识别与智能系统 Pattern Recognition and Intelligent Systems导航、制导与控制 Navigation, Guidance and Control计算机科学与技术 Computer Science and Technology计算机软件与理论 Computer Software and Theory计算机系统结构 Computer Systems Organization计算机应用技术 Computer Applied Technology建筑学 Architecture建筑历史与理论 Architectural History and Theory建筑设计及其理论 Architectural Design and Theory城市规划与设计(含风景园林规划与设计) Urban Planning and Design (including Landscape Planning and Design)建筑技术科学 Building Technology Science土木工程 Civil Engineering岩土工程 Geotechnical Engineering结构工程 Structural Engineering市政工程 Municipal Engineering供热、供燃气、通风及空调工程 Heating, Gas Supply, Ventilating and Air Conditioning Engineering防灾减灾工程及防护工程 Disaster Prevention and Reduction Engineering and Protective Engineering桥梁与隧道工程 Bridge and Tunnel Engineering水利工程 Hydraulic Engineering水文学及水资源 Hydrology and Water Resources水力学及河流动力学 Hydraulics and River Dynamics水工结构工程 Hydraulic Structure Engineering水利水电工程 Hydraulic and Hydro-Power Engineering港口、海岸及近海工程 Harbor, Coastal and Offshore Engineering测绘科学与技术 Surveying and Mapping大地测量学与测量工程 Geodesy and Survey Engineering摄影测量与遥感 Photogrammetry and Remote Sensing地图制图学与地理信息工程 Cartography and Geographic Information Engineering化学工程与技术 Chemical Engineering and Technology化学工程 Chemical Engineering化学工艺 Chemical Technology生物化工 Biochemical Engineering应用化学 Applied Chemistry工业催化 Industrial Catalysis地质资源与地质工程 Geological Resources and Geological Engineering矿产普查与勘探 Mineral Resource Prospecting and Exploration地球探测与信息技术 Geodetection and Information Technology地质工程 Geological Engineering矿业工程 Mineral Engineering采矿工程 Mining Engineering矿物加工工程 Mineral Processing Engineering安全技术及工程 Safety Technology and Engineering石油与天然气工程 Oil and Natural Gas Engineering油气井工程 Oil-Gas Well Engineering油气田开发工程 Oil-Gas Field Development Engineering油气储运工程 Oil-Gas Storage and Transportation Engineering纺织科学与工程 Textile Science and Engineering纺织工程 Textile Engineering纺织材料与纺织品设计 Textile Material and Textiles Design纺织化学与染整工程 Textile Chemistry and Dyeing and Finishing Engineering服装设计与工程 Clothing Design and Engineering轻工技术与工程 The Light Industry Technology and Engineering制浆造纸工程 Pulp and Paper Engineering制糖工程 Sugar Engineering发酵工程 Fermentation Engineering皮革化学与工程 Leather Chemistry and Engineering交通运输工程 Communication and Transportation Engineering道路与铁道工程 Highway and Railway Engineering交通信息工程及控制 Traffic Information Engineering & Control交通运输规划与管理 Transportation Planning and Management载运工具运用工程 Vehicle Operation Engineering船舶与海洋工程 Naval Architecture and Ocean Engineering船舶与海洋结构物设计制造 Design and Construction of Naval Architecture and Ocean Structure轮机工程 Marine Engine Engineering水声工程 Underwater Acoustics Engineering航空宇航科学与技术 Aeronautical and Astronautical Science and Technology飞行器设计 Flight Vehicle Design航空宇航推进理论与工程 Aerospace Propulsion Theory and Engineering航空宇航器制造工程 Manufacturing Engineering of Aerospace Vehicle人机与环境工程 Man-Machine and Environmental Engineering兵器科学与技术 Armament Science and Technology武器系统与运用工程 Weapon Systems and Utilization Engineering兵器发射理论与技术 Armament Launch Theory and Technology火炮、自动武器与弹药工程 Artillery, Automatic Gun and Ammunition Engineering军事化学与烟火技术 Military Chemistry and Pyrotechnics核科学与技术 Nuclear Science and Technology核能科学与工程 Nuclear Energy Science and Engineering核燃料循环与材料 Nuclear Fuel Cycle and Materials核技术及应用 Nuclear Technology and Applications辐射防护及环境保护 Radiation and Environmental Protection农业工程 Agricultural Engineering农业机械化工程 Agricultural Mechanization Engineering农业水土工程 Agricultural Water-Soil Engineering农业生物环境与能源工程Agricultural Biological Environmental and Energy Engineering农业电气化与自动化 Agricultural Electrification and Automation林业工程 Forestry Engineering森林工程 Forest Engineering木材科学与技术 Wood Science and Technology林产化学加工工程 Chemical Processing Engineering of Forest Products环境科学与工程 Environmental Science and Engineering环境科学 Environmental Science环境工程 Environmental Engineering生物医学工程 Biomedical Engineering食品科学与工程 Food Science and Engineering食品科学 Food Science粮食、油脂及植物蛋白工程 Cereals, Oils and Vegetable Protein Engineering农产品加工及贮藏工程 Processing and Storage of Agriculture Products水产品加工及贮藏工程 Processing and Storage of Aquatic Products农学 Agriculture作物学 Crop Science作物栽培学与耕作学 Crop Cultivation and Farming System作物遗传育种学 Crop Genetics and Breeding园艺学 Horticulture果树学 Pomology蔬菜学 Olericulture茶学 Tea Science农业资源利用学 Utilization Science of Agricultural Resources土壤学 Soil Science植物营养学 Plant Nutrition植物保护学 Plant Protection植物病理学 Plant Pathology农业昆虫与害虫防治 Agricultural Entomology and Pest Control农药学 Pesticide Science畜牧学 Animal Science动物遗传育种与繁殖 Animal Genetics, Breeding and ReproductionScience动物营养与饲料科学 Animal Nutrition and Feed Science草业科学 Practaculture Science特种经济动物饲养学(含蚕、蜂等) The Rearing of Special-type EconomicAnimals (including Silkworm, Honeybees, etc.)兽医学 Veterinary Medicine基础兽医学 Basic Veterinary Medicine预防兽医学 Preventive Veterinary Medicine临床兽医学 Clinical Veterinary Medicine林学 Forestry林木遗传育种学 Forest Tree Genetics and Breeding森林培育学 Silviculture森林保护学 Forest Protection森林经理学 Forest Management野生动植物保护与利用 Wildlife Conservation and Utilization园林植物与观赏园艺 Ornamental Plants and Horticulture水土保持与荒漠化防治 Soil and Water Conservation and Desertification Combating 水产学 Fisheries Science水产养殖学 Aquaculture Science捕捞学 Fishing Science渔业资源学 Science of Fisheries Resources医学 Medicine基础医学 Basic Medicine人体解剖与组织胚胎学 Human Anatomy, Histology and Embryology免疫学 Immunology病原生物学 Pathogenic Organisms病理学与病理生理学 Pathology and Pathophysiology法医学 Forensic Medicine放射医学 Radiation Medicine航空航天与航海医学 Aerospace and Nautical medicine临床医学 Clinical Medicine内科学(含心血管病学、血液病学、呼吸系病学、消化系病学、内分泌与代谢病学、肾脏病学、风湿病学、传染病学) Internal medicine (including Cardiology, Hematology, Respiratory, Gastroenterology, Endocrinology and Metabolism, Nephrology, Rheuma-tology, Infectious Diseases)儿科学 Pediatrics老年医学 Geriatrics神经病学 Neurology精神病与精神卫生学 Psychiatry and Mental Health皮肤病与性病学 Dermatology and Venereology影像医学与核医学 Imaging and Nuclear Medicine临床检验诊断学 Clinical Laboratory Diagnostics护理学 Nursing外科学(含普通外科学、骨外科学、泌尿外科学、胸心血管外科学、神经外科学、整形外科学、烧伤外科学、野战外科学) Surgery (General Surgery, Orthopedics, Urology, Cardiothoracic Surgery, Neurosurgery, Plastic Surgery, Burn Surgery, Field Surgery) 妇产科学 Obstetrics and Gynecology眼科学 Ophthalmic Specialty耳鼻咽喉科学 Otolaryngology肿瘤学 Oncology康复医学与理疗学 Rehabilitation Medicine & Physical Therapy运动医学 Sports Medicine麻醉学 Anesthesiology急诊医学 Emergency Medicine口腔医学 Stomatology口腔基础医学 Basic Science of Stomatology口腔临床医学 Clinical Science of Stomatology公共卫生与预防医学 Public Health and Preventive Medicine流行病与卫生统计学 Epidemiology and Health Statistics劳动卫生与环境卫生学 Occupational and Environmental Health营养与食品卫生学 Nutrition and Food Hygiene儿少卫生与妇幼保健学 Maternal, Child and Adolescent Health卫生毒理学 Hygiene Toxicology军事预防医学 Military Preventive Medicine中医学 Chinese Medicine中医基础理论 Basic Theories of Chinese Medicine中医临床基础 Clinical Foundation of Chinese Medicine中医医史文献 History and Literature of Chinese Medicine方剂学 Formulas of Chinese Medicine中医诊断学 Diagnostics of Chinese Medicine中医内科学 Chinese Internal Medicine中医外科学 Surgery of Chinese Medicine中医骨伤科学 Orthopedics of Chinese Medicine中医妇科学 Gynecology of Chinese Medicine中医儿科学 Pediatrics of Chinese Medicine中医五官科学 Ophthalmology and Otolaryngoloy of Chinese Medicine针灸推拿学 Acupuncture and Moxibustion and Tuina of Chinese medicine民族医学 Ethnomedicine中西医结合医学 Chinese and Western Integrative Medicine中西医结合基础医学 Basic Discipline of Chinese and Western Integrative中西医结合临床医学 Clinical Discipline of Chinese and Western Integrative Medicine 药学 Pharmaceutical Science药物化学 Medicinal Chemistry药剂学 Pharmaceutics生药学 Pharmacognosy药物分析学 Pharmaceutical Analysis微生物与生化药学 Microbial and Biochemical Pharmacy药理学 Pharmacology中药学 Science of Chinese Pharmacology军事学 Military Science军事思想学及军事历史学 Military Thought and Military History军事思想学 Military Thought军事历史学 Military History战略学 Science of Strategy军事战略学 Military Strategy战争动员学 War Mobilization战役学 Science of Operations联合战役学 Joint Operation军种战役学(含第二炮兵战役学) Armed Service Operation (including Operation of Strategic Missile Force)战术学 Science of Tactics合同战术学 Combined-Arms Tactics兵种战术学 Branch Tactics军队指挥学 Science of Command作战指挥学 Combat Command军事运筹学 Military Operation Research军事通信学 Military Communication军事情报学 Military Intelligence密码学 Cryptography军事教育训练学(含军事体育学) Military Education and Training (including Military Physical Training)军制学 Science of Military System军事组织编制学 Military Organizational System军队管理学 Military Management军队政治工作学 Science of Military Political Work军事后勤学与军事装备学 Science of Military Logistics and Military Equipment军事后勤学 Military Logistics后方专业勤务 Rear Special Service军事装备学 Military Equipment管理学 Management Science管理科学与工程 Management Science and Engineering工商管理学 Science of Business Administration会计学 Accounting企业管理学(含财务管理、市场营销学、人力资源管理学) Corporate Management (including Financial Management, Marketing, and Human Resources Management)旅游管理学 Tourist Management技术经济及管理学 Technology Economy and Management农林经济管理学 Agricultural and Forestry Economics & Management农业经济管理学 Agricultural Economics & Management林业经济管理学 Forestry Economics & Management公共管理学 Science of Public Management行政管理学 Administration Management社会医学与卫生事业管理学 Social Medicine and Health Management教育经济与管理学 Educational Economy and Management社会保障学 Social Security土地资源管理学 Land Resource Management图书馆、情报与档案学 Science of Library, Information and Archival图书馆学 Library Science情报学 Information Science档案学 Archival Science.. .. .. ..参考.资料。
合肥工业大学各学院、专业名称及其英文翻译

合肥工业大学各学院、专业名称及其英文翻译仪器科学与光电工程学院 School of Instrument Science and Opto-electronic Engineering1、测控技术与仪器 Measurement & Control Technology and Instrument2、光信息科学与技术 Optic Information Science & Technology机械与汽车工程学院 School of Machinery and Automobile Engineering3、车辆工程 Vehicles Engineering4、工业工程 Industrial Engineering5、工业设计 Industry Design6、过程装备与控制工程 Process Equipment & Control Engineering7、机械设计制造及其自动化 Machine Design & Manufacture & Its Automation8、交通工程 Transportation Engineering9、热能与动力工程 Thermal Energy & Power Engineering材料科学与工程学院 School of Material Science and Engineering10、金属材料工程 Metal Materials Engineering11、材料物理 Materials Physics12、无机非金属材料工程 Inorganic Non-metallic Materials Engineering13、材料成型及控制工程 Material Forming & Control Engineering电气与自动化工程学院 School of Electric Engineering and Automation14、电气工程及其自动化 Electric Engineering and Automation15、生物医学工程 Biomedical Engineering16、自动化 Automation计算机与信息学院 School of Computer and Information17、计算机科学与技术 Computer Science & Technology18、电子信息工程 Electronic Information Engineering19、电子信息科学与技术 Electronic Information Science & Technology20、通信工程 Communications Engineering21、信息安全Information Security化学工程学院 School of Chemical Engineering22、高分子材料与工程 Macromolecule Material and Engineering23、化学工程与工艺 Chemical Engineering and Technics24、制药工程 Pharmacy Engineering25、应用化学 Applied Chemistry土木建筑工程学院 School of Civil Engineering26、给排水工程 Water Supply & Drainage Engineering27、工程力学 Engineering Mechanics28、水利水电工程 Hydraulic and Hydro-Power Engineering29、土木工程 Civil Engineering30、建筑环境与设备工程 Architectural Environment & Equipment Engineering建筑与艺术学院 School of Architecture and Arts31、城市规划 Urban Planning32、建筑学 Architecture33、艺术设计 Artistic Design资源与环境学院 School of Resources and Environment34、地理信息系统 Geographic Information System35、环境工程 Environment Engineering36、勘查技术与工程 Exploration Technology & Engineering37、资源勘查工程 Resources Exploration Engineering理学院 School of Sciences38、电子科学与技术 Electronic Science & Technology39、数学与应用数学 Applied Mathematics40、微电子学 Microelectronics41、信息与计算科学 Science of Information & Computation42、应用物理学 Applied Physics管理学院 School of Management43、电子商务 Electronic Commerce44、会计学 Accounting45、工商管理 Business Management46、劳动与社会保障 Labour and Social Security47、信息管理与信息系统 Information Management & System48、旅游管理 Tourism Management49、市场营销 Marketing人文经济学院 School of Humanities and Economics50、财政学 Finance51、广告学 Advertisement52、国际经济与贸易 International Economy & Trade53、经济学 Economics54、思想政治教育 Education in Ideology and Politics55、英语 English56、法学 Law57、社会工作 Social Work生物与食品工程学院 School of Biotechnology and Food Engineering58、生物工程 Bioengineering59、生物技术 Biotechnology60、食品科学与工程 Food Science and Engineering。
力学专业英语词汇翻译

力学专业英语词汇翻译牛顿力学Newtonian mechanics经典力学classical mechanics工程力学engineering mechanics固体力学solid mechanics一般力学general mechanics应用力学applied mechanics流体力学fluid mechanics理论力学theoretical mechanics静力学statics运动学kinematics动力学dynamics材料力学materials mechanics结构力学structural mechanics实验力学experimental mechanics计算力学computational mechanics力force作用点point of action作用线line of action力系system of forces力系的简化reduction of force system等效力系equivalent force system刚体rigid body力的可传性transmissibility of force平行四边形定则parallelogram rule力三角形force triangle力多边形force polygon零力系null-force system平衡equilibrium力的平衡equilibrium of forces平衡条件equilibrium condition平衡位置equilibrium position平衡态equilibrium state分析力学analytical mechanics拉格朗日乘子Lagrange multiplier拉格朗日[量] Lagrangian循环积分cyclic integral哈密顿[量] Hamiltonian哈密顿函数Hamiltonian function正则方程canonical equation正则摄动canonical perturbation正则变换canonical transformation正则变量canonical variable哈密顿原理Hamilton principle作用量积分action integral哈密顿--雅可比方程Hamilton-Jacobi equation作用--角度变量action-angle variables泊松括号poisson bracket边界积分法boundary integral method运动稳定性stability of motion轨道稳定性orbital stability渐近稳定性asymptotic stability结构稳定性structural stability倾覆力矩capsizing moment拉力tensile force正应力normal stress切应力shear stress静水压力hydrostatic pressure集中力concentrated force分布力distributed force线性应力应变关系linear relationship between stress and strain 弹性模量modulus of elasticity横向力lateral force transverse force轴向力axial force拉应力tensile stress压应力compressive stress平衡方程equilibrium equation静力学方程equations of static比例极限proportional limit应力应变曲线stress-strain curve拉伸实验tensile test‘屈服应力yield stress极限应力ultimate stress轴shaft梁beam纯剪切pure shear横截面积cross-sectional area挠度曲线deflection curve曲率半径radius of curvature曲率半径的倒数reciprocal of radius of curvature纵轴longitudinal axis悬臂梁cantilever beam简支梁simply supported beam微分方程differential equation惯性矩moment of inertia静矩static moment扭矩torque moment弯矩bending moment弯矩对x的导数derivative of bending moment with respect to x弯矩对x的二阶导数the second derivative of bending moment with respect to x 静定梁statically determinate beam静不定梁statically indeterminate beam相容方程compatibility equation补充方程complementary equation中性轴neutral axis圆截面circular cross section两端作用扭矩twisted by couples at two ends刚体rigid body扭转角twist angle静力等效statically equivalent相互垂直平面mutually perpendicular planes通过截面形心through the centroid of the cross section一端铰支pin support at one end一端固定fixed at one end弯矩图bending moment diagram剪力图shear force diagram剪力突变abrupt change in shear force、旋转和平移rotation and translation虎克定律hook’s law边界条件boundary condition初始位置initial position、力矩面积法moment-area method绕纵轴转动rotate about a longitudinal axis横坐标abscissa扭转刚度torsional rigidity拉伸刚度tensile rigidity剪应力的合力resultant of shear stress正应力的大小magnitude of normal stress脆性破坏brittle fail对称平面symmetry plane刚体的平衡equilibrium of rigid body约束力constraint force重力gravitational force实际作用力actual force三维力系three-dimentional force system合力矩resultant moment标量方程scalar equation、矢量方程vector equation张量方程tensor equation汇交力系cocurrent system of forces任意一点an arbitrary point合矢量resultant vector反作用力reaction force反作用力偶reaction couple转动约束restriction against rotation平动约束restriction against translation运动的趋势tendency of motion绕给定轴转动rotate about a specific axis沿一个方向运动move in a direction控制方程control equation共线力collinear forces平面力系planar force system一束光 a beam of light未知反力unknown reaction forces参考框架frame of reference大小和方向magnitude and direction几何约束geometric restriction刚性连接rigidly connected运动学关系kinematical relations运动的合成superposition of movement固定点fixed point平动的叠加superposition of translation刚体的角速度angular speed of a rigid body质点动力学particle dynamics运动微分方程differential equation of motion 工程实际问题practical engineering problems变化率rate of change动量守恒conservation of linear momentum 定性的描述qualitative description点线dotted line划线dashed line实线solid line矢量积vector product点积dot product极惯性矩polar moment of inertia角速度angular velocity角加速度angular accelerationinfinitesimal amount 无穷小量definite integral 定积分a certain interval of time 某一时间段kinetic energy 动能conservative force 保守力damping force 阻尼力coefficient of damping 阻尼系数free vibration 自由振动periodic disturbance 周期性扰动viscous force 粘性力forced vibration 强迫震动general solution 通解particular solution 特解transient solution 瞬态解steady state solution 稳态解second order partial differential equation 二阶偏微分方程external force 外力internal force 内力stress component 应力分量state of stress 应力状态coordinate axes 坐标系conditions of equilibrium 平衡条件body force 体力continuum mechanics 连续介质力学displacement component 位移分量additional restrictions 附加约束compatibility conditions 相容条件mathematical formulations 数学公式isotropic material 各向同性材料sufficient small 充分小state of strain 应变状态unit matrix 单位矩阵dilatation strain 膨胀应变the first strain invariant 第一应变不变量deviator stress components 应力偏量分量the first invariant of stress tensor 应力张量的第一不变量bulk modulus 体积模量constitutive relations 本构关系linear elastic material 线弹性材料mathematical derivation 数学推导a state of static equilibrium 静力平衡状态Newton‘s first law of motion 牛顿第一运动定律directly proportional to 与……成正比stress concentration factor 应力集中系数state of loading 载荷状态st venant’ principle 圣维南原理uniaxial tension 单轴拉伸cylindrical coordinates 柱坐标buckling of columns 柱的屈曲critical value 临界值stable equilibrium 稳态平衡unstable equilibrium condition 不稳定平衡条件critical load 临界载荷a slender column 细长杆fixed at the lower end 下端固定free at the upper end 上端自由critical buckling load 临界屈曲载荷potential energy 势能fixed at both ends 两端固定hinged at both ends 两端铰支tubular member 管型杆件transverse dimention 横向尺寸stability of column 柱的稳定axial force 轴向力elliptical hole 椭圆孔plane stress 平面应力nominal stress 名义应为principal stress directions 主应力方向axial compression 轴向压缩dynamic loading 动载荷dynamic problem 动力学问题inertia force 惯性力resonance vibration 谐振static states of stress 静态应力dynamic response 动力响应time of contact 接触时间length of wave 波长resonance frequency 谐振频率自由振动free vibration固有振动natural vibration暂态transient state环境振动ambient vibration反共振anti-resonance衰减attenuation库仑阻尼Coulomb damping参量[激励]振动parametric vibration模糊振动fuzzy vibration临界转速critical speed of rotation阻尼器damper半峰宽度half-peak width相平面法phase plane method相轨迹phase trajectory解谐detuning耗散函数dissipative function硬激励hard excitation硬弹簧hard spring, hardening spring谐波平衡法harmonic balance method久期项secular term自激振动self-excited vibration软弹簧soft spring ,softening spring软激励soft excitation模态分析modal analysis固有模态natural mode of vibration同步synchronization频谱frequency spectrum基频fundamental frequency缓冲器buffer风激振动aeolian vibration嗡鸣buzz倒谱cepstrum颤动chatter蛇行hunting阻抗匹配impedance matching机械导纳mechanical admittance机械效率mechanical efficiency机械阻抗mechanical impedance随机振动stochastic vibration, random vibration 隔振vibration isolation减振vibration reduction方位角azimuthal angle多体系统multibody system静平衡static balancing动平衡dynamic balancing静不平衡static unbalance动不平衡dynamic unbalance现场平衡field balancing不平衡unbalance不平衡量unbalance质量守恒conservation of mass动量守恒conservation of momentum能量守恒conservation of energy动量方程momentum equation能量方程energy equation结构分析structural analysis结构动力学structural dynamics拱Arch三铰拱three-hinged arch抛物线拱parabolic arch圆拱circular arch穹顶Dome空间结构space structure空间桁架space truss雪载[荷] snow load风载[荷] wind load土压力earth pressure地震载荷earthquake loading弹簧支座spring support支座位移support displacement支座沉降support settlement超静定次数degree of indeterminacy机动分析kinematic analysis结点法method of joints截面法method of sections结点力joint forces共轭位移conjugate displacement影响线influence line三弯矩方程three-moment equation单位虚力unit virtual force刚度系数stiffness coefficient柔度系数flexibility coefficient力矩分配moment distribution力矩分配法moment distribution method力矩再分配moment redistribution分配系数distribution factor矩阵位移法matri displacement method单元刚度矩阵element stiffness matrix单元应变矩阵element strain matrix总体坐标global coordinates高斯--若尔当消去法Gauss-Jordan elimination Method屈曲模态buckling mode线弹性断裂力学linear elastic fracture mechanics, LEFM 弹塑性断裂力学elastic-plastic fracture mechanics, EPFM 断裂Fracture脆性断裂brittle fracture解理断裂cleavage fracture蠕变断裂creep fracture裂纹Crack裂缝Flaw缺陷Defect割缝Slit微裂纹Microcrack折裂Kink椭圆裂纹elliptical crack深埋裂纹embedded crack损伤力学damage mechanics损伤Damage连续介质损伤力学continuum damage mechanics细观损伤力学microscopic damage mechanics损伤区damage zone 疲劳Fatigue低周疲劳low cycle fatigue应力疲劳stress fatigue随机疲劳random fatigue蠕变疲劳creep fatigue腐蚀疲劳corrosion fatigue疲劳损伤fatigue damage疲劳失效fatigue failure疲劳断裂fatigue fracture疲劳裂纹fatigue crack疲劳寿命fatigue life疲劳破坏fatigue rupture疲劳强度fatigue strength交变载荷alternating load交变应力alternating stress应力幅值stress amplitude应变疲劳strain fatigue应力循环stress cycle应力比stress ratio安全寿命safe life过载效应overloading effect循环硬化cyclic hardening循环软化cyclic softening环境效应environmental effect裂纹片crack gage裂纹扩展crack growth, crack Propagation裂纹萌生crack initiation循环比cycle ratio实验应力分析experimental stress Analysis工作[应变]片active[strain] gage基底材料backing material应力计stress gage零[点]飘移zero shift, zero drift应变测量strain measurement应变计strain gage应变指示器strain indicator应变花strain rosette应变灵敏度strain sensitivity机械式应变仪mechanical strain gage直角应变花rectangular rosette引伸仪Extensometer应变遥测telemetering of strain横向灵敏系数transverse gage factor横向灵敏度transverse sensitivity焊接式应变计weldable strain gage平衡电桥balanced bridge粘贴式应变计bonded strain gage粘贴箔式应变计bonded foiled gage粘贴丝式应变计bonded wire gage桥路平衡bridge balancing电容应变计capacitance strain gage补偿片compensation technique补偿技术compensation technique基准电桥reference bridge电阻应变计resistance strain gage温度自补偿应变计self-temperature compensating gage 半导体应变计semiconductor strain Gage计算结构力学computational structural mechanics加权残量法weighted residual method有限差分法finite difference method有限[单]元法finite element method配点法point collocation里茨法Ritz method广义变分原理generalized variational Principle最小二乘法least square method胡[海昌]一鹫津原理Hu-Washizu principle赫林格-赖斯纳原理Hellinger-Reissner Principle修正变分原理modified variational Principle约束变分原理constrained variational Principle混合法mixed method杂交法hybrid method边界解法boundary solution method有限条法finite strip method半解析法semi-analytical method协调元conforming element非协调元non-conforming element混合元mixed element杂交元hybrid element边界元boundary element强迫边界条件forced boundary condition 自然边界条件natural boundary condition 离散化Discretization离散系统discrete system连续问题continuous problem坐标变换transformation of Coordinates 广义位移generalized displacement广义载荷generalized load广义应变generalized strain广义应力generalized stress界面变量interface variable节点node, nodal point[单]元Element角节点corner node边节点mid-side node内节点internal node无节点变量nodeless variable杆元bar element桁架杆元truss element梁元beam element二维元two-dimensional element一维元one-dimensional element三维元three-dimensional element轴对称元axisymmetric element板元plate element壳元shell element厚板元thick plate element三角形元triangular element四边形元quadrilateral element四面体元tetrahedral element曲线元curved element二次元quadratic element线性元linear element三次元cubic element四次元quartic element等参[数]元isoparametric element单元分析element analysis单元特性element characteristics刚度矩阵stiffness matrix几何矩阵geometric matrix等效节点力equivalent nodal force节点位移nodal displacement节点载荷nodal load位移矢量displacement vector载荷矢量load vector质量矩阵mass matrix集总质量矩阵lumped mass matrix相容质量矩阵consistent mass matrix阻尼矩阵damping matrix瑞利阻尼Rayleigh damping刚度矩阵的组集assembly of stiffness Matrices 载荷矢量的组集consistent mass matrix质量矩阵的组集assembly of mass matrices单元的组集assembly of elements局部坐标系local coordinate system局部坐标local coordinate面积坐标area coordinates体积坐标volume coordinates曲线坐标curvilinear coordinates静凝聚static condensation形状函数shape function试探函数trial function检验函数test function权函数weight function样条函数spline function节点号node number单元号element number带宽band width带状矩阵banded matrix变带状矩阵profile matrix带宽最小化minimization of band width波前法frontal method子空间迭代法subspace iteration method行列式搜索法determinant search method逐步法step-by-step method增量法incremental method初应变initial strain初应力initial stress切线刚度矩阵tangent stiffness matrix割线刚度矩阵secant stiffness matrix模态叠加法mode superposition method 平衡迭代equilibrium iteration子结构Substructure子结构法substructure technique网格生成mesh generation结构分析程序structural analysis program 前处理pre-processing后处理post-processing网格细化mesh refinement应力光顺stress smoothing组合结构composite structure。
学科英文翻译

中文学科、专业名称英文学科、专业名称哲学Philosophy哲学Philosophy马克思主义哲学Philosophy of Marxism中国哲学Chinese Philosophy外国哲学Foreign Philosophies逻辑学Logic伦理学Ethics美学Aesthetics宗教学Science of Religion科学技术哲学Philosophy of Science and Technology经济学Economics理论经济学Theoretical Economics政治经济学Political Economy经济思想史History of Economic Thought经济史History of Economic西方经济学Western Economics世界经济World Economics人口、资源与环境经济学Population, Resources and Environmental Economics应用经济学Applied Economics国民经济学National Economics区域经济学Regional Economics财政学(含税收学)Public Finance (including Taxation)金融学(含保险学)Finance (including Insurance)产业经济学Industrial Economics国际贸易学International Trade劳动经济学Labor Economics统计学Statistics数量经济学Quantitative Economics中文学科、专业名称英文学科、专业名称国防经济学National Defense Economics法学Law法学Science of Law法学理论Jurisprudence法律史Legal History宪法学与行政法学Constitutional Law and Administrative Law刑法学Criminal Jurisprudence民商法学(含劳动法学、社会保障法学) Civil Law and Commercial Law (including Science of Labour Law and Science of Social Security Law )诉讼法学Science of Procedure Laws经济法学Science of Economic Law环境与资源保护法学Science of Environment and Natural Resources Protection Law国际法学(含国际公法学、国际私法学、国际经济法学、) International law (including International Public law, International Private Law and International Economic Law)精选文库军事法学Science of Military Law政治学Political Science政治学理论Political Theory中外政治制度Chinese and Foreign Political Institution科学社会主义与国际共产主义运动Scientific Socialism and InternationalCommunist Movement中共党史(含党的学说与党的建设) History of the Communist Party of China(including the Doctrine of China Party and Party Building)马克思主义理论与思想政治教育Education of Marxist Theory and Education in Ideology and Politics国际政治学International Politics国际关系学International Relations外交学Diplomacy社会学Sociology社会学Sociology人口学Demography人类学Anthropology民俗学(含中国民间文学) Folklore (including Chinese Folk Literature)民族学Ethnology民族学Ethnology马克思主义民族理论与政策Marxist Ethnic Theory and Policy中国少数民族经济Chinese Ethnic Economics中国少数民族史Chinese Ethnic History中国少数民族艺术Chinese Ethnic Art教育学Education教育学Education Science教育学原理Educational Principle课程与教学论Curriculum and Teaching Methodology教育史History of Education比较教育学Comparative Education学前教育学Pre-school Education高等教育学Higher Education成人教育学Adult Education职业技术教育学V ocational and Technical Education特殊教育学Special Education教育技术学Education Technology心理学Psychology基础心理学Basic Psychology发展与心理学Developmental and Educational Psychology应用心理学Applied Psychology体育学Science of Physical Culture and Sports体育人文社会学Humane and Sociological Science of Sports运动人体科学Human Movement Science体育教育训练学Theory of Sports Pedagogy and Training精选文库民族传统体育学Science of Ethnic Traditional Sports文学Literature中国语言文学Chinese Literature文艺学Theory of Literature and Art语言学及应用语言学Linguistics and Applied Linguistics汉语言文字学Chinese Philology中国古典文献学Study of Chinese Classical Text中国古代文学Ancient Chinese Literature中国现当代文学Modern and Contemporary Chinese Literature中国少数民族语言文学Chinese Ethnic Language andLiterature比较文学与世界文学Comparative Literature and World Literature外国语言文学Foreign Languages and Literatures英语语言文学English Language and Literature俄语语言文学Russian Language and Literature法语语言文学French Language and Literature德语语言文学German Language and Literature日语语言文学Japanese Language and Literature印度语言文学Indian Language and Literature西班牙语语言文学Spanish Language and Literature阿拉伯语语言文学Arabic Language and Literature欧洲语言文学European Language and Literature亚非语言文学Asian-African Language and Literature外国语言学及应用语言学Linguistics and Applied Linguistics inForeign Languages新闻传播学Journalism and Communication新闻学Journalism传播学Communication艺术学Art艺术学Art Theory音乐学Music美术学Fine Arts设计艺术学Artistic Design戏剧戏曲学Theater and Chinese Traditional Opera电影学Film广播电视艺术学Radio and television Art舞蹈学Dance历史学History历史学History史学理论及史学史Historical Theories and History of Historical Science考古学及博物馆学Archaeology and Museology历史地理学Historical Geography历史文献学(含敦煌学、古文字学) Studies of Historical Literature (includingPaleography and Studies of Dunhuang)精选文库专门史History of Particular Subjects中国古代史Ancient Chinese History中国近现代史Modern and Contemporary Chinese History世界史World History理学Natural Science数学Mathematics基础数学Fundamental Mathematics计算数学Computational Mathematics概率论与数理统计Probability and Mathematical Statistics应用数学Applied mathematics运筹学与控制论Operational Research and Cybernetics物理学Physics理论物理Theoretical Physics粒子物理与原子核物理Particle Physics and Nuclear Physics原子与分子物理Atomic and Molecular Physics等离子体物理Plasma Physics凝聚态物理Condensed Matter Physics声学Acoustics光学Optics无线电物理Radio Physics化学Chemistry无机化学Inorganic Chemistry分析化学Analytical Chemistry有机化学Organic Chemistry物理化学(含化学物理)Physical Chemistry (including Chemical Physics)高分子化学与物理Chemistry and Physics of Polymers天文学Astronomy天体物理Astrophysics天体测量与天体力学Astrometry and Celestial Mechanics地理学Geography自然地理学Physical Geography人文地理学Human Geography地图学与地理信息系统Cartography and Geography Information System大气科学Atmospheric Sciences气象学Meteorology大气物理学与大气环境Atmospheric Physics and Atmospheric Environment海洋科学Marine Sciences物理海洋学Physical Oceanography海洋化学Marine Chemistry海洋生理学Marine Biology海洋地质学Marine Geology地球物理学Geophysics固体地球物理学Solid Earth Physics空间物理学Space Physics精选文库地质学Geology矿物学、岩石学、矿床学Mineralogy, Petrology, Mineral Deposit Geology地球化学Geochemistry古生物学与地层学(含古人类学)Paleontology and Stratigraphy (including Paleoanthropology)构造地质学Structural Geology第四纪地质学Quaternary Geology生物学Biology植物学Botany动物学Zoology生理学Physiology水生生物学Hydrobiology微生物学Microbiology神经生物学Neurobiology遗传学Genetics发育生物学Developmental Biology细胞生物学Cell Biology生物化学与分子生物学Biochemistry and Molecular Biology生物物理学Biophysics生态学Ecology系统科学Systems Science系统理论Systems Theory系统分析与集成Systems Analysis and Integration科学技术史History of Science and Technology工学Engineering力学Mechanics一般力学与力学基础General and Fundamental Mechanics固体力学Solid Mechanics流体力学Fluid Mechanics工程力学Engineering Mechanics机械工程Mechanical Engineering机械制造及其自动化Mechanical Manufacture and Automation机械电子工程Mechatronic Engineering机械设计与理论Mechanical Design and Theory车辆工程Vehicle Engineering光学工程Optical Engineering仪器科学与技术Instrument Science and Technology精密仪器及机械Precision Instrument and Machinery测试计量技术及仪器Measuring and Testing Technologies and Instruments材料科学与工程Materials Science and Engineering材料物理与化学Materials Physics and Chemistry材料学Materialogy材料加工工程Materials Processing Engineering冶金工程Metallurgical Engineering冶金物理化学Physical Chemistry of Metallurgy钢铁冶金Ferrous Metallurgy有色金属冶金Non-ferrous Metallurgy动力工程及工程热物理Power Engineering and Engineering Thermophysics工程热物理Engineering Thermophysics热能工程Thermal Power Engineering动力机械及工程Power Machinery and Engineering流体机械及工程Fluid Machinery and Engineering制冷及低温工程Refrigeration and Cryogenic Engineering化工过程机械Chemical Process Equipment电气工程Electrical Engineering电机与电器Electric Machines and Electric Apparatus电力系统及其自动化Power System and its Automation高电压与绝缘技术High V oltage and Insulation Technology电力电子与电力传动Power Electronics and Power Drives电工理论与新技术Theory and New Technology of Electrical Engineering电子科学与技术Electronics Science and Technology物理电子学Physical Electronics电路与系统Circuits and Systems微电子学与固体电子学Microelectronics and Solid State Electronics电磁场与微波技术Electromagnetic Field and Microwave Technology信息与通信工程Information and Communication Engineering通信与信息系统Communication and Information Systems信号与信息处理Signal and Information Processing控制科学与工程Control Science and Engineering控制理论与控制工程Control Theory and Control Engineering检测技术与自动化装置Detection Technology and Automatic Equipment系统工程Systems Engineering模式识别与智能系统Pattern Recognition and Intelligent Systems导航、制导与控制Navigation, Guidance and Control计算机科学与技术Computer Science and Technology计算机软件与理论Computer Software and Theory计算机系统结构Computer Systems Organization计算机应用技术Computer Applied Technology建筑学Architecture建筑历史与理论Architectural History and Theory建筑设计及其理论Architectural Design and Theory城市规划与设计(含风景园林规划与设计)Urban Planning and Design (including Landscape Planning and Design)建筑技术科学Building Technology Science土木工程Civil Engineering岩土工程Geotechnical Engineering结构工程Structural Engineering市政工程Municipal Engineering供热、供燃气、通风及空调工程Heating, Gas Supply, Ventilating and Air Conditioning Engineering防灾减灾工程及防护工程Disaster Prevention and Reduction Engineering and Protective Engineering桥梁与隧道工程Bridge and Tunnel Engineering水利工程Hydraulic Engineering水文学及水资源Hydrology and Water Resources水力学及河流动力学Hydraulics and River Dynamics水工结构工程Hydraulic Structure Engineering水利水电工程Hydraulic and Hydro-Power Engineering港口、海岸及近海工程Harbor, Coastal and Offshore Engineering测绘科学与技术Surveying and Mapping大地测量学与测量工程Geodesy and Survey Engineering摄影测量与遥感Photogrammetry and Remote Sensing地图制图学与地理信息工程Cartography and Geographic Information Engineering化学工程与技术Chemical Engineering and Technology化学工程Chemical Engineering化学工艺Chemical Technology生物化工Biochemical Engineering应用化学Applied Chemistry工业催化Industrial Catalysis地质资源与地质工程Geological Resources and Geological Engineering矿产普查与勘探Mineral Resource Prospecting and Exploration地球探测与信息技术Geodetection and Information Technology地质工程Geological Engineering矿业工程Mineral Engineering采矿工程Mining Engineering矿物加工工程Mineral Processing Engineering安全技术及工程Safety Technology and Engineering石油与天然气工程Oil and Natural Gas Engineering油气井工程Oil-Gas Well Engineering油气田开发工程Oil-Gas Field Development Engineering油气储运工程Oil-Gas Storage and Transportation Engineering纺织科学与工程Textile Science and Engineering纺织工程Textile Engineering纺织材料与纺织品设计Textile Material and Textiles Design纺织化学与染整工程Textile Chemistry and Dyeing and Finishing Engineering服装设计与工程Clothing Design and Engineering轻工技术与工程The Light Industry Technology and Engineering制浆造纸工程Pulp and Paper Engineering制糖工程Sugar Engineering发酵工程Fermentation Engineering皮革化学与工程Leather Chemistry and Engineering交通运输工程Communication and Transportation Engineering道路与铁道工程Highway and Railway Engineering交通信息工程及控制Traffic Information Engineering & Control交通运输规划与管理Transportation Planning and Management载运工具运用工程Vehicle Operation Engineering船舶与海洋工程Naval Architecture and Ocean Engineering船舶与海洋结构物设计制造Design and Construction of Naval Architecture and Ocean Structure轮机工程Marine Engine Engineering水声工程Underwater Acoustics Engineering航空宇航科学与技术Aeronautical and Astronautical Science and Technology飞行器设计Flight Vehicle Design航空宇航推进理论与工程Aerospace Propulsion Theory and Engineering航空宇航器制造工程Manufacturing Engineering of Aerospace Vehicle人机与环境工程Man-Machine and Environmental Engineering兵器科学与技术Armament Science and Technology武器系统与运用工程Weapon Systems and Utilization Engineering兵器发射理论与技术Armament Launch Theory and Technology火炮、自动武器与弹药工程Artillery, Automatic Gun and Ammunition Engineering军事化学与烟火技术Military Chemistry and Pyrotechnics核科学与技术Nuclear Science and Technology核能科学与工程Nuclear Energy Science and Engineering核燃料循环与材料Nuclear Fuel Cycle and Materials核技术及应用Nuclear Technology and Applications辐射防护及环境保护Radiation and Environmental Protection农业工程Agricultural Engineering农业机械化工程Agricultural Mechanization Engineering农业水土工程Agricultural Water-Soil Engineering农业生物环境与能源工程Agricultural Biological Environmental and Energy Engineering农业电气化与自动化Agricultural Electrification and Automation林业工程Forestry Engineering森林工程Forest Engineering木材科学与技术Wood Science and Technology林产化学加工工程Chemical Processing Engineering of Forest Products环境科学与工程Environmental Science and Engineering环境科学Environmental Science环境工程Environmental Engineering生物医学工程Biomedical Engineering食品科学与工程Food Science and Engineering食品科学Food Science粮食、油脂及植物蛋白工程Cereals, Oils and Vegetable Protein Engineering农产品加工及贮藏工程Processing and Storage of Agriculture Products水产品加工及贮藏工程Processing and Storage of Aquatic Products农学Agriculture作物学Crop Science精选文库作物栽培学与耕作学Crop Cultivation and Farming System作物遗传育种学Crop Genetics and Breeding园艺学Horticulture果树学Pomology蔬菜学Olericulture茶学Tea Science农业资源利用学Utilization Science of Agricultural Resources土壤学Soil Science植物营养学Plant Nutrition植物保护学Plant Protection植物病理学Plant Pathology农业昆虫与害虫防治Agricultural Entomology and Pest Control农药学Pesticide Science畜牧学Animal Science动物遗传育种与繁殖Animal Genetics, Breeding and ReproductionScience动物营养与饲料科学Animal Nutrition and Feed Science草业科学Practaculture Science特种经济动物饲养学(含蚕、蜂等)The Rearing of Special-type EconomicAnimals (including Silkworm, Honeybees, etc.)兽医学Veterinary Medicine基础兽医学Basic Veterinary Medicine预防兽医学Preventive Veterinary Medicine临床兽医学Clinical Veterinary Medicine林学Forestry林木遗传育种学Forest Tree Genetics and Breeding森林培育学Silviculture森林保护学Forest Protection森林经理学Forest Management野生动植物保护与利用Wildlife Conservation and Utilization园林植物与观赏园艺Ornamental Plants and Horticulture水土保持与荒漠化防治Soil and Water Conservation and Desertification Combating水产学Fisheries Science水产养殖学Aquaculture Science捕捞学Fishing Science渔业资源学Science of Fisheries Resources医学Medicine基础医学Basic Medicine人体解剖与组织胚胎学Human Anatomy, Histology and Embryology免疫学Immunology病原生物学Pathogenic Organisms病理学与病理生理学Pathology and Pathophysiology法医学Forensic Medicine放射医学Radiation Medicine精选文库航空航天与航海医学Aerospace and Nautical medicine临床医学Clinical Medicine内科学(含心血管病学、血液病学、呼吸系病学、消化系病学、内分泌与代谢病学、肾脏病学、风湿病学、传染病学)Internal medicine (including Cardiology, Hematology, Respiratory, Gastroenterology, Endocrinology and Metabolism, Nephrology, Rheuma-tology, Infectious Diseases)儿科学Pediatrics老年医学Geriatrics神经病学Neurology精神病与精神卫生学Psychiatry and Mental Health皮肤病与性病学Dermatology and Venereology影像医学与核医学Imaging and Nuclear Medicine临床检验诊断学Clinical Laboratory Diagnostics护理学Nursing外科学(含普通外科学、骨外科学、泌尿外科学、胸心血管外科学、神经外科学、整形外科学、烧伤外科学、野战外科学)Surgery (General Surgery, Orthopedics, Urology, Cardiothoracic Surgery, Neurosurgery, Plastic Surgery, Burn Surgery, Field Surgery)妇产科学Obstetrics and Gynecology眼科学Ophthalmic Specialty耳鼻咽喉科学Otolaryngology肿瘤学Oncology康复医学与理疗学Rehabilitation Medicine & Physical Therapy运动医学Sports Medicine麻醉学Anesthesiology急诊医学Emergency Medicine口腔医学Stomatology口腔基础医学Basic Science of Stomatology口腔临床医学Clinical Science of Stomatology公共卫生与预防医学Public Health and Preventive Medicine流行病与卫生统计学Epidemiology and Health Statistics劳动卫生与环境卫生学Occupational and Environmental Health营养与食品卫生学Nutrition and Food Hygiene儿少卫生与妇幼保健学Maternal, Child and Adolescent Health卫生毒理学Hygiene Toxicology军事预防医学Military Preventive Medicine中医学Chinese Medicine中医基础理论Basic Theories of Chinese Medicine中医临床基础Clinical Foundation of Chinese Medicine中医医史文献History and Literature of Chinese Medicine方剂学Formulas of Chinese Medicine中医诊断学Diagnostics of Chinese Medicine中医内科学Chinese Internal Medicine中医外科学Surgery of Chinese Medicine中医骨伤科学Orthopedics of Chinese Medicine中医妇科学Gynecology of Chinese Medicine中医儿科学Pediatrics of Chinese Medicine中医五官科学Ophthalmology and Otolaryngoloy of Chinese Medicine针灸推拿学Acupuncture and Moxibustion and Tuina of Chinese medicine民族医学Ethnomedicine中西医结合医学Chinese and Western Integrative Medicine中西医结合基础医学Basic Discipline of Chinese and Western Integrative中西医结合临床医学Clinical Discipline of Chinese and Western Integrative Medicine药学Pharmaceutical Science药物化学Medicinal Chemistry药剂学Pharmaceutics生药学Pharmacognosy药物分析学Pharmaceutical Analysis微生物与生化药学Microbial and Biochemical Pharmacy药理学Pharmacology中药学Science of Chinese Pharmacology军事学Military Science军事思想学及军事历史学Military Thought and Military History军事思想学Military Thought军事历史学Military History战略学Science of Strategy军事战略学Military Strategy战争动员学War Mobilization战役学Science of Operations联合战役学Joint Operation军种战役学(含第二炮兵战役学)Armed Service Operation (including Operation of Strategic Missile Force)战术学Science of Tactics合同战术学Combined-Arms Tactics兵种战术学Branch Tactics军队指挥学Science of Command作战指挥学Combat Command军事运筹学Military Operation Research军事通信学Military Communication军事情报学Military Intelligence密码学Cryptography军事教育训练学(含军事体育学)Military Education and Training (including Military Physical Training)军制学Science of Military System军事组织编制学Military Organizational System军队管理学Military Management军队政治工作学Science of Military Political Work军事后勤学与军事装备学Science of Military Logistics and Military Equipment军事后勤学Military Logistics后方专业勤务Rear Special Service军事装备学Military Equipment管理学Management Science管理科学与工程Management Science and Engineering工商管理学Science of Business Administration会计学Accounting企业管理学(含财务管理、市场营销学、人力资源管理学)Corporate Management (including Financial Management, Marketing, and Human Resources Management)旅游管理学Tourist Management技术经济及管理学Technology Economy and Management农林经济管理学Agricultural and Forestry Economics & Management农业经济管理学Agricultural Economics & Management林业经济管理学Forestry Economics & Management公共管理学Science of Public Management行政管理学Administration Management社会医学与卫生事业管理学Social Medicine and Health Management教育经济与管理学Educational Economy and Management社会保障学Social Security土地资源管理学Land Resource Management图书馆、情报与档案学Science of Library, Information and Archival图书馆学Library Science情报学Information Science档案学Archival Science。
工程力学专业英语翻译

A necessary condition for Eq.(1) to be valid is that the stress ζ must be uniform over the cross section of the bar. This condition will be realized if the axial force P acts through the centroid of the cross section. When the load P does not act at the centroid, bending of the bar will result, and a more complicated analysis is necessary. At present, however, it is assumed that all axial forces are applied at the centroid of the cross section unless specifically stated to the contrary. Also, unless stated otherwise, it is generally assumed that the weight of the object itself is neglected, as was done when discussing the bar in Fig.1.
When a material exhibits a linear relationship between stress and strain, it is said to be linear elastic. This is an extremely important property of many solid materials, including most metals, plastics, wood, concrete, and ceramics. The linear relationship between stress and strain for a bar in tension can be expressed by the simple equation ζ=Eε (3) in which E is a constant of proportionality known as the modulus of elasticity for the material. 当一种材料的应力与应变表现出线性关系时,我们称这种材 料为线弹性材料。这是许多固体材料的一个极其重要的性质,这 些材料包括大多数金属,塑料,木材,混凝土和陶瓷。对于被拉 伸的梁来说,这种应力与应变之间的线性关系可以用简单方程(3) ζ= Eε 来表示,这里E是一个已知的比例常数,即该材料的弹性模 量。
力学名词英语翻译

力学名词英语翻译力学名词英语翻译力学名词英语翻译力学mechanics 牛顿力学newtonian mechanics经典力学classical mechanics静力学statics运动学kinematics动力学dynamics动理学kinetics宏观力学macroscopic mechanics,macromechanics 细观力学mesomechanics微观力学microscopic mechanics,micromechanics 一般力学general mechanics固体力学solid mechanics流体力学fluid mechanics理论力学theoretical mechanics应用力学applied mechanics工程力学engineering mechanics实验力学experimental mechanics计算力学computational mechanics理性力学rational mechanics物理力学physical mechanics地球动力学geodynamics力force作用点point of action作用线line of action力系system of forces力系的简化reduction of force system 等效力系equivalent force system刚体rigid body力的可传性transmissibility of force 平行四边形定则parallelogram rule 力三角形force triangle力多边形force polygon零力系null-force system平衡equilibrium力的平衡equilibrium of forces平衡条件equilibrium condition平衡位置equilibrium position平衡态equilibrium state分析力学analytical mechanics拉格朗日乘子lagrange multiplier拉格朗日[量] lagrangian拉格朗日括号lagrange bracket循环坐标cyclic coordinate循环积分cyclic integral哈密顿[量] hamiltonian哈密顿函数hamiltonian function正则方程canonical equation正则摄动canonical perturbation正则变换canonical transformation正则变量canonical variable哈密顿原理hamilton principle作用量积分action integral哈密顿--雅可比方程hamilton-jacobi equation 作用--角度变量action-angle variables阿佩尔方程appell equation劳斯方程routh equation拉格朗日函数lagrangian function诺特定理noether theorem泊松括号poisson bracket边界积分法boundary integral method并矢dyad运动稳定性stability of motion轨道稳定性orbital stability李雅普诺夫函数lyapunov function渐近稳定性asymptotic stability结构稳定性structural stability久期不稳定性secular instability弗洛凯定理floquet theorem倾覆力矩capsizing moment自由振动free vibration固有振动natural vibration暂态transient state环境振动ambient vibration反共振anti-resonance衰减attenuation库仑阻尼coulomb damping同相分量in-phase component非同相分量out-of-phase component超调量overshoot参量[激励]振动parametric vibration模糊振动fuzzy vibration临界转速critical speed of rotation阻尼器damper半峰宽度half-peak width集总参量系统lumped parameter system相平面法phase plane method相轨迹phase trajectory等倾线法isocline method跳跃现象jump phenomenon负阻尼negative damping达芬方程duffing equation希尔方程hill equationkbm方法kbm method, krylov-bogoliu-bov-mitropol'skii method马蒂厄方程mathieu equation平均法averaging method组合音调combination tone解谐detuning耗散函数dissipative function硬激励hard excitation硬弹簧hard spring, hardening spring谐波平衡法harmonic balance method久期项secular term自激振动self-excited vibration分界线separatrix亚谐波subharmonic软弹簧soft spring ,softening spring软激励soft excitation邓克利公式dunkerley formula瑞利定理rayleigh theorem分布参量系统distributed parameter system优势频率dominant frequency模态分析modal analysis固有模态natural mode of vibration同步synchronization超谐波ultraharmonic范德波尔方程van der pol equation频谱frequency spectrum基频fundamental frequencywkb方法wkb method, wentzel-kramers-brillouin method 缓冲器buffer风激振动aeolian vibration嗡鸣buzz倒谱cepstrum颤动chatter蛇行hunting阻抗匹配impedance matching机械导纳mechanical admittance机械效率mechanical efficiency机械阻抗mechanical impedance随机振动stochastic vibration, random vibration 隔振vibration isolation减振vibration reduction应力过冲stress overshoot喘振surge摆振shimmy起伏运动phugoid motion起伏振荡phugoid oscillation驰振galloping陀螺动力学gyrodynamics陀螺摆gyropendulum陀螺平台gyroplatform陀螺力矩gyroscoopic torque陀螺稳定器gyrostabilizer陀螺体gyrostat惯性导航inertial guidance姿态角attitude angle方位角azimuthal angle舒勒周期schuler period机器人动力学robot dynamics多体系统multibody system多刚体系统multi-rigid-body system机动性maneuverability凯恩方法kane method转子[系统]动力学rotor dynamics转子[一支承一基础]系统rotor-support-foundation system 静平衡static balancing动平衡dynamic balancing静不平衡static unbalance动不平衡dynamic unbalance现场平衡field balancing不平衡unbalance不平衡量unbalance互耦力cross force挠性转子flexible rotor分频进动fractional frequency precession半频进动half frequency precession油膜振荡oil whip转子临界转速rotor critical speed自动定心self-alignment亚临界转速subcritical speed涡动whirl连续过程continuous process碰撞截面collision cross section通用气体常数conventional gas constant 燃烧不稳定性combustion instability稀释度dilution完全离解complete dissociation火焰传播flame propagation组份constituent碰撞反应速率collision reaction rate燃烧理论combustion theory浓度梯度concentration gradient阴极腐蚀cathodic corrosion火焰速度flame speed火焰驻定flame stabilization火焰结构flame structure着火ignition湍流火焰turbulent flame层流火焰laminar flame燃烧带burning zone渗流flow in porous media, seepage达西定律darcy law赫尔-肖流hele-shaw flow毛[细]管流capillary flow过滤filtration爪进fingering不互溶驱替immiscible displacement不互溶流体immiscible fluid互溶驱替miscible displacement互溶流体miscible fluid迁移率mobility流度比mobility ratio渗透率permeability孔隙度porosity多孔介质porous medium比面specific surface迂曲度tortuosity空隙void空隙分数void fraction注水water flooding可湿性wettability地球物理流体动力学geophysical fluid dynamics 物理海洋学physical oceanography大气环流atmospheric circulation海洋环流ocean circulation海洋流ocean current旋转流rotating flow平流advection埃克曼流ekman flow埃克曼边界层ekman boundary layer大气边界层atmospheric boundary layer大气-海洋相互作用atmosphere-ocean interaction 埃克曼数ekman number罗斯贝数rossby unmber罗斯贝波rossby wave斜压性baroclinicity正压性barotropy内磨擦internal friction海洋波ocean wave盐度salinity环境流体力学environmental fluid mechanics斯托克斯流stokes flow羽流plume理查森数richardson number污染源pollutant source污染物扩散pollutant diffusion噪声noise噪声级noise level噪声污染noise pollution排放物effulent工业流体力学industrical fluid mechanics流控技术fluidics轴向流axial flow并向流co-current flow对向流counter current flow横向流cross flow螺旋流spiral flow旋拧流swirling flow滞后流after flow混合层mixing layer抖振buffeting风压wind pressure附壁效应wall attachment effect, coanda effect简约频率reduced frequency爆炸力学mechanics of explosion终点弹道学terminal ballistics动态超高压技术dynamic ultrahigh pressure technique 流体弹塑性体hydro-elastoplastic medium热塑不稳定性thermoplastic instability空中爆炸explosion in air地下爆炸underground explosion水下爆炸underwater explosion电爆炸discharge-induced explosion激光爆炸laser-induced explosion核爆炸nuclear explosion点爆炸point-source explosion殉爆sympathatic detonation强爆炸intense explosion粒子束爆炸explosion by beam radiation 聚爆implosion起爆initiation of explosion爆破blasting霍普金森杆hopkinson bar电炮electric gun电磁炮electromagnetic gun爆炸洞explosion chamber轻气炮light gas gun马赫反射mach reflection基浪base surge成坑cratering能量沉积energy deposition爆心explosion center爆炸当量explosion equivalent火球fire ball爆高height of burst蘑菇云mushroom侵彻penetration规则反射regular reflection崩落spallation应变率史strain rate history流变学rheology聚合物减阻drag reduction by polymers 挤出[物]胀大extrusion swell, die swell无管虹吸tubeless siphon剪胀效应dilatancy effect孔压[误差]效应hole-pressure[error]effect 剪切致稠shear thickening剪切致稀shear thinning触变性thixotropy反触变性anti-thixotropy超塑性superplasticity粘弹塑性材料viscoelasto-plastic material 滞弹性材料anelastic material本构关系constitutive relation麦克斯韦模型maxwell model沃伊特-开尔文模型voigt-kelvin model宾厄姆模型bingham model奥伊洛特模型oldroyd model幂律模型power law model应力松驰stress relaxation应变史strain history应力史stress history记忆函数memory function衰退记忆fading memory应力增长stress growing粘度函数voscosity function相对粘度relative viscosity复态粘度complex viscosity拉伸粘度elongational viscosity拉伸流动elongational flow第一法向应力差first normal-stress difference第二法向应力差second normal-stress difference 德博拉数deborah number魏森贝格数weissenberg number动态模量dynamic modulus振荡剪切流oscillatory shear flow宇宙气体动力学cosmic gas dynamics等离[子]体动力学plasma dynamics电离气体ionized gas行星边界层planetary boundary layer阿尔文波alfven wave泊肃叶-哈特曼流] poiseuille-hartman flow哈特曼数hartman number生物流变学biorheology生物流体biofluid生物屈服点bioyield point生物屈服应力bioyield stress电气体力学electro-gas dynamics铁流体力学ferro-hydrodynamics血液流变学hemorheology, blood rheology血液动力学hemodynamics磁流体力学magneto fluid mechanics磁流体动力学magnetohydrodynamics, mhd磁流体动力波magnetohydrodynamic wave磁流体流magnetohydrodynamic flow磁流体动力稳定性magnetohydrodynamic stability 生物力学biomechanics生物流体力学biological fluid mechanics生物固体力学biological solid mechanics宾厄姆塑性流bingham plastic flow开尔文体kelvin body沃伊特体voigt body可贴变形applicable deformation可贴曲面applicable surface边界润滑boundary lubrication液膜润滑fluid film lubrication向心收缩功concentric work离心收缩功eccentric work关节反作用力joint reaction force微循环力学microcyclic mechanics微纤维microfibril渗透性permeability生理横截面积physiological cross-sectional area 农业生物力学agrobiomechanics纤维度fibrousness硬皮度rustiness胶粘度gumminess粘稠度stickiness嫩度tenderness渗透流osmotic flow易位流translocation flow蒸腾流transpirational flow过滤阻力filtration resistance压扁wafering风雪流snow-driving wind停滞堆积accretion遇阻堆积encroachment沙漠地面desert floor流沙固定fixation of shifting sand 流动阈值fluid threshold力学名词英语翻译相关内容:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
When a material exhibits a linear relationship between stress and strain, it is said to be linear elastic. This is an extremely important property of many solid materials, including most metals, plastics, wood, concrete, and ceramics. The linear relationship between stress and strain for a bar in tension can be expressed by the simple equation ζ=Eε (3) in which E is a constant of proportionality known as the modulus of elasticity for the material. 当一种材料的应力与应变表现出线性关系时,我们称这种材 料为线弹性材料。这是许多固体材料的一个极其重要的性质,这 些材料包括大多数金属,塑料,木材,混凝土和陶瓷。对于被拉 伸的梁来说,这种应力与应变之间的线性关系可以用简单方程(3) ζ= Eε 来表示,这里E是一个已知的比例常数,即该材料的弹性模 量。
方程(1) 用于求解在梁中均匀分布的应力问题。它表示了应力 的单位是力除以面积。正如我们在图1中所看到的,当梁被力P拉 伸的时候,生成的应力是拉应力;如果力的方向被颠倒,导致梁 被压缩时,产生的应力被称为压应力。
A necessary condition for Eq.(1) to be valid is that the stress ζ must be uniform over the cross section of the bar. This condition will be realized if the axial force P acts through the centroid of the cross section. When the load P does not act at the centroid, bending of the bar will result, and a more complicated analysis is necessary. At present, however, it is assumed that all axial forces are applied at the centroid of the cross section unless specifically stated to the contrary. Also, unless stated otherwise, it is generally assumed that the weight of the object itself is neglected, as was done when discussing the bar in Fig.1.
Note that E has the same units as stress. The modulus of elasticity is sometimes called Young’s modulus, after the English scientist Thomas Young (1773-1829) who studied the elastic behavior of bars. For most materials the modulus of elasticity in compression is the same as in tension. 注意,弹性模量的单位跟应力的单位相同。在研究梁的弹性 行为的英国科学家Thomas Young (1773-1829)出现之后,弹性模
布在横截面上,类似于在水平面下的静水压力的连续分布。
The intensity of force, that is, the force per unit area, is called the stress and is commonly denoted by the Greek letter ζ. Assuming that the stress has a uniform distribution over the cross section [see Fig.1(b)], we can readily see that its resultant is equal to the intensity ζ times the cross-sectional area A of the bar. Furthermore, from the equilibrium of the body shown in Fig.1(b), we can also see that this resultant must be equal in magnitude and opposite in direction to the force P. Hence, we obtain ζ = P/A. (1) 力的强度,也就是说单位面积上的力,被称为应力,通常用 希腊字母ζ来表示。假定应力在横截面上均匀分布[见图1 ( b )], 那么我们可以很容易的看出它的合力等于强度 ζ乘以梁的横截面 积A。而且,从图1上显示的物体的平衡来看,我们可以发现这个 合力是跟拉力 P在数值上相等,方向相反的。因此,我们得到方 程(1)ζ = P/A。
illustration the bar is assu forces P that produce a uniform stretching, or tension, of the bar. 应力和应变的概念可以通过考虑一根矩形梁的拉伸的简单方 法来举例说明。如图1所示,这根矩形梁可以看作是由遍及长度 方向的连续横截面所组成,这些横截面垂直于它的轴向。在这个 例子中,这根矩形梁被假定在它两端施加了一对使它发生均匀拉 伸的轴向力P。
Translation
The concepts of stress and strain can be illustrated in an elementary way by considering the extension of a prismatic bar. As shown in Fig. 1, a prismatic bar is one that has constant cross section throughout its length and a straight axis. In this
By making an artificial cut (section mm) through the bar at right angles to its axis, we can isolate part of the bar as a free body [see Fig.1(b)]. At the left-hand end the tensile force P is applied, and at the other end there are forces representing the action of the removed portion of the bar upon the part that remains. These forces will be continuously distributed over the part cross section, analogous to the continuous distribution of hydrostatic pressure over a submerged surface. 假设在梁的轴向上做一个垂直截面(截面mm),可以分离出 一部分自由的梁[见图1(b)]。在该梁的左端,有拉力P,而在另一 端有相应的力可以替代梁的分离部分对它的作用。这些力连续分
The total elongation of a bar carrying an axial force will be denoted by the Greek letter δ[see Fig.1(a)], and the elongation per unit length, or strain, is then determined by the equation ε=δ/L (2). Where L is the total length of the bar. Note that the strain ε is a non-dimensional quantity. It can be obtained accurately from Eq.(2) as long as the strain is uniform throughout the length of the bar. If the bar is in tension, the strain is a tensile strain, representing an elongation or stretching of the material; if the bar is in compression, the strain is a compressive strain, which means that adjacent cross section of the bar move closer to one another. 在轴向力作用下,梁的总伸长用希腊字母 δ来表示[见图1(a)], 单位伸长量或者说应变将由方程 (2)决定,这里 L是指梁的总长度。 注意,这里应变ε是一个无量纲量,只要应变在梁的长度上各处是 均匀的,那么它可以通过方程(2)精确获得。如果梁被拉伸,那么 得到拉应变,表现为材料的延长或者拉伸;如果梁被压缩,那么 得到压应变,意味着梁的横截面将彼此更加靠近。
方程(1) 成立的必要条件是应力ζ在梁的横截面上是均匀分布 的。如果轴向力 P通过横截面的形心,那么这个条件是可以实现 的。如果轴向力 P不通过横截面的形心,则会导致梁的弯曲,必 须经过更复杂的分析。然而,目前除非特定说明,都假定所有的 轴向力都通过横截面的形心。同样,除非是另外说明,一般我们 不考虑物体自重,正如我们在图1中讨论的梁一样。
