用分形方法预测股票指数
分形的基本原理与炒股应用

分形的基本原理与炒股应用1. 什么是分形分形是一种数学概念,描述了自相似性的特征,在自然界和人类创造的事物中广泛存在。
简单来说,分形是指物体的一部分或整体的结构在不同的尺度下具有相似的形状或图案。
分形的研究已经在许多领域得到了应用,如自然科学、艺术、金融等。
2. 分形的基本原理分形的基本原理可以概括为以下几点:2.1 自相似性自相似性指的是物体的一部分与整体的结构相似。
这意味着无论在什么尺度上观察,物体都会呈现出相似的形状或图案。
例如,树枝的分支形状、山脉的形态和脑部神经元的结构都呈现出自相似性。
2.2 不规则性分形的形状通常是不规则的,并且无法用简单的几何形状来描述。
分形对象的边界是复杂且粗糙的,没有固定的线条或曲线。
这种不规则性使得分形对象在尺度放大或缩小时产生非常丰富的细节。
2.3 不可压缩性分形的不可压缩性指的是无法用有限的信息来完全描述分形对象。
无论尺度有多小,分形对象的细节都是无限的,因此无法通过有限的数据来完全描述。
这使得分形研究成为一个复杂而有挑战性的领域。
3. 分形在炒股中的应用分形理论在金融领域的应用非常广泛,特别是在炒股中的技术分析中经常使用。
以下是分形在炒股中的一些应用:3.1 分形图形模式识别分形的自相似性特点可以用于识别股票价格图中的重要模式。
分形图形模式通常被认为是价格趋势的标志,可以帮助炒股者预测股票价格的未来走势。
例如,股票价格图中的分形形态可以用来确定重要的转折点或趋势的延续。
3.2 分形维度的计算分形维度是描述分形对象的尺度不变性的一个指标。
在炒股中,可以通过计算股票价格图的分形维度来评估价格波动的复杂性和随机性。
较高的分形维度表示价格波动较为复杂,可能需要更多的技术分析来预测未来走势。
3.3 分形振荡指标的应用分形振荡指标是基于分形理论的技术指标,用于判断股票价格的超买和超卖情况。
通过计算价格波动波峰和波谷之间的比例可以得到分形振荡指标的数值。
炒股者可以根据分形振荡指标的数值来执行买入或卖出交易策略。
分形几何在统计物理建模中的应用指标

分形几何在统计物理建模中的应用指标在统计物理建模中,分形几何是一个重要的工具,它可以帮助我们理解和描述复杂系统的结构和行为。
分形几何是一种研究自相似性的数学工具,可以揭示隐藏在大量数据背后的规律和模式。
本文将介绍分形几何在统计物理建模中的应用指标。
一、分形维数分形维数是分形几何中用来描述自相似性的基本指标。
在统计物理建模中,分形维数可以用来度量物理系统的非线性特征和空间结构的复杂性。
常见的分形维数有Hausdorff维数和盒维数。
Hausdorff维数是一种度量集合空间填充性的维数,它可以用来描述系统的粗糙度和分形结构的程度。
在统计物理建模中,Hausdorff维数可以帮助我们判断系统的多尺度特性和相变现象。
盒维数是另一种常用的分形维数,它是通过计算集合中所需的最小盒子数来描述集合的几何结构。
在统计物理建模中,盒维数可以用来度量系统的分形特性和相变过程中的临界现象。
通过比较相同系统在不同温度下的盒维数,我们可以研究系统的相变行为和临界指数。
二、分形分析方法除了分形维数,还有一些其他的分形分析方法也被广泛应用于统计物理建模中。
分形谱是一种用来分析信号和时间序列的工具,它可以揭示系统的周期性和非周期性的特征。
在统计物理建模中,分形谱可以用来研究系统的相变行为和临界指数,以及系统的动力学特性。
分形模拟是一种通过随机生成分形图形来模拟物理系统的方法。
通过分形模拟,我们可以生成与实际系统相类似的分形图形,从而研究系统的分形特性和宏观行为。
分形统计是一种通过分析统计数据的分形特征来研究系统的结构和行为的方法。
通过分形统计,我们可以提取出数据的分形维数和分形特征,从而研究系统的自相似性和非线性特性。
三、分形几何在统计物理建模中的应用分形几何在统计物理建模中有广泛的应用,可以帮助我们理解和解释多种物理现象和现象。
在相变研究中,分形几何可以用来研究系统的临界现象和相变行为。
通过计算系统的分形维数和分形特征,我们可以预测系统在临界点的行为,以及相变点的位置和形式。
基于改进的分形插值与SVM的股指预测模型

吉 首 大 学 学 报 (自 然 科 学 版 ) JournalofJishouUniversity (NaturalScienceEdition)
Vol.39 No.3 May2018
文章编号:1007 2985(2018)03 0014 06
第3期 黎 红,等:基于改进的分形插值与 SVM 的股指预测模型
15
1 时间序列的 R/S分析方法与SVM 预测模型
1.1R/S 分 析 方 法
R/S分析方法是 Hurst提出的一种非参数统计分析方 法.该 方 法 通 过 Hurst指 数 来 判 断 时 间 序 列 的 不同波动状态,其步骤如下:对于时间序列{xt,t=1,2,…,T},设 x- 是 该 序 列 的 均 值,则 该 序 列 的 累 积 离
∗ 收稿日期:2017 09 15 基金项目:教 育 部 人 文 社 科 规 划 基 金 (12YJAZH020);南 京 财 经 大 学 现 代 服 务 业 协 同 创 新 中 心 资 助 项 目 (ZWFXT14001);江 苏 省 普 通 高 校 学 术 学 位 研 究 生 科 研 创 新 计 划 项 目 (KYLX16_1337) 通信作者:王宏勇(1963—),男,江苏扬州人,南京财经大学应 用 数 学 学 院 教 授,硕 士 生 导 师,主 要 从 事 分 形 理 论 与 金 融应用研究.
意味着序列具有分形特征.其中:0≤ H <0.5说明序列存在反持续性;0.5< H ≤1说明序列存在状态持
验
研
究
发
现
,重
标
极
差(R/S)T 满足幂律关系(R/S)T =cTH ,其中 H 是 Hurst指数,c 是与参数T 无关的正常数.时间序列的
通达信分形指标

通达信分形指标分形理论在技术分析领域中占据着重要地位。
通达信分形指标是一种常用的技术指标,能够帮助投资者识别市场趋势的转折点,提供有效的买卖信号。
本文将介绍通达信分形指标的原理、应用方法以及实例分析,以帮助读者更好地理解和应用该指标。
一、通达信分形指标的原理通达信分形指标基于分形理论,该理论认为市场的走势具有自相似的特征,即小的价格波动模式与大的价格波动模式相似。
分形指标通过检测市场价格图表中的极值点,来捕捉和识别趋势的转折点。
分形是指市场中的价格波动形态,具有以下特征:1)每一个分形都有自己明确的顶点或者底点;2)它们是非对称的,即上升趋势中的分形形态与下降趋势中的分形形态不同;3)分形具有扩散特性,也就是说,一个分形的形状会在未来的价格波动中重复出现。
通达信分形指标通过寻找市场价格图表中的极值点,来确认分形的形成。
一般情况下,上升趋势中的分形由上下两个相邻的高点和低点组成,而下降趋势中的分形则由上下两个相邻的低点和高点组成。
二、通达信分形指标的应用方法通达信分形指标的应用方法较为简单,以下是一些常见的应用方法:1. 识别趋势转折点:当市场价格形成一个完整的分形时,可以判断该分形是一个高点还是一个低点。
如果市场形成的是一个上升趋势的分形,说明市场即将出现下降趋势;如果形成的是一个下降趋势的分形,说明市场即将出现上升趋势。
2. 确定波段交易的买卖点:根据分形的形成和变化规律,可以确定波段交易的买卖点。
当一个上升趋势的分形形成后,投资者可以在其顶点附近做空;当一个下降趋势的分形形成后,投资者可以在其底点附近做多。
3. 结合其他指标确认交易信号:分形指标可以与其他技术指标结合使用,以确认交易信号的有效性。
例如,结合移动平均线指标,当分形信号与移动平均线的黄金交叉或死亡交叉同时出现,可以增强买卖信号的可靠性。
三、通达信分形指标的实例分析下面通过一个实例来演示通达信分形指标的具体应用。
以某股票的日线图为例,当市场形成一个完整的上升趋势分形时,投资者可以在分形的顶点附近设定卖出点,以获取较好的收益。
分形维度和Hurst指数的实验分析

分形维度和Hurst指数的实验分析本文将实验探究分形维度和Hurst指数的相关性和实际应用。
在这项实验中,我们将应用分形几何学和金融工程领域中的Hurst指数来分析时间序列数据的长期依赖性和复杂性。
首先让我们来了解一下分形维度。
在分形几何学中,分形维度是用来描述具有自相似性质的几何图形的维度。
自相似是指图形的不同尺度的部分具有相似的结构和形状,同时仍然保持图形原有的整体性质。
分形维度可以用来描述许多自然和人工产生的形态,如树枝、山脉、云雾等等。
在本实验中,我们将使用分形维度来分析时间序列数据的长期依赖性和复杂性。
接下来让我们来了解一下Hurst指数。
Hurst指数是用来衡量时间序列数据长期依赖性的指标。
在金融工程领域中,Hurst指数常常被用来分析股价、汇率等时间序列数据的走势。
在一些自然现象中,如地震、洪水等,也可以使用Hurst指数来评估出现这些现象的概率。
Hurst指数的取值范围在0与1之间,大于0.5的Hurst指数表明时间序列数据存在长期正相关性,小于0.5的Hurst指数则表明时间序列数据存在长期负相关性。
为了验证分形维度和Hurst指数的相关性和实际应用,我们从一个有代表性的数据集中收集了与沪深300指数相关的时间序列数据。
该数据集包含了2010年至今的中国股市指数收盘价和成交量数据。
我们首先通过Box Counting方法计算出该时间序列数据的分形维度,并使用R语言绘制了分形维度的图像。
结果表明该时间序列数据的分形维度约为1.53。
接下来我们将计算Hurst指数来验证我们对该时间序列数据的假设。
我们使用R/S分析法对时间序列数据进行分析,并计算出该时间序列数据的Hurst指数。
结果表明,该时间序列数据的Hurst指数约为0.53,大于0.5,表明该时间序列数据具有长期正相关性。
我们进一步分析了该时间序列数据的拟合模型,并使用自回归移动平均模型(ARMA)对其进行预测。
ARMA模型是一种经典的自回归模型,在金融领域中广泛应用于时间序列数据的预测和建模。
fractals指标

fractals指标Fractals指标是基于“分形几何”理论的技术分析指标。
所谓分形,是指在任何比例上的自相似性,即某个结构中的一部分在其它层次的结构中也有出现,而且出现的方式和规律相同。
Fractals指标利用这种分形特征,通过寻找市场重要的高低点,来提供交易指示。
举个例子,我们可以看一看日图中的全球最大资本管理公司:贝莱德,分形指示的效果。
从图中可以看出分形指标的效果非常不错,几乎在每个市场波动中,都有明显的高低点形成。
(图1:贝莱德点差日线图)图中显示的圆圈就表示了分形点,当市场走势突破分形点时,就会有较大的概率进一步走向相反的方向。
因此,分形指标可以被看作是一种密实的支撑和阻力水平的交叉确认技术,可以帮助交易者确认市场的趋势和方向,从而更好地制定交易策略并做出决策。
Fractals指标通过寻找市场中的“波峰”和“波谷”来确定价格的发展方向。
在图表中,每个波峰和波谷都被认为是一个分形点。
分形点有两种形式:上行的分形点(表示市场中的“波峰”)和下行的分形点(表示市场中的“波谷”)。
在一个典型的分形指标中,至少需要四个连续的价格点才能形成一个波峰或波谷。
在分形指标中,波峰通常表示最高价,并伴随着分形点的出现。
波谷则表示最低价,通常也会有分形点的存在。
通过寻找这些分形点,分形指标可以提供有关价格的重要信息:市场的高低点和未来价格的方向。
在计算分形指标时,我们需要寻找这里所说的“运行最高价”和“运行最低价”。
在确定“运行最高价”时,我们需要首先找到当前价格周期中的最高价。
然后,我们需要观察此价格点左侧的两个价格点。
如果当前最高价比这两个价格点都高,那么我们就找到了一个波峰点,表示当前市场的高点。
反之,如果当前最高价并不比这两个价格点都高,那么我们将跳过这个点,继续寻找下一个点。
相应地,当我们确定“运行最低价”时,我们需要找到当前价格周期中的最低价。
然后,我们需要观察此价格点左侧的两个价格点。
如果当前最低价比这两个价格点都低,那么我们就找到了一个波谷点,表示当前市场的低点。
fractal分型指标

fractal分型指标
Fractal分型指标,也称为分形指标,是一种由Bill Williams发明的技术分析工具。
它用于识别市场中可能的转折点,即高峰或低谷。
以下是关于分型指标的几个关键点:
1. 定义:分型指标是由至少五个连续的柱状图组成,其中中间的柱状图必须是最高的高点或最低的低点。
如果中间柱图最高,两边较低,这通常被视为熊市分型;相反,如果中间柱图最低,两边较高,则被视为牛市分型。
2. 阈值:分形指标中有一个概念叫做“分形阈值”。
当分形指标下穿1.00阈值时,预期市场价格会出现结构性突破,即短期反转向上,这可能是空头平仓并转为做多的信号。
3. 市场应用:分形指标可以帮助交易者发现市场的高峰或低谷,它们通常出现在所有市场和时间范围内,是一种自然且重复出现的模式。
4. 结合使用:分形指标经常与其他技术分析工具一起使用,以提高交易决策的准确性。
例如,它常与比尔·威廉姆斯的另一个指标——鳄鱼指标结合使用。
5. 交易策略:存在一些基于分形指标的交易策略,这些策略利用分形来识别市场的反转点,并为交易者提供宝贵的见解。
总的来说,分型指标是交易者用来分析市场趋势和预测未来价格
变动的有力工具。
通过识别分型模式,交易者可以更好地理解市场动态,并据此制定相应的交易策略。
然而,任何技术分析工具都不是百分之百准确的,因此在使用分型指标时,应结合其他市场信息和分析方法,以形成更全面的交易决策。
基于分形插值与机器学习模型的股指分析和预测

条件:
棕i
éê x0 ëê y0
ùú ûú
=
éê x i ëê y i
-1 -1
ùú ûú
,棕i
éê x N ëê y N
ùú ûú
=
éê x i ëê y i
ùú ûú
i = 1,2,…,N,
(2)
由式(1) 、式(2) 可得:
摇 摇 收稿日期:2019-02-19;修回日期:2019-03-05. 摇* 基金项目:教育部人文社科规划基金项目(12YJAZH020) ;江苏省研究生科研与实践创新计划项目( KYCX19_1632) . 作者简介:朱婷(1995— ) ,女,江苏靖江人,硕士研究生,从事分形理论与金融应用研究.
关键词:分形插值;SVM;BP 神经网络;股指序列;预测 中图分类号:F224郾 9, F830郾 9摇 摇 摇 文献标志码:A摇 摇 摇 文章编号:1672-058X(2019)06-0057-08
0摇 引摇 言
型和 R / S 分析法研究上证综指日收盘数据的变化 规 律 和 结 构 特 征, 预 测 股 指 短 期 的 变 化 趋 势。
第 36 卷第 6 期摇 摇 摇 摇 摇 摇 Vol郾 36摇 No郾 6
摇
J
重庆工商大学学报( 自然科学版)
Chongqing Technol & Business Univ( Nat Sci
Ed) 摇
摇 摇 摇 摇 摇 摇 2019 年 12 月 Dec郾 2019
doi:10郾 16055 / j郾 issn郾 1672-058X郾 2019郾 0006郾 010
势是金融市场分析中的重要课题。 然而,许多研究 代函数系的纵向尺度因子对数据拟合与预测的效
分形理论和股票价格秘密

分形理论及其发展历程被誉为大自然的几何学的分形(Fractal)理论,是现代数学的一个新分支,但其本质却是一种新的世界观和方法论。
它与动力系统的混沌理论交叉结合,相辅相成。
它承认世界的局部可能在一定条件下、过程中、在某一方面(形态,结构,信息,功能,时间,能量等)表现出与整体的相似性,它承认空间维数的变既可以是离散的也可以是连续的,因而拓展了视野。
一、分形几何的概念是美籍法国数学家曼德尔布罗特(B.B.Mandelbrot)1975年首先提出的,但最早的工作可追朔到1875年,德国数学家维尔斯特拉斯(K.Weierestrass)构造了处处连续但处处不可微的函数,集合论创始人康托(G.Cantor,德国数学家)构造了有许多奇异性质的三分康托集。
1890年,意大利数学家皮亚诺(G.Peano)构造了填充空间的曲线。
1904年,瑞典数学家科赫(H.von Koch)设计出类似雪花和岛屿边缘的一类曲线。
1915年,波兰数学家谢尔宾斯基(W.Sierpinski)设计了像地毯和海绵一样的几何图形。
这些都是为解决分析与拓扑学中的问题而提出的反例,但它们正是分形几何思想的源泉。
1910年,德国数学家豪斯道夫(F.Hausdorff)开始了奇异集合性质与量的研究,提出分数维概念。
1928年布利干(G.Bouligand)将闵可夫斯基容度应用于非整数维,由此能将螺线作很好的分类。
1932年庞特里亚金(L.S.Pontryagin)等引入盒维数。
1934年,贝塞考维奇(A.S.Besicovitch)更深刻地提示了豪斯道夫测度的性质和奇异集的分数维,他在豪斯道夫测度及其几何的研究领域中做出了主要贡献,从而产生了豪斯道夫-贝塞考维奇维数概念。
以后,这一领域的研究工作没有引起更多人的注意,先驱们的工作只是作为分析与拓扑学教科书中的反例而流传开来。
二、1960年,曼德尔布罗特在研究棉价变化的长期性态时,发现了价格在大小尺度间的对称性。
k线图的分形

k线图的分形蜡烛图上的分形指标,作为⼀种特殊的K线组合形态,通过对价格的⼀系列的⾼低点的描述,辅助识别出市场潜在的突破和反转点,预判后期⾛势。
顶分形:相邻的五根K线,若中间那根K线最⾼价为这五根K线的最⾼价,则这根K线的最⾼点为顶分形。
底分形:相邻的五根K线,若中间那根K线最低价为这五根K线的最低价,则这根K线的最低点为底分形。
特殊情况:若相邻的两根或两根以上的K线⾼(低)点价格⼀样,则把K线合并来对待,以最右边的K线来判定是否为分形点。
注意:由于该分形指标是由5根k线组合的形态,因此,对于⼀个完整的分形,其第五根k线必须关闭,以确保该分形是确定的。
使⽤⽅法:1. 寻找被突破的分形,判断后期⾛势。
当价格突破了⼀个确定的分形的最⾼价或最低价,我们视该分形为已被突破。
如果价格突破了⼀个上分形,那么市场⾛势视为向上;如果价格突破了下分形,那么市场⾛势视为向下。
2. 利⽤分形设置⽌损点。
操盘⼿也经常⽤分形来确定要在何处设置⽌损点。
例如,当买⼊⼀个短头⼨时,可以⽤最近的上分形来设置⽌损点。
当买⼊⼀个长头⼨时,可以⽤最近的下分形来设置⽌损点。
但是,在实践中,我发现在较⼩周期,对于⼤多的品种,分形反复震荡出现,杂波较多,不太适合⽤于特定的组合形态识别,或者是判断后期⼀段较长的价格⾛势。
因此考虑对分形后的信号点再进⾏⼀次分形:即若当前顶分形的最⾼价⾼于前⼀个顶分形的最⾼价,且当前顶分形的最⾼价⾼于后⼀个顶分形的最⾼价,则视为有效顶分形保留,反之遗弃;若当前底分形的最低价低于前⼀个底分形的最低价,且当前底分形的最低价低于后⼀个底分形的最低价,则视为有效底分形保留,反之遗弃。
这样进⾏⼀次滤波后,保留的分形形态⼤致能够体现出市场当前的⾛势情况。
再通过分析极值点的震荡过程,希望能够得出⼀些有益结论。
极值点的震荡过程:在分析区间震荡与突破时,往往需要⾼低点相间排列。
通过上述⽅法,有时会打破这⼀要求,因此,在对初始的⾼低分形进⾏⼀次滤波后,还需要对⼀些缺失点进⾏⼆次补充,使其更易分析。
如何利用分形把握股票买点汇总

如何利用分形把握股票买点【核心提示】分形是在多空双方力量的对比原理上建立的理论。
为了大家能够理解分形,请大家把自己的手掌伸出来,观察自己五根手指的结构。
当你把手举起来的时候,中间的手指一定是最高的,两边依次下降,这就是典型的上分形,反之当你把手掌指尖冲下的时候就是典型的下分形。
下面我们将具体讲解分形的原理以及如何利用分形来把握股票的买点方面的知识。
一、分形的原理与分形的确立在股市中分形的构成就像我们的手指一样,最少由5根K线构成,以中间的K线为准,前后的两根K线最高点都低于中间K线的高点为上分形,前后的两根低点都高于中间K线的低点为下分形。
需要注意的是在确定分形时,如果当天的K线高点与前一高点(或当日K 线的低点与前一低点相同时,当天的K线将不列入5根K线之内,需等待第6根K线的确认。
二、关注涨停板之后的分形涨停的股票是这个市场中强势的股票,有主力的可能性较大,当天的涨停也主要是主力发力的作用,因此它的位置对后期的影响很大。
如果后期股价回调能够在这个涨停板的K 线范围之内止跌,就是我们要重点关注的股票。
一旦股价在后期的调整之中形成下分形,就需要投资者及时把握。
笔者再次强调涨停的目的,是为了强调强势,只有强势的股票才更容易给投资者带来收益,正所谓“强者恒强”。
三、买点的把握1.静态上的买点(1涨停板之后下分形出现的买点一只股票在不断的上升趋势中总是会有回调的时候,只是回调的幅度有的时候无法判断。
下分形的出现是上升趋势中回调止跌企稳的位置,它给我们提供的是股价二次拉升的买入点。
注意此买点只适合于上升趋势。
图1——双钱股份(60062309年8月12日—10月16日日线图如图1所示,图中A、B处就是下分形出现的位置,随后该股都出现了连续的拉升。
需要说明的是利用下分形买入并不是每次都能成功,如果下分形出现之后股价下跌,那么原有的下分形的低点位置就是我们考虑风险控制的位置,因为后期股价跌破了这个分形的低点,就会在股价的走势上面形成高点下降低点也同时下降的走势,这样股价就会形成下降趋势。
分形及顶底预测

下面对于三个目标位有什么指导意义作一说明:
以上升趋势测顶为例:当股价到达第一目标位时,很有 可能向第二目标位前进,但是如果没有到达第二目标位, 反而回落到第一目标位时,要考虑到减仓,同理,当股价 达到第二目标位,向第三目标位前进时,如果没有到达第 三目标位,反而回落到第二目标位时,要考虑减仓,同理 当股价超越了第三目标位,但很快又回落到第三目标位时, 要考虑减仓。
一般牛市只测上涨,不测下跌,但可以在 五分钟线上操作,权证可在一分钟线上操作
测大盘
从2007.10.16 10:05到13:15测出三个目标 位 5859.26 5818.41 5777.56 在10.19 日的10:10到第三目标位,反弹 在10.22日破位后进入更大级别调整
测权证
伊利CWB1在一分钟线测算,从07.10.26的 10:00到10:09测出三个目标位20.383 20.255 20.127 在11:27到达第一目标位反 弹,13:23下探开始向上运行,调整结束
注意:为保证分形的有效性,在做顶底预测时,必须 将鳄鱼线调用出来,以此来辨别分形的有效性。同时,顶 底预测也可以在分时或长周期中进行操作。
老股票的上涨
加上鳄鱼线,找到股票的起涨点,既有效下分 形,拉到离它最近的有效上分形
例如600029南方航空,周线 2006年8月11日 到2007年6月22,测出的三个目标位30.22; 34.55; 38.87
顶底预测的用法:
在做顶底预测时,必须遵循两个原则,一个是相邻 原则,一个是突破原则。所谓的相邻原则就是一个上分 形和前面的相邻的下分形作预测,当所预测的结果都已 经被当前股价超越,则再次选择的上分形必须遵循突破 原则(即突破前期分形的另一个级别更高的上分形)。 同时,在做预测时,首先确定价格运行的趋势(上 涨或下跌),如果是上升趋势,我们要预测的是股价的 顶,如果是下跌趋势,我们要预测的是股价的底。在做 顶底预测时,必须找到有效的上分形和有效的下分形, 两点一画,预测的目标位就被显示出来,在显示的三个 目标位中,第一和第二目标位容易到达,第三目标位因 为是运用于期货中的所以在当前证券市场不易达到,但 是一旦达到,并能有效上攻,则后期涨幅将会非常巨大。
基于分型理论的股价多角度分析

基于分型理论的股价多角度分析股市是一个充满变幻和不确定性的世界。
在投资股票的过程中,很难凭借肉眼或者感性判断来作出正确的决策。
这就需要我们借助一些有效的分析方法来帮助我们预测股票价格的走势,进而制定出科学、切实可行的投资策略。
其中一种比较有趣和实用的方法就是分析分型理论,本文将从多个角度出发,深入浅出地介绍股价分型理论的应用。
1. 什么是分型理论?分型理论是由著名的股票分析大师比尔·威廉姆斯 (Bill Williams)所提出的一种技术分析方法。
它的基本含义是,股票走势的波动呈现出一种规律性的周期性变化,通常是由一连串不同级别的高点和低点组成。
这些高点和低点称为“分型”,而这些分型就是市场价格在不同时间段内呈现出的各种趋势转换的信号。
这些信号对投资者来说十分重要,因为它们可以提供有效的买卖信号并预测未来的价格走势。
2. 如何识别股价分型?为了有效地利用分型理论,我们首先需要学会识别分型。
做法就是通过观察股票价格曲线中出现的高点和低点,从中找出一些规律性和周期性的波动。
根据比尔·威廉姆斯的理论,分型可以分为上涨分型和下跌分型。
上涨分型是由一组更高的高点和低点组成,而下跌分型则是由一组更低的高点和低点组成。
这些分型可以在股票价格走势曲线中自然形成。
当我们发现某支股票出现了明显的分型时,就可以按照分型理论来进行分析。
3. 如何利用分型理论进行多角度分析?一旦我们能够识别出股价中的分型,就可以从多个角度来进行分析。
以下就是几个常见的多角度分析方法:(1)时间周期分析在分型理论中,我们可以通过跨越不同时间周期的分型来发现市场的走势变化。
比如,我们可以选用一个天、一个周或者一个月的时间周期来观察股票价格。
当我们从每个时间周期中找到分型,然后将它们合并到一起,就能形成一个更完整的市场走势。
这种分析方法可以帮助我们更全面地了解市场的大趋势以及短期波动的变化。
(2)K线图形分析K线图也是一种常用的股票价格分析工具。
基于变维分形的股票指数预测模型

A r c s d l f t c d xb s d o a ib ed me so r ca f e at o mo e o k i e a e n v ra l i n in fa t l o s n
DONG u s e g M A n Ch n h n . Li g
( l g f ce c , io i g e h ia ie s y F xn 1 3 0 , hn Col e in e L a n n c nc l v ri , u i 2 0 0 C ia) e oS T Un t
Ab t a t n o d rt n n e s y t mp o e t e a c r c f s o t e m t c n e o e a t t i p p r sr c :I r e o f d a a y wa o i r v h c u a y o r- r so k i d x f r c s, h s a e i h t p o o e e d t n l ss meh d b p l i g v ra l i n i n f c a,a c mu a i n a d ta so a in r p s s a n w a a a ay i t o y a p y n a ib e d me so r tl c u lto r n f r t a n m o me o s h t d .Us g t e r w a a fo S a g a t c c a g ,a s re fta so m a i n n t e r w aa a e i a d t r m h n h n h iS o k Ex h n e e is o n f r t s o h a d t r r o p r o e n e t a s o a i n i e e td b s d o e o t l t e s o t emo e . eb s ta so a in e f r d a d ab s n f r t s lc e a e n t p i n s d 1 Th e t n f r to m r t m o s h ma f i t h r m i t e s d t ee i e t e c r e p n i g fa t lp r mee s u s q e t , h r ca it b to su e o s h n u e o d tr n o r s o d n c a a a t r .S b e u n l t e fa t ld sr u in i s d t m h r y i
基于分形市场预测股价波动

本科生毕业论文(设计)题目: 基于分形市场预测股价波动趋势姓名: 黄篁学院: 数理信息工程学院专业: 信息与计算科学班级:2011级2班学号: 1884110207指导教师: 余宏杰职称: 副教授2014 年 11 月 18 日安徽科技学院教务处制第一章绪论微观经济学是以一定的假设条件作为前提的。
在微观经济分析中,根据所研究的问题和所要建立的理论的不同需要,假设条件存在着差异。
但是,在众多的不同经济理论的各自不同的假设田建忠,有一个假设条件是所有经济理论均具备的一个基本的假设条件,这个微观经济学的基本假设条件就是“合乎理性的人”的假设条件[1]。
所谓“合乎理性人”的前提也就是所研究的经济对象所从事的经济活动都是利己的,都是试图采取有效的方法规避风险,从而取得最大的收益。
同样,在以证券市场也是如此。
随着人们对股票价格研究的不断深入,研究者逐渐认识到投资人在投资和接收到投资信息反馈的时间是不是同步的,存在一定的延迟,这也就说明股票的收益风险不是稳定的,而是不短变化甚至是无穷的,股票收益表现出尖峰、厚尾、时变性和长期相关等特性,在此基础上分形市场被不断提出。
1.1 研究目的与意义股票市场在我国不断发展壮大,已经成为金融行业不可或缺的重要组成部分。
所以,有效准确的对股票价格进行预测在金融投资领域占有非常重要的地位。
但是由于股票受到经济、政策、以及投资人心理状态等诸多复杂的因素影响,所以股价是一个典型的非线性系统,传统的线性预测并不能得到理想的效果。
与此同时,股票一方面作为资源配置的一种手段,在资源配置中起着重要的作用,不仅与普通百姓的切身利益相关,更能反映一个国家宏观经济的发展状况,是关乎国计民生的大问题。
但是另外一个方面,我国证券市场建立于1986年,虽然只有二十几年的历史却先后出现了大概五次左右较大的股价暴涨暴跌现象。
2008年下半年沪指突破6000点大关迅速回落至1700多点,而这一“牛”“熊”的大幅跳水也只是近年来的一个缩影而已。
分形预测,真正的顶底先知

分形预测,真正的顶底先知分形预测,真正的顶底先知SEO论坛推广 2016-09-17 18:24:25 相对论,量子理论,混沌理论,并称为现代三大突破性理论。
这些理论的出现,打破了人们的传统世界观,看世界的方法和角度有了新的进展。
它们既是对传统科学的挑战,也是对传统科学的发展。
其中混沌理论是研究事物从无序到有序的一系列变化。
在这一变化过程中会出现异动,就是初始条件十分微小的变化经过不断放大,对其未来的状态都会造成极大的差别。
混沌理论的价值突出体现在初始敏感性和分形。
所谓初始敏感性体现在一个微小的变化可能会引起巨大的波动,这就是著名的蝴蝶效应。
混沌理论认为在混沌系统中,初始条件十分微小的变化,经过不断放大,对其未来状态会造成极其巨大的差别。
我们可以用在西方世界流传的一首民谣对此作形象的说明。
这首民谣说:丢失一个钉子,坏了一只蹄铁;坏了一只蹄铁,折了一匹战马;折了一匹战马,伤了一位骑士;伤了一位骑士,输了一场战斗;输了一场战争,亡了一个帝国。
蝴蝶效应:“一只南美洲亚马孙河流域热带雨林中的蝴蝶,偶尔扇动几下翅膀,可以在两周以后引起美国德克萨斯州的一场龙卷风。
”其原因就是蝴蝶扇动翅膀的运动,导致其身边的空气系统发生变化,并产生微弱的气流,而微弱的气流的产生又会引起四周空气或其他系统产生相应的变化,由此引起一个连锁反应,最终导致其他系统的极大变化。
那么为什么要了解这些呢,了解这些对于做股票有什么作用?通过运用分形几何学能够做到预测不同时间阶段股价波动的规律。
主要是用来测算股价波段涨跌目标位,它揭示的是股市最大的秘密:“顶”和“底”。
知道了底和顶,就可以实现股市的终极操作方法:“低买高卖”。
当你不知道哪里是真正的低,哪里是真正的高时,现在你将有一个指路明灯了。
何为分形,请看下图:一系列至少五根连续的线,中间的那一根线的最高价比左右两根的都高, 为上分形。
一系列至少五根连续的线,中间的那一根线的最低价比左右两根的都低, 为下分形。
分形_股价(10328107)

读“华尔街上的多分形走动”有感描述海岸线形状和星系模式的几何学也可以解释股票价格如何疯涨与暴跌这是Benoit B.Mandelbrot 写的一篇关于用分形和多分形方法来刻画股份变动的文章,阅读至哈尔滨方舟非线性系统研究所。
这篇文章主要是对传统的金融理论进行了辨正的分析,认为证券理论虽然能够解释在股价比较平静的时候股价总体的变化趋势,“证券理论或许能解释市场在95%的时间里发生的情况。
然而,如果人们承认重大的事件就包含在剩下的5%内的话,那么这个理论所描述的图景就没有反映实际情况。
”于是作者就用自己多年从事分形研究的成果来试图完善股价的模拟,去掉在经典理论中对股价作的太多假设和限定。
我以前很少接触分形理论,接触过的也极不系统,不知道分形理论能做什么事情,这篇文章叙述了分形在模拟股价方面的用处,让我从感性上又对分形理论认识增加了。
简单地说,用分形来刻画股价最基本的方法是:第一步是用1条直的走势线来表示某一价格(见图1)。
然后用1条称为生成元(generator)的折线来产生对应于金融市场的牌价上下波动情况的图形。
生成元由3段组成,沿着直的价格走势线插入,即内插。
(如果使用少于3段的生成元,则不能模拟可以上下变动的价格。
)在画出了初始生成元之后,它的3段再分别用3个较短的生成元来内插。
重复这些过程,就在缩小了的尺度上重新得出生成元(或价格曲线)的形状。
水平轴(时间尺度)和竖直轴(价格尺度)都被压缩了,以便同生成元每一段的水平边界和竖直边界相配合。
图表 1M4)。
在这个生成元的第1段所代表的时间区间中,市场活动的速度加快,而在对应于第2段的时间区间中,市场活动的速度放慢(见图3)。
图表 2 可以看出这种方法是简章但令人匪夷所思的,它可以产生出股价的上下变动趋势,展示出十分丰富的结构。
据说这也是分形几何学与混沌理论的基础之一。
显然,这种形状的图形不是传统的证券理论所能带给我们的,它不仅能复现证券理论中所描述的平稳市场所持有的模式,更能复现最近几个月中剧烈振荡的金融交易状况。
分形的计算图示
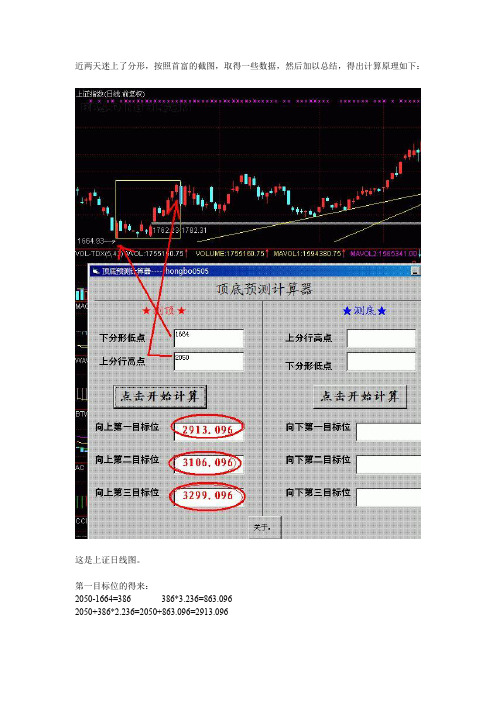
近两天迷上了分形,按照首富的截图,取得一些数据,然后加以总结,得出计算原理如下:这是上证日线图。
第一目标位的得来:2050-1664=386 386*3.236=863.0962050+386*2.236=2050+863.096=2913.096第二目标位的得来:2050+(2050-1664)*2.236+(2050-1664)/ 2=2050+863.096+193=3106.096第三目标位的得来:2050+(2050-1664)*2.236+(2050-1664)=2050+863.096+386=3299.096这是一支个股的(新华医疗):第一目标位的得来:7.15-5.15=2 2*2.236=4.4727.15+(7.15-5.15)*2.236=7.15+4.172=11.622第二目标位的得来:7.15+(7.15-5.15)*2.236+(7.15-5.15)/ 2=7.15+4.472+1=12.622第三目标位的得来:7.15+(7.15-5.15)*2.236+(7.15-5.15)=7.15+4.472+2=13.622以上是上涨的计算,下面市下跌的计算:这是大盘5分钟的下跌度量第一目标位的得来:2663.89-2628.67=35.22 35.22*2.236=78.752628.67-(2663.89-2628.67)*2.236=2628.67-78.75=2549.92第二目标位的得来:2628.67-(2663.89-2628.67)*2.236-(2663.89-2628.67)/ 2=2628.67 - 78.75 – 17.61=2532.31第三目标位的得来:2628.67-(2663.89-2628.67)*2.236-(2663.89-2628.67)=2514.70以上是分形的计算原理,其中的三个目标位所反映的是市场的强弱程度。
另,附上关于分形预测顶底的基础理论:顶底预测:顶底预测功能是用来测算股价波段涨跌目标位的,它揭示的是股市最大的秘密:“顶”和“底”。
基于分形插值方法的股票价格模拟

基于分形插值方法的股票价格模拟
陈晓红
【期刊名称】《安徽大学学报(自然科学版)》
【年(卷),期】2008(032)003
【摘要】分形插值方法是分形插值函数由迭代函数系统实现的一种方法,它可以看成是一种发展了的科学工作的通用语言.利用分形插值方法可以构造股票价格变化的分形函数,股票价格变化的规律属于非线性的,用此方法拟合Hausdorff度量空间中的经验数据,并可以利用Matlab软件实现.本文阐述的是利用分形插值方法对网上实时深发展股票价格变化曲线进行模拟.通过多次的参数调节,模拟图形效果较好.【总页数】3页(P26-28)
【作者】陈晓红
【作者单位】合肥工业大学理学院,安徽合肥230009
【正文语种】中文
【中图分类】O174
【相关文献】
1.基于分形插值方法的油气管道腐蚀灰色预测 [J], 孙春一;石彬
2.使用递归分形插值方法模拟真实感地貌景观 [J], 王燕平;刘永和
3.基于分形插值方法的城市轨道交通车站客流拟合与仿真 [J], 乐逸祥;周磊山;齐向春
4.基于多重分形理论的地表高程插值方法研究 [J], 严磊
5.基于分形插值方法的长江口深水航道回淤量计算 [J], 潘昀;窦希萍;焦增祥;王玉丹;丁磊
因版权原因,仅展示原文概要,查看原文内容请购买。
分形理论和股票价格

分形理论和股票价格分形理论的创始人美籍法国数学家Mandelbrot1967年在美国《科学》杂志上发表了“英国的海岸线有多长”的划时代的论文。
1975年他出版了分形几何的第一部著作《分形:形状、机遇和维数》,标志着分形理论的诞生。
分形是用以描述那种不规则的、破碎的、琐屑的几何特征。
分形是相对于整形而言的,它的基本特征是不可微性、不可切性、不光滑性,甚至是不连续性。
很多学者研究了我国股票市场的混沌特征,不仅说明了股市运行过程中的混沌特征,而且还给出了混沌特征的数量指标。
但他们并没有给出混沌吸引子的结构,而它却是混沌状态的基本特征,是描述混沌的基本工具。
混沌吸引子具有分形结构,混沌与分形是密切相关的。
本论文以上海股市为例,来分析我国股票市场的分形特征。
股市混沌吸引子的分形维我国股市具有复杂的混沌结构,而且我们还给出了股票指数收益率序列的混沌结构的数量指标。
“这些数量指标都是混沌度的特征指标”。
混沌的另一个特征是具有混沌吸引子,吸引子是一个分形,而分形维是刻划分形最重要的指标。
分形维数有多种定义,两种最常用的分形维数是豪斯道夫(Hausdorff)维数和盒维数。
1983年,Grassberger和Procaccia利用了嵌入理论和相空间重构技术,提出了从时间序列直接计算关联维数的算法。
本文也是用此法来计算我国股市混沌吸引子的分形维。
设{xk:k=1,…N}是观测某一系统得到的时间序列,将其嵌入到m 维欧氏空间中,得该空间中的点集,其元素为:xn(m,τ)=(xn,xn+τ,…,xn+(m-1)τ),n=1,…Nm,其中:Nm=N-(m-1)τ.从Nm个点中任选一个点xi计算其余每个点到该点的距离rij,对所有xi(i=1,…,Nm)重复这一过程,可得到关联积分函数其中的H(x)当x>0时取1,当x≤0时取0,关联维数D为当r→0时函数logCm(r)/logr的极限。
Grassberger和Procaccia证明了当嵌入维数大于分形维时,所求的分形维不因嵌入维数的增加而增加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S214 = 781921.6 S215 = 894285 (12)
由于 S11 ~ S113 , S21 ~ S213 都是已知的,根据(12)式之值,应用下述公式
S1i = S2i - S2i-1 (13)
在建立坐标系时,令8月13日为第一天,8月14日为第二天,等。将r取为各天的编号,即r1 = 1,r2 = பைடு நூலகம் 等。N值取为各日的恒指收市之值。r和N的取值见表1。
现在就可以计算由(Ni, ri)(i=1~13)以及(S1i, ri)(i=1~13)等确定的分段分形参数。
先分析有关的数据。关于分维数D及D1~D4等的结果见表1,其中Di,i+1表示根据上述方法选择Ni时,在(N,r)坐标系中,由第i个和第i+1个数据点组成的分形直线的分维数。……D4i,i+1表示根据(9)式选择S4i时,在(S4,r)坐标系中,由第i个和第i+1个数据点组成的分形直线的分维数。与D及D1~D4相对应的常数分别用 C及C1~C4来表示。
用分形方法预测股票指数
摘 要 应用常维或变维分形模型 N = C/rD (D为常量或变量)预测股票指数。预测时先将原始数据进行一系列变换,从中选出一种变换,使变换后的数据能与分形模型符合良好。在本文中应用N的各阶累计和来构造系列变换,并给出上海和香港股市股票指数的预测实例。
关键词 分形,常维分形,变维分形,预测,股票指数
8月21日 6 7527 -0.268 -1.065 -1.917 -2.676 -3.356
8月24日 7 7845 -0.043 -1.061 -1.934 -2.719 -3.429
8月25日 8 7890 0.060 -1.047 -1.945 -2.752 -3.488
表1,恒生指数分形模型的计算结果
------------------------------------------------------------------
日期 ri Ni Di,i+1 D1i,i+1 D2i,i+1 D3i,i+1 D4i,i+1
8月31日 12 7275 0.371 -0.938 -1.946 -2.828 -3.638
9月1日 13 7062
------------------------------------------------------------------
8月26日 9 7834 -0.106 -1.052 -1.955 -2.779 -3.536
8月27日 10 7922 0.124 -1.036 -1.961 -2.801 -3.577
8月28日 11 7829 0.843 -0.962 -1.954 -2.817 -3.610
而实际值为:
N14 = 7355 N15 = 7318
上述预测结果还可以用下述方法进行改进。
先将原始数据进行平移,然后再用分形方法进行处理,效果很好。经过试算,如果将全部N值都先加上500,即N1......N13 = 7160......7562,此时得到的(S2,r)坐标系中的后5条直线的分维数极为接近,依此为:-1.942061, -1.952193, -1.957868, -1.952093, -1.944866。特别是最后两条直线的D2之值仅相差0.007227。然后按上述方法进行处理,预测出N值之后再减去500,则得到如下预测结果
D = -1.946145 (10)
C = 4598.671 (11)
将上述参数及r = 14,15分别代入(1)式(将N改为S2),得到
{S1i}= {N1, N1+N2, N1+N2+N3 ......} (i=1,2......n)(6)
{S2i}= {S11, S11+S12, S11+S12+S13 ......} (i=1,2......n)(7)
{S3i}= {S21, S21+S22, S21+S22+S23 ......} (i=1,2......n)(8)
分形方法自1967年问世以来,虽然只有短短几十年的历史,然而已在一些领域获得成功应用,它被用来揭示复杂现象中深藏的有组织结构。许多科学家预言,在21世纪之中,无论是自然科学领域还是社会科学领域,应用分形方法都将取得重大成果。分形方法的特点是引入了分维数的概念。在传统的几何学中,维数为整数,例如点为0维,直线为1维,平面为2维等。而在分形方法中,分维数D突破了整数的限制,例如海岸线的分维数D值可以取为1.02,1.25等[1]。但是,在原有的分形方法中,分维数为常量,而自然界中根本不存在严格满足这种分形关系的现象。因此大量的复杂现象无法用原有的分形(可称为常维分形)模型来描述。为克服这一困难,我们采用了变维分形[2]的概念,亦即分维数是可变的量。应用变维分形及原有的常维分形方法预测股票指数,已经取得了初步成果。
第一步,将原始数据点(Ni, ri)(i=1~n)绘于双对数坐标上,一般情况下它们不能与分形分布模型符合良好,于是可将Ni排成一个基本序列,即有:
{Ni}= {N1, N2 , N3 ......} (i=1,2......n) (5)
其他的序列均可以根据基本序列构造。例如构造一阶累计和序列S1,其中S11 =N1,S12 =N1+N2,S13 =N1+N2+N3 等等,依类推可构造二阶、三阶累计和等等,即有:
Ni = S1i - S1i-1 (14)
可得如下预测结果
N14(9月2日收市值)= 7375.625
N15(9月3日收市值)= 7345.74
解出r可得
r = [C/f(R)]1/D (4)
亦即将R经过上式的变换而得到分形分布的形式。
2 变换形成的分形
前面已经说明,对于任一函数关系,均可转化为分形分布的形式。然而在实际应用中,往往只给出一些数据点,而函数关系则是未知的,因此变换的具体形式也就无法求出。在这种情况下,只能用尝试的方法来寻找恰当的变换方法。既然是尝试的方法,就可以变换R,也可以变换N。经过选择,发现了一种施行累计和的系列变换,可以将数据进行一系列变换,从中选出一种变换,使变换后的数据能与分形分布模型符合良好,亦即使变换后的数据能用分形分布来处理。该法可简介如下。
从上述结果可以看出,如果对N值不进行处理,则所得分维数D值有正有负,比较分散。而经过累计和处理之后,分维数就比较接近,尤其以2阶累计和的效果最好。由13个数据点组成的12条分段直线中,后面的5条直线的分维数很接近,其中最后两条直线的D2之值相差0.008118。如果选择由第12和第13个数据点组成的最后一条直线的分形参数作为有代表性的分形参数,并将其D2,C2之值记为D,C,则有:
需要指出的是,本文只讨论用分形方法对股票指数进行短期预测。
1 分形分布的有关公式
分形分布可用如下幂指数分布定义[3]
N = (1)
式中:r为特征线度,如时间,长度等;N 为与 r 有关的物体数目,如价格,指数等;C为待定常数,D为分维数。
D = ln(Ni/Nj)/ln(rj/ri) (2)
C = NirD (2’)
由于负数不能进行对数计算,所以当Ni中有负数时,必须将全部N值加一个常数以消除负数,亦即将全部数据点先进行一下平移处理。有时为了使分析和预测的结果更好,也可以先将全部数据点进行一下平移处理。
8月18日 3 7210 -0.193 -1.072 -1.823 -2.447 -2.978
8月19日 4 7622 -0.070 -1.070 -1.871 -2.552 -3.144
8月20日 5 7742 0.154 -1.029 -1.892 -2.622 -3.264
但是对于双对数坐标上非直线的函数关系,原有的分形方法就无法处理。为克服这一困难,我们采用了变维分形[2]的概念,亦即分维数D是可变的量。
现在我们说明,对于N与R之间的任一函数关系N = f(R),均可转化为分形分布 N = C/rD 的形式。为此只需令
f(R) = (3)
------------------------------------------------------------------
8月13日 1 6660 -0.117 -1.060 -1.625 -2.030 -2.346
8月14日 2 7224 0.005 -1.032 -1.742 -2.290 -2.736
在本文中r取为时间的编号,例如规定某一天为第一天,则有r1 =1,第二天的r2 =2,等。N为股票指数,例如可以将N1 取为第一天的收市指数,N2 取为第二天的收市指数,等。
在目前一般应用的分形方法中,D为常数,这种分形可称为常维分形。它在双对数坐标上是一条直线。根据该直线上的任意两个数据点(Ni,ri)和(Nj,rj),可以确定该段直线的分形参数,亦即分维数D 和常数C 。将两个数据点的坐标代入(1)式后可以解出
第三步,选择效果最好的变换并确定其相应的分形参数。
将各阶累计和构成的数据点分别绘于双对数坐标上之后与某一分形分布模型进行对比,即可选择效果最好的变换并确定其相应的分形参数。
分形分布模型确定之后,即可用外插计算的方法进行预测。
3 应用实例
例1,已知1998年香港股市世纪大战期间,自8月13日~9月1日恒生指数依次收于6660,7224,7210,7622,7742,7527,7845,7890,7834,7922,7829,7275,7062,试用分形方法预测9月2日和9月3日恒指收市之值。
{S4i}= {S31, S31+S32, S31+S32+S33 ......} (i=1,2......n)(9)
